第4章 狭义相对论(3)
大学物理上 第4章 狭义相对论基础

1. 爱因斯坦的理论是牛顿理论的发展 2.光速不变否定了绝对时空概念。不存在绝对运动或 .光速不变否定了绝对时空概念。 绝对静止。 绝对静止。
10
§4.3
狭义相对论时空观
4.3.1 同时的相对性 由于光速不变, 由于光速不变,在某一个惯性系中同时发生的两 个事件, 个事件,在另一相对它运动的其它惯性系中并不一定 是同时发生的,这个结论称为“同时的相对性” 是同时发生的,这个结论称为“同时的相对性”。
v x = v′ + u x v y = v′y vz = v′ z
y = y′
x
P
x'
ut
o z
o'
x′
u
x
伽利略速度变换 v′ = vx − u x S ' 系 v′ = v y y v' z = v z
z'
S系
r r r v = v '+u
经典时空中速度满足速度叠加原理。 经典时空中速度满足速度叠加原理。
17
.
慢 双生子佯谬
慢 .
.
1971年,美空军用两组Cs(铯)原子钟作实验。 年 美空军用两组 ( 原子钟作实验。 实验值: 实验值:绕地球一周的运动 钟变慢: 钟变慢:203± 10ns ± 理论值:绕地球一周的运动 理论值: 钟变慢: 184 ± 23 ns 钟变慢: 实验值和理论值在误差 范围内是一致的。 范围内是一致的。 实验验证了孪生子效应确实是存在的。 实验验证了孪生子效应确实是存在的。
9
4.2.2 狭义相对论的基本原理 1.狭义相对性原理:一切物理规律在任何惯性系中 1.狭义相对性原理: 狭义相对性原理 都具有相同的形式。 都具有相同的形式。即:物理定律与惯性系的选择无 对物理定律来说,所有惯性系都是等价的。 关,对物理定律来说,所有惯性系都是等价的。 2.光速不变原理:在所有惯性系中, 2.光速不变原理:在所有惯性系中,光在真空中的 光速不变原理 速率相同,与惯性系之间的相对运动无关,也与光源、 速率相同,与惯性系之间的相对运动无关,也与光源、 观察者的运动无关。 观察者的运动无关。 说明: 说明:
第4章 狭义相对论
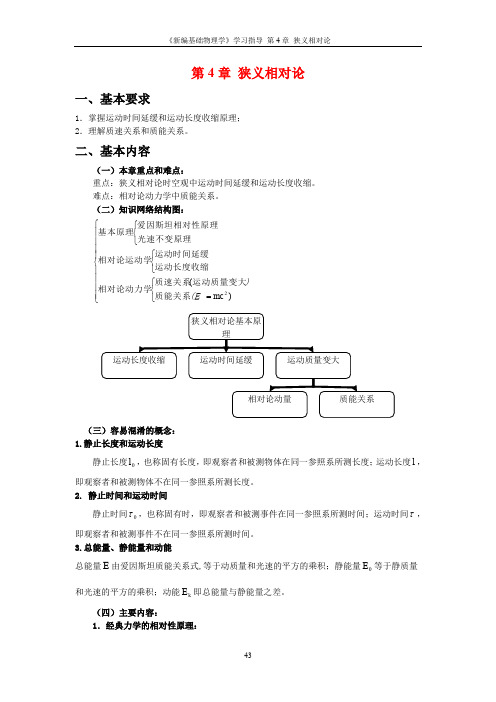
第4章 狭义相对论一、基本要求1.掌握运动时间延缓和运动长度收缩原理; 2.理解质速关系和质能关系。
二、基本内容(一)本章重点和难点:重点:狭义相对论时空观中运动时间延缓和运动长度收缩。
难点:相对论动力学中质能关系。
(二)知识网络结构图:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎩⎨⎧=⎩⎨⎧⎩⎨⎧)(2mc (E )质能关系运动质量变大质速关系相对论动力学运动长度收缩运动时间延缓相对论运动学光速不变原理爱因斯坦相对性原理基本原理(三)容易混淆的概念: 1.静止长度和运动长度静止长度0l ,也称固有长度,即观察者和被测物体在同一参照系所测长度;运动长度l ,即观察者和被测物体不在同一参照系所测长度。
2. 静止时间和运动时间静止时间0τ,也称固有时,即观察者和被测事件在同一参照系所测时间;运动时间τ,即观察者和被测事件不在同一参照系所测时间。
3.总能量、静能量和动能总能量E 由爱因斯坦质能关系式,等于动质量和光速的平方的乘积;静能量0E 等于静质量和光速的平方的乘积;动能k E 即总能量与静能量之差。
(四)主要内容:1.经典力学的相对性原理:一切彼此相对作匀速直线运动的诸惯性系中的力学规律是一样的。
即力学规律的数学形式都是相同的。
2.狭义相对论基本原理:(1)爱因斯坦相对性原理:物理定律在所有惯性参考系内都是等价的。
(2)光速不变原理:在所有惯性系中,光在真空中的速度恒等于c 。
3.洛伦兹变换:若S S 、'分别为两惯性系,S 系相对S '系以v 沿x 轴运动,在0='=t t 时两系重合,则一质点(或一事件)在S 系中的时空坐标(x 、y 、z 、t )与在S '系中的时空坐标(x '、y '、z '、t ')之间的关系为洛伦兹时空变换。
(1)洛伦兹时空变换同一事件在S 系中时空坐标(x 、y 、z 、t )与在S '系中的时空坐标(x '、y '、z '、t ')之间的关系为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧='='--='--='z z y y c v vt x x c v x c v t t 222)(1)(1逆变换为:⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧'='=-+'=-+=z z y y c v vtx x c v x c v t t 222)(1)(1(2)洛伦兹速度变换某质点相对于S 系速度u ,与相对S '系速度u '之间的关系为:PcE 021c vu v u u x x x--=';221)(1c v u c v u u x y y --=';221)(1c v u cvu u x z z --='逆变换为:21c vu v u u x xx '++'=;221)(1c v u c v u u x y y '+-'=;221)(1c v u c v u u x z z '+-'=4.狭义相对论时空观:(为简化公式,可令:22221,11c v cv -=-=βγ) (1)运动时间延缓公式:2201c v -=ττ其中:0τ为静止时间,也称固有时,即观察者和被测事件在同一参照系所测时间;τ为运动时间,即观察者和被测事件不在同一参照系所测时间。
4.3 相对论动力学

作者 杨 鑫
4.3 相对论动力学
第4章 狭义相对论基础
8
二、相对论能量 1.相对论动能 1.相对论动能
2
动能增量= 动能增量=合外力作功
E ⋅ d(mv) v ⋅ d(mv ) =∫ dt ⋅vdt =v⋅(mdv +vdm) =∫ v⋅ d( m v ) =mvdv+ v dm Ek= ∫1 F dr Ek0 = 0
2
静 能 总能量
E0 = m0c
2
E = mc
∆E = ∆ m c
作者 杨 鑫
质量和能量都是物 2 质的属性,两者之 间在量值上的联系 , 2 绝不等于它们可以 相 互 转 化
演示: 演示:弹簧振子 演示: 演示:加热
=常 量 ∑mi = 常 量
4.3 相对论动力学
第4章 狭义相对论基础
13
4.相对论能量和动量的关系 4.相对论能量和动量的关系
m=
是不 定的
m0 v 1− 2 c
2
只有静止质量= 只有静止质量 = 0 的物体 才 能 以 光 速 c 运 动 光 子
作者 杨
光子、中微子 光子、
E0 = 0 P = E c = mϕ c= h λ E = Pc
鑫
m0 = 0 m = E c2 = hν c2 ϕ
4.3 相对论动力学
第4章 狭义相对论基础
作者 杨 鑫
4.3 相对论动力学
第4章 狭义相对论基础
5
4.3 相对论动力学
一、相 对 论 质 量 与 动 量 二、相 对 论 能 量
三、光子的能量、质量和动量 光子的能量、
作者 杨 鑫
4.3 相对论动力学
第4章 狭义相对论基础
4.3 狭义相对论基本原理 相对时空观

Guangxi university
S
y S' O
u y' O' c c c x' c x
在S系中, 若按伽利略变换: 往左:v=c-u 往右:v=c+u
Guangxi university
讨论:
1 Einstein 的相对性理论 是 Newton理论的发展 一切物理规律 力学规律
解1:以地面为参照系 介子寿命延长。 用经典时空观 介子所走路程
y 0.998c 0 8 6 y 0.998 3 10 2.15 10 644(m )
还没到达地面,就已经衰变了。但实际探测 仪器不仅在地面,甚至在地下 3km 深的矿井 中也测到了 介子。
Guangxi university
S
S
u
弟 a. e f 弟 0 .
x
x
x
) 花开事件:( x, t1 S 系x处发生两个事件 ) ( x, t 2 花谢事件:
t1 (寿命) t t2
在S系中观察者测量花的寿命是多少?
Guangxi university
S
第三节
狭义相对论基本原理 相对时空观
Guangxi university
返回
一、 狭义相对论的两条基本原理
爱因斯坦在1905年发表的《论动体的电动力学》 论文中提出了狭义相对论两条基本原理 1.相对性原理
所有物理规律在一切惯性系中都具有相同形式。 (所有惯性系都是平权的,在它们之中所有物理规 律都一样) 2.光速不变原理
2 光速不变与伽利略变换 与伽利略的速度相加原理不相容
【大学物理上册课后答案】第4章 狭义相对论时空观

习 题4-1 一辆高速车以0.8c 的速率运动。
地上有一系列的同步钟,当经过地面上的一台钟时,驾驶员注意到它的指针在0=t ,他即刻把自己的钟拨到0'=t 。
行驶了一段距离后,他自己的钟指到6 us 时,驾驶员看地面上另一台钟。
问这个钟的读数是多少? 【解】s)(10)/8.0(16/12220μ=-μ=-∆=∆c c s cu t t所以地面上第二个钟的读数为)(10's t t t μ=∆+=4-2 在某惯性参考系S 中,两事件发生在同一地点而时间间隔为4 s ,另一惯性参考系S′ 以速度c u 6.0=相对于S 系运动,问在S′ 系中测得的两个事件的时间间隔和空间间隔各是多少?【解】已知原时(s)4=∆t ,则测时(s)56.014/1'222=-=-∆=∆s cu t t由洛伦兹坐标变换22/1'c u ut x x --=,得:)(100.9/1/1/1'''8222220221012m c u t u c u ut x c u ut x x x x ⨯=-∆=-----=-=∆4-3 S 系中测得两个事件的时空坐标是x 1=6×104 m ,y 1=z 1=0,t 1=2×10-4 s 和x 2=12×104 m ,y 2=z 2=0,t 2=1×10-4 s 。
如果S′ 系测得这两个事件同时发生,则S′ 系相对于S 系的速度u 是多少?S′ 系测得这两个事件的空间间隔是多少?【解】(m)1064⨯=∆x ,0=∆=∆z y ,(s)1014-⨯-=∆t ,0'=∆t0)('2=∆-∆γ=∆c xu t t 2c x u t ∆=∆⇒ (m /s )105.182⨯-=∆∆=⇒xtc u (m)102.5)('4⨯=∆-∆γ=∆t u x x4-4 一列车和山底隧道静止时等长。
4-3 狭义相对论基本原理 洛伦兹变换

dt '
u c2
dx'
dy' dt '
1 2
1
u c2
dx' dt '
v'y 1 2
1
u c2
v'x
同理
vz
v'z 1 2
1
u c2
v'x
第4章 相对论
第3节
大学物理学(第4版) 9
由 S→S'系
由 S'→S系
v
' x
vx u
1
u c2
vx
✓ 和光速不变紧密联系在一起的是:在某一惯性系中 同时发生的两个事件,在相对于此惯性系运动的另一 惯性系中观察,并不一定是同时发生的 .
说明同时具有相对性,时间的量度是相对的 .
第4章 相对论
第3节
二、洛伦兹变换
S系和S′系是两个相对 作匀速直线运动的惯性 系
大学物理学(第4版) 3
S→S′
x' (x ut)
第3节 一、狭义相对论的两条基本原理
大学物理学(第4版) 1
相对性原理:所有物理定律在一切惯性系中都具有 相同的形式。或者说所有惯性系都是平权的,在它 们之中所有物理规律都一样。
光速不变原理:所有惯性系中测量到的真空中光速 沿各方向都等于c,与光源的运动状态无关。
第4章 相对论
第3节
大学物理学(第4版) 2
y
'
y
z' z
t '
(t
第4章 狭义相对论基础

S系
m11 m2 2 m110 m2 20
利用伽利略变换
S 系
m11 m2 2 m110 m2 20
动量守恒定律在伽利略变换下形式不变。 在两相互作匀速直线运动的惯性系中,牛顿运 动定律具有相同的形式。
5
4.1 伽利略变换 经典力学的相对性原理
y' y
z' z
y y'
v x' c2 t 2 1 v 2 c t '
z z'
1) x ' , t '与 x, t成线性关系,但比例系数不等于1。 2) 时间不独立,t 和 x 变换相互交叉。 3)
v c
时,洛伦兹变换
伽利略变换。
13
4.2 狭义相对论的基本假设 洛仑兹变换
tt
'
t t 2 t1 t 2 t1 t '
6
4.1 伽利略变换 经典力学的相对性原理
空间间隔度量绝对不变
' x' x2 x1' ( x2 ut2 ) ( x1 ut1 )
x2 x1 x
t 2 t1
( S系中必须同时测量长度两端 ) 牛顿力学的相对性原理
1)满足相对性原理和光速不变原理。 2)当质点速率远小于真空光速 c 时,该变换应能
使伽利略变换重新成立。
o 设 : t ' 0 时, ,o' 重合 ; 事件 P 的时空坐标如图所示。 t
x' x vt v2 1 c
2
y' y
v x c2 t' 2 1 v 2 c t
4-1 狭义相对论基本原理 洛伦兹变换

持不变 . 这种不变显示出物理定律对匀速直线运动 的对称性 —— 相对论对称性 .
第四章 狭义相对论
速度变换公式
u' x = u x v
u' y = u y u'z = uz
加速度变换公式
s
y
y
s'
y'
v
y'
vt
o
x'
P ( x, y , z ) * ( x' , y ' , z ' )
z z
o' z' z'
x
x' x
a'x = a x
a' y = a y
a = a' F = ma ' F = ma
实践已证明,绝对时空观是不正确的 实践已证明,绝对时空观是不正确的 . 不正确
4 – 1 狭义相对论基本原理 洛伦兹变换
第四章 狭义相对论
2 伽利略变换 当 t = t′ = 0 时 o 与 o' 重合 坐标变换公式
s
y
y
s'
y'
v
yx, y , z ) * ( x' , y ' , z ' )
4 – 1 狭义相对论基本原理 洛伦兹变换
第四章 狭义相对论
二
狭义相对论的基本原理
Albert Einstein ( 1879 – 1955 ) 20世纪最伟大的物理学家,于 世纪最伟大的物理学家, 世纪最伟大的物理学家 1905年和 年和1915年先后创立了狭义相 年和 年先后创立了狭义相 对论和广义相对论,他于1905年提 对论和广义相对论,他于 年提 出了光量子假设,为此他于1921年 出了光量子假设,为此他于 年 获得诺贝尔物理学奖, 获得诺贝尔物理学奖,他还在量子 理论方面具有很多的重要的贡献 . 爱因斯坦的哲学观念: 爱因斯坦的哲学观念:自然 哲学观念 界应当是和谐而简单的 . 理论特色: 理论特色:出于简单而归于 深奥 .
第04章(狭义相对论)习题答案

1 1 - ( u / c ) 2
(SI) ]
解:由题意,车厢上的观察者测得的这两个痕迹之间的距离为固有长度 L 0 ,而地面上 的观察者测看来,这两个痕迹是随车厢一起运动的,测得长度会发生相对论长度收缩,则
L 0 =
1 1 u 2 c 2
4-5 在惯性系 S 中,有两事件发生于同一地点,且第二事件比第一事件晚发生Dt =2s;而 在另一惯性系 S'中,观测第二事件比第一事件晚发生Dt¢=3s.那么在 S'系中发生两事件 8 的地点之间的距离是多少?[6.72×10 m] 解: 设两惯性系的相对运动速度为 u , 由题意, S 系中测得的两事件的时间间隔 Dt = 2 s 为固有时间,根据相对论时间膨胀效应, S ¢ 系测得的时间间隔
¢= Dt
Dt 1 u c 2
2
即: 3 =
2 1 u c 2
2
解得: u =
5 c 3
则 S ¢ 系中发生的这两事件的地点之间的距离 L 为:
L = u Dt =
5 8 c ´ 3 » 6.71´ 10 m 3
4-6
一体积为 V0,质量为 m0 的立方体沿其一棱的方向相对于观察者 A 以速度 v 运动.观
t 0
1 u 2 c 2
则 5 =
4 1 u 2 c 2
解得: u =
3 c 5
4-2
-6 m 子是一种基本粒子,在相对于 m 子静止的坐标系中测得其寿命为 t 0 =2×10 s.如
果 m 子相对于地球的速度为v = 0.988c (c 为真空中光速),则在地球坐标系中测出的 m 子的 寿命是多长?[1.29×10 5 s] 解:由题意, m 子的固有寿命为 t 0 = 2 ´10 s ,根据相对论时间膨胀效应,对于地面 参考系运动的 m 子的寿命为: t=
狭义相对论

狭义相对论狭义相对论(Special Relativity)是主要由爱因斯坦创立的时空理论,是对牛顿时空观的改造。
伽利略变换与电磁学理论的不自洽到 19 世纪末,以麦克斯韦方程组为核心的经典电磁理论的正确性已被大量实验所证实,但麦克斯韦方程组 在经典力学的伽利略变换下不具有协变性。
而经典力学中的相对性原理则要求一切物理规律在伽利略变换下都具有协变性。
迈克尔孙寻找以太的实验 为解决这一矛盾,物理学家提出了“以太假说”,即放弃相对性原理,认为麦克斯韦方程组只对一个绝对参 考系(以太)成立。
根据这一假说,由麦克斯韦方程组计算得到的真空光速是相对于绝对参考系(以太) 的速度;在相对于“以太”运动的参考系中,光速具有不同的数值。
实验的结果——零结果 但斐索实验和迈克耳逊-莫雷实验表明光速与参考系的运动无关。
洛仑兹坐标变换 洛仑兹变换是描述狭义相对论空间中各参考系间关系的变换。
它最早由洛仑兹从以太说推出,用以解决经典力学与经典电磁学间的矛盾(即迈克尔孙-莫雷实验的零结果)。
后被爱因斯坦用于狭义相对论。
1632 年,伽利略出版了他的名著《关于托勒密和哥白尼两大世界体系的对话》。
书中那位地动派的“萨尔维阿蒂”对上述问题给了一个彻底的回答。
他说:“把你和一些朋友关在一条大船甲板下的主舱里,让你们 带着几只苍蝇、蝴蝶和其他小飞虫,舱内放一只大水碗,其中有几条鱼。
然后,挂上一个水瓶,让水一滴 一滴地滴到下面的一个宽口罐里。
船鱼向各个方向随便游动,水滴滴进下面的罐口,你把任何东西扔给你 的朋友时,只要距离相等,向这一方向不必比另一方向用更多的力。
你双脚齐跳,无论向哪个方向跳 过的 距离都相等。
当你仔细地观察这些事情之后,再使船以任何速度前进,只要运动是匀速,也不忽左忽右地 摆动,你将发现,所有上述现象丝毫没有变化。
你也无法从其中任何一个现象来确定,船是在运动还是停 着不动。
即使船运动得相当快,你跳向船尾也不会比跳向船头来得远。
(精品)第4讲狭义相对论

a11 a44
x 0, x vt 代入(a)第一式 a14 va11
关于四个系数的方程尚缺一个
28
( 2 )‘光速不变原理
t = t‘ = 0 时刻,从坐标原点发出一光波为事件1,事件 2为在x轴另一点接收到光信号。根据光速不变原理, 在两个参考系中,光波向各方向传播到达的时空点, 即位置与时间满足球面方程:
爱因斯坦与他不同,是从狭义相对性原理和光速不变原 理导出洛仑兹变换,使之成为狭义相对论中具有基础地 位的关系式。
24
为什么是线性变换?
由相对性原理,一个惯性系中的匀速运动在另一个 惯性系看来也必须是匀速运动。惯性系可以传递, 只有时空坐标变换是线性的才能保证这一点。
从数学上看, S系和S‘系是等价的,S 系和S’ 系之 间时空坐标变换必须是相同性质的变换,只有线性 变换的逆变换仍然是线性变换
“以太”幽灵
至十九世纪上半叶,当光具有波动性被大 多数物理学家承认时,以太假说又获得了新的支 持,于是十九世纪末的物理学界,牢固地确立了 一种思想,认为有一种到处存在的、能穿透一切 的介质,并充满所有物质的内部和它们之间的空 间,它的作用是作为传播光波的基础。惠更斯把 它叫作“以太”(光以太),后来又被叫做法拉 第管(电磁以太),被认为是引起带电体和磁化 物体之间相互作用的原因。
11
二、狭义相对论基本原理
经典物理学
I. Newton (1642-1727)
J. C. Maxwell (1831-1879)
物理学的大综合
力
热
声
光
电
磁
12
狭义相对论以前的力学和时空观
描述物体的运动需要选择参考系,并在参考系中建立坐 标系。 事件:物体在某一时刻处于某一位置
2016第四章狭义相对论

论 过渡到经典力学.经典力学是相对论力学的一种特
例或近似.
3
§4.1 伽利略变换 经典力学的时空观
普
通
物 狭义相对论和广义相对论
理
教 程
狭义相对论是关于高速情况下的时空观理论;
广义相对论是关于引力和时空结构的理论.
狭义相对论适用于一切惯性参考系,而广义
第 四
相对论适用于一切参考系.
章
相对论和时空观
伽利略坐标变换
当u c 变换无意义 速度有极限
12
普
通
物
理 教
作业: 普通物理教程(上):
程
习题4 P97
第 四
三、计算题
章
狭
2 、3 、6
义
相
对
论
13
普 §4.3 狭义相对论的时空观
通 物
理 4.3.1 同时性的相对性
教
程 在牛顿力学中,时间是绝对的。如两事
件在S系中被同时观察到,那么在S′中也是
普 通 物 理 教 程
第四章 狭义相对论
北京建筑工程学院 理学院 应用物理系
1
第四章 狭义相对论
普
通
物
理
教 程
§4.1
伽利略变换
经典力学的时空观
§4.2 狭义相对论的基本原理 洛伦兹变换
第
四 §4.3 狭义相对论的时空观
章
狭 §4.4 狭义相对论动力学基础
义 相 对 论
2
§4.1 伽利略变换 经典力学的时空观
15
普 §4.3 狭义相对论的时空观
通
物 理
设 S系中x1、x2两处发生两事件,时间
教 程
间隔为Δt t2 t1 .问 S′系中这两事件
狭义相对论3个重要结论

狭义相对论3个重要结论狭义相对论是20世纪最重要的理论之一。
它影响着宇宙学、量子力学、人类行为之类的诸多学科,引领了研究宇宙的新方向,并取得了广泛的成就。
其最重要的三个结论是:(1)能量和质量之间的关系:狭义相对论的第一个重要结论是,能量和质量之间具有等价的关系,也就是著名的质能关系”:E = mc2。
这意味着能量和质量可以互相转化,只要有足够的能量,质量可以从有形的物质变为无形的能量,反之亦然。
(2)时空变形:狭义相对论第二个重要结论是,物体在弯曲的时空中会遭受时空坐标的变形。
物体在引力影响下会变形,而无论是谁在观察,这种变形都是相同的。
因此,它提出了时间和空间是相对而不是绝对的概念。
(3)光子的重力:狭义相对论的最后一个重要结论是,光子也受到重力的作用,它的运动受到时空的影响,而且其在弯曲的时空中的行为与其他物体相同。
这是因为万有引力作用于所有的物体,而不仅仅是质量物体,这个事实证明了物质的能量和质量的同一性。
以上就是狭义相对论的三个重要结论。
它改变了人类对宇宙的理解,使物体在引力场中受到时空坐标的影响,根据这个理论,宇宙可能是有极限的。
近几十年来,狭义相对论的证据已经被普遍认可,它也在各种场合中不断得到验证和支持。
它的重要性不仅表现在物理上,而且也影响到社会科学和文化,因为它反映了宇宙的真实面貌,改变了人类对宇宙的理解,使人们能够更好地理解宇宙,进而深入地研究宇宙,挖掘它的秘密。
在宇宙学、物理学和数学等学科方面,狭义相对论贡献巨大。
它使物理学有了质能转换的基础,促进了宇宙学的发展,并且在现代物理学中仍然占有相当重要的地位。
随着对狭义相对论的不断深入研究,人们对它的研究也越来越深入,相信不久的将来,它必将带来更大的惊喜。
就像波恩说的:“时空终将改变我们对宇宙的看法,这样就可以改变宇宙,而另一个改变将会发生,这也是狭义相对论最强大、最深远的影响!”总之,狭义相对论是20世纪最重要的理论之一,其最重要的三个结论是:能量和质量之间的关系,时空变形,以及光子的重力。
4-3 相对论基础

第4章 相对论
在相对论中,物体的质量与运动密切相关。根据动 量守恒定律和相对论速度变换关系,从理论上可以证明 物体的质量随物体运动速度 v 而变化,其关系式为
m
m0 1 (v c )
2
m0 —— 静止质量 m —— 运动质量 ——质速关系式
上式揭示了物质与运动的不可分割性。
当物体的速度接近光速时,如电子的速度 v = 0.98c m0 时,其运动质量 m 5m0 2 1 (0.98) 现代电子加速器可使电子的速度达到 v = 0.999 999 9997c, 此时电子的运动质量
氢弹就是氢核聚变的产物。由于氘核 和氚核质量较轻,单位质量的氘核数或氚 核数约为重核的几百倍,所以轻核聚变释 放的能量比重核裂变大许多。这就是氢弹 比原子弹威力更大的原因。 1967年6月17日,中国第一颗氢弹爆 炸成功。
23
大 学 物理学
第4章 相对论
4.4.3 动量与能量的关系
将 E = mc2 写作
E ( m )c
2
③ 反之,当物体的能量改变时,其质量也必然随 之改变,这是相对论的又一极其重要的推论。
11
大 学 物理学
第4章 相对论
相对论的质能关系为开创原子能时代提供了理论 基础,这是一个具有划时代意义的理论公式。
相对论质能关系的正确性,已在核能的应用中得到 证明。
12
大 学 物理学
N E 2.56 1021 3.29 1011 J E 8.42 1010 J
15
大 学 物理学
第4章 相对论
链式反应:
在热中子轰击铀-235核时,生成物中有多于 一个的中子,若它们被其它的铀核所俘获,将会 发生新的裂变,这一连串的裂变称为链式反应。 利用链式反应可制成多种型号和用途的反应堆。
大学物理A1 课件 第4章 狭义相对论

x = ax + bt + e t = ct + dx + f
v
o
P x , y , z , t
x x
S系看 x =0点,
设 t = t =0 时,在o=o点 发出一光信号, 在两个参考 代入以上方程组可得 系中测得的光到达某时空 x = a(x vt)(1)点的事件为p和p '
(2) 长度收缩是“测量”结果,不是“视觉”效 应。
例4-2. 静系中子的平均寿命为2.210-6s。 据报导,在一组高能物理实验中,当它 的速度为u=0.9966c时通过的平均距离为 8km。试说明这一现象:(1) 用经典力学 计算与上述结果是否一致;(2) 用时间膨 胀说明;(3) 用尺缩效应说明。
1 v2 c 2
l l0 1 v c
2
2
原长:在相对于观察者静止 l 的参考系中测得的物体长度。 0
长度收缩:运动物体的长度小于原长, l
当
l0
v c l l0
注意:长度收缩只发生在运动的方向上。
结论:
(1) 相对于观察者运动物体沿运动方向长度缩短了— — 长度收缩 (动尺缩短)
事件 1 A M 发生
B
k
事件 2 发生
K’系:1、2 两事件同时发生
K 系1事件先于2 事件发生
结论:“同时性”具有相对性 ——光速不变原理的直接结果
4.2.2 时间延缓
火车系:
S 系
理想实验:爱因斯坦火车 M y
d
o
A'
, t1 ) I(x1
x1
x
, t2 ) II(x1
0
1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x,t
1 1
到达: x2,t2
x,t
2 2
由题意: t2 t1 10s
Δx uΔt
x2 x1 100 m
u 0.6c
由洛仑兹空间间隔与时间间隔变换式:
100 0.6c 10 x' 2.25 108 m 0.8 1 β 2 u 0.6c Δt 2 Δx 10 2 100 c c t' 12.5s 2 0.8 1 β
质量亏损, 释放结合能.
应用:原子弹、氢弹、核电站 ……
2013-1-28
狭义相对论
相对论的质能关系为开创 原子能时代提供了理论基 础 , 这是一个具有划时 代意义的理论公式 . 开启天堂的钥匙也能打开地狱的大门
1967年6月17日,中国 第一颗氢弹爆炸成功
1941年12月6日,美国总统罗斯福根据爱因斯坦的思想, 批准了代号“曼哈顿工程”的研究项目。由奥本海默领导了一 批世界著名的物理、化学、数学、气象学家和工程专家,进行 原子弹研究。 1945年7月16日5:30 第一颗原子弹爆炸。
σ
S
S
f
' 动系
哥
u
地球和飞船参 考系不对称
哥
弟. a 弟 e
0
σ
x'
x
2013-1-28
狭义相对论
4.4.3 高速物体的视觉效应
1. 汤普金斯先生的错误
汤普金斯先生是《物理世界 奇遇记》里的主人翁. 那本书的 作者盖莫夫说, 汤普金斯先生来 到一座奇异的城市, 由于在这城 市里极限速度 (相应于真实世界 中的光速) 异乎寻常地小, 因此, 他很容易看到各种相对论效应. 汤普金斯先生说, 当他以高速骑 自行车时, 他发现这个城市的一 切都像右图那样变短了.
2013-1-28
狭义相对论
4.4 几个经典佯谬
4.4.1 因果关系 开枪 事件1:
v
鸟死 事件2:
由洛仑兹变换 u 开枪 1, t1) 鸟死 2, t2) t (t 2 x) (x (x c u x t t2 t1 0 t (1 2 ) c Δt 即事件1 先发生,
2013-1-28
狭义相对论
例:计算核聚变中释放出的能量. 质子+中子=氘核
mp 1.67265 1027 kg 质子:
mD 3.34365 1027 kg 氘核:
mn 1.67496 1027 kg 中子:
m mp mn mD 3.96 1030 kg 质量亏损:
2013-1-28
狭义相对论
2. 看不到汤普金斯先生所说的景象 运动尺的缩短, 并不能证明汤普金斯先生将看 到一个变扁的世界. 关键在于尺缩是根据“同时” 进行拍照而得到的. 汤普金斯先生的 “看” , 恰恰 不符合这个要求. 因为当眼睛 “看” 到一个物体时, 意味着物体各部分发射的光子同时到达眼睛. 形成 了像. 这样, 这些光子就不可能是在同一时刻发射出 来的, 因为物体距眼睛的距离不同. 离开观察者较远 的点,必定有较早的发射时刻. 近的点则有较迟的发 射时刻. 这就同尺长测量中要求的“同时”是矛盾 的.
度增大情况.
讨论
(1) 普遍性: v << c时,m(v)=m0 v c 时,m (2) 相对性: 质量具有相对性.
2013-1-28
牛顿力学 c 是极限速度
狭义相对论
2. 动量
p mv
m0 v 1 2 c
2
v
当v c时 v c 0 m m0
相对论力学退化为经典力学.
2013-1-28
dv dm F m v dt dt
狭义相对论
4.5.3 相对论能量 1. 相对论动能 经典力学 相对论力学 2 m0 m0v 2 Ek v Ek ? 2 2 2 2 1v / c dp dW F dr dr dp v vdm mdv v c 2dm dt 两边微分 m0 m m dm 2 v dv 2 2 1 β c v m 2 2 2 c v dm mv dv Ek F d r c d m
L
m0
Ek mc m0c
2
2013-1-28
2
相对论的动能表达式
狭义相对论
讨论
注意相对论动能与经典力学动能的区别和联系 2 2 Ek mc m0c Ek m0v 2 / 2
当v << c 时, 0, 有
m0 Ek c m0 2 2 1v / c
2
1 v 2 3v 4 m0c 2 (1 2 4 1) 2c 8c m0v 2 牛顿力学中的动能公式 2
2013-1-28
狭义相对论
2. 质能关系
Ek mc 2 m0 c 2
定义: 静止能量: 总 能 量:
mc 2 m0 c 2 Ek
E0 m0c 2
p m0v
光子:
m0 0 , v c
p mc
2013-1-28
狭义相对论
4.5.2 力和加速度的关系
dp d(mv ) d m0v F dt dt dt 1 v 2 c 2
dv 当v c时 F m0 dt 即在低速时,有: F ma
任何宏观静止 物体具有能量
E mc 2 ------质能关系
物体的相对论总能量与物体的总质量成正比 —— 质量与能量不可分割. 讨论 (1) 质能关系统一了质量守恒定律和能量守恒定律;
E mc c m
2 2
2013-1-28
狭义相对论
(2) 静能E0=m0c2表征物体静止时的总内能; 分子间相互作用势能 分子运动动能 原子间结合在一起的化学能 原子核与电子结合在一起的电磁能 原子核内基本粒子间的结合能 (3) 质能关系是人类打开核能宝库的钥匙. 裂变:重核分裂为中等质量的核 聚变:轻核聚合为中等质量的核
2013-1-28
狭义相对论
3. 能量和动量的关系 由质速关系: m
m0 v2 1 2 c
v2 m 1 2 m0 c
两边平方: 两边同乘c4 :
2
v2 m 2 1 2 c
2 4
2 m0
2 4 0
m c m v c m c
2 2 2
E (m0c ) p c
x'2 , y' 2 , z' 2 , t' 2
x' x'2 x'1 y' y'2 y'1 z' z' 2 z'1 t' t'2 t'1
Δ x uΔ t x' 1 β 2
2013-1-28
y' Δ y
z' Δ z
u Δt 2 Δx c t' 1 β 2
2
狭义相对论
mA
mB v' A 1 2 c
2
c2 v'2 A u ( 1 2 1) v' A c
S’系: 静止质量: m0=mB,
m m0 v2 1 2 c
运动质量: m=mA . ----质速关系
2013-1-28
狭义相对论
质速关系反映了物质与
运动的不可分割性.
右图曲线表示质量随速
狭义相对论
洛伦兹空间间隔与时间间隔变换式:
事 件1 事 件2 空间间隔 时间间隔 S x1, y1, z1, t1 S' x'1, y'1, z'1, t'1
x2 , y2 , z2 , t2
x x2 x1 y y2 y1 z z2 z1 t t2 t1
2013-1-28
x'ut ' x 2 u 1 2 c y y' 逆 变 z z' 换 t ' u x' t c 2 u2 1 2 c
狭义相对论
3. 洛伦兹速度变换 vx ' u vx u dx' dx udt vx v x ' u dt ' dt u dx 1 u v 1 2 vx ' 2 2 x c c c 2 u2 u vy ' 1 2 vy 1 2 正 逆 c c 变 v y ' dy ' 变 v y u u dt ' 换 换 1 2 vx ' 1 2 vx c c 2 u2 u vz ' 1 2 vz 1 2 dz ' c c vz v z ' dt ' u u 1 2 vx ' 1 2 vx c c
狭义相对论
例: 在惯性系S中, 有两事件同时发生在 xx’ 轴上相距 1.0103m处, 从S系观察到这两事件相距2.0103m. 求: 由S’系测得此两事件的时间间隔为多少?
解: 由洛仑兹变换得:
x
x ut 1 u c
2
x 1 u c
2
u t 2 x c t 2 1 u c
与物体运动无关
F持续作用
要求:
dp d ( mv ) F dt dt
p 持续
但 v 的上限是 c
m 随速率增大而增大
m m(v)
2013-1-28
S系:
t=0时刻, M, v=0, t 时刻, mA=mB=M/2, vA=-u, vB=u. 由洛伦兹速度变换: vA u 2u ' vA u u2 1 2 vA 1 2 c c
