12动量矩定理wy分析
合集下载
理论力学 12 动量矩定理

轴转动(zhuàn dòng)。已知均质杆 OA 长为 l ,质 C1 量为 m 1,均质圆盘 C 2 的半径为 r ,质量为 m 2,
试求复摆对 O 轴的动量矩。
A
C2 r
解: J O 的计算(jìsuàn):
JO
1 12
m1
l
2
m1
l 2
2
1 2 m2
r2
m2
l
r
2
图 12-9
由几何关系知: r R h z
h 薄圆片对 y 轴转动惯量 d J y 为:
1 r2 dm 4
精品资料
dJ y
1 4
r 2dm
z 2dm
1 4
r2
z2
r 2dz
1
4
R4 h4
h
z 4
R2 h2
h
z 2
z2
dz
整个(zhěnggè)圆锥体对于 y 轴的转动惯量为:
J y
h 0
1 4
底圆直径的转动惯量。已知圆锥体质量为 M ,
z
底圆半径为 R ,高为 h ,如图12-6所示。 r
h z dz
解:把圆锥体分成许多(xǔduō)厚度为 d z 的薄圆片,该薄圆片的质量为
d m r2d z
为圆锥体的密度,r为薄圆片的半径。
O
y
R
x
图 12-6
圆锥体的质量为
M 1R2h
3
薄圆片对自身直径的转动惯量为
精品资料
12.1 转动惯量、平行(píngxíng) 轴定1理2.1.1 转动惯量
质点系的运动,不仅(bùjǐn)与作用在质点系上的力有关, 还与质点系各质点的质量其及分布情况有关。质心是描述质 点系质量分布的一个特征量,转动惯量(Moment of inertia)则 是描述质点系质量分布的另一个特征量。
理论力学12—动量矩定理解析

又因为
z
F mv
Q
r
y
O
v mv 0, r F M O (F )
所以
d M O (mv) M O (F )
dt
x 质点对某定点的 动量矩对时间的一阶 导数,等于作用力对 同一点的矩。
12.2.1 质点的动量矩定理
将上式投影在直角坐标轴上,并将对点的动量 矩与对轴的动量矩的关系代入,得
d d t M x (mv) M x (F )
z
4 定轴转动刚体的动量矩
Lz mz (mivi ) miviri miri2
令 Jz=Σmiri2 称为刚体对 z 轴的转动惯 量, 于是得
ri mivi Mi
Lz J z
即:绕定轴转动刚体对其转轴的动量矩等于刚体对 转轴的转动惯量与转动角速度的乘积。
质点系的动量矩
例1 均质圆盘可绕轴O转动,其上缠有一 绳,绳下端吊一重物A。若圆盘对转轴O的转
n i 1
MO (Fi(i) )
由于内力总是成对出现,因此上式右端的底二项
n
MO (Fi(i) ) 0
i 1
12.2.2 质点系的动量矩定理
上式左端为
n
i 1
d dt
MO (mivi )
d dt
n i 1
MO (mivi )
d dt
LO
于是得
d
dt
LO
n i 1
MO (Fi(e) )
d dt
M
y
(mv)
M
y
(F
)
d dt
M
z
(mv)
M
z
(F
)
质点对某 固定轴的动量 矩对时间的一 阶导数等于质 点所受的力对 同一轴的矩。
12动量矩定理

图12.7 钟摆
第12章 动量矩定理
12.1 转 动 惯 量
【例12.5】 匀质圆盘与匀质杆组成的钟摆如图12.7所示。已知圆盘质量m1, 直径d,杆的质量m2,长l,试求钟摆对悬挂轴O的转动惯量J0。
解:钟摆由匀质杆和匀质盘组成,所以有 = JO JO杆 + JO
其中
JO
=J c
+
m1
l
+
d 2
平方的乘积,即
12.7
J=z J zc + md 2
(12.7)
第12章 动量矩定理
12.1 转 动 惯 量
证明:如图12.5所示,设刚体总的质量为m,轴zc通过质心C,z与zc平行且 相距为d。不失一般性,可令y与yc重合,在刚体内任取一质量为mi的质点Mi,它 至zc轴和z轴的距离分别为ric和ri。刚体对于z、zc轴的转动惯量分别为
12.9
第12章 动量矩定理
12.1 转 动 惯 量
【例12.4】 质量为m,长为l的匀质杆如图12.6所示,求杆对yc的转动惯量。
解:由例12.1知
Jy
=
1 ml2 3
,根据平行轴定理式(12.7)有
J yc
=J y
−
md 2
=1 ml2 3
−
m
l
2
2
=1 12
ml 2
12.10
图12.6 匀质杆
在工程问题上,计算刚体的转动惯量时,常应用下面公式
12.3
第12章 动量矩定理
12.1 转 动 惯 量
Jz
=
mρ
2 z
(12.2)
ρ 其中m为整个刚体的质量, z 为刚体对z轴的回转半径,它具有长
第十二章 动量矩定理

Lz=Jzω
§2 动量矩定理
一、质点的动量矩定理
设质点质量为m, 受力F, MO(mv) 动量mv,定坐标系Oxyz , 根据质点的动量定理 z
F
B
mv
r
o A y
MO(F)
d (mv ) F dt
等式两边同时与矢径r作矢量积, 即 x
d (mv ) r F r dt
MO(F)
?
d (mv ) r F 为求等式 r 左边项,先来看 dt d (r mv ) dr mv r d (mv ) dt dt dt v ( r d ( v mv∵O为定点!)mv ) dt MO(mv) =0
第十二章
动量矩定理
z
§1 动量矩的概念
一、质点的动量矩
F r
o
B A m
y
回顾: 力对点的矩 Mo(F)= r×F 若 r=xi+yj+zk F=Fxi+Fyj+Fzk
则 i M o (F ) x Fx
j y Fy k z Fz
MO(F)
x
大小:│Mo(F) │ =2S△OAB
方向:按右手螺旋规则定。
[Mo(mv)]z= M z(mv)
代数量
• 动量矩的量刚为 ML2T-1 (kg· 2/S) m
二、质点系的动量矩
质点系对固定点O的动量矩等于各质点对同 一点O的动量矩的矢量和(即质点系动量对点O 的主矩):
对定点
Lo M o (mi vi )
i 1
n
矢量
质点系对固定轴z的动量矩等于各质点对同一 轴z的动量矩的代数和,即
vC
C
Lo = M o(Mvc)
动量矩定理公式总结

动量矩定理公式总结
动量矩定理是物理学中的重要概念,它描述了物体在受到外力作用时的运动状态变化。
在本文中,将介绍动量矩定理的概念和公式,并探讨其在物理学研究中的应用。
动量矩定理是指,物体在受到外力作用时,它的动量随时间的变化率等于作用在物体上的合外力矩。
换句话说,动量矩定理描述了物体受到外力矩作用时的转动运动状态变化。
动量矩定理的公式为:dL/dt = M,其中dL/dt表示物体动量的变化率,M表示作用在物体上的合外力矩。
这个公式可以用来计算物体运动时的动量变化情况,以及外力矩对运动状态的影响。
除了上述公式,动量矩定理还可以用向量形式表示。
具体而言,物体的角动量L等于它的动量p与位置向量r的叉积,即L = r × p。
在这种情况下,动量矩定理可以表示为dL/dt = M × r,其中M表示外力矩。
动量矩定理在物理学研究中有着广泛的应用。
例如,在机械工程中,动量矩定理可用于计算机械系统的运动状态,以及预测其运动轨迹。
在天体物理学中,动量矩定理可用于研究行星、恒星等天体的旋转运动状态。
总之,动量矩定理是物理学中的重要概念,它描述了物体在受到外力作用时的运动状态变化。
通过了解动量矩定理的概念和公式以及其在物理学研究中的应用,我们可以更好地理解物体的运动状态变化和物理规律。
12动量矩定理wy

Lc
Jc
1 2
mR 2
1 2
mRvc
vc R
Jc
1 mR2 2
D
思考:对速度瞬心 D 的动量矩 ?
答案:
LD J D JC mR 2 或
LD LC mvC R JC mvC R
§ 12-3 动量矩定理
一、质点的动量矩定理
MO(mv)=r mv
将上式两端对时间求一阶导数,得:
dt
M z (F)
——质点系动量矩定理及其守恒
◆ 对某固定点O的动量矩定理:
dLO
dt
mO F e
质点系内力不能改变质点系的动量矩, 只有外力才是系统动量矩改变的原因。
即:质点系对某固定点O 的动量矩Lo 对时间的导数,等于作用于该 质点系的所有外力对于同一点之矩的矢量和(即外力系对O 点的主 矩)。
直杆OA和质量为 m 半径为 R的 均质园盘 A在 A点刚接 , 如图所 示.求系统对垂直于图面且过 O 点的轴的转动惯量。
O A
R
解:
JO = JOA + J盘
J OA
1 3
ml 2
O
J 盘 J A m (OA)2
1 mR2 m (OA)2
2
A
1 mR2 ml 2
R
2
JO
4 3
ml2
LO M BvB R M AvA R 0
B
vB vA
VA
又因为二人在同一高度上,从静止开始向上爬,
MAg
所以二人同时到达顶端。
VB MBg
——应用举例 例七 已知:水平匀质圆台重G ,半径为R ,无摩擦地绕通 过其中心的铅直轴OZ 转动。重为P 的人以不变的相对速度
第12章 动量矩定理

M
i 1
n
o
( Fi ) 0
(e)
Lo (t ) Lo (t0 )
M
i 1
n
x
( Fi ) 0
(e)
Lx (t ) Lx (t0 )
质点系动量矩守恒举例:
O
若两猴等重 ,轮无 质量。谁爬得快?
离合器传动
图示为运送矿石的卷扬机系统。已知鼓轮的半径 例: 为R ,重量为 P mg ,绕轴 O 转动。小车和矿石总
LO l m v l m lω m l2 θ
v
只有 m g 对O点有矩
MO (F ) mgsin l
图中 角的正方向,便规定了取 矩的正方向。
根据动量矩定理列方程
d 2 ( ml ) mg sin l dt
l g sin 0
——线性化
第13章 动量矩定理
动量矩定理表达了动量矩(机械运动 的一种度量)与力矩之间的关系。
本章首先介绍动量矩定理。在引进 转动惯量的概念之后,将定理应用于研 究刚体的定轴转动,得出刚体定轴转动 的微分方程。最后,将相对质心的动量 矩定理与前述质心运动定理结合,给出 刚体的平面运动微分方程。
§13-1 动量矩定理
d( ri mi vi ) ri Fi (e) ri Fi (i) (i 1,2,, n) dt n n n d( ri mi vi ) (e) (i) ri Fi ri Fi 相加得 dt i 1 i 1 i 1
其中 ri Fi
重量为 P1 m1 g 。配重 P2 m2 g 。作用在鼓轮上的力 偶矩为 M ,鼓轮对转轴的转动惯量为 J ,轨道的倾角 为 。不计绳的质量及各处摩擦。求小车的加速度。
十二章动量矩定理

F mv
M0(F)
o
Q
y
x
由牛顿第二定律
m
dv dt
F
d dt
(mv)
F
r
d dt
(mv)
r
F
d (r mv) r d(mv) dr mv
dt
ห้องสมุดไป่ตู้
dt dt
理论力学电子教程
第十二章 动量矩定理
d (r mv) r F dt
M0(mv) m0(F)
理论力学电子教程
第十二章 动量矩定理
C
m2
IOZ M
式中
M
m1
O
IOZ
1 3
m1L2
1 2
m2
r
2
m2L2
理论力学电子教程
第十二章 动量矩定理
代入已知值得:
IOZ
1 10 0.32 3
1 40 0.152 2
40 0.32
4.35kg m2
M 20 4.6rad / s2
IOZ 4.35
理论力学电子教程
第十二章 动量矩定理
dt
M y (mv)]
my (Fe )
d [
dt
M z (mv)]
mz (Fe )
理论力学电子教程
第十二章 动量矩定理
【典型题精解】
例12-1 滑块A,B质量分别为2Kg,0.5Kg,用长1
米的绳连接,在水平光滑滑竿上滑动,绳和竿的质量不计。
竿绕铅垂轴转动,轴的摩擦也不计。当 rA 0.6m 时,滑块 A以速度0.4m/S沿竿向外运动,竿的角速度 0.5rad / s
求此时竿的角加速度。
1m
B rB
第12章-动量矩定理

它表达为刚体质量 m 与某一长度ρ z 旳平方
旳乘积: J z m z2
细直杆 均质圆环 均质圆板
J z /m 1 / 3 l2 z 0.5774 l
J z /m R2 z R
J z /m 1 / 2 R2 z 0.7071R
z 假如把刚体旳质量全部集中在与 轴相距为ρ z 旳点
上,则此质点对 z 轴旳转动惯量与原刚体相同。
四、平行轴定理
J z J z md 2
定理:刚体对任意轴旳转动惯量,等于刚体对 于经过质心、并与该轴平行旳轴旳转动惯量, 加上刚体旳质量与两轴间距离平方旳乘积。
z
O
z
d
ri
ri
C
O
mi
zi
y( y)
C点为质心;
O z 为质心轴,O z
为与之平行旳任
xi
一轴,距离为 d 。
x d x yi J z mi ri2 mi ( xi2 yi2 )
d dt
(
J
z
)
Jz
Mz
dω dt
(Fi
)M
M z (Fi )
z
(
FN
i
)
Fi
或
Jz
d2
dt2
M z (Fi )
或 J z M z (Fi )
FNi
与 m a Fi 比较
例:已知滑轮半径为 R ,转动惯量为 J ,带动滑轮
旳皮带拉力分别为 F1 和 F2 。求滑轮旳角加速度 。
F2 解:根据定轴转动微分方程
d(ri
mivi ) dt
ri
F (e) i
ri
Fi(i)
(i 1,2,, n)
相加得
旳乘积: J z m z2
细直杆 均质圆环 均质圆板
J z /m 1 / 3 l2 z 0.5774 l
J z /m R2 z R
J z /m 1 / 2 R2 z 0.7071R
z 假如把刚体旳质量全部集中在与 轴相距为ρ z 旳点
上,则此质点对 z 轴旳转动惯量与原刚体相同。
四、平行轴定理
J z J z md 2
定理:刚体对任意轴旳转动惯量,等于刚体对 于经过质心、并与该轴平行旳轴旳转动惯量, 加上刚体旳质量与两轴间距离平方旳乘积。
z
O
z
d
ri
ri
C
O
mi
zi
y( y)
C点为质心;
O z 为质心轴,O z
为与之平行旳任
xi
一轴,距离为 d 。
x d x yi J z mi ri2 mi ( xi2 yi2 )
d dt
(
J
z
)
Jz
Mz
dω dt
(Fi
)M
M z (Fi )
z
(
FN
i
)
Fi
或
Jz
d2
dt2
M z (Fi )
或 J z M z (Fi )
FNi
与 m a Fi 比较
例:已知滑轮半径为 R ,转动惯量为 J ,带动滑轮
旳皮带拉力分别为 F1 和 F2 。求滑轮旳角加速度 。
F2 解:根据定轴转动微分方程
d(ri
mivi ) dt
ri
F (e) i
ri
Fi(i)
(i 1,2,, n)
相加得
动量矩定理12章
)2
0
z
B
D
例: 均质圆盘,其绕轴O的转动惯量为J ,可绕通
过其中心的轴无摩擦地转动,另一质量为 m2
的人由 B 点按规律 s 1 at 2 沿距 O 轴半径
为 r 的圆周运动。初始2时,圆盘与人均静止。
求圆盘的角速度与角加速度。
解: 圆盘与人一起 —— 研究对象
受力分析: M z (Fi ) 0
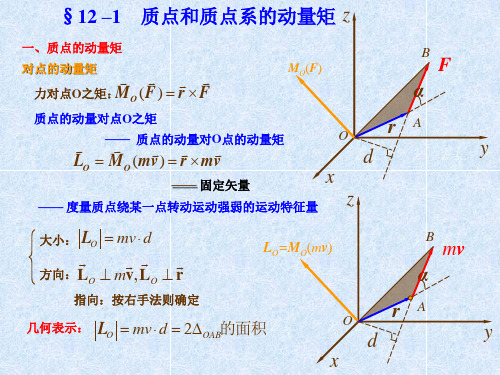
大小: LO mv d
方向:LO mv, LO r
LO=MO(mv)
B
mv α
指向:按右手法则确定
几何表示: LO mv d 2OAB的面积
O
rA
d
y
x
对轴的动量矩
类似于力对点之矩与力对轴之矩的关系: MO (F ) x M x (F ) yFz zFy
质点的动量 mv 对 x 轴之矩 :
§12 –1 质点和质点系的动量矩 z
一、质点的动量矩
对点的动量矩 力对点O之矩:MO (F ) r F
MO(F)
B
F α
质点的动量对点O之矩
—— 质点 的动量对O点的动量矩 LO MO (mv) r mv
—— 固定矢量
O
rA
d
x
y
—— 度量质点绕某一点转动运动强弱的运动特征量
z
LOz (JO m1r12 m2r22 )
(b)
外力主矩仅由重力 m1g 和 m2g 产生,有
m0g
A
B
v2 m2g
v1 m1g
MOz (m1r1 m2r2 )g
(c)
(b)
例题
dLOz dt
M Oz
(a)
LOz (JO m1r12 m2r22 )
12.动量矩定理

By
FNx
B B R J2
G2
FBx
a
FN y
由对B点的动量矩定理 由对 点的动量矩定理
z2 r2 α1 ∴ α1 = iα2 Q = =i = z1 r1 α2
M −m i gR α2 = J1i 2 + J2 + m 2 R
J2α2 + mR2α2 = FNx ⋅ r2 − mgR (2)
r2 = ir1
n d (J zω) = ∑Mz (F i ) dt i =1
去掉微分符号即是 J zα = ∑Mz (Fi )
i =1 n
n
&& : 用角坐标的导数可写成 J zϕ = ∑Mz (F i )
i =1
上式称为刚体绕定轴转 动的微分方程
通风机的转动部分以初角速度ωo 绕中心轴转 例一 . (书上 习12 – 9 )通风机的转动部分以初角速度 书上 通风机的转动部分以初角速度 空气的阻力矩与角速度成正比, 为常数. 动 , 空气的阻力矩与角速度成正比 即 M = kω , k为常数 若转动部 为常数 分对转轴的转动惯量为J 分对转轴的转动惯量为 . 问: 经过多少时间其转动的角速度减少为初角速度的一半 ? 又在此 时间内共转了多少转 ?
v
O
取整个系统为研究对象, 解: 取整个系统为研究对象 受力及运 动分析如图
θ
v
O 由对 点的动量矩定理 M d (JOω + m2vR) = −m2 gRsinθ + M Fy dt R ω a JO + m2 R⋅ a = M − m2 gRsinθ R O Fx M − m2 gR2 sinθ R M a= JO + m2 R2 m1 g
FNx
B B R J2
G2
FBx
a
FN y
由对B点的动量矩定理 由对 点的动量矩定理
z2 r2 α1 ∴ α1 = iα2 Q = =i = z1 r1 α2
M −m i gR α2 = J1i 2 + J2 + m 2 R
J2α2 + mR2α2 = FNx ⋅ r2 − mgR (2)
r2 = ir1
n d (J zω) = ∑Mz (F i ) dt i =1
去掉微分符号即是 J zα = ∑Mz (Fi )
i =1 n
n
&& : 用角坐标的导数可写成 J zϕ = ∑Mz (F i )
i =1
上式称为刚体绕定轴转 动的微分方程
通风机的转动部分以初角速度ωo 绕中心轴转 例一 . (书上 习12 – 9 )通风机的转动部分以初角速度 书上 通风机的转动部分以初角速度 空气的阻力矩与角速度成正比, 为常数. 动 , 空气的阻力矩与角速度成正比 即 M = kω , k为常数 若转动部 为常数 分对转轴的转动惯量为J 分对转轴的转动惯量为 . 问: 经过多少时间其转动的角速度减少为初角速度的一半 ? 又在此 时间内共转了多少转 ?
v
O
取整个系统为研究对象, 解: 取整个系统为研究对象 受力及运 动分析如图
θ
v
O 由对 点的动量矩定理 M d (JOω + m2vR) = −m2 gRsinθ + M Fy dt R ω a JO + m2 R⋅ a = M − m2 gRsinθ R O Fx M − m2 gR2 sinθ R M a= JO + m2 R2 m1 g
第12章 动量矩定理

§12-3 动量矩定理
例 题 5
两个鼓轮固连在一起,其总质量是 m,对水平转轴O的
转动惯量是 JO ;鼓轮的半径是 r1 和 r2 。绳端悬挂的重物 A和 B 质量分别是 m1 和 m2 ,且 m1 > m2。试求鼓轮的角 加速度(与例12-1类似)。
r1 r2
w
A
B
§12-3
动量矩定理
例 题 5
解: 1、选系统(含鼓轮,重物 A , B)为研究对象
2、运动分析 设鼓轮的角速度为w, 物 A的速度:v1= r1w 物 B的速度:v2= r2w
2
y
FO
r1 r2
w
mg
3、受力分析 重力 mg,m1g , m2g 轴O处约束力 FO
LOz ( J O m1r1 m2 r2 )w
2
v1 A m1 g v2
y
m
w
C
平面运动=随C平动+绕C转动
ri
O
rC
x
LC J C ωk , 为动量偶
第12章 动量矩定理
§12-2 刚体对轴的转动惯量
§12-2 刚体对轴的转动惯量
z
2-1 定义
J z ri mi
2
ri
vi
mi
i
均质连续体:
w
O x
y
J z M r dm
2
单位:kg· m2
3、 质点系动量矩守恒定理
若
e M O ( Fi ) 0 e M z ( Fi ) 0
dL O e MO dt
则 LO 常矢 则 Lz 常量
即:当质系所受合外力对某定点(或某定轴)的 矩为零,则质系对该点(或该轴)的动量矩保持 不变 —— 质系动量矩守恒定律。
第十二动量矩定理-资料

Jy
m 12
(b 2
c2)
y
1 (b 2 c 2 ) 12
abc
JZ
m 12
(a 2
b2)
Jy
m 12
a2
Jy
m 12
b2
z
1 (a 2 b2) 12
x 0 .289 a
y 0 .289 b
abh
§12-5 质点系相对于质心的动量矩定理
1.对质心的动量矩
L z M z(m iv i) m iv ir i
m i riri m iri2
转动惯量
Jz miri2
Lz Jz
§12-2 动量矩定理
1.质点的动量矩定理
设O为定点,有
ddtMO(mv)ddt(rmv)
drmvrd(mv)
dt
dt
其中:
d (mv) F dt d r v (O为定点) dt
例12-3:已知 m, J O , m 1 , m 2 ,r1 , r2 ,不计摩擦.
求:(1)
(2)O处约束力 F N
(3)绳索张力 F T1 ,F T 2
解: (1) L O J O m 1 v 1 r 1 m 2 v 2 r 2
(JOm 1r12m 2r2 2)
dt
d A 称面积速度.
dt
面积速度定理:质点在有心力作用下其面积速度守恒.
例12-4:两小球质量皆为m,初始角速度 0 求:剪断绳后, 角时的.
解: 0 时,
Lz12ma 0a2m2 a0
0 时,
由
Lz2 2m (alsin )2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章:动量矩定理
§ 12-1 动量矩 § 12-2 动量矩定理 § 12-3 转动惯量 § 12-4 刚体绕定轴转动的微分方程
动量定理揭示了质点和质点系动量变化与外力主矢的关 系;质心运动定理揭示了质心运动与外力主矢的关系。但 它们无法描述质点系机械运动的全貌。
均质轮受外力作用而绕其质心O作定轴转 动,它有角速度和角加速度,但对于轮 的动量为:
mz
(F
i i
)
(1)
(i=1,2,….n)
将n个方程求和:
x
n
i 1
dmz (mivi ) dt
n i 1
mz
(Fie )
n i 1
mz
(F
i i
)
m1
mi Fei
y
mn m2
mi vi mj fij fji Fii
d
dt
mz (mivi )
mz (Fie )
dLz
dt
mz (Fie )
方向:垂直于r、mv所在的平面, 指向由右手螺旋法则判定。
(2)质点对固定轴的动量矩
M x (mv) [r mv]x y mv z z mv y M y (mv) [r mv] y z mv x x mv z M z (mv) [r mv]z x mv y y mv x
= ( -yi i +xi j )
y
mi
C ri
x
Lcr = ri mivri
= (xi i +yi j)mi( -yi i +xi j ) = k mi (xi2+yi2 ) = JC k = Lc
Lcz = JC
例题11-1. 边长为a 质量为m的正方体沿平直轨道滑动如 图所示。已知质心C的速度为v。求: (1) 正方体对轨道上 固定点O的动量矩; (2) 正方体的绝对运动对质心 C的动量 矩; (3) 正方体的相对运动对质心C的动量矩。
(3) 质点系的动量矩
质点系中所有质点的动量对于固定轴的矩的代数和, 称为质点系对固定轴的动量矩。
LZ = LZi = MZ(mivi)
=
xi
mivyi
yi
mivxi
(4) 定轴转动刚体对转轴的动量矩
M
z
mivi
mivi ri mi ri2
Lz M z mivi Miri2
LCr
1 2
mr
22
vC = vB + vCB= r1 + r2
A
rc
C B
2
rC OA AB BC rC P 2mr 2 (1 2 )
vC
LOC mr 2 (21 2.52 )
LOO 2.5mr 2 (1 2 )
§ 12-2 动量矩定理
一、质点的动量矩定理
MO(mv)=r mv
O
A
O 可绕通过点 O 的水平轴转动。 1
一绳绕在圆柱O上, 绳的另一端
绕在圆柱 C上。求圆柱下落其角
速度分别为 1和2时系统对O点 的动量矩。
C B
2
解: 圆柱体O作定轴转动
O
1
圆柱体C作平面运动B为瞬心(相对).
LO = LOO + LOC
LOO
1 2
mr 21
LOC = rc P + Lcr
dM z (mv)
dt
M z (F)
二、质点系对固定轴的动量矩定理
第i个质点:质量为mi 动量为mivi:
z
力 外力 Fei 内力 Fii
m1 mi
Fei
mn
m2
mi vi mj
Fii
y
x
根据质点对固定轴的动量矩定理:
第i个质点:
dmz (mivi ) dt
mz (Fi )
z
mz
(Fie
)
将上式两端对时间求一阶导数,得:
dM o (mv)
dt
d dt
(r
mv)
dr dt
mv
r
d (mv) dt
v mv r F
MO (F)
质点对固定点的动量矩定理:
d
M
o (mv)
dt
M
o
(
F
)
(1)
将(1)式两端投影到固定的轴上,可得到
质点对固定轴的动量矩定理:
d M o (mv)z
dt
[Mo(F)]z
P mvC mvO 0
不能用动量定理来描述轮绕其质心的定轴转动。
§ 12-1 动 量 矩
(1) 质点的动量矩
mv
质量为m的质点A ,t 时刻动量 为mv, O为空间任一固定点,
MO(mv)
d
A
则mv 对O点的矩定义为质
O
r
点的动量矩:
MO(mv)=r mv
动量矩是一个矢量.
大小: MO (mv) r mv r mv sin mv d
Miri2
令
miri2 JZ
LZ=Jz •ω
其中: JZ称为刚体对转轴的转动惯量。 ω为刚体转动的角速度。
例题11-3. 有对称面的刚体在 平行于对称面的平面内作平面 运动,角速度为。求:刚体对过 质心且垂直于对称面的轴的动 量矩。
C
解: 取坐标如图
vri = ri =k(xi i +yi j)
质点系对固定轴的动量矩定理:
dLz
dt
mz (Fie )
三、动量矩守恒定律
若
Mz (Fie) 0 , 则Lz = C(恒量)
例11-5
图示卷扬机鼓轮质量为m1,半径为r,可绕过鼓 轮中心O的水平轴转动。鼓轮上绕一绳,绳的一端 悬挂一质量为m2的重物。鼓轮视为匀质,并令其 对O轴的转动惯量为JO。今在鼓轮上作用一不变力 矩M,试求重物上升的加速度。
解:研究质点系----鼓轮与重物
v
r
M m1g
O
Fox
v
系统对O轴的动量矩:
Foy
LO
JO
m2vr
JO r
m2r v
m2g
由动量矩定理
dLo
dt
mo (Fie )
代入数据得:
JO r
m2r
dv dt
M
m2gr
M m1g
O
Fox
v
Foy
m2g
解得
a
M m2gr
Jo r
m2r
§ 12-3 转动惯量 Zc Z
L
J
Z
1 3
ML2
平行移轴公式
J
CZ
1 12
C
v
O
解: 建立直角
y
坐标系Oxy
O
rc
C
v
x A
(1)LO = ri mivi = ( mi ri )v = m rcv = - 0.5amvk
(2) Lc = ri mivi = ( mi ri )v = 0
(3) vri = 0
Lcr = 0
例题11- 4. 均质圆柱体O和C的
质量均为m,半径相等均为 r.圆柱
(1)刚体对轴的转动惯量
Jz = miri2
m1
ri
mi
od
C
若刚体的质量为M,则:
mn
m = mi
若C点为刚体的质心
(2)平行轴定理 Jz1 = Jcz + md 2
m2 yc y
mj
(3)几种常见均质物体的转动惯量
细直杆
Z/
Z
则:由定义 dm m dxl
l
0
x2dx
1 ml2 3
§ 12-1 动量矩 § 12-2 动量矩定理 § 12-3 转动惯量 § 12-4 刚体绕定轴转动的微分方程
动量定理揭示了质点和质点系动量变化与外力主矢的关 系;质心运动定理揭示了质心运动与外力主矢的关系。但 它们无法描述质点系机械运动的全貌。
均质轮受外力作用而绕其质心O作定轴转 动,它有角速度和角加速度,但对于轮 的动量为:
mz
(F
i i
)
(1)
(i=1,2,….n)
将n个方程求和:
x
n
i 1
dmz (mivi ) dt
n i 1
mz
(Fie )
n i 1
mz
(F
i i
)
m1
mi Fei
y
mn m2
mi vi mj fij fji Fii
d
dt
mz (mivi )
mz (Fie )
dLz
dt
mz (Fie )
方向:垂直于r、mv所在的平面, 指向由右手螺旋法则判定。
(2)质点对固定轴的动量矩
M x (mv) [r mv]x y mv z z mv y M y (mv) [r mv] y z mv x x mv z M z (mv) [r mv]z x mv y y mv x
= ( -yi i +xi j )
y
mi
C ri
x
Lcr = ri mivri
= (xi i +yi j)mi( -yi i +xi j ) = k mi (xi2+yi2 ) = JC k = Lc
Lcz = JC
例题11-1. 边长为a 质量为m的正方体沿平直轨道滑动如 图所示。已知质心C的速度为v。求: (1) 正方体对轨道上 固定点O的动量矩; (2) 正方体的绝对运动对质心 C的动量 矩; (3) 正方体的相对运动对质心C的动量矩。
(3) 质点系的动量矩
质点系中所有质点的动量对于固定轴的矩的代数和, 称为质点系对固定轴的动量矩。
LZ = LZi = MZ(mivi)
=
xi
mivyi
yi
mivxi
(4) 定轴转动刚体对转轴的动量矩
M
z
mivi
mivi ri mi ri2
Lz M z mivi Miri2
LCr
1 2
mr
22
vC = vB + vCB= r1 + r2
A
rc
C B
2
rC OA AB BC rC P 2mr 2 (1 2 )
vC
LOC mr 2 (21 2.52 )
LOO 2.5mr 2 (1 2 )
§ 12-2 动量矩定理
一、质点的动量矩定理
MO(mv)=r mv
O
A
O 可绕通过点 O 的水平轴转动。 1
一绳绕在圆柱O上, 绳的另一端
绕在圆柱 C上。求圆柱下落其角
速度分别为 1和2时系统对O点 的动量矩。
C B
2
解: 圆柱体O作定轴转动
O
1
圆柱体C作平面运动B为瞬心(相对).
LO = LOO + LOC
LOO
1 2
mr 21
LOC = rc P + Lcr
dM z (mv)
dt
M z (F)
二、质点系对固定轴的动量矩定理
第i个质点:质量为mi 动量为mivi:
z
力 外力 Fei 内力 Fii
m1 mi
Fei
mn
m2
mi vi mj
Fii
y
x
根据质点对固定轴的动量矩定理:
第i个质点:
dmz (mivi ) dt
mz (Fi )
z
mz
(Fie
)
将上式两端对时间求一阶导数,得:
dM o (mv)
dt
d dt
(r
mv)
dr dt
mv
r
d (mv) dt
v mv r F
MO (F)
质点对固定点的动量矩定理:
d
M
o (mv)
dt
M
o
(
F
)
(1)
将(1)式两端投影到固定的轴上,可得到
质点对固定轴的动量矩定理:
d M o (mv)z
dt
[Mo(F)]z
P mvC mvO 0
不能用动量定理来描述轮绕其质心的定轴转动。
§ 12-1 动 量 矩
(1) 质点的动量矩
mv
质量为m的质点A ,t 时刻动量 为mv, O为空间任一固定点,
MO(mv)
d
A
则mv 对O点的矩定义为质
O
r
点的动量矩:
MO(mv)=r mv
动量矩是一个矢量.
大小: MO (mv) r mv r mv sin mv d
Miri2
令
miri2 JZ
LZ=Jz •ω
其中: JZ称为刚体对转轴的转动惯量。 ω为刚体转动的角速度。
例题11-3. 有对称面的刚体在 平行于对称面的平面内作平面 运动,角速度为。求:刚体对过 质心且垂直于对称面的轴的动 量矩。
C
解: 取坐标如图
vri = ri =k(xi i +yi j)
质点系对固定轴的动量矩定理:
dLz
dt
mz (Fie )
三、动量矩守恒定律
若
Mz (Fie) 0 , 则Lz = C(恒量)
例11-5
图示卷扬机鼓轮质量为m1,半径为r,可绕过鼓 轮中心O的水平轴转动。鼓轮上绕一绳,绳的一端 悬挂一质量为m2的重物。鼓轮视为匀质,并令其 对O轴的转动惯量为JO。今在鼓轮上作用一不变力 矩M,试求重物上升的加速度。
解:研究质点系----鼓轮与重物
v
r
M m1g
O
Fox
v
系统对O轴的动量矩:
Foy
LO
JO
m2vr
JO r
m2r v
m2g
由动量矩定理
dLo
dt
mo (Fie )
代入数据得:
JO r
m2r
dv dt
M
m2gr
M m1g
O
Fox
v
Foy
m2g
解得
a
M m2gr
Jo r
m2r
§ 12-3 转动惯量 Zc Z
L
J
Z
1 3
ML2
平行移轴公式
J
CZ
1 12
C
v
O
解: 建立直角
y
坐标系Oxy
O
rc
C
v
x A
(1)LO = ri mivi = ( mi ri )v = m rcv = - 0.5amvk
(2) Lc = ri mivi = ( mi ri )v = 0
(3) vri = 0
Lcr = 0
例题11- 4. 均质圆柱体O和C的
质量均为m,半径相等均为 r.圆柱
(1)刚体对轴的转动惯量
Jz = miri2
m1
ri
mi
od
C
若刚体的质量为M,则:
mn
m = mi
若C点为刚体的质心
(2)平行轴定理 Jz1 = Jcz + md 2
m2 yc y
mj
(3)几种常见均质物体的转动惯量
细直杆
Z/
Z
则:由定义 dm m dxl
l
0
x2dx
1 ml2 3
