浙江省2009年1月高等教育自学考试 工程数学(一)试题 课程代码07961
浙江2009年1月高等教育自学考试

浙江省 2009 年 1 月高等教育自学考试汽车构造试题 课程代码: 02576本试卷分 A 、B 卷,使用 佃97年版本教材的考生请做 A 卷,使用2008年版本教材的 考生请做 B 卷;若 A 、 B 两卷都做的,以 B 卷记分。
A 卷、单项选择题(本大题共 15 小题,每小题 2 分,共 30 分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的 括号内。
错选、多选或未选均无分。
1. 四冲程发动机在进行压缩行程时( A. 进气门开启、排气门开启 C •进气门开启、排气门关闭2. 下列各零件不属于气门传动组的是( A. 凸轮轴 C •气门弹簧3.将推杆或凸轮传来的力改变方向传给气门使其开启的零件是( )A.凸轮轴 B.挺柱 C •气门弹簧 D.摇臂4. 不属于气门组的机件是( )A.气门挺柱 B.气门 C •气门弹簧D.气门导管5•过量空气系数 a 值在0.85~0.95之间,这是( )A.功率成分混合气 B.经济成分混合气C.浓混合气D.稀混合气 6•将燃油喷在每缸进气门的外侧,贮存并汽化,以便进气门开启时涌入气缸是( A.多点喷射 B.同时喷射 C.分组喷射 D.顺序喷射7•发动机正常工作时,其冷却水的温度应在多少度之间?()A.50 C ~60 CB.60 C ~70CC.70 C ~80CD.80 C ~90C 8•柱塞式喷油泵的压油过程是指( )A. 柱塞下移至进油孔以下的下止点位置时B. 柱塞从下止点向上移动到将进油孔关闭时C. 柱塞上移到螺旋槽或斜槽上限高出进油孔的下沿时D. 柱塞上移到上止点时9•汽车有四个车轮,其中两个后轮为驱动轮时,则其驱动形式可表示为( )A.2 X 1 C.4 X 2D.4 X 4)B •进气门关闭、排气门开启 D •进气门关闭、排气门关闭 ) B.挺柱 D.摇臂轴B.2 X 210. 下列关于变速器传动比的叙述不正确的是(A. 等于所有从动齿轮齿数的连乘积/所有主动齿轮齿数的连乘积B. 等于各级齿轮传动比的连乘积C•既是变速比又是变扭比D .降速则降扭,增速则增扭11. 为了防止换档时同时挂上两个档,因此在变速箱内设置了()A.定位装置B•自锁装置C. 互锁装置D.倒档锁装置12. 使汽车两侧车轮以不同的转速旋转,适应汽车转弯及在不平路面上行驶的部件是()A.主减速器B.差速器C.半轴D.桥壳13•根据普通差速器的工作原理可以知道,当n i=0,n2=2n。
全国2009年1月高等教育自学考试线性代数试题

全国2009年1月高等教育自学考试线性代数试题课程代码:02198试卷说明:在本卷中,A T 表示矩阵A 的转置矩阵,A *表示矩阵A 的伴随矩阵,E 表示单位矩阵,|A |表示方阵A 的行列式,A -1表示矩阵A 的逆矩阵,秩(A )表示矩阵A 的秩.一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是最符合题目要求的。
请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设A 为n 阶方阵,若A 3=O ,则必有( )A. A =OB.A 2=OC. A T =OD.|A |=02.设A ,B 都是n 阶方阵,且|A |=3,|B |=-1,则|A T B -1|=( )A.-3B.-31C. 31 D.3 3.设A 为5×4矩阵,若秩(A )=4,则秩(5A T )为( )A.2B.3C.4D.54.设向量α=(4,-1,2,-2),则下列向量中是单位向量的是( ) A.31α B.51α C.91α D.251α 5.二次型f (x 1,x 2)=522213x x +的规范形是( ) A.y 21-y 22B. -y 21-y 22C.-y 21+y 22D. y 21+y 226.设A 为5阶方阵,若秩(A )=3,则齐次线性方程组Ax =0的基础解系中包含的解向量的个数是( )A.2B.3C.4D.57.向量空间W ={(0,x ,y ,z ) |x +y =0}的维数是( )A.1B.2C.3D.48.设矩阵A =⎪⎪⎭⎫ ⎝⎛3421,则矩阵A 的伴随矩阵A *=( )A.⎪⎪⎭⎫ ⎝⎛1423 B. ⎪⎪⎭⎫ ⎝⎛--1423 C. ⎪⎪⎭⎫ ⎝⎛1243 D. ⎪⎪⎭⎫ ⎝⎛--1243 9.设矩阵A =⎪⎪⎪⎪⎪⎭⎫ ⎝⎛3000130011201111,则A 的线性无关的特征向量的个数是( ) A.1 B.2C.3D.410.设A ,B 分别为m ×n 和m ×k 矩阵,向量组(I )是由A 的列向量构成的向量组,向量组(II )是由(A ,B )的列向量构成的向量组,则必有( )A.若(I )线性无关,则(II )线性无关B.若(I )线性无关,则(II )线性相关C.若(II )线性无关,则(I )线性无关D.若(II )线性无关,则(I )线性相关二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案,错填、不填均无分。
2009年考研数学一试题与答案解析

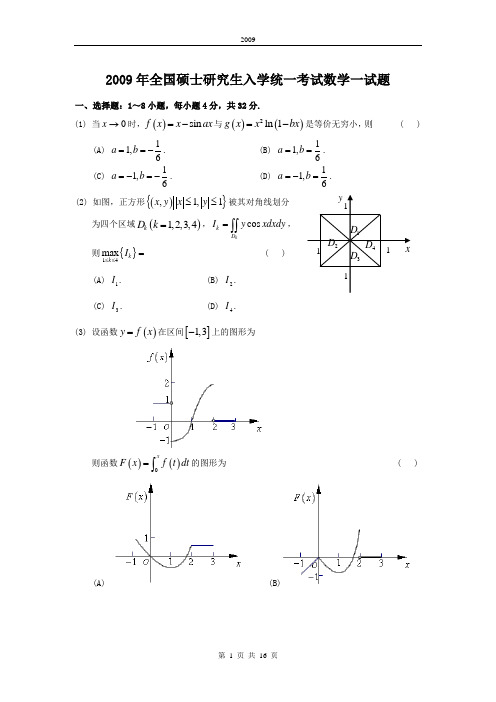
2009年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则(A)11,6a b ==- (B)11,6a b ==(C)11,6a b =-=-(D)11,6a b =-=(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=(A)1I(B)2I (C)3I(D)4I(3)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)(4)设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则(A)当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B)当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时,221n nn a b∞=∑收敛. (D)当1nn b∞=∑发散时,221n nn a b∞=∑发散.(5)设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基12233,,+++αααααα的过渡矩阵为 (A)101220033⎛⎫⎪ ⎪ ⎪⎝⎭(B)120023103⎛⎫⎪⎪ ⎪⎝⎭(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭(D)111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭(6)设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3==A B ,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭(B)**23OB A O ⎛⎫⎪⎝⎭(C)**32O A BO ⎛⎫ ⎪⎝⎭(D)**23O A BO ⎛⎫⎪⎝⎭(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =(A)0 (B)0.3(C)0.7(D)1(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为(A)0(B)1(C)2 (D)3二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ . (10)若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12e xy C C x =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .(11)已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .(12)设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .(13)若3维列向量,αβ满足2T=αβ,其中T α为α的转置,则矩阵Tβα的非零特征值为 .(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .三、解答题(15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值. (16)(本题满分9分)设n a 为曲线n y x =与()11,2,.....n y x n +==所围成区域的面积,记122111,n n n n S a S a ∞∞-====∑∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. (1)求1S 及2S 的方程. (2)求1S 与2S 之间的立体体积.(18)(本题满分11分)(1)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(2)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分) 计算曲面积分()32222xdydz ydzdx zdxdyI xy z++=∑++⎰⎰,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分)设111111042--⎛⎫⎪=- ⎪ ⎪--⎝⎭A ,1112-⎛⎫ ⎪= ⎪ ⎪-⎝⎭ξ (1)求满足21=A ξξ的2ξ.231=A ξξ的所有向量2ξ,3ξ. (2)对(1)中的任意向量2ξ,3ξ证明123,,ξξξ无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-.(1)求二次型f 的矩阵的所有特征值;(2)若二次型f 的规范形为2212y y +,求a 的值.(22)(本题满分11分)袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(1)求{}10p X Z ==.(2)求二维随机变量(),X Y 概率分布. (23)(本题满分11 分)设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,1X ,2X ,…n X 是来自总体X 的简单随机样本.(1)求参数λ的矩估计量.(2)求参数λ的最大似然估计量.2009年考研数学试题答案与解析(数学一)一、选择题:1~8小题,每小题4分,共32分.(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则(A)11,6a b ==-. (B)11,6a b ==. (C)11,6a b =-=-. (D)11,6a b =-=.【答案】 A.【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a axg x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除(B)、(C). 另外201cos lim3x a axbx →--存在,蕴含了1cos 0a ax -→()0x →故 1.a =排除(D).所以本题选(A ). (2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max kk I ≤≤=(A)1I .(B)2I . (C)3I .(D)4I .【答案】 A.【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.24,D D 两区域关于x 轴对称,而(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,而(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰; {}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为(A).x(3)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征:①[]0,1x ∈时,()0F x ≤,且单调递减. ②[]1,2x ∈时,()F x 单调递增. ③[]2,3x ∈时,()F x 为常函数.④[]1,0x ∈-时,()0F x ≤为线性函数,单调递增. ⑤由于F(x)为连续函数结合这些特点,可见正确选项为(D ).(4)设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则(A )当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B )当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时,221n nn a b∞=∑收敛. (D)当1nn b∞=∑发散时,221n nn a b∞=∑发散.【答案】C. 【解析】方法一:举反例:(A)取(1)nn n a b ==- (B )取1n n a b n ==(D )取1n n a b n==故答案为(C ).方法二:因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时,有1n a <又因为1nn b∞=∑收敛,可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时,有1n b <从而,当12n N N >+时,有22n nn a b b <,则由正项级数的比较判别法可知221n nn a b∞=∑收敛.(5)设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基 122331,,αααααα+++的过渡矩阵为(A)101220033⎛⎫⎪ ⎪ ⎪⎝⎭.(B)120023103⎛⎫⎪⎪ ⎪⎝⎭.(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.(D)111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. 【答案】A.【解析】因为()()1212,,,,,,n n A ηηηααα=,则A 称为基12,,,n ααα到12,,,nηηη的过渡矩阵. 则由基12311,,23ααα到122331,,αααααα+++的过渡矩阵M 满足 ()12233112311,,,,23M ααααααααα⎛⎫+++= ⎪⎝⎭12310111,,22023033ααα⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A).(6)设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为()A **32O B A O ⎛⎫ ⎪⎝⎭.()B **23O B A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭. 【答案】B.【解析】根据CC C E *=,若111,C C C CC C*--*==分块矩阵O A B O ⎛⎫ ⎪⎝⎭的行列式221236O A A B B O ⨯=-=⨯=(),即分块矩阵可逆11116601O B BO A O A O A OB B O B B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O BOB AO A O ****⎛⎫⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为(B ).(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX = (A)0.(B)0.3. (C)0.7.(D)1.【答案】C.【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭, 所以()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭, 所以()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰而()0x x dx +∞-∞'Φ=⎰,()()11221222x x x dx u u u du +∞+∞-∞-∞--⎛⎫''Φ=+Φ= ⎪⎝⎭⎰⎰ 所以00.3520.7EX =+⨯=.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为 (A)0.(B)1.(C)2.(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)1[(0)(1)]21[(00)(1)]2Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=,X Y 独立1()[(0)()]2Z F z P X z P X z ∴=⋅≤+≤(1)若0z <,则1()()2Z F z z =Φ(2)当0z ≥,则1()(1())2Z F z z =+Φ0z ∴=为间断点,故选(B ).二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9)设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ . 【答案】"'"12222xf f xyf ++.【解析】''12z f f y x∂=+⋅∂,2"'""'"1222212222z xf f yx f xf f xyf x y ∂=++⋅=++∂∂. (10)若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = . 【答案】2xy xe x =-++.【解析】由12()xy c c x e =+,得121λλ==,故2,1a b =-=微分方程为''2'y y y x -+=设特解*y Ax B =+代入,',1y A A ==220,2A AxB x B B -++=-+==∴ 特解 *2y x =+∴ 12()2xy c c x e x =+++把 (0)2y = , '(0)0y =代入,得120,1c c ==- ∴ 所求2xy xe x =-++ (11)已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .【答案】136【解析】由题意可知,2,,0x x y x x ==≤≤,则ds ==,所以()21148Lxds x ==+⎰11386==(12)设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .【答案】415π. 【解析】 方法一:2122220sin cos z dxdydz d d d ππθϕρϕρϕρ=⎰⎰⎰⎰⎰⎰()21240cos cos d d d ππθϕϕρρ=-⎰⎰⎰30cos 1423515d πϕπϕπ=⋅-⋅=⎰方法二:由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydz Ω⎰⎰⎰ 所以,()21222240011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰14002214sin sin 33515d r dr d πππππϕϕϕϕ=⋅⋅=⎰⎰⎰(13)若3维列向量,αβ满足2Tαβ=,其中Tα为α的转置,则矩阵Tβα的非零特征值为 .【答案】2.【解析】2Tαβ=()2T T βαββαββ∴==⋅, T βα∴的非零特征值为2.(14)设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = . 【答案】1-. 【解析】2X kS -+为2np 的无偏估计22()E X kX np -∴+=2(1)1(1)(1)11np knp p np k p pk p p k ∴+-=∴+-=∴-=-∴=-三、解答题:15~23小题,共94分. (15)(本题满分9分) 求二元函数()22(,)2ln f x y x y y y =++的极值.【解析】2(,)2(2)0x f x y x y '=+= 2(,)2ln 10y f x y x y y '=++=故10,x y e= =2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ = 则12(0,)12(2)xxef e ''=+,1(0,)0xyef ''=,1(0,)yy ef e ''=.0xxf ''>而2()0xy xx yy f f f ''''''-< ∴二元函数存在极小值11(0,)f e e=-.(16)(本题满分9分)设n a 为曲线ny x =与()11,2,.....n y x n +==所围成区域的面积,记122111,n n n n S a S a ∞∞-====∑∑,求1S 与2S 的值.【解析】由题意,n y x =与n+1y=x 在点0x =和1x =处相交,所以112111111a ()()001212n n n n n x x dx x x n n n n +++=-=-=-++++⎰, 从而1111111111S lim lim(-)lim()23122+22Nn nN N N n n a a N N N ∞→∞→∞→∞=====-++=-=++∑∑2211111111111111=)22+1232N 2N+123456n n n S a n n ∞∞-====--++-=-+-+∑∑()( 由2(1)1(1)2nn x x n-++-+ln(1+x)=x- 取1x =得22111ln(2)1()11ln 2234S S =--+=-⇒=-.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成.(Ⅰ)求1S 及2S 的方程(Ⅱ)求1S 与2S 之间的立体体积.【解析】(I )1S 的方程为222143x y z ++=, 过点()4,0与22143x y +=的切线为122y x ⎛⎫=±- ⎪⎝⎭, 所以2S 的方程为222122y z x ⎛⎫+=- ⎪⎝⎭.(II )1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差,其中22135(4)44V x dx ππ=-=⎰.故所求体积为9544πππ-=.(18)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.【解析】(Ⅰ)作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----,易验证()x ϕ满足:()()a b ϕϕ=;()x ϕ在闭区间[],a b 上连续,在开区间(),a b 内可导,且''()()()()f b f a x f x b aϕ-=--.根据罗尔定理,可得在(),a b 内至少有一点ξ,使'()0ϕξ=,即'()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--(Ⅱ)任取0(0,)x δ∈,则函数()f x 满足:在闭区间[]00,x 上连续,开区间()00,x 内可导,从而有拉格朗日中值定理可得:存在()()000,0,x x ξδ∈⊂,使得()0'00()(0)x f x f f x ξ-=-……()*又由于()'lim x f x A +→=,对上式(*式)两边取00x +→时的极限可得:()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====- 故'(0)f +存在,且'(0)f A +=.(19)(本题满分10分)计算曲面积分()32222xdydz ydzdx zdxdyI xy z++=∑++⎰⎰,其中∑是曲面222224x y z ++=的外侧.【解析】2223/2()xdydz ydxdz zdxdy I x y z ∑++=++⎰⎰,其中222224x y z ++= 2222223/22225/22(),()()x y z x x x y z x y z ∂+-=∂++++①2222223/22225/22(),()()y x z y y x y z x y z ∂+-=∂++++② 2222223/22225/22(),()()z x y z z x y z x y z ∂+-=∂++++③ ∴①+②+③=2223/22223/22223/2()()()0()()()x y zx x y z y x y z z x y z ∂∂∂++=∂++∂++∂++ 由于被积函数及其偏导数在点(0,0,0)处不连续,作封闭曲面(外侧)222211:.016x y z R R ∑++=<<有 1132223/233313434()3xdydz ydxdz zdxdyxdydz ydxdz zdxdy R dV x y z R R R ππ∑∑∑Ω++++====⋅=++⎰⎰⎰⎰⎰⎰⎰⎰⎰(20)(本题满分11分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭ 1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足21A ξξ=的2ξ. 231A ξξ=的所有向量2ξ,3ξ.(Ⅱ)对(Ⅰ)中的任意向量2ξ,3ξ证明1ξ,2ξ,3ξ无关. 【解析】(Ⅰ)解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量,令32x =,由0Ax =解得,211,1x x =-= 求特解,令120x x ==,得31x =故21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,其中1k 为任意常数.解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭故有两个自由变量,令21x =-,由20A x =得131,0x x ==求特解21200η⎛⎫⎪ ⎪= ⎪ ⎪⎪⎝⎭故 321121000k ξ⎛⎫ ⎪⎛⎫ ⎪ ⎪=-+ ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭ ,其中2k 为任意常数.(Ⅱ)证明:由于12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠ 故123,,ξξξ 线性无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+- (Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值.【解析】(Ⅰ) 0101111a A aa ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+(Ⅱ) 若规范形为2212y y +,说明有两个特征值为正,一个为0.则1) 若10a λ==,则 220λ=-< ,31λ= ,不符题意 2) 若20λ= ,即2a =,则120λ=>,330λ=>,符合3) 若30λ= ,即1a =-,则110λ=-< ,230λ=-<,不符题意 综上所述,故2a =.(22)(本题满分11分)袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数. (Ⅰ)求{}10p X Z ==;(Ⅱ)求二维随机变量(),X Y 概率分布.【解析】(Ⅰ)在没有取白球的情况下取了一次红球,利用压缩样本空间则相当于只有1个红球,2个黑球放回摸两次,其中摸了一个红球12113324(10)9C P X Z C C ⨯∴====⋅.(Ⅱ)X ,Y 取值范围为0,1,2,故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======(23)(本题满分11 分) 设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,1X ,2X ,…,n X 是来自总体X 的简单随机样本.(Ⅰ)求参数λ的矩估计量; (Ⅱ)求参数λ的最大似然估计量【解析】 (1)由EX X =而22022ˆx EX x e dx X Xλλλλ+∞-===⇒=⎰为总体的矩估计量 (2)构造似然函数()()12111L ,.....,;;nii nnx nn i i i i x x f x x eλλλλ=-==∑==⋅⋅∏∏取对数11ln 2ln ln n ni i i i L n x x λλ===+-∑∑令111ln 222001n i n n i i i i i d L n n x d x x n λλλ====⇒-=⇒==∑∑∑故其最大似然估计量为2Xλ''=。
浙江省2009年1月高等教育自学考试统计法规概论试题

浙江省2009年1月高等教育自学考试统计法规概论试题第一篇:浙江省2009年1月高等教育自学考试统计法规概论试题浙江省2009年1月高等教育自学考试统计法规概论试题课程代码:00251一、单项选择题(本大题共20小题,每小题1分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.在统计行政诉讼中,被告统计局的局长参加庭审的身份为()A.被告B.第三人C.被告的委托代理人D.被告的法定代表2.某市人民政府制定的《该市统计工作管理办法》属于()A.法律B.地方性法规C.政府规章D.行政法规3.进行民间统计调查活动应遵循的原则是()A.简洁、全面B.系统、综合C.合法、科学、客观、公正D.协调、一致、引导、规划4.下列属于经常性调查的是()A.固定资产总值调查B.生产设备调查C.普查D.产量调查5.统计行政诉讼法中,审判监督程序和第二审程序不同点之一是()A.提起主体不同B.提起客体不同C.内容不同D.地点不同6.统计违法案件的查处程序为()A.立案、审查、处理和结案B.立案、检查、处理和结案C.立案、调查、处理和结案D.调查、立案、处理和结案7.行政处分是一种内部具体行政行为。
当事人对所受行政处分不服时,可以要求(A.行政复议 B.提出行政诉讼C.通过申诉程序解决D.辩论解决8.瞒报统计资料在主观方面,表现为()A.故意B.有过错C.过失D.恶意9.统计工作的统一性,最关键的是()A.统计标准B.统计制度C.统计调查方法D.统计管理体制10.以下属于组织主体的是()A.个人B.自由工作者C.个体商贩D.国家机关11.民间统计调查采用的方法是()A.实地观察法B.调查研究法C.科学研究法D.统计方法12.涉外社会调查与民间统计调查在管理内容上,是()A.并列关系B.包容关系C.交叉关系D.同一关系13.统计资料是国家和社会的()A.重要信息资源B.统计观察保障)C.重要法律资料D.重要组成部分14.统计资料的统一管理和公布,可以保证统计资料公布的()A.合法性B.同一性C.组织性D.有序性15.下列各项属于统计专业职务的是()A.总统计师B.统计局长C.统计调研员D.统计员16.地方各级人民政府各部门的统计机构和统计负责人在统计业务上由()A.该地人民政府指导B.上级主管部门指导C.该地政府统计机构指导D.国家统计局指导17.统计的认识功能是指()A.对客观事物特征进行分析B.对客观事物进行决策C.对客观事物质与量的认识D.对客观事物进行调查18.《中华人民共和国统计法》的修订时间是()A.1996年B.1982年C.1979年D.1977年19.统计人员有权()A.对违反统计法的政府机关进行罚款B.对违反统计法的个人实施罚款C.公布调查数据D.检查资料的准确性,要求改正不准确的资料20.统计行政管理相对人在法定期限内未申请复议也未起诉而又不履行行政决定的,统计行政机关可以()A.起诉B.申请人民法院强制执行C.依法强制执行D.与统计管理相对人协商解决二、多项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的五个备选项中至少有两个是符合题目要求的,请将其代码填写在题后的括号内。
2009年1月浙江高等教育自学考试管理试题

2009年1月浙江高等教育自学考试管理试题一、填空题(本大题共10小题,每空1分,共20分)请在每小题的空格中填上正确答案。
错填、不填均无分。
1.教育管理学学科体系有两个维度:__________维度和__________维度。
2.作为社会现象的管理,它具有两个重要的职能:一个是组织和开发__________的职能,另一个是协调和控制__________的职能。
3.什么是好教育?什么是__________?这是教育或学校的__________价值观。
4.目标是制定和选择__________的__________。
5.调动教师的__________和创造性是办好教育的__________。
6.教育行政的管理职能是指__________所需要的__________的管辖使用等,以维持教育活动的顺利进行。
7.督政即把督导__________的教育工作作为__________任务。
8.教师考核的方法,按形式分有__________法、学生评价法、__________评价法。
9.美国著名管理专家__________提出,管理由计划、执行、检查、__________等四个环节组成。
10.从过程角度分,可以将学生工作质量分为__________质量、__________和结果质量。
二、判断题(本大题共10小题,每小题1分,共10分)判断下列各题,正确的在题后括号内打“√”,错的打“╳”。
11.集权度主要是指组织中决策权力的分布情况。
( )12.教育管理主要是解决教育、教学过程中师生的矛盾和问题。
( )13.人的积极性是处于能动状态的心理活动针对一定目标的外在表现。
( )14.实施教师考核的两项原则,即公正、客观、准确的原则和自评相结合的原则。
( )15.决策的权力只集中于领导层而下属人员无权参与被称为高度集权。
( )16.学校的文化环境是指学校的情感氛围,校风、学风、优良传统。
( )17.教育行政上的分权制最大的长处在于,可以使教育行政管理具有弹性,避免一刀切,因地制宜地发展教育事业,可使教育适应各地的实际需要。
工程数学试卷与答案汇总(完整版)

1.某人打靶3发,事件Ai 表示“击中i 发”,i=0,1,2,3. 那么事件A=A1∪A2∪A3表示( )。
A. 全部击中.B. 至少有一发击中.C. 必然击中D. 击中3发2.对于任意两个随机变量X 和Y ,若E(XY)=E(X)E(Y),则有( )。
A. X 和Y 独立。
B. X 和Y 不独立。
C. D(X+Y)=D(X)+D(Y)D. D(XY)=D(X)D(Y)3.下列各函数中可以作为某个随机变量的概率密度函数的是( )。
A . 其它1||0|)|1(2)(≤⎩⎨⎧-=x x x f 。
B. 其它2||05.0)(≤⎩⎨⎧=x x f C. 00021)(222)(<≥⎪⎪⎩⎪⎪⎨⎧=--x x e x f x σμπσ D. 其它00)(>⎩⎨⎧=-x e x f x , 4.设随机变量X ~)4,(2μN , Y ~)5,(2μN , }4{1-≤=μX P P ,}5{2+≥=μY P P , 则有( )A. 对于任意的μ, P 1=P 2B. 对于任意的μ, P 1 < P 2C. 只对个别的μ,才有P 1=P 2D. 对于任意的μ, P 1 > P 25.设X 为随机变量,其方差存在,c 为任意非零常数,则下列等式中正确的是( )A .D(X+c)=D(X). B. D(X+c)=D(X)+c.C. D(X-c)=D(X)-cD. D(cX)=cD(X)6. 设3阶矩阵A 的特征值为-1,1,2,它的伴随矩阵记为A*, 则|A*+3A –2E|= 。
7.设A= ⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--10000002~011101110x ,则x = 。
8.设有3个元件并联,已知每个元件正常工作的概率为P ,则该系统正常工作的概率为 。
9.设随机变量X 的概率密度函数为其它A x x x f <<⎩⎨⎧=002)(,则概率二、填空题(每空3分,共15分)=≥)21(X P 。
2009-数一标准答案及解析

= P( XY ≤ z ) = P( XY ≤ z Y= 0) P(Y= 0) + P( XY ≤ z Y= 1) P(Y= 1) FZ ( z ) 1 = [ P( XY ≤ z Y = 0) + P( XY ≤ z Y = 1)] 2 1 = [ P( X ⋅ 0 ≤ z Y = 0) + P( X ≤ z Y = 1)] 2
+∞
−∞
x −1 xΦ′ dx 2
∫
+∞
−∞
+∞ +∞ x −1 x −1 ′ ( u ) du 2 xΦ′ ( x ) dx = 0 , ∫ xΦ′ dx = u 2 ∫ ( 2u + 1) Φ= −∞ −∞ 2 2
所以 EX = 0 + 0.35 × 2 = 0.7 . ( 8 ) 设 随 机 变 量 X 与 Y 相 互 独 立 , 且 X 服 从 标 准 正 态 分 布 N ( 0,1) , Y 的 概 率 分 布 为
x −1 , 2
0.7 x − 1 Φ′ , 2 2
所以 EX =
∫
+∞
−∞
xF ′ ( x= )dx
∫
+∞
−∞
x − 1 x 0.3Φ′ ( x ) + 0.35Φ′ dx 2
= 0.3∫
而
+∞
−∞
xΦ′ ( x ) dx + 0.35∫
所以 I1
2
{( x , y ) y ≥ x ,0≤ x≤1}
∫∫
y cos xdxdy > 0 ;
梅花香自苦寒来,岁月共理想,人生齐高飞! 第 - 6 - 页 共 19 页
2009年1月数量方法试题及答案

2009年1月高等教育自学考试中英合作商务管理专业与金融管理专业考试数量方法试题 课程代码:0799第一部分 必答题(满分60分)一、 单项选择题(本题包括1-20二十个小题,每小题1分,共20分) 1. 某保温瓶胆厂一年内各月产量的次品数为50 30 10 40 40 30 10 30 70 30 30 30 则该厂全年月次品数的众数是A. 10B. 30C. 40D. 50 2. 以下是根据10个销售员一个月销售某产品的数据作的茎叶图: 7 4 4 28 9 7 6 3 5 9 1 0 则销售数量的极差为A. 5B. 6C. 7D. 193. 随机抽取某大学6名大学生,对其收看某选秀节目的收视时间(单位:小时)做调查,得到样本数据为 0.5,0,1.2,4.3,1.2,2.3则大学生收看选秀节目的时间中位数为A. 0B. 0.5C. 1.2D. 1.674. 对某小学学生进行近视眼防治抽样调查,先将所有学生按年级划分,然后在各年级随机抽取学生班级,对抽中班级的所有学生进行调查,这种抽样方法属于A. 简答随机抽样B. 整群抽样C. 分层抽样D. 等距抽样5. 甲乙两人独立地先后射击目标一次,甲命中目标的概率为0.5,乙命中目标的概率为0.8,则目标被击中的概率为A. 0.3B. 0.4C. 0.9D. 16. 北京大学统计系06级3班共有60名同学。
至少有2名同学生日相同的概率为(一年按365天计算)A. 6060!365B. 6036560365PC. 603653651PD. 60365601365P - 7. 振安商场黄金部营业员接待一位顾客并做成一笔生意的概率是0.4,在某天他接待了5位顾客,则做成3笔生意的概率是A. 3255(0.4)0.6CB. 50.4C. 3525(0.4)0.6CD. 30.68. 红星游乐园入口处的每辆汽车的载客人数服从2λ=的泊松分布,今任意观察一辆到达公园门口的汽车,车中无乘客的概率为A. 2e - B. 2 C. 2e D. 22!e -9. 某食品超市的牛奶销售量服从正态分布,每天平均销售200公斤,标准差为20公斤。
高等教育自学考试线性代数经管类真题2009年1月_真题-无答案

高等教育自学考试线性代数(经管类)真题2009年1月(总分100,考试时间150分钟)课程代码:04184一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.2.3.4. 设A,B分别为m×n和m×k矩阵,向量组(I)是由A的列向量构成的向量组,向量组(Ⅱ)是由(A,B)的列向量构成的向量组,则必有()A. 若(I)线性无关,则(Ⅱ)线性无关B. 若(I)线性无关,则(Ⅱ)线性相关C. 若(Ⅱ)线性无关,则(I)线性无关D. 若(Ⅱ)线性无关,则(I)线性相关5. 设A为5阶方阵,若秩(A)=3,则齐次线性方程组Ax=0的基础解系中包含的解向量的个数是()A. 2B. 3C. 4D. 56.7. 对非齐次线性方程组Am×nx=b,设秩(A)=r,则()A. r=m时,方程组Ax=b有解B. r=n时,方程组Ax=b有唯一解C. m=n时,方程组Ax=b有唯一解D. r<n时,方程组Ax=b有无穷多解8.9.10.二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
错填、不填均无分。
11.12.13.14.15.16.17.18.19.20.三、计算题(本大题共6小题,每小题9分,共54分)21.22.23.24.25.26.四、证明题(本大题共1小题,6分)27.。
浙江2009年1月高等教育自学考试

浙江省2009年1月高等教育自学考试机械制造基础试题课程代码:02189一、填空题(本大题共12小题,每空1分,共16分)请在每小题的空格中填上正确答案。
错填、不填均无分。
1.由于所加载荷不同,所引起金属变形方式也不同,常见的变形方式有:拉伸与压缩、弯曲、__________、剪切等。
2.常用的硬度试验方法有布氏硬度、__________和维氏硬度三种。
3.组成合金的独立的最基本的单元称为__________。
4.合金中凡是结构、成分和性能相同并且与其它部分有界面分开的均匀组成部分称为__________。
5.若凝固后的固态物质是晶体,则这种凝固过程称为__________。
6.所谓共晶转变是指__________的液相在一定的温度下,同时结晶出两种不同固相的转变。
7.在一个晶粒内部化学成分不均匀的现象叫__________。
8.铸铁具有优良的__________、__________、减磨性及减振性等,而且熔炼铸铁的工艺设备简单,成本低廉,因此是制造各种铸件最常用的材料。
9.可锻铸铁中的碳以__________的形态存在于铸铁中,所以其力学性能较灰铸铁高。
10.在滑动轴承中,制造__________和__________的合金称为轴承合金。
11.塑料的品种很多,按合成树酯的热性能,分为__________塑料和__________塑料两类。
12.根据热处理的目的和工序位置的不同,热处理可分为__________热处理和__________热处理两大类。
二、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.金属材料在静载荷作用下抵抗变形和断裂的能力()A.塑性B.强度C.弹性D.韧性2.纯铁的熔点为()A.1148℃B.1227℃C.1450℃D.1538℃3.金属的晶粒大小对金属力学性能有重要的影响,下列细化晶粒的方法中不.正确的是()A.变质处理B.附加振动C.减小过冷度D.降低浇注速度4.碳含量为0.5%的铁碳合金,在950℃时的组织为()A.珠光体B.奥氏体C.铁素体加珠光体D.渗碳体加珠光体5.调质处理就是__________的热处理。
2009年浙江省专升本《高等数学(一)》试卷及答案

------------------------2009年浙江省普通高校“专升本”联考《高等数学(一)》试卷--------------------2009年浙江省普通高校《高等数学(一)》试卷考试说明:1、考试时间为150分钟;2、满分为150分;3、答案请写在试卷纸上,用蓝色或黑色墨水的钢笔、圆珠笔答卷,否则无效;4、密封线左边各项要求填写清楚完整。
一. 选择题(每个小题给出的选项中,只有一项符合要求.本题共有5个小题,每小题4分,共20分)1函数1arccos2x y +=的定义域是 ( ) .A 1x < .B ()3,1-.C {}{}131x x x <⋂-≤≤ .D 31x -≤≤.2.极限sin 3limx xx→∞等于 ( ).A 0 .B 13.C 3 .D 1.3.下列函数中,微分等于1ln dx x x的是 ( ) .A ln x x c + .B ()ln ln y x c =+ .C 21ln 2x c + .D ln x c x+.4.()1cos d x -=⎰( ).A 1cos x - .B cos x c -+.C sin x x c -+ .D sin x c +. 5.方程2222x y z a b=+表示的二次曲面是 ( ).A 椭球面.B 圆锥面.C 椭圆抛物面 .D 柱面.报考学校:______________________报考专业:______________________姓名: 准考证号: ------------------------------------------------------------------------------------------密封线---------------------------------------------------------------------------------------------------二.填空题(只须在横线上直接写出答案,不必写出计算过程, 本题共有10个小题,每小题4分,共40分)1.2226lim _______________.4x x x x →+-=-2.设函数(),,x e f x a x ⎧=⎨+⎩00x x ≤>在点0x =处连续,则________________a =.3.设函数xy xe =,则()''0__________________y =.4.函数sin y x x =-在区间[]0,π上的最大值是_____________________.5.sin 1_______________________.4dx π⎛⎫+= ⎪⎝⎭⎰6.()() ____________________________.aax f x f x dx -+-=⎡⎤⎣⎦⎰7.设()() xa x F x f t dt x a=-⎰,其中()f t 是连续函数,则()lim _________________.x aF x +→=8.设32, 2a i j k b i j k =--=+-,则____________________.a b ⋅=9.设()2,yz x y =+则()0,1____________________________.zx ∂=∂ 10.设(){},01,11,D x y x y =≤≤-≤≤则_____________________.Ddxdy =⎰⎰三.计算题( 本题共有10个小题,每小题6分,共60分)1.计算0lim.x xx e e x-→-2.设函数y =求.dy3.计算1xxe dx e +⎰.4.设 2 02sin cos tx u du y t⎧=⎪⎨⎪=⎩⎰,求.dy dx5.计算 2.22dxx x +∞-∞++⎰6. 设曲线()y f x =在原点与曲线sin y x =相切,求n7.求微分方程'tan 3y x y +=-满足初值条件02y π⎛⎫= ⎪⎝⎭的特解. .8.设(),z z x y =是由方程2224x y z z ++=所确定的隐函数,求.z x∂∂ 9.求D⎰⎰,其中区域(){}2222,4D x y x y ππ=≤+≤.10.求幂级数21113n nn x ∞-=∑的收敛域._姓名: 准考证号:--------------------------------------------------------------------------------------四.综合题(本题有3个小题,共30分,其中第1题14分,第2题8分,第3题8分) 1.求函数21x y x +=的单调区间,极值及其图形的凹凸区间. (本题14分)2.设()f x 在[]0,1上可导,()()00,11f f ==,且()f x 不恒等于x ,求证:存在()0,1ξ∈使得()' 1.f ξ> (本题8分)3.设曲线22y x x =-++与y 轴交于点P ,过P 点作该曲线的切线,求切线与该曲线及x 轴围成的区域绕x 轴旋转生成的旋转体的体积. (本题8分)2009年浙江省普通高校“专升本”联考《高等数学(一)》参考答案及评分标准一. 选择题(每小题4分,共20分)1.D ,2.A ,3.B ,4.B ,5.C . 二. 填空题(每小题4分,共40分) 1.54 , 2.1 , 3.2 , 4.0 , 5.sin 14x c π⎛⎫++ ⎪⎝⎭ ,6.0 ,7.()af a ,8.3 ,9.2 , 10.2 . 三. 计算题(每小题6分,共60分) 1.解.00lim lim 1x x x xx x e e e e x --→→-+=5分2.=6分2.解.()3221',1y x ==+5分故()3221+dxdy x =.6分3.解.原式=()11x xd e e ++⎰3分()ln 1.x e c =++6分4.解法1.dy dy dtdx dxdt= 3分222sin 2.sin t t t t-==-6分解法 2.因为22sin ,2sin dx t dt dy t t dt==-,4分 故2.dyt dx=- 6分5.解.原式()()2111d x x +∞-∞+=++⎰3分=()tan 1arc x +∞-∞+5分 =.π6分6.解. 由条件推得()()'00,1 1.f f ==2分于是()1220lim 220n n f f n n →∞⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎢⎥=⎢⎥-⎢⎥⎣⎦5分(第1页,共3页)==6分注:若按下述方法:原式()()112200'lim lim 1f x f x x ++→→⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭解答者,只给4分. 7.解法1.分离变量,得到 cot ,3dyxdx y=-+2分积分得到ln 3ln sin y x c +=-+或 ()3 .sin cy c x =-∈4分代入初值条件02y π⎛⎫= ⎪⎝⎭,得到3c =.于是特解为33.sin y x=-6分解法2.由()()(),p x dx p x dxy e q x e dx c -⎡⎤⎰⎰=+⎢⎥⎣⎦⎰ 其中()()13,tan tan p x q x x x ==-,得到 ()3 .sin c y c x =-∈4分代入初值条件02y π⎛⎫=⎪⎝⎭,得到3c =.于是特解为 3 3.sin y x=-6分8.解.方程两边对x 求偏导数,得到 224,z zx zx x∂∂+=∂∂ 4分故.2z x x z∂=∂-6分 9.解.原式2 2 0sin d r rdr πππθ=⎰⎰3分 = 22 2cos cos r r rdr πππππ⎡⎤-+⎢⎥⎣⎦⎰5分 =26.π-6分10.解.由121121321131lim lim3n nn n n n n nx ax a x +++-→∞→∞==,可知 收敛半径R =,4分又当x =,对应数项级数的一般项为级数均发散,故该级数的收敛域为(.6分(第2页,共3页)四. 综合题(第1小题14分,第2小题8分, 第3小题8分,共30分) 1.解.定义域()(),00,-∞⋃+∞,()34232',",x x y y x x++=-= 令'0,y =得驻点12x =-,5分 令"0,y =得23x =-,10分 函数的单调增加区间为()2,0,-单调减少区间为(),2-∞-及()0,,+∞ 在2x =-处,有极小值14-.其图形的凹区间为(),2-∞-及()0,+∞,凸区间为(),3.-∞-14分2.证明.由于()f x 不恒等于x ,故存在()00,1,x ∈使得()00.f x x ≠2分如果()00,f x x >根据拉格朗日定理,存在()00,,x ξ∈使得 ()()()0000'10f x f x f x xξ-=>=-,5分若()00,f x x <根据拉格朗日定理,存在()0,1,x ξ∈使得 ()()()000011'111f f x x f x x ξ--=>=--.8分注:在“2分”后,即写“利用微分中值定理可证得,必存在ξ,使得()'1f ξ>”者共得3分.3.解.P 点处该曲线的切线方程为2y x =+,且与x轴的交于点()2,0A -2分曲线与x 轴的交点()1,0B -和()2,0C ,因此区域由直线PA 和AB 及曲线弧PB所围成.4分该区域绕x 旋转生成的旋转体的体积() 02218292330V x x dx πππ-=--++=⎰.8分注:若计算由直线PA 与AC 及曲线弧PC 所围成,从而() 222 081362315V x x dx πππ=+-++=⎰者得6分.。
浙江省2011年10月高等教育自学考试 工程数学(一)试题 课程代码07961

07961# 工程数学(一)试题 第 1 页 共 5 页浙江省201 1年10月高等教育自学考试工程数学(一)试题课程代码:07961一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设事件A 与B 相互独立,且P (A )>0,P (B )>0,则一定有( ) A.()1()P A B P A =- B. ()0P A B = C.P (A )=1-P (B )D. ()()P A B P B =2.掷2颗骰子,记事件A={2颗骰子出现点数之和等于7},则事件A 的概率为( ) A.16 B. 56 C.112D. 153.下列各函数中可以作为某个随机变量的分布函数的是( )A.1() 0,1x f x x <=≥⎩B. 1() 0,1x f x x <=≥⎩C. 21,11() 0,1x x f x x ⎧<⎪+=⎨⎪≥⎩D. 22,11() 0,1x x f x x ⎧<⎪+=⎨⎪≥⎩4.设随机变量X题4表则P ({0<X ≤3}-{X >2})=( ) A.0 B.0.2 C.0.5D.0.75.已知随机变量(X ,Y )服从二维正态分布,且E (X )=E (Y )=0,D (X )=1,D (Y )=4,ρXY =12,若07961# 工程数学(一)试题 第 2 页 共 5 页Z =aX +Y 与Y 的协方差为0,则a 等于( )A.2B.-2C.4D.-46.设二维连续随机变量(X 1,Y 1)与(X 2,Y 2)的概率密度为f 1(x ,y )与f 2(x ,y ),令f (x ,y )=af 1(x ,y )+bf 2(x ,y ),要使函数f (x ,y )是某个二维随机变量的概率密度,则a ,b 应满足( )A.a +b =1B.a ≥0,b ≥0且a +b =1C.0≤a ≤1,0≤b ≤1D.a >0,b >07.设随机变量X ~B (10,0.2),Y ~P (5),则E (2X +Y )等于( ) A.215 B.7 C.9D.1158.设随机变量X 1,X 2,…,X n ,…相互独立,且X i (i =1,2,…,n,…)都服从参数为3的指数分布,则当n 充分大时,随机变量Z n =11ni i X n =∑的概率分布近似服从( )A.N (11,39)B.N (11,39n)C.N (3,9)D.N (3,9n) 9.设总体X ~N (μ,σ2),X 1,X 2,…,X n 为样本,X 为样本均值,S 为样本标准差,则服从t (n -1)分布的统计量是( )A.C.10.设α,β分别是假设检验中第一、第二类错误的概率,且H 0,H 1分别为原假设和备择假设,则P {拒绝H 0\H 0为真}=( ) A.α B.βC.1-αD.1-β07961# 工程数学(一)试题 第 3 页 共 5 页二、填空题(本大题共15小题,每小题2分,共30分)请在每小题的空格中填上正确答案。
高等数学试卷-00023 2009年01月真题及答案

2009年1月高等教育自学考试全国统一命题考试高等数学(工本)试题课程代码:00023一、单项选择题(本大题共5小题,每小题3分,共15分)在每小题列出的四个备选项中只有一个是最符合题目要求的。
请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.平面x +2y -z +1=0的法向量为( )A.{1,-2,-1}B.{2,4,2}C.{-1,2,-1}D.{2,4,-2}2.设函数f (x ,y )=y x y x -+,则f (y,x 11)=( ) A.x y x y +- B. y x y x -+ C. x y x y -+ D. yx y x +- 3.设积分区域D 由|x +y |=1和|x -y |=1所围成,则二重积分⎰⎰D dxdy =( ) A.1B.2C.3D.4 4.微分方程y ′=y 的通解为( )A.y =e CxB.y =Ce xC.y =C + 2x eD.y =C 2x e 5.无穷级数∑∞=+-+-1n 1n nn21)(21)(( ) A.绝对收敛 B.条件收敛C.发散D.敛散性不确定二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6.向量α={1,2,1}的模为_______.7.设函数z =3xy 2+2x 2y ,则x z ∂∂=_______. 8.二次积分dy y x 4dx 2220x 402--⎰⎰-的值等于_______.9.微分方程y ″+3(y ′)4-3x +1=0的阶数是_______.10.无穷级数Λ+++=∑∞=4332211n n u 的通项u n=_______. 三、计算题(本大题共12小题,每小题5分,共60分)11.求直线⎩⎨⎧=-=-32z y y x 与平面2x +3y -z +1=0的交点坐标.12.求曲面z =2-x 2-y 2在点(1,2,-3)处的切平面方程.13.求函数f (x ,y ,z )=xyz 2在点(1,-1,2)处的梯度.14.设函数z=(xy+y 2)arctany ,求y x z ∂∂∂2. 15.计算积分I =dx e dy y x ⎰⎰1102. 16.计算三重积分⎰⎰⎰Ωxdxdydz y cos ,其中积分区域Ω:0≤x ≤2π,0≤y ≤1,-1≤z ≤1. 17.计算对坐标的曲线积分⎰++(3,2))01(.dy )x-y (dx )y x (.18.计算对面积的曲面积分⎰⎰∑--+dS )2z y x(222,其中∑是z =22y x +中0≤z ≤1的部分.19.求微分方程y ″+y =x +1的通解.20.求微分方程xy ′+y =xe x 的通解.21.判断无穷级数∑∞=1n n n!n 3n 的敛散性. 22.求幂函数∑∞=-1)2(2n n nx n 的收敛区间. 四、综合题(本大题共3小题,每小题5分,共15分)23.求函数f (x ,y )=5x 2-4xy +y 2+2x +1的极值.24.求上半球面z =224y x --含在柱面x 2+y 2=2x 内部的面积S .25.将函数f (x )=x+21展开为x -2的幂级数.。
2009考研数一真题及解析
2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分.(1) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A) 11,6a b ==-. (B) 11,6a b ==. (C) 11,6a b =-=-. (D) 11,6a b =-=.(2) 如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤= ( )(A) 1I .(B) 2I .(C) 3I .(D) 4I .(3) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为 ( )(A) (B)-1-111x y 1D2D3D4D(C)(D)(4) 设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则 ( )(A) 当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B) 当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C) 当1nn b∞=∑收敛时,221n nn a b∞=∑收敛. (D) 当1nn b∞=∑发散时,221n nn a b∞=∑发散.(5) 设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基122331,,αααααα+++的过渡矩阵为 ( )(A) 101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭.(B) 120023103⎛⎫⎪⎪ ⎪⎝⎭.(C) 111246111246111246⎛⎫- ⎪ ⎪ ⎪-⎪ ⎪ ⎪- ⎪⎝⎭.(D) 111222111444111666⎛⎫-⎪ ⎪⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. (6) 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为 ( ) (A) **32O B A O ⎛⎫⎪⎝⎭. (B) **23O B A O ⎛⎫⎪⎝⎭.(C) **32O A BO ⎛⎫⎪⎝⎭.(D) **23OA BO ⎛⎫⎪⎝⎭.(7) 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布的分布函数,则EX = ( ) (A) 0. (B) 0.3. (C) 0.7. (D) 1.(8) 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====.记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为 ( ) (A) 0. (B) 1. (C) 2. (D) 3.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ .(10) 若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12x y C C x e =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .(11) 已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .(12) 设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .(13) 若3维列向量,αβ满足2Tαβ=,其中T α为α的转置,则矩阵T βα的非零特征值为. (14) 设12,,,m X X X 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值.(16)(本题满分9分)设n a 为曲线n y x =与()11,2,n y xn +==所围成区域的面积,记11,n n S a ∞==∑2211n n S a ∞-==∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是由过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. (Ⅰ)求1S 及2S 的方程; (Ⅱ)求1S 与2S 之间的立体体积. (18)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分)计算曲面积分()32222xdydz ydzdx zdxdyI xy z∑++=++⎰⎰,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ; (Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明:123,,ξξξ线性无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. (22)(本题满分11分)袋中有1个红球,2个黑球与3个白球.现有放回地从袋中取两次,每次取一个球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(Ⅰ)求{}10P X Z ==;(Ⅱ)求二维随机变量(),X Y 的概率分布. (23)(本题满分11 分)设总体X 的概率密度为2,0,()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,12,,,n X X X 是来自总体X 的简单随机样本.(Ⅰ) 求参数λ的矩估计量;(Ⅱ )求参数λ的最大似然估计量.2009年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分. (1) 【答案】(A)【解析】()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim 36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bxa ax ab axb →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛 即36a b =-,故排除B ,C.另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选A.(2) 【答案】(A)【解析】本题利用二重积分区域的对称性及被积函数的奇偶性.令(,)cos f x y y x =,24,D D 两区域关于x 轴对称,(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}{}1(,),013(,),012cos 0,2cos 0.x y y x x x y y x x I y xdxdy I y xdxdy ≥≤≤≤-≤≤=>=<⎰⎰⎰⎰所以正确答案为(A). (3) 【答案】(D)【解析】此题为定积分的应用知识考核,由()y f x =的图形可以看出,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出下面几个方面的特征:① []1,0x ∈-时,()0F x ≤为线性函数,单调递增;② []0,1x ∈时,()0F x ≤,且单调递减; ③ []1,2x ∈时,()F x 单调递增; ④ []2,3x ∈时,()F x 为常函数; ⑤ ()F x 为连续函数.结合这些特点,可见正确选项为(D). (4) 【答案】C【解析】解法1 举反例:取(1)nn n a b ==-,则lim 0n n a →∞=,1n n b ∞=∑是收敛的,但111n n n n a b n ∞∞===∑∑发散,排除(A);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但2111n n n n a b n ∞∞===∑∑收敛,排除(B);取1n n a b n ==,则lim 0n n a →∞=,1n n b ∞=∑是发散的,但224111n n n n a b n ∞∞===∑∑收敛,排除(D),故答案为(C).解法2 因为lim 0,n n a →∞=则由定义可知1,N ∃使得1n N >时,有1n a <;又因为1nn b∞=∑收敛,可得lim 0,n n b →∞=则由定义可知2,N ∃使得2n N >时,有1n b <,从而,当12n N N >+时,有22n nn a b b <,则由正项级数的比较判别法可知221n nn a b∞=∑收敛.(5) 【答案】(A)【解析】根据过渡矩阵的定义,知由基12311,,23ααα到122331,,αααααα+++的过渡矩阵M 满足:()12233112312311,,,,2310111,,220,23033M αααααααααααα⎛⎫+++= ⎪⎝⎭⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭ ⎪⎝⎭所以此题选(A). (6) 【答案】(B) 【解析】分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O⨯=-=⨯=(),即分块矩阵可逆,且1116112366.1132O A O A O A O B B O B O B O A O O B O B B O B A O A O A O A *---******⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫ ⎪ ⎪⎛⎫⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪⎝⎭⎝⎭故答案为(B).(7) 【答案】(C)【解析】因为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,所以 ()()0.710.322x F x x -⎛⎫'''=Φ+Φ ⎪⎝⎭, 因此, ()()10.30.352x EX xF x dx x x dx +∞+∞-∞-∞⎡-⎤⎛⎫'''==Φ+Φ ⎪⎢⎥⎝⎭⎣⎦⎰⎰()10.30.352x x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ ⎪⎝⎭⎰⎰.由于()x Φ为标准正态分布的分布函数,所以()0x x dx +∞-∞'Φ=⎰,()()()()11221222222,x x x dx u u u du u u du u du +∞+∞-∞-∞+∞+∞-∞-∞--⎛⎫''Φ=+Φ ⎪⎝⎭''=Φ+Φ=⎰⎰⎰⎰()10.30.3500.3520.72x EX x x dx x dx +∞+∞-∞-∞-⎛⎫''=Φ+Φ=+⨯= ⎪⎝⎭⎰⎰.(8) 【答案】(B)【解析】(){}{0}{0}{1}{1}11{0}{1}2211{00}{1},22Z F z P XY z P XY z Y P Y P XY z Y P Y P XY z Y P XY z Y P X z Y P X z Y =≤=≤==+≤===≤=+≤==⋅≤=+≤=由于,X Y 相互独立,所以11(){0}{}22Z F z P X z P X z =⋅≤+≤. (1) 当0z <时,1()()2Z F z z =Φ;(2) 当0z ≥时,11()()22Z F z z =+Φ,因此,0z =为间断点,故选(B).二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 【答案】12222xf f xyf '''''++ 【解析】12zf f y x∂''=+⋅∂, 21222212222zxf f yx f xf f xyf x y∂''''''''''=++⋅=++∂∂. (10) 【答案】(1)2xx e -+【解析】由常系数线性齐次微分方程0y ay by '''++=的通解为()12xy C C x e =+可知1x y e =,2x y xe =为其两个线性无关的解,代入齐次方程,有111222(1)010,[2(1)]020,x x y ay by a b e a b y ay by a a b x e a '''++=++=⇒++='''++=++++=⇒+=从而可见2,1a b =-=,非齐次微分方程为2y y y x '''-+=.设特解*y Ax B =+,代入非齐次微分方程,得2A Ax B x -++=,即11(2)202A A Ax A B x A B B ==⎧⎧+-+=⇒⇒⎨⎨-+==⎩⎩所以特解*2y x =+,通解()122xy C C x e x =+++.把()()02,00y y '==代入通解,得120,1C C ==-.所以所求解为2(1)2x x y xe x x e =-++=-+.(11)【答案】136【解析】由题意可知,2,0y x x =≤≤,则ds ==,所以()21148Lxds x ==+⎰11386==. (12) 【答案】415π 【解析】解法1:()212222002124013500sin cos cos cos cos 42.3515z dxdydz d d d d d d πππππθϕρϕρϕρθϕϕρρϕρππΩ==-⎛⎫=⋅-⋅= ⎪⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰⎰解法2:由轮换对称性可知2z dxdydz Ω=⎰⎰⎰2x dxdydz Ω=⎰⎰⎰2y dxdydz Ω⎰⎰⎰所以,()212222400011sin 33z dxdydz x y z dxdydz d d r dr ππϕθϕΩΩ=++=⎰⎰⎰⎰⎰⎰⎰⎰⎰ 14002214sin sin 33515d r dr d ππππϕϕϕϕπ==⋅⋅=⎰⎰⎰. (13) 【答案】2【解析】2T αβ=,()2T Tβαββαββ∴==⋅,又由于0β≠,T βα∴的非零特征值为2.(14) 【答案】1-【解析】由于2X kS +为2np 的无偏估计量,所以22()E X kS np +=,即2222()()()E X kS np E X E kS np +=⇒+=2(1)1(1)(1)1 1.np knp p np k p pk p p k ⇒+-=⇒+-=⇒-=-⇒=-三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)【解析】 2(,)2(2)x f x y x y '=+,2(,)2ln 1y f x y x y y '=++.令(,)0,(,)0,x y f x y f x y ⎧'=⎪⎨'=⎪⎩解得唯一驻点1(0,)e .由于212(0,)1(0,)21(0,)11(0,)2(2)2(2),1(0,)40,11(0,)(2),xxexye yy eA f y e eB f xy eC f x e e y ''==+=+''===''==+= 所以 2212(2)0,B AC e e-=-+<且0A >. 从而1(0,)f e 是(,)f x y 的极小值,极小值为11(0,)f e e=-.(16)(本题满分9分) 【解析】曲线ny x =与1n y x+=的交点为(0,0)和(1,1),所围区域的面积112111111()()001212n n n n n a x x dx x x n n n n +++=-=-=-++++⎰, 111lim 1111111lim()lim(),2312222Nn nN n n N N S a a N N N ∞→∞==→∞→∞===-++-=-=+++∑∑22111211111111(1)22123456nn n n n S a nn n∞∞∞-=====-=-+-++=-+∑∑∑(). 考查幂级数1(1)n nn x n ∞=-∑,知其收敛域为(1,1]-,和函数为ln(1)x -+.因为2(1)()ln(1)n nn S x x x x n ∞=-==-+∑,令1x =,得2211(1)1ln 2n n S a S ∞-====-∑.(17)(本题满分11分)【解析】(I)椭球面1S 的方程为222143x y z ++=. 设切点为00(,)x y ,则22143x y +=在00(,)x y 处的切线方程为00143x x y y +=. 将4,0x y ==代入切线方程得01x =,从而032y ==±. 所以切线方程为142x y ±=,从而圆锥面2S 的方程为222(1)44x y z +-=,即222(4)440x y z ---=.(II)1S 与2S 之间的体积等于一个底面半径为32、高为3的锥体体积94π与部分椭球体体积V 之差,其中22135(4)44V x dx ππ=-=⎰.故所求体积为9544πππ-=.(18)(本题满分11分) 【解析】(Ⅰ)取()()()()()f b f a F x f x x a b a-=---,由题意知()F x 在[],a b 上连续,在(),a b 内可导,且()()()()()(),()()()()()().f b f a F a f a a a f a b af b f a F b f b b a f a b a -=--=--=--=-根据罗尔定理,存在(),a b ξ∈,使得()()()()0f b f a F f b aξξ-''=-=-,即()()()()f b f a f b a ξ'-=-.(Ⅱ)对于任意的(0,)t δ∈,函数()f x 在[]0,t 上连续,在()0,t 内可导,由右导数定义及拉格朗日中值定理()()000()0()0lim lim lim ()0t t t f t f f tf f t tξξ++++→→→-'''===-,其中()0,t ξ∈. 由于()0lim t f t A +→'=,且当0t +→时,0ξ+→,所以0lim ()t f A ξ+→'=,故(0)f +'存在,且(0)f A +'=.(19)(本题满分10分)【解析】取2221:1x y z ∑++=的外侧,Ω为∑与1∑之间的部分.()()()11322223322222222.xdydz ydzdx zdxdyI xy zxdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zxy z∑∑-∑∑++=++++++=+++++⎰⎰⎰⎰⎰⎰根据高斯公式()13222200xdydz ydzdx zdxdydxdydz x y z∑-∑Ω++==++⎰⎰⎰⎰⎰.()1122232222134.x y z xdydz ydzdx zdxdyxdydz ydzdx zdxdyxy zdxdydz π∑∑++≤++=++++==⎰⎰⎰⎰⎰⎰⎰所以4I π=.(20)(本题满分11分) 【解析】(Ⅰ)对矩阵1()Aξ施以初等行变换()11110221111111111012204220000A ξ⎛⎫-- ⎪---⎛⎫⎪ ⎪⎪=-→ ⎪ ⎪ ⎪---⎪⎝⎭ ⎪ ⎪⎝⎭可求得 2122122k kk ξ⎛⎫-+ ⎪ ⎪ ⎪=- ⎪ ⎪⎪ ⎪⎝⎭,其中k 为任意常数.又2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭,对矩阵21()A ξ施以初等行变换()211110220122201000044020000A ξ⎛⎫- ⎪-⎛⎫⎪ ⎪=--→ ⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭, 可求得 312a a b ξ⎛⎫-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,其中,a b 为任意常数.(Ⅱ)解法1 由(Ⅰ)知12311122211,,102222ka ka kbξξξ--+--=-=-≠-, 所以123,,ξξξ线性无关.解法2 由题设可得10A ξ=.设存在数123,,k k k ,使得1122330k k k ξξξ++=, ①等式两端左乘A ,得22330k A k A ξξ+=,即21330k k A ξξ+=, ②等式两端再左乘A ,得2330k A ξ=,即310k ξ=.由于10ξ≠,于是30k =,代入②式,得210k ξ=,故20k =.将230k k ==代入①式,可得10k =,从而1,ξ23,ξξ线性无关.(21)(本题满分11分) 【解析】(Ⅰ)二次型f 的矩阵101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭.由于01||01()((1))((2))111aE A aa a a a λλλλλλλ---=-=--+----+,所以A 的特征值为123,1,2a a a λλλ==+=-.(Ⅱ)解法1 由于f 的规范形为2212y y +,所以A 合同于100010000⎛⎫⎪ ⎪ ⎪⎝⎭,其秩为2,故 1230A λλλ==,于是0a =或1a =-或2a =.当0a =时,1230,1,2λλλ===-,此时f 的规范形为2212y y -,不合题意. 当1a =-时,1231,0,3λλλ=-==-,此时f 的规范形为2212y y --,不合题意. 当2a =时,1232,3,0λλλ===,此时f 的规范形为2212y y +. 综上可知,2a =.解法2 由于f 的规范形为2212y y +,所以A 的特征值有2个为正数,1个为零. 又21a a a -<<+,所以2a =.(22)(本题满分11分)【解析】(Ⅰ) 12211{1,0}463(10)1{0}9()2C P X Z P X Z P Z ⋅========. (Ⅱ)由题意知X 与Y 的所有可能取值均为0,1,2.()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0,461112,0,0,1,36311,1,2,10,910,2,91,20,2,20,C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======故(,)X Y 的概率分布为(23)(本题满分11 分) 【解析】(Ⅰ)2202().x EX xf x dx x e dx λλλ+∞+∞--∞===⎰⎰令X EX =,即2X λ=,得λ的矩估计量为12Xλ=. (Ⅱ)设12,,,(0,1,2,,)n i x x x x i n >=为样本观测值,则似然函数为()12121,,,;,nii nx nn i i L x x x ex λλλ=-=∑=⋅∏11ln 2ln ln nni i i i L n x x λλ===-+∑∑,由1ln 20ni i d L n x d λλ==-=∑,得λ的最大似然估计量为22Xλ=.。
自-浙江省2009年10月高等教育自学考试工程数学(一)试题课程代码07961

浙江省2009年10月高等教育自学考试工程数学(一)试题课程代码:07961一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设A ,B是随机事件,且A ⊂B ,则B A ⋃=( ) A.AB.BC.AB ﻩD.A ∪B2.现有10节电池,其中7件正品,3件次品,任意抽取两节电池,每次抽一节,抽取后不再放回,则2次抽出的均是正品的概率为( )A .51ﻩB.5021 C .157ﻩD.1073.随机变量X ,Y 独立同分布:P{X =-1}=P {Y=-1}=21,P {X =1}=P{Y =1}=21,则下列各式中成立的是( )A.P {X =Y }=21ﻩB .P{X =Y}=1 C.P {X +Y =0}=41D.P{XY =1}=41 4.设随机变量X ,Y 相互独立,且D(X)=D (Y)=2,则D (X -Y)=( )A.0 B.2ﻩC.4ﻩD.85.如果函数f (x )=⎩⎨⎧≤≤.,0,,其他b x a x 是某连续型随机变量X 的概率密度,则区间[a,b]可以是( )A.[0,1]ﻩB.[0,2]C.[1,2]D.[1,3]6.设随机变量X 1,X 2独立同分布,且其方差为σ2>0.令随机变量Y =21(X 1+X 2),则下列各项中正确的是( )A.Cov(X1,Y )=22σﻩB.Cov(X 1,Y)=2σC.Cov(X 1,Y )=22σD.Cov(X 1,Y )=223σ 7.设(X,Y )为二维连续随机变量,则X 与Y 不相关的充分必要条件是( ) A.X与Y 相互独立ﻩB .E (XY )=E (X )E (Y ) C.E (X+Y )=E(X )+E(Y )D.(X ,Y )~N (μ1,μ2;21σ,22σ;0)8.设随机变量X 1,X2,…X n …相互独立,且X i(i =1,2,…,n ,…)都服从参数为2的泊松分布,则当n 充分大时,随机变量Z n =∑=ni i X n 11的概率分布近似服从( )A.N(2,4) B.N (2,n2)ﻩ C.N (n21,21)ﻩD.N (2n ,4n ) 9.设X1,X2,…X n是来自正态总体N (0,σ2)的样本,X 为样本均值, s 2为样本方差, 则下列统计量中, 服从自由度为n -1的t 分布的是( ) A .sXn B.sXn ﻩ C.2s Xn D.2s Xn 10.与总体方差的置信区间优劣无关的是 ( ) A.样本容量B.区间长度ﻩC.总体方差ﻩD.总体均值二、填空题(本大题共15小题,每小题2分,共30分)请在每小题的空格中填上正确答案。
浙江省1月高等教育自学考试高等数学(工专)试题及答案解析历年试卷及答案解析

浙江省2018年1月高等教育自学考试高等数学(工专)试题课程代码:00022一、单项选择题(在每小题的四个备选答案中选出一个正确答案,并将其号码填在题后的括号内。
每小题2分,共20分)1.设f -1(x)=2x 12x-1+,则:f(x)=( ) A. x)2(1x-1+ B. x 1x -1+ C. x 212x -1+ D. x212x1-+ 2.0x lim → tg2x sin3x =( )A.3B.23C.21D.13.过原点作曲线y=e x 的切线,则:切线的方程为( )A.y=e xB.y=e xC.y=xD.y=2ex4.设f(x)=x(x-1)(x-2)(x-3),则:方程f ′(x)=0,在〔0,3〕内的根的个数为( )A.1B.2C.3D.45.设f(x)的一个原函数为x 3,则:∫xf(1-x 2)dx=( )A.(1-x 2)3+CB.-21(1-x 2)3+C C.-61(1-x 2)3+C D.x 3+C6.设⎰x02dt )t (f =2x 3,则: ⎰10dx )x (f ( )A.1B.2C.3D.47.如果广义积分⎰-x0P 2dx x 收敛,则( )A.P>1B.P<1C.P>3D.P<3.8.函数Z=f(x,y)在点(x 0,y 0)处连续是z=f(x,y),在点(x 0,y 0)处存在一阶偏导数的() A.充分条件 B.必要条件C.充要条件D.既非充分,又非必要条件9.方程y xdx dy-=的通解为( )A.x 2-y 2=CB.xy=CC.x 2+y 2=CD.x+y=C10.下列级数中绝对收敛的级数是( )A. ∑∞=-1n n )1( 1n 1+B.∑∞=1n tg 2n 1C. ∑∞=-1n n )1( 32n 1n 2++D.∑∞=1n ln(1+n 1)二、填空题(每格2分,共20分)11.∞→n lim (n n 2n 2-+)=______. 12.设f(x)=⎪⎩⎪⎨⎧-+2x 1ax 1 0)(x 0)(x =≠ ,在点x=0处连续,则:a=_____. 13.设y=xcos2x ,则:f ′(x)=______. 14.设x=⎪⎩⎪⎨⎧==--t 3t 2ey e x ,则:dx dy =_____. 15.⎰++-)x 1(x x x 122dx=______. 16.⎰2x 0dt )t (f dx d =______. (f(t)为连续函数) 17.⎰--+1123dx x 12x =______.18.设z=x y (x>0),则:dz=______.19.设D :x 2+y 2≤a 2,则:⎰⎰+D 22dxdy )y x ( =______.20.幂级数∑∞=1n n n x 2n 的收敛半径是______.三、计算题(每题6分,共42分)21. 设y=2xarctg2x-ln 24x 1+,求:22dx x d ,dx dy . 22. 求0x lim →(1e 1sinx 1x --). 23. 设y 是由方程e y +xy=e 所确定的x 的函数,求:dx dy 、0x dx dy = 24. ∫xsin 2xdx25. ∫a 0x 3dx x a 22- (a>0) 26. 求过直线2 1-x =y+2=2- 3-z 且平行于直线33z 2 1-y 0 1x +==+的平面方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
07961# 工程数学(一)试题 第 1 页 共 4 页
浙江省2009年1月高等教育自学考试
工程数学(一)试题
课程代码:07961
一、单项选择题(本大题共10小题,每小题2分,共20分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.以A 表示事件“甲种产品畅销,乙种产品滞销”,则事件A 为( ) A.甲种产品滞销,乙种产品畅销 B.甲、乙两种产品均畅销 C.甲种产品滞销
D.甲种产品滞销或乙种产品畅销
2.若两事件A 和B 同时出现的概率P (AB )=0,则( ) A. A 和B 不相容 B. AB 是不可能事件 C. AB 未必是不可能事件
D. P (A )=0或P (B )=0
3.设随机变量X 和Y 相互独立,且都服从0-1分布:
则下列结论正确的是( ) A. X =Y B. P (X =Y )=1 C. p (X ≠Y )=0.24
D. P (X =Y )=0.52
4.设随机变量X 的概率密度函数f (x )=⎩⎨⎧≤≤+其他,
020,x b ax ,且已知X 的分布函数F (1)=41,则
有( )
A. a =21
,b =0
B. a =0,b =2
1 C. a =1,b =
21 D. a =
41,b =4
1 5.设某人练习射击,每次命中率为p ,重复射击n 次,这n 次中的命中次数记为X ,若E (X )=8,D (X )=1.6,则( ) A. n =40,p =0.
2 B. n =25,p =0.32 C. n =20,p =0.4 D. n =10,p =0.8
07961# 工程数学(一)试题 第 2 页 共 4 页
6.设随机变量X ~N (0,1),X 的分布函数为Φ(x ),则P {|X |>2}的值为( ) A. 2[1-Φ(2)] B. 2Φ(2)-1
C. 2-Φ(2)
D. 1-2Φ(2)
7.对任意两个随机变量X 和Y ,若E (XY )=E (X )E (Y ),则( ) A. X 和Y 相互独立 B. X 和Y 不相关 C. D (XY )=D (X )D (Y )
D. X 和Y 不独立
8.设总体X 的数学期望是μ,X 1,X 2,…X n 为来自该总体的一个样本,则下列结论正确的是
( )
A. 不能确定
B. X 2是μ的无偏估计量
C. X 2不是μ的估计量
D. X 2是μ的极大似然估计量
9.在假设检验中,显著性水平α指( ) A. P (接受H 0|H 0为假)=α B. P (接受H 1|H 1为假)=α C. P (拒绝H 0|H 0为真)=α
D. P (拒绝H 1|H 1为真)=α 10.假设检验时,当样本容量一定,如果缩小犯第一类错误的概率,则犯第二类错误的概率
( )
A.变小
B.变大
C.不变
D.不确定
二、填空题(本大题共15小题,每小题2分,共30分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
11.事件A 和B 互不相容,且P (A )=31
,P (B )=41,P (A |B )=_______。
12.设X 和Y 相互独立且都服从N (0,1),则D (2X -3Y +1)=_______。
13.设离散型随机变量X 的分布律为P (X =k )=c
k
(k =1,2,…5),则c =_______。
14.设二维随机变量(X ,Y )的联合概率密度函数为⎪⎩⎪⎨⎧>>=--其他,
00,0,),(43y x ke
y x f y x ,则
k =_______。
15.设X 表示10次独立重复射击中命中目标的次数,且每次命中目标的概率为0.4,则E (X 2)=_______。
16.设随机变量X 与Y 的相关系数为0.9,若Z =X -0.4,则ρ
YZ =_______。
07961# 工程数学(一)试题 第 3 页 共 4 页
17.设321,,θθθ 是总体分布中参数θ的无偏估计量,32132θθθθ
+-=a ,当a =_______时,θ
也是θ的无偏估计量。
18.功率为40W ,60W ,100W 的灯泡分别有3箱、5箱、2箱,次品率分别为10%,4%,5%,随机取一箱,再从该箱内随机取一只灯泡,则取出的灯泡为次品的概率是_______。
19.设随机变量X ~P (λ),λ>0,且P (X ≤1)=4P (X =2),则λ=_______。
20.若随机变量X ~U [1,6],则方程x 2+Xx +1=0有实根的概率为_______。
21.某射手在两次射击中至少命中一次的概率为0.75,则该射手在一次射击中命中的概率是_______。
22.若设随机变量X ~N (2,σ2),且已知P (2<X <4)=0.3.则P (X <0)=_______。
23.设总体X ~N (0,σ2
),X 1,X 2,X 3,X 4是来自总体为X 样本,则V =
∑=4
1
2
2
1i X σ
~_______。
24.设总体X 服从参数为λ泊松分布,其中λ为未知参数,x 2,x 2,…x n 为来自该总体的样本观测值,x 为总体X 样本均值,则λ的矩估计为_______。
25.设总体X ~N (μ,1),x 1,x 2,…x n 为总体X 的样本观测值,x 为总体X 样本均值,s 2为总体X 样本方差,检验正态总体均值μ时,H 0∶μ=μ0,H 1∶μ≠μ0在显著水平α下的拒绝域是_______。
三、计算题(本大题共2小题,每小题8分,共16分)
26.为防止意外,某矿井内同时设有两种报警系统A 与B ,每种系统单独使用时其有效运行的概率,系统A 为0.92,系统B 为0.93,而在A 失灵的条件下,B 有效的概率为0.85,求 (1)发生意外时这两种报警系统同时有效的概率; (2)发生意外时这两种报警系统至少一个有效的概率。
27.设连续随机变量X 的概率密度为f (x )=⎪⎩⎪⎨⎧<<其他
,010x ,Ax B ,且E (X )=32,求
(1)系数A 与B ;
(2)X 的分布函数F (x ); (3)D (X )。
07961# 工程数学(一)试题 第 4 页 共 4 页
四、综合题(本大题共2小题,每小题12分,共24分)
28.设(X ,Y )的可能取值为(0,0),(-1,1),(-1,2),(2,0),(2,2),相应的概率为61
,121,31,61,a . (1)列表表示其联合分布律; (2)求X 与Y 边缘分布律; (3)求Cov (X ,Y )。
29.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩
⎨⎧<<<<其他,00,10,x
y x Ax ,
(1)确定系数A ;
(2)求边缘概率密度f X (x ),f Y (y ); (3)判别X 与Y 的独立性。
五、应用题(本大题10分)
30.设总体X 服从泊松分布P (λ),其中λ为未知参数。
如果取得样本观测值为x 1,x 2,……,x n ,求参数λ的矩估计值和极大似然估计值。
