运筹学教学课件 第一章 线性规划与单纯形法
合集下载
运 筹 学 课 件
12/3 4
z
1 2
x4
x5 42
x3
2 3
x4
1 3
x5
4
新典式
主元化 为1，主 元所在
x2
1 2
x4
6
列的其 余元素
x1
2 3
x4
1 3
x5
4
化为0
观察最后一个典式，所有检验数均为非负， 故其对应的基本可行解为最优解，即
X * 4,6,6,0,0T z* 42
去掉引入变量，得原问题的最优解为：
运筹学课件
目录
运筹学概论 第一章 线性规划基础 第二章 单纯形法 第三章 LP对偶理论 第四章 灵敏度分析 第五章 运输问题 第六章 整数规划 第七章 动态规划 第八章 网络分析
第二章 单纯形法
(SM-Simplex Method)
1947年，美国运筹学家Dantzig提出，原理是 代数迭代。
单纯形法中的单纯形的这个术语，与该方法毫 无关系，它源于求解方法的早期阶段所研究的一 个特殊问题，并延用下来。
CB B1b B1b
z
CB B1N CN X N X B B1NX N
CB B1b B1b
上述方程组的矩阵形式为
10
0 I
CB
B1N B1N
CN
z XB XN
CB B1b B1b
上式的系数增广阵称为对应于基B的单纯形表：
T(B)
CB B1b B1b
0 I
CB
B1N B1N
CN
形式的LP问题，必须解决三个问题： ⑴初始基本可行解的确定； ⑵解的最优性检验； ⑶基本可行解的转移规则。 这里先放一下⑴，研究⑵和⑶，为此，
运筹学课件1-4单纯形法计算步骤
b 21 4
9 4
3 x1 1 -1 3 4 -1 12
9 x2 3 1 9 0 1 0
0 x3 1 0 0 1 0 0
0 x4 0 1 0 -3 1 -9
θ 7 4
9/4 -
所以把x3换出为非基变量，x1为换入变量即新的基变量。
第20页
cj
CB 0 0
0 9 3
XB x3 x4 cj-zj x3 x2 cj-zj x1
cj-zj
x3 x1 x5 cj-zj
6
0 1 0
5
5/2 1/2 1
0
1 0 0
0
-1/2 1/2 -1
0
0 0 1
75 5
0
2
0
-3
0
5
x2
5
0
1
0
-1
1
第10页
cj CB 0 0 0 0 6 0 XB x3 x4 x5 b 90 75 80 105/2 75/2 5
6 x1 1 2 2
5 x2 3 1 2
9/4
-
3 9
9/4 25/4
1 0 0
25
第24页
cj CB 0 0 XB x3 x4 cj-zj b 21 4
3 x1 1 -1 3
9 x2 3 1 9
0 x3 1 0 0
0 x4 0 1 0 θ 7 4
0
9
x3
x2 cj-zj x1 x2 cj-zj
9
4
4
-1 12
0
1 0 0 1 0
1
0 0 1/4 1/4 -3
i 1
第1页
单纯形表求解线性规划问题
运筹学 (2)ppt课件
《辞海》对运筹学解释为：“二十世纪四十年代开始形成的一门 科学，主要研究经济活动与军事活动中能用数量来表达的有关运 用，筹划与管理方面的问题，它根据问题的要求，通过数学的分 析与运算，作出综合性的合理的安排，以达到较经济、较有效地 使用人力、物力。近年来，它在理论与应用方面都有较大发展。 其主要分枝有规划论、对策论、排队论及质量控制等。”
后来田忌的谋士孙膑献了一计：在每次开赛前要求对方先报马名， 由此区分对方参赛的是上马、中马还是下马；然后以自己的上马 对对方的中马、自己的中马对对方和下马、自己的下马对对方的 上马。这样，两胜一负每天赢得一千金。
6
1．赛马与桂陵之战
不久，即公元前354年，魏国以庞涓为将率军伐赵，兵围邯郸。 次年，邯郸在久困之下已岌岌可危，而魏军因久攻不下，损失也很 大。齐国应赵国的要求，以田忌为将，孙膑为军师，率军击魏救赵。 孙膑令一部轻兵乘虚直趋魏都大梁，而以主力埋伏于庞涓大军归途 必经的桂陵之地。魏国因主力远征，都城十分空虚。魏惠王见齐军 逼进，急令庞涓回师自救。刚刚攻下邯郸的庞涓闻大梁告急，急率 疲惫之师回救。
8
2．晋国公重建皇城
距今约1000年前，开封一场 大火，北宋皇城毁于一旦。宋真 宗命晋国公丁渭，主持重建全部 宫室殿宇。
当时，皇城都是砖木结构的， 建筑材料必须从远地通过汴水运 来。由于时间紧、任务重，按一 般的操作法肯定不能按时完成。 丁渭深思熟虑，规划并实施了一 个至今令人拍案叫绝的施工方案。
运筹学
1
内容提要
绪论 线性规划与单纯形法 线性规划的进一步研究 运输问题 动态规划 存储论 排队论
2
绪论
3
第一节 运筹学的产生和发展
运筹学，英国称Operational Research，美国称Operations Research，直译作“作业研究”或“运用研究”，简称OR。中文 “运筹”二字取自《史记•高祖本记》中，刘邦“夫运筹帷幄之中， 决胜于千里之外，吾不如子房”。由此可见，它是一门决策科学， 优化科学。
后来田忌的谋士孙膑献了一计：在每次开赛前要求对方先报马名， 由此区分对方参赛的是上马、中马还是下马；然后以自己的上马 对对方的中马、自己的中马对对方和下马、自己的下马对对方的 上马。这样，两胜一负每天赢得一千金。
6
1．赛马与桂陵之战
不久，即公元前354年，魏国以庞涓为将率军伐赵，兵围邯郸。 次年，邯郸在久困之下已岌岌可危，而魏军因久攻不下，损失也很 大。齐国应赵国的要求，以田忌为将，孙膑为军师，率军击魏救赵。 孙膑令一部轻兵乘虚直趋魏都大梁，而以主力埋伏于庞涓大军归途 必经的桂陵之地。魏国因主力远征，都城十分空虚。魏惠王见齐军 逼进，急令庞涓回师自救。刚刚攻下邯郸的庞涓闻大梁告急，急率 疲惫之师回救。
8
2．晋国公重建皇城
距今约1000年前，开封一场 大火，北宋皇城毁于一旦。宋真 宗命晋国公丁渭，主持重建全部 宫室殿宇。
当时，皇城都是砖木结构的， 建筑材料必须从远地通过汴水运 来。由于时间紧、任务重，按一 般的操作法肯定不能按时完成。 丁渭深思熟虑，规划并实施了一 个至今令人拍案叫绝的施工方案。
运筹学
1
内容提要
绪论 线性规划与单纯形法 线性规划的进一步研究 运输问题 动态规划 存储论 排队论
2
绪论
3
第一节 运筹学的产生和发展
运筹学，英国称Operational Research，美国称Operations Research，直译作“作业研究”或“运用研究”，简称OR。中文 “运筹”二字取自《史记•高祖本记》中，刘邦“夫运筹帷幄之中， 决胜于千里之外，吾不如子房”。由此可见，它是一门决策科学， 优化科学。
运筹学第01章课件
12
运筹学在管理中的应用
• 财务和会计：包括预测、贷款、成 财务和会计：包括预测、贷款、 本分析、定价、证券管理、 本分析、定价、证券管理、现金管 理等。 理等。 • 其他：设备的维修、更新，科学项 其他：设备的维修、更新， 工程项目的选择与评价， 目、工程项目的选择与评价，工程 优化设计、管理等。 优化设计、管理等。
6
运筹学概况简述
运筹学能够对经济管理系统中 的人力、物力、 的人力、物力、财力等资源进行统 筹安排， 筹安排，为决策者提供有依据的最 优方案，以实现最有效的管理。 优方案，以实现最有效的管理。 通常以最优、 通常以最优、最佳等作为决策 目标，避开最劣的方案。 目标，避开最劣的方案。
7
运筹学的产生和发展
16
运筹学解决问题的过程
1）提出问题：认清问题。 提出问题：认清问题。 2）寻求可行方案：建模、求解。 寻求可行方案：建模、求解。 3）确定评估目标及方案的标准或方 途径。 法、途径。 4）评估各个方案：解的检验、灵敏 评估各个方案：解的检验、 性分析等。 性分析等。
17
运筹学解决问题的过程
5）选择最优方案：决策。 ）选择最优方案：决策。 6）方案实施：回到实践中。 ）方案实施：回到实践中。 7）后评估：考察问题是否得到完 ）后评估： 满解决。 满解决。
10
运筹学在管理中的应用
生产计划：生产作业的计划、 生产计划：生产作业的计划、日程表
的编排、合理下料、配料问题、 的编排、合理下料、配料问题、物料 管理等。 管理等。
库存管理：多种物资库存量的管理， 库存管理：多种物资库存量的管理，
库存方式、库存量等。 库存方式、库存量等。
运输问题：确定最小成本的运输线路、 运输问题：确定最小成本的运输线路、
运筹学在管理中的应用
• 财务和会计：包括预测、贷款、成 财务和会计：包括预测、贷款、 本分析、定价、证券管理、 本分析、定价、证券管理、现金管 理等。 理等。 • 其他：设备的维修、更新，科学项 其他：设备的维修、更新， 工程项目的选择与评价， 目、工程项目的选择与评价，工程 优化设计、管理等。 优化设计、管理等。
6
运筹学概况简述
运筹学能够对经济管理系统中 的人力、物力、 的人力、物力、财力等资源进行统 筹安排， 筹安排，为决策者提供有依据的最 优方案，以实现最有效的管理。 优方案，以实现最有效的管理。 通常以最优、 通常以最优、最佳等作为决策 目标，避开最劣的方案。 目标，避开最劣的方案。
7
运筹学的产生和发展
16
运筹学解决问题的过程
1）提出问题：认清问题。 提出问题：认清问题。 2）寻求可行方案：建模、求解。 寻求可行方案：建模、求解。 3）确定评估目标及方案的标准或方 途径。 法、途径。 4）评估各个方案：解的检验、灵敏 评估各个方案：解的检验、 性分析等。 性分析等。
17
运筹学解决问题的过程
5）选择最优方案：决策。 ）选择最优方案：决策。 6）方案实施：回到实践中。 ）方案实施：回到实践中。 7）后评估：考察问题是否得到完 ）后评估： 满解决。 满解决。
10
运筹学在管理中的应用
生产计划：生产作业的计划、 生产计划：生产作业的计划、日程表
的编排、合理下料、配料问题、 的编排、合理下料、配料问题、物料 管理等。 管理等。
库存管理：多种物资库存量的管理， 库存管理：多种物资库存量的管理，
库存方式、库存量等。 库存方式、库存量等。
运输问题：确定最小成本的运输线路、 运输问题：确定最小成本的运输线路、
运筹学线性规划与单纯形法
整理课件
16
Max Z= x1-2x2+3x3' -3x3" + 0x4 +0x5 s.t. x1+x2+ x3' - x3" +x4 =7
x1-x2+ x3' - x3" -x5=2
-3x1+x2+2x3' -2x3" =5 x1, x2,x3',x3", x4,x5 0
第一节小结：建立模型；三个组成要素；四种形式； 化为标准形（4个条件5点）
.
9x1+4x2 ≤ 360
90 80 60 40 20
4x1+5x2 ≤200
B C
HI G
Z=70x1+120x2 3x1+10x2 ≤300
0
20 D40 E 60
80 1F00 x1
整理课件
30
二、解的几种可能情况
1．唯一最优解。目标函数直线与凸多边形只有 一个切点； 2．无穷多最优解，目标函数图形与某个约束条 件平行。 3．无界解（无最优解）----可行域无界。一般是 漏了一些约束条件。 4．无可行解----可行域为空。
Ⅰ
Ⅱ 计划期可用能力
2
2
12
1
2
8
4
0
16
0
4
12
2
3
问：应如何安排生产计划，才能使总利润最大？
整理课件
3
解：用数学的语言进行描述:
1.决策变量：设产品I、II的产量分别为 x1、x2 2.目标函数：问题要求获取利润最大，该公司获取
利润为2 x1 + 3 x2，令z = 2 x1 + 3 x2，则max z = 2 x1 + 3 x2， max z 是该公司获取利润的目标 值，它是变量x1、 x2的函数，称为目标函数。
运筹学第1章：线性规划问题及单纯型解法
原料甲 原料乙 最低含量 VA 0.5 0.5 2 VB1 1.0 0.3 3 VB2 0.2 0.6 1.2 VD 0.5 0.2 2 0.3 0.5 单价
分别代表每粒胶丸中甲, 设 x1, x2分别代表每粒胶丸中甲, 乙两种原料的用量
5
例3,合理下料问题 , 分别代表采用切割方案1~8的套数, 的套数, 设 xj 分别代表采用切割方案 的套数
19
( f(x
)= 3
6
1.2.2 单纯型法的基本思路
确定初试基础可行解
检查是否为 最优解? 最优解?
是
求最优解的目标函数值
否 确定改善方向
求新的基础可行解
20
1.2.3 单纯型表及其格式
IV CB III XB II x1 b c1 a11 a21 c1′′= cn+1 xn+1 b1 c2′′= cn+2 xn+2 b2 x2 … xn c2 … cn a12 … a1n a22 … a2n I xn+1 cn+1 1 0 0 zn+1 xn+2 cn+2 0 1 0 zn+2 … … … … … … xn+m cn+m 0 0 1 zn+m
OBJ : max f ( x) = 6x1 + 4x2 2x1 + x2 ≤ 10 铜资源约束 x1 + x2 ≤ 8 铅资源约束 s.t. x2 ≤ 7 产量约束 x1, x2 ≥ 0 产量不允许为负值 最优解: x1 = 2, x2 = 6, max f ( x) = 36.
4
例2,配料问题(min, ≥) ,配料问题(
2 max 1 O 1 2 3 4 D 5 6 7 H 8
(完整版)运筹学胡运权第五版课件(第1章)
四运筹学研究的基本特点?系统的整体优化?多学科的配合?模型方法的应用五五运筹学研究的基本步骤运筹学研究的基本步骤?分析与表述问题?建立数学模型?对问题求解?对模型和模型导出的解进行检验?建立对解的有效控制?方案的实施第一章线性规划及单纯形法linearprogrammingandsimplexmethodggp11一般线性规划问题的数学模型11问题的提出例1用一块边长为a的正方形铁皮做一个无盖长方体容器应如何裁剪可使做成的容器的容积最大
（3）L.P. 的顶点与基可行解一一对应。
§1.3 单纯形法（Simplex Method）原理
3-1 预备知识：凸集与顶点
（1）凸集：对于集合C中任意两点连线段上的点，若全在C内， 则称集合C为凸集。
直观特征：图形从内部向外部凸出。
凸集
非凸集
（2）顶点：凸集中不在任意两点的连线段内部的点。
X1
转化为
（2）若约束条件为不等式，
则依次引入松弛变量或剩余变量（统称为松弛变量），
转化为等式约束条件。
约束为≥不等式，减去松弛变量，化为等式约束条件；
多 退
约束为≤不等式，加上松弛变量，化为等式约束条件。
少 补
注意：松弛变量在目标函数中系数全为0。
例：max z=2 x1+3 x2
2 x1+2 x2 12
s.t.
4x1
16
5 x2 15
x10， x2 0
标准化
max z 2x1 3x2 0x3 0x4 0x5
2x1 2x2 x3
12
s.t.
4
x1
5 x2
x4 16 x5 15
x1, x2 , x3, x4 , x5 0
（3）若决策变量xj≤0，则令
（3）L.P. 的顶点与基可行解一一对应。
§1.3 单纯形法（Simplex Method）原理
3-1 预备知识：凸集与顶点
（1）凸集：对于集合C中任意两点连线段上的点，若全在C内， 则称集合C为凸集。
直观特征：图形从内部向外部凸出。
凸集
非凸集
（2）顶点：凸集中不在任意两点的连线段内部的点。
X1
转化为
（2）若约束条件为不等式，
则依次引入松弛变量或剩余变量（统称为松弛变量），
转化为等式约束条件。
约束为≥不等式，减去松弛变量，化为等式约束条件；
多 退
约束为≤不等式，加上松弛变量，化为等式约束条件。
少 补
注意：松弛变量在目标函数中系数全为0。
例：max z=2 x1+3 x2
2 x1+2 x2 12
s.t.
4x1
16
5 x2 15
x10， x2 0
标准化
max z 2x1 3x2 0x3 0x4 0x5
2x1 2x2 x3
12
s.t.
4
x1
5 x2
x4 16 x5 15
x1, x2 , x3, x4 , x5 0
（3）若决策变量xj≤0，则令
运筹学教学课件(全)
实用举例
某公司通过市场调研，决定生产高中档新型拉杆箱。 某分销商决定买进该公司3个月内的全部产品。拉杆箱生 产需经过原材料剪裁、缝合、定型、检验和包装4过程。
通过分析生产过程，得出：生产中档拉杆箱需要用 7/10小时剪裁、5/10小时缝合、1小时定型、1/10小时检 验包装；生产高档拉杆箱则需用1小时剪裁、5/6小时缝合、 2/3小时定型、1/4小时检验包装。由于公司生产能力有限， 3月内各部的最大生产时间为剪裁部630小时、缝合部600 小时、定型部708小时、检验包装部135小时。
D {x | Ax b, x (x1,, xi ,, xn ) 0}
是凸集（凸多面体）。
引理2.1：线性规划的可行解 x (x1 ,, xn )T 为基本可行解的 充分必要条件是x的正分量所对应的系数列向量是线性无关的， 即每个正分量都是一个基变量。
定理2.2：线性规划问题的基本可行解x对应于可行域的顶点
通过分析生产过程，得出：生产中档拉杆箱需要用
7/10小时可剪裁以、通5/1过0小线时性缝合规、划1小求时定解型！、1/10小时
检验包装；生产高档拉杆箱则需用1小时剪裁、5/6小时 缝合、2/3小时定型、1/4小时检验包装。由于公司生产 能力有限，3月内各部的最大生产时间为剪裁部630小时、 缝合部600小时、定型部708小时、检验包装部135小时。
x2
L1：x1=6 L3：2x1+3x2=18
B 可行域
L2：x2=4 最优解
x1
4x1+3x2
解的特殊情况——解的特殊情况——无界解
线性规划的基本性质
若线性规划有最 优解，则最优解必在可 行域的顶点上达到。
X
可行域内部的点 • 可行解? 是 • 最优解? 不
第一章线性规划及单纯形法
第一章线性规划及单纯形法6.6单纯形法小结Drawingontheexampl,thetwoaxisinterceptsareplotted.2、求初始基可行解并进行最优性检验Cj比值CBXBb 检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000令非基变量x1=0，x2=0，找到一个初始基可行解：x1=0，x2=0，x3=8，x4=12，x5=36，σj＞0，此解不是最优（因为z=3x1+5x2+0x3+0x4+0x5)即X0=(0,0,8,12,36)T，此时利润Z=03、寻找另一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9主元首先确定入基变量再确定出基变量检验数?j81010060101/2012300-21x3x2x5050-30300-5/20Cj比值CBXBb检验数?jx1x2x3x4x53500081010012020103634001x3x4x5000035000-12/2=636/4=9令x1=0，x4=0，得x2=6，x3=8，x5=12，即得基可行解X1=(0,6,8,0,12)T此时Z＝30σ1=3＞0，此解不是最优迭代4、寻找下一基可行解Cj比值CBXBb检验数?jx1x2x3x4x53500081010060101/2012300-21x3x2x5050-30300-5/208-4检验数?j40012/3-1/360101/204100-2/31/3x3x2x1053-42000-1/2-1令x4=0，x5=0，得x1=4，x2=6，x3=4，即X0=(4,6,4,0,0)T?j＜0最优解:X=(4,6,4,0,0)T最优值:Z=42小结：单纯形表格法的计算步骤①将线性规划问题化成标准型。
②找出或构造一个m阶单位矩阵作为初始可行基，建立初始单纯形表。
运筹学基础教学课件PPT
都江堰水利工程
Page 4
川西太守李冰 父子主持修建， 其目标是利用 岷江上游的水 资源灌溉川西 平原，追求的 效益还有防洪 与航运。其总 体构思是系统 思想的杰出运 用
北宋丁谓主持修复皇宫
Page 5
例2、北宋丁谓主持修复皇宫 面临的问题：木材、石材、 砖瓦等建筑材料如何取得？
修建如何进行？
大街 开封 皇宫
2、策略集
策 略：在对策中，局中人在整个决策过程中针对一系 列行动制定的完整行动方案。
策略集：每个局中人策略的全体集合。 局 势：每个局中人从自己的策略集合中选择一个策
略，构成一个局势。
3、赢得函数
利用全部局势集合上的一个实值函数，来描述 每个局势完结后局中人的得失的报酬数值。
对策的分类
Page 23
目标函数: 约束条件:1原材料的限制 2工时的限制 3座椅的限制 4非负限制 数学模型:
图解法
x2
1000
5x1+2.5x2≤2500
x1=400
800
Z=2600
600
400
Z=1800
Page 20
max Z=4x1+3x2
2x1 2x2 1600 5x1x1420.05x2 2500 x1 0、x2 0
线平衡率 秒表法/PTS
动作和方法研究
动改法
成本控制 设施规划
双手操作法 人机配合法
物流分析
防错法
PMP体系
PAC体系
系统设计
……
工作抽样法 流程程序法
五五法 其它
1工程学 2人机学(人因工程学) 3材料学 4管理学 5统计学 6运筹学 7系统工程学 8材料力学 9工程力学 10物流与设施规划
运筹学第一章
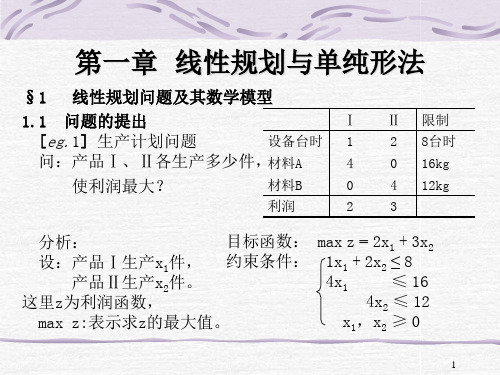
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数，
4x2 ≤ 12
max z:表示求z的最大值。
x1，x2 ≥ 0
1
[eg.2]污水处理问题
环保要求河水含污低于2‰，河水可自身净化20%。 问：化工厂1、2每天各处理多少污水，使总费用最少？
分析：
500万m3
化工厂1
2万m3 1000元/万m3 化工厂2
(2)不等式(≤，≥) 对于“≤”情况：在“≤”左边加上一个松弛变量（非
负），变为等式； 对于“≥”情况：在“≥”左边减去一个剩余变量（非
负），变为等式。 注意：松弛变量、剩余变量在目标函数中的价值系数为0。
(3)无约束变量 令xk = xk’ - xk”，xk’,xk” ≥ 0，代入即可。
13
[eg.7]将下述问题化为标准型
22
3、人工基
[eg.10]max z = x1 + 2x2 + 3x3
x1 + 3x2 + 2x3 = 3 2x1 + x2 + x3 = 4 x1,x2,x3 ≥ 0 分析： A= 1 3 2 211 ∵ 找不到单位矩阵基 ∴ 引入人工变量为初始基变量（2个）
23
3.2 最优性的检验与解的判别
min z = -x1+2x2-3x3 x1+ x2+ x3 ≤ 7 ① x1- x2+ x3 ≥ 2 ②
-3x1+ x2+2x3 = 5 ③ x1,x2 ≥ 0，x3无约束
解：令x3 = x3’-x3”，x3’,x3” ≥ 0；
①式加上一个松弛变量x4；②式减去一个剩余变量x5； 令z’ = -z
第1章线性规划与单纯形法
26
线性规划问题的数学模型
7. 线性规划问题的解
线性规划问题
n
max Z cj xj (1) j 1
s.t
n j 1
aij
xj
bi
(i 1, 2,
, m) (2)
x
j
0,
j
1, 2,
, n (3)
求解线性规划问题，就是从满足约束条件(2)、(3)的方程组 中找出一个解，使目标函数(1)达到最大值。
解： Max z = 3x1–5x2’+5x2”–8x3 +7x4 s.t. 2x1–3x2’+3x2”+5x3+6x4+x5= 28 4x1+2x2’-2x2”+3x3-9x4-x6= 39 -6x2’+6x2”-2x3-3x4-x7 = 58 x1 ,x2’,x2”,x3 ,x4 ,x5 ,x6 ,x7 ≥ 0
x1 , x2 0, x3无约束
解:（１）因为x3无符号要求 ，即x3取正值也可取负值，标准 型中要求变量非负，所以
用 x3 x3 替换 x3 ，且 x3 , x3 0
20
线性规划问题的数学模型
(2) 第一个约束条件是“≤”号，在“≤”左端加入松驰变量x4， x4≥0,化为等式；
(3) 第二个约束条件是“≥”号，在“≥”左端减去剩余变量x5， x5≥0；
11
线性规划问题的数学模型
3. 建模条件 (1) 优化条件：问题所要达到的目标能用线型函数描述，且 能够用极值 （max 或 min）来表示；
(2) 限定条件：达到目标受到一定的限制，且这些限制能够 用决策变量的线性等式或线性不等式表示；
(3) 选择条件：有多种可选择的方案供决策者选择，以便找 出最优方案。
线性规划问题的数学模型
7. 线性规划问题的解
线性规划问题
n
max Z cj xj (1) j 1
s.t
n j 1
aij
xj
bi
(i 1, 2,
, m) (2)
x
j
0,
j
1, 2,
, n (3)
求解线性规划问题，就是从满足约束条件(2)、(3)的方程组 中找出一个解，使目标函数(1)达到最大值。
解： Max z = 3x1–5x2’+5x2”–8x3 +7x4 s.t. 2x1–3x2’+3x2”+5x3+6x4+x5= 28 4x1+2x2’-2x2”+3x3-9x4-x6= 39 -6x2’+6x2”-2x3-3x4-x7 = 58 x1 ,x2’,x2”,x3 ,x4 ,x5 ,x6 ,x7 ≥ 0
x1 , x2 0, x3无约束
解:（１）因为x3无符号要求 ，即x3取正值也可取负值，标准 型中要求变量非负，所以
用 x3 x3 替换 x3 ，且 x3 , x3 0
20
线性规划问题的数学模型
(2) 第一个约束条件是“≤”号，在“≤”左端加入松驰变量x4， x4≥0,化为等式；
(3) 第二个约束条件是“≥”号，在“≥”左端减去剩余变量x5， x5≥0；
11
线性规划问题的数学模型
3. 建模条件 (1) 优化条件：问题所要达到的目标能用线型函数描述，且 能够用极值 （max 或 min）来表示；
(2) 限定条件：达到目标受到一定的限制，且这些限制能够 用决策变量的线性等式或线性不等式表示；
(3) 选择条件：有多种可选择的方案供决策者选择，以便找 出最优方案。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
资源限量 8 台时 16kg 12kg
上页
下页
返回
该计划的数学模型
目标函数 约束条件 Max Z = 2x1 + 3x2 x1 + 2x2 8 4x1 16 4x2 12 x1、 x2 0
x1
x2
上页 下页 返回
•基本概念
决策变量（Decision variables） 目标函数（Objective function） 它是决策变量的函数 约束条件（Constraint conditions） 指决策变量取值时受到 符号约束 的各种资源条件的限制 可行域（Feasible region) ，通常表达为含决策变 量的等式或不等式。 最优解（Optimal solution)
用科学（系统化的知识）代替凭经验 的方法
上页 下页 返回
运筹学的主要内容
第一章 线性规划与单纯形法 第二章 对偶理论与灵敏度分析 第三章 运输问题 第四章 目标规划 第五章 整数规划 第十章 图与网络分析 第十二章 排队论
上页 下页 返回
运筹学学习方法
1、课前预习 2、认真听课，适当笔记 3、认真作业
上页 下页 返回
例4
人事管理问题
1. 一个企业每周七天都要生产或营业 2. 每个工作人员每周连续5天
3. 据分析每天的上班人数分别60、40、
50、30、65、70和75人 4. 问该企业至少需要多少个职工？
上页
下页
返回
模型建立
1、设(未知数)决策变量
设从星期一开始上班的人数为x1,星期二开始上班的人数为 x2，星期三开始上班的人数为x3，星期四开始上班的人数为 x4,星期五开始上班的人数为x5 ，星期六开始上班的人数为x6， 星期日开始上班的人数为x7。
上页 下页 返回
设决策变量的原则
1、将决策者想知道但还不知道的设为未 知数； （返回） 2、所取决策变量要便于表达目标函数和 约束条件。 3、当将决策者想知道但还不知道的是由 多个部分组成时，则应将最基本的部分 取为决策变量。(作业)
上页 下页 返回
建立线性规划数学模型的步骤
1、选择适当的决策变量
上页
下页
返回
建模型之前的分析和计算
设：
化工厂1每天处理的污水量为x1万立方米； 化工厂2每天处理的污水量为x2万立方米
( 2 x1 ) 2 经第2工厂前的水质要求： 500 1000 经第2工厂后的水质要求： [ 0.8( 2 x1 ) ( 1.4 x2 )] 2 700 1000
上页 下页 返回
线性规划中的两类数学模型1
1、max 总收入或总利润 总成本≤b
返回
上页 下页 返回
线性规划中的两类数学模型2
2、min 总成本 总收入≥b
返回
2）表格单纯形法
上页 下页 返回
第一章 重点与难点
1、将实际生产问题、管理问题建立线性规 划的数学模型。 2、线性规划数学模型的一般形式
3、一组约束条件
决策变量的线性等式或不等式组
xj≥０
上页 下页 返回
4、通常变量有符号约束
P38例11 配料问题
产 品 A B D 原材料 供应量 原材料 价格 100 65 100 25 60 35 原材料 C ≥50% ≥ 25% P ≤ 25% ≤ 50% H 产价 品格 50 35 25
继续
返回
1.1 问题的提出
线性规划是运筹学的一个重要分支。线性 规划在理论上比较成熟，在实用中的应用 日益广泛与深入。特别是在电子计算机能 处理成千上万个约束条件和决策变量的线 性规划问题之后，线性规划的适用领域更 为广泛了。从解决技术问题的最优化设计 到工业、农业、商业、交通运输业、军事、 经济计划和管理决策等领域都可以发挥作 用。它已是现代科学管理的重要手段之一。
设按Ⅰ方案下料的原材料根数为x1,Ⅱ方案为x2，Ⅲ方案为x3， Ⅳ方案为x4,Ⅴ方案为x5 ，Ⅵ方案为x6，Ⅶ方案为x7,Ⅷ方案为 x8 。
2、用决策变量表达目标函数 min z= x1+ x2 + x3 + x4 + x5 + x6 + x7 + x8 3、用决策变量表达全部的约束条件 4、注意符号约束
运筹学有一定难度，该课程有一定的研 究性特征；以线性代数和概率论为基础
上页 下页 返回
运筹学 解决问题的主要程序
生产问题 管理问题 建立数学模型 （线性规划数 学模型）
分析求解结果 （对偶问题与 灵敏度分析）
求解数学模型 （图解法与单 纯形法）
上页 下页 返回
第一章
§1 §2 §3 §4
法
线性规划与单纯形法
能够求出最优解为：
x1=10 ，x2 =50 ，x4 =30 (最优值)minz=90
上页
下页
返回
教材上的模型说明
min z 0 x1 0.1x2 0.2 x3 0.3x4 0.8 x5 x4 100 x1 2 x2 2 x3 2 x4 x5 100 3x5 100 3x1 x2 2 x3 x1 , x2 , x3 , x4 , x5 0
可行域中使目标 函数达到最优的 决策变量的值 满足约束条件的决 策变量的取值范围
上页 下页 返回
问题中要确定的未知量，表 明规划中的用数量表示的方 案、措施，可由决策者决定 和控制。
建立线性规划数学模型的步骤
1、选择适当的决策变量
设决策变量的原则
2、用决策变量表达目标函数
收入或利润极大化 成本或支出极小化
设决策变量的原则
2、用决策变量表达目标函数
收入或利润极大化 成本或支出极小化
3、用决策变量表达所有的约束条件 4、注意变量的符号约束返回
上页 下页 返回
线性规划数学模型 的特点
1、一组决策变量(x1,x2,…,xn)
决策者可选择
2、一个目标函数
极大化或极小化 是决策变量的线性函数 Max(或min) z=c1x1+c2x2+…+cnxn
1）决策变量 2）目标函数 3）约束条件 4）符号约束
上页
下页
返回
重点与难点
3、两个自变量的线性规划的图解法 4、线性规划数学模型的标准形式 5、*一般线性规划的单纯形法基础
1）线性规划解的基本概念 可行解 最优解 基 基解 基可行解 可行基
上页
下页
返回
重点与难点
2）线性规划的几何意义 凸集 k个点的凸组合 凸集的顶点 线性规划可行域是凸集 3）基可行解的特征 可行解是基可行解的充分必要条件是其非零分 量的系数列向量线性无关 基可行解对应于可行域的顶点
旋转
上页
下页
返回
重点与难点
7、*单纯形法的其它问题
1）最优性的判断 唯一最优解判断 无穷多最优解判断 无界解判断 2）检验数的公式法
σj=cj-zj=cj-CBPj’
3）最小化问题的最优性判 断与换基 所有检验数都非负为最
上页
下页
返回
§1 线性规划问题
及其数学模型
1. 2. 3. 4. 5. 线性规划问题的数学模型 线性规划的数学模型的一般形式 两个自变量线性规划的图解法 线性规划问题的标准形式 线性规划问题的解的概念
x1 元钢 Ⅰ
2.9m
2.1m 1.5m
2
0 1
1
2 0
1
1 1
1
0 3
0
3 0
0
2 2
0
1 3
0
0 4
0.1 0.3 0.9 余料 2.1m的元钢不少于100根：
0
1.1
0.4
上页
0.8
下页
1Байду номын сангаас4
返回
2x2 + x3 + 3x5 +2 x6 + x7 + x8 ≥100
模型建立
1、设(未知数)决策变量
上页
下页
返回
数学模型为
min z= x1+ x2 + x3 + x4 + x5 + x6 + x7 + x8 2x1+ x2 + x3 + x4≥100 2x2 + x3 + 3x5 +2 x6 + x7 + x8 ≥100 x1 + x3 + 3x4 + x5 + 2x6 +3 x7 + 4x8 ≥100 xj ≥0， xj 为整数，j=1,2,…,8
上页 下页 返回
整理得到本问题的数学模型为：
目标函数 min z 1000x1 800x2 约束条件 x1 x1 1 2 x2 1.4 x1 , x2 0
上页 下页 返回
0.8 x1 x2 1.6
例3 合理下料问题
书上P38例10 2.9m 2.1m 1.5m 一套钢架 任务：100套钢架
上页 下页 返回
重点与难点
4）线性规划的基本定理 若线性规划有最优解则最优值一定可在某基可行解 处取到，即包含一个基可行解（顶点）为最优解。 K个最优解的凸组合都是最优解。 线性规划的枚举法及其缺点。
6、*线性规划单纯形法
1）线性规划单纯形法的步骤 找一个基可行解作为初始解 最优解的判断 换基
上页 下页 返回
1、线性规划问题的提出
将生产经营和管理过程中的决策问题 ——转化成数学模型
上页
下页
返回
•例1: 生产计划问题(步骤)