邻补角、对顶角、同位角、内错角、同旁内角经典习题-一对一专用

合集下载

同位角、内错角、同旁内角(习题及答案)

∴∠ABE=∠DBE（角平分线的定义）
∵∠DBE=∠A（______________________________）
∴_______=∠A（______________________________）
∴BE_____AC（______________________________）
6.已知：如图，E为DF上的点，B为AC上的点，∠1=∠2，AC∥DF．
推理就是由一个或几个已知的判断（前提），推导出一个未知的结论的思维过程．其作用是从已知的知识得到未知的知识，特别是可以得到不可能通过感觉经验掌握的未知知识．几何推理是我们中学接触最多的一种推理形式．
要想进行严格的几何推理，首先要有一些对应前提．这些前提我们叫做“基本事实”或“定理”，比如我们学过的“同位角相等，两直线平行”、“两点确定一条直线”等都是一些基本事实．这些作为大前提，是我们进行推理的主要依据．而根据这些“基本事实”或“定理”，我们对某个句子进行判断或说明的过程就是证明．
例如，如下的推理：
已知：如图，∠ABC=∠1．
求证：AD∥BC．
证明：如图，
∵∠ABC=∠1（已知）
∴AD∥BC（同位角相等，两直线平行）
我们分析可知，每一个判断都有自己的条件和结论．上述推理中的条件就是∠ABC=∠1，代表着一组同位角相等，而结论就是AD∥BC．由条件得到结论的过程叫做证明，而这个证明必须依据基本事实．我们把基本事实放在结论后的括号中，表明我们是以此为依据进行推理的．
6.已知
对顶角相等
等量代换
同位角相等，两直线平行
两直线平行，同位角相等
已知
两直线平行，内错角相等
思考小结
1.同位角相等，两直线平行（或内错角相等，两直线平行，或同旁内角互补，两直线平行）

同位角、内错角、同旁内角练习(含答案)

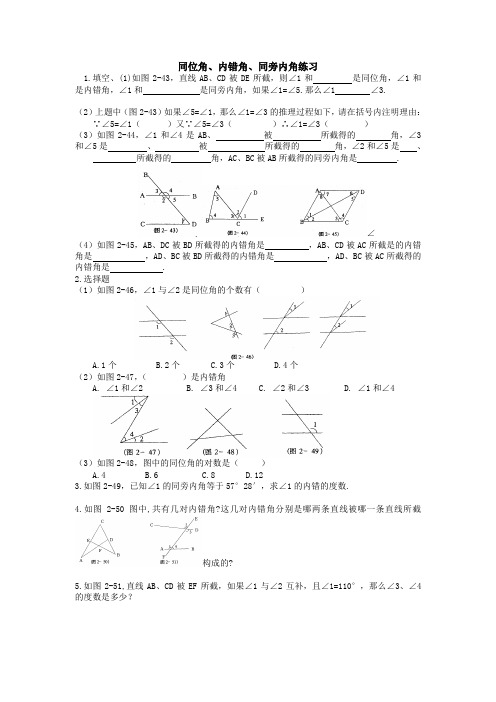
同位角、内错角、同旁内角练习1.填空、(1)如图2-43，直线AB、CD被DE所截，则∠1和是同位角，∠1和是内错角，∠1和是同旁内角，如果∠1=∠5.那么∠1 ∠3.（2）上题中（图2-43）如果∠5=∠1，那么∠1=∠3的推理过程如下，请在括号内注明理由：∵∠5=∠1（）又∵∠5=∠3（）∴∠1=∠3（）（3）如图2-44，∠1和∠4是AB、被所截得的角，∠3和∠5是、被所截得的角，∠2和∠5是、所截得的角，AC、BC被AB所截得的同旁内角是 .∠（4）如图2-45，AB、DC被BD所截得的内错角是，AB、CD被AC所截是的内错角是，AD、BC被BD所截得的内错角是，AD、BC被AC所截得的内错角是 .2.选择题（1）如图2-46，∠1与∠2是同位角的个数有（）A.1个B.2个C.3个D.4个（2）如图2-47，（）是内错角A. ∠1和∠2B. ∠3和∠4C. ∠2和∠3D. ∠1和∠4（3）如图2-48，图中的同位角的对数是（）A.4B.6C.8D.123.如图2-49，已知∠1的同旁内角等于57°28′，求∠1的内错的度数.4.如图2-50图中,共有几对内错角?这几对内错角分别是哪两条直线被哪一条直线所截构成的?5.如图2-51,直线AB、CD被EF所截，如果∠1与∠2互补，且∠1=110°，那么∠3、∠4的度数是多少？1、如图，∠1的内错角是，它们是直线、被直线所截得的；∠1的同位角是，它们是直线、被直线所截得的；∠1的同旁内角是，它们是直线、被直线所截的；2．如图，下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是…………………………………（）（A）①、②、③（B）①、②、④（C）②、③、④（D）①、②、③、④3、如图，图中的同位角共有……………………………………………………………（）（A）6对（B）8对（C）10对（D）12对4．下面四个图形中，∠1与∠2是对顶角的图形的个数是（）A．0 B．1 C．2 D．3121212125．三条直线两两相交于同一点时，对顶角有m对，交于不同三点时，对顶角有n对，则m与n的关系是（）A．m = n B．m＞n C．m＜n D．m + n = 10 6．如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD = 38°，则∠AOC = ，∠COB = 。

同位角、内错角、同旁内角练习题及答案

同位角、错角、同旁角测试题A卷一、填空题1.如图1，直线a、b被直线c所截，∠1和∠2是，∠3和∠4是，∠3和∠2是。

2.如图2，∠1和∠2是直线和直线被直线所截得的角。

3.如图3，∠1的错角是，∠A的同位角是，∠B的同旁角是。

4.如图4，和∠1构成错角的角有个；和∠1构成同位角的角有个；和∠1构成同旁角的角有个。

5.如图5，指出同位角是，错角是，同旁角是。

二、选择题6.如图6，和∠1互为同位角的是( )(A)∠2； (B)∠3；(C)∠4； (D)∠5。

7.如图7，已知∠1与∠2是错角，则下列表达正确的是( )(A)由直线AD、AC被CE所截而得到的；(B)由直线AD、AC被BD所截而得到的；(C)由直线DA、DB被CE所截而得到的；(D)由直线DA、DB被AC所截而得到的。

8.在图8中1和2是同位角的有( )(A)(1)、(2)； (B)(2)、(3)； (C)(1)、(3)； (D)(2)、(4)。

9.如图9，在指明的角中，下列说法不正确的是( )(A)同位角有2对； (B)同旁角有5对；(C)错角有4对； (D)∠1和∠4不是错角。

10.如图10，则图中共有( )对错角(A)3； (B)4； (C)5； (D)6。

三、简答题11.如图11(1)说出∠1与∠2互为什么角？(2)写出与∠1成同位角的角；(3)写出与∠1成错角的角。

12.如图12(1)说出∠A与∠1互为什么角？(2) ∠B与∠2是否是同位角；(3)写出与∠2成错角的角。

13.如图13，指出同位角、错角、同旁角。

B卷一、填空题1.如图1，∠1和∠2可以看作直线和直线被直线所截得的角。

2.如图2，∠1和∠2是直线和直线被直线被直线所截得的角。

3.如图3，直线DE、BC被直线AC所截得的错角是；∠B与∠C可以看作直线、被直线所截得的角。

4.如图4，与∠EFC构成错角的是；与∠EFC构成同旁角的是。

5.如图5，与∠1构成错角的角有个；与∠1构成同位角的角有个；与∠1构成同旁角的角有个。

七年级数学下册同位角、内错角、同旁内角练习题

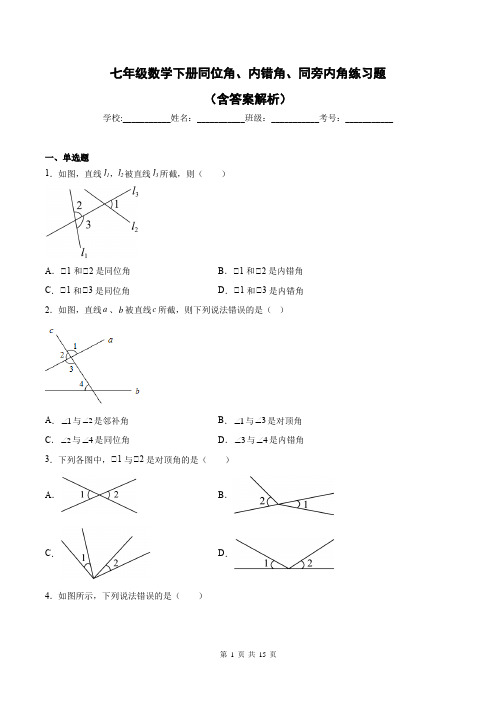
七年级数学下册同位角、内错角、同旁内角练习题（含答案解析）学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，直线l 1，l 2被直线l 3所截，则（）A ．∠1和∠2是同位角B ．∠1和∠2是内错角C ．∠1和∠3是同位角D ．∠1和∠3是内错角2．如图，直线a 、b 被直线c 所截，则下列说法错误的是（）A ．1∠与2∠是邻补角B ．1∠与3∠是对顶角C ．2∠与4∠是同位角D ．3∠与4∠是内错角3．下列各图中，∠1与∠2是对顶角的是（）A ．B ．C ．D ．4．如图所示，下列说法错误的是（）A．∠1和∠3是同位角B．∠1和∠5是同位角C．∠1和∠2是同旁内角D．∠5和∠6是内错角5．给出下列说法：（1）两条直线被第三条直线所截，同位角相等；（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；（3）相等的两个角是对顶角；（4）从直线外一点到这条直线的垂线段，叫作这点到直线的距离．其中正确的有（）A．0个B．1个C．2个D．3个6．在下图中，1∠和2∠是同位角的是（）A．（1）、（2）B．（1）、（3）C．（2）、（3）D．（2）、（4）7．下列四幅图中，1∠和2∠是同位角的是（）A．（1）（2）B．（3）（4）C．（1）（2）（3）D．（1）（3）（4）8．如图，下列两个角是同旁内角的是（）A ．1∠与2∠B ．1∠与3∠C ．1∠与4∠D ．2∠与4∠9．如图所示，下列说法正确的是（）A ．∠2与∠1是内错角B ．∠2与∠3是同位角C ．∠3与∠B 是同旁内角D ．∠A 与∠3是内错角10．下列图形中，1∠与2∠是同位角的是（）A ．B ．C ．D ．11．下列所示的四个图形中，∠1和∠2是同位角的是（）A ．∠∠B ．∠∠∠C ．∠∠∠D ．∠∠12．下列说法正确的是（）A ．同位角相等B ．在同一平面内，如果a ∠b ，b ∠c ，则a ∠cC ．相等的角是对顶角D ．在同一平面内，如果a ∠b ，b ∠c ，则a ∠c二、填空题13．如图所示，（1）1∠和2∠是直线______和直线_______被第三条直线_______所截而成的_______角；（2）2∠和3∠是直线______和直线_______被第三条直线______所截而成的______角；（3）4∠和A ∠是直线______和直线______被第三条直线______所截而成的_______角．14．如图，直线,AB CD 与直线,EF GH 分别相交，图中的同旁内角共有_______对．15．如图，∠1和∠B 是直线____和直线____被直线____所截得到的_____角；∠2和∠4是直线____和直线____被直线____所截得到的_____角；∠D和∠4是直线___和直线___被直线___所截得到的_____角.16．如图，四边形ABCD是正方形，点E在BC上，∠ABE绕正方形的中心经顺时针旋转后与∠DAF重合，则∠DGE=______度．17．回顾之前所学内容填空：同位角：图中∠1与∠5，这两个角分别在直线AB，CD的同一方（上方），并且都在直线EF的同侧（右侧），具有这种位置关系的一对角叫做__________．图中还有同位角：__________．内错角：∠3与∠5，这两个角分别在直线AB，CD之间，并且分别在直线EF两侧，（∠3在直线EF左侧，∠5在直线EF右侧），具有这种位置关系的一对角叫做__________．图中还有内错角：__________．同旁内角：∠3与∠6，这两个角分别在直线AB，CD之间，但它们在直线EF的同一旁（左侧），具有这种位置关系的一对角叫做__________．图中还有同旁内角：__________．18．如图所示，1∠与2∠是________角，2∠与4∠是______角，2∠与3∠是__________角．19．空间两条不重合的直线的位置关系有________、________、________三种．三、解答题20．如图中，共有几对内错角？这几对内错角分别是哪两条直线被哪一条直线所截构成的？21．根据图形填空：（1）若直线,ED BC 被直线AB 所截，则1∠和_____是同位角；（2）若直线,ED BC 被直线AF 所截，则3∠和_____是内错角；（3）1∠和3∠是直线,AB AF 被直线______所截构成的内错角；（4）2∠和4∠是直线AB ，______被直线BC 所截构成的_____角．22．如图∠1、∠2、∠3、∠4、∠5中，哪些是同位角？哪些是内错角？哪些是同旁内角？参考答案：1．C【分析】两条直线a、b被第三条直线c所截，在截线c的同旁，被截两直线a、b的同一侧的角（都在左侧或者都在右侧），把这样的两个角称为同位角；根据定义分别判断即可．【详解】解：∠1和∠2既不是同位角，也不是内错角，故选项A、B错误；∠1和∠3是同位角，故选项C正确，选项D错误；故答案为：C．【点睛】本题考查了同位角、内错角、同旁内角，掌握同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形是解题的关键．2．D【分析】利用邻补角、对顶角、同位角、同旁内角定义解答即可．【详解】解：A 、1∠与2∠是邻补角，故原题说法正确；B 、1∠与3∠是对顶角，故原题说法正确；C 、2∠与4∠是同位角，故原题说法正确；D 、3∠与4∠是同旁内角，故原题说法错误；答案：D ．【点睛】此题主要考查了邻补角、对顶角、同位角、同旁内角，关键是掌握各种角的定义．3．A【分析】根据对顶角的定义，即可一一判定．【详解】解：A 、∠1与∠2是对顶角，故A 选项正确；B 、∠1与∠2不是对顶角，故B 选项错误；C 、∠1与∠2不是对顶角，故C 选项错误；D 、∠1与∠2不是对顶角，故D 选项错误．故选：A ．【点睛】本题主要考查了对顶角的定义，熟记对顶角的图形是解题的关键．4．B【分析】根据同位角、内错角、同旁内角的意义：两条直线被第三条直线所截，在截线的同旁，在被截的两直线的同一侧的角叫做同位角；两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间的两个角叫做内错角；两条直线被第三条直线所截，在截线同旁，且在被截两条直线之内的两角叫做同旁内角，可得答案．【详解】解：A 、∠1和∠3是同位角，故此选项不符合题意；B 、∠1和∠5不存在直接联系，故此选项符合题意；C 、∠1和∠2是同旁内角，故此选项不符合题意；D 、∠1和∠6是内错角，故此选项不符合题意；故选B ．【点睛】本题考查了同位角、内错角、用旁内角，利用同位角、内错角、同旁内角的意义是解题关键． 5．B【分析】正确理解对顶角、同位角、相交线、平行线、点到直线的距离的概念，逐一判断．【详解】解：（1）同位角只是一种位置关系，只有两条直线平行时，同位角相等，错误；（2）强调了在平面内，正确；（3）不符合对顶角的定义，错误；（4）直线外一点到这条直线的垂线段的长度，叫做点到直线的距离，不是指点到直线的垂线段的本身，而是指垂线段的长度．故选：B．【点睛】本题主要考查了对顶角、同位角、相交线、平行线、点到直线的距离，正确理解相关概念是解题的关键．6．B【分析】根据同位角的特征：两条直线被第三条直线所截形成的角中，两个角都在两条被截直线的同侧，并且在第三条直线（截线）的同旁，由此判断即可．【详解】解：∠∠1和∠2是同位角；∠∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角；∠∠1和∠2是同位角；∠∠1的两边所在的直线没有任何一条和∠2的两边所在的直线公共，∠1和∠2不是同位角．故选：B．【点睛】本题考查三线八角中的某两个角是不是同位角，同位角完全由两个角在图形中的相对位置决定．在复杂的图形中判别同位角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形．7．A【分析】互为同位角的两个角，都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角．【详解】解：根据同位角的定义，图（1）、（2）中，∠1和∠2是同位角；图（3）∠1、∠2的两边都不在同一条直线上，不是同位角；图（4）∠1、∠2不在被截线同侧，不是同位角．故选：A．【点睛】本题考查同位角的概念，是需要熟记的内容．即两个都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角．8．B【分析】根据同旁内角的概念求解即可．【详解】解：由图可知，∠1与∠3是同旁内角，∠1与∠2是内错角，∠4与∠2是同位角，故选：B ．【点睛】本题考查了同旁内角的概念，属于基础题，熟练掌握同位角，同旁内角，内错角的概念是解决本题的关键．9．C【分析】根据内错角、同位角、同旁内角的定义进行判断即可．【详解】∠2与∠1不是内错角，A 选项错误，不符合题意；∠2与∠3是邻补角，B 选项错误，不符合题意；∠3与∠B 是同旁内角，C 选项正确，符合题意；∠A 与∠3是同位角，D 选项错误，不符合题意；故选：C ．【点睛】本题考查了内错角、同位角、同旁内角的定义，即同位角：在截线的同旁，在被截两直线的同方向；内错角：在截线的两旁，在被截两直线的内部；同旁内角：在截线的同一侧，夹在被截两直线的之间；熟练掌握知识点是解题的关键．10．D【分析】根据同位角的定义解答．【详解】A 、B 、C 中的1∠与2∠不是同位角，D 中的1∠与2∠是同位角；故选：D ．【点睛】此题考查同位角的定义，熟记定义是解题的关键．11．C【分析】在截线的同侧，并且在被截线的同一方的两个角是同位角，所以∠∠∠符合要求．【详解】解：图∠、∠、∠中，∠1与∠2在截线的同侧，并且在被截线的同一方，是同位角；图∠中，∠1与∠2的两条边都不在同一条直线上，不是同位角．故选：C ．【点睛】此题主要考查了内错角、同位角和同旁内角的定义，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．12．D【分析】根据同位角的定义、垂线的性质、对顶角的性质、平行公理依次判断．【详解】解：A. 同位角不一定相等，故该项不符合题意；B. 在同一平面内，如果a ∠b ，b ∠c ，则a //c ，故该项不符合题意；C. 相等的角不一定是对顶角，故该项不符合题意；D. 在同一平面内，如果a//b，b//c，则a//c，故该项符合题意；故选：D．【点睛】此题考查了语句的判断，正确掌握同位角的定义、垂线的性质、对顶角的性质、平行公理是解题的关键．13．BA CE BD同位BA CA BD同旁内BA CE AC内错【分析】根据同位角、内错角及同旁内角的定义：两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形即可得出答案．【详解】解：由图可知：（1）1∠和2∠是直线BA和直线CE被第三条直线BD所截而成的同位角；∠是直线BA和直线CA被第三条直线BD所截而成的同旁内角；（2）2∠和3（3）4∠和A∠是直线BA和直线CE被第三条直线AC所截而成的内错角，故答案为：BA；CE；BD；同位；BA；CA；BD；同旁内；BA；CE；AC；内错．【点睛】此题考查了同位角、内错角及同旁内角的知识，属于基础题，掌握定义是关键．14．16【分析】根据同旁内角的定义：两直线被第三条直线所截，在截线的同一侧，被截线的内部的两个角是同旁内角，注意每一个“三线八角”基本图形都有两对同旁内角，从对原图形进行分解入手即可求得答案．【详解】解：直线AB、CD被EF所截有2对同旁内角；直线AB、CD被GH所截有2对同旁内角；直线CD、EF被GH所截有2对同旁内角；直线CD、GH被EF所截有2对同旁内角；直线GH、EF被CD所截有2对同旁内角；直线AB、EF被GH所截有2对同旁内角；直线AB、GH被EF所截有2对同旁内角；直线EF、GH被AB所截有2对同旁内角．共有16对同旁内角．故答案为：16．【点睛】此题考查了同旁内角的知识，属于基础题，掌握定义是关键．15．（1）AD（2）BC（3）AB（4）同位（5）AB（6）CD（7）AC（8）同位（9）AC（10）AD（11）CD（12）同旁内【分析】根据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形解答．【详解】∠1和∠B是直线AD和直线BC被直线A所截得到的同位角；∠2和∠4是直线AB和直线CD被直线AC所截得到的同位角；∠D和∠4是直线AC和直线AD被直线DC所截得到的同旁内角.【点睛】本题主要考查了三线八角的问题，熟记同位角、内错角、同旁内角的位置关系是解决此类问题的关键．16．90【分析】由旋转的性质得∠ADF=∠BAE，再根据正方形的性质，得∠DAF=90°，从而得∠AFD+∠ADF=90°，即∠AFD+∠BAE=90°，再由三角形内角和定理得出∠AGF=90°，即可由对顶角相等求得答案．【详解】解：∠△ABE绕正方形的中心经顺时针旋转后与△DAF重合，∠∠ADF=∠BAE，∠四边形ABCD是正方形，∠∠DAF=90°，∠∠AFD+∠ADF=90°，∠∠AFD+∠BAE=90°，∠∠AFD+∠BAE+∠AGF=180°，∠∠AGF=90°，∠∠DGE=∠AGF=90°，故答案为：90．【点睛】本题考查旋转的性质，三角形内角和定理，对顶角性质，熟练掌握旋转的性质是解题的关键．17．同位角∠2和∠6；∠3和∠7；∠4和∠8内错角∠4和∠6同旁内角∠4和∠5【解析】略18．同位同旁内内错【分析】根据同位角、内错角及同旁内角的定义：两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形即可得出答案．【详解】解：由图形可得，∠1与∠2是同位角；∠2与∠4是同旁内角；∠2与∠3是内错角．故答案为：同位、同旁内、内错．【点睛】此题考查了同位角、内错角及同旁内角的知识，属于基础题，掌握定义是关键．19．相交平行异面【分析】在空间，直线与直线的位置关系有平行、相交、异面三种，在同一平面内两条不重合的直线的位置关系是平行或相交，根据两条直线所在的空间解答即可.【详解】在空间，直线与直线的位置关系有相交、平行、异面，故答案为：相交、平行、异面.【点睛】此题考查相交于平行的特征及性质，关键是要明确两条直线所在的平面是在空间或是在同一平面内.20．BC、BE被DF截得的两对内错角；∠DFB和∠CDF；∠FDB和∠FDB；AC、AD被BE截得的两对内错角：∠AFE和∠CEF，∠AEF和∠EFD【分析】根据内错角的定义：两条直线被第三条直线所截形成的角中，若两个角都在两直线之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．所以由图形可得答案．【详解】∠DFB和∠CDF，∠FDB和∠FDB 是BC、BE被DF截得的内错角；∠AFE和∠CEF，∠AEF和∠EFD是AC、AD被BE截得的内错角.【点睛】本题主要考查了内错角的定义，三线八角中的某两个角是不是内错角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别内错角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．内错角的边构成“Z“形，认真识图是关键．21．（1）2∠；（3）ED；（4）AF，同位∠；（2）4【分析】（1）根据图形及同位角的概念可直接进行求解；（2）根据图形及内错角的概念可直接进行求解；（3）根据图形及内错角的概念可直接进行求解；（4）根据图形及同位角的概念可直接进行求解．【详解】解：由图可得：（1）若直线,ED BC 被直线AB 所截，则1∠和2∠是同位角；故答案为2∠；（2）若直线,ED BC 被直线AF 所截，则3∠和4∠是内错角；故答案为4∠；（3）1∠和3∠是直线,AB AF 被直线ED 所截构成的内错角；故答案为ED ；（4）2∠和4∠是直线AB ，AF 被直线BC 所截构成的同位角；故答案为AF ，同位．【点睛】本题主要考查内错角及同位角的概念，熟练掌握同位角及内错角的概念是解题的关键． 22．同位角有∠1和∠5；∠4和∠3；内错角有∠2和∠3；∠1和∠4；同旁内角有∠3和∠5；∠4和∠5；∠4和∠2．【分析】同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．依此即可得出答案．【详解】解：∠∠1和∠5在截线AC 同侧，在被截直线BE ，CE 同方向所成的角；∠4和∠3，在截线CE 的上方，被截直线DB 、EB 的左侧，∠同位角有∠1和∠5；∠4和∠3，共2对；∠∠2和∠3在截线BD 两侧，被截直线AC 与CE 内部；∠1和∠4在截线BE 两侧，被截直线AC 与CE 内部， ∠内错角有∠2和∠3；∠1和∠4,共2对；∠∠3和∠5在截线CD 同侧，被截直线CB 与DB 内部；∠4和∠5在截线CE 同侧，被截直线CB 与EB 的内部；∠4和∠2在截线BE 同侧，被截直线DB 与DE 的内部，∠同旁内角有∠3和∠5；∠4和∠5；∠4和∠2，共3对.【点睛】本题考查了同位角、内错角、同旁内角，三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．。

5.1.3 同位角、内错角、同旁内角100题(含解析)

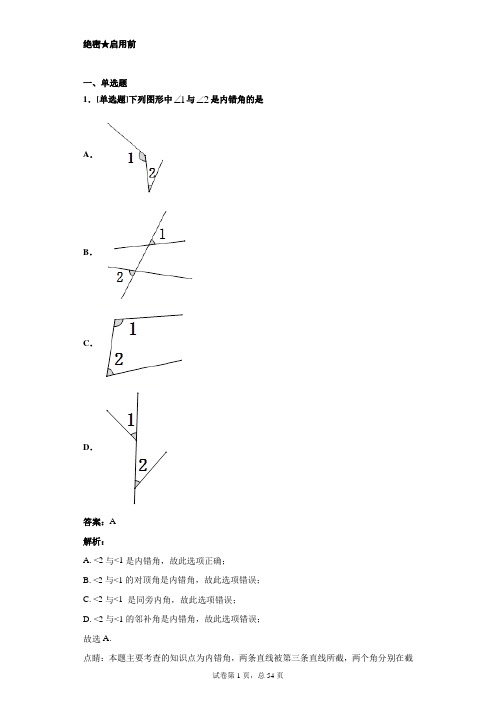
绝密★启用前一、单选题1．[单选题]下列图形中1∠与2∠是内错角的是A ．B ．C ．D ．答案：A 解析：A. <2与<1是内错角，故此选项正确；B. <2与<1的对顶角是内错角，故此选项错误；C. <2与<1 是同旁内角，故此选项错误；D. <2与<1的邻补角是内错角，故此选项错误；线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角.掌握内错角的定义是解答本题的关键.2．[单选题]已知如图AB 、BE 被AC 所截，下列说法不正确的是（）A ．1∠与2∠是同旁内角B ．1∠与ACE ∠是内错角C ．B 与ACB ∠是同位角D ．1∠与3∠不是同位角答案：C 解析：解析：根据同位角、内错角、同旁内角的定义可以直接得到答案. 【详解】解：A. 1∠与2∠是同旁内角，正确但不符合题意；B. 1∠与ACE ∠是内错角，正确但不符合题意；C. B ∠与ACB ∠是同位角，错误符合题意；D.1∠与3∠不是同位角，正确但不符合题意.故选：C. 【点睛】本题主要考查了三线八角.3．[单选题]如图，∠1与∠2不能构成同位角的图形的是（）A ．B．C．D．答案：D解析：解析：根据同位角的定义来分析判断即可，两条直线被第三条直线所截,在截线的同旁,被截两直线的同一方,把这种位置关系的角称为同位角.【详解】由同位角的定义可知图A、B、C中的∠1和∠2可以构成同位角，D中的∠1和∠2构不成同位角.故本题答案为：D.【点睛】同位角的定义是本题的考点，根据同位角的定义正确识别同位角是解题的关键. 4．[单选题]如图，下列说法错误的是（）A．∠1与∠3是对顶角B．∠3与∠4是内错角C．∠2与∠6是同位角D．∠3与∠5是同旁内角答案：C解析：根据对顶角定义、内错角定义、同位角定义、同旁内角定义进行分析即可．【详解】A、∠1与∠3是对顶角，故A说法正确；B、∠3与∠4是内错角，故B说法正确；C、∠2与∠6不是同位角，故C说法错误；D、∠3与∠5是同旁内角，故D说法正确；故选：C．【点睛】本题考查对顶角、内错角、同位角和同旁内角的定义，掌握其定义是选择本题答案的关键．5．[单选题]下列选项中，∠ 5和∠6不是同旁内角的是（）A．B．C．D．答案：B解析：根据同旁内角的定义:两条直线被第三条直线所截，在截线同旁，且在被截线之内的两角，叫做同旁内角.进行解答【详解】A. ∠5和∠6是同旁内角,不合题意,故此选项错误.B.∠5和∠6不是同旁内角,符合题意,故此选项正确C.∠5和∠6是同旁内角,不合题意,故此选项错误D.∠5和∠6是同旁内角,不合题意,故此选项错误【点睛】本题考查同旁内角的定义,理解掌握同旁内角定义是解题关键6．[单选题]如图，直线1l和2l被直线3l所截，则（）A ．1∠和2∠是同位角B ．1∠和2∠是内错角C ．1∠和3∠是同位角D ．1∠和3∠是内错角答案：C 解析：根据同位角和内错角的定义进行分析即可．【详解】同位角是位于两直线及截线的同侧，内错角是位于两直线内侧及截线两侧，故1∠和3∠是同位角；故选：C ．【点睛】本题考查了同位角和内错角的判断，熟练掌握基本概念是解决这类问题的关键． 8．[单选题]如图，点D 、E 分别为三角形ABC 边BC 、AC 上一点，作射线DE ，则下列说法错误的是（）A ．∠1与∠3是对顶角B ．∠2与∠A 是同位角C ．∠2与∠C 是同旁内角D ．∠1与∠4是内错角解析：根据同位角、内错角以及同旁内角的概念进行判断．【详解】解：A、∠1与∠3是对顶角，说法正确；B、∠2与∠A是同位角，说法正确；C、∠2与∠C是同旁内角，说法正确；D、∠2与∠4是内错角，说法错误．故选：D．【点睛】考查了同位角、内错角以及同旁内角，解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．9．[单选题]如图，下列结论正确的是（）.A．∠5与∠2是对顶角；B．∠1与∠3是同位角；C．∠2与∠3是同旁内角；D．∠1与∠2是同旁内角.根据对顶角即三线八角的特征可得∠1与∠2是同旁内角，故选D。

《同位角、内错角、同旁内角》练习题(含答案)

5.1.3 同位角、内错角、同旁内角1.如图，有以下判断：①∠1与∠3是内错角；②∠2与∠3是内错角；③∠2与∠4是同旁内角；④∠2与∠3是同位角.其中说法正确的有__________(填序号).2.看图填空：(1)∠1和∠3是直线__________被直线__________所截得的__________；(2)∠1和∠4是直线__________被直线__________所截得的__________；(3)∠B和∠2是直线__________被直线__________所截得的__________；(4)∠B和∠4是直线__________被直线__________所截得的__________.3.如图所示,若∠1=∠2,在①∠3和∠2；②∠4和∠2；③∠3和∠6；④∠4和∠8中相等的有( )A.1对B.2对C.3对D.4对4.如图,如果∠1＝40°,∠2＝100°,那么∠3的同位角等于__________,∠3的内错角等于__________,∠3的同旁内角等于__________.5.如图，下列说法错误的是( )A.∠1和∠3是同位角B.∠A和∠C是同旁内角C.∠2和∠3是内错角D.∠3和∠B是同旁内角6.如图所示，∠B与∠CAD是由直线__________和直线__________被直线__________所截得到的__________角.7.如图，__________是∠1和∠6的同位角，__________是∠1和∠6的内错角，__________是∠6的同旁内角.8.根据图形说出下列各对角是什么位置关系？(1)∠1和∠2；(2)∠1和∠7；(3)∠3和∠4；(4)∠4和∠6；(5)∠5和∠7.9.如图，∠1和∠2是哪两条直线被哪一条直线所截形成的？它们是什么角？∠1和∠3是哪两条直线被哪一条直线所截形成的？它们是什么角？10.探究题：(1)如图1,两条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对；(2)如图2,三条水平的直线被一条竖直的直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对；(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有__________对,内错角有__________对,同旁内角有__________对.(用含n的式子表示)5.2平行线及其判定参考答案1.①③2.(1)AB，BC AC 同旁内角(2)AB，BC AC 同位角(3)AB，AC BC 同位角(4)AC，BC AB 内错角3.C4.80° 80° 100°5.A6.BC AC BD 同位7.∠3 ∠5 ∠48.(1)∠1和∠2是同旁内角；(2)∠1和∠7是同位角；(3)∠3和∠4是内错角；(4)∠4和∠6是同旁内角；(5)∠5和∠7是内错角.9.∠1和∠2是直线EF，DC被直线AB所截形成的同位角，∠1和∠3是直线AB，CD被直线EF所截形成的同位角.10.(1)4 2 2(2)12 6 6(3)2n(n-1) n(n-1) n(n-1)。

同位角,内错角,同旁内角同步练习

5.1.3同位角,内错角,同旁内角同步练习(含答案)(总6页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2同位角内错角同旁内角班级姓名座号月日主要内容:同位角、内错角、同旁内角的认识一、课堂练习:1.下列图形中,1∠和2∠不是同位角的是( B )2.如图,属于内错角的是( D )A.∠1和∠2B.∠2和∠3 C .∠1和∠4 D.∠3和∠43.看图填空:(1)如图1,同位角一共有对,分别是；内错角一共有对,分别是；同旁内角一共有对,分别是； (2)如图2,同位角一共有对,分别是；内错角一共有对,分别是；第2题3421A B C12121212同旁内角一共有对,分别是 .4.如图,1∠与哪个角是内错角,与哪个角是同旁内角 2∠与哪个角是内错角,与哪个角是同旁内角(只需写一个角)它们分别是哪两条直线被哪一条直线所截形成的二、课后作业: 5.看图填空 (1)如右图:①∠1和∠4是邻补角； ②∠1和∠3是对顶角； ③∠2和∠D 是内错角； ④∠3和∠D 是同旁内角； ⑤∠4和∠D 是同位角； ⑥∠4和∠B 是同位角. (2)如右图:①∠ABC 与是同位角； ②∠ADB 与是内错角； ③∠ABC 与是同旁内角. 6.如图所示,同位角一共有对, 分别是；cA BCDE ABC DEF123412A BCDE同旁内角一共有对,分别是 . 7.如图,∠1和∠2,∠3和∠4各是哪两条直线被哪一条直线所截形成的它们各是什么角8.如图,用数字标注的角中,共有四对内错角,请把它们一一写出,并说明是哪两条直线被哪一条直线所截得的内错角.三、新课预习:9.画图回答问题:如图,P、Q分别是直线EF外两点,(1)过P画AB∥EF,过Q画CD∥EF.E FPQA B图1 图245(2)过点P 能画几条直线与EF 平行为什么解:过点P 只能画一条直线与EF 平行.理由:经过直线外一点,有且只有一条直线与这条直线平行.(3)AB 与CD 平行吗为什么解:AB 与CD 平行.理由:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.参考答案一、课堂练习:1.下列图形中,1∠和2∠不是同位角的是( B )2.如图,属于内错角的是( D )A.∠1和∠2B.∠2和∠3 C .∠1和∠4 D.∠3和∠43.看图填空:(1)如图1,同位角一共有 4 对,分别是 ∠l 和∠5,∠2和∠6,∠3和∠7,∠4和∠8 ；第2题 3421A B C121212126内错角一共有 2 对,分别是 ∠3和∠6,∠4和∠5 ；同旁内角一共有 2 对,分别是 ∠3和∠5,∠4和∠6 ；(2)如图2,同位角一共有 2 对,分别是 ∠l 和∠3,∠2和∠4 ；内错角一共有 0 对,分别是；同旁内角一共有 1 对,分别是 ∠2和∠3 .4.如图,1∠与哪个角是内错角,与哪个角是同旁内角 2∠与哪个角是内错角,与哪个角是同旁内角(只需写一个角)它们分别是哪两条直线被哪一条直线所截形成的解:1∠与DAB ∠是内错角,它是直线DE 、BC 被直线AB所截形成的；1∠与EAB ∠是同旁内角,它是直线DE 、BC 被直线AB 所截形成的；1∠与2∠是同旁内角,它是直线AB 、AC 被直线BC 所截形成的； 1∠与BAC ∠是同旁内角,它是直线BC 、AC 被直线AB 所截形成的； 2∠与EAC ∠是内错角,它是直线DE 、BC 被直线AC 所截形成的； 2∠与BAC ∠是同旁内角,它是直线AB 、BC 被直线AC 所截形成的.(2∠与DAC ∠是同旁内角,它是直线DE 、BC 被直线AC 所截形成的.)二、课后作业:c12A BCD E75.看图填空 (1)如右图:①∠1和∠4是邻补角； ②∠1和∠3是对顶角；③∠2和∠D 是内错角； ④∠3和∠D 是同旁内角； ⑤∠4和∠D 是同位角； ⑥∠4和∠B 是同位角.(2)如右图:①∠ABC 与 ∠EAD 是同位角；②∠ADB 与 ∠DBC 、 ∠EAD 是内错角； ③∠ABC 与 ∠DAB 、 ∠BCD 是同旁内角. 6.如图所示,同位角一共有 6 对,分别是 ∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8,∠7和∠9,∠4和∠9 ；同旁内角一共有 4 对分别是 ∠1和∠6, ∠1和∠9, ∠4和∠7, ∠6和∠9 .7.如图,∠1和∠2,∠3和∠4各是哪两条直线被哪一条直线所截形成的它们各是什么角解:如图1中,∠1和∠2是直线AB 、CD 被直线BD 所截, 它们是内错角；∠3和∠4是直线AD 、CB 被直线BD 所截, 它们也是内错角. 如图2中,∠1和∠2是直线AB 、CD 被直线BC 所截,它们是同旁内角；AB CDEABC D EF1234A B 图1 图28∠3和∠4是直线AD 、CB 被直线AB 所截,它们是同位角.8.如图,用数字标注的角中,共有四对内错角,请把它们一一写出,并说明是哪两条直线被哪一条直线所截得的内错角.解:∠1和∠5是内错角,它们是由直线AD 、BC 被直线AC∠2和∠6是内错角,它们是由直线AB 、CD 被直线AC 所截形成的； ∠3和∠7是内错角,它们是由直线AB 、CD 被直线BD 所截形成的； ∠4和∠8是内错角,它们是由直线AD 、BC 被直线BD 所截形成的.三、新课预习: 9.画图回答问题:如图,P 、Q 分别是直线EF 外两点, (1)过P 画AB ∥EF ,过Q 画CD ∥EF .(2)过点P 能画几条直线与EF 平行为什么解:过点P 只能画一条直线与EF 平行.理由:经过直线外一点,有且只有一条直线与这条直线平行.(3)AB 与CD 平行吗为什么解:AB 与CD 平行.理由:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.A B C DEFPQ。

邻补角、对顶角、同位角、内错角、同旁内角经典习题-一对一专用

邻补角、对顶角、同位角、内错角、同旁内角一、学习目标1、了解两条直线相交所构成的角，理解并掌握邻补角、对顶角的概念和性质；2、理解并掌握垂线的概念和性质；3、了解同位角、内错角、同旁内角的概念并会辨别二、主要内容1、邻补角：两直线相交所成的四个角中，有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角。

2、对顶角：两直线相交所成的四个角中，有一个公共顶点，并且一个角的两边分别是另一个角两边的反向延长线，具有这种关系的两个角，互为对顶角；对顶角的性质：对顶角相等。

注意：1、对顶角是成对出现的，对顶角是具有特殊位置关系的两个角；2、如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角3、如果∠α与∠β互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α与∠β不一定是邻补角。

4、两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个。

习题巩固1．下面四个图形中，∠1与∠2是对顶角的图形的个数是（）A．0 B．1 C．2 D．3121212122、下面各图中∠1和∠2是对顶角的是（）A．B．C．D．3、下列语句正确的是（）.A、相等的角是对顶角B、相等的两个角是邻补角C、对顶角相等D、邻补角不一定互补，但可能相等4、下列语句错误的有（）个.（1）两个角的两边分别在同一条直线上，这两个角互为对顶角（2）有公共顶点并且相等的两个角是对顶角（3）如果两个角相等，那么这两个角互补（4）如果两个角不相等，那么这两个角不是对顶角A、1B、2C、3D、45、已知∠1与∠2是邻补角，∠2是∠3的邻补角，那么∠1与∠3的关系是（）.A、对顶角B、相等但不是对顶角C、邻补角D、互补但不是邻补角6、下列说法正确的是（）.A、有公共顶点的两个角是对顶角B、两条直线相交所成的两个角是对顶角C、有公共顶点且有一条公共边的两个角是邻补角D、两条直线相交所成的无公共边的两个角是对顶角7、已知：如图所示，AB⊥CD，垂足为点O，EF为过点O•的一条直线，则∠1与∠2的关系一定成立的是（）A．相等 B．互余 C．互补 D．互为对顶角8、下列判断正确的个数是_____个。

对顶角、邻补角、同位角、内错角练习

O F E D C B A 34D C B A 12O D C B A 12O D C B A（一）邻补角、对顶角的内容一、邻补角、对顶角的定义1、（1）∠AOC 和∠BOC 有一条公共边．．．．．OC ，它们的另一边互为，称这两个角互为。

用量角器量一量这两个角的度数，会发现它们的数量关系是（2）∠AOC 和∠BOD （有或没有）公共边，但∠AOC 的两边分别是∠BOD两边的，称这两个角互为2.如图3所示,AB 与CD 相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.(3) (4) (5)3.如图3所示,若∠1=25°,则∠2=_______,∠3=______,∠4=_______.4.如图4所示,直线AB,CD,EF 相交于点O,则∠AOD 的对顶角是_____,∠AOC 的邻补角是_______;若∠AOC=50°,则∠BOD=______,∠COB=_______.5.如图5所示,直线AB,CD 相交于点O,若∠1-∠2=70,则∠BOD=_____,∠2=____.二、邻补角、对顶角的性质1、邻补角的性质：邻补角。

注意：邻补角是互补的一种特殊的情况，数量上，位置上有一条。

2、对顶角。

3、如图，已知直线a 、b 相交。

∠1＝40°，求∠2、∠3、∠4的度数解：∠3＝∠1＝40°（）。

∠2＝180°－∠1＝180°－40°＝140°（）。

∠4＝∠2＝140°（）。

4、如图,直线AB 、CD 相交于点O (1)若∠AOC+∠BOD=100°,求各角的度数. (2)若∠BOC 比∠AOC 的2倍多33°,求各角的度数（二）同位角、内错角、同旁内角（一）如图,直线AB、CD与EF相交（或两条直线AB、CD被第三条直线EF所截）构成个角。

我们来研究其中没有公共顶点．．．．．．的两个角的关系。

同位角、内错角、同旁内角练习题及答案

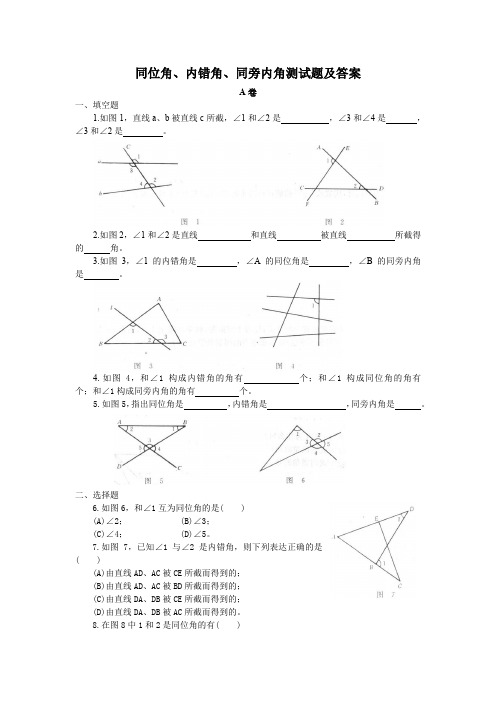
同位角、内错角、同旁内角测试题及答案A卷一、填空题1.如图1，直线a、b被直线c所截，∠1和∠2是，∠3和∠4是，∠3和∠2是。

2.如图2，∠1和∠2是直线和直线被直线所截得的角。

3.如图3，∠1的内错角是，∠A的同位角是，∠B的同旁内角是。

4.如图4，和∠1构成内错角的角有个；和∠1构成同位角的角有个；和∠1构成同旁内角的角有个。

5.如图5，指出同位角是，内错角是，同旁内角是。

二、选择题6.如图6，和∠1互为同位角的是( )(A)∠2； (B)∠3；(C)∠4； (D)∠5。

7.如图7，已知∠1与∠2是内错角，则下列表达正确的是( )(A)由直线AD、AC被CE所截而得到的；(B)由直线AD、AC被BD所截而得到的；(C)由直线DA、DB被CE所截而得到的；(D)由直线DA、DB被AC所截而得到的。

8.在图8中1和2是同位角的有( )(A)(1)、(2)； (B)(2)、(3)； (C)(1)、(3)； (D)(2)、(4)。

9.如图9，在指明的角中，下列说法不正确的是( )(A)同位角有2对； (B)同旁内角有5对；(C)内错角有4对； (D)∠1和∠4不是内错角。

10.如图10，则图中共有( )对内错角(A)3； (B)4； (C)5； (D)6。

三、简答题11.如图11(1)说出∠1与∠2互为什么角？(2)写出与∠1成同位角的角；(3)写出与∠1成内错角的角。

12.如图12(1)说出∠A与∠1互为什么角？(2) ∠B与∠2是否是同位角；(3)写出与∠2成内错角的角。

13.如图13，指出同位角、内错角、同旁内角。

B卷一、填空题1.如图1，∠1和∠2可以看作直线和直线被直线所截得的角。

2.如图2，∠1和∠2是直线和直线被直线被直线所截得的角。

3.如图3，直线DE、BC被直线AC所截得的内错角是；∠B与∠C可以看作直线、被直线所截得的角。

4.如图4，与∠EFC构成内错角的是；与∠EFC构成同旁内角的是。

同位角,内错角,同旁内角练习题

5.1.3同位角、内错角、同旁内角练习题一、选择题1.如图，∠1和∠2不是同位角的是( )2．如图，∠1和∠2是内错角，可看成是由直线( )．(A)AD，BC被AC所截构成(B)AB，CD被AC所截构成(C)AB，CD被AD所截构成(D)AB，CD被BC所截构成3.如图,与∠α构成同旁内角的角有()个个个个4.如右图所示(1) ∠1与∠4是内错角；(2) ∠1与∠2是同位角；(3) ∠2与∠4是内错角；(4) ∠4与∠5是同旁内角；(5) ∠3与∠4是同位角；(6) ∠2与∠5是内错角。

其中正确的共有( )45321(A)1个(B)2个(C)3个(D)4个5.如右图，下列说法中错误的是( )A．13∠∠、是同位角B．12∠∠、是同旁内角C．15∠∠、是同位角D．56∠∠、是内错角6.如图中共有内错角（）A. 2对B. 3对C. 4对D. 5对7.如图所示，图中有( )对同旁内角．对．对．对．对．二．填空题8．如右图所示，图中用数字标出的角中，同位角有______ ；内错角有______ ；同旁内角有______ ．9．如图所示，(1)∠AED和∠ABC可看成是直线______、______被直线_____ _所截得的____ ___角；(2)∠EDB和∠DBC可看成是直线______、______被直线____ ___所截得的____ __角；(3)∠EDC和∠C可看成是直线_______、____被直线__ ___所截得的___ _ __角．三.简答题10.(1)说出∠1与∠2互为什么角(2)写出与∠1成同位角的角；(3)写出与∠1成同旁内角的角。

11.如图, 直线DE截AB, AC, 构成八个角:21HNMFEDCBANMGFEDCBA87654321E DCBA①指出图中所有的同位角、内错角、同旁内角.②∠A与∠5, ∠A与∠6, ∠A与∠8,分别是哪一条直线截哪两条直线而成的什么角。

同位角,内错角,同旁内角的题型

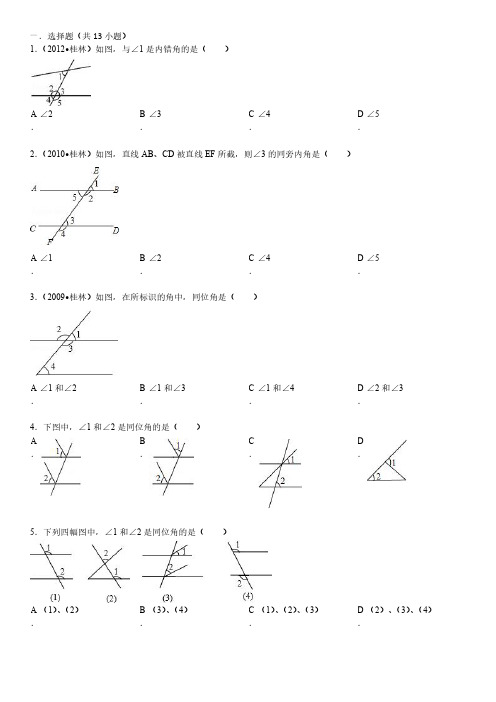
一．选择题（共13小题）1．（2012•桂林）如图，与∠1是内错角的是（）A ．∠2B ．∠3C ．∠4D ．∠52．（2010•桂林）如图，直线AB 、CD 被直线EF 所截，则∠3的同旁内角是（）A ．∠1B ．∠2C ．∠4D ．∠53．（2009•桂林）如图，在所标识的角中，同位角是（）A ．∠1和∠2B ．∠1和∠3C ．∠1和∠4D ．∠2和∠34．下图中，∠1和∠2是同位角的是（）A ．B ．C ．D ．5．下列四幅图中，∠1和∠2是同位角的是（）A ．（1）、（2）B ．（3）、（4）C ．（1）、（2）、（3）D ．（2）、（3）、（4）6．若∠1与∠2是同旁内角，∠1=30°，则（）A ．∠2=150°B．∠2=30°C ．∠2=150°或30°D．∠2的大小不能确定7．在图中，∠1与∠2是同位角的有（）A ．①②B．①③C．②③D．②④8．下列说法中正确的有（）个①对顶角的角平分线成一条直线；②相邻二角的角平分线互相垂直；③同旁内角的角平分线互相垂直；④邻补角的角平分线互相垂直．A ．1个B．2个C．3个D．4个9．如图所示，下列说法不正确的是（）A ．∠1与∠B是同位角B．∠1与∠4是内错角C ．∠3与∠B是同旁内角D．∠C与∠A不是同旁内角10．如图，射线c，b被a所截，则∠1与∠2是（）A ．同位角B．内错角C．同旁内角D．对顶角11．如图，下列判断错误的是（）A ．∠1与∠2是同旁内角B．∠3与∠4是内错角C ．∠5与∠6是同旁内角D．∠5与∠8与是同位角12．下列命题中，真命题有（）（1）直线外一点与直线上各点连接的所有线段中，垂线段最短；（2）两条直线被第三条直线所截，内错角相等；（3）经过两点有一条直线，并且只有一条直线；（4）如果一条直线和两条直线中的一条垂直，那么这条直线也和另一条垂直．A ．1个B．2个C．3个D．4个13．如图所示，下列说法错误的是（）A ．∠A和∠B是同旁内角B．∠A和∠3是内错角C ．∠1和∠3是内错角D．∠C和∠3是同位角二．填空题（共15小题）14．如图，标有角号的7个角中共有_________对内错角，_________对同位角，_________对同旁内角．15．如图，如果∠1=40°，∠2=100°，那么∠3的同位角等于_________度，∠3的内错角等于_________度，∠3的同旁内角等于_________度．16．如图，按角的位置关系填空：∠A与∠1是_________；∠A与∠3是_________；∠2与∠3是_________．17．如图，图中内错角的对数是_________．18．如图，∠A的同位角是_________，∠1的内错角是_________，∠2的同旁内角是_________．19．如图，∠1和∠3是直线_________，_________被直线_________所截得到的_________角；∠3和∠2是直线_________，_________被直线_________所截得到的_________角；∠1和∠2是直线_________，_________被直线_________所截得到的_________角．20．如图，按角的位置关系填空：∠A与∠1是_________，是由直线_________与_________被_________所截构成的；∠A与∠3是_________，是由直线_________与_________被_________所截构成的；∠2与∠3是_________，是由直线_________与_________被_________所截构成的．21．如图，在直线DE与∠O的两边相交，则∠O的同位角是_________，∠8的内错角是_________，∠1的同旁内角是_________．22．请在图中任意找出一对内错角可以为：_________与_________（或_________与_________）．23．如图，在∠1、∠2、∠3、∠4、∠5、∠B、∠D、∠ACE中，与∠D是同位角的是_________；与∠2是内错角的是_________．24．如图填空．（1）若ED，BC被AB所截，则∠1与_________是同位角．（2）若ED，BC被AF所截，则∠3与_________是内错角．（3）∠1与∠3是AB和AF被_________所截构成的_________角．（4）∠2与∠4是_________和_________被BC所截构成的_________角．25．如图，与∠1构成同位角的是_________，与∠2构成内错角的是_________．26．如图，直线AB，CD与直线EF相交，∠5和_________是同位角，和_________是内错角，和_________是同旁内角．∠2和_________是直线_________、_________被_________所截而形成的同位角．27．如图，在图上标出∠β的所有同位角，并标上数字_________．28．如图，∠1的同旁内角是_________．三．解答题（共1小题）29．（1）如果把图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？∠2与∠3呢？（2）如果把图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对什么角？∠5与∠6呢？参考答案与试题解析一．选择题（共13小题）1．（2012•桂林）如图，与∠1是内错角的是（）A ．∠2B．∠3C．∠4D．∠5考点：同位角、内错角、同旁内角．分析：根据内错角的定义找出即可．解答：解：根据内错角的定义，∠1的内错角是∠3．故选B．点评：本题考查了“三线八角”问题，确定三线八角的关键是从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．2．（2010•桂林）如图，直线AB、CD被直线EF所截，则∠3的同旁内角是（）A ．∠1B．∠2C．∠4D．∠5考点：同位角、内错角、同旁内角．分析：解答此题的关键是理解同旁内角的定义：“同旁”指在截线的同侧；“内”指在被截两条线之间．可据此进行判断．解答：解：由图知：∠3和∠2在截线EF的同侧，且都在被截直线AB、CD的内侧，所以∠3和∠2是同旁内角，故选B．点评：熟练掌握“三线八角”的含义，是解答此类题目的关键．3．（2009•桂林）如图，在所标识的角中，同位角是（）A ．∠1和∠2B．∠1和∠3C．∠1和∠4D．∠2和∠3考点：同位角、内错角、同旁内角．分析：同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角．解答：解：根据同位角、邻补角、对顶角的定义进行判断，A 、∠1和∠2是邻补角，错误；B 、∠1和∠3是邻补角，错误；C 、∠1和∠4是同位角，正确；D 、∠2和∠3是对顶角，错误．故选C ．点评：解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．4．下图中，∠1和∠2是同位角的是（）A ．B ．C ．D ．考点：同位角、内错角、同旁内角．分析：本题考查同位角的定义，在截线的同侧，并且在被截线的同一方的两个角是同位角．根据定义，逐一判断．解答：解：A 、∠1、∠2的两边都不在同一条直线上，不是同位角；B 、∠1、∠2的两边都不在同一条直线上，不是同位角；C 、∠1、∠2的两边都不在同一条直线上，不是同位角；D 、∠1、∠2有一边在同一条直线上，又在被截线的同一方，是同位角．故选D ．点评：判断是否是同位角，必须符合三线八角中，在截线的同侧，并且在被截线的同一方的两个角是同位角．5．下列四幅图中，∠1和∠2是同位角的是（）A ．（1）、（2）B ．（3）、（4）C ．（1）、（2）、（3）D ．（2）、（3）、（4）考点：同位角、内错角、同旁内角．分析：互为同位角的两个角，都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角．解答：解：根据同位角的定义，图（1）、（2）中，∠1和∠2是同位角；图（3）∠1、∠2的两边都不在同一条直线上，不是同位角；图（4）∠1、∠2不在被截线同侧，不是同位角．故选A ．点评：本题考查同位角的概念，是需要熟记的内容．即两个都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角．6．若∠1与∠2是同旁内角，∠1=30°，则（）A ．∠2=150°B ．∠2=30°C ．∠2=150°或30°D ．∠2的大小不能确定考点：同位角、内错角、同旁内角．分析：两直线平行时同旁内角互补，不平行时无法确定同旁内角的大小关系．解答：解：同旁内角只是一种位置关系，并没有一定的大小关系，只有两直线平行时，同旁内角才互补．故选D．点评：特别注意，同旁内角互补的条件是两直线平行．7．在图中，∠1与∠2是同位角的有（）A ．①②B．①③C．②③D．②④考点：同位角、内错角、同旁内角．分析：根据同位角的定义：在截线的同侧，并且在被截线的同一方的两个角是同位角，所以只有②③是同位角．解答：解：①图中，∠1与∠2的两边都不在同一条直线上，不是同位角，②图中，∠1与∠2有一条边在同一条直线上，另一条边在被截线的同一方，是同位角，③图中，∠1与∠2有一条边在同一条直线上，另一条边在被截线的同一方，是同位角，④图中，∠1与∠2的两边都不在同一条直线上，不是同位角．故选C．点评：判断是否是同位角，必须符合三线八角中，在截线的同侧，并且在被截线的同一方的两个角是同位角．8．下列说法中正确的有（）个①对顶角的角平分线成一条直线；②相邻二角的角平分线互相垂直；③同旁内角的角平分线互相垂直；④邻补角的角平分线互相垂直．A ．1个B．2个C．3个D．4个考点：同位角、内错角、同旁内角；角平分线的定义；对顶角、邻补角．分析：本题考查几个类别图形的角平分线的关系，要从两个角的位置及大小上，进行判断．解答：解：①因为对顶角相等，其角平分线所分得的角也相等，可构成新的对顶角，故对顶角的角平分线成一条直线，正确；②相邻二角互补时角平分线互相垂直，其它情况下就不垂直，错误；③同旁内角互补时角平分线互相垂直，其它情况下就不垂直，错误；④由于邻补角互补，又有位置关系，故邻补角的角平分线互相垂直，正确．故选B．点评：对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义，要善于区分不同概念之间的联系和区别．9．如图所示，下列说法不正确的是（）A ．∠1与∠B是同位角B．∠1与∠4是内错角C ．∠3与∠B是同旁内角D．∠C与∠A不是同旁内角考点：同位角、内错角、同旁内角．分析：本题考查同位角、内错角、同旁内角的概念，要根据概念判断，分清楚截线与被截线．解答：解：A、∠1与∠B是两直线DE、BC被直线AB所截的同位角，正确；B、∠1与∠4是两直线AB、AC被直线DE所截的内错角，正确；C、∠3与∠4是两直线AB、AC被直线DE所截的同旁内角，正确；D、∠C与∠A是两直线AB、BC被直线AC所截的同旁内角，判断错误．故选D．点评：对概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义，要善于区分不同概念之间的联系和区别．10．如图，射线c，b被a所截，则∠1与∠2是（）A ．同位角B．内错角C．同旁内角D．对顶角考点：同位角、内错角、同旁内角．分析：根据同位角的定义作答．解答：解：∵射线c，b被a所截，∠1与∠2在截线a的同侧，在两条被截直线c，b的同旁，∴∠1与∠2是同位角．故选A．点评：两条直线被第三条直线所截，在截线的同侧，在两条被截直线的同旁的两个角是同位角．如果两个角是同位角，那么它们一定有一条边所在的直线公共．11．如图，下列判断错误的是（）A ．∠1与∠2是同旁内角B．∠3与∠4是内错角C ．∠5与∠6是同旁内角D．∠5与∠8与是同位角考点：同位角、内错角、同旁内角．分析：根据同位角、内错角和同旁内角的定义，结合图形判断．解答：解：因为∠5与∠6没有位置上的直接联系，不是三线八角问题，错误；故选C．点评：本题主要考查“三线八角”问题，正确掌握各种角的定义是解题的关键．12．下列命题中，真命题有（）（1）直线外一点与直线上各点连接的所有线段中，垂线段最短；（2）两条直线被第三条直线所截，内错角相等；（3）经过两点有一条直线，并且只有一条直线；（4）如果一条直线和两条直线中的一条垂直，那么这条直线也和另一条垂直．A ．1个B．2个C．3个D．4个考点：同位角、内错角、同旁内角；直线、射线、线段；垂线；垂线段最短．分析：根据所学公理和性质定理，对各选项分析判断后再计算个数．解答：解：（1）直线外一点与直线上各点连接的所有线段中，垂线段最短，正确；（2）应为两条平行直线被第三条直线所截，内错角相等，故本选项错误；（3）经过两点有一条直线，并且只有一条直线，正确；（4）应为如果一条直线和两条平行直线中的一条垂直，那么这条直线也和另一条垂直，故本选项错误．所以（1）（3）两项是真命题．故选B．点评：本题主要是对公理和定理的考查，熟记公理定理是解题的关键．13．如图所示，下列说法错误的是（）A ．∠A和∠B是同旁内角B．∠A和∠3是内错角C ．∠1和∠3是内错角D．∠C和∠3是同位角考点：同位角、内错角、同旁内角．分析：内错角的定义，两个角分别在截线的两侧，且在两条被截线之间，具有这样位置关系的一对角叫做内错角．∠A和∠3不是在截线的两侧，不是内错角．解答：解：根据内错角、同旁内角和同位角的定义可知：A、C、D均是正确的，只有B错误．故选B．点评：判断是否是内错角，必须符合三线八角中，两个角分别在截线的两侧，且在两条被截线之间，具有这样位置关系的一对角叫做内错角．二．填空题（共15小题）14．如图，标有角号的7个角中共有4对内错角，2对同位角，4对同旁内角．考点：同位角、内错角、同旁内角．分析：根据内错角，同位角及同旁内角的定义即可求得此题．解答：解：如图，共有4对内错角：分别是∠1和∠4，∠2和∠5，∠6和∠1，∠5和∠7；2对同位角：分别是∠7和∠1，∠5和∠6；4对同旁内角：分别是∠1和∠5、∠3和∠4、∠3和∠2、∠4和∠2．点评：此题主要考查了内错角，同位角，同旁内角的定义．15．如图，如果∠1=40°，∠2=100°，那么∠3的同位角等于80度，∠3的内错角等于80度，∠3的同旁内角等于100度．考点：同位角、内错角、同旁内角；对顶角、邻补角．专题：计算题．分析：在截线的同旁找同位角和同旁内角，在截线的两旁找内错角．要结合图形，熟记同位角、内错角、同旁内角的位置特点，比较它们的区别与联系．解答：解：∵∠1=40°，∠2=100°，∴∠3的同位角=∠4=180°﹣∠2=180°﹣100°=80°．∠3的内错角=∠5=180°﹣∠2=180°﹣100°=80°．∠3的同旁内角=∠6=∠2=100°．点评：两条直线被第三条直线所截，构成八个角（简称“三线八角”），其中同位角4对，内错角2对，同旁内角2对．本题同时考查了邻补角和对顶角的定义．16．如图，按角的位置关系填空：∠A与∠1是同旁内角；∠A与∠3是同位角；∠2与∠3是内错角．考点：同位角、内错角、同旁内角．分析：根据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形找出即可．解答：解：根据图形，∠A与∠1是直线AC、MN被直线AB所截形成的同旁内角，∠A与∠3是直线AC、MN 被直线AB所截形成的同位角，∠2与∠3是直线AC、AB被直线MN所截形成的内错角．故应填：同旁内角，同位角，内错角．点评：本题考查了三线八角中的同旁内角，同位角，内错角的概念，知同位角、内错角、同旁内角是两直线被第三条直线所截而成的角．17．如图，图中内错角的对数是4．考点：同位角、内错角、同旁内角．专题：几何图形问题．分析：根据内错角是在截线两旁，被截线之内的两角，内错角的边构成”Z“形作答．解答：解：由内错角定义，直线AB、CD被BC所截，内错角有：∠ABC与∠DCB；直线EC、AB被BC所截，内错角有：∠ABC与∠ECB为内错角；直线FB、CD被BC所截，内错角有：∠FBC与∠DCB；直线EC、FB被BC所截，内错角有：∠FBC与∠ECB为内错角．共有4对．故答案为：4．点评：本题主要考查内错角的定义，要灵活掌握变形直线相交所成的内错角．18．如图，∠A的同位角是∠BFG，∠CGF，∠1的内错角是∠CGF，∠2的同旁内角是∠CGF或∠B 或∠A．考点：同位角、内错角、同旁内角．分析：准确识别同位角、内错角、同旁内角的关键，是弄清哪两条直线被哪一条线所截．也就是说，在辨别这些角之前，要弄清哪一条直线是截线，哪两条直线是被截线．解答：解：∠A与∠BDG是直线AC、DE被直线AB所截形成的同位角，∠A与∠CGF是直线AB、DE被直线AC所截形成的同位角；∠1与∠CGF是直线AC、AB被直线DE所截形成的内错角；∠A与∠2是直线AB、BC被直线AC所截形成的同旁内角，∠2与∠B是直线AC、AB被直线BC所截形成的同旁内角，∠2与∠CGF是直线BC、DE被直线AC所截形成的同位角；故∠A的同位角是∠BFG，∠CGF，∠1的内错角是∠CGF，∠2的同旁内角是∠CGF或∠B或∠A．点评：在复杂的图形中识别同位角、内错角、同旁内角时，应当沿着角的边将图形补全，或者把多余的线暂时略去，找到三线八角的基本图形，进而确定这两个角的位置关系．19．如图，∠1和∠3是直线a，b被直线c所截得到的同旁内角；∠3和∠2是直线a，c被直线b所截得到的内错角角；∠1和∠2是直线b，c被直线a所截得到的同位角角．考点：同位角、内错角、同旁内角．分析：根据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形解答．解答：解：∠1和∠3是直线a，b被直线c所截得到的同旁内角；∠3和∠2是直线a，c被直线b所截得到的内错角；∠1和∠2是直线b，c被直线a所截得到的同位角．故填：a，b，c，同旁内角；a，c，b，内错角；b，c，a，同位角．点评：本题主要考查了三线八角的问题，熟记同位角、内错角、同旁内角的位置关系是解决此类问题的关键．20．如图，按角的位置关系填空：∠A与∠1是同旁内角，是由直线AC与DE被AB所截构成的；∠A与∠3是同位角，是由直线AC与DE被AB所截构成的；∠2与∠3是内错角，是由直线AC 与AB被DE所截构成的．考点：同位角、内错角、同旁内角．专题：几何图形问题．分析：根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角作答．解答：解：图中：∠A与∠1是同旁内角，是由直线AC与DE被AB所截构成的；∠A与∠3是同位角；是由直线AC与DE被AB所截构成的；∠2与∠3是内错角，是由直线AC与AB被DE所截构成的．故答案为：同旁内角，AC，DE，AB；同位角，AC，DE，AB；内错角，AC，AB，DE．点评：本题考查了同位角、内错角、同旁内角的概念．三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．21．如图，在直线DE与∠O的两边相交，则∠O的同位角是∠2和∠5，∠8的内错角是∠2，∠1的同旁内角是∠8和∠O．考点：同位角、内错角、同旁内角．分析：准确识别同位角、内错角、同旁内角的关键，是弄清哪两条直线被哪一条线所截．也就是说，在辨别这些角之前，要弄清哪一条直线是截线，哪两条直线是被截线．解答：解：∠O与∠2在截线OB和ED的同侧，被截线OA的同侧，∠O与∠5在截线OA和ED的同侧，被截线OB的同侧，故∠O的同位角是∠2和∠5；∠8与∠2在截线OA和OB的内部，被截线DE的两侧，故∠8与∠2是内错角；∠1与∠8在截线OA和OB的内部，被截线DE的同侧，故∠1与∠8是同旁内角，∠1与∠O在截线DE 和OB的内部，被截线OA的同侧，故∠1与∠O是同旁内角．故∠O的同位角是∠2和∠5；∠8的内错角是∠2；∠1的同旁内角是∠8和∠O．点评：本题考查同位角、内错角和同旁内角的定义，是需要熟记的内容．22．请在图中任意找出一对内错角可以为：∠1与∠3（或∠3与∠4）．考点：同位角、内错角、同旁内角．专题：开放型．分析：根据内错角是在截线两旁，被截线之内的两角，内错角的边构成”Z“形作答．解答：解：如图：一对内错角有∠1与∠3（或∠3与∠4）．故答案为：∠1，∠3（或∠3，∠4）．点评：本题考查了内错角的定义，正确记忆内错角的定义是解决本题的关键．23．如图，在∠1、∠2、∠3、∠4、∠5、∠B、∠D、∠ACE中，与∠D是同位角的是∠5、∠ACE；与∠2是内错角的是∠4、∠ACE．考点：同位角、内错角、同旁内角．专题：应用题．分析：根据同位角的定义，以及内错角的定义，在截线的两旁找内错角，即可得出答案．解答：解：根据图形可知：与∠D是同位角的是∠5、∠ACE，与∠2是内错角的是∠4、∠ACE，故答案为∠5、∠ACE，∠4、∠ACE．点评：本题主要考查了同位角与内错角的定义，同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角，内错角就是在截线的两旁，比较简单．24．如图填空．（1）若ED，BC被AB所截，则∠1与∠2是同位角．（2）若ED，BC被AF所截，则∠3与∠4是内错角．（3）∠1与∠3是AB和AF被ED所截构成的内错角．（4）∠2与∠4是AB和AF被BC所截构成的同位角．考点：同位角、内错角、同旁内角．分析：根据同位角、内错角的定义进行分析解答即可，两个角分别在截线的两侧，且在两条直线之间，具有这样位置关系的一对角互为内错角，两个角都在截线的同旁，又分别处在被截的两条线的同侧，具有这样位置关系的一对角叫做同位角．解答：解：（1）如图：若ED，BC被AB所截，则∠1与∠2是同位角，（2）若ED，BC被AF所截，则∠3与∠4是内错角，（3）∠1与∠3是AB和AF被ED所截构成的内错角，（4）∠2与∠4是AB和AF被BC所截构成的同位角．故答案为∠2；∠4；ED，内错；AB，AF，同位．点评：本题主要考查内错角、同位角的定义，解答此类题确定三线八角是关键，可直接从截线入手．25．如图，与∠1构成同位角的是∠B，与∠2构成内错角的是∠BDE．考点：同位角、内错角、同旁内角．分析：两个角分别在被截线的同一方，并且都在截线的同侧，具有这种位置关系的两个角叫做同位角，与∠1构成同位角的是∠B；两个角都在被截线之间，并且都在截线的两侧，具有这种位置关系的两个角，叫做内错角，与∠2构成内错角的是∠BDE．解答：解；根据同位角、内错角的定义，与∠1构成同位角的是∠B，与∠2构成内错角的是∠BDE．点评：正确记忆同位角以及内错角的定义是解决本题的关键．26．如图，直线AB，CD与直线EF相交，∠5和∠1是同位角，和∠3是内错角，和∠2是同旁内角．∠2和∠6是直线AB、CD被EF所截而形成的同位角．考点：同位角、内错角、同旁内角．分析：根据两直线被第三条直线所截，在截线的同一侧，被截线的同一方向的两个角是同位角；在截线的两侧，被截线的内部的两个角是内错角；在截线的同一侧，被截线的内部的两个角是同旁内角，结合图形解答．解答：解：根据图形∠5与∠1是同位角，和∠3是内错角，和∠2是同旁内角．∠2和∠6是直线AB、CD被EF 所截而形成的同位角．故应填：∠1，∠3，∠2，∠6，AB，CD，EF．点评：本题主要考查同位角、内错角和同旁内角的定义，从图形中准确找出同位角、内错角或同旁内角是考查的重点之一．27．如图，在图上标出∠β的所有同位角，并标上数字1、2、3．考点：同位角、内错角、同旁内角．专题：推理填空题．分析：同位角的判断要把握几个要点：①分析截线与被截直线；②作为同位角要把握两个相同，在截线同旁，在被截直线同侧．解答：解：根据同位角的定义标出∠β的所有同位角，如图：故答案为：1、2、3．点评：此题考查的知识点是同位角，此类题的解题要点在概念的掌握．28．如图，∠1的同旁内角是∠3，∠GEN．考点：同位角、内错角、同旁内角．分析：根据同旁内角的定义即两个内角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互为同旁内角进行解答即可．解答：解：根据同旁内角的定义可知∠1的同旁内角是∠3，∠GEN．故答案为：∠3，∠GEN．点评：本题主要考查了同旁内角的定义．解答此题时要结合图形和同旁内角的定义进行解答，比较简单．三．解答题（共1小题）29．（1）如果把图看成是直线AB，EF被直线CD所截，那么∠1与∠2是一对什么角？∠2与∠3呢？（2）如果把图看成是直线AB，CD被直线EF所截，那么∠4与∠5是一对什么角？∠5与∠6呢？考点：同位角、内错角、同旁内角．专题：计算题．分析：根据同位角、同旁内角、同位角、对顶角的定义进行判断．解答：解：（1）内错角，同旁内角；（2）同位角，对顶角．点评：解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．。

同位角、内错角、同旁内角练习(含答案)

同位角、内错角、同旁内角练习1.填空(1)如图2-43，直线AB、CD被DE所截，则∠1和是同位角，∠1和是内错角，∠1和是同旁内角，如果∠1=∠5.那么∠1 ∠3.（2）上题中（图2-43）如果∠5=∠1，那么∠1=∠3的推理过程如下，请在括号内注明理由：∵∠5=∠1（）又∵∠5=∠3（）∴∠1=∠3（）（3）如图2-44，∠1和∠4是AB、被所截得的角，∠3和∠5是、被所截得的角，∠2和∠5是、所截得的角，AC、BC被AB所截得的同旁内角是 .∠（4）如图2-45，AB、DC被BD所截得的内错角是，AB、CD被AC所截是的内错角是，AD、BC被BD所截得的内错角是，AD、BC被AC所截得的内错角是 .2.选择题（1）如图2-46，∠1与∠2是同位角的个数有（）A.1个B.2个C.3个D.4个（2）如图2-47，（）是内错角A. ∠1和∠2B. ∠3和∠4C. ∠2和∠3D. ∠1和∠4（3）如图2-48，图中的同位角的对数是（）A.4B.6C.8D.123.如图2-49，已知∠1的同旁内角等于57°28′，求∠1的内错的度数.1.如图1，直线a、b被直线c所截，∠1和∠2是，∠3和∠4是，∠3和∠2是。

2.如图2，∠1和∠2是直线和直线被直线所截得的角。

3.如图3，∠1的内错角是，∠A的同位角是，∠B的同旁内角是。

4.如图4，和∠1构成内错角的角有个；和∠1构成同位角的角有个；和∠1构成同旁内角的角有个。

5.如图5，指出同位角是，内错角是，同旁内角是。

二、选择题6.如图6，和∠1互为同位角的是( )(A)∠2； (B)∠3；(C)∠4； (D)∠5。

8.在图8中1和2是同位角的有( )(A)(1)、(2)； (B)(2)、(3)； (C)(1)、(3)； (D)(2)、(4)。

人教版七年级下第五章同位角、内错角、同旁内角同步练习题含解析

综上可知，平面内四条直线共有三个交点，则这四条直线中最多有三条平行线.
故答案为三.
20．图1中同位角有：∠1与∠5，∠2与∠6，∠3与∠7，∠4与∠8；内错角有：∠3与∠6，∠4与∠5；同旁内角有：∠3与∠5，∠4与∠6.；图2中同位角有：∠1与∠3，∠2与∠4；同旁内角有：∠3与∠2．
【分析】根据两直线被第三条直线所截，两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角是同位角，可得同位角；两个角在截线的两侧，被截两直线的中间的角是内错角，可得内错角；两个角在截线的同侧，被截两直线的中间的角是同旁内角，可得同旁内角．
17．指出图中各对角的位置关系：
（1）∠C和∠D是_____角；
（2）∠B和∠GEF是____角；
（3）∠A和∠D是____角；
（4）∠AGE和∠BGE是____角；
（5）∠CFD和∠AFB是____角．
18．如图，直线AB，CD被直线EF所截，如果∠2=100°，那么∠1的同位角等于____度．
19．平面内四条直线共有三个交点，则这四条直线中最多有________条平行线．
【详解】解：∵题目并未告诉，∠1和∠2是属于两条平行线被截的同旁内角，
∴∠2的度数大小不能确定，
故选D．
【点睛】本题主要考查了同旁内角的定义，解题的关键在于能够熟练掌握相关知识进行求解．
9．C
【分析】根据对顶角、邻补角、同位角、内错角的定义分别分析即可．
【详解】解：A、∠1与∠2是邻补角，故原题说法错误；
内错角有2对，它们是与，与；
同旁内角有2对，它们是与，与；
对顶角有4对，它们是与，与，与，与．
故答案为：4；与，与，与，与；2；与，与；2；与，与；4；与，与，与，与

《同位角、内错角、同旁内角》练习题(含答案)

同位角、内错角、同旁内角经典练习题(附答案)

同位角、内错角、同旁内角经典练习题1.如图，点D E ，分别为ABC △边BC AC ，上一点，作射线DE ，则下列说法错误的是（）第1题图第2题图A ．1∠与3∠是对顶角B ．2∠与A ∠是同位角C ．2∠与C ∠是同旁内角D ．1∠与4∠是内错角2.如图，已知1∠与2∠是内错角，则下列表述正确的是( )A.由直线AD BC ，被AC 所截而得到的B.由直线AB CD ，被BC 所截而得到的C.由直线AB CD ，被AC 所截而得到的D.由直线AD BC ，被CD 所截而得到的3.如图，直线AD BE ，被直线BF 和AC 所截，则1∠的同位角和5∠的内错角分别是( )A.42∠∠，B.26∠∠，C.54∠∠，D.24∠∠，4.如图，B ∠的同位角可以是( )A.1∠B.2∠C.3∠D.4∠5.如图所示，以下几种说法，其中正确的个数是( )①3∠和4∠是同位角；②6∠和7∠是同位角；③4∠和5∠是内错角；④2∠和5∠是同旁内角⑤2∠和7∠是同位角；⑥1∠和2∠是同位角A.3B.4C.5D.66.如图所示，与∠A 是同旁内角的角共有个.7.如图，2∠的内错角是，3∠与B ∠是角，B ∠的同旁内角是 .第7题图第8题图8.如图（1）找出直线DC AC ，被直线BE 所截形成的同旁内角；（2）指出DEF ∠与CFE ∠是由哪两条直线被哪一条直线所截形成的什么角；（3）试找出图中与DAC ∠是同位角的所有角.答案以及解析1.答案：D解析：根据同位角、内错角以及同旁内角的概念进行判断：A 、B 、C 、正确D 错误.2.答案：C解析：因为1∠的两边为AB AC ，，2∠的两边为AC CD ，，所以1∠与2∠是由直线AB CD ，被AC 所而得到的，故选C3.答案：B解析：由题意，知1∠的同位角是25∠∠，的内错角是6∠，故选B.4.答案：D解析：根据同位角的特征可知，∠B 的同位角可以是4∠.故选D.5.答案：B解析：根据同位角、内错角、同旁内角的特征可知，3∠和4∠是同位角，1∠和2∠是同位角，4∠和5∠是内错角，2∠和5∠是同旁内角，6∠和7∠不是同位角，2∠和7∠不是同位角则正确的为③④①，共4个，故选B6.答案：4解析：与A ∠是同旁内角的有,,,ABC ADC ADE AED ∠∠∠∠,共4个.7.答案：C ∠ 内错 1∠或DAB ∠或C ∠解析：2∠和C ∠在被截线AD 和BC 的内部，截线AC 的两侧，故2∠的内错角是C ∠；3∠与B ∠在被截线AE 和BC 的内部，截线AB 的两侧，故3∠与B ∠是内错角；B ∠的同旁内角是1∠或DAB ∠或C ∠8.答案：解:（1）FBC ∠和CFB ∠，DFB ∠和FBA ∠是直线DC AC ，被直线BE 所截形成的同旁内角.（2）DEF ∠与CFE ∠是由直线AG DF ，被直线EF 所截形成的内错角.（3）DAC ∠的同位角有EBH DCH EDF GEF ∠∠∠∠，，，.。

同位角、内错角、同旁内角专项练习41题(有答案)

同位角.内错角.同旁内角专项练习50题知识点:1、两条直线被第三条直线所截形成八个角，它们构成了同位角、内错角与同旁内角。

如图，直线“上被直线/所截①Z1与Z5在截线/的同侧，同在被截直线（"的上方,叫做同位角（位置相同）②Z5与Z3在截线/的两旁（交错），在被截直线4b之间（内），叫做内错角（位置在内且交错）③Z5与Z4在截线/的同侧，在被截直线之间（内），叫做同旁内角“④三线八角也可以成模型中看出。

同位角是"A”型；内错角是“Z”型：同旁内角是“U”型。

2、如何判别三线八角判别同位角.内错角或同旁内角的关键是找到构成这两个角的“三线S有时需要将有关的部分“抽出”或把无关的线略去不看，有时又需要把图形补全。

例如：A 1如图,判断下列各对角的位置关系:（DZ1与Z2：（2）Z1与Z7：（30 与ZBAD：（4）Z2与Z6：（5）/5与Z8。

我们将各对角从图形中抽岀来（或者说略去与有关角无关的线），得到下列各图。

如图所示，不难看出Z1与Z2是同旁内角：Z1与Z7是同位角：Z1与ZBAD是同旁内角；Z2与Z6是内错角：Z5与Z8对顶角。

专项练习:所截得的角,AC 、BC 被AB 所截得的同旁内角是8、如图2・45, AB. DC 被BD 所截得的内错角是 _________ 是 ____________ ，AD 、BC 被BD 所截得的内错角是 Z • AB 、______ 所角。

12、如图2-49,已知Z1的同旁内角等于57° 28’，求Z1的内错的度数.13、如图1, Z1和Z2可以看作直线 _________ 和直线 _________ 被直线 _______ 所截得的角。

15、如图3,直线DE 、BC 被直线AC 所截得的内错角是 ______ : ZB 与ZC 可以看作直线 __________ 、 __________ 被E ）是内错角个 10.如图 2-47,( 11、如图2-48,图中的同位角的对数是（ )14、如图2, Z1和Z2是直线和直线被直线直线 ________ 所截得的________ 角o图316、如图4.与ZEFC构成内错角的是.2 1、如下图6,和Z1互为同位角的是(图I______________ :与ZEFC构成同旁内角的____ 个；与Z2构成同位角的角有 _______ 个:个。

七年级数学下册-同位角、内错角、同旁内角练习含答案

同位角、内错角、同旁内角练习要求：熟悉并掌握三线八角。

Ａ卷一、填空题1．如图1，直线a、ｂ被直线c所截，∠１和∠2是，∠3和∠4是，∠３和∠2是。

２.如图2,∠１和∠2是直线和直线被直线所截得的角。

3.如图3，∠１的内错角是，∠A的同位角是，∠B的同旁内角是。

４.如图４，和∠1构成内错角的角有个;和∠1构成同位角的角有个;和∠1构成同旁内角的角有个。

５．如图5，指出同位角是，内错角是，同旁内角是。

二、选择题６.如图６，和∠１互为同位角的是( )(A）∠2; (B)∠3；(C)∠4；（D）∠５。

７．如图７，已知∠１与∠2是内错角，则下列表达正确的是( ）(A)由直线ＡD、AC被ＣＥ所截而得到的;(B)由直线AD、AＣ被BD所截而得到的；(C)由直线DＡ、DＢ被ＣＥ所截而得到的；（D）由直线ＤA、DB被AＣ所截而得到的。

8.在图8中1和2是同位角的有( )(Ａ）(1)、(2）; (B）(2)、(3）; (C)(１）、（3); (Ｄ)(2)、(4)。

9．如图9，在指明的角中，下列说法不正确的是( )（A）同位角有２对; (Ｂ）同旁内角有5对;(Ｃ)内错角有4对; （Ｄ)∠1和∠4不是内错角。

1０．如图１0,则图中共有( )对内错角 (A)3；（B)4； (Ｃ)５； (Ｄ）6。

三、简答题1１.如图1１(１）说出∠１与∠２互为什么角?(2)写出与∠１成同位角的角;（3)写出与∠1成内错角的角。

12．如图12(1)说出∠Ａ与∠1互为什么角?(2) ∠B与∠2是否是同位角；(３）写出与∠２成内错角的角。

B卷一、填空题１．如图1,∠1和∠2可以看作直线和直线被直线所截得的角。

2.如图2，∠1和∠2是直线和直线被直线被直线所截得的角。

3．如图3,直线DE、BＣ被直线AC所截得的内错角是；∠B与∠C可以看作直线、被直线所截得的角。

４.如图4,与∠EFC构成内错角的是；与∠EFC构成同旁内角的是。

５.如图5，与∠1构成内错角的角有个;与∠1构成同位角的角有个；与∠１构成同旁内角的角有个。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

邻补角、对顶角、同位角、内错角、同旁内角
一、学习目标
1、了解两条直线相交所构成的角，理解并掌握邻补角、对顶角的概念和性质；
2、理解并掌握垂线的概念和性质；
3、了解同位角、内错角、同旁内角的概念并会辨别二、主要内容
1、邻补角：两直线相交所成的四个角中，有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角。

图形顶点边的关系大小关系对顶角
∠1与∠2 有公共顶点
∠1的两边与∠2的两边互为反向延长线
对顶角相等即∠1=∠2
邻补角
∠3与∠4
有公共顶点
∠3与∠4有一条边公共，另一边互为反向延长线。

∠3+∠4=180°
注意：
1、对顶角是成对出现的，对顶角是具有特殊位置关系的两个角；
2、如果∠α与∠β是对顶角，那么一定有∠α=∠β；反之如果∠α=∠β，那么∠α与∠β不一定是对顶角
3、如果∠α与∠β互为邻补角，则一定有∠α+∠β=180°；反之如果∠α+∠β=180°，则∠α与∠β不一定是邻补角。

4、两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个。

习题巩固
1．下面四个图形中，∠1与∠2是对顶角的图形的个数是（） A ．0 B ．1 C ．2 D ．3
12
1
2
1
2
1
2
2、下面各图中∠1和∠2是对顶角的是（）
1 2 4 3
A．B．C．D．
3、下列语句正确的是（）.
A、相等的角是对顶角
B、相等的两个角是邻补角
C、对顶角相等
D、邻补角不一定互补，但可能相等
4、下列语句错误的有（）个.
（1）两个角的两边分别在同一条直线上，这两个角互为对顶角
（2）有公共顶点并且相等的两个角是对顶角
（3）如果两个角相等，那么这两个角互补
（4）如果两个角不相等，那么这两个角不是对顶角
A、1
B、2
C、3
D、4
5、已知∠1与∠2是邻补角，∠2是∠3的邻补角，那么∠1与∠3的关系是（）.
A、对顶角
B、相等但不是对顶角
C、邻补角
D、互补但不是邻补角
6、下列说法正确的是（）.
A、有公共顶点的两个角是对顶角
B、两条直线相交所成的两个角是对顶角
C、有公共顶点且有一条公共边的两个角是邻补角
D、两条直线相交所成的无公共边的两个角是对顶角
7、已知：如图所示，AB⊥CD，垂足为点O，EF为过点O•的一条直线，则∠1与∠2的关系一定成立的是（）
A．相等 B．互余 C．互补 D．互为对顶角
8、下列判断正确的个数是_____个。

⑴如果两个角相等，那么这两个角是对顶角。

⑵如果两个角有共公顶点，且角平分线互为反向延长线，那么这两个角是对顶角。

⑶对顶角的平分线在同一条直线上。

⑷以同一个角为邻补角且不重合的两个角是对顶角。

9、如图，直线AB 、CD 相交于点O ，∠1＝∠2．则∠1的对顶角是_____，∠4的邻补角是______．∠2的补角是_________．
10、如图，已知直线AB 、CD 相交于点O ，∠AOC ＝50°，求∠BOD 、∠AOD 、∠BOC 的度数.
解：∵∠BOD 与∠AOC 是对顶角 ∴ ＝＝ °（）
∵ 与是邻补角 ∴∠AOD ＝180°－∠AOC ＝180°－50°＝130° ∵ 与是对顶角 ∴∠BOC ＝∠AOD ＝130°
11、如图所示，直线AB ，CD 相交于点O ，∠BOE=90°，若∠COE=55°，•求∠BOD 的度数．
C
O
E D B
A
12、如图所示，直线AB 与CD 相交于点O ，OE 平分∠AOD ，∠AOC=•120•°. 求∠BOD ，∠AOE 的度数．
50
O
A
D C B
13、如图，直线AB 、CD 相交于点O ，OE 平分∠BOC.已知∠BOE=65°,求∠AOD 、∠AOC 的度数.
3、两直线相交所成的四个角中，如果有一个角是直角，那么就称这两条直线相互垂直；垂线的性质：⑴过一点有且只有一条直线与已知直线垂直。

⑵连接直线外一点与直线上各点的所在线段中，垂线段最短。

习题巩固
1、下列说法中正确的是（）
A ．有且只有一条直线垂直于已知直线。

B ．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离。

C ．互相垂直的两条直线一定相交。

D ．直线c 外一点A 与直线c 上各点连接而成的所有线段中，最短线段的长是3cm ，则点A 到直线c
的距离是3cm 。

2、点到直线的距离是指这点到这条直线的（）
A 、垂线段
B 、垂线的长
C 、长度
D 、垂线段的长
4、两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，
⑴如果两个角分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做同位角； ⑵如果两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做内错角； ⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做同旁内角。

习题巩固
1．如图，若直线a ，b 被直线c 所截，在所构成的八个角中指出，下列各对角之间是属于哪种特殊位置关系的角?
(1)∠1与∠2是_______；(2)∠5与∠7是______；
(3)∠1与∠5是_______；(4)∠5与∠3是______；
(5)∠5与∠4是_______；(6)∠8与∠4是______；
(7)∠4与∠6是_______；(8)∠6与∠3是______；
(9)∠3与∠7是______；(10)∠6与∠2是______．
E
65
O A
D
C B
2、如图所示，
(1)∠AED 和∠ABC 可看成是直线______、______被直线_____ _所截得的____ ___角；
(2)∠EDB 和∠DBC 可看成是直线______、______被直线____ ___所截得的____ __角；
(3)∠EDC 和∠C 可看成是直线_______、____ 被直线__ ___所截得的___ _ __角．
3、已知图①～④，
图① 图② 图③ 图④ 在上述四个图中，∠1与∠2是同位角的有( )． (A)①②③④ (B)①②③ (C)①③ (D)①
4、如图，下列结论正确的是( )． (A)∠5与∠2是对顶角 (B)∠1与∠3是同位角
(C)∠2与∠3是同旁内角 (D)∠1与∠2是同旁内角
5、如图，∠1和∠2是内错角，可看成是由直线( )． (A)AD ，BC 被AC 所截构成 (B)AB ，CD 被AC 所截构成
(C)AB ，CD 被AD 所截构成 (D)AB ，CD 被BC 所截构成 6、下列图形中,1∠和2∠不是同位角的是( )
A B C D
1
2
1
2
1
21
2
7、如图,属于内错角的是( )
A.∠1和∠2
B.∠2和∠3 C .∠1和∠4 D.∠3和∠4
8、如图所示,同位角一共有对,
分别是；内错角一共有对,
分别是；
同旁内角一共有对,
分别是 .
3
42
1a
b
c
1
2
3456
789。