(完整版)余角、补角、对顶角的概念和习题答案
余角、补角、对顶角(通用版)(含答案)

余角、补角、对顶角(通用版)试卷简介:考查学生对余角、补角、对顶角的定义以及对同角(或等角)的余角相等、同角(或等角)的补角相等、对顶角相等的掌握情况,并利用这些进行简单的计算.一、单选题(共16道,每道6分)1.如图,∠1,∠2是对顶角的是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:对顶角的定义2.下列语句正确的是( )A.若两个角不是对顶角,则这两个角不相等B.若两角相等,则这两个角是对顶角C.若两个角是对顶角,则这两个角相等D.以上判断都不对答案:C解题思路:试题难度:三颗星知识点:对顶角相等3.下面四个图形中,∠1=∠2一定成立的是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:对顶角相等4.如果一个角的补角是120°,那么这个角的余角是( )A.130°B.60°C.30°D.20°答案:C解题思路:试题难度:三颗星知识点:补角的定义5.如果一个角的余角是50°,那么这个角的补角是( )A.130°B.140°C.150°D.160°答案:B解题思路:试题难度:三颗星知识点:补角的定义6.已知∠1与∠2互余,且∠1=35°,则∠2的补角的度数为( )A.145°B.115°C.135°D.125°答案:D解题思路:试题难度:三颗星知识点:补角的定义7.如图,∠AOB=15°,∠AOC=90°,点B,O,D在同一直线上,则∠COD的度数为( )A.75°B.15°C.105°D.165°答案:C解题思路:试题难度:三颗星知识点:补角的定义8.如图,OC⊥AB,∠COD=45°,则图中互为补角的角共有( )A.1对B.2对C.3对D.4对答案:C解题思路:试题难度:三颗星知识点:补角的定义9.如图,OA⊥OB,OC⊥OD,则( )A.∠AOC=∠AODB.∠AOC=∠BODC.∠AOD=∠BODD.以上结论都不对答案:B解题思路:试题难度:三颗星知识点:余角的定义10.如果∠α和∠β互余,则下列式子中:①180°-∠β;②∠α+2∠β;③90°+∠α;④2∠α+∠β.能表示∠β补角的有( )A.①③B.①④C.①③④D.①②③④答案:C解题思路:试题难度:三颗星知识点:补角的定义11.如图,∠AOC=∠BOD=90°,若∠AOB=150°,则∠DOC的度数为( )A.30°B.40°C.50°D.60°答案:A解题思路:试题难度:三颗星知识点:余角的定义12.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )A.25°B.35°C.45°D.55°答案:D解题思路:试题难度:三颗星知识点:对顶角相等13.如图,∠COD为平角,AO⊥OE,,则∠EOD的度数为( )A.30°B.45°C.60°D.75°答案:A解题思路:试题难度:三颗星知识点:平角的定义14.如图,已知AB⊥CD,垂足为点O,EF过点O,则图中∠FOB与∠EOD的关系是( )A.∠FOB+∠EOD=180°B.∠FOB+∠EOD=90°C.∠FOB=∠EODD.无法确定答案:B解题思路:试题难度:三颗星知识点:补角的定义15.若∠α与∠β互余,∠β与∠γ互余,则∠α与∠γ的关系是( )A.互余B.互补C.相等D.不确定答案:C解题思路:试题难度:三颗星知识点:补角的定义16.如果∠A与∠B互补,∠B与∠C互余,则∠A与∠C的关系是( )A.互余B.互补C.∠A-∠C=90°D.∠A-∠C=180°答案:C解题思路:试题难度:三颗星知识点:补角的定义。
考点06 余角和补角(解析版)

考点06 余角和补角1.(甘肃省肃南县第一中学2019—2020学年七年级上学期期末试题(一))如果两个角互为补角,而其中一个角是另一个角的5倍,那么这两个角是( )A .15o ,75oB .20o ,100oC .10o ,50oD .30o ,150o【答案】D【分析】设较小的角为x ,则较大的角5x ,根据这两个角互为补角可得关于x 的方程,解方程即可求出x ,进而可得答案.【详解】解:设较小的角为x ,则较大的角5x ,根据题意得:x+5x=180°,解得:x=30°,5×30°=150°;所以这两个角是:30°,150°.故选:D .【点睛】本题考查了互补两角的概念和简单的一元一次方程的应用,属于基础题型,正确理解题意、熟练掌握上述知识是解题的关键.2.(河北省新乐市2020-2021学年七年级上学期期中数学试题)若90αθ∠+∠=︒,βθ∠=∠,则α∠与β∠的关系是( ) A .α∠与β∠互余B .α∠与β∠互补C .α∠与β∠相等D .α∠大于β∠【答案】A 【分析】根据等角的余角相等可直接进行排除选项.【详解】解:∵90αθ∠+∠=︒,βθ∠=∠,∴90αβ∠+∠=︒,故选A .【点睛】本题主要考查余角,熟练掌握余角的性质是解题的关键.3.(广东省珠海市香洲区紫荆中学2020-2021学年七年级上学期期中数学试题)已知一个角是30°,那么这个角的补角的度数是( )A .120°B .150°C .60°D .30°【答案】B【分析】根据互补的两角之和为180°即可得出这个角的补角.【详解】解:这个角的补角18030150=︒-︒=︒.故答案为:B .【点睛】本题考查了补角的知识,属于基础题,掌握互补的两角之和为180°是关键.4.(广东省揭阳市2019-2020学年七年级下学期期中数学试题)已知115A ∠=︒,B 是A ∠的补角,则B 的余角的度数是( )A .65︒B .115︒C .15︒D .25︒【答案】D【分析】根据余角与补角的定义逐步解答即可.【详解】解:由题意得,180B A ∠=︒-∠18011565=︒-︒=︒, ∴B 的余角为906525︒-︒=︒.故选:D.【点睛】本题考查了余角和补角的定义与计算,熟练掌握定义是解答关键.5.(河北省石家庄市灵寿县2019-2020学年七年级上学期期末数学试题)已知A ∠是它的补角的4倍,那么A ∠=( )A .144︒B .36︒C .90︒D .72︒【答案】A【分析】根据A ∠的补角是180A ∠︒-,结合A ∠是它的补角的4倍,列方程求解即可.【详解】∵A ∠的补角是180A ∠︒-,依题意得:()4180A A ∠∠=︒-,解得:144A ∠=︒.故选:A .【点睛】本题主要考查了补角的概念,正确得出等量关系是解题关键.6.(陕西省榆林市清涧县2019-2020学年七年级上学期期末数学试题)如图,AOB ∠为平角,且14AOC BOC ∠=∠,则BOC ∠的度数是( )A .144︒B .36︒C .45︒D .135︒【答案】A 【分析】根据平角的性质得到180AOC BOC ∠+∠=︒,再根据这两个角之间的比例关系求出BOC ∠.【详解】解:∵AOB ∠是平角,∴180AOC BOC ∠+∠=︒, ∵14AOC BOC ∠=∠, ∴41801445BOC ∠=︒⨯=︒. 故选:A .【点睛】本题考查平角的性质,解题的关键是利用平角的性质和角度之间的比例求角度.7.(甘肃省肃南县第一中学2019—2020学年七年级上学期期末试题(一)231745'''︒的余角是_________________,补角是___________________.【答案】664215'''︒ 1564215'''︒【分析】根据互为余角、互为补角的定义进行计算即可求得答案.【详解】解:∵90231745895960231745664215''''''''''''︒-︒=︒-︒=︒∴231745'''︒的余角是664215'''︒;∵18023174517959602317451564215''''''''''''︒-︒=︒-︒=︒∴231745'''︒的补角是1564215'''︒.故答案是:664215'''︒;1564215'''︒【点睛】本题考查了余角、补角的概念,掌握基本概念是解决问题的关键.8.(河北省张家口市宣化区2020-2021学年七年级上学期期中(冀教版)试题如果∠α=26°,那么∠α的余角等于__________ .【答案】64°【分析】根据互为余角的两个角的和等于90°列式计算即可的解.【详解】∵∠α=26°,∴∠α的余角=90°-26°=64°.故答案为:64°【点睛】本题考查了余角的定义,是基础题,熟记互为余角的两个角的和等于90°是解题的关键.9.(黑龙江省大兴安岭塔河县2019-2020学年七年级上学期期末数学试题)已知∠α=36°14′,则∠α的余角的度数是_____.【答案】53°46′【分析】直接利用互为余角的定义结合度分秒的转化得出答案.【详解】解:∵∠α=36°14′,则∠α的余角的度数是:90°-36°14′=89°60′-36°14′=53°46′;故答案为:53°46′.【点睛】此题主要考查了互为余角的定义结合度分秒的转化,正确把握相关定义是解题关键.10.(河北省唐山市乐亭县第三初级中学2020-2021学年七年级上学期期末数学试题)6250'°的余角等于______.【答案】2710'°【分析】根据余角的定义、角的四则运算即可得.【详解】6250'°的余角为906250896062502710''''︒-︒=︒-︒=︒,故答案为:2710'°.【点睛】本题考查了余角、角的四则运算,熟练掌握余角的定义是解题关键.11.(浙江省宁波市江北外国语学校2020-2021学年七年级上学期期中数学试题)30°角的补角是______度.【答案】150【分析】根据互补的两角之和为180°,即可得出答案.【详解】解:30°的补角为18030150︒︒︒-=.故答案为:150【点睛】本题考查了余角和补角的知识,互余的两角之和为90°,互补的两角之和为180°,是需要我们熟练记忆的内容.12.(江西省赣州市定南县2019-2020学年七年级下学期期末数学试题)∠1的对顶角等于50︒,∠1的余角等于_______________.【答案】40°【分析】根据余角的概念进行解答即可.【详解】解:∠1的对顶角等于50︒,∠1=50︒,则∠1的余角等于90°-50°=40°.故答案为:40°.【点睛】本题主要考查了余角的概念,注意:如果两个角的和等于90°,就说这两个角互为余角.13.(河北省保定市曲阳县2020-2021学年七年级上学期期中数学试题)已知α∠和β∠互补,且αβ∠>∠,则有下列式子:①90β︒-∠;②90α∠-︒;③()12αβ∠+∠;④()12αβ∠-∠;⑤()1902α∠-︒;其中,表示β∠的余角的式子有______(填序号).【答案】①②④【分析】根据余角和补角的定义,把式子进行变形即可确定答案.【详解】解:∵α∠和β∠互补,∴α∠+β∠=180°,∴β∠=180°-α∠,根据余角定义①正确,②90α∠-︒=180°-β∠-90°=90°-β∠所以②正确,③()12αβ∠+∠=1180902⨯︒=︒故③错误,④()12αβ∠-∠=12(180°-β∠-β∠)=12(180°-2β∠)=90°-β∠故④正确,⑤()1902α∠-︒=()()1118090=9022ββ-︒--∠∠故⑤错误; 故答案为:①②④.【点睛】本题考查余角和补角相关计算以及余角和补角的定义,熟练进行式子的变形是解题的关键. 14.(湖南省长沙市2019-2020年七年级下学期第三次教学质量检测联考数学试题)如图所示,A 、O 、B 三点在同一条直线上,AOC ∠与AOD ∠互余,已知20AOD ∠=︒,则BOC ∠=______.【答案】110︒【分析】根据余角的性质,先解出AOC ∠的度数,再由邻补角的性质即可计算出BOC ∠度数.【详解】A 、O 、B 三点在同一条直线上,AOC ∠与AOD ∠互余, ∴AOC ∠+AOD ∠=90︒20AOD ∠=︒902070AOC ∴∠=︒-︒=︒AOC ∠+180BOC ∠=︒18070110BOC ∴∠=︒-︒=︒故答案为:110︒.【点睛】本题考查余角与补角,是基础考点,难度较易,掌握相关知识是解题关键.15.(河北省石家庄市栾城区2020-2021学年七年级上学期期中考试数学试题)如图,90BOC ∠=°,45COD ∠=︒,则图中互为补角的角共有______对.【答案】3对【分析】根据题意,补角的定义是两个角的和为180°即可得出结论.【详解】由题意知,∵90BOC ∠=°,45COD ∠=︒,∴∠BOD=45°,∠AOD=135°,∴互补的角为:∠BOD 和∠AOD ,∠COD 和∠AOD ,∠AOC 和∠BOC,共3对,故答案为:3对.【点睛】本题考查了补角的定义,掌握补角的定义是解题的关键.16.(江西省赣州市定南县2019-2020学年七年级上学期期末数学试题)一个角的余角是5134',这个角的补角是__________. 【答案】14134'【分析】根据余角、补角和度分秒的性质计算即可;【详解】∵一个角的余角是5134',所以这个角是9051343826''︒-︒=︒,∴这个角的补角为180382614134''︒-︒=︒; 故答案是14134'︒.【点睛】本题主要考查了余角和补角的性质,准确利用度分秒计算是解题的关键.17.(河南省新乡市原阳县2020-2021学年七年级上学期第二次月考数学试题)一个角的余角的度数为7028'47''︒,则这个角等于__________.【答案】1931'13''【分析】相加等于90°的两角称作互为余角,也作两角互余,即一个角是另一个角的余角.因而,已知一个角的余角,求这个角,就可以用90°减去它余角的度数.【详解】解:这个角的度数为907028'47''1931'13''-︒=,故答案为:1931'13''【点睛】本题主要考查余角的定义,是一个基本的题目,注意角度的单位换算1=60',1'60''=是本题的解题关键.18.(内蒙古乌兰察布市四子王旗2019-2020学年七年级上学期期末数学试题)已知∠α= 29°18′,则∠α的余角的补角等于_________.【答案】119°18´【分析】利用互余和互补两角的关系即可求出答案.【详解】解:∵∠α= 29°18′,∴∠α的余角=90°-29°18′=60°42′,∴∠α的余角的补角=180°-60°42′=119°18´.【点睛】本题考查了余角和补角.正确把握相关定义是解题的关键.19.(吉林省长春外国语学校2020-2021学年七年级上学期第二次月考数学试题)若A ∠=52°16′,则A ∠的补角为_____.【答案】127°44′【分析】根据补角的定义解题即可.【详解】A ∠的补角为180180521612744A ''︒-∠=︒-︒=︒故答案为:127°44′【点睛】本题考查补角,是基础考点,难度较易,掌握相关知识是解题关键.20.一个角的余角比它的补角的14还少12︒,则这个角的度数为_______. 【答案】76︒【分析】设这个角为x ,则它的余角为90x ︒-,补角为180x ︒-,根据题意列出方程即可求解.【详解】设这个角为x ,则它的余角为90x ︒-,补角为180x ︒- ()190180124x x ∴-=-- 19045124x x -=-- 3574x =4573x =⨯ 76x =︒即这个角为76︒故答案为76︒.【点睛】此题主要考查角度的计算,解题的关键是根据题意列出方程求解.21.(云南省保山市第九中学2020-2021学年七年级上学期第三次月考数学试题)如果∠1=60°,∠1的余角等于__________【答案】30°【分析】根据余角的概念进行解答即可.【详解】如果∠1=60°,则∠1的余角等于90°-60°=30°.故答案为:30°.【点睛】本题主要考查了余角的概念,注意:如果两个角的和等于90°,就说这两个角互为余角. 22.(湖南省长沙市雅礼实验中学2020-2021学年七年级上学期第三次月考数学试题)已知,∠A =46°28',则∠A 的余角=_____.【答案】43°32′【分析】根据余角的定义求解即可.【详解】解:∵∠A =46°28′,∴∠A 的余角=90°﹣46°28′=43°32′.故答案为:43°32′.【点睛】本题考查了余角的定义,熟知余角的定义是解答的关键.23.(河北省唐山市乐亭县第三初级中学2020-2021学年七年级上学期期末数学试题)如图,O 为直线AB 上一点,50AOC ∠=︒,OD 平分AOC ∠,90DOE ∠=︒.(1)图中有______个小于平角的角.(2)求COE ∠、∠BOE 的度数.【答案】(1)9;(2)6565COE BOE ∠=∠=︒°,.【分析】(1)根据平角的定义即可得;(2)先根据角平分线的定义可得1252COD AOC ∠=∠=︒,再根据余角的定义可得COE ∠的度数,然后根据平角的定义可得∠BOE 的度数.【详解】(1)图中小于平角的角为,,,,,,,,AOD AOC AOE DOC DOE DOB COE COB EOB ∠∠∠∠∠∠∠∠∠,共有9个,故答案为:9;(2)因为OD 平分AOC ∠,50AOC ∠=︒, 所以1252COD AOC ∠=∠=︒, 因为90DOE ∠=︒,所以902565COE DOE COD ∠=∠-∠=︒-︒=︒,所以180180506565BOE AOC COE ∠=︒-∠-∠=︒-︒-︒=︒.【点睛】本题考查了余角、平角、角平分线的定义,熟练掌握角的相关概念是解题关键.24.(广东省深圳市福田区石厦学校2020-2021学年七年级上学期期中数学试题)已知:如图1,OB 、OC 分别为锐角AOD ∠内部的两条动射线,当OB 、OC 运动到如图的位置时,100AOC BOD ∠+∠=︒,40AOB COD ∠+∠=︒.(1)求BOC ∠的度数.(2)如图2,射线OM 、ON 分别为AOB ∠、COD ∠的平分线,求MON ∠的度数.(3)如图3,若OE 、OF 是AOD ∠外部的两条射线,且90EOB COF ∠=∠=︒,OP 平分EOD ∠,OQ 平分AOF ∠,当BOC ∠绕着点A 旋转时,POQ ∠的大小是否会发生变化,若不变,求出其度数,若变化,说明理由.【答案】(1)BOC ∠的度数为30︒;(2)MON ∠的度数为50︒;(3)POQ ∠的大小不变,110∠=︒POQ【分析】(1)根据角的和与差即可得出答案;(2)根据角平分线的性质及角的和与差即可得出答案;(3)根据90EOB COF ∠=∠=︒,可得出60COE BOF ∠=∠=︒,进而求出EOF ∠,再根据OP 平分DOE ∠,OQ 平分AOF ∠,即可得出答案.【详解】(1)∵100AOC BOD ∠+∠=︒,∴100AOB BOC BOC COD ∠+∠+∠+∠=︒,∴2100AOB COD BOC ∠+∠+∠=︒,∵40AOB COD ∠+∠=︒,∴260BOC ∠=︒,∴30BOC ∠=︒.答:BOC ∠的度数为30︒.(2)∵OM 平分AOB ∠, ∴12BOM AOB ∠=∠, ∵ON 平分COD ∠, ∴12CON COD ∠=∠, ∴()12BOM CON AOB COD ∠+∠=∠+∠, ∵40AOB COD ∠+∠=︒,30BOC ∠=︒,∴302050MON BOM BOC CON ∠=∠+∠+∠=︒+︒=︒.答:MON ∠的度数为50︒.(3)∵90EOB COF ∠=∠=︒,30BOC ∠=︒,∴60COE BOF ∠=∠=︒,又150EOF COE BOF BOC ∠=∠+∠+∠=︒,70AOD ∠=°,1507080DOE AOF ∠+∠=︒-︒=︒,∵OP 平分DOE ∠,OQ 平分AOF ∠, ∴()1402POQ AOQ DOE AOF ∠+∠=∠+∠=︒, ∴4070110POQ POD AOQ AOD ∠=∠+∠+∠=︒+︒=︒.故POQ ∠的大小不变.【点睛】本题考查了角平分线的定义、余角和补角的意义,掌握角平分线的定义以及角的和差关系是正确解答的前提.25.(江苏省南通市崇川区南通田家炳中学2020-2021学年七年级上学期12月月考数学试题)如图,点O是直线AB上的一点,∠COD是一个直角,OE平分∠BOC.(1)如图1,当∠AOC=30°,求∠DOE的度数;(2)如图2,若∠AOC=x°,求∠DOE的度数.(用含有x的代数式表示)【答案】(1)15°;(2)12x【分析】(1)根据互补求出∠BOC,再根据角平分线求出∠COE,再用互余,求出结果即可;(2)方法同(1),把角度用未知数表示,相应的角度用含有x的代数式表示即可.【详解】(1)∵∠AOC=30°,∴∠BOC=180°﹣∠AOC=150°,又∵OE平分∠BOC,∴∠BOE=∠COE=12∠BOC=75°,又∵∠COD=90°,∴∠DOE=∠COD﹣∠COE=15°;(2)∵∠AOC=x°,∴∠BOC=180°﹣∠AOC=(180﹣x)°,又∵OE平分∠BOC∴∠BOE=∠COE=12∠BOC=12(180﹣x)°,又∵∠COD=90°∴∠DOE=∠COD﹣∠COE=90°﹣12(180﹣x)°=12x°【点睛】本题考查角平分线、互为余角、互为补角的意义,通过图形直观得出各个角之间的关系是正确解答的关键.26.(吉林省白山市临江2019-2020学年七年级上学期期末数学试题)已知两个角的大小之比是7:3,它们的差是36°,这两个角是否互余?请说明理由.【答案】两角互余,理由见解析.【分析】由两角之比是7:3,即可设这两个角分别为:7x°,3x°,又由它们的差是36°,即可得方程:7x°-3x°=36°,解此方程即可求得答案.【详解】两角互余.理由:设两角分别为7x°,3x°,由题得7x°-3x°=36,解得x°=9°,则7x°=63°,3x°=27°,∵63°+27°=90°∴这两个角互余.【点睛】此题考查了角的计算.解题时注意掌握方程思想的应用.。
余角、补角、对顶角的概念和习题答案

余角和补角和对顶角余角:如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A补角:如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A对顶角:一个角的两边分别是另一个角的反向延长线,这两个角是对顶角。
两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线相交,构成两对对顶角。
对顶角相等.对顶角与对顶角相等.对顶角是对两个具有特殊位置的角的名称; 对顶角相等反映的是两个角间的大小关系。
补角的性质:同角的补角相等。
比如:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B。
等角的补角相等。
比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:同角的余角相等。
比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。
比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
注意:①钝角没有余角;②互为余角、补角是两个角之间的关系。
如∠A+∠B+∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A+∠B+∠C=180°,不能说∠A、∠B、∠C互为补角;③互为余角、补角只与角的度数相关,与角的位置无关。
只要它们的度数之和等于90°或180°,就一定互为余角或补角。
余角与补角概念认识提示:(1)定义中的“互为”一词如何理解如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 ,同样∠2的补角是∠1。
对顶角余角和补角的定义

对顶角余角和补角的定义
顶角、余角和补角是在几何学和三角学中常见的概念。
顶角指的是两条直线相交时,形成的相对的两个角,这两个角的顶点是同一个点。
余角是指一个角的补角,即与该角相加为90度的角。
而补角则是两个角的和为90度的角。
从几何学的角度来看,顶角是指两条直线相交时形成的相对的两个角,它们共享一个公共顶点。
例如,在一个三角形中,顶角通常指的是三角形的顶点所对的角。
余角是指一个角的补角,也就是与该角相加为90度的角。
例如,如果一个角的度数是x度,那么它的余角就是90度减去x度。
补角是指两个角的和为90度的角。
例如,如果一个角的度数是x度,那么它的补角就是90度减去x度。
从三角学的角度来看,顶角、余角和补角也有特定的定义。
在三角函数中,余角是指角A的余角是90度减去角A的度数。
补角是指两个角的和为90度的角,例如,如果角A的度数是x度,那么角A的补角就是90度减去x度。
这些概念在解题和推导三角函数的过程中经常被用到。
总的来说,顶角、余角和补角是几何学和三角学中非常基础和
重要的概念,它们帮助我们理解角的关系,解决各种几何和三角学问题。
通过理解这些概念,我们能更好地应用它们解决实际问题,并且在数学推导和证明中起到重要的作用。
七年级数学上册6.3余角、补角、对顶角什么叫余角、补角?它们的性质是什么?素材苏科版

什么叫余角、补角?它们的性质是什么?难易度:★★★★关键词:角答案:(1)余角:如果两个角的和等于90°(直角),就说这两个角互为余角。
即其中一个角是另一个角的余角。
(2)补角:如果两个角的和等于180°(平角),就说这两个角互为补角。
即其中一个角是另一个角的补角。
(3)性质:等角的补角相等。
等角的余角相等。
(4)余角和补角计算的应用,常常与等式的性质、等量代换相关联。
注意:余角(补角)与这两个角的位置没有关系。
不论这两个角在哪儿,只要度数之和满足了定义,则它们就具备相应的关系。
【举一反三】典例:已知一个角的补角比这个角的余角的3倍大10°,求这个角的度数.思路引导:主要考查了余角和补角的概念以及运用.互为余角的两角的和为90°,互为补角的两角之和为180度.解此题的关键是能准确的从图中找出角之间的数量关系,从而计算出结果.利用题中“一个角的补角比这个角的余角的3倍大10°"作为相等关系列方程求解即可.设这个角是x,则(180°-x)—3(90°-x)=10°,解得x=50°.故答案为50°.标准答案:50°尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
苏科版七年级上《6.3余角、补角、对顶角》同步测试含答案(共2份)第1课时余角和补角

第 1 页 共 9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可6.3 第1课时 余角和补角知识点 1 余角、补角的概念1.2017·广东已知∠A =70°,则∠A 的补角为( )A .110°B .70°C .30°D .20°2.下列选项中,能与30°角互补的是( )图6-3-13.如图6-3-2,点O 在直线AB 上,若∠1=40°,则∠2的度数是( )图6-3-2A .50°B .60°C .140°D .150°4. 如果一个角是36°,那么( )A .它的余角是64°B .它的补角是64°C .它的余角是144°D .它的补角是144°5.现有下列说法:①锐角的余角是锐角;②钝角没有余角;③直角的补角是直角;④两个锐角互余.其中正确说法的个数是( )A .4B .3C .2D .16.52°34′的余角是__________,补角是__________.7.若一个锐角的余角与这个角相等,则这个角等于________°.8.已知∠1和∠2互余,∠2和∠3互补,如果∠1=63°,那么∠3=________°.9.一个角的补角比它的余角的4倍少15°,求这个角的度数.第 2 页 共 9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可知识点 2 余角、补角的性质10.若∠1+∠2=90°,∠1+∠3=90°,则________=________,理由是__________________________________;若∠1+∠2=180°,∠3+∠4=180°,∠1=∠3,则________=________,理由是_________________________________________________.11.若∠1与∠2互补,∠2与∠3互补,∠1=50°,则∠3等于( )A .50°B .130°C .40°D .140°12.如图6-3-3所示,一副三角板(直角顶点重合)摆放在桌面上,若∠AOC =65°,则∠BOD 等于( )图6-3-3A .45°B .55° C.60° D .65°13.下列说法错误的是( )A .若两角互余,则这两角均为锐角B .若两角相等,则它们的补角也相等C .互为余角的两个角的补角相等D .两个钝角不能互补14.如图6-3-4,已知∠BOC =90°,∠DOA =90°,∠1=50°,求∠2的度数.第 3 页 共 9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可图6-3-415.如图6-3-5所示,点A ,O ,E 在一条直线上,从点O 引射线OB ,OC ,OD ,∠AOC =∠COE =∠BOD =90°,那么图中互补的角有哪几对?图6-3-516.如果一个角等于它的余角的2倍,那么这个角是它的补角的( )A .2倍 B.12 C .5倍 D.1517.已知:如图6-3-6,∠AOB =∠COD =90°,则∠1与∠2的关系是( )图6-3-6A .互余B .互补第 4 页 共 9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可C .相等D .无法确定18.如图6-3-7,O 为直线AB 上一点,∠AOC =α,∠BOC =β,则β的余角可表示为( )图6-3-7A.12(α+β)B.12α C.12(α-β) D.12β 19.如图6-3-8,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD =150°,则∠BOC =________°.图6-3-8 20.如图6-3-9,将一副三角尺的直角顶点重合在一起.(1)若∠DOB 与∠DOA 的度数之比是2∶11,求∠BOC 的度数;(2)若叠合所成的∠BOC =n °(0<n <90),则∠DOA 的补角的度数与∠BOC 的度数之比是多少?图6-3-921.如图6-3-10,O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.(1)写出与∠AOE互补的角;(2)若∠AOD=36°,求∠DOE的度数;(3)当∠AOD=x°时,请直接写出∠DOE的度数.图6-3-1022.如图6-3-11,已知O为直线AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.(1)∠COD与∠AOB相等吗?请说明理由;(2)试求∠AOC与∠AOB的度数.第 5 页共9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可图6-3-11第 6 页共9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可第 7 页 共 9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可详解详析1.A 2.D 3.C4.D [解析] 如果一个角是36°,那么它的余角是90°-36°=54°,补角是180°-36°=144°.故选D.5.B6.37°26′ 127°26′ [解析] 90°-52°34′=37°26′,180°-52°34′=127°26′.7.458.153 [解析] 因为∠1和∠2互余,所以∠1+∠2=90°.又因为∠1=63°,所以∠2=27°.因为∠2和∠3互补,所以∠2+∠3=180°,即27°+∠3=180°,所以∠3=153°.9.解:设这个角为x °,由题意得180°-x °=4(90°-x °)-15°,解得x =55.即这个角的度数为55°.10.∠2 ∠3 同角的余角相等 ∠2 ∠4等角的补角相等11.A12.D [解析] ∵∠AOC 和∠BOD 都是∠BOC 的余角,∴∠AOC =∠BOD .∵∠AOC =65°,∴∠BOD =65°.故选D.13.C [解析] 若两角互余,则这两角均为锐角,选项A 正确;若两角相等,则它们的补角也相等,选项B 正确;30°与60°的角互余,30°角的补角是150°,60°角的补角是120°,则互为余角的两个角的补角不一定相等,选项C 错误;两个钝角不能互补,选项D 正确.14.解:因为∠AOD =90°,所以∠1+∠BOD =90°.因为∠BOC =90°,所以∠2+∠BOD =90°.根据同角的余角相等,可得∠2=∠1=50°.15.解:∠AOD 与∠DOE 互补,∠BOC 与∠DOE 互补,∠BOE 与∠AOB 互补,∠DOC 与∠AOB 互补,∠AOC 与∠BOD 互补,∠AOC 与∠COE 互补,∠BOD 与∠COE 互补.16.B [解析] 设这个角为α,它的余角为β,它的补角为γ,则α=2β,∵α+β=90°,∴α+12α=90°,∴α=60°.∵α+γ=180°,∴γ=120°,∴α=12γ.故选B.第 8 页 共 9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可17.B18.C [解析] 由邻补角的定义,得α+β=180°,两边都除以2,得12(α+β)=90°,β的余角是12(α+β)-β=12(α-β).故选C. 19.30[解析] ∵∠AOB =∠COD =90°,∠AOD =150°,∴∠BOC =∠AOB +∠COD -∠AOD =90°+90°-150°=30°.20.解:(1)设∠DOB =2x ,则∠DOA =11x .因为∠AOB =∠COD =90°,所以∠AOC =∠DOB =2x ,∠BOC =7x .又因为∠DOA =∠AOB +∠COD -∠BOC =180°-∠BOC ,可得方程11x =180°-7x ,解得x =10°,所以∠BOC =70°.(2)因为∠DOA =∠AOB +∠COD -∠BOC =180°-∠BOC ,所以∠DOA 与∠BOC 互补,则∠DOA 的补角的度数是n °,则∠DOA 的补角的度数与∠BOC 的度数之比是1∶1.21.解:(1)∵OE 平分∠BOC ,∴∠BOE =∠COE .∵∠AOE +∠BOE =180°,∴∠AOE +∠COE =180°,∴与∠AOE 互补的角是∠BOE ,∠COE .(2)∵OD ,OE 分别平分∠AOC ,∠BOC ,第 9 页 共 9 页为了成功地生活,少年人必须学习自立,铲除埋伏各处的障碍,在家庭要教养他,使他具有为人所认可∴∠COD =∠AOD =36°,∠COE =∠BOE =12∠BOC ,∠AOC =2×36°=72°, ∴∠BOC =180°-72°=108°,∴∠COE =12∠BOC =54°, ∴∠DOE =∠COD +∠COE =90°.(3)当∠AOD =x °时,∠DOE =90°.22.解:(1)∠COD =∠AOB .理由:因为∠AOC 与∠AOB 互补,所以∠AOC +∠AOB =180°.又因为∠AOC +∠COD =180°,所以∠COD =∠AOB .(2)因为OM 和ON 分别是∠AOC 和∠AOB 的平分线,所以∠AOM =12∠AOC ,∠AON =12∠AOB , 所以∠MON =∠AOM -∠AON =12∠AOC -12∠AOB =12(∠AOC -∠AOB )=12∠BOC . 因为∠MON =40°,所以∠BOC =80°,所以∠COD +∠AOB =180°-80°=100°.又因为∠AOB =∠COD ,所以∠AOB =∠COD =50°,所以∠AOC =180°-∠COD =130°.。
余角、补角、对顶角

互为余角90°
互为补角180°
通过练习进一步巩固今天所学的知识。培养学生自主学习能力。整理知识,检验目标的实施情况
板书设计
情境创设
1、
2、
例1:……
……
……
例2:……
……
……
习题……
……
……
作业布置
课后随笔
互补,互余是一种特殊的数量关系
答:∠2与∠3相等
因为∠1与∠2互余,∠1与∠3互余
所以∠2=90°—∠1,∠3=90°—∠1
所以∠2=∠3
引导学生交流得出结论,
同角(或等角)的余角相等
同角(或等角)的补角相等。
通过具体情景让学生探索和发现,在不断提出问题和解决问题的氛围中发展空间观念。使学生了解余角、补角的概念和由来,培养学生的观察力和归纳能力
课时编号
备课时间
课题
6.3余角、补角、对顶角(1)
教学目标
1、在具体情景了解余角、补角,概念
2、知道等角的余角相等,等角的补角相等
3、经历观察—操作—说理,交流等过程,进一步发展宽间的观念
教学重点
余角、补角,概念
教学难点
同角(等角)的余角相等,同角(等角)的补角相等
教学过程
教学内容
教师活动
学生活动
用一副三角尺,在实际操作中,演示课本中的图
如果两个角的和是一个直角,这两个的角叫做互为余角,简称互余,其中一个是另一个的余角。
如果两个角的和是一个平角,这两个的角叫做互为补角,简称互补,其中一个是另一个的补角。
思考:同一块三角板上有两个锐角互余吗?
如果∠α+∠β=90°那么∠α与∠β互余
62 角、余角、补角以及对顶角(解析版)

2021-2022学年七年级数学上册同步课堂专练(苏科版)6.2角、余角、补角以及对顶角一、单选题1.下列说法中正确的是()A.射线AB与射线BA是同一条射线B.两条射线组成的图形叫做角C.各边都相等的多边形是正多边形D.连接两点的线段的长度叫做两点之间的距离【答案】D【详解】解:A、射线AB与射线BA不是同一条射线,故此选项错误;B、有公共端点是两条射线组成的图形叫做角,故此选项错误;C、各边都相等、各角都相等的多边形是正多边形,故此选项错误;D、连接两点的线段的长度叫做两点之间的距离,故此选项正确.故选:D.2.如图,直线AB,CD相交于点O,分别作∠AOD,∠BOD的平分线OE,OF.将直线CD绕点O旋转,下列数据与∠BOD大小变化无关的是()A.∠AOD的度数B.∠AOC的度数C.∠EOF的度数D.∠DOF的度数【详解】 解:OE ,OF 平分∠AOD ,∠BOD11,22AOE EOD AOD DOF FOB BOD ∴∠=∠=∠∠=∠=∠180AOD BOD ∠+∠=︒111()90222EOD DOF AOD BOD AOD BOD ∴∠+∠=∠+∠=∠+∠=︒90EOF ∴∠=︒180AOD BOD ∴∠=︒-∠1,2AOC BOD DOF BOD ∴∠=∠∠=∠都与∠BOD 大小变化有关,只有∠EOF 的度数与∠BOD 大小变化无关, 故选:C .3.如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,12740'∠=︒,则2∠的余角是( )A .1720'︒B .3220︒'C .3320'︒D .5820︒'【答案】B解:由题意可得:∠2+∠EAC =90° ∠∠2的余角是∠EAC∠∠EAC =601602740'3220'︒-∠=︒-︒=︒ 故选:B .4.设一个锐角与这个角的补角的差的绝对值为α,则( ) A .090α︒<<︒或90180α︒<<︒ B .0180α︒<<︒ C .090α︒<<︒ D .090α︒<≤︒【答案】B 【详解】解:设这个角的为x 且0<x <90°,根据题意可知180°-x -x =α, ∠α=180°-2x ,∠180°-2×90°<α<180°-2×0°, 0°<α<180°. 故选:B .5.如图,直线a 、b 被直线c 所截,则下列说法错误的是( )A .1∠与2∠是邻补角B .1∠与3∠是对顶角C .2∠与4∠是同位角D .3∠与4∠是内错角【答案】D 【详解】解:A 、1∠与2∠是邻补角,故原题说法正确;B 、1∠与3∠是对顶角,故原题说法正确;C 、2∠与4∠是同位角,故原题说法正确;D 、3∠与4∠是同旁内角,故原题说法错误;答案:D .6.下列推理错误的是( )A .因为1223∠=∠∠=∠,,所以13∠=∠B .因为12123∠=∠∠+∠=∠,,所以321∠=∠C .因为1223∠+∠=∠,所以1323∠=∠∠=∠,D .因为1∠与2∠互补,13∠=∠,所以2∠与3∠互补 【答案】C 【详解】解:A .因为∠1=∠2,∠2=∠3,所以∠1=∠3(等量代换),故原说法正确; B .因为∠1=∠2,∠1+∠2=∠3,所以∠3=∠1+∠1=2∠1,故原说法正确; C .当∠1+∠2=2∠3时,∠1,∠2不一定等于∠3,故原说法错误; D .因为∠1与∠2互补,∠1=∠3,所以∠2与∠3互补,故说法正确. 故选:C .7.下列说法正确的是( )A.如果∠1+∠2+∠3=90º,那么∠1、∠2、∠3三个互余B.过一点有且只有一条直线与已知直线平行C.不相等的两个角一定不是对顶角D.若两条直线被第三条所截,则同位角相等【答案】C【详解】如果两个角的和是90°,称这两个角互为余角,所以选项A说法错误;过直线外一点有且只有一条直线与已知直线平行,所以选项B说法错误;对顶角永远相等,所以不相等的两个角一定不是对顶角,所以选项C正确;若两条平行直线被第三条所截,则同位角相等,所以选项D说法错误;故选C.8.在下列说法中,正确的是()A.连接A,B就得到AB的距离B.延长AOB∠的平分线C.一个有理数不是整数就是分数D.23-a是单项式【答案】C 【详解】解:A. 连接A ,B 就得到线段AB ,而线段AB 的长度叫做的距离,故原说法错误,不符合题意; B. AOB ∠的平分线就是射线,若延长也只能反向延长,故原说法错误,不符合题意; C. 一个有理数不是整数就是分数,原说法正确,符合题意; D.23-a 是多项式,故原说法错误,不符合题意; 故选:C . 二、填空题9.已知,//MN PQ ,将一副三角板按照如图方式摆放在平行线之间,且线段BC 落在直线MN 上,线段DE 落在直线PQ 上,其中60ACB ∠=︒,45AED ∠=︒,CO 平分ACB ∠,EO 平分AED ∠,两条角平分线相交与点O ,则COE ∠=________︒.【答案】52.5 【详解】延长CO 交PQ 于点F ,则∠COE =∠CFE +∠OEF ,∠60ACB ∠=︒,45AED ∠=︒,CO 平分ACB ∠,EO 平分AED ∠, ∠∠BCF =30°,∠OEF =22.5°, ∠//MN PQ , ∠∠BCF =∠CFE ,∠∠COE =30°+22.5°=52.5°,故答案为:52.5°.10.如图是某城市一座古塔底部平面图,在不能进入塔内测量的情况下,学习兴趣小组设计了如图所示的一种测量方案,学习兴趣小组认为测得COD ∠的度数就是AOB ∠的度数.其中的数学原理是__________.【答案】对顶角相等 【详解】解:∠∠COD 与∠AOB 互为对顶角 ∠∠COD =∠AOB 故答案为:对顶角相等11.如图,AB 和CD 交于点O ,则AOC ∠的邻补角是___;AOC ∠的对顶角是___;若40AOC ∠=︒,则BOD ∠=___,AOD ∠=___,BOC ∠=___.【答案】AOD ∠和BOC ∠ BOD ∠ 40° 140° 140° 【详解】解:AB 和CD 交于点O ,则AOC ∠的邻补角是AOD ∠和BOC ∠;AOC ∠的对顶角是BOD ∠,40AOC ∠=︒,40BOD AOC ∴∠=∠=︒,180********AO D AO C ∴∠=︒-∠=︒-︒=︒, 140BO C AO D ∴∠=∠=︒.故答案为:AOD ∠和BOC ∠;BOD ∠;40︒;140︒;140︒.12.如图,某海域有三个小岛A ,B ,O ,在小岛O 处观测到小岛A 在它北偏东62°的方向上,观测到小岛B 在它南偏东38°12'的方向上,则∠AOB 的补角的度数是_____.【答案】100°12′. 【详解】解:∠OA 是表示北偏东62°方向的一条射线,OB 是表示南偏东38°12′方向的一条射线, ∠∠AOB =180°-62°-38°12′=79°48′,∠∠AOB 的补角的度数是180°-79°48′=100°12′. 故答案是:100°12′. 三、解答题13.如图,已知直线AB,CD相交于点O,射线OE把∠AOC分成两部分.(1)写出图中∠AOC的对顶角,∠COE的补角是;(2)已知∠AOC=60°,且∠COE:∠AOE=1:2,求∠DOE的度数.【答案】(1)∠BOD,∠DOE;(2)160°【详解】解:(1)由图形可知,∠AOC的对顶角是∠BOD,∠COE的补角是∠DOE;(2)设∠COE=x,则∠AOE=2x,∠∠AOC=60°,∠x+2x=60,解得x=20,即∠COE=20°,∠AOE=40°,∠∠AOC+∠AOD=180°,∠∠AOD=120°,∠∠DOE=∠AOE+∠AOD=40°+120°=160°.14.在同一平面内已知∠AOB=150°,∠COD=90°,OE平分∠BOD.(1)当∠COD的位置如图1所示时,且∠EOC=35°,求∠AOD的度数;(2)当∠COD的位置如图2所示时,作∠AOC的角平分线OF,求∠EOF的度数;(3)当∠COD的位置如图3所示时,若∠AOC与∠BOD互补,请你过点O作射线OM,使得∠COM为∠AOC的余角,并求出∠MOE的度数.(题中的角都是小于平角的角)【答案】(1)40°;(2)150°;(3)见解析,∠MOE的度数为105°或135°.【详解】解:(1)∠∠COD=90°,∠EOC=35°,∠∠EOD=55°,∠OE平分∠BOD,∠∠BOD=2∠EOD=110°,∠∠AOD=∠AOB﹣∠BOD=40°;(2)∠∠AOB=150°,∠COD=90°,∠∠AOC+∠BOD=360°﹣150°﹣90°=120°,∠OF平分∠AOC,OE平分∠BOD,∠∠COF=12∠AOC,∠DOE=12∠BOD,∠∠COF+∠DOE=60°,∠∠EOF=60°+90°=150°;(3)设∠AOC=α,∠∠AOB=150°,∠COD=90°,∠∠AOD=90°﹣α,∠BOC=150°﹣α,∠∠AOC与∠BOD互补,∠∠AOC+∠BOD=180°,∠∠AOD+∠BOC=180°,∠90°﹣α+150°﹣α=180°,∠α=30°,即∠AOC=30°,∠∠BOD=150°,∠OE平分∠BOD,∠∠DOE=∠BOE=75°,如图3,∠∠COM为∠AOC的余角,∠∠COM=60°,∠∠DOM=30°,∠∠MOE=∠MOD+∠DOE=30°+75°=105°,如备用图,∠∠COM为∠AOC的余角,∠∠COM=60°,∠BOM=60°,∠∠MOE =∠BOM +∠BOE =60°+75°=135°;综上所述,∠MOE 的度数为105°或135°.15.已知直线AB 与CD 相交于点O .(∠)如图1,若90AOM ∠=︒,OC 平分AOM ∠,则AOD ∠=_________.(∠)如图2,若90AOM ∠=︒,4BOC BON ∠=∠,OM 平分CON ∠,求MON ∠的大小;(∠)如图3,若AOM α∠=,4BOC BON ∠=∠,OM 平分CON ∠,求MON ∠的大小(用含α的式子表示).【答案】(∠)135°;(∠)54°;(∠)54035α︒- 【详解】解(∠)90AOM =︒∠,OC 平分AOM ∠,11904522AOC AOM ∴∠=∠=⨯︒=︒, 180AOC AOD ∠+∠=︒,180********AOD AOC ∴∠=-∠=︒-︒︒=︒,即AOD ∠的度数为135︒;(∠)4BOC NOB ∠=∠∴设NOB x ∠=︒,4BOC x ∠=︒,43CON COB BON x x x ∴∠=∠-∠=︒-︒=︒,OM 平分CON ∠,1322COM MON CON x ∴∠=∠=∠=︒, 3902BOM x x ∠=︒+︒=︒, 36x ∴=︒,33365422MON x ∴∠=︒=⨯︒=︒, 即MON ∠的度数为54︒;(∠)4BOC NOB ∠=∠∴设NOB x ∠=︒,4BOC x ∠=︒,43CON COB BON x x x ∴∠=∠-∠=︒-︒=︒, OM 平分CON ∠,1322COM MON CON x ∴∠=∠=∠=︒, 31802BOM x x α∠=︒+︒=︒-, 36025x α︒-∴=, 336025403255MON αα︒-︒-∴∠=⨯=.。
余角、补角、对顶角的相关计算(人教版)(含答案)

余角、补角、对顶角的相关计算(人教版)一、单选题(共15道,每道6分)1.如果一个角的余角是50°,那么这个角的补角是( )A.130°B.140°C.150°D.160°答案:B解题思路:试题难度:三颗星知识点:补角的定义2.已知∠1与∠2互余,且∠1=35°,则∠2的补角的度数为( )A.145°B.115°C.135°D.125°答案:D解题思路:试题难度:三颗星知识点:补角的定义3.若∠α是它的余角的2倍,则∠α=( )A.30°B.45°C.60°D.120°答案:C解题思路:试题难度:三颗星知识点:余角4.若∠α和∠β互余,则下列式子:①180°-∠β;②∠α+2∠β;③90°+∠α;④2∠α+∠β.其中能表示∠β补角的有( )A.①③B.①④C.①③④D.①②③④答案:C解题思路:试题难度:三颗星知识点:补角5.如图,已知AB⊥CD,垂足为点O,EF过点O,则图中∠FOB与∠EOD的关系是( )A.∠FOB+∠EOD=180°B.∠FOB+∠EOD=90°C.∠FOB=∠EODD.无法确定答案:B解题思路:试题难度:三颗星知识点:补角的定义6.如图,∠AOB=15°,∠AOC=90°,点B,O,D在同一直线上,则∠COD的度数为( )A.75°B.15°C.105°D.165°答案:C解题思路:试题难度:三颗星知识点:补角的定义7.如图,OA⊥OB,OC⊥OD,则( )A.∠AOC=∠AODB.∠AOC=∠BODC.∠AOD=∠BODD.以上结论都不对答案:B解题思路:试题难度:三颗星知识点:余角的定义8.如图,∠AOC=∠BOD=90°,若∠AOB=150°,则∠DOC的度数为( )A.30°B.40°C.50°D.60°答案:A解题思路:试题难度:三颗星知识点:余角的定义9.如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOD的度数是( )A.25°B.35°C.45°D.55°答案:D解题思路:试题难度:三颗星知识点:对顶角相等10.如图所示,∠AOC=90°,∠COB=α,OD平分∠AOB,则∠COD的度数为( )A. B.C.45°-αD.90°-α答案:B解题思路:试题难度:三颗星知识点:角平分线定义11.如图,∠COD为平角,AO⊥OE,∠DOE=∠AOC,则∠DOE的度数为( )A.30°B.45°C.60°D.75°答案:A解题思路:试题难度:三颗星知识点:补角12.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,则下列结论错误的是( )A.∠A=∠BCDB.∠A与∠ACD互余C.∠A与∠BCD互余D.∠B=∠ACD答案:C解题思路:试题难度:三颗星知识点:同角或等角的余角相等13.如图,OC⊥AB,∠COD=45°,则图中互为补角的角共有( )A.1对B.2对C.3对D.4对答案:C解题思路:试题难度:三颗星知识点:补角14.若∠α与∠β互余,∠β与∠γ互余,则∠α与∠γ的关系是( )A.互余B.互补C.相等D.不确定答案:C解题思路:试题难度:三颗星知识点:补角的定义15.如果∠A与∠B互补,∠B与∠C互余,则∠A与∠C的关系是( )A.互余B.互补C.∠A-∠C=90°D.∠A-∠C=180°答案:C解题思路:试题难度:三颗星知识点:补角的定义。
第一节 余角与补角、对顶角

第一节 余角、补角与对顶角1.互为余角:如果两个角的和是直角,那么称这两个角互为余角。
注:互为余角仅仅表明了两个角之间的度量关系,与角的位置无关。
2.互为补角:如果两个角的和是平角,那么称这两个角互为补角。
注:和是平角,说明了互为补角仅仅表明了两个角之间的度量关系,与角的位置无关。
3.对顶角直线AB 与CD 相交于点O ,∠AOC 与∠BOD 有公共顶点O ,它们的两边互为反向延长线,这样的两个角叫做对顶角。
注:(1)两条直线相交;(2)有公共顶点;(3)无公共边(4)对顶角是成对的,是具有特殊位置的两个角。
4.角的重要性质:(1)同角或等角的余角相等。
(2)同角或等角的补角相等。
(3)对顶角相等。
例1:判断题(1).若∠1+∠2=90°,则∠1与∠2互余.( ) (2).若∠A 与∠B 互补,则∠A +∠B =180°.( )(3).若∠1与∠2互补,∠2与∠3互补,则∠1与∠3互补.( ) (4).若∠AOB +∠BOC =180°,则点A 、O 、C 必在同一直线上.( ) (5).若∠α+∠β+∠γ=90°,则∠α、∠β、∠γ互余.( )例2:如图1,直线l 1与l2相交,∠1=50°,则∠2=_________,∠3=_________.图1 图2例3:如图2,直线AB 与CD 相交于O 点,且∠AOD =90°,则∠AOC =_________=_________=_________=_________.例4:如图3,若AO ⊥CO ,BO ⊥DO ,∠BOC=150°,则∠DOC=________,∠AOD =________.图3 图4 图5AOBCA BCODOBA C例5:如图4,直线AB 与CD 相交于O ,∠EOD =90°,正确填写下列两角关系的名称.∠1与∠2:______________________ ∠2与∠3:______________________ ∠2与∠4:______________________ ∠1与∠4:______________________ 例6:如图5,AO ⊥BO ,直线CD 经过点O ,∠AOC =30°,求∠BOD 的度数. 例7:两条直线相交于一点,则共有对顶角的对数为( )A.1对B.2对C.3对D.4对例8:下面说法正确的个数为( )①对顶角相等 ②相等的角是对顶角 ③若两个角不相等,则这两个角一定不是对顶角 ④若两个角不是对顶角,则这两个角不相等A.1个B.2个C.3个D.4个例9:若∠1和∠2互余,∠2与∠3互余,∠1=40°,则∠3等于( )A.40°B.130°C.50°D.140°例10:如图,∠1和∠2是对顶角的图形有( )A.(1)(3)B.(2)(3)C.(3)D.(3)(4)例11:如图,已知直线AB 、CD 相交于点O ,OE 平分∠BOD ,OF 平分∠COB ,:4:1AOD DOC ∠∠=,AOF ∠的度数。
七年级数学上册知识讲义-6.3认识余角、补角、对顶角-苏科版
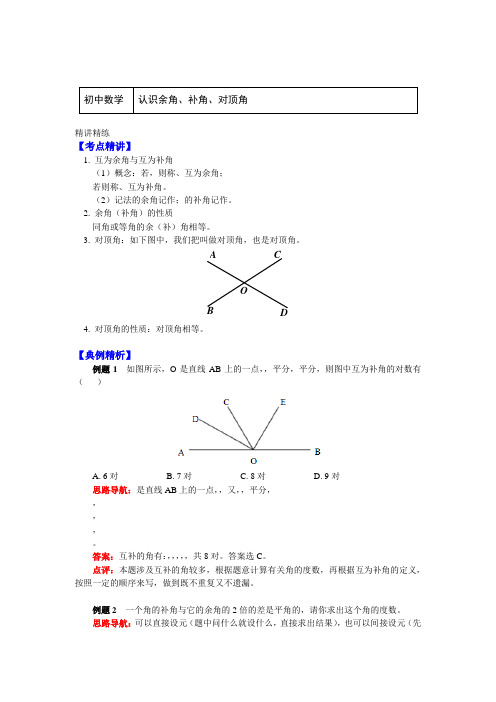
初中数学认识余角、补角、对顶角精讲精练【考点精讲】1. 互为余角与互为补角(1)概念:若,则称、互为余角;若则称、互为补角。
(2)记法的余角记作;的补角记作。
2. 余角(补角)的性质同角或等角的余(补)角相等。
3. 对顶角:如下图中,我们把叫做对顶角,也是对顶角。
OADBC4. 对顶角的性质:对顶角相等。
【典例精析】例题1 如图所示,O是直线AB上的一点,,平分,平分,则图中互为补角的对数有()A. 6对B. 7对C. 8对D. 9对思路导航:是直线AB上的一点,,又,,平分,,,,。
答案:互补的角有:,,,,,共8对。
答案选C。
点评:本题涉及互补的角较多,根据题意计算有关角的度数,再根据互为补角的定义,按照一定的顺序来写,做到既不重复又不遗漏。
例题2 一个角的补角与它的余角的2倍的差是平角的,请你求出这个角的度数。
思路导航:可以直接设元(题中问什么就设什么,直接求出结果),也可以间接设元(先求出这个角,再求出它的余角),然后列方程求解。
答案:设这个角的度数为,则它的补角、余角分别为,(),根据题意得,解得,所以这个角的度数为60度。
点评:有关余角和补角的计算题目,常设未知数,根据题意列方程求解。
所设的未知数不同,所得到的方程也不同。
例题3 如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线。
D(1)求∠2和∠3的度数;(2)OF平分∠AOD吗?为什么?思路导航:(1)根据邻补角的定义,即可求得∠2的度数,根据角平分线的定义和平角的定义即可求得∠3的度数;(2)根据OF分得∠AOD的两部分角的度数即可说明。
答案:(1)∵∠BOC+∠2=180°,∠BOC=80°,∴∠2=180°-80°=100°;∵OE是∠BOC的角平分线,∴∠1=40°。
∵∠1+∠2+∠3=180°,∴∠3=180°-∠1-∠2=180°-40°-100°=40°。
对顶角 互补 互余

第二章相交线与平行线1 两条直线的位置关系第1课时对顶角、补角和余角【知识与技能】在具体情境中了解相交线、平行线、补角、余角、对顶角的定义,知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等,并能解决一些实际问题.【过程与方法】经历操作、观察、猜想、交流、推理等获取信息的过程,进一步发展空间观念、推理能力和有条理表达的能力.【情感态度】激发学生学习数学的兴趣,认识到现实生活中蕴含着大量的数量和图形的有关问题,这些问题可以抽象成数学问题,用数学方法予以解决.【教学重点】1.余角、补角、对顶角的概念.2.理解等角的余角相等、等角的补角相等、对顶角相等.【教学难点】对“在同一平面内的两条直线”含义的理解.理解等角的余角相等,等角的补角相等.一、情景导入,初步认知向同学们展示一些生活中的图片,让学生观察生活中的两条直线之间的位置关系.【教学说明】数学来源于生活,通过课前开放,引导学生从身边熟悉的图形出发,体会数学与生活的联系,总结出同一平面内两条直线的基本位置关系,体会本章内容的重要性和在生活中的广泛应用,为引入新课做好准备.通过亲身经历提炼有关数学信息的过程,可以让学生在直观有趣的问题情境中学到有价值的数学.二、思考探究,获取新知探究1:相交线、平行线1.从上面的图片中,你能找出两条直线有几种位置关系吗?2.请各组同学每人拿出两支笔,用它们代表两条直线,在同一平面内,随意移动笔,观察笔与笔有几种位置关系?各种位置关系,分别叫做什么?.【归纳结论】同一平面内的两条直线的位置关系有平行和相交两种;若两条直线只有一个公共点,我们称这两条直线为相交线;同一平面内不相交的两条直线叫做平行线.【教学说明】让学生用两支笔动手操作,不但培养了学生的动手能力,还能让学生更深层次的体会到平行线的含义,进一步明确同一平面内两条直线的位置关系.探究2:对顶角的概念和性质请先画一画:两条直线直线AB和CD,交于点O,再回答下列问题1.观察:∠1和∠2的位置有什么关系?大小有何关系?为什么?小组合作交流,尝试用自己的语言描述对顶角的定义.2.剪刀可以看成两直线相交,那么剪刀在剪东西的过程中,∠1和∠2还保持相等吗?∠3和∠4呢?你有何结论?【归纳结论】两个角的两边互为反向延长线,则这两个角叫做对顶角.对顶角相等.探究3:余角、补角的概念和性质1.用量角器,量出∠1、∠2、∠3、∠4的度数,观察∠1与∠3有什么关系?2.图中还有哪些角,具有这种关系?【归纳结论】如果两个角的和是180°,那么称这两个角互为补角.类似的,如果两个角的和是90°,那么称这两个角互为余角.3.打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图抽象成几何图形,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.小组合作交流,解决下列问题:问题1:哪些角互为补角?哪些角互为余角?问题2:∠3与∠4有什么关系?为什么?问题3:∠AOC与∠BOD有什么关系?为什么?你还能得到哪些结论?【归纳结论】同角或等角的余角相等.同角或等角的补角相等.【教学说明】概括归纳得到猜想和规律,并加以验证,是创新的重要方法.结合具体的学习内容,设计有效的数学探究活动,使学生经历数学的发生发展过程,积累数学活动经验.三、运用新知,深化理解1.在下列4个判断中:①在同一平面内,不相交的两条线段一定平行;②不相交的两条直线一定平行;③在同一平面内,不平行的两条射线一定相交;④在同一平面内,不平行的两条直线一定相交.其中正确的个数是(D)A.4B.3C.2D.12.如果一个角的补角是150°,那么这个角的余角的度数是60°3.已知∠α=24°,且∠α与∠β互余,∠β与∠γ互余,则∠γ的余角和补角的度数分别为66°,156°.4.判断.(1)一个角有余角也一定有补角.()(2)一个角有补角也一定有余角.()(3)一个角的补角一定大于这个角.()答案:(1)√(2)×3)×5.填表:从中,你发现一个锐角的补角比它的余角大.答案:表格第一行:58°,148°;第二行:27°37′,117°37′;第三行:90°-x,180°-x;空格:90°.6.已知一个角的补角是它的余角的4倍,求这个角的度数.分析:可以利用方程思想解决这道题.解:设这个角为x°,则180-x=4(90-x),∴x=60.答:这个角是60°.7.如图,E、F是直线DG上两点,∠1=∠2,∠3=∠4=90°,找出图中相等的角并说明理由.解:∠5=∠6,理由是:等角的余角相等.8.如图,已知AOB是一直线,OC是∠AOB的平分线,∠DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?解:互余:∠1与∠2,∠1与∠4,∠2与∠3,∠4与∠3;互补:∠1与∠EOB,∠3与∠EOB,∠4与∠AOD,∠2与∠AOD,∠AOC 与∠BOC,∠AOC与∠DOE,∠BOC与∠DOE.相等:∠AOC=∠BOC=∠DOE,∠1=∠3,∠2=∠4.【教学说明】巩固本节课的知识点,检验学生的掌握程度.四、师生互动,课堂小结1.你学到了哪些知识点?2.你学到了哪些方法?3.你还有哪些困惑?1.布置作业:教材“习题2.1”中第1、2、3题.2.完成同步练习册中本课时的练习.本节的教学是非常成功的一节课,学生的积极性、主动性完全迸发,整个课堂完全就是和谐统一的有机整体.仔细想想,从中得出:对于新旧知识具有类似内容的情况可以用类比的方法,这样省时高效;对于几何命题的验证,可通过多种方法证明,如本节的“等角的余角相等”,可以通过测量、叠合法、逻辑证明等方法,这样可以让不同的学生得到清晰而深刻的理解;更重要的是通过本节学习知道说明一个几何命题的过程是怎样的,须经历“猜想—推理—结论”这样一个过程,为以后的学习做了铺垫.。
(完整版)初一平行线与相交线经典试题

第一章:平行线与相交线考点1:余角、补角、对顶角一、考点讲解:1.余角:如果两个角的和是直角,那么称这两个角互为余角.2.补角:如果两个角的和是平角,那.么称这两个角互为补角.3.对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.4.互为余角的有关性质:①∠1+∠2=90°,则∠1、∠2互余.反过来,若∠1,∠2互余.则∠1+∠2=90○.②同角或等角的余角相等,如果∠l十∠2=90○,∠1+∠3= 90○,则∠2= ∠3.5.互为补角的有关性质:①若∠A +∠B=180○则∠A、∠B互补,反过来,若∠A、∠B 互补,则∠A+∠B=180○.②同角或等角的补角相等.如果∠A +∠C=18 0○,∠A+∠B=18 0°,则∠B=∠C.6.对顶角的性质:对顶角相等.二、经典考题剖析:【考题1-1】(2004、厦门,2分)已知:∠A= 30○,则∠A的补角是________度.解:150○点拨:此题考查了互为补角的性质.【考题1-2】(2004、青海,3分)如图l-2-1,直线AB,CD相交于点O,OE⊥AB 于点O,OF平分∠AOE,∠1=15○30’,则下列结论中不正确的是()A.∠2 =45○B.∠1=∠3C.∠AOD与∠1互为补角D.∠1的余角等于75○30′解:D 点拨:此题考查了互为余角,互为补角和对顶角之间的综合运用知识.三、针对性训练:(30 分钟) (答案:220 ) 1._______的余角相等,_______的补角相等.2.∠1和∠2互余,∠2和∠3互补,∠1=63○,∠3=__3.下列说法中正确的是()A.两个互补的角中必有一个是钝角B.一个角的补角一定比这个角大C.互补的两个角中至少有一个角大于或等于直角D.相等的角一定互余4.轮船航行到C处测得小岛A的方向为北偏东32○,那么从A处观测到C处的方向为()A.南偏西32○B.东偏南32○C.南偏西58○D.东偏南58○5.若∠l=2∠2,且∠1+∠2=90○则∠1=___,∠2=___.6.一个角的余角比它的补角的九分之二多1°,求这个角的度数.7.∠1和∠2互余,∠2和∠3互补,∠3=153○,∠l=_8.如图l-2-2,AB⊥CD,AC⊥BC,图中与∠CAB互余的角有()A.0个B.l个C.2个D.3个9.如果一个角的补角是150○,那么这个角的余角是____________10.已知∠A和∠B互余,∠A与∠C互补,∠B与∠C的和等于周角的13,求∠A+∠B+∠C的度数.11.如图如图1―2―3,已知∠AOC与∠B都是直角,∠BOC=59○.(1)求∠AOD的度数;(2)求∠AOB和∠DOC的度数;(3)∠A OB与∠DOC有何大小关系;(4)若不知道∠BOC的具体度数,其他条件不变,这种关系仍然成立吗?考点2:同位角、内错角、同旁内角的认识及平行线的性质一、考点讲解:1.同一平面内两条直线的位置关系是:相交或平行.2.“三线八角”的识另:三线八角指的是两条直线被第三条直线所截而成的八个角.正确认识这八个角要抓住:同位角位置相同,即“同旁”和“同规”;内错角要抓住“内部,两旁”;同旁内角要抓住“内部、同旁”.3.平行线的性质:(1)两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.(2)过直线外一点有且只有一条直线和已知直线平行.(3)两条平行线之间的距离是指在一条直线上任意找一点向另一条直线作垂线,垂线段的长度就是两条平行线之间的距离.二、经典考题剖析:【考题2-1】(2004贵阳,3分)如图1―2―4,直线a ∥b,则∠A CB=________解:78○点拨:过点C作CD平行于a,因为a∥b,所以CD∥b.则∠A C D=2 8○,∠DCB=5 0○.所以∠ACB=78○.【考题2-2】(2004、开福,6分)如图1―2―5,AB∥CD,直线EF分别交A B、CD于点E、F,EG平分∠B EF,交CD于点G,∠1=5 0○求∠2的度数.解:65○点拨:由AB∥CD,得∠BEF=180○-∠1=130○,∠BEG=∠2.又因为EG平分∠BEF,所以∠2=∠BEG=12∠BEF=65°(根据平行线的性质)三、针对性训练:( 40分钟) (答案:220 ) 1.如图1-2-6,AB∥CD,AC⊥BC,图中与∠CAB互余的角有()A.l个B.2个C.3个D.4个2.下列说法中正确的个数是()(1)在同一平面内不相交的两条直线必平行;(2)在同一平面内不平行的两条直线必相交;(3)两条直线被第三条直线所截,所得的同位角相等;(4)两条平行线被第三条直线所截,一对内错角的平分线互相平行。
对顶角、余角和补角

探讨一
1、归纳对顶角的概念与性质. 定义:有_公__共__顶点,且两边互为反向延长线的两个 角叫做_对__顶__角___. 性质:对顶角_相__等__.
例题分析:
下列图形中,∠1与∠2是对顶角的是( )
如图,直线AB、CD,EF相交于点O,∠1=40°, ∠BOC=110°,求∠2的度数.
2、两直线的位置关系与对顶角
【归纳】 1.概念:(1)如果两个角的和是_9_0_°__,那 么称这两个角互为余角. (2)如果两个角的和是_1_8_0_°__,那么称这两个角互为 补角. 2.性质:同角或等角的余角_相__等__,同角或等角的补 角_相__等__.
【思考】 1.任何角都有余角吗? 提示:由余角的定义可知,只有小于直角的角才有余角. 2.“相等的角是对顶角”这句话对吗? 提示:不对,对顶角是与两角的位置有关系的,必须是 有公共顶点,且两边互为反向延长线的两个角叫对顶角.
巩固训练 1.同一平面内有三条直线,如果只有两条互相平 行,那么它们的交点个数为( ) (A)0 (B)1 (C)2 (D)3 【解析】选C.同一平面内有三条直线,如果只 有两条互相平行,那么第三条直线与这两条直 线相交,所以共有2个交点.
首页
2.下列各图中,∠1与∠2互为对顶角的是( )
【解析】选C.对顶角必备的两个要素:有公共的 顶点,两边互为反向延长线.
分线吗?并简述理由;
(2)如图②,若∠ECD=α,CD在∠BCE的内部,请你猜想∠ACE
与∠DCB是否相等?并简述理由;
(3)在(2)的条件下,请问∠ECD与∠ACB的和是多少?并简述理由 解析:(1)首先根据直角三角板的特点得到 ∠ACD=90°,∠ECB=90°.再根据角平 分线的定义计算出∠ECD和∠DCB的度数 即可; (2)∠ACE与∠DCB相等,根据“等角的余角 相等”即可得到答案; (3)根据角的和差关系进行等量代换即可.
角的数量关系(余角,补角)练习题及解析

角的数量关系(余角,补角)练习题及解析下面是角的数量关系(余角,补角)的相应练习题。
有兴趣的同学可以做一做。
①如果一个角的余角和这个角的补角互补,那么这个角的度数是多少。
②若∠A与∠B互为余角,且∠A比∠B大,则∠B的补角是( )。
A:2(∠A-∠B) B:2(∠A+∠B) C:2∠A+∠B D:∠A+2∠B③一个角的补角的16分之一是6°15′,则这个角是多少度。
④如果∠AOC与∠BOD都是直角,已知∠BOC:∠AOD=5:7,求∠AOB的度数。
⑤∠A与∠B互余,∠A与∠C互补,已知∠B=12°34′56″ 那么∠C= 。
(用度分秒表示)⑥∠A的补角是∠B的补角的3倍,且∠A比∠B的一半大15°,求∠A的度数。
①答案:45°解析:设这个角是x度,根据等量关系列方程90-x+(180-x)=180 解得x=45②答案:C解析:∠A与∠B互为余角,所以∠A+∠B=90°∠B的补角是180°-∠B = 2(∠A+∠B)-∠B=2∠A+∠B③答案:80°解析:这个角的补角是6°15′× 16 = 100°所以这个角是180°-100°=80°④答案:15°解析:∠AOB=∠COD(根据它俩都与∠BOC互余),∠BOC:(∠BOC+2∠AOB)=5:7得到∠BOC:∠AOB=5:1,它们的和是90°,所以∠AOB=90°÷6=15°⑤答案:102°34′56″解析:∠A=90°-∠B∠C=180°-∠A=180°-(90°-∠B)=∠B+90°=102°34′56″⑥答案:90°解析:根据第一个条件,180°-∠A=3(180°-∠B)根据第二个条件,∠A=0.5∠B+15°,即∠B=2(∠A-15°)代入第一个方程,解得∠A=90°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
余角和补角和对顶角余角:如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A补角:如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A的补角=180°-∠A对顶角:一个角的两边分别是另一个角的反向延长线,这两个角是对顶角。
两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线相交,构成两对对顶角。
对顶角相等.对顶角与对顶角相等.对顶角是对两个具有特殊位置的角的名称; 对顶角相等反映的是两个角间的大小关系。
补角的性质:同角的补角相等。
比如:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B。
等角的补角相等。
比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:同角的余角相等。
比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。
比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
注意:①钝角没有余角;②互为余角、补角是两个角之间的关系。
如∠A+∠B+∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A+∠B+∠C=180°,不能说∠A、∠B、∠C互为补角;③互为余角、补角只与角的度数相关,与角的位置无关。
只要它们的度数之和等于90°或180°,就一定互为余角或补角。
余角与补角概念认识提示:(1)定义中的“互为”一词如何理解?如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 ,同样∠2的补角是∠1。
(2)互余、互补的两角是否一定有公共顶点或公共边?两角互余或互补,只与角的度数有关,与位置无关。
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、∠3 互余(互补)吗?不能,互余或互补是两个角之间的数量关系。
已知∠A 与∠B 互余,∠B 与∠C 互补,若∠A=50°,则∠C 的度数是 [ D ] A .40° B .50° C .130° D .140° 如果∠A 的补角是它的余角的4倍,则∠A=______度.设∠A 为x ,则∠A 的余角为90°-x ,补角为180°-x ,根据题意得,180°-x=4(90°-x ), 解得x=60°. 故答案为:60.已知∠ α=50°17',则∠α的余角和补角分别是 [ B ]A .49°43',129°43'B .39°43',129°43'C .39°83',129°83'D .129°43′,39°43′两个角的比是6:4,它们的差为36°,则这两个角的关系是( )A .互余B .相等C .互补D .以上都不对设一个角为6x ,则另一个角为4x , 则有6x-4x=36°,∴x=18°,则这两个角分别为108°,72°, 而108°+72°=180°∴这两个角的关系为互补. 故选C .如果∠A=35°18′,那么∠A 的余角等于______.如果∠A=35°18′,那么∠A 的余角等于90°-35°18′=54°42′. 故填54°42′.已知∠1和∠2互补,∠3和∠2互余,求证:∠3= =21(∠1-∠2).证明:由题意得:∠2+∠3=90°,∠1+∠2=180°, ∴2(∠2+∠3)=∠1+∠2,故可得:∠3=21(∠1-∠2) 如图,∠1的邻补角是[ ]A.∠BOCB.∠BOC 和∠AOFC.∠AOFD.∠BOE 和∠AOF两个角互为补角,那么这两个角大小 [ D ]A.都是锐角B.都是钝角C.一个锐角,一个钝角D.无法确定如果两个角互为补角,那么这两个角一定互为邻补角,证明此命题真——加原因如果两个角互为补角,那么这两个角一定互为邻补角,这是假命题.如果两个角互为领补角,那么这两个角一定互为补角,这是真命题.譬如说,两直线平行,同旁内角互补,但互为同旁内角的两个角一定不互为领补角.如果两个角互补,那它们是邻补角”——————为什么说这个是假命题?两条平行线切出的同旁内角也互补,但是它们不是邻补角.所以说:“如果两个角互补,那它们是邻补角”是假命题!因为邻补角是相邻的两个角互补,那么这两个角是互为邻补角,而互补的两个角有不相邻的,比如四边形的两个对角互补,则这四点共圆如果一个角是36°,那么[ D ].它的余角是64°B.它的补角是64°C.它的余角是144°D.它的补角是144°下列说法中:①同位角相等;②两点之间,线段最短;③如果两个角互补,那么它们是邻补角;④两个锐角的和是锐角;⑤同角或等角的补角相等.正确的个数是()A.2个B.3个C.4个D.5个①同位角相等,说法错误;②两点之间,线段最短,说法正确;③如果两个角互补,那么它们是邻补角,说法错误;④两个锐角的和是锐角,说法错误;⑤同角或等角的补角相等,说法正确;说法正确的共有2个,故选:A.下列说法正确的是()A.小于平角的角是锐角B.相等的角是对顶角C.邻补角的和等于180°D.同位角相A、小于平角的角有:锐角、直角、钝角,故本选项错误;B、对顶角相等,相等的角不一定是对顶角,故本选项错误;C、邻补角的和等于180°正确,故本选项正确;D、只有两直线平行,才有同位角相等,故本选项错误.故选C.下列说法正确的是()A.相等的角是对顶角B.对顶角相等C.同位角相等D.锐角大于它的余角A、相等的角是对顶角,说法错误;B、对顶角相等,说法正确;C、同位角相等,说法错误;D、锐角大于它的余角,说法错误;故选:B.下列说法中,正确的是()A.对顶角相等B.内错角相等C.锐角相等D.同位角相等A、对顶角相等,说法正确;B、内错角相等,说法错误,只有两直线平行时,内错角才相等;C、锐角相等,说法错误,例如30°角和20°角;D、同位角相等,说法错误,只有两直线平行时,同位角才相等;故选:A.三条直线相交于一点可以构成几对对顶角?两条直线出现2*(2-1)=2对对顶角三条直线出现3*(3-1)=6对对顶角四条直线出现4*(4-1)=12对对顶角依次类推,n条直线相交于一点有n*(n-1)对对顶角三条直线相交于一点,共可组成______对对顶角.如图,单个的角是对顶角的有3对,两个角的复合角是对顶角的有3对,所以,共有对顶角3+3=6对.故答案为:6.三条直线相交与一点,能构成几对对顶角?四条呢?五条呢?N条呢?我要方法和答案!三条直线相交与一点,6对;四条直线相交与一点,12对;五条直线相交与一点,20对;N条直线相交与一点,N(N-1)对;如果有n条直线相交于一点,有多少对对顶角?n的平方减去2条数个数2 2=2x13 6=3x24 12=4x35 20=5x4…………n n(n-1)三条直线相交于一点,对顶角最多有______对.把三条直线相交于一点,拆成三种两条直线交于一点的情况,因为两条直线相交于一点,形成两对对顶角,所以三条直线相交于一点,有3个两对对顶角,共6对对顶角两条直线相交,有一个交点。
三条直线相交,最多有多少个交点?四条直线呢?你能发现什么规律吗?这个其实就是组合问题。
因为两条线构成一个交点,所以三条线时,从三条线中取两条线,有3*2/2=3种取法,所以有3个交点。
四条线中取两条,有4*3/2=6种取法,所以有6个交点。
n条线中取两条,有n(n-1)/2种取法,所以有n(n-1)/2个交点。
邻补角是互补的角是真命题吗当然是,邻补角相加等于180度就是互补啊互补的角是邻补角是真命题还是假命题若是真命题,请举反例两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角称为互为邻补角.可以随便画两个没有公共边的角,比如1个60度,另一个120度,显然它们是互补的,但是并不是邻补角所以互补的角是邻补角这是一个假命题应该说邻补角是互补的角,这才是真命题既相邻又互补的两个角是邻补角吗两条平行线切出的同旁内角也互补,但是它们不是邻补角。
所以说:“如果两个角互补,那它们是邻补角”是假命题!成互补关系的两个角互为邻补角是对还是错不对相邻的两个角互补称之为邻补角像两直线平行,同旁内角互补(这两个互补的角不相邻)、互补的两个角是邻补角用因为所以答因为两个角是邻补角所以两个角互补反过来不成立。
