四位2421码转余三码方法
常用编码(BCD编码、余3码、格雷反射码、奇偶校验码)

常用编码(BCD编码、余3码、格雷反射码、奇偶校验码)常用编码1、BCD编码 例 写出十进数563.97D对应的8421BCD码。
563.97D=0101 0110 0011 . 1001 01118421BCD 例 写出8421BCD码1101001.010118421BCD对应的十进制数。
1101001.010118421BCD=0110 1001 . 0101 10008421BCD=69.58D 在使用8421BCD码时一定要注意其有效的编码仅十个,即:0000~1001。
四位二进制数的其余六个编码1010,1011,1100,1101,1110,1111不是有效编码。
2、余3码 余3码也是一种BCD码,但它是无权码,但由于每一个码对应的8421BCD码之间相差3,故称为余3码,其一般使用较少,故正须作一般性了解,具体的编码如下表。
十进制数8421BCD码2421BCD码余3码0000000000011100010001010020010001001013001100110110401000100011150101101110006011011001001701111101101081000111010119100111111100100001,00000001,00000100,00113、格雷反射码(循环码)iddle">十进制数二进制数格雷码十进制数二进制数格雷码000000000810001100100010001910011101200100011101010111140100011012110010105010101111311011011601100*************70111010015111110004、奇偶校验码在数据的存取、运算和传送过程中,难免会发生错误,把“1”错成“0”或把“0”错成“1”。
奇偶校验码是一种能检验这种错误的代码。
它分为两部分;信息位和奇偶校验位。
余3码至8421BCD码的转换

有逻辑函数画出逻辑电路图如下:
又例如 00011100,(这表示 8 位的二进制数)如将其视为二进制数,其值 为 28,但不能当成 BCD 码,因为在 8421BCD 码中,它是个非法编码 。 右图为十进制数和 8421BCD 编码的对应关系表: 二:余 3 码 由 8421 码加 3 后形成的余 3 码是一种 BCD 码,它是由 8421 码加 3 后形 成的(即余 3 码是在 8421 码基础上每位十进制数 BCD 码再加上二进制数 0011 得到的)。因为 8421 码中无 1010~1111 这 6 个代码,所以余 3 码中无 0000~0010、1101~1111 这 6 个代码。余 3 码不具有有权性,但具有自补 性,余 3 码是一种“对 9 的自补码” 8421 码是中国大陆的叫法, 即 BCD 代码。Binary-Coded Decimal,简称 BCD,称 BCD 码或二-十进 制代码,亦称二进码十进数。是一种二进制的数字编码形式,用二进制编码 的十进制代码。这种编码形式利用了四个位元来储存一个十进制的数码,使 二进制和十进制之间的转换得以快捷的进行。这种编码技巧,最常用于会计 系统的设计里,因为会计制度经常需要对很长的数字串作准确的计算。相对 于一般的浮点式记数法,采用 BCD 码,既可保存数值的精确度,又可免却使
余三码表示的十进制数相加时,能正确产生进位信号,但对“和”必须修正。 修正的方法是:如果有进位,则结果加 3;如果无进位,则结果减 3。 8421BCD 码转换成余 3 码 通过 WEWB32 软件实验,输入 BCD 码转换成余三码的逻辑函数为: 输入端口 a,b,c,d,输出端口 e,f,g,h,用 G3,G2,G1,G0 表 示: G3=A’BC+A’BD+ABC’ G2=A’B’C+A’BC’D’+B’C’D G1=A’C’D’+A’CD+B’C’D’ G0=A’D’+B’C’D’
8421BCD码与余三码地相互转换

《数字逻辑电路》课程设计报告书2018年6月课程设计报告书设计 目 的1.掌握组合逻辑电路的基本概念与结构。
2.认识基本门电路74LS08、74LS32、74LS04、74LS48、74LS27、74LS86的各端口,并能够正确的使用。
3.了解8421BCD 码转换成余3码及余3码转换成8421BCD 码的工作原理,调试及故障排除方法。
4.掌握芯片间的逻辑关系,准确的进行连线。
设计 内容 及 功能 说明设计内容:使用“与”门(74LS08)、“或”门(74LS32)、非门(74LS04)、七段数码管译码器驱动器(74LS48)、三输入“或”门74LS27、“异或门”74LS86,设计8421BCD 码转换成余3码及余3码转换成8421BCD 码。
根据题意,要将8421BCD 码转换成余3码及余3码转换成8421BCD 码就必须得根据转换的规则来实现。
其中8421BCD 码转换成余三码时,8421BCD 码有0000—0110七种输入,另外有1101—1111是3种输入,这三种输入转换成余三码后用单个数码管无法进行显示;余3码转换成8421BCD 码时,余三码有0011—1111十三种输入,另外有0000—0010是三种输入单一数码管无法显示的,因此我们可以用这些无关小项来化简逻辑函数,从而得到优化的逻辑电路,正确的完成设计的要求。
功能说明:集成电路名称及引脚符号74LS08与门 74LS32或门74LS04非门 74LS27三输入“或”门内容及功能说明74LS48七段数码管译码器驱动器设 计 步 骤“8421BCD 码转余3码”“余3码转8421BCD 码”根据卡诺图,逻辑函数化简结果如下所示。
“8421BCD 码转余3码”DD C B A O D C CD D C B A O D B D C B C B D C B A O BC BD A D C B A O =+=++=++=),,,(0),,,(1),,,(2),,,(3“余3码转8421BCD 码”DD C B A Y D C D C D C B A Y D C B BCD C B D C B A Y ACD AB D C B A Y =+=++=+=),,,(0),,,(1),,,(2),,,(34.画出组合逻辑电路5.调试从A,B,C,D端输入8421BCD码得到的O3,O2,O1,O0和输入余3码得到的Y3,Y2,Y1,Y0如图所示,与预期结果相同。
8421BCD—余3码转换

8421BCD—余3码转换VHDL程序并行语句的应用一、实训目的1.巩固编译、仿真VHDL文件的方法。
2.掌握VHDL程序并行语句的应用。
二、实训器材计算机与Quartus ?工具软件。
三、实训指导(一) 实训原理8421BCD-余3码转换电路的真值表如表3-1所示。
表3-1 8421BCD-余3码转换电路的真值表输入输出a3 a2 a1 a0 y3 y2 y1 y00 0 0 0 0 0 1 10 0 0 1 0 1 0 00 0 1 0 0 1 0 10 0 1 1 0 1 1 00 1 0 0 0 1 1 10 1 0 1 1 0 0 00 1 1 0 1 0 0 10 1 1 1 1 0 1 01 0 0 0 1 0 1 11 0 0 1 1 1 0 0 (二)实训步骤1.设计输入VHDL文件(1)建立工程项目。
(2)建立VHDL文件。
(3)用条件信号赋语句或选择信号赋值语句等并行语句设计VHDL文件。
VHDL 代码如下:LIBRARY ieee;USE ieee.std_logic_1164.ALL; ENTITY ysmzh ISPORT(a:IN STD_LOGIC_VECTOR(3 DOWNTO 0);y:OUT STD_LOGIC_VECTOR(3 DOWNTO 0));END ysmzh;ARCHITECTURE a OF ysmzh IS BEGINPROCESS(a)BEGINCASE a ISWHEN "0000"=>y<="0011";WHEN "0001"=>y<="0100";WHEN "0010"=>y<="0101";WHEN "0011"=>y<="0110";WHEN "0100"=>y<="0111";WHEN "0101"=>y<="1000";WHEN "0110"=>y<="1001";WHEN "0111"=>y<="1010";WHEN "1000"=>y<="1011";WHEN "1001"=>y<="1100";WHEN OTHERS=>NULL;END CASE;END PROCESS;END a;2.编译仿真VHDL文件(1)编译VHDL文件。
8421码到余三循环码的转换电路仿真课设报告材料

东北大学分校计算机与通信工程院电子线路课程设计具有数显的数码转换电路(8421码—余3循环码)课程设计任务书专业:通信工程学号:4101015 学生:吴玉新设计题目:具有数显的码制转换电路8421码—余3循环码一、设计实验条件高频实验室二、设计任务及要求1. 要求输入为8421码。
输出为余三循环码2. 输出要具有数显功能三、设计报告的容1.前言数字电路课程设计是继“数字电路”课后开出的实践环节课程其目的是训练学生综合运用学过的数字电路的基本知识独立设计比较复杂的数字电路能力。
设计建立在硬件和软件两个平台的基础上。
硬件平台是可编程逻辑器件所选器件可保存在一片芯片上设计出题目要求的数字电路。
软件平台是multisim通过课程设计学生要掌握使用EDA电子设计自动化工具设计数字电路的方法包括设计输入便宜软件仿真下载及硬件仿真等全过程。
数字电路课程设计在于更好的让学生掌握这门课程并且了解其实用性知道该门课程和我们的生活息息相关并且培养学生的动手能力让学生对该门课程产生浓厚的兴趣。
2.设计容及其分析(1)方案一1.设计思路设计8421转余三循环码主要是考虑怎样找到二者之间的联系。
列出真值表后,根据值为1的那些项列出表达式,用最小项之和表示。
然后根据卡诺图进行化简,得出最简表达式。
最后根据表达式,在Multisim上画图仿真,用灯的灭(表示0)和亮(表示1)来表示码制的转换。
即可得到8421码对余三循环码的转换。
真值表:表1 8421转余三循环码真值表根据真值表得出表达式:X4=A——CX3=B——C——+ A——BCD+A——B——D——X2=A B——C——D——+A——B+A——C+A——DX1=A B——C——+A——BD+A——BC根据表达式画出逻辑电路图:图0 8421码转余3循环码逻辑电路图2.所用主要器件及芯片1.电源;2.导线若干,开关4个;3.白炽灯(5v 1w)4个;4.芯片:74ls04 2片74ls08 1片74ls11 2片74ls20 1片74ls32 2片3.线路运行介绍J1.J2.J3.J4端为输入8421码端,J1端是最高位,依次下排。
数字逻辑设计-至少3种方法2421码转余三码(纯原创)

3. 设计2421码转余3码的码制转换电路,至少用3种不同的方法(必须包括用加法器的方法),如:卡诺图化简,利用与非门实现;✹用译码器(如138)和若干门实现;✹用多路复用器(如151)和反相器实现;✹用加法器加辅助电路(如比较器、各类门)实现;✹用其它方法实现;不论用哪种方法,注意未使用项的处理,分析电路延迟和成本;写出详细的设计文档,并用相关软件画出原理图。
分工:李柳完成问题三的设计和记录,10月18号完成后在小组成员讨论组里给康钊未和白欣逸讲解,最后由白欣逸整理成文档,李柳制作ppt讲稿并代表小组担任主讲。
首先:设:以X3-X0分别表示2421码中的由高到低的各位,以F3-F0分别表示余三码中由高到低的各位。
3.1方案一:卡诺图化简,利用与非门实现。
将2421码转换成余三码,利用与非门实现。
具体步骤:1、列真值表2、卡诺图化简(多输出函数)3、电路处理,得到电路图:“与-或”式转换成“与非-与非”式3.1.1真值表表3.1.1.1 2421码转换成余三码真值表将真值表用卡诺图化简(多输出函数)表3.1.1.2 2421码转换成余三码卡诺图F0:F0=X0’F1:F2:F3:F3=X3得到关于F的函数:F3=X3F2=X3’X2+X2X1X0+X3’X1F1=X3’X1’X0’+X2X1’X0+X3’X1X0+X2X1X0’F0=X0’将F化简成与非门形式的函数:F3=X3F2=[(X3’X2)’(X2X1X0)’(X3’X1)’]’F1=[(X3’X1’X0’)’(X2X1’X0)’(X3’X1X0)’(X2X1X0’)’]’F0=X0’3.1.2 Multisim仿真将以上的函数化简成与非电路的形式,用Multisim仿真绘制原理图如下:图3.1.2 2421码转换成余三码卡诺图实现仿真图注意:未使用项:在右侧的6输入与非门中有输入未使用,根据与非门的性质,未使用项应该接高电平,这样不会影响电路性质,所以将所以未使用项都接上拉电阻接高电平,如原理图所示。
余三码

余三码实验目的设计一位十进制数的余三码编码的加法器单元电路。
实验基本要求在做本实验之前,需要具备几点要求:1)知道二进制是如何加减运算的;2)知道二进制和十进制之间的关系及相互之间的转化;3)知道逻辑门电路图符号代表什么含义及其功能特性是如何;以上3点是做本实验的基础,如有一点不满足,请先自学相关内容。
实验过程首先,我们要了解什么是余三码?余三码(余3码)【计算机】是由8421码加上0011形成的一种无权码,由于它的每个字符编码比相应的8421码多3,故称为余三码。
BCD码的一种。
那什么是8421码呢?8421码,即BCD代码,是一种二进制的数字编码形式,用二进制编码的十进制代码。
这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。
以上都是一些比较专业的定义,下面来讲一下我的理解。
首先,不管是余三码还是8421码都是由四位长度的二进制来表示的。
四位二进制能表示是数值范围是0000(0)-1111(15),8421码呢,为了方便人的十进制思维,只选取了0000(0)-1001(9)分别和十进制下的0-9一一对应,1010(10)-1111(15)这一部分不要了。
由此可以看出,8421码选择的二进制数转化为十进制得到的数值也是从0到9的,和它要对应的十进数数值完全吻合。
而余三码呢,它选取0011(3)-1100(12)来和十进制下的0-9一一对应,由于它选取的二进制数转化为十进制得到的数值是从3到12的,比它要对应的十进数数值都大3,故称为余三码。
下图更为直观的表现了余三码,8421码与十进制数的对应关系:表1-1接着,我们应该了解它这样做的好处是什么以及是如何计算的?余三码是一种对9的自补代码,因而可给运算带来方便。
其次,在将两个余三码表示的十进制数相加时,能正确产生进位信号,但对“和”必须修正。
修正的方法是:如果有进位,则结果加上0011(3);如果无进位,则结果加上1101(13)(或则减去0011(3)),即得和数的余三码,最终的进位要看修正时候的进位。
8421BCD码、格雷码、余3码编码方法

8421BCD码、格雷码、余3码编码方法
数字系统只能识别0和1两种不同的状态,只能识别二进制数。
实际传递和处理的信息很复杂,因此为了能使二进制数码表示更多、更复杂的信息,把0、1按一定的规律编制在一起表示信息,这个过程称为编码。
最常见的编码为二-十进制编码。
所谓二十进制编码是用4位二进制数表示0~9的10个十进制数,也称BCD码。
常见的BCD码有8421码、格雷(Gray)码、余3码、5421码、2421码等编码。
其中8421码、5421码和2421码为有权码,其余为无权码。
1.8421BCD码
8421BCD码是最常用的BCD码,为有权码,各位的权从左到右为8、4、2、1。
在8421BCD 码中利用4位二进制数的16种组合0000~1111 中的前10种组合0000~1001 代表十进制数的0~9,后6种组合1010~1111为无效码。
例:把十进制数78表示为8421BCD码的形式。
解:(78)10=(0111 1000)8421
(78)10=(1010 1011)5421
(78)10=(1101 1110)2421
2.格雷码(Gray)
格雷码最基本的特性是任何相邻的代码间仅有一位数码不同。
在信息传输过程中,若计数电路按格雷码计数时,每次状态更新仅有一位发生变化,因此减少了出错的可能性。
格雷码为无权码。
3.余3码
因余3码是将8421BCD码的每组加上0011(即十进制数3)即比它所代表的十进制数多3,因此称为余3码。
余3码的另一特性是0与9、1和8等互为反码。
四位2421码转余三码方法分析

1
01
0
11
0
10
1
01 11 10
111 000 000 111
Y3=A’C’D+A’CD+AC’D+ACD’
Y4=D’
2020/10/23
• (2)
2421BCD码
余三码
A B C D Y1 Y2 Y3 Y4
真值表:
0
0
0
0
0
0
1
1
0
0
0
1
0
1
0
0
(不采用无关 0
0
1
0
0
1
0
1
项,最小风险
0 0
1
0
1
0
1
1
1
0
1
1
0
1
0
0
0
1
0
0
1
1
00
1
1
0
1
0
1
0
1
0
1
0
1
1
1
011源自1000
1
1
0
0
1
0
0
1
1
1
0
1
1
0
1
0
1
1
1
0
1
0
1
1
1
1
1
1
1
1
0
0
①采用无关项d,最小成本法
化简后的卡诺图:
AB 00 01 11 10
CD
00
0011
01
0011
11
0011
10
数字逻辑与数字系统设计习题参考答案

2.3解:根据逻辑图可直接写出逻辑表达式:(a) F= ;(b) F=
解:设3个输入变量分别为A、B、C,输出为F,按题意,其中有奇数个为1,则输出F=1,因此可写出其逻辑表达式为F= 。根据逻辑表达式可绘制逻辑习题2.3图如下:
习题2.3图
2.4解:根据逻辑图可直接写出逻辑表达式:(a) F= ;(b) F=
2.5解:
(1)若A+B=A+C,则B=C
不正确。若A=1,B和C为不同值(如B=0,C=1或B=1,C=0),A+B=A+C仍然成立。
(2)若AB=BC,则A=C
不正确。若B=0,A和C为不同值,等式仍然成立。
(3)若1+A=B,则A+AB=B
1.6(1)(117)8=(1001111)2=(79)10
(2)(7456)8=(111100101110)2=(3886)10
(3)(23765.64)8=(10 0111 1111 0101.1101)2=(10229.8125)10
(4)(0.746)8=(0.11111)2=(0.96875)10
W=A+BD+BCX= Y= Z=
= = = =
根据化简并变换后的逻辑表达式可绘制逻辑习题4-12图所示下:
4.13解:
//4.6的VerilogHDL描述
module ex6(a,b,s,f);//
input a,b,s;
output f;
assign f=(s?b:a);
endmodule
2421转余3码的多种实现方法

2421转余3码的多种实现方法
通过计算机程序实现2421转余3码主要有以下几种方法:
1.通过除法和取余运算:
这种方法是最简单的方法,可以通过不断进行除法和取余操作,将2421转为余3码。
具体操作如下:
-将2421不断除以4,直到商为0,得到的余数序列即为余3码的逆序。
例如,2421除以4的商为605,余数为1,所以第一个余数为1 -继续将商继续除以4,得到的余数序列即为余3码的逆序。
例如,605除以4的商为151,余数为1,所以第二个余数为1
-重复以上步骤,直到商为0,得到的逆序序列即为余3码。
例如,最后得到的逆序序列为1101,将其反转得到余3码为1011
2.通过二进制转换:
这种方法将2421转为二进制,再将二进制转为余3码。
具体操作如下:
3.通过查表法:
这种方法事先建立一个查表,将2421的各个数位对应的余3码保存在表中,通过表查找来实现2421转余3码。
具体操作如下:
-建立一个含有0到9的十个元素的数组,数组中的元素分别对应0到9的余3码。
-将2421的各个数位对应的余3码保存在数组中。
例如,2对应的余3码是+1,4对应的余3码是-1,2对应的余3码是-10,1对应的余3码是+1
-遍历2421的各位数字,根据数组中保存的余3码,得到对应的余3码序列。
需要注意的是,余3码有多种表示方法,可以根据实际需求和具体情况选择合适的转换方法。
以上是三种常见的实现方法,通过这些方法可以实现2421转余3码。
2421转余3码的多种实现方法

2421转余3码的多种实现方法1、实现2421码转换为余3码(输入不允许为非2421码),画出电路图 (1)使用74X151和逻辑门实现 (2)使用74X138和逻辑门实现(3)使用比较器(74X85)和加法器(74X283)等(例如74X157)实现(4)是否有其他实现方法,如果有请给出1.功能分析1.1转换关系表1.2真值表 十进制数 第几项 2421码 Excess-3码 x3 x2 x1 x0y3 y2 y1 y00 0 0 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 0 0 2 2 0 0 1 0 0 1 0 1 3 3 0 0 1 1 0 1 1 0 4 4 0 1 0 0 0 1 1 1 d 5 0 1 0 1 d d d d d 6 0 1 1 0 d d d d d71 11dd dd十进制数 2421码Excess-3码 x3x2x1x0y3y2 y1y00 0 0 0 0 0 0 1 1 1 0 0 0 1 0 1 0 0 2 0 0 1 0 0 1 0 1 3 0 0 1 1 0 1 1 0 4 0 1 0 0 0 1 1 1 5 1 0 1 1 1 0 0 0 6 1 1 0 0 1 0 0 1 7 1 1 0 1 1 0 1 0 8 1 1 1 0 1 0 1 1 9111111d 8 1 0 0 0 d d d dd 9 1 0 0 1 d d d dd 10 1 0 1 0 d d d d5 11 1 0 1 1 1 0 0 06 12 1 1 0 0 1 0 0 17 13 1 1 0 1 1 0 1 08 14 1 1 1 0 1 0 1 19 15 1 1 1 1 1 1 0 01.3卡诺图y3=x3y3=∑(11,12,13,14,15)y2=x3'x0+x2x1x0+x3'x2'x1y2=∑(1,2,3,4,15)y1=x3'x2'x1'x0'+x3'x 2'x1x0+x3'x2x1'x0+x3x2x1'x0'+x3x2x1x0'y1=∑(0,3,4,13,14)2.实现2.1使用74X151和逻辑门实现2.1.1实现思路74X151为8路多路复用器,有三个控制输入端,一个使能端。
具有数显的数码转换电路 8421码—余3循环码 数字电路课设

东北大学秦皇岛分校计算机与通信工程学院电子线路课程设计具有数显的数码转换电路(8421码—余3循环码)专业名称通信工程班级学号姓名指导老师设计时间课程设计任务书专业:通信工程学号:学生姓名:设计题目:具有数显的码制转换电路8421码—余3循环码一、设计实验条件高频实验室二、设计任务及要求1. 要求输入为8421码。
输出为余三循环码2. 输出要具有数显功能三、设计报告的内容1.前言数字电路课程设计是继“数字电路”课后开出的实践环节课程其目的是训练学生综合运用学过的数字电路的基本知识独立设计比较复杂的数字电路能力。
设计建立在硬件和软件两个平台的基础上。
硬件平台是可编程逻辑器件所选器件可保存在一片芯片上设计出题目要求的数字电路。
软件平台是multisim通过课程设计学生要掌握使用EDA电子设计自动化工具设计数字电路的方法包括设计输入便宜软件仿真下载及硬件仿真等全过程。
数字电路课程设计在于更好的让学生掌握这门课程并且了解其实用性知道该门课程和我们的生活息息相关并且培养学生的动手能力让学生对该门课程产生浓厚的兴趣。
2.设计内容及其分析1.设计思路设计8421转余三循环码主要是考虑怎样找到二者之间的联系。
列出真值表后,根据值为1的那些项列出表达式,用最小项之和表示。
然后根据卡诺图进行化简,得出最简表达式。
最后根据表达式,在Multisim上画图仿真,用灯的灭(表示0)和亮(表示1)来表示码制的转换。
即可得到8421码对余三码的转换。
真值表:表1 8421转余三循环码真值表十进制数8421码余3循环码0 0000 00101 0001 01102 0010 01113 0011 01014 0100 01005 0101 11006 0110 11017 0111 11118 1000 11109 1001 1010根据真值表得出表达式:X4=A——CX3=B——C——+ A——BCD+A——B——D——X2=A B——C——D——+A——B+A——C+A——DX1=A B——C——+A——BD+A——BC根据表达式画出逻辑电路图:图0 8421码转余3循环码逻辑电路图2.所用主要器件及芯片1.电源;2.导线若干,开关4个;3.白炽灯(5v 1w)4个;4.芯片:74ls04 2片74ls08 1片74ls11 2片74ls20 1片74ls32 2片3.线路运行介绍J1.J2.J3.J4端为输入8421码端,J1端是最高位,依次下排。
码制转换
G1 B3B2B1B0 B3B2B1B0 B3B2B1B0 B3B2B1B0 B3B2B1B0 B3B2B1B0 B3B2B1B0 B3B2B1B0 B3B0(B2 B1) B3B0(B2 B1) B3B0(B2 B1) B3B0(B2 B1) B2 B1
分配管脚:即把设计的电路输入输出端口分配到CPLD指定的I/O口,设定步骤如下 Assignments菜单中选择Pins ,打开PIN PLANNER对话框,在相应端口Location栏双 击打开可选择管脚编号的下拉框进行选择。(注意:时序逻辑电路的触发脉冲输入端口 只能从12、14、62、64中选择);由于实验板接线孔分布较为紧凑,分配管脚时注意 相邻节点不要因为太靠近而在接线时发生短路故障。再次对工程项目进行编译,使管脚 分配生效,但凡修改原理图或改变管脚,完成后都要重新编译,使改动生效。
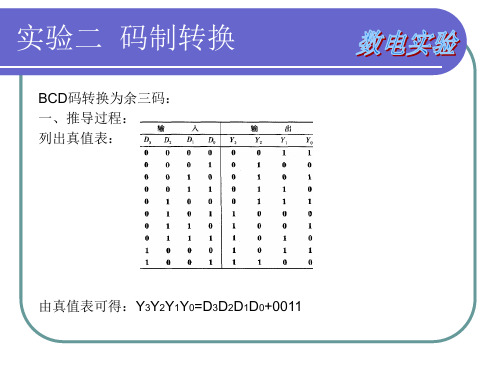
实验二 码制转换
实验电路原理图:
实验二 码制转换
二、用CPLD实现设计的实验电路
CPLD开发的四个基本步骤:
输入
图形输入
文本输入
编译 下载
仿真
实验二 码制转换
1、开发软件QuartusII的操作 1)用图形输入法输入实验电路原理图: 点击File->New或直接点击工具栏New按钮,打开New对话框,Device Design Files选 项卡中Block Diagram/Schematic File,点”OK”进入原理图编辑界面。
实验二 码制转换
三、静态逻辑功能测试 下载完成后,找到各个分配的管脚对应的接线孔,D3、D2、D1、D0分别连接4个电平 开关,Y3、Y2、Y1、Y0分别连接4组逻辑指示灯,将测试结果记录在真值表中。
2421码是什么意思

2421码是什么意思
2421码用4位二进制数来表示1位十进制数中的0到9这10个数码,是一种二进制的数字编码形式,即通常的十进制转化为二进制对应的一种码。
二进制编码的十进制数(BinaryCodeDecimal,BCD)。
通常采用4位二进制数来表示一位十进制数中的0到9这十个数。
这种编码可以使二进制和十进制之间的转换得以快速进行。
但是二进制数可以组合出16种代码,故必有6种为冗余状态。
将十进制的数转换成bcd码必须要先装换成二进制。
它是一种无权码,实在8421码的基础上加上(0011)形成的,即是8421码加上3,有上溢出和下溢出的空间。
二进制代码与格雷码相互转换

二进制代码与格雷码相互转换格雷码(Gray Code,简称G码)是典型的循环码,它是由二进制码(Binary,简称B码)导出的。
特点是序号相邻的两组代码只有一位码不同(包括头尾两组代码),且具有循环性。
上述特点使全部码组按序循环相邻,若以循环码表示一个循环过程中按顺序发生的状态,则任何状态变化只对应有一个变量发生变化,这个特点有助于提高电路的可靠性。
电路实现:3个异或门和两个2输入数据选择器MUX,设置方式控制端M:当M = 0 时,G码→B码;当M = 1时,B码→G码。
十进制数的二进制编码在人机交互过程中,为了既满足系统中使用二进制数的要求,又适应人们使用十进制数的习惯,通常用4位二进制代码对十进制数字符号进行编码,简称为二-十进制代码,或称BCD(Binary Coded Decimal)码。
它既有二进制的形式,又有十进制的特点。
常用的BCD码有8421码、2421码和余3码3种,它们与十进制数字符号对应的编码如表1.4所示。
表1.4 常用的3种BCD码进制字符8421码2421码余3码0 0000 0000 00111 0001 0001 01002 0010 0010 01013 0011 0011 01104 0100 0100 01115 0101 1011 10006 0110 1100 10017 0111 1101 10108 1000 1110 10119 1001 1111 1100一、8421码8421码是最常用的一种有权码,其4位二进制码从高位至低位的权依次为23、22、21、20,即为8、4、2、1,故称为8421码。
按8421码编码的0~9与用4位二进制数表示的0~9完全一样,所以,8421码是一种人机联系时广泛使用的中间形式。
注意:※ 8421码中不允许出现1010~1111四种组合,因为没有十进制数字符号与其对应。
※ 十进制数字符号的8421码与相应ASCII码的低四位相同,这一特点有利于简化输入输出过程中BCD码与字符代码的转换。
bcd码表示方法

bcd码表示方法【最新版3篇】《bcd码表示方法》篇1BCD 码是一种用四位二进制数表示十进制数的编码方式。
由于十进制数共有0、1、2,...,9 十个数码,因此,至少需要4 位二进制码来表示1 位十进制数。
常见的BCD 编码有8421BCD 码、2421BCD 码、余3 码等。
其中,8421BCD 码是最常用的一种,它用 4 位二进制数表示1 位十进制数,从左到右的权为8、4、2、1。
例如,十进制数37 用8421BCD 码表示为001121。
BCD 码的转换方式包括pack 和unpack 两种。
pack 是将十进制数转换为BCD 码,unpack 则是将BCD 码转换回十进制数。
在pack 过程中,首先用四位二进制数表示个位,然后用四位二进制数表示十位,以此类推,直到最高位。
在unpack 过程中,从右往左每四位二进制数转换为一个十进制数,然后依次排列得到原始十进制数。
需要注意的是,BCD 码仅能表示0~9 这10 个数码,因此,其他字符或数字需要通过其他编码方式来表示。
《bcd码表示方法》篇2BCD 码是一种用四位二进制数表示十进制数的编码方式。
由于十进制数共有0、1、2,...,9 十个数码,因此,至少需要4 位二进制码来表示1 位十进制数。
常见的BCD 编码有8421BCD 码、2421BCD 码、余3 码等。
其中,8421BCD 码是最常用的一种,它用 4 位二进制数表示1 位十进制数中的0~9 这10 个数码,从左到右的权为8、4、2、1。
例如,十进制数37 的8421BCD 码为001121。
BCD 码的转换方式包括pack 和unpack 两种。
pack 是将十进制数转换为BCD 码,unpack 则是将BCD 码转换回十进制数。
在pack 过程中,首先用四位二进制数表示个位,然后用四位二进制数表示十位,以此类推,直到最高位。
在unpack 过程中,从右往左每四位二进制数转换为一个十进制数,然后依次排列得到原始十进制数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数电第二次讨论
二、设计四位2421码转四位余三码的电路
(1)要求用最小成本和最小风险两种方法设计该电路,列出真值表,化简卡诺图,写出表达式,并画出电路。
(提示:两种方法的区别在于:对没有出现的输入(无关项),输出应该怎么确定?如果无关项对应的输出取任意值d,并且在化简卡诺图的时候根据需求使用了某些d项,此时设计方法为最小代价法(也叫最小成本法);如果d项不参与卡诺图化简,此方法为最小风险法))
(2)由设计好的电路重新列出真值表,比较此时的真值表或卡诺图与化简前的原始真值表或卡诺图有何异同,请解释不同的原因
答:
(1).原始真值表:
①用无关项d,最小成本法卡诺图化简:
①用无关项d,最小成本法画出电路图:
②采用无关项,最小风险法卡诺图化简:
③采用无关项,最小风险法
画出电路图:
(2)
真值表:(采用无关项,最小成本法)
①用无关项d,最小成本法:
化简后的卡诺图:
Y2=A’D+A’C+A’B+BCD
Y3=A’C’D+A’CD+AC’D+ACD’
Y4=D’
(2)
真值表:(不采用无关项,最小风险法)
②采用无关项,最小风险法
化简后的卡诺图:
Y1=AB+ACD
Y3=A’C’D’+ABC’D+ABCD’+A’B’CD
Y4=A’B’D’+A’C’D’+ABD’
不同的原因:
(1)无关项d在进行卡诺图运算时根据其位置填入1或0,并写出相应的真值表。
(2)若不采用无关项d则电路所需的器件更多,电路更复杂。
不同的方法设计的电路图不同,真值表和卡诺图可能不同。
同一设计方法若卡诺图化简时的括圈方式不同,则化简表达式不同,电路图不同,从而真值表也可能不相同。
