精品数学讲义—映射

合集下载

映射的概念精品PPT课件

•３.设集合Ａ＝｛１,－３,２,３,－１,－２｝，集合Ｂ＝｛９，０，４，１，５｝,对应关系是：集合Ａ中的每一个数，在集合Ｂ中都有一个其对应的平方数.
*
思考5:有人说映射有“三性”，即“有序性”， “存在性”和“唯一性”，对此你是怎样理解的？
①“有序性”：映射是有方向的，A到B的映射与B到A的映射往往不是同一个映射；
解: （１）将x= 2代入对应关系，可得其在Ｂ
中的对应元素为（ 2 1，2）
x+1=2
（２）由题意得：
x2=1
∴x=1
即 (2,1)在Ａ中的对应元素为１
*
练习：下列对应是否为从集合A到集合B的映射？
(1) A R, B {y | y 0}, f : x | x |;
*
小结：
1、映射的概念 2、映射与函数的区别与联系
映射的概念
*
复习:函数的概念
一般地，设A、B是两个非空的数集，
如果按某种对应法则f，对于集合A中的每一个数x，在集合B中都有唯一的数y和它对应，这样的对应叫做集合A到集合B的一个函数．
函数的本质：
建立在两个非空数集上的特殊对应
*
复习:函数的概念
这种“特殊对应”有何特点： 1.可以是“一对一” 2.可以是“多对一” 3.不能“一对多” 4.A中不能有剩余元素 5.B中可以有剩余元素
A
B
A
B
a
1
b
c
22
（１）
A
B
1
a
2
3
b
*
(3)
1
a
b
2
c
（２）
A
B
a
1
b
c

《映射的概念》课件

《映射的概念》ppt课件
CONTENTS
• 映射的定义 • 一一映射 • 连续映射 • 映射的应用
01
映射的定义
什么是映射
01
映射是指将一个集合的元素按照某种规则一一对应到另一个集合中的元素，建立元素之间的对应关系。
02
映射通常用函数来表示，函数是从一个集合到另一个集合的映射，表示输入和输出之间的对应关系。
机器学习
在机器学习中，输入数据与输出结果的聆听
THANKS
一一映射的例子
要点一
总结词
例如，将一组数或集合中的元素一一对应地映射到另一组数或集合中的元素。
要点二
详细描述
在实际应用中，一一映射的例子很多。例如，在数学中，可以将一组数或集合中的元素一一对应地映射到另一组数或集合中的元素。在计算机科学中，文件系统中的文件名到文件内容的映射、数据库中的记录到数据的映射等都是一一映射的例子。此外，在现实生活中，一对一的约会、一对一的商品交易等也可以看作是一一映射的实例。
详细描述
一一映射是一种特殊的映射关系，它要求每个原像都与一个唯一的像相对应，并且每个像也都有其唯一的原像。也就是说，在映射过程中，每一个元素都不被重复地映射到同一个像上，也不存在未被映射的原像。
一一映射的性质
总结词
一一映射具有可逆性、一一对应性和确定性等性质。
详细描述
一一映射是一种可逆的过程，即通过映射的反向操作可以找到原像。同时，一一映射确保了每个原像都与一个唯一的像相对应，并且每个像也都有其唯一的原像。此外，一一映射还具有确定性，即每个原像都映射到唯一的像上，没有歧义或不确定性。
拓扑学
在拓扑学中，映射用于研究空间之间的连续变换和不变性。

高考数学考点一-映射的概念

高考数学考点一-映射的概念高考数学考点一、映射的概念1.了解对应大千世界的对应共分四类，分别是：一对一多对一一对多多对多2.映射：设A和B是两个非空集合，如果按照某种对应关系f，对于集合A 中的任意一个元素_，在集合B中都存在的一个元素y与之对应，那么，就称对应f：A→B为集合A到集合B的一个映射(mapping).映射是特殊的对应，简称“对一”的对应。

包括：一对一多对一高考数学考点二、函数的概念1.函数：设A和B是两个非空的数集，如果按照某种确定的对应关系f，对于集合A中的任意一个数_，在集合B中都存在确定的数y与之对应，那么，就称对应f：A→B为集合A到集合B的一个函数。

记作y=f(_),_A.其中_叫自变量，_的取值范围A叫函数的定义域;与_的值相对应的y的值函数值，函数值的集合叫做函数的值域。

函数是特殊的映射，是非空数集A到非空数集B的映射。

2.函数的三要素：定义域、值域、对应关系。

这是判断两个函数是否为同一函数的依据。

3.区间的概念：设a,bR,且a①(a,b)={_a⑤(a,+∞)={__a}⑥[a,+∞)={__≥a}⑦(-∞,b)={__高考数学考点三、函数的表示方法1.函数的三种表示方法列表法图象法解析法2.分段函数：定义域的不同部分，有不同的对应法则的函数。

注意两点：①分段函数是一个函数，不要误认为是几个函数。

②分段函数的定义域是各段定义域的并集，值域是各段值域的并集。

考点四、求定义域的几种情况①若f(_)是整式，则函数的定义域是实数集R;②若f(_)是分式，则函数的定义域是使分母不等于0的实数集;③若f(_)是二次根式，则函数的定义域是使根号内的式子大于或等于0的实数集合;④若f(_)是对数函数，真数应大于零。

⑤.因为零的零次幂没有意义，所以底数和指数不能同时为零。

⑥若f(_)是由几个部分的数学式子构成的，则函数的定义域是使各部分式子都有意义的实数集合;⑦若f(_)是由实际问题抽象出来的函数，则函数的定义域应符合实际问题高中地理知识点分析(1)位置：①经纬度位置：(100E-140E)(10S-20N)②海陆位置：东临太平洋，西临印度洋，是亚洲和大洋洲的过渡地带(2)范围：东南亚包括中南半岛和马来群岛两大部分，是亚洲纬度最低的地区。

第3-4节映射

(2)如果BY，则由f和B唯一确定了X的一个子集。 {xf(x)B，xX}
这个子集习惯上用f-1(B)表示。f-1(B)是X中在f下的象落在B里的那些元素组成的。
f-1(B)叫做在f下B的原象。利用这种方法，由f又得到一个2Y到2X的一个映射，记为f-1。
16/25
集合与图论例1：设X={1,2,3,4}，Y={a,b,c,d,e}，f：XY： f(1)=a，f(2)=b，f(3)=b，f(4)=c。令A={1,2}，B={b,c,d}，求f(A)，f-1(B)，f-1({d})， f-1({b})。解：f(A) ={a,b} f-1(B) ={2,3,4}。
24/25
集合与图论
逆映射的性质
定理4.1 设f:XY，则f是可逆的充分必要条件是f为双射（一一对应）。定理4.2 设f:XY，则如果f是可逆的，则f的逆映射是唯一的。f的逆记作f-1。定理4.3 设f:XY，g:YZ都是可逆的，则gf 也可逆且(gf)-1=f-1g-1，(f-1)-1=f。定理4.4 设f:XY，则: (1)f左可逆的充分必要条件是f为单射； (2)f右可逆的充分必要条件是f为满射。
18/25
集合与图论例2：设X={1,2,3,4},Y={a,b,c,d,e}。 f:XY： f(1)=a,f(2)=b,f(3)=b,f(4)=c。令A={1,2},B={3,4} ，求f(A∩B)， f(A)∩f(B)。解: f(A∩B) =, f(A)∩f(B) ={b}
例3：设X={a,b,c},Y={1,2,3}。f:XY： f(a)=1,f(b)=f(c)=2。令A={a,b},B={c}，求f(AB)，f(A)f(B)。解：f(AB)=f((A\B)∪(B\A)) =f({a,b,c})={1,2} f(A)f(B) ={1,2}{2}={1}

人教版高一数学课件-映射

其中集合A中的元素x稱為原象，在集合B 中與x對應的元素y稱為象.
思考3:下圖中的對應是不是映射？為什麼？
A
B
圖1
A
B
圖2
思考4:在我們的生活中處處有映射，你能舉一個實例嗎？
知識探究（二）
思考1:函數一定是映射嗎？映射一定是函數嗎？
思考2:映射有哪幾種對應形式？
一對一，多對一
思考3:設集合A=N，B={x|x是非負偶數}，你能給出一個對應關係f，使從集合A到集合B的對應是一個映射嗎？並指出其對應形式.
（3）集合A={x|x是三角形},集合B={x|x是圓}，對應關係f：每一個三角形都對應它的內切圓；
（4）集合A={x|x是師大附中的班級}，集合 B={x|x是師大附中的學生}，對應關係f：每一個班級都對應班裏的學生;
（5）集合A={1,2,3,4}, B={3，4，5，6，7， 8，9}，對應關係f：x→2x+1
思考4:圖1是從集合A到集合B的一個映射嗎？圖2 是從集合B到集合A的一個映射嗎？
A
B
圖1
A
B
圖2
思考5:有人說映射有“三性”，即“有序性”， “存在性”和“唯一性”，對此你是怎樣理解的？
①“有序性”：映射是有方向的，A到B的映射與B到A的映射往往不是同一個映射；
②“存在性”：對於集合A中的任何一個元素，集合B中都存在元素和它對應；
③“唯一性”：對於集合A中的任何一個元素，在集合B中和它對應的元素是唯一的.
理論遷移
例1 試判斷下麵給出的對應是否為從集合A到集合 B的映射？（1）集合A={P|P是數軸上的點}，集合B=R，對應關係f：數軸上的點與它所代表的實數對應；
（2）集合A={P|P是平面直角坐標系中的點}，集合B={(x,y)|x∈R,y∈R}，對應關係f：平面直角坐標系中的點與它的座標對應；

映射(高中数学)

映射定义：设X,Y 是两个非空集合，如果按照一定的对应关系f 使对于集合X 中的任意一个元素x ，在集合Y 中都有唯一的对应元素y 与之对应，那么就称对应f ：X →Y 为集合X 到集合Y 的一个映射。

其中，元素y 称为元素x （在映射f 下）的像，记作f （x ），即y=f （x ）；而元素x 称为元素y （在映射f 下）的一个原像。

映射的三要素：① 定义域：集合X 称为映射f 的定义域，记作fD,即fD=X ；② 值域：集合X 中所有元素的像组成的集合成为映射f 的值域，记作fR或f （x ），且fRY ；③ 对应法则f ：使每一个元素x ∈X 都有唯一确定的元素y 与之对应。

注意：对于每一个x ∈X ，与之对应的像y 是唯一的;但对于每一个y ∈fR ，与之对应的原像x 不一定是唯一的。

分类：① 单射：对于集合X 中的任意两个不同元素1x ≠2x ，它们的像f （1x ）≠f （2x ），则称f 为X 到Y 单射； ② 满射：若集合Y 中的任意一元素y 都是集合X 中某元素的像，即f R=Y ；③ 双射：若f 既是单射，又是满射，则称f 为一一映射（双射）。

逆映射：若f 是集合X 到集合Y 的单射，则有定义可得，对于每一个y ∈fR，都有唯一的x ∈X 与之对应，我们就可以定义一个新映射g ：fR →x 。

对于每个y ∈fR，规定g （y ）=x ，且这个x 满足f （x ）=y ，就称映射g 为映射f 的逆映射，记作1-f，其定义域1-fD=fR，值域1-fR=X 。

复合映射：设有两个映射f ：X →1Y g ：2Y→Z,其中1Y⊂2Y，则由映射g 和f 可以定出一个从X 到Z 的对应法则，它将每个x ∈X 映成f [g （x ）]，这个映射称为映射g 和映射f 的复合映射，记作f 。

g ，即f 。

g ：X →Z 。

（注意：映射g 与f 构成复合映射的条件是：g 的值域必须包含在f 的定义域中，即gR⊂fD。

必修1映射

练 1. 下列对应是否是集合 A 到集合 B 的映射？（ 1） A={1，2，3，4}，B={3，4，5，6，7，8，9}，对应法则 f : x 2 x 1 （ 2） A N * , B {0,1} ，对应法则 f : x x 除以 2 得的余数；（ 3） A N ， B {0,1, 2} ， f : x x 被 3 除所得的余数；
1、映射的概念及表示方法
① A {1, 4,9} , B {3, 2, 1,1, 2,3} ，对应法则：开平方；
② A {3, 2, 1,1, 2,3} ， B {1, 4,9} ，对应法则：平方；
2 3 1 ③ A {30, 45, 60} , B {1, , , }, 2 2 2 对应法则：求正弦
1 1 1 （ 4）设 X {1, 2,3, 4}, Y {1, , , } 2 3 4 1 f :x ； x （ 5） A {x | x 2, x N }, B N ， f : x 小于 x 的最大质数 .
练 2. 已知集合 A a, b , B 1,0,1 , 从集合 A 到集合 B 的映射，试问能构造出多少映射？
A a B -1 0 1
Байду номын сангаас
b
小结： 1. 映射的概念； 2. 判定是否是映射主要看两条：一是A集合中的元素都要有对应，但B中元素未必要有对应；二是A中元素与B中元素只能出现 “一对一”或“多对一”的对应形式
作业：P23 练习 2、4
一般地，设 A、 B 是两个非空的集合，如果按某一个确定的对应法则 f，使对于集合 A 中的任意一个元素 x，在集合 B 中都有唯一确定的元素 y 与之对应，那么就称对应 f : A B 为从集合 A 到集合 B 的一个映射（ mapping）．记作“ f : A B ”

第二讲映射及映射法

第二讲映射及映射法知识、方法、技能1．映射的定义设A ，B 是两个集合，如果按照某种对应法则f ，对于集合A 中的任何一个元素，在集合B 中都有惟一的元素和它对应，这样的对应叫做从集合A 到集合B 的映射，记作.:B A f →（1）映射是特殊的对应，映射中的集合A ，B 可以是数集，也可以是点集或其他集合，这两个集合有先后次序，从A 到B 的映射与从B 到A 的映射是截然不同的.（2）原象和象是不能互换的，互换后就不是原来的映射了.（3）映射包括集合A 和集合B ，以及集合A 到B 的对应法则f ，三者缺一不可.（4）对于一个从集合A 到集合B 的映射来说，A 中的每一个元素必有惟一的，但B 中的每一个元素都不一定都有原象.如有，也不一定只有一个.2．一一映射一般地，设A 、B 是两个集合，.:B A f →是集合A 到集合B 的映射，如果在这个映射下，对于集合A 中的不同元素，在集合B 中有不同的象，而且B 中每一个元素都有原象，那么个这个映射叫做A 到B 上的一一映射.3．逆映射如果f 是A 与B 之间的一一对应，那么可得B 到A 的一个映射g ：任给B b ∈，规定 a b g =)(，其中a 是b 在f 下的原象，称这个映射g 是f 的逆映射，并将g 记为f —1.显然有（f —1）—1= f ，即如果f 是A 与B 之间的一一对应，则f —1是B 与A 之间的一一对应，并且f —1的逆映射是f .事实上，f —1是B 到A 的映射，对于B 中的不同元素b 1和b 2，由于它们在f 下的原象不同，所以b 1和b 2在f —1下的像不同，所以f —1是1－1的. 任给b a f A a =∈)(,设，则a b f=-)(1.这说明A 中每个元素a 在f —1都有原象.因此，f —1是映射上的.这样即得f —1是B 到A 上的1－1映射，即f —1是B 与A 之间一一对应.从而f —1有逆映射.:B A h →由于任给b a h A a =∈)(,设，其中b 是a 在f —1下的原象，即f —1(b)=a ，所以，f(a)=b ，从而f h a f b a h ===得),()(，这即是f —1的逆映射是f .赛题精讲Ⅰ映射关映射的高中数学竞赛题是常见题型之一，请看下述试题.例1：设集合},,,,|),,,{(},,110|{M d c b a d c b a F x x x M ∈=∈≤≤=集合Z 映射f ：F →Z.使得v u y x v x y u y x v u cd ab d c b a ff f ,,,,66),,,(,39),,,(.),,,(求已知→→-→的值.【思路分析】应从cd ab d c b a f -→),,,(入手，列方程组来解之.【略解】由f 的定义和已知数据，得 ⎩⎨⎧∈=-=-).,,,(66,39M y x v u xv uy xy uv 将两式相加，相减并分别分解因式，得.27))((,105))((=+-=-+x u v y x u v y显然，},110|{,,,,0,0Z ∈≤≤∈≥-≥-x x x v u y x v y x u 在的条件下，,110≤-≤v u ,21)(,15)(,105|)(,2210,221]11105[21=+=++≤+≤≤+≤+v y v y v y v y v y 可见但即对应可知.5)(,7)(21=-=-x u x u 同理，由.9)(,3)(223,221]1127[,11021=+=+≤+≤≤+≤+≤-≤x u x u x u x u v y 又有知对应地，.3)(,9)(21=-=-v y v y 于是有以下两种可能：（Ⅰ）⎪⎪⎩⎪⎪⎨⎧=-=+=-=+;3,9,7,15v y x u x u x y （Ⅱ）⎪⎪⎩⎪⎪⎨⎧=-=+=-=+.3,9,5,21v y x u x u v y 由（Ⅰ）解出x =1，y=9，u =8，v =6；由（Ⅱ）解出y=12，它已超出集合M 中元素的范围.因此，（Ⅱ）无解.【评述】在解此类问题时，估计x u v y x u v y +--+,,,的可能值是关键，其中，对它们的取值范围的讨论十分重要.例2：已知集合}.0|),{(}333|),{(><<=x y y x x y y x A 和集合求一个A 与B 的一一对应f ，并写出其逆映射.图Ⅰ－1－2－1【略解】从已知集合A ，B 看出，它们分别是坐标平面上两直线所夹角形区域内的点的集合（如图Ⅰ－1－2－1）.集合A 为直线x y x y 333==和所夹角内点的集合，集合B 则是第一、三象限内点的集合.所要求的对应实际上可使A 区域拓展成B 区域，并要没有“折叠”与“漏洞”.先用极坐标表示集合A 和B ：},36,,0|)sin ,cos {(πθπρρθρθρ<<∈≠=R A }.20,,0|)sin ,cos {(πϕρρϕρϕρ<<∈≠=R B令).6(3),sin ,cos ()sin ,cos (πθϕϕρϕρθρθρ-=→f 在这个映射下，极径ρ没有改变，辐角之间是一次函数23πθϕ-=，因而ϕθ和之间是一一对应，其中),3,6(ππθ∈ ).2,0(πϕ∈所以，映射f 是A 与B 的一一对应. 逆映射极易写，从略.【评述】本题中将下角坐标问题化为极坐标问题，颇具特色.应注意理解掌握.Ⅱ映射法应用映射知识往往能巧妙地解决有关集合的一些问题.例3：设X={1，2，…，100}，对X 的任一非空子集M ，M 中的最大数与最小数的和称为M 的特征，记为).(M m 求X 的所有非空子集的特征的平均数.【略解】设.}|101{,:,X A a a A A A f X A ≠≠⊂∈-=''→⊂令于是A A f '→:是X 的非空子集的全体（子集组成的集），Y 到X 自身的满射，记X 的非空子集为A 1，A 2，…，A n （其中n=2100－1），则特征的平均数为.))()((21)(111∑∑=='+=ni i i n i i A m A m n A m n 由于A 中的最大数与A ′中的最小数的和为101，A 中最小数与A ′中的最大数的和也为101，故,202)()(='i i A m A m 从而特征平均数为 .10120221=⋅⋅n n如果A ，B 都是有限集合，它们的元素个数分别记为).(),(B card A card 对于映射B A f →:来说，如果f 是单射，则有)()(B card A card ≤；如果f 是满射，则有)()(B card A card ≥；如果f 是双射，则有)()(B card A card =.这在计算集合A 的元素的个数时，有着重要的应用.即当)(A card 比较难求时，我们就找另一个集合B ，建立一一对应B A f →:，把B 的个数数清，就有)()(B card A card =.这是我们解某些题时常用的方法.请看下述两例.例4：把△ABC 的各边n 等分，过各分点分别作各边的平行线，得到一些由三角形的边和这些平行线所组成的平行四边形，试计算这些平等四边形的个数.【略解】如图Ⅰ－1－2－2所示，我们由对称性，先考虑边不行于BC 的小平行四边形.把AB 边和AC 边各延长一等分，分别到B ′，C ′，连接 B ′C ′.将A ′B ′的n 条平行线分别延长，与B ′C ′相交，连同B ′，C ′共有n+2个分点，从B ′至C ′依次记为1，2，…，n+2.图中所示的小平行四边形所在四条线分别交B ′C ′于i ，j ，k ，l .记A={边不平行于BC 的小平行四边形}，}.21|),,,{(+≤<<<≤=n l k j i l k j i B把小平行四边形的四条边延长且交C B ''边于四点的过程定义为一个映射：B A f →:. 下面我们证明f 是A 与B 的一一对应，事实上，不同的小平行四边形至少有一条边不相同，那么交于C B ''的四点亦不全同.所以，四点组),,,(l k j i 亦不相同，从而f 是A 到B 的1－1的映射.任给一个四点组21),,,,(+≤<<<≤n l k j i l k j i ，过i ，j 点作AB 的平行线，过k ，l 作AC 的平行线，必交出一个边不平行于BC 的小平行四边形，所以，映射f 是A 到B 的满射. 总之f 是A 与B 的一一对应，于是有.)()(42+==n C B card A card加上边不平行于AB 和AC 的两类小平行四边形，得到所有平行四边形的总数是.342+n C 例5：在一个6×6的棋盘上，已经摆好了一些1×2的骨牌，每一个骨牌都恰好覆盖两上相邻的格子，证明：如果还有14个格子没有被覆盖，则至少能再放进一个骨牌.【思路分析】还有14个空格，说明已经摆好了11块骨牌，如果已经摆好的骨牌是12块，图Ⅰ－1－2－3所示的摆法就说明不能再放入骨牌.所以，有14个空格这一条件是完全必要的.我们要证明当还有14个空格时，能再放入一个骨牌，只要能证明必有两个相邻的空格就够了.如果这种情况不发生，则每个空格的四周都有骨牌，由于正方形是对称的，当我们选定一个方向时，空格和骨牌就有了某种对应关系，即可建立空格到骨牌的一种映射，通过对空格集合与骨牌集合之间的数量关系，可以得到空格分布的一个很有趣的结论，从而也就证明了我们的命题.【略解】我们考虑下面5×6个方格中的空.如果棋盘第一行（即最上方的一行）中的空格数多于3个时，则必有两空格相邻，这时问题就得到解决.现设第一行中的空格数最多是3个，则有11314)(=-≥X card ，另一方面全部的骨牌数为11，即.11)(=Y card 所以必有),()(Y card X card =事实上这是一个一一映射，这时，将发生一个很有趣的现象：最下面一行全是空格，当然可以放入一个骨牌.【评述】这个题目的证明是颇具有特色的，从内容上讲，这个题目具有一定的综合性，既有覆盖与结构，又有计数与映射，尤其是利用映射来计数，在数学竞赛中还较少见.当然这个题目也可以用其他的方法来解决.例如，用抽屉原则以及用分组的方法来讨论其中两行的结构，也能比较容易地解决这个问题，请读者作为练习.例6：设N={1，2，3，…}，论证是否存一个函数N N f →:使得2)1(=f ，n n f n f f +=)())((对一切N ∈n 成立，)1()(+<n f n f 格，即除去第一行后的方格中的空格.对每一个这样的空格，考察它上方的与之相邻的方格中的情况.（1）如果上方的这个方格是空格，则问题得到解决.（2）如果上方的这个方格被骨牌所占，这又有三种情况.（i ）骨牌是横放的，且与之相邻的下方的另一个方格也是空格，则这时有两空格相邻，即问题得到解决；（ii ）骨牌是横放的，与之相邻的下方的另一个方格不是空格，即被骨牌所覆盖；（iii ）骨牌是竖放的.现在假设仅发生（2）中的（ii ）和（iii ）时，我们记X 为下面5×6个方格中的空格集合，Y 为上面5×6个方格中的骨牌集合，作映射Y X →:ϕ，由于每个空格（X 中的）上方都有骨牌（Y 中的），且不同的空格对应于不同的骨牌.所以，这个映射是单射，于是有 )()(Y card X card ≤，对一切N ∈n 成立.【解法1】存在，首先有一条链.1→2→3→5→8→13→21→… ①链上每一个数n 的后继是)(n f ，f 满足n n f n f f +=)())(( ②即每个数是它产面两个数的和，这种链称为f 链.对于①中的数m>n ，由①递增易知有n m n f m f -≥-)()( ③我们证明自然数集N 可以分析为若干条f 链，并且对任意自然数m>n ，③成立（从而)()1(n f n f >+），并且每两条链无公共元素）.方法是用归纳法构造链（参见单壿著《数学竞赛研究教程》江苏教育出版社）设已有若干条f 链，满足③，而k+1是第一个不在已有链中出现的数，定义1)()1(+=+k f k f ④这链中其余的数由②逐一确定.对于m>n ，如果m 、n 同属于新链，③显然成立，设m 、n 中恰有一个属于新链.若m 属于新链，在m=k+1时，,1)(1)()()(n m n k n f k f n f m f -=+-≥-+=-设对于m ，③成立，则n m f m n m n f m m f n f m f f -≥+-≥-+=-)()()()())(([由②易知)(2m f m ≥]. 即对新链上一切m ，③成立.若n 属于新链，在n=k+1时，.11)()()()(n m k m k f m f n f m f -=--≥--=-设对于n ，③成立，在m>n 时，m 不为原有链的链首。

高一数学最新课件-映射1 精品

1.已知A＝{a,b},B＝{1,2},那么从A到B可以构成（）个映射
2.点集A＝B {(x, y│) x, y R}, f : (x, y) (x y, x y)
(1)求A中元素（1，3）的象
(2)求B中元素（1，3）的原象
映射
映射概念：
设A, B是两个集合，如果按照某个对应法则f ，使集合A中的任何一个元素，在集合B中都有唯一的元素f(x)跟它对应，那么，这样的对应（包括集合A、B以及从A到B的对应关系f ）, 叫做从集合A到集合B的映射.记作：f : A B
函数概念：设A, B是非空的数集，如果按照某个对应关系f ，使集合A中的任何一个数x，在集合B 中都有唯一确定的数f(x)跟它对应，那么就称 f : A B为从集合A到集合B的一个函数. 记作：y f (x), x A
Hale Waihona Puke 注意：1.方向性 : 映射f : A B与f : B A不同 2.任意性： A中元素无剩余，B中可以有剩余
3.唯一性：不能一对多，但能多对一
映射举例：
1.集合A＝{x│x是三角形}，B＝{y│y>0} f:计算三角形面积
2.集合A＝{x│x是高一某班同学}， B＝{y│0 y 100} f:月考数学成绩
3.集合M＝{x│0 x 6}， P＝{y│0 y 3} f:x y=x
口答：已知映射f : A B,下列中正确的有（）个
（1）A中的每一个元素在B中都有象（2）B中的每一个元素在A中都有原象（3）A中不同的元素在B中都有不同的象（4）B中不同的象在A中都有不同的原象
练习：

高数课件-映射与函数

义的一切实数组成的合集，这种定义域称为函数的自然定义域。在这种约定之下，一
般的用算是表达的函数可用“y=∱（x）”表达，而不必再出Df。
例如，函数y=
1- x 2 的定义域是封闭间 -1，1 ，函数y=
1 的定义域是开区间 1- x2
（-1，1）。
表示函数的主要方法有三种：表格法、图形法、解析法（公式法）。其中，用图形法表下）的像，并记作∱（χ）,即
y=∱（χ）, 而元素χ称为元素y（在映射∱下）的一个原像；集合X称为映射∱的定义域，记作Df，即Df=X；X中所有元素的像所组成的集合称为映射∱的值域，记作Rf或者∱（χ），即
Rf=∱(X)= f(x) I χ∈X
在上述映射的定义中，需要注意的是：
映射
与
主讲人：日期 :
函数
第一节映射与函数
映射是现代数学中的一个基本概念，而函数是微积分的研究对象，也是映射的一种。本节主要介绍映射、函数及有关概念，函数的性质与运算等。
一.映射
1.映射概念定义设X、Y是两个非空集合，如果存在一个法则∱，使得对X中的每个元素χ，按法则∱，在Y中有唯一确定的元素y与之对应，那么称∱为从X到Y的映射，记作
由复合映射的定义可知，映射ℊ和∱构成复合映射的条件是：ℊ的值域Rg必须包含在∱的定义域内，即Rg⊂Df,否则，不能构成复合映射。由此可以知道，映射ℊ和∱的复合是有顺序的，∱∘ℊ有意义并不表示ℊ∘∱也有意义。即使∱∘ℊ与ℊ∘∱都有意义，复合映射∱∘ℊ与ℊ∘∱也未必相同。
例4
设有映射ℊ：R→ -1，1 ，对每个x∈R，ℊ（x)=sinx；映射∱： -1，1 → 0，1 ，对每个 u∈ -1，1 ，∱（u)= 1- u2,则映射ℊ和∱构成的复合映射∱∘ℊ：R→ 0，1

映射的概念分析

映射的概念分析映射是数学中的一个重要概念，它描述了一个集合中的每个元素与另一个集合中的元素之间的对应关系。

在数学中，我们可以将映射理解为函数，其中一个集合是定义域，另一个集合是值域。

映射可以用于描述数学模型、图论、集合论等各种数学领域中的概念与关系。

映射有很多种形式，可以分为单射、满射和双射三种类型。

首先，单射是指一个集合中的不同元素在映射的结果中有不同的映射元素。

换句话说，映射的结果中不存在重复的映射元素。

对于集合A到集合B的映射f：A →B，如果对于集合A中的任意两个不同的元素a1和a2，有f(a1)≠f(a2)，那么这个映射就是单射。

可以通过绘制函数图像来判断一个映射是否为单射，如果函数的图像没有任何两点在同一水平线上，那么这个函数是单射。

其次，满射是指映射的结果包含了值域中的每一个元素。

也就是说，对于集合A 到集合B的映射f：A→B，如果对于集合B中的任意一个元素b，存在集合A 中的元素a，使得f(a)=b，那么这个映射就是满射。

可以通过在值域上滑动水平线来判断一个映射是否为满射，如果水平线与函数的图像相交于每个y值上至少一个点，那么这个函数就是满射。

最后，双射是指一个集合中的每个元素与另一个集合中的元素存在唯一的对应关系。

也就是说，对于集合A到集合B的映射f：A→B，既是单射又是满射，那么这个映射就是双射。

可以通过绘制函数的图像并判断是否为一一映射来判断一个映射是否为双射。

映射还有一些衍生的概念。

首先是像、原像和逆映射。

对于映射f：A→B，如果b是集合B中的一个元素，a是集合A中满足f(a)=b的元素，那么b是元素a的像，元素a是元素b的原像。

逆映射是指如果映射f：A→B是双射，那么可以构造一个逆映射f^(-1)：B →A，满足f^(-1)(f(x))=x和f(f^(-1)(y))=y。

其次是复合映射。

如果映射f：A→B和映射g：B→C都存在，那么可以定义一个复合映射h：A→C，使得h(x)=g(f(x))。

高一数学必修教学课件第二章映射

02 一一映射与逆映射
一一映射的定义及性质
一一映射定义
设A和B是两个非空集合，如果存在一个从A到B的映射f，使得B中的每一个元素都有A中的唯一元素与之对应，则称f为从A到B的一一映射。
一一映射的性质
一一映射具有单射和满射的性质，即每个元素都有唯一的像，且像集B中的每个元素都有原像。
逆映射的概念及求法
方程的图像可以看作是定义域到值域的一个映射关系的图形表示，通过映射的性质可以研究方程的图像的形状和性质。
方程的变换与映射关系
通过映射的变换可以研究方程之间的内在联系和相互转化。
映射在不等式中的应用
不等式的解集与映射关系
不等式的解集可以看作是定义域到值域的一个映射关系的集合表示，通过映射的性质可以研究不等式的解集的存在性和范围。
映射的表示方法
通常用箭头图或表格来表示映射。在箭头图中，箭头表示元素之间的对应关系；在表格中，第一行列出原像集合的元素，第一列列出像集合的元素，表格中的其余部分表示对应关系。
映射的性质与分类
有向性
映射是有方向的，即A中的元素通过对应关系f对应到B中的元素。
唯一性
对于A中的任何一个元素，通过对应关系f在B中有唯一确定的元素与之对应。
不等式的图像与映射关系
不等式的图像可以看作是定义域到值域的一个映射关系的图形表示，通过映射的性质可以研究不等式的图像的形状和性质。
不等式的证明与映射关系
通过映射的性质可以证明一些不等式，例如利用单调性证明不等式等。
05 映射的拓展与应用前景
拓展映射的概念及应用
拓展映射的定义
在原有映射的基础上，通过引入新的元素或规则，对映射关系进行扩展和深化，以适应更广泛的应用场景。

离散数学,映射

定义1.3.7
设A，B是任意两个集合。
(1)称A的基数小于等于B的基数，记为A B，如果有A到B单射σ或有B到A满射σ。 (2) 称A的基数小于B的基数，记为AB，如果AB且AB。换句话说，若A与B的某一子集有1-1对应关系，则AB；若A与B的某一子集有1-1 对应关系，且A与B不存在1-1对应关系，则 AB。
数无穷集，作 :Z+B， (x)=x2 整数的集合Z是可数无穷集，
作 : Z+ Z，
x 2 ( x) x 1 2 x为偶数 x为奇数
定理1.3.2
可数集合的子集仍为可数集合。
证明：如果此可数集合是有限集合，则它的子集也有限，当然可数。如果此可数集合是无穷集合，则此集合的元素可写成a1, a2, …, an, …的形式。它的子集可以这样得到：从左向右，第一个是子集中元素的记为ai1，第二个是子集中元素的记为ai2, …，于是，此子集的元素可排列为： ai1, ai2, …, ain, …。所以，此子集是可数集合。
定义1.3.5
映射的乘积
设是集合Ａ到集合Ｂ内的映射，是集
合Ｂ到集合Ｃ内的映射，对任意aA，规定 ( )(a)＝ ( (a)) 显然是集合Ａ到集合Ｃ内的映射，我们称此映射为映射与映射的乘积。不难证明：映射的乘积满足结合律，但是不满足交换律。
例：
设A={1,2,3,4},B={a,b,c,d},
A 1 2 3 4 B a b c d
逆映射(inverse mapping)
若是集合A到集合B的1–1映射，则对于
B中每个元素b都对应着A中以b为映象（在下）的那个元素，这个对应显然是集合B 到A上的映射，我们称这个映射为的逆映射，记为 -1 。显然， -1也是1-1映射，并且对任意aＡ，都有 -1 ((a))＝a

第3讲映射的定义和性质

• 编写C语言程序主要就是编写函数: 从main 开始.
• Def 任意给定两个集合A和B, 若存在对应法则f, 使得对于任意 xA, 均存在唯一的yB 与它对应, 则称f是集合A到B的映射, 或称其为A到B的函数, 记为 f : A B
f
y
A
x
B
• 为何讨论映射? • 集合之间的对应关系.
• 其他理解方式:
x
f
y
• 映射的两个特点:
– (1)全函数. – (2)唯一性.
• 注意区别函数 f 与 f(x). • y = f(x)?
• 函数符号的选取:
– f, g,…, – F,G,…,
– ,,…,
– sin, exp, main, – add, average, hanoi, delete_string, …
离散数学
第3讲映射的定义和性质
第1章集合、映射与运算
1.2 映射的有关概念
本讲内容
1
映射的定义
2
映射的性质
1.2 映射的有关概念
• 1. 映射的定义 • 映射(mapping) = 函数(function).
• y = f(x) = x2 , ceiling function x , floor function x , …
• 例1-8
f :ZN
Z :...,3,2,1,0,1,2,3,...
N : 0,1,2,3,4,5,6,...
• 例1-9
f : (0,1) R
x tan x 1 π. 2
O
1
• Def 1-11 有限集合A上自身的双射称为A上的置换(permutation).
A
A
• 例1-10

人教版高中数学必修一课件：集合-映射

8
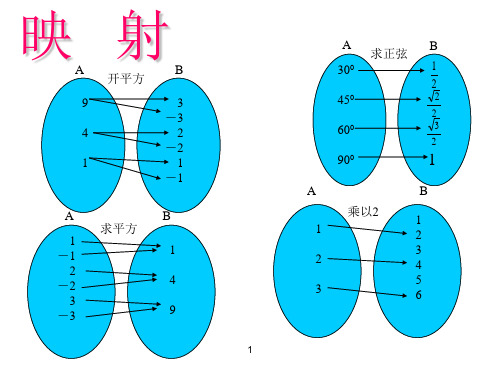
已知 ⑴
的映A射有多{1少,个2?,3},取,适B当的{对5应,法6}则
A到B ⑵以为定义域, 为值域的函数有多少个?
⑶在所有的以为定义域, 为值域的函数中,
满足 A
B 的函数有多少个?
A
B
f (1) f (2) f (3)
9
A B {a,b,c, d,e,, x, y, z}
A {a, b, c, d ,, x , y , z } B {a, b, c, d , , x , y , z }
考察下面的问题,集合A,B与集合C之间有什么关系?
(1)A={2,4,6,8,10}, B={3,5,8,12} ,C={8}； (2)A={x|x是我班的女同学},
B={x|x是我班戴眼镜的同学}, C={x|x是我班戴眼镜的女同学}.
发现：集合C是由集合A中和集合B中的公共元素所组成的.
交集
一一映射：设A，B是两个集合，f : A B 是集合A到集合B
的映射，如果在这个映射下，对于A中的不同元素，在集合B中有不同的象，而且B中每一个元素都有原象，那么这个映射叫做 A到B上的一一映射
7
• 答：主要有两点区别： • (1) 映射要求A中的元素在B中有唯一的象，
而一一映射不仅要求A中的元素在B中有唯一的象，还要求A中不同的元素在B中有不同的象； • (2) 映射不需要B中的元素都有原象，而一一映射则要求B中的每一个元素都必须有原象。
映射
A 开平方
B93来自－342－2
1
1
－1
A
B
求平方
1
－1
1
2
－2
4
3
－3
9
A 求正弦 B