二元一次不等式(组)所表示的平面区域PPT
合集下载
【数学课件】二元一次不等式
若C≠0，则直线定界,原点定域
特殊点(0,0)
画出下列不等式表示的平面区 域：
(1) x-y+1<0 ;
(2) x+ y>0；
(3) 2x+5y-10≥0 ;
（1）x-y+1<0
y x-y+1=0
1
-1
o
取(0,0) 0-0+1>0
x
（2）x+ y>0
y
1
o
直线过（0，0）
取（0，1）
0+1>0
Y
x+y-1>0
x+y-1<10XO Nhomakorabea1
l
点集{(x,y)|x+y-1>0}表示直线x+y-1=0右上方平面区域 点集{(x,y)|x+y-1<0}表示直线x+y-1=0左下方平面区域
（1）Ax+By+C>0在平面直角坐标系中 表示直线Ax+By+C=0某一侧所有点组成的平面区域。
（2）在确定区域时，在直线的某一侧取一个特殊点
－１ Ｄ
l 右上方的点(x,y), x+y-1>0成立
l 左下方的点(x,y), x+y-1<成立
证明:如图,设M(x,y)为 l
右上方区域内任一点
P YM
过M作MP平行于x轴交 l
于点P (x0 , y0 )
则 x x0 , y y0
x y x0 y0
1
X
O1
l
x+y-1=0
问3 在平面直角坐标系下作出A(1,1),B(1,2),
特殊点(0,0)
画出下列不等式表示的平面区 域：
(1) x-y+1<0 ;
(2) x+ y>0；
(3) 2x+5y-10≥0 ;
（1）x-y+1<0
y x-y+1=0
1
-1
o
取(0,0) 0-0+1>0
x
（2）x+ y>0
y
1
o
直线过（0，0）
取（0，1）
0+1>0
Y
x+y-1>0
x+y-1<10XO Nhomakorabea1
l
点集{(x,y)|x+y-1>0}表示直线x+y-1=0右上方平面区域 点集{(x,y)|x+y-1<0}表示直线x+y-1=0左下方平面区域
（1）Ax+By+C>0在平面直角坐标系中 表示直线Ax+By+C=0某一侧所有点组成的平面区域。
（2）在确定区域时，在直线的某一侧取一个特殊点
－１ Ｄ
l 右上方的点(x,y), x+y-1>0成立
l 左下方的点(x,y), x+y-1<成立
证明:如图,设M(x,y)为 l
右上方区域内任一点
P YM
过M作MP平行于x轴交 l
于点P (x0 , y0 )
则 x x0 , y y0
x y x0 y0
1
X
O1
l
x+y-1=0
问3 在平面直角坐标系下作出A(1,1),B(1,2),
二元一次不等式(组)与平面区域 课件
|AB|＝|3×1＋－32×－1＋6|＝ 122.
∴S△ABC＝12×
12 × 2
122＝36.
(2)画出2x－3＜y≤3表示的区域，并求所有的正整数解．
【思路分析】
原不等式等价于
y＞2x－3 y≤3.
而求正整数解，则意味着x，y还有限制条件，即求：
xy＞ ＞00 y＞2x－3，
y≤3
的整数解．
例3 画出不等式组2x＋x＋2yy－－51≤＞00 ，所表示的平面区域． y＜x＋2
【思路分析】 解决这种问题的关键在于正确地描绘出边 界直线，再根据不等号的方向，确定所表示的平面区域．
【解析】 先画直线x＋2y－1＝0，由于是大于号，从而将 直线画成虚线，∵0＋0－1<0，∴原点在它的相反区域内．
如图中阴影部分中横坐标、纵坐标均为整数的点．
探究5 充分利用已知条件，找出不等关系，画出适合条件 的平面区域，然后在该平面区域内找出符合条件的点的坐 标．实际问题要注意实际意义对变量的限制．必要时可用表格 的形式列出限制条件．
思考题6 一工厂生产甲、乙两种产品，生产每吨产品的资
源需求如下表：
品种 电力/kW·h 煤/t 工人/人
(2)设直线l方程为Ax＋By＋C＝0(A＞0)，则 ①Ax＋By＋C＞0表示l右侧平面区域． ②Ax＋By＋C＜0表示l左侧平面区域．
思考题1 (1)不等式x－2y≥0所表示的平面区域是下图中的 ()
【解析】
x－2y＝0的斜率为
1 2
，排除C、D.又大于0表示直
线右侧，选B.
【答案】 B
(2)不等式x＋3y－6＜0表示的平面区域在直线x＋3y－6＝0的
【解析】 如图，在其区域内的整数解为(1,1)、(1,2)、 (1,3)、(2,2)、(2,3)，共五组．
3.3.1二元一次不等式(组)与平面区域(一)
企业和个人贷款，希望这笔贷款至少可带来3万元的收益， 其中从企业贷款中获益12%，从个人贷款中获益10%.那 么，信贷部应如何分配资金呢？
x y 2500, 12 x 10 y 300 x 0, y0
1. 我们把含有两个未知数，并且未知数的次数是1的不
满足 x y 6 的点集在坐标平面上是怎样的图形？
l:x-y=6
问题一
满足 x y 6 的点集{( x, y) x y 6}在坐标平面上 是怎样的图形？
l:x-y=6
二元一次不等式 x－y＜6所表示的图形.
在直角坐标系中，所有点被直线l : x－y＜6分成三类: ①在直线l上的点;
确定.
一般地
C≠0时，常用点(0,0)确定.
C=0时，常用点(0,1)或(1,0)确定.
二元一次不等式Ax＋By＋C>0表示的平面区域常用 “直线定界，特殊点定域”的方法，即画线—取点—判 断.
例1. 画出x＋4y＜4表示的平面区域.
练习
教材P86练习第1、2题
x 3 y 6 0 例2. 画出 表示的平面区域. x y 2 0
l:x-y=6
问题一
满足 x y 6 的点集{( x, y) x y 6}在坐标平面上 是怎样的图形？
问题二
满足 Ax By C 0 的点集 {(x, y) Ax By C 0}
在坐标平面上是怎样的图形？
( A, B不同时为0)
问题三
满足 Ax 2 Bx C 0 的点集源自Ax 2 Bx C 0 的同
(1) x y 1
1.判断下列式子是不是二元一次不等式？ 2
(2) x y 1
人教a版必修五课件：二元一次不等式(组)与平面区域(62页)
2．点(x0，y0)在直线Ax＋By＋C＝0的右上方，则一定 有Ax0＋By0＋C>0吗？
提示：不一定．与系数B的符号有关．
3．若A(x1，y1)，B(x2，y2)两点在直线Ax＋By＋C＝0的 同侧或两侧应满足什么条件？
提示：同侧(Ax1＋By1＋C)(Ax2＋By2＋C)>0.异侧(Ax1＋ By1＋C)(Ax2＋By2＋C)<0.
新知初探
1．二元一次不等式及其解集的意义 (1)二元一次不等式 含有两 个未知数，并且含未知数的项的最高次数是 1 的不等式称为二元一次不等式． 二元一次不等式的一般形式是Ax＋By＋C>0，Ax＋By ＋C<0，Ax＋By＋C≥0，Ax＋By＋C≤0，其中A，B不同 时为零．
(2)二元一次不等式组 由几个 二元一次不等式 组成的不等式组称为二元一次 不等式组． (3)二元一次不等式(组)的解集 满足二元一次不等式(组)的x和y的取值构成有序数对 (x，y)，所以这样的有序数对(x，y)构成的集合称为二元一 次不等式(组)的解集．一个二元一次不等式，它的解是一些 数对(x，y)，因此，它的解集不能用数轴上一个区间表示， 而应是平面上的一个区域．
By＋C＝0划分平面成两个半平面的区域，分别由不等式Ax ＋By＋C>0与Ax＋By＋C<0决定．因此，如同前面所学平面 内的直线可以视为二元一次方程的几何表示一样，半平面 就是二元一次不等式的几何表示．
思考感悟
1．每一个二元一次不等式(组)都能表示平面上的一个 区域吗？ 提示：不一定．当不等式组的解集为空集时，不等式 组不表示任何图形．
7 答案：4
类型三 [例3]
点与平面区域的关系 已知点P(1，－2)及其关于原点的对称点中有
2020版人教A数学必修5 课件：3.3.1 二元一次不等式(组)与平面区域
即时训练3-1:某家具厂制造甲、乙两种型号的桌子,每张桌子需木工和 漆工两道工序完成.已知木工做一张甲、乙型号的桌子分别需要1 h和 2 h,漆工油漆一张甲、乙型号的桌子分别需要3 h和1 h.又木工、漆工 每天工作分别不得超过8 h和9 h.请列出满足生产条件的数学关系式,并 画出相应的平面区域.
3.3 二元一次不等式(组)与简单的线性规划 问题
3.3.1 二元一次不等式(组)与平面区域
[目标导航]
1.知道什么是二元一次不等式及二元一次不等式组. 2.了解二元一次不等式的几何意义,并会画其表示的平面 课标要求 区域. 3.能从实际情境中抽象出二元一次不等式组,并能用平面 区域表示二元一次不等式组的解.
x y 2 1 0,
x ky k 0
(2)将图中阴影部分表示的平面区域,用不等式表示出来.
(2)解:由图(1)可知,其边界所在的直线在 x 轴和 y 轴上的截距均为 1,故边界所在的直线 方程为 x+y-1=0, 将原点(0,0)代入直线方程 x+y-1=0 的左边,得 0+0-1<0, 故所求的不等式为 x+y-1≤0;
思考1:不等式2x-3y>0是二元一次不等式吗? 答案:是,符合二元一次不等式的两个特征. 2.二元一次不等式表示的平面区域
表示直线 Ax+By+C=0
某一侧
二元一次不等式Ax+By+C>0 所有点组成的平面区域,我们把直线画 成 虚线 ,以表示区域 不包括 边界
表示直线 Ax+By+C=0
某一侧
y
1)
0,
表示的平面区
域的面积等于( )
二元一次不等式(组)表示的平面区域
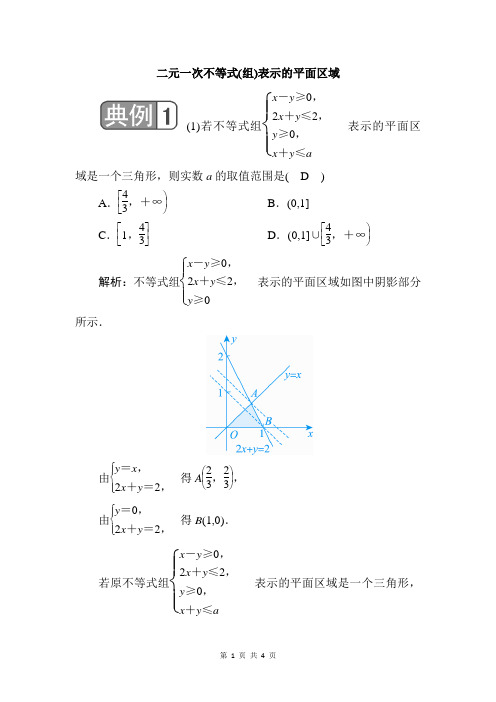
二元一次不等式(组)表示的平面区域(1)若不等式组⎩⎪⎨⎪⎧x －y ≥0，2x ＋y ≤2，y ≥0，x ＋y ≤a表示的平面区域是一个三角形，则实数a 的取值范围是( D )A ．⎣⎢⎡⎭⎪⎫43，＋∞ B ．(0,1]C ．⎣⎢⎡⎦⎥⎤1，43D ．(0,1]∪⎣⎢⎡⎭⎪⎫43，＋∞解析：不等式组⎩⎪⎨⎪⎧x －y ≥0，2x ＋y ≤2，y ≥0表示的平面区域如图中阴影部分所示．由⎩⎪⎨⎪⎧y ＝x ，2x ＋y ＝2，得A ⎝ ⎛⎭⎪⎫23，23，由⎩⎪⎨⎪⎧y ＝0，2x ＋y ＝2，得B (1,0)． 若原不等式组⎩⎪⎨⎪⎧x －y ≥0，2x ＋y ≤2，y ≥0，x ＋y ≤a表示的平面区域是一个三角形，则直线x ＋y ＝a 中a 的取值范围是0＜a ≤1或a≥43.(2)若不等式组⎩⎪⎨⎪⎧x ≥0，x ＋3y ≥4，3x ＋y ≤4所表示的平面区域的面积被直线y＝kx ＋43分为2∶1两部分，则k 的值是1或5.解析：不等式组表示的平面区域如图所示．由于直线y ＝kx ＋43过定点⎝ ⎛⎭⎪⎫0，43.因此只有直线过AB 的三等分点时，直线y ＝kx ＋43能把平面区域分为2∶1两部分．因为A (1,1)，B (0,4)，所以AB 靠近A 的三等分点为⎝ ⎛⎭⎪⎫23，2，靠近B 的三等分点为⎝ ⎛⎭⎪⎫13，3，当y ＝kx ＋43过点⎝ ⎛⎭⎪⎫23，2时，k ＝1，当y ＝kx ＋43过点⎝ ⎛⎭⎪⎫13，3时，k ＝5.1.二元一次不等式(组)表示平面区域的判断方法直线定界，测试点定域． 2．求平面区域的面积(1)首先画出不等式组表示的平面区域，若不能直接画出，应利用题目的已知条件转化为不等式组问题，从而再作出平面区域；(2)对平面区域进行分析，若为三角形应确定底与高，若为规则的四边形(如平行四边形或梯形)，可利用面积公式直接求解，若为不规则四边形，可分割成几个三角形分别求解再求和．(1)不等式组⎩⎪⎨⎪⎧2x ＋y －6≤0，x ＋y －3≥0，y ≤2表示的平面区域的面积为( B ) A ．4 B ．1 C ．5D ．无穷大解析：不等式组⎩⎪⎨⎪⎧2x ＋y －6≤0，x ＋y －3≥0，y ≤2表示的平面区域如图所示(阴影部分)，△ABC 的面积即所求，求出点A ，B ，C 的坐标分别为A (1,2)，B (2,2)，C (3,0)，则△ABC 的面积为S＝12×(2－1)×2＝1.(2)若函数y ＝2x 图象上存在点(x ，y )满足约束条件⎩⎪⎨⎪⎧x ＋y －3≤0，x －2y －3≤0，x ≥m ，则实数m 的最大值为( B )A ．12 B ．1 C ．32D ．2解析：在同一直角坐标系中作出函数y ＝2x 的图象及⎩⎪⎨⎪⎧x ＋y －3≤0，x －2y －3≤0所表示的平面区域，如图阴影部分所示．由图可知，当m ≤1时，函数y ＝2x 的图象上存在点(x ，y )满足约束条件，故m 的最大值为1.。
高考数学一轮复习课件：二元一次不等式表示的平面区域
变式:画出不等式 2x+y-6≥0表示的平面区域。
y
6
o
3
x
2x+y-6=0
若不等式中带等号时,其表示的区域包含边界，边界线应 画成实线;不带等号时,不包含边界，边界线画成虚线. 若不便于画成虚线（如坐标轴），应通过文字加以说明.
探究拓展 y
Y 6
2x+y-6≥0
6
O
3
X
o
3
x
2x+y-6＜0
2x+y-6=0 2x+y-6=0
Y想 一 想 ？来自取原点（0,0),代入2x+y-6， 因为2×0+0-6=-6 ＜0，
所以，原点在2x+y-6＜0 O 表示的平面区域内,不等 式 2x+y-6＜0表示的区域 2x+y-6＜0 为直线下方区域如图所示。
画出不等式 6 2x+y-6≥0表 示的平面区 域?
3 X
2x+y-6=0
点评:该题属给出不等式画出其所表示的平面区域问题 常采用“直线定界,特殊点定域”的方法
(1,0)点定域 若C=0，则 直线定界 _________、_________.
(3)注意事项: 若不等式中不含等号，则 ______________________ 边界画成虚线，否则画成实线 ____________________________________________
口 诀 ： 同 号 在 上 ， 异 号 在 下
O
X
x-y+5=0
x=3
自主归纳总结
(1)二元一次不等式Ax+By+C>0在平面直角 直线Ax+By+C=0某一侧所 坐标系中表示 ______________________ 有点组成的 __________平面区域。 (2)不等式所表示平面区域的确定步骤： 直线定界 特殊点定域 __________、____________ 直线定界 原点定域 若C≠0，则 _________、_________.
高考数学一轮复习课件：二元一次不等式(组)
由x2＋ x＋2yy－ －24＝ ＝00， ， 得A(2，0)． 由42xx－ ＋yy＋ －14＝ ＝00，. 得点B(12，3)， ∴zmax＝3×2－0＝6，zmin＝3×12－3＝－32. 故z的取值范围是[－32，6]．
【答案】 [－32，6]
x≥0， 若不等式组 x＋3y≥4， 所表示的平面区域被直线y 3x＋y≤4
(1)求z＝x－y的最小值和最大值；
(2)若z＝ x2＋y2，求z的取值范围．
•【审题视点】 明确目标函数z的几何意义， 数形结合找最优解，代入求值．
x≥0， 【尝试解答】 作约束条件 x＋2y≥3，
2x＋y≤3. 域，如图所示为△ABC及其内部．
联立x2＋x＋2yy＝＝33，. 得A(1，1)．
当直线l：y＝－m1 x＋mz 在y轴 上的截距最大时，目标函数取最大值． 平移直线l，当l过点B时，z有最大值．
因此z＝x＋my的最大值zmax＝12＋m2 . 依题意，12＋m2 ＜2(m＞1)，得1＜m＜3. 故实数m的取值范围是(1，3)．
•【答案】 C
•错因分析：(1)忽视条件m＞1，没能准确判 定直线l的斜率范围，导致错求最优解，从而 错得实数m的取值范围．
•【解析】 可行域如图 中阴影部分所示．先画出 直线l0：y＝－3x，平移 直线l0，当直线过A点时z ＝3x＋y的值最大，
由xy＝－2y－，1＝0，得xy＝＝23.， ∴A点坐标为(3，2)．∴z最大＝3×3＋2＝11.
•【答案】 B
x≥1， 3．在平面直角坐标系中，不等式组 x＋y≤0， 表示
•2．解线性规划应用问题的一般步骤是：(1) 分析题意，设出未知量；(2)列出线性约束条 件和目标函数；(3)作出可行域并利用数形结 合求解；(4)作答．
【数学】3.5.1《二元一次不等式(组)所表示的平面区域》课件(新人教B版必修5)
否则应画成实线。
2、画图时应非常准确，否则将得不到正确结果。 3、熟记“直线定界、特殊点定域”方法的内涵。
x＋y－1≥0 在平面直角坐标系中，若不等式组x－1≤0 ax－y＋1≥0 常数)所表示的平面区域内的面积等于 2，求 a 的值．
[解题过程] 如图可得阴影区域为不等式组
x＋y－1≥0 x－1≤0
解：设开设初中班x个，高中班y个。因办学规模 以20～30个班为宜，所以， 20≤x＋y≤30 而由于资金限制，26x＋54y＋2×2x＋2×3y≤1200 另外，开设的班级不能为负，则x≥0，y≥0。
把上面四个不等式合在一起，得限制条件用数学关系式表示为
y
20 x＋y 30 30 x＋2y 40 20 x0 y 0
y
左上方 x-y+1<0
1
x-y+1=0
-1
o
x
（x。，y。） x0>x，y=y0 x0-y0+1> x-y+1
(x，y）
右下方 x-y+1>0
问题：一般地，如何画不等式 AX+BY+C>0表示的平面区域？
（1）二元一次不等式Ax+By+C>0在平面 直角坐标系中表示直线Ax+By+C=0某一侧 所有点组成的平面区域。
（2）由于对直线同一侧的所有点(x,y)，把 它代入Ax+By+C，所得实数的符号都相同， 所以只需在此直线的某一侧取一个特殊点 (x0,y0) ，从Ax0+By0+C的正负可以判断出 Ax+By+C>0表示哪一侧的区域。 一般在C≠0时，取原点作为特殊点。
二元一次不等式所表示的平面区域
当堂检测
1、不等式x – 2y + 6 > 0表示的区域在直线
x – 2y + 6 = 0的（ B ） （A）右上方 （B）右下方
（C）左上方 （D）左下方
2、不等式3x + 2y – 6 ≤0表示的平面区 域是（ D ）
x 3 y 6 0 3、不等式组 x y 2 0
解：
3 2 1
y 2x-3y+2=0
-1 O 2y+1=0 -1 -2
1
2
3 x-3=0
例3．一个化肥厂生产甲、乙两种混合肥料，生产1 车皮甲种肥料需用的主要原料是磷酸盐4吨，硝酸盐 18吨，生产1车皮乙种肥料需用的主要原料是磷酸盐 1吨，硝酸盐15吨，现有库存磷酸盐10吨，硝酸盐66 吨。如果在此基础上进行生产，设x，y分别是计划 生产甲、乙两种混合肥料的车皮数，请列出满足生 产条件的数学关系式，并画出相应的平面区域。 解：x和y所满足的数学关系式为 4 x y ≤ 10 18 x 15 y ≤ 66 x≥0 y≥0
表示的平面区域是（ B ）
4：画出下面不等式组所表示的平面区域 y
解：依次画出三个不 等式 x－y+5≥0, x+y≥0, x≤3所表示的 平面区域
x y 5≥ 0 x y ≥ 0 x ≤ 3
x+y=0
O
x
x-y+5=0 x=3
所以,不x+y－1=0。 在直线l的上方和下方取一些点： y 5 上方：(0，2)，(1，3)，
(0，5)，(2，2)； 下方：(－1，0), (0，0),
(0，－2), (1，－1) 结论: 在l上方的点的坐标 使式子的值都大于0。 在l下方的点的坐标 使式子的值都小于0。
3.3.1二元一次不等式(组)与平面区域(第二课时)
典例分析
解：设需要截第一种钢板x张，第二种钢板 张，则 设需要截第一种钢板 张 第二种钢板y张
y
2x+y≥15 X+2y≥18 X+3y ≥27 x ≥0 y ≥0 图形表示如右
18 16 14 12 10 8 6 4 2
X+3y=27
2 4 6 8 10 12 14 16 18 20 22 24 26 28
y
x-y=0 x+2y-4=0 2 4
y
4
o
-2
x
y+2=0
o
3
x
4x+3y-12=0
思 考
2x+y -2=0 x+2y+1=0
画出不等式(x+2y+1)(2x+y -2)<0 画出不等式 表示的平面区域. 表示的平面区域
y
原不等式等价于 x + 2 y +1 > 0 x + 2 y +1 < 0 (1) 或(2) 2x + y − 2 < 0 2x + y − 2 > 0
分别为计划生产甲、 解：设x、y分别为计划生产甲、乙两种混合 、 分别为计划生产甲 肥料的车皮数，于是满足条件的数学关系式是： 肥料的车皮数，于是满足条件的数学关系式是：
典例分析
＋ 4x y ≤10 18x＋ 15y ≤ 66 x ≥ 0 y ≥ 0 条件表示的平面区域为图中红 色阴影种大小不同的钢板截成A、B、C三种规 格，每张钢板可同时截得三种规格的小钢板的块 数如下表示： 数如下表示： 钢型 第一种钢板 第二种钢板 规格
A 规格
2 1
B 规格
高考理科数学《二元一次不等式(组)》课件
殊图形分别求解再求和．
(1)(2016·郑州模拟)在平面直角坐标系 xOy 中，满足
不
等
式
组
|x|≤|y|，
|x|＜1
的
点
(x
，
y)
的
集
合
用
阴
影
表
示
为
下
列
图
中
的
()
解：|x|＝|y|把平面分成四部分，|x|≤|y|表示含 y 轴的两个区域；|x|＜1 表示 x＝±1 所夹含 y 轴的区
域．故选 C．
x－y＋1≥0， (2018·石家庄质检)若 x，y 满足约束条件x－2≤0， 则
x＋y－2≥0，
z＝yx的最大值为________．
解：作出不等式组表示的平面区域如图阴影部分所 示，z＝yx＝yx－－00，表示区域内的点与原点连线的斜率，易
知 zmax＝kOA．由xx－＋yy＋－12＝＝00，，得 A12，32，所以 kOA＝3，
________边界直线，则把边界直线画成________．
(2)由于对直线 Ax＋By＋C＝0 同一侧的所有点(x，y)，把它的 坐标(x，y)代入 Ax＋By＋C，所得的符号都________，所以只需在 此直线的同一侧取一个特殊点(x0，y0)(如原点)作为测试点，由 Ax0 ＋By0＋C 的________即可判断 Ax＋By＋C＞0 表示的是直线 Ax
() D．45
解：作出可行域如图中阴影部分所示，
结合目标函数的几何意义可知，目标函数在点 A 处取得最大值．联
立直线方程x＋y＝5， －x＋y＝1，
可得点
A
的坐标为
A(2，3)，据此可知目标
函数的最大值 zmax＝3×2＋5×3＝21．故选 C．
(1)(2016·郑州模拟)在平面直角坐标系 xOy 中，满足
不
等
式
组
|x|≤|y|，
|x|＜1
的
点
(x
，
y)
的
集
合
用
阴
影
表
示
为
下
列
图
中
的
()
解：|x|＝|y|把平面分成四部分，|x|≤|y|表示含 y 轴的两个区域；|x|＜1 表示 x＝±1 所夹含 y 轴的区
域．故选 C．
x－y＋1≥0， (2018·石家庄质检)若 x，y 满足约束条件x－2≤0， 则
x＋y－2≥0，
z＝yx的最大值为________．
解：作出不等式组表示的平面区域如图阴影部分所 示，z＝yx＝yx－－00，表示区域内的点与原点连线的斜率，易
知 zmax＝kOA．由xx－＋yy＋－12＝＝00，，得 A12，32，所以 kOA＝3，
________边界直线，则把边界直线画成________．
(2)由于对直线 Ax＋By＋C＝0 同一侧的所有点(x，y)，把它的 坐标(x，y)代入 Ax＋By＋C，所得的符号都________，所以只需在 此直线的同一侧取一个特殊点(x0，y0)(如原点)作为测试点，由 Ax0 ＋By0＋C 的________即可判断 Ax＋By＋C＞0 表示的是直线 Ax
() D．45
解：作出可行域如图中阴影部分所示，
结合目标函数的几何意义可知，目标函数在点 A 处取得最大值．联
立直线方程x＋y＝5， －x＋y＝1，
可得点
A
的坐标为
A(2，3)，据此可知目标
函数的最大值 zmax＝3×2＋5×3＝21．故选 C．
人教新课标版数学高二B必修5课件 3.5.1 二元一次不等式(组)所表示的平面区域
明目标、知重点
探要点·究所然 情境导学 在前面我们学习了等差数列，其特点是从第2项起，每一 项与它前一项的差等于同一常数，在生活中也常见从第2 项起，每一项与它前一项的比等于同一常数的数列，本节 我们就来研究这类数列.
探究点一 二元一次不等式(组)的有关概念 思考1 不等式x＋y>700,10x＋12y≤8 000有什么特点？ 答 都含有两个未知数，且未知数的最高次数为1.
2x＋y≥15，
x＋2y≥18，
x＋3y≥27，
x≥0， y≥0.
用图形表示以上限制条件，
得到如下图的平面区域(阴影部分).
当堂测·查疑缺
1234
1.不在不等式3x＋2y<6表示的平面区域内的一个点是( D )
A.(0,0)
B.(1,1) C.(0,2)
D.(2,0)
解析 将四个点的坐标分别代入不等式中， 其中点(2,0)代入后不等式不成立， 故此点不在不等式3x＋2y<6表示的平面区域内，故选D.
(2)y≥－2x＋3. 解 先画出直线2x＋y－3＝0(画成实线).取原点(0,0)， 代入2x＋y－3，∵2×0＋0－3<0， ∴原点不在2x＋y－3≥0表示的平面区域内， 不等式y≥－2x＋3所表示的平面区域如图所示.
例2 画出下列不等式组所表示的平面区域：
2x－y＋1>0
(1)
，
x＋y－1≥0
(3)不等式表示的区域(也称不等式的 图象 ) 以不等式解(x，y)为坐标的所有点构成的 集合 叫做不等式 表示的区域(或不等式的图象). (4)二元一次不等式组所表示的平面区域是每一个不等式所 表示的平面区域的交集，就是二元一次不等式组所表示的 平面区域.
2.平面区域内的点 直线l：Ax＋By＋C＝0把在坐标平面内不在直线l上的点分 为两部分，直线l的同一侧的点的坐标使式子Ax＋By＋C的 值具有 相同 的符号，并且两侧的点的坐标使Ax＋By＋C的 值的符号 相反，一侧都大于0，另一侧都小于0.
4.1二元一次不等式(组)与平面区域
§4 简单线性规划
-1-
4.1 二元一次不等式(组)与平面区域
-2-
目标导航
Z D 知识梳理 HISHISHULI
典例透析
IANLITOUXI
S随堂演练 UITANGYANLIAN
1.能从实际情境中抽象出二元一次不等式组,了解二元一次不等 式的几何意义.
2.能用平面区域表示二元一次不等式组,并能利用二元一次不等 式(组)所表示的平面区域解决简单的实际问题.
(2)将y≤-2x+3变形为2x+y-3≤0, 画出直线2x+y-3=0(画成实线),
取点(0,0),代入2x+y-3,得2×0+0-3=-3<0,
故y≤-2x+3表示的区域是直线2x+y-3=0及其左下方的平面区域,
如图②阴影部分所示.
-22-
目标导航
Z D 知识梳理 HISHISHULI
典例透析
S随堂演练 UITANGYANLIAN
题型一 画二元一次不等式表示的平面区域 【例1】 (1)画出不等式3x-4y-12≥0表示的平面区域; (2)画出不等式3x+2y<0表示的平面区域. 分析:(1)先画直线,再取原点分析;(2)先画直线,再取点(1,0)分析. 解:(1)先画直线3x-4y-12=0,取原点(0,0),代入3x-4y-12,得-12<0, 所以原点不在3x-4y-12≥0表示的平面区域内,
另外，还有x 0, y 0. 综上所述，x, y应满足以下不等式组
3x 5y 150 5x 2y 200
2x 8y 160，
3x 5y 150， 5x 2 y 200，
2x 8y 160
-1-
4.1 二元一次不等式(组)与平面区域
-2-
目标导航
Z D 知识梳理 HISHISHULI
典例透析
IANLITOUXI
S随堂演练 UITANGYANLIAN
1.能从实际情境中抽象出二元一次不等式组,了解二元一次不等 式的几何意义.
2.能用平面区域表示二元一次不等式组,并能利用二元一次不等 式(组)所表示的平面区域解决简单的实际问题.
(2)将y≤-2x+3变形为2x+y-3≤0, 画出直线2x+y-3=0(画成实线),
取点(0,0),代入2x+y-3,得2×0+0-3=-3<0,
故y≤-2x+3表示的区域是直线2x+y-3=0及其左下方的平面区域,
如图②阴影部分所示.
-22-
目标导航
Z D 知识梳理 HISHISHULI
典例透析
S随堂演练 UITANGYANLIAN
题型一 画二元一次不等式表示的平面区域 【例1】 (1)画出不等式3x-4y-12≥0表示的平面区域; (2)画出不等式3x+2y<0表示的平面区域. 分析:(1)先画直线,再取原点分析;(2)先画直线,再取点(1,0)分析. 解:(1)先画直线3x-4y-12=0,取原点(0,0),代入3x-4y-12,得-12<0, 所以原点不在3x-4y-12≥0表示的平面区域内,
另外，还有x 0, y 0. 综上所述，x, y应满足以下不等式组
3x 5y 150 5x 2y 200
2x 8y 160，
3x 5y 150， 5x 2 y 200，
2x 8y 160
高中数学 第三章 不等式 3.5.1 二元一次不等式(组)所表示的平面区域课件 新人教B版必修5
界)，且 A(1，1)，B(0，4)，C0，43，直线 y＝a(x＋1)恒过点 P(－1，0)，且斜率为 a，
由斜率公式可知 kAP＝12，
kBP＝4. 若直线 y＝a(x＋1)与区域 D 有公共点，
数形结合可得12≤a≤4. 【答案】 (1)(－∞，2)∪(5，＋∞)
(2)12，4
1.若点 P(a2，a)不在不等式 x＋2y＋1≤0 表示的 平面区域内，则 a 的取值范围是________． 解析：因为点 P(a2，a)不在不等式 x＋2y＋1≤0 表示的平面区 域内， 所以 a2＋2a＋1>0，即(a＋1)2>0，解得 a≠－1. 所以 a 的取值范围是{a∈R|a≠－1}． 答案：{a∈R|a≠－1}
2．不等式(x－y)(x＋2y－2)≥0 表示的平面区域的大致图形是 ()
解析：选 B.原不等式等价于xx－ ＋y2≥y－0， 2≥0 或xx－ ＋y2≤y－0， 2≤0. 故原不等式表示的区域由这两个不等式组表示的区域组成．
3.平面直角坐标系中，不等式组23xx＋ －23yy－ ＋14≥ ≥00， ，表示的平面区 x≤2
(1)画二元一次不等式组表示平面区域的一般步骤
(2)求平面区域面积的方法 求平面区域的面积，先画出不等式组表示的平面区域，然后根 据区域的形状求面积． ①若画出的平面区域是规则的，则直接利用面积公式求解． ②若平面区域是不规则的，可采用分割的方法，将平面区域分 成几个规则图形求解．
1.不等式组xx－ ＋yy≤ ≤00，表示的平面区域是(
1．二元一次不等式的概念 (1)二元一次不等式是指含有_两__个___未知数，且未知数的最高次 数为一次的不等式． (2)一般形式为 Ax＋By＋C>0 或 Ax＋By＋C<0.其中 A2＋B2≠ 0.
《二元一次不等式组与平面区域》
（4）二元一次不等式（组）的解集与平面直角 坐标系内的点之间的关系：
二元一次不等式（组）的解集是有序实数对， 而点的坐标也是有序实数对，因此，有序 实数对就可以看成是平面内点的坐标， 进而，二元一次不等式（组）的解集就 可以看成是直角坐标系内的点构成的集合。
（5）探究二元一次不等式（组）的解集表示的 图形 （1）回忆、思考 回忆：初中一元一次不等式（组）的解 集 所表示的图形 思考：在直角坐标系内，二元一次不 等式（组）的解集表示什么图形？
3.3.1《二元一次不等式 (组）与平面区域》
二元一次不等式和二元一次不等式组的定义
（1）二元一次不等式：
含有两个未知数，并且未知数的最高次数是1的 不等式叫做二元一次不等式 ;
（2）二元一次不等式组：
由几个二元一次不等式组成的不等式组 称为二元一次不等式组。
（3）二元一次不等式（组）的解集：
满足二元一次不等式（组）的x和y的取 值构成有序实数对（x,y），所有这样的 有序实数（x,y）构成的集合称为二元一 次不等式（组）的解集。
归纳：不等式组表示的平面区域是各 个不等式所表示的平面点集的交集， 因而是各个不等式所表示的平面区域 的公共部分。
2．画出下列不等式组所表示的平面区域： （1）2 x y 1 0 解：（1）在同一个直角坐标系中，
x y 1≥ 0
作出直线2x－y+1=0(虚线)，
x+y－1=0(实线)。 用例1的选点方法，分别作出不等式2x－ y+1>0，x+y－1≥0所表示的平面区域，
则它们的交集就是已知不等式组所 表示的区域。
y 3 2 1 -1 O 2y+1=0 -1 -2 1 2 3 x-3=0 2x-3y+2=0
二元一次不等式(组)与平面区域nbsp课件1
例3 、要将两种大小不同的钢板截成Ａ．Ｂ．Ｃ三种规格，每张钢板可同时 截得三种规格的小钢板的块数如下表所示： 规格类型 钢板类型 第一种钢板 第二种钢板
A规格 2 1
Ｂ规格 1 2
Ｃ规格 1 3
今需要Ａ．Ｂ．Ｃ三种规格的成品分别为15，18，27块，用数 学关系式和图形表示上述要求。
解：设需要截第一种钢板x张，第二种
2、画图时应非常准确，否则将得不到正确结果。 3、熟记“直线定界、特殊点定域”方法的内涵。
作业：
Ｐ93
A
1, 2.B1,2
平面区域的确定常采 用“直线定界，特殊 x 点定域”的方法。
x+4y<4
练习：
1、不等式x－2y+6>0表示的平面区域在直线的x －2y+6=0的（ Ｂ ） A. 右上方 B. 右下方 C、左上方 D、左下方 3 -6 ） Ｄ y -3 图（1） y y
x
2、不等式3x+2y-6≤0表示的平面区域是（ Y y
归纳：
对于直线Ax + By + C = O
（1）若A>0,B<0 (2)A>0,B>0 y y Ax+By+C<0在左上方 Ax +B y+ C>0在右上方
0 0 x Ax +B y+ C>0在右下方 Ax+By+C<0在左 下方
x
应该注意的几个问题：
1、若不等式中不含0，则边界应画成虚线，
否则应画成实线。
钢板y张，则
2x+y≥15 X+2y≥18 X+3y ≥27 x ≥0 y ≥0
18 16
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：（1）所求的平面区域不包括直线， 用虚线画直线l：2x－y－3=0， 将原点坐标(0，0)代入2x－y－3，得 2×0－0－3=－3<0，
这样，就可以判定不等式2x－y－
3>0所表示的区域与原点位于直线2x－y －3=0的异侧，即不包含原点的那一侧。
y 2 1
2x-y-3=0
x -1 O -1 -2 1 2
则它们的交集就是已知不等式组所表示
的区域。
y 3
2x-y+1=0
2
1
x
-1 O -1 1 2 x+y-1=0
2x 3 y 2 0 （2） 2 y 1 ≥ 0 x 3≤ 0
解：（2）在同一个直角坐标系中，作出 直线2x－3y+2=0(虚线)，2y+1=0(实线)， x－3=0(实线)，
Ax By C 0 ( 0 ) 或 Ax By C 0 ( 0 )
3、已知直线l：Ax+By+C=0，它把平面分 为两部分，每个部分叫做开半平面，开半 平面与l的并集叫做闭半平面。 4、不等式的解(x，y)为坐标的所有点构 成的集合，叫做不等式表示的平面区域 或不等式的图象。
二元一次不等式（组）所表 示的平面区域
高二数学备课组
预习检测
y
2x-y-3=0
x-y-1=0 0 x
【学习目标】 1、了解二元一次不等式（组）的概念， 理解其解集的几何意义； 2、会画二元一次不等式（组）所表示的 平面区域。
预习案作业优秀学生
知识梳理 1、含有两个未知数，且未知数的最高次 数为1，我们称这样的不等式为二元一次 不等式 2、二元一次不等式的一般形式为
当堂检测
1、A 2、C
4 y 3 2 1 3x+2y-6 0 -1 O -1 1 2 x 3x+2y-6=0
例2．画出下列不等式组所表示的平面区域：
2x y 1 0 （1） x y 1≥ 0
解：（1）在同一个直角坐标系中，
作出直线2x－y+1=0(实线)，
x+y－1=0(实线)。
用例1的选点方法，分别作出不等式2x－ y+1 ≥ 0，x+y－1≥0所表示的平面区域，
解：设x，y分别是计划生产甲、乙两种混 合肥料的车皮数，则x，y所满足的数学关 系式为
4 x y ≤ 10 1 8 x 1 5 y ≤ 6 6 x≥ 0 y≥ 0
分别画出不等式组中， 各不等式所表示的区域.
然后取交集，就是不等式组所表示的区域。
y 10 9 8 7 6 5 4 3 2 1 O
则它们的交集就是已知不等式组所表示 的区域。 用例1的选点方法，分别作出不等式
2x－3y+2>0，2y+1≥0，x－3≤0
所表示的平面区域，
y 3 2 1 -1 O 2y+1=0 -1 -2 1 2 3 x-3=0 2x-3y+2=0
例3．一个化肥厂生产甲、乙两种混合肥 料，生产1车皮甲种肥料需用的主要原料 是磷酸盐4吨，硝酸盐18吨，生产1车皮乙 种肥料需用的主要原料是磷酸盐1吨，硝 酸盐15吨，现有库存磷酸盐10吨，硝酸盐 66吨。如果在此基础上进行生产，设x，y 分别是计划生产甲、乙两种混合肥料的车 皮数，请列出满足生产条件的数学关系式， 并画出相应的平面区域。
4x+y=10
18x+15y=66 x 1 2 3 4
课堂小结
画平面区域的步骤： （1）先画不等式对应的方程所表示的直线 （包括直线时，把直线画成实线；不包括直 线时，把直线化成虚线） 简称“直线定界” （2）再通过选点法判定在直线的哪一侧，选 点法中常选的点有（0,0），（1，0）或 （0,1）等， 简称“特殊点定域”
二元一次不等式的几何意义
直线l：Ax+By+C=0把坐标平面内不在
直线l上的点分为两部分，直线l同一侧的点
的坐标使式子Ax+By+C的值具有相同的符 号，并且两侧的点的坐标使Ax+By+C的值 的符号相反，一侧都大于零，另一侧都小 于零。
例1．画出下面二元一次不等式表示的平 面区域： （1）2x－y－3>0； （2）3x+2y－6≤0.
2x-y-3>0
（2）画出3x+2y－6≤0的平面区域.
解：（2）所求的平面区域包括直线，用 实线画直线l：3x+2y－6=0， 将原点坐标(0，0)代入3x+2y－6，得 3×0+2×0－6=－6<0，
这样，就可以判定不等式3x+2y－6≤0所 表示的区域与原点位于直线2x－y－3=0的 同侧，即包含原点的那一侧（包含直线l）。
这样，就可以判定不等式2x－y－
3>0所表示的区域与原点位于直线2x－y －3=0的异侧，即不包含原点的那一侧。
y 2 1
2x-y-3=0
x -1 O -1 -2 1 2
则它们的交集就是已知不等式组所表示
的区域。
y 3
2x-y+1=0
2
1
x
-1 O -1 1 2 x+y-1=0
2x 3 y 2 0 （2） 2 y 1 ≥ 0 x 3≤ 0
解：（2）在同一个直角坐标系中，作出 直线2x－3y+2=0(虚线)，2y+1=0(实线)， x－3=0(实线)，
Ax By C 0 ( 0 ) 或 Ax By C 0 ( 0 )
3、已知直线l：Ax+By+C=0，它把平面分 为两部分，每个部分叫做开半平面，开半 平面与l的并集叫做闭半平面。 4、不等式的解(x，y)为坐标的所有点构 成的集合，叫做不等式表示的平面区域 或不等式的图象。
二元一次不等式（组）所表 示的平面区域
高二数学备课组
预习检测
y
2x-y-3=0
x-y-1=0 0 x
【学习目标】 1、了解二元一次不等式（组）的概念， 理解其解集的几何意义； 2、会画二元一次不等式（组）所表示的 平面区域。
预习案作业优秀学生
知识梳理 1、含有两个未知数，且未知数的最高次 数为1，我们称这样的不等式为二元一次 不等式 2、二元一次不等式的一般形式为
当堂检测
1、A 2、C
4 y 3 2 1 3x+2y-6 0 -1 O -1 1 2 x 3x+2y-6=0
例2．画出下列不等式组所表示的平面区域：
2x y 1 0 （1） x y 1≥ 0
解：（1）在同一个直角坐标系中，
作出直线2x－y+1=0(实线)，
x+y－1=0(实线)。
用例1的选点方法，分别作出不等式2x－ y+1 ≥ 0，x+y－1≥0所表示的平面区域，
解：设x，y分别是计划生产甲、乙两种混 合肥料的车皮数，则x，y所满足的数学关 系式为
4 x y ≤ 10 1 8 x 1 5 y ≤ 6 6 x≥ 0 y≥ 0
分别画出不等式组中， 各不等式所表示的区域.
然后取交集，就是不等式组所表示的区域。
y 10 9 8 7 6 5 4 3 2 1 O
则它们的交集就是已知不等式组所表示 的区域。 用例1的选点方法，分别作出不等式
2x－3y+2>0，2y+1≥0，x－3≤0
所表示的平面区域，
y 3 2 1 -1 O 2y+1=0 -1 -2 1 2 3 x-3=0 2x-3y+2=0
例3．一个化肥厂生产甲、乙两种混合肥 料，生产1车皮甲种肥料需用的主要原料 是磷酸盐4吨，硝酸盐18吨，生产1车皮乙 种肥料需用的主要原料是磷酸盐1吨，硝 酸盐15吨，现有库存磷酸盐10吨，硝酸盐 66吨。如果在此基础上进行生产，设x，y 分别是计划生产甲、乙两种混合肥料的车 皮数，请列出满足生产条件的数学关系式， 并画出相应的平面区域。
4x+y=10
18x+15y=66 x 1 2 3 4
课堂小结
画平面区域的步骤： （1）先画不等式对应的方程所表示的直线 （包括直线时，把直线画成实线；不包括直 线时，把直线化成虚线） 简称“直线定界” （2）再通过选点法判定在直线的哪一侧，选 点法中常选的点有（0,0），（1，0）或 （0,1）等， 简称“特殊点定域”
二元一次不等式的几何意义
直线l：Ax+By+C=0把坐标平面内不在
直线l上的点分为两部分，直线l同一侧的点
的坐标使式子Ax+By+C的值具有相同的符 号，并且两侧的点的坐标使Ax+By+C的值 的符号相反，一侧都大于零，另一侧都小 于零。
例1．画出下面二元一次不等式表示的平 面区域： （1）2x－y－3>0； （2）3x+2y－6≤0.
2x-y-3>0
（2）画出3x+2y－6≤0的平面区域.
解：（2）所求的平面区域包括直线，用 实线画直线l：3x+2y－6=0， 将原点坐标(0，0)代入3x+2y－6，得 3×0+2×0－6=－6<0，
这样，就可以判定不等式3x+2y－6≤0所 表示的区域与原点位于直线2x－y－3=0的 同侧，即包含原点的那一侧（包含直线l）。