2020届全国100所名校高三最新高考模拟示范卷(六)数学(理)试题解析
2020全国100所名校高考模拟金典卷理科数学试卷及答案解析(13页)

2020全国100所名校高考模拟金典卷理科数学试卷理科数学试卷(120分钟 150分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合2|01x A x x +⎧⎫=≤⎨⎬-⎩⎭,[]{}2|log (2)(1)B x y x x ==-+,则A B =I ( ) A.[-2,2) B.(-1,1) C.(-1,1] D.(-1,2) 2.复数21iz i=-,则z 在复平面内的对应点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3.设等差数列{}n a 的前n 项和为n S ,若242, 16a S ==,则5a =( ) A.10 B .12 C .13 D .144.给出下列说法: ①“tan 1x =”是“4x π=”的充分不必要条件;②定义在[a, b]上的偶函数2()(5)f x x a x b =+++的最大值为30; ③命题“0001,2x x x ∃∈+R …”的否定形式是“1,2x x x∀∈+>R ”. 其中错误说法的个数为( ) A.0 B.1 C.2 D.35.已知点()2,3A ,且点B 为不等式组00260y x y x y ⎧⎪-⎨⎪+-⎩…„„,所表示平面区域内的任意一点,则||AB 的最小值为( )A.12D.1 6.函数2()sin f x x x x =-的图象大致为( )A. B. C. D.7.3ax ⎛ ⎝⎭的展开式中,第三项的系数为1,则11a dx x =⎰( )A.2ln2B.ln2C.2D.18.执行如图所示的程序框图,若输出的120S =,则判断框内可以填入的条件是( ) A.4?k > B .5?k > C.6?k > D.7?k >9.河图是上古时代神话传说中伏羲通过黄河中浮出龙马身上的图案,与自己的观察而画出的“八卦”,而龙马身上的图案就叫做“河图”,把一到十分为五组,如图所示,其口诀:一六共宗,为水居北;二七同道,为火居南;三八为朋,为木居东;四九为友,为金居西;五十同途,为土居中.现从这十个数中随机抽取4个数,则能成为两组的概率是( )A.13 B .110C.121D.125210.如图,正方形网格纸中的实线图形是一个多面体的三视图,则该多面体各表面所在平面互相垂直的有( ) A.2对B.3对C.4对D.5对11.已知直线:2l y x b =+被抛物线2:2(0)C y px p =>截得的弦长为5,直线l 经过C 的焦点,M 为C 上的一个动点,设点N 的坐标为()4,0,则MN 的最小值为( ) A.C.12.已知数列{}n a 满足:()()2*112,10n n n a a S S n +=+-=∈N ,其中n S 为数列{}n a 的前n 项和. 设()()()12111()1n S S S f n n +++=+L ,若对任意的n 均有(1)()f n kf n +<成立,则k 的最小整数值为( )A.2B.3C.4D.5二、填空题:本题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.已知A B C ,,为圆O 上三点,且2CO BA BC =-u u u r u u u r u u u r ,则BA BC ⋅=u u u r u u u r_____________.14.已知函数()2sin()0,,2f x x πωϕωϕπ⎛⎫⎡⎤=+>∈ ⎪⎢⎥⎣⎦⎝⎭的部分图象如图所示,其中()01f =,5||2MN =,则点M 的坐标为_____________.15.如图,点A 为双曲线2222:1(0,0)x y C a b a b-=>>的右顶点,右焦点为()2,0F ,点P 为双曲线上一点,作PB x ⊥轴,垂足为B ,若A 为线段OB 的中点,且以A 为圆心,AP 为半径的圆与双曲线C 恰有三个公共点,则双曲线C 的方程为____________.16.已知在三棱锥A BCD -中,平面ABD ⊥平面BCD ,4BC CD BC CD AB AD ⊥====,,,则三棱锥A BCD -的外接球的体积为____________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤第17~21题为必考题,每个试题考生都必须作答.第2、23题为选考题,考生根据要求作答. (一)必考题:共60分.17.在ABC △中,角A B C ,,所对的边分别为a b c ,,,sin ()sin sin a A a b B c C ++=,ABC △的面积S abc =. (1)求角C 的大小;(2)求ABC △周长的取值范围.18.如图,在多面体ABCGDEF 中,AB AC AD ,,两两垂直,四边形ABED 是边长为2的正方形,AC DG EF ∥∥,且12AC EF DG ===,.(1)证明:CF ⊥平面BDG . (2)求二面角F BC A --的余弦值.19.某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推岀两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次,每次收取维修费2000元; 方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次,每次收取维修费1000元.某医院准备一次性购买2台这种机器,现需决策在购买机器时应购买哪种延保方案,为此搜集并整理50台这种机器超过质保期后延保两年内维修的次数,如下表:以这50台机器维修次数的频率代替1台机器维修次数发生的概率.记X 表示准备购买的2台机器超过质保期后延保两年内共需维修的次数. (1)求X 的分布列;(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更划算?20.已知O 为坐标原点,椭圆22221(0)x y a b a b +=>>的右焦点为()1,0F ,,过点F 的直线l 与C 相交于A B 、两点,点M 为线段AB 的中点.(1)当l 的倾斜角为45︒时,求直线OM 的方程;(2)试探究在x 轴上是否存在定点Q ,使得QA QB ⋅u u u r u u u r为定值?若存在,求出点Q 的坐标;若不存在,请说明理由.21.已知函数2()2(1)ln(1)2f x x x x x =++--. (1)判断函数()f x 的单调性; (2)已知数列{}n a ,()*123ln(1),1n n n n a T a a a a n n +==∈+N L L ,求证:[]ln (2)12n nn T +<-. (二)选考题:共10分.请考生在第22、23两题中任选一题作答.如果多做,则按所做的第一题计分. 22.[选修4-4:坐标系与参数方程]在直角坐标系xOy 中,曲线1C 的参数方程为2cos 3sin x y θθ=⎧⎨=⎩(θ为参数).在以原点O 为极点,x 轴正半轴为极轴建立的极坐标系中,曲线2C 的极坐标方程为24sin 5ρρθ=+. (1)写出曲线1C 的普通方程和2C 的直角坐标方程; (2)若P Q ,分别为曲线12C C ,上的动点,求PQ 的最大值. 23.[选修4-5:不等式选讲] 已知函数()|2||36|f x x x =-++. (1)解不等式()34f x x ≥-+;(2)若函数()f x 的最小值为a ,且2(0,0)m n a m n +=>>,求11m n+的最小值.1.答案 B命题意图 本题考查解不等式与集合的运算. 解题分析 不等式201x x +≤-,等价于()()210x x +-≤且10x -≠,解得21x -≤<,即集合{}|21A x x =-<„ ,函数2log [(2)(1)]y x x =-+的定义域为(2)(1)0x x -+>,解得12x -<<,即集合{|12}B x x =-<<,所以()1,1A B =-I .2答案B命题意图 本题考查复数的运算及几何意义. 解题分析 由222(1)111i i i z i i i +===-+--,知对应点的坐标为()1,1-,所以对应点在第二象限. 3.答案D命题意图 本题考查等差数列的通项公式与前n 项和公式.解题分 由题意得211412246164a a d a S a d d =+=⎧=-⎧⎪⇒⎨⎨=+==⎪⎩⎩,则524414a =-+⨯=.4.答案 C命题意图 本题考查命题及充分、必要条件. 解题分析 对于①,当4x π=时,一定有tan 1x =但是当tan 1x =时,,4x k k ππ=+∈Z ,所以“tan 1x =”是“4x π=”的必要不充分条件,所以①不正确;对于②,因为()f x 为偶函数,所以5a =-.因为定义域为[],a b ,所以5b =, 所以函数2()5,[5,5]f x x x =+∈-的最大值为(5)(5)30f f -==,所以②正确; 对于③,命题“0001,2x x x ∃∈+R …”的否定形式是“1,2x x x∀∈+<R ”,所以③是错误的; 故错误说法的个数为2. 5.答案 C命题意图 本题考查线性规划及点到直线的距离公式.解题分析 结合不等式,绘制可行域,如图.由0260x y x y -=⎧⎨+-=⎩,得22x y =⎧⎨=⎩,即()2,2C ,点A 的位置如图所示,计算A 点到该区域的最小值,即计算点A 到直线260x y +-=的距离,所以min ||AB ==6.答案 A命题意图 本题考查函数的奇偶性与单调性,函数导数的应用.解题分析()f x 为偶函数,排除选项B ;2()sin (sin )f x x x x x x x =-=-,设()sin g x x x =-, 则()1cos 0g x x '=-≥恒成立,所以()g x 单调递增,所以当0x >时,()()00g x g >=, 所以当0x >时,()()0f x xg x =>,且()f x 单调递增,故选A 项. 7.答案 A命题意图 本题考查二项式定理及定积分.解题分析根据二项式3ax ⎛ ⎝⎭的展开式的通项公式得221213()4a T C ax x +⎛== ⎝⎭. Q 第三项的系数为1,1,44aa ∴=∴=,则4111111d d ln 2ln 2ax x x xx ===⎰⎰.8.答案 B命题意图 本题考查程序框图.解题分析 模拟执行如图所示的程序框图如下:1,1k S ==; 2,4k S ==; 3,11k S ==; 4,26k S ==; 5,57k S ==;6,120k S ==,此时满足条件5k >,输出120S =. 所以判断框内可以填入的条件是5?k >. 9.答案 C命题意图 本题考查古典概型.解题分析 现从这十个数中随机抽取4个数,基本事件总数140n C =,能成为两组包含的基本事件个数52m C =,则能成为两组的概率25410121C m P n C ===.10.答案 C命题意图 本题考查三视图,线面垂直和面面垂直的判定.解题分析 该几何体是一个四棱锥,其直观图如图所示,易知平面PAD ⊥平面ABCD ,作PO AD ⊥于O ,则PO ⊥平面ABCD ,PO CD ⊥,又AD CD ⊥,所以CD ⊥平面PAD ,所以平面PCD ⊥平面PAD ,同理可证平面PAB ⊥平面PAD ,由三视图可知PO AO OD ==,所以AP PD ⊥,又AP CD ⊥,所以AP ⊥平面PCD ,所以平面PAB ⊥平面PCD ,所以该多面体各表面所在平面互相垂直的有4对.11.答案 C命题意图 本题考查抛物线方程及过焦点的弦.解题分析 由题意得22224(42)02y x bx b p x b y px=+⎧⇒+-+=⎨=⎩, 则()22222512424b p b ⎡⎤-⎛⎫=+-⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦,又直线l 经过C 的焦点,则22b p-=,b p ∴=-. 由此解得2p =,所以抛物线方程为24y x =.设()00,M x y ,则204y x =, ()()()2222200000||444212MN x y x x x ∴=-+=-+=-+,故当02x =时,||MN取得最小值.12.答案 A命题意图 本题考查数列的综合应用. 解题分析 当1n ≥时,有条件可得()211n n n nS S S S +--=-,从而111n n nS S S +--=,故111111111n n n n n S S S S S +-=-=----,又1111121S ==--,11n S ⎧⎫∴⎨⎬-⎩⎭是首项、公差均为1的等差数列, 11n n S ∴=-,1n n S n +=,由()()()12111()1n S S S f n n +++=+L , 得()1(1)1(1)23152,2()2223n n S f n n f n n n n +++++⎡⎫===-∈⎪⎢+++⎣⎭, 依题意知(1)()f n k f n +>, min 2k ∴=.13.答案0命题意图 本题考查平面向量的数量积.解题分析 11()22CO BA BC CA =-=u u u r u u u r u u u r u u u r Q ,∴圆心O 为线段AC 的中点,因而90ABC ∠=︒,故0BA BC ⋅=u u u r u u u r .14.答案 ()1,2-命题意图 本题考查三角函数的图象及解析式.解题分析 函数()2sin()0,,2f x x πωϕωϕπ⎛⎫⎡⎤=+>∈ ⎪⎢⎥⎣⎦⎝⎭的部分图象如图所示.(0)2sin 1f ϕ==Q ,56πϕ=Q .又5||2MN ==3πω∴=,即函数5()2sin 36f x x ππ⎛⎫=+ ⎪⎝⎭. 令52sin 236x ππ⎛⎫+= ⎪⎝⎭,结合图象得5362x πππ+=,解得1x =-,故点M 的坐标为()1,2-. 五步导解 解↔答15.答案 221x y -=命题意图 本题考查双曲线的标准方程、离心率和渐近线方程.解题分析 由题意可得(),0A a ,又A 为线段OB 的中点,所以(2,0)B a ,令2x a =,代入双曲线的方程可得y =,可设()2,3P a b -,由题意和结合图形可得圆A 经过双曲线的左顶点(),0a -,即||2AP a =,即2a =a b =,又c =222a b c +=,得1a b ==,故双曲线C 的方程为221x y -=.16.答案 36π命题意图 本题考查多面体与球.解题分析 如图取BD 的中点E ,连接AE CE ,,则AE BD CE BD ⊥⊥,. Q 平面ABD ⊥平面BCD ,平面ABD I 平面BCD BD =,AE ∴⊥平面BCD .又CEC Q 平面BCD ,AE CE ∴⊥.设ABD △的外接圆的圆心为O ,半径为r .AB AD ∴=, ∴圆心O 在AE 所在的直线上,22222()r BE OE BE r AE ∴=+=+-. Q在Rt BCD △中,BD =BE EC ∴==在Rt ABE △中,2AE ,()2282r r ∴=+-,解得,3,1r OE =∴=. Q在Rt OEC △中,3OC ==,3OA OB OC OD ∴====,∴点O 是三棱锥A BCD -的外接球的球心,且球的半径3R =,∴球的体积34363V R ππ==.17.命题意图 本题考查正、余弦定理及三角恒等变换.解题分析(1)由sin ()sin sin a A a b B c C ++=及正弦定理得222a b ab c ++=,又由余弦定理得1cos 2C =-,23C π∴=. (2)由1sin 2S abc ab C ==,可知2sin c C =,2sin ,2sin a A b B ∴==,ABC △的周长为1(sin sin sin )2a b c A B C ++=++1sin sin 23A A π⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦11sin sin 22A A A ⎛⎫=+- ⎪ ⎪⎝⎭11sin 22A A ⎛⎫= ⎪ ⎪⎝⎭1sin 23A π⎛⎫=+ ⎪⎝⎭.0,3A π⎛⎫∈ ⎪⎝⎭Q ,2,333A πππ⎛⎫∴+∈ ⎪⎝⎭,sin 3A π⎤⎛⎫∴+∈⎥ ⎪⎝⎭⎝⎦,ABC ∴△周长的取值范围为⎝⎦.18.命题意图 本题考查空间点线、面关系及线面垂直、二面角.解题分析(1)证明:因为AB AC AD ,,两两垂直,AC DG AB DE ∥,∥, 所以DG AD DG DE ⊥⊥,,所以DG ⊥平面ABED ,因为AE ⊂平面ABED ,所以DG AE ⊥,因为四边形ABED 为正方形,所以AE BD ⊥,因为BD DG D =I ,所以AE ⊥平面BDG ,因为AC EF ∥所以四边形AEFC 为平行四边形,所以AE CF ∥,所以CF ⊥平面BDG .(2)由(1)知DE DG DA ,,互相垂直,故以D 为坐标原点,以DE DG DA ,,所在直线分别为x y z ,,轴建立如图所示的空间直角坐标系D xyz -, 则(0,0,0),(0,0,2),(2,0,2),(0,1,2),(2,1,0)D A B C F , 所以(0,1,2),(2,1,0)FB CB =-=-u u u r u u u r.设(),,m a b c =u r 为平面BCF 的法向量,则2020m FB b c m CB a b ⎧⋅=-+=⎪⎨⋅=-=⎪⎩u r u u u r u r u u u r , 令1a =,则21b c ==,,所以()1,2,1m =u r.又因为AD ⊥平面ABC ,所以()0,0,2DA =u u u r为平面ABC 的一个法向量,所以()cos ,m DA ==u r u u u r 由图可知二面角F BC A --是钝角,所以二面角F BC A --的余弦值为. 19.命题意图 本题考查离散型随机变量的期望和方差以及方案的确定. 解题分析 (1)X 的所有可能取值为0,1,2,3,4,5,6111(0)1010100P X ==⨯=,111(1)210525P X ==⨯⨯=,11213(2)25551025P X ==⨯+⨯⨯=, 131211(3)2210105550P X ==⨯⨯+⨯⨯=,22317(4)25510525P X ==⨯+⨯⨯=, 236(5)251025P X ==⨯⨯=,339(6)1010100P X ==⨯=,X ∴的分布列为(2)所选延保方案一,所需费用1Y 元的分布列为()117117697000900011000130001500010720100502525100E Y =⨯+⨯+⨯+⨯+⨯=(元) 选择延保方案二,所需费用2Y 元的分布列为()267691000011000120001042010025100E Y =⨯+⨯+⨯=(元)()()12E Y E Y >Q ,∴该医院选择延保方案二较划算.20.命题意图 本题考查椭圆有关的定值、定点问题.解题分析由题得1c e c a ===,解得a =222a b c =+,得1b =,故椭圆方程为2212x y +=. 设()()1122,,,A x y B x y ,易知直线l 的方程为1x y =+,由22112x y x y =+⎧⎪⎨+=⎪⎩,得23210y y +-=, 于是12122313y y y y ⎧+=-⎪⎪⎨⎪⋅=-⎪⎩, 从而1212423x x y y +=++=,故211,,332CM M k ⎛⎫-=- ⎪⎝⎭, 所以直线OM 的方程为12y x =-. (2)①当直线l 的斜率不为0时,设()0,0Q x ,直线l 的方程为1x my =+,由22112x my x y =+⎧⎪⎨+=⎪⎩, 得()222210m y my ++-=,所以1221222212m y y m y y m ⎧+=-⎪⎪+⎨⎪=-⎪+⎩, 所以()()()()()210201************OA QB x x x x y y my my x my my x y y =⋅=--+=++-++++u u u r u u u r ()()()()()2222121200000022121121112122m m y y m y y x x x m m x x x m m --=+⋅++-+-+=+⋅+⋅-+-+=++ ()202002231212x m x x m --+-++, 由023112x --=,得054x =, 故此时点57,0,416Q QA QB ⎛⎫⋅=- ⎪⎝⎭u u u r u u u r ; ②当直线l 的斜率为0时,2257416QA QB ⎛⎫⋅=-=- ⎪⎝⎭u u u r u u u r . 综上,在x 轴上存在定点5,04Q ⎛⎫ ⎪⎝⎭,使得QA QB ⋅u u u r u u u r 为定值. 21.命题意图 本题考查导数综合.解题分析 (1)()f x 的定义域为()1,-+∞,()2ln(1)2f x x x '=+-.设()()212g x ln x x =+-. ∵2()1x g x x -'=+,∴当()1,0x ∈-时,()0g x '>;当,()0x ∈+∞时,()0g x '<, ∴()g x 在()1,0-上单调递增,在(0,)+∞上单调递减,∴()g x 在0x =处取得最大值.又∵()00g =,∴对任意的1,()x ∈-+∞,()()00g x g ≤=恒成立,即对任意的1,()x ∈-+∞,都有()f x ' ()2120ln x x =+-≤恒成立,故()f x 在定义域()1,-+∞上是减函数.(2)由()f x 是减函数,且()00f =可得,当0x >时,()0f x <,∴()0f n <,即22(1)ln(1)2n n n n ++<+,两边同除以22(1)n +得ln(1)121211n n n n n n ++<⋅⋅+++,即12211n n n a n n +<⋅⋅++, 从而1231112334521222341234121n n n n n n n T a a a a n n n +++⎛⎫⎛⎫=⋅<⋅⋅⋅⋅⋅⋅⋅⋅⋅=⋅ ⎪⎪+++⎝⎭⎝⎭⋅L L L , 所以[]21(2)ln (2)ln 2ln(2)ln(1)(1)ln 22(1)n n n n T n n n n +⎡⎤++<=+-+-+⎢⎥+⎣⎦. ① 下面证2ln(2)ln(1)(1)ln 2102n n n n +-+-++-<. 记()2ln(2)ln(1)(1)ln 212x h x x x x =+-+-++-,[1,)x ∈+∞, ∴2211111()ln 2ln 2ln 2221232223x h x x x x x x x'=--+=-+=-+++++++. ∵2y x x=+在[2,)+∞上单调递减,而1111(2)ln 2(23ln 2)(2ln8)06233h '=-+=-=-<, ∴当[2,)x ∈+∞时,()0h x '<恒成立,∴()h x 在[2,)+∞上单调递减,即[2,)x ∈+∞,()(2)2ln 4ln33ln 2ln 2ln30h x h =--=-<„,∴当2n …时,()0h n <.∵19(1)2ln3ln 22ln 2ln 028h =---=-, ∴当*n ∈N 时,()0h n <,即2ln(2)ln(1)(1)ln 212n n n n +-+-+<-. ② 综合①②可得,[]ln (2)12n n n T +<-. 22.命题意图 本题考查参数方程、极坐标方程的应用及两点间距离的求法.解题分析 (1)曲线1C 的普通方程为22149x y +=, 曲线2C 的直角坐标方程为2245x y y +=+,即22(2)9x y +-=.(2)设P 点的坐标为(2cos ,3sin )θθ.2||333PQ PC +„,当sin 1θ=-时,max ||538PQ =+=.23.命题意图 本题考查绝对值不等式的解法及基本不等式.解题分析 (1)44,2()|2||36|28,22,44,2x x f x x x x x x x --<-⎧⎪=-++=+-⎨⎪+>⎩剟当2x <-时,4434x x -≥-+,即8x ≤-;当22x -≤≤时,2834x x +≥-+,即45x ≥-,可得425x -≤≤; 当2x >时,4434x x +≥-+,即0x ≥,可得2x >, ∴不等式的解集为4|8 5x x x ⎧⎫≤-≥-⎨⎬⎩⎭或 . (2)根据函数44,2()28,22,44,2x x f x x x x x --<-⎧⎪=+-≤≤⎨⎪+>⎩可知当2x =-时,函数取得最小值(2)4f -=,可知4a =, 8,0,0m n m n ∴+=>>,11111111()11(22)8882n m m n m n m n m n ⎛⎫⎛⎫∴+=⋅++=⋅++++= ⎪ ⎪⎝⎭⎝⎭…> 当且仅当n m m n =,即4m n ==时,取“=”,∴11m n +的最小值为12.。
2020年普通高等学校招生全国统一考试模拟六数学理试题Word版含答案

2017年普通高等学校招生全国统一考试模拟试题数学(理科)(六)第丨卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知集合A = {xI(x-2)(x +1) <0},5 = {x G ZI-1 <^< 1},则=A. {—1,0}B. {0,1}C. {—1,0,1}D. {—1,2} 2•方程〃 + 6x +13 = 0的一个根是A. —3 + 2i B・ 3 + 2/ C. —2 + 3/ D・ 2 + 3z3.已知f(x)是定义在R上的偶函数,且在区间(-co,0)上单调递增,若实数"满足/(2M)>/(-V2),实数"的取值范围是A. B.4.如图,设区域Z) = {(^.y)IO<A:<l,O<y<l},向区域内随机投一点,且投入到区域内任一点都是等可能的,则点落到由曲线y = ^与y =X2所围成阴影区域内的概率是A. -B. -C.丄D.-6 3 2 35.执行如图所示的程序框图,若输出的5 = 86,则判断框内的正整数的值为A.7B. 6,7C. 6,7,8D. &95=1*=■0.6.向量讥满足p +片=2辰,且(方―可门=0,则方』的夹角的余弦值为j=r+2*A. 0B. -C. -D.—3 2 2G古束)第II 卷 (非选择题共90分)二.填空题:本大题共4小题,每小题5分,共20分.10.在体积为*的三棱锥S 一 ABC 中.AB = BC = 2.ZABC = 120 ,SA = SC 9且平面 SAC 丄平面ABC 9若该三棱锥的四个顶点都在同一球面上,则该球的体积为2 211.已知点人迅是双曲线C$-计=1(“>0小>0)的左、右焦点,0为坐标原点,点P 在双曲线C 的右支上,且满足再鸟= 引13|啓则双曲线C 的离心率的取值范围为A. (1,+co)B.1 — 11 — xL X G (—2 ),则函数 g(X)= f(X)-COS7TX 在区间[0,8] 3/(x-2),xe[2,+oo) 内所有零点的和为 A. 16 B. 30 C. 327. 已知等差数列{©}中,S “为其前"项和,若= an 2+4“+a—4(d w R),记数列、孑、n “的前项和为人,则心=&已知aj^c 均为正数,且(d+c)(Z? + c) = 2,则a + 2b+3c 的最小值是A. y/2B. 2>/2C. 4D. 89•某几何体的三视图如下图所示,且该几何体的体积为 芈则正视图和的值为A” B. 2 亦C. £2D.- 320逅兀A. -----------3B.芈C. 20龙 D&12•已知函数/(兀)=彳D. 40C.D.\+y-2<013.已知满足约束条件x-2y-2<0,若2x+y + A:>0恒成立,则实数斤的取值范2x-y+2>0围为________________ .14.若(1 — 2x) = a()+ ciyX + • • • +(x € R) 9则q + 2d? + …+ 201 厶勺仍= _______ •2 215.已知点A,F分别是椭圆C:-^- + p- = l(«>/7>0)的上顶点和左焦点,若AF与圆O:x2+y2=4相切于点T,且点T是线段AF靠近点A的三等分点,则椭圆C的标准方程为________________ .16.若数列{①}满足a2一% > a3 -①> 5 -佝> …〉冷+1 -则称数列{。
2020届全国百所名校金典卷 理数 1-6(含答案)
已知&"#'是等差数列(&$#'是由正数组成的等比数列(且"*+%,($!+-("($!+%'.(",/$, +&.! #'$求数列&"#'(&$#'的通项公式) #!$记%#+$#%"#(求数列&%#'的前# 项和!
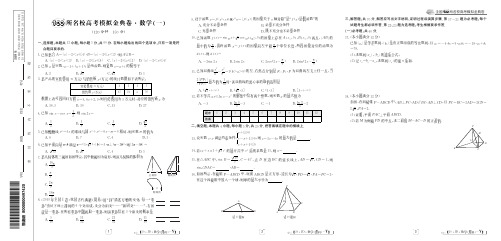
'.!#本小题满分'!分$ 如图(在四棱锥 &%'()* 中('(&)('*()('*)*(且 &)+()+!'*+!)*+
(则,!&的值为
+!"
,!%3"
-!3"
$!&&"
(!某调查机构对全国互联网行业进行调查统计(得到整个互联网行业从业者年龄分布饼状图,
3"后从事互联网行业者岗位分布条形图(则下列结论中一定正确的是
#注+3"后指&33"年及以 后 出 生(1" 后 指 &31"%&313 年 之 间 出 生(1" 前 指 &363 年 及 以 前
!##++**!#+#! 最大值为4+(时&该双曲线的离心率的取值范围是
(!#槡!&/5$
)!#槡!&0*
*!#+&0*
$!+0&/5$
+!!若不等式($%6.$%$! 的解集中恰有两个整数&则实数(的最大值为
2020届全国高考三卷模拟试卷数学(理)试题(六)解析版

是区域
xy
1 y
0 1
0
内一动点,点
B
是圆
x y 1 0
点,则 AB 的最小值为
.
上—
图1
由约束条件画出可行域如图 1 所示,记圆心 (2,1) 到直线 x y 1 0 的距离为
3
d,则 d 2 2 ,所以 | AB | 的最小值为 2 1 . 2
线方程为
y
y0
1 k
(x
x0 )
,令
y
0
,得
x
ky0
x0
,即
|
OP
|
ky0
x0
,由点差法得
ky0
2
,所以
2(| OP | | MN |) 2x0 4 (2x0 2) 2 . 三、解答题(共 70 分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分 12 分)等差数列{an} 的前 项和为 Sn ,若 a4 a5 16, S6 36
由程序框图知,输出 a,b,c 中最大的数,
2
1
1
∵a 0.54 0.254 b 0.94 , c 0 ,所以 b 最大,故选 B.
9.已知 a, b
R
,定义运算“
”,
a
b
a, a b, a
b b
,设函数
f
(x)
(2x
2)
(1 log 2x , x (0, 2) ,
2 ,故选 A.
(全国100所名校最新高考模拟示范卷)2020年普通高等学校招生全国统一考试理科数学模拟测试试题(含答案)

2020年普通高等学校招生考试数学模拟测试一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={0,1,2,3},B={2,3,4,5},则A ∪B= A.{1,2,3,4,5}B.{0,1,4,5}C.{2,3}D.{0,1,2,3,4,5}2.i 是虚数单位,z=2—i,则|z|=B.23.已知向量a =(1,2),b =(-1,λ),若a ∥b ,则实数λ等于 A.-1B.1C.-2D.24.设命题p:∀x ∈R ,x 2>0,则p ⌝为A.∀x ∈R ,x 2≤0B.∀x ∈R ,x 2>0C.∃x ∈R ,x 2>0D.∃x ∈R ,x 2≤05.51(1)x-展开式中含x -2的系数是 A.15B.-15C.10D.-106.若双曲线22221(0,x y a b a b -=>>)的左、右焦点分别为F 1、F 2,离心率为53,点P(b,0),为则12||||PF PF =A.6B.8C.9D.107.图为祖冲之之子祖暅“开立圆术”中设计的立体模型.祖暅提出“祖氏原理”,他将牟合方盖的体积化成立方体与一个相当于四棱锥的体积之差,从而求出牟合方盖的体积等于32(3d d 为球的直径),并得到球的体积为16V d π=,这种算法比外国人早了一千多年,人们还用过一些类似的公式,根据π=3.1415926…,判断下列公式中最精确的一个是A.d ≈3B .d ≈√2V 3C.d≈√300157V3D .d≈√158V 38.已知23cos cos ,2sin sin 2αβαβ-=+=则cos(a+β)等于 A.12B.12-C.14D.14-二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法正确的是A.第一场得分的中位数为52 B.第二场得分的平均数为193C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等10.已知正方体的外接球与内切球上各有一个动点M 、N,若线段MN 1,则 A.正方体的外接球的表面积为12π B.正方体的内切球的体积为43πC.正方体的边长为2D.线段MN 的最大值为11.已知圆M 与直线x 十y +2=0相切于点A(0,-2),圆M 被x 轴所截得的弦长为2,则下列 结论正确的是A.圆M 的圆心在定直线x-y-2=0上B.圆M 的面积的最大值为50πC.圆M 的半径的最小值为1D.满足条件的所有圆M 的半径之积为1012.若存在m,使得f(x)≥m 对任意x ∈D 恒成立,则函数f(x)在D 上有下界,其中m 为函数f(x)的一个下界;若存在M,使得f(x)≤M 对任意x ∈D 恒成立,则函数f(x)在D 上有上界,其中M 为函数f(x)的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.下列说法正确的是A.1不是函数1()(0)f x x x x=+>的一个下界 B.函数f(x)=x l nx 有下界,无上界C.函数2()xe f x x=有上界有,上无界下,界无下界D.函数2sin ()1xf x x =+有界 三、填空题:本题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.设f(x)是定义在R 上的函数,若g(x)=f(x)+x 是偶函数,且g(-2)=-4,则f(2)=___. 14.已知函数f(x)=sin(ωx+φ)(ω>0),点2(,0)3π和7(,0)6π是函数f(x)图象上相邻的两个对称中心,则ω=___.15.已知F 1,F 2分别为椭圆的221168x y +=左、右焦点,M 是椭圆上的一点,且在y 轴的左侧,过点F 2作∠F 1MF2的角平分线的垂线,垂足为N,若|ON|=2(О为坐标原点),则|MF 2|-|MF 1|=___,|OM|=__.(本题第一空2分,第二空3分)16.在正三棱柱ABC-A 1B 1C 1中,AB =1=2,E,F 分别为AB 1,A 1C 1的中点,平面α过点C 1,且平面α∥平面A 1B 1C ,平面α∩平面A 1B 1C 1=l ,则异面直线EF 与l 所成角的余弦值为__·四、解答题:本题共6小题,共70分。
2020届全国100所名校高三最新高考模拟示范卷(一)模拟测试数学(理)试题(解析版)

2020届全国100所名校高三最新高考模拟示范卷(一)模拟测试数学(理)试题一、单选题1.已知集合{|24,}A x x x =-≤≤∈Z ,{|2,}B x x k k ==∈Z ,则A B =( )A .{0,2,4}B .{2,0,2,4}-C .{2,2,4}-D .{2,4}【答案】B【解析】注意集合B 是偶数集. 【详解】由题可知{2,0,2,4}A B ⋂=-. 故选:B. 【点睛】本题考查集合的交集运算,考查学生的基本计算能力,是一道容易题. 2.设复数2z ai =+,若z z =,则实数a =( ) A .0 B .2C .1-D .2-【答案】A【解析】利用共轭复数及复数相等的定义即可得到答案. 【详解】因为z z =,所以22ai ai +=-,解得0a =. 故选:A. 【点睛】本题考查复数的概念,考查学生的基本运算能力,是一道容易题. 3.设命题p :存在3,3a a a ∈>R ,则p ⌝为( ) A .存在3,3a a a ∈≤R B .不存在3,3a a a ∈>R C .对任意3,3a a a ∈≤R D .对任意3,3a a a ∉≤R【答案】C【解析】,()x M p x ∃∈的否定为,()x M p x ∀∈⌝. 【详解】由于特称命题的否定是全称命题,知“存在3,3a a a ∈>R ”的否定为“对任意3,3a a a ∈≤R ”.故选:C. 【点睛】本题考查含量词命题的否定,考查学生对特称命题否定的理解,只需将存在改为任意,“>”改为“≤”即可. 4.222cos cos 105ππθθ⎛⎫⎛⎫--+-= ⎪ ⎪⎝⎭⎝⎭( ) A .12B .2C .1D .32【答案】C 【解析】注意到2()5210πππθθ-=-+,结合同角三角函数的基本关系即可得到答案. 【详解】22222cos cos cos cos 10510210πππππθθθθ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫--+-=++-+ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦22cos sin 11010ππθθ⎛⎫ ⎪⎝⎛⎫=+++= ⎪⎝⎭⎭.故选:C. 【点睛】本题考查三角函数的恒等变换,涉及到配角的知识,是一道容易题.5.科赫曲线是一种外形像雪花的几何曲线,一段科赫曲线可以通过下列操作步骤构造得到,任画一条线段,然后把它均分成三等分,以中间一段为边向外作正三角形,并把中间一段去掉,这样,原来的一条线段就变成了4条小线段构成的折线,称为“一次构造”;用同样的方法把每条小线段重复上述步骤,得到16条更小的线段构成的折线,称为“二次构造”,…,如此进行“n 次构造”,就可以得到一条科赫曲线.若要在构造过程中使得到的折线的长度达到初始线段的1000倍,则至少需要通过构造的次数是( ).(取lg30.4771≈,lg 20.3010≈)A .16B .17C .24D .25【答案】D【解析】由折线长度变化规律可知“n 次构造”后的折线长度为43na ⎛⎫ ⎪⎝⎭,由此得到410003n⎛⎫≥ ⎪⎝⎭,利用运算法则可知32lg 2lg 3n ≥⨯-,由此计算得到结果. 【详解】记初始线段长度为a ,则“一次构造”后的折线长度为43a ,“二次构造”后的折线长度为243a ⎛⎫ ⎪⎝⎭,以此类推,“n 次构造”后的折线长度为43na ⎛⎫ ⎪⎝⎭, 若得到的折线长度为初始线段长度的1000倍,则410003na a ⎛⎫≥ ⎪⎝⎭,即410003n⎛⎫≥ ⎪⎝⎭,()()44lg lg lg 4lg32lg 2lg3lg1000333nn n n ⎛⎫∴==-=-≥= ⎪⎝⎭,即324.0220.30100.4771n ≥≈⨯-,∴至少需要25次构造.故选:D . 【点睛】本题考查数列新定义运算的问题,涉及到对数运算法则的应用,关键是能够通过构造原则得到每次构造后所得折线长度成等比数列的特点.6.已知直线10ax y +-=将圆22:(1)(2)4C x y -++=平分,则圆C 中以点,33a a ⎛⎫-⎪⎝⎭为中点的弦的弦长为( ).A .2B .C .D .4【答案】C【解析】由直线平分圆可知其过圆心,从而求得a ,根据圆心与弦中点连线垂直于弦,可利用勾股定理求得半弦长,进而得到弦长. 【详解】直线10ax y +-=平分圆C ,∴直线10ax y +-=过圆C 的圆心()1,2C -,210a ∴--=,解得:3a =,∴圆心()1,2C -到点,33a a ⎛⎫- ⎪⎝⎭1=,∴所求弦长为=.故选:C . 【点睛】本题考查直线被圆截得弦长的求解,关键是熟练掌握圆的性质,即圆心与弦中点连线垂直于弦.7.关于函数()sin f x x x =,[,]x ππ∈-,有下列三个结论:①()f x 为偶函数;②()f x 有3个零点;③43f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,其中所有正确结论的编号是( ) A .①② B .①③C .②③D .①②③【答案】D【解析】依次对①②③进行验证即可. 【详解】()sin()sin ()f x x x x x f x -=--==,①正确;令()0f x =,得0x =或sin 0x =,解得0x =或x π=±,②正确:因为42483236f f ππππ⎛⎫⎛⎫=⨯=<=⨯= ⎪ ⎪⎝⎭⎝⎭, 所以③正确. 故选:D. 【点睛】本题考查函数的基本性质,涉及到函数的奇偶性、函数的零点、函数值大小,是一道容易题.8.已知抛物线2:2(0)C x py p =>的焦点为F ,C 的准线与对称轴交于点H ,直线2p y =-与C 交于A ,B 两点,若||AH =,则||AF =( ) A .3 B .83C .2D .4【答案】C【解析】注意到直线2py =-过点H ,利用||||AM AH =tan AHM ∠=||AH =||2AM =,再利用抛物线的定义即可得到答案. 【详解】连接AF ,如图,过A 作准线的垂线,垂足为M ,易知点0,,0,22p p F H ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭.易知直 线32p y x =-过点H ,tan 3,3AHM AHM π∠=∠=,则||3,||2AM AH =又43||3AH =, 所以||2AM =,由抛物线的定义可得||AF =||2AM =.故选:C. 【点睛】本题考查直线与抛物线的位置关系,涉及到利用抛物线的定义求焦半径,考查学生转化与化归的思想,是一道中档题.二、多选题9.下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法错误的是( )A .私人类电动汽车充电桩保有量增长率最高的年份是2018年B .公共类电动汽车充电桩保有量的中位数是25.7万台C .公共类电动汽车充电桩保有量的平均数为23.12万台D .从2017年开始,我国私人类电动汽车充电桩占比均超过50% 【答案】ABC【解析】根据统计图表分别对选项A 、B 、C 、D 验证即可. 【详解】私人类电动汽车充电桩保有量增长率最高的年份是2016年,A 错误;这5次统计的公共类电动汽车充电桩保有量的中位数是21.4万台,B 错误; 因为4.914.121.43044.723.025++++=,故C 项错误,D 项显然正确. 故选:D. 【点睛】本题考查统计图表与用样本估计总体,涉及到中位数、平均数等知识,是一道基础题. 10.若1021001210(21),x a a x a x a x x R +=+++∈,则( )A .01a =B .00a =C .10012103a a a a ++++=D .012103a a a a ++++=【答案】AC【解析】根据选项的特点,采用赋值法求解. 【详解】 因为1021001210(21),x a a x a x a x x R +=+++∈,令0x =得01a =,故A 正确. 令1x =得10012103a a a a ++++=,故C 正确.故选:AC 【点睛】本题主要考查二项式定理展开式的项的系数和系数的和,一般采用通项公式和赋值法,属于中档题.,11.在直四棱柱1111ABCD A B C D -中,底面ABCD 是边长为4的正方形,13AA =,则( )A .异面直线1AB 与11B D 所成角的余弦值为225B .异面直线1A B 与11B D 所成角的余弦值为35C .1//A B 平面11BD C D .点1B 到平面11BD A 的距离为125【答案】ACD【解析】根据11//A B D C ,得到11B D C ∠即为 异面直线1A B 与11B D 所成角,再用余弦定理求解判断A ,B 的正误.根据11//A B DC ;利用线面平行的判定定理判断.C 的正误..利用等体积法,有111111B A BD B A BD V V --= 计算判断D 的正误. 【详解】因为11//A B D C ,所以11B D C ∠即为 异面直线1A B 与11B D 所成角, 又因为111142,5,5B D D C B C === ,所以222111111111c 22os 25B D DC B C BD C B D D C +-∠==⨯,故A 正确.因为111//,A B D C A B ⊄平面11B D C 1D C ⊂平面11B D C , 所以1//A B 平面11B D C ,故C 正确.因为111111B A B D B A BD V V --= , 即1111111111113232A B A D B B A B A D h ⨯⨯⨯⨯=⨯⨯⨯⨯ , 解得125h =,故D 正确. 故选:ACD 【点睛】本题主要考查异面直线所成的角,线面平行的判定定理,等体积法求三棱锥的高,综合性强,属于中档题.12.已知ln 2,0()12,02x x x f x x ->⎧⎪=⎨-≤⎪⎩,存在实数m 满足()12(())12f m f f m ++=,则( )A .()0f m ≤B .()f m 可能大于0C .(,1]m ∈-∞-D .(2(,1]0,e m ⎤∈-∞-⋃⎦【答案】AD【解析】若()0f m >,()1ln[()]2()22f m f m f m -<<-,不满足题意;若()0f m ≤,2(())1f f m +()12(2)+1=2f m =-()12f m +,故只需解不等式()0f m ≤即可.【详解】由()12(())12f m f f m ++=,可得()1(())22f m f f m =-. 若()0f m >,则()1ln[()]222f m f m -=-,∵ln 1x x ≤-,2x x >, ∴ln 23x x -≤-,112122x xx -<-<-,∴1ln 23122xx x x -≤-<-<-,∴方程无解;若()0f m ≤,2(())1f f m +()12(2)+1=2f m =-()12f m +,故只需解()0f m ≤即可, 当0m ≤时,由1()202mf m =-≤,解得1m ≤-; 当0m >时,由()ln 20f m m =-≤,解得20e m <≤.综上所述,当(2(,1]0,e m ⎤∈-∞-⋃⎦时,()0f m ≤,满足()12(())12f m f f m ++=. 故选:AD. 【点睛】本题考查函数与方程的综合,涉及到分类讨论思想在分段函数中的应用,考查学生的运算求解能力,是一道中档题.三、填空题13.曲线1()e xf x x=+在1x =处的切线斜率为_________. 【答案】e 1-【解析】利用导数的几何意义即可解决. 【详解】∵21()e xf x x '=-,∴'(1)e 1f =-.由导数的几何意义知曲线1()e x f x x=+在1x =处的切线斜率为e 1-. 故答案为:e 1- 【点睛】本题考查导数的几何意义,考查学生的基本计算能力,是一道基础题. 14.如图,在平行四边形ABCD 中,E 为BC 的中点,F 为DE 的中点,若12AF AB nAD =+,则n =_________.【答案】34【解析】1()2AF AD AE =+,将12=+=+AE AB BE AB AD 代入即可得到答案.【详解】连接AE ,11113()22224AF AD AE AD AB AD AB AD ⎛⎫=+=++=+ ⎪⎝⎭, 则34n =. 故答案为:34. 【点睛】本题考查平面向量的基本定理的应用,考查学生简单的数学运算能力,是一道容易题.15.已知双曲线222:1(0)4x y C b b-=>的左、右顶点分别为A 、B ,点P 在双曲线C 上,且直线PA 与直线PB 的斜率之积为1,则双曲线C 的焦距为__________.【答案】【解析】设()00,P x y ,利用斜率乘积为1和P 在双曲线上可构造方程组求得2b ,进而得到2c ,求得焦距. 【详解】由双曲线方程知:()2,0A -,()2,0B , 设()00,P x y ,则200020001224PA PBy y y k k x x x ⋅=⋅==+--,即2204x y -=,又2200214x y b-=,24b ∴=,2228c a b ∴=+=,∴双曲线C 的焦距为2c =.故答案为:【点睛】本题考查双曲线焦距的求解问题,关键是能够利用斜率关系和点在双曲线上构造方程求得双曲线标准方程中的未知量.四、双空题16.已知圆锥SC 的底面半径、高、体积分别为2、3、V ,圆柱OM 的底面半径、高、体积分别为1、h 、V ,则h =_________,圆锥SC 的外接球的表面积为_________. 【答案】41699π【解析】利用圆锥和圆柱的体积相等可得圆柱的高h ,再利用勾股定理,即222(3)2R R -+=即可得到半径R ,从而求得外接球表面积.【详解】依题有221231,3V h ππ=⨯⨯=⨯⋅解得4h =.设圆锥SC 的外接球的半径为R ,则有222(3)2R R -+=,解得136R =,则圆锥SC 的外接球的表面积为213169469ππ⎛⎫=⎪⎝⎭. 故答案为: (1) 4 ; (2) 1699π. 【点睛】本题考查圆锥、圆柱的体积以及圆锥的外接球问题,考查学生的运算求解能力,是一道中档题.五、解答题17.在①34b a =,②333a b =,③224a b =这三个条件中任选一个,补充在下面问题中,再判断{}n c 是否是递增数列,请说明理由.已知{}n a 是公差为1的等差数列,{}n b 是正项等比数列,111a b ==,__________,*()n n n c a b n =∈N .判断{}n c 是否是递增数列,并说明理由.注:如果选择多个条件分别解答,按第一个解答计分. 【答案】见解析【解析】只需分别对所选番号进行等差、等比数列基本量的运算,得到n c ,再作商1n n c c +与1比较大小即可. 【详解】因为{}n a 是公差为1,首项为1的等差数列,所以11n a n n =+-=. 设{}n b 的公比为q ,若选①,由34b a =,得11344,2,2,2n n n n b a q b c n --=====⋅,1121(1)22(1)n n n n c n n c n n -+⋅==<+⋅+,则1n n c c +<,所以{}n c 是递增数列. 若选②,由3333a b ==,得31,1,1,n n b q b c n ====, 则11n n c n c n +=<=+,所以{}n c 是递增数列. 若选③,由2242a b ==,得211111,,,2222n n n n nb q bc --====, 11221(1)21n n n n c n nc n n -+⋅==+⋅+,则1n n c c +≥,所以{}n c 不是递增数列.【点睛】本题考查等差、等比数列的基本量的计算,是一道开放性试题,属于容易题. 18.已知ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,21sin cos 22A A A π⎛⎫-=+ ⎪⎝⎭.(1)求角A 的大小;(2)若ABC ,周长为3a ,求a 的值. 【答案】(1)3π(2)1a = 【解析】(1)21sin cos 22A A A π⎛⎫-=+⇒ ⎪⎝⎭22cos 1cos221222A A A +==+⇒sin 216A π⎛⎫-= ⎪⎝⎭解方程即可;(2)由1sin 2ABC S bc A ==△可得a bc =,由余弦定理以及周长为3a ,联立解方程组即可. 【详解】(121sin cos 22A A A π⎛⎫-=+⎪⎝⎭,所以22cos 1cos221222A AA +==+,即sin 216A π⎛⎫-= ⎪⎝⎭,因为(0,)A π∈,所以112,666A πππ⎛⎫-∈- ⎪⎝⎭,所以2,623A A πππ-==.(2)因为1sin 2ABC S bc A ===△,所以a bc =. 又因为2222222cos()3,33a b c bc b c bc b c bc a b c a π=+-=+-=+-++=,所以222,43b c a a a a +==-,解得1a =或0a =(舍),故1a =. 【点睛】本题考查二倍角公式、辅助角公式以及余弦定理解三角形,考查学生的运算求解能力,是一道容易题.19.如图,在四棱锥M ABCD -中,AB AD ⊥,2AB AM AD ===,22MB MD ==.(1)证明:AM ⊥平面ABCD .(2)若E 是BM 的中点,CD ∥,2AB CD AB =,求平面ECD 与平面ABM 所成锐二面角的余弦值.【答案】(1)见解析(2)55【解析】(1)要证AM ⊥平面ABCD ,只需证AD AM ⊥,AB AM ⊥即可; (2)分别求出平面ECD 与平面ABM 的法向量,m n ,然后利用||cos ||||m n m n θ⋅=⋅计算即可. 【详解】(1)因为2228AB AM BM +==,所以AB AM ⊥, 同理2228AD AM DM +==可得AD AM ⊥. 因为AD AB A ⋂=,所以AM ⊥平面ABCD .(2)因为AB AD ⊥,所以AD 、AM 、AB 两两垂直,以A 为坐标原点, 建立如图所示的空间直角坐标系,因为2AB AM AD ===,所以(0,0,0),(2,0,0),(0,2,0),(0,0,2)A D M B , 因为E 是BM 的中点,所以(0,1,1)E , 因为,2CD AB CD AB =∥,所以(2,0,1)C . 所以(2,1,0),(0,0,1)CE DC =-=, 设平面ECD 的一个法向量为()111,,m x y z =,由()()111111,,(0,0,1)0,,(2,1,0)0m DC x y z m CE x y z ⎧⋅=⋅=⎪⎨⋅=⋅-=⎪⎩,得111020z x y =⎧⎨-+=⎩,取11x =,得(1,2,0)m =.易知平面ABM 的一个法向量为(2,0,0)n AD ==,设平面ECD 与平面ABM 所成锐二面角的平面角为θ,所以||(1,2,0)cos 5||||1m n m n θ⋅===⋅,所以平面ECD 与平面ABM . 【点睛】本题考查线面垂直的证明以及向量法求二面角,考查学生的数学运算能力,此题解题关键是准确写出点的坐标,属于中档题.20.已知直线l 与椭圆22:162x y C +=交于不同的两点A ,B .(1)若线段AB 的中点为11,2⎛⎫⎪⎝⎭,求直线l 的方程; (2)若l 的斜率为k ,且l 过椭圆C 的左焦点F ,AB 的垂直平分线与x 轴交于点N ,求证:||||FN AB 为定值. 【答案】(1)4670x y +-=;(2)证明见解析【解析】(1)利用点差法可求得直线l 的斜率,进而求得直线l 的方程;(2)设():2l y k x =+,与椭圆方程联立得到韦达定理的形式,进而表示出AB 中点坐标;当0k =时,易求得||||FN AB 的值;当0k ≠时,可得AB 垂直平分线方程,进而求得N 点坐标和FN ,利用弦长公式求得AB ,进而求得||||FN AB 的值;综合两种情况可知||||FN AB 为定值. 【详解】(1)设()11,A x y ,()22,B x y ,则22112222162162x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩,两式作差得:2112211213y y x x x x y y -+=-⨯-+, AB 中点为11,2⎛⎫⎪⎝⎭,2121l y y k x x -=-,12233l k ∴=-⨯=-,∴直线l 的方程为:()12123y x -=--,即:4670x y +-=. (2)由椭圆方程知:()2,0F -,可设直线l 的方程:()2y k x =+,联立()222162y k x x y ⎧=+⎪⎨+=⎪⎩得:()222213121260k x k x k +++-=,设()11,A x y ,()22,B x y ,则21221213k x x k +=-+,212212613k x x k -=+,()3121222124441313k ky y k x x k k k k∴+=++=-+=++, 21226213x x k k+∴=-+,1222213y y k k +∴=+, 当0k =时,AB =,2FN =,6FN AB∴=; 当0k ≠时,AB 的垂直平分线方程为:2222161313k k y x k k k ⎛⎫-=-+ ⎪++⎝⎭,令0y =得:22413k x k =-+,224,013k N k ⎛⎫∴- ⎪+⎝⎭,()222221421313k k FN k k +∴=-+=++,1AB ==)22113kk+=+,()22221613kFNABk+∴==+;综上所述:FNAB【点睛】本题考查直线与椭圆综合应用问题,涉及到中点弦所在直线方程、定值问题的求解;求解中点弦问题的常用方法是点差法的方式;求解定值问题的关键是能够通过某一变量表示出所求值,通过化简消元得到定值.21.已知函数()lnf x a x x=-,其中a为常数.(1)讨论函数()y f x=的单调性;(2)当a e=(e为自然对数的底数),[1,)x∈+∞时,若方程(1)()1b xf xx-=+有两个不等实数根,求实数b的取值范围.【答案】(1)当0a≤时,()f x在()0,∞+上单调递减;当0a>时,()f x在()0,a上单调递增,在(),a+∞上单调递减;(2)[)1,1-【解析】(1)分别在0a≤和0a>两种情况下,根据()f x'的正负确定()f x的单调性;(2)将问题转化为当[)1,x∈+∞时,()()21lne x x xg xx+-=与y b=有两个不同交点的问题,通过导数可求得()g x的单调性和最值,进而得到函数图象,通过数形结合的方式可确定b的范围.【详解】(1)由题意得:()f x定义域为()0,∞+,()1a a xf xx x-'=-=,当0a≤时,()0f x'<,则()f x在()0,∞+上单调递减;当0a>时,令()0f x'=,解得:x a=,∴当()0,x a∈时,()0f x'>;当(),x a∈+∞时,()0f x'<,()f x∴在()0,a上单调递增,在(),a+∞上单调递减.综上所述:当0a ≤时,()f x 在()0,∞+上单调递减;当0a >时,()f x 在()0,a 上单调递增,在(),a +∞上单调递减. (2)当a e =时,()1ln 1b x e x x x --=+有两个不等实根,方程可化为()21ln e x x x b x+-=, 令()()21ln e x x x g x x+-=,则()22ln x ex e e xg x x -++-'=, 令()2ln h x x ex e e x =-++-,则()222e x ex eh x x e x x-+-'=-+-=,当[)1,x ∈+∞时,22x ex e -+-20≤-<,即()h x '<0()h x ∴在[)1,+∞上单调递减, ()()11221h x h e e ∴≤=-+=-,且()220h e e e e e =-++-=()h x ∴在[)1,+∞上有且仅有一个零点x e =,∴当[)1,x e ∈时,()0h x >,即()0g x '>;当(),x e ∈+∞时,()0h x <,即()0g x '<,()g x ∴在[)1,e 上单调递增,在(),e +∞上单调递减, ()()max 11g x g e e e ∴==+-=,()11g =-,由此可得()g x 图象如下图所示:则当[)1,x ∈+∞时,方程()()11b x f x x -=+有两个不等实数根等价于当[)1,x ∈+∞时,()g x 与y b =有两个不同交点,由图象可知:[)1,1b ∈-.【点睛】本题考查导数在研究函数中的应用,涉及到利用导数讨论含参数函数的单调性、根据方程根的个数求解参数范围的问题;求解方程根的个数问题的关键是能够将问题转化为两个函数图象交点个数的求解问题,利用数形结合的方式求得结果.22.小芳、小明两人各拿两颗质地均匀的骰子做游戏,规则如下:若掷出的点数之和为4的倍数,则由原投掷人继续投掷;若掷出的点数之和不是4的倍数,则由对方接着投掷.(1)规定第1次从小明开始.(ⅰ)求前4次投掷中小明恰好投掷2次的概率;(ⅱ)设游戏的前4次中,小芳投掷的次数为X ,求随机变量X 的分布列与期望. (2)若第1次从小芳开始,求第n 次由小芳投掷的概率n P .【答案】(1)(ⅰ)3964(ⅱ)见解析,2716(2)1122nn P ⎛⎫=-- ⎪⎝⎭【解析】(1)(ⅰ)一人投掷两颗骰子,向上的点数之和为4的倍数的概为91364=,前4次投掷中小明恰好投掷2次有三种情况:小明,小明,小芳,小芳;小明,小芳,小明,小芳;小明,小芳,小芳,小明,分别计算概率相加即可;(ⅱ)小芳投掷的次数X 的所有可能的取值为0,1,2,3,分别求出相应的概率即可;(2)若第1次从小芳开始,则第n 次由小芳投掷骰子有两种情况:1.第1n -次由小芳投掷,第n 次继续由小芳投掷,2.第1n -次由小明投掷,第n 次由小芳投掷. 【详解】(1)一人投掷两颗骰子,向上的点数之和为4的倍数的概为91364=. (ⅰ)因为第1次从小明开始,所以前4次投掷中小明恰好投掷2次的概率,1313333133944444444464P =⨯⨯+⨯⨯+⨯⨯=. (ⅱ)设游戏的前4次中,小芳投掷的次数为X ,依题意,X 可取0,1,2,3, 所以1111(0)44464P X ==⨯⨯=,33113311321(1)44444444464P X ==⨯⨯+⨯⨯+⨯⨯=, 39(2)64P X ==,3113(3)44464P X ==⨯⨯=.所以X 的分布列为所以12139327()01236464646416E X =⨯+⨯+⨯+⨯=. (2)若第1次从小芳开始,则第n 次由小芳投掷骰子有两种情况: ①第1n -次由小芳投掷,第n 次继续由小芳投掷,其概率为111(2)4n n P P n -=; ②第1n -次由小明投掷,第n 次由小芳投掷, 其概率为()21113311(2)444n n n P P P n --⎛⎫=--=- ⎪⎝⎭. 因为①②两种情形是互斥的,所以1211113313(2)44424n n n n n n P P P P P P n ---=+=+-=-+, 所以1111(2)222n n P P n -⎛⎫-=-- ⎪⎝⎭.因为11P =,所以12n P ⎧-⎫⎨⎬⎩⎭是以12为首项, 12-为公比的等比数列,所以1111222n n P -⎛⎫-=- ⎪⎝⎭,即1122nn P ⎛⎫=-- ⎪⎝⎭.【点睛】本题考查随机变量的分布列与数列综合应用,涉及到利用递推数列求通项公式,考查学生逻辑推理与运算能力,是一道有一定难度的综合题.。
2020年高考全真模拟卷理科数学06(含解析)

2020年高考全真模拟卷(6)数学(理)(考试时间:120分钟 试卷满分:150分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数z =21i+在复平面内对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限2.已知集合{}230,{|17},M x x x N x x =->=≤≤,则()R C M N =I ( )A .{}37x x <≤B .{}37x x ≤≤C .{}13x x ≤≤D .{}13x x ≤<3.下列叙述中正确的是( )A .函数222()2f x x x =++的最小值是2 B .“04m <„”是“210mx mx ++…”的充要条件C .若命题2:,10p x R x x ∀∈-+≠,则2000:,10p x R x x ⌝∃∈-+=D .“已知,x y R ∈,若1xy <,则,x y 都不大于1”的逆否命题是真命题4.已知双曲线22221(0,0)x y a b a b-=>>的焦距为且两条渐近线互相垂直,则该双曲线的实轴长为( )A .2B .4C .6D .85.函数3x xe e y x x--=-的图像大致是( )A .B .C .D .6.一个几何体的三视图如右图所示,且其左视图是一个等边三角形,则这个几何体的体积为( )A B C D .(4π+7.设a =20.1,b =ln 12,c =log 32,则a ,b ,c 的大小关系是( )A .a >b >cB .a >c >bC .b >a >cD .b >c >a8.执行如图所示的程序框图,则输出S 的值为( )A .213log 32+B .2log 3C .2D .39.设函数()3sin 2cos 244f x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,则( ) A .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递增,其图象关于直线4x π=对称B .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递增,其图象关于直线2x π=对称C .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递减,其图象关于直线4x π=对称D .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递减,其图象关于直线2x π=对称10.6(1)(1)ax x -+的展开式中,3x 项的系数为-10,则实数a 的值为( )A .23B .2C .2-D .23-11.已知球O 的半径为R ,,,A B C 三点在球O 的球面上,球心O 到平面ABC 的距离为12R ,2AB AC ==,120BAC ︒∠=,则球O 的表面积为( )A .169π B .163π C .649π D .643π 12.若存在0a >,使得函数2()6ln f x a x =与2()4g x x ax b =--的图象在这两个函数图象的公共点处的切线相同,则b 的最大值为( ) A .213e -B .216e -C .216e D .213e 二、填空题:本题共4小题,每小题5分,共20分.13.若,x y 满足2030x y x y x -≤⎧⎪+≤⎨⎪≥⎩,则2z x y =+的最大值为 .14.已知向量()()1,,2,4a k b =-=-v v ,若()3//a b a +v v v,则实数k = .15.已知抛物线C :22y px =(0p >)的焦点为F ,准线为l ,过F 的直线交抛物线C 于P ,Q 两点,交l 于点A ,若3PF FQ =u u u r u u u r ,则AQQF= . 16.在ABC ∆中,AB AC =,D 为AC 边上的点,且AC 3AD =,4BD =,则ABC ∆面积的最大值为 .三、解答题:(本大题共6小题,共计70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知数列{}n a 为等差数列,7210a a -=,且1621a a a ,,依次成等比数列. (I )求数列{}n a 的通项公式; (II )设11n n n b a a +=,数列{}n b 的前n 项和为n S ,若225n S =,求n 的值.18.(本小题满分12分)某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图所示.(I)试估计该校学生在校月消费的平均数;(II)根据校服务部以往的经验,每个学生在校的月消费金额x(元)和服务部可获得利润y(元),满足关系式:10,200400,30,400800,50,8001200,xy xx≤<⎧⎪=≤<⎨⎪≤≤⎩根据以上抽样调查数据,将频率视为概率,回答下列问题:(i)将校服务部从一个学生的月消费中,可获得的利润记为ξ,求ξ的分布列及数学期望.(ii)若校服务部计划每月预留月利润的14,用于资助在校月消费低于400元的学生,估计受资助的学生每人每月可获得多少元?19.(本小题满分12分)如图,在多面体ABCDEF 中,四边形ABCD 为菱形,//AF DE ,AF AD ⊥,且平面BED ⊥平面ABCD .(I )求证:AF CD ⊥;(II )若60BAD ∠=o ,12AF AD ED ==,求二面角A FB E --的余弦值.20.(本小题满分12分)设直线l 与抛物线22x y =交于A ,B 两点,与椭圆22143x y +=交于C ,D 两点,直线OA ,OB ,OC ,OD (O 为坐标原点)的斜率分别为1k ,2k ,3k ,4k ,若OA OB ⊥.(I )是否存在实数t ,满足1234()k k t k k +=+,并说明理由; (II )求OCD ∆面积的最大值.21.(本小题满分12分) 设函数()ln 1af x x x =+-,()0a > (I )当130a =时,求函数()f x 的单调递增区间; (II )若()f x 在10,e ⎛⎫⎪⎝⎭内有极值点,当()10,1x ∈,()21,x ∈+∞,求证:()()21423f x f x e ->-.()2.71828e =⋯请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程(本小题满分10分)在直角坐标系xOy 中,曲线C 的参数方程为2cos (22sin x y ααα=⎧⎨=+⎩为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (I )求曲线C 的极坐标方程;(II )设,A B 为曲线C 上不同两点(均不与O 重合),且满足4AOB π∠=,求OAB ∆的最大面积.23.选修4-5:不等式选讲(本小题满分10分) 设函数()|2||2|f x x x =+-- (I )解不等式()2f x ≥;(II )当x ∈R ,01y <<时,证明:11|2||2|1x x y y+--≤+-.一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数z =21i+在复平面内对应的点位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】D【解析】由题意得22(1)2(1)11(1)(1)2i i z i i i i --====-++-,∴复数21iz =+在复平面内对应的点的坐标为(1,1)-,位于第四象限,故选D .2.已知集合{}230,{|17},M x x x N x x =->=≤≤,则()R C M N =I ( )A .{}37x x <≤ B .{}37x x ≤≤C .{}13x x ≤≤D .{}13x x ≤<【答案】C【解析】由{}{2303M x x x x x =->=>或}0x <,∴{}03R C M x x =≤≤,又{|17}N x x =≤≤,(){}13R C M N x x ∴⋂=≤≤,故选C .3.下列叙述中正确的是( )A .函数222()2f x x x =++的最小值是2 B .“04m <„”是“210mx mx ++…”的充要条件C .若命题2:,10p x R x x ∀∈-+≠,则2000:,10p x R x x ⌝∃∈-+=D .“已知,x y R ∈,若1xy <,则,x y 都不大于1”的逆否命题是真命题 【答案】C【解析】对于A :()2222222222f x x x x x =+=++-++2≥中,22222x x +=+的等号不成立,A 错;当0m =时210mx mx ++≥也成立,B 错;当13x =,2y =时1xy <也成立,又原命题与逆否命题真假性一致,∴D 错,故选C .4.已知双曲线22221(0,0)x y a b a b-=>>的焦距为且两条渐近线互相垂直,则该双曲线的实轴长为( )A .2B .4C .6D .8【答案】B【解析】∵双曲线22221(0,0)x y a b a b -=>>的两条渐近线为b y x a=±,∵两条渐近线互相垂直,∴21b a ⎛⎫-=- ⎪⎝⎭,得a b =,∵双曲线焦距为,∴c =222c a b =+可知228a =,∴2a =,∴实轴长为24a =,故选B .5.函数3x xe e y x x--=-的图像大致是( )A .B .C .D .【答案】A【解析】令()3x xe ef x x x--=-,则()()f x f x -=,故函数为偶函数,图像关于y 轴对称,排除C 选项.由30x x -≠,解得0x ≠且1x ≠±.()0.50.510.500.1250.5e e f -=<-,排除D 选项.()10101101100010e ef -=>-,故可排除B 选项.故选A .6.一个几何体的三视图如右图所示,且其左视图是一个等边三角形,则这个几何体的体积为( )ABCD.(4π+【答案】B【解析】该几何体是圆锥的一半与一四棱锥的组合体.圆锥底半径为1,四棱锥的底面是边长为2的正方形,高均为B . 7.设a =20.1,b =ln 12,c =log 32,则a ,b ,c 的大小关系是( )A .a >b >cB .a >c >bC .b >a >cD .b >c >a【答案】B【解析】由题意得a =20.1>1,b =ln 12<0,c =log 32∈(0,1),∴a >c >b ,故选B . 8.执行如图所示的程序框图,则输出S 的值为( )A .213log 32+ B .2log 3C .2D .3【答案】C【解析】模拟程序的运行,可得s =3,i=1;满足条件i 3≤,执行循环体s =3+log i=2;满足条件i 3≤,执行循环体s =3+log +log ,i=3;满足条件i 3≤,执行循环体,s =3+log +4log log +=,i=4;不满足条件i 3≤,退出循环,输出s 的值为s =242log =;故选C . 9.设函数()3sin 2cos 244f x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,则( ) A .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递增,其图象关于直线4x π=对称B .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递增,其图象关于直线2x π=对称C .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递减,其图象关于直线4x π=对称D .()y f x =在,04π⎛⎫-⎪⎝⎭上单调递减,其图象关于直线2x π=对称【答案】B【解析】∵()3sin 2cos 2244f x x x x ππ⎛⎫⎛⎫=++-= ⎪ ⎪⎝⎭⎝⎭, 由222,πππ-+≤≤∈k x k k Z 得,2πππ-+≤≤∈k x k k Z ,由222,k x k k Z πππ≤≤+∈得,2πππ≤≤+∈k x k k Z ,即()y f x =的单调递增区间为,,2πππ⎡⎤-+∈⎢⎥⎣⎦k k k Z ;单调递减区间为,,2πππ⎡⎤+∈⎢⎥⎣⎦k k k Z ;∴()y f x =在,04π⎛⎫-⎪⎝⎭上单调递增;由2,π=∈x k k Z 得,2k x k Z π=∈;即函数()y f x =的对称轴为:,2k x k Z π=∈;因此其图象关于直线2x π=对称,故选B .10.6(1)(1)ax x -+的展开式中,3x 项的系数为-10,则实数a 的值为( ) A .23B .2C .2-D .23-【答案】B【解析】6(1)x +展开式的通项公式为16r r r T C x +=,分别令2,3x x ==,可求得2x 的系数为2615C =,3x 的系数为3620C =,故6(1)(1)ax x -+的展开式中,3x 项的系数为1201510a ⨯-=-,解得2a =,故选B .11.已知球O 的半径为R ,,,A B C 三点在球O 的球面上,球心O 到平面ABC 的距离为12R ,2AB AC ==,120BAC ︒∠=,则球O 的表面积为( )A .169π B .163π C .649π D .643π 【答案】D【解析】在ABC V 中,2120AB AC BAC ==∠=︒Q ,,BC ∴==正弦定理可得平面ABC 截球所得圆的半径(即ABC V 的外接圆半径),2r ==,又∵球心到平面ABC 的距离12d R =, ∴球的O半径2163R R =∴=,故球O 的表面积26443S R ππ==, 故选D . 12.若存在0a >,使得函数2()6ln f x a x =与2()4g x x ax b =--的图象在这两个函数图象的公共点处的切线相同,则b 的最大值为( ) A .213e-B .216e-C .216eD .213e【答案】D【解析】设曲线()y f x =与()y g x =的公共点为()00,x y ,∵26(),a f x x'=()24g x x a '=-,∴200624a x a x -=,则220230x ax a --=,解得0x a =-或3a , 又00x >,且0a >,则03x a =.∵()()00f x g x =,∴2200046ln x ax b a x --=,2236ln 3b a a a =--(0)a >.设()h a b =,∴()12(1ln3)h a a a '=-+,令()0h a '=,得13ea =. ∴当103e a <<时,()0'>h a ;当13e a >时,()0h a '<,∴b 的最大值为2113e 3eh ⎛⎫= ⎪⎝⎭,故选D . 二、填空题:本题共4小题,每小题5分,共20分.13.若,x y 满足2030x y x y x -≤⎧⎪+≤⎨⎪≥⎩,则2z x y =+的最大值为 .【答案】4【解析】当直线z =2x +y 经过直线2x -y =0与直线x +y =3的交点(1,2)时,z 取最大值2×1+2=4.14.已知向量()()1,,2,4a k b =-=-v v ,若()3//a b a +v v v,则实数k = .【答案】2.【解析】由题意,得()()()331,2,45,34a b k k +=-+-=--r r,∵()3//a b a +r r r ,∴()()13450k k ⨯----=,解得2k =,故答案为:2.15.已知抛物线C :22y px =(0p >)的焦点为F ,准线为l ,过F 的直线交抛物线C 于P ,Q 两点,交l 于点A ,若3PF FQ =u u u r u u u r ,则AQQF= .【答案】2【解析】过P ,Q 分别作PM ,QN 垂直准线l 于,M N ,如图,3PF FQ =u u u r u u u rQ ,1||||4QF PQ ∴=,由抛物线定义知,||||,||||PM PF QF QN ==,||3||PM QN ∴=,//PM QN Q ,||||1||||3AQ QN AP PM ∴==, 11||||4||2||22AQ QP QF QF ∴==⨯=,2AQ QF ∴=,故答案为:2.16.在ABC ∆中,AB AC =,D 为AC 边上的点,且AC 3AD =,4BD =,则ABC ∆面积的最大值为 . 【答案】9【解析】∵AC 3AD =,∴3ABC ABD S S ∆∆=,设AD x =,则3AB x =,由343x x x x +>>-得12x <<,222291658cos 233x x x A x x x +--==⋅⋅,sin A ==11sin 322ABDS AB AD A x ∆=⋅=⋅⋅==,∵12x <<,∴252x =时,ABD S ∆取得最大值3=,∴ABC S ∆最大值为9,故答案为:9. 三、解答题:(本大题共6小题,共计70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知数列{}n a 为等差数列,7210a a -=,且1621a a a ,,依次成等比数列. (I )求数列{}n a 的通项公式; (II )设11n n n b a a +=,数列{}n b 的前n 项和为n S ,若225n S =,求n 的值. 【解析】(I )设数列{a n }为公差为d 的等差数列,a 7﹣a 2=10,即5d =10,即d =2, a 1,a 6,a 21依次成等比数列,可得a 62=a 1a 21,即(a 1+10)2=a 1(a 1+40),解得a 1=5, 则a n =5+2(n ﹣1)=2n +3. (II )b n ()()111123252n n a a n n +===++(112325n n -++), 即有前n 项和为S n 12=(11111157792325n n -+-++-++L )12=(11525n -+)()525n n =+, 由S n 225=,可得5n =4n +10,解得n =10. 18.(本小题满分12分)某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图所示.(I )试估计该校学生在校月消费的平均数;(II )根据校服务部以往的经验,每个学生在校的月消费金额x (元)和服务部可获得利润y (元),满足关系式:10,200400,30,400800,50,8001200,x y x x ≤<⎧⎪=≤<⎨⎪≤≤⎩根据以上抽样调查数据,将频率视为概率,回答下列问题:(i )将校服务部从一个学生的月消费中,可获得的利润记为ξ,求ξ的分布列及数学期望. (ii )若校服务部计划每月预留月利润的14,用于资助在校月消费低于400元的学生,估计受资助的学生每人每月可获得多少元?【解析】(I )学生月消费的平均数113(300500700400010001000x =⨯+⨯+⨯ 119001100)20068020004000+⨯+⨯⨯=. (II )(i )月消费值落入区间[)200,400、[)400,800、[]800,1200的频率分别为0.05、0.80、0.15, 因此()100.05P ξ==,()300.80P ξ==,()500.15P ξ==, 即ξ的分布列为ξ的数学期望值()100.05300.80500.1532E ξ=⨯+⨯+⨯=.(ii )服务部的月利润为32200064000⨯=(元),受资助学生人数为20000.05100⨯=, 每个受资助学生每月可获得1640001001604⨯÷=(元). 19.(本小题满分12分)如图,在多面体ABCDEF 中,四边形ABCD 为菱形,//AF DE ,AF AD ⊥,且平面BED ⊥平面ABCD .(I )求证:AF CD ⊥;(II )若60BAD ∠=o ,12AF AD ED ==,求二面角A FB E --的余弦值. 【解析】(I )证明:连接AC ,由四边形ABCD 为菱形可知AC BD ⊥,∵平面BED ⊥平面ABCD ,且交线为BD ,∴AC ⊥平面BED ,∴AC ED ⊥, 又//AF DE ,∴AF AC ⊥,∵,AF AD AC AD A ⊥⋂=,∴AF ⊥平面ABCD ,∵CD ⊂平面ABCD ,∴AF CD ⊥. (II )解:设AC BD O ⋂=,过点O 作DE 的平行线OG ,由(I )可知,,OA OB OG 两两互相垂直, 则可建立如图所示的空间直角坐标系O xyz -,设()1202AF AD ED a a ===>,则)())(),0,0,0,,0,,0,2,0,,4A B a F a E a a -,∴()()()),,0,0,0,2,0,2,4,,,2AB a AF a BE a a BF a a ===-=-u u u v u u u v u u u v u u u v,设平面ABF 的法向量为(),,m x y z v=,则·0·0m AB m AF ⎧=⎨=⎩u u u v v u u u v v ,即020y z ⎧+=⎪⎨=⎪⎩,取y =则()m =v 为平面ABF 的一个法向量,同理可得()0,2,1n =v为平面FBE的一个法向量,则cos ,5m n ==, 又二面角A FB E --的平面角为钝角,则其余弦值为.20.(本小题满分12分)设直线l 与抛物线22x y =交于A ,B 两点,与椭圆22143x y +=交于C ,D 两点,直线OA ,OB ,OC ,OD (O 为坐标原点)的斜率分别为1k ,2k ,3k ,4k ,若OA OB ⊥.(I )是否存在实数t ,满足1234()k k t k k +=+,并说明理由; (II )求OCD ∆面积的最大值.【解析】设直线l 方程为y kx b =+,()11,A x y ,()22,B x y ,()33,C x y ,()44,D x y ,联立y kx b =+和22x y =,得2220x kx b --=,则122x x k +=,122x x b =-,21480k b ∆=+>.由OA OB ⊥,∴12120x x y y +=,得2b =.联立2y kx =+和223412x y +=,得()22341640kxkx +++=,∴3421634k x x k +=-+,342434x x k =+.由22192480k ∆=->,得214k >. (I )∵121212y y k k k x x +=+=,3434346y y k k k x x +=+=-,∴123416k k k k +=-+.(II)根据弦长公式34CD x =-,得:CD =.根据点O 到直线CD的距离公式,得d =,∴21234OCDS CD d k∆=⋅=+0t =>,则24OCD S t ∆=≤+,∴当2t =,即5k =±时,OCD S ∆21.(本小题满分12分) 设函数()ln 1af x x x =+-,()0a > (I )当130a =时,求函数()f x 的单调递增区间; (II )若()f x 在10,e ⎛⎫⎪⎝⎭内有极值点,当()10,1x ∈,()21,x ∈+∞,求证:()()21423f x f x e ->-.()2.71828e =⋯【解析】(I )函数()f x 的定义域为()()0,11,+∞U ,当130a =时,()()25665'1x x f x x x ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭=-, 令()'0f x >,得:65x >或56x <,∴函数单调增区间为:50,6⎛⎫ ⎪⎝⎭,6,5⎛⎫+∞ ⎪⎝⎭. (II )证明:()()()()222211'11x a x af x x x x x -++=-=--, 令()()()()2210g x x a x x m x n =-++=--=,∴2m n a +=+,1mn =,若()f x 在10,e ⎛⎫ ⎪⎝⎭内有极值点,不妨设10m e<<,则1n e m =>,且122a m n e e =+->+-, 由()'0f x >得:0x m <<或x n >;由()'0f x <得:1m x <<或1x n <<, ∴()f x 在()0,m 递增,(),1m 递减;()1,n 递减,(),n +∞递增,当()10,1x ∈时,()()1ln 1af x f m m m ≤=+-; 当()21,x ∈+∞时,()()2ln 1af x f n n ≥=+-,∴()()()()2111ln ln 2ln 1111a a f x f x f n f m n m n a n m n m ⎛⎫-≥-=+--=+- ⎪----⎝⎭12ln n n n =+-,n e >.设()12ln F n n n n =+-,n e >,则()222'10F n n n =++>,∴()F n 是增函数,∴()()12F n F e e e>=+-. 又()()23131411031032203333e e e e e e e e e e e ----+-⎛⎫+---=--+==> ⎪⎝⎭,∴()()21423f x f x e ->-.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分. 22.选修4-4:坐标系与参数方程(本小题满分10分)在直角坐标系xOy 中,曲线C 的参数方程为2cos (22sin x y ααα=⎧⎨=+⎩为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系. (I )求曲线C 的极坐标方程;(II )设,A B 为曲线C 上不同两点(均不与O 重合),且满足4AOB π∠=,求OAB ∆的最大面积.【解析】(I )设曲线C 上任意点的极坐标为(,)ρθ,由题意,曲线C 的普通方程为22(2)4x y +-=,即2240x y y +-=,则24sin ρρθ=,故曲线C 的极坐标方程为4sin ρθ=.(II )设1(,)A ρθ,则2(,)4B πρθ+,故3(0,)4πθ∈, ∵点,A B 在曲线C 上,则14sin ρθ=,24sin()4πρθ=+,1sin 2AOB S OA OB AOB ∆∴=∠ ()23sin 4sin sin cos 2sin 22cos 22220,444θθθθθθθθθ⎛⎫πππ⎛⎫⎛⎫⎛⎫=+=+=-+=-+∈ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,故38πθ=时,OAB ∆取到最大面积为2. 23.选修4-5:不等式选讲(本小题满分10分) 设函数()|2||2|f x x x =+-- (I )解不等式()2f x ≥;(II )当x ∈R ,01y <<时,证明:11|2||2|1x x y y+--≤+-. 【解析】(I )由已知可得:()4,22,224,2x f x x x x ≥⎧⎪=-<<⎨⎪-≤-⎩,当2x ≥时,42>成立;当22x -<<时,22x ≥,即1x ≥,则12x ≤<. ∴()2f x ≥的解集为{|1}x x ≥. (II )由(I )知,224x x +--≤,由于01y <<,则()1111112224111y yy y y y y y y y⎛⎫-⎡⎤+=++-=++≥+= ⎪⎣⎦---⎝⎭,当且仅当1=1y y y y --,即12y =时取等号,则有11221x x y y +--≤+-.。
【试卷】【金太阳】2020年全国100所名校最新高考模拟示范卷 理科数学(六)

2020年全国100所名校最新高考模拟示范卷理科数学(六)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|2,2,},{|(2)9}Z P x x k k k Q x x ==∈=+<≥,则P Q = ( ) A .{4,2,0,1}--B .{4,2,0}--C .{|41}x x -<≤D .{|45}x x -<≤2.已知复数z 满足1i z z +-=,在复平面内对应的点为(,)x y ,则( ) A .1y x =+B .y x =C .2y x =-D .y x =-3.已知1311531log ,log ,363a b c π-===,则,,a b c 的大小关系是( )A .b a c <<B .a c b <<C .c b a <<D .b c a <<4.中国折叠扇有深厚的文化底蕴.如图(2),在半圆O 中作出两个扇形OAB 和OCD ,用扇环ABDC (图中阴影部分)制作折叠扇的扇面.记扇环形ABDC 的面积为1S ,扇形OAB 的面积为2S ,当1S 与2S 的比OCD 的半径与半圆O 的半径之比为( ) ABC.3 D25.函数ln ()sin xf x x x=+的部分图象大致是( )6.“车走直、马走日、炮打隔子、象飞田、小卒过河赛大车”,这是中国象棋中的部分下棋规则.其中“马走日”是指马走“日”字的对角线,如棋盘中,马从点A 处走出一步,只能到点B 或点C 或点D 或点E .设马从点A 出发,必须经过点M ,N (点M ,N 不考虑先后顺序)到达点P ,则至少需走的步数为( ) A .5 B .6 C .7 D .87.已知,a b 是单位向量,且(1,1)a b +=-, 则a 与a b -的夹角为( )A .6πB .4πC .3πD .23π8.执行如图所示的程序框图,则输出的S =( ) A .414 B .325 C .256 D .759.已知等差数列{}n a 的前n 项和为n S ,满足3213,22(3)n n n a S S S n --=+=+≥,则( ) A .2n n S na n-=B .2n n S na n+=C .21n n S a n-=D .21n n S a n+=10.已知双曲线2221(0)3x y a a -=>的右焦点为F ,圆222x y c +=(c 为双曲线的半焦距)与双曲线C 的一条渐近线交于,A B 两点,且线段AF 的中点M 落在另一条渐近线上,则双曲线C 的方程是( )A .22143x y -=B .22133x y -=C .22123x y -=D .2213y x -=11.在三棱锥P ABC -中,PA ⊥平面ABC ,AB BC ⊥,且2AB =.若三棱锥P ABC -的外接球的体积为36π,则当该三棱锥的体积最大时,其表面积为( )A .6+B .8+C .8+D .6+12.已知函数()2sin 6f x x πω⎛⎫=- ⎪⎝⎭的图象的一条对称轴为x π=,其中ω为常数,且(0,1)ω∈,给出下述四个结论:①函数()f x 的最小正周期为3π;②将函数()f x 的图象向左平移6π所得图象关于原点对称;③函数()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上单调递增;④函数()f x 在区间(0,100)π上有67个零点.其中所有正确结论的编号是( ) A .①② B .①③C .①③④D .①②④二、填空题:本题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13.函数2()(0)2xf x x x =>+的最大值为 . 14.已知等比数列{}n a中,13543,a a a a ==24461335a a a a a a a a +=+ .15.已知7件产品有5件合格品,2件次品.为找出这2件次品,每次任取一件检验,检验后不放回,则第一次和第二次都检验出次品的概率为 ;恰好在第一次检验出正品而在第四次检验出最后一件次品的概率为 .16.椭圆22221(0)x y a b a b +=>>的左焦点为F ,过点F的直线l 与椭圆交于,A B 两点(点B在第一象限),与y 轴交于E 点,若AF EB =,则椭圆的离心率为 .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(本小题满分12分) 已知ABC △的内角,,A B C 的对边分别为,,a b c ,设cos cos a B b A c -=. (1)求A ; (2)若a =,ABC △的面积为1,求以,2,2a b c 为边的111A B C △的面积.18.(本小题满分12分)在长方体1111ABCD A B C D -中,1//,1,3,EF AD AA AF AB AD ====.(1)求证:平面1C EF ⊥平面1D EF . (2)求二面角11C D F E --的大小.119.(本小题满分12分)已知抛物线2:()N C y px p +=∈的焦点为F ,点P 在抛物线C 上,其纵坐标为1p +,174PF =, 且(0,2),(1,0)M N . (1)求抛物线C 的方程;(2)过M 的直线l 与抛物线C 交于,A B 两点,若AN BN ⊥,求直线l 的斜率. 20.(本小题满分12分)已知函数()sin ,()()x f x x x g x e f x =-=. (1)求证:函数()g x 是30,2π⎡⎤⎢⎥⎣⎦上的增函数. (2)若不等式()x e af x ≥对,2x ππ⎡⎤∀∈-⎢⎥⎣⎦恒成立,求实数a 的取值范围. 21.(本小题满分12分)在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,现对已借阅了科技类图书的市民(以下简称为“问卷市民”)进行随机问卷调查,若不借阅时政类图书记1分,若借阅时政类图书记2分,每位市民选择是否借阅时政类图书的概率均为12,市民之间选择意愿相互独立.(1)从问卷市民中随机抽取4人,记总得分为随机变量ξ,求ξ的分布列和数学期望;(2)(i )若从问卷市民中随机抽取()N m m +∈人,记总分恰为m 分的概率为m A ,求数列{}m A 的前10项和;(ii )在对所有问卷市民进行随机问卷调查过程中,记已调查过的累计得分恰为n 分的概率为n B (比如:1B 表示累计得分为1分的概率,2B 表示累计得分为2分的概率,N n +∈),试探求n B 与1n B -之间的关系,并求数列{}n B 的通项公式.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所作的第一题计分. 22.【选修4—4:坐标系与参数方程】(本小题满分10分) 在平面直角坐标系xOy 中,点(2,0)A -,直线l 的参数方程为2cos sin x t y t ϕϕ=-+⎧⎨=⎩(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为22(13cos )4ρθ+=.(1)当2πϕ=时,判断直线l 与曲线C 的位置关系;(2)若直线l 与曲线C 相切于点B ,求AB 的值. 23.【选修4—5:不等式选讲】(本小题满分10分) 已知222,,,1R a b c a b c ∈++=. (1)证明:112ab bc ca -++≤≤. (2)证明:2222222222()()()3a b c b c a c a b +++++≤.2020年全国100所名校最新高考模拟示范卷理科数学(五)参考答案1.答案:B解析:2{|20}{|(2)(1)0}{|12}A x x x x x x x x=--=-+=-≤≤≤≤,{|21}B x x=-<≤,所以{|22}A B x x=-<≤.2.答案:C 解析:2i2i2i,1i1i1iz z=∴====---,公式:11121222,zzz z z zz z⋅=⋅=.3.答案:D 解析:因为70412212π≈,故选D.4.答案:B 解析:当0a≤时,1()f x axx=+在(2,)+∞上单调递减,当0a>时,1()f x axx=+在⎛⎝上单调递减,在⎫+∞⎪⎭2,即14a≥.5.答案:A 解析:①正确;②正确;③由()6E X =,可得(25)2()52657E X E X -=-=⨯-=,故错误.当3a =-时,26a x y a -=即为963x y -=-,即3210x y -+=,所以方程组232106x y a x y a-+=⎧⎨-=⎩有无穷多解,④正确.6.答案:A解析:105445511551,1log log 2,log 2log 22a b c =>=>=>==<=,故a b c >>.7.答案:A解析:234cos 12sin ,sin 255C C C =-=-∴=;1,a c ==由余弦定理可得2222cos c a b ab C =+- 即263105b b +-=,31(5)05b b ⎛⎫-+= ⎪⎝⎭,5b =,114sin 152225ABC S ab C ∴==⨯⨯⨯=△. 8.答案:C 解析:由 1.3522.35x x -=-,设 1.35t x =-,得21t t =-,作出函数2t y =和1y t =-的图象,可知0t =,即 1.35x =.俯视图的面积为1.3513(5.4 1.35)13.5⨯+⨯-=,正视图面积为5.4,所以俯视图的面积是正视图面积的2.5倍. 9.答案:A 解析:因为当[0,2]x ∈π时,2555x πππω+ωπ+≤≤,由()f x 在[0,2]π有且仅有5个零点.则265x ππω+<π5≤,解得1229510ω⎡⎫∈⎪⎢⎣⎭,. 10.答案:C解析:设221122(2,),(2,)A t t B t t ,12t t ≠,由24x y =,得2xy '=,所以切线12,l l 的斜率分别为11k t =,22k t =, 所以21111:(2)l y t t x t -=-,即211y t x t =-,同理2222:l y t x t =-,联立2112223y t x t y t x t y ⎧=-⎪=-⎨⎪=-⎩,得12123x t t y t t =+⎧⎨==-⎩,22121212222ABt t t tk t t -+==-,21211:(2)2AB t t l y t x t +-=-,即12122t t y x t t +=-,即1232t t y x +=+,即直线AB 恒过定点(0,3),即直线AB 过圆心(0,3),则直线AB 截圆22650x y y +-+=所得弦长为4. 解法二:不妨设(0,3)P -,设切线方程为3y kx =-,将其代入24x y =,得24120x kx -+=, 则216480k ∆=-=,解得k =,当k =2120x -+=,解得x =故A ,同理可得(B -,所以直线AB 的方程为3y =,直线AB 过圆心(0,3), 则直线AB 截圆22650x y y +-+=所得弦长为4. 11.答案:D解析:a 与b 为函数()3x f x =的“线性对称点”,所以333a ba b +=+=≥,故34a b +≥(当且仅当a b =时取等号).又a b +与c 为函数()3x f x =的“线性对称点”,所以3333abca b c++++=,所以33314313131313a b a b ca b a b a b +++++===+---≤,从而c 的最大值为334log log 413=-.12.答案:B 解析:设正方体的棱长为1,延长1D N ,与AB 的延长线交于点F ,则1BF =,连接FM并延长,交BC 于点P ,交AD 于点Q ,取AB 中点G ,连接MG ,则23BP BF GM FG ==, 12,233BP AQ BP ∴===,连接PN ,并延长交11B C 于点H ,连接1D H ,则113HC =,平面1HD QP 即为截面,取PC 中点E ,连接1,C E QE ,则点C 所在的多面体的体积1111111111111123233D DQ C CE C D H EQP V V V --⎛⎫⎛⎫=+=⨯⨯⨯+⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭,点1A 所在的多面体的体积1221211,332V V V =-=∴=.13.答案:160- 解析:612x x ⎛⎫- ⎪⎝⎭的展开式中常数项为33361(2)160C x x ⎛⎫⋅⋅-=- ⎪⎝⎭. 14 解析:2,1a b == ,cos 13a b a bπ⋅=⋅=,所以222244164113a b a a b b -=-⋅+=-+= ,所以2a b -=15.答案:0解析:()1ln ,(1)1,(1)2f x x f f a ''=+==-,切线1l 的方程:21y a x +=-,又1l 过原点,所以21a =-,221111()ln 1,()ln ,()x f x x x g x x g x x x x x-'=+=+=-=,当(0,1)x ∈时,()0,()g x g x '<单调递减,当(1,)x ∈+∞时,()0,()g x g x '>单调递增,故()()f x g x x=的最小值为(1)1g =,所以1,20m m a =+=. 16.答案:2或43 解析:设直线倾斜角为α,则7tan cos 8αα==.P 在第一象限, 12F PF △是等腰三角形,所以112F P F F =或212F P F F =.若112F P F F =,则11212,22F P F F c F P c a ===-,由余弦定理得222244(22)788c c x a c +--=,整理得23840e e -+=,解得2e =或23e =(舍去).…………………………………………………………3分250(221288)5.56 3.84130202030K ⨯⨯-⨯=≈>⨯⨯⨯,所以有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关联.…………………………………………………………………………………………………6分(2)年龄在[55, 65)的被调查者共5人,其中了解新高考的有2人,则抽取的3人中了解新高考的人数X 可能取值为0,1,2,则31121323233335551633(0),(1),(2)1010510C C C C C P X P X P X C C C ==========.………………………9分 所以X 的分布列为1336()012105105E X =⨯+⨯+⨯=.……………………………………………………………………12分18.解析:(1)由题意可得4121114614(2)(6)S a d a d a a d =+=⎧⎨+=+⎩ ,即1212372a d d a d +=⎧⎨=⎩,…………………………3分 又因为0d ≠,所以12,1a d ==,所以1n a n =+.……………………………………………………6分 (2)因为111(2)(1)11(1)(2)(1)(2)12n n n n a a n n n n n n ++-+===-++++++,………………………………9分 所以11111111233412222(2)n n T n n n n ⎛⎫⎛⎫⎛⎫=-+-++-=-=⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭ .…………………………12分 19.解析:(1)设AC 与BD 的交点为O ,连接MO .因为//OD EF ,OD ⊄平面CEF ,EF ⊂平面CEF ,所以//OD 平面CEF .……………………………………………………………………………………2分 又OM 是ACE △的中位线,所以//OM CE ,又OM ⊄平面CEF ,CE ⊂平面CEF ,所以//OM 平面CEF .……………………………………………………………………………………………………4分 又OM OD O = ,所以平面//OMD 平面CEF .又MD ⊂平面OMD ,故//MD 平面CEF .…5分 (2)因为DE DC ⊥,平面CDE ⊥平面ABCD ,平面CDE 平面,ABCD CD DE =⊂平面CDE ,所以ED ⊥平面ABCD .连接OF ,则EF OD ,故四边形ODEF 是平行四边形,故//ED OF , 从而OF ⊥平面ABCD .……………………………………………………………………………………6分 以O 为坐标原点,,,OA OB OF 分别为x 轴,y 轴,z 轴,建立空间直角坐标系,则(0,1,0),(0,0,1),(0,1,1)A B F E -,则(0,1,0),((0,1,1)EF AF BF ===-,设平面AEF 的法向量为(,,)n x y z =,则0n EF y n AF z ⎧⋅==⎪⎨⋅=+=⎪⎩,取n = ,…………8分则cos ,n BF n BF n BF⋅==⋅BF则cos sin ,n BF θ== ,所以直线BF 与平面AEF ………………………………………………12分 20.解析:(1)由题知,2110,()mx x f x mx x x-'>=-+=,…………………………………………1分 ①当0≤m 时,21()0mx f x x -'=<,所以()f x 在(0,)+∞上单调递减,没有极值;………………3分②当0m >时,令21()0mx f x x -'==,得x =,当x⎛∈ ⎝时,()0,()f x f x '<单调递减,当x ⎫∈+∞⎪⎭时,()0,()f x f x '>单调递增,故()f x 在x=处取得极小值111ln 222f m m =+-,无极大值.…………………………5分 (2)不妨令11111()x x x e x h x x e xe----=-=,不难证明10≥x e x --,当且仅当1x =时取等号, 所以当(1,)x ∈+∞时,()0h x >,由(1)知,当0,1≤m x >时,()f x 在(1,)+∞上单调递减,()(1)0f x f <=恒成立; 所以若要不等式111()x f x x e->-在(1,)+∞上恒成立,只能0m >. 当01m <<1>,由(1)知,()f x 在⎛ ⎝上单调递减, 所以(1)0f f<=,不满足题意.……………………………………………………………………8分 当1≥m 时,设21111()(1)ln 2x F x m x x x e-=---+, 因为1,1≥m x >,所以11111,1,01,10≥x x x mx x e e e---><<-<-<,32221222111111(1)(1)()10x x x x x x F x mx x x x e x x x x---+-+'=-++->-++-==>, 所以()F x 在(1,)+∞上单调递增,又(1)0F =,所以当(1,)x ∈+∞时,()0F x >恒成立,即()()0f x h x ->恒成立,故存在1≥m ,使得不等式111()x f x x e->-在(1,)+∞上恒成立.此时m 的最小值是1.…………12分21.解析:(1)由2b =b =,又由22222214c a b e a a -===,得2234a b =, 则224,3a b ==,故椭圆C 的方程为22143x y +=.……………………………………………………4分(2)由(1)知(1,0)F ,①当直线12,l l 的斜率都存在时,由对称性不妨设直线1l 的方程为(1)y k x =-,1k ≠±, 由222222(1)(43)8412034120y k x k x k x k x y =-⎧⇒+-+-=⎨+-=⎩,……………………………………5分设1122(,),(,)P x y Q x y ,则2221212228412,,144(1)04343k k x x x x k k k -+==∆=+>++,…………6分则2212(1)34k PQ k +==+,由椭圆的对称性可设直线2l 的斜率为11k k +-, 则22221121224(1)17(1)21341k k k MN k k k k +⎛⎫+⋅ ⎪+-⎝⎭==+++⎛⎫+⋅ ⎪-⎝⎭,……………………………………………………8分 222222212(1)7(1)27(1)27873424(1)6882432PQ k k k k k k MN k k k k ++++++=⋅==+++++, 令87t k =+,则78t k -=,当0t =时,78k =-,78PQ MN =, 当0t ≠时,22724322432197878722t k t k t t-⎛⎫+ ⎪+⎝⎭==+-+, 若0t >,则1977722t t +--,若0t <,则1977722≤t t+-2872432≤k k ++,即2872432k k ++,≤PQ MN ,且87PQ MN ≠.………………………………………………10分 ②当直线12,l l 的斜率其中一条不存在时,由对称性不妨设直线1l 的方程为1y x =-, 则2242,37b PQ MN a ===,此时87PQ MN =∈⎣⎦. 若设2l 的方程为1y x =-,则78PQMN =∈⎣⎦, 综上可知,PQMN的取值范围是⎣⎦.……………………………………………12分 22.解析:(1)由122cos :2sin x C y αα=+⎧⎨=⎩(α为参数),得1C 的普通方程为22(2)4x y -+=; 由sin 13πρθ⎛⎫-= ⎪⎝⎭,得1sin cos 12ρθρθ=cos sin 20θρθ-+=,又由cos ,sin x y ρθρθ==,得曲线220C y -+=.…………………………………………5分(2)由题意,可设点P 的直角坐标为(22cos ,2sin )αα+,因为2C 是直线,所以PQ 的最小值,即为P 到2C 的距离()d α的最小值,()2cos 16d παα⎛⎫=+++ ⎪⎝⎭.………………………………8分 当且仅当52,6Z k k παπ=+∈时,()d α1-, 此时P的直角坐标为(2.…………………………………………………………………………10分23.解析:(1)3,11()2112,1213,2≥≤x x f x x x x x x x ⎧⎪⎪⎪=++-=+-<<⎨⎪⎪--⎪⎩,…………………………………………1分 当1≥x 时,39≤x ,得13≤≤x ;………………………………………………………………………2分 当112x -<<时,29≤x +,解得7≤x ,故112x -<<;…………………………………………3分 当12≤x -时,39≤x -,解得3≥x -,故132≤≤x --.……………………………………………4分 综上,原不等式的解集为{|33}≤≤x x -.………………………………………………………………5分(2)36,1()91244,12≤x x g x x x x x +-⎧⎪=-+--=+-<<⎨⎪,在同一坐标系内画出函数()f x 和()g x 的图象,10分。
2020届全国100所名校高考模拟金典卷(六)数学(理)试题解析

绝密★启用前2020届全国100所名校高考模拟金典卷(六)数学(理)试题注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、单选题1.已知集合{}2|20A x x x =--≥,{|13}B x x =<<,则()R A B =U ð()A .{|13}x x -<<B .{|11}x x -<<C .{|12}x x <<D .{|23}x x << 答案:A由集合A 求出A R ð,进而求出()R A B ðU 即可.解:∵{}2|20{|12}R x x x x A x =--<=-<<ð,∴(){|13}R B x A x ⋃=-<<ð. 故选:A点评:本题主要考查集合的运算,考查学生的运算求解能力.2.已知复数z 满足(1)4z i +=,则1z -=()A .2B C .3 D答案:B先求出z ,再计算1z -.解:由(1)4(1)(1)4(1)z i z i i i +=⇒+-=-得22z i =-,则|1||12|z i -=-==故选:B点评:本题主要考查了复数的运算,复数的模的计算,考查学生的基本运算能力.3.已知函数()f x =A ,则函数21()()2x g x x A -⎛⎫=∈ ⎪⎝⎭的值域为()A .(,0]-∞B .(,1]-∞C .(1,)+∞D .[1,)+∞答案:D 先求出集合A ,再判断出函数()g x 的单调性,从而求出函数()g x 的值域. 解:由310log (1)0x x ->⎧⎨-≥⎩得2x ≥,所以[)2,A =+∞ 又因为函数()g x 在R 上单调递增,所以当x A ∈时,()1g x ≥.故选:D点评:本题主要考查了对数函数,指数函数的性质,考查了函数单调性的判断,考查了学生的运算求解能力.4.若x 、y 满足约束条件4201x y x y y +≤⎧⎪-+≥⎨⎪≥⎩,目标函数2z x y =+取得的最大值为()A .5B .6C .7D .8答案:C作出不等式组所表示的可行域,平移直线2z x y =+,找出使得直线2z x y =+在x 轴上截距最大时对应的最优解,代入目标函数计算即可得出结果.解: 作出不等式组4201x y x y y +≤⎧⎪-+≥⎨⎪≥⎩所表示的可行域如下图所示:联立140y x y =⎧⎨+-=⎩,得31x y =⎧⎨=⎩,得点()3,1A , 平移直线2z x y =+,当该直线经过可行域的顶点A 时,直线2z x y =+在x 轴上的截距最大,此时z 取最大值,即max 2317z =⨯+=.故选:C.点评:本题考查简单的线性规划问题,考查线性目标函数的最值问题,一般利用平移直线的方法找出最优解,考查数形结合思想的应用,属于基础题.5.已知ABC ∆的面积为4,且2sin sin sin A B C =,则AB 的长为()A .4B .C .2D 答案:A由正弦定理得2sin BC B AB ⋅=,又1sin 42BC AB B ⋅⋅=,故可求得AB . 解: Q 2sin sin sin A B C =,由正弦定理得2sin BC B AB ⋅=, 又1sin 42BC AB B ⋅⋅=, ∴216AB =,得4AB =.故选:A点评:本题主要考查了正弦定理的应用,三角形的面积公式,考查了学生运算求解能力.6.我国古代数学著作《九章算术》有如下问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,始与岸齐,问水深、葭长各几何?”意思是说:“有一个边长为1丈的正方形水池,在池的正中央长着一根芦苇,芦苇露出水面1尺.若将芦苇拉到池边中点处,芦苇的顶端恰好到达水面.问水有多深?芦苇多长?”该题所求的水深为()A .12尺B .10尺C .9尺D .14尺答案:A设水深为x 尺,根据题意列出有关x 的方程,进而可求得x 的值,即可得出结论. 解:设水深为x 尺,依题意得()22215x x +-=,解得12x =.因此,水深为12尺.故选:A.点评:本题考查中国数学史,考查考生的逻辑推理能力与运算求解能力,属于基础题.7.某三棱锥的三视图如图所示,则该三棱锥最长棱的长为()A .22B .3C .23D .4答案:C 作出三棱锥的直观图,结合三视图中的数据计算出三棱锥各条棱的棱长,进而可得出结果.解:该三棱锥直观图如图所示,其中2BD =,2215AC CB CD ===+=,222222AB =+=,2223AD AB BD =+=,因此,该三棱锥的最长棱的棱长为23AD =.故选:C.点评:本题考查三视图,考查考生的空间想象能力,属于中等题.8.已知抛物线2:4C y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是线段PF 与抛物线C 的一个交点,若3PF FQ =u u u r u u u r ,则点Q 到y 轴的距离为()。
2020届全国100所名校最新高考模拟示范卷(二)高三模拟测试数学(理)试题(解析版)

(1)因为 ,
利用正弦定理可得, ,
即 ,因为 ,
所以 ,即 ,
因为 ,所以 , ,
因为 ,所以 .
(2)由(1)及余弦定理可得,
,即 ,
所以 ,当且仅当 时等号成立,
所以 的最大值为 .
【点睛】
本题考查利用正余弦定理解三角形、两角和的正弦公式及利用基本不等式求最值;考查运算求解能力和知识迁移能力;属于中档题、常考题型.
18.如图,在四棱锥 中, 底面 ,底面 为直角梯形, , ∥ , , , , , 分别为线段 , , 的中点.
(1)证明:平面 ∥平面 .
(2)求直线 与平面 所成角的正弦值.
【答案】(1)证明见解析;(2)
【解析】(1)连接 ,设 与 相交于点 ,利用线面平行的判定定理和面面平行的判定定理即可证明;
以 为原点, 所在的直线为 轴, 轴, 轴,
建立空间直角坐标系,如图所示:
则 , , , ,
所以 ,
11.已知数列 满足条件 , , ,则 的最小值为()
A.3B.2C.1D.0
【答案】C
【解析】利用 可得 ,即 ,结合 可得 ,利用累加法可得, ,只需求出 的最小值即可,结合 ,即 ,分 两种情况分别代入递推式,依次求出 的值,求出使 最小的对应的 的值即可.
【详解】
因为 , ,
所以 ,即 ,
又 ,所以 ,
,即 , .
故答案为: .
【点睛】
本题考查正弦型函数对称性和周期性的综合应用问题,关键是明确正弦型函数相邻的两个对称中心横坐标间隔为半个最小正周期.
15.若 , 满足约束条件 ,则 的最大值为__________.
【答案】
【解析】作出不等式组表示的平面区域,平移直线 ,根据目标函数的几何意义知,向下平移直线 到最高点时,目标函数 有最大值,据此求出目标函数 最大值即可.
2020届百校联盟(全国卷)高三第六次调研考试数学(理)试题

2020届百校联盟(全国卷)高三第六次调研考试高三数学(理科) ★祝考试顺利★ 注意事项:1、考试范围:高考范围。
2、试题卷启封下发后,如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况,应当立马报告监考老师,否则一切后果自负。
3、答题卡启封下发后,如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象,应当马上报告监考老师,否则一切后果自负。
4、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
5、选择题的作答:每个小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
6、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
7、保持答题卡卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
8、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
第I 卷(选择题 共60分)一、选择题(本题共12小题,每小题5分,共60分,每题只有一个正确选项) 1.设全集为R ,集合{02}A x x =<<,{1}B x x =≥,则()R A C B I ( ) A .{01}x x <≤ B .{01}x x << C .{12}x x ≤<D .{02}x x <<2.已知集合{|01,}A x x x N =≤≤∈,则集合A 的子集个数为( ) A .1 B .2 C .3 D .43.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB =uur( )A .3144AB AC -uuu r uuu rB .1344AB AC -uuu r uuu rC .3144AB AC +uuu r uuu rD .1344AB AC +uuu r uuu r4.已知向量(1,7)m =与向量(tan ,18tan )n αα=+平行,则tan 2α的值为( ) A .43-B .43C .34-D .345.已知函数3()sin(2)2f x x π=+(x R ∈),下面结论错误的是( ) A .函数()f x 的最小正周期为π B .函数()f x 是偶函数C .函数()f x 的图象关于直线4x π=对称 D .函数()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上是增函数6.△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,已知a =b =6A π∠=,则B ∠=( ) A .4π B .4π或34π C .3π或23π D .3π7.已知命题:p 对任意()480,,log log x x x ∈+∞<,命题:q 存在x R ∈,使得tan 13xx =-,则下列命题为真命题的是( )A .p q ∧B .()()p q ⌝∧⌝C .()p q ∧⌝D .()p q ⌝∧ 8.已知()f x 是定义在R 上的偶函数,且在区间(,0)-∞上单调递增,若实数a 满足|1|(2)(a f f ->,则a 的取值范围是( )A .1(,)2-∞ B .1(,)2-∞3(,)2+∞ C .13(,)22 D .3(,)2+∞9.函数y=2|x|sin2x 的图像可能是( )10.已知定义在R 上的函数()f x 满足:(1)y f x =-的图象关于(1,0)点对称,且当0x ≥时恒有31()()22f x f x -=+,当[0,2)x ∈时,()1xf x e =-,则(2016)(2015)f f +-=( )A .1e -B .1e -C .1e --D .1e +11.已知a 为常数,函数32()3(3)1xf x ax ax x e =---+在(0,2)内有两个极值点,则实数a的取值范围为( )A .(,)3e -∞B .2(,)3e eC .2(,)36e eD .(,)3e+∞12.已知21()ln (0)2f x a x x a =+>,若对任意两个不等的正实数12,x x ,都有1212()()2f x f x x x ->-恒成立,则实数a 的取值范围是( )A . (0,1]B . (1,)+∞C .(0,1)D .[1,)+∞第II 卷(非选择题 共90分)二、填空题(每小题5分,共20分.把答案填在答题卷的横线........上) 13.已知⎭⎬⎫⎩⎨⎧---∈3,2,1,21,21,1,2α,若幂函数αx x f =)(为奇函数,且在0+∞(,)上单调递减,则α=_________14.已知曲线3ln y x x =-,则其在点(1,3)处的切线方程是_______________15.在平面直角坐标系中,已知点A (-1,0),B (2,0),E ,F 是y 轴上的两个动点,且|EF uu v|=2,则AE uu u v ·BF uu v的最小值为 __________.16.若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点,则()f x 在[1,1]-上的最大值与最小值的和为__________三、解答题:(本题共6个小题,共70分,解答应写出文字说明,证明过程和演算步骤)17.(本小题满分12分)设常数a R ∈,函数f x ()=x x a 2cos 22sin + (1)若f x ()为偶函数,求a 的值; (2)若4f π〔〕1=,求方程1f x =-()ππ-[,]上的解. 18.(本小题满分12分)记(),()f x g x ''分别为函数(),()f x g x 的导函数.若存在0x ∈R ,满足00()()f x g x =且00()()f x g x ''=,则称0x 为函数()f x 与()g x 的一个“S 点”.(1)证明:函数()f x x =与2()22g x x x =+-不存在“S 点”;(2)若函数2()1f x ax =-与()ln g x x =存在“S 点”,求实数a 的值19.(本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,(sin ,sin sin )m A B C =-,(3,)n a b c =-+,且m n ⊥.(1)求角C 的值;(2)若ABC ∆为锐角三角形,且1c =b -的取值范围. 20. (本小题满分12分) 已知函数1()ln f x x a x x=-+. (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点12,x x ,证明:()()12122f x f x a x x -<--.21.(本小题满分12分)某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时,某地上班族S 中的成员仅以自驾或公交方式通勤,分析显示:当S 中()%0100x x <<的成员自驾时,自驾群体的人均通勤时间为⎪⎩⎪⎨⎧<<-+≤<=10030,9018002300,30)(x x x x x f (单位:分钟), 而公交群体的人均通勤时间不受x 影响,恒为40分钟,试根据上述分析结果回答下列问题:(1)当x 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族S 的人均通勤时间g x ()的表达式;讨论g x ()的单调性,并说明其 实际意义.22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C 的方程为||2y k x =+.以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为22cos 30ρρθ+-=.(1)求2C 的直角坐标方程;(2)若1C 与2C 有且仅有三个公共点,求1C 的方程.高三数学(理科)试卷参考答案与评分标准一、选择题(12小题,每题5分,共60分) 二、填空题(4小题,每题5分,共20分)13.1- 14.210x y -+= 15. 3- 16.3-三、解答题:(本题共6个小题,共70分,解答应写出文字说明,证明过程和演算步骤) 17.解:(1)11cos 22sin )(2+-+=x x a x f =12cos 2sin ++x x a ,1)2cos()2sin()(+-+-=-x x a x f 12cos 2sin ++-=x x a当)(x f 为偶函数时:)()(x f x f -=,则a a -=,解得0=a 。
【金太阳】2020年全国100所名校最新高考模拟卷理科数学试卷(六)

.
a1a3 a3a5
15.已知 7 件产品有 5 件合格品,2 件次品.为找出这 2 件次品,每次任取一件检验,检验后不放回,则
第一次和第二次都检验出次品的概率为
;恰好在第一次检验出正品而在第四次检验出最后一件
次品的概率为
.
x2 y2
2
16.椭圆 1(a b 0) 的左焦点为 F ,过点 F 且斜率为 的直线 l 与椭圆交于 A, B 两点(点 B
A. 6 6 3
B.8 6 3
C.8 8 5
D. 6 8 5
12.已知函数
f
(x)
2sin x
6
的图象的一条对称轴为
x
,其中
为常数,且
(0,1)
,给出
下述四个结论:
①函数 f (x) 的最小正周期为 3 ;②将函数 f (x) 的图象向左平移 所得图象关于原点对称;
6
③函数
f
20.(本小题满分 12 分)
已知函数 f (x) x sin x, g(x) ex f (x) .
3 (1)求证:函数 g(x) 是 0, 2 上的增函数.
(2)若不等式
e
x
≥
af
(
x)
对
x
,
2
恒成立,求实数
a
的取值范围.
21.(本小题满分 12 分)
在学习强国活动中,某市图书馆的科技类图书和时政类图书是市民借阅的热门图书.为了丰富图书资源,
一条渐近线交于 A, B 两点,且线段 AF 的中点 M 落在另一条渐近线上,则双曲线 C 的方程是( )
x2 y2 A. 1
43
x2 y2 B. 1
33
普通高等学校招生全国统一考试2020届高三模拟考试数学(理)试题含解析

【解析】
【分析】
设 , ,根据中点坐标公式可得 坐标,利用 可得到 点坐标所满足的方程,结合直线斜率可求得 ,进而求得 ;将 点坐标代入双曲线方程,结合焦点坐标可求得 ,进而得到离心率。
【详解】 左焦点为 , 双曲线的半焦距 .
设 , , , ,
, ,即 , ,即 ,
又直线 斜率 ,即 , , ,
【答案】D
【解析】
【分析】
利用余弦定理角化边整理可得结果。
【详解】由余弦定理得: ,
整理可得: , .
故选: .
【点睛】本题考查余弦定理边角互化的应用,属于基础题。
7.已知 , , ,则( )
A. B.
C. D.
【答案】C
【解析】
【分析】
根据指数运算法则、指数函数函数和对数函数单调性,可通过临界值比较出大小关系。
【详解】取 中点 ,连接 ,
, ,即 。
, ,
,
则 .
故选: 。
【点睛】本题考查平面向量数量积的求解问题,涉及到平面向量的线性运算,关键是能够将所求向量进行拆解,进而利用平面向量数量积的运算性质进行求解。
9。已知 是定义在 上的奇函数,且当 时, .若 ,则 的解集是( )
A. B.
C。 D.
【答案】B
【详解】取 中点 ,由 , 可知: ,
为三棱锥 外接球球心,
过 作 平面 ,交平面 于 ,连接 交 于 ,连接 , , ,
, , , 为 的中点
由球的性质可知: 平面 , ,且 .
设 ,
, ,
, 在 中, ,
即 ,解得: ,
三棱锥 的外接球的半径为: ,
三棱锥 外接球的表面积为 .
2020届全国100所名校最新高考模拟示范卷(二)高三模拟测试数学(理)试题解析

绝密★启用前2020届全国100所名校最新高考模拟示范卷(二)高三模拟测试数学(理)试题注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、单选题1.若集合{}|22A x x =-<≤,{}|13B x x =-<<,则A B =U ( )A .[)2,3-B .(]1,2-C .(]2,2-D .()2,3-答案:D利用集合的并运算求解即可.解:因为集合{}|22A x x =-<≤,{}|13B x x =-<<,由集合的并运算可得,()2,3A B =-U .故选:D点评:本题考查集合的并运算;考查运算求解能力;属于基础题.2.i 是虚数单位,2z i =-,则||z =( )A B .2 C D 答案:C由复数模长的定义可直接求得结果.解:2z i =-Q ,z ∴==故选:C . 点评:本题考查复数模长的求解问题,属于基础题. 3.若双曲线()222210,0x y a b a b-=>>的离心率为53,则该双曲线的渐近线方程为( )A .45y x =±B .54y x =±C .43y x =±D .34y x =? 答案:C 由双曲线的离心率,结合,,a b c 的关系求出,a b 的关系,代入双曲线的渐近线方程即可求解.解: 因为双曲线的离心率为53,即53c e a ==, 所以53c a =,又222c a b =+, 所以43b a =,因为双曲线的渐近线方程为b y x a=±, 所以该双曲线的渐近线方程为43y x =±. 故选:C点评:本题考查双曲线的标准方程及其几何性质;考查运算求解能力;属于基础题.4.已知数列{}n a 是等差数列,其前n 项和为n S ,若1166S =,则6a =( )A .6B .4C .11D .3答案:A利用等差数列的性质和等差数列前n 项和公式即可求解.解:因为1166S =,由等差数列前n 项和公式可得, ()1111111662a a S +==,解得11112a a +=, 由等差数列的性质可得,11162a a a +=,所以66a =.故选:A点评:本题考查等差数列的性质和等差数列前n 项和公式;考查运算求解能力;灵活运用等差数列的性质和等差数列的前n 项和公式是求解本题的关键;属于基础题.5.511x ⎛⎫- ⎪⎝⎭展开式中含2x -的系数是( ) A .15 B .15- C .10 D .10-由二项展开式通项公式可确定3r =,由此可求得系数. 解:511x ⎛⎫- ⎪⎝⎭展开式的通项()()55155111r r r r r r r T C C x x --+⎛⎫=⋅-=-⋅ ⎪⎝⎭, 当3r =时,3224510T C x x --=-=-,即2x -的系数为10-.故选:D .点评: 本题考查二项展开式指定项系数的求解问题,关键是熟练掌握二项展开式通项公式的形式.6.函数()()21e ln 11e xx f x x x -=+-+的图象大致为( ) A . B .C .D .答案:B根据题意,利用函数奇偶性的定义判断函数()f x 的奇偶性排除选项,C D ;利用()20f >排除选项A 即可.解:由题意知,函数())21e ln 11e xxf x x x -=++的定义域为R ,其定义域关于原点对称, 因为())21ln 11xx e f x x x e----=++)21ln 11x x e x x e -=++ 又因为)))1222ln 1ln 1ln 1x x x x x x -+=+=-+, 所以()()f x f x -=,即函数()f x 为偶函数,故排除,C D ; 又因为())2212ln 5201e f e-=->+,故排除A. 故选:B本题考查函数解析式较复杂的图象的判断;利用函数奇偶性、特殊值符号的正负等有关性质进行逐一排除是解题的关键;属于中档题.7.某几何体的三视图如图所示,三个视图中的曲线都是圆弧,则该几何体的体积为( )A .152πB .12πC .112πD .212π 答案:A由三视图可知,该几何体为由18的球体和14的圆锥体组成,结合三视图中的数据,利用球和圆锥的体积公式求解即可.解:由三视图可知,该几何体为由18的球体和14的圆锥体组成, 所以所求几何体的体积为11+84V V V =球圆锥, 因为31149=3=8832V ππ⨯⨯球, 221111=34344312V r h πππ⨯⨯=⨯⨯⨯=圆锥, 所以915322V πππ=+=,即所求几何体的体积为152π. 故选:A点评:本题考查三视图还原几何体及球和圆锥的体积公式;考查学生的空间想象能力和运算求解能力;三视图正确还原几何体是求解本题的关键;属于中档题、常考题型.8.图为祖冲之之子祖暅“开立圆术”中设计的立体模型.祖暅提出“祖氏原理”,他将牟合方盖的体积化成立方体与一个相当于四棱锥的体积之差,从而求出牟合方盖的体积等于323d (d 为球的直径),并得到球的体积为316V d π=,这种算法比外国人早了一千多年,人们还用过一些类似的公式,根据 3.1415926π=⋅⋅⋅,判断下列公式中最精确的一个是( )A .3169d V ≈B .32d V ≈C .3300157d V ≈D .3158d V ≈答案:C利用选项中的公式化简求得π,找到最精确的选项即可.解: 由316V d π=得:36V dπ=. 由A 得:3916V d ≈,69 3.37516π=∴⨯≈;由B 得:312V d ≈,632π∴≈=; 由C 得:3157300V d ≈,6157 3.14300π⨯∴≈=;由D 得:3815V d ≈,68 3.215π⨯∴≈=, C ∴的公式最精确.故选:C .点评:本题考查数学史与立体几何的知识,关键是能够对选项中的公式进行准确化简求得π的近似值.9.已知1F ,2F 分别为椭圆221168x y +=的左、右焦点,M 是椭圆上的一点,且在y 轴的左侧过点2F 作12F MF ∠的角平分线的垂线,垂足为N ,若2ON =(O 为坐标原点)则21MF MF -等于( )A .4B .2C 3D 33答案:A延长2F N 交1MF 的延长线于点P ,根据题意作出图形,利用三角形全等和三角形中位线的性质即可求解.解:延长2F N 交1MF 的延长线于点P ,作图如下:因为MN 为12F MF ∠的角平分线,且2F N MN ⊥, 所以2MF MP =, 所以2111MF MF MP MF F P -=-=,因为,O N 分别为122,F F F P 的中点,所以ON 为12PF F ∆的中位线, 所以1122ON F P ==, 所以21124MF MF F P ON -===.故选:A点评:本题考查椭圆方程和直线与椭圆的位置关系;考查数形结合思想和运算求解能力;根据题意作出图形,三角形中位线的性质的运用是求解本题的关键;属于中档题.10.若存在m ,使得()f x m ≥对任意x D ∈恒成立,则函数()f x 在D 上有下界,其中m 为函数()f x 的一个下界;若存在M ,使得()f x M ≤对任意x D ∈恒成立,则函数()f x 在D 上有上界,其中M 为函数()f x 的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.下述四个结论:①1不是函数()()10f x x x x=+>的一个下界;②函数()ln f x x x =有下界,无上界;③函数()2e xf x x=有上界,无下界;④函数()2sin 1x f x x =+有界. 其中所有正确结论的编号是( )A .①②B .②④C .③④D .② 答案:B根据函数上界、下界及有界的概念,利用导数判断函数的单调性并求最值,结合选项,利用排除法,对结论①②③④进行逐项判断即可.解:。
2020年全国100所名校高考模拟金典卷理科数学试卷及其答案(六)

初高中数学学习资料的店1 初高中数学学习资料的店100所名校高考模拟金典卷·数学(六)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2|20A x x x =--≥,{|13}B x x =<<,则()A B ⋃=R ð( ).A .{|13}x x -<<B .{|11}x x -<<C .{|12}x x <<D .{|23}x x << 2.已知复数z 满足(1)4z i +=,则|1|z -=( ).A .2 BC .3D3.已知函数()f x =A ,则函数21()()2x g x x A -⎛⎫=∈ ⎪⎝⎭的值域为( ). A .(,0]-∞ B .(,1]-∞ C .(1,)+∞D .[1,)+∞ 4.若x 、y 满足约束条件4201x y x y y +≤⎧⎪-+≥⎨⎪≥⎩,目标函数2z x y =+取得的最大值为( ).A .5B .6C .7D .85.已知ABC △的面积为4,且2sin sin sin A B C =,则AB 的长为( ).A .4 B.C .2 D6.我国古代数学著作《九章算术》有如下问题:“今有池方一丈,葭生其中央,出水一尺,引葭赴岸,始与岸齐,问水深、葭长各几何?”意思是说:“有一个边长为1丈的正方形水池,在池的正中央长着一根芦苇,芦苇露出水面1尺.若将芦苇拉到池边中点处,芦苇的顶端恰好到达水面.问水有多深?芦苇多长?”该题所求的水深为( ).A .12尺B .10尺C .9尺D .14尺7.某三棱锥的三视图如图所示,则该三棱锥最长棱的长为( ).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前
2020届全国100所名校高三最新高考模拟示范卷(六)数学
(理)试题
注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上 一、单选题
1.已知集合{}
|2,2,P x x k k k Z ==≤∈,(){
}
2
|29Q x x =+<,则P Q =I ( ) A .{}4,2,0,1-- B .{}4,2,0-- C .{}|41x x -≤< D .{}|45x x -≤<
答案:B
可求出{}4,2,0,2,4P =--,{}|51Q x x =-<<,然后进行交集的运算即可. 解:
解:{}
{}|2,2,4,2,0,2,4P x x k k k Z ==≤∈=--,
(){
}
{}2
|29|51Q x x x x =+<=-<<,
所以{}4,2,0P Q =--I . 故选:B. 点评:
本题考查交集的运算,属于基础题.
2.已知复数z 满足1z i z +-=,在复平面内对应的点为(),x y ,则( ) A .1y x =+ B .y x =
C .2y x =-
D .y x =-
答案:A
由已知可列式子()()2
2
2211x y x y ++-=+,整理化简即可. 解:
解:由1z i z +-=,得()()2
2
2211x y x y ++-=+, 化简整理得1y x =+. 故选:A. 点评:
本题考查复数的模的求法和几何意义,属于基础题.
3.已知
1
3 11
53
1
log
,log,3
63
a b c
π-
===,则,,
a b c的大小关系是( )
A.b a c
<<B.a c b
<<C.c b a
<<D.b c a
<<
答案:D
利用对数函数和指数函数的单调性判断.
解:
11
55
11
log log1,
65
a=>=
11
33
log log10,
3
b
π
=<=
1
30
331
c-<
==,则01
c
<<,所以b c a
<<.
故选:D.
点评:
本题考查指对数值大小比较.
指数函数值大小比较:常化为同底或同指,利用指数函数的单调性,图象或1,0等中间量进行比较.
对数函数值大小比较:
(1)单调性法:在同底的情况下直接得到大小关系,若不同底,先化为同底;
(2)中间量过渡法:寻找中间数联系要比较的两个数,一般是用“0”,“1”或其他特殊值进行“比较传递”;
(3)图象法:根据图象观察得出大小关系.
4.中国折叠扇有着深厚的文化底蕴.如图(2),在半圆O中作出两个扇形OAB和OCD,用扇环形ABDC(图中阴影部分)制作折叠扇的扇面.记扇环形ABDC的面积为1S,扇形OAB的面积为2S,当1S与2S的比值为
51
-
时,扇面的形状较为美观,则此时扇形OCD的半径与半圆O的半径之比为( )
A.
51
4
B.
51
2
C.35
-D52
答案:B
扇环形ABDC的面积1S等于扇形OAB的面积减扇形OCD的面积;设半径代入求解.
解:
设AOBθ
∠=,半圆O的半径为r,扇形OCD的半径为1r,
依题意,有
22
1
2
11
51
22
12
2
r r
r
θθ
θ
--
=,即
22
1
2
51
r r
r
--
=,
所以
2
2
1
2
3562551
()
r
r
---
===,得1
51
r
r
-
=.
故选:B.
点评:
本题考查弧度制下扇形面积计算问题.
其解题策思路:
(1)明确弧度制下扇形面积公式,在使用公式时,要注意角的单位必须是弧度.
(2)分析题目已知哪些量、要求哪些量,然后灵活地运用弧长公式、扇形面积公式直接求解,或合理地利用圆心角所在三角形列方程(组)求解.
5.函数
ln
()sin
x
f x x
x
=+的部分图象大致是( )
A.B.
C.D.
答案:C
先判断函数的奇偶性,根据奇偶函数图象特征排除,再利用特值验证排除可得解. 解:
因为
ln||
0,()sin()()
x
x f x x f x
x
-
≠-=-+=-
-
,
ln
()sin x
f x x
x
∴=+奇函数,图象关于原点对称,所以排除选项D;
因为
2ln
2
()10
2
f
π
π
π
=+>,所以排除选项A;
因为
ln
()00
f
π
π
π
=+>,所以排除选项B;因此选项C正确.
故选:C. 点评:
本题考查函数图象识别问题.
其解题思路:由解析式确定函数图象:
①由函数的定义域,判断图象左右的位置,由函数的值域,判断图象的上下位置; ②由函数的单调性,判断图象的变化趋势; ③由函数的奇偶性,判断图象的对称性; ④由函数的周期性,判断图象的循环往复. 函数图象识别有时常用特值法验证排除
6.“车走直、马走日、炮打隔子、象飞田、小卒过河赛大车”,这是中国象棋中的部分下棋规则.其中“马走日”是指马走“日”字的对角线,如棋盘中,马从点A 处走出一步,只能到点B 或点C 或点D 或点E .设马从点A 出发,必须经过点,M N (点,M N 不考虑先后顺序)到达点P ,则至少需走的步数为( )
A .5
B .6
C .7
D .8
答案:B
分步计算,第一步从点A 经过点M ,第二步从点M 经过点N ,第三步从点N 到达点
P ,
解:
由图可知,从N 到P 只需1步,从M 到N 至少需走2步,从A 到M 至少需走3步,从A 到N 至少需走3步.所以要使得从点A 经过点,M N 到点P 所走的步数最少,只需从点A 先到点M ,再到点N ,最后到点P ,这样走的步数为6. 故选:B. 点评:
本题考查分步乘法计数原理.
(1)利用分步乘法计数原理解决问题时要注意按事件发生的过程来合理分步,即分步是有先后顺序的,并且分步必须满足:完成一件事的各个步骤是相互依存的,只有各个步骤都完成了,才算完成这件事.
(2)谨记分步必须满足的两个条件:一是各步骤互相独立,互不干扰;二是步与步确保连续,逐步完成.
7.已知a r ,b r 是单位向量,且()1,1a b +=-r r ,则a r 与a b -r r
的夹角为( )
A .
π6
B .
π4
C .
π3
D .
2π3
答案:B
由()1,1a b +=-r r ,两边平方,得:()222
22112a b a b ++⋅=+-=r r r r ,因为a r ,b r 是单
位向量,所以求得0a b ⋅=r r
,进而得出a b -=r r 求得a r 与a b -r r
的夹角.
解:
由()1,1a b +=-r r ,两边平方,得:()222
22112a b a b ++⋅=+-=r r r r ,
因为a r ,b r 是单位向量,所以1122a b ++⋅=r r ,得0a b ⋅=r r
,
则22222a b a b a b -=+-⋅=r r r r r r
,
∴a b -=r r
所以(
)
2cos ,2a a b a a b a a b
⋅--====⋅-r r r r r r r r r r r r ,
所以a r 与a b -r r 的夹角为π
4
.
故选:B. 点评:
本题考查两个向量的数量积的定义和公式,属于基础题. 8.执行如图所示的程序框图,则输出的S =( )
A .414
B .325
C .256
D .75
答案:A 根据题意()3
m
n m =∈N ,由2020n <,得1m =,2,3,4,5,6,分别算出相
应值即可得出结果. 解: 解:()3
m
n m =∈N ,由2020n <,得1m =,2,3,4,5,6.
所以S 的值依次为()16115S =-⨯=,()25226S =-⨯=,()36339S =-⨯=,
()494420S =-⨯=,()5205575S =-⨯=,()67566414S =-⨯=.
故选:A. 点评:
本题主要考查程序框图和算法,属于基础题.
9.已知等差数列{}n a 的前n 项和为n S ,满足33a =,()21223n n n S S S n --+=+≥,则( )
A .2n n S n
a n -= B .2n n S n
a n +=
C .21
n n S a n
-=
D .21
n n S a n
+=
答案:B
由已知得31222S S S +=+,即123222222a a a a a ++=++,进而求出公差2d =,再利用求和公式列式,化简得出结论. 解:。
