解处奇异凸的极小化问题的正规化牛顿法
牛顿法推导

牛顿法推导(一)牛顿法推导的概念牛顿法,又被称为牛顿-拉夫逊方法,是17世纪由艾萨克·牛顿提出的一种在实数域和复数域上近似求解方程的方法。
牛顿法的基本思想是用迭代点的梯度信息和二阶导数对目标函数进行二次函数逼近,然后将这个二次函数的极小值或极大值作为新的迭代点。
这个过程会不断重复进行,直至找到满足要求的迭代解。
在实际应用中,例如机器学习领域,牛顿法和梯度下降法等都是主要的优化算法。
假设我们需要求解函数f(x)在某区间[a, b]上的零点,初始点为x0。
迭代公式如下:x_{k+1} = x_k - f(x_k)/f'(x_k)其中,f'(x_k)表示的是函数在x_k处的一阶导数,f''(x_k)表示的是函数在x_k 处的二阶导数。
而我们要求的就是使得上述公式趋向于零的解x,也就是极小值点或者极大值点。
然而在实际应用中,由于海塞矩阵的逆矩阵计算较为复杂,因此有了拟牛顿法用来简化这一过程。
(二)牛顿法推导的优缺点牛顿法的优点主要包括收敛速度快,具有二阶收敛性。
对于二次正定函数,迭代一次便可以得到最优解,对于非二次函数,若函数二次性较强或迭代点已经进入最优点的较小邻域,则收敛速度也很快。
然而,牛顿法也存在一些缺点。
首先,牛顿法是迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
此外,如果目标函数的海森矩阵无法保持正定,牛顿法可能会失效。
其次,牛顿法对函数要求较为苛刻,函数必须具有连续的一、二阶偏导数,并且海森矩阵必须正定。
另外,当初始点离最优解较远时,可能会导致牛顿法发散或者效率降低。
最后,由于牛顿法是一种基于二次近似的算法,可能产生一定的误差,这就需要反复进行迭代。
为了克服这些问题,拟牛顿法被提出,通过不直接使用二阶偏导数而构造出可以近似海森矩阵或者海森矩阵的逆的正定对称阵,来优化目标函数。
(三)牛顿法推导的意义牛顿法的意义在于,它是一种强大的数学工具,可以求解函数的极值问题以及方程的根。
最优化理论方法——牛顿法
牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
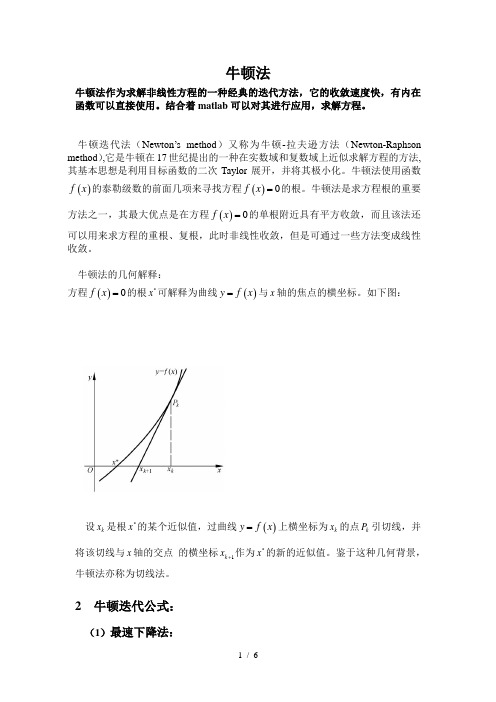
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()Tk k k k fx f x x x f x x x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0Tk k d g <的方向k d 是下降方向。
当α取定后,Tk k d g 的值越小,即T kk d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:T k k kk d g d g ≤,故当且仅当k k d g =-时,Tk k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。
牛顿法求极值

牛顿法求极值极值理论是拉格朗日在1897年发表的《拉格朗日函数原理与极值问题》中首次提出的,是数学分析中最重要的主题之一。
它涉及多元函数中的极大值和极小值的求解问题。
牛顿法是现代数值分析的一种重要的方法,它主要用来解决非线性方程组和极值问题。
它是在17世纪由英国数学家牛顿首先提出的,因此得名“牛顿法”。
二、牛顿法的基本原理牛顿法是一种迭代算法,它的基本原理是:以某点为基点,求解点处的极大值和极小值时,首先考虑函数在该点处的切线,然后计算出该切线与x轴之间的交点,并用这个交点做新的基点,再求出它的切线,重复以上过程,直至切线的斜率不再发生变化,即收敛,得到极值点。
牛顿法主要用于求解一元函数的极值问题,当然也可以用于求解多元函数的极值问题,但是由于较复杂,使用起来就比较麻烦。
三、牛顿法的优缺点(1) 优点:牛顿法比其他计算方法效率更高,有时可以求得更接近极值的值。
(2)点:牛顿法对函数的限制较多,它只能处理可导函数,且函数的二阶导数不能出现奇点。
四、牛顿法的步骤(1)定初始点:用x0作为初始点,求原函数f(x0)的一阶导数和二阶导数;(2)造牛顿迭代式:计算牛顿步长Δx=-f′(x0)/f″(x0;(3)新点:x1=x0+Δx;(4)测是否满足收敛条件:确定是否满足要求的收敛条件,如果满足,则将x1作为极值点,否则本次计算结束,将x1作为下一次计算的初始点,重复以上步骤。
五、应用实例以f(x) = x3 - 4x2 + x + 2为例,用牛顿法求极值:令x0 = 1,求f′(x0)和f″(x0),得f′(x0) = 3 - 8 + 1 = -4,f″(x0) = 6;根据牛顿迭代式,计算Δx=-f′(x0)/f″(x0)=-4/6=-2/3;确定新点x1=x0+Δx=1+(-2/3)=-1/3;检测收敛条件,计算f′(x1)和f″(x1),得f′(x1) = -2/3,f″(x1) = 6,可知条件满足,x1=-1/3就是函数f(x)的极值点。
修正牛顿法详解

修正牛顿法(Modified Newton's Method)是一种优化算法,通常用于解决非线性最小化问题。
它是基于牛顿法(Newton's Method)的一种变种,用于解决牛顿法可能会出
现的一些问题。
在牛顿法中,我们希望通过在每一步迭代中
求解一个二阶导数矩阵(Hessian Matrix)的逆来寻找函数
的最小值。
然而,在某些情况下,这个二阶导数矩阵可能不
是正定的,这会导致算法出现问题。
为了克服这个问题,修
正牛顿法使用了一个修正项来调整牛顿法中的二阶导数矩阵
的逆。
这个修正项可以保证矩阵的正定性,从而确保算法的
稳定性和可靠性。
修正牛顿法的每一次迭代都需要计算函数的一阶导数和二
阶导数矩阵,因此它的计算复杂度比其他一些优化算法高,
但是它通常能够更快地收敛到最小值,并且可以处理更广泛
的优化问题。
在具体实现上,修正牛顿法通常包括以下步骤:
初始化:选择一个初始点x_0,以及一个足够小的正数ε。
计算一阶导数:计算函数在x_0点的一阶导数。
判断是否满足牛顿条件:如果一阶导数的范数小于ε,则
认为已经找到了最小值,结束算法。
计算修正项:如果一阶导数的范数大于ε,则计算修正项,使得矩阵正定。
更新迭代点:使用修正项更新迭代点,然后返回步骤2。
需要注意的是,修正牛顿法虽然能够保证算法的稳定性和可靠性,但是在某些情况下可能收敛较慢或者无法收敛到最小值。
因此,在实际应用中,需要结合具体问题选择合适的优化算法。
牛顿法原理

牛顿法原理
牛顿法是一种可以将非线性收敛到最小值的迭代法,是以传统意义上的函数最小值求解和极值求解具有重要意义的数值解法之一。
牛顿法(Newton's Method)或称牛顿迭代法,由英国数学家牛顿提出。
它是一种以逐步逼近的方式来求解极值,也就是最优求解法。
它可以帮助求解数学中连续函数极值及根的值,是近代数值分析的重要组成部分,也是当今最重要的最优方法之一。
牛顿法的基本思想是,如果一个连续函数的图像在某一点处有极值,那么该点处函数的导数为零,它即为函数的极值点。
根据这一思想,牛顿法寻找极值点,即就是不断从起点开始,计算梯度并根据梯度计算新的点,然后继续重复上面的步骤,直到收敛为止。
牛顿法的具体步骤有:
(1)确定变量的初始值,使用方程组求解;
(2)计算变量的一阶偏导数;
(3)根据一阶偏导数的函数值更新变量的值;
(4)用新值计算梯度,若精度满足要求,则可结束;若未满足要求,则重复步骤2和3。
在求解函数极值时,牛顿法优于迭代法。
牛顿法不仅使函数值逐渐收敛到极值,而且保持精度高。
其收敛速度快,收敛精度高,且稳定性好,而迭代法则收敛缓慢,而且收敛精度也不高。
总之,牛顿法是通过不断迭代计算求取函数极值的一种简便有效的求解方法,利用它求解特定类型函数的极值及其根可以弥补非线性方程其他求解方法的盲点,大大的提高了求解的效率。
牛顿法、拟牛顿法、高斯-牛顿法、共轭梯度法推导总结

牛顿法、拟牛顿法、高斯-牛顿法、共轭梯度
法推导总结
一、牛顿法
牛顿法是一种求解非线性方程的迭代方法。
牛顿法的基本思想是:在当前点附近,用一次泰勒展开式近似原函数,然后求解近似函数的极值点。
牛顿法每次迭代所需要的计算量较大,但其收敛速度较快。
二、拟牛顿法
拟牛顿法是一种求解无约束极值问题的优化算法。
拟牛顿法是将牛顿法中Hessian矩阵用近似Hessian矩阵Bk表示的算法。
拟牛顿法的计算量比牛顿法小,但是收敛速度较牛顿法慢。
三、高斯-牛顿法
高斯-牛顿法是求解非线性最小二乘问题的一种迭代算法。
该算法假设误差服从高斯分布,利用牛顿法求解目标函数的局部极小值,以最小化残差平方和。
高斯-牛顿法在处理非线性最小二乘问题时具有很好的收敛性。
四、共轭梯度法
共轭梯度法是解决对称正定线性方程组的迭代算法。
该算法通过对一个对称正定矩阵进行迭代求解,寻找线性方程组的解。
共轭梯度法的优点是可以使用较少的内存和计算量实现高效的求解。
以上算法都是数值优化中比较常用的算法,它们各自具有不同的优缺点,可根据实际问题的特点来选择合适的算法。
牛顿法

牛顿法牛顿法(英语:Newton's method)又称为牛顿-拉弗森方法(英语:Newton-Raphson method),它是一种在实数域和复数域上近似求解方程的方法。
方法使用函数的泰勒级数的前面几项来寻找方程的根。
起源:牛顿法最初由艾萨克·牛顿在《流数法》(Method of Fluxions,1671年完成,在牛顿去世后的1736年公开发表)中提出。
约瑟夫·鲍易也曾于1690年在Analysis Aequationum中提出此方法。
原理:二阶逼近牛顿法对局部凸函数找到极小值,对局部凹函数找到极大值,对局部不凸不凹函数可能找到鞍点牛顿法要求估计二阶导数。
牛顿法据称比直接计算要快了4 倍。
其中的两次迭代(第二步迭代被注释掉了)就是用的牛顿法来求解方程,也就是的根。
牛顿法的思想其实很简单,给定一个初始点,使用在该点处的切线来近似函数,然后寻找切线的根作为一次迭代。
比如对于这个例子,令,给定初始点,在该点处的导数是,由此可以得到该处的切线为,求解得到正是代码中的迭代。
当然代码的重点其实不在这里,而在0x5f3759df这个奇怪的magic number,用于得到一个好的初始点。
这个神奇的数字到底是谁发现的,根据wikipedia 上的说法似乎至今还没有定论。
xkcd 还为此画了一条漫画,讽刺说每次我们惊奇地发现工业界里不知道哪个无名人士写出了0x5f3759df之类的神奇数字,背后都有成千上万的其他无名人士我们无从知晓,说不定他们中的某一个人已经解决了P=NP 的问题,但是那人却还在调某个自动打蛋器的代码所以我们至今仍无知晓。
:D回到我们今天的话题,从这段代码中我们可以看到两点:牛顿法收敛非常快,对于精度要求不是特别高的情况,比如上面的图形学相关的计算中,甚至只用了一次计算迭代。
另一方面,初始值的选取非常重要,我们接下去将会看到,初始值选得不好有可能会直接导致算法不收敛。
牛顿法

牛顿法以伟大的英国科学家牛顿命名,牛顿不仅是伟大的物理学家,是近代物理的奠基人,还是伟大的数学家,他和德国数学家莱布尼兹并列发明了微积分,这是数学历史上最有划时代意义的成果之一,奠定了近代和现代数学的基石。
在数学中,也有很多以牛顿命名的公式和定理,牛顿法就是其中之一。
牛顿法不仅可以用来求解函数的极值问题,还可以用来求解方程的根,二者在本质上是一个问题,因为求解函数极值的思路是寻找导数为0的点,这就是求解方程。
在本文中,我们介绍的是求解函数极值的牛顿法。
在SIGAI之前关于最优方法的系列文章“理解梯度下降法”,“理解凸优化”中,我们介绍了最优化的基本概念和原理,以及迭代法的思想,如果对这些概念还不清楚,请先阅读这两篇文章。
和梯度下降法一样,牛顿法也是寻找导数为0的点,同样是一种迭代法。
核心思想是在某点处用二次函数来近似目标函数,得到导数为0的方程,求解该方程,得到下一个迭代点。
因为是用二次函数近似,因此可能会有误差,需要反复这样迭代,直到到达导数为0的点处。
下面我们开始具体的推导,先考虑一元函数的情况,然后推广到多元函数。
牛顿法在每次迭代时需要计算出Hessian矩阵,然后求解一个以该矩阵为系数矩阵的线性方程组,这非常耗时,另外Hessian矩阵可能不可逆。
为此提出了一些改进的方法,典型
的代表是拟牛顿法(Quasi-Newton)。
凸优化证明题

凸优化证明题摘要:一、引言二、凸优化基本概念1.凸函数2.凸优化问题三、凸优化证明方法1.解析法2.梯度下降法3.牛顿法四、凸优化证明题实例解析1.解析法实例2.梯度下降法实例3.牛顿法实例五、结论正文:一、引言凸优化是运筹学中的一个重要分支,它在很多领域都有广泛的应用,例如机器学习、信号处理、经济学等。
凸优化问题的解决可以帮助我们找到最优解,从而提高效率和降低成本。
在解决凸优化问题时,证明是一个关键环节。
本文将介绍凸优化证明题的解题方法。
二、凸优化基本概念1.凸函数凸函数是指在其定义域内,任意两点之间的函数值都大于等于这两点连线的函数。
凸函数的图像呈现出一种向上凸起的形状。
2.凸优化问题凸优化问题是指在给定凸函数目标函数和凸约束条件下,寻找一个最优解的问题。
凸优化问题的解具有最优性,即任意其他解都至少和最优解一样差。
三、凸优化证明方法1.解析法解析法是凸优化证明中最常用的方法。
它主要通过分析目标函数和约束条件的性质,推导出最优解的存在性和唯一性。
2.梯度下降法梯度下降法是一种迭代优化算法,它是解决凸优化问题的有效工具。
通过计算目标函数的梯度,并不断更新解的方向,最终可以收敛到最优解。
3.牛顿法牛顿法是一种二阶优化算法,它具有更快的收敛速度。
牛顿法通过计算目标函数的二阶梯度,并更新解的方向,同样可以收敛到最优解。
四、凸优化证明题实例解析1.解析法实例假设我们要解决以下凸优化问题:最小化:f(x) = x^2约束条件:g(x) = x - 1 ≤ 0我们可以通过解析法证明,该问题的最优解为x=1。
2.梯度下降法实例我们继续以上述凸优化问题为例,使用梯度下降法求解。
初始解:x0 = 2学习率:α= 0.1迭代次数:T = 100通过梯度下降法,我们可以得到最优解x≈1.0000。
3.牛顿法实例我们再以上述凸优化问题为例,使用牛顿法求解。
初始解:x0 = 2迭代次数:T = 10通过牛顿法,我们可以得到最优解x≈1.0000。
牛顿迭代法的基本原理知识点

牛顿迭代法的基本原理知识点牛顿迭代法是一种求解方程近似解的数值计算方法,通过不断逼近方程的根,以获得方程的解。
它基于牛顿法则和泰勒级数展开,被广泛应用于科学和工程领域。
本文将介绍牛顿迭代法的基本原理和相关知识点。
一、牛顿迭代法的基本原理牛顿迭代法的基本原理可以总结为以下几个步骤:1. 假设要求解的方程为 f(x) = 0,给定一个初始近似解 x0。
2. 利用泰勒级数展开,将方程 f(x) = 0 在 x0 处进行二阶近似,得到近似方程:f(x) ≈ f(x0) + f'(x0)(x - x0) + 1/2 f''(x0)(x - x0)^23. 忽略近似方程中的高阶无穷小,并令f(x) ≈ 0,得到近似解 x1:0 ≈ f(x0) + f'(x0)(x1 - x0) + 1/2 f''(x0)(x1 - x0)^2求解上述方程,得到近似解 x1 = x0 - f(x0)/f'(x0)。
4. 通过反复迭代的方式,不断更新近似解,直到满足精度要求或收敛于方程的解。
二、牛顿迭代法的收敛性与收敛速度牛顿迭代法的收敛性与收敛速度与初始近似解 x0 的选择和方程本身的性质有关。
1. 收敛性:对于某些方程,牛顿迭代法可能无法收敛或者收敛到错误的解。
当方程的导数为零或者初始近似解离根太远时,迭代可能会发散。
因此,在应用牛顿迭代法时,需要对方程和初始近似解进行合理的选择和判断。
2. 收敛速度:牛顿迭代法的收敛速度通常较快,二阶收敛的特点使其在数值计算中得到广泛应用。
在满足收敛条件的情况下,经过每一次迭代,近似解的有效数字将至少加倍,迭代次数的增加会大幅提高精度。
三、牛顿迭代法的优点与局限性1. 优点:1) 收敛速度快:牛顿迭代法的二阶收敛特性决定了它在求解方程时的高效性和快速性。
2) 广泛适用:牛顿迭代法可以用于求解非线性方程、方程组和最优化问题等,具有广泛的应用领域。
牛顿法数学原理

牛顿法数学原理引言牛顿法是一种常用的数值优化算法,用于求解非线性方程的根或最优化问题的极值点。
牛顿法的优势在于快速收敛速度和高精度的计算结果。
本文将介绍牛顿法的数学原理和相关推导。
牛顿法的思想和目标牛顿法的核心思想是通过迭代逼近函数曲线的根,进而找到方程的解或者函数的极值点。
牛顿法的目标是通过一系列迭代步骤,逐渐接近函数的根或极值点。
具体而言,对于求解方程的根,牛顿法通过迭代逼近方程的解;而对于求解函数的极值点,牛顿法通过迭代逼近函数的驻点。
牛顿法的原理设函数f(x)在点x0处可导,对应的切线方程为:y=f′(x0)(x−x0)+f(x0)。
牛顿法的基本思想是通过切线的零点逼近函数的根,即求出切线方程与x轴的交点,假设为x1。
迭代过程中,不断使用这种方法来求出更接近函数根的近似解。
为了推导牛顿法的迭代公式,考虑切线方程与x轴的交点x1,即切线方程的函数值为零:f′(x0)(x1−x0)+f(x0)=0将切线方程的一般式表示为:$$x_1=x_0-\\frac{f(x_0)}{f'(x_0)}$$根据以上推导可得到牛顿法的迭代公式:$$x_{n+1}=x_n-\\frac{f(x_n)}{f'(x_n)}$$其中,x n表示第n次迭代得到的结果,f(x n)表示函数f(x)在点x n上的函数值,f′(x n)表示函数f(x)在点x n上的导数值。
牛顿法的收敛性分析牛顿法在某些条件下具有快速的收敛性。
首先,我们需要确保迭代的初始点足够接近函数的根或极值点,否则可能会出现不收敛情况。
其次,我们需要满足以下两个条件:1.函数f(x)2.在区间[a,b]3.上连续,且在区间内存在唯一的根或极值点。
4.函数f(x)5.在区间[a,b]6.上具有对应的导数,且导数连续。
在满足以上条件的情况下,根据牛顿法的迭代公式可以推导出以下结论:•当函数f(x)•在根或极值点的附近具有二阶连续导数时,牛顿法具有二阶收敛性,即每次迭代后的误差的平方至少减小一个常数倍。
极大化和极小化函数的方法

极大化和极小化函数的方法极大化和极小化函数的方法主要是指将函数最终达到极大值或极小值的计算过程。
一般来说可以采用梯度下降法(gradient descent)、牛顿法(Newton's Method)、拉格朗日法(Lagrange Multipliers)、或者其他的优化方法来实现极大化和极小化函数的目标。
梯度下降法是一种基于步长搜索的独立变量函数最小化法,它通过使用梯度指示器对对函数进行逐步迭代来搜索最小点。
每一次迭代,它会考虑在梯度方向上的升降来选择下次迭代的位置,并按照梯度的大小来改变迭代的步长大小。
当梯度的值接近于零时,会收敛到最优值。
弊端是当函数处于非凸空间时,求解出的结果会受到起始点的影响,可能得到的答案不是最优的。
牛顿法是用于求解非线性函数极值的方法,它使用x在函数f(x)附近的一阶导数和二阶导数来确定跳跃位置。
它最大的优点是可以在收敛速度上快于梯度下降法,并且可以从任何一点开始,例如局部极值。
然而,这种方法也有一些局限性,牛顿法不适合处理多维空间,它只能处理单元素函数,并且当函数极值有许多个点时,牛顿法可能会陷入局部极小值点而不是全局极小值点。
拉格朗日法是一种在极大化和极小化函数时常见的优化方法。
它结合了梯度下降法和牛顿法,可以发现函数极值的极小点。
它的基本思想是,对于给定的对偶变量Λ,把原始函数改写成一个新的函数F,然后根据牛顿法或梯度下降法求解F的极值。
这种方法能够从不同的角度考虑最优化问题,避免陷入局部极小值。
另外,还有一些其他的优化方法,可以用来求解极大化和极小化函数的极值,比如:Simulated Annealing Algorithm(模拟退火算法), Genetic Algorithm(遗传算法), Particle Swarm Optimization(粒子群优化)等。
所有这些方法都旨在找出函数最优解,不同优化算法有一定的适用范围,在不同场景下,需要选择合适的优化方法,以达到最优解。
优化 数学 牛顿法

优化数学牛顿法优化数学牛顿法引言:牛顿法是一种常用的数值逼近方法,用于求解方程的根。
它以牛顿迭代公式为基础,通过不断逼近函数的零点来求解方程。
然而,牛顿法在某些情况下存在一些不足之处,需要进行优化,以提高收敛速度和稳定性。
本文将介绍几种优化牛顿法的方法。
一、牛顿法的原理和应用范围牛顿法是一种迭代方法,通过在初始点处对函数进行线性近似,求得近似零点,并以此作为下一次迭代的初始点,反复迭代直至收敛。
牛顿法在求解非线性方程、最优化和插值等问题中广泛应用。
二、牛顿法的不足之处1. 初始点的选择对收敛性有较大影响:牛顿法对初始点的选择十分敏感,不同的初始点可能导致不同的迭代结果,甚至可能无法收敛。
2. 收敛速度慢:在某些情况下,牛顿法的收敛速度较慢,需要进行多次迭代才能达到精度要求。
3. 不稳定性:当函数的二阶导数为0或接近0时,牛顿法可能发散或陷入震荡。
三、优化牛顿法的方法为了克服牛顿法的不足,人们提出了一系列优化方法,旨在提高收敛速度和稳定性。
以下是几种常见的优化方法:1. 初始点的优化选择为了提高牛顿法的收敛性,可以采用合理的初始点选择策略。
例如,可以根据函数的性质和图像来选择初始点,使得初始点更接近函数的零点。
此外,还可以利用其他数值方法的结果作为初始点进行迭代,以提高收敛性。
2. 防止迭代过程发散为了避免迭代过程发散,可以引入合适的收敛判据。
例如,可以设置最大迭代次数,当迭代次数超过一定阈值时,停止迭代并输出结果。
此外,还可以通过判断函数值的变化情况来判断是否发散,如果函数值发散,则调整步长或迭代方法。
3. 改进迭代步长的选择牛顿法的迭代步长对于收敛速度起着重要作用。
为了提高收敛速度,可以采用自适应步长的方法,根据函数的性质和导数的大小来选择合适的步长。
此外,还可以使用加速技术,如割线法和拟牛顿法等,来改进迭代步长的选择。
4. 针对特殊情况的优化方法对于某些特殊的函数或方程,可以采用针对性的优化方法。
最优化算法(牛顿、拟牛顿、梯度下降)
最优化算法(⽜顿、拟⽜顿、梯度下降)1、⽜顿法 ⽜顿法是⼀种在实数域和复数域上近似求解⽅程的⽅法。
⽅法使⽤函数f (x)的泰勒级数的前⾯⼏项来寻找⽅程f (x) = 0的根。
⽜顿法最⼤的特点就在于它的收敛速度很快。
具体步骤: ⾸先,选择⼀个接近函数f (x)零点的x0,计算相应的f (x0) 和切线斜率f ' (x0)(这⾥f ' 表⽰函数f 的导数)。
然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和x 轴的交点的x坐标,也就是求如下⽅程的解: 我们将新求得的点的x 坐标命名为x1,通常x1会⽐x0更接近⽅程f (x) = 0的解。
因此我们现在可以利⽤x1开始下⼀轮迭代。
迭代公式可化简为如下所⽰: 已经证明,如果f ' 是连续的,并且待求的零点x是孤⽴的,那么在零点x周围存在⼀个区域,只要初始值x0位于这个邻近区域内,那么⽜顿法必定收敛。
并且,如果f ' (x)不为0, 那么⽜顿法将具有平⽅收敛的性能. 粗略的说,这意味着每迭代⼀次,⽜顿法结果的有效数字将增加⼀倍。
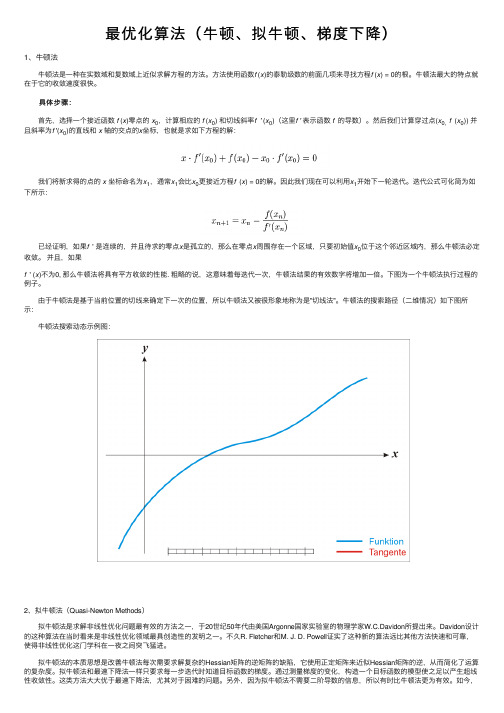
下图为⼀个⽜顿法执⾏过程的例⼦。
由于⽜顿法是基于当前位置的切线来确定下⼀次的位置,所以⽜顿法⼜被很形象地称为是"切线法"。
⽜顿法的搜索路径(⼆维情况)如下图所⽰: ⽜顿法搜索动态⽰例图:2、拟⽜顿法(Quasi-Newton Methods) 拟⽜顿法是求解⾮线性优化问题最有效的⽅法之⼀,于20世纪50年代由美国Argonne国家实验室的物理学家W.C.Davidon所提出来。
Davidon设计的这种算法在当时看来是⾮线性优化领域最具创造性的发明之⼀。
不久R. Fletcher和M. J. D. Powell证实了这种新的算法远⽐其他⽅法快速和可靠,使得⾮线性优化这门学科在⼀夜之间突飞猛进。
拟⽜顿法的本质思想是改善⽜顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使⽤正定矩阵来近似Hessian矩阵的逆,从⽽简化了运算的复杂度。
凸优化算法之牛顿法
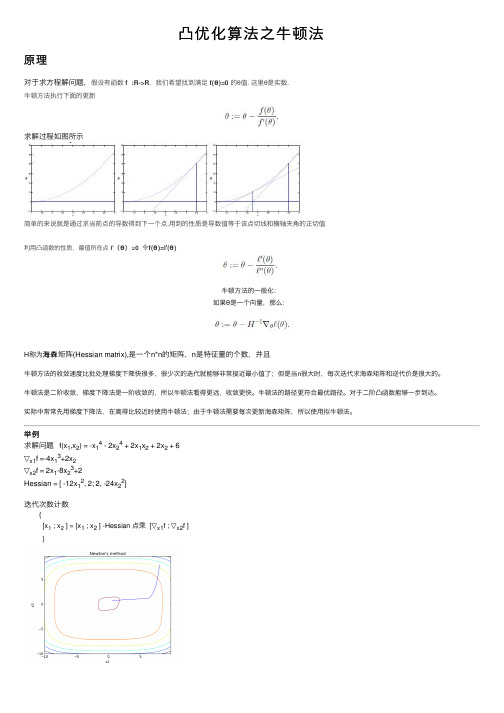
凸优化算法之⽜顿法原理对于求⽅程解问题,假设有函数f :R->R,我们希望找到满⾜f(θ)=0 的θ值. 这⾥θ是实数.⽜顿⽅法执⾏下⾯的更新求解过程如图所⽰简单的来说就是通过求当前点的导数得到下⼀个点.⽤到的性质是导数值等于该点切线和横轴夹⾓的正切值利⽤凸函数的性质,最值所在点 l'(θ)=0 令f(θ)=l'(θ)⽜顿⽅法的⼀般化:如果θ是⼀个向量,那么:海森矩阵(Hessian matrix),是⼀个n*n的矩阵,n是特征量的个数,并且H称为海森⽜顿⽅法的收敛速度⽐批处理梯度下降快很多,很少次的迭代就能够⾮常接近最⼩值了;但是当n很⼤时,每次迭代求海森矩阵和逆代价是很⼤的。
⽜顿法是⼆阶收敛,梯度下降法是⼀阶收敛的,所以⽜顿法看得更远,收敛更快。
⽜顿法的路径更符合最优路径。
对于⼆阶凸函数能够⼀步到达。
实际中常常先⽤梯度下降法,在离得⽐较近时使⽤⽜顿法;由于⽜顿法需要每次更新海森矩阵,所以使⽤拟⽜顿法。
举例求解问题 f(x1,x2) = -x14 - 2x24 + 2x1x2 + 2x2 + 6▽x1f =-4x13+2x2▽x2f = 2x1-8x23+2Hessian = [ -12x12, 2; 2, -24x22]迭代次数计数{[x1 ; x2 ] = [x1 ; x2 ] -Hessian 点乘 [▽x1f; ▽x2f ]}1. # -*- coding: utf-8 -*-2. """3. Created on Wed Apr 12 23:56:25 20174.5. @author: LoveDMR6.7. ⽜顿⽅法8. """9.10. import numpy as np11. import matplotlib.pyplot as plt12. delta =0.2513. x1 = np.arange(-10,10, delta )14. x2 = np.arange(-10,10, delta )15. X1 , X2 = np.meshgrid( x1 , x2 )16.17. Y =2*X1*X2+2*X2-X1**4-2*X2**4+618. plt.figure()19. bg_fig = plt.contour(X1,X2,Y)20.21. theta = np.array([8,8])22. a , b =[],[]23.24. a.append(theta[0])25. b.append(theta[1])26.27. H = np.array([[2,3],[3,10]])28. Hi= np.linalg.inv(H)29. for i in xrange(1,50):30. t = np.array([theta[0]**3*(-4)+2*theta[1]**2,(-8)*theta[1]**3+2*theta[0]+2])31. H = np.array([[(-12)*theta[0]**3,2],[2,(-24)*theta[1]**2]])32. Hi= np.linalg.inv(H)33. theta = theta - np.dot(Hi,t )34. a.append(theta[0])35. b.append(theta[1])36.37. plt.plot(a , b)38. plt.title("Newton's method")39. plt.xlabel('x1')40. plt.ylabel('x2')41. plt.show()。
凸优化处理方法

凸优化处理方法凸优化是数学中的一种重要方法,广泛应用于工程、经济学、运筹学等领域。
凸优化处理方法是指在解决凸优化问题时所采用的一系列算法和技巧。
本文将介绍几种常用的凸优化处理方法,并分析其特点和适用范围。
一、梯度下降法梯度下降法是一种常用的凸优化处理方法,通过迭代的方式逐步优化目标函数。
其基本思想是沿着目标函数的负梯度方向进行搜索,不断更新参数,直到达到最优解。
梯度下降法具有收敛性好、计算简单等优点,适用于解决大规模的凸优化问题。
二、牛顿法牛顿法是一种基于二阶导数信息的凸优化处理方法。
其核心思想是利用目标函数的二阶导数矩阵信息进行迭代优化,通过求解线性方程组来更新参数。
牛顿法收敛速度较快,适用于解决高维、非线性的凸优化问题。
三、内点法内点法是一种近年来发展起来的凸优化处理方法,通过引入人工内点,将原凸优化问题转化为一系列的线性规划问题。
内点法具有全局收敛性和多项式时间复杂度等优点,适用于解决大规模的凸优化问题。
四、分裂算法分裂算法是一种将原凸优化问题分解为多个子问题进行求解的凸优化处理方法。
其基本思想是将原问题分解为几个较小的子问题,并通过迭代的方式逐步优化子问题,最终得到原问题的解。
分裂算法适用于解决具有一定结构的凸优化问题,能够提高算法的效率和收敛速度。
五、次梯度法次梯度法是一种求解非光滑凸优化问题的处理方法。
在非光滑凸优化问题中,目标函数可能不是处处可微的,此时无法使用传统的梯度下降法等方法。
次梯度法通过引入次梯度的概念,对非光滑点进行处理,从而求解非光滑凸优化问题。
六、对偶法对偶法是一种将原凸优化问题转化为对偶问题进行求解的凸优化处理方法。
通过构造拉格朗日函数和对偶函数,将原问题转化为对偶问题,并通过求解对偶问题来获取原问题的解。
对偶法能够有效地求解具有特殊结构的凸优化问题,提高算法的效率和精度。
七、凸松弛法凸松弛法是一种将原非凸优化问题转化为凸优化问题进行求解的处理方法。
通过对原问题进行适当的松弛,将其转化为一个凸优化问题,并利用凸优化方法来求解。
解非凸函数的方法

解非凸函数的方法
解非凸函数的方法有多种,以下是一些常见的方法:
1. 梯度下降法:通过不断沿着函数梯度的负方向更新变量,逐渐逼近函数的局部最小值。
具体实现时可以采用批量梯度下降或随机梯度下降等方法。
2. 牛顿法:通过求解函数的Hessian矩阵(二阶导数矩阵)和梯度矩阵的线性方程组来迭代逼近函数的最小值。
相比于梯度下降法,牛顿法通常更快,但需要计算和存储Hessian矩阵。
3. 拟牛顿法:是牛顿法的改进,通过构造一个近似Hessian矩阵来代替真实的Hessian矩阵,从而在保持牛顿法的优点的同时减小计算和存储的开销。
4. 共轭梯度法:结合了梯度下降法和牛顿法的思想,通过迭代更新方向和步长,在每一步都沿着当前方向的最优步长进行搜索,从而快速收敛到函数的最小值。
5. 坐标下降法:将多维问题分解为多个一维问题逐一解决,每次只对一个变量进行优化,其他变量保持不变。
这种方法在处理大规模稀疏问题时特别有效。
6. 遗传算法:模拟生物进化过程的自然选择和遗传机制,通过种群迭代的方式搜索最优解。
遗传算法对非线性、多峰值、离散和非凸函数等问题具有较强的鲁棒性。
7. 模拟退火算法:借鉴物理中的退火过程,通过随机接受一定概率的较差解来避免陷入局部最优解。
模拟退火算法适用于处理大规模、离散和非凸函数优化问题。
这些方法各有优缺点,选择哪种方法取决于具体的问题和要求。
在实际应用中,通常需要根据问题的性质和规模进行实验和比较,以确定最适合的方法。
最优化理论与方法——牛顿法

牛顿法牛顿法作为求解非线性方程的一种经典的迭代方法,它的收敛速度快,有内在函数可以直接使用。
结合着matlab 可以对其进行应用,求解方程。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
牛顿法的几何解释:方程()0f x =的根*x 可解释为曲线()y f x =与x 轴的焦点的横坐标。
如下图:设k x 是根*x 的某个近似值,过曲线()y f x =上横坐标为k x 的点k P 引切线,并将该切线与x 轴的交点 的横坐标1k x +作为*x 的新的近似值。
鉴于这种几何背景,牛顿法亦称为切线法。
2 牛顿迭代公式:(1)最速下降法:以负梯度方向作为极小化算法的下降方向,也称为梯度法。
设函数()f x 在k x 附近连续可微,且()0k k g f x =∇≠。
由泰勒展开式: ()()()()()Tk k k k fx f x x x f x x x ο=+-∇+- (*)可知,若记为k k x x d α-=,则满足0Tk k d g <的方向k d 是下降方向。
当α取定后,Tk k d g 的值越小,即T kk d g -的值越大,函数下降的越快。
由Cauchy-Schwartz 不等式:T k k kk d g d g ≤,故当且仅当k k d g =-时,Tk k d g 最小,从而称k g -是最速下降方向。
最速下降法的迭代格式为: 1k k k k x x g α+=-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
where µk > 0 is a parameter and I is the identity matrix, and proved that if g (x ) provides a local error bound for problem (1.3) and µ is chosen as µk = g (xk ) 2 , then the LevenbergMarquardt method retains a quadratic convergence property. The concept of a local error bound is defined as follows. Definition 1.1. A function F : R n → R is said to provide a local error bound for problem ¯ ∈ X is there exist a neighborhood (x ¯ ) of x ¯ and a constant m > 0 such that (1.2) near x ¯) for all x ∈ (x F (x ) ≥ m dist(x , X ), where dist(x , X ) denotes the distance from point x to the solution set X . In the remaining part of the paper, we will omit the phrase “for problem (1.2)” when ¯ }, and we talk about a local error bound. It is clear that if X is a singleton, i.e., X = {x ¯ ) is nonsingular, then g (x ) provides a local error bound near x ¯. the Hessian matrix G (x However, the converse is not true in general. An example is given in [1], which shows that (1.5)
The classical Newton method is quite a way of solving (1.2) and (1.3). An attractive feature ¯ ) is nonsingular at a of Newton’s method lies in its local quadratic convergence when G (x ¯ . We call a solution x ¯ of problem (1.2) or (1.3) nonsingular if G (x ¯ ) is a nonsingular solution x ¯ singular. It is clear that a nonsingular solution is locally isolated. matrix. Otherwise we call x We are particularly interested in the case where problem (1.2) may have singular solutions. When Newton’s method is applied to such a problem, the quadratic rate of convergence may no longer be guaranteed. Recently, there has been some progress in convergence analysis of Newton-type methods for problem (1.3) with singular solutions. Yamashita and Fukushima [5] studied the Levenberg-Marquardt method for solving (1.3), in which the subproblem is the system of linear equations (G (xk )T G (xk ) + µk I )d + G (xk )T g (xk ) = 0, (1.4)
132 for all x , y ∈ S . Consider the minimization problem min f (x ), x ∈ R n .
LI ET AL.
(ppose that f is convex and that the solution set X of (1.2) is nonempty and contained in S . It is clear that X is convex. Denote by g (x ) = ∇ f (x ) and G (x ) = ∇ 2 f (x ) the gradient and the Hessian matrix of f at x , respectively. It is well-known that f is convex if and only if G (x ) is positive semidenfinite for all x ∈ R n . Moreover, if f is convex, then x is a solution of (1.2) if and only if it is a solution of the system of nonlinear equations g (x ) = 0. (1.3)
REGULARIZED NEWTON METHODS FOR CONVEX MINIMIZATION PROBLEMS
133
¯ ). Note also that the the local error bound condition is weaker than nonsingularity of G (x ¯ . More specifically, let the condition in Definition 1.1 depends on a particular choice of x function f : R 2 → R be defined by f (x ) = with 4 (x2 − 1) φ (x2 ) = 0 (x2 + 1)4 if x2 ∈ [1, +∞) if x2 ∈ (−1, 1) if x2 ∈ (−∞, −1]. 1 2 x + φ (x2 ) 2 1
Abstract. This paper studies convergence properties of regularized Newton methods for minimizing a convex function whose Hessian matrix may be singular everywhere. We show that if the objective function is LC2 , then the methods possess local quadratic convergence under a local error bound condition without the requirement of isolated nonsingular solutions. By using a backtracking line search, we globalize an inexact regularized Newton method. We show that the unit stepsize is accepted eventually. Limited numerical experiments are presented, which show the practical advantage of the method. Keywords: minimization problem, regularized Newton methods, global convergence, quadratic convergence, unit step
∗ The author is partially supported by the National Natural Science Foundation of China via Grant 10171030 and a Hong Kong Polytechnic University Postdoctoral Fellowship. ∗∗ The author is partially supported by a Grant-in-Aid for Scientific Research from the Ministry of Education, Science, Sports and Culture of Japan. † The author is partially supported by the Research Grant Council of Hong Kong. ‡ The author is partially supported by a Grant-in-Aid for Scientific Research from the Ministry of Education, Science, Sports and Culture of Japan.
Computational Optimization and Applications, 28, 131–147, 2004 c 2004 Kluwer Academic Publishers. Manufactured in The Netherlands.
Regularized Newton Methods for Convex Minimization Problems with Singular Solutions
