数学---辽宁省大连市瓦房店高中2016-2017学年高一(下)期末试卷(理)(解析版)
辽宁省瓦房店市高级中学2016-2017学年高一下学期期末考试英语试题含答案

2016-2017学年度下学期瓦房店市高级中学期末考试高一英语试题命题人:邵美玲第二部分阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该项涂黑。
ADream home in magical Lucas Valley. Room is rented for the summer. Would like to sign lease(租约)with the right person who is healthy and eco conscious.PREFER to offer rent reduction option for the right person, see below。
.。
3 beautiful bedrooms,about 10’ x 11' with 4’ window faces morning sun and beautiful view of courtyard garden and flowers. Can be furnished or unfurnished。
Home features sunny island kitchen,floor to ceiling glass with garden views。
Share use of all amenities of home,beautiful sunny yard,organic gardens,picnic table。
Great outdoor pool, yoga and tennis 2 blocks away, 2 great farmers markets weekly 5 minutes away at SR Civic Center. Peaceful quiet neighborhood,easy parking right outside,1。
辽宁省瓦房店市高级中学2016-2017学年高二下学期期末

2016-2017学年度下学期瓦房店市高级中学期末考试高二数学试题(理科)考试时间:120分钟试卷满分:150分命题与校对:虞政华一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 是虚数单位,复数的共轭复数是( )A. 2-iB. 2+iC. -1+2iD. -1-2i【答案】B【解析】,那么它的共轭复数为,故选B.2. 设全集 ( )A. (0,1]B. [-1,1]C. (1,2]D. (-∞,-1]∪[1,2]【答案】C【解析】由中不等式解得:,即,,由中不等式变形得:,解得:则,故选C.3. 设等差数列取最小值时,等于( )A. 9B. 8C. 7D. 6【答案】D【解析】由等差数列的性质可得,解得,又,设公差为,所以,解得,则,所以,所以当时,取最小值,故选D.4. 若,则 ( )A. B. C. D.【答案】A【解析】,,故选A.5. 的 ( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】B【解析】,时必有,当时,不一定成立,即的必要不充分条件,故选B.6. 已知满足线性约束条件:,则目标函数的取值范围是()A. B. C. D.【答案】C【解析】画出性约束条件:表示的可行域,如图,由图由得由得,因为经过点时,,经过时,所以的取值范围是,故选C.【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.7. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( )A. 192 里B. 96 里C. 48 里D. 24 里【答案】B【解析】记每天走的路程里数为,易知是公比为的等比数列,由题意知,故选B.8. 把函数的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象上所有点向左平移个单位长度,得到图象的函数解析式为( )A. B.C. D.【答案】C【解析】将函数的图象上所有点的横坐标变为原来的倍(横坐标不变),可得的图象;再将所得到的图象上所有点向左平移个单位,所得函数图象的解析式为,故选C.9. 在△ABC中,若,且则A=( )A. B. C. D.【答案】A【解析】因为在中,,由正弦定理可得,,即,解得,所以由余弦定理可得,,故选A.10. 已知命题,;命题,使则下列命题中为真命题的是( )A. B.p∧(q) C. D.【答案】D【解析】由题意可知,命题为假命题,则为真命题;命题为真命题,则为假命题,所以由真值表可得,为真命题,为假命题,为假命题,为假命题,故选D...................11. 已知函数,若,,使得,则实数的取值范围是( )A. (-∞,1]B. [1,+∞)C. (-∞,2]D. [2,+∞)【答案】A【解析】当时,由得,,令,解得,令,解得,在单调递减,是函数的最小值,当时,为增函数,是函数最小值,又,都在,使得,可得在的最小值不小于在的最小值,即,解得,故选A.【方法点睛】本题主要考查函数的最值、全称量词与存在量词的应用.属于难题.解决这类问题的关键是理解题意、正确把问题转化为最值和解不等式问题,全称量词与存在量词的应用共分四种情况:(1)只需;(2),只需;(3),只需;(4),,.12. 设正实数满足.则当取得最大值时,的最大值为( )A. 0B.C. 1D. 3【答案】C【解析】,又均为正实数,(当且仅当时取“=”),,此时,,,当且仅当时取得“=”,满足题意,的最大值为,故选C.【易错点晴】本题主要考查利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).二、填空题:本题共4小题,每小题5分,共20分。
辽宁省瓦房店市高级中学高一数学下学期期末考试试题理

2015——2016学年度下学期高一期末考试数学试题(理科)一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求.1. 向量a =(13,tanα),b =(cosα,1),且a ∥b ,则锐角α的余弦值为( )A.13 B .23 C.23 D .223 2.)190sin(160sin 2350cos ︒-︒-︒=( )A .- 3B .-32 C.32D . 3 3. 函数f(x)=sin2x -4sin 3x·cosx(x∈R )的最小正周期为( )A.π2 B .π4 C.π8D .π 4. 在△ABC 中,acos 2C 2+ccos 2A2=32b ,则( )A .a ,b ,c 依次成等差数列B .b ,a ,c 依次成等差数列C .a ,c ,b 依次成等差数列D .a ,b ,c 既成等差数列,也成等比数列 5. 已知{a n }为等差数列,若a 1+a 5+a 9=8π,则cos(a 3+a 7)的值为( )A.32 B .-32 C. 12 D .-126.函数y =log 2x +log x 2x )10(≠>x x 且的值域是( )A .(-∞,-1]B .[3,+∞)C .[-1,3]D .(-∞,-1]∪[3,+∞)7. 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)的部分图象如图所示,则将y =f(x)的图象向右平移π6个单位后,得到的图象的解析式为( )A .y =sin2xB .y =cos2xC .y =sin(2x +2π3)D .y =sin(2x -π6)8. 《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布( )A .30尺B .90尺C .150尺D .180尺 9.在平面直角坐标系xOy 中,过定点)1,1(Q 的直线l 与曲线1-=x xy 交于N M 、点,则 =⋅-⋅OQ MO OQ ON ( )A.2B.4C.6D.810. 已知向量,为平面向量,若+与的夹角为3π,+与的夹角为4π,则=( )A .33 B .46 C .35 D .3611. 在斜三角形ABC 中,sinA =-2cosB·cosC,且tanB·tanC=1-2,则角A 的值为( )A.π4 B .π3 C. π2 D .3π412. 已知不等式组⎪⎩⎪⎨⎧≤-≥-≥+224x y x y x 表示的平面区域为D ,点)0,1(),0,0(A O ,若点M 是D 上的动点,则的最小值是( )A .10103 B .55 C .22D .1010二.填空题:本大题共4小题,每小题5分13. 已知向量,夹角为︒45,1=102=a=_________.14. 在由正数组成的等比数列{a n }中,若a 3a 4a 5=3π,则sin(log 3a 1+log 3a 2+…+log 3a 7)的值为_____.15. 已知等差数列{a n }的前n 项和为S n ,a 2=4,S 10=110,则S n +64a n 的最小值为_________.16. 在ABC ∆中,角C B A ,,的对边分别为c b a ,,,若B c B A b tan 2)tan (tan =+,BC 边的中线长为1,则a 的最小值为______________.三.解答题:解答应写出文字说明,证明过程或演算步骤. 17. 如图,平面四边形ABCD中,AB =AD =CD =,30CBD ∠=,120BCD ∠=,求(1)ADB ∠; (2)ADC ∆的面积S .18. 在△ABC 中,角A,B,C 所对的边分别是c b a ,,,且cos cos sin A B Ca b c+=. (1)证明:sin sin sin A B C =; (2)若22265b c a bc +-=,求tan B .19.某同学用“五点法”画函数2,0,0,)sin()(πϕωϕω<>>++=A B x A x f 在某一个周期的图象时,列表并填入了部分数据,如下表:(1)请求出上表中的1x , 2x ,3x ,并直接写出函数f (x )的解析式;ABDC(2)将f (x )的图象沿x 轴向右平移32个单位得到函数g (x ),若函数g (x )在],0[m x ∈(其中)4,2(∈m )上的值域为]3,3[-,且此时其图象的最高点和最低点分别为P ,Q ,求OQ 与QP 夹角θ的大小.20. 已知函数21)6sin()(+-=πx x f (1)若⎥⎦⎤⎢⎣⎡∈2,0πx ,1011)(=x f ,求x cos 的值; (2)在ABC ∆中,角C B A ,,的对边分别是c b a ,,,且满足a c A b 32cos 2-≤, 求)(B f 的取值范围.21. 已知等比数列{}n a 的首项18a =,公比为q (1q ≠),n S 是数列{}n a 的前n 项和. (1)若3S ,42S ,53S 成等差数列,求{}n a 的通项公式n a ;(2)令2log n n b a =,n T 是数列{}n b 的前n 项和,若3T 是数列{}n T 中的唯一最大项,求q 的取值范围.22. 设各项均为正数的数列{a n }的前n 项和为S n ,满足a 2n +1=4S n +4n +1,n∈N *,且a 2,a 5,a 14恰好是等比数列{b n }的前三项. (1)求数列{a n },{b n }的通项公式;(2)记数列{b n }的前n 项和为T n ,若对任意的n∈N *,(T n +32)k≥3n-6恒成立,求实数k 的取值范围.2015——2016学年度下学期高一期末考试数学(理科)参考答案一、选择题二、填空题 13、23 14、23 15、21716、222- 三、解答题17、解:(1)在BCD ∆中,由正弦定理得:sin 3sin 2CD BD BCD CBD =⋅∠==∠, …………………2分在ABD ∆中,由余弦定理得:222cos 2AD BD AB ADB AD BD +-∠=⋅==…………………4分 所以45ADB ∠= …………………5分 (2)因为30CBD ∠=,120BCD ∠=,所以30CDB ∠=因为6sin sin(4530)ADC ∠=+=…………………7分 所以1sin2S AD CD ADC=⋅⋅∠12=⨯=………………10分 18、解:(1)根据正弦定理,设sin a A =sin b B =sin c C=k(k>0). 则a=ksin A ,b=ksin B ,c=ksin C . 代入cos A a +cos B b =sin C c 中,有cos sin A k A +cos sin B k B =sin sin Ck C,变形可得 sin Asin B=sin Acos B+cos Asin B=sin(A+B).在△ABC 中,由A+B+C=π,有sin(A+B)=sin(π–C)=sin C ,所以sin Asin B=sin C .………………6分(2)由已知,b 2+c 2–a 2=65bc ,根据余弦定理,有cos A=2222b c a bc +-=35.………8分所以=45.………………9分 由(Ⅰ),sin Asin B=sin Acos B+cos Asin B ,所以45sin B=45cos B+35sin B , 故tan B=sin cos BB=4.………………12分 19、解:(1)由⎪⎩⎪⎨⎧=+=+2337231πϕωπϕω,得⎪⎩⎪⎨⎧==32πϕπω.∴⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+=+ππππππππ23232032321x x x ,∴321-=x ,342=x ,3103=x . 又∵)32sin(3)(,0,3ππ+===x x f B A .…………………6分 (2)将f (x )的图象向右平移32个单位得到函数x x g 2sin 3)(π=, 由于g (x )在],0[m x ∈(其中)4,2(∈m )上的值域为]3,3[-,则3≥m ,……8分 故最高点为)3,1(P ,最低点为)3,3(-Q .则)3,3(-=,)32,2(-=,…………………10分则23cos -==θ,故πθ65=.…………………12分20、解:(1)由11()10f x =,∴3sin()65x π-=;…………………1分又∵[0,]2x π∈,∴[,]663x πππ-∈-,即4cos()65x π-=………………2分3cos cos[()]cos()cos sin()sin 6666661010x x x x ππππππ∴=-+=---=- (6)分22bcosA2c2sin cos2sin2sin cos2sin()2sin cos2[sin cos cos sin]2sin cos cos(0,]6B A c AB A A B AB A A B A B AA B A B Bπ≤≤⇒≤+⇒≤+⇒≥⇒≥⇒∈()由得:…………………10分∴1sin()(,0]62Bπ-∈-,即11()sin()()(0,]622f B B f Bπ=-+⇒∈…………………12分21、解:(1)由题意,43543S S S=+,得qqaqqaqqa--+--=--1)1(31)1(1)1(4513141,∴13q=或1=q(舍),所以1183nna-⎛⎫=⨯ ⎪⎝⎭………………4分(2)()22log31logn nb a n q==+-,∴{}n b成等差数列,………………6分3T是数列{}n T中的唯一最大项,所以2log0q<………………8分且3224032log033log0b qqb>+>⎧⎧⇒⎨⎨+<<⎩⎩,………………10分解得:142q⎛⎫∈ ⎪⎪⎝⎭,∴q的取值范围是142⎛⎫⎪⎪⎝⎭………………12分22、解:(1)当n≥2时,4S n-1=a2n-4(n-1)-1,4a n=4S n-4S n-1=a2n+1-a2n-4,∴a2n+1=a2n+4a n+4=(a n+2)2.∵a n>0,∴a n+1=a n+2. …………2分∴当n≥2时,{a n}是公差为2的等差数列.∵a2,a5,a14构成等比数列,∴a25=a2a14,∴(a2+6)2=a2(a2+24),解得a2=3.由条件可知,4S1=4a1=a22-5=4,∴a1=1. …………3分∵a2-a1=3-1=2,∴{a n}是首项为1,公差为2的等差数列.∴数列{a n}的通项公式为a n=2n-1,…………4分数列{b n}的通项公式为b n=3n. …………6分(2)T n=3n+1-32,…………8分∴(3n +1-32+32)k ≥3n -6对n ∈N *恒成立, ∴k ≥2n -43n 对n ∈N *恒成立.…………9分令c n =2n -43n ,c n -c n -1=2n -43n -2n -63n -1=n n 3414-.…………10分 当n ≤3时,c n >c n -1;当n ≥4时,c n <c n -1, 即 >>><<54321c c c c c∴(c n )max =c 3=227,∴k ≥227.…………12分。
2016-2017学年辽宁省大连市瓦房店高中高二(下)期末数学试卷(理科)(解析版)

2016-2017学年辽宁省大连市瓦房店高中高二(下)期末数学试卷(理科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)i是虚数单位,复数的共轭复数为()A.2+i B.2﹣i C.﹣1+i D.﹣1﹣2i2.(5分)设全集U=R,已知集合A={x||x|≤1},B={x|log2x≤1},则(∁U A)∩B=()A.(0,1]B.[﹣1,1]C.(1,2]D.(﹣∞,﹣1]∪[1,2]3.(5分)设等差数列{a n}的前n项和为S n,若a1=﹣11,a3+a7=﹣6,则当S n取最小值时,n等于()A.9B.8C.7D.64.(5分)若,则sin(π+2α)=()A.B.C.D.5.(5分)“x<0”是“﹣1<x<0”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.(5分)已知x,y满足线性约束条件:,则目标函数z=y﹣3x的取值范围是()A.B.(﹣3,﹣1)C.D.7.(5分)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了()A.192 里B.96 里C.48 里D.24 里8.(5分)把函数y=sin x(x∈R)的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象上所有点向左平移个单位长度,得到图象的函数解析式为()A.y=sin(2x﹣)B.y=sin(2x+)C.y=sin(x+)D.y=sin(x+)9.(5分)在△ABC中,若,且=2,则A=()A.B.C.D.10.(5分)已知命题p:∀x∈R,x+≥2;命题q:∃x0∈[0,],使sin x0+cos x0=,则下列命题中为真命题的是()A.p∨(¬q)B.p∧(¬q)C.(¬p)∧(¬q)D.(¬p)∧q 11.(5分)已知函数f(x)=x+,g(x)=2x+a,若∀x1∈[,1],∃x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是()A.(﹣∞,1]B.[1,+∞)C.(﹣∞,2]D.[2,+∞)12.(5分)设正实数x,y,z满足x2﹣3xy+4y2﹣z=0.则当取得最大值时,的最大值为()A.0B.1C.D.3二、填空题:本题共4小题,每小题5分,共20分.13.(5分)函数的最小正周期为.14.(5分)设函数f(x)=,则函数f(x)的值域是.15.(5分)△ABC中,若b=2,A=120°,三角形的面积,则三角形外接圆的半径为.16.(5分)若函数f(x)=﹣x3+x2+2ax在[,+∞)上存在单调递增区间,则a的取值范围是.三、解答题:共70分.解答应写出文字说明、解答过程或演算步骤.17.(10分)在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l 的极坐标方程是,圆C的极坐标方程是ρ=4sinθ.(Ⅰ)求l与C交点的极坐标;(Ⅱ)设P为C的圆心,Q为l与C交点连线的中点,已知直线PQ 的参数方程是(t为参数),求a,b的值.18.(12分)已知函数f(x)=2sin x sin(x +).(1)求函数f(x)的最小正周期和单调递增区间;(2)当x∈[0,]时,求f(x)的值域.19.(12分)已知数列{a n}满足a1=﹣1,na n+1=S n+n(n+1)(n∈N*),S n是数列{a n}的前n 项和.(1)求数列{a n}的通项公式a n;(2)令b n =,求数列{b n}的前n项和T n.20.(12分)为了研究家用轿车在高速公路上的车速情况,交通部门对100名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在55名男性驾驶员中,平均车速超过100km/h的有40人,不超过100km/h的有15人.在45名女性驾驶员中,平均车速超过100km/h的有20人,不超过100km/h的有25人.(Ⅰ)完成下面的列联表,并判断是否有99.5%的把握认为平均车速超过100km/h的人与性别有关.(Ⅱ)以上述数据样本来估计总体,现从高速公路上行驶的大量家用轿车中随机抽取3辆,记这3辆车中驾驶员为男性且车速超过100km/h的车辆数为X,若每次抽取的结果是相互独立的,求X的分布列和数学期望.参考公式与数据:Χ2=,其中n=a+b+c+d21.(12分)在直三棱柱ABC﹣A'B'C'中,底面ABC是边长为2的正三角形,D'是棱A'C'的中点,且AA'=2.(1)试在棱CC'上确定一点M,使A'M⊥平面AB'D';(2)当点M在棱CC'中点时,求直线AB'与平面A'BM所成角的正弦值.22.(12分)设f(x)=e x﹣2ax﹣1.(Ⅰ)讨论函数f(x)的极值;(Ⅱ)当x≥0时,e x≥ax2+x+1,求a的取值范围.2016-2017学年辽宁省大连市瓦房店高中高二(下)期末数学试卷(理科)参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解答】解:复数==2﹣i,故它的共轭复数为2+i,故选:A.2.【解答】解:集合A={x||x|≤1}=[﹣1,1],B={x|log2x≤1}=(0,2],∵全集U=R,∴∁U A=(﹣∞,﹣1)∪(1,+∞)∴(∁U A)∩B=(1,2],故选:C.3.【解答】解:由等差数列的性质可得a3+a7=2a5=﹣6,解得a5=﹣3.又a1=﹣11,设公差为d,所以,a5=a1+4d=﹣11+4d=﹣3,解得d=2.则a n=﹣11+2(n﹣1)=2n﹣13,所以S n==n2﹣12n=(n﹣6)2﹣36,所以当n=6时,S n取最小值.故选:D.4.【解答】解:∵,可得:(cosα﹣sinα)=,∴两边平方可得:1﹣2sinαcosα=,解得:sin2α=,∴sin(π+2α)=﹣sin2α=﹣.故选:A.5.【解答】解:由﹣1<x<0⇒x<0;反之不成立.∴“x<0”是“﹣1<x<0”的必要不充分条件.故选:B.6.【解答】解:由z=y﹣3x得y=3x+z,作出不等式组,对应的平面区域如图,平移直线y=3x+z,由图象可知当直线y=3x+z,过点B时,直线y=3x+z的截距最小,此时z最小,由,解得,即B(1,0).代入目标函数z=y﹣3x,得z=0﹣3=﹣3,∴目标函数z=x﹣2y的最小值是﹣3.当直线y=3x+z,过点A时,直线y=3x+z的截距最大,此时z最大,由,解得A(,).代入目标函数z=y﹣3x,得z==,∴目标函数z=y﹣3x的最大值是.目标函数z=y﹣3x的取值范围是(﹣3,]故选:C.7.【解答】解:由题意可知此人每天走的步数构成为公比的等比数列,由题意和等比数列的求和公式可得=378,解得a1=192,∴第此人二天走192×=96里,∴第二天走了96里,故选:B.8.【解答】解:∵函数y=sin x(x∈R),图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y=sin x,图象上所有点向左平行移动个单位长度,得到y=sin(x+)=sin(x+),x∈R.故选:C.9.【解答】解:∵在△ABC中,==2,由正弦定理可得:=2,即:c=2b,∵=b(a×+b×),∴整理可得:a2﹣b2=bc,∴a2﹣b2=b×2,解得:a2=7b2,∴由余弦定理可得:cos A===,∵A∈(0,π),∴A=.故选:A.10.【解答】解:对于命题p:当x≤0时,x+≥2不成立,∴命题p是假命题,则¬p是真命题;对于命题q:sin x+cos x=sin(x+)∈[1,],则q是真命题,所以(¬p)∧q.故选:D.11.【解答】解:满足题意时应有:f(x)在的最小值不小于g(x)在x2∈[2,3]的最小值,由对勾函数的性质可知函数在区间上单调递减,f(x)在的最小值为f(1)=5,当x2∈[2,3]时,g(x)=2x+a为增函数,g(x)在x2∈[2,3]的最小值为g(2)=a+4,据此可得:5⩾a+4,解得:a⩽1,实数a的取值范围是(﹣∞,1],故选:A.12.【解答】解:∵x2﹣3xy+4y2﹣z=0,∴z=x2﹣3xy+4y2,又x,y,z均为正实数,∴==≤=1(当且仅当x=2y时取“=”),∴=1,此时,x=2y.∴z=x2﹣3xy+4y2=(2y)2﹣3×2y×y+4y2=2y2,∴+﹣=+﹣=﹣+1≤1,当且仅当y=1时取得“=”,满足题意.∴的最大值为1.故选:B.二、填空题:本题共4小题,每小题5分,共20分.13.【解答】解:函数的最小正周期为:=π.故答案为:π.14.【解答】解:①x>1时,f(x)=;∴;即0<f(x)<1;②x≤1时,f(x)=﹣x﹣2;∴﹣x≥﹣1;∴﹣x﹣2≥﹣3;即f(x)≥﹣3;∴函数f(x)的值域为(0,1)∪[﹣3,+∞).故答案为:(0,1)∪[﹣3,+∞).15.【解答】解:=sin120°,解得c=2.∴c=b=2,又A=120°.∴B=C=30°.解得a=2,∴2R===4,解得R=2.故答案为:2.16.【解答】解:函数f(x)=﹣x3+x2+2ax,f′(x)=﹣x2+x+2a=﹣(x﹣)2++2a.当x∈[,+∞)时,f′(x)的最大值为f′()=2a+,令2a+>0,解得a,所以a的取值范围是.故答案为:.三、解答题:共70分.解答应写出文字说明、解答过程或演算步骤.17.【解答】解:(Ⅰ)ρ=4sinθ代入,得sinθcosθ=cos2θ.所以cosθ=0或tanθ=1,取,.再由ρ=4sinθ得ρ=4,或.所以l与C 交点的极坐标是,或.…(5分)(Ⅱ)参数方程化为普通方程得.由(Ⅰ)得P,Q的直角坐标分别是(0,2),(1,3),代入解得a=﹣1,b=2.…(10分)18.【解答】解:(1)f(x)=2sin x sin(x+)=2sin x(sin x+cos x)=sin2x+sin x cos x=+sin2x=+sin(2x﹣)则函数f(x)的最小正周期T==π,由2k≤2kπ+,k∈Z,解得,kπ﹣≤x≤kπ+,k∈Z,则f(x)的单调递增区间为[kπ﹣,kπ+],k∈Z;(2)当x∈[0,]时,2x ﹣∈[﹣,],sin(2x ﹣)∈[﹣,1],则f(x)的值域为[0,1+].19.【解答】解:(1)na n+1=S n+n(n+1)(n∈N*),n≥2时,(n﹣1)a n=S n﹣1+n(n﹣1),∴na n+1﹣(n﹣1)a n=a n+2n,化为:a n+1﹣a n=2,又a1=﹣1,∴数列{a n}是等差数列,公差为2,首项为﹣1.∴a n=﹣1+2(n﹣1)=2n﹣3.(2)b n ==,∴数列{b n}的前n项和T n =﹣+++…+,=++…++,∴=﹣+﹣=﹣2×﹣,可得:T n =﹣.20.【解答】解:(Ⅰ)因为,所以有99.5%的把握认为平均车速超过100km/h与性别有关.…(6分)(Ⅱ)根据样本估计总体的思想,从高速公路上行驶的大量家用轿车中随机抽取1辆,驾驶员为男性且车速超过100km/h的车辆的概率为.X可取值是0,1,2,3,,有:,,,,分布列为.…(12分)21.【解答】解:(1)取AC边中点为O,∵底面ABC是边长为2的正三角形,∴OB⊥AC,连接OD',∵D'是边A'C'的中点,∴OD'⊥AC,OD'⊥OB,建立以O为坐标原点,OB为x轴,OC为y轴,OD'为z轴如图所示的空间直角坐标系…(2分)则有O(0,0,0),A(0,﹣1,0),B(,0,0),C(0,1,0),B'(,0,2),A'(0,﹣1,2),D'(0,0,2),C'(0,1,2),设M(0,1,t),则=(0,2,t﹣2),=(0,1,2),=(,1,2)…(4分)若A'M⊥平面AB'D',则有A'M⊥AD',A'M⊥AB',∴,解得t=,即当CM=时,A'M⊥平面AB'D'.…(6分)(2)当点M在棱CC'中点时,M(0,1,),∴=(﹣),=(0,2,﹣),设平面A′BM的一个法向量=(x,y,z),∴,令z=,得=(),…(9分)设直线AB'与平面A'BM所成角为θ,则sinθ==.∴直线AB'与平面A'BM所成角的正弦值为.…(12分)22.【解答】解:(Ⅰ)f'(x)=e x﹣2a,若a≤0,则f'(x)>0,f(x)在g(x)上单调递增,没有极值.…(2分)若a>0,令f'(x)=0,x=ln2a,列表所以当x=ln2a时,f(x)有极小值f(2a)=2a﹣2aln2a﹣1,没有极大值.…(6分)(Ⅱ)方法1设g(x)=e x﹣ax2﹣x﹣1,则g'(x)=e x﹣2ax﹣1=f(x).从而当2a≤1,即时,f'(x)>0(x≥0),g'(x)≥g'(0)=0,g(x)在[0,+∞)单调递增,于是当x≥0时,g(x)≥g(0)=0.…(8分)当时,若x∈(0,ln2a),则f'(x)<0,g'(x)<g'(0)=0,g(x)在(0,ln2a)单调递减,于是当x∈(0,ln2a)时,g(x)<g(0)=0.综合得a的取值范围为.…(12分)(Ⅱ)方法2由(Ⅰ)当时,f(x)≥f(2)=0,得e x≥1+x.(Ⅱ)设g(x)=e x﹣ax2﹣x﹣1,则g'(x)=e x﹣2ax﹣1≥x(1﹣2a).从而当2a≤1,即时,g'(x)≥0(x≥0),而g'(0)=0,于是当x≥0时,g(x)≥0.…(8分)由e x>1+x(x≠0)可得,e﹣x>1﹣x,即x>1﹣e﹣x(x≠0),从而当时,g'(x)<e x﹣2a(1﹣e﹣x)﹣1=e x(e x﹣1)(e x﹣2a).故当x∈(0,ln2a)时,g'(x)<0,而g(0)=0,于是当x∈(0,ln2a)时,g(x)<g(0)=0.综合得a的取值范围为.…(12分)。
辽宁省瓦房店市高级中学2016-2017学年高一下学期期末考试物理试题Word版含答案

2016-2017学年度高一下学期期末物理试题一.选择题(1.-.7.单选..,8.-.12..多选..。
每题4分,共48分.)1.质量为1kg的质点在xy平面上做曲线运动,在x方向的速度图象和y方向的位移图象如图,下列说法正确的是()A.质点的初速度为3 m/sB.质点所受的合外力为1.5 NC.质点初速度的方向与合外力方向垂直D.2 s末质点速度大小为6 m/s2.一个物体从某一确定的高度以v0的初速度水平抛出,已知它落地时的速度为v t,重力加速度为g,下列说法正确的是()A.用θ表示它的速度方向与水平夹角,则B.它的运动时间是C.它的竖直方向位移是D.它的位移是3.如图,细线的一端固定于O点,另一端系一小球. 在水平拉力作用下,小球以恒定速率在竖直平面内由点B.运动到点A. . 下列说法正确的是()A.小球所受合力为0B.绳子拉力做负功C.重力的功率逐渐增大D.水平拉力逐渐减小4.质量为m的小球由轻绳a和b分别系于一轻质细杆的A点和B点,如图,绳a与水平方向成θ角,绳b在水平方向且长为l,当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是( )A.b绳拉力不可能为零B.a绳的拉力随角速度的增大而增大C.当角速度ω>gl tan θ,b绳将出现拉力D.若b绳突然被剪断,则a绳的拉力一定发生变化5.如图,两质量相同的小球A、B,分别用细线悬挂在等高的O1、O2点,A球的悬线比B的长,把两球均拉到悬线水平后将小球由静止释放,则两球经最低点时(以悬点为零势能点),说法正确的是( )A.机械能A球大于B球B.悬绳对球的拉力A球大于B球C. 向心加速度A球等于B球D. A球的速度等于B球的速度6.如图,a、b、c、d是在地球大气层外的圆形轨道上匀速运行的四颗人造卫星,其中a、c 的轨道相交于P,b、d在同一个圆轨道上,某时刻b卫星恰好处于c卫星的正上方。
下列说法中正确的是()A.b、d存在相撞危险B.a、c的加速度大小相等,且大于b的加速度C.b、c的角速度大小相等,且小于a的角速度D.a、c的线速度大小相等,且小于d的线速度7.如图,光滑水平面上有半径相同的A、B两球在同一直线上运动.两球质量关系为m B=2m A,规定向右为正方向,A、B两球的动量均为6 kgm/s,运动中两球发生碰撞,碰撞后A球的动量增量为-4 kgm/s,则( )A.左方是A球,碰撞后A、B两球速度大小之比为2∶5B.左方是A球,碰撞后A、B两球速度大小之比为1∶5C.右方是A球,碰撞后A、B两球速度大小之比为2∶5D.右方是A球,碰撞后A、B两球速度大小之比为1∶108.如图水平的木板B托着木块A一起在竖直平面内做匀速圆周运动,从水平位置a沿逆时针方向运动到最高点b的过程中()A.B对A的支持力越来越大B.B对A的支持力越来越小C.B对A的摩擦力越来越大D.B对A的摩擦力越来越小9.质量为m的汽车在平直路面上启动,启动过程的速度图象如图,其中OA为过原点的直线。
【全国百强校】辽宁省2016-2017学年高一下学期期末考试数学试题

辽宁省2016-2017学年高一下学期期末考试数学试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知向量,则向量的单位向量是()A. B. C. D.2. 为了了解全校240名学生的身高情况,从中抽取40名学生进行测量,下列说法正确的是()A. 总体是240B. 个体是每一个学生C. 样本是40名学生D. 样本容量是403. ()A. 2B.C.D.4. 已知2弧度的圆心角所对的弦长为2,则这个圆心角所对的弧长是()A. 2B.C.D.5. 在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如频率分布直方图所示.若该处高速公路规定正常行驶速度为,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有()A. 30辆B. 300辆C. 170辆D. 1700辆6. 关于向量下列说法错误的是()A. 如果,则B. 如果,则C. ,当且仅当与共线时取等D. ,当且仅当与共线时取等7. 在中,角所对的边分别为,若,则()A. B. C. D.8. 设向量满足,,则等于()A. B. 1 C. D. 29. 如图所示的程序框图给出了求某多项式值的一个实例,若输入的值分别为3,2,则输出的值为()A. 9B. 18C. 20D. 3510. 设都是锐角,且,则()A. B. C. 或 D. 或11. 在锐角中,,则的取值范围为()A. B. C. D.12. 设为函数的对称中心,且满足,则这样的有()A. 61个B. 63个C. 65个D. 67个第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 计算:__________.14. 如图,在中,,点在边上,,则的值为__________.15. 已知等腰梯形中,,且,设,用表示,则__________.16. 在直角坐标系中,已知任意角以坐标原点为顶点,以轴的非负半轴为始边,若其终边经过点,且,定义:,称“”为“的正余弦函数”,若,则__________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 设两个非零向量与不共线.(1)若,,求证:三点共线;(2)试确定实数,使与共线.18. 在中,分别为内角的对边,.(1)求的大小;(2)若,求的面积.19. 某中学对高三学生进行体能测试,已知高三某文科班有学生30人,立定跳远的测试成绩用茎叶图表示如图(单位:);男生成绩在以上(包括)定义为“合格”,成绩在以下(不包括)定义为“不合格”;女生成绩在以上(包括)定义为“合格”,成绩在以下(不包括)定义为“不合格.(1)求女生立定跳远测试成绩的中位数;(2)若在男生中按成绩是否合格进行分层抽样,抽取6人,求抽取成绩为“合格”的学生人数;(3)若从(2)中抽取的6名男生中任意选取4人,求这4人中至少有3人“合格”的概率.20. 已知,点,(1)以为对角线作正方形/(点依次逆时针排列),求出的坐标,并求出点的坐标;(2)设为与垂直的单位向量,求向量的坐标,并求边上的高的长.21. 如图,已知四边形中,,设.(1)设边的长为,将表示成的函数,(写成的形式),并求出的取值范围;(2)将该四边形进行某种翻折,判断:①与是否可能会重合;②与是否可能会重合.并请说明你做出上述两个判断的理由.22. 已知,且,向量,.(1)求函数的解析式,并求当时,的单调递增区间;(2)当时,的最大值为5,求的值;(3)当时,若不等式在上恒成立,求实数的取值范围.。
2016-2017年辽宁省大连市庄河高中高一(下)期末数学试卷(理科)(解析版)

2016-2017学年辽宁省大连市庄河高中高一(下)期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)在△ABC,已知a cos A=b cos B,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形2.(5分)两个相关变量满足如表关系:根据表格已得回归方程:=9.4x+9.2,表中有一数据模糊不清,请推算该数据是()A.37B.38.5C.39D.40.53.(5分)某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则老年人、中年人、青年人分别应抽取的人数是()A.7,11,18B.6、12、18C.6、13、17D.7、14、21 4.(5分)函数y=2sin(﹣2x)的单调递增区间是()A.B.C.D.5.(5分)盒中共有形状大小完全相同的5个球,其中有2个红球和3个白球.若从中随机取2个球,则概率为的事件是()A.都不是红球B.恰有1个红球C.至少有1个红球D.至多有1个红球6.(5分)如图圆C内切于扇形AOB,∠AOB=,若在扇形AOB内任取一点,则该点在圆C内的概率为()A.B.C.D.7.(5分)在△ABC中,a,b,c分别为三个内角A,B,C所对的边,设向量,若,则角A的大小为()A.B.C.D.8.(5分)下列命题中,假命题是()A.若a,b∈R且a+b=1,则a•b≤B.若a,b∈R,则≥()2≥ab恒成立C.(x∈R)的最小值是2D.∃x0,y0∈R,x02+y02+x0y0<09.(5分)在△ABC中,N为AC的四分之一等分点(靠近A点),点P在线段BN上,若,则实数m的值为()A.B.C.1D.310.(5分)已知圆C1:(x﹣2)2+(y+1)2=1,圆C2与圆C1关于直线x﹣y﹣2=0对称,则圆C2的方程为()A.(x﹣1)2+y2=1B.x2+(y﹣1)2=1C.(x+1)2+y2=1D.x2+(y+1)2=111.(5分)函数的图象与函数y=2sinπx(﹣4≤x≤6)的图象所有交点的横坐标之和等于()A.18B.14C.16D.1212.(5分)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,l2与l3间的距离是2,正三角形ABC的三顶点分别在l1、l2、l3上,则△ABC的边长是()A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)某四棱柱的三视图如图所示,则该四棱柱的体积为.14.(5分)已知tan(θ﹣π)=2,则sin2θ+sinθcosθ﹣2cos2θ+3的值为.15.(5分)已知圆C的圆心是直线x+y+1=0与直线x﹣y﹣1=0的交点,直线3x+4y﹣11=0与圆C相交于A,B两点,且|AB|=6,则圆C的方程为.16.(5分)等腰△ABC的顶角A=,|BC|=2,以A为圆心,1为半径作圆,PQ为该圆的一条直径,则•的最大值为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)已知函数f(x)=4cos x sin(x)﹣1.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间[﹣,]上的最大值和最小值.18.(12分)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.19.(12分)在三角形ABC中,角A,B,C及其对边a,b,c满足:c cos B=(2a﹣b)cos C.(1)求角C的大小;(2)求函数y=2sin2B﹣cos2A的值域.20.(12分)在△ABC中,a,b,c分别为角A,B,C的对边,设f(x)=a2x2﹣(a2﹣b2)x﹣4c2.(1)若f(1)=0,且,求角C的大小;(2)若f(2)=0,求角C的取值范围.21.(12分)已知圆C:x2+(y﹣4)2=4,直线l:(3m+1)x+(1﹣m)y﹣4=0(Ⅰ)求直线l所过定点A的坐标;(Ⅱ)求直线l被圆C所截得的弦长最短时m的值及最短弦长;(Ⅲ)已知点M(﹣3,4),在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有为一常数,试求所有满足条件的点N的坐标及该常数.22.(12分)已知向量,,且向量∥.(Ⅰ)求函数y=f(x)的解析式及函数的定义域;(Ⅱ)若函数g(θ)=﹣cos2θ﹣a sinθ+2,存在a∈R,对任意,总存在唯一,使得f(x1)=g(θ0)成立,求实数a的取值范围.2016-2017学年辽宁省大连市庄河高中高一(下)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)在△ABC,已知a cos A=b cos B,则△ABC的形状是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形【考点】HP:正弦定理.【解答】解:根据正弦定理可知∵a cos A=b cos B,∴sin A cos A=sin B cos B,∴sin2A=sin2B,∴A=B,或2A+2B=180°即A+B=90°,所以△ABC为等腰或直角三角形.故选:D.2.(5分)两个相关变量满足如表关系:根据表格已得回归方程:=9.4x+9.2,表中有一数据模糊不清,请推算该数据是()A.37B.38.5C.39D.40.5【考点】BK:线性回归方程.【解答】解:=,∴=9.4×4+9.2=46.8.设看不清的数据为a,则25+a+50+56+64=5=234.解得a=39.故选:C.3.(5分)某单位有老年人27人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为42的样本,则老年人、中年人、青年人分别应抽取的人数是()A.7,11,18B.6、12、18C.6、13、17D.7、14、21【考点】B3:分层抽样方法.【解答】解:由题意,老年人、中年人、青年人比例为1:2:3.由分层抽样的规则知,老年人应抽取的人数为×42=7人,中年人应抽取的人数为×42=14人,青年人应抽取的人数为×42=21人.故选:D.4.(5分)函数y=2sin(﹣2x)的单调递增区间是()A.B.C.D.【考点】HJ:函数y=Asin(ωx+φ)的图象变换.【解答】解:,由于函数的单调递减区间为的单调递增区间,即故选:B.5.(5分)盒中共有形状大小完全相同的5个球,其中有2个红球和3个白球.若从中随机取2个球,则概率为的事件是()A.都不是红球B.恰有1个红球C.至少有1个红球D.至多有1个红球【考点】CC:列举法计算基本事件数及事件发生的概率.【解答】解:盒中共有形状大小完全相同的5个球,其中有2个红球和3个白球,从中随机取2个球,基本事件总数n==10,都不是红球的概率为:=;恰有1个红球的概率为:=;至少有1个红球的概率为:1﹣=;至多有1个红球的概率为:+=.∴概率为的事件是恰有1个红球.故选:B.6.(5分)如图圆C内切于扇形AOB,∠AOB=,若在扇形AOB内任取一点,则该点在圆C内的概率为()A.B.C.D.【考点】CF:几何概型;G8:扇形面积公式.【解答】解:由题意知本题是一个等可能事件的概率,设圆C的半径为r,试验发生包含的事件对应的是扇形AOB,满足条件的事件是圆,其面积为⊙C的面积=π•r2,连接OC,延长交扇形于P.由于CE=r,∠BOP=,OC=2r,OP=3r,则S扇形AOB==;∴⊙C的面积与扇形OAB的面积比是.∴概率P=,故选:C.7.(5分)在△ABC中,a,b,c分别为三个内角A,B,C所对的边,设向量,若,则角A的大小为()A.B.C.D.【考点】9T:数量积判断两个平面向量的垂直关系.【解答】解:因为,所以,即:b2﹣bc+c2﹣a2=0即:b2﹣bc+c2=a2;,所以cos A=,A=故选:B.8.(5分)下列命题中,假命题是()A.若a,b∈R且a+b=1,则a•b≤B.若a,b∈R,则≥()2≥ab恒成立C.(x∈R)的最小值是2D.∃x0,y0∈R,x02+y02+x0y0<0【考点】2K:命题的真假判断与应用.【解答】解:A.a,b∈R且a+b=1,考虑a,b>0时,,则a•b≤正确;B.a,b∈R,∵a2+b2≥2ab,∴2(a2+b2)≥(a+b)2,则≥()2≥ab恒成立;C.=,当且仅当x2=1时取等号,因此(x∈R)的最小值是2,正确;D.x02+y02+x0y0=≥0.∴不∃x0,y0∈R,使得x02+y02+x0y0<0成立.综上可知:只有D是假命题.故选:D.9.(5分)在△ABC中,N为AC的四分之一等分点(靠近A点),点P在线段BN上,若,则实数m的值为()A.B.C.1D.3【考点】9H:平面向量的基本定理.【解答】解:N为线段AC上接近A点的四等分点,∴=,设=λ,=+=(1﹣λ)+,由=(m+)+=m+,∴,即λ=,m=,故选:A.10.(5分)已知圆C1:(x﹣2)2+(y+1)2=1,圆C2与圆C1关于直线x﹣y﹣2=0对称,则圆C2的方程为()A.(x﹣1)2+y2=1B.x2+(y﹣1)2=1C.(x+1)2+y2=1D.x2+(y+1)2=1【考点】J6:关于点、直线对称的圆的方程.【解答】解:圆C1:(x﹣2)2+(y+1)2=1的圆心为C1(2,﹣1),半径为1,设圆心C1(2,﹣1)关于直线x﹣y﹣2=0的对称点为C2(m,n),则由,求得,故C2(1,0),再根据半径为1,可得圆C2的方程为(x﹣1)2+y2=1,故选:A.11.(5分)函数的图象与函数y=2sinπx(﹣4≤x≤6)的图象所有交点的横坐标之和等于()A.18B.14C.16D.12【考点】53:函数的零点与方程根的关系.【解答】解:如图,做出函数y=2sin2πx,以及函数y=的图象,并且它们的图象都关于点(1,0)对称,且当x=时,y=sin2πx的图象在y=的下方,并且交点也关于(1,0)对称成对出现,每一对对称的点的横坐标的和为2,共6对,因此12个根的和为6×2=12,故选:D.12.(5分)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,l2与l3间的距离是2,正三角形ABC的三顶点分别在l1、l2、l3上,则△ABC的边长是()A.B.C.D.【考点】IU:两条平行直线间的距离.【解答】解:作高AE,BG,CF(如图),设AD=x,则AC=3x,于是DG=x﹣x=,BG=•3x=x,∵∠BDG=∠CDF,∠BGD=∠CFD=90°,∴Rt△BDG∽Rt△CDF,∴,即,∴DF=,∴DE=,∵AD2=AE2+DE2=1+=,∴AD=,∴AC=3x=3×=.故选:D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)某四棱柱的三视图如图所示,则该四棱柱的体积为.【考点】L!:由三视图求面积、体积.【解答】解:由已知中的三视图可得:该几何体上部是一个以俯视图为底面四棱柱,棱柱的底面面积S=×(1+2)×1=,棱柱的高为1,故棱柱的体积V=,故答案为:14.(5分)已知tan(θ﹣π)=2,则sin2θ+sinθcosθ﹣2cos2θ+3的值为.【考点】GG:同角三角函数间的基本关系;GS:二倍角的三角函数.【解答】解:∵已知tan(θ﹣π)=2=tanθ,则sin2θ+sinθcosθ﹣2cos2θ+3=+3=+3=+3=,故答案为.15.(5分)已知圆C的圆心是直线x+y+1=0与直线x﹣y﹣1=0的交点,直线3x+4y﹣11=0与圆C相交于A,B两点,且|AB|=6,则圆C的方程为x2+(y+1)2=18.【考点】J1:圆的标准方程;J9:直线与圆的位置关系.【解答】解:由得,得直线x+y+1=0与直线x﹣y﹣1=0的交点坐标为(0,﹣1),即圆心的坐标为(0,﹣1);圆心C到直线AB的距离d==3,∵|AB|=6,∴根据勾股定理得到半径r==3,∴圆的方程为x2+(y+1)2=18.故答案为:x2+(y+1)2=1816.(5分)等腰△ABC的顶角A=,|BC|=2,以A为圆心,1为半径作圆,PQ为该圆的一条直径,则•的最大值为.【考点】9O:平面向量数量积的性质及其运算.【解答】解:如图:由已知==;故答案为:.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(10分)已知函数f(x)=4cos x sin(x)﹣1.(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间[﹣,]上的最大值和最小值.【考点】H1:三角函数的周期性;HW:三角函数的最值.【解答】解:(Ⅰ)∵f(x)=4cos x sin(x+)﹣1,=4cos x(sin x+cos x)﹣1=sin2x+2cos2x﹣1=sin2x+cos2x=2sin(2x+),所以函数的最小正周期为π;(Ⅱ)∵﹣≤x≤,∴﹣≤2x+≤,∴当2x+=,即x=时,f(x)取最大值2,当2x+=﹣时,即x=﹣时,f(x)取得最小值﹣1.18.(12分)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.【考点】CB:古典概型及其概率计算公式.【解答】解(1)从袋中随机取两个球,其一切可能的结果组成的基本事件有1,4和2,1和3,1和4,2和3,2和4,3,共6个.从袋中取出的球的编号之和不大于4的事件共有1,3和2,1两个.因此所求事件的概率P==.(2)先从袋中随机取一个球,记下编号为m,放回后,再从袋中随机取一个球,记下编号为n,其一切可能的结果(m,n)有:(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.又满足条件n≥m+2的事件为:(1,3),(1,4),(2,4),共3个,所以满足条件n≥m+2的事件的概率为P1=.故满足条件n<m+2的事件的概率为1﹣P1=1﹣=.19.(12分)在三角形ABC中,角A,B,C及其对边a,b,c满足:c cos B=(2a﹣b)cos C.(1)求角C的大小;(2)求函数y=2sin2B﹣cos2A的值域.【考点】GF:三角函数的恒等变换及化简求值;GL:三角函数中的恒等变换应用;HW:三角函数的最值.【解答】解:(1)c cos B=(2a﹣b)cos C.由正弦定理化简:得sin C cos B=2sin A cos C﹣sin B cos C即sin(B+C)=2sin A cos C∵A+B+C=π∴sin A=2sin A cos C∵0<A<π,sin A≠0∴cos C=.∵0<C<π,∴C=.(2)函数y=2sin2B﹣cos2A=1﹣cos2B﹣cos2A,∵A+B=∴B=.则y=1﹣cos()﹣cos2A=1﹣cos(﹣2A)﹣cos2A=1+cos(﹣2A)﹣cos2A=1+cos2A+sin2A﹣cos2A=sin2A﹣cos2A+1=sin(2A﹣)+1.∵0<A<∴<2A﹣<得<sin(2A﹣)≤1.故得函数y=2sin2B﹣cos2A的值域为(,2].20.(12分)在△ABC中,a,b,c分别为角A,B,C的对边,设f(x)=a2x2﹣(a2﹣b2)x﹣4c2.(1)若f(1)=0,且,求角C的大小;(2)若f(2)=0,求角C的取值范围.【考点】HR:余弦定理.【解答】解:(1)由f(1)=0,得a2﹣a2+b2﹣4c2=0,∴b=2c,又由正弦定理,得b=2R sin B,c=2R sin C,将其代入上式,得sin B=2sin C,∵,∴,将其代入上式,得,∴,整理得:,∴.∵角C是三角形的内角,∴.(2)∵f(2)=0,∴4a2﹣2a2+2b2﹣4c2=0,即a2+b2﹣2c2=0,由余弦定理,得,∴(当且仅当a=b时取等号).∴,∠C是锐角,又∵余弦函数在上递减,∴.21.(12分)已知圆C:x2+(y﹣4)2=4,直线l:(3m+1)x+(1﹣m)y﹣4=0(Ⅰ)求直线l所过定点A的坐标;(Ⅱ)求直线l被圆C所截得的弦长最短时m的值及最短弦长;(Ⅲ)已知点M(﹣3,4),在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有为一常数,试求所有满足条件的点N的坐标及该常数.【考点】J9:直线与圆的位置关系;JE:直线和圆的方程的应用.【解答】解:(Ⅰ)依题意得,m(3x﹣y)+(x+y﹣4)=0,令3x﹣y=0且x+y﹣4=0,得x=1,y=3∴直线l过定点A(1,3),(Ⅱ)当AC⊥l时,所截得弦长最短,由题知C(0,4),r=2,∴,得,∴由得m=﹣1,∴圆心到直线的距离为,∴最短弦长为.(Ⅲ)法一:由题知,直线MC的方程为y=4,假设存在定点N(t,4)满足题意,则设P(x,y),,得|PM|2=λ2|PN|2(λ>0),且(y﹣4)2=4﹣x2∴(x+3)2+(y﹣4)2=λ2(x﹣t)2+λ2(y﹣4)2∴(x+3)2+4﹣x2=λ2(x﹣t)2+λ2(4﹣x2)整理得,(6+2tλ2)x﹣(λ2t2+4λ2﹣13)=0∵上式对任意x∈[﹣2,2]恒成立,∴6+2tλ2=0且λ2t2+4λ2﹣13=0解得或t=﹣3,λ=1(舍去,与M重合)综上可知,在直线MC上存在定点,使得为常数法二:设直线MC上的点N(t,4)取直线MC与圆C的交点P1(﹣2,4),则取直线MC与圆C的交点P2(2,4),则令,解得或t=﹣3(舍去,与M重合),此时若存在这样的定点N满足题意,则必为,下证:点满足题意,设圆上任意一点P(x,y),则(y﹣4)2=4﹣x2∴==,∴综上可知,在直线MC上存在定点,使得为常数.22.(12分)已知向量,,且向量∥.(Ⅰ)求函数y=f(x)的解析式及函数的定义域;(Ⅱ)若函数g(θ)=﹣cos2θ﹣a sinθ+2,存在a∈R,对任意,总存在唯一,使得f(x1)=g(θ0)成立,求实数a的取值范围.【考点】GL:三角函数中的恒等变换应用.【解答】解:(Ⅰ)…(2分)有意义则∴,k∈z解得,定义域为,k∈z…(4分)(Ⅱ)=,∵,∴﹣3≤log3x≤1∴函数f(x)的值域为[0,4].…(5分)g(θ)=﹣cos2θ﹣a sinθ+2=sin2θ﹣a sinθ+1,t=sinθ则ϕ(t)=g(θ)=t2﹣at+1,﹣1≤t ≤1由题意知:[0,4]⊆{y|y=t2﹣at+1,﹣1≤t≤1},且对任意y∈[0,4],总存在唯一,使得y=g(θ0),即存在唯一t0∈[﹣1,1],使得y=ϕ(t0)…(8分)以下分三种情况讨论:①当即a≤﹣2时,则,解得a≤﹣2;…(9分)②当时,则,解得a≥2;…(10分)③当时,则或解得a∈φ…(11分)综上a≥2或a≤﹣2…(12分)。
辽宁省瓦房店市高级中学2016-2017学年高二下学期期末考试数学(理)试题

试卷第1页,共6页绝密★启用前辽宁省瓦房店市高级中学2016-2017学年高二下学期期末考试数学(理)试题试卷副标题考试范围:xxx ;考试时间:66分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、设正实数 满足.则当 取得最大值时,的最大值为( )A .0B .C .1D .32、已知函数,若,,使得,则实数的取值范围是( )A .(-∞,1]B .[1,+∞)C .(-∞,2]D .[2,+∞)3、已知命题 ,;命题,使则下列命题中为真命题的是( )试卷第2页,共6页A .B .p ∧(q )C .D .4、在△ABC 中,若,且则A =( )A .B .C .D .5、把函数 的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象上所有点向左平移个单位长度,得到图象的函数解析式为( )A .B .C .D .6、中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( ) A .192 里 B .96 里 C .48 里 D .24 里7、已知满足线性约束条件:,则目标函数的取值范围是( )A .B .C .D .8、的 ( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件试卷第3页,共6页9、若,则( )A .B .C .D .10、设等差数列 取最小值时, 等于( )A .9B .8C .7D .611、设全集( )A .(0,1]B .[-1,1]C .(1,2]D .(-∞,-1]∪[1,2]12、 是虚数单位,复数的共轭复数是( )A .2-iB .2+iC .-1+2iD .-1-2i试卷第4页,共6页第II 卷(非选择题)二、填空题(题型注释)13、若函数在上存在单调递增区间,则的取值范围是________.14、在中,若,三角形的面积,则三角形外接圆的半径为________.15、函数的值域是________.16、函数的最小正周期为___________ .三、解答题(题型注释)17、设. (1)讨论函数的极值;(2)当时,,求的取值范围.18、(本小题满分15分)在直三棱柱中,底面是边长为2的正三角形,是棱的中点,且.试卷第5页,共6页(1)试在棱上确定一点,使平面;(2)当点在棱中点时,求直线与平面所成角的大小的正弦值。
辽宁省大连市第二十高级中学2016-2017学年高一数学下学期期末考试试卷

3
(Ⅰ)关于 x 的不等式 (m 3) x 2 (m 3) x 1 0 的解集为 R ,求实数 m 的取值范围 ; (Ⅱ) 关于 x 的不等式 x 2 ax 4 0 的解集为 {x | x b} ,求 a, b 的值.
18.(本小题满分12分) 已知 (0, ), sin cos (Ⅰ) 求 sin cos 的值; (Ⅱ) 求 sin( 2
1 3 ,则 cos( ) 3 2
(C) 8
(D) 10
(A)
2 2 3
(B)
2 2 3
(C)
1 3
(D)
1 3
5. tan105 (A) 2 3 (B) 1 3 (C)
3 3 3
( D) 2 3
6.若等比数列前 n 项和为 S n ,且满足 S 9 S 6 S 3 ,则公比 q 等于 (A) 1 (B) 1 1 (C) 1 (D) 不存在
(,7) (24,)
(C) (7,24) (D) (,24) (7,) 9. 在等差数列 a n 前 n 项和为 S n ,若 S 4 1, S 8 4 ,则 a17 a18 a19 a 20 的值为 (A) 9
17
(B) 12
(C) 16
(D)
(D)
卷Ⅱ 二、填空题:本大题共4小题,每小题5分,共20分. 13. 已知非零向量 a , b 满足| a b |=| a b |,则< a , b >=
.
14. 在 ABC 中,若 sin A ∶ sin B ∶ sin C 7 ∶ 8 ∶ 13 ,则 C ________
10. 在 ABC 中,角 A、B、C 对边分别为 a、b、c , A 60 , b 1 ,这个三角形的面积 为 3 ,则 ABC 外接圆的直径是 (A) 39
学16—17学年下学期高一期末考试英语试题(附答案)(3)

2016-2017学年度下学期瓦房店市高级中学期末考试高一英语试题第二部分阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的四个选项(A、B、C和D)中,选出最佳选项,并在答题卡上将该项涂黑。
ADream home in magical Lucas Valley. Room is rented for the summer. Would like to sign lease(租约)with the right person who is healthy and eco conscious.PREFER to offer rent reduction option for the right person, see below...3 beautiful bedrooms, about 10‟ x 11‟ with 4‟ window faces morning sun and beautiful view of courtyard garden and flowers. Can be furnished or unfurnished.Home features sunny island kitchen, floor to ceiling glass with garden views. Share use of all amenities of home, beautiful sunny yard, organic gardens, picnic table.Great outdoor pool, yoga and tennis 2 blocks away, 2 great farmers markets weekly 5 minutes away at SR Civic Center. Peaceful quiet neighborhood, easy parking right outside, 1.5 miles from 101, great access to all Bay Area.Please be healthy and environmentally conscious, clean and considerate, no smoking, no drugs, no pets. Quiet and friendly prof F (author, healer, consultant) —works from home p/t, 1 dog, NO cats, sorry NO pets possible - dog is NOT pet friendly.Partial rent reduction option available for the right person — read more if interested:Holistic health author seeking great reliable help with routine home and office help (filing, organizing papers) garden watering and dog walking (up to 5 hours per week, prefer 1 hour available each morning between 7-9am) or time on Saturdays, see details below, please leave your phone number in response.PLEASE PUT in your EMAIL:* your phone number* what date you are available to move in* what skills you can contribute21. What is the advantage of living in the advertised room?A. You can swim without leaving home.B. You can save some money by helping the owner.C. You can form a habit of protecting environment.D. You can enjoy the setting sun through the window.22. Who may be the right person to share the house with the author?A. Mary, an outgoing girl who loves animals and raises a cat.B. Mr Green, a warm-hearted man who smokes occasionally.C. Tom, a student who is thoughtful and helpful.D. Jim, a healthy young man who hates animals.23. How far is the house from 101, great access to all Bay Area?A. 2 blocks away.B. 5 minut es‟ walk.C. 1.5 miles.D. 2 miles.24. How can you get in touch with the author?A. By email.B. By telephone.C. In person.D.By fax.BYou‟re in a department store and you see a couple of attractive young women looking at a sweater.You listen to their conversation:“I can‟t believe it-a Lorenzo Bertolla! They are almost impossible to find.Isn‟t it beautiful? And it‟s a lot cheaper than the one Sara bought in Rome.”They leave and you go over to see this incredible sweater.It‟s nice an d the price is right.You‟ve never heard of Lorenzo Bertolla, but those girls looked really stylish.They must know.So, you buy it.You never realize that those young women are employees of an advertising agency.They are actually paid to go from store to store, talking loudly about Lorenzo Bertolla clothes.Every day we notice what people are wearing, driving and eating.If the person looks cool, the product seems cool, too.This is the secret of undercover marketing.Companies from Ford to Nike are starting to use it.Undercover marketing is important because it reaches people that don‟t pay attention to traditional advertising.This is particularly true of the MTV generation-consumers between theage of 18 and 34.It is a golden group.They have a lot of money to spend, but they don‟t trust ads.So advertising agencies hire young actors to “perform” in bars and other places here young adults go.Some people might call this practice deceptive(骗人的), but marketing executive Jonathan Ressler calls it creative.“Look at traditional advertising.Its effectiveness is decreasing.”However, one might ask what exactly is “real” about young women pretending to be enthusiastic about a sweater? Advertising executives would say it‟s no less real than an ad.The difference is that you know an ad is trying to persuade you to buy something.You don‟ t know when a conversation you overhear is just a performance.25.The two attractive young women were talking so that they could _____.A.get the sweater at a lower price B.be heard by people aroundC.be admired by other shoppers D.decide on buying the sweater26.The underlined words Lorenzo Bertolla is _____.A.a very popular male singer B.an advertising agencyC.a clothing company in Rome D.the brand name of a sweater27.Which of the following can be inferred from the passage?A.The two girls are in fact employed by the Lorenzo Bertolla Company.B.The MTV generation tend to be more easily influenced by ads.C.Traditional advertising is becoming less effe ctive because it‟s too direct.D.Undercover marketing will surely be banned soon by the government.28.Which of the following would be the best title for the text?A.Two Attractive Shoppers B.Lorenzo Bertolla SweatersC.Ways of Advertising D.Undercover MarketingCWe have two dogs and offer them good food and a comfortable bed. However, they always try to run away. One day as I was walking them along the river, Cady broke away from me. I called for her to return, but she didn‟t. I got unhappy and didn‟t run after her.That afternoon I picked my daughter up from school and I told her that Cady might be missing. “If she has done something wrong, I will not be paying her fines this time,” I said. Mydaughter asked for the reason. I insisted that I would not keep a disobedient (不听话的) dog.I took a glance over my daughter. It seemed that the thought of losing the dog was very painful to her. I think I have given Cady a good living environment. If she is silly enough to leave all that behind, then “bye-b ye” is my attitude.In a warm and tender moment that brings tears to my eyes, my daughter said, “Dad, you don‟t understand. Cady is not pretty and not even well trained. If she is missing, no one will adopt her. That means she will die.”Then I remembered that the reason why I kept the stray (流浪的) dog in the first place was that we could not find a home for her and did not want her to be destroyed. My heart softened.As we pulled into the driveway, there stood Cady in the backyard with a lovely expression. My neighbor told me that she was clever enough to find her way back. My daughter jumped with joy.29. Which of the following is TRUE according to the second paragraph?A. The owner will be fined if his dog does something wrong.B. The author had difficulty getting along with the dog.C. The author wanted to get rid of the dog on purpose.D. The author was quite worried after the dog lost.30. What the author‟s daughter said in the fourth paragraph suggested that __________.A. she was angry with the stupid dogB. she wanted to train the dog wellC. she was sure the dog would returnD. she was quite worried about the dog31. What was the author reminded of after hearing his daughter‟s words?A. How his daughter loved Cady.B. When Cady became his friend.C. Why they adopted Cady.D. Where Cady was trained.32. We can infer from the text that __________ .A. the author was happy about the dog‟s returnB. it‟s the author‟s job to collect stray dogsC. the author has no experience in keeping dogsD. the author didn‟t want the dog to come backDPeople are being attracted to Facebook with the promise of a fun, free service withoutrealizing they‟re paying for it by giving up large amounts of personal information. F acebook then attempts to make money by selling their data to advertisers that want to send targeted messages.Most Facebook users don‟t realize this is happening. Even if they know what the company is up to, they still have no idea what they‟re paying for Facebook because people don‟t really know what their personal information is worth.The biggest problem, however, is that the company keeps changing the rules. Early on, you keep everything private. That was the great thing about Facebook — you could create your own little private network. Last year, the company changed its privacy rules so that many things —your city, your photo, your friends‟ names—were set, by default (默认) to be shared with everyone on the Internet.According to Facebook‟s vice-president Elliot Schrage, the company is simply making changes to improve its service, and if people don‟t share information, they have a "less satisfying experience".Some people think this is more about Facebook looking to make more money. Its original business model, which was about selling ads and putting them at the side of the page, totally failed. Who wants to look at ads when they‟re online connecting with their friends?The privacy issue has already landed Facebook in hot water in Washington. In April, Senator Charles Schumer called on Facebook to change its privacy policy. He also urged the Federal Trade Commission to set guidelines for social-networking sites. "I think the senator rightly communicated that we had not been clear about what the new products were and how people could choose to use them or not to use them,"Schrage admits.I think that whatever Facebook has done so far to invade our privacy is only the beginning, which is why I‟m considering stopping using it. Facebook is a convenient site, but I‟m upset by the idea that my information is in the hands of people I don‟t know. That‟s too high a price to pay.33. What is the main idea of the passage?A. Facebook is becoming a more useful site.B. Facebook is improving its service gradually.C. Facebook is stealing and selling users‟ information.D. Facebook is losing more customers.34. What did Facebook‟s business model include at the beginning?A. Selling its service.B. Selling ads.C. Selling its products.D. Selling personal information.35. According to the writer, why Facebook make changes to its rule?A. To provide better service to its users.B. To follow the Federal guidelines.C. To encourage its users‟ communication.D.To gain its users‟ more personal information.第二节(共5小题;每小题2分,满分10分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项。
辽宁省瓦房店市2016-2017学年高二数学下学期期末考试试题 理(含解析)

2016-2017学年度下学期瓦房店市期末考试高二数学试题(理科)考试时间:120分钟试卷满分:150分一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 是虚数单位,复数的共轭复数是( )A. 2-iB. 2+iC. -1+2iD. -1-2i【答案】B【解析】,那么它的共轭复数为,故选B.2. 设全集 ( )A. (0,1]B. [-1,1]C. (1,2]D. (-∞,-1]∪[1,2]【答案】C【解析】由中不等式解得:,即,,由中不等式变形得:,解得:则,故选C.3. 设等差数列取最小值时,等于( )A. 9B. 8C. 7D. 6【答案】D【解析】由等差数列的性质可得,解得,又,设公差为,所以,解得,则,所以,所以当时,取最小值,故选D.4. 若,则 ( )A. B. C. D.【答案】A【解析】,,故选A.5. 的 ( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】B【解析】,时必有,当时,不一定成立,即的必要不充分条件,故选B.6. 已知满足线性约束条件:,则目标函数的取值范围是()A. B. C. D.【答案】C【解析】画出性约束条件:表示的可行域,如图,由图由得由得,因为经过点时,,经过时,所以的取值范围是,故选C.【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值,属简单题.求目标函数最值的一般步骤是“一画、二移、三求”:(1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.7. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( )A. 192 里B. 96 里C. 48 里D. 24 里【答案】B【解析】记每天走的路程里数为,易知是公比为的等比数列,由题意知,故选B.8. 把函数的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象上所有点向左平移个单位长度,得到图象的函数解析式为( )A. B.C. D.【答案】C【解析】将函数的图象上所有点的横坐标变为原来的倍(横坐标不变),可得的图象;再将所得到的图象上所有点向左平移个单位,所得函数图象的解析式为,故选C.9. 在△ABC中,若,且则A=( )A. B. C. D.【答案】A【解析】因为在中,,由正弦定理可得,,即,解得,所以由余弦定理可得,,故选A.10. 已知命题,;命题,使则下列命题中为真命题的是( )A. B. p∧(q) C. D.【答案】D【解析】由题意可知,命题为假命题,则为真命题;命题为真命题,则为假命题,所以由真值表可得,为真命题,为假命题,为假命题,为假命题,故选D...................11. 已知函数,若,,使得,则实数的取值范围是( )A. (-∞,1]B. [1,+∞)C. (-∞,2]D. [2,+∞)【答案】A【解析】当时,由得,,令,解得,令,解得,在单调递减,是函数的最小值,当时,为增函数,是函数最小值,又,都在,使得,可得在的最小值不小于在的最小值,即,解得,故选A.【方法点睛】本题主要考查函数的最值、全称量词与存在量词的应用.属于难题.解决这类问题的关键是理解题意、正确把问题转化为最值和解不等式问题,全称量词与存在量词的应用共分四种情况:(1)只需;(2),只需;(3),只需;(4),,.12. 设正实数满足.则当取得最大值时,的最大值为( )A. 0B.C. 1D. 3【答案】C【解析】,又均为正实数,(当且仅当时取“=”),,此时,,,当且仅当时取得“=”,满足题意,的最大值为,故选C.【易错点晴】本题主要考查利用基本不等式求最值,属于难题.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用或时等号能否同时成立).二、填空题:本题共4小题,每小题5分,共20分。
2016-2017学年高一下学期期末考试数学试题(有答案)
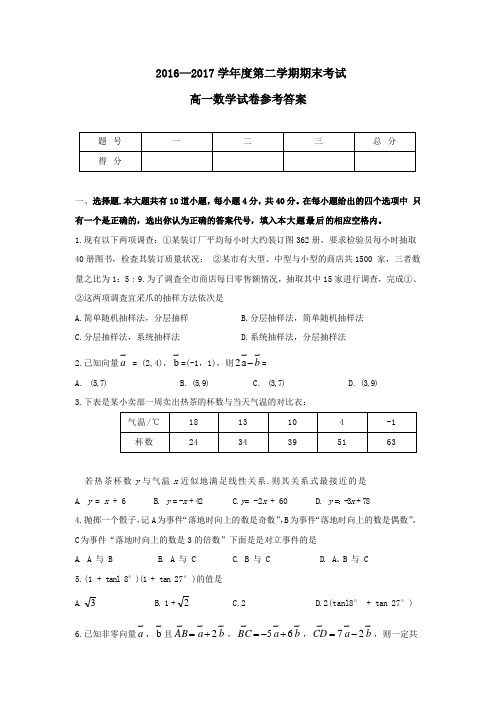
2016—2017学年度第二学期期末考试高一数学试卷参考答案一、选择题.本大题共有10道小题,每小题4分,共40分。
在每小题给出的四个选项中只有一个是正确的,选出你认为正确的答案代号,填入本大题最后的相应空格内。
1.现有以下两项调查:①某装订厂平均每小时大约装订图362册,要求检验员每小时抽取40册图书,检査其装订质量状况;②某市有大型、中型与小型的商店共1500 家,三者数量之比为1:5 : 9.为了调査全市商店每日零售额情况,抽取其中15家进行调查,完成①、②这两项调査宜采爪的抽样方法依次是A.简单随机抽样法,分层抽样B.分层抽样法,简单随机抽样法C.分层抽样法,系统抽样法D.系统抽样法,分层抽样法2.己知向量→a = (2,4),→b=(-1,1),则→→a2b-=A. (5,7)B. (5,9)C. (3,7)D. (3,9)3.下表是某小卖部一周卖出热茶的杯数与当天气温的对比衣:若热茶杯数y与气温x近似地满足线性关系.则其关系式最接近的是A. y = x + 6B. y =-x+42C.y= -2x + 60D. y=:-3x+784.抛掷一个骰子,记A为事件“落地时向上的数是奇数”,B为事件“落地时向上的数是偶数”,C为事件“落地时向上的数是3的倍数”下面是是对立事件的是A. A 与 BB. A 与 CC. B 与 CD. A、B 与 C5.(1 + tanl 8°)(1 + tan 27°)的值是A.3B.1+2C.2D.2(tanl8° + tan 27°)6.已知非零向量→a,→b且→→→2baAB+=,→→→65baBC+-=,→→→27baCD-=,则一定共线的三点 是A. A 、B 、DB. A 、B 、CC. B 、C 、DD. A 、C 、D7.如图,是由一个圆、一个三角形和一个长方形构成的组合体,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则三个形状颜色不全相同的概率为A.43B.83C.41D.818.阅读程序框图,若输入m=4, n=6,则输出a ,i 分别是 A.a =12,i = B.a =12,i =3 C.a =8,i =4 D.a =8,i =3 9.若α,β为锐角,且满足cos α=54,cos (α+β)=135。
2016-2017高一下期末数学试题(7)

2016-2017学年高一下期期末考试试卷(7)数学(120分钟 150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长是( )A .2B .sin2 C.2sin1D .2sin12.如图所示是一样本的频率分布直方图,则由图形中的数据, 可以估计众数、中位数与平均数分别为( )A .10 13 12 B. 12.5 13 12 C .12.5 13 13 D. 12.5 15 123.在区间[1,1]-上任取三点,则它们到原点O 的距离平方和小于1的概率为( )A. π/9B. π/8C. π/6D. π/44.设a ,b 是两个非零向量.( )A.若||||||a b a b +=-,则a b ⊥B.若a b ⊥,则||||||a b a b +=-C.若||||||a b a b +=-,则存在实数λ,使得a b λ=D.若存在实数λ,使得a b λ=,则||||||a b a b +=-5.以下给出的是计算12+14+16+…+120的值的一个程序框图,其中判断框内应填入的条件是( )A .i<20?B .i>10?C .i<10?D .i≤10?6.若将函数cos()sin()(0,0)66y A x x A ππωω=-⋅+>>的图像向左平移6π个单位后得到的图像关于原点对称,则ω的值可能为( )A.2B.3C.4D.57.在两个袋内,分别装着写有0,1,2,3,4,5六个数字的6张卡片,今从每个袋中各任取一张卡片,则两数之和等于5的概率为( ) A.31 B.61 C.91 D.121 气温/℃ 18 13 10 4 -1 杯数2434395163若热茶杯数y 与气温x 近似地满足线性关系,则其关系式最接近的是( ) A.y=x+6 B.y=-x+42 C.y=-2x+60 D.y=-3x+789.若,A B 是锐角ABC ∆的两个内角,则点P (cos sin ,sin cos )B A B A --在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 10.函数22()cos 2cos 2xf x x =-的一个单调增区间是( ) A.2()33ππ,B.()62ππ,C.(0)3π,D.()66ππ-,11.()22sin 50sin1013tan102sin 80⎡⎤︒+︒+︒︒=⎣⎦( )A. 22B. 23C. 15D. 612.已知向量(2,0)OB =,向量(2,2)OC =,向量(2cos ,2sin )CA αα=,则向量OA 与向量OB 的夹角的取值范围是( )A.[0,]4πB.5[,]412ππC.5[,]122ππD.5[,]1212ππ二、填空题(本大题共4小题,每小题5分,共20分)13.已知锐角α终边上一点P 的坐标是(4sin 3,4cos3),-则α等于 . 14.设1,e 2e 为单位向量,且1,e 2e 的夹角为3π,若123a e e =+,12b e =,则向量a 在b 方向上的投影为 .15.已知[0,],()sin(cos )x f x x π∈=的最大值为,a 最小值为,()cos(sin )b g x x =的最大值为,c 最小值为d ,则,,,a b c d 的大小关系为 .16.设两个向量22(2,cos )a λλα=+-和(,sin )2mb m α=+,其中,,m λα为实数.若2a b =,则mλ的取值范围是 .三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤)17.(本小题10分)在郑州外国语学校举行的电脑知识竞赛中,将高一两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40. (1)求第二小组的频率,并补全这个频率分布直方图; (2)求这两个班参赛的学生人数是多少?(3)这两个班参赛学生的成绩的中位数应落在第几小组内? (不必说明理由) .18.已知向量(cos ,3cos )33x x m =,(sin,cos )33x xn =,()f x m n =⋅. (1)求函数()f x 的单调区间;(2)如果先将()f x 的图象向左平移(0)ϕϕ>个单位,再保持纵坐标不变,横坐标变为原来的13倍,得到函数()g x 的图象,若()g x 为偶函数,求ϕ的最小值.19.随机地把一根长度为8的铁丝截成3段.(1)若要求三段的长度均为正整数,求恰好截成三角形三边的概率. (2)若截成任意长度的三段,求恰好截成三角形三边的概率.20.已知ABC ∆的面积S 满足13S ≤≤,且2,AC CB ACB θ⋅=-∠= ; (1)求函数()sin 42sin cos cos 244f ππθθθθθ⎛⎫⎛⎫=-+-+- ⎪ ⎪⎝⎭⎝⎭的最大值;(2)若 ()()sin 2,cos2,cos2,sin 2m A A n B B ==,求23m n -的取值范围.甲 82 82 79 95 87 乙9575809085(2)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;(3)现要从甲、乙两人中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参赛更合适?并说明理由.22.如图,开发商欲对边长为1km 的正方形ABCD 地段进行市场开发,拟在该地段的一个角建设一个景观,需要建一条道路EF (点,E F 分别在,BC CD 上),根据规划要求CEF ∆的周长为2km . (1)设,BAE DAF αβ∠=∠=,试证明4παβ+=.(2)欲使EAF ∆的面积最小,试确定点,E F 的位置.2016-2017学年高一下期期末考试试卷答案一.选择题CCCCD DBCBA DD 二.填空题 13.32π-; 14.52; 15.c a d b >>>; 16.[6,1]- 三.解答题17.解: (1)各小组的频率之和为1.00,第一、三、四、五小组的频率分别是0.30,0.15,0.10,0.05. ∴第二小组的频率为:1.00-(0.30+0.15+0.10+0.05)=0.40.∴落在59.5~69.5的第二小组的小长方形的高=频率组距=0.4010=0.04.则补全的直方图如图所示.(2)设九年级两个班参赛的学生人数为x 人. ∵第二小组的频数为40人,频率为0.40, ∴40x=0.40,解得x =100(人). 所以九年级两个班参赛的学生人数为100人. (3)∵0.3×100=30,0.4×100=40,0.15×100=15,0.10×100=10,0.05×100=5,即第一、第二、第三、第四、第五小组的频数分别为30,40,15,10,5,所以九年级两个班参赛学生的成绩的中位数应落在第二小组内.18.解:(1)21232323()cos sin 3cos sin cos sin()33323333x x x x x x f x π=+=++=++由2222332x k k πππππ-≤+≤+,得533()44k x k k Z ππππ-≤≤+∈ ∴ 函数()f x 的单调递增区间为5[3,3]()44k k k Z ππππ-+∈ 由23222332x k k πππππ+≤+≤+,得733()44k x k k Z ππππ+≤≤+∈ ∴函数()f x 的单调递增区间为7[3,3]()44k k k Z ππππ++∈. (2)由题意图象变换,得23()sin(2)33g x x πϕ=+++ ∵()g x 是偶函数,∴2332k ππϕπ+=+,3,24k k Z ππϕ=+∈∵0ϕ>,∴当0k =时,ϕ有最小值4π. 19.解:(1)试验发生包含的基本事件数为21种情况,可以列举出所有结果: (1,1,6),(1,2,5),(1,3,4),(1,4,3), (1,5,2),(1,6,1),(2,1,5),(2,2,4), (2,3,3),(2,4,2),(2,5,1),(3,1,4), (3,2,3),(3,3,2),(3,4,1),(4,1,3), (4,2,2),(4,3,1),(5,1,2),(5,2,1), (6,1,1),记事件A 为“能构成三角形”,有3种情况:(2,3,3),(3,2,3),(3,3,2). ∴所求的概率是31()217P A ==. (2)设把铁丝分成任意的三段,其中第一段为x ,第二段为y ,则第三段为8x y --,⎪⎩⎪⎨⎧>-->>0800y x y x记事件A 为“能构成三角形”,如果要构成三角形,则必须满足:84(8)4.(8)4x y x y x y x x y y y y x y x x +>--+>⎧⎧⎪⎪+--><⎨⎨⎪⎪+--><⎩⎩,即∴所求的概率为11612.14642()P A ⨯=⨯=20.解:(1)如图:由2,CA CB ACB θ⋅=∠=;得sin 2ab θ=,1sin tan 2S ab θθ==∵1S ≤≤∴1tan θ≤≤()0,θπ∈;∴43ππθ≤≤; ∵ ())2sin cos 22f θθθθ=--;sin cos 4t πθθθ⎛⎫=-=- ⎪⎝⎭;∵43ππθ≤≤ ∴0412ππθ≤-≤从而0t ⎡∈⎢⎣⎦∴())212f t θ=+--;22=+ ;∵104t ⎡=∈⎢⎣⎦;∴当14t =时,()f t 有最大值()f t =(2)∵()()sin 2,cos2,cos2,sin 2m A A n B B == ; (3) ∴22sin 2cos 21,1m A A n =+==sin 2cos 2cos 2sin 2m n A B A B ⋅=+ ()()sin 2sin 22A B C π=+=-sin 2sin 2C θ=-=- ∴22234129m n m m n n -=-⋅+1312sin 2θ=+∵43ππθ≤≤∴2223ππθ≤≤; 235m n -≤故23m n -的取值范围为⎤⎥⎦21.解:(1)茎叶图略;(2)取甲乙两人的成绩,所有可能的基本事件有:(82,95)(82,75)(82,80)(82,90)(82,85)(82,95)(82,75)(82,80)(82,90)(82,85)(79,95)(79,75)(79,80)(79,90)(79,85)(95,95)(95,75)(95,80)(95,90)(95,85)(87,95)(87,75)(87,80)(87,90)(87,85)共25个, 记“甲的成绩比乙的成绩高”为事件A ,事件A 包含的基本事件数为12个,所以2512)(=A P (3).s s 50s 6.31s 85852222参赛比较合适甲的成绩较稳定,派甲,;,,,,乙甲乙甲乙甲乙甲∴<=====x x x x22.解: (1)设,(01,01),CE x CF y x y ==<≤<≤则tan 1,tan 1,x y αβ=-=-由已知得,2,x y +=即2()2x y xy +-=,tan tan 2()tan()1,0,.1tan tan 24x y x y xy αβππαβαβαβαβ+-+∴+===<+<∴+=-+-(2)由(1)可知,11sin 244cos cos EAF S AE AF EAF AE AF αβ∆=⋅⋅∠=⋅=⋅2111.4sin 22coscos cos())144ππααααα=⋅==+-++0,2,4428ππππααα<<∴+=∴=时,EAF ∆的面积最小,最小面积为 1.-22tan8tan,tan 1,481tan 8ππππ=∴=-故此时1,BE DF == 所以,当1BE DF ==时,EAF ∆的面积最小.。
数学卷·2019届辽宁省大连市高一下学期期末考试(2017.07)(必修3,4)

2016~2017学年度第二学期期末考试试卷高一数学第Ⅰ卷选择题(共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.求值tan()为( )A.1B.C.D.2.对于线性回归方程,下列说法中不正确...的是()A.叫做回归系数B.当>0,每增加一个单位,平均增加个单位C. 回归直线必经过点D.叫做回归系数3.某公司生产三种型号的轿车,产量分别是1600辆、6000辆和2000辆,为检验公司的产品质量,现从这三种型号的轿车中抽取48辆进行检验,这三种型号的轿车应抽取的数量依次为()A.16,16,16B.8,30,10C.4,33,11D.12,27,94.已知点A(2,3),B(,1),C(,2),若∥,则( )A.3B.2C.-2D.15.执行如图所示的程序框图,若输出的b的值为16,则图中判断框内①处应填的值为( )A.3B.4C.5D.26.已知sin α=,sin(α-β)=-,α,β均为锐角,则等于( )A. B.1 C. D.7.把函数y =sin x (x ∈R )的图象上所有点向左平行移动个单位长度,再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所表示的函数是( )A.y =sin ,x ∈RB.y =sin ,x ∈RC.y =sin ,x ∈RD.y =sin ,x ∈R8.以下程序运行的结果是( )A.60137B.60133C.60131D.601219.在平行四边形ABCD 中,E 、F 分别是边和的中点,若其中R ,则( )A. B.2 C. D.110.在斜三角形ABC 中,( )A.1B.C.2D.11.在△ABC 中,若,则△ABC 的形状是( )A.锐角三角形 B .直角三角形 C.钝角三角形 D.等腰直角三角形12.设函数.若存在的一条对称轴,满足成立,则的取值范围是( )A.B.C. D.第Ⅱ卷非选择题(共90分)二.填空题(本大题共4小题,每小题5分,共20分,把答案填在答卷卡的相应位置上)13.已知角的终边经过则.14.函数y=Asin(ωx+φ)部分图象如图,则函数解析式为.15.向量a、b ,已知a=(2,1),a·b=10,|a+b|=5,则|b|=.16.在上随机取一个值,使得关于的方程有实根的概率为.三.解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)同时抛掷甲、乙两颗骰子.(1)求事件A“甲的点数大于乙的点数”的概率;(2)若以抛掷甲、乙两颗骰子点数m,n作为点P的坐标(m,n),求事件B“P落在圆内”的概率.18.(本小题满分12分)如图,在平面直角坐标系中,角的终边OP与单位圆交于点P,角的终边OQ与单位圆交于点Q.(1)写出P、Q两点的坐标;(2)试用向量的方法证明关系式:.19.(本小题满分12分)某赛季甲、乙两名篮球运动员每场比赛得分情况如下表:(1)绘制两人得分的茎叶图;(2)分析并比较甲、乙两人七场比赛的平均得分及得分的稳定程度.20.(本小题满分12分)如图,在△ABC中,角A,B,C所对的边分别为a,b,c,且.(1)求角A的大小;(2)若是的角平分线,,求的长.21.(本小题满分12分)如图,两条公路AP与AQ夹角A为钝角,其正弦值是.甲乙两人从A点出发沿着两条公路进行搜救工作,甲沿着公路AP方向,乙沿着公路AQ方向.(1)当甲前进5km的时候到达P处,同时乙到达Q处,通讯测得甲乙两人相距km,求乙在此时前进的距离AQ;(2)甲在5公里处原地未动,乙回头往A方向行走至M点收到甲发出的信号,此时M点看P、Q两点的张角为(张角为QMP),求甲乙两人相距的距离MP的长.22.(本小题满分12分)已知函数的图象与直线y=2相交,且两相邻交点之间的距离为.(1)求;(2)已知函数,若对任意的,均有,求的取值范围.2016~2017学年度第二学期期末考试试卷高一数学参考答案:一、选择题DDBCA CCACB BA二、填空题13. 14. 15. 5 16.17.基本事件空间{(1,1),(1,2)…(6,6)}共36个…………………………………2分(1)事件A包括(2,1)(3,1)(3,2)(4,1)(4,2)(4,3)(5,1)(5,2)(5,3)(5,4)(6,1)(6,2)(6,3)(6,4)(6,5)共15个所以,P(A)= ………………………………………………………………..6分(2)事件B包括(1,1)(1,2)(1,3)(1,4)(2,1)(2,2)(2,3)(2,4)(3,1)(3,2)(3,3)(4,1)(4,2)共13个所以P(B)= ………………………………………………………………………..10分18.(1)P(),Q()…………………………… ..……2分(2)19.解:(1)如图…………………………….4分(2)甲的平均得分方差……………………7分乙的平均得分方差 ………………10分∴,则这七场比赛甲的平均得分低于乙,但甲的得分更稳定一些…12分20.解(1)2a cos C -c =2b ,由正弦定理得 2sin A cos C -sin C =2sin B ,2sin A cos C -sin C =2sin(A +C ) =2sin A cos C +2cos A sin C ,…………….2分 ∴-sin C =2cos A sinC ,∵sin C ≠0,∴cos A =-2 1, …………… …4分 而A ∈(0, π),∴A =32π. ……………………………………6分(2)在△ABC 中,由余弦定理得,21.解:(1)在△APQ 中,由余弦定理得,…………………………..4分代入上式, 则 ………………………..……………….…6分(2)在△APM 中,可知………………………………………………………..….….12分22.解:(1)与直线y=2的图象的两相邻交点之间的距离为.则T=.所以单调增区间……………………………….. ..6分(2)由,得……………………………………….……8分,当时,,要使恒成立,只需,解得………………………………………………10分当时,,要使恒成立,只需,矛盾.综上的取值范围是…………………………………………………12分。
辽宁省瓦房店市高级中学2016-2017学年高二下学期期末考试数学(理)试题含答案

2016-2017学年度下学期瓦房店市高级中学期末考试高二数学试题(理科)考试时间:120分钟 试卷满分:150分 命题与校对:虞政华一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. i 是虚数单位,复数错误!的共轭复数是( )A .2-iB . 2+iC .-1+2iD .-1-2i2。
设全集U =R ,已知集合A ={x ||x |≤1},B ={x |log 2x ≤1},则(∁U A )∩B =( )A .(0,1]B .C .(1,2]D .(-∞,-1]∪3。
设等差数列{a n }的前n 项和为S n ,若a 1=-11,a 3+a 7=-6,则当S n 取最小值时,n 等于( )A .9B .8C .7D .64. 若3sin()45πα-=,则=+)2sin(απ ( ) A .725-B .725C .15-D .155. “x <0”是“-1< x <0”的 ( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6。
已知,x y 满足线性约束条件:1022010x y x y x -+≥⎧⎪+-≥⎨⎪-<⎩,则目标函数x y z 3-=的取值范围是( )A .)31,1(-- B .)1,3(-- C . ]31,3(- D . ]31,3[- 7. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了( ) A .192 里 B .96 里 C .48 里 D .24 里8. 把函数y =sin x (x ∈R)的图象上所有点的横坐标变为原来的2倍(纵坐标不变),再把所得图象上所有点向左平移3π个单位长度,得到图象的函数解析式为( )A .y =sin 错误!B .y =sin 错误!C .y =sin 错误!D .y =sin 错误!9. 在△ABC 中,若)cos cos (322A b B a b b a +=-,且错误!=2错误!, 则A =( )A.错误! B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
辽宁省大连市瓦房店高中2016-2017学年高一(下)期末数学试卷(理)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求)1.(5分)已知全集U={0,1,2,3,4,5},集合A={1,2,3,5},B={2,4},则(∁U A)∪B为()A.{0,2,3,4} B.{4} C.{1,2,4} D.{0,2,4}2.(5分)已知l,m为直线,α为平面,l∥α,m⊂α,则l与m之间的关系是()A.平行B.垂直C.异面D.平行或异面3.(5分)设x1,x2,…,x n的平均数为,标准差是s,则另一组数2x1﹣3,2x2﹣3,…,2x n﹣3的平均数和标准差分别是()A.2,4s B.2﹣3,4s C.2﹣3,2s D.2,s4.(5分)幂函数f(x)=(m2﹣2m+1)x2m﹣1在(0,+∞)上为增函数,则实数m的值为()A.0 B.1 C.2 D.1或25.(5分)已知向量,,且与的夹角为钝角,则实数x的取值范围为()A.B. C.D.且6.(5分)设a=sin33°,b=cos55°,c=tan35°,则()A.a>b>c B.b>c>a C.c>b>a D.c>a>b7.(5分)我国古代名著《九章算术》中有这样一段话:“今有金锤,长五尺,斩本一尺,重四斤.斩末一尺,重二斤.”意思是:“现有一根金锤,头部的1尺,重4斤;尾部的1尺,重2斤;且从头到尾,每一尺的重量构成等差数列.”则下列说法错误的是()A.该金锤中间一尺重3斤B.中间三尺的重量和是头尾两尺重量和的3倍C.该金锤的重量为15斤D.该金锤相邻两尺的重量之差的绝对值为0.5斤8.(5分)在区间[0,π]上随机取一实数x,则事件“”发生的概率为()A.B.C.D.9.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若a cos B+b cos A=c sin C,S=(b2+c2﹣a2),则∠B=()A.90°B.60°C.45°D.30°10.(5分)若[x]表示不超过x的最大整数,则图中的程序框图运行之后输出的结果为()A.49850 B.49900 C.49800 D.4995011.(5分)已知sinα﹣sinβ=1﹣,cosα﹣cosβ=,则cos(α﹣β)=()A.﹣B.﹣ C.D.12.(5分)已知函数f(x)=cos2+sinωx﹣(ω>0),x∈R,若f(x)在区间(π,2π)内没有零点,则ω的取值范围是()A.(0,] B.(0,]∪[,)C.(0,] D.(0,]∪[,]二、填空题(本大题共4小题,每小题5分)13.(5分)从编号为0,1,2,…,79的80件产品中,采用系统抽样的方法抽取容量为5的一个样本,若编号为42的产品在样本中,则该样本中产品的最小编号为.14.(5分)与向量=(3,4)垂直且模长为2的向量为.15.(5分)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为.16.(5分)三角形ABC中,BC=4,且sin AcotB+cos A=,则三角形ABC面积最大值为.三、解答题(解答应写出文字说明,证明过程或演算步骤)17.(10分)已知.(1)求tan x;(2)求的值.18.(12分)△ABC的内角A,B,C的对边分别为a,b,c,已知2c﹣a=2b cos A.(1)求角B的大小;(2)若b=2,求a+c的最大值.19.(12分)2017年高考特别强调了要增加对数学文化的考查,为此瓦房店市高级中学高三年级数学组特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[50,60),[60,70),…,[90,100]分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).(1)求频率分布直方图中的x的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表,中位数请用分数表示);(2)若高三年级共有700名学生,试估计高三学生中这次测试成绩不低于70分的人数;(3)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求后两组中至少有1人被抽到的概率.20.(12分)如图,在四棱锥P﹣ABCD中,P A⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(1)证明:BE∥面APD;(2)证明BE⊥CD;(3)求三棱锥P﹣BDE的体积.21.(12分)已知等差数列{a n}的前n项和为S n,a3=7,S9=27.(1)求数列{a n}的通项公式;(2)若b n=|a n|,求数列{b n}的前n项和T n.22.(12分)已知圆O:x2+y2=r2(r>0)与直线x﹣y+2=0相切.(1)求圆O的方程;(2)过点(1,)的直线l截圆所得弦长为2,求直线l的方程;(3)设圆O与x轴的负半轴的交点为A,过点A作两条斜率分别为k1,k2的直线交圆O于B,C两点,且k1k2=﹣2,试证明直线BC恒过一个定点,并求出该定点坐标.【参考答案】一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求)1.D【解析】全集U={x∈N|x≤4}={0,1,2,3,4}∵A={0,1,3},B={1,3,4},∴A∩B={1,3},∴∁U(A∩B)={0,2,4},故选D.2.D【解析】∵l,m为直线,α为平面,l∥α,m⊂α,∴由线面平行的性质定理得l与m平行或异面.故选D.3.C【解析】设x1,x2,…,x n的平均数为,标准差是s,则另一组数2x1﹣3,2x2﹣3,…,2x n﹣3的平均数为,标准差为=2s.故选C.4.C【解析】∵幂函数f(x)=(m2﹣2m+1)x2m﹣1在(0,+∞)上为增函数,∴,解得m=2.故选C.5.D【解析】向量,,且,即x≠,•=2x﹣21,那么:向量,夹角的余弦值为<0即2x﹣21<0,解得:x,∴x且x≠,故选D.6.C【解析】由诱导公式可得b=cos55°=cos(90°﹣35°)=sin35°,由正弦函数的单调性可知b>a,而c=tan35°=>sin35°=b,∴c>b>a故选C.7.B【解析】由题意可知等差数列中a1=4,a5=2,则d=,∴,a1+a5=6,.∴S5=15.∴A正确,B错误,C正确,D正确.故选B.8.A【解析】由题意,在区间[0,π]上满足事件“”的x范围是[]∪[],由几何概型的公式得到所求概率为;故选A.9.C【解析】由正弦定理可知a cos B+b cos A=2R sin A cos B+2R sin B cos A=2R sin(A+B)=2R sin C=2R sin C•sin C∴sin C=1,C=.∴S=ab=(b2+c2﹣a2),解得a=b,因此∠B=45°.故选C.10.A【解析】根据题意,得;[x]表示不超过x的最大整数,且[]=[50.4]=50;所以,该程序框图运行后输出的结果中是39个0与40个1,40个2,40个3,…,40个49,0.4×4+1=17个50的和;所以输出的结果为S=40××49+(0.4×40+1)×50=49850.故选A.11.D【解析】∵sinα﹣sinβ=1﹣,cosα﹣cosβ=,∴(cosα﹣cosβ)2=,(sinα﹣sinβ)2=﹣.两式相加,得2﹣2cos(α﹣β)=2﹣.∴cos(α﹣β)=.故选D.12.D【解析】函数f(x)=cos2+sinωx﹣=cosωx+sinωx=sin(ωx+),可得T=≥π,0<ω≤2,f(x)在区间(π,2π)内没有零点,函数的图象如图两种类型,结合三角函数可得:或,解得ω∈(0,]∪[,].故选D.二、填空题(本大题共4小题,每小题5分)13.10【解析】样本间隔为80÷5=16,∵42=16×2+10,∴该样本中产品的最小编号为10,故答案为10.14.(,﹣)或(﹣,)【解析】设所求向量为(x,y),则3x+4y=0且=2,联立解得或故答案为(,﹣)或(﹣,)15.96+4(﹣1)π【解析】由三视图可知几何体为边长为4的正方体挖去一个圆锥得到的,圆锥的底面半径为2,高为2,∴圆锥的母线长为2;∴该正方体的平面面积为6×42﹣π×22=96﹣4π;又圆锥体的侧面面积为π×2×2=4π.∴该几何体的表面积为96﹣4π+4π=96+4(﹣1)π.故答案为96+4(﹣1)π.16.4【解析】三角形ABC中,sin AcotB+cos A=,可得:,即,由正弦定理可得:c=.BC=4,可得a=4.由余弦定理得:(b)2=a2+b2﹣4a•b cos C,即2b2+16b cos C﹣16=0,即b2+8b cos C﹣8=0∴cos C=,∴sin2C=1﹣cos2C=﹣,∵S△ABC=b•a sin C=×4b sin C=2b sin C,∴(S△ABC)2=4b2sin2C=4b2(﹣)=5b2﹣4﹣b4=96﹣(b2﹣40)2.当b2=40,即b=2时,三角形ABC面积取得最大值∴(S△ABC)2max=96,∴三角形ABC的面积的最大值为4.故答案为4.三、解答题(解答应写出文字说明,证明过程或演算步骤)17.解:(1)由题意可得:,∴,∴.(2)=====.18.解:(1)∵2c﹣a=2b cos A,∴根据正弦定理,得2sin C﹣sin A=2sin B cos A,∵A+B=π﹣C,可得sin C=sin(A+B)=sin B cos A+cos B sin A,∴代入上式,得2sin B cos A=2sin B cos A+2cos B sin A﹣sin A,化简得(2cos B﹣1)sin A=0∵A是三角形的内角可得sin A>0,∴2cos B﹣1=0,解得cos B=,∵B∈(0,π),∴B=;(2)由余弦定理b2=a2+c2﹣2ac cos B,得12=a2+c2﹣ac.∴(a+c)2﹣3ac=12,∴12≥(a+c)2﹣ac,(当且仅当a=c=2时)∴a+c≤4,∴a+c的最大值为4.19.解:(1)由频率分布直方图可得第4组的频率为1﹣0.1﹣0.3﹣0.3﹣0.1=0.2,故x=0.02.故可估计所抽取的50名学生成绩的平均数为:(55×0.01+65×0.03+75×0.03+85×0.02+95×0.01)×10=74(分).由于前两组的频率之和为0.1+0.3=0.4,前三组的频率之和为0.1+0.3+0.3=0.7,故中位数在第3组中.设中位数为t分,则有(t﹣70)×0.03=0.1,所以,即所求的中位数为(或写成)分.(2)由(1)可知,50名学生中成绩不低于70分的频率为0.3+0.2+0.1=0.6,由以上样本的频率,可以估计高三年级700名学生中成绩不低于70分的人数为700×0.6=420.(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在[70,80)这组的3名学生分别为a,b,c,成绩在[80,90)这组的2名学生分别为d,e,成绩在[90,100]这组的1名学生为f,则从中任抽取3人的所有可能结果为:(a,b,c),(a,b,d),(a,b,e),(a,b,f),(a,c,d),(a,c,e),(a,c,f),(a,d,e),(a,d,f),(a,e,f),(b,c,d),(b,c,e),(b,c,f),(b,d,e),(b,d,f),(b,e,f),(c,d,e),(c,d,f),(c,e,f),(d,e,f)共20种.其中后两组中没有人被抽到的可能结果为(a,b,c),只有1种,故后两组中至少有1人被抽到的概率为.20.(1)证明:取PD中点F,连接AF,EF,∵E,F分别是PC,PD的中点,∴∵,∴EF∥AB,EF=AB∴四边形ABEF是平行四边形,∴BE∥AF,又BE⊄面P AD,AF⊂面P AD∴BE∥面P AD,(2)证明:由P A⊥面ABCD,DC⊂面ABCD,∴P A⊥DC.,∴,∴AF⊥DC,且AF∥BE,∴BE⊥CD;(3)解:∵点E为棱PC的中点,P A⊥底面ABCD,∴.21.解:(1)等差数列{a n}的前n项和为S n,a3=7,S9=27.可得a1+2d=7,9a1+36d=27,解得a1=11,d=﹣2,∴a n=﹣2n+13;(2)因为a n=﹣2n+13,所以,a6=1,a7=﹣1,当n≤6且n∈N*时,T n=a1+a2+…+,当n≥7且n∈N*时,T n=(a1+a2+…+a6)﹣(a7+a8+…+a n)=n2﹣12n+72,综上,22.解:(1)∵圆O:x2+y2=r2(r>0)与直线x﹣y+2=0相切,∴圆心O到直线的距离d==2=r,∴圆O的方程为x2+y2=4;(2)若直线l的斜率不存在,直线l为x=1,此时直线l截圆所得弦长为2,符合题意;若直线l的斜率存在,设直线为y﹣=k(x﹣1),即3kx﹣3y+﹣3k=0,由题意知,圆心到直线的距离为d==1,解得:k=﹣,此时直线l为x+y﹣2=0,则所求的直线为x=1或x+y﹣2=0;(3)由题意知,A(﹣2,0),设直线AB:y=k1(x+2),与圆方程联立得:,消去y得:(1+k12)x2+4k12x+(4k12﹣4)=0,∴x A•x B=,∴x B=,y B=,即B(,),∵k1k2=﹣2,用代替k2得:C(,),∴直线BC方程为y﹣=(x﹣),即y﹣=(x﹣)(k12≠2),整理得:y=x+=(x+)(k12≠2),则直线BC定点(﹣,0).。
