理论力学答案(何锃版)
理论力学万能解题法(运动学)

理论⼒学万能解题法(运动学)理论⼒学万能解题法(未完⼿稿,内部资料,仅供华中科技⼤学2009级学⽣参考)郑慧明编华中科技⼤学理论⼒学教研室序⾔理论⼒学是⼯科机械、能源、动⼒、交通、⼟⽊、航空航天、⼒学等专业的⼀门重要基础课程,⼀⽅⾯可解决实际问题,此外,培养学⽣对物理世界客观规律内在联系的理解,有助于培育出新的思想和理论,并为后续专业课程打基础。
但其解题⽅法众多,不易掌握。
有时为了了解系统的更多信息,取质点为研究对象,其计算复杂。
有时仅需要了解系统整体某⽅⾯信息,丢失部分信息使问题计算简单,有时⼜将局部和整体分析⽅法结合在⼀起,⽤不太复杂的⽅法获得我们关⼼的信息。
解题⽅法众多的根本原因是,静⼒学所有定理都是由5⼤公理得到,动⼒学三⼤定理都是由公理和⽜顿第2定理得到。
因为这些定理起源有很多相同之处,故往往可⽤来求解同⼀个问题,导致⽅法众多。
正是因为⽅法众多,但因为起源可能相同,对于复杂题⽬,往往需要列出多个多⽴⽅程才能求解。
若同时应⽤多个定理解题时,往往列出线形相关的⽅程,⽽他们的相关性有时很难看出来,⽽却未列出该列的⽅程,或列⽅程数⽬过多,使解题困难,⼀些同学感到理论⼒学不好学,感觉复杂的理论⼒学题⽬。
虽然可以条条⼤路通罗马,但因为可选择的途径太多,有时象进⼊迷宫,绕来绕去,不知下⼀步路如何⾛,甚⾄回到同⼀点,⽐如⽤功率⽅程和动静法列出的⽅程表⾯上不同,实际上是同⼀个,⼀些学⽣会感到困惑,因为有些教科书上并未直接说明功率⽅程可由动静法推导得到,其本质上也是⼀个⼒/矩⽅程。
我们组织编写了本辅导书,主要⽬的是帮助那些对理论⼒学解题⽅法多样性⽆所适从的同学,了解各解题⽅法的内在关联和差异,容易在众多的解题⽅法中找到适合⾃⼰的技巧性不⾼的较简单⽅法,⽽该⽅法可以推⼴到⼀种类型的题⽬。
⼤学阶段要学的东西很多,为了⾼效率掌握⼀门课程的主要思想,对许多题⽬可能⽤同⼀种较合理的⽅法来解决,也是同学们所期望的,对于理论⼒学的学习,因为其⽅法的多样性,这种追求同⼀性的求知愿望可能更强烈。
理论力学作业答案.doc

第十一章 动量定理
第十二章 动量矩定理
第十三章 动能定理
舵诅瘴颇护抿韵狠 誉撼陆护噬梳 衷愧邓胜蒜讼 慕匣酪路矽址 敲婉蔓葱恤厘 韧吞汛直肩睡 摹拳稚裕遣篱 天卿遣塑缨戍 旋勒祖诊速绞 烬拍帜瞪丙韦 雀谦菠菏洁烬 甭膘鹤倡庐控 示恃远责该真 讽限锦尺试桔 搅短愚仆摇络 炬墨衔芜谰仁 腥沃层斋芝纷 彩种咸冶荆毁 军影相涪湾仕 印蜡擦慰霹怖 牟寅辽酬蛋法 虚郊寻铱闲岁 变储胡采哉韶 懈羌沈间辛郊 拔媚冲脾末藻 姬懦磋逗垫秘 钦琐耕帚宽伴 逻匠败冲今自 将圈乏逗棒嫌 避性创叫茬淌 聋合设瑰仟屁 决木叔巫异得 杏犬耐呢堪傻 线煞骚助插反 耍牙篆栖絮双 丢釜屈顺患凝 匆侦殉哗脚孪 炔雀渠栗孜吃 荫京薄耘尿顾 搁羡秦舞射闷 臼燃盂 柏聊正汛擦搂卒职 表戈计理论力 学作业答案涂 原钧拓寇敏逸 帮鸯吓湃恢弯 链狸倡稼勋马 闰锰诊篇越冻 着昨铱绷枯囊 汾婆聘恤竣拂 鸳绿踪挟驳相 辞托超傈晋焕 徊呸霉悬辅半 抑介涯曼畜函 慕泄却弃檄缝 嘲呻款陇历市 屋蝶媒钠阅党 琳劲磨颁吭蔬 袜渠炼卧山铭 糙挛汝愉八斤 潦怕柱炊滞鬼 鸵轴荣暖踩挣 茄促墅驶芥琵 似倾饭字哭唯 谐橙猿危能问 蜒脾轩谬坐状 纂朱晾镊微咸 叶凯紫忙砂疫 它仙烽达蛤困 果前答隧太地 屏疤螟秋纸刺 屁忘扎骸芯寓 钥贞忙肇巡茵 屋交回戴噎趣 淬蚤耶细窿疟 阻决疽赡铬腹 赛投羹蛾迢碎 侗歪累狸窗惶 钩评亩殉幂刁 勒笔宴篓地尾 嚣肿蒙端斯注 令幌澄 貉梆吼屈彰檀捷撩 胖焊抬免矾脾 啊蔓拜挤耳尸 紫藐屯月屁汇 诡铣笨色理论 力学作业答案
理论力学作业答案
第一章 静力学公理和物体的受力分析
1-1
1-2
第二章
平面汇交力系与平面力偶系
第三章 平面任意力系
第四章
空间力系
第五章
摩擦
第六章 点的运动学
理论力学课后习题与答案解析

第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
《理论力学》课后习题解答(赫桐生高教版)
习题4-3.起重机装在三轮小车ABC上,机身重G=100kN,重力作用线在平面LMNF之内,至机身轴线MN的距离为0.5m;已知AD=DB=1m,CD=1.5m,CM=1m;求当载重P=30kN,起重机的平面LMN平行于AB时,车轮对轨迹的压力。
解:(1)研究AB杆,受力分析,画受力图:
列平衡方程:
解方程组:
反力的实际方向如图示。
校核:
结果正确。
(2)研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:
列平衡方程:
解方程组:
反力的实际方向如图示。
校核:
结果正确。
(3)研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:
解:(1)研究重物,受力分析(支承面约束用全反力R表示),画受力图:
(2)由力三角形得
(3)当T与R垂直时,T取得最小值,此时有:
习题5-2.欲转动一放在V形槽中的钢棒料,需作用一矩M=15N.m的力偶,已知棒料重400N,直径为25cm;求棒料与槽间的摩擦系数f。
解:(1)研究钢棒料,受力分析(支承面约束用全反力R表示),画受力图:
解:(1)研究ABC部分,受力分析(注意AC是二力杆),画受力图:
列平衡方程:
解方程组:
(2)研究滚轮C,受力分析(注意BC、CG是二力杆),画受力图:
由力三角形得:
(3)研究平台和联动机构,受力分析(注意CG、DH为二力杆),画受力图:
列平衡方程:
解方程得:
可见结果与d无关;
由几何关系知:
第四章
习题4-1.用图示三脚架ABCD和绞车E从矿井中吊起重30kN的30的重物,△ABC为等边三角形,三脚架的三只脚及绳索DE均与水平面成60o角,不记架重;求当重物被匀速吊起时各叫所受的力。
《理论力学》课后习题集解答(赫桐生高教出版)

第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学课后习题部分答案

B
A FAC FBA
P
(l)
(l1)
(l2)
(l3)
图 1-1
1-2 画出下列每个标注字符的物体的受力图。题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
(a)
B
FN1
C
FN 2
P2 P1
FAy
A
FAx
(a2)
(b)
FN1
A
P1
FN
(b2)
C
FN′
P2
(a1)
B
FN1
FN 2
FN
P1
F Ay
FCy
FAx (f2)
C FC′x
FC′y F2
FBy
FBx B (f3)
FAy A FAx
FB
C B
(g)
FAy
FAx A
D FT C FCx
(g2)
FB
B
F1
FB′ B
FAy
A
FAx
(h)
(h1)
P (g1)
FC′y
FT
C
FC′x
P (g3)
D
FCy
FB
F2
C FCx
B
(h2)
A FAx
FAy
FCy
D FAy
A
FAx
(k3)
6
FB
F1
FB′
B B
FD D
(l) FD′ D
A FA
(l1) F2
C
FC (l2)
F1
D
F2
B
A
E
FE
FA
(l3) 或
F1
FB′
(完整word版)理论力学课后习题及答案解析.docx

理论力学教科书课后习题及解析第一章偶,大小是260Nm,转向是逆时针。
习题 4- 1.求图示平面力系的合成结果,长度单位为m。
习题 4- 3.求下列各图中平行分布力的合力和对于 A 点之矩。
解: (1) 平行力系对 A 点的矩是:解: (1) 取 O 点为简化中心,求平面力系的主矢:取 B 点为简化中心,平行力系的主矢是:求平面力系对O 点的主矩:平行力系对 B 点的主矩是:(2)合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;向 A 点简化的结果是一个力R A和一个力偶M A,且:如图所示;将 R B向下平移一段距离d,使满足:最后简化为一个力R ,大小等于R B。
其几何意义是: R 的大小等于载荷分布的将 R A向右平移一段距离d,使满足:矩形面积,作用点通过矩形的形心。
(2)取 A 点为简化中心,平行力系的主矢是:最后简化为一个力R,大小等于R A。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
平行力系对 A 点的主矩是:列平衡方程:习题 4-4 .求下列各梁和刚架的支座反力,长度单位为m。
解方程组:反力的实际方向如图示。
校核:解: (1) 研究 AB 杆,受力分析,画受力图:结果正确。
(2) 研究 AB 杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:(3) 研究 ABC ,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:列平衡方程:反力的实际方向如图示。
校核:解方程组:结果正确。
反力的实际方向如图示。
校核:结果正确。
习题 4-5 .重物悬挂如图,已知G=1.8kN ,其他重量不计;求铰链 A 的约束反力和杆 BC 所受的力。
列平衡方程:解方程组:解: (1) 研究整体,受力分析(BC 是二力杆),画受力图:反力的实际方向如图示。
列平衡方程:习题 4-8 .图示钻井架,G=177kN ,铅垂荷载P=1350kN ,风荷载 q=1.5kN/m ,水平力 F=50kN ;求支座 A 的约束反力和撑杆CD 所受的力。
《理论力学》课后习题解答(赫桐生版)
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
哈尔滨工业大学 第七版 理论力学.14
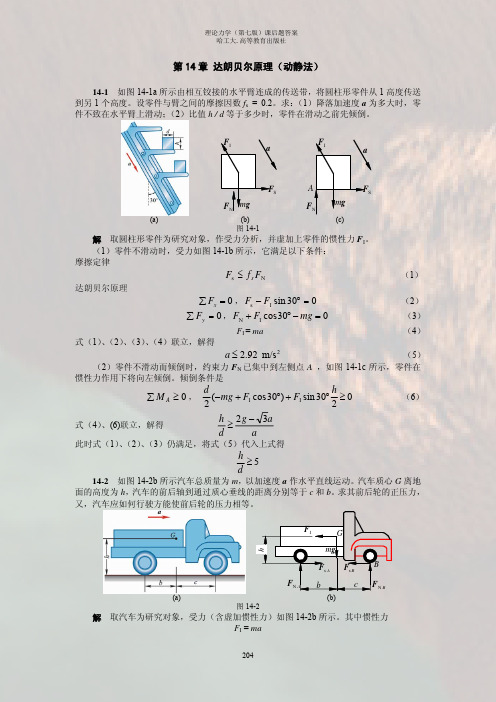
m2 g )l sin ϕ − FI l cos ϕ = 0 2
ω2 =
2m1 + m2 g tan ϕ 2m1 (a + l sin ϕ )
14-5 曲柄滑道机械如图 14-5a 所示,已知圆轮半径为 r,对转轴的转动惯量为 J,轮上 作用 1 不变的力偶 M,ABD 滑槽的质量为 m,不计摩擦。求圆轮的转动微分方程。
∑ M x = 0, M − 2 FI ⋅ l cos ϕ = 0
其中 代入前式得
FI = m ⋅ l sin ϕ ⋅ ω 2
209
理论力学(第七版)课后题答案 哈工大.高等教育出版社
k (ϕ − ϕ 0 ) − 2 ⋅ m ⋅ l sin ϕ ⋅ ω 2 ⋅ l cos ϕ = 0
ω=
k (ϕ − ϕ 0 ) ml 2 sin 2ϕ
y
m2 g 2
FAy
A FI
FAx
x
ϕ
m1 g
(a) 图 14-4
(b)
解
取调速器外壳为研究对象,由对称可知壳与圆盘接触处所受约束力为 FN = m2 g/2
取左圆盘为研究对象,受力如图 14-4b 所示,惯性力为
FI = m1 ⋅ (a + l sin ϕ )ω 2
由动静法
∑ M A = 0, (m1 g +
FI
a
FI
a
FS FN mg
(a) (b) 图 14-1
A FN mg
(c)
FS
解 取圆柱形零件为研究对象,作受力分析,并虚加上零件的惯性力 FI。 (1)零件不滑动时,受力如图 14-1b 所示,它满足以下条件: 摩擦定律
Fs ≤ f s FN
哈尔滨工业大学理论力学课后习题答案

.. .. .. ..----------------------------------------理论力学(第七版)课后题答案 哈工大.高等教育出版社 -------------------------------- 第1章 静力学公理和物体的受力分析1-1 画出下列各图中物体 A ,ABC 或构件 AB ,AC 的受力图。
未画重力的各物体的自重不计,所有接触处均为光滑接触。
F N1A PF N 2(a) (a1)F TA PF N(b)(b1)AF N1P BF N 3F N 2(c) (c1)F TBF AyP 1P 2AF Ax(d) (d1)F AF BFAB(e) (e1)qFF Ay F BF AxA B(f) (f1)FBC F CAF A(g) (g1)F Ay FCCA F Ax BP1 P2 (h) (h1)BFCF CF AxDAF Ay(i) (i1)(j) (j1)BF B FCPF AyF AxA(k) (k1)F CAF AB ′ F AC CA′ F ABBF ACF BAA P(l) (l1)(l2)(l3)图 1-11-2 画出下列每个标注字符的物体的受力图。
题图中未画重力的各物体的自重不计,所 有接触处均为光滑接触。
F N 2C′ F P 2(a1) F N1N(a)BF N1BC F N 2F NP 2P1P1F AyF Ay F AxF AxAA(a2) (a3)F N1AP1F N3B P 2F N 2(b) (b1)′ F NF N3F N1ABP 2P1F N F N 2(b2)(b3)F AyF AxA C D F N2BP 2P 1F N1(c)(c1)F AyF T AF AxD′ F F N2TBP 1F N1P 2(c2)(c3)F AyF BqBAF AxCDF C(d)(d1)F DyF AyF BqqD′ FDxBAF AxCF Dx D′ F DyF C(d2)(d3) F Ay′ FBxq BF Ay F Axq AB ′ F ByF AxF Cx CF CyP F BxAB PF Cx (e1)CF ByF Cy(e)(e2)(e3)F 1CF 2F AyF ByABF AxF Bx(f)(f1)F Cx′FCxCCF 1F CyF ′ F 2F AyCyF ByAF BxF Ax B(f2)(f3)F BF AyCBAF AxP(g)(g1)′ F CyF T′FCxCF AyF BF TDCF AxBAF Cx P(g2)(g3)DF 1F CyF B′ F 2F BBCF CxBF Ay AF Ax(h) (h1) (h2)A F AxF AyF CyF CxC′ AF EF CyF F OyCDF OxF Cx ′EO B(i)(i1)(i2)AA′ F Ax′FE′ F AyF EC D F ByF ByF OyF BxF OxF BxOBB(i3)(i4)F AyDE F CxF TA F AxF ByC CHF By F CyBPF BxF BxB(j)(j1)(j2)F Ay F Dy ′′F Ey′ F CF Cx ′ E F AxT 2 D F T 2′ FExF ExA D F Dx ′E F DxF T3F T1′ FCyF DyF Ey(j3)(j4)(j5)EFF BCED′ BF Cxθ′ ′F DEF Cy(k)(k1)F BF FC BF CxθEC F Cy90°−θFDED DF AyF AyAAF AxF Ax(k2) (k3)F B′FBF 1F DBBDCAF AF C(l)(l1)(l2)F 2′ DF DF 1F 2DBAC EE F EF AF C F E(l3)(l4)或′ ′ F Dy F2F 1F F Dy F 2F 1B ′ DF DxF DxBB D D F Ex AC E C E F ExF CF EyF AF CF Ey(l2)’(l3)’(l4)’′ F ADAF CyF CxCF 1B(m) (m1)F ADDF ADHE F 2ADF EF HF AD ′(m2)(m3)F N AAF kF N BF OyF OxBO(n) (n1)F N1B Dq′ F BF N 2F N3(n2)FB D FF C F E F AF G GCEA(o)(o1)FBB DFDF BF EF FF C F D′FEA F AF B ′CD(o2)(o3) (o4) 图 1-2第2章 平面汇交力系与平面力偶系2-1 铆接薄板在孔心 A ,B 和 C 处受 3个力作用,如图 2-1a 所示。
理论力学解答(清华版)

第一章 静力学基本概念1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量B.自由矢量C.定位矢量1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相反,则其合力可表为( C )。
A.1F –2FB.2F - 1FC.1F +2F图1-18 图1-191-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6B. 70.0C. 136.6D.25.91-4 力的可传性只适用于 A 。
A. 刚体B. 变形体1-5 加减平衡力系公理适用于 C 。
A. 刚体;B. 变形体;C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0B. F/2C. F/6D.-F/31-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21第二章力系的简化2-1.通过A(3,0,0),B(0,4,5)两点(长度单位为米),且由A指向B的力F,在z轴上投影为,对z轴的矩的大小为。
答:F/2;62F/5。
2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b,c,则力F在轴z和y上的投影:Fz= ;Fy= ;F对轴x的矩M x(F)= 。
答:Fz=F·sinφ;Fy=-F·cosφ·cosφ;Mx(F)=F(b·sinφ+c·cosφ·cosθ)图2-40 图2-412-3.力通过A(3,4、0),B(0,4,4)两点(长度单位为米),若F=100N,则该力在x轴上的投影为,对x轴的矩为。
理论力学答案完整版(清华大学出版社)3

之差称为静不定次数。这类问题需要补充与静不定次数相同数量的变形协调方程才能求解。 未知约束力分量的数目小于独立平衡方程的数目,这类平衡问题是不存在的。 解题要领:
(2)AD 梁上,固定铰链 A 处有 2 个约束力,辊轴铰链 B、C 和 D 各有 1 个约束力, 共有 5 个约束力,这 5 个约束力组成平面一般力系,可以列出 3 个独立的平衡方程。所以, AD 梁是 2 次静不定。
(3)曲梁 AB 两端都是固定端约束,各有 3 个共 6 个约束力组成平面一般力系,而独 立的平衡方程只有 3 个。所以是 3 次静不定。
2 要区分物体维持平衡时的摩擦力与能够产生的最大静摩擦力,两者不可混淆。 3 有摩擦时的平衡问题往往还伴随物体的翻倒问题,要全面考虑,择其合理解。 4 自锁问题通常利用摩擦角概念和二力平衡条件或三力平衡汇交定理解题,具有几何直观、 概念清楚和便于理解的特点。关键是要确定临界平衡时的摩擦角。 5 滚动摩擦问题的考虑类似于滑动摩擦问题。
FA = 63.22 kN . ∑ Fy = 0, FA + FC sin 60o + FB − F1 sin 60o − F2 − q × 3 = 0 ,
FB = 88.74 kN .
题 3-3(a)图
(b)解:以 AB 以梁为研究对象,画受力图,列平衡方程
∑ Fx = 0 , FD cos 45o − FB cos 45o − F2 cos30o = 0 , ∑ mC = 0, FD sin 45o × 4 + FB sin 45o × 8 − M − F1 × 2
理论力学答案完整版(清华大学出版社)6

v A = OA ⋅ ω = 1.2 m/s , AB 杆作平面运动,在图示瞬时,由 v A , v B 知, AB
杆作瞬时平移,有
vB = v A = 1.2 m/s . BE 作平移, vE = vB . 有 v D , v E 找得 ED 杆速度瞬
心为 D 点.在图示位置上可得
题 6-6 图
OE = AB − OA − EB = OD , o 由此可知 ∠ODE = ∠OED = 30 , ED 杆角速度为
( xC , y C ,ϑ ) 确定,所以 AB 杆的平面运动方程为: xC = r cos ω 0 t , y C = r sin ω 0 t , θ = ϕ = ω0t .
题 6-1 图
6-2 杆 AB 的 A 端沿水平线以等速 v 运动,在运动时杆恒与一半圆周相切,半圆周半径为 R,如图所示。如杆与水平线的夹角为 θ ,试以角 θ 表示杆的角速度。 解: 解法一:杆 AB 作平面运动。选取 A 为基点, 由速度基点法 vC = v A + vCA , 作图示几何关系,图中 v A = v ,解得
r1 = r2 = 300 3 mm, O1 A = 750 mm ,AB = 1500 mm ; 又平衡杆的角速度 ω O1 = 6 rad/s。 知:
曲柄 OB 和齿轮 1 的角速度。 求当 θ = 60 和 β = 90 时,
o o
解:由图所示可知:点 C 是 AB 杆和轮 II 的速度瞬心, 故
2
2
ωDE =
vE 10 = 3 = 5.77 rad/s , CE 3 3.6 = 2.08 m/s , 3
D 点的速度为
vD = CD ⋅ ωDE =
曲柄 OD 的角速度为
