湖北省黄冈中学自主招生考试数学试卷
2021年湖北省黄冈中学自主招生数学试题

2021年湖北省黄冈中学自主招生数学试题2021年黄冈中学自主招生考试数学试题一、填空题(每小题5分,共50分)1、已知四个不等实数a、b、c、d任意三个实数和为2、4、5、7,则abcd=__________.二、解答题(本大题共70分)11、(本题12分)已知A(-5,0),B(5,0),P点为直线y?为a,若∠APB为钝角,求a的取值范围.A B x P y l 15x?上的一个动点,P点的横坐标33143a(a?2)2、已知a???2,则a??__________.aaaa?bb?aab3、已知x?2?b?a有四个不同的解,则????__________.a?bb?aab4、已知如图∠B=90°,AB=4,BC=3,点D为边AB上的一动点,DE⊥AB于E,DF⊥BC于F,当EF最长时cos∠EFD=__________.5、 x-x+x+1被x-1整除,则余式是__________________.6、如图,△ABC中2643212、(本题12分)已知函数y?kx?2(k?1)x?k?3,(1)若该函数的图像与x轴有交点,求k的取值范围;22ADAE1?x,?y, S△ABC的面积为2,且y-x=,则△BED的最大面积为__________. ABAC2227、已知①x+ax+b=0, ②x+bx+c=0, ③x+cx+a=0,方程①②有公共根p,②③有公共根q, ①③有公共根r,则abc=___________.8、有一个实数n,若n为偶数则除以2,若n为奇数则乘以3再加1.例如:6进行8次上述操作后结果为1.问进行8次上述操作后结果为1的数有_______个. 9、如图为一个无穷数表,则表中2021出现的次数为__________次. 10、已知a(3x?2y)?a(4y?3z)?4y?3z?2y?3x,则x?y=_______.xy?yz?xz4 7 5 9 6 7 … 22(2)已知kx1?2(k?1)x2?k?3?4x1x2,当-1?x?1时y的最大值与最小值分别为多少?A E D D A 2 3 E 4 5 6 3 5 7 911 13 … 10 13 16 19 … 13 17 21 25 … 11 16 21 26 31 … 13 19 25 31 37 …B FC B C7 … … … … … … … 第4题图第6题图第9题表113、(本题14分)如图,EA为△ABC外接圆的切线,AB=AC, BD//AC, AE=35, BD=4.求FC的长. E AB F CD14、(本题14分)已知AB为⊙O的直径,Q为BC的中点,PB、PC为⊙O的切线.求证:AB-AQ=AC-AP. AC OQ BD15、(本题18分)有25张标有1,2,3,4,5,…,25的卡片,甲乙两人各持有其中的一部分.若甲将15号卡片给乙则甲所有卡片的平均数上升0.25,乙所有的卡片的平均数也上升0.25.求甲、乙两人原来各持有多少卡片,并写出一种甲可能持有卡片的情况.2感谢您的阅读,祝您生活愉快。
黄冈高中自招试题及答案

黄冈高中自招试题及答案试题一:数学1. 已知函数 \(f(x) = 3x^2 - 2x + 1\),求导数 \(f'(x)\)。
2. 解不等式 \(2x^2 - 5x + 3 > 0\)。
3. 已知圆的方程为 \((x-3)^2 + (y-4)^2 = 25\),求圆心和半径。
试题二:语文1. 解释“不以物喜,不以己悲”的含义。
2. 根据题目给出的古文段落,分析作者的写作手法和表达的情感。
3. 写作题:以“时间的价值”为题,写一篇不少于800字的议论文。
试题三:英语1. 将下列句子翻译成英文:“这个城市的交通非常便利。
”2. 根据所给的短文内容,回答下列问题:- What is the main idea of the passage?- How does the author describe the importance of teamwork?3. 写作题:以“My Hometown”为题,写一篇不少于120词的短文。
试题四:物理1. 一个质量为2kg的物体,受到一个大小为10N的力,求物体的加速度。
2. 已知一个电路中的电阻为20Ω,电流为0.5A,求电压。
3. 描述牛顿第三定律,并给出一个生活中的例子。
试题五:化学1. 写出水的化学式,并解释其分子结构。
2. 解释什么是摩尔质量,并给出一个具体元素的摩尔质量。
3. 写出一个简单的化学反应方程式,并解释其反应类型。
答案:试题一:数学1. \(f'(x) = 6x - 2\)2. 解得 \(x < \frac{1}{2}\) 或 \(x > 3\)3. 圆心为 (3, 4),半径为5试题二:语文1. “不以物喜,不以己悲”意味着不因外界事物的变化而感到高兴或悲伤,保持内心的平和。
2. 略(根据具体段落分析)3. 略(根据题目要求写作)试题三:英语1. The transportation in this city is very convenient.2. - The main idea is to emphasize the importance of environmental protection.- The author describes the importance of teamwork by giving examples of successful projects that were achieved through collaborative efforts.3. 略(根据题目要求写作)试题四:物理1. 加速度 \(a = \frac{F}{m} = \frac{10N}{2kg} = 5 m/s^2\)2. 电压 \(V = I \times R = 0.5A \times 20Ω = 10V\)3. 牛顿第三定律指出,对于每一个作用力,都有一个大小相等、方向相反的反作用力。
2020年黄冈中学自主招生考试数学试题(含答案)

第1页共11页数学试题试卷满分120分,考试时间120分钟一、选择题(本大题8小题,每小题4分,共32分)在每小题列出的四个选项中,只有一个是正确的,请选出正确选项,在答题卡上相应位置用2B 铅笔涂黑.1.2020年的春天至今,一种被称为新型冠状病毒肺炎的肺部疾病在全球爆发,这次突如其来的疫情给世界各国人民生命安全和身体健康带来严重威胁,对世界经济社会发展带来严重冲击.疫情严重,请尽量不要聚会,避免出入公共场所.截止7月10日,全球大约有12300000人感染新冠肺炎.12300000用科学计数法表示为()A .612.310⨯B .512310⨯C .80.12310⨯D .71.2310⨯2.一把直尺和一块三角板ABC (含45︒角)按如图1所示摆放,直尺一边与三角板的两直角边分别交于点D 和点E ,另一边与三角板的两直角边分别交于点F 和点A ,25CED ∠=︒,则BFA ∠的大小为()A .115︒B .110︒C .105︒D .120︒3.已知a ,b 两数在数轴上的位置如图2所示,则化简222b a a b ab a b -++--的结果是()A .1a b --B .1a b -++C .1a b +-D .1a b --+4.假期里王老师有一个紧急通知,要用电话尽快通知给50个同学,假设每通知一个同学需要1分钟时间,同学接到电话后也可以相互通知,那么要使所有同学都接到通知最快需要的时间为()A .8分钟B .7分钟C .6分钟D .5分钟5.构建几何图形解决代数问题体现了“数形结合”的重要思想.在计算tan15︒时,如图3,在Rt ACB ∆中,90C ∠=︒,30ABC ∠=︒,延长CB 使BD AB =,连接AD ,得15D ∠=︒,所以123tan152323(23)(23)AC CD -︒====-++-.类比这种方法,计算tan 22.5︒的值为()A .21+B .21-C .2D .126.设,,a b c 分别是ABC ∆的三条边,对应的角分别为,,A B C ,若3,2,30b c C === ,则可以作出符合条图2图3图1第2页共11页件的三角形的个数为()A .0B .1C .2D .不确定7.如图4,有一电路连着三个开关,每个开关闭合与断开是等可能的,若不考虑元件的故障因素,则电灯点亮的概率为()A .12B .34C .23D .388.数独是源自18世纪瑞士的一种数学游戏.如图5是数独的一个简化版,由3行3列9个单元格构成.玩该游戏时,需要将数字1,2,3(各3个)全部填入单元格,每个单元格填一个数字,要求每一行、每一列均有1,2,3这三个数字,则不同的填法有()A .12种B .24种C .72种D .216种二、填空题(本大题8小题,每小题4分,共32分)请把下列各题正确的答案填写在答题卡的相应的位置上.9.若函数6xy x =-在实数范围内有意义,则函数x 的取值范围是_____________.10.某商场销售额4月份为25万元,6月份为36万元,该商场5、6两个月销售额的平均增长率是%.11.已知3232x -=+,3232y +=-,则22x y x y ++=_____________.12.设非零实数a ,b ,c 满足2302340a b c a b c ++=⎧⎨++=⎩,则222ab bc ca a b c ++++的值为.13.若[]x 表示不超过x 的最大整数(例如[2.3]=2),{}[]x x x =-,方程2{}3[]x x x +=的解为.14.如图6,ABC ∆的顶点是正方形网格的格点,则sin A 的值为________.15.如图7,在锐角三角形ABC 中,8AB =,ABC ∆的面积为40,BD 平分ABC ∠,若M 、N 分别是BD 、BC 上的动点,则CM MN +的最小值为________.16.n 个单位小立方体叠放在桌面上,所得几何体的主视图和俯视图均如图8所示.那么n 的最大值与最小值的积是.三、解答题(一)(本大题4小题,每小题8分,共32分).图5图6图7图4图8。
黄冈中学自主招生预录数学模拟试题

黄冈中学自主招生预录数学试题一、 选择题(每小题5分,共20分)1. 方程023x =+-x x 实根个数为( )A 1B 2C 3D 4 2.=+++=-=6,231,23122b a b a 则( ) A 3 B 4 C 5 D 63.已知一个六边形六个内角都是1200,连续四条边长依次是1,3,3,2则该六边形的周长是( )A 13B 15C 14D 164.实数a,b 满足()()111a 22=----b b a ,说法:(1)a=b, (2)a=-b, (3)ab=1,(4)ab=-1中正确的有( )个A 1B 2C 3D 4 二、填空题(每小题5分,共40分)5.若a,b 都是正实数,0111=+--b a b a ,则=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛33b a a b 6.不论m 为任何实数,抛物线1222-+++=m m mx x y 的顶点都在一条直线上,则这条直线的解析式是7.甲从A 地到B 地,乙从B 地到A 地,甲,乙同时出发相向匀速而行,经t 小时相遇于C 地,相遇后二人继续前进,甲又用了4小时到达B 地,乙又用了9小时到达A 地,则t= 8.75+的小数部分是a ,75-的小数部分是b ,则ab-2a+3b-12=9.设a ax -=1,则24x x += 10.如果一个三位数,百位数字与个位数字都大于十位数字,则称这个三位数为“凹数”,从所有三位数中任取一个三位数是“凹数”的概率是11.化简:=++⎪⎪⎭⎫ ⎝⎛+--+-+-b a ab ab a a ab b b b ab a 21b 12.同心圆半径分别为6,8,AB 为小圆的弦,CD 为大圆的弦,且ABCD 为矩形,圆心在矩形ABCD 内,当矩形ABCD 面积最大时,矩形ABCD 的周长为三、解答题(13、14题各13分,15题14分)13.一号列车从甲站开往乙站,一小时后二号列车从乙站开往甲站,二号列车每小时比一号列车多行10千米,两列车刚好在甲乙两站中点处相遇。
湖北省黄冈中学初中数学自主招生预录考试训练试题二(

湖北省黄冈中学2016年初中数学自主招生预录考试训练试题二(理科实验班)预录考试数学训练题(二) 参考答案一、选择题(共4小题,每小题5分,共20分) 1.D . 2.B . 3.A . 解析:CPE∆∽CBA ∆222PE CP CP bPE AB a b AB BC BC a ⇒=⇒=⋅=+222b EF PE a b a ⇒==+.4.C .二、填空题(共8小题,每小题5分,共40分) 5.3. 6.10. 7.23 . 8.33332x --<<. 解析:由26<0x mx +-,2222424122224m mm mx m m+++-<<=++解得 -.当1≤m ≤3时,22241241=322m m ++++- -的最大值为-,221212333=2243243m m-++++的最小值为. 所以,当1≤m ≤3时,y <0即260x mx +-<恒成立时, x 的取值范围是33332x --<<. 9.25.解析:由题意知(a -b )2=1,∴a 2-2ab + b 2=1,又∵a 2+ b 2=13,∴2ab =12,∴(a +b )2=a +2ab + b 2=13+12=25. 10.2018.解析:由题意知m 2-2016m +1=0,∴m 2-2015m =m -1,m 2+1= 2016m ,∴原式=m -1+20162016m +3= m -1+1m+3=2+1m m +2=2016m m +2=2016+2=2018.11.9.解析:从俯视图知该立体图形从前到后共排了三排小正方体,各位置上小正方体的个数如图所示. 12.-10.解析:[5]+3[-π]=2+3×(-4)=2-12=-10. 三、解答题(本大题共4小题,共60分)QBC A P 13.(本小题14分)由题意知,3+2=3a +b ,且3= -a +b ,解得a =3-1,b =23-1. ∴2-c =ac +b =(3-1)c +(23-1),解得c =3-2. ∴a -b = -3,b -c =3+1,c -a = -1. ∴a 2+b 2+c 2-ab -bc -ca =21[(a -b )2+(b -c )2+(c-a )2]=21[(-3)2+(3+1)2+(-1)2]=4+3. 14.(本小题16分)(1)连接EP ,FP ,∵四边形ABCD 为正方形,∴∠BAD=90°,∠BPA=90°,∴∠FPE=90°,∴∠BPF=∠APE , 又∵∠FBP=∠PAE=45°,∴△BPF ≌△APE ,∴BF=AE ,而AB=AD ,∴DE=AF ; (2)连EF ,∵∠BAD=90°,∴EF 为⊙O 的直径,而⊙O 的半径为23,∴EF=3, ∴AF 2+AE 2=EF 2=(3)2=3,而DE=AF ,故DE 2+AE 2=3 ①;又∵AD=AE+ED=AB ,∴AE+ED= 12+ ②,由①②联立起来组成方程组,解得AE=1,ED=2或AE= 2,ED=1,所以ED AE= 222或. 15.(本小题12分)(1)当0x a <≤时,PCQ PBQ PBC S S S S ∆∆∆==-=ax x x a a x a x a 4343)(2321)(23)(212+-=-•--•+,当x a >时,PCQ PBQ PBC S S S S ∆∆∆==-=ax x a x a a x x a 4343)(2321)(23)(212-=-•--•+, ⎪⎪⎩⎪⎪⎨⎧>-≤<+-=∴)(4343)0(434322a x ax x a x ax x S ; (2)2213sin602ABC S a a ∆=︒=,若ABC PCQ S S ∆∆=,则 当0x a <≤时,有22333444x ax a -+=QACB P即220xax a -+=,解得,此方程无实根;当x a >时,有22333444x ax a -= 即220xax a --=解得,121515 22x a a x a a +-=>=<,(舍去)所以,当152APa +=时, △PCQ 的面积和△ABC 的面积相等.16.(本小题18分)(1)设过B 、A 、A ′三点的抛物线的函数表达式为y=ax 2+bx+c . ∵抛物线过点B (﹣1,0),A (0,2),A ′(1,1),∴021a b c c a b c -+=⎧⎪=⎨⎪++=⎩,解得32122a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩. ∴过B 、A 、A ′三点的抛物线的函数表达式为y=32-x 2+12x+2; (2)存在,E (﹣2,1);(3)如图,△ABO 向下平移到△AB 1O 1,△B A ′B ′向左平移到B 2 A ′B ′,AB 1交x 轴于点C ,B A ′交y 轴于点D ,AB 1交B A ′于点E ,连接O E . 移动t 秒时,A(0,2﹣t ),C(22t -,0),B 2 (﹣1﹣t ,0),D(0,12t+), 设直线A C 的解析式为y=k 1x+b 1,则1112202b ttk b =-⎧⎪⎨-+=⎪⎩,解得1122k b t =⎧⎨=-⎩,故y=2x+2﹣t ; 设直线B 2D 的解析式为y=k 2x+b 2,则122012t k b t b +=⎧⎪⎨+=⎪⎩(-1-),解得221212k t b ⎧=⎪⎪⎨+⎪=⎪⎩,故y=12 x+12t +; 由221122y x tty x =+-⎧⎪⎨+=+⎪⎩得112222t x t x ++-=+,4421x t x t +-=++,333x t =-,1x t =-,故E(t ﹣1,t ).0设△ABO 与△B A ′B ′重叠面积为S ,则S=S△COE +S△DOE=12OC·︱y E︱+12OD·︱x E︱=12·22t-·t+12·12t+·(1﹣t) =14(2 t﹣t2)+14(1﹣t2)=﹣12t2+12t+14=﹣12(t﹣12)2+38.∵﹣12<0,∴当t=12时,△ABO与△B A′B′重叠面积的最大值为38.。
湖北省黄冈中学初中数学自主招生预录考试训练试题五(

湖北省黄冈中学2016年初中数学自主招生(理科实验班)预录考试训练试题五高中预录考试数学训练题(五) 参考答案一、选择题(共4小题,每小题5分,共20分) 1.B . 2.C . 3.A . 4.C .解析:设第n 层的最高点到水平线的距离记为:a n (n =1,2,3,…,10). 由题意,得224412132435411111;();();();();2222a a a a a a a a a ==+=+=+=+66106576109111();();...;();222a a a a a a =+=+=+把这10个式子左右相加,得2468101010111111170512[()()()()()]()2222221024a =+⨯++++-=. 二、填空题(共8小题,每小题5分,共40分)5.6. 6.5个. 7.4196. 8.45.解析:记2n ≥张卡片至多经过n a 次操作后,能将它们按从小到大顺序排列,则232431091;2;3;............9.a a a a a a a ==+=+=+所以10123.....945a =++++=.9.0. 10.36.解析:每隔3cm 剪一刀共剪72÷3-1=24-1=23刀,每隔4cm 剪一刀,共剪72÷4-1=17刀,所以应共剪23+17=40刀,但其中重复位置的刀数为:72÷12-1=5刀,因此互不重复的刀数为40-5=35刀,所以72cm 长的绳子按要求被剪的段数为35+1=36段. 11.6.解析:∵a <3,b >3,∴a -3<0,b -3>0,∴(a -3)(b -3)<0,∴ab -3(a +b )+9<0, 又∵a +b =k -1,ab =3,代入上述不等式,得3-3(k -1) +9<0,解得k >5. 12.130.解析:由30350x y z x y z ++=⎧⎨+-=⎩用x 来表示y ,z ,得y =40-2x ,z =x -10,又由y ≥0,z ≥0,得402x x -≥0⎧⎨-10≥0⎩,解得10≤x ≤20, 又把y =40-2x ,z =x -10代入M =5x +4y +2z ,得M =-x +140,显然M 是关于x 的一次函数,且M 随x 增大而减小,所以当x =10时,M 的最大值为130. 三、解答题(本大题共4小题,共60分) 13.(本题满分14分)过点A 作AN ⊥BC 交DG 于M ,交BC 于N ,设AN=h ,DE=x=MN=DG , 则121=⋅h BC ,2h BC =,由DG ∥BC 知△ADG ∽△ABC ,故AN AM BC DG =,即h xh hx -=2,∴222+=h h x . 记正方形DEFG 的面积为S ,则212222222222222=⎪⎭⎫⎝⎛≤⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎭⎫⎝⎛+=h h h h S . 当2=h 时,正方形DEFG 面积的最大值为21. 14.(本题满分12分)由题意知0)1)(5(56)12(4)13(222≥--=+-=---=∆a a a a a a , ∴5≥a 或1≤a .由根与系数的关系知12,3122121-=-=+a x x a x x .故21221212221212116)(310)(3)3)(3(x x x x x x x x x x x x -+=-+=--8019185)12(16)31(3222-=+--=---=a a a a .∴31=a (舍)或5332-=a . ∴所求的实数533-=a . 15.(本题满分16分)(1)当x = c 时,y = 0,即20, (1)0ac bc c c ac b ++=++=,又c>1,所以 10ac b ++=.设一元二次方程20ax bx c ++=两个实根为1212,()x x x x ≤.由120cx x a⋅=>,及x = c >1,得120 0x x >>,. 又因为当0<x <c 时,0y >,所以1x c =, 于是二次函数2y ax bx c =++的对称轴:2bx c a=-≥ 即2b ac ≤-. 所以12b ac ac =--≤-,即1ac ≤.(2)因为0<x=1<c 时,0y >,所以0a b c ++>. 由1ac ≤及0,1a c >>得:01a <<. 因为22()(23)2()(223)221(1)(2)(1)(2)a b c a b c x a b c x c a b c x a ac c x cx x x x x x x x x +++++++++--++++==++++++ 而0a b c ++>,01a <<,1c >,223(1)(21)(1)0a ac c a c c --+=--+->,所以当x >0时,2()(232)20(1)(2)a b c x a ac c x c x x x +++-+-+>++,即021a b cx x x++>++.16.(本题满分18分)(Ⅰ)当020,()60x v x ≤≤=时;当20200,()x v x ax b <≤=+时设,由题意得1,2000,32060,200.3a a b a b b ⎧=-⎪+=⎧⎪⎨⎨+=⎩⎪=⎪⎩解得∴320031)(+=x x v .故函数()v x 的表达式为60,(020),()1(200),(20200)3x v x x x ≤≤⎧⎪=⎨-<≤⎪⎩.(Ⅱ)由题意得60,(020),()1(200),(20200)3x x f x x x x ≤<⎧⎪=⎨-<≤⎪⎩.当020x ≤≤时,当20x =时,()f x 的最大值为60×20=1200;当20200x <≤时,21110000()(200)(100)333f x x x x =-=--+,∵13-<0,∴当100x =时,()f x 的最大值为1000033333≈. 综上所述,当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.。
2021年湖北省黄冈中学(黄冈预录)自主招生数学模拟试卷(三)

2021年湖北省黄冈中学(黄冈预录)自主招生数学模拟试卷(三)一、选择题(每小题5分,共30分)1.设a=,则的整数部分为()A.1B.2C.3D.42.已知△ABC中,∠ACB=90°,∠ABC=15°,则tan B=()A.B.C.D.3.正整数构成的数列a1,a2,…,a n,…满足:①数列递增,即a1<a2<…a n<…;②a n=a n﹣1+a n﹣2(n ≥3),则称为“类斐波那契数列”,例如:3,4,7,11,18,29,…,则满足a5=61的“类斐波那契数列”有()A.3种B.4种C.5种D.6种4.如图正方形ABCD的顶点A在第二象限y=图象上,点B、点C分别在x轴、y轴负半轴上,点D在第一象限直线y=x的图象上,若S阴影=,则k的值为()A.﹣1B.C.D.﹣25.如图所示,正方形ABCD中,E,F分别是AB,BC上的点,DE交AC于点M.AF交BD于点N,若AF平分∠BAC,DE⊥AF;记,则有()A.x>y>z B.x=y=z C.x=y<z D.x=y>z6.如图所示,已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x 轴的平行线交二次函数图象于点B,分别过点B,A作x轴的垂线、垂足分别为C,D,连接P A,PD,PD交AB于点E,则()A.P A=PD﹣PE B.PD=P A•PE C.PD=PE+AD D.P A2=PE•PD二、填空题(每小题5分,共30分)7.关于x,y的方程组的解是.8.已知直角三角形的三边长都是整数,且其面积与周长在数值上相等,若将全等的三角形都作为同一个,那么这样的直角三角形的个数是个.9.若关于x的方程(x﹣4)(x2﹣6x+m)=0的三个根恰好可以组成某直角三角形的三边长,则m的值为.10.如图,矩形ABCD中,AB=10,BC=12,M为AB中点,N为BC边上一动点,将△MNB沿MN折叠,得到△MNB',则CB'的最小值为.11.如图,四边形ABHK是边长为6的正方形,点C、D在边AB上,且AC=DB=1,点P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作正方形AMNP和正方形BRQP,E、F分别为MN、QR 的中点,连接EF,设EF的中点为G,则当点P从点C运动到点D时,点G移动的路径长为.12.如图,△ABC中,∠ACB=90°,sin A=,AC=8,将△ABC绕点C顺时针旋转90°得到△A′B′C,P为线段A′B′上的动点,以点P为圆心,P A′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为.三、解答题(共60分)13设互不相等的非零实数a,b,c满足,求的值.14如图,在平面直角坐标系中已知四边形ABCD为菱形,且A(0,3),B(﹣4,0).(1)求过点C的反比例函数表达式;(2)设直线l与(1)中所求函数图象相切,且与x轴,y轴的交点分别为M,N,O为坐标原点.求证:△OMN的面积为定值.15如图,在△ABC中,D是BC的中点,过D的直线交AC于E,交AB的延长线于F,AB=mAF,AC=nAE.求:(1)m+n的值;(2)的取值范围.16如图1,P为第象限内一点,过P、O两点的⊙M交x轴正半轴于点A,交y轴正半轴于点B,∠OP A=45°.(1)求证:PO平分∠APB;(2)作OH⊥P A交弦P A于H.①若AH=2,OH+PB=8,求BP的长;②若BP=m,OH=n,把△POB沿y轴翻折,得到△P′OB(如图2),求AP′的长.17如图,已知抛物线y=x2+2bx+2c(b,c是常数,且c<0)与x轴分别交于点A,B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(﹣1,0).(1)点B的坐标为(结果用含c的代数式表示);(2)连接BC,过点A作直线AE∥BC,与抛物线y=x2+2bx+2c交于点E,点D是x轴上的一点,其坐标为(2,0).当C,D,E三点在同一直线上时,求抛物线的解析式;(3)在(2)条件下,点P是x轴下方的抛物线上的一个动点,连接PB,PC,设所得△PBC的面积为S.①求S的取值范围;②若△PBC的面积S为整数,则这样的△PBC共有个.。
湖北省黄冈中学(黄冈预录)自主招生数学模拟试卷(卷尾含答案解析)

2021年湖北省黄冈中学(黄冈预录)自主招生数学模拟试卷(二)1.已知过点(2,3)的直线y=ax+b(a≠0)不经过第四象限,设s=a−2b,则s的取值范围是( )A. 32≤s<6 B. −3<s≤3 C. −6<s≤32D. 32≤s≤52.有下列四个命题:①若x2=4,则x=2;②若22x−1=44x2−1,则x=12;③命题“若a>b,则am2>bm2”的逆命题;④若一元二次方程ax2+bx+c=0的两根是1和2,则方程cx2−bx+a=0的两根是−1和−12.其中真命题的个数是( )A. 1个B. 2个C. 3个D. 4个3.若函数y=12(x2−100x+271+|x2−100x+271|),当自变量取1,2,3,…,100个自然数时,函数值的和是( )A. 374B. 390C. 765D. 5784.如图,在矩形ABCD中,E是BC上的点,F是CD上的点,,则S△AEFS△CEF=( )A. 3B. 92C. 5 D. 1125.如图,Rt三角形ABC位于第一象限,AB=4,AC=2,直角顶点A在直线y=x上,其中点A的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若函数y=kx(k≠0)的图象与△ABC有交点,则k的最大值是( )A. 5B. 498C.12124D. 46. 如图,已知⊙O 上的两条弦AC 和BC 互相垂直于点C ,点D 在弦BC 上,点E 在弦AC 上,且BD =AE ,连接AD 和BE ,点P 为BE 中点,点Q 为AD 中点,射线QP 与线段BC 交于点N ,若∠A =30∘,NQ =2√6,则DQ 的长为( )A. √6B. √5C. 52D. 47. 已知α为锐角,tan α2=23,则tanα=______.8. 方程|1−|x +1||−3k =kx 有三个实数根,则k =______.9. 从−3,−2,−1,−12,0,12,1,2,3这9个数中随机抽取一个数,记为m ,若数m 使关于x 的不等式组{13(2x +7)≥3x −m <0无解,且使关于x 的分式方程x x+3+m−2x+3=−1有非负整数解,那么从这9个数中抽到满足条件的m 的概率是______.10. 把1,2,3,4,5,6,7,8,9,10这10个数分为A 、B 两个部分,其中A 部分的元素之和等于B 部分的元素之积,则A 部分的数是______,B 部分的数是______. 11. 如图,设ABCDE 是正五边形,五角星ACEBD(阴影部分)的面积为2,设AC 与BE的交点为P ,BD 与CE 的交点为Q ,则四边形APQD 的面积等于______.12. 如图,正方形ABCD 中,AB =4,E 是BC 中点,CD 上有一动点M ,连接EM 、BM ,将△BEM 沿着BM 翻折得到△BFM ,连接DF ,CF ,则DF +12FC 的最小值为______.13. 已知正整数x ,y 满足2xy +x +y =117,求x +y 的值.14. 已知一列数如下规律排列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项20,接下来的两项20,21,再接下来的三象20,21,22,依此类推. (1)第10个1是这列数的第几项; (2)该列数的第2018项为多少?(3)求满足如下条件的最小整数N :N >100且该列数的前N 项和为2的整数幂.(参考公式:1+q ++q 2+…+q n )={1−q n+11−q (q ≠1)n +1(q =1)15.如图,△ABC中,P为BC边上一点,E为线段PC的中垂线与边AC的交点,D为线段BP的中垂线与边AB的交点,点P关于直线DE的对称点为点Q.(1)证明:A,Q,D,E四点共圆;(2)证明:A,Q,B,C四点共圆.16.在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“特别距离”,给出如下定义:若|x1−x2|≥|y1−y2|,则点P1与点P2的“特别距离”为|x1−x2|;若|x1−x2|<|y1−y2|,则点P1与点P2的“特别距离”为|y1−y2|.例如:点P1(1,2),点P2(3,5),因为|1−3|<|2−5|,所以点P1与点P2的“特别距离”为|2−5|=3,也就是图(1)中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).,0),B为y轴上的一个动点.(1)已知点A(−12①若点A与点B的“特别距离”为3,写出一个满足条件的点B的坐标______;②直接写出点A与点B的“特别距离”的最小值______;(2)已知C是直线y=4x+4上的一个动点,如图(2),点D的坐标是(0,1),求点C3与点D的“特别距离”的最小值及相应的点C的坐标.17.如图,在平面直角坐标系xOy中,一次函数y=54x+m的图象与x轴交于A(−1,0),与y轴交于点C.以直线x=2为对称轴的抛物线C1:y=ax2+bx+c(a≠0)经过A、C两点,并与x轴正半轴交于点B.(1)求m的值及抛物线C1:y=ax2+bx+c(a≠0)的函数表达式.(2)设点D(0,2512),若F是抛物线C1:y=ax2+bx+c(a≠0)对称轴上使得△ADF的周长取得最小值的点,过F任意作一条与y轴不平行的直线交抛物线C1于M1(x1,y1),M2(x2,y2)两点,试探究1M1F +1M2F是否为定值?请说明理由.(3)将抛物线C1作适当平移,得到抛物线C2:y2=−14(x−ℎ)2,ℎ>1.若当1<x≤m 时,y2≥−x恒成立,求m的最大值.答案和解析1.【答案】C【解析】解:∵过点(2,3)的直线y =ax +b(a ≠0)不经过第四象限, ∴a >0,b ≥0,将(2,3)代入直线y =ax +b , 3=2a +b ,b =3−2a∴{a >03−2a ≥0,解得0<a ≤32,s =a −2b =a −2×(3−2a)=5a −6, a =0时,s =−6, a =32,s =32, 故−6<s ≤32.故选:C.根据题意得出a >0,b ≥0,即可推出得0<a ≤32,从而求得s 的取值范围. 本题考查了一次函数图象上点的坐标特征,得出当b =0时,s =a +2b 有最小值是关键.2.【答案】B【解析】解:①若x 2=4,则x =±2,本小题说法是假命题; ②x =12时,2x −1=0,22x−1=44x 2−1无意义,本小题说法是假命题;③“a >b ,则若am 2>bm 2”的逆命题是“若am 2>bm 2,则a >b ”,本小题说法是真命题;④若一元二次方程ax 2+bx +c =0的两根是1和2,则方程为(x −1)(x −2)=0,即x 2−3x +2=0, ∴a =1,b =−3,c =2,∴方程cx 2−bx +a =0为2x 2−3x +1=0, 解得:x 1=−1和x 2=−12,本小题说法是真命题.故选:B.利用一元二次方程的解法、分式方程的解法、不等式的性质等知识分别判断后即可确定正确的选项.本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.3.【答案】C【解析】解:令x2−100x+271=0,解得:x1=50−√2229<3,x2=50+√2229>97,∴当x从3到97时,|x2−100x+271|=−(x2−100x+271),则y=0;当x=1时,y=12(x2−100x+271+|x2−100x+271|)=172;当x=2时,y=12(x2−100x+271+|x2−100x+271|)=75;当x=98时,y=12(x2−100x+271+|x2−100x+271|)=75;当x=99时,y=12(x2−100x+271+|x2−100x+271|)=172;当x=100时,y=12(x2−100x+271+|x2−100x+271|)=271;故所求和为172+75+75+172+271=765.故选:C.由x2−100x+271=(x−50−√2229)(x−50+√2229),可知当x从3到97时,函数值为0,再分别求出x=1、2、98、99、100时的函数值即可.本题考查函数值的知识,有一定难度,关键是将x2−100x+271分解为(x−50−√2229)(x−50+√2229),进行解答.4.【答案】A【解析】解:,即12BE⋅AB=12AD⋅DF=14AB⋅BC=14AD⋅CD,∴BE=12BC,DF=12DC,∴EC=12BC,CF=12CD,,,∴S△AEF S △CEF=3,故选:A.由面积关系可得BE =12BC ,DF =12DC ,可求,可求S △EFC 的面积,即可求解.本题考查了矩形的性质,求出△CFE 的面积是解题的关键.5.【答案】B【解析】解:在y =x 中,令x =1,则y =1,则A 的坐标是(1,1), 把(1,1)代入y =kx 得:k =1; C 的坐标是(1,3),B 的坐标是(5,1), 设直线BC 的解析式是y =kx +b , 则{k +b =35k +b =1, 解得:{k =−12b =72,则函数的解析式是:y =−12x +72,根据题意,得:k x =−12x +72,即x 2−7x +2k =0, Δ=49−8k ≥0, 解得:k ≤498.故k 的最大值为498, 故选:B.把A 点的坐标代入即可求出k 的最小值;当反比例函数和直线BC 相交时,求出b 2−4ac 的值,得出k 的最大值.本题主要考查了反比例函数,用待定系数法求一次函数的解析式,根的判别式等知识点,解此题的关键是理解题意进而求出k 的值.题目较好,难度适当.6.【答案】D【解析】解:连接AB,OP,OQ,∵AC⊥BC,∴∠ACB=90∘,∴AB为直径,∵P为BE的中点,Q为AD的中点,∴OP//AC,OP=12AE,OQ//BD,OQ=12BD,∴OP⊥OQ,∴∠POQ=90∘,∵BD=AE,∴OP=OQ,∴∠OPQ=∠OQP=45∘,∵∠A=30∘,∴∠CDA=60∘,∴∠NDQ=120∘,∴∠OQA=120∘,∴∠NQD=15∘,∴∠DNQ=45∘,过点Q作QM⊥BC交BC于M,则△NQM为等腰直角三角形,∵NQ=2√6,∴MQ=2√3,在Rt△DMQ中,∠MDQ=60∘,∴DQ=MQsin60∘=4,故选:D.连接AB,OP,OQ,根据AC⊥BC可确定AB为直径,则OP,OQ为中位线,利用中位线的性质可求得∠PQO=45∘,根据∠A=30∘,可求出∠CDA=60∘,∠DNQ=45∘,过点Q作QM⊥BC交BC于M,则△NQM为等腰直角三角形,进而求出MQ的长度,解直角三角形MQD即可求解.本题考查了圆周角定理,圆心角、弦、弧之间的关系等知识,本题解题的关键:(1)连接AB,OP,OQ,利用中位线的性质,圆周角定理和圆心角、弦、弧之间的关系求出∠DNQ=45∘,(2)过点Q作QM⊥BC交BC于M,构造等腰直角三角形.7.【答案】125【解析】解:tana=2tanα21−tan2α2=2×231−(23)2=125.故答案为:125.根据正切公式进行计算即可得出答案.本题主要考查了正切公式,熟练应用公式进行求解是解决本题的关键.8.【答案】12【解析】解:原方程整理,可得|1−|x+1||=kx+3k,∵方程|1−|x+1||一3k=kx有三个实数根,∴函数y1=|1−|x+1||和y2=kx+3k有三个交点,当x≥−1时,y1=|x|,当x<−1时,y1=|x+2|,如图:当函数y1=|1−|x+1||和y2=kx+3k有三个交点时,直线y2=kx+3k必经过点(−3,0),点(−1,1),将(−1,1)代入y2=kx+3k中,可得:−k+3k=1,解得:k=12,故答案为:12.将原方程变形为|1−|x +1||=kx +3k ,然后结合一次函数y 1=|1−|x +1||和y 2=kx +3k 有三个交点,利用数形结合思想解题.本题考查一次函数的交点问题,理解一次函数与一元一次方程的关系,利用数形结合思想解题关键.9.【答案】29【解析】解:解不等式13(2x +7)≥3,得:x ≥1, 解不等式x −m <0,得:x <m ,∵不等式组无解,∴m ≤1,∴符合此条件的有−3,−2,−1,−12,0,12,1这7个数,解分式方程得x =−m−12,∵方程有非负整数解,∴在以上7个数中,符合此条件的有−3、−1这2个,∴从这9个数中抽到满足条件的m 的概率是29,故答案为:29. 解不等式组中每个不等式,根据不等式组无解得出m 的取值范围,从而确定9个书中符合此条件的数;再解分式方程,结合分式有非负整数解确定符合条件的m 的值,由概率公式求解即可.此题考查了概率公式、分式方程的解,解一元一次不等式以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.10.【答案】1、2、3、4、5、8、9、10 6、7【解析】解:∵1+2+3+4+5+6+7+8+9+10=55,所以B 部分的元素之积小于55,而1+2+3+4+5+8+9+10=6×7=42,∴A 部分的数是1、2、3、4、5、8、9、10;B 部分的数是:6、7.故答案为:1、2、3、4、5、8、9、10;:6、7.根据有理数的加法法则以及有理数的乘法法则求解即可.本题考查了有理数的加法与乘法,求出B部分的元素之积的范围是解答本题的关键.11.【答案】1【解析】解:设AD与BE交于点R,AC与BD交于点H,AD与CE交于点J,连接RQ,如图所示:∵由五角星的性质可知:△APR≌△BHP≌△CQH≌△DJQ≌△ERJ,AP=AR,JR=JQ=HQ=HP,AR=CQ,∴RQ//AC,同理:PQ//AD,∴四边形APQR为平行四边形,∵AP=AR,∴四边形APQR为菱形,∴△APR与△PQR面积相等,PQ=RQ,在△HPQ和△JRQ中,{HP=JR HQ=JQ PQ=RQ,∴△HPQ≌△JRQ(SSS),∴△HPQ和△JRQ的面积相等,设△APR的面积为S1,△HPQ的面积为S2,则2=6S1+2S2,∴S APQD=3S1+S2=1,故答案为:1.设AD与BE交于点R,AC与BD交于点H,AD与CE交于点J,连接RQ,证明四边形APQR为菱形,再由菱形的性质可得出△APR与△PQR面积相等,由SSS证得△HPQ≌△JRQ,由五角星的性质得出△APR≌△BHP≌△CQH≌△DJQ≌△ERJ,设△APR的面积为S1,△HPQ的面积为S2,则2=6S1+2S2,进而可得出S APQD=3S1+S2=1,即可得出结果.本题考查了正多边形和圆、五角星的性质、平行四边形的判定、菱形的判定与性质、全等三角形的判定与性质等知识;解答此题的关键是由五角星的性质得出△APR≌△BHP≌△CQH≌△DJQ≌△ERJ,四边形APQR为平行四边形,再证明△HPQ≌△JRQ.12.【答案】5【解析】解:如图所示:取BG=1,连接FG.∵BC=4,E是BC的中点,∴BE=2.由翻折的性质可知BF=BE=2.∵BF=2,BC=4,GB=1,∴BF2=BC⋅GB.∴BFCB=GBFB.又∵∠FBG=∠FBC,∴△BGF∽△BFC,∴FGFC =BFBC=12,∴FG=12FC.∴DF+12FC=DF+FG≥DG=√DC2+CG2=5.∴DF+12FC的最小值为5.故答案为:5.取BG=1,连接FG,首先证明△BGF∽△BFC,从而可得到FG=12FC,然后依据三角形的三边关系可知DF+12FC=DF+FG≥DG,然后依据勾股定理求得DG的值即可.题主要考查的是相似三角形的性质和判定、正方形的性质、三角形的三边关系,够造△BGF使△BGF∽△BFC是解题的关键.13.【答案】解:∵2xy+x+y=117,∴y=117−x2x+1≥1,可得x≤1163,结合正整数的条件可得{x =2y =23或{x =23y =2, ∴x +y =25.【解析】首先用含x 的式子表示出y ,再根据正整数的条件逐个分析可得答案. 本题考查代数式求值,根据已知条件得到用含x 的代数式表示y 是解题关键.14.【答案】解:(1)由题意可知,第1个1是第1项,第2个1是第1+1=2项,第3个1是第1+2+1=4项,第4个1是第1+2+3+1=7项,…由此规律可知:第10个1是第1+2+3+…+9+1=46项,故第10个1是第46项;(2)将其数列分组,使每组第一项均为1,第一组:20,第二组:20,21,第三组:20,21,22,…第k 组:20,21,22,…,2k−1,共有项数为1+2+3+…+k =k(k+1)2, 当k =63时,63×(63+1)2=2016,则2018项应该为第64组的第二项,∴该列数的第2018项为2;(3)由题意得,前n 组的和为:S =20+21+22+,…,+2n−1=2n+1−n −2 2n+1为2的整数幂,只需将−2−n 消去即可.∴第n +1组为:1,2,4,8, (2)∴前n +1组的和为:2n+2−n −3∴只需要再加上第n +2组的前两项即可消除,此时共有项数:1+2+3+…+n +n +1+2=(n+1)(n+2)2+2∵N>100,∴令(n+1)(n+2)+2≥1002∴n≥14,由题意2+n=2k+1−1,可得n的最小值为29,k的最小值为4,+5=440,此时N=29×302综上所述,N的最小值为440.【解析】(1)根据第1个1是第1项,第2个1是第2项,第3个1是第4项,第4个1是第7项,…,这个规律推算结果便可;(2)根据“1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…”将其数列分组,使每组第一项均为1,第一组:20,第二组:20,21,第三组:20,21,22,…,第k组:20,21,22,…,2k−1,由此得到此数列前n项和计算即可;(3)由题意求得数列的每一项,及前n项和S n=2n+1−2−n,及项数,由题意可知:2n+1为2的整数幂,只需将−2−n消去即可求得N的值.本题主要考查找规律,熟练掌握规律形式是解答本题的关键.15.【答案】证明:(1)连接QA,QD,QE,QP,PD,PE,根据对称性可知:DQ=DP,EQ=EP,∴∠1=∠2,∠3=∠4,∴∠EQD=∠1+∠3=∠2+∠4=∠DPE,∵E为线段PC的中垂线与边AC的交点,D为线段BP的中垂线与边AB的交点,∴EC=EP,DB=DP,∴∠C=∠5,∠B=∠6,∠A+∠B+∠C=180∘,∠DPE+∠6+∠5=180∘,∴∠A=∠DPE=∠EQD,∴A,Q,D,E四点共圆;(2)连接QB,QC,∵A,Q,D,E四点共圆,∴∠7=∠8,∴∠BDQ=∠QEC,BD=PD=QD,QE=PE=CE,∴△BDQ∽△CEQ,∴∠BQD=∠CQE,∴∠BQC =∠DQE =∠DPE =∠A ,∴A ,Q ,B ,C 四点共圆.【解析】(1)连接QA ,QD ,QE ,QP ,PD ,PE ,根据对称性和中垂线的性质得到∠A =∠DPE =∠EQD ,可证A ,Q ,D ,E 四点共圆;(2)连接QB ,QC ,根据四点共圆的性质,相似三角形的判定与性质可得∠BQC =∠DQE =∠DPE =∠A ,可证A ,Q ,B ,C 四点共圆.本题考查了四点共圆,中垂线的性质,对称性,等腰三角形的性质,相似三角形的判定与性质,是综合题型,难度较大,关键是作出辅助线.16.【答案】(0,3)12【解析】解:(1)①∵B 为y 轴上的一个动点,∴设点B 的坐标为(0,y).∵|−12−0|=12≠3, ∴|0−y|=3,解得y =3或y =−3;∴点B 的坐标是(0,3)或(0,−3),故答案为:(0,3);②设点B 的坐标为(0,y),当点A 与点B 的“特别距离”取最小值时,根据运算定义可知|x 1−x 2|=|y 1−y 2|, ∴|−12−0|=|0−y|,∴当|y|≤12时,点A 与点B 的“特别距离”最小,最小值为12;故答案为:12;(2)当点C 与点D 的“特别距离”取最小值时,根据运算定义可知|x 1−x 2|=|y 1−y 2|, ∵C 是直线y =43x +4上的一个动点,点D 的坐标是(0,1),∴设点C 的坐标为(x 0,43x 0+4),∴|x 1−x 2|=−x 0,|y 1−y 2|=43x 0+4−1,∴−x 0=43x 0+3,此时,x 0=−97, ∴43x 0+4=167,∴点C 与点D 的“特别距离”的最小值为:|x 0|=97,此时C(−97,167). (1)①根据点B 位于y 轴上,可以设点B 的坐标为(0,y),由“特别距离”的定义可以确定|0−y|=3,据此可以求得y 的值;②设点B 的坐标为(0,y).根据|x 1−x 2|≥|y 1−y 2|,“特别距离”为|x 1−x 2|即可求得最小值;(2)设点C 的坐标为(x 0,43x 0+4).根据材料可知C 、D 两点的“特别距离”取最小值时,|x 1−x 2|=|y 1−y 2|,据此可以求得最小值和点C 的坐标.本题考查了一次函数综合题,正确理解“特别距离”的定义是解题的关键.17.【答案】解:(1)∵一次函数y =54x +m 的图象与x 轴交于A(−1,0)∴0=−54+m ∴m =54. ∴一次函数的解析式为y =54x +54.∴点C 的坐标为(0,54).∵y =ax 2+bx +c(a ≠0)经过A 、C 两点且对称轴是x =2,∴{a −b +c =0c =54−b 2a =2,解得{a =−14b =1c =54 ∴y =−14x 2+x +54. ∴m 的值为54,抛物线C 1的函数表达式为y =−14x 2+x +54.(2)要使△ADF 的周长取得最小,只需AF +DF 最小连接BD 交x =2于点F ,因为点B 与点A 关于x =2对称,根据轴对称性质以及两点之间线段最短,可知此时AF +DF 最小.令y =−14x 2+x +54中的y =0,则x =−1或5∴B(5,0)∵D(0,25 12 )∴直线BD解析式为y=−512x+2512,∴F(2,54).令过F(2,54)的直线M1M2解析式为y=kx+b1,则54=2k+b1,∴b1=54−2k则直线M1M2的解析式为y=kx+54−2k.解法一:由{y=−14x2+x+54y=kx+54−2k得x2−(4−4k)x−8k=0∴x1+x2=4−4k,x1x2=−8k∵y1=kx1+54−2k,y2=kx2+54−2k∴y1−y2=k(x1−x2)∴M1M2=√(x1−x2)2+(y1−y2)2=√(x1−x2)2+k2(x1−x2)2=√1+k2√(x1−x2)2=√1+k2√(x1+x2)2−4x1x2=√1+k2√(4−4k)2+32k=4(1+k2)M1F=√(x1−2)2+(y1−54)2=√(x1−2)2+(kx1+54−2k−54)2 =√1+k2√(x1−2)2同理M2F=√1+k2√(x2−2)2∴M1F⋅M2F=(1+k2)√(x1−2)2(x2−2)2=(1+k2)√[x1x2−2(x1+x2)+4]2=(1+k 2)√[−8k −2(4−4k)+4]2=4(1+k 2)=M 1M 2∴1M 1F +1M 2F =M 1F +M 2F M 1F ⋅M 2F =M 1M 2M 1F⋅M 2F =1;解法二:∵y =−14x 2+x +54=−14(x −2)2+94,∴(x −2)2=9−4y设M 1(x 1,y 1),则有(x 1−2)2=9−4y 1. ∴M 1F =√(x 1−2)2+(54−y 1)2=√(54−y 1)2+9−4y 1=134−y 1; 设M 2(x 2,y 2),同理可求得:M 2F =134−y 2. ∴1M 1F +1M 2F =M 1F+M 2FM 1F⋅M 2F =(134−y 1)+(134−y 2)(134−y 1)⋅(134−y 2)=132−(y 1+y 2)16916−134(y 1+y 2)+y 1y 2 ①.直线M 1M 2的解析式为y =kx +54−2k ,即:y −54=k(x −2). 联立y −54=k(x −2)与抛物线(x −2)2=9−4y ,得: y 2+(4k 2−52)y +2516−9k 2=0, ∴y 1+y 2=52−4k 2,y 1y 2=2516−9k 2,代入①式,得:1M 1F +1M 2F =4k 2+44k 2+4=1.(3)设y 2与y =−x 的两交点的横坐标分别为x 0,x 0′, ∵抛物线C 2:y 2=−14(x −ℎ)2可以看成由y =−14x 2左右平移得到,观察图象可知,随着图象向右移,x 0,x 0′的值不断增大 ∴当1<x ≤m ,y 2≥−x 恒成立时,m 最大值在x 0′处取得 ∴当x 0=1时,对应的x 0′即为m 的最大值 将x 0=1代入y 2=−14(x −ℎ)2=−x 得(1−ℎ)2=4, ∴ℎ=3或−1(舍)将ℎ=3代入y 2=−14(x −ℎ)2=−x 有−14(x −3)2=−x∴x0=1,x0′=9.∴m的最大值为9.【解析】(1)只需将A点坐标代入一次函数关系式即可求出m值,利用待定系数法和二次函数的图象与性质列出关于a、b、c的方程组求出a、b、c的值就可求出二次函数关系式;(2)先运用轴对称的性质找到点F的坐标,再运用一元二次方程根与系数的关系及平面直角坐标系中两点之间的距离公式求出M1M2、M1F、M2F,证出M1F⋅M2F=M1M2,最后可求1M1F +1M2F=1;(3)设y2与y=−x的两交点的横坐标分别为x0,x0,因为抛物线C2:y2=−14(x−ℎ)2可以看成由y=−14x2左右平移得到,观察图象可知,随着图象向右移,x0,x0的值不断增大,所以当1<x≤m,y2≥−x恒成立时,m最大值在x0处取得,根据题意列出方程求出x0,即可求解.本题主要考查运用待定系数法求函数解析式、一元二次方程根与系数的关系及平面直角坐标系中两点距离公式的综合运用,对计算要求较高.第21页,共21页。
2023-2024学年湖北省黄冈中学自主招生数学模拟试卷+答案解析

2023-2024学年湖北省黄冈中学自主招生数学模拟试卷一、选择题:本题共8小题,每小题4分,共32分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.在数轴上和有理数a,b,c对应的点的位置如图示,有下列四个结论:;;;其中正确的结论有个.()A.4B.3C.2D.12.如图,在中,,,点C在边AB上,且,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为()A.B.C.D.3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量单位:万人的数据,绘制了如图所示的折线图.根据该折线图,有下列四个结论:月接待游客量逐月增加;年接待游客量逐年增加;各年的月接待游客量高峰期大致在7,8月;各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,其中正确的结论有个.()A.4B.3C.2D.14.对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数有两个相异的不动点,,且,则c的取值范围是()A. B. C. D.5.如图,在中,,,点D为内一点,,,连接BD,将绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为()A. B. C. D.6.如图①,在矩形ABCD中,,对角线AC,BD相交于点O,动点P由点A出发,沿向点D运动.设点P的运动路程为x,的面积为y,y与x的函数关系图象如图②所示,则AC边的长为()A.3B.4C.5D.67.对于实数x,符号表示不超过x的最大整数,如,若有正整数解,则正实数a的取值范围是()A.或B.或C.或D.或8.已知非零实数a,b,c满足,,,则()A. B. C. D.二、填空题:本题共8小题,每小题4分,共32分。
9.一个不透明的口袋中有四个完全相同的小球,其上分别标有数字1,2,4,8,随机摸取一个小球后不放回,再随机摸取一个小球,则两次取出的小球上数字之积等于2或16的概率是______.10.如图所示,在中,D是边AC上的点,且,,,则的值为______.11.如图,在平面直角坐标系中,直线:与直线:交于点,过作x轴的垂线,垂足为,过作的平行线交于,过作x轴的垂线,垂足为,过作的平行线交于,过作x轴的垂线,垂足为…按此规律,则点的纵坐标为______.12.如图,正方形ABCD和,,,连接BF,DE,若绕点A旋转,当最大时,的面积=______.13.如图,平行四边形OABC的顶点A在反比例函数的图象上,顶点B,C在反比例函数的图象上,则平行四边形OABC的面积为______.14.如图,、都是等腰直角三角形,,,将绕点B逆时针方向旋转后得,当点恰好落在线段上时,则______.15.因式分解:______.16.已知二次函数的图象与x轴交于不同的两点A、B,C为二次函数的图象的顶点,,若是边长为3的等边三角形,则______.三、解答题:本题共7小题,共56分。
湖北省黄冈中学2020年春自主招数学模拟试题及参考答案

黄冈中学2020年春自主招生模拟试题数 学 试 题(考试时间:120分钟 总分120分)一、选择题(每题3分,共24分)1.一元二次方程x 2+bx+c=0的一实根是另一实根的2倍,则以下结论错误的是( )A.b 2-4c ≥0B.b ≤0C.c ≥0D.2b 2=9c2.关于x 的不等式组1532223x x x x a ⎧+>-⎪⎪⎨+⎪<+⎪⎩,只有4个整数解,则a 的取值范围是( )A.-5≤a ≤143-B.-5≤a ≤143-C. -5<a ≤143-D. -5≤a<143- 3.双曲线y=k x (k<0)上有A ,B 两点,直线AB 交y 轴于点D ,交x 轴于点C ,且OD=OC ,若A (43-,1),则点B 的坐标为( )A.(-1,43) B.(-1,34) C.(-1,23) D .(-1,32)4.已知函数f(x)=x 2+λx ,p ,q ,r 为△ABC 的三边,且P<q<r ,若所有的正整数p ,q ,r 都满足f(p)<f(q)<f(r),则λ的取值范围是( )A. λ>-2B. λ>-3C. λ>-4D. λ>-55.如图,△ABC 的面积为60,点D 在BC 上,BD=2CD ,连接AD 点E 为AD 中点,连接BE 并工交AC 于点,则△AEF 的面积为( )A. 2B. 4C. 5D. 86.记S n =a 1+a 2+…+a n , 令T n =12nS S S n+++,称T n 为a 1,a 2…,a n 这列数的“理想数”.已知a 1,a 2,…,a 500的“理想数”为2004,那么8,a 1,a 2,…,a 500的“理想数”为( )A. 2004B.2006C. 2008D. 20107.如图,△ABC 内接于⊙O ,且AB=AC ,直线AD 交BC 于点E ,F 是OE 的中点,如果BD ∥CF ,BC=25,则线段CD 的长为( )A. 2B.5C.6D. 238.已知x ,y ,z ,a ,b 均为非零的实数,且满足331xy x y a b =+-,31yz y z a =+,331xz x z a b=++,112xyz xy yz zx =++,则a 的值为( ) A. 2 B.-2 C.1 D. -1二、填空题(每题3分,共24分)9.已知a+b+c=0, a 2+b 2+c 2=6,那么a 4+b 4+c 4的值为_________.第5题图第7题图10.用三种边长相等的正多边形地转铺地,其顶点在一起,刚好能完全铺满地面,已知正多边形的边数为x、y、z,则111x y z++的值为.11.将一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b,则使关于x,y的方程组322ax byx y+=⎧⎨+=⎩,只有正数解的概率为.12.如图,在平面直角坐标系中,四边形ABCD是平行四边形,顶点B在的反比例函数y=2(0)xx-<上,点A在反比例函数3(0)y xx=>上,C,D在x轴上,则平行四边形ABCD的面积是_______.13. 设[x]表示不超过x的最大整数(例如:[2]=2,[1.25]=1),则方程3x-2[x]+4=0的解为________ .14.使不等式|2x3-|+k<x有解的实数k的取值范围是______.15.如图,⊙O中,直径AB=10,C,D是上半圆⌒AB上的两个动点,弦AC与BD交于点E,则AE·AC+BE·BD=__________.16.如图所示,点A、C都在函数y=2(0)xx>的图象上,点B,D都在x轴上,且使得△OAB,△BCD都是等腰直角三角形,则D点的坐标为________.三、解答题17.(8分)已知实数x,y满足(2x+1)2+y2+(y-2x)2=13,求x+y.18.(8分)设m是不小于-1的实数,关于x的方程x2+2(m-2)x+m2-3m+3=0有两个不相等的实数根x1,x2(1)若22126x x+=,求m的值;(2)求22121211mx mxx x+--的最大值.第16题图第15题图2yx=-3yx=第12题图19.(8分)如图,已知△ABC,D是BC的延长线上的点,F是AB延长线上的点,∠ACD的平分线交BA的延长线于点E,∠FBC的平分线交AC的延长线于点E,∠FBC的平分线交AC的延长线于点G,若CE=BC=BG,求∠ABC.20.(8分)如图,已知A,B两点的坐标分别为A(0,23),B(2,0),直线AB与反比例函数y=mx的图象交于点C和点D(-1,a).(1)求直线AB和反比例函数的解析式;(2)求∠ACO的度数.21.(9分)如图,在锐角△ABC中,AC是最短边,以AC的中点O为圆心,12AC长为半径作⊙O,交BC于点E,过O作OD∥BC交O于点D,连结AE、AD、DC.(1)求证:D是⌒AE的中点;(2)求证:∠DAO=∠B+∠BAD;(3)若=12CEFOCDSS∆∆=,且AC=4,求CF的长.22.(9分)提高过江大桥的车辆通行能力可改善整个城市的交通状况。
2020年黄冈中学自主招生考试数学试题答案
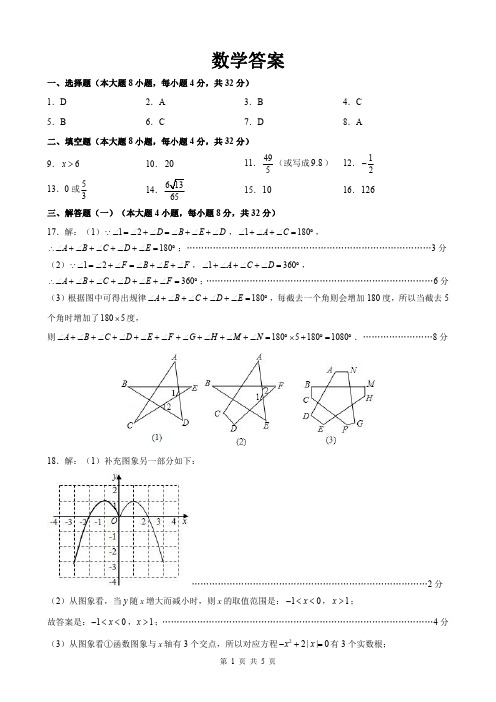
数学答案一、选择题(本大题8小题,每小题4分,共32分)1.D2.A 3.B 4.C 5.B 6.C 7.D 8.A二、填空题(本大题8小题,每小题4分,共32分)9.6x >10.2011.495(或写成8.9)12.12-13.0或5314.6515.1016.126三、解答题(一)(本大题4小题,每小题8分,共32分)17.解:(1)12D B E D ∠=∠+∠=∠+∠+∠ ,1180A C ∠+∠+∠=︒,180A B C D E ∴∠+∠+∠+∠+∠=︒;…………………………………………………………………………3分(2)12F B E F ∠=∠+∠=∠+∠+∠ ,1360A C D ∠+∠+∠+∠=︒,360A B C D E F ∴∠+∠+∠+∠+∠+∠=︒;……………………………………………………………………6分(3)根据图中可得出规律180A B C D E ∠+∠+∠+∠+∠=︒,每截去一个角则会增加180度,所以当截去5个角时增加了1805⨯度,则180********A B C D E F G H M N ∠+∠+∠+∠+∠+∠+∠+∠+∠+∠=︒⨯+︒=︒.……………………8分18.解:(1)补充图象另一部分如下:………………………………………………………………………2分(2)从图象看,当y 随x 增大而减小时,则x 的取值范围是:10x -<<,1x >;故答案是:10x -<<,1x >;…………………………………………………………………………………4分(3)从图象看①函数图象与x 轴有3个交点,所以对应方程22||0x x -+=有3个实数根;②方程22||1x x -+=-有2个实数根;③若关于x 的方程22||x x n -+=有4个实数根,则n 的取值范围是01n <<,故答案为:3,3;2;01n <<.(注:一个1分)…………………………………………………………8分19.解:(1)证明:如图,连接OC ,20.AB 是O 的直径,C 是弧AB 的中点,OC AB∴⊥CD AC = ,OA OB =,OC ∴为ABD ∆的中位线,//OC BD ∴,BD AB ∴⊥,BD ∴是O 的切线;……………………………………………………………………………………………………………………4分(2)E 是OB 的中点,OE BE ∴=,//OC BD ,OCE BFE ∴∆∆∽,∴OC OE BF BE=,1BF = ,1OC ∴=,∴在Rt ABF ∆中,2AB =,1BF =,由勾股定理得:AF ==AB 是O 的直径,90AHB ∴∠=︒,1122AF BH AB BF = ,BH ∴==BH ∴的长为5.……………………………………8分20.解:(1)如图,作AH x ⊥轴于H .在Rt AOH ∆中,OA = 1tan2AOH ∠=,2AH ∴=,4OH =,(4,2)A ∴-,(4,2)A - 在k y x=的图象上,8k ∴=-,……………………………2分(,4)B m - ,在8y x =-的图象上上,2m ∴=,把A 、B 坐标代入y kx b =+,则4224k b k b -+=⎧⎨+=-⎩,解得12k b =-⎧⎨=-⎩,∴反比例函数的解析式为8y x=-,一次函数的解析式为2y x =--.……………………………………………………………………………………………………………………4分(2)由2y x =--,令0x =,则2y =-;令0y =,则2x =-,(0,2)D ∴-,(2,0)C -,12(42)62AOB AOD BOD S S S ∆∆∆∴=+=⨯⨯+=,若点E 在y 轴上,设(0,)E y ,则|(2)|DE y =--.由3AED AOB S S ∆∆=,可得1|(2)|4362y ⨯--⨯=⨯.解得7y =或11-,∴点E 的坐标为(0,7)或(0,11)-;……………………6分若点E 在x 轴上,设(,0)E x ,则|(2)|CE x =--.由2AED AOB S S ∆∆=,可得1|(2)|4362x ⨯--⨯=⨯.解得7x =或11-,∴点E 的坐标为(7,0)或(11,0)-;综上所述,点E 的坐标为(0,7)或(0,11)-或(7,0)或(11,0)-.………………………………………………8分四、解答题(二)(本大题2小题,每小题12分,共24分).21.解:(1)∵10BC =,∴=5AB ①当点D 落在线段AB上,52BD AB AD =-=-,当点D 落在线段BD 的延长线上时,52BD AB AD =+=+,BD ∴的长为52-或52+.……………………………………………………………………………2分②显然ABD ∠不能为直角,当ADB ∠为直角时,222AD BD AB +=,∴3BD =,当BAD ∠为直角时,222AB AD BD +=,∴7BD =,BD ∴长为3或7.…………………………………………………………………………………………4分(2)如图1,连接12D D ,1D C ,则△12AD D 为等腰直角三角形,∴12122D D AD ==,12AD AD ∴=,AB AC =,21BAC D AD ∠=∠ ,21BAD CAD ∴∠=∠,在2ABD ∆和1ACD ∆中,2121AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩,21()BAD CAD SAS ∴∆≅∆,21BD CD ∴=,……………………………………………………………………6分又2135AD C ∠=︒ ,122211354590D D C AD C AD D ∴∠=∠-∠=︒-︒=︒,∴2212125CD CD D D =+=,∴25BD =.………………………………………………………………8分(3)存在最大值和最小值.理由:如图2,所示,连接1CD ,点P 、M 分别是2CD ,21D D 的中点,∴112PM CD =,1//PM CD , 点N 、P 分别是BC ,2CD 的中点,∴212PN BD =,2//PN BD ,21BD CD = ,PM PN ∴=,MPN ∴∆是等腰三角形,1//PM CD ,221D PM D CD ∴∠=∠,2//PN BD ,2PNC D BC ∴∠=∠,2222D PN D CB PNC D CB D BC ∠=∠+∠=∠+∠ ,22MPN D PM D PN ∴∠=∠+∠2122D CD D CB D BC =∠+∠+∠12BCD D BC =∠+∠12ACB ACD D BC=∠+∠+∠22ACB ABD D BC =∠+∠+∠ACB ABC =∠+∠.90BAC ∠=︒ ,90ACB ABC ∴∠+∠=︒,90MPN ∴∠=︒.MPN ∴∆为等腰直角三角形.……………10分∴212PMN S PN ∆==2211()22BD =,∴当2BD 取最大时,PMN ∆的面积最大,此时最大面积2117[228S +==;当2BD 取最小时,PMN ∆的面积最小,此时最小面积2117[228S -==.……………12分22.解:(1)对于抛物线211433y x x =-++,令0y =得2114033x x -++=,解得3x =-或4.令0x =得4y =,(3,0)A ∴-,(4,0)B ,(0,4)C ,5x = 时,83y =-,8(5,)3E ∴-,设直线AD 的解析式为y kx b =+,则有30853k b k b -+=⎧⎪⎨+=-⎪⎩,解得131k b ⎧=-⎪⎨⎪=-⎩,∴直线AD 的解析式为113y x =--.…………………………………………………………………………4分(2)如图1中,设211(,4)33F m m m -++,则1(,1)3G m m --,212533FG m m =-++,//FG CD ,//FH AC ,FHD CAD ∴∠=∠,FGH CDA ∠=∠,FGH ∴∠,FHG ∠是定值,∴当FG 最大时,FGH ∆的周长最短,22121165(1)3333FG m m m =-++=--+ ,103-< ,1m ∴=时,FG 有最大值,此时(1,4)F ,………………………………………………………6分作点F 关于y 轴的对称点F ',连接AF ',由此AF '交y 轴于T ,此时||TA TF -最大,(3,0)A - ,(1,4)F '-,∴直线AF '的解析式为26y x =+,∴点T 坐标(0,6).………………………………………………………………………………………………8分(3)①如图2中,当90MNP ∠=︒,重叠部分是MNP ∆是直角三角形,FMN COA ∆∆ ∽,∴FN FM CO AC =,211433FN m m =-++ ,25511(4)4433FM PM PG FN m m ∴====-++,2FN PG FG += ,22211511122(4)(4)53343333m m m m m m ∴-+++-++==-++,整理得295960m m --=,解得329m =或3-(舍弃),图22132132236(43939243FN ∴=-+⨯+=.…………………………………………………………………………10分②如图3中,当PM GF ⊥时,重叠部分是MNK ∆是直角三角形.::3:4:5KM FK FM = ,PM PG =,:2:5PK PG ∴=,:2KG PK ∴=,21111(1):(3)43233m m m ∴+-++=,(3):(3)(4)4m m m ∴++-+=,解得421m =-或3-(舍弃),166363FK ∴=.::5:3FN NK FM MK == ,510863FN FK ∴==.③当90NMF ∠=︒,不可能得到PM PG =,故此种情形不存在.综上所述,当PMN ∆与FGH ∆重叠部分图形为直角三角形,且PM PG =时,线段FN 的长为2362431063.………………………………………………………12分。
初中数学黄岗试卷及答案

一、选择题(每题4分,共40分)1. 下列数中,不是整数的是()A. -3B. 0.5C. 3D. -2答案:B2. 下列图形中,不是轴对称图形的是()A. 正方形B. 等腰三角形C. 圆D. 长方形答案:D3. 如果a > b,那么下列不等式中正确的是()A. a - b > 0B. a + b > 0C. a - b < 0D. a + b < 0答案:A4. 已知三角形ABC中,∠A = 90°,∠B = 30°,则∠C的度数是()A. 60°B. 30°C. 45°D. 90°答案:C5. 下列代数式中,完全平方公式适用的是()A. (x + 2)^2B. (x - 3)^2C. (x + 3)(x - 2)D. (x + 1)(x + 2)答案:B6. 下列方程中,无解的是()A. 2x + 3 = 7B. 3x - 5 = 2x + 1C. 5x - 3 = 0D. 2x + 4 = 3x + 1答案:C7. 下列函数中,是反比例函数的是()A. y = 2x + 1B. y = 3/xC. y = x^2D. y = 4x - 5答案:B8. 在平面直角坐标系中,点A(2,3)关于x轴的对称点坐标是()A.(2,-3)B.(-2,3)C.(-2,-3)D.(2,-3)答案:A9. 下列数中,能被3整除的是()A. 27B. 28C. 29D. 30答案:A10. 下列图形中,周长最小的是()A. 正方形B. 长方形C. 等腰三角形D. 圆答案:D二、填空题(每题4分,共40分)11. 0.2的倒数是______。
答案:512. 下列各数中,负数是______。
答案:-1/213. 在直角坐标系中,点B(-3,4)关于原点的对称点坐标是______。
答案:(3,-4)14. 如果x = 2,那么2x + 3的值是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省黄冈中学自主招生考试数学试卷2011年湖北省黄冈中学自主招生考试数学试卷一、填空题(5×8=40分)1.(5分)(2012•乐平市校级自主招生)方程组的解是.2.(5分)(2011•罗田县校级自主招生)若对任意实数x不等式ax>b都成立,那么a,b的取值范围为.3.(5分)(2013•武汉校级自主招生)设﹣1≤x≤2,则|x﹣2|﹣|x|+|x+2|的最大值与最小值之差为.4.(5分)(2011•罗田县校级自主招生)两个反比例函数y=,y=在第一象限内的图象如图所示.点P1,P2,P3、…、P2007在反比例函数y=上,它们的横坐标分别为x1、x2、x3、…、x2007,纵坐标分别是1,3,5…共2007个连续奇数,过P1,P 2,P3、…、P2007分别作y轴的平行线,与y=的图象交点依次为Q1(x1′,y1′)、Q1(x2′,y2′)、…、Q2(x2007′,y2007′),则|P2007Q2007|=.5.(5分)(2011•罗田县校级自主招生)如图,圆锥的母线长是3,底面半径是1,A是底面圆周上一点,从A点出发绕侧面一周,再回到A 点的最短的路线长是.6.(5分)(2012•金阊区校级自主招生)有一张矩形纸片ABCD,AD=9,AB=12,将纸片折叠使A、C两点重合,那么折痕长是.7.(5分)(2011•罗田县校级自主招生)已知3,a,4,b,5这五个数据,其中a,b是方程x2﹣3x+2=0的两个根,则这五个数据的标准差是.8.(5分)(2015•黄冈中学自主招生)若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为.二、选择题(5×8=40分)9.(5分)(2015•黄冈中学自主招生)如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于()A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:1010.(5分)(2012•涪城区校级自主招生)若一直角三角形的斜边长为c,内切圆半径是r,则内切圆的面积与三角形面积之比是()A. B.C. D.11.(5分)(2002•济南)抛物线y=ax2与直线x=1,x=2,y=1,y=2围成的正方形有公共点,则实数a的取值范围是()A .≤a ≤1B .≤a ≤2C .≤a ≤1D .≤a ≤212.(5分)(2015•黄冈中学自主招生)有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需( )A .1.2元B .1.05元C .0.95元D .0.9元13.(5分)(2014•余姚市校级自主招生)设关于x 的方程ax 2+(a+2)x+9a=0,有两个不相等的实数根x 1、x 2,且x 1<1<x 2,那么实数a 的取值范围是( )A .B .C .D .14.(5分)(2015•黄冈中学自主招生)如图,正方形ABCD 的边AB=1,和都是以1为半径的圆弧,则无阴影两部分的面积之差是( )A .B .1﹣C .﹣1D .1﹣15.(5分)(2015•黄冈中学自主招生)已知锐角三角形的边长是2,3,x ,那么第三边x 的取值范围是( )A.1<x<B. C.D.16.(5分)(2012•涪城区校级自主招生)某工厂第二季度的产值比第一季度的产值增长了x%,第三季度的产值又比第二季度的产值增长了x%,则第三季度的产值比第一季度的产值增长了()A.2x% B.1+2x% C.(1+x%)x%D.(2+x%)x%三、解答题17.(15分)(2015•永春县自主招生)设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2,(1)若x12+x22=6,求m值;(2)求的最大值.18.(15分)(2013•茶陵县自主招生)如图,开口向下的抛物线y=ax2﹣8ax+12a与x轴交于A、B两点,抛物线上另有一点C在第一象限,且使△OCA∽△OBC,(1)求OC的长及的值;(2)设直线BC与y轴交于P点,点C是BP 的中点时,求直线BP和抛物线的解析式.19.(15分)(2013•茶陵县自主招生)某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高最高产值是多少?(以千元为单位)20.(10分)(2013•茶陵县自主招生)一个家庭有3个孩子,(1)求这个家庭有2个男孩和1个女孩的概率;(2)求这个家庭至少有一个男孩的概率.21.(15分)(1999•福州)如图,已知⊙O和⊙O′相交于A、B两点,过点A作⊙O′的切线交⊙O 于点C,过点B作两圆的割线分别交⊙O、⊙O′于E、F,EF与AC相交于点P.(1)求证:PA•PE=PC•PF;(2)求证:;(3)当⊙O与⊙O′为等圆时,且PC:CE:EP=3:4:5时,求△PEC与△FAP的面积的比值.2011年湖北省黄冈中学自主招生考试数学试卷参考答案与试题解析一、填空题(5×8=40分)1.(5分)(2012•乐平市校级自主招生)方程组的解是和.【解答】解:设x+1=a,y﹣1=b,则原方程可变为,由②式又可变化为=26,把①式代入得=13,这又可以变形为(+)2﹣3=13,再代入又得﹣3=9,解得ab=﹣27,又因为a+b=26,所以解这个方程组得或,于是(1),解得;(2),解得.故答案为和.2.(5分)(2011•罗田县校级自主招生)若对任意实数x不等式ax>b都成立,那么a,b的取值范围为a=0,b<0.【解答】解:∵如果a≠0,不论a大于还是小于0,对任意实数x不等式ax>b都成立是不可能的,∴a=0,则左边式子ax=0,∴b<0一定成立,∴a,b的取值范围为a=0,b<0.3.(5分)(2013•武汉校级自主招生)设﹣1≤x≤2,则|x﹣2|﹣|x|+|x+2|的最大值与最小值之差为1.【解答】解:∵﹣1≤x≤2,∴x﹣2≤0,x+2>0,∴当2≥x≥0时,|x﹣2|﹣|x|+|x+2|=2﹣x﹣x+x+2=4﹣x;当﹣1≤x<0时,|x﹣2|﹣|x|+|x+2|=2﹣x+x+x+2=4+x,当x=0时,取得最大值为4,x=2时取得最小值,最小值为3,则最大值与最小值之差为1.故答案为:14.(5分)(2011•罗田县校级自主招生)两个反比例函数y=,y=在第一象限内的图象如图所示.点P1,P2,P3、…、P2007在反比例函数y=上,它们的横坐标分别为x1、x2、x3、…、x2007,纵坐标分别是1,3,5…共2007个连续奇数,过P1,P 2,P3、…、P2007分别作y轴的平行线,与y=的图象交点依次为Q1(x1′,y1′)、Q1(x2′,y2′)、…、Q2(x2007′,y2007′),则|P2007Q2007|=.【解答】解:由题意可知:P2007的坐标是(Px2007,4013),又∵P2007在y=上,∴Px 2007=. 而Qx 2007(即Px 2007)在y=上,所以Qy 2007===,∴|P2007Q 2007|=|Py 2007﹣Qy 2007|=|4013﹣|=.故答案为:.5.(5分)(2011•罗田县校级自主招生)如图,圆锥的母线长是3,底面半径是1,A 是底面圆周上一点,从A 点出发绕侧面一周,再回到A 点的最短的路线长是 3 .【解答】解:∵图中扇形的弧长是2π,根据弧长公式得到2π=∴n=120°即扇形的圆心角是120° ∴弧所对的弦长是2×3sin60°=36.(5分)(2012•金阊区校级自主招生)有一张矩形纸片ABCD,AD=9,AB=12,将纸片折叠使A、C两点重合,那么折痕长是.【解答】解:如图,由勾股定理易得AC=15,设AC的中点为E,折线FG与AB交于F,(折线垂直平分对角线AC),AE=7.5.∵∠AEF=∠B=90°,∠EAF是公共角,∴△AEF∽△ABC,∴==.∴EF=.∴折线长=2EF=.故答案为.7.(5分)(2011•罗田县校级自主招生)已知3,a,4,b,5这五个数据,其中a,b是方程x2﹣3x+2=0的两个根,则这五个数据的标准差是.【解答】解:由方程x2﹣3x+2=0解方程的两个根是1,2,即a=1,b=2故这组数据是3,1,4,2,5其平均数(3+1+4+2+5)=3方差S 2=[(3﹣3)2+(1﹣3)2+(4﹣3)2+(2﹣3)2+(5﹣3)2]=2故五个数据的标准差是S==故本题答案为:.8.(5分)(2015•黄冈中学自主招生)若抛物线y=2x2﹣px+4p+1中不管p取何值时都通过定点,则定点坐标为(4,33).【解答】解:y=2x2﹣px+4p+1可化为y=2x2﹣p (x﹣4)+1,分析可得:当x=4时,y=33;且与p的取值无关;故不管p取何值时都通过定点(4,33).二、选择题(5×8=40分)9.(5分)(2015•黄冈中学自主招生)如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于()A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10【解答】解:连接EM,CE:CD=CM:CA=1:3∴EM平行于AD∴△BHD∽△BME,△CEM∽△CDA∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3∴AH=(3﹣)ME,∴AH:ME=12:5∴HG:GM=AH:EM=12:5设GM=5k,GH=12k,∵BH:HM=3:2=BH:17k∴BH=K,∴BH:HG:GM=k:12k:5k=51:24:10 故选D.10.(5分)(2012•涪城区校级自主招生)若一直角三角形的斜边长为c,内切圆半径是r,则内切圆的面积与三角形面积之比是()A. B.C. D.【解答】解:设直角三角形的两条直角边是a,b,则有:S=,又∵r=,∴a+b=2r+c,将a+b=2r+c代入S=得:S=r=r(r+c).又∵内切圆的面积是πr2,∴它们的比是.故选B.11.(5分)(2002•济南)抛物线y=ax2与直线x=1,x=2,y=1,y=2围成的正方形有公共点,则实数a的取值范围是()A.≤a≤1 B.≤a≤2 C.≤a≤1 D.≤a≤2【解答】解:由右图知:A(1,2),B(2,1),再根据抛物线的性质,|a|越大开口越小,把A点代入y=ax2得a=2,把B点代入y=ax 2得a=,则a的范围介于这两点之间,故≤a≤2.故选D.12.(5分)(2015•黄冈中学自主招生)有铅笔、练习本、圆珠笔三种学习用品,若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本8本,圆珠笔2支共需4.2元,那么,购铅笔、练习本、圆珠笔各1件共需()A.1.2元B.1.05元C.0.95元D.0.9元【解答】解:设购一支铅笔,一本练习本,一支圆珠笔分别需要x,y,z元,根据题意得,②﹣①得x+y+z=1.05(元).故选:B.13.(5分)(2014•余姚市校级自主招生)设关于x 的方程ax 2+(a+2)x+9a=0,有两个不相等的实数根x 1、x 2,且x 1<1<x 2,那么实数a 的取值范围是( ) A . B . C . D .【解答】解:∵方程有两个不相等的实数根,则△>0,∴(a+2)2﹣4a ×9a=﹣35a 2+4a+4>0, 解得﹣<a <,∵x 1+x 2=﹣,x 1x 2=9, 又∵x 1<1<x 2, ∴x 1﹣1<0,x 2﹣1>0, 那么(x 1﹣1)(x 2﹣1)<0, ∴x 1x 2﹣(x 1+x 2)+1<0, 即9++1<0, 解得<a <0,最后a 的取值范围为:<a <0.故选D .14.(5分)(2015•黄冈中学自主招生)如图,正方形ABCD的边AB=1,和都是以1为半径的圆弧,则无阴影两部分的面积之差是()A.B.1﹣ C.﹣1 D.1﹣【解答】解:如图:正方形的面积=S1+S2+S3+S4;①两个扇形的面积=2S3+S1+S2;②②﹣①,得:S3﹣S4=S扇形﹣S正方形=﹣1=.故选:A.15.(5分)(2015•黄冈中学自主招生)已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是()A.1<x<B. C.D.【解答】解:因为32﹣22=5,32+22=13,所以5<x 2<13,即.故选B.16.(5分)(2012•涪城区校级自主招生)某工厂第二季度的产值比第一季度的产值增长了x%,第三季度的产值又比第二季度的产值增长了x%,则第三季度的产值比第一季度的产值增长了()A.2x% B.1+2x% C.(1+x%)x%D.(2+x%)x%【解答】解:第三季度的产值比第一季度的增长了(1+x%)×(1+x%)﹣1=(2+x%)x%.故选D.三、解答题17.(15分)(2015•永春县自主招生)设m是不小于﹣1的实数,关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x1、x2,(1)若x12+x22=6,求m值;(2)求的最大值.【解答】解:∵方程有两个不相等的实数根,∴△=b2﹣4ac=4(m﹣2)2﹣4(m2﹣3m+3)=﹣4m+4>0,∴m<1,结合题意知:﹣1≤m<1.(1)∵x2+x22=(x1+x2)2﹣2x1x2=4(m﹣2)2﹣21(m2﹣3m+3)=2m2﹣10m+10=6∴,∵﹣1≤m<1,∴;(2)==(﹣1≤m <1).∴当m=﹣1时,式子取最大值为10.18.(15分)(2013•茶陵县自主招生)如图,开口向下的抛物线y=ax2﹣8ax+12a与x轴交于A、B两点,抛物线上另有一点C在第一象限,且使△OCA∽△OBC,(1)求OC的长及的值;(2)设直线BC与y轴交于P点,点C是BP 的中点时,求直线BP和抛物线的解析式.【解答】解:(1)由题设知a<0,且方程ax2﹣8ax+12a=0有两二根,两边同时除以a得,x2﹣8x+12=0原式可化为(x﹣2)(x﹣6)=0x1=2,x2=6于是OA=2,OB=6∵△OCA∽△OBC∴OC2=OA•OB=12即OC=2而===,故(2)因为C是BP的中点∴OC=BC从而C点的横坐标为3又∴设直线BP的解析式为y=kx+b,因其过点B(6,0),,则有∴∴又点在抛物线上∴∴∴抛物线解析式为:.19.(15分)(2013•茶陵县自主招生)某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高最高产值是多少?(以千元为单位)【解答】解:设每周应生产空调、彩电、冰箱的数量分别为x台、y台、z台,则有,①﹣②×4得3x+y=360,总产值A=4x+3y+2z=2(x+y+z)+(2x+y)=720+(3x+y)﹣x=1080﹣x,∵z≥60,∴x+y≤300,而3x+y=360,∴x+360﹣3x≤300,∴x≥30,∴A≤1050,即x=30,y=270,z=60.最高产值:30×4+270×3+60×2=1050(千元)20.(10分)(2013•茶陵县自主招生)一个家庭有3个孩子,(1)求这个家庭有2个男孩和1个女孩的概率;(2)求这个家庭至少有一个男孩的概率.【解答】解:画树状图得:则一共有8种等可能的情况,(1)∵2个女孩和1个男孩的3种,∴这个家庭有2个男孩和1个女孩的概率为:;(2)∵这个家庭至少有一个男孩的有7种情况,∴这个家庭至少有一个男孩的概率为:.21.(15分)(1999•福州)如图,已知⊙O和⊙O′相交于A、B两点,过点A作⊙O′的切线交⊙O 于点C,过点B作两圆的割线分别交⊙O、⊙O′于E、F,EF与AC相交于点P.(1)求证:PA•PE=PC•PF;(2)求证:;(3)当⊙O与⊙O′为等圆时,且PC:CE:EP=3:4:5时,求△PEC与△FAP的面积的比值.【解答】(1)证明:连接AB,∵CA切⊙O'于A,∴∠CAB=∠F.∵∠CAB=∠E,∴∠E=∠F.∴AF∥CE.∴.∴PA•PE=PC•PF.(2)证明:∵,∴=.∴.再根据切割线定理,得PA2=PB•PF,∴.(3)解:连接AE,由(1)知△PEC∽△PFA,而PC:CE:EP=3:4:5,∴PA:FA:PF=3:4:5.设PC=3x,CE=4x,EP=5x,PA=3y,FA=4y,PF=5y,∴EP2=PC2+CE2,PF2=PA2+FA2.∴∠C=∠CAF=90°.∴AE为⊙O的直径,AF为⊙O'的直径.∵⊙O与⊙O'等圆,∴AE=AF=4y.∵AC2+CE2=AE2∴(3x+3y)2+(4x)2=(4y)2即25x2+18xy﹣7y2=0,∴(25x﹣7y)(x+y)=0,∴.∴.参与本试卷答题和审题的老师有:liume。
