2010年上海春考数学试卷
2010年上海高考数学文科试卷带详解

2010年普通高等学校招生全国统一考试(上海卷)数学(文科)一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分. 1.已知集合{}1,3,A m =,{}3,4B =,{}1,2,3,4AB =则m = .【测量目标】集合的基本运算.【考查方式】直接给出两个集的并集,根据集合的定义求元素. 【参考答案】2【试题解析】显然m =2. 2.不等式204xx ->+的解集是 . 【测量目标】解一元二次不等式.【考查方式】直接给出分数不等式,求不等式的解集. 【参考答案】{}24|<<-x x 【试题解析】204xx ->+等价于(x -2)(x +4)<0,所以4x -<<2. 3.行列式ππcossin 66ππsin cos 66的值是 .【测量目标】行列式的运算.【考查方式】直接给出行列式,根据行列式运算法则求值. 【参考答案】0.5 【试题解析】ππcossin66ππsin cos 66=πππππ1cos cos sin sin cos 666632-==.4.若复数12i z =-(i 为虚数单位),则z z z += .【测量目标】复数的基本运算.【考查方式】直接给出复数z ,求其共轭复数,进而根据运算法则求值. 【参考答案】62i -【试题解析】z z z +=(12i)(12i)12i 62i -++-=-.5.将一个总数为A 、B 、C 三层,其个体数之比为5:3:2.若用分层抽样方法抽取容量为100的样本,则应从C 中抽取 个体. 【测量目标】分层抽样.【考查方式】给出样本,根据分层抽样求样本的个体. 【参考答案】20【试题解析】从C 中抽取20102100=⨯. 6.已知四棱椎P ABCD -的底面是边长为6 的正方形,侧棱PA ⊥底面ABCD ,且8PA =则该四棱椎的体积是 . 【测量目标】锥的体积.【考查方式】直接给出四棱锥的底面边长和高的值,利用椎体体积公式求体积. 【参考答案】96 【试题解析】9683631=⨯⨯=V . 7.圆22:2440C x y x y +--+=的圆心到直线3440x y ++=的距离d = . 【测量目标】点到直线的距离公式.【考查方式】给出圆一般方程,得到圆心坐标,根据点到直线的距离公式求解. 【参考答案】3【试题解析】圆心(1,2)到直线3440x y ++=距离为3542413=+⨯+⨯.8.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为 . 【测量目标】抛物线的定义及其标准方程.【考查方式】给出符合抛物线定义的动点数据,利用代数关系求动点的轨迹方程. 【参考答案】y 2=8x【试题解析】P 的轨迹是以(2,0)F 为焦点的抛物线,p =2所以其方程为y 2=8x. 9.函数3()log (3)f x x =+的反函数的图像与y 轴的交点坐标是 . 【测量目标】反函数的概念和性质.【考查方式】直接给出函数,求其反函数,进而得出交点坐标. 【参考答案】(0,-2)【试题解析】函数3()log (3)f x x =+的反函数为33-=xy ,另x =0,有y =2-.10. 从一副混合后的扑克牌(52张)中随机抽取2张,则“抽出的2张均为红桃”的概率 为 (结果用最简分数表示). 【测量目标】随机事件与概率.【考查方式】给出等可能事件,利用排列组合求概率.【参考答案】351【试题解析】“抽出的2张均为红桃”的概率为213252C 3C 51=.11. 2010年上海世博会园区每天9:00开园,20:00停止入园.在右边的框图中,S 表示上海世博会官方网站在每个整点报道的入园总人数,a 表示整点报道前1个小时内入园人数,则空白的执行框内应填入 .【测量目标】循环结构的程序框图.【考查方式】根据程序框图的逻辑结构,得到S 与a 的数量关系. 【参考答案】S ←S +a.【试题解析】依步骤得S ←S +a.12.在n 行m 列矩阵12321234113*********n n n n n n n n n n ⋅⋅⋅--⎛⎫ ⎪⋅⋅⋅- ⎪⎪⋅⋅⋅ ⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪ ⎪⋅⋅⋅---⎝⎭中,第11 题图 记位于第i 行第j 列的数为(,1,2,)ij a i j n =⋅⋅⋅.当9n =时,11223399a a a a +++⋅⋅⋅+= . 【测量目标】矩阵的定义.【考查方式】给出矩阵的行和列,求出各对角元素值,最后求和. 【参考答案】45【试题解析】11223399a a a a +++⋅⋅⋅+=1+3+5+7+9+2+4+6+8=45.13.在平面直角坐标系中,双曲线Γ的中心在原点,它的一个焦点坐标为(5,0),1(2,1)e =、2(2,1)e =-分别是两条渐近线的方向向量.任取双曲线Γ上的点P ,若12OP ae be =+(a 、b ∈R ),则a 、b 满足的一个等式是 . 【测量目标】双曲线的几何性质,平面向量的线性运算.【考查方式】根据给出的方向向量,求出渐进线的方程,从而得到双曲线的标准方程,再利 用平面向量得到点到坐标原点的向量坐标求出啊,a ,b 关系. 【参考答案】4ab =1.【试题解析】1(2,1)e =、2(2,1)e =-是渐进线方向向量,所以双曲线渐近线方程 为.x y 21±=,又1,2,5==∴=b a c (步骤1) 双曲线方程为1422=-y x ,12OP ae be =+=),22(b a b a -+,1)(4)22(22=--+∴b a b a ,化简得4ab =1 . (步骤2)14.将直线1:10l x y +-=、2:0l nx y n +-=、3:0l x ny n +-=(n ∈*N ,2n)围成的三角形面积记为n S ,则lim n n S →∞= .【测量目标】简单的极限运算.【考查方式】直接给出直线方程,观察图形得出可行域代数关系,利用极限求最小值.【参考答案】12【试题解析】B )1,1(++n nn n 所以BO AC ⊥,(步骤1) n S =)1(21)2221(221+-=-+⨯⨯n n n n 所以lim n n S →∞=12 . (步骤2)二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生必须 在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.满足线性约束条件23,23,0,0x y x y x y +⎧⎪+⎪⎨⎪⎪⎩的目标函数z x y =+的最大值是 ( )A .1B .32C.2D.3 【测量目标】线性规划求目标函数的最值.【考查方式】直接给出约束条件,利用线性规划求目标函数的最大值.【参考答案】C 【试题解析】当直线z x y =+过点B (1,1)时,z 最大值为2. 16.“()π2π4x k k =+∈Z ”是“tan 1x =”成立的 ( )A.充分不必要条件B.必要不充分条件C.充分条件D.既不充分也不必要条件 【测量目标】充要条件的判定. 【考查方式】充分,必要条件. 【参考答案】A【试题解析】ππtan(2π)tan144k +==,所以充分;但反之不成立,如5πtan 14=. 17.若0x 是方程式 lg 2x x +=的解,则0x 属于区间 ( ) A.(0,1) B.(1,1.25) C.(1.25,1.75) D.(1.75,2)【测量目标】二分法的计算.【考查方式】根据给出的函数,构造新的函数,将选项带入新函数得到答案. 【参考答案】D【试题解析】04147lg)47()75.1(,2lg )(<-==-+=f f x x x f 由构造函数.02lg )2(>=f 知0x 属于区间(1.75,2).18.若ABC △的三个内角满足sin :sin :sin 5:11:13A B C =,则ABC △ ( ) A.一定是锐角三角形 B.一定是直角三角形C.一定是钝角三角形D.可能是锐角三角形,也可能是钝角三角形 【测量目标】正弦定理,余弦定理.【考查方式】给出三角形内角正弦的比值,从而得到三角形边长的比值,利用余弦定理得到 余弦值,最后判断角的大小. 【参考答案】C【试题解析】由sin :sin :sin 5:11:13A B C =及正弦定理得::a b c =5:11:13由余弦定理得22251113cos 02511C +-=<⨯⨯,所以角C 为钝角. 三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的 规定区域内写出必要的步骤. 19.(本题满分12分) 已知π02x <<,化简: 2πlg(cos tan 12sin )lg[2cos()]lg(1sin 2)24x x x x x +-+--+.【测量目标】三角函数的诱导公式,对数的化简和计算.【考查方式】给出计算式,通过三角函数的变换,化简,再根据对数的基本运算求值. 【试题解析】原式=2lg(sin cos )lg(cos sin )lg(sin cos )0x x x x x x +++-+=.20.(本满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).(1)当圆柱底面半径r 取何值时,S 取得最大值?并求出该 最大值(结果精确到0.01平方米);(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出 用于灯笼的三视图(作图时,不需考虑骨架等因素).【测量目标】平面图形的直观图和三视图,柱体的面积.【考查方式】写出含未知量底面积代数式,利用函数的知识求最值,根据空间想像能力绘制 较为准确三视图.【试题解析】(1) 设圆柱形灯笼的母线长为l ,则l =1.2-2r (0<r <0.6), (2) 23π(0.4)0.48πS r =--+, (步骤1) (3) 所以当r =0.4时,S 取得最大值约为1.51平方米; (4) 当r =0.3时,l =0.6,作三视图. (步骤2)21.(本题满分14分)本题共有2个小题,第一个小题满分6分,第2个小题满分8分.已知数列{}n a 的前n 项和为n S ,且585n n S n a =--,n ∈*N(1)证明:{}1n a -是等比数列;(2)求数列{}n S 的通项公式,并求出使得1n n S S +>成立的最小正整数n . 【测量目标】数列的通项公式与前n 项和n S 的关系.【考查方式】给出数列前n 项和的代数关系式,证明等比数列,进而求出等比数列的前n 和, 利用比较大小求解.【试题解析】(1) 当n =1时,a 1=-14;当2n时,a n =S n -S n -1=-5a n +5a n -1+1,所以151(1)6n n a a --=-, (步骤1)又a 1-1=-15≠0,所以数列{a n -1}是等比数列;(2) 由(1)知:151156n n a -⎛⎫-=- ⎪⎝⎭,得151156n n a -⎛⎫=- ⎪⎝⎭(步骤2)从而1575906n n S n -⎛⎫=+- ⎪⎝⎭ (n ∈*N ); (步骤3)由S n +1 > S n ,得156522,log 114.96525n n -⎛⎫<>+ ⎪⎝⎭≈,最小正整数n =15.(步骤4) 22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分. 若实数x 、y 、m 满足x m y m -<-,则称x 比y 接近m . (1)若21x -比3接近0,求x 的取值范围;(2)对任意两个不相等的正数a 、b ,证明:22a b ab +比33a b +接近2(3)已知函数()f x 的定义域{}π,,D x x k k x ≠∈∈Z R .任取x D ∈,()f x 等于1sin x +和1sin x -中接近0的那个值.写出函数()f x 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).【测量目标】解一元二次不等式,不等式的基本性质,函数的单调性与最值,奇偶性和周期..【考查方式】给出条件求符合条件自变量的取值范围.满足条件的绝对不等式相互之间比较大小.根据函数的奇偶,周期性,以及最小值求解函数的单调区间.【试题解析】(1) x ∈(-2,2); (步骤1)(2) 对任意两个不相等的正数a 、b,有223322a b ab a b +>+>(步骤2)因为2233222()()0a b ab a b a b a b +--+-=-+-<,(步骤3)所以223322a b ab a b +-<+-,即a 2b +ab 2比a 3+b 3接近2(3) 1sin ,(2ππ,2π)()1|sin |,π1sin ,(2π,2ππ)x x k k f x x x k x x k k +∈-⎧==-≠⎨-∈+⎩,k ∈Z ,(步骤4) f (x )是偶函数,f (x )是周期函数,最小正周期T =π,函数f (x )的最小值为0,(步骤5) 函数f (x )在区间π(π,π)2k k -单调递增,在区间π(π,π+)2k k 单调递减,k ∈Z .(步骤6) 23(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.已知椭圆Γ的方程为22221(0)x y a b a b+=>>,(0,)A b 、(0,)B b -和(,0)Q a 为Γ的三顶点.(1)若点M 满足1()2AM AQ AB =+,求点M 的坐标; (2)设直线11:l y k x p =+交椭圆Γ于C 、D 两点,交直线22:l y k x =于点E .若2122b k k a=-,证明:E 为CD 的中点;(3)设点P 在椭圆Γ内且不在x 轴上,如何构作过PQ 中点F 的直线l ,使得l 与椭圆Γ的两个交点1P 、2P 满足12PP PP PQ +=12PP PP PQ +=?令10a =,5b =,点P 的坐标是(-8,-1),若椭圆Γ上的点1P 、2P 满足12PP PP PQ +=,求点1P 、2P 的坐标.【测量目标】平面向量的线性运算,直线方程和椭圆标准方程,直线和椭圆的位置关系,椭圆中的探索性问题.【考查方式】通过向量坐标的基本运算求M.根据直线方程和椭圆方程的位置关系,解出两直线的斜率代数关系,再进行证明.根据向量等式的关系以及直线和椭圆方程的线性关系求出坐标. 【试题解析】(1) (,)22ab M -;(步骤1)(2) 由方程组122221y k x p x y a b=+⎧⎪⎨+=⎪⎩,消y 得方程2222222211()2()0a k b x a k px a p b +++-=,因为直线11l y k x p =+:交椭圆Γ于C 、D 两点,所以∆>0,即22221a k b p +->0,设C (x 1,y 1)、D (x 2,y 2),CD 中点坐标为(x 0,y 0),(步骤2)则212102221201022212x x a k px a k b b p y k x p a k b ⎧+==-⎪+⎪⎨⎪=+=⎪+⎩,由方程组12y k x py k x =+⎧⎨=⎩,消y 得方程(k 2-k 1)x =p ,(步骤3)又因为2221b k a k =-,所以2102222112202221a k p px x k k a k b b p y k x ya kb ⎧==-=⎪-+⎪⎨⎪===⎪+⎩,(步骤4)故E 为CD 的中点;(3) 因为点P 在椭圆Γ内且不在x 轴上,所以点F 在椭圆Γ内,可以求得直线OF 的斜率k 2,由12PP PP PQ +=知F 为P 1P 2的中点,根据(2)可得直线l 的斜率2122b k a k =-,从而得直线l 的方程.(步骤5)1(1,)2F -,直线OF 的斜率212k =-,直线l 的斜率212212b k a k =-=-,解方程组22112110025y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩,消y :x 2-2x -48=0,解得P 1(-6,-4)、P 2(8,3).(步骤6)。
高中数学2010上海市春季高考试卷试题

高中数学2010上海市春季高考试卷 试题 2019.091,已知复数1z i =+,则2zz -=____________.2,设{0,1,2,3}U =,2{|0}A x U x mx =∈+=,若C {1,2}U A =,则实数m =________.3,某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至少命中一次的概率为1625,则该队员每次罚球的命中率为____________.4,已知以F 为焦点的抛物线24y x =上的两点A 、B 满足3AF FB =,则弦AB 的中点到准线的距离为____________.5,已知函数()f x 满足:1(1)4f =,4()()()(),(,)f x f y f x y f x y x y R =++-∈,则(2010)f =____________.6,本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)设函数22()cos()2cos ,32xf x x x Rπ=++∈.(Ⅰ) 求()f x 的值域;(Ⅱ) 记△ABC 的内角A 、B 、C 的对边长分别为a 、b 、c ,若()1f B =,1b =,c =a 的值.7,在甲、乙等6个单位参加的一次“唱读传讲”赛出活动中,每个单位的节目集中安排在一起.若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求:(Ⅰ) 甲、乙两单位的演出序号至少有一个为奇数的概率; (Ⅱ) 甲、乙两单位之间的演出单位个数ξ的分布列与期望.8,已知函数1()ln(1)x f x x x a -=+++,其中实数1a ≠-(Ⅰ) 若2a =,求曲线()y f x =在点(0,(0))f 处的切线方程;(Ⅱ) 若()f x 在1x =处取得极值,试讨论()f x 的单调性.9,如题(19)图,四棱锥P -ABCD 中,底面ABCD 为矩形,PA ⊥底面ABCD ,PA =AB,点E 是棱PB 的中点. (Ⅰ) 求直线AD 与平面PBC 的距离;(Ⅱ) 若ADA -EC -D 的平面角的余弦值.题(19)图10,已知以原点O 为中心,F 为右焦点的双曲线C 的离心率e =.(Ⅰ)求双曲线C 的标准方程及其渐近线方程;(Ⅱ)如题(20)图,已知过点11(,)M x y 的直线1l :1144x x y y +=与过点22(,)N x y (其中21x x ≠)的直线2l :2244x x y y +=的交点E 在双曲线C 上,直线MN 与双曲线的两条渐近线分别交于G 、H 两点,求△OGH 的面积.11, 在数列{}n a 中,11a =,1*1(21),()n n n a ca c n n N ++=++∈其中实数0c ≠.(Ⅰ) 求{}n a 的通项公式;(Ⅱ) 若对一切*k N ∈有221k k a a ->,求c 的取值范围.12,函数1sin 22y x=的最小正周期T = 。
2010年高考上海文科数学试卷及答案

2010年普通高等学校招生全国统一考试(上海卷)数学(文科)考生注意:1.答卷前,考生务必在答题纸上将姓名、高考准考证号填写清楚,并在规定的区域内贴上条形码2.本试卷共有23道试题,满分150分,考试时间120分钟。
一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.已知集合{}1,3,A m =,{}3,4B =,{}1,2,3,4A B = 则m = 。
2.不等式204xx ->+的解集是 。
3.行列式cossin 66sincos66ππππ的值是 。
4.若复数12z i =-(i 为虚数单位),则z z z ⋅+= 。
5.将一个总数为A 、B 、C 三层,其个体数之比为5:3:2。
若用分层抽样方法抽取容量为100的样本,则应从C 中抽取 个个体。
6.已知四棱椎P ABCD -的底面是边长为6 的正方形,侧棱PA ⊥底面ABCD ,且8PA =, 则该四棱椎的体积是 。
7.圆22:2440C x y x y +--+=的圆心到直线3440x y ++=的距离d = 。
8.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为 。
9.函数3()log (3)f x x =+的反函数的图像与y 轴的交点坐标是 。
10. 从一副混合后的扑克牌(52张)中随机抽取2张,则“抽出的2张均为红桃”的概率为 (结果用最简分数表示)。
11. 2010年上海世博会园区每天9:00开园,20:00停止入园。
在右边的框图中,S 表示上海世博会官方网站在每个整点报道的入园总人数,a 表示整点报道前1个小时内入园人数,则空白的执行框内应填入 。
12.在n 行m 列矩阵12321234113*********n n n n n n n n n n ⋅⋅⋅--⎛⎫ ⎪⋅⋅⋅- ⎪⎪⋅⋅⋅ ⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪ ⎪⋅⋅⋅---⎝⎭中,记位于第i 行第j 列的数为(,1,2,)ij a i j n =⋅⋅⋅。
上海市普通高等学校2010届高三春季招生考试(大综合)

上海市普通高等学校2010届高三春季招生考试综合能力测试题本试卷分第I卷和第II卷两部分,满分为150分。
考试时间为120分钟。
第Ⅰ卷(共72分)考生注意:1.答第I卷前,考生务必在试卷和答题卡上用钢笔或圆珠笔清楚填写姓名、准考证号、校验码,并用铅笔把答题卡上正确涂写准考证号和校验码。
2.第I卷(1—24题)为单选项,由机器阅卷,答案必须全部涂写在答题卡上。
考生应将代表正确答案的小方格用铅笔涂黑。
注意试题题号和答题卡编号一一对应,不能错位。
答案需要更改时,必须将原选项用橡皮擦去,重新选择。
答案涂写在试卷上一律不给分。
1.针对当前市政建设造成的交通拥堵,上海市政府承诺尽最大努力把施工对市民出行和生产生活的影响降到最低程度,并对市民所给予的理解和支持表示衷心的感谢。
这体现了政府()A.坚持依法治国方略B.完善社会保障制度C.实践为人民服务宗旨D.行使经济调节职能2.“我们选居委会主任,一定要选有头脑、有思路,能团结小区群众搞好社会和谐,让小区的环境更美,让小区一年比一年更有魅力的主任。
”这是上海市居民张女士拿着“居委会选举通知书”向记者透露的她心目中居委会主任的标准。
张女士对居委会主任有如此高的要求,因为民委会是居民()A.直接行使民主权利的基层政权组织B.自我管理的基层自治组织C.管理公共事务的基层社会组织D.维护自身权益的基层社区组织3.一次,钱学森为解决导师交给他的难题,前后写了五份演算文稿。
当他把定稿装入文件袋后,特意在封面上工工整整写道“Final”(定稿),但他马上又觉得不妥,便在旁边补了一行“Nothing is final!!!”(没有什么认识是最后的)。
这句“Nothing is final!!!”体现的哲学道理是()A.真理是客观的B.真理是绝对的C.真理是发展的D.真理是普遍的4.截至2009年7月6日,国内某知名购物网站上支付宝(第三方电子支付机构)日交易额峰值已达7亿元,交易700万笔。
2010数学真题卷及答案
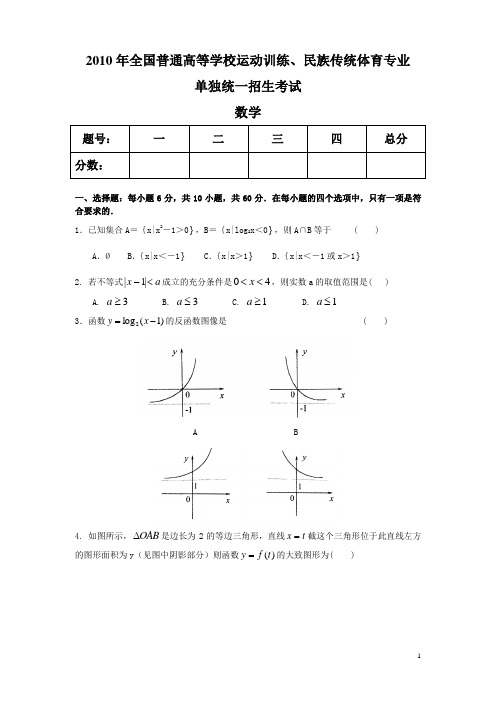
2010年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学一、选择题:每小题6分,共10小题,共60分.在每小题的四个选项中,只有一项是符合要求的.1.已知集合A ={x|x 2―1>0},B ={x|log 2x <0},则A ∩B 等于 ( )A .ØB .{x|x <-1}C .{x|x >1}D .{x|x <-1或x >1}2. 若不等式||x a -<1成立的充分条件是04<<x ,则实数a 的取值范围是( ) A. a ≥3B. a ≤3C. a ≥1D. a ≤13.函数)1(log 2-=x y 的反函数图像是 ( )A B4. 如图所示,∆OAB 是边长为2的等边三角形,直线x t =截这个三角形位于此直线左方的图形面积为y (见图中阴影部分)则函数y f t =()的大致图形为( )5.已知a 、b 是非零向量且满足(a -2b )⊥a ,(b -2a )⊥b ,则a 与b 的夹角是( )A .6π B .3π C .32π D .65π6椭圆22143x y +=的右焦点到直线y x =的距离是 ( )A.127. 过圆锥曲线C 的一个焦点F 的直线l 交曲线C 于A 、B 两点,且以AB 为直径的圆与F 相应的准线相交,则曲线C 为A. 双曲线B. 抛物线C. 椭圆D. 以上都有可能 8.若αααααcos sin cos 3sin ,2tan +-=则的值是( )A .31-B .-35C .31 D .35 9.直线052)3(057)3()1(2=-+-=-+-++y x m m y m x m 与直线垂直的充要条件是( )A .2-=mB .3=mC .31=-=m m 或D .23-==m m 或10.已知1(2)2x f x x ++=+,则1(2)f x -+= ( ) A.12x x -+ B.11x -+ C.211x x +-- D.21x x +-+二、填空题:每小题5分,共8小题,共计40分.将答案填在题中的横线上。
2010上海市春季高考数学试卷(全解全析)

2010上海市春季高考数学试卷一、填空题(本大题满分56分)本大题共有14题,考生应在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1、函数1sin 22y x =的最小正周期T = 。
答案:π解析:由周期公式得222T πππω===。
2、已知函数2()2f x ax x =+是奇函数,则实数a = 。
答案:0解析:由奇函数定义有()()0f x f x -+=得222()2()220a x x ax x ax -+-++==,故0a =。
3、计算:21ii=+ (i 为虚数单位) 答案:1i +解析:22(1)2211(1)(1)2i i i i i i i i -+===+++-。
4、已知集合1{|||2},{|0}1A x xB x x =<=>+,则A B ⋂= 。
答案:{|12}x x -<<解析:由题知{|22}A x x =-<<,{|1}B x x =>-,故{|12}A B x x ⋂=-<<.5、若椭圆2212516x y +=上一点P 到焦点1F 的距离为6,则点P 到另一个焦点2F 的距离是 答案:4解析:由椭圆的定义知12||||210PF PF a +==,1||6PF =,故2||4PF =。
6、某社区对居民进行上海世博会知晓情况的分层抽样调查。
已知该社区的青年人、中年人和老年人分别有800人、1600人、1400人。
若在老年人中的抽样人数是70,则在中年人中的抽样人数应该是 。
答案:80。
解析:由题可知抽取的比例为701140020k ==,故中年人应该抽取人数为116008020N =⨯=。
7、已知双曲线C 经过点(1,1),它的一条渐近线方程为y =,则双曲线C 的标准方程是 。
答案:223122x y -=。
解析:设双曲线的方程为223(0)y x λλ-=≠,将点(1,1)代入可得2λ=-。
2010年上海市春季高考数学试卷标准答案与解析

2010年上海市春季高考数学试卷参考答案与试题解析一、填空题:(本大题满分56分,每小题4分)本大题共有14小题,考生应在答题纸相应的编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.上海)函数的最小正周期T=π..(4分)(2010? 1【考点】三角函数的周期性及其求法.【专题】计算题.【分析】直接利用三角函数的周期公式,求出函数的周期即可.【解答】解:由三角函数的周期公式可知,T==πsin2x的最小正周期为函数y=故答案为:π.【点评】本题考查三角函数的周期公式的应用,是基础题,送分题.函数f(x)=Asin(ωx+φ)T=.的最小正周期为;2.+2x是奇函数,则实数a=0=ax.(4分)(2010?上海)已知函数f(x)2【考点】奇函数.【分析】由奇函数定义入手寻找特殊值是解决此问题的最简解法.,﹣f(x)【解答】解:由奇函数定义有f(﹣x)= ,=﹣(a+2))=a﹣2=﹣f(1)(﹣则f1 解得a=0.【点评】本题考查奇函数定义.上海)计算:=1+i((2010?i为虚数单位).43.(分)【考点】复数代数形式的乘除运算.【专题】计算题.【分析】复数分子、分母同乘分母的共轭复数,化简为a+bi(a,b∈R)的形式.==1+i【解答】.解:=故答案为:1+i【点评】本题考查复数代数形式的乘除运算,是基础题.B={x|>0},则A∩B={x|﹣,已知集合2010?上海)A={x||x|<2}1<x<2}.(4.4(分)【考点】交集及其运算.【专题】计算题.【分析】利用绝对值不等式及分式不等式的解法,我们易求出集合A,B,再根据集合交集运算法则,即可求出答案.【解答】解:∵集合A={x||x|<2}=(﹣2,2)1∞)(﹣1,+B={x|>0}=2} <x={x|﹣1<A∩B=(﹣1,2)∴2}<﹣1<x故答案为:{x|本题考查的知识点是交集及其运算,其中根据绝对值不等式及分式不等式的解法,【点评】,是解答本题的关键.求出集合A,B到另一个P的距离为6,则点上海)若椭圆+=1上一点P到焦点5.(4分)(2010?F1.4焦点F的距离是2椭圆的简单性质.【考点】计算题.【专题】| |=6,进而可求|PF|+|PF【分析】根据椭圆的定义|PF|=2a,已知|PF2211 |PF|=4.|+|PF|=2a=10,|PF|=6,故【解答】解:由椭圆的定义知|PF21124故答案为【点评】本题主要考查了椭圆的性质.属基础题.上海)某社区对居民进行上海世博会知晓情况分层抽样调查.已知该社区2010?.(4分)(6人,若在老年人中的抽样人数是人、1400的青年人、中年人和老年人分别有800人、1600 .70,则在中年人中的抽样人数应该是80【考点】分层抽样方法.【分析】根据老年人抽取的人数计算抽取比例,再根据这个比例求中年人中需抽取的人数.N=1600.解:由题可知抽取的比例为×k==80=,故中年人应该抽取人数为【解答】80故答案为:属基解决分层抽样的关键是抓住各层抽取的比例相等,【点评】本题考查基本的分层抽样,本题.则它的一条渐近线方程为.(1,1),20107.(4分)(?上海)已知双曲线C经过点C.的标准方程是C双曲线【考点】双曲线的标准方程.【专题】计算题.2﹣Cy的一条渐近线方程为,则可将双曲线的方程设为【分析】根据题意,双曲线2坐标代入可得λ的值,进而可得答案.0λ(λ≠),将点C=3x的一条渐近线方程为【解答】解:根据题意,双曲线C,22 0),λ≠3x则可设双曲线的方程为y﹣=λ(2,﹣λ11C将点(,)代入可得=.2故答案为:.要求学【点评】本题考查双曲线的方程,涉及双曲线的方程与其渐近线的方程之间的关系,生熟练掌握,注意题意要求是标准方程,答案必须写成标准方程的形式.62 +)的二项展开式中,常数项是60.8.(4分)(2010?上海)在(2x【考点】二项式定理.【专题】计算题.0的值,即可求得常数项.,求出r【分析】在二项展开式的通项公式中,令x的幂指数等于2rr21266﹣﹣﹣x?T 2=?x?【解答】解:在(2x+)的二项展开式中,通项公式为r+13rr12﹣?x.= ,3r=0,解得r=412令﹣故展开式的常数项为,=60 60故答案为.求展开式中某项的系数,【点评】本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于中档题.(.值(结果用数(4分)2010?上海)连续两次掷骰子,出现点数之和等于4的概率为9.表示)【考点】古典概型及其概率计算公式.【专题】计算题.个,满足条件的事【分析】本题是一个古典概型,试验发生包含的事件总的试验结果为36 ,可以列举出共3个,根据古典概型的概率公式得到结果.件是点数和为的结果为4 【解答】解:由题意知本题是一个古典概型,36个,试验发生包含的事件总的试验结果为4,满足条件的事件是点数和为的结果为个,1)共33(2,2),(,,1可以列举出(,3)=由古典概型概率计算公式可得P=.=.故答案为解题过程中要用到列举法本题考查古典概型,考查分步计数问题,是一个基础题,【点评】来做出事件所包含的事件数,注意列举时,做到不重不漏..1的正四棱锥的体积V=上海)各棱长为2010分)(10.4(?棱柱、棱锥、棱台的体积.【考点】计算题.【专题】3【分析】先求出正四棱锥的斜高,再求出它的高,然后利用体积公式求解即可.h=,h′,则=【解答】解:由题知斜高V=?Sh=1=?.故故答案为:【点评】本题考查棱锥的体积,考查空间想象能力,计算能力,是基础题.上海)方程=0的解集为{﹣3,2}.411.(分)(2010?【考点】三阶矩阵.【专题】计算题.【分析】利用矩阵的化简方法把方程的左边化简,得到一个一元二次方程,解出即可.22 18=0,12﹣4x+3x﹣【解答】=9x+2x解:﹣2即x+x﹣6=0,故x=﹣3,x=2.21故方程的解集为{﹣3,2}.【点评】考查学生化简行列的方法,解方程的方法,写解集的方法.12.(4分)(2010?上海)根据所示的程序框图(其中[x]表示不大于x的最大整数),输出r=.【考点】程序框图.4【专题】图表型.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算变更r的值,模拟程序的运行,用表格对程序运行过程中各变量的值进行分析,不难得到输出结果.【解答】解:由框图的算法原理可知:b=,a=,﹣<1;﹣a)=n=1,n(b﹣)<1)=2;(n=2,n(b﹣a﹣)>1=3,(n=3,n(b﹣a)m=[3]=6此时,,=,r= =r=.故输出故答案为:【点评】根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)?②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.13.(4分)(2010?上海)在如图所示的斜截圆柱中,已知圆柱底面的直径为40cm,母线长2最短50cm,最长80cm,则斜截圆柱的侧面面积S=2600πcm.【考点】棱柱、棱锥、棱台的体积.【专题】计算题;压轴题.【分析】将相同的两个几何体,对接为圆柱,然后求出新圆柱侧面积的一半即可.【解答】解:将相同的两个几何体,对接为圆柱,则圆柱的侧面展开,2 cm.×=2600ππ×50+80侧面展开图的面积S=()×202 π故答案为:2600 本题考查圆柱的侧面积,考查计算能力,是基础题.【点评】阶方阵上海)设2010分)(14.4(?n5= A n任取A中的一个元素,记为x;划去x所在的行和列,将剩下的元素按原来的位置关系组1n1成n﹣1阶方阵A,任取A中的一个元素,记为x;划去x所在的行和列,…;将最2nn112﹣﹣,则=1…+x.=x+x+…+x,则S=x+x+S后剩下的一个元素记为x,记n2n2n11nn【考点】高阶矩阵;数列的极限.【专题】综合题;压轴题.2【分析】不妨取x=1,x=2n+3,x=4n+5,…,x=2n﹣1,故S=1+(2n+3)+(4n+5)+…+nn21332.)=n,故可求(2n﹣12【解答】解:不妨取x=1,x=2n+3,x=4n+5,…,x=2n﹣1,n31222故S=1+(2n+3)+(4n+5)+…+(2n﹣1)=[1+3+5+…+(2n﹣1)]+[2n+4n+…+(n﹣1)2n]=n+n23(n﹣1)×n=n,==1,故=故答案为:1.【点评】本题考查高阶矩阵和数列的极限,解题时要认真审题,仔细解答,避免不必要的错误.二、选择题:(本大题20分)本大题共有4小题,每题有且只有一个正确答案,考生应在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.(5分)(2010?上海)若空间三条直线a、b、c满足a⊥b,b⊥c,则直线a与c()A.一定平行B.一定相交C.一定是异面直线D.平行、相交、是异面直线都有可能【考点】空间中直线与直线之间的位置关系.【专题】空间位置关系与距离.【分析】利用正方体的棱与棱的位置关系及异面直线所成的角的定义即可得出,若直线a、b、c 满足a⊥b、b⊥c,则a∥c,或a与c相交,或a与c异面.【解答】解:如图所示:a⊥b,b⊥c,a与c可以相交,异面直线,也可能平行.从而若直线a、b、c满足a⊥b、b⊥c,则a∥c,或a与c相交,或a与c异面.故选D.6熟注意全面考虑.【点评】本题考查空间中直线与直线之间的位置关系,解题时要认真审题,练掌握正方体的棱与棱的位置关系及异面直线所成的角的定义是解题的关键.M=a,记1)∈(0,,)已知a,a1+a﹣a,N=a201016.(5分)(?上海)(上海春卷16221112)则M与N的大小关系是(.不确定.M=N DM>N CA.M<N B.不等式比较大小.【考点】计算题.【专题】根据题意,利用作差法进行求解.【分析】+1 ﹣aN=aa﹣a解:由【解答】M﹣2112 0,a﹣1)>=(a﹣1)(21 N,故M>B.故选【点评】此题考查大小的比较,利用作差法进行求解,是一道基础题.2与抛物线“直线lk,“≠0”是分)(2010?上海)已知抛物线C:y=x与直线l:y=kx+l517.()C有两个不同交点”的(B.必要不充分条件;A.充分不必要条件.充要条件D.既不充分也不必要条件C 【考点】必要条件、充分条件与充要条件的判断.【专题】压轴题.从而判定有两个不同交点的条件是:方程组有两个不同实数根,【分析】直线l与抛物线C 该题.22222,0=﹣4k+1>=(2k﹣1)﹣4k,x【解答】解:由(kx+1)=x即k+(2k﹣1)x+1=0△有两C直线l与抛物线有两个不同的交点与抛物线C”,但“0则.故“k≠”推不出“直线l .≠0”个不同的交点”则必有“k .故选B第三0是第二点,0>还是△≥【点评】本题突破口在直线l与抛物线C有两个不同交点,△是充要条件的判断.对称,则P=()已知函数fx)的图象关于点(上海春卷(.18(5分)2010?上海)18 的坐标是()点P0,)0.BA..C.D(函数的图象与图象变化.【考点】7【专题】压轴题.【分析】利用对称性质和中点坐标公式进行求解.【解答】解:设P(m,n),任意给点M(x,y)关于P(m,n)的对称点为N(2m﹣x,2n﹣y),,联立方程组:由,解这个方程组得到,故选C.【点评】巧妙运用对称性质,合理借助中点坐标公式是求解对称问题的重要方法.三、解答题:(本大题74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.,求的值.>1)上海)已知tanθ=a,(a?19.(12分)(2010【考点】两角和与差的正弦函数;弦切互化;二倍角的正切.【专题】计算题.化简,【分析】利用两角和与差的正弦函数,以及二倍角的正切,代入tanθ=a,求出结果即可.【解答】解:原式=.===.即:【点评】本题是基础题,考查弦切互化,二倍角的正切,考查计算能力,常考题型.x 1)≠a>0且a2((2010(.14分)(?上海)已知函数fx)=log8﹣)(20a的值;x)的反函数是其本身,求a((1)若函数f )的最大值.(﹣)(时,求函数>)当(2a1y=fx+fx8【考点】反函数;函数的最值及其几何意义.【专题】计算题.【分析】(1)先求出反函数的解析式,利用反函数和原函数的解析式相同,求出a的值.(2)当a>1时,先求出函数的定义域,化简函数的解析式,利用基本不等式求出最值.xx fx)(x=,),∴8﹣2=a ,)【解答】解:(1)∵函数f(x=log(8﹣2ax.,∴故反函数为y=,∴log(8﹣2)a=2=ax(2)当a>1时,由题意知,8﹣2>0,∴x<3,函数y=f(x)+f(﹣x)的定义域(﹣3,3),x=+,(8﹣2)+f函数y=f(x)(﹣x)=log axxxx﹣﹣∴2+2≥2,当且仅当x=0时,取等号.∴0<65﹣8(2+2 )≤49,当a>1时,函数y=f(x)+f(﹣x)在x=0处取得最大值log49.a【点评】本题考查求函数的反函数的方法,对数式的运算性质,基本不等式的应用.21.(14分)(2010?上海)已知地球半径约为6371千米.上海的位置约为东经121°、北纬31°,大连的位置约为东经121°、北纬39°,里斯本的位置约为西经10°、北纬39°.(1)若飞机以平均速度720千米/小时,飞行,则从上海到大连的最短飞行时间约为多少小时(飞机飞行高度忽略不计,结果精确到0.1小时)?(2)求大连与里斯本之间的球面距离(结果精确到1千米)【考点】球面距离及相关计算.【专题】计算题;综合题.【分析】(1)先求两地的球心角,求出球面距离,然后求飞行时间.(2)求出两点的距离,求出球心角,然后求球面距离.【解答】解:(1)∵上海与大连在同一经线上,∴它们在地球的同一个大圆上.设地球的球心为O,上海、大连分别为点A、B.由上海、大连的经、纬度知∠AOB=8°地球半径r≈6371千米×6371 的弧长:经计算得AB889.56÷720≈1.2(小时)∴从上海到大连的最短飞行时间约为1.2(小时)(2)设里斯本为C,过B作与赤道平面平行的球面的截面,设其圆心为O′,由已知得9∠BO′C=121°+10°=131°,∠OBO′=39°OB=OC=rO′C=O′B=OBcos∠OBO′=rcos39°由余弦定理可得22222BC=O′B+O′C﹣2O′B?O′Ccos131°=2rcos39°(1﹣cos131°)BOC=∠cos4﹣﹣1.87×10≈BOC≈90.01°∴∠为于是大圆的弧长BC∴大连与里斯本之间的球面距离约为10009千米.【点评】本题考查球面距离及其他计算,余弦定理的应用,是中档题.=,定义,对任意向量16分)(2010?﹣上海)在平面上,给定非零向量22.(.,求;3)),=(﹣1(1,)若=(2,3上,则位置向量Ax+By+C=0,证明:若位置向量的终点在直线(2,1)的(2)若=终点也在一条直线上;2终点=y上时,位置向量,当位置向量的终点在抛物线C3(:)已知存在单位向量x2与向量满足什么关系?l ′关于直线l对称,问直线C总在抛物线′:y=x上,曲线C和C【考点】向量在几何中的应用.【专题】压轴题;函数的性质及应用;平面向量及应用.,代入=10)根据题意,算出=7的表达式并化简整理,即可得【分析】(1,(;,﹣)到=的表达式解出=(xAx+By+C=0,上,由题中y),终点在直线(2)设=(x',y')满足的关系式,从而得到点)在直线Ax+By+C=0(上,化简整理得到直线(,3A+4B)x+(4A﹣,说明向量5C=0﹣3B)y的终点也在一条直线上;,解出θ)cosθ,sin,3))设=(xy),单位向量θyx关于、和的坐标形式,结=((22终点在抛物线y=x上,建立关于x=y的终点在抛物线合x上且、y和θ的方程,化简10满l的方向向量l:y=x对称,算出(.再由曲线,)C和C′整理得到=±关于直线垂直.与向量?=0,从而得到直线足l),(﹣1,(=2,3)3,【解答】解:(1=)∵=,(﹣)=(﹣1,∴=73,=10),可得)()﹣(﹣;,)因此==,﹣﹣=(2,3上),终点在直线Ax+By+C=0)设=(x',y'(2,)=(=(2算出=2x'+y'=5,,,1,),=)﹣((∴,=)﹣=(x',y')),y,得到,满足因此,若=(x Ax+By+C=0∵点(上,)在直线,﹣)y5C=03A+4B∴A)×x++B×(4A﹣3B+C=0,化简得(不全为零,可得以上方程是一条直线的方程A、B由的终点也在一条直线上;即向量3是单位向量,)∵(θ,=xcosθθ,sinθ)+ysin,可得?cosx∴设=(,y),=()θ+ycos2θ,θ=(﹣xcos2﹣ysin2θ﹣2xsin2θθ(﹣所以=﹣=2xcos+ysin)22 =x=y的终点在抛物线∵x上,且终点在抛物线y上,112,+ycos2θ)θ=(﹣2xsin2θθ∴﹣xcos2﹣ysin2θ==﹣,θsin=,sinθ=﹣或cosθ化简整理,通过比较系数可得cos,()∴=±,∵曲线C和C′关于直线l:y=x对称,的方向向量=(1,1).∴l与向量垂直.l,即可得⊥?=0,因此直线终点在一条直线上时,向量的终点也在本题给出向量的关系式,求证当向量【点评】一条直线上等问题.着重考查了向量的数量积运算、向量的坐标运算和曲线与方程的讨论等知识,属于中档题.=(ax为常数).2010?上海)已知首项为x的数列{x}满足23.(18分)(n+1n1*(1)若对于任意的x≠﹣1,有x=x对于任意的n∈N都成立,求a的值;n1n+2(2)当a=1时,若x>0,数列{x}是递增数列还是递减数列?请说明理由;n1(3)当a确定后,数列{x}由其首项x确定,当a=2时,通过对数列{x}的探究,写出“{x}nnn1是有穷数列”的一个真命题(不必证明).说明:对于第3题,将根据写出真命题所体现的思维层次和对问题探究的完整性,给予不同的评分.【考点】数列递推式.【专题】计算题;综合题;压轴题;探究型.22时,由n=1+xa+1)x,当,代入xx化简后等于x,得到ax=(【分析】(1)求出nn+2nn+1nn的值即可;x的任意性得得到a1<﹣xx﹣x==﹣>a=1(2)数列为递减数列,因为当且x>1得到x0,而nn+1n1n 0,所以得证;﹣得到即可.}{x是有穷数列,可以令x=满足得到数列3()由a=2{x}x=,因为1n+1nn==x=)∵解:(1x =【解答】nn+222,∴a=﹣x的任意性得1.时,由,当+xxa+1=x∴a()n=11nnn(}{x)数列2是递减数列.n120. x>∵1** N∈,﹣<0,=﹣﹣∈>∴x0,nN又xx=xn nnnn+1是递减数列.}故数列{x n﹣,则{x}是有穷数列.=x=满足})满足条件的真命题为:数列(3{xx,若nn+11n【点评】考查学生会利用数列的递推式解决数学问题,会判断一个数列是递减或递增数列.13。
2010年上海市普通高等学校春季招生考试数学试卷

2010年上海市普通高等学校春季招生考试数学试卷考生注意:1.答卷前,考生务必将姓名、高考座位号、校验码等填写清楚.2.本试卷共有22道试题,满分150分.考试时间120分钟.一. 填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每题填对得4分,否则一律得零分.1.已知集合{1A x x =<-或}23x ≤<,{}24B x x =-≤<,则A B = .2.计算:131lim 32n n nn +→∞+=+ . 3.函数()1f x x =-的定义域是 . 4.方程2cos 14x π⎛⎫-= ⎪⎝⎭在区间(0,)π内的解是 . 5.已知数列{}n a 是公差不为零的等差数列,11a =. 若125a a a 、、成等比数列,则n a =.6.化简:cos sin 36ππαα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭. 7.已知P 是双曲线22219x y a -=右支上的一点,双曲线的一条渐近线方程为30x y -=. 设 12F F 、分别为双曲线的左、右焦点. 若23PF =,则1PF = .8.已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如右图所示,则该凸多面体的体积V = .9.已知无穷数列{}n a 前n 项和113n n S a =-,则数列{}n a 的各项和为 . 10.古代“五行”学说认为:“物质分金、木、土、水、火五种属性,金克木,木克土,土克水,水克火,火克金.”将五种不同属性的物质任意排成一列,设事件A 表示“排列中属性相克的两种物质不相邻”,则事件A 出现的概率是 (结果用数值表示).11.已知12,,,n a a a ;12,,,n b b b (n 是正整数),令112n L b b b =+++,223L b b =+ ,n b ++,n n L b =. 某人用右图分析得到恒等式: 1122n n a b a b a b +++=11223a L c L c L +++k k c L + n n c L ++,则k c = (2)k n ≤≤.12.已知(1,2),(3,4)A B ,直线1l :20,:0x l y ==和3:l x +3y 10-=. 设i P 是i l (1,2,3)i =上与A 、B 两点距离平方和最小的点,则△123PP P 的面积是 .二.选择题(本大题满分16分)本大题共有4题,每题都给出四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得 4分,否则一律得零分.13.已知向量(2,3),(3,)a b λ=-=,若//a b ,则λ等于 [答] ( ) (A )23. (B )2-. (C )92-. (D )23-. 14.已知椭圆221102x y m m +=--,长轴在y 轴上. 若焦距为4,则m 等于 [答]( ) (A )4. (B )5. (C )7. (D )8.15.已知函数()()f x g x 、定义在R 上,()()()h x f x g x =⋅,则“()()f x g x 、均为奇函 数”是“()h x 为偶函数”的 [答] ( )(A )充分不必要条件. (B )必要不充分条件. (C )充要条件. (D )既不充分也不必要条件.16.已知C z ∈,且22i 1,i z --=为虚数单位,则22i z +-的最小值是 [答] ( )(A )2. (B )3.(C )4. (D )5.三.解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.17. (本题满分12分)已知cos ,32πθθπ⎛⎫=-∈ ⎪⎝⎭,求2cos sin 2sin θθθ-的值.18. (本题满分12分)在平面直角坐标系xOy 中,A B 、分别为直线2x y +=与x y 、轴的交点,C 为AB 的中点. 若抛物线22(0)y px p =>过点C ,求焦点F 到直线AB 的距离.19. (本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.已知函数()2()log 21x f x =+.(1)求证:函数()f x 在(,)-∞+∞内单调递增;(2)记1()-f x 为函数()f x 的反函数. 若关于x 的方程1()()f x m f x -=+在[1,2]上有解,求m 的取值范围.20. (本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.某厂根据市场需求开发折叠式小凳(如图所示). 凳面为三角形的尼龙布,凳脚为三根细钢管. 考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:①凳子高度为30cm,②三根细钢管相交处的节点O与凳面三角形ABC重心的连线垂直于凳面和地面. (1)若凳面是边长为20cm的正三角形,三只凳脚与地面所成的角均为45,确定节点O分细钢管上下两段的比Array值(精确到0.01);(2)若凳面是顶角为120的等腰三角形,腰长为24cm,节点O分细钢管上下两段之比为2:3. 确定三根细钢管的长度(精确到0.1cm).题满分8分.在直角坐标平面xOy 上的一列点()()11221,,2,,,A a A a (,),n n A n a ,简记为{}n A . 若由1n n n b A A j +=⋅构成的数列{}n b 满足1,1,2,n n b b n +>=,其中j 为方向与y 轴正方向相同的单位向量,则称{}n A 为T 点列.(1) 判断()123111,1,2,,3,,,23A A A ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭1,,n A n n ⎛⎫ ⎪⎝⎭,是否为T 点列,并说明理由; (2)若{}n A 为T 点列,且点2A 在点1A 的右上方. 任取其中连续三点1k k A A +、、2k A +,判断△12k k k A A A ++的形状(锐角三角形、直角三角形、钝角三角形),并予以证明;(3)若{}n A 为T 点列,正整数1m n p q ≤<<<满足m q n p +=+,求证:>n q m p A A j A A j ⋅⋅.题满分8分.已知z 是实系数方程220x bx c ++=的虚根,记它在直角坐标平面上的对应点为(Re ,Im )z P z z .(1)若(,)b c 在直线20x y +=上,求证:z P 在圆1C :22(1)1x y -+=上;(2)给定圆C :222()x m y r -+=(R m r ∈、,0r >),则存在唯一的线段s 满足:①若z P 在圆C 上,则(,)b c 在线段s 上;② 若(,)b c 是线段s 上一点(非端点),则z P 在圆C 上. 写出线段s 的表达式,并说明理由;(3)由(2)知线段s 与圆C 之间确定了一种对应关系,通过这种对应关系的研究,填写表一(表中1s 是(1)中圆1C 的对应线段).表一线段s 与线段1s 的关系 m r 、的取值或表达式s 所在直线平行于1s 所在直线s 所在直线平分线段1s线段s 与线段1s 长度相等2008年上海市普通高等学校春季招生考试数学试卷参考答案及评分标准说明1. 本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.2. 评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅. 当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.3. 第17题至第22题中右端所注的分数,表示考生正确做到这一步应得的该题累加分数.4. 给分或扣分均以1分为单位.答案及评分标准一.(第1至12题)每一题正确的给4分,否则一律得零分. 1. {}4x x <. 2. 13. 3. [2,1)(1,3]-. 4. 712x π=.5. 21n a n =-.6. cos α.7. 5.8. 16+. 9. 1-. 10. 112. 11. 1k k a a --. 12. 32. .17. [解] 原式2cos 2sin cos sin θθθθ=- …… 2分 21cos sin sin cos cos θθθθθ-==. …… 5分又 cos ,32πθθπ⎛⎫=-∈ ⎪⎝⎭,sin 3θ∴==, …… 9分2c o s 4s i n 2s i n 2θθθ∴-=-. …… 12分 18. [解] 由已知可得 (2,0),(0,2),(1,1)A B C , …… 3分 解得抛物线方程为 2y x =. …… 6分于是焦点 1,04F ⎛⎫ ⎪⎝⎭. …… 9分 ∴ 点F 到直线AB 的距离为8=. …… 12分 19. [证明](1)任取12x x <,则()()11221222221()()log 21log 21log 21x x x x f x f x +-=+-+=+, 1212,02121x x x x <∴<+<+,11222212101,log 02121x x x x ++∴<<<++, 12()()f x f x ∴<,即函数()f x 在(,)-∞+∞内单调递增. …… 6分[解](2)()12()log 21(0)x f x x -=->, …… 9分[解法一]1()()m f x f x -∴=- =()()22log 21log 21x x --+ 22212log log 12121x x x -⎛⎫==- ⎪++⎝⎭, …… 11分 当12x ≤≤时,222123,152133215x x ≤≤∴≤-≤++, m ∴的取值范围是2213log ,log 35⎡⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. …… 14分 [解法二] 解方程()()22log 21log 21x x m -=++,得 221log 12m m x ⎛⎫+= ⎪-⎝⎭, …… 11分 22112,1log 212m m x ⎛⎫+≤≤∴≤≤ ⎪-⎝⎭, 解得 2213log log 35m ⎛⎫⎛⎫≤≤ ⎪ ⎪⎝⎭⎝⎭.m ∴的取值范围是2213log ,log 35⎡⎤⎛⎫⎛⎫ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦. …… 14分 20. [解](1)设△ABC 的重心为H ,连结OH .由题意可得,3BH =. 设细钢管上下两段之比为λ.已知凳子高度为30. 则301OH λλ=+. …… 3分 节点O 与凳面三角形ABC 重心的连线与地面垂直,且凳面与地面平行.∴ OBH ∠就是OB 与平面ABC 所成的角,亦即45OBH ∠=.303,1BH OH λλ=∴=+解得,0.63λ=≈. …… 6分 即节点O 分细钢管上下两段的比值约为0.63.(2)设120,24B AB BC ∠=∴==,AC = 设△ABC 的重心为H,则8,BH AH ==, …… 10分 由节点O 分细钢管上下两段之比为2:3,可知12OH =.设过点A B C 、、的细钢管分别为AA BB CC '''、、,则560.82AA CC OA ''====≈,536.12BB OB '===≈, ∴ 对应于A B C 、、三点的三根细钢管长度分别为60.8cm , 36.1cm 和60.8cm . …… 14分 21. [解](1) 1n a n=, 1111(1)n b n n n n -∴=-=++,显然有1n n b b +>, ∴ {}n A 是T 点列. …… 3分(2)在△12k k k A A A ++中,()()1112211,,1,k k k k k k k k A A a a A A a a ++++++=--=-, ()()1122111k k k k k k k k A A A A a a a a ++++++⋅=-+--. …… 5分点2A 在点1A 的右上方,1210b a a ∴=->,/{}n A 为T 点列,10n b b ∴≥>, ()()21110k k k k k k a a a a b b ++++∴--=-<,则1120k k k k A A A A +++⋅<. ∴ 12k k k A A A ++∠为钝角,∴ △12k k k A A A ++为钝角三角形. …… 8分(3)[证明] 1,m n p q m q n p ≤<<<+=+,0q p n m ∴-=->. ①1121q p q q q q p p a a a a a a a a ---+-=-+-++- 12()q q p p b b b q p b --=+++≥-. ② 同理n m a a -=121()n n m n b b b n m b ---+++≤-. ③ …… 12分由于{}n A 为T 点列,于是1p n b b ->, ④由①、②、③、④可推得q p n m a a a a ->-, …… 15分∴->-q n p m a a a a ,即 >⋅⋅n q m p A A j A A j . …… 16分22. [证明](1)由题意可得 20b c +=,解方程2220x bx b +-=,得z b =-±, …… 2分∴ 点(),z P b -或(),z P b -, 将点z P 代入圆1C 的方程,等号成立,∴ z P 在圆1C :22(1)1x y -+=上. …… 4分(2)[解法一] 当0∆<,即2b c <时,解得z b =-,∴ 点(),z P b -或(),z P b -, 由题意可得222()b m c b r --+-=,整理后得 222c mb r m =-+-, …… 6分()240b c ∆=-<,222()b m c b r ++-=,(,)b m r m r ∴∈---+.∴ 线段s 为: 222c mb r m =-+-,[,]b m r m r ∈---+.若(,)b c 是线段s 上一点(非端点),则实系数方程为222220,(,)x bx mb r m b m r m r +-+-=∈---+.此时0∆<,且点(),z P b -、(),z P b -在圆C 上. …… 10分[解法二] 设i =+z x y 是原方程的虚根,则2(i)2(i)0++++=x y b x y c ,解得22,2,x b y x bx c =-⎧⎨=++⎩①② 由题意可得,222()x m y r -+=. ③解①、②、③ 得 222c mb r m =-+-. …… 6分以下同解法一.[解](3)表一线段s 与线段1s 的关系 、m r 的取值或表达式 得分s 所在直线平行于1s 所在直线 1m =,1r ≠ 12分s 所在直线平分线段1s 22(1)1r m --=,1m ≠ 15分线段s 与线段1s 长度相等 ()22145m r +=18分卖炭翁白居易(唐) 字乐天号香山居士卖炭翁,伐薪烧炭南山中。
2010年上海高考数学文科试卷带详解

2010年普通高等学校招生全国统一考试(上海卷)数学(文科)一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.1.已知集合{}1,3,A m =,{}3,4B =,{}1,2,3,4A B = 则m = . 【测量目标】集合的基本运算.【考查方式】直接给出两个集的并集,根据集合的定义求元素. 【参考答案】2【试题解析】显然m =2. 2.不等式204xx ->+的解集是 . 【测量目标】解一元二次不等式.【考查方式】直接给出分数不等式,求不等式的解集. 【参考答案】{}24|<<-x x 【试题解析】204xx ->+等价于(x -2)(x +4)<0,所以4x -<<2. 3.行列式ππcossin 66ππsin cos 66的值是 .【测量目标】行列式的运算.【考查方式】直接给出行列式,根据行列式运算法则求值. 【参考答案】0.5 【试题解析】ππcossin66ππsin cos 66=πππππ1cos cos sin sin cos 666632-==.4.若复数12i z =-(i 为虚数单位),则z z z += .【测量目标】复数的基本运算.【考查方式】直接给出复数z ,求其共轭复数,进而根据运算法则求值. 【参考答案】62i -【试题解析】z z z += (12i)(12i)12i 62i -++-=-.5.将一个总数为A 、B 、C 三层,其个体数之比为5:3:2.若用分层抽样方法抽取容量为100的样本,则应从C 中抽取 个体. 【测量目标】分层抽样.【考查方式】给出样本,根据分层抽样求样本的个体. 【参考答案】20【试题解析】从C 中抽取20102100=⨯. 6.已知四棱椎P ABCD -的底面是边长为6 的正方形,侧棱PA ⊥底面ABCD ,且8PA =则该四棱椎的体积是 . 【测量目标】锥的体积.【考查方式】直接给出四棱锥的底面边长和高的值,利用椎体体积公式求体积. 【参考答案】96 【试题解析】9683631=⨯⨯=V . 7.圆22:2440C x y x y +--+=的圆心到直线3440x y ++=的距离d = . 【测量目标】点到直线的距离公式.【考查方式】给出圆一般方程,得到圆心坐标,根据点到直线的距离公式求解. 【参考答案】3【试题解析】圆心(1,2)到直线3440x y ++=距离为3542413=+⨯+⨯.8.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为 .【测量目标】抛物线的定义及其标准方程.【考查方式】给出符合抛物线定义的动点数据,利用代数关系求动点的轨迹方程. 【参考答案】y 2=8x【试题解析】P 的轨迹是以(2,0)F 为焦点的抛物线,p =2所以其方程为y 2=8x. 9.函数3()log (3)f x x =+的反函数的图像与y 轴的交点坐标是 . 【测量目标】反函数的概念和性质.【考查方式】直接给出函数,求其反函数,进而得出交点坐标. 【参考答案】(0,-2)【试题解析】函数3()log (3)f x x =+的反函数为33-=xy ,另x =0,有y =2-. 10. 从一副混合后的扑克牌(52张)中随机抽取2张,则“抽出的2张均为红桃”的概率 为 (结果用最简分数表示). 【测量目标】随机事件与概率.【考查方式】给出等可能事件,利用排列组合求概率.【参考答案】351【试题解析】“抽出的2张均为红桃”的概率为213252C 3C 51=.11. 2010年上海世博会园区每天9:00开园,20:00停止入园.在右边的框图中,S 表示上海世博会官方网站在每个整点报道的入园总人数,a 表示整点报道前1个小时内入园人数,则空白的执行框内应填入 . 【测量目标】循环结构的程序框图.【考查方式】根据程序框图的逻辑结构,得到S 与a 的数量关系. 【参考答案】S ←S +a.【试题解析】依步骤得S ←S +a.12.在n 行m 列矩阵12321234113*********n n n n n n n n n n ⋅⋅⋅--⎛⎫ ⎪⋅⋅⋅- ⎪⎪⋅⋅⋅⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪ ⎪⋅⋅⋅---⎝⎭中, 第11 题图 记位于第i 行第j 列的数为(,1,2,)ij a i j n =⋅⋅⋅.当9n =时,11223399a a a a +++⋅⋅⋅+= . 【测量目标】矩阵的定义.【考查方式】给出矩阵的行和列,求出各对角元素值,最后求和. 【参考答案】45【试题解析】11223399a a a a +++⋅⋅⋅+=1+3+5+7+9+2+4+6+8=45.13.在平面直角坐标系中,双曲线Γ的中心在原点,它的一个焦点坐标为,1(2,1)e =、 2(2,1)e =-分别是两条渐近线的方向向量.任取双曲线Γ上的点P ,若12OP ae be =+ (a 、 b ∈R ),则a 、b 满足的一个等式是 .【测量目标】双曲线的几何性质,平面向量的线性运算.【考查方式】根据给出的方向向量,求出渐进线的方程,从而得到双曲线的标准方程,再利 用平面向量得到点到坐标原点的向量坐标求出啊,a ,b 关系. 【参考答案】4ab =1.【试题解析】1(2,1)e = 、2(2,1)e =-是渐进线方向向量,所以双曲线渐近线方程为.x y 21±=,又1,2,5==∴=b a c (步骤1) 双曲线方程为1422=-y x ,12OP ae be =+ =),22(b a b a -+,1)(4)22(22=--+∴b a b a ,化简得4ab =1 . (步骤2)14.将直线1:10l x y +-=、2:0l nx y n +-=、3:0l x ny n +-=(n ∈*N ,2n …)围 成的三角形面积记为n S ,则lim n n S →∞= .【测量目标】简单的极限运算.【考查方式】直接给出直线方程,观察图形得出可行域代数关系,利用极限求最小值. 【参考答案】12【试题解析】B )1,1(++n n n n 所以BO AC ⊥,(步骤1) n S =)1(21)2221(221+-=-+⨯⨯n n n n 所以lim n n S →∞=12 . (步骤2)二.选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案.考生必须 在答题纸的相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.15.满足线性约束条件23,23,0,0x y x y x y +⎧⎪+⎪⎨⎪⎪⎩…………的目标函数z x y =+的最大值是 ( )A .1B .32C.2D.3 【测量目标】线性规划求目标函数的最值.【考查方式】直接给出约束条件,利用线性规划求目标函数的最大值.【参考答案】C 【试题解析】当直线z x y =+过点B (1,1)时,z 最大值为2. 16.“()π2π4x k k =+∈Z ”是“tan 1x =”成立的 ( )A.充分不必要条件B.必要不充分条件C.充分条件D.既不充分也不必要条件 【测量目标】充要条件的判定. 【考查方式】充分,必要条件. 【参考答案】A 【试题解析】ππtan(2π)tan 144k +==,所以充分;但反之不成立,如5πtan 14=. 17.若0x 是方程式 lg 2x x +=的解,则0x 属于区间 ( ) A.(0,1) B.(1,1.25) C.(1.25,1.75) D.(1.75,2)【测量目标】二分法的计算.【考查方式】根据给出的函数,构造新的函数,将选项带入新函数得到答案. 【参考答案】D【试题解析】04147lg)47()75.1(,2lg )(<-==-+=f f x x x f 由构造函数. 02lg )2(>=f 知0x 属于区间(1.75,2).18.若ABC △的三个内角满足sin :sin :sin 5:11:13A B C =,则ABC △ ( ) A.一定是锐角三角形 B.一定是直角三角形C.一定是钝角三角形D.可能是锐角三角形,也可能是钝角三角形 【测量目标】正弦定理,余弦定理.【考查方式】给出三角形内角正弦的比值,从而得到三角形边长的比值,利用余弦定理得到 余弦值,最后判断角的大小. 【参考答案】C【试题解析】由sin :sin :sin 5:11:13A B C =及正弦定理得::a b c =5:11:13由余弦定理得22251113cos 02511C +-=<⨯⨯,所以角C 为钝角. 三、解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的 规定区域内写出必要的步骤. 19.(本题满分12分) 已知π02x <<,化简:2πlg(cos tan 12sin ))]lg(1sin 2)24x x x x x +-+--+ .【测量目标】三角函数的诱导公式,对数的化简和计算.【考查方式】给出计算式,通过三角函数的变换,化简,再根据对数的基本运算求值. 【试题解析】原式=2lg(sin cos )lg(cos sin )lg(sin cos )0x x x x x x +++-+=.20.(本满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用S 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).(1)当圆柱底面半径r 取何值时,S 取得最大值?并求出该 最大值(结果精确到0.01平方米);(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出 用于灯笼的三视图(作图时,不需考虑骨架等因素).【测量目标】平面图形的直观图和三视图,柱体的面积.【考查方式】写出含未知量底面积代数式,利用函数的知识求最值,根据空间想像能力绘制 较为准确三视图. 【试题解析】(1) 设圆柱形灯笼的母线长为l ,则l =1.2-2r (0<r <0.6), (2) 23π(0.4)0.48πS r =--+, (步骤1) (3) 所以当r =0.4时,S 取得最大值约为1.51平方米; (4) 当r =0.3时,l =0.6,作三视图. (步骤2)21.(本题满分14分)本题共有2个小题,第一个小题满分6分,第2个小题满分8分. 已知数列{}n a 的前n 项和为n S ,且585n n S n a =--,n ∈*N(1)证明:{}1n a -是等比数列;(2)求数列{}n S 的通项公式,并求出使得1n n S S +>成立的最小正整数n . 【测量目标】数列的通项公式与前n 项和n S 的关系.【考查方式】给出数列前n 项和的代数关系式,证明等比数列,进而求出等比数列的前n 和, 利用比较大小求解.【试题解析】(1) 当n =1时,a 1=-14;当2n …时,a n =S n -S n -1=-5a n +5a n -1+1,所以151(1)6n n a a --=-, (步骤1)又a 1-1=-15≠0,所以数列{a n -1}是等比数列;(2) 由(1)知:151156n n a -⎛⎫-=- ⎪⎝⎭ ,得151156n n a -⎛⎫=- ⎪⎝⎭(步骤2)从而1575906n n S n -⎛⎫=+- ⎪⎝⎭(n ∈*N ); (步骤3)由S n +1 > S n ,得156522,log 114.96525n n -⎛⎫<>+ ⎪⎝⎭≈,最小正整数n =15.(步骤4) 22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分.若实数x 、y 、m 满足x m y m -<-,则称x 比y 接近m . (1)若21x -比3接近0,求x 的取值范围;(2)对任意两个不相等的正数a 、b ,证明:22a b ab +比33a b +接近2 (3)已知函数()f x 的定义域{}π,,D x x k k x ≠∈∈Z R .任取x D ∈,()f x 等于1sin x +和1sin x -中接近0的那个值.写出函数()f x 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明). 【测量目标】解一元二次不等式,不等式的基本性质,函数的单调性与最值,奇偶性和周期.. 【考查方式】给出条件求符合条件自变量的取值范围.满足条件的绝对不等式相互之间比较大小.根据函数的奇偶,周期性,以及最小值求解函数的单调区间. 【试题解析】(1) x ∈(-2,2); (步骤1)(2) 对任意两个不相等的正数a 、b,有223322a b ab a b ab +>+>(步骤2)因为2233222()()0a b ab a b a b a b +--+-=-+-<,(步骤3)所以223322a b ab a b +-<+-,即a 2b +ab 2比a 3+b 3接近2(3) 1sin ,(2ππ,2π)()1|sin |,π1sin ,(2π,2ππ)x x k k f x x x k x x k k +∈-⎧==-≠⎨-∈+⎩,k ∈Z ,(步骤4) f (x )是偶函数,f (x )是周期函数,最小正周期T =π,函数f (x )的最小值为0,(步骤5) 函数f (x )在区间π(π,π)2k k -单调递增,在区间π(π,π+)2k k 单调递减,k ∈Z .(步骤6) 23(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.已知椭圆Γ的方程为22221(0)x y a b a b+=>>,(0,)A b 、(0,)B b -和(,0)Q a 为Γ的三顶点.(1)若点M 满足1()2AM AQ AB =+,求点M 的坐标;(2)设直线11:l y k x p =+交椭圆Γ于C 、D 两点,交直线22:l y k x =于点E .若2122b k k a=- ,证明:E 为CD 的中点;(3)设点P 在椭圆Γ内且不在x 轴上,如何构作过PQ 中点F 的直线l ,使得l 与椭圆Γ的两个交点1P 、2P 满足12PP PP PQ += 12PP PP PQ +=?令10a =,5b =,点P 的坐标是(-8,-1),若椭圆Γ上的点1P 、2P 满足12PP PP PQ +=,求点1P、2P 的坐标. 【测量目标】平面向量的线性运算,直线方程和椭圆标准方程,直线和椭圆的位置关系,椭圆中的探索性问题.【考查方式】通过向量坐标的基本运算求M.根据直线方程和椭圆方程的位置关系,解出两直线的斜率代数关系,再进行证明.根据向量等式的关系以及直线和椭圆方程的线性关系求出坐标.【试题解析】(1) (,)22ab M -;(步骤1)(2) 由方程组122221y k x p x y a b=+⎧⎪⎨+=⎪⎩,消y 得方程2222222211()2()0a k b x a k px a p b +++-=,因为直线11l y k x p =+:交椭圆Γ于C 、D 两点, 所以∆>0,即22221a k b p +->0,设C (x 1,y 1)、D (x 2,y 2),CD 中点坐标为(x 0,y 0),(步骤2)则212102221201022212x x a k px a k b b p y k x p a k b ⎧+==-⎪+⎪⎨⎪=+=⎪+⎩, 由方程组12y k x py k x=+⎧⎨=⎩,消y 得方程(k 2-k 1)x =p ,(步骤3)又因为2221b k a k =-,所以2102222112202221a k p px x k k a k b b p y k x ya kb ⎧==-=⎪-+⎪⎨⎪===⎪+⎩,(步骤4) 故E 为CD 的中点;(3) 因为点P 在椭圆Γ内且不在x 轴上,所以点F 在椭圆Γ内,可以求得直线OF 的斜率k 2,由12PP PP PQ += 知F 为P 1P 2的中点,根据(2)可得直线l 的斜率2122b k a k =-,从而得直线l 的方程.(步骤5)1(1,)2F -,直线OF 的斜率212k =-,直线l 的斜率212212b k a k =-=-,解方程组22112110025y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩,消y :x 2-2x -48=0,解得P 1(-6,-4)、P 2(8,3).(步骤6)。
【春考卷】整合版

【出现问题】 出现问题】
【解题思路】 解题思路】
1、“原则”、“做法”没有读懂; 原则” 做法”没有读懂; 原样保留”是对“老电厂”的改造方法, 2、“原样保留”是对“老电厂”的改造方法,对“老粮仓 的改造方法则是“一切还原” 剥离附属物等)。 ”的改造方法则是“一切还原”(剥离附属物等)。
2010年上海市春季高考试卷 2010年上海市春季高考试卷 讲 评 2010. 2010.1.5
1、第③段中“有形的载体”指的是 段中“有形的载体” 【解题思路】 解题思路】 题型: 题型:指代题 关键:把握对应关系(偏正短语) 关键:把握对应关系(偏正短语) 【出现问题】 出现问题】 过分具体 苏州河畔的老厂房与…… 具体: 过分具体:苏州河畔的老厂房与…… 【参考答案】 参考答案】 旧工业文明的老建筑。 旧工业文明的老建筑。
9、(3分)第⑦段对“我”步态的描述富于变化, 、(3 步态的描述富于变化, 富于变化 语言表达的角度作赏析 的角度作赏析。 从语言表达的角度作赏析。
我开始稀奇古怪地走,先走他一个老太太赶集: 比较舒缓的语言节奏细描四种步态 的语言节奏细描四种步态, 先用我开始稀奇古怪地走,先走他一个老太太赶集:脚尖向 比较舒缓的语言节奏细描四种步态, 化 外一撇,脚跟狠狠着地,臀部撅起来;再走他一个老头赶路: 外一撇,脚跟狠狠着地,臀部撅起来;再走他一个老头赶路: 短句、短语组成排比概述其他步态 组成排比概述其他步态, 的 再用短句、短语组成排比概述其他步态, ; 双膝一弯,两手一背——老头走路是两条腿的僵硬和平衡; ——老头走路是两条腿的僵硬和平衡 双膝一弯,两手一背——老头走路是两条腿的僵硬和平衡 过 节奏越来越快, 节奏越来越快 : 走他一个小姑娘上学:单用一只脚着地转着圈儿地走; 程 走他一个小姑娘上学,单用一只脚着地转着圈儿地走;走他 一个秧歌步:胳膊摆起和肩一样平,进三步退一步, 一个秧歌步:胳膊摆起和肩一样平,进三步退一步 最后用不确定的语气, 最后用不确定的语气,想象自己的步态,嘴里得 着“ ”; 着“ , ”;走个 ,走个时 的、 的、 表 ,走个 ,再走一个 。 的、 的、 表 的、 自己 的, 得 进 , 的, 走一 背 的、 走的 不走个小 最 ——变化的 后我 地 定走个 。我” 我是 ,我是 。 变化的 的变化。 ,我是 “ 的变化 和 来 着走 最最 , 富 的 我自己。 我 于 我自己。
2010年高考数学上海卷(秋季)文科全解析

2010年普通高等学校招生全国统一考试(上海卷)数学(文科)一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.已知集合{}1,3,A m =,{}3,4B =,{}1,2,3,4A B =则m = 2 。
解析:考查并集的概念,显然m=22.不等式204xx ->+的解集是 {}24|<<-x x 。
解析:考查分式不等式的解法204xx ->+等价于(x-2)(x+4)<0,所以-4<x<23.行列式cossin 66sincos66ππππ的值是 0.5 。
解析:考查行列式运算法则cossin 66sincos66ππππ=213cos 6πsin 6πsin 6πcos6πcos ==-π 4.若复数12z i =-(i 为虚数单位),则z z z ⋅+ i 26- 。
解析:考查复数基本运算z z z ⋅+=i i i i 2621)21)(21(-=-++-5.将一个总数为A 、B 、C 三层,其个体数之比为5:3:2。
若用分层抽样方法抽取容量为100的样本,则应从C 中抽取 20 个个体。
解析:考查分层抽样应从C 中抽取20102100=⨯6.已知四棱椎P ABCD -的底面是边长为6 的正方形,侧棱PA ⊥底面ABCD ,且8PA =,则该四棱椎的体积是 96 。
解析:考查棱锥体积公式9683631=⨯⨯=V 7.圆22:2440C x y x y +--+=的圆心到直线3440x y ++=的距离d = 3 。
解析:考查点到直线距离公式圆心(1,2)到直线3440x y ++=距离为3542413=+⨯+⨯8.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为y 2=8x 。
解析:考查抛物线定义及标准方程定义知P 的轨迹是以(2,0)F 为焦点的抛物线,p=2所以其方程为y 2=8x9.函数3()l o g (3)f x x=+的反函数的图像与y 轴的交点坐标是(0,-2) 。
上海市春季高考数学试卷(含答案).doc

上海市普通高等学校春季招生考试数学试卷一•填空题(本大题满分36分)本大题共有12题,要求直接填写结果,每题填对得3分,否则一律得0分。
1.函数y = log2(x + 2)的定义域是 _________________2.方程2v = 8的解是_________________3.抛物线/=8x的准线方程是___________________4.函数y = 2sin x的最小正周期是_________________5.已知向量5 = (1, k),方= (9M —6)。
若万〃方,则实数k= _______________6.函数j = 4sinx + 3cosx的最大值是__________________7.复数2 + 3/ (d是虚数单位)的模是__________________8.在AABC中,角A、B、C所对边长分别为a、b、c ,若a = 5,/? = & 3 = 60°,贝ijb二—9.在如图所示的正方体ABCD_A、B\C\D\中,异面直线A/与所成角的大小为 ____________________________ 110.从4名男同学和6名女同学屮随机选取3人参加某社团活动,选岀的3人屮男女同学都有的概率为________ (结果用数值表示)。
11.若等差数列的前6项和为23,前9项和为57,则数列的前"项和»二_________________ o12.36的所有正约数之和可按如下方法得到:因为36=22X32,所以36的所有正约数之和为(1+3+32)+(2+2X3+2X32)+(22+22X3+22X32)=(1+2+22)(1+3+32)=91参照上述方法,可求得2000的所有正约数之和为________________________________二.选择题(本大题满分36分)本大题共有12题,每题都给出四个结论,其中有且只有一个结论是正确的。
2010年上海市普通高等学校春季招生考试数学试卷
的距离为 6 ,则 点 P 到 另一 个 焦 点 F 的 距 离 是 2
的分层抽样调查. 已知该社 区有青年人、巾年人 和老年人分别有 80 0 人、10 人、10 人. 60 40 若在 老年人中的抽样人数是 7 , 0 则在中年人中的抽样 人 数 应该 是 — — . 7 已知双 曲线 经过 点 (, ) 它的一条渐 . 1 1, 近 线方 程为 Y= 、3 则 双 曲 线 的标 准方 程是 , , /
2骝 一
数. 学 学教
2 1年第 2 00 期
n 阶方阵 一 , 一1 1任取A 一 中的一个元素, 1 记 为x ; 2 划去 x 所在的行和列, … ; 2 … 将最后剩 下的一个元素记为 . 记 =x + +… + 1 2
n )
() 函数 fx 的反 函数是其本身, 的 1若 () 求a 值; () 2当a>1 求函数 =fx +_一 ) 时, () 厂 的 (
1 . n阶方 阵 A = 4设
8 \ ) 二 展 式 , 数 . 十 /的 项 开 中 常 项 在f 2 x
是— — .
In f4 l /+ I n1 +
\
…
4+ n3
…
3 4+ …6二. , n - I n5 1
… … …
分6 . 分
1. 8已知函数 . 厂 )= (4一来自, 的图像关于点
P对称, 则点P的坐标是
【 () 答】
c() c2 . A2. B , , 圭 ()
一
1 1 1 方 程 l 方程I
.
z zI 0 = 的解集为— — .
2010年普通高等学校招生全国统一考试数学文科试题(上海卷)真题解析

2010年普通高等学校招生全国统一考试(上海卷)数学(文科)答案及解析考生注意:1.答卷前,考生务必在答题纸上将姓名、高考准考证号填写清楚,并在规定的区域内贴上条形码.2.本试卷共有23道试题,满分150分,考试时间120分钟.一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.已知集合{}1,3,A m =,{}3,4B =,{}1,2,3,4A B =,则m = .【解析】∵{}1,2,3,4AB =,∴{}21,3,m ∈,于是2m =.故答案为:2.【点评】本题考查集合的概念和运算,属基础概念题.2.不等式204xx ->+的解集是 . 【解析】20(4)(2)0(4)(2)0424xx x x x x x->⇔+->⇔+-<⇔-<<+,故答案为:)2,4(-.或由2020404x xx x ->⎧->⇔⎨+>+⎩或2040x x -<⎧⎨+<⎩,解得42x -<<,故答案为:)2,4(-. 【点评】本题考查分式不等式的解法,常规方法是化为整式不等式或不等式组求解.3.行列式cossin 66sincos66ππππ的值是 .【解析】cossin 166coscossinsincos()cos 66666632sincos66πππππππππππ=-=+==,答案为:12. 【点评】本题考查二阶行列式的计算方法与和角的余弦公式以及特殊角的三角函数值,符合在知识交汇处命题原则,属基础题.4.若复数12z i =-(i 为虚数单位),则z z z ⋅+= .【解析】∵12z i =-,∴(12)(12)1251262z z z i i i i i ⋅+=-++-=+-=-,故答案为:i 26-【点评】本题考查复数的基本概念与运算,属基础概念题.5.将一个总数分为A 、B 、C 三层,其个体数之比为5:3:2.若用分层抽样方法抽取容量为100的样本,则应从C 中抽取 个个体.【解析】设A 、B 、C 三层的个体数为5k ,3k ,2k (0k >),则分层抽样方法知:从C 中应抽取100220532k k k k⨯=++个个体,故答案为:20.【点评】本题改编自09年湖南的一道高考题,主要考查分层抽样的基本知识.6.已知四棱椎P ABCD -的底面是边长为6 的正方形,侧棱PA ⊥底面ABCD ,且8PA =, 则该四棱椎的体积是 . 【解析】四棱椎的体积2168963V =⨯⨯=,故答案为:96. 【点评】本题考查棱椎的概念、性质和体积计算公式,属基础题.7.圆22:2440C x y x y +--+=的圆心到直线3440x y ++=的距离d = . 【解析】由044222=+--+y x y x ,得22(1)(2)1x y -+-=,则圆心为(1,2),故22|31424|334d ⨯+⨯+==+,答案为:3.【点评】本题考查圆的标准方程、点到直线的距离公式以及计算能力,是课本习题的变式题.8.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为 .【解析】由抛物线定义知:P 的轨迹为抛物线,易知焦参数4p =,所以点P 的轨迹方程为x y 82=.【点评】本题考查抛物线定义和轨迹方程的求法之——直接法,属基础概念题. 9.函数3()log (3)f x x =+的反函数的图像与y 轴的交点坐标是 ______.【解析】因函数3()log (3)f x x =+图象与x 轴的交点是(2,0)-,所以其反函数的图像与y 轴的交点坐标是(0,2)-,故答案为:)2,0(-.【点评】反函数是高考常考的知识点,一般难度都不大.当与反函数图像有关时,要注意反函数与原函数的图象关于直线y x =对称.10. 从一副混合后的扑克牌(52张)中随机抽取2张,则“抽出的2张均为红桃”的概率为 ____________(结果用最简分数表示).【解析】由等可能事件的概率计算公式,得213252117C P C ==,故答案为:117.【点评】本题考查等可能事件的概率及其计算,解本类问题的关键是弄清基本事件的总数. 11. 2010年上海世博会园区每天9:00开园,20:00停止入园.在右边的框图中,S 表示上海世博会官方网站在每个整点报道的入园总人数,a 表示整点报道前1个小时内入园人数,则空白的执行框内应填入 .【解析】依题意,S 表示上海世博会官方网站在每个整点报道的入园总人数,a 表示整点报道前1个小时内入园人数,可知程序的执行框内应填:a S S +←.【点评】本题主要考查算法的程序框图.由题意确定算式是基础,弄清算法流程图的逻辑结构是解题关键.12.在n 行m 列矩阵12321234113451212321n n n n n n n n n n ⋅⋅⋅--⎛⎫ ⎪⋅⋅⋅- ⎪⎪⋅⋅⋅⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪ ⎪⋅⋅⋅---⎝⎭中,记位于第i 行第j 列的数为(,1,2,)ij a i j n =⋅⋅⋅.当9n =时,11223399a a a a +++⋅⋅⋅+= _____.【解析】当9n =时,由矩阵的结构可知:111a =,223a =,335a =,447a =,559a =,662a =,774a =,886a =,998a =,∴1122339912945a a a a +++⋅⋅⋅+=+++=,故答案为:45.【点评】矩阵是上海高考常考的知识点,也是一大亮点.本题考查矩阵元素的构成规律和等差数列的前n 项和公式.13.在平面直角坐标系中,双曲线Γ的中心在原点,它的一个焦点坐标为(5,0),1(2,1)e =、2(2,1)e =-分别是两条渐近线的方向向量。
上海2010-2017年春季高考客观题难题解析汇总

上海近八年春考客观题难题解析汇总2010年 春考13、在右图所示的斜截圆柱中,已知圆柱底面的直径为40cm ,母线长最短50cm ,最长80cm ,则斜截圆柱的侧面面积S=______cm 2。
【详解】法一:在此题斜截圆柱上再补一个同样形状的斜截圆锥,最后拼凑成一个底面半径为20 cm ,高130 cm 的圆柱,则侧面面积为122013026002ππ⨯⨯⨯=. 法二:几何体的50cm 到80cm 处的截去的部分的面积和余下的面积相等, 将几何体侧面展开,上部分面积为ππ6003020221=⨯⨯⨯, 下部分面积为ππ200050202=⨯⨯,由此可知:斜截圆柱的侧面面积为2600π,故选C .【教法指导】在无法直接求形状不规则的几何体的体积和面积时,我们经常采用割补法,将不规则的几何图形经过分割、切拼,补充成一个规则的图形,该题充分利用了这一方法。
14、设n 阶方阵⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-+-+-+--+++-+++-=125)1(23)1(21)1(21654341414523212125312n n n n n n n n n n n n n n n n A n ,任取n A 中的一个元素,记为1x ;划去1x 所在的行和列,将剩下的元素按原来的位置关系组成1-n 阶方阵1-n A ,任取1-n A 中的一个元素,记为2x ;划去2x 所在的行和列,……;将最后剩下的一个元素记为n x ,记n n x x x S +++= 21,则1lim 3+∞→n S nn =______________。
【详解】根据题意n S 用n 来表示是确定的,不妨将12,,,n x x x 分别取n A 中主对角线上的值21,23,45,,21n n n ++-,所以:21(23)(45)(21)n S n n n =++++++-[135(21)][24(1)2]n n n n n =++++-++++-2323n n n n =+-=.这里计算n S ,也可以把这些数看成公差为22n +的等差数列,(1)(22)2n n n S n n -=++=3n . 故33331lim lim lim 11111n n n n S n n n n→∞→∞→∞===+++,故答案为1. 【教法指导】因为是小题,题目中所取的是不同行不同列的数,所以可以取特殊位置的数,答案中给的是取主对角线,为了方便可以这样取,所以在教学中这种特殊值的思想要讲给学生.18、已知函数1()42xf x =-的图像关于点P 对称,则点P 的坐标是 【答】( ) (A ))21,2(;(B ))41,2(; (C ))81,2(; (D )(0,0)【详解】法一:利用结论若()f x 的图像关于点(),a b 对称,则有()(2)2f x f a x b +-=.然后把函数解析式带入,则有21124242x a xb -+=--,化简得()2228223222822a x x a a x x b b b ----=+∙-+,由等式的恒成立可得1,28b a ==.法二:利用选项,找特殊点。
上海春考数学20题

上海春考数学20题1.一个正整数的个位数是7,十位数是6,百位数是3,这个数是多少?2. 一个圆的周长为30π,它的直径是多少?3. 如果x+2y=10,2x-y=8,那么x和y的值分别是多少?4. 已知等比数列的首项是2,公比是3,前n项的和为242,求n的值。
5. 在平面直角坐标系中,A(-5,0),B(5,0),C(5,3),D (-5,3)是一个矩形的四个顶点,它的面积是多少?6. 在一个平行四边形中,对角线交点的坐标为(-1,5),它的底边长为8,高为3,它的面积是多少?7. 已知两个有理数的和为-3,差为7,它们的积是多少?8. 已知三角形的三边长分别为4、5、6,它是否为等腰三角形?9. 已知直角三角形的斜边长为10,其中一个直角边的长为6,求另一个直角边的长。
10. 已知一个等差数列的首项是2,公差是3,前n项的和为35,求n的值。
11. 一辆汽车以每小时100公里的速度行驶,它经过一段路程,用时5小时,这段路程有多长?12. 在一个四边形中,两对相邻角的度数分别是30°、60°和110°、130°,它的对角线相交的点与四个顶点的连线呈菱形,它的面积是多少?13. 已知一组数据为3、4、5、6、7、8,求这组数据的平均数和中位数。
14. 一件商品原价为120元,现在打8折出售,它的售价是多少?15. 若x+y=25,x>0,y<0,那么sinx+cosy的值为多少?16. 已知直角三角形的两条直角边分别为3和4,求斜边长。
17. 在一个平行四边形中,一条对角线的长为6,它的面积是24,求另一条对角线的长。
18. 若x+y=6,x-y=4,那么x-y的值是多少?19. 已知一组数据为2、3、4、5、6,求这组数据的方差。
20. 已知正方形ABCD的边长为x,其中点E、F、G、H分别是AB、BC、CD、DA的中点,求四边形EFGH的面积。
2010年普通高等学校招生全国统一考试(上海卷)数学(文科)

2010年普通高等学校招生全国统一考试(上海卷)数学(文科)考生注意:1.答卷前,考生务必在答题纸上将姓名、高考准考证号填写清楚,并在规定的区域内贴上条形码2.本试卷共有23道试题,满分150分,考试时间120分钟。
一、填空题(本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分。
1.已知集合{}1,3,A m =,{}3,4B =,{}1,2,3,4A B =U 则m = 。
2.不等式204xx ->+的解集是 。
3.行列式cossin 66sincos66ππππ的值是 。
4.若复数12z i =-(i 为虚数单位),则z z z ⋅+= 。
5.将一个总数为A 、B 、C 三层,其个体数之比为5:3:2。
若用分层抽样方法抽取容量为100的样本,则应从C 中抽取 个个体。
6.已知四棱椎P ABCD -的底面是边长为6 的正方形,侧棱PA ⊥底面ABCD ,且8PA =, 则该四棱椎的体积是 。
7.圆22:2440C x y x y +--+=的圆心到直线3440x y ++=的距离d = 。
8.动点P 到点(2,0)F 的距离与它到直线20x +=的距离相等,则P 的轨迹方程为 。
9.函数3()log (3)f x x =+的反函数的图像与y 轴的交点坐标是 。
10. 从一副混合后的扑克牌(52张)中随机抽取2张,则“抽出的2张均为红桃”的概率为 (结果用最简分数表示)。
11. 2010年上海世博会园区每天9:00开园,20:00停止入园。
在右边的框图中,S表示上海世博会官方网站在每个整点报道的入园总人数,a 表示整点报道前1个小时内入园人数,则空白的执行框内应填入 。
12.在n 行m 列矩阵12321234113*********n n n n n n n n n n ⋅⋅⋅--⎛⎫ ⎪⋅⋅⋅- ⎪⎪⋅⋅⋅ ⎪⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ⎪ ⎪⋅⋅⋅---⎝⎭中,记位于第i 行第j 列的数为(,1,2,)ij a i j n =⋅⋅⋅。
