福建省漳州市长泰县第一中学2015-2016学年高二数学3月月考试题-文
福建省漳州市长泰县第一中学2015_2016学年高二化学3月月考试题

福建省漳州市长泰县第一中学2015-2016学年高二化学3月月考试题满分100分,时间90分钟可能用到的相对原子质量:H :1 C :12 N :14 O :16第I卷(选择题,共60分)一、选择题(每题3分,共60分。
每小题只有一个....选项符合题意。
)1.碳氢化合物是一种大气污染物,下列现象的产生与碳氢化合物有关的是( )A.臭氧空洞B.光化学烟雾C.酸雨D.火山爆发2.某市曾经发生了一起震惊全国的特大投毒案,犯罪分子在食品中投入了毒鼠剂——毒鼠强,导致多人中毒死亡。
已知毒鼠强的结构简式如上图,有关毒鼠强(化学名:四亚甲基二砜四胺)的下列相关说法正确的是( )A.毒鼠强的分子式为C4H8N4S2O4B.毒鼠强属于烃C.毒鼠强分子内含SO2分子,因而具有毒性D.毒鼠强属于无机物3.乙烷、乙烯、乙炔共同具有的性质是( )A.都能使溴水和酸性高锰酸钾溶液褪色B.都能发生加聚反应生成高分子化合物C.都不溶于水,且密度比水小D.分子中各原子都处于同一平面上4.下列物质由于发生反应,不能使溴水褪色,但能使酸性KMnO4溶液褪色的是( )A.异丁烷B.1戊烯C.苯D.甲苯5.利用红外光谱对有机化合物分子进行测试并记录,可以初步判断该有机物分子拥有的( ) A.同分异构体数B.原子个数C.基团种类 D.共价键种类6.下列各组物质的沸点,前者高于后者的是( )A.丙烷丁烷 B.新戊烷正戊烷C.对-二甲苯间-二甲苯 D.碘干冰7.下列说法正确的是( )A.有机物中都存在同分异构现象B.只要含有的官能团种类相同就是同系物C.14C和14Si是同位素D.C2H5Cl没有同分异构体8.下列物质的命名错误的是( )9.分子中碳与氢两元素的质量比为24∶5的烃的一氯代物共有A.2种B.3种C.4种D.5种10.下列实验,能获得成功的是( )A.用溴水鉴别苯、乙醇、苯乙烯B.苯、溴水、铁粉混合制溴苯C.用分液漏斗分离苯和乙醇D.加浓溴水,然后过滤除去苯中混有的少量己烯11.(2013·茂名高二质检)将CH4和C2H4的混合气体15 g通入盛有足量溴水的容器中,溴水的质量增加了7 g,则混合气体中CH4和C2H4的体积比为( )A.1∶2 B.2∶1C.3∶2 D.2∶312.E(C5H5)2的结构如图,其中氢原子的化学环境完全相同。
数学上学期期中试题-长泰一中高二2015-2016学年上学期期中考试数学试题及答案(理)

长泰一中2015-2016学年上学期期中考试高二理科数学试卷一、选择题 (本大题共12小题,每小题5分,合计60分,答案用2B 铅笔在机读答题卡上填涂。
)1.已知命题p :∀x ∈R ,x >sin x ,则p 的否定形式为( )A .p ⌝:∃x ∈R ,x <sin xB .p ⌝:∀x ∈R ,x ≤sin xC .p ⌝:∃x ∈R ,x ≤sin xD .p ⌝:∀x ∈R ,x <sin x2.方程(x -y )2+(xy -1)2=0表示的是( )A .一条直线和一条双曲线B .两条双曲线C .两个点D .以上答案都不对3.对于给定的两个变量的统计数据,下列说法正确的是( )A .都可以分析出两个变量的关系B .都可以用一条直线近似地表示两者的关系C .都可以作出散点图D .都可以用确定的表达式表示两者的关系 4. 口袋中有100个大小相同的红球、白球、黑球,其中红球45个,从口袋中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为( ) A .0.45B .0.67C .0.64D .0.325.已知p :x 2-x <0,那么p 的一个必要不充分条件是( )A .0<x <1B .-1<x <1 C. 12<x <23D. 12<x <2 6.某学校举办了一次以班级为单位的广播操比赛,9位评委给高一(1)班打出的分数如茎叶图所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现 有一个数字(茎叶图中的x )无法看清,若记分员计算无误,则数字x 应该是( )A .2B .3C .4D .57.在如图的程序框图中,输入n =60,按程序运行后输出的结果是( )A .0B .3C .4D .58.已知焦点在x 轴上的双曲线的渐近线方程是y =±4x ,则该双曲线的离心率是( )A.17B.15C.174 D.1549.将一根长10 cm 的铁丝用剪刀剪成两段,然后再将每一段剪成等长的两段,并用这四段铁丝围成一个矩形,则围成的矩形面积大于6 cm 2的概率等于( ) A.15 B.25 C.35 D.4510.已知命题p :∃x ∈R ,(m +1)(x 2+1)≤0,命题q :∀x ∈R ,x 2+mx +1>0恒成立. 若p ∧q 为假命题,则实数m 的取值范围为( )A .m ≥2B .m ≤-2或m >-1C .m ≤-2或m ≥2D .-1<m ≤211.已知F 1、F 2分别是双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,P 为双曲线上一点,过F 1作∠F 1PF 2的平分线的垂线,垂足为H ,则点H 的轨迹为( )A .椭圆B .双曲线C .圆D .抛物线12.已知抛物线y 2=4x 上两个动点B 、C 和点A (1,2),且∠BAC =90°,则动直线BC 必过定点( )A .(2,5)B . (-2,5)C .(5,-2)D .(5,2)二、填空题(本大题共4小题,每小题5分,共20分.把正确答案直接写在答题卷相应位置上。
福建省长泰一中2015-2016年度高二上学期期中考试理科数学试卷

长泰一中2015/2016学年上学期期中考试高二理科数学试卷一、选择题 (本大题共12小题,每小题5分,合计60分,答案用2B 铅笔在机读 答题卡上填涂。
)1.已知命题p :∀x ∈R ,x >sin x ,则p 的否定形式为A .p ⌝:∃x ∈R ,x <sin xB .p ⌝:∀x ∈R ,x ≤sin xC .p ⌝:∃x ∈R ,x ≤sin xD .p ⌝:∀x ∈R ,x <sin x2.方程(x -y )2+(xy -1)2=0表示的是A .一条直线和一条双曲线B .两条双曲线C .两个点D .以上答案都不对3.对于给定的两个变量的统计数据,下列说法正确的是A .都可以分析出两个变量的关系B .都可以用一条直线近似地表示两者的关系C .都可以作出散点图D .都可以用确定的表达式表示两者的关系4. 口袋中有100个大小相同的红球、白球、黑球,其中红球45个,从口袋中摸出一个球,摸出 白球的概率为0.23,则摸出黑球的概率为 A .0.45B .0.67C .0.64D .0.325.已知p :x 2-x <0,那么p 的一个必要不充分条件是A .0<x <1B .-1<x <1 C. 12<x <23D. 12<x <2 6.某学校举办了一次以班级为单位的广播操比赛,9位评委给高一(1)班打出的分数如茎叶图 所示,统计员在去掉一个最高分和一个最低分后,算得平均分为91,复核员在复核时,发现 有一个数字(茎叶图中的x )无法看清,若记分员计算无误,则数字x 应该是A .2B .3C .4D .57.在如图的程序框图中,输入n =60,按程序运行后输出的结果是A .0B .3C .4D .58.已知焦点在x 轴上的双曲线的渐近线方程是y =±4x ,则该双曲线的离心率是A.17B.15C.174 D.1549.将一根长10 cm 的铁丝用剪刀剪成两段,然后再将每一段剪成等长的两段, 并用这四段铁丝围成一个矩形,则围成的矩形面积大于6 cm 2的概率等于A.15B.25C.35D.4510.已知命题p :∃x ∈R ,(m +1)(x 2+1)≤0,命题q :∀x ∈R ,x 2+mx +1>0恒成立. 若p ∧q 为假命题,则实数m 的取值范围为A .m ≥2B .m ≤-2或m >-1C .m ≤-2或m ≥2D .-1<m ≤211.已知F 1、F 2分别是双曲线x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点,P 为双曲线上一点,过F 1作∠F 1PF 2的平分线的垂线,垂足为H ,则点H 的轨迹为A .椭圆B .双曲线C .圆D .抛物线12.已知抛物线y 2=4x 上两个动点B 、C 和点A (1,2),且∠BAC =90°,则动直线BC 必过定点A .(2,5)B .(-2,5)C .(5,-2)D .(5,2)二、填空题(本大题共4小题,每小题5分,共20分.把正确答案直接写在答题卷相应位置上。
福建省漳州市长泰县第一中学高二数学下学期期中试题

长泰一中2015-2016学年下学期期中考高二文科数学试卷一、单项选择(每小题12分,共5分,合计60分) 1、已知{}{}1,022-==<-=x y x N x x x M ,则=)(N C M R I ( )A .{}10<<x xB .{}20<<x xC .{}1<x x D .φ 2、已知集合},3,1{m A =,},1{m B =,A B A =Y ,则=m ( ) A .0或3 B .0或3C .1或3D .1或33、下列函数中,在其定义域内既是奇函数又是减函数的是( ) A.x y 1=B.1y x x =+C.tan y x =D. xx y +-=11lg 4、曲线2,14x t y t=⎧⎨=+⎩(t 为参数)与圆22sin ρθ=的位置关系为( )A 、相离B 、相切C 、相交D 、不确定5、命题“对任意x ∈R ,都有2240x x -+≤”的否定为( )A.对任意x ∈R ,都有2240x x -+≥B.对任意x ∈R ,都有2240x x -+≤C.存在0x ∈R ,使得200240x x -+> D.存在0x ∈R ,使200240x x -+≤ 6、已知直线t ty t x (12⎩⎨⎧+=+=为参数)与曲线C :03cos 42=+-θρρ交于B A ,两点,则=AB ( )A .1B .21C .22D .27、若f(x)=x 2+2mx+m 2-2m 在(-∞,3]上单调递减,则实数m 的取值范围是( ) A.(-∞,-3] B.[-3,+∞) C.(-∞,3] D.[3,+∞)8、若关于x 的不等式12a x x ≥++-存在实数解,则实数a 的取值范围是( ) A .(,3]-∞- B .[)3,+∞ C .[]3,3- D .[)(,3]3,-∞-+∞U9、函数y=a x+3﹣2(a >0,且a≠1)的图象恒过定点A ,且点A 在直线mx+ny+1=0上(m >0,n >0),则的最小值为( )A .12B . 10C .8D .14 10、函数)6(log )(231x x x f --=的单调递增区间是( )A .(),2-∞B .1,22⎡⎫-⎪⎢⎣⎭ C .13,2⎛⎤-- ⎥⎝⎦ D .()3,+∞11、若k R ∈,则“1k >”是方程“22111x y k k -=-+”表示双曲线的( ) A .充分不必要条件 B .必要不充分条件C .充要条件 D .既不充分也不必要条件 12、下列命题中正确的是(A .若p q ∨为真命题,则p q ∧为真命题B .“0a >,0b >”是“2b aa b+≥”的充分必要条件 C .命题“若2320x x -+=,则1x =或2x =”的逆否命题为“若1x ≠或2x ≠,则2320x x -+≠”D .命题:p 0R x ∃∈,使得20010x x +-<,则:p ⌝R x ∀∈,使得210x x +-≥二、填空题(每小题4分,共4题,合计16分)13、.已知y =f(x)在定义域(-1,1)上是减函数,且f(1-a)<f(3a -1),则a 的取值范围是________. 14、已知圆的极坐标方程ρ=2cos θ,直线的极坐标方程为ρcos θ﹣2ρsin θ+7=0,则圆心到直线距离为 .15、已知命题2:,210p x R ax ax ∃∈++≤.若命题p ⌝是真命题,则实数a 的取值范围是 .16、定义全集U 的子集M 的特征函数为1,()0,M U x M f x x C M ∈⎧=⎨∈⎩,这里U C M 表示集合M 在全集U 中的补集,已,M U N U ⊆⊆,给出以下结论:①若M N ⊆,则对于任意x U ∈,都有()()M N f x f x ≤;②对于任意x U ∈都有()1()U C M M f x f x =-;③对于任意x U ∈,都有()()()M N M N f x f x f x =⋅I ;④对于任意x U ∈,都有()()()M N M N f x f x f x =⋅U .则结论正确的是三、解答题(5*12+14=74分)17、(本小题12分)已知不等式ax 2+x+c>0的解集为{x|1<x<3}. (1)求a ,c 的值.(2)若“ax 2+2x+4c>0”是“x+m>0”的充分不必要条件,求实数m 的取值范围.18、(本小题12分)在直角坐标系xoy 中,直线l 的参数方程为12x t y t =-⎧⎨=+⎩,(t 为参数),在以原点O 为极点,x 轴的正半轴为极轴的极坐标系中,曲线C 的极坐标方程为2312cos ρθ=+.MABXYO.(Ⅰ)直接写出直线l 、曲线C 的直角坐标方程;(Ⅱ)设曲线C 上的点到与直线l 的距离为d ,求d 的取值范围.19、(本小题12分)已知函数()|1|||f x x x a =-+-. (Ⅰ)当2a =时,解不等式()4f x ≥;(Ⅱ)若不等式()2f x a ≥恒成立,求实数a 的取值范围.20、(本小题12分)函数+=+2()1ax b f x x 是定义在-∞+∞(,)上的奇函数,且=12()25f . (1)求实数,a b ,并确定函数()f x 的解析式; (2)用定义证明()f x 在(1,1)-上是增函数;(3)写出()f x 的单调减区间,并判断()f x 有无最大值或最小值?如有,写出最大值或最小值.(本小问不需说明理由)21、(本小题12分)已知椭圆E :12222=+by a x )(0>>b a 的半焦距为c ,原点O 到经过两点(c ,0),(0,b )的直线的距离为21c , (1)求椭圆E 的离心率;(2)如图,AB 是圆M:(x+2)2+(y-1)2=25的一条直径,若椭圆E 经过A ,B 两点,求椭圆E 的方程22、(本小题14)已知函数2()ln (1)2a f x x x a x =+-+. (1)若曲线()y f x =在1x =处的切线方程为2y =-,求()f x 的单调区间; (2)若0x >时,()()2f x f x x '<恒成立,求实数a 的取值范围.。
漳州市长泰县第一中学2015-2016学年高二下学期期中考试英语试题含答案试题

长泰一中2015-2016学年下学期期中考高二英语试卷第一部分听力(共两节,满分30 分)第一节听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What is Jack's hobby?A. Attending concerts.B. Playing football.C. Seeing films.2. What does the number refer to?A. A telephone number.B. A room number.C. A flight number.3. Where does Bob study now?A. At Clark High School.B. At Searing High School.C. At Melrose Community College.4. What can we learn from the conversation?A. The man wants to travel by train.B. The speakers will have a long trip.C. The woman thinks the train is tiring.5. What does the man mean?A. He will sell the car.B. The car is in good condition.C. He got tired of the car years ago.第二节听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟作答时间。
福建省长泰县第一中学高二数学上学期期末考试试题 文

长泰一中2015/2016学年上学期期末考试高二年文科数学试卷考试范围: 必修3, 选修1-1 选修1-2 时间:120分钟 满分:150分一、选择题:本大题共12个小题,每小题5分,共60分 1.“(1)(3)0x x +-<”是“1->x ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件2.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点,公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为(1);在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为(2)。
则完成(1)、(2)这两项调查宜采用的抽样方法依次是( )A 、分层抽样法,系统抽样法B 、分层抽样法,简单随机抽样法C 、系统抽样法,分层抽样法D 、简单随机抽样法,分层抽样法3.一个物体的运动方程为21t t s +-=其中s 的单位是米,t 的单位是秒,那么物体在3秒末的瞬时速度是( )A .7米/秒B .6米/秒C .5米/秒D .8米/秒4.已知双曲线C 的焦点、实轴端点分别恰好是椭圆2212516x y +=的长轴端点、焦点,则双曲线C 的渐近线方程为 ( )A .430x y ±=B .340x y ±=C .450x y ±=D .540x y ±=5.甲、乙2人下棋,下成和棋的概率是21,乙获胜的概率是31,则甲胜的概率是( )A. 21B.65C.61D.326. 已知ABC ∆的顶点C B 、在椭圆131222=+y x 上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则ABC ∆的周长是( )A . 38 B. 6 C. 34 D. 127.若函数21()ln 2f x x a x =-+在区间(1,)+∞上是减函数,则实数a 的取值范围为( )A .[1,)+∞B .(1,)+∞C .(,1]-∞D .(,1)-∞8.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )分数 5 4 3 2 1 人数201030301011题A 、3B 、210C 、3D 、859.函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内的图象如图所示, 则函数)(x f 在开区间),(b a 内有极小值点( )abxy)(x f y ?=OA .1个B .2个C .3个D .4个10.在长为10 cm 的线段AB 上任取一点P ,并以线段AP 为边作正方形,这个正方形的面积介于25 cm2与49 cm 2之间的概率为( ) A 、103 B 、51 C 、52 D 、5411、下图给出的是计算201614121+⋅⋅⋅+++的值的一个程 序框图,其中判断框内应填入的条件是( ) A.i>10 B.i<10 C.i>20 D.i<2012、用反证法证明命题“三角形中最多只有一个内角是钝角”时,结论的否定是( )A 、没有一个内角是钝角B 、有两个内角是钝角C 、有三个内角是钝角D 、至少有两个内角是钝角二、填空题:本大题共4个小题,每小题4分,共16分。
福建省长泰高三下学期第一次月考文科数学试题

长泰2016届高三年级第一次月考数 学 试 卷(文)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合}06|{2≤--=x x x A ,{|14}B x x x =<->或,则集合A B 等于 A . {}|34x x x >或≤ B .{}|13x x -<≤C .{}|34x x <≤D .{}|21x x --<≤2.已知复数z 满足(1﹣i)z=i 2015(其中i 为虚数单位),则的虚部为( ) A .- B .C .iD .﹣i3.已知3tan =θ,则θθθθ22cos 2cos sin sin -+等于( ) A .1 B .45 C .43-D .54 4.已知向量a 与向量b 夹角为6π,且||3a =,(2)a a b ⊥-,则||b =( )AB .1C .D .25. 执行如图所示的程序框图, 输出的S 值为( ) A .2 B .4C .8D .166.直线l 过抛物线x 2=2py (p >0)的焦点,且与抛物线交于A 、B 两点,若线段AB 的长是6,A B 的中点到x 轴的距离是1,则此抛物线方程是( ) A .x 2=4y B .x 2=12y C . x 2=6y D .x 2=8y7.将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为( )8.已知函数f(x)(x ∈R)满足f(1)=1,且f ′(x)<1,则不等式f(1g 2x)<1g 2x 的解集为( ) A .B .C .D . (10,+∞)9.已知正项等差数列{}n a 满足120152a a +=,则2201411a a +的最小值为( ) A .2014 B .2015 C .1 D .2 10.下列4个命题:①命题“若20x x -=,则1x =”的逆否命题为“若1x ≠,则20x x -≠”; ②若“p ⌝或q ”是假命题,则“p 且q ⌝”是真命题;③若p :(2)0x x -≤,q :2log 1x ≤,则p 是q 的充要条件;④若命题p :存在x R ∈,使得22x x <,则p ⌝:任意x R ∈,均有22x x ≥; 其中正确命题的个数是( ) A .1个B .2个C .3个D .4个11.平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )(A)6π (B)43π (C)46π (D)63π12.在长为20cm 的线段AB 上任取一点P ,并且以线段AP 为边作正三角形,则2与2之间的概率为 ( )A .15B .25C .35D .310二.填空题:本大题共4小题,每小题5分,共20分。
【数学】福建省漳州市长泰县第二中学2015-2016学年高二下学期第一次月考(文)
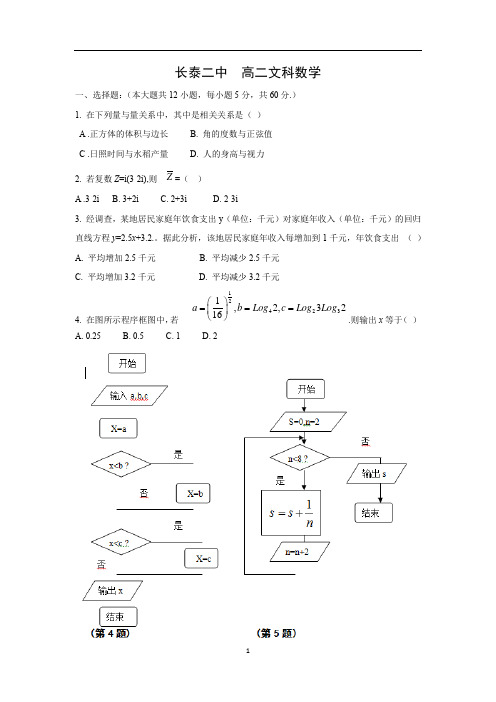
长泰二中高二文科数学一、选择题:(本大题共12小题,每小题5分,共60分.)1. 在下列量与量关系中,其中是相关关系是()A .正方体的体积与边长 B. 角的度数与正弦值C .日照时间与水稻产量 D. 人的身高与视力2. 若复数Z=i(3-2i),则Z=()A .3-2i B. 3+2i C. 2+3i D. 2-3i3. 经调查,某地居民家庭年饮食支出y(单位:千元)对家庭年收入(单位:千元)的回归直线方程y=2.5x+3.2.。
据此分析,该地居民家庭年收入每增加到1千元,年饮食支出()A. 平均增加2.5千元 B. 平均减少2.5千元C. 平均增加3.2千元D. 平均减少3.2千元4. 在图所示程序框图中,若124231,2,3216a b Log c Log Log⎛⎫===⎪⎝⎭.则输出x等于()A. 0.25B. 0.5C. 1D. 25. 如上图所示,执行程序框图,输出结果( )A .512 B. 712 C. 1112 D. 16. 推理“(1)矩形是平行四边形” “(2)正方形是矩形” “(3)所以正方形是平行四边形”。
其中小前提是( )A.(1)B.(2)C.(3)D.(1)和(2) 7. 在等差数列 {}n a 中,若n a >0,公差d >0,则有4637a a a a >。
类比上述性质,在等比数列{}n b 中,若n b >0,公比q >1,则4578,,,b b b b 一个不等关系是( )A.4857b b b b +>+B.5748b b b b +>+C.4758b b b b +>+ D.4578b b b b +>+8. 已知1()f x Sinx Cosx =+,1()n f x +是()n f x 导函数,即21()()f x f x '=,32()()f x f x '=,1()(),n n f x f x n N *+'=∈,则2015()f x =( )A. sinx +cosxB. -sinx - cosxC. sinx -cosxD. -sinx +cosx 9. 已知复数Z 满足( Z-i)i=2+3i, 求Z=( )B. C. 10 D. 1810. 设a,b,c (,)o ∈-∞,则111,,a b c b c a +++( )A. 都不大于 -2B. 都不小于 -2B. 至少有一个不大于 -2 D.至少有一个不小于 -211. 若函数f(x)= 1aLnx x +在区间(1,+ ∞)上单调递增,则实数a 取值范围( )A.(],2-∞- B. (],1-∞- C. [)1,+∞ D. [)2,+∞12. 某公司在甲,乙二地销售一种车,利润(单位:万元),分别为21 5.060.15L x x =-和22L x =,其中x 为销售量(单位:辆)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A.2B. 13C.12D. 112.(普通班做)设,,x y z 均大于0,则三个数:111,,x y z y z x+++的值 ( C )A. 都大于2B.至少有一个不大于2C. 至少有一个不小于2D. 都小于212.(实验班做) 若R b a ∈,且b a ≠,则在 ① 22b b a >+;② 322355b a b a b a+>+;③ ();1222--≥+b a b a④ 2>+baa b . 这四个式子中一定成立的有 ( C ) A. 4个 B. 3个 C. 2个D. 1个二、填空题:本大题共4个小题,每小题5分,共20分。
13、函数2ln 1y x =+在点(1,1)处的切线方程为 210x y --= .14. 在直角坐标平面内,以坐标原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,已知直线l 的极坐标方程为cos()14πθ+=,曲线C 的参数方程为()13cos sin x y ααα⎧=+⎪⎨=⎪⎩为参数,点M 是曲线C 上的动点 ,则点M到直线l 最大值为 2.15. 设函数()3f x x x a =-+-,如果对任意,()4x R f x ∈≥,则a 的取值范围是_____()()7,,1+∞⋃-∞-_____.16.已知命题p :存在x ∈R ,使tan x =22,命题q :x 2-3x +2<0的解集是{x |1<x <2},下列结论:①命题“p 且q ”是真命题;②命题“p 且q ⌝”是假命题;③命题“p ⌝或q ”是真命题;④命题“p ⌝或q ⌝”是假命题,其中正确的是 ①②③④三、解答题:本大题共6个小题,共70分, 解答应写出文字说明或演算步骤。
17. (本小题满分12分) 已知曲线C 的极坐标方程是2COS ρθ=,直线l 的参数方程是22,3253x t y t ⎧=-+⎪⎨⎪=-⎩(t 为参数).(1)将曲线C 的极坐标方程化为直角坐标方程; (2)设直线l 与y 轴的交点是M ,N 是曲线C 上一动点,求MN 的最小值. 解:(1)曲线C 的极坐标方程可化为22cos ρρθ=又222,cos ,x y x ρρθ+==……………………………………2分所以曲线C 的直角坐标方程2220x y x +-=………………4分(2)将直线l 的参数方程化为直角坐标方程,得3y x =-- …………6分令x 0=得3y =-,即M 点的坐标为(0,-3). ……………………8分又曲线C 为圆,圆C 的圆心坐标为(1,0),半径1r =,则MC =,1MN MC r ≥-=………………………………11分所以MN的最小值为1…………………………………………12分18.(本小题满分12分)在研究色盲与性别的关系调查中,调查了男性400人,其中有30人患色盲,调查的600名女性中有20人患色盲.(1)根据以上数据建立一个2×2列联表;(2)有多大把握认为“性别与患色盲有关系”? 参考公式及数据:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )附临界值参考表:x 02.7063.841 5.024 6.635 7.87910.828解:(1)性别与色盲的2×2列联表建立如下:患色盲 不患色盲总计男 30 370 400 女 20 580 600 总计50 950 1 000…… ……… ……………………………………5分 (2)假设H 0:“性别与患色盲没有关系”,根据(1)中2×2列联表中数据,可求得()22100030580203708.77250950400600K ⨯-⨯=≈⨯⨯⨯ ………………… ……………8分又P (K 2≥7.879)=0.005,即H 0成立的概率不超过0.005,…………10分 故若认为“性别与患色盲有关系”,则出错的概率不超过0.005.所以有99.5%的把握认为“性别与患色盲有关系”………………………………12分. 19. (本小题满分12分)已知椭圆的两焦点为10()1,F -、()21,0F ,p 为椭圆上一点,且122F F = 12.PF PF +(1)求此椭圆的方程;(2)若点P 在第二象限,∠F 2F 1P =120°,求△PF 1F 2的面积.解:(1)依题意得|F 1F 2|=2, 又2|F 1F 2|=|PF 1|+|PF 2|,∴|PF 1|+|PF 2|=4=2a .∴a =2,c =1, b2=3.∴所求椭圆的方程为x24+y23=1.(2)设P 点坐标为(x ,y ),∵∠F 2F 1P =120°, ∴PF 1所在直线的方程为y =(x +1)·tan 120°,即y =-3(x +1).解方程组⎩⎪⎨⎪⎧y =-3x +1,x 24+y23=1,又∵x <0,y >0,可得⎩⎪⎨⎪⎧x =-85,y =335.∴12PF F S∆=12|F 1F 2|·335=335. 20. (本小题满分12分)解不等式:(1)411x x -<- ; (2)124x x -++>解:(1)、(,1)(1,3)-∞- (2)、5(,)(2,)2-∞-+∞20、(实验班做)(本小题满分12分)已知函数()212f x x x a=-++,()3g x x =+.(Ⅰ)当2a =-时,求不等式()()f x g x <的解集;(Ⅱ)设1a >-,且当1,22a x ⎡⎫∈-⎪⎢⎣⎭时,()()f x g x ≤,求a 的取值范围.解:(1)当2a =-时,不等式()()f x g x <化为212230x x x -+---<…1分设函数21223y x x x =-+--- 则15()212(1)236(1)x x y x x x x ⎧-<⎪⎪⎪=--≤≤⎨⎪->⎪⎪⎩……………………………4分其图像如图所示,从图像可知, 当且仅当(0,2)x ∈时,0y <………5分所以原不等式的解集是{}02x x |<<………………6分(2)当1,22a x ⎡⎫∈-⎪⎢⎣⎭时,()1f x a =+………………………………………6分不等式()()f xg x ≤化为13a x +≤+………………… …………………7分所以2x a ≥-对1,22a x ⎡⎫∈-⎪⎢⎣⎭都成立……………………………………9分故22aa -≥-,即43a ≤………………………………………………11分从而a 的取值范围是41,3⎛⎤- ⎥⎝⎦…………………………………………12分 21.(普通班做)(本小题满分12分)已知函数32()f x x ax bx c=+++在23x =-与1x =时都取得极值. (1) 求a ,b 的值与函数()f x 的单调区间; (2) 若对[1,2]x ∈-,不等式2()f x c <恒成立,求c 的取值范围.解:(1)f(x)=x 3+ax 2+bx +c , f′(x)=3x 2+2ax +b ,由f′⎝ ⎛⎭⎪⎫-23=129-43a +b =0,f′(1)=3+2a +b =0得a =-12,b =-2.f′(x)=3x 2-x -2=(3x +2)(x -1), 令f′(x )>0,得x<-23或x>1, 令f′(x)<0,得-23<x<1.所以函数f(x)的递增区间是⎝⎛⎭⎪⎫-∞,-23和(1,+∞),递减区间是⎝ ⎛⎭⎪⎫-23,1.(2)f(x)=x 3-12x 2-2x +c ,x∈[-1,2],由(1)知,当x =-23时,f ⎝ ⎛⎭⎪⎫-23=2227+c 为极大值,而f(2)=2+c ,则f(2)=2+c 为最大值, 要使f(x)<c 2,x∈[-1,2]恒成立, 则只需要c 2>f(2)=2+c ,得c<-1或c>2.21. (实验班做)(本小题满分12分)已知函数()ln f x x a x=+,在1x =处的切线l 与直线20x y += 垂直,函数21()().2g x f x xbx =+-(1) 求实数a 的值;(2) 若函数()g x 存在单调递减区间,求实数b 的取值范围;(3) 设1212,()x x xx >是函数()g x 的两个极值点,若72b ≥,求12()()g x g x - 的最小值。
解:(Ⅰ)()ln ()1af x x a x f x x'=+∴=+,,20l x y +=与直线垂直,1|12x k y a ='∴==+=,1a ∴=(Ⅱ)21()ln (1)(0)2g x x x b x x =+-->21(1)1()(1)x b x g x x b x x--+'=+--=设2()(1)1x xb x μ=--+,则(0)10μ=>只须21013231(1)40b b b b b b -⎧>>⎧⎪⇒⇒>⎨⎨><-⎩⎪∆=-->⎩或b∴的取值范围为(3,)+∞(Ⅲ)令21212()0(1)101,1g x xb x x x b x x '=--+=∴+=-=得,2222111212121212122211()()ln()(1)()ln ()()()22x x g x g x x x b x x x x x x x x x x -=+----=+--+-2211211221222111ln ln ()22x x x x x x x x x x x x -=-=--11220,01x t x x t x =<<∴<<,,又212221212121()1725,(1)2(1)241x x b x x b t x x t x x ⎧+=-+⎪=-++≥-=⎨=⎪⎩得2141740,04t t t ∴-+≥∴<≤,令111()ln ()(0)24h t t t t t =--<≤ 222111(1)()(1)022t h t t t t -'=-+=-<,1()(0,]4h t ∴在单减 115()()2ln 248h t h ≥=-故12()()g x g x -的最小值为152ln 28-22.(本小题满分10分)提示:本小题为选作题①(选修4-1:几何证明选讲)如图设M 为线段AB 中点,AE 与BD 交于点C ,∠DME=∠A=∠B=α,且DM 交AC 于F ,EM 交BD 于G.(Ⅰ)写出图中三对相似三角形,并对其中一对作出证明;(Ⅱ)连结FG ,设α=45°,AB=42,AF=3,求FG 长.②(选修4—4:坐标系与参数方程)平面直角坐标系中,已知曲线221:1C x y +=,将曲线1C 上所有点横坐标,纵坐标分别伸长为原来的2倍和3倍后,得到曲线2C(Ⅰ)试写出曲线2C 的参数方程;(Ⅱ)在曲线2C 上求点P ,使得点P 到直线:450l x y +-=的距离最大,并求距离最大值.③(选修4—5:不等式选讲)设()2|||3|.f x x x =-+ (Ⅰ)求不等式()7f x ≤的解集S ;(Ⅱ)若关于x 不等式()|23|0f x t +-≤有解,求参数t 的取值范围.解:①(I ) △AME ∽△MFE ,△BMD ∽△MGD , △AMF ∽△BGM ……3分∵∠AMD =∠B+∠D ,∠BGM=∠DMG+∠D , 又∠B=∠A=∠DME=α∴∠AMF=∠BGM ∴△AMF ∽△BGM …………6分(II )由(1)△AMF ∽△BGM , AF BM AM BG =, 38=BG ,∠α=45°∴△ABC 为等腰直角三角形AB=24,AC=BC=4,CF=AC -AF=1,CG=4-3438=,35)34(1222=+=+=GC FC FG …12分② (1)曲线1C 的参数方程为cos (sin x y θθθ=⎧⎨=⎩为参数), 由23x x y y⎧'=⎪⎨'=⎪⎩得2cos 3sin x y θθ⎧'=⎪⎨'=⎪⎩ ,∴2C 的参数方程为2cos (3sin x y θθθ⎧=⎪⎨=⎪⎩为参数)……6分(2)由(1)得点()2cos ,3sin P θθ,点P到直线l的距离()2cos 3sin 455cos 4522d θθθϕ+---==, 2tan 3ϕ=,max5551022d ==,此时2535,P ⎛⎫-- ⎪ ⎪⎝⎭点的坐标为 ……12分。
