福建省龙岩市2009年普通高中毕业班单科质量检查
2009年龙岩市普通高中毕业班单科质量检查

2009年龙岩市普通高中毕业班单科质量检查物理试题(考试时间:90分钟满分:100分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卷上.2.第Ⅰ卷(选择题)每小题选出答案后,请把答案填在答题卷上.3.第Ⅱ卷(非选择题)必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷上各题目指定区域内相应位置;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效.4.考生必须保持答题卷的整洁,考试结束后,将答题卷交回.第Ⅰ卷(选择题共40分)一、本题共10 小题,每小题4 分,共40分。
在每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得4 分,选对但不全的得2 分,有错选或不答的得0 分。
1.四个同学分别画出质点的位移-时间或速度-时间图像,如图所示。
不管质点如何运动,但可以肯定已画错的是()2. 如图所示,a、b、c、d四个图是不同的单色光形成的双缝干涉或单缝衍射图样。
分析各图样的特点可以得出的正确结论是()A. a、b是光的干涉图样;B. c、d是光的干涉图样;C.形成a图样光的波长比形成b图样光的波长短D.形成c图样光的波长比形成d图样光的波长短3. 许多科学家在物理学发展过程中做出了重要贡献,他们的研究应用了许多科学的物理思想 和方法,下列表述正确的是( )A. 卡文迪许在测量“万有引力常量”时用到了“放大法”B. 伽利略用“理想实验”的方法推理得出“力是物体运动的原因”C. 法拉第从大量的实验中归纳得出电磁感应产生的条件D. 库仑用类比的方法发现了库仑定律4. 如右图所示,质子以一定的初速度v 0从边界ab 上的A 点水平向右射入 竖直、狭长的矩形区域abcd (不计质子的重力)。
当该区域内只加竖直 向上的匀强电场时,质子经过t 1时间从边界cd 射出;当该区域内只加水 平向里的匀强磁场时,质子经过t 2时间从边界cd 射出,则 ( ) A. t 1>t 2B. t 1<t 2C. t 1=t 2D. t 1、t 2的大小关系与电场、磁场的强度有关5. 如图所示,O 是波源,a 、b 、c 、d 是波传播方向上处于平衡位置的四个质点,且oa =ab =bc =cd =2m ,开始时各质点均静止在平衡位置,在t =0时刻,波源O 开始沿y 轴正方向做简谐振动,振幅是0.1m ,波沿x 轴正方向传播,波长λ=8m 。
2009年福建普通高中毕业班单科质量检查

2009 年福建省普通高中毕业班单科质量检查英语试卷本试卷分第i 卷(选择题)和第n 卷(非选择题)两部分,满分 150分。
考试时间120分钟。
第i 卷第一部分 听力(共两节,满分 30 分)第一节(共 5 小题;每小 1.5 分,满分 7.5 分)听下面 5 段对话。
每段对话后有一个小题,从题中所给的 听下面 5 段对话或独白。
每段对话或独白后有几个小题,从题中所给的 A 、B 、C 三个 选项中选出最佳选项, 并标在试卷的相应位置。
听每段对话或独白前, 你将有时间阅读各个 小题,每小题 5 秒钟;听完后,各小题给出 5 秒钟的作答时间。
每段对话或独白读两遍。
A 、B 、C 三个选项中选出最 佳选项,并标在试卷的相应位置。
听完每段对话后,你都有 和阅读下一小题。
每段对话仅读一遍。
例: How much is the shirt?A .£ 19.15.B .£ 9.15.答案是 B 。
1 . In which room is the meeting held?A . In Room 405.B .In Room 504.2 . What does the man want to do?A . Put in enough money.B . Open a checking account.C . Write out his checks.3 . How will the man probably go to work?A . By bus.B .By car.4 . What does the man want?A . A pair of trousers.B . A pair of gloves.5 . What does the woman think the man should do?10 秒钟的时间来回答有关小题C .£ 9.18.C .In Room 404.C .By taxi.C . A pair of socks.C . Take an exam.听第 6 段材料,回答第6、7 题。
2009年龙岩市高中毕业班质量检查

2009年龙岩市高中毕业班质量检查1949年中华人民共和国成立,为中国进行“基本制度选择”提供了条件。
新中国初期建立或选择的政治制度不包括...25.之所以作出上述选择,从《生活与哲学》角度看,符合A.物质决定意识B.实践决定于认识C.矛盾的普遍性D.事物发展的原因26.2009年2月28日,温家宝总理来到中国政府网考察并与网友在线交流,当有网友抱怨道:“我是一个返乡农民工,现在哪都找不到工作了!”温总理回答:“无论是农民工就业,还是大学生就业,以及城镇零就业家庭就业,都时刻摆在我心里。
”这就要求政府A.全力发展高科技产业和资本密集型产业B.树立自主择业观、竞争就业观和职业平等观C.通过扩大生产规模为劳动者提供更多就业机会D.营造有助于促进就业和鼓励自主创业的良好环境27.2009年2月5日,国家财政部公布了2009年关键期限记账式国债发行计划,其中国债发行规模将达2008年的2倍左右,即在1.4万亿和1.6万亿元之间。
发行当天,居民踊跃购买。
对下列观点,你赞同的是①发行国债是积极财政政策的重要内容②发行国债是适度宽松货币政策的重要内容③购买债券收益比股票高④购买债券风险比股票小A.①③B.③④C.②③ D.①④28.图8描述的是某商品的价格走势,下列对Array该图理解错误..的是A.该商品很可能出现供不应求的现象B.生产者可能会缩小该商品生产规模C.该商品的互补商品需求量会有所增加D.该商品的替代商品需求量会有所增加29.从2008年9月开始,福建省委认真贯彻中央的部署,全面开展深入学习实践科学发展观活动,坚持“海西应先行”,取得了较好成效。
这体现了A.坚持行使国家职能,积极推进海峡西岸经济区建设B.坚持科学执政,促进我省经济社会的可持续发展C.坚持民主执政,在经济建设各个环节发挥核心作用D.坚持依法执政,发挥党总揽全局协调各方面的核心作用30.西藏实行民主改革的50年,是西藏自治区经济、政治、文化、社会事业全面发展进步的50年,如2008年西藏生产总值是1959年的227倍,100%的农牧民享有免费医疗,藏民 信教自由得到了切实保障等。
龙岩市普通高中毕业班单科质量检查

2009年龙岩市普通高中毕业班单科质量检查2009年龙岩市普通高中毕业班单科质量检查语文试题(考试时间:150分钟;满分:150分)考生注意:请在卷末的“答题纸”上作答一、古诗文阅读(27分)(一)默写常见的名句名篇(6分)1.补写出下列名句名篇中的空缺部分。
(任选三题)(6分)(1)风急天高猿啸哀,。
(杜甫《登高》)君子博学而日参省乎己,。
(荀子《劝学》)(2) 但见悲鸟号古木,。
(李白(蜀道难))曲终收拨当心画,。
(白居易《琵琶行》)(3)小楼昨夜又东风,。
(李煜《虞美人》)制芰荷以为衣兮,。
(屈原《离骚》)(4)羽扇纶巾,谈笑间。
(苏轼《念奴娇•赤壁怀古.五步一楼,十步一阁;、檐牙高啄。
(杜牧《阿房宫赋》)(二)文言文阅读(15分)阅读下面的文言文,完成24题。
王守仁,字伯安,余姚人。
守仁娠十四月而生。
祖母梦神人自云中送儿下,因名云。
五岁不能言,异人拊之,更名守仁,乃言。
登弘治十二年进士。
兵部尚书王琼素奇守仁才。
十一年八月擢右佥都御史,巡抚南、赣。
当是时,福建大帽山贼詹师富等起,前巡抚文森托疾避去,贼掠大庾,攻南康、赣州,赣县主簿吴玭战死。
守仁至,知左右多贼耳目,乃呼老黠隶诘之。
隶战栗不敢隐,因贳其罪,令诇①,贼动静无勿知。
于是檄福建、广东会兵,先讨大帽山贼。
明年正月,督副使扬璋等破贼长富村。
逼之象湖山,指挥覃桓、县丞纪镛战死。
守仁亲率锐卒屯上杭。
佯退师,出不意捣之,连破四十余寨,俘斩七千有奇。
十四年六月,命勘福建叛军。
行至丰城而宁王宸濠反。
守仁急趋吉安,与伍文定征调兵食,治器械舟揖,传檄暴宸濠罪,俾守令各率吏士勤王。
乃多遣间谍,佯言所部合十六万,直捣南昌。
七月,袭下九江、南康,出大江,薄安庆,宥胁从,安士民。
丙辰复战,官军却,守仁斩先却者。
诸军殊死战,贼复大败。
明日,宸濠方晨朝其群臣,官军奄至。
以小舟载薪,乘风纵火,宸濠舟胶浅,仓卒易舟遁,王冕所部兵追执之。
凡三十五日而贼平。
2009年福建省高中毕业班单科质量检查考试

2009年福建省高中毕业班单科质量检查考试思想政治学科质量分析一、命题思路介绍2009年省质检单科思想政治试卷命题目标在于全面了解我省新课程普通高中毕业班思想政治学科教学情况,检查高三上学期的复习效果,发现教学和复习问题,同时,为新课程首届毕业班师生提供一份可参考的试题样式,引导全省下一阶段复习,提高毕业班的教学质量。
为此,试题反映了2009年福建省高考考试说明的精神,在命题指导思想、考试内容、考核能力目标、试卷形式等方面遵循了省颁考试说明的要求。
全卷分I卷选择题和II卷非选择题,具体的考试内容以省颁考试说明为准,考查了四个必修模块内容,符合考试说明规定的要求(见表一),具体内容不超出《考试说明》范围。
表一:思想政治试卷题型、内容结构表纵观2009年省质检单科政治试卷,注意新课程基本理念的贯彻落实,呈现以下几个特点:1.基础性本次质检定位在第一轮教学复习(实际上不少学校还没有完成一轮的教学复习),故以考生接受高等教育必须具备的基本知识和基本能力为主要考核内容,全面考查考生对所学基础知识、基本技能的掌握程度,所选考点多属核心概念和主干知识,覆盖到各个单元,基本上做到不偏不怪(见表二)。
表二:思想政治试题直接考查的考点2. 能力性本次考试在注重考查“双基”的基础上,适当地体现了能力立意为主线的思想,表现在:其一,全部试题都是运用情景材料设计,要求考生能够通过阅读材料,从中提取有用信息,并在答题中运用这些信息,考查信息收集处理能力;其二,试题要求考生通过对试题中事实因素和意识因素的认识,考核考生对基本事实、基本概念和观点的内涵的理解并做出合理判断,包括对选择题素材的理解判断和对主观题中的经济数据、社会现象、基本结论的比较分析,考核理解判断能力;第三,试题要求考生通过对社会热点、生活实际和历史现象的具体分析,明确事物存在和发展的意义,分析事物的成因,归纳出社会政治、经济和思维领域的科学结论,考核分析归纳能力;第四,试题要求考生在掌握知识间的内在联系的基础上,运用不同知识综合解决较为复杂的现实问题,提出解决问题的方法,考核综合运用能力。
2009年福建普通高中毕业班单科质量检查物理试题

2009年福建省普通高中毕业班单科质量检查物理试题(满分:100分考试时间:90分钟)本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)第1卷(选择题共40分)一、本题共10小题,每小题4分,共40分。
在每小题的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确。
全部选对的得4分,选对但不全的得2分,有选错的得0分。
1.吹肥皂泡是同学们小时候经常玩的一种游戏。
在阳光下,肥皂泡表面呈现出五颜六色的花纹,这是光的( )A.反射现象B.干涉现象c.色散现象D.折射现象2.物体A、B在同一直线上做匀变速直线运动,它们的υ图像如图所示,则( )t-A.物体A、B运动方向一定相反B.物体A、B在O-4s内的位移相同C.物体A、B在t=4s时的速度相同D.物体A的加速度比物体B的加速度大3.如图所示,人竖直站在自动扶梯的水平踏板上,随扶梯一起匀速斜向下运动。
以下分析正确的是( )A.人受到重力和支持力的作用B.人受到摩擦力的方向水平向左C.人受到重力、支持力和摩擦力的作用D.人受到与速度方向相同的合外力4.雷达是是运用电磁波来工作的,它发射的电磁波频率多在300MHz至1000MHz的范围内,已知真空中光速c=3×108m/s,下列说法正确的是( )A.电磁波可由恒定不变的电场和磁场产生B.电磁波可由周期性变化的电场或磁场产生C.雷达发射的电磁波在真空中的波长范围多在0.3m至l m之间D.雷达与目标之间的距离可由电磁波从发射到接收的时间间隔确定5⋅”汶川大地震,牵动了全国人民的心。
一架装载救灾物资的直升飞机,以lOm/s 5.“12的速度水平飞行,在距地面l80m的高度处,欲将救灾物资准确投放至地面目标,若不计空气阻力,g取10m/s2,则( )A.物资投出后经过6s到达地面目标B.物资投出后经过18s到达地面目标c .应在距地面目标水平距离60m 处投出物资 D .应在距地面目标水平距离180m 处投出物资6.如图所示,地面上竖立着一轻质弹簧,小球从其正上方某一高度处自由下落到弹簧上。
2009年福建普通高中毕业班单科质量检查理

2009年福建省普通高中毕业班单科质量检查数学试卷(理)本试卷分第I 卷(选择题)和第II 卷(非选择题),全卷满分150分,考试时间120分钟。
参考公式:样本数据n x x x ,,,21 的标准差:x x x x x x x ns n 其中,])()()[(122221-++-+-=为样本平均数; 柱体体积公式:Sh V =,其中S 为底面面积,h 为高;锥体体积公式:Sh V 31=,其中S 为底面面积,h 为高; 球的表面积、体积公式:3234,4R V R S ππ==,其中R 为球的半径。
第Ⅰ卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案填在题目后面的括号内。
1.复数)1)(3(i i z -+=在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 2.命题:“02,2≥+-∈∀x x x R ”的否定是 ( )A .02,2≥+-∈∃x x x R B .02,2≥+-∈∀x x x RC .02,2<+-∈∃x x x RD .02,2<+-∈∀x x x R3.某几何体的三视图如图所示,则该几何体的体积等于 ( )A .π328 B .π316 C .834+πD .12π4.函数||log 2x y =的图象大致是 ( )5.已知},31|{},034|{2x x y x Q x x x P -++==≤+-=则“P x ∈”是“Q x ∈”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件6.下图是计算1+3+5+…+99的值的算法程序框图,那么在空白的判断中,应该填入下面四个选项中的 ( )A .101≤iB .99≤iC .97≤iD .50≤i7.为了得到函数x x x y cos sin 3sin 2+=的图象,可以将函数x y 2sin =的图象( )A .向左平移6π个单位长度,再向下平移21个单位长度B .向右平移6π个单位长度,再向上平移21个单位长度C .向左平移12π个单位长度,再向下平移21个单位长度D .向右平移12π个单位长度,再向上平移21个单位长度8.函数1sin )(3++=x x x f 的图象 ( )A .关于点(1,0)对称B .关于点(0,1)对称C .关于点(—1,0)对称D .关于点(0,—1)对称9.已知抛物线x y 42=的焦点为F ,准线与x 轴的交点为M ,N 为抛物线上的一点,且NMF MN NF ∠=则|,|23||= ( )A .6πB .4π C .3π D .125π 10.定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系xOy 中,若21ye xe +=(其中e 1、e 2分别是斜坐标系x 轴、y 轴正方向上的单位向量,x 、R ∈y ,O 为坐标系原点),则有序数对(y x ,)称为点P 的斜坐标。
2009年福建省普通高中毕业班单科质量检查

2009年福建省普通高中毕业班单科质量检查生物试题第I卷(选择题共50分)本卷共30小题,其中第1~10题,每小题1分;第11~30题,每小题2分,共50分。
每小题的四个选项中。
只有一个是正确的。
1.有关生物体细胞组成元素的叙述,错误..的是( )A.在不同生物的体细胞内,组成它们的化学元素种类大体相同B.组成细胞的最基本元素是CC.在同一生物的不同体细胞内,各种化学元素的含量相同D.组成生物体细胞的化学元素,在无机自然界中都能找到2.下列不属于细胞凋亡现象的是( )①霜冻导致香蕉植株死亡②蝌蚪发育成为青蛙过程中尾部消失③寄主细胞因病毒的增殖释放而死亡④花瓣的自然凋落A.①②B.①③C.②④D.③④3.下列有关人体细胞的叙述,正确的一组是( )①细胞内水分减少,代谢速度减慢是衰老细胞的主要特征之一②癌变是细胞的正常基因突变成原癌基因的过程③细胞膜表面的糖蛋白参与细胞间的信息交流④癌细胞容易在体内转移,与其细胞膜上糖蛋白等物质减少有关A.②⑧④B.①②⑧C.①②④D.①③④4.DNA分子片段复制的情况如图所示,图中a、b、c、d表示脱氧核苷酸链的片段。
如果没有发生变异,下列说法错误..的是( )A.b和c的碱基序列可以互补B.a和c的碱基序列可以互补C.a中(A+T)/(G+C)的比值与b中(A+T)/(G+C)的比值相同D.a中(A+G)/(T+C)的比值与d中(A+G)/(T+C)的比值一般不相同5.现代生物进化理论认为( )A.生物多样性的形成也就是新物种不断形成的过程B.自然界中种群的基因频率一定会发生变化C.生殖隔离一定是地理隔离的结果D.种群中产生的变异是定向的6.下列有关育种的叙述,正确的是( )A.用γ射线照射作物种子,获得所需性状的频率很低B.可用杂交育种的方法获得新的基因C.三倍体植物不能由受精卵发育而来D.诱变获得的突变体多数能表现出优良性状7.下列有关生态系统结构的叙述,正确的是( )A.每种动物在生态系统中只能处在一个营养级上B.在生态系统的食物链中,营养级越高的生物体型就越大C.自养生物都是生产者,是生态系统的主要成分D.细菌和真菌都是分解者8.下列有关群落演替的叙述,不正确...的是( )A.群落的演替是指一个群落替代另一个群落的过程B.草原地区的农田在弃耕后开始出现次生演替C.群落的初生演替速度通常非常慢D.火灾过后的森林发生的演替是初生演替9.下列选项中,不属于...生态系统的信息传递在农业生产中应用的是( )A.利用人工合成的化学信息素吸引昆虫为作物传粉B.向田间喷洒杀虫剂杀灭害虫C.延长光照时间来提高家禽的产蛋量D.利用音响设备发出不同的声信号来驱赶鸟类10.右图为人体局部内环境物质交换的示意图,下列有关说法错误..的是( )HCO和A.①中液体的pH能保持稳定。
2009年福建省普通高中毕业班单科质量检查思想政治试题

2009年福建省普通高中毕业班单科质量检查思想政治试题(满分:100分考试时间:90分钟)本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I卷1至6页,第Ⅱ卷7至10页。
第I卷(选择题共48分)在下列各题的选项中,只有一项是最符合题意的。
(每小题2分,共48分)国家决定自2008年12月1日起推行新的“家电下乡”试点,公布了“家电下乡”中标企业名单。
农户购买“家电下乡”产品可享受13%的财政补贴。
回答1—3题。
1.柳某是一家中标的家电企业老总,他要从这项惠农政策中提高收益,你认为他应该采取的措施是( )A.提高社会劳动生产率B.减少个别劳动时间C.增加商品的价值量D.提高商品的使用价值2.材料中,财政补贴发挥的作用主要有( )①保证城乡居民收入同步增长②改善农民的生活质量③保障农村经济的平稳运行④促进资源的合理配置A.①③B.①④C.②③D.②④3.农民消费不足一直是制约我国内需扩大的瓶颈之一。
在未来的四年里,这项政策的实施大约可以撬动农民消费9000多亿元。
这表明( )A.消费对生产具有巨大的反作用B.拉动内需离不开国家的宏观调控C.行政手段是最直接最有效的调控办法D.提高农民消费水平主要依靠政府补贴当前正在全国推进的集体林权制度改革,是继家庭联产承包责任制之后中国农村经营制度的又一重大变革。
回答4—5题。
4.集体林权制度改革是在保持集体林地所有权不变的前提下,将林地经营权交给农民,使农民不仅具有经营的主体地位,而且享有对林木的所有权、处置权、收益权。
这样做有利于( )A.鼓励多种所有制经济共同发展B.改变我国农村的基本经济制度C.完善和发展我国农村经济制度D.发挥农村集体经济的主导作用5.杨大伯准备承包本村后山几百亩林地。
假如你是他的亲戚,你会提醒他( )①了解《农村土地承包法》、《森林法》等法律规定②利用林地人股与房地产公司合作开发商品房③聘请林业部门的技术人员指导自己的生产④与村里和有关部门签订林地承包经营合同A.①②③B.①②④C.①③④D.②③④2008年12月18日,国务院印发了《关于实施成品油价格和税费改革的通知》。
2009年福建省普通高中毕业班单科质量检查语

2009年福建省普通高中毕业班单科质量检查语文试题(本试卷分六大题,共8页。
满分150分,考试时间150分钟。
)一、古代诗文阅读(27分)(一)默写常见的名句名篇。
(6分)1.补写出下列名句名篇中的空缺部分。
(只选三小题)(6分)(1)剑阁峥嵘而崔嵬,,。
(李白《蜀遭难》)(2)别有幽愁暗恨生,。
银瓶乍破水浆迸,。
(白居易《琵琶行》)(3)故不积跬步,;,无以成江海。
(荀子《劝学》)(4)歌台暖响,;舞殿冷袖,。
(杜牧(阿房宫赋))(二)文言文阅读(15分)阅读下面的文言文,完成2—4题。
(建武二十七年)秋,七月,武陵蛮寇临沅。
遣李嵩、中山太守马成讨之,不克。
马援请行,帝悯其老,未许,援曰:“臣尚能被甲上马。
”帝令试之。
援据鞍顾眄,以示可用,帝笑曰:“矍铄哉是翁!”遂遣援率中郎将马武、耿舒等将四万余人征五溪。
援谓友人杜愔曰:“吾受厚恩,年迫日索,常恐不得死国事;今获所愿,甘心瞑目,但畏长者家儿或在左右,或与从事,殊难得调,介介独恶是耳!”马援军至临乡,击破蛮兵,斩获二千余人。
初,援尝有疾,虎贲中郎将梁松来候之,独拜床下,援不答。
松去后,诸子问曰:“梁伯孙,帝婿,贵重朝庭,公卿已下莫不惮之,大人奈何独不为礼?”援曰:“我乃松父友也,虽贵,何得失其序乎!”松由是恨援。
及援讨武陵蛮,军次下隽,有两道可入:从壶头则路近而水险,从充则涂夷而运远。
耿舒欲从充道,援以为弃日费粮,不如进壶头,扼其喉咽,充贼自破。
以事上之,帝从援策。
进营壶头,贼乘高守隘,水疾,船不得上。
会暑甚,士卒多疫死,援亦中病,乃穿岸为室以避炎气。
贼每升险鼓噪,援辄曳足以观之,左右哀其壮意,莫不为之流涕。
耿舒与兄好畤侯弇书曰:“前舒上书当先击充,粮虽难运而兵马得用,军人数万,争欲先奋。
今壶头竟不得进,大众怫郁行死,诚可痛惜!前到临乡,贼无故自致,若夜击之,即可殄灭。
伏波[注]类西域贾胡,到一处辄止,以是失利。
今果疾疫,皆如舒言。
”弇得书奏之,帝乃使梁松乘驿责问援,因代监军。
福建省龙岩市普通高中毕业班单科质量检查(文)

2009年福建省龙岩市普通高中毕业班单科质量检查数学试卷(文科)参考公式:样本数据x 1,x 2, …,x n 的标准差:其中x 为样本平均数; 柱体体积公式:V =Sh , 其中S 为底面面积,h 为高;锥体体积公式:V =31Sh ,其中S 为底面面积,h 为高; 球的表面积、体积公式:24S R =π,343V R =π,其中R 为球的半径.第I 卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案填在题目的括号内。
1.已知i 是虚数单位,实数y x ,满足(i)i 12i x y ++=+,则y x -的值为 ( )A .-1B .0C .1D .22.为了求函数22)(x x f x-=的一个零点,某同学利用计算器,得到自变量x 和函数值)(x f 的部分对应值(精确到0.01)如下表所示:则函数f (x )的一个零点所在的区间是( )A .(0.6,1.0)B .(1.4,1.8)C .(1.8,2.2)D .(2.6,3.0)3.下图所示的几何体(下底面是正六边形),其侧视图正确的是( )A .B .C .D .4.已知函数⎩⎨⎧≤>=),0(2),0(log )(2x x x x f x 若21)(=a f ,则a 的值为( )A .1-B .2C .1-或21D .1-或25.对某校400名学生的体重(单位:kg )进行统计,得到如图所示的频率分布直方图,则学生体重在60kg 以上的人数为( )A .200B .100C .40D .206.已知椭圆)0(12222>>=+b a b y a x 的焦点分别为1F 、2F ,4=b ,椭圆的离心率为53,过1F 的直线交椭圆于A 、B 两点,则2ABF ∆的周长为 ( )A .10B .12C .16D .20 7.下图的程序运行后,输出的结果为( )A .13,7B .7,4C .9,7D .9,58.已知函数1cos 22sin )(2-+=x x x f ,将函数)(x f y =的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数)(x g y =的图象,则)(x g 的解析式为 ( )A .)8sin(2π+x B .)4sin(2π+xC .)44sin(2π+xD .x 4cos 2 9.下列说法正确的是( )A .若0≠x ,则21≥+x xB .函数)62sin(2π-=x y 的图象的一条对称轴是直线12π=xC .1=a 是直线0=-ay x 与直线0=+ay x 互相垂直的充要条件D .若命题P :“存在R x ∈,012>--x x ”,则命题P 的否定:“任意R x ∈,012≤--x x10.设m 、n 是两条不同直线,α、β、γ是三个不同平面,给出下列四个命题: ①若α⊥m ,α//n ,则n m ⊥ ②若βα//,γβ//,α⊥m ,则γ⊥m③若α//m ,β//m ,则βα//④若γα⊥,γβ⊥,则βα//其中正确命题的序号是 ( )A .①和②B .②和③C .③和④D .①和④11.对任意两个正整数m 、n 定义某种运算○+:()()m n m n m n mn m n +⎧⊕=⎨⎩与奇偶性相同与奇偶性不同,则集合*P (,|8,,N a b a b a b ⊕=∈={)}中元素的个数为( )A .5B .7C .9D .1112.若变量x 、y 满足条件10,40,1,x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩则y xx y +的取值范围是( )A .[]2,+∞B .102,3⎡⎤⎢⎥⎣⎦C .3410,153⎡⎤⎢⎥⎣⎦ D .5,33⎡⎤⎢⎥⎣⎦第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.请把正确答案填在后面横线上. 13.圆03222=-+-y x x 的圆心到直线033=-+y x 的距离为 .14.设向量)3,2(=,b (1,2)=,若向量λa + b 与向量c (4,1)=-垂直,则λ= .15.已知函数()f x 为R 上的奇函数,当0x ≥时,()(1)f x x x =+.若()2f a =-,则实数a = .16.对任意正整数n ,定义n 的阶乘!n 如下:123)2)(1(!⨯⨯⨯⨯--= n n n n .例如4!=4×3×2×1. 现有四个命题: ①2!×3!= 6!;② 2009!的个位数字为0; ③(a +b )!=a !+b !(a ,b ∈ N *);④n ·n !=(n +1)!- n !(n ∈N *).其中所有正确命题的序号是 .三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知),2(ππα∈,且sincos223αα+=. (Ⅰ)求αcos 的值;(Ⅱ)若53)sin(-=+βα,)2,0(πβ∈,求βsin 的值.18.(本小题满分12分)晚会上,主持人前面放着A 、B 两个箱子,每箱均装有3个完全相同的球,各箱的三个球分别标有号码1,2,3。
福建省普通高中毕业班单科质量检查
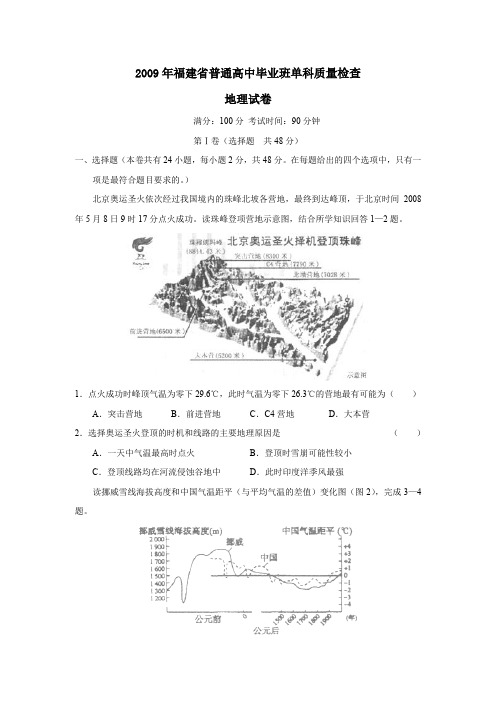
2009年福建省普通高中毕业班单科质量检查地理试卷满分:100分考试时间:90分钟第Ⅰ卷(选择题共48分)一、选择题(本卷共有24小题,每小题2分,共48分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
)北京奥运圣火依次经过我国境内的珠峰北坡各营地,最终到达峰顶,于北京时间2008年5月8日9时17分点火成功。
读珠峰登项营地示意图,结合所学知识回答1—2题。
1.点火成功时峰顶气温为零下29.6℃,此时气温为零下26.3℃的营地最有可能为()A.突击营地B.前进营地C.C4营地D.大本营2.选择奥运圣火登顶的时机和线路的主要地理原因是()A.一天中气温最高时点火B.登顶时雪崩可能性较小C.登顶线路均在河流侵蚀谷地中D.此时印度洋季风最强读挪威雪线海拔高度和中国气温距平(与平均气温的差值)变化图(图2),完成3—4题。
3.中国从15世纪到20世纪的近500年中,气候处于温暖期的是()A.1470-1520年B.1620-1720年C.1840-1890年D.1910-1950年4.图示公元后挪威雪线降低时期,我国可能出现的现象是()A.水稻种植范围向北扩展B.野象栖息地的最北界北迁C.热带范围扩大D.北方河流结冰期变长读两区域示意图,回答5—7题。
5.飞机从乙地沿着最近距离飞往甲地,其方向是()A.由西北向东南 B.由东北向西南C.由西南向东北D.由东向西6.甲、乙两地附近的气候状况是()A.甲地受信风、山脉的影响,形成热带雨林气候B.甲地深受洋流、山脉的影响,气候带呈南北狭长分布C.乙地主要受海陆热力性质的影响,夏季降水丰沛D.乙地受东北信风、山脉的影响,形成热带沙漠气候7.甲、乙两地沿海海域的洋流流向大致相同时,下列现象可信的是()A.尼罗河中上游正值汛期B.澳大利亚多数居民身穿羽绒服欢度圣诞节C.墨西哥湾沿岸飓风活动频繁D.地中海沿岸温和多雨读2001-2005年广东省三个区域国内生产总值增长率变化图,完成8—9题。
投稿:福建省龙岩市2009年普通高中毕业班单科质量检查(生物)

福建省龙岩市2009年普通高中毕业班单科质量检查生物试题2009.03(考试时间:90分钟满分:100分)第Ⅰ卷(选择题共50分)(本卷共35小题,其中第1~20题,每小题1分;第21~35题,每小题2分,共50 分。
每小题的四个选项中,只有一个最佳选项,选出并填入第5页下方的答题表中)1.下列物质合成过程中需要供给氮源的是A.肝糖元B.纤维素C.性激素D.胰岛素2.下列各项中,符合以自然选择学说为核心的现代生物进化理论观点的是A.不可遗传的变异为生物进化提供了原材料B.生物进化的实质是种群基因型频率的改变C.新物种形成的必要条件是地理隔离D.自然选择决定生物进化的方向3.下列关于DNA结构与功能的说法,不正确...的是A.DNA分子中G与C这一碱基对含量较高,其结构稳定性相对较大B.DNA分子脱氧核苷酸序列的多样性是DNA分子多样性的主要原因C.DNA转录和翻译的产物不同,说明DNA分子具有特异性D.基因突变频率低的重要原因是碱基互补配对原则保证DNA复制准确进行4.赫尔希和蔡斯分别用35S和32P标记T2噬菌体的蛋白质和DNA组分,下列被标记的部位组合正确的是A.①④B.①③C.①②D.②④5.同一个体内的各类活细胞所含酶的A.种类有差异,数量相同B.种类有差异,数量不同C.种类无差异,数量相同D.种类无差异,数量不同6.下列关于呼吸作用的叙述中,正确的是A.微生物的发酵就是无氧呼吸B.哺乳动物成熟的红细胞可运输O2,也可进行有氧呼吸C.剧烈运动时,人体内产生的CO2是有氧呼吸和无氧呼吸的共同产物D.细胞呼吸时,有机物中的能量是逐步释放的7.下列有关硝化细菌的叙述,正确的是A.能形成细胞壁和合成蛋白质B.可遗传变异的来源有突变和基因重组C.能遵循孟德尔遗传定律D.能以有丝分裂方式进行增殖8.如右图所示,不能够...表达的生理过程是A.突触小体释放神经递质B.胰岛B细胞分泌胰岛素C.肝细胞产生RNA聚合酶D.肠腺细胞分泌消化酶细胞膜①②③④O O HN H2H C9.激素从释放到消失(即灭活)所经过的代谢时间称为该激素的半衰期。
投稿:福建省龙岩市2009年普通高中毕业班单科质量检查(数学理科)
福建省龙岩市2009年普通高中毕业班单科质量检查 数学(理科)试题 2009.03(考试时间:120分钟;满分:150分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共8页.参考公式:样本数据x 1,x 2,…,x n 的标准差:其中x 为样本平均数 ;柱体体积公式:V =Sh ,其中S 为底面面积,h 为高;锥体体积公式:V =31Sh ,其中S 为底面面积,h 为高; 球的表面积、体积公式:24S R =π,343V R =π,其中R 为球的半径.第I 卷(选择题 共50分)一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一 项是符合题目要求的,请把正确答案填在题目后面的括号内.1. 已知i 是虚数单位,实数y x ,满足(i)i 12i x y ++=+,则y x -的值为 ( ) A.-1 B. 0 C. 1 D. 22. 计算dx x 2402-⎰的结果是 ( )A. π4B. π2C. πD.2π 3. 对某校400名学生的体重(单位:kg )进行统计,得到如图所示的频率分布直方图,则 学生体重在60kg 以上的人数为 ( ) A. 200 B. 100 C. 40 D. 204. 右边的程序运行后,输出的结果为 ( ) A. 13,7 B. 7,4 C. 9,7 D. 9,55. 已知椭圆)0(12222>>=+b a b y a x 的焦点分别为1F 、2F ,4=b ,离心率为53.过1F 的直线交椭圆于A 、B 两点,则2ABF ∆的周长为 ( )A. 10B. 12C. 16D. 206. 已知函数1cos 22sin )(2-+=x x x f ,将)(x f 的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再将所得图象向右平移4π个单位,得到函数)(x g y =的图象,则)(x g 的解 析式为( ) A. x sin 2 B. x cos 2C. )434sin(2π-x D. x 4cos 2. 7. 下列说法正确的是( )A. 函数)62sin(2π-=x y 的图象的一条对称轴是直线12π=xB. 若命题P :“存在R x ∈,012>--x x ”,则命题P 的否定:“任意R x ∈,012≤--x x ”C. 若0≠x ,则21≥+xxD. “1=a ”是“直线0=-ay x 与直线0=+ay x 互相垂直”的充要条件 8. 设m 、n 是两条不同直线,α、β、γ是三个不同平面,给出下列四个命题:①若α⊥m ,α//n ,则n m ⊥ ②若βα//,γβ//,α⊥m ,则γ⊥m ③若α//m ,β//m ,则βα// ④若γα⊥,γβ⊥,则βα//其中正确命题的序号是( ) A. ①和② B. ②和③C. ③和④D. ①和④9. 对任意两个正整数m 、n 定义某种运算○+:()()m n m n m n m n mn+⎧⊕=⎨⎩与奇偶性相同与奇偶性不同,则集合P (,|20,,a b a b a b ⊕=∈={)N *}中元素的个数为( ) A. 21B. 22C. 23D. 2410. 把正整数按一定的规则排成了如图所示的三角形数表.设ij a (i ,j ∈N *)是位于这个三角形数表中从上往下数第i 行、从左往右数第j 个数,如42a =8. 若ij a =2009,则i 与j 的和为( ) A. 105 B. 106 C. 107D. 108第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分,请把正确答案填在后面横线上. 11. 袋中有3个黑球,1个红球.从中任取2个,取到一个黑球得0分,取到一个红球得2分,则所得分数ξ的数学期望=ξE .12. 已知二项式62)(xa x +的展开式中的常数项为15,则实数a 为 . 13. 设向量a ,b 满足| a -b |=2,| a |=2,且a -b 与a 的夹角为3π,则| b |= .14. 已知函数)(x f 是定义在R 上的奇函数,当x ≥0时,)1(log )(2+=x x f . 若2)(-<m f ,则实数m 的取值范围是 .15. 对任意正整数n ,定义n 的双阶乘!!n 如下:当n 为偶数时,!!(2)n n n =-(4)n -642⨯⨯⨯⨯; 当n 为奇数时,135)4)(2(!!⨯⨯⨯⨯--= n n n n .现有四个命题:①(2009!!)·(2008!!)=2009!; ② 2008·2008!!=2009!!- 2008!!; ③ 2009!!的个位数字为5;④(a +b )!! = a !!+b !!(a 、b ∈ N *)其中所有正确命题的序号是 .三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分13分)已知),2(ππα∈,且262cos2sin=+αα. (Ⅰ)求αcos 的值;(Ⅱ)若53)sin(-=-βα,),2(ππβ∈,求cos β的值.17.(本小题满分13分)如图,在体积为1的三棱柱111C B A ABC -中,侧棱⊥1AA 底面ABC ,AB AC ⊥,11==AA AC ,P 为线段AB 上的动点.(Ⅰ)求证:P C CA 11⊥;(Ⅱ)当AP 为何值时,二面角111A PB C --的 大小为4π?APBA 1C 1B 1C18. (本小题满分13分)近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了,车容影响了市容市 貌. 今年该市决定引进一种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A 经过测算,如果全市的汽车总量是x ,那么一年内在该洗车行洗车的平均辆次是x 41,该洗车行每年的其他费用是20000元. 问: 洗车行A 从今年开始至少经过多少年才能收回购买净化器的成本? (注:洗车行A 买一台污水净化器就能满足洗车净水需求)19.(本小题满分13分)已知抛物线C:)0(22>=p px y 上横坐标为4的点到焦点的距离为5. (Ⅰ)求抛物线C 的方程;(Ⅱ)设),(11y x A ,),(22y x B 是抛物线C 上任意两点,且a y y =-||21(0>a ,且a 为常数). 过弦AB 的中点M 作垂直于y 轴的直线交抛物线于点D ,连结AD 、BD 得到ABD ∆,求证:ABD ∆的面积为定值;(Ⅲ)在(Ⅱ)的条件下,分别过弦AD 、BD 的中点作垂直于y轴的直线依次交抛物线于点E 、F ,连结AE 、DE 和BF 、 DF ,得到ADE ∆和BDF ∆,并按此方法继续下去. 若设ABD S a ∆=1, ,2BDF ADE S S a ∆∆+=,n a 是第n 次操作时得到的12-n 个三角形面积的和,记n n a a a S +++= 21,求证:243a S n <.O20.(本小题满分14分)设函数1()(2)ln 2f x a x ax x=-++(a ∈R ). (Ⅰ)当0=a 时,求)(x f 的极值;(Ⅱ)当0≠a 时,求)(x f 的单调区间;(Ⅲ)当2=a 时,对于任意正整数n ,在区间⎥⎦⎤⎢⎣⎡++n n 16,21上总存在m +4个数12,,a a 31234,,,,,,,m m m m m a a a a a a ++++使得<+++)()()(21m a f a f a f 1()m f a ++234()()()m m m f a f a f a +++++成立,试问:正整数m 是否有最大值?若有求其最大值;否则,说明理由.21. 本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分. (1)(本小题满分7分)选修4-2:矩阵与变换已知矩阵P=⎪⎪⎭⎫⎝⎛020a ,Q=⎪⎪⎭⎫⎝⎛010b ,若矩阵PQ 对应的变换把直线04:1=+-y x l 变为直线04:2=++y x l ,求a 、b 的值.(2)(本小题满分7分)选修4-4:坐标系与参数方程已知直线l 的极坐标方程是01sin cos =-+θρθρ.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,椭圆C的参数方程是⎩⎨⎧==θθsin ,cos 2y x (θ为参数),求直线l 和椭圆C相交所成弦的弦长. (3)(本小题满分7分)选修4-5:不等式选讲已知实数c b a 、、满足12=++c b a ,1222=++c b a ,求证:213c -≤≤.2009年龙岩市普通高中毕业班单科质量检查数学(理科)试题参考答案及评分标准说明:一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分. 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基本知识和基本运算,每小题5分,满分50分. 1. B 2. C 3. B 4.C 5.D 6.A 7. B 8. A 9. C 10. C 二、填空题:本题考查基本知识和基本运算,每小题4分,满分20分. 11. 112. 1±13. 214. (,3)-∞-15. ①③三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.16. 本题主要考查三角函数的倍角公式、两角和公式等基本知识,考查学生的运算求解能力. 满分13分.解:(Ⅰ)因为sin cos22αα+=两边同时平方得 1sin 2α=. ………………………………………(4分) 又2παπ<<,所以cos 2α=-. ………………………………………(6分) (Ⅱ)因为2παπ<<,2πβπ<<,所以2ππβ-<-<-,得22ππαβ-<-<.又3sin()5αβ-=-,知4cos()5αβ-=. …………………(9分)cos cos[()]cos cos()sin sin()βααβααβααβ=--=-+-413()525=+⨯-=………………………………………(13分)17. 本题主要考查线线位置关系,二面角的求法等基本知识,考查空间想像能力,运算求解能力和推理论证能力. 满分13分. 解:(Ⅰ)证明:连结1AC ,侧棱1AA ⊥底面ABC ,1AA AB ∴⊥,又AB AC ⊥.AB ∴⊥平面11A ACC .又1CA ⊂平面11A ACC ,1AB CA ∴⊥ . ………(3分) 11AC AA ==,∴四边形11A ACC 为正方形,11AC CA ∴⊥. 1AC AB A =, 1CA ∴⊥平面1AC B .又1C P ⊂平面1AC B ,11CA C P ∴⊥. …………(6分) (Ⅱ)1111111,,C A AA C A A B ⊥⊥1111AA A B A =.∴11C A ⊥平面11ABB A .又11111112ABC A B C V AB -=⨯⨯⨯=, 2AB ∴=. 如图,以1A 为原点,建立空间直角坐标系1A -xyz ,设AP=x ,则 1(0,0,0)A 、1(0,2,0)B 、1(0,0,1)C 、(1,,0)P x .知面11A PB 的一个法向量为11(0,0,1)A C =,……(9分) 设面11C PB 的一个法向量为(,,)n a b c =,1(1,2,0)B P x =- ,11C B (0,2,1)=- .由1110n B P n C B ⎧⋅=⎪⎨⋅=⎪⎩ 得(2)020a x b b c +-=⎧⎨-=⎩令1,2,2b c a x ===-则, (2,1,2)n x ∴=-………(11分)依题意:1111cos4||(2n AC n AC π⋅==⋅=2解得12x =,22x =2AP ∴=时,二面角111C PB A --的大小为4π. …………(13分) yCBA 1Az xC 1B 1PCB 118.本题主要考查数列与不等式等基本知识,考查运用数学知识分析问题与解决问题的能力,考查应用意识. 满分13分.解:设第一年(今年)的汽车总量为1a ,第n 年的汽车总量为n a ,则180000a = 282000a =,…80000(1)2000n a n =+-⋅.数列{}n a 构成的首项为80000,公差为2000的等差数列,12(1)8000020002n n n n S a a a n -=++⋅⋅⋅+=+⋅. ………………………(4分) 若洗车行A 从今年开始经过n 年可以收回购买净化设备的成本. 则((1)8000020002n n n -+⋅)184⋅⋅-20000n ≥900000,………………………(8分) 整理得,2694500,n n +-≥ (6)(75)0,n n -+≥因为0n >,所以 6n ≥.答:至少要经过6年才能收回成本. …………………………………………(13分)19.本题主要考查直线与抛物线的位置关系、等比数列求和等基本知识,考查运算求解能力和分析问题、解决问题的能力. 满分13分 解:(Ⅰ)依题意得:452p+=,解得2p =. 所以抛物线方程为24y x = . ………………………………………………(3分) (Ⅱ)若12x x =,即直线AB 垂直于x 轴,不防设12y y >,由12,y y a -=又由抛物线对称性可得:12ay =.又2114y x =,得 2116a x = ,故S △ABD =332a . …………………………(4分)若12x x ≠,设直线AB 方程:y kx b =+,由方程组2,4,y kx b y x =+⎧⎨=⎩消去x 得:2440ky y b -+=.(※)依题意可知:0k ≠. 由已知得124y y k +=,124b y y k=. ……………………………………(5分) 由12y y a -=,得221212()4y y y y a +-=,即221616b a k k-=,整理得221616kb a k -=. 所以2216(1)a k kb =- . …………………………………………(6分)AB 中点222(,)bk M k k-,所以点212(,)D k k, 依题意知12211122ABD bkS DM y y a k -=-=⨯⨯. 又因为方程(※)中判别式16160kb =->,得10kb ->.所以2112ABD bkS a k -=⨯⨯ ,又22116a k bk -=, 所以23121632ABDa a Sa =⨯⨯=. 又a 为常数,故ABDS的面积为定值. …………………………………(9分)(Ⅲ)依题意得:31,32a a =3323()()242,4,3232a a a a =⨯=⨯…,311()2232n n n a a --⨯=. 故332n a S =⨯111416⎡+++⎢⎣…2212n -⎤+⎥⎦311()413214n a -=⋅- 311()244n a ⎡⎤=-⎢⎥⎣⎦<324a . ………………………………(13分) 注:本题第(Ⅱ)问另解,参照本标准给分;第(Ⅲ)问若用定积分证明,同样给分. 20. 本题主要考查函数的单调性、极值、最值、不等式等基本知识,考查运用导数研究函数性质的方法,考查分类与整合及化归与转化等数学思想. 满分14分.解:(Ⅰ)依题意,知()f x 的定义域为(0,)+∞.当0a =时,1()2ln f x x x =+ ,222121()x f x x x x -'=-=. 令()0f x '=,解得12x =. 当102x <<时,()0f x '<;当12x >时,()0f x '> . 又1()22ln 22f =-,所以()f x 的极小值为22ln 2-,无极大值 . …………………………(3分)(Ⅱ)221()2a f x a x x-'=-+ 222(2)1ax a x x +--= .令()0f x '=,解得1211,2x x a =-=. …………………………(4分)若0a >,令()0f x '<,得102x <<;令()0f x '>,得12x > . 若0a <,①当2a <-时,112a -<, 令()0f x '<,得10x a <<-或12x >;令()0f x '>,得112x a -<<.②当2a =-时,22(21)()0x f x x -'=-≤. ③当20a -<<时,得112a ->,令()0f x '<,得102x <<或1x a >-;令()0f x '>,得112x a<<-.综上所述,当0a >时,()f x 的递减区间为1(0,)2,递增区间为1(,)2+∞. 当2a <-时,()f x 的递减区间为11(0,),(,)2a -+∞;递增区间为11(,)2a -. 当2a =-时,()f x 递减区间为(0,)+∞.当20a -<<时,()f x 的递减区间为11(0,),(,)2a -+∞,递增区间为11(,)2a-. …………………………(9分)(Ⅲ)当2a =时,1()4f x x x=+,由222141()4x f x x x -'=-+=,知11,62x n n ⎡⎤∈++⎢⎥⎣⎦时,()0f x '≥ . 1()()42f x f ==min ,1()(6)f x f n n =++max .依题意得:11()4(6)2mf f n n <++ 对一切正整数成立. ……………(11分)令16k n n=++ ,则8k ≥(当且仅当1n =时取等号).又()f k 在区间1[6,)n n +++∞单调递增,得min 1()328f k =,故1328m <,又m 为正整数,得32m ≤,当32m =时,存在123212a a a ==⋅⋅⋅==,12348m m m m a a a a ++++====,对所有n 满足条件.所以,正整数m 的最大值为32. …………………………………(14分)21. (1)本题主要考查矩阵乘法与变换等基本知识,考查运算求解能力,考查函数与方程思想. 满分7分.解:PQ =020120000b a b a ⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭, PQ 矩阵表示的变换T :(,)(,)P x y P x y '''满足条件 '20'0x b x y a y ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.所以'2,',x bx y ay =⎧⎨=⎩ ………………………(3分)直线40x y -+=任取点(),x y ,则点()2,bx ay 在直线40x y ++=上,故240bx ay ++=,又40x y -+=,得21,1,b a =⎧⎨=-⎩所以1,1.2a b =-⎧⎪⎨=⎪⎩ ………………………………………(7分)(2)本题主要考查直线极坐标方程和椭圆参数方程等基本知识,考查运算求解能力,考查化归与转化思想. 满分7分.解:由题意知直线和椭圆方程可化为:10x y +-=, ①2214x y +=. ② …………………………(2分)①②联立,消去y 得:2580x x -=,解得10x =,285x =. 设直线与椭圆交于A 、B 两点,则12AB x =-5=.故所求的弦长为5. …………………………(7分)(3)本题主要考查不等式证明等基本知识,考查化归与转化思想. 满分7分.解:因为22221,1a b c a b c ++=++=, 所以22221,1a b c a b c +=-+=-. 由柯西不等式:22222(12)()(2)a b a b ++≥+ , …………………………(3分)225(1)(1)c c -≥-,整理得,2320c c --≤,解得21 3c-≤≤.∴213c-≤≤.…………………………(7分)。
投稿:福建省龙岩市2009年普通高中毕业班单科质量检查(政治)

福建省龙岩市2009年普通高中毕业班单科质量检查政治试题2009.03(考试时间:90分钟满分:100分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至6页,第Ⅱ卷7至10页。
第Ⅰ卷选择题(共24小题,48分。
)在下列各题的选项中,只有一项是最符合题意的。
(每小题2分,共48分)。
2008年12月以来,我国液晶电视价格大幅度下跌,业内人士认为,液晶电视价格大幅度下跌是市场发展的必然。
而到了2009年元旦期间,液晶电视销量大增。
回答1—2题:1.“液晶电视价格大幅度下跌是市场发展的必然”说明①市场竞争激烈,供求关系发生变化②商家为了抢占市场,让利给消费者③个别劳动生产率的提高使单位商品的价值量降低④社会劳动生产率提高,生产商品的社会必要劳动时间缩短A.①③B.①④C.②③D.②④2.2009年元旦期间,液晶电视销量大增,这说明A.供求与价格之间存在相互影响、制约的关系B.生活必需品的需求受价格变动的影响比较大C.高档耐用消费品的需求受价格变动的影响小D.价格变动促使商品生产者扩大液晶电视生产3.2009年国家公务员考试竞争将极为惨烈。
2009年国家公务员考试共计报名确认人数为775418人,比2008年增加了133600人,增长了21%。
其中,国家环保部竞争最激烈的职位招录比例达到834∶1。
面对严峻的就业形势,劳动者应该①树立竞争就业观②改善劳动就业环境③树立职业平等观④树立多种方式就业观A.①②③B.①②④C.②③④D.①③④4.2008年下半年以来,由美国次贷危机引发的金融危机愈演愈烈,国际经济环境急转直下,我国经济下行压力加大。
为应对挑战,保持增长,我国国务院决定实施积极的财政政策和适度宽松的货币政策,出台扩大内需的十大措施。
上述材料表明政府应用的宏观调控手段是:A.行政手段B.经济手段C.财政手段D.货币手段5.2008年中国对外贸易、吸收外资、对外投资总体情况表上表主要说明:A.更好地发挥利用外资作用B.积极参与区域经济交流与合作C.我国全面提高对外开放水平D.我国坚持“引进来”和“走出去”相结合6.2009年中央一号文件指出:“扩大内需、实施积极财政政策,要把‘三农’作为投入重点。
福建省龙岩市普通高中毕业班单科质量检查数学(文科)试题
2009年福建省龙岩市普通高中毕业班单科质量检查数学(文科)试题(考试时间:120分钟;满分:150分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共8页.参考公式:样本数据x 1,x 2, …,x n 的标准差:其中x 为样本平均数 ;柱体体积公式:V =Sh ,其中S 为底面面积,h 为高;锥体体积公式:V =31Sh ,其中S 为底面面积,h 为高; 球的表面积、体积公式:24S R =π,343V R =π,其中R 为球的半径.第I 卷(选择题 共60分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一 项是符合题目要求的,请把正确答案填在题目的括号内.1.已知i 是虚数单位,实数y x ,满足(i)i 12i x y ++=+,则y x -的值为 ( )A .-1B . 0C .1D .22.为了求函数22)(x x f x -=的一个零点,某同学利用计算器,得到自变量x 和函数值)(x f 的部分对应值(精确到0.01)如下表所示:) A .(0.6,1.0) B .(1.4,1.8) C .(1.8,2.2) D .(2.6,3.0)3.右图所示的几何体(下底面是正六边形),其侧视图正确的是 ( )A BC D4.已知函数⎩⎨⎧≤>=),0(2),0(log )(2x x x x f x 若21)(=a f ,则a 的值为 ( )A .1-B .2C .1-或21D .1-或2正视 侧视俯视5.对某校400名学生的体重(单位:kg ) 进行统计,得到如图所示的频率分布直 方图,则学生体重在60kg 以上的人数 为 ( ) A .200 B .100 C .40 D .206.已知椭圆)0(12222>>=+b a by a x 的焦点分别为1F 、2F ,4=b ,椭圆的离心率为53,过1F 的直线交椭圆于A 、B 两点,则2ABF ∆的周长为 ( )A .10B .12C .16D .207.右图的程序运行后,输出的结果为( )A .13,7B .7,4C .9,7D .9,58.已知函数1cos 22sin )(2-+=x x x f ,将函数)(x f y =的图象上各点的横坐标伸长到原 来的2倍,纵坐标不变,得到函数)(x g y =的图象,则)(x g 的解析式为 ( ) A .)8sin(2π+x B .)4sin(2π+xC .)44sin(2π+xD .x 4cos 29.下列说法正确的是 ( ) A .若0≠x ,则21≥+xxB .函数)62sin(2π-=x y 的图象的一条对称轴是直线12π=xC .1=a 是直线0=-ay x 与直线0=+ay x 互相垂直的充要条件D .若命题P :“存在R x ∈,012>--x x ”,则命题P 的否定:“任意R x ∈,012≤--x x10.设m 、n 是两条不同直线,α、β、γ是三个不同平面,给出下列四个命题:①若α⊥m ,α//n ,则n m ⊥ ②若βα//,γβ//,α⊥m ,则γ⊥m ③若α//m ,β//m ,则βα//④若γα⊥,γβ⊥,则βα//其中正确命题的序号是 ( ) A .①和②B .②和③C .③和④D .①和④kg )11.对任意两个正整数m 、n 定义某种运算○+:()()m n m n m n mnm n +⎧⊕=⎨⎩与奇偶性相同与奇偶性不同,则集合*P (,|8,,N a b a b a b ⊕=∈={)}中元素的个数为 ( ) A .5B .7C .9D .1112.若变量x 、y 满足条件10,40,1,x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩则y xx y +的取值范围是 ( )A .[]2,+∞B .102,3⎡⎤⎢⎥⎣⎦C .3410,153⎡⎤⎢⎥⎣⎦D .5,33⎡⎤⎢⎥⎣⎦第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.请把正确答案填在后面横线上. 13.圆03222=-+-y x x 的圆心到直线033=-+y x 的距离为 . 14.设向量a (2,3)=,b (1,2)=,若向量λa+ b 与向量c (4,1)=-垂直,则λ= . 15.已知函数()f x 为R 上的奇函数,当0x ≥时,()(1)f x x x =+.若()2f a =-,则实数a = .16.对任意正整数n ,定义n 的阶乘!n 如下:123)2)(1(!⨯⨯⨯⨯--= n n n n .例如4!=4×3×2×1. 现有四个命题: ①2!×3!= 6!;② 2009!的个位数字为0;③(a +b )!=a !+b !(a ,b ∈ N *); ④n ·n !=(n +1)!- n !(n ∈ N *).其中所有正确命题的序号是 .三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知),2(ππα∈,且sincos22αα+=. (Ⅰ)求αcos 的值;(Ⅱ)若53)sin(-=+βα,)2,0(πβ∈,求βsin 的值.晚会上,主持人前面放着A 、B 两个箱子,每箱均装有3个完全相同的球,各箱的三个球 分别标有号码1,2,3.现主持人从A 、B 两箱中各摸出一球.(Ⅰ)若用),(y x 分别表示从A 、B 两箱中摸出的球的号码,请写出数对),(y x 的所有情形,并回答一共有多少种;(Ⅱ)求所摸出的两球号码之和为5的概率;(Ⅲ)请你猜这两球的号码之和,猜中有奖.猜什么数获奖的可能性大?说明理由.19.(本小题满分12分)已知n S 为数列}{n a 的前n 项的和,且n n S n -=2. (Ⅰ)求数列}{n a 的通项公式; (Ⅱ)若*1(2N )n nb n n na =≥∈且,记n n b b b T +++= 32,求证:21<n T .如图,在体积为1的三棱柱111C B A ABC -中,侧棱⊥1AA 底面ABC ,AB AC ⊥,11==AA AC ,P 为线段AB 上的动点. (Ⅰ)求证:P C CA 11⊥;(Ⅱ)线段AB 上是否存在一点P ,使四面体11C AB P -的体积为61?若存在,请确定点P 的位置;若不存在,请说明理由.21.(本小题满分12分)已知抛物线C:)0(22>=p px y 上横坐标为4的点到焦点的距离为5. (Ⅰ)求抛物线C 的方程;(Ⅱ)设直线b kx y +=与抛物线C 交于两点),(11y x A ,),(22y x B ,且a y y =-||21(0>a ,且a 为常数).过弦AB 的中点M 作平行于x 轴的直线交抛物线于点D ,连结AD 、BD 得到ABD ∆. (ⅰ)求证:)1(1622kb k a -=; (ⅱ)求证:ABD ∆的面积为定值.CB 1设函数1()(2)ln 2(R)f x a x ax a x=-++∈. (Ⅰ)当0=a 时,求)(x f 的极值; (Ⅱ)当0<a 时,求)(x f 的单调区间;(Ⅲ)若对任意)2,3(--∈a 及]3,1[,21∈x x ,恒有|)()(|3ln 2)3ln (21x f x f a m ->-+成立,求m 的取值范围.2009年龙岩市普通高中毕业班单科质量检查数学(文科)试题参考答案及评分标准说明: 一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则.二、对计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有较严重的错误,就不再给分. 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.四、只给整数分数,选择题和填空题不给中间分.一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分.1. B2. C3. A4. D5. B6. D7. C8. B9. D 10. A 11.C 12. C 二、填空题:本题考查基础知识和基本运算,每小题4分,满16分. 13. 114. 25-15. 1-16. ②④三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤. 17. 本题主要考查三角函数的基本公式,考查运算能力. 满分12分.解:(Ⅰ)因为sincos22αα+=,所以412sin cos 223αα+=,1sin 3α=. ………………………………(2分)因为(,)2παπ∈,所以cos α==. …………………………(6分)(Ⅱ)因为(,),(0,)22ππαπβ∈∈,所以3(,)22ππαβ+∈又3sin()5αβ+=-,得4cos()5αβ+=-. ……………………………(9分) []sin sin ()βαβα=+-sin()cos cos()sin αβααβα=+⋅-+⋅341()()()5353=-⋅---⋅415=. ……………………………………………………(12分) 18.本题主要考查概率的基本知识,考查应用意识. 满分12分.解:(Ⅰ)数对(,)x y 的所有情形为:(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)共9种.答:一共有9种. ……………………………………………………(4分) (Ⅱ)记“所摸出的两球号码之和为5”为事件A ,则事件A 包括的基本结果有:(2,3),(3,2)共2个,所以P (A )=29. 答:所摸出的两球号码之和为5的概率为29. ………………………(8分)(Ⅲ)记“所摸出的两球号码之和为i ”为事件i A (i =2,3,4,5,6)由(Ⅰ)中可知事件A 2的基本结果为1种,事件A 3的基本结果为2种,事件A 4的基本结果为3种,事件A 5的基本结果为2种,事件A 6的基本结果为1种,所以21()9P A =,32()9P A =,43()9P A =,52()9P A =,61()9P A =. 故所摸出的两球号码之和为4的概率最大.答:猜4获奖的可能性大. ……………………………………………(12分)19. 本题主要考查等差数列,不等式等基本知识,考查运算求解能力及推理论证能力. 满分12分.解:(1)当1n =时,110a S ==; …………………………………………………(1分)当2n ≥时,1n n n a S S -=-22(1)(1)n n n n =---+-22n =-. ………(4分)因为10a =满足22n a n =-,所以22n a n =- . …………………………(6分) (2)因为1(2)n nb n na =≥, 所以12(1)n b n n =-111()21n n=-- . ………………………………………(8分)23n T b b =++…n b +1111(12223=-+-+…11)1n n +--111(1)22n =-<, 即12n T <. ………………………………………………………………(12分)20. 本题主要考查直线与平面的位置关系,考查空间想像能力,推理论证能力和运算求解能力.满分12分. 解:(Ⅰ)证明:连结1AC ,侧棱1AA ⊥底面ABC ,1AA AB ∴⊥又AB AC ⊥.AB ∴⊥平面11A ACC .又1CA ⊂平面11A ACC ,1AB CA ∴⊥ . ………(3分) 11AC AA ==,∴四边形11A ACC 为正方形, 11AC CA ∴⊥.1AC AB A ⋂=, 1CA ∴⊥平面1AC B . ………………………………(5分)又1C P ⊂平面1AC B ,11CA C P ∴⊥. ………………………………………(6分) (Ⅱ)设在线段AB 上存在一点P ,使1116P AB C V -=. 11111112ABC A B C V AB -=⨯⨯⨯=, 2AB ∴= . …………………………(7分)又1,AC AB AA AC ⊥⊥且11C A ⊥平面11,ABB A BB AB ⊥,由111116P AB C C PAB V V --==, 知11111111111332326PAB S C A PA BB PA ⋅=⨯⋅=⨯⨯⨯=, 解得1PA =,∴存在AB 的中点P ,使1116P AB C V -= . …………………(12分)21.本题主要考查直线与抛物线的位置关系等基本知识,考查运算求解能力和分析问题、解决问题的能力. 满分12分 解:(Ⅰ)依题意得:452p+=,解得2p =. 所以抛物线方程为24y x = . ………………………………………………(4分)(Ⅱ)由方程组2,4,y kx b y x =+⎧⎨=⎩消去x 得:2440ky y b -+=.(※)依题意可知:0k ≠.CB 1由已知得124y y k +=,124b y y k=. ……………………………………(6分) 由12y y a -=,得221212()4y y y y a +-=, 即221616ba k k-=,整理得221616kb a k -=. 所以2216(1)a k kb =- . ………………(8分) (Ⅲ)由(Ⅱ)知AB 中点222(,)bk M k k-, 所以点212(,)D k k,依题意知12211122ABD bkS DM y y a k-=-=⨯⨯. 又因为方程(※)中判别式16160kb =->,得10kb ->. ………(10分)所以2112ABD bk S a k -=⨯⨯ ,由(Ⅱ)可知22116a k bk -=,所以23121632ABD a a S a =⨯⨯=. …………………………………………(11分) 又a 为常数,故ABD S的面积为定值. …………………………………(12分)22.本题主要考查函数的单调性、极值、最值、不等式等基本知识,考查运用导数研究函数性质的方法,考查分类与整合及化归与转化等数学思想. 满分14分. 解:(Ⅰ)依题意,知()f x 的定义域为(0,)+∞.当0a =时,1()2ln f x x x =+ ,222121()x f x x x x-'=-=. 令()0f x '=,解得12x =. 当102x <<时,()0f x '<;当12x >时,()0f x '> . 又1()22ln 22f =-,所以()f x 的极小值为22ln 2-,无极大值 . …………………………(4分)(Ⅱ)221()2a f x a x x-'=-+ 222(2)1ax a x x +--=当2a <-时,112a -<, 令()0f x '<,得1x a <-或12x >,令()0f x '>,得112x a -<<; 当20a -<<时,得112a ->,令()0f x '<,得102x <<或1x a >-,令()0f x '>,得112x a<<-;当2a =-时,22(21)()0x f x x -'=-≤. 综上所述,当2a <-时,()f x 的递减区间为11(0,),(,)2a -+∞;递增区间为11(,)2a -. 当2a =-时,()f x 在(0,)+∞单调递减. 当20a -<<时,()f x 的递减区间为11(0,),(,)2a -+∞;递增区间为11(,)2a-.…………………………………(9分)(Ⅲ)由(Ⅱ)可知,当(3,2)a ∈--时,()f x 在[]1,3单调递减.当1x =时,()f x 取最大值;当3x =时,()f x 取最小值.所以121()()(1)(3)(12)(2)ln 363f x f x f f a a a ⎡⎤-≤-=+--++⎢⎥⎣⎦24(2)ln 33a a =-+-.………………(11分) 因为12(ln3)2ln3()()m a f x f x +->-恒成立, 所以2(ln 3)2ln 34(2)ln 33m a a a +->-+-, 整理得243ma a >-. 又0a < 所以243m a<-, 又因为32a -<<- ,得122339a -<<-, 所以132384339a -<-<- 所以133m ≤- . ……………………………………………………………(14分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
福建省龙岩市2009年普通高中毕业班单科质量检查 数学(理科)试题 2009.03(考试时间:120分钟;满分:150分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题),共8页.第I 卷(选择题 共50分)一、选择题:本题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一 项是符合题目要求的,请把正确答案填在题目后面的括号内.1. 已知i 是虚数单位,实数y x ,满足(i)i 12i x y ++=+,则y x -的值为 ( ) A.-1 B. 0 C. 1 D. 22. 计算dx x 2402-⎰的结果是 ( )A. π4B. π2C. πD.2π 3. 对某校400名学生的体重(单位:kg )进行统计,得到如图所示的频率分布直方图,则 学生体重在60kg 以上的人数为 ( ) A. 200 B. 100 C. 40 D. 204. 右边的程序运行后,输出的结果为 ( ) A. 13,7 B. 7,4 C. 9,7 D. 9,55. 已知椭圆)0(12222>>=+b a by a x 的焦点分别为1F 、2F ,4=b ,离心率为53.过1F 的直线交椭圆于A 、B 两点,则2ABF ∆的周长为 ( ) A. 10B. 12C. 16D. 206. 已知函数1cos 22sin )(2-+=x x x f ,将)(x f 的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再将所得图象向右平移4π个单位,得到函数)(x g y =的图象,则)(x g 的解 析式为( ) A. x sin 2 B. x cos 2C. )434sin(2π-x D. x 4cos 2. 7. 下列说法正确的是( )A. 函数)62sin(2π-=x y 的图象的一条对称轴是直线12π=xB. 若命题P :“存在R x ∈,012>--x x ”,则命题P 的否定:“任意R x ∈,012≤--x x ”C. 若0≠x ,则21≥+xxD. “1=a ”是“直线0=-ay x 与直线0=+ay x 互相垂直”的充要条件 8. 设m 、n 是两条不同直线,α、β、γ是三个不同平面,给出下列四个命题:①若α⊥m ,α//n ,则n m ⊥ ②若βα//,γβ//,α⊥m ,则γ⊥m ③若α//m ,β//m ,则βα// ④若γα⊥,γβ⊥,则βα//其中正确命题的序号是( ) A. ①和② B. ②和③C. ③和④D. ①和④9. 对任意两个正整数m 、n 定义某种运算○+:()()m n m n m nm n mn+⎧⊕=⎨⎩与奇偶性相同与奇偶性不同,则集合P (,|20,,a b a b a b ⊕=∈={)N *}中元素的个数为( ) A. 21B. 22C. 23D. 2410. 把正整数按一定的规则排成了如图所示的三角形数表.设ij a (i ,j ∈N *)是位于这个三角形数表中从上往下数第i 行、从左往右数第j 个数,如42a =8. 若ij a =2009,则i 与j 的和为( )A. 105B. 106C. 107D. 108第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题4分,共20分,请把正确答案填在后面横线上. 11. 袋中有3个黑球,1个红球.从中任取2个,取到一个黑球得0分,取到一个红球得2分,则所得分数ξ的数学期望=ξE .12. 已知二项式62)(xa x +的展开式中的常数项为15,则实数a 为 . 13. 设向量a ,b 满足| a -b |=2,| a |=2,且a -b 与a 的夹角为3π,则| b |= .14. 已知函数)(x f 是定义在R 上的奇函数,当x ≥0时,)1(log )(2+=x x f . 若2)(-<m f , 则实数m 的取值范围是 .15. 对任意正整数n ,定义n 的双阶乘!!n 如下:当n 为偶数时,!!(2)n n n =-(4)n -642⨯⨯⨯⨯ ; 当n 为奇数时,135)4)(2(!!⨯⨯⨯⨯--= n n n n . 现有四个命题:①(2009!!)·(2008!!)=2009!; ② 2008·2008!!=2009!!- 2008!!; ③ 2009!!的个位数字为5;④(a +b )!! = a !!+b !!(a 、b ∈ N *)其中所有正确命题的序号是 .三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分13分)已知),2(ππα∈,且262cos 2sin=+αα. (Ⅰ)求αcos 的值;(Ⅱ)若53)sin(-=-βα,),2(ππβ∈,求cos β的值.17.(本小题满分13分)如图,在体积为1的三棱柱111C B A ABC -中,侧棱⊥1AA 底面ABC ,AB AC ⊥,11==AA AC ,P 为线段AB 上的动点.(Ⅰ)求证:P C CA 11⊥;(Ⅱ)当AP 为何值时,二面角111A PB C --的 大小为4π?18. (本小题满分13分)近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了,车容影响了市容市 貌. 今年该市决定引进一种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A 经过测算,如果全市的汽车总量是x ,那么一年内在该洗车行洗车的平均辆次是x 41,该洗车行每年的其他费用是20000元. 问: 洗车行A 从今年开始至少经过多少年才能收回购买净化器的成本? (注:洗车行A 买一台污水净化器就能满足洗车净水需求)19.(本小题满分13分)已知抛物线C:)0(22>=p px y 上横坐标为4的点到焦点的距离为5. (Ⅰ)求抛物线C 的方程;(Ⅱ)设),(11y x A ,),(22y x B 是抛物线C 上任意两点,且a y y =-||21(0>a ,且a 为常数). 过弦AB 的中点M 作垂直于y 轴的直线交抛物线于点D ,连结AD 、BD 得到ABD ∆,求证:ABD ∆的面积为定值;(Ⅲ)在(Ⅱ)的条件下,分别过弦AD 、BD 的中点作垂直于y轴的直线依次交抛物线于点E 、F ,连结AE 、DE 和BF 、 DF ,得到ADE ∆和BDF ∆,并按此方法继续下去. 若设ABD S a ∆=1, ,2BDF ADE S S a ∆∆+=,n a 是第n 次操作时得到的12-n 个三角形面积的和,记n n a a a S +++= 21,求证:243a S n <.20.(本小题满分14分)设函数1()(2)ln 2f x a x ax x=-++(a ∈R ). (Ⅰ)当0=a 时,求)(x f 的极值; (Ⅱ)当0≠a 时,求)(x f 的单调区间;(Ⅲ)当2=a 时,对于任意正整数n ,在区间⎥⎦⎤⎢⎣⎡++n n 16,21上总存在m +4个数12,,a a 31234,,,,,,,m m m m m a a a a a a ++++ 使得<+++)()()(21m a f a f a f 1()m f a ++234()()()m m m f a f a f a +++++成立,试问:正整数m 是否有最大值?若有求其最大值;否则,说明理由.OAPBA 1C 1B 1C21. 本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分. (1)(本小题满分7分)选修4-2:矩阵与变换已知矩阵P=⎪⎪⎭⎫⎝⎛020a ,Q=⎪⎪⎭⎫⎝⎛010b ,若矩阵PQ 对应的变换把直线04:1=+-y x l 变为直线04:2=++y x l ,求a 、b 的值.(2)(本小题满分7分)选修4-4:坐标系与参数方程已知直线l 的极坐标方程是01sin cos =-+θρθρ.以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,椭圆C的参数方程是⎩⎨⎧==θθsin ,cos 2y x (θ为参数),求直线l 和椭圆C相交所成弦的弦长. (3)(本小题满分7分)选修4-5:不等式选讲已知实数c b a 、、满足12=++c b a ,1222=++c b a ,求证:213c -≤≤.2009年龙岩市普通高中毕业班单科质量检查数学(理科)试题参考答案及评分标准一、选择题:本题考查基本知识和基本运算,每小题5分,满分50分. 1. B 2. C 3. B 4.C 5.D 6.A 7. B 8. A 9. C 10. C 二、填空题:本题考查基本知识和基本运算,每小题4分,满分20分. 11. 112. 1±13. 214. (,3)-∞-15. ①③三、解答题:本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤.16. 本题主要考查三角函数的倍角公式、两角和公式等基本知识,考查学生的运算求解能力. 满分13分. 解:(Ⅰ)因为sin cos222αα+=两边同时平方得1sin 2α=. ………………………………………(4分) 又2παπ<<,所以cos 2α=-. ………………………………………(6分) (Ⅱ)因为2παπ<<,2πβπ<<,所以2ππβ-<-<-,得22ππαβ-<-<.又3sin()5αβ-=-,知4cos()5αβ-=. …………………(9分)cos cos[()]cos cos()sin sin()βααβααβααβ=--=-+-413()525=+⨯-=. ………………………………………(13分)17. 本题主要考查线线位置关系,二面角的求法等基本知识,考查空间想像能力,运算求解能力和推理论证能力. 满分13分. 解:(Ⅰ)证明:连结1AC ,侧棱1AA ⊥底面ABC , 1AA AB ∴⊥,又AB AC ⊥ .AB ∴⊥平面11A ACC .又1CA ⊂ 平面11A ACC ,1AB CA ∴⊥ . ………(3分) 11AC AA == ,∴四边形11A ACC 为正方形,CB 111AC CA ∴⊥.1AC AB A = , 1CA ∴⊥平面1AC B .又1C P ⊂平面1AC B ,11CA C P ∴⊥. …………(6分) (Ⅱ)1111111,,C A AA C A A B ⊥⊥ 1111AA A B A = .∴11C A ⊥平面11ABB A .又11111112ABC A B C V AB -=⨯⨯⨯= , 2AB ∴=.如图,以1A 为原点,建立空间直角坐标系1A -xyz ,设AP=x ,则 1(0,0,0)A 、1(0,2,0)B 、1(0,0,1)C 、(1,,0)P x .知面11A PB 的一个法向量为11(0,0,1)A C = ,……(9分) 设面11C PB 的一个法向量为(,,)n a b c =,1(1,2,0)B P x =- ,11C B(0,2,1)=- .由1110n B P n C B ⎧⋅=⎪⎨⋅=⎪⎩ 得(2)020a x b b c +-=⎧⎨-=⎩令1,2,2b c a x ===-则, (2,1,2)n x ∴=-………(11分)依题意:1111cos 4||n AC n AC π⋅==⋅解得12x =,22x =2AP ∴=111C PB A --的大小为4π. …………(13分) 18.本题主要考查数列与不等式等基本知识,考查运用数学知识分析问题与解决问题的能力,考查应用意识. 满分13分.解:设第一年(今年)的汽车总量为1a ,第n 年的汽车总量为n a ,则180000a =282000a =,…80000(1)2000n a n =+-⋅.数列{}n a 构成的首项为80000,公差为2000的等差数列,12(1)8000020002n n n n S a a a n -=++⋅⋅⋅+=+⋅. ………………………(4分) 若洗车行A 从今年开始经过n 年可以收回购买净化设备的成本. 则((1)8000020002n n n -+⋅)184⋅⋅-20000n ≥900000,………………………(8分) 整理得,2694500,n n +-≥(6)(75)0,n n -+≥因为0n >,所以 6n ≥.答:至少要经过6年才能收回成本. …………………………………………(13分)19.本题主要考查直线与抛物线的位置关系、等比数列求和等基本知识,考查运算求解能力和分析问题、解决问题的能力. 满分13分 解:(Ⅰ)依题意得:452p+=,解得2p =. 所以抛物线方程为24y x = . ………………………………………………(3分) (Ⅱ)若12x x =,即直线AB 垂直于x 轴,不防设12y y >,由12,y y a -=又由抛物线对称性可得:12ay =.又2114y x =,得 2116a x = ,故S △ABD =332a . …………………………(4分)若12x x ≠,设直线AB 方程:y kx b =+,由方程组2,4,y kx b y x =+⎧⎨=⎩消去x 得:2440ky y b -+=.(※)依题意可知:0k ≠. 由已知得124y y k +=,124b y y k=. ……………………………………(5分) 由12y y a -=,得221212()4y y y y a +-=, 即221616b a k k-=,整理得221616kb a k -=. 所以2216(1)a k kb =- . …………………………………………(6分)yCB A 1 A zx C 1B 1PAB 中点222(,)bk M k k -, 所以点212(,)D k k,依题意知12211122ABD bkS DM y y a k -=-=⨯⨯ .又因为方程(※)中判别式16160kb =-> ,得10kb ->.所以2112ABD bk S a k -=⨯⨯ ,又22116a k bk -=,所以23121632ABDa a S a =⨯⨯= . 又a 为常数,故ABD S 的面积为定值. …………………………………(9分)(Ⅲ)依题意得:31,32aa =3323()()242,4,3232a a a a =⨯=⨯…,311()2232n n n a a --⨯=. 故332n a S =⨯111416⎡+++⎢⎣…2212n -⎤+⎥⎦311()413214n a -=⋅- 311()244n a ⎡⎤=-⎢⎥⎣⎦<324a . ………………………………(13分) 注:本题第(Ⅱ)问另解,参照本标准给分;第(Ⅲ)问若用定积分证明,同样给分. 20. 本题主要考查函数的单调性、极值、最值、不等式等基本知识,考查运用导数研究函数性质的方法,考查分类与整合及化归与转化等数学思想. 满分14分.解:(Ⅰ)依题意,知()f x 的定义域为(0,)+∞.当0a =时,1()2ln f x x x =+ ,222121()x f x x x x -'=-=. 令()0f x '=,解得12x =. 当102x <<时,()0f x '<;当12x >时,()0f x '> . 又1()22ln 22f =-,所以()f x 的极小值为22ln 2-,无极大值 . …………………………(3分)(Ⅱ)221()2a f x a x x-'=-+ 222(2)1ax a x x +--= .令()0f x '=,解得1211,2x x a =-=. …………………………(4分)若0a >,令()0f x '<,得102x <<;令()0f x '>,得12x > .若0a <,①当2a <-时,112a -<,令()0f x '<,得10x a <<-或12x >;令()0f x '>,得112x a -<<.②当2a =-时,22(21)()0x f x x -'=-≤. ③当20a -<<时,得112a ->,令()0f x '<,得102x <<或1x a >-;令()0f x '>,得112x a<<-.综上所述,当0a >时,()f x 的递减区间为1(0,)2,递增区间为1(,)2+∞.当2a <-时,()f x 的递减区间为11(0,),(,)2a -+∞;递增区间为11(,)2a -.当2a =-时,()f x 递减区间为(0,)+∞.当20a -<<时,()f x 的递减区间为11(0,),(,)2a -+∞,递增区间为11(,)2a-. …………………………(9分)(Ⅲ)当2a =时,1()4f x x x=+, 由222141()4x f x x x -'=-+=,知11,62x n n ⎡⎤∈++⎢⎥⎣⎦时,()0f x '≥ . 1()()42f x f ==min ,1()(6)f x f n n =++max .依题意得:11()4(6)2mf f n n <++ 对一切正整数成立. ……………(11分)令16k n n=++ ,则8k ≥(当且仅当1n =时取等号).又()f k 在区间1[6,)n n+++∞单调递增,得min 1()328f k =,故1328m <,又m 为正整数,得32m ≤,当32m =时,存在123212a a a ==⋅⋅⋅==,12348m m m m a a a a ++++====,对所有n 满足条件.所以,正整数m 的最大值为32. …………………………………(14分)21. (1)本题主要考查矩阵乘法与变换等基本知识,考查运算求解能力,考查函数与方程思 想. 满分7分. 解:PQ =020120000b a b a ⎛⎫⎛⎫⎛⎫= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,PQ 矩阵表示的变换T :(,)(,)P x y P x y ''' 满足条件'20'0x b x y a y ⎛⎫⎛⎫⎛⎫= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭.所以'2,',x bx y ay =⎧⎨=⎩………………………(3分)直线40x y -+=任取点(),x y ,则点()2,bx ay 在直线40x y ++=上,故240bx ay ++=,又40x y -+=,得21,1,b a =⎧⎨=-⎩所以1,1.2a b =-⎧⎪⎨=⎪⎩ ………………………………………(7分)(2)本题主要考查直线极坐标方程和椭圆参数方程等基本知识,考查运算求解能力,考查化归与转化思想. 满分7分.解:由题意知直线和椭圆方程可化为:10x y +-=,①2214x y +=. ② …………………………(2分)①②联立,消去y 得:2580x x -=,解得10x =,285x =. 设直线与椭圆交于A 、B 两点,则12AB x =-5=故所求的弦长为5. …………………………(7分)(3)本题主要考查不等式证明等基本知识,考查化归与转化思想. 满分7分.解:因为22221,1a b c a b c ++=++=, 所以22221,1a b c a b c +=-+=-. 由柯西不等式:22222(12)()(2)a b a b ++≥+ , …………………………(3分)225(1)(1)c c -≥-,整理得,2320c c --≤, 解得213c -≤≤. ∴213c -≤≤. …………………………(7分)。
