Mathematica软件在高等数学教学中的应用
Mathematica软件在高等数学教学中的应用

Mathematica软件在高等数学教学中的应用【摘要】Mathematica软件是一套专门进行数学计算的软件,具有形象性、直观性、互动性和时效性。
在高等数中引入Mathematica软件进行辅助教学,有利于激发学生的学习兴趣,培养学生基本计算及用数学方法解决实际应用问题的能力。
【关键词】高等数学;Mathematica软件;应用0.引言数学软件Mathematica是处理数学问题的一种应用软件,它的功能非常强大,不仅可以用于符号运算和数值计算,还可以用来方便地绘制一元和二元函数的图形。
运用数学软件作为平台,进行数学实验,把数学软件作为认知工具、计算工具和应用工具,不仅丰富了教学手段,也给传统的数学教学注入了活力。
教师利用数学软件将传统教学中的粉笔加黑板、教师一言堂这种枯燥的教学过程制作成课件,通过计算机呈现给学生,使学生多种感观并用,增强学生的好奇心,吸引学生的注意力,提高对信息的吸收率。
同时,在高等数学教学中适当使用数学软件,能对抽象的数学概念和烦琐的数学运算加以几何解释和简化,通过图形的动态变化使“死”的知识活起来,真正将形与数有机地结合起来,把运动和变化呈现在学生面前,加深对知识的理解,充分调动学生学习的积极性和主动性。
1.Mathematica软件在数学教学中的运用高等数学内容十分丰富,包括微积分、空间解析几何和微分方程等。
高等数学涉及大量的数学计算,Mathematica强大的计算功能,能很好地解决高等数学中的计算问题。
利用Mathematica软件的计算功能,可以提高学生的计算能力。
1.1用Mathematica求极限计算极限命令格式:Limt[函数表达式,自变量→定值]如计算,只要利用Mathematica“基本输入工具栏”,在其“工作窗口”中输入:Limit[Log[1+x]/2x,x->0],运行软件,即可得到计算结果。
1.2用Mathematica求导数计算导数的命令格式:D[f[x],x] (求f(x)一阶导数)D[f[x],{x,n}] (求f(x)n阶导数)D[f[x,y],x,y] (求f(x,y)的二阶混合偏导数f’’xy(x,y))如已知y=xex,求y’。
Mathematica软件在高等数学教学中的应用

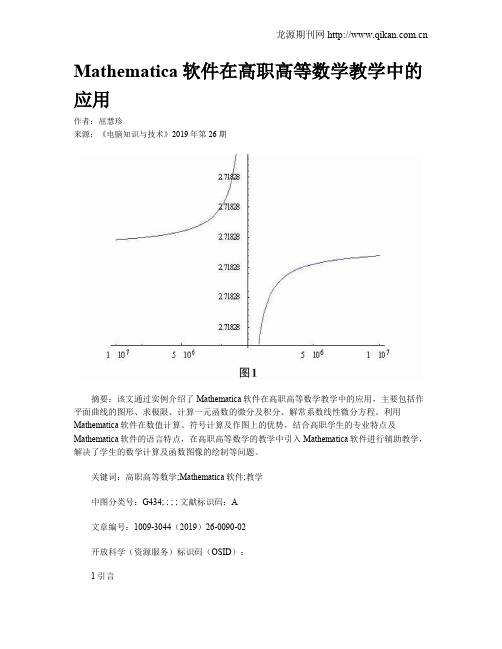
在 同 济版 的 高 等 数 学 教 材 中 .数 列 极 限 的 引入 借 用 的是 刘徽 的 割 圆 术 . 即利 用 圆 内接 正 多边 形 来 推 算 圆 的 面 积 . 体 具 过程如下 : 设 有 半 径 为 r 圆 . 先 作 内接 正 六 边 形 . 它 的 面 积 记 的 首 把 为A,再 作 内接 正 十 二 边 形 , 面 积 为 A ; 此 下 去 。 ; 其 ,循 每次 边 数
“
(= , n 3
n
1 - 1
4 5 … ) 当n 限 增 大 时 , 一 限逼 近 S ,, , 无 A无 。上 述 的 文字 叙 述 过 程 在 课 本 中非 常 繁 琐 , 果 我 们 只 用 语 言 表 达 , 生 理 解 起 来 会 如 学 比较 吃 力 , 因 为他 们 看 不 到n 限增 大 时 , 逼 近 的程 度 。 无 A 与S 如 果 用 Ma e ai 软件 , 图 1 用 动 画 的 方 式 将 上 述 过 程 演 t m ta h c 在 中 示 出来 , 生 就会 更 加 直 观 地 看 到 上 述 逼 近 的过 程 . 而 对 极 学 从 限概 念 有 一 个 更 直 接 的感 官 认 识 。用 这样 的 几 何 直 观 再 配 合 理 论 推 导 , 生反 映普 遍 较 好 , 得 了 比较 明显 的教 学 效 果 。 学 取
Байду номын сангаас
加倍 , 般 的把 内接 正6 2 边形 的 面 积 记 为 A 。 当n 大 , 一 ×… 越 内
接 正1 形 与 圆 的差 别 就 越 小 . 而 用 其 内接 正n 形 的 面 积 3 . 边 从 边 A 逼 近 圆 面积 S 由图 1 过 计 算 可知 A = i c s , 经 n s o n
Mathematica软件在高等数学教学中的应用研究

Mathematica 软件在高等数学教学中的应用研究摘要:文章根据高等数学的教学现状,探讨了Mathematica 软件在高等数学教学中的应用。
实践证明:利用数学软件辅助教学有利于激发学生的学习兴趣,培养学生探索知识的能力,改善教师课堂教学效率。
关键词:Mathematica 软件;高等数学;教学效果中图分类号:G642.0文献标志码:A 文章编号:1674-9324(2020)05-0254-03刘熙娟,刘云*(塔里木大学信息工程学院,新疆阿拉尔843300)收稿日期:2019-04-26基金项目:塔里木大学青年创新资金项目(TDZKQN201823);塔里木大学重点课程《高等数学》(220101405)作者简介:刘熙娟(1988-),女,讲师,主要从事生态数学研究。
*通讯作者:刘云。
一、引言高等数学是各类高等院校多种专业(包括许多文科专业)开设的一门重要基础理论课,对学生后续课程的学习以及思维素质的培养起着非常重要的作用。
高等数学课程教学的目的在于让学生掌握数学的基本理论、方法和技能,同时还要培养学生自觉运用高等数学的理论知识解决实际应用问题的数学能力。
然而高等数学中大量复杂的计算往往使学生望而生畏,部分学生对数学的抽象性感到困惑,对枯燥的理论推导感到厌烦,从而对高等数学的学习失去信心。
传统的数学教育过分强调形式化的逻辑推导,缺乏体现数学与其他学科的横向联系,使得充满活力、充满生机、充满美感的数学成了内容多负担重的习题、结论和公式的堆积,也难以将数学知识运用到实际生活中去。
在高等数学教学中若能采用一些数学软件解决机械的数值计算与符号演算,把更多的精力用于加强“本质”性问题的学习,让学生亲身体会数学知识在生产、经营和管理活动中的应用,使得高等数学课程从“学数学”向“用数学”转变,从“理论教学”到“应用教学”转变,充分领略数学的“工具性”与“应用性”,同时革新教学手段和教学方法,定能充分调动学生的学习兴趣,加深对理论知识的理解,培养应用数学的能力,以期达到教学效果的最优化。
Mathematica软件在高等数学教学中的应用

1072016年/第三十期/十月(下)Mathematica 软件在高等数学教学中的应用郭灿(广东培正学院计算机系广东・广州510830)摘要为了改变高等数学难教难学的现状,提高学生对高等数学的学习效率,利用Mathematica 软件在符号运算、数值计算、函数作图等方面的强大功能,从而实现使用Mathematica 这一软件辅助进行高等数学的教学。
关键词Mathematica 软件计算绘图高等数学中图分类号:G424文献标识码:ADOI:10.16400/ki.kjdkx.2016.10.052The Application of Mathematica Software in the Teaching of Higher MathematicsGUO Can(Department of Computer Science and Engineering,Guangdong Pei Zheng College,Guangzhou,Guangdong 510830)Abstract In order to change the situation of the higher mathematics course is hard to teach and learn,We need to improve stu-dents'learning efficiency of higher mathematics,so we use the powerful function of the software Mathematical in symbolic computation,numerical computing,function mapping,etc.to achieve using Mathematica software assisted teaching of higher mathematics.KeywordsMathematica software;calculation and drawing;advanced mathematics高等数学是一门重要基础课,它既是学习专业的后续课程与工程计算的工具,又是学生探索和创新的必备素养。
Mathematica软件在高等数学教学中的运用

文章编号:100924873(2005)022*******ΞMat hematica 软件在高等数学教学中的运用王玉苏, 吴素敏(石家庄职业技术学院基础部,河北石家庄 050081)摘 要:Mathematica 软件具有强大的数值计算、符号计算、绘图、程序设计等功能,高等数学教学中引入Math 2ematica 软件作为教学的辅助工具,可解决学生数学运算问题,函数的图形绘制问题等,提高学生的数学分析能力和解决综合应用问题的能力.关键词:Mathematica 软件;极限;导数;图像;综合应用问题中图分类号:G 642.0 文献标识码:A 随着科学技术的迅猛发展和教育改革的深入,传统的高等数学教学内容及方法不断受到冲击.适时地进行教学改革,运用现代信息技术,使其跟上科技发展的步伐,为现代化建设输送合格的人才,已势在必行.为此,我们在机电系的高等数学教学中引入了Mathematica 软件进行教学.Mathematica 是用计算机处理数学问题的工作平台,具有简单易学的交互式操作方式、强大的数值计算功能、符号计算功能、绘图功能、人工智能列表处理功能以及像c 语言、Pascal 语言那样的结构化程序设计功能,如何将它与高等数学有机地结合,起到促进教学改革和提高教学效果的作用,是我们努力追寻和探讨的目标.1 充分利用Mathematica 的计算功能,解决学生数学运算中的问题高等数学同初等数学在教学内容和方法上有着本质的不同,高等数学面对的是刚进学校的学生,在学习中学生感到不适应,常会觉得一些概念比较抽象,难以理解,导致运算出现错误,Mathematica 的计算功能恰能解决数学运算中的问题.极限概念是高等数学入门的基本概念,也是初学者感到抽象、难以理解的概念之一,用Mathemat 2ica 进行极限的运算则非常简单,写出表达式,便可直接得出结果.如求解limx →0e x -1x,用Mathematica 只要输入Limit [(Exp [x ]-1)/x ,x >0]便可得到极限结果.求函数的导数,特别是求复合函数的导数,同样也是学生运算出错率较高之处.Mathematica 对解决如y =ln tanx2-cos x ln tan x 等类型的复合函数求导问题也很容易.Mathematica 还可解决导数应用题、计算一元函数的积分、解常微分方程等方面的数学运算问题.众所周知,数学运算是教学中的重要环节,是提高学生素质的重要手段.在引进Mathematica 进行计算的同时,我们并没有忽视学生的数学运算能力.我们清醒地认识到,如果学生过分依赖计算机,而忽视数学基本运算能力的培养,反而不利于教学质量的提高.因此,我们是在基本概念、基本运算按大纲要求讲解完成后,将Mathematica 作为巩固已学知识、提高学生知识运用能力的有利工具.2 利用Mathematica 的绘图功能,作函数的图形图形能为重要的概念和关系提供洞察和形象的表示.在高等数学教学中,描绘函数的图形是必不可少的内容.在Mathematica 中,可以直观准确地绘出二维和三维图形,还可以用动画形式来演示函数图形连续变化过程,激发学生的兴趣,达到好的教学效果.在导数的应用一章中专门讨论了画函数的图形问题,[1]其方法是利用高等数学中一阶导数、二阶导学、函数的单调区间、凹凸区间、极值、拐点的知识及相关的初等数学知识,利用描点作图法,画出函数的图形,由于此方法综合性较强及描点作图只能作Ξ收稿日期:20041007作者简介:王玉苏(1961),女,河北丰润人,石家庄职业技术学院副教授.2005年4月第17卷第2期石家庄职业技术学院学报Journal of Shijiazhuang Vocational Technology Institute Apr.2005Vol.17 No.2草图,一般教学中选择简单的具有代表性的图形进行绘制,而Mathematica 的绘图功能给了我们强有力的支持,只要我们正确的输入函数,其图像就能很标准地显现出来,可使学生对函数本身有更深入的了解,对学生掌握相应的概念很有帮助.3 用Mathematica 解决综合应用问题,提高学生分析问题和解决问题的能力长期以来,高等数学一直是基础教学的重要学科,而学生对它的认识一般只停留在传统观念及为了进一步深造的必考科目上.这是因为,高等数学直接为实际所应用同教学往往是脱节的,纠其原因,一些综合应用问题,计算量及计算难度较大,教学中往往难以进行.利用Mathematica 的数值计算功能、符号计算功能、人工智能列表处理功能,使学生在学习抽象数学的同时,对数学的应用价值和应用方法有所了解.通过求解梯子长度问题、陈酒出售的最佳时机问题、放射性废料的处理问题给出了三个综合应用问题,这三个问题实际上是求函数的极值问题.对这类问题教科书上虽有明确的做题方法,但要解决上述三个问题,其求解层次较多,计算量偏大,课堂教学中难以实现.利用Mathematica 对上述问题的解决,使学生开阔了眼界,加深了对数学理论及数学概念的理解,了解了微积分和自然科学、工程技术之间的联系与应用,激发了学生学习数学、应用数学的兴趣.总之,引入Mathematica 软件进行高等数学教学,给传统的教学注入了活力.它正在以下方面改变着高等数学教学的现状:(1)突出学生在解题过程中的主体地位;(2)为解决来自实际的问题扫清了冗长繁杂计算的障碍;(3)可以创设更具吸引力的数学问题情景;(4)提供了理想的问题求解的环境.今后我们将对Mathematica 软件如何深入地与教学相结合问题做进一步探讨,通过培养学生数学应用能力,让学生了解数学的真谛,从而激发他们的创新意识,培养他们的创新能力.参考文献:[1] 侯凤波.高等数学[M ].北京:高等教育出版社,2000.责任编辑:金 欣Application of mathematicasoft w are in advanced mathematics teachingWAN G Yu 2su , WU Su 2min(Department of Basic Education ,Shijiazhuang Vocational Technology Institure ,Shijiazhuang 050081,China )Abstract :Mathematica softwane has powerful numerical computation functions ,maths symbols function ,drawing function and procedure design function.Mathematica software is introduced in advanced mathematics teaching as a teaching aid tool.So in this way ,a kind of new energy is put into the teaching.And at the same time the students can improve their ability of maths analysis and the ability of settling comprehensive applying problems.K ey w ords :mathematica software ;limit ;derivative ;image ;comprehensive applying problems55第2期王玉苏等:Mathematica 软件在高等数学教学中的运用。
Mathematica高数

u 1,0 x, y
x u x, y y v x, y , v 1,0 x, y x2 y2
y u x, y x v x, y x2 y2
u 0,1 x, y
y u x, y x v x, y , v 0,1 x, y x2 y2
x u x, y y v x, y
x2 y2
结果见Math界面
【例】观察f(x) = 4x3-5x2+x-2的单调性、 凹凸性与f '(x),f "(x)符号的关系。
若该储户每季度结算一次,则每季度利率为:0.005
4
故第一季度后储户本息共计:100,000(1 0.005;) 第二季
度后储户本息共计:100,000(1 0.005)2……
4
依此,一年后该储户
4
本息共计:100,000(1 0.005)4. 若该储户每月结算4一次,月利率为:0.005 按上面的方法
12 知一年后储户本息共计:100,000(1 0.005)12
12
若该储户等间隔结算n次,则一年后本息共计:100,000(1 0.005)n
n
随着结算次数的无限增加,即在上式中n->∞,故一年后本
息共计:lim100,000(1 n
0.005) n n
程序如下: a[n_]:=100000(1+0.005/n)^n; Limit[a[n],n->Infinity]
TableForm[%]
f[100]
Limit[f[n],n->Infinity]
1 . 9523.81 3. 27232.5 5 . 43294.8 7. 57863.7 9. 71078.2 11 . 83064.1 13. 93935.7 15. 103797 17. 112741 19. 120853 20. 124622
谈数学软件Mathematica的使用

且自成一体 。Mathematica 软件是一个数学计算软件系统 , 更确切 地说 , Mathematica软件是一种通用符号计算系统 。它功能较为齐全 ,包括符号运 数的某些特性 。如绘制参数方程
的图形 。用手工绘制
算 ,数值计算 ,平面 、立体图形的描绘演示和结构化编程等多种功能 。同时 简单易学 ,采用交互式操作方式 ,每发出一个命令 ,就执行相应的数学运 算 ,给出运算结果 ,而且有适应于各种操作系统的不同版本 ,还能和几种常 用算法语言相互转换 。国外有许多大学应用符号软件进行科学研究 ,并将 其应用于数学教学中 ,而将这一系统应用于中学数学教学中的却不多 。我 国广东一些教学单位曾以选修课的形式 ,使用 Mathematica在学生中作了一 项实验 ,以探讨它对数学学习的影响 。从总体情况来看 ,试验组在期末考 试中的优势表现在两个方面 ,一是图形的知觉较好 ; 另一是对一些抽象概 念理解较深 。
此外 ,软件还可以做出等值线图 ,密度图 ,二 、三维数据图等多种类型 的图形 ,丰富了教学手段 ,提高了教学内容的可视性 ,从而提高教学质量 。 许多在课堂教学中无法短时间内描绘的图形 ,可以轻松迅捷地展现在学生 眼前 ,使抽象的数学式子与直观形象的图形之间建立有效的联系 ,增强学 生对所学知识的理解 、记忆和深化 。
京 :北京大学出版社 , 1994. [ 3 ]高锐灵. 高中是否需要数学微积分 [ J ]. 数学教学 , 2000, ( 4 ) : 51
- 53. [ 4 ]罗强. 倡导以操作为主的 CA I模式 [ J ]. 中学数学月刊 , 2002, ( 1 ) :
85 - 86. [ 5 ]王莱用. Mathematica处理和分析实验数据 [ J ]. 核电子学与探测技
Mathematica在《高等数学》教学中的应用

Mathematica在《高等数学》教学中的应用作者:乌兰其其格来源:《赤峰学院学报·自然科学版》 2011年第10期(赤峰学院数学与统计学院,内蒙古赤峰 024000)摘要:把计算机和数学软件引入高等数学教学中,进行多媒体教学实践是提高教学质量的重要措施.文章介绍了Mathematica在《高等数学》教学中的应用,借助Mathematica数学软件可以使《高等数学》教学更加形象化、生动化,减轻学生计算负担,培养学生的创新能力,提高学生的综合能力.关键词:Mathematica;高等数学;应用中图分类号:G642文献标识码:A文章编号:1673-260X(2011)10-0240-02Mathematica是最优秀的数学软件之一,是借助于计算机数学软件强大的数值计算、符号运算、图形和动画功能,为一引些抽象概念加入有实际意义的背景材料和几何解释,可以提高学生的学习兴趣,尤其可以提高学生运用数学知识解决实际问题的能力.本文主要介绍Mathematica在《高等数学》的应用.1 概念形象化利用Mathematica绘制图形,可以使学生直观地、形象地了解《高等数学》中一些概念.例1 作y=x2-1在[-2,2]内的图像和作y=lgx在[0.3,4]内的图像,其输入和输出如图1.1平时我们作图时,两个坐标轴的单位长度应该一致,即1:1.但在Mathematica系统中根据美学原理系统默认的纵横之比为1:0.618,而将参数AspectRatio的值设置为Automatic(自动的)时可使纵横比为1:1.例2 (1)作y=sinx和y=cosx在[0,2π]内的图像,且两坐标轴上的单位比为0.618.(2)作y=sinx和y=cosx在[0,2π]内的图像,且两坐标轴上的单位比为1:1.其输入和输出如图1.2.例3 作y=sinx和y=cosx在[0,2π]内的图像,且两坐标轴上的单位比为1:1,线条用蓝色虚线.输入:Plot[{Sin[x],Cos[x]},{x,0,2Pi},AspectRatio->Automatic,PlotStyle->{{RGBColor[0,0,1],Dashing[{0.02,0.05}]}}]输出如图1.3.2 简化计算过程例4 已知二元函数f(x,y)=x2y+y2,求f对x,y的一阶和二阶偏导.解输入:In[1]:=f[x_,y_]=x^2*y+y^2In[2]:=D[f[x,y],x]In[3]:=D[f[x,y],y]In[4]:=D[f[x,y],x,y]In[4]:=D[f[x,y],{x,2}]In[5]:=D[f[x,y],{y,2}]得:结果为2.通过程序的编写,大量减少计算,学生可以把大量的精力用于思考解决问题的方法上,提高学生的逻辑思维能力,为学习数学打下良好的基础.参考文献:〔1〕刘谦.教学软件在教学中的作用[J].计算机与现代化,2001(1):98-102.〔2〕赖兴珲.Mathematica在高校教学中的应用[J].玉林师范学院学报,2003(4):36-38.〔3〕侯风波.高等数学[M].北京:高等教育出版社,2002.。
Mathematica在大学数学教学中的应用

GAOJIAO SHIYE高教视野17数学学习与研究2019.17Mathematica 在大学数学教学中的应用◎蔡浩江1房敏1王婧嘉2(1.西安石油大学理学院,陕西西安710065;2.中南大学交通运输工程学院,湖南长沙410075)【摘要】随着现代信息技术以及计算机辅助教学的蓬勃发展,最新的信息技术已经在高等院校的日常教学中越来越普及.在大学数学的教学领域中,信息技术的应用,可以使艰深、复杂的数学理论和公式变得简单直观.将Mathematica 这款非常实用的数学软件与传统教学相结合,构建符合学生认知规律的教学模式是提高大学数学教学质量的有效方法.实践证明这种教学模式的建立对培养学生的数学思维,激发学生的学习主动性,提高教学效果有着非常重要的作用.【关键词】计算机辅助教学;数学软件;Mathematica 一、目的与意义高校的数学教学中,传统的教学方法强调数学理论的连续与严谨,采用以教师为主导的灌输式的数学教学模式,使原本就比较抽象难懂的数学定义与概念变得难上加难.信息时代的到来,移动终端的使用,使传统教学模式受到了强烈冲击.当前,学生获取知识的渠道变得更为丰富,各种MOOC 、微课学习视频及其他丰富的网络教学资源都为学生的课外学习提供了条件.但是与传统教学相似,各种网络教学资源仍注重于学生掌握严谨的数学理论和计算能力,忽略了理论知识的推导以及创新思维的培养,淡化了理论推导过程中的猜想、观察、实验、归纳、类比、抽象等环节,忽视了学生的主体地位,弱化了学生自主探索的学习过程,不利于培养学生的应用与创新能力.对大多数学生而言,这些资源的利用虽然能够在一定程度上提高他们的学习效率,但仍然无法将所学的数学知识应用于其他课程及解决实际问题,学生的逻辑思维能力、创新与应用能力并没有显著提高.教学实践证明,数学软件与传统课堂教学的有机结合,是提高学生创新思维和应用能力的一条行之有效的途径.一方面,数学软件可以使用图像展现数学深奥的理论,可以加强学生对抽象知识的理解.另一方面,为了贯彻实施素质教育,教师还可以设计数学课程的实验教学环节:提出典型实际问题,引发学生思考,培养学生的数学思维;在教师的启发下分析问题、探索问题,从而提高学生的创新精神和实践能力;利用数学软件进行数学实验,使学生对教学内容有了直观认识,从而提升学习兴趣,提高研究能力.学生在使用数学软件解决问题的过程中找到了理论与实际的结合点,体验到了“学”和“用”的和谐统一,获得了学习带来的成就感,学习兴趣和动力会得到长效的保持.二、计算机辅助教学的可行性教学硬件的改善为软件的使用提供了保障条件.Matlab 、Mathematica 、Maple 并称为三大数学软件.Matlab 是Math Works 公司出品的数学软件,用于算法开发、数据分析以及数值计算;Mathematica 是由美国的Wolfram Research 公司开发的数学软件,其在图形、数值、代数等方面应用广泛;Maple 是由加拿大Waterloo 大学开发的科学计算软件,拥有优秀的符号计算和数值计算能力.它们各有所长,但就高校计算机辅助教学及实验教学而言,Mathematica 更具优势,原因有:第一,Mathematica 有与数学教材完全相同的基本数学符号输入界面,见图1,不需要太多的课堂时间讲解,学生即可上手使用;第二,自定义函数的写法,各类函数的输入和输出,更接近语言的表达顺序,简单易懂;第三,绘制的三维图形可以方便地调整观察视角,有利于学生对空间图形的直观认识;第四,符号运算方便、简洁,容易掌握.图1Mathematica 数学符号输入界面因此,将Mathematica 数学软件引入数学教学中具有很好的可行性.通过它,可以将复杂抽象的计算问题按照人们习惯的书写格式输入和输出,学生容易掌握,还可将复杂的函数关系用图形的形式展现出来,便于将抽象的问题具体化、可视化.本文将以Mathematica 的几个辅助实验为例说明与传统教学相结合的教学模式对提高大学数学教学效果的积极作用.三、Mathematica 软件在辅助教学的应用(一)在观察数列变化趋势中的使用在高等数学的教学过程中,极限作为微积分学的基础,无疑是最重要、最基础的环节.但在通常的教学中,大部分学生并不容易发现数列规律.借助Mathematica 程序给出的直观图示,可以帮助他们发现数列的规律,进而理解数列收敛的本质.例如,可以从复利问题引入重要极限lim n →ɕ1+1()nn,激发学生的学习兴趣,再借助Mathematica 程序绘出数列变化的直观图示,如图2所示:图2数列变化图示学生从图像中观察到了数列变化的特点,直观的感受使学生对公式首先有了感性认识,以此为基础,再利用二项展开式进行公式的推导和理论证明,从而使学生上升到理性认识.此过程遵循了猜想、观察、实验、归纳、类比、抽象的环节,重在思维方式的启发与培养,引导学生独立思考并提升了学生学习的积极性和主动性.(二)在函数绘图中的使用在传统的高数课堂教学中,由于缺乏对复杂函数图像的描绘等教学环节,对很多学生而言,曲线的直角坐标方程、极坐标方程及参数方程3种表达方式之间相互转化;不同坐标系下的三重积分的计算;线、面积的计算;隐函数的概念等知识点一直以来是都是难点问题.“数”与“形”之间不能完美的结合,使得部分学生缺乏直观认知,造成概念混淆,无法深入理解相关知识.但是在计算机辅助教学中,我们就可以借助Mathematica 中的绘图软件,在教学过程中绘制复杂函数的图像,“数”与“形”的有机结合,可以使抽象函数具体化,加深学生对函数以及相关知识的理解.使用高教视野GAOJIAO SHIYE18数学学习与研究2019.17Plot 、PolarPlot 、ParametricPlot 函数绘制一元函数、极坐标函数、参数方程表示的二维图形,使用Plot3D 、RevolutionPlot3D 、SphericalPlot3D 、ParametricPlot3D 函数绘制二元函数、柱坐标函数、球坐标函数、参数方程表示的三维图形,使用ContourPlot 绘制隐函数图形.还可以通过CoordinateTransform 函数实现直角坐标Cartesian ,极坐标Polar ,柱坐标Cylindrical ,球坐标Spherical 之间的相互转换.如图3绘制了极坐标方程ρ=cos2θ表示的四叶玫瑰线和方程x 3+y 3-3xy =0确定的函数曲线.图3图形图示还可以通过Animate 函数绘制动画,演示摆线、旋转曲面等图形的形成过程,如图4所示,帮助学生更好地理解所学内容并增强学生的学习兴趣.图4旋转曲面示例(三)在定积分和二重积分定义中的使用积分在数学、物理、机械、电子、军事等方面均有着广泛应用,但积分的概念对大部分学生而言却是难以理解的.在教学中,我们一般通过求曲边梯形面积和曲顶柱体体积的问题引入,需要经过“分割、近似代替、求和、取极限”四个步骤进行.其中“取极限”这一环节,课堂教学仅通过语言描述表达,没有相关的实验环节,学生缺乏直观的感性认知以及从具体到抽象的思维过程,无法深入、透彻地理解相关概念,难以获得较好的教学效果.通过Mathematica 绘制具体例子的图示,如图5所示,以图形直观的方式呈现,远胜于教师的口头讲解,有助于学生加深印象并理解概念.图5定积分与二重积分引例图示(四)在大数定律中的使用大数定律是概率统计中的重要定理,揭示了n 个相互独立的随机变量的算术平均值当n →ɕ时依概率收敛于其数学期望.为了帮助学生更好地理解大数定律,可以利用Mathematica 给出直观演示.例如,在讲授辛钦大数定律时,利用Mathematica 的Random 和NormalDistribution 函数,产生n 个相互独立且服从正态分布N (1,22)的随机变量X 1,X 2,…,X n ,考查当随机变量个数n 逐渐增多时,它们的算术平均值的变化情况.图6分别给出了当n =10,100,1000,10000四种情况下,重复试验50次,n 个随机变量的算术平均值的分布情况.图6大数定律图示从图6可以明显看出,当n =10时,10个相互独立的随机变量的算术平均值与μ=1有很大偏差,但随着n 越来越大,n 个相互独立的随机变量的算术平均值越来越密集在μ=1这条直线附近.由此可见,传统教学中复杂、艰深的数学定理,借助于数学软件的帮助,以直观易懂的图形图像展示给学生,使得复杂抽象的理论知识变得简单、具体,让学生印象深刻,从而取得较好的教学效果.四、计算机辅助教学的优点(一)有利于学生自主学习数学课程的教学强调进行交互式教学以及以学生为中心的自主学习,在课前、课中和课后都以学生为主体、教师为主导.数学软件辅助教学,使得作为主体的学生,对课程知识的获取和掌握不再完全依赖于任课教师的课堂教学,可以利用更多的课外时间自主学习.(二)有利于学习成绩的提高在运用计算机辅助的交互教学过程中,将Mathematica 软件引入到数学课堂,使抽象的概念、函数、公式变得直观形象,学生在数学模型的动态展现中更加深刻地理解理论知识,提高课堂的教学效率,提升学生的学习兴趣.学生在学习过程中遇到难题,也可以通过讨论,查找资料,编写程序等多种方式加以解决.(三)有利于实践能力的培养在课程教学中,我们运用Mathematica 软件进行交互教学,让学生通过自主学习的方式不仅掌握有关定理、公式,而且能够熟练掌握一门数学软件.既增强了学生的自学能力,还提高了学生的动手能力,也培养了学生的实践应用能力.五、结束语在数学课程中运用Mathematica 软件进行辅助教学,充分利用数学软件的计算和绘图功能,加强了数学教学的简便性和直观性,使得“数”与“形”有机结合,“教”与“学”相得益彰,不仅有助于提高课堂教学效果,还有助于培养学生利用数学软件探究问题的意识.学生在课后利用课外教学资源自主学习、表达和解决实际问题时,也可以方便地使用软件辅助,既促进了学生学习成绩的提高,也培养了学生理论联系实际的能力.教学实践证明,在数学教学中充分利用辅助软件是一种比较科学有效的教学方法,能够激发学生的学习兴趣,活跃课堂氛围,提高课堂教学效果.【参考文献】[1]同济大学数学系.高等数学(上册):第7版[M ].北京:高等教育出版社,2014.[2]同济大学数学系.高等数学(下册):第7版[M ].北京:高等教育出版社,2014.[3]朱开永,王升瑞,李媛.概率论与数理统计[M ].上海:同济大学出版社,2013.[4]Wolfram S.Mathematica 全书[M ].赫孝良,周仓义,译.西安:西安交通大学出版社,2002.[5]王绍恒,王艺静.Mathematica 软件在大学数学课程教学中的应用[J ].教育理论与实践,2013(21):39-40.[6]刘雄伟.基于Mathematica 的高等数学教学过程研究与实践[J ].大学教育,2016(2):136-138.。
Mathematica软件在高职高等数学教学中的应用
Mathematica软件在高职高等数学教学中的应用作者:屈慧珍来源:《电脑知识与技术》2019年第26期摘要:该文通过实例介绍了Mathematica软件在高职高等数学教学中的应用,主要包括作平面曲线的图形、求极限、计算一元函数的微分及积分、解常系数线性微分方程。
利用Mathematica软件在数值计算、符号计算及作图上的优势,结合高职学生的专业特点及Mathematica软件的语言特点,在高职高等数学的教学中引入Mathematica软件进行辅助教学,解决了学生的数学计算及函数图像的绘制等问题。
关键词:高职高等数学;Mathematica软件;教学中图分类号:G434; ; ; ; 文献标识码:A文章编号:1009-3044(2019)26-0090-02开放科学(资源服务)标识码(OSID):1 引言Mathematica软件是由美国Wolfram公司生产研究的一种数学分析型的软件,以符号运算为主,也具有高精度的数值计算功能和强大的图形功能,详情见参考文献[1-2]。
对高职学生来说,不需要掌握特別复杂的计算机知识,只需要了解Mathematica软件的基本使用语句,就可以很好地使用该软件[3]。
而且,近年来,由于国内教育体制不断改革,高校生源不断扩招,导致高职学生文化基础越来越差,特别是数学基础。
另一方面,高等数学中大部分内容抽象性强、逻辑性高,内容多而学时少。
综合各方面的原因,将Mathematica软件运用到高等数学教学中,能够增加教学内容的直观性,让学生对数学知识有更直观的认识,还能培养学生的实践动手能力,激发学生的学习兴趣,从而提高教学的质量和效率[4]。
2 Mathematica软件在高等数学教学中的应用举例本文给出具体例题的操作演示,学生可以体验到利用Mathematica软件可以非常简单的解决计算极限、导数、微分、积分、解方程与函数图形的绘制等问题。
让学生不需要牢记大量的数学公式和法则,就能轻松地计算出各种复杂难题。
mathematica在高等数学课程教学中的应用

mathematica在高等数学课程教学中的应用
Mathematica是由Wolfram Research公司开发的著名的高等数学软件。
它不仅可以处理常见的数学表达式和积分、微积分示范操作,而且还可以进行符号和计算机代码处理,以及多维可视化应用,为高等数学课程的教学提供不可忽视的突出的优势。
首先,Mathematica在处理公式方面具有极强的表现能力,它可以根据简单的输入即可自动生成信息精确且易读的表示形式,并能够准确描述数学关系和含义,在高等数学课程中可以大大提高教学质量和学生的学习效果,特别是在计算复杂公式和绘制许多基本结构图形图例方面能够得心应手。
其次,Mathematica也可以利用它独特的函数式程序化语言构建软件,从而在对于复杂的数学问题进行探索和分析的同时也避免了错综复杂的代码和多余的代码,因此可以使学生更加轻松、高效的完成任务,所有任务都将能够在更短的时间内编写,因此有利于提升学生的计算能力和模型构建能力。
此外,Mathematica还提供了数学领域的多维可视化功能,可以帮助学生快速而清晰的总结具有复杂数学代数或几何关系的各类函数,这不仅有助于同学及时把握、理解学习内容,还能很好的让老师呈现教学内容,以便学生们更好的掌握,而且在一定程度上会提高学生的知识掌握能力。
总之,Mathematica是一款十分实用的高等数学软件,它可以极大的提高学生学习数学的效果,有效的缩短学习的时间,而在这种情况下,高等数学课程的教学也离不开它的重要性。
Mathematica软件在数学教学与科研中的应用

( 东华理工大学数学与信息科学学院 , 江西 抚州 344000 )
[ 摘 要] Mat hematica 自面世以来 ,在科技及其他领域产生了深刻影响 ,现已被广泛应用于解决各种数学 的应用型问题 ,特别对于大型的数值计算更是一个不可缺少的工具 。本文基于数学软件 Mat hematica5. 2 的特 点 ,结合数学教学与科研的需求 ,讨论 Mat hematica 在数学教学与科研中的应用 。
xy 的交线 。可得因 k x 2 + y2 值的不同 , 交线为高度不断变化的水平直线 , 可见函数 f ( x , y) 当 ( x , y) 以不同的方向趋于 ( 0 , 0 ) 时趋于不同的值 ,
3/ 2
1/ 2
1/ 2 - 3/ 2 圆曲线 ,从图 5 、 图 6 可以看出正交变换使图形在原坐标系 下的位置发生了旋转 ,而图形不改变 。
x2
25
+
y2
9
= 1 进行正交变换
x y
=
图6 类似的其它数学课程如计算方法 、 微分方程等也可通 过 Mat hematica 辅助教学 ,许多高校教师讨论过这个问题 , 可参阅文献 [ 5 ] [ 6 ] 。 二、 Mathematica 在数学科研中的应用 Mat hematica 软件也是数学科研工作者的好帮手 , 它 强大的符号与数值计算功能已经广泛地应用于社会的许多 领域 。对于数学领域 , 许多数学工作者已辅助 Mat hemati2 ca 展开了大量的研究工作 。倪致祥将 Mat hematica 称为科 [7 ] 研的有力工具 。 张栋恩用 Mat hematica 解一个系统的优 [8] 化设计问题 , 通过对各容差搭配方案下目标值 y 的方差 估计和计算机随机模拟两种方法 , 得到该系统的最优设计 方案 。孙哲等利用三个线性方程组与 Mat hematica 软件 , 给出求解古典自然数幂和公式 S k ( n) ( k ≥0 , n ∈ N + ) 以及 现代自然数幂和公式 T k ( n) ( k ≥0 , n ∈ N + ) 的若干新的机 械计算方法 。还有许多如微分方程的定性理论等问题都可 以用 Mat hematica 软件辅助研究 。 对于 Mat hematica5. 2 版 , 就函数 NDSolve 而言 , 可用 来求解多种微分代数方程 , 这对于科研过程中处理实际问 题有很重要的作用 。现简单列举实例如下 : ( t) = A . X ( t) , 初值条件 例1 求解矩阵微分方程 X′ 为 X ( 0) = X 0 ,其中 1 2 3 1 0 0 A = - 4 5 6 , X0 = 0 1 0 . 7 8 9 0 0 1 [ 析 ]用 N D S ol ve 可以得到其近似解 , 图 7 中表示微分 方程的解 X ( t) 的范数随着 t 的变化 。 求解矩阵微分方程程序代码如下 : A = {{ - 1 , - 2 , - 3} ,{ - 4 , - 5 , - 6} ,{ - 7 , - 8 , - 9}} ; X0 = {{1 ,0 ,0} ,{0 ,1 ,0} ,{0 ,0 ,1}} ; ( t ) = = - A. X ( t ) , X ( 0) = = X0} , X NDSolve[ { X’ ( t ) ,{t ,0 ,3} ] 例2 求解微分代数方程组 : 4 y′ 1 (t) = 10 y2 (t) y3 (t) - 0. 04y1 (t) , y′ 107 y2 ( t ) 2 - 104 y2 ( t ) y3 ( t ) + 0. 04y1 ( t ) , 2 (t) = = 3 × y′ 1 ( t ) + y2 ( t ) + y3 ( t ) = 1 , y1 ( 0) = 1 ,y2 ( 0) = 0 ,y3 ( 0) = 0. [ 析 ] 用 NDSolve 可以得到其近似解 , 图 8 中表示微分 代数方程组的解所描述的图形 ,程序代码如下 : ( t ) = 104 y2 ( t ) y3 ( t ) - 0. 04 y1 ( t ) , NDSolve[ {y1’ (t) y2’ = - 3 107 y2(t)^2 - 104 y2 (t) y3(t) + 0. 04 y1 (t) , y1 ( t ) + y2 ( t ) + y3 ( t ) = = 1 , y1 ( 0 ) = 1 , y2 ( 0 ) = 0 ,y3 ( 0) = 0} ,{y1 ,y2 ,y3} ,{t ,0 ,1000000} ]
Mathematica软件在高等数学教学中应用

Mathematica软件在高等数学教学中应用摘要:本文通过一些具体的例子,介绍了Mathematica 软件在高等数学教学中的应用。
说明在高等数学教学中融入软件的学习,不仅使得抽象概念变得形象生动,而且能避免冗长繁杂的计算,从而激发学生学习高等数学的兴趣。
关键字:Mathematica软件高等数学教学应用一、引言极限、导数、定积分等概念,可以说是高等数学中最重要、最具有代表性的概念,它们体现了应用微积分的思想和方法,其应用几乎涵盖了所有的自然学科。
但上述概念对于学生来说也是最难理解的,因为从本质上来说它们有三种表示形态:逻辑形态、算法形态和直观形态。
大学老师呈现最多的是前两种形态,因此造成大部分学生觉得高等数学的学习抽象枯燥,运算繁琐冗长。
为了帮助学生解决认知中的困难,首先通过数学软件的直观演示,加深学生对一些重要概念的理解,然后再详细地介绍它们的逻辑形态和算法形态,这样使得抽象概念的学习更加形象生动。
下面就Mathematica软件在教学中的具体应用谈谈心得体会。
二、Mathematica软件在高等数学教学中的应用1.运用软件演绎极限的概念在同济版的高等数学教材中,数列极限的引入借用的是刘徽的割圆术,即利用圆内接正多边形来推算圆的面积,具体过程如下:设有半径为r的圆,首先作内接正六边形,把它的面积记为A■;再作内接正十二边形,其面积为A■;循此下去,每次边数加倍,一般的把内接正6×2■边形的面积记为A■。
当n越大,内接正n边形与圆的差别就越小,从而用其内接正n边形的面积A■逼近圆面积S,由图1经过计算可知A■=nr■sin■cos■ (n=3,4,5,…),当n无限增大时,A■无限逼近S。
上述的文字叙述过程在课本中非常繁琐,如果我们只用语言表达,学生理解起来会比较吃力,因为他们看不到n无限增大时,A■与S逼近的程度。
如果用Mathematica 软件,在图1中用动画的方式将上述过程演示出来,学生就会更加直观地看到上述逼近的过程,从而对极限概念有一个更直接的感官认识。
mathematica软件在高等数学教学中的运用

mathematica软件在高等数学教学中
的运用
今天,计算机科学和计算技术正在越来越广泛地应用于高等数学的教学和研究中。
在讲授高等数学课程中,mathematica软件是一种非常有效的辅助工具,具有
丰富的图形和数据分析功能,可以更好地帮助学生理解数学的概念,学习解题技巧。
Mathematica软件提供了用户一个强大而且完整的高等数学计算环境,它具有
高精度的计算能力,可以在解决数学课程问题时帮助学生快速找到正确的结论。
它可以以可视化和动画的形式呈现复杂的数学问题。
同时,mathatica拥有实用的可
视化工具,给出了直接而清晰的结论。
因此,学生能够以更深刻的理解以及更好的希望来解决复杂的数学问题,更加形象化地研究概念的联系。
除此之外,mathatica的强大的编辑功能还可以帮助教师顺利完成高等数学的
复杂课程设计,大大提高了校园教学的效率。
由于mathatica拥有多种数学功能,它可以更好地帮助学生记忆数学知识,掌握解决数学问题的方法。
总之,mathatica软件可以更好地帮助学生和教师更准确地完成数学的教学和
研究,更快地步入数学的学习世界。
Mathematica软件在高等数学教学中的应用

Mathematica软件在高等数学教学中的应用——孔垂冕(学号2008212077)摘要:Mathematica软件是一套专门进行数学计算的软件,在高等数学中引入Mathematica软件进行辅助教学,有利于增强教学的直观性,激发学生学习兴趣,提高学生解决数学综合问题的能力。
关键词:Mathematica软件;高等数学;计算;数学建模;综合问题1引言随着现代教育技术的发展和教学改革的不断深入,传统的高等数学教学内容及方法不断的受到挑战。
在高等数学教学过程中适时地进行教学改革,引入现代化的教学手段,提高高等数学教学水平,增强学生学习数学的兴趣和应用数学知识的能力已势在必行。
本学期在我校赵东方老师得课堂学习数学模型课,亲身体会到Mathematica在数学建模中的重大地位和它的强大功能,下面就谈谈其在高等数学的几个应用。
2 Mathematica软件简介Mathematica是由位于美国伊利诺州的伊利诺大学香槟(Champaign)分校附近的WolframReseareh公司开发的一套专门进行数学计算的软件,目前最新的发布版是Mathematiea 5.0。
该软件功能较为齐全,包括数值计算、符号计算、函数绘图以及象C 语言一样的结构化程序设计功能。
同时,它具有图形化用户界面,采用交互式操作方式,易学易用。
将Mathematiea软件与高等数学教学有机结合,有利于促进数学教学改革,提高教学效果,增强学生利用计算机解决数学实际问题的能力。
3 Mathematica软件在高等数学教学中的应用(1)、利用Mathematiea的计算功能,提高学生计算能力高等数学教学内容十分丰富,包括微积分、空间解析几何和微分方程等知识,内容无论在深度还是广度上都远远超过初等数学。
其中较为特殊的一点是,高等数学涉及大量的数学计算。
这些对于刚进校园的大一新生来说,如同面对比高考更难、更复杂的计算型“题海”,以致在学习中会感觉不适应,常常出现运算错误。
将Mathematica软件融入高等数学教学的探讨

的理论 就会感 到困惑和不解 。因此 , 教学过程 中我们需要借助于 在
一
定的教学 手段将 这种数学现象重 现, 创造 出 良 好数学意境 。如在
维普资讯
极 i f .
2 0 .8 0 80
( 中旬于 ) l j
将 Mah maia软 件 融 高 等 数 学 教 学 的 探讨 te t c
口 程
( 南工业 大 学理 学院 河
摘 要
作用。
涛
河南・ 州 郑 400 ) 50 1
结合 Ma e t a t mac 软件在 高等数学教 学中的运用 ,分几个方面探 讨 了Ma e ta h i t ma c 软件在高等数 学教学过程 中的 h i 高等数学 计算能力
和定量刻画的基础上 , 步抽 象概念 , 逐 形成方法 和理论 , 并进行应用
的过程 。在这种严谨 的理论体系包装下 , 数学 家发现 问题 、 决问 解
题的思维轨迹往往 被掩盖了。导 致学生 在学 习的过程 中, 对于现存
m ta a e 软件融入 高等数学教学 中, i 不仅可 以调 动学生学习高等数学 的积极 性 , 加深学 生对课 堂教学内容 的理解 , 而且还可 以提 高学生 的计算 能力和 分析 、 决 问题 的能力 , 解 改善 教学效果 和质量 , 进一 步加强学生运用 计算机 软件的能力 。 M t m ta a e a c 是美 国 Wo r h i la f m研究公 司开发的一种 数学分 析型 的软件 , 以符号计算见 长 , 具有高精度 的数值 计算功能 和强大的 也 图形功能 。 近年来 , a e ac 软 件在数学 、 M t m ta h i 物理学 、 工程计算等方 面 的应 用 日益深入 ,在许 多重要科学 中的发现 中扮演着 重要 的角
Mathematica软件在高职数学教学中的应用

Mathematica软件在高职数学教学中的应用孙静茹【摘要】Mathematica数学软件具有强大的作图功能、计算功能、模型的动态性以及编程功能,等等.高等数学作为高职院校的公共基础课,其教学目标是培养学生的数学方法和数学思维且能够运用所学知识为专业服务.高职学生的数学基础薄弱,而高等数学中的一些定义、概念和计算比较抽象,将Mathematica数学软件应用到高职数学教学中,使教学内容更直观,可激发学生的学习兴趣,提高课堂的教学质量.【期刊名称】《黑龙江科学》【年(卷),期】2018(009)017【总页数】2页(P74-75)【关键词】Mathematica;数学软件;高等数学【作者】孙静茹【作者单位】长春汽车工业高等专科学校,长春130013【正文语种】中文【中图分类】G434Mathematica以其卓越的技术和简单的使用方法成为国内外大学数学实验教学中广泛使用的教学软件之一。
高等数学中,以教师为主导的灌输式的数学教学模式,忽视了学生的主体地位,弱化了学生自主探索的学习过程,使原本就比较抽象难懂的数学定义与概念变得难上加难。
教学硬件的改善为软件使用提供了保障条件,因此,将Mathematica数学软件引入高等数学教学中,具有较强的可行性。
1 Mathematica软件在绘制函数图形中的应用在高等数学的学习中,两个重要极限的证明烦琐难懂,对高职院校学生的学习难度较大,采用Mathematica软件教学,能够加深其对知识点的理解与应用。
案例1 :作出和g(x)=1在区间[-20,20]内的函数图像。
在[a,b]上画出函数f(x)的图像的基本命令是Plot[f,{x,a,b},选项]在Mathematica软件中输入命令:Plot[{Sin[x]/x,1},{x,-20,20}]则输出的函数图像见图1。
图1 Mathematica输出的函数图像Fig.1 Function image of Mathematica output由图1可知,当自变量x无限接近于0时,函数值y则无限接近于1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函 数 功 能
% ! ’ ; % , 6 % * + K & % 6 . T! T < 1 ,! ( ! ’ ! ( & T < T < 1 ,! < T P P P
按照 E! G 的值作. 的等值线图
!* ’ 实现图形的动画效果 )
近几年 # 我们在高等数学 教 学 中 积 极 地 开 展 教 学内容和教 学 方 法 的 改 革 # 尝试利用 N 6 9 0 < 6 1 : 软件来解决教学中的一些计 算 ( 验证 和 绘 制 复 杂 图 形等问题 # 既 节 省 时 间# 又增加了教学内容的几何 直观 # 为学生提供丰富的 感知材 料 ’ 下 面 笔 者 将 结 合二元函数极值与无穷级数 这两部 分 的 教 学 内 容 # 来介绍 N 6 9 0 < 6 1 : - 软件在教学中的应用 ’
-
E# c= . G$ E" # 得到各 " # $ . G E G c=
N 6 9 0 < 6 1 : -是 美 国 D % & . + <G 0 5 0 + : 9公司 开发的一个功能强大的计算 机软件 系 统 # 不仅能进 行数值计算 # 还可解决各种 领域内 涉 及 的 复 杂 的 符 号计算 ’ 除了计算功能 # 它还 具备 较 强 的 图 形 绘 制 功能 # 可绘制各种复杂的平 面 ( 立 体 图 形# 而且还可 以对它们进 行 翻 转 ( 旋 转# 甚至还能够轻而易举地
K 4 " ( ) C 4 " , 1 4 软件在高等数学教学中的应用
张二艳
" 北京印刷学院 # 北京 ! $ = # > = =
摘 ! 要 !二元函数极值与无 穷 级 数 这 两 部 分 教 学 内 容 抽 象 难懂 ! 利用 N 6 9 0 < 6 1 : -软 件 强 大 的 符 号 计 算 和 图 形 处 理 功能 ! 可以加强这部分教学内 容 的 几 何 直 观 ! 弥补学生空间 想象能力的不足 " 实践证明 ! 教学中多辅以一些这 类 软 件! 借助于多 媒 体 技 术 实 现 抽 象 数 学 概 念 和 理 论 的 直 观 可 视 化! 不仅可以提 高 学 生 的 学 习 兴 趣 和 加 深 对 教 学 内 容 的 理 解! 而且还可以提高学生运用计算机软件的能力 " 关键词 !N 高等数学 # 教学研究 6 9 0 < 6 1 : -软件 # 中图分类号 ! V ! ] #% 7 > " # 文章编号 ! $ % ! = = " A C > # > # = = > = # A = = ] ] A = " 文献标识码 !?
表 :! 二元函数极值判定表
< ’ZB 4=
# # < ’ZB c= # < ’ZB 5=
# = = @ A = C A = ] !! 收稿日期 !
万方数据
<4= 极小值
<5= 极大值
失效
不是极值
] C
北 京 印 刷 学 院 学 报
# = = >年
" # 求S 的 极 值 点 E !! 例 !! 设 ScE ZC G\# G ZW! 和极值 "
并且通过变化函数的值域分别绘制出函数的远景 图形 + 近景图形进行观察 " 输入命令 ! ’ ( ! ’ ! ( ! !cK & % 6 W ‘% U T! Z"! " Z>! > P 3 & $ K & % 6 K % 1 , 6 5 Z 4# = ( & $ !! K & % 6 G , 0 Z 4’ Z# =! W #cb 9 % S% 3 3 3 & $ Wcb 9 % S% #! ; & 1 e 1 & & Z 4( % , 0 3 8 3 输出 W 个图 形 ! 分 别 是 远 景 图 !! 近 景 图 #! 去 掉平台的近景图 W" 从图 W 观察可知 J) ! 为极小 Z#! Z"* #! "* () 值点 ! * 不是极值点 " =! = T) : ; =! 利用 K 4 " ( ) C 4 " , 1 4 绘制出等值线来观察极值 N 6 9 0 < 6 1 : -还提供了另外几个表达式作图函 数! 如函数 ; % , 6 % * + K & % 6能 够 绘 制 空 间 曲 面 的 等 值 线图 " 函数的等值线图类似地理 上 的 等 高 线 图 ! 它
驻点的坐标 # 对每一个驻 点 " # 求出二阶偏导 E G =# =$
# # # )S # )S’ 然 后 # 数 <c)S # 对每一个驻 ’c # # Bc E E ) ) G ) ) G
点" # 计算判别式 < 根据判别式 E ’ZB# 的 值 # G =# =$ 结论如表 !’ 的符号进行判别 #
S ( )4 5 , 1 4 " , & ’& .C 4 " ( ) C 4 " , 1 40 & . " 6 4 / ) + + , ’" ) 4 1 ( , ’ .4 $ 3 4 ’ 1 ) $C 4 " ( 0 -&
d 9 , + A , 3a P
" / 0 1 1 , , 5 6 1 6 * 6 0% .7 + 9 1 :; % << * , 1 : 6 1 % ,# 2 34 8 $ / 0 1 1 , = # > = =# ; 9 1 , 2 3!
:! K 4 " ( ) C 4 " , 1 4软件在二元函数的自由极 值教学中的应用
高 等 数 学, 中的重要 !! 多元函数 的 自 由 极 值 是 + 教学内容 # 是教学的一个难点 ’ 由 于 多 元 函 数 的 复 杂性 # 教师只 能 画 出 简 单 函 数 的 图 像 # 大部分的图 只能靠学 生的想 像 能 力 和 文 字 像很难用手工描绘 # 不能像一元函数的极值 那样借 助 函 数 图 像 直 说明 # 观地理解极值的概念 ’ 为此 # 我们利用 N 6 9 0 < 6 1 A 软件讲授这部分内容 # 加强了这部 分教学 内容 的 : 几何直观 # 弥 补 了 学 生 空 间 想 像 能 力 的 不 足# 使多 元函数的自 由 极 值 的 学 习 更 加 直 观 ( 生 动 和 全 面# 改善了教学效果 ’ : ; :! 利用 K 4 " ( ) C 4 " , 1 4 计算二元函数的极值 根据二元函数极值的必要 条 件 和 充 分 条 件 # 求 多元函数极值的步骤可归纳如下 ! 对于多元函数 # 求解正 规方程 组 Sc." E# G$
!! 下 面 通 过 绘 制 例 ! 中 函 数 的 等 值 线 图 来 观 察 极值 " % ! ’ ( ! ’ ! ( ! "c; % , 6 % * + K & % 6 U T! Z"! " Z>! > 3 P ( ! K & % 6 G , 0 Z 4’ Z# =! @ = 3 & $ K & % 6 K % 1 , 6 5 Z 4W = % ! & ; & 0 + U !! #! W! " 3 3 3 3 输出等值线图 ! 见图 "" 观察发现 ! 随着图形灰 度的逐渐加 深 ! 函 数 值 逐 渐 减 小! 图形中明显有两 * 和 () * " 个极小点 # Z#! Z" #! " J) 在多元函数的微积分教学 中 ! 常常会遇到各种 空间立体图形的绘制 ! 这类图形的绘 制 往 往 繁 冗 复 杂! 仅凭 手 工 绘 制 难 以 达 到 观 察 效 果 " 如 果 使 用 则能 N 6 9 0 < 6 1 : - 软件来解 决 所 遇 到 的 图 形 问 题 ! 达到事半功倍的效果 "
! 8 7 0 " / 4 1 " a T 6 + 0 < 0R & * 0% .I 1 , + * , : 6 1 % ,, O1 , . 1 , 1 6 05 0 A P. + 1 0 5+ 0 6 % %I 5 6 + : 6 , OO 1 . . 1 : * & 6 6 %* , O 0 + 5 6 , O J B 9 08 % S 0 + A . * & . * , : 6 1 % , 5% . 5 < I % & : % < * 6 1 , , O3 + 9 1 :8 + % : 0 5 5 1 , . P 8 38 3% N 6 9 0 < 6 1 : -b % . 6 S + 0: ,1 < + % R 06 9 03 0 % < 0 6 + 1 :% I 0 : 6% . 8 2 &S 0 M , 0 5 5 0 5 1 ,5 : 0 6 9 0 5 06 S %8 + 6 5 6 %: % * , 6 0 + : 6 5 6 * O 0 , 6 5 8 #1 1 < 1 , 6 1 % , J? 58 + : 6 1 : 09 58 + % R 0 O ,6 0 : 9 1 , .O A 3 3% R , : 0 O< 6 9 5 6 9 0 5 0M 1 , O 5% . 5 % . 6 S + 0S 1 6 96 9 09 0 & .< * & 6 1 A 8% < 0 O 1 -6 0 : 9 , % & % ,R 1 5 * & 1 U 06 9 0I 5 6 + : 6: % , : 0 6 5, O 3 P: 8 #S & + 1 , : 1 & 0 5 9 1 : 9S 1 & &5 * + 0 & , 9 , : 05 6 * O 0 , 6 5 1 , 6 0 + 0 5 61 , 8 8 P0 < 6 9 5& 0 + , 1 , , O9 0 & 9 0 <6 %I 0 6 6 0 +* , O 0 + 5 6 , O6 9 0 386 6 0 : 9 1 , % , 6 0 , 6, O1 < + % R 06 9 0 1 +I 1 & 1 6 ,< M 1 , 5 0% . 3: 8 P1 3* : % < * 6 0 +5 % . 6 S + 05S 0 & & J 8 !N % % 9 ) & / $ 0 6 9 0 < 6 1 : -b % . 6 S + 0 O R , : 0 O< 6 9 5 6 0 : 9 A %6 1 , , O+ 0 5 0 + : 9 3-
