气体动理论
气体动理论

2.两种不同种类的理想气体,压强相同,温度相同,体积不同, 试
问单位体积内的分子数是否相同?
(答案:相同)
3.两瓶不同种类的气体,分子平均平动动能相同,但气体的分 子数密度不同,试问他们的压强是否相同? (答案:不同)
4.两瓶不同种类的气体,体积不同,但温度和压强相同,问气体 分子的平均平动动能是否相同?单位体积中的分子的总平动 动能是否相同?方均根速率是否相同?(答案:相同,相同,不同)
2. 理想气体的内能包括哪些? 理想气体的内能=所有气体分子动能量的总和;
3. 内能与机械能有什么区别?
机械能可以为零,而内能永不为零。
一摩尔理想气体的内能:
Emol N
i KT i RT
2
2
M千克理想气体的内能: E M i RT i vRT
M mol 2
2
问题:
1.三个容器内分别储有1mol氦气(He),1mol氢气(H2),1mol氨 气(NH3)( 三种气体均 视为刚性分子的理想气体),若它们的 温度都升高 1K , 则三种气体内能的增加分别是多少? (答案:12.5J, 20.8J, 24.9J) 2.写出下列各量的表达式:
(2) 分子沿各个方向运动的机会是均等的,没有任何一个 方向上气体分子的运动比其它方向更占优势。即沿着各 个方向运动的平均分子数应该相等;
(3) 分子速度在各个方向的分量的各种平均值相等。
五、气体动理论的统计方法 (statistical metheds)
用对大量分子的平均性质的了解代替个别分子的 真实性质。对个别分子(或原子)运用牛顿定律求 出其微观量,如:质量、速度、能量等,再用统计的 方法,求出大量分子关于微观量的统计平均值,并 用来解释在实验中直接观测到的物体的宏观性质, 如:温度、压强、热容等。
气体动理论

每个分子的速度指向任何方向的概率是一样的。
∑ni vxi ∑ vx = i ni
i
vx = vy = vz = 0
∑n v2 i xi
∑ v
2 x
=
i
ni
i
v
2 x
=
v
2 y
=
vz2
=
v2 3
二、理想气体压强公式的推导
1. 压强宏观意义
p= F S
F S
2. 气体压强微观意义
气体压强等于气体对单位面积器壁的压力,气体对容器壁 的压力是气体分子对器壁频繁碰撞的总的平均效果。
理想气体的压强∗∗ 温度的微观意义∗∗ 能量均分定理∗∗ 麦克斯韦速率分布律∗∗
§ 理想气体的压强
一、理想气体的微观模型 T不变 PV = C
理想气体:在各种压强下都严格遵守玻意耳定律的气体。 1. 对单个分子的力学性质的假设
分子当作质点,不占体积; 分子之间,分子和器壁之间无相互作用,但可 以通过碰撞交换能量动量 ; 弹性碰撞(能量动量守恒); 分子运动服从牛顿力学。
pV = m RT M
pV =ν ⋅ RT
R为普适气体常数
R = p0Vm,0 = 1.013 × 105 × 22.4 × 10−3
T0
273.15
= 8.31(Jmol⋅K)
若写成 ν = N
NA
N为气体分子总数
N A = 6.023 × 1023 / mol 阿伏伽德罗常量
pV = μ N RT = N R T
εk
=
5 2
kT
E 转动
=
1 2
J
ω2
xx
+
1 2
大学物理气体动理论

气体分子之间的相互作用力产生的势能, 由于气体分子之间的距离非常大,因此气 体分子的势能通常可以忽略不计。
分子动理论的基本假设
分子之间无相互作用力
气体分子之间不存在相互作用的力,它们之间只 存在微弱的范德华力。
分子运动速度服从麦克斯韦分布
气体分子的运动速度服从麦克斯韦分布,即它们 的速度大小和方向都是随机的。
分子碰撞的统计规律
分子碰撞的随机性
01
气体分子之间的碰撞是随机的,碰撞事件的发生和结果都是随
机的。
分子碰撞频率
02
单位时间内分子之间的碰撞次数与分子数密度、分子平均速度
和分子碰撞截面有关。
碰撞结果的统计规律
03
碰撞后分子的速度方向和大小的变化遵循一定的统计规律,可
以用概率密度函数来描述。
热现象的统计解释
大学物理气体动理论
• 引言 • 气体动理论的基本概念 • 气体动理论的基本定律 • 气体动理论的统计解释 • 气体动理论的应用 • 结论
01Biblioteka 引言主题简介气体动理论
气体动理论是通过微观角度研究气体 运动状态和变化的学科。它以分子运 动论为基础,探究气体分子运动的规 律和特性。
分子模型
气体动理论中,将气体分子视为弹性 小球,相互之间以及与器壁之间发生 弹性碰撞。通过建立分子模型,可以 更好地理解气体分子的运动特性。
对未来研究的展望
随着科学技术的发展,气体动理 论仍有很大的发展空间和应用前
景。
未来研究可以进一步探索气体分 子间的相互作用和气体在极端条 件下的行为,例如高温、高压或
低温等。
气体动理论与其他领域的交叉研 究也将成为未来的一个重要方向, 例如与计算机模拟、量子力学和
大学物理-气体动理论
求: (1) 容器的容积,
(2) 漏去了多少氧气?
解: (1)
pv M RT
VM P RT8.21(升)
(2) 设漏气后的压力、温度、质量分别为 p' T' M'
p'V M' RT'
M' p'V0.06K 7 g
RT'
M 0 .1 0 0 .0 6 0 .0 7 K 3 3 g
平衡态: 在不受外界影响的条件下,一个系统的宏观性质不随时间
改变的状态。热动平衡
平衡过程:气体从一个状态变化到另一个状态,其间所经历的
过渡方式称为状态变化的过程.
如果过程所经历的所有中间状态都无限接近平衡状态,
该过程称为平衡过程.
2020/5/2
2
二、状态参量:
1、气体所占的体积 V: m 3
2、压强 P:
总的分子数密度为
n
n i
i
设 dA 法向为 x 轴
dA
一次碰撞单分子动量变化
vi dt
2 mvix
x 在 dt 时间内与dA碰撞的分子数
2020/5/2
ni vix dt dA 斜柱体体15积
dt 时间内传给 dA 的冲量为
dI = 2 mnivix2 dt dA
(vix>0)vx2= Nhomakorabeai
ni
vxi2
第三章 气体动理论
理想气体状态方程
麦克斯韦速率分布律
气体动理论的压强公式 玻耳兹曼分布律
气体动理论的温度公式
能量均分定理
2020/5/2
1
气体动理论

17
§2.1.3理想气体的温度
1.宏观意义:冷热程度,是决定某一系统 与另一系统是否处于热平衡的宏观标志。
2.微观意义:由状态方程可得
pV = N RT NA
状态方程:
p=
N V
R NA
T = nkBT
波尔兹曼常数:
kB
=
R NA
= 1.38 10-23 J
K -1
18
温度的统计意义
p = 2 nω 3
p = nkT
ω = 3 kT 2
此式称为理想气体分子温度公式. 温度的统计意义:
(1)温度是分子平均平动动能的量度,反映无 规则热运动的剧烈程度;
(2)温度是大量分子集体表现,对个别分子 温度没有意义。
相等。
2.气体分子沿各方向运动的概率相等 即分子速度在各方向上分量的各种平均值相
等。
在直角坐标系中有: vx2 = vy2 = vz2
vx2 + vy2 + vz2 = v2
vx2
=
vy2
=
vz2
=
1 v2 3
11
§2.1.2理想气体的压强
1.产生
固体、液体的 :重力原因 气体压强:大量分子不断碰撞的结果。
单个分子碰撞器壁的作用力是不 连续的、偶然的、不均匀的。从 总的效果上来看,分子碰撞对器 壁产生一个持续的平均作用力。
PA=F/SA
12
2 .理想气体压强公式的导出
公式导出 见图:
PA=F/SA
长方形容器内分子总数为N。
设分子质量为m,速率为vx、vy、vz;
第十二章 气体动理论

1 2 v = v 3
2 x
1 ε k = mv2 2
理想气体压强公式: 第十二章:气体动理论
2 p = nε k 3
压强的物理意义
统计关系式 宏观可观测量
2 p = nε k 3
微观量的统计平均值
理想气体的压强公式是力学原理和统计方法相结合得出 的统计规律。
第十二章:气体动理论
理想气体分子平均平动动能与温度的关系
T = 273.15 + t
此外还包含:气体的质量,密度等
表示大量分子集体特征的物理量,可直接测量! 第十二章:气体动理论
微观角度: 研究气体分子的热运动
质量 m 坐标 (x, y, z) 气体分子 的: 精确求解所有分子的运动方程? 不可能! 分子数目太大! 相互作用复杂! 不能直接观测!
v 速度 v
1 3 2 ε k = m v = kT 2 2
i ε = kT 2
分子的平均能量:
i 1 mol 理想气体的内能: E = N Aε = RT 2
第十二章:气体动理论
εk ∝ T
第十二章:气体动理论
方均根速率
1 3 2 ε k = m v = kT 2 2
vrms
3kT 3RT = v = = m M
2
气体分子的方均根速率和质量的平方根成反比
第十二章:气体动理论
注意
热运动与宏观运动的区别: 温度所反映的是分子的无规则运动,它和物体的整体 运动无关,物体的整体运动是其中所有分子的一种有 规则运动的表现. 当温度 T = 0 时,气体的平均平动动能为零,这时气 体分子的热运动将停止。然而,事实上绝对零度是不 可能达到的,因而分子的热运动是永不停息的。
单个分子遵循力学规律:
气体动理论

气体动理论(kinetic theory of gases)是19世纪中叶建立的以气体热现象为主要研究对象的经典微观统计理论。
气体由大量分子组成,分子作无规则的热运动,分子间存在作用力,分子的运动遵循经典的牛顿力学。
根据上述微观模型,采用统计平均的方法来考察大量分子的集体行为,为气体的宏观热学性质和规律,如压强、温度、状态方程、内能、比热以及输运过程(扩散、热传导、黏滞性)等提供定量的微观解释。
气体动理论揭示了气体宏观热学性质和过程的微观本质,推导出宏观规律,给出了宏观量与微观量平均值的关系。
它的成功印证了微观模型和统计方法的正确性,使人们对气体分子的集体运动和相互作用有了清晰的物理图像,标志着物理学的研究第一次达到了分子水平。
9.0气体动理论

温度的数值表示法 ——温标。
3. 温度(T) :
冰点 273.15K, 绝对零度:T = 0 K,
热力学(开氏)温标: 水三相点(气态、液态、固态的共存 状 国际单位:开尔文(K) 态)273.16 K
摄氏温标和开氏温标的关系
4. 热力学第零定律——
t = T-273.15
测温原理
热平衡 :
在不受外界影响的
3kT
v 2 3kT 3RT 1.73 RT
M
M
v 2 1.73 RT M
f(v)
3. d f (v ) 0
3. 最概然速率 (最可几
dv
速率)
vp
2kT
vp 1.41
RT M
O
2RT 1.41 RT
vp
v
M
M
三、三个统计速率 1. 平均速率
v 1.60 RT M
2. 方均根速率
假设要测定中国足球队队员的平均体
重,怎么测?
G G1 G2 Gi G22
22
22 G i i1 22
设系统由N个分子组成,要测量分子
的平均速率v,若测得N个分子的v值分别
为:v1、v2、…vi、…vN ,则v的平均值为:
v v1 v2 vi vN
N
N vi i1 N
如果足球队中有4个人的体重70公斤,
P
n vx2
1 3
n v 2
2 3
n
1 2
v2
2 3
n kt
其中
kt
1 2
v2
称为气体分子的平均平动动能。
§9-6 温度的微观本 质
由理想气体状态方程
p nk T n为单位体积内的分子数
第7章 气体动理论

碰后折回来需用的时间:
2x vx
t vxt 2x / vx 2x
一个分子在 t 时间内碰撞器壁的总冲量:
I1
2mv
x
t
2x / v x
mv
2 x
t
x
(3) N 个分子在 t 时间内
碰撞器壁的总冲量:
IN
N
mv
2 ix
t
x i 1
m x
t
N i 1
v2 ix
y
A1
vy
m
(4) I Ft P F / s
kr
1 2
mvc2x
1 2
mvc2y
1 2
mvc2z
1 2
J yc2y
1 2
J zc2z
1 2
J x c2x
2.能量均分定理(Boltzmann 假设)
t
1 2
mv2
3 2
kT
v
2 x
v
2 y
v
2 z
1 3
v2
1 2
mv
2 x
1 2
m
v
2 y
1 2
mvz2
1 ( 1 mv2 ) 32
1 kT 2
φ
确定刚体转轴的方位: 需要二个自由度(α,β);
β P(x,y,z)
α
γo
X
确定刚体绕转轴转过的角度, Z
需要一个自由度(φ);
刚体位置的确定共需要六个自由度。
3.气体分子模型自由度 ①单原子分子: 如氦原子 He 需要三个平动自由度 i=t=3;
②刚性双原子分子: 如氧气分子
O2
质心需要三个平动自由度;两原子连线方位需要
第四章 气体动理论

§4-1
分子动理论的基本观点
一、物质微观结构的物理图象 1、物质是由大量的微观粒子——原子或分子组 成的; 2、分子在作永不停息的无规则运动; 3、分子之间有相互作用力。 综上所述,一切宏观物体(不论它是气体、 液体、还是固体)都是由大量的原子或分子组 成的;所有分子都在不停的、无规则运动中; 分子之间有相互作用力。这就是关于物质微观 结构的三个基本观点。
(s t )
C2 引力: f1 t , C2、t均 0 r 斥力: f C 1 , C 、s均 0 2 1 s r t:4 ~ 7 s : 9 ~ 13
2、图线
(f—r图线)
三、分子间的势能曲线(Ep—r图线)
1、分子间的势能: dE p fdr
C1 C2 E p fdr ( s t )dr r r C1 C2 s 1 t 1 ( s 1)r (t 1)r
N pV RT NA
p nkT
温度 T 的物理意义
1 2 3 平 m v kT 2 2
1) 温度是分子平均平动动能的量度 平 T (反映热运动的剧烈程度).
2)温度是大量分子的集体表现,个别分子无意义.
3)在同一温度下,各种气体分子平均平动动能均 相等。 注意 热运动与宏观运动的区别:温度所反 映的是分子的无规则运动,它和物体的整 体运动无关,物体的整体运动是其中所有 分子的一种有规则运动的表现.
由于热力学方法的局限性,我们对平衡态下系统内 部的情况不了解,从而对温度和理想 气体的理解 也很肤浅,对气体的压强更是一无所知,因此,为 了全面了解平衡态下的基本热学信息,我们必须用 分子物理学的方法从微观本质上加以认识。
• 气体动理论是统计物理学的基础; • 气体动理论是从微观的观点来研究气体的热学 性质; • 解释气体的温度、压强、热容、内能等的微观 本质; • 建立统计的概念。
气体动理论

1 k m0 v 2 2 3kT 3 RT 2 v T, 3 m0 M k kT 2 2 称为方均根速率 (root-mean-square speed) v
例 . 在273K时: 3 k kT 5.65 10 21 J 2
2
3.53 10 eV
i E RT 2
pV RT
i E pV 2
i E NkT 2
i E RT 2
蓝皮书p50:35
若理想气体的体积为V,压强为p,温度为T,一个分子 的质量为m,/ m . (B) pV / (kT). (C) pV / (RT). (D) pV / (mT).
10-2 理想气体状态方程的微观解释
一 理想气体压强的统计意义
前提: 平衡态, 忽略重力, 分子看成质点 (即只考虑分子的平动); 讨论对象: 同 一种气体,分子质量为 m0 , N…… 总分子数, ……体积, V
N ……分子数密度(足够大), n V
设第i 组分子的速度在 vi vi d vi
一定量某理想气体按pV2=恒量的规律膨胀,则膨胀后 理想气体的温度 (A) 将升高. (B) 将降低. (C) 不变. (D)升高还是降低,不能确定.
把所有分子按速度分为若干组,在每一 组内的分子速度大小,方向都几乎相等。
区间内。
Ni 速度为第 组的分子数密度, i ni V N N i , n ni
压强公式的推导步骤:
i i
器壁
一个分子对器壁的冲量
一组分子对器壁的冲量 各组分子对器壁的冲量
i
dS
x
整个气体对器壁的压强
3 k kT 2 m m R N NA M M k
第2章 气体动理论

按位置的分布是均匀的:
dN N n dV V
包含足够多分子 “宏观小微观大”
每个分子运动速度取向沿任意方向的概率都相等,即分 子速度平方按方向的分布是均匀的:
1 2 v v v v 3
2 x 2 y 2 z
v
2
2 2 2 vx v y vz
2 x
2 ix N i i
, vN 1, x , vN , x
第 i 组的Ni个分子具有相同的速度分量,记为vix: v N1 ,, Ni1 1x v N1 ,, Ni1 2x v N1 ,, Ni x vix 且有 N1 N2 Ni N 或
§2-1 理想气体的压强
道尔顿分压定律
设几种气体储于一密闭容器中,并处于平衡态, 且分子数密度分别为 n1 、n2 、 n3 、 … , 则 混合气体的分子数密度为
n n1 n2
温度相同,故
1 2 ...
混合气体的压强为
p1 p2
2 2 2 p n n11 n2 2 3 3 3
定理——在温度为T 的平衡态下,气体分子每一个自由度
的平均动能都相等,且等于 1 kT。 2 一般地:
在温度 T 的平衡态下,分子能量表达式中任何 一个平方项的统计平均值都等于 1 kT 。 2
§2-3 能均分定理
一个分子的能量,总能写成关于坐标和速度 的平方项之和:
2 1 质心平动动能: m (v x v 2 v z2 ) y
第二章 气体动理论
Kinetic Theory of Gases
本章主要内容
§2-1 §2-2 §2-3 §2-4 §2-5 §2-6 §2-7 §2-8 §2-9 理想气体的压强 温度的微观意义 能均分定理 Maxwell速率分布律 Boltzmann分布律 实际气体等温线 Van der Waals方程 平均碰撞频率和平均自由程 输运过程
气体动理论

2 x
2 y
2 z
1 2
3
二、理想气体的压强公式
对压强的统计解释
气体的压强是由大量分子 在和器壁碰撞中不断给器 壁以力的作用所引起的, 压强是气体分子给容器壁 冲量的统计平均量。
例: 雨点对伞的持续作用。
压强公式的推导:
单位时间内分子a作用在A面上的作用力:
l3 l2 z
y
v a vx A
Fa 2mvx vx 2l
§1 气体的微观图像
一、原子(atom)
“假如在一次浩劫中所有的科学知识都被摧毁, 只剩下一句话留给后代,什么语句可用最少的 词包含最多的信息?我相信,这是原子假说,即 万物由原子(微小粒子)组成.”——费曼
道尔顿确立 了原子概念
原子是化学元素的基本单元
现代的仪器已可以观察和测量原子的大小 以及它们在物体中的排列情况, 例如 X 光 分析仪,电子显微镜, 扫描隧道显微镜等.
引言
气体动理论是从气体分子热运动的观点出发, 运用统计方法研究大量气体分子的宏观性质和统 计规律的科学,它是统计物理学最基本的内容。 本章将根据气体分子模型,研究气体的压强与温 度等宏观性质和分子速率分布规律与能量分布规 律等统计规律,从微观角度揭示这些性质和规律 的本质,同时穿插介绍这些理论的一些应用.
2 x
2 y
2 z
v y
o
vv x
2
2 x
2 y
2 z
v z
12
2 1x
12y
12z
22
2 2x
22y
2 2z
……
N112 N112x N112y N112z N222 N222x N222y N222z
……
气体动理论

三Hale Waihona Puke 、 压 强 推 导上一张 下一张
返回
具有速度 vi 的Ni 个分子作用:
上一张 下一张 返回
上一张 下一张 返回
压强公式的推导过程:
• 对象:理想气体的微观模型。
• 状态:平衡态。
• 方法:个别分子服从力学规律,
•
大量分子服从统计规律。
• 结论:P = n m v 2/ 3
即:
(1) f (v) dN Ndv
f (v)表示在速率v 附近 单位速率间隔内的分子数 占总分子数的比率.
(2) f (v)dv dN N
表示速率在 v~v+dv 区间 内的分子数占总分子数的比 率,即阴影1 面积。
(3) v2 f (v)dv N
v1
N
表示速率在 v1~ v2 区间 内的分子数占总分子数的 比率, 即阴影2 面积。
• Q:系统与外界的热交换。 Q>0表示系统从外界吸热;Q<0表示系统向外 界放热。
• E:系统内能的改变量。 E>0表示系统内能增加(若是理想气体,则 温度升高);E<0表示系统内能减少。
• A:系统对外界的做功情况。 A>0表示系统对外界作正功,如体积膨胀的过 程;A<0表示系统对外界作负功,亦即外界对 系统做功。
不可逆 可逆.
上一张 下一张 返回
有关物质结构与运动规律的 三条基本定理
• 宏观物体有大量微粒组成。 • 分子间存在相互作用力。 • 分子永不停息地无规运动。
上一张 下一张 返回
气体分子运动的特点:
• 看作是惯性支配下的自由运动。 • 分子间存在频繁碰撞。 • 服从统计规律。
气体动理论

0
a vd v Nv0
2 v0
v0
a dv 1 N
2N a 3v0
八 热学
1 N N Nf ( v ) d v a d v av0 2 3 1.5 v0 1 .5 v 0
2 v0 2 v0
a 2 v vf ( v ) d v v dv Nv0 0 0
T ( K),t ( o C)
平衡态
t T 273.15
若某种气体处于热平衡、力学平衡与化学平衡之中, 就说它处在热力学平衡状态。
八 热学
与外界没有能量交换,内部没有能量转换,
也没有外场作用。 气体分子的热运动和相互碰撞永不停息,
在宏观上表现为热动平衡状态——
密度均匀、温度均匀、压强均匀。
M mol N A m
M 代入 pV RT M mol
分子数密度
M Nm
N R p T V NA
N n V
p nkT
R 玻尔兹曼常量 k 1.38 10 23 J/K NA
八 热学 2 理想气体的压强公式和温度公式 分子热运动的统计规律 分子热运动具有无序性与统计性。 气体处在平衡状态时,在容器中密度处处 均匀,因此—— 沿各个方向运动的分子数目相等,分子速 度在各个方向的分量的各种平均值也相等。
8 RT M mol RT 1.60 M mol
八 热学 2)方均根速率2 Nhomakorabeav
0
2
v v 2 f ( v) d v
v
2
3k T m
3RT RT 1.73 M mol M mol
八 热学
3)最概然速率 v p
大学物理 气体动理论

二、 能量按自由度均分定理
1 3 2 W m v kT 2 2
v x v y vz
2 2
2
1 2 v 3
1 1 1 1 1 2 2 2 2 mv x mv y mv z ( mv ) 2 2 2 3 2
1 2 1 2 1 2 1 mvx mv y mvz kT 2 2 2 2
(kT )
(RT )
(m T )
讨论
一瓶氦气和一瓶氮气密度相同,分子平均平动动 能相同,而且它们都处于平衡状态,则它们 (A)温度相同、压强相同。 (B)温度、压强都不同。 (C)温度相同,但氦气的压强大于氮气的压强. (D)温度相同,但氦气的压强小于氮气的压强. 解
Nm k k T T p nkT V m m
M i E R T 2
是温度的单值函数E=f(T)
§3.4 麦克斯韦速率分布律
Maxwells law of distribution of speeds
对于由大量分 子组成的热力学系 统从微观上加以研 究时,必须用统计 的方法 .
小球在伽 尔顿板中的分 布规律 .
单个粒子行为--- 偶然 大量粒子行为--- 必然
Kinetic Theory of Gases
第三章 气体动理论
主要内容
§3-1 气体动理论的基本概念 §3-2 理想气体的压强和温度 §3-3 能量按自由度均分定理 §3-4 麦克斯韦速率分布律 §3-5 气体分子的平均碰撞频率和平均自由程 §3-6 输运过程
热学概述
与热现象有关的性质和规律。
P P2 P3 ... 1
在一定温度下,混合气体的总压强等 于相混合的各种气体的分压强之和。
气体动理论

第四章气体动理论一、基本要求1. 理解理想气体微观模型。
理解理想气体压强、温度的概念及其微观本质。
掌握理想气体压强、温度的公式并会做相应计算。
通过推导气体压强公式,了解气体动理论的基本研究思想和方法。
2. 理解能量均分定理,掌握理想气体内能的概念、公式及有关计算。
3. 了解麦克斯韦速率分布律、速率分布函数和速率分布曲线的物理意义,了解气体分子热运动三种统计速率。
4. 了解玻耳兹曼能量分布律。
二、内容概要(一)统计概念1.理想气体压强(1)压强概念 垂直作用于器壁单位面积上的压力。
(2)压强公式 p=n 32ε=231_v nm 为分子平均平动动能。
(4-1) (3)适用条件 理想气体(大量分子组成),处于平衡态。
(4)微观本质①由大量气体分子对器壁的碰撞所产生,表示单位时间内气体分子作用于器壁单位面积上的平均冲量。
②一定温度的平衡态下,单位体积内的气体分子数(分子数密度n)越多,或分子平均平动动能(-ε)越大,压强就越高。
-n 、-ε为气体分子微观量的统计平均值。
2. 理想气体温度(1) 温度概念 表征系统处于热平衡态的物理量。
(2) 温度公式 -ε=kT 23 (3) 适用条件 理想气体(由大量分子组成)处于平衡态。
(4) 微观本质 反映了大量分子热运动的剧烈程度,是分子平均平动动能的量度。
(二)统计规律1. 能量均分定理(1) 内容要点物质分子每个自由度的平均动能kT 21 每个分子的平均动能 -k ε=kT i 2vmol 理想气体内能 E=v RT i 2 气体自由度 i=()()()⎪⎩⎪⎨⎧刚性多原子分子刚性双原子分子单原子分子653(2) 适用条件. 式 (4-2) (4-3)----任何物质分子,温度为 T 的平衡态。
式 (4-4)----理想气体,温度为 T (室温附近)的平衡态。
2. 麦克斯韦速率分布律(1) 气体速率分布函数f(v)=Ndv dN (4-6) 表示速率v 在附近单位速率区间内的分子分布概率(即分子数占总分子数的比率)。
第六章 气体动理论 (Kinetic theory of gases)

(Kinetic theory of gases)
从分子热运动观点出发,依赖微观 粒子的力学规律,运用统计方法研究气 体分子热运动的宏观性质和变化规律。 寻求宏观量与微观量之间的关系,揭示 气体宏观热现象及其规律的微观本质。
§ 6 . 1 状态、过程与理想气体 States, Process and Ideal gas
•二、气体的状态参量 State parameter of gas • 把描述系统状态的变量称为状态参量。 状态参量分为宏观量与微观量
1. 宏观量 macro variable 从整体上描述系统的状态量,一般可以直接测量。 如 M、V、E 等----可以累加,称为广延量 extensive variable P、T 等----不可累加,称为强度量 intensity variable 2. 微观量 microcosmic variable 描述系统内微观粒子的物理量。 如分子的质量m、 直径 d 、速度 v、动量 p、能量 等。 微观量与宏观量有一定的内在联系。 例如,气体的压强是大量分子撞击器壁的平均效果, 它与大量分子对器壁的冲力的平均值有关。
p nkT
混合气体
n...
p p1 p 2 p 3 ...
• 四、理想气体状态方程
State equation of ideal gas • 1、理想气体:是一种理想化的物理模型。 • 2、理想气体的状态方程:(克拉珀龙方程)
M pV vRT RT M mol
( =M / Mmol : 摩尔数)
3、实际气体:压强不太大(与大气压相比),温 度不太低(与室温相比)的条件下,可近似地看成 理想气体。
• 三、平衡态与平衡过程
• Equilibrium state and equilibrium process • 1、平衡态:在没有外界影响的条件下,系统各个 部分的宏观性质长时间内不发生变化的状态。 (系统与外界没有作功或传热等方式的能量交换) • 2、热动平衡:热力学中的平衡是一种热动平衡, 系统的分子作永不停息的热运动,而且因为碰撞, 每个分子的速度经常在变,但是系统的宏观量不 随时间改变。宏观上表现为平衡态。 • 3、平衡态是一个理想化的概念,实际上不存在完 全不受外界影响的系统,也就不存在宏观性质绝 对不变化的系统。
大学物理第十章 气体动理论

分子间的相互作用力,
f
称分子力。此力为短程力,
引力、斥力视距离而定
斥
力
当 r = r0(r0 10-10 m)时 f = 0
当 r < r0 时 f 为斥力 当 r > r0 时 f 为引力 当 r > 10-9 m 时,分子力可忽略。
o
引 r0
力
r
§6-2气体的状态参量、平衡状态、理想气体状态方程
p
F A1
F l2l3
m l1 l 2 l 3
N
v
2 ix
i 1
1 mN V
v
2 ix
N
1 V
mN
v
2 x
v
2 x
1 v2
3
1
N
mv 2
3V
分子数密度n
理想气体压强公式
p 1 nmv 2 3
p 1 nmv 2 3
2 3
1 n(
2
mv2 )
2 3
得 P M RT Nm RT N R T nkT
V
VN 0 m
V N0
N0m
波尔兹曼常数
由压强公式
p nkT
p
2 3
n
k
k
3 kT 2
可见:从微观角度看,温度是分子
大小的量度,表征大
k
量气体分子热运动剧烈程度,是一统计平均值,对个别分子无
意义。
§6—5 能量按自由度均分原则、理想气体的内能
一、运动自由度:
确定运动物体在空间位置所需要的独立坐标数目,称为 该物体的自由度
第4章气体动理论
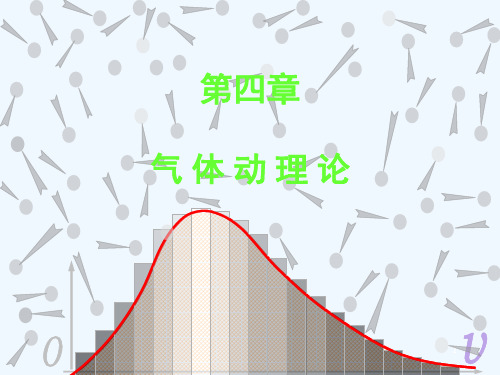
小球每次落入哪个狭槽是不
完全相同的,这表明在一次
实验中小球落入哪个狭槽中 是偶然的。 尽管一个小球落入哪个槽中 是偶然的,但大量小球的分 布规律则是确定的,即遵从
统计分布规律。
7
统计规律:当小球数N 足够大时小球的分布具有统计规律。
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
子,如果分子有 t 个平动自由度,r 个转动自由度,则气体分 子的平均动能为
1 i ( t r ) kT kT 2 2
单原子分子
双原子分子
多原子分子
3 kT 2
5 kT 2
6 kT 2
27
★ 理想气体的内能 实际气体的内能 气体分子热运动的各种形式的动能和势能的总和。 平动动能 分子动能 转动动能 振动动能 分子振动势能
i i
于1,称为概率的归一化条件。
6
小球在伽尔顿板中的分布规律
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
单位: 8.31J · mol-1 · K-1
4
★ 统计规律
一定条件下,大量偶然随机事件的整体具有确定的规律
性,这种规律称为统计规律。
对单个分子运用力学规律,对大量分子求统计平均值, 从而建立大量分子微观量的统计平均值与系统宏观量之 间的关系。这种关系就是所要寻求的统计规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
18
一个系统处于一定的宏观状态时,还可以处于许多 不同的微观状态,且这些微观态还在不断地变化着。
测量描述系统宏观状态的某宏观量M时,由于系统的 微观状态变化,各次实验测得的值不尽相同,若:
系统处于微观态A而出现测量值为MA的次数为NA, 系统处于微观态B而出现测量值为MB的次数为NB….. 实验总次数为:
以阿佛加德罗常数 N0 =6.02×1023计。 热学系统以外的物体称为外界。
例:
若汽缸内气体为系统, 则其它为外界
本课程中热学的主要研究对象——理想气体
10
三. 平衡状态(equilibrium state)
在不受外界影响的条件下,系统的宏观性质 不随时间改变的状态,称为平衡态。 a. 系统处于平衡态时,大量分子仍作无序热运动, 但系统的宏观量不随时间改变——动态平衡
§11.1 气体分子的运动图象 平衡态 状态方程 一. 气体分子的热运动 1. 分子运动的基本概念:
状态参量
一切物体都是由大量分子或原子组成; 分子都在永不停息地作无序热运动; 分子之间有相互作用的分子力。
2. 气体分子的热运动图象
3 1019 个 / cm3 分子的密度:
分子间距很大,有一定的作用力;
dI 2 p n t 理想气体的压强公式 dtdA 3
1 2 其中 t v 2
24
1 2 分子的平均平动动能 t v 是大量分子热运动平动动能的 2 统计平均值
是一个统计规律; 2 p n t 3 p , n , t 是三个统计平均量
压强是统计概念, 是大量分子无规热运动时与器壁不断碰撞的集体 平均效果。 只适用于大量分子组成的系统,对个别分子或 25 少量分子无“压强”概念。
15
§11.2
理想气体的压强
一. 统计规律和统计假设
1. 什么是统计规律和统计方法
大量偶然事件从整体上反映出来的一种规律性。
定义: 某一事件 i 发生的概率为 Pi
Ni Pi lim N N
Ni ——事件 i 发生的次数 N ——各种事件发生的总次数 归一化条件 表演实验:伽耳顿板
16
f ( p,V , T ) 0
理想气体的状态方程:
M pV RT RT M mol
14
六. 准静态过程(quasi-State process)
系统从一种状态变化到另一种状态,其间所经历的 过渡方式称为状态变化的过程
准静态过程——过程所经历的所有中间状态 都无限接近于平衡态 理想气体、平衡态、准静态过程都是理想模型。
i
Pi 1
例: 扔硬币
•统计方法:用统计平均方法从微观量求出宏观量; •统计规律:是大量偶然事件的总体所服从的必然规律
•统计规律所反映的是与某宏观量相关的微观量 的统计平均值; •统计规律的特点:
(1)只对大量偶然的事件才有意义. (2)它是不同于个体规律的整体规律(量变到质变). (3)总是伴随着涨落.
单个分子速率不可预知,但平衡态下大量分子的速率 26 分布遵循确定的统计规律.
二. 分子速率分布的实验测定**
蒸汽源 (蒸气温度固定) 检测器 R
l r
O
抽气
R
L
圆柱体相当于 速率选择器
D 抽气
细槽入口与出口狭缝夹 角
L 给定,只有满足 的分子,才能通过细槽到达D。 v L L l v 2 2 v L ( l r ) r
3
热学的研究方法
1. 微观法.
物质的微观结构 + 统计方法——称为统计物理学 其初级理论称为气体分子运动论(气体动理论) 优点:揭示了热现象的微观本质。 微观量:表征个别分子特性的量
2. 宏观法.
最基本的实验规律逻辑推理——称为热力学。 优点:可靠、普遍。 缺点:未揭示微观本质。 宏观量:实验中测得的表征大量分子集体特性的量
dt 时间内各种速度的分子传给 dA 的总冲量为
dI
n( v x 0 ) 2 2 ( 2v x dtdA)dn dtdA v x dn
n
N 1 2 2 dtdA v x dN dtdA nv x V NN
2 2 1 2 n( v )dtdA n t dtdA 3 3 2
k 1.38 1023 J K 1 —Boltzman常量
v 2
是每个分子质量,
f(v)
面积 f ( v )dv dN N
v
v v+dv
28
速率在v~v+dv内的分子数占总分子数的百分比为:
麦克斯韦 dN 3 / 2 2 kT 2 f (v )dv 4 ( ) e v dv 速率分布率 N 2kT
分子热运动的平均速率约 v 500 m / s
z 1010 次/ 秒 分子的平均碰撞次数约
8
3. 气体分子热运动的微观模型
—— 理想气体分子模型 •(1)分子当作质点,不占体积; (因为分子的线度<<分子间的平均距离) •(2)分子之间除碰撞的瞬间外,无相互作用力。 相邻两次碰撞间的运动是自由运动(忽略重力) •(3)弹性碰撞(动能不变) •(4)服从牛顿力学 (但分子数目太多,且频繁碰撞,各分子运动 情况瞬息万变,故必须用统计方法来研究。)
v 2
摩尔气体常数(普适气体恒量)与Boltzman常量: 23 1 k 1.38 10 J K —Boltzman常量
物质宏观热现象及其有关规律的本质,并确立宏观量
与微观量之间的关系。
5
统计物理学基本观点: (1)宏观量与微观量之间必然存在着应有的内 在联系; (2)虽然个别分子的运动是无规则的,随机的、 但就大量分子的集体表现来看,却存在着 一定的统计规律。
统计物理学是微观理论; 热力学是宏观理论。 二者相辅相成。
v v x v y vz
v v x v y vz
21
二.理想气体的压强公式
压强是大量分子和容器壁不断碰撞结果的宏观表现, 量值上等于单位时间内与器壁碰撞的所有分子作用 于器壁单位面积的总冲量。 对任意形状容器(容积V)中一定质量的处于平衡态 的某种理想气体,把所有N个分子按速度分为若干组, 在每一组内的分子速度大小、方向都差不多。
1. 体积 2. 压强
1atm 1.01325 105 Pa 76cm Hg 1工 程 大 气 压 9.80665 10 Pa
4
3. 温度
宏观上:物体的冷热程度; 微观上:反映物质内部分子运动剧烈程度;
12
温标—温度的分度方法 热力学温标T(K)
摄氏温标 t( 0C )
华氏温标 tF ( F ) 等
v x dt
设每个分子质量为,
速度在 v ~ v dv 的每个分子与dA碰撞一次的动量 改变为 2v x 速度在 v ~ v dv 间,dt 时间内与dA碰撞的分子数 v x dtdA dn , 它们传给dA的冲量为:
斜柱体体积
2 2v x v x dtdA dn 2v x 同的温度
c. 平衡态不一定是均匀态
A C
温度测量
设 A 和 B、B 和 C 分别热平衡, 则 A 和 C 一定热平衡。
B
(热力学第零定律)
11
四. 状态参量(state parameter)
——表示热学系统在平衡态下的宏观性质的物理量
对一定量气体的某一平衡态,用三个状态参 量表征:( p, V, T)
综上:理想气体可看作是自由的、无规则 运动着的弹性分子质点的集合
一般实际气体在压强不太大(与大气压比较)、 9 温度不太低(与室温比较)时,都可近似地看成理想气体。
二. 热学系统(thermodynamic system)与 外界(surroundings)
热学研究的对象——热学系统
它包含极大量的分子、原子:
§ 11.3 麦克斯韦速率分布律 一. 分子速率分布和分布函数
设总分子数N, 分子速率v的可能取值范围:0 ~ , 将分子速率划分为无穷多微小区间, 设速率区间 v ~ v+dv内分子数为 dN
dN —速率在v~v+dv内的分子数占总分子数的百分比 N
dN 令 f (v ) 速率 v 附近单位速率区间内分子数 Ndv 占总分子数的百分比—速率分布函数
2 vx
2 N i vix
N
i
i
20
注意:对任意一个分子i,
vi v xi i v yi j v zi k
2 2 2
v v x , v v y , v vz
2 x 2 y 2 z
v v
2
2
2 2 v2 vx v2 vz2 v 2 v x v 2 vz2 y y
dN N n dV V
dV——体积元(宏观小,微观大)
(3)平衡态时分子的速度按方向的分布是各向均匀的
v x v y vz 0
1 2 v v v v 3
2 x 2 y 2 z
vx
N v N
i i i i
i ix
1 vx dN N 1 2 v x dN N
统计物理学和热力学都是有关热学的理论
4
统计物理学和热力学的关系
二者研究对象相同:物质热现象和热运动规律
但二者的研究方法和出发点不同。 热力学的研究方法:以观测和实验事实为依据,主要
从能量观点出发,分析研究物态变化过程中有关热功 转换的关系和条件。 统计物理学的研究方法:以物质的分子原子结构概念 和分子热运动概念为基础,用统计方法,解释与揭示
, 相应于一定的,通过细槽的分子速率在 v v v区间内 改变,可让不同速率区间的分子通过细槽,测D上 27 金属层的沉积厚度,就可测气体分子速率分布规律。
