大学物理基础学(习岗)第二章 气体动理论 能量均分定理
大学物理温度和气体动理论-2(清华大学出版社

能量按自由度均分定理:
在温度 T 的平衡态下,物质(气体、液体和
固体)分子的每一个自由度的平均能量都相
等,而且都等于
1 2
kT
。
11
推论:气体平衡态时,分子任何一自由度的平均能量
相分等子,的均平为均能12 量kT :——( 能i 量k 均T 分定理()i tr)
2 单原子分子: i3(t3,r0) 3 kT
17.5 能量均分定理
一、自由度 二、能量按自由度均分定理 三、理想气体的内能
1
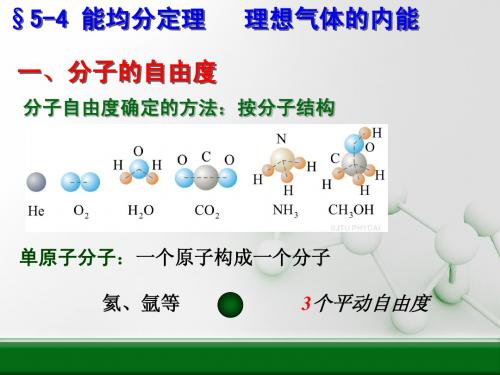
一、自由度 ( i )
确定一个物体的空间位置所需要的独立坐标数。 质点的自由度 在空间自由运动的质点: 三个独立坐标 自由度 i =3
在曲面上运动的质点:
二个独立坐标 自由度 i =2
质点沿直线或曲线运动: 一个独立坐标 自由度 i =1
v
L
2
(3) 沉积在检测器上相应的金
属层厚度必定正比相应速率下
的分子数
19
模拟装置:
20
氧气分子在273K时的分布情况 N
Nv
速率区间 分子数的百分比
100以下
1.4
100~200
8.1
200~300
16.5
300~400
21.4
N
400~500
20.6
Nv
500~600
15.1
600~700
·分布的概念
例:学生人数按年龄的分布
16
年龄
人数按年龄 的分布
人数比率按 年龄的分布
15 ~16 2000 20%
17 ~ 18 3000 30%
19 ~20 4000 40%
21~22 1000 10%
大学物理课件-能量均分定理

摩爾數
3
M3 M mol3
0.289 40
0.007
1mol 空氣在標準狀態下的內能
E
i1 2
1RT
i2 2
2RT
i3 2
3
RT
1 2
(i11
i2 2
i3 3 )RT
1
(5 0.789 5 0.208 3 0.007) 8.31 273
2
5.68103 J
練習十四
t kT 2
r kT 2
s kT 2
總動能 = 平均平動動能 + 平均轉動動能 + 平均振動動能
E t kT r kT s kT ?
222
為什麼均分到各自由度所對應的運動能量都是KT/2呢?
答:主要是分子不斷碰撞以達到平衡態的結果。
三、理想氣體的內能
1、內能:氣體分子各種形式能量的總和。
包括分子平動動能+轉動動能+振動(動能、勢能)
1例5如–:8氫氣多(普H2勒)在效高应溫下兩氫原子之間第就十有五章 机械波
振動,氯氣(Cl2)在常溫下便有振動。 這時可以看作由兩質點組成的彈性諧振子
對雙原子分子----6個自由度(加了 確定兩原子之間相對位置的自由度)
對多原子系統(N3)
3個平動自由度(t)
3N個自由度
3個轉動自由度(r)
(3N-6)個振動自由度(s)
例1 貯存有氮氣的容器以速度100米/秒運動。 若該容器突然停止,問容器中溫度將升多少?(假
設無能量損耗) 已知: v 100m / s
i 5 28103 kg / mol 求: T ?
解:依能量守恆,氮氣的宏觀動能將轉化為其 內能。
1 2
Mv 2
大物课件-均能分定理
解: 设 v 500ms1 , dv 1ms1
题目要求的是速率在v—v+dv内的分子数dN,而
dN NfБайду номын сангаас(v)dv
P 1.013 10 25 3 n 2.7 10 m 23 kT 1.38 10 273.15
5
M mol 28 10 3 26 m 4.65 10 kg 23 NA 6.022 10
四. 气体的三种统计速率
(1)最概然速率: 速率分布函数 f (v)中的极大值对应 的分子速率 v p 。
极值条件
m f (v) 4 e 2kT
2
d f (v ) 0 dv 3
mv
2 2 kT v 2
vp
2 kT 2RT 2RT 1.41 RT mN A M mol M mol m
立坐标;
( x, y, z )
2:再确定H原子还需要1个角度
x
y
6自由度= 5+1= 3 平动自由度+ 2 转动自由度+ 1 转动自由度
二. 能量按自由度均分定理
椐理想气体温度公式,分子平均平动动能与温 度关系为
1 3 2 k mv kT 2 2
2 z 2
v v v v , v2 v2 v2 v x y z 3 1 1 1 1 2 2 2 mvx mv y mvz kT 2 2 2 2
2 x 2 y
2
分子在每一个自由度上具有相等的平均平动动 能,其大小等于 1 kT 。 2
在温度为T 的平衡态下,物质(气体、液体、 固体)分子的每一个自由度都具有相等的平均动能, 1 其大小等于 kT 。
大学物理课件-能量均分定理
3 kT 2
3 1.38 1023 273 J 2
5.6 1021J
分子的平均轉動動能:
2 kT 1.38 1023 273 J 3.7 10 21 J
2
(3)單位體積內的分子數:n p
kT
Ek
n
3 2
kT
3 2
p
3 2
0.011.013 105 J
1.5103 J
(4)根據內能公式
E m i RT 0.3 5 8.31 273J 1.7 103 J
M2
2
例2 體積為2×10-3m3的剛性雙原子分子理想氣體,其內能
為6.75×102J.(1)求氣體的壓強; (2)設分子總數為5.4×1022個,
求分子的平均平動動能和氣體的溫度.
解: (1)
E m i RT M2
pV m RT
結論:
一定量理想氣體的 內能僅取決於T
理想氣體的內能只是溫度的單值函數
例1. 容器內有某種理想氣體,氣體溫度為273K,壓強為0.01 atm ( 1atm = 1.013×105 Pa ),密度為1.24×10-2 kg·m-3。試 求:(1) 氣體的摩爾品質,並確定它是什麼氣體;
(2) 氣體分子的平均平動動能和平均轉動動能各是多少;
為 kT 2 。
分子平均動能:
k
i 2
kT
單原子分子: i 3
雙原子分子: 多原子分子:
i5
i6
能量均分是統計結果
“i”為分子自由度數
3 k 2 kT
5
k
kT 2
6 k 2 kT
能量均分定理是分子間頻繁碰撞的必然結果
能量均分定理不僅適用於氣體,也適用於液體和固體,
大学物理:2气体动理论

4
2、关于分子集体运动的统计假设 (1)通过碰撞分子速度不断变化
(2)无外场时,平衡态分子按位置均匀分布
n
dN dV
N V
(3)平衡态分子速度取向各方向等概率
vx vy vz 0
v
2
x
v
2
y
vz2
1 3
v
2
5
二、理想气体压强公式的推导
平衡态 忽略重力 分子看成质点
kT。
13
一、气体分子的自由度(degree of freedom) 力学对自由度的定义:确定物体空间位置的
独立坐标的数目。
这里,只考虑那些对能量有贡献的自由度。
分子能量表达式中平方项的数目与自由度有关。
1、单原子分子(如 He,Ne)
质点,只有平动自由度 t 3 , (x, y, z)
能量表达式中包括 3 个平方项。
热学
Heat
第2章 气体动理论
2005年秋季学期 编
目 录 △:自学 §2.1理想气体的压强
【演示】气体压强模拟 §2.2 温度的微观意义 §2.3 能量均分定理 §2.4 麦克斯韦速率分布律
【演示】伽尔顿板 速率分布
△§2.5 麦克斯韦速率分布律的实验验证 §2.6 玻耳兹曼分布 能量均分定理的证明(补充)
△§2.7 实际气体等温线
2
§2.8 范德瓦耳斯方程 §2.9 气体分子的平均自由程 △§2.10 输运过程 【演示】空气粘滞(卧式转盘)
3
§2.1 理想气体的压强 【演示】气体压强模拟
一、理想气体的微观假设
1、关于每个分子力学性质的假设
(1)质点 (分子线度<<分子间平均距离) (2)遵从牛顿力学规律 (3)除碰撞瞬间,分子间、分子与器壁间无相
大学物理(12.4.1)--能量均分定理理想气体内能

一、自由度力学中要确定一个物体在空间的位置所需要的独立坐标数目,叫做这个物体的自由度。
在热力学中一般不涉及原子内部的运动,仍将原子当作质点而将分子当作是由原子质点构成的。
一个要确定一个自由运动质点的空间位置需要3个独立坐标,因此单原子分子的自由度是3,即它有3个平动自由度。
对于刚性(原子间的相对位置不变)双原子分子气体,可看作两个原子(质点)被一条直线连接,需要用3个坐标确定其质心的位置,再用2个坐标确定其连线的方位,因此刚性双原子分子气体的自由度为5。
对于刚性多原子分子,具有3个平移自由度和3个转动自由度,总自由度为6。
二、能量按自由度均分定理1.能量按自由度均分定理理想气体分子平均平动动能 kT k 23=ε 222221212121z y x k v m v m v m v m ++==ε 又 222231v v v v z y x === 有 kT v m v m v m z y x 21212121222===这表明,气体分子沿x 、y 、z 三个方向的平均平动动能都相等,且都等于kT /2。
因为在温度公式中的分子是看作质点的,它只有三个自由度,而这个结果说明,每个分子的平均平动动能是均匀地分配给每个自由度,即每个自由度都均匀地分配了kT /2的能量。
这个现象可以这样解释:气体平衡态的建立和维持,是靠分子无规则运动和频繁碰撞实现的,在碰撞过程中,能量可以从一个分子传到另一个分子,也可以由一种运动形式转化成另一种运动形式,也可以从一个自由度转移到另一个自由度,这些转变是无规则的,但总的趋势是各种形式的平均能量趋于相等,这一结论是否可以推广到转动和振动上呢?经典统计物理已经证明了这一点:在温度为T 的平衡状态下,分子的每一个自由度上都具有相同的平均能量,其大小都为kT /2。
2.说明:1)能量均分定理是统计规律,是大量分子的整体表现。
对单个分子而言,分子的能量并不一定是均分分配的,但由于分子间的相互碰撞,在相互碰撞中分子可以交换能量;对于某一自由度来说,其上的能量也不一定均匀的,但由于分子的无规则运动和分子间的相互碰撞,使得在各个自由度上的能量不断“搅拌”,最后达到均匀。
大物 2 气体动理论

1 理想气体的微观模型
(1)分子可视为质点; 线度
9 r 10 m , d r ; 间距
d 10
10
m
(2)除碰撞瞬间, 分子间无相互作用力; (3)弹性质点(碰撞均为完全弹性碰撞); (4)分子的运动遵从经典力学的规律 .
1
2. 统计规律性
对于由大量分子组成的气体,虽然每个分子的运动 遵守动力学规律,但因分子间频繁的碰撞,使得单 个分子的运动具有偶然性。正是单个分子的运动的 偶然性,才使大量分子的整体出现了规律性,这种 规律性具有统计平均的意义,称统计规律性。 对大量分子组成的气体系统的统计假设 (1)气体处在平衡态时,分子在容器中的空间分布 平均来说是均匀的
i 5 1 5 6 由E vRT , EO2 RT RT , EH 2O RT 3RT , 2 2 2 4 2 5 5 3 则E EH 2 EO2 EH 2O ( 3) RT RT 2 4 4
E 100% 25% E H 2O
24
v v v
2 x 2 y
2 z
v v v v
2 2 x 2 y
2 z
1 2 v 3
4
3、理想气体压强公式
设 n :分子数密度
ni 单位体积内速度为 vi 的分子数
m :分子质量
i dt 时间内速度为vi 的分子撞到dS 面上的个数为:
n ni
ni vix dtdS
1 i k (t r s )kT kT 2 2 1 每个振动自由度上均分有 的振动势能
2 kT
18
1 1 k s kT (t r 2 s )kT 2 2
能量均分定理

3、理想气体的内能
气体内能 = 分子各种运动形式的动能 + 分子间相互作
用的势能
无相互作用势能 理想气体:分子间相互作用力忽略不计, 1 mol 理想气体的内能
i i E0 N A ( kT ) RT 2 2
质量为 m ,摩尔质量为 M 的理想气体的内能
m i E RT M 2
m i E RT M 2
(T1 , T2 ) K dl (T ) dT
此电流过程K作正功 吸热——转化成电势能
此电流过程K作负功
电势能降低——放热
汤姆孙效应是热——电转换效应 可逆(不同于焦耳热) (T)与材料的性质有关 用同种金属,只依靠汤姆孙电动 势,也不能在闭合回路内建立恒定 电流。
即:理想气体的内能只与状态参量 — 温度有关,是温度 T 的单值函数。
单原子分子
m 3 E RT M 2
m 5 E RT M 2
刚性双原子分子
刚性多原子分子
m 6 E RT M 2
例: 摩尔数相同的氧气和水蒸气气体(视为理想气体),如
果它们的温度相同,则两气体
A. 内能相等;
B. 分子的平均动能相同; C. 分子的平均平动动能相同; D. 分子的平均转动动能相同。
3 相等。换言之,气体分子的平均平动动能 kT 均匀分配到 2 1 每个平动自由度上,每个平动自由度上分到的能量为 kT 。 2
上式说明: 分子沿 x, y, z 三个方向运动的平均平动动能
上述结论推广到转动自由度上,即
温度为T的平衡态下,气体分子每一个自由度(包括平动 自由度和转动自由度)都具有相同的平均动能,其大小都等
—— 1 mol 气体的内能
气体动理论第2讲——理想气体的压强 温度和能量均分定理

fx
m l1
i 1
N
2 ix
6
N 1 N 2 2 压强 Px ix m ix . V N i 1 l 2 l 3 l 1 l 2 l 3 i 1 N 1 N 2 2 V l 1 l 2 l 3 , n , x ix . V N i 1
1 2 , 3
2 x 2 y 2 z
4
2、理想气体压强公式的推导
设容器边长为 l 1 、 和 l 3 , l2 B 内有 N 个质量同为 m 的气体分子。
Y
O X 第 i个分子以 i与 A 面碰,速 l3 l1 度变为 i , Z 完全弹性: ix ix , iy iy , iz iz 第 i 个分子碰 A 一次,给予 A 的冲量: mix 2
思考: 道尔顿分压定律
1 1 P P1 P2 P1 P 2 2 2 1 ( P1 P 2) ??? 2
19
作
业
题: 、8.7 、8.9
习题8.6 预习内容:
8.4 — 8.8 复习内容:本讲
20
1 单个分子的平均总能量: (t r 2 s )kT 2
12
3、理想气体的内能
热力学系统的内能 E = 分子热运动能量 + 分子间势能。 不考虑系统中的化学能和核能。 理想气体:
1 E N A N A (t r 2s)kT 2 M 1 (t r 2 s) RT . 2
P:宏观量;
k 、 2: n、
微观量的统计平均值;
压强是大量分子对器壁碰撞的统计平 均的结果,是对大量分子就空间、时间求平均。
能量均分定理

能量均分定理能量均分定理1能量均分定理2理想气体的内能2t 12m ε=v kT 23=222212121z y x m m m v v v ==kT 21=2kT 在温度为T 的平衡态下,物质(气体、液体和固体)分子的每一个自由度都具有相同的平均动能,其值为这一结论称为能量按自由度均分定理。
12kT 一个分子的平均平动动能为一、能量均分定理(Theorem of equi-partition ofenergy )(1) 能量按自由度均分是大量分子统计平均的结果,是分子 间的频繁碰撞而致。
说明(3) 若某种气体分子具有t 个平动自由度和r 个转动自由度, s 个振动自由度,1()2t r s kT ++则每个气体分子的平均总动能为每个气体分子的平均势能为 ,2s kT 因此(2) 一般也适用液体和固体。
1(2)22i t r s kT kT ε=++=一个气体分子的平均总能量为对于刚性分子(常温)0s =1()2t r kT ε=+二、理想气体的内能理想气体的内能:气体内所有分子的动能和分子内原子间振动势能的总和。
1mol 理想气体的内能为 质量为m 、摩尔质量为M m 的理想气体的内能为m 2m i U RT M =m A A 22i i U N N kT RT ε==⋅=说明一定质量的理想气体内能完全取决于分子运动的自由度数和气体的温度,而与气体的体积和压强无关。
对于给定气体,i 是确定的,所以其内能就只与温度有关,这与宏观的实验观测结果是一致的。
焦耳定律单原子分子气体 ,32V m C R =双原子分子气体 ,52V mC R =多原子分子气体 ,3V m C R=Ø理想气体的摩尔热容理想气体的定体摩尔热容为,d d 2m V m U i C R T ==2m i U RT =理想气体的摩尔内能为在温度为T 的平衡态下,物质(气体、液体和固体)分子的每一个自由度都具有相同的平均动能,其值为这一结论称为能量按自由度均分定理。
能量均分定理理想气体内能

要3个平动自由度, 确定连线, 要2个转动自由度;确定沿连线的简谐振动,
要1个动能和1个势能自由度,所以共有7个自由度。
非刚性双原子分子的能量: kt kr kv
•
多原子气体分子(原子数n3)
C
刚性: 6个自由度(3个平动自由度, 3个转动自由度);
非刚性:有3n个自由度,其中3个是平动的,3个是转动的,其 余3n-6是振动的。
教程
二 能量均分定理(玻耳兹曼假设) 气体处于平衡态时,分子任何一个自由
度的平均能量都相等,均为 1 kT ,这就是 能量按自由度均分定理 . 2
分子的平均能量 i kT
2
5
物理学
7-5 能量均分定理 理想气体内能
教程
三 理想气体的内能
1.气体的内能 理想气体的动能、振动势能、分子间相互作用势能的和
刚性双原子气体
Emol
5 2
RT
6
刚性多原子气体 Emol 2 RT 6
物理学
7-5 能量均分定理 理想气体内能
教程
例 设有一恒温容器,其内储有某种理想
气体,若容器发生缓慢漏气,问:
(1)气体的压强是否变化?为什么? (2)容器内气体分子的平均平动动能是否变化? 为什么?
(3)气体的内能是否变化?为什么?
p(2V)=(v1+v2)RT
解得:
T p1 p2 p1 p2
T1 T2
9
物理学
7-5 能量均分定理 理想气体内能
教程
例:水蒸汽分解为同温度的氢气与氧气,即
H 2O
H2
1 2
O2
求:此过程中内能的增量(不记振动自由度)
解:H2O,O2,H2分子的自由度分别为 6,5,5
能量均分定理

在重力场中气体分子的密度n随高度 的增加按指数而减小。 在重力场中气体分子的密度 随高度Z的增加按指数而减小。 随高度 的增加按指数而减小 分子的质量m越大 越大, 的减小就越迅速, 分子的质量 越大,重力的作用就越显著 ,n的减小就越迅速, 的减小就越迅速 气体的温度越高,分子的无规则运动越剧烈, 的减小就越缓 气体的温度越高,分子的无规则运动越剧烈, n的减小就越缓 慢。
鞍山科技大学 姜丽娜 8
§2.6 玻尔兹曼分布律 重力场中粒子按高度的分布 1. 玻尔兹曼分布律 玻尔兹曼把麦克斯韦速率分布律推广到气体分子在任意力 场中运动的情形 。 当气体处于平衡状态时,在一定温度下 在速度分布间隔 当气体处于平衡状态时 在一定温度下,在速度分布间隔 在一定温度下
和坐标分布间隔
鞍山科技大学 姜丽娜 5
三、理想气体的内能 问题: 问题: 1. 气体的内能包括哪些? 气体的内能包括哪些? 气体的内能=气体分子的总能量 气体的内能 气体分子的总能量 + 分子间相互作用势能 2. 理想气体的内能包括哪些? 理想气体的内能包括哪些? 理想气体的内能=所有气体分子各种运动能量的总和 理想气体的内能 所有气体分子各种运动能量的总和 3. 内能与机械能有什么区别? 内能与机械能有什么区别? 机械能可以为零,而内能永不为零。 机械能可以为零,而内能永不为零。 一摩尔理想气体的内能
7
);
摩尔气体分子的总转动动能( ⑷1摩尔气体分子的总转动动能 摩尔气体分子的总转动动能 摩尔气体的内能( ⑸1摩尔气体的内能 摩尔气体的内能 )。 。
鞍山科技大学 姜丽娜
3.有一个处于恒温条件下的容器 其内贮有 有一个处于恒温条件下的容器,其内贮有 某种理想气体, 有一个处于恒温条件下的容器 其内贮有1mol某种理想气体 某种理想气体 若容器发生缓慢漏气,试问容器内气体分子的平均平动动能是 若容器发生缓慢漏气 试问容器内气体分子的平均平动动能是 否改变?气体的内能是否改变 气体的内能是否改变? 否改变 气体的内能是否改变 (答案: 不变 变) 答案 不变,变 4.两个容器中分别贮有理想气体氦和氧,已知氦气的压强是氧 两个容器中分别贮有理想气体氦和氧, 两个容器中分别贮有理想气体氦和氧 气的1/2,氦气的容积是氧气的 倍。试问氦气的内能是氧气内能 氦气的容积是氧气的2倍 气的 氦气的容积是氧气的 的多少倍? 的多少倍 (答案:3 /5倍) 答案 倍 5.质量相等的的理想气体氧和氦 分别装 在两个容积相等的容 质量相等的的理想气体氧和氦,分别装 质量相等的的理想气体氧和氦 器内,在温度相同的情况下 在温度相同的情况下,氧和氦的压强之比为 ;氧 器内 在温度相同的情况下 氧和氦的压强之比为 氧 ;氧和氦内能之 氧和氦内能之 分子和氦分子的平均平动动能之比为 比为_________. 比为 (答案 1:8; 1:1; 5:24) 答案: 答案
6气体动理论-2能量均分
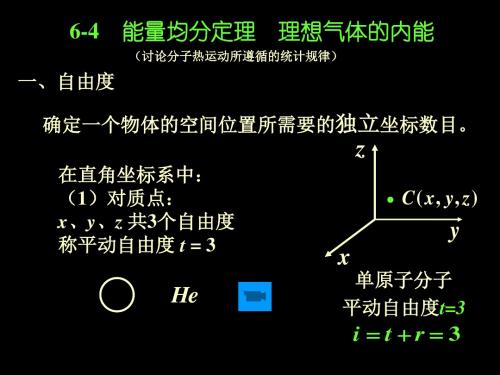
3
3
3 3 M 28 . 9 10 1 % 0 . 289 10 kg Ar质量 3
M3 0.289 摩尔数 n3 0.007 M mol 3 40 1mol空气在标准状态下的内能
i3 i1 i2 E n1 RT n2 RT n3 RT 2 2 2 1 ( i1 n1 i2 n2 i3 n3 )RT 2
6 kT 2
k 5 2 kT
分子平均动能按自由度均分的原则是统计规律
(1)分子平均平动动能 t 按自由度均分 (2)分子平均动能 k 按自由度均分
能量 (气体的内能) 按自由度均分原理 气 体 内 能 分子平均动能的总和(平动、振动、转动)
i k kT 2
19
原子间振动平均位能的总和(对理想气体,忽略)
在标准状态下,几种气体分子的平均自由程
气体 氢
7 10
氮
氧
7
空气
7
(m ) 1.13 10
d (m )
0.599 10 3.10 10
0.647 10 2.90 10
7.0 10
8 10
2.30 10
10
10
3.70 10
注意:气体容器线度小于平均自由程计算值时,实际平均 自由程就是容器线度的大小。
6-4
一、自由度
能量均分定理
理想气体的内能
(讨论分子热运动所遵循的统计规律)
确定一个物体的空间位置所需要的独立坐标数目。
z
在直角坐标系中: (1)对质点: x、y、z 共3个自由度 称平动自由度 t = 3
C ( x, y, z )
y
x
单原子分子 平动自由度t=3
第2章气体动理论

第2章气体动理论♦本章学习目标了解:玻耳兹曼分布率;范德瓦耳斯方程和输运过程。
理解:理想气体的压强,温度的微观意义;能量均分定理,麦克斯韦速率分布律及其统计意义;麦克斯韦速率分布律的实验验证,实际气体等温线;气体分子的平均自由程的概念。
掌握:理想气体的压强,能量均分定理,麦克斯韦速率分布律及其统计意义;实际气体等温线;气体分子的平均自由程的概念。
♦本章教学内容1、理想气体压强公式2、温度的微观意义3、能量均分定理4、麦克斯韦速率分布律5、麦克斯韦速率分布律的实验验证*6、玻尔兹曼分布率♦本章重点压强和温度的微观实质和意义、理想气体的内能、速率分布函数以及理想气体平衡态的特征速率等。
♦本章难点压强和温度的微观实质和意义速率分布函数的物理意义以及相关的计算2.1 理想气体的压强一、理想气体模型1.关于单个分子的力学性质的假设在宏观上我们知道,理想气体是一种在任何情况下都遵守玻意耳定律、盖-吕萨克定律和查理定律的气体。
但从微观上看什么样的分子组成的气体才具有这种宏观特性呢?气体分子的运动是肉眼看不见的,所以理想气体的微观模型是通过对宏观实验结果的分析和综合提出的一个假说。
通过这个假说得到的结论与宏观实验结果进行比较来判断模型的正确性。
通过前人多年的努力,我们现在知道理想气体的微观模型具有以下特征:(1 )分子与容器壁和分子与分子之间只有在碰撞的瞬间才由相互作用,其它时候的相互作用可以忽略不计。
(2)分子本身的体积在气体中可以忽略不计,即对分子可采用质点模型。
(3 )而分子与容器壁以及分子与分子之间的碰撞属于牛顿力学中的完全弹性碰撞。
实验证明,实际气体中分子本身占的体积约只占气体体积的千分之一,在气体中分子之间的平均距离远大于分子的几何尺寸,所以将分子看成质点是完全合理的从另一个方面看,对已达到平衡态的气体如果没有外界影响,其温度、压强等态参量都不会因分子与容器壁以及分子与分子之间的碰撞而发生改变,气体分子的速度分布也保持不变,因而分子与容器壁以及分子与分子之间的碰撞是完全弹性碰撞也是理所当然的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
R 8 . 314 J mol
1
K
1
解:已知条件,把这些气体看成理想气体刚性分子, He为单原子分子,自由度i=3, i H2,N2为双原子分子,自由度i=5, E0 RT 2 NO2为多原子分子,自由度i=6, 温度T=273 K,
各种气体内能分别为: He气体: H2,N2: NO2:
E E 2 E1 M i
2
R T 2 T1
i 2
( P2V 2 P1V 1 )
PV
M
RT
已知系统从初态(p1V1T1) 变 化 到 末 态 (p2V2T2) , 内能的变化:
补充例题:当温度为0C时,分别求1 mol的氦(He),氢(H2), 氮(N2)和二氧化氮(NO2)等气体的内能。当温度升高1 K时, 内能各增加多少?
E0 3 2 5 2 6 2 RT RT RT 3 2 5 2 6 2 8 . 31 273 6 . 81 10
3
8 . 31 273 8 . 31 273
3 . 40 10 5 . 67 10
3
J
E0 E0
3
J
J
平动自由度 t 3 转动自由度 r 0 总自由度 i t r 3 0 3
x
z
P (x , y, z )
o
y
2.双原子分子气体 例如:氢气(H2)、氧气(O2)等为双原子分子 气体。其模型可用两个刚性质点模型来代替。 平动自由度 t 3 转动自由度 r 2 总自由度 i t r 3 2 5 3.多原子分子气体
E0
6 2
J
补充例题2 : 2升的容器中盛有某刚性双原子分子理想气体,在 常温下,压强为1.5105 Pa,求该气体的内能?
E M i RT
2
M
E
i 2
PV
PV
i 2
RT
5 2
E
PV
1 . 5 10 2 10
5
3
7 . 5 10
2
如果气体分子具有i个自由度,则每个分子的总平均动 i 能为: 23 kT k 1.38 10 J / K
2
推广之,气体分子有t个平动自由度、r个转 动自由度、s个振动自由度,则分子的平动、转动、 振动动能分别为:
t 2 kT , r 2 kT , s 2 kT
气体分子的平均总动能为: t r s kT
例如: 物体沿一维直线运动,最 少只需一个坐标,则自由度数为1 轮船在海平面上行驶,要描 写轮船的位置至少需要两维坐 标,则自由度为 2。
x
但对于火车在轨道上行驶时 自由度是多少呢?自由度是 1, 由于受到轨道限制有一维坐标 不独立。
飞机在天空中飞翔,要描写 飞机的空间位置至少需要三维 坐标,则自由度为 3。
自由运动的刚体有:三个平 动自由度,三个转动自由度,共 6个自由度.
2、理想气体分子自由度
理想气体刚性分子的自由度为:分子的平动、转动自 由度之和。(刚性:组成分子的原子之间无相对位置变化) 气体分子的自由度依分子的结构不同而不同。
1.单原子分子气体 例如:He、Ne、Ar。其模型可用一个质点来代替。
内能的增量: E
i 2
RT
RT 5 2 3 2 8 . 31 1 20 . 8 J 8 . 31 1 25 8 . 31 1 12 . 5 J
He气体:
H2,N2: NO2:
E0 E0 5 2 6 2
3 2
RT RT
(J)
2. 体积V=1L,压强p=105Pa的单原子气体分子的内能 为( )
B.150 J;
1)该定理是统计规律,只适用于大量分子组成的系统。 2)微观上是由于大量分子无规则碰撞的结果。 由于分子的激烈碰撞(几亿次/秒),使平动动能 与转动动能不断转换, 平动动能 转动动能
使平动动能与转动动能达到相同,即每个自由度上也
平均分配了kT/2能量。
(二)、理想气体的内能
1. 实际气体的内能
气体内能:所有气体分子 的动能和势能的总和。
刚性双原子分子气体: E 刚性多原子分子理 想气体,它的内 能只是温度的函 数而且与热力学 温度成正比。
E
RT
2
当温度变化dT时 dE
i 2
RdT
说明: 理想气体的内能E 为状态量
E
M i
2
RT
对一定质量的理想气体,内能由自由度和热力学温度共 同决定。 如果分子的自由度在状态变化过程中保持不变,则内能 只与温度有关。 由于温度是状态量,所以理想气体的内能是状态量,为 温度的单值函数。
x
z
o
y
例如:二氧化碳气体(CO2)、水蒸气(H2O)、甲 烷气体(CH4)等为多原子分子气体。其模型可用多 个刚性质点来代替。 平动自由度 t 3 转动自由度 r 3 总自由度 i t r 3 3 6
实际上,双原子分子和多原子分子都是非刚性的,分 子内原子的相对位置会发生变化,存在振动自由度。
双原子分子有一个振动自由度;
多原子分子(设原子数为n)最多可以有3n个自由度,其中3个 是平动、3个是转动,其余的3n-6个都是振动自由度。
理想气体分子的自由度为分子的平动、转动和振动
自由度之和。
3、能量按自由度均分定理
在温度为T的热平衡系统,物质(气体、液体和 等概率假设:在热运动中,任何一种运动形式都不 固体)中分子的每一个自由度都具有相同的平均动能, 会比另一种运动更占优势,(平动、转动、振动)各 且等于kT/2。这就是能量按自由度均分定理,简称能 种运动形式机会均等。 量均分定理。
内能——气体中所有分子各自由度的动能(平动、转 动、振动)与分子内部原子间的相互作用势能(振动 势能),还包含分子间的相互作用势能。
2. 理想气体的内能
由理想气体的微观模型可知,理想气体分子间没 有相互作用势能,故其内能为所有理想气体分子的总 平均动能和分子内部势能之和。 3. 常温下,理想气体刚性分子的自由度为i=t+r,忽 略了分子内部的振动动能和势能,则每个分子的平均 i 1 总能量为平动动能和转动动能之和:
§2-6 能量均分定理 理想气体的内能
分子的无规则热运动:分子作为质点,仅考虑分子 的平动; 实际上,一般分子具有:平动、转动、原子振动; 现讨论分子热运动的能量所遵循的统计规律;
内能
(一).能量按自由度均分原理
1.自由度
自由度是描述物体运动自由程度的物理量。
在力学中,自由度是指决定一个物体的空间位置所 需要的独立坐标数. 所谓独立坐标数是指描写物体位置所需的最少 的坐标数。
kT 2 2
( t r ) kT
1).一个分子的内能为: 2 kT 2).1 mol气体分子的内能为: 3). M 千克气体的内能:
E 单原子分子气体: 3 2
i
E0 N
E M i
A
i 2
kT
i 2
i 2
RT
2
RT
RT
RT
5 2 6 2 i
█ 一个质点在空间自由运动需要三个独立坐标(x,y,z)才能确定 其位置,因此质点具有三个自由度。 █ 若一个质点被限制在曲面或平面上运动,则只需两个独立 坐标,自由度数为2; █ 若质点被限制在直线或曲线上运动,则 只有一个自由度; 一个刚体的空间运动可以分解为质心平动和绕通过质心轴的 转动。 刚体位置的确定: ①. 质心位置的确定(x,y,z); ②. 转轴的方位的确定(两个独立的方位角,或); ③. 旋转角的确定; cos 2 cos 2 cos 2 1
2
1
分子的振动势能与振动动能相等,则分子总 能量为:
1
t
r 2 s kT
2
注意:本章中把气体分子都视为刚性分子来 处理,忽略其振动。
单原子分子气体(i=3)
双原子分子气体(i=5) 多原子分子气体(i=6)
3 2 kT
5 2
6 2
kT
只和温度 有关
kT
能量均分定理的说明:
