弯矩 曲率关系
混凝土结构复习重点

以混凝土为主制成的结构成为混凝土结构。
包括素混凝土结构,钢筋混凝土结构,预应力混凝土结构等。
钢筋混凝土结构的主要优点如下:取材容易;合理用材;耐久性较好;耐火性好;可模型好;整体性好。
也存在着一些缺点,主要是:自重较大,抗裂性较差,钢筋混凝土结构的施工复杂、工序多、隔热隔声性能较差。
建筑结构的功能包括安全性,适用性,耐久性三个方面,简称“三性”。
承载力计算与变形、裂缝宽度验算是分别为了满足安全性与适用性要求的。
恒荷载的荷载分项系数rg一般取1.2 ;活荷载的荷载分项系数rq一般取1.4。
混凝土的立方体抗压强度Fcu,k以立方体强度值作为混凝土强度的基本指标,并把立方体抗压强度作为评定混凝土强度等级的标准。
规定以变长为150mm的立方体为标准试件,标准立方体试件在(20+3)°C的温度和相对湿度90%以上的潮湿空气中养护28d,按照标准试验方法测得的抗压强度作为混凝土的立法抗压强度,单位N/mm2。
结构或材料承受的应力不变,而应变随时间增长的现象称为徐变。
影响徐变的因素有:骨料比例大,徐变小;水泥用量大,水多,徐变大;养护温度高,湿度大,徐变小;加载龄期早,徐变大;骨料弹性模量越大,徐变小。
混凝土凝结硬化过程中,体积减小的现象称为混凝土的收缩。
影响混凝土收缩的因素有:水泥的品种;水泥的用量;骨料的性质;养护条件;混凝土的制作方法;使用环境;构件的体积与表面积比值。
热轧钢筋根据其力学指标的高低分为四个种类:HPB235级,HRB35级,HRB00 级,RRB400级。
钢筋的疲劳是指钢筋在承受重复、周期性的动荷载作用下,经过一定次数后,突然脆性断裂的现象。
纵向受拉钢筋的最小配筋率是这样确定的:按|||a阶段计算钢筋混凝土受弯构件正截面受弯承载力与由素混凝土受弯构件计算得到的正截面受弯承载力两者相等时的配筋率。
双筋截面:如果在受压区配置的纵向受压钢筋数量比较多,不仅起架立钢筋的作用,而且在正截面受弯承载力的计算中必须考虑它的作用,这样配筋的截面称为双筋截面。
名师名校勘测设计注册工程师讲义【土木工程材料考前复习指导】第83讲第十六章结构设计(二十九)

二、受弯构件(梁)1.强度计算1)抗弯强度在主平面内受弯的实腹构件,其抗弯强度应按下式计算(17-204)式中:M x、M y——分别为同一截面绕x轴和y轴的弯矩(对工字形截面,x轴为强轴,y轴为弱轴);M nx、M ny——分别为对x轴和y轴的净截面模量;当截面板件宽厚比等级为S1、S2、S3或S4级时,应取全截面模量,当截面板件宽厚比等级为S5级时,应取有效截面模量,均匀受压翼缘有15ε,腹板有效截面可按《钢结构设计标准》第8.4.2条的规定采用(mm3);效外伸宽度可取kγx、γy——分别为沿x轴、y轴的截面塑性发展系数,对工字形截面,γx=1.05,γy=1.20,对箱形截面γx=γy=1.05,对需要计算疲劳的梁,宜取γx=γy=1.0,对其他截面,可按《钢结构设计标准》中6.1.2条采用。
2)抗剪强度(17-205)式中:V——计算截面沿腹板平面作用的剪力;S——计算剪应力处以上毛截面对中和轴的面积矩;I——毛截面惯性矩;t w——腹板厚度;ƒv——钢材的抗剪强度设计值。
3)局部抗压强度当梁上翼缘作用有沿腹板平面的集中荷载,且该荷载又未设置支承加劲肋时,腹板计算高度上边缘的局部抗压强度按下式计算:(17-206)式中:F——集中荷载,对动力荷载应考虑动力系数;ψ——集中荷载增大系数,对重级工作制吊车梁,ψ=l.35,对其他梁,ψ=l.O;l z——集中荷载按45°扩散在腹板计算高度上边缘的假定分布长度,其值应根据支座具体尺寸确定。
梁的支座处,当不设置支承加劲肋时,也应按式(17-206)计算腹板计算高度下边缘的局部压应力,但ψ取1.0。
【例17-17/2014真题】设计一悬臂钢架,最合理的截面形式是:解:根据悬臂梁的受力特点可知,上翼縁承受拉应力,下翼縁承受压应力,钢材的抗拉、抗压强度相同,故应选择上、下翼縁面积相同的截面形式。
答案:B2.截面板件宽厚比等级截面板件宽厚比是指截面板件平直段的宽度和厚度之比,受弯或压弯构件腹板平直段的高度与腹板厚度之比也可称为板件高厚比。
型钢加固钢筋混凝土梁弯矩—曲率关系的研究

l 0
道
建
筑
De e e , 0 8 c mb r 2 0
Ral y En ie rn i wa gn eig
文章编 号 :0 319 (0 8 1. 1。3 10 .95 2o )20 00 0
型钢 加 固钢 筋 混 凝 土梁 弯 矩一 曲率 关 系的研 究
王 尧 燕 , 宏 文 周
12 本 构 关 系 .
型钢 加 固钢 筋混凝 土 梁 的截 面 弯矩一 曲率 (
) 能 性
1 混凝 土应 力一应 变关 系 )
进行 分析 , 包括初 始弯 矩 、 型钢截 面高 度 h 。和原钢
筋混 凝土梁 配筋率 等 , 型钢加 固钢筋 混凝 土 梁 的 对
采 用《 凝 土 结 构设 计 规 范 》 G 50 0 2 0 ) 混 ( B 0 1- 0 2 中
第 二次受 力 ( 即加 固后再 次旌加 外荷 载 ) 时才 开始工 作 的 。因此 , 型钢 加 固钢筋混 凝 土梁 截 面 的 M- ( 系 分 p关 两个 阶段 考虑 。具体 计算 步骤 是 : 设 置初 始 条 件 : ①
= ; O ②每 次取 : 曲率 = +△ ③ 假定某 一 规定截 面 ; 的应 变 ; 求 出各 条带 的应 变 e ⑤ 按钢 筋 和混 凝 土 ④ ; 的应力 一应 变关 系 求 对 应 于应 变 e的应 力 ; 如 已 ⑥
关系) , 时 为简化 计算 采用 以下基本 假定 : 1 平截 面假定 ; ) 2 不考 虑剪 切变形 的影 响 ; )
3 不考 虑型 钢失稳 破坏 ; )
4 截 面破坏 条件 为 : 受 压 混凝 土 边 缘应 变 达 到 ) ① 混 凝土极 限应 变 ; 型钢或 钢筋应 变达 到极 限应变 。 ②
《弯矩曲率关系》课件

曲率的定义
曲率:描述曲线弯曲程度的量, 定义为曲线上任一点处切线方向 角的变化量与经过的弧长的比值
。
在数学上,曲率是用来衡量曲线 上某一点附近的小弧段弯曲程度
的量。
对于直线,其曲率为0;对于圆 ,其曲率是一个常数,等于圆的
半径倒数。
曲率的计算
曲率计算公式:K = lim(Δs->0) [Δs / (Δt)^2] / lim(Δt>0) [Δs / Δt]
在机械工程中的应用
传动系统设计
在机械传动系统中,弯矩曲率关系对于齿轮、轴等部件的设计和优化具有指导意义。了解弯矩与曲率的关系有助 于提高传动系统的效率和稳定性。
疲劳分析
在机械部件的疲劳分析中,弯矩曲率关系是评估其疲劳寿命的重要因素之一。通过对弯矩和曲率的变化规律进行 分析,可以预测部件的疲劳寿命和潜在的疲劳断裂风险。
在工程结构中,弯矩和曲率是密切相关的。例如,在桥梁、建筑和机械设计中,需 要考虑到结构的弯曲程度和弯矩之间的关系。
当结构受到外力作用时,会发生弯曲变形,曲率会发生变化,同时弯矩也会随之改 变。因此,在设计时需要考虑到结构的承载能力和稳定性。
了解弯矩与曲率的关系有助于工程师更好地设计结构,确保其安全性和稳定性。
需要研究弯矩曲率关系在不同温度、湿度等环境 条件下的变化规律。
需要探索弯矩曲率关系在复合材料、智能材料等 新型材料中的应用。
对学习者的建议
学习者应该深入理解弯矩和曲 率的定义及测量方法。
学习者应该掌握弹性力学和 材料力学的基本原理,以便 更好地理解弯矩曲率关系。
学习者可以通过实验和实践来 加深对弯矩曲率关系的理解和
应用。THANΒιβλιοθήκη S感谢观看详细描述
弯矩是材料力学中一个重要的概念,用于描述弯曲变形过程 中截面所受到的力矩作用。在材料受到弯曲时,截面上会产 生剪力和弯矩,弯矩的大小与剪力和中性轴距离有关。
弯矩曲率关系
1. 基本假定
混凝土受压时的应力-应 变关系
n
2
1 60
(
fcu
50),当n
2时,取n
2
当应力较小时,如 c 0.3 fc时,可取 c Ecc
c fc
c
f
c
1
1
c 0
n
o
0
0 0.002 0.5 fcu 50105
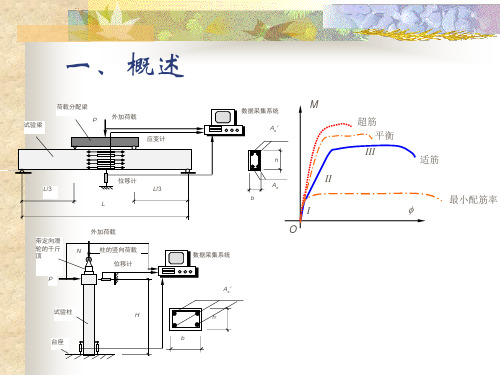
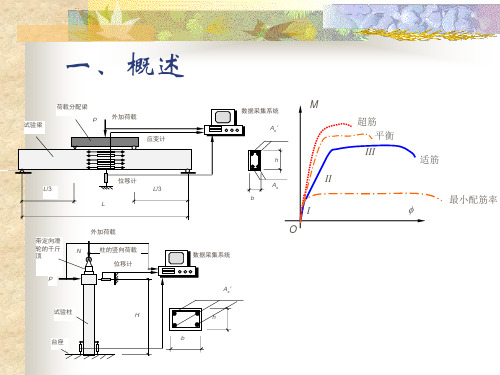
四、受弯构件的试验研究
2. 试验结果
最小配筋率
四、受弯构件的试验研究
2. 试验结果 P
M
超筋 平衡
III
适筋
L/3 L
II 少筋 I O
最小配筋率
c
c
c
c
L/3
(c’<u) c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
As
as
h/2as h h/2as
as
1
i
Zi
截面中心线 s n
As
b
c1 s ci M
N
X 0,
n
ci Ai
' s
As'
s As
N
0
i 1
sAs ci
sAs
M 0,
荷载分 配梁 P
第二章弯矩曲率关系
n
i 1
ci
Ai s' As' s As N 0
n
2) 假定和 值
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )=0 2 2
3) 由相容方程求出各条带混凝土的应变及钢筋的应变; 4) 由物理关系求出相应的应力,拉区混凝土条带的应变 超过其极限受拉应变时,应对其进行处理;
2) 假定 值
X 0,
n
i 1
ci
Ai s' As' s As N 0
n
M 0,
M ci Ai Z i s As (
i 1
h h a s ) s As (a s )=0 2 2
3) 由相容方程求出各条带混凝土的应变及钢筋的应变; 4) 由物理关系求出相应的应力,拉区混凝土条带的应变 超过其极限受拉应变时,应对其进行处理;
5) 将各应力值代入第一平衡方程,判断是否满足平衡条件: 如不满足,需要调整 值直至满足为止,如满足平衡条件, 则由第二平衡方程求出M,然后重复步骤1~5
6) 当符合破坏条件时,停止计算。
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
M - 关系的计算方法之二 :分级加荷载法
1) 取M=M+M
h h/2as
as b
n
As
对钢筋混凝土柱, 有时也可能会出现 s < 0
s s ( s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的平衡方程
as h/2as h h/2as as b 1 i Zi 截面中心线 n As As
第3章钢筋混凝土受弯构件习题和思考题及答案

第三章钢筋混凝土受弯构件问答题1. 适筋梁正截面受弯全过程可划分为几个阶段?各阶段的主要特点是什么?与计算有何联系?1。
答:适筋梁正截面受弯全过程可划分为三个阶段—混凝土开裂前的未裂阶段、混凝土开裂后至钢筋屈服前的裂缝阶段和钢筋开始屈服前至截面破坏的破坏阶段.第Ⅰ阶段的特点是:1)混凝土没有开裂;2)受压区混凝土的应力图形是直线,受拉区混凝土的应力图形在第Ⅰ阶段前期是直线,后期是曲线;3)弯矩与截面曲率基本上是直线关系.a I 阶段可作为受弯构件抗裂度的计算依据。
第Ⅱ阶段的特点是:1)在裂缝截面处,受拉区大部分混凝土推出工作,拉力主要由纵向受拉钢筋承担,但钢筋没有屈服;2)受压区混凝土已有塑性变形,但不充分,压应力图形为只有上升段的曲线;3)弯矩与截面曲率是曲线关系,截面曲率与挠度的增长加快了.阶段Ⅱ相当于梁使用时的受力状态,可作为使用阶段验算变形和裂缝开展宽度的依据。
第Ⅲ阶段的特点是:1)纵向受拉钢筋屈服,拉力保持为常值;裂缝截面处,受拉区大部分混凝土已退出工作,受压区混凝土压应力曲线图形比较丰满,有上升曲线,也有下降段曲线;2)由于受压区混凝土合压力作用点外移使内力臂增大,故弯矩还略有增加;3)受压区边缘混凝土压应变达到其极限压应变实验值0cu 时,混凝土被压碎,截面破坏;4)弯矩—曲率关系为接近水平的曲线。
第Ⅲ阶段末可作为正截面受弯承载力计算的依据。
2. 钢筋混凝土梁正截面受力全过程与匀质弹性材料梁有何区别?2.答:钢筋混凝土梁正截面受力全过程与匀质弹性材料梁的区别有:钢筋混凝土梁从加载到破坏的全过程分为三个阶段;从第Ⅱ阶段开始,受拉区混凝土就进入塑性阶段,梁就开始带裂缝工作,受拉区拉力都由钢筋来承担,直到第Ⅲ阶段末整个梁破坏,而匀质弹性材料梁没有这两个阶段,始终是在弹性阶段内工作的.3.钢筋混凝土梁正截面有哪几种破坏形态?各有何特点?3。
答:钢筋混凝土梁正截面有适筋破坏、超筋破坏和少筋破坏三种。
简支梁挠度方程

简支梁挠度方程简支梁挠度方程是描述简支梁在外力作用下产生的挠度变形的方程。
简支梁是一种常见的结构形式,广泛应用于桥梁、楼板等工程中。
在工程设计和结构分析中,了解简支梁的挠度方程对于确定结构的稳定性和安全性至关重要。
简支梁挠度方程的推导基于弹性力学的基本原理。
在外力作用下,简支梁会发生弯曲变形,产生挠度。
挠度方程是通过分析简支梁受力平衡和变形关系得到的,可以用来计算梁的挠度。
我们假设简支梁在外力作用下弯曲变形后的挠度为y(x),其中x表示梁上的任意一点的位置。
根据弹性力学的基本原理,梁受力平衡时,外力和内力之和为零。
在简支梁上,内力主要包括弯矩和剪力。
在简支梁上,弯矩的大小与梁的曲率有关。
曲率越大,弯矩越大。
根据受力平衡条件,弯矩的变化率等于单位长度上的剪力,即M(x) = -V'(x),其中M(x)表示梁上任意一点的弯矩,V(x)表示梁上任意一点的剪力。
根据弯矩和曲率之间的关系,我们可以得到简支梁上的挠度方程。
根据弯矩-曲率关系,曲率等于挠度的二阶导数,即κ(x) = y''(x),其中κ(x)表示梁上任意一点的曲率。
由此,我们可以得到简支梁的挠度方程:M(x) = -EIy''(x),其中E表示梁的弹性模量,I表示梁的截面惯性矩。
这个方程描述了简支梁受力平衡和变形关系。
在实际应用中,我们可以根据挠度方程进行简支梁的挠度计算。
根据梁的几何形状和受力情况,我们可以确定梁的弯矩分布,进而计算出梁的挠度分布。
通过挠度计算,我们可以评估简支梁的结构稳定性和安全性,为工程设计和结构分析提供依据。
总结起来,简支梁挠度方程是描述简支梁在外力作用下产生的挠度变形的方程。
根据弹性力学的基本原理,通过分析梁的受力平衡和变形关系,可以得到简支梁的挠度方程。
挠度方程在工程设计和结构分析中具有重要的应用价值,可以用来计算简支梁的挠度,评估结构的稳定性和安全性。
了解简支梁挠度方程的原理和应用,有助于工程师进行结构设计和分析工作,确保工程的可靠性和安全性。
材料力学知识点

第六章弯曲变形知识要点1、弯曲变形的概念1)、挠曲线弯曲变形后梁的轴线变为挠曲线。
平面弯曲时,挠曲线为外力作用平面内的平面曲线。
2)、平面弯曲时的变形在小变形情况下,梁的任意二横截面绕各自的中性轴作相对转动,杆件的轴线变为平面曲线,其变形程度以挠曲线的曲率来度量。
1》纯弯曲时,弯矩—曲率的关系(由上式看出,若弯曲刚度EI为常数则曲率为常数,即挠曲线为圆弧线)2》横力弯曲时,弯矩—曲率的关系3)、平面弯曲时的位移1》挠度——横截面形心在垂直于梁轴线方向上的线位移,以表示。
2》转角——横截面绕其中性轴旋转的角位移,以表示。
挠度和转角的正负号由所选坐标系的正方向来确定。
沿y轴正方向的挠度为正。
转角的正负号判定规则为,将x轴绕原点旋转90°而与y轴重合,若转角与它的转向相同,则为正,反之为负。
4)、挠曲线近似微分方程5)、受弯曲构件的刚度条件,2、积分法求梁的挠度和转角由积分常数C、D由边界条件和连续性条件确定。
对于梁上有突变载荷(集中力、集中力偶、间断性分布力)的情况,梁的弯矩M(x)不是光滑连续函数,应用上式时,应分段积分,每分一段就多出现两个积分常数。
因此除了用边界条件外,还要用连续性条件确定所有的积分常数。
边界条件:支座对梁的位移(挠度和转角)的约束条件。
连续条件:挠曲线的光滑连续条件。
悬臂梁边界条件:固定端挠度为0,转角为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等简支梁边界条件:固定绞支座或滑动绞支座处挠度为0连续条件:在载荷分界处(控制截面处)左右两边挠度相等,转角相等连接铰链处,左右两端挠度相等,转角不等3、叠加原理求梁的挠度和转角1)、叠加原理各载荷同时作用下梁任一截面的挠度和转角等于各个载荷单独作用时同一截面挠度和转角的代数和。
2)、叠加原理的限制叠加原理要求梁某个截面的挠度和转角与该截面的弯矩成线性关系,因此要求:1》弯矩M和曲率成线性关系,这就要求材料是线弹性材料2》曲率与挠度成线性关系,这就要求梁变形为小变形4、弯曲时的超静定问题——超静定梁1)、超静定梁约束反力数目多于可应用的独立的静力平衡方程数的梁称为超静定梁,它的未知力不能用静力平衡方程完全确定,必须由变形相容条件和力与变形间的物理关系建立补充方程,然后联立静力平衡方程与补充方程,求解所有的未知数。
midas计算弯矩曲率曲线

midas计算弯矩曲率曲线计算弯矩曲率曲线通常涉及使用MIDAS(Multiple Indicator Dilution and Multiple Indicator Dilution Analysis)方法,这是一种用于血流动力学研究的技术。
弯矩曲率曲线描述了横截面上各点的弯矩和曲率的关系,是一个重要的结构力学参数。
以下是一般的步骤,用于计算弯矩曲率曲线:
1. 获取横截面几何信息:
•首先,您需要获取结构的横截面几何信息,包括横截面的形状、尺寸、截面积等。
这些信息将在后续的计算中使用。
2. 计算截面惯性矩:
•使用横截面的几何信息,计算相对于截面中心的横截面惯性矩。
横截面惯性矩在计算弯矩时是一个重要的参数。
3. 应用弯矩公式:
•根据横截面上各点的弯矩公式计算弯矩。
弯矩�M 与曲率�k 的关系通常可以表示为�=�⋅�⋅�M=E⋅I⋅k,其中�E 是材料的弹性模量,�I 是横截面的惯性矩,�k 是曲率。
4. 绘制弯矩曲率曲线:
•将得到的弯矩和曲率的数据进行图形化处理,绘制弯矩曲率曲线。
通常,曲率沿着横轴,弯矩沿着纵轴。
这是一个简化的描述,实际情况可能更为复杂,具体取决于结构的几何形状和加载条件。
在实际应用中,通常会使用专业的结构分析软件,如 MIDAS Civil,进行弯矩曲率曲线的计算和绘制。
请确保在进行结构分析时,了解和遵循适用的结构力学理论和标准。
勘察设计类注册工程师专业基础精讲第十六章结构设计(二十九)08

二、受弯构件(梁) 1.强度计算1)抗弯强度在主平面内受弯的实腹构件,其抗弯强度应按下式计算(17-204)式中:M x 、M y ——分离为同一截面绕x 轴和y 轴的弯矩(对工字形截面,x 轴为强轴,y 轴为弱轴);M nx 、M ny ——分离为对x 轴和y 轴的净截面模量;当截面板件宽厚比等级为S1、S2、S3或S4级时,应取全截面模量,当截面板件宽厚比等级为S5级时,应取有效截面模量,匀称受压翼缘有效外伸宽度可取k 15ε,腹板有效截面可按《钢结构设计标准》第8.4.2条的规定采用(mm 3);γx 、γy ——分离为沿x 轴、y 轴的截面塑性发展系数,对工字形截面,γx =1.05,γy =1.20,对箱形截面γx =γy =1.05,对需要计算疲劳的梁,宜取γx =γy =1.0,对其他截面,可按《钢结构设计标准》中6.1.2条采用。
2)抗剪强度(17-205)式中:V ——计算截面沿腹板平面作用的剪力; S ——计算剪应力处以上毛截面向中和轴的面积矩; I ——毛截面惯性矩; t w ——腹板厚度;ƒv ——钢材的抗剪强度设计值。
3)局部抗压强度当梁上翼缘作用有沿腹板平面的扩散荷载,且该荷载又未设置支承加劲肋时,腹板计算高度上边缘的局部抗压强度按下式计算:(17-206)式中:F ——扩散荷载,对动力荷载应考虑动力系数;ψ——扩散荷载增大系数,对重级工作制吊车梁,ψ=l.35,对其他梁,ψ=l .O ;l z ——扩散荷载按45°蔓延在腹板计算高度上边缘的假定分布长度,其值应按照支座详细尺寸决定。
梁的支座处,当不设置支承加劲肋时,也应按式(17-206)计算腹板计算高度下边缘的局部压应力,但ψ取1.0。
【例17-17/2014真题】设计一悬臂钢架,最合理的截面形式是:解:按照悬臂梁的受力特点可知,上翼縁承受拉应力,下翼縁承受压应力,钢材的抗拉、抗压强度相同,故应挑选上、下翼縁面积相同的截面形式。
有粘结预应力混凝土梁的弯矩-曲率关系

1 预 应力混凝 土梁的建模
1 . 1 梁方 案设计
性 行 为非常重 要 。普 通 非 预应 力 混 凝 土 梁 ( 以下 简 称普 通梁 ) 的弯矩 一 曲率关 系 可 以通过 纤 维模 型
法得 到 , 即根 据平截 面假 定 , 由曲率 得到 各小 条处 的应 变 , 从 而得 到 应 力 , 进 而得 到 轴 力 和 弯矩 [ 1 1 。 预应 力 混凝 土 梁 ( 以下 简称 预应 力 梁 ) 同样 可 通
第3 1 卷 第1 期
2 0 1 3年 2月
江
西
科
学
Vo 1 . 3l No. 1
J I ANGXI S C I E NC E
Fe b. 2 0l 3
文章编号 : 1 0 0 1 — 3 6 7 9 ( 2 0 1 3 ) 0 1 —0 0 7 3— 0 6
有粘 结 预 应 力 混 凝 土梁 的弯 矩 一 曲率关 系
周 颖彬 , 苏 小 卒
( 同济 大学建筑工程 系, 上海 2 0 0 0 9 2 )
摘 要: 研究 了有粘结顸应 力混凝土 梁中各参数对其 弯矩. 曲率关 系的影响。通过 有限元方 法对不 同参数 的有
粘结预应力混凝土梁进行求解 , 可得到相应 的 弯矩一 曲率关 系。结合 理论 分析 , 并针对 力筋偏心距对 弯矩一 曲
本 文运 用 A N S Y S软 件 对 有 粘结 预 应 力 混 凝
土 简支 梁 建模 从 而进行 其 弯矩一 曲率关 系的求 解 。
通过 建 立纯 弯段 ( 如图 1 所示 , 对 称加 载 , 加 载 点 为 l / 3跨 处 ) , 可避 开 加载 点 ( 若 单点 加 载 则 为唯
弯矩设计值计算公式

弯矩设计值计算公式在计算弯矩设计值之前,首先需要了解一些基本概念和假设条件。
在弯矩设计值的计算中,常用的假设条件有弹性假设、平面截面假设和截面标准态假设。
弹性假设是指结构在外力作用下发生弯曲时,结构元素内部的应力和应变处于弹性阶段,不考虑塑性变形。
弹性假设一般适用于小的变形情况下。
平面截面假设是指结构元素截面在弯曲过程中不产生剪切变形,即假设结构元素截面在整个弯曲过程中保持平面。
这个假设适用于工程中大多数结构元素。
截面标准态假设是指结构元素在弯曲时假设截面形状和材料性质处于标准状态,不考虑截面的不规则形状和材料的非均匀性。
根据这些假设条件,可以得到弯矩设计值的计算公式。
根据结构力学理论,弯矩M与外力P和结构特性EI(抗弯刚度)之间的关系可以表示为:M=EI*δ/ρ其中,M代表弯矩设计值,E代表材料的弹性模量,I代表结构截面的惯性矩,δ代表结构的挠度,ρ代表结构的曲率半径。
挠度δ的计算可以根据结构力学理论和边界条件进行求解。
多数情况下采用分布载荷的挠度计算方法,该方法可以根据载荷的分布情况和边界条件,得到结构的挠度表达式。
曲率半径ρ的计算也是结构力学理论中重要的内容。
对于不同的结构形状和加载方式,计算曲率半径有不同的方法,其中一种常用的计算方法是根据结构截面形状和挠度得到曲率半径的表达式。
弯矩设计值的计算公式通常需要结合具体工程设计中的情况,考虑结构的载荷分布、边界条件、结构形状和材料等因素。
在实际设计中,为了确保结构的安全性和可靠性,设计师需要根据公式计算出弯矩设计值,并根据弯矩设计值选择合适的结构材料和尺寸。
总之,弯矩设计值的计算公式是工程设计中重要的理论基础,通过合理的计算可以确保结构的稳定性和安全性。
然而,在实际工程设计中,除了弯矩设计值的计算,还需要考虑其他因素,如轴力、剪力等,以全面评估结构的性能和可靠性。
因此,在实际工程设计中,需要综合考虑各种影响因素,进行综合分析和计算。
结构力学的梁的挠度与挠曲分析探究

结构力学的梁的挠度与挠曲分析探究梁是工程结构中常见的构件之一,对于梁的挠度与挠曲分析,是结构设计和计算中不可忽视的重要内容。
本文将探究梁的挠度和挠曲分析方法,从而深入了解梁的结构特性和应用。
一、梁的挠度分析方法1. 等载荷假设法等载荷假设法是最常用的梁的挠度分析方法之一。
在该方法中,假设梁在全跨度范围内承受着均匀分布的荷载或集中力,通过求解梁的弯矩和剪力方程,最终得到梁的挠度分布。
2. 差分法差分法是另一种常见的梁的挠度分析方法。
该方法通过将梁的分析区域划分为若干个小段,对每个小段进行简单的弯矩和剪力计算,然后通过积分求和的方式得到整个梁的挠度分布。
3. 叠加原理法叠加原理法是一种较为灵活的梁的挠度分析方法。
该方法通过将各种不同类型的载荷作用于梁上,并利用叠加原理进行挠度计算。
例如,可以将均匀分布载荷和集中力分别作用于梁上,然后将其挠度分布叠加得到最终的挠度结果。
二、梁的挠曲分析方法1. 弯矩-曲率法弯矩-曲率法是常用的梁的挠曲分析方法之一。
该方法通过建立梁的弯矩-曲率关系,推导出梁的挠曲方程,并通过求解该方程得到梁的挠曲形状和挠曲量。
2. 弯矩传递法弯矩传递法是一种简化的梁的挠曲分析方法。
该方法假设梁上截面的切线方向和挠曲方向相同,并利用弯矩传递原理求解梁的挠曲形状和挠曲量。
虽然该方法存在一定的近似性,但在一些简化计算中仍然得到了广泛应用。
3. 高斯消元法高斯消元法是一种利用矩阵运算进行梁的挠曲分析的方法。
该方法通过建立梁的刚度矩阵和载荷矩阵,通过矩阵运算求解梁的位移分布,从而得到梁的挠曲形状和挠曲量。
三、梁的挠度与挠曲分析的应用梁的挠度与挠曲分析在结构设计和计算中具有广泛的应用。
通过对梁的挠度和挠曲进行分析,可以评估梁的结构安全性以及承载性能。
在工程实践中,合理的梁的挠度和挠曲分析有助于优化结构设计,提高结构的稳定性和承载能力。
此外,梁的挠度与挠曲分析也是结构调整和改造的重要依据。
在对已有结构进行改进或加固时,对梁的挠度和挠曲进行分析有助于确定结构的强度和刚度要求,从而指导工程师进行适当的结构调整和加固措施。
t型剪力墙骨架曲线计算方法及试验验证

t型剪力墙骨架曲线计算方法及试验验证T型剪力墙是一种常用的结构墙体,能够承受地震力和风荷载。
对于T型剪力墙的设计和计算,需要确定骨架曲线。
本文将介绍T型剪力墙骨架曲线的计算方法及试验验证。
首先,T型剪力墙的骨架曲线是指墙体在受力时的整体形变曲线。
根据结构力学理论,可以将T型剪力墙简化为一个力矩和剪力作用下的梁柱体系。
因此,可以采用弯矩-曲率关系来计算T型剪力墙的骨架曲线。
计算T型剪力墙骨架曲线的步骤如下:1.确定剪力墙的几何尺寸和材料力学性质。
2.根据墙体的受力情况,计算剪力墙底部的弯矩分布。
根据结构力学理论,可以采用弯矩分布的经验公式或数值计算方法。
3.计算剪力墙底部的弯矩与曲率的关系,可以采用材料的本构关系。
4.根据弯矩-曲率关系,可以得到剪力墙骨架曲线。
为了验证计算得到的T型剪力墙骨架曲线的准确性,可以进行试验验证。
试验验证的步骤如下:1.按照设计的T型剪力墙样式,搭建试验模型。
试验模型的尺寸和材料力学性质应与实际工程一致。
2.对试验模型施加一定的荷载,可以是模拟地震荷载或风荷载。
同时,测量墙体各部位的位移和变形。
3.根据试验得到的数据,计算墙体的骨架曲线。
4.将试验计算得到的骨架曲线与理论计算结果进行比较,看两者是否吻合。
通过以上的计算和试验验证,可以得到T型剪力墙的骨架曲线。
这种方法能够较为准确地描述剪力墙在受力过程中的整体形变情况。
根据骨架曲线的计算结果,可以进一步分析和设计剪力墙的结构性能,确保墙体在地震和风荷载下的安全性。
综上所述,T型剪力墙骨架曲线的计算方法及试验验证是一个重要的设计步骤。
通过计算和试验的相互验证,可以获得准确的骨架曲线,为工程结构的设计和分析提供重要依据。
UCfber在钢筋混凝土截面弯矩_曲率计算中的应用

4 混凝土二次衬砌
为保证二次衬砌进度,并做到内实、外美,采用
2 台 9m 长整体钢模衬砌台车,台车总重量达 60t,主 骨架部分在厂家生产,现场安装后,焊接顶面钢板, 为保证模板周转使用不变形,采用 8mm 厚钢板,现 场安装需要一个月时间。二次衬砌要做到仰拱先行 创造环境,适时衬砌保安全。7 月初开始衬砌,在雨 季前完成进出口二次衬砌,施工安全得到保证。
Moment/kN*m Moment/kN*m
244800。如果该桥梁在罕遇地震顺桥向作用下,固定 墩墩底截面弯矩小于 92710,则说明固定墩墩底截 面处于弹性工作状态;如果固定墩墩底截面弯矩大 于 92710 但小于 476000,说明固定墩墩底截面已经 达到屈服状态但是尚未破坏,上述两种状态证明该
ρx,ρy—分别为箍筋在 x, y 的体积含筋率。由公
式(5)计算。
ρx
=
Asx s×dc
(5a)
ρy
=
Asy s×bc
(5b)
其中:
dc —矩形截面沿 Y 轴方向算到箍筋外缘的宽;
bc —矩形截面沿 X 轴方向算到箍筋外缘的宽;
S—纵向箍筋的间距。
算出 f′lx 和 f′ly 之后,就可以利用约束应力与约
开裂弯矩 /kN·m 28460 77040 67690 144900 92710 186300
表 1 各墩墩底截面弯矩 - 曲率计算结果
开裂曲率 /rad·m-1 1.237e-4 4.837e-5 1.124e-4 4.747e-5 9.684e-5 4.539e-5
屈服弯矩 /kN·m 90100 237500 171300 375000 223200 476000
混凝土结构设计原理复习答案

混凝土结构设计原理复习答案1.结构有哪些功能要求?简述承载能力极限状态和正常使用极限状态的概念。
结构的功能要求:安全性,适用性,耐久性。
承载力极限状态:结构或构件达到最大承载能力或者变形达到不适于继续承载的状态;正常使用极限状态:结构或构件达到正常使用或耐久性能中某项规定限度的状态。
2.单向受力状态下,混凝土的强度与哪些因素有关?混凝土轴心受压应力--应变曲线有何特点?常用的表示应力--应变关系的数学模型有哪几种?适筋梁正截面受弯全过程可划分为三个阶段—混凝土开裂前的未裂阶段、混凝土开裂后至钢筋屈服前的裂缝阶段和钢筋开始屈服前至截面破坏的破坏阶段。
第Ⅰ阶段的特点是:1)混凝土没有开裂;2)受压区混凝土的应力图形是直线,受拉区混凝土的应力图形在第Ⅰ阶段前期是直线,后期是曲线;3)弯矩与截面曲率基本上是直线关系。
阶段可作为受弯构件抗裂度的计算依据。
第Ⅱ阶段的特点是:1)在裂缝截面处,受拉区大部分混凝土推出工作,拉力主要由纵向受拉钢筋承担,但钢筋没有屈服;2)受压区混凝土已有塑性变形,但不充分,压应力图形为只有上升段的曲线;3)弯矩与截面曲率是曲线关系,截面曲率与挠度的增长加快了。
阶段Ⅱ相当于梁使用时的受力状态,可作为使用阶段验算变形和裂缝开展宽度的依据。
第Ⅲ阶段的特点是:1)纵向受拉钢筋屈服,拉力保持为常值;裂缝截面处,受拉区大部分混凝土已退出工作,受压区混凝土压应力曲线图形比较丰满,有上升曲线,也有下降段曲线;2)由于受压区混凝土合压力作用点外移使内力臂增大,故弯矩还略有增加;3)受压区边缘混凝土压应变达到其极限压应变实验值时,混凝土被压碎,截面破坏;4)弯矩—曲率关系为接近水平的曲线。
第Ⅲ阶段末可作为正截面受弯承载力计算的依据。
3.什么是混凝土的徐变?徐变对混凝土构件有何影响?通常认为影响徐变的主要因素有哪些?如何减少徐变?结构或材料承受的荷载或应力不变,而应变或变形随时间增长的现象称为徐变。
徐变对混凝土结构和构件的工作性能有很大影响,它会使构件的变形增加,在钢筋混凝土截面中引起应力重分布的现象,在预应力混凝土结构中会造成预应力损失。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c0 0.00,2cu0.0033
11.0
1
0.8, 0.7,
fcu 50Mpa fcu 50Mpa
线性插值(《混凝土结构设计
规范》GB50010 )
六、受弯构件正截面简化分析
1. 压区混凝土等效矩形应力图形(极限状态下)
定义:
x h0
xn=nh
0
1c0
yc C
x=1xn
对试验梁,已知b、h0、As、fc、fy、Es, Mu
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(ct =tu)
s<y
sAs
s= fyAs
y
fyAs s>y
四、受弯构件的试验研究
2. 试验结果
结论
•适筋梁具有较好的变形能力,超筋梁和少筋梁的破坏具有突然性,设计 时应予避免
•在适筋和超筋破坏之间存在一种平衡破坏。其破坏特征是钢筋屈服的同 时,混凝土压碎
二、骨架曲线的弯矩-曲率关系
1. 基本假定
P
平截面假定----平均应变意义上
As’
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
as b
s
b c
(1-n)h0
忽略剪切变形对梁、柱构件变形的影响
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的相容关系
as h/2as h h/2as
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理
As
as 1
h/2-
i
as
Zi
h h/2-
as
截面中心线 s
n
as
As
b
c1 s ci M
N
sAs ci
sAs
ci > t0
该条带混 凝土开裂
ci > tu
该条带混凝 土退出工作
ci = 0
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
t t Ec
s s Es
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
ct
c
h0 h
M
s b c
As b
xn
sAs
(E-1)As
s t
s Ess E Ecst Et
用材料力学的方法求解
TsAsEAst
将钢筋等效成混凝土
五、受弯构件正截面受力分析
2. 弹性阶段的受力分析
当cb =tu时,认为拉区混凝土开裂并退出工作(约束受拉)
X 0
A
s
0.5ctbcxr0.5Ectu(hxcr) sAs
xn=n h0 h0 h
c
M
s
t0
cb= tu
b
ct
C xn=xc
r
T
c
sAs
设EE Ecs ,近似认 s 为 tu
xcr
1 2 E As
bh
1 E As
h 2
bh
对一般钢筋混凝土梁 As / bh 0.5 ~ 2%,
E 6 ~ 7
在试验中测得s及Mu,于是:
sAs
M0 X 0
Mu EssAsh0(12)
21
Mu
Ess Ash0
1c 0h 0 b E ssA s11 fch 0 b
11 1fcc0hh00bbE 1fscshA0sb
六、受弯构件正截面简化分析
1. 压区混凝土等效矩形应力图形(极限状态下)
1c0
11 1fcc0hh00bbE 1fscshA0sb
c
c
净距30mm 钢筋直径d
净距30mm 钢筋直径d
h h0=h-60
c25mm d
c
b
净距25mm 钢筋直径d
h h0=h-35
b
h b
2~3.5(矩形截)面 2.5~4.0(T形截面 )
d 1~ 0 2m 0(桥 m 1 梁 ~ 4 4m 中 0)m
三、截面尺寸和配筋构造
1. 板
c15mm d
1 3
c0 t
c
)
yc
n h0 (1
1 2
1 12
c0
t c
1
1 3
c0
t c
2 )
五、受弯构件正截面受力分析
4. 破坏阶段的受力分析
对适筋梁,达极限状态时,
xn=nh
0
c t cu0.00,3s 3fy
M
X 0
n
1.253s
fy
c0
ct= c0
ct
yc
c
C
0
sAs(fyAs)
M0
MfyAsh0(10.412 n) c0b0h2n(0.7980.32n 9)
平衡破坏 适筋破坏
cu xn
b
h0
y
超筋破坏
xb 矩形应力图形的 压界 区限 高受 度
b 矩形应力图形的 压界 区限 相受 对高度
bh x0 bh 10 xbc 1 ucu y1 1cyu1 E1 sfycu
六、受弯构件正截面简化分析
2. 界限受压区高度
fcu50Mp时 a :
b
1
0.8 fy
0.0033Es
b即 nnb
b即 nnb
b即 nnb
拉区混凝土开裂后的处理
P
P
曲率
平均应变分布
即使在纯弯段也只可能在几个截面上出现裂 缝,裂缝间混凝土的拉应变不相等
?
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
拉区混凝土开裂后的处理--Considère(1899)试验
N (kN)
200
混凝土:fc=30.8MPa; ft=1.97MPa;
六、受弯构件正截面简化分析
1. 压区混凝土等效矩形应力图形(极限状态下)
c0=1fc
1c0
由C的大小不变
xn=nh
0
yc C
xn=nh
0
yc C
x=1xn
Mu
Mu
C1fcbnh0(113cc0u)11fc1nbh0
sAs
sAs
1
1
1
(11c0) 3cu
由C的位 置不变
ycnh0(11 2 11 11 32c cc c00uu2)0.51nh0,113 21c c 0u1 3 1 6c c0uc c0u2
由大量试验结果,
xn=nh
0
Mu
yc C
x=1xn
sAs
根据统计分析
1
1.0 0.94
fcu50Mpa fcu80Mpa
中间线性插值
六、受弯构件正截面简化分析
2. 界限受压区高度
cu
xnb 界限受压区高度
平衡破坏
xn
b
nb 界限受压区相对高度 适筋破坏
h0
nb
xn b h0
cu cuy
y
超筋破坏
as b
ci Zi
As
1
i
Zi
截面中心线 s n
As
c1 s ci M
N
sAs ci
sAs
s '
(h 2
as
'
)
s
(h 2
a s )
二、骨架曲线的弯矩-曲率关系
2. 短期荷载下的弯矩-曲率关系
截面的物理方程(对物理方程的处理)
cic(ci) cic(ci)
s s ( s )
s s (s )
•界限配筋率、最小配筋率是区分适筋破坏、超筋破坏和少筋破坏的定量 指标
五、受弯构件正截面受力分析
1. 基本假定 P
平截面假定----平均应变意义上
As’
as’
dy
y
h
L/3
L/3
ct
L
c
s’ nh0
As
(1-n)h0
s
b c
as
b
nh c t0ycnh0s 'as'(1sn)h0
五、受弯构件正截面受力分析
E1nnctAs
n 22En2E0
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
ct
ct
xn=n
c
h0
A
h0 h
y
M
s
s
yc C xn
sAs
cb
b
M较大时, c按曲 线性分布,需要进 行积分计算(略)
M0
M 0 .5c tbn h 0 2 (1 1 3n )sA sh 0 (1 1 3n )
1. 基本假定
混凝土受压时的应力-应 变关系
当应力较小 c时 0.3f, c时如 ,可 c Ecc
n26 1(0fcu5)0当 ,n2时, n2取
c fc
c
fc 110c
n
o
0
00.0020.5fcu501 05
00.00时 2 , 0取 0.002
c u
u 0.0033fcu50105
u 0.00时 33,u取 0.003
五、受弯构件正截面受力分析
3. 开裂阶段的受力分析
ct
ct
xn=n
c
h0
A
h0 h
y
M
s
s
yc C xn
sAs
cb
b
M较小时, c可以认为 是按线性分布,忽略拉
