Dijkstra算法求解最短路径的设计与实现
Dijkstra算法原理详细讲解

Dijkstra算法原理详细讲解
Dijkstra算法是图论中的一种贪心算法,用于求解最短路径问题。
该算法的贪心策略是:每次选择当前距离起点最近的节点作为中间节点,并更新起点到其它节点的距离。
通过不断选择距离起点最近的节点,并逐步更新起点到各个节点的距离,最终得到起点到终点的最短路径。
Dijkstra算法的具体实现包括以下几个步骤:
1. 初始化:将起点到各个节点的距离记为无穷大或者一个较大的值,将起点到自己的距离记为0。
2. 选择当前距离起点最近的节点作为中间节点。
这个过程可以通过维护一个距离起点最近的节点集合来实现,初始时集合中只包含起点。
3. 更新起点到与中间节点相邻的节点的距离,即对于每个与中间节点相邻的节点,如果从起点到中间节点的距离加上中间节点到该节点的距离小于起点到该节点的距离,则更新起点到该节点的距离为从起点到中间节点的距离加上中间节点到该节点的距离。
4. 重复步骤2和步骤3,直到起点到终点的距离不再更新。
5. 最终得到起点到终点的最短路径。
Dijkstra算法的时间复杂度为O(N^2),其中N为节点的数目。
如果使用优先队列来维护距离起点最近的节点集合,则算法的时间复杂度可以降为O(NlogN),但是实际应用中优先队列的实现可能较为复杂。
Dijkstra算法可以用于有向图和无向图,但是不能处理带有负权边的图。
如果图中存在负权边,则可以使用Bellman-Ford算法来求解最短路径。
Dijkstra最短路径算法的实现及优化

Dijkstra最短路径算法的实现及优化 施培港 厦门信息港建设发展股份有限公司 厦门市槟榔路1号联谊广场五层 361004 Email:spg@xminfoport.com 摘要:最短路径算法种类繁多,比较有名的算法包括:Dijkstra算法、Ford算法、Floyd算法、Moore算法、A*算法、K值算法,而即使同一种算法也有多种不同的实现方式。
本文就Dijkstra算法的两种实现方式做一定的分析,并采用一种新的实现方法达到对算法优化的目的。
关键字:Dijkstra算法 最短路径 网络分析 地理信息系统(GIS) 1. 何谓最短路径 所谓最短路径就是网络中两点之间距离最短的路径,这里讲的距离可以是实际的距离,也可以引申为其它的度量,如时间、运费、流量等。
因此,从广义上讲,最短路径算法就是指从网络中找出两个点之间最小阻抗路径的算法。
2. Dijkstra算法介绍 Dijkstra算法本身是一种贪婪算法,它通过分步的方法来求最短路径。
首先,初始产生源点到它自身的路径,其长度为零,然后在贪婪算法的每一步中,产生一个到达新的目的顶点的最短路径。
其算法描述如下(算法中以有向图表示网络结构): 对于有向图G =(V,E),图中有n个顶点,有e条弧,其中V为顶点的集合,E为弧的集合,求源点VS到终点VT的最短路径。
(1) 用带权的邻接矩阵L来表示有向图,L(X,Y)表示弧<X,Y>的权值,若弧<X,Y>不存在,则设L(X,Y)=∞;用D(X)表示源点VS到顶点X的距离,除源点VS的值为0外,其余各点设为∞;用S表示已找到的从源点VS出发的最短路径的顶点的集合,其初始状态为空集;用V-S表示未找到最短路径的顶点的集合; (2) 选择源点VS做标记,令Y = VS,S = S ∪ {VS}; (3) 对于V-S中各顶点, 若D(X) > D(Y) + L(Y,X),则修改D(X)为 D(X) = D(Y) + L(Y,X) 其中Y是己确定作标记的点; (4) 选择Vj,使得D(j) = min{ D(i) | Vi ∈ V-S } 若D(j)为∞,则说明VS到V-S中各顶点都没有通路,算法终止;否则,Vj就是当前求得的一条从源点VS出发的最短路径的终点,对Vj做标记,令Y = Vj,并把Vj放入集合S中,即令S = S ∪ {Vj}; (5) 如果Y等于VT,则说明已经找到从VS到VT的最短路径,算法终止;否则,转到3继续执行。
最短路径dijkstra算法流程

最短路径dijkstra算法流程最短路径算法是计算在带权有向图或者无向图中起点到所有其他点最短路径的一种算法,其中最短路径指的是边权值之和最少的路径。
目前最常用的算法是Dijkstra算法,它是由荷兰计算机科学家Edsger W. Dijkstra于1959年提出的。
下面将介绍Dijkstra算法的流程。
1. 初始化首先,需要将起点到每个点的最短距离都初始化为无穷大,除了起点自己的最短距离为0。
其中,起点是指算法的起点节点。
同时,需要创建一个集合S,用于记录已经确定了最短距离的点。
2. 找出未确定最短路径的节点中最小的距离,并将其标记为已确定最短路径在第一步中,只有起点节点的最短距离是确定的。
接下来,在集合S中找出剩余未确定最短路径的节点中距离最小的节点u,并将其标记为已经确定了最短路径。
在第一次执行该步骤时,节点u即为起点节点。
3. 更新最短距离将节点u所有邻居的距离进行更新。
假设节点v是节点u的邻居,其距离为d(u,v),则:如果 d(u,v) + dist(u) < dist(v),则更新节点v的最短距离为d(u,v) + dist(u),其中dist(u)表示起点节点到节点u的最短距离。
重复执行上述步骤,直到集合S中包含所有节点。
4. 输出每个节点的最短距离执行完第三步之后,每个节点的最短距离都已经确定。
此时,可以输出每个节点的最短距离。
以上就是Dijkstra算法的流程。
此外,这个算法还可以通过堆优化来提高效率。
具体来说,可以将还未确定最短距离的节点按照距离从小到大存储在堆中,每次取出堆中距离最小的节点。
(这部分由于是在原算法的基础之上的优化模型,所以该模型不友好于百科网站的格式要求,如果您有需要,也可以决定不包括,并以此作为描述结尾)总的来说,Dijkstra算法是求解最短路径问题的有效方法之一。
它适用于只有正权边的有向或者无向图,并且能够计算出起点到所有其他节点的最短路径。
因此,它可以用于路线规划、制订地图等应用情景中。
最短路径算法dijkstra算法python

最短路径算法dijkstra算法python Dijkstra算法是一种用于求解图中两点之间最短路径的经典算法。
该算法由荷兰计算机科学家Edsger Dijkstra于1956年提出,至今仍然被广泛运用于各个领域,例如路由算法、网络优化、地图导航等。
本文将以Python 语言为基础,详细介绍Dijkstra算法的原理和实现过程。
一、Dijkstra算法的原理Dijkstra算法的核心思想是利用贪心策略逐步构建最短路径树。
该算法首先将起始节点的距离设置为0,将其他节点的距离设置为无穷大。
然后在每一轮选择距离起始节点最近的节点,并更新其周围节点的距离。
通过不断选择距离最近的节点,并更新距离,直到找到终点节点或所有节点都被访问完毕,即可得到起始节点到终点节点的最短路径。
二、算法的实现步骤下面将详细介绍Dijkstra算法的实现步骤。
1. 创建一个空的顶点集合visited和距离集合distance,并初始化起始节点的距离为0,其他节点的距离为无穷大。
2. 选择起始节点,并将其加入visited集合。
3. 遍历起始节点的邻居节点,计算起始节点到每个邻居节点的距离,并更新distance集合。
4. 在distance集合中选择距离起始节点最短的节点,将其加入visited 集合。
5. 重复步骤3和步骤4,直到终点节点被加入visited集合或所有节点都被访问完毕。
6. 根据visited集合和distance集合,可以得到起始节点到终点节点的最短路径。
三、Dijkstra算法的Python实现下面将使用Python语言实现Dijkstra算法,并解决一个具体的例子。
首先,创建一个图的类,包含节点和边的信息,并定义一些基本的方法。
其中,节点信息包括标识符、邻居节点和距离,边的信息包括起始节点、终点节点和权重。
pythonclass Graph:def __init__(self):self.nodes = []self.edges = []def add_node(self, node):self.nodes.append(node)def add_edge(self, start, end, weight):edge = (start, end, weight)self.edges.append(edge)接下来,实现Dijkstra算法的主要函数,用于求解最短路径。
最短路径问题dijkstra求解过程

Dijkstra算法是一种用于求解最短路径问题的常用算法,适用于带权有向图。
以下是Dijkstra 算法的求解过程:
初始化:将起始节点标记为当前节点,并将起始节点到所有其他节点的距离初始化为无穷大(表示暂时未知)。
将起始节点到自身的距离设置为0,表示起始节点到自身的最短路径长度为0。
遍历所有节点:
选择当前节点的邻接节点中,距离最小且尚未被访问的节点。
更新该邻接节点的最短路径长度。
如果经过当前节点到达该邻接节点的路径比当前记录的最短路径更短,则更新最短路径长度。
继续遍历未访问的节点,直到所有节点都被访问。
重复步骤3,直到所有节点都被访问或者没有可达节点。
最终得到起始节点到其他节点的最短路径长度。
在Dijkstra算法的求解过程中,使用一个距离表(distances)来记录起始节点到各个节点的当前最短路径长度,一个访问表(visited)来标记节点是否已被访问。
同时,使用优先队列(例如最小堆)来选取下一个距离最小且尚未被访问的节点。
具体的实现可以使用迭代或递归的方式,根据实际情况来选择合适的数据结构和算法实现。
在实际编程中,可能还需要考虑处理边的权重、处理节点的邻接关系和路径记录等细节。
Dijkstra算法要求图中的边权重非负,且无法处理负权边的情况。
对于含有负权边的图,可以考虑使用其他算法,如Bellman-Ford算法或SPFA(Shortest Path Faster Algorithm)等。
dijkstra算法代码实现

Dijkstra算法是一种用于解决单源最短路径问题的经典算法,由荷兰计算机科学家艾兹赫尔·迪克斯特拉在1956年提出。
该算法主要用于计算一个顶点到其余各个顶点的最短路径。
Dijkstra算法的基本思想是:假设图G中顶点集合为V,边集合为E,从源点s开始,初始时只有s的已知最短路径,用集合S记录已找到最短路径的顶点。
利用S中顶点的最短路径来更新其余顶点的最短路径,直到找到从s到其余所有顶点的最短路径。
Dijkstra算法具体实现过程如下:1. 创建两个集合,一个用来保存已找到最短路径的顶点集合S,另一个用来保存未找到最短路径的顶点集合V-S。
2. 初始化距离数组dist[],将源点到各个顶点的距离初始化为无穷大,源点到自身的距离初始化为0。
3. 从源点s开始,将s加入S集合,更新源点到其余各个顶点的距离,如果存在边(u,v),使得dist[v] > dist[u] + w(u,v),则更新dist[v] = dist[u] + w(u,v),其中w(u,v)表示边(u,v)的权值。
4. 重复第3步,直到将所有顶点加入S集合为止,此时dist数组即为源点到各个顶点的最短路径。
根据以上实现思路,我们可以使用代码来实现Dijkstra算法。
以下是Python语言的Dijkstra算法实现示例:```pythondef dijkstra(graph, src):dist = [float('inf')] * len(graph)dist[src] = 0visited = [False] * len(graph)for _ in range(len(graph)):u = min_distance(dist, visited)visited[u] = Truefor v in range(len(graph)):if graph[u][v] > 0 and not visited[v] and dist[v] > dist[u] + graph[u][v]:dist[v] = dist[u] + graph[u][v]print_solution(dist)def min_distance(dist, visited):min_dist = float('inf')min_index = -1for v in range(len(dist)):if dist[v] < min_dist and not visited[v]:min_dist = dist[v]min_index = vreturn min_indexdef print_solution(dist):print("顶点\t最短距离")for i in range(len(dist)):print(f"{i}\t{dist[i]}")```在上面的示例代码中,我们首先定义了一个dijkstra函数,该函数接受图的邻接矩阵表示和源点的索引作为参数。
matlab dijkstra算法求解最短路径例题

matlab dijkstra算法求解最短路径例题摘要:一、Dijkstra 算法简介1.Dijkstra 算法背景2.Dijkstra 算法原理二、MATLAB 实现Dijkstra 算法求解最短路径1.创建图对象2.计算最短路径3.可视化结果三、Dijkstra 算法应用示例1.例题描述2.解题步骤3.结果分析正文:一、Dijkstra 算法简介Dijkstra 算法是一种经典的图论算法,用于计算图中两个节点之间的最短路径。
它是由荷兰计算机科学家Edsger W.Dijkstra 于1956 年提出的,其基本思想是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra 算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
可以用堆优化来提高效率。
二、MATLAB 实现Dijkstra 算法求解最短路径1.创建图对象首先,我们需要使用MATLAB 的graph 函数创建一个图对象,指定节点和边的信息。
例如,我们创建一个简单的图,包含4 个节点和3 条边:```matlabG = graph(4, 3);```其中,4 表示图中有4 个节点,3 表示图中有3 条边。
2.计算最短路径接下来,我们可以使用MATLAB 的shortestpath 函数计算两个节点之间的最短路径。
例如,我们计算节点1 到节点3 的最短路径:```matlabSP = shortestpath(G, 1, 3);```3.可视化结果最后,我们可以使用MATLAB 的plot 函数将最短路径可视化。
例如,我们绘制节点和边以及最短路径:```matlabplot(G, SP);```三、Dijkstra 算法应用示例以下是一个使用Dijkstra 算法求解最短路径的例题:在一个图中,有4 个节点和3 条边,如下所示:```1 --2 -- 3| /| /| /| /|/4```请问,节点1 到节点4 的最短路径是多少?。
dijkstra最短路径算法详解

dijkstra最短路径算法详解
Dijkstra最短路径算法是一种常用的图算法,用于求解带权图中的单源最短路径问题,即从一个固定的源节点到图中的其他节点的最
短路径。
以下是详细的算法步骤:
1. 初始化
一开始,将源节点的距离设为0,其余节点的距离设置为正无穷,在未访问的节点集合中把源节点压入堆中。
2. 确定最短路径
从堆中取出未访问节点集合中距离源节点最近的节点v,标记其
为已访问。
之后,对于v的邻居节点w,计算从源节点到v再到w的距离,如果经过v的路径比已经计算得到的路径短,则更新路径。
更新
后的距离先暂时放入堆中,如果后边有更短的路径,则更新。
3. 重复第2步
重复第2步,直到取出的节点为终点节点,或者堆为空。
4. 算法结束
算法结束后,各节点的距离就是从源节点到它们的最短距离。
Dijkstra算法的复杂度是O(NlogN),其中N是节点个数。
其优
势在于只需要算一次即可得到所有最短路径,但是要求所有边的权值
必须非负,否则会导致算法不准确。
总之,Dijkstra算法是一种简单有效的最短路径算法,其实现也比较直观。
在处理如飞机和火车等交通路径规划问题中有较好的应用。
路由算法中的Dijkstra算法实现原理

路由算法中的Dijkstra算法实现原理路由算法是计算机网络中的一项重要技术,它指导着数据在网络中的传输过程。
路由算法中的Dijkstra算法是其中一种比较常用的算法,它通过计算最短路径来选择数据传输方案,进而实现高效稳定的数据传输。
本文将详细介绍Dijkstra算法的实现原理。
一、Dijkstra算法的概述Dijkstra算法是一种用于计算带权图最短路径的算法。
它的基本思想是:维护一个当前已知的最短路径集合S和距离源点最短的节点v,然后以v为基础扩展出一些新的节点,并计算这些节点到源点的距离并更新路径集合S。
重复这一过程,一直到源点到所有节点的最短路径集合已经确定为止。
该算法求解的是一个有向带权图中一个节点到其他所有节点的最短路径问题,其中「带权」表示图的边权值是一个非负实数。
二、Dijkstra算法的实现Dijkstra算法可以使用多种数据结构的实现,常见的有数组、链表、堆等。
这里我们以使用优先队列为例进行实现。
首先,定义一个数组distance用于存储源点至所有节点的最短距离。
初始状态下,将源点与其它节点的距离初始化为正无穷大。
同时,构建一个优先队列,用于维护已经遍历过的节点。
具体实现过程如下:1. 初始化distance数组和优先队列。
将源点源加入优先队列中,与源点相邻的节点按照距离增序加入队列中。
2. 从队列中取出距离源点最短的节点u,然后遍历所有与节点u相邻的节点v。
通过计算distance[u] + w(u,v)可得到源点到节点v的距离。
如果这个距离比已经存储在distance[v]中的距离更短,则更新distance[v]的值,同时将节点v加入到优先队列中。
3. 重复步骤2,直到所有节点都已经加入到队列中,并且所有节点的最短路径都已经被确定。
三、Dijkstra算法的时间复杂度分析Dijkstra算法的时间复杂度主要取决于寻找当前距离源点最短的节点的过程。
如果使用数组实现,该过程的时间复杂度为O(n^2),n为节点数量。
dijkstra算法 java最短路径

dijkstra算法java最短路径Dijkstra算法是一种用于寻找图中两个节点之间最短路径的算法。
它采用的是贪心策略,将图中的节点分为两个集合:已访问节点集S和未访问节点集T。
算法从源节点开始,每次从T中选择到源节点距离最短的节点加入S集合,并更新S集合中各节点到源节点的最短路径。
直到T集合中的节点全部加入S集合,算法结束。
Dijkstra算法的Java实现如下:●public class Dijkstra{●public static void main(String[]args){●创建图●Graph graph=new Graph();●graph.addVertex("A");●graph.addVertex("B");●graph.addVertex("C");●graph.addEdge("A","B",10);●graph.addEdge("A","C",20);●graph.addEdge("B","C",30);●计算最短路径●dijkstra(graph,"A");}●private static void dijkstra(Graph graph,String startVertex){●初始化●Set<String>visited=new HashSet<>();●Map<String,Integer>distances=new HashMap<>();●for(String vertex:graph.getVertices()){●distances.put(vertex,Integer.MAX_VALUE);}●distances.put(startVertex,0);●遍历所有节点●for(String vertex:graph.getVertices()){●找到未访问节点中距离源节点最小的节点●String nearestVertex=findNearestVertex(distances,visited);●将该节点加入已访问节点集合●visited.add(nearestVertex);●更新该节点到其他节点的最短路径●for(String neighbor:graph.getAdjacentVertices(nearestVertex)){●intnewDistance=distances.get(nearestVertex)+graph.getEdgeWeight(nearestVertex,neighbor ●if(newDistance<distances.get(neighbor)){●distances.put(neighbor,newDistance);}}}●输出结果●System.out.println("从"+startVertex+"到其他节点的最短路径:");●for(String vertex:graph.getVertices()){●System.out.println(vertex+"的最短路径是:"+distances.get(vertex));}}●private static String findNearestVertex(Map<String,Integer>distances,Set<String>visited){●int minDistance=Integer.MAX_VALUE;●String nearestVertex=null;●for(String vertex:distances.keySet()){●if(!visited.contains(vertex)&&distances.get(vertex)<minDistance){●minDistance=distances.get(vertex);●nearestVertex=vertex;}}●return nearestVertex;}}该算法的工作原理如下:1.初始化距离表,将所有节点的距离初始化为无穷大。
最短路dijkstra算法详解

最短路dijkstra算法详解最短路问题是图论中的一个经典问题,其目标是在给定图中找到从一个起点到其他所有节点的最短路径。
Dijkstra算法是解决最短路问题的一种常用算法,本文将详细介绍Dijkstra算法的原理、实现以及时间复杂度等相关内容。
一、Dijkstra算法的原理Dijkstra算法是一种贪心算法,其基本思想是从起点开始,逐步扩展到其他节点。
具体而言,Dijkstra算法通过维护一个集合S来记录已经找到了最短路径的节点,以及一个数组dist来记录每个节点到起点的距离。
初始时,S集合为空,dist数组中除了起点外所有节点都被初始化为无穷大。
接下来,重复以下步骤直到所有节点都被加入S集合:1. 从dist数组中选择距离起点最近的未加入S集合的节点u;2. 将u加入S集合;3. 更新与u相邻的未加入S集合的节点v的距离:如果从起点出发经过u可以得到更短的路径,则更新v对应位置上dist数组中存储的值。
重复以上步骤直至所有节点都被加入S集合,并且dist数组中存储了每个节点到起点的最短距离。
最后,根据dist数组中存储的信息可以得到起点到任意节点的最短路径。
二、Dijkstra算法的实现在实现Dijkstra算法时,需要使用一个优先队列来维护未加入S集合的节点,并且每次从队列中选择距离起点最近的节点。
由于C++标准库中没有提供优先队列,因此需要手动实现或者使用第三方库。
以下是一个基于STL堆实现的Dijkstra算法代码示例:```c++#include <iostream>#include <vector>#include <queue>using namespace std;const int INF = 0x3f3f3f3f;vector<pair<int, int>> adj[10001];int dist[10001];void dijkstra(int start) {priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;pq.push(make_pair(0, start));dist[start] = 0;while (!pq.empty()) {int u = pq.top().second;pq.pop();for (auto v : adj[u]) {if (dist[u] + v.second < dist[v.first]) {dist[v.first] = dist[u] + v.second;pq.push(make_pair(dist[v.first], v.first));}}}}int main() {int n, m, start;cin >> n >> m >> start;for (int i = 1; i <= n; i++) {dist[i] = INF;}for (int i = 1; i <= m; i++) {int u, v, w;cin >> u >> v >> w;adj[u].push_back(make_pair(v, w));}dijkstra(start);for (int i = 1; i <= n; i++) {if (dist[i] == INF) {cout << "INF" << endl;} else {cout << dist[i] << endl;}}return 0;}```以上代码中,adj数组用于存储图的邻接表,dist数组用于存储每个节点到起点的最短距离。
dijkstra算法最短路径

《求解最短路径:应用迪杰斯特拉算法》一、介绍Dijkstra算法的概念和基本原理Dijkstra算法是一种用于解决最短路径问题的算法,它由荷兰计算机科学家Edsger Dijkstra在1959年发明,用于求解从源点到其他所有结点的最短路径。
它的基本原理是:在一张图中,从源点到每一个结点的最短路径是从源点开始,经过最少的边到达每一个结点的路径。
Dijkstra算法的实现过程中,首先要建立一个有向图,该图由顶点和边组成,每条边都有一个权值,表示从一个顶点到另一个顶点的距离。
然后,从源点开始,每次选择最小权值的边,继续查找下一个顶点,直到找到终点。
最后,将所有路径之和求出,即为源点到目标点的最短路径。
举例来说,假如有一张有向图,其中有A,B,C,D四个结点,以及AB,AC,BD,CD四条边,其中AB,AC,BD边的权值分别为2,3,1,CD边的权值为4。
如果要求求出从A到D的最短路径,则可以使用Dijkstra算法,首先从A出发,选择权值最小的边,即BD,则A-B-D的路径长度为3,接着从B出发,选择权值最小的边,即CD,则A-B-D-C的路径长度为7,因此,从A到D的最短路径为A-B-D,路径长度为3。
Dijkstra算法的优点是算法简单,实现方便,时间复杂度低,它可以用于解决路径规划,车辆调度,网络路由等问题,同时,它也可以用于解决复杂的最短路径问题。
因此,Dijkstra算法在计算机科学中有着重要的应用价值。
二、讨论Dijkstra算法的应用及其优势Dijkstra算法是一种用于解决最短路径问题的算法,它的应用和优势非常广泛。
首先,Dijkstra算法可以用于解决交通路网中的最短路径问题。
例如,在一个城市的交通路网中,如果一个乘客要从一个地方到另一个地方,那么他可以使用Dijkstra算法来查找最短的路径。
这样可以节省乘客的时间和金钱,也可以减少拥堵。
此外,Dijkstra算法还可以用于解决计算机网络中的最短路径问题。
Dijkstra算法求解单源最短路径问题
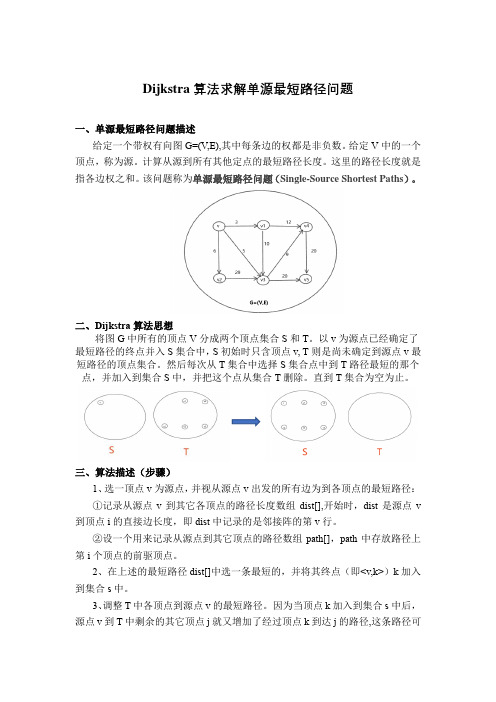
Dijkstra算法求解单源最短路径问题一、单源最短路径问题描述给定一个带权有向图G=(V,E),其中每条边的权都是非负数。
给定V中的一个顶点,称为源。
计算从源到所有其他定点的最短路径长度。
这里的路径长度就是指各边权之和。
该问题称为单源最短路径问题(Single-Source Shortest Paths)。
二、Dijkstra算法思想将图G中所有的顶点V分成两个顶点集合S和T。
以v为源点已经确定了最短路径的终点并入S集合中,S初始时只含顶点v, T则是尚未确定到源点v最短路径的顶点集合。
然后每次从T集合中选择S集合点中到T路径最短的那个点,并加入到集合S中,并把这个点从集合T删除。
直到T集合为空为止。
三、算法描述(步骤)1、选一顶点v为源点,并视从源点v出发的所有边为到各顶点的最短路径:①记录从源点v到其它各顶点的路径长度数组dist[],开始时,dist是源点v到顶点i的直接边长度,即dist中记录的是邻接阵的第v行。
②设一个用来记录从源点到其它顶点的路径数组path[],path中存放路径上第i个顶点的前驱顶点。
2、在上述的最短路径dist[]中选一条最短的,并将其终点(即<v,k>)k加入到集合s中。
3、调整T中各顶点到源点v的最短路径。
因为当顶点k加入到集合s中后,源点v到T中剩余的其它顶点j就又增加了经过顶点k到达j的路径,这条路径可能要比源点v到j原来的最短的还要短。
调整方法是比较dist[k]+g[k,j]与dist[j],取其中的较小者。
4、再选出一个到源点v路径长度最小的顶点k,从T中删去后加入S中,再回去到第三步,如此重复,直到集合S中的包含图G的所有顶点。
四、算法实现(数据结构)1、算法实现输入:一个大于1的整数n.输出:●一个随机生成的有向图G=(V,E),对于每一条边,有一个非负数字c(u,v)与之相关。
●对于每个顶点v∈V,得到从v0到v的最短路径的长度。
Dijkstra算法步骤详述

Dijkstra算法步骤详述Dijkstra算法是一种经典的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
本文将详细介绍Dijkstra算法的步骤和实现。
1. 初始化首先,我们需要将算法的输入进行初始化。
假设我们有一个带权重的有向图,其中节点集合为V,边的集合为E。
对于每个节点v ∈ V,我们设置初始距离d[v]为正无穷大(INF),表示从起点到节点v的距离为无穷大;同时,我们设置起点s的初始距离d[s]为0,表示从起点到自身的距离为0。
2. 确定最短路径接下来,我们将在图中逐步确定起点到其他节点的最短路径。
首先,我们从起点s开始,将s标记为当前节点。
然后,对于s的所有邻居节点v,我们更新其当前最短路径,并标记v为下一个当前节点。
这一步骤可以通过以下过程实现:a. 对于节点s的所有邻居节点v,计算通过s到达v的距离。
如果该距离小于d[v],则将d[v]更新为该距离,并将s作为节点v的前驱节点(即最短路径上v的前一个节点)。
b. 从剩余的未标记节点中选择一个距离最短的节点作为下一个当前节点。
具体而言,从未标记节点中选择一个节点u,使得d[u]最小,并将其标记为当前节点。
3. 更新最短路径在上一步中,我们确定了起点到一个节点的最短路径。
现在,我们将以已选择的当前节点继续执行第2步,直到所有节点都被标记为止。
具体而言,重复进行以下步骤:a. 在当前节点的所有邻居节点中,更新其最短路径并选择下一个当前节点,过程与第2步相同。
b. 如果不存在未标记节点,则算法终止。
4. 输出最短路径当算法终止时,我们可以得到从起点到达所有节点的最短路径。
对于每个节点v,最短路径可以通过回溯每个节点的前驱节点得到。
具体而言,从目标节点开始,通过前驱节点一直回溯到起点,即可得到最短路径。
总结:Dijkstra算法通过逐步确定起点到其他节点的最短路径,从而找到整个图中的最短路径。
它的步骤包括初始化、确定最短路径和更新最短路径。
最短路径算法―Dijkstra(迪杰斯特拉)算法分析与实现(

Dijkstra( 迪杰斯特拉算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra 算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra 算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。
一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。
设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。
Dijkstra 算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S 中,同时对数组dist作必要的修改。
一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
例如,对下图中的有向图,应用Dijkstra 算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。
Dijkstra 算法的迭代过程:主题好好理解上图!以下是具体的实现(C/C++:A ]***************************************2.* About: 有向图的Dijkstra 算法实现3. * Author: Tanky Woo4. * Blog: 6.7. #i nclude8. using n amespace std;9.9. con st i nt maxnum = 100;10. con st i nt maxi nt = 999999;12.13.11. void Dijkstra(i nt n, int v, int *dist, int *prev, int c[max nu m][max num]12. {13. bool s[maxnum]; // 判断是否已存入该点到 S 集合中14. for(i nt i=1; i<=n; ++i15. {16. dist[i] = c[v][i];17. s[i] = 0; // 初始都未用过该点18. if(dist[i] == maxi nt19. prev[i] = 0;20. else21. prev[i] = v;22. }23. dist[v] = 0;24. s[v] = 1;28.29. // 依次将未放入S 集合的结点中,取 dist[] 最小值的结点,放入结合 S 中5. *************************************30. // 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度31.for(i nt i=2; i<=n; ++i32.{33.i nt tmp = maxi nt;34.i nt u = v;35.// 找出当前未使用的点j的dist[j] 最小值36.for(int j=1; j<=n; ++j37.if((!s[j] && dist[j]38.{39.u = j; // u 保存当前邻接点中距离最小的点的号码40.tmp = dist[j];41.}42.s[u] = 1; // 表示u点已存入S集合中43.43.// 更新dist44.for(i nt j=1; j<=n; ++j45.if((!s[j] && c[u][j]46.{47.int newdist = dist[u] + c[u][j];48.if( newdist < dist[j]49.{50.dist[j] = n ewdist;51.prev[j] = u;52.}53.}54.}55.}58.void searchPath(i nt *prev,i nt v, int u59.{60.int que[max nu m];61.i nt tot = 1;62.que[tot] = u;63.tot++;64.int tmp = prev[u];65.while(tmp != v66.{67.que[tot] = tmp;68.tot++;69.tmp = prev[tmp];70.}71.que[tot] = v;72.for(int i=tot; i>=1; --i73.if(i != 174.cout << que[i] << "-> ";75.else76.cout << que[i] << en dl;77.}78.78.int main(79.{80.freopen("input.txt", "r", stdin;81.II各数组都从下标1开始82.i nt dist[max num]; II 表示当前点到源点的最短路径长度83.i nt prev[max nu m]; II 记录当前点的前一个结点记录图的两点间路径长度84.i nt c[max nu m][max nu m]; II87.88. II输入结点数89. cin >> n;90. II输入路径数91. cin >> line;92. i nt p, q, le n; II 输入p, q93.94. II 初始化c[][] 为maxi nt95. for(i nt i=1; i<=n; ++i96. for(i nt j=1; j<=n; ++j97. c[i][j] = maxi nt;98.99. for(i nt i=1; i<=li ne; ++i100. {101. cin >> p >> q >> len;102. if(len < c[p][q] II 有重边103. {104. c[p][q] = le n; II p 指向q 105. c[q][p] = le n; II q指向p,106. }107. }108.109. for(int i=1; i<=n; ++i110. dist[i] = maxi nt;111. for(i nt i=1; i<=n; ++i112. {113. for(i nt j=1; j<=n; ++j 两点及其路径长度这样表示无向图114.printf("%8d", c[i][j];115.prin tf("\n";116.}117.117.Dijkstra(n, 1, dist, prev, c;119.118.// 最短路径长度119.cout << " 源点到最后一个顶点的最短路径长度:"<< dist[ n] << endl;122.120.// 路径121.cout << " 源点到最后一个顶点的路径为:";122.searchPath(prev, 1, n;123.}复制代码输入数据:571 2 101 4 301 5 1002 3 503 5 104 3 204 5 60输出数据:999999 10 999999 30 10010 999999 50 999999 999999 999999 50 999999 20 1030 999999 20 999999 60100 999999 10 60 999999源点到最后一个顶点的最短路径长度: 60 源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5。
最短路径 算法

最短路径算法在计算机科学和图形学中,最短路径算法是一种用于找到一组节点之间最短路径的算法。
这些算法广泛应用于路由算法、GIS系统、模拟导航系统等领域。
在许多实际应用中,最短路径算法提供了许多实用的功能,如确定两点之间的距离和导航路径等。
下面将介绍几种最短路径算法的基本原理和实现方法。
一、Dijkstra算法Dijkstra算法是一种基于贪婪策略的最短路径算法,适用于图中不含负权边的图。
该算法的基本思想是从一个源节点开始,逐步计算源节点到其他节点的最短路径。
算法的核心思想是每次选择当前已知最短路径的节点,并更新其邻居节点的距离。
实现步骤如下:1. 初始化:将源节点的距离设为0,将所有其他节点的距离设为无穷大。
2. 遍历所有与源节点相邻的节点,并更新其到源节点的距离。
3. 对于每个相邻节点,如果通过源节点到达该节点的距离小于当前距离,则更新该节点的距离。
4. 重复步骤2和3,直到所有节点的距离都得到更新。
二、Bellman-Ford算法Bellman-Ford算法是一种适用于包含负权边的图的最短路径算法。
该算法通过多次迭代来更新节点的距离,并使用松弛操作来检测负权环。
该算法的时间复杂度为O(n),其中n是图中节点的数量。
实现步骤如下:1. 初始化:将源节点的距离设为0,并将所有其他节点的距离设为可能的最长距离(例如正无穷)。
2. 对于每个相邻节点u,从图中移除边(u, v),并更新v的距离(如果存在)。
3. 在没有剩余边的情况下,重新初始化所有节点的距离。
4. 重复步骤2和3,直到所有边的长度被增加到所有v的权重的加和+ε或被更改为新权重的节点变为可达状态。
如果某个节点的权重减小或为负数(因此没有负权环),那么就从结果集中移除它,并将邻居的权重减小对应的数量到其它节点中对应邻居的权重处(对权重相同的情况仍然可采用轮转机制确保统一更新)以优化该点下一步的可能选择空间和对应的下一个邻居的可能状态下的可能性一致。
最短路径问题(Dijkstra算法)和最小生成树(Kruskal算法和Prim算法)

t(j)=tmin;
end
end
end
ifk==n
break;
end
end
T;
c;
Prim算法程序:
function[T c] =Primf(a)
%a表示权值矩阵
%c表示生成树的权和
%T表示生成树的边集合
l=length(a);
a(a==0)=inf;
k=1:l;
listV(k)=0;
上机实验1、2
1.最短路径问题(Dijkstra算法)
2.最小生成树(Kruskal算法和Prim算法)
一、最短路径问题(Dijkstra算法)
实验问题描述:如图的交通网络,每条弧上的数字代表车辆在该路段行驶所需的时间,有向边表示单行道,无向边表示可双向行驶。若有一批货物要从1号顶点运往11号顶点,问运货车应沿哪条线路行驶,才能最快地到达目的地。
listV(1)=1;
e=1;
while(e<l)
min=inf;
fori=1:l
iflistV(i)==1
forj=1:l
iflistV(j)==0&min>a(i,j)
min=a(i,j);b=a(i,j);
s=i;d=j;
end
end
end
end
listV(d)=1;
distance(e)=b;
T =
3 4 1 2
4 5 3 5
c =
10
>> a=[0 5 3 7 inf;5 0 8 inf 4;3 8 0 1 6;7 inf 1 0 2;inf 4 6 2 0];
>> [T c] =Primf(a)
dijkstra最短路径算法步骤

dijkstra最短路径算法步骤Dijkstra最短路径算法是一种用于在加权图中查找两个节点之间最短路径的算法。
它是由荷兰计算机科学家Edsger W. Dijkstra于1956年提出的。
该算法通过维护一个距离数组,记录每个节点到源节点的距离,并不断更新距离数组来寻找最短路径。
一、基本概念在介绍Dijkstra算法的具体步骤之前,我们需要了解一些基本概念。
1.加权图:加权图是指每条边都有一个权值的图。
2.距离数组:距离数组是指记录每个节点到源节点的当前最短距离的数组。
3.已访问集合:已访问集合是指已经找到最短路径的节点集合。
二、算法步骤1.初始化首先,我们需要将所有节点的距离初始化为无穷大,表示当前还没有找到任何一条路径。
同时,将源节点的距离设为0,表示从源节点到自己的距离为0。
2.选择最小值接下来,在未访问集合中选择一个当前距离最小的点,加入已访问集合中。
这个点就是当前最优解所在位置。
3.更新邻居节点然后,我们需要更新所有与该节点相邻的节点的距离。
具体来说,对于每个相邻节点,我们需要计算从源节点到该节点的距离是否比当前距离更短。
如果更短,则更新距离数组中该节点的值。
4.重复步骤2和3重复执行步骤2和3,直到所有节点都被加入已访问集合中。
此时,距离数组中存储的就是源节点到所有其他节点的最短路径。
三、示例假设我们有以下加权图:现在我们要从A点出发,找到到达其他各点的最短路径。
1.初始化首先,我们将所有点的距离初始化为无穷大,除了A点为0。
2.选择最小值我们从未访问集合{B,C,D,E}中选择当前距离最小的B点,并将其加入已访问集合中。
3.更新邻居节点接下来,我们需要更新与B相邻的所有点(C和D)的距离。
Dijkstra算法的实现和复杂度分析最短路径问题的解决方案

Dijkstra算法的实现和复杂度分析最短路径问题的解决方案最短路径问题一直是图论中的经典问题。
为了解决最短路径问题,荷兰计算机科学家Dijkstra提出了一种被广泛应用的算法。
本文将介绍Dijkstra算法的实现过程,并进行复杂度分析。
一、Dijkstra算法的简介Dijkstra算法是一种用于解决带有非负权重边的带权重有向图中单源最短路径问题的贪心算法。
该算法以源节点为中心逐步计算到其他节点的最短路径。
在每一步中,选择具有最小路径长度的节点作为下一次循环的起点,并使用该节点更新其邻接节点的路径长度。
二、Dijkstra算法的实现Dijkstra算法的实现分为以下步骤:1. 创建一个距离集合,用于存储起点到每个节点的路径长度。
将起点的距离初始化为0,其他节点的距离初始化为无穷大。
2. 创建一个已访问集合,用于标记已经计算过最短路径的节点。
3. 在未访问的节点中选择距离最小的节点作为下一次循环的起点,并标记为已访问。
4. 对于该节点的所有出边,更新其邻接节点的路径长度。
如果经过当前节点到达邻接节点的路径长度小于已存储的路径长度,则更新路径长度。
5. 重复步骤3和步骤4,直到所有节点都被访问过或者没有可以访问的节点为止。
三、Dijkstra算法的复杂度分析Dijkstra算法的复杂度可以分为两个部分进行分析:初始化和迭代更新。
1. 初始化在初始化阶段,需要为每个节点初始化其路径长度和已访问状态。
对于有n个节点的图来说,初始化的时间复杂度为O(n)。
2. 迭代更新迭代更新的次数不会超过节点数量n次。
在每次迭代中,需要在未访问的节点中找到路径长度最小的节点,这个过程的时间复杂度为O(n)。
然后,需要更新该节点的所有邻接节点的路径长度,这一步的时间复杂度为O(m),其中m为边的数量。
所以,迭代更新的时间复杂度为O(n*m)。
综上所述,Dijkstra算法的时间复杂度为O(n^2)。
在稠密图中,即m接近于n^2的情况下,算法的效率较低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Dijkstra算法求解最短路径的设计与实现
作者:刘敏
来源:《电脑知识与技术》2012年第12期
摘要:对任意图,选择合适的数据结构表示图,在此基础上实现求解最短路径的Dijkstra 算法。
对所设计的图的数据结构,提供必要的基本功能。
建立图的表示模块,顶点的插入和删除操作模块;在建立图之后从单源点开始求最短路径并显示。
实现的功能有建立有向图,排除和增加目的地,方便找出最短路径,在建立好的有向图中,显示出来从顶点到各个顶点的最短路径。
关键词:最短路径;有向图;数据结构
中图分类号:TP313文献标识码:A文章编号:1009-3044(2012)12-2759-03
1设计问题的提出
1.1对于最短路径问题
最短路径是在实际应用中非常有用的工具,将该问题细分,可以分为点到点最短路径,单源点的最短路径,所有点到所有点以及带负边情况下的最短路径。
1.2 Dijkstra算法的主要思想
Dijkstra算法的基本思路是:假设每个点都有一对标号(dj, pj),其中dj是从起源点s到点j 的最短路径的长度(从顶点到其本身的最短路径是零路(没有弧的路),其长度等于零);pj则是从s到j的最短路径中j点的前一点。
求解从起源点s到点j的最短路径算法的基本过程如下:
1)初始化。
起源点设置为:①ds=0, ps为空;②所有其他点: di=∞, pi=;③标记起源点s,记k=s,其他所有点设为未标记的。
2)检验从所有已标记的点k到其直接连接的未标记的点j的距离,并设置:dj=min[dj, dk+lkj]式中,lkj是从点k到j的直接连接距离。
3)选取下一个点。
从所有未标记的结点中,选取dj中最小的一个i:di=min[dj,所有未标记的点j]点i就被选为最短路径中的一点,并设为已标记的。
4)找到点i的前一点。
从已标记的点中找到直接连接到点i的点j*,作为前一点,设置:
i=j* 5)标记点i。
如果所有点已标记,则算法完全退出,否则,记k=i,转到2)再继续。
2概要设计
在任意图中实现求最短路径问题,首先是要能成功的在内存中输入图的信息,图的信息有两个,一是顶点个数,二是每两点之间的权值信息。
当建立图之后,对图进行遍历才能使用Dijkstra算法求出最短路径,所以,建立图这一步很关键。
在实际使用当中,顶点的信息是成千上万,而且是随时可能产生变动,故建图模块要实现顶点的删除和插入操作;在完成了图的建立之后,用Dijkstra算法的思想,从单源点开始,求出到各个顶点的最短路径,并能够实现显示功能,这也是程序实际化的要求。
3建图过程
能把一个带有顶点和权值的数据结构图输入电脑首先要用到数组,存储每个顶点信息以及每两个顶点构成的线路的权值。
在建图的过程中,图的信息不是一成不变的,所以在实现初步输入图的信息后,要有删除和插入操作。
需要插入顶点的时候,回归到初始建图模块,但是这个操作是在已建立的图上操作,而非在清除内存之后进行插入,所以,要实现插入的高效和实用性。
在删除顶点的时候,在已建立的图上进行删除,首先对图进行遍历,只要是和欲删除的顶点有关联的边值都要删除掉,这样就实现了顶点的删除操作,目的是提高用户使用程序的效率,对已知或者误录入的顶点进行排除,增加了程序的人性化。
4 Dijkstra求最短路径的基本思想
把顶点分成两组,第一组是已确定最短路径的结点的集合,第二组是尚未确定最短路径的结点的集合。
按路径长度递增的次序逐个把第二组的顶点放到第一组中。
设求从v1到其它各顶点间的最短路径,则在任意时刻,从v1到第一组各顶点间的最短路径都不大于从v1到第二组各顶点间的最短路径。
4.1 Dijkstra求最短路径的步骤
设图以邻接矩阵cost存储,矩阵中各元素的值为各边的权值。
顶点间无边时其对应权值用无穷大表示。
从顶点v1到其它各顶点间的最短路径的具体步骤如下:
1)初始化:s[MAX]。
设一dist向量,其下标是各顶点,元素值是顶点v0到各顶点的边的权值。
若v0到某顶点无边,dist向量中的对应值为无穷大。
2)选dist中最小的权值,将其顶点s[V0]加入s集合。
3)修改从顶点V0到集合s[MAX]中各顶点的最短路径长度,如果
dist[u]+cost[u][j]
则修改dist[k]为
dist[k]=dist[u]+cost[u][j]
4)重复(2)、(3)n-1次。
由此求得v1到图上其余各顶点得最短路径。
4.2存储结构体:用于存储经过的顶点和顶点数以及权值
struct
{int num;
int pnode[MAX]; }path[MAX]; //path为从V0到各顶点的最短路径
4.3建图子函数:
void creatgraph()//创建带权有向图
{ int i,j,s,e,len,contin=1;
printf("请输入点个数:");
scanf("%d",&n); for(i=0;i
{for(j=0;j
cost[i][j]=up;
cost[j][i]=up;}
cost[i][i]=0;}
4.4显示所建的邻接矩阵图
void display(int n1)//显示用户输入的信息
{ int i,j;
printf("\n********所建图的邻接矩阵*******\n____");
for(i=0;i
printf("____%d____",i);
printf("\n");
for(i=0;i
{
printf("%d",i);
for(j=0;j
printf("\t%6d<%d,%d>",cost[i][j],i,j);</p> printf("\n");
4.5求最短路径模块
void shortdjs()//求最短路径
{ int s[MAX];
int mindis,dis,i,j,v0=0,u=0;
for(i=0;i
{ dist[i]=cost[v0][i];//初始化dist[]数组
path[i].pnode[0]=v0;//顶点都为0
path[i].num=0;//记录经过的结点数都为0 s[i]=0;}
4.6输出最短路径
void dispath()//输出最短路径
{{printf("(V0->%d): ",i);
if(dist[i]
printf("\t %d\t(",dist[i]);
else
printf("\t∝\t(");//显示无穷大
for(j=0;j
printf("V%d->",path[i].pnode[j]);
printf("V%d>\n",path[i].pnode[path[i].num]);}
}
在这里还没有设计建图过程中,顶点的插入和删除功能,这两个功能可加到Creargraph ()中。
5结束语
这个程序广泛用在社会交通当中,用v0~V20表示不同的地点信息,供出行者参考,具体使用方法如下:
1)输入顶点个数:最大不能超过20,请输入罗马数字,若输入其他符号,会显示警告;
2)以“数字数字数字”的格式输入图的信息,第一次输入的第一个数字为源点,也就是我们的出发点,求最短路径会从这个顶点开始,每一次输入的第二个数字也是顶点,第三个数字是前两个顶点间的距离,或者说是权值,当输入“0 0 0”时,将停止录入功能;
3)在录入图的信息之后,屏幕中会出现一个矩阵来核实用户录入的图正确与否,程序将会提示用户是否进行添加顶点,如果想添加顶点请按“Y”或者“y”,若不添加顶点请按“N”或“n”退出添加顶点系统;
4)添加顶点的过程和Step1中录入方式相同,同样以“0 0 0”结束录入。
这时系统将提醒用户是否要删除顶点,以防止误入图的信息;
5)类似于Step3中方法进入删除顶点信息,系统根据用户输入的顶点序号删除其对应的所有信息,在完成修改之后系统将显示顶点到其他各点的最短路径,以供用户查询参考。
参考文献:
[1]王昆仑,李红.数据结构与算法[M].北京:中国铁道出版社,2006.
[2]苏仕华.数据结构与算法解析[M].合肥:中国科学技术大学出版社,2004.
[3]王昆仑,李红.数据结构与算法[M].北京:中国铁道出版社,2007.
[4]郭嵩山.国际大学生程序设计竞赛例题解[M].北京:电子工业出版社,2008.
[5]刘大有,唐海鹰.数据结构[M].北京:高等教育出版社,2001.
[6]徐孝凯.数据结构实用教程[M].北京:清华大学出版社,1999.
[7]严蔚敏,陈文博.数据结构及算法教程[M].北京:清华大学出版社,2001.
[8]刘振安,刘燕君. C程序设计课程设计[M].北京:机械工业出版社,2004.。
