山东省青岛市2010届高三上学期期中考试(数学理)
山东省青州市2010届高三上学期期中考试(基本能力)

高三基本能力5说明:本试卷共12页,分第Ⅰ卷和第Ⅱ卷两部分。
满分100分。
第Ⅰ卷 选择题(共30分)注意事项:1. 每题选出答案后,用2B 铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再改涂其它答案标号。
不涂答题卡,只答在试卷上的不得分。
2.第Ⅰ卷共30小题,全部为单项选择题,每小题1分,共30分。
一、金秋的阳光温馨恬静,家乡的秋风和煦轻柔,蓝天白云飘逸悠扬。
1.春华秋实,“秋”是成熟的季节,是收获的季节。
下列有关“秋”的描写错误的是A .蓝蓝的天,白白的云,大雁成群往南行B .葡萄紫、柿子红,一串一串像灯笼C .菊花黄,麦花香,天高云淡天气爽D .缤纷的落叶,五彩的菊,五彩缤纷是秋季2.某校高三举行“金秋十月”作文大赛,要求参赛者以电子稿件WORD 的形式上交作品。
右图是李华制作作品的一页,若要对其进一步编辑,下列操作不能实现的是 A .右击图片→设置图片格式→版式→嵌入型 B .点击“文件”菜单→页面设置→纸张→A4 C .在“格式”→“分栏”中选择栏数为“两栏” D .点击“视图”菜单→全选→左击全选内容→字体3.“别愁逢夏果,归与入秋蝉”,从夏天到秋天知了的叫声一直陪伴着我们。
用心聆听,知了的叫声是有节奏的,下面节奏符合其叫声规律的是 4.一年好景君须记,最是橙黄橘绿时。
自然界的绚丽色彩是艺术的重要源泉,下列有关色彩的叙述错误的是A .一束灿烂的阳光照到三棱镜上,可以观察到七色光B .印象主义流派画家根据光色原理对绘画色彩进行了大胆革新C .护士服由原来的白色改为粉红色是因为粉红色为暖色,给人以温暖、温馨的感觉D .用颜料三原色可以调配出绝大多数色彩,同样其他颜色也能调配出三原色5.秋高气爽是人们户外运动、锻炼的黄金季节。
如图所示为某球类运动比赛过程中,球运动到边线附近的垂直投影示意图。
下列说法不正确的是A .如果球在空中无任何接触而且是篮球运动,则三球均为出界B .如果球未落地而且是足球运动,则不能判定球③出界C .如果球已落地而且是篮球运动,则三球均已出界D .如果球已落地而且是排球运动,则球①②未出界,球③出界6. “喜迎中秋庆团圆,欢乐笑语万里传。
山东省青岛市2010届高三教学质量检测(三)数学(文)

山东省青岛市2010届高三教学质量检测(三)数 学 试 题(文)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分,考试时间120分钟。
注意事项:1.答卷前,考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合},2|{},8,4,2,0{M a a x x N M ∈===,则集合N M 等于 ( )A .{2,4,8,16}B .{0,2,4,8}C .{2,4,8}D .{0,4,8}2.若复数ii a 212+-(i R a ,∈为虚数单位)是纯虚数,则实数a 的值为( )A .4B .-4C .1D .-13.右图是2010年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m 为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为21,a a ,则一定有 ( )A .21a a >B .12a a >C .21a a =D .21,a a 的大小与m 的值有关4.函数x x x y 2cos3cos sin +=的图象的一个对称中心是( )A .)23,3(-πB .)23,32(-π C .)23,32(π D .)23,3(π5.设F 1,F 2是双曲线12422=-yx 的两个焦点,P 是双曲线上的一点,且||4||321PF PF =,则21F PF ∆的面积等于( )A .24B .38C .24D .486.在区间],0[π内随机取两个数分别记为a 、b ,则使得函数π+-+=222)(b ax x x f 有零点的概率为 ( )A .87B .43C .21D .417.一个算法的程序框图如图所示,该程序输出的结果为( ) A .98 B .109C .1110D .12118.若函数)(log )(b x x f a +=的大致图象如右图,其中a , b (10≠>a a 且)为常数,则函数b a x g x +=)(的大 致图象是 ( )9.已知函数)10(log )(≠>+=a a x a x f a x 且在[1,2]上的最大值与最小值之和为62log +a,则a 的值为( )A .21 B .41C .2D .4110.设点M (a ,b )是曲线2ln 21:2++=x x y C 上的任意一点,直线l 是曲线C 在点M 处的切线,那么直线l 斜率的最小值为( )A .-2B .0C .2D .411.已知直线0=+-a y x 与圆122=+y x 交于不同两点A 、B ,O 为坐标原点,则"1"=a 是“向量OB OA ,满足||||OB OA OB OA -=+”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件12.数列}{n a 满足⎪⎪⎩⎪⎪⎨⎧<≤-<≤=+121,12210,21nn n n n a a a a a,若20101,53a a 则== ( )A .51 B .52 C .53 D .54第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分把答案写在题中的横线上。
重庆市2010届高三上学期期末测试(数学理)

高2010级(上)期末测试卷数学(理工类)数学试题卷(理工农医类)共4页。
满分150分。
考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试卷上答题无效。
5.考试结束,将试卷和答题卡一并收回。
参考公式:当事件A 、B 互斥时,那么P(A+B) = P(A)+P(B) 当事件A 、B 互相独立时,那么P(A ·B) = P(A)·P(B)如果事件A 在一次实验中发生的概率是P ,那么n 次独立重复实验中恰好发生K 次的概率k n kk n n p p c k p --=)1()(.一.选择题:本大题10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项符合题目要求.1. 设集合A={a ,b },则满足A B={a ,b ,c ,d }的所有集合B 的个数是A.1B.4C.8D.162. 函数lg(1)y x =+的反函数的图像为3. 在等差数列{n a }中, 1328,3a a a ⋅== , 则公差d =DxCABA. 1B. -1C. ±1D. ±24. 直线1l 在x 轴和y 轴上的截距分别为3和1,直线2l 的方程为022=+-y x ,则直线1l 到2l 的角为A .71arctanB .45C .135D .45或1355. 已知3sin tan 2=⋅αα,02<<-απ,则)6cos(πα-的值是A .0B .23C .1D .216. 把函数)(x y 3lg =的图像按向量a 平移,得到函数)1lg(+=x y 的图像,则a为A . )3lg ,1(-B . )3lg ,1(-C .)3lg ,1(--D .)0,31(7. 已知x a x f =)(,x b x g =)(,当3)()(21==x g x f 时,21x x >,则a 与b 的大小关系不可能成立.....的是 A .1>>a bB .01>>>b aC.10<<<b aD .01>>>a b8. 双曲线)1(122>=-n y nx 的两焦点为21,F F ,点P 在双曲线上,且满足:2221+=+n PF PF ,则21F PF ∆的面积是A .1B .21C .2D .49. 称||),(d -=为两个向量、间的“距离”.若向量、满足: ① 1||=; ② ≠;③ 对任意的R t ∈,恒有),(),(d t d ≥则 A. ⊥B. )(-⊥C. )(-⊥D.)()(-⊥+10. 关于x 的方程0)1(122=++++b x x a xx 有实数根,则22b a +的最小值是 A.52B. 1C. 54D. 52二.填空题:(本大题共5小题,共25分,把答案填写在答题卡相应位置上) 11. 抛物线022=+y x 的焦点坐标是_____________. 12. 不等式2|log 1|2>+x 的解集是_____________.13.已知正数x 、y 满足⎩⎨⎧≥+-≤-05302y x y x ,则yx z )21()41(⋅=的最小值为_____________.14. 已知数列}{n a 满足11,211221++-==-n na n n a a n n ,则数列}{n a 的通项=n a _____________.15. 如图,一条螺旋线是用以下方法画成:ΔABC 是边长为1的正三角形,曲线11223,,CA A A A A 分别以A 、B 、C 为圆心,AC 、1BA 、2CA 为半径画的弧,曲线123CA A A 称为螺旋线旋转一圈.然后又以A 为圆心3AA 为半径画弧,这样画到第n 圈,则所得螺旋线的长度n l =_____________.(用π表示即可)三. 解答题:(本大题共6小题,共75分)(各题解答必须写出必要的文字说明、演算步骤和推理过程). 16. (本小题满分13分)已知向量)3,5(),3,6(),4,3(m m ---=-=-=. (Ⅰ)若C B A ,,三点共线,求实数m 的值; (Ⅱ)若ABC ∠为锐角,求实数m 的取值范围.A 3A 2A 1CA B17. (本小题满分13分)已知函数x x b x a x f cos sin cos 2)(2+=)0,0>>b a (,)(x f 的最大值为a +1,最小值为21-. (Ⅰ)求)(x f 的最小正周期; (Ⅱ)求)(x f 的单调递增区间.18. (本小题满分13分)已知数列}{n a 中,11=a ,113--⋅=n n n a a ),2(*N n n ∈≥.数列}{n b 的前n 项和)9(log 3n nn a S =)(*N n ∈. (Ⅰ)求数列}{n b 的通项公式; (Ⅱ)求数列|}{|n b 的前n 项和. 19. (本小题满分12分)已知22()log a xf x x a--=-是奇函数.(Ⅰ) 求a 的值;(Ⅱ) 若关于x 的方程1()2x f x m --=⋅有实解,求m 的取值范围.20. (本小题满分12分)已知点()1,1A 是椭圆()012222>>=+b a by a x 上一点,21,F F 是椭圆的两焦点,且满足421=+AF AF .(Ⅰ)求椭圆的两焦点坐标;(Ⅱ)设点B 是椭圆上任意一点,如果AB 最大时,求证A 、B 两点关于原点O 不对称;(Ⅲ)设点C 、D 是椭圆上两点,直线AC 、AD 的倾斜角互补,试判断直线CD 的斜率是否为定值?若是定值,求出定值;若不是定值,说明理由.21. (本小题满分12分)已知曲线C :xy =1,过C 上一点),(n n n y x A 作一斜率为21+-=n n x k 的直线交曲线C 于另一点),(111+++n n n y x A ,点列),3,2,1( =n A n 的横坐标构成数列{n x },其中7111=x . (Ⅰ)求证:{3121+-n x }是等比数列;(Ⅱ)求证:)1,(1)1()1()1()1(33221≥∈<-++-+-+-n N n x x x x n n .高2010级(上)期末测试卷 数学(理工类)(参考答案)一.选择题:本大题10小题,每小题5分,共50分. 1~5 BDCBA 6~10 CDACC 10. 令t xx =+1,则原方程化为022=-++b at t ,其中2||≥t ,此方程有根有以下情形对于图)(),(),(c b a ,易知0)2(≤-f 和0)2(≤f 中至少有一个成立 即有022≤++-b a 或022≤++b a由线性规划知识可知,),(b a 满足的平面区域如图阴影部分所示且点O 到直线的距离为5252002=++⨯Oxyxyxxxx)(a )(b )(c )(d )(e故此时5422≥+b a ,其中当52,54-=±=b a 时取等号 对于图)(),(e d ,显然有4≥a ,此时1622≥+b a ,故有22b a +的最小值为54. 二.填空题:本大题共5小题,共25分.11. )81,0(- 12. ),2()81,0(+∞ 13.116 14. 12+n n 15.π)3(2n n +三. 解答题:本大题共6小题,共75分. 16.(13分)解:(1)已知向量))3(,5(),3,6(),4,3(m m OC OB OA +--=-=-=),1,2(),1,3(m m AC AB --== 由三点共线知m m -=-2)1(3∴实数21=m 时,满足的条件…………6分(2)由题设知),1(),1,3(m m BC BA ---=--=ABC ∠ 为锐角,43033->⇒>++=⋅∴m m m …………12分又由(1)可知,当21=m 时, 0=∠ABC ,故),21()21,43(∞+-∈ m …………13分17.(13分)解:(1)a x b a x b x a x f +++=++=)2sin(42sin 2)2cos 1()(22ϕ,由题设知214,142222-=+-=+b a a b a ,所以21=a ,3=b (4)分所以21)62sin(212cos 212sin 23)(++=++=πx x x x f , 所以)(x f 的最小正周期为π…………7分 (2)由63226222πππππππππ+≤≤-⇒+≤+≤-k x k k x k ,所以)(x f 单调增区间为]6,3[ππππ+-k k )(Z k ∈…………13分18.(13分)解:(1)11333log log --⋅=n n n a a ,)1(log log 133-+=-n a a n n)1(21log log 133-+++=-n a a n 2)1(-=n n ,n a 3log 2)1(-=n n , )9(log 3n n n a S =252nn -=)(*N n ∈…………4分211-==S b ,当2≥n 时,31-=-=-n S S b n n n ,∴数列}{n b 的通项公式3-=n b n )(*N n ∈.…………7分(2)设数列|}{|n b 的前n 项和为n T ,当03≤-=n b n 即3≤n 时,n n S T -=252n n -=; 当3>n 时,32S S T n n -=21252+-=n n .…………13分19(12分)解: (Ⅰ)由20a xx a-->-得:2a x a -<<…………2分()f x 为奇函数,2 1.a a a ∴-=-⇒=经验证可知:1=a 时,)(x f 是奇函数,1=a 为所求…………5分(Ⅱ)12121()log ,().121x x x f x f x x -+-=∴=-+ …………8分 法一:由1()2x f x m --=⋅得:22(2)2(21)3(21)22121x x x x x xm -+-++==++ 2(21)3 3.21xx =++-≥+当且仅当2log 1)x =时,min 3m =所以m 的取值范围是3,)+∞…………12分 法二:原方程即2(2)(1)20x xm m -+-=设2xt =,则2(1)0t m t m -+-=原方程有实解,等价于方程2(1)0t m t m -+-=有正实解…………6分令2()(1)g t t m t m =-+-则(0)0g <或(0)0102g m =⎧⎪⎨+>⎪⎩或⎪⎪⎩⎪⎪⎨⎧>+≥++=∆>02104)1(0)0(2m m m g …………10分 0m ⇒>或0m =或30m ≤<所以m的取值范围是3,)+∞…………12分20.(12分) 解:(I )由椭圆定义知:42=a ∴2=a ∴14222=+b y x 把()1,1代入得11412=+b∴ 342=b 则椭圆方程为134422=+y x ∴ 38344222=-=-=b a c ∴ 362=c 故两焦点坐标为)0,362(),0,362(-.…………3分 (II ) 用反证法 : 假设A 、B 两点关于原点O 对称,则B 点坐标为()1,1-- ,此时22=AB 取椭圆上一点()0,2-M ,则10=AM ∴AB AM >.从而此时AB 不是最大,这与AB 最大矛盾,所以命题成立.…………7分(III )设AC 方程为:()11+-=x k y 联立⎪⎩⎪⎨⎧=++-=14341)1(22y x x k y 消去y 得()()01631631222=--+--+k k x k k xk ∵点()1,1A 在椭圆上∴1316322+--=k k k x C …………9分∵ 直线AC 、AD 倾斜角互补 ∴ AD 的方程为()11+--=x k y同理 1316322+-+=k k k x D …………10分又()()11,11+--=+-=D D C C x k y x k y()k x x k y y D C D C 2-+=-所以31=--=D C D C CD x x y y k 即直线CD 的斜率为定值31.…………12分21.(12分)过C :xy 1=上一点),(n n n y x A 作斜率为n k 的直线交C 于另一点1+n A , 则2111111111+-=⋅-=--=--=+++++n n n n n n n n n n n n x x x x x x x x x y y k , 于是有:21+=+n n n x x x . …………2分记3121+-=n n x a ,则n n nn n n a x x x x a 2)3121(231221312111-=+--=+-+=+-=++,因为023121,711111≠-=+-==x a x 而, 因此数列{3121+-n x }是等比数列. ………… 6分(3)由(2)可知:31)2(12,)2(--+=-=n n nn x a 则,31)1(212)1()1(⋅--+⋅-=-n n n n n x .当n 为偶数时有:- 11 - =-+---n n n n x x )1()1(11 =n n n n n n n n n n n n 21212222)312)(312(2231213121111111+<⋅+<-++=-++------, 于是①在n 为偶数时有:12121212121)1()1()1(432221<+++++<-++-+-n n n x x x .…………10分 ②在n 为奇数时,前n -1项为偶数项,于是有: n n n n x x x x )1()1()1()1(11221-+-++-+--- 131211)31)2(12(11)1(1<++-=--+-=-=-+<n n n n n x x .…………12分综合①②可知原不等式得证.。
高三上学期物理单元测试1-力、物体的平衡、直线运动

2010届《英才宝典》高考导航系列试题高三上学期物理单元测试(1)[原人教版] 命题范围 力 物体的平衡 直线运动本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共100分考试用时90分钟第Ⅰ卷(选择题共40分)一、本题共10小题,每小题4分,共40分.在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确.全部选对的得4分,选不全的得2分,有选错或不答的得0分.1.如图所示,一木块在垂直于倾斜天花板平面方向的推力F 作用下处于静止状态,下列判断正确的是 ( ) A .天花板与木块间的弹力可能为零 B .天花板对木块的摩擦力一定不为零 C .逐渐增大F 的过程,木块将始终保持静止 D .木块受到天花板的摩擦力随推力F 的增大而变化2.小球从空中自由下落,与水平地面碰后弹到空中某一高度,其速度随时间变化的关系如图2所示。
取g =10m/s 2。
则( ) A .小球第一次反弹初速度的大小为3 m/s B .小球第一次反弹初速度的大小为5 m/s C .小球能弹起的最大高度为0.45m D .小球能弹起的最大高度为1.25m3.物体沿一直线运动,在t 时间内通过的路程为s ,它在中间位置s 21处的速度为v 1,在中间时刻t 21时的速度为v 2,则v 1和v 2的关系为 ( ) A .当物体作匀加速直线运动时,v 1>v 2 B .当物体作匀减速直线运动时,v 1>v 2 C .当物体作匀速直线运动时,v 1=v 2D .当物体作匀减速直线运动时,v 1<v 24.甲乙两车在一平直道路上同向运动,其v t -图像如图所示,图中OPQ ∆和OQT ∆的面积分别为1s 和2s ()21s s >.初始时,甲车在乙车前方0s 处。
( )A .若012s s s =+,两车不会相遇2B .若01s s <,两车相遇2次C .若01s s =,两车相遇1次D .若02s s =,两车相遇1次5.如图所示,粗糙的斜面M 放在粗糙的水平面上,物块m 恰好能在斜面体上沿斜面匀速下滑,斜面静止不动。
2010长春市十一高中高三上学期期中考试(数学理)

长春市十一高中2010届高三上学期期中考试数 学 试 题(理科)(本试卷分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分.答题时间120分钟, 满分150分.)第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,共60分.每小题给出的4个选项中,只有一项是符合题目要求的.1.0sin 330的值是 ( )A .B .12-C .12D 2.复数32(1)i i +等于 ( )A .2B .2-C .2iD .2i -3.已知全集{}1,2,3,4,5U =,集合{}{}1,3,3,4,5A B ==,则集合()U C A B 等于( )A .{}3B .{}4,5C .{}3,4,5D .{}1,2,4,54.设A 为ABC ∆的最小内角,则cos sin A A +的取值范围是 ( )A .(B .⎡⎣C .(D .( 5.直线2y x =与抛物线23y x =-围成的封闭图形的面积是 ( )A .B .2C .323 D .353 6.已知平面向量20a b =≠ ,且关于x 的方程20x a x a b ++∙= 有实根,则a 与b 的夹角的取值范围是 ( )A .0,6π⎡⎤⎢⎥⎣⎦B .,3ππ⎡⎤⎢⎥⎣⎦C .2,33ππ⎡⎤⎢⎥⎣⎦D .,6ππ⎡⎤⎢⎥⎣⎦7.设()ln f x x x =,若0()2f x '=,则0x 等于 ( )A 2eB eC l n 22D l n 28. 0203sin 702cos 10-- 等于 ( )A 12B 2C 2D 29.若函数()y f x =的定义域是[]0,2,则函数(2)()1f xg x x =-的定义域为 ( ) A .[]0,1 B . [)0,1 C .[)(]0,11,4 D . ()0,110.已知0.90.7 1.1log 0.8,log 0.9, 1.1a b c ===,则 ( )A .c b a >>B .b c a >>C .c a b >>D .b a c >>11.函数()321f x ax a =-+在[]1,1-上存在一个零点,则a 的取值范围为 ( )A .15a ≥B .1a ≤-C .115a -≤≤D .15a ≥或1a ≤- 12.函数2()lg()1f x a x =+-是奇函数,且在0x =处有意义,则使()0f x <的x 的取值范围为 ( )A (1,0)-B (0,1)C (,0)-∞D ()(,0)1,-∞+∞第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.方程223x x -+=的实数解的个数为 .14.已知曲线3y x bx c =++上一点(1,2)A 的切线为1,y x =+则22b c += .15.下列命题:①,,R αβ∃∈cos()cos sin αβαβ+=+;②630,ln ln 10x x x ∀>++>;③,R ϕ∀∈函数sin(2)y x ϕ=+都不是偶函数;④,m R ∃∈使243()(1)m m f x m x -+=-是幂函数,且在(0,)+∞上递减.其中真命题有 (把你认为正确的序号都填上).16.等比数列{}n a 的前n 项和为n S ,已知1S ,22S ,33S 成等差数列,则{}n a 的公比为 .三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)已知函数()2cos (sin cos )1,f x x x x x R =-+∈(1)求函数()f x 的最小正周期;(2)求函数()f x 的值域.18.(本小题满分12分)已知向量(cos ,sin ),(cos ,sin ),a b a b ααββ==-= (1)求cos()αβ-的值;(2)若50,sin 2213ππβαβ-<<<<=-,求sin α的值.19.(本小题满分12分)设()f x 是定义在()0,+∞上的单调增函数,满足()()(),(3)1f xy f x f y f =+=.(1)求(1)f 的值;(2)若()(8)2f x f x +-≤,求x 的取值范围.20.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,且*22,()n n n a S n N -=∈.(1)求证:数列{}12-⋅-n n n a 是等比数列;(2)求数列{}n a 的通项公式.21.(本小题满分12分)已知函数32()31()f x ax x x a R =+-+∈.(1)当3a =-时,求证:()f x 在R 上是减函数;(2)如果对任意x R ∈,不等式()4f x x '≤恒成立,求实数a 的取值范围.22.(本小题满分12分)已知数列{}n a 的前n 项和为n S ,点(,)n S n n 在直线11122y x =+上,数列{}n b 满足*2120()n n n b b b n N ++-+=∈, 311b =,且{}n b 的前9项和为153.(1)求数列{}n a 和{}n b 的通项公式;(2)设3,(211)(21)n n n c a b =--记数列{}n c 的前n 项和为n T ,求使不等式57n k T >对一切*n N ∈都成立的最大正整数k 的值.(本页不交,答案写到答题纸上)数学(理科)参考答案及评分标准一、选择题(每小题5分,共60分)1.B 2.A 3.D 4.D 5.C 6.B7.B 8.C 9.B 10.C 11.D 12.A二、填空题(每小题4分,共16 分)13.2 14.13 15.①②④ 16.13三、解答题(共6小题,共70分)17.解:2()2cos sin 2cos 1f x x x x =-+sin 2cos 2))4x x x π=-=- ……………………………………………2分 (1)()f x 的最小正周期T π= ………………………………………………6分(2)()f x的值域为⎡⎣ …………………………………………10分18.解:(1)∵a b -= ,∴22425a a b b -+= 又(cos ,sin ),(cos ,sin ),a b ααββ== ∴42351,cos()25a b a b αβ-===-== ………………………6分 (2)∵50,sin 2213ππβαβ-<<<<=- ∴0αβπ<-<,由(1)得()3cos ,5αβ-=从而()4sin 5αβ-= 又5sin 13β=-,得12cos 13β=代入,可得 []33sin sin ()65ααββ=-+= …………………………………12分19.解:(1) 令1x y ==,得(1)0f = …………………………………………4分(2) 由(3)(3)2,(9)2f f f +=∴=,又由()(8)2f x f x +-≤得()()89f x x f -≤⎡⎤⎣⎦∵()f x 是定义在()0,+∞上的单调增函数∴080(8)9x x x x >⎧⎪->⎨⎪-≤⎩解得 89x <≤ ……………12分 20.解:(1)∵22n n n a S -=,∴11122n n n a S +++-=两式相减,得122n n n a a +=+,∴1(1)222(1)2n n n n n a n a n +-+=+-+ ∴11(1)222nn n n a n a n +--+=- ,又由已知得12,a =从而1111210a --=≠ ∴数列{}12n n a n -- 是首项为1,公比为2的等比数列 …………………8分 (2)由(1)1122n n n a n ---= ,∴1(1)2n n a n -=+……………………12分 21.解:(1)2213,()9619()03a f x x x x '=-∴=-+-=--≤恒成立 ∴()f x 在R 上是减函数 ………………………………………………6分(2)2()361f x ax x '=+-,由()4f x x '≤恒成立,∴23210ax x +-≤, ① 当0a =时,不成立② 由0a ≠时, 得 04120a a <⎧⎨∆=+≤⎩ ∴13a ≤- 综上,实数a 的取值范围是1,3⎛⎤-∞- ⎥⎝⎦…………12分 22.解:(1)由题意2111111,2222n n S n S n n n =+=+ 当2n ≥时 ,15n n n a S S n -=-=+,当1n =时,116a S ==也适合上式∴*5()n a n n N =+∈ ………………………4分 ∵*2120()n n n b b b n N ++-+=∈∴数列{}n b 是等差数列,由{}n b 的前9项和为153得199()1532b b +=, 从而5191()172b b b =+=,又311b =,得13,5d b ==,∴32n b n =+ ………………………………………………6分(2)3111()(21)(63)22121n c n n n n ==--+-+, ∴11[1]221n T n =-+,数列{}n T 是递增数列, ∴只要11357k T =>,∴19k < ∴max 18k = ……………………………………………………………12分。
高三第一学期期终测评(数学理)

上海市黄浦区2010届高三上学期期终基础学业测评高三数学试卷(理科) (2010.1.20)考生注意:1.每位考生应同时收到试卷和答题卷两份材料,解答必须在答题卷上进行,写在试卷上的解答一律无效;2.答卷前,考生务必将姓名、准考证号等相关信息在答题卷上填写清楚; 3.本试卷共23道试题,满分150分;考试时间120分钟.命题人:冯志勇 审核人:李小平 校对:胡泊一.填空题(本大题满分56分) 本大题共有14题,考生应在答题卷的相应编号的空格内直接填写结果,每题填对得4分,否则一律得零分.1.已知函数在,,且点的反函数是)12()(1)(1x f y a x xa x f -=---=)(1x f y -=的图像上,则实数=a .2.)02()12(,与,,非零向量、已知-=++=∈βαb a a R b a 平行,则a 、b 满足的条件是 .3.已知随机事件A 、B 是互斥事件,若18.0)(25.0)(==B P A P ,, 则)(B A P ⋃= . 4.不等式1|11|≥-+x x 的解集是 . 5.方程1)49(log 3+=-x x的解=x .6.已知角α(πα<<0)的顶点在原点,始边与x 轴正半轴重合,点P )34(,-是角α终边上一点,则2cosα= .7.方程1sin 3cos =+x x 的解集是 .8.=∈++++=∞→*22)]([)(lim )(321)(n f n f N n n n f n ,则若 .9.下面是用行列式解二元一次方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的程序框图,请在(1)、(2)、(3)处分别填上合适的指令.10.如图1所示,点A 、B 是单位圆(圆心在原点,半径为1的圆)上两点,OA 、OB 与x 轴正半轴所成的角分别为.和βα-,,记)sin (cos αα=,,))sin()(cos(ββ--=用两种方法计算⋅后,利用等量代换可以得到的等式是 .11.在cm AB cm BC cm AC ABC 543===∆,,中,,现以BC 边所在的直线为轴把ABC ∆(及其内部)旋转一周后,所得几何体的全面积是 2cm .12.掷一枚质地均匀的硬币可能出现图案向上,也可能出现文字向上.现将一枚质地均匀的硬币连续掷3次,表示若用随机变量ξ3次中出现图案向上的次数ξE ,则数学期望= .13.给出下列4个命题,其中正确命题的序号是 . (1)在大量的试验中,事件A 出现的频率可以作为事件A 出现的概率的估计值;(2)样本标准差)2(1)()()(22221≥--++-+-=n n x x x x x x S n 可以作为总体标准差的点估计值;(3)随机抽样就是使得总体中每一个个体都有同样的可能性被选入样本的一种抽样方法;(4)分层抽样就是把总体分成若干部分,然后在每个部分指定某些个体作为样本的一种抽样方法.14.已知数列{},的值是奇数的值是偶数 ,是正整数满足⎪⎩⎪⎨⎧-==+)(13)(2)(11n nn nn n a a a a a m m a a 若的所有可能的值是,则m a 24= .二.选择题(本大题满分16分) 本大题共有4题,每题有且只有一个正确答案,考生应在答题卷的相应编号上,将代表答案的小方格涂黑,选对得4分,否则一律得零分.15.已知{}”成立的”是“,,则“,且、a x a a x a R x a =-∈≠∈||0[答]( )A .充要条件.B .充分非必要条件.C .必要非充分条件.D .非充分非必要条件.16.定义两种运算xx x f b a b a b a b a ⊕-⊗=-=⊗-=⊕222)(||22,则函数,的解析式是[答]( )A .)22(4)(2,,-∈-=x x x x f . B .)22(4)(2,,-∈--=x xx x f .C .)2()2(4)(2∞+⋃--∞∈-=,,,x x x x f .D .)2()2(4)(2∞+⋃--∞∈--=,,,x x xx f .17.在空间中,给出下列4个命题(其中c b a 、、表示直线,β表示平面),则正确命题的序号是[答]( )(1)三个点确定一个平面; (2)若;,则,b a c b c a ||||||(3)在空间中,若角21θθ与角的两边分别平行,则21θθ=; (4)若ββ⊥⊂⊥⊥≠a cbc a b a,则、,,.A .(1)、(2)、(4).B .(2).C .(2)、(3).D .(2)、(3)、(4).18.已知函数0)()()1(1)1(|1|1)(2=++⎪⎩⎪⎨⎧=≠-=c x bf x f x x x x x f 的方程,若关于 有且仅有3个实数根=++232221321x x x x x x ,则、、[答]( )A .5.B .2222b b +.C .3.D .2222c c +.三.解答题(本大题满分78分) 本大题共有5题,解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤.19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.如图3所示,已知长方体中1111D C B A ABCD -,431===AA AB AD ,,M 是11B A 的中点.(1)求1ACD BM 与平面所成的角; (2)求点M 到平面1CD A 的距离.20.(本题满分14分)的值.、,求,,,且中,在c a c a b C A C B A ABC 5644222=-==>>∆21.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.已知a 、b 是正整数,函数)(2)(b x bx ax x f -≠++=的图像经过点)31(,. (1)求函数f (x )的解析式;(2)判断函数f (x )在]01(,-上的单调性,并用单调性定义证明你的结论.22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.某生产旅游纪念品的工厂,拟在2010年度将进行系列促销活动.经市场调查和测算,该纪念品的年销售量x 万件与年促销费用t 万元之间满足3-x 与t +1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2010年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为:“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x 与t 所满足的关系式;(2)请把该工厂2010年的年利润y 万元表示成促销费t 万元的函数; (3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.已知数列{}.,满足)(22111*+∈+==N n a a a a n n n n (1)证明数列{};的通项公式列是等差数列,并求出数n n n n a a a ⎭⎬⎫⎩⎨⎧2 (2)求等差数列{}11231201)(++*=++++∈n nn n n n n n a C b C b C b C b N n b ,使对*∈N n 都成立;(3)M a c a c a c a c M N n nb c nn n n <++++∈=* 332211)(,使,是否存在正常数令*∈N n 对恒成立,并证明你的结论.黄浦区2009学年度第一学期期末教学质量检测数学试卷(理科)(2010年1月20日)参考答案和评分标准说明:1、本解答仅列出试题的一种解法,如果考生的解法与所列解答不同,可参考解答中的评分精神进行评分。
山东省滨州阳信二中2010届高三上学期第二次 数学理
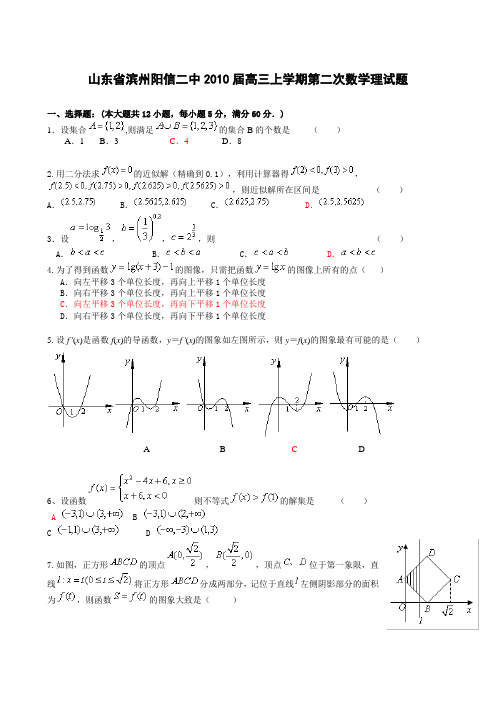
山东省滨州阳信二中2010届高三上学期第二次数学理试题一、选择题:(本大题共12小题,每小题5分,满分60分.)1.设集合,则满足的集合B的个数是()A.1 B.3 C.4 D.82.用二分法求的近似解(精确到0.1),利用计算器得,,则近似解所在区间是()A. B. C. D.3.设,,,则()A. B. C.D.4.为了得到函数的图像,只需把函数的图像上所有的点()A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度5.设f '(x)是函数f(x)的导函数,y=f '(x)的图象如左图所示,则y=f(x)的图象最有可能的是()A B C D6、设函数则不等式的解集是()A BC D7.如图,正方形的顶点,,顶点位于第一象限,直线将正方形分成两部分,记位于直线左侧阴影部分的面积为,则函数的图象大致是()8.已知是定义在R上的偶函数,在上为增函数,且则不等式的解集为()A. B. C. D.9.在上定义的函数是偶函数,且,若在区间是减函数,则函数()A.在区间上是增函数,区间上是增函数B.在区间上是增函数,区间上是减函数C.在区间上是减函数,区间上是增函数D.在区间上是减函数,区间上是减函数10.设函数定义在实数集上,则函数与的图象关于()A. 直线对称 B.直线对称 C. 直线对称 D.直线对称11.对于幂函数,若,则,大小关系是()A.B.C.D.无法确定12.是定义在R上的偶函数,且,则方程=0在区间(0,6)内解的个数的最小值是A.5B.4 C.3 D.2二、填空题:(本大题共4小题,每小题4分,满分16分.)13.已知为奇函数,当时,,则当时,的解析式为_________. 14.已知,,,则与的大小关系是_________.15.函数的单调减区间为值域为16.若,规定:,例如:,则的奇偶性为三、解答题:(本大题共6小题,前5题每小题12分,第6题16分,满分74分.)17.(本小题满分12分)设集合,(1)求集合;(2)若不等式的解集为B,求的值。
山东省胶州市2010届高三上学期期末考试(数学文)word版

胶州市第三中学高三模块测试数学(文)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。
考试时间120分钟。
注意事项:1.考生务必将姓名、准考证号、考试科目、试卷类型填涂在答题卡、纸规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
答案不能答在试题卷上。
3.第Ⅱ卷答案必须写在答题纸各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案。
不按以上要求作答的答案无效。
第Ⅰ卷(选择题 共60分)一、选择题:本题共12个小题,每小题5分,共60分;在每小题给出的四个选项中只有一...个.是符合题目要求的。
1.若集合{3},{xM y y P y y -====||则M P ⋂= A .{1}y y >|B .{1}y y ≥|C .{0}y y >|D .{0}y y ≥|2.某体育彩票规定:从01号到36号中任意抽取7个构成一注。
某人要求从01号到10号中任意抽取2个连续的号。
从21号到30号中任意抽取1个号,从31号到36号中任意抽取1个号,形成一注,那么此人采用的抽样方法是 A .简单随机抽样 B .分层抽样 C .系统抽样 D .抽签法3.已知平面向量(1,3),(4,2),a b a b λ=-=-+ 与a垂直,则λ等于A .-1B .1C .-2D .24.命题:“若21x <,则11x -<<”的逆否命题是 A .若21x ≥,则1x ≥,或1x ≤- B .若11x -<<,则21x < C .若1x >,或1x <-,则21x >D .若1x ≥,或1x ≤-,则21x ≥5.设a R ∈;若函数,xy e ax x R =+∈有大于零的极值点,则A .1a <-B .1a >-C .1a e <-D .1a e>-6.己知函数()y f x =||的图象如下图所示,则函数()y f x =的图象不可能...的是7.能使函数)sin(3)y x x ϕϕ=+--为奇函数的ϕ的一个取值为 A .6πB .2πC .23πD .3π 8.在等差数列{}n a 中,若 4681012120a a a a a ++++=,则91113a a -的值为 A .14B .15C .16D .179.已知有m n 、为两条不同的直线,αβ、为两不同的平面,则下列命题中正确的命题是 A .若,,//,//,m n m n ααββ⊂⊂则//αβ B .若,,//,m n αβαβ⊂⊂则//m n C .若,,m m n α⊥⊥则//n α D .若//,,m n n α⊥则m α⊥ 10腰三角形,俯视图是半径为1的半圆,则该几何体的体积是 A .23πB .3πC .πD .2π11.若定义运算()f a b *= ,则函数22(log (1)log (1))f x x +*-值域是A .(1,1)-B .[0,1)C .(,0]-∞D .[0,)+∞12.圆223:204C x x y -++=上满足条件:到点1(,0)16F 的距离与到直线116x =-的距离相等的点的个数为A .0B .1C .2D .4第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每题4分,共16分,把答案写在答题纸上。
山东省实验中学2010届高三上学期第一次诊断性测试数学理

山东省实验中学2010届高三第一次诊断性测试数学理试题注意事项:1.本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.第I 卷1至2页.第II 卷3至6页.共150分.考试时间120分钟.2.考生一律不准使用计算器.第Ⅰ卷(选择题 共60分)一、 选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若集合⎭⎬⎫⎩⎨⎧≤-+=032x x x A ,{}0432≤--=x x x B ,则 (R C )等于 ( )A .{3≤x x 或}4>xB .}31|{≤<-x xC .}43|{<≤x xD .}12|{-<≤-x x2.若b a c b a >∈,R 、、,则下列不等式成立的是 ( ) A.ba 11<. B. 22b a >. C. 1122+>+c b c a . D. ||||c b c a >. 3. 已知点)cos 2 ,cos (sin ααα⋅P 在第四象限, 则角的终边在 ( )A .第一象限B .第二象限C .第三象限D .第四象限 4.下列函数既是奇函数,又在区间[]1,1-上单调递减的是 ( )A .31)(x x f = B .()1f x x =-+C .2()ln2x f x x -=+ D .()1()2x xf x a a -=+ 5.已知函数54)(--=x x x f ,则当方程a x f =)(有三个根时,实数的取值范围是( )A .15-<<-aB .15-≤≤-aC .5-<aD .1->a6.设函数⎩⎨⎧<+≥+-=0,60,64)(2x x x x x x f 则不等式)1()(f x f >的解集是 ( )A .)3,1()3,( --∞B .),3()0,3(+∞-C . ),3()1,1(+∞-D . ),3()1,3(+∞-7.下列四个函数中,图像如右图所示的只能是 ( ) A .x x y lg += B .x x y lg -=C .x x y lg +-=D .x x y lg --=8.若对(,0)a ∀∈-∞,R ∈∃θ,使a a ≤θsin 成立,则)6cos(πθ-的值为 ( )A .12 B .12- C .32 D .32- 9.已知函数0)1(),0()(2=>++=f a c bx ax x f ,则“a b 2>”是“0)2(<-f ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件10.函数|log |)(3x x f =在区间[]b a ,上的值域为[]1,0,则a b -的最小值为( )A . 31B. 32C.D.11.已知函数)0( log )(2>=x x x f 的反函数为,,且有8)()()(111=⋅---b f a f x f 若0>a 且0>b ,则ba 41+的最小值为 ( )A .B .3C .6D .912.已知定义在上的函数)(x f y =满足下列三个条件:①对任意的R x ∈都有);()2(x f x f -=+②对于任意的2021≤<≤x x ,都有),()(21x f x f <③)2(+=x f y 的图象关于y 轴对称,则下列结论中,正确的是 ( )A .)7()5.6()5.4(f f f <<B . )5.6()7()5.4(f f f <<C .)5.6()5.4()7(f f f <<D . )5.4()5.6()7(f f f <<第Ⅱ卷(非选择题 共90分)题号 二 三总分17 18 19 20 21 22分数二、 填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.13.函数x x x x f -++-=16)(2的定义域是_________________________.14.函数)32(log )(221--=x x x f 的单调递增区间是_____________________________.15.若,53)cos(,51)cos(=-=+βαβα则______________________tan tan =⋅βα. 16.已知实数y x ,满足)0(,1255334>+=⎪⎩⎪⎨⎧≥≤+-≤-a y ax z x y x y x 设,若633当取最大值时对应的点有无数多个,则= .三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知集合{}1≤-=a x x A ,{}0452≥+-=x x x B . (1)若3a =,求;(2)若A B =∅ ,求实数的取值范围 .18.(本小题满分12分)已知3sin cos sin 2cos =-+xx xx .(1)求x tan ; (2)求xx x sin )4cos(22cos ⋅+π的值.19.(本小题满分12分)已知函数()32f x x ax bx c =-+++图像上的点))1(,1(f P 处的切线方程为31y x =-+,函数3)()(2+-=ax x f x g 是奇函数. (1)求函数)(x f 的表达式; (2)求函数)(x f 的极值.20.(本小题满分12分)已知20,1413)cos(,71cos παββαα<<<=-=且. (1)求α2tan 的值; (2)求β.21.(本小题满分12分)已知命题:在]2,1[∈x 内,不等式022>-+ax x 恒成立;命题:函数)32(log )(231a ax x x f +-=是区间),1[+∞上的减函数. 若命题“q p ∨”是真命题,求实数的取值范围.22. (本小题满分14分)已知函数x ax x x f ln )(2-+=, .a R ∈ (1)若函数)(x f 在[]2,1上是减函数,求实数的取值范围;(2)令2)()(x x f x g -=,是否存在实数,当∈x ],0(e (是自然常数)时,函数)(x g 的最小值是3,若存在,求出的值;若不存在,说明理由; (3)当∈x ],0(e 时,证明: x x x x e ln )1(2522+>-.山东省实验中学2007级第一次诊断性测试数 学 试 题(理科)答案 2009.10一、选择题1-5 DCCCA 6-10 DBAAB 11-12 BB 二、填空题11、 {12<≤-x x 或}31≤<x 12、)1,(--∞ 13、21 14、53. 三、解答题:本大题共6小题,共80分,解答应写出文字说明、演算步骤或推证过程.17.解:(I )当3a =,由13≤-x 得131≤-≤-x解得42≤≤x {}42≤≤=x x A …………………4分(2)由1≤-a x 得11+≤≤-a x a {}11+≤≤-=a x a x A …………………. 6分 由0452≥+-x x 解得41≥≤x x 或{}41≥≤=x x x B 或 ……….8分A B =∅ , ⎩⎨⎧<+>-4111a a 得 32<<a即的取值范围是32<<a .……………………………………………………………12分18.解:(1)3sin cos sin 2cos =-+x x xx , 3tan 1tan 21=-+x x 52tan =x ……4分 (2) 原式=x x x xx sin )sin 22cos 22(2sin cos 22--………………………………………8分xx x x x x x sin )sin (cos )sin )(cos sin (cos -+-=x xx sin sin cos += ……10分1cot +=x =27. ……12分19.解:(1) ()'232f x x ax b =-++, …………………1分函数()f x 在1x =处的切线斜率为-3, ()'1323f a b =-++=-,即20a b +=, 又()112f a b c =-+++=-得1a b c ++=-,………………………………3分 又函数3)(3+++-=c bx x x g 是奇函数,0)0(=g .3-=∴c2,4,3a b c =-==-, ………………………………6分()32243f x x x x =--+-. ………………………………7分(2))2)(23(443)(2'+--=+--=x x x x x f ,令,0)(=x f 得32=x 或2-=x ,()2,-∞-2-⎪⎭⎫ ⎝⎛-322,32⎪⎭⎫⎝⎛∞+,32 ()'f x 0- ()f x递减极小值递增极大值递减,极小11)2()(-=-=f x f .2741)32()(-==f x f 极大.………………………………… 12分20.解:(1)由1cos ,072παα=<<, 34tan =α, ∴()222tan 24383tan 21tan 47143ααα⨯===---………………………………………………………… 4分(2)由20παβ<<<,得02παβ<-<又∵()13cos 14αβ-=,∴1433)sin(=-βα…………………………………………………… 6分由()βααβ=--得:()cos cos βααβ=--⎡⎤⎣⎦()()cos cos sin sin ααβααβ=-+-113433317147142=⨯+⨯=.3πβ=………………………………………………………………… 12分21.解 : ]2,1[∈x 时,不等式022>-+ax x 恒成立x x x x a -=->222在[]2,1∈x 上恒成立,令x xx g -=2)(,则)(x g 在[]2,1上是减函数,1)1()(max ==∴g x g , .1>∴a 即若命题真,则;1>a ……………………………5分又函数)32(log )(231a ax x x f +-=是区间),1[+∞上的减函数,[)[)⎩⎨⎧∞+>+-=∞++-=上恒成立,在上的增函数,是1032)(132)(22a ax x x u a ax x x u ⎩⎨⎧>≤∴0)1(1u a 11≤<-∴a .即若命题真,则.11≤<-a ……………………… 10分若命题“q p ∨”是真命题,得.1->a ………………………………………………………………… 12分22.解:(1)01212)(2'≤-+=-+=xax x x a x x f 在[]2,1上恒成立, 令 12)(2-+=ax x x h ,有⎩⎨⎧≤≤0)2(0)1(h h 得,271⎪⎩⎪⎨⎧-≤-≤a a ……………………… 4分得27-≤a ……………………………………………………………………………5分(2)假设存在实数,使x ax x g ln )(-=(],0(e x ∈)有最小值3,x a x g 1)('-=xax 1-= ……………………………………………6分 ① 当0≤a 时,)(x g 在],0(e 上单调递减,31)()(min =-==ae e g x g ,ea 4=(舍去),②当e a <<10时,)(x g 在)1,0(a 上单调递减,在],1(e a上单调递增 3ln 1)1()(min =+==a ag x g ,2e a =,满足条件.③当e a ≥1时,)(x g 在],0(e 上单调递减,31)()(min =-==ae e g x g ,ea 4=(舍去), 综上,存在实数2e a =,使得当],0(e x ∈时)(x g 有最小值3. ……………………10分 (3)令x x e x F ln )(2-=,由(2)知,3)(min =x F .令25ln )(+=x x x ϕ,2'ln 1)(xxx -=ϕ, 当e x ≤<0时,0)('≥x ϕ,()h x 在],0(e 上单调递增 ∴32521251)()(max =+<+==e e x ϕϕ ,25ln ln 2+>-∴x x x x e 即x x e 2522-x x ln )1(+>.………14分。
山东省济南市历城区2010届高三上学期期中考试(数学理)

高三数学试题(理科)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知定义在R 上的奇函数()f x ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数则 A .(25)f -(11)(80)f f << B .(80)(11)(25)f f f <<-C .(11)(80)(25)f f f <<-D .(25)(80)(11)f f f -<<2.若A 是ABC ∆的一个内角,且2sin cos 3A A +=,∆ABC 的形状是 A .锐角三角形B .直角三角形C .钝角三角形D .不确定3.设n S 是等差数列{}n a 的前n 项和,已知263,11a a ==,则7S 等于A .13B .35C .49D .634.定义在R 上的函数()f x 满足()f x =2log (4),0(1)(2),0x x f x f x x -≤⎧⎨--->⎩则(3)f 的值为A .-1B .-2C .1D .25.函数log a y x =在[2,)x ∈+∞上总有||1y >,则a 的取值范围是 A .102a <<或12a << B .112a <<或12a <<C .12a <<D .102a <<或2a >6.若函数()(1)cos ,02f x x x x π=+≤<,则()f x 的最大值是A .1B .2C 1D 27.不等式2(2)2(2)40a x a x -+--<对x R ∈恒成立,则实数a 的取值范围是A .(,2)-∞B .[2,2]-C .(2,2]-D .(,2)-∞-8.已知等比数列{}n a 满足0,1,2,...n a n >=,且25252(3)nn a a n -∙=≥,则当1n ≥时2123221log log ...log n a a a -+++=A .(21)n n -B .2(1)n +C .2nD .2(1)n -9.已知偶函数()f x 在区间[0,)+∞单调增加,则满足1(21)()3f x f -<的x 取值范围是A .12(,)33B .12[,)33C .12(,)23D .12[,)2310.若(1,),(2,3)a x b x ==,那么222||||aba b +的取值范围是A .(,2-∞B .[0,2C .[22-D .]2+∞ 11.已知a 是实数,则函数()1sin f x a ax =+的图像不可能是12.函数cos(2)26y x π=+-的图像F 按向量a 平移到'F ,'F 的解析式(),y f x =当()y f x =为奇函数时,向量a 可以等于A .(,2)6π-B .(,2)6πC .(,2)6π--D .(,2)6π-二、填空题(把答案填填在题中横线上,本大题共4小题,每小题4分,共16分) 13.已知a 、b 、c 为等比数列,b 、m 、a 和b 、n 、c 是两个等差数列,则a cm n+= 。
2012届高三上学期期中考试(数学理)

2012届高三上学期期中考试试题数学(理科)一.选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1 .若集合{},{}x A x x B xx-2=-1≤2+1≤3=≤1,则B A =A. {}x x -1≤<0B. {}x x 0<≤1C. {}x x 0≤≤2D. {}x x 0≤≤1 2.下面四个条件中,使a b >成立的充分而不必要的条件是A .1a b +>B .1a b ->C .22a b >D .33a b >3.已知函数⎩⎨⎧≤>=)0(2)0(log)(2x x x x f x,若21)(=a f ,则实数a 的值为A .-1 B.2 C .-1或2 D .1或2-4.已知等差数列{a n }的公差为d (d ≠0),且a 3+a 6+a 10+a 13=32,若a m =8,则m 为A .12B .8C .6D .45.函数y =ln1|2x -3|的大致图象为()6.在平行四边形ABCD 中,AE →=13AB →,AF →=14AD →,CE 与BF 相交于G 点.若AB →=a ,AD →=b ,则 AG →=A.27a +17bB.27a +37bC.37a +17bD.47a +27b 7.设,x y 满足约束条件04312x y x x y ≥⎧⎪≥⎨⎪+≤⎩,则221y x ++的最大值是A. 5B. 6C. 8D. 108.函数11x y x +=-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于A .2B . 4C . 6D .8二.填空题:本大题共6小题,考生做答6小题,每小题5分, 共30分. (一)必做题(9~12题)9.不等式212-<-x x 的解集为 .10.若6x x ⎛- ⎝⎭展开式的常数项为60,则常数a 的值为 . 11 .已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m =(1,3-),n =(cos A ,sin A ).若m ⊥n ,且C c A b B a sin cos cos =+,则角B = .12.已知8,0,0=++>>ab b a b a ,,则b a +的最小值是 .13.如图,M 是正方体ABCD -A 1B 1C 1D 1的棱DD 1的中点,给出下列四个命题:①过M 点有且只有一条直线与直线AB ,B 1C 1都相交; ②过M 点有且只有一条直线与直线AB ,B 1C 1都垂直; ③过M 点有且只有一个平面与直线AB ,B 1C 1都相交; ④过M 点有且只有一个平面与直线AB ,B 1C 1都平行. 其中真命题是是 _______.(填写真命题的序号) (二)选做题:(14~15题,考生只能从中选做一题)14.(坐标系与参数方程选做题)在极坐标系中,曲线C 的极坐标方程为3)6sin(=-πθρ,点)3, 2(πA 到曲线C 上点的距离的最小值 .15.如图,EB 、EC 是⊙O 的两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E =460,∠DCF =320,则∠A 的大小为 .三.解答题:本大题共6小题,满分80分. 解答须写出文字说明、证明过程或演算步骤. 16.(本题满分12分)在ABC ∆中,内角,,A B C 所对的边长分别是,,a b c , 已知4A π=,4cos 5B =.(I )求cos C 的值;(II )若10,B C D =为A B 的中点,求CD 的长.17.(本题满分12分)图乙图甲M 已知等差数列{a n }满足a 2=0,a 6+a 8= -10 (I )求数列{a n }的通项公式; (II )求数列12n n a -⎧⎫⎨⎬⎩⎭的前n 项和.18. (本题满分14分)如图甲,直角梯形ABCD 中,//AB CD ,2D AB π∠=,点M 、N 分别在A B ,CD 上,且MN AB ⊥,MC CB ⊥,2BC =,4M B =,现将梯形ABCD 沿MN 折起,使平面AMND 与平面MNCB 垂直(如图乙).(Ⅰ)求证://AB 平面DNC ;(Ⅱ)当DN 的长为何值时,二面角D BC N --的大小为30︒?19. ((本题满分14分)本着健康、低碳的生活理念,租自行车骑游的人越来越多。
山东省青岛市2010届高三第一次模拟考试数学理科试题

青岛市高三教学质量统一检测数学试题(理科) 2010.3本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟. 注意事项:1.答卷前,考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1 (i 为虚数单位)等于A .1B .1-C .iD .i -2.若集合}11,|{31≤≤-==x x y y A ,}1{x y x B -==,则A B =A .(]1,∞-B .]1,1[-C .φD .{1}3.设p 和q 是两个简单命题,若p ⌝是q 的充分不必要条件,则p 是q ⌝的 A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.计算机执行下面的程序段后,输出的结果是1=a 3=b b a a += b a b -= PRINT b a ,A .1 3 B .4 1 C . 0 0 D .605.若dx x a ⎰=22sin π,dx x b ⎰=1cos ,则a 与b 的关系是A .b a <B .b a >C .b a =D .0=+b a 6.圆222210x y x y +--+=上的点到直线2=-y x 的距离的最大值是A .2 B. 1+C .2+D. 1+ 学|科|7.已知抛物线2x ay =的焦点恰好为双曲线222y x -=的上焦点,则a 的值为A .1B .4C .8D .168.将奇函数()sin()(0,0,)22f x A x A ππωφωφ=+≠>-<<的图象向左平移6π个单位得到的图象关于原点对称,则ω的值可以为A .2B .3C .4D .6 9.已知281(0,0)x y x y+=>>,则x y +的最小值为A .12B .14C .16D .1810.过原点的直线与函数xy 2=的图像交于B A ,两点,过B 作y 轴的垂线交于函数xy 4=的图像于点C ,若直线AC 平行于y 轴,则点A 的坐标是A .)2,1(B .)4,2(C .)2,21( D .)1,0(11.在数列}{n a 中,a a a n n +=+1(a n ,N *∈为常数),若平面上的三个不共线的非零向量,,满足a a 20101+=,三点C B A ,,共线且该直线不过O 点,则2010S 等于A .1005B .1006C .2010D .201212.平面α外有两条直线m 和n ,如果m 和n 在平面α内的射影分别是直线1m 和直线1n ,给出下列四个命题: ①1m ⊥1n ⇒m ⊥n ; ②m ⊥n ⇒1m ⊥1n ; ③1m 与1n 相交⇒m 与n 相交或重合; ④1m 与1n 平行⇒m 与n 平行或重合; 其中不正确...的命题个数是 A.1 B. 2 C.3 D. 4 Zxxk第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.13.若nxx )1(+展开式中第2项与第6项的系数相同,那么展开式的中间一项的系数为 ;14.已知区域}0,5,0|),{(},0,0,10|),{(≥≤≥-=≥≥≤+=Ωy x y x y x A y x y x y x ,若向区域Ω上随机投1个点,则这个点落入区域A 的概率()P A = ; 15.关于x 的不等式|2||1|5x x ++-<的解集为 ;16.已知函数⎩⎨⎧=x x x f 3log )(2)0()0(≤>x x ,且关于x 的方程0)(=-+a x x f 有且只有一个实根,则实数a 的范围是 .三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)已知向量)cos ,2sin 3(x t x m +=,)cos 2,1(x n =,设函数n m x f ⋅=)(. (Ⅰ)若21)32cos(=-πx ,且⊥,求实数t 的值; (Ⅱ)在ABC ∆中,c b a ,,分别是角C B A ,,的对边,若1,3)(==b A f ,且ABC ∆的面积为23,实数1=t ,求边长a 的值.18.(本小题满分12分)某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从2种服装商品, 2种家电商品, 3种日用商品中,选出3种商品进行促销活动.(Ⅰ)试求选出的3种商品中至多有一种是家电商品的概率;(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高x 元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为40元的奖券.假设顾客每次抽奖时获奖的概率都是21,若使促销方案对商场有利,则x 最少为多少元?19.(本题满分共12分)下图分别为三棱锥ABC S -的直观图与三视图,在直观图中,SA SC =,N M 、分别为SB AB 、的中点.(Ⅰ)求证:SB AC ⊥; 学。
山东省青岛三中2010届高三上学期第二次月考数学试题

山东省青岛三中2010届高三上学期第二次月考数学注意事项:1.本卷共150分,考试时间120分钟 2.将答案写在答题卡的相应位置一、选择题( 12 小题,每小题 5 分)1.设集合{}{}|2,|3Mx x P x x =>=<,那么“x M ∈,或x P ∈”是“x MP ∈”的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件2.已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数,则( ).A.(25)(11)(80)f f f -<<B. (80)(11)(25)f f f <<-C. (11)(80)(25)f f f <<-D. (25)(80)(11)f f f -<<3.已知数列{}n a 的通项公式是)(lg 2a n +∈+=N n n n,前n 项和为S n ,当2008S n-取得最小值时,n 的值是( )A. 9B. 10 C .11 D.124.从高出海面hm 的小岛A 处看正东方向有一只船B ,俯角为30看正南方向的一船C 的俯角为45,则此时两船间的距离为( ).A .2hmB D .5.已知向量(6,4),(0,2),,a b OC a b λ===+r r uuu r r r 若点C 在函数sin 12y x π=的图象上,则实数λ的值为( )A.52 B.32 C.52- D.32-6.下列各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共面...的一个图是OPRSSQRPQQSSP PQSS(A)(B)(C)(D)7.若过原点的直线与圆2x+2y+x4+3=0相切,若切点在第三象限,则该直线的方程是()A.xy3=B.xy3-=C.xy33=D.xy33-=8.如图,过抛物线)(022>=ppxy的焦点F的直线l交抛物线于点A.B,交其准线于点C,若BFBC2=,且3=AF,则此抛物线的方程为()A.xy232=B.xy32=C.xy292=D.xy92=9.一套重要资料锁在一个保险柜中,现有n把钥匙依次分给n名学生依次开柜,但其中只有一把真的可以打开柜门,平均来说打开柜门需要试开的次数为()A.1 B.n C.21+nD.21-n10.复数cos sinZ iθθ=+((0,2)θπ∈)在复平面上所对应的点在第二象限上,则θ的取值范围是()A.(0,2πB. (,)2ππ C.3(,2ππ D.3(,2)2ππ11.从1、2、3、4、5这五个数字中,任取三个组成无重复数字的三位数,但当三个数字中有2和3时,2需排在3前面(不一定相邻),这样的三位数有( )A.9个B.15个C.42个D.51个12.给出下面四个类比结论()①实数,,ba若0=ab则0=a或0=b;类比向量,,若0=⋅ba,则0=a或0=b②实数,,ba有;2)(222bababa++=+类比向量,,有2222)(+⋅+=+③向量2=;类比复数z,有22zz=④实数ba,有022=+ba,则0==ba;类比复数z,2z有02221=+zz,则21==z z 其中类比结论正确的命题个数为( )A 、0B 、1C 、2D 、3二、填空题( 4 小题,每小题 5 分)13.若函数xf x f x x x f x ∆+-∆+=→∆2)1()1(lim,1)(03则= .14.在△AOB 的边OA 上有5个点,边OB 上有6个点,加上O 点共个点,以这12个点为顶点的三角形有 个.15.已知两个实数集},,,{},,,,{5211021b b b B a a a A ==,若从A 到B 的映射f 使得B中的每个元素都有原象,且)()()(1021a f a f a f ≥≥≥ 则这样的映射共有_____16.已知函数()2|2|f x x ax b =-+()x R ∈.给了下列命题:①()f x 必是偶函数②当()()02f f =时, ()f x 的图象必关于直线1x =对称;③若20a b -≤,则()f x 在区间[),a +∞上是增函数;④()f x 有最大值2||a b -.其中正确的命题的序号是______________________.三、解答题( 6 小题,共70分)17.(10分)已知向量(cos ,sin )a αα=,(cos ,sin )b ββ=,25a b -=. (Ⅰ)求cos()αβ-的值;(Ⅱ)若02πα<<,02πβ-<<,且5sin 13β=-,求sin α的值.18.(10分)在数列{}n a 中,c c a a a n n (,111+==+为常数,)*∈N n ,且521,,a a a 成公比不等于1的等比数列.(Ⅰ)求c 的值; (Ⅱ)设11+=n n n a a b ,求数列{}n b 的前n 项和n S19.(12分)已知向量()1,3,2sin ,2cos ,23sin ,23cos -=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=c x x b x x a(1)当b a ⊥时,求x 的值的集合; (2)求c a-的最大值.20.(12分)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD AC CD ⊥⊥,,60ABC ∠=°,PA AB BC ==,E 是PC 的中点.(Ⅰ)求PB 和平面PAD 所成的角的大小; (Ⅱ)证明AE ⊥平面PCD ;(Ⅲ)求二面角A PD C --的正弦值.21.(12分)甲、乙、丙3位大学生同时应聘一个用人单位的职位,3人能被选中的概率分别为31,43,52,且各自能否被选中是无关的。
山东省青岛市2010届高三上学期期中考试英语试题

山东省青岛市2010届高三上学期期中考试英语试题本试卷分第Ⅰ卷和第Ⅱ卷两部分,共14页,满分150分。
考试时间120分钟。
考试结束后,将答题卡和答题纸一并交回。
注意事项:1.答卷前,考生务必用2B铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
答案不能答在试题卷上。
3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题纸各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
第Ⅰ卷(共105分)第一部分:听力(共两节,满分30分)该部分分为第一、第二两节。
注意:回答听力部分时,请先将答案标在试卷上。
听力部分结束前,你将有两分钟的时间将你的答案转涂到客观题答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.15.C.£9.18. 答案是B。
1. What day is probably today?A. Sunday.B. Tuesday.C. Wednesday.2. Which place are the speakers probably talking about?A. An office building.B. A football field.C. A concert hall.3. What kind of weather will they have tomorrow?A. Snowy.B. Fairly warm.C. A little cold.4. What do we know about the man?A. He may not go home for the New Year.B. He will stay at home for the vacation.C. He will graduate this month.5. What is the relationship between the speakers?A. Doctor and patient.B. Boss and secretary.C. Brother and sister.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
青岛市高三教学质量检测高中数学 (理科) 2009.11本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟. 注意事项:1.答卷前,考生务必用2B 铅笔和0.5毫米黑色签字笔(中性笔)将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上.2.第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案不能答在试题卷上.3.第Ⅱ卷必须用0.5毫米黑色签字笔(中性笔)作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若全集R U =,集合{}|22M x x =-≤≤,{}2|30N x x x =-≤,则()U M N ð=A.[2,0]-B. [2,0)-C.[0,2]D. (0,2]2. 已知sin 0α<且tan 0α>,则α是A .第一象限角B . 第二象限角C . 第三象限角D . 第四象限角3. 有下列四个命题 ①“若0x y +=,则,x y 互为相反数”的逆命题; ②“全等三角形的面积相等”的否命题;③“若1q ≤,则220x x q ++=有实根”的逆否命题;④“不等边三角形的三个内角相等”的逆命题.其中真命题为A .①②B .②③C .①③D .③④4.设111222,,,,,a b c a b c 均为非零实数,不等式21110a x b x c ++<和22220a x b x c ++<的解集分别为集合M 和N ,那么“111222a b ca b c ==”是“M N =” A .充分非必要条件 B .必要非充分条件C .充要条件D .既非充分又非必要条件5. 函数21()221xx f x +=+-的值域是A .(2,)-+∞B .(1,)-+∞C .(1,)+∞ D.(2,)+∞6. 函数3()31f x x x =-+在闭区间[3,0]-上的最大值、最小值分别是A .1,1-B .3,17-C .1,17-D .9,19-7. 设1232,2()log (1) 2.x e x f x x x -⎧<⎪=⎨-≥⎪⎩,,,则((2))f f 的值为 A. 0 B. 1 C. 2 D. 3 8.已知3sin()45x π-=,则sin 2x 的值为 A .1925 B .1625 C .1425 D .7259.设0,0a b >>,则以下不等式中不.一定成立的是 A.2a bb a +≥ B. ln(1)0ab +> C. 22222a b a b ++≥+ D. 3322a b ab+≥10.函数bx a x f -=)(的图象如图,其中a 、b 为常数,则下列结论正确的是 A .1,0a b >< B .1,0a b >> C .01,0a b <<>D .01,0a b <<<11.某纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的10%以下,则至少需过滤的次数为(参考数据lg 20.3010=) A. 10 B. 11 C. 12D. 1312.数列{}n a 满足15a =,22211n n n n aa a a +=++ (*N n ∈),则{}n a 的前10项和为 A .50 B .100 C .150 D .200第10题图第Ⅱ卷(非选择题 共90分)二、填空:本大题共4小题,每小题4分,共16分.13.已知2{|log (1)(1)}M x y x x ==-+,3{|,N y y x x ==+[0,1]}x ∈,则M N = ;14.20(2)x x e dx -=⎰;15.设n S 是各项均不为零的等差数列{}n a 的前n 项和,且387,k S S S S ==,则k的值为 ;16.已知函数()f x =⎪⎩⎪⎨⎧<--≥+-)0()0(22x x x x x x ,则不等式()20f x +>的解集是____________.三、解答题:本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分) 在ABC ∆中,3,4cos 2cos 23BC AC A C ==-=. (Ⅰ)求AB 的值; (Ⅱ)求sin(2)4A π-的值.18. (本小题满分12分)已知2(),Z f x x x k k =-+∈,若方程()2f x =在3(1,)2-上有两个不相等的实数根.(Ⅰ)确定k 的值;(Ⅱ)求2[()]4()f x f x +的最小值及对应的x 值.19. (本小题满分12分) 设函数2()sin(2)2cos 16f x x x πωω=--+,若()f x 的最小正周期为8。
(Ⅰ)求ω的值;(Ⅱ)若函数()y g x =与()y f x =的图象关于直线1x =对称,求当[0,2]x ∈时()y g x =的最小值. 20.(本小题满分12分)已知数列{}n a 的前n 项和n S 与通项n a 满足1(1)(N )3n n S a n *=-∈. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求证:13n S <;(Ⅲ)设函数2()log f x x =,12()()()n n b f a f a f a =+++,求1231111nb b b b ++++. 21. (本小题满分12分)据调查,某地区300万从事传统农业的农民,人均年收入6000元,为了增加农民的收入,当地政府积极引进资金,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有)0(>x x 万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高%x ,而进入企业工作的农民的人均年收入为6000a 元(2)a ≥.(Ⅰ) 在建立加工企业后,要使从事传统农业的所有农民的年总收入不低于加工企业建立前的农民的年总收入,试求x 的取值范围;(Ⅱ)在(Ⅰ)的条件下,当地政府应该如何引导农民(即x 多大时),能使这300万农民的人均年收入达到最大. 22. (本小题满分14分)已知函数()ln 3(R)f x a x ax a =--∈. (Ⅰ)求函数)(x f 的单调区间;(Ⅱ)若函数)(x f y =的图象在点))2(,2(f 处的切线的倾斜角为︒45,对于任意的]2,1[∈t ,函数]2)('[)(23mx f x x x g ++=在区间)3,(t 上总不是单调函数,求m 的取值范围; (Ⅲ)求证:ln 2ln 3ln 4ln 1(2,N )234n n n n n*⨯⨯⨯⨯<≥∈.青岛市高三教学质量检测高中数学 (理科)答案 2009.11一、选择题:本大题共12小题.每小题5分,共60分BCCDB BCDDD BA二、填空题:本大题共4小题,每小题4分,共16分.13. )1,0[; 14. 25e -; 15.4或7; 16.(2,2)- 三、解答题:本大题共6小题,共74分. 17.(本小题满分12分)解:(Ⅰ)在ABC ∆中,4cos2cos23A C -=224(12sin )(12sin )3A C ---=………………2分224sin sin A C =2sin sin A C =………………4分根据正弦定理,ABCC AB sin sin = 于是AB =522sin sin ==BC BC AC………………6分(Ⅱ)在ABC ∆中,根据余弦定理,得cos A =2222AB AC BC AB AC +-=⋅…8分于是 sin A =55cos 12=-A 从而4sin 22sin cos 5A A A ==223cos 2cos sin 5A A A =-=……………10分所以 sin(2)sin 2coscos 2sin44410A A A πππ-=-=……………12分 18.(本小题满分12分)解:(Ⅰ)设2()()22g x f x x x k =-=-+-由题设有(1)035()02494013(1,)22g k g k k -=>⎧⎪⎪=->⎪⎨∆=->⎪⎪--∈-⎪⎩-------------4分5944k ⇒<<,又Z k ∈∴2k =--------------------6分 (Ⅱ)∵2k =,∴2217()2()024f x x x x =-+=-+>--------------------8分∴2[()]4()()f x f x f x +=+4()f x≥4=当且仅当()f x =4()f x ,即2[()]4f x =时取等号. ---------------------10分 ∵()0f x >,∴()2f x =时取等号.即222x x -+=,解得x =0或1.当x =0或1时,2[()]4()f x f x +取最小值4. ---------12分19.(本小题满分12分) 解:(Ⅰ)()f x =sin 2coscos 2sincos 266x x x ππωωω--32cos 22x x ωω-)3x πω----------------------4分()f x 的最小正周期为282T πω==,故8πω=--------------------6分 (Ⅱ)由(Ⅰ)知:()sin()43f x x ππ=- 在()y g x =的图象上任取一点(,())x g x ,它关于1x =的对称点(2,())x g x - . 由题设条件,点(2,())x g x -在()y f x =的图象上,从而 ()(2)sin[(2)]43g x f x x ππ=-=--sin[]243x πππ--)43x ππ+-------------------8分当02x ≤≤时,53436x ππππ≤+≤, 因此当2x =时,()y g x =在区间[0,2]上取得最小值为:m i n 53()62g x π==----------------------12分 20. (本小题满分12分) 解:(Ⅰ)当2n ≥时111111(1)(1)3333n n n n n a a a a a --=---=-+,13n n n a a a -=-+∴114n n a a -=---------------------2分 由1111(1)3S a a ==-得114a = ∴数列{}n a 是首项114a =、公比为14的等比数列,∴1111()()444n nn a -=⨯=---4分(Ⅱ) 由1(1)3n n S a =-得11[1()]34nn S =---------------------5分11()14n -<,∴111[1()]343n -<∴13n S <-------------------------8分(Ⅲ)2()log f x x =21222log log log n n b a a a ∴=+++=212log ()n a a a=1221log ()2(12)(1)4nn n n +++=-+++=-+-------------------10分∵1111(1)1n b n n n n=-=-++ ∴12111n b b b +++=11111(1)()()2321n n -+-++-+1nn =-+-----12分 21. (本小题满分12分)解:(I )由题意得(300)6000(1%)3006000x x -⨯⨯+≥⨯……………3分 即22000x x -≤解得0200x ≤≤又∵0>x ,∴0200x <≤……………………………………………………5分 (II) 设这300万农民的人均年收入为y 元则(300)6000(1%)6000300x x axy -⨯⨯++=……………………8分20.220(2)6000x a x =-+++………………………………10分20(2)2,50(2)2002(0.2)a a a +≥∴-=+≥⨯-所以函数20.220(2)6000y x a x =-+++在(0,200]上是增函数.∴当200x =时,2max 0.220020(2)2006000y a =-⨯++⨯+60004000a =+万元…………………………………12分22. (本小题满分14分)(Ⅰ))0()1()('>-=x xx a x f --------------------2分 当0>a 时,)(x f 的单调增区间为(]0,1,减区间为[)1,+∞; 当0<a 时,)(x f 的单调增区间为[)1,+∞,减区间为(]0,1; 当0=a 时,)(x f 不是单调函数--------------------4分(Ⅱ)12)2('=-=af 得2-=a ,32ln 2)(-+-=x x x f ∴x x m x xg 2)22()(23-++=,∴2)4(3)('2-++=x m x x g -------------------6分∵)(x g 在区间)3,(t 上总不是单调函数,且()02'g =-∴⎩⎨⎧><0)3('0)('g t g ----------8分由题意知:对于任意的]2,1[∈t ,'()0g t <恒成立,所以,'(1)0'(2)0'(3)0g g g <⎧⎪<⎨⎪>⎩,∴9337-<<-m -------------------10分(Ⅲ)令1-=a 此时3ln )(-+-=x x x f ,所以2)1(-=f ,由(Ⅰ)知3ln )(-+-=x x x f 在),1(+∞上单调递增,∴当),1(+∞∈x 时)1()(f x f >,即01ln >-+-x x ,∴1ln -<x x 对一切),1(+∞∈x 成立,-----------------12分 ∵2,N*n n ≥∈,则有1ln 0-<<n n ,∴nn n n 1ln 0-<<ln 2ln 3ln 4ln 12311(2,N )234234n n n n n n n*-∴⋅⋅⋅⋅<⋅⋅⋅⋅=≥∈…………………14分。
