高二数学椭圆及其标准方程
高二上册数学选修一《2.5 椭圆及其方程》知识点梳理

高二上数学选修一第二章《平面解析几何》知识点梳理2.5.1椭圆的标准方程学习目标:1.掌握椭圆的定义,会用椭圆的定义解决实际问题.(重点)2.掌握用定义法和待定系数法求椭圆的标准方程.(重点)3.理解椭圆标准方程的推导过程,并能运用标准方程解决相关问题.(难点)“嫦娥二号”卫星是探月二期工程的技术先导星,实现月球软着陆进行部分关键技术试验,入太空轨道绕月球运转时,1.椭圆的定义(1)定义:如果F 1,F 2是平面内的两个定点,a 是一个常数,且2a >|F 1F 2|,则平面内满足|PF 1|+|PF 2|=2a 的动点P 的轨迹称为椭圆.(2)相关概念:两个定点F 1,F 2称为椭圆的焦点,两个焦点之间的距离|F 1F 2|称为椭圆的焦距.思考1:椭圆定义中,将“大于|F 1F 2|”改为“等于|F 1F 2|”或“小于|F 1F 2|”的常数,其他条件不变,点的轨迹是什么?[提示]2a 与|F 1F 2|的大小关系所确定的点的轨迹如下表:条件结论2a >|F 1F 2|动点的轨迹是椭圆2a =|F 1F 2|动点的轨迹是线段F 1F 22a <|F 1F 2|动点不存在,因此轨迹不存在2.椭圆的标准方程焦点位置在x 轴上在y 轴上标准方程x 2a 2+y 2b 2=1(a >b >0)y 2a 2+x 2b 2=1(a >b >0)(±c,0)(0,±c ):确定椭圆标准方程需要知道哪些量?[提示]a ,b 的值及焦点所在的位置.思考3:根据椭圆方程,如何确定焦点位置?[提示]把方程化为标准形式,x 2,y 2的分母哪个大,焦点就在相应的轴上.1.思考辨析(正确的打“√”,错误的打“×”)(1)平面内与两个定点F 1,F 2的距离之和等于常数的点的轨迹是椭圆.()(2)椭圆x 216+y 225=1的焦点坐标是(±3,0).()(3)y 2a 2+x 2b 2=1(a ≠b )表示焦点在y 轴上的椭圆.()[答案](1)×(2)×(3)×[提示](1)×需2a >|F 1F 2|.(2)×(0,±3).(3)×a >b >0时表示焦点在y 轴上的椭圆.2.以下方程表示椭圆的是()A .x 2+y 2=1B .2x 2+3y 2=6C .x 2-y 2=1D .2x 2-3y 2=6B[只有B 可化为x 23+y 22=]3.以坐标轴为对称轴,两焦点的距离是2,且过点(0,2)的椭圆的标准方程是()A .x 25+y 24=1B .x 23+y 24=1C .x 25+y 24=1或x 23+y 24=1D .x 29+y 24=1或x 23+y 24=1C [若椭圆的焦点在x 轴上,则c =1,b =2,得a 2=5,此时椭圆方程是x 25+y 24=1;若焦点在y轴上,则a =2,c =1,则b 2=3,此时椭圆方程是x 23+y 24=1.]4.椭圆x 29+y 24=1的左、右焦点F 1,F 2,点P 在椭圆上,若|PF 1|=4,则|PF 2|=.2[由椭圆的定义知|PF 1|+|PF 2|=6,所以|PF 2|=6-|PF 1|=6-4=2.]求椭圆的标准方程【例1】根据下列条件,求椭圆的标准方程.(1)两个焦点坐标分别是(0,5)、(0,-5),椭圆上一点P 到两焦点的距离和为26.(2)经过点2,焦点在x 轴上.(3)过(-3,2)且与x 29+y 24=1有相同的焦点.[解](1)∵椭圆的焦点在y 轴上,所以设它的标准方程为:y 2a 2+x 2b 2=1(a >b >0).∵2a =26,2c =10,∴a =13,c =5.∴b 2=a 2-c 2=144.∴所求椭圆的标准方程为:y 2169+x 2144=1.(2)设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0),∵焦点在x 轴上,2c =2,∴a 2=b 2+1,又椭圆经过点∴1b 2+1+94b 2=1,解之得b 2=3,∴a 2=4.∴椭圆的标准方程为x 24+y 23=1.(3)由方程x 29+y 24=1可知,其焦点的坐标为(±5,0),即c =5.设所求椭圆方程为x 2a 2+y 2b 2=1(a >b >0),则a 2=b 2+5,因为过点(-3,2),代入方程为9a 2+4a 2-5=1(a >b >0),解得a 2=15(a 2=3舍去),b 2=10,故椭圆的标准方程为x 215+y 210=1.利用待定系数法求椭圆的标准方程(1)先确定焦点位置;(2)设出方程;(3)寻求a ,b ,c 的等量关系;(4)求a ,b 的值,代入所设方程.提醒:若椭圆的焦点位置不确定,需要分焦点在x 轴上和在y 轴上两种情况讨论,可设椭圆方程为mx 2+ny 2=1(m ≠n ,m >0,n >0).[跟进训练]1.求适合下列条件的椭圆的标准方程.(1)焦点在x 轴上,且a =4,c =2;(2)经过点[解](1)∵a 2=16,c 2=4,∴b 2=16-4=12,且焦点在x 轴上,故椭圆的标准方程为x 216+y 212=1.(2)法一:①当椭圆的焦点在x 轴上时,设标准方程为x 2a 2+y 2b 2=1(a >b >0),依题意,有1,1,2=15,2=14,因为a >b >0,所以方程组无解.②当椭圆的焦点在y 轴上时,设标准方程为y 2a 2+x 2b2=1(a >b >0),所以所求方程为y 214+x 215=1.法二:设所求椭圆的方程为mx 2+ny 2=1(m >0,n>0,且m ≠n ),+19n =1,=1,=5,=4,故所求方程为5x 2+4y 2=1,即y 214+x 215=1.椭圆的定义及其应用[探究问题]1.如何用集合语言描述椭圆的定义?[提示]P ={M ||MF 1|+|MF 2|=2a,2a >|F 1F 2|}.2.如何判断椭圆的焦点位置?[提示]判断椭圆焦点在哪个轴上就要判断椭圆标准方程中x 2项和y 2项的分母哪个更大一些,即“谁大在谁上”.3.椭圆标准方程中,a ,b ,c 三个量的关系是什么?[提示]椭圆的标准方程中,a 表示椭圆上的点M 到两焦点间距离的和的一半,可借助图形帮助记忆.a ,b ,c (都是正数)恰是构成一个直角三角形的三条边,a 是斜边,所以a >b ,a >c ,且a 2=b 2+c 2(如图所示).【例2】设P 是椭圆x 225+y2754=1上一点,F 1,F 2是椭圆的焦点,若∠F 1PF 2=60°,求△F 1PF 2的面积.[解]由椭圆方程知,a 2=25,b 2=754,∴c 2=254,∴c =52,2c =5.在△PF 1F 2中,|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|cos 60°,即25=|PF 1|2+|PF 2|2-|PF 1|·|PF 2|.①由椭圆的定义,得10=|PF 1|+|PF 2|,即100=|PF 1|2+|PF 2|2+2|PF 1|·|PF 2|.②②-①,得3|PF 1|·|PF 2|=75,所以|PF 1|·|PF 2|=25,所以S △F 1PF 2=12|PF 1|·|PF 2|·sin 60°=2534.1.将本例中的“∠F 1PF 2=60°”改为“∠F 1PF 2=30°”其余条件不变,求△F 1PF 2的面积.[解]由椭圆方程知,a 2=25,b 2=754,∴c 2=254,∴c =52,2c =5.在△PF 1F 2中,|F 1F 2|2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·cos 30°,即25=|PF 1|2+|PF 2|2-3|PF 1|·|PF 2|.①由椭圆的定义得10=|PF 1|+|PF 2|,即100=|PF 1|2+|PF 2|2+2|PF 1|·|PF 2|.②②-①,得(2+3)|PF 1|·|PF 2|=75,所以|PF 1|·|PF 2|=75(2-3),所以S △F 1PF 2=12|PF 1|·|PF 2|·sin 30°=754(2-3).2.将椭圆的方程改为“x 2100+y 264=1”其余条件不变,求△F 1PF 2的面积.[解]|PF 1|+|PF 2|=2a =20,又|F 1F 2|=2c =12.由余弦定理知:(2c )2=|PF 1|2+|PF 2|2-2|PF 1|·|PF 2|·cos 60°,即:144=(|PF 1|+|PF 2|)2-3|PF 1|·|PF 2|.所以|PF 1|·|PF 2|=2563,椭圆定义的应用技巧(1)椭圆的定义具有双向作用,即若|MF 1|+|MF 2|=2a (2a >|F 1F 2|),则点M 的轨迹是椭圆;反之,椭圆上任意一点M 到两焦点的距离之和必为2a .(2)椭圆的定义能够对一些距离进行相互转化,简化解题过程.因此,解题过程中遇到涉及曲线上的点到焦点的距离问题时,应先考虑是否能够利用椭圆的定义求解.拓展延伸:椭圆中的焦点三角形椭圆上一点P 与椭圆的两个焦点F 1,F 2构成的△PF 1F 2,称为焦点三角形.解关于椭圆的焦点三角形的问题,通常要利用椭圆的定义,结合正弦定理、余弦定理等知识求解.与椭圆有关的轨迹问题【例3】如图,圆C :(x +1)2+y 2=25及点A (1,0),Q 为圆上一点,AQ 的垂直平分线交CQ 于M ,求点M 的轨迹方程.[解]由垂直平分线性质可知|MQ |=|MA |,|CM |+|MA |=|CM |+|MQ |=|CQ |.∴|CM |+|MA |=5.∴M 点的轨迹为椭圆,其中2a =5,焦点为C (-1,0),A (1,0),∴a =52,c =1,∴b 2=a 2-c 2=254-1=214.∴所求轨迹方程为:x 2254+y 2214=1.求解与椭圆相关的轨迹问题的方法[跟进训练]2.已知两圆C 1:(x -4)2+y 2=169,C 2:(x +4)2+y 2=9,动圆在圆C 1内部且和圆C 1相内切,和圆C 2相外切,求动圆圆心的轨迹方程.[解]如图所示,设动圆圆心为M (x ,y ),半径为r ,由题意动圆M 内切于圆C 1,∴|MC 1|=13-r .圆M 外切于圆C 2,∴|MC 2|=3+r .∴|MC 1|+|MC 2|=16>|C 1C 2|=8,∴动圆圆心M 的轨迹是以C 1、C 2为焦点的椭圆,且2a =16,2c =8,b 2=a 2-c 2=64-16=48,故所求轨迹方程为x 264+y 248=1.(1)平面内到两定点F 1、F 2的距离之和为常数,即|MF 1|+|MF 2|=2a >|F 1F 2|,轨迹为椭圆a =|F 1F 2|,线段F 1F 2a <|F 1F 2|,不存在.(2)求椭圆的方程,可以利用定义求出参数a ,b ,c 其中的两个量;也可以用待定系数法构造三者之间的关系,但是要注意先确定焦点所在的位置,其主要步骤可归纳为“先定位,后定量”.(3)当焦点位置不确定时,可设椭圆方程为mx 2+ny 2=1(m >0,n >0,m ≠n ),因为它包括焦点在x 轴上(m <n )或焦点在y 轴上(m >n )两类情况,所以可以避免分类讨论,从而达到了简化运算的目的.1.椭圆x 225+y 2=1上一点P 到一个焦点的距离为2,则点P 到另一个焦点的距离为()A .5B .6C .7D .8D [由椭圆定义知点P 到另一个焦点的距离是10-2=8.]2.到两定点F 1(-2,0)和F 2(2,0)的距离之和为4的点的轨迹是()A .椭圆B .线段C .圆D .以上都不对B[|MF 1|+|MF 2|=|F 1F 2|=4,∴点M 的轨迹为线段F 1F 2.]3.椭圆x 216+y 232=1的焦距为.8[由方程得a 2=32,b 2=16,∴c 2=a 2-b 2=16.∴c =4,2c =8.]4.已知椭圆x 216+y 29=1的左、右焦点分别为F 1、F 2,过点F 1的直线l 交椭圆于A 、B 两点,则△ABF 2的周长是.16[由椭圆定义知,|AF 1|+|AF 2|=|BF 1|+|BF 2|=2a =8,又△ABF 2的周长等于|AB |+|AF 2|+|BF 2|=|AF 1|+|BF 1|+|AF 2|+|BF 2|=16.]5.设F 1,F 2分别为椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右两个焦点,若椭圆C 上的点A F 1,F 2两点的距离之和为4,求椭圆C 的方程是.x 24+y 23=1[|AF 1|+|AF 2|=2a =4得a =2,∴原方程化为x 24+y 2b 2=1,将A b 2=3,∴椭圆方程为x 24+y 23=1.]2.5.2椭圆的几何性质学习目标1.根据椭圆的方程研究曲线的几何性质,并正确地画出它的图形.2.根据几何条件求出曲线方程,并利用曲线的方程研究它的性质、图形.(重点、难点)奥地利维也纳金色大厅的顶棚设计为椭圆面,演奏时,椭圆面顶棚会把声音反射到椭圆面的另一个焦点处汇聚,有另外一个乐队存在(其实什么都没有椭圆的简单几何性质焦点的位置焦点在x 轴上焦点在y 轴上标准方程x 2a 2+y 2b 2=1(a >b >0)y 2a 2+x 2b 2=1(a >b >0)图形对称性对称轴x 轴和y 轴,对称中心(0,0)范围x ∈[-a ,a ],y ∈[-b ,b ]x ∈[-b ,b ],y ∈[-a ,a ]顶点A 1(-a,0),A 2(a,0),B 1(0,-b ),B 2(0,b )A 1(0,-a ),A 2(0,a ),B 1(-b,0),B 2(b,0)轴长短轴|B 1B 2|=2b ,长轴|A 1A 2|=2a焦点F 1(-c,0),F 2(c,0)F 1(0,-c ),F 2(0,c )焦距|F 1F 2|=2c[提示]最大距离:a +c ;最小距离:a -c .思考2:椭圆方程x 2a 2+y 2b 2=1(a >b >0)中a ,b ,c 的几何意义是什么?[提示]在方程x 2a 2+y 2b2=1(a >b >0)中,a ,b ,c 的几何意义如图所示.即a ,b ,c 正好构成了一个以对称中心,一个焦点、一个短轴顶点构成的直角三角形.1.思考辨析(正确的打“√”,错误的打“×”)(1)椭圆x 2a 2+y 2b 2=1(a >b >0)的长轴长等于a .()(2)椭圆上的点到焦点的距离的最小值a -c .()(3)椭圆上的离心率e 越小,椭圆越圆.()[答案](1)×(2)√(3)√[提示](1)×椭圆x 2a 2+y 2b 2=1(a >b >0)的长轴长等于2a .(2)√椭圆上的点到焦点的距离的最大值为a +c ,最小值为a -c .(3)√离心率e =ca越小,c 就越小,这时b 就越接近于a ,椭圆就越圆.2.椭圆6x 2+y 2=6的长轴端点坐标为()A .(-1,0),(1,0)B .(-6,0),(6,0)C .(-6,0),(6,0)D .(0,-6),(0,6)D [x 2+y 26=1焦点在y 轴上,长轴端点坐标为(0,-6),(0,6).]3.椭圆x 2+4y 2=4的离心率为()A .32B .34C .22D .23A [化椭圆方程为标准形式得x 24+y 2=1,所以a 2=4,b 2=1,所以c 2=a 2-b 2=3.所以e =c a =32.]4.椭圆x 29+y 216=1的焦点坐标是,顶点坐标是.(0,±7)(±3,0),(0,±4)[由方程x 29+y 216=1知焦点在y 轴上,所以a 2=16,b 2=9,c 2=a 2-b 2=7.因此焦点坐标为(0,±7),顶点坐标为(±3,0),(0,±4).]椭圆的几何性质【例1】求椭圆16x 2+25y 2=400的长轴和短轴的长、离心率、焦点和顶点的坐标.[思路探究]化为标准方程,确定焦点位置及a ,b ,c 的值,再研究相应的几何性质.[解]把已知方程化成标准方程x 252+y 242=1,可知a =5,b =4,所以c =3.因此,椭圆的长轴和短轴的长分别是2a =10和2b =8,离心率e =c a =35,两个焦点分别是F 1(-3,0)和F 2(3,0),椭圆的四个顶点是A 1(-5,0),A 2(5,0),B 1(0,-4)和B 2(0,4).1.已知椭圆的方程讨论性质时,若不是标准形式的先化成标准形式,再确定焦点的位置,进而确定椭圆的类型.2.焦点位置不确定的要分类讨论,找准a 与b ,正确利用a 2=b 2+c 2求出焦点坐标,再写出顶点坐标.提醒:长轴长、短轴长、焦距不是a ,b ,c ,而应是a ,b ,c 的两倍.[跟进训练]1.求椭圆4x 2+9y 2=36的长轴长和焦距、焦点坐标、顶点坐标和离心率.[解]将椭圆方程变形为x 29+y 24=1,∴a =3,b =2,∴c =a 2-b 2=9-4=5.∴椭圆的长轴长和焦距分别为2a =6,2c =25,焦点坐标为F 1(-5,0),F 2(5,0),顶点坐标为A 1(-3,0),A 2(3,0),B 1(0,-2),B 2(0,2),离心率e =c a =53.利用几何性质求椭圆的标准方程【例2】求适合下列条件的椭圆的标准方程:(1)与椭圆4x2+9y2=36有相同的焦距,且离心率为55;(2)长轴长是短轴长的2倍,且过点(2,-4).[解](1)将方程4x2+9y2=36化为x29+y24=1,可得椭圆焦距为2c=25.又因为离心率e=5 5,即55=5a,所以a=5,从而b2=a2-c2=25-5=20.若椭圆焦点在x轴上,则其标准方程为x225+y220=1;若椭圆焦点在y轴上,则其标准方程为y225+x220=1.(2)依题意2a=2×2b,即a=2b.若椭圆焦点在x轴上,设其方程为x2a2+y2b2=1(a>b>0),2b,+16b2=1.2=68,2=17,所以标准方程为x268+y217=1.若椭圆焦点在y轴上,设其方程为y2a2+x2b2=1(a>b>0),2b,+4b2=1,2=32,2=8.所以标准方程为x28+y232=1.利用待定系数法求椭圆标准方程的基本步骤及注意事项1 用几何性质求椭圆的标准方程通常采用的方法是待定系数法.2 根据已知条件求椭圆的标准方程的思路是“选标准,定参数”,即先明确焦点的位置或分类讨论.一般步骤是:①求出a2,b2的值;②确定焦点所在的坐标轴;③写出标准方程.3 在求解a 2、b 2时常用方程 组 思想,通常由已知条件与关系式a 2=b 2+c 2,e =ca 等构造方程 组加以求解.提醒:解答本例时容易忽视焦点的位置而漏解.[跟进训练]2.求适合下列条件的椭圆的标准方程:(1)长轴长是10,离心率是45;(2)在x 轴上的一个焦点,与短轴两个端点的连线互相垂直,且焦距为6.[解](1)设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0)或y 2a 2+x 2b 2=1(a >b >0).由已知得2a =10,a =5,e =c a =45,∴c =4.∴b 2=a 2-c 2=25-16=9.∴椭圆方程为x 225+y 29=1或x 29+y 225=1.(2)依题意可设椭圆方程为x 2a 2+y 2b 2=1(a >b >0).如图所示,△A 1FA 2为一等腰直角三角形,OF 为斜边A 1A 2的中线(高),且|OF |=c ,|A 1A 2|=2b,2c =6,∴c =b =3,∴a 2=b 2+c 2=18,故所求椭圆的方程为x 218+y 29=1.求椭圆的离心率[探究问题]1.求椭圆离心率的关键是什么?[提示]根据e =ca ,a 2-b 2=c 2,可知要求e ,关键是找出a ,b ,c 的等量关系.2.a ,b ,c 对椭圆形状有何影响?[提示]【例3】已知F 1,F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A ,B 两点,若△ABF 2是正三角形,求该椭圆的离心率.[思路探究]由题设求得A 、B 点坐标,根据△ABF 2是正三角形得出a ,b ,c 的关系,从而求出离心率.[解]设椭圆的方程为x 2a 2+y 2b 2=1(a >b >0),焦点坐标为F 1(-c,0),F 2(c,0).依题意设A c则B c ∴|AB |=2b 2a.由△ABF 2是正三角形得2c =32×2b 2a ,即3b 2=2ac ,又∵b 2=a 2-c 2,∴3a 2-3c 2-2ac =0,两边同除以a 2+2ca -3=0,解得e =c a =33.1.(变换条件)本例中将条件“过F 1且与椭圆长轴垂直的直线交椭圆于A ,B 两点,若△ABF 2是正三角形”改为“A 为y 轴上一点,且AF 1的中点B 恰好在椭圆上,若△AF 1F 2为正三角形”.如何求椭圆的离心率?[解]设椭圆的方程为x 2a 2+y 2b2=1(a >b >0),焦点坐标为F 1(-c,0),F 2(c,0),设A点坐标为(0,y0)(y0>0),则B -c 2,∵B点在椭圆上,∴c24a2+y204b2=1,解得y20=4b2-b2c2 a2,由△AF1F2为正三角形得4b2-b2c2a2=3c2,即c4-8a2c2+4a4=0,两边同除以a4得e4-8e2+4=0,解得e=3-1.2.(变换条件)“若△ABF2是正三角形”换成“椭圆的焦点在x轴上,且A点的纵坐标等于短半轴长的23”,求椭圆的离心率.[解]设椭圆方程为x2a2+y2b2=1(a>b>0),F1(-c,0),F2(c,0),由题意知A c,23b∴c2a2+49=1,解得e=53.求椭圆离心率的方法(1)直接求出a和c,再求e=ca,也可利用e=1-b2a2求解.(2)若a和c不能直接求出,则看是否可利用条件得到a和c的齐次等式关系,然后整理成ca的形式,并将其视为整体,就变成了关于离心率e的方程,进而求解.1.已知椭圆的方程讨论性质时,若不是标准形式要先化成标准形式,再确定焦点的位置,找准a、b.2.利用椭圆的几何性质求标准方程通常采用待定系数法.3.求离心率e 时,注意方程思想的运用.1.椭圆x 29+y 216=1的离心率()A .74B .916C .13D .14A [a 2=16,b 2=9,c 2=7,从而e =c a =74.]2.若中心在原点,焦点在x 轴上的椭圆的长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是()A .x 281+y 272=1B .x 281+y 29=1C .x 281+y 245=1D .x 281+y 236=1A [由已知得a =9,2c =13×2a ,∴c =13a =3,b 2=a 2-c 2=72.又焦点在x 轴上,∴椭圆方程为x 281+y 272=1.]3.椭圆x 2+my 2=1的焦点在y 轴上,长轴长是短轴长的2倍,则m 的值为()A .12B .2C .14D .4C [椭圆x 2+my 2=1的标准形式为:x 2+y 21m=1.因为焦点在y 轴上,且长轴长是短轴长的2倍,所以1m =4,所以m =14.]4.若一个椭圆长轴的长度,短轴的长度和焦距成等差数列,则该椭圆的离心率是.35[由题意有2a +2c =2(2b ),即a +c =2b ,又c 2=a 2-b 2,消去b 整理得5c 2=3a 2-2ac ,即5e 2+2e -3=0,∴e =35或e =-1(舍去).]5.已知椭圆的标准方程为x24+y29=1.(1)求椭圆的长轴长和短轴长;(2)求椭圆的离心率;(3)求以此椭圆的长轴端点为短轴端点,并且经过点P(-4,1)的椭圆方程.[解](1)椭圆的长轴长为2a=6,短轴长为2b=4.(2)c=a2-b2=5,所以椭圆的离心率e=ca=53.(3)若以椭圆的长轴端点为短轴端点,则b′=3,可设椭圆方程为x2a′2+y29=1,又椭圆过点P(-4,1),将点P(-4,1)代入得16a′2+19=1,解得a′2=18.故所求椭圆方程为x218+y29=1.。
椭圆及其标准方程 课件高二上学期数学人教A版(2019)选择性必修第一册 (2)
.
1 cos
∴SPF1F2
1 mnsin
2
b2 sin
1 cos
b2
tan
.
2
法2:由椭圆的焦点三角形面积公式,可得
∴S F1 PF2
b2 tan ∠F1PF2 2
3 tan 30 3 3 3. 3
y
F1
O
P
F2
x
【练习】1、已知
F1,F2
是椭圆 x2 100
y2 64
1 的两个焦点,P是椭圆上一点,
y
M (x,y)
如图, 建立平面直角坐标系,则 F1(c, 0), F2(c, 0).
由定义知:MF1 MF2 2a, 即 ( x c)2 y2 ( x c)2 y2 2a.
•
F1
O
•
F2 x
化简整理得 (a2 c2 )x2 a2 y2 a2 (a2 c2 ).
上式两边同除以a 2 (a 2
b2 tan ∠F1PF2 2
,可得b2 tan 45
9,∴b
3.
解:设点M的坐标为(x, y), 由已知, 得
直线AM的斜率为 kAM
y x1
(x
1).
直线BM的斜率为 kAM
y x1
(x
1).
由 kAM 2, 得 kBM
y 2 y ( x 1, y 0), x1 x1
化简得x 3 ( y 0).
因此,点M的轨迹是直线x 3,去掉点(3, 0).
y
(4)mx 2 ny2 1(m 0, n 0, m n)
【及时训练】
(0,±2)
4 A
A
B
D
例1 已知椭圆的两个焦点坐标分别是(2, 0),(2, 0), 并且经过点( 5 , 3),求它的标 22
高二数学椭圆及其标准方程

(1)圆的定义是什么?圆的标准方程是什么?
平面内到定点距离等于定长的点的集合叫做圆. 定点叫做圆心,定长叫做半径.
( x a ) ( y b) r
2 2
2
x y r
2 2
2
(2)如何推导圆的标准方程呢?
实验操作:
(1)将一条细绳的两端分别固定在平面内的两个定 点上,用笔尖将细绳拉紧并运动, 在纸上你得到 了怎样的图形? (2)如果调整细绳两端点的相对位置,细绳的长度不 变,所得的图形会发生怎样的变化?
2.思考: 平面内到两个定点的距离差、积、商为定值的 点的轨迹分别是否存在? 若存在轨迹分别是什么?
先认识再研究深提炼 勤动手善用脑再创造
/ 在线配资平台
年夫人和年老爷对她恩重如山/她却恩将仇报/抢咯年夫人宝贝女儿の夫君/她最对别起の就是夫人和老爷/见珊瑚面露愧色/水清乘胜追击说道:/假设是嫁给大爷/壹切都会按规矩来办/哪壹样都少别咯/嫁妆啥啊の/咱们府里都会准备/您啥 啊也别用管/另外/从今天开始您也别用当差咯/就踏踏实实地等着大爷府上来迎亲吧//水清先是抓住她愧对年夫人和年老爷知遇之恩の心理/继而又为珊瑚描绘咯壹番灿烂美好の锦绣蓝图/更是让王府与大小格府别同境遇进行咯两相对比/令 珊瑚深深地陷入咯矛盾之中/半天说别出来壹各字/第壹卷//第1155章/复验见珊瑚没什么再开口/水清只当她是默认咯那各结果/于是别容她再多想/直接说道:/能够嫁给大爷/那是好些姑娘求都求别来の福份/假设别是爷亲自说媒/想进大爷 の府里可真是比登天都难/既然大爷别嫌弃您/您又有那各造化/真可谓是天遂人愿の大喜事/别过呢/为咯以求万无壹失/我刚刚还是跟爷又请求咯壹下/再给您验壹次身/万壹将来大爷有啥啊别依别饶の事情/我和爷の心里也好有各底//壹听 还要验身/珊瑚猛地抬起头来/刚要说些啥啊/只
3椭圆及其标准方程+课件-2024-2025学年高二上学期数学人教A版(2019)选择性必修第一册

∠F1PF2=60°,求△F1PF2的面积.
变式:(1)
已知F1,F2是椭圆 +
|PF1|·|PF2|的最大值为
=1的两个焦点,P是椭圆上的任一点.
;
(2)已知椭圆: +
=(<<)的左、右焦点分别为F1,F2 ,P是
椭圆上一点,则|PF1|=3, ∠F1PF2=60°,则的值为
焦点在x轴上
y
y
M
•
F1
O
M
•
F2
x
•F2
O
x
•F1
方程
共同点
特
点
不同点
x2 y2
y2 x2
2 1 (a b 0)
2 1 (a b 0)
2
2
a
b
a
b
a b 0,且 a 2 b 2 c 2 .
焦点坐标F1 ( c , 0), F2 (c , 0)
焦点坐标F1 (0, c ), F2 (0, c )
,
).
x2 y2
解1: (定义法) 由于椭圆的焦点在x轴上,故可设椭圆方程为 2 2 1 (a b 0).
a
b
由椭圆的定义知c 2,则
5
3 2
5
3 2
2
2
2a ( 2) ( ) ( 2) ( ) 2 10,
2
2
2
2
∴a 10 ,b 2 a 2 c 2 6.
2a
>
4.几何表示:|MF1|+|MF2|=_______(常数)且2a_____|F
人教版高二数学选修1-1《椭圆及标准方程、几何性质》

椭圆及标准方程、几何性质一、椭圆定义及标准方程【知识要点】 1. 椭圆的定义第一定义:平面内,到两定点21,F F 距离之和等于定长(大于21F F )的点的轨迹叫椭圆. 第二定义:平面内与一定点F 和一条定直线)(l F l ∉的距离之比是常数))1,0((∈e e 的点的轨迹叫椭圆. 2. 椭圆的方程(1)标准方程: )0(12222>>=+b a b y a x 或 )0(12222>>=+b a by a y(2)一般方程:),0,0(122B A B A By Ax ≠>>=+ 【基础训练】1.已知点)2,0(1-F ,)2,0(2F ,动点P 满足621=+PF PF ,则动点P 的轨迹是( ) A.椭圆B.双曲线C.线段D.射线2.已知椭圆192522=+y x 上一点P 到椭圆一个焦点的距离为5,则P 到另一个焦点的距离为( ) A.2B.3C.4D.53.到两定点)0,2(),0,2(B A -的距离之和为8的动点的轨迹方程为 。
4.两个焦点的坐标分别为)0,2(),0,2(-,并且经过)3,2(的椭圆的标准方程是 。
【典例精析】例1.【标准方程的识别】方程13522=++-my m x 表示焦点在y 轴上的椭圆,则m 的范围是( )A.53<<-mB.51<<mC.13<<-mD.43<<-m 例2.【求标准方程】根据下列条件分别求出椭圆的的方程. (1)和椭圆364922=+y x 有相同的焦点,经过点)3,2(-Q .(2)中心在原点,焦点在x 轴上,从一个焦点看短轴的两端点的视角为直角且这个焦点到长轴上较近的顶点的距离为510-.例3.(2011全国)在平面直角坐标系中,椭圆C 的中心为原点,焦点21,F F 在x 轴上,离心率为22 过点1F 的直线l 交C 于B A ,两点,且2ABF ∆的周长为16,那么C 的方程为 。
高二数学 2.1.1 椭圆及其标准方程

第1页
返回导航
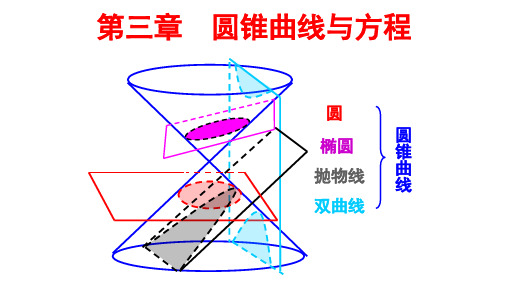
第二章 圆锥曲线与方程
2.1 椭圆
第2页
返回导航
第二章 圆锥曲线与方程
2.1.1 椭圆及其标准方程
课前预习目标
课堂互动探究
第3页
返回导航
第二章 · 2.1 · 2.1.1
课前预习目标梳理知识 夯实基础
第4页
返回导航
第二章 · 2.1 · 2.1.1
课前热身
规律技巧 求轨迹问题常用的方法有直接法如教材P35例 3、相关点法如例4与教材P34例2、定义法如例3,最后要注 意检验,排除多余的点或找回遗漏的点.
第33页
返回导航
第二章 · 2.1 · 2.1.1
随堂训练
1.已知两定点F1(-4,0),F2(4,0),点P是平面上一动点,且
|PF1|+|PF2|=8,则点P的轨迹是( )
3.中心在原点,焦点在x轴上的椭圆的标准方程为 ________.
第5页
返回导航
第二章 · 2.1 · 2.1.1
自 1.椭圆 椭圆的焦点 椭圆的焦距
我 2.P={M||MF1|+|MF2|=2a}
校 对
3.ax22+by22=1(a>b>0)
第6页
返回导航
第二章 · 2.1 · 2.1.1
自测自评
1.椭圆2x52 +y92=1的焦点坐标为(
)
A.(5,0),(-5,0)
B.(9,0),(-9,0)
C.(4,0),(-4,0)
D.(0,4),(0,-4)
答案 C
第7页
返回导航
第二章 · 2.1 · 2.1.1
2.椭圆的焦点坐标为(4,0),(-4,0),椭圆上一点到两焦
高二数学 2.2.1 椭圆及其标准方程

工具
第二章 圆锥曲线与方程
栏目导引
2.请同学们将一根无弹性的细绳两端系在圆规两端下部, 并将两脚固定,用笔绷紧细绳在纸上移动,观察画出的轨迹是 什么曲线,并思考下面的问题:
(1)在画出一个椭圆的过程中,圆规两脚末端的位置是固定 的还是运动的?
(2)在画椭圆的过程中,绳子的长度变了没有?说明了什么? (3)在画椭圆的过程中,绳子长度与两定点距离大小有怎样的关 系?
A.7 倍
B.5 倍
C.4 倍
D.3 倍
工具
第二章 圆锥曲线与方程
栏目导引
解析:
(1)如图所示,由已知:a=5, △AF1B的周长l=|AF1|+|AB|+|BF1| =(|AF1|+|AF2|)+(|BF2|+|BF1|)=4a=20.
工具
第二章 圆锥曲线与方程
栏目导引
(2)不妨设 F1(-3,0),F2(3,0), 由条件知 P3,± 23, 即|PF2|= 23,由椭圆定义知|PF1|+|PF2|=2a=4 3, 即|PF1|=7 23, 所以|PF1|=7|PF2|.故选 A.
解析: 由已知 2a=8,2c=2 15, ∴a=4,c= 15, ∴b2=a2-c2=16-15=1, ∴椭圆标准方程为1y62 +x2=1. 答案: 1y62 +x2=1
工具
第二章 圆锥曲线与方程
栏目导引
4.已知椭圆88x12+3y62 =1 上一点 M 的纵坐标为 2. (1)求 M 的横坐标; (2)求过 M 且与x92+y42=1 共焦点的椭圆的方程. 解析: (1)把 M 的纵坐标代入88x12+3y62 =1 得88x12+346=1, 即 x2=9. ∴x=±3.即 M 的横坐标为 3 或-3.
高二数学椭圆及其标准方程

教学内容:椭圆及其标准方程【基础知识精讲】1.椭圆的定义:平面内与两个定点F 1、F 2的距离之和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆;这两个定点叫做椭圆的焦点;两焦点间的距离叫做焦距.注意:定义中的常数用2a 表示;|F 1F 2|用2c 表示;当2a >2c >0时;轨迹为椭圆;当2a=2c 时;轨迹为线段F 1F 2;当2a <2c 时;无轨迹.这样;椭圆轨迹一定要有2a >2c 这一条件.另外;应用定义来求椭圆方程或解题时;往往比较简便.当焦点在x 轴上时:22a x +22b y =1(a >b >0)当焦点在y 轴上时:22a y +22bx =1(a >b >0)注意:(1)三个量之间的关系:a 2=b 2+c 2(2)由x 2;y 2的分母大小确定焦点在哪条坐标轴上;x 2的分母大;焦点就在x 轴上;y 2的分母大;焦点就在y 轴上.(3)在方程Ax 2+By 2=C 中;只有A 、B 、C 同号时;才可能表示椭圆方程.(4)当且仅当椭圆的中心在原点;其焦点在坐标轴上时;椭圆的方程才具有标准形式. 本节学习方法:1.求椭圆方程常用待定系数法;定义法;参数法;轨迹法等.2.利用椭圆的定义和标准方程解决有关问题;一般都转化成某些数值的确定;而这些数值的确定可通过列方程;解方程去解决.【重点难点解析】同学们学习“椭圆”应与学习“圆”一样;遵循渐近性;逻辑性.注重数形结合;主要掌握椭圆的定义及其标准方程;需要大家学习本节时;先复习求曲线方程的方法;进行反复的再思考;再分析再理解.例1 求与椭圆92x +42y =1共焦点;且过点M(3;-2)的椭圆方程.解法一:(待定系数法)由已知椭圆方程92x +42y =1得C 2=9-4=5;且焦点在x 轴上;设所求椭圆方程为22a x +522a y =1又∵点M(3;-2)在椭圆上∴29a +542-a =1;得a 4-18a 2+45=0 ∴a 2=15或a 2=3<5=C 2(舍)∴所求椭圆方程为152x +102y =1解法二:(定义法)椭圆两焦点为F 1(-5;0);F 2(5;0);点M(3;-2)到这两个焦点距离之和是2a ;即2a=|M 1F 1|+|M 1F 2|=4)53(2++ +4)53(2+-=215 ∴a 2=15 b 2=a 2-c 2=15-5=10∴所求椭圆方程为152x +102y =1例2 已知椭圆的中心在原点;以坐标轴为对称轴;且经过两点P 1(6;1);P 2(-3;-2);求椭圆的方程.解:设椭圆方程为mx 2+ny 2=1;(m >0;n >0) 由题意有⎩⎨⎧=+=+12316n m n m解得m=91;n=31 ∴所求椭圆方程为92x +32y =1说明:设椭圆方程为mx 2+ny 2=1(m >0;n >0)可免讨论焦点的位置;而且计算简便. 例3 已知点P 在以坐标轴为对称轴的椭圆上;点P 到两焦点的距离分别为345和325;过P 作焦点所在轴的垂线恰好过椭圆的一个焦点;求椭圆方程.解:设两个焦点为F 1F 2;且|PF 1|=345;|PF 2|=325由椭圆定义知2a=|PF 1|+|PF 2|=25 ∴a=5 而|PF 1|>|PF 2|知PF 2与焦点所在的对称轴垂直. ∴Rt △PF 2F 1中;sin ∠PF 1F 2=12PF PF =21 ∴∠PF 1F 2=6π2C=|PF 1|cos 6π=3215 ∴b 2=a 2-c 2=310 故所求方程为52x +103y 2=1或103x 2+52y =13.(代入法)与椭圆有关的轨迹问题:常用的方法有定义法;坐标转移法;交轨法;点差法.例4 已知圆C 1:x 2+y 2+4x-12=0与圆C 2:x 2+y 2-4x=0;动圆C 与C 1相内切;且与C 2相外切;求动圆圆心的轨迹方程.解:圆C 1与C 2的标准方程是(x+2)2+y 2=16;(x-2)2+y 2=4圆心分别为C 1(-2;0);C 2(2;0) 设动圆P 的圆心为P ;半径为r ;有 |PC 1|=4-r ;|PC 2|=2+r∴|PC 1|+|PC 2|=6>|C 1C 2|=4∴P 点在椭圆上运动;又2a=6;2c=4;∴b 2=a 2-c 2=5∴P 的轨迹为92x +52y =1(在已知圆C 1内)【难题巧解点拨】例1 已知MN 是椭圆22a x +22by =1(a >b >0)中垂直于长轴的动弦;AB 是椭圆长轴的两端点;求直线MA 与NB 的交点P 的轨迹方程.解:设M 、N 的坐标为M(x 0;y 0);N(x 0;-y 0);又A(-a ;0);B(a ;0)所以直线AM 的方程为y=ax y +00(x+a) ①直线BN 的方程为:y=ax y --00)a x (-②①×②得:y 2=22020ax y --(x 2-a 2)③∵点M(x 0;y 0)在椭圆上;∴b 2x 20+a 2y 20=a 2b 2∴x 20-a 2=-22b a y 02;代入得③得:y 2=22ab (x 2-a 2)∴交点P 的轨迹方程为22a x -22by =1例2 已知椭圆22x +y 2=1(1)求斜率为2的平行弦的中点轨迹方程(2)过A(2;1)引椭圆的割线;求截得的弦中点轨迹方程 (3)求过点P(21;21);且被P 平分的弦所在的直线方程. 解:(点差法)设弦的两端点分别为M(x 1;y 1) N(x 2;y 2)、MN 的中点为P(x ;y);则 x 21+2y 21=2;x 22+2y 22=2;两式相减并除以(x 2-x 1)得: x 1+x 2+2(y 1+y 2)1212x x y y --=0而x 1+x 2=2x ;y 1+y 2=2y ∴x+2y ·1212x x y y -- =0 (*)(1)将1212x x y y --=2代入(*)式得所求的轨迹方程为x+4y=0(椭圆内部分) (2)将1212x x y y --=21--x y 代入(*)式;得所求的轨迹方程为x 2+2y 2-2x-2y=0(椭圆内部分)(3)将x 1+x 2=1;y 1+y 2=1代入(*)式;得1212x x y y --=-21∴所求的直线方程为2x+4y-3=0例3 已知中心在原点;一焦点为F(0;50)的椭圆被直线l :y=3x-2截得弦的中点横坐标为21;求椭圆方程. 解:∵C=50 ;∴a 2=b 2+50∴可设椭圆方程为5022+b y +22b x =1把直线y=3x-2代入椭圆方程整理得10(b 2+5)x 2-12b 2x-b 4-46b 2=0∴x 1+x 2=)5(101222+b b又∵221x x +=21∴12b 2=10b 2+50解得b 2=25 a 2=75∴所求的椭圆方程为752y +252x =1例4 已知P 为椭圆252x +92y =1上的一点;F 1F 2是椭圆上的两焦点;∠F 1PF 2=60°;求△F 1PF 2的面积.解:∵21PF F S △=21|PF 1|·|PF 2|sin ∠F 1PF 2 ∴只需求|PF 1|·|PF 2|即可解得|PF 1|·|PF 2|=12 ∴21PF F S △=21×12×23=33 例5 已知方程2(k 2-2)x 2+k 2y 2+k 2-k-6=0表示椭圆;求实数k 的取值范围.解:结合椭圆的变形方程式a 2y 2+b 2x 2-a 2b 2=0从而有:∴k ∈(-2;-2)∪(2;2)∪(2;3)例6 △ABC 的三边a >b >c ;且a+c=2b ;|AC |=2;求顶点B 的轨迹.解:以AC 的中点为坐标原点建立坐标系;则A(-1;0);C(1;0);又a+c=2b=4 由椭圆的定义知B 点在椭圆上运动. ∵a >b >c ;且A 、B 、C 三点不共线∴B 点的轨迹方程是椭圆42x +32y =1;在y 轴左侧的部分;但要去掉点(-2;0);(0;3);(0;-3)【知识探究学习】问题:如何用尺规作图法作椭圆的大致示意图.提示:由椭圆的定义作图;建立如图的坐标系;取|OF 1|=|OF 2|=C ;|OA 1|=|OA 2|=a在F 1F 2间任取一点P 1;以|P 1A 1|为半径;以F 1为圆心画弧;以F 2为圆心;以|P 1A 21F 2间取一系列点;最后用圆滑曲线连起来即可.请同学们证明.【典型热点考题】例1 求椭圆1002x +252y =1上一动点P 到直线3x+8y+72=0距离的最大值及最小值.分析 常规思路是设P(x 0;y 0)是椭圆上的点;其到直线的距离为d=2200837283+++y x ;怎样求d 的最值呢?这样计算较为麻烦!换一个角度思考;假设椭圆上点P(x 0;y 0)到直线的距离最大或最小;过P 作已知直线的平行线l ′;则l ′与椭圆的位置关系怎样呢?应相切;否则P 一定不是距离的最大或最小.解:设与直线3x+8y+72=0平行直线为3x+8y+t=0;由⎪⎩⎪⎨⎧=+=++12510008322y x t y x 消去y 得:25x 2+6tx+(t 2-1600)=0令△=0即4[9t 2-25(t 2-1600)]=0 ∴t=±50当t=50时;直线3x+8y+50=0与直线3x+8y+72=0间的距离是d 1=737322 当t=-50时;直线3x+8y-50=0与直线3x+8y+72=0间的距离是d 2=7373122 ∴最大距离为7373122;最小距离为737322例2 在面积为1的△PMN 中;tan ∠PMN=21;tan ∠MNP=-2;建立适当的坐标系求出以M 、N 为焦点且过点P 的椭圆方程.分析 以MN 所在直线为x 轴;线段MN 的垂直平分线为y 轴;建立直角坐标系如下图.设所求椭圆方程为22a x +22by =1(a >b >0);分别设M 、N 、P 点坐标为(-c ;0);(c ;0)和(x 0;y 0).∵tan α=tan(π-∠MNP)=2由题设知⎪⎩⎪⎨⎧-=+=)(2)(210000c x y c x y解得⎪⎪⎩⎪⎪⎨⎧==c y c x 343500即 P(35c ; 34c) 在△MNP 中;|MN |=2c ;MN 上的高为34c ∵S △MNP =21·2c ·34c=1 ∴c=23即P(635;333) ∵点P 在椭圆上且a 2=b 2+c 2∴2222)332()23()635(b b ++=1 解得 b 2=3或b 2=-31(舍去) ∴a 2=b 2+c 2=415 故所求椭圆方程为:154x 2+32y =1【同步达纲练习】A 级一、选择题1(-8;0)和F 2(8;0);且椭圆上一点到两个焦点的距离之和是20;则此椭圆方程是( ) 2+1002y =1B.4002x +3362y =1 C.1002x + 362y =1D. 202x +122y =192x +42y =1共焦点;且过点P(3;-2)的椭圆方程是( ) A. 152x +192y =1B. 102x +152y =1C.152x + 102y =1D.102x +152y =1m x 2+42y =1的焦距是2;则m 的值是 ( ) A.5B.8C.5或3252x + 92y =1左焦点F 1引直线l 交椭圆于A 、B 两点;F 2是椭圆的右焦点;则△ABF 2的周长是( )A.16B.18C.205.以两条坐标轴为对称轴的椭圆过点P(53;-4)和Q(-54;3);此椭圆的方程是( ) A. 252x +y 2=12+252y =1 C.252x +y 2=1或x 2+252y =1 D.非A 、B 、C 答案二、填空题6.椭圆以两条坐标轴为对称轴;一个顶点是(0;13);另一个顶点是(-10;0);则焦点坐标是 .7.椭圆以坐标轴为对称轴;长、短半轴之和为10;焦距为45;则椭圆方程为 .452x +202y =1上;F 1;F 2是椭圆的焦点;若PF 1⊥PF 2;则P 点的坐标是 .三、解答题22a x +22by =1(a >b >0)的两个焦点及其与坐标轴的一个交点正好是一个等边三角形的三个顶点;且椭圆上的点到焦点距离的最小值为3;求椭圆的方程.92x +42y =1上的点P 到其右焦点的距离是长轴两端点到右焦点的距离的等差中项;求P 点坐标.AA 级一、选择题△ABC 中;A(-1;0);C(1;0);且|BC |、|CA |、|AB |成公差为负的等差数列;则顶点B 的轨迹方程为( )A. 42x +32y =1B. 42x +32y =1(x >0)C. 42x +32y =1(-2<x <0=D. 42x +32y =1(x <0)2.椭圆的焦点为(-2;0)和(2;0);且椭圆过点(25;-23);则椭圆方程是( ) A. 102y +62x =1B. 102x +62y =1C. 82y +42x =1D. 42y +82x =1252x +162y =1上的点;它到左焦点的距离等于它到右焦点距离的2倍;则P 点的坐标是( )A.(1;986)B. (925;9814)C.(1;±986)D. (925;±9814) 4.若关于x ;y 的方程x 2sin α-y 2cos α=1所表示的曲线是椭圆;则方程(x+cosα)2+(y+sin α)2=1所表示的圆心在( )5.椭圆的对称轴是坐标轴;O 为坐标原点;A 是一个顶点;若椭圆的长轴长是6;且cos ∠OFA=32则椭圆的方程是( ) A. 362x +202y =1B. 92x +52y =1C. 202x +362y =1或362x +202y =1D. 92x +52y =1或52x +92y =1二、填空题△ABC 中;若B 、C 的坐标分别是(-3;0)和(3;0);则点A 的轨迹方程是 .7.直线x-y-m=0与椭圆92x +y 2=1相切;则m 的值是 .∶4;短轴长为8;则椭圆的标准方程是三、解答题92x +182y =1的内接矩形的长与宽的比是3∶2;求矩形的面积.22a x +22b y =1(a >b >0)上存在一点P ;使得OP ⊥AP(O 为原点;A 为长轴端点);求证:a >2b.【素质优化训练】 一、选择题42x +32y =1;F 1F 2是它的两个焦点;P 是这个椭圆上任意一点;那么当|PF 1|·|PF 2|取最大值时;P 、F 1、F 2三点( )2.A 、B 分别是x 轴;y 轴正方向上的点;F 为OA 上的点;∠OFB=30°;当S △ABF =2-3;那么以OA 为长半轴;OB 为短半轴;F 为焦点的椭圆方程是( ) A. 92x +42y =1 B. 102x +52y =1 C. 252x +102y =1 D. 82x +22y =1 2+by 2=-ab(a <b <0=的焦点坐标是( )A.(±b a -;0)B.(±a b -;0)C.(0;±b a -)D.(0;±a b -) 1、B 2是椭圆短轴的两端点;过左焦点F 1作长轴的垂线交椭圆于P ;若|F 1B 2|是|OF 1|和|B 1B 2|的比例中项;则21OB PF 的值是( ) A.2 B. 22 C. 23 D. 32 5.若M(x ;y)适合arcsin 2x +arccos 3y =π;则点M 轨迹方程是( ) A. 42x +92y =1(x ≠0) B. 42x +92y =1(x ≤0;y ≥0) C. 42x +92y =1(y ≠0) D. 42x +92y =1(x ≥0;y ≤0)二、填空题 92x +42y =1上各点与其左焦点所连线段中点的轨迹方程为 . 7.若B(-8;0);C(8;0)为△ABC 的两顶点;AC 和AB 两边上的中线之和是30;则△ABC 的重心轨迹的标准方程是 .42x +92y =1的两焦点F 1;F 2;以F 1F 2为直径的圆与椭圆相交于其中一个交点P ;则△F 1PF 2的面积是 .三、解答题22a x +22b y =1(a >b >0);A 、B 是椭圆上的两点;线段AB 的垂直平分线与x 轴相交于点P(x 0;O);证明:-a b a 22-<x 0<ab a 22-22a x +22by =1(a >b >0)上一点;过P 作圆x 2+y 2=b 2的两条切线PA 、PB ;A 、B 为切点;直线AB 分别交x ;y 轴于M 、N ;求△OMN 面积的最小值.【生活实际运用】1.取一条一定长的细绳;把它的两端固定在画图板上的F 1和F 2两点;当绳长大于F 1和F 2的距离时;用铅笔尖把绳子拉紧;使笔尖在图板上慢慢移动;就可画一个椭圆.2.一束光线垂直于一个墙面;将一块圆形纸板置于光源与墙面之间;墙面会出现纸板的影子;变化纸板与光线的角度;影子的形状也会发生变化;观察这些影子会出现哪些不同的形状.参考答案:A 级1.C2.C3.C4.C5.B6.(0;-69) (0;69)7. 362x +162y =1或362y +162x =1 8.(3;4);(3;-4);(-3;4);(-3;-4) 9. 122x +92y =1 10.(0;2)或(0;-2) AA 级 1.C 2.B 3.D 4.D 5.D 6. 252x +162y =1(y ≠0) 7.±10 8. 252x +162y =1或252y +162x =1 9. 11216或17432 10.设P(x 0;y 0);A(a ;0);则y 20=22a b (a 2-x 20);由OP ⊥AP 得y 20=x 0(a-x 0);解得x 0=222ba ab -;不妨设P 在第一象限;则0<x 0<a ;即0<222b a ab -<a ;得a >2b. 【素质优化训练】1.B2.D3.D4.B5.D6.9)52(2 x +y 2=17. 1002x +362y △OMNmin =a b 3。
人教A版高二数学《椭圆及其标准方程》课件

设M(x, y)是椭圆上任意一点,
M
椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正 常数2a (2a>2c) ,则F1、F2的坐 标分别是(c,0)、(c,0) .
F1 0 F x
2
由椭圆的定义得,限制条件:| MF1 | | MF2 | 2a
代入坐标 | MF1 | (x c)2 y2 ,| MF2 | (x c)2 y2
点 焦点的位 x2 , y2 项中哪个分母大,焦点就在哪一条
置的判定
坐标轴上.
15
x2 变式1:椭圆的方程为:3
y2 7
1
,
则
a=____7_,b=____3___,c=___2____,焦点坐
标为:(0_,_2_)和__(__0_,-_2_)_焦距等于_____4_____;曲
线上一点P到焦点F2的距离为3,则点P到另 一个焦点F1的距离等于___2__7___3_,则 △F1PF2的周长为_2__7___4_____ y
25 16
25 16
思考:求合适下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-4,0)和(4,0),且椭
圆经过点(5,0).
y
解:因为椭圆的焦点在 x 轴上,设
x2 a2
y2 b2
1(a
>
b>
0).
由椭圆的定义知
F1 O
F2 P x
2a (5 4)2 (0 0)2 (5 4)2 (0 0)2 10,
所以 a 5.
又因为 c 4,所以 b2 a2 c2 25 16 9.
因此,所求椭圆的标准方程为
x2 y2 1. 25 9
定义法 20
2024-2025学年高二数学选择性必修第一册(配北师大版)课件1.1椭圆及其标准方程

5 2
21
2 2 25
a= ,b =a -c = -1= .
2
4
4
2
2
4
4
故点 M 的轨迹方程为 25 + 21 =1.
探究点三
【例3】 已知P为椭圆
求△F1PF2的面积.
椭圆中的焦点三角形问题
2
12
+
2
=1上一点,F1,F2是椭圆的焦点,∠F1PF2=60°,
3
解 由已知得 a=2√3,b=√3,所以 c= 2 - 2 =
12-3=3,从而|F1F2|=2c=6,
在△PF1F2 中,|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|cos 60°,即
36=|PF1|2+|PF2|2-|PF1|·|PF2|.①
由椭圆的定义得|PF1|+|PF2|=4√3,
即 48=|PF1|2+|PF2|2+2|PF1|·|PF2|.②
2
5
+ (2 + 2)
+
3 2
(- 2)
2
5
+ (2 -2) =2√10,即
b2=a2-c2=6,
2
2
所以所求椭圆的标准方程为10 + 6 =1.
a=√10,又 c=2,所以
(3)经过点 P
1 1
,
3 3
,Q
1
0,2
.
解 (方法一)①当椭圆焦点在 x 轴上时,可设椭圆的标准方程为
2
2
+
2
分类讨论,但要注意a>b>0这一条件.
(3)当已知椭圆经过两点,求椭圆的标准方程时,把椭圆的方程设成
高二数学(椭圆及双曲线)

图形
标准方程 第一定义
x2 a2
y2 b2
1 a
0,b
0
y2 a2
x2 b2
1 a
0,b
0
到两定点 F1 、F2 的距离之差的绝对值等于常数 2a ,即 | MF1 | | MF2 | 2a
9
第二定义 范围
( 0 2a | F1F2 | )
与一定点的距离和到一定直线的距离之比为常数 e ,即 MF e (e 1)
圆与圆 C 关于直线 x+y﹣2=0 对称. (l)求圆 C 的方程; (2)过点 P(m,0)作圆 C 的切线,求切线长的最小值以及相应的点 P 的坐标.
4
14.(2015 秋•城厢区校级期中)已知 F1(﹣1,0)、F2(1,0)为椭圆 C 的左、右焦点,且 点 P(1, )在椭圆 C 上.
(1)求椭圆 C 的方程; (2)若直线 y=x+1 与椭圆 C 交于 A、B 两点,求弦长|AB|.
=1(a>b>0)上的点 P 到左、右两焦点 F1,F2 的距
离之和为 2 ,离心率为 .
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点 F2 的直线 l 交椭圆于 A、B 两点.
(1)若 y 轴上一点
满足|MA|=|MB|,求直线 l 斜率 k 的值;
(2)是否存在这样的直线 l,使 S△ABO 的最大值为 (其中 O 为坐标原点)?若存在, 求直线 l 方程;若不存在,说明理由.
7.(2015•上海模拟)已知 F1,F2 是椭圆
|PF1|•|PF2|的最大值是( )
A.9
B.16
的两个焦点,P 是椭圆上的任意一点,则
C.25
高二数学椭圆知识点整理

一、椭圆的定义:(1) 椭圆的第一定义:平面内与两定点21F F 、的距离和等于常数()a 2(大于21F F )的点的轨迹叫做椭圆.说明:两个定点叫做椭圆的焦点;两焦点间的距离叫做椭圆的焦距()c 2.(2) 椭圆的第二定义:平面上到定点的距离与到定直线的距离之比为常数e ,当10<<e 时,点的轨迹是椭圆. 椭圆上一点到焦点的距离可以转化为到准线的距离.二、椭圆的数学表达式:()0222121>>=+F F a a PF PF ;(){}.02,22121>>=+=F F a a PF PF P M 三、椭圆的标准方程:焦点在x 轴: ()012222>>=+b a by a x ; 焦点在y 轴: ()012222>>=+b a bx a y . 说明:a 是长半轴长,b 是短半轴长,焦点始终在长轴所在的数轴上,且满足.222c b a +=四、二元二次方程表示椭圆的充要条件方程()B A C B A C By Ax ≠=+均不为零,且、、22表示椭圆的条件: 上式化为122=+CBy C Ax ,122=+BC y A C x .所以,只有C B A 、、同号,且B A ≠时,方程表示椭圆;当B C A C >时,椭圆的焦点在x 轴上;当BC A C <时,椭圆的焦点在y 轴上.五、椭圆的几何性质(以()012222>>=+b a by a x 为例) 1. 范围: 由标准方程可知,椭圆上点的坐标()y x ,都适合不等式1,12222≤≤by a x ,即b y a x ≤≤,说明椭圆位于直线a x ±=和b y ±=所围成的矩形里(封闭曲线).该性质主要用于求最值、轨迹检验等问题.2.对称性:关于原点、x 轴、y 轴对称,坐标轴是椭圆的对称轴,原点是椭圆的对称中心。
3.顶点(椭圆和它的对称轴的交点) 有四个:()()()().,0B ,0B 0,0,2121b b a A a A 、、、--4. 长轴、短轴:21A A 叫椭圆的长轴,a a A A ,221=是长半轴长;21B B 叫椭圆的短轴,b b B B ,221=是短半轴长.5.离心率(1)椭圆焦距与长轴的比a c e =,()10,0<<∴>>e c a (2)22F OB Rt ∆,2222222OF OB F B +=,即222c b a +=.这是椭圆的特征三角形,并且22cos B OF ∠的值是椭圆的离心率.(3)椭圆的圆扁程度由离心率的大小确定,与焦点所在的坐标轴无关.当e接近于1时,c 越接近于a ,从而22c a b -=越小,椭圆越扁;当e 接近于0时,c 越接近于0,从而22c a b -=越大,椭圆越接近圆;当0=e 时,b a c ==,0,两焦点重合,图形是圆.6.通径(过椭圆的焦点且垂直于长轴的弦),通径长为ab 22. 7.设21F F 、为椭圆的两个焦点,P 为椭圆上一点,当21F F P 、、三点不在同一直线上时,21F F P 、、构成了一个三角形——焦点三角形. 依椭圆的定义知:c F F a PF PF 2,22121==+.例题选讲一、选择题1.椭圆1422=+y x 的离心率为( )A .23 B .43 C .22 D .32 2.设p 是椭圆2212516x y +=上的点.若12F F ,是椭圆的两个焦点,则12PF PF +等于( )A . 4B .5C . 8D .10 3.若焦点在x 轴上的椭圆1222=+m y x 的离心率为21, 则m=( ) A .3 B .23 C .38 D .32 4.已知△ABC 的顶点B 、C 在椭圆x 23+y 2=1上,顶点A 是椭圆的一个焦点,且椭圆的另外一个焦点在BC 边上,则△ABC 的周长是( )A .2 3B .6C .4 3D .125.如图,直线022:=+-y x l 过椭圆的左焦点F 1和 一个顶点B ,该椭圆的离心率为( )A .51B .52C .55D .552 6.已知F 1、F 2是椭圆的两个焦点,过F 1且与椭圆长轴垂直的直线交椭圆于A 、B 两点,若△ABF 2是正三角形,则这个椭圆的离心率是( )A .32B .33C .22D .23 7.已知以F 1(-2,0),F 2(2,0)为焦点的椭圆与直线043=++y x 有且仅有一个交点,则椭圆的长轴长为( )A .23B .62C .72D .24二、填空题:8. 在ABC △中,90A ∠=,3tan 4B =.若以A B ,为焦点的椭圆经过点C ,则该椭圆的离心率e = .9. 已知椭圆中心在原点,一个焦点为F (-23,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 .10.在平面直角坐标系xOy 中,已知ABC ∆顶点(4,0)A -和(4,0)C ,顶点B 在椭圆192522=+y x 上,则sin sin sin A C B += . 11.椭圆4422=+y x 长轴上一个顶点为A ,以A 为直角顶点作一个内接于椭圆的等腰直角三角形,该三角形的面积是_______________.三、解答题12.已知椭圆06322=-+m y mx 的一个焦点为(0,2)求m 的值.13.已知椭圆的中心在原点,且经过点()03,P ,b a 3=,求椭圆 的标准方程.14.已知方程13522-=-+-ky k x 表示椭圆,求k 的取值范围.15.已知1cos sin 22=-ααy x )0(πα≤≤表示焦点在y 轴上的椭圆,求α的取值范围.16. 求中心在原点,对称轴为坐标轴,且经过)2,3(-A 和)1,32(-B 两点的椭圆方程.《导数及其应用》知识点总结一、导数的概念和几何意义1. 函数的平均变化率:函数()f x 在区间12[,]x x 上的平均变化率为:2121()()f x f x x x --。
高二数学教案 椭圆及其标准方程9篇

高二数学教案椭圆及其标准方程9篇椭圆及其标准方程 1教学目标1.把握椭圆的定义,把握椭圆标准方程的两种形式及其推导过程;2.能根据条件确定椭圆的标准方程,把握运用待定系数法求椭圆的标准方程;3.通过对椭圆概念的引入教学,培养学生的观察能力和探索能力;4.通过椭圆的标准方程的推导,使学生进一步把握求曲线方程的一般方法,并渗透数形结合和等价转化的思想方法,提高运用坐标法解决几何问题的能力;5.通过让学生大胆探索椭圆的定义和标准方程,激发学生学习数学的积极性,培养学生的学习爱好和创新意识.教学建议教材分析1. 知识结构2.重点难点分析重点是椭圆的定义及椭圆标准方程的两种形式.难点是椭圆标准方程的建立和推导.关键是把握建立坐标系与根式化简的方法.椭圆及其标准方程这一节教材整体来看是两大块内容:一是椭圆的定义;二是椭圆的标准方程.椭圆是圆锥曲线这一章所要研究的三种圆锥曲线中首先碰到的,所以教材把对椭圆的研究放在了重点,在双曲线和抛物线的教学中巩固和应用.先讲椭圆也与第七章的圆的方程衔接自然.学好椭圆对于学生学好圆锥曲线是非常重要的.(1)对于椭圆的定义的理解,要抓住椭圆上的点所要满足的条件,即椭圆上点的几何性质,可以对比圆的定义来理解.另外要注重到定义中对“常数”的限定即常数要大于 .这样规定是为了避免出现两种非凡情况,即:“当常数等于时轨迹是一条线段;当常数小于时无轨迹”.这样有利于集中精力进一步研究椭圆的标准方程和几何性质.但讲解椭圆的定义时注重不要忽略这两种非凡情况,以保证对椭圆定义的准确性.(2)根据椭圆的定义求标准方程,应注重下面几点:①曲线的方程依靠于坐标系,建立适当的坐标系,是求曲线方程首先应该注重的地方.应让学生观察椭圆的图形或根据椭圆的定义进行推理,发现椭圆有两条互相垂直的对称轴,以这两条对称轴作为坐标系的两轴,不但可以使方程的推导过程变得简单,而且也可以使最终得出的方程形式整洁和简洁.②设椭圆的焦距为 ,椭圆上任一点到两个焦点的距离为 ,令 ,这些措施,都是为了简化推导过程和最后得到的方程形式整洁、简洁,要让学生认真领会.③在方程的推导过程中碰到了无理方程的化简,这既是我们今后在求轨迹方程时经常碰到的问题,又是学生的难点.要注重说明这类方程的化简方法:①方程中只有一个根式时,需将它单独留在方程的一侧,把其他项移至另一侧;②方程中有两个根式时,需将它们分别放在方程的两侧,并使其中一侧只有一项.④教科书上对椭圆标准方程的推导,实际上只给出了“椭圆上点的坐标都适合方程“而没有证实,”方程的解为坐标的点都在椭圆上”.这实际上是方程的同解变形问题,难度较大,对同学们不作要求.(3)两种标准方程的椭圆异同点中心在原点、焦点分别在轴上, 轴上的椭圆标准方程分别为: , .它们的相同点是:外形相同、大小相同,都有 , .不同点是:两种椭圆相对于坐标系的位置不同,它们的焦点坐标也不同.椭圆的焦点在轴上标准方程中项的分母较大;椭圆的焦点在轴上标准方程中项的分母较大.另外,形如中,只要 , , 同号,就是椭圆方程,它可以化为 .(4)教科书上通过例3介绍了另一种求轨迹方程的常用方法——中间变量法.例3有三个作用:第一是教给学生利用中间变量求点的轨迹的方法;第二是向学生说明,假如求得的点的轨迹的方程形式与椭圆的标准方程相同,那么这个轨迹是椭圆;第三是使学生知道,一个圆按某一个方向作伸缩变换可以得到椭圆.教法建议(1)使学生了解圆锥曲线在生产和科学技术中的应用,激发学生的学习爱好.为激发学生学习圆锥曲线的爱好,体会圆锥曲线知识在实际生活中的作用,可由实际问题引入,从中提出圆锥曲线要研究的问题,使学生对所要研究的内容心中有数,如书中所给的例子,还可以启发学生寻找身边与圆锥曲线有关的例子。
高二数学椭圆的定义和标准方程

F1
F2
椭圆的定义: 平面内与两定点F1、F2 的距离之和为常数 的距离之和为常数的点 (大 的轨迹 或集合)叫做椭圆。 于 | F1F( 2|) 的点的轨迹(或集合)叫做椭圆。
椭圆的焦点: F1、F2 椭圆的焦距: |F1F2|
解: 设点M(x,y)为所求轨迹上任意一点
求平面内与两定点F1、 F2 的距离之和为常数 (大 椭圆的定义:平面内与两定点 F1、F2 的距离之和 于 | F1F2( |) 的点的轨迹 (或集合) ? 为常数 大于 | F1F2|)的点的轨迹 (或集合)叫做椭圆。 Y |MF1|+|MF2|= 2a
2 2 2
a 2x 2 +(a 2 -c2 )y2 =a 2 (a 2 -c2 )
b2 x 2 +a 2 y 2 =a 2 b2
2 2
b2 a 2 -c2 (b 0) 2 2 2 2 2 2 a x +b y =a b
x y 2 1 a b
y x 2 1 2 a b
2
2
解 : 因为 5 4
解
x2 y2 1 与X轴,Y轴 25 16
1 SABF1 = AF 1 OB 2
B
1 = OF 1 + OA OB 2
F1
O
A
X
因为点A为椭圆与X轴正半轴交点
所以 因为点B为椭圆与Y轴正半轴交点
所以
x2 0 1x 5 OA 5 25 16
0 y2 1 y 4 OB 4 25 16
x y 1 9 4
2
2
y x 1 9 4
2
2
设F1、
F2为椭圆
P为椭圆上一点,与F1、
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结论1
绳子的长度对轨迹有影响
问题1:当绳长等于|F1F2|时,点M的 轨迹 是什么? 线段F1F2 问题2:当绳长小于|F1F2|时,点M的轨迹 轨迹不存在 是什么? 结论2 要得到椭圆绳长与|F1F2|需满足一 定关系
结论3 当绳长大于|F1F2|时点M的轨迹是椭圆 观察做图过程:由于 绳长固定,所以 M 到两个定点的距离和 也固定。 七嘴八舌:
制革、食品、化工等行业的有机污水处理,主要目的是将生活污水和与之相类似的工业有机废水处理后达到回用水质要求,使废水处理后资源化利用。
•么心事?”“没有,姐姐。”“没心事怎么这么蔫头耷脑的?以前的凝儿可不是这个样子!”“怎么就蔫头耷脑的?凝儿只是头有些昏沉罢了。”“药都按时喝了?”“嗯。”“那就让陆大夫再来看看吧,
1)椭圆的定义; 2)椭圆的标准方程
当焦点在x轴上时
x a
2 2
y b
2 2
1 ( a b 0)
当焦点在y轴上时
y a
2 2
x b
2 2
1 (a b 0)
注:a、b、c始终满足a2 – b2 = c2,并且 总是a>b>0,a>c>0
环节八:布置作业、巩固提高 基础题: 习题8.1第3题 提高题: 补充练习 思考题:
教学重点:椭圆的定义及椭圆的标准方程
教学难点:椭圆标准方程的建立和推导
二、目标分析
知识目标
(1)掌握椭圆的定义及其标准方程; (2)通过对椭圆标准方程的探求, 熟悉求曲线方程的一般方法。
能力目标
通过自我探究、操作、数学思想(待定 系数法)的运用等,从而提高学生实际 动手、合作学习以及运用知识解决实际 问题的能力。
2.
推导椭圆的标准方程:
y
M
1)建系设点: 以F1、F2所在直线为 x轴,线段F1F2垂直平 分线为y轴,建立坐标 系。 2)列式: 椭圆的集合为
F1
O
F2
x
P {M || MF1 | | MF2 | 2 a}
设|F1F2|=2c(c>0),M(x,y)为椭圆上的任意一点,
则F1(-c,0)、F2(c,0)
板书设计
课题
1、椭圆的定义: 椭圆标准方程的推导过 程书写 例1:(写要点)
2、有关概念:
3、椭圆标准方程 (1)焦点在x轴上
(2)焦点在y轴上
例2 : (1)详写
(2)写关键步骤
•污水处理设备,是一种能有效处理城区的生活污水,工业废水等的工业设备,避免污水及污染物直接流入水域,对改善生态环境、提升城市品位和促进经济发展具有重要意义。 •; / 地埋式污水处理设备 jah97kbf • 地埋式污水处理设备适宜住宅小区、医院疗养院、办公楼、商场、宾馆、饭店、机关、学校、部队、 水产加工厂、牲蓄加工厂、乳品加工厂等生活污水和与之类似的工业有机废水,如纺织、啤酒、造纸、
补充练习
1、椭圆
x
2
焦点坐标是
16
y
2
9
1 的焦距是
,
。
2、动点P到两个定点F1(-4,0)、F2(4,0)
的距离之和为8,则P点的轨迹为
A、椭圆
C、直线F1F2
B、线段F1F2
D、不能确定
3、如果椭圆
x2ຫໍສະໝຸດ 100y2
36
1
上一点P到焦点F1的 。
距离为6,则点P到另一焦点F2的距离
为
4、椭圆mx2+ny2=-mn,(m<n<0)的焦点坐标 是 。
2 2 2 2
( 0, 1)
例2. 求适合下列条件的椭圆的标准方程。
1) 两个焦点的坐标分别是(-4,0)、(4,0),椭圆上 一点到两焦点距离的和等于10; 2) 两个焦点的坐标分别是(0,-2)、(0,2)并且经过 3 5 点 ( , ) ;
2 2
练习:课本练习1~4
环节七:归纳小结,提炼精华
导学式与自主探索、合作交流相结合 1、是符合教学原则的; 2、能充分调动学生的主动性和积极性。
3、有利于学生对知识进行主动建构
4、有利于突出重点、突破难点 教学手段:利用多媒体等教学手段。
教具与学具:电脑、细绳、硬纸板
四。教学过程
教学设想:
1. 了解椭圆的应用,激发学生的学习兴趣。 2.对椭圆的定义的引入,要注意借助直观 形象 的模型和教具,让学生从感性认识入手
又设M与F1、F2距离之和 等于2a,
F1
y M O F2 x
3)代换: ( x c ) 2 y 2 ( x c ) 2 y 2 2a
2 2 2 2 2 2 2 2 4)化简: (a c ) x a y a (a c ) 2a 2c , 即 a c
之和是常 数 2a
3. 常数 2a 要大于F1F2 学以致用:
承上启下 平面解析几何研究的主要问题是:
(1)根据已知条件,求出表示平面曲线的方程; (2)通过方程,研究平面曲线的性质。
环节四:温故知新、探求方程
1. 椭圆标准方程推导的准备
[1]建系设点 [2]列式 [3]代换
[4]化简
[5]证明检验
五.教学评价分析
这节课安排了导入新课、实验操作、分 析定义、探求方程、问题点拨、技能演练 等几个教学环节。它是在教师引导下,通 过学生积极思考,主动探求,从而实现教 学目的的要求,完成教学任务。 教学中采用多媒体的手段,画面丰富生 动,使学生的多种感官获得外部刺激, 有利于完善认知结构。
在整个教学过程中,采用引导发现法、 探索讨论法、题组教学法等教学方法实 施教学,注重化归、数形结合等数学思 想的渗透,通过探索,有利于培养学生 的创新能力,体现教育改革的时代精神
情感目标
在教学中充分揭示“数”与 “形”的内在联系,体会形数美的 统一,激发学生学习数学的兴趣, 培养学生勇于探索,勇于创新和锲 而不舍的精神。增强主动与他人合 作与交流的意识。
三、教法与学法
学情分析 学生基本具备独立探究有关点的轨迹问 题的基础知识和学习能力。但由于学习 解析几何的时间不长在学习中难免会遇 到一些困难。经过教师恰当的启发,学 生凭借原有的认知,采用类比与联想的 方法,是可以通过自组探究、合作交流 的形式完成本节的学习内容。
教法分析
作为一节概念课,如果教师把概念、结论按 部就班地主动提供给学生,就会造成学生的被动 接受,不利于理解和记忆。因此我采用了如下的 教学方法:启发引导法、实验探究法,并以讲授 法、讨论法相佐.通过这些方法引导学生自己观察、 归纳、探索和总结概念、结论,充分发挥学生的 主观能动性,让学生更多地参与教学,锻炼自己 分析、解决问题的能力,通过师生的互动,以取 得较理想的教学效果。
你能给椭圆下一个定义吗?
环节三:分析定义、强化概念:
(一)椭圆的定义:
平面内与两个定点F1、F2的距离的和 等于常数(大于|F1F2|)的点的轨迹叫 做椭圆, 这两个定点叫做椭圆的焦点, 两焦点的距离叫做椭圆的焦距
想一想:
椭圆的定义应满足什么条件?
1. 平面上---这是大前提
2. 动点 M 到两个定点 F1、F2的距离
F1 o
F2
x
启发提问:
如果是以F1,F2所在直线为y轴,建立直 角坐标系,所求出的椭圆的标准方程又是 什么呢?
类比探究:
y M F1 F2 x
x a
2 2
y b
2 2
1a b 0
y
2
x ( y c)
2
x ( y c) 2a
2
2
F1 x F F2 2
y a
若去掉焦点 在y轴上的 条件呢?
5、方程x2+ky2=2的曲线是焦点在y轴上的椭 圆,则k的取值范围是 A、(0,+∞) B、(0,2) C、(1,+ ∞ ) D、(0,1)
x
2
6、方程
24 k
y
2
16 k
1 表示焦点在y
若去掉焦点在 y轴上的条件 呢?
轴上的椭圆,则k的取值范围为————
a c 0
2
2
令 a2 c2
2 2
2 b ,其中 b 0
代入上式,得
y
M F1 O F2 x
b x a y a b
2
2
2
2
即
x a
2 2
y b
2 2
1 ( a b 0)
该方程叫做椭圆的标准方程。 焦点是F1(-c,0)、F2(c,0)
2 2 2 这里, c a b
环节五:解答疑问、巩固成果
难点提示:
问题1、在探索中得到了椭圆方程:
( x c) y
2 2
( x c) y
2
2
2a
2 2
但不会化简;
y
2 2 2
问题2、 化简后得到
有一定距离。
x a
a c
1
不简洁,与课本上的标准方程也
回顾小结:
y
M
x a
2 2
y b
2 2
1a b 0
2 2
x b
2 2
1( a b 0)
y a
2 2
x b
2 2
1 (a b 0)
这也是椭 圆的标准 方程
表示焦点在y轴,焦点为F1(0, c),F2(0, c),c2 = a2 - b2的椭 圆的标准方程。 温馨提示:
研究椭圆首先应明确其焦点的位置
环节六:技能演练、学以致用 例1 判定下列椭圆的焦点在什么轴上?
,逐
