2018中考数学一轮复习4.1基本平面图形课件及随堂演练(德州市)最新版
2018年山东省德州市中考数学试卷-答案

2018年山东省德州市初中学业水平考试数学答案解析第Ⅰ卷一、选择题1.【答案】C【解析】3的相反数是.3-【考点】相反数.2.【答案】B【解析】A 项,是中心对称图形.B 项,既是轴对称图形又是中心对称图形.C 项,是轴对称图形.D 项,既不是轴对称图形也不是中心对称图形.【考点】轴对称图形和中心对称图形的定义.3.【答案】D【解析】亿1.4968=149600000=1.49610.⨯【考点】科学记数法.4.【答案】C【解析】A 项,B 项,C 项,正确.D 项, 325.a a a = ()326.a a -=-23.mn mn mn --=-【考点】考查了整式的运算.5.【答案】A【解析】由平均数是6,得,解得.将这组数据按从小到大的顺序排列,为2,6,7,7,8,6+2+8++7=65x ⨯7x =所以中位数是7.【考点】平均数,中位数.6.【答案】A【解析】图①,,即与互余.图②,由同角的余角相等,得.图+=1809090αβ∠∠︒-︒=︒α∠β∠=αβ∠∠③,图④,由平角的定义,得.==18045135.αβ∠∠︒-︒=︒+=180αβ∠∠︒【考点】两角互余的性质及判定.7.【答案】B【解析】A 项,由抛物线开口向上,知;由直线经过第一、二、四象限,知,不符合题意.B 项,0a >0a <由抛物线开口向上,知,对称轴为,在轴的右侧;由直线经过第一、三、四象限,知0a >10x a=>y,符合题意.C 项,由抛物线开口向上,知,对称轴为,应在轴的右侧,不符合题意.D 0a >0a >10x a=>y 项,由抛物线开口向下,知;由直线经过第一、三、四象限,知,不符合题意.0a <0a >【考点】二次函数和一次函数的图象与性质.8.【答案】D【解析】方程两边同时乘最简公分母,得,解得检验:当()()12x x -+()()()2123x x x x +--+= 1.x =1x =时,,所以是原方程的增根,故原方程无解.()()12=0x x -+1x =【考点】了解分式方程.9.【答案】A【解析】如图,连接是的直径, .90,AC ABC AC ∠=︒∴ O 2m.,45,AC BA BC BAC ==∴∠=︒)sin 2sin 45m .BC AC BAC ∴=∠=⨯︒= ()2m 2ABC S π∴==扇形(第9题)【考点】圆周角的性质、解直角三角形、扇形的面积公式.10.【答案】B【解析】①当时,随的增大而减小.②当时,32,30,y x k =-+=-<∴ 1x >y x 3,30,y k x==>∴ 1x >y 随的增大而减小.③函数图象开口向上,对称轴为轴,当时,随的增大而x 22,20,y x a ==> y ∴1x >y x 增大.④当时,随的增大而增大.3,30,y x k ==>∴ 1x >y x 【考点】一次函数、反比例函数、二次函数的图象的增减性.11.【答案】B【解析】用“杨辉三角”的规律展开,从左起各项系数分别为1,8,28,56,70,56,28,8,1,的()8a b +()8a b ∴+展开式中从左起第四项的系数为56.【考点】找规律.12.【答案】C【解析】①如图1,连接点是等边三角形的中心,,.OB OC O ABC ,30,120,OB OC DBO OBC ECO BOC ∴=∠=∠=∠=︒∴∠=︒120.120,BOE EOC FOG ∴∠+∠=︒∠=︒ 故①正确.()120,.,.BOE DOB DOB EOC DOB EOC ASA OD OE ∴∠+∠=︒∴∠=∠∴≅∴=△△(第12题)②如图2,当绕点旋转到使时,是等边三角FOG ∠O ,OF AB OG BC ⊥⊥2,60,BD BE B BDE ==∠=︒∴△形.是等腰三角形.易得,OD OE ODE =∴ △22,.ODE BDE S S ==△△.故②错误. 22,CDE BDE S S <∴≠△△(第12题)③如图3,连接,过点做,垂足为点.,OB OC O OH BC ⊥H ,,DOB BOE EOC BOE DOB EOC S S S S H ≅∴+=+ △△△四边形△△1., 2.2BOC ODBE S S OH BC HC BC ∆∴=⊥∴== 四边形130,tan 22OCH ACB OH CH OCH ∠=∠=︒∴=∠==故③正确. 11422BOC S BC OH ∴==⨯= △(第12题)④如图1,的周长为,,DOB EOC BD CE BDE ≅∴=∴ △△△要使的周长最小,则的长最小.当绕4.BD BE DE CE BE DE BC DE DE ++=++=+=+BDE △DE FOG ∠点旋转到使时,垂足分别为点,如图2,则由垂线段最短可得的长最小,O ,OF AB OG BC ⊥⊥,D E ,OD OE 的长最小,这时周长的最小值为故④正确.DE ∴ 2.BD BE DE BDE ===∴∆4+42 6.DE =+=【考点】等边三角形的性质与判定、全等三角形的性质与判定、等边三角形中心的性质、解直角三角形、三角形的面积及求最小值.第Ⅱ卷二.填空题13.【答案】1 【解析】231 1.-+==【考点】整式的运算及绝对值.14.【答案】3-【解析】是一元二次方程的两个实数根,12,x x 220x x +-=12121,2,x x x x ∴+=-=-()121212 3.x x x x ∴++=-+-=-【考点】一元二次方程的根与系数的关系.15.【答案】3【解析】由勾股定理,得根据角平分线上的点到角两边的距离相等,,5,4,CM OB OC OM ⊥==∴ 3.CM =得点到射线的距离为3.C OA 【考点】勾股定理、角平分线的性质.16. 【解析】由勾股定理,得,,2223425AB =+=2222222420,125AC BC =+==+=是直角三角形,2225,,AB BC AC BC AB ∴==+=ABC∴∆90,sin BC ACB BAC AB ∠=︒∴∠==【考点】直角三角形的判定、解直角三角形.17.【答案】60 【解析】解方程组得 48,229,x y x y -=⎧⎨+=⎩5,12.x y =⎧⎨=⎩560.,12y x x y x y <∴==⨯= ◆【考点】了解二元一次方程组及对新定义的阅读理解.18.【答案】或()4,3--()2,3-【解析】解得如图1,当是平行四边形的3,2,y x y x ⎧=⎪⎨⎪=-⎩12121,3,3, 1.x x y y =-=⎧⎧⎨⎨=-=⎩⎩()1,3.A ∴--()3,0, 3.B OB -∴= OB 一边时,则点到轴的距离是或点的坐标为或3,,AP OB AP OB ==∴∥P y 1+3=4312,-=∴P ()4,3--.点在轴左侧,()2,3- P y ()4,3.P ∴--(第18题)如图2,当是平行四边形的对角线时,过点作,过点作,垂足分别为点,OB A AC OB ⊥P PD OB ⊥C .,四边形是平行四边形,D ()1,3A -- ()1, 3.3,0, 3.OC AC B OB ∴==-∴= OABP 由全等三角形对应高相等,得 ,.,.PB AO OP BA BO OB PBO AOB ∴===∴∆≅∆ 3.,PD AC PB AO === ,,1,312Rt PBD Rt AOC BD OC OD OB BD ∴≅∴==∴=-=-=△△()2,3.P ∴-。
2018中考数学一轮复习《3.2一次函数》和随堂演练(德州市)精选优质PPT课件

知识点一 一次函数和正比例函数的概念 1.一次函数:一般地,形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数. 2.当b=__0__时,y=kx(k≠0)为正比例函数,正比例函数 是一种特殊的一次函数.
正比例函数一定是一次函数,但一次函数不一定是正比例 函数.
知识点二 一次函数的图象与性质
求出k,b的值即可.
2.一次函数图象的平移 一次函数y=kx+b(k≠0)的图象平移分为沿x轴平移和沿y 轴平移: (1)若沿x轴向右平移a个单位长度,则解析式为y=k(x-a) +b;若沿x轴向左平移a个单位长度,则解析式为_y_=__k_(_x__ +a)+b .
(2)若沿y轴向上平移a个单位长度,则解析式为y=kx+b+a; 若沿y轴向下平移a个单位长度,则解析式为__y_=__k_x_+__b_-__a__.
3
①当0<m<50时,y随x的增大而减小, ∴当x=34时,y取最大值, 即商店购进34台A型电脑和66台B型电脑的销售利润最大.
②m=50时,m-50=0,y=15 000, 即商店购进A型电脑数量满足33 1 ≤x≤70的整数时,均获
3
得最大利润.
③当50<m<100时,m-50>0,y随x的增大而增大,
2
考点三 一次函数与方程、不等式的关系 (5年0考) 例4 (2016·东营)如图,直线y=x+b与直线y=kx+6交于 点P(3,5),则关于x的不等式x+b>kx+6的解集是 .
【分析】 方法一:利用已知求出k,b的值,然后解不等式;
方法二:利用图象确定x的取值范围.
【自主解答】 方法一:∵直线y=x+b与直线y=kx+6交于 点P(3,5),∴k=- 1 ,b=2.
山东省德州市中考数学一轮复习《第一章第2讲》课件

5.[2015·德州,T4,3分]下列运算正确的是( D )
6.[2015·德州,T5,3分]关联考题见第5讲“过真题”T1.
类型1 整式的运算 1.[2018·潍坊]下列计算正确的是( C )
2.[2018·吉林]下列计算结果为a6的是( C ) A.a2×a3 B.a12÷a2 C.(a2)3 D.(-a2)3
考点2 整式及有关概念
整式 单项式和多项式统称为整式
单项式 系数:① 数字 因数;次数:所有字母的② 指数 和
多项式
项:每个单项式叫做多项式的项,不含字母的项叫做③常数项 ;次数:④次数最高项 的次数
考点3 整式的运算 6年6考 1.整式的加减
同类项 所含字母相同,并且相同字母的指数也相同 把括号和它前面的“+”号去掉,括号里面各项的
(am)n=⑤ amn (m,n为整数)
积的乘方
(ab)n=⑥ anbn (n为整数)
整式 单项式乘以单项式 系数相乘,同底数的幂相乘 的乘 单项式乘以多项式 a(m+n-p)=am+an-ap
法 多项式乘以多项式 (a+m)(b-n)=ab-an+bm-mn
整式的 除法
单项式除以 单项式
多项式除以 单项式
类型3 求代数式的值
C
7 2a+1
解题要领:①利用乘法公式,求代数式的值时,常常用到完全平方公式的变形:a2+ b2=(a+b)2-2ab,2ab=(a+b)2-(a2+b2);②把要求的代数式变形,再把已知的 代数式的值代入.
2019考向过预测
1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月5日星期六下午3时20分39秒15:20:3922.3.5 2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那
2018年日照市中考一轮复习《4.1基本平面图形》(含答案)
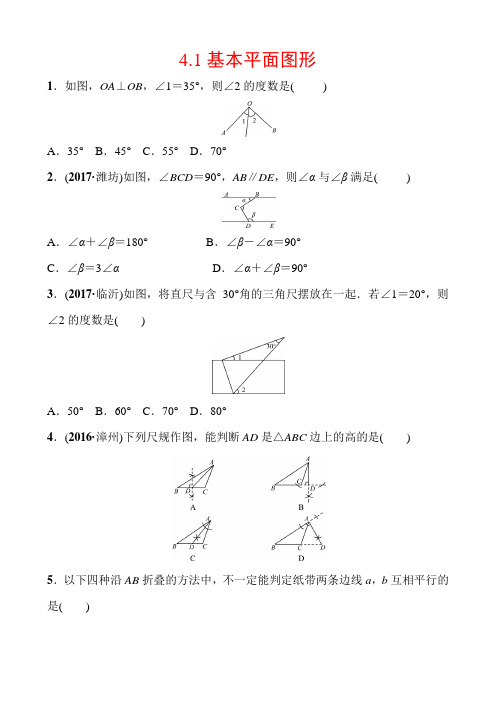
4.1基本平面图形1.如图,OA⊥OB,∠1=35°,则∠2的度数是( )A.35°B.45°C.55°D.70°2.(2017·潍坊)如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )A.∠α+∠β=180°B.∠β-∠α=90°C.∠β=3∠αD.∠α+∠β=90°3.(2017·临沂)如图,将直尺与含30°角的三角尺摆放在一起.若∠1=20°,则∠2的度数是( )A.50°B.60°C.70°D.80°4.(2016·漳州)下列尺规作图,能判断AD是△ABC边上的高的是( )5.以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )A.如图1,展开后测得∠1=∠2B.如图2,展开后测得∠1=∠2且∠3=∠4C.如图3,测得∠1=∠2D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD6.(2017·德州)如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是______________________.7.(2017·威海)如图,直线l1∥l2,∠1=20°,则∠2+∠3=__________.8.(2016·淄博)如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.参考答案1.C 2.B 3.A 4.B 5.C6.同位角相等,两直线平行7.200°8.解:AC∥OB,BC∥OA.理由如下:∵∠1=∠2,∴AC∥OB.∵∠2+∠3=180°,∴BC∥OA.。
《线段、射线、直线》基本平面图形PPT课件

a
●
●
A
B
(2) 射线:
用两个大写字母(端点和射线上另 外一点,端
点必须写在前面)表示。 如:射线 OA ,但不能记为射线AO.
端点字母必须 写在前面
●
●
O
A
(3)直线:
用两个大写字母(直线上任意两点)表示,如:直 线AB或直线BA。 用一个小写字母表示。如:直线a
4A
B 记作:线段BA ( √ )
5 请用两种方式分别表示图中的两条直线.
m
n
O
A
B
6 如图,直线 AB和直线AC表示的是同一条直线吗?
AB C
7 怎样表示图中以O为端点的射线?
OA B C
8
射线OB和射线BO是同一条射线吗? 为什么?
( 要求:画图说明)
B O
B O
射线OB
B O
射线BO
例2 如图所示,下列说法正确的是 (C) A.直线AB和直线CD是不同的直线 B.射线AB和射线BA是同一条射线 C.线段AB和线段BA是同一条线段 D.以上说法均不正确
3.如图,图中的直线可以表示为___直__线__A_B_(_或__直__线__B_A_)或 ____直__线__m__.
4.新学期开学整理教室时,老师总是先把每一列最前面和 最后面的课桌摆好,然后依次摆中间的课桌,一会儿一列 课桌就整齐地摆在一条直线上了,这是因为 ____两__点__确__定__一__条__直__线.
解:(1)如图 (1),这种情况下只能画一条直线. (2)如图 (2),这种情况下能画四条直线. (3)如图 (3),这种情况下能画六条直线.
课堂小结
线段:A
山东省德州市2018年中考数学复习第4章图形的认识与三角形第14讲三角形与全等三角形课件

中位线
连接三角形任意两边④中点三角形的中位线⑤平行于第三边,
的线段
且等于第三边的⑥一半
考点3 三角形的边角关系
三角形的三边关 三角形任意两边之和①大于第三边;任意两边之差②小于
系
第三边
三角形内角和定 理
三角形三个内角的和等于③180°
(1)三角形的外角④等于与它不相邻的两个内角的和;(2)
三角形内角和定 理的推论
⑤相等;面积⑥相等
2.全等三角形的判定
简称
“⑦边角边”或
“SAS”
一般三角形 的全等判定
“⑨角边角”或
“ASA”
判定内容
两边和它们的夹角⑧分别相等的两个三 角形全等
两角和它们的夹边分别相等的两个三角 形全等
“⑩角角边”或
“AAS”
两角和其中一个角的对边分别相等的两 个三角形全等
“? 边边边”或
“SSS”
直角三角形两条高为两条直角边,
斜边上的高在三角形内
中线
三角形三条中线相交于一点,交点
连接三角形的顶点与对边中叫做①重心,都在三角形内;三角
点的线段
形的任意一条中线将这个三角形分
为两个面积②相等的三角形
角平分线
三角形顶点出发的角的平分三角形的三条角平分线相交于一点, 线与对边交点间的线段 交点叫做③内心,都在三角形内
变式运用? [2017·苏州模拟 ]如图,在△ABC中,AB=CB,∠ABC= 90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE,DE, DC.
(1)求证:△ABE≌△CBD; (2)若∠CAE=30°,求∠BDC的度数.
解:(1)证明:在△ABE和△CBD中,
∴△ABE≌△CBD(SAS). (2)∵△ABE≌△CBD, ∴∠AEB=∠BDC. ∵∠AEB为△AEC的外角, ∴∠AEB=∠ACB+∠CAE=30°+45°=75°, 则∠BDC=75°
18年山东省德州市中考数学试卷及详细答案

2018年山东省德州市中考数学试卷及详细答案2018年山东省德州市中考数学试卷一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个均记零分。
1.3的相反数是A.3 B.C.﹣3 D.﹣2.下列图形中,既是轴对称图形又是中心对称图形的是A.B.C.D.3.一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即亿km,用科学记数法表示亿是A.×107 B.×108 C.×108 D.×108 4.下列运算正确的是A.a3?a2=a6 B.3=a6 C.a7÷a5=a2 D.﹣2mn﹣mn=﹣mn 5.已知一组数据:6,2,8,x,7,它们的平均数是6,则这组数据的中位数是A.7 B.6 C.5 D.4 6.如图,将一副三角尺按不同的位置摆放,下列方式中∠α与∠β互余的是A.图①B.图②C.图③D.图④7.如图,函数y=ax2﹣2x+1和y=ax﹣a 在同一平面直角坐标系的图象可能是第1页A.B.C.D.8.分式方程﹣1=D.无解的解为A.x=1 B.x=2 C.x=﹣1 9.如图,从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为A.2 B.C.πm2 D.2πm2 10.给出下列函数:①y=﹣3x+2;②y=;③y=2x2;④y=3x,上述函数中符合条作“当x>1时,函数值y随自变量x增大而增大“的是A.①③B.③④C.②④D.②③11.我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式n 的展开式的各项系数,此三角形称为“杨辉三角” 根据”杨辉三角”请计算8的展开式中从左起第四项的系数为第2页A.84 B.56 C.35 D.28 12.如图,等边三角形ABC 的边长为4,点O是△ABC的中心,∠FOG=120°,绕点O旋转∠FOG,分别交线段AB、BC于D、E两点,连接DE,给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③四边形ODBE的面积始终等于周长的最小值为6.上述结论中正确的个数是;④△BDE A.1 B.2 C.3 D.4 二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题填对得4分。
2018年山东省德州市中考数学试卷(含答案与解析)

数学试卷 第1页(共28页) 数学试卷 第2页(共28页)绝密★启用前山东省德州市2018年初中学业水平考试数 学(考试时间120分钟,满分150分)第Ⅰ卷(选择题 共48分)一、选择题(本大题共12小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.3的相反数是( ) A .3B .13C .3-D .13-2.下列图形中,既是轴对称图形又是中心对称图形的是( )ABCD3.一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.496亿km.用科学记数法表示1.496亿是 ( ) A .71.49610⨯B .814.9610⨯C .80.149610⨯D .81.49610⨯4.下列运算正确的是( )A .326=a a aB .()326a a -=C .752=a a a ÷D .2mn mn mn --=- 5.已知一组数据:6,2,8,x ,7,它们的平均数是6,则这组数据的中位数是 ( ) A .7B .6C .5D .46.如图,将一副三角尺按不同的位置摆放,下列摆放方式中,α∠与β∠互余的是( )(第6题)A .图①B .图②C .图③D .图④7.函数221y ax x =-+和y ax a =-(a 是常数,且0a ≠)在同一平面直角坐标系中的图象可能是( )ABC D8.分式方程()()31112x x x x -=--+的解为( )A .1x =B .2x =C .1x =-D .无解9.如图,从一块直径为2 m 的圆形铁皮上剪出一个圆心角为90︒的扇形,则此扇形的面积为( )A .2m 2πB2mC .2m πD .22m π(第9题)10.给出下列函数:①32y x =-+;②3y x=;③22y x =;④3y x =.上述函数中符合条件“当1x >时,函数值y 随自变量x 增大而增大”的是( )A .①③B .③④C .②④D .②③11.我国南宋数学家杨辉所著的《详解九章算法》一书中,用如图的三角形解释二项式()na b +的展开式的各项系数,此三角形称为“杨辉三角”.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共28页) 数学试卷 第4页(共28页)()()()()()()012345111121 133114641 15101051a b a b a b a b a b a b +⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅⋅(第11题)请根据“杨辉三角”计算()8a b +的展开式中从左起第四项的系数为 ( )A .84B .56C .35D .2812.如图,等边三角形ABC 的边长为4,点O 是ABC △的中心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB ,BC 于D ,E 两点,连接DE ,给出下列四个结论:①OD OE =;②ODE BDE S S =△△;③四边形ODBEBDE △周长的最小值为6.其中正确结论的个数是( )A .1B .2C .3D .4(第12题)第Ⅱ卷(非选择题 共102分)二、填空题(本大题共6小题,每小题4分,共24分)13.计算:23-+= .14.若1x ,2x 是一元二次方程220x x +-=的两个实数根,则1212x x x x ++= .15.如图,OC 为AOB ∠的平分线,CM OB ⊥,5OC =,4OM =,则点C 到射线OA 的距离为 .(第15题)16.如图,在44⨯的正方形方格图形中,小正方形的顶点称为格点,ABC △的顶点都在格点上,则BAC ∠的正弦值是 .(第16题)17.对于实数a ,b ,定义运算“◆”:,,.a b a b ab a b ≥=<⎪⎩◆例如4◆3,因为43>,所以4◆.若x ,y 满足方程组48,229,x y x y -=⎧⎨+=⎩则=x ◆y .18.如图,反比例函数3y x=与一次函数2y x =-在第三象限交于点A ,点B 的坐标为()3,0-,点P 是y 轴左侧的一点,若以点A ,O ,B ,P 为顶点的四边形为平行四边形,则点P 的坐标为 .(第18题)数学试卷 第5页(共28页) 数学试卷 第6页(共28页)三、解答题(本大题共7小题,共78分.解答应写出必要的文字说明、证明过程或演算步骤.)19.(本小题满分8分) 先化简,再求值:2233111211x x x x x x --⎛⎫÷-+ ⎪-++-⎝⎭,其中x 是不等式组()5331,131922x x x x ⎧->+⎪⎨-<-⎪⎩的整数解.20.(本小题满分10分)某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.(第20题)请根据以上信息,解答下列问题: (1)这次被调查的学生共有多少人? (2)请将条形统计图补充完整.(3)若该校约有1 500名学生,请估计全校学生中喜欢娱乐节目的有多少人. (4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁4名学生中选取2名,求恰好选中甲、乙两名学生的概率(用画树状图或列表的方法解答).21.(本小题满分10分)如图,两座建筑物的水平距离BC 为60 m ,从C 点测得A 点的仰角α为53︒,从A 点测得D 点的俯角β为37︒,求两座建筑物的高度.(参考数据:343434s i n 37,c o s 37,t a n 37,s i n 53,c o s 53,t a n 53554553︒≈︒≈︒≈︒≈︒≈︒≈)(第21题)22.(本小题满分12分)如图,AB 是O 的直径,直线CD 与O 相切于点C ,且与AB 的延长线交于点E ,点C 是BF 的中点.(1)求证:AD CD ⊥.(2)若30CAD ∠=︒,O 的半径为3,一只蚂蚁从点B 出发,沿着BE —EC —CB爬回至点B ,求蚂蚁爬过的路程.(结果保留一位小数.参考数据: 1.73π≈≈)(第22题)-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________ 姓名________________ 考生号________________________________ _____________23.(本小题满分12分)为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.(1)求年销售量y与销售单价x的函数关系式.(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10 000万元的年利润,则该设备的销售单价应是多少万元?24.(本小题满分12分)再读教材:宽与长的比是0.618)的矩形叫作黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计.下面,我们用宽为2的矩形纸片折叠黄金矩形.(提示:2MN=)第一步,在矩形纸片一端,利用图1的方法折出一个正方形,然后把纸片展平.第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平.(第24题)第三步,折出内侧矩形的对角线AB,并把AB折到图3中所示的AD处.第四步,展平纸片,按照所得的点D折出DE,使DE ND⊥,则图4中就会出现黄金矩形.(第24题)问题解决:(1)图3中AB=(保留根号).(2)如图3,判断四边形BADQ的形状,并说明理由.(3)请写出图4中所有的黄金矩形,并选择其中一个说明理由.实际操作:(4)结合图4.请在矩形BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.25.(本小题满分14分)如图1,在平面直角坐标系中,直线1y x=-与抛物线2y x bx c=-++交于A,B两点,其中(),0A m,()4,B n,该抛物线与y轴交于点C,与x轴交于另一点D.(1)求m,n的值及该抛物线的解析式.(2)如图2,若点P为线段AD上的一动点(不与点A,D重合),分别以AP,DP 为斜边,在直线AD的同侧作等腰直角三角形APM和等腰直角三角形DPN,连接MN,试确定MPN∆面积最大时点P的坐标.(3)如图3,连接BD,CD,在线段CD上是否存在点Q,使得以A,D,Q为顶点的三角形与ABD∆相似?若存在,请直接写出点Q的坐标;若不存在,请说明理由.(第25题)数学试卷第7页(共28页)数学试卷第8页(共28页)数学试卷第9页(共28页)数学试卷第10页(共28页)数学试卷 第11页(共28页) 数学试卷 第12页(共28页)2018年山东省德州市初中学业水平考试数学答案解析第Ⅰ卷一、选择题 1.【答案】C【解析】3的相反数是3-. 【考点】相反数. 2.【答案】B【解析】A 项,是中心对称图形.B 项,既是轴对称图形又是中心对称图形.C 项,是轴对称图形.D 项,既不是轴对称图形也不是中心对称图形. 【考点】轴对称图形和中心对称图形的定义. 3.【答案】D【解析】1.496亿8=149600000=1.49610.⨯ 【考点】科学记数法. 4.【答案】C【解析】A 项,325.a a a =B 项,()326.a a -=-C 项,正确.D 项,23.mn mn mn --=-【考点】考查了整式的运算. 5.【答案】A【解析】由平均数是6,得6+2+8++7=65x ⨯,解得7x =.将这组数据按从小到大的顺序排列,为2,6,7,7,8,所以中位数是7. 【考点】平均数,中位数. 6.【答案】A【解析】图①,+=1809090αβ∠∠︒-︒=︒,即α∠与β∠互余.图②,由同角的余角相等,得=αβ∠∠.图③,==18045135.αβ∠∠︒-︒=︒图④,由平角的定义,得+=180αβ∠∠︒.【考点】两角互余的性质及判定. 7.【答案】B【解析】A 项,由抛物线开口向上,知0a >;由直线经过第一、二、四象限,知0a <,不符合题意.B 项,由抛物线开口向上,知0a >,对称轴为10x a=>,在y 轴的右侧;由直线经过第一、三、四象限,知0a >,符合题意.C 项,由抛物线开口向上,知0a >,对称轴为10x a=>,应在y 轴的右侧,不符合题意.D 项,由抛物线开口向下,知0a <;由直线经过第一、三、四象限,知0a >,不符合题意. 【考点】二次函数和一次函数的图象与性质. 8.【答案】D【解析】方程两边同时乘最简公分母()()12x x -+,得()()()2123x x xx +--+=,解得 1.x =检验:当1x =时,()()12=0x x -+,所以1x =是原方程的增根,故原方程无解.【考点】了解分式方程. 9.【答案】A【解析】如图,连接.90,A C A B C A C ∠=︒∴是O 的直径,2m.,45,AC BA BC BAC ==∴∠=︒)sin 2sin 45m .BC AC BAC ∴=∠=⨯︒=()2290m 3602ABC S ππ⨯⨯∴==扇形(第9题)【考点】圆周角的性质、解直角三角形、扇形的面积公式. 10.【答案】B【解析】①32,30,y x k =-+=-<∴当1x >时,y 随x 的增大而减小.②数学试卷 第13页(共28页) 数学试卷 第14页(共28页)3,30,y k x==>∴当1x >时,y 随x 的增大而减小.③22,20,y x a ==>函数图象开口向上,对称轴为y 轴,∴当1x >时,y 随x 的增大而增大.④3,30,y x k ==>∴当1x >时,y 随x 的增大而增大.【考点】一次函数、反比例函数、二次函数的图象的增减性. 11.【答案】B【解析】用“杨辉三角”的规律展开()8a b +,从左起各项系数分别为1,8,28,56,70,56,28,8,1,()8a b ∴+的展开式中从左起第四项的系数为56.【考点】找规律. 12.【答案】C【解析】①如图1,连接,.OB OC 点O 是等边三角形ABC 的中心,,30,120,OB OC DBO OBC ECO BOC ∴=∠=∠=∠=︒∴∠=︒120.120,BOE EOC FOG ∴∠+∠=︒∠=︒()120,.,.BOE DOB DOB EOC DOB EOC ASA OD OE ∴∠+∠=︒∴∠=∠∴≅∴=△△故①正确.(第12题)②如图2,当FOG ∠绕点O 旋转到使,OF AB OG BC ⊥⊥时,2,60,BD BE B BDE ==∠=︒∴△是等边三角形.,OD OE ODE =∴△是等腰三角形.易得22,.ODE BDE S S =△△223,CDE BDE OD DE S S <∴≠△△.故②错误.(第12题)③如图3,连接,OB OC ,过点O 做OH BC ⊥,垂足为点H .,DOB BOE EOC BOE DOB EOC S S S S H ≅∴+=+△△△四边形△△,1., 2.2BOC ODBE S S OH BC HC BC ∆∴=⊥∴==四边形132330,tan 22OCH ACB OHCH OCH ∠=∠=︒∴=∠=⨯=1142233BOC S BC OH ∴==⨯⨯=△故③正确.(第12题)④如图1,,,DOB EOC BD CE BDE ≅∴=∴△△△的周长为4.BD BE DE CE BE DE BC DE DE ++=++=+=+要使BDE △的周长最小,则DE 的长最小.当FOG ∠绕点O 旋转到使,OF AB OG BC ⊥⊥时,垂足分别为点,D E ,如图2,则由垂线段最短可得,OD OE 的长最小,DE ∴的长最小,这时2.BD BE DE BDE ===∴∆周长的最小值为4+42 6.DE =+=故④正确.数学试卷 第15页(共28页) 数学试卷 第16页(共28页)【考点】等边三角形的性质与判定、全等三角形的性质与判定、等边三角形中心的性质、解直角三角形、三角形的面积及求最小值.第Ⅱ卷二.填空题 13.【答案】1【解析】231 1.-+== 【考点】整式的运算及绝对值. 14.【答案】3- 【解析】12,x x 是一元二次方程220x x +-=的两个实数根,12121,2,x x x x ∴+=-=-()121212 3.x x x x ∴++=-+-=-【考点】一元二次方程的根与系数的关系. 15.【答案】3【解析】,5,4,CM OB OC OM ⊥==∴由勾股定理,得 3.CM =根据角平分线上的点到角两边的距离相等,得点C 到射线OA 的距离为3. 【考点】勾股定理、角平分线的性质. 16.【解析】由勾股定理,得2223425AB =+=,2222222420,125AC BC =+==+=,2225,,AB BC AC BC AB ∴==+=ABC∴∆是直角三角形,90,sin BC ACB BAC AB ∠=︒∴∠=【考点】直角三角形的判定、解直角三角形. 17.【答案】60【解析】解方程组48,229,x y x y -=⎧⎨+=⎩得5,12.x y =⎧⎨=⎩560.,12y x x y x y <∴==⨯=◆【考点】了解二元一次方程组及对新定义的阅读理解.18.【答案】()4,3--或()2,3-【解析】解3,2,y x y x ⎧=⎪⎨⎪=-⎩得12121,3,3, 1.x x y y =-=⎧⎧⎨⎨=-=⎩⎩()1,3.A ∴--()3,0, 3.B OB -∴=如图1,当OB 是平行四边形的一边时,则3,,AP OB AP OB ==∴∥点P 到y 轴的距离是1+3=4或312,-=∴点P 的坐标为()4,3--或()2,3-.点P 在y 轴左侧,()4,3.P ∴--(第18题)如图2,当OB 是平行四边形的对角线时,过点A 作AC OB ⊥,过点P 作PD OB ⊥,垂足分别为点C ,D .()1,3A --,()1, 3.3,0, 3.OC AC B OB ∴==-∴=四边形OABP 是平行四边形,,.,.PB AO OP BA BO OB PBO AOB ∴===∴∆≅∆由全等三角形对应高相等,得 3.,PD AC PB AO ===,1,312Rt PBD Rt AOC BD OC OD OB BD ∴≅∴==∴=-=-=△△,()2,3.P ∴-(第18题)【考点】求图象交点的坐标,平行四边形的性质及全等三角形的判定与性质. 三、解答题数学试卷 第17页(共28页) 数学试卷 第18页(共28页)19.【答案】解:原式()()()21311=113111=111.1x x x x x x x x x x x x x +--⎛⎫-+ ⎪-+---⎝⎭+---=- 解不等式组:()533113192.2x x x x ⎧->+⎪⎨-<-⎪⎩①,② 解不等式①,得3x >.解不等式②,得5x <.∴不等式组的解集是35x <<.x 是整数,∴=4.x 原式11==4-13. 【解析】解:原式()()()21311=113111=111.1x x x x x x x x x x x x x +--⎛⎫-+ ⎪-+---⎝⎭+---=- 解不等式组:()533113192.2x x x x ⎧->+⎪⎨-<-⎪⎩①,② 解不等式①,得3x >.解不等式②,得5x <.∴不等式组的解集是35x <<.x 是整数,∴=4.x 原式11==4-13. 20.【答案】(1)从喜欢动画节目人数可得1530%=50÷(人). 答:这次被调查的学生共有50人. (2)5041518310----=(人) 补全条形统计图如图所示.(第20题)(3)181500=54050⨯(人). 答:估计全校学生中喜欢娱乐节目的有540人.(4)列表如下:(画树状图法略)由列表可知,共有12种结果,且每种结果出现的可能性相同,其中恰好选中甲、乙两名学生的结果有2种,P ∴(恰好选中甲、乙两名学生)21==.126【解析】(1)从喜欢动画节目人数可得1530%=50÷(人). 答:这次被调查的学生共有50人.(2)5041518310----=(人)数学试卷 第19页(共28页) 数学试卷 第20页(共28页)补全条形统计图如图所示.(第20题)(3)181500=54050⨯(人). 答:估计全校学生中喜欢娱乐节目的有540人. (4)列表如下:(画树状图法略)由列表可知,共有12种结果,且每种结果出现的可能性相同,其中恰好选中甲、乙两名学生的结果有2种,P ∴(恰好选中甲、乙两名学生)21==.12621.【答案】解:如图,过点D 作DE AB ⊥交AB 于点E ,则=60m.DE BC =4=53tan53,3α︒︒,在Rt ABC ∆中,tan ,AB BC α=4,3AB BC ∴=即4,603AB =解得80m.AB =又337,tan37,4ADE β∠==︒︒≈在Rt ADE ∆中,3tan ,,4AE AE ADE DE DE ∠=∴=即3,604AE =解得45AE =,80B EA B A E B E =-∴=-=(),C D B E =35CD ∴= 答:建筑物AB 的高度为80m ,建筑物CD 的高度为35m .【解析】如图,过点D 作DE AB ⊥交AB 于点E ,则=60m.DE BC =4=53tan53,3α︒︒,在Rt ABC ∆中,tan ,AB BC α=4,3AB BC ∴=即4,603AB =解得80m.AB =又337,tan37,4ADE β∠==︒︒≈在Rt ADE ∆中,3tan ,,4AE AE ADE DE DE ∠=∴=即3,604AE =解得45AE =,80B EA B A E B E =-∴=-=(),C D B E=35CD ∴= 答:建筑物AB 的高度为80m ,建筑物CD 的高度为35m . 22.【答案】(1)证明:如图,连接.OC(第22题)∵直线CD 是O 的切线 ∴OC CD ⊥. ∴=90OCE ∠.∵点C 是BF 的中点. ∴CAD CAB ∠=∠ ∵OA OC =, ∴CAB ACO ∠=∠ ∴CAD ACO ∠=∠ ∴AD CO ∥∴==90ADC OCE ∠∠, ∴AD CD ⊥(2)解:∵=30CAD ∠, ∴=30CAB ACO ∠-∠ ∴+60COE CAB ACO ∠=∠∠= ∵直线CD 是O 的切线 ∴OC CD ⊥ ∴=90OCE ∠∴180906030E ∠-︒︒=-= ∵3OC = ∴2=6OE OC - ∴=3BE OE OB =-在Rt OCE △中,由勾股定理,得:CE ===.BC 的长603.180l ππ⨯⨯==∴蚁蚂爬过的路程为11.3.π≈ 【解析】(1)证明:如图,连接.OC(第22题)∵直线CD 是O 的切线 ∴OC CD ⊥. ∴=90OCE ∠. ∵点C 是BF 的中点.∴CAD CAB ∠=∠ ∵OA OC =, ∴CAB ACO ∠=∠ ∴CAD ACO ∠=∠ ∴AD CO ∥∴==90ADC OCE ∠∠, ∴AD CD ⊥(2)解:∵=30CAD ∠, ∴=30CAB ACO ∠-∠ ∴+60COE CAB ACO ∠=∠∠= ∵直线CD 是O 的切线 ∴OC CD ⊥ ∴=90OCE ∠∴180906030E ∠-︒︒=-= ∵3OC = ∴2=6OE OC - ∴=3BE OE OB =-在Rt OCE △中,由勾股定理,得:CE .BC 的长603.180l ππ⨯⨯==∴蚁蚂爬过的路程为11.3.π≈23.【答案】(1)∵此设备的年销售量y (单位:台)和销售单价x (单位:万元)成一次函数关系,∴可设()0y kx b k =+≠.根据题意,得40600,45550,k b k b +-⎧⎨+=⎩解得:10,1000,k b =-⎧⎨=⎩∴年销售量y 与销售单价x 的函数关系式是101000.y x =-+ (2)∵此设备的销售单价是x 万元,成本价是30方元, ∴该设备的单件利润为()30x -万元. 由题意,得()()3010100010000x x --+= 解得:12=80,=50.x x∵销售单价不得高于70万元,即70x ≤, ∴180x =不符合题意,舍去.∴50.x =答:该公可若想获得10 000万元的年利润,则该设备的销售单价应是50万元. 【解析】(1)∵此设备的年销售量y (单位:台)和销售单价x (单位:万元)成一次函数关系,∴可设()0y kx b k =+≠.根据题意,得40600,45550,k b k b +-⎧⎨+=⎩解得:10,1000,k b =-⎧⎨=⎩∴年销售量y 与销售单价x 的函数关系式是101000.y x =-+ (2)∵此设备的销售单价是x 万元,成本价是30方元, ∴该设备的单件利润为()30x -万元. 由题意,得()()3010100010000x x --+= 解得:12=80,=50.x x∵销售单价不得高于70万元,即70x ≤, ∴180x =不符合题意,舍去.∴50.x =答:该公可若想获得10 000万元的年利润,则该设备的销售单价应是50万元. 24.【答案】(1(2)四边形BADQ 是菱形. 理由如下:∵四边形ACBF 是矩形, ∴BQ AD ∥ ∴=BQA QAD ∠∠由折叠的性质,得=,BAQ QAD AB AD ∠∠=,∴,BQA BAQ ∠=∠ ∴.BQ AB = ∴,BQ AD = ∴,BQ AD ∥∴四边形BADQ 是平行四边形. 又∵AB AD =, ∴BADQ 是菱形.(3)图4中的黄金矩形有矩形BCDE 、矩形MNDE . 以黄金矩形BCDE 为例,理由如下:∵1,AD AB AN AC ===∴1CD AD AC =-,又∵2BC =.∴CD BC -∴矩形BCDE 是黄金矩形.(4)如图,在矩形BCDE 上添加线段GH ,使四边形 G CDH 为正方形,此时四边形BGHE 为所要作的黄金矩形,长1GH ,宽3HE =(第24题))1,213DH GH CD HE DE DH ∴==∴=-=-=HE GH ∴==∴矩形BGHE 是黄金矩形. 【解析】(1)由题意,得12,1,90,2BM MN AF BF BM AFB AB =====∠=︒∴===(2)四边形BADQ 是菱形. 理由如下:∵四边形ACBF 是矩形,∴BQ AD ∥ ∴=BQA QAD ∠∠由折叠的性质,得=,BAQ QAD AB AD ∠∠=, ∴,BQA BAQ ∠=∠ ∴.BQ AB = ∴,BQ AD = ∴,BQ AD ∥∴四边形BADQ 是平行四边形. 又∵AB AD =, ∴BADQ 是菱形.(3)图4中的黄金矩形有矩形BCDE 、矩形MNDE . 以黄金矩形BCDE 为例,理由如下:∵1,AD AB AN AC ===∴1CD AD AC =-=,又∵2BC =.∴12CD BC -. ∴矩形BCDE 是黄金矩形.(4)如图,在矩形BCDE 上添加线段GH ,使四边形 G CDH 为正方形,此时四边形BGHE 为所要作的黄金矩形,长1GH ,宽3HE =(第24题)51CD =,四边形GCDH 是正方形,DH G∴=)1,213DH GH CD HE DE DH ∴==∴=-=-=1.2HE GH ∴=∴矩形BGHE 是黄金矩形. 25.【答案】(1)把点,0A m ()、4,B n ()代入1y x =-得1, 3.m n ==∴()()1,0,4,3.A B∵抛物线2y x bx c =-++过点A 、B ,∴10,1643,b c b c -++=⎧⎨-++=⎩解得:6,5,b c =⎧⎨=-⎩∴该抛物线的解释式为26 5.y x x =-+-(2)如图1,∵APM △和DPN △为等直角三角形,∴=45,APM DPN ∠∠= ∴90,MPN ∠= ∴MPN △为直角三角形.令2650x x -+-=,解得:121, 5.x x == ∴()5,0, 4.D AD = 设AP k =,则4,DP k =-,PM)4.PN k =-∴)11422MPN S PM PN k ∆==⨯- =214k k -+=()21214k --+ ∴当2k =,即2AP =时,MPN S ∆最大,此时3OP =,∴()3,0.P(3)存在,点Q 坐标为23(,-)或7833⎛⎫ ⎪⎝⎭,-. 【解析】(1)把点,0A m ()、4,B n ()代入1y x =-得1, 3.m n == ∴()()1,0,4,3.A B∵抛物线2y x bx c =-++过点A 、B ,∴10,1643,b c b c -++=⎧⎨-++=⎩解得:6,5,b c =⎧⎨=-⎩∴该抛物线的解释式为26 5.y x x =-+-(2)如图1,∵APM △和DPN △为等直角三角形,∴=45,APM DPN ∠∠= ∴90,MPN ∠= ∴MPN △为直角三角形.令2650x x -+-=,解得:121, 5.x x == ∴()5,0, 4.D AD = 设AP k =,则4,DP k =-,PM)4.PN k =-∴)11422MPN S PM PN k ∆==⨯- =214k k -+=()21214k --+ ∴当2k =,即2AP =时,MPN S ∆最大,此时3OP =,∴()3,0.P (3)存在,点Q 坐标为23(,-)或7833⎛⎫ ⎪⎝⎭,-.。
【数学课件】2018年中考数学一轮复习2.4一元一次不等式组课件和随堂演练(德州市)

知识点三 一元一次不等式组及其解法 1.一元一次不等式组:一般地,关于同一未知数的几个一 元一次不等式合在一起,就组成一个一元一次不等式组. 2.一元一次不等式组的解法 (1)解一元一次不等式组的一般步骤:先求出这个不等式组 中每个一元一次不等果不等式 集是x<2,那么m的取值范围是( D )
的解
A.m=2
C.m<2
B .m> 2
D.m≥2
6.若关于x的一元一次不等式组 m的取值范围是( D ) A.m≥2 C.m≤2 B.m>2 D.m<2
有解,则
考点三 一元一次不等式的应用
(5年0考)
例4 山地自行车越来越受到中学生的喜爱,各种品牌相继 投放市场.某车行经营的A型车去年销售总额为5万元,今 年每辆销售价比去年降低400元,若卖出的数量相同,销售 总额将比去年减少20%. (1)今年A型车每辆售价多少元?(用列方程的方法解答)
第四节 一元一次不等式(组)
知识点一 不等式的概念及其性质
1.不等式的概念:用符号“<”或“>”表示大小关系的式 子,叫做不等式. 未知数 的值,叫做不等 2.不等式的解:使不等式成立的_______ 式的解.
3.不等式的解集:一个含有未知数的不等式的所有的解, 组成这个不等式的解集. 4.不等式的性质 (1)不等式的性质1:不等式两边加(或减)同一个数(或式
3.(2014·德州)不等式组 可表示为( D )
的解集在数轴上
4.(2017·德州)不等式组
的解集是( B )
A.x≥-3 C.-3≤x<2
B.-3≤x<4 D .x>4
命题角度❷
由解集求字母系数的值或范围
例3 (2017·武城一模)若不等式组 则实数a的取值范围是( A.a≥-1 C.a≤1 ) B.a<-1 D.a≤-1
【数学课件】2018中考数学一轮复习《1.3分式》课件及随堂演练(德州市)

【分析】 先根据分式混合运算的法则把原式进行化简, 再把a的值代入求解. 【自主解答】 原式=
讲:
分式化简求值的易错点
在分式的化简求值过程中,需要注意的有以下两点:
(1)分式化简的最终结果必须是最简分式或整式;(2)代入
的数值必须使原来的分式有意义.
练:链接变式训练9
7.(2015·德州),再求值:
其中a=2sin 60°-tan 45°,b=1.
解:原式
9.(2017·武城一模)先化简,再求值: 其中x满足x2+x-2=0.
解:原式
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文
D.缩小到原来的 1 10
4.不改变分式的值,把分式
分子、分母各项的系数
3x 2y
都化为整数后,分式变为__9_x _6_y__.
考点三 分式的四则运算 (5年1考)
例3 (2016·德州)化简
等于( )
【分析】 原式第二项约分后,两项通分并利用同分母分 式的加法法则计算即可得到结果. 【自主解答】 原式=
上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱
好好学习,天天向上。 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基
4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种
山东省德州市中考数学一轮复习《第一章第4讲》课件

You made my day!
我们,还在路上……
一般地,被开方数不含④_分__母__,也不含⑤_能__开__得__尽__方 的因数或因式,这样的二次根式称为最简二次根式
≥0
(a≥0)
最简二次根式
同类二次根式
考情分析►二次根式单独考查的频率低,一般与整式或分式的运算,在运用勾股定理 或锐角三角函数求线段长度时一并考查. 预测►结合分式的化简求值考查,或整合在图形与几何中一并考查.
第4讲 二次根式及其运算
考点1 二次根式的概念及性质 6年1考
概念
一般地,形如① 叫做被开方数
(a意义,则②_a_≥__0_
同类二次根式
几个二次根式化为最简二次根式后,如果③_被__开__方__数_ 相同,那么这几个二次根式就叫做同类二次根式
最简二次根式
D
2019 考向过预测
1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月5日星期六下午3时21分29秒15:21:2922.3.5 2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那
些善于独立思考的人,给那些具有锲而不舍的人。2022年3月下午3时21分22.3.515:21March 5, 2022 3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022年3月5日星期六3时21分29秒15:21:295 March 2022 4、享受阅读快乐,提高生活质量。下午3时21分29秒下午3时21分15:21:2922.3.5
命题点1 二次根式的性质
命题点2 二次根式的运算
4.[2015·德州,T18,6分]关联考题见第3讲“过真题”T4. 5.[2014·德州,T18,6分]关联考题见第3讲“过真题”T5. 6.[2013·德州,T18,6分]关联考题见第3讲“过真题”T6. 类型1 二次根式的性质
2018年中考数学一轮复习2.1一次方程(组)和随堂演练(德州市)精选优质PPT课件

考点二 解二元一次方程组 (5年0考)
例2 已知方程组
则 x-y的值为 .
【分析】 方法一:根据代入消元法分别求出x,y的值,
然后得到x-y的值;方法二:两个方程做差,直接得出x-
y的值.
【自主解答】 方法一:
由①得x=1-2y. ③
把③代入②,得2(1-2y)+y=3,解得y=- 1 .
3
把y=- 1 代入③,得x= 5 .∴x-y= 5 + 1 =2.
知识点三 一次方程(组)的应用 1.用一次方程(组)解决日常生活中的行程问题、工程问 题、营销中的利润问题、储蓄问题、折扣问题和其他一些 常见问题.
2.列方程(组)解应用题的一般步骤为:(1)审,即审清题 意,分清题中的已知量和未知量;(2)设,即设出关键未知 数;(3)列,即找出题干中的等量关系,列方程(组);(4) 解,即解方程(组);(5)验,即检验结果是否正确或是否有 实际意义;(6)答,回归题中,规范作答.
解一元一次方程的实质是利用等式的基本性质将方程两边 进行恒等变形.
知识点二 二元一次方程(组)及其解法 1.二元一次方程:含有_两__个__未知数,并且含有未知数的 项的次数都是__1__,像这样的方程叫做二元一次方程. 2.二元一次方程组:方程组中有两个未知数,含有每个未 知数的项的次数都是1,并且一共有两个方程,像这样的方 程组叫做二元一次方程组. 3.二元一次方程组的解:一般地,二元一次方程组的两个 方程的公共解,叫做二元一次方程组的解.
第二章 方程与不等式 第一节 一次方程(组)
知识点一 一元一次方程及其解法 1.方程:含有_未__知__数__的等式叫做方程. 2.方程的解:使方程左、右两边的值相等的_未__知__数__的值, 叫做方程的解.
2018年中考数学一轮复习1.1实数及其运算和随堂演练(德州市)精选优质PPT课件

13.(2017·齐河一模)计算:( 2015 )0+2sin 45°- 8 =__1____2_.
在此输入您的封面副标题
【分析】 先根据负整数指数幂的运算法则求出2-2的值,
然后根据0次幂的定义求出( 3 )0的值,最后求和即可.
【自主解答】 2-2+( 3 )0= 1 +1= 1 +1= 5 ,故答案为
22
4
4
5.
4
在实数的运算过程中,经常遇到的公式有以下几种:a-p=
(a-1)p= 1 ,a0=1(a≠0),同时注意与实数的绝对值、二
【自主解答】 477万=4 770 000=4.77×106,故选C.
讲:
科学记数法的表示及误区
科学记数法的表示形式为a×10n的形式,其中1≤|a|<
10,n为整数.确定n的值时,要看把原数变成a时,小数点
移动了多少位,n的绝对值与小数点移动的位数相同.当原
数绝对值>1时,n是正数;当原数的绝对值<1时,n是负
cos45°,tan 30°,…;(3)类似循环小数型,如1.010
010 001…,4.151 151 115…,…;(4)π 型,如 ,
4π ,3 ,….
2
4
知识点二 实数的有关概念 1.数轴:规定了_原__点__、_单__位__长__度__、_正__方__向__的直线叫做数 轴,实数与数轴上的点是一一对应的. 2.相反数:只有_符__号__不同的两个数叫做互为相反数.特别 地,0的相反数还是0;a+b=0⇔a,b互为相反数;在数轴 上,表示相反数的两个点位于原点两侧,且到原点的距离 _相__等__.
9.(2017·东营)下列四个数中,最大的数是( D )
A.3 C.0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.性质与判定 (1)同位角_相__等__⇔两直线平行. (2)内错角相等⇔两直线_平__行__. (3)同旁内角_互__补__⇔两直线平行.
知识点五 定义、命题与定理 1.命题 (1)命题:判断一件事情的语句,叫做命题,命题由_题__设__ 和_结__论__两部分组成.命题可分为真命题和假命题两类. (2)互逆命题:在两个命题中,如果一个命题的题设和结论 分别是另一个命题的_结__论__和_题__设__,那么这两个命题称 为互逆命题,其中一个命题称为另一个命题的逆命题. 2.定理:经过证明的真命题叫做定理.
4.如图,直线AB与CD相交于点O,若∠1+∠2=80°,则 ∠3等于( C )
A.100° B.120° C.140° D.160°
5.如图,有下列判断:①∠A与∠1是同位角;②∠A与∠B 是同旁内角;③∠4与∠1是内错角;④∠1与∠3是同位角. 其中正确的是__①__②___(填序号).
考点三 平行线的性质与判定 (5年4考) 例3 (2017·庆云一模)如图,直线a∥b,一块含60°角的直 角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°, 则∠2的度数为( )
知识点六 尺规作图 1.尺规作图:我们把只能使用_圆__规___和_没__有__刻__度__的直尺 这两种工具去作几何图形的方法称为尺规作图.
2.常见的五种基本作图: (1)作一条线段等于已知线段; (2)作一个角等于已知角; (3)作角平分线; (4)过一点作已知直线的垂线; (5)作线段的垂直平分线.
A.105° B.110° C.115° D.120°
2.角的分类 (1)按照角的大小,角可分为锐角、_直__角__、_钝__角__、平角和 周角. (2)1周角=360°=2平角=4直角;1°=60′,1′=60″.
3.余角、补角 (1)余角:如果两个角的和是90°,就说这两个角互为余 角.即若α +β =90°,则α ,β 互为余角.同角或等角 的余角_相__等___. (2)补角:如果两个角的和是180°,就说这两个角互为补 角.即α +β =180°,则α ,β 互为补角.同角或等角的 补角__相__等__.
4.角的平分线:从一个角的顶点出发,把这个角分成两个 _相__等__的角的射线,叫做这个角的平分线.
知识点三 相交线 1.对顶角的性质:对顶角相等. 2.三线八角(如图) (1)同位角:∠1与∠5,∠2与∠6,∠4与_∠__8_,∠3与_∠__7_. (2)内错角:∠2与_∠__8_,∠3与∠5. (3)同旁内角:∠3与∠8,∠2与_∠__5_.
第四章 几何初步与三角形 第一节 几何的初步认识
知识点一 直线、射线与线段 1.直线、射线与线段的区别 直线_没__有__端点,射线有1个端点,线段有__2__个端点.
2.基本事实 (1)经过两点有一条直线,并且只有一条直线,即_两__点__确定 一条直线. (2)两点的所有连线中,___段__最短.简单说成:两点之间, 线段最短.
3.垂直的性质 (1)在同一平面内,过一点 _有__且__只__有__一条直线与已知直线 垂直. (2)连接直线外一点与直线上各点的所有线段中,_垂__线__段__ 最短. 4.点到直线的距离:直线外一点到这条直线的垂线段的长 度,叫做点到直线的距离.
知识点四 平行线 1.平行公理 (1)经过直线外一点,_有__且__只__有__一条直线与这条直线平行. (2)如果两条直线都与第三条直线平行,那么这两条直线也互 相_平__行__.
考点一 线与角 (5年1考) 例1 (2017·夏津一模)如图,将一副三角板叠放在一起, 使直角的顶点重合于O,则∠AOC+∠DOB=( )
A.90° B.120° C.160° D.180°
【分析】 因为本题中∠AOC始终在变化,因此可以采用 “设而不求”的解题技巧进行求解. 【自主解答】 设∠AOD=α , ∴∠AOC=90°+α ,∠BOD=90°-α ,
考点二 相交线 (5年0考) 例2 如图,直线a,b,c两两相交于A,B,C三点,则图中 有 对对顶角;有 对同位角;有 对内错角;有
对同旁内角.
【分析】 根据3条直线两两相交,共有3个交点,据此可 判断对顶角、同位角、内错角、同旁内角的对数. 【自主解答】 3条直线两两相交,共有3个点,每个点有2 对对顶角,任意两条直接被第三条截有12对同位角,6对内 错角,6对同旁内角,所以对顶角有6对,12对同位角,6对 内错角,6对同旁内角.故答案为6,12,6,6.
3.两点的距离 连接两点间的线段的_长__度__,叫做这两点的距离.
4.线段的中点:点M把线段AB分成相等的两条线段AM与MB, 点M叫做线段AB的中点.这时AM=BM= 1 AB(或AB=2AM=
2
2BM).
知识点二 角 1.角的定义 (1)有公共端点的_两__条__射__线__组成的图形叫做角.这个公共 端点是角的顶点,这两条射线是角的两条边. (2)一条射线绕着它的端点旋转而形成的图形也叫做角.
∴∠AOC+∠BOD=90°+α +90°-α =180°.故选D.
涉及角度或线段的计算时,经常用到角平分线、线段的中 点的性质.尤其在角的计算中,还需要注意余角、补角性 质的运用,同时,注意三角尺的角是30°,45°,60°, 90°等隐含条件的应用.
1.如图,点O在直线AB上,射线OC,OD在直线AB的同侧, ∠AOD=40°,∠BOC=50°,OM,ON分别平分∠BOC和 ∠AOD,则∠MON的度数为( A )
A.135° B.140° C.152° D.45°
2.(2013·德州)如图,为抄近路践踏草坪是一种不文明的 现象.请你用数学知识解释出现这一现象的原因:__两__点__之__ _间__线__段__最__短__.
3.已知∠1的补角是133°21′,则它的余角是__4_3_°__2_1_′_; 下午14点半,钟面上的时针与分针的夹角是__1_0_5__度.
