吉林省东北师范大学附中2016届高三上学期第二次模拟数学(文)试卷
吉林省东北师范大学附属中学净月校区高三数学上学期第

吉林省东北师范大学附属中学净月校区2016届高三数学上学期第二次模拟考试试题理一、选择题(本大题包括12小题,每小题5分,共60分)1.已知集合A=错误!未找到引用源。
,B=错误!未找到引用源。
,则A错误!未找到引用源。
B=()A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
2.已知数列错误!未找到引用源。
满足错误!未找到引用源。
,错误!未找到引用源。
,则数列错误!未找到引用源。
的前6项和为()A.63 B.127 C.错误!未找到引用源。
D.错误!未找到引用源。
3.若错误!未找到引用源。
,错误!未找到引用源。
是第三象限的角,则错误!未找到引用源。
错误!未找到引用源。
( )A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
4.已知错误!未找到引用源。
是两个不同的平面,错误!未找到引用源。
是两条不同的直线,则下列命题不正确的是()A.若错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
B.若错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
C.若错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
D.若错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
错误!未找到引用源。
错误!未找到引用源。
5.已知正项数列错误!未找到引用源。
中,错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
等于()A.错误!未找到引用源。
B.4 C.8 D.166.已知两定点错误!未找到引用源。
,错误!未找到引用源。
,点P在椭圆错误!未找到引用源。
上,且满足错误!未找到引用源。
=2,则错误!未找到引用源。
为()A.-12 B.12 C.一9 D.9俯视图侧视图正视图7.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积是()A.2B.错误!未找到引用源。
【百强校】2016届吉林东北师大附中高三上第二次摸底考语文试卷(带解析)

绝密★启用前【百强校】2016届吉林东北师大附中高三上第二次摸底考语文试卷(带解析)试卷副标题考试范围:xxx ;考试时间:106分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、依次填入下面一段文字横线处的语句,衔接最恰当的一组是(3分)一如胡应麟所说“独钓寒江雪,五字极闹”,这个“闹”字很刁,一下子点化了柳宗元《江雪》一诗中的昂扬活力。
所谓的枯寂,不过是一种表象。
_________,__________,__________。
或许,___________,___________;____________,_____________。
那片苍茫的空阔,并非一无所有,而是如国画中留出的空白,意味深远。
①诱人的芭蕉正在雪天里挺立 ②只有雪野的空旷③君不见,恍若轻绸的溪泉正在冰雪下面漾动 ④才能凸显生命的充实 ⑤方能反衬人心的温热 ⑥只有雪天的凄冷 ⑦江上小舟,亦正在无声中悠然地划行A .①⑦③②④⑥⑤B .③①⑦②④⑥⑤C .①⑦③⑥⑤②④D .③①⑦⑥⑤②④2、下列各句中,没有语病的一项是(3分)A .马克思、恩格斯、列宁的著作不容易译好,它要求翻译人员具有相当高的政治水平试卷第2页,共11页和业务水平才能胜任。
B .中国大量的音乐暴发户不惜自掏腰包也要在维也纳金色大厅献演,是因为金色大厅的权威性,足够蒙骗不知底细的中国人和音乐新秀。
C .《澄衷蒙学堂字课图说》是中国近代教育史上非常具有代表性的教材,它对每一个与人精神状况有关的字的解释,都是合乎情理的。
D .作家喜欢把相反的力量、个性加诸一人身上,让他面目不清、身份游移,现实生活中许多人就是这样。
3、依次填入下列各句横线处的成语,最恰当的一组是(3分)①在那荒唐的十年中间,说谎的艺术发展到了____________的程度,谎言变成了真理,说真话倒犯了大罪。
2016届吉林省东北师大附中等校高三联考数学(文)试题(解析版)

2016届吉林省东北师大附中等校高三联考数学(文)试题一、选择题1.设全集{}8≤∈=x N x U ,集合{}7,3,1=A ,{}8,3,2=B ,则=)()(B C A C U U ( )A .{}8,7,2,1B .{}6,5,4C .{}6,5,4,0D .{}6,5,4,3,0 【答案】C【解析】试题分析:{}{}80,1,2,3,4,5,6,8U x N x =∈≤= ,(){}()()0,4,5,6U U U C A C B C A B ∴=⋃= ,故选C .【考点】集合交、并、补的运算. 2.已知复数i z +=11,i z -=22,则=iz z 21( ) A .i 31- B .i 31+- C .i 21+ D .i 21- 【答案】A【解析】试题分析:根据题意:()()()122123313i i i iz z i i i i i i+-++====-,故选A . 【考点】复数的运算.3.若实数数列:81,,1a 成等比数列,则圆锥曲线122=+ay x 的离心率是( ) A .10或322 B .3或36 C .322 D .31或10【答案】A【解析】试题分析:因为1,,81a 成等比数列,所以281a =,即9a =±.当9=a 时,圆锥曲线表示的是椭圆,所以离心率3c e a a ===;当9-=a 时,圆锥曲线表示的双曲线,1091=+=c ,所以离心率10==ace ,故选A . 【考点】等比数列中项性质,椭圆和双曲线的离心率. 4.函数2)(1-=-x ax f )1,0(≠>a a 的图象恒过定点A ,若点A 在直线01=--ny mx 上,其中 0,0>>n m ,则nm 21+的最小值为( )A .4B .5C .6D .223+ 【答案】D【解析】试题分析:因为函数2)(1-=-x a x f )1,0(≠>a a 的图象恒过定点A ,所以()1,1A -,又因为点A 在直线01=--ny mx 上,所以1m n +=,所以()121223n mm n m n m n m n⎛⎫+=++=++⎪⎝⎭,又 0,0>>n m ,∴2n m m n +≥且仅当2n m m n =时,即1,2m n =取=,∴123m n+≥+故选D . 【考点】基本不等式.5.如图为某几何体的三视图,则该几何体的表面积为( )俯视图侧视图正视图12222A .π220+B .π320+C .π224+D .π324+ 【答案】B【解析】试题分析:根据三视图的特征,得到该几何体是一个半圆柱和正方体的组合体.其底面积的面积:22282S ππ⎛⎫=⨯+=+⎪⎝⎭;底面周长:6C π=+;侧面面积:()62122ππ+⨯=+.所以几何体的表面积:()()8123203πππ+++=+,故选B . 【考点】三视图的识别,几何体的表面积计算.6.气象意义上从春季进入夏季的标志为:“连续5天每天日平均温度不低于C ︒22”,现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数,单位C ︒) ①甲地:5个数据的中位数为24,众数为22; ②乙地:5个数据的中位数为27,平均数为24;③丙地:5个数据中有一个数据是32,平均数为26,方差为2.10.则肯定进入夏季的地区有( )A .0个B .1个C .2个D .3 【答案】C【解析】试题分析:甲地肯定进入, 丛数为22,∴22至少出现两次,若有一天低于22,则中位数不可能为24;丙地也进入,根据方差的定义:()()()()()222221234126262626322610.25x x x x ⎡⎤-+-+-+-+-=⎣⎦,即()()()()222212342626262615x x x x -+-+-+-=,显然1234,,,x x x x 都要大于22,才能成立,乙地不一定进入,比如12,23,27,29,29,故选C . 【考点】中位数、平均数、众数的概念及运用.7.已知条件p :3-=k ,条件q :直线2+=kx y 与圆122=+y x 相切,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】A【解析】试题分析:条件q :直线2+=kx y 与圆122=+y x 相切,1=,得k =,所以p q ⇒,但是q p ≠>,所以p 是q 的充分不必要条件. 【考点】充要条件.8.平面α截球O 所得的截面圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A .π6 B . C .π64 D .π36 【答案】B【解析】试题分析:根据题意可得:球的半径R =,球的体积334433r V ππ===.【考点】球的体积.9.若如图所示的程序框图输出的S 是126,则条件①可为( )A .?5≤nB .?6≤nC .?7≤nD .?8≤n 【答案】B【解析】试题分析:根据题意,该程序表示的是首项为2,公比为2的数列求和,即232222n S =++++122126n +=-=,∴6n =,故选B .【考点】程序框图.10.若函数2(2)()m xf x x m-=+的图象如图所示,则m 的范围为( )A .)1,(--∞B .)2,1(-C .)2,0(D .)2,1( 【答案】D【解析】试题分析:根据图象可知,函数图象过原点,即()00f =,所以0m ≠.当0x >时,()0f x >,所以20m ->,即2m <;函数()f x 在[]1,1-是单调递增的,所以()0f x '>在[]1,1-恒成立,()()()()()()()2222222222()0m x m x m x m x m f x xm xm -+----'==>++, 20m -<,∴只需要20xm -<在[]1,1-上恒成立,∴()2max0x m -<,∴1m >,综上所述:12m <<,故选D .【考点】函数图象.【方法点晴】本题主要考查的是根据函数图象,求函数的性质,进而求参数范围.属于中档题.解决这类问题,主要是观察函数图象,根据函数图象推断出函数的性质,比如:函数过特殊点、函数的奇偶性、在某段上函数值的符号以及函数的单调性.11.过双曲线)0,0(12222>>=-b a by a x 的左焦点1F ,作圆222a y x =+的切线交双曲线右支于点P ,切点为T ,1PF 的中点M 在第一象限,则以下结论正确的是( )A .MT MO a b -=-B .MT MO a b ->-C .MT MO a b -<-D .MT MO a b +=- 【答案】A【解析】试题分析:因为T 是切点,所以连接OT ,则1OT PF ⊥,在TO F1∆中,1TF b =.连接2PF ,在12PFF ∆中,O 、P 分别是12F F 、1PF 的中点,所以212OM PF =,2111122MO MT PF PF TF ⎛⎫∴-=-- ⎪⎝⎭()()2111222PF PF b a b b a =-+=-+=-,故选A . 【考点】双曲线的定义,直线与圆相切.【思路点晴】本题主要考查的是双曲线的定义、直线与圆相切的性质和三角形中位线的综合运用,属于难题.解题的关键是根据相切,得到1OT PF ⊥,再根据双曲线的性质,求出1TF b =;又因为M 点是中点,在焦点三角形12PFF ∆中,运用中位线定理得212OM PF =,再结合双曲线定义122PF PF a -=,最终求出答案. 12.已知函数)(x f 定义在R 上的奇函数,当0<x 时,()(1)xf x e x =+,给出下列命题:①当0>x 时,()(1)xf x e x =-②函数)(x f 有2个零点③0)(>x f 的解集为),1()0,1(+∞- ④R x x ∈∀21,,都有2)()(21<-x f x f ,其中正确的命题是( )A .①③B .②③C .③④D .②④ 【答案】C【解析】试题分析:① 函数()f x 在R 上的奇函数,∴()()f x f x =--,令()0,x ∈+∞,则(),0x -∈-∞,()()(1)(1)x x f x f x e x e x --=--=--=-,故①错;②当0<x 时,()(1)0xf x e x =+=,0x e > ,∴1x =-是函数的一个零点,同理可以求出当0>x ,1x =是函数的一个零点, 函数()f x 是奇函数,∴()00f =,综上所述函数()f x 有3个零点,故②错;由①可知函数()(1)000(1)0x xe x xf x x e x x -⎧+<⎪⎪=⎨⎪->⎪⎩,0)(>x f 的解集为),1()0,1(+∞- ,故③正确;④当0<x 时,()()(1)2xxx f x e x e e x '=++=+,当()2,0x ∈-时,()0f x '>,()f x 单增;当(),2x ∈-∞-时,()0f x '<,()f x 单减;∴在0<x ,函数有最小值()()2m i n2f x f e -=-=-.同理在0x >时,函数有最大值()()2max 2f x f e -==.∴Rx x ∈∀21,,都有()()212ma x min ()()2f x f x f x f x e --<-=, 201e -<<,∴222e -<,故()0,x ∈+∞④正确.【考点】函数性质.【方法点晴】本题主要综合考查奇函数的性质,属于难题.①求奇函数在()0,x ∈+∞的解析式,关键是令()0,x ∈+∞,再利用奇函数的性质()()f x f x =--求出()0,x ∈+∞的解析式;在奇函数的性质中当0属于定义域是一定会有()00f =,这是最容易遗忘的.二、填空题13.向量1=a ,2=b ,)2()(b a b a -⊥+,则向量a 与b的夹角为 .【答案】2π 【解析】试题分析: )2()(-⊥+,∴()(2)0a b a b +⋅-=,即222c o s ,0a ab a b b +⋅-=, ∴cos ,0a b = ,即向量与的夹角为2π.【考点】向量的乘积运算. 14.已知0θπ<<,1tan()47πθ+=,那么sin cos θθ+= . 【答案】15-【解析】试题分析:sin cos 4πθθθ⎛⎫+=+ ⎪⎝⎭ ,0θπ<< ,∴5444πππθ<+<,又 1t a n ()47πθ+=,∴544πππθ<+<,根据同角三角函数基本关系得sin 410πθ⎛⎫+=- ⎪⎝⎭∴1sin cos 5θθ+=-. 【考点】同角三角函数基本关系和辅助角公式.15.若y x ,满足条件⎪⎩⎪⎨⎧≤-≥+≤-2212x y y x y x ,目标函数y x z 23+-=的最小值为 .【答案】1-【解析】试题分析:不等式组⎪⎩⎪⎨⎧≤-≥+≤-2212x y y x y x 表示的可行域如图ABC ∆,当目标函数y x z 23+-=经过()1,1A 有最小值,且最小值是31211-⨯+⨯=-.【考点】线性规划求目标函数的最值.【方法点晴】本主要考查线性规划中已知可行域求目标函数的最值,属于容易题.本题关键是在坐标系上画出可行域,然后利用数形结合的方法求出目标函数的最大值,如果可行域是一个封闭的图形,目标函数的最值一般在交点处取得,分别把交点求出来,代入目标函数中就可以.在直角坐标系画可行域时要注意“直线定界,点定域”的原则. 16..若X 是一个集合,τ是一个以X 的某些子集为元素的集合,且满足:①X 属于τ,空集∅属于τ;②τ中任意多个元素的并集属于τ;③τ中任意多个元素的交集属于τ.则称τ是集合X 上的一个拓扑.已知集合{,,}X a b c =,对于下面给出的四个集合τ:① {,{},{},{,,}}a c a b c τ=∅; ② {,{},{},{,},{,,}}b c b c a b c τ=∅; ③ {,{},{,},{,}}a a b a c τ=∅; ④ {,{,},{,},{},{,,}}a c b c c a b c τ=∅. 其中是集合X 上的一个拓扑的集合τ的所有序号是 . 【答案】②④【解析】试题分析:①{,{},{},{,,}}a c a b c τ=∅,但是{}{}{},a c a c τ⋃=∉,所以①错;②④都满足集合X 上的一个拓扑的集合τ的三个条件.所以②④正确;③{}{}{,}a a b b τ⋃=∉,故错.所以答案②④.【考点】集合包含关系的判定及应用.【方法点晴】本题主要考查的关于集合的新定义题型,属于基础题.需要准确的把握集合包含的判定方法,及集合的子集间的交并补的关系.本题关键是需要学生准确理解集合X 上的一个拓扑τ所要满足的三个条件,需要学生认真分析题干,准确把握信息.对于这种开放性题目,需要考生准确理解和快速掌握新知识的能力.三、解答题17.在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,面积为S ,已知b Ac C a 252cos 22cos 222=+.(Ⅰ)求证:b c a 3)(2=+;(Ⅱ)若41cos =B ,15=S ,求b . 【答案】(Ⅰ)证明见解析;(Ⅱ)4=b .【解析】试题分析:(Ⅰ)利用二倍角公式去平方;再由()sin sin sin cos cos sin B A C A C A C =+=+,结合正弦定理,得到b Ac C a =+cos cos ,化简可证明b c a 3)(2=+;(II )1sin 2ABC S ac B ∆=,利用余弦定理,再结合b c a 3)(2=+,最终可以算出b . 试题解析:解:(Ⅰ)由条件:b A c C a 25)cos 1()cos 1(=+++, 由于:b A c C a =+cos cos ,所以:b c a 23=+, 即:b c a 3)(2=+(Ⅱ)41cos =B ,所以:415sin =B , 151581sin 21===ac B ac S ,8=ac 又:)cos 1(2)(cos 22222B ac c a B ac c a b +-+=-+=, 由b c a 3)(2=+,所以:)411(16452+=b ,所以:4=b 【考点】正弦定理和余弦定理的运用.【方法点晴】本题主要考查解三角形,正弦定理和余弦定理得综合运用,属于基础题.解三角形中,常用的的技巧“边化角”或者“角化边”,特别是当遇到题干有每项都含有边的齐次式的等式时,多选择边化角.题上出现三角形面积时要合理利用公式111sin sin sin 222ABC S ab C bc A ac B ∆===. 18.如图所示,该几何体是由一个直三棱柱BCF ADE -和一个正四棱锥ABCD P -组合而成,AF AD ⊥,2==AD AE . PF EDC BA(Ⅰ)证明:平面⊥PAD 平面ABFE ;(Ⅱ)求正四棱锥ABCD P -的高h ,使得该四棱锥的体积是三棱锥ABF P -体积的4倍.【答案】(Ⅰ)证明见解析(Ⅱ)2=h . 【解析】试题分析:(Ⅰ)根据题意可以证明:AD ⊥平面ABFE ,所以能证明到:平面⊥PAD 平面ABFE ;(Ⅱ) AD ⊥平面ABFE ,∴P 到平面ABF 的距离刚好是12AD =,求出23P ABF V -=,再用h 表示P ABCD V -,由于4P ABCD P ABF V V --=,求出h . 试题解析:(Ⅰ)证明:直三棱柱BCF ADE -中,⊥AB 平面ADE , 所以:AD AB ⊥,又AF AD ⊥,所以:⊥AD 平面ABFE ,⊂AD 平面PAD , 所以:平面⊥PAD 平面ABFE (Ⅱ)P 到平面ABF 的距离1=d所以:11122213323P ABF ABF V S d -∆==⨯⨯⨯⨯=而:118224333P ABCD ABCD P ABF V S h h V --==⨯⨯==,所以2h =【考点】面面垂直,锥体的体积.【方法点晴】证明面面垂直问题时要主要转化成线面垂直去证明;三棱锥是一个比较特殊的几何体,三个面都可以作为底面,特别是在求三棱锥体积时,一定要选择容易找出三棱锥高的面作为我们的底面;有时几何体的面积直接求比较困难时,需要我们转化成间接的方式求.19.甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:(Ⅰ)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;(Ⅱ)现要从中选派一人参加该项竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由. 【答案】(Ⅰ)1225;(Ⅱ)派甲参赛比较合适. 【解析】试题分析:(Ⅰ)用列举的方法把基本事件一一列举出来得到基本事件总数,再找出甲的成绩比乙高的的事件总数,求出这两个的比值就是甲的成绩比乙高的概率;(Ⅱ)分别求出甲、乙的方差,方差越小的越稳定.试题解析:(Ⅰ)记甲被抽到的成绩为x ,乙被抽到的成绩为y ,用数对),(y x 表示基本事件:(82,95) (82,75) (82,80) (82,90) (82,85) (82,95) (82,75) (82,80) (82,90) (82,85)(79,95) (79,75) (79,80) (79,90) (79,85) (95,95) (95,75) (95,80) (95,90) (95,85)(87,95) (87,75) (87,80) (87,90) (87,85) 基本事件总数25n =9甲 乙 7 8 975 2 20 5 055记“甲的成绩比乙高”为事件A,事件A 包含的基本事件: (82,75) (82,80) (82,75) (82,80) (79,75) (95,75) (95,80) (95,90) (95,85) (87,75) (87,80) (87,85) 事件A 包含的基本事件数是12m = 所以12()25m P A n == (Ⅱ)派甲参赛比较合适.理由如下:85=甲x ,85=乙x ,6.312=甲s ,502=乙s =甲x 乙x ,<2甲s 2乙s 甲的成绩较稳定,派甲参赛比较合适【考点】茎叶图、概率和方差.20.椭圆1C 与2C 的中心在原点,焦点分别在x 轴与y 轴上,它们有相同的离心率22=e ,并且2C 的短轴为1C 的长轴,1C 与2C 的四个焦点构成的四边形面积是22. (Ⅰ)求椭圆1C 与2C 的方程;(Ⅱ)设P 是椭圆2C 上非顶点的动点,P 与椭圆1C 长轴两个顶点A ,B 的连线PA ,PB 分别与椭圆1C 交于点E ,F .(1)求证:直线PA ,PB 斜率之积为常数;(2)直线AF 与直线BE 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.【答案】(Ⅰ)1C :1222=+y x ,2C :14222=+y x ;(Ⅱ)(1)证明见解析;(2)18-.【解析】试题分析:(Ⅰ)根据离心率c e a ==和222a b c -=分别设出出双曲线1C 、2C 的标准方程,再根据1C 与2C 的四个焦点构成的四边形面积是22,分别求1C 、2C的标准方程;(Ⅱ)(1)设出P 点坐标()00,x y ,带入2C 中得到1422020=+y x ,用P 点坐标分别表示出直线PA ,PB 斜率,最后化简算出定值.(2)的思路和(1)一样.试题解析:解:(Ⅰ)依题意22=e ,设1C :122222=+by b x ,2C :1422222=+b y b x ,由对称性,四个焦点构成的四边形为菱形,且面积2222221=⨯⨯=b b S ,解得:12=b ,所以椭圆1C :1222=+y x ,2C :14222=+y x (Ⅱ)(1)设),(00y x P ,则142220=+y x ,)0,2(-A ,)0,2(B 200+=x y k PA ,200-=x y k PB所以:2224220202020-=--=-=⋅x x x y k k PBPA , 直线PA ,PB 斜率之积为常数2-(2)设),(11y x E ,则122121=+y x , 211+=x y k EA ,211-=x y k EB ,所以:212211220212121-=--=-=⋅x x x y k k EBEA ,同理:21-=⋅FB FA k k 所以:41.=⋅⋅FB FA EB EA k k k k ,由PA EA k k =,PB FB k k =,结合(1)有81-=⋅FB EA k k 【考点】椭圆标准方程、直线与椭圆相交. 21.设函数1ln )(-+=x ax x f (0>a ). (Ⅰ)当301=a 时,求函数)(x f 的单调区间; (Ⅱ)当21≥a ,),1(+∞∈x 时,求证:11ln >-+x ax . 【答案】(Ⅰ)函数单调增区间为:)65,0(,),56(+∞,单调减区间为:)1,65(,)56,1(;(Ⅱ)证明见解析.【解析】试题分析:(Ⅰ)求出函数()f x 的导函数,根据()0f x '>,对应的是函数的单调递增区间;0)(>'x f ,对应的是函数的单调递减区间;(Ⅱ)若证11ln >-+x ax ,)1,21(>≥x a 成立,只需证ln ln 1a x x x +≥- 112(1)x +>-,即2(1)l n 12(x x x -+>-当1>x 时成立.构造函数()()21l n 2(1)1g x x xx =---+ (1)x >,只需要()()min 01g x x >>.试题解析:(Ⅰ)函数)(x f 的定义域为),1()1,0(+∞ , 当301=a 时,2)1()56)(65()(---='x x x x x f , 令:0)(>'x f ,得:56>x 或65<x ,所以函数单调增区间为:)65,0(,),56(+∞0)(<'x f ,得:5665<<x ,所以函数单调减区间为:)1,65(,)56,1((Ⅱ)若证11ln >-+x a x ,)1,21(>≥x a 成立,只需证:1)1(21ln 1ln >-+≥-+x x x a x 即:)1(21ln )1(2->+-x x x 当1>x 时成立 设()g x =()21ln 2(1)1(1)x x x x ---+>∴())1(ln 2xx x g -=',显然)(x g '在),1(+∞内是增函数 且02)1(<-='g ,0)212(ln 2)2(>-='g∴)(x g '=0在(1,2)内有唯一零点0x ,使得:01ln 00=-x x , 且当x ∈(1,0x ),)(x g '<0; 当x ∈(0x ,+∞),)(x g '>0.∴)(x g 在(1,0x )递减,在(0x ,+∞)递增()()11ln 12)()(000min+--==x x x g x g =()1111200+⎪⎪⎭⎫ ⎝⎛--x x =)1(2500x x +-∵()2,10∈x ∴251200<+<x x ∴0)(min >x g ∴11ln >-+x ax 成立 【考点】利用导函数求单调区间,函数不等式的证明. 22.选修4——1几何证明选讲如图,P 是圆O 外一点,PA 是圆O 的切线,A 为切点,割线PBC 与圆O 交于B ,C ,PA PC 2=,D 为PC 中点,AD 的延长线交圆O 于点E ,证明:(Ⅰ)EC BE =; (Ⅱ)22PB DE AD =⋅.【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析.【解析】试题分析:(Ⅰ)连接AB ,AC ,因为PD PA =,故PDA PAD ∠=∠,又因为:DCA DAC PDA ∠+∠=∠,PAB BAD PAD ∠+∠=∠,根据弦切角等于同弦所对的圆周角:PAB DCA ∠=∠,所以:BAD DAC ∠=∠,从而弧BE =弧EC ,因此:EC BE =;(II )由切割线定理得:PC PB PA ⋅=2和DC PD PA ==,能得到PB DC 2=,PB BD =,再根据相交弦定理得:DC BD DE AD ⋅=⋅,所以22PB DE AD =⋅.试题解析:(Ⅰ)证明:连接AB ,AC ,由题设知PD PA =,故PDA PAD ∠=∠ 因为:DCA DAC PDA ∠+∠=∠,PAB BAD PAD ∠+∠=∠, 由弦切角等于同弦所对的圆周角:PAB DCA ∠=∠,所以:BAD DAC ∠=∠,从而弧BE =弧EC ,因此:EC BE =(Ⅱ)由切割线定理得:PC PB PA ⋅=2,因为DC PD PA ==,所以:PB DC 2=,PB BD =由相交弦定理得:DC BD DE AD ⋅=⋅ 所以:22PB DE AD =⋅【考点】圆的性质.23.选修4——4 坐标系与参数方程在直角坐标系中,曲线C 的参数方程为⎩⎨⎧==ϕϕsin 15cos 5y x ,(ϕ为参数),直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 23321,(t 为参数).以原点为极点,x 轴的正半轴为极轴建立极坐标系,点P 的极坐标为)2,3(π.(Ⅰ)求点P 的直角坐标,并求曲线C 的普通方程;(Ⅱ)设直线l 与曲线C 的两个交点为A ,B ,求PB PA +的值.【答案】(Ⅰ))3,0(P ,115522=+y x ;(Ⅱ)6. 【解析】试题分析:(Ⅰ)根据点的极坐标化直角坐标的公式,求出点P ;结合参数方程得到cos sin φφ⎧=⎪⎪⎨⎪=⎪⎩,再根据22cos sin 1φφ+=求出曲线C 的普通方程;(Ⅱ)点P 在直线上,联立直线的参数方程代入曲线C 的普通方程求解. 试题解析:(Ⅰ)由极值互化公式知:点P 的横坐标02cos3==πx ,点P 的纵坐标32sin3==πx所以)3,0(P ;消去参数ϕ的曲线C 的普通方程为:115522=+y x (Ⅱ)点P 在直线l 上,将直线的参数方程代入曲线C 的普通方程得:0822=-+t t ,设其两个根为1t ,2t ,所以:221=+t t ,821-=t t ,由参数t 的几何意义知:64)(2122121=-+=-=+t t t t t t PB PA .【考点】坐标系与参数方程,直线与曲线相交. 24.选修4——5 不等式选讲 已知函数5)(++-=x a x x f .(Ⅰ)若1=a ,解不等式:52)(+≥x x f ; (Ⅱ)若8)(≥x f 恒成立,求a 的取值范围. 【答案】(Ⅰ){}2-≤x x ;(Ⅱ)3≥a 或13-≤a .【解析】试题分析:(Ⅰ)当1=a 时,写出不等式,运用零点分区间的方法,讨论当3≥x 时,当21≤x 时,当321<<x 时,去掉绝对值解不等式,然后取并集;(Ⅱ)因为55+≥++-a x a x ,所以将8)(≥x f 转化85≥+a 就可以解出来.试题解析:(Ⅰ)当1=a 时,0)51)(42(5152)(≥---+⇔+≥-⇒+≥x x x x x x x f解得:2-≤x ,所以原不等式解集为{}2-≤x x(Ⅱ)5)5(5)(+=+--≥++-=a x a x x a x x f ,若8)(≥x f 恒成立, 只需:85≥+a 解得:3≥a 或13-≤a 【考点】不等式求解.。
2016年吉林省吉林大学附中高考数学二模试卷(文科)(解析版)
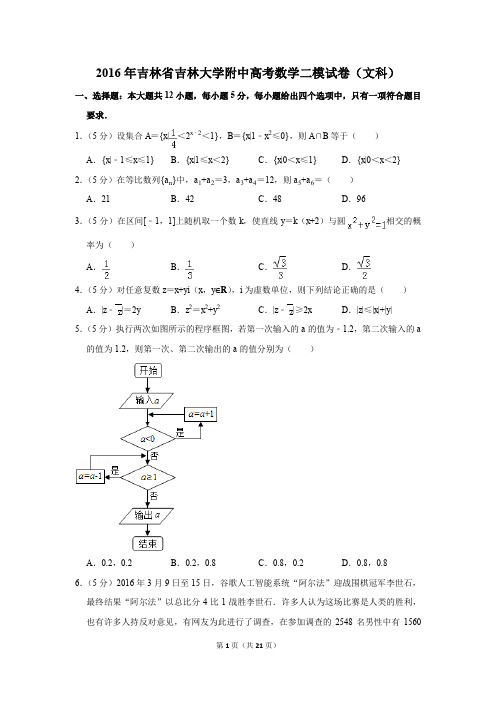
2016年吉林省吉林大学附中高考数学二模试卷(文科)一、选择题:本大题共12小题,每小题5分,每小题给出四个选项中,只有一项符合题目要求.1.(5分)设集合A={x|<2x﹣2<1},B={x|1﹣x2≤0},则A∩B等于()A.{x|﹣1≤x≤1}B.{x|1≤x<2}C.{x|0<x≤1}D.{x|0<x<2} 2.(5分)在等比数列{a n}中,a1+a2=3,a3+a4=12,则a5+a6=()A.21B.42C.48D.963.(5分)在区间[﹣1,1]上随机取一个数k,使直线y=k(x+2)与圆相交的概率为()A.B.C.D.4.(5分)对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是()A.|z﹣|=2y B.z2=x2+y2C.|z﹣|≥2x D.|z|≤|x|+|y| 5.(5分)执行两次如图所示的程序框图,若第一次输入的a的值为﹣1.2,第二次输入的a 的值为1.2,则第一次、第二次输出的a的值分别为()A.0.2,0.2B.0.2,0.8C.0.8,0.2D.0.8,0.86.(5分)2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是()A.茎叶图B.分层抽样C.独立性检验D.回归直线方程7.(5分)下列函数既是奇函数,又在区间(0,1)上单调递减的是()A.f(x)=x3B.f(x)=﹣|x+1|C.f(x)=ln D.f(x)=2x+2﹣x8.(5分)已知一个几何体可切割成一个多面体及一个旋转体的一部分,其三视图如图所示,则该几何体的体积是()A.πB.π+1C.π+D.π9.(5分)给定两个命题p,q.若¬p是q的必要而不充分条件,则p是¬q的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件10.(5分)将所有正偶数按如图方式进行排列,则2 016位于()A.第30行B.第31行C.第32行D.第33行11.(5分)已知四棱锥P﹣ABCD的顶点都在球O的球面上,底面ABCD是矩形,AB=2AD =4,平面P AD⊥底面ABCD,△P AD为等边三角形,则球面O的表面积为()A.B.32πC.64πD.12.(5分)已知集合{f(x)|f(x)=ax2﹣|x+1|+2a<0,x∈R}为空集,则实数a的取值范围是()A.[,+∞)B.[,+∞)C.[,+∞)D.(﹣∞,)二、填空题:本大题共4小题,每小题5分.13.(5分)若实数x,y满足的最小值是.14.(5分)已知正方形ABCD的边长为2,E为CD的中点,则•=.15.(5分)函数f(x)的图象如图所示,f′(x)是f(x)的导函数,设a=f′(﹣2),b =f′(﹣3),c=f(﹣2)﹣f(﹣3),则a,b,c由小到大的关系为.16.(5分)已知数列满足:a1=1,a n+1=,(n∈N*),若b n+1=(n﹣λ)(+1),b1=﹣λ,且数列{b n}是单调递增数列,则实数λ的取值范围为.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知△ABC的内角A,B,C的对边分别为a,b,c,且满足=2+2cos (A+B).(Ⅰ)求的值;(Ⅱ)若a=1,c=,求△ABC的面积.18.(12分)如图,直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面B1BCC1;(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F﹣AEC的体积.19.(12分)已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩拉样统计,先将800人按001,002,…,800进行编号.(1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了第7行至第9行)(2)抽取取100人的数学与地理的水平测试成绩如表:成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求a,b的值.(3)在地理成绩为及格的学生中,已知a≥10,b≥18,求数学成绩为优秀的人数比及格的人数少的概率.20.(12分)已知点H(﹣6,0),点P(0,b)在y轴上,点Q(a,0)在x轴的正半轴上,且满足⊥,点M在直线PQ上,且满足﹣2=,(Ⅰ)当点P在y轴上移动时,求点M的轨迹C的方程;(Ⅱ)过点T(﹣1,0)作直线l与轨迹C交于A、B两点,线段AB的垂直平分线与x轴的交点为E(x0,0),设线段AB的中点为D,且2|DE|=|AB|,求x0的值.21.(12分)已知函数f(x)=,g(x)=alnx﹣x(a≠0).(Ⅰ)求函数f(x)的单调区间;(Ⅱ)求证:当a>0时,对于任意x1,x2∈(0,e],总有g(x1)<f(x2)成立.请考生在第22、23、24题任选一题作答,如果多做,则按所做的第一题计分.作答时请写清楚题号.[选修4-1:几何证明选讲]22.(10分)如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=AC,作直线AF与圆E相切于点F,连结EF交BC于点D,已知圆E的半径为2,∠EBC=30°.(Ⅰ)求AF的长;(Ⅱ)求的值.[选修4-4:坐标系与参数方程]23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(1)把C1的参数方程化为极坐标方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).[选修4-5:不等式选讲]24.(Ⅰ)求不等式2x+2|x|≥2的解集;(Ⅱ)已知实数m>0,n>0,求证:+≥.2016年吉林省吉林大学附中高考数学二模试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,每小题给出四个选项中,只有一项符合题目要求.1.(5分)设集合A={x|<2x﹣2<1},B={x|1﹣x2≤0},则A∩B等于()A.{x|﹣1≤x≤1}B.{x|1≤x<2}C.{x|0<x≤1}D.{x|0<x<2}【解答】解:集合A={x|<2x﹣2<1}={x|﹣2<x﹣2<0}={x|0<x<2},B={x|1﹣x2≤0}={x|x≤﹣1或x≥1},所以A∩B={x|1≤x<2}.故选:B.2.(5分)在等比数列{a n}中,a1+a2=3,a3+a4=12,则a5+a6=()A.21B.42C.48D.96【解答】解:设等比数列{a n}的公比为q,则a3+a4=a1q2+a2q2=(a1+a2)q2=3q2=12,解之可得q2=4,故a5+a6=a3q2+a4q2=(a3+a4)q2=12×4=48故选:C.3.(5分)在区间[﹣1,1]上随机取一个数k,使直线y=k(x+2)与圆相交的概率为()A.B.C.D.【解答】解:圆x2+y2=1的圆心为(0,0)圆心到直线y=k(x+2)的距离为要使直线y=k(x+2)与圆x2+y2=1相交,则解得﹣<k<∴在区间[﹣1,1]上随机取一个数k,使直线y=k(x+2)与圆x2+y2=1有公共点的概率为P==故选:C.4.(5分)对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是()A.|z﹣|=2y B.z2=x2+y2C.|z﹣|≥2x D.|z|≤|x|+|y|【解答】解:由于复数z=x+yi(x,y∈R),i为虚数单位,∴|z﹣|=|2yi|=2|y|,故(A)错误.由z2 =x2﹣y2+2xyi,故(B)错误.由|z﹣|=2|y|,不一定大于或等于2x,故(C)错误.由|z|=≤=|x|+|y|,故(D)正确.故选:D.5.(5分)执行两次如图所示的程序框图,若第一次输入的a的值为﹣1.2,第二次输入的a 的值为1.2,则第一次、第二次输出的a的值分别为()A.0.2,0.2B.0.2,0.8C.0.8,0.2D.0.8,0.8【解答】解:若第一次输入的a的值为﹣1.2,满足上面一个判断框条件a<0,第1次循环,a=﹣1.2+1=﹣0.2,第2次判断后循环,a=﹣0.2+1=0.8,第3次判断,满足上面一个判断框的条件退出上面的循环,进入下面的循环,不满足下面一个判断框条件a≥1,退出循环,输出a=0.8;第二次输入的a的值为1.2,不满足上面一个判断框条件a<0,退出上面的循环,进入下面的循环,满足下面一个判断框条件a≥1,第1次循环,a=1.2﹣1=0.2,第2次判断后不满足下面一个判断框的条件退出下面的循环,输出a=0.2;故选:C.6.(5分)2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是()A.茎叶图B.分层抽样C.独立性检验D.回归直线方程【解答】解:在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,可得:K2==83.88>10.828,故有理由“性别”对判断“人机大战是人类的胜利”是否有关系时,故利用独立性检验的方法最有说服力,故选:C.7.(5分)下列函数既是奇函数,又在区间(0,1)上单调递减的是()A.f(x)=x3B.f(x)=﹣|x+1|C.f(x)=ln D.f(x)=2x+2﹣x【解答】解:A.f(x)=x3在(0,1)上单调递增,∴该选项错误;B.f(x)=﹣|x+1|的定义域为R,且f(0)=﹣1≠0;∴f(x)不是奇函数,∴该选项错误;C.的定义域为(﹣1,1),且;∴f(x)为奇函数;;在(﹣1,1)上单调递减,y=lnt单调递增;∴f(x)在(0,1)上单调递增;∴该选项正确;D.f(x)的定义域为R,且f(﹣x)=f(x);∴f(x)为偶函数;∴该选项错误.故选:C.8.(5分)已知一个几何体可切割成一个多面体及一个旋转体的一部分,其三视图如图所示,则该几何体的体积是()A.πB.π+1C.π+D.π【解答】解:根据三视图可知几何体是组合体:左边是直三棱柱、右边是半个圆柱,直三棱柱的底面是等腰直角三角形,直角边是1,侧棱长是2,圆柱的底面半径是1,母线长是2,∴该几何体的体积V==π+1,故选:B.9.(5分)给定两个命题p,q.若¬p是q的必要而不充分条件,则p是¬q的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:∵¬p是q的必要而不充分条件,∴q是¬p的充分不必要条件,即q⇒¬p,但¬p不能⇒q,其逆否命题为p⇒¬q,但¬q不能⇒p,则p是¬q的充分不必要条件.故选:A.10.(5分)将所有正偶数按如图方式进行排列,则2 016位于()A.第30行B.第31行C.第32行D.第33行【解答】解:由于题意可得:第n行的最后一个数为2[n(n+1)].令n=31,最后一个数为1984.令n=32,最后一个数为2112.∴2 016位于第32行.故选:C.11.(5分)已知四棱锥P﹣ABCD的顶点都在球O的球面上,底面ABCD是矩形,AB=2AD =4,平面P AD⊥底面ABCD,△P AD为等边三角形,则球面O的表面积为()A.B.32πC.64πD.【解答】解:令△P AD所在圆的圆心为O1,则圆O1的半径r=,因为平面P AD⊥底面ABCD,所以OO1=AB=2,所以球O的半径R==,所以球O的表面积=4πR2=.故选:D.12.(5分)已知集合{f(x)|f(x)=ax2﹣|x+1|+2a<0,x∈R}为空集,则实数a的取值范围是()A.[,+∞)B.[,+∞)C.[,+∞)D.(﹣∞,)【解答】解:∵集合{f(x)|f(x)=ax2﹣|x+1|+2a<0,x∈R}为空集,∴ax2﹣|x+1|+2a≥0恒成立,∴,设,故a≥g(x)max.令t=x+1,则.①当t=0时,g(x)=φ(t)=0,∴a≥0.②当t>0时,g(x)=φ(t)==≤,∴a≥;③当t<0时,g(x)=φ(t)=﹣=≤,∴a≥.综上,取交集得a≥.故选:B.二、填空题:本大题共4小题,每小题5分.13.(5分)若实数x,y满足的最小值是1.【解答】解:令t=x+2y作出不等式组表示的平面区域,如图所示由于t=x+2y可得y=,根据直线在y轴上的截距越大,t越大∴直线t=x+2y平移到点O(O,0)时,t取得最小值0,此时,z=1故答案为:114.(5分)已知正方形ABCD的边长为2,E为CD的中点,则•=2.【解答】解:∵已知正方形ABCD的边长为2,E为CD的中点,则=0,故=()•()=()•()=﹣+﹣=4+0﹣0﹣=2,故答案为2.15.(5分)函数f(x)的图象如图所示,f′(x)是f(x)的导函数,设a=f′(﹣2),b =f′(﹣3),c=f(﹣2)﹣f(﹣3),则a,b,c由小到大的关系为a<c<b.【解答】解:c=f(﹣2)﹣f(﹣3)=,表示(﹣2,f(﹣2))、(﹣3,f(﹣3))两点连线的斜率,a=f′(﹣2)表示(﹣2,f(﹣2))处的切线斜率,b=f′(﹣3)表示(﹣3,f(﹣3))处的切线斜率,结合函数f(x)的图象:由图可知f′(﹣2)<<f′(﹣3),即a<c<b,故答案为:a<c<b.16.(5分)已知数列满足:a1=1,a n+1=,(n∈N*),若b n+1=(n﹣λ)(+1),b1=﹣λ,且数列{b n}是单调递增数列,则实数λ的取值范围为λ<2.【解答】解:∵数列{a n}满足:a1=1,a n+1=,(n∈N*),∴,化为,∴数列是等比数列,首项为+1=2,公比为2,∴,∴b n+1=(n﹣λ)(+1)=(n﹣λ)•2n,∵数列{b n}是单调递增数列,∴b n+1>b n,∴n≥2时,(n﹣λ)•2n>(n﹣1﹣λ)•2n﹣1,化为λ<n+1,∵数列{n+1}为单调递增数列,∴λ<3.n=1时,b2=(1﹣λ)×2>﹣λ=b1,解得λ<2.综上可得:实数λ的取值范围为λ<2.故答案为:λ<2.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)已知△ABC的内角A,B,C的对边分别为a,b,c,且满足=2+2cos (A+B).(Ⅰ)求的值;(Ⅱ)若a=1,c=,求△ABC的面积.【解答】解:(Ⅰ)∵,∴sin(2A+B)=2sin A+2sin A cos(A+B),∴sin[A+(A+B)]=2sin A+2sin A cos(A+B),∴sin(A+B)cos A﹣cos A sin(A+B)=2sin A,…(2分)∴sin B=2sin A,…(4分)∴b=2a,∴.…(6分)(Ⅱ)∵,,∴b=2,∴,∴.…(10分)∴,即△ABC的面积的.…(12分)18.(12分)如图,直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面B1BCC1;(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F﹣AEC的体积.【解答】(Ⅰ)证明:∵几何体是直棱柱,∴BB1⊥底面ABC,AE⊂底面ABC,∴AE⊥BB1,∵直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E分别是BC的中点,∴AE⊥BC,BC∩BB1=B,∴AE⊥平面B1BCC1,∵AE⊂平面AEF,∴平面AEF⊥平面B1BCC1;(Ⅱ)解:取AB的中点G,连结A1G,CG,由(Ⅰ)可知CG⊥平面A1ABB1,直线A1C与平面A1ABB1所成的角为45°,就是∠CA1G,则A1G=CG=,∴AA1==,CF=.三棱锥F﹣AEC的体积:×==.19.(12分)已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩拉样统计,先将800人按001,002,…,800进行编号.(1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了第7行至第9行)(2)抽取取100人的数学与地理的水平测试成绩如表:成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求a,b的值.(3)在地理成绩为及格的学生中,已知a≥10,b≥18,求数学成绩为优秀的人数比及格的人数少的概率.【解答】(本小题满分12分)解:(1)依题意,最先检测的3个人的编号依次为785,667,199.…(3分)(2)由=0.3,解得a=14,…(5分)∵7+9+a+20+18+4+5+6+b=100,∴b=17.…(7分)(3)由题意,知a+b=31,且a≥10,b≥18,∴满足条件的(a,b)有:(10,21),(11,20),(12,19),(13,18),(14,17),(15,16),(16,15),(17,14),(18,13),(19,12),(20,11),(21,10),(22,9),(23,8)共14组,且每组出现的可能性相同.….…(9分)其中数学成绩为优秀的人数比及格的人数少有:(10,21),(11,20),(12,19),(13,18),(14,17),(15,16)共6组.…(11分)∴数学成绩为优秀的人数比及格的人数少的概率为.…(12分)20.(12分)已知点H(﹣6,0),点P(0,b)在y轴上,点Q(a,0)在x轴的正半轴上,且满足⊥,点M在直线PQ上,且满足﹣2=,(Ⅰ)当点P在y轴上移动时,求点M的轨迹C的方程;(Ⅱ)过点T(﹣1,0)作直线l与轨迹C交于A、B两点,线段AB的垂直平分线与x轴的交点为E(x0,0),设线段AB的中点为D,且2|DE|=|AB|,求x0的值.【解答】解:(Ⅰ)设点M的坐标为(x,y),则,,,,由⊥,得6a﹣b2=0.由﹣2=0,得,则由6a﹣b2=0得y2=x,故点M的轨迹C的方程为y2=x(x>0);(Ⅱ)由题意知直线l:y=k(x+1),设A(x1,y1),B(x2,y2),联立得k2x2+(2k2﹣1)x+k2=0(k≠0),由△=(2k2﹣1)2﹣4k4=1﹣4k2>0,解得﹣<k<,∴,∴,∴,,令y=0,解得,∴,∴,∴,∵,故有,则,化简得,此时.21.(12分)已知函数f(x)=,g(x)=alnx﹣x(a≠0).(Ⅰ)求函数f(x)的单调区间;(Ⅱ)求证:当a>0时,对于任意x1,x2∈(0,e],总有g(x1)<f(x2)成立.【解答】解:(Ⅰ)函数f(x)的定义域为R,.当a>0时,当x变化时,f'(x),f(x)的变化情况如下表:当a<0时,当x变化时,f'(x),f(x)的变化情况如下表:综上所述,当a>0时,f(x)的单调递增区间为(﹣1,1),单调递减区间为(﹣∞,﹣1),(1,+∞);当a<0时,f(x)的单调递增区间为(﹣∞,﹣1),(1,+∞),单调递减区间为(﹣1,1).…(5分)(Ⅱ)由(Ⅰ)可知,当a>0时,f(x)在(0,1)上单调递增,f(x)在(1,e]上单调递减,又f(0)=a,f(e)=所以f(x)min=a,同样地,当a>0时,g(x)在(0,a)上单调递增,g(x)在(a,e]上单调递减,所以g(x)max=g(a)=alna﹣a,因为a﹣(alna﹣a)=a(2﹣lna)>a(2﹣lne)=a>0,所以对于任意x1,x2∈(0,e],总有g(x)max=g(e)=alna﹣a<a=f(x)min.所以对于任意x1,x2∈(0,e],仍有x1,x2∈(0,e].综上所述,对于任意x1,x2∈(0,e],总有g(x1)<f(x2)成立.…(13分)请考生在第22、23、24题任选一题作答,如果多做,则按所做的第一题计分.作答时请写清楚题号.[选修4-1:几何证明选讲]22.(10分)如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=AC,作直线AF与圆E相切于点F,连结EF交BC于点D,已知圆E的半径为2,∠EBC=30°.(Ⅰ)求AF的长;(Ⅱ)求的值.【解答】解:(Ⅰ)如图,延长BE交圆E于点M,连结CM,则∠BCM=90°,又BM=2BE=4,∠EBC=30°,所以,又,可知,所以.根据切割线定理得,即AF=3.(Ⅱ)过E作EH⊥BC于H,则△EDH∽△ADF,从而有,又由题意知所以EH=1,因此.[选修4-4:坐标系与参数方程]23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(1)把C1的参数方程化为极坐标方程;(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).【解答】解:(1)将,消去参数t,化为普通方程(x﹣4)2+(y﹣5)2=25,即C1:x2+y2﹣8x﹣10y+16=0,将代入x2+y2﹣8x﹣10y+16=0,得ρ2﹣8ρcosθ﹣10ρsinθ+16=0.∴C1的极坐标方程为ρ2﹣8ρcosθ﹣10ρsinθ+16=0.(2)∵曲线C2的极坐标方程为ρ=2sinθ.∴曲线C2的直角坐标方程为x2+y2﹣2y=0,联立,解得或,∴C1与C2交点的极坐标为()和(2,).[选修4-5:不等式选讲]24.(Ⅰ)求不等式2x+2|x|≥2的解集;(Ⅱ)已知实数m>0,n>0,求证:+≥.【解答】解:(Ⅰ)①当x≥0时,有,由,解得.②当x<0时,有,即.解得或,又x<0,解得,则原不等式解集为{x |或}.(Ⅱ)证明:==,则,当且仅当na=mb时等号成立.第21页(共21页)。
2016届东北三省四市教研联合体高三第二次模拟数学(文)试题(图片版,)

2016年二模文科数学答案13、4 14、6 15、①② 16、117. (I )设数列}{n a 的公差为d ,数列}{n b 的公比为q由题意可得,2,91-==d a …………(2分) n a n 211-=…………(3分),211==q b …………(5分) nn b ⎪⎭⎫⎝⎛=21…………(6分)(II )|211|||n a n -=,…………(7分)当2105n n T n n -=≤时,,…………(9分) 当501062+-=≥n n T n n 时,,…………(11分)所以⎪⎩⎪⎨⎧≥+-≤-=6,50105,1022n n n n n n T n …………(12分)18. (I …………(3分); …………(6分) (II )喜欢运动的女志愿者有6人,分别设为A 、B 、C 、D 、E 、F ,其中A 、B 、C 、D 懂得医疗救护,则从这6人中任取2人有AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15种取法,…………(8分)其中两人都懂得医疗救护的有AB,AC,AD,BC,BD,CD ,共6种. …………(10分) 2人都能胜任医疗救护工作”为事件A ,…………(12分) 19. (Ⅰ)连接ED ,MN ∥ED …………(2分)又EFDA MN 平面⊄,EFDA ED 平面⊂ 所以MN ∥EFDA 平面…………(5分) (Ⅱ)由题意EFDA 平面⊥EFCB 平面⋂EFDA 平面EF EFCB =平面,CF ⊥EF ,⊂CF EFCB 平面 所以CF ⊥EFDA 平面…………(8分) 又EFDA c EFDA M V V --=21…………(9分) 4=EFDA S …………(10分)所以2=-EFDA M V …………(12分)20. (Ⅰ) 解:设),(),,(n m A y x C⎪⎪⎩⎪⎪⎨⎧+=+=2022n y m x …………(1分)所以⎩⎨⎧-=-=y n xm 4…………(2分)又4)4(2--=m n …………(3分)所以所求方程为y x 42= …………(4分)(Ⅱ)假设存在点),(00y x P设)4,(211x x A ,)4,(222x x B ,直线AB 的方程为1+=kx y联立⎩⎨⎧=+=yx kx y 412 ,得0442=--kx x ,…………(5分) 则⎩⎨⎧-==+442121x x kx x …………(6分)切线PA 的方程为)(241121x x x x y -=-点),(00y x P 代入化简得04200121=+-y x x x 同理得04200222=+-y x x x …………(7分)所以知21,x x 是方程042002=+-y x x x的两根…………(9分)则44021-==y x x …………(10分)所以10-=y ,代入圆方程得00=x …………(11分) 所以存在点)1,0(-P …………(12分)21. 解:(I )因为函数()x f 的定义域为()∞+,0. …………(2分)()x xx x f -=-='111,. …………(3分) 令 ()0111>-=-='x xx x f ,得10<<x令 ()0111<-=-='x xx x f ,得1>x . …………(4分)所以函数()x f 的单调递增区间为()10,, 函数()x f 的单调递减区间为()∞+,1. …………(5分) (II )证明:根据题意,()1ln (0)2g x x m x x=+->, 因为1x ,2x 是函数()1ln 2g x x m x=+-的两个零点, 所以111ln 02x m x +-=,221ln 02x m x +-=. 两式相减,可得122111ln22x x x x =-, …………7分 即112221ln 2x x x x x x -=,故1212122lnx x x x x x -=.那么1211212ln x x x x x -=,2121212ln x x x x x -=.令12x t x =,其中01t <<,则1211112ln 2ln 2ln t t t t x x t t t---+=+=. 构造函数1()2ln (01)h t t t t t=--<<, ……………10分则22(1)'()t h t t -=.因为01t <<,所以'()0h t >恒成立,故()(1)h t h <,即12ln 0t t t--<.可知112ln t t t->,故121x x +>. ……………12分 22. (Ⅰ)由题意可知BDC CBD ∠=∠…………(1分)所以DAC CAB ∠=∠…………(2分)由角分线定理可知,AB BM AD MD =,即AB MD AD BM⋅=⋅得证. …………(4分)(Ⅱ)由题意BM CP MD CB =,即AB CP AD CB =,. …………(4分)由四点共圆有BAD BCP ∠=∠. …………(5分)所以BCP ∆∽BAD ∆.. …………(6分) 所以ADB CBP ∠=∠. …………(7分)又BAC CBP ∠=∠,ADB ACB ∠=∠. …………(8分) 所以ACB BAC ∠=∠. …………(9分) 所以AC AB =. …………(10分)23. 解:(I)曲线C 的直角坐标方程为141222=+y x …………(1分)左焦点)0,22(-F 代入直线AB 的参数方程 得22-=m …………(2分)直线AB 的参数方程是⎪⎪⎩⎪⎪⎨⎧=+-=t y t x 222222(为参数t ) 代入椭圆方程得0222=--t t …………(3分) 所以||||FB FA ⋅=2…………(4分)(Ⅱ) 设椭圆C 的内接矩形的顶点为)sin 2,cos 32(θθ,)sin 2,cos 32(θθ-,)sin 2,cos 32(θθ-,)20)(sin 2,cos 32(πθθθ<<--…………(6分) 所以椭圆C 的内接矩形的周长为θθsin 8cos 38+=)3sin(16πθ+…………(8分)当23ππθ=+时,即6πθ=时椭圆C 的内接矩形的周长取得最大值16…………(10分)24. 解析:(I)错误!未找到引用源。
吉林省实验中学2016届高三上学期第二次模拟考试文数试

考试时间:(120分钟 ) 试卷满分:(150分 )第Ⅰ卷 (选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四 个选项中,只有一项是符合题目要求的.)1. 已知集合{}1log |2<=x x A ,{}02|2<-+=x x x B ,则A ∪B =( )A .()2,∞-B .()10,C .()22,-D .()1,∞- 【答案】C 【解析】试题分析:由已知{|02}A x x =<<,{|21}B x x =-<<,所以{|22}A B x x =-<<,故选C .考点:集合的运算.2. 下列命题中正确的是( ) A .若p ∨q 为真命题,则p ∧q 为真命题B .“x =5”是“x 2-4x -5=0”的充分不必要条件C .命题“若x <-1,则x 2-2x -3>0”的否定为:“若x ≥-1,则x 2-2x -3≤0” D .已知命题p :∃x ∈R ,x 2+x -1<0,则⌝p :∃x ∈R ,x 2+x -1≥0 【答案】B考点:命题的真假判断.3. 当0<x <1时,2212)(,)(,)(-===x x h x x g x x f 的大小关系是( ) A.)()()(x f x g x h << B.)()()(x g x f x h <<C.)()()(x f x h x g <<D.)()()(x h x g x f << 【答案】D考点:比较大小.4.设复数z =a +b i(a ,b ∈R),若z1+i=2-i 成立,则点P (a ,b )在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 【答案】A 【解析】试题分析:(2)(1)2213z i i i i i =-+=+-+=+,所以(,)(3,1)a b =,点P 在第一象限,故选A .考点:复数的运算,复数的几何意义. 5. 已知k yx==72,411=-yx ,则k 的值是( ) A .472⎪⎭⎫ ⎝⎛ B .4172⎪⎭⎫⎝⎛ C .415 D .4127⎪⎭⎫⎝⎛ 【答案】B 【解析】试题分析:由题意2log x k =,7log y k =,所以2711112log 2log 7log 4log log 7k k k x y k k -=-=-==,427k =,142()7k =,故选B .考点:对数的运算,换底公式.6.下列区间中,函数|)2ln(|)(x x f -=在其上为增函数的是 ( )A .(-,1∞]B .41,3⎡⎤-⎢⎥⎣⎦ C .)30,2⎡⎢⎣D .[)1,2【答案】D【解析】试题分析:ln(2),1()ln(2),12x x f x x x -≤⎧=⎨--<<⎩,只有ln(2)y x =--是增函数,因此()f x 的增区间为[1,2),故选D . 考点:函数的单调性.7. 如图,函数()x f 的图象在P 点处的切线方程是172+-=x y ,若点P 的横坐标是5,则(5)'(5)f f +=( )A .5B .5-C .10D .10-【答案】A考点:导数的几何意义.8.设函数()()212log ,0log ,0x x f x x x >⎧⎪=⎨-<⎪⎩,若()()f a f a >-,则实数a 的取值范围是A .()01,-∪()10,B .()1-∞-,∪()∞+,1 C .()01,-∪()∞+,1D .()1-∞-,∪()10,【答案】C 【解析】试题分析:0a >时,212log log a a >,1a >,当0a <时,122log ()log ()a a ->-,01a <-<,10a -<<,所以有101a a -<<>或,故选C .考点:对数函数的性质,分段函数.9.函数y =x2-2sin x 的图象大致是 ( )【答案】C考点:函数的图象.【名师点晴】解数学选择题的很多,常见的解法有直接法、数形结合法、特例法、验证法(代入法)、排除法(筛选法、淘汰法)、估算法、极限法等等,具体解题时可以把多种方法结合起来,会使题目的求角过程简单化.解选择题时既要看到各种常规题的解题思想方法,又要充分挖掘题目的“个性”特征,寻求简便解法,充分利用选择题的暗示作用,迅速地指出正确的选择,可以迅速、准确地得出正确答案,还可以提高解题速度,为后续解题节省时间,对于选择题一定要“小题小做,小题巧做”,切忌小题大做.10.定义在R 上的函数)(x f 满足)()4(),()(x f x f x f x f =--=-且)0,1(-∈x 时,512)(+=x x f ,则=)20(log 2f ( )A.1-B.54- C.54 D.1【答案】A 【解析】试题分析:由()()f x f x -=-知()f x 是奇函数,由(4)()f x f x -=知()f x 是周期函数,且周期为4,又24l o g 205<<,所以22222164(log 20)(log 204)(4log 20)(log )(log )205f f f f f =-=--=-=-=24log 51(2)15-+=-,故选A . 考点:函数的奇偶性、周期性,对数的运算. 11. 设函数xx x f +=1)(,则使得()(21)f x f x >-成立的x 的取值范围是( )A .1,13⎛⎫ ⎪⎝⎭B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C .11,33⎛⎫- ⎪⎝⎭D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭【答案】A考点:函数的奇偶性与单调性.【名师点晴】解函数不等式()()f m f n >的方法一般是利用函数的单调性,直接去掉符号""f ,化为()m n m n ><或,如果函数()f x 为奇函数,题目形式为12()()0f x f x +>形式,化为22()()f x f x >-,如果函数()f x 为偶函数,题目形式为12()()f x f x >形式,化为12()()f x f x >.12. 若a 、b分别是方程lg 4x x +=与104x x +=的解,函数()()22,02,0x a b x x f x x ⎧+++≤=⎨>⎩,则关于x 的方程()f x x =的解的个数是( )A .1B .2C .3D .4【答案】C 【解析】试题分析:两方程lg 4x x +=与104x x +=化为lg 4x x =-和104xx =-,因此两方程lg 4x x +=与104x x +=的解可以看作是函数lg y x =和10x y =分别与直线4y x =-的交点的横坐标,而函数lg y x =和10xy =互为反函数,它们的图象关于直线y x =对称,又直线4y x =-与直线y x =垂直,交点为(2,2),所以有4a b +=,当0x >时,()f x x =的解为2x =,当0x ≤时,方程242x x x ++=有两解1-和2-,因此方程()f x x =有三解,故选C .考点:函数与方程的应用.【名师点晴】判断函数零点个数最常用的方法是令f(x)=0,转化为方程根的个数,解出方程有几个根,函数y =f(x)就有几个零点,如果方程的根解不出,还有两种方法判断:方法一是基本方法,是利用零点的存在性原理,要注意参考单调性可判定零点的唯一性;方法二是数形结合法,要注意作图技巧.本题中求a b +,就是把两方程lg 4x x +=与104x x +=的解转化为函数lg y x =和10x y =分别与直线4y x =-的交点的横坐标.第Ⅱ卷 (非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13. 若函数f(x)=xln ()为偶函数,则a= 【答案】1考点:函数的奇偶性.14.函数f (x )=ax 3+bx 2+cx +d 的部分数值如下表:则函数y =lg f (x )的定义域为__________. 【答案】),2()1,1(+∞⋃- 【解析】试题分析:由表格可知函数()f x 的图象的变化趋势如图所示,则()0f x >的解为112x x -<<>或.考点:函数的图象,函数的定义域.15.已知:函数m x g x x f x-==)21()(,)(2,若对][][,2,0,2,121∈∃-∈∀x x 使得)()(21x g x f >,则实数m 的取值范围__________【答案】41>m考点:不等式恒成立,函数的最值.【名师点晴】不等式恒成立问题经常转化为求函数的最值,这时我们要注意题中量词“对于任意的”、“存在”,如x R ∀∈,()f x m >恒成立,则m 小于()f x 的最小值,x R ∃∈,()f x m >恒成立,则m 小于()f x 的最大值等等.16. 对于函数x x f )31()(=定义域中的任意)(,2121x x x x ≠,有如下结论: ①);()()(2121x f x f x x f ∙=+②);()()(2121x f x f x x f +=⋅③0)()(2121<--x x x f x f ;④2)()()2(2121x f x f x x f +<+.上述结论中正确结论的序号是 . 【答案】①③④ 【解析】试题分析:12121212111()()()()()()333x x x x f x x f x f x ++==⋅=,①正确,又1212111()()()333x x x x ≠+,②错,函数1()()3x f x =是减函数,③正确,12121221111()()[()()]23233x x x x x x f ++==+12()()2f x f x +=,④正确.考点:命题的真假判断,指数函数的性质.【名师点晴】本题考查命题真假判断,实质上是考查函数的性质.对于这种给出具体函数式的问题,只要把函数式代入一一验证即可,解决此类问题不能限入误区,认为这类问题都是有难度,没处下手,事实上最简单的方法反而是最好的方法.三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或 演算步骤)17.(本题满分12分) 已知函数ππ1()cos()cos()sin cos 334f x x x x x =+--+ (1)求函数)(x f 的最小正周期和最大值;(2)求函数()f x 单调递增区间【答案】(1)最小正周期为 T π=,最大值为2;(2)5[,],88k k k z ππππ--∈考点:三角函数的周期、最值、单调区间. 18. (本小题满分12分)已知数列{}n a 满足首项为12a =,12n n a a +=,*()n ∈N .设23lo g 2n n b a =- *()n ∈N ,数列{}n c 满足n n n b a c =.(Ⅰ)求证:数列{}n b 成等差数列; (Ⅱ)求数列{}n c 的前n 项和n S .【答案】(Ⅰ)见解析;(Ⅱ)110(53)2n n S n +=--⋅考点:等比数列通项公式,等差数列的证明,错位相减法求和. 【名师点晴】1.一般地,如果数列{n a }是等差数列,{n b }是等比数列,求数列{n n a b ⋅ }的前n 项和时,可采用错位相减法.2.用乘公比错位相减法求和时,应注意:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式. 19.(本题满分12分)四棱锥P ABCD -底面是平行四边形,面PAB ⊥面ABCD ,12PA PB AB AD ===,060BAD ∠=,,E F 分别为,AD PC 的中点. (1)求证://EF PAB 面 (2)求证:EF PBD ⊥面【答案】证明见解析.DB AG⊥-----------------------②---------------------------------10分由 ①②可知,,AG PB AG BD AG PBD ⊥⊥∴⊥面//,EF AG EF PBD ∴⊥又面-----------------------------------------------12分考点:线面平行与线面垂直的判断.20. 为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500 ml 以上为常喝,体重超过50 kg 为肥胖.已知在这30人中随机抽取1人,抽到肥胖的学生的概率为415.(1)请将上面的列联表补充完整.(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.(3)现从常喝碳酸饮料且肥胖的学生(其中有2名女生)中,抽取2人参加电视节目,则正好抽到1男1女的概率是多少? 参考数据:参考公式:K 2=))()()(()(2d b c a d c b a cb ad n ++++-,其中n =a +b +c +d.【答案】(1)见解析;(2)有关;(3)815.试题解析:(1)设常喝碳酸饮料且肥胖的学生有x 人,则x +230=415,解得x =6.列联表如下:(2)由已知数据可得K 2=10×20×8×22≈8.523>7.879,因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.(3)设常喝碳酸饮料且肥胖的男生为A ,B ,C ,D ,女生为E ,F ,则任取2人有AB ,AC ,AD ,AE ,AF ,BC ,BD ,BE , BF ,CD ,CE ,CF ,DE ,DF ,EF ,共15种.其中是1男1女的有AE ,AF ,BE ,BF ,CE ,CF ,DE ,DF ,共8种, 故正好抽到1男1女的概率P =.考点:古典概型,独立性检验.21.设()()256ln f x a x x =-+,其中a R ∈,曲线()y f x =在点()()1,1f 处的切线与y 轴相交于点()0,6. (1)确定a 的值;(2)求函数()f x 的单调区间与极值. 【答案】(1)12a =;(2)()f x 在(0,2),(3,)+∞上为增函数,在(2,3)为减函数.极大值9(2)6ln 22f =+,极小值(3)26ln 3f =+.考点:导数的几何意义,函数的单调性、极值.【名师点晴】1.曲线的切线的求法:若已知曲线过点P(x0,y0),求曲线过点P的切线则需分点P(x0,y0)是切点和不是切点两种情况求解.(1)点P(x0,y0)是切点的切线方程为y-y0=f′(x0)(x-x0).(2)当点P(x0,y0)不是切点时可分以下几步完成:第一步:设出切点坐标P′(x1,f(x1));第二步:写出过P′(x1,f(x1))的切线方程为y-f(x1)=f′(x1)(x-x1);第三步:将点P的坐标(x0,y0)代入切线方程求出x1;第四步:将x1的值代入方程y-f(x1)=f′(x1)(x-x1)可得过点P(x0,y0)的切线方程.2.求可导函数单调区间的一般步骤和方法:(1)确定函数f(x)的定义域;(2)求f′(x),令f′(x)=0,求出它在定义域内的一切实根;(3)把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来,然后用这些点把函数f(x)的定义区间分成若干个小区间;(4)确定f′(x)在各个开区间内的符号,根据f′(x)的符号判定函数f(x)在每个相应小开区间内的增减性.3.可导函数极值存在的条件:(1)可导函数的极值点x0一定满足f′(x0)=0,但当f′(x1)=0时,x1不一定是极值点.如f(x)=x 3,f′(0)=0,但x =0不是极值点.22.在直角坐标xOy 中,直线l的参数方程为132(x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数),以原点为极点,x 轴的正半轴为极轴建立极坐标系,C的极坐标方程为ρθ=.(Ⅰ)写出C 的直角坐标方程;直线l 的直角坐标方程(Ⅱ)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求点P 的坐标. 【答案】(Ⅰ)22(3x y +=;(Ⅱ)(3,0).考点:极坐标方程与直角坐标方程的互化,直线参数方程的应用,两点间的距离公式.。
2016届吉林大学附中高三第二次模拟考试数学(文)试题(解析版)

2016届吉林大学附中高三第二次模拟考试数学(文)试题一、选择题1.设集合221{|21}{|10}4x A x B x x -=<<=-,…,则A B 等于( ) (A ){|11}x x -≤… (B ){|12}x x <≤ (C ){|01}x x <≤ (D ){|02}x x <<【答案】B【解析】试题分析:对于集合A ,21214x -<<等价于220222,02x x --<<<<,对于集合B ,解得1,1x x ≤-≥,所以[)1,2A B ⋂=.【考点】1.集合交集;2.指数不等式;3.一元二次不等式.【易错点晴】高考对集合知识的考查要求较低,均是以小题的形式进行考查,一般难度不大,要求考生熟练掌握与集合有关的基础知识.纵观近几年的高考试题,主要考查以下两个方面:一是考查具体集合的关系判断和集合的运算.解决这类问题的关键在于正确理解集合中元素所具有属性的含义,弄清集合中元素所具有的形式以及集合中含有哪些元素.二是考查抽象集合的关系判断以及运算.注意区间端点的取舍. 2.已知等比数列{a n }中,123a a +=,3412a a +=,则56a a +=( ) (A )3 (B )15 (C )48 (D )63 【答案】C【解析】试题分析:234124a a q a a +==+,所以()2563448a a a a q +=+⋅=.【考点】等比数列.3.在区间[11]-,上随机取一个数k ,使直线(2)y k x =+与圆221x y +=相交的概率为( )(A )12 (B )13(C(D【答案】C【解析】试题分析:直线与圆相交,则圆心到直线的距离小于半径,即21,31,d k k =<<<<232=. 【考点】1.几何概型;2.直线与圆的位置关系.4.设复数i z x y =+ (x ,y ∈R ),i 为虚数单位,则下列结论正确的是( ) (A )|z -z |=2y (B )z 2=x 2+y 2(C )|z -z |2x ? (D )|z|… |x|+|y|【答案】D【解析】试题分析:2z z y -=,故A ,C 选项不正确,2222z x y xyi =-+,故B 选项不正确,故选D. 【考点】复数运算.5.执行两次下图所示的程序框图,若第一次输入的a 的值为 1.2-,第二次输入的a 的值为1.2,则第一次、第二次输出的a 的值分别为( )(A )0.2,0.2 (B )0.2,0.8 (C )0.8,0.2 (D )0.8,0.8 【答案】C【解析】试题分析:第一次, 1.20, 1.210.20,0.210.8a a a =-<=-+=-<=-+=,输出0.8a =;第二次, 1.21, 1.210.2a a =>=-=,输出0.2a =,故选C.【考点】算法与程序框图.6.2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见, 2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是( ) (A )茎叶图 (B )分层抽样 (C )独立性检验 (D )回归直线方程 【答案】C 【解析】试题分析:这是独立性检验,因为这里有两个分类变量,一个是性别分为男女,一个是意见分为支持和反对,这样就构成一个22⨯联表,用独立性检验来验证“人机大战是人类的胜利”是否有关系. 【考点】概率统计.7.下列函数既是奇函数,又在区间(01),上单调递减的是( ) (A )3()f x x = (B )()|1|f x x =-+ (C )1()ln1xf x x-=+ (D )()22x x f x -=+ 【答案】C【解析】试题分析:A 为增函数,B 为非奇非偶函数,D 为偶函数,故C 正确. 【考点】函数单调性8.给定两个命题p ,q ,若⌝p 是q 的必要而不充分条件,则p 是⌝q 的( ) (A )充分而不必要条件 (B )必要而不充分条件 (C )充要条件 (D )既不充分也不必要条件 【答案】A【解析】试题分析:若p ⌝是q 的必要而不充分条件,说明p ⌝是大范围,q 是小范围.故p 是小范围,q ⌝是大范围.所以p 是q ⌝的充分不必要条件.【考点】充要条件. 9.已知四棱锥P ABCD -的顶点都在球O 的球面上,底面ABCD 是矩形,24AB AD ==,平面PAD ⊥底面ABCD ,PAD △为等边三角形,则球面O 的表面积为( ) (A )323π (B )32π (C )64π (D )643π【答案】D【解析】试题分析:将四棱锥P ABCD -补成正三棱柱,则四棱锥P ABCD -的外接球就是正三棱柱的外接球,PAD ∆是边长为4的等边三角形,由此可得外接球球的半径为3,故表面积为26443R ππ=.【考点】球的内接几何体.【思路点晴】常见的图形有正三角形,直角三角形,矩形,它们的外心可用其几何性质求;而其它不规则图形的外心,可利用正弦定理来求.若长方体长宽高分别为,,a b c 则其体长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心.10.已知集合2{()|()|1|20}f x f x ax x a x =-++<∈R ,为空集,则实数a 的取值范围是( ) (A)+)∞ (B)+)∞ (C)+)∞ (D)(-∞ 【答案】B【解析】试题分析:原不等式可化为212x a x +<+,由于解集为空集,即212x a x +≥+恒成立,故可先排除D 选项.令()212x g x x +=+,当1x =-时,()10g -=;当1x >-时()212x g x x +=+,()()()222221'2x x x g x x +-+=+()222222x x x --+=+,令()'0,g x x ==,故())1g x g≤=,所以a ≥;同理可求的,当1x <-时,()21124x g x x --=≤+,14a ≥,综上所述选B . 【考点】导数与不等式.【思路点晴】恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.不等式的恒成立问题和有解问题、无解问题是联系函数、方程、不等式的纽带和桥梁,也是高考的重点和热点问题,往往用到的方法是依据不等式的特点,等价变形,构造函数,借助图像观察,或参变分离,转化为求函数的最值问题来处理.二、填空题11.将所有正偶数按如下方式进行排列,则2 016位于( ) 第1行:2 4第2行:6 8 10 12第3行:14 16 18 20 22 24第4行:26 28 30 32 34 36 38 40 …… …… ……(A )第30行 (B )第31行 (C )第32行 (D )第33行 【答案】C【解析】试题分析:201610082=,每行的项数是行数的两倍,故第n 行有2n 个数,前n 行有()2222n n n n +=+项,代入选项验证可知,C 正确.【考点】数列12.若实数x ,y 满足1000x y x y x -+⎧⎪+⎨⎪⎩≥,≥,≤,则z=3x+2y的最小值是 .【答案】1【解析】试题分析:画出可行域如下图所示,由图可知,目标函数在点()0,0取得最小值为031=.【考点】线性规划.13.已知正方形ABCD 的边长为2,E 为CD 的中点,则AE BD ⋅=__________.【答案】2【解析】试题分析:()14222AE BD AD AB AD AB ⎛⎫⋅=+⋅-=-= ⎪⎝⎭.【考点】向量运算.14.函数()f x 的图象如图所示,()f x '是()f x 的导函数,设(2)a f '=-,(3)b f '=-,(2)(c f f =---,则a b c ,,由小到大的关系为 .【答案】a c b <<【解析】试题分析:设()()()()2,2,3,3A f B f ----,(2)(3)2(3)f f c ---=---,故c 的几何意义是AB 两点的斜率,a 的几何意义是在A 点切线的斜率,b 的几何意义是在B 点切线的斜率,由图象可知a c b <<. 【考点】函数与导数.【思路点晴】导数的几何意义就是函数在某点切线的斜率,本题中,,A B 两点切线的斜率分别为()'2f -和()'3f -,这样我们在图像上就可以发现这两个值的大小关系.本题的难点在于c ,观察c ,(2)(3)c f f =---,注意到()231---=,我们就可以将c 转化为(2)(3)2(3)f f c ---=---,其表示的几何意义就是过AB 两点割线的斜率.15.已知数列{a n }满足a 1=1,1*()2n n n a a n a +=∈+N .若111()(1)n nb n b a λλ+=-+=-,,且数列{b n }是递增数列,则实数λ的取值范围是 .【答案】(2)-∞,【解析】试题分析:易知1121n n a a +=+,所以111121n n a a +⎛⎫+=+ ⎪⎝⎭,又11a =,故111222n nna -+=⋅=,所以()()112,12n n n nb n b n λλ-+=-⋅=--⋅,当1n =是,上式也符合,所以()11120n n n b b n λ-+-=-+⋅>所以1n λ+>,故2λ<.【考点】数列与不等式.【思路点晴】这些题都是由递推公式推导通项公式,由1a 和递推关系求通项公式,可观察其特点,一般常利用“化归法”、“累加法”、“累乘法”、“构造等比数列”、“迭代”等方法.递推公式推导通项公式方法:(1)累加法:1()n n a a f n +-=(2)累乘法:1()n na f n a +=(3)待定系数法:1n n a pa q +=+(其中,p q 均为常数,)0)1((≠-p pq )解法:把原递推公式转化为:)(1t a p t a n n -=-+,其中pqt -=1,再利用换元法转化为等比数列求解.三、解答题16.已知ABC △的内角A B C ,,的对边分别为a b c ,,,且满足sin(2)22cos()sin A B A B A+=++.(Ⅰ)求ba的值;(Ⅱ)若1a c =,ABC △的面积.【答案】(I )2ba=;(II 【解析】试题分析:(I )利用两角和的正弦、余弦公式,化简sin(2)22cos()sin A B A B A+=++,得到sin 2sin B A =,利用正弦定理得到2ba=;(II )由(I )可求得2b =,先求出一个角的余弦值,再求其正弦值,最后利用三角形面积公式求面积. 试题解析:解析:(Ⅰ)∵sin(2)22cos()sin A B A B A+=++,∴s i n (2)2s i n 2s i n c o s ()A B A A A B +=++, ∴sin[()]2sin 2sin cos()A A B A A A B ++=++,∴s i n (A B A AA B+-+=, ∴sin 2sin B A =,∴2b a =,∴2ba=.(Ⅱ)∵1a c ==,,2ba =,∴2b =,∴2221471cos 242a b c C ab +-+-===-,∴23C π=.∴11sin 1222ABC S ab C ==⋅⋅=△ABC △ 【考点】三角函数与解三角形.17.如图,直三棱柱ABC -A 1B 1C 1的底面是边长为2的正三角形,E ,F 分别是BC ,CC 1的中点.(Ⅰ)证明:平面AEF⊥平面B 1BCC 1;(Ⅱ)若直线A 1C 与平面A 1ABB 1所成的角为45°,求三棱锥F -AEC 的体积.【答案】(I )证明见解析;(II )12【解析】试题分析:(I )要证明面面垂直,实际上就是要证明线面垂直,由图像可知,只需证明AE ⊥平面11B BCC ,注意到几何体为直棱柱,侧棱和底面垂直,加上底面三角形为等边三角形,第一问就可以证明出来了;(II )先作出直线1AC 与平面11A ABB 所成的角,由此求出高2FC =,进而求出体积为12试题解析:(Ⅰ)证明:如图,因为三棱柱ABC A 1B 1C 1是直三棱柱,所以AE⊥BB 1. 又E 是正三角形ABC 的边BC 的中点,所以AE⊥BC. 又1BC BB B = ,因此AE⊥平面B 1BCC 1. 而AE ⊂平面AEF ,所以平面AEF⊥平面B 1BCC 1.(Ⅱ)设AB 的中点为D ,连接A 1D ,CD. 因为△ABC 是正三角形,所以CD⊥AB.又三棱柱ABC A 1B 1C 1是直三棱柱,所以CD⊥AA 1. 又1AB AA A = ,因此CD⊥平面A 1ABB 1, 于是∠CA 1D 为直线A 1C 与平面A 1ABB 1所成的角. 由题设,∠CA 1D =45°,所以A 1D =CD在Rt△AA 1D 中,AA 1FC =12AA 1故三棱锥F AEC 的体积V =13S △AEC ·FC=13×【考点】立体几何.18.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩抽样统计,先将800人按001002003,,,,L 进行编号. (Ⅰ)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了第7行 至第9行)84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 7663 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54(Ⅱ)抽的100人的数学与地理的水平测试成绩如下表:成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有2018442++=人,若在该样本中,数学成绩优秀率为30%,求a b ,的值.(Ⅲ)将108a b ≥,≥的a b ,表示成有序数对()a b ,,求“在地理成绩为及格的学生中,数学成绩为优秀的人数比及格的人数少”的数对()a b ,的概率. 【答案】(I )785667199,,;(II )14,17a b ==;(III )37. 【解析】试题分析:(I )按随机数表法,最先检测的3个人的编号依次为785667199,,;(II )由790.3100a++=,得14a =,因为792018456100a b ++++++++=,所以17b =;(III )由题意,知31a b +=,且108a b ≥,≥,列举出所有可能有14中,其中符合题意的有6种,故概率为37. 试题解析:(Ⅰ)依题意,最先检测的3个人的编号依次为785667199,,. (Ⅱ)由790.3100a++=,得14a =, 因为792018456100a b ++++++++=,所以17b =.(Ⅲ)由题意,知31a b +=,且108a b ≥,≥. 故满足条件的()a b ,有:(1021)(1120)(1219)(1318)(1417)(1516),,,,,,,,,,,, (1615),,(1714)(1813)(1912)(2011)(2110)(229)(238),,,,,,,,,,,,,共14组. ……9分其中数学成绩为优秀的人数比及格的人数少有:(1021)(1120)(1219)(1318),,,,,,,, (1417),,(1516),共6组. ∴数学成绩优秀的人数比及格的人数少的概率为63147=. 【考点】概率统计.19.已知点(60)H -,,点(0)P b ,在y 轴上,点(0)Q a ,在x 轴的正半轴上,且满足HP ⊥PQ ,点M 在直线PQ 上,且满足PM -2MQ=0,(Ⅰ)当点P 在y 轴上移动时,求点M 的轨迹C 的方程;(Ⅱ)过点(10)T -,作直线l 与轨迹C 交于A 、B 两点,线段AB 的垂直平分线与x 轴的交点为0(0)E x ,,设线段AB 的中点为D,且2|||DE AB ,求0x 的值. 【答案】(I )2(0)y x x =>;(II )053x =. 【解析】试题分析:(I )设点M 的坐标为()x y ,,由HP PQ ⊥,得:260a b -=,将坐标代入20PM MQ -= ,消去,a b ,即可求得轨迹方程为2y x =;(II )由题意知直线:(1)l y k x =+,联立直线方程和抛物线的方程,结合跟与系数的关系,可求得211(1)22D k k -,,211(0)22E k -,,由弦长公式得到12|||AB x x -,代入2|||DE AB 可解出2313k =,此时053x =.试题解析:(Ⅰ)设点M 的坐标为()x y ,,则 (6)HP b = ,,()PQ a b =- ,,()PM x y b =-,,()MQ a x y =-- ,, 由HP ⊥PQ,得:260a b -=.由PM -2MQ =0得:32()223x a x a xy b y b y⎧=-=⎧⎪⇒⎨⎨-=-⎩⎪=⎩,则由260a b -=得2y x =,故点M 的轨迹C 的方程为2y x =(0)x >.(Ⅱ)由题意知直线:(1)l y k x =+,设A 11()x y ,,B 22()x y ,,则 联立2(1)y k x y x =+⎧⎨=⎩,,得2222(21)0(0)k x k x k k +-+=≠,2140k ∆=->. ∴12122121x x x x k +=-=,,∴12122y y k +=,∴211(1)22D k k-,, 2111:(1)22DE l y x k k k =--++,令0y =,解得022111112222x k k =-+=-, ∴211(0)22E k -,,∴||DE ==∴12|||AB x x =-==,∵2|||DE AB21||k +=1||k =,化简得2313k =,此时053x =. 【考点】直线与圆锥曲线的位置关系.【方法点晴】直线与圆锥曲线位置关系的判断、有关圆锥曲线弦的问题等能很好地渗透对函数方程思想和数形结合思想的考查,一直是高考考查的重点,特别是焦点弦和中点弦等问题,涉及中点公式、根与系数的关系以及设而不求、整体代入的技巧和方法,也是考查数学思想方法的热点题型.涉及弦长的问题中,应熟练地利用根与系数关系、设而不求法计算弦长;涉及垂直关系时也往往利用根与系数关系、设而不求法简化运算;涉及过焦点的弦的问题,可考虑用圆锥曲线的定义求解. 20.已知函数2()1axf x a x =++,g (x )=aln x -x (a ≠0). (Ⅰ)求函数f (x )的单调区间;(Ⅱ)证明:当a > 0时,对于任意x 1,x 2∈(0,e],总有g (x 1) < f (x 2)成立,其中e 2.71828= 是自然对数的底数.【答案】(I )当0a >时,()f x 的单调递增区间为()1,1-,单调递减区间为(),1-∞-,()1,+∞,当0a <时,()f x 的单调递增区间为(),1-∞-,()1,+∞,单调递减区间为()1,1-;(II )证明见解析. 【解析】试题分析:(I )先求导()()()()2211'1a x x f x x-+=+,由此,对a 进行分类讨论,0a >时,开口向下,0a <时,开口向上,分别画出对应导函数的图象,从而得出单调区间.(II )由(I )当0a >时,()f x 在()0,1是正函数,在()1,e 上为减函数.()()f x f e a >>.用(I )的方法,对()g x 求导后进行分类讨论,利用导数证明()max g x a <恒成立即可.试题解析:(Ⅰ)函数f (x )的定义域为R ,f ′(x )=()()22211a x x-+=()()()22111a x x x-++.综上所述,当a>0时,f (x )的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);当a<0时,f (x )的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).(Ⅱ)由(Ⅰ)可知,当a>0时,f (x )在区间(0,1)上单调递增,f (x )>f (0)=a ;f (x )在区间(1,e]上单调递减,且f (e )=21aee ++a>a ,所以当x∈(0,e]时,f (x )>a.因为g (x )=aln x -x ,所以g′(x )=ax-1,令g′(x )=0,得x =a. ①当a≥e 时,g′(x )≥0在区间(0,e]上恒成立,所以函数g (x )在区间(0,e]上单调递增,所以g (x )max =g (e )=a -e<a. 所以对于任意x 1,x 2∈(0,e],仍有g (x 1)<f (x 2).②当0<a<e 时,由g′(x )>0,得0<x<a ;由g′(x )<0,得e≥x>a,所以函数g (x )在区间(0,a )上单调递增,在区间(a ,e]上单调递减.所以g (x )max =g (a )=aln a -a.因为a -(aln a -a )=a (2-ln a )>a (2-ln e )=a>0, 所以对任意x 1,x 2∈(0,e],总有g (x 1)<f (x 2).综上所述,对于任意x 1,x 2∈(0,e],总有g (x 1)<f (x 2). 【考点】1.函数导数与不等式;2.不等式存在性问题与恒成立问题.【方法点晴】不等式的恒成立问题和有解问题、无解问题是联系函数、方程、不等式的纽带和桥梁,也是高考的重点和热点问题,往往用到的方法是依据不等式的特点,等价变形,构造函数,借助图象观察,或参变分离,转化为求函数的最值问题来处理.含参数的不等式()()f x g x >恒成立、有解、无解的处理方法:①()y f x =的图象和()y g x =图象特点考考虑;②构造函数法,一般构造()()()F x f x g x =-,转化为()F x 的最值处理;③参变分离法,将不等式等价变形为()a h x >,或()a h x <,进而转化为求函数()h x 的最值.21.选修4-1:几何证明选讲如图,过圆E 外一点A 作一条直线与圆E 交于B C ,两点,且13AB AC =,作直线AF 与圆E 相切于点F ,连结EF 交BC 于点D ,已知圆E 的半径为2,30EBC ∠=︒.CA(Ⅰ)求AF 的长; (Ⅱ)求EDAD的值. 【答案】(I )3AF =;(II )13ED AD =. 【解析】试题分析:(I )延长BE 交圆E 于点M ,连结CM ,则90BCM ∠=︒,结合已知条件可得AC =,利用切割线定理得29AF AB AC =⋅=;(II )过E 作EH BC ⊥于H ,则EDH ADF △∽△,对应边成比例ED EH AD AF =,由此求得13ED AD =.试题解析:(Ⅰ)延长BE 交圆E 于点M ,连结CM ,则90BCM ∠=︒, 又2430BM BE EBC ==∠=︒,,所以BC =, 又13AB AC=,可知12AB BC =AC =.根据切割线定理得29AF AB AC =⋅,即3AF =. (Ⅱ)过E 作EH BC ⊥于H ,则EDH ADF △∽△,从而有ED EHAD AF=,又由题意知122CH BC EB ===,所以1EH =,因此13ED AD =. 【考点】几何证明选讲.22.选修4-4:坐标系与参数方程已知曲线1C 的参数方程为45cos 55sin x ty t =+⎧⎨=+⎩(t 为参数),以坐标原点为极点,x 轴非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=. (Ⅰ)把1C 的参数方程化为极坐标方程;(Ⅱ)求1C 与2C 交点的极坐标(其中002ρθπ<≥≤,).【答案】(I )28cos 10sin 160ρρθρθ--+=;(II))4π,(2)2π,.【解析】试题分析:(I )先消去参数t 化为直角坐标方程22(4)(5)25x y -+-=,利用cos sin x y ρθρθ=⎧⎨=⎩代入上式可得极坐标方程为28cos 10sin 160ρρθρθ--+=;(II )由222281016020x y x y x y y ⎧+--+=⎪⎨+-=⎪⎩,,解得11x y =⎧⎨=⎩或02x y =⎧⎨=⎩,再化为极坐标为)4π,(2)2π,. 试题解析:(Ⅰ)将45cos 55sin x ty t=+⎧⎨=+⎩消去参数t ,化为普通方程22(4)(5)25x y -+-=,即221:810160C x y x y +--+=.将cos sin x y ρθρθ=⎧⎨=⎩,,代入22810160x y x y +--+=, 得28cos 10sin 160ρρθρθ--+=.所以1C 的极坐标方程为28cos 10sin 160ρρθρθ--+=. (Ⅱ)2C 的普通方程为2220x y y +-=.由222281016020x y x y x y y ⎧+--+=⎪⎨+-=⎪⎩,,解得11x y =⎧⎨=⎩或02x y =⎧⎨=⎩.所以1C 与2C交点的极坐标分别为)4π,(2)2π,.【考点】坐标系与参数方程. 23.选修4-5:不等式选讲(Ⅰ)求不等式||22x x +≥(Ⅱ)已知实数00m n >>,,求证:222()a b a b m n m n+++….【答案】(I))21|log 12x x x ⎧⎫≤≥⎨⎬⎩⎭或;(II )证明见解析. 【解析】试题分析:(I )由于题目含有绝对值,所以分成两类来讨论,当0x ≥时,原不等式化为1222x≥,解得12x ≥.当0x <时,原不等式化为2(2)210x x -+≥,解得)2log 1x ≤;(II )将原不等式做差,然后化简得2222()()0()a b a b na mb m n m n mn m n +-+-=++≥. 试题解析:(Ⅰ)①当0x ≥时,有22xx+≥1222x≥,解得12x ≥.②当0x <时,有22x x -+≥,即2(2)210x x -+≥.解得21x 或21x ,又0x <,∴2log 1)x ≤,∴原不等式解集为为1{|2x x ≥或2log 1)}x ≤.(Ⅱ)∵2222()(()a b a b na mb a b m n na mb mn a b m n m n mn m n mn m n +++++-++-=-=+++22222()n a m b mnab mn m n +-=+2()0()na mb mn m n -=+≥,∴222()a b a b m n m n +++≥,当且仅当na mb =时等号成立. 【考点】不等式选讲.。
2016届吉林省实验中学高三上学期第二次模拟考试文数试题 解析版

考试时间:(120分钟 ) 试卷满分:(150分 )第Ⅰ卷 (选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四 个选项中,只有一项是符合题目要求的.)1. 已知集合{}1log |2<=x x A ,{}02|2<-+=x x x B ,则A ∪B =( )A .()2,∞-B .()10,C .()22,-D .()1,∞- 【答案】C 【解析】试题分析:由已知{|02}A x x =<<,{|21}B x x =-<<,所以{|22}A B x x =-<< ,故选C .考点:集合的运算.2. 下列命题中正确的是( ) A .若p ∨q 为真命题,则p ∧q 为真命题B .“x =5”是“x 2-4x -5=0”的充分不必要条件C .命题“若x <-1,则x 2-2x -3>0”的否定为:“若x ≥-1,则x 2-2x -3≤0” D .已知命题p :∃x ∈R ,x 2+x -1<0,则⌝p :∃x ∈R ,x 2+x -1≥0 【答案】B考点:命题的真假判断.3. 当0<x <1时,2212)(,)(,)(-===x x h x x g x x f 的大小关系是( )A.)()()(x f x g x h <<B.)()()(x g x f x h <<C.)()()(x f x h x g <<D.)()()(x h x g x f << 【答案】D考点:比较大小.4.设复数z =a +b i(a ,b ∈R),若z1+i=2-i 成立,则点P (a ,b )在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 【答案】A 【解析】试题分析:(2)(1)2213z i i i i i =-+=+-+=+,所以(,)(3,1)a b =,点P 在第一象限,故选A .考点:复数的运算,复数的几何意义. 5. 已知k yx==72,411=-yx ,则k 的值是( ) A .472⎪⎭⎫ ⎝⎛ B .4172⎪⎭⎫⎝⎛ C .415 D .4127⎪⎭⎫⎝⎛ 【答案】B 【解析】试题分析:由题意2log x k =,7log y k =,所以2711112log 2log 7log 4log log 7k k k x y k k -=-=-==,427k =,142()7k =,故选B .考点:对数的运算,换底公式.6.下列区间中,函数|)2ln(|)(x x f -=在其上为增函数的是 ( )A .(-,1∞]B .41,3⎡⎤-⎢⎥⎣⎦ C .)30,2⎡⎢⎣D .[)1,2【答案】D 【解析】试题分析:ln(2),1()ln(2),12x x f x x x -≤⎧=⎨--<<⎩,只有ln(2)y x =--是增函数,因此()f x 的增区间为[1,2),故选D . 考点:函数的单调性.7. 如图,函数()x f 的图象在P 点处的切线方程是172+-=x y ,若点P 的横坐标是5,则(5)'(5)f f +=( )A .5B .5-C .10D .10-【答案】A考点:导数的几何意义.8.设函数()()212log ,0log ,0x x f x x x >⎧⎪=⎨-<⎪⎩,若()()f a f a >-,则实数a 的取值范围是A .()01,-∪()10,B .()1-∞-,∪()∞+,1 C .()01,-∪()∞+,1D .()1-∞-,∪()10,【答案】C 【解析】试题分析:0a >时,212log log a a >,1a >,当0a <时,122log ()log ()a a ->-,01a <-<,10a -<<,所以有101a a -<<>或,故选C .考点:对数函数的性质,分段函数.9.函数y =x2-2sin x 的图象大致是 ( )【答案】C考点:函数的图象.【名师点晴】解数学选择题的很多,常见的解法有直接法、数形结合法、特例法、验证法(代入法)、排除法(筛选法、淘汰法)、估算法、极限法等等,具体解题时可以把多种方法结合起来,会使题目的求角过程简单化.解选择题时既要看到各种常规题的解题思想方法,又要充分挖掘题目的“个性”特征,寻求简便解法,充分利用选择题的暗示作用,迅速地指出正确的选择,可以迅速、准确地得出正确答案,还可以提高解题速度,为后续解题节省时间,对于选择题一定要“小题小做,小题巧做”,切忌小题大做.10.定义在R 上的函数)(x f 满足)()4(),()(x f x f x f x f =--=-且)0,1(-∈x 时,512)(+=x x f ,则=)20(log 2f ( )A.1-B.54- C.54D.1【答案】A 【解析】试题分析:由()()f x f x -=-知()f x 是奇函数,由(4)()f x f x -=知()f x 是周期函数,且周期为4,又24l o g 205<<,所以22222164(log 20)(log 204)(4log 20)(log )(log )205f f f f f =-=--=-=-= 24log 51(2)15-+=-,故选A . 考点:函数的奇偶性、周期性,对数的运算. 11. 设函数xx x f +=1)(,则使得()(21)f x f x >-成立的x 的取值范围是( )A .1,13⎛⎫ ⎪⎝⎭B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C .11,33⎛⎫- ⎪⎝⎭D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭【答案】A考点:函数的奇偶性与单调性.【名师点晴】解函数不等式()()f m f n >的方法一般是利用函数的单调性,直接去掉符号""f ,化为()m n m n ><或,如果函数()f x 为奇函数,题目形式为12()()0f x f x +>形式,化为22()()f x f x >-,如果函数()f x 为偶函数,题目形式为12()()f x f x >形式,化为12()()f x f x >.12. 若a 、b 分别是方程lg 4x x +=与104x x +=的解,函数()()22,02,0x a b x x f x x ⎧+++≤=⎨>⎩,则关于x 的方程()f x x =的解的个数是( )A .1B .2C .3D .4【答案】C 【解析】试题分析:两方程lg 4x x +=与104x x +=化为lg 4x x =-和104xx =-,因此两方程lg 4x x +=与104x x +=的解可以看作是函数lg y x =和10x y =分别与直线4y x =-的交点的横坐标,而函数lg y x =和10xy =互为反函数,它们的图象关于直线y x =对称,又直线4y x =-与直线y x =垂直,交点为(2,2),所以有4a b +=,当0x >时,()f x x =的解为2x =,当0x ≤时,方程242x x x ++=有两解1-和2-,因此方程()f x x =有三解,故选C .考点:函数与方程的应用.【名师点晴】判断函数零点个数最常用的方法是令f(x)=0,转化为方程根的个数,解出方程有几个根,函数y =f(x)就有几个零点,如果方程的根解不出,还有两种方法判断:方法一是基本方法,是利用零点的存在性原理,要注意参考单调性可判定零点的唯一性;方法二是数形结合法,要注意作图技巧.本题中求a b +,就是把两方程lg 4x x +=与104x x +=的解转化为函数lg y x =和10x y =分别与直线4y x =-的交点的横坐标.第Ⅱ卷 (非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)13. 若函数f(x)=xln (a= 【答案】1考点:函数的奇偶性.14.函数f (x )=ax 3+bx 2+cx +d 的部分数值如下表:则函数y =lg f (x )的定义域为__________. 【答案】),2()1,1(+∞⋃- 【解析】试题分析:由表格可知函数()f x 的图象的变化趋势如图所示,则()0f x >的解为112x x -<<>或.考点:函数的图象,函数的定义域.15.已知:函数m x g x x f x-==)21()(,)(2,若对][][,2,0,2,121∈∃-∈∀x x 使得)()(21x g x f >,则实数m 的取值范围__________【答案】41>m考点:不等式恒成立,函数的最值.【名师点晴】不等式恒成立问题经常转化为求函数的最值,这时我们要注意题中量词“对于任意的”、“存在”,如x R ∀∈,()f x m >恒成立,则m 小于()f x 的最小值,x R ∃∈,()f x m >恒成立,则m 小于()f x 的最大值等等.16. 对于函数x x f )31()(=定义域中的任意)(,2121x x x x ≠,有如下结论: ①);()()(2121x f x f x x f ∙=+②);()()(2121x f x f x x f +=⋅③0)()(2121<--x x x f x f ;④2)()()2(2121x f x f x x f +<+.上述结论中正确结论的序号是 . 【答案】①③④ 【解析】试题分析:12121212111()()()()()()333x x x x f x x f x f x ++==⋅=,①正确,又1212111()()()333x x x x ≠+,②错,函数1()()3x f x =是减函数,③正确,12121221111()()[()()]23233x x x x x x f ++==≤+12()()2f x f x +=,④正确.考点:命题的真假判断,指数函数的性质.【名师点晴】本题考查命题真假判断,实质上是考查函数的性质.对于这种给出具体函数式的问题,只要把函数式代入一一验证即可,解决此类问题不能限入误区,认为这类问题都是有难度,没处下手,事实上最简单的方法反而是最好的方法.三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或 演算步骤)17.(本题满分12分) 已知函数ππ1()cos()cos()sin cos 334f x x x x x =+--+ (1)求函数)(x f 的最小正周期和最大值;(2)求函数()f x 单调递增区间【答案】(1)最小正周期为 T π=,最大值为2;(2)5[,],88k k k z ππππ--∈考点:三角函数的周期、最值、单调区间. 18. (本小题满分12分)已知数列{}n a 满足首项为12a =,12n n a a +=,*()n ∈N .设23l o g 2n n b a =- *()n ∈N ,数列{}n c 满足n n n b a c =.(Ⅰ)求证:数列{}n b 成等差数列; (Ⅱ)求数列{}n c 的前n 项和n S .【答案】(Ⅰ)见解析;(Ⅱ)110(53)2n n S n +=--⋅考点:等比数列通项公式,等差数列的证明,错位相减法求和. 【名师点晴】1.一般地,如果数列{n a }是等差数列,{n b }是等比数列,求数列{n n a b ⋅ }的前n 项和时,可采用错位相减法.2.用乘公比错位相减法求和时,应注意:(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式. 19.(本题满分12分)四棱锥P ABCD -底面是平行四边形,面PAB ⊥面ABCD ,12PA PB AB AD ===,060BAD ∠=,,E F 分别为,AD PC 的中点. (1)求证://EF PAB 面 (2)求证:EF PBD ⊥面【答案】证明见解析.DB AG⊥-----------------------②---------------------------------10分由 ①②可知,,AG PB AG BD AG PBD ⊥⊥∴⊥面//,EF AG EF PBD ∴⊥又面-----------------------------------------------12分考点:线面平行与线面垂直的判断.20. 为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500 ml 以上为常喝,体重超过50 kg 为肥胖.已知在这30人中随机抽取1人,抽到肥胖的学生的概率为415.(1)请将上面的列联表补充完整.(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由.(3)现从常喝碳酸饮料且肥胖的学生(其中有2名女生)中,抽取2人参加电视节目,则正好抽到1男1女的概率是多少? 参考数据:参考公式:K 2=))()()(()(2d b c a d c b a cb ad n ++++-,其中n =a +b +c +d.【答案】(1)见解析;(2)有关;(3)815.试题解析:(1)设常喝碳酸饮料且肥胖的学生有x 人,则x +230=415,解得x =6.列联表如下:(2)由已知数据可得K 2=10×20×8×22≈8.523>7.879,因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.(3)设常喝碳酸饮料且肥胖的男生为A ,B ,C ,D ,女生为E ,F ,则任取2人有AB ,AC ,AD ,AE ,AF ,BC ,BD ,BE , BF ,CD ,CE ,CF ,DE ,DF ,EF ,共15种.其中是1男1女的有AE ,AF ,BE ,BF ,CE ,CF ,DE ,DF ,共8种, 故正好抽到1男1女的概率P =.考点:古典概型,独立性检验.21.设()()256ln f x a x x =-+,其中a R ∈,曲线()y f x =在点()()1,1f 处的切线与y 轴相交于点()0,6. (1)确定a 的值;(2)求函数()f x 的单调区间与极值. 【答案】(1)12a =;(2)()f x 在(0,2),(3,)+∞上为增函数,在(2,3)为减函数.极大值9(2)6ln 22f =+,极小值(3)26ln 3f =+.考点:导数的几何意义,函数的单调性、极值.【名师点晴】1.曲线的切线的求法:若已知曲线过点P(x0,y0),求曲线过点P的切线则需分点P(x0,y0)是切点和不是切点两种情况求解.(1)点P(x0,y0)是切点的切线方程为y-y0=f′(x0)(x-x0).(2)当点P(x0,y0)不是切点时可分以下几步完成:第一步:设出切点坐标P′(x1,f(x1));第二步:写出过P′(x1,f(x1))的切线方程为y-f(x1)=f′(x1)(x-x1);第三步:将点P的坐标(x0,y0)代入切线方程求出x1;第四步:将x1的值代入方程y-f(x1)=f′(x1)(x-x1)可得过点P(x0,y0)的切线方程.2.求可导函数单调区间的一般步骤和方法:(1)确定函数f(x)的定义域;(2)求f′(x),令f′(x)=0,求出它在定义域内的一切实根;(3)把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来,然后用这些点把函数f(x)的定义区间分成若干个小区间;(4)确定f′(x)在各个开区间内的符号,根据f′(x)的符号判定函数f(x)在每个相应小开区间内的增减性.3.可导函数极值存在的条件:(1)可导函数的极值点x0一定满足f′(x0)=0,但当f′(x1)=0时,x1不一定是极值点.如f(x)=x 3,f′(0)=0,但x =0不是极值点.22.在直角坐标xOy 中,直线l的参数方程为132(x t t y ⎧=+⎪⎪⎨⎪=⎪⎩为参数),以原点为极点,x 轴的正半轴为极轴建立极坐标系,C的极坐标方程为ρθ=. (Ⅰ)写出C 的直角坐标方程;直线l 的直角坐标方程(Ⅱ)P 为直线l 上一动点,当P 到圆心C 的距离最小时,求点P 的坐标. 【答案】(Ⅰ)22(3x y +=;(Ⅱ)(3,0).考点:极坐标方程与直角坐标方程的互化,直线参数方程的应用,两点间的距离公式.。
吉林省吉林大学附中高考数学二模试卷文(含解析)

吉林省吉林大学附中2016年高考数学二模试卷(文科)(解析版)一、选择题:本大题共12小题,每小题5分,每小题给出四个选项中,只有一项符合题目要求.1.设集合A={x|<2x﹣2<1},B={x|1﹣x2≤0},则A∩B等于()A.{x|﹣1≤x≤1} B.{x|1≤x<2} C.{x|0<x≤1} D.{x|0<x<2}2.在等比数列{a n}中,a1+a2=3,a3+a4=12,则a5+a6=()A.21 B.42 C.48 D.963.在区间[﹣1,1]上随机取一个数k,使直线y=k(x+2)与圆相交的概率为()A.B.C.D.4.对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是()A.|z﹣|=2y B.z2=x2+y2C.|z﹣|≥2x D.|z|≤|x|+|y|5.执行两次如图所示的程序框图,若第一次输入的a的值为﹣1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为()A.0.2,0.2 B.0.2,0.8 C.0.8,0.2 D.0.8,0.86.2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是()A.茎叶图B.分层抽样 C.独立性检验D.回归直线方程7.下列函数既是奇函数,又在区间(0,1)上单调递减的是()A.f(x)=x3B.f(x)=﹣|x+1| C.f(x)=ln D.f(x)=2x+2﹣x8.已知一个几何体可切割成一个多面体及一个旋转体的一部分,其三视图如图所示,则该几何体的体积是()A.π B.π+1 C.π+D.π9.给定两个命题p,q.若¬p是q的必要而不充分条件,则p是¬q的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件10.将所有正偶数按如图方式进行排列,则2 016位于()A.第30行B.第31行C.第32行D.第33行11.已知四棱锥P﹣ABCD的顶点都在球O的球面上,底面ABCD是矩形,AB=2AD=4,平面PAD ⊥底面ABCD,△PAD为等边三角形,则球面O的表面积为()A.B.32π C.64π D.12.已知集合{f(x)|f(x)=ax2﹣|x+1|+2a<0,x∈R}为空集,则实数a的取值范围是()A.[,+∞)B.[,+∞)C.[,+∞)D.(﹣∞,)二、填空题:本大题共4小题,每小题5分.13.(5分)(2014马鞍山三模)若实数x,y满足的最小值是.14.已知正方形ABCD的边长为2,E为CD的中点,则= .15.函数f(x)的图象如图所示,f′(x)是f(x)的导函数,设a=f′(﹣2),b=f′(﹣3),c=f(﹣2)﹣f(﹣3),则a,b,c由小到大的关系为.16.已知数列满足:a1=1,a n+1=,(n∈N*),若b n+1=(n﹣λ)(+1),b1=﹣λ,且数列{b n}是单调递增数列,则实数λ的取值范围为.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知△ABC的内角A,B,C的对边分别为a,b,c,且满足=2+2cos(A+B).(Ⅰ)求的值;(Ⅱ)若a=1,c=,求△ABC的面积.18.如图,直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面B1BCC1;(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F﹣AEC的体积.19.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩拉样统计,先将800人按001,002,…,800进行编号.(1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了第7行至第9行)(2)抽取取100人的数学与地理的水平测试成绩如表:成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求a ,b的值.(3)在地理成绩为及格的学生中,已知a ≥10,b ≥18,求数学成绩为优秀的人数比及格的人数少的概率.20.已知点H (﹣6,0),点P (0,b )在y 轴上,点Q (a ,0)在x 轴的正半轴上,且满足⊥,点M 在直线PQ 上,且满足﹣2=,(Ⅰ)当点P 在y 轴上移动时,求点M 的轨迹C 的方程;(Ⅱ)过点T (﹣1,0)作直线l 与轨迹C交于A 、B 两点,线段AB 的垂直平分线与x 轴的交点为E (x 0,0),设线段AB 的中点为D ,且2|DE|=|AB|,求x 0的值.21.已知函数f (x )=,g (x )=alnx ﹣x (a ≠0).(Ⅰ)求函数f (x )的单调区间;(Ⅱ)求证:当a >0时,对于任意x 1,x 2∈(0,e],总有g (x 1)<f (x 2)成立.请考生在第22、23、24题任选一题作答,如果多做,则按所做的第一题计分.作答时请写清楚题号.[选修4-1:几何证明选讲]22.如图,过圆E 外一点A 作一条直线与圆E 交于B ,C 两点,且AB=AC ,作直线AF 与圆E 相切于点F ,连结EF 交BC 于点D ,已知圆E 的半径为2,∠EBC=30°. (Ⅰ)求AF 的长;(Ⅱ)求的值.[选修4-4:坐标系与参数方程]23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)[选修4-5:不等式选讲]24.求不等式2x+2|x|≥2的解集;(Ⅱ)已知实数m>0,n>0,求证: +≥.2016年吉林省吉林大学附中高考数学二模试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,每小题给出四个选项中,只有一项符合题目要求.1.设集合A={x|<2x﹣2<1},B={x|1﹣x2≤0},则A∩B等于()A.{x|﹣1≤x≤1} B.{x|1≤x<2} C.{x|0<x≤1} D.{x|0<x<2}【分析】化简集合A、B,计算A∩B即可.【解答】解:集合A={x|<2x﹣2<1}={x|﹣2<x﹣2<0}={x|0<x<2},B={x|1﹣x2≤0}={x|x≤﹣1或x≥1},所以A∩B={x|1≤x<2}.故选:B.【点评】本题考查了集合的化简与运算问题,是基础题目.2.在等比数列{a n}中,a1+a2=3,a3+a4=12,则a5+a6=()A.21 B.42 C.48 D.96【分析】设等比数列{a n}的公比为q,由题意可得q2=4,而a5+a6=(a3+a4)q2,代入计算可得.【解答】解:设等比数列{a n}的公比为q,则a3+a4=a1q2+a2q2=(a1+a2)q2=3q2=12,解之可得q2=4,故a5+a6=a3q2+a4q2=(a3+a4)q2=12×4=48故选C【点评】本题考查等比数列的性质,涉及整体代入的思想,属中档题.3.在区间[﹣1,1]上随机取一个数k,使直线y=k(x+2)与圆相交的概率为()A.B.C.D.【分析】利用圆心到直线的距离小于等于半径可得到直线与圆相交,可求出满足条件的k,最后根据几何概型的概率公式可求出所求.【解答】解:圆x2+y2=1的圆心为(0,0)圆心到直线y=k(x+2)的距离为要使直线y=k(x+2)与圆x2+y2=1相交,则解得﹣<k<∴在区间[﹣1,1]上随机取一个数k,使直线y=k(x+2)与圆x2+y2=1有公共点的概率为P==故选C.【点评】本题主要考查了几何概型的概率,以及直线与圆相交的性质,解题的关键弄清概率类型,同时考查了计算能力,属于基础题.4.对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是()A.|z﹣|=2y B.z2=x2+y2C.|z﹣|≥2x D.|z|≤|x|+|y|【分析】根据|z﹣|=|2yi|=2|y|,可得 A、C不正确,根据z2=x2﹣y2﹣2xyi,可得B不正确,由|z|=可得D正确.【解答】解:由于复数z=x+yi(x,y∈R),i为虚数单位,∴|z﹣|=|2yi|=2|y|,故(A)错误.由z2=x2﹣y2+2xyi,故(B)错误.由|z﹣|=2|y|,不一定大于或等于2x,故(C)错误.由|z|=≤=|x|+|y|,故(D)正确.故选:D.【点评】本题考查两个复数代数形式的乘法,虚数单位i的幂运算性质,复数的模的定义,准确理解复数的模的定义,是解题的关键,属于基础题.5.执行两次如图所示的程序框图,若第一次输入的a的值为﹣1.2,第二次输入的a的值为1.2,则第一次、第二次输出的a的值分别为()A.0.2,0.2 B.0.2,0.8 C.0.8,0.2 D.0.8,0.8【分析】计算循环中a的值,当a≥1时不满足判断框的条件,退出循环,输出结果即可.【解答】解:若第一次输入的a的值为﹣1.2,满足上面一个判断框条件a<0,第1次循环,a=﹣1.2+1=﹣0.2,第2次判断后循环,a=﹣0.2+1=0.8,第3次判断,满足上面一个判断框的条件退出上面的循环,进入下面的循环,不满足下面一个判断框条件a≥1,退出循环,输出a=0.8;第二次输入的a的值为1.2,不满足上面一个判断框条件a<0,退出上面的循环,进入下面的循环,满足下面一个判断框条件a≥1,第1次循环,a=1.2﹣1=0.2,第2次判断后不满足下面一个判断框的条件退出下面的循环,输出a=0.2;故选C.【点评】本题考查循环结构的应用,注意循环的结果的计算,考查计算能力.6.2016年3月9日至15日,谷歌人工智能系统“阿尔法”迎战围棋冠军李世石,最终结果“阿尔法”以总比分4比1战胜李世石.许多人认为这场比赛是人类的胜利,也有许多人持反对意见,有网友为此进行了调查,在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,在运用这些数据说明“性别”对判断“人机大战是人类的胜利”是否有关系时,应采用的统计方法是()A.茎叶图B.分层抽样 C.独立性检验D.回归直线方程【分析】这是一个独立性检验应用题,处理本题时要注意根据在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,计算出K2的值,并代入临界值表中进行比较,不难得到答案.【解答】解:在参加调查的2548名男性中有1560名持反对意见,2452名女性中有1200名持反对意见,可得:K2==83.88>10.828,故有理由“性别”对判断“人机大战是人类的胜利”是否有关系时,故利用独立性检验的方法最有说服力,故选:C.【点评】本题考查独立性检验知识,考查学生的计算能力,属于基础题.7.下列函数既是奇函数,又在区间(0,1)上单调递减的是()A.f(x)=x3B.f(x)=﹣|x+1| C.f(x)=ln D.f(x)=2x+2﹣x【分析】根据奇函数、偶函数的定义,奇函数在原点有定义时,f(0)=0,以及函数单调性的定义,复合函数单调性的判断便可判断每个选项的正误,从而找出正确选项.【解答】解:A.f(x)=x3在(0,1)上单调递增,∴该选项错误;B.f(x)=﹣|x+1|的定义域为R,且f(0)=﹣1≠0;∴f(x)不是奇函数,∴该选项错误;C.的定义域为(﹣1,1),且;∴f(x)为奇函数;;在(﹣1,1)上单调递减,y=lnt单调递增;∴f(x)在(0,1)上单调递增;∴该选项正确;D.f(x)的定义域为R,且f(﹣x)=f(x);∴f(x)为偶函数;∴该选项错误.故选:C.【点评】考查奇函数和偶函数的定义及判断方法,奇函数f(x)在原点有定义时,f(0)=0,对数函数、反比例函数的单调性,复合函数单调性的判断.8.已知一个几何体可切割成一个多面体及一个旋转体的一部分,其三视图如图所示,则该几何体的体积是()A.π B.π+1 C.π+D.π【分析】由三视图知该几何体是组合体:左边是直三棱柱、右边是半个圆柱,由三视图求出几何元素的长度,由柱体的体积公式求出几何体的体积.【解答】解:根据三视图可知几何体是组合体:左边是直三棱柱、右边是半个圆柱,直三棱柱的底面是等腰直角三角形,直角边是1,侧棱长是2,圆柱的底面半径是1,母线长是2,∴该几何体的体积V==π+1,故选:B.【点评】本题考查由三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.9.给定两个命题p,q.若¬p是q的必要而不充分条件,则p是¬q的()A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件【分析】根据互为逆否命题真假性相同,可将已知转化为q是¬p的充分不必要条件,进而根据逆否命题及充要条件的定义得到答案.【解答】解:∵¬p是q的必要而不充分条件,∴q是¬p的充分不必要条件,即q⇒¬p,但¬p不能⇒q,其逆否命题为p⇒¬q,但¬q不能⇒p,则p是¬q的充分不必要条件.故选A.【点评】本题考查的知识点是充要条件的判断,其中将已知利用互为逆否命题真假性相同,转化为q是¬p的充分不必要条件,是解答的关键.10.将所有正偶数按如图方式进行排列,则2 016位于()A.第30行B.第31行C.第32行D.第33行【分析】由于题意可得:第n行的最后一个数为2[n(n+1)].分别令n=31,令n=32,即可判断出结论.【解答】解:由于题意可得:第n行的最后一个数为2[n(n+1)].令n=31,最后一个数为1984.令n=32,最后一个数为2112.∴2 016位于第32行.故选:C.【点评】本题考查了等差数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.11.已知四棱锥P﹣ABCD的顶点都在球O的球面上,底面ABCD是矩形,AB=2AD=4,平面PAD ⊥底面ABCD,△PAD为等边三角形,则球面O的表面积为()A.B.32π C.64π D.【分析】求出△PAD所在圆的半径,利用勾股定理求出球O的半径R,即可求出球O的表面积.【解答】解:令△PAD所在圆的圆心为O1,则圆O1的半径r=,因为平面PAD⊥底面ABCD,所以OO1=AB=2,所以球O的半径R==,所以球O的表面积=4πR2=.故选:D.【点评】本题考查球O的表面积,考查学生的计算能力,比较基础.12.已知集合{f(x)|f(x)=ax2﹣|x+1|+2a<0,x∈R}为空集,则实数a的取值范围是()A.[,+∞)B.[,+∞)C.[,+∞)D.(﹣∞,)【分析】由题意知 ax2﹣|x+1|+2a≥0恒成立,再化恒成立问题为函数的最值问题,利用换元法化简.从而讨论去绝对值号并确定函数的最值.【解答】解:∵集合{f(x)|f(x)=ax2﹣|x+1|+2a<0,x∈R}为空集,∴ax2﹣|x+1|+2a≥0恒成立,∴,设,故a≥g(x)max.令t=x+1,则.①当t=0时,g(x)=φ(t)=0,∴a≥0.②当t>0时,g(x)=φ(t)==≤,∴a≥;③当t<0时,g(x)=φ(t)=﹣=≤,∴a≥.综上,取交集得a≥.故选B.【点评】本题考查了不等式的恒成立问题及转化思想的应用,同时考查了换元法与分类讨论的思想方法应用.二、填空题:本大题共4小题,每小题5分.13.(5分)(2014马鞍山三模)若实数x,y满足的最小值是 1 .【分析】令t=x+2y,要求z的最小值,只要求解t的最小值,作出不等式组表示的平面区域,由于t=x+2y,可知直线在y轴上的截距越大,t越大,可求t的最小值,进而可求z的最小值【解答】解:令t=x+2y作出不等式组表示的平面区域,如图所示由于t=x+2y可得y=,根据直线在y轴上的截距越大,t越大∴直线t=x+2y平移到点O(O,0)时,t取得最小值0,此时,z=1故答案为:1【点评】本题主要考查了线性规划的简单应用,解题的关键是明确目标函数的几何意义14.已知正方形ABCD的边长为2,E为CD的中点,则= 2 .【分析】根据两个向量的加减法的法则,以及其几何意义,可得要求的式子为()(),再根据两个向量垂直的性质,运算求得结果.【解答】解:∵已知正方形ABCD的边长为2,E为CD的中点,则=0,故=()()=()()=﹣+﹣=4+0﹣0﹣=2,故答案为 2.【点评】本题主要考查两个向量的加减法的法则,以及其几何意义,两个向量垂直的性质,属于中档题.15.函数f(x)的图象如图所示,f′(x)是f(x)的导函数,设a=f′(﹣2),b=f′(﹣3),c=f(﹣2)﹣f(﹣3),则a,b,c由小到大的关系为a<c<b .【分析】利用导数的几何意义,数形结合可作出大小比较.【解答】解:c=f(﹣2)﹣f(﹣3)=,表示(﹣2,f(﹣2))、(﹣3,f(﹣3))两点连线的斜率,a=f′(﹣2)表示(﹣2,f(﹣2))处的切线斜率,b=f′(﹣3)表示(﹣3,f(﹣3))处的切线斜率,结合函数f(x)的图象:由图可知f′(﹣2)<<f′(﹣3),即a<c<b,故答案为:a<c<b.【点评】本题考查函数单调性的性质,考查数形结合思想,属中档题.16.已知数列满足:a1=1,a n+1=,(n∈N*),若b n+1=(n﹣λ)(+1),b1=﹣λ,且数列{b n}是单调递增数列,则实数λ的取值范围为λ<2 .【分析】数列{a n}满足:a1=1,a n+1=,(n∈N*),两边取倒数可得,化为,利用等比数列的通项公式可得,于是b n+1=(n﹣λ)(+1)=(n﹣λ)2n,由于b1=﹣λ,且数列{b n}是单调递增数列,可得b n+1>b n,解出即可.【解答】解:∵数列{a n}满足:a1=1,a n+1=,(n∈N*),∴,化为,∴数列是等比数列,首项为+1=2,公比为2,∴,∴b n+1=(n﹣λ)(+1)=(n﹣λ)2n,∵b1=﹣λ,且数列{b n}是单调递增数列,∴b n+1>b n,∴(n﹣λ)2n>(n﹣1﹣λ)2n﹣1,化为λ<n+1,∵数列{n+1}为单调递增数列,∴λ<2.∴实数λ的取值范围为λ<2.故答案为:λ<2.【点评】本题考查了变形利用等比数列的通项公式的方法、单调递增数列,考查了推理能力与计算能力,属于中档题.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.已知△ABC的内角A,B,C的对边分别为a,b,c,且满足=2+2cos(A+B).(Ⅰ)求的值;(Ⅱ)若a=1,c=,求△ABC的面积.【分析】(Ⅰ)根据正弦定理进行转化即可求的值;(Ⅱ)若a=1,c=,根据三角形的面积公式即可求△ABC的面积.【解答】解:(Ⅰ)∵,∴sin(2A+B)=2sinA+2sinAcos(A+B),∴sin[A+(A+B)]=2sinA+2sinAcos(A+B),∴sin(A+B)cosA﹣cosAsin(A+B)=2sinA,…(2分)∴sinB=2sinA,…(4分)∴b=2a,∴.…(6分)(Ⅱ)∵,,∴b=2,∴,∴.…(10分)∴,即△ABC的面积的.…(12分)【点评】本题主要考查正弦定理的应用,根据三角形的面积公式以及正弦定理进行转化是解决本题的关键.18.如图,直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,(Ⅰ)证明:平面AEF⊥平面B1BCC1;(Ⅱ)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F﹣AEC的体积.【分析】(Ⅰ)证明AE ⊥BB 1,AE ⊥BC ,BC∩BB 1=B ,推出AE ⊥平面B 1BCC 1,利用平面余平米垂直的判定定理证明平面AEF ⊥平面B 1BCC 1;(Ⅱ)取AB 的中点G ,说明直线A 1C 与平面A 1ABB 1所成的角为45°,就是∠CA 1G ,求出棱锥的高与底面面积即可求解几何体的体积.【解答】(Ⅰ)证明:∵几何体是直棱柱,∴BB 1⊥底面ABC ,AE ⊂底面ABC ,∴AE ⊥BB 1, ∵直三棱柱ABC ﹣A 1B 1C 1的底面是边长为2的正三角形,E 分别是BC 的中点, ∴AE ⊥BC ,BC∩BB 1=B ,∴AE ⊥平面B 1BCC 1, ∵AE ⊂平面AEF ,∴平面AEF ⊥平面B 1BCC 1;(Ⅱ)解:取AB 的中点G ,连结A 1G ,CG ,由(Ⅰ)可知CG ⊥平面A 1ABB 1,直线A 1C 与平面A 1ABB 1所成的角为45°,就是∠CA 1G ,则A 1G=CG=,∴AA 1==,CF=.三棱锥F ﹣AEC 的体积:×==.【点评】本题考查几何体的体积的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力.19.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现学校决定利用随机数表法从中抽取100人进行成绩拉样统计,先将800人按001,002,…,800进行编号. (1)如果从第8行第7列的数开始向右读,请你依次写出最先检测的3个人的编号;(下面摘取了第7行至第9行)(2)抽取取100人的数学与地理的水平测试成绩如表:成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人,若在该样本中,数学成绩优秀率为30%,求a ,b 的值.(3)在地理成绩为及格的学生中,已知a ≥10,b ≥18,求数学成绩为优秀的人数比及格的人数少的概率.【分析】(1)利用随机数表法直接求解. (2)由=0.3,能求出a ,再由7+9+a+20+18+4+5+6+b=100,能求出b .(3)由题意,知a+b=31,且a ≥10,b ≥18,满足条件的(a ,b )有14组,其中数学成绩为优秀的人数比及格的人数少有6组,由此能求出数学成绩为优秀的人数比及格的人数少的概率.【解答】(本小题满分12分)解:(1)依题意,最先检测的3个人的编号依次为785,667,199.…(3分) (2)由=0.3,解得a=14,…(5分)∵7+9+a+20+18+4+5+6+b=100,∴b=17.…(7分) (3)由题意,知a+b=31,且a ≥10,b ≥18, ∴满足条件的(a ,b )有:(10,21),(11,20), (12,19),(13,18),(14,17),(15,16), (16,15),(17,14),(18,13),(19,12), (20,11),(21,10),(22,9),(23,8)共14组, 且每组出现的可能性相同.….…(9分) 其中数学成绩为优秀的人数比及格的人数少有: (10,21),(11,20),(12,19),(13,18), (14,17),(15,16)共6组.…(11分) ∴数学成绩为优秀的人数比及格的人数少的概率为.…(12分)【点评】本题考查随机数表法的应用,考查统计表的应用,考查概率的求法,是中档题,解题时要注意列举法的合理运用.20.已知点H(﹣6,0),点P(0,b)在y轴上,点Q(a,0)在x轴的正半轴上,且满足⊥,点M在直线PQ上,且满足﹣2=,(Ⅰ)当点P在y轴上移动时,求点M的轨迹C的方程;(Ⅱ)过点T(﹣1,0)作直线l与轨迹C交于A、B两点,线段AB的垂直平分线与x轴的交点为E(x0,0),设线段AB的中点为D,且2|DE|=|AB|,求x0的值.【分析】(Ⅰ)设点M的坐标为(x,y),求得、、、的坐标,运用向量垂直的条件:数量积为0,向量共线的坐标表示,运用代入法,即可得到所求轨迹方程;(Ⅱ)由题意知直线l:y=k(x+1),设A(x1,y1),B(x2,y2),联立抛物线的方程,运用韦达定理和中点坐标公式,以及弦长公式,化简整理,解方程即可得到所求值.【解答】解:(Ⅰ)设点M的坐标为(x,y),则,,,,由⊥,得6a﹣b2=0.由﹣2=0,得,则由6a﹣b2=0得y2=x,故点M的轨迹C的方程为y2=x(x>0);(Ⅱ)由题意知直线l:y=k(x+1),设A(x1,y1),B(x2,y2),联立得k2x2+(2k2﹣1)x+k2=0(k≠0),由△=(2k2﹣1)2﹣4k4=1﹣4k2>0,解得﹣<k<,∴,∴,∴,,令y=0,解得,∴,∴,∴,∵,故有,则,化简得,此时.【点评】本题考查轨迹方程的求法,注意运用向量共线和垂直的条件,考查直线和抛物线的方程联立,运用韦达定理和弦长公式,考查化简整理的运算能力,属于中档题.21.已知函数f(x)=,g(x)=alnx﹣x(a≠0).(Ⅰ)求函数f(x)的单调区间;(Ⅱ)求证:当a>0时,对于任意x1,x2∈(0,e],总有g(x1)<f(x2)成立.【分析】(I)先求函数f(x)的导数,再对字母a进行分类讨论,根据导数大于0函数单调递增,导数小于0时函数单调递减可得答案.(Ⅱ)欲证当a>0时,对于任意x1,x2∈(0,e],总有g(x1)<f(x2)成立,只须证明对于任意x1,x2∈(0,e],总有g(x)max<f(x)min.由(Ⅰ)可知,当a>0时,f(x)在(0,1)上单调递增,f(x)在(1,e]上单调递减,从而有f(x)min=a,同样地利用导数可得,当a>0时,g(x)在(0,a)上单调递增,g(x)在(a,e]上单调递减,从而g(x)max=g (a)=alna﹣a,最后利用作差法即可得到g(x)max<f(x)min.【解答】解:(Ⅰ)函数f(x)的定义域为R,.当a>0时,当x变化时,f'(x),f(x)的变化情况如下表:当a<0时,当x变化时,f'(x),f(x)的变化情况如下表:综上所述,当a>0时,f(x)的单调递增区间为(﹣1,1),单调递减区间为(﹣∞,﹣1),(1,+∞);当a<0时,f(x)的单调递增区间为(﹣∞,﹣1),(1,+∞),单调递减区间为(﹣1,1).…(5分)(Ⅱ)由(Ⅰ)可知,当a>0时,f(x)在(0,1)上单调递增,f(x)在(1,e]上单调递减,又f(0)=a,f(e)=所以f(x)min=a,同样地,当a>0时,g(x)在(0,a)上单调递增,g(x)在(a,e]上单调递减,所以g(x)max=g(a)=alna﹣a,因为a﹣(alna﹣a)=a(2﹣lna)>a(2﹣lne)=a>0,所以对于任意x1,x2∈(0,e],总有g(x)max=g(e)=alna﹣a<a=f(x)min.所以对于任意x1,x2∈(0,e],仍有x1,x2∈(0,e].综上所述,对于任意x1,x2∈(0,e],总有g(x1)<f(x2)成立.…(13分)【点评】本题考查导数知识的运用,考查函数的单调性与最值,考查学生分析解决问题的能力,属于中档题.请考生在第22、23、24题任选一题作答,如果多做,则按所做的第一题计分.作答时请写清楚题号.[选修4-1:几何证明选讲]22.如图,过圆E外一点A作一条直线与圆E交于B,C两点,且AB=AC,作直线AF与圆E 相切于点F,连结EF交BC于点D,已知圆E的半径为2,∠EBC=30°.(Ⅰ)求AF的长;(Ⅱ)求的值.【分析】(Ⅰ)可延长BE并交圆E于M,并连接CM,从而画出图形,根据条件便可求出BC 的长,进而求出AC的长,从而根据切割线定理求出AF的长;(Ⅱ)可过E作EH⊥BC,从而可得出△EDH与△ADF相似,从而有,再根据题意即可得出EH的长,从而便可求出的值.【解答】解:(Ⅰ)如图,延长BE交圆E于点M,连结CM,则∠BCM=90°,又BM=2BE=4,∠EBC=30°,所以,又,可知,所以.根据切割线定理得,即AF=3.(Ⅱ)过E作EH⊥BC于H,则△EDH∽△ADF,从而有,又由题意知所以EH=1,因此.【点评】考查直径所对圆周角为直角,三角函数定义,以及切割线定理,三角形相似的判定,相似三角形的对应边的比例关系.[选修4-4:坐标系与参数方程]23.已知曲线C1的参数方程为(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.(Ⅰ)把C1的参数方程化为极坐标方程;(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)【分析】(Ⅰ)对于曲线C1利用三角函数的平方关系式sin2t+cos2t=1即可得到圆C1的普通方程;再利用极坐标与直角坐标的互化公式即可得到C1的极坐标方程;(Ⅱ)先求出曲线C2的极坐标方程;再将两圆的方程联立求出其交点坐标,最后再利用极坐标与直角坐标的互化公式即可求出C1与C2交点的极坐标.【解答】解:(Ⅰ)曲线C1的参数方程式(t为参数),得(x﹣4)2+(y﹣5)2=25即为圆C1的普通方程,即x2+y2﹣8x﹣10y+16=0.将x=ρcosθ,y=ρsinθ代入上式,得.ρ2﹣8ρcosθ﹣10ρsinθ+16=0,此即为C1的极坐标方程;(Ⅱ)曲线C2的极坐标方程为ρ=2sinθ化为直角坐标方程为:x2+y2﹣2y=0,由,解得或.∴C1与C2交点的极坐标分别为(,),(2,).【点评】本题主要考查了参数方程化成普通方程,点的极坐标和直角坐标的互化.熟练掌握极坐标与直角坐标的互化公式、两圆的位置关系是解题的关键.[选修4-5:不等式选讲]24.求不等式2x+2|x|≥2的解集;(Ⅱ)已知实数m>0,n>0,求证: +≥.【分析】(Ⅰ)讨论①当x≥0时,②当x<0时,去绝对值,运用指数函数的单调性,计算即可得到所求解集;(Ⅱ)运用作差法,因式分解,配方,由完全平方式非负,即可得证.【解答】解:(Ⅰ)①当x≥0时,有,由,解得.②当x<0时,有,即.解得或,又x<0,解得,则原不等式解集为{x|或}.(Ⅱ)证明:==,则,当且仅当na=mb时等号成立.【点评】本题考查不等式的解法和证明,注意运用分类讨论和作差法,考查化简整理的运算能力,属于中档题.。
吉林省吉林大学附属中学2016届高三第二次模拟考试理数试题 含解析

一、选择题(本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1、已知{|12}{|3}U M x x N x x ==-=R ,≤≤,≤,则()UM N =( )(A ){|23}x x ≤≤(B){|23}x x <≤(C ){|1x x -≤或23}x ≤≤(D){|1x x <-或23}x <≤ 【答案】D 【解析】 试题分析:{}1,2UCM x x =<->或,(){}1,23U C M N x x ⋂=<-<≤或.考点:集合交集、并集和补集.【易错点晴】高考对集合知识的考查要求较低,均是以小题的形式进行考查,一般难度不大,要求考生熟练掌握与集合有关的基础知识.纵观近几年的高考试题,主要考查以下两个方面:一是考查具体集合的关系判断和集合的运算.解决这类问题的关键在于正确理解集合中元素所具有属性的含义,弄清集合中元素所具有的形式以及集合中含有哪些元素.二是考查抽象集合的关系判断以及运算.注意区间端点的取舍。
2、已知复数2i 1iz +=+,则复数z 在复平面内对应的点在( )(A )第一象限 (B )第二象限(C )第三象限 (D )第四象限【答案】D 【解析】试题分析:()()()()21231112i i i i z ii i +-+-===++-,故在第四象限。
考点:复数运算.3、在等差数列{}na 中,15487a aa +==,,则5a =( )(A )11 (B )10 (C )7(D)3 【答案】B 【解析】试题分析:依题意,有11148,37a a d a d ++=+=,解得1512,3,410a d a a d =-==+=.考点:等差数列.4、下列说法中正确的是( )(A )“(0)0f =”是“函数()f x 是奇函数”的充要条件 (B)若20:10p x xx ∃∈-->R ,,则2:10p x xx ⌝∀∈--<R ,(C )若p q ∧为假命题,则p ,q 均为假命题(D )命题“若6απ=,则1sin 2α="的否命题是“若6απ≠,则1sin 2α≠”【答案】D 【解析】试题分析:A 是不充分不必要条件;B 应该是≤;C 是,p q 至少有一个假命题,故D 正确。
【全国百强校】吉林省东北师范大学附属中学2016届高三上学期第二次模拟考试文数试题(原卷版)

吉林省东北师范大学附属中学2016届高三上学期第二次模拟考试文数试题一、选择题:(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.212log log 2= ( )(A )12 (B )12- (C )32 (D )32-2.命题“2,320x R x x ∃∈-+=”的否定是( )(A )2,320x R x x ∀∈-+= (B )2,320x R x x ∃∈-+≠(C )2,320x R x x ∀∈-+≠ (D )2,320x R x x ∃∈-+>3.若0.23a =,3log π=b ,3log c =,则( )(A )b c a >> (B )b a c >>(C )a b c >> (D )c a b >>4.已知函数()sin cos ,(0,)f x x x x π=+∈,且'()0f x =,则x =( )(A )4π(B )34π(C )3π (D )6π5.已知幂函数{}(),2,1,1,3n f x x n =∈--的图象关于y 轴对称,则下列选项正确的是( )(A )(2)(1)f f -> (B )(2)(1)f f -<(C )(2)(1)f f = (D )(2)(1)f f ->-6.“a b >”是“22a b >”的( )(A )充分非必要条件. (B )必要非充分条件.(C )充要条件. (D )既非充分又非必要条件.7.曲线()(,)n f x ax a n R =∈在点(1,2)处的切线方程是42y x =-,则下列说法正确的是()(A )函数()f x 是偶函数且有最大值 (B )函数()f x 是奇函数且有最大值(C )函数()f x 是偶函数且有最小值 (D )函数()f x 是奇函数且有最小值8.若()f x 是R 上周期为5的奇函数,且满足(1)1,(2)2f f ==,(23)(14)f f +-=( )(A )1- (B )1 (C )2- (D )29.函数2()1x f x x=-的图象大致是( )10.已知函数22()22,()f x x x g x ax bx c =-+=++,若这两个函数的图象关于(2,0)对称,则()f c = ( )(A )122 (B )5 (C )26 (D )12111.如果一个正方体的体积在数值上等于V ,表面积在数值上等于S ,且0V S m --≥恒成立,则实数m 的 范围是( )(A )(,16]-∞- (B )(,32]-∞- (C )[32,16]-- (D )以上答案都不对12.若函数)(x f 满足:在定义域D 内存在实数0x ,使得)1()()1(00f x f x f +=+成立,则称函数)(x f 为 “1的饱和函数”.给出下列五个函数:①x x f 2)(=;②x x f 1)(=;③21()lg()2f x x =-;④21()xx f x e -=. 其中是“1的饱和函数”的所有函数的序号为( )(A )①②④ (B )②③④ (C )①②③ (D )①③④第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.已知2,,m a e b e -==且1a b ⋅=,则m = .14.已知集合{}{}23,,0,,1A a B b a ==-,且{}1AB =,则A B = . 15.若命题“2,20x R ax ax ∀∈--<”是真命题,则实数a 的取值范围是 .16.若函数22()243f x x a x a =++-有三个不同的零点,则函数()()(1)g x f x f a a =-++的零点个数 是________个. 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分) 已知函数27(),(4).2m f x x f x =-=且 (Ⅰ)判断()f x 的奇偶性;(Ⅱ)写出不等式()1f x >的解集(不要求写出解题过程).18.(本小题满分12分)已知函数()2sin(2)1f x x φ=++的图象过点(0,0),且02πφ-<<. (Ⅰ)求φ的值;(Ⅱ)求函数()f x 的最大值,并求此时x 的值.19.本小题满分12分)已知等比数列{}n a ,253,81a a ==.(Ⅰ)求7a 和公比q ;(Ⅱ)设3log n n n b a a =+,求数列{}n b 的前n 项的和.20.(本小题满分12分)设关于x 的方程2220()x ax a R --=∈)的两个实根为()αβαβ<、,函数14)(2+-=x a x x f . (Ⅰ)求()f α,()f β的值(结果用含有a 的最简形式表示);(Ⅱ)函数)(x f 在R 上是否有极值,若有,求出极值;没有,说明理由.21.(本小题满分12分)已知M 是椭圆22221(0)x y a b a b +=>>上一点,椭圆的离心率12e =. (Ⅰ)求椭圆的方程;(Ⅱ)过点(0,3)P 的直线m 与椭圆交于,A B 两点.若A 是PB 的中点,求直线m 的方程.22.(本小题满分12分)已知函数2()ln ,()(1)1()f x x x g x ax a x a R ==-++∈.(Ⅰ)当0a =时,求()()f x g x +的单调区间;(Ⅱ)当1x ≥时,()()ln f x g x x ≤+,求实数a 的取值范围.:。
高三数学月考试题及答案-东北师范大学附属中学净月校区2016届高三上学期第二次模拟考试(文)

东北师范大学附属中学净月校区2016届高三上学期第二次模拟考试数学试卷(文)一、选择题(本大题包括12小题,每小题5分,共60分) 1.已知集合A ={}22320x x x -->,B ={}2ln(1)x y x =-,则AB =( )A .(2,1)--B . (,2)(1,)-∞-+∞ C .1(1,)2- D . (2,1)(1,)--+∞2.不等式组36020x y x y -+≥⎧⎨-+<⎩表示的平面区域是( )3.已知数列{}n a 满足11a =,12(2,)n n a a n n N *-=≥∈,则数列{}n a 的前6项和为( )A .63B .127C .6332D .127644.若4cos 5α=-,α是第三象限的角,则sin()4πα+=( ) A .210-B.210C .7210- D.7210 5.已知,αβ是两个不同的平面,,m n 是两条不同的直线,则下列命题不正确的是( ) A .若m //n ,m α⊥,则n α⊥ B .若m α⊥,m β⊥,则αβC .若m α⊥,m β⊂,则αβ⊥D .若//m α,n αβ=,则m //n6.已知正项数列{}n a 中,11a =,22a =,222112(2)n n n a a a n +-=+≥,则6a 等于( ) A .22 B .4 C .8 D .167.已知两定点(0,2)A -,(0,2)B ,点P 在椭圆2211216x y +=上,且满足||||AP BP -=2,则AP BP 为( )A .-12 B.12 C .一9 D .98.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面 积是( )A .B .3226+ C.32222++ D. 3222+9.点为椭圆22221(0)x y a b a b+=>>的一个焦点,若椭圆上存在点A 使AOF ∆为正三角形,那么椭圆的离心率为( )A .22B .32C .312-D .31-10.已知抛物线28y x =的焦点F 到双曲线C :22221(0,0)y x a b a b-=>>渐近线的距离为455,点P 是抛物线28y x =上的一动点,P 到双曲线C 的上焦点1(0,)F c 的距离与到直线2x =-的距离之和的最小值为3,则该双曲线的方程为( )A .22123y x -= B .2214x y -= C .2214y x -= D .22132y x -= 11.已知M 是ABC ∆内的一点,且23,30,AB AC BAC =∠=若,MBC MCA ∆∆和MAB ∆的面积分别为1,,2x y ,则14x y+的最小值是( )A .20B .18C .16D .912.已知圆C :1)()(22=-+-b y a x ,平面区域Ω:⎪⎩⎪⎨⎧≥≥+-≤-+00307y y x y x .若圆心Ω∈C ,且圆C与x 轴相切,则22b a +的最大值为( )A.49B.37C.29D.5二、填空题(本大题包括4小题,每小题5分,共20分)13.在边长为1的正三角形ABC 中,设2,3BC BD CA CE ==,则AD BE =__________.2F14.若等比数列{}n a 的各项均为正数,且510119122a a a a e +=,则1220ln ln ln a a a ++=________.15.利用一个球体毛坯切削后得到一个四棱锥P ABCD -,其中底面四边形是边长为1的正方形,1PA =,且PA ⊥平面ABCD ,则球体毛坯体积的最小值应为 . 16.已知函数⎩⎨⎧<<-≤<=63),6(30,lg )(x x f x x x f ,设方程()2()x f x b b R -=+∈的四个实根从小到大依次1234,,,x x x x ,对于满足条件的任意一组实根,下列判断中正确的为 . (请填所有正确命题的序号)(1)1201x x <<或()()340661x x <--<;(2)1201x x <<且()()34661x x -->; (3)1219x x <<或34925x x <<; (4)1219x x <<且342536x x <<.三、解答题(本大题包括6小题,共70分,解答应写出证明过程或演算步骤) 17.(本小题12分)在锐角ABC ∆中,,,a b c 分别为角,,A B C 所对的边,且32sin a c A = (Ⅰ)确定角C 的大小; (Ⅱ)若7c =,且ABC ∆的面积为332,求a b +的值.18.(本小题12分)已知数列{}n a 的前n 项和为n S ,若()14211n n S n a +=-+(*n ∈N ),且11=a . (Ⅰ)求证:数列{}n a 为等差数列; (Ⅱ)设1n n nb a S =,数列{}n b 的前n 项和为n T ,证明:32n T <(*n ∈N ).19.(本小题12分)如图所示,四棱锥P ABCD -的底面ABCD 是直角梯形, AD BC //,AB AD ⊥,13AB BC AD ==,PA ⊥底面ABCD ,过BC 的平面交PD 于M ,交PA 于N (N 与A 不重合). (Ⅰ)求证:BC MN //; (Ⅱ)如果BM AC ⊥,求此时PMPD的值.20.(本小题12分)已知椭圆M :2221(0)3x y a a +=>的一个焦点为(1,0)F -,左右顶点分别为A ,B . 经过点F 的直线l 与椭圆M 交于C ,D 两点. (Ⅰ)求椭圆方程;(Ⅱ)记ABD ∆与ABC ∆的面积分别为1S 和2S ,求12||S S -的最大值.21.(本小题12分)已知函数. x ee xf m xln )(-=(Ⅰ)设1x =是函数)(x f 的极值点,求m 的值并讨论)(x f 的单调性; (Ⅱ)当2≤m 时,证明:0)(>x f .请考生在第22,23,24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B 铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题10分)选修4-1:几何证明选讲CNMPDBA如图所示,AC 为O 的直径,D 为BC 的中点,E 为BC 的中点.(Ⅰ)求证://DE AB ;(Ⅱ)求证:2AC BC AD CD =.23.(本小题10分)选修4—4:坐标系与参数方程平面直角坐标系中,直线l 的参数方程是3x ty t=⎧⎪⎨=⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴,建立极坐标系,已知曲线C 的极坐标方程为2222cos sin ρθρθ+-2sin 30ρθ-=.(Ⅰ)求直线l 的极坐标方程;(Ⅱ)若直线l 与曲线C 相交于A 、B 两点,求||AB .24.(本小题10分)选修4-5:不等式选讲设函数()214f x x x =+--. (Ⅰ)解不等式0)(>x f ;(Ⅱ)若()34f x x m +->对一切实数x 均成立,求实数m 的取值范围.参考答案1-12 ACCDB DDDCB BA13 ﹣ ; 14. 50; 15. 32π; 16.(1),(2),(3)17.(本小题10分)解(1)由及正弦定理得,是锐角三角形,…………5分(2)解法1:由面积公式得由余弦定理得由②变形得解法2:前同解法1,联立①、②得消去b 并整理得解得所以故…………10分18.解(Ⅰ) 由题设()14211n n S n a +=-+,则21413a S =-=,3234115,a S =-=35a =. 当2n ≥时,()14231n n S n a -=-+,两式相减得()()12121n n n a n a ++=-, …………2分 方法一:由()()12121n n n a n a ++=-,得12121n n a a n n +=+-,且2131a a=.则数列21n a n ⎧⎫⎨⎬-⎩⎭是常数列,即1121211n a a n ==-⨯-,也即21n a n =- ………6分 所以数列{}n a 是首项为1,公差为2的等差数列 ………………………7分 方法二:由()()12121n n n a n a ++=-,得()()122321n n n a n a +++=+, 两式相减得212n n n a a a +++=,且1322a a a += …………………6分所以数列{}n a 等差数列. …………………7分 (Ⅱ) 由(Ⅰ)得12-=n a n ,()21212n n n S n +-==,()121nbn n =-, …………9分当1=n 时,1312T =<成立;………………………………………………10分 当2n ≥时,()()111111121212122n b n n n n n n n n ⎛⎫==<=- ⎪---⎛⎫⎝⎭- ⎪⎝⎭ ……12分所以1111111122231n T n n ⎡⎤⎛⎫⎛⎫⎛⎫<+-+-++- ⎪ ⎪ ⎪⎢⎥-⎝⎭⎝⎭⎝⎭⎣⎦1113111222n ⎛⎫=+-<+= ⎪⎝⎭综上所述,命题得证.19.证明:(1)因为梯形ABCD ,且AD BC //, 又因为⊄BC 平面PAD ,⊂AD 平面PAD ,所以//BC 平面PAD . 因为平面 BCNM 平面PAD =MN , 所以BC MN //. …………4分(2)过M 作//MK PA 交AD 于K ,连结BK . 因为PA ⊥底面ABCD , 所以MK ⊥底面ABCD . 所以MK AC ⊥. 又因为BM AC ⊥,BM MK M =,所以⊥AC 平面BMK , 所以AC BK ⊥.CNMPDBAK ABDPMC知13AK AD =, 所以13PM PD =. …………12分20.(本小题满分12分)解:(I )因为(1,0)F -为椭圆的焦点,所以1,c =又23,b =所以24,a =所以椭圆方程为22143x y +=…………………………4分(Ⅱ)当直线l 无斜率时,直线方程为1x =-,此时33(1,),(1,)22D C ---, ,ABD ABC ∆∆面积相等,12||0S S -= …………5分 当直线l 斜率存在(显然0k ≠)时,设直线方程为(1)(0)y k x k =+≠,设1122(,),(,)C x y D x y和椭圆方程联立得到22143(1)x y y k x ⎧+=⎪⎨⎪=+⎩,消掉y 得2222(34)84120k x k x k +++-= 显然0∆>,方程有根,且221212228412,3434k k x x x x k k -+=-=++ ………………8分此时122121|||2||||||2||S S y y y y -=-=+212|(1)(1)|k x k x =+++21212||2|()2|34k k x x k k =++=+ ………………………………10分因为0k ≠,上式1212123332124||24||||||k k k k =≤==+,(32k =±时等号成立)所以12||S S -的最大值为3 ………………………………12分另解:(Ⅲ)设直线l 的方程为:1-=my x ()R m ∈,则由⎪⎩⎪⎨⎧=+-=134122y x my x 得,()0964322=--+my y m .设()11y ,x C ,()22y ,x D ,则436221+=+m m y y ,0439221<+-=⋅m y y . ………………8分 所以,2121y AB S ⋅=,1221y AB S ⋅=,()21122142121y y y y AB S S +⨯⨯=-=-43122+=m m ……………………10分 当0=m 时,=-21S S 343212431222=⨯≤+=mmm m ()R m ∈. 由432=m ,得 332±=m . 当0=m 时,3021<=-S S 从而,当332±=m 时,21S S -取得最大值3.…………………………12分(21)(本小题满分12分) 解证:(Ⅰ)1()x m f x e x-'=-,由1x =是)(x f 的极值点得(1)0f '=, 即110m e --=,所以1m =. ………………………………2分 于是1()ln 0x f x e x x -=->,(),11()x f x e x-'=-, 由121()0x f x e x-''=+>知 ()f x '在(0,)x ∈+∞上单调递增,且(1)0f '=, 所以1x =是()0f x '=的唯一零点. ……………………………4分因此,当(0,1)x ∈时,()0f x '<;当(1,)x ∈+∞时,()0f x '>,所以,函数)(x f 在(0,1)上单调递减,在(1,)+∞上单调递增. ……………………………5分 (Ⅱ)当2≤m ,(0,)x ∈+∞时,2x m x e e --≥,又1+≥x e x ,所以12-≥≥--x e e x m x . ………………………………………8分取函数()1ln (0)h x x x x =-->)0(>x ,xx h 11)('-=,当10<<x 时,0)('<x h ,)(x h 单调递减;当1>x 时,0)('>x h ,)(x h 单调递增,得函数()h x 在1=x 时取唯一的极小值即最小值为(1)ln 2h =-. ……10分所以2()ln ln 1ln 0x m x f x e x e x x x --=-≥-≥--≥,而上式三个不等号不能同时成立,故>0.…………………………………12分22【证明】: (Ⅰ)连接OE ,因为D 为的中点,E 为BC 的中点,所以OED 三点共线.………………………… …2分 因为E 为BC 的中点且O 为AC 的中点,所以OE ∥AB ,故DE ∥AB.………………………… …5分 (Ⅱ)因为D 为的中点,所以∠BAD =∠DAC ,又∠BAD =∠DCB ∠DAC =∠DCB .又因为AD ⊥DC ,DE ⊥CE △DAC ∽△ECD .………… …8分 AC CD =ADCEAD ·CD =AC ·CE 2AD ·CD =AC ·2CE2AD ·CD =AC ·BC .……………………………10分23.(本小题满分10分)选修4—4:坐标系与参数方程解:(Ⅰ)消去参数得直线l 的直角坐标方程:x y 3=---------2分由⎩⎨⎧==θρθρsin cos y x 代入得 θρθρcos 3sin =)(3R ∈=⇒ρπθ.( 也可以是:3πθ=或)0(34≥=ρπθ)---------------------5分 (Ⅱ)⎪⎩⎪⎨⎧==--+303sin 2sin cos 2222πθθρθρθρ 得 0332=--ρρ-----------------------------7分设)3,(1πρA ,)3,(2πρB , 则154)(||||2122121=--=-=ρρρρρρAB .---------10分 (若学生化成直角坐标方程求解,按步骤对应给分)24.解:(I )当x 4≥ 时, f (x )=2x +1-(x -4)=x +5>0,得x >-5,所以x 4≥成立. 当421<≤-x 时,f (x )=2x +1+x -4=3x -3>0,得x >1,所以1<x <4成立. EBOACD当21-<x 时, f (x )=-x -5>0,得x <-5,所以x <-5成立. 综上,原不等式的解集为{x |x >1或x <-5} . …………5分 (II)f (x )+43-x =|2x +1|+2|x -4|9|)82(12|=--+≥x x . 当时等号成立或214-≤≥x x ,所以m <9. …………10分。
2016届东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)高考数学二模试卷(文科)解析版

2016年东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)高考数学二模试卷(文科)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)(2016•辽宁校级二模)已知集合A={x∈R|1≤x≤5},B={x∈R|x<2},则A∩B 为()A.{x∈R|1≤x<2}B.{x∈R|x<1}C.{x∈R|2<x≤5}D.{x∈R|2≤x≤5} 2.(5分)(2016•辽宁校级二模)已知i是虚数单位,若1+i=z(1﹣i),则z=()A.﹣1 B.1 C.﹣i D.i3.(5分)(2016•辽宁校级二模)已知数列{a n}为等差数列,a2+a3=1,a10+a11=9,则a5+a6=()A.4 B.5 C.6 D.74.(5分)(2016•辽宁校级二模)已知双曲线﹣y2=1(a>0)的离心率为,则其渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x5.(5分)(2016•辽宁校级二模)一个算法的流程图如图所示,若输入x的值为1,则输出y的值是()A.0 B.﹣1 C.﹣D.﹣36.(5分)(2016•辽宁校级二模)函数f(x)=Acos(ωx+φ)在区间[0,π]上的图象如图所示,则函数f(x)的解析式可能是()A.f(x)=2cos(2x+)B.f(x)=﹣cos(x﹣)C.f(x)=﹣cos(2x﹣)D.f(x)=cos(2x﹣)7.(5分)(2016•辽宁校级二模)已知m,n表示不同的直线,α,β表示不同的平面,则下列命题正确的个数是()①若m⊥α,n⊥α,则m∥n;②若m⊥n,n⊥α,则m∥α;③若m⊥β,α⊥β,则m∥α;④若m⊥α,m⊥β,则α∥β.A.1 B.2 C.3 D.48.(5分)(2016•辽宁校级二模)已知命题p:若奇函数y=f(x)(x∈R)满足f(x+2)=f (x),则f(6)=0;命题q:不等式log2x﹣1>﹣1的解集为{x|x<2},则下列结论错误的是()A.p∧q真B.p∨q真C.(¬p)∧q为假D.(¬p)∧(¬q)为真9.(5分)(2016•辽宁校级二模)已知某几何体的三视图如图所示,则该几何体的表面积为()A.4+B.4+3π C.4+πD.4++10.(5分)(2016•辽宁校级二模)若向量=(1,﹣1),|=||,•=﹣1,则向量与﹣夹角为()A.B.C. D.11.(5分)(2016•辽宁校级二模)已知圆心为C1的圆(x+2)2+y2=1,圆心为C2的圆(x ﹣4)2+y2=4,过动点P向圆C1和圆C2引切线,切点分别为M,N,若|PM|=2|PN|,则△PC1C2面积最大值为()A.3B.3C.3D.1512.(5分)(2016•辽宁校级二模)设函数f′(x)是函数f(x)(x≠0)的导函数f′(x)<,函数y=f(x)(x≠0)的零点为1和﹣2,则不等式xf(x)<0的解集为()A.(﹣∞,﹣2)∪(0,1)B.(﹣∞,﹣2)∪(1,+∞)C.(﹣2,0)∪(0,1)D.(﹣2,0)∪(1,+∞)二、填空题(本大题共有4小题,每小题5分)13.(5分)(2016•辽宁校级二模)函数f(x)=的定义域是.14.(5分)(2016•辽宁校级二模)已知实数x,y满足,则目标函数z=的最大值为.15.(5分)(2016•辽宁校级二模)设正三角形ABC的外接圆内随机取一点,则此点落在正三角形ABC内的概率为.16.(5分)(2016•辽宁校级二模)设数列{a n}的前n项和为S n,a1=2,若S n+1=S n,则数列{}的前2016项和为.三、解答题(解答应写出文字说明,证明过程或演算步骤)17.(12分)(2016•辽宁校级二模)已知向量=(sin,1),=(cos,),f(x)=•.(I)求f(x)的最大值,并求此时x的值;(Ⅱ)在△ABC中,内角A,B,C的对边分别是a,b,c,满足f(B)=,a=2,c=3,求sinA的值.18.(12分)(2016•辽宁校级二模)在甲、乙两个训练队的体能测试中,按照运动员的测试关系;(Ⅱ)采用分层抽样的方法在两个训练队成绩优秀的120名运动员中抽取名运动员组成集训队.现从这6名运动员中任取2名运动员参加比赛,求这2名运动员分别来自于甲、乙两个不同训练队的概率.(参考公式:K2=,其中n=a+b+c+d)19.(12分)(2016•辽宁校级二模)三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.(Ⅰ)求证:平面B1FG∥平面BDE;(Ⅱ)求三棱锥B1﹣BDE的体积.20.(12分)(2016•辽宁校级二模)已知抛物线C:y=x2,直线l:y=x﹣1,设P为直线l上的动点,过点P作抛物线的两条切线,切点分别为A、B(Ⅰ)当点P在y轴上时,求线段AB的长;(Ⅱ)求证:直线AB恒过定点.21.(12分)(2016•辽宁校级二模)已知函数f(x)=lnx+a(x2﹣3x)(a∈R)(Ⅰ)当a=1时,求函数f(x)的极值;(Ⅱ)讨论函数f(x)的单调性.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-1:几何证明选讲]22.(10分)(2016•辽宁校级二模)如图,AB为⊙O的直径,∠ABD=90°,线段AD交半圆于点C,过点C作半圆切线与线段BD交于点M,与线段BA延长线交于点F.(Ⅰ)求证:M为BD的中点;(Ⅱ)已知AB=4,AC=,求AF的长.五、[选修4-4:坐标系与参数方程]23.(2016•辽宁校级二模)直角坐标系xOy中,直线l的参数方程是(t为参数,0≤α<π),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程ρ=﹣4cosθ,圆C的圆心到直线l的距离为.(Ⅰ)求α的值;(Ⅱ)已知P(1,0),若直线l于圆C交于A、B两点,求+的值.[选修4-5:不等式选讲].24.(2016•辽宁校级二模)已知a,b,c为正数,且a+b+c=1(Ⅰ)求++的最小值;(Ⅱ)求证:++≥++.2016年东北三省三校(哈尔滨师大附中、东北师大附中、辽宁省实验中学)高考数学二模试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
2019年吉林省长春市东北师大附中高2019届高2016级数学二模试卷文科数学试题及详细解析

2019年吉林省长春市东北师大附中高2019届高2016级数学二模试卷文科数学试题及详解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={x|﹣1<x<1},B={x|0<x<2},则A∪B=()A.{x|﹣1<x<1}B.{x|﹣1<x<2}C.{x|0<x<2}D.{x|0<x<1}2.(5分)i是虚数单位,=()A. B. C. D.3.(5分)已知向量=(2,x),=(1,2),若∥,则实数x的值为()A.1B.2C.3D.44.(5分)设sinθ+cosθ=,则sin2θ=()A. B.﹣ C. D.5.(5分)函数的零点所在的区间是()A. B.(1,2) C.(2,e) D.(e,3)6.(5分)下列有关命题的说法正确的是()A.若“p∧q”为假命题,则p,q均为假命题B.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C.命题“若x>1,则”的逆否命题为真命题D.命题“∃x0∈R使得x02+x0+1<0”的否定是:“∃x∈R,均有x2+x+1≥0”7.(5分)元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=()A. B. C. D.8.(5分)若三角形ABC中,sin(A+B)sin(A﹣B)=sin2C,则此三角形的形状是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形9.(5分)函数y=x+cos x的大致图象是()A. B.C. D.10.(5分)已知函数满足对任意x1≠x2,都有成立,则实数a的取值范围是()A.(0,)B.(0,]C.(0,)D.(1,+∞)11.(5分)已知f(x)=﹣x3+x在区间(a,10﹣a2)上有最大值,则实数a的取值范围是()A.a<﹣1B.﹣2≤a<3C.﹣2≤a<1D.﹣3<a<112.(5分)在等腰直角△ABC中,AC=BC,D在AB边上且满足:,若∠ACD=60°,则t的值为()A. B. C. D.二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)若sin(+α)=﹣,α∈(0,π),则sinα=.14.(5分)已知向量=(λ,3),=(3,﹣2),如果与的夹角为直角,则λ=15.(5分)已知函数y=log2(ax﹣1)在(﹣2,﹣1)上单调递减,则a的取值范围是.16.(5分)设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4)=f(x),且当x∈[﹣2,0]时,f(x)=()x﹣6.若在区间(﹣2,6]内关于x的方程f(x)﹣log a(x+2)=0(a>1)恰有3个不同的实数根,则实数a的取值范围是.三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.17.(12分)已知函数f(x)=cos2x+sin2x+m.(1)求f(x)的最小正周期;(2)当x∈[0,]时,f(x)的最小值为5,求m的值.18.(12分)已知在△ABC中,角A,B,C的对边分别为a,b,c,且a sin B+b cos A=0.(1)求角A的大小;(2)若,求△ABC的面积.19.(12分)如图,在四棱锥P﹣ABCD中,棱P A⊥底面ABCD,且AB⊥BC,AD∥BC,P A=AB=BC=2AD=2,E是PC的中点.(1)求证:ED∥平面P AB;(2)求三棱锥A﹣PDE的体积.20.(12分)已知椭圆C:的左、右焦点分别是E、F,离心率,过点F的直线交椭圆C于A、B两点,△ABE的周长为16.(1)求椭圆C的方程;(2)已知O为原点,圆D:(x﹣3)2+y2=r2(r>0)与椭圆C交于M、N两点,点P为椭圆C上一动点,若直线PM、PN与x轴分别交于G、H两点,求证:|OG|•|OH|为定值.21.(12分)已知函数f(x)=xlnx﹣ax(a∈R).(1)求函数f(x)的单调区间;(2)若f(x)+a≥0恒成立,求a的值.[选修4-4:坐标系与参数方程]22.(10分)直角坐标系xOy中,曲线C1的参数方程为(α为参数),曲线.(1)在以O为极点,x轴的正半轴为极轴的极坐标系中,求C1,C2的极坐标方程;(2)射线与C1异于极点的交点为A,与C2的交点为B,求|AB|.[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣3|.(1)若f(t)+f(2t)<9,求t的取值范围;(2)若存在x∈[2,4],使得f(2x)+|x+a|≤3成立,求a的取值范围.2019年吉林省长春市东北师大附中高2019届高2016级数学二模试卷文科数学试题及详解析参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若集合A={x|﹣1<x<1},B={x|0<x<2},则A∪B=()A.{x|﹣1<x<1}B.{x|﹣1<x<2}C.{x|0<x<2}D.{x|0<x<1}【解答】解:∵集合A={x|﹣1<x<1},B={x|0<x<2},∴A∪B={x|﹣1<x<2}.故选:B.2.(5分)i是虚数单位,=()A. B. C. D.【解答】解:i是虚数单位,=,故选:A.3.(5分)已知向量=(2,x),=(1,2),若∥,则实数x的值为()A.1B.2C.3D.4【解答】解:向量=(2,x),=(1,2),∥,可得x=4.故选:D.4.(5分)设sinθ+cosθ=,则sin2θ=()A. B.﹣ C. D.【解答】解:∵sinθ+cosθ=,∴平方可得1+2sinθcosθ=1+sin2θ=,则sin2θ=﹣,故选:B.5.(5分)函数的零点所在的区间是()A. B.(1,2) C.(2,e) D.(e,3)【解答】解:∵函数(x>0),∴y′=+1+>0,∴函数y=lnx+x﹣﹣2在定义域(0,+∞)上是单调增函数;又x=2时,y=ln2+2﹣﹣2=ln2﹣<0,x=e时,y=lne+e﹣﹣2=+e﹣﹣2>0,因此函数的零点在(2,e)内.故选:C.6.(5分)下列有关命题的说法正确的是()A.若“p∧q”为假命题,则p,q均为假命题B.“x=﹣1”是“x2﹣5x﹣6=0”的必要不充分条件C.命题“若x>1,则”的逆否命题为真命题D.命题“∃x0∈R使得x02+x0+1<0”的否定是:“∃x∈R,均有x2+x+1≥0”【解答】解:若“p∧q”为假命题,则p,q至少有一个为假命题,故A错误;x=﹣1可得x2﹣5x﹣6=0,反之不成立,x=6也成立,“x=﹣1”是“x2﹣5x﹣6=0”的充分不必要条件,故B错误;“若x>1,则”为真命题,其逆否命题为真命题,故C正确;命题“∃x0∈R使得x02+x0+1<0”的否定是:“∀x∈R,x2+x+1≥0”,故D错误.故选:C.7.(5分)元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=()A. B. C. D.【解答】解:由题意,解方程:2[2(2x﹣1)﹣1]﹣1=0,解得x=,故选:B.8.(5分)若三角形ABC中,sin(A+B)sin(A﹣B)=sin2C,则此三角形的形状是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形【解答】解:∵△ABC中,sin(A+B)=sin C,∴已知等式变形得:sin C sin(A﹣B)=sin2C,即sin(A﹣B)=sin C=sin(A+B),整理得:sin A cos B﹣cos A sin B=sin A cos B+cos A sin B,即2cos A sin B=0,∴cos A=0或sin B=0(不合题意,舍去),∴A=90°,则此三角形形状为直角三角形.故选:B.9.(5分)函数y=x+cos x的大致图象是()A. B.C. D.【解答】解:由于f(x)=x+cos x,∴f(﹣x)=﹣x+cos x,∴f(﹣x)≠f(x),且f(﹣x)≠﹣f(x),故此函数是非奇非偶函数,排除A、C;又当x=时,x+cos x=x,即f(x)的图象与直线y=x的交点中有一个点的横坐标为,排除D.故选:B.10.(5分)已知函数满足对任意x1≠x2,都有成立,则实数a的取值范围是()A.(0,)B.(0,]C.(0,)D.(1,+∞)【解答】解:对任意的实数x1≠x2,都有成立,可得函数图象上任意两点连线的斜率小于0,说明函数为减函数,可得:,解得a∈(0,].故选:B.11.(5分)已知f(x)=﹣x3+x在区间(a,10﹣a2)上有最大值,则实数a的取值范围是()A.a<﹣1B.﹣2≤a<3C.﹣2≤a<1D.﹣3<a<1【解答】解:由题意得f(x)=﹣x3+x,所以f′(x)=﹣x2+1=﹣(x+1)(x﹣1),当x<﹣1或x>1时,f′(x)<0;当﹣1<x<1时,f′(x)>0,故x=1是函数f(x)的极大值点,所以由题意应有,解得﹣2≤a<1.故选:C.12.(5分)在等腰直角△ABC中,AC=BC,D在AB边上且满足:,若∠ACD=60°,则t的值为()A. B. C. D.【解答】解:∵,∴A,B,D三点共线,∴由题意建立如图所示坐标系,设AC=BC=1,则C(0,0),A(1,0),B(0,1),直线AB的方程为x+y=1,直线CD的方程为y=x,故联立解得,x=,y=,故D(,),故=(,),=(1,0),=(0,1),故t+(1﹣t)=(t,1﹣t),故(,)=(t,1﹣t),故t=,故选:A.二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)若sin(+α)=﹣,α∈(0,π),则sinα=.【解答】解:∵sin(+α)=cosα=﹣,α∈(0,π),∴sinα===.故答案为:.14.(5分)已知向量=(λ,3),=(3,﹣2),如果与的夹角为直角,则λ=2【解答】解:∵与的夹角为直角,∴=0,即3λ﹣6=0,∴λ=2.故答案为:2.15.(5分)已知函数y=log2(ax﹣1)在(﹣2,﹣1)上单调递减,则a的取值范围是(﹣∞,﹣1).【解答】解:∵已知函数y=log2(ax﹣1)在(﹣2,﹣1)上单调递减,∴a<0,且﹣a﹣1>0,求得a<﹣1,故答案为:(﹣∞,﹣1).16.(5分)设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4)=f(x),且当x∈[﹣2,0]时,f(x)=()x﹣6.若在区间(﹣2,6]内关于x的方程f(x)﹣log a(x+2)=0(a>1)恰有3个不同的实数根,则实数a的取值范围是.【解答】解:由f(x+4)=f(x),即函数f(x)的周期为4,∵当x∈[﹣2,0]时,f(x)=()x﹣6.∴若x∈[0,2],则﹣x∈[﹣2,0],则f(﹣x)=()﹣x﹣6=3x﹣6,∵f(x)是偶函数,∴f(﹣x)=3x﹣6=f(x),即f(x)=3x﹣6,x∈[0,2],由f(x)﹣log a(x+2)=0得f(x)=log a(x+2),作出函数f(x)的图象如图:当a>1时,要使方程f(x)﹣log a(x+2)=0恰有3个不同的实数根,则等价为函数f(x)与g(x)=log a(x+2)有3个不同的交点,则满足,即,解得,故a的取值范围是,故答案为:.三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.17.(12分)已知函数f(x)=cos2x+sin2x+m.(1)求f(x)的最小正周期;(2)当x∈[0,]时,f(x)的最小值为5,求m的值.【解答】解:(1)由题意知:f(x)=cos2x+sin2x+m=2sin(2x+)+m,所以f(x)的最小正周期为T=π(2)由(1)知:f(x)=2sin(2x+)+m,当x∈[0,]时,2x+∈[,]所以当2x+=时,f(x)的最小值为﹣+m又∵f(x)的最小值为5,∴﹣+m=5,即m=5+.18.(12分)已知在△ABC中,角A,B,C的对边分别为a,b,c,且a sin B+b cos A=0.(1)求角A的大小;(2)若,求△ABC的面积.【解答】解:(1)在△ABC中,由正弦定理得sin A sin B+sin B cos A=0,…(2分)即sin B(sin A+cos A)=0,又角B为三角形内角,sin B≠0,所以sin A+cos A=0,即,…(4分)又因为A∈(0,π),所以.…(6分)(2)在△ABC中,由余弦定理得:a2=b2+c2﹣2bc•cos A,则…(8分)即,解得或,…(10分)又,所以.…(12分)19.(12分)如图,在四棱锥P﹣ABCD中,棱P A⊥底面ABCD,且AB⊥BC,AD∥BC,P A=AB=BC=2AD=2,E是PC的中点.(1)求证:ED∥平面P AB;(2)求三棱锥A﹣PDE的体积.【解答】证明:(1)取PB中点H,连接AH、EH,∵E,H分别为面PC,PB的中点,∴HE∥BC,且HE=BC,又∵AD∥BC,且AD=BC,∴AD∥HE,且AD=HE,∴四边形AHED是平行四边形,∴AH∥DE,又AH⊂平面P AB,又DE⊄平面P AB,∴DE∥平面P AB.…(6分)解:(2)由(1)知,BC⊥PB,∴AD⊥PB,又PB⊥AH,且AH∩AD=A,∴PB⊥平面ADEH,∴PH是三棱锥P﹣ADE的高,又可知四边形ADEH为矩形,且AD=1,AH=,…(9分)∴三棱锥A﹣PDE的体积:V A﹣PDE=V P﹣ADE====.…(12分)20.(12分)已知椭圆C:的左、右焦点分别是E、F,离心率,过点F的直线交椭圆C于A、B两点,△ABE的周长为16.(1)求椭圆C的方程;(2)已知O为原点,圆D:(x﹣3)2+y2=r2(r>0)与椭圆C交于M、N两点,点P为椭圆C上一动点,若直线PM、PN与x轴分别交于G、H两点,求证:|OG|•|OH|为定值.【解答】解:(1)由题意和椭圆的定义得|AF|+|AE|+|BF|+|BE|=4a=16,则a=4,由,解得,则b2=a2﹣c2=9,所以椭圆C的方程为;(2)证明:由条件可知,M,N两点关于x轴对称,设M(x1,y1),P(x0,y0),则N(x1,﹣y1),由题可知,,,所以,.又直线PM的方程为,令y=0得点G的横坐标,同理可得H点的横坐标,所以|OG|•|OH|=|•|=||==16,即|OG|•|OH|为定值.21.(12分)已知函数f(x)=xlnx﹣ax(a∈R).(1)求函数f(x)的单调区间;(2)若f(x)+a≥0恒成立,求a的值.【解答】解:(1)f(x)的定义域是(0,+∞),f′(x)=lnx+1﹣a,令f′(x)>0,解得:x>e a﹣1,令f′(x)<0,解得:0<x<e a﹣1,故f(x)在(0,e a﹣1)递减,在(e a﹣1,+∞)递增;(2)f(x)+a≥0恒成立,即a(x﹣1)≤xlnx恒成立,x>1时,即a≤在(1,+∞)恒成立,令h(x)=,(x>1),h′(x)=,令y=﹣lnx+x﹣1,则y′=﹣+1=>0,故y=﹣lnx+x﹣1在(1,+∞)递增,故y>0,故h′(x)=>0,故h(x)在(1,+∞)递增,由=(lnx+1)=1,故a≤1,x=1时,显然成立,0<x<1时,即a≥在(0,1)恒成立,令m(x)=,(0<x<1),m′(x)=<0,故m(x)在(0,1)递增,由=(lnx+1)=1,故a≥1,综上,a=1.[选修4-4:坐标系与参数方程]22.(10分)直角坐标系xOy中,曲线C1的参数方程为(α为参数),曲线.(1)在以O为极点,x轴的正半轴为极轴的极坐标系中,求C1,C2的极坐标方程;(2)射线与C1异于极点的交点为A,与C2的交点为B,求|AB|.【解答】解:(Ⅰ)曲线C1:(α为参数)化为普通方程为x2+y2=2x,所以曲线C1的极坐标方程为ρ=2cosθ,曲线C2的极坐标方程为ρ2(1+2sin2θ)=3.(Ⅱ)射线与曲线C1的交点的极径为,射线与曲线C2的交点的极径满足,解得,所以.[选修4-5:不等式选讲]23.已知函数f(x)=|x﹣3|.(1)若f(t)+f(2t)<9,求t的取值范围;(2)若存在x∈[2,4],使得f(2x)+|x+a|≤3成立,求a的取值范围.【解答】解:(1)由f(t)+f(2t)<9得|t﹣3|+|2t﹣3|<9,∴,或,或,解得﹣1<t<5.(2)当x∈[2,4]时,f(2x)+|x+a|=2x﹣3+|x+a|,∴存在x∈[2,4],使得|x+a|≤6﹣2x即2x﹣6≤x+a≤6﹣2x成立,∴存在x∈[2,4],使得成立,∴,∴a∈[﹣4,0].。
吉林省东北师大附中2016年高考数学模拟试卷(文科)(六) 含解析

2016年吉林省东北师大附中高考数学模拟试卷(文科)(六)一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i是虚数单位,则(1﹣2i)(2+i)=()A.4﹣3i B.3﹣4i C.﹣3﹣4i D.﹣4+3i2.已知集合A={a,4},B={2,a2},且A∩B={4},则A∪B=()A.{2,4} B.{﹣2,4}C.{﹣2,2,4}D.{﹣4,2,4}3.已知命题p:∃x0>0,2x0=3,则¬p是() A.∀x∈R,2x≠3 B.∀x>0,2x≠3 C.∀x≤0,2x=3 D.∀x≤0,2x≠34.已知向量,的夹角的余弦值是,且满足||=||=1,则|+|=( )A.B.C.D.5.已知A+B=π,B∈(,π),且sinB=,则tanA=()A.B.C.2D.6.执行如图所示的程序框图,输出的S值为()A.2 B.4 C.6 D.127.已知等比数列{a n}(a1≠a2)的公比为q,且a7,a1,a4成等差数列,则q=()A.1或B. C.1或 D.18.已知抛物线y2=2x的焦点为F,准线为l,且l与x 轴交于点E,A是抛物线上一点,AB⊥l,垂足为B,|AF|=,则四边形ABEF的面积等于()A.19 B.38 C.18 D.369.已知函数f(x)(x∈R),满足f(﹣x)=﹣f(x),f (3﹣x)=f(x),则fA.0 B.3 C.﹣3 D.不确定10.甲、乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜时间内随机到达,试求这两艘船中至少有一艘在停靠泊位时必须等待的概率是() A.B.C.D.11.如图,一个几何体的三视图是三个直角三角形,则该几何体的最长的棱长等于()A.2B.3 C.3D.912.过双曲线﹣=1(a>0,b>0)的左焦点F(﹣,0)作圆(x﹣)2+y2=1的切线,切点在双曲线上,则双曲线的离心率等于( )A.2 B.C.D.二.填空题:本大题共4小题,每小题5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013级高三年级第二次摸底考试(数学文)学科试题考试时间: 120分钟试卷满分: 150分命题人:邢昌振审题人:戴有刚孙明侠第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)212log log2+=(A)12(B)12-(C)32(D)32-(2)命题“2,320x R x x∃∈-+=”的否定是(A)2,320x R x x∀∈-+=(B)2,320x R x x∃∈-+≠(C)2,320x R x x∀∈-+≠(D)2,320x R x x∃∈-+>(3)若0.23a=,πlog3b=,3logc=,则(A)b c a>>(B)b a c>>(C)a b c>>(D)c a b>>(4)已知函数()sin cos,(0,)f x x x xπ=+∈,且'()0f x=,则x=(A)4π(B)34π(C)3π(D)6π(5)已知幂函数{}(),2,1,1,3nf x x n=∈--的图象关于y轴对称,则下列选项正确的是(A)(2)(1)f f->(B)(2)(1)f f-<(C)(2)(1)f f=(D)(2)(1)f f->-(6)“a b>”是“22a b>”的(A)充分非必要条件.(B)必要非充分条件.(C)充要条件.(D)既非充分又非必要条件.(7)曲线()(,)nf x ax a n R=∈在点(1,2)处的切线方程是42y x=-,则下列说法正确的是(A )函数()f x 是偶函数且有最大值 (B )函数()f x 是奇函数且有最大值(C )函数()f x 是偶函数且有最小值 (D )函数()f x 是奇函数且有最小值(8)若()f x 是R 上周期为5的奇函数,且满足(1)1,(2)2f f ==,(23)(14)f f +-=(A )1-(B )1 (C )2- (D )2(9)函数2()1x f x x=-的图象大致是(10)已知函数22()22,()f x x x g x ax bx c =-+=++,若这两个函数的图象关于(2,0)对称,则()f c =(A )122 (B )5 (C )26 (D )121(11)如果一个正方体的体积在数值上等于V ,表面积在数值上等于S ,且0V S m --≥恒成立,则实数m 的范围是(A )(,16]-∞- (B )(,32]-∞- (C )[32,16]-- (D )以上答案都不对(12)若函数)(x f 满足:在定义域D 内存在实数0x ,使得)1()()1(00f x f x f +=+成立, 则称函数)(x f 为“1的饱和函数”.给出下列五个函数:① x x f 2)(=;②xx f 1)(=;③21()lg()2f x x =-;④21()x x f x e -=. 其中是“1的饱和函数”的所有函数的序号为(A )①②④ (B )②③④ (C )①②③ (D )①③④第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分。
(13)已知2,,m a e b e -==且1a b ⋅=,则m = .(14)已知集合{}{}23,,0,,1A a B b a ==-,且{}1A B = ,则A B = .(15)若命题“2,20x R ax ax ∀∈--<”是真命题,则实数a 的取值范围是 .(16)若函数22()243f x x a x a =++-有三个不同的零点,则函数()()(1)g x f x f a a =-++的零点个数是________个.三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.(17)(本小题满分10分) 已知函数27(),(4).2m f x x f x =-=且 (Ⅰ)判断()f x 的奇偶性;(Ⅱ)写出不等式()1f x >的解集(不要求写出解题过程).(18)(本小题满分12分)已知函数()2sin(2)1f x x φ=++的图象过点(0,0),且02πφ-<<. (Ⅰ)求φ的值;(Ⅱ)求函数()f x 的最大值,并求此时x 的值.(19)(本小题满分12分)已知等比数列{}n a ,253,81a a ==.(Ⅰ)求7a 和公比q ;(Ⅱ)设3log n n n b a a =+,求数列{}n b 的前n 项的和.(20)(本小题满分12分)设关于x 的方程2220()x ax a R --=∈)的两个实根为()αβαβ<、,函数14)(2+-=x a x x f . (Ⅰ)求()f α,()f β的值(结果用含有a 的最简形式表示);(Ⅱ)函数)(x f 在R 上是否有极值,若有,求出极值;没有,说明理由.(21) (本小题满分12分)已知A 是椭圆22221(0)x y a b a b +=>>上一点,椭圆的离心率12e =. (Ⅰ) 求椭圆的方程;(Ⅱ) 过点(0,3)P 的直线m 与椭圆交于,A B 两点.若A 是PB 的中点,求直线m 的方程.(22)(本小题满分12分)已知函数2()ln ,()(1)1().f x x x g x ax a x a R ==-++∈.(Ⅰ)当0a =时,求()()f x g x +的单调区间;(Ⅱ)当1x ≥时,()()ln f x g x x ≤+,求实数a 的取值范围;文科数学参考答案一 、选择题 BCCAB ACABA BD二、填空题 13.2 14. {}0,1,2,315. (8,0]- 16. 4三、解答题17. (Ⅰ)可得 1,()(),m f x f x =-=-奇函数.(Ⅱ)(1,0)(2,).-+∞18.解析:(Ⅰ) 有已知得1sin ,2φ=-又02πφ-<<,所以.6πφ=- (Ⅱ)解:由(Ⅰ)得 ()2sin(2)16f x x π=-+,所以 max ()3,f x = 此时由222,().623x k x k k Z πππππ-=+=+∈得 19.解: (Ⅰ)253,813,a a q ==∴= 可求公比 7729.a =(Ⅱ)由已知可得13,n n a -=设{}n b 的前n 项的和为n S ,3log n n n b a a =+13(1)n n -=+-, 213(1)31.1322n n n n n n n S n -++--=+-=-则 20.解析:(Ⅰ)αβ==()()f f αβ==== (Ⅱ)设2()22g x x ax =--,2222222(4)(1)(4)(1)4(1)2(4)'()(1)(1)x a x x a x x x x a f x x x ''-+--++--==++222222(22)2()(1)(1)x ax g x x x ---==-++. 因为当x α<时, ()0g x >,所以'()0f x <;当x αβ<<时,()0g x <,'()0f x >当x β>时,()0g x >,'()0f x <.∴函数)(x f 在(,)α-∞是减函数.在()βα,上是增函数.在(),β+∞上是减函数.所以()f x有极小值()f α=极大值()f β=. 21.解:(Ⅰ) 椭圆的方程为221.43x y +=; (Ⅱ)设11(,)A x y ,由A 是PB 的中点,得11(2,23)B x y -.因为,A B 在椭圆上,所以 得22112211143(2)(23)143x y x y ⎧+=⎪⎪⎨-⎪+=⎪⎩,解得11132x y =±⎧⎪⎨=⎪⎩ 所以,直线m 的斜率3.2k =±直线的方程3 3.2y x =±+22.解析:(Ⅰ)设()()()ln 1,h x f x g x x x x =+=-+'()ln .h x x ∴=由'()0,(0,1)h x x <∈得;由'()0,(1,)h x x >∈+∞得()h x 在(0,1)单调递减,在(1,)+∞单调递增.(Ⅱ)(法一)由()()ln f x g x x ≤+,得(1)ln (1)(1)x x ax x -≤--, 因为1,x ≥ 所以:ⅰ)当1x =时,.a R ∈ⅱ)当1x >时,可得ln 1x ax ≤-,令()ln 1h x ax x =--,则只需()ln 10h x ax x =--≥即可.因为1'()h x a x =-.且 101x<< ⅰ)当0a ≤时,()0h x '<,得()h x 在(1,)+∞单调递减,且可知()20h e ae =-<这与()ln 10h x ax x =--≥矛盾,舍去;ⅱ)当1a ≥时, ()0h x '>得()ln 1h x ax x =--在(1,)+∞上是增函数,此时()ln 1(1)10h x ax x h a =-->=-≥.iii )当01a <<时,可得 ()h x 在1(1,)a 单调递减,在1(,)a +∞单调递增,min 1()()ln 0h x h a a ∴==<矛盾。
综上:当1a ≥时,()()ln f x g x x ≤+恒成立.(法二)(分离常数)略。
