机械设计基础:第8章回转件的平衡
机械设计基础-第八章平衡和调速

显然,动能变化量相同时,飞轮的转动惯量越大,角速度 波动越小。
南京航空航天大学 机电学院
College of Mechanical and Electrical Engineering
Nanjing University of Aeronautics and Astronautics
2、非周期性速度波动
南京航空航天大学 机电学院
College of Mechanical and Electrical Engineering
Nanjing University of Aeronautics and Astronautics
措施:安装转动惯量较大的回转件——飞轮(转动惯量较大 的盘形零件)。 原理:盈功时飞轮储存能量,飞轮的动能增加,使主轴 角速度上升的幅度减小; 亏功时飞轮释放其能量,飞轮动能减少,使主轴 角速度下降的幅度减小
南京航空航天大学 机电学院
College of Mechanical and Electrical Engineering
Nanjing University of Aeronautics and Astronautics
机械设计基础
之
第八章 调速和平衡
南京航空航天大学 机电学院
College of Mechanical and Electrical Engineering
南京航空航天大学 机电学院
College of Mechanical and Electrical Engineering
南京航空航天大学 机电学院
College of Mechanical and Electrical Engineering
Nanjing University of Aeronautics and Astronautics
机械设计基础答案77438
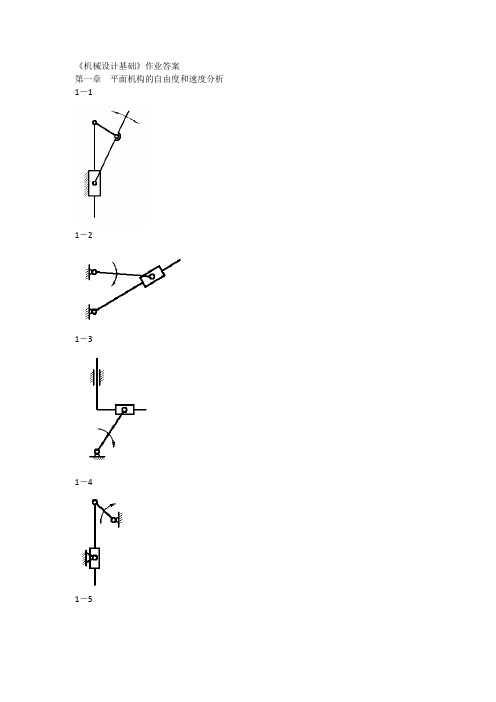
《机械设计基础》作业答案第一章平面机构的自由度和速度分析1-11-21-31-41-5自由度为:11 19211)0192(73')'2(3=--=--+⨯-⨯=--+-=FPPPnFHL或:1182632 3=-⨯-⨯=--=HLPPnF1-6自由度为11)01122(93')'2(3=--+⨯-⨯=--+-=FPPPnFHL或:11 22241112832 3=--=-⨯-⨯=--=HLPPnF1-10自由度为:1128301)221142(103')'2(3=--=--⨯+⨯-⨯=--+-=F P P P n F H L或: 122427211229323=--=⨯-⨯-⨯=--=HL P P n F1-1122424323=-⨯-⨯=--=HL P P n F1-13:求出题1-13图导杆机构的全部瞬心和构件1、3的角速度比。
1334313141P P P P ⨯=⨯ωω11314133431==P P ω1-14:求出题1-14图正切机构的全部瞬心。
设s rad /101=ω,求构件3的速度3v 。
s mm P P v v P /20002001013141133=⨯===ω1-15:题1-15图所示为摩擦行星传动机构,设行星轮2与构件1、4保持纯滚动接触,试用瞬心法求轮1与轮2的角速度比21/ωω。
构件1、2的瞬心为P 12P 24、P 14分别为构件2与构件1相对于机架的绝对瞬心1224212141P P P P ⨯=⨯ωω121214122421r P P ==ω 1-16:题1-16图所示曲柄滑块机构,已知:s mm l AB /100=,s mm l BC /250=,s rad /101=ω,求机构全部瞬心、滑块速度3v 和连杆角速度2ω。
在三角形ABC 中,BCA AB BC∠=sin 45sin 0,52sin =∠BCA ,523cos =∠BCA , 045sin sin BCABC AC=∠,mm AC 7.310≈s mm BCA AC P P v v P /565.916tan 1013141133≈∠⨯===ω1224212141P P P P ωω=s rad AC P P P P /9.21002101001122412142≈-⨯==ωω1-17:题1-17图所示平底摆动从动件凸轮1为半径20=r 的圆盘,圆盘中心C 与凸轮回转中心的距离mm l AC 15=,mm l AB 90=,s rad /101=ω,求00=θ和0180=θ时,从动件角速度2ω的数值和方向。
第8章平衡答题

第八章答题:第八章课程名:机械设计基础 (第八章) 题型 计算题 考核点:静平衡计算、动平衡计算1. 某汽轮机转子质量为1吨,由于材质不匀及叶片安装误差致使质心偏离回转轴线0.4mm ,当该转子以5000r/min 的转速转动时,其离心力有多大?离心力是它本身重力的几倍?(8分)解:离心力:F =mr ω2=N 109662)6050002(100014.0100012=⨯⨯⨯⨯⨯π 离心力是它本身重力的倍数:109662/(1000×9.8)=11.9倍*2.图示盘形回转件经静平衡试验得知,其不平衡质径积mr 等于2kg.m ,方向沿图中方向 。
由于结构限制,,只允许在和方向各加一个质径积来进行平衡,求D D c c r m r m 和的数值。
(12分)解:依题意列方程︒=︒=︒+︒60sin 30sin 60cos 30cos D D c c A A D D c c r m r m r m r m r m代入已知数:232122123DD c c D D cc r m r m r m r m ==+ 解得:mkg r m m kg r m c c D D ⋅=⋅=732.11*3图示盘形回转件上存在四个偏置质量;已知m1=10kg, m2=l4kg ,m3=l6kg, m4=10kg ,r1=50mm ,r2=100mm ,r3=75mm ,r4=50mm ,设所有不平衡质量分布在同一回转面内,问应在什么方位上加多大的平衡质径积才能达到平衡?(12分)解:依题意:设沿r1方向为X 正方向,沿r2方向为Y 正方向。
列方程m1r1-m3r3+mxrx=0m2r2-m4r4+myry=0 10×0.05-16×0.075+m x r x =0 m x r x =0.7kg ·m14×0.1-10×0.05+m y r y =0 m y r y =-0.9kg ·m 平衡质径积为:kgm14.1=52..125°YX*4图示盘状转子上有两个不平衡质量:m1=1.5kg, m2=0.8kg, r1=140mm, r2=180mm, 相位如图。
杨可桢《机械设计基础》(第5版)笔记和课后习题(回转件的平衡)

第8章 回转件的平衡8.1 复习笔记一、回转件平衡的目的机械中有许多构件是绕固定轴线回转的,这类作回转运动的构件称为回转件(或称转子)。
1.不平衡的原因由于回转件的结构不对称、材质不均匀或是制造不准确等因素,使回转件在转动时产生离心力系的不平衡,使离心力系的合力和合力偶矩不等于零。
2.不平衡的危害(1)在运动副中产生附加的动压力,从而增大构件中的内应力和运动副中的摩擦,加剧运动副的磨损,降低机械效率和使用寿命;(2)使机械产生周期性振动,降低工作可靠性和精度、零件材料的疲劳损坏以及令人厌倦的噪声。
3.回转件平衡的目的调整回转件的质量分布,使转子工作时的离心力达到平衡,以消除附加动压力,尽可能减轻有害振动,改善机构工作性能。
二、回转件的平衡计算根据组成回转件各质量的不同分布,可分两种情况。
1.质量分布在同一回转面内轴向尺寸很小的回转件(B/D <0.2),将其质量看作是分布在同一平面内,如风扇叶轮、飞轮、砂轮等。
对于这类转子,利用在刚性转子上重心的另一侧加上一定的质量,或在重心同侧去掉一些质量,使质心位置落在回转轴线上,从而使离心惯性力达到平衡,即平衡条件为:b 0=+∑=i F F F式中,F 、b F 、i F ∑分别表示总离心力、平衡质量的离心力、原有质量的离心力。
写成质径积的形式为:b b 0=+∑=i i me m r m r特点:若重心不在回转轴线上,则在静止状态下,无论其重心初始在何位置,最终都会落在轴线的铅垂线的下方,这种不平衡现象在静止状态下就能表现出来,故称为静平衡。
静平衡的条件:分布于回转件上各个质量的质径积的向量和为零,即:b b 0+∑=i i m r m r2.质量分布不在同一回转面内 对于轴向尺寸较大(B/D ≥0.2)的回转件,如内燃机中的曲轴和凸轮轴、电机转子、机床主轴等,其质量的分布不能再近似地认为是位于同一回转面内,而应看作分布在垂直于轴线的许多互相平行的回转平面内,离心惯性力将形成一个不汇交空间力系,因此必须使各质量产生的离心力的合力和合力偶都等于零,才能达到平衡,即平衡条件为:0F ∑= 0M ∑=平衡方法:对于动不平衡的转子,无论其具有多少个偏心质量以及分布在多少个回转平面内,只要将各不平衡质量产生的惯性力分别分解到两个选定的平衡基面内,则动平衡即转化为在两平衡基面内的静平衡计算问题。
机械设计基础(机工版)教案:机械平衡

第二节机械平衡一、机械平衡的目的:尽量减小惯性力所引起的附加动压力,减轻机械振动,改善机械工作性能,延长机械使用寿命。
二、机械平衡的种类:(1)回转件的平衡1)刚性回转件的平衡:工作转速低于一阶临界转速的回转件的平衡。
轴线变形忽略不计。
2)挠性回转件的平衡:工作转速高于一阶临界转速的回转件的平衡。
(2)机构的平衡:往复运动和平面复合运动的构件系统的平衡。
三、静平衡1.静不平衡:对轴向尺寸较小的回转件,可近似地认为其不平衡质量分布在同一回转平面内。
若其质心不在回转轴线上,质心对轴线产生静力矩,称为静不平衡。
2.静平衡:质心与回转轴线重合,在任何位置都静止。
3.结论:(1) 静平衡的条件:各个偏心质量的离心惯性力的合力为零或质径积的向量和为零。
(2) 对于静不平衡的回转件,无论它有多少个偏心质量,都只需要适当地增加一个平衡质量即可获得平衡,即对于静不平衡的转子,需加平衡质量的最少数目为1。
四、动平衡1 动不平衡:对于质量不能再视为分布在同一平面内,由于各惯性力不在同一回转平面内,因而将形成惯性力偶,即使质心在回转轴线上,仍然是不平衡的。
这种不平衡只有在转子运动时才显示出来,故称其为动不平衡。
2 动平衡计算:动平衡措施:将每个平面的惯性力平衡。
3 结论:(1)动平衡的条件:转子上分布在不同平面内的各个质量所产生的空间离心惯性力系的合力及合力矩均为零。
(2)对于动不平衡的转子,无论它有多少个偏心质量,都只需要在任选的两个平衡平面内各增加或减少一个合适的平衡质量即可使转子获得动平衡,即对于动不平衡的转子,需加平衡质量的最少数目为2。
因此,动平衡又称为双面平衡,而静平衡则称为单面平衡。
由于动平衡同时满足静平衡条件,所以经过动平衡的转子一定静平衡的;反之,经过静平衡的转子则不一定是动平衡的。
五、本章小结周期性速度波动调节方法:安装飞轮。
非周期性速度波动的调节方法:1)当机械的原动机所发出的驱动力矩是速度的函数且具有下降的趋势时,机械具有自动调节非周期性速度波动的能力。
机械设计基础 第8章 回转件的平衡

2,静平衡计算 静平衡计算主要是针对由于结构所引起的静不平衡的转子而 进行平衡的计算. 根据其结构,计算确定需增加或除去的平衡质量,使其在设 计时获得静平衡. F
F i1 1 FF2 i
2
m1 mb
r1
r2 r3 rb
m2 m3
F 3F3
m3r3 3 F
m3r3
m2r2 m F r
22 2
mbbbbb m F rr m1111r1 m Fr
增大运动副中摩擦和构件中的内应力,降低机械效率和使用 寿命,影响机械本身的正常工作,也必将引起机械及其基础产生 强迫振动,甚至产生共振. 会导致工作机械及其厂房建筑受到破 坏.不平衡惯性力也可以利用.
附加的动压力
振动(源)
噪音,精度↓, 可靠性↓,寿命 ↓,效率↓.
一,平衡的目的:完全或部分地消除惯性合力和惯性合力偶 尽量减小惯性力所引起的附加动压力. 二,平衡的分类 刚性回转件平衡 回转件的平衡: 柔性回转件平衡 (有专门学科)
§8-3 刚性转子的平衡试验
对于经平衡计算在理论上已经平衡的转子,由于其制造精度 和装配的不精确,材质的不均匀等原因,就会产生新的不平衡. 但这种无法用计算来进行平衡,而只能借助于实验平衡. 平衡实验是用实验的方法来确定出转子的不平衡量的大小和 方位,然后利用增加或除去平衡质量的方法予以平衡. 1.静平衡实验 (1)实验设备
§8-1 回转件平衡的目的
回转件:绕定轴回转的构件,也称转子. 机械在运转时,构件所产生的不平衡惯性力将在运动副中引 起附加的动压力. n=6000r/min 例 磨削工作的砂轮 FⅠ A S B e=1mm
其方向作周期性变化 FⅠ在转动副中引起的附加反力是砂轮自重的40倍.
机械设计基础课件08回转件的平衡

求平衡质量的大小和向径的方法有三种:解析法、图解法和 试验法。解析法精确,图解法直观,试验法实用。下面由例题 简述解析法和图解法的具体求解方法。
式中P、Pb和Pi分别表示总离心力、平衡质量的离心力和原有质量离心力的 合力。代入离心力计算式,并消除ω后,可得
式中,m、e为回转件的总质量和总质心向径,mb、rb为平衡质量及其质心 的向径,mi、ri为原有各质量及其质心的向径。
由上式可知,当回转速度ω一定时,离心力的大小和方向只 与各个质量的大小和向径有关,我们把质量与向径的乘积称为 质径积。
为了使转子达到动平衡,通常采用动平衡试验法,即将回 转件在动平衡试验机上运转,然后在两个选定的平面内分别找 出所需的质径积的大小和方位,通过逐步调整,最终使转子达 到动平衡。
显然动平衡条件中包含了静平衡条件,也就是说动平衡的转子一定也是静平衡的,
但静平衡的转子不一定是动平衡的。
为了使转子达到动平衡,通常采用动平衡试验法,即将回转件在动平衡试验机 上运转,然后在两个选定的平面内分别找出所需的质径积的大小和方位,通过逐步 调整,最终使转子达到动平衡。
上述动平衡机的结构和测试方法都比较简陋,因而灵敏度
和平衡精度都较低。目前已有大量的机电一体的动平衡机,关 于这些动平衡机的详细情况,请读者参阅有关的文献和资料。
导轨式静平衡加简单可靠,其精度也能满足一般机械生 产的需要。
8.2.2 质量分布不在同一回转面内
对于轴向尺寸较大的回转件,即称为轴类零件,如电动机的转子、机床 主轴等,其质量分布不能近似地认为是位于同一回转面内。这类回转件转 动时产生的离心力不再是平面力系,而是空间力系。因此,单靠在某一回 转面内加一平衡质量的静平衡方法不能使这类回转件转动时达到平衡。
机械设计基础习题及答案
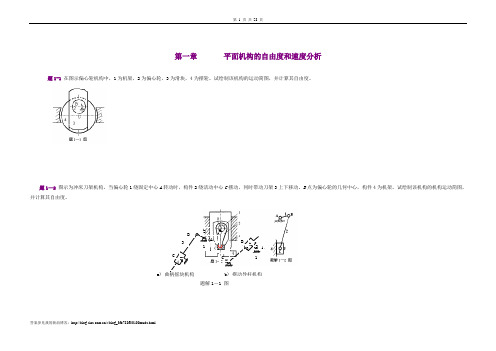
第一章平面机构的自由度和速度分析题1-1在图示偏心轮机构中,1为机架,2为偏心轮,3为滑块,4为摆轮。
试绘制该机构的运动简图,并计算其自由度。
题1—2图示为冲床刀架机构,当偏心轮1绕固定中心A转动时,构件2绕活动中心C摆动,同时带动刀架3上下移动。
B点为偏心轮的几何中心,构件4为机架。
试绘制该机构的机构运动简图,并计算其自由度。
题1—3计算题1-3图a)与图b)所示机构的自由度(若有复合铰链,局部自由度或虚约束应明确指出)。
题1-3图a)题1-3图b)题1—4计算题1—4图a、图b所示机构的自由度(若有复合铰链,局部自由度或虚约束应明确指出),并判断机构的运动是否确定,图中画有箭头的构件为原动件。
题1—5 计算题1—5图所示机构的自由度(若有复合铰链,局部自由度或虚约束应明确指出),并标出原动件。
题1—5图 题解1—5图题1-6 求出图示的各四杆机构在图示位置时的全部瞬心。
第二章 连杆机构题2-1在图示铰链四杆机构中,已知 l BC =100mm ,l CD =70mm ,l AD =60mm ,AD 为机架。
试问:(1)若此机构为曲柄摇杆机构,且AB 为曲柄,求l AB 的最大值;(2)若此机构为双曲柄机构,求l AB 最小值; (3)若此机构为双摇杆机构,求l AB 的取值范围。
题2-2 如图所示的曲柄滑块机构: (1)曲柄为主动件,滑块朝右运动为工作 行程,试确定曲柄的合理转向,并简述其理由;(2)当曲柄为主动件时,画出极位夹角θ,最小传动角g min ; (3)设滑块为主动件,试用作图法确定该机构的死点位置 。
D题2-1图题2-3图示为偏置曲柄滑块机构,当以曲柄为原动件时,在图中标出传动角的位置,并给出机构传动角的表达式,分析机构的各参数对最小传动角的影响。
题2-4设计一曲柄摇杆机构,已知机构的摇杆DC长度为150mm,摇杆的两极限位置的夹角为45°,行程速比系数K=1.5,机架长度取90mm。
第8章平衡

第八章 转子的平衡8.1 考点提要8.1.1 重要概念及术语静平衡,动平衡,长径比,质径积 8.1.2 动平衡和静平衡的区别对于轴向长度和直径的比值(长径比)小于或等于0.2的转子,可以被视为一个薄片圆盘,不平衡质量都看作在一个端面上。
这样的圆盘上如果有不平衡的偏心质量,则不需要输入动力转矩,只要用手松开转子,转子就会转动,直至不平衡质量的重心在正下方为止。
由于不需要输入动力就可以看出不平衡,所以称为静不平衡。
对于轴向长度和直径的比值(长径比)大于0.2的转子,即使实现了静平衡,由于不平衡质量分布在轴类构件的不同端面上,在输入力矩后会产生不平衡的力偶,这种现象称为动不平衡。
8.1.3. 静平衡的校正对与质量分布在同一回转面的圆盘,只要进行力平衡,在圆盘上增加一个配重,使各不平衡质量产生的离心力互相抵消即可实现平衡。
设圆盘上有n 个不平衡质量,某个不平衡质量的半径为i r ,某个不平衡质量i m ,配重质量b m ,配重半径b r ,则所有离心力的矢量和应为零:0)(21=+∑= i ni i b b r m r m约去角速度得:01=+∑=i ni i bb r m r m既质量和半径的乘积(质径积)的矢量和为零。
图8.1 静平衡的校正建立坐标系,如图8.1所示(图中有三个不平衡质径积,一个配平衡的质径积),把各向量对X,Y 轴方向投影得:∑=+0cos cos θθb b b i i i r m r m ∑=+0sin sin θθb b b i i i r m r m 得:∑∑-+-=22)sin ()cos (θθi i i i i i b b r m r m r m (8-1)∑-∑-=θθθii i i i i b r m r m cos sin (8-2) 角度再根据坐标系中X ,Y 坐标方向分量的正负号确定象限并调整即可。
8.1.4. 动平衡的校正把轴向各个不平衡质量保持方向不变,向两个准备安装配重的校正面利用力矩相等的原则分解, 以图8.2为例:221)()()(L r m L L r m i i A i i =+ 121)()()(L r m L L r m i i B i i =+这样就把i i r m 分解为校正面上的A i i r m )(和B i i r m )(,方向不变。
机械设计基础8回转件的平衡

如果想用Fb’, Fb’’ 来取代Fb ,
则:
Fb Fb Fb Fb l Fb l
l l l ,代入上式得:
∵
l Fb Fb l l Fb Fb l
消去等式两边的公因子2得:
l mb rb mb rb l l mb rb mb rb l
Fb
me mb rb mi ri 0
对于所需平衡面上不能安装平衡质量的回转件,可另选 两个回转面安装平衡质量。 例:已知,一曲轴的回转平面如图所示,试在距原平衡面为 l’,l’’ 的两侧T’,T’’面上配平衡质量。 解: 设在T’,T’’面上分别配上平衡质量mb’, mb’’,向径分别为 rb’, rb’’,且mb’, mb’’都处于经过mb的质心且包含回转轴线的平 面内。 那么产生离心力 Fb’, Fb’’ Fb 为 互相平行的力。
F1
F --- ---- 总离心力,
Fi ----
原有质量离心力的合力
Fb
即:
得:
me 2 mb rb 2 mi ri 2 0 me mb rb mi ri 0
m --- 总质量
e ----总质心的向径 mb --- 平衡质量
F1
rb ---平衡质心的向径
l l m1 1 m1 m1 1 m1 l l l2 l2 m2 m2 m2 m2 l l l3 l3 m3 m3 m3 m3 l l
对回转面T’,平衡方程为:
mb rb m1 r1 m2 r2 m3 r3 0
设:不平衡质量m1, m2分布在相距为l 的两个回转平面内, 而且, m1 = m2,r1 =-r2, 该回转件的质心虽然在回转轴上, 且满足:m1r1 +m2r2 = 0 静平衡条件; 但由于m1,m2不在同一个回转面内,回转 件回转时会产生力偶,回转件仍处于动
机械设计基础课件第八章回转件的平衡

回转件是指在运动中具有旋转不对称性的机械零件,回转件的平衡性是机械 设计中非常关键的问题。
回转件的定义
常见的回转件
钻孔加工机,车削加工机,制动盘,离合器曲 轴等等。
重心与惯性矩
回转件的平衡与其重心位置和惯性矩有关,理 解这些概念有助于确定平衡条件。
特殊的回转件
手表的自动上弦装置,自行车的飞轮等,这些 回转件的平衡问题需要特殊考虑。
平衡的概念与判定条件
1 平的定义
指回转件在运动过程中,不外力不产生力矩。
2 判定条件
回转件的平衡需要满足两个条件:对重心的合外力与合外力矩均为零。
3 举个例子
一辆自行车,骑行过程中不会翻倒,就是因为车轮的平衡可以满足平衡条件。
平衡解法的基本原理
1
受力分析
分解合外力,计算受力点至重心的距离
2
力矩计算
动平衡
回转件在运动状态下的平衡状态,即回转件所受 合外力矩仍然为零。
静平衡与动平衡的判定条件
1
静平衡的判定条件
寻找合力的作用点和力矩的方向,可用物理方法求解。
2
动平衡的判定条件
刚体转动惯量必须大于等于对象所受扭矩的一部分,常用解析法求解。
3
复杂的案例
比如飞机的旋翼系统、燃气轮机的转子系统等,需要结合实验证验验证平衡性。
实例分析与课后习题
实例分析
分析一些实际的产品的平衡性,如汽车发动机的销轴、建筑杆塔的吊臂等等。
课后习题
巩固所学知识,设计一些有挑战性的习题帮助学生掌握平衡原理。
计算受力点的力矩,与重心至该点的距离相乘
3
平衡条件
平衡条件为合外力与合外力矩均为零,利用方程组求解
《机械设计基础》答案
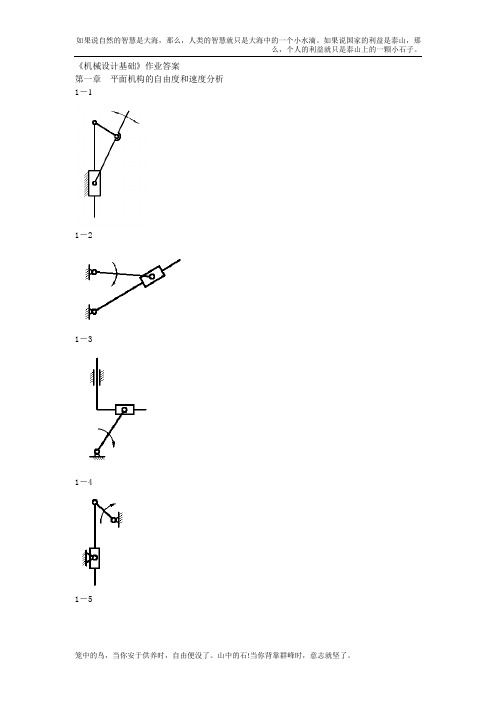
《机械设计基础》作业答案第一章平面机构的自由度和速度分析1-11-21-31-41-5自由度为:11 19211)0192(73')'2(3=--=--+⨯-⨯=--+-=FPPPnFHL或:1182632 3=-⨯-⨯=--=HLPPnF1-6自由度为11)01122(93')'2(3=--+⨯-⨯=--+-=FPPPnFHL或:11 22241112832 3=--=-⨯-⨯=--=HLPPnF1-10自由度为:1128301)221142(103')'2(3=--=--⨯+⨯-⨯=--+-=F P P P n F H L或:122427211229323=--=⨯-⨯-⨯=--=H L P P n F1-1122424323=-⨯-⨯=--=H L P P n F 1-13:求出题1-13图导杆机构的全部瞬心和构件1、3的角速度比。
1334313141P P P P ⨯=⨯ωω11314133431==P P ω1-14:求出题1-14图正切机构的全部瞬心。
设s rad /101=ω,求构件3的速度3v 。
s mm P P v v P /20002001013141133=⨯===ω1-15:题1-15图所示为摩擦行星传动机构,设行星轮2与构件1、4保持纯滚动接触,试用瞬心法求轮1与轮2的角速度比21/ωω。
构件1、2的瞬心为P 12P 24、P 14分别为构件2与构件1相对于机架的绝对瞬心1224212141P P P P ⨯=⨯ωω121214122421r P P ==ω 1-16:题1-16图所示曲柄滑块机构,已知:s mm l AB /100=,s mm l BC /250=,s rad /101=ω,求机构全部瞬心、滑块速度3v 和连杆角速度2ω。
在三角形ABC 中,BCAAB BC ∠=sin 45sin 0,52sin =∠BCA ,523cos =∠BCA ,45sin sin BC ABCAC =∠,mm AC 7.310≈s mm BCA AC P P v v P /565.916tan 1013141133≈∠⨯===ω1224212141P P P P ωω=s rad AC P P P P /9.21002101001122412142≈-⨯==ωω1-17:题1-17图所示平底摆动从动件凸轮1为半径20=r 的圆盘,圆盘中心C 与凸轮回转中心的距离mm l AC 15=,mm l AB 90=,s rad /101=ω,求00=θ和0180=θ时,从动件角速度2ω的数值和方向。
《机械设计基础》第8章%20回转件的平衡

16
30°
画有向线段: S C 160 2 B o
W2 60°
1
120
Wb =80mm(量得)
WC
水平线
WB
αBb =121.7°
(量得)
17
则
mbrb = µmr Wb =20×80=1600 kg.mm
故应加平衡质量为: mbrb 1600 mb = = =16 kg rb 100 其相位为: 逆时针 αBb =121.7°
15
mB=2kg rB=120mm mC=2kg rC=160mm m2=10kg r2=120mm 相位
解:平衡条件: mBrB + mCrC + m2r2 + m b rb =0 质径积: mBrB =2×120=240 kg.mm mCrC =2×160=320 kg.mm m2r2 =10×120=1200 kg.mm kg.mm 取比例尺µmr =20 mm mBrB 240 有向线段: WB= µmr = 20 =12mm mCrC 320 WC= µ = =16mm 20 mr m2r2 1200 W2= µ = =60mm 20 mr
2
回转件平衡的目的
回转件: 回转件 是指绕固定轴线作回转运动的构
件。 若回转件质心 偏离回转中心, 则,产生离心 力。 P=mr ω2
p ω r m
(其方向为周期性变化)
3
离心力给机械带来的不良影响: 离心力给机械带来的不良影响: 1、在运动副中引起动压力,增大运动副 的摩擦力和构件的应力; 2、降低机械效率; 3、引起机器振动,工作质量下降,使 机器甚至厂房受到影响或破坏; 4、由于离心力随转速增加而急剧增加, 故对现代高速机械影响更严重。
《机械设计基础》第8章 回转件的平衡

D
它们的质量可以视为分 布在垂直于轴线的同一回转 面内,如其质心不在回转轴 线上,则其偏心质量产生的 惯性力不平衡。这种不平衡 现象在回转件静态时就会表 现出来,故称为静不平衡。
F=me 2 m e
B
D
F=me 2 m e
B
回转件的静平衡,就是利用在回转件上增加或除去一 平衡质量的方法,使其质心回到回转轴线上,从而使回转 件的惯性力得到平衡(即∑F = 0)的一种平衡措施。 其平衡的原理:利用理论力学平面汇交力系的平衡理论。
2)分别把每个偏心质量
mi用两个平面上的质量
mi′和mi″来代替; 分解公式为: mi′= mi li″/l
图8-4 a)
mi″= mi li′/l
其中 li′为mi到平衡基面T′的距离, li″为mi到平衡基面
T″的距离, l=li′+li″为两平衡基面平面汇交力
质量不能再近似地认为是分布在同一回转面内,而应该看 作是分布在垂直轴线的多个相互平行的回转面内。
如图所示的发动机曲轴, 其不平衡质量m1、m2、m3是 分布在3个回转面内。
这类回转件转动时所产生的离心力系不再是平面汇交 力系,而是空间力系。因此,单靠在某一回转面内加一平 衡质量并不能消除这类回转件转动时的不平衡。
图8-1
∴ ∑miω2ri+ mbω2rb=0 即∑miri+ mbrb=0——静平衡条件:质径积的向量和为0。
式中:miri称为质径积,是矢量。它相对地表达了各 质量在同一转速下的离心力的大小和方向。
mbrb的大小和方向可根据图解法来求。
求解步骤如下:
1)写出质径积的矢量平衡方程式:
m1r1+ m2r2+ …+mbrb=0 2)计算各偏心质量的质径积的大小;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ω ω
ω
平衡原理:在重心的另一侧加上一定的质量,或在重 心同侧去掉一些质量,使质心位置落在回转轴线上, 而使离心惯性力达到平衡。
自用盘编号JJ321002
平衡计算方法: 同一平面内各重物所产生的离心惯性力构成一个平 面汇交力系: Fi
F2 m2
如果该力系不平衡,那么合力: ∑Fi≠0 增加一个重物 Gb 后,可使新
F’3 m’2r2 m’1r1
m’b F’b
l’1
m”3r3
m”2r2
作图法求解
m’br’b + m’1r1 + m’2r2+ m’3r3 = 0 m”br”b + m”1r1 + m”2r2+ m”3r3 = 0
空间力系的平衡
自用盘编号JJ321002
m”1r1 m”br”b
两个平面汇交力系的平衡问题。
F”3
将三个不同回转 面内的离心惯性 力往平面Ⅰ和Ⅱ 上分解。
F’3
" ' l1 l1 F1' F1 F1" F1 l l ' " l3 l3 F3' F3 F3" F3 l l
自用盘编号JJ321002
" l2 F2' F2 l
' l2 F2" F2 l
T” F”2
T' F’2
自用盘编号JJ321002
§12-2 回转件的平衡计算
D 一、质量分布在同一回转面内 B 适用范围:轴向尺寸较小的盘形转子 (B/D<0.2),如风扇叶轮、飞轮、砂轮等回转件,
特点:若重心不在回转轴线 上,则在静止状态下,无论 其重心初始在何位置,最终 都会落在轴线的铅垂线的下 方这种不平衡现象在静止状 态下就能表现出来,故称为 静平衡。 如自行车轮
m2 T”
Fb' l ' Fb" l "
将 l l ' l " 代入求解,得:
l" F Fb l l' " Fb Fb l
' b
消去公因子 ω2,得:
r’b
F’b
rb
F”b Fb
r”b
l" m r mb rb l l' " " mb rb mb rb l
' ' b b ' b
的力系之合力: F = Fb+∑Fi = 0
Fb r2 r1 r3 m3
F3
偏心
m1 F1
ω
设各偏心质量分别为mi,偏心距为ri ,转子以ω 等速 回转, 产生的离心惯性力为:
Fi = miω2ri
自用盘编号JJ321002
=> ∑Fi= miω2ri
平衡配重所产生的离心惯性力为: Fb=mbω2rb
任意空间力系的平衡条件为: ∑Fi = 0,
∑Mi=0
自用盘编号JJ321002
动平衡计算方法:首先在转子上选定两个回转平面Ⅰ和Ⅱ作为平 衡基面,该平面用来加装或去掉平衡质量。
T’
F’2 F2 m2 r2 F’1
T”
F”2
F”1
r1
m1 F 1 l’3 l’2 l’1 l
r3 m3 F3 l”1 l”2 l”3
自用盘编号JJ321002
成正比
μ = Z’0/m0’r’0
α T” 1 T’ r’ m’
r” m” 2
3
ω1 ω1 ω1
T’ T’ T’ O’2 O’ O’2 m’ O’1
5
4
确定相位差 摆架位于最高点时,不平衡质量不在 正上方,而是处在沿回转方向超前角 α的位置,α称为强迫振动相位差。
自用盘编号JJ321002
P2
m2
Pb
总离心惯性力的合力为:
r2 rb r1 r 3
m1 P1
P3 m3 ω
F = Fb +∑Fi = 0
mω2e = mbω2rb + m1ω2r1 + m2ω2r2+ m3ω2r3 =0
约掉公因式
me = mbrb + m1r1 + m2r2+ m3r3 = 0 称miri为质径积
? ? √ √ √ √ √ √
第8章
回转件的平衡
§8-1 回转件平衡的目的 §8-2 回转件的平衡计算
§8-3 回转件的平衡试验
自用盘编号JJ321002
§8-1 回转件平衡的目的
回转件(或转子) ----- 绕定轴作回转运动的构件。 当质心离回转轴的距离为r 时,离心力为: F=mrω2 举例:已知图示转子的重量为G=10 N, 重心与回转轴线的距离为1 mm,转速 为n=3000 rpm, 求离心力F的大小。
ω1 α1
H1
ω2
H2 α2
ω1
α1
H1
α2 (a) (b) (c)
H2 ω2
将图(b)转动 2π -2α后与图(a)叠加, 不平衡质量位于连线的中垂线上。
自用盘编号JJ321002
本章重点
①掌握静平衡和动平衡的计算方法。
②熟悉静平衡和动平衡的实验方法。
自用盘编号JJ321002
②产生有害的振动,使机械的工作性能恶化。
③降低机械效率。 平衡的目的:研究惯性力分布及其变化规律,并采 取相应的措施对惯性力进行平衡,从而减小或消除 所产生的附加动压力、减轻振动、改善机械的工作 性能和提高使用寿命。 本章重点介绍刚性转子的平衡问题。
所谓刚性转子的不平衡,是指由于结构不对称、材料缺陷以及制造误差等原因而使质量分布不均匀,致使中心惯性主轴与回 转轴线不重合,而产生离心惯性力系的不平衡。根据平衡条件的不同,又可分为静平衡和动平衡两种情况。
Q Q Q Q Q
导轨式静平衡架
自用盘编号JJ321002
滚子式平衡架:
特点: 使用方便,但精 度较低。
Q
Q
单摆式平衡架:
特点:工作效率高。
Q Q
自用盘编号JJ321002
二、动平衡实验 m’
T” r” m” 2
1
T’ r’
5 3 4
Z’
根据强迫振动理论有:Z’=μ m’r’ 用标准转子测得:Z’0=μ m0’r’0 不平衡质径积: m’r’= Z’/μ
F
e
N21
F=ma=Geω2/g
=10×10-3[2π×3000/60]2/9.8 =100 N
ω
G N 21
ω θ G N21 F
如果转速增加一倍: n=6000 rpm F=400 N 由此可知:不平衡所产生的惯性力对 机械运转有很大的影响。 大小方向变化
自用盘编号JJ321002
离心力P力的大小方向始终都在变化,将对运动副产 生动压力。 附加动压力会产生一系列不良后果: ①增加运动副的摩擦,降低机械的使用寿命。
自用盘编号JJ321002
§12-3 刚性转子的平衡实验
一、静平衡实验 导轨式平衡架
特点:结构简单、精度高,但两刀口平行、调整困难,且要 求两轴端直径相同。一般要经过多次实验才能找准,工作效 率低,不适合批量生产。
O OO S S S O O O O S S S Q QQ Q Q
S S
O OO
S S
F2
L
F1
这种在静止状态下处于平衡,而运动状态下呈现不平 衡,称为动不平衡。对此类转子的平衡,称为动平衡。
自用盘编号JJ321002
适用对象:轴向尺寸较大(B/D≥0.2)的转子,如内燃 机中的曲轴和凸轮轴、电机转子、机床主轴等都必须 按动平衡来处理。
理由:此类转子由于质量分布不在同一个平面内,离 心惯性力将形成一个不汇交空间力系,故不能按静平 衡处理。
m3r3 mbrb
可用图解法求解此矢量方程 (选定比例μw)。
自用盘编号JJ321002
m1r1
m2r2
me = mbrb + m1r1 + m2r2+ m3r3 = 0
很显然,回转件平衡后:
e=0
回转件质量对轴线产生的静力矩:
从理论上讲,对于偏心质量分布在多个运 动平面内的转子,对每一个运动按静平衡 的方法来处理(加减质量),也是可以达 到平衡的。问题是由于实际结构不允许在 偏心质量所在平面内安装平衡配重,也不 允许去掉不平衡重量(如凸轮轴、曲轴、电 机转子等)。解决问题的唯一办法就是:r’b=r”b=rb ,则有:
自用盘编号JJ321002
l" m mb l l' " mb mb l
重要结论: 某一回转平面内的不平衡质量m, 可以在两个任选的回转平面内进 行平衡。
二、质量分布不在同一回转面内
m
m1
T’ mb
m2 T”
图示凸轮轴的偏心质量不在同一 ω 回转平面内,但质心在回转轴上, 在任意静止位置,都处于平衡状 态。 运动时有:F1+F2 = 0 惯性力偶矩: M=F1L=F1L≠0
结论: 对于动不平衡的转子,无论其具有多少个偏心质量以
及分布在多少个回转平面内,都只要在选定的平衡基
面内加上或去掉平衡质量,即可获得完全平衡。故动
平衡又称为双面平衡。
经过计算,在理论上是平衡的转子,由于制造误差、材质不均匀、安装误差等因素,使实际转子存在不平衡量。要彻底消除 不平衡,只有通过实验方法测出其不平衡质量的大小和方向。然后通过增加或除去平衡质量的方法予以平衡。
m’2 m’1 m’3 F’3 l’1
F2 m2 r2
m”2 m”3 l”3 l”2 F”3 m”1 F”
r1
F’
1
r3 m3 F3 l”1 l
1
m1 F 1 l’3 l’2
