14.3.1提公因式法因式分解
14.3.1 提公因式法因式分解

2、下列因式分解错误的是 (
2 2
B
)
A、x y ( x y )( x y ) B、x 6 x 9 ( x 3)
2 2
C、x 2 xy x( x y ) D、x 2 y 2 ( x y )2
• • • •
1、因式分解是整式乘法的逆变形。 2、因式分解的对象应是多项式。 3、因式分解的结果一定是积的形式。 4、结果中的每一个因式都必须是整式 。 • 5、要分解到再也不能分解为止。
4、提公因式法分解因式应注意的问题: (1)公因式要提尽; (2)小心漏掉1; (3)提出负号时,要注意变号.
课堂小结
符号规律: (1)(a–b)与(b–a)互为相反数:
①当n为偶数时, (a–b)n=(b–a)n ; ②当n为奇数时, (a–b)n= – (b–a)n 。
(2)(a–b)与(–a–b)互为相反数: ①当n为偶数时, (a–b)n=(–a–b)n ; ②当n为奇数时, (a–b)n= – (–a–b)n 。 (3)(a+b)与(b+a)是相同的数: 当n为整数时, (a–b)n=(b+a)n 。
=328-327-326
=326(32-3-1)
=326×5
=325×45 ∴817-279-913能被45整除.
1.分解因式: x( x y )(a b) y ( y x)(b a ); 2.解关于x的方程: 5 x( x 2) 4( x 2) 0.
2m n 3 不解方程组 , 求: 5n(2m n)2 2(n 2m)3的值. 4m 3n 1
做
计算下列个式:
(1) 3x(x-1)= _____ (2) m(a+b+c) = _____ (3) (m+4)(m-4)= ____ (4) (x-3)2= _______ (5) a(a+1)(a-1)= ____
14.3.1因式分解(提公因式法)八年级数学上册课件(人教版)

拓展训练
人教版数学八年级上册
3.△ABC的三边长分别为a、b、c,且a+2ab=c+2bc,请 判断△ABC是等边三角形、等腰三角形还是直角三角形?并 说明理由. 解:整理a+2ab=c+2bc得,a+2ab-c-2bc=0,
(a-c)+2b(a-c)=0,(a-c)(1+2b)=0,
∴a-c=0或1+2b=0,
解:原式=-(a2-ab+ac)=-2a(a-2b+3c) (6)-2x3+4x2-2x
解:原式=-(2x3-4x2+2x)=-2x(x2-2x+1)
人教版数学八年级上册
拓展训练
人教版数学八年级上册
1.已知m-4n=-2,mn=5,求-m3n+8m2n2-16mn3的值. 解:-m3n+8m2n2-16mn3=-mn(m2-8mn+16n2)=-mn(m-4n)2 .
典例精析
例1 把8a3b2+12ab3c分解因式.
分析:找公因式
1.系数的最大公约数 4
2.找相同字母
ab
3.相同字母的最低指数 a1b2
公因式为:4ab2
解:8a3b2+12ab3c =4ab2•2a2+4ab2•3bc =4ab2(2a2+3bc)
人教版数学八年级上册
典例精析
人教版数学八年级上册
复习引入
人教版数学八年级上册
单项式与多项式相乘的法则:单项式与多项式相乘,就是 用单项式去乘多项式的每一项,再把所得的积相加.
p(a+b+c)=pa+pb+pc
多项式与多项式相乘的法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个 多项式的每一项,再把所得的积相加.
第十四章 14.3 14.3.1 提公因式法

(x-3y)2(9x-6y)=3(x-3y)2(3x-2y). 又3x-x-32y=y=1,6, ∴7x(x-3y)2-2(3y-x)3=3×12×6=18.
第十四章 整式的乘法与因式分解 14.3 因式分解
14.3.1 提公因式法
1. 把一个多项式化为几个 整式的积的形式 ,叫 做因式分解.
2. 运用提公因式法因式分解的关键是确定多项式各 项的公因式,公因式是指各项系数的 最大公约数 , 各项公有字母的 最低次幂 .
知识点 因式分解的定义 1. (2017·常德)下列各式由左到右的变形中,属于分解 因式的是( C ) A.a(m+n)=am+an B.a2-b2-c2=(a-b)(a+b)-c2 C.10x2-5x=5x(2x-1) D.x2-16+6x=(x+4)(x-4)+6x
(2)若因式分解 1+x+x(x+1)+x(x+1)2+…+x(x+ 1)2017,则需应用上述方法 2017 次,结果是 (1+x)2018 ;
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+x(x+ 1)n(n 为正整数).
解:原式=(1+x)n+1.
1.确定公因式的方法:①系数:取各项系数的最大 公约数;②字母:取各项都含有的相同字母;③指数: 取相同字母的最低次幂.
【解析】∵2x2+bx+c=2(x-3)(x+1)=2(x2-2x-3) =2x2-4x-6,∴b=-4,c=-6.
2. 阅读下面因式分解的过程,再回答问题: 1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]= (1+x)2(1+x)=(1+x)3. (1)上述因式分解的方法是 提公因式法 ,共应用了 2 次;
14.3.1提公因式法 四环节

=3a(a-3b)
温馨提示
3a 3a a
2
9ab 3a 3b
分两步 第一步,找出公因式; 第二步,提取公因式 , (即将多项式化为两个因式的 乘积)
小颖解的有误吗?
把 8 a 3 b2 –12ab 3 c + ab分解因式.
解: 8 a 3 b2 –12ab 3 c + ab
=ab•8a2 b-ab • 12 b2 c+ab • 1
☞
把下列各式分解因式
(1) x(x+y)-y(x+y) (2) am+an+bm+bn
把下列各式分解因式: 1.2a-4b; 2.ax2+ax-4a; 3.3ab2-3a2b; 4.2x3+2x2-6x; 5.7x2+7x+14; 6.-12a2b+24ab2; 7.xy-x2y2-x3y3; 8.27x3+9x2y.
2)3 x +9xy
3) a2 b – 2a b2 + ab
4) 4xy2-6xy+8x3y
ab
2xy
(2)多项式中的公因式是如何确定的? (交流探索)
过关秘密武器:
正确找出多项式各项公因式的关键是:
公因式的系数是多项式各项系数的 定系数: 最大公约数。 定字母: 字母取多项式各项中都含有的相同 的字母。
3
2
当多项式第一项系 数是负数,通常先 提出“-”号,使 括号内第一项系数 变为正数,注意括 号内各项都要变号。
练一练
把下列各多项式因式分解
1)
-4a3b3+6a2b-2ab 2) -9a2b3-12ab4+15ab5 3) -4x3y+2x2y2+xy3 4 ) -x4y2-2x2y-xy
14.3.1提公因式法

(1) 24x3y-18x2y (2) 7ma+14ma2 (3)-16x4+32x3-56x2 (4)- 7ab-14abx+49aby (5)2a(y-z)-3b(y-z) (6)p(a2+b2)-q(a2+b2)
解因式的方法叫做提公因式法.
提公因式法一般步骤: 1、确定各项公因式(第一项是负的,先提取 一个负号,再确定公因式.) 2、利用整式除法把多项式各项写成公因式与 另一项乘积的形式 3、提取公因式
例 1、 用提取公因式法因式分 解:
①9a b 15ab c
2 2
② 12s t 8st 4st ③ 5a(x-y)-10b(y-x)
⑥ 4.3x199.8+0.76x1998-1.9x199.8 ⑦ 2a(y-z)-3ab(y-z) ⑧ 4p(a2+b2)-pq(a2+b2) ⑨ 12b(a-b)2 – 18(b-a)3
⑩ 2(a+b)2 – a-b
pa + pb + pc
在多项式中,每一个项都含有的 因式,叫做公因式.
找公因式的方法: 1. 所有项的系数的最大公约数
2. 取每一项都有的字母,且字母的指数取最 低的. 3.系数与相同字母的最低次幂相乘的积. 注:1.第一项是负的,先提取一个负号,
再确定公因式.
2.公因式可以是单项式或多项式.
指出下列各多项式中各项的公因式
①ax+ay+a 2 ②3mx-6nx ③4a2b+10ab2 2 ④3x -6xy+x ⑤12x2yz-9x3y2
pa + pb + pc = p ( a + b + c )
14.3.1 提公因式法
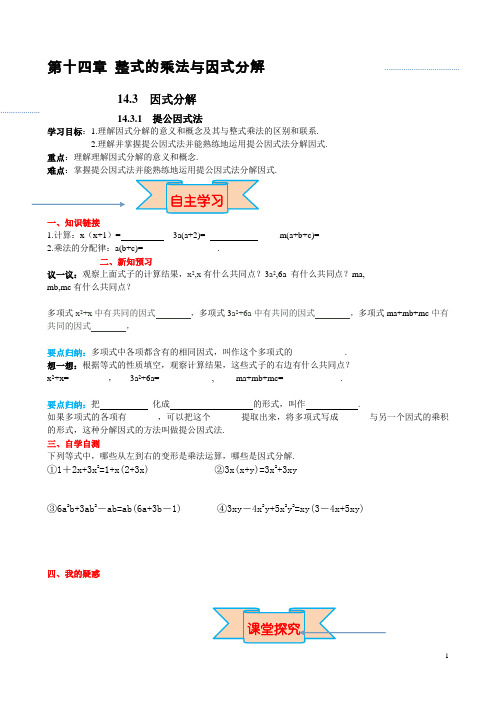
第十四章整式的乘法与因式分解14.3 因式分解14.3.1 提公因式法学习目标:1.理解因式分解的意义和概念及其与整式乘法的区别和联系.2.理解并掌握提公因式法并能熟练地运用提公因式法分解因式.重点:理解理解因式分解的意义和概念.难点:掌握提公因式法并能熟练地运用提公因式法分解因式.一、知识链接1.计算:x(x+1)= 3a(a+2)= m(a+b+c)=2.乘法的分配律:a(b+c)=_________________.二、新知预习议一议:观察上面式子的计算结果,x2,x有什么共同点?3a2,6a 有什么共同点?ma,mb,mc有什么共同点?多项式x2+x中有共同的因式,多项式3a2+6a中有共同的因式,多项式ma+mb+mc中有共同的因式,要点归纳:多项式中各项都含有的相同因式,叫作这个多项式的____________.想一想:根据等式的性质填空,观察计算结果,这些式子的右边有什么共同点?x2+x=_________,3a2+6a=____________, ma+mb+mc=_____________.要点归纳:把化成的形式,叫作.如果多项式的各项有_______,可以把这个_______提取出来,将多项式写成_______与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.三、自学自测下列等式中,哪些从左到右的变形是乘法运算,哪些是因式分解.①1+2x+3x2=1+x(2+3x) ②3x(x+y)=3x2+3xy③6a2b+3ab2-ab=ab(6a+3b-1) ④3xy-4x2y+5x2y2=xy(3-4x+5xy)四、我的疑惑___________________________________________________________________________________________ ___________________________________________________________一、要点探究探究点1:因式分解例1:下列从左到右的变形中是因式分解的有()①x2-y2-1=(x+y)(x-y)-1;②x3+x=x(x2+1);③(x-y)2=x2-2xy+y2;④x2-9y2=(x+3y)(x-3y).A.1个B.2个C.3个D.4个方法总结:因式分解与整式乘法是相反方向的变形,即互逆运算,二者是一个式子的不同表现形式.因式分解的右边是两个或几个因式积的形式,整式乘法的右边是多项式的形式.辩一辩:在下列等式中,从左到右的变形是因式分解的有___________,不是的,请说明为什么?①am+bm+c=m(a+b)+c ____________________________________;②24x2y=3x ·8xy ____________________________________;③x2-1=(x+1)(x-1) ____________________________________;④(2x+1)2=4x2+4x+1 ____________________________________;⑤x2+x=x2(1+1x) ____________________________________;⑥2x+4y+6z=2(x+2y+3z) ____________________________________.探究点2:公因式问题1:如何确定一个多项式的公因式?找一找:3x 2- 6 xy的公因式.(1)多项式3x 2- 6 xy有____项,分别为__________、_________,它们的系数分别是______、_______,最大公约数是____________,它们含有的共同字母是___________,该字母的指数分别为____、_____. (2)该多项式的公因式为______________.方法归纳:正确找出多项式的公因式的步骤:1.定系数:公因式的系数是多项式各项系数的_______________.2.定字母:字母取多项式各项中都含有的________的字母.3.定指数:相同字母的指数取各项中______的一个,即字母最_____次数.填一填:下列各多项式的公因式是什么?将其填在横线上.(1) 3x+6y ___________; (2)ab-2ac ___________;(3) a2 - a3 ___________ ; (4)4 (m+n) 2 +2(m+n) ___________;(5)9m2n-6mn ___________; (6)-6x2y-8 xy 2 ___________;探究点3:用提公因式法分解因式例2:把下列各式分解因式(1)8a3b2+12ab3c;(2)2a(b+c)-3(b+c);(3)(a+b)(a-b)-a-b.方法总结:提公因式法步骤(分两步)第一步:找出公因式;第二步:提取公因式,即将多项式化为两个因式的乘积.辩一辩:下列同学分解因式的结果正确吗?不正确的话,请说明理由,并改正.(1)分解因式12x2y+18xy2=3xy(4x + 6y). ____________(填“正确”或“错误”)理由:_______________________________正解:________________________________(2)分解因式3x2 - 6xy+x =x(3x-6y).____________(填“正确”或“错误”)理由:_______________________________正解:________________________________(3)- x 2+xy-xz= - x(x+y-z)____________(填“正确”或“错误”)理由:_______________________________正解:________________________________易错归纳:(1)提取公因式后,多项式中各项还含有公因式.(2)提取公因式后,漏掉另一个因式中商是1的项;(3)找底数互为相反数的幂的公因式时符号出错;例3:计算:(1)39×37-13×91;(2)29×20.16+72×20.16+13×20.16-20.16×14.方法总结:在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.例4: 已知a +b =7,ab =4,求a 2b +ab 2的值.方法总结:含a ±b ,ab 的求值题,通常要将所求代数式进行因式分解,将其变形为能用a ±b 和ab 表示的式子,然后将a ±b ,ab 的值整体带入即可.1.下列各式变形中,是因式分解的是( )A.a 2-2ab +b 2-1=(a -b )2-1 B.)11(22222xx x x +=+ C .(x +2)(x -2)=x 2-4 D.x 4-1=(x 2+1)(x +1)(x -1)2.多项式6ab 2c -3a 2bc +12a 2b 2中各项的公因式是( )A .abcB .3a 2b 2C .3a 2b 2cD .3ab3.把a 2-4a 多项式分解因式,结果正确的是( )A .a (a-4)B .(a+2)(a-2)C .a (a+2)(a-2)D .(a-2)2-44.当a ,b 互为相反数时,代数式a 2+ab-2的值为( )A .2B .0C .-2D .-15.分解因式(1)a 2b –2ab 2+ab ; (2)2(a-b )-4(b-a);(3)a 2b (a -b )+3ab (a -b ); (4)y 2(2x +1)+y (2x +1)2.A.5mn B.5m2n2 C.5m2n D.5mn22.把多项式(x+2)(x-2)+(x-2)提取公因式(x-2)后,余下的部分是()A.x+1 B.2x C.x+2 D.x+33.下列多项式的分解因式,正确的是()A.12xyz-9x2y2=3xyz(4-3xyz)B.3a2y-3ay+6y=3y(a2-a+2)C.-x2+xy-xz=-x(x2+y-z)D.a2b+5ab-b=b(a2+5a)4.把下列各式分解因式:(1)8 m2n+2mn=_____________;(2)12xyz-9x2y2=_____________;(3)p(a2 + b2 )- q(a2 + b2 )=_____________;(4) -x3y3-x2y2-xy=_______________;(5)(x-y)2+y(y-x)=_____________.5.若9a2(x-y)2-3a(y-x)3=M·(3a+x-y),则M等于_____________.6.简便计算:(1) 1.992+1.99×0.01 ; (2)20132+2013-20142; (3)(-2)101+(-2)100.7.(1)已知: 2x+y=4,xy=3,求代数式2x2y+xy2的值.(2)化简求值:(2x+1)2-(2x+1)(2x-1),其中x=12. .拓展提升8.△ABC的三边长分别为a、b、c,且a+2ab=c+2bc,请判断△ABC是等边三角形、等腰三角形还是直角三角形?并说明理由.。
人教版八年级数学上册 14.3.1因式分解 (提公因式法)

因式分解( 提公因式法)1. 因式分解的概念因式分解:把一个多项式化成几个整式的乘积的形式,这就叫做把这个多项式因式分解,也可称为将这个多项式分解因式。
2. 提取公因式确定公因式的方法是:先取各项数字系数的最大公约数,再取各项相同字母的最低次幂,合起来就是这个多项式的公因式。
如果多项式的首项系数是负的,提公因式时要将负号提出,使括号内第一项的系数是正的,并且注意括号内其它各项要变号。
如果公因式是多项式时,只要把这个多项式整体看成一个字母,按照提字母公因式的办法提出。
总结 ①公因式的系数:②字母:③相同字母的指数:例1 下列从左到右的变形,属于分解因式的是( )A. (x+3)(x -2)=x 2+x -6B. ax -ay+1=a(x -y)+1C. x 2-21y=(x+y 1)(x -y 1) D. 3x 2+3x=3x(x+1) 例2 写出下列多项式中的公因式:(1)3525x x + (2)121m n m n ab a b -+-(3)253243143521x y x y x y +- (4)()()23a a b a b a --- (5)()()2222n m n m m nm n + (6)3223232125a b c ab c a b c +-例3利用提公因式法分解因式:(1)33xy y x - (2)32318x x -例4 把a 2﹣4a 多项式分解因式,结果正确的是( )A .a (a ﹣4) B . (a+2)(a ﹣2) C . a (a+2)(a ﹣2) D . (a ﹣2)2﹣4例5把多项式(m+1)(m ﹣1)+(m ﹣1)提取公因式(m ﹣1)后,余下的部分是( )A . m+1B . 2mC . 2D . m+2例6已知(19x ﹣31)(13x ﹣17)﹣(13x ﹣17)(11x ﹣23)可因式分解成(ax+b )(8x+c ),其中a ,b ,c 均为整数,则a+b+c=( )A . ﹣12B . ﹣32C . 38D . 721.下列变形中,属于因式分解的是 ( )A .(a +b )(a -b )=a 2-b 2B .x 2-y 2+4y -4=(x +y )(x -y )+4(y -1)C .a 3-b 3=(a -b )(a +ab +b )D .a 2-10a +10=a (a -10)+102. 49x 3y z 3+14x 2y 2z 2-21xy 2z 2在分解因式时应提取的公因式是 ( )A .7x 3y z 3B .7x 2y 2z 2C .7xy 2z 2D .7xy z 23. 多项式0.5x(a -b)-0.25y(b -a)中,可提取公因式 ( )A .0.5x+0.25yB .0.5x+0.25yC .a+bD .0.25(a -b)4. (-a )m +a (-a )m -1的值是 ( )A .1B .-1C .0D .(-1)x+15. 下列各恒等变形中,是因式分解的是 ( )A .a 2-2ab +b 2=(a -b )2B .(a +b )2=a 2+2ab +b 2C .a 2b +ab 2+c=ab (a +b )+cD .a 2-2ab +b 2-c=(a -b )2-c。
人教版数学八年级上册14.3.1因式分解-提取公因式 课件

针对训练:
(1)-x2y+yx-xy2 (2)-4x2+8ax+2x (3)-3ab+6abx-9aby
例2 、因式分解 2(a-b)2 -a+b =2(a-b)2-(a-b) =(a-b)[2(a-b)-1] =(a-b)(2a-2b-1)
点拨:提公因式时,将因式改变符号后,才能看出公因式。 针对训练:
提公因式法: 其中一个因式是各项的公因式m另一个因式 (a+b+c)是m(a+b+c)除以m所得的商.像这 种分解因式的方法叫做提公因式。 归纳:如果多项式各项都有公因式,可以把 这个公因式提出来,将多项式写成积的形式, 这就叫做提公因式分解因式。
指出下列各多项式中各项的公因式
⑴5xy-10x ⑵9y2+12y ⑶7x3y2-42x2y3 ⑷7(a-3)-b(a-3) 注意:1.公因式系数为各项系数的最 大公约数。 2.取各项相同的字母。 3.找出相同字母的最低次幂。
14.3 因式分解 14.3.1 提公因式
• 1.了解公因式的概念和因式分解的意义,培 养逆向思维的能力;
• 2.通过独立思考、小组交流,探究整式乘法 与因式分解的区别和联系;
• 3.掌握如何用提公因式来分解因式。
运用已学过的知识填空:
⑴ x(x-2)= X2-2x ;
⑵ (x+2)(x-2)= x2-4 ;
(1) a(x-y)-x+y (2) 7(x-3)-x(3-x) (3) (a-2)2-2a(2-a) (4)(x+y-z)(x-y+z)-(y+z-x)(z-x-y)
归纳总结: 分解因式的一般步骤:
1. 找出,找出应提取的公因式。 2. 除以,用多项式去除以公因式。 3. 整理,把多项式写成因式积的
课件1:14.3.1提公因式法

ma+mb +mc =m(a+b +c)
分解因式4m2-8mn
解: 4m2-8mn
=4m•m-4m•2n
确定公因式
=4m(m-n)
提取公因式
例1 把 8a3b2+12ab3c 分解因式.
解: 8a3b2 +12ab3c =4ab2 2a2+4ab2 3bc =4ab(2 2a2+3bc).
例2 把 2(a b+c)-(3 b+c)分解因式.
整
式
14.3 因式分解
的 乘
法
14.3.1 提公因式法
与 因
式
分
解
教学目标
(1)初步了解因式分解的意义,知道因式分解与整 式乘法是互逆运算。 (2)会找公因式 (3)会用提公因式法分解因式 (4)体会数学知识之间是相互联系的,是可以相互 转化的。 (5)进一步培养学生观察、分析、归纳等能力。
重点 、难点、 关 键 重点:提公因式法是因式分解最基本最常用的方
提出问题:两个等式的左边各项有何共同特点?
Ⅱ.讲解新课
练习1:找出下列各多项式中各项的公因式:
(1)ax+ay
(2)6a+14b (3)2a2+4a
(4)4m2-8mn (5)8a2x+6ax2-12a3x3
(1)a(x+y)
(2)2(3a+7b) (3)2a(a+2)
(4)4m(m-2n) (5)2ax(4a+3x-6a2x2)
因式分解(分解因式):把一个多项式化成几个整 式积的形式叫因式分解
⑶设问:整式乘法和因式分解有什么关系? 因式分解就是将多项式 化成几个整式的积
人教版数学八年级上册14.3.1提公因式法因式分解-课件

例1 把8a3b212ab3c分解因
分析:应先找出
与
的公因式,再提公因式进行分解.
例 2 分解因式
2a(bc)3(bc)
分析:(b+c)是这两个式子的公因式,
可以直接提出.
解 2a(b : c)3(bc)
(bc)2 (a . 3)
因式分解:
(1)24x3y-18x2y ;
(2)7ma+14ma2 ;
(3)-16x4+32x3-56x2 ; (4)- 7ab-14abx+49aby ; (5)2a(y-z)-3b(y-z) ; (6)p(a2+b2)-q(a2+b2).
1.20042+2004能被2005整除吗?
2.先分解因式,再求值
4a2(x7)3(x7),其中 a5,x3.
• 小结: • 本节课你有何收获?还有哪些困惑?
14.3.1 提公因式法
:整式的乘法
计算下列各式:
x(x+1)= x2 + x ; (x+1)(x-1)= x2-1 .
请把下列多项式写成整式乘积的形式.
(1) x 2 x x(x1)
(2) x 2 1 (x1)(x1)
把一个多项式化成几个整式 积的形式,这种变形叫做把这个 多项式因式分解(或分解因式).
想一想:因式分解与整式 乘法有何关系?
x2-y2 因式分解 (x+y)(x-y)
整式乘法
因式分解与整式乘法是互逆过程.
练习一 理解概念
判断下列各式哪些是整式乘法?哪 些是因式分解?
(1) x2-4y2=(x+2y)(x-2y);因式分解 (2) 2x(x-3y)=2x2-6xy 整式乘法 (3) (5a-1)2=25a2-10a+1 ;整式乘法
14.3.1提公因式法分解因式

【教学重点】了解因式分解的意义,感受其作用,掌握用提公因式法把多项式分解因式.
【教学难点】整式乘法与因式分解之间的关系;正确地确定多项式的最大公因式.
【教具准备】“121”导学稿、ppt课件.
教学过程
教师/学生活动
(2)3x2+x3=()();
(3)ma+mb+mc=()().
3.归纳:“回忆”的是已熟悉的运算,而要“探索”的问题,其过程正好与“回忆”,它是把一个多项式化为几个整式的乘积形式,这就是因式分解(也叫分解因式).
由上可知,整式乘法与因式分解是的变形.在下面变形的箭头上填上适当的变形方法.
x(x-1)
※多项式各项都含有的,叫做这个多项式各项的公因式.
6.提公因式法分解因式.
如果一个多项式的各项含有公因式,那么就可以,从而将多项式化成两个的乘积的形式,这种分解因式的方法叫做提公因式法.如:ma+mb+mc=m(a+b+c)
【重难点过关】
1.辨一辨:下列各式从左到右的变形,哪是因式分解?
(1)4a(a+2b)=4a2+8ab;(2)6ax-3ax2=3ax(2-x);
个案调整
【预习交流】
问题一:1.回忆:运用前两节所学的知识填空:
(1)2(x+3)=___________________;(2)x2(3+x)=_________________;
(3)m(a+b+c)=_______________________.
2.探索:你会做下面的填空吗?
(1)2x+6=()();
3.把下列各式分解因式:
⑴8m2n+2mn⑵12xyz-9xy2⑶2a(y-z)-3b(z-y)
人教版八年级数学上册课件:14.3.1提公因式法

9.将下列各式因式分解: (1)-9x2y-6xyz;
解:原式=-3xy(3x+2z);
(2)4x2-12x2y+12x3y2; 解:原式=4x2(1-3y+3xy2);
(3)9a3x2-18a5x2-36a4x4; 解:原式=9a3x2(1-2a2-4ax2);
(4)-28m4n3+42m2n3-14m2n; 解:原式=-14m2n(2m2n2-3n2+1);
2.多项式4a2b(a-b)-6ab2(b-a)的公因式是( D ) A.4ab B.2ab C.ab(a-b) D.2ab(a-b)
3.下列各式由左边到右边的变形中,属于分解因式的是 ( C)
A.a(x+y)=ax+ay B.x2-4x+4=x(x-4)+4 C.10x2-5x=5x(2x-1) D.x2-16+6x=(x+4)(x-4)+6x
同多项式因式); (3)定指数,即各项相同字母因式(或相同多项式因式)的
指数的最小值.
3.提公因式法:如果一个多项式的各项有公因式,那么 可把该公因式提取出来进行因式分解,这种因式分解 的方法,叫做提公因式法.
提公因式的一般步骤:第一步找出公因式;第二步确定 另一个因式;第三步写成积的形式.
1.多项式12ab3c-8a3b的公因式是( D ) A.4ab2 B.-4abc C.-4ab2 D.4ab
(4)因式分解是有范围的,无特殊说明,一般在有理数范
围内分解,有时也要求在实数范围内分解;
(5)整式乘法与因式分解的关系:整式的乘法与因式分解 一个是积化和差、一个是和差化积,是两种互逆的变 形.即:
多项式
整式的乘积.
14.3.1提公因式法
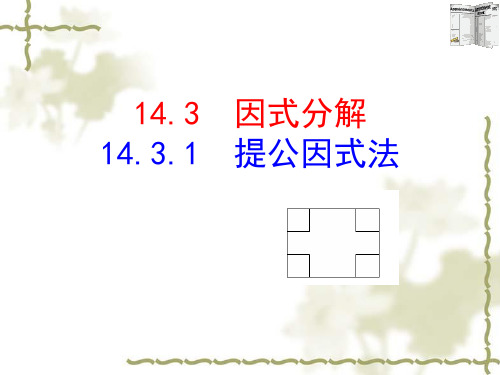
(1) x2-4y2=(x+2y)(x-2y);因式分解 (2) 2x(x-3y)=2x2-6xy 整式乘法 (3) (5a-1)2=25a2-10a+1 ; 整式乘法 (4) x2+4x+4=(x+2)2 ;因式分解 (5) (a-3)(a+3)=a2-9 整式乘法 因式分解 (6) m2-4=(m+2)(m-2) ; (7) 2πR+ 2πr= 2π(R+r). 因式分解
注意:公因式可以是数字,字母,也 =(x-y)(a-b). 可以是单项式,还可以是多项式。
=a(x-y)-b(x-y)
【课堂练习】
2. 6(m-n)3-12(n-m)2 【解析】6(m-n)3-12(n-m)2 =6(m-n)3-12[-(m-n)]2 =6(m-n)3-12(m-n)2 =6(m-n)2(m-n-2).
这些在分解因式时,符号都可当做公因式,但要注意符号
【课堂练习】
2.(苏州·中考)分解因式 a2-a=
【解析】 a2-a=a(a-1). 答案:a(a-1) 3.(盐城·中考)因式分解 2a 2 4a ______. 【解析】用提公因式法因式分解:2 a 4 a 2 a (a 2)
讨论点拨
叫做把这 个多项式因式分解,也叫把这个多项式分解因式。 2、与整式乘法的关系:是整式乘法的 变形 逆
1、 把一个多项式化成几个整式积的形式
讨论点拨
因式分解 x2-1 (x+1)(x-1)
整式乘法
因式分解与整式乘法是方向相反的变形.
自学指导2
看课本第P114--115页练习以上的内容,并思
确定公因式的方法
(1)系数——取各项的最大公约数 (2)字母——取各项相同字母 (3)指数——取各项相同字母的最低次幂 提公因式法分解因式的步骤
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14.3.1 提公因式法
:整式的乘法
计算下列各式:
x(x+1)= x2 + x ; 2-1 (x+1)(x-1)= x .
讨论
630能被哪些数整除?
在小学我们知道,要解决这个问题, 需要把630分解成质数乘积的形式.
630 2 3 5 7
2
类似地,在式的变形中,有时需 要将一个多项式写成几个整式的乘积 的形式.
请把下列多项式写成整式乘积的形式.
(1) x x x( x 1) 2 ( 2) x 1 ( x 1)( x 1)
2
把一个多项式化成几个整式 积的形式,这种变形叫做把这个 多项式因式分解(或分解因式).
想一想:Biblioteka 因式分解与整式乘法有何关系?
2-y2 因式分解 x 整式乘法
分析:(b+c)是这两个式子的公因式, 可以直接提出.
例3:分解因式 2a(y-z)-3b(z-y) ;
因式分解:
3y-18x2y (1)24x
; 2; (2)7ma+14ma 4+32x3-56x2 ; (3)-16x (4)- 7ab-14abx+49aby ; (5)2a(y-z)-3c(y-z) ; 2+b2)-q(a2+b2). (6)p(a
注意:各项系数都是整数时,因式的 系数应取各项系数的最大公约数;字 母取各项的相同的字母,而且各字母 的指数取次数最低的.
例1
把8a b 12ab c分解因式
3 2 3
分析:应先找出 与 的公因式,再提公因式进行分解.
例 2 分解因式
2a(b c) 3(b c)
解:a(b c) 3(b c) 2 (b c)(2a 3)
2+2004能被2005整除吗? 1.2004
2.先分解因式,再求值 4a ( x 7) 3( x 7), 其中a 5, x 3.
2
这节课你学到了什么?
因式分解 方法:提公因式法
怎样分解因式: ma mb mc . 公因式:多项式中各项都有的 因式,叫做这个多项式的公因式;
把多项式ma+mb+mc分解成 m(a+b+c)的形式,其中m是各项的公因 式,另一个因式(a+b+c)是ma+mb+mc 除 以m的商,像这种分解因式的方法,叫 做提公因式法.
说出下列多项式各项的公因式: (1)ma + mb ; m (2)4kx- 8ky ; 4k (3)5y3+20y2 ; 5y2 (4)a2b-2ab2+ab . ab
(x+y)(x-y)
因式分解与整式乘法是互逆过程.
练习一 理解概念 判断下列各式哪些是整式乘法?哪 些是因式分解? 因式分解 (1) x2-4y2=(x+2y)(x-2y); (2) 2x(x-3y)=2x2-6xy 整式乘法 整式乘法 (3) (5a-1)2=25a2-10a+1 ; (4) x2+4x+4=(x+2)2 ; 因式分解 (5) (a-3)(a+3)=a2-9 整式乘法 因式分解 (6) m2-4=(m+2)(m-2) ; (7) 2πR+ 2πr= 2π(R+r). 因式分解
