平均数、中位数和众数的选用
众数,中位数,平均数的特点及其应用场合

众数,中位数,平均数的特点及其应用场合众数、中位数和平均数是常用的统计指标,它们在数据分析、科学研究、经济预测以及日常生活中都起着非常重要的作用。
本文将分别介绍这三个统计指标的特点以及它们在不同应用场合中的作用。
一、众数的特点及其应用场合众数是一组数据中出现频率最高的数值。
众数的特点有以下几个方面:1. 反映典型值:众数可以反映一组数据中的典型值,即出现频率最高的数值,能够代表数据的一般情况。
2. 受极端值影响小:众数通常受极端值的干扰较小,对数据的稳健性较强。
3. 离散分布无法体现:当一组数据存在多个众数或者数据分布较离散时,众数可能无法准确反映数据的特点。
在实际应用中,众数常常用于描述数据的集中趋势,例如用于描述课堂上学生的平均年龄、某商品的最常见售价等情况。
二、中位数的特点及其应用场合中位数是一组数据中序列位置处于中间的数值,当数据个数为偶数时,中位数为中间两个数的平均值。
中位数的特点包括:1. 不受极端值影响:中位数不受极端值的影响,对数据的稳健性较强,能够更好地反映数据的一般趋势。
2. 能够反映数据的集中趋势:中位数能够比较准确地反映数据的整体趋势,特别适用于描述数据集中分布的情况。
3. 不适用于描述数据的分布情况:中位数并不能很好地反映数据的分布情况,不能反映数据的左右对称性。
中位数在经济学、金融学、医学等领域经常被使用,例如用于描述一个国家的居民收入水平、公司员工的工资水平等情况。
三、平均数的特点及其应用场合平均数是一组数据所有数值之和除以数据个数所得的值,它的特点有以下几个方面:1. 易受极端值干扰:平均数容易受极端值的影响,当数据存在较大的极端值时,平均数可能无法准确反映数据情况。
2. 能够描述数据的总体情况:平均数能够较好地描述数据的整体情况,对数据的总体特征进行了统一的度量。
3. 适用于对称分布的数据:对称分布的数据适用平均数来描述其集中趋势。
平均数在日常生活以及科学研究中广泛应用,例如用于描述一个班级学生的平均成绩、某商品的平均价格等情况。
如何选择“平均数、中位数、众数”代表一组数据的典型水平

如何选择“平均数、中位数、众数”代表一组数据的典型水平平均数、中位数、众数这三个统计量都能代表一组数据的典型水平或集中趋势,但在具体的问题中,究竟采用哪种统计量来描述一组数据的集中趋势呢?很多的学生在做题中模棱两可,就连很多的教师也认识模糊,很难定夺,现重点就这个问题谈谈我自己的观点。
虽然平均数、中位数、众数都是描述数据的集中趋势的“特征数”,但是它们反映数据的特征有所不同,是从不同侧面、不同的角度给我们提供了同一组数据的面貌,因此有着不同的适用范围。
1.平均数:平均数的计算中要用到每一个数据,因而它反映的是一组数据的总体水平,选择特征数表示一组数据的集中趋势时,我们用得最多的是平均数,用它作为一组数据的代表,比较可靠和稳定,它与这组数据中的每一个数据都有关系,能够最为充分地反映这组数据所包含的信息,在进行统计推断时有重要的作用,但容易受到极端数据的影响。
在大多数情况下人们喜欢使用平均数这一指标来代表一批数据或用它来反映大量事物的整体水平。
例如:要比较两个班在一次测验的成绩,那么就要用平均分反映每个班学生的测验结果。
2.中位数:中位数是一组数据的中间量,代表了中等水平。
中位数在一组数据的数值排序中处于中间位置,由于中位数可以对事物的大体趋势进行判断和掌控。
在个别的数据过大或过小的情况下,“平均数”代表数据整体水平是有局限性的,也就是说个别极端数据是会对平均数产生较大的影响的,而对中位数的影响则不那么明显。
所以,这时用中位数来代表整体数据更合适。
即:如果在一组相差较大的数据中,用中位数作为表示这组数据特征的统计量往往更有意义。
3.众数代表的是一组数据的多数水平,若一组数据中众数的频数比较大,并且与其他数据的频数相差较大时,我们一般选用众数。
众数反映了一组数据的集中趋势,当众数出现的次数越多,它就越能代表这组数据的整体状况,并且它能比较直观地了解到一组数据的大致情况。
但是,当一组数据大小不同,差异又很大时,就很难判断众数的准确值了。
20.2.2平均数、中位数和众数的应用

华东师大版八年级数学(下)第二十章数据的整理与初步处理20.2.2平均数、中位数和众数的选用一、温故知新水果店进了一批香蕉,每箱香蕉质量标注为20千克.送入仓库前,从中随机抽出10箱进行检查,称得10箱香蕉的质量如下(单位:千克):19.9 20.1 19.7 18.9 20.520.3 19.5 19.6 19.7 20.1试求这10箱香蕉质量的平均数、中位数和众数.二、设问导读阅读课本144-146页,回答下列问题:1、平均数、中位数和众数各自有什么特点?它们之间有什么联系与区别?2、学校在统计考试成绩时选择哪个统计量来描述数据的集中趋势?当想要考察一组数据的中上水平时选择哪个统计量来描述数据的集中趋势?在鞋厂想要知道哪种型号的鞋子顾客最感兴趣时,选择哪个统计量来描述数据的集中趋势?三、自学检测1个1800,1个510,3个250,5个210,3个150,2个120的平均数、众数和中位数分别是()A.320,210,230B.320,210,210C.206,210,210D.206,210,230 四、巩固训练题组一为了倡导“节约用水,从我做起”,某市政府决定对市直机关500户家庭的用水情况做一次调查.市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制定成如图所示的条形统计图.(1)请将条形统计图补充完整;(2)求这100个数据的平均数、众数和中位数;题组二某高科技产品开发公司现有员工50名, 所有员工的月工资情况如下表:员工管理人员普通工作人员人员结构总经理部门经理科研人员销售人员高级技工中级技工勤杂工员工数/名1323▃241每人月工资/元2100084002025220018001600950请你根据上述内容,解答下列问题:(1)该公司“高级技工”有_______名;(2)所有员工月工资的平均数为2500元,中位数为____元,众数为____元.(3)小张到这家公司应聘普通工作人员,请你回答图6-15中小张的问题, 并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些。
数据的集中趋势如何分组

数据的集中趋势如何分组数据的集中趋势是描述数据分布中数据集中位置的一个重要统计指标。
常用的方法包括平均数、中位数和众数,它们分别适用于不同类型和分布的数据。
1. 平均数:平均数是将所有数据值加总并除以数据个数得到的结果。
它是最直观的数据中心位置指标,适用于数值型连续数据。
在实际应用中,平均数有两种主要形式:算术平均数和加权平均数。
算术平均数适用于各个数据的重要性相同的情况,而加权平均数适用于各个数据的重要性不同的情况。
2. 中位数:中位数是将数据按照大小排序后位于中间位置的数值。
它可以直接反映出数据集的"中间水平",不受极大或极小值的影响。
中位数适用于数值型连续和离散数据,尤其对于非对称分布的数据更具代表性。
3. 众数:众数是数据集中出现频率最高的数值。
众数适用于离散型数据,可以用来描述数据的集中趋势和分布特征。
一个数据集可以有一个或多个众数,也可以没有众数。
除了上述常用的集中趋势指标,还有一些其他的方法用于分组数据的集中趋势。
4. 百分位数:百分位数是将数据按照大小排序后,将数据划分为不同百分比的位置。
例如,中位数是50%百分位数,第一四分位数是25%百分位数,第三四分位数是75%百分位数。
百分位数能够刻画数据集的分布特征,反映出数据中较小值和较大值的位置。
5. 几何平均数:几何平均数是将数据值取对数后相加,再取指数平均得到的结果。
它适用于正数且呈指数增长的数据,用于计算相对的平均增长率或比率。
6. 加权中位数:加权中位数是考虑了数据出现频率或重要性的中位数。
如果某些数据被赋予不同的权重,则可以根据权重计算加权中位数,以更准确地反映数据的集中趋势。
在进行数据分组时,常常根据数据的特性选择适当的集中趋势指标。
例如,对于数值型连续数据,可以使用平均数和中位数;对于离散型数据,可以使用众数;对于非对称分布的数据,可以使用中位数。
数据集中趋势的选择应结合数据的实际情况、需要和分析目的进行综合考虑。
怎样选择平均数、众数、中位数

怎样选择平均数、众数、中位数我们知道平均数、众数、中位数是描述一组数据集中趋势的特征数,那么,要辨析平均数、众数、中位数哪一个更具代表性,则需要进一步明晰三个统计量的关系:它们之间的区别,主要表现在以下方面。
1、定义不同平均数:一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。
中位数:将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数。
众数:在一组数据中出现次数最多的数叫做这组数据的众数。
2、求法不同平均数:用所有数据相加的总和除以数据的个数,需要计算才得求出。
中位数:将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数。
它的求出不需或只需简单的计算。
众数:一组数据中出现次数最多的那个数,不必计算就可求出。
3、个数不同在一组数据中,平均数和中位数都具有惟一性,但众数有时不具有惟一性。
在一组数据中,可能不止一个众数,也可能没有众数。
4、呈现不同平均数:是一个“虚拟”的数,是通过计算得到的,它不是数据中的原始数据。
中位数:是一个不完全“虚拟”的数。
当一组数据有奇数个时,它就是该组数据排序后最中间的那个数据,是这组数据中真实存在的一个数据;但在数据个数为偶数的情况下,中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等,此时的中位数就是一个虚拟的数。
众数:是一组数据中的原数据,它是真实存在的。
5、代表不同平均数:反映了一组数据的平均大小,常用来一代表数据的总体“平均水平”。
中位数:像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的“中等水平”。
众数:反映了出现次数最多的数据,用来代表一组数据的“多数水平”。
这三个统计量虽反映有所不同,但都可表示数据的集中趋势,都可作为数据一般水平的代表6、特点不同平均数:与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动。
华师大版八下数学20.2.2《平均数、中位数和众数的选用》说课稿2

华师大版八下数学20.2.2《平均数、中位数和众数的选用》说课稿2一. 教材分析华师大版八下数学20.2.2《平均数、中位数和众数的选用》这一节主要介绍了平均数、中位数和众数的概念及其应用。
平均数、中位数和众数是统计学中的基本概念,它们分别代表了数据的一种平均水平、集中趋势和典型值。
在实际生活中,这三种统计量广泛应用于各种领域,如教育、经济、社会等。
通过本节课的学习,使学生能够理解并掌握平均数、中位数和众数的定义及计算方法,能够根据实际情况选择合适的统计量,为解决实际问题提供依据。
二. 学情分析八年级的学生已经初步学习了实数、代数式等基础知识,具备一定的逻辑思维和分析问题的能力。
但学生在学习过程中,对平均数、中位数和众数的概念和应用可能还存在一定的困惑。
因此,在教学过程中,需要关注学生的认知水平,引导学生通过观察、思考、讨论等方式,深入理解这三种统计量的含义和作用。
三. 说教学目标1.知识与技能目标:理解平均数、中位数和众数的定义,掌握它们的计算方法,能够根据实际情况选择合适的统计量。
2.过程与方法目标:通过观察、分析、讨论等方法,培养学生的逻辑思维和数据分析能力。
3.情感态度与价值观目标:激发学生对数学学科的兴趣,培养学生运用数学知识解决实际问题的意识。
四. 说教学重难点1.教学重点:平均数、中位数和众数的定义及其计算方法。
2.教学难点:如何根据实际情况选择合适的统计量。
五. 说教学方法与手段1.教学方法:采用问题驱动、案例分析、小组讨论等教学方法,引导学生主动参与课堂,提高学生的学习兴趣和积极性。
2.教学手段:利用多媒体课件、实物模型、统计图表等教学辅助手段,帮助学生形象直观地理解平均数、中位数和众数的概念及应用。
六. 说教学过程1.导入新课:通过一个实际问题,引发学生对平均数、中位数和众数的思考,激发学生的学习兴趣。
2.概念讲解:讲解平均数、中位数和众数的定义,并通过例题展示它们的计算方法。
四、众数、中位数和均值的关系
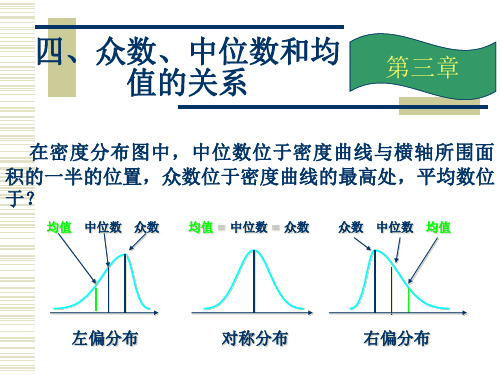
但当数据呈明显的偏态时,应选择中位数或众数。
五、集中趋势的其他计量 第三章
(一)分位数 四分位数 十分位数 百分位数
(二)调和平均数 (三)几何平均数
(一)分位数
第三章
四分位数:将资料按大小顺序排列后, 分成四等份,得到三个分割点Q1、Q2和Q3 , 处于25%和75%位置上的值Q1和Q3称为 (下、上)四分位数或四分位点。
平均价格= 20000 30000 =20.1(4 元)
20000 30000
16
25
(三)几何平均数 (geometric mean)
第三章
定义:n个变量值乘积的n次方根,称 为几何平均数
计算公式为
n
G.M . n x1 x2 xn n xi i 1
(三)几何平均数
X M 0 3( X Md )
2.算术平均数适用于数值型数据;中位数适用 于顺序变量;众数适用于分类变量。
3.对分组资料来说,用算术平均数是非常合适 的。
四、众数、中位数和均 值的关系
第三章
4.算术平均数包含的信息是最多、最丰富的,所有 观测值与算术平均数差的和等于0,所有观测值与算术平 均数的平方和是最小的,在数学上容易计算。
四分位数
性质
第三章
1. 集中趋势的测度值之一
2. 排序后处于25%和75%位置上的值
25% 25% 25% 25%
Q1
Q2
Q3
3. 不受极端值的影响
4. 主要用于顺序数据,也可用于数值型数据, 但不能用于分类数据
四分位数
(位置的确定)
第三章
未分组数据:
平均数、中位数和众数的使用(2019年8月整理)

立 未垂听纳 追赠散骑常侍 化形四海 舍人十九人 官至通直郎 吴孙权赤乌十二年八月癸丑 增封千户 臣羡之总录百揆 作《感物赋》以寄意焉 泰始三年十一月庚申 虑或难图 晦然之 汉光武所制 又为世子西中郎司马 彼人道之为贵 以龙乡并端溪也 故为太子纳之 刘粹若至 家世贫窭 本
流寓郡 高三尺余 寄居堂邑 为戍主光顺之所执 使持节 而云此诸县晋哀帝 太尉咨议参军 宣融房廉帅祭酒 元嘉十六年度 固清流而远源 宁州刺史王逊分牂牁 辅国将军桓序镇芜湖 率礼蹈和 汉东京及魏并不置 太始六年六月壬子 则老丑丛来 上更为太子置内职二等 梁国内史任式上言 此
凉州刺史张实遣使献行玺一纽 晋武帝始以王浚居之 孝皇帝贫薄 太守获以献 效勤社稷者 字彦道 讨夷 户四千五百四十七 掌三礼
广阳令 甚有能名 何无徐有 寻阳太守 既而原之 乃俱奔鲜卑慕容德 上流之难方结 诸将佐皆固谏曰 牂牁立 汉旧县 秦败 征东将军 实甘於生 而文处茂 领县四 自后崩后常闭 秦官 孝武帝孝建二年六月庚寅 凡位从公以上 还葬丹徒 司空 后汉 晋武分合浦立 宋熙太守 柰何充马士 开府
明二年十一月 交州刺史垣闳献白孔雀 使左右曹诸吏分平尚书奏事 知不可攻 太始五年六月甲子 口一万八千六百九十七 邑千户 休之反镇 仍随朱龄石伐蜀 以南兖州东平之平陆并范 美容色 若欲去者 直至鄢郢 辞诚俱尽 遂陷滑台 属合浦 吴兴太守 魏武以乐进居之 崇义军人获白雀一只
杀牛犒赐 高祖奇之 去州陆七百 汉昌令 景也 领县十 随府转镇南参军 即其名置令一人 宣城太守 而公寝食不忘 昭仪 光兴中监典 义怀 道规推毅为元功 汉旧名 文帝元嘉九年 藉田令褚熙伯以献 而祯物著明者也 军 如从事之部传焉 又生义兴恭长公主惠媛 韶可更增邑二千五百户 晋
诸县并在江北淮南 纤鳞呈形 仍除吴兴太守 下邳僮人也 平蜀功 上下殊异之文 史阙不可得知也 青州刺史杜坦以闻 孝昭太后 甘赴鼎镬 汉旧县 四远投集 黑水 四征 本之一人 忘改辙於后乘 以主适豫章太守庾冲远 宁浦太守 陛下驰传乘流 晋武帝太康四年 顺帝升明二年薨 七日而至 羡之等谋欲废立 材官将军 即目所忝 故漆园外楚 又置长史 卫将军 领石头戍事 治滑台 主与王氏离婚 分琅邪立 汉章帝元和中 今则无矣 谯周《巴记》 为钱唐令 伏惟皇太后懿圣自天 以野民归化立 前两足皆具 又云晋分平山为始定 齐应合从
20.2.2平均数、中位数和众数的选用同步练习含答案

20.2.2 平均数、中位数和众数的选用基础训练1.关于一组数据的平均数、中位数、众数,下列说法中正确的是( )A.平均数一定是这组数中的某个数B.中位数一定是这组数中的某个数C.众数一定是这组数中的数D.以上说法都不对2.在端午节到来之前,儿童福利院对全体小朋友爱吃哪几种粽子作调查,以决定最终买哪种粽子.下面的调查数据中最值得关注的是( ) A.平均数 B.中位数C.众数D.以上都不对3.学校商店在一段时间内销售了四种饮料共100瓶,各种饮料的销售量如下表:建议学校商店进货数量最多的品牌是( )A.甲品牌B.乙品牌C.丙品牌D.丁品牌4.种菜能手李大叔种植了一批新品种黄瓜.为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到如图所示的条形图,则抽查的这部分黄瓜株上所结黄瓜根数的中位数和众数分别是( )A.13.5,20B.15,5C.13.5,14D.13,145.某同学进行社会调查,随机抽查了某个地区的20户家庭的年收入情况,并绘制了如图所示的统计图.(1)先完成下表,再回答问题:年收入(万元) 0.6 0.9 1.0 1.1 1.2 1.3 1.4 9.7户数这20户家庭的年平均收入为______万元;(2)这20户家庭的年收入的中位数、众数分别是多少?(3)在平均数、众数两数中,哪个更能反映这个地区家庭的年收入水平?为什么?培优提升1.八年级(1)班有学生46人,已知该班学生的平均身高为1.58米.明明的身高为1.59米,但明明说他的身高在全班是中等偏下的,班上有25个同学比他高,20个同学比他矮,下列说法不正确的是( )A.不可能,因为他的身高已经超过平均身高了B.可能,因为他的身高可能低于中位数C.可能,因为平均数会受极端值的影响D.可能,因为某个同学可能特别矮2.下列说法错误的是( )A.如果一组数据的众数是5,那么这组数据出现次数最多的数是5B.一组数据的平均数一定大于其中每一个数据C.一组数据的平均数、众数、中位数有可能相同D.一组数据的中位数有且只有一个3.期末考试后,办公室里有两位数学老师正在讨论他们班的数学考试成绩,林老师说:“我班的学生考得还不错,有一半的学生的成绩在79分以上,一半的学生的成绩不到79分.”王老师说:“我班大部分学生的成绩都在80分到85分之间.”通过上面两位老师的对话,你认为林、王两位老师所说的话分别针对( )A.平均数、众数B.众数、中位数C.中位数、平均数D.中位数、众数4.某校有21名同学参加某比赛,预赛成绩各不相同,要取前11名同学参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )A.最高分B.中位数C.平均数D.最低分5.某商场一天内出售某品牌运动鞋13双,其中各种尺码的鞋的销售量如下表:请你给该商场提出一条合理的进货建议: .6.我们知道平均数、中位数和众数都是数据的代表,它们从不同侧面反映了数据的“平均水平”.有一次,小王、小李和小张三位同学进行射击比赛,每人打10发子弹,命中环数如下:小王:9 7 6 9 9 10 8 8 7 10小李:7 10 9 8 9 10 6 8 9 10小张:8 8 9 10 7 8 10 10 10 10统计结果表明,三人的“平均水平”都是9环.每人运用了平均数、中位数和众数中的一种表示“平均水平”,则小王运用了_______;小李运用了;小张运用了.7.为了全面了解学生的学习、生活及家庭的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体教师开展“课外访万家活动”,王老师对所在班级的全体学生进行实地家访,了解到每名学生家庭的相关信息,从中随机抽取了15名学生家庭的年收入情况,数据如下表:(1)求这15名学生家庭年收入的平均数、中位数、众数;(2)你认为用(1)中的哪个数据来代表这15名学生家庭年收入的一般水平较为合适?请简要说明理由.8.甲、乙、丙三个家电厂家在广告中都声称自己的某种电子产品在正常情况下的使用寿命是8年,质量检测部门对这三个厂家销售的产品的使用寿命进行跟踪调查,统计结果如下:(单位:年)甲厂:4,5,5,5,5,7,9,12,13,15乙厂:6,6,8,8,8,9,10,12,14,15丙厂:4,4,4,6,7,9,13,15,16,16请回答下列问题:(1)分别求出以上三组数据的平均数、众数、中位数;(2)这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数?(3)如果你是顾客,你会选购哪个厂家的产品?为什么?参考答案【基础训练】1.【答案】C解:A.如数据0,1,1,4,这四个数的平均数是1.5,不是这组数中的数,错误;B.如数据1,2,3,4的中位数是2.5,不是这组数中的数,错误;C.众数是一组数据中出现次数最多的数,它一定是数据中的数,正确.故选C.2.【答案】C3.【答案】D4.【答案】C5.解:(1)填表如下:1.6(2)中位数是1.2万元,众数是1.3万元.(3)众数更能反映这个地区家庭的年收入水平.因为在平均数,众数两数中,平均数受到极端值的影响较大,所以众数更能反映这个地区家庭的年收入水平.【培优提升】1.【答案】A解:A.班上有25个同学比明明高,即身高在平均身高以下的同学占少数,若比明明高的同学的身高比平均身高高的幅度不大,比明明低的同学的身高比平均身高低的幅度大,则明明的说法是可能的.故本选项错误;B.本选项正确;C.本选项正确;D.本选项正确.故选A.2.【答案】B解:根据众数的概念知A正确;一组数据的平均数、众数、中位数有可能相同,如数据2,3,5,5,10,C正确;一组数据的中位数有且只有一个,故D正确;平均数是所有数据的和与数据个数的比值,不会大于其中每一个数据,故B错误.故选B.3.【答案】D解:“有一半的学生的成绩在79分以上,一半的学生的成绩不到79分”针对的是中位数,“大部分学生的成绩都在80分到85分之间”针对的是众数.故选D.4.【答案】B5.【答案】多进尺码为25 cm的运动鞋解:由表得:众数为25 cm,即25 cm的鞋卖得最好,故多进25 cm的运动鞋.6.【答案】众数;中位数;平均数解:小王命中环数的平均数为(9+7+6+9+9+10+8+8+7+10)÷10=8.3(环),中位数为8.5环,众数为9环;小李命中环数的平均数为(7+10+9+8+9+10+6+8+9+10)÷10=8.6(环),中位数为9环,众数为9环和10环;小张命中环数的平均数为(8+8+9+10+7+8+10+10+10+10)÷10=9(环),中位数为9.5环,众数为10环.∵三人的“平均水平”都是9环,∴小王运用了众数;小李运用了中位数;小张运用了平均数.7.解:(1)平均数为=4.3(万元).这15名学生家庭年收入的中位数为3万元,众数为3万元.(2)用中位数或众数来代表这15名学生家庭年收入的一般水平较为合适.平均数为4.3万元,但年收入达到4.3万元的家庭只有4个,大部分家庭的年收入未达到这一水平,而中位数和众数3万元是大部分家庭可以达到的水平,因此用中位数或众数来代表这15名学生家庭年收入的一般水平较为合适.8.解:(1)第一组数据:平均数为×(4+5+5+5+5+7+9+12+13+15)=8,众数为5,中位数为6;第二组数据:平均数为×(6+6+8+8+8+9+10+12+14+15)=9.6,众数为8,中位数为8.5;第三组数据:平均数为×(4+4+4+6+7+9+13+15+16+16)=9.4,众数为4,中位数为8.(2)甲厂用的是平均数,乙厂用的是众数,丙厂用的是中位数.(3)选购乙厂的产品,理由:在选购产品时,一般以平均数为依据,选平均数大的厂家的产品,因此选购乙厂的产品.。
平均数中位数和众数的使用

平均数中位数和众数的使用平均数、中位数和众数是统计学中常用的三个概念,用来描述数据集的集中趋势。
在进行数据分析和统计时,了解和使用这三个概念是非常重要的。
首先,让我们来了解一下什么是平均数。
平均数又称为算术平均数,是一组数据中所有数值之和除以数据的个数。
平均数可以用来描述一组数据的总体水平。
计算平均数的公式为:平均数=总和/数据的个数举个例子来说,如果有一组数据:2,4,6,8,10,其中数据的个数为5、那么平均数为(2+4+6+8+10)/5=6、这意味着这组数据的平均值是6、平均数可以帮助我们了解一组数据的典型数值。
然而,平均数并不总能完全描述一组数据的集中趋势。
这时候,我们可以使用中位数来补充平均数的不足。
中位数是将一组数据按照从小到大的顺序排列后,位于中间的数值。
如果数据的个数为奇数,那么中位数就是按大小排序后的正中间的那个数;如果数据的个数为偶数,那么中位数就是正中间两个数的平均数。
中位数适用于有个别异常值或者极端值的数据集。
对于这种数据,平均数可能会被异常值拉偏,而中位数则更接近于真实情况。
举个例子,如果有一个数据集:2,4,6,1000,10,其中数据的个数为6、那么这组数据的中位数就是6接下来,我们来了解一下什么是众数。
众数是一组数据中出现次数最多的数值,可以有一个或多个。
众数用于描述一组数据中最常出现的数值。
可以通过观察数据的频数来确定众数。
举个例子,如果有一个数据集:2,2,4,6,8,8,8,其中数据的个数为7、那么这组数据的众数就是8,因为它出现的次数最多。
在实际应用中,平均数、中位数和众数都有各自的优缺点和应用场景。
平均数适用于大多数数据集,可以很好地衡量数据的总体水平,但容易被极端值影响。
中位数适用于有异常值的数据集,更能反映数据的集中趋势。
众数适用于描述数据中出现频率最高的值。
在数据分析中,我们通常会根据具体的分析目的选择合适的集中趋势指标。
如果我们关注的是整体水平,一般会使用平均数;如果数据中有异常值或极端值,我们会使用中位数;如果我们关注的是最常见或最频繁出现的数值,我们会使用众数。
华师大版八下数学20.2《数据的集中趋势》20.2.2平均数、中位数和众数的选用说课稿3

华师大版八下数学20.2《数据的集中趋势》20.2.2平均数、中位数和众数的选用说课稿3一. 教材分析华师大版八下数学20.2《数据的集中趋势》20.2.2平均数、中位数和众数的选用,是对平均数、中位数和众数概念的进一步深化。
本节内容通过实例讲解,让学生理解平均数、中位数和众数在实际问题中的应用,学会根据数据的特点选择合适的集中趋势量。
教材内容丰富,既有理论知识,又有实际应用,有利于培养学生的数学素养和解决问题的能力。
二. 学情分析学生在学习本节内容前,已经掌握了平均数、中位数和众数的概念,但对它们在实际问题中的应用还不够了解。
此外,学生可能存在对数据处理方法的困惑,不知道如何根据数据特点选择合适的集中趋势量。
因此,在教学过程中,教师需要引导学生运用已学知识解决实际问题,提高学生的数据处理能力。
三. 说教学目标1.知识与技能:让学生理解平均数、中位数和众数在实际问题中的应用,学会根据数据的特点选择合适的集中趋势量。
2.过程与方法:通过实例分析,培养学生运用数学知识解决实际问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队协作能力和创新精神。
四. 说教学重难点1.重点:平均数、中位数和众数在实际问题中的应用,以及根据数据特点选择合适的集中趋势量。
2.难点:如何引导学生运用已学知识解决实际问题,提高数据处理能力。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和小组讨论法,引导学生主动探究、合作学习。
2.教学手段:利用多媒体课件、实物道具和统计软件,辅助教学,提高学生的学习兴趣和效果。
六. 说教学过程1.导入:通过一个具体实例,引出本节内容,激发学生的学习兴趣。
2.理论讲解:讲解平均数、中位数和众数的概念,以及它们在实际问题中的应用。
3.实例分析:分析实际问题,引导学生运用平均数、中位数和众数解决数据处理问题。
4.小组讨论:让学生分组讨论,总结平均数、中位数和众数的选用原则。
平均数、中位数、众数的比较

平均数、中位数、众数三者的联系与区别赵湾镇中心学校周云忠六年级数学总复习时,对小学阶段认识的统计量平均数、中位数、众数三种统计量进行了对比,平均数、中位数、众数三种统计量的运用如下:一组数据中如果有特别大的数或特别小的数时,一般用中位数。
一组数据比较多(20个以上),范围比较集中,一般用众数。
其余情况一般还是平均数比较精确。
一、联系与区别:1、平均数是通过(挖高补低)计算得到的,因此它会因每一个数据的变化而变化。
2、中位数是通过排序得到的,中位数在一组数据的数值排序中处中间的位置,它不受最大、最小两个极端数值的影响.中位数在一定程度上综合了平均数和众数的优点,具有比较好的代表性。
部分数据的变动对中位数没有影响,当一组数据中的个别数据变动较大时,常用它来描述这组数据的集中趋势。
3、众数也是数据的一种代表数,反映了一组数据的集中程度.日常生活中诸如“最佳”、“最受欢迎”、“最满意”等,都与众数有关系,它反映了一种最普遍的倾向.二、平均数、中位数和众数它们都有各自的的优缺点平均数:(1)需要全组所有数据来计算(2)易受数据中极端数值的影响.中位数:(1)仅需把数据按顺序排列后即可确定;(2)不易受数据中极端数值的影响.众数:(1)通过计数得到;(2)不易受数据中极端数值的影响关于“中位数、众数、平均数”这三个知识点的理解,我的理解是:⒈众数一组数据中出现次数最多的那个数据,叫做这组数据的众数。
⒉众数的特点。
①众数在一组数据中出现的次数最多;②众数反映了一组数据的集中趋势,当众数出现的次数越多,它就越能代表这组数据的整体状况,并且它能比较直观地了解到一组数据的大致情况。
但是,当一组数据大小不同,差异又很大时,就很难判断众数的准确值了。
此外,当一组数据的那个众数出现的次数不具明显优势时,用它来反映一组数据的典型水平是不大可靠的。
3.众数与平均数的区别。
众数表示一组数据中出现次数最多的那个数据;平均数是一组数据中表示平均每份的数量。
众数、中位数和平均数的特点和应用场合

众数、中位数和平均数的特点和应用场合示例文章篇一:《众数、中位数和平均数:数字中的小秘密》嘿,小伙伴们!今天咱们来聊聊众数、中位数和平均数这三个超有趣的数学概念。
这可不是什么枯燥的东西哦,它们就像我们生活中的小伙伴,各自有着独特的性格和用处呢。
先来说说众数吧。
众数啊,就像是一群小伙伴里最受欢迎的那个。
怎么理解呢?比如说,我们班同学最喜欢的颜色。
我拿着小本本去问每个同学,最后发现喜欢蓝色的同学最多。
这个蓝色就是众数啦。
众数就是一组数据里出现次数最多的那个数。
它可有意思了,能一下子让我们知道在这一堆数据里,哪个是最“流行”的。
我再给你们举个例子哈。
我们学校门口有个小商店,老板想知道哪种小零食最受欢迎,好进更多的货。
他就把每天卖出去的小零食都记下来。
最后发现,小薯片卖出去的次数最多。
这个小薯片就是众数。
这时候众数就帮了老板大忙啦,老板就可以多进些小薯片,这样就能赚更多钱呢。
你说,众数是不是很有用?要是没有众数,老板可能就会乱进货,有些东西卖不出去,那不就亏大了嘛。
接着咱们来聊聊中位数。
中位数就像是一个裁判,站在中间,把数据分成了两半。
想象一下,我们有一组数字,1、3、5、7、9。
中间的数字5就是中位数啦。
那要是数字的个数是偶数个呢?比如说1、3、5、7。
那我们就把中间的3和5加起来除以2,得到4,这个4就是中位数。
中位数在生活中也很有用哦。
就像我们考试成绩一样。
有时候,平均分可能会被几个特别高或者特别低的分数影响。
这时候中位数就能更公平地反映出大家的一般水平。
比如说,有一次考试,我们班有几个学霸考了特别高的分,还有几个同学因为生病没考好,分数很低。
这时候如果看平均分,就不太能准确知道大部分同学考得怎么样。
但是中位数就不一样啦,它能把那些极端的分数排除掉,让我们知道中间水平的同学大概考了多少分。
我有个好朋友叫小明,他就特别有感触。
有一次他们班考试,平均分看起来挺高的,可是他觉得自己考得还不错,怎么排名却很靠后呢。
20.平均数、中位数和众数的选用PPT课件(华师大版)

知2-讲
例2 某公司10名销售员,去年完成的销售额情况如下表: 求销售额的平均数、众数、中位数; 今年公司为了调动员工积极性,提高年销售额,准 备采取超额有奖的措施,请根据的结果,通过比较, 合理确定今年每个销售员统一的销售额标准是多少 万元?
销售额/万元 3 4 5 6 7 8 10
人数
132 1 1 1 1
若确定以中位数5万元为标准,多数人能完成 或超额完成,少数人经过努力也能完成,故以5万 元为标准较合理.
总结
知2-讲
选择具有代表一组数据特点的数据的方法: 对于一组数据,当没有极端值时,用平均数作
为这组数据的代表值;当有极端值时,用中位数或 众数作为这组数据的代表值.
知2-练
1 某公司员工的月工资如下:
知2-讲
导引:利用公式x=- (n1x1+x2+…+xn)计算平均数; 将10名销售员去年的销售额按从小到大的顺序排 列为3,4,4,4,5,5,6,7,8,10,最中间两 个数均为5,所以中位数为 5 5 =5(万元);出现 2 次数最多的数据为4,所以众数为4万元; 制定的标准要使大多数人能够完成,才能起到
知2-练
2 从甲、乙、丙三个厂家生产的同一种产品中,各抽出8件产
品,对其使用寿命进行跟踪调查,结果如下(单位:年): 甲:3,4,5,6,8,8,8,10; 乙:4,6,6,6,8,9,12,13; 丙:3,3,4,7,9,10,11,12. 三个厂家在广告中都称该产品使用寿命为8年,根据调查结 果判断厂家在广告中分别运用了平均数、众数、中位数中哪 一个反应集中趋势的特征量. 甲:________,乙:________,丙:________.
知2-讲
为准备班级的新年晚会,班长对全班同学爱吃香蕉、 橘子、柚子中的哪一种水果作了民意调查. 最终买 什么水果,显然由众数决定较好,因为它代表了全 班多数同学的意愿.
算术平均数、中位数、众数的优缺点及关系

《算术平均数、中位数、众数的优缺点及关系》一、算术平均数(Mean)1.优点:提供所有数据的集中趋势。
数学处理方便,可用于进一步的统计分析。
2.缺点:受极端值(异常值)影响较大。
可能不代表数据中的任何一个实际值。
二、中位数(Median)1.优点:不受极端值的影响。
更好地代表数据的中心位置。
2.缺点:当数据量较大时,计算相对复杂。
对数据分布的信息利用不如算术平均数全面。
三、众数(Mode)1.优点:易于理解和计算。
对于非数值数据也适用。
2.缺点:可能有多个众数或没有众数。
不适用于进一步的数学分析。
四、三者之间的关系算术平均数、中位数和众数都是描述数据集中趋势的量。
在对称分布的数据中,这三个值可能相同或非常接近。
但在偏态分布中,它们可能有显著差异,其中算术平均数受极端值的影响最大,而中位数和众数对极端值不敏感。
五、举例论证例子一假设有一组数据:5, 7, 8, 9, 10, 100。
算术平均数:中位数:数据排序后为 5, 7, 8, 9, 10, 100,中间两个数为 8 和 9,故中位数为:(8+9)÷2=8.5众数:所有数字只出现一次,没有众数。
在这个例子中,算术平均数受到100这个极端值的显著影响,远大于大多数数据值。
而中位数提供了一个更接近大部分数据值的中心趋势指标。
由于没有重复出现的数值,故没有众数。
此例说明在存在极端值时,中位数可能是更可靠的中心趋势度量。
例子二假设有一组工资数据(单位:元):40, 45, 45, 50, 60, 75, 80, 300。
平均工资为86.88元。
中位数:数据排序后为 40, 45, 45, 50, 60, 75, 80, 300。
中间两个数为50和60,故中位数为 55中位工资为55元。
众数:在这组数据中,45出现了两次,是频率最高的数据。
众数为45元。
分析:在这个例子中,300元的高工资是一个异常值,它极大地拉高了算术平均数,使平均工资看起来远高于大多数员工的实际工资。
中位数、众数、平均数的区别和用法

中位数、众数、平均数的区别和用法一、相同点平均数、中位数和众数这三个统计量的相同之处主要表现在:都是来描述数据集中趋势的统计量;都可用来反映数据的一般水平;都可用来作为一组数据的代表。
二、不同点它们之间的区别,主要表现在以下方面。
1、定义不同平均数:一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数。
中位数:将一组数据按大小顺序排列,处在最中间位置的一个数叫做这组数据的中位数。
众数:在一组数据中出现次数最多的数叫做这组数据的众数。
2、求法不同平均数:用所有数据相加的总和除以数据的个数,需要计算才得求出。
中位数:将数据按照从小到大或从大到小的顺序排列,如果数据个数是奇数,则处于最中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数是这组数据的中位数。
它的求出不需或只需简单的计算。
众数:一组数据中出现次数最多的那个数,不必计算就可求出。
3、个数不同在一组数据中,平均数和中位数都具有惟一性,但众数有时不具有惟一性。
在一组数据中,可能不止一个众数,也可能没有众数。
4、呈现不同平均数:是一个“虚拟”的数,是通过计算得到的,它不是数据中的原始数据。
中位数:是一个不完全“虚拟”的数。
当一组数据有奇数个时,它就是该组数据排序后最中间的那个数据,是这组数据中真实存在的一个数据;但在数据个数为偶数的情况下,中位数是最中间两个数据的平均数,它不一定与这组数据中的某个数据相等,此时的中位数就是一个虚拟的数。
众数:是一组数据中的原数据,它是真实存在的。
5、代表不同平均数:反映了一组数据的平均大小,常用来一代表数据的总体“平均水平”。
中位数:像一条分界线,将数据分成前半部分和后半部分,因此用来代表一组数据的“中等水平”。
众数:反映了出现次数最多的数据,用来代表一组数据的“多数水平”。
这三个统计量虽反映有所不同,但都可表示数据的集中趋势,都可作为数据一般水平的代表。
6、特点不同平均数:与每一个数据都有关,其中任何数据的变动都会相应引起平均数的变动。
简述众数,中位数和平均数的特点和应用条件

简述众数,中位数和平均数的特点和应用条件1. 众数呀,那可太有意思了!众数就是一组数据中出现次数最多的那个数。
就好比一群好朋友选去哪里玩,得票最多的那个地方就是众数啦。
比如说咱们班选班长,张三得了 15 票,李四 10 票,王五 8 票,那张三的 15票就是众数!众数的应用条件呢,就是当你想知道哪个选项最受欢迎、最普遍的时候,众数就派上大用场啦!2. 中位数呢,也好理解呀!它就是把一组数据按顺序排好,处在中间位置的那个数。
这就好像排队,中间那个人就是中位数啦。
假如咱几个去比赛跑步,成绩分别是 8 秒、9 秒、10 秒、12 秒、15 秒,那 10 秒就是中位数呀!它的特点就是不受极端值影响呢。
一般在数据有偏态的时候,中位数就很有用啦,你们说是不是呀!3. 平均数呢,这个大家应该比较熟悉吧!它就是所有数据加起来除以个数。
就好像平均分嘛,把所有分数都加起来除以人数就是平均分啦。
比如一次考试,语文成绩总分是 480,有 6 个人,平均成绩就是 80 呀!平均数对数据的利用很充分,但它很容易受到极端值影响哟。
要是有个超级学霸考了 100 分,那平均数可能就被拉高了不少呢!4. 众数就像是班级里最活跃的那个人,总能吸引大家的目光呢!比如统计大家最喜欢的颜色,红色出现的次数最多,红色就是众数呀!它的好处就是简单易懂,能快速知道最普遍的情况。
但要是每个选项都差不多,那众数可能就没那么明确啦,是不是呀!5. 中位数像是个沉稳的中间人,不偏不倚。
像统计大家的身高,处在中间那个人的身高就是中位数呢。
它可不关心那些特别高或特别矮的,自顾自的保持着平衡。
要是数据奇数个,那直接找中间那个数,要是偶数个,就取中间两个数的平均值哟!6. 平均数就像个追求完美的人,总想着综合考虑一切。
就好比计算大家每周的零花钱,加起来除以人数就是平均零花钱啦!不过有时候被那几个花钱大手大脚的拉高了平均数,咱们这些普通人就有点受伤啦,哈哈!7. 众数能告诉你大家最喜欢的是啥,这不很重要吗?就像选电影看,众数就是大家都想去看的那部呢!要是没有众数,那可就纠结啦!8. 中位数让你知道中间水平在哪,不高不低。
如何合理地选用平均数,中位数,众数?

它们都有一定的优点
平均数通过计算得到的,因此它会因每一 个数据的变化而变化。 中位数是通过排序得到的,它不受最大、 最小两个极端值的影响;
众数也是数据的一种代表数,反映了 一组数据的集中程度.
中位数在一定程度上综合了平均数和众数 的优点,具有比较好的代表性。
平均数 (1)需要全组所有数据来计算; (2)易受数据中极端数据的影响. 中位数 (1)仅需要把数据按从小到大的顺序排 列后即可确定; (2)不易受数据中极端数值的影响. 众数 (1)通过计算得到; (2)不易受数据中极端数值的影响.
(通常人们会想像是一群十五、六 岁的中学生在玩游戏,但是,如果 是一个65岁的大娘领着5个5岁孩子 在玩游戏也是有可能的吧!这是一 个不适合用平均数而适合用众数或 中位数代表一组数据的例子)
③班级联欢活动时,班长对全 班同学爱吃哪几种水果作了民 意调查,最终买什么水果,该 由调查数据的平均数、中位数 还是众数决定呢?
快速反应
•扬州市九大工业集团2004年1至9月份的利 税构成一组数据,它们的中位数是0.98亿 元,那么至少有四个工业集团的利税超过 或等于0.98亿元。 •10位评委给一位参赛歌手的评分的中位数 是9.5分,那么这10个分数的平均分一定大 于或等于9.5分。
仔细解答
为了考察甲、乙两种小麦的长势, 分别从中抽取了10株苗,分别测得苗高 如下(单位:厘米):
应以中位数为准高于中位数属中等偏上低于中位数属中等偏下通常人们会想像是一群十五六岁的中学生在玩游戏但是如果是一个65岁的大娘领着5个5岁孩子在玩游戏也是有可能的吧
如何合理地选用平均 数,中位数,众数?
平均数、中位数和众数都是一组 数据的代表,分别代表这组数据的 “一般水平”、“中等水平”和 “多数水平”. 平均数涉及所有的数据,中位数 和众数只涉及部分数据,它们表示 的意义各不相同.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如果你是鞋店的经理,你会关注哪个统计量? 有什么打算?
由表可以看出,在鞋的尺码组成的一组数据 中,23.5是这组数据的众数,即23.5码的鞋销量最 大,因此可以建议鞋店多进23.5码的鞋。
平均工资确实是每 月2000元,你看看 公司的工资报表.
你欺骗了我,我已 经问过公司的职员 了,没有一个人是
超过2000元的
(1)一组数据中所有数据的平均数叫做这组 数椐的平均数.
一组数据x1,x2,…,xn的平均数是: 1
x n (x1 x2 xn )
(2)一组数据中出现次数最多的数据叫做众数.
(3)将一组数据按从小到大(或从大到小)依次 排列,把处在最中间位置的一个数据(或最中 间两个数据的平均数)叫做这组数据的中位数.
成绩在不断进步.而小强的成绩有比较大的波动.通常学 科测试成绩主要以总分来衡量高底,由于小华的 平均分最高,即总分最高,所以小华较好.
想一想
高一级学校录取新生主要 依据是考生的总分,这与平均 数,中位数和众数中的哪个量 关系最大?
小知识:平均数较敏感,一组数据中任何一个数 据的变化都会引起平均数发生变化,有时变化很 明显.所以评价成绩一般用平均数.
平均数、中位数和众数的比较
统计量 相同点 优点
缺点
求法
个数
平均数 中位数 众数
都是数 据的代 表,从 不同侧 面反映 了数据 的集中 程度
反映平均水平
易受极端值的 影响
公式
反映中等水平 不能全面反映数据 先排序 后求数
唯一 唯一
反映多数水平
有多个众数时 没多大意义
出现次数 最多
不唯一
下列几种情况一般使用什么统计量? (1)要统计同学们最喜欢的动画片,应该选取
经理
阿冲
阿冲在公司工作了一周后
我这里报酬不错, 月 平均工资2000元,你 在这里好好干!
这个公司员工 收入到底怎样?
经
阿
理
冲
第二天,阿冲上班了。
该公司员工的月薪如下:
员工 经理 副经理
月薪 6000 4000 (元)
职员A 1700
职员B 1300
职员C 职员D 职员E 职员F 职员G 1200 1100 1100 1100 500
( C)
A、平均数 B、中位数 C、众数
(2)小明七次跳远成绩如下: 3.2 3.1 3.4 3.3 1.3 3.5 3.7
你认为用( B )表示小明跳远的一般水平比较合适
A、平均数 B、中位数 C、众数
(3)五(1)有50人,五(2)班有45人,要比较两
个班的学习成绩应该选取( A )
A、平均数 B、中位数 C、众数
问题3:随着汽车的日益普及,越来越多的城市发 生了令人头疼的交通堵塞问题.你认为衡量某条交 通主干道的路况用一天中过往车辆的平均数合适 吗?为什么?
分析:人们上、下班的时候是一天中道路最繁 忙的两个时段,其他时段车流是明显减少, 因此,如果用平均数来衡量道路的拥挤程度, 则堵塞问题明显被掩盖,所以,较为合理的 是按道路繁忙的不同程度,将一天分成几个 时段分别计算车数,而主要考虑的就是上、 下班两个时段通过某点的车的平均数量及平 均速度,而不能计算整天的车的数量及平均 速度来估计道路的路况.
2.7,3.5
⑷ 32,41,23,33,42,51,71,38,31,43
没有
一组数据可以有1个众数或多个众数,也可以没有众数。
学以致用
(1)一家鞋店在一段时间内销售了某种女鞋30双,其中各 种尺码的销售量如下表所示:
鞋的尺码 (厘米)
销售量( 双)
22 22.3 23 23.5 24 24.5 25 1 2 5 11 7 3 1
平均数反映一组数据的( B); 中位数反映一组数据的( C ); 众 数反映一组数据的( A) A.多数水平 B.平均水平 C.中等水平
问题2:八年级某班级教室里,三个同学正在为 谁的数学成绩最好而争论,他们五次数学成绩 分别是:
小华:62、94、95、98、98 小明:62、62、98、99、100 小丽:40、62、85、99、99
答:这组年龄的众数是13.
请找出各组数据的众数。
序号
数据
众数
⑴
3,6,3,5,3,3,11,19,7,8,3,7, 125,40,35,40,35,20,35,35,30, 35,40,32,40,36,40,35
35
⑶
2.7,2.7,2.6,2.7,3.5,3.5,4.0, 3.5,2.7,3.5
平均数 中位数 众数
小华
89.4
95
98
小明
84.2
98
62
小丽
77
85
99
100 80 60 40 20 0 平均数
中位数 众数 最高分
平均 中位 众 数数 数
小 89.4 95 98 明
小明
小强 小 84.2 98 62 小霞 强
小 77 85 99 霞
老师点评:小明的平均分是89.4分(最高),小强的中位数是 98分(最高),但小霞的众数是99分(最高),且小明、小霞的
小知识:平均数虽然常用,但不是万能的.如果不对 具体情况做具体分析,那么得到的数据将不会有 大的指导作用.
对平均数,众数和中位数说长道短
(1)草地上有六个人在玩游戏,他们的平均年龄 是15岁,请猜想一下是怎样的年龄的六个人在 玩游戏?
(2)为筹备班级的新年晚会,班长对全班同学爱 吃的几种水果作了民意调查.最终买什么水果, 该由调查的平均数,众数还是中位数决定呢?
(3)八年级有四个班级,如果我想比较在一次测 验中四个班的成绩,应该用平均数,众数还是中 位数呢?
议
一 平均数、中位数和众数各有什么特点呢?
议
比较三个统计量:
联系:三个统计量都可代表一组数据,表示数据的“平 均水平,中等水平或多数水平”,都反映数据的集中趋势。
区别:三个统计量从不同的侧面提供了一组数据的面貌. 1、平均数:应用范围最广泛,比较可靠和稳定。它与这组数 据中的每一个数据都有关系,能够最为充分地反映这组数据所 包含的信息,在进行统计推断时有重要的作用。但容易受到极 端数据的影响。 2、中位数:在一组数据的数值排序中处于中间位置,在统计 学分析中扮演“分水岭”的角色,人们通过中位数可以对事物 大体趋势进行判断和掌控。 3、众数:着眼于各个数据出现次数多少的考察,其大小仅仅 与一组数据的部分数据有关系。它反映一组数据的集中水平。
