河南省郑州市2012-2013学年高二下学期期末考试文科数学试题(有答案)(高清扫描版)
河南省郑州市2012年-2013年高二下学期期末考试(数学文)扫描版

郑州市2012 —2013学年下期期末番试高二数学(文)试题卷注載事项;車试卷分第I卷〔选择題[和第U卷[菲选释题)闯部分.垮试时pel 120分娜•満分I甜分.弔生应首先阅渎袴題咔上的文字信总.擀后在容趣卡上你答.在试裁巻上作菩无效.空椎时只交碧題卡*•奇公式"■烛事性检捡临界值pa*>k)0. 500H00, 25a is0.100t050.025h 005,6 00110. 4550. 7C5L3232, 706 3. Ml 5.024隹635匸枕:l(k 828H (巧一壬“小-j?)工百卅一嚨y乙方程占=»辰4:•葛中M ------------------------------------- -- ----------------£ J:'nr11 欝. _______ …緘齐Q十訂〔£■+旳G+R (0+必'4.棹关指数:押=1— ------------------£<X-J)a第I卷(选择题,共60分)一、选择麵(本大融韭丘小题■辩小压5分.共棚分•在魁小聽给出的创彳选项中.貝有一项见符合題目要壊的」在第&x9U2曆中均展逸做一題、参选刚按4 t判分・)昇疑散彳、,的廉晶虚£ 1 I 1謂B* C* ―甘2 •已頼不与了之间的一组数摇:T01-1 -2§y135T則了与止的线性回归方程必过佥A. (2t2)B. <1. 5 .4)CA1.5 .0)D, (1*2)E在販烟与患餉病迖两牛井类變轨的计算中*贰列说薩疋嗚的尺扎若K z的观嗣值为自=氏鉅时夷们冇99%的把握认为吸烟与患肺病有捷亲*那么衣1( 0个陨烟的人中必有的人恿有肺材鬲二数学(文》试剧卷幫[頁< « S «)区从独立性检验可知看的把握.认为畏呷与思肺辆有关尿』扎菲帕说某人吸惆・ 那么他市gg%的可能患有脑牺「苦从竦计議中求出前95謁的把握认勾礙哪弓空怖櫛有芜痰.提摺有7,的町能性便得按判出规错课vm ()AB 等于扎zC.fi[x-=V> *(4一弟与豔數方程彳_ (?为齧数}尊价的普通方程为扎护卜耳口民护4呂MlfOGW 】』盂应2」44(4-5>不糠武匕〒31 + 1芒一岔VS 的轉劇是 A. (-rl-3^r<2) & 0C. RIX " | 疋< —3 威,arAZ)丨用反证怯讣Jtr 若门一甘r< 3.则。
河南省郑州市2012-2013学年高二下学期期末考试理科数学试题(有答案)(高清扫描版)

因为
a a 2 4a a a 2 4a 0 ,令 t ,则 t 0 , 2 2
所以当 0 x t 时 g ( x) 0 ,当 x t 时 g ( x) 0 , 即函数 g ( x) 的减区间为 (0, t ) ,增区间为 (t , ) , 又因为当 x 0, x 时均有 g ( x) , 所以 g ( x) 0 有唯一解 g (t ) 0 , 注意到 g (t ) 0 ,所以 ---------8 分
2 3
2 3
2 3
2 3
20 , 27
所以所求概率为
20 .-------4 分 27
⑵由题意可知, 的所有可能取值为 0,10, 20, 25, 40 , 用 Ai (i 1, 2,3) 表示事件“第 i 次击中目标” , 则 P ( 0) P ( X 0)
1 3
-------10 分
m 2 0 ,即 m 8 为所求. 4
18.解:⑴随机抽查这个班的一名学生,共有 50 种不同的抽查方法, 其中积极参加班级工作的学生有 18+6=24 人,即有 24 种不同的抽法, 由古典概型的计算公式可得抽到积极参加班级工作的学生的概率是 P 1
24 12 . 50 25 19 . 50
t 2 2at 2a ln t 0, 2 t at a 0,
3
1 , 27
2 2 1 2 P( 10) P( X 1) C3 (1 ) 2 , 3 3 9 2 1 2 4 , P( 20) P( A1 A2 A3 ) 3 3 3 27 8 , P( 25) P( X 2) P( 20) 27
河南省郑州市2013-2014学年高中二年级下学期期末考试数学(文)试题(扫描版)

高中二年级数学(文科)参考答案三、解答题18.(4-1)证明:由△ABC≌△BAD得∠ACB=∠BDA,故A、B、C、D四点共圆.….4分从而∠CAB=∠CDB.再由△ABC≌△BAD得∠CAB=∠DBA..….8分因此∠DBA=∠CDB,所以AB∥CD..….12分(4-4)解:直线的参数方程为33,()1,2xsy s⎧=-+⎪⎪⎨⎪=⎪⎩为参数,………………………..3分曲线1,()1x tt ty tt⎧=+⎪⎪⎨⎪=-⎪⎩为参数可以化为224x y-=.……………………6分将直线的参数方程代入上式,得263100s s-+=.……………….9分设A、B对应的参数分别为12s s,,∴121212636863,10.s s s s s s±=+==、AB 12s s =-=.…………………………..12分(4-5)(I )略 ………………. 6分(II )由条件得:()()|21||25|6,f x g x x x +=++-=121256,,215()()21256,,22521256,,2x x x f x g x x x x x x x ⎧---+=<-⎪⎪⎪∴+=+-+=-≤≤⎨⎪⎪++-=>⎪⎩15.22x x ⎧⎫∴-≤≤⎨⎬⎩⎭…………………12分 19. (Ⅰ)70,66,x y ==∑∑====5125124750,23190i ii ii xyx 36.01221=--=∑∑==ni ini iixn xyx n yx b ,8.40=a ,回归直线方程为ˆ0.3640.8.yx =+……………6分 (Ⅱ)∑==-ni i iy y10)(,所以为”优拟方程”. ………12分20. 解:分由表中数据得K 2的观测值k =42×(16×12-8×6)224×18×20×22=25255≈4.582>3.841.所以,据此统计有95%的把握认为选做“几何类”或“代数类”与性别有关. 12分 21. 解:(Ⅰ)选择(2)式,计算如下:sin 215°+cos 215°-sin15°cos15°=1-12sin30°=1-14=34. 2分(Ⅱ)三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-a )=34. 5分证明如下:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=sin 2α+(cos30°cos α+sin30°sin α)2-sin α(cos30°cos α+sin 30°sin α) =sin 2α+34cos 2α+32sin αcos α+14sin 2α-32sin αcos α-12sin 2α22333sin cos .444αα=+= 22.(4-1)解:BC AB ACB ==∠,30, 30=∠∴CAB .又因AB 是⊙O 的直径,所以 90=∠ADB , 60=∠ABD . 又因OD OB =,BD OD OB AB 222===∴,3==DC AD .所以2=AB .1===∴BD OD OB . …………………………6分30=∠ACB ,23,60==∠∴DE CDE . OD OA = , 30=∠∴ADO , 90=∠∴ODE , 371.42OE ∴=+=……12分(4-5) 解:(Ⅰ)不等式()10f x a +->即为|2|10.x a -+-> 当1a =时,解集为2x ≠,即(,2)(2,)-∞+∞;当1a >时,解集为全体实数R ;当1a <时,解集为(,1)(3,)a a -∞+-+∞ ……6分(Ⅱ)()f x 的图象恒在函数()g x 图象的上方,即为|2||3|x x m ->-++对任意实数x 恒成立,即|2||3|x x m -++>恒成立,又对任意实数x 恒有|2||3||(2)(3)|5x x x x -++--+=≥,于是得5m <, 即m 的取值围是(,5)-∞ …………… 12分。
2012学年第二学期高二文科数学期末试题及答案-(1)

试卷类型:A肇庆市中小学教学质量评估 2012—2013学年第二学期统一检测试题高二数学(文科)本试卷共4页,20小题,满分150分。
考试用时120分钟 注意事项:1. 答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名、班别、座位号、考号 填写在答题卷上密封线内相对应的位置上。
2. 选择题每小题选出答案后,用2B 铅笔把答题卷上对应题目的答案标号涂黑;如需要改动,用橡皮擦干净后,再选涂其它答案,答案不能写在试卷或草稿纸上。
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内相应的位置上;如需改动,先划掉原来的答案,然后再在答题区内写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知点P 的极坐标为)3,2(π,则点P 的直角坐标为A.(1,3)B.(1,-3)C.(3,1)D.(3,-1) 2. 计算=+2)1(iA. 2B. -2C. 2iD. -2i 3. 一物体作直线运动,其运动方程为t t t s 2)(2+-=,则t =1时其速度为A. 4B. -1C. 1D. 0 4. 若i x x x )23()1(22+++-是纯虚数,则实数x =A. -1B. 1C. -1或1D. 05. 曲线⎩⎨⎧-=+=34,12t y t x (t 为参数)与x 轴交点的直角坐标是A.(1,4)B.(1,-3)C.(1625,0)D.(1625±,0) 6. 设函数x ex f x3)(2+=(R x ∈),则)(x fA. 有最大值B. 有最小值C. 是增函数D. 是减函数 7. 用反证法证明命题“三角形的内角至少有一个不大于60︒”时,应该先A. 假设三内角都不大于60︒B. 假设三内角都大于60︒C. 假设三内角至多有一个大于60︒D. 假设三内角至多有两个大于60︒ 8. 若函数x x a x f sin cos )(+=在4π=x 处取得极值,则a 的值等于A. 3-B.3C. -1D. 1 9. 复数i i+-11与i 31-在复平面上所对应的向量分别是,,O 为原点,则这两个向量的夹角∠AOB = A. 6π B. 4π C. 3π D. 2π10. 已知数列{n a }的通项公式2)1(1+=n a n ,记)1()1)(1)(1()(321n a a a a n f ----= ,通过计算)1(f ,)2(f ,)3(f ,)4(f 的值,猜想)(n f 的值为A.2)1(12+-n n B. )1(2++n n n C. 12++n n D. )1(22++n n 二、填空题:本大题共4小题,每小题5分,共20分. 11. i 是虚数单位,则=+-21ii▲ . 12. 若直线l 经过点M (1,5),且倾斜角为32π,则直线l 的参数方程为 ▲ . 13. 圆心在)4,1(πA ,半径为1的圆的极坐标方程是 ▲ .14. 观察下列等式:1=1 2+3+4=9 3+4+5+6+7=25 4+5+6+7+8+9+10=49……照此规律,第五个等式应为 ▲ .三、解答题:本大题共6小题,共80分,解答应写出证明过程或演算步骤. 15.(本小题满分12分)某地有两所中学,为了检验两校初中毕业生的语文水平,从甲、乙两校九年级学生中各随机抽取20%的学生(即占各自九年级学生总数的20%)进行语文测验. 甲校32人,有21人及格;乙校24人,有15人及格.(1)试根据以上数据完成下列2⨯2列联表;(2)判断两所中学初中毕业生的语文水平有无显著差别?附:))()()(()(22d b c a d c b a bc ad n K++++-=.16.(本小题满分12分)某产品的广告费用支出x 与销售额y 之间有如下的对应数据:(1)求回归直线方程;(2)据此估计广告费用为10时销售收入y 的值.附:线性回归方程a x b yˆˆˆ+=中系数计算公式∑∑∑∑====-⋅-=---=ni ini ii ni ini i ix n xy x n yx x xy y x xb 1221121)())((ˆ,x b y aˆˆ-=,其中x ,y 表示样本均值.17.(本小题满分14分)已知函数x x x x f --=23)(. (1)求函数)(x f 的单调区间;(2)求曲线)(x f y =在点P (-1,f (-1))处的切线方程.18.(本小题满分14分)已知复数1z 满足:i z i 34)21(1+=+,i z z n n 221+=-+(*N n ∈). (1)求复数1z ;(2)求满足13||≤n z 的最大正整数n .19.(本小题满分14分)设数列}{n a 的前n 项和为n S ,且n n a n S -=2(*N n ∈). (1)求1a ,2a ,3a ,4a 的值; (2)猜想n a 的表达式,并加以证明.20.(本小题满分14分)已知x x a x f ln )(+=, xxx g ln )(=,(]e x ,0∈,其中e 是无理数且e …,R a ∈. (1)若a =1,求)(x f 的单调区间与极值; (2)求证:在(1)的条件下,21)()(+>x g x f ; (3)是否存在实数a ,使)(x f 的最小值是-1?若存在,求出a 的值;若不存在,说明理由.2012—2013学年第二学期统一检测题 高二数学(文科)参考答案及评分标准二、填空题11. 1-i 12. ⎪⎪⎩⎪⎪⎨⎧+=-=,235,211t y t x (t 为参数)(其它正确答案同样给分)13. )4cos(2πθρ-= (其它正确答案同样给分) 14. 5+6+7+8+9+10+11+12+13=81三、解答题 15.(本小题满分12分) 解:(2)058.020362432)1511921(56))()()(()(22≈⨯⨯⨯⨯-⨯=++++-=d c b a d b c a bc ad n k . (10分) 因为455.0058.0<≈k ,所以两所中学初中毕业生的语文水平无显著差别. (12分)16.(本小题满分12分) 解:(1)5586542=++++=x , (1分)5057050604030=++++=y , (2分)∑==⨯+⨯+⨯+⨯+⨯=511380708506605404302i ii yx , (3分)∑==++++=512145643625164i ix, (4分)5.65514550551380ˆ21221=⨯-⨯⨯-=--=∑∑==ni ini ii x n xyx n yx b, (6分) 5.1755.650ˆˆ=⨯-=-=x b y a, (8分) 所以回归直线方程为5.175.6ˆ+=x y. (9分) (2)x ⨯10+17.5=82.5. (12分)17.(本小题满分14分)解:(1)函数)(x f 的定义域为(-∞,+∞). (1分))1)(31(3123)(2-+=--='x x x x x f . (4分)当)31,(--∞∈x 时,0)(>'x f ,此时)(x f 单调递增; (5分)当)1,31(-∈x 时,0)(<'x f ,此时)(x f 单调递减; (6分) 当),1(+∞∈x 时,0)(>'x f ,此时)(x f 单调递增. (7分) 所以函数)(x f 的单调增区间为)31,(--∞与),1(+∞,单调减区间为)1,31(-. (9分) (2)因为11)1()1()1(23-=+---=-f , (10分)41)1(2)1(3)1(2=--⨯--⨯=-'f , (12分)所以所求切线方程为)1(41+=+x y ,即34+=x y . (14分) 18.(本小题满分14分)解:(1)设),(1R b a bi a z ∈+=,则bi a z -=1. (1分) 因为i bi a i 34))(21(+=-+,所以i i b a b a 34)2()2(+=-++. (3分)于是⎩⎨⎧=-=+,32,42b a b a 解得⎩⎨⎧==.1,2b a (5分)故i z +=21. (6分) (2)由i z z n n 221+=-+(*N n ∈)得:i z z 2212+=-,i z z 2223+=-,┅,i z z n n 221+=--(2≥n ) (7分)累加得i n n z z n )1(2)1(21-+-=-,i n n z n )12(2-+=(2≥n ). (9分) 因为i i z )112(1221-⨯+⨯=+=,所以i n n z n )12(2-+=(*N n ∈). (10分) 故148)12(4||222+-=-+=n n n n z n (11分)令13||≤n z ,即1691482≤+-n n ,解得5433711<+≤≤n , (13分) 因此n 的最大正整数取值是4. (14分) 19.(本小题满分14分)解:(1)因为n n a n S -=2,n n a a a S +++= 21,*N n ∈ (1分)所以,当1=n 时,有112a a -=,解得012121-==a ; (2分)当2=n 时,有22122a a a -⨯=+,解得1221223-==a ; (3分) 当3=n 时,有332132a a a a -⨯=++,解得2321247-==a ; (4分)当4=n 时,有4432142a a a a a -⨯=+++,解得34212815-==a . (5分)(2)猜想1212--=n n a (*N n ∈) (9分)由n n a n S -=2(*N n ∈),得11)1(2----=n n a n S (2≥n ), (10分) 两式相减,得12-+-=n n n a a a ,即1211+=-n n a a (2≥n ). (11分) 两边减2,得)2(2121-=--n n a a , (12分) 所以{2-n a }是以-1为首项,21为公比的等比数列,故1)21(12-⨯-=-n n a , (13分)即1212--=n n a (*N n ∈). (14分)20.(本小题满分14分) 解:(1)当a =1时,x x x f ln 1)(+=,21)(xx x f -=',(]e x ,0∈ (1分) 令01)(2=-='xx x f ,得x =1. 当)1,0(∈x 时,0)(<'x f ,此时)(x f 单调递减; (2分) 当),1(e x ∈时,0)(>'x f ,此时)(x f 单调递增. (3分) 所以)(x f 的单调递减区间为(0,1),单调递增区间为(1,e ),)(x f 的极小值为1)1(=f . (4分) (2)由(1)知)(x f 在(]e ,0上的最小值为1. (5分) 令21ln 21)()(+=+=x x x g x h ,(]e x ,0∈,所以2ln 1)(x xx h -='. (6分) 当),0(e x ∈时,0)(>'x h ,)(x h 在(]e ,0上单调递增, (7分)所以min max )(12121211)()(x f e e h x h ==+<+==. 故在(1)的条件下,21)()(+>x g x f . (8分)(3)假设存在实数a ,使x xax f ln )(+=((]e x ,0∈)有最小值-1. 因为221)(xax x x a x f -=+-=', (9分) ①当0≤a 时,0)(>'x f ,)(x f 在(]e ,0上单调递增,此时)(x f 无最小值; (10分)②当e a <<0时,当),0(a x ∈时,0)(<'x f ,故)(x f 在(0,a )单调递减;当),(e a x ∈时,0)(>'x f ,故)(x f 在(a ,e )单调递增; (11分) 所以1ln )()(min -=+==a a a a f x f ,得21ea =,满足条件; (12分) ③当e a ≥时,因为e x <<0,所以0)(<'x f ,故)(x f 在(]e ,0上单调递减.1ln )()(min -=+==e e ae f x f ,得e a 2-=(舍去); (13分) 综上,存在实数21e a =,使得)(xf 在(]e ,0上的最小值为-1. (14分)。
河南省郑州市高二下学期期末考试数学(文)试题-含答案

下期期末考试 高二数学(文)试题卷 第Ⅰ卷(选择题,共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.复数111ii-++的虚部是( ) A .i - B .1- C .1i - D .12.用反证法证明某命题时,对其结论:“自然数a ,b ,c 中恰有一个偶数”正确的反设为( ) A .a ,b ,c 都是奇数 B .a ,b ,c 都是偶数 C .a ,b ,c 中至少有两个偶数D .a ,b ,c 中至少有两个偶数或都是奇数 3.在下列说法中,真命题的个数是( )①随机误差是引起预报值与真实值之间误差的原因之一; ②残差平方和越小,预报精度越高;③用相关指数刻画回归的效果,2R 的值越接近1,说明模型的拟合效果越好;④因为由任何一组观测值都可以求得一个回归直线方程,所以没有必要进行相关性检验. A .1 B .2 C .3 D .4 4.(选修4-4:坐标系与参数方程)下列极坐标方程表示圆的是( ) A .1ρ= B .2πθ=C .sin 1ρθ=D .(sin cos )1ρθθ+=(选修4-5:不等式选讲)不等式113x <+<的解集为( ) A .(4,2)(0,2)--U B .(2,0)(2,4)-U C .(4,0)- D .(0,2)5.某地财政收入x 与支出y 满足线性回归方程y bx a e =++(单位:亿元),其中0.8b =,2a =,0.5e ≤,如果今年该地区财政收入是10亿元,年支出预计不会超过( )A .9亿元B .9.5亿元C .10亿元D .10.5亿元6.设1111333b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,则( )A .a b a a a b <<B .a a b a b a <<C .b a a a a b <<D .b a a a b a << 7.若z C ∈且221z i +-=,则22z i --的最小值是( )A .2B .3C .4D .5 8.(选修4-4:坐标系与参数方程)已知直线l :1x ty t =⎧⎨=+⎩(t 为参数),圆C :2cos ρθ=,则圆心C 到直线l 的距离是( )A .2B .3C .2D .1 (选修4-5:不等式选讲)已知01a b <<<,下面不等式中一定成立的是( ) A .log log 20a b b a ++> B .log log 20a b b a +-> C .log log 20a b b a ++≤ D .log log 20a b b a ++≥9.下面是电影《达芬奇密码》中的一个片段,女主角欲输入一个由十个数字按一定规律组成的密码,但当她果断地依次输入了前八个数字11235813,欲输入最后两个数字时她犹豫了,也许是她真的忘记了最后的两个数字、也许…….请你依据上述相关信息推测最后的两个数字最有可能的是( )A .18B .20C .21D .31 10.执行如图所示的程序框图(算法流程图),输出的n 为( )A .3B .4C .5D .6 11.(选修4-4:坐标系与参数方程)若(2,1)P -为圆O :15cos 5sin x y θθ=+⎧⎨=⎩(02)θπ≤<的弦的中点,则该弦所在直线l 的方程是( )A .30x y --=B .20x y +=C .10x y +-=D .250x y --= (选修4-5:不等式选讲)已知a ,b ,c 为三角形的三边,且222S a b c =++,P ab bc ca =++,则( )A .2P S P ≤<B .2P S P <<C .S P >D .2S P ≥ 12.已知3,()3,x a x a f x x a x a-++≥⎧=⎨-+<⎩,2()g x x =,若关于x 的不等式()()f x g x >至少有一个负数解,则实数a 的取值范围是( ) A .13(3,)4- B .13(,3)4- C .(3,3)- D .1313(,)44- 第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.某饮料店的日销售收入y (单位:百元)与当天平均气温x (单位:C o )之间有下列数据:甲、乙、丙三位同学对上述数据进行了研究,分别得到了x 与y 之间的三个线性回归方程:①$3y x =-+;②$ 2.8y x =-+;③$ 2.6y x =-+;④$ 2.8y x =+,其中正确方程的序号是 . 14.在复平面上,复数23(2)i -对应的点到原点的距离为 . 15.,a b R ∈,若112a b a b ++-+-≤,则a b +的取值范围为 .16.近几年,人工智能技术得到了迅猛发展,某公司制造了一个机器人,程序设计师设计的程序是让机器人每一秒钟前进一步或后退一步,并且以先前进3步,然后再后退2步的规律前进.如果将机器人放在数轴的原点,面向正的方向在数轴上前进(1步的距离为1个单位长度).令()P n 表示第n 秒时机器人所在位置的坐标,且记(0)0P =,则下列结论中正确的是 .(请将正确的序号填在横线上)①(3)3P =;②(5)1P =;③(2018)(2019)P P <;④(2017)(2018)P P <;⑤(2003)(2018)P P =.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.已知z 是复数,2z i +,2z i-均为实数(i 为虚数单位),且复数2()z mi +在复平面上对应的点在第一象限. (1)求复数z ;(2)求实数m 的取值范围.18.随着炎热的夏天到,在海边旅游的人们都喜欢潜水这项活动.某潜水中心调查了200名男性与200名女性下潜至距离水面5米时是否会耳鸣,如图为其等高条形图:(1)绘出22⨯列联表;(2)利用独立性检验的方法,能否在犯错误的概率不超过0.001的前提下认为性别与耳鸣有关?参考数据及公式:20()P K k ≥0.050 0.010 0.001 0k3.8416.63510.82822()()()()()n ad bc K a b c d a c b d -=++++,n a b c d =+++.19.选修4-4:坐标系与参数方程已知直线l 的参数方程为2x a t y t =-⎧⎨=⎩(t 为参数),圆C 的参数方程为4cos 4sin x y θθ=⎧⎨=⎩(θ为参数).(1)求直线l 与圆C 的普通方程;(2)若直线l 与圆C 有公共点,求实数a 的取值范围. 选修4-5:不等式选讲已知函数()21f x x =-.(1)若对任意,,()a b c R a c ∈≠,都有()a b b cf x a c-+-≤-恒成立,求x 的取值范围;(2)解不等式()3f x x ≤. 20.证明:(1)已知a ,b 为实数,且1a <,1b <,求证:1ab a b +>+;(2)已知a ,b ,c 均为实数,且1a <,1b <,1c <,求证:2abc a b c +>++.(提示:可利用第一问的结论进行证明) 21.选修4-4:坐标系与参数方程在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,圆C的极坐标方程为)4πρθ=+,直线l的参数方程为1x ty =⎧⎪⎨=-+⎪⎩t 为参数),直线l 和圆C 交于A ,B 两点,P 是圆C 上不同于A ,B 的任意一点.(1)求圆心的极坐标; (2)求PAB ∆面积的最大值. 选修4-5:不等式选讲设关于x 的不等式2324x a x x -++≥+的解集为A . (1)若1a =,求A ;(2)若A R =,求a 的取值范围.22.某公司为了确定下一年度投入某种产品的宣传费,需要了解年宣传费x (单位:万元),对年销售量y (单位:t )和年利润z (万元)的影响,为此,该公司对近7年宣传费i x 和年销售量(1,2,,7)i y i ==⋅⋅⋅的数据进行了初步处理,得到了如图所示的散点图和表中的统计量的值.xyk721()ii x x =-∑ 721()ii kk =-∑71()()iii x x y y =--∑71()()ii i kk k k =--∑17.4082.303.6140 9.7 2935.1 35.0其中ln i i k y =,7117i i k k ==∑.(1)根据散点图判断,y bx a =+与21c xy c e=哪一个更适宜作为年销售量y 关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程; (3)已知这种产品年利润z 与x ,y 的关系为 2.50.110z e y x -=-+,当年宣传费为28万元时,年销售量及年利润的预报值分别是多少?附:①对于一组具有有线性相关关系的数据(,)(1,2,3,,)i i i n μυ=⋅⋅⋅,其回归直线u υβα=+的斜率和截距的最小二乘估计分别为µ121()()()niii nii u u u u υυβ==--=-∑∑,$µau υβ=-. ②2.5e - 0.75ee3e 7e0.08 0.47 2.7220.09 1096.63。
河南省郑州市2013-学年高二下学期期末考试数学(文)试题(扫描版).pdf

高中二年级 数学 参考答案 三、解答题 18.….4分 从而∠CAB=∠CDB.再由△ABC≌△BAD得∠CAB=∠DBA..….8分 因此∠DBA=∠CDB,所以AB∥CD..….12分 (4-4)解:直线的参数方程为, ………………………..3曲线可以化为. ……………………6将直线的参数方程代入上式,得.……………….9设A、B对应的参数分别为,∴ AB=.…………………………..12………………. 6分 (II)由条件得: …………………12分 19. (Ⅰ) ,,回归直线方程为……………6分 (Ⅱ),所以为”优拟方程”. ………12分 20. 解: 几何类代数类总计男同学16622女同学81220总计241842………………..4由表中数据得K的观测值k 所以,据此统计有95的把握认为选做“几何类”或“代数类”与性别有关. 12 21. 解:选择(2)式,计算如下: sin215°+cos215°-sin15°cos15°=1-sin30°=1-=.三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-a)=.证明如下: sin2α+cos2(30°-α)-sinαcos(30°-α) =sin2α+(cos30°cosα+sin30°sinα)2-sinα(cos30°cosα+sin30°sinα) =sin2α+cos2α+sinαcosα+sin2α-sinαcosα-sin2α 22.(4-1)解:,. 又因AB是⊙O的直径,所以,. 又因,,. 所以.. …………………………6分 ,. ,,, ……12分 即为 当时,解集为,即; 当时,解集为全体实数; 当时,解集为 ……6分 (Ⅱ)的图象恒在函数图象的上方,即为对任意实数恒成立,即恒成立, 又对任意实数恒有,于是得, 即的取值范围是 …………… 12分。
2012-2013学年度第二学期高二年级调研测试数学文科试卷(含答案)

2012~2013学年度第二学期高二年级调研测试数学试题(文科)一、填空题:(本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡...相应位置上.)1.若集合{}{}{}0,,2,3,3A m B A B ===I ,则实数=m ▲. 答案:32.已知“凡是9的倍数的自然数都是3的倍数”和“自然数n 是9的倍数”,根据三段论推理规则,我们可以得到的结论是 ▲ . 答案:n 是3的倍数.3.函数0y =的定义域为 ▲ .答案:{}2,x 4x x >-≠且4.用反证法证明命题“若210x -=,则1x =-或1x =”时,假设命题的结论不成立的正确叙述是“ ▲ ”. 答案:假设x ≠-1且x ≠1.5.已知复数22(815)(918)i z m m m m =-++-+为纯虚数,则实数m 的值为 ▲ . 答案: 5.6.已知函数3(0)()(0)xx f x x x ⎧≤⎪=⎨>⎪⎩,则1()4f f ⎡⎤-⎢⎥⎣⎦= ▲ .答案: -12.7.已知集合{}3(,)1,,,(,)2,,4y A x y x R y R B x y y ax x R y R x ⎧-⎫==∈∈==+∈∈⎨⎬-⎩⎭,若A B ⋂=∅,则实数a 的值为 ▲ . 答案:148.已知方程3log 5x x =-的解所在区间为(,1)()k k k N *+ ∈,则k = ▲ . 答案: 3.9.对于大于1的自然数m 的n 次幂可用奇数进行如图所示的“分裂”,仿此,记36的“分裂”中最小的数为a ,而26的“分裂”中最大的数是b ,则a +b = ▲ . 答案:4210.在矩形ABCD 中,5AB =,2BC =,现截去一个角PCQ ∆,使P Q 、分别落在边BC CD 、上,且PCQ ∆的周长为8,设PC x =,CQ y =,则用x 表示y 的表达式为y = ▲ .答案:y=8328x x --(0<x ≤2). 11.给出下列命题:①在区间(0,)+∞上,函数1y x -=,12y x =,2(1)y x =-,3y x =中有三个是增函数;②若log 3log 30m n <<,则01m n <<<;③若函数()f x 是奇函数,则(1)f x -的图象关于点(1,0)A 对称;④函数()()21f x x x x =⋅+--有2个零点. 其中正确命题的序号..为 ▲ . 答案:③④A BCDPQ12.当(34)x ∈,时,不等式240x mx ++<恒成立,则m 的取值范围是 ▲ . 答案:m ≤-5.13.设1a >,若函数2()log ()a f x ax x =-在区间1,62⎡⎤⎢⎥⎣⎦上是增函数,则a 的取值范围是▲ . 答案: a>2.14.设不等式2(1)0x px p p +--≥对任意正整数x 都成立,则实数p 的取值范围是 ▲ .答案:≤p ≤二、解答题:本大题共6小题,共90分.(解答应写出必要的文字说明,证明过程或演算步骤)15. (本小题满分14分)设全集是实数集R ,22{|2730},{|0}A x x x B x x a =-+≤=+<,(1) 当4a =-时,求A B ; (2) 若()R A B B =r ð,求负数a 的取值范围.解:(1)1{|3}2A x x =≤≤ ………………………………………………4分 当4a =-时,{|22}B x x =-<< …………………………………………………4分{|23}A B x x =-<≤ ………………………………………………… 8分(2) 1{|}2R A x x =<或x>3r ð ………………………………………10分∵0a <,∴{|B x x =<, …………………… 12分当()R A B B =r ð时,有R B A ⊆r ð,要使R B A ⊆r ð,12≤成立, 解得104a -≤<………………14分 16.(本题满分14分)已知复数22(4sin )2(cos 1)z a i θθ=-++,其中a +∈R,),0(πθ∈,i 为虚数单位,且z 是方程2220x x ++=的一个根.(1)求θ与a 的值;(2)若w x yi =+(,x y 为实数),求满足1zw z i-≤+的点(,)x y 表示的图形的面积. 解:(1)由方程x 2+2x+2=0得x=-1±i ………………………………………2分 2(cos 1)0θ+≥∴z=-1+I ……………………………………………………………………4分又z=(a 2-42sin θ)+2(cos θ+1)i∴22a -4sin 1 2(cos 1)1θθ⎧=-⎨+=⎩ …………………………………………………………………… 6分 a ∈(0,+∞),),0(πθ∈∴θ=23π, …………………………………………………………………… 8分(2)1125z i z i i --==+-+ …………………………………………………… 10分∴1w -≤(1,0)为圆心,5为半径的圆,………………………… 12分∴面积为22(55ππ= ………………………… 14分 17.(本题满分14分)已知定义域为R 的函数2()2x x bf x a-=+是奇函数.(1)求,a b 的值;(2) 利用定义判断函数()y f x =的单调性;(3)若对任意[0,1]t ∈,不等式22(2)()0f t kt f k t ++->恒成立,求实数k 的取值范围.解: (1)1101(0)011111(1)(1)221bb a f a a b f f a a -⎧-=⎧⎪===⎧⎪⎪+∴+⎨⎨⎨=⎩⎪⎪-=-=⎩⎪++⎩得(需验证)………………4分 (其它解法酌情给分)12122(22)(21)(21)x x x x -=++(2)由(Ⅰ)知121221(),21x xf x x x R x x -=∀∈<+、,且 121212121221212(22)()()2121(21)(21)x x x x x x x x f x f x ----=-=++++则 12121212,22220,210,210x x x x x x x x <∴<∴-<+>+>1212()()0()()f x f x f x f x ∴-<∴<()y f x R ∴=在上为增函数………………9分(求导数方法酌情给分) (3)22(2)()0f t kt f k t ++->22(2)()f t kt f k t ∴+>--22()()()f x f k t f t k ∴--=-是奇函数22(2)()f t kt f t k ∴+>-()f x 为增函数2222(1)t kt t k k t t ∴∴+>-∴+>-…………10分 [][]220.111,211t t t t k k t t ∈∴+∈∴>-∴<++恒成立-222(1)1(1)11111220111111t t t t t t t t t t t -+-==+=-+=++-≥=++++++……12分 当且仅当0t =时等号成立。
2012-2013学年度第一学期期末考试试卷 高二 数学 文科(含参考答案)

2012-2013学年度第一学期期末考试试卷 高二 数学 文科(含参考答案)一、选择题(本大题共12小题,每小题5分,共60分) 1.计算机执行下面的程序段后,输出的结果是( ) A. 1,3 B. 4,1 C. 0,0 D. 6,0 2.抛物线2y ax =的焦点坐标为( ) A. 1(,0)4aB. (,0)4a C. 1(0,)4aD. (0,)4a3.设双曲线的焦点在x 轴上,两条渐近线为12y x=±,则该双曲线的离心率等于( )A. 5B.C.2D.544.在学校举行的一次歌咏比赛中,已知七位评委为某班的节目评定分数的茎叶图如右,图中左边为十位数,右边为个位数,去掉一个最高分和一个最低分,所剩数据的平均数和方差分别为( ) A. 84,4.84 B. 84,1.6 C. 85,1.6 D. 85,45.曲线34y x x =-在点(1,3)--处的切线方程是( )A. 72y x =+B. 74y x =+C. 2y x =-D. 4y x =-6.在11111(2),110(5),45(8),40这四个各种进制数中,最小的数是( )A. 11111(2)B. 110(5)C. 45(8)D. 407.为了了解某校学生的体重情况,抽取了一个样本,将所得的数据整理后,画出了频率分布直方图(如右图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的学生人数为( ) A. 46 B. 48 C. 50 D. 608.从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )A. 至少有一个黑球与都是黑球B. 至少有一个黑球与都是红球C. 至少有一个黑球与至少有一个红球D. 恰有一个黑球与恰有两个黑球9.若一动圆与圆22650x y x +++=外切,同时与圆226910x y x +--=内切,则动圆圆心的轨迹为( )A. 椭圆B. 双曲线一支C.抛物线D. 圆10.函数2()2ln f x x x =-的单调减区间是( )A. (0,1]B. [1,)+∞C. (,1]-∞-及(0,1]D. [1,0)-及(0,1]11.若椭圆221(1)xy m m+=>与双曲线221(0)xy n n-=>有相同的焦点12,F F ,P 是两曲线的一个交点,则12F P F ∆的面积是( )A. 4B. 3C. 1D. 2 12.下列命题中的假命题是( )A.“2b ac =” 是“,,a b c 成等比数列”的充要条件B. 命题“200,10x R x ∃∈+<”的否定是“2,10x R x ∀∈+≥”C. “若a b >,则22ac bc >”的否命题D. 若命题“p ⌝”和“p q ∨”均为真,则命题q 为真二、填空题(本大题共4个小题,每小题5分,共20分)13.公共汽车站每5分钟有一辆汽车通过,乘客到达汽车站的任一时刻是等可能的,则乘客候车不超过3分钟的概率是3514.周长为20cm 的矩形,绕一边旋转成一个圆柱,则圆柱体积的 最大值为100027π15.读下面程序,该程序所表示的函数是101x y x -+⎧⎪=⎨⎪+,0,0,0x x x <=>16.对于曲线22:141xyC kk +=--,给出下面四个命题:①曲线C 不可能表示椭圆;②当14k <<时,曲线C 表示椭圆;③若曲线C 表示双曲线,则1k <或4k >;④若曲线C 表示焦点在x 轴上的椭圆,则512k <<其中所有正确命题的序号为③④三。
河南省郑州市2012-2013高二上期期末数学(文科)试题(必修5+选修1-1)(含答案)(高清扫描版)

z 3x 800 2 3 y 6000 1200(2 x 3 y) 6000
1200 2 6 xy 6000 150000...........8分
高二理科数学
第 5页
共7页
当且仅当 2 x
高二理科数学
第 1页
共7页
高二理科数学
第 2页
共7页
高二理科数学
第 3页
共7页
高二理科数学
第 4页
共7页
2012—2013 学年上期期末考试
高中二年级
一、选择题 题号 答案 1 A 2 D 3 D 4 B 5 C
文科数学
6 B 7 C 8 A
参考答案
9 B 10 A 11 C 12 C
二、填空题 13. 31; 14. 45 ; 15.
f ( x) 的导数 f ( x) 1 ln x .
1 1 ;令 f ( x) 0 ,解得 0 x . e e 1 1 从而 f ( x) 在 0, 单调递减,在 ,+ 单调递增. e e
令 f ( x) 0 ,解得 x
1 1 时, f ( x ) 取得最小值 . ………………………… 6 分 e e (Ⅱ)依题意,得 f ( x) ax 1 在 [1 ) 上恒成立, ,
1 1 1 0 , x x
所以 g ( x) 的最小值是 g (1) 1 , …………………………………………12 分
故 g ( x) 是 (1 ) 上的增函数, , 所以 a 的取值范围是 (, . 1]
22.解: (Ⅰ)由题设知:2a = 4,即 a = 2, 将点 (1, ) 代入椭圆方程得 得 b2 = 3, ∴c2 = a2-b2 = 4-3 = 1 ,故椭圆方程为 x y 1 , 4 3 焦点 F1、F2 的坐标分别为(-1,0)和(1,0). 分 (Ⅱ)由(Ⅰ)知 A(2,0), B(0, 3 ) , k PQ k AB ∴PQ 所在直线方程为 y 3 ( x 1) , 2
2012下学期高二文科(含答案)

2012年下学期期末质量测试卷高二 数学(文科)一.选择题:请把正确选项填在答题栏中.(本题共8个小题,每题5分,共40分) 1. 命题“若b a >,则c b c a +>+”的逆否命题为( D )A .若b a <,则c b c a +<+.B .若b a ≤,则c b c a +≤+.3.在中,,,,则等于( D ).A. 4.已知,,,a b c m R ∈,则下列推证中正确的是( C )A.22a b am bm >⇒>B.a ba b c c>⇒> C.11,0a b ab a b >>⇒< D.2211,0a b ab a b>>⇒<5.函数3125y x x =-+在[1,3]上的最大值和最小值分别是( C )A. 6-,11-B. 6-,12-C. 4-,11-D. 4-,12-6.与双曲线2214y x -=有共同的渐近线,且过点的双曲线方程为(C )A .221312y x -= B .22128y x -= C .22128x y -= D .221312x y -= 7.已知点(2,3)-与抛物线22(0)y px p =>的焦点的距离是5,则p 的值是(B )A .2B .4C .8D .168. 已知p :函数2()1f x x m x =++有两个零点,q :x R ∀∈,244(2)10x m x +-+>.若p q ∨为真,p q ∧为假,则实数m 的取值范围为(B )A .(,2)[3,)-∞-+∞B .(,2)(1,2][3,)-∞-+∞C .(1,2][3,)+∞D .(,2)(1,2]-∞-选择题答题栏:9.在ABC ∆中,角,A B 均为锐角,且,sincos B A >则ABC ∆的形状是钝角三角形. 10.数列1234,,,,24816 的前10项和10S =_____509256____. 11.给出以下四个判断:①一个命题的逆命题为真,它的否命题也一定为真; ②在ABC ∆中,“︒=∠60B ”是“C B A ∠∠∠,,三个角成等差数列”的充要条件 ;③12x y >⎧⎨>⎩是32x y xy +>⎧⎨>⎩的充要条件; ④(1)(2)0x x ++=是2x =-的充要条件.以上说法中,判断错误..的有_③ ④_.12.给出平面区域(如图所示),若使目标函数:(0)z ax y a =+>取得最大值的最优解有无数多个,则a 的值为35.13. 函数25()(ln 2)log 5log xf x x e =-(其中e 为自然对数的底数)的导函数为1()5xf x x'=-. 14.二次方程22(1)20x a x a +++-=,有一个根比1大,另一个根比1-小,则a 的取值范围是10a -<< .15.椭圆1422=+y x 上到点(1,0)A 的距离最近的点P 的坐标是(35,34±)。
河南省郑州市2012-2013学年高二下学期期末考试理科数学试题(有答案)(word版)

河南省郑州市2012-2013学年下期期末试题高二数学(理科)第I 卷(选择题,共60分)一.选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知复数11z i=+,则z 在复平面上对应的点在A .第一象限B .第二象限C .第三象限D .第四象限2.如果随机变量2~(2,)N ξσ-,且(31)0.4P ξ-≤≤-=,则(1)P ξ≥-=A .0.7B .0.6C .0.3D .0.23.用反证法证明“若3a b c ++<,则,,a b c 中至少有一个小于1”时,“假设”应为A .假设,,a b c 至少有一个大于1B .假设,,a b c 都大于1C .假设,,a b c 至少有两个大于1D .假设,,a b c 都不小于14.下列求导正确的是A .211()'1x x x+=+B .22log (log )'ex x=C .3(3)'3log x x e =D .32(sin 2)'6sin 2x x =5.曲线2x y e =在点2(4,)e 处的切线与坐标轴所围成的三角形的面积为A .292eB .24eC .22eD .2e6.函数32()343x f x x x =+--在[0,2]上的最小值是A .173-B .103-C .4-D .1-7.甲、乙、丙三位同学独立地解决同一个问题,已知三位同学能够正确解决这个问题的概率分别为111,,234,则有人能够解决这个问题的概率为 A .1312 B .34 C .14D .1248.某同学为了解秋冬季节用电量(y 度)与气温(x ℃)的关系,曾由下表数据计算出回归直线方程为ˆ260yx =-+,现表中有一个数据被污损,则被污损的数据为 A .40 B .39C .38D .379.甲同学参加一次英语口语考试,已知在备选的10道试题中,甲能答对其中的5道题.规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才算合格.则甲合格的概率为A .512B .21 C .32 D .5610.用1,2,3三个数字组成一个四位数,规定这三个数必须都使用,且同一数字不能相邻出现,这样的四位数共有A .18个B .9个C .12个D .24个11.函数10()cos ,02x f x x x π-≤<=⎨≤≤⎪⎩与x 轴围成的封闭图形的面积为A .14π+ B .54π C .54D .1π+12.已知点P 、Q 分别为函数ln(1)1y x =-+和11x y e -=+图象上的动点,O 为坐标原点,当||PQ 最小时,直线OQ 交函数11x y e-=+的图象于点00(,)R x y (异于Q 点),则0y x = A .011x -BC .2D .3第II 卷(非选择题,共90分)二.填空题(本大题共4小题,每小题5分,共20分.)13.袋中有3个白球2个黑球共5个小球,现从袋中每次取一个小球,每个小球被抽到的可能性均相同,不放回地抽取两次,则在第一次取到白球的条件下,第二次仍取到白球的概率是 .14.已知i 为虚数单位,则232013i i i i++++= .。
郑州市2013-2014高二下期(文)word版

2013-2014学年下期期末考试 高二数学(文)试题卷参考公式:若()11,x y ,…,(),n n x y 为样本点,ˆˆˆybx a =+为回归直线,则 1111,n ni i i i x x y y n n ====∑∑ ()()()1122211ˆn niii ii i nni ii i x x y y x y nx ybx x xnx====---==--∑∑∑∑,ˆˆay bx =- ()()()()()22n ad bc K a b c d a c c d -=++++,其中n 为样本容量参考数据:一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个答案中,只有一项是符合题目要求的)1. 若复数z 满足12z i =-,则z 的虚部为( )A. 2i -B. 2iC. 2-D. 22. 经过对2K 的统计量研究,得到若干个临界值,当23.841K ≥时,我们( )A. 有95%的把握认为A 与B 有关B. 有99%的把握认为A 与B 有关C. 没有充分理由说明事件A 与B 有关D. 有97.5%的把握认为A 与B 有关3. 利用回归分析的方法研究两个具有线性相关关系的变量时,下列说法中表达错误的是( ) A. 相关系数r 满足1r ≤,并且r 越接近1,变量间的相关程度越大;r 越接近0,变量间的相关程度越小B. 可以用2R 来刻画回归效果,对于已获取的样本数据,2R 越小,模型的拟合效果越好C. 如果残差点比较均匀地落在含有x 轴的水平的带状区域内,那么选用的模型比较合适;这样的带状区域越窄,回归方程的预报精度越高D. 不能期望回归方程得到的预报值就是预报变量的精确值 4. 某车间加工零件的数量x 与加工时间y 的统计数据如下表:现已求得上表数据的回归方程ˆˆˆybx a =+中的ˆ0.9b =,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )A. 84分钟B. 94分钟C. 102分钟D. 112分钟5.(4—1)如图,在ABC ∆中,90,,ACB CD AB D ∠=︒⊥为垂足,若6,:1:2CD cm AD DB ==,则AD 的值是( )A. 6cmB.C. 18cmD.(4—4)曲线22x ty t =⎧⎨=⎩(t 为参数)的焦点坐标为( ) A. ()1,0 B. ()0,1 C. ()1,0- D. ()0,1- (4—5)不等式5310x x -++≥的解集是( )A. []5,7-B. (,4][6,)-∞-+∞C. (,5][7,)-∞-+∞D. []4,6- 6. 下面几种推理是类比推理的是( )A. 两条直线平行,同旁内角互补,如果A ∠和B ∠是两条平行直线的同旁内角,则180A B ∠+∠=︒B. 由平面三角形的性质,推测空间四边形的性质C. 某校高二年级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员D. 一切偶数都能被2整除,1002是偶数,所以1002能被2整除7. 某市质量监督局计量认证审查流程图如图所示,从右图可得在审查过程中可能不被通过审查的环节有 处 A.1 B. 2 C. 3 D. 48. 用反证法证明:“若,,a b c 都是正数,则三个数111,,a b c b c a+++中至少有一个不小于2”时,“假设”应为( )A. 假设111,,a b c b c a +++至少有一个大于2B. 假设111,,a b c b c a +++都不大于2C. 假设111,,a b c b c a +++至多有两个不小于2D. 假设111,,a b c b c a+++都小于29.(4—1)如图,AB 是O 的直径,,PB PE 分别切O 于,B C ,若40ACE ∠=︒,则P ∠=( )A. 60︒B. 70︒C. 80︒D. 90︒ (4—4)在极坐标系中,曲线()cos sin 202ρθρθθπ+=≤≤与4πθ=的交点的极坐标为( )A. ()1,1B. 1,4π⎛⎫ ⎪⎝⎭ C. 4π⎫⎪⎭ D.4π⎛⎫ ⎪⎝⎭(4—5)若不等式26ax +<的解集为()1,2-,则实数a 等于( ) A. 8 B. 2 C. 4- D. 8- 10. 12i -+是下列哪个实系数方程的一个根( )A. 2450x x -+= B. 2450x x ++= C. 2250x x -+= D. 2250x x ++=11. 如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按顺时针方向绕圆周从一个点跳到另一个点. 若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点. 该青蛙从5这个点跳起,经2014次跳后它将停在的点是( )A. 1B. 2C. 3D. 412.(4—1)正方形ABCD 的边长为3,点E 在边AB 上,点F 在边BC 上,1AE BF ==,动点P 从E 出发沿直线向F 运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,当点P 第一次碰到E 时,P 与正方形的边碰撞的次数为( )A. 8B. 6C. 4D. 3(4—4)已知曲线1C 的参数方程2cos 3sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立坐标系,曲线2C 的极坐标方程是2ρ=,正方形ABCD 的顶点都在2C 上,且,,,A B C D 依逆时针次序排列,点A 的极坐标为2,3π⎛⎫⎪⎝⎭,设P 为1C 上任意一点,则2222PA PB PC PD +++的取值范围是( )A. []12,52B. []32,52C. []12,32D. []20,32 (4—5)若存在实数x 使13x a x -+-≤成立,则实数a 的取值范围是( ) A. ()2,4- B. []2,4- C. ()2,3- D. []1,4第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分)13. 对于一组数据的两个函数模型,其残差平方和分别为153.4和200,若从中选取一个拟合程度较好的函数模型,应选残差平方和为 的那个.14. 若复数z 满足()3443i z i -=+,则z 在复平面内所对应的点到原点的距离为 . 15. ()11123f n =+++…()*1n N n +∈,计算可得()()()352,42,822f f f =>>,()163f >,()7322f >,推测当2n ≥时,有 . 16.(4—1)如图,,AB CD 是半径为a 的圆O 的两条弦,它们相交于AB 的中点P ,23aPD =,30OAP ∠=︒,则CP = .(4—4)在以O 为极点的极坐标系中,直线l 的极坐标方程是cos 20ρθ-=,直线l 与极轴相交于点M ,则以OM 为直径的圆的极坐标方程是 .(4—5)若,,x y a R +∈a 的最小值是 .三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤) 17. 已知z 是复数,2z i +与2z i-均为实数(i 为虚数单位),且复数()2z ai +在复平面上对应点在第一象限.(I )求z 的值;(II )求实数a 的取值范围.18.(4—1)如图,在四边形ABCD 中,ABC BAD ∆≅∆. 求证:||AB CD .(4—4)过点()3,0P -且倾斜角为30︒的直线和曲线11x t ty t t ⎧=+⎪⎪⎨⎪=-⎪⎩(t 为参数)相交于,A B 两点,求线段AB 的长.(4—5)已知函数()()21,25f x x g x x =+=-.(I )画出函数()()y f x g x =-的图象; (II )解方程:()()6f x g x +=19. 已知某校5个学生的数学和物理成绩如下表(I )通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系,用x 表示数学成绩,用y 表示物理成绩,求y 与x 的回归方程;(II )利用残差分析回归方程的拟合效果,若残差和在()0.1,0.1-范围内,则称回归方程为“优拟方程”,问:该回归方程是否为“优拟方程”?参考公式:残差和公式为:20. 在一次数学测验中,教师对选答题的选题情况进行了统计,如下表:(单位:人)在统计结果中,如果把《几何证明选讲》和《坐标系与参数方程》称为几何类,把《不等式选讲》称为代数类,请列出如下22⨯列联表:(单位:人)据此判断是否有95%的把握认为选做“几何类”或“代数类”的人数与性别有关?21. 某同学在一次研究性学习中发现:以下五个式子的值都等于同一个常数:(1)22sin 13cos 17sin13cos17︒+︒-︒︒; (2)22sin 15cos 15sin15cos15︒+︒-︒︒; (3)22sin 18cos 12sin18cos12︒+︒-︒︒; (4)()()22sin 18cos 48sin 18cos48-︒+︒--︒︒;(5)()()22sin 25cos 55sin 25cos55-︒+︒--︒︒.(I )试从上述五个式子中选择一个,求出这个常数;(II )根据(I )的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论. 22.(4—1)如图,已知ABC ∆中,AB BC =,以AB 为直径的O 交AC 于点D ,过D 作DE BC ⊥,垂足为E ,连接OE .若30CD ACB =∠=︒,分别求,AB OE 的长. (4—4)在直角坐标系xOy 中,以O 为极点,x 轴正半轴为极轴建立极坐标系,直线l的极坐标方程为sin 42πρθ⎛⎫+= ⎪⎝⎭,圆O的参数方程为cos 2sin x r y r θθ⎧=-+⎪⎪⎨⎪=+⎪⎩(θ为参数,0r >). (I )求圆心的极坐标;(II )当r 为何值时,圆上的点到直线l 的最大距离为3. (4—5)设函数()()2,3f x x g x x m =-=-++. (I )解关于x 的不等式()()10f x a a R +->∈;(II )若函数()f x 的图象恒在函数()g x 图象的上方,求m 的取值范围.2013—2014学年下期期末学业水平测试高中二年级 数学(文科) 参考答案一、选择题1.C 2.A 3.B 4.C 5.B 6.B 7.C 8.D 9.C 10.D 11.A 12.B 二、填空题13. 153.4; 14.1; 15121(2),(2)22nn n n f f -++>>或;16.9(41);(44)2cos ;(45)8aρθ--=-三、解答题2z i x +=),12)(5x ++18.(4-1)证明:由△ABC ≌△BAD 得∠ACB =∠BDA ,故A、B 、C 、D 四点共圆.….4分 从而∠CAB =∠CDB .再由△ABC ≌△BAD 得∠CAB =∠DBA..….8分 因此∠DBA =∠CDB ,所以AB ∥CD..….12分(4-4)解:直线的参数方程为3,()1,2x s y s ⎧=-⎪⎪⎨⎪=⎪⎩为参数, ………………………..3分曲线1,()1x t t t y t t ⎧=+⎪⎪⎨⎪=-⎪⎩为参数可以化为224x y -=. ……………………6分将直线的参数方程代入上式,得2100s -+=.……………….9分设A 、B 对应的参数分别为12s s ,,∴12121210.s s s s s s =+==、AB 12s s =-…………………………..12分(4-5)(I )略 ………………. 6分(II )由条件得:()()|21||25|6,f x g x x x +=++-=121256,,215()()21256,,22521256,,2x x x f x g x x x x x x x ⎧---+=<-⎪⎪⎪∴+=+-+=-≤≤⎨⎪⎪++-=>⎪⎩15.22x x ⎧⎫∴-≤≤⎨⎬⎩⎭…………………12分19. (Ⅰ)70,66,x y ==∑∑====5125124750,23190i i i ii x yx 36.01221=--=∑∑==ni ini ii xn xyx n yx b ,8.40=a ,回归直线方程为ˆ0.3640.8.yx =+……………6分 (Ⅱ)∑==-ni i i y y 10)(,所以为”优拟方程”. ………12分20. 解:4分由表中数据得K 2的观测值k =42×(16×12-8×6)224×18×20×22=25255≈4.582>3.841.所以,据此统计有95%的把握认为选做“几何类”或“代数类”与性别有关. 12分 21. 解:(Ⅰ)选择(2)式,计算如下:sin 215°+cos 215°-sin15°cos15°=1-12sin30°=1-14=34. 2分(Ⅱ)三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-a )=34. 5分证明如下:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=sin 2α+(cos30°cos α+sin30°sin α)2-sin α(cos30°cos α+sin30°sin α) =sin 2α+34cos 2α+32sin αcos α+14sin 2α-32sin αcos α-12sin 2α22333sin cos .444αα=+= 22.(4-1)解:BC AB ACB ==∠,30 , 30=∠∴CAB .又因AB 是⊙O 的直径,所以 90=∠ADB , 60=∠ABD . 又因OD OB =,BD OD OB AB 222===∴,3==DC AD .所以2=AB .1===∴BD OD OB . …………………………6分30=∠ACB ,23,60==∠∴DE CDE . OD OA = , 30=∠∴ADO , 90=∠∴ODE,OE ∴==……12分 (4-4) (1)圆心坐标为)22,22(--设圆心的极坐标为),(θρ,则1,ρ== 所以圆心的极坐标为5(1,).4π………………4分(2)直线l的极坐标方程为)ρθθ+= ∴直线l 的普通方程为10.x y +-= …………………8分圆上的点到直线l的距离|cos sin 1|r r d θθ-+-+-=即|sin()1|d πθ+-=∴圆上的点到直线l3.=2r = ………….12分 (4-5) 解:(Ⅰ)不等式()10f x a +->即为|2|10.x a -+-> 当1a =时,解集为2x ≠,即(,2)(2,)-∞+∞;当1a >时,解集为全体实数R ; 当1a <时,解集为(,1)(3,)a a -∞+-+∞ ……6分(Ⅱ)()f x 的图象恒在函数()g x 图象的上方,即为|2||3|x x m ->-++对任意实数x 恒成立,即|2||3|x x m -++>恒成立,又对任意实数x 恒有|2||3||(2)(3)|5x x x x -++--+=≥,于是得5m <, 即m 的取值范围是(,5)-∞ …………… 12分。
2012、2013年河南省高考文科数学试题及答案

2013年普通高等学校招生全国统一考试 文科数学注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至3页,第Ⅱ卷3至5页。
2. 答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3. 全部答案在答题卡上完成,答在本试题上无效。
4. 考试结束,将本试题和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题。
每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的一项。
(1)已知集合{1,2,3,4}A =,2{|,}B x x n n A ==∈,则A B =I ( )(A ){0} (B ){-1,,0} (C ){0,1} (D ){-1,,0,1}(2)212(1)i i +=-( ) (A )112i -- (B )112i -+ (C )112i + (D )112i -(3)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )(A )12 (B )13 (C )14 (D )16(4)已知双曲线2222:1x y C a b-=(0,0)a b >>的离心率为5,则C 的渐近线方程为( ) (A )14y x =±(B )13y x =± (C )12y x =±(D )y x =±(5)已知命题:p x R ∀∈,23xx<;命题:q x R ∃∈,321x x =-,则下列命题中为真命题的是:( ) (A )p q ∧(B )p q ⌝∧(C )p q ∧⌝ (D )p q ⌝∧⌝(6)设首项为1,公比为23的等比数列{}n a 的前n 项和为n S ,则( ) (A )21n n S a =- (B )32n n S a =- (C )43n n S a =- (D )32n n S a =-(7)执行右面的程序框图,如果输入的[1,3]t ∈-,则输出的S 属于(A )[3,4]- (B )[5,2]- (C )[4,3]- (D )[2,5]-(8)O 为坐标原点,F 为抛物线2:42C y x =的焦点,P 为C 上一点,若||42PF =,则POF ∆的面积为( ) (A )2(B )22(C )23(D )4(9)函数()(1cos )sin f x x x =-在[,]ππ-的图像大致为( )(10)已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ,223cos cos 20A A +=,7a =,6c =,则b =( )(A )10(B )9(C )8(D )5(11)某几何函数的三视图如图所示,则该几何的体积为( )(A )168π+ (B )88π+ (C )1616π+ (D )816π+(12)已知函数22,0,()ln(1),0x x x f x x x ⎧-+≤=⎨+>⎩,若|()|f x ax ≥,则a 的取值范围是( )(A )(,0]-∞ (B )(,1]-∞ (C) [2,1]- (D) [2,0]-第Ⅱ卷本卷包括必考题和选考题两个部分。
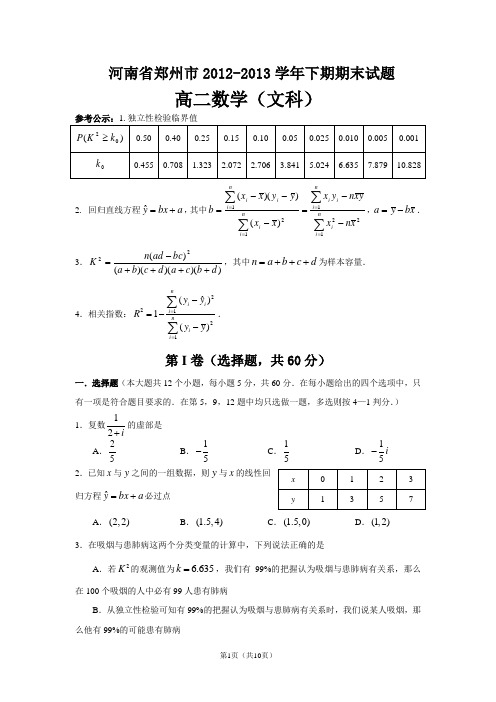
河南省郑州市2012-2013学年高二下学期期末考试文科数学试题(有答案)(word版)
河南省郑州市2012-2013学年下期期末试题高二数学(文科)2. 回归直线方程a bx y +=ˆ,其中∑∑∑∑====--=---=ni ini ii ni ini i ix n xyxn yx x xy y x xb 1221121)())((,x b y a -=.3.))()()(()(22d b c a d c b a bc ad n K ++++-=,其中d c b a n +++=为样本容量.4.相关指数:22121ˆ()1()niii nii y yR y y ==-=--∑∑.第I 卷(选择题,共60分)一.选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.在第5,9,12题中均只选做一题,多选则按4—1判分.)1.复数12i +的虚部是 A .25 B .15- C .15D .15i - 2.已知x 与y 之间的一组数据,则y 与x 的线性回归方程a bx y+=ˆ必过点A .(2,2)B .(1.5,4)C .(1.5,0)D .(1,2)3.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是A .若2K 的观测值为 6.635k =,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病B .从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病C .若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误D .以上三种说法都不正确4.某自动化仪表公司组织结构如右图,的直接领导是A .副总经理(甲)BC .总经理D .董事会5.(4—1)如图,AB 是圆O 的直径,P 是延长线上的一点,过P 作圆O 的切线,切点为C ,30PC CAB =∠= ,则圆O 的直径AB 等于A .2B .4C .6D .(4—4)与参数方程x y ⎧=⎪⎨=⎪⎩t 为参数)等价的普通方程为A .2214y x +=B .221(01,02)4y x x y +=≤≤≤≤C .221(02)4y x y +=≤≤D .221(01)4y x x +=≤≤ (4—5)不等式|3||2|5x x ++-<的解集是A .{|32}x x -≤<B .∅C . RD .{|3x x <-,或2}x >6.用反证法证明“若3a b c ++<,则,,a b c 中至少有一个小于1”时,“假设”应为A .假设,,a b c 至少有一个大于1B .假设,,a b c 都大于1C .假设,,a b c 至少有两个大于1D .假设,,a b c 都不小于17.“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是A .完全归纳推理B .演绎推理C .类比推理D .归纳推理8.某工厂的某种产品产量x (千件)与单位成本y (元)满足线性回归方程ˆ77.36y=- 1.82x ,则以下说法中正确的是。
河南省高二(下)期末数学试卷(文科)(含参考答案)

河南省高二(下)期末数学试卷(文科)一、选择题(每小题5分,共60分)1.集合A={﹣1,0,1},B={y|y=cosx,x∈A},则A∩B=()A.{0}B.{1}C.{0,1}D.{﹣1,0,1}2.下列有关选项正确的是()A.若p∨q为真命题,则p∧q为真命题是“x2﹣4x﹣5=0”的充分不必要条件B.“x=5”C.命题“若x<﹣1,则x2﹣2x﹣3>0”的否定为:“若x≥﹣1,则x2﹣3x+2≤0”D.已知命题p:?x∈R,使得x2+x﹣1<0,则?p:?x∈R,使得x2+x﹣1≥03.已知a=log32,那么log38﹣2log36用a表示是()A.5a﹣2 B.a﹣2 C.3a﹣(1+a)2D.3a﹣a2﹣14.设F(x)=f(x)+f(﹣x),x∈R,若[﹣π,﹣]是函数F(x)的单调递增区间,则一定是F(x)单调递减区间的是()A.[﹣,0]B.[,0]C.[π,π]D.[,2π]5.设y1=40.9,y2=80.48,y3=,则()A.y3>y1>y2B.y2>y1>y3C.y1>y3>y2D.y1>y2>y36.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是()A.B.C.D.7.已知函数f(x)=lnx+ln(2﹣x),则()A.f(x)在(0,2)单调递增B.f(x)在(0,2)单调递减C.y=f(x)的图象关于直线x=1对称D.y=f(x)的图象关于点(1,0)对称8.设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是()A.函数f(x)有极大值f(2)和极小值f(1)B.函数f(x)有极大值f(2)和极小值f(﹣2)C.函数f(x)有极大值f(﹣2)和极小值f(1)D.函数f(x)有极大值f(﹣2)和极小值f(2)9.函数y=2x3﹣3x2﹣12x+5在[0,3]上的最大值、最小值分别是()A.5,﹣4 B.5,﹣15 C.﹣4,﹣15 D.5,﹣1610.函数y=x2﹣lnx的单调递减区间为()A.(﹣1,1]B.(0,1]C.[1,+∞)D.(0,+∞)11.已知奇函数f(x)在R上是增函数.若a=﹣f(),b=f(log24.1),c=f(20.8),则a,b,c的大小关系为()A.a<b<c B.b<a<c C.c<b<a D.c<a<b12.函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点()A.1个 B.2个 C.3个 D.4个二、填空题(每小题5分,共20分)13.曲线y=x2+在点(1,2)处的切线方程为.14.要使函数f(x)=x2+3(a+1)x﹣2在区间(﹣∞,3]上是减函数,则实数a的取值范围.15.若曲线y=x2+ax+b在点(0,b)处的切线方程是x﹣y+1=0,则a,b的值分别为.16.y=的定义域是.三、解答题(请写出必要的文字说明和推演步骤,第17题10分,其他每题12分,共70分)17.已知A={x|﹣2≤x≤5},B={x|m+1≤x≤2m﹣1},B?A,求m的取值范围.18.求值:lg500+lg﹣lg64+50(lg2+lg5)2.19.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.(1)求y=f(x)的解析式;(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.20.求f(x)=x3﹣12x在[﹣3,5]上的最值.21.设a,b∈R,|a|≤1.已知函数f(x)=x3﹣6x2﹣3a(a﹣4)x+b,g(x)=e x f(x).(Ⅰ)求f(x)的单调区间;(Ⅱ)已知函数y=g(x)和y=e x的图象在公共点(x0,y0)处有相同的切线,求证:f(x)在x=x0处的导数等于0.22.设函数f(x)=lnx+x2+ax(1)若x=时,f(x)取得极值,求a的值;(2)若f(x)在其定义域内为增函数,求a的取值范围.河南省安阳市洹北中学高二(下)期末数学试卷(文科)参考答案与试题解析一、选择题(每小题5分,共60分)1.集合A={﹣1,0,1},B={y|y=cosx,x∈A},则A∩B=()A.{0}B.{1}C.{0,1}D.{﹣1,0,1}【考点】1E:交集及其运算.【分析】求出B={cos1,1},利用两个集合的交集的定义求得A∩B.【解答】解:∵A={﹣1,0,1},∴B={y|y=cosx,x∈A}={cos1,1},则A∩B={1 },故选B.2.下列有关选项正确的是()A.若p∨q为真命题,则p∧q为真命题B.“x=5”是“x2﹣4x﹣5=0”的充分不必要条件C.命题“若x<﹣1,则x2﹣2x﹣3>0”的否定为:“若x≥﹣1,则x2﹣3x+2≤0”D.已知命题p:?x∈R,使得x2+x﹣1<0,则?p:?x∈R,使得x2+x﹣1≥0【考点】2L:必要条件、充分条件与充要条件的判断;2J:命题的否定.【分析】本题需要逐一判断,到满足题意的选项为止,(选择题四选一);可以采用先熟悉后生疏的策略判定解答.【解答】解:由复合命题真值表知:若p∨q为真命题,则p、q至少有一个为真命题,有可能一真一假,也可能两个都真,推不出p∧q为真命题∴选项A错误;由x=5可以得到x2﹣4x﹣5=0,但由x2﹣4x﹣5=0不一定能得到x=5,∴选项B成立;选项C错在把命题的否定写成了否命题;选项D错在没有搞清楚特称命题的否定是全称命题.故选B.3.已知a=log32,那么log38﹣2log36用a表示是()A.5a﹣2 B.a﹣2 C.3a﹣(1+a)2D.3a﹣a2﹣1【考点】4H:对数的运算性质.【分析】利用对数的幂的运算法则及积的运算法则将log38﹣2log36用log32,从而用a表示.【解答】解:∵log38﹣2log36=3log32﹣2(1+log32)=log32﹣2=a﹣2故选B.4.设F(x)=f(x)+f(﹣x),x∈R,若[﹣π,﹣]是函数F(x)的单调递增区间,则一定是F(x)单调递减区间的是()A.[﹣,0]B.[,0]C.[π,π]D.[,2π]【考点】3D:函数的单调性及单调区间.【分析】根据条件先判断函数F(x)的奇偶性,结合函数奇偶性和单调性之间的关系进行求解即可.【解答】解:∵F(x)=f(x)+f(﹣x),∴F(﹣x)=f(﹣x)+f(x)=F(x),则函数F(x)是偶函数,若[﹣π,﹣]是函数F(x)的单调递增区间,则[,π]是函数F(x)的单调递递减区间,∵[,0]?[,π],∴[,0]是函数F(x)的单调递递减区间,故选:B.5.设y1=40.9,y2=80.48,y3=,则()A.y3>y1>y2B.y2>y1>y3C.y1>y3>y2D.y1>y2>y3【考点】4B:指数函数的单调性与特殊点.【分析】化简这三个数为2x的形式,再利用函数y=2x在R上是增函数,从而判断这三个数的大小关系.【解答】解:∵=21.8,=(23)0.48=21.44,=21.5,函数y=2x在R上是增函数,1.8>1.5>1.44,∴21.8>21.5>21.44,故y1>y3>y2,故选C.6.设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是()A.B.C.D.【考点】6A:函数的单调性与导数的关系.【分析】先根据导函数的图象确定导函数大于0 的范围和小于0的x的范围,进而根据当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减确定原函数的单调增减区间.【解答】解:由y=f'(x)的图象易得当x<0或x>2时,f'(x)>0,故函数y=f(x)在区间(﹣∞,0)和(2,+∞)上单调递增;当0<x<2时,f'(x)<0,故函数y=f(x)在区间(0,2)上单调递减;故选C.7.已知函数f(x)=lnx+ln(2﹣x),则()A.f(x)在(0,2)单调递增B.f(x)在(0,2)单调递减C.y=f(x)的图象关于直线x=1对称D.y=f(x)的图象关于点(1,0)对称【考点】35:函数的图象与图象变化.【分析】由已知中函数f(x)=lnx+ln(2﹣x),可得f(x)=f(2﹣x),进而可得函数图象的对称性.【解答】解:∵函数f(x)=lnx+ln(2﹣x),∴f(2﹣x)=ln(2﹣x)+lnx,即f(x)=f(2﹣x),即y=f(x)的图象关于直线x=1对称,故选:C.8.设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是()A.函数f(x)有极大值f(2)和极小值f(1)B.函数f(x)有极大值f(2)和极小值f(﹣2)C.函数f(x)有极大值f(﹣2)和极小值f(1)D.函数f(x)有极大值f(﹣2)和极小值f(2)【考点】6A:函数的单调性与导数的关系.【分析】利用函数的图象,判断导函数值为0时,左右两侧的导数的符号,即可判断极值.【解答】解:由函数的图象可知,f′(﹣2)=0,f′(2)=0,并且当x<﹣2时,f′(x)>0,当﹣2<x<1,f′(x)<0,函数f(x)有极大值f(﹣2).又当1<x<2时,f′(x)<0,当x>2时,f′(x)>0,故函数f(x)有极小值f(2).故选:D.9.函数y=2x3﹣3x2﹣12x+5在[0,3]上的最大值、最小值分别是()A.5,﹣4 B.5,﹣15 C.﹣4,﹣15 D.5,﹣16【考点】6E:利用导数求闭区间上函数的最值.【分析】对函数求导,利用导数研究函数y=2x3﹣3x2﹣12x+5在[0,3]上的单调性,判断出最大值与最小值位置,代入算出结果.【解答】解:由题设知y'=6x2﹣6x﹣12,令y'>0,解得x>2,或x<﹣1,故函数y=2x3﹣3x2﹣12x+5在[0,2]上减,在[2,3]上增,当x=0,y=5;当x=3,y=﹣4;当x=2,y=﹣15.由此得函数y=2x3﹣3x2﹣12x+5在[0,3]上的最大值和最小值分别是5,﹣15;故选B.10.函数y=x2﹣lnx的单调递减区间为()A.(﹣1,1]B.(0,1]C.[1,+∞)D.(0,+∞)【考点】6B:利用导数研究函数的单调性.【分析】由y=x2﹣lnx得y′=,由y′<0即可求得函数y=x2﹣lnx的单调递减区间.【解答】解:∵y=x2﹣lnx的定义域为(0,+∞),y′=,∴由y′≤0得:0<x≤1,∴函数y=x2﹣lnx的单调递减区间为(0,1].故选:B.11.已知奇函数f(x)在R上是增函数.若a=﹣f(),b=f(log24.1),c=f(20.8),则a,b,c的大小关系为()A.a<b<c B.b<a<c C.c<b<a D.c<a<b【考点】3N:奇偶性与单调性的综合.【分析】根据奇函数f(x)在R上是增函数,化简a、b、c,即可得出a,b,c的大小.【解答】解:奇函数f(x)在R上是增函数,∴a=﹣f()=f(log25),b=f(log24.1),c=f(20.8),又1<20.8<2<log24.1<log25,∴f(20.8)<f(log24.1)<f(log25),即c<b<a.故选:C.12.函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点()A.1个 B.2个 C.3个 D.4个【考点】6D:利用导数研究函数的极值.【分析】由图象得:导函数f′(x)=0有3个根,只有在b附近的根满足根的左边为负值,根的右边为正值,故函数只有1个极小值点.从而问题得解.【解答】解:由图象得:导函数f′(x)=0有3个根,只有在b附近的根满足根的左边为负值,根的右边为正值,故函数只有1个极小值点,故选:A.二、填空题(每小题5分,共20分)13.曲线y=x2+在点(1,2)处的切线方程为x﹣y+1=0.【考点】6H:利用导数研究曲线上某点切线方程.【分析】求出函数的导数,求出切线的斜率,利用点斜式求解切线方程即可.【解答】解:曲线y=x2+,可得y′=2x﹣,切线的斜率为:k=2﹣1=1.切线方程为:y﹣2=x﹣1,即:x﹣y+1=0.故答案为:x﹣y+1=0.14.要使函数f(x)=x2+3(a+1)x﹣2在区间(﹣∞,3]上是减函数,则实数a的取值范围(﹣∞,1] .【考点】3W:二次函数的性质.【分析】函数f(x)=x2+3(a+1)x﹣2在区间(﹣∞,3]上是减函数,即说明(﹣∞,3]是函数f(x)的减区间的子集.【解答】解:函数f(x)=x2+3(a+1)x﹣2的单调减区间为(﹣∞,﹣],又f(x)在区间(﹣∞,3]上是减函数,所以有(﹣∞,3]?(﹣∞,﹣],所以3≤﹣,解得a≤1,即实数a的取值范围为(﹣∞,1].故答案为:(﹣∞,1].15.若曲线y=x2+ax+b在点(0,b)处的切线方程是x﹣y+1=0,则a,b的值分别为1,1.【考点】6H:利用导数研究曲线上某点切线方程.【分析】求出函数的导数,求得切线的斜率,由已知切线方程,可得切线的斜率和切点,进而得到a,b的值.【解答】解:y=x2+ax+b的导数为y′=2x+a,即曲线y=x2+ax+b在点(0,b)处的切线斜率为a,由于在点(0,b)处的切线方程是x﹣y+1=0,则a=1,b=1,故答案为:1,1.16.y=的定义域是(] .【考点】33:函数的定义域及其求法.【分析】由根式内部的代数式大于等于0,然后求解对数不等式得答案.【解答】解:由,得0<3x﹣2≤1,∴,∴y=的定义域是(].故答案为:(].三、解答题(请写出必要的文字说明和推演步骤,第17题10分,其他每题12分,共70分)17.已知A={x|﹣2≤x≤5},B={x|m+1≤x≤2m﹣1},B?A,求m的取值范围.【考点】18:集合的包含关系判断及应用.【分析】解决本题的关键是要考虑集合B能否为空集,先分析满足空集的情况,再通过分类讨论的思想来解决问题.同时还要注意分类讨论结束后的总结.【解答】解:当m+1>2m﹣1,即m<2时,B=?,满足B?A,即m<2;当m+1=2m﹣1,即m=2时,B=3,满足B?A,即m=2;当m+1<2m﹣1,即m>2时,由B?A,得即2<m≤3;综上所述:m的取值范围为m≤3.18.求值:lg500+lg﹣lg64+50(lg2+lg5)2.【考点】4H:对数的运算性质.【分析】利用对数的性质和运算法则求解.【解答】解:lg500+lg﹣lg64+50(lg2+lg5)2=lg+50=2+50=52.19.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.(1)求y=f(x)的解析式;(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.【考点】6H:利用导数研究曲线上某点切线方程;62:导数的几何意义;IG:直线的一般式方程.【分析】(1)已知曲线上的点,并且知道过此点的切线方程,容易求出斜率,又知点(2,f (2))在曲线上,利用方程联立解出a,b(2)可以设P(x0,y0)为曲线上任一点,得到切线方程,再利用切线方程分别与直线x=0和直线y=x联立,得到交点坐标,接着利用三角形面积公式即可.【解答】解析:(1)方程7x﹣4y﹣12=0可化为,当x=2时,,又,于是,解得,故.(2)设P(x0,y0)为曲线上任一点,由知曲线在点P(x0,y0)处的切线方程为,即令x=0,得,从而得切线与直线x=0的交点坐标为;令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0);所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为.故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.20.求f(x)=x3﹣12x在[﹣3,5]上的最值.【考点】6E:利用导数求闭区间上函数的最值.【分析】求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可.【解答】解:函数f(x)定义域为R,f′(x)=3(x+2)(x﹣2),令f′(x)=0,得x=±2,当x>2或x<﹣2时,f′(x)>0,∴函数在(﹣∞,﹣2)和(2,+∞)上是增函数;当﹣2<x<2时,f′(x)<0,∴函数在(﹣2,2)上是减函数.∴当x=﹣2时,函数有极大值f(﹣2)=16,当x=2时,函数有极小值f(2)=﹣16,f(﹣3)=9 f(5)=65,因此函数的最大值是f(5)=65,最小值是f(2)=﹣16.21.设a,b∈R,|a|≤1.已知函数f(x)=x3﹣6x2﹣3a(a﹣4)x+b,g(x)=e x f(x).(Ⅰ)求f(x)的单调区间;(Ⅱ)已知函数y=g(x)和y=e x的图象在公共点(x0,y0)处有相同的切线,求证:f(x)在x=x0处的导数等于0.【考点】6H:利用导数研究曲线上某点切线方程.【分析】(Ⅰ)求出函数f(x)的导函数,得到导函数的零点,由导函数的零点对定义域分段,列表后可得f(x)的单调区间;(Ⅱ)求出g(x)的导函数,由题意知,求解可得,得到f(x)在x=x0处的导数等于0.【解答】(Ⅰ)解:由f(x)=x3﹣6x2﹣3a(a﹣4)x+b,可得f'(x)=3x2﹣12x﹣3a(a﹣4)=3(x﹣a)(x﹣(4﹣a)),令f'(x)=0,解得x=a,或x=4﹣a.由|a|≤1,得a<4﹣a.当x变化时,f'(x),f(x)的变化情况如下表:x(﹣∞,a)(a,4﹣a)(4﹣a,+∞)f'(x)+﹣+f(x)↗↘↗∴f(x)的单调递增区间为(﹣∞,a),(4﹣a,+∞),单调递减区间为(a,4﹣a);(Ⅱ)证明:∵g'(x)=e x(f(x)+f'(x)),由题意意知,即求解可得,∴f(x)在x=x0处的导数等于0.22.设函数f(x)=lnx+x2+ax(1)若x=时,f(x)取得极值,求a的值;(2)若f(x)在其定义域内为增函数,求a的取值范围.【考点】6D:利用导数研究函数的极值;6B:利用导数研究函数的单调性.【分析】(1)先求函数的导函数,根据若时,f(x)取得极值得f′()=0,解之即可;(2)f(x)在其定义域内为增函数可转化成只需在(0,+∞)内有2x2+ax+1≥0恒成立,建立不等关系,解之即可;【解答】解:,(1)因为时,f(x)取得极值,所以,即2+1+a=0,故a=﹣3.(2)f(x)的定义域为(0,+∞).方程2x2+ax+1=0的判别式△=a2﹣8,①当△≤0,即时,2x2+ax+1≥0,f'(x)≥0在(0,+∞)内恒成立,此时f(x)为增函数.②当△>0,即或时,要使f(x)在定义域(0,+∞)内为增函数,只需在(0,+∞)内有2x2+ax+1≥0即可,设h(x)=2x2+ax+1,由得a>0,所以.由①②可知,若f(x)在其定义域内为增函数,a的取值范围是.。
2012下.高二文科

2012年下学期期终考试试卷高二文科数学一、选择题:本大题共8小题,每小题5分,共40分. 1. 椭圆123222=+y x 的两焦点之间的距离为A .210B 10C .22D 22.等差数列{}n a :1,4,7,……中,当298m a =时,序号m 等于A .99B .100C .96D .101 3. 如果命题“p q ∨”为假命题,则A .,p q 均为假命题B .,p q 中至少有一个真命题C .,p q 均为真命题D .,p q 中只有一个真命题4. 在同一坐标系中,方程22221x y a b+=与20ax by += (a >b > 0 )的曲线大致是5. 不等式23100x x --≥的解集是A . (,2][5,)-∞-+∞UB . [2,5]-C . (,)-∞+∞D . φ 6.函数()y f x =在定义域3(,3)2-内可导,其图像如图所示.记()y f x =的导函数为 ()y f x '=,则不等式()0f x '≤的解集为A .1[,1][2,3)3-UB .148[1,][,]233-UC .31[,][1,2)22-UD .31148(,][,][,3)23233--U U7. 对变量,x y 有观测数据(,)(1,2,i i x y i =…,10),得散点图(1)所示.对变量,u v 有观测数据(,)(1,2i i u v i =,…,10),得散点图(2).由这两个散点图可以判断A. 变量x 与y 正相关, u 与v 正相关 B . 变量x 与y 正相关, u 与v 负相关 C . 变量x 与y 负相关, u 与v 正相关 D . 变量x 与y 负相关, u 与v 负相关 8.某人从2009年起,每年1月1日到银行新存入a 元(一年定期),若年利率为r 保持不变,且每年到期存款和利息自动转为新的一年定期,到2012年底将所有存款及利息全部取回,则可取回的钱数(元)为A .5[(1)(1)]ar r r+-+ B .4[(1)(1)]a r r r+-+ C .6(1)a r +D .5(1)a r +二、填空题: 本大题共7小题,每小题5分,共35分. 9. 计算:21ii=- . 10. 全称命题:1,2>∈∀x R x 的否定是 . 11.当函数14y x x=+(x >0)取最小值时相应的x 的值等于 12.若抛物线x y 42=上一点),(00y x P 到其焦点F 的距离等于4,则=0x13. 当点00(,)x y 在直线0x y +=上运动时,0022xyS =+的最小值是 14.在数列{}n a 中, 1121,2nn na a a a +==+,通过计算234,,a a a 的值,可猜想出这个数列的通项公式为n a =15. 如图(3),若射线,PM PN 上分别存在点,A B '与,B A ',则三角形面积之比PBPA B P A P S S PAB B A P ⋅'⋅'=∆''∆,如图(4)若不在同一平面内的射线,PD PE 和PF 上分别存在点,,A B '点,C C '和点,B A ',则三棱锥体积之比=-'''-ABCP C B A P V V三、解答题: 本大题共6小题,满分75分. 16. (本题满分12分)某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视(1) 由表中数据直观分析,收看新闻节目的观众是否与年龄有关?(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应抽取几名? 17. (本题满分12分)设{}n a 是公差2d =的等差数列,{}n b 是各项都为正数的等比数列,且11b =,7,233254=+=+b a b a .(1)求数列{}n a 和{}n b 的通项公式;(2)设31(1,2,3,n n C b n -==…),求数列}{n C 的前n 项和n S .18. (本题满分12分) (本题满分12分)某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台.已知生产这些家电产品每台所需问每周生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少千元?19. (本题满分13分)一艘轮船在航行中每小时的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时8元,而其他与速度无关的费用是每小时128元.(1)求轮船航行一小时的总费用W 与它的航行速度x (公里/小时)的函数关系式; (2)问此轮船以多大的速度航行时,能使每公里的总费用最少?20. (本题满分13分)已知椭圆2222:1x y C a b+=的左焦点1F 的坐标为(, 2F 是它的右焦点,点M 是椭圆C 上一点, 12MF F ∆的周长等于4+ (1)求椭圆C 的方程;(2)过定点(0,2)P 作直线l 与椭圆C 交于不同的两点,A B ,且OA OB ⊥(其中O 为坐标原点),求直线l 的方程.21. (本题满分13分)设函数d cx bx ax x f +++=23)((,,,)a b c d R ∈满足:R x ∈∀都有0)()(=-+x f x f ,且1x =时,)(x f 取极小值.32- (1))(x f 的解析式;(2)当]1,1[-∈x 时,证明:函数图象上任意两点处的切线不可能互相垂直;(3)设()()F x xf x =, 当(x ∈时,求函数()F x 的最小值,并指出当()F x 取最小值时相应的x 值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学(文科)
参考答案
二、填空题 13. 1 ;
2
14. i ;
2 2
( 15. 3 R ) =4 R ;16.(4-1)4;
3 2
2
4
(4-4) 6 cos 7 sin 8 ;
(4-5)4.
三、解答题(本大题共 6 小题,共 70 分,解答应写出文字说明、证明过程或演算步骤.) 17.(10 分) 解:⑴由题意
y , x y 0 ,上式也成立.
综上知,原不等式成立.…………12 分 本题可用综合法,分析法,等方法. 19. 解:⑴随机抽查这个班的一名学生,共有 50 种不同的抽查方法, 其中积极参加班级工作的学生有 18+6=24 人,即有 24 种不同的抽法, 由古典概型的计算公式可得抽到积极参加班级工作的学生的概率是 P 1 同理可得,抽到不太主动参加班级工作且学习积极性一般的概率是
x y ) xy ( x y ) xy , y x
即 x x y y x y y x ,整理得 当 x y 0 时, x y ,则 x 当 x y 0 时, x y ,则 x
x y
x y 0 .…………4 分
y , x y 0 ,所以上式成立;
2 1, an 1 ;…………8 分 n ..…………12 分
21. 解:(1)由数据求得, x =12, y =27,…………3 分
高二文科数学
第 8页
共 10 页
5 ^ 由公式求得: b = , a = y -b x =-3. …………8 分 2
5 所以 y 关于 x 的线性回归方程为 y = x-3. …………9 分 2
^ 5 (2)当 x=10 时,y= ×10-3=22,|22-23|<2; 2 ^ 5 当 x=8 时,y= ×8-3=17,|17-16|<2. 2 所以该研究所得到的线性回归方程是可靠的.…………12 分 22.(4-1) (Ⅰ)证明: AB 为直径, ACB
∴圆 C 的圆心坐标为(1,0), …………………6 分 ∵圆 C 经过点 P
2,
, 4
∴圆 C 的半径为 PC
2
2
12 2 1 2 cos
4
=1 , …………………9 分
∴圆 C 经过极点.∴圆 C 的极坐标方程为 =2cos . …………………12 分 (4-5) 证 : 因为 x, y 皆为正数, 所以原不等式等价于 (
…………………10 分
5 ∴BC=2x=15,AB=AC= x=12.5, 3 ∴△ABC 的周长为 40cm. …………………12 分
3 (4-4)解∵圆 C 圆心为直线 sin 与极轴的交点, 3 2
高二文科数学 第 7页 共 10 页
3 ∴在 sin 中令 =0 ,得 1 , …………………3 分 3 2
2
, CAB ABC
2
,
P C
PAC ABC PAC CAB
2
.
PA AB, AB 为直径, PA 为圆的切线.………… 4 分
(Ⅱ) CE 6k , ED 5k , , AE 2m, EB 3m ,
A E
.
O
B
AE EB CE ED m 5k , BD 3m D BD 4 5 . AEC ∽ DEB 8 6k BC 2 25m 2 64 3k 2 5 . ( ) 2 m 2, k CEB ∽ AED 2 2 m 5 AD 25m 80 BD 4 5 2 5 . AB 10, BD 4 5 在直角三角形 ADB 中 sin BAD AB 10 5
高二文科数学
第 1页
共 10 页
高二文科数学
第 2页
共 10 页
高二文科数学
第 3页
共 10 页
高二文科数学
第 4页
共 10 页
高二文科数学
第 5页
共 10 页
高二文科数学
第 6页
共 10 页
2012—2013 学年度下学期期末考试 高中二年级
一、选择题 1---12 BBCBB DDAAD CC
BCE BAD sin BCE
m 2 0 ,即 m 8 为所求. 4
18.(本题满分 12 分) (4-1)(1)证明:在△ADC 和△BEC 中, ∵∠ADC=∠BEC=90°,∠C=∠C,∴△ADC∽△BEC, ∴
AC AD 5 . BC BE 6
∵AD 是等腰三角形 ABC 底边 BC 的高线, ∴BC=2BD,又 AB=AC, ∴
12 , 25
P2
2
19 . 50
-----4 分
50 (18 19 6 7) 2 11.538 ,------8 分 ⑵由 K 统计量的计算公式得: K 24 26 25 25
2
由于 11.538 10.828 , 所以有 99.9%的把握认为“学生的学习积极性与对待班级工作的 态度有关系”. --------12 分 20. (1) a1 1, a 2 (2) a n (3) S n
a 2 a 3b 0,
a 2 0, 所以 z 2 2i 为所求.
⑵由⑴得 z 所以
解之得
a 2, b 2,
-------5 分
m m m(1 i) 2 2i 2 2i R , z 2 2i 4
-------10 分
AC AB 5 AB 5 , . BC 2BD 6 BD 3
…………………6 分
5 (2)设 BD=x,则 AB= x, 3 在 Rt△ABD 中,∠ADB=90°, 2 2 2 根据勾股定理,得 AB =BD +AD , 5 2 2 2 ∴3x =x +10 ,解得 x=7.5.
