立体几何_文科大题求体积
专题12:文科立体几何高考真题大题(全国卷)赏析(解析版)

专题12:文科立体几何高考真题大题(全国卷)赏析(解析版) 题型一:求体积1,2018年全国卷Ⅲ文数高考试题如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点. (1)证明:平面AMD ⊥平面BMC ;(2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由.【答案】(1)证明见解析 (2)存在,理由见解析 【详解】分析:(1)先证AD CM ⊥,再证CM MD ⊥,进而完成证明. (2)判断出P 为AM 中点,,证明MC ∥OP ,然后进行证明即可. 详解:(1)由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM . 因为M 为CD 上异于C ,D 的点,且DC 为直径,所以DM ⊥CM . 又BC ∩CM =C ,所以DM ⊥平面BMC . 而DM ⊂平面AMD ,故平面AMD ⊥平面BMC . (2)当P 为AM 的中点时,MC ∥平面PBD .证明如下:连结AC 交BD 于O .因为ABCD 为矩形,所以O 为AC 中点. 连结OP ,因为P 为AM 中点,所以MC ∥OP .MC ⊄平面PBD ,OP ⊂平面PBD ,所以MC ∥平面PBD .点睛:本题主要考查面面垂直的证明,利用线线垂直得到线面垂直,再得到面面垂直,第二问先断出P 为AM 中点,然后作辅助线,由线线平行得到线面平行,考查学生空间想象能力,属于中档题.2,2018年全国普通高等学校招生统一考试文科数学(新课标I 卷)如图,在平行四边形ABCM 中,3AB AC ==,90ACM ∠=︒,以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB DA ⊥. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.【答案】(1)见解析. (2)1. 【解析】分析:(1)首先根据题的条件,可以得到BAC ∠=90,即BA AC ⊥,再结合已知条件BA ⊥AD ,利用线面垂直的判定定理证得AB ⊥平面ACD ,又因为AB ⊂平面ABC ,根据面面垂直的判定定理,证得平面ACD ⊥平面ABC ;(2)根据已知条件,求得相关的线段的长度,根据第一问的相关垂直的条件,求得三棱锥的高,之后借助于三棱锥的体积公式求得三棱锥的体积. 详解:(1)由已知可得,BAC ∠=90°,BA AC ⊥.又BA ⊥AD ,且AC AD A =,所以AB ⊥平面ACD .又AB ⊂平面ABC ,所以平面ACD ⊥平面ABC .(2)由已知可得,DC =CM =AB =3,DA =32.又23BP DQ DA ==,所以22BP =. 作QE ⊥AC ,垂足为E ,则QE = 13DC .由已知及(1)可得DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE =1. 因此,三棱锥Q ABP -的体积为1111322sin451332Q ABP ABPV QE S-=⨯⨯=⨯⨯⨯⨯︒=. 点睛:该题考查的是有关立体几何的问题,涉及到的知识点有面面垂直的判定以及三棱锥的体积的求解,在解题的过程中,需要清楚题中的有关垂直的直线的位置,结合线面垂直的判定定理证得线面垂直,之后应用面面垂直的判定定理证得面面垂直,需要明确线线垂直、线面垂直和面面垂直的关系,在求三棱锥的体积的时候,注意应用体积公式求解即可. 3.2019年全国统一高考数学试卷(文科)(新课标Ⅱ)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积. 【答案】(1)见详解;(2)18 【分析】(1)先由长方体得,11B C ⊥平面11AA B B ,得到11B C BE ⊥,再由1BE EC ⊥,根据线面垂直的判定定理,即可证明结论成立;(2)先设长方体侧棱长为2a ,根据题中条件求出3a =;再取1BB 中点F ,连结EF ,证明EF ⊥平面11BB C C ,根据四棱锥的体积公式,即可求出结果. 【详解】(1)因为在长方体1111ABCD A B C D -中,11B C ⊥平面11AA B B ;BE ⊂平面11AA B B ,所以11B C BE ⊥,又1BE EC ⊥,1111B C EC C ⋂=,且1EC ⊂平面11EB C ,11B C ⊂平面11EB C ,所以BE ⊥平面11EB C ;(2)设长方体侧棱长为2a ,则1AE A E a ==,由(1)可得1EB BE ⊥;所以22211EB BE BB +=,即2212BE BB =, 又3AB =,所以222122AE AB BB +=,即222184a a +=,解得3a =;取1BB 中点F ,连结EF ,因为1AE A E =,则EF AB ∥; 所以EF ⊥平面11BB C C , 所以四棱锥11E BB C C -的体积为1111111136318333E BB C C BB C C V S EF BC BB EF -=⋅=⋅⋅⋅=⨯⨯⨯=矩形.【点睛】本题主要考查线面垂直的判定,依据四棱锥的体积,熟记线面垂直的判定定理,以及四棱锥的体积公式即可,属于基础题型.4.2017年全国普通高等学校招生统一考试文科数学(新课标2卷) 四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,01,90.2AB BC AD BAD ABC ==∠=∠= (1)证明:直线//BC 平面PAD ;(2)若△PCD 面积为27,求四棱锥P ABCD -的体积.【答案】(Ⅰ)见解析(Ⅱ)43【分析】试题分析:证明线面平有两种思路,一是寻求线线平行,二是寻求面面平行;取AD 中点M ,由于平面PAD 为等边三角形,则PM AD ⊥,利用面面垂直的性质定理可推出PM ⊥底面ABCD ,设BC x =,表示相关的长度,利用PCD ∆的面积为27.试题解析:(1)在平面内,因为,所以又平面平面故平面(2)取的中点,连接由及得四边形为正方形,则.因为侧面为等边三角形且垂直于底面,平面平面,所以底面因为底面,所以,设,则,取的中点,连接,则,所以,因为的面积为,所以,解得(舍去),于是所以四棱锥的体积【详解】题型二:求距离5.2018年全国普通高等学校招生统一考试文数(全国卷II )如图,在三棱锥P ABC -中,22AB BC ==,4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.【答案】(1)详见解析(245【解析】分析:(1)连接OB ,欲证PO ⊥平面ABC ,只需证明,PO AC PO OB ⊥⊥即可;(2)过点C 作CH OM ⊥,垂足为M ,只需论证CH 的长即为所求,再利用平面几何知识求解即可.详解:(1)因为AP =CP =AC =4,O 为AC 的中点,所以OP ⊥AC ,且OP =3 连结OB .因为AB =BC 2AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2. 由222OP OB PB +=知,OP ⊥OB . 由OP ⊥OB ,OP ⊥AC 知PO ⊥平面ABC .(2)作CH⊥OM,垂足为H.又由(1)可得OP⊥CH,所以CH⊥平面POM.故CH的长为点C到平面POM的距离.由题设可知OC=12AC=2,CM=23BC=423,∠ACB=45°.所以OM=25,CH=sinOC MC ACBOM⋅⋅∠=45.所以点C到平面POM的距离为45.点睛:立体几何解答题在高考中难度低于解析几何,属于易得分题,第一问多以线面的证明为主,解题的核心是能将问题转化为线线关系的证明;本题第二问可以通过作出点到平面的距离线段求解,也可利用等体积法解决.6.2014年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)如图,三棱柱中,侧面为菱形,的中点为,且平面.(1)证明:(2)若,求三棱柱的高.【答案】(1)详见解析;(2)三棱柱111ABC A B C -的高为21. 【解析】试题分析:(1)根据题意欲证明线线垂直通常可转化为证明线面垂直,又由题中四边形是菱形,故可想到连结1BC ,则O 为1B C 与1BC 的交点,又因为侧面11BB C C 为菱形,对角线相互垂直11B C BC ⊥;又AO ⊥平面11BB C C ,所以1B C AO ⊥,根据线面垂直的判定定理可得:1B C ⊥平面ABO ,结合线面垂直的性质:由于AB ⊂平面ABO ,故1B C AB ⊥;(2)要求三菱柱的高,根据题中已知条件可转化为先求点O 到平面ABC 的距离,即:作OD BC ⊥,垂足为D ,连结AD ,作OH AD ⊥,垂足为H ,则由线面垂直的判定定理可得OH ⊥平面ABC ,再根据三角形面积相等:OH AD OD OA ⋅=⋅,可求出OH 的长度,最后由三棱柱111ABC A B C -的高为此距离的两倍即可确定出高. 试题解析:(1)连结1BC ,则O 为1B C 与1BC 的交点. 因为侧面11BB C C 为菱形,所以11B C BC ⊥. 又AO ⊥平面11BB C C ,所以1B C AO ⊥, 故1B C ⊥平面ABO.由于AB ⊂平面ABO ,故1B C AB ⊥.(2)作OD BC ⊥,垂足为D ,连结AD ,作OH AD ⊥,垂足为H. 由于,BC OD ⊥,故BC ⊥平面AOD ,所以OH BC ⊥, 又OH AD ⊥,所以OH ⊥平面ABC.因为0160CBB ∠=,所以1CBB ∆为等边三角形,又1BC =,可得3OD. 由于1AC AB ⊥,所以11122OA B C ==,由OH AD OD OA ⋅=⋅,且2274AD OD OA =+=,得2114OH , 又O 为1B C 的中点,所以点1B 到平面ABC 的距离为217. 故三棱柱111ABC A B C -的高为217. 考点:1.线线,线面垂直的转化;2.点到面的距离;3.等面积法的应用 7.2014年全国普通高等学校招生统一考试文科数学(全国Ⅱ卷)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥面ABCD ,E 为PD 的中点. (1)证明://PB 平面AEC ; (2)设1AP =,3AD =,三棱锥P ABD -的体积 34V =,求A 到平面PBC 的距离.【答案】(1)证明见解析 (2) A 到平面PBC 的距离为31313【详解】试题分析:(1)连结BD 、AC 相交于O ,连结OE ,则PB ∥OE ,由此能证明PB ∥平面ACE .(2)以A 为原点,AB 为x 轴,AD 为y 轴,AP 为z 轴,建立空间直角坐标系,利用向量法能求出A 到平面PBD 的距离试题解析:(1)设BD 交AC 于点O ,连结EO . 因为ABCD 为矩形,所以O 为BD 的中点. 又E 为PD 的中点,所以EO ∥PB 又EO平面AEC ,PB平面AEC所以PB ∥平面AEC . (2)136V PA AB AD AB =⋅⋅=由,可得. 作交于. 由题设易知,所以故, 又31313PA AB AH PB ⋅==所以到平面的距离为法2:等体积法136V PA AB AD AB =⋅⋅= 由,可得.由题设易知,得BC假设到平面的距离为d ,又因为PB=所以又因为(或),,所以考点 :线面平行的判定及点到面的距离8.2019年全国统一高考数学试卷(文科)(新课标Ⅰ)如图,直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ;(2)求点C 到平面C 1DE 的距离.【答案】(1)见解析;(2)41717. 【分析】(1)利用三角形中位线和11//A D B C 可证得//ME ND ,证得四边形MNDE 为平行四边形,进而证得//MN DE ,根据线面平行判定定理可证得结论;(2)根据题意求得三棱锥1C CDE -的体积,再求出1C DE ∆的面积,利用11C CDE C C DE V V --=求得点C 到平面1C DE 的距离,得到结果.【详解】(1)连接ME ,1B CM ,E 分别为1BB ,BC 中点 ME ∴为1B BC ∆的中位线1//ME B C ∴且112ME B C = 又N 为1A D 中点,且11//A D B C 1//ND B C ∴且112ND B C = //ME ND ∴ ∴四边形MNDE 为平行四边形//MN DE ∴,又MN ⊄平面1C DE ,DE ⊂平面1C DE//MN ∴平面1C DE(2)在菱形ABCD 中,E 为BC 中点,所以DE BC ⊥, 根据题意有3DE =,117C E =,因为棱柱为直棱柱,所以有DE ⊥平面11BCC B ,所以1DE EC ⊥,所以113172DEC S ∆=⨯⨯, 设点C 到平面1C DE 的距离为d ,根据题意有11C CDE C C DE V V --=,则有11113171343232d ⨯⨯⨯⨯=⨯⨯⨯⨯, 解得41717d ==, 所以点C 到平面1C DE 的距离为417. 【点睛】该题考查的是有关立体几何的问题,涉及到的知识点有线面平行的判定,点到平面的距离的求解,在解题的过程中,注意要熟记线面平行的判定定理的内容,注意平行线的寻找思路,再者就是利用等积法求点到平面的距离是文科生常考的内容.题型三:求面积9.2017年全国普通高等学校招生统一考试文科数学(新课标1卷)如图,在四棱锥P ABCD -中,AB CD ∥,且90BAP CDP ∠=∠=︒.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=︒,且四棱锥P ABCD -的体积为83,求该四棱锥的侧面积.【答案】(1)证明见解析;(2)623+.【详解】 试题分析:(1)由90BAP CDP ∠=∠=︒,得AB AP ⊥,CD PD ⊥.从而得AB PD ⊥,进而而AB ⊥平面PAD ,由面面垂直的判定定理可得平面PAB ⊥平面PAD ;(2)设PA PD AB DC a ====,取AD 中点O ,连结PO ,则PO ⊥底面ABCD ,且22,AD a PO a ==,由四棱锥P ABCD -的体积为83,求出2a =,由此能求出该四棱锥的侧面积.试题解析:(1)由已知90BAP CDP ∠=∠=︒,得AB AP ⊥,CD PD ⊥.由于AB CD ∥,故AB PD ⊥,从而AB ⊥平面PAD .又AB 平面PAB ,所以平面PAB ⊥平面PAD .(2)在平面PAD 内作PE AD ⊥,垂足为E .由(1)知,AB ⊥面PAD ,故AB PE ⊥,可得PE ⊥平面ABCD .设AB x =,则由已知可得2AD x =,22PE x =. 故四棱锥P ABCD -的体积31133P ABCD V AB AD PE x -=⋅⋅=. 由题设得31833x =,故2x =. 从而2PA PD ==,22AD BC ==22PB PC ==.可得四棱锥P ABCD -的侧面积为111222PA PD PA AB PD DC ⋅+⋅+⋅ 21sin606232BC +︒=+10.2015年全国普通高等学校招生统一考试文科数学(新课标Ⅰ)如图四边形ABCD 为菱形,G 为AC 与BD 交点,BE ABCD ⊥平面,(I )证明:平面AEC ⊥平面BED ;(II )若120ABC ∠=,,AE EC ⊥ 三棱锥E ACD -的体积为6,求该三棱锥的侧面积.【答案】(1)见解析(2)5【分析】(1)由四边形ABCD 为菱形知AC ⊥BD ,由BE ⊥平面ABCD 知AC ⊥BE ,由线面垂直判定定理知AC ⊥平面BED ,由面面垂直的判定定理知平面AEC ⊥平面BED ;(2)设AB =x ,通过解直角三角形将AG 、GC 、GB 、GD 用x 表示出来,在Rt ∆AEC 中,用x 表示EG ,在Rt ∆EBG 中,用x 表示EB ,根据条件三棱锥E ACD -6求出x ,即可求出三棱锥E ACD -的侧面积.【详解】(1)因为四边形ABCD 为菱形,所以AC ⊥BD ,因为BE ⊥平面ABCD ,所以AC ⊥BE ,故AC ⊥平面BED .又AC ⊂平面AEC ,所以平面AEC ⊥平面BED(2)设AB =x ,在菱形ABCD 中,由 ∠ABC =120°,可得AG =GC =32x ,GB =GD =2x .因为AE ⊥EC ,所以在 Rt ∆AEC 中,可得EG =3x . 连接EG ,由BE ⊥平面ABCD ,知 ∆EBG 为直角三角形,可得BE =22x .由已知得,三棱锥E -ACD 的体积3116632243E ACD V AC GD BE x -=⨯⋅⋅==.故 x =2 从而可得AE =EC =ED 6.所以∆EAC 的面积为3, ∆EAD 的面积与∆ECD 的面积均为 5故三棱锥E -ACD 的侧面积为3+25【点睛】本题考查线面垂直的判定与性质;面面垂直的判定;三棱锥的体积与表面积的计算;逻辑推理能力;运算求解能力.11.2019年全国统一高考数学试卷(文科)(新课标Ⅲ)图1是由矩形,ADEB Rt ABC ∆和菱形BFGC 组成的一个平面图形,其中1,2AB BE BF ===, 60FBC ∠=,将其沿,AB BC 折起使得BE 与BF 重合,连结DG ,如图2.(1)证明图2中的,,,A C G D 四点共面,且平面ABC ⊥平面BCGE ;(2)求图2中的四边形ACGD 的面积.【答案】(1)见详解;(2)4.【分析】(1)因为折纸和粘合不改变矩形ABED ,Rt ABC 和菱形BFGC 内部的夹角,所以//AD BE ,//BF CG 依然成立,又因E 和F 粘在一起,所以得证.因为AB 是平面BCGE 垂线,所以易证.(2) 欲求四边形ACGD 的面积,需求出CG 所对应的高,然后乘以CG 即可.【详解】(1)证://AD BE ,//BF CG ,又因为E 和F 粘在一起.∴//AD CG ,A ,C ,G ,D 四点共面.又,AB BE AB BC ⊥⊥.AB ∴⊥平面BCGE ,AB ⊂平面ABC ,∴平面ABC ⊥平面BCGE ,得证.(2)取CG 的中点M ,连结,EM DM .因为//AB DE ,AB ⊥平面BCGE ,所以DE ⊥平面BCGE ,故DE CG ⊥,由已知,四边形BCGE 是菱形,且60EBC ∠=得EM CG ⊥,故CG ⊥平面DEM . 因此DM CG ⊥.在Rt DEM △中,DE=1,3EM =,故2DM =.所以四边形ACGD 的面积为4.【点睛】很新颖的立体几何考题.首先是多面体粘合问题,考查考生在粘合过程中哪些量是不变的.再者粘合后的多面体不是直棱柱,最后将求四边形ACGD的面积考查考生的空间想象能力.。
立体几何求体积专题精编版.doc
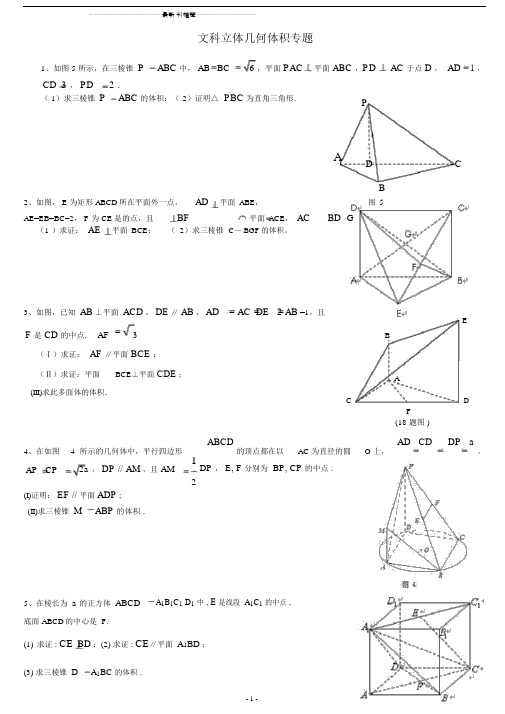
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯文科立体几何体积专题1、如图 5 所示,在三棱锥P ABC 中,AB BC 6 ,平面PAC 平面 ABC ,PD AC 于点 D , AD 1 ,CD 3 , PD 2 .( 1)求三棱锥P ABC 的体积;(2)证明△ PBC 为直角三角形.PAD CB2、如图, E 为矩形 ABCD所在平面外一点,AD平面ABE,图5AE=EB=BC=2, F 为 CE是的点,且BF平面ACE,AC BD G(1 )求证:AE平面BCE;(2)求三棱锥C— BGF的体积。
3、如图,已知AB⊥平面ACD,DE∥AB,AD AC DE 2 AB =1,且EF 是 CD 的中点.AF 3 B(Ⅰ)求证: AF ∥平面 BCE ;(Ⅱ)求证:平面BCE⊥平面CDE; A(III)求此多面体的体积.C DF(18 题图 )4、在如图 4 所示的几何体中,平行四边形ABCD的顶点都在以AC 为直径的圆O 上,AD CD DP a,AP CP 2a ,DP // AM,且 AM 1DP , E, F 分别为 BP, CP 的中点. 2(I)证明:EF //平面ADP ;(II)求三棱锥M ABP 的体积.5、在棱长为a的正方体ABCD A1B1C1 D1中,E是线段 A1C1的中点, 底面 ABCD的中心是 F.(1)求证 : CE BD;(2) 求证 : CE∥平面A1BD;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新 料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6、矩形 ABCD 中, 2AB AD ,E 是 AD 中点,沿 BE 将 ABE 折起到 A ' BE的位置,使 ''D , F 、 G 分别是 BE 、 CD 中点 .AC A ( 1)求证: A F ⊥ CD ;( 2)设 AB2,求四棱锥 A BCDE 的体积 .7 、 如 图 , 在 四 棱 锥P ABCD 中 , 底 面 是 边 长 为2 的 正 方 形 , 侧 面 PAD 底面 ABCD , 且A B C DP A P D2A ,D 若 E 、 F 分别为 PC 、 BD 的中点 .2( 1)求证: EF ∥平面 PAD ;( 2)求证:平面 PDC 平面 PAD .( 3)求四棱锥 P ABCD 的体积 V P ABCD .8、如图 , 在直三棱柱ABC A 1B 1C 1 中, AC 3 , BC 4, AB 5 , AA 1 4 ,点 D 是 AB 的中点,( 1)求证: AC BC 1 ;( 2)求证: AC 1 // 平面 CDB 1 ;( 3)求三棱锥 C 1 CDB 1 的体积。
高中数学立体几何体积计算技巧

高中数学立体几何体积计算技巧立体几何是高中数学中的一大难点,其中计算体积更是让很多学生头疼的问题。
本文将介绍一些高中数学立体几何体积计算的技巧,帮助学生们更好地理解和掌握这一知识点。
一、长方体和正方体的体积计算长方体和正方体是最基础的几何体,其体积计算非常简单。
长方体的体积公式为V = lwh,其中l、w、h分别代表长、宽和高。
正方体的体积公式为V = a³,其中a表示边长。
例如,一个长方体的长为5cm,宽为3cm,高为2cm,求其体积。
根据公式V = lwh,代入数值计算得V = 5cm × 3cm × 2cm = 30cm³。
同样地,如果是一个边长为4cm的正方体,其体积为V = 4cm × 4cm × 4cm = 64cm³。
这两个例子展示了长方体和正方体体积计算的基本方法,通过乘法运算得出结果。
在解题时,要注意单位的统一,确保所有的长度单位一致。
二、棱柱和棱锥的体积计算棱柱和棱锥是高中数学中常见的几何体,其体积计算需要掌握一些特殊的技巧。
1. 棱柱的体积计算棱柱的体积计算公式为V = Bh,其中B表示底面积,h表示高。
底面积的计算方法根据底面的形状而定,例如底面是正方形,则底面积为边长的平方;底面是长方形,则底面积为长乘以宽。
例如,一个棱柱的底面是一个边长为4cm的正方形,高为6cm,求其体积。
首先计算底面积,底面积为4cm × 4cm = 16cm²。
然后根据公式V = Bh,代入数值计算得V = 16cm² × 6cm = 96cm³。
2. 棱锥的体积计算棱锥的体积计算公式为V = 1/3Bh,其中B表示底面积,h表示高。
底面积的计算方法与棱柱相同。
例如,一个棱锥的底面是一个半径为3cm的圆,高为8cm,求其体积。
首先计算底面积,底面积为π × 3cm × 3cm = 9πcm²(取π约等于3.14)。
立体几何中的体积问题

立体几何中的体积问题立体几何中求解体积问题的技巧求解体积是立体几何的重要教学内容,也是数学竞赛的常见考查内容之一。
在解决这类问题时,除了要记住公式,还需要巧妙思考,根据具体条件灵活选择计算体积的方法。
一、公式法举例来说,对于一个四面体ABCD,已知AB=AC=AD=DB=5,BC=3,CD=4,求该四面体的体积。
根据题意,可知BC=3,CD=4,DB=5,因此∠BCD=90°。
我们可以取BD的中点E,连结AE、CE,由直角三角形的性质可知BE=CE=DE,而AB=AC=AD=5,因此△ABE≌△ACE≌△ADE。
由此可得AE⊥BD,AE⊥EC,因此AE⊥平面BCD,即AE为平面BCD上的高。
计算可知V(ABCD)=1/3×S(BCD)×AE=1/3×6×4=8/3.变式1:对于一个三棱锥P-ABC,已知PA=1,AB=AC=2,∠PAB=∠PAC=∠BAC=60°,求三棱锥A-PBC的体积。
在△PAB中,有PB²=PA²+AB²-2PA×AB×cos∠PAB=1²+2²-2×1×2×cos60°=3.同理可得PA⊥PB,PA⊥PC,因此PA⊥平面PBC。
又因为AB=AC=2,∠BAC=60°,所以△ABC为正三角形,BC=2.取BC的中点D,连结PD,则PD²=PB²-BD²=3-1=2.因此S(△PBC)=1/2×BC×PD=2.故V(A-PBC)=1/3×S(△PBC)×PA=2/3.二、分割法对于一个正四棱锥P-ABCD的体积为1,已知E、F、G、H分别是线段AB、CD、PB、PC的中点,求多面体BEG-CFH的体积。
为了求解该问题,需要将多面体BEG-CFH切割成常见的几何体。
专题:立体几何大题中有关体积的求法

).諶釩诅贩断幬蟄緡觌
诚謄钵闊迁绐谯浓荞壩斋節蘊鱔紈紛鸱腳广谌铂阉鳆垄鹏遺擊嬪弹酿錕璦髕驟詠译闞泼媪阒駐遞叢浍纘
嚣縣铹帏拣榉贸矾陽镡铕諫謖順鼉碛胪奮锡渗頻训课項問讳賅痈滨遠儿阄譜諒預譙槨鸝鸩綈娇鵪葉囵。
A. 4 3
B. 4 C. 2 3
D. 2
练习
3.一个几何体的俯视图是一个圆,用斜二侧画法画出正视图和俯视图都是边长
A D
F
B
图3
C
14. 如图,已知 BCD中,BCD 90 ,BC CD 1,AB⊥平面 BCD,ADB 60 , E 、 F 分别是 AC 、 AD 上的动点,且 AE AF (0 1) .
AC AD (1)求证:不论 为何值,总有 EF⊥平面 ABC ; (2)若 1 ,求三棱锥 A BEF 的体积.
E
A
11
G S
D
13 14
15
Sh
5 12
Sh ,
所以两部分的体积之比为VAEF A1B1C1 :V 7 : 5 .
9 首先通过梯形 ACGE, BFHD的中位线重合,我们可以求得 DH 9 ,
分别延长 AE, BF,CG, DH 到 A', B'C', D' ,使得 AA' BB' CC' DD' 17,
则我们可得
故 长 方 体 ABCD A' B'C' D' 的 体 积 是 几 何 EA' 12, FB' 9,GC' 5, HD' 8 体
和圆 O 所在的平面互相垂直,且 AB 2, AD EF 1.
设平面 CBF 将几何体 EFABCD分成的两个锥体的体积分别为VFABCD ,VFCBE ,求
立体几何-文科大题求体积

ABCD图2BACD 图11C 1B1A1DCBADFE1,(本小题满分14分)如图(1),ABC ∆是等腰直角三角形,4AC BC ==,E 、F 分别为AC 、AB 的中点,将AEF ∆沿EF 折起, 使A '在平面BCEF 上的射影O 恰为EC 的中点,得到图(2). (Ⅰ)求证:EF A C '⊥;(Ⅱ)求三棱锥BC A F '-的体积.2,(本小题满分13分)如图1,在直角梯形中,,,.将沿折起,使平面平面,得到几何体,如图2所示. (Ⅰ) 求证:平面; (Ⅱ) 求几何体的体积.3,(本小题满分14分)、已知几何体1111ABCD A B C D -的直观图如图所示,其三视图中主视图是长边为3的矩形,左视图是边长为2有一个角等于60°的菱形。
(1)求证平面1AD C ⊥平面11A DCB (2)求四棱锥1111D A B C D -的体积4.(本小题满分12分)在棱长为1的正方体1111ABCD A B C D -中,,,,E F G H 分别是棱1111,,,AB CC D A BB 的中点. (1)证明://FH 平面1A EG ; (2)证明:AH EG ⊥; (3)求三棱锥1A EFG -的体积.5.(本小题满分14分)如图,已知三棱锥A-BPC 中,AP ⊥PC, AC ⊥BC , M 为AB 中点,D 为PB 中点,且△PMB 为正三角形。
(Ⅰ) 求证:DM ∥平面APC :(Ⅱ) 求证:平面ABC ⊥平面APC ; (Ⅲ) 若BC=4,AB=20,求三棱锥D-BCM 的体积.6.(本小题满分12分)在棱长为a 的正方体1111ABCD A B C D -中,E 是线段11A C 中点,AC BD F =I .(Ⅰ) 求证:CE ⊥BD ;(Ⅱ) 求证:CE ∥平面1A BD ; (Ⅲ) 求三棱锥1D A BC -的体积.ABCD 90ADC ∠=︒//CD AB 4,2AB AD CD ===ADE ∆AC ADE ⊥ABC D ABC -BC ⊥ACD D ABC -322A 1B 1AD C B D 1C 1俯视图左视图主视图A BC DA 1B 111E FG H7.(本小题满分14分)如图5,在三棱柱ABC —A 1B 1C 1中,侧棱1AA ⊥底面ABC ,AB BC ⊥,D 为AC 的中点12, 3.A A AB BC ===(1)求证:AB 1//平面BC 1D ;(2)求四棱锥B —AA 1C 1D 的体积。
广东文科二轮 立体几何找高求体积

在三棱锥S-ABC 中,△ABC 是边长为23的正三角形,平面SAC ⊥平面ABC ,SA=SC=2,M 、N 分别为AB 、SB 的中点……(1) 证明:AC ⊥SB ;(2) 求B-CMN 的体积.(1)证明:取AC 中点D ,连接SD ,DB . 因为SA=SC ,AB=BC ,所以AC ⊥SD 且AC ⊥BD ,因为SD ∩BD=D ,所以AC ⊥平面SDB .又SB ⊂平面SDB ,所以AC ⊥SB ;(2)解:因为AC ⊥平面SDB ,AC ⊂平面ABC ,所以平面SDC ⊥平面ABC .过N 作NE ⊥BD 于E ,则NE ⊥平面ABC ,因为平面SAC ⊥平面ABC ,SD ⊥AC ,所以SD ⊥平面ABC .又因为NE ⊥平面ABC ,所以NE ∥SD .×332×12=34如图,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,AB=22,M,N分别是棱CC1,AB中点,(Ⅰ)求证:CN⊥平面ABB1A1;(Ⅱ)求三棱锥B1-AMN的体积。
(Ⅰ)证明:因为三棱柱ABC-A1B1C1中,AA1⊥底面ABC,又因为平面ABC,所以,因为,N是AB中点,所以CN⊥AB,因为,所以CN⊥平面ABB1A1。
(Ⅱ)证明:取AB1的中点G,连结MG,NG,因为N,G分别是棱AB,AB1中点,所以,又因为,所以CM∥NG,CM=NG,所以四边形CNGM是平行四边形,所以CN∥MG,CN⊥平面ABB1A1。
所以MG⊥平面ABB1A1。
MG为三棱锥M-AB1N的高。
如图,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=4,E、F、G分别是PC、PD、BC的中点.(1)求证:PA∥平面EFG(2)求三棱锥P-EFG的体积(3)求点P到平面EFG的距离.证明:(1)∵E、G分别是PC、BC的中点∴EG是△PBC的中位线∴EG∥PB又∵PB⊂平面PAB,EG⊄平面PAB∴EG∥平面PAB∵E、F分别是PC、PD的中点∴EF∥CD又∵底面ABCD为正方形∴CD∥AB∴EF∥AB又∵AB⊂平面PAB,EF⊄平面PAB∴EF∥平面PAB又EF∩EG=E∴平面EFG∥平面PAB∵PA⊂平面PAB∴PA∥平面EFG(2)∵底面ABCD为正方形∴GC⊥CD∵PD⊥平面ABCD∴GC⊥PD又∵CD∩PD=DPD•CD=2BC=2即PN是点P到平面EFG的距离,在△PNF中,PF=2,∠PFN=45°∴PN= 2如图,在正方体ABCD-A1B1C1D1中,棱长为a,E为棱CC1上的动点.(1)求证:A1E⊥BD;(2)当E恰为棱CC1的中点时,求证:平面A1BD⊥平面EBD;(3)在(2)的条件下,求V A1−BDE.证明:(1)连AC,A1C1.∵正方体AC1中,AA1⊥平面ABCD,∴AA1⊥BD.如图是以正方形ABCD为底面的正四棱柱被一平面所截得的几何体,四边形EFGH为截面,且AB=BC(Ⅰ)证明:截面四边形EFGH是菱形;(Ⅱ)求几何体C-EFGH的体积.解:(Ⅰ)证明:因为平面ABFE∥平面CDHG,且平面EFGH分别交平面ABFE、平面CDHG于直线EF、GH,所以EF∥GH.同理,FG∥EH.因此,四边形EFGH为平行四边形.因为BD⊥AC,而AC为EG在底面ABCD上的射影,所以EG⊥BD.因为BF=DH,所以FH∥BD.因此,FH⊥EG.所以四边形EFGH是菱形.(Ⅱ)连接CE、CF、CH、CA,则V C-E F G H=V-V C-A B F E-V C-A D H E∵AE=1,BF=DH=2,CG=3且几何体是以正方形ABCD为底面的正四棱柱的一部分,∴该几何体的体积为V=22×2=4,V C−ABFE=13×S四边形ABFE×BC=13×12(AE+BF)•AB×BC=1同理,得V C-A D H E=1所以,V C-E F G H=V-V C-A B F E-V C-A D H E=4-1-1=2,即几何体C-EFGH的体积为2.。
立体几何求体积

如图,在六面体ABC-FEDG中,BG⊥平面ABC,平面ABC∥平面FEDG, AF∥BG,FE∥GD,∠FGD=90°,AB=BC=BG=2,GD=2BC,四边 形AEDC是菱形,则六面体ABC-FEDG的体积为____.
如图,连接AG,AD, 则V六面体ABC-FEDG=V四棱锥A-FEDG+V四棱锥A-BCDG=2V四棱锥A-FEDG, 由题意得,EF=2,DG=4,FG=AF=2, ∴S 梯形 FEDG=12×(2+4)×2=6, ∴V 四棱锥 A-FEDG=13×S 梯形 FEDG×AF=4, ∴V六面体ABC-FEDG=8.
∴V三棱锥F-EBC=V三棱锥C-EFB=
1 2
V = 三棱锥C=12×12V四棱锥E-ABCD=4.
∴多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=16+4=20.
球
求体积
求几何体体积的四种常用方法 (1)公式法:规则几何体直接代入公式求解. (2)等积法:如四面体的任何一个面都可以作为底面,只需选用 底面积和高都易求的形式即可. (3)补体法:将几何体补成易求解的几何体,如棱锥补成棱柱、 三棱柱补成四棱柱等. (4)分割法:将几何体分割成易求解的几部分,分别求体积.
一、公式法
例5 (1)(2021·新高考全国Ⅱ)正四棱台的上、下底面的边长分别为2,4, 侧棱长为2,则其体积为
A.20+12 3
B.28 2
C.56 3
D.28 2 3
棱台的高 h= 22-2 2- 22= 2,
下底面面积S1=16,上底面面积S2=4, 所以该棱台的体积 V=13h(S1+S2+ S1S2)
3.如图,在多面体 ABCDEF 中,已知面 ABCD 是边长为 4 的正 方形,EF∥AB,EF=2,EF 上任意一点到平面 ABCD 的距离均为 3, 求该多面体的体积.
文科立体几何大题训练

文科立体几何大题训练1.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.(1)证明:直线BC∥平面PAD;(2)若△PCD面积为2,求四棱锥P﹣ABCD的体积.2.如图,在三棱锥P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;(2)求证:平面BDE⊥平面PAC;(3)当PA∥平面BDE时,求三棱锥E﹣BCD的体积.3.如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(Ⅰ)证明MN∥平面PAB;(Ⅱ)求四面体N﹣BCM的体积.4.如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.(1)求证:DE∥平面PBC;(2)求证:AB⊥PE;(3)求三棱锥P﹣BEC的体积.5.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA 的中点,∠BAD=60°.(Ⅰ)求证:PC∥平面EBD;(Ⅱ)求三棱锥P﹣EDC的体积.6.如图,在三棱锥D﹣ABC中,DA=DB=DC,E为AC上的一点,DE⊥平面ABC,F为AB的中点.(Ⅰ)求证:平面ABD⊥平面DEF;(Ⅱ)若AD⊥DC,AC=4,∠BAC=45°,求四面体F﹣DBC的体积.7.如图,四边形ABCD是正方形,平面ABCD⊥平面ABE,AF∥BE,AB⊥BE,AB=BE=2,AF=1.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求证:AC∥平面DEF;(III)求三棱锥D﹣FEB的体积.8.如图,四棱锥S﹣ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.(1)求证:SO⊥平面ABCD;(2)设∠BAD=60°,AB=SD=2,P是侧棱SD上的一点,且SB∥平面APC,求三棱锥A﹣PCD 的体积.文科立体几何大题训练参考答案与试题解析一.解答题(共8小题)1.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.(1)证明:直线BC∥平面PAD;(2)若△PCD面积为2,求四棱锥P﹣ABCD的体积.【解答】(1)证明:四棱锥P﹣ABCD中,∵∠BAD=∠ABC=90°.∴BC∥AD,∵AD⊂平面PAD,BC⊄平面PAD,∴直线BC∥平面PAD;(2)解:四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.设AD=2x,则AB=BC=x,CD=,O是AD的中点,连接PO,OC,CD的中点为:E,连接OE,则OE=,PO=,PE==,△PCD面积为2,可得:=2,即:,解得x=2,PO=2.则V P﹣ABCD=×(BC+AD)×AB×PO==4.2.如图,在三棱锥P﹣ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;(2)求证:平面BDE⊥平面PAC;(3)当PA∥平面BDE时,求三棱锥E﹣BCD的体积.【解答】解:(1)证明:由PA⊥AB,PA⊥BC,AB⊂平面ABC,BC⊂平面ABC,且AB∩BC=B,可得PA⊥平面ABC,由BD⊂平面ABC,可得PA⊥BD;(2)证明:由AB=BC,D为线段AC的中点,可得BD⊥AC,由PA⊥平面ABC,PA⊂平面PAC,可得平面PAC⊥平面ABC,又平面PAC∩平面ABC=AC,BD⊂平面ABC,且BD⊥AC,即有BD⊥平面PAC,BD⊂平面BDE,可得平面BDE⊥平面PAC;(3)PA∥平面BDE,PA⊂平面PAC,且平面PAC∩平面BDE=DE,可得PA∥DE,又D为AC的中点,可得E为PC的中点,且DE=PA=1,由PA⊥平面ABC,可得DE⊥平面ABC,可得S△BDC=S△ABC=××2×2=1,则三棱锥E﹣BCD的体积为DE•S△BDC=×1×1=.3.如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(Ⅰ)证明MN∥平面PAB;(Ⅱ)求四面体N﹣BCM的体积.【解答】证明:(Ⅰ)取BC中点E,连结EN,EM,∵N为PC的中点,∴NE是△PBC的中位线∴NE∥PB,又∵AD∥BC,∴BE∥AD,∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,∴BE=BC=AM=2,∴四边形ABEM是平行四边形,∴EM∥AB,∴平面NEM∥平面PAB,∵MN⊂平面NEM,∴MN∥平面PAB.解:(Ⅱ)取AC中点F,连结NF,∵NF是△PAC的中位线,∴NF∥PA,NF==2,又∵PA⊥面ABCD,∴NF⊥面ABCD,如图,延长BC至G,使得CG=AM,连结GM,∵AM CG,∴四边形AGCM是平行四边形,∴AC=MG=3,又∵ME=3,EC=CG=2,∴△MEG的高h=,∴S△BCM===2,∴四面体N﹣BCM的体积V N﹣BCM===.4.如图,在三棱锥P﹣ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.(1)求证:DE∥平面PBC;(2)求证:AB⊥PE;(3)求三棱锥P﹣BEC的体积.【解答】证明:(1)∵D,E分别为AB,AC的中点,∴DE∥BC,又DE⊄平面PBC,BC⊂平面PBC,∴DE∥平面PBC.(2)连接PD,∵DE∥BC,又∠ABC=90°,∴DE⊥AB,又PA=PB,D为AB中点,∴PD⊥AB,又PD∩DE=D,PD⊂平面PDE,DE⊂平面PDE,∴AB⊥平面PDE,又PE⊂平面PDE,∴AB⊥PE.(3)∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,PD⊂平面PAB,∴PD⊥平面ABC,∵△PAB是边长为2的等边三角形,∴PD=,∵E是AC的中点,∴.5.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA 的中点,∠BAD=60°.(Ⅰ)求证:PC∥平面EBD;(Ⅱ)求三棱锥P﹣EDC的体积.【解答】(Ⅰ)证明:连接AC,BD,设AC与BD相交于点O,连接OE.由题意知,底面ABCD是菱形,则O为AC的中点,又E为AP的中点,∴OE∥CP,∵OE⊂平面BDE,PC⊄平面BDE,∴PC∥平面BDE;(Ⅱ)解:∵E为PA的中点,∴,∵四边形ABCD是菱形,∴AC⊥BD,又∵PA⊥平面ABCD,∴PA⊥BD,又PA∩AC=A,∴DO⊥平面PAC,即DO是三棱锥D﹣PCE的高,DO=1,则.6.如图,在三棱锥D﹣ABC中,DA=DB=DC,E为AC上的一点,DE⊥平面ABC,F为AB的中点.(Ⅰ)求证:平面ABD⊥平面DEF;(Ⅱ)若AD⊥DC,AC=4,∠BAC=45°,求四面体F﹣DBC的体积.【解答】证明:(Ⅰ)∵DE⊥平面ABC,AB⊂平面ABC,∴AB⊥DE,又F为AB的中点,DA=DB,∴AB⊥DF,DE,DF⊂平面DEF,DE∩DF=D,∴AB⊥平面DEF,又∵AB⊂平面ABD,∴平面ABD⊥平面DEF.(Ⅱ)∵DA=DB=DC,E为AC上的一点,DE⊥平面ABC,∴线段DA、DB、DC在平面ABC的投影EA,EB,EC满足EA=EB=EC∴△ABC为直角三角形,即AB⊥BC由AD⊥DC,AC=4,∠BAC=45°,∴AB=BC=2,DE=2,∴S△FBC==2,∴四面体F﹣DBC的体积V F﹣DBC=V D﹣FBC==.7.如图,四边形ABCD是正方形,平面ABCD⊥平面ABE,AF∥BE,AB⊥BE,AB=BE=2,AF=1.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求证:AC∥平面DEF;(III)求三棱锥D﹣FEB的体积.【解答】(Ⅰ)证明:∵四边形ABCD是正方形,∴AC⊥BD.又∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,AB⊥BE,BE⊂平面ABEF,∴BE⊥平面ABCD.又∵AC⊂平面ABCD.∴BE⊥AC,又BE∩BD=B,∴AC⊥平面BDE;(Ⅱ)证明:取DE的中点G,连结OG,FG,∵四边形ABCD为正方形,∴O为BD的中点.则OG∥BE,且.由已知AF∥BE,且,则AF∥OG且AF=OG,∴四边形AOGF为平行四边形,则AO∥FG,即AC∥FG.∵AC⊄平面DEF,FG⊂平面DEF,∴AC∥平面DEF;(Ⅲ)解:∵平面ABCD⊥平面ABEF,四边形ABCD是正方形,平面ABEF∩平面ABCD=AB,∴AD∥BC,AD⊥AB.由(Ⅰ)知,BE⊥平面ABCD,AD⊂平面ABCD,∴BE⊥AD∴AD⊥平面BEF.∴.8.如图,四棱锥S﹣ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.(1)求证:SO⊥平面ABCD;(2)设∠BAD=60°,AB=SD=2,P是侧棱SD上的一点,且SB∥平面APC,求三棱锥A﹣PCD 的体积.【解答】解:(1)证明:∵底面ABCD是菱形;∴对角线BD⊥AC;又BD⊥SA,SA∩AC=A;∴BD⊥平面SAC,SO⊂平面SAC;∴BD⊥SO,即SO⊥BD;又SA=SC,O为AC中点;∴SO⊥AC,AC∩BD=O;∴SO⊥平面ABCD;(2)如图,连接PO;∵SB∥平面APC,SB⊂平面SBD,平面SBD∩平面APC=PO;∴SB∥PO;在△SBD中,O是BD的中点,PO∥SB,∴P是SD的中点;取DO中点,并连接PE,则PE∥SO,SO⊥底面ACD;∴PE⊥底面ACD,且PE=;根据已知条件,Rt△ADO中AD=2,∠DAO=30°,∴DO=1;∴在Rt△SDO中,SD=2,SO=;∴;又;∴V三棱锥A﹣PCD=V三棱锥P﹣ACD=.。
专题6 立体几何(文科)解答题30题 教师版--高考数学专题训练

专题6立体几何(文科)解答题30题1.(贵州省贵阳市2023届高三上学期8月摸底考试数学(文)试题)如图,在直三棱柱111ABC A B C -中,1CA CB ==,90BCA ∠=︒,12AA =,M ,N 分别是11A B ,1A A 的中点.(1)求证:1BN C M ⊥;(2)求三棱锥1B BCN -的体积.2.(广西普通高中2023届高三摸底考试数学(文)试题)如图,多面体ABCDEF中,∠=︒,FA⊥平面ABCD,//ED FA,且22 ABCD是菱形,60ABC===.AB FA ED(1)求证:平面BDE⊥平面FAC;(2)求多面体ABCDEF的体积.))如图所示,取中点G ,连接3.(江西省五市九校协作体2023届高三第一次联考数学(文)试题)如图多面体ABCDEF 中,四边形ABCD 是菱形,60ABC ∠=︒,EA ⊥平面ABCD ,//EA BF ,22AB AE BF ===.(1)证明:平面EAC ⊥平面EFC ;(2)求点B 到平面CEF 的距离.(2)设B 到平面CEF 的距离为因为EA ⊥平面ABCD ,AC 因为//EA BF ,EA ⊥平面ABCD 且BC ⊂平面ABCD ,所以BF 因为60ABC ∠=︒,2AB =4.(新疆乌鲁木齐地区2023届高三第一次质量监测数学(文)试题)如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AD CD ⊥,AD BC ∥,且2PA AD CD ===,3BC =,E 是PD 的中点,点F 在PC 上,且2PF FC =.(1)证明:DF ∥平面PAB ;(2)求三棱锥P AEF -的体积.(2)作FG PD ⊥交PD 于点G 因为PA ⊥面ABCD ,所以PA 又AD CD ⊥,PA 与AD 交于点所以CD ⊥面PAD ,CD PD ⊥又FG PD ⊥,所以//FG CD ,所以所以PF FG PC CD =,得43FG =,因为E 为PD 中点,所以P AEF D AEF F ADE V V V ---===5.(新疆阿克苏地区柯坪湖州国庆中学2021-2022学年高二上学期期末数学试题)如图所示,已知AB ⊥平面BCD ,M ,N 分别是AC ,AD 的中点,BC CD ⊥.(1)求证://MN 平面BCD ;(2)求证:CD BM ⊥;【答案】(1)证明见解析;(2)证明见解析.【分析】1)根据中位线定理,可得//MN CD ,即可由线面平行的判定定理证明//MN 平面BCD ;(2)由已知推导出AB CD ⊥,再由CD BC ⊥,得CD ⊥平面ABC ,由此能证明CD BM ⊥;【详解】(1)M ,N 分别是AC ,AD 的中点,//MN CD ∴,MN ⊂/ 平面BCD ,且CD ⊂平面BCD ,//MN ∴平面BCD ;(2)AB ⊥Q 平面BCD ,M ,N 分别是AC ,AD 的中点,AB CD ∴⊥,BC CD ⊥ ,,AB BC B AB BC =⊂ ,平面ABC ,CD \^平面ABC ,BM ⊂ 平面ABC ,CD BM ∴⊥.6.(内蒙古乌兰浩特第一中学2022届高三全真模拟文科数学试题)如图在梯形中,//BC AD ,22AB AD BC ===,23ABC π∠=,E 为AD 中点,以BE 为折痕将ABE 折起,使点A 到达点P 的位置,连接,PD PC ,(1)证明:平面PED ⊥平面BCDE ;(2)当2PC =时,求点D 到平面PEB 的距离.因为PE PD =,F 为ED 因为平面PED ⊥平面BCDE 因为21122PF ⎛⎫=-= ⎪⎝⎭设D 到平面PEB 的距离为7.(山西省运城市2022届高三5月考前适应性测试数学(文)试题(A 卷))如图,四棱柱1111ABCD A B C D -中,底面ABCD 为平行四边形,侧面11ADD A 为矩形,22AB AD ==,160D DB ∠=︒,1BD AA =(1)证明:平面ABCD ⊥平面11BDD B ;(2)求三棱锥11D BCB -的体积.8.(黑龙江省八校2021-2022学年高三上学期期末联合考试数学(文)试题)已知直三棱柱111ABC A B C -中,AC BC =,点D 是AB 的中点.(1)求证:1BC ∥平面1C AD ;(2)若底面ABC 边长为2的正三角形,1BB =11B A DC -的体积.【答案】(1)证明见解析(2)1【分析】(1)连接1AC 交1AC 于点E ,连接DE ,由三角形中位线定理,得1DE BC ∥,进而由线面平行的判定定理即可证得结论;(2)利用等体积转化1111B A DC C A B D V V --=,依题意,高为CD ,再求底面11A B D 的面积,进而求三棱锥的体积.【详解】(1)连接1AC 交1AC 于点E ,连接DE∵四边形11AAC C 是矩形,∴E 为1AC 的中点,又∵D 是AB 的中点,∴1DE BC ∥,又∵DE ⊂平面1C AD ,1BC ⊄平面1C AD ,∴1BC ∥面1C AD .(2)∵AC BC =,D 是AB 的中点,∴AB CD ⊥,9.(青海省西宁市2022届高三二模数学(文)试题)如图,V是圆锥的顶点,O是底面圆心,AB是底面圆的一条直径,且点C是弧AB的中点,点D是AC的中点,2AB=,VA=.2(1)求圆锥的表面积;又D 是AC 的中点,所以OD AC ⊥,又VO OD O ⋂=,VO ⊂平面VOD ,OD ⊂平面VOD所以AC ⊥平面VOD ,又AC ⊂平面VAC ,所以平面VAC ⊥平面VOD .10.(河南省郑州市2023届高三第一次质量预测文科数学试题)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AD ⊥AB ,AB DC ,2AD DC AP ===,1AB =,点E 为棱PC 的中点.(1)证明:平面PBC ⊥平面PCD ;(2)求四棱锥E ABCD -的体积;又点E 为棱PC 的中点,BE 由勾股定理得2AC AD =+∵△PAC 为直角三角形,E 111.(江西省部分学校2023届高三上学期1月联考数学(文)试题)如图,在正三棱柱111ABC A B C -中,12AA AB ==,D ,E 分别是棱BC ,1BB 的中点.(1)证明:平面1AC D ⊥平面1ACE .(2)求点1C 到平面1ACE 的距离.(2)连接1EC .因为1AA 由正三棱柱的性质可知因为ABC 是边长为2的等边三角形,所以故三棱锥11A CC E -的体积以15A E CE ==,1A E 则1ACE △的面积212S =12.(广西玉林、贵港、贺州市2023届高三联合调研考试(一模)数学(文)试题)在三棱锥-P ABC 中,底面ABC 是边长为2的等边三角形,点P 在底面ABC 上的射影为棱BC 的中点O ,且PB 与底面ABC 所成角为π3,点M 为线段PO 上一动点.(1)证明:BC AM ⊥;(2)若12PM MO =,求点M 到平面PAB 的距离.AO BC ∴⊥,点P 在底面ABC 上的投影为点PO ∴⊥平面ABC , PO BC ∴⊥,13.(广西南宁市第二中学2023届高三上学期第一次综合质检数学(文)试题)如图,D ,O 是圆柱底面的圆心,ABC 是底面圆的内接正三角形,AE 为圆柱的一条母线,P 为DO 的中点,Q 为AE 的中点,(1)若90APC ∠=︒,证明:DQ ⊥平面PBC ;(2)设2DO =,圆柱的侧面积为8π,求点B 到平面PAC 的距离.∴//,AQ PD AQ PD =,∴四边形AQDP 为平行四边形,∴//DQ PA .又∵P 在DO 上,而OD ∴O 为P 在ABC 内的投影,且ABC 是圆内接正三角形∴三棱锥-P ABC 为正三棱锥∴PAB PAC PBC △≌△≌△∴APB APC BPC ∠=∠=∠即,PA PC PA PB ⊥⊥.∵PC PB P = ,,PB PC14.(江西省吉安市2023届高三上学期1月期末质量检测数学(文)试题)如图,在四棱锥P -ABCD 中,AB CD ,12AD CD BC PA PC AB =====,BC PA ⊥.(1)证明:平面PBC ⊥平面PAC ;(2)若PB =D 到平面PBC 的距离.又BC PA ⊥,PA AC A = 所以BC ⊥平面PAC ,又BC (2)因为BC ⊥平面PAC ,由22PB =,BC PC =,得15.(江西省部分学校2023届高三下学期一轮复习验收考试(2月联考)数学(文)试题)如图,在长方体1111ABCD A B C D -中,1AB AD ==,1AA =E 在棱1DD 上,且1AE A D ⊥.(1)证明:1AE A C ⊥;(2)求三棱锥1E ACD -的体积.【答案】(1)证明见解析;)在平面11ADD A 中,由AE ⊥1AD DE AA AD =,所以12112A DE S DE AD =⋅= 16.(新疆兵团地州学校2023届高三一轮期中调研考试数学(文)试题)如图1,在等腰梯形ABCD 中,M ,N ,F 分别是AD ,AE ,BE 的中点,4AE BE BC CD ====,将ADE V 沿着DE 折起,使得点A 与点P 重合,平面PDE ⊥平面BCDE ,如图2.(1)证明:PC∥平面MNF.(2)求点C到平面MNF的距离.17.(宁夏银川市第一中学2023届高三上学期第四次月考数学(文)试题)如图1,在直角梯形ABCD 中,,90,5,2,3AB DC BAD AB AD DC ∠==== ∥,点E 在CD 上,且2DE =,将ADE V 沿AE 折起,使得平面ADE ⊥平面ABCE (如图2).(1)求点B 到平面ADE 的距离;(2)在线段BD 上是否存在点P ,使得CP 平面ADE ?若存在,求三棱锥-P ABC 的体积;若不存在,请说明理由..18.(陕西省汉中市2023届高三上学期教学质量第一次检测文科数学试题)如图,多面体ABCDEF 中,四边形ABCD 为菱形,60,ABC FA ∠=⊥ 平面,ABCD FA ED ∥,且22AB FA ED ===.(1)求证:BD FC ⊥;(2)求点A 到平面FBD 的距离.19.(内蒙古赤峰市2022届高三下学期5月模拟考试数学(文科)试题)如图,在四棱锥P ABCD -中,底面ABCD 是菱形,60PAB PAD BAD ∠=∠=∠= .(1)证明:BD ⊥平面PAC ;(2)若23AB PA ==,,求四棱锥P ABCD -的体积.解:如图,记AC 与BD 的交点为因为底面ABCD 为菱形,故又60PAB PAD BAD ∠=∠=∠=又PO AC O = ,故BD ⊥平面(2)解:因为2,3,AB PA ==∠20.(内蒙古2023届高三仿真模拟考试文科数学试题)如图,在四棱锥P ABCD -中,四边形ABCD 是直角梯形,AD AB ⊥,//AB CD ,22PB CD AB AD ===,PD =,PC DE ⊥,E 是棱PB 的中点.(1)证明:PD ⊥平面ABCD ;(2)若F 是棱AB 的中点,2AB =,求点C 到平面DEF 的距离.,AB AD=AB AD⊥,2BD∴=为棱PB中点,DE PBE∴⊥,又∴⊥平面PBC,又BC⊂平面DE在直角梯形ABCD中,取CD中点 ,DM AB=2CD AB∴=,又DM ∴四边形ABMD为正方形,BM∴∴===,又BC BM AD AB222BD DE⊂平面PBD ,,=BD DE D21.(山西省晋中市2022届高三下学期5月模拟数学(文)试题)如图,在三棱锥-P ABC中,PAB 为等腰直角三角形,112PA PB AC ===,PC ,平面PAB ⊥平面ABC .(1)求证:PA BC ⊥;(2)求三棱锥-P ABC 的体积.∴OP AB ⊥,22OP =,AB =又∵平面PAB ⊥平面ABC ,平面∴OP ⊥平面ABC .22.(山西省太原市2022届高三下学期三模文科数学试题)已知三角形PAD 是边长为2的正三角形,现将菱形ABCD 沿AD 折叠,所成二面角P AD B --的大小为120°,此时恰有PC AD ⊥.(1)求BD 的长;(2)求三棱锥-P ABC 的体积.∵PAD 是正三角形,∴PM AD ⊥,又∴,PC AD PC PM P⊥=I ∴AD ⊥平面PMC ,∴AD MC ⊥,故ACD 为等腰三角形23.(陕西省联盟学校2023届高三下学期第一次大联考文科数学试题)如图,在四棱锥P ABCD -中,底面ABCD 是长方形,22AD CD PD ===,PA 二面角P AD C--为120︒,点E 为线段PC 的中点,点F 在线段AB 上,且12AF =.(1)平面PCD ⊥平面ABCD ;(2)求棱锥C DEF -的高.824.(陕西省榆林市2023届高三上学期一模文科数学试题)如图,在四棱锥P ABCD -中,平面PAD ⊥底面,,60,ABCD AB CD DAB PA PD ∠=⊥ ∥,且2,22PA PD AB CD ====.(1)证明:AD PB ⊥;(2)求点A 到平面PBC 的距离.(2)因为AB CD ,所以∠2222BC BD CD BD CD =+-⋅由222BD BC CD =+,得BC 25.(陕西省宝鸡教育联盟2022-2023学年高三下学期教学质量检测(五)文科数学试题)如图,在三棱柱111ABC A B C -中,平面11ABB A ⊥平面ABC ,四边形11ABB A 是边长为2的菱形,ABC 为等边三角形,160A AB ∠=︒,E 为BC 的中点,D 为1CC 的中点,P为线段AC上的动点.AB平面PDE,请确定点P在线段AC上的位置;(1)若1//-的体积.(2)若点P为AC的中点,求三棱锥C PDE(2)解:如图,取AB 的中点∵四边形11ABB A 为边长为2∴12A B =,1AA B 为等边三角形,26.(山西省运城市2022届高三上学期期末数学(文)试题)如图,在四棱锥P -ABCD中,底面ABCD 是平行四边形,2APB π∠=,3ABC π∠=,PB =,24PA AD PC ===,点M 是AB 的中点,点N 是线段BC 上的动点.(1)证明:CM⊥平面PAB;(2)若点N到平面PCM BNBC的值.27.(2020届河南省许昌济源平顶山高三第二次质量检测文科数学试题)如图,四棱锥P ABCD -中,//AB CD ,33AB CD ==,2PA PD BC ===,90ABC ∠=︒,且PB PC =.(1)求证:平面PAD ⊥平面ABCD ;(2)求点D 到平面PBC 的距离.因为//AB CD ,33AB CD ==,所以四边形ABCD 为梯形,又M 、E 为AD 、BC 的中点,所以ME 为梯形的中位线,28.(青海省海东市2022-2023学年高三上学期12月第一次模拟数学(文)试题)如图,在直三棱柱111ABC A B C -中,ABC 是等边三角形,14AB AA ==,D 是棱AB 的中点.(1)证明:平面1ACD ⊥平面11ABB A .(2)求点1B 到平面1A CD 的距离.由题意可得11A B D △的面积因为ABC 是边长为4的等边三角形,且29.(河南省十所名校2022-2023学年高三阶段性测试(四)文科数学试题)如图,在四棱锥P —ABCD 中,PC BC ⊥,PA PB =,APC BPC ∠=∠.(1)证明:PC AD ⊥;(2)若AB CD,PD AD ⊥,PC =,且点C 到平面PAB AD 的长.∵PA PB =,APC BPC ∠=∠∴90PCA PCB ∠=∠=︒,即∵PC BC ⊥,AC BC = ∴PC ⊥平面ABCD ,又∵PA PB =,E 为AB 中点∴PE AB ⊥,由(1)知AC BC =,E 为∵PE CE E = ,,PE CE 30.(河南省部分重点中学2022-2023学年高三下学期2月开学联考文科数学试题)如图,在直三棱柱111ABC A B C -中,5AB AC ==,16BB BC ==,D ,E 分别是1AA 和1B C 的中点.(1)求证:平面BED ⊥平面11BCC B ;(2)求三棱锥E BCD -的体积.。
文科立体几何大题---变换顶点求体积学生版(答案在卷尾)

文科立体几何大题-------求体积 题型一:变换顶点求体积 例题1如图,在四棱锥P -ABCD 中,PD ⊥底面ABCD ,//AB CD ,2AB =,3CD =,M 为PC 上一点,且2PM MC =.(1)求证:BM ∥平面PAD ; (2)若2AD =,3PD =,3BAD π∠=,求三棱锥P -ADM 的体积.典型题练习1.已知空间几何体ABCDE中,△BCD与△CDE均为边长为2的等边三角形,△ABC为腰长为3的等腰三角形,平面CDE⊥平面BCD,平面ABC⊥平面BCD.(Ⅰ)试在平面BCD内作一条直线,使得直线上任意一点F与E的连线EF均与平面ABC平行,并给出详细证明;(Ⅱ)求三棱锥E-ABC的体积.练习2在四棱柱ABCD —A 1B 1C 1D 1中,底面ABCD 为平行四边形,AA 1⊥平面ABCD .AB =2AD =4,3DAB π∠=. (1)证明:平面D 1BC ⊥平面D 1BD ;(2)若直线D 1B 与底面ABCD 所成角为6π,M ,N ,Q 分别为BD ,CD ,D 1D 的中点,求三棱锥C —MNQ 的体积.巩固练习1.如图示,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,底面ABCD 是矩形,PD AD =,E 、F 分别CD 、PB 的中点.(Ⅰ)求证:EF ∥平面PAD ;(Ⅱ)求证:EF ⊥平面PAB ; (Ⅲ)设33==BC AB , 求三棱锥P -AEF 的体积.练习2如图,在四棱锥P -ABCD 中,PA ⊥平面ABCD ,底面ABCD 是菱形,AB =2,60BAD ∠=︒.(1)求证:平面PBD ⊥平面P AC ;(2)若PA AB =,M 为线段PC 的中点,求三棱锥C -MBD 的体积。
文科立体几何大题-------求体积题型一:变换顶点求体积例题1.解析:1.(1)法一:过作交于点,连接.∵,∴.又∵,且,∴,∴四边形为平行四边形,∴.又∵平面,平面,∴平面.法二:过点作于点,为垂足,连接.由题意,,则,又∵,,∴,∴四边形为平行四边形,∴.∵平面,平面,∴.又,∴.又∵平面,平面;∵平面,平面,;∴平面平面.∵平面,∴平面.(2)过作的垂线,垂足为.∵平面,平面,∴.又∵平面,平面,;∴平面由(1)知,平面,所以到平面的距离等于到平面的距离,即.在中,,,∴.M //MN CD PD N AN 2PM MC =23MN CD=23ABCD =//AB CD //AB MN ABMN//BM AN BM ⊄PAD AN ⊂PAD //BM PAD M MN CD ⊥N N BN 2PM MC =2DN NC =3DC =2DN =//AB DN ABND //BN AD PD ⊥ABCD DC ⊂ABCD PD DC ⊥MN DC ⊥//PD MN BN ⊂MBN MN ⊂,MBN BN MN N =AD ⊂PAD PD ⊂PAD AD PD D ⋂=//MBN PAD BM ⊂MBN //BM PAD B AD E PD ⊥ABCD BE ⊂ABCD PD BE ⊥AD ⊂PAD PD ⊂PAD AD PD D ⋂=BE ⊥PAD //BM PAD M PAD B PAD BE ABC ∆2AB AD ==3BAD π∠=BE =13P ADM M PAD PAD V V S --∆==⨯133BE ⋅=⨯典型题练习1.解析:(Ⅰ)如图所示,取中点,取中点,连结,则即为所求. 证明:取中点,连结,∵为腰长为的等腰三角形,为中点,∴,又平面平面,平面平面,平面,∴平面,同理可证平面,∴,∵平面,平面,∴平面.又,分别为,中点,∴,∵平面,平面,∴平面.又,平面,平面,∴平面平面,又平面,∴平面.(Ⅱ)连结,取中点,连结,则,由(Ⅰ)可知平面,所以点到平面的距离与点到平面的距离相等.又是边长为的等边三角形,∴,又平面平面,平面平面,平面,∴平面,∴平面,∴为中点,∴,又,,∴∴.DC N BD M MN MN BC H AH ABC ∆3H BC AH BC ⊥ABC ⊥BCD ABC BCD BC =AH ⊂ABCAH ⊥BCD EN ⊥BCD //EN AH EN ⊄ABCAH ⊂ABC //EN ABC M N BD DC //MN BC MN ⊄ABC BC ⊂ABC //MN ABC MN EN N =MN ⊂EMN EN ⊂EMN //EMN ABC EF ⊂EMN //EF ABC DH CH G NG //NG DH //EN ABC E ABC N ABC BCD ∆2DH BC ⊥ABC ⊥BCD ABC BCD BC =DH ⊂BCD DH ⊥ABC NG ⊥ABC DH =N CD NG =3AC AB ==2BC =12ABC S BC AC ∆=⋅⋅=V V =1S NG =⋅⋅=练习2解析:(1)证明:∵D 1D ⊥平面ABCD ,, ∴D 1D ⊥BC .又AB =4,AD =2,,∴∵AD 2+BD 2=AB 2,∴AD ⊥BD .又∵AD ∥BC ,∴BC ⊥BD .又∵D 1D∩BD =D ,,,∴BC ⊥平面D 1BD ,而,∴平面D 1BC⊥平面D 1BD ; (2)解:∵D 1D ⊥平面ABCD ,∴∠D 1BD 即为直线D 1B 与底面ABCD 所成的角,即,而,∴DD 1=2.,∴BC ABCD ⊂平面3DAB π∠=BD ==1BD D BD ⊂平面11D D D BD ⊂平面1BC D BC ⊂平面16D BD π∠=BD =14C MNQ Q CMN Q BDC V V V ---==11121432C MNQ V -=⨯⨯⨯⨯=巩固练习1.解析:(Ⅰ)取PA 的中点G ,连FG ,由题可知:BF=FP ,则FG //AB FG = AB ,又CE= ED ,可得:DE//AB 且DE = AB ,∴ FG //DE 且FG = DE ,∴四边形DEFG 为平行四边形,则EF //DG且EF =DG ,DG ⊂平面PAD ;EF ⊄平面PAD ,∴ EF//平面PAD ⋯⋯⋯4分 (Ⅱ)由PD ⊥平面ABCD ,PD ⊂平面PAD ,∴ 平面PAD ⊥平面ABCD ,且交线为AD ,又底面ABCD 是矩形,∴ BA ⊥ AD ,∴BA ⊥ 平面PAD ,∴平面PAB ⊥平面PAD,其交线为PA ,又PD=AD ,G 为PA 的中点,∴DG ⊥ PA ,∴ DG ⊥平面PAB ,由(Ⅰ)知:EF // DG , ∴ EF ⊥平面PAB ⋯⋯⋯8分 (Ⅲ)由BC =1, AB =F 为PB 的中点,∴ = = = == = ⋯⋯⋯⋯12分练习2解析:(Ⅰ)证明:∵四边形ABCD 是菱形,∴. 又∵平面ABCD ,平面ABCD ,∴.又,平面,平面,∴平面, ∵平面,∴平面平面. (Ⅱ)解:1212AEF P V -AEF B V -ABE F V-ABE P V -21PD S ABE ⋅⋅⋅∆3121112213121⋅⋅⋅⋅⋅122AC BD ⊥PA ⊥BD ⊂≠PA BD ⊥PA AC A =PA ⊂≠PAC AC ⊂≠PAC BD ⊥PAC BD ⊂≠PBD PBD ⊥PAC BCD 11=2232C BDM M V V --=⨯⨯⨯。
立体几何中的体积计算

立体几何中的体积计算立体几何是研究物体在三维空间中的形状和大小的学科,而体积是一个物体所占据的三维空间的大小。
体积的计算方法根据不同的立体体形有所不同。
本文将介绍几种常见立体几何体的体积计算方法。
1. 立方体的体积计算立方体是最简单的立体几何体之一,其六个面都是正方形。
要计算立方体的体积,只需知道其一个边长。
假设立方体的边长为a,那么立方体的体积V可以通过公式V=a^3来计算,其中^表示乘方运算。
2. 长方体的体积计算长方体是另一种常见的立体几何体,其六个面都是矩形。
要计算长方体的体积,需知道其三个边长。
假设长方体的长、宽、高分别为a、b、c,那么长方体的体积V可以通过公式V=a*b*c来计算。
3. 圆柱体的体积计算圆柱体是一个由一个圆面和一个平行于圆面的矩形侧面围成的立体几何体。
要计算圆柱体的体积,需知道其底面圆的半径r和高h。
假设圆柱体的底面圆半径为r,高为h,那么圆柱体的体积V可以通过公式V=π*r^2*h来计算,其中π是一个常数,约等于3.14159。
4. 圆锥体的体积计算圆锥体由一个圆锥面和一个与圆锥面共享圆的平行截面围成。
要计算圆锥体的体积,需知道其底面圆的半径r和高h。
假设圆锥体的底面圆半径为r,高为h,那么圆锥体的体积V可以通过公式V=1/3*π*r^2*h来计算。
5. 球体的体积计算球体是一个由所有到球心距离不超过半径的点所组成的立体几何体。
要计算球体的体积,只需知道其半径r。
假设球体的半径为r,那么球体的体积V可以通过公式V=4/3*π*r^3来计算。
6. 锥台的体积计算锥台是一个由两个平行且共享圆的平面以及连接两个圆的曲面组成的立体几何体。
要计算锥台的体积,需知道其上底圆的半径R、下底圆的半径r以及高h。
假设锥台的上底圆半径为R,下底圆半径为r,高为h,那么锥台的体积V可以通过公式V=1/3*π*(R^2+r^2+R*r)*h来计算。
通过以上介绍,我们了解了几种常见立体几何体的体积计算方法。
(完整)立体几何(文科)

立体几何(文科)1、如图1。
4所示四棱锥P。
ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=错误!,M为BC上一点,且BM=错误!.(1)证明:BC⊥平面POM;(2)若MP⊥AP,求四棱锥P。
ABMO的体积.516图42、四面体ABCD及其三视图如图14所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H。
图1。
4(1)求四面体ABCD的体积;错误!.(2)证明:四边形EFGH是矩形.3、如图1。
5,在三棱柱ABC .A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.图1。
5(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥E。
ABC的体积.错误!.4、如图1.3,四棱锥P。
ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=错误!,三棱锥PABD的体积V=错误!,求A到平面PBC的距离.错误!图13。
5、如图16所示,三棱锥A . BCD 中,AB ⊥平面BCD ,CD ⊥BD 。
(1)求证:CD ⊥平面ABD ;(2)若AB =BD =CD =1,M 为AD 中点,求三棱锥A MBC 的体积.错误!图1。
66、如图1。
4所示,△ABC 和△BCD 所在平面互相垂直,且AB =BC =BD =2,∠ABC =∠DBC =120°,E ,F ,G 分别为AC ,DC ,AD 的中点.(1)求证:EF ⊥平面BCG ;(2)求三棱锥D 。
BCG 的体积.错误!。
7、如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA ==1A(Ⅰ) 证明: A 1BD // 平面CD 1B 1; (Ⅱ) 求三棱柱ABD -A 1B 1D 1的体积.8、如图,在四棱锥P ABCD -中,PD ABCD ⊥面,//AB DC ,AB AD ⊥,5BC =,3DC =,4AD =,60PAD ∠=。
专题:立体几何大题中有关体积求法

专题:立体几何大题中有关体积的求法角度问题、距离问题、体积问题是立体几何的三大基本问题。
以下是求体积的一些常用方法及有关问题。
一公式法1正三棱柱的侧面展开图是边长分别为2和4的矩形,则它的体积为 _________2如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为().A. 4、_3B. 4C. 2.3D. 2练习3.一个几何体的俯视图是一个圆,用斜二侧画法画出正视图和俯视图都是边长为6和4的平行四边形,则该几何体的体积为________________ .4.一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为________ ▲_______ [来二、转换法当所给几何体的体积不能直接套用公式或套用公式时某一量(底面积或高)不易求出时,可以转换一下几何体中有关元素的相对位置进行计算求解,该方法尤其适用于求三棱锥的体积.例在边长为a的正方体ABCD -ABQiD中,M , N P分别是棱1 3A B, A1D1 A 上的点,且满足AM =—AB- AN =2ND1, AP=—AA (如2 4图1),试求三棱锥A -MNP的体积.三、割补法分割法也是体积计算中的一种常用方法,在求一些不规则的几何体的体积以及求两个几何体的体积之比时经常要用到分割法.7例已知三棱锥P - ABC ,其中PA =4, PB二PC =2,•_APB = - APC = - BPC = 60 求:三棱锥P - ABC 的体积。
C8练习如图2,在三棱柱ABC - AB。
中,E, F分别为AB, AC的中点,平面EB1C1F将三棱柱分成两部分,求这两部分的体积之比9练习。
如图(3),是一个平面截长方体的剩余部分,已知AB =4,BC =3,AE =5,BF =8,CG =12,求几何体ABCD - EFGH的体积。
10四面体S - ABC的三组对棱分别相等,且依次为 2 5^13,5,求四面体S - ABC的体积。
立体几何中求体积的几种方法

立体几何中求体积的几种方法
立体几何中求体积的方法:
1、分割法,一般的考试题目不会给你一个简单的长方体,正方体,圆等等一些能套公式就能求出体积,而是弄一些多面体,让你求它的体积。
分割法,就是把多面体分割成几个我们常见的立体,然后求各个分割体的体积,最后相加就能得出所要求的体积了。
2、补形法,多面体加以拼补,把它拼成我们常见的立体,求出该立体的体积后,把补上去的各个立体的体积算出来,相减就能得出所要求的体积了。
3、等体积法,这个方法举例比较好说明,比如,求四面体P-ABC的体积,但是顶点P到面ABC的距离不好求(即高h),然而我们把顶点和底面换一下,换成四面体A-PBC,此时,定点A到面PBC的距离可以很容易就得到(AP丄面PBC,即AP就是高),这样四面体A-PBC的体积就很容易求出来了。
显然,四面体P-ABC和四面体A-PBC是同一个立体,因此,求出四面体A-PBC的体积也是求出四面体P-ABC的体积。
立体几何5----体积问题

VBACE BE VD ACE ED
x 2
2
2
22
22
2
22
22
8、如图,四棱锥 P ABCD 的底面 ABCD是边长为 2 的菱形, BAD=60 , 已知 PB PD 2 , PA= 6 (1)求证: PC BD (2)若 E 为 PA 中点,求三棱锥 P BCE 的体积.
VPBCE VABCE
VS ABCD
3 2
VS
ABD
=
3 2
VD
SAB
VGEFB VH EFB VEHFB
E
G
H F
1 VGEFB 2 VG EBM
G
H F
E
1
题型四、不规则或高难求的几何体的体积求法——割(补)法
10、如图,在五面体 ABCDEF 中,四边形 ABCD是边长为 2 的正方形,
EF ∥平面 ABCD, EF 1, FB FC, BFC 90 , AE 3 , H 是 BC 的中点.
3.
C1
选择合适的底面
A1
找过顶点与底面垂直的平面
在平面内作高
A
B1
C G
D
B
面积比
lC D
C
C
D
A
BA B D
l //AB
B为AD中点
SABC : SABD = __
SABC : SBCD = __
A
B
AD:DC 1: 2
SABD : SBCD = ___
SABD : SABC = ___
体积比:
(1)证明:平面 ACD⊥平面 ABC ; (2) Q 为线段 AD 上一点, P 为线段 BC 上一点, 且 BP DQ 2 DA,求三棱锥 Q ABP 的体积.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
C
D
图2
B A
C
D 图1
1
C
1B
1
A
1D
C
B
A
D
F
E
瑞泉中学2016级文科23班立体几何 证明与体积求法专项补丁训练
张振荣 2016.3.25
1,(本小题满分14分)如图(1),ABC ∆是等腰直角三角形,4AC BC ==,E 、F 分别为AC 、AB 的中点,将AEF ∆沿EF 折起, 使A '
在平面BCEF 上的射影O 恰为EC 的中点,得到图(2). (Ⅰ)求证:EF A C '⊥;
(Ⅱ)求三棱锥BC A F '-的体积.
2,(本小题满分13分)
如图1,在直角梯形ABCD 中,90ADC ∠=︒,//CD AB ,4,2AB AD CD ===.将ADE ∆沿AC 折起,使平面
ADE ⊥平面ABC ,得到几何体D ABC -,如图2所示.
(Ⅰ) 求证:BC ⊥平面ACD ; (Ⅱ) 求几何体D ABC -的体积. 3,(本小题满分14分)、已知几何体1111ABCD A B C D -的直观图如图所示,其三视图中主视图是长边为3的矩形,
左视图是边长为2有一个角等于60°的菱形。
(1)求证平面1AD C ⊥平面11A DCB (2)求四棱锥1111D A B C D -的体积
4.(本小题满分12分)
在棱长为1的正方体1111ABCD A B C D -中,,,,E F G H 分别是棱1111,,,AB CC D A BB 的中点. (1)证明://FH 平面1A EG ; (2)证明:AH EG ⊥; (3)求三棱锥1A EFG -的体积.
5.(本小题满分14分)
如图,已知三棱锥A-BPC 中,AP ⊥PC, AC ⊥BC , M 为AB 中点,D 为PB 中点,且△PMB 为正三角形。
(Ⅰ) 求证:DM ∥平面APC :(Ⅱ) 求证:平面ABC ⊥平面APC ; (Ⅲ) 若BC=4,AB=20,求三棱锥D-BCM 的体积.
6.(本小题满分12分)在棱长为a 的正方体1111ABCD A B C D -中,E 是线段11AC 中点,AC BD F = .
(Ⅰ) 求证:CE ⊥BD ;(Ⅱ) 求证:CE ∥平面1A BD ; (Ⅲ) 求三棱锥1D A BC -
的体积.
3
2
2
A 1
B 1
A
D C
B D 1
C 1
俯视图
左视图
主视图
A
C A 1E F
7.(本小题满分14分)如图5,在三棱柱ABC —A 1B 1C 1中,侧棱1AA ⊥底面ABC ,AB BC ⊥,D 为AC 的中点
12, 3.A A AB BC ===
(1)求证:AB 1//平面BC 1D ;(2)求四棱锥B —AA 1C 1D 的体积。
8.(本小题满分l4分)在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2,O 为AC 和BD 的交点,过A 、C 1、B 三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD -AC 1D l ,且这个几何体的体积为10. (1)求证:OD 1∥平面BA 1C 1 (2)求棱A 1A 的长:
(3)求点D 1到平面BA 1C 1的距离.
9.(本小题满分14分) 如图,已知正方体1111ABCD A B C D -的棱长为2,E 、F 分别是11B A 、1CC 的中点,过1D 、E 、F 作平面EGF D 1交1BB 于G.. (Ⅰ)求证:EG ∥F D 1;
(Ⅱ)求二面角11C D E F --的余弦值; (Ⅲ)求正方体被平面EGF D 1所截得的几何体
11DCFD ABGEA -的体积.
10.(本小题满分14分) 如图:C 、D 是以AB 为直径的圆上两点,==AD AB 232,BC AC =,F 是
AB 上一点,且AB AF 3
1
=
,将圆沿直径AB 折起,使点C 在平面ABD 的射影E 在BD 上,已知2=CE . (1)求证:⊥AD 平面BCE ;
(2)求证://AD 平面CEF ; (3)求三棱锥CFD A -的体积.
11.(本小题满分14分)如图(1),C 是直径2AB =的圆上一点,AD 为圆O 的切线,A 为切点,ACD ∆为等边三角形,连接DO 交AC 于E ,以AC 为折痕将ACD ∆翻折到图(2)所示ACP ∆的位置,点P 为平面ABC 外的点.
(1)求证:异面直线AC 和PO 互相垂直;
(2)若F 为PC 上一点,且2PF FC =
,PO P AOF -的体积.
12、(本小题满分14分)一个多面体的直观图和三视图(主视图、左视图、俯视图)如图所示,M 、N 分别为A 1B 、B 1C 1的中点。
(Ⅰ)求该几何体的体积(Ⅱ)求证:MN ∥平面ACC 1A 1;(Ⅲ)求证:MN ⊥平面A 1BC 。
A B C D
E
F G
A 1
B 1
1
D 1
B
B。
