最新最全立体几何 文科大题复习求体积完整版.doc
立体几何求体积大题

立体几何中有关体积问题一、知识归纳一、知识归纳1、柱体体积公式:.V S h =2、椎体体积公式:1.3V S h =3、球体体积公式:343V R π=二、点到平面的距离问题二、点到平面的距离问题 求解方法:求解方法:1、几何法:等体积法求h2、向量法:、向量法: 点A 到面α的距离AB nd n•=u u u u r r r其中,n →是底面的法向量,点B 是面α内任意一点。
内任意一点。
题型分析:题型分析:1、如图,在三棱柱111ABC A B C -中,AC BC ⊥,1AB BB ⊥12AC BC BB ===,D 为AB 中点,且1CD DA ⊥(1)求证:1BB ABC ⊥平面 (2)求证:1BC ∥平面1CA D (3)(3)求三棱椎求三棱椎11-A B DC 的体积的体积2、如图,在四棱锥E ABCD -中,ADE ∆是等边三角形,侧面ADE ABCD ⊥地面,AB ∥DC ,且,且2435BD DC AD AB ====,,.(1)若F 是EC 上任意一点,求证:面BDF ADE ⊥面(2)(2)求三棱锥求三棱锥C BDE -的体积。
的体积。
3、如图,在棱长为2的正方体中,,E F 分别为1DD DB 、的中点。
的中点。
(1)求证:EF ∥平面11ABC D (2) (2)求证求证1EF B C ⊥ (2)求三棱锥1B EFC -的体积。
1A 1B 1C A DCB1A 1B 1C AECBDF1D A ECBDF4、如图,已知四棱锥P ABCD -的底面为等腰梯形,AB ∥CD ,AC BD ⊥,垂足为H ,PH 是四棱锥的高。
(Ⅰ)证明:平面PAC ⊥ 平面PBD ; (Ⅱ)若6AB =,APB ADB ∠=∠=60°,求四棱锥P ABCD -的体积。
的体积。
5、如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥;(II )设PD=AD=1,求棱锥D-PBC 的高.的高.6、如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点。
立体几何求体积专题精编版.doc
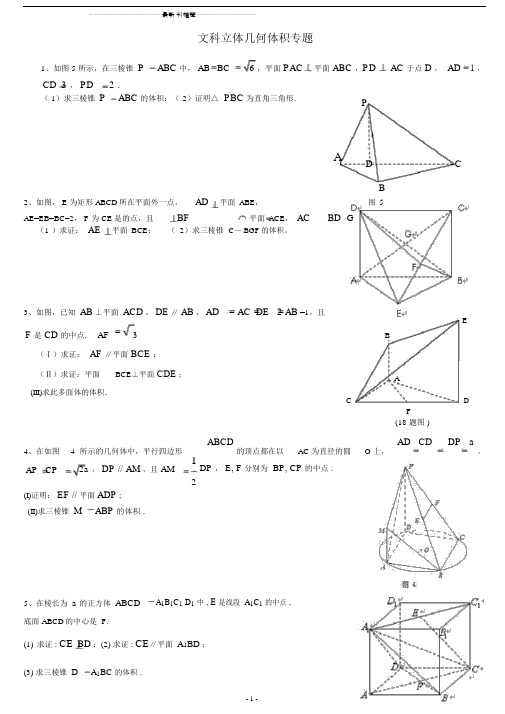
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯文科立体几何体积专题1、如图 5 所示,在三棱锥P ABC 中,AB BC 6 ,平面PAC 平面 ABC ,PD AC 于点 D , AD 1 ,CD 3 , PD 2 .( 1)求三棱锥P ABC 的体积;(2)证明△ PBC 为直角三角形.PAD CB2、如图, E 为矩形 ABCD所在平面外一点,AD平面ABE,图5AE=EB=BC=2, F 为 CE是的点,且BF平面ACE,AC BD G(1 )求证:AE平面BCE;(2)求三棱锥C— BGF的体积。
3、如图,已知AB⊥平面ACD,DE∥AB,AD AC DE 2 AB =1,且EF 是 CD 的中点.AF 3 B(Ⅰ)求证: AF ∥平面 BCE ;(Ⅱ)求证:平面BCE⊥平面CDE; A(III)求此多面体的体积.C DF(18 题图 )4、在如图 4 所示的几何体中,平行四边形ABCD的顶点都在以AC 为直径的圆O 上,AD CD DP a,AP CP 2a ,DP // AM,且 AM 1DP , E, F 分别为 BP, CP 的中点. 2(I)证明:EF //平面ADP ;(II)求三棱锥M ABP 的体积.5、在棱长为a的正方体ABCD A1B1C1 D1中,E是线段 A1C1的中点, 底面 ABCD的中心是 F.(1)求证 : CE BD;(2) 求证 : CE∥平面A1BD;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新 料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6、矩形 ABCD 中, 2AB AD ,E 是 AD 中点,沿 BE 将 ABE 折起到 A ' BE的位置,使 ''D , F 、 G 分别是 BE 、 CD 中点 .AC A ( 1)求证: A F ⊥ CD ;( 2)设 AB2,求四棱锥 A BCDE 的体积 .7 、 如 图 , 在 四 棱 锥P ABCD 中 , 底 面 是 边 长 为2 的 正 方 形 , 侧 面 PAD 底面 ABCD , 且A B C DP A P D2A ,D 若 E 、 F 分别为 PC 、 BD 的中点 .2( 1)求证: EF ∥平面 PAD ;( 2)求证:平面 PDC 平面 PAD .( 3)求四棱锥 P ABCD 的体积 V P ABCD .8、如图 , 在直三棱柱ABC A 1B 1C 1 中, AC 3 , BC 4, AB 5 , AA 1 4 ,点 D 是 AB 的中点,( 1)求证: AC BC 1 ;( 2)求证: AC 1 // 平面 CDB 1 ;( 3)求三棱锥 C 1 CDB 1 的体积。
专题立体几何大题中有关体积的求法.docx

专题:立体几何大题中有关体积的求法角度问题、距离问题、体积问题是立体儿何的三大基本问题。
以下是求体积的一•些常用方法及有关问题。
一公式法1.正三棱柱的侧面展开图是边长分别为2和4的矩形,则它的体积为___________ •2如图,某儿何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为().A. 4迟B. 4C. 2巧D. 2练习3. 一个几何体的俯视图是一个圆,用斜二侧画法画出正视图和俯视图都是边长为6和4的平行四边形,则该几何体的体积为________________ •4•一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为▲二、转换法当所给几何体的体积不能直接套用公式或套用公式吋某一量(底面积或高)不易求出吋, 可以转换一下几何体中冇关元素的相对位置进行计算求解,该方法尤其适用于求三棱锥的体积.例在边长为d的正方体ABCD-A^C^中,M, N, P分别是棱1 3A Bp 4/上的点,且满足A l M=-A lB lf fN = 2ND\, =($n2图1),试求三棱锥A.-MNP的体枳.三、割补法分割法也是体积计算中的一种常用方法,在求一些不规则的儿何体的体积以及求两个儿何体的体积之比时经常要用到分割法.7例已知三棱锥P-ABC,其中= 4, PB=PC = 2,A APB = ZAPC = ZBPC = 60°求:三棱锥P-ABC的体积。
C8练习如图2,在三棱柱ABC-AjB.C,中,E, F分别为AB, AC的中点,平而EBQF将三棱柱分成两部分,求这两部分的体积之比9练习。
如图(3 ),是一个平面截长方体的剩余部分,已知A3 = 4, BC = 3,AE = 5,BF = 8, CG = ]2,求几何体ABCD-EFGH的体积。
10四面体S-ABC的三纟fl对棱分别相等,且依次为2^5, V13,5 , 求四面体S-ABC的体积。
立体几何-文科大题求体积

ABCD图2BACD 图11C 1B1A1DCBADFE1,(本小题满分14分)如图(1),ABC ∆是等腰直角三角形,4AC BC ==,E 、F 分别为AC 、AB 的中点,将AEF ∆沿EF 折起, 使A '在平面BCEF 上的射影O 恰为EC 的中点,得到图(2). (Ⅰ)求证:EF A C '⊥;(Ⅱ)求三棱锥BC A F '-的体积.2,(本小题满分13分)如图1,在直角梯形中,,,.将沿折起,使平面平面,得到几何体,如图2所示. (Ⅰ) 求证:平面; (Ⅱ) 求几何体的体积.3,(本小题满分14分)、已知几何体1111ABCD A B C D -的直观图如图所示,其三视图中主视图是长边为3的矩形,左视图是边长为2有一个角等于60°的菱形。
(1)求证平面1AD C ⊥平面11A DCB (2)求四棱锥1111D A B C D -的体积4.(本小题满分12分)在棱长为1的正方体1111ABCD A B C D -中,,,,E F G H 分别是棱1111,,,AB CC D A BB 的中点. (1)证明://FH 平面1A EG ; (2)证明:AH EG ⊥; (3)求三棱锥1A EFG -的体积.5.(本小题满分14分)如图,已知三棱锥A-BPC 中,AP ⊥PC, AC ⊥BC , M 为AB 中点,D 为PB 中点,且△PMB 为正三角形。
(Ⅰ) 求证:DM ∥平面APC :(Ⅱ) 求证:平面ABC ⊥平面APC ; (Ⅲ) 若BC=4,AB=20,求三棱锥D-BCM 的体积.6.(本小题满分12分)在棱长为a 的正方体1111ABCD A B C D -中,E 是线段11A C 中点,AC BD F =I .(Ⅰ) 求证:CE ⊥BD ;(Ⅱ) 求证:CE ∥平面1A BD ; (Ⅲ) 求三棱锥1D A BC -的体积.ABCD 90ADC ∠=︒//CD AB 4,2AB AD CD ===ADE ∆AC ADE ⊥ABC D ABC -BC ⊥ACD D ABC -322A 1B 1AD C B D 1C 1俯视图左视图主视图A BC DA 1B 111E FG H7.(本小题满分14分)如图5,在三棱柱ABC —A 1B 1C 1中,侧棱1AA ⊥底面ABC ,AB BC ⊥,D 为AC 的中点12, 3.A A AB BC ===(1)求证:AB 1//平面BC 1D ;(2)求四棱锥B —AA 1C 1D 的体积。
(完整word版)文科立体几何平行、垂直加体积

1、在平行六面体ABCD—A1B1C1D1中,AA1=AB,AB1⊥B1C1。
求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.2、如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A 1C1⊥A1B1.求证:(1)直线DE∥平面A1C1 F;(2)平面B1D E⊥平面A1C1F。
3、如图,在正方体ABCD —A 1B 1C 1D 1中,E,F ,P,Q,M,N 分别是棱AB ,AD,DD 1,BB 1,A 1B 1,A 1D 1的中点。
求证:(1)直线BC 1∥平面EFPQ; (2)直线AC 1⊥平面PQMN 。
4、如图,ABCD 与ADEF 为平行四边形,M ,N ,G 分别是AB ,AD,EF 的中点。
(1)求证:BE∥平面DMF; (2)求证:平面BDE∥平面MNG 。
中点, 5、如图,在三棱柱111ABC A B C -中,D 是AC 的于点E .1A D ⊥平面ABC ,=AB BC ,平面1BB D 与棱11AC 交(Ⅰ)求证:1AC A B ⊥;(Ⅱ)求证:平面1BB D ⊥平面11AAC C ; (Ⅲ)求证:1B B DE ∥.EABCB 1C 1A 1D6、如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD。
求证:(1)EF∥平面ABC;(2)AD⊥AC。
7、如图①所示,已知直角△ABC,其中∠ABC=90°,D,E分别是AB,AC边上的中点,现沿DE将△ADE 翻折,使得A与平面ABC外一点P重合,得到如图②所示的几何体.(1)证明:平面PBD⊥平面BCED;(2)记平面PDE与平面PBC的交线为l,探究:直线l与BC是否平行.若平行,请给出证明;若不平行,请说明理由.8、如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(1)证明:平面AEC⊥平面BED;(2)若∠ABC=120°,AE⊥EC,三棱锥E—ACD的体积为,求该三棱锥的侧面积.9、如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD。
完整版)体积计算题

完整版)体积计算题本文档将介绍如何计算不同几何体的体积,并提供一系列实际的问题,以应用所学的体积计算知识。
通过这些实际问题的练,读者将更好地理解和掌握体积计算方法。
在几何学中,体积是一个非常重要的概念。
它代表了一个物体所占据的空间量。
计算体积不仅有助于我们理解物体的大小和形状,还可以在许多实际问题中发挥作用,如建筑设计、容量计算、物流规划等。
下面是一些常见几何体的体积计算方法:立方体的体积公式:V = a^3,其中a表示边长。
长方体的体积公式:V = lwh,其中l、w、h分别表示长、宽和高。
圆柱体的体积公式:V = πr^2h,其中r表示底面半径,h表示高度。
球体的体积公式:V = (4/3)πr^3,其中r表示半径。
圆锥体的体积公式:V = (1/3)πr^2h,其中r表示底面半径,h表示高度。
以下是一些实际应用示例,通过这些例子可以更好地理解如何应用体积计算方法:假设我们需要设计一个水箱,用来存储一定量的水。
根据需求,我们预计水箱的长、宽、高分别为3m、2m、1.5m,请计算水箱的容量。
根据长方体的体积公式:V = lwh。
代入数据:V = 3m * 2m * 1.5m = 9m^3.因此,水箱的容量为9立方米。
假设我们有一个圆桶,底面半径为1.5m,高度为2m,请计算圆桶的容量。
根据圆柱体的体积公式:V = πr^2h。
代入数据:V = π * (1.5m)^2 * 2m = 4.5πm^3.因此,圆桶的容量约为14.137m^3.本文介绍了常见几何体的体积计算方法,并通过实际应用示例演示了如何应用这些计算方法。
通过对体积计算的研究和实践,我们可以更好地理解和应用几何学的知识,以解决实际问题。
体积计算是应用数学的一个重要方面,在工程、建筑、设计等领域具有广泛的应用,读者可以通过不断练习和掌握这些计算方法,提升自己的数学和解决问题的能力。
高中数学立体几何体积复习 题集附答案

高中数学立体几何体积复习题集附答案高中数学立体几何体积复习题集附答案一、填空题1. 已知四棱锥的底面是一个边长为6cm的正方形,且侧棱长为8cm,求四棱锥的体积。
解答:四棱锥的体积公式为V = (1/3)×底面积×高。
底面积为6^2 = 36cm^2,高为8cm。
所以四棱锥的体积为V = (1/3)×36cm^2×8cm = 96cm^3。
2. 圆柱的底面半径为5cm,高为12cm,求圆柱的体积。
解答:圆柱的体积公式为V = 底面积×高。
底面积为π×5^2 = 25πcm^2,高为12cm。
所以圆柱的体积为V = 25πcm^2×12cm = 300πcm^3。
3. 正方体的体积为64cm^3,求正方体的边长。
解答:正方体的体积公式为V = 边长^3。
已知V = 64cm^3,代入公式可得:64 = 边长^3。
求解得边长 = 4cm。
4. 球的半径为10cm,求球的体积。
解答:球的体积公式为V = (4/3)π×半径^3。
已知半径为10cm,代入公式可得:V = (4/3)π×10^3。
所以球的体积为V = (4/3)π×1000 = 4000πcm^3。
二、选择题1. 下列几何体中,体积最大的是:A. 正方体的棱长为10cmB. 长方体的长、宽、高分别为6cm、8cm、10cmC. 圆柱的底面半径为5cm,高为14cmD. 球的半径为7cm解答:选项C。
计算各几何体的体积,可得:A. 正方体的体积为V = 10^3 = 1000cm^3B. 长方体的体积为V = 6cm×8cm×10cm = 480cm^3C. 圆柱的体积为V = π×5^2×14cm = 350πcm^3D. 球的体积为V = (4/3)π×7^3 = 1434πcm^3可见,C选项的体积最大。
立体几何求体积

如图,在六面体ABC-FEDG中,BG⊥平面ABC,平面ABC∥平面FEDG, AF∥BG,FE∥GD,∠FGD=90°,AB=BC=BG=2,GD=2BC,四边 形AEDC是菱形,则六面体ABC-FEDG的体积为____.
如图,连接AG,AD, 则V六面体ABC-FEDG=V四棱锥A-FEDG+V四棱锥A-BCDG=2V四棱锥A-FEDG, 由题意得,EF=2,DG=4,FG=AF=2, ∴S 梯形 FEDG=12×(2+4)×2=6, ∴V 四棱锥 A-FEDG=13×S 梯形 FEDG×AF=4, ∴V六面体ABC-FEDG=8.
∴V三棱锥F-EBC=V三棱锥C-EFB=
1 2
V = 三棱锥C=12×12V四棱锥E-ABCD=4.
∴多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=16+4=20.
球
求体积
求几何体体积的四种常用方法 (1)公式法:规则几何体直接代入公式求解. (2)等积法:如四面体的任何一个面都可以作为底面,只需选用 底面积和高都易求的形式即可. (3)补体法:将几何体补成易求解的几何体,如棱锥补成棱柱、 三棱柱补成四棱柱等. (4)分割法:将几何体分割成易求解的几部分,分别求体积.
一、公式法
例5 (1)(2021·新高考全国Ⅱ)正四棱台的上、下底面的边长分别为2,4, 侧棱长为2,则其体积为
A.20+12 3
B.28 2
C.56 3
D.28 2 3
棱台的高 h= 22-2 2- 22= 2,
下底面面积S1=16,上底面面积S2=4, 所以该棱台的体积 V=13h(S1+S2+ S1S2)
3.如图,在多面体 ABCDEF 中,已知面 ABCD 是边长为 4 的正 方形,EF∥AB,EF=2,EF 上任意一点到平面 ABCD 的距离均为 3, 求该多面体的体积.
文科立体几何大题---变换顶点求体积学生版(答案在卷尾)

文科立体几何大题-------求体积 题型一:变换顶点求体积 例题1如图,在四棱锥P -ABCD 中,PD ⊥底面ABCD ,//AB CD ,2AB =,3CD =,M 为PC 上一点,且2PM MC =.(1)求证:BM ∥平面PAD ; (2)若2AD =,3PD =,3BAD π∠=,求三棱锥P -ADM 的体积.典型题练习1.已知空间几何体ABCDE中,△BCD与△CDE均为边长为2的等边三角形,△ABC为腰长为3的等腰三角形,平面CDE⊥平面BCD,平面ABC⊥平面BCD.(Ⅰ)试在平面BCD内作一条直线,使得直线上任意一点F与E的连线EF均与平面ABC平行,并给出详细证明;(Ⅱ)求三棱锥E-ABC的体积.练习2在四棱柱ABCD —A 1B 1C 1D 1中,底面ABCD 为平行四边形,AA 1⊥平面ABCD .AB =2AD =4,3DAB π∠=. (1)证明:平面D 1BC ⊥平面D 1BD ;(2)若直线D 1B 与底面ABCD 所成角为6π,M ,N ,Q 分别为BD ,CD ,D 1D 的中点,求三棱锥C —MNQ 的体积.巩固练习1.如图示,在四棱锥P -ABCD 中,PD ⊥平面ABCD ,底面ABCD 是矩形,PD AD =,E 、F 分别CD 、PB 的中点.(Ⅰ)求证:EF ∥平面PAD ;(Ⅱ)求证:EF ⊥平面PAB ; (Ⅲ)设33==BC AB , 求三棱锥P -AEF 的体积.练习2如图,在四棱锥P -ABCD 中,PA ⊥平面ABCD ,底面ABCD 是菱形,AB =2,60BAD ∠=︒.(1)求证:平面PBD ⊥平面P AC ;(2)若PA AB =,M 为线段PC 的中点,求三棱锥C -MBD 的体积。
文科立体几何大题-------求体积题型一:变换顶点求体积例题1.解析:1.(1)法一:过作交于点,连接.∵,∴.又∵,且,∴,∴四边形为平行四边形,∴.又∵平面,平面,∴平面.法二:过点作于点,为垂足,连接.由题意,,则,又∵,,∴,∴四边形为平行四边形,∴.∵平面,平面,∴.又,∴.又∵平面,平面;∵平面,平面,;∴平面平面.∵平面,∴平面.(2)过作的垂线,垂足为.∵平面,平面,∴.又∵平面,平面,;∴平面由(1)知,平面,所以到平面的距离等于到平面的距离,即.在中,,,∴.M //MN CD PD N AN 2PM MC =23MN CD=23ABCD =//AB CD //AB MN ABMN//BM AN BM ⊄PAD AN ⊂PAD //BM PAD M MN CD ⊥N N BN 2PM MC =2DN NC =3DC =2DN =//AB DN ABND //BN AD PD ⊥ABCD DC ⊂ABCD PD DC ⊥MN DC ⊥//PD MN BN ⊂MBN MN ⊂,MBN BN MN N =AD ⊂PAD PD ⊂PAD AD PD D ⋂=//MBN PAD BM ⊂MBN //BM PAD B AD E PD ⊥ABCD BE ⊂ABCD PD BE ⊥AD ⊂PAD PD ⊂PAD AD PD D ⋂=BE ⊥PAD //BM PAD M PAD B PAD BE ABC ∆2AB AD ==3BAD π∠=BE =13P ADM M PAD PAD V V S --∆==⨯133BE ⋅=⨯典型题练习1.解析:(Ⅰ)如图所示,取中点,取中点,连结,则即为所求. 证明:取中点,连结,∵为腰长为的等腰三角形,为中点,∴,又平面平面,平面平面,平面,∴平面,同理可证平面,∴,∵平面,平面,∴平面.又,分别为,中点,∴,∵平面,平面,∴平面.又,平面,平面,∴平面平面,又平面,∴平面.(Ⅱ)连结,取中点,连结,则,由(Ⅰ)可知平面,所以点到平面的距离与点到平面的距离相等.又是边长为的等边三角形,∴,又平面平面,平面平面,平面,∴平面,∴平面,∴为中点,∴,又,,∴∴.DC N BD M MN MN BC H AH ABC ∆3H BC AH BC ⊥ABC ⊥BCD ABC BCD BC =AH ⊂ABCAH ⊥BCD EN ⊥BCD //EN AH EN ⊄ABCAH ⊂ABC //EN ABC M N BD DC //MN BC MN ⊄ABC BC ⊂ABC //MN ABC MN EN N =MN ⊂EMN EN ⊂EMN //EMN ABC EF ⊂EMN //EF ABC DH CH G NG //NG DH //EN ABC E ABC N ABC BCD ∆2DH BC ⊥ABC ⊥BCD ABC BCD BC =DH ⊂BCD DH ⊥ABC NG ⊥ABC DH =N CD NG =3AC AB ==2BC =12ABC S BC AC ∆=⋅⋅=V V =1S NG =⋅⋅=练习2解析:(1)证明:∵D 1D ⊥平面ABCD ,, ∴D 1D ⊥BC .又AB =4,AD =2,,∴∵AD 2+BD 2=AB 2,∴AD ⊥BD .又∵AD ∥BC ,∴BC ⊥BD .又∵D 1D∩BD =D ,,,∴BC ⊥平面D 1BD ,而,∴平面D 1BC⊥平面D 1BD ; (2)解:∵D 1D ⊥平面ABCD ,∴∠D 1BD 即为直线D 1B 与底面ABCD 所成的角,即,而,∴DD 1=2.,∴BC ABCD ⊂平面3DAB π∠=BD ==1BD D BD ⊂平面11D D D BD ⊂平面1BC D BC ⊂平面16D BD π∠=BD =14C MNQ Q CMN Q BDC V V V ---==11121432C MNQ V -=⨯⨯⨯⨯=巩固练习1.解析:(Ⅰ)取PA 的中点G ,连FG ,由题可知:BF=FP ,则FG //AB FG = AB ,又CE= ED ,可得:DE//AB 且DE = AB ,∴ FG //DE 且FG = DE ,∴四边形DEFG 为平行四边形,则EF //DG且EF =DG ,DG ⊂平面PAD ;EF ⊄平面PAD ,∴ EF//平面PAD ⋯⋯⋯4分 (Ⅱ)由PD ⊥平面ABCD ,PD ⊂平面PAD ,∴ 平面PAD ⊥平面ABCD ,且交线为AD ,又底面ABCD 是矩形,∴ BA ⊥ AD ,∴BA ⊥ 平面PAD ,∴平面PAB ⊥平面PAD,其交线为PA ,又PD=AD ,G 为PA 的中点,∴DG ⊥ PA ,∴ DG ⊥平面PAB ,由(Ⅰ)知:EF // DG , ∴ EF ⊥平面PAB ⋯⋯⋯8分 (Ⅲ)由BC =1, AB =F 为PB 的中点,∴ = = = == = ⋯⋯⋯⋯12分练习2解析:(Ⅰ)证明:∵四边形ABCD 是菱形,∴. 又∵平面ABCD ,平面ABCD ,∴.又,平面,平面,∴平面, ∵平面,∴平面平面. (Ⅱ)解:1212AEF P V -AEF B V -ABE F V-ABE P V -21PD S ABE ⋅⋅⋅∆3121112213121⋅⋅⋅⋅⋅122AC BD ⊥PA ⊥BD ⊂≠PA BD ⊥PA AC A =PA ⊂≠PAC AC ⊂≠PAC BD ⊥PAC BD ⊂≠PBD PBD ⊥PAC BCD 11=2232C BDM M V V --=⨯⨯⨯。
数学综合算式专项练习题立体几何中的体积计算

数学综合算式专项练习题立体几何中的体积计算在数学学科中,立体几何是一个重要的部分。
对于学生来说,掌握立体几何的知识点和计算方法,不仅可以提高数学综合能力,还可以帮助解决实际问题。
本文将重点介绍立体几何中的体积计算,通过专项练习题的形式,帮助读者掌握相关知识。
练习题一:长方体的体积计算1. 已知一个长方体的长为10cm,宽为5cm,高为8cm,求该长方体的体积。
解析:长方体的体积计算公式为V = 长 ×宽 ×高,将已知的数值代入公式计算即可。
解答:V = 10cm × 5cm × 8cm = 400cm³。
练习题二:正方体的体积计算2. 已知一个正方体的边长为6cm,求该正方体的体积。
解析:正方体的体积计算公式为V = 边长³,将已知的数值代入公式计算即可。
解答:V = 6cm³ = 216cm³。
练习题三:圆柱体的体积计算3. 已知一个圆柱体的底面半径为4cm,高度为10cm,求该圆柱体的体积。
解析:圆柱体的体积计算公式为V = π × 半径² ×高度,将已知的数值代入公式计算即可。
其中,圆周率π取3.14。
解答:V = 3.14 × 4cm² × 10cm = 125.6cm³。
练习题四:金字塔的体积计算4. 已知一个金字塔的底面为边长为6cm的正方形,高度为8cm,求该金字塔的体积。
解析:金字塔的体积计算公式为V = 底面积 ×高度 ÷ 3,将已知的数值代入公式计算即可。
解答:V = 6cm × 6cm × 8cm ÷ 3 = 96cm³。
练习题五:球体的体积计算5. 已知一个球体的半径为5cm,求该球体的体积。
圆周率π取3.14。
解析:球体的体积计算公式为V = 4/3 × π × 半径³,将已知的数值代入公式计算即可。
(完整)立体几何(文科)

立体几何(文科)1、如图1。
4所示四棱锥P。
ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=错误!,M为BC上一点,且BM=错误!.(1)证明:BC⊥平面POM;(2)若MP⊥AP,求四棱锥P。
ABMO的体积.516图42、四面体ABCD及其三视图如图14所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H。
图1。
4(1)求四面体ABCD的体积;错误!.(2)证明:四边形EFGH是矩形.3、如图1。
5,在三棱柱ABC .A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.图1。
5(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥E。
ABC的体积.错误!.4、如图1.3,四棱锥P。
ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设AP=1,AD=错误!,三棱锥PABD的体积V=错误!,求A到平面PBC的距离.错误!图13。
5、如图16所示,三棱锥A . BCD 中,AB ⊥平面BCD ,CD ⊥BD 。
(1)求证:CD ⊥平面ABD ;(2)若AB =BD =CD =1,M 为AD 中点,求三棱锥A MBC 的体积.错误!图1。
66、如图1。
4所示,△ABC 和△BCD 所在平面互相垂直,且AB =BC =BD =2,∠ABC =∠DBC =120°,E ,F ,G 分别为AC ,DC ,AD 的中点.(1)求证:EF ⊥平面BCG ;(2)求三棱锥D 。
BCG 的体积.错误!。
7、如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA ==1A(Ⅰ) 证明: A 1BD // 平面CD 1B 1; (Ⅱ) 求三棱柱ABD -A 1B 1D 1的体积.8、如图,在四棱锥P ABCD -中,PD ABCD ⊥面,//AB DC ,AB AD ⊥,5BC =,3DC =,4AD =,60PAD ∠=。
立体几何求体积方法

立体几何求体积方法宝子们,立体几何求体积可是个有趣又有点小挑战的事儿呢。
咱先来说说最基本的公式法。
对于正方体,那体积就是棱长的立方,就像一个小方块,棱长是a的话,体积V = a³,超级好记对吧。
长方体呢,体积就是长×宽×高,要是长是a,宽是b,高是c,那体积V = a×b×c,就像算一个盒子能装多少东西一样直观。
圆柱的体积也不难哦。
它的体积公式是V = πr²h,r是底面半径,h是高。
你可以想象圆柱是由好多好多同样大小的圆片堆起来的,每个圆片的面积是πr²,堆了h那么高,就得出体积啦。
还有圆锥,圆锥的体积是等底等高圆柱体积的三分之一呢。
所以圆锥体积公式就是V = 1/3πr²h。
这就像是圆锥是圆柱的小跟班,体积只有圆柱的三分之一,是不是很可爱的关系呀。
棱锥的体积计算和圆锥类似哦。
对于三棱锥、四棱锥等,它们的体积都是与它们等底等高棱柱体积的三分之一。
再来说说分割法。
有时候一个复杂的立体图形,咱们可以把它分割成几个简单的立体图形,然后分别求出体积,再把这些体积加起来就好啦。
比如说一个奇怪形状的组合体,看起来像个大怪兽,咱们把它切成几个正方体、长方体、圆锥之类的小零件,再分别计算体积,就像拆了大怪兽的零件一样,最后一加就得到总体积啦。
补形法也很有用呢。
要是遇到一个不完整的立体图形,咱们可以把它补成一个完整的、我们熟悉的立体图形,然后用完整图形的体积减去补上去那部分的体积。
就像是给一个残缺的小玩偶补上缺失的部分,然后再算出原来残缺部分的体积。
宝子们,立体几何求体积其实没那么可怕啦,只要把这些方法都掌握好,就像拥有了魔法一样,不管遇到什么立体图形,都能轻松算出它的体积哟。
最新--立体几何(文科体积部分) 精品
1.(2018重庆一模)已知三棱锥A﹣BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.(1)求证:DM∥平面APC;(2)求证:平面ABC⊥平面APC;(3)若BC=4,AB=20,求三棱锥D﹣BCM的体积.2在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.(Ⅰ)证明:PA∥平面BMQ;(Ⅱ)已知PD=DC=AD=2,求点P到平面BMQ的距离.3.(2018•北京)如图,在三棱锥P﹣ABC中,AB⊥BC,D,E分别是AB,AC的中点,且PE⊥平面ABC.求证:(1)BC∥平面PDE;(2)AB⊥平面PDE.4.(2014•福建)如图,三棱锥A﹣BCD中,AB⊥平面BCD,CD⊥BD.(Ⅰ)求证:CD⊥平面ABD;(Ⅱ)若AB=BD=CD=1,M为AD中点,求三棱锥A﹣MBC的体积.5.(2014•山东)如图,四棱锥P﹣ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=AD,E,F分别为线段AD,PC的中点.(Ⅰ)求证:AP∥平面BEF;(Ⅱ)求证:BE⊥平面PAC.6.(2014•江苏)如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.7.(2018•贵州)如图,几何体EF﹣ABCD中,CDEF为边长为2的正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,AD=2,AB=4,∠ADF=90°.(1)求异面直线DF和BE所成角的大小;(2)求几何体EF﹣ABCD的体积..(2014•南京)如图,六面体ABCDE中,面DBC⊥面ABC,AE⊥面ABC.(1)求证:AE∥面DBC;(2)若AB⊥BC,BD⊥CD,求证:AD⊥DC.9.(2014•孝感)如图,已知四棱锥P﹣ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.(Ⅰ)求证:AB∥平面PCD;(Ⅱ)求证:BC⊥平面PAC;(Ⅲ)若M是PC的中点,求三棱锥M﹣ACD的体积.10.(2014•黄山)如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2,E、F分别是AB、PD的中点.(1)求证:AF∥平面PCE;(2)求证:平面PCE⊥平面PCD;(3)求四面体PEFC的体积.11.(2014•安庆)如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.(1)求证:AB1∥平面BC1D;(2)若BC=3,求三棱锥D﹣BC1C的体积.12.(2014•吉林)在四棱锥V﹣ABCD中,底面ABCD是正方形,侧面V AD是正三角形,平面V AD⊥底面ABCD.(Ⅰ)如果P为线段VC的中点,求证:V A∥平面PBD;(Ⅱ)如果正方形ABCD的边长为2,求三棱锥A﹣VBD的体积.14.(2014•甘肃)如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.(Ⅰ)证明:PA∥平面EDB;(Ⅱ)求三梭锥A一BDP的体积.15.(2014•青岛)如图,在四棱锥E﹣ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE 的中点.(Ⅰ)求证:BE∥平面ACF;(Ⅱ)求四棱锥E﹣ABCD的体积.16.(2014•潍坊)如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.(Ⅰ)求证:AE⊥平面BCE;(Ⅱ)求证;AE∥平面BFD;(Ⅲ)求三棱锥C﹣BGF的体积.17.(2014•江门)如图,三棱柱ABC﹣A1B1C1中,侧棱垂直底面,AC⊥BC,D是棱AA1的中点,AA1=2AC=2BC=2(1)证明:C1D⊥平面BDC;(2)求三棱锥C﹣BC1D的体积.18.(2014•包头)如图,直三棱柱ABC﹣A1B1C1中,AA1=2AC=2BC,D是AA1的中点,CD⊥B1D.(1)证明:CD⊥B1C1;(2)平面CDB1分此棱柱为两部分,求这两部分体积的比.19.(2014•长春)如图,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.(1)求证:BC⊥D1E;(2)若AA1=,求三棱锥D1﹣B1CB的体积.20.(2014•濮阳)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠ADC=90°,∠BAD=120°,AD=AB=1,AC交BD于O点.(1)求证:平面PBD⊥平面PAC;(2)求三棱锥D﹣ABP和三棱锥B﹣PCD的体积之比.21.(2014•安徽)已知在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=,AB=1,AD=2,∠BAD=120°,E,G,H分别是BC,PC,AD的中点.(Ⅰ)求证:PH∥平面GED;(Ⅱ)求证:平面PAE⊥平面PDE;(Ⅲ)求三棱锥P﹣GED的体积.22.(2014•齐齐哈尔)如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在CE上,无论点F运动到何处时,总有BF⊥AE.(Ⅰ)求证:平面ADE⊥平面BCE;(Ⅱ)求三校锥的D﹣ACE体积.23.(2014•惠州)如图所示,在棱长为2的正方体ABCD﹣A1B1C1D1中,E、F分别为DD1、DB的中点.(1)求证:EF∥平面ABC1D1;(2)求证:EF⊥B1C;(3)求三棱锥的体积.24.(2014江苏)在四棱锥P﹣ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.(1)求证:PC⊥AE;(2)求证:CE∥平面PAB;(3)求三棱锥P﹣ACE的体积V.25.(2018•许昌)如图,多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AB=CD=1,,G为AD的中点.(1)求证;AC⊥CE;(2)在线段CE上找一点F,使得BF∥平面ACD,并给予证明;(3)求三棱锥V G﹣BCE的体积.。
高考文科数学复习空间几何体的表面积、体积共46页文档

16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔 积、体积
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
7、心急吃不了热汤圆。
•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
C
D
图2
B
A
C
D 图1
1
C
1B
1
A
1D
C
B
A
D
F
E
1,(本小题满分14分)如图(1),ABC ∆是等腰直角三角形,4AC BC ==,E 、F 分别为AC 、AB 的中点,将AEF ∆沿EF 折起, 使A '在平面BCEF 上的射影O 恰为EC 的中点,得到图(2). (Ⅰ)求证:EF A C '⊥;
(Ⅱ)求三棱锥BC A F '-的体积.
2,(本小题满分13分)
如图1,在直角梯形中,,,.将沿折起,使平面
平面,得到几何体,如图2所示. (Ⅰ) 求证:平面; (Ⅱ) 求几何体的体积.
3,(本小题满分14分)、已知几何体1111ABCD A B C D -的直观图如图所示,其三视图中主视图是长边为3的矩形,左视图是边长为2有一个角等于60°的菱形。
(1)求证平面1AD C ⊥平面11A DCB (2)求四棱锥1111D A B C D -的体积
4.(本小题满分12分)
在棱长为1的正方体1111ABCD A B C D -中,,,,E F G H 分别是棱1111,,,AB CC D A BB 的中点. (1)证明://FH 平面1A EG ; (2)证明:AH EG ⊥; (3)求三棱锥1A EFG -的体积.
5.(本小题满分14分)
如图,已知三棱锥A-BPC 中,AP ⊥PC, AC ⊥BC , M 为AB 中点,D 为PB 中点,且△PMB 为正三角形。
(Ⅰ) 求证:DM ∥平面APC :(Ⅱ) 求证:平面ABC ⊥平面APC ; (Ⅲ) 若BC=4,AB=20,求三棱锥D-BCM 的体积.
6.(本小题满分12分)在棱长为a 的正方体1111ABCD A B C D -中,E 是线段11A C 中点,AC
BD F =.
(Ⅰ) 求证:CE ⊥BD ;(Ⅱ) 求证:CE
∥平面1A BD ; (Ⅲ) 求三棱锥1D A BC -的体积.
ABCD 90ADC ∠=︒//CD AB 4,2AB AD CD ===ADE ∆AC
ADE ⊥ABC D ABC -BC ⊥ACD D ABC -3
2
2
A 1
B 1
A
D C B D 1
C 1
俯视图
左视图
主视图
A
C A 1E F
7.(本小题满分14分)如图5,在三棱柱ABC —A 1B 1C 1中,侧棱1AA ⊥底面ABC ,AB BC ⊥,D 为AC 的中点
12, 3.A A AB BC ===
(1)求证:AB 1//平面BC 1D ;(2)求四棱锥B —AA 1C 1D 的体积。
8.(本小题满分l4分)在长方体ABCD-A 1B 1C 1D 1中,AB=BC=2,O 为AC 和BD 的交点,过A 、C 1、B 三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD -AC 1D l ,且这个几何体的体积为10. (1)求证:OD 1∥平面BA 1C 1 (2)求棱A 1A 的长:
(3)求点D 1到平面BA 1C 1的距离.
9.(本小题满分14分) 如图,已知正方体的棱长为2,E 、F 分别是、的中点,过、E 、F 作平面交于G.. (Ⅰ)求证:∥;
(Ⅱ)求二面角的余弦值; (Ⅲ)求正方体被平面所截得的几何体
的体积.
10.(本小题满分14分) 如图:C 、D 是以AB 为直径的圆上两点,==AD AB 232,BC AC =,F 是
AB 上一点,且AB AF 3
1
=
,将圆沿直径AB 折起,使点C 在平面ABD 的射影E 在BD 上,已知2=CE . (1)求证:⊥AD 平面BCE ; (2)求证://AD 平面CEF ; (3)求三棱锥CFD A -的体积.
11.(本小题满分14分)如图(1),是直径的圆上一点,为圆O 的切线,为切点,为等边三角形,连接交于,以为折痕将翻折到图(2)所示的位置,点P 为平面ABC 外的点.
(1)求证:异面直线和互相垂直; (2)若为上一点,且,,求三棱锥的体积.
12、(本小题满分14分)一个多面体的直观图和三视图(主视图、左视图、俯视图)如图所示,M 、N 分别为A 1B 、B 1C 1的中点。
(Ⅰ)求该几何体的体积(Ⅱ)求证:MN ∥平面ACC 1A 1;(Ⅲ)求证:MN ⊥平面A 1BC 。
1111ABCD A B C D -11B A 1CC 1D EGF D 11BB EG F D 111C D E F --EGF D 111DCFD ABGEA -C 2AB =AD A ACD ∆DO AC E AC ACD ∆ACP ∆AC PO F PC 2PF FC
=PO =
P AOF
-A B C D
E
F G
A 1
B 1
1
D 1
B
B
赠送以下资料
5以内的加减法口算练习题
姓名得分
2+2= 3+2= 0+2= 0+1= 3-1= 2+1= 2+3= 1 +4= 1-0= 2+2= 0-0= 3+2= 3-1= 2-1= 2+ 2= 4-3= 3+2= 2+2= 5-4= 3-1= 0+4= 4+1 = 1+0= 0+0= 5-2= 3+2= 4-3= 2+2= 1+2 = 5-2= 1+2= 2-0= 1+2= 4+1= 2+2= 2-0 = 1-1= 2+2= 2-0= 1-0= 3+0= 4-2= 2-0= 3-0= 0+1= 4-1= 4+1= 3-1= 4-3= 2-0= 3-1= 1+3= 2-0= 1-0= 3+0= 1+2= 5-4= 1-1 = 2+0= 3-1= 2-0= 0+1= 1+4= 2+3= 2-1 = 3-1= 0+0= 2+2= 2-0= 3-1= 1+0= 1+2
= 2+2= 1+3= 5-4= 0+2= 2+3= 1-0= 5-2=
3-3= 1+2= 2-1= 3-3= 3-0= 4-4= 5-4= 2 +2= 3-2= 3-0= 3+1= 2+1= 3-3= 4-4= 2-0= 4-0= 3-2=
3-0= 4-3= 5-2= 5+0=
家长签名。
