函数与方程-高考理科数学试题
高考数学专题练习 1函数与方程思想 理 试题

高考小题专项练 训练1 函数与方程思想(推荐时间:45分钟)一、选择题1.已知向量a =(3,2),b =(-6,1),而(λa +b )⊥(a -λb ),则实数λ等于( )A .1或2B .2或-12C .2D .02.若2x+5y≤2-y+5-x,则有( ) A .x +y ≥0 B .x +y ≤0 C .x -y ≤0 D .x -y ≥03.若函数f (x )、g (x )分别为R 上的奇函数、偶函数,且满足f (x )-g (x )=e x,则有( ) A .f (2)<f (3)<g (0) B .g (0)<f (3)<f (2) C .f (2)<g (0)<f (3) D .g (0)<f (2)<f (3)4.设a >1,若对于任意的x ∈[a,2a ],都有y ∈[a ,a 2]满足方程log a x +log a y =3,这时a 的取值的集合为( ) A .{a | 1<a ≤2} B .{a | a ≥2} C .{a | 2≤a ≤3} D .{2,3}5.对任意a ∈[-1,1],函数f (x )=x 2+(a -4)x +4-2a 的值总大于零,则x 的取值范围是 ( ) A .1<x <3 B .x <1或x >3 C .1<x <2 D .x <1或x >26.f (x )是定义在R 上的以3为周期的奇函数,f (2)=0,则函数y =f (x )在区间(-1,4)内的零点个数为( )A .2B .3C .4D .57.函数f (x )=ax 2+bx +c (a ≠0)的图象关于直线x =-b2a对称.据此可推测,对任意的非零实数a ,b ,c ,m ,n ,p ,关于x 的方程m [f (x )]2+nf (x )+p =0的解集都不可能是( )A .{1,2}B .{1,4}C .{1,2,3,4}D .{1,4,16,64}8.设函数f (x )=x 3+sin x ,若0≤θ≤π2时,f (m cos θ)+f (1-m )>0恒成立,则实数m 的取值范围是( )A .(0,1)B .(-∞,0)C .(-∞,1)D.⎝⎛⎭⎪⎫-∞,12 9.若不等式ax -1x +b >0的解集为{x |-1<x <2},则不等式bx +1ax +1<0的解集是( )A .{x |12<x <1}B .{x |x <12,或x >2}C .{x |-12<x <1}D .{x |x <-1,或x >2}10.(2011·宜昌模拟)方程x 2-32x -m =0在x ∈[-1,1]上有实根,则m 的取值范围是( )A .m ≤-916B .-916<m <52C .m ≥52D .-916≤m ≤52二、填空题11.已知函数f (x )是定义在实数集R 上的不恒为零的偶函数,且对任意实数x 都有xf (x +1)=(1+x )f (x ),则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫52的值是________. 12.若关于x 的方程(2-2-|x -2|)2=2+a 有实根,则实数a 的取值范围是________.13.当x ∈(1,2)时,不等式x 2+mx +4<0恒成立,则m 的取值范围为__________.14.若y =1-sin 2x -m cos x 的最小值为-4,则m 的值为________.15.已知等差数列{a n }共有10项,其奇数项的和为15,偶数项的和为30,则它的公差d =________. 16.已知圆x 2+y 2+2x -4y +1=0关于直线2ax -by +2=0(a ,b ∈R )对称,则ab 的取值范围是____________.17.对于满足0≤p ≤4的实数p ,使x 2+px >4x +p -3恒成立的x 的取值范围是__________. 答案1.B 2.B 3.D 4.B 5.B 6.D 7.D 8.C 9.A 10.D 11.0 12.[-1,2) 13.(-∞,-5] 14.±5 15.3 16.(-∞,14]17.(-∞,-1)∪(3,+∞)。
高二数学函数与方程试题

高二数学函数与方程试题1.若函数满足,且时,,函数,则函数在区间内的零点的个数为()A.8B.9C.10D.13【答案】B【解析】函数满足知函数的周期,判断函数的零点个数,就是判断和图像的在区间交点个数,因此零点的个数为9个.【考点】函数的零点与函数图像的交点的个数.2.函数的零点必落在区间()A.B.C.D.(1,2)【答案】B【解析】要验证函数的零点存在区间,只需验证在区间有即可,经验证B符合条件.【考点】函数零点所在区间验证.3.方程x3﹣6x2+9x﹣4=0的实根的个数为()A.0B.1C.2D.3【答案】C【解析】方程x3﹣6x2+9x﹣4=0的实根的个数就是函数的零点个数.对函数求导,得,可得在为增函数,在时为减函数,又当时,当时,结合图象可知函数的零点有个,故方程有根.【考点】函数的零点,数形结合.4.已知函数(),若函数在上有两个零点,则的取值范围是()A.B.C.D.【答案】D【解析】显然当x>0时只有一个零点,所以当x≤0时有且只有一个零点,根据指数函数函数值的分布可知a的取值范围是.【考点】(1)函数的零点;(2)函数的性质.5.根据表格中的数据,可以判定函数的一个零点所在的区,则的值为()A.-1 B.0 C.1 D.2【答案】C【解析】由给出的数据,求出对应的函数值f(-1),f(0),f(1),f(2),f(3),根据零点存在性定理:函数是连续不断的,当f(a)f(b)<0时,f(x)在区间(a,b)存在零点,来判断零点所在的区间.解:因为f(-1)=0.37-1<0;f(0)=1-2<0;f(1)=2.72-3<0;f(2)=7.39-4>0;f(3)=20.09-5>0,所以f(1)f(2)<0;所以f(x)在区间(1,2)上有零点.故答案为C【考点】函数零点点评:本题考查了函数零点存在性定理的应用,求出函数在各端点值的符号是解题的关键.6.下列函数在其定义域内,既是奇函数又存在零点的是:()A.B.C.D.【答案】C【解析】函数是奇函数需满足,验证四个选项得B,C满足,当时当时,所以函数不存在零点,因此选C【考点】函数奇偶性即函数零点点评:函数满足在定义域内有,则函数是奇函数,若满足则是偶函数。
高三数学函数与方程试题答案及解析

高三数学函数与方程试题答案及解析1.已知函数,若存在唯一的零点,且,则的取值范围是A.B.C.D.【答案】C【解析】试题分析:根据题中函数特征,当时,函数显然有两个零点且一正一负; 当时,求导可得:,利用导数的正负与函数单调性的关系可得:和时函数单调递增; 时函数单调递减,显然存在负零点; 当时,求导可得:,利用导数的正负与函数单调性的关系可得:和时函数单调递减; 时函数单调递增,欲要使得函数有唯一的零点且为正,则满足:,即得:,可解得:,则.【考点】1.函数的零点;2.导数在函数性质中的运用;3.分类讨论的运用2.已知实数、、满足,,则的最大值为为_______.【答案】【解析】因为,所以,所以,所以,由,解得,故实数的最大值为.【考点】一元二次方程的根的判别式,容易题.3.给出定义:若m-<x≤m+(其中m为整数),则m叫做离实数x最近的整数,记作{x}=m,在此基础上给出下列关于函数f(x)=|x-{x}|的四个命题:①函数y=f(x)的定义域为R,值域为[0,];②函数y=f(x)在[-,]上是增函数;③函数y=f(x)是周期函数,最小正周期为1;④函数y=f(x)的图象关于直线x= (k∈Z)对称.其中正确命题的序号是________.【答案】①③④【解析】m=1时,x∈(,],f(x)=|x-1|=f1(x),m=2时,x∈(,],f(x)=|x-2|=f2(x),显然,f2(x)的图象是由f1(x)的图象右移1个单位而得,一般地,m=k时,x∈(,],f(x)=|x-k|=fk (x),m=k+1时,x∈(,],f(x)=|x-k-1|=fk+1(x),f k+1(x)的图象是由fk(x)的图象右移1个单位而得,于是可画出f(x)的图象如下:4.若函数f(x)=x3-ax2(a>0)在区间上是单调增函数,则使方程f(x)=1 000有整数解的实数a的个数是________.【答案】4【解析】令f′(x)=3x2-2ax>0,则x>或x<0.由f(x)在区间上是单调增函数知⊆,从而a∈(0,10].由f(x)=1 000得a =x-,令g(x)=x-,则g(x)在(0,+∞)上单调递增,且与x轴交于点(10,0),在同一直角坐标系中作出函数g(x)与y=a(0<a≤10)的大致图像(如图所示).当a=10时,由f(x)=1 000得x3-10x2-1 000=0.令h(x)=x3-10x2-1 000,因为h(14)=-216<0,h(15)=125>0,所以方程x3-10x2-1 000=0在区间(14,15)上存在根x0,因此从图像可以看出在(10,x]之间f(x)=1000共有4个整数解.5.已知函数f(x)=2x,x∈R.当m取何值时方程|f(x)-2|=m有一个解?两个解?【答案】两个解【解析】解:令F(x)=|f(x)-2|=|2x-2|,G(x)=m,画出F(x)的图像如图所示.由图像看出,当m=0或m≥2时,函数F(x)与G(x)的图像只有一个交点,原方程有一个解;当0<m<2时,函数F(x)与G(x)的图像有两个交点,原方程有两个解.6.设,则函数的零点位于区间()A.(-1,0)B.(0,1)C.(1,2)D.(2,3)【答案】C【解析】,选C.【考点】零点的定义.7.已知函数,若函数恰有两个不同的零点,则实数的取值范围为.【答案】【解析】,的解为,时,,当时,,从而在区间和上是减函数,在区间和上是减函数,,当时,.如图是的图象,,,方程的解就是函数的图象与直线的交点的横坐标,当或或时,有两个交点,即方程有两个解,或称有两个零点,或或.【考点】函数的零点,函数的图象与性质,直线与曲线相交.8.已知函数f(x)=||x-1|-1|,若关于x的方程f(x)=m(m∈R)恰有四个互不相等的实根x1,x2,x 3,x4,则x1x2x3x4的取值范围是________.【答案】(-3,0)【解析】f(x)=||x-1|-1|=方程f(x)=m的解就是y=f(x)的图象与直线y=m交点的横坐标,由图可知,x2=-x1,x3=2+x1,x4=2-x1,且-1<x1<0.设t=x1x2x3x4=(-2)2-4,则t=(-2)2-4,易得-3<t<0.9.对于实数a和b,定义运算“”:a b=设f(x)=(2x-1)(x-1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则x1、x2、x3的取值范围是________.【答案】【解析】由新定义得f(x)=作出函数f(x)的图象,由图可知,当0<m<时,f(x)=m(m∈R)恰有三个互不相等的实数根x1、x2、x3,不妨设x1<x2<x3,易知x2>0,且x2+x3=2×=1,∴x2x3<.令解得x=或x= (舍去),∴<x1<0,∴<x1x2x3<0.10.已知f(x)=2x,g(x)=3-x2,试判断函数y=f(x)-g(x)的零点个数.【答案】两个【解析】在同一坐标系内作出函数f(x)=2x与g(x)=3-x2的图象,两图象有两个交点,∴函数y=f(x)-g(x)有两个零点.11.关于x的方程x3-3x2-a=0有三个不同的实数解,则实数a的取值范围是________.【答案】(-4,0)【解析】由题意知使函数f(x)=x3-3x2-a的极大值大于0且极小值小于0即可,又f′(x)=3x2-6x=3x(x-2),令f′(x)=0,得x1=0,x2=2.当x<0时,f′(x)>0;当0<x<2时,f′(x)<0;当x>2时,f′(x)>0,所以当x=0时,f(x)取得极大值,即f(x)极大值=f(0)=-a;当x=2时,f(x)取得极小值,即f(x)极小值=f(2)=-4-a,所以解得-4<a<0.,12.的零点个数为()A.4B.5C.6D.7【答案】B【解析】∵,∴,图像如图所示,由图像看出与有5个交点,∴的零点个数为5个.【考点】1.函数零点问题;2.函数图像.13.设函数,集合=,设,则A.9B.8C.D.6【答案】A【解析】,注意总共只有7个根,且这些根都为正整数,任一方程的两根之和都为8,所以这些根为1、7,2、6,3、5,4.所以,.【考点】1、函数的零点;2、二次方程根与系数的关系.14.已知关于X的方程的解集为P,则P中所有元素的和可能是()A.3,6,9B.6,9,12C.9,12,15D.6,12,15【答案】B【解析】函数的图像如图所示,直线,当时,;当时,;当时,;当时,;综上可得:P中所有元素的和可能是6,9,12.【考点】1.函数图像;2.中点坐标公式.15.若函数有极值点,且,则关于的方程的不同实根个数是 .【答案】3【解析】函数有极值点,说明方程的两根为,不妨设,即是极大值点,是极小值点,方程的解为或,由于,所以是极大值,有两解,,只有一解.因此共有3解.【考点】函数的极值与方程的解.16.设方程的两个根为,则()A.B.C.D.【答案】D【解析】依题意,,,分别作出函数和函数的图像.则图像中两函数交点的横坐标即方程的两个根.由图可知,两根中一个大于1,一个大于0小于1.不妨设,则,.所以,故.【考点】函数与方程、对数函数与指数函数的图像和性质17.若为偶函数,且当时,,则的零点个数为()A.B.C.D.无穷多个【答案】C【解析】当时,,所以【考点】函数的零点18.设,(1)若的图像关于对称,且,求的解析式;(2)对于(1)中的,讨论与的图像的交点个数.【答案】(1);(2)见解析.【解析】(1)因为函数图象关于对称,故为二次函数且对称轴为∴,又,代入可求得函数解析式;(2)将问题转化为有几个解的问题,令,利用导数讨论其增减区间,当时,与的图像无交点;当时,与的图像有一个交点;当时,与的图像有两个交点.试题解析:(1)∵的图像关于对称∴为二次函数且对称轴为∴又∵∴∴(2)即即令当时∵∴即在递增当时∵∴即在递减,∵当时当时∴①当时,与的图像无交点;②当时,与的图像有一个交点;③当时,与的图像有两个交点.【考点】利用导数研究函数的单调区间、函数与方程思想、函数解析式的求法.19.函数的零点一定位于区间( )A.(1, 2)B.(2, 3)C.(3, 4)D.(4, 5)【答案】B【解析】因为,,所以,根据根的存在性定理可知,函数的零点在区间内.【考点】零点存在性定理.20.设,则函数的零点位于区间()A.(0 ,1)B.(-1, 0) C.(1, 2) D.(2 ,3)【答案】A【解析】因为,由零点存在性定理知,在内有零点,有为单调函数,故存在唯一零点,选A.【考点】零点存在定理.21.设函数(1)设,,证明:在区间内存在唯一的零点;(2) 设,若对任意,有,求的取值范围;(3)在(1)的条件下,设是在内的零点,判断数列的增减性.【答案】(1) 见解析;(2);(3)见解析.【解析】(1) 先根据零点存在性定理判断在在内存在零点,在利用导数说明函数在上是单调递增的,从而说明在区间内存在唯一的零点;(2)此问可用两种解法:第一种,当时,,根据题意判断出在上最大值与最小值之差,据此分类讨论如下:(ⅰ)当;(ⅱ)当;(ⅲ)当,综上可知,;第二种,用表示中的较大者,直接代入计算即可;(3)先设出零点,然后根据在上是递增的得出结论.试题解析:(1),时,∵,∴在内存在零点. 又当时, ,∴在上是单调递增的,所以在内存在唯一零点.(2)当时,,对任意都有等价于在上最大值与最小值之差,据此分类讨论如下:(ⅰ)当,即时, ,与题设矛盾(ⅱ)当,即时, 恒成立(ⅲ)当,即时, 恒成立.综上可知,注:(ⅱ)(ⅲ)也可合并证明如下:用表示中的较大者.当,即时,恒成立 .(3)证法一设是在内的唯一零点,,于是有又由(1)知在上是递增的,故, 所以,数列是递增数列.证法二设是在内的唯一零点则的零点在内,故,所以,数列是递增数列.【考点】1.零点存在性定理;2.利用导数判断函数单调性;3.利用函数单调性判断大小.22.定义在上的函数满足下列两个条件:⑴对任意的恒有成立;⑵当时,;记函数,若函数恰有两个零点,则实数的取值范围是()A.B.C.D.【答案】D【解析】当时,,所以,同理可得,,直线恒过定点,所以函数恰有两个零点时需满足.【考点】1.函数的解析式;2.函数的零点.23.若定义在R上的偶函数满足且时,则方程的零点个数是()A.2个B.3个C.4个D.多于4个【答案】C【解析】试题分析:函数f(x)是以2为周期的周期函数,且是偶函数,根据上的解析式,图象关于y轴对称,可以绘制上的图象,根据周期性,可以绘制上的图象,而是个偶函数,绘制其在y轴右侧图象可知两图象右侧有两个交点,根据对称性可得共有四个交点,故选B.【考点】函数与方程.24.函数所有零点的和等于( )A.6B.7.5C.9D.12【答案】C【解析】函数所有零点转化为两个函数图像的交点的横坐标,画出函数的图像,根据图像可知有6个交点,且两两关于直线对称,故所以零点的和为【考点】函数的零点.25.若函数且有两个零点,则实数的取值范围是.【答案】【解析】构造函数且,要保证两个函数图象有不同的两个交点,则需.【考点】函数的图象.26.已知函数,则关于的方程的实根的个数是___ _【答案】5【解析】根据题意,由于函数,则关于的方程,的实根的个数即为的方程的根的个数,那么结合解析式,由于,而对于,,故可知满足题意的方程的解为5个,故答案为5.【考点】函数与方程点评:主要是考查了函数与方程的根的问题的综合运用,属于中档题。
2023-2024学年高考数学一元二次函数、方程与不等式专项练习题(含答案)

2023-2024学年高考数学一元二次函数、方程与不等式小专题一、单选题1.下列命题正确的是( )A .若,则B .若,则a b >22ac bc>a b >-a b ->C .若,则D .若,则ac bc >a b>a b >a c b c->-2.若不等式的解集是,则不等式的解集是( 220ax x c ++<11(,)(,)32-∞-⋃+∞220cx x a -+≤ )A .B .11,23⎡⎤-⎢⎥⎣⎦11,32⎡⎤-⎢⎥⎣⎦C .D .[]2,3-[]3,2-3.若,且,则的最小值是( )0x >0y >21x y +=1xx y +A .B .C .2D .122+322+324.若正实数,满足,且恒成立,则实数的取值范围为( )x y 4x y xy +=234yx a a +>-a A .B .C .D .[]1,4-()1,4-[]4,1-()4,1-5.若对于任意,都有成立,则实数的取值范围是( )[],1x m m ∈+210x mx +-<m A .B .2,03⎛⎫- ⎪⎝⎭2,02⎛⎫- ⎪ ⎪⎝⎭C .D .2,03⎡⎤-⎢⎥⎣⎦2,02⎡⎤-⎢⎥⎣⎦6.已知,若关于的不等式在上恒成立,则的最小值为0a >x 31ax x +≥+()1,x ∈-+∞a ( )A .1B .2C .4D .87.若命题“”为假命题,则m 的取值范围是( )2000R,220x x mx m ∃∈+++<A .B .][(),12,-∞-⋃+∞()(),12,-∞-+∞ C .D .[]1,2-()1,2-8.设集合,.若中恰含有一个整数,{}260A x x x =+->{}210,0B x xax a =--≤>A B ⋂则实数的取值范围是( )a A .B .C .D .80,3⎛⎫⎪⎝⎭815,34⎡⎫⎪⎢⎣⎭8,3⎡⎫+∞⎪⎢⎣⎭815,34⎡⎤⎢⎥⎣⎦二、多选题9.下列说法正确的有( )A .的最小值为21x y x +=B .已知,则的最小值为1x >4211y x x =+--421+C .若正数x 、y 满足,则的最小值为323x y xy +=2x y +D .设x 、y 为实数,若,则的最大值为2291x y xy ++=3x y +221710.若正实数x ,y 满足x +y =1,且不等式有解,则实数m 的取值范围241312m mx y +<++是错误的是( )A .m <-3或m >B .-3<m <3232C .m ≤-3或m ≥D .-3≤m ≤323211.已知关于的不等式的解集为或,则下列结论中,正确结论x 20ax bx c ++≥{|3x x ≤}4x ≥的序号是( )A .0a >B .不等式的解集为0bx c +<{}4|x x <-C .不等式的解集为或20cx bx a -+<1|4x x ⎧<-⎨⎩13x ⎫>⎬⎭D .0a b c ++>12.若,,,则下列不等式对一切满足条件的,恒成立的是( )0a >0b >2a b +=a b A .B .1ab ≤2a b +≤C .D .222a b +≥112a b+≥三、填空题13.已知关于x 一元二次方程有两个实根,,(1)若比3大,比3240x x a -+=1x 2x 1x 2x 小,则a 的取值范围是 ;(2)把写成用含a 表达式为 .12x x -14.已知都是实数,一元二次方程有两个非零实根,且,则,,a b c 20ax bx c ++=12,x x 2b c == .1211+x x 15.已知函数,当时,恒成立,则的最大值为.()222=+-b a f x ax x []1,1x ∈-()12f x ≥-a b +16.中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有一个三角形,边长分别为a ,b ,c ,三角形的面积S 可由公式求得,其中p 为三角形()()()S p p a p b p c =---周长的一半,这个公式也被称为海伦—秦九韶公式,现有一个三角形的边长满足,5a b +=,则此三角形面积的最大值为.3c =答案:1.D【分析】根据不等式的性质,令,可以判断A 的真假;由不等式的性质3,可以判断0c =B ,C 的真假;由不等式的性质1,可以判断D 的真假,进而得到答案.【详解】当时,若,则,故A 错误;0c =a b >22ac bc =若,则,故B 错误;a b >-a b -<若,当时,则;当时,则,故C 错误;ac bc >0c >a b >0c <a b <若,则,故D 正确a b >a c b c ->-故选:D 2.C【分析】依题意和是方程的两个实数根,利用韦达定理得到方程组13-12220ax x c ++=,即可求出,再解一元二次不等式即可.112321132a c a ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩12,2a c =-=222120x x --≤【详解】因为不等式的解集是:,220ax x c ++<11(,)(,)32-∞-⋃+∞所以和是方程的两个实数根,13-12220ax x c ++=由,解得:,112321132a ca ⎧-+=-⎪⎪⎨⎪-⨯=⎪⎩12,2a c =-=故不等式,即为,220cx x a -+≤222120x x --≤解不等式,得:,260x x --≤23x -≤≤所求不等式的解集是.[]23-,故选:C .3.A【分析】利用基本不等式可得答案.【详解】因为,且,0x >0y >21x y +=所以,1121222221++=++=++≥⨯=+x x x xx y x y x y x y x y y y当且仅当时等号成立,221,12x y =-=-故选:A.4.B【分析】根据题意,结合基本不等式的运算,由系数“1”的妙用可得,然后求解不等44yx +≥式,即可得到结果.【详解】因为正实数,满足,所以,x y 4x y xy +=411y x +=则,144422244444y y y x y xx x x y x y x y ⎛⎫⎛⎫+=++=++≥+⋅= ⎪ ⎪⎝⎭⎝⎭当且仅当时,即时,等号成立,此时取得最小值4,44411y x x y y x ⎧=⎪⎪⎨⎪+=⎪⎩2,8x y ==因为恒成立,所以,解得.234yx a a +>-243a a >-14a -<<实数的取值范围为.a ()1,4-故选:B 5.B【分析】利用一元二次函数的图象与性质分析运算即可得解.【详解】由题意,对于都有成立,[],1x m m ∀∈+2()10f x x mx =+-<∴,解得:,()()()()2221011110f m m m f m m m m ⎧=+-<⎪⎨+=+++-<⎪⎩202m -<<即实数的取值范围是.m 2,02⎛⎫- ⎪ ⎪⎝⎭故选:B.6.C【分析】利用基本不等式求解.【详解】因为,,1x >-10x +>所以,()1121121111a aax x x a x x x +=++-≥+⋅-=-+++当且仅当,即时,取得等号,11ax x +=+1x a =-所以有最小值为,1ax x ++21a -因为不等式在上恒成立,31ax x +≥+()1,x ∈-+∞所以,解得,所以的最小值为4,213a -≥4a ≥a 故选:C.7.C【分析】由题意结合命题和它的否定的真假性关系,以及一元二次不等式恒成立问题的充要条件即可求解.【详解】由题意命题“”为真命题,2000R,220x x mx m ∀∈+++≥所以当且仅当,()()22442420m m m m ∆=-+=--≤解得,即m 的取值范围是.12m -≤≤[]1,2-故选:C.8.B【分析】求出A 中的不等式的解集确定出A ,由A 与B 交集中恰有一个整数,求出的范围a 即可.【详解】解:,因为函数图象的对称{}{}26023A x x x x x x =+->=><-或()21f x x ax =--轴为直线,,根据对称性可知,要使中恰含有一个整数,02ax =>()3380f a -=+>A B ⋂则这个整数为3,所以有且,即,即,所以实数的取()30f ≤()40f >8301540a a -≤⎧⎨->⎩83154a a ⎧≥⎪⎪⎨⎪<⎪⎩a 值范围为.815,34⎡⎫⎪⎢⎣⎭故选:B 9.BCD【分析】利用基本不等式一一计算即可.【详解】显然当时,,故A 错误;=1x -102x y x +==<原式可化为:,()()44211221142111y x x x x =-++≥-⋅+=+--当且仅当即时取得等号,故B 正确;()4211x x -=-21x =+由,1223133x y xy y x +=⇒+=所以,()12225225222333333333x y x y x y x y y x y x y x ⎛⎫+=++=++≥⋅+= ⎪⎝⎭当且仅当即时取得等号,故C 正确;2233x yy x =1x y ==由,()()22225591315143131212x y xy x y xy x y x y ++=⇒+=+=+⨯⨯⨯≤++则,当且仅当时取得等号,()27122213131277x y x y +≤⇒+≤=2137x y ==故D 正确.故选:BCD 10.BCD【分析】使不等式有解,大于的最小值,根据题意先利241312m m x y+<++232m m+411x y ++用基本不等式求的最小值,再解不等式求m 的取值范围.411x y ++【详解】因为正实数x ,y 满足,所以,1x y +=(1)2x y ++=则=,411x y ++)1=44[2(1111(5)](211)y x y x x y y x ≥++++++++1119(52)=(54)22241x y y x +⋅+++=当且仅当,即时等号成立.411y x x y +=+1323x y ⎧=⎪⎪⎨⎪=⎪⎩因为不等式有解,所以,241312m m x y+<++23922m m +>即,,239022m m +->0()3)(32m m +>-解得或.3m <-32m >故选:BCD.11.AD【分析】根据不等式的解集,即可判断A 项;根据三个二次之间的关系,结合韦达定理可得出,进而代入不等式,化简、求解不等式,即可判断B 、C 、D 项.712b a c a =-⎧⎨=⎩【详解】对于A 项,由不等式的解集范围为两边,即可得出二次函数开口向上,即,0a >故A 项正确;对于B 项,由已知可得,3、4即为的两个解.20ax bx c ++=由韦达定理可得,,解得,34712ba c a ⎧-=+=⎪⎪⎨⎪=⎪⎩712b ac a =-⎧⎨=⎩代入可得.7120ax a -+<又,所以,所以解集为,故B 项错误;0a >127x >12|7x x ⎧⎫>⎨⎬⎩⎭对于C 项,由B 知,,,,7b a =-12c a =0a >代入不等式可得,21270ax ax a ++<化简可得,212710x x ++<解得,1134x -<<-所以,不等式的解集为,故C 项错误;20cx bx a -+<11|34x x ⎧⎫-<<-⎨⎬⎩⎭对于D 项,由已知可得,当时,有,故D 项正确.1x =71260a b c a a a a ++=-+=>故选:AD.12.ACD【分析】分别根据基本不等式即可求出.【详解】,当且仅当时取等号,故A 成立;2()12a b ab +≤=1a b ==假设,则,则,与已知矛盾,故B 不成立;2a b +≤22a b ab ++≤0ab ≤,当且仅当时取等号,故C 成立;2222()242()4222a b a b a b ab ++=+-≥-⨯=-=1a b ==,由A 可得,当且仅当时取等号,故D 成立.112a b a b ab ab ++==1122a b ab +=≥1a b ==故选:ACD .13.且3a <164a -4a ≤【分析】(1)设,则由题意可得,由此求得a 的范围;()24ax x x f =-+()330f a =-<(2)用韦达定理即可求解;【详解】(1)设,因为的图象是开口向上的抛物线,()24ax x x f =-+()24ax x x f =-+又一元二次方程有两个实根,,且 比3大,比3小,240x x a -+=1x 2x 1x 2x 所以,求得,()330f a =-<3a <(2)由关于x 一元二次方程有两个实根、,且,240x x a -+=1x 2x 1640a ∆=-≥所以,,且,得,124x x +=12x x a =4a ≤()21212124164x x x x x x a-=+-=-故;且3a <164a -4a ≤14.2-【分析】由根与系数关系得,再由及已知即可求值.1212,b c x x x x a a +=-=12121211x x x x x x ++=【详解】由题设,且,0a ≠1212,b cx x x x a a +=-=而,,则.12121211x x b x x x x c ++==-2b c =12112x x +=-故2-15.2【分析】将函数化简可得,结合题目要求的最大值,故考虑()2122x f x a x b⎛⎫=-+⋅ ⎪⎝⎭a b +,得出关于的不等式,进而取特殊值判断是否满足满足取等条件求解即可.2122xx -=a b +【详解】函数,对恒成立,令()221122222b a x f x ax x a x b ⎛⎫=+-=-+⋅≥- ⎪⎝⎭[]1,1x ∈-,则或,故,得,当时,2122xx -=12x =-1x =112442a b f ⎛⎫-=--≥- ⎪⎝⎭2a b +≤24,33a b ==满足,则的最大值为2.()2222121113333222f x x x x ⎛⎫=+-=+-≥-⎪⎝⎭a b +故216.3【分析】计算出,得到,由基本不等式求出.4p =24S ab =-243S ab =-≤【详解】因为,,所以,5a b +=3c =53422a b c p +++===故,()()()()()()44443244216424S a b a b a b ab ab =---=--=-++=-因为,当且仅当时,等号成立,()22544a b ab +≤=52a b ==故,25242434S ab =-≤⨯-=故3。
函数与方程试题及解答

函数与方程试题及解答1. 函数题(1)已知函数f(x) = x^2 - 4x + 3,求f(2)的值。
解答:将x = 2代入函数f(x),得到f(2) = 2^2 - 4*2 + 3 = 4 - 8 + 3 = -1。
所以f(2)的值为-1。
(2)已知函数g(x) = 3x - 5,求满足g(x) = 10的x的值。
解答:将g(x) = 10代入函数表达式,得到3x - 5 = 10。
解这个方程,将常数项移到右边,得到3x = 15。
再将方程两边除以3,得到x = 5。
所以满足g(x) = 10的x的值为5。
2. 方程题(1)解方程3x + 5 = 8。
解答:将常数项移到右边,得到3x = 8 - 5 = 3。
再将方程两边除以3,得到x = 1。
所以方程3x + 5 = 8的解为x = 1。
(2)解方程2(x - 3) = 4x + 5。
解答:先将方程两边展开,得到2x - 6 = 4x + 5。
将2x移动到右边,将4x移动到左边,得到-6 - 5 = 4x - 2x。
计算得到-11 = 2x。
再将方程两边除以2,得到x = -5.5。
所以方程2(x - 3) = 4x + 5的解为x = -5.5。
3. 综合题有一个数列,前两项为1,第三项开始,每一项是前两项的和。
求这个数列的第10项。
解答:根据数列的定义,可以得到数列的前几项为1, 1, 2, 3, 5, 8, 13, 21, 34,接下来可以继续计算得到第10项为34。
所以这个数列的第10项为34。
4. 应用题某公司销售一种产品,根据市场调研,每降低产品售价1元,销量就会增加1000件。
已知该产品售价为20元时,销量为20000件。
问降低售价至多少元时,销量可以达到40000件?解答:假设降价x元时,销量为40000件。
根据已知条件,可以得到方程20 - x = 40000/1000。
将方程简化,得到20 - x = 40。
将常数项移到右边,得到-x = 40 - 20 = 20。
高二数学函数与方程试题答案及解析

高二数学函数与方程试题答案及解析1.已知函数有零点,则的取值范围是.【答案】【解析】由题意知有解,即方程有解,可转化为直线与方程所表示的曲线有交点,用数形结合思想可得的取值范围。
【考点】函数的零点与相应的方程根的关系及数形结合思想的应用。
2.已知是定义在上且周期为3的函数,当时,,若函数在区间上有10个零点(互不相同),则实数的取值范围是.【答案】【解析】由于函数在区间上有10个零点(互不相同),因此与函数有10个不同的交点,由于函数周期为3,所以与函数在一个周期内交点个数为4,对于函数,当时,,为翻折之后抛物线的顶点,由于恒成立,要使在一个周期内的交点为4,满足,此时,函数在区间上有10个零点(互不相同).【考点】函数的交点.3.下列图象表示的函数能用二分法求零点的是()【答案】C【解析】函数在区间上存在零点,满足两条:一是函数在区间连续,二是,满足这两条的是【考点】函数的零点.4.函数的零点所在区间为()A.B.C.D.【答案】A【解析】,;则,所以函数的零点所在区间为.【考点】零点存在定理.5.已知符号表示不超过的最大整数,若函数有且仅有3个零点,则的取值范围是()A.B.C.D.【答案】C【解析】因为,有且仅有3个零点,则方程在(0,+∞)上有且仅有3个实数根,且 a>0.∵x>0,∴[x]≥0;若[x]=0,则=0;若[x]≥1,因为[x]≤x<[x]+1,∴<<1,∴<a≤1,且随着[x]的增大而增大.故不同的[x]对应不同的a值,故有[x]=1,2,3,4.若[x]=1,则有<≤1;若[x]=2,则有<≤1;若[x]=3,则有<≤1;若[x]=4,则有<≤1;综上所述,<a≤,故选C.考点:函数零点,对新概念的理解,分类整合思想6.函数的零点个数为 ( )A.0B.1C.2D.3【答案】B【解析】在同一个直角坐标系中画出的图像,易知两图像的交点只有一个,故选B。
【考点】利用函数图像判断函数零点的个数。
高三数学函数与方程试题

高三数学函数与方程试题1.函数f(x)=lnx-x-a有两个不同的零点,则实数a的取值范围是()A.(-∞,-1]B.(-∞,-1)C.[-1,+∞)D.(-1,+∞)【答案】B【解析】函数f(x)=lnx-x-a的零点,即为关于x的方程lnx-x-a=0的实根,将方程lnx-x-a=0,化为方程lnx=x+a,令y1=lnx,y2=x+a,由导数知识可知,直线y2=x+a与曲线y1=lnx相切时有a=-1,若关于x的方程lnx-x-a=0有两个不同的实根,则实数a的取值范围是(-∞,-1).故选B.2.已知函数f(x)=-x2+2ex+m-1,g(x)=x+ (x>0).(1)若g(x)=m有实数根,求m的取值范围;(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.【答案】(1)m≥2e(2)(-e2+2e+1,+∞)【解析】解:(1)∵g(x)=x+≥2=2e等号成立的条件是x=e,故g(x)的值域是[2e,+∞),因此,只需m≥2e,g(x)=m就有实数根.(2)若g(x)-f(x)=0有两个相异的实根,即g(x)与f(x)的图象有两个不同的交点,作出g(x)与f(x)的大致图象.∵f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2,∴其图象的对称轴为x=e,开口向下,最大值为m-1+e2.故当m-1+e2>2e,即m>-e2+2e+1时,g(x)与f(x)有两个交点,即g(x)-f(x)=0有两个相异实根.∴m的取值范围是(-e2+2e+1,+∞).3.设函数,,则函数的零点有个.【答案】4【解析】由得所以由,在同一坐标系内作和图像,可知有4个交点.故答案为4【考点】函数的解析式;函数与方程.4.已知函数f(x)=|ax-2|+bln x(x>0,实数a,b为常数).(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;(2)若a≥2,b=1,求方程f(x)=在(0,1]上解的个数.【答案】(1)[2,+∞).(2)0【解析】解:(1)当a=1时,f(x)=|x-2|+bln x①当0<x<2时,f(x)=-x+2+bln x,f′(x)=-1+.由条件得-1+≥0恒成立,即b≥x恒成立.所以b≥2;②当x≥2时,f(x)=x-2+bln x,f′(x)=1+.由条件得1+≥0恒成立,即b≥-x恒成立.所以b≥-2.因为函数f(x)的图像在(0,+∞)上不间断,综合①②得b的取值范围是[2,+∞).(2)令g(x)=|ax-2|+ln x-,即当0<x<时,g(x)=-ax+2+ln x-,g′(x)=-a++.因为0<x<,所以>,则g′(x)>-a++=≥0,即g′(x)>0,所以g(x)在上是单调增函数;当x>时,g(x)=ax-2+ln x-,g′(x)=a++>0,所以g(x)在上是单调增函数.因为函数g(x)的图像在(0,+∞)上不间断,所以g(x)在(0,+∞)上是单调增函数.因为g=ln-,而a≥2,所以ln≤0,则g<0,g(1)=|a-2|-1=a-3.①当a≥3时,因为g(1)≥0,所以g(x)=0在(0,1]上有唯一解,即方程f(x)=解的个数为1;②当2≤a<3时,因为g(1)<0,所以g(x)=0在(0,1]上无解,即方程f(x)=解的个数为0.5.已知函数,,的零点分别为,则()A.B.C.D.【答案】D【解析】令,,分别得,,,则分别为函数的图象与函数,,的图象交点的横坐标,在同一平面直角坐标系下作出它们的图象,易得,,,故选.【考点】函数图象、零点的概念.6.若函数f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是()A.(-2,2)B.[-2,2]C.(-1,1)D.[-1,1]【答案】A【解析】函数f(x)=x3-3x+a有3个不同的零点方程x3-3x+a=0有三个不同的根a=-x3+3x函数g(x)=a与函数F(x)=-x3+3x的图象有三个不同的交点∵F′(x)=-3x2+3=-3(x2-1)=-3(x-1)(x+1)∴即F(x)在x=1处取得极大值2,在x=-1处取得极小值-2∵直线g(x)=a与函数F(x)=-x3+3x的图象有三个不同的交点∴a∈(-2,2)7.已知二元一次方程组的增广矩阵是,若该方程组无解,则实数的值为___________.【答案】【解析】二元一次方程组的增广矩阵就是把方程组中两个方程的未知数的系数及常数项分别对应的写成一行形成的矩阵.当然时,该方程组是有解的,时,该方程组无解等价于,解得.【考点】方程组的增广矩阵及方程组解的判定.8.方程的实数解的个数为___________.【答案】【解析】由题意可令函数和,分别作图如下,不难发现它们有三个交点,则方程有三个实数解.【考点】1.函数的图象;2.函数与方程的关系9.若、是方程,的解,函数,则关于的方程的解的个数是()A.B.C.D.【答案】C【解析】由题意知,、是方程,的实数根,作出函数,与函数的图象如下图所示,则函数与函数交于点,函数与函数交于点,由于函数与函数关于直线对称,且直线与垂直,且交于点,故点、也关于直线对称,且其中点为点,因此,当时,,解方程,即,解得或;当时,,解方程,故关于的方程的实根个数为,故选C.【考点】1.函数的零点;2.函数的图象;3.分段函数10.设,(1)若的图像关于对称,且,求的解析式;(2)对于(1)中的,讨论与的图像的交点个数.【答案】(1);(2)见解析.【解析】(1)因为函数图象关于对称,故为二次函数且对称轴为∴,又,代入可求得函数解析式;(2)将问题转化为有几个解的问题,令,利用导数讨论其增减区间,当时,与的图像无交点;当时,与的图像有一个交点;当时,与的图像有两个交点.试题解析:(1)∵的图像关于对称∴为二次函数且对称轴为∴又∵∴∴(2)即即令当时∵∴即在递增当时∵∴即在递减,∵当时当时∴①当时,与的图像无交点;②当时,与的图像有一个交点;③当时,与的图像有两个交点.【考点】利用导数研究函数的单调区间、函数与方程思想、函数解析式的求法.11.已知函数(为常数,为自然对数的底数)的图象在点处的切线与该函数的图象恰好有三个公共点,则实数的取值范围是【答案】【解析】函数在点处的切线的方程为,因此原条件转化为直线与曲线有两个公共点,即方程有两个小于1的根,设,则有,解得实数的取值范围是实数的取值范围是【考点】导数的几何意义、函数与方程、一元二次方程根的分布.12.下列几个命题:①方程有一个正实根,一个负实根,则;②函数是偶函数,但不是奇函数;③设函数定义域为R,则函数与的图象关于轴对称;④一条曲线和直线的公共点个数是,则的值不可能是.其中正确的有_______________.【答案】①④【解析】方程有一个正实根,一个负实根,则当时,,故,故①正确;对于②,函数化为,是常函数,且其既为偶函数也为奇函数,故②错;对于③,与的图象对称轴为,故③错;对于④,和直线的公共点个数可以是不可能是,故④正确.答案为:①④.【考点】函数与方程、函数的奇偶性、函数的对称性.13.“函数在上存在零点”的充要条件是 .【答案】或【解析】函数在上存在零点等价于直线在上与轴有交点,则或,即或.【考点】函数的零点,充要条件.14.若函数在上有两个零点,则实数的取值范围是________.【答案】【解析】函数在上有两个零点即直线与函数的图象有两个交点,,所以在是减函数,在上是增函数,,所以实数的取值范围是.【考点】函数零点、函数的最值.15.设函数,则其零点所在的区间为()A.(-1,0)B.(0,1)C.(1,2)D.(2,3)【答案】C【解析】因为,,,,,且,所以,函数的零点在区间(1,2)内.【考点】函数零点的判定16.若方程在[1,4]上有实数解,则实数的取值范围是( )A.[4,5]B.[3,5]C.[3,4]D.[4,6]【答案】A【解析】,解得.【考点】根的分布.17.若定义在R上的偶函数满足且时,则方程的零点个数是()A.2个B.3个C.4个D.多于4个【答案】C【解析】试题分析:函数f(x)是以2为周期的周期函数,且是偶函数,根据上的解析式,图象关于y轴对称,可以绘制上的图象,根据周期性,可以绘制上的图象,而是个偶函数,绘制其在y轴右侧图象可知两图象右侧有两个交点,根据对称性可得共有四个交点,故选B.【考点】函数与方程.18.定义在上的偶函数,满足,,则函数在区间内零点的个数为()A.个B.个C.个D.至少个【答案】D【解析】∵是定义在上的偶函数,且周期是3,,∴,即.∴,,所以方程在内,至少有4个解,选D.【考点】函数的性质,函数的零点.19.若是函数的两个零点,且,则的最小值是 .【答案】【解析】因为是函数的两个零点,所以,,.【考点】函数零点问题.20.根据下表中的数据,可以判断函数的一个零点所在区间为,则=01230.37A.2 B.1 C.0 D.-1【答案】B【解析】由表可知,故,故选B.【考点】本题考查了零点存在性定理点评:熟练掌握零点的概念及零点存在性定理是解决此类问题的关键,属基础题21.已知函数,,则函数的零点个数是A.4B.3C.2D.1【解析】根据题意,由于函数,那么可知函数的零点,即为f(f(x)+1=0的解得个数,因为结合图像可知,满足f(f(x)=-1,则可知f(x)=-2,或者f(x)=,因此可知满组每个方程的解有2个,则可知解有4个,故选A.。
2020年高考浙江版高考理科数学 2.7 函数与方程
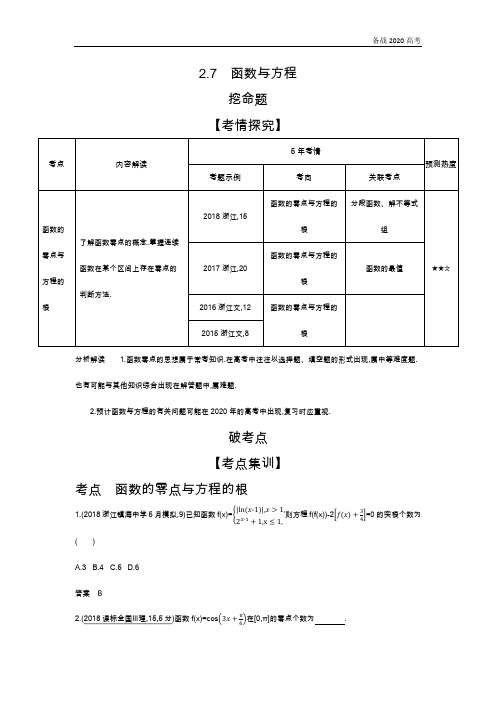
2.7 函数与方程挖命题【考情探究】分析解读 1.函数零点的思想属于常考知识.在高考中往往以选择题、填空题的形式出现,属中等难度题.也有可能与其他知识综合出现在解答题中,属难题.2.预计函数与方程的有关问题可能在2020年的高考中出现,复习时应重视.破考点【考点集训】考点函数的零点与方程的根1.(2018浙江镇海中学5月模拟,9)已知函数f(x)=--则方程f(f(x))-2=0的实根个数为( )A.3B.4C.5D.6答案B2.(2018课标全国Ⅲ理,15,5分)函数f(x)=cos在[0,π]的零点个数为.答案 33.(2018天津理,14,5分)已知a>0,函数f(x)=若关于x的方程f(x)=ax恰有2个互异的实--数解,则a的取值范围是.答案(4,8)炼技法【方法集训】方法1 判断函数零点所在区间和零点的个数的方法1.(2018浙江新高考调研卷三(杭州二中),5)函数f(x)=ln x-x|x-e|的零点的个数是( )A.0B.1C.2D.3答案C2.(2017浙江镇海中学模拟卷三,9)已知x1,x2为函数f(x)=(x2+ax+b)·e x+c的极值点(其中a,b,c为实常数).若f(x1)=x1<x2,则关于x的方程f2(x)+(a+2)·f(x)+a+b=0的不同实根的个数为( )A.1B.2C.3D.4答案C方法2 函数零点的应用(2017浙江名校协作体,17)设函数f(x)=x2-2ax+15-2a,x∈(0,+∞)的两个零点分别为x1,x2,且在区间(x1,x2)上恰好有两个正整数,则实数a的取值范围是.答案过专题【五年高考】统一命题、省(区、市)卷题组考点函数的零点与方程的根1.(2018课标全国Ⅰ理,9,5分)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )A.[-1,0)B.[0,+∞)C.[-1,+∞)D.[1,+∞)2.(2017课标全国Ⅲ理,11,5分)已知函数f(x)=x2-2x+a(e x-1+e-x+1)有唯一零点,则a=( )A.-B.C. D.1答案C3.(2017山东理,10,5分)已知当x∈[0,1]时,函数y=(mx-1)2的图象与y=+m的图象有且只有一个交点,则正实数m的取值范围是( )A.(0,1]∪[2,+∞)B.(0,1]∪[3,+∞)C.(0,]∪[2,+∞)D.(0,]∪[3,+∞)答案B4.(2015天津,8,5分)已知函数f(x)=--函数g(x)=b-f(2-x),其中b∈R.若函数y=f(x)-g(x)恰有4个零点,则b的取值范围是( ) A.∞ B.-∞C. D.答案D5.(2015北京,14,5分)设函数f(x)=---①若a=1,则f(x)的最小值为;②若f(x)恰有2个零点,则实数a的取值范围是.答案①-1 ②∪[2,+∞)6.(2015湖北,12,5分)函数f(x)=4cos2cos--2sin x-|ln(x+1)|的零点个数为.教师专用题组考点函数的零点与方程的根1.(2015安徽,2,5分)下列函数中,既是偶函数又存在零点的是( )A.y=cos xB.y=sin xC.y=ln xD.y=x2+1答案A2.(2017江苏,14,5分)设f(x)是定义在R上且周期为1的函数,在区间[0,1)上, f(x)=∈其中集合D=-∈,则方程f(x)-lg x=0的解的个数是.答案83.(2015江苏,13,5分)已知函数f(x)=|ln x|,g(x)=--则方程|f(x)+g(x)|=1实根的个数为.答案 44.(2015湖南,15,5分)已知函数f(x)=若存在实数b,使函数g(x)=f(x)-b有两个零点,则a的取值范围是.答案(-∞,0)∪(1,+∞)5.(2014天津,14,5分)已知函数f(x)=|x2+3x|,x∈R.若方程f(x)-a|x-1|=0恰有4个互异的实数根,则实数a的取值范围为.答案(0,1)∪(9,+∞)6.(2016江苏,19,16分)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)-2有且只有1个零点,求ab的值.解析(1)因为a=2,b=,所以f(x)=2x+2-x.①方程f(x)=2,即2x+2-x=2,亦即(2x)2-2×2x+1=0,所以(2x-1)2=0,于是2x=1,解得x=0.②由条件知f(2x)=22x+2-2x=(2x+2-x)2-2=(f(x))2-2.因为f(2x)≥mf(x)-6对于x∈R恒成立,且f(x)>0,所以m≤对于x∈R恒成立.而=f(x)+≥2·=4,且=4,所以m≤4,故实数m的最大值为4.(2)因为函数g(x)=f(x)-2只有1个零点,而g(0)=f(0)-2=a0+b0-2=0,所以0是函数g(x)的唯一零点.因为g'(x)=a x ln a+b x ln b,又由0<a<1,b>1知ln a<0,ln b>0,所以g'(x)=0有唯一解x0=lo-.令h(x)=g'(x),则h'(x)=(a x ln a+b x ln b)'=a x(ln a)2+b x(ln b)2,从而对任意x∈R,h'(x)>0,所以g'(x)=h(x)是(-∞,+∞)上的单调增函数.于是当x∈(-∞,x0)时,g'(x)<g'(x0)=0;当x∈(x0,+∞)时,g'(x)>g'(x0)=0.因而函数g(x)在(-∞,x0)上是单调减函数,在(x0,+∞)上是单调增函数.下证x0=0.若x0<0,则x0<<0,于是g<g(0)=0.又g(log a2)=+-2>-2=0,且函数g(x)在以和log a2为端点的闭区间上的图象不间断,所以在和log a2之间存在g(x)的零点,记为x1.因为0<a<1,所以log a2<0. 又<0,所以x1<0,与“0是函数g(x)的唯一零点”矛盾.若x0>0,同理可得,在和log b2之间存在g(x)的非0的零点,矛盾.因此,x0=0.于是-=1,故ln a+ln b=0,所以ab=1.评析本题主要考查指数函数、基本不等式、利用导数研究基本初等函数的单调性及零点问题,考查综合运用数学思想方法分析与解决问题以及逻辑推理能力.【三年模拟】一、选择题(每小题4分,共28分)1.(2019届衢州、湖州、丽水三地教学质量检测,9)已知函数f(x)=ax2+bx-(a>0)有两个不同的零点x1,x2,则( )A.x1+x2<0,x1x2<0B.x1+x2>0,x1x2>0C.x1+x2<0,x1x2>0D.x1+x2>0,x1x2<0答案A-若两个函数的图象只有一个交2.(2019届浙江高考模拟试卷(四),7)已知函数f(x)=ax+1,g(x)=点,则实数a的取值范围为( )A. B.C.∪-D.-答案C3.(2018浙江新高考调研卷三(杭州二中),4)a=1是方程x2-cos x+|a|=0有唯一根的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案A4.(2018浙江新高考调研卷一(诸暨中学),7)已知实数a∈(1,),则方程-+|x|=的不同解的个数为( )A.0B.2C.3D.4答案D设方程f(x)=t(t∈R)的四5.(2018浙江金丽衢十二校第三次联考(5月),9)已知函数f(x)=-个不等实根从小到大依次为x1,x2,x3,x4,则下列判断中错误的是( )A.x1+x2+x3+x4=40B.x1x2=1C.x3x4=361D.x3x4-20(x3+x4)+399=0答案C6.(2018浙江湖州、衢州、丽水高三质检,8)已知函数f(x)=|x-1|+|x|+|x+1|,则方程f(2x-1)=f(x)所有根的和是( )A. B.1 C. D.2答案C7.(2018浙江嘉兴高三期末,8)若f(x)=x2+bx+c在(m-1,m+1)内有两个不同的零点,则f(m-1)和f(m+1)( )A.都大于1B.都小于1C.至少有一个大于1D.至少有一个小于1答案D二、填空题(单空题4分,多空题6分,共8分)8.(2019届浙江高考模拟试卷(四),17)函数f(x)=x2+ax+b(a,b∈R)在(0,2)上有两个零点x1,x2,且|x1-x2|≥1,则a2+a-3b的取值范围为.答案-9.(2018浙江诸暨高三5月适应性考试,17)已知a,b,c∈R+(a>c),关于x的方程|x2-ax+b|=cx恰有三个不等实根,且函数f(x)=|x2-ax+b|+cx的最小值是c2,则= .答案 5。
压轴题09 基本初等函数、函数与方程(原卷版)--2023年高考数学压轴题专项训练(全国通用)

压轴题09基本初等函数、函数与方程题型/考向一:基本初等函数的图像与性质题型/考向二:函数的零点题型/考向三:函数模型及其应用○热○点○题○型一基本初等函数的图像与性质1.指数函数y =a x (a >0,且a ≠1)与对数函数y =log a x (a >0,且a ≠1)互为反函数,其图象关于y =x 对称,它们的图象和性质分0<a <1,a >1两种情况,着重关注两个函数图象的异同.2.幂函数y =x α的图象和性质,主要掌握α=1,2,3,12,-1五种情况.一、单选题1.若125()3a -=,121log 5b =,3log 7c =,则a ,b ,c 的大小关系为()A .a b c>>B .b c a >>C .c a b>>D .c b a>>2.已知函数()2121x f x =-+,则()A .()f x 是偶函数且是增函数B .()f x 是偶函数且是减函数C .()f x 是奇函数且是增函数D .()fx 是奇函数且是减函数3.下列函数中,既是偶函数又是区间(0,)+∞上的增函数的是()A .y =B .21y x =C .lg y x=D .332x xy --=4.已知函数()2,0,1,0,2x x x f x x ⎧≥⎪=⎨⎛⎫-<⎪ ⎪⎝⎭⎩若()()6f a f a <-,则实数a 的取值范围是()A .()3,-+∞B .(),3-∞-C .()3,+∞D .(),3-∞5.函数()2eln 2x f x x=的图象大致是()A .B .C .D .6.指数函数x y a =的图象如图所示,则2y ax x =+图象顶点横坐标的取值范围是()A .1,2⎛⎫-∞- ⎪⎝⎭B .1,02⎛⎫- ⎪⎝⎭C .10,2⎛⎫⎪⎝⎭D .1,2⎛⎫-+∞ ⎪⎝⎭7.已知实数1a ≠,函数()4,0,2,0,x a x x f x x -⎧≥=⎨<⎩若(1)(1)f a f a -=-,则a 的值为()A .12B .12-C .14D .14-8.函数()()()ln 1ln 1f x x x x =+--⎡⎤⎣⎦的部分图象大致是()A .B .C .D .二、填空题9.已知函数()2()e e x x f x x -=-⋅,若实数m 满足))2(1)f f m f -≤,则实数m的取值范围是____________.10.已知函数()|ln(1)||ln(1)|f x x x =--+,则函数()f x 的最小值为___________.11.已知,,1x y a ∈>R ,若2x y a a a +=,且x y +的最大值为103,则函数()()212log 2f x x ax a =-++的最小值为______12.幂函数y=xa ,当a 取不同的正数时,在区间[0,1]上它们的图象是一组美丽的曲线(如图),设点A (1,0),B (0,1),连接AB ,线段AB 恰好被其中的两个幂函数y=xa ,y=xb 的图象三等分,即有BM =MN =NA ,那么ab =______.○热○点○题○型二函数的零点判断函数零点个数的方法:(1)利用零点存在定理判断.(2)代数法:求方程f (x )=0的实数根.(3)几何法:对于不易求根的方程,将它与函数y =f (x )的图象联系起来,利用函数的性质找出零点或利用两个函数图象的交点求解.在利用函数性质时,可用求导的方法判断函数的单调性.一、单选题1.函数()243xf x x =+-的零点所在的区间是()A .1,04⎛⎫- ⎪⎝⎭B .10,4⎛⎫ ⎪⎝⎭C .11,42⎛⎫ ⎪⎝⎭D .13,24⎛⎫ ⎪⎝⎭2.已知函数()2cos 1f x a x x =--有且只有1个零点,则实数a 的值是()A .0B .1C .2D .33.已知()0,2πθ∈,若函数()()2sin cos sin 2f x x x x θ=-+在π0,4⎛⎫⎪⎝⎭上无零点,则θ的值可能为()A .π6B .π4C .11π12D .6π54.若函数22,0()1,0x x f x x x -⎧≤=⎨+>⎩,则函数()()2g x f x =-的零点的个数是()A .1B .2C .3D .45.已知函数()2ln 1212x x x f x mx mx x +>⎧⎪=⎨-+≤⎪⎩,,,若()()g x f x m =-有三个零点,则实数m 的取值范围是()A .71,4⎛⎤⎥⎝⎦B .(]1,2C .41,3⎛⎤ ⎥⎝⎦D .[]1,36.()f x 是定义在R 上的奇函数,当[]1,1x ∈-时,()f x x =,()()11f x f x +=-,令()()lg g x f x x =-,则函数()g x 的零点个数为()A .4B .5C .6D .77.已知函数()41,0141,02x x x f x x ⎧+-≤⎪=⎨⎛⎫->⎪ ⎪⎝⎭⎩,关于x 的方程()()()22110f x t f x t +-+-=有6个不等实数根,则实数t 的取值范围是()A.7,5⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪ ⎪⎝⎭⎝⎭B.7,5⎡⎫⎛⎫-∞-+∞⎪⎢ ⎪⎪⎝⎭⎣⎭C .7,52⎛-- ⎝⎦D .7,522⎛⎛⎫-- ⎪ ⎪⎝⎭⎝⎭8.已知()f x 是定义域为{}0x x ≠的偶函数且2ln 1()(0)ex f x x x =->,则函数()f x 零点个数是()A .6B .5C .4D .3二、多选题9.已知偶函数()f x 满足()()()126f x f x f -+=,()11e f -=+,且当[)0,6x ∈时,()e 1x f x a -=+,则下列说法正确的有()A .2e a =B .()f x 在[]18,24上为增函数C .()320231ef -=-D .()f x 在[]2023,0-上共有169个零点10.定义在R 上的偶函数()f x 满足()()22f x f x -=+,且当[]0,2x ∈时,()2e 1,01,44,1 2.x x f x x x x ⎧-≤≤=⎨-+<≤⎩若关于x 的不等式()m x f x ≤的整数解有且仅有9个,则实数m的取值可以是()A .e 16-B .e 17-C .e 18-D .e 19-三、填空题11.已知函数()131,0ln ,0x x f x x x +⎧-≤⎪=⎨>⎪⎩,若函数()()()2221g x f x af x a =-+-⎡⎤⎣⎦恰有4个不同的零点,则a 的取值范围是__________.12.已知函数11,02()2(2),28x x f x f x x ⎧--≤≤=⎨-<≤⎩,若方程()f x kx =恰好有四个实根,则实数k 的取值范围是___.○热○点○题○型三函数模型及其应用应用函数模型解决实际问题的一般程序和解题关键:(1)一般程序:――→读题文字语言⇒――→建模数学语言⇒――→求解数学应用⇒――→反馈检验作答(2)解题关键:解答这类问题的关键是确切地写出相关函数解析式,然后应用函数、方程、不等式和导数的有关知识加以综合解答.一、单选题1.垃圾分类,一般是指按一定规定或标准将垃圾分类储存、分类投放和分类搬运,从而变成公共资源的一系列活动的总称.已知某种垃圾的分解率ν与时间t (月)满足函数关系式t v a b =⋅(其中a ,b 为非零常数).若经过6个月,这种垃圾的分解率为5%,经过12个月,这种垃圾的分解率为10%,那么这种垃圾完全分解(分解率为100%)至少需要经过()(参考数据lg 20.3≈)A .20个月B .40个月C .28个月D .32个月2.大西洋鲑鱼每年都要逆流而上游回产地产卵,研究鲑鱼的科学家发现鲑鱼的游速(单位:m /s )可以表示为31log 2100Qv =,其中Q 表示鲑鱼的耗氧量的单位数.当一条鲑鱼以3ln2m /s ln3的速度游动时,其耗氧量是静止时耗氧量的倍数为()A .83B .8C .32D .643.0C 表示生物体内碳14的初始质量,经过t 年后碳14剩余质量01()2th C t C ⎛⎫= ⎪⎝⎭(0t >,h 为碳14半衰期).现测得一古墓内某生物体内碳14含量为00.4C ,据此推算该生物是距今约多少年前的生物(参考数据lg 20.301≈).正确选项是()A .1.36hB .1.34hC .1.32hD .1.30h4.2023年1月底,由马斯克、彼得泰尔等人创立的人工智能研究公司openAI 发布的名为“ChatGTP ”的人工智能聊天程序进入中国,迅速以其极高的智能化水平引起国内关注.深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的,在神经网络优化中,指数衰减的学习率模型为0G G L L D=,其中L 表示每一轮优化时使用的学习率,0L 表示初始学习率,D 表示衰减系数,G 表示训练迭代轮数,0G 表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.5,衰减速度为18,且当训练迭代轮数为18时,学习率衰减为0.4,则学习率衰减到0.2以下(不含0.2)所需的训练迭代轮数至少为()(参考数据:1g20.3010≈)A .72B .74C .76D .785.血氧饱和度是呼吸循环的重要生理参数.人体的血氧饱和度正常范围是95%~100%,当血氧饱和度低于90%时,需要吸氧治疗,在环境模拟实验室的某段时间内,可以用指数模型:0()e KtS t S =描述血氧饱和度()S t 随给氧时间t (单位:时)的变化规律,其中0S 为初始血氧饱和度,K 为参数.已知060%S =,给氧1小时后,血氧饱和度为80%.若使得血氧饱和度达到90%,则至少还需要给氧时间(单位:时)为()(精确到0.1,参考数据:ln 2069ln 3110≈≈.,.)A .0.3B .0.5C .0.7D .0.96.某企业为了响应并落实国家污水减排政策,加装了污水过滤排放设备,在过滤过程中,污染物含量M (单位:mg /L )与时间t (单位:h )之间的关系为0e ktM M -=(其中0,M k 是正常数).已知在处理过程中,该设备每小时可以清理池中残留污染物10%,则过滤一半的污染物需要的时间最接近()(参考数据:lg20.30≈,lg30.48≈)A .6小时B .8小时C .10小时D .12小时7.著名物理学家牛顿在17世纪提出了牛顿冷却定律,描述温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律.统计学家发现网络热搜度也遵循这样的规律,即随着时间的推移,热搜度会逐渐降低.假设事件的初始热搜度为()000N N >,经过t (天)时间之后的热搜度变为()0etN t N α-=,其中α为冷却系数.若设某事件的冷却系数0.3α=,则该事件的热搜度降到初始的50%以下需要的天数t 至少为().(ln 20.693≈,t 取整数)A .7B .6C .4D .38.针对“台独”分裂势力和外部势力勾结的情况,为捍卫国家主权和领土完整,维护中华民族整体利益和两岸同胞切身利益,解放军组织多种战机巡航台湾.已知海面上的大气压强是760mmHg ,大气压强P (单位:mmHg )和高度h (单位:m )之间的关系为760e hk P -=(e为自然对数的底数,k 是常数),根据实验知500m 高空处的大气压强是700mmHg ,则当歼20战机巡航高度为1000m ,歼16D 战机的巡航高度为1500m 时,歼20战机所受的大气压强是歼16D 战机所受的大气压强的()倍.A .0.67B .0.92C .1.09D .1.5二、多选题9.如图,某池塘里浮萍的面积y (单位:2m )与时间t (单位:月)的关系为t y a =,关于下列说法正确的是()A .浮萍每月的增长率为3B .浮萍每月增加的面积都相等C .第4个月时,浮萍面积超过280m D .若浮萍蔓延到2224m 2m 8m 、、所经过的时间分别是123t t t 、、,则2132t t t =+10.泊松分布适合于描述单位时间(或空间)内随机事件发生的次数.如某一服务设施在一定时间内到达的人数,显微镜下单位分区内的细菌分布数等等.其概率函数为()e !kP X k k λλλ-==,参数λ是单位时间(或单位面积)内随机事件的平均发生次数.现采用某种紫外线照射大肠杆菌,大肠杆菌的基因组平均产生3个嘧啶二体.设大肠杆菌的基因组产生的嘧啶二体个数为Y ,()P Y k =表示经该种紫外线照射后产生k 个嘧啶二体的概率.已知Y 服从泊松分布,记为()Y Pois λ~,当产生的嘧啶二体个数不小于1时,大肠杆菌就会死亡,下列说法正确的有()(参考数据:3e 0.049-=⋅⋅⋅,恒等式0e !inxi x i ==∑)A .大肠杆菌a 经该种紫外线照射后,存活的概率约为5%B .设()()f k P Y k λ==,则,(1)()0,()f k f k k λ∀∈+->∈N NC .如果()X pois λ~,那么(!)X E X λ=,X 的标准差σλ=D .大肠杆菌a 经该种紫外线照射后,其基因组产生的嘧啶二体个数的数学期望为311.(多选)甲同学家到乙同学家的途中有一座公园,甲同学家到公园的距离与乙同学家到公园的距离都是2km.如图所示表示甲同学从家出发到乙同学家经过的路程y (km)与时间x (min)的关系,下列结论正确的是()A.甲同学从家出发到乙同学家走了60minB.甲从家到公园的时间是30minC.甲从家到公园的速度比从公园到乙同学家的速度快D.当0≤x≤30时,y与x的关系式为y=1 15 x12.尽管目前人类还无法准确预报地震,但科学家经过研究,已经对地震有所了解,例如,地震时释放的能量E(单位:焦耳)与地震里氏震级M之间的关系为lg E=4.8+1.5M,则下列说法正确的是()A.地震释放的能量为1015.3焦耳时,地震里氏震级约为七级B.八级地震释放的能量约为七级地震释放的能量的6.3倍C.八级地震释放的能量约为六级地震释放的能量的1000倍D.记地震里氏震级为n(n=1,2,···,9,10),地震释放的能量为an,则数列{an}是等比数列。
高三数学函数及其表示试题答案及解析

高三数学函数及其表示试题答案及解析1.设常数,函数,若,则.【答案】3【解析】由题意,则,所以.【考点】函数的定义.2.在函数y=|x|(x∈[-1,1])的图象上有一点P(t,|t|),此函数与x轴、直线x=-1及x=t围成图形(如图阴影部分)的面积为S,则S与t的函数关系图象可表示为()【答案】B【解析】当t∈[-1,0]时,S增速越来越平缓,当t∈[0,1]时,S增速越来越快,选B项.3.若函数f(x)=,则(1)=________.(2)f(3)+f(4)+…+f(2 012)+++…+=________.【答案】(1)-1(2)0【解析】(1)∵f(x)+f=+=0,∴=-1(x≠±1),∴=-1.(2)又f(3)+f=0,f(4)+=0,…f(2 012)+f=0,∴f(3)+f(4)+…+f(2 012)+f+…+f=0.4.已知复数z+i,在映射f下的象是,则﹣1+2i的原象为()A.﹣1+3i B.2﹣i C.﹣2+i D.2【答案】D【解析】由题意:z+i→∴﹣1+2i=,z=2﹣i所以z+i=2﹣i+i=2.故选D.5.下列图象表示函数关系y=f(x)的有________.(填序号)【答案】①④【解析】根据函数定义,定义域内任意的一个自变量x的值都有唯一一个y与之对应.6.设函数f(x)=其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.(1)求函数f(x)的表达式;(2)若方程f(x)=x+a(a∈R)至少有两个不相同的实数根,求a取值的集合.【答案】(1)f(x)=(2)【解析】(1)∵当且仅当x=-2时,函数f(x)取得最小值-2.∴二次函数y=x2+bx+c的对称轴是x=-=-2.且有f(-2)=(-2)2-2b+c=-2,即2b-c=6.∴b=4,c=2.∴f(x)=(2)记方程①:2=x+a(x>0),方程②:x2+4x+2=x+a(x≤0).分别研究方程①和方程②的根的情况:(ⅰ)方程①有且仅有一个实数根a<2,方程①没有实数根a≥2.(ⅱ)方程②有且仅有两个不相同的实数根,即方程x2+3x+2-a=0有两个不相同的非正实数根.∴-<a≤2;方程②有且仅有一个实数根,即方程x2+3x+2-a=0有且仅有一个非正实数根.∴2-a<0或Δ=0,即a>2或a=-.综上可知,当方程f(x)=x+a(a∈R)有三个不相同的实数根时,-<a<2;当方程f(x)=x+a(a∈R)有且仅有两个不相同的实数根时,a=-或a=2.∴符合题意的实数a取值的集合为7.已知函数,对任意都有,且是增函数,则【答案】6【解析】本题看起来很难,好像没处下手,事实上,我们只要紧紧抓住函数的定义,从的初始值开始,如,首先,否则不合题意,其次若,则与是增函数矛盾,当然更不可能(理由同上),因此,,.【考点】函数的定义与性质.8.是上的奇函数,当时,,则当时,()A.B.C.D.【答案】C【解析】∵,∴,∴,又∵是上的奇函数,∴,∴.【考点】1.函数的奇偶性;2.函数解析式.9.设函数的定义域为,若存在闭区间,使得函数满足:①在上是单调函数;②在上的值域是,则称区间是函数的“和谐区间”.下列结论错误的是()A.函数()存在“和谐区间”B.函数()不存在“和谐区间”C.函数)存在“和谐区间”D.函数()不存在“和谐区间”【答案】B【解析】根据“和谐区间”的定义,我们只要寻找到符合条件的区间即可,对函数(),“和谐区间”,函数是增函数,若存在“和谐区间” ,则,因为方程有两个不等实根和,故,即区间是函数的“和谐区间”,B错误,选B,根据选择题的特征,下面C,D显然应该是正确的(事实上,函数)的“和谐区间”为,在其定义域内是单调增函数,若有“和谐区间”,则方程有两个不等实根,但此方程无实根,因此函数不存在“和谐区间”).【考点】新定义的理解,函数的单调性,方程的解.10.设函数的定义域为,若存在闭区间,使得函数满足:①在上是单调函数;②在上的值域是,则称区间是函数的“和谐区间”.下列结论错误的是()A.函数()存在“和谐区间”B.函数()不存在“和谐区间”C.函数)存在“和谐区间”D.函数(,)不存在“和谐区间”【答案】D【解析】根据“和谐区间”的定义,我们只要寻找到符合条件的区间即可,对函数(),“和谐区间”,函数是增函数,若存在“和谐区间” ,则,因此方程至少有两个不等实根,考虑函数,由,得,可得在时取得最小值,而,即的最小值为正,无实根,题设要求的不存在,因此函数()不存在“和谐区间”,函数)的“和谐区间”为,当然此时根据选择题的设置方法,知道应该选D,事实上,在其定义域内是单调增函数,“和谐区间”为,故D中的命题是错误的.【考点】新定义的理解,函数的单调性,方程的解.11.若对任意,,(、)有唯一确定的与之对应,称为关于、的二元函数. 现定义满足下列性质的二元函数为关于实数、的广义“距离”:(1)非负性:,当且仅当时取等号;(2)对称性:;(3)三角形不等式:对任意的实数z均成立.今给出个二元函数:①;②;③;④.则能够成为关于的、的广义“距离”的函数的所有序号是 .【答案】(1)【解析】对于①,f(x,y)=|x-y|≥0满足(1),f(x,y)=|x-y|=f(y,x)=|y-x|满足(2);f(x,y)=|x-y|=|(x-z)+(z-y)|≤|x-z|+|z-y|=f(x,z)+f(z,y)满足(3)故①能够成为关于的x、y的广义“距离”的函数;对于②不满足(3);对于③不满足(2);对于④不满足(1)(2),故答案为①【考点】1.函数的概念及其构成要素.12.已知函数的导函数为偶函数,则()A.0B.1C.2D.3【答案】A【解析】对所给函数求导得:,由偶函数定义知:,即,所以.【考点】1.函数的导数;2.偶函数的定义13.已知函数, 则的值是 .【答案】【解析】由分段函数解析式得.【考点】1.分段函数;2.函数值的求法14.若曲线y=上存在三点A,B,C,使得,则称曲线有“中位点”,下列曲线(1)y=cosx,,(2),(3),(4)有“中位点”的是()A.(2)(4)B.(1)(3)(4)C.(1)(2)(4) C.(2)(3)D.(2)(3)(4)【答案】B【解析】若曲线y=上存在三点A,B,C,使得,则称曲线有“中位点”,此时函数图象上必然有三点共线,函数y=cosx的图象上(0,1),(,0),(π,-1)三点显然共线,函数的图象上(-1,-4),(0,-2),(1,0)三点和函数的图象上(-1,-1),(0,0),(1,1)三点显然共线,均有三点共线,而没有,故选B.【考点】1.数形结合的思想方法;2.新定义的理解15.已知函数且,其中为奇函数, 为偶函数,若不等式对任意恒成立,则实数的取值范围是 .【答案】【解析】∵h(x)为定义在R上的偶函数,g(x)为定义在R上的奇函数∴g(-x)=-g(x),h(-x)=h(x), 又∵由h(x)+g(x)=2x, h(-x)+g(-x)=h(x)-g(x)=2-x,∴h(x)= (2x+2−x),g(x)=(2x−2−x), 不等式2ag(x)+h(2x)≥0在[1,2]上恒成立,化简为:a(2x−2−x)+(22x+2−2x)≥0,x∈[1,2], ∵1≤x≤2∴2x-2-x>0,令t=2-x-2x,整理得:,由t=2-x-2x得在上单调递增,故意当时,即实数a的取值范围为.【考点】1.函数不等式的恒成立问题;2.换元法;3.基本不等式16.设为实常数,是定义在R上的奇函数,当时,.若“,”是假命题,则的取值范围为 .【答案】【解析】是定义在R上的奇函数,故可求解析式为又“”是假命题,则是真命题,当时,,解得,①当时,,结合均值不等式有,得或,②①②取交集得的取值范围是.【考点】1.根据奇偶性求函数解析式;2.特称命题的否定;3.不等式恒成立问题.17.已知,则___________.【答案】2【解析】因为,所以,又因为,所以.【考点】求分段函数的函数值.18.已知,则的值等于.【答案】2014【解析】令,则所以,,故【考点】指数式与对数式的互化.19.已知函数满足.(1)求常数的值;(2)解不等式.【答案】(1) ;(2)【解析】(1)显然,所以,代入相应解析式求出;(2)由(1)确定函数解析式,对在不同段上的讨论.试题解析:(1)因为,所以;由,即,. 4分(2)由(1)得,由得, 6分当时,解得; 8分当时,解得. 10分所以的解集为. 12分【考点】1.分段函数;2.不等式.20.下列各组函数是同一函数的是()①与;②与;③与;④与。
高二数学函数与方程试题

高二数学函数与方程试题1.已知函数若方程有两个不相等的实根,则实数的取值范围是()A.B.C.D.【答案】B【解析】由于要使有两个不相等的实根,则与的图象有两个交点,当,,代入得,解得,此时有一个交点;当,此时有一个交点,要使与的图象有两个交点,则.【考点】函数图象的交点.2.已知函数,若存在唯一的零点,且,则的取值范围是( ). A.B.C.D.【答案】C【解析】显然当时,不符合题意;因为,所以;当时,令,得,则在处取得极大值,若存在唯一的零点,且,则(舍去);当时,令,得,则在处取得极小值,若存在唯一的零点,且,则,即.考点:函数的零点.3.方程有两个根,则的范围为【答案】【解析】注意到,方程有两个根等价于函数的图象与直线有两个不同的交点,如图,所以有:从而得到:.【考点】函数的图象与方程的根.4.函数f(x)=2x+x3-2在区间(0,1)内的零点个数是( )A.0B.1C.2D.3【答案】B【解析】,在范围内,函数为单调递增函数.又,,,故在区间存在零点,又函数为单调函数,故零点只有一个.【考点】导函数,函数的零点.5.已知函数,方程有五个不同的实数解时,的取值范围为.【答案】;【解析】方程有五个不同的实数解,等价于有五个不同的实数解;有函数的图象知有两个不同的解,有三个不同的实数解,则.【考点】函数的零点、数形结合思想.6.若函数有极值点,且,则关于的方程的不同实根的个数是()A.3B.4C.5D.6【答案】A【解析】函数有极值点,说明方程的两根为,所以方程的解为或,若,即是极大值点,是极小值点,由于,所以是极大值,有两解,,只有一解,所以此时只有3解;若,即是极小值点,是极大值点,由于,所以是极小值,有2解,,只有一解,所以此时只有3解;综上可知,选A.【考点】函数的极值与方程的解.7.如图是函数的大致图象,则等于A.B.C.D.【答案】D【解析】由图象知f(x)=0的根为0,-1,2,∴d=0.∴.∴的两个根为-1和2.∴b=-1,c=-2.∴.∴.∵x1,x2为的两根,∴.∴,故选D.【考点】函数的导数与零点.8.若函数在区间上存在一个零点,则的取值范围是( )A.B.或C.D.【答案】B【解析】因为函数为一次函数或常数函数,又函数在区间上存在一个零点,所以函数只能是一次函数,根据一次函数的图像可知,要在区间上存在一个零点,只须即即,解是或,故选B.【考点】1.一次函数的图像与性质;2.函数的零点;3.二次不等式.9.在下列区间中,函数的零点所在的区间为()A.(-,0)B.(0,)C.(,)D.(,)【答案】C【解析】由函数零点存在定理,将选项代入检验,故选C。
高三数学函数与方程试题

高三数学函数与方程试题1.方程的解属于区间 ( )A.B.C.D.【答案】C【解析】试题分析:记f(x)=,有f(2)=ln2-2<0,f(3)=ln3-1>0,故零点一定在(2,3)内,选C【考点】函数的零点2.已知是定义在上且周期为3的函数,当时,,若函数在区间上有10个零点(互不相同),则实数的取值范围是 .【答案】【解析】作出函数的图象,可见,当时,,,方程在上有10个零点,即函数和图象与直线在上有10个交点,由于函数的周期为3,因此直线与函数的应该是4个交点,则有.【考点】函数的零点,周期函数的性质,函数图象的交点问题.3.若平面直角坐标系内两点P,Q满足条件:①P,Q都在函数f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数f(x)的一个“友好点对”(点对(P,Q)与点对(Q,P)为同一个“友好点对”).已知函数f(x)=,则f(x)的“友好点对”有________个.【答案】2【解析】设x<0,则问题转化为关于x的方程(2x2+4x+1)+=0,即e x=-x2-2x-有几个负数解问题.记y1=e x,y2=-(x+1)2+,当x=-1时, <,所以函数y1的图象与y2的图象有两个交点(如图),且横坐标均为负数,故所求“友好点对”共有2个.4.若关于x的方程x2-(a2+b2-6b)x+a2+b2+2a-4b+1=0的两个实数根x1,x2满足x 1<0<x2<1,则a2+b2+4a+4的取值范围是________.【答案】【解析】由题意得即利用线性规划的知识,问题转化为求区域上的点到点(-2,0)的距离的平方的取值范围.由图可知,所求的最大距离即为点(-2,0)与圆心(-1,2)的连线交圆与另一端点的值,即+2.所求的最小距离即为点(-2,0)到直线a+b+1=0的距离,即为=,所以a2+b2+4a+4∈,即a2+b2+4a+4∈.5.已知方程x=的解x∈,则正整数n=________.【答案】2【解析】在同一直角坐标系中画出函数y=x,y=的图像,如图所示.由图可得x∈(0,1),设f(x)=x-,因为f=-<0,f=->0,故n=2.6.(5分)(2011•天津)对实数a与b,定义新运算“⊗”:a⊗b=.设函数f(x)=(x2﹣2)⊗(x﹣1),x∈R.若函数y=f(x)﹣c的图象与x轴恰有两个公共点,则实数c的取值范围是()A.(﹣1,1]∪(2,+∞)B.(﹣2,﹣1]∪(1,2]C.(﹣∞,﹣2)∪(1,2]D.[﹣2,﹣1]【答案】B【解析】根据定义的运算法则化简函数f(x)=(x2﹣2)⊗(x﹣1),的解析式,并画出f(x)的图象,函数y=f(x)﹣c的图象与x轴恰有两个公共点转化为y=f(x),y=c图象的交点问题,结合图象求得实数c的取值范围.解:∵,∴函数f(x)=(x2﹣2)⊗(x﹣1)=,由图可知,当c∈(﹣2,﹣1]∪(1,2]函数f(x)与y=c的图象有两个公共点,∴c的取值范围是(﹣2,﹣1]∪(1,2],故选B.点评:本题考查二次函数的图象特征、函数与方程的综合运用,及数形结合的思想.属于基础题.7.若关于的方程在区间上有两个不同的实数解,则的取值范围为 .【答案】【解析】原方程变形为,作出函数的图象,它在上单调递增,函数值取值范围是,在单调递减,函数值取值范围是,从图中可以看出当时,直线与函数的图象有两个交点,即原方程有两解.【考点】方程的解与函数的图象.8.已知()(1)若方程有3个不同的根,求实数的取值范围;(2)在(1)的条件下,是否存在实数,使得在上恰有两个极值点,且满足,若存在,求实数的值,若不存在,说明理由.【答案】(1);(2)不存在,参考解析【解析】(1)由已知(),若方程有3个不同的根,则可得到或对两个方程分别讨论即可到结论.(2)在(1)的条件下,是否存在实数,使得在上恰有两个极值点,通过对函数求导,判断导函数的根的情况,通过换元使得等式简洁些.要满足,由于,所以可得,通过验证根是否存在.即可得到结论.(1)解:由得:或可得或且∵方程有3个不同的根,∴方程有两个不同的根∴又∵,且要保证能取到0∴即∴.(2)解:∵令,设∴∵∴∴∵∴,∴∴存在,使得,另外有,使得假设存在实数,使得在上恰有两个极值点,且满足则存在,使得,另外有,即∴,∴,即即(*)设∴∵∴∴∴在上是增函数∴∴方程(*)无解,即不存在实数,使得在上恰有两个极值点,且满足【考点】1.函数与x轴的交点与方程的根的问题.2.函数的极值.3.等价转化的思想.4.函数的最值问题.9.函数的零点所在的区间是()A.B.C.D.【答案】C【解析】∵函数,∴,=<<0,=>>0,∴,所以函数的零点所在区间是.【考点】函数的零点.10.某同学为了研究函数的性质,构造了如图所示的两个边长为的正方形和,点P是边BC上的一个动点,设CP=x,则.(1);(2)函数的零点个数是.【答案】(1);(2).【解析】(1)由题意可得函数=,当共线,即时,;(2)函数的零点个数,即的图象与交点的个数. 由(1),当P与B或C重合,即或时,.结合图象可知,交点个数为,故函数零点的个数是.【考点】函数的应用问题,函数的零点,函数的图象.11.方程lgx=2-x在区间(n,n+1)(n∈Z)有解,则n的值为________.【答案】1【解析】令f(x)=lgx+x-2,由f(1)=-1<0,f(2)=lg2>0,知f(x)=0的根介于1和2之间,即n=1.12.函数f(x)=ln x- (x>1)的零点所在的区间为()A.B.C.D.【答案】C【解析】f(2)=ln 2-1<0,f=ln-,由125>8e2得>,所以f=ln->0,因此f(2)f<0,所以其中的一个零点区间为.13.我们把形如y= (a>0,b>0)的函数因其图象类似于汉字中的“囧”字,故生动地称为“囧函数”,若当a=1,b=1时的“囧函数”与函数y=lg|x|的交点个数为n,则n=________.【答案】4【解析】由题意知,当a=1,b=1时,y==在同一坐标系中画出“囧函数”与函数y=lg|x|的图象如图所示,易知它们有4个交点..14.存在实数x,使,则a的取值范围是_________【答案】【解析】存在实数x,使,即方程有解,,解得或.【考点】逻辑用语,一元二次方程的解.15.某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为立方米,且.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为千元,设该容器的建造费用为千元.(Ⅰ)写出关于的函数表达式,并求该函数的定义域;(Ⅱ)求该容器的建造费用最小时的.【答案】(Ⅰ);(Ⅱ)当时,建造费用最小时当时,建造费用最小时.【解析】(Ⅰ)由圆柱和球的体积的表达式,得到l和r的关系.再由圆柱和球的表面积公式建立关系式,将表达式中的l用r表示.并注意到写定义域时,利用l≥2r,求出自变量r的范围;(Ⅱ)用导数的知识解决,注意到定义域的限制,在区间(0,2]中,极值未必存在,将极值点在区间内和在区间外进行分类讨论.试题解析:(I)设容器的容积为V,由题意知故3分由于因此.所以建造费用因此5分..(II)由(I)得由于当所以.7分令;(1)当时,所以是函数y的极小值点,也是最小值点。
函数与方程高考试题汇编

函数与方程高考试题汇编一、选择题1.(2018全国卷Ⅰ)已知函数0()ln 0⎧=⎨>⎩,≤,,,x e x f x x x ()()=++g x f x x a .若()g x 存在2个零点,则a 的取值范围是 A .[1,0)-B .[0,)+∞C .[1,)-+∞D .[1,)+∞2.(2017新课标Ⅲ)已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .13.(2017山东)已知当[0,1]x ∈时,函数2(1)y mx =-的图象与y m =的图象有且只有一个交点,则正实数m 的取值范围是 A .(])0,123,⎡+∞⎣B .(][)0,13,+∞ C.()23,⎡+∞⎣D .([)3,+∞4.(2016年天津)已知函数()f x =2(4,0,log (1)13,03)a x a x a x x x ⎧+<⎨++≥-+⎩(0a >,且1a ≠)在R 上单调递减,且关于x 的方程|()|2f x x =-恰好有两个不相等的实数解,则a 的取值范围是 A .(0,23] B .[23,34] C .[13,23]{34} D .[13,23){34}5.(2015安徽)下列函数中,既是偶函数又存在零点的是A .y cos x =B .y sin x =C .y ln x =D .21y x =+6.(2015福建)若,a b 是函数()()20,0f x x px q p q =-+>> 的两个不同的零点,且,,2a b - 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p q +的值等于 A .6 B .7 C .8 D .97.(2015天津)已知函数()()22,22,2x x f x x x ⎧-≤⎪=⎨->⎪⎩ 函数()()2g x b f x =-- ,其中 b R ∈ ,若函数()()y f x g x =- 恰有4个零点,则b 的取值范围是A .7(,)4+∞ B .7(,)4-∞ C .7(0,)4 D .7(,2)48.(2015陕西)对二次函数2()f x ax bx c =++(a 为非零整数),四位同学分别给出下列结论,其中有且仅有一个结论是错误的,则错误的结论是A .-1是()f x 的零点B .1是()f x 的极值点C .3是()f x 的极值D .点(2,8)在曲线()y f x =上9.(2014山东)已知函数()12+-=x x f ,()kx x g =.若方程()()f x g x =有两个不相等的实根,则实数k 的取值范围是A .),(210B .),(121C .),(21D .),(∞+210.(2014北京)已知函数()26log f x x x=-,在下列区间中,包含()f x 零点的区间是 A .()0,1 B .()1,2 C .()2,4 D .()4,+∞11.(2014重庆)已知函数13,(1,0]()1,(0,1]x f x x x x ⎧-∈-⎪=+⎨⎪∈⎩, 且()()g x f x mx m =--在(1,1]-内有且仅有两个不同的零点,则实数m 的取值范围是A .]21,0(]2,49(⋃--B .]21,0(]2,411(⋃-- C .]32,0(]2,49(⋃-- D .]32,0(]2,411(⋃--12.(2014湖北)已知()f x 是定义在R 上的奇函数,当0x ≥时,2()=3f x x x -.则函数()()+3g x f x x =-的零点的集合为A .{1,3}B .{3,1,1,3}-- C.{23} D.{21,3}- 13.(2013安徽)已知函数32()f x x ax bx c =+++有两个极值点12,x x ,若112()f x x x =<,则关于x 的方程23(())2()0f x af x b ++=的不同实根个数为A .3B .4C .5D .614.(2013重庆)若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间A .(),a b 和(),b c 内B .(),a -∞和(),a b 内C .(),b c 和(),c +∞内D .(),a -∞和(),c +∞内15.(2013湖南)函数()2ln f x x =的图像与函数()245g x x x =-+的图象的交点个数为A .3B .2C .1D .016.(2013天津)函数0.5()2|log |1x f x x =-的零点个数为A .1B .2C .3D .417.(2012北京)函数121()()2xf x x =-的零点个数为A .0B .1C .2D .3 18.(2012湖北)函数2()cos f x x x =在区间[0,4]上的零点个数为A .4B .5C .6D .719.(2012辽宁)设函数)(x f ()x R ∈满足()()f x f x -=,()(2)f x f x =-,且当[]0,1x ∈时,()3=f x x .又函数()()=cos g x x x π,则函数()()()h x g x f x =-在13[,]22-上的零点个数为A .5B .6C .7D .8 20.(2011天津)对实数a 与b ,定义新运算“⊗”:,1,, 1.a ab a b b a b -≤⎧⊗=⎨->⎩ 设函数()()22()2,.f x x x x x R =-⊗-∈若函数()y f x c =-的图像与x 轴恰有两个公共点,则实数c 的取值范围是A .(]3,21,2⎛⎫-∞-⋃- ⎪⎝⎭ B .(]3,21,4⎛⎫-∞-⋃-- ⎪⎝⎭C .11,,44⎛⎫⎛⎫-∞⋃+∞ ⎪⎪⎝⎭⎝⎭ D .311,,44⎛⎫⎡⎫--⋃+∞ ⎪⎪⎢⎝⎭⎣⎭21.(2011福建)若关于x 的方程210x mx ++=有两个不相等的实数根,则实数m 的取值范围是A .(-1,1)B .(-2,2)C .(-∞,-2)∪(2,+∞)D .(-∞,-1)∪(1,+∞) 22.(2011全国新课标)函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于A .2B .4C .6D .823.(2011山东)已知()f x 是R 上最小正周期为2的周期函数,且当02x <≤时,3()f x x x =-,则函数()y f x =的图象在区间[0,6]上与x 轴的交点的个数为 A .6 B .7 C .8 D .924.(2010年福建)函数223,0()2ln ,0x x x f x x x ⎧+-=⎨-+>⎩≤,的零点个数为A .0B .1C .2D .325.(2010天津)函数()23xf x x =+的零点所在的一个区间是A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2) 26.(2010广东)“14m <”是“一元二次方程20x x m ++=有实数解”的 A .充分非必要条件 B .充分必要条件 C .必要非充分条件 D .非充分非必要条件27.(2010浙江)设函数()4sin(21)f x x x =+-,则在下列区间中函数()f x 不.存在零点的是 A .[]4,2-- B .[]2,0- C .[]0,2 D .[]2,428.(2019全国Ⅱ理12)设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦C .5,2⎛⎤-∞ ⎥⎝⎦D .8,3⎛⎤-∞ ⎥⎝⎦29.(2019浙江9)已知,a b ∈R ,函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩,若函数()y f x ax b =--恰有3个零点,则 A .a <-1,b <0B .a <-1,b >0C .a >-1,b <0D .a >-1,b >0二、填空题1.(2018全国卷Ⅲ)函数()cos(3)6f x x π=+在[0,]π的零点个数为________.2.(2018天津)已知0a >,函数222,0,()22,0.x ax a x f x x ax a x ⎧++=⎨-+->⎩≤若关于x 的方程()f x ax =恰有2个互异的实数解,则a 的取值范围是 .3.(2018江苏)若函数32()21()f x x ax a =-+∈R 在(0,)+∞内有且只有一个零点,则()f x 在[1,1]-上的最大值与最小值的和为 . 4.(2018浙江)已知λ∈R ,函数24,()43,x x f x x x x λλ-⎧=⎨-+<⎩≥,当2λ=时,不等式()0f x <的解集是_____.若函数()f x 恰有2个零点,则λ的取值范围是______.5.(2018浙江)我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一.凡百钱,买鸡百只,问鸡翁、母、雏各几何?”设鸡翁,鸡母,鸡雏个数分别为x ,y ,z ,则1001531003x y z x y z ++=⎧⎪⎨++=⎪⎩,当81z =时,x = ,y = . 6.(2017江苏)设()f x 是定义在R 且周期为1的函数,在区间[0,1)上,2,(),x x Df x x x D⎧∈=⎨∉⎩其中集合1{|,}n D x x n n-==∈*N ,则方程()lg 0f x x -=的解的个数是 . 7.(2016年山东)已知函数2||,()24,x x m f x x mx m x m⎧=⎨-+>⎩≤ 其中0m >,若存在实数b ,使得关于x 的方程()f x b =有三个不同的根,则m 的取值范围是_________.8.(2015湖北)函数2π()4coscos()2sin |ln(1)|22x f x x x x =---+的零点个数为 . 9.(2015北京)设函数()()()2142 1.xa x f x x a x a x ⎧-<⎪=⎨--⎪⎩≥‚‚‚①若1a =,则()f x 的最小值为;②若()f x 恰有2个零点,则实数a 的取值范围是.10.(2015湖南)已知函数32,(),x x af x x x a⎧=⎨>⎩≤,若存在实数b ,使函数()()g x f x b =-有两个零点,则a的取值范围是 .11.(2014江苏)已知)(x f 是定义在R 上且周期为3的函数,当)3,0[∈x 时,|212|)(2+-=x x x f .若函数a x f y -=)(在区间]4,3[-上有10个零点(互不相同),则实数a 的取值范围是 .12.(2014福建)函数()⎩⎨⎧>+-≤-=0,ln 620,22x x x x x x f 的零点个数是_________.13.(2014天津)已知函数2()|3|f x x x =+,x ∈R .若方程()|1|0f x a x --=恰有4个互异的实数根,则实数a 的取值范围为__________.14.(2012福建)对于实数a 和b ,定义运算“*”:22,,,,a ab a b a b b ab a b ⎧-*=⎨->⎩设()f x =(21)(1)x x -*-,且关于x 的方程为()f x m =(m ∈R )恰有三个互不相等的实数根123,,x x x ,则123x x x 的取值范围是____________.15.(2011北京)已知函数32,2()(1),2x f x x x x ⎧≥⎪=⎨⎪-<⎩,若关于x 的方程()f x =k 有两个不同的实根,则数k 的取值范围是_______.16.(2011辽宁)已知函数a x e x f x +-=2)(有零点,则a 的取值范围是_____.17.(2019江苏14)设(),()f x g x 是定义在R 上的两个周期函数,()f x 的周期为4,()g x 的周期为2,且()f x 是奇函数.当2(]0,x ∈时,()f x =(2),01()1,122k x x g x x +<≤⎧⎪=⎨-<≤⎪⎩,其中k >0.若在区间(0,9]上,关于x 的方程()()f x g x =有8个不同的实数根,则k 的取值范围是 .。
第8节 函数与方程--2025年高考数学复习讲义及练习解析

第八节函数与方程课标解读考向预测1.理解函数的零点与方程解的联系,掌握函数的零点、方程的根、图象交点(横坐标)三者之间的灵活转化.2.理解函数零点存在定理,并能简单应用.3.会用二分法求方程的近似解.从近三年高考情况来看,函数零点(方程的根)个数的判断、由零点存在定理判断零点(方程的根)是否存在、利用函数零点(方程的根)确定参数的取值范围等是考查的热点.本节内容也可与导数结合考查,难度较大.预计2025年高考函数与方程仍会出题,可能以选择题或填空题考查三种形式的灵活转化,也可能与导数结合考查,难度较大.必备知识——强基础1.函数的零点对于函数y =f (x ),我们把使f (x )=0的实数x 叫做函数y =f (x )的零点.2.方程的根与函数零点的关系方程f (x )=0有实数解⇔函数y =f (x )有零点⇔函数y =f (x )的图象与x 轴有公共点.3.函数零点存在定理如果函数y =f (x )在区间[a ,b ]上的图象是一条连续不断的曲线,且有01f (a )f (b )<0,那么,函数y =f (x )在区间(a ,b )内至少有一个零点,即存在c ∈(a ,b ),使得f (c )=0,c 也就是方程f (x )=0的解.4.二分法对于在区间[a ,b ]上连续不断且02f (a )f (b )<0的函数y =f (x ),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点的近似值的方法叫做二分法.求方程f (x )=0的近似解就是求函数y =f (x )零点的近似值.函数零点的相关技巧:(1)若连续函数f (x )在定义域上是单调函数,则f (x )至多有一个零点.(2)连续不断的函数f (x ),其相邻的两个零点之间的所有函数值同号.(3)连续不断的函数f (x )通过零点时,函数值不一定变号.(4)连续不断的函数f (x )在闭区间[a ,b ]上有零点,不一定能推出f (a )f (b )<0.1.概念辨析(正确的打“√”,错误的打“×”)(1)函数的零点就是函数的图象与x轴的交点.()(2)连续函数y=f(x)在区间(a,b)内有零点,则f(a)f(b)<0.()(3)函数y=f(x)为R上的单调函数,则f(x)有且仅有一个零点.()(4)二次函数y=ax2+bx+c(a≠0),若b2-4ac<0,则f(x)无零点.()答案(1)×(2)×(3)×(4)√2.小题热身(1)(人教A必修第一册4.5.1例1改编)已知函数f(x)=23x+1+a的零点为1,则实数a的值为()A.-2B.-12D.2C.12答案B(2)下列函数图象与x轴都有公共点,其中不能用二分法求图中函数零点近似值的是()答案A解析根据题意,利用二分法求函数零点的条件是函数在零点的左、右两侧的函数值符号相反,即图象穿过x轴,据此分析,知选项A中的函数不能用二分法求零点.故选A. (3)(人教A必修第一册习题4.5T2改编)已知函数y=f(x)的图象是一条连续不断的曲线,部分对应关系如表所示,则该函数的零点个数至少为()x123456y126.115.15-3.9216.78-45.6-232.64A.2B.3C.4D.5解析由表可知,f (2)f (3)<0,f (3)f (4)<0,f (4)f (5)<0,所以函数f (x )在区间[1,6]上至少有3个零点.故选B.(4)若函数f (x )=kx +1在[1,2]上有零点,则实数k 的取值范围是________.答案-1,-12考点探究——提素养考点一函数零点所在区间的判断例1(1)(2024·湖南长沙长郡中学高三月考)函数f (x )=5-2x -lg (2x +1)的零点所在的区间是()A .(0,1)B .(1,2)C .(2,3)D .(3,4)答案C解析因为函数f (x )=5-2x -lg (2x +1)-12,+,所以函数f (x )最多只有一个零点,因为f (0)f (1)=5(3-lg 3)>0,f (1)f (2)=(3-lg 3)(1-lg 5)>0,f (2)f (3)=(1-lg 5)(-1-lg 7)<0,f (3)f (4)=(-1-lg 7)×(-3-lg 9)>0,所以函数f (x )=5-2x -lg (2x +1)的零点所在的区间是(2,3).故选C.(2)用二分法求函数f (x )=3x -x -4的一个零点,其参考数据如下:f (1.6000)≈0.200f (1.5875)≈0.133f (1.5750)≈0.067f (1.5625)≈0.003f (1.5562)≈-0.029f (1.5500)≈-0.060据此数据,可得方程3x -x -4=0的一个近似解为________(精确度为0.01).答案 1.56(答案不唯一,在[1.5562,1.5625]上即可)解析注意到f (1.5562)≈-0.029和f (1.5625)≈0.003,显然f (1.5562)f (1.5625)<0,又|1.5562-1.5625|=0.0063<0.01,所以近似解可取1.56.【通性通法】确定函数零点所在区间的常用方法(1)利用函数零点存在定理:首先看函数y =f (x )在区间[a ,b ]上的图象是否连续,再看是否有f (a )f (b )<0.若有,则函数y =f (x )在区间(a ,b )内必有零点.(2)数形结合法:通过画函数图象,观察图象与x 轴在给定区间上是否有交点来判断.【巩固迁移】1.(2023·广东梅州高三二模)用二分法求方程log 4x -12x=0的近似解时,所取的第一个区间可A.(0,1)B.(1,2) C.(2,3)D.(3,4)答案B解析令f(x)=log4x-12x,因为函数y=log4x,y=-12x在(0,+∞)上都是增函数,所以函数f(x)=log4x-12x在(0,+∞)上是增函数,f(1)=-12<0,f(2)=log42-14=12-14=14>0,所以函数f(x)=log4x-12x在区间(1,2)上有唯一零点,所以用二分法求方程log4x-12x=0的近似解时,所取的第一个区间可以是(1,2).故选B.2.已知2<a<3<b<4,函数y=log a x与y=-x+b的交点为(x0,y0),且x0∈(n,n+1),n∈N*,则n=________.答案2解析依题意,x0为方程log a x=-x+b的解,即为函数f(x)=log a x+x-b的零点,∵2<a<3<b<4,∴f(x)在(0,+∞)上单调递增,又f(2)=log a2+2-b<0,f(3)=log a3+3-b>0,∴x0∈(2,3),即n=2.考点二函数零点个数的判断例2(1)已知函数f(x)2-4,x≤1,2(x-1),x>1,则函数y=f(x)零点的个数为________.答案2解析当x≤1时,由f(x)=x2-4=0,可得x=2(舍去)或x=-2;当x>1时,由f(x)=log2(x -1)=0,可得x=2.综上所述,函数y=f(x)零点的个数为2.(2)方程ln x+cos x=13在(0,1)上的实数根的个数为________.答案1解析解法一:ln x+cos x=13,即cos x-13=-ln x,在同一平面直角坐标系中,分别作出函数y=cos x-13和y=-ln x的大致图象,如图所示,在(0,1)上两函数的图象只有一个交点,即方程ln x+cos x=13在(0,1)上的实数根的个数为1.解法二:令f(x)=ln x+cos x-13,则f′(x)=1x-sin x,显然在(0,1)上f′(x)>0,所以函数f(x)在(0,1)上单调递增,又ln 1e +cos 1e -13=-1-13+cos 1e <0,f (1)=ln 1+cos1-13=0+cos1-13>cos π3-13=12-13>0,所以在(0,1)上函数f (x )的图象和x 轴有且只有一个交点,即方程ln x +cos x =13在(0,1)上的实数根的个数为1.【通性通法】求解函数零点个数的基本方法(1)直接法:令f (x )=0,方程有多少个解,则f (x )有多少个零点.(2)构造函数法:判断函数的性质,并结合零点存在定理判断.(3)图象法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后观察求解,此时需要根据零点个数合理寻找“临界”情况,特别注意边界值的取舍.【巩固迁移】3.(2024·江苏无锡模拟)函数f (x )2-2,x ≤0,x -6+lg x ,x >0的零点的个数为________.答案2解析当x ≤0时,f (x )=x 2-2,根据二次函数的性质可知,此时f (x )单调递减,零点为x =-2;当x >0时,f (x )=2x -6+lg x ,∵y =2x -6单调递增,y =lg x 单调递增,∴f (x )=2x -6+lg x 单调递增.f (1)=-4<0,f (3)=lg 3>0,由零点存在定理知,在区间(1,3)必有唯一零点.综上所述,函数f (x )的零点的个数为2.4.函数f (x )|-|log 2x |的零点有________个.答案2解析f (x )|-|log 2x ||=|log 2x |的根的个数,即为y |与y =|log 2x |图象交点的个数,画出大致图象如图所示,则由图象可知交点有2个,即函数f (x )的零点有2个.考点三函数零点的应用(多考向探究)考向1利用零点比较大小例3已知函数f (x )=3x +x ,g (x )=log 2x +x ,h (x )=x 3+x 的零点分别为a ,b ,c ,则a ,b ,c 的大小顺序为()A .a <c <bB .a <b <cC.b<a<c D.b<c<a答案A解析解法一:因为函数y=3x,y=x均为R上的增函数,故函数f(x)=3x+x为R上的增函数,因为f(-1)=13-1<0,f(0)=1>0,所以-1<a<0.因为函数y=log2x,y=x在(0,+∞)上均为增函数,故函数g(x)=log2x+x在(0,+∞)上为增函数,因为1+12<0,g(1)=1>0,所以12<b<1.由h(c)=c(c2+1)=0可得c=0,因此a<c<b.故选A.解法二:由题设,3a=-a,log2b=-b,c3=-c,所以问题可转化为直线y=-x与y=3x,y=log2x,y=x3的图象的交点问题,函数图象如图所示,由图可知a<c=0<b.故选A.【通性通法】(1)直接利用方程研究零点.(2)利用图象交点研究零点.(3)利用零点存在定理研究零点.【巩固迁移】5.(2023·江西南昌模拟预测)已知函数f(x)=2x+x-4,g(x)=e x+x-4,h(x)=ln x+x-4的零点分别是a,b,c,则a,b,c的大小顺序是()A.a<b<c B.c<b<aC.b<a<c D.c<a<b答案C解析由已知条件得f(x)的零点可以看成y=2x的图象与直线y=4-x的交点的横坐标,g(x)的零点可以看成y=e x的图象与直线y=4-x的交点的横坐标,h(x)的零点可以看成y=ln x 的图象与直线y=4-x的交点的横坐标,在同一坐标系内分别画出函数y=2x,y=e x,y=ln x,y=4-x的图象,如图所示,由图可知b<a<c.故选C.考向2根据零点个数求参数例4(2023·山东济南高三三模)已知函数f (x )x +1)2,x ≤0,x |,x >0,若函数g (x )=f (x )-b 有四个不同的零点,则实数b 的取值范围为()A .(0,1]B .[0,1]C .(0,1)D .(1,+∞)答案A解析依题意,函数g (x )=f (x )-b 有四个不同的零点,即f (x )=b 有四个解,转化为函数y =f (x )与y =b 的图象有四个交点,由函数y =f (x )可知,当x ∈(-∞,-1]时,函数单调递减,y ∈[0,+∞);当x ∈(-1,0]时,函数单调递增,y ∈(0,1];当x ∈(0,1)时,函数单调递减,y ∈(0,+∞);当x ∈[1,+∞)时,函数单调递增,y ∈[0,+∞).结合图象,可知实数b 的取值范围为(0,1].故选A.【通性通法】根据零点个数求参数的方法(1)直接法:直接根据题设条件构建关于参数的不等式(组),再通过解不等式(组)确定参数范围.(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.一是转化为两个函数y =g (x ),y =h (x )的图象的交点个数问题,画出两个函数的图象,其交点的个数就是函数零点的个数,二是转化为y =a ,y =g (x )的图象的交点个数问题.【巩固迁移】6.(2024·安徽蚌埠高三摸底)已知函数f (x )=2|x |+x 2+a 有唯一的零点,则实数a 的值为()A .1B .-1C .0D .-2答案B解析函数f (x )=2|x |+x 2+a 的定义域为R ,f (-x )=2|-x |+(-x )2+a =f (x ),即函数f (x )为偶函数,当x ≥0时,f (x )=2x +x 2+a ,则f (x )在[0,+∞)上单调递增,在(-∞,0)上单调递减,则当x =0时,f (x )min =a +1,由函数f (x )=2|x |+x 2+a 有唯一的零点,得a +1=0,解得a =-1,所以实数a 的值为-1.故选B.7.设a ∈R ,对任意实数x ,记f (x )=min{|x |-2,x 2-ax +3a -5}.若f (x )至少有3个零点,则实数a 的取值范围为________.答案[10,+∞)解析设g (x )=x 2-ax +3a -5,h (x )=|x |-2,由|x |-2=0可得x =±2.要使得函数f (x )至少有3个零点,则函数g (x )至少有一个零点,则Δ=a 2-12a +20≥0,解得a ≤2或a ≥10.①当a =2时,g (x )=x 2-2x +1,作出函数g (x ),h (x )的图象如图所示,此时函数f (x )只有2个零点,不符合题意;②当a <2时,设函数g (x )的2个零点分别为x 1,x 2(x 1<x 2),要使得函数f (x )至少有3个零点,则x 2≤-2,-2,-2)=4+5a -5≥0,无解;③当a =10时,g (x )=x 2-10x +25,作出函数g (x ),h (x )的图象如图所示,由图可知,函数f (x )的零点个数为3,符合题意;④当a >10时,设函数g (x )的2个零点分别为x 3,x 4(x 3<x 4),要使得函数f (x )至少有3个零点,则x 3≥2,,=4+a -5≥0,解得a >4,所以a >10.综上所述,实数a 的取值范围是[10,+∞).考向3根据零点范围求参数例5已知函数f (x )=log 2(x +1)-1x +m 在区间(1,3]上有零点,则实数m 的取值范围为________.答案-53,解析由于函数y =log 2(x +1),y =m -1x在区间(1,3]上单调递增,所以函数f (x )在(1,3]上单调递增,由于函数f (x )=log 2(x +1)-1x +m 在区间(1,3]上有零点,,≥0,<0,+53≥0,解得-53≤m <0.因此实数m 的取值范围是-53,【通性通法】根据零点范围求参数的方法(1)利用零点存在定理构建不等式(组)求解.(2)分离参数后转化为函数的值域(最值)问题求解.(3)转化为两个熟悉的函数图象的上下关系问题,从而构建不等式(组)求解.【巩固迁移】8.(2024·湖北荆州中学高三月考)已知f (x )是定义在R 上且周期为3的函数,当x ∈[0,3)时,f (x )=|x 2-2x +12|,若函数y =f (x )-a 在区间[-3,4]上有10个零点(互不相同),则实数a 的取值范围是________.答案解析作出函数f (x )=|x 2-2x +12|,x ∈[0,3)的图象,可见f (0)=12,当x =1时,f (x )极大值=12,方程f (x )-a =0在[-3,4]上有10个零点,即函数y =f (x )的图象与直线y =a 在[-3,4]上有10个交点,由于函数f (x )的周期为3,因此直线y =a 与函数f (x )=|x 2-2x +12|,x ∈[0,3)的图象有4个交点,则有a课时作业一、单项选择题1.(2024·江苏扬中第二高级中学高三期初检测)函数f (x )=2x +3x 的零点所在的一个区间是()A .(-2,-1)B .(-1,0)C .(0,1)D .(1,2)答案B解析因为函数f (x )=2x +3x 在定义域内单调递增,f (-1)=12-3=-52<0,f (0)=1+0=1>0,所以由函数零点存在定理可知,函数f (x )的零点所在的区间为(-1,0).故选B.2.已知函数f (x )x -1,x ≤1,+log 2x ,x >1,则函数f (x )的零点为()A .2B .-2,0C.12D .0答案D解析当x ≤1时,令f (x )=2x -1=0,解得x =0;当x >1时,令f (x )=1+log 2x =0,解得x=12(舍去).综上所述,函数f (x )的零点为0.故选D.3.函数f (x )=e x |ln x |-1的零点个数是()A .1B .2C .3D .4答案B解析令f (x )=e x |ln x |-1=0,即|ln x |=e -x ,则函数f (x )=e x |ln x |-1的零点个数等价于两个函数y =e -x 与y =|ln x |图象的交点个数,y =e -x 与y =|ln x |的图象如图所示,由图可知,两个函数的图象有2个交点,故函数f (x )=e x |ln x |-1的零点个数是2.故选B.4.(2023·河南扶沟期末)若关于x 的方程log 12x =m1-m在区间m 的取值范围是()(1,+∞)答案B解析y =log 12x,则1<y <2,即1<m 1-m<2,解得12<m <23.故选B.5.已知三个函数f (x )=2x -1+x -1,g (x )=e x -1-1,h (x )=log 2(x -1)+x -1的零点依次为a ,b ,c ,则a ,b ,c 的大小关系是()A .a >b >c B .a >c >b C .c >a >b D .c >b >a答案D解析∵函数f (x )=2x -1+x -1为增函数,又f (0)=2-1-1=-12<0,f (1)=1>0,∴a ∈(0,1),由g (x )=e x -1-1=0,得x =1,即b =1,∵h (x )=log 2(x -1)+x -1在(1,+∞)上单调递增,又log +32-1=-12<0,h (2)=log 2(2-1)+2-1=1>0,∴32<c <2,∴c >b >a .故选D.6.若方程m x -x -m =0(m >0,且m ≠1)有两个不同的实数根,则实数m 的取值范围是()A .(0,1)B .(2,+∞)C .(0,1)∪(2,+∞)D .(1,+∞)答案D解析方程m x -x -m =0有两个不同的实数根等价于函数y =m x 与y =x +m 的图象有两个不同的交点,当m >1时,如图1所示,由图可知,当m >1时,函数y =m x 与y =x +m 的图象有两个不同的交点,满足题意;当0<m <1时,如图2所示,由图可知,当0<m <1时,函数y =m x 与y =x +m 的图象有且仅有一个交点,不满足题意.综上所述,实数m的取值范围为(1,+∞).故选D.7.已知函数f (x )x ,x ≤0,x ,x >0,若函数g (x )=f (x )+x -m 恰有两个不同的零点,则实数m 的取值范围是()A .[0,1]B .(-1,1)C .[0,1)D .(-∞,1]答案D解析由题意,函数f (x )x ,x ≤0,x ,x >0,当x ≤0时,函数f (x )=e x 为增函数,其中f (0)=1,当x >0时,函数f (x )=ln x 为增函数,且f (1)=0,又由函数g (x )=f (x )+x -m 恰有两个不同的零点,即为g (x )=0有两个不等的实数根,即y =f (x )与y =-x +m 的图象有两个不同的交点,如图所示,当y =-x +m 恰好过点(1,0),(0,1)时,两函数的图象有两个不同的交点,结合图象,要使得函数g (x )=f (x )+x -m 恰有两个不同的零点,实数m 的取值范围是(-∞,1].故选D.8.已知函数f (x )x |,0<x ≤10,-12x +6,x >10,若a ,b ,c 均不相等,且f (a )=f (b )=f (c ),则abc 的取值范围是()A .(1,10)B .(5,6)C .(10,12)D .(20,24)答案C解析函数f (x )的图象如图所示,不妨设a <b <c ,则-lg a =lg b =-12c +6∈(0,1),所以ab=1,0<-12c +6<1,所以ab =1,10<c <12,所以10<abc <12.故选C.二、多项选择题9.下列说法正确的是()A .函数y =x 2-3x -4的零点是(4,0),(-1,0)B .方程e x =3+x 有两个解C .函数y =3x ,y =log 3x 的图象关于直线y =x 对称D .用二分法求方程3x +3x -8=0在x ∈(1,2)内的近似解的过程中得到f (1)<0,f (1.5)>0,f (1.25)<0,则方程的根落在区间(1.25,1.5)上答案BCD解析对于A ,令y =x 2-3x -4=0,解得x =-1或x =4,所以函数y =x 2-3x -4的零点是-1和4,故A错误;对于B,分别作出y=e x,y=3+x的图象,y=e x与y=3+x的图象有两个交点,即方程e x=3+x有两个解,故B正确;对于C,因为同底数的指数函数和对数函数的图象关于直线y=x对称,所以函数y=3x,y=log3x的图象关于直线y=x对称,故C正确;对于D,因为y=3x+3x-8单调递增,由零点存在定理知,因为f(1)<0,f(1.5)>0,f(1.25)<0,所以方程的根落在区间(1.25,1.5)上,故D正确.故选BCD.10.若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1<x2,则下列结论正确的是()A.当m=0时,x1=2,x2=3B.m>-14C.当m>0时,2<x1<x2<3D.二次函数y=(x-x1)(x-x2)+m的零点为2和3答案ABD解析对于A,易知当m=0时,(x-2)(x-3)=0的根为2,3,故A正确;对于B,设y=(x-2)(x-3)=x2-5x+6-14≥-14,因为y=(x-2)(x-3)的图象与直线y=m有两个交点,所以m>-14,故B正确;对于C,当m>0时,y=(x-2)(x-3)-m的图象由y=(x-2)(x-3)的图象向下平移m个单位长度得到,x1<2<3<x2,故C错误;对于D,由(x-2)(x-3)=m 展开得,x2-5x+6-m=0,利用根与系数的关系求出x1+x2=5,x1x2=6-m,代入y=(x-x1)(x-x2)+m可得y=(x-x1)(x-x2)+m=(x-2)(x-3)-m+m=(x-2)(x-3),所以二次函数y=(x-x1)(x-x2)+m的零点为2和3,故D正确.故选ABD.11.已知函数f(x)x-1|,x<1,4x2+16x-13,x≥1,函数g(x)=f(x)-a,则下列结论正确的是()A.若g(x)有3个不同的零点,则a的取值范围是[1,2)B.若g(x)有4个不同的零点,则a的取值范围是(0,1)C.若g(x)有4个不同的零点x1,x2,x3,x4(x1<x2<x3<x4),则x3+x4=4D.若g(x)有4个不同的零点x1,x2,x3,x4(x1<x2<x3<x4),则x3x4答案BCD解析令g(x)=f(x)-a=0,得f(x)=a,所以g(x)的零点个数即为函数y=f(x)与y=a图象的交点个数,故作出函数y =f (x )的图象如图,由图可知,若g (x )有3个不同的零点,则a 的取值范围是[1,2)∪{0},故A 错误;若g (x )有4个不同的零点,则a 的取值范围是(0,1),故B 正确;若g (x )有4个不同的零点x 1,x 2,x 3,x 4(x 1<x 2<x 3<x 4),此时x 3,x 4关于直线x =2对称,所以x 3+x 4=4,故C 正确;由C 项可知x 3=4-x 4,所以x 3x 4=(4-x 4)x 4=-x 24+4x 4,由于g (x )有4个不同的零点,a 的取值范围是(0,1),故0<-4x 24+16x 4-13<1,所以134<-x 24+4x 4<72,故D 正确.故选BCD.三、填空题12.已知函数f (x )=log 2(x -1)+a 在区间(2,3)上有且仅有一个零点,则实数a 的取值范围为________.答案(-1,0)解析由对数函数的性质,可得f (x )为增函数,又函数f (x )在(2,3)上有且仅有一个零点,所以f (2)f (3)<0,即a (a +1)<0,解得-1<a <0,所以实数a 的取值范围是(-1,0).13.已知函数f (x )x -1|+1,x >0,x 2-2x ,x ≤0,若函数y =f (x )-kx -1有m 个零点,函数y =f (x )-1k x-1有n 个零点,且m +n =7,则非零实数k 的取值范围是________.答案,13∪[3,+∞)解析f (x )的图象与直线y =kx +1和y =1kx +1共7个交点,f (x )的图象如图所示,所以①k <3,3,解得0<k ≤13;0<1k <3,≥3,解得k ≥3.综上,非零实数k ,13∪[3,+∞).14.(2024·河北衡水中学高三月考)已知函数f (x )=x -1x -2与g (x )=1-sinπx ,则函数F (x )=f (x )-g (x )在区间[-2,6]内所有零点的和为________.答案16解析令F (x )=f (x )-g (x )=0,得f (x )=g (x ),在同一平面直角坐标系中分别画出函数f (x )=1+1x -2与g (x )=1-sinπx 的图象,如图所示,又f (x ),g (x )的图象都关于点(2,1)对称,结合图象可知f (x )与g (x )的图象在[-2,6]上共有8个交点,交点的横坐标即F (x )=f (x )-g (x )的零点,由对称性可得,所有零点的和为4×2×2=16.15.已知函数f (x )+1x ,x <0,x ,x >0,则方程f (f (x ))+3=0的解的个数为()A .3B .4C .5D .6答案C解析已知函数f (x )+1x ,x <0,x ,x >0,∴令f (x )=-3,则当x >0时,ln x =-3,解得x =1e 3;当x <0时,x +1x =-3,解得x =-3±52.∵f (f (x ))+3=0,即f (f (x ))=-3,则f (x )=1e 3或f (x )=-3±52.由f (x )=1e 3,得ln x =1e 3,此方程只有一个根,∵当x <0时,f (x )=x +1x ≤-2,当且仅当x =-1时,等号成立,∴f (x )=-3+52仅在x >0时有一个根,f (x )=-3-52在x <0时有两个根,在x >0时有一个根.综上,方程f (f (x ))+3=0的解的个数为5.故选C.16.(多选)(2024·湖北荆州模拟)已知函数f (x )|log 12x |,0<x<4,4≤x ≤14,若方程f (x )=m 有四个不等的实根x 1,x 2,x 3,x 4,且x 1<x 2<x 3<x 4,则下列结论正确的是()A .0<m <2B .x 1x 2=12C .x 3x 4∈(48,55)D .x 1x 3∈(1,5)答案ACD解析对于A ,当0<x <1时,log 12x >0,则f (x )=log 12x ,易得f (x )在(0,1)上单调递减,且f (x )>f (1)=0,当1≤x <4时,log 12x ≤0,则f (x )=-log 1x ,易得f (x )在[1,4)上单调递增,且f (1)≤f (x )<f (4),即0≤f (x )<2,当4≤x ≤14时,f (x )=则由f (x )=x ∈[4,14]的图象,可知f (x )在[4,8)上单调递减,在[8,14]上单调递增,且f (4)=2,f (5)=0,f (8)=4,f (11)=0,f (14)==4,从而利用对数函数与正弦函数的性质,画出f (x )的图象,如图所示,因为方程f (x )=m 有四个不等实根,所以f (x )与y =m 的图象有四个交点,所以0<m <2,故A 正确;对于B ,结合A 项分析可得log 12x 1=-log 12x 2,所以log 12(x 1x 2)=0,则x 1x 2=1,故B 错误;对于C ,D ,由正弦函数的性质及结合图象可知(x 3,m )与(x 4,m )关于直线x =8对称,所以x 3+x 4=16,又当0<x <1时,f (x )=log 12x ,令f (x )=2,得x =14,所以14<x 1<1,4<x 3<5,所以x 1x 3∈(1,5),x3x 4=x 3(16-x 3)=-x 23+16x 3=-(x 3-8)2+64,因为x 3∈(4,5),所以x 3x 4∈(48,55),故C ,D 正确.故选ACD.17.已知定义在R 上的奇函数y =f (x )满足f (1+x )=f (1-x ),当-1≤x <0时,f (x )=x 2,则方程f (x )+12=0在[-2,6]内的所有根之和为________.答案12解析因为f (1+x )=f (1-x ),所以y =f (x )的图象关于直线x =1对称,又函数y =f (x )在R 上为奇函数,且当-1≤x <0时,f (x )=x 2,由此画出f (x )在区间[-2,6]上的图象如图所示.f (x )+12=0⇒f (x )=-12,由图可知,y =-12与f (x )的图象有4个交点,其中两个关于直线x =1对称,两个关于直线x =5对称,所以方程f (x )+12=0在[-2,6]内的所有根之和为2×1+2×5=12.18.(2024·山东泰安高三期末)已知函数f (x )2(x +1),x >3,x +3|,-9≤x ≤3,若x 1<x 2,x 1<x 3,且f (x 1)=f (x 2),f (x 1)+f (x 3)=4,则x 3x 1+x 2的取值范围是________.答案-52,-12解析对于f (x )2(x +1),x >3,+3|,-9≤x ≤3,当x >3时,f (x )>2,当-9≤x ≤3时,0≤f (x )≤2,并且图象关于直线x =-3对称,函数f (x )的图象如下图所示,如果x 1>3,则f (x 1)=f (x 2)不成立,∴x 1∈[-9,3],x 2∈[-9,3],并且有x 1+x 2=-6,0<f (x 1)≤2.由f (x 1)+f (x 3)=4可知,2≤f (x 3)<4,∴2≤log 2(x 3+1)<4,3≤x 3<15.∴x 3x 1+x 2=-16x 3-52,-12.。
高二数学函数与方程试题

高二数学函数与方程试题1.已知二次函数的二次项系数为,且不等式的解集为,(1)若方程有两个相等的实根,求的解析式;(2)若的最大值为正数,求的取值范围.【答案】(1);(2)【解析】(1)抓住二次函数的图像与横坐标的交点、二次不等式解集的端点值、二次方程的根是同一个问题.解决与之相关的问题时,可利用函数与方程的思想、化归的思想将问题转化,(2)结合二次函数的图象来解决是当不等式对应的方程的根个数不确定时,讨论判别式与0的关系,(3)当a>0时,配方法最大值,也可用顶点坐标,或在对称轴处取得最大值试题解析:由题意可设,且,即, 2分(1),即有两个相等的实根,得,即,而,得,即,整理得. 6分(2),即,而,得,即, 9分,或,而,得的取值范围为. 12分【考点】二次函数和一元二次不等式解的关系及二次函数的最值2.函数的零点所在区间为()A.B.C.D.【答案】C【解析】已知,可计算,,所以可得零点所在的区间是,故选C.【考点】函数零点存在性定理.3.已知函数,若函数恰有4个零点,则实数的取值范围为.[来【答案】 1 < a< 2【解析】由函数解析式可知函数为基本初等函数,故先绘出函数图象:要使有四个零点,即函数的图象与的图象有四个交点。
由图形特点可知.无论取多少都在轴左侧有两个及其以上交点。
当时,两图像在左侧有一个交点。
当的图象与在左侧相切时,即,则.当时,共有5个交点;当时,共有3个交点.故.【考点】函数零点,函数图象,函数交点三者关系4.若函数满足,且时,,函数,则函数在区间内的零点的个数为()A.8B.9C.10D.13【答案】B【解析】函数满足知函数的周期,判断函数的零点个数,就是判断和图像的在区间交点个数,因此零点的个数为9个.【考点】函数的零点与函数图像的交点的个数.5.已知f(x)是定义在R上的奇函数,当时,,则函数的零点的集合为A.B.C.D.【答案】D【解析】设x<0,则-x>0,从而有,又因为f(x)是定义在R上的奇函数,所以有,从而得到:,则函数,令解得:,故选D.【考点】1.函数的奇偶性;2.函数的零点.6.设函数,若,,则关于的方程的解的个数为()A.1B.2C.3D.4【答案】C.【解析】由,可得,当时,有两个解,当时,显然有一个解,故选C.【考点】分段函数.7.一轮船行驶时,单位时间的燃料费u与其速度v的立方成正比,若轮船的速度为每小时10km 时,燃料费为每小时35元,其余费用每小时为560元,这部分费用不随速度而变化.已知该轮船最高速度为25km/h, 则轮船速度为 km/h时,轮船航行每千米的费用最少.【答案】20【解析】设轮船的燃料费u与速度v之间的关系是:u=kv3(k≠0),由已知,当v=10时,u=35,∴⇒k=,∴∴轮船行驶1千米的费用当且仅当,即v=20(km/h)时,等号成立.【考点】正比例函数、均值不等式的应用,函数模型的选择与应用.8.设函数中,为奇数,均为整数,且均为奇数.求证:无整数根。
高三数学理科测试题函数、导数、三角函数、解三角形(供参考)

高三数学《函数与导数、三角函数与解三角形》测试题(理科)一、选择题1.设2:f x x →是集合A 到集合B 的映射,若{}1,2B =,则AB 为( ) A .∅B .{1}C .∅或{2}D .∅或{1}2.函数x x x f ln )(+=的零点所在的区间为( ) A .(-1,0)B .(0,1)C .(1,2)D .(1,e )3.若函数2()log (3)a f x x ax =-+在区间(,]2a -∞上为减函数,则a 的取值范围是( )A .(0,1)B .(1,+∞)C .(1,23)D .(0,1)∪(1,23)4.若0()ln 0xe x g x xx ⎧≤=⎨>⎩,则1(())2g g = ( )A .12B .1C .12e D .ln 2-5.已知32()f x ax bx cx d =+++的图象如图所示,则有 ( ) A .0b < B .01b <<C .12b <<D .2b >6. 已知函数()f x 定义域为R ,则下列命题:①若()y f x =为偶函数,则(2)y f x =+的图象关于y 轴对称. ②若(2)y f x =+为偶函数,则()y f x =关于直线2x =对称. ③若函数(21)y f x =+是偶函数,则(2)y f x =的图象关于直线12x 对称. ④若(2)(2)f x f x -=-,则则()y f x =关于直线2x =对称. ⑤函数(2)y f x =-和(2)y f x =-的图象关于2x =对称.其中正确的命题序号是 ( ) A.①②④ B.①③④ C.②③⑤ D.②③④ 7.y =(sin x +cos x )2-1是( ) A .最小正周期为2π的偶函数 B .最小正周期为2π的奇函数 C .最小正周期为π的偶函数D .最小正周期为π的奇函数8.把函数y =sin(ωx +φ)(ω>0,|φ|<π)的图象向左平移π6个单位,再将图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)所得的图象解析式为y =sin x ,则( )xA .ω=2,φ=π6B .ω=2,φ=-π3C .ω=12,φ=π6D .ω=12,φ=π129.若函数f (x )=sin ωx +cos ωx (ω>0)的最小正周期为1,则它的图像的一个对称中心为( )A.⎝⎛⎭⎫-π8,0 B.⎝⎛⎭⎫π8,0 C .(0,0)D.⎝⎛⎭⎫-π4,0 10.函数y =cos(ωx +φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如右图所表示,A 、B 分别为最高与最低点,并且两点间的距离为22,则该函数的一条对称轴为( )A .x =2πB .x =π2C .x =1D .x =211.tan10°+tan50°+tan120°tan10°·tan50°的值应是( )A .-1B .1C .- 3D.3 12. 函数)(x f 在定义域R 内可导,若)2()(x f x f -=,且当)1,(-∞∈x 时,0)()1(<'-x f x ,设).3(),21(),0(f c f b f a ===则 ( )A .c b a <<B .b a c <<C .a b c <<D .a c b <<二、填空题13.设()f x 是定义在R 上且以3为周期的奇函数,若(1)1f ≤,23(2)1a f a -=+,则实数a 的取值范围是 .14.已知函数xx x f 2)(+=,x x x g ln )(+=,1)(--=x x x h 的零点分别为,,21x x 3x ,则321,,x x x 的大小关系是 .15.已知f (x )=2sin ⎝⎛⎭⎫2x -π6-m 在x ∈[0,π2]上有两个不同的零点,则m 的取值范围是________.16.对于函数f (x )=2cos 2x +2sin x cos x -1(x ∈R )给出下列命题:①f (x )的最小正周期为2π;②f (x )在区间[π2,5π8]上是减函数;③直线x =π8是f (x )的图像的一条对称轴;④f (x )的图像可以由函数y =2sin2x 的图像向左平移π4而得到.其中正确命题的序号是________(把你认为正确的都填上). 三、简答题17.在△ABC 中,A 、B 、C 的对边分别为a 、b 、c ,已知a +b =5,c =7,且4sin 2A +B2-cos2C =72.(1)求角C 的大小; (2)求△ABC 的面积.18.在△ABC 中,内角A ,B ,C 对边的边长分别是a ,b ,c ,已知c =2,C =π3.(1)若△ABC 的面积等于3,求a ,b ;(2)若sin C +sin(B -A )=2sin2A ,求△ABC 的面积.19.向量m =(a +1,sin x ),n =(1,4cos(x +π6)),设函数g (x )=m ·n (a ∈R ,且a 为常数).(1)若a 为任意实数,求g (x )的最小正周期;(2)若g (x )在[0,π3)上的最大值与最小值之和为7,求a 的值.20.设函数22()(1)ln(1)f x x x =+-+ (1)求函数)(x f 的单调区间;(2)当]1,11[--∈e ex 时,不等式()f x m <恒成立,求实数m 的取值范围; (3)关于x 的方程2()f x x x a =++在[0,2]上恰有两个相异实根,求a 的取值范围. 21.设函数bx xex f xa +=-)(,曲线)(x f y =在点(2,)2(f )处的切线方程为4)1(+-=x e y .(1)求a ,b 的值; (2)求)(x f 的单调区间. 22.答案解析选择题 1—5 DBCAA 6—12 CDBAC CB填空题 13. 213aa <-≥或 14. 321x x x >> 15.[-1,2] 16.②③ 简答题17.[解析] (1)∵A +B +C =180°,4sin 2A +B 2-cos2C =72.∴4cos 2C 2-cos2C =72,∴4·1+cos C 2-(2cos 2C -1)=72,∴4cos 2C -4cos C +1=0,解得cos C =12,∵0°<C <180°,∴C =60°. (2)∵c 2=a 2+b 2-2ab cos C , ∴7=(a +b )2-3ab ,解得ab =6. ∴S △ABC =12ab sin C =12×6×32=332.18.[解析] (1)由余弦定理及已知条件得,a 2+b 2-ab =4,又因为△ABC 的面积等于3,所以12ab sin C=3,得ab =4.联立方程组⎩⎨⎧a 2+b 2-ab =4,ab =4,解得a =2,b =2.(2)由题意得sin(B +A )+sin(B -A )=4sin A cos A ,即sin B cos A =2sin A cos A , 当cos A =0时,A =π2,B =π6,a =433,b =233,当cos A ≠0时,得sin B =2sin A ,由正弦定理得b =2a ,联立方程组⎩⎨⎧a 2+b 2-ab =4,b =2a ,解得a =233,b =433. 所以△ABC 的面积S =12ab sin C =233.19.[解析] g (x )=m ·n =a +1+4sin x cos(x +π6)=3sin2x -2sin 2x +a +1 =3sin2x +cos2x +a =2sin(2x +π6)+a(1)g (x )=2sin(2x +π6)+a ,T =π.(2)∵0≤x <π3,∴π6≤2x +π6<5π6当2x +π6=π2,即x =π6时,y max =2+a .当2x +π6=π6,即x =0时,y min =1+a ,故a +1+2+a =7,即a =2.20. (1)函数定义域为),1()1,(+∞---∞ ,,1)2(2]11)1[(2)(++=+-+='x x x x x x f 由,0)(>'x f 得210x x -<<->或 ;由,0)(<'x f 得.012<<--<x x 或则递增区间是(2,1),(0,)--+∞递减区间是(,2),(1,0)-∞--。
高考数学(理)二轮试题:第2章《函数与方程》(含答案)

精品题库试题理数1.(2014山东,8,5分)已知函数f(x)=|x-2|+1,g(x)=kx.若方程f(x)=g(x)有两个不相等的实根,则实数k的取值范围是()A. B. C.(1,2) D.(2,+∞)1.B1.f(x)=如图,作出y=f(x)的图象,其中A(2,1),则k OA=.要使方程f(x)=g(x)有两个不相等的实根,则函数f(x)与g(x)的图象有两个不同的交点,由图可知,<k<1.2.(2014课表全国Ⅰ,11,5分)已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x 0,且x0>0,则a 的取值范围是()A.(2,+∞)B.(1,+∞)C.(-∞,-2)D.(-∞,-1)2.C2.(1)当a=0时,显然f(x)有两个零点,不符合题意.(2)当a≠0时, f '(x)=3ax2-6x,令f '(x)=0,解得x1=0,x2=.当a>0时,>0,所以函数f(x)=ax3-3x2+1在(-∞,0)与上为增函数,在上为减函数,因为f(x)存在唯一零点x0,且x0>0,则f(0)<0,即1<0,不成立.当a<0时,<0,所以函数f(x)=ax3-3x2+1在和(0,+∞)上为减函数,在上为增函数,因为f(x)存在唯一零点x0,且x0>0,则f>0,即a·-3·+1>0,解得a>2或a<-2,又因为a<0,故a的取值范围为(-∞,-2).选C.3.(2014重庆一中高三下学期第一次月考,7)已知函数的图像与轴恰好有三个不同的公共点,则实数的取值范围是()(A)(B)(C)(D)3. C3. , 当或时, 可得; 当时,, 所以函数的极小值为, 极大值为, 由题意可得, 解得.4. (2014山西太原高三模拟考试(一),12) 已知方程在(0,+∞)上有两个不同的解,(<),则下面结论正确的是( )4. C4. 由题意可得上有两个不同的解,(<),结合数形结合可得直线与曲线相切于点,且,则根据导数的几何意义可得切线的斜率为,根据两点间的斜率公式可得,由此可得,即,两边同除可得2故选C.5. (2014福州高中毕业班质量检测, 9) 若定义在上的函数满足,, 且当时, 其图象是四分之一圆(如图所示), 则函数在区间上的零点个数为( )A. 5B. 4C. 3D. 25. B5. 因为定义在上的函数满足, ,所以函数是偶函数,且关于对称,又因为函数的定义域是, 所以,令得,由表中数据可知的单调减区间为,单调增区间为,当时,函数的极小值为,所以在时取得极大值,且函数在上是增函数,所以当时由3个交点;时只有一个交点,故函数在区间上的零点个数为4.6. (2014河北石家庄高中毕业班复习教学质量检测(二),11) 已知函数其中为自然对数的底数,若关于的方程有且只有一个实数解,则实数的取值范围为( )A. B. C. D.6. B6. 先令,则,所以,从而方程只有一个解,即的图像与的图像只有一个交点. 由数形结合可知:当时,应满足;当时交点有且只有一个;综上所述,实数的取值范围为.选B.7. (2014贵州贵阳高三适应性监测考试, 8) 下列命题中假命题的是()A. ,,使B. ,函数都不是偶函数C. ,使D. >0, 函数有零点7.B7.当时,为偶函数,所以是假命题. , , 显然为真.8. (2014山东实验中学高三第一次模拟考试,8) 已知函数的零点分别为的大小关系是()A. B. C. D.8.A8. 由已知分别是,,的根, 作出,,,的图像,如图所示,由图像可得.9. (2014广东广州高三调研测试,8) 对于实数和,定义运算“*” :*设*,且关于的方程为恰有三个互不相等的实数根,,,则的取值范围是()A.B.C.D.9.A9. 由已知可得,作出的图像,不妨设,由图像可得,且,由重要不等式。
高考数学(理科)-函数与方程-专题练习(含答案与解析)

)()2,+∞)()2,+∞(名师押题)已知函数,x0<() g x)4,3⎛⎫+∞ ⎪⎝⎭)4,23⎛⎫ ⎪⎝⎭17-1(1)17-1(2)B.12D.8()=有两个不同的零点y f x0,1,).}(∞+ )()g x x =+等号成立的条件是因而只需2,m e g ≥()21,f x e =--+其最大值为m -即m e >-()故函数f(x)有两个零点.]=-2(正根舍去),B.y=b的图象,如图所示从而函数f(x)=|2x-2|-b的图象,如图所示,当直线g 有两个不相等的实根时,k 的范围为所以函数f (x )的图象关于直线⎭⎫12|x |在[-3,3]上的图象,由图可知上的奇函数,所以当-1≤x <0时,的图象的对称轴为x =2k 与函数f (x )的图象在(0,6)内的零点之和为2×1+2×5==1或a >2,即0<a <x =0不是y =f (x )-g (x )的零点.内的零点个数即方程f (x )=g (x )(-+2x ;即k =4cos πx .⎧2上有且仅有三个零点, ∞)上只有三个交点, ⎩⎪⎨⎪⎧-x 2+-x -1-x-1,1-x >0⎩⎪⎨⎪⎧x 2-4x +2,x ≥1,-x -x ≥1时,函数g (.D [当>0时x -x 2,x )的图象,结合函数图象可知⎪⎪x -2-由题意知方程a =f (x )在[-3,4]上有由图可知a ∈⎝⎛⎭⎫0,12.]7.10 [问题可转化为y =⎝⎛⎭⎫12|x -⎦⎤n n -2×9和(n ,+∞)内都恰有一个零点=1f x +-1⎩⎪⎨⎪⎧1x +1--1<,xx ,由图象可知0<m ≤k AB =13.] 是周期等于3的周期函数f (x )与函数y =1|x |的交点的个数⎩⎪⎨-x ,f x +x <的图象如图所示,l ,观察可得函数y =f (x )的图象与直线l :有且只有两个不相等的实数根时,a <1,故选C .] ))=0,个交点,从小到大依次设为x1,x2,x3,x4,x5,=f(-x),所以log4(4-1+e2,其最大值为m-1 ,。
高一数学函数与方程试题

高一数学函数与方程试题1.函数的图象与轴的交点个数是()A.4B.3C.1D.0【答案】B.【解析】首先将函数化简为,然后根据函数与方程的关系知,要求“函数的图像与轴的交点的个数”就转化为求“方程的实数根的个数”,于是对其进行分类讨论:①当时,令,解得,,此时方程有两个实数根满足题意;②当时,令,解得,,因为,不满足,故舍去,所以此时方程有且仅有一个实数根满足题意. 综上所述,方程的实数根的个数有3个,即函数的图像与轴的交点的个数有3个,故选B.【考点】函数与方程.2.已知关于x的方程有两个不同的实数根,则实数k的取值范围是 .【答案】.【解析】首先利用换元法令,则问题“方程有两个不同的实数根”转化为“方程有两个不同的正实数根”,然后根据二次函数的根的分布知,应满足条件:且,解之得:.即为所求.【考点】一元二次方程的根的判断.3.一艘船上午在A处,测得灯塔S在它的北偏东300处,且与它相距海里,之后它继续沿正北方向匀速航行,上午到达B处,此时又测得灯塔S在它的北偏东750,此船的航速是()海里/小时。
A.B.C.D.【答案】D【解析】由题意得在三角形中,,由正弦定理得,即,得,因此航行的速度.【考点】正弦定理在三角形中的应用.4.关于的方程的两根分别在区间与内,求的取值范围.【答案】.【解析】(1)理解常用代数式的意义:表示的是到点的距离;表示点与点连线的斜率;(2)利用线性规划求目标函数的最值一般步骤:一画、二移、三求,其关键是准确的作出可行域,理解目标函数的意义;(3)在线性约束条件下,线性目标函数只有在可行域的顶点或者边界上取得最值.在解答选择题和填空题时可以根据可行域的顶点直接进行检验.试题解析:解:可以转化为点与连线的斜率.由题知两根在(0,1)与(1,2)内,可令必满足,即,由线性规划可知:点M(1,2)与阴影部分连线的斜率k的取值范围为∵(-3,1),(-1,0),【考点】线性规划的应用.5.方程实根的个数为( )A.6B.5C.4D.3【答案】A【解析】本题主要考查实根个数. 令在时是单调递增的,且值域为,值域为,且具有周期性的;所以可以考虑,有交点时的最大允许范围是(-10,10)1、当时,与只有一个交点;2、当时,与有两个交点;3、当时,与只有一个交点;4、当时,与有两个交点所以方程相等的实数根的个数为6个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(十一) 函数与方程[小题对点练——点点落实]对点练(一) 函数的零点问题1.(2018·河北武邑中学基础训练)方程ln(x +1)-2x =0(x >0)的根存在的大致区间是( )A .(0,1)B .(1,2)C .(2,e)D .(3,4)解析:选B 令f (x )=ln(x +1)-2x ,则f (1)=ln(1+1)-2=ln 2-2<0,f (2)=ln 3-1>0,所以函数f (x )的零点所在大致区间为(1,2).故选B.2.(2018·四川双流中学必得分训练)函数f (x )=2x +2x 的零点所处的区间是( ) A .[-2,-1] B .[-1,0] C .[0,1]D .[1,2]解析:选B f (-2)=2-2+2×(-2)<0,f (-1)=2-1+2×(-1)<0,f (0)=20+0>0,由零点存在性定理知,函数f (x )的零点在区间[-1,0]上.故选B.3.(2018·云南大理州统测)函数f (x )=⎩⎪⎨⎪⎧ln x ,x >0,-x (x +2),x ≤0的零点个数是( )A .0B .1C .2D .3解析:选D 当x >0时,令f (x )=0可得x =1;当x ≤0时,令f (x )=0可得x =-2或x =0.因此函数的零点个数为3.故选D.4.关于x 的方程|x 2-2x |=a 2+1(a >0)的解的个数是( ) A .1 B .2 C .3D .4解析:选B ∵a >0,∴a 2+1>1.而y =|x 2-2x |的图象如图所示,∴y =|x 2-2x |的图象与y =a 2+1的图象总有2个交点,即方程|x 2-2x |=a 2+1(a >0)的解的个数是2.5.函数f (x )=2sin πx -x +1的零点个数为( ) A .4 B .5 C .6D .7解析:选B 令2sin πx -x +1=0,得2sin πx =x -1,令h (x )=2sin πx ,g (x )=x -1,则f (x )=2sin πx -x +1的零点个数问题就转化为函数h (x )与g (x )的图象的交点个数问题.h (x )=2sin πx 的最小正周期为T =2ππ=2,画出两个函数的图象,如图所示,因为h (1)=g (1),h ⎝⎛⎭⎫52>g ⎝⎛⎭⎫52,g (4)=3>2,g (-1)=-2,所以两个函数图象的交点共5个,所以f (x )=2sin πx -x +1的零点个数为5.对点练(二) 函数零点的应用问题1.已知函数f (x )=log 3x +2x -a 在区间(1,2)内有零点,则实数a 的取值范围是( ) A .(-1,-log 32) B .(0,log 52) C .(log 32,1)D .(1,log 34)解析:选C ∵单调函数f (x )=log 3x +2x -a 在区间(1,2)内有零点,∴f (1)·f (2)<0,即(1-a )·(log 32-a )<0,解得log 32<a <1,故选C.2.(2018·甘肃天水一中月考)已知函数f (x )=ln x -ax 2+ax 恰有两个零点,则实数a 的取值范围为( )A .(-∞,0)B .(0,+∞)C .(0,1)∪(1,+∞)D .(-∞,0)∪{1}解析:选C 由题意,显然x =1是函数f (x )的一个零点,取a =-1,则f (x )=ln x +x 2-x ,f ′(x )=2x 2-x +1x =2⎝⎛⎭⎫x -142+78x>0恒成立.则f (x )仅有一个零点,不符合题意,排除A 、D ;取a =1,则f (x )=lnx -x 2+x ,f ′(x )=1-2x 2+x x =(1+2x )(1-x )x,f ′(x )=0得x =1,则f (x )在(0,1)上递增,在(1,+∞)上递减,f (x )max =f (1)=0,即f (x )仅有一个零点,不符合题意,排除B ,故选C.3.已知函数f (x )=⎩⎪⎨⎪⎧sin πx ,0≤x ≤1,log 2 017x ,x >1,若a ,b ,c 互不相等,且f (a )=f (b )=f (c ),则a+b +c 的取值范围是( )A .(1,2 017)B .(1,2 018)C .[2,2 018]D .(2,2 018)解析:选D 作出函数f (x )的图象与直线y =m ,如图所示,不妨设a <b <c ,当0≤x ≤1时,函数f (x )的图象与直线y =m 的交点分别为A ,B ,由正弦曲线的对称性,可得A (a ,m )与B (b ,m )关于直线x =12对称,因此a +b =1,当直线y =m =1时,由log 2 017x =1,解得x =2 017.若满足f (a )=f (b )=f (c ),且a ,b ,c 互不相等,由a <b <c 可得1<c <2 017,因此可得2<a +b +c <2 018,即a +b +c ∈(2,2 018).故选D.4.(2018·孝感模拟)若函数f (x )=(m -2)x 2+mx +(2m +1)的两个零点分别在区间(-1,0)和区间(1,2)内,则实数m 的取值范围是( )A.⎝⎛⎭⎫-12,14B.⎝⎛⎭⎫-14,12 C.⎝⎛⎭⎫14,12D.⎣⎡⎦⎤-14,12 解析:选C 依题意并结合函数f (x )的图象可知,⎩⎪⎨⎪⎧m ≠2,f (-1)·f (0)<0,f (1)·f (2)<0,即⎩⎪⎨⎪⎧m ≠2,[m -2-m +(2m +1)](2m +1)<0,[m -2+m +(2m +1)][4(m -2)+2m +(2m +1)]<0,解得14<m <12.5.(2018·广东七校联合体联考)若函数f (x )=2x +a 2x -2a 的零点在区间(0,1)上,则实数a 的取值范围是( )A.⎝⎛⎭⎫-∞,12 B .(-∞,1) C.⎝⎛⎭⎫12,+∞D .(1,+∞)解析:选C 易知函数f (x )的图象连续,且在(0,1)上单调递增.∴f (0)f (1)=(1-2a )(2+a 2-2a )<0,解得a >12.6.已知x 0是f (x )=⎝⎛⎭⎫12x +1x 的一个零点,x 1∈(-∞,x 0),x 2∈(x 0,0),则( ) A .f (x 1)<0,f (x 2)<0 B .f (x 1)>0,f (x 2)>0 C .f (x 1)>0,f (x 2)<0D .f (x 1)<0,f (x 2)>0解析:选C 在同一坐标系下作出函数f (x )=⎝⎛⎭⎫12x ,f (x )=-1x 的图象(图略),由图象可知当x ∈(-∞,x 0)时,⎝⎛⎭⎫12x >-1x ;当x ∈(x 0,0)时,⎝⎛⎭⎫12x <-1x ,所以当x 1∈(-∞,x 0),x 2∈(x 0,0)时,有f (x 1)>0,f (x 2)<0.7.(2018·龙岩质检)已知f (x )是奇函数,且是R 上的单调函数,若函数y =f (2x 2+1)+f (λ-x )只有一个零点,则实数λ的值是________.解析:令y =f (2x 2+1)+f (λ-x )=0,则f (2x 2+1)=-f (λ-x )=f (x -λ),因为f (x )是R 上的单调函数,所以2x 2+1=x -λ,即2x 2-x +1+λ=0只有一个实根,则Δ=1-8(1+λ)=0,解得λ=-78.答案:-788.已知函数f (x )=⎩⎪⎨⎪⎧log 2(x +1),x >0,-x 2-2x ,x ≤0,若函数g (x )=f (x )-m 有3个零点,则实数m 的取值范围是________.解析:函数g (x )=f (x )-m 有3个零点,转化为f (x )-m =0的根有3个,进而转化为y =f (x ),y =m 的交点有3个.画出函数y =f (x )的图象,则直线y =m 与其有3个公共点.又抛物线顶点为(-1,1),由图可知实数m 的取值范围是(0,1).答案:(0,1)[大题综合练——迁移贯通]1.已知a 是正实数,函数f (x )=2ax 2+2x -3-a .如果函数y =f (x )在区间[-1,1]上有零点,求a 的取值范围.解:f (x )=2ax 2+2x -3-a 的对称轴为x =-12a. ①当-12a ≤-1,即0<a ≤12时,须使⎩⎪⎨⎪⎧ f (-1)≤0,f (1)≥0,即⎩⎪⎨⎪⎧a ≤5,a ≥1,∴无解.②当-1<-12a <0,即a >12时,须使⎩⎪⎨⎪⎧ f ⎝⎛⎭⎫-12a ≤0,f (1)≥0,即⎩⎪⎨⎪⎧-12a -3-a ≤0,a ≥1,解得a ≥1,∴a 的取值范围是[1,+∞).2.(2018·德州模拟)已知函数f (x )=-x 2-2x .g (x )=⎩⎪⎨⎪⎧x +14x ,x >0,x +1,x ≤0.(1)求g [f (1)]的值;(2)若方程g [f (x )]-a =0有4个实数根,求实数a 的取值范围. 解:(1)∵f (1)=-12-2×1=-3,∴g [f (1)]=g (-3)=-3+1=-2.(2)令f (x )=t ,则原方程化为g (t )=a ,易知方程f (x )=t 在t ∈(-∞,1)内有2个不同的解,则原方程有4个解等价于函数y =g (t )(t <1)与y =a 的图象有2个不同的交点,作出函数y =g (t )(t <1)的图象,如图所示,由图象可知,当1≤a <54时,函数y =g (t )(t <1)与y =a 有2个不同的交点,即所求a 的取值范围是⎣⎡⎭⎫1,54. 3.(2018·信阳模拟)已知函数f (x )=log 2(2x +1). (1)求证:函数f (x )在(-∞,+∞)上单调递增;(2)若g (x )=log 2(2x -1)(x >0),且关于x 的方程g (x )=m +f (x )在[1,2]上有解,求m 的取值范围.解:(1)证明:∵函数f (x )=log 2(2x +1),任取x 1<x 2,则f (x 1)-f (x 2)=log 2(2x 1+1)-log 2(2x 2+1)=log 22x 1+12x 2+1,∵x 1<x 2,∴0<2x 1+12x 2+1<1,∴log 22x 1+12x 2+1<0,∴f (x 1)<f (x 2),∴函数f (x )在(-∞,+∞)上单调递增. (2)∵g (x )=m +f (x ), ∴m =g (x )-f (x )=log 2(2x -1)-log 2(2x +1) =log 22x -12x +1=log 2⎝⎛⎭⎫1-22x +1,∵1≤x ≤2,∴2≤2x ≤4, ∴log 213≤log 2⎝⎛⎭⎫1-22x +1≤log 235,故m 的取值范围为⎣⎡⎦⎤log 213,log 235.。
