广东省2016届高三数学一轮复习专题突破训练立体几何理

合集下载

高三数学一轮复习【立体几何】练习题

高三数学一轮复习【立体几何】练习题1.空间中，用a，b，c表示三条不同的直线，γ表示平面，则下列说法正确的有()A.若a∥b，b∥c，则a∥cB.若a⊥γ，b⊥γ，则a∥bC.若a∥γ，b∥γ，则a∥bD.若a⊥b，b⊥c，则a⊥c答案AB解析根据空间平行直线的传递性可知A正确；由直线与平面垂直的性质定理知B正确；若a∥γ，b∥γ，则a，b可能平行、相交或异面，故C错误；若a⊥b，b⊥c，则a，c可能相交、平行或异面，故D错误.2.对于两条不同直线m，n和两个不同平面α，β，下列选项正确的为()A.若m⊥α，n⊥β，α⊥β，则m⊥nB.若m∥α，n∥β，α⊥β，则m⊥n或m∥nC.若m∥α，α∥β，则m∥β或m⊂βD.若m⊥α，m⊥n，则n∥α或n⊂α答案ACD解析对A，令m，n分别为直线m，n的方向向量，因为m⊥α，n⊥β，所以m⊥α，n⊥β，又α⊥β，所以m⊥n，即m⊥n，所以选项A正确；对B，如图所示，在正方体ABCD-A1B1C1D1中，令平面ABCD为平面α，平面ABB1A1为平面β，直线A1C1为m，直线C1D为n，满足α⊥β，m∥α，n∥β，但m与n既不平行也不垂直，所以选项B错误；对C，若m⊄β，过m作一平面γ分别与平面α和平面β相交，且交线分别为a，b，则m∥a，a∥b，所以m∥b，所以m∥β；若m⊂β，符合题意，所以选项C 正确；对D，若n⊂α，符合题意；若n⊄α，过直线n作一平面β与平面α相交，设交线为b，因为b⊂α，m⊥α，所以m⊥b，又m⊥n，且n，b在同一平面内，所以n∥b，所以n∥α，所以选项D正确.综上，选ACD.3.如图是一个正方体的平面展开图，则在该正方体中()A.AE∥CDB.CH∥BEC.DG⊥BHD.BG⊥DE答案BCD解析由正方体的平面展开图还原正方体如图，连接AH，DE，BG，BH，DG，HC.由图形可知，AE⊥CD，故A错误；因为HE∥BC，HE＝BC，所以四边形BCHE为平行四边形，所以CH∥BE，故B正确；因为DG⊥HC，DG⊥BC，HC∩BC＝C，HC，BC⊂平面BHC，所以DG⊥平面BHC，又BH⊂平面BHC，所以DG⊥BH，故C正确；因为BG∥AH，而DE⊥AH，所以BG⊥DE，故D正确.故选BCD.4.用一个平面截正方体，所得的截面不可能是()A.锐角三角形B.直角梯形C.有一个内角为75°的菱形D.正五边形答案BCD解析对于A，如图1，截面的形状可能是正三角形，故A可能；图1图2对于B，首先考虑平面截正方体得到的截面为梯形，且QR与AA1不平行，如图2所示，不妨假设PQ⊥QR，因为AA1⊥平面A1B1C1D1，PQ⊂平面A1B1C1D1，所以AA1⊥PQ，从而有PQ⊥平面A1ABB1，这是不可能的，故B不可能；对于C，当平面截正方体得到的截面为菱形(非正方形)时，只有如下情形，如图3，其中P，R为所在棱的中点，易知当菱形为PBRD1时，菱形中的锐角取得最小值，即∠PD1R最小.设正方体的棱长为2，则PD1＝RD1＝5，PR＝22，则由余弦定理，得cos∠PD1R＝PD21＋RD21－PR22PD1·RD1＝5＋5－82×5×5＝15<6－24＝cos 75°，所以∠PD1R>75°，故C不可能；图3对于D，假设截面是正五边形，则截面中的截线必然分别在5个面内，由于正方体有6个面，分成两两平行的三对，故必然有一对平行面中有两条截线，而根据面面平行的性质可知这两条截线互相平行，但正五边形的边中是不可能有平行的边的，故截面的形状不可能是正五边形，故D不可能.综上所述，选BCD.5.已知正方体ABCD-A1B1C1D1的棱长为2，M为AA1的中点，平面α过点D1且与CM垂直，则()A.CM⊥BDB.BD∥平面αC.平面C1BD∥平面αD.平面α截正方体所得的截面图形的面积为9 2答案ABD解析如图，连接AC，则BD⊥AC.因为BD⊥AM，AM∩AC＝A，AM，AC⊂平面AMC，所以BD⊥平面AMC，又CM⊂平面AMC，所以BD⊥CM，故A正确；取AD的中点E，连接D1E，DM，由平面几何知识可得D1E⊥DM，又CD⊥D1E，DM∩CD＝D，DM，CD⊂平面CDM，所以D1E⊥平面CDM，又CM⊂平面CDM，所以D1E⊥CM.连接B1D1，过点E作EF∥BD，交AB于F，连接B1F，所以CM⊥EF，又D1E∩EF＝E，D1E，EF⊂平面D1EFB1，所以CM⊥平面D1EFB1，所以平面α截正方体所得的截面图形即梯形D1EFB1.由EF∥BD，BD⊄平面α，EF⊂平面α，得BD∥平面α，故B正确；连接AB1，AD1，易知平面AB1D1∥平面C1BD，而平面AB1D1∩平面α＝B1D1，所以平面C1BD与平面α不平行，故C不正确；截面图形为等腰梯形D1EFB1，EF＝2，B1D1＝22，D1E＝B1F＝5，所以截面图形的面积S＝12×(2＋22)×（5）2－⎝⎛⎭⎪⎫22－222＝92，故D正确.6.在正方体ABCD-A1B1C1D1中，N为底面ABCD的中心，P为线段A1D1上的动点(不包括两个端点)，M为线段AP的中点，则()A.CM与PN是异面直线B.CM>PNC.平面PAN⊥平面BDD1B1D.过P，A，C三点的正方体的截面一定是等腰梯形答案BCD解析对于选项A，如图，连接NC，PC，则A，N，C三点共线.又M为AP的中点，N为AC的中点，所以CM与PN共面，故A错误；对于选项B，因为P为线段A1D1上的动点(不包括两个端点)，所以AC>AP.在△MAC中，CM2＝AC2＋AM2－2AC·AM cos∠MAC＝AC2＋14AP2－AC·AP·cos∠MAC.在△PAN中，PN2＝AP2＋AN2－2AP·AN cos∠PAN＝AP2＋1 4AC 2－AP ·AC cos ∠PAN ，则CM 2－PN 2＝34(AC 2－AP 2)>0，所以CM >PN ，故B 正确；对于选项C ，在正方体ABCD-A 1B 1C 1D 1中，易知AC ⊥平面BDD 1B 1，即AN ⊥平面BDD 1B 1，又AN ⊂平面PAN ，所以平面PAN ⊥平面BDD 1B 1，故C 正确；对于选项D ，连接A 1C 1，在平面A 1B 1C 1D 1内作PK ∥A 1C 1，交C 1D 1于K ，连接KC .在正方体中，A 1C 1∥AC ，所以PK ∥AC ，PK ，AC 共面，所以四边形PKCA 就是过P ，A ，C 三点的正方体的截面，AA 1＝CC 1，A 1P ＝C 1K ，所以AP ＝CK ，即梯形PKCA 为等腰梯形，故D 正确.故选BCD.7.如图，在正四棱柱ABCD-A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是( )A.直线PB 1∥平面BC 1DB.三棱锥P-BC 1D 的体积为13C.三棱锥D 1-BC 1D 外接球的表面积为3π2D.直线PB 1与平面BCC 1B 1所成角的正弦值的最大值为53 答案 ABD解析对于A 选项，连接B 1D 1，AB 1，根据正四棱柱的性质可知AD 1∥BC 1，BD ∥B 1D 1，因为BC 1⊄平面AB 1D 1，AD 1⊂平面AB 1D 1，所以BC 1∥平面AB 1D 1，同理得BD ∥平面AB 1D 1，又BC 1∩BD ＝B ，所以平面AB 1D 1∥平面BC 1D ，又PB 1⊂平面AB 1D 1，所以PB 1∥平面BC 1D ，所以A 选项正确；对于B 选项，易知AD 1∥平面BC 1D ，所以V P-BC 1D ＝V A-BC 1D ＝V C 1-ABD ＝13×12×1×1×2＝13，所以B 选项正确；对于C 选项，三棱锥D 1-BC 1D 的外接球即正四棱柱ABCD-A 1B 1C 1D 1的外接球.设外接球的半径为R ，则4R 2＝12＋12＋22＝6，所以外接球的表面积为4πR 2＝6π，所以C 选项错误；对于D 选项，过P 作PE ∥AB ，交BC 1于点E ，则PE ⊥平面BCC 1B 1，连接B 1E ，则∠PB 1E 即直线PB 1与平面BCC 1B 1所成的角，当B 1E 最小时，∠PB 1E 最大，此时B 1E ⊥BC 1，由等面积法得S △BB 1C 1＝12BC 1·B 1E ＝12BB 1·B 1C 1，解得B 1E ＝25，在Rt △PB 1E 中，PE ＝AB ＝1，所以PB 1＝12＋⎝ ⎛⎭⎪⎫252＝35，所以∠PB 1E 的正弦值的最大值为PE PB 1＝53，所以D 选项正确.故选ABD.8.如图，已知正方体ABCD-A 1B 1C 1D 1的棱长为2，E ，F ，G 分别为BC ，CC 1，BB 1的中点，则( )A.直线D1D与直线AF垂直B.直线A1G与平面AEF平行C.平面AEF截正方体ABCD-A1B1C1D1所得的截面的面积为9 2D.点A1和点D到平面AEF的距离相等答案BCD解析对于选项A，假设AF与D1D垂直，又D1D⊥AE，AE∩AF＝A，AE，AF⊂平面AEF，所以D1D⊥平面AEF.因为EF⊂平面AEF，所以D1D⊥EF，这显然是错误的，所以假设不成立，故A错误；图1对于选项B，取B1C1的中点N，连接A1N，GN，如图1所示，易知A1N∥AE，又AE⊂平面AEF，A1N⊄平面AEF，所以A1N∥平面AEF.因为GN∥EF，EF⊂平面AEF，GN⊄平面AEF，所以GN∥平面AEF.又A1N，GN⊂平面A1GN，A1N∩GN＝N，所以平面A1GN∥平面AEF.因为A1G⊂平面A1GN，所以A1G∥平面AEF，故B正确；对于选项C，连接AD1，FD1，如图2所示，因为AD1∥EF，所以四边形AD1FE 为平面AEF截正方体ABCD-A1B1C1D1所得的截面，又AD1＝22＋22＝22，图2EF ＝12＋12＝2，D 1F ＝AE ＝12＋22＝5，所以四边形AD 1FE 为等腰梯形，高为（5）2－⎝ ⎛⎭⎪⎫222＝322，则S 梯形AD 1FE ＝12×(2＋22)×322＝92，故C 正确；对于选项D ，连接A 1D ，如图2所示，由选项C 可知A 1D 与平面AEF 相交且交点为A 1D 的中点，所以点A 1和点D 到平面AEF 的距离相等，故D 正确.综上，选BCD.9.已知棱长为a 的正方体ABCD-A 1B 1C 1D 1中，M 是B 1C 1的中点，点P 在正方体的表面上运动，且总满足MP ⊥MC ，则下列结论中正确的是( ) A.点P 的轨迹中包含AA 1的中点B.点P 在侧面AA 1D 1D 内的轨迹的长为5a4 C.MP 长度的最大值为21a4D.直线CC 1与直线MP 所成角的余弦值的最大值为55 答案 BCD解析如图，取A 1D 1的中点E ，分别取A 1A ，B 1B 上靠近A 1，B 1的四等分点F ，G ，连接EM ，EF ，FG ，MG ，易知EM ∥FG 且EM ＝FG ，所以E ，M ，F ，G 四点共面.连接GC ，因为MG 2＝⎝ ⎛⎭⎪⎫a 22＋⎝ ⎛⎭⎪⎫a 42＝5a 216，MC 2＝⎝ ⎛⎭⎪⎫a 22＋a 2＝5a 24，GC 2＝⎝ ⎛⎭⎪⎫3a 42＋a 2＝25a 216，因此MG 2＋MC 2＝GC 2，所以MG ⊥MC ，易知ME ⊥MC ，又MG ∩ME ＝M ，MG ，ME ⊂平面MEFG ，所以MC ⊥平面MEFG ，即点P 的轨迹为四边形MEFG (不含点M )，易知点P 在侧面AA 1D 1D 内的轨迹为EF ，且EF ＝MG ＝5a4，所以A 选项错误，B 选项正确；根据点P 的轨迹可知，当P 与F 重合时，MP 最长，易知FG ⊥平面BB 1C 1C ，则FG ⊥MG ，连接MF ，所以MF ＝a 2＋5a 216＝21a4，故C 选项正确；由于点P 的轨迹为四边形MEFG (不含点M )，所以直线CC 1与直线MP 所成的最小角就是直线CC 1与平面MEFG 所成的角，又向量CC 1→与平面MEFG 的法向量CM →的夹角等于∠C 1CM ，且sin ∠C 1CM ＝a25a 2＝55，所以直线CC 1与平面MEFG 所成角的余弦值为55，即直线CC 1与直线MP 所成角的余弦值的最大值等于55，故D 选项正确.10.如图，长方体ABCD-A 1B 1C 1D 1中，AB ＝BC ＝1，AA 1＝2，M 为AA 1的中点，过B 1M 作长方体的截面α交棱CC 1于N ，则( )A.截面α可能为六边形B.存在点N，使得BN⊥截面αC.若截面α为平行四边形，则1≤CN≤2D.当N与C重合时，截面图形的面积为36 4答案CD解析设N0为棱CC1的中点，当N从C1移动到C时，其过程中存在以下几种情况，如图1，当点N在线段C1N0上时，截面α为平行四边形；当点N在线段N0C上(不包括点N0，C)时，截面α为五边形；当点N与点C重合时，截面α为梯形.图1图2由以上分析可知，对于A，截面α不可能为六边形，所以A错误；对于B，假设BN⊥截面α，因为B1M⊂α，所以BN⊥B1M，所以必有点N，C重合，而BC与平面B1CQM不垂直，所以B错误；对于C，当截面α为平行四边形时，点N在线段C1N0上，则1≤CN≤2，所以C 正确；对于D，当点N与点C重合时，截面α为梯形，如图2，过M作MM′⊥B1C，垂足为M′.设梯形的高为h，B1M′＝x，则在Rt△B1MM′中，由勾股定理，得h2＝(2)2－x2，①同理h 2＝⎝ ⎛⎭⎪⎫522－⎝ ⎛⎭⎪⎫52－x 2，② 由①②，解得x ＝255，h ＝65，所以截面α的面积等于12×⎝⎛⎭⎪⎫5＋52·h ＝12×352×65＝364，所以D 正确. 综上可知，选CD.。

广东省2016届高三数学一轮复习专题突破训练数列理

广东省2016届高三数学理一轮复习专题突破训练数列2016年广东省高考将采用全国卷，下面是近三年全国卷的高考试题及2015届广东省部分地区的模拟试题，供同学们在复习时参考。

一、选择、填空题1、（2013年全国I 卷）设等差数列{a n }的前n 项和为S n ，1m S -＝－2，m S ＝0，1m S +＝3，则m ＝ ( ) A 、3B 、4C 、5D 、62、（2013年全国I 卷）若数列{n a }的前n 项和为S n ＝2133n a +，则数列{n a }的通项公式是n a =______. 3、（佛山市2015届高三二模）已知等差数列{}n a 满足1243=+a a ，523a a =，则=6a . 4、（广州市2015届高三二模）设(),P x y 是函数()y f x =的图象上一点，向量()()51,2x =-a ，()1,2y x =-b ，且//a b .数列{}n a 是公差不为0的等差数列，且()()()12936f a f a f a ++⋅⋅⋅+=，则129a a a ++⋅⋅⋅+=A.0B.9C.18D.365、（茂名市2015届高三二模）已知等差数列{}n a 的前n 项和为n S ，12,242==S a ，则=3a ( ).A ． 2B ．3C ．4D ．56、（梅州市2015届高三一模）已知等比数列{n a }的公比为正数，且239522,1a a a a ==，则1a ＝＿＿＿7、（汕头市2015届高三二模）已知等差数列{}n a 满足24201220148a a a a +++=，n S 是该数列的前n 项的和，则2015S =8、（深圳市2015届高三二模）设等差数列}{n a 的前n 项和为n S ，已知153=S ，1539=S ，则=6S ．9、（揭阳市2015届高三上期末）已知数列}{n a 的前n 项和212n S n n =+，则2232a a -的值为 A ．9 B ．18 C ．21 D ．11210、（汕尾市2015届高三上期末）已知{}n a 为等差数列，且388a a +=，则10S 的值为（） A ．40B ．45C ．50D ．5511、（深圳市2015届高三上期末）如果自然数a 的各位数字之和等于8，我们称a 为“吉祥数”。

届数学一轮复习第七章立体几何第三节空间图形的基本关系与公理课时规范练文含解析

第七章立体几何第三节空间图形的基本关系与公理课时规范练A组—-基础对点练1．若直线a⊥b，且直线a∥平面α，则直线b与平面α的位置关系是()A．bαB．b∥αC．bα或b∥αD．b与α相交或bα或b∥α解析：b与α相交或bα或b∥α都可以．答案：D2．(2020·江西景德镇模拟）将图①中的等腰直角三角形ABC沿斜边BC上的中线折起得到空间四面体ABCD(如图②)，则在空间四面体ABCD中，AD与BC的位置关系是()A．相交且垂直B．相交但不垂直C．异面且垂直D．异面但不垂直解析:在题图①中，AD⊥BC,故在题图②中,AD⊥BD，AD⊥DC,又因为BD∩DC＝D,所以AD⊥平面BCD,又BC平面BCD，D不在BC上，所以AD⊥BC，且AD与BC异面，故选C。

答案：C3．(2020·湖北荆州模拟)设α，β是两个不同的平面,a，b是两条不同的直线，则下列命题正确的是(）A．若a⊥b，b⊥α,则a∥αB．若aα,bβ，α∥β，则a与b是异面直线C．若a⊥α,b⊥β，a⊥b，则α⊥βD．若α∩β＝b,a∥b,则a∥α且a∥β解析：选项A，a可能在α内，故A错；选项B，a与b可能平行可能异面,故B错；选项D,a可能在α或β内,故D错．故选C.答案：C4．（2020·安徽安庆模拟）在正方体ABCD。

A1B1C1D1中,点P是线段BC1上任意一点，则下列结论中正确的是（)A．AD1⊥DP B．AC1⊥DPC．AP⊥B1C D．A1P⊥B1C解析:在正方体ABCD。

A1B1C1D1中，∵B1C⊥BC1,B1C⊥AB,BC1∩AB＝B，∴B1C⊥平面ABC1D1，∵点P是线段BC1上任意一点，∴AP平面ABC1D1，∴AP⊥B1C.故选C.答案：C5．(2020·河北模拟）若a，b是不同的直线,α,β是不同的平面，则下列命题中正确的是（)A．若a∥α，b∥β,a⊥b，则α⊥βB．若a∥α，b∥β，a∥b，则α∥βC．若a⊥α，b⊥β，a∥b，则α∥βD．若a∥α，b⊥β，a⊥b，则α∥β解析：∵a∥b,a⊥α,∴b⊥α，又b⊥β，∴α∥β.故选C.答案:C6. (2020·广东东莞模拟）如图，在三棱柱ABC.A1B1C1中，侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形，E是BC的中点，则下列叙述正确的是（)A．CC1与B1E是异面直线B．AC⊥平面ABB1A1C．AE，B1C1为异面直线，且AE⊥B1C1D．A1C1∥平面AB1E解析：因为CC1与B1E都在平面CC1B1B内，且CC1与B1E是相交直线,所以选项A错误．假设AC⊥平面ABB1A1，则AC⊥AB,即∠CAB＝90°，从而可得∠C1A1B1＝90°，这与题设“底面三角形A1B1C1是正三角形”矛盾，故假设错误，即选项B错误．因为点B1∉AE，直线B1C1交平面AEB1于点B1，所以AE,B1C1为异面直线；由题意可知△ABC是正三角形，又E是BC的中点，所以AE⊥BC，结合BC∥B1C1可得AE⊥B1C1,故选项C正确．因为直线AC交平面AB1E于点A，又AC∥A1C1，所以直线A1C1与平面AB1E相交，故选项D错误．综上，选C。

高考数学(理)一轮总复习课件：第八章立体几何 8-8-2

思考题 1 (1)如图，四面体 A－BCD 的三视图如图所示，其中正视图是一个正三角形，设二面角 A－BC－D 的大小为 θ，则 sin2θ＝________．
【解析】设 BD 中点为 E，则由侧视图知面 ABD⊥面 BCD，
∴AE⊥平面 BCD，由 E 作 EO⊥BC 于 O，连接 OA，则∠AOE
连接 OD，易知 PO⊥平面 ABC，所以 PO⊥ AB，所以 AB⊥平面 POD，则 AB⊥OD，所以∠PDO 为二面角 P－AB－C 的平面角．又 OD＝12BC＝ 2，PD＝ PO2＋OD2＝ 6，则 sinθ＝sin∠PDO＝PPOD ＝ 36，故选 C.
【答案】 C
★状元笔记★ 如果由已知易作出二面角的平面角，则可采取定义法求解，其步骤是：作→证→求→答．
第 2 学时二面角
授人以渔
题型一定义法求二面角 (1)(2019·台州一模)在边长为 a 的等边三角形 ABC 中， AD⊥BC 于点 D，沿 AD 折成二面角 B－AD－C，若此时 BC＝12 a，则二面角 B－AD－C 的大小为________．
【解析】在边长为 a 的等边三角形 ABC 中，AD⊥BC 于
【答案】 C
★状元笔记★ 二面角的平面角实质上就是两个向量的夹角！这两个向量的起点都在棱上，且分别在两个半平面内垂直于棱！
思考题 2 (1)设平面 α 的一个法向量为 n1＝(1，2，－2)，平面 β 的一个法向量为 n2＝(－2，－4，k)，若 α 和 β 所成的锐二面角的余弦值为23，则 k＝________．
【解析】 (1)证明：如图，取 A1C1 的中点 D，连接 B1D，CD.
∵C1C＝A1A＝A1C，∴CD⊥A1C1. ∵底面△ABC 是边长为 2 的正三角形， ∴AB＝BC，∴A1B1＝B1C1， ∴B1D⊥A1C1. 又∵B1D∩CD＝D，∴A1C1⊥平面 B1CD， ∴A1C1⊥B1C.

广东省2016届高三数学一轮复习专题突破训练平面向量理

广东省2016届高三数学理一轮复习专题突破训练平面向量2016年广东省高考将采用全国卷，下面是近三年全国卷的高考试题及2015届广东省部分地区的模拟试题，供同学们在复习时参考。

一、选择题1、（2015年全国I 卷）设D 为ABC 所在平面内一点3BC CD =，则（）（A ）1433AD AB AC =-+ (B)1433AD AB AC =- （C ）4133AD AB AC =+ (D)4133AD AB AC =- 2、（佛山市2015届高三二模）已知向量a ()32, 0-=，b ()3, 1=，则向量a 在b 上的投影为（）A ．3-B ．3-C ．3D ．33、（惠州市2015届高三4月模拟）在ABC ∆中，2=AB ，3=AC ，3AB AC ⋅=，则=BC ( )A C 4、（茂名市2015届高三二模）在△ABC 中,54sin =A ,6=∙AC AB ,则△ABC 的面积为（）. A ．3B ．125C ．6D ．45、（深圳市2015届高三二模）平面向量(1,2)=-a ，(2,)x =-b ，若a // b ，则x 等于A ．4B ．4-C ．1-D ．2 6、（河北保定2015届高三11月模拟）在△ABC 中，若•=•=•，且||=||=||=2，则△ABC 的周长为（）A ．B ． 2C ． 3D ． 67、（冀州中学2015届高三上学期第一次月考）已知向量,a b 的夹角为45︒，且1a =，210a b -=，则b =（）（A （B ）2 （C ）（D ）8、（开封市2015()2,2,a b a b a ==-⊥，则,a b 的夹角是9、（洛阳市2015届高三上学期期中考试）已知向量=（2，0），向量=（2，2），向量=（cos α，sin α），则向量与向量的夹角范围为（） A ． [0，] B ． [，] C ． [，] D ． [，]10、（潮州市2015届高三上期末）若向量()2,1a =-，()0,2b =，则以下向量中与a b +垂直的是（）A ．()1,2-B ．()1,2C ．()2,1D ．()0,2 11、（佛山市2015届高三上期末）已知两个单位向量12,e e 的夹角为45︒,且满足()121λ⊥-e e e ,则实数λ的值是( )A ．1BCD ．2 12、（广州市2015届高三上期末）设向量(,1)x =a ，(4,)x =b , 若,a b 方向相反, 则实数x 的值是A ．0B ．2±C ．2D ．2-13、（肇庆市2015届高三上期末）设a ，b 为非零向量，||2||a b =，两组向量4321,,,x x x x 和4321,,,y y y y 均由2个a 和2个b 排列而成. 若44332211y x y x y x y x ⋅+⋅+⋅+⋅所有可能取值中的最小值为2||4a ，则a 与b 的夹角为 A ．32π B ．2π C ．3π D ．6π二、填空题1、（2014年全国I 卷）已知A ，B ，C 是圆O 上的三点，若1()2AO AB AC =+，则AB 与AC 的夹角为 .2、（2013年全国I 卷）已知两个单位向量a ，b 的夹角为60°，c ＝t a ＋(1－t)b ，若b ·c =0，则t =_____.3、（广州市2015届高三二模）在边长为1的正方形ABCD 中，以A 为起点，其余顶点为终点的向量分别为1a ，2a ，3a ；以C 为起点，其余顶点为终点的向量分别为1c ，2c ，3c ．若m 为()()i j s t +∙+a a c c 的最小值，其中{}{},1,2,3i j ⊆，{}{},1,2,3s t ⊆，则m = ． 4、（惠州市2015届高三上期末）已知(1,2)a =，(0,1)b =，(,2)c k =-，若(2)a b c +⊥，则实数k =______5、（汕头市2015届高三上期末）下列关于向量c b a ,,的命题中，正确的有。

2016届高三数学一轮总复习课件：第七章立体几何7-4

行).
符号语言
l⊄α
a⊂α ⇒l∥α a∥l
第六页，编辑于星期五：二十点十二分。
2.性质定理：文字语言
如果一条直线和一个平性面平行，经过这条直线质的平面和这个平面相定交，那么这条直线就和理交线平行(简记线面平行
⇒线线平行).
图形语言
符号语言
a∥α
a⊂β ⇒a∥b α∩β＝b
答案平行
第十三页，编辑于星期五：二十点十二分。
知识点二
平面与平面平行
4.设l为直线，α，β是两个不同的平面．下列命题中正确的是
() A．若l∥α，l∥β，则α∥β
B．若l⊥α，l⊥β，则α∥β
C．若l⊥α，l∥β，则α∥β
D．若α⊥β，l∥α，则l⊥β
第十四页，编辑于星期五：二十点十二分。
解析 l∥α，l∥β，则α与β可能平行，也可能相交，故A项错；由面面平行的判定定理可知B项正确；由l⊥α，l∥β可知α⊥ β，故C项错；由α⊥β，l∥α可知l与β可能平行，也可能相交，故 D项错．
第二十页，编辑于星期五：二十点十二分。
问题3 证明面面平行有哪些常见的方法？ (1)利用定义：即证两个平面没有公共点(不常用)． (2)利用面面平行的判定定理(主要方法)． (3)利用垂直于同一条直线的两平面平行(客观题可用)． (4)利用平面平行的传递性，即两个平面同时平行于第三个平面，则这两个平面平行(客观题可用)．
第十九页，编辑于星期五：二十点十二分。
问题2 证明线面平行有哪些常见的方法？ (1)利用线面平行的定义(无公共点)； (2)利用线面平行的判定定理(a⊄α，b⊂α，a∥b⇒a∥α)； (3)利用面面平行的性质(α∥β，a⊂α⇒a∥β)； (4)利用面面平行的性质(α∥β，a⊄α，a⊄β，a∥α⇒a∥β)．

广东省2016届高三数学一轮复习专题突破训练复数与框图文

广东省2016届高三数学文一轮复习专题突破训练复数与框图2016年广东省高考将采用全国卷，下面是近三年全国卷的高考试题及2015届广东省部分地区的模拟试题，供同学们在复习时参考。

一、复数1、（2015年全国I 卷）已知复数z 满足(1)1z i i -=+，则z =（）（A ） 2i -- （B ）2i -+ （C ）2i - （D ）2i +（3）2、（2014年全国I 卷）设i iz ++=11，则=||z A.21 B. 22 C. 23 D. 2 3、（2013年全国I 卷）1＋2i（1－i ）2＝( )A ．－1－12iB ．－1＋12iC ．1＋12iD ．1－12i4、（佛山市2015届高三二模）若复数z 满足(1)i z i -=，其中i 为虚数单位，则在复平面上复数z 对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限5、（广州市2015届高三一模）已知i 为虚数单位，复数i z a b =+(),a b ∈R 的虚部b 记作Im ()z ，则Im 11i ⎛⎫=⎪+⎝⎭A ．12-B ．1-C ．12D ．16、（华南师大附中2015届高三三模）设i 为虚数单位,若复数()()2282i z m m m =+-+-是纯虚数,则实数m =(***)A ．4-B ．4-或2C ．-2或4D ．27、（潮州市2015届高三上期末）复数()()11z i i =+-在复平面内对应的点的坐标为（） A ．()1,0 B ．()0,2 C ．()0,1 D ．()2,08、（东莞市2015届高三上期末）设复数z 满足2z i i =-，i 是虚数单位，则z ＝（） A 、2－i B 、1＋2i C 、－1＋2i D 、－1－2i9、（江门市2015届高三上期末）已知 i 是虚数单位，若复数bi a Z +=（a ，R b ∈）在复平面内对应的点位于第四象限，则复数 i Z ⋅在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限10、（清远市2015届高三上期末）若a，b∈R，i是虚数单位，若（1＋i）i＝a＋bi，则（）A、a＝1，b＝1B、a＝－1，b＝1C、a＝－1，b＝－1D、a＝1，b＝－1二、框图1、（2015年全国I卷）执行右面的程序框图，如果输入的0.01t=，则输出的n=（）（A）5（B）6（C）10（D）122、（2014年全国I卷）执行下图的程序框图，若输入的,,a b k分别为1,2,3，则输出的M=A.203B.165C.72D.1583、（2013年全国I卷）如图1－1所示的程序框图，如果输入的t∈[－1，3]，则输出的s属于( )图1－1A．[－3，4]B．[－5，2]C ．[－4，3]D ．[－2，5]4、（佛山市2015届高三二模）某班有49位同学玩“数字接龙”游戏，具体规则按如图所示的程序框图执行（其中a 为座位号），并以输出的值作为下一轮输入的值。

高三数学一轮复习立体几何知识点突破训练含答案解析

精品基础教育教学资料，仅供参考，需要可下载使用！第八章⎪⎪⎪立体几何第一节空间几何体的三视图、直观图、表面积与体积突破点(一) 空间几何体的三视图和直观图基础联通抓主干知识的“源”与“流” 1．空间几何体的结构特征 (1)多面体的结构特征多面体结构特征棱柱有两个面平行，其余各面都是四边形且每相邻两个面的交线都平行且相等棱锥有一个面是多边形，而其余各面都是有一个公共顶点的三角形棱台棱锥被平行于底面的平面所截，截面和底面之间的部分叫做棱台几何体旋转图形旋转轴圆柱矩形矩形任一边所在的直线圆锥直角三角形一条直角边所在的直线圆台直角梯形或等腰梯形直角腰所在的直线或等腰梯形上下底中点的连线球半圆或圆直径所在的直线(1)三视图的名称几何体的三视图包括：正视图、侧视图、俯视图． (2)三视图的画法①在画三视图时，能看见的轮廓线和棱用实线表示，重叠的线只画一条，不能看见的轮廓线和棱用虚线表示．②三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体的正投影图．3．空间几何体的直观图空间几何体的直观图常用斜二测画法来画，其规则是：本节主要包括3个知识点：1.空间几何体的三视图和直观图；2.空间几何体的表面积与体积；3.与球有关的切、接应用问题.(1)原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴，y′轴的夹角为45°或135°，z′轴与x′轴和y′轴所在平面垂直．(2)原图形中平行于坐标轴的线段，直观图中仍分别平行于坐标轴；平行于x轴和z轴的线段在直观图中保持原长度不变；平行于y轴的线段在直观图中长度为原来的一半．考点贯通抓高考命题的“形”与“神”空间几何体的结构特征[例1](1)用任意一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是()A．圆柱B．圆锥C．球体D．圆柱、圆锥、球体的组合体(2)下列说法正确的是()A．有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱B．四棱锥的四个侧面都可以是直角三角形C．有两个平面互相平行，其余各面都是梯形的多面体是棱台D．棱台的各侧棱延长后不一定交于一点[解析](1)截面是任意的且都是圆面，则该几何体为球体．(2)A错，如图(1)；B正确，如图(2)，其中底面ABCD是矩形，PD⊥平面ABCD，可证明∠PAB，∠PCB，∠PDA，∠PDC都是直角，这样四个侧面都是直角三角形；C错，如图(3)；D错，由棱台的定义知，其侧棱的延长线必相交于同一点．[答案](1)C(2)B[方法技巧]解决与空间几何体结构特征有关问题的三个技巧(1)把握几何体的结构特征，要多观察实物，提高空间想象能力；(2)紧扣结构特征是判断的关键，熟悉空间几何体的结构特征，依据条件构建几何模型，如例1(2)中的A，C两项易判断失误；(3)通过反例对结构特征进行辨析．空间几何体的三视图1.画三视图的规则长对正、高平齐、宽相等，即俯视图与正视图一样长；正视图与侧视图一样高；侧视图与俯视图一样宽．2．三视图的排列顺序先画正视图，俯视图放在正视图的下方，侧视图放在正视图的右方．[例2](1)(2017·贵州七校联考)如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形，按正视图，侧视图，俯视图的顺序排列)()A．①②⑥B．①②③C．④⑤⑥D．③④⑤(2)(2016·天津高考)将一个长方体沿相邻三个面的对角线截去一个棱锥，得到的几何体的正视图与俯视图如图所示，则该几何体的侧(左)视图为()[解析](1)正视图应该是边长为3和4的矩形，其对角线左下到右上是实线，左上到右下是虚线，因此正视图是①；侧视图应该是边长为5和4的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此侧视图是②；俯视图应该是边长为3和5的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此俯视图是③.(2)先根据正视图和俯视图还原出几何体，再作其侧(左)视图．由几何体的正视图和俯视图可知该几何体为图①，故其侧(左)视图为图②.[答案](1)B(2)B[方法技巧]三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图注意正视图、侧视图和俯视图的观察方向；注意能看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的视图解决此类问题，可先根据已知的一部分视图，还原、推测直观图的可能形式，然后再找其剩下部分视图的可能形式．当然作为选择题，也可将选项逐项代入检验．(3)由几何体的三视图还原几何体的形状要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．空间几何体的直观图直观图与原图形面积的关系按照斜二测画法得到的平面图形的直观图与原图形面积的关系：(1)S直观图＝24S原图形．(2)S原图形＝22S直观图．[例3]用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是()[解析]由直观图可知，在直观图中多边形为正方形，对角线长为2，所以原图形为平行四边形，位于y轴上的对角线长为2 2.[答案] A能力练通抓应用体验的“得”与“失”1．[考点一]如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下四个命题中，假命题是()A．等腰四棱锥的腰与底面所成的角都相等B．等腰四棱锥的侧面与底面所成的二面角都相等或互补C．等腰四棱锥的底面四边形必存在外接圆D．等腰四棱锥的各顶点必在同一球面上解析：选B因为“等腰四棱锥”的四条侧棱都相等，所以它的顶点在底面的射影到底面的四个顶点的距离相等，故A，C是真命题；且在它的高上必能找到一点到各个顶点的距离相等，故D是真命题；B是假命题，如底面是一个等腰梯形时结论就不成立．2．[考点二]一几何体的直观图如图，下列给出的四个俯视图中正确的是()解析：选B由直观图可知，该几何体由一个长方体和一个截角三棱柱组成．从上往下看，外层轮廓线是一个矩形，矩形内部是一条水平线段连接两个三角形．3．[考点二]已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为()解析：选C当正视图为等腰三角形时，则高应为2，且应为虚线，排除A，D；当正视图是直角三角形时，由条件得一个直观图如图所示，中间的线是看不见的线PA形成的投影，应为虚线，故答案为C.4．[考点三]用斜二测画法画出的某平面图形的直观图如图，边AB平行于y轴，BC，AD平行于x轴．已知四边形ABCD的面积为2 2 cm2，则原平面图形的面积为()A．4 cm2B．4 2 cm2C．8 cm2D．8 2 cm2解析：选C 依题意可知∠BAD ＝45°，则原平面图形为直角梯形，上下底面的长与BC ，AD 相等，高为梯形ABCD 的高的22倍，所以原平面图形的面积为8 cm 2.5．[考点二](2017·南昌模拟)如图，在正四棱柱ABCD -A 1B 1C 1D 1中，点P 是平面A 1B 1C 1D 1内一点，则三棱锥P -BCD 的正视图与侧视图的面积之比为( )A ．1∶1B ．2∶1C ．2∶3D ．3∶2解析：选A 根据题意，三棱锥P -BCD 的正视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高；侧视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高．故三棱锥P -BCD 的正视图与侧视图的面积之比为1∶1.突破点(二) 空间几何体的表面积与体积基础联通抓主干知识的“源”与“流” 1．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r ＋r ′)l圆柱、圆锥、圆台侧面积间的关系：S 圆柱侧＝2πrl ――→r ′＝rS 圆台侧＝π(r ＋r ′)l ――→r ′＝0S 圆锥侧＝πrl . 2．空间几何体的表面积与体积公式名称几何体表面积体积柱体 (棱柱和圆柱)S 表面积＝S 侧＋2S 底V ＝Sh 锥体 (棱锥和圆锥)S 表面积＝S 侧＋S 底V ＝13Sh台体 (棱台和圆台)S 表面积＝S 侧＋S 上＋S 下V ＝13(S 上＋S 下＋S 上S 下)h球S ＝4πR 2V ＝43πR 3考点贯通抓高考命题的“形”与“神”空间几何体的表面积[例1] (1)(2017·安徽江南十校联考)某几何体的三视图如图所示，其中侧视图的下半部分曲线为半圆弧，则该几何体的表面积为( )A ．4π＋16＋4 3B ．5π＋16＋4 3C ．4π＋16＋2 3D ．5π＋16＋2 3(2)一个四面体的三视图如图所示，则该四面体的表面积是( )A ．1＋ 3B ．2＋ 3C ．1＋2 2D ．2 2[解析] (1)由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体，三棱柱的两个侧面面积之和为2×4×2＝16，两个底面面积之和为2×12×2×3＝23；半圆柱的侧面积为π×4＝4π，两个底面面积之和为2×12×π×12＝π，所以几何体的表面积为5π＋16＋23，故选D.(2)根据三视图还原几何体如图所示，其中侧面ABD ⊥底面BCD ，另两个侧面ABC ，ACD 为等边三角形，则有S 表面积＝2×12×2×1＋2×34×(2)2＝2＋3.[答案] (1)D (2)B[方法技巧]求空间几何体表面积的常见类型及思路(1)求多面体的表面积，只需将它们沿着棱“剪开”展成平面图形，利用求平面图形面积的方法求多面体的表面积．(2)求旋转体的表面积，可以从旋转体的形成过程及其几何特征入手，将其展开后求表面积，但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系．(3)求不规则几何体的表面积时，通常将所给几何体分割成基本的柱体、锥体、台体，先求出这些基本的柱体、锥体、台体的表面积，再通过求和或作差，求出所给几何体的表面积．空间几何体的体积柱体、锥体、台体体积间的关系[例2] (1)(2016·北京高考)某三棱锥的三视图如图所示，则该三棱锥的体积为( )A.16B.13C.12D ．1 (2)某几何体的三视图如图所示，则该几何体的体积为( )A.13＋2π B.13π6 C.7π3D.5π2[解析] (1)通过三视图可还原几何体为如图所示的三棱锥P -ABC ，通过侧视图得高h ＝1，通过俯视图得底面积S ＝12×1×1＝12，所以体积V ＝13Sh ＝13×12×1＝16.(2)由三视图可知，该几何体是一个圆柱和半个圆锥组合而成的几何体，其体积为π×12×2＋12×13π×12×1＝13π6.[答案] (1)A (2)B [方法技巧]求空间几何体体积的常见类型及思路(1)若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，等积转换法多用来求三棱锥的体积．(2)若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解．(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．能力练通抓应用体验的“得”与“失”1．[考点二](2016·山东高考)一个由半球和四棱锥组成的几何体，其三视图如图所示，则该几何体的体积为( )A.13＋23πB.13＋23πC.13＋26π D ．1＋26π 解析：选C 由三视图知，四棱锥是底面边长为1，高为1的正四棱锥，结合三视图可得半球半径为22，从而该几何体的体积为13×12×1＋12×4π3×⎝⎛⎭⎫223＝13＋26π.故选C. 2．[考点二]已知一个几何体的三视图如图所示，则该几何体的体积为( )A.5π3 cm 3 B ．2π cm 3 C.7π3cm 3 D ．3π cm 3解析：选C 该几何体为一个圆柱挖去半个球得到的几何体，其体积V ＝π×12×3－12×4π×133＝7π3(cm 3)．3.[考点一]某几何体的三视图如图所示，则它的表面积为( )A ．125＋20B ．242＋20C ．44D ．12 5解析：选A 由三视图得，这是一个正四棱台，且上、下底面的边长分别为2,4，则侧面梯形的高h ＝ 22＋⎝⎛⎭⎫4－222＝5，所以该正四棱台的表面积S ＝(2＋4)×52×4＋22＋42＝125＋20.4．[考点一]某几何体的三视图如图所示，则该几何体的表面积等于( )A ．8＋2 2B ．11＋2 2C ．14＋2 2D ．15解析：选B 由三视图知，该几何体是一个直四棱柱，上、下底面为直角梯形，如图所示．直角梯形斜腰长为12＋12＝2，所以底面周长为4＋2，侧面积为2×(4＋2)＝8＋22，两底面的面积和为2×12×1×(1＋2)＝3，所以该几何体的表面积为8＋22＋3＝11＋2 2.5．[考点二]中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升，其三视图如图所示(单位：寸)：若π取3，其体积为12.6(立方寸)，则图中的x 的值为________．解析：由三视图知，商鞅铜方升由一圆柱和一长方体组合而成，由题意得：(5.4－x )×3×1＋π·⎝⎛⎭⎫122x ＝12.6，解得x ＝1.6.答案：1.6突破点(三) 与球有关的切、接应用问题1.球的表面积和体积是每年高考的热点，且多与三视图、多面体等综合命题，常以选择题、填空题的形式出现.解决此类问题时，一是要善于把空间问题平面化，把平面问题转化到直角三角形中处理；二是要将变化的模型转化到固定的长方体或正方体中.2.与球有关的组合体问题主要有两种，一种是内切问题，一种是外接问题.解题时要认真分析图形，明确切点和接点的位置，确定有关“元素”间的数量关系，并作出合适的截面图.考点贯通抓高考命题的“形”与“神”多面体的内切球问题[例1] 若一个正四面体的表面积为S 1，其内切球的表面积为S 2，则S 1S 2＝________.[解析] 设正四面体棱长为a ，则正四面体表面积为S 1＝4×34·a 2＝3a 2，其内切球半径为正四面体高的14，即r ＝14×63a ＝612a ，因此内切球表面积为S 2＝4πr 2＝πa 26，则S 1S 2＝3a 2π6a 2＝63π. [答案] 63π[方法技巧]处理与球有关内切问题的策略解答此类问题时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．多面体的外接球问题处理与球有关外接问题的策略把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．[例2] (1)(2017·抚顺模拟)已知直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( )A.3172 B ．210 C.132D ．310(2)正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为( )A.81π4 B ．16π C ．9πD.27π4(3)一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为2的正方形)，则该几何体外接球的体积为________．[解析] (1)如图所示，由球心作平面ABC 的垂线，则垂足为BC 的中点M .又AM ＝12BC ＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA ＝⎝⎛⎭⎫522＋62＝132.(2)如图所示，设球半径为R ，底面中心为O ′且球心为O ， ∵正四棱锥P -ABCD 中AB ＝2， ∴AO ′＝ 2. ∵PO ′＝4，∴在Rt △AOO ′中，AO 2＝AO ′2＋OO ′2， ∴R 2＝(2)2＋(4－R )2，解得R ＝94，∴该球的表面积为4πR 2＝4π×⎝⎛⎭⎫942＝81π4.(3)依题意可知，新的几何体的外接球也就是原正方体的外接球，球的直径就是正方体的体对角线，∴2R ＝23(R 为球的半径)，∴R ＝3， ∴球的体积V ＝43πR 3＝43π.[答案] (1)C (2)A (3)43π [方法技巧]与球有关外接问题的解题规律(1)直棱柱外接球的球心到直棱柱底面的距离恰为棱柱高的12.(2)正方体外接球的直径为正方体的体对角线的长．此结论也适合长方体，或由同一顶点出发的两两互相垂直的三条棱构成的三棱柱或三棱锥．(3)求多面体外接球半径的关键是找到由球的半径构成的三角形，解三角形即可．能力练通抓应用体验的“得”与“失”1．[考点一]一块石材表示的几何体的三视图如图所示，将该石材切削、打磨、加工成球，则能得到的最大球的半径等于( )A ．1B ．2C ．3D ．4解析：选B 该几何体为直三棱柱，底面是边长分别为6,8,10的直角三角形，侧棱长为12，故能得到的最大球的半径等于底面直角三角形内切圆的半径，其半径为r ＝2Sa ＋b ＋c ＝2×12×6×86＋8＋10＝2，故选B.2．[考点二]如图是某几何体的三视图，则该几何体的外接球的表面积为( )A ．200πB ．150πC ．100πD ．50π解析：选D 由三视图知，该几何体可以由一个长方体截去4个角后得到，此长方体的长、宽、高分别为5,4,3，所以外接球半径R 满足2R ＝42＋32＋52＝52，所以外接球的表面积为S ＝4πR 2＝4π×⎝⎛⎭⎫5222＝50π，故选D. 3．[考点二](2016·太原模拟)如图，平面四边形ABCD 中，AB ＝AD ＝CD ＝1，BD ＝2，BD ⊥CD ，将其沿对角线BD 折成四面体A ′-BCD ，使平面A ′BD ⊥平面BCD ，若四面体A ′-BCD 的顶点在同一个球面上，则该球的表面积为( )A ．3πB.32π C ．4π D.34π 解析：选A 由图示可得BD ＝A ′C ＝2，BC ＝3，△DBC 与△A ′BC 都是以BC 为斜边的直角三角形，由此可得BC 中点到四个点A ′，B ，C ，D 的距离相等，即该三棱锥的外接球的直径为3，所以该外接球的表面积S ＝4π×⎝⎛⎭⎫322＝3π. 4．[考点二]设一个球的表面积为S 1，它的内接正方体的表面积为S 2，则S 1S 2的值等于( )A.2πB.6πC.π6D.π2解析：选D 设球的半径为R ，其内接正方体的棱长为a ，则易知R 2＝34a 2，即a ＝233R ，则S 1S 2＝4πR 26×⎝⎛⎭⎫233R 2＝π2.[全国卷5年真题集中演练——明规律] 1．(2016·全国甲卷)如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为( )A ．20πB ．24πC ．28πD ．32π解析：选C 由三视图知该几何体是圆锥与圆柱的组合体，设圆柱底面圆半径为r ，周长为c ，圆锥母线长为l ，圆柱高为h .由图得r ＝2，c ＝2πr ＝4π，h ＝4，由勾股定理得，l ＝22＋(23)2＝4，S 表＝πr 2＋ch ＋12cl ＝4π＋16π＋8π＝28π.2．(2016·全国丙卷)在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球．若AB ⊥BC ，AB ＝6，BC ＝8，AA 1＝3，则V 的最大值是( )A ．4πB.9π2C ．6πD.32π3解析：选B 设球的半径为R ，∵△ABC 的内切圆半径为6＋8－102＝2，∴R ≤2.又2R ≤3，∴R ≤32，∴V max ＝43×π×⎝⎛⎭⎫323＝9π2.故选B. 3．(2015·新课标全国卷Ⅱ)一个正方体被一个平面截去一部分后，剩余部分的三视图如下图，则截去部分体积与剩余部分体积的比值为( )A.18 B.17 C.16 D.15解析：选D 由已知三视图知该几何体是由一个正方体截去了一个“大角”后剩余的部分，如图所示，截去部分是一个三棱锥．设正方体的棱长为1，则三棱锥的体积为V 1＝13×12×1×1×1＝16，剩余部分的体积V 2＝13－16＝56.所以V 1V 2＝1656＝15，故选D. 4．(2015·新课标全国卷Ⅱ)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O -ABC 体积的最大值为36，则球O 的表面积为( )A ．36πB ．64πC ．144πD ．256π解析：选C 如图，设球的半径为R ，∵∠AOB ＝90°，∴S △AOB ＝12R 2.∵V O -ABC ＝V C -AOB ，而△AOB 面积为定值，∴当点C 到平面AOB 的距离最大时，V O -ABC 最大，∴当C 为与球的大圆面AOB 垂直的直径的端点时，体积V O -ABC 最大，为13×12R 2×R ＝36，∴R ＝6，∴球O 的表面积为4πR 2＝4π×62＝144π.故选C.5．(2015·新课标全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16＋20π，则r ＝( )A ．1B ．2C ．4D ．8解析：选B 如图，该几何体是一个半球与一个半圆柱的组合体，球的半径为r ，圆柱的底面半径为r ，高为2r ，则表面积S ＝12×4πr 2＋πr 2＋4r 2＋πr ·2r ＝(5π＋4)r 2.又S ＝16＋20π，∴(5π＋4)r 2＝16＋20π，∴r 2＝4，r ＝2，故选B.6．(2015·新课标全国卷Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺．问：积及为米几何？”其意思为：“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米约有( )A ．14斛B ．22斛C ．36斛D ．66斛解析：选B 设米堆的底面半径为r 尺，则π2r ＝8，所以r ＝16π，所以米堆的体积为V＝14×13π·r 2·5＝π12×⎝⎛⎭⎫16π2×5≈3209(立方尺)．故堆放的米约有3209÷1.62≈22(斛)．故选B. 7．(2014·新课标全国卷Ⅱ)如图，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解析：选C 原毛坯的体积V ＝(π×32)×6＝54π(cm 3)，由三视图可知该零件为两个圆柱的组合体，其体积V ′＝V 1＋V 2＝(π×22)×4＋(π×32)×2＝34π(cm 3)，故所求比值为1－V ′V ＝1027.8．(2013·新课标全国卷Ⅰ)某几何体的三视图如图所示，则该几何体的体积为( )A．16＋8π B．8＋8πC．16＋16π D．8＋16π解析：选A根据三视图可以判断该几何体由上、下两部分组成，其中上面部分为长方体，下面部分为半个圆柱，所以组合体的体积为2×2×4＋12×22×π×4＝16＋8π，故选A.9．(2012·新课标全国卷)已知三棱锥S-ABC的所有顶点都在球O的球面上，△ABC是边长为1的正三角形，SC为球O的直径，且SC＝2，则此棱锥的体积为()A.26 B.36 C.23 D.22解析：选A由于三棱锥S-ABC与三棱锥O-ABC底面都是△ABC，O是SC的中点，因此三棱锥S-ABC的高是三棱锥O-ABC高的2倍，所以三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍．在三棱锥O-ABC中，其棱长都是1，如图所示，S△ABC＝34×AB2＝34，高OD＝12－⎝⎛⎭⎫332＝63，所以V S-ABC＝2V O-ABC＝2×13×34×63＝26.[课时达标检测] 重点保分课时——一练小题夯双基，二练题点过高考[练基础小题——强化运算能力]1．下列结论正确的是()A．各个面都是三角形的几何体是三棱锥B．以三角形的一条边所在直线为旋转轴，其余两边绕旋转轴旋转形成的曲面所围成的几何体叫圆锥C．棱锥的侧棱长与底面多边形的边长都相等，则该棱锥可能是六棱锥D．圆锥的顶点与底面圆周上的任意一点的连线都是母线解析：选D A错误，如图①是由两个相同的三棱锥叠放在一起构成的几何体，它的各个面都是三角形，但它不是三棱锥；B 错误，如图②，若△ABC 不是直角三角形，或△ABC 是直角三角形但旋转轴不是直角边，所得的几何体都不是圆锥；C 错误，若该棱锥是六棱锥，由题设知，它是正六棱锥．易证正六棱锥的侧棱长必大于底面边长，这与题设矛盾．2.如图是一个空间几何体的三视图，其中正视图、侧视图都是由边长为4和6的矩形以及直径等于4的圆组成，俯视图是直径等于4的圆，该几何体的体积是( )A.41π3B.62π3C.83π3D.104π3解析：选D 由题意得，此几何体为球与圆柱的组合体，其体积V ＝43π×23＋π×22×6＝104π3. 3．某空间几何体的三视图如图所示，则该几何体的表面积为( )A ．12＋4 2B ．18＋8 2C ．28D ．20＋8 2解析：选D 由三视图可知该几何体是底面为等腰直角三角形的直三棱柱，如图．则该几何体的表面积为S ＝2×12×2×2＋4×2×2＋22×4＝20＋82，故选D.4．《九章算数》中，将底面是直角三角形的直三棱柱称为“堑堵”，已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”的侧面积为( )A ．2B ．4＋2 2C ．4＋4 2D ．6＋4 2解析：选C 由题可知，该几何体的底面为等腰直角三角形，等腰直角三角形的斜边长为2，腰长为2，棱柱的高为2.所以其侧面积S ＝2×2＋22×2＝4＋42，故选C.5．已知一个正方体的所有顶点在一个球面上，若球的体积为9π2，则正方体的棱长为________．解析：设正方体棱长为a ，球半径为R ，则43πR 3＝9π2，∴R ＝32，∴3a ＝3，∴a ＝ 3.答案： 3[练常考题点——检验高考能力]一、选择题1．已知圆锥的表面积为a ，且它的侧面展开图是一个半圆，则这个圆锥的底面直径是( )A.a2 B.3πa3πC.23πa 3πD.23a 3π解析：选C 设圆锥的底面半径为r ，母线长为l ，由题意知2πr ＝πl ，∴l ＝2r ，则圆锥的表面积S 表＝πr 2＋12π(2r )2＝a ，∴r 2＝a 3π，∴2r ＝23πa 3π.2．在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3B.4π3C.5π3D ．2π解析：选C 过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，如图所示，该几何体的体积为V ＝V 圆柱－V 圆锥＝π·AB 2·BC －13·π·CE 2·DE ＝π×12×2－13π×12×1＝5π3，故选C. 3．一个几何体的三视图如图所示，则该几何体的体积为( )A.163B.203C.152D.132解析：选D 该几何体可视为正方体截去两个三棱锥所得，如图所示，所以其体积为23－13×12×2×2×2－13×12×1×1×1＝132.故选D.4．已知正四面体的棱长为2，则其外接球的表面积为( ) A ．8π B ．12π C.32π D ．3π 解析：选D 如图所示，过顶点A 作AO ⊥底面BCD ，垂足为O ，则O 为正三角形BCD 的中心，连接DO 并延长交BC 于E ，又正四面体的棱长为2，所以DE ＝62，OD ＝23DE ＝63，所以在直角三角形AOD 中，AO ＝AD 2－OD 2＝233.设正四面体外接球的球心为P ，半径为R ，连接PD ，则在直角三角形POD 中，PD 2＝PO 2＋OD 2，即R 2＝⎝⎛⎭⎫233－R 2＋⎝⎛⎭⎫632，解得R ＝32，所以外接球的表面积S ＝4πR 2＝3π. 5．(2017·郑州质检)如图所示是一个几何体的三视图，则这个几何体外接球的表面积为( )A ．8πB ．16πC ．32πD ．64π解析：选C 还原三视图可知该几何体为一个四棱锥，将该四棱锥补成一个长、宽、高分别为22，22，4的长方体，则该长方体外接球的半径r ＝(22)2＋(22)2＋422＝22，则所求外接球的表面积为4πr 2＝32π.6．已知四棱锥P -ABCD 的三视图如图所示，则四棱锥P -ABCD 的四个侧面中面积的最大值是( )A ．6B ．8C ．2 5D ．3解析：选A 四棱锥如图所示，作PN ⊥平面ABCD ，交DC 于点N ，PC ＝PD ＝3，DN ＝2，则PN ＝32－22＝5，AB ＝4，BC ＝2，BC ⊥CD ，故BC ⊥平面PDC ，即BC ⊥PC ，同理AD ⊥PD .设M 为AB 的中点，连接PM ，MN ，则PM ＝3，S △PDC ＝12×4×5＝25，S △PBC ＝S△PAD＝12×2×3＝3，S △PAB ＝12×4×3＝6，所以四棱锥P -ABCD 的四个侧面中面积的最大值是6.二、填空题7．在棱长为3的正方体ABCD -A 1B 1C 1D 1中，P 在线段BD 1上，且BP PD 1＝12，M 为线段B 1C 1上的动点，则三棱锥M -PBC 的体积为________．解析：∵BP PD 1＝12，∴点P 到平面BC 1的距离是D 1到平面BC 1距离的13，即三棱锥P -MBC 的高h ＝D 1C 13＝1.M 为线段B 1C 1上的点， ∴S △MBC ＝12×3×3＝92，∴V M -PBC ＝V P -MBC ＝13×92×1＝32. 答案：328．一个几何体的三视图如图所示(单位：m)，则该几何体的体积为________m 3.。

高考数学(广东专用,文科)大一轮复习配套课时训练：第七篇立体几何第6节空间直角坐标系(含答案)

第6节空间直角坐标系课时训练练题感提知能【选题明细表】A组一、选择题1.点(2,0,3)在空间直角坐标系中的位置是( C )(A)y轴上 (B)xOy平面上(C)xOz平面上(D)x轴上解析:因为点(2,0,3)的纵坐标为0,横坐标、竖坐标都不为0,所以点(2,0,3)在x轴、z轴所确定的平面上.故选C.2.点B是点A(1,2,3)在坐标平面yOz内的射影,则B点的坐标是( B )(A)(1,2,0) (B)(0,2,3) (C)(1,0,3) (D)(1,0,0)解析:点在yOz平面的横坐标为0,其他坐标与A点相同,所以B点坐标为(0,2,3).故选B.3.已知空间一点A(-3,1,4),则点A关于原点对称的点的坐标为( C )(A)(1,-3,-4) (B)(-4,1,-3)(C)(3,-1,-4) (D)(4,-1,3)解析:关于原点对称的点的坐标的特点是横、纵、竖坐标全部变为原来的相反数.故选C.4.正方体不在同一表面上的两个顶点为A(-1,2,-1),B(3,-2,3),则正方体的体积为( C )(A)8 (B)27 (C)64 (D)128解析:由于A、B是正方体不在同一个平面上的两个顶点,所以A、B必为正方体一体对角线的两顶点,由于|AB|==4,故正方体的边长为4,体积为43=64.故选C.5.以棱长为1的正方体ABCD A1B1C1D1的棱AB、AD、AA1所在的直线为坐标轴,建立空间直角坐标系,如图所示,则正方形AA1B1B的对角线交点的坐标为( B )(A)(B)(C)(D)解析:连接AB1和A1B交于点O.据题意知AB1与A1B的交点即为AB1的中点.由题意得A(0,0,0),B1(1,0,1),∴AB1的中点坐标为,故选B.二、填空题6.在空间直角坐标系中,点M(2,1,-3)关于坐标原点的对称点为M′,则M′在平面xOz上的射影M″的坐标是.解析:点M(2,1,-3)关于原点的对称点为M′(-2,-1,3),点M′在平面xOz上的射影M″的坐标是(-2,0,3).答案:(-2,0,3)7.已知点A(1,-2,1)关于平面xOy的对称点为A1,则|AA1|= .解析:易知A1(1,-2,-1),所以|AA1|==2.答案:28.已知点A(1,2,3),B(2,-1,4),点P在y轴上,且|PA|=|PB|,则点P的坐标为.解析:设P(0,b,0),因为|PA|=|PB|,所以=,解得b=-.答案:（0,-,0）9.在空间直角坐标系中,点M(-2,4,-3),且MN⊥xOz面,垂足为N,则N点关于原点的对称点的坐标是.解析:因为点M(-2,4,-3),且MN⊥xOz面,垂足为N,所以N(-2,0,-3),所以N点关于原点的对称点的坐标是(2,0,3).答案:(2,0,3)三、解答题10. 如图所示,在长方体OABC O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=2,E是BC的中点,作OD⊥AC于点D,求线段B1E的长度及顶点O1到点D的距离.解:以O为坐标原点,以OA,OC,OO1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则O(0,0,0),O1(0,0,2),B1(2,3,2),E(1,3,0),∴|B=.设D(x,y,0),在Rt△AOC中,|OA|=2,|OC|=3,|AC|=,∴|OD|2=（）2=,∴|O 1D|===.11. 在棱长为1的正方体ABCD A1B1C1D1中,F是BD的中点,G在CD上,且|CG|=|CD|,E 为C1G的中点,求EF的长.解:如图所示,建立空间直角坐标系,由题意得F,C1(0,1,1),G,所以E,所以|EF|===.即EF的长为.B组12.已知空间直角坐标系Oxyz中有一点A(-1,-1,2),点B是平面xOy内的直线x+y=1上的动点,则A、B两点的最短距离是( B )(A) (B) (C)3 (D)解析:法一因为点B在平面xOy内的直线x+y=1上,故可设点B为(x,-x+1,0),所以|AB|===,所以当x=,即B时,|AB|取得最小值.故选B.法二设点A在平面xOy内的射影为A′(-1,-1,0),则A′、B的最短距离等于平面直角坐标系中A″(-1,-1)到直线x+y=1的距离d,则d=.又|A′A|=2,则|AB|min==.故选B.13.如图所示,正四面体A BCD的棱长为1,E、F分别是棱AB、CD的中点.(1)建立适当的空间直角坐标系,写出顶点A,B,C,D的坐标;(2)求EF的长.解:(1)设底面正三角形BCD的中心为O,连接AO,DO,延长DO交BC于点M,则AO⊥平面BCD,M是BC的中点,且DM⊥BC,过O作ON∥BC,交CD于点N,则ON⊥DM.以O为坐标原点,OM,ON,OA所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系.则|OD|=|DM|=×=,|OM|=|DM|=,|OA|===,所以A（0,0,）,B（,-,0）,C（,,0）,D（-,0,0）.(2)由(1)及中点坐标公式得E（,-,）,F（-,,0）,∴|EF|==.。

广东省高三数学(理)一轮复习专题训练：《立体几何》Word版含答案

立体几何1.【2014广东（理）高考7】若空间中四条直线两两不同的直线1l .2l .3l .4l ，满足12l l ⊥，23//l l ，34l l ⊥，则下列结论一定正确的是( )A .14l l ⊥B .14//l lC .1l .4l 既不平行也不垂直D .1l .4l 的位置关系不确定【答案】D2.【2013广东（理）高考5】某四棱台的三视图如图所示,则该四棱台的体积是( ).A .4B .143C .163D .6 【答案】B3.【2013广东（理）高考6】设m ,n 是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是( ).A .若α⊥β,m ⊂α,n ⊂β,则m ⊥nB .若α∥β,m ⊂α,n ⊂β,则m ∥nC .若m ⊥n ,m ⊂α,n ⊂β,则α⊥βD .若m ⊥α,m ∥n ,n ∥β,则α⊥β 【答案】D4.【2012广东（理）高考6】某几何体的三视图如图1所示，它的体积为( ) A .12π B .45π C .π57 D .π81【答案】C5.【2014广东（理）高考18】 (本小题满分13分)如图4，四边形ABCD 为正方形，PD ⊥平面ABCD ，30DPC ∠=，AF PC ⊥于点F ，//FE CD ，交PD 于点E . (1)证明：CF ADF ⊥平面； (2)求二面角D AF E --的余弦值.【答案】(1)详见解析；. （１）PD ⊥平面ABCD ，PD AD ∴⊥，又CD AD ⊥，PD CD D =， AD ∴⊥平面PCD ，AD PC ∴⊥，又AF PC ⊥，PC ∴⊥平面ADF ，即CF ADF ⊥平面；（２）设1AB =，则Rt PDC ∆中，1CD =，又DPC ∠=2PC ∴=，PD =，由（１）知CF DF ⊥DF ∴=AF ==12CF ∴==，又//FE CD ，14DE CF PD PC ∴==，DE ∴=，同理3344EF CD ==，如图所示，以D 为原点，建立空间直角坐标系，则(0,0,1)A ，E，3,0)4F，P ，(0,1,0)C ，设(,,)m x y z =是平面AEF 的法向量，则m AE m EF ⎧⊥⎨⊥⎩，又3(AE EF ⎧=⎪⎨=⎪⎩，所以300m AE x z m EF⎧⋅=-=⎪⎨⋅==⎪⎩，令4x =，得z =，m =，由（１）知平面ADF 的一个法向量(PC =，设二面角D AF E --的平面角为θ，可知θ为锐角，||cos |cos ,|||||m PCm PC m PC ⋅=<>==⋅θ=，即所求．6.【2013广东（理）高考18】 (本小题满分14分)如图(1),在等腰直角三角形ABC 中,∠A ＝90°,BC ＝6,D ,E 分别是AC ,AB 上的点,CD ＝BE,O 为BC 的中点.将△ADE 沿DE 折起,得到如图(2)所示的四棱锥A ′BCDE ,其中A ′O .图(1)图(2)(1)证明：A ′O ⊥平面BCDE ；(2)求二面角A ′CDB 的平面角的余弦值. 【答案】(1)详见解析 (2(Ⅰ) 在图1中,易得3,OC AC AD === 连结,OD OE ,在OCD ∆中,由余弦定理可得OD ==由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD的延长线于H ,连结A H', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角. 结合图1可知,H 为AC 中点,故OH =,从而A H '==所以cos OH A HO A H '∠==',所以二面角A CD B '--向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y ⎧+=⎪⎨-++=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量, 所以cos ,3n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦值为7.【2012广东（理）高考18】 (本小题满分13分)如图所示，在四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，点E 在线段PC 上，PC ⊥平面BDE .(1)证明：BD ⊥平面PAC ；(2)若1,2PA AD ==，求二面角B PC A --的正切值；【答案】（1）证明：因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以BD ⊥PA又因为PC⊥平面BDE，BD⊂平面BDE，BD⊥PC而PA∩PC=P，BD⊥平面PAC.（2）由（1）BD⊥平面PAC，得BD⊥AC，所以矩形ABCD为正方形设AC交BD于点O, 由PC⊥平面BDE,得PC垂直OE和BE所以∠BEO为二面角B－PC－A的平面角1,23PA AD AC BO OC PC==∴===∴==OE COOEPA PC===又所以在直角三角形BEO中，tan∠BEO3BOEO===，即二面角B-PC-A的正切值为3.8．（广东省湛江市湖光中学2014届高三上学期入学考试数学（理）试题）设三棱锥的三个侧面两两互相垂直,且侧棱长均为则其外接球的表面积为（）A．48πB．36πC．32πD．12π【答案】B9错误！未指定书签。

高考数学一轮复习第七篇立体几何与空间向量专题7.3 直线、平面平行的判定及性质练习(含解析)-

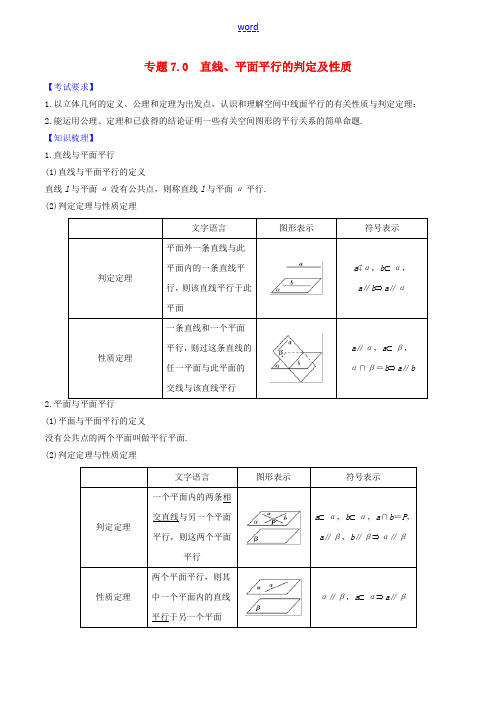
专题7.0 直线、平面平行的判定及性质【考试要求】1.以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理；2.能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题.【知识梳理】1.直线与平面平行(1)直线与平面平行的定义直线l与平面α没有公共点，则称直线l与平面α平行.(2)判定定理与性质定理文字语言图形表示符号表示判定定理平面外一条直线与此平面内的一条直线平行，则该直线平行于此平面a⊄α，b⊂α，a∥b⇒a∥α性质定理一条直线和一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行a∥α，a⊂β，α∩β＝b⇒a∥b2.平面与平面平行(1)平面与平面平行的定义没有公共点的两个平面叫做平行平面.(2)判定定理与性质定理文字语言图形表示符号表示判定定理一个平面内的两条相交直线与另一个平面平行，则这两个平面平行a⊂α，b⊂α，a∩b＝P，a∥β，b∥β⇒α∥β性质定理两个平面平行，则其中一个平面内的直线平行于另一个平面α∥β，a⊂α⇒a∥β如果两个平行平面同时和第三个平面相交，那么它们的交线平行α∥β，α∩γ＝a，β∩γ＝b⇒a∥b平行关系中的三个重要结论(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.(2)平行于同一平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.(3)两个平面平行，则其中任意一个平面内的直线与另一个平面平行.【疑误辨析】1.判断下列结论正误(在括号内打“√”或“×”)(1)若一条直线和平面内一条直线平行，那么这条直线和这个平面平行.( )(2)若直线a∥平面α，P∈α，则过点P且平行于直线a的直线有无数条.( )(3)如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行.( )(4)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面.( )【答案】(1)×(2)×(3)×(4)√【解析】(1)若一条直线和平面内的一条直线平行，那么这条直线和这个平面平行或在平面内，故(1)错误.(2)若a∥α，P∈α，则过点P且平行于a的直线只有一条，故(2)错误.(3)如果一个平面内的两条直线平行于另一个平面，则这两个平面平行或相交，故(3)错误.【教材衍化】2.(必修2P61A1(2)改编)下列说法中，与“直线a∥平面α”等价的是( )A.直线a上有无数个点不在平面α内B.直线a与平面α内的所有直线平行C.直线a与平面α内无数条直线不相交D.直线a与平面α内的任意一条直线都不相交【答案】 D【解析】因为a∥平面α，所以直线a与平面α无交点，因此a和平面α内的任意一条直线都不相交，故选D.3.(必修2P61A1(1)改编)下列命题中正确的是( )A.若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α，那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a，b和平面α满足a∥b，a∥α，b⊄α，则b∥α【答案】 D【解析】根据线面平行的判定与性质定理知，选D.【真题体验】4.(2018·某某模拟)已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是( )A.m∥α，n∥α，则m∥nB.m∥n，m∥α，则n∥αC.m⊥α，m⊥β，则α∥βD.α⊥γ，β⊥γ，则α∥β【答案】 C【解析】A中，m与n平行、相交或异面，A不正确；B中，n∥α或n⊂α，B不正确；根据线面垂直的性质，C正确；D中，α∥β或α与β相交，D错.5.(2019·某某月考)若平面α∥平面β，直线a∥平面α，点B∈β，则在平面β内且过B点的所有直线中( )A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一与a平行的直线【答案】 A【解析】当直线a在平面β内且过B点时，不存在与a平行的直线，故选A.6.(2019·十八中开学考试)如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH 的形状为________.【答案】平行四边形【解析】∵平面ABFE∥平面DCGH，又平面EFGH∩平面ABFE＝EF，平面EFGH∩平面DCGH＝HG，∴EF∥HG.同理EH∥FG，∴四边形EFGH是平行四边形.【考点聚焦】考点一与线、面平行相关命题的判定【例1】 (1)在空间中，a，b，c是三条不同的直线，α，β是两个不同的平面，则下列命题中的真命题是( )A.若a⊥c，b⊥c，则a∥bB.若a⊂α，b⊂β，α⊥β，则a⊥bC.若a∥α，b∥β，α∥β，则a∥bD.若α∥β，a⊂α，则a∥β(2)(2019·聊城模拟)下列四个正方体中，A，B，C为所在棱的中点，则能得出平面ABC∥平面DEF的是( )【答案】(1)D (2)B【解析】(1)对于A，若a⊥c，b⊥c，则a与b可能平行、异面、相交，故A是假命题；对于B，设α∩β＝m，若a，b均与m平行，则a∥b，故B是假命题；对于C，a，b可能平行、异面、相交，故C是假命题；对于D，若α∥β，a⊂α，则a与β没有公共点，则a∥β，故D是真命题.(2)在B中，如图，连接MN，PN，∵A，B，C为正方体所在棱的中点，∴AB∥MN，AC∥PN，∵MN∥DE，PN∥EF，∴AB∥DE，AC∥EF，∵AB∩AC＝A，DE∩EF＝E，AB，AC⊂平面ABC，DE，EF⊂平面DEF，∴平面ABC∥平面DEF.【规律方法】 1.判断与平行关系相关命题的真假，必须熟悉线、面平行关系的各个定义、定理，无论是单项选择还是含选择项的填空题，都可以从中先选出最熟悉最容易判断的选项先确定或排除，再逐步判断其余选项.2.(1)结合题意构造或绘制图形，结合图形作出判断.(2)特别注意定理所要求的条件是否完备，图形是否有特殊情况，通过举反例否定结论或用反证法推断命题是否正确.【训练1】 (1)下列命题正确的是( )A.若两条直线和同一个平面平行，则这两条直线平行B.若一条直线与两个平面所成的角相等，则这两个平面平行C.若一条直线与两个相交平面都平行，则这条直线与这两个平面的交线平行D.若两个平面垂直于同一个平面，则这两个平面平行(2)在正方体ABCD －A 1B 1C 1D 1中，M ，N ，Q 分别是棱D 1C 1，A 1D 1，BC 的中点，点P 在BD 1上且BP ＝23BD 1，则下面说法正确的是________(填序号).①MN ∥平面APC ；②C 1Q ∥平面APC ；③A ，P ，M 三点共线；④平面MNQ ∥平面APC . 【答案】 (1)C (2)②③【解析】 (1)A 选项中两条直线可能平行也可能异面或相交；对于B 选项，如图，在正方体ABCD －A 1B 1C 1D 1中，平面ABB 1A 1和平面BCC 1B 1与B 1D 1所成的角相等，但这两个平面垂直；D 选项中两平面也可能相交.C 正确.(2)如图，对于①，连接MN ，AC ，则MN ∥AC ，连接AM ，，易得AM ，交于点P ，即MN ⊂平面APC ，所以MN∥平面APC 是错误的. 对于②，由①知M ，N 在平面APC 内，由题易知AN∥C 1Q ，且AN ⊂平面APC ， C 1Q ⊄平面APC.所以C 1Q ∥平面APC 是正确的.对于③，由①知，A ，P ，M 三点共线是正确的.对于④，由①知MN ⊂平面APC ，又MN ⊂平面MNQ ，所以平面MNQ ∥平面APC 是错误的. 考点二直线与平面平行的判定与性质角度1 直线与平面平行的判定【例2－1】 (2019·东北三省四市模拟)在如图所示的几何体中，四边形ABCD 是正方形，PA ⊥平面ABCD ，E ，F 分别是线段AD ，PB 的中点，PA ＝AB ＝1.【答案】见解析【解析】(1)证明：EF ∥平面PDC ； (2)求点F 到平面PDC 的距离.(1)证明取PC 的中点M ，连接DM ，MF ，∵M，F 分别是PC ，PB 的中点，∴MF∥CB，MF ＝12CB ，∵E 为DA 的中点，四边形ABCD 为正方形， ∴DE∥CB，DE ＝12CB ，∴MF∥DE，MF ＝DE ，∴四边形DEFM 为平行四边形， ∴EF∥DM，∵EF ⊄平面PDC ，DM ⊂平面PDC ， ∴EF ∥平面PDC . (2)解 ∵EF ∥平面PDC ，∴点F 到平面PDC 的距离等于点E 到平面PDC 的距离.∵PA ⊥平面ABCD ，∴PA ⊥DA ，在Rt△PAD 中，PA ＝AD ＝1，∴DP ＝ 2. ∵PA ⊥平面ABCD ，∴PA ⊥CB ，∵CB ⊥AB ，PA ∩AB ＝A ，∴CB ⊥平面PAB ， ∴CB ⊥PB ，则PC ＝3，∴PD 2＋DC 2＝PC 2， ∴△PDC 为直角三角形， ∴S △PDC ＝12×1×2＝22.连接EP ，EC ，易知V E －PDC ＝V C －PDE ，设E 到平面PDC 的距离为h ， ∵CD ⊥AD ，CD ⊥PA ，AD ∩PA ＝A ，∴CD ⊥平面PAD ，则13×h ×22＝13×1×12×12×1，∴h ＝24， ∴点F 到平面PDC 的距离为24. 角度2 直线与平面平行性质定理的应用【例2－2】 (2018·某某模拟)如图所示，在正方体ABCD －A 1B 1C 1D 1中，棱长为2，E ，F 分别是棱DD 1，C 1D 1的中点.(1)求三棱锥B 1－A 1BE 的体积；(2)试判断直线B 1F 与平面A 1BE 是否平行，如果平行，请在平面A 1BE 上作出与B 1F 平行的直线，并说明理由. 【答案】见解析【解析】(1)如图所示，V B 1－A 1BE ＝V E －A 1B 1B ＝13S △A 1B 1B · DA ＝13×12×2×2×2＝43.(2)B 1F ∥平面A 1BE .延长A 1E 交AD 延长线于点H ，连BH 交CD 于点G ，则BG 就是所求直线.证明如下：因为BA 1∥平面CDD 1C 1，平面A 1BH ∩平面CDD 1C 1＝GE ，所以A 1B ∥GE . 又A 1B ∥CD 1，所以GE ∥CD 1.又E 为DD 1的中点，则G 为CD 的中点. 故BG ∥B 1F ，BG 就是所求直线.【规律方法】 1.利用判定定理判定线面平行，关键是找平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线.2.在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”；而在应用性质定理时，其顺序恰好相反.【训练2】 (2017·某某卷)如图，在三棱锥A －BCD 中，AB ⊥AD ，BC ⊥BD ，平面ABD ⊥平面BCD ，点E ，F (E 与A ，D 不重合)分别在棱AD ，BD 上，且EF ⊥AD .求证：(1)EF ∥平面ABC ； (2)AD ⊥AC . 【答案】见解析【解析】证明 (1)在平面ABD 内，AB⊥AD，EF⊥AD，则AB∥EF.∵AB ⊂平面ABC ，EF ⊄平面ABC ，∴EF∥平面ABC.(2)∵BC⊥BD，平面ABD∩平面BCD＝BD，平面ABD⊥平面BCD，BC⊂平面BCD，∴BC⊥平面ABD.∵AD⊂平面ABD，∴BC⊥AD.又AB⊥AD，BC，AB⊂平面ABC，BC∩AB＝B，∴AD⊥平面ABC，又因为AC⊂平面ABC，∴AD⊥AC.考点三面面平行的判定与性质【例3】 (经典母题)如图所示，在三棱柱ABC－A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：(1)B，C，H，G四点共面；(2)平面EFA1∥平面BCHG.【答案】见解析【解析】证明(1)∵G，H分别是A1B1，A1C1的中点，∴GH是△A1B1C1的中位线，则GH∥B1C1.又∵B1C1∥BC，∴GH∥BC，∴B，C，H，G四点共面.(2)∵E，F分别为AB，AC的中点，∴EF∥BC，∵EF⊄平面BCHG，BC⊂平面BCHG，∴EF∥平面BCHG.又G，E分别为A1B1，AB的中点，A1B1平行且等于AB，∴A1G平行且等于EB，∴四边形A1EBG是平行四边形，∴A1E∥GB.∵A1E⊄平面BCHG，GB⊂平面BCHG，∴A1E∥平面BCHG.又∵A1E∩EF＝E，∴平面EFA1∥平面BCHG.【迁移探究1】在本例中，若将条件“E，F，G，H分别是AB，AC，A1B1，A1C1的中点”变为“D1，D分别为B1C1，BC的中点”，求证：平面A1BD1∥平面AC1D.【答案】见解析【解析】证明如图所示，连接A 1C 交AC 1于点M ， ∵四边形A 1ACC 1是平行四边形， ∴M 是A 1C 的中点，连接MD ， ∵D 为BC 的中点， ∴A 1B∥DM. ∵A 1B ⊂平面A 1BD 1， DM ⊄平面A 1BD 1， ∴DM∥平面A 1BD 1，又由三棱柱的性质知，D 1C 1平行且等于BD ， ∴四边形BDC 1D 1为平行四边形， ∴DC 1∥BD 1.又DC 1⊄平面A 1BD 1，BD 1⊂平面A1BD1， ∴DC 1∥平面A 1BD 1，又DC 1∩DM＝D ，DC 1，DM ⊂平面AC1D ，因此平面A 1BD 1∥平面AC 1D .【迁移探究2】在本例中，若将条件“E ，F ，G ，H 分别是AB ，AC ，A 1B 1，A 1C 1的中点”变为“点D ，D 1分别是AC ，A 1C 1上的点，且平面BC 1D ∥平面AB 1D 1”，试求AD DC的值. 【答案】见解析【解析】连接A 1B 交AB 1于O ，连接OD 1.由平面BC 1D ∥平面AB 1D 1，且平面A 1BC 1∩平面BC 1D ＝BC 1，平面A 1BC 1∩平面AB 1D 1＝D 1O ，所以BC 1∥D 1O ，则A 1D 1D 1C 1＝A 1OOB＝1.又由题设A 1D 1D 1C 1＝DC AD， ∴DC AD ＝1，即ADDC＝1. 【规律方法】 1.判定面面平行的主要方法 (1)利用面面平行的判定定理.(2)线面垂直的性质(垂直于同一直线的两平面平行). 2.面面平行条件的应用(1)两平面平行，分析构造与之相交的第三个平面，交线平行. (2)两平面平行，其中一个平面内的任意一条直线与另一个平面平行.【提醒】利用面面平行的判定定理证明两平面平行，需要说明是在一个平面内的两条直线是相交直线. 【训练3】 (2019·某某二模)如图，四棱锥P －ABCD 中，底面ABCD 是直角梯形，AB ∥CD ，AB ⊥AD ，AB ＝2CD ＝2AD ＝4，侧面PAB 是等腰直角三角形，PA ＝PB ，平面PAB ⊥平面ABCD ，点E ，F 分别是棱AB ，PB 上的点，平面CEF ∥平面PAD .(1)确定点E ，F 的位置，并说明理由； (2)求三棱锥F －DCE 的体积. 【答案】见解析【解析】(1)因为平面CEF ∥平面PAD ，平面CEF ∩平面ABCD ＝CE ，平面PAD ∩平面ABCD ＝AD ，所以CE ∥AD ，又AB ∥DC ，所以四边形AECD 是平行四边形，所以DC ＝AE ＝12AB ，即点E 是AB 的中点.因为平面CEF ∥平面PAD ，平面CEF ∩平面PAB ＝EF ，平面PAD ∩平面PAB ＝PA ，所以EF ∥PA ，又点E 是AB 的中点，所以点F 是PB 的中点.综上，E ，F 分别是AB ，PB 的中点.(2)连接PE ，由题意及(1)知PA ＝PB ，AE ＝EB ，所以PE ⊥AB ，又平面PAB ⊥平面ABCD ，平面PAB ∩平面ABCD ＝AB ，所以PE ⊥平面ABCD . 又AB ∥CD ，AB ⊥AD ，所以V F －DEC ＝12V P －DEC ＝16S △DEC ×PE ＝16×12×2×2×2＝23. 【反思与感悟】1.转化思想：三种平行关系之间的转化其中线面平行是核心，线线平行是基础，要注意它们之间的灵活转化.2.直线与平面平行的主要判定方法(1)定义法；(2)判定定理；(3)面面平行的性质.3.平面与平面平行的主要判定方法(1)定义法；(2)判定定理；(3)推论；(4)a⊥α，a⊥β⇒α∥β.【易错防X 】1.在推证线面平行时，一定要强调直线不在平面内，否则，会出现错误.2.面面平行的判定中易忽视“面内两条相交线”这一条件.3.如果一个平面内有无数条直线与另一个平面平行，易误认为这两个平面平行，实质上也可以相交.4.运用性质定理，要遵从由“高维”到“低维”，但也要注意，转化的方向总是由题目的具体条件而定，决不可过于“模式化”.【分层训练】【基础巩固题组】(建议用时：40分钟)一、选择题1.若直线l 不平行于平面α，且l ⊄α，则( )A.α内的所有直线与l 异面B.α内不存在与l 平行的直线C.α与直线l 至少有两个公共点D.α内的直线与l 都相交【答案】 B【解析】因为l ⊄α，直线l 不平行于平面α，所以直线l 只能与平面α相交，于是直线l 与平面α只有一个公共点，所以平面α内不存在与l 平行的直线.2.(2019·某某双基测试)已知直线l ，m ，平面α，β，γ，则下列条件能推出l∥m 的是( )A.l ⊂α，m ⊂β，α∥β B .α∥β，α∩γ＝l ，β∩γ＝mC.l∥α，m⊂αD.l⊂α，α∩β＝m【答案】 B【解析】选项A中，直线l，m也可能异面；选项B中，根据面面平行的性质定理，可推出l∥m，B正确；选项C中，直线l，m也可能异面；选项D中，直线l，m也可能相交.故选B.3.(2018·长郡中学质检)如图所示的三棱柱ABC－A1B1C1中，过A1B1的平面与平面ABC交于DE，则DE与AB 的位置关系是( )A.异面B.平行C.相交D.以上均有可能【答案】 B【解析】在三棱柱ABC－A1B1C1中，AB∥A1B1，∵AB⊂平面ABC，A1B1⊄平面ABC，∴A1B1∥平面ABC，∵过A1B1的平面与平面ABC交于DE.∴DE∥A1B1，∴DE∥AB.4.(2018·某某六校联考)设a，b是两条不同的直线，α，β是两个不同的平面，则α∥β的一个充分条件是( )A.存在一条直线a，a∥α，a∥βB.存在一条直线a，a⊂α，a∥βC.存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥αD.存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α【答案】 D【解析】对于选项A，若存在一条直线a，a∥α，a∥β，则α∥β或α与β相交，若α∥β，则存在一条直线a，使得a∥α，a∥β，所以选项A的内容是α∥β的一个必要条件；同理，选项B、C的内容也是α∥β的一个必要条件而不是充分条件；对于选项D，可以通过平移把两条异面直线平移到一个平面中，成为相交直线，则有α∥β，所以选项D的内容是α∥β的一个充分条件.故选D.5.(2019·某某模拟)若平面α截三棱锥所得截面为平行四边形，则该三棱锥与平面α平行的棱有( )A.0条B.1条C.2条D.1条或2条【答案】 C【解析】如图所示，四边形EFGH为平行四边形，则EF∥GH.∵EF⊄平面BCD，GH⊂平面BCD，∴EF∥平面BCD.又∵EF⊂平面ACD，平面BCD∩平面ACD＝CD，∴EF∥CD.又EF⊂平面EFGH，CD⊄平面EFGH.∴CD∥平面EFGH，同理，AB∥平面EFGH，所以与平面α(面EFGH)平行的棱有2条.二、填空题6.(2018·某某模拟)如图，在正方体ABCD－A1B1C1D1中，AB＝2，E为AD的中点，点F在CD上，若EF∥平面AB1C，则EF＝________.【答案】 2【解析】根据题意，因为EF∥平面AB1C，所以EF∥AC.又E是AD的中点，所以F是CD的中点.因为在Rt△DEF中，DE＝DF＝1，故EF＝ 2.7.如图，平面α∥平面β，△ABC，△A′B′C′分别在α，β内，线段AA′，BB′，CC′共点于O，O在α，β之间，若AB＝2，AC＝1，∠BAC＝60°，OA∶OA′＝3∶2，则△A′B′C′的面积为________.【答案】23 9【解析】相交直线AA′，BB′所在平面和两平行平面α，β相交于AB，A′B′，所以AB∥A′B′.同理BC∥B′C′，CA∥C′A′.所以△ABC与△A′B′C′的三内角相等，所以△ABC∽△A′B′C′，A′B′AB＝OA ′OA ＝23.S △ABC ＝12×2×1×32＝32，所以S △A ′B ′C ′＝32×⎝ ⎛⎭⎪⎫232＝32×49＝239. 8.(2019·某某调研)设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题： ①若m ⊂α，n ∥α，则m ∥n ；②若α∥β，β∥γ，m ⊥α，则m ⊥γ；③若α∩β＝n ，m ∥n ，m ∥α，则m ∥β；④若m ∥α，n ∥β，m ∥n ，则α∥β.其中是真命题的是________(填上正确命题的序号).【答案】 ②【解析】①m ∥n 或m ，n 异面，故①错误；易知②正确；③m ∥β或m ⊂β，故③错误；④α∥β或α与β相交，故④错误.三、解答题9.(2019·某某模拟)已知四棱锥P －ABCD 的底面ABCD 是平行四边形，侧面PAB ⊥平面ABCD ，E 是棱PA 的中点.(1)求证：PC ∥平面BDE ；(2)平面BDE 分此棱锥为两部分，求这两部分的体积比.【答案】见解析【解析】(1)证明在平行四边形ABCD 中，连接AC ，设AC ，BD 的交点为O ，则O 是AC 的中点. 又E 是PA 的中点，连接EO ，则EO 是△PAC 的中位线，所以PC∥EO，又EO ⊂平面EBD ，PC ⊄平面EBD ，所以PC∥平面EBD.(2)解设三棱锥E －ABD 的体积为V 1，高为h ，四棱锥P －ABCD 的体积为V ，则三棱锥E －ABD 的体积V 1＝13×S △ABD ×h ，因为E 是PA 的中点，所以四棱锥P －ABCD 的高为2h ，所以四棱锥P －ABCD 的体积V ＝13×S 四边形ABCD ×2h ＝4×13S △ABD ×h ＝4V 1，所以(V －V 1)∶V 1＝3∶1，所以平面BDE 分此棱锥得到的两部分的体积比为3∶1或1∶3.10.如图，ABCD 与ADEF 均为平行四边形，M ，N ，G 分别是AB ，AD ，EF 的中点.求证：(1)BE∥平面DMF；(2)平面BDE∥平面MNG.【答案】见解析【解析】证明(1)连接AE，则AE必过DF与GN的交点O，连接MO，则MO为△ABE的中位线，所以BE∥MO.又BE⊄平面DMF，MO⊂平面DMF，所以BE∥平面DMF.(2)因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN，又DE⊄平面MNG，GN⊂平面MNG，所以DE∥平面MNG.又M为AB的中点，所以MN为△ABD的中位线，所以BD∥MN，又MN⊂平面MNG，BD⊄平面MNG，所以BD∥平面MNG，又DE，BD⊂平面BDE，DE∩BD＝D，所以平面BDE∥平面MNG.【能力提升题组】(建议用时：20分钟)11.(2019·某某模拟)过三棱柱ABC－A1B1C1的任意两条棱的中点作直线，其中与平面ABB1A1平行的直线共有( )A.4条B.6条C.8条D.12条【答案】 B【解析】如图，H，G，F，I是相应线段的中点，故符合条件的直线只能出现在平面HGFI中，有FI，FG，GH，HI，HF，GI共6条直线.12.已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是( )A.若α，β垂直于同一平面，则α与β平行B.若m，n平行于同一平面，则m与n平行C.若α，β不平行，则在α内不存在与β平行的直线D.若m，n不平行，则m与n不可能垂直于同一平面【答案】 D【解析】A项，α，β可能相交，故错误；B项，直线m，n的位置关系不确定，可能相交、平行或异面，故错误；C项，若m⊂α，α∩β＝n，m∥n，则m∥β，故错误；D项，假设m，n垂直于同一平面，则必有m∥n与已知m，n不平行矛盾，所以原命题正确，故D项正确.13.在正四棱柱ABCD－A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，则点Q满足条件________时，有平面D1BQ∥平面PAO.【答案】Q为CC1的中点【解析】如图所示，设Q为CC1的中点，因为P为DD1的中点，所以QB∥PA.连接DB，因为P，O分别是DD1，DB的中点，所以D1B∥PO，又D1B⊄平面PAO，QB⊄平面PAO，PO⊂平面PAO，PA⊂平面PAO，所以D1B∥平面PAO，QB∥平面PAO，又D1B∩QB＝B，所以平面D1BQ∥平面PAO.故Q为CC1的中点时，有平面D1BQ∥平面PAO.14.(2018·某某六市三模)已知空间几何体ABCDE中，△BCD与△CDE均是边长为2的等边三角形，△ABC是腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD.(1)试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出证明；(2)求三棱锥E－ABC的体积.【答案】见解析【解析】(1)如图所示，取DC的中点N，取BD的中点M，连接MN，则MN即为所求.证明：连接EM，EN，取BC的中点H，连接AH，∵△AB C是腰长为3的等腰三角形，H为BC的中点，∴AH⊥BC，又平面ABC⊥平面BCD，平面ABC∩平面BCD＝BC，AH⊂平面ABC，∴AH⊥平面BCD，同理可证EN⊥平面BCD，∴EN∥AH，∵EN⊄平面ABC，AH⊂平面ABC，∴EN∥平面ABC.又M，N分别为BD，DC的中点，∴MN∥BC，∵MN⊄平面ABC，BC⊂平面ABC，∴MN∥平面ABC.又MN∩EN＝N，MN⊂平面EMN，EN⊂平面EMN，∴平面EMN∥平面ABC，又EF⊂平面EMN，∴EF∥平面ABC，即直线MN上任意一点F与E的连线EF均与平面ABC平行.(2)连接DH，取CH的中点G，连接NG，则NG∥DH，由(1)可知EN∥平面ABC，∴点E到平面ABC的距离与点N到平面ABC的距离相等，又△BCD 是边长为2的等边三角形， ∴DH⊥BC，又平面ABC⊥平面BCD ，平面ABC∩平面BCD ＝BC ，DH ⊂平面BCD ，∴DH ⊥平面ABC ，∴NG ⊥平面ABC ，易知DH ＝3，又N 为CD 中点，∴NG ＝32，又AC ＝AB ＝3，BC ＝2，∴S △ABC ＝12·BC ·AH ＝12×2×32－12＝22， ∴V E －ABC ＝V N －ABC ＝13·S △ABC ·NG ＝63. 【新高考创新预测】15.(【答案】不唯一型)如图所示，在正四棱柱ABCD －A 1B 1C 1D 1中，E ，F ，G ，H 分别是棱CC 1，C 1D 1，D 1D ，DC 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 只需满足条件________时，就有MN ∥平面B 1BDD 1.(注：请填上你认为正确的一个条件即可，不必考虑全部可能情况)【答案】点M 在线段FH 上(或点M 与点H 重合)【解析】连接HN ，FH ，FN ，则FH∥DD 1，HN∥BD，易知平面FHN∥平面B1BDD 1，只需M∈FH，则MN ⊂平面FHN ，∴MN∥平面B 1BDD 1.。

高三理科数学一轮复习讲义,复习补习资料：第八章立体几何8.5直线平面垂直的判定与性质(解析版)

§8.5直线、平面垂直的判定与性质考纲展示►1.能以立体几何中的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质和判定定理．2．能运用公理、定理和已获得的结论证明一些有关空间图形的位置关系的简单命题．考点1 直线与平面垂直的判定与性质直线与平面垂直(1)直线和平面垂直的定义：直线l与平面α内的________直线都垂直，就说直线l与平面α互相垂直．(2)直线与平面垂直的判定定理及性质定理：答案：(1)任意一条(2)两条相交直线a，b⊂αa∩b＝O l⊥al⊥b平行a⊥αb⊥α(1)[教材习题改编]下列命题中不正确的是( )A．如果平面α⊥平面β，且直线l∥平面α，则直线l⊥平面βB．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βC．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βD．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥γ答案：A(2)[教材习题改编] 如图，在三棱锥V－ABC中，∠VAB＝∠VAC＝∠ABC＝90°，则构成三棱锥的四个三角形中直角三角形的个数为________．答案：4[典题1] (1)[2019·上海六校联考]已知m和n是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m⊥β的是( )A．α⊥β且m⊂αB．α⊥β且m∥αC．m∥n且n⊥βD．m⊥n且α∥β[答案] C[解析]由线线平行性质的传递性和线面垂直的判定定理，可知C正确．(2)如图所示，在四棱锥P－ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点．求证：①CD⊥AE；②PD⊥平面ABE.[证明]①在四棱锥P－ABCD中，∵PA⊥底面ABCD，CD⊂平面ABCD，∴PA⊥CD.∵AC⊥CD，PA∩AC＝A，∴CD⊥平面PAC.而AE⊂平面PAC，∴CD⊥AE.②由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.∵E是PC的中点，∴AE⊥PC.由①知，AE⊥CD，且PC∩CD＝C，∴AE⊥平面PCD.而PD⊂平面PCD，∴AE⊥PD.∵PA⊥底面ABCD，∴PA⊥AB.又AB⊥AD，且PA∩AD＝A，∴AB⊥平面PAD，而PD⊂平面PAD，∴AB⊥PD.又AB∩AE＝A，∴PD⊥平面ABE.[点石成金] 直线和平面垂直判定的四种方法(1)利用判定定理；(2)利用判定定理的推论(a∥b，a⊥α⇒b⊥α)，如典题1的第(1)题中选项C；(3)利用面面平行的性质(a⊥α，α∥β⇒a⊥β)；(4)利用面面垂直的性质．当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面.[2019·湖北武汉调研]如图所示，在四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE.(1)求证：BD⊥平面PAC；(2)若PA＝1，AD＝2，求三棱锥E－BCD的体积．(1)证明：∵PA⊥平面ABCD，BD⊂平面ABCD，∴PA⊥BD.∵PC ⊥平面BDE ，BD ⊂平面BDE ， ∴PC ⊥BD . 又PA ∩PC ＝P ， ∴BD ⊥平面PAC .(2)解：如图所示，设AC 与BD 的交点为O ，连接OE .∵PC ⊥平面BDE ，∴PC ⊥OE . 由(1)知，BD ⊥平面PAC ， ∴BD ⊥AC .由题设条件知，四边形ABCD 为正方形．由AD ＝2，得AC ＝BD ＝22，OC ＝ 2. 在Rt △PAC 中，PC ＝PA 2＋AC 2＝12＋22＝3.易知Rt △PAC ∽Rt △OEC ， ∴OE PA ＝CE AC ＝OC PC ，即OE 1＝CE 22＝23， ∴OE ＝23，CE ＝43. ∴V E －BCD ＝13S △CEO ·BD＝13·12OE ·CE ·BD ＝16×23×43×22＝827. 考点2 平面与平面垂直的判定与性质平面与平面垂直的判定定理与性质定理答案：垂线l⊂βl⊥α交线α⊥βl⊂βα∩β＝a l⊥a定理的应用：注意由平面到空间的思维的变化．(1)已知直线a，b，c，若a⊥b，b⊥c，则a与c的位置关系为________．答案：平行、相交或异面解析：在同一个平面内，由题设条件可得a∥c，在空间中，则直线a与c的位置关系不确定，即平行、相交、异面都有可能．(2)已知直线a和平面α，β，若α⊥β，a⊥β，则a与α的位置关系为________．答案：a∥α或a⊂α解析：易得a∥α或a⊂α.垂直关系的证明及应用：直接法．(1)如图所示，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°.将△ADB 沿BD折起，使平面ABD⊥平面BCD，构成三棱锥A－BCD，则在三棱锥A－BCD中，平面ADC________平面ABC.答案：⊥解析：在四边形ABCD中，由已知可得BD⊥CD，又平面ABD⊥平面BCD，且平面ABD∩平面BCD＝BD，所以CD⊥平面ABD，所以CD⊥AB.又AD⊥AB，AD∩CD＝D，所以AB⊥平面ADC，所以平面ABC⊥平面ADC.(2)如图所示，在长方体ABCD－A1B1C1D1中，AB＝AD＝3，AA1＝2，则四棱锥A－BB1D1D的体积为________．答案：6解析：连接AC，交BD于点O，在长方体ABCD－A1B1C1D1中，因为AB＝AD＝3，所以BD＝32，且AC⊥BD.又因为BB1⊥底面ABCD，所以BB1⊥AC.又DB∩BB1＝B，所以AC⊥平面BB1D1D，所以AO 为四棱锥A －BB 1D 1D 的高，且AO ＝12BD ＝322.因为矩形BB 1D 1D 的面积S ＝BD ·BB 1＝32×2＝62，所以四棱锥A －BB 1D 1D 的体积V ＝13S ·AO ＝13×62×322＝6.[典题2] 如图，四棱锥P －ABCD 中，AB ⊥AC ，AB ⊥PA ，AB ∥CD ，AB ＝2CD ，E ，F ，G ，M ，N 分别为PB ，AB ，BC ，PD ，PC 的中点．求证：(1)CE ∥平面PAD ； (2)平面EFG ⊥平面EMN .[证明] (1)证法一：取PA 的中点H ，连接EH ，DH .因为E 为PB 的中点，所以EH ∥AB ，EH ＝12AB .又AB ∥CD ，CD ＝12AB ，所以EH ∥CD ，EH ＝CD ，因此四边形DCEH 是平行四边形．所以CE ∥DH .又DH ⊂平面PAD ，CE ⊄平面PAD ，所以CE ∥平面PAD . 证法二：连接CF .因为F 为AB 的中点，所以AF ＝12AB .又CD ＝12AB ，所以AF ＝CD .又AF ∥CD ，所以四边形AFCD 为平行四边形．因此CF ∥AD .又CF ⊄平面PAD ，AD ⊂平面PAD ，所以CF ∥平面PAD .因为E ，F 分别为PB ，AB 的中点，所以EF ∥PA .又EF ⊄平面PAD ，PA ⊂平面PAD ，所以EF ∥平面PAD . 因为CF ∩EF ＝F ，故平面CEF ∥平面PAD . 又CE ⊂平面CEF ，所以CE ∥平面PAD .(2)因为E ，F 分别为PB ，AB 的中点，所以EF ∥PA .又AB ⊥PA ，所以AB ⊥EF . 同理可证AB ⊥FG .又EF ∩FG ＝F ，EF ⊂平面EFG ，FG ⊂平面EFG ，因此AB ⊥平面EFG .又M ，N 分别为PD ，PC 的中点，所以MN ∥CD .又AB∥CD，所以MN∥AB，所以MN⊥平面EFG.又MN⊂平面EMN，所以平面EFG⊥平面EMN.[题点发散1] 在本例条件下，证明：平面EMN⊥平面PAC.证明：因为AB⊥PA，AB⊥AC，且PA∩AC＝A，所以AB⊥平面PAC.又MN∥CD，CD∥AB，所以MN∥AB，所以MN⊥平面PAC.又MN⊂平面EMN，所以平面EMN⊥平面PAC.[题点发散2] 在本例条件下，证明：平面EFG∥平面PAC.证明：因为E，F，G分别为PB，AB，BC的中点，所以EF∥PA，FG∥AC.又EF⊄平面PAC，PA⊂平面PAC，所以EF∥平面PAC.同理，FG∥平面PAC.又EF∩FG＝F，所以平面EFG∥平面PAC.[点石成金] 1.判定面面垂直的方法(1)面面垂直的定义；(2)面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．2．在已知平面垂直时，一般要用性质定理进行转化．在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直.如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD.E 和F分别是CD和PC的中点．求证：(1)PA⊥底面ABCD；(2)BE∥平面PAD；(3)平面BEF⊥平面PCD.证明：(1)∵平面PAD∩平面ABCD＝AD，又平面PAD⊥平面ABCD，且PA⊥AD，PA⊂平面PAD，∴PA⊥底面ABCD.(2)∵AB∥CD，CD＝2AB，E为CD的中点，∴AB∥DE，且AB＝DE.∴四边形ABED为平行四边形．∴BE∥AD.又BE⊄平面PAD，AD⊂平面PAD，∴BE∥平面PAD.(3)∵AB⊥AD，且四边形ABED为平行四边形，∴BE⊥CD，AD⊥CD.由(1)知，PA⊥底面ABCD，CD⊂平面ABCD，则PA⊥CD，又PA∩AD＝A，∴CD⊥平面PAD.又PD⊂平面PAD，从而CD⊥PD，又E，F分别为CD，CP的中点，∴EF∥PD，故CD⊥EF.∵EF⊂平面BEF，BE⊂平面BEF，且EF∩BE＝E，∴CD⊥平面BEF.又CD⊂平面PCD.∴平面BEF⊥平面PCD.考点3 平行与垂直的综合问题[考情聚焦] 空间线、面的平行与垂直的综合考查一直是高考必考热点．主要有以下几个命题角度：角度一证明多面体中的平行与垂直关系[典题3] 如图所示，E是以AB为直径的半圆弧上异于A，B的点，矩形ABCD所在平面垂直于该半圆所在的平面．(1)求证：AE⊥EC；(2)设平面ECD与半圆弧的另一个交点为F.求证：EF∥AB.[证明](1)∵E是半圆上异于A，B的点，∴AE⊥EB.又∵平面ABCD⊥平面ABE，平面ABCD∩平面ABE＝AB，CB⊥AB，∴CB⊥平面ABE.又∵AE⊂平面ABE，∴CB⊥AE.∵CB∩BE＝B，∴AE⊥平面CBE.又∵EC⊂平面CBE，∴AE⊥EC.(2)∵CD∥AB，AB⊂平面ABE，∴CD∥平面ABE.又∵平面CDE∩平面ABE＝EF，∴CD∥EF.又∵CD∥AB，∴EF∥AB.角度二探索性问题中的平行与垂直关系[典题4] 如图，在三棱台ABC－DEF中，CF⊥平面DEF，AB⊥BC.(1)设平面ACE ∩平面DEF ＝a ，求证：DF ∥a ；(2)若EF ＝CF ＝2BC ，试问在线段BE 上是否存在点G ，使得平面DFG ⊥平面CDE ？若存在，请确定点G 的位置；若不存在，请说明理由．(1)[证明] 在三棱台ABC －DEF 中，AC ∥DF ，AC ⊂平面ACE ，DF ⊄平面ACE ， ∴DF ∥平面ACE . 又∵DF ⊂平面DEF ，平面ACE ∩平面DEF ＝a ， ∴DF ∥a .(2)[解] 线段BE 上存在点G ，且BG ＝13BE ，使得平面DFG ⊥平面CDE .证明如下：取CE 的中点O ，连接FO 并延长交BE 于点G ，连接GD ， ∵CF ＝EF ，∴GF ⊥CE .在三棱台ABC －DEF 中，AB ⊥BC ⇒DE ⊥EF . 由CF ⊥平面DEF ⇒CF ⊥DE . 又CF ∩EF ＝F ，∴DE ⊥平面CBEF ，∴DE ⊥GF .⎭⎪⎬⎪⎫GF ⊥CE ，GF ⊥DE ，CE ∩DE ＝E ⇒GF ⊥平面CDE . 又GF ⊂平面DFG ， ∴平面DFG ⊥平面CDE . 此时，如平面图所示，∵O 为CE 的中点，EF ＝CF ＝2BC ，由平面几何知识易证△HOC ≌△FOE ， ∴HB ＝BC ＝12EF .由△HGB ∽△FGE 可知，BG GE ＝12，即BG ＝13BE .角度三折叠问题中的平行与垂直关系[典题5] 如图所示，在矩形ABCD 中，AB ＝3，BC ＝4，E ，F 分别在线段BC ，AD 上，EF∥AB ，将矩形ABEF 沿EF 折起，记折起后的矩形为MNEF ，且平面MNEF ⊥平面ECDF .(1)求证：NC ∥平面MFD ； (2)若EC ＝3，求证：ND ⊥FC ； (3)求四面体N －EFD 体积的最大值．(1)[证明] ∵平行四边形MNEF 和EFDC 都是矩形， ∴MN ∥EF ，EF ∥CD ，MN ＝EF ＝CD ， ∴MN ∥CD .∴四边形MNCD 是平行四边形． ∴NC ∥MD .∵NC ⊄平面MFD ，MD ⊂平面MFD ，∴NC ∥平面MFD .(2)[证明] 连接ED ，交FC 于点O .∵平面MNEF ⊥平面ECDF ，且NE ⊥EF ，平面MNEF ∩平面ECDF ＝EF ，NE ⊂平面MNEF ，∴NE ⊥平面ECDF .∵FC ⊂平面ECDF ，∴FC ⊥NE . ∵EC ＝CD ，∴四边形ECDF 为正方形，∴FC ⊥ED . 又∵ED ∩NE ＝E ，ED ，NE ⊂平面NED ， ∴FC ⊥平面NED .∵ND ⊂平面NED ，∴ND ⊥FC .(3)[解] 设NE ＝x ，则FD ＝EC ＝4－x ，其中0<x <4.由(2)得NE ⊥平面FEC ， ∴四面体N －EFD 的体积为V N －EFD ＝13S △EFD ·NE ＝12x (4－x )．∴V N －FED ≤12⎣⎢⎡⎦⎥⎤x ＋－x 22＝2，当且仅当x ＝4－x ，即x ＝2时，四面体N －FED 的体积最大，最大值为2. [点石成金] 平行与垂直的综合应用问题处理的两个策略(1)探索性问题一般是先根据条件猜测点的位置再给出证明，探索点存在问题，点多为中点或三等分点中某一个，也可以根据相似知识建点．(2)折叠问题中的平行与垂直关系的处理关键是结合图形弄清折叠前后变与不变的数量关系，尤其是隐含着的垂直关系.[方法技巧] 1.三种垂直关系的证明(1)判定线线垂直的方法①定义：两条直线所成的角为90°；②平面几何中证明线线垂直的方法；③线面垂直的性质：a⊥α，b⊂α⇒a⊥b；④线面垂直的性质：a⊥α，b∥α⇒a⊥b.(2)判定线面垂直的常用方法①利用线面垂直的判定定理；②利用“两平行线中的一条与平面垂直，则另一条也与这个平面垂直”；③利用“一条直线垂直于两平行平面中的一个，则与另一个也垂直”；④利用面面垂直的性质．(3)判定面面垂直的方法①利用定义：两个平面相交，所成的二面角是直二面角；②判定定理：a⊂α，a⊥β⇒α⊥β.2．线面垂直、面面垂直的常见性质(1)垂直于同一条直线的两个平面平行．(2)过一点有且只有一条直线与已知平面垂直．(3)过一点有且只有一个平面与已知直线垂直．3．三种垂直关系的转化在证明两平面垂直时，一般先从现有的直线中寻找平面的垂线，若图中不存在这样的直线，则可通过作辅助线来解决．如有平面垂直时，一般要用性质定理，在一个平面内作交线的垂线，使之转化为线面垂直，然后进一步转化为线线垂直．[易错防范] 在用线面垂直的判定定理证明线面垂直时，考生易忽视说明平面内的两条直线相交，而导致被扣分，这一点在证明中要注意．口诀：线不在多，重在相交．真题演练集训1．[2019·浙江模拟]已知互相垂直的平面α，β交于直线l.若直线m，n满足m∥α，n⊥β，则( )A．m∥l B．m∥nC．n⊥l D．m⊥n答案：C解析：因为α∩β＝l，所以l⊂β，又n⊥β，所以n⊥l.故选C.2．[2019·天津模拟]如图，已知△ABC，D是AB的中点，沿直线CD将△ACD翻折成△A′CD，所成二面角A′－CD－B的平面角为α，则( )A．∠A′DB≤α B．∠A′DB≥αC．∠A′CB≤α D．∠A′CB≥α答案：B解析：∵A′C和BC都不与CD垂直，∴∠A′CB≠α，故C，D错误．当CA＝CB时，容易证明∠A′DB＝α.不妨取一个特殊的三角形，如Rt△ABC，令斜边AB＝4，AC＝2，BC＝23，如图所示，则CD＝AD＝BD＝2，∠BDH＝120°，设沿直线CD将△ACD折成△A′CD，使平面A′CD⊥平面BCD，则α＝90°.取CD中点H，连接A′H，BH，则A′H⊥CD，∴A′H⊥平面BCD，且A′H＝3，DH＝1.在△BDH中，由余弦定理可得BH＝7.在Rt△A′HB中，由勾股定理可得A′B＝10.在△A′DB中，∵A′D2＋BD2－A′B2＝－2<0，可知cos∠A′DB<0，∴∠A′DB为钝角，故排除A.故选B.3．[2019·重庆模拟]α，β是两个平面，m，n是两条直线，有下列四个命题：①如果m⊥n，m⊥α，n∥β，那么α⊥β.②如果m⊥α，n∥α，那么m⊥n.③如果α∥β，m⊂α，那么m∥β.④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．其中正确的命题有________．(填写所有正确命题的编号)答案：②③④解析：对于命题①，可运用长方体举反例证明其错误：如图，不妨设AA′为直线m，CD 为直线n，ABCD所在的平面为α，ABC′D′所在的平面为β，显然这些直线和平面满足题目条件，但α⊥β不成立；命题②正确，证明如下：设过直线n的某平面与平面α相交于直线l，则l∥n，由m⊥α知m⊥l，从而m⊥n，结论正确；由平面与平面平行的定义知，命题③正确；由平行的传递性及线面角的定义知，命题④正确．4．[2019·江苏模拟]如图，在直三棱柱ABC－A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且B1D⊥A1F，A1C1⊥A1B1.求证：(1)直线DE∥平面A1C1F；(2)平面B1DE⊥平面A1C1F.证明：(1)在直三棱柱ABC－A1B1C1中，A1C1∥AC.在△ABC中，因为D，E分别为AB，BC的中点，所以DE∥AC，于是DE∥A1C1.又DE⊄平面A1C1F，A1C1⊂平面A1C1F，所以直线DE∥平面A1C1F.(2)在直三棱柱ABC－A1B1C1中，A1A⊥平面A1B1C1.因为A1C1⊂平面A1B1C1，所以A1A⊥A1C1.又A1C1⊥A1B1，A1A⊂平面ABB1A1，A1B1⊂平面ABB1A1，A1A∩A1B1＝A1，所以A1C1⊥平面ABB1A1.因为B1D⊂平面ABB1A1，所以A1C1⊥B1D.又B1D⊥A1F，A1C1⊂平面A1C1F，A1F⊂平面A1C1F，A1C1∩A1F＝A1，所以B1D⊥平面A1C1F.因为直线B1D⊂平面B1DE，所以平面B1DE⊥平面A1C1F.5．[2019·成都一诊]如图，在以A，B，C，D，E，F为顶点的五面体中，面ABEF为正方形，AF＝2FD，∠AFD＝90°，且二面角D－AF－E与二面角C－BE－F都是60°.(1)证明：平面ABEF⊥平面EFDC；(2)求二面角E－BC－A的余弦值．(1)证明：由已知可得AF⊥DF，AF⊥FE，所以AF⊥平面EFDC.又AF⊂平面ABEF，故平面ABEF⊥平面EFDC.(2)解：过D 作DG ⊥EF ，垂足为G ，由(1)知DG ⊥平面ABEF .以G 为坐标原点，GF →的方向为x 轴正方向，|GF →|为单位长，建立如图所示的空间直角坐标系G －xyz.由(1)知∠DFE 为二面角D －AF －E 的平面角，故∠DFE ＝60°，则DF ＝2，DG ＝3，可得A (1,4,0)，B (－3,4,0)，E (－3,0,0)，D (0,0，3)．由已知，AB ∥EF ，所以AB ∥平面EFDC . 又平面ABCD ∩平面EFDC ＝ CD ，故AB ∥CD ，CD ∥EF .由BE ∥AF ，可得BE ⊥平面EFDC ，所以∠CEF 为二面角C －BE －F 的平面角，∠CEF ＝60°. 从而可得C ( －2,0，3)．连接AC ，则EC →＝(1,0，3)，EB →＝(0,4,0)，AC →＝(－3，－4，3)，AB →＝(－4,0,0)．设n ＝(x ，y ，z )是平面BCE 的法向量，则 ⎩⎪⎨⎪⎧n ·EC →＝0，n ·EB →＝0，即⎩⎨⎧x ＋3z ＝0，4y ＝0，所以可取n ＝(3,0，－3)．设m 是平面ABCD 的法向量，则⎩⎪⎨⎪⎧m ·AC →＝0，m ·AB →＝0，同理可取m ＝(0，3，4)．则cos 〈n ，m 〉＝n·m |n||m|＝－21919.故二面角E －BC －A 的余弦值为－21919.课外拓展阅读立体几何证明问题中的转化思想[典例] 如图所示，M ，N ，K 分别是正方体ABCD －A 1B 1C 1D 1的棱AB ，CD ，C 1D 1的中点．求证：(1)AN ∥平面A 1MK ； (2)平面A 1B 1C ⊥平面A 1MK .[审题视角] (1)要证线面平行，需证线线平行；(2)要证面面垂直，需证线面垂直，要证线面垂直，需证线线垂直．[证明] (1)如图所示，连接NK . 在正方体ABCD －A 1B 1C 1D 1中，∵四边形AA 1D 1D ，DD 1C 1C 都为正方形， ∴AA 1∥DD 1，AA 1＝DD 1，C 1D 1∥CD ，C 1D 1＝CD . ∵N ，K 分别为CD ，C 1D 1的中点， ∴DN ∥D 1K ，DN ＝D 1K ，∴四边形DD 1KN 为平行四边形． ∴KN ∥DD 1，KN ＝DD 1， ∴AA 1∥KN ，AA 1＝KN .∴四边形AA 1KN 为平行四边形， ∴AN ∥A 1K .∵A 1K ⊂平面A 1MK ，AN ⊄平面A 1MK ， ∴AN ∥平面A 1MK .- 21 -(2)如图所示，连接BC 1.在正方体ABCD －A 1B 1C 1D 1中，AB ∥C 1D 1，AB ＝C 1D 1.∵M ，K 分别为AB ，C 1D 1的中点，∴BM ∥C 1K ，BM ＝C 1K .∴四边形BC 1KM 为平行四边形，∴MK ∥BC 1.在正方体ABCD －A 1B 1C 1D 1中，A 1B 1⊥平面BB 1C 1C ，BC 1⊂平面BB 1C 1C ，∴A 1B 1⊥BC 1.∵MK ∥BC 1，∴A 1B 1⊥MK .∵四边形BB 1C 1C 为正方形，∴BC 1⊥B 1C .∴MK ⊥B 1C .∵A 1B 1⊂平面A 1B 1C ，B 1C ⊂平面A 1B 1C ，A 1B 1∩B 1C ＝B 1，∴MK ⊥平面A 1B 1C .又∵MK ⊂平面A 1MK ，∴平面A 1B 1C ⊥平面A 1MK .方法点睛1．线面平行、垂直关系的证明问题的指导思想是线线、线面、面面关系的相互转化，交替使用平行、垂直的判定定理和性质定理．2．线线关系是线面关系、面面关系的基础．证明过程中要注意利用平面几何中的结论，如证明平行时常用的中位线、平行线分线段成比例，证明垂直时常用的等腰三角形的中线等．3．证明过程一定要严谨，使用定理时要对照条件，步骤书写要规范．。

【2016年高考数学】2016年高考数学(理)一轮复习精品立体几何

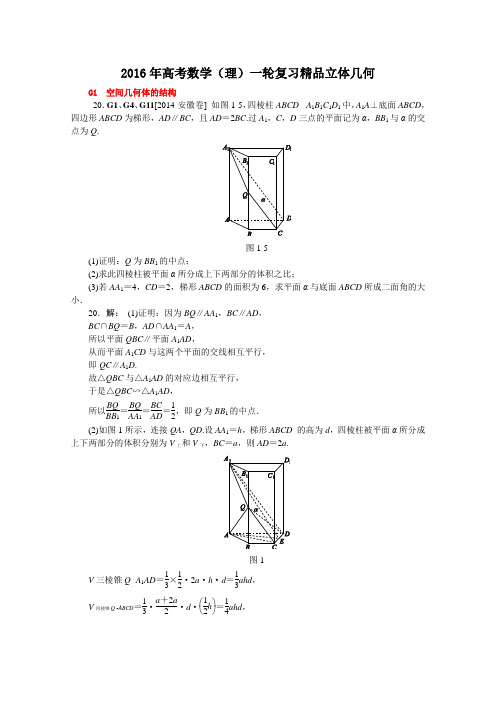
2016年高考数学（理）一轮复习精品立体几何G1 空间几何体的结构 20．G1、G4、G11[2014·安徽卷] 如图1-5，四棱柱ABCD - A 1B 1C 1D 1中，A 1A ⊥底面ABCD ，四边形ABCD 为梯形，AD ∥BC ，且AD ＝2BC .过A 1，C ，D 三点的平面记为α，BB 1与α的交点为Q .图1-5(1)证明：Q 为BB 1的中点；(2)求此四棱柱被平面α所分成上下两部分的体积之比；(3)若AA 1＝4，CD ＝2，梯形ABCD 的面积为6，求平面α与底面ABCD 所成二面角的大小．20．解： (1)证明：因为BQ ∥AA 1，BC ∥AD ， BC ∩BQ ＝B ，AD ∩AA 1＝A ，所以平面QBC ∥平面A 1AD ，从而平面A 1CD 与这两个平面的交线相互平行，即QC ∥A 1D .故△QBC 与△A 1AD 的对应边相互平行，于是△QBC ∽△A 1AD ，所以BQ BB 1＝BQ AA 1＝BC AD ＝12，即Q 为BB 1的中点．(2)如图1所示，连接QA ，QD .设AA 1＝h ，梯形ABCD 的高为d ，四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下，BC ＝a ，则AD ＝2a .图1V 三棱锥Q -A 1AD ＝13×12·2a ·h ·d ＝13ahd ，V 四棱锥Q -ABCD＝13·a ＋2a 2·d ·⎝⎛⎭⎫12h ＝14ahd ，所以V 下＝V 三棱锥Q -A 1AD ＋V 四棱锥Q -ABCD ＝712ahd . 又V 四棱柱A 1B 1C 1D 1 ABCD ＝32ahd ，所以V 上＝V 四棱柱A 1B 1C 1D 1 ABCD －V 下＝32ahd －712ahd ＝1112ahd ，故V 上V 下＝117.(3)方法一：如图1所示，在△ADC 中，作AE ⊥DC ，垂足为E ，连接A 1E .又DE ⊥AA 1，且AA 1∩AE ＝A ，所以DE ⊥平面AEA 1，所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角．因为BC ∥AD ，AD ＝2BC ，所以S △ADC ＝2S △BCA . 又因为梯形ABCD 的面积为6，DC ＝2，所以S △ADC ＝4，AE ＝4.于是tan ∠AEA 1＝AA 1AE ＝1，∠AEA 1＝π4.故平面α与底面ABCD 所成二面角的大小为π4.方法二：如图2所示，以D 为原点，DA ，DD 1→分别为x 轴和z 轴正方向建立空间直角坐标系．设∠CDA ＝θ，BC ＝a ，则AD ＝2a .因为S 四边形ABCD ＝a ＋2a2·2sin θ＝6，所以a ＝2sin θ.图2从而可得C (2cos θ，2sin θ，0)，A 1⎝⎛⎭⎫4sin θ，0，4，所以DC ＝(2cos θ，2sin θ，0)，DA 1→＝⎝⎛⎭⎫4sin θ，0，4.设平面A 1DC 的法向量n ＝(x ，y ，1)，由⎩⎨⎧DA 1→·n ＝4sin θx ＋4＝0，DC →·n ＝2x cos θ＋2y sin θ＝0，得⎩⎪⎨⎪⎧x ＝－sin θ，y ＝cos θ，所以n ＝(－sin θ，cos θ，1)．又因为平面ABCD 的法向量m ＝(0，0，1)，所以cos 〈n ，m 〉＝n·m|n||m|＝22，故平面α与底面ABCD 所成二面角的大小为π4.8．G1[2014·湖北卷] 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：“置如其周，令相乘也．又以高乘之，三十六成一．”该术相当于给出了由圆锥的底面周长L 与高h ，计算其体积V 的近似公式V ≈136L 2h .它实际上是将圆锥体积公式中的圆周率π近似取为3.那么，近似公式V ≈275L 2h 相当于将圆锥体积公式中的π近似取为( )A.227B.258C.15750D.3551138．B [解析] 设圆锥的底面圆半径为r ，底面积为S ，则L ＝2πr ，由题意得136L 2h ≈13Sh ，代入S ＝πr 2化简得π≈3；类比推理，若V ＝275L 2h ，则π≈258.故选B.7．G2、G1[2014·辽宁卷] 某几何体三视图如图1-1所示，则该几何体的体积为( )A ．8－2πB ．8－πC ．8－π2D ．8－π4图1-17．B [解析] 根据三视图可知，该几何体是正方体减去两个体积相等的圆柱的一部分⎝⎛⎭⎫占圆柱的14后余下的部分，故该几何体体积为2×2×2－2×14×π×2＝8－π.G2 空间几何体的三视图和直观图 7．G2[2014·安徽卷] 一个多面体的三视图如图1-2所示，则该多面体的表面积为( )A ．21＋ 3B ．8＋ 2C ．21D ．18图1-27．A [解析] 如图，由三视图可知该几何体是棱长为2的正方体截去两个小三棱锥后余下的部分，其表面积S ＝6×4－12×6＋2×12×2×62＝21＋ 3.2．G2[2014·福建卷] 某空间几何体的正视图是三角形，则该几何体不可能是( ) A ．圆柱 B ．圆锥 C ．四面体 D ．三棱柱2．A [解析] 由空间几何体的三视图可知，圆柱的正视图、侧视图、俯视图都不可能是三角形．5．G2[2014·湖北卷] 在如图1-1所示的空间直角坐标系O xyz 中，一个四面体的顶点坐标分别是(0，0，2)，(2，2，0)，(1，2，1)，(2，2，2)．给出编号为①，②，③，④的四个图，则该四面体的正视图和俯视图分别为( )图1-1A ．①和②B ．①和③C ．③和②D ．④和②5．D [解析] 由三视图及空间直角坐标系可知，该几何体的正视图显然是一个直角三角形且内有一条虚线(一锐角顶点与其所对直角边中点的连线)，故正视图是④；俯视图是一个钝角三角形，故俯视图是②. 故选D.7．G2、G8[2014·湖南卷] 一块石材表示的几何体的三视图如图1-2所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于( )图1-2A ．1B ．2C ．3D ．47．B [解析] 由三视图可知，石材为一个三棱柱(相对应的长方体的一半)，故可知能得到的最大球为三棱柱的内切球．由题意可知正视图三角形的内切圆的半径即为球的半径，可得r ＝6＋8－102＝2.5．G2[2014·江西卷] 一几何体的直观图如图1-1所示，下列给出的四个俯视图中正确的是( )图1-1A B C D图1-25．B [解析] 易知该几何体的俯视图为选项B 中的图形． 7．G2、G1[2014·辽宁卷] 某几何体三视图如图1-1所示，则该几何体的体积为( )A ．8－2πB ．8－πC ．8－π2D ．8－π4图1-17．B [解析] 根据三视图可知，该几何体是正方体减去两个体积相等的圆柱的一部分⎝⎛⎭⎫占圆柱的14后余下的部分，故该几何体体积为2×2×2－2×14×π×2＝8－π.3．G2[2014·浙江卷] 几何体的三视图(单位：cm)如图1-1所示，则此几何体的表面积是( )图1-1A ．90 cm 2B ．129 cm 2C ．132 cm 2D ．138 cm 23．D [解析] 此几何体是由长方体与三棱柱组合而成的，其直观图如图，所以该几何体的表面积为2(4×3＋6×3＋6×4)＋2×12×3×4＋4×3＋3×5－3×3＝138(cm 2)，故选D.12．G2[2014·新课标全国卷Ⅰ] 如图1-3，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为( )图1-3A ．6 2B ．6C ．4 2D ．412．B [解析] 该几何体是如图所示的棱长为4的正方体内的三棱锥E - CC 1D 1(其中E 为BB 1的中点)，其中最长的棱为D 1E ＝（4 2）2＋22＝6.6．G2[2014·新课标全国卷Ⅱ] 如图1-1，网格纸上正方形小格的边长为1(表示1 cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3 cm ，高为6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )图1-1A.1727B.59C.1027D.136．C [解析] 该零件是一个由两个圆柱组成的组合体，其体积为π×32×2＋π×22×4＝34π(cm 3)，原毛坯的体积为π×32×6＝54π(cm 3)，切削掉部分的体积为54π－34π＝20π(cm 3)，故所求的比值为20π54π＝1027.17．G2[2014·陕西卷] 四面体ABCD 及其三视图如图1-4所示，过棱AB 的中点E 作平行于AD ，BC 的平面分别交四面体的棱BD ，DC ，CA 于点F ，G ，H .(1)证明：四边形EFGH 是矩形；(2)求直线AB 与平面EFGH 夹角θ的正弦值．图1-417．解：(1)证明：由该四面体的三视图可知， BD ⊥DC ，BD ⊥AD ，AD ⊥DC ， BD ＝DC ＝2，AD ＝1.由题设，BC ∥平面EFGH ，平面EFGH ∩平面BDC ＝FG ，平面EFGH ∩平面ABC ＝EH ， ∴BC ∥FG ，BC ∥EH ，∴FG ∥EH . 同理EF ∥AD ，HG ∥AD ，∴EF ∥HG . ∴四边形EFGH 是平行四边形．又∵AD ⊥DC ，AD ⊥BD ，∴AD ⊥平面BDC ， ∴AD ⊥BC ，∴EF ⊥FG ， ∴四边形EFGH 是矩形．(2)方法一：如图，以D 为坐标原点建立空间直角坐标系，则D (0，0，0)，A (0，0，1)，B (2，0，0)，C (0，2，0)，DA ＝(0，0，1)，BC ＝(－2，2，0)，BA ＝(－2，0，1)．设平面EFGH 的法向量n ＝(x ，y ，z )， ∵EF ∥AD ，FG ∥BC ， ∴n ·DA ＝0，n ·BC ＝0，得⎩⎪⎨⎪⎧z ＝0，－2x ＋2y ＝0，取n ＝(1，1，0)， ∴sin θ＝|cos 〈BA →，n 〉|＝⎪⎪⎪⎪BA ·n |BA ||n |＝25×2＝105.方法二：如图，以D 为坐标原点建立空间直角坐标系，则D (0，0，0)，A (0，0，1)，B (2，0，0)，C (0，2，0)，∵E 是AB 的中点，∴F ，G 分别为BD ，DC 的中点，得E ⎝⎛⎭⎫1，0，12，F (1，0，0)，G (0，1，0)．∴FE →＝⎝⎛⎭⎫0，0，12，FG ＝(－1，1，0)， BA ＝(－2，0，1)．设平面EFGH 的法向量n ＝(x ，y ，z )，则n ·FE ＝0，n ·FG ＝0，得⎩⎪⎨⎪⎧12z ＝0，－x ＋y ＝0，取n ＝(1，1，0)，∴sin θ＝|cos 〈BA →，n 〉|＝⎪⎪⎪⎪⎪⎪BA ·n |BA →||n |＝25×2＝105.10．G2[2014·天津卷] 一个儿何体的三视图如图1-3所示(单位：m)，则该几何体的体积为________m 3.图1-310.20π3 [解析] 由三视图可得，该几何体为圆柱与圆锥的组合体，其体积V ＝π×12×4＋13π×22×2＝20π3.7．G2[2014·重庆卷] 某几何体的三视图如图1-2所示，则该几何体的表面积为( )图1-2A ．54B ．60C ．66D ．727．B [解析] 由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥所得，三棱柱的底面是一个两直角边长分别为3和4的直角三角形，高为5，截去的锥体的底面是两直角边的边长分别为3和4的直角三角形，高为3，所以表面积为S ＝12×3×4＋3×52＋2＋52×4＋2＋52×5＋3×5＝60.G3 平面的基本性质、空间两条直线 4．G3[2014·辽宁卷] 已知m ，n 表示两条不同直线，α表示平面．下列说法正确的是( ) A ．若m ∥α，n ∥α，则m ∥n B ．若m ⊥α，n ⊂α，则m ⊥n C ．若m ⊥α，m ⊥n ，则n ∥α D ．若m ∥α，m ⊥n ，则n ⊥α4．B [解析] B [解析] 由题可知，若m ∥α，n ∥α，则m 与n 平行、相交或异面，所以A 错误；若m ⊥α，n ⊂α，则m ⊥n ，故B 正确；若m ⊥α，m ⊥n ，则n ∥α或n ⊂α，故C 错误．若m ∥α，m ⊥n ，则n ∥α或n ⊥α或n 与a 相交，故D 错误．17．G3、G5、G11[2014·福建卷] 在平面四边形ABCD 中，AB ＝BD ＝CD ＝1，AB ⊥BD ，CD ⊥BD .将△ABD 沿BD 折起，使得平面ABD ⊥平面BCD ，如图1-5所示．(1)求证：AB ⊥CD ；(2)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值．图1-517．解：(1)证明：∵平面ABD ⊥平面BCD ，平面ABD ∩平面BCD ＝BD ，AB ⊂平面ABD ，AB ⊥BD ，∴AB ⊥平面BCD .又CD ⊂平面BCD ，∴AB ⊥CD .(2)过点B 在平面BCD 内作BE ⊥BD .由(1)知AB ⊥平面BCD ，BE ⊂平面BCD ，BD ⊂平面BCD ，∴AB ⊥BE ，AB ⊥BD . 以B 为坐标原点，分别以BE →，BD →，BA →的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图所示)．依题意，得B (0，0，0)，C (1，1，0)，D (0，1，0)，A (0，0，1)，M ⎝⎛⎭⎫0，12，12. 则BC →＝(1，1，0)，BM →＝⎝⎛⎭⎫0，12，12，AD →＝(0，1，－1)．设平面MBC 的法向量n ＝(x 0，y 0，z 0)，则⎩⎪⎨⎪⎧n ·BC →＝0，n ·BM →＝0，即⎩⎪⎨⎪⎧x 0＋y 0＝0，12y 0＋12z 0＝0，取z 0＝1，得平面MBC 的一个法向量n ＝(1，－1，1)．设直线AD 与平面MBC 所成角为θ，则sin θ＝||cos 〈n ，AD →〉＝|n ·AD →||n |·|AD →|＝63.即直线AD 与平面MBC 所成角的正弦值为63. 11．G3[2014·新课标全国卷Ⅱ] 直三棱柱ABC -A 1B 1C 1中，∠BCA ＝90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC ＝CA ＝CC 1，则BM 与AN 所成角的余弦值为( )A.110B.25C.3010D.22 11．C [解析] 如图，E 为BC 的中点．由于M ，N 分别是A 1B 1，A 1C 1的中点，故MN ∥B 1C 1且MN ＝12B 1C 1，故MN 綊BE ，所以四边形MNEB 为平行四边形，所以EN 綊BM ，所以直线AN ，NE 所成的角即为直线BM ，AN 所成的角．设BC ＝1，则B 1M ＝12B 1A 1＝22，所以MB ＝1＋12＝62＝NE ，AN ＝AE ＝52，在△ANE 中，根据余弦定理得cos ∠ANE ＝64＋54－542×62×52＝3010.18．G3，G4，G5，G11[2014·四川卷] 三棱锥A -BCD及其侧视图、俯视图如图1-4所示．设M，N分别为线段AD，AB的中点，P为线段BC上的点，且MN⊥NP.(1)证明：P是线段BC的中点；(2)求二面角A -NP -M的余弦值．图1-418．解：(1)如图所示，取BD的中点O，连接AO，CO.由侧视图及俯视图知，△ABD，△BCD为正三角形，所以AO⊥BD，OC⊥BD.因为AO，OC⊂平面AOC，且AO∩OC＝O，所以BD⊥平面AOC.又因为AC⊂平面AOC，所以BD⊥AC.取BO的中点H，连接NH，PH.又M，N，H分别为线段AD，AB，BO的中点，所以MN∥BD，NH∥AO，因为AO⊥BD，所以NH⊥BD.因为MN⊥NP，所以NP⊥BD.因为NH，NP⊂平面NHP，且NH∩NP＝N，所以BD⊥平面NHP.又因为HP⊂平面NHP，所以BD⊥HP.又OC⊥BD，HP⊂平面BCD，OC⊂平面BCD，所以HP∥OC.因为H为BO的中点，所以P为BC的中点．(2)方法一：如图所示，作NQ⊥AC于Q，连接MQ.由(1)知，NP∥AC，所以NQ⊥NP.因为MN⊥NP，所以∠MNQ为二面角A -NP -M的一个平面角．由(1)知，△ABD ，△BCD 为边长为2的正三角形，所以AO ＝OC ＝ 3. 由俯视图可知，AO ⊥平面BCD .因为OC ⊂平面BCD ，所以AO ⊥OC ，因此在等腰直角△AOC 中，AC ＝ 6. 作BR ⊥AC 于R因为在△ABC 中，AB ＝BC ，所以R 为AC 的中点，所以BR ＝AB 2－⎝⎛⎭⎫AC 22＝102.因为在平面ABC 内，NQ ⊥AC ，BR ⊥AC ，所以NQ ∥BR .又因为N 为AB 的中点，所以Q 为AR 的中点，所以NQ ＝BR 2＝104.同理，可得MQ ＝104. 故△MNQ 为等腰三角形，所以在等腰△MNQ 中， cos ∠MNQ ＝MN 2NQ ＝BD 4NQ ＝105.故二面角A - NP - M 的余弦值是105. 方法二：由俯视图及(1)可知，AO ⊥平面BCD .因为OC ，OB ⊂平面BCD ，所以AO ⊥OC ，AO ⊥OB . 又OC ⊥OB ，所以直线OA ，OB ，OC 两两垂直．如图所示，以O 为坐标原点，以OB ，OC ，OA 的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系O -xyz .则A (0，0，3)，B (1，0，0)，C (0，3，0)，D (－1，0，0)．因为M ，N 分别为线段AD ，AB 的中点，又由(1)知，P 为线段BC 的中点，所以M ⎝⎛⎭⎫－12，0，32，N ⎝⎛⎭⎫12，0，32，P ⎝⎛⎭⎫12，32，0，于是AB ＝(1，0，－3)，BC ＝(－1，3，0)，MN ＝(1，0，0)，NP ＝⎝⎛⎭⎫0，32，－32. 设平面ABC 的一个法向量n 1＝(x 1，y 1，z 1)，由⎩⎪⎨⎪⎧n 1⊥AB ，n 1⊥BC ，得⎩⎪⎨⎪⎧n 1·AB ＝0，n 1·BC ＝0，即⎩⎨⎧（x 1，y 1，z 1）·（1，0，－3）＝0，（x 1，y 1，z 1）·（－1，3，0）＝0，从而⎩⎨⎧x 1－3z 1＝0，－x 1＋3y 1＝0.取z 1＝1，则x 1＝3，y 1＝1，所以n 1＝(3，1，1)．设平面MNP 的一个法向量n 2＝(x 2，y 2，z 2)，由，⎩⎪⎨⎪⎧n 2⊥MN ，n 2⊥NP ，得⎩⎪⎨⎪⎧n 2·MN ＝0，n 2·NP ＝0，即⎩⎪⎨⎪⎧（x 2，y 2，z 2）·（1，0，0）＝0，（x 2，y 2，z 2）·⎝⎛⎭⎫0，32，－32＝0，从而⎩⎪⎨⎪⎧x 2＝0，32y 2－32z 2＝0. 取z 2＝1，则y 2＝1，x 2＝0，所以n 2＝(0，1，1)．设二面角A - NP - M 的大小为θ，则cos θ＝⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|＝⎪⎪⎪⎪⎪⎪（3，1，1）·（0，1，1）5×2＝105. 故二面角A -NP -M 的余弦值是105.G4 空间中的平行关系 20．G1、G4、G11[2014·安徽卷] 如图1-5，四棱柱ABCD - A 1B 1C 1D 1中，A 1A ⊥底面ABCD ，四边形ABCD 为梯形，AD ∥BC ，且AD ＝2BC .过A 1，C ，D 三点的平面记为α，BB 1与α的交点为Q .图1-5(1)证明：Q 为BB 1的中点；(2)求此四棱柱被平面α所分成上下两部分的体积之比；(3)若AA 1＝4，CD ＝2，梯形ABCD 的面积为6，求平面α与底面ABCD 所成二面角的大小．20．解： (1)证明：因为BQ ∥AA 1，BC ∥AD ， BC ∩BQ ＝B ，AD ∩AA 1＝A ，所以平面QBC ∥平面A 1AD ，从而平面A 1CD 与这两个平面的交线相互平行，即QC ∥A 1D .故△QBC 与△A 1AD 的对应边相互平行，于是△QBC ∽△A 1AD ，所以BQ BB 1＝BQ AA 1＝BC AD ＝12，即Q 为BB 1的中点．(2)如图1所示，连接QA ，QD .设AA 1＝h ，梯形ABCD 的高为d ，四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下，BC ＝a ，则AD ＝2a .图1V 三棱锥Q -A 1AD ＝13×12·2a ·h ·d ＝13ahd ，V 四棱锥Q -ABCD＝13·a ＋2a 2·d ·⎝⎛⎭⎫12h ＝14ahd ，所以V 下＝V 三棱锥Q -A 1AD ＋V 四棱锥Q -ABCD ＝712ahd . 又V 四棱柱A 1B 1C 1D 1 ABCD ＝32ahd ，所以V 上＝V 四棱柱A 1B 1C 1D 1 ABCD －V 下＝32ahd －712ahd ＝1112ahd ，故V 上V 下＝117.(3)方法一：如图1所示，在△ADC 中，作AE ⊥DC ，垂足为E ，连接A 1E .又DE ⊥AA 1，且AA 1∩AE ＝A ，所以DE ⊥平面AEA 1，所以DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角．因为BC ∥AD ，AD ＝2BC ，所以S △ADC ＝2S △BCA . 又因为梯形ABCD 的面积为6，DC ＝2，所以S △ADC ＝4，AE ＝4.于是tan ∠AEA 1＝AA 1AE ＝1，∠AEA 1＝π4.故平面α与底面ABCD 所成二面角的大小为π4.方法二：如图2所示，以D 为原点，DA ，DD 1→分别为x 轴和z 轴正方向建立空间直角坐标系．设∠CDA ＝θ，BC ＝a ，则AD ＝2a .因为S 四边形ABCD ＝a ＋2a2·2sin θ＝6，所以a ＝2sin θ.图2从而可得C (2cos θ，2sin θ，0)，A 1⎝⎛⎭⎫4sin θ，0，4，所以DC ＝(2cos θ，2sin θ，0)，DA 1→＝⎝⎛⎭⎫4sin θ，0，4.设平面A 1DC 的法向量n ＝(x ，y ，1)，由⎩⎨⎧DA 1→·n ＝4sin θx ＋4＝0，DC →·n ＝2x cos θ＋2y sin θ＝0，得⎩⎪⎨⎪⎧x ＝－sin θ，y ＝cos θ，所以n ＝(－sin θ，cos θ，1)．又因为平面ABCD 的法向量m ＝(0，0，1)，所以cos 〈n ，m 〉＝n·m|n||m|＝22，故平面α与底面ABCD 所成二面角的大小为π4.17．G4、G11[2014·北京卷] 如图1-3，正方形AMDE 的边长为2，B ，C 分别为AM ，MD 的中点．在五棱锥P - ABCDE 中，F 为棱PE 的中点，平面ABF 与棱PD ，PC 分别交于点G ，H .(1)求证：AB ∥FG ；(2)若P A ⊥底面ABCDE ，且P A ＝AE ，求直线BC 与平面ABF 所成角的大小，并求线段PH 的长．图1-317．解：(1)证明：在正方形AMDE 中，因为B 是AM 的中点，所以AB ∥DE . 又因为AB ⊄平面PDE ，所以AB ∥平面PDE .因为AB ⊂平面ABF ，且平面ABF ∩平面PDE ＝FG ，所以AB ∥FG .(2)因为P A ⊥底面ABCDE ，所以P A ⊥AB ，P A ⊥AE .建立空间直角坐标系Axyz ，如图所示，则A (0，0，0)，B (1，0，0)，C (2，1，0)，P (0，0，2)，F (0，1，1)，BC →＝(1，1，0)．设平面ABF 的法向量为n ＝(x ，y ，z )，则 ⎩⎪⎨⎪⎧n ·AB →＝0，n ·AF →＝0，即⎩⎪⎨⎪⎧x ＝0，y ＋z ＝0.令z ＝1，则y ＝－1.所以n ＝(0，－1，1)．设直线BC 与平面ABF 所成角为α，则 sin α＝|cos 〈n ，BC →〉|＝⎪⎪⎪⎪⎪⎪n ·BC →|n ||BC →|＝12.因此直线BC 与平面ABF 所成角的大小为π6.设点H 的坐标为(u ，v ，w )．因为点H 在棱PC 上，所以可设PH →＝λPC →(0<λ<1)．即(u ，v ，w －2)＝λ(2，1，－2)，所以u ＝2λ，v ＝λ，w ＝2－2λ. 因为n 是平面ABF 的一个法向量，所以n ·AH →＝0，即(0，－1，1)·(2λ，λ，2－2λ)＝0，解得λ＝23，所以点H 的坐标为⎝⎛⎭⎫43，23，23. 所以PH ＝⎝⎛⎭⎫432＋⎝⎛⎭⎫232＋⎝⎛⎭⎫－432＝2.19．G4、G10、G11、G12[2014·湖北卷] 如图1-4，在棱长为2的正方体ABCD -A 1B 1C 1D 1中，E ，F ，M ，N 分别是棱AB ，AD ，A 1B 1，A 1D 1的中点，点P ，Q 分别在棱DD 1，BB 1上移动，且DP ＝BQ ＝λ(0<λ<2)．(1)当λ＝1时，证明：直线BC 1∥平面EFPQ .(2)是否存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由．图1-419．解：方法一(几何方法)：(1)证明：如图①，连接AD 1，由ABCD A 1B 1C 1D 1是正方体，知BC 1∥AD 1.当λ＝1时，P 是DD 1的中点，又F 是AD 的中点，所以FP ∥AD 1，所以BC 1∥FP . 而FP ⊂平面EFPQ ，且BC 1⊄平面EFPQ ，故直线BC 1∥平面EFPQ .图① 图②(2)如图②，连接BD .因为E ，F 分别是AB ，AD 的中点，所以EF ∥BD ，且EF ＝12BD .又DP ＝BQ ，DP ∥BQ ，所以四边形PQBD 是平行四边形，故PQ ∥BD ，且PQ ＝BD ，从而EF ∥PQ ，且EF ＝12PQ .在Rt △EBQ 和Rt △FDP 中，因为BQ ＝DP ＝λ，BE ＝DF ＝1，于是EQ ＝FP ＝1＋λ2，所以四边形EFPQ 也是等腰梯形．同理可证四边形PQMN 也是等腰梯形．分别取EF ，PQ ，MN 的中点为H ，O ，G ，连接OH ，OG ，则GO ⊥PQ ，HO ⊥PQ ，而GO ∩HO ＝O ，故∠GOH 是面EFPQ 与面PQMN 所成的二面角的平面角．若存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角，则∠GOH ＝90°. 连接EM ，FN ，则由EF ∥MN ，且EF ＝MN 知四边形EFNM 是平行四边形．连接GH ，因为H ，G 是EF ，MN 的中点，所以GH ＝ME ＝2.在△GOH 中，GH 2＝4，OH 2＝1＋λ2－⎝⎛⎭⎫222＝λ2＋12， OG 2＝1＋(2－λ)2－⎝⎛⎭⎫222＝(2－λ)2＋12，由OG 2＋OH 2＝GH 2，得(2－λ)2＋12＋λ2＋12＝4，解得λ＝1±22，故存在λ＝1±22，使面EFPQ 与面PQMN 所成的二面角为直二面角．方法二(向量方法)：以D 为原点，射线DA ，DC ，DD 1分别为x ，y ，z 轴的正半轴建立如图③所示的空间直角坐标系．由已知得B (2，2，0)，C 1(0，2，2)，E (2，1，0)，F (1，0，0)，P (0，0，λ)．图③BC 1→＝(－2，0，2)，FP ＝(－1，0，λ)，FE ＝(1，1，0)． (1)证明：当λ＝1时，FP ＝(－1，0，1)，因为BC 1→＝(－2，0，2)，所以BC 1→＝2FP →，即BC 1∥FP .而FP ⊂平面EFPQ ，且BC 1⊄平面EFPQ ，故直线BC 1∥平面EFPQ .(2)设平面EFPQ 的一个法向量为n ＝(x ，y ，z )，则由⎩⎪⎨⎪⎧FE →·n ＝0，FP →·n ＝0可得⎩⎪⎨⎪⎧x ＋y ＝0，－x ＋λz ＝0.于是可取n ＝(λ，－λ，1)．同理可得平面MNPQ 的一个法向量为m ＝(λ－2，2－λ，1)．若存在λ，使面EFPQ 与面PQMN 所成的二面角为直二面角，则m ·n ＝(λ－2，2－λ，1)·(λ，－λ，1)＝0，即λ(λ－2)－λ(2－λ)＋1＝0，解得λ＝1±22.故存在λ＝1±22，使面EFPQ 与面PQMN 所成的二面角为直二面角．18．G4、G10[2014·新课标全国卷Ⅱ] 如图1-3，四棱锥P -ABCD 中，底面ABCD 为矩形，P A ⊥平面ABCD ，E 为PD 的中点．(1)证明：PB ∥平面AEC ； (2)设二面角D -AE -C 为60°，AP ＝1，AD ＝3，求三棱锥E -ACD 的体积．图1-318．解：(1)证明：连接BD 交AC 于点O ，连接EO . 因为ABCD 为矩形，所以O 为BD 的中点．又E 为PD 的中点，所以EO ∥PB . 因为EO ⊂平面AEC ，PB ⊄平面AEC ，所以PB ∥平面AEC .(2)因为P A ⊥平面ABCD ，ABCD 为矩形，所以AB ，AD ，AP 两两垂直．如图，以A 为坐标原点，AB →，AD ，AP 的方向为x 轴、y 轴、z 轴的正方向，|AP →|为单位长，建立空间直角坐标系A -xyz ，则D ()0，3，0，E ⎝⎛⎭⎫0，32，12，AE →＝⎝⎛⎭⎫0，32，12.设B (m ，0，0)(m >0)，则C (m ，3，0)，AC →＝(m ，3，0)．设n 1＝(x ，y ，z )为平面ACE 的法向量，则⎩⎪⎨⎪⎧n 1·AC →＝0，n 1·AE →＝0，即⎩⎪⎨⎪⎧mx ＋3y ＝0，32y ＋12z ＝0，可取n 1＝⎝⎛⎭⎫3m ，－1，3.又n 2＝(1，0，0)为平面DAE 的法向量，由题设易知|cos 〈n 1，n 2〉|＝12，即33＋4m 2＝12，解得m ＝32. 因为E 为PD 的中点，所以三棱锥E -ACD 的高为12.三棱锥E -ACD 的体积V ＝13×12×3×32×12＝38. 17．G4，G11[2014·山东卷] 如图1-3所示，在四棱柱ABCD -A 1B 1C 1D 1中，底面ABCD 是等腰梯形，∠DAB ＝60°，AB ＝2CD ＝2，M 是线段AB 的中点．图1-3(1)求证：C 1M ∥平面A 1ADD 1；(2)若CD 1垂直于平面ABCD 且CD 1＝3，求平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值．17．解：(1)证明：因为四边形ABCD 是等腰梯形，且AB ＝2CD ，所以AB ∥DC ，又M 是AB 的中点，所以CD ∥MA 且CD ＝MA .连接AD 1.因为在四棱柱ABCD - A 1B 1C 1D 1中，CD ∥C 1D 1，CD ＝C 1D 1，所以C 1D 1∥MA ，C 1D 1＝MA ，所以四边形AMC 1D 1为平行四边形，因此，C 1M ∥D 1A .又C 1M ⊄平面A 1ADD 1，D 1A ⊂平面A 1ADD 1，所以C 1M ∥平面A 1ADD 1. (2)方法一：连接AC ，MC .由(1)知，CD ∥AM 且CD ＝AM ，所以四边形AMCD 为平行四边形，所以BC ＝AD ＝MC .由题意∠ABC ＝∠DAB ＝60°，所以△MBC 为正三角形，因此AB ＝2BC ＝2，CA ＝3，因此CA ⊥CB .设C 为坐标原点，建立如图所示的空间直角坐标系C xyz .所以A (3，0，0)，B (0，1，0)，D 1(0，0，3)．因此M ⎝⎛⎭⎫32，12，0，所以MD 1→＝⎝⎛⎭⎫－32，－12，3，D 1C 1→＝MB →＝⎝⎛⎭⎫－32，12，0.设平面C 1D 1M 的一个法向量n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·D 1C 1→＝0，n ·MD 1→＝0，得⎩⎨⎧3x －y ＝0，3x ＋y －2 3z ＝0，可得平面C 1D 1M 的一个法向量n ＝(1，3，1)．又CD 1→＝(0，0，3)为平面ABCD 的一个法向量．因此cos 〈CD 1→，n 〉＝CD 1→·n |CD 1→||n |＝55，所以平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值为55. 方法二：由(1)知，平面D 1C 1M ∩平面ABCD ＝AB ，点过C 向AB 引垂线交AB 于点N ，连接D 1N.由CD 1⊥平面ABCD ，可得D 1N ⊥AB ，因此∠D 1NC 为二面角C 1 AB C 的平面角．在Rt △BNC 中，BC ＝1，∠NBC ＝60°，可得CN ＝32，所以ND 1＝CD 21＋CN 2＝152. 在Rt △D 1CN 中，cos ∠D 1NC ＝CN D 1N ＝32152＝55，所以平面C 1D 1M 和平面ABCD 所成的角(锐角)的余弦值为55. 18．G3，G4，G5，G11[2014·四川卷] 三棱锥A - BCD 及其侧视图、俯视图如图1-4所示．设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN ⊥NP .(1)证明：P 是线段BC 的中点； (2)求二面角A - NP - M 的余弦值．图1-418．解：(1)如图所示，取BD 的中点O ，连接AO ，CO . 由侧视图及俯视图知，△ABD ，△BCD 为正三角形，所以AO ⊥BD ，OC ⊥BD .因为AO ，OC ⊂平面AOC ，且AO ∩OC ＝O ，所以BD ⊥平面AOC .又因为AC ⊂平面AOC ，所以BD ⊥AC . 取BO 的中点H ，连接NH ，PH .又M ，N ，H 分别为线段AD ，AB ，BO 的中点，所以MN ∥BD ，NH ∥AO ，因为AO ⊥BD ，所以NH ⊥BD . 因为MN ⊥NP ，所以NP ⊥BD .因为NH ，NP ⊂平面NHP ，且NH ∩NP ＝N ，所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ，所以BD ⊥HP .又OC ⊥BD ，HP ⊂平面BCD ，OC ⊂平面BCD ，所以HP ∥OC . 因为H 为BO 的中点，所以P 为BC 的中点．(2)方法一：如图所示，作NQ ⊥AC 于Q ，连接MQ.由(1)知，NP ∥AC ，所以NQ ⊥NP .因为MN ⊥NP ，所以∠MNQ 为二面角A - NP - M 的一个平面角．由(1)知，△ABD ，△BCD 为边长为2的正三角形，所以AO ＝OC ＝ 3. 由俯视图可知，AO ⊥平面BCD .因为OC ⊂平面BCD ，所以AO ⊥OC ，因此在等腰直角△AOC 中，AC ＝ 6. 作BR ⊥AC 于R因为在△ABC 中，AB ＝BC ，所以R 为AC 的中点，所以BR ＝AB 2－⎝⎛⎭⎫AC 22＝102.因为在平面ABC 内，NQ ⊥AC ，BR ⊥AC ，所以NQ ∥BR .又因为N 为AB 的中点，所以Q 为AR 的中点，所以NQ ＝BR 2＝104.同理，可得MQ ＝104. 故△MNQ 为等腰三角形，所以在等腰△MNQ 中， cos ∠MNQ ＝MN 2NQ ＝BD 4NQ ＝105.故二面角A - NP - M 的余弦值是105. 方法二：由俯视图及(1)可知，AO ⊥平面BCD .因为OC ，OB ⊂平面BCD ，所以AO ⊥OC ，AO ⊥OB . 又OC ⊥OB ，所以直线OA ，OB ，OC 两两垂直．如图所示，以O 为坐标原点，以OB ，OC ，OA 的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系O -xyz .则A (0，0，3)，B (1，0，0)，C (0，3，0)，D (－1，0，0)．因为M ，N 分别为线段AD ，AB 的中点，又由(1)知，P 为线段BC 的中点，所以M ⎝⎛⎭⎫－12，0，32，N ⎝⎛⎭⎫12，0，32，P ⎝⎛⎭⎫12，32，0，于是AB ＝(1，0，－3)，BC ＝(－1，3，0)，MN ＝(1，0，0)，NP ＝⎝⎛⎭⎫0，32，－32. 设平面ABC 的一个法向量n 1＝(x 1，y 1，z 1)，由⎩⎪⎨⎪⎧n 1⊥AB ，n 1⊥BC ，得⎩⎪⎨⎪⎧n 1·AB ＝0，n 1·BC ＝0，即 ⎩⎨⎧（x 1，y 1，z 1）·（1，0，－3）＝0，（x 1，y 1，z 1）·（－1，3，0）＝0，从而⎩⎨⎧x 1－3z 1＝0，－x 1＋3y 1＝0.取z 1＝1，则x 1＝3，y 1＝1，所以n 1＝(3，1，1)．设平面MNP 的一个法向量n 2＝(x 2，y 2，z 2)，由，⎩⎪⎨⎪⎧n 2⊥MN ，n 2⊥NP ，得⎩⎪⎨⎪⎧n 2·MN ＝0，n 2·NP ＝0，即⎩⎪⎨⎪⎧（x 2，y 2，z 2）·（1，0，0）＝0，（x 2，y 2，z 2）·⎝⎛⎭⎫0，32，－32＝0，从而⎩⎪⎨⎪⎧x 2＝0，32y 2－32z 2＝0.取z 2＝1，则y 2＝1，x 2＝0，所以n 2＝(0，1，1)．设二面角A - NP - M 的大小为θ，则cos θ＝⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|＝⎪⎪⎪⎪⎪⎪（3，1，1）·（0，1，1）5×2＝105. 故二面角A -NP -M 的余弦值是105.G5 空间中的垂直关系 17．G3、G5、G11[2014·福建卷] 在平面四边形ABCD 中，AB ＝BD ＝CD ＝1，AB ⊥BD ，CD ⊥BD .将△ABD 沿BD 折起，使得平面ABD ⊥平面BCD ，如图1-5所示．(1)求证：AB ⊥CD ；(2)若M 为AD 中点，求直线AD 与平面MBC 所成角的正弦值．图1-517．解：(1)证明：∵平面ABD ⊥平面BCD ，平面ABD ∩平面BCD ＝BD ，AB ⊂平面ABD ，AB ⊥BD ，∴AB ⊥平面BCD .又CD ⊂平面BCD ，∴AB ⊥CD .(2)过点B 在平面BCD 内作BE ⊥BD .由(1)知AB ⊥平面BCD ，BE ⊂平面BCD ，BD ⊂平面BCD ，∴AB ⊥BE ，AB ⊥BD . 以B 为坐标原点，分别以BE →，BD →，BA →的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图所示)．依题意，得B (0，0，0)，C (1，1，0)，D (0，1，0)，A (0，0，1)，M ⎝⎛⎭⎫0，12，12. 则BC →＝(1，1，0)，BM →＝⎝⎛⎭⎫0，12，12，AD →＝(0，1，－1)．设平面MBC 的法向量n ＝(x 0，y 0，z 0)，则⎩⎪⎨⎪⎧n ·BC →＝0，n ·BM →＝0，即⎩⎪⎨⎪⎧x 0＋y 0＝0，12y 0＋12z 0＝0，取z 0＝1，得平面MBC 的一个法向量n ＝(1，－1，1)．设直线AD 与平面MBC 所成角为θ，则sin θ＝||cos 〈n ，AD →〉＝|n ·AD →||n |·|AD →|＝63.即直线AD 与平面MBC 所成角的正弦值为63. 18．G5、G11[2014·广东卷] 如图1-4，四边形ABCD 为正方形，PD ⊥平面ABCD ，∠DPC ＝30°，AF ⊥PC 于点F ，FE ∥CD ，交PD 于点E .(1)证明：CF ⊥平面ADF ； (2)求二面角D - AF - E 的余弦值．图1-419．G5、G11[2014·湖南卷] 如图1-6所示，四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等，AC ∩BD ＝O ，A 1C 1∩B 1D 1＝O 1，四边形ACC 1A 1和四边形BDD 1B 1均为矩形．(1)证明：O 1O ⊥底面ABCD ；(2)若∠CBA ＝60°，求二面角C 1OB 1D 的余弦值．图1-619．解：(1)如图(a)，因为四边形ACC 1A 1为矩形，所以CC 1⊥AC .同理DD 1⊥BD . 因为CC 1∥DD 1，所以CC 1⊥BD .而AC ∩BD ＝O ，因此CC 1⊥底面ABCD . 由题设知，O 1O ∥C 1C .故O 1O ⊥底面ABCD .(2)方法一：如图(a)，过O 1作O 1H ⊥OB 1于H ，连接HC 1.由(1)知，O 1O ⊥底面ABCD ，所以O 1O ⊥底面A 1B 1C 1D 1，于是O 1O ⊥A 1C 1.图(a)又因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等，所以四边形A 1B 1C 1D 1是菱形，因此A 1C 1⊥B 1D 1，从而A 1C 1⊥平面BDD 1B 1，所以A 1C 1⊥OB 1，于是OB 1⊥平面O 1HC 1. 进而OB 1⊥C 1H .故∠C 1HO 1是二面角C 1OB 1D 的平面角．不妨设AB ＝2.因为∠CBA ＝60°，所以OB ＝3，OC ＝1，OB 1＝7.在Rt △OO 1B 1中，易知O 1H ＝OO 1·O 1B 1OB 1＝237.而O 1C 1＝1，于是C 1H ＝O 1C 21＋O 1H 2＝1＋127＝197.故cos ∠C 1HO 1＝O 1HC 1H ＝237197＝25719.即二面角C 1OB 1D 的余弦值为25719.方法二：因为四棱柱ABCD -A 1B 1C 1D 1的所有棱长都相等，所以四边形ABCD 是菱形，因此AC ⊥BD .又O 1O ⊥底面ABCD ，从而OB ，OC ，OO 1两两垂直．图(b)如图(b)，以O 为坐标原点，OB ，OC ，OO 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系O xyz ，不妨设AB ＝2.因为∠CBA ＝60°，所以OB ＝3，OC ＝1，于是相关各点的坐标为O (0，0，0)，B 1(3，0，2)，C 1(0，1，2)．易知，n 1＝(0，1，0)是平面BDD 1B 1的一个法向量．设n 2＝(x ，y ，z )是平面OB 1C 1的一个法向量，则⎩⎪⎨⎪⎧n 2·OB →1＝0，n 2·OC →1＝0，即⎩⎨⎧3x ＋2z ＝0，y ＋2z ＝0.取z ＝－3，则x ＝2，y ＝23，所以n 2＝(2，23，－3)．设二面角C 1OB 1D 的大小为θ，易知θ是锐角，于是cos θ＝|cos 〈n 1，n 2〉|＝⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|＝2319＝25719.故二面角C 1OB 1D 的余弦值为25719.19．G5、G7、G11[2014·江西卷] 如图1-6，四棱锥P - ABCD 中，ABCD 为矩形，平面P AD ⊥平面ABCD .图1-6(1)求证：AB ⊥PD .(2)若∠BPC ＝90°，PB ＝2，PC ＝2，问AB 为何值时，四棱锥P - ABCD 的体积最大？并求此时平面BPC 与平面DPC 夹角的余弦值．19．解：(1)证明：因为ABCD 为矩形，所以AB ⊥AD . 又平面P AD ⊥平面ABCD ，平面P AD ∩平面ABCD ＝AD ，所以AB ⊥平面P AD ，故AB ⊥PD .(2)过P 作AD 的垂线，垂足为O ，过O 作BC 的垂线，垂足为G ，连接PG . 故PO ⊥平面ABCD ，BC ⊥平面POG ，BC ⊥PG . 在Rt △BPC 中，PG ＝2 33，GC ＝2 63，BG ＝63.设AB ＝m ，则OP ＝PG 2－OG 2＝43－m 2，故四棱锥P - ABCD 的体积为V ＝13×6·m ·43－m 2＝m38－6m 2. 因为m 8－6m 2＝8m 2－6m 4＝－6⎝⎛⎭⎫m 2－232＋83，所以当m ＝63，即AB ＝63时，四棱锥P - ABCD 的体积最大．此时，建立如图所示的空间直角坐标系，各点的坐标分别为O (0，0，0)，B ⎝⎛⎭⎫63，－63，0，C ⎝⎛⎭⎫63，263，0，D ⎝⎛⎭⎫0，263，0，P ⎝⎛⎭⎫0，0，63，故PC →＝⎝⎛⎭⎫63，263，－63，BC →＝(0，6，0)，CD ＝⎝⎛⎭⎫－63，0，0.设平面BPC 的一个法向量为n 1＝(x ，y ，1)，则由n 1⊥PC →，n 1⊥BC →，得⎩⎪⎨⎪⎧63x ＋2 63y －63＝0，6y ＝0，解得x ＝1，y ＝0，则n 1＝(1，0，1)．同理可求出平面DPC 的一个法向量为n 2＝⎝⎛⎭⎫0，12，1. 设平面BPC 与平面DPC 的夹角为θ，则cos θ＝|n 1·n 2||n 1||n 2|＝12·14＋1＝105.19．G5、G11[2014·辽宁卷] 如图1-5所示，△ABC 和△BCD 所在平面互相垂直，且AB ＝BC ＝BD ＝2，∠ABC ＝∠DBC ＝120°，E ，F 分别为AC ，DC 的中点．(1)求证：EF ⊥BC ； (2)求二面角E -BF -C 的正弦值．图1-519．解：(1)证明：方法一，过点E 作EO ⊥BC ，垂足为O ，连接OF .由△ABC ≌△DBC可证出△EOC ≌△FOC ，所以∠EOC ＝∠FOC ＝π2，即FO ⊥BC .又EO ⊥BC ，EO ∩FO ＝O ，所以BC ⊥平面EFO .又EF ⊂平面EFO ，所以EF ⊥BC .图1方法二，由题意，以B 为坐标原点，在平面DBC 内过B 作垂直BC 的直线，并将其作为x 轴，BC 所在直线为y 轴，在平面ABC 内过B 作垂直BC 的直线，并将其作为z 轴，建立如图所示的空间直角坐标系，易得B (0，0，0)，A (0，－1，3)，D (3，－1，0)，C (0，2，0)，因而E (0，12，32)，F (32，12，0)，所以EF →＝(32，0，－32)，BC →＝(0，2，0)，因此EF →·BC →＝0，从而EF →⊥BC →，所以EF ⊥BC .图2(2)方法一，在图1中，过点O 作OG ⊥BF ，垂足为G ，连接EG .因为平面ABC ⊥平面BDC ，所以EO ⊥面BDC ，又OG ⊥BF ，所以由三垂线定理知EG ⊥BF ，因此∠EGO 为二面角E -BF -C 的平面角．在△EOC 中，EO ＝12EC ＝12BC ·cos 30°＝32.由△BGO ∽△BFC 知，OG ＝BO BC ·FC ＝34，因此tan ∠EGO ＝EOOG＝2，从而得sin ∠EGO＝255，即二面角E -BF -C 的正弦值为2 55.方法二，在图2中，平面BFC 的一个法向量为n 1＝(0，0，1)．设平面BEF 的法向量n 2＝(x ，y ，z )，又BF →＝(32，12，0)，BE →＝(0，12，32)，所以⎩⎪⎨⎪⎧n 2·BF →＝0，n 2·BE →＝0，得其中一个n 2＝(1，－3，1)．设二面角E -BF -C 的大小为θ，且由题知θ为锐角，则cos θ＝|cos 〈n 1，n 2〉|＝⎪⎪⎪⎪n 1·n 2|n 1||n 2|＝15，因此sin θ＝25＝2 55，即所求二面角正弦值为2 55.19．G 5、G 11[2014·新课标全国卷Ⅰ] 如图1-5，三棱柱ABC -A 1B 1C 1中，侧面BB 1C 1C 为菱形，AB ⊥B 1C .图1-5(1)证明：AC ＝AB 1；(2)若AC ⊥AB 1，∠CBB 1＝60°，AB ＝BC ，求二面角A -A 1B 1 C 1的余弦值．19．解：(1)证明：连接BC 1，交B 1C 于点O ，连接AO ，因为侧面BB 1C 1C 为菱形，所以B 1C ⊥BC 1，且O 为B 1C 及BC 1的中点．又AB ⊥B 1C ，所以B 1C ⊥平面ABO . 由于AO ⊂平面ABO ，故B 1C ⊥AO . 又B 1O ＝CO ，故AC ＝AB 1.(2)因为AC ⊥AB 1，且O 为B 1C 的中点，所以AO ＝CO .又因为AB ＝BC ，所以△BOA ≌ △BOC .故OA ⊥OB ，从而OA ，OB ，OB 1两两垂直．以O 为坐标原点，OB 的方向为x 轴正方向，|OB |为单位长，建立如图所示的空间直角坐标系O xyz .因为∠CBB 1＝60°，所以△CBB 1为等边三角形，又AB ＝BC ，则A ⎝⎛⎭⎫0，0，33，B (1，0，0)，B 1⎝⎛⎭⎫0，33，0，C ⎝⎛⎭⎫0，－33，0. AB 1→＝⎝⎛⎭⎫0，33，－33，A 1B 1→＝AB ＝⎝⎛⎭⎫1，0，－33，B 1C →1＝BC ＝⎝⎛⎭⎫－1，－33，0.设n ＝(x ，y ，z )是平面AA 1B 1的法向量，则 ⎩⎨⎧n ·AB 1＝0，n ·A 1B 1→＝0，即⎩⎨⎧33y －33z ＝0，x －33z ＝0.所以可取n ＝(1，3，3)．设m 是平面A 1B 1C 1的法向量，则⎩⎪⎨⎪⎧m ·A 1B 1→＝0，m ·B 1C 1→＝0，同理可取m ＝(1，－3，3)．则cos 〈n ，m 〉＝n ·m |n ||m |＝17.所以结合图形知二面角A -A 1B 1 C 1的余弦值为17.18．G3，G4，G5，G11[2014·四川卷] 三棱锥A - BCD 及其侧视图、俯视图如图1-4所示．设M ，N 分别为线段AD ，AB 的中点，P 为线段BC 上的点，且MN ⊥NP .(1)证明：P 是线段BC 的中点； (2)求二面角A - NP - M 的余弦值．图1-418．解：(1)如图所示，取BD 的中点O ，连接AO ，CO . 由侧视图及俯视图知，△ABD ，△BCD 为正三角形，所以AO ⊥BD ，OC ⊥BD .因为AO ，OC ⊂平面AOC ，且AO ∩OC ＝O ，所以BD ⊥平面AOC .又因为AC ⊂平面AOC ，所以BD ⊥AC . 取BO 的中点H ，连接NH ，PH .又M ，N ，H 分别为线段AD ，AB ，BO 的中点，所以MN ∥BD ，NH ∥AO ，因为AO ⊥BD ，所以NH ⊥BD . 因为MN ⊥NP ，所以NP ⊥BD .因为NH ，NP ⊂平面NHP ，且NH ∩NP ＝N ，所以BD ⊥平面NHP . 又因为HP ⊂平面NHP ，所以BD ⊥HP .又OC ⊥BD ，HP ⊂平面BCD ，OC ⊂平面BCD ，所以HP ∥OC .因为H 为BO 的中点，所以P 为BC 的中点．(2)方法一：如图所示，作NQ ⊥AC 于Q ，连接MQ.由(1)知，NP ∥AC ，所以NQ ⊥NP .因为MN ⊥NP ，所以∠MNQ 为二面角A - NP - M 的一个平面角．由(1)知，△ABD ，△BCD 为边长为2的正三角形，所以AO ＝OC ＝ 3. 由俯视图可知，AO ⊥平面BCD .因为OC ⊂平面BCD ，所以AO ⊥OC ，因此在等腰直角△AOC 中，AC ＝ 6. 作BR ⊥AC 于R因为在△ABC 中，AB ＝BC ，所以R 为AC 的中点，所以BR ＝AB 2－⎝⎛⎭⎫AC 22＝102.因为在平面ABC 内，NQ ⊥AC ，BR ⊥AC ，所以NQ ∥BR .又因为N 为AB 的中点，所以Q 为AR 的中点，所以NQ ＝BR 2＝104.同理，可得MQ ＝104. 故△MNQ 为等腰三角形，所以在等腰△MNQ 中， cos ∠MNQ ＝MN 2NQ ＝BD 4NQ ＝105.故二面角A - NP - M 的余弦值是105. 方法二：由俯视图及(1)可知，AO ⊥平面BCD .因为OC ，OB ⊂平面BCD ，所以AO ⊥OC ，AO ⊥OB . 又OC ⊥OB ，所以直线OA ，OB ，OC 两两垂直．如图所示，以O 为坐标原点，以OB ，OC ，OA 的方向为x 轴，y 轴，z 轴的正方向，建立空间直角坐标系O -xyz .则A (0，0，3)，B (1，0，0)，C (0，3，0)，D (－1，0，0)．因为M ，N 分别为线段AD ，AB 的中点，又由(1)知，P 为线段BC 的中点，所以M ⎝⎛⎭⎫－12，0，32，N ⎝⎛⎭⎫12，0，32，P ⎝⎛⎭⎫12，32，0，于是AB ＝(1，0，－3)，BC ＝(－1，3，0)，MN ＝(1，0，0)，NP ＝⎝⎛⎭⎫0，32，－32. 设平面ABC 的一个法向量n 1＝(x 1，y 1，z 1)，由⎩⎪⎨⎪⎧n 1⊥AB ，n 1⊥BC ，得⎩⎪⎨⎪⎧n 1·AB ＝0，n 1·BC ＝0，即 ⎩⎨⎧（x 1，y 1，z 1）·（1，0，－3）＝0，（x 1，y 1，z 1）·（－1，3，0）＝0，从而⎩⎨⎧x 1－3z 1＝0，－x 1＋3y 1＝0.取z 1＝1，则x 1＝3，y 1＝1，所以n 1＝(3，1，1)．设平面MNP 的一个法向量n 2＝(x 2，y 2，z 2)，由，⎩⎪⎨⎪⎧n 2⊥MN ，n 2⊥NP ，得⎩⎪⎨⎪⎧n 2·MN ＝0，n 2·NP ＝0，即⎩⎪⎨⎪⎧（x 2，y 2，z 2）·（1，0，0）＝0，（x 2，y 2，z 2）·⎝⎛⎭⎫0，32，－32＝0，从而⎩⎪⎨⎪⎧x 2＝0，32y 2－32z 2＝0. 取z 2＝1，则y 2＝1，x 2＝0，所以n 2＝(0，1，1)．设二面角A - NP - M 的大小为θ，则cos θ＝⎪⎪⎪⎪⎪⎪n 1·n 2|n 1|·|n 2|＝⎪⎪⎪⎪⎪⎪（3，1，1）·（0，1，1）5×2＝105. 故二面角A -NP -M 的余弦值是105. 17．G5、G11[2014·天津卷] 如图1-4所示，在四棱锥P - ABCD 中，P A ⊥底面ABCD,AD ⊥AB ，AB ∥DC ，AD ＝DC ＝AP ＝2，AB ＝1，点E 为棱PC 的中点．(1)证明：BE ⊥DC ；(2)求直线BE 与平面PBD 所成角的正弦值；(3)若F 为棱PC 上一点，满足BF ⊥AC ，求二面角F - AB - P 的余弦值．图1-417．解：方法一：依题意，以点A 为原点建立空间直角坐标系(如图所示)，可得B (1，0，0)，C (2，2，0)，D (0，2，0)，P (0，0，2)．C 由E 为棱PC 的中点，得E (1，1，1)．(1)证明：向量BE ＝(0，1，1)，DC ＝(2，0，0)，故BE ·DC ＝0，所以BE ⊥DC .(2)向量BD ＝(－1，2，0)，PB ＝(1，0，－2)．设n ＝(x ，y ，z )为平面PBD 的法向量，则⎩⎪⎨⎪⎧n ·BD ＝0，n ·PB ＝0，即⎩⎪⎨⎪⎧－x ＋2y ＝0，x －2z ＝0. 不妨令y ＝1，可得n ＝(2，1，1)为平面PBD 的一个法向量．于是有 cos 〈n ，BE 〉＝n ·BE |n |·|BE |＝26×2＝33，所以直线BE 与平面PBD 所成角的正弦值为33. (3) 向量BC ＝(1，2，0)，CP ＝(－2，－2，2)，AC ＝(2，2，0)，AB ＝(1，0，0)．由点F 在棱PC 上，设CF ＝λCP →，0≤λ≤1.故BF ＝BC ＋CF ＝BC ＋λCP →＝(1－2λ，2－2λ，2λ)．由BF ⊥AC ，得BF ·AC ＝0，因此2(1－2λ)＋2(2－2λ)＝0，解得λ＝34，即BF ＝⎝⎛⎭⎫－12，12，32.设n 1＝(x ，y ，z )为平面F AB 的法向量，则⎩⎪⎨⎪⎧n 1·AB ＝0，n 1·BF ＝0，即⎩⎪⎨⎪⎧x ＝0，－12x ＋12y ＋32z ＝0.不妨令z ＝1，可得n 1＝(0，－3，1)为平面F AB 的一个法向量．取平面ABP 的法向量n 2＝(0，1，0)，则cos 〈n 1，n 2〉＝n 1·n 2|n 1|·|n 2|＝－310×1＝－31010.易知二面角F - AB - P 是锐角，所以其余弦值为31010.方法二：(1)证明：如图所示，取PD 中点M ，连接EM ，AM .由于E ，M 分别为PC ，PD 的中点，故EM ∥DC ，且EM ＝12DC .又由已知，可得EM ∥AB 且EM ＝AB ，故四边形ABEM为平行四边形，所以BE ∥AM .。

高三数学理一轮复习专题突破训练立体几何Word版含解析

山东省届高三数学理一轮复习专题突破训练
立体几何
一、选择、填空题
、（年山东高考）
在梯形中，,,.将梯形绕
所在的直线旋转一周而形成的曲面所围成的几何体的体积为
()()()()
、（年山东高考）三棱锥中，分别为的中点，记三棱锥的
体积为，的体积为，则。

、（年山东高考）已知三棱柱－的侧棱与底面垂直，体积为，底面是边长为的正三角形．若为底面的中心，则与平面所成角的大小为( )．
．．．．
、（德州市届高三二模）一个几何体的三视图如图所示，该几何体体积为.
、（菏泽市届高三二模）一个几何体的三视图如图所示，则该几何体的体积的是（）
．．．．
、（青岛市届高三二模）某三棱锥的三视图如图所示，该三棱锥的体积是；
、（潍坊市届高三二模）设是不同的直线，是不同的平面，下列命题中正确的是．若，则；．若，则；．若，则；．若，则；
、（莱州市届高三上期末）如右图放置的六条棱长都相等的三棱锥，则这个几何体的侧视图是
.等腰三角形.等边三角形.直角三角形.无两边相等的三角形
、（临沂市届高三上期末）已知某几何体的三视图，则该几何体的体积是
、（青岛市届高三上期末）
若圆台两底面周长的比是：，过高的中点作平行于底面的平面，则圆台被分成两部分的体积比是
：：
：：
、（泰安市届高三上期末）已知为不同的直线，为不同的平面，则下列说法正确的是
..。

广东省高三数学一轮复习专题突破训练立体几何文-人教版高三全册数学试题

广东省2016届高三数学文一轮复习专题突破训练立体几何2016年广东省高考将采用全国卷，下面是近三年全国卷的高考试题及2015届广东省部分地区的模拟试题，供同学们在复习时参考。

一、选择、填空题1、（2015年全国I卷）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问”积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放的米有（）（A）14斛（B）22斛（C）36斛（D）66斛2、（2015年全国I卷）圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体的三视图中的正视图和俯视图如图所示，若该几何体的表面积为+，则r=( )1620π（A）1（B）2（C）4（D）83、（2014年全国I卷）如图，网格纸的各小格都是正方形，粗实线画出的事一个几何体的三视图，则这个几何体是（）A.三棱锥B.三棱柱C.四棱锥D.四棱柱4、（2013年全国I卷）某几何体的三视图如图1－3所示，则该几何体的体积为( )图1－3A．16＋8π B．8＋8πC．16＋16π D．8＋16π5、（佛山市2015届高三二模）已知a，b，c均为直线，α，β为平面，下面关于直线与平面关系的命题：（1）任意给定一条直线与一个平面α，则平面α内必存在与a垂直的直线；（2）a∥β，β内必存在与a相交的直线；（3）α∥β，a⊂α，b⊂β，必存在与a，b都垂直的直线；（4）α⊥β，cαβ=，a⊂α，b⊂β，若a不垂直c，则a不垂直b。

其中真命题的个数为（）A．1 B．2 C． 3 D．46、（广州市2015届高三一模）已知某锥体的正视图和侧视图如图2，其体积为233，则该锥体的俯视图可以是7、（华南师大附中2015届高三三模）某三棱锥的三视图如下图所示，则该三棱锥的四个面中，面积最大的面的面积是(***)A．2 B． 3 C．7 D．18、（惠州市2015届高三4月模拟）已知某几何体的三视图如上图所示，则该几何体的体积为 ( ) A ．12 B ．1 C ．32D ．39、（茂名市2015届高三二模）已知平面α⊥平面β，=l αβ，点,A A l α∈∉，作直线AC l ⊥，现给出下列四个判断：（1）AC 与l 相交，（2）AC α⊥，（3）AC β⊥，（4）//AC β. 则可能．．成立的个数为（） A. 1B. 2C. 3D. 410、（梅州市2015届高三一模）若某几何体的三视图如右图所示，则此几何体的体积等于A 、30B 、12C 、24D 、411、（深圳市2015届高三二模）已知直线l ，平面,,αβγ，则下列能推出//αβ的条件是 A.l α⊥，//l β B.//l α，//l β C.α⊥γ，γβ⊥ D.//αγ，//γβ12、（湛江市2015届高三二模）一个几何体的三视图如图，正视图和侧视图都是由一个半圆和一个边长为2的正方形组成，俯视图是一个圆，则这个几何体的表面积是（）A ．5πB ．6πC ．7πD ．9π13、（深圳市2015届高三二模）.某几何体的三视图如图3所示，其中俯视图为半径为2的四分之一个圆弧，则该几何体的体积为．14、（珠海市2015届高三二模）l m 、是空间两条直线，αβ、是空间两个平面，则 A ．m l //，l α⊂，m β⊂，则βα// B ．l m ⊥，l α⊂，m β⊂，则αβ⊥ C ．αβ⊥，α//l ，β//m ，则l m ⊥ D ．l α⊥，m l //，m β⊂，则αβ⊥ 15、（潮州市2015届高三上期末）已知某几何体的三视图如图所示，则该几何体的体积是（）A ．233π+ B ．323π+ C ．3π D ．232π二、解答题1、（2015年全国I 卷）如图四边形ABCD 为菱形，G 为AC 与BD 交点，BE ABCD ⊥平面，（I ）证明：平面AEC ⊥平面BED ；（II ）若120ABC ∠=，,AE EC ⊥ 三棱锥E ACD -的体积为63，求该三棱锥的侧面积.2、（2014年全国I 卷）如图，三棱柱111C B A ABC -中，侧面C C BB 11为菱形，C B 1的中点为O ，且⊥AO 平面C C BB 11. （I ）证明：;1AB C B ⊥（II ）若1AB AC ⊥,,1,601==∠BC CBB求三棱柱111C B A ABC -的高.3、（2013年全国I 卷）如图1－5所示，三棱柱ABC－A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°.(1)证明：AB⊥A 1C ；(2)若AB ＝CB ＝2，A 1C ＝6，求三棱柱ABC －A 1B 1C 1的体积．图1－54、（佛山市2015届高三二模）如图4，平面ABCD ⊥平面PAB ，且四边形ABCD 为正方形，△PAB 为正三角形，M 为PD 的中点，E 为线段BC 上的动点.（1）若E 为BC 的中点，求证：AM ⊥平面PDE ；AD C BEM图4（2）若三棱锥A —PEM 的体积为33，求正方形ABCD 的边长.5、（广州市2015届高三一模）如图4，在边长为4的菱形ABCD 中，60DAB ︒∠=，点E ，F 分别是边CD ，CB 的中点，ACEF O =．沿EF 将△CEF 翻折到△PEF ，连接PA,PB,PD ，得到如图5的五棱锥P ABFED -，且10PB =. （1）求证：BD ⊥平面POA ；（2）求四棱锥P BFED -的体积.6、（华南师大附中2015届高三三模）如图，111111ABCDEF A B C D E F -是底面半径为1的圆柱的内接正六棱柱（底面是正六边形，侧棱垂直于底面），过FB 作圆柱的截面交下底面于11C E ，已知113FC =. （1）证明：四边形11BFE C 是平行四边形；（2）证明：1FB CB ⊥；（3）求三棱锥1A A BF -的体积.7、（惠州市2015届高三4月模拟）如图所示，在所有棱长都为2a 的三棱柱111ABC A B C -中，侧棱1AA ABC ⊥底面，D 点为棱AB 的中点．(1)求证：1AC ∥平面1CDB ； (2)求四棱锥111C ADB A -的体积．ABCDA 1B 1C 18、（茂名市2015届高三二模）右图为一简单组合体，其底面ABCD 为正方形，PD ⊥平面ABCD ，//EC PD ，且22PD AD EC ===，N 为线段PB 的中点. （1）证明：NE PD ⊥；（2）求四棱锥B CEPD -的体积.9、（梅州市2015届高三一模）如图，△ABC 是等腰直角三角形，∠ACB ＝90°，AC ＝2a ，D ，E 分别为AC ，AB 的中点，沿DE 将△ADE 折起，得到如图所示的四棱锥'A BCDE -，F 是'A B 的中点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

广东省2016届高三数学理一轮复习专题突破训练立体几何2016年广东省高考将采用全国卷，下面是近三年全国卷的高考试题及2015届广东省部分地区的模拟试题，供同学们在复习时参考。

立体几何在全国卷中占据着重要的位置，既在选择或填空题出现，又在解答题中出现，一般考试2-3题，既考查立体几何知识，又考试立体几何知识在实际问题中的应用。

一、选择、填空题1、（2015年全国I卷）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。

问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧度为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（）A.14斛B.22斛C.36斛D.66斛2、（2015年全国I卷）圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示。

若该几何体的表面积为16 + 20 ，则r=（A ）1（B ）2（C ）4（D ）83、（2014年全国I 卷）12.如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的个条棱中，最长的棱的长度为A .B .C .6D .44、（2013年全国I 卷）如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为 ( )A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 35、（2013年全国I 卷）某几何体的三视图如图所示，则该几何体的体积为A .168π+B .88π+C .1616π+D .816π+6、（佛山市2015届高三二模）已知a , b , c 均为直线，α, β为平面.下面关于直线与平面关系的命题：（1）任意给定一条直线a 与一个平面α，则平面α内必存在与a 垂直的直线；（2）任意给定的三条直线a , b , c ，必存在与a , b , c 都相交的直线；（3）α//β，βα⊂⊂b a , ，必存在与a , b 都垂直的直线；（4）βαβαβα⊂⊂=⊥b a c , , , ，若a 不垂直c ，则a 不垂直b .其中真命题的个数为（）A ． 1B ． 2C ．3D ．47、（广州市2015届高三二模）．如图2，圆锥的底面直径2AB =，母线长3VA =，点C 在母线VB 上，且1VC =，有一只蚂蚁沿圆锥的侧面从点A 到达点C ，则这只蚂蚁爬行的最短距离是ABC．3D．28、（华南师大附中2015届高三三模）某三棱锥的三视图如图二所示，正视图、侧视图均为直角三角形，则该三棱锥的四个面中，面积最大的面的面积是*** .9、（惠州市2015届高三4月模拟）多面体MN ABCD的底面ABCD矩形，其正（主）视图和侧（左）视图如图，其中正（主）视图为等腰梯形，侧（左）视图为等腰三角形，则该多面体的体积为 ( )A．163BC．203D．610、（茂名市2015届高三二模）某三棱锥的三视图如图所示，则该几何体的体积为（）.A．23B．43C．83D．411、（梅州市2015届高三一模）若某几何体的三视图如右图所示，则此几何体的体积等于A、30B、12C、24D、422 24A B CDM N12、（汕头市2015届高三二模）某师傅用铁皮制作一封闭的工件，其三视图如图所示（单位长度：cm ，图中水平线与竖线垂直），则制作该工件用去铁皮的面积为（制作过程中铁皮的损耗和厚度忽略不计）A．(21003cmB. (22003cmC. (23003cm +D. 2300cm13、（深圳市2015届高三二模）如图1，已知某品牌墨水瓶的外形三视图和尺寸，则该墨水瓶的容积为（瓶壁厚度忽略不计）A ．π8+B ．π48+C ．π16+D ．π416+14、（汕尾市2015届高三上期末）已知直线l ⊥平面α，直线m ⊆平面β，则下列四个结论：①若//αβ，则l m ⊥ ②若αβ⊥，则//l m③若//l m ，则αβ⊥ ④若l m ⊥，则//αβ。

其中正确的结论的序号是（） A.①④ B.②④ C.①③ D.②③15、（韶关市2015届高三上期末）如图，一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的侧面积为（）A ．2B ．6 C． D．2+ 二、解答题102010俯视图左视图主视图图11正视图侧视图俯视图1、（2015年全国I 卷）如图，，四边形ABCD 为菱形，∠ABC=120°，E ，F 是平面ABCD 同一侧的两点，BE ⊥平面ABCD ，DF ⊥平面ABCD ，BE=2DF ，AE ⊥EC 。

（1）证明：平面AEC ⊥平面AFC（2）求直线AE 与直线CF 所成角的余弦值[2、（2014年全国I 卷）如图三棱柱111ABC A B C -中，侧面11BB C C 为菱形，1AB B C ⊥. (Ⅰ) 证明：1AC AB =；（Ⅱ）若1AC AB ⊥，o 160CBB ∠=，AB=BC 求二面角111A A B C --的余弦值.3、（2013年全国I 卷）如图，三棱柱ABC-A 1B 1C 1中，CA=CB ，AB=A A 1，∠BA A 1=60°. （Ⅰ）证明AB⊥A 1C;（Ⅱ）若平面ABC ⊥平面AA 1B 1B ，AB=CB=2，求直线A 1C 与平面BB 1C 1C 所成角的正弦值。

4、（佛山市2015届高三二模）如图2，在直三棱柱ABC －A 1B 1C 1中，AB ＝BC ＝2，∠ABC ＝1200，D 为AC 的中点，P 为棱A 1B 上的动点.（1）探究：AP 能否与平面A 1BC 垂直？（2）若AA 1＝6，求二面角A 1－BD －B 1的余弦值.5、（广州市2015届高三二模）如图5，已知六棱柱111111ABCDEF A BC D E F -的侧棱垂直于底面，侧棱长与底面边长都为3，M ，N 分别是棱AB ，1AA 上的点，且1AM AN ==．（1）证明：M ，N ，1E ，D 四点共面；（2）求直线BC 与平面1MNE D 所成角的正弦值．6、（华南师大附中2015届高三三模）如图，已知斜三棱柱111ABC A B C -,90BCA ∠=︒,2AC BC ==,1A 在底面ABC 上的射影恰为AC 的中点D , 又知11BA AC ⊥． (Ⅰ) 求证：1AC ⊥平面1A BC ； (Ⅱ) 求1CC 到平面1A AB 的距离；(Ⅲ) 求二面角1A A B C --的平面角的余弦值．7、（惠州市2015届高三4月模拟）如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，1ABA 1B 1D 1CDN EF E 1F 1图5BAC1A 1B1C D//AD BC ，90ADC ∠=︒，平面PAD ⊥底面ABCD ，Q 为AD 的中点，M 是棱PC 上的点，2PA PD AD ===，1BC =，CD =．（1）求证：平面PQB ⊥平面PAD ；（2）若二面角M BQ C --为 30，设PM t MC =⋅，试确定 t 的值．8、（茂名市2015届高三二模）在四棱锥P ABCD -中, AD ⊥平面PDC , PD DC ⊥,底面ABCD 是梯形, AB ∥DC ，1,2AB AD PD CD ====（1）求证:平面PBC ⊥平面PBD ; （2）设Q 为棱PC 上一点,PQ PC λ=,试确定λ的值使得二面角Q BD P --为60º.9、（梅州市2015届高三一模）如图，△ABC 是等腰直角三角形，∠ACB ＝90°，AC ＝2a ，D ，E 分别为AC ，AB 的中点，沿DE 将△ADE 折起，得到如图所示的四棱锥'A BCDE -，F 是'A B 的中点。

（1）求证：EF ∥平面'A CD ；（2）当四棱锥'A BCDE -的体积取最大值时，求平面'A CD 与平面'A BE 夹角的余弦值。

10、（汕头市2015届高三二模）如图，在三棱锥P-ABC 中，PA ⊥平面ABC ，P∠BAC=1200，且AB=AC=AP，M是PB的中点，N在BC上，且BN=13 BC。

（1）求证：MN⊥AB，（2）求二面角P-AN-M的余弦值。

11、（深圳市2015届高三二模）如图4，已知三棱锥O ABC-的三条侧棱OA，OB，OC两两垂直，△ABC为等边三角形，M为△ABC内部一点，点P在OM的延长线上，且PBPA=．（1）证明：OBOA=；（2）证明：平面⊥PAB平面POC；（3）若PA=，OP，求二面角BOAP--的余弦值．12、（珠海市2015届高三二模）如图为一多面体ABCDE ，四边形ACDE 是边长为2 的菱形，其所在平面与平面ABC垂直，AB = BCEAC =3π，F、G分别是AC 、BD中点．O图4BCPM∙F（1）求证： FG //平面ABE ；（2）求二面角 A -BE - D 的正弦值．13、（韶关市2015届高三上期末）如图，ABCD 是边长为3的正方形，ABEF 是矩形，平面ABCD ⊥平面ABEF ,G 为EC 的中点．(1)求证：AC //平面BFG ；(2)若三棱锥C DGB -的体积为94，求二面角E BF G --14、（深圳市2015届高三上期末）在三棱锥P ABC -中，已知平面PBC ⊥平面ABC ，AB 是底面△ABC 最长的边．三棱锥P ABC -的三视图如图5所示，其中侧视图和俯视图均为直角三角形．（1）请在图6中，用斜二测画法，把三棱锥P ABC -的直观图补充完整（其中点P 在xOz 平面内），并指出三棱锥P ABC -的哪些面是直角三角形；（2）求二面角B PA C --的正切值；（3）求点C 到面PAB 的距离．15、（肇庆市2015届高三上期末）如图，四棱柱1111D C B A ABCD -中，A A 1⊥底面ABCD ，且41=A A . AD //BC ，AD =2BC ，CD =2.平面DCE A 1与B B 1交于点E . 正视图图5（1）证明：EC //D A 1；（2）求三棱锥AB A C 1-的体积；（3）求二面角A DC A --1的大小.参考答案一、选择、填空题 1、【答案】B考点：圆锥的体积公式 2、【答案】B考点：简单几何体的三视图；球的表面积公式；圆柱的测面积公式 3、【答案】：C【解析】：如图所示，原几何体为三棱锥D ABC -，其中4,AB BC AC DB DC =====6DA ==，故最长的棱的长度为6DA =，选C4、【命题意图】本题主要考查球的截面圆性质、球的体积公式，是容易题. 【解析】设球的半径为R ，则由题知球被正方体上面截得圆的半径为4，球心到截面圆的距离为R-2，ABCDEA 1B 1C 1D 1则222(2)4R R =-+，解得R=5，∴球的体积为3453π⨯=500π33cm ，故选A. 5、【命题意图】本题主要考查简单组合体的三视图及简单组合体体积公式，是中档题.【解析】由三视图知，该几何体为放到的半个圆柱底面半径为2高为4，上边放一个长为4宽为2高为2长方体，故其体积为21244222π⨯⨯+⨯⨯ =168π+，故选A .6、B （1），（3）正确；当a//b ，且a, b α⊂，c //α时（2）错误；若a b b c b ⊥⇒⊥⇒⊥α故（4）错误。