四川省攀枝花市高二下学期期末调研检测数学(文)试题-含答案
2017-2018学年四川省攀枝花市高二(下)期末数学试卷(文科)(解析版)
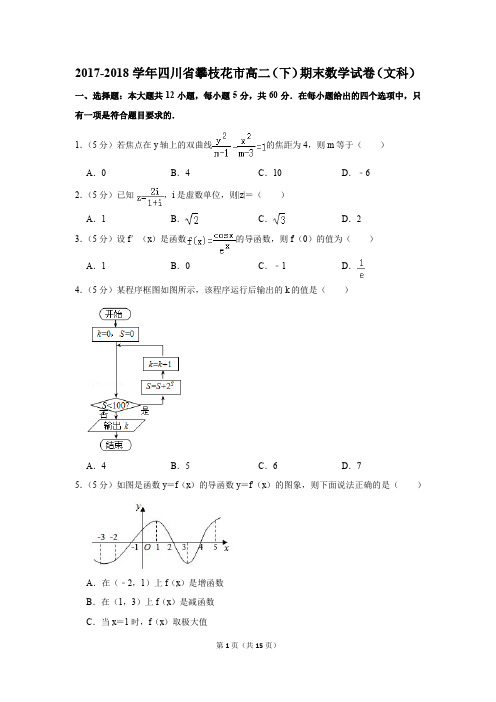
2017-2018学年四川省攀枝花市高二(下)期末数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)若焦点在y轴上的双曲线的焦距为4,则m等于()A.0B.4C.10D.﹣62.(5分)已知,i是虚数单位,则|z|=()A.1B.C.D.23.(5分)设f′(x)是函数的导函数,则f'(0)的值为()A.1B.0C.﹣1D.4.(5分)某程序框图如图所示,该程序运行后输出的k的值是()A.4B.5C.6D.75.(5分)如图是函数y=f(x)的导函数y=f'(x)的图象,则下面说法正确的是()A.在(﹣2,1)上f(x)是增函数B.在(1,3)上f(x)是减函数C.当x=1时,f(x)取极大值D.当x=2时,f(x)取极大值6.(5分)将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的侧面积为()A.4πB.C.D.2π7.(5分)若a∈[1,5],则函数在区间[2,+∞)内单调递增的概率是()A.B.C.D.8.(5分)函数y=x3﹣x的图象与直线y=ax+2相切,则实数a=()A.﹣1B.1C.2D.49.(5分)设m、n是两条不同的直线,α、β是两个不同的平面,下列命题中正确的是()A.若m∥α,n∥β,且α∥β,则m∥nB.若α⊥β,m⊥α,则m∥βC.若m⊥α,n⊥β,α⊥β,则m⊥nD.若m∥α,n⊥β,且α⊥β,则m∥n10.(5分)某空间几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.11.(5分)正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为,此时四面体ABCD的外接球的表面积为()A.6πB.C.5πD.12.(5分)设函数f′(x)是奇函数f(x)(x∈R)的导函数,当x>0时,,则使得(x2﹣1)f(x)<0成立的x的取值范围是()A.(﹣∞,﹣1)∪(1,+∞)B.(﹣∞,﹣1)∪(0,1)C.(﹣1,0)∪(0,1)D.(﹣1,0)∪(1,+∞)二、填空题:本大题共4小题,每小题5分,共20分.13.(5分)已知椭圆C的中心在坐标原点,焦点在x轴上,离心率等于,它的一个顶点恰好是抛物线x2=4y的焦点,则椭圆C的标准方程为.14.(5分)如图,在三棱柱ABC﹣A1B1C1中,CC1⊥底面ABC,∠ACB=90°,CA=CB =CC1,D是CC1的中点,则直线AC1与BD所成角的余弦值为15.(5分)在推导等差数列前n项和的过程中,我们使用了倒序相加的方法,类比可求得sin21°+sin22°+…+sin289°=.16.(5分)已知函数(a∈R),g(x)=ex,若f(x)与g(x)的图象恰好有三个公共点,则实数a的取值范围是.三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)已知函数f(x)=ax2+blnx在x=1处有极值.(1)求a,b的值;(2)求f(x)的单调区间.18.(12分)2018年至2020年,第六届全国文明城市创建工作即将开始.在2017年9月7日召开的攀枝花市创文工作推进会上,攀枝花市委明确提出“力保新一轮提名城市资格、确保2020年创建成功”的目标.为了确保创文工作,今年初市交警大队在辖区开展“机动车不礼让行人整治行动”.表是我市一主干路口监控设备抓拍的5个月内“驾驶员不礼让斑马线”行为统计数据:(Ⅰ)请利用所给数据求违章人数y与月份x之间的回归直线方程;(Ⅱ)预测该路口7月份不“礼让斑马线”违章驾驶员的人数;(Ⅲ)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查“驾驶员不礼让斑马线”行为与驾龄的关系,得到如下2×2列联表:能否据此判断有97.5%的把握认为“礼让斑马线”行为与驾龄有关?参考公式:.(其中n=a+b+c+d)19.(12分)如图1、2,在边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点,点M是AD上的点,且.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P,连接EF,PB(Ⅰ)求证:PD⊥EF;(Ⅱ)求证:PB∥平面EFM20.(12分)如图,在三棱柱ABC﹣A1B1C1中,侧面AA1B1B⊥底面ABC,AA1=AB,∠ABC =90°.(Ⅰ)求证:AB1⊥平面A1BC;(Ⅱ)设BB1中点为D点,若AB=2,∠A1AB=60°,且A1C与平面BB1C1C所成的角为30°,求三棱锥D﹣A1C1C的体积.21.(12分)已知函数(其中a∈R,e为自然对数的底数)(Ⅰ)若函数f(x)是R上的单调增函数,求实数a的取值范围(Ⅱ)当x>0时,证明:(e x﹣1)ln(x+1)>x2[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系中,曲线C1的普通方程为.以坐标原点O为极点,x 轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=﹣2sinθ.(Ⅰ)求曲线C1的参数方程和C2的普通方程;(Ⅱ)若P、Q分别是曲线C1、C2上的动点,求|PQ|的最大值.[选修4-5:不等式选讲]23.已知函数f(x)=|x+a|+|x﹣1|.(1)若a=1,解不等式f(x)<4;(2)对任意满足m+n=1的正实数m,n,若总存在实数x0,使得成立,求实数a的取值范围.2017-2018学年四川省攀枝花市高二(下)期末数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【解答】解:焦点在y轴上的双曲线的焦距为4,可得:,解得m=4.故选:B.2.【解答】解:∵已知==i(1﹣i)=1+i,∴|z|=,故选:B.3.【解答】解:根据题意,,其导数f′(x)==﹣,则f'(0)=﹣1;故选:C.4.【解答】解:当S=0时,满足继续循环的条件,故S=1,k=1;当S=1时,满足继续循环的条件,故S=3,k=2;当S=3时,满足继续循环的条件,故S=11,k=3;当S=11时,满足继续循环的条件,故S=2059,k=4;当S=2049时,不满足继续循环的条件,故输出的k值为4,故选:A.5.【解答】解:在(﹣2,1)上,f'(x)<0,f(x)是减函数,故A错误;在(1,2)上,f'(x)>0,f(x)是增函数,故B错误;在(﹣1,2)上,f'(x)>0,f(x)是增函数,故1不是函数的极大值点,故C错误;在(﹣1,2)上,f'(x)>0,f(x)是增函数,在(2,4)上,f'(x)<0,f(x)是减函数,故当x=2时,f(x)取极大值;故选:D.6.【解答】解:将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周,所形成几何体是底面半径为r=1,母线长为l=的圆锥,∴该几何体的侧面积S=πrl==.故选:C.7.【解答】解:∵函数y=x+在区间[2,+∞)内单调递增,∴≤2,∵a∈[1,5],∴a∈[1,4],∴函数y=x+在区间[2,+∞)内单调递增的概率是,故选:A.8.【解答】解:设切点为(m,n),y=x3﹣x的导数为y′=3x2﹣1,可得切线的斜率为k=3m2﹣1=a,又n=am+2=m3﹣m,解得m=﹣1,a=2,故选:C.9.【解答】解:在A中,若m∥α,n∥β,且α∥β,则m与n平行或异面,故A错误;在B中,若α⊥β,m⊥α,则m∥β或m⊂β,故B错误;在C中,若m⊥α,n⊥β,α⊥β,则由线面垂直、面面垂直的性质定理得m⊥n,故C正确;在D中,若m∥α,n⊥β,且α⊥β,则m与n相交、平行或异面,故D错误.故选:C.10.【解答】解:由三视图得该几何体是从四棱锥P﹣ABCD中挖去一个半圆锥,四棱锥的底面是以2为边长的正方形、高是2,圆锥的底面半径是1、高是2,∴所求的体积V==,故选:B.11.【解答】解:根据题意可知三棱锥B﹣ACD的三条侧棱BD⊥AD、DC⊥DA,底面是等腰直角三角形,它的外接球就是它扩展为三棱柱的外接球,求出三棱柱的底面中心连线的中点到顶点的距离,就是球的半径,三棱柱CDB﹣C'AB'的中,底面边长为1,1,,由题意可得:三棱柱上下底面中点连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,∴三棱柱CDB﹣C'AB'的外接球的球心为O,外接球的半径为r,球心到底面的距离为1,底面中心到底面三角形的顶点的距离为:∴球的半径为r==.外接球的表面积为:4πr2=5π故选:C.12.【解答】解:根据题意,设g(x)=lnx•f(x)(x>0),其导数g′(x)=(lnx)′f(x)+lnxf′(x)=f(x)+lnxf′(x),又由当x>0时,,则有g′(x)=f(x)+lnxf′(x)<0,即函数g(x)在(0,+∞)上为减函数,又由g(1)=ln1•f(x)=0,则在区间(0,1)上,g(x)=lnx•f(x)>0,又由lnx<0,则f(x)<0,在区间(1,+∞)上,g(x)=lnx•f(x)<0,又由lnx>0,则f(x)<0,则f(x)在(0,1)和(1,+∞)上,f(x)<0,又由f(x)为奇函数,则在区间(﹣1,0)和(﹣∞,﹣1)上,都有f(x)>0,(x2﹣1)f(x)<0⇒或,解可得:x>1或﹣1<x<0,则x的取值范围是(﹣1,0)∪(1,+∞).故选:D.二、填空题:本大题共4小题,每小题5分,共20分.13.【解答】解:∵椭圆C的中心在坐标原点,焦点在x轴上,离心率等于,它的一个顶点恰好是抛物线x2=4y的焦点.由题意,设椭圆方程为(a>b>0),则有,解得a=,b=c=1,∴椭圆C的方程:.故答案为:.14.【解答】解:∵在三棱柱ABC﹣A1B1C1中,CC1⊥底面ABC,∠ACB=90°,CA=CB =CC1,D是CC1的中点,∴以C为原点,CA为x轴,CB为y轴,CC1为z轴,建立空间直角坐标系,设CA=CB=CC1=2,则A(2,0,0),C1(0,0,2),B(0,2,0),D(0,0,1),=(﹣2,0,2),=(0,﹣2,1),设直线AC1与BD所成角为θ,则cosθ===.∴直线AC1与BD所成角的余弦值为.故答案为:.15.【解答】解:设S=sin21°+sin22°+…+sin289°,则S=sin289°+sin288°+…+sin21°,两式倒序相加,得:2S=(sin21°+sin289°)+(sin22°+sin288°)+…+(sin289°+sin21°)=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin289°+cos s289°)=89,∞S=44.5.故答案为:44.5.16.【解答】解:由x≥0时,y=e x﹣ex的导数为y′=e x﹣e,当x>1时,函数y=e x﹣ex递增,当x<1时,函数y=e x﹣ex递减,可得函数y=e x﹣ex在x=1处取得最小值0,可得e x﹣ex=0在x≥0时仅有一解x=1;由题意可得x<0时,a﹣﹣ex=0两个不等的负数解,可得ex2﹣ax+1=0,即有,即,解得a<﹣2,故答案为:(﹣∞,﹣2).三、解答题:本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.【解答】解:(1)∵f′(x)=2ax+.又f(x)在x=1处有极值,∴即解得a=,b=﹣1.(2)由(1)可知f(x)=x2﹣lnx,其定义域是(0,+∞),f′(x)=x﹣=.由f′(x)<0,得0<x<1;由f′(x)>0,得x>1.∴函数y=f(x)的单调减区间是(0,1),单调增区间是(1,+∞).18.【解答】(本小题满分12分)解:(Ⅰ)由表中数据知:∴,,∴所求回归直线方程为.…………………(5分)(Ⅱ)由(Ⅰ)知,令x=7,则人.…………………(7分)(Ⅲ)由表中数据得,根据统计有97.5%的把握认为“礼让斑马线”行为与驾龄有关.…………………(12分)19.【解答】(Ⅰ)证明:∵折叠前AD⊥AE,DC⊥CF∴折叠后PD⊥PE,PD⊥PF又∵PE∩PF=P∴PD⊥平面PEF,而EF⊂平面PEF∴PD⊥EF.(Ⅱ)连接BD交EF于N,连接NM,在正方形ABCD中,连接AC交BD于O,则,所以,又,即,在△PBD中,,∴PB∥MN,PB⊄平面EFM,MN⊂平面EFM,∴PB∥平面EFM.20.【解答】解:(Ⅰ)由侧面AA1B1B⊥底面ABC,CB⊥CA,CB⊂底面ABC,得到CB⊥侧面AA1B1B,又因为AB1⊂侧面AA1B1B,所以AB1⊥CB,又由已知AA1=AB,侧面AA1B1B为菱形,所以对角线AB1⊥A1B,即AB1⊥CB,AB1⊥A1B,且A1B∩CB=B,所以AB1⊥平面A1BC.…………………(6分)(Ⅱ)因为∠A1AB=60°,易知△A1BB1为等边三角形,中线A1D⊥BB1,由(Ⅰ)CB⊥侧面AA1B1B,所以CB⊥A1D,得到A1D⊥平面BB1C1C,∴∠A1CD即为A1C与平面BB1C1C所成的角,∴A 1B=2,,,,得到;,.…………………(12分)21.【解答】(Ⅰ)解:f'(x)=e x﹣x﹣a,∵函数f(x)是R上的单调递增函数,∴f'(x)≥0在x∈R上恒成立,即e x﹣x≥a在x∈R 时恒成立,令g(x)=e x﹣x,则g'(x)=e x﹣1.∴g(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增.则g(x)min=g(0)=1∴实数a的取值范围是(﹣∞,1];(Ⅱ)证明:由(Ⅰ)可知,当a=1时,当x>0时,f(x)>f(0)=0,即.欲证(e x﹣1)ln(x+1)>x2,只需证>x2,即证即可.构造函数h(x)=ln(x+1)﹣(x>0),则恒成立,故h(x)在(0,+∞)单调递增,从而h(x)>h(0)=0.即,亦即.故(e x﹣1)ln(x+1)>x2.[选修4-4:坐标系与参数方程]22.【解答】解:(Ⅰ)曲线C1的普通方程为.整理得:曲线C1的参数方程为(α为参数).曲线C2的极坐标方程为ρ=﹣2sinθ,即ρ2=﹣2ρsinθ,∴曲线C2的直角坐标方程为x2+y2=﹣2y,即x2+(y+1)2=1.(Ⅱ)法一:设P(2cosα,sinα),则P到曲线C2的圆心(0,﹣1)的距离:,=,=,∵sinα∈[﹣1,1],∴当时,.∴|PQ|max=d max+r=.法二:设P(x,y),则P到曲线C2的圆心(0,﹣1)的距离,∵y∈[﹣1,1],∴当时,.∴|PQ|max=d max+r=.[选修4-5:不等式选讲]23.【解答】解:(1)f(x)=|x+1|+|x﹣1|,当x≤﹣1时,由f(x)=﹣2x<4,得x>﹣2,则﹣2<x≤﹣1;当﹣1<x≤1时,f(x)=2<4恒成立;当x>1时,由f(x)=2x<4,得x<2,则1<x<2.综上,不等式f(x)<4的解集为{x|﹣2<x<2};(2)由题意+=(+)(m+n)=2++≥4,由绝对值不等式得f(x)=|x+a|+|x﹣1|≥|a+1|,当且仅当(x+a)(x﹣1)≤0时取等号,故f(x)的最小值为|a+1|,由题意得4≥|a+1|,解得:﹣5≤a≤3.。
四川高二下学期期末检测数学文试题

高二(下)期末数学试卷(文科)、选择题(共12小题,每小题5分,满分60分) 1. (1 i)(2 i)0.45,既用现金支付也用非现金支付的概率为 0.15,则不用现金支付的概率为 A . 0.3B . 0.4C . 0.6D . 0.73. 已知复数z 满足(1+2i ) z=3+4i ,则| . |等于( )A . 2B. 5C.干 D . ... ■4. (2018衡水三调)来自英、法、日 德的甲、乙、丙、丁四位客人,刚好碰在一起.他们除懂本国语言外,每人还会说其他三国语言中的一种.有一种语言是三个人会说的,但没有一种语言四人 都懂,现知道:①甲是日本人,丁不会说日语,但他俩能自由交谈;②四人中没有一个人既能用日 语交谈,又能用法语交谈;③乙、丙、丁交谈时,不能只用一种语言;④乙不会说英语,当甲与丙 交谈时,他能做翻译.针对他们懂的语言,正确的推理是( )A .甲日德、乙法德、丙英法、丁英德B .甲日英、乙日德、丙德法、丁日英C .甲日德、乙法德、丙英德、丁英德D .甲日法、乙英德、丙法德、丁法英5.已知函数f (x ) =x 3+x 2+e x ,则曲线y=f (x )在点(0, f (0))处的切线方程是( )A . x+2y+仁0 B. x - 2y+1=0 C. x+y -仁0D . x - y+仁06 .从2 018名学生中选取50名学生参加全国数学联赛,若采用以下方法选取:先用简单随机抽样法从2 018名学生中剔除18名学生,剩下的2 000名学生再按系统抽样的方法抽取,则每名学生入 选的概率A .3 iB .3 i C. 3 i D . 3 i2.若某群体中的成员只用现金支付的概率为A .不全相等B .均不相等C .都相等,且为50 2 0187. 函数f (x ) =x ^ - 8lnx 的单调递减区间为( )A . [2, +x )B. (-X, 2]C. (0, 2] D . (- 2, 2)X8. 如图所示,在扇形AOB 中,/ AOB 牙,圆C 内切于扇形 内投一点,则该点落在圆C 外的概率为()0 7 S 1 0 7x92 2 19.如图是某位篮球运动员 8场比赛得分的茎叶图,其中一个数据染上污渍用 x 代替,那么这位运动()员这8场比赛的得分平均数不小于得分中位数的概率为()A •有90%以上的把握认为“该市居民能否做到’光盘’与性别有关”B •在犯错误的概率不超过 1%的前提下,认为“该市居民能否做到’光盘’与性别无关”C •在犯错误的概率不超过 1%的前提下,认为“该市居民能否做到’光盘’与性别有关”D •有90%以上的把握认为“该市居民能否做到‘光盘’与性别无关”11.我州某高中从高二年级甲、乙两个班种各选出 7名学生参加2017年全国高中数学联赛(四川初赛),他们取得的成绩(满分140分)的茎叶图如图所示,其中甲班学生 成绩的中位数是81,乙班学生成绩的平均数是86,若正实数a 、b 满足:a , G , b 成等1 4差数列且x , G, y 成等比数列,则一V 的最小值为()N D4 9A .石 B. 2 C. 丁 D . 8 12.已知函数 f (x ) =axlnx^x 3则实数a 的取值范围是()25 9 25 zz9A. [0, —]B.[ 2,—]C. (-x, 4] D. (-x,豆]二、填空题(共4小题,每小题5分,满分20 分)13. ______________________________________ 曲线y 2lnx 在点(1,0)处的切线方程为 .A.5C .510.春节期间,“厉行节约,反对浪费”之风悄然吹开,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:则下面的正确结论是( )附表及公式:K 2=做不到“光盘”能做到“光盘”男 45 10 女3015P(K 2> k °)0.100 0.050 0.010 0.001 k 02.7063.8416.63510.828n ad — bea +bc +d a +e b + dax 2,当 x € 苗,5]时,恒有 f'( x ) ?x -f (x )> 0,n = a + b + c +d.14. 某企业三月中旬生产 A , B , C 三种产品共3 000件,根据分层抽样的结果,业统计员制作了如下的统计表格:比C 产品的样本容量多10,根据以上信息,可得 C 的产品数量是 _____________ 件.15. (2018湖北八校联考)祖暅是我国南北朝时代的数学家,是祖冲之的儿子•他提出了一条原理:“幕势既同,则积不容异.”这里的“幕”指水平截面的面积,“势”指高•这句话的意思是:两 个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆a 2+b 2=1(a>b>0)所围成的平面图形绕 y 轴旋转一周后,得一橄榄状的几何体 (称为椭球体)如图所示,课本中介绍了应用祖暅原理求球体体积公式的方法,请类比此法,求出椭球体体积,其体积等于 __________ .116.设函数f (x )= In x -2ax 2— bx ,若x = 1是f (x )的极大值点,贝V a 的取值范围为 _______三、解答题(共5小题,满分60分)17. (12 分)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式•为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位: min )绘制了如下茎叶图:第-种生产方式第二种生产方式8 r 6 5 5 6 »9 9 76 27 0 1 2 2 3 4 56 6 89X7765433 28 14 452 110 0 9 0(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由; (2)求40名工人完成生产任务所需时间的中位数 m ,并将完成生产任务所需时间超过 m 和不超过m 的工人数填入下面的列联表:超过m”不超过m第种生产方式第二种生产方式(3)根据(2)中的列联表,能否 有99%的把握认为两种生产方式的效率有差异?产品类别 A B C产品数量(件)1 300样本容量(件)130A 产品的样本容量附: K 22n(ad be)(a b)(e d)(a e)(b d)2P(Kkk) 0.050 0.010 0.0013.841 6.635 10.828企18. (12分)为了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照[27.5,32.5),[32.5,37.5), [37.5,42.5) , [42.5,47.5),[47.5,52.5]分为 5 组,其频率分布直方图如图所示.(1) 求图中a的值;(2) 估计这种植物果实重量的平均数x和方差s1 2 3( );(3)已知这种植物果实重量不低于32.5克的即为优质果实•若所取样本容量n = 40,从该样本分布在[27.5,32.5)和[47.5,52.5]的果实中,随机抽取2个,求抽到的都是优质果实的概率.19. (12分)某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取100名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试•测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离)•无酒状态与酒后状态下的试验数据分别列于表1和表2.停车距离(10,20](20,30](30,40](40,50](50,60] d(米)频数26m n82平均每毫升血液酒精含量x(毫克) 1030507090平均停车距离y(米) 3050607090已知表1数据的中位数估计值为26,回答以下问题.2 若x= 3时,y = f(x)有极值.(1) 求a, b, c的值.(2) 求y = f(x)在[—3,1]上的最大值和最小值.21.设函数f(x)= mx2—(2m + 1)x+ In x, m€ R.(1) 当m= 3时,求f(x)的极值;(2) 设m>0,讨论函数f(x)的单调性.22. (12分)已知函数f (x) =£亡x2+mx在x=1处有极小值,2 3g (x) =f (x)-亍x3x2+x- alnx.20. (12 分)已知函数f(x)= x3+ ax2+ bx+ c,曲线y= f(x)在点x= 1 处的切线为1: 3x—y+ 1 = 0, (1)求函数f (x)的单调区间;呂(戈1)-吕〔X?) (2)是否存在实数a,对任意的X1、X2€( 0, +x),且X1M X2,有----------------- >1X]-戈2恒成立?若存在,求出a的取值范围;若不存在,说明理由.请考生在第22、23两题中任选一题作答【选修4-4:坐标系与参数方程】22. (10分)在直角坐标系中,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为p si( 怙)罟,曲线C的参数方程为(尸后;山口(a为参数).(1) 求直线l的普通方程;(2) 若P是曲线C上的动点,求点P到直线l的最大距离及点P的坐标.【选修4-5:不等式选讲】23. 已知函数f (x) =| 2x- a| , g (x) =x+1.(1)若a=1,求不等式f (x)< 1的解集;(2)对任意的x€ R, f (x) +| g (x) | >a2+2a (a>0)恒成立,求实数a的取值范围.高二(下)期末数学试卷(文科)参考答案一、选择题(共12小题,每小题5分,满分60分) 1.D 2. B 3. D 4. A 5. D 6. C 7 .C 8. A 9. B 10 .A 11. C12. C4题解析:选A 分析题目和选项,由①知,丁不会说日语,排除B 选项;由②知,没有人既 会日语又会法语,排除 D 选项;由③知乙、丙、丁不会同一种语言,排除C 选项,故选A.6题解析:选C 从N 个个体中抽取 M 个个体,则每个个体被抽到的概率都等于 N ,故每名学17 + 10+ x 27 + x9题解析:选B 由茎叶图可知 0< x < 9且x € N ,中位数是 --------- 2 ----- =二—,这位运动员这 1 1 1 27+ x 8 场比赛的得分平均数为 8(7 + 8 + 7+ 9+ x + 3+ 1+ 10X 4+ 20X 2) = -(x + 115),由§(x + 115)》 —2100X 675 — 300疋3.030.因为2.706<3.030<3.841,所以有90%以上的把握认为 “该市居民能否做到 55X45 X 75X 25‘光盘'与性别有关”.二、填空题(共4小题,每小题5分,满分20分)13. y =2x -214. 800 . 15. 4 n )2a 16. (— 1,+^ )14题解析:设样本容量为X ,则3"00^ 1 300= 130,二x = 300.••• A 产品和C 产品在样本中共有 300 — 130 = 170(件).设C 产品的样本容量为 y ,贝U y + y + 10= 170,• y = 80.• C 产品的数量为 驾严乂 80= 800(件).300 15题解析:椭圆的长半轴长为 a ,短半轴长为b ,现构造两个底面半径为 b ,高为a 的圆柱,然后在 圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,根据祖 暅原理得出椭球体的1 4体积 V = 2(V 圆柱一 V 圆锥)=2 nX b 2X a — 3 nX b 2X a = 4 n )2a.3 3生入选的概率都相等,且为50 2 018.310.10题解选 A 由列联表得到 a = 45,b = 10,c = 30,d = 15,则 a + b = 55,c + d = 45,a +c = 75, b +d = 25, ad = 675, bc = 300,a +bc +d a+ c b + d 得3x < 7,即x = 0,1,2,所以这位运动员这8场比赛的得分平均数不小于得分中位数的概率为n = 100,计算得K 2的观测值k = n ad — bc 2116 题解析:•/ f(x)的定义域为(0 ,+^), f' (x) = -― ax—b,X由f' (1) = 0,得b = 1 —a.1 —ax2+ 1 + ax —x/• f' (x)=——ax + a—1 =x xax + 1 x—1x .①若a> 0,当0v x v 1时,f' (x)> 0, f(x)单调递增;当x > 1时,f' (x) v 0,f(x)单调递减;所以x = 1是f(x)的极大值点.1②若 a v 0,由f' (x)= 0,得x = 1 或x =—-.a因为x = 1是f(x)的极大值点,所以一1 > 1,解得一1 v a v 0.a综合①②得a的取值范围是(一1,+^).答案:(—1 ,+^ )三、解答题(共5小题,满分60分)17解:(1 )第二种生产方式的效率更高.理由如下:(i)由茎叶图可知:用第一种生产方式的工人中,有75%的工人完成生产任务所需时间至少80分钟,用第二种生产方式的工人中,有75%的工人完成生产任务所需时间至多79分钟.因此第二种生产方式的效率更高.(ii)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间的中位数为85.5分钟,用第二种生产方式的工人完成生产任务所需时间的中位数为73.5分钟•因此第二种生产方式的效率更高.(iii)由茎叶图可知:用第一种生产方式的工人完成生产任务平均所需时间高于80分钟;用第二种生产方式的工人完成生产任务平均所需时间低于80分钟,因此第二种生产方式的效率更高.(iv)由茎叶图可知:用第一种生产方式的工人完成生产任务所需时间分布在茎8上的最多,关于茎8大致呈对称分布;用第二种生产方式的工人完成生产任务所需时间分布在茎7上的最多,关于茎7大致呈对称分布,又用两种生产方式的工人完成生产任务所需时间分布的区间相同,故可以认为用第二种生产方式完成生产任务所需的时间比用第一种生产方式完成生产任务所需的时间更少,因此第二种生产方式的效率更高.学科%网以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分.(2)由茎叶图知m 79 8180 .2列联表如下:(3)由于K2 4°(15 15 5 5)10 6 635,所以有99%的「把握认为两种生产方式的效率有20 20 20 20差异.18. 解:⑴组距为d = 5,由5X (0.020 + 0.040 + 0.075+ a + 0.015) = 1,得a = 0.050.⑵各组中值和相应的频率依次为:所以x = 30 X 0.1 +s2= (- 10)2X 0.1+ (- 5)2X 0.2+ 02X 0.375+ 52X 0.25 + 102X 0.075= 28.75.⑶由已知,果实重量在[27.5,32.5)和[47.5,52.5]内的分别有4个和3个,分别记为A1, A2, A3, A4和B1, B2, B3,从中任取2个的取法有:A1A2, A1A3, A1A4, A1B1, A1B2, A1B3, A2A3,A2A4, A2B1, A2B2, A2B3, A3A4, A3B1, A3B2,A3B3, A4B1, A4B2, A4B3, B1B2, B1B3, B2B3,共21种取法,其中都是优质果实的取法有B1B2, B1B3, B2B3,共3种取法,所以抽到的都是优质果实的概率P=21=119. 解:解:(1)依题意,得:60m= 50- 26,解得m = 40, 又m+ n + 36= 100,解得n = 24.故停车距离的平均数为15 X 捡+ 25X 组+ 35 X 坐+ 45 乂旦+ 55X2 =右.100 100 100 100 100⑵依题意,可知x = 50, y = 60,11x i y i = 10X 30 + 30X 50 + 50 X 60+ 70 X 70+ 90 X 90= 17 800,i = 15x 2= 102+ 302+ 502 + 702 + 902= 16 500,17 800— 5X 50X 6016 500 — 5X 502 :=60— 0.7X 50= 25,所以回归直线方程为 y = 0.7x + 25. (3)由(1)知当y>81时认定驾驶员是 “醉驾”.令y>81,得0.7x +25>81,解得x>80,当每毫升血液酒精含量大于 80毫克时认定为“醉驾”.20. 解:(1)由 f(x) = x 3 + ax 2 + bx + c ,得 f ' (x) = 3x 2+ 2ax + b.当x = 1时,切线I 的斜率为3,可得2a + b = 0,①可得 4a + 3b + 4= 0,② 由①②,解得a = 2, b =一 4.由于切点的横坐标为 1,纵坐标为4,所以f(1) = 4. 所以 1 + a + b + c = 4,得 c = 5. ⑵由(1)可得 f(x) = x 3 + 2x 2- 4x + 5, f ' (x)= 3x 2+ 4x - 4.2 令 f ' (x) = 0,解得 x = — 2 或 x = 3.当x 变化时,f ' (x), f(x)的取值及变化情况如表所示:x —3 (—3,— 2)—22 ,11 f ' (x) ++—++ f(x)813495所以y = f(x)在[—3,1]上的最大值为13,最小值为27.21.解:(1)当 m = 3 时,f(x)= 3x 2— 7x + In x(x>0),1 (6x — 1(x — 1/• f ' (x) = 6x — 7 + x = x .由 f ' (x)>0,得 0<x<6或 x>1; 1由 f ' (x)<0,得 6<x<1 ,1 1•••函数f(x)在6和(1,+^ )上单调递增,在,1上单调递减,所以b =23- X2y = f(x)有极值,则 f ' 3= 0,1121 13•函数f(x)的极大值为f6 =- 12- In 6,极小值为f(1) = -4. (2)由题意知,函数f(x)的定义域为(0,+^ ),1 (2mx — 1(x — 1 f ' (x)= 2mx — (2m + 1) + x = x . 1 由 f ' (x) = 0,得 x = 2n 或 x = 1.1 1① 当2m = 1,即卩m = 2时,f ' (x)> 0恒成立,•函数f(x)在(0,+s )上单调递增;1 1② 当2m>1,即0<m<2时,1 由 f ' (x)>0,得 0<x<1 或 x>2m1由 f ' (x)<0,得 1<x<2m1 1•函数f(x)在(0,1)和,+8上单调递增,在2m 上单调递减; 1 1③ 当0<2m<1,即m>2时, 1由 f ' (x)>0,得 0<x<2m 或 x>1, 1由 f ' (x)<0,得 2m<x<1 ,1 1•函数f(x)在2m 和(1 ,+s )上单调递增,在,1上单调递减.22.解:(1)v f (x ) =x 3^x 2+mx ,A f'( x ) =3x 2+3x+m ,3■/ f (x ) =x 3^x 2+mx 在 x=1 处有极小值,• f'(1) =6+m=0,得 m=- 6. • f (x ) =x 3^x 2 - 6x ,贝U f (x ) =3 (x 2+x - 2) =3 (x - 1) (x+2).•当 x €(-x,- 2)U( 1, +x)时,f (x )>0,当 x € (- 2, 1)时,f'(x )V 0,则f (x )的单调增区间为(-x,- 2), (1, +x),单调减区间为(-2, 1);ii1( Xn)假设存在实数a 使得对任意的 x i , X 2€( 0, +x),且X I M x ?,有 ---------------- - > 1恒 成立,不妨设 O v X i v x 2,只要 g (x i ) — g (X 2)V x i — X 2, 即:g ( x i )— x i v g ( X 2)— X 2.令h (x ) =g (x )— x ,只要h (乂)在(0, +x )为增函数即可. 又函数 h (x ) =g (x )— x»J- —匸:y 訂口,则 f ( X ) =、一L 一=—[八:■■-.£ XZX要使h' (x )> 0在(0, +X )上恒成立,则需 2x 3+3x 2 — i2x — 2a >0在(0, +^)上恒 成立, 即 2a < 2x 3+3x 2 — i2x .令 t (x ) =2x 3+3x 2 — i2x ,贝U t'( x ) =6x 2+6x — i2=6 (x+2) (x- i ). •••当x €(0, i )时,t (x )单调递减,当x €( i , +x )时,t (x )单调递增, 则 t ( X ) min =t ( i ) = — 7 . • 2a < — 7,得 a 龙* ..7 ( X 2) •••存在实数 a W 「7,对任意的 x i 、X 2€( 0, +x),且X I M X 2,有 ---------------- >i 恒邑X I -兀2成立.(1) 求m , n 的值,并估计驾驶员无酒状态下停车距离的平均数;(2) 根据最小二乘法,由表 2的数据计算y 关于x 的回归方程J = bx + a ; (3) 该测试团队认为:驾驶员酒后驾车的平均“停车距离” y 大于(1)中无酒状态下的停车距离平 均数的3倍,则认定驾驶员是“醉驾” •请根据 (2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(附:对于一组数据(x 1, y 1), (x 2, y 2),…,(x n , y n ),其回归直线y = bx + a 的斜率和截距的最小n__ __________ n__ ___X i — x y i — y X i y i — n x y..... ................... A 尸1尸1 A _ A_二乘估计分另U 为 b == , a = y — b x )n ——nx i — x 2x 2 — nx 2i = 1i = 1—alnx=・'J — 5x — alnx .x 2+x — alnx (2) g (x ) =f (x )23。
四川省攀枝花市2022高二数学下学期期末考试试题(含解析)

A. B. C. D.
【答案】A
【解析】
【分析】
令 ,构造 ,要使函数 有三个不同的零点 (其中 ),则方程 需要有两个不同的根 ,则 ,解得 或 ,结合 的图象,并分 , 两个情况分类讨论,可求出 的值.
【详解】令 ,构造 ,求导得 ,当 时, ;当 时, ,
(Ⅰ)求实数 的值及样本容量 ;
(Ⅱ)根据历史成绩是否优秀,利用分层抽样的方法从这 名学生中抽取5名,再从这5名学生中随机抽取2名,求这2名学生的历史成绩均优秀的概率;
(Ⅲ)请将 列联表补充完整,并判断是否有 的把握认为历史成绩是否优秀与性别有关?
男生
女生
合计
优秀
良好
20
合计
60
参考公式及数据: (其中 ).
故选A.
【点睛】本题考查了空间组合体的三视图,考查了学生的空间想象能力,属于基础题.
10.函数 与它的导函数 的大致图象如图所示,设 ,当 时, 单调递减的概率为( )
A. B. C. D.
【答案】B
【解析】
【分析】
结合图象可得到 成立的x的取值范围,从而可得到 的单调递减区间,即可选出答案.
【详解】由图象可知, 轴左侧上方图象为 的图象,下方图象为 的图象,
又
本题正确选项:
【点睛】本题考查椭圆几何性质的应用,关键是能够熟练掌握椭圆通径长和对称性,属于基础题.
8.设 是两条不同的直线, 是两个不同的平面,下列命题中正确的是( )
A. 若 , ,则 B. 若 , ,则
C. 若 , ,则 D. 若 , ,则
【答案】C
【解析】
分析】
在A中, 与 相交或平行;在B中, 或 ;在C中,由线面垂直的判定定理得 ;在D中, 与 平行或 .
2023-2024学年四川省攀枝花市米易县攀莲中学高二数学文下学期期末试题含解析

2023-2024学年四川省攀枝花市米易县攀莲中学高二数学文下学期期末试题专业课理论基础部分一、选择题:1.下列函数中,奇函数是()A. y=xB. y=x³C. y=|x|D. y=√x2.已知函数f(x)=2x+1,下列函数是f(x)的反函数的是()A. f⁻¹(x)=1/2x+1B. f⁻¹(x)=1/2x-1C. f⁻¹(x)=2x-1D. f⁻¹(x)=2x+13.设函数f(x)=ax²+bx+c,且f(1)=3,f(-1)=5,f(2)=11,则a+b+c的值为()A. 8B. 9C. 10D. 114.下列等式中,正确的是()A. (a+b)²=a²+2ab+b²B. (a+b)³=a³+3a²b+3ab²+b³C. (a+b)⁴=a⁴+4a³b+6a²b²+4ab³+b⁴D.(a+b)⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵5.已知函数f(x)=x²-4x+3,下列函数是f(x)的复合函数的是()A. f(g(x))B. g(f(x))C. f(x)²D. (f(x))²答案:1.A 2.A 3.C 4.B 5.A二、判断题:1.若两个函数互为反函数,则它们的定义域相同。
()2.函数f(x)=2x+1在x=1处的导数为2。
()3.函数f(x)=x²在(-∞,0)上的单调递减。
()4.若a>0,则函数f(x)=ax²在(-∞,+∞)上单调递增。
()5.若两个函数的图象关于y轴对称,则这两个函数互为反函数。
()答案:1.√ 2.× 3.√ 4.× 5.×三、填空题:1.若函数f(x)的定义域为R,且f(-x)=-f(x),则函数f(x)为________函数。
四川省攀枝花市数学高二下学期文数期末考试试卷

四川省攀枝花市数学高二下学期文数期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分) (2017高二下·曲周期末) 下列关于残差的叙述正确的是()A . 残差就是随机误差B . 残差就是方差C . 残差都是正数D . 残差可用来判断模型拟合的效果2. (2分) (2019高一上·阜新月考) 不等式的解集是()A . .B .C .D .3. (2分) (2015高二下·福州期中) 有一段“三段论”推理是这样的:对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为函数f(x)=x3在x=0处的导数值f′(x0)=0,所以,x=0是函数f (x)=x3的极值点.以上推理中()A . 大前提错误B . 小前提错误C . 推理形式错误D . 结论正确4. (2分) (2017高二下·淄川期末) 在复平面内,复数g(x)满足,则z的共轭复数对应的点位于()A . 第一象限B . 第二象限C . 第三象限D . 第四象限5. (2分)如图是一个结构图,在□处应填入()A . 对称性B . 解析式C . 奇偶性D . 图象交换6. (2分) (2018高二下·西宁期末) 在直角坐标系中,曲线的参数方程为(为参数),在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点,以轴正半轴为极轴)中,曲线的方程为,则与的交点个数为().A .B .C .D .7. (2分)(2017·内江模拟) 设z=1﹣i(i为虚数单位),若复数﹣z2在复平面内对应的向量为,则向量的模是()A .B . 2C .D .8. (2分)设a,b,c大于0,则3个数:a+ ,b+ ,c+ 的值()A . 都大于2B . 至少有一个不大于2C . 都小于2D . 至少有一个不小于29. (2分) (2018高二下·通许期末) 下列关于残差图的描述错误的是()A . 残差图的横坐标可以是编号B . 残差图的横坐标可以是解释变量和预报变量C . 残差点分布的带状区域的宽度越窄相关指数越小D . 残差点分布的带状区域的宽度越窄残差平方和越小10. (2分) (2019高一下·丽水月考) 设,下列命题正确的是()A . 若,则B . 若,则C . 若,则D . 若,则11. (2分)已知点的坐标满足条件,那么的取值范围为()A .B .C .D .12. (2分)(2017·朝阳模拟) “现代五项”是由现代奥林匹克之父顾拜旦先生创立的运动项目,包含射击、击剑、游泳、马术和越野跑五项运动.已知甲、乙、丙共三人参加“现代五项”.规定每一项运动的前三名得分都分别为a,b,c(a>b>c且a,b,c∈N*),选手最终得分为各项得分之和.已知甲最终得22分,乙和丙最终各得9分,且乙的马术比赛获得了第一名,则游泳比赛的第三名是()A . 甲B . 乙C . 丙D . 乙和丙都有可能二、填空题 (共4题;共5分)13. (2分)按照图的工序流程,从零件到成品最少要经过________ 道加工和检验程序,导致废品的产生有________ 种不同的情形.14. (1分) (2019高二下·青浦期末) 若复数z满足,则的取值范围是________.15. (1分) (2020高三上·浙江月考) 已知函数,,设的最大值为,若时,则的取值范围为________.16. (1分) (2018高二下·黑龙江期中) 关于下列说法:①由平面三角形的性质推测空间四面体的性质,这是一种合情推理;②归纳推理得到的结论不一定正确,类比推理得到的结论一定正确;③演绎推理是由特殊到特殊的推理;④演绎推理在大前提、小前提和推理形式都正确时,得到的结论一定正确.其中正确的是________.(填所有正确说法的序号)三、解答题 (共6题;共65分)17. (20分) (2016高二下·晋中期中) 已知m∈R,复数z= +(m2+2m﹣3)i,当m为何值时,(1)z∈R;(2) z是纯虚数;(3) z对应的点位于复平面第二象限;(4)(选做)z对应的点在直线x+y+3=0上.18. (10分) (2017高二下·太原期中) 已知数列{an}的前n项和为Sn ,且满足a1= ,2Sn﹣SnSn﹣1=1(n≥2).(1)猜想Sn的表达式,并用数学归纳法证明;(2)设bn= ,n∈N* ,求bn的最大值.19. (10分)(2017·吉安模拟) 选修4-4:坐标系与参数方程在直角坐标系xOy中,曲线,曲线C2的参数方程为:,(θ为参数),以O 为极点,x轴的正半轴为极轴的极坐标系.(1)求C1 , C2的极坐标方程;(2)射线与C1的异于原点的交点为A,与C2的交点为B,求|AB|.20. (10分) (2019高一上·普宁期中) 已知且,函数(1)解关于的不等式(2)当时,求证:方程在区间内至少有一个根21. (5分)(2020·南昌模拟) 在极坐标系中,曲线,以极点O为旋转中心,将曲线C逆时针旋转得到曲线 .(Ⅰ)求曲线的极坐标方程;(Ⅱ)求曲线C与曲线的公共部分面积.22. (10分) (2019高二下·葫芦岛月考) 某高中尝试进行课堂改革.现高一有两个成绩相当的班级,其中班级参与改革,班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过分的为进步明显,得到如下列联表.进步明显进步不明显合计班级班级合计(1)是否有的把握认为成绩进步是否明显与课堂是否改革有关?(2)按照分层抽样的方式从班中进步明显的学生中抽取人做进一步调查,然后从人中抽人进行座谈,求这人来自不同班级的概率.附:,当时,有的把握说事件与有关.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共5分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共65分) 17-1、17-2、17-3、17-4、18-1、18-2、19-1、19-2、20-1、20-2、21-1、22-1、22-2、第11 页共11 页。
2018~2019学年四川省攀枝花市高二下学期期末调研检测数学(文)试题及答案

绝密★启用前四川省攀枝花市2018~2019学年高二下学期期末调研检测数学(文)试题2019年7月本试题卷分第一部分(选择题)和第二部分(非选择题).第一部分1至2页,第二部分3至4页,共4页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分.考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.注意事项:1.选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上.2.本部分共12小题,每小题5分,共60分.第一部分(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 抛物线x y 82=的焦点为( )(A )(2,0) (B )(2,0)- (C )(0,2) (D )(0,2)-2. 复数z 满足12z i i ⋅=+ (i 为虚数单位),则复数z 在复平面内所对应的点在( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限3.如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 分别为10,14,则输出的a =( )(A )6 (B )4(C )2 (D )04. 已知函数()f x 在R 上可导,且2()2(1)f x x xf '=+,则(1)f '=( ) (A )2- (B )2 (C )4 (D )4-5.若圆锥的高为3,底面半径为4,则此圆锥的表面积为( )(A )40π (B )36π (C )26π (D )20π6.函数321()3f x ax x a =-+在[1,2]上单调递增,则实数a 的取值范围是( ) (A )1a > (B )1a ≥ (C )2a >(D )2a ≥ 7. 已知O 为坐标原点,点1F 、2F 分别为椭圆22:143x y C +=的左、右焦点,A 为椭圆C 上的一点,且212AF F F ⊥,1AF 与y 轴交于点B ,则||OB 的值为( )(A )32 (B )34 (C )52 (D )548. 设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )(A )若//m α,//m β,则//αβ (B )若m α⊥,m n ⊥,则n α⊥(C )若m α⊥,//m n ,则n α⊥ (D )若αβ⊥,m α⊥,则//m β9. 某几何体的三视图如图所示,则该几何体的体积为( )(A )43 (B )53(C )73 (D )52 10. 函数()f x 与它的导函数()f x '的大致图象如图所示,设()g x =当(0,5)x ∈时,()g x 单调递减的概率为( )(A )15(B )25 (C )35 (D )45 11. 在三棱柱111C B A ABC -中,ABC AA 底面⊥1,12,43BAC AA π∠==,32==AC AB ,则三棱柱111C B A ABC -的外接球的表面积为( )(A )π32 (B )48π (C )π64 (D )π7212. 已知函数2()()x x x ax f x a e e=+-有三个不同的零点321,,x x x (其中321x x x <<),则)1)(1()1(3213221x x x ex e x e x ---的值为( ) (A )1 (B )1- (C )a (D )a -。
四川省攀枝花市2022届数学高二下期末达标测试试题含解析

四川省攀枝花市2022届数学高二(下)期末达标测试试题一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意)1====,则,a b 的值分别是( )A .48,7B .61,7C .63,8D .65,82.已知非空集合,A B ,全集U A B =⋃,集合M A B =⋂, 集合()()U U N B A =⋃痧则( ) A .M N M =UB .M N ⋂=∅C .M N =D .M N ⊆ 3.函数()ln x f x e x =在1x =处的切线方程是()A .()1y e x =-B .1y ex =-C .()21y e x =-D .e y x =-4.观察2'()2x x =,4'3()4x x =,'(cos )sin x x =-,由归纳推理可得:若定义在R 上的函数()f x 满足()()f x f x -=,记()g x 为()f x 的导函数,则()g x -=A .()f xB .()f x -C .()g xD .()g x -5.已知函数()()f x x R ∈满足()()=f x f a x -,若函数25y x ax =--与()y f x =的图像的交点为()11,x y ,()22,x y ,…,(),m m x y ,且12mi i x m ==∑,则a =( )A .1B .2C .3D .46.4名同学分别从6所大学中选择一所参观,则不同选法有( )A .64种B .46种C .46A 种D .46C 种7.已知()f x 为定义在R 上的奇函数,且满足(1)(1)f x f x +=-,则(10)f 的值为 ( ) A .0 B .2 C .5 D .108.若关于x 的一元二次不等式20ax bx c ++<的解集为R ,则( )A .00a >⎧⎨∆>⎩B .00a >⎧⎨∆<⎩C .00a <⎧⎨∆>⎩D .00a <⎧⎨∆<⎩9.对于函数()f x 和()g x ,设(){|0}x f x α∈=,(){|0}x g x β∈=,若存在α,β,使得1αβ-…,则称()f x 与()g x 互为“零点相邻函数”.若函数()12x f x ex -=+-与()23g x x ax a =--+互为“零点相邻函数”,则实数a 的取值范围为( )10.设()f x 是定义在R 上恒不为零的函数,对任意实数,x y R ∈,都有()()()f x f y f x y =+,若112a =,()()n a f n n N +=∈,则数列{}n a 的前n 项和n S 的取值范围是( )A .1,12⎡⎫⎪⎢⎣⎭ B .1,22⎡⎫⎪⎢⎣⎭ C .1[,2]2 D .1[,1]211.已知定义在R 上的函数()f x 的导函数为()f x ',若()()20f x f x '->,且()1f e =,则不等式()211x f x e-<的解集为( ) A .(),1-∞ B .(),e -∞ C .()1,+∞ D .(),e +∞12.执行如右图所示的程序框图,则输出的s 的值是( )A .7B .6C .5D .3二、填空题(本题包括4个小题,每小题5分,共20分)13.已知复数2(12i)z =-(i 为虚数单位),则z 的实部为____.14. “直线l 与平面α内无数条直线垂直”是“l α⊥”的______条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分又不必要”)15.已知命题p :∃x∈R,e x -mx =0,q :∀x∈R,x 2-2mx +1≥0,若p∨(q)为假命题,则实数m 的取值范围是________.16.复数12i iz +=(i 是虚数单位)的虚部是_______. 三、解答题(本题包括6个小题,共70分) 17.已知{()}n f x 满足12()(0)1f x x x =>+,11()(())n n f x f f x +=.(2)用数学归纳法证明对()n f x 的猜想.18.已知函数32()2f x x ax b =-+.(1)讨论()f x 的单调性;(2)是否存在,a b ,使得()f x 在区间[0,1]的最小值为1-且最大值为1?若存在,求出,a b 的所有值;若不存在,说明理由.19.(6分)已知函数()21f x x a x =-+-,a R ∈.()1若不等式()21f x x ≤--有解,求实数a 的取值范围;(2)当2a <时,函数()f x 的最小值为3,求实数a 的值.20.(6分)已知曲线 y = x 3 + x -2 在点 P 0 处的切线1l 平行于直线4x -y -1=0,且点 P 0 在第三象限,⑴求P 0的坐标;⑵若直线1l l ⊥, 且 l 也过切点P 0 ,求直线l 的方程.21.(6分)已知命题p :对[1,1]x ∀∈-,函数()2()lg 4()f x a ax x a =--∈R 总有意义;命题q :函数321()43()3g x x ax x a =-++∈R 在[1,)+∞上是增函数.若命题“p q ∨”为真命题且“p q ∧”为假命题,求实数a 的取值范围.22.(8分)若n 1n 21(1,2,3,)a a n +=+=⋯,且11a =.(1)求2345,,,a a a a ;(2)归纳猜想通项公式n a .参考答案一、单选题(本题包括12个小题,每小题35,共60分.每小题只有一个选项符合题意)1.C【解析】【分析】【详解】 由222233+=, 333388+=, 4444, (1515)+=, 归纳可得2211n n n n n n +=--, 故当8n =时,28,8163b a ==-=, 故选C.【点睛】本题通过观察几组等式,归纳出一般规律来考查归纳推理,属于中档题.归纳推理的一般步骤: 一、通过观察个别情况发现某些相同的性质. 二、从已知的相同性质中推出一个明确表述的一般性命题(猜想). 2.B【解析】分析:根据题意画出图形,找出M 与 N 的并集,交集,判断M 与 N 的关系即可详解:Q 全集U A B =⋃,集合M A B =⋂, 集合()()U U N B A =⋃痧M N U ∴⋃=,M N ⋂=∅,M N ≠故选B点睛:本题主要考查的是交集,并集,补集的混合运算,根据题目画出图形是解题的关键,属于基础题。
四川省攀枝花市2022届数学高二第二学期期末达标测试试题含解析

四川省攀枝花市2022届数学高二第二学期期末达标测试试题一、选择题:本题共12小题,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知数列{}n a 满足1111,||3n n n a a a -=-=(,2)n N n ∈≥,且21{}n a -是递减数列,2{}n a 是递增数列,则1012a = A .10163-B .9163-C .101113- D .91113- 【答案】D 【解析】试题分析:由n n n a a 311=--可得:n n n a a 212231=--,又{}12-n a 是递减数列,2{}n a 是递增数列,所以01212<--+n n a a ,0222>-+n n a a 即0222<-+n n a a ,由不等式的性质可得:1222122++--<-n n n n a a a a ,又因为2223131+>n n ,即1222122++-->-n n n n a a a a ,所以0122<--n n a a ,即nn n a a 212231-=--,同理可得:1221231++=-n n n a a ;当数列{}n a 的项数为偶数时,令()*∈=N k k n ,2,可得:k k k k k k a a a a a a a a 212212221232321231,31,,31,31-=-=-=--=----- ,将这12-k 个式子相加得:⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛+++-=--125324212313131313131k kk a a ,所以12121111112211992791124431199kk k ma a -⎛⎫⎛⎫--⎪ ⎪⎝⎭⎝⎭=-+=-⋅--,则910103111314124221212-=⎪⎭⎫ ⎝⎛⋅-=a ,所以选D .考点:1.裂项相消法求和;2.等比数列求和;2.已知函数()()()()2102ln 10x x x f x x x ⎧-+<⎪=⎨⎪+≥⎩,若函数()y f x kx =-有3个零点,则实数k 的取值范围为( ) A .10,2⎛⎫ ⎪⎝⎭B .()1,2C .1,12⎛⎫ ⎪⎝⎭D .()2,+∞【答案】C 【解析】 【分析】求导计算0x =处导数,画出函数()f x 和y kx =的图像,根据图像得到答案. 【详解】当0x ≥时,()()ln 1f x x =+,则()1'1f x x =+,()'01f =; 当0x <时,()212f x x x =-+,则()1'22f x x =-+,当0x →时,()1'2f x →;画出()f x 和y kx =函数图像,如图所示:函数有3个交点,根据图像知112k <<. 故选:C .【点睛】本题考查了根据函数零点个数求参数,意在考查学生的计算能力和应用能力,画出函数图像是解题的关键. 3.某研究性学习小组调查研究学生使用智能手机对学习的影响,部分统计数据如表(参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.)附表:20()P K k ≥0.15 0.10 0.05 0.025 0.010 0.005 0.0010k2.072 2.7063.841 5.024 6.635 7.879 10.828则下列选项正确的是( )A .有99.5%的把握认为使用智能手机对学习有影响B .有99.5%的把握认为使用智能手机对学习无影响C .有99.9%的把握认为使用智能手机对学习有影响D .有99.9%的把握认为使用智能手机对学习无影响 【答案】A【解析】分析:根据列联表中数据利用公式求得2K ,与邻界值比较,即可得到结论. 详解:根据卡方公式求得()223081281020101218K -==⨯⨯⨯,27.89710.828K <<,∴该研究小组有99.5%的把握认为中学生使用智能手机对学生有影响,故选A.点睛:独立性检验的一般步骤:(1)根据样本数据制成22⨯列联表;(2)根据公式()()()()()22n ad bc K a b a d a c b d -=++++计算2K 的值;(3) 查表比较2K 与临界值的大小关系,作统计判断. 4.如图,在矩形OABC 中的曲线分别是sin y x =,cos y x =的一部分,,02A π⎛⎫⎪⎝⎭,()0,1C ,在矩形OABC 内随机取一点,则此点取自阴影部分的概率为( )A .()421π-B .()321π-C .()221π-D .21-【答案】A 【解析】 【分析】先利用定积分计算阴影部分面积,再用阴影部分面积除以总面积得到答案. 【详解】曲线分别是sin y x =,cos y x =的一部分则阴影部分面积为:4102(cos sin )2(sin cos )22240S x x dx x x ππ=-=+=-⎰总面积为:122S ππ=⨯=14(21)S P S π-==【点睛】本题考查了定积分,几何概型,意在考查学生的计算能力. 5.已知全集,,,则集合( )A .B .C .D .【答案】D 【解析】试题分析:因为A ∪B={x|x≤0或x≥1},所以,故选D.考点:集合的运算.6. “0x ∀>,2sin x x >”的否定是( ) A .0x ∀>,2sin x x < B .0x ∀>,2sin x x ≤C .00x ∃≤,002sin x x ≤D .00x ∃>,002sin x x ≤【答案】D 【解析】 【分析】通过命题的否定的形式进行判断. 【详解】因为全称命题的否定是特称命题,故“0x ∀>, 2sin x x >”的否定是“00x ∃>, 002sin x x ≤”. 故选D. 【点睛】本题考查全称命题的否定,属基础题.7.设a b c d R ∈、、、,且a bc d ><,,则下列结论中正确的是( ) A .a c b d +>+ B .a c b d ->-C .ac bd >D .a bd c> 【答案】B 【解析】 【分析】利用不等式性质判断或者举反例即可. 【详解】对A,当1,0,2,4a b c d ====时a c b d +<+不满足对B,因为,a b c d ><则a d b c +>+⇒a c b d ->-成立.故B 正确. 对C,当1,0,1,2a b c d ===-=时不满足ac bd >,故不成立. 对D,当3,2,1,2a b c d ====时不满足,故不成立. 故选:B 【点睛】本题主要考查了不等式的性质运用等,属于基础题型. 8.设123log 2,ln 2,5a b c -===则 A .a b c << B .b c a <<C .c a b <<D .c b a <<【答案】C 【解析】 【分析】由ln 2ln 2ln 3a b =<=及311log ,22a c >==<=可比较大小. 【详解】∵2031a ln ln =>,>,∴ln 2ln 2ln 3a b =<=,即a b <.又3311log 2log ,22a c =>==<=.∴a c >.综上可知:c ab << 故选C. 【点睛】本题主要考查了指数与对数的运算性质及对数函数的单调性比较大小,属于中档题. 9.在△ABC 中,若AB=2,AC=3,∠A=60°,则BC 的长为( )A B C .3D 【答案】D 【解析】 【分析】在ABC ∆中,由,AB AC ,以及cos A 的值,利用余弦定理,即可求解,得到答案. 【详解】由题意,在ABC ∆中,由2,3,60AB AC A ===,由余弦定理可得2222cos 4967BC AB AC AB AC A =+-⋅=+-=,则BC = D.【点睛】本题主要考查了余弦定理的应用,以及余弦定理是解答特殊角的三角函数值的应用,其中熟练掌握余弦定理是解答本题的关键,着重考查了运算与求解能力,属于基础题. 10.已知在R 上的可导函数()f x 的导函数为'()f x ,满足'()()f x f x <,且(5)f x +为偶函数,(10)1f =,则不等式()xf x e <的解集为( )A .(0,)+∞B .(1,)+∞C .(5,)+∞D .(10,)+∞【答案】A 【解析】 【分析】 【详解】分析:构造新函数()()x f x g x e=,利用已知不等式确定()g x 的单调性, 详解:设()()x f x g x e=,则'()()'()x f x f x g x e -=,由已知'()()f x f x <得)'(0g x <,∴()g x 是减函数.∵(5)f x +是偶函数,∴()f x 的图象关于直线5x =对称, ∴(0)(10)1f f ==,0(0)(0)1f g e ==,()()1xf xg x e=<的解集为(0,)+∞,即()xf x e <的解集为(0,)+∞.故选A .点睛:本题考查用导数研究函数的单调性,解题关键是是构造新函数()()x f x g x e=,对于含有'(),()f x f x 的已知不等式,一般要构造新函数如()()g x xf x =,()()f x g x x =,()()xg x e f x =,()()x f x g x e=等等,从而能利用已知条件确定()g x 的单调性,再解出题中不等式的解集. 11.已知随机变量X 服从正态分布()22,N σ且P (X ≤4)=0.88,则P (0<X <4)=( )A .0.88B .0.76C .0.24D .0.12【答案】B 【解析】 【分析】正态曲线关于x μ=对称,利用已知条件转化求解概率即可. 【详解】因为随机变量X 服从正态分布2(2,)N σ,2μ=,得对称轴是2X =,(4)0.88P X ≤=,(4)(0)10.880.12P X P X ∴≥=≤=-=,(04)12(4)10.240.76P X P X ∴<<=-≥=-=,故选B .【点睛】本题在充分理解正态分布的基础上,充分利用正态分布的对称性解题,是一道基础题.12.用反证法证明:若整系数一元二次方程20(0)ax bx c a ++=≠有有理数根,那么a 、b 、c 中至少有一个偶数时,下列假设正确的是( ) A .假设a 、b 、c 都是偶数B .假设a 、b 、c 都不是偶数C .假设a 、b 、c 至多有一个偶数D .假设a 、b 、c 至多有两个偶数 【答案】B 【解析】 【分析】根据反证法的概念,可知假设应是所证命题的否定,即可求解,得到答案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(下)调研检测 2018.07高二数学(文科)本试题卷分第一部分(选择题)和第二部分(非选择题).第一部分1至2页,第二部分3至4页,共4页.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.满分150分.考试时间120分钟.考试结束后,将本试题卷和答题卡一并交回.注意事项:1.选择题必须使用2B 铅笔将答案标号填涂在答题卡上对应题目标号的位置上. 2.本部分共12小题,每小题5分,共60分.第一部分(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若焦点在y 轴上的双曲线22113y xm m -=--的焦距为4,则m 等于( )(A )0 (B )4 (C )10 (D )6- 2.已知复数2i1iz=+(i 为虚数单位),则||z =( ) (A )3 (B )2 (C )3 (D )2 3. 设)(x f '是函数cos ()x xf x e=的导函数,则(0)f '的值为( ) (A )1 (B )0 (C )1- (D )1e4. 某程序框图如图所示,该程序运行后输出的k 的值是( ) (A )4(B )5(C )6 (D )75. 如图是函数()y f x =的导函数()y f x '=的图象,则下面说法正确的是( ) (A )在(2,1)-上()f x 是增函数 (B )在(1,3)上()f x 是减函数 (C )当1x =时,()f x 取极大值 (D )当2x =时,()f x 取极大值6.将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成的几何体的侧面积为( ) (A )4π(B )22π(C )2π(D )2π7. 若[1,5]a ∈,则函数()af x x x=+在区间[2,+)∞内单调递增的概率是( ) (A )34 (B )24 (C )14 (D )458.函数3y x x =-的图象与直线2y ax =+相切,则实数a 的值为( ) (A )1- (B )1 (C )2(D )49. 设m 、n 是两条不同的直线,α、β是两个不同的平面,下列命题中正确的是( ) (A )若//,//m n αβ,且//αβ,则//m n (B )若,m αβα⊥⊥,则//m β(C )若,m n αβ⊥⊥,αβ⊥,则m n ⊥ (D )若//,m n αβ⊥,且αβ⊥,则//m n10. 某空间几何体的三视图如图所示,则该几何体的体积为( )(A )83 (B )83π-(C )73 (D )73π-11. 正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C 2,此时四面体ABCD 外接球表面积为( ) (A 55(B 77 (C )5π (D )7π 12.设函数)(x f '是奇函数))((R x x f ∈的导函数,当0x >时,()()ln f x f x x x'⋅<-,则使得2(1)()0x f x -<成立的x 的取值范围是( )(A )(,1)(1,)-∞-+∞U (B )(,1)(0,1)-∞-U (C )(1,0)(0,1)-U (D )(1,0)(1,)-+∞U1122正视图侧视图俯视图第二部分(非选择题 共90分)注意事项:1.必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷上无效.2.本部分共10小题,共90分.二、填空题:本大题共4小题,每小题5分,共20分. 13. 已知椭圆C 的中心在坐标原点,焦点在轴上,离心率等于2,它的一个顶点 恰好是抛物线24x y =的焦点,则椭圆C 的标准方程为________.14.如图,在三棱柱111ABC A B C -中,1CC ⊥底面ABC ,90ACB ∠=o ,1CA CB CC ==,D 是1CC 的中点,则直线1AC 与BD 所成角的余弦值为__________.15. 在推导等差数列前n 项和的过程中,我们使用了倒序相加的方法,类比可以求得222sin 1sin 2sin 89+++=o o o L .16.已知函数1,0(),0x a x f x x e x ⎧-<⎪=⎨⎪≥⎩()a R ∈,()g x ex =,若()f x 与()g x 的图象恰好有三个公共点,则实数a 的取值范围是__________.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知函数2()ln f x ax b x =+在1x =处有极值12. (Ⅰ)求a 、b 的值;(Ⅱ)求函数()y f x =的单调区间.18. (本小题满分12分)2018年至2020年,第六届全国文明城市创建工作即将开始.在2017年9月7日召开的攀枝花市创文工作推进会上,攀枝花市委明确提出“力保新一轮提名城市资格、确保2020年创建成功”的目标.为了确保创文工作,今年初市交警大队在辖区开展“机动车不礼让行人整治行动” .下表是我市一主干路口监控设备抓拍的5个月内 “驾驶员不礼让斑马线”行为统计数据:月份 1 2 3 4 5违章驾驶员人数120 105 100 90 85(Ⅰ)请利用所给数据求违章人数与月份之间的回归直线方程ˆˆˆybx a =+; (Ⅱ)预测该路口7月份不“礼让斑马线”违章驾驶员的人数;(Ⅲ)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查“驾驶员不礼让斑马线”行为与驾龄的关系,得到如下22⨯列联表:不礼让斑马线礼让斑马线合计驾龄不超过1年 22 8 30 驾龄1年以上8 1220 合计302050能否据此判断有97.5%的把握认为“礼让斑马线”行为与驾龄有关?参考公式:1122211()()ˆˆˆ,()n ni iiii i nniii i x y nx y x x y y bay bx xnxx x ====---===---∑∑∑∑. 22()()()()()n ad bc K a b c d a c b d -=++++(其中n a b c d =+++)2()P K k ≥0.150 0.100 0.050 0.025 0.010 0.005 0.001 k2.0722.7063.8415.0246.6357.87910.82819.(本小题满分12分)如图,在边长为2的正方形ABCD 中,点E 是AB 的中点,点F 是BC 的中点,点M 是AD 上的点, 且13AM MD =.将△AED ,△DCF 分别沿DE ,DF 折起, 使A ,C 两点重合于P ,连接EF ,PB . (Ⅰ) 求证:PD EF ⊥; (Ⅱ)求证://PB 平面EFM .20.(本小题满分12分)如图,在三棱柱111ABC A B C -中,侧面11AA B B ⊥底面ABC ,1AA AB =,90ABC ∠=o .(Ⅰ)求证:1AB ⊥平面1A BC ;(Ⅱ)设1BB 中点为D 点,若2AB =,160A AB ∠=o, 且1A C 与平面11BB C C 所成的角为30o ,求三棱锥11D A C C -的体积.21.(本小题满分12分)已知函数21()e 12xf x x ax =---(其中a ∈R ,e 为自然对数的底数).(Ⅰ)若函数()f x 是R 上的单调增函数,求实数a 的取值范围;(Ⅱ)当0x >时,证明:2(e 1)ln(1)x x x -+>.E BAM gPE FM请考生在22~23三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B 铅笔在答题卡上把所选题目对应题号右侧的方框涂黑. 22.(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系中,曲线1C 的普通方程为2214x y +=.以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=-. (Ⅰ)求曲线1C 的参数方程和2C 的普通方程;(Ⅱ)若P 、Q 分别是曲线1C 、2C 上的动点,求PQ 的最大值.23.(本小题满分10分)选修4-5:不等式选讲已知函数()1f x x a x =++-. (Ⅰ)若1a =,解不等式()4f x <;(Ⅱ)对任意满足1m n +=的正实数m 、n ,若总存在实数0x ,使得011()f x m n+≥成立,求实数a 的取值范围.攀枝花市(下)调研检测 2018.07高二数学(文)参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1~5)BDCAD (6~10)CABCB (11~12)CD二、填空题:本大题共4小题,每小题5分,共20分.13、2212x y += 14、10 15、8944.5()2或 16、三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17、(本小题满分12分)解:(Ⅰ)'()2bf x ax x =+,则2(1)201(1)1ln12f a b f a b '=+=⎧⎪⎨=⋅+=⎪⎩ 121a b ìïï=ï\íïï=-ïî.…………………6分(Ⅱ)21()ln 2f x x x =-的定义域为(0,)+∞,211'()x f x x x x-=-=,令'()0f x =,则1x =或1x =-(舍去)\当01x <<时,'()0f x <,()f x 递减;当1x >时,'()0f x >,()f x 递增, \()f x 的单调递减区间是(0,1),单调递增区间是(1,)+∞.…………………12分18、(本小题满分12分)解:(Ⅰ)由表中数据知:3,100x y ==∴1221141515008.55545ni ii ni i x y nx ybx nx==--===---∑∑$,ˆ125.5a y bx =-=$, ∴所求回归直线方程为ˆ8.5125.5yx =-+.…………………5分 (Ⅱ)由(Ⅰ)知,令7x =,则ˆ8.57125.566y=-⨯+=人. …………………7分(Ⅲ)由表中数据得2250(221288)505.556 5.024*********K ⨯⨯-⨯==≈>⨯⨯⨯,根据统计有97.5%的把握认为“礼让斑马线”行为与驾龄有关.…………………12分19、(本小题满分12分)(Ⅰ)证明:∵折叠前A D AE ⊥,DC CF ⊥…………2分 ∴折叠后PD PE ⊥,PD PF ⊥…………3分 又∵PE PF P =I∴PD ⊥平面PEF ,而EF ⊂平面PEF ∴PD EF ⊥.…………………5分(Ⅱ)连接BD 交EF 于N ,连接NM ,在正方形ABCD 中,连接AC 交BD 于O , 则1124BN BO BD ==,所以13BN ND =,…………………9分 又13AM MD =,即13PM DM =,在PBD ∆中,13PM BN MD ND ==, 所以//PB MN ,PB ⊄平面EFM ,MN ⊂平面EFM ,所以//PB 平面EFM .…………………12分20、(本小题满分12分)解:(Ⅰ)由已知侧面11AA B B ⊥底面ABC ,CB CA ⊥, CB ⊂底面ABC ,得到CB ⊥侧面11AA B B ,又因为1AB ⊂侧面11AA B B ,所以1AB CB ⊥,又由已知1AA AB =,侧面11AA B B 为菱形,所以对角线11AB A B ⊥,即1AB CB ⊥,11AB A B ⊥,1A B CB B =I ,所以1AB ⊥平面1A BC .…………………6分(Ⅱ)因为160A AB ∠=o,易知11A BB V 为等边三角形,中线1A D ⊥1BB ,由(Ⅰ)CB ⊥侧面11AA B B ,所以1CB A D ⊥,得到1A D ⊥平面11BB C C ,1A CD ∠即为1A C 与平面11BB C C 所成的角,12A B = ,13A D =,123AC =, 22211CB A C A B =-,得到22CB =111222DC C S CC BC ==V 1111111263D A C C A DCC DC C V V A D S --===V (12)PE FMNEAM gON分21、(本小题满分12分) 解:(Ⅰ)a x e x f x--=')(Θ函数()f x 是R 上的单调递增函数,0)(≥'∴x f 在R x ∈上恒成立,即a x e x ≥-在Rx ∈时恒成立,令x e x g x-=)(,则1)(-='xe x g ;所以)(x g 在()0-,∞上单调递减,在()∞+,0上单调递增;1)0()(min ==g x g所以实数a 的取值范围是(,1]-∞.……………………5分(Ⅱ)由(Ⅰ)可知,当1a =时,当0x >时,()(0)0f x f >=,即212xx e x ->+.欲证(e 1)ln(1)xx -+>2x ,只需证2ln(1)2xx x +>+即可. 构造函数()h x =ln(1)x +-22xx +(0x >), 则22214()01(2)(1)(2)x h x x x x x '=-=>++++恒成立,故()h x 在(0,)+∞单调递增, 从而()(0)0h x h >=.即2ln(1)02x x x +->+,亦即2ln(1)2xx x +>+. 得证2(e 1)ln(1)xx x -+>. ……………………12分请考生在22~23三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B 铅笔在答题卡上把所选题目对应题号右侧的方框涂黑. 22.(本小题满分10分)选修4-4:坐标系与参数方程 解:(Ⅰ)曲线1C 的参数方程为2cos sin x y αα=⎧⎨=⎩(α为参数). ……………………2分曲线2C 的极坐标方程为2sin ρθ=-,即22sin ρρθ=-,∴曲线2C 的直角坐标方程为222x y y +=-,即()2211x y ++=. ……………………5分(Ⅱ)法一:设()2cos ,sin P αα,则P 到曲线2C 的圆心()0,1-的距离()224cos sin 1d αα=++23sin 2sin 5αα-++21163(sin )33α=--+,∵[]sin 1,1α∈-,∴当1sin 3α=时,max 433d =. ∴max max PQ d r =+434331+=+=. ……………………10分 法二:设(),P x y ,则P 到曲线2C 的圆心()0,1-的距离222222116(1)44(1)3253()33d x y y y y y y =++=-++=-++=--+,∵[]1,1y ∈-,∴当13y =时,max 43d =. ∴max max PQ d r =+43433133+=+=. ……………………10分23.(本小题满分10分)选修4-5:不等式选讲 解:(Ⅰ)1a =时,()11f x x x =++-法一:由绝对值不等式的几何意义得不等式的解集为(2,2)x ∈-. 法二:当1x ≤-时,由()24f x x =-<得2x >-,则21x -<≤-;当11x -<≤时,()24f x =<恒成立;当1x >时,由()24f x x =<得2x <,则12x <<.综上,不等式()4f x <的解集为{}|22x x -<<. ……………………5分 (Ⅱ)由题意1111()()114n mm n m n m n m n+=++=+++≥,……………………7分 由绝对值不等式得()11f x x a x a =++-≥+,当且仅当()(1)0x a x +-≤时取等号,故()f x 的最小值为1a +.……………………9分由题意得41a ≥+,解得53a -≤≤. ……………………10分。
