DEA的Matlab程序 - 360文档中心

DEA算法学习系列之三：一次性求解CCR模型所有DMU参数——效率、规模效益、有效性特征、调整值的matlab代码

DEA算法学习笔记系列（三）一次性求解CCR模型所有DMU参数——效率、规模效益、有效性特征、调整值的matlab代码目录1 编写目的 (4)1.1E XCEL一次只能计算一个DMU (4)1.2M A TLAB编程一次性计算所有DMU的效率、有效性、调整值 (5)2 MATLAB求解线性规划 (5)2.1系统函数说明 (5)2.1.1 调用格式： (5)2.1.2 输入参数说明 (5)2.1.3 返回值说明 (6)2.2简单例子，用代码求解 (7)2.2.1 例1 (7)2.2.2 例2： (8)2.2.3 例题3（无解的例子） (9)2.2.4 例4（需要标准化的例子，一个等式的例子） (10)2.2.5 例5 (11)2.2.6 例子6：松弛变量为基变量——用等式重解例1 (13)2.3自定义M A TLAB函数求解线性规划（从EXCEL读数据） (14)2.3.1 简单版：MyLinprog——读取给定文件中数据，返回计算结果 (14)3 DEA模型之CCR简介 (16)3.1CCR理论模型 (16)4 CCR模型计算过程——一个决策单元的计算过程 (18)4.1例题说明 (18)4.2基于理论构建模型——湖南省 (19)4.3调整形式，以利于线性规划函数求解 (19)4.4按照自定义函数，构造EXCEL文件 (20)4.4.1 矩阵A的格式和说明 (20)4.4.2 价值向量系数矩阵C的格式和说明 (20)4.4.3 资源限制矩阵b的格式和说明 (21)4.4.4 X取值条件的限制 (21)4.5调用自定义函数（M Y L INPROG）求解指定决策单元模型 (22)4.6计算结果评价 (22)4.6.1 最优值 (22)4.6.2 各变量的值 (23)4.6.3 模型效率分析 (24)4.7调整方案 (24)5 计算CCR模型的MATLAB函数——所有决策单元 (25)5.1程序代码（可直接运行） (25)5.2存放数据的EXCEL文件格式说明 (27)5.2.1 第一个：投入产出数据 (27)5.2.2 第二个数据：价值变量系数矩阵（不需准备） (27)5.2.3 第三个数据：资源限制矩阵（不需要准备） .................................................................. 28 5.2.4 第四个数据：决策变量的取值范围（不需要准备） ...................................................... 28 5.2.5 范例数据 .............................................................................................................................. 28 5.3 计算所有DMU 的函数 .............................................................................................................. 28 5.3.1 函数输入参数 ...................................................................................................................... 28 5.3.2 返回参数1：每个DMU 效率、规模效益、是否弱有效 ................................................ 28 5.3.3 返回参数2：每个DMU 的所有值 (29)5.3.4 返回参数3：增加的松弛变量 ........................................................................................... 29 5.3.5 返回参数4：非DEA 有效DMU 调整后的投入产出矩阵 .............................................. 29 5.3.6 返回参数5：非DEA 有效DMU 各个指标调整值 .......................................................... 29 5.4 返回参数例子 ............................................................................................................................. 29 5.4.1 返回参数1：每个DMU 效率、规模效益、是否弱有效 ................................................ 29 5.4.2 返回参数2：每个DMU 的所有值 (30)5.4.3 返回参数3：增加的松弛变量 ........................................................................................... 30 5.4.4 返回参数4：非DEA 有效DMU 调整后的投入产出矩阵 .............................................. 30 5.4.5 返回参数5：非DEA 有效DMU 各个指标调整值 .......................................................... 30 6 补充知识 ............................................................................................................................................ 30 6.1 自定义MA TLAB 函数 .................................................................................................................. 30 6.2 M A TLAB 向量操作 ....................................................................................................................... 32 6.2.1 读取矩阵第一列 .................................................................................................................. 32 6.3 M A TLAB 操作EXCEL 数据 ........................................................................................................... 32 6.3.1 读入excel 数据 .................................................................................................................... 32 6.3.2 写内容到xls ........................................................................................................................ 33 6.4 M A TLAB 的FOR 循环语句............................................................................................................ 35 7 参考资料 .. (35)λλ1 编写目的1.1 Excel 一次只能计算一个DMUDEA 的CCR 模型，他的对偶模型如下图：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥=-+++=-+++=++++=++++=++++=++---无约束θθθθθλλλλλλλλλλλλλλλλλλλλλ,004.165921.266204.165922.93009.219620.144410.18120.144760.4929.17920.443000.46120.44320.24980.40131.84940.144431.84964.58145.98084.93656.130684.93608.58366.932..min 2432114321343212432114321jDs s s s s Vt s 很多人通过EXCEL 提供的一个插件进行计算，如下图所示：但是，这种方法有以下不足：（1）每次只能计算一个DMU ，如果有多个DMU ，那么需要人工重复计算过程多次；（2）通过Excel 计算，只能得到θ，没法得到各个，所以，也无法直接判断是规模效益递增还是递减；λ（3）没发直接得到ss ii、+-的值，也无法直接判断DMU 是弱DEA 有效，还是DEA 有效1.2 Matlab 编程一次性计算所有DMU 的效率、有效性、调整值文章通过编写Matlab 程序，实现一次性对所有DMU 计算效率θ、有效性（根据θ以及所有的汇总值）、调整值（根据ss ii、+-）。

DEA算法学习系列之三：一次性求解CCR模型所有DMU参数——效率、规模效益、有效性特征、调整值的matlab代码

DEA算法学习笔记系列（三）一次性求解CCR模型所有DMU参数——效率、规模效益、有效性特征、调整值的matlab代码目录1 编写目的 (4)1.1E XCEL一次只能计算一个DMU (4)1.2M A TLAB编程一次性计算所有DMU的效率、有效性、调整值 (5)2 MATLAB求解线性规划 (5)2.1系统函数说明 (5)2.1.1 调用格式： (5)2.1.2 输入参数说明 (5)2.1.3 返回值说明 (6)2.2简单例子，用代码求解 (7)2.2.1 例1 (7)2.2.2 例2： (8)2.2.3 例题3（无解的例子） (9)2.2.4 例4（需要标准化的例子，一个等式的例子） (10)2.2.5 例5 (11)2.2.6 例子6：松弛变量为基变量——用等式重解例1 (13)2.3自定义M A TLAB函数求解线性规划（从EXCEL读数据） (14)2.3.1 简单版：MyLinprog——读取给定文件中数据，返回计算结果 (14)3 DEA模型之CCR简介 (16)3.1CCR理论模型 (16)4 CCR模型计算过程——一个决策单元的计算过程 (18)4.1例题说明 (18)4.2基于理论构建模型——湖南省 (19)4.3调整形式，以利于线性规划函数求解 (19)4.4按照自定义函数，构造EXCEL文件 (20)4.4.1 矩阵A的格式和说明 (20)4.4.2 价值向量系数矩阵C的格式和说明 (20)4.4.3 资源限制矩阵b的格式和说明 (21)4.4.4 X取值条件的限制 (21)4.5调用自定义函数（M Y L INPROG）求解指定决策单元模型 (22)4.6计算结果评价 (22)4.6.1 最优值 (22)4.6.2 各变量的值 (23)4.6.3 模型效率分析 (24)4.7调整方案 (24)5 计算CCR模型的MATLAB函数——所有决策单元 (25)5.1程序代码（可直接运行） (25)5.2存放数据的EXCEL文件格式说明 (27)5.2.1 第一个：投入产出数据 (27)5.2.2 第二个数据：价值变量系数矩阵（不需准备） (27)5.2.3 第三个数据：资源限制矩阵（不需要准备） .................................................................. 28 5.2.4 第四个数据：决策变量的取值范围（不需要准备） ...................................................... 28 5.2.5 范例数据 .............................................................................................................................. 28 5.3 计算所有DMU 的函数 .............................................................................................................. 28 5.3.1 函数输入参数 ...................................................................................................................... 28 5.3.2 返回参数1：每个DMU 效率、规模效益、是否弱有效 ................................................ 28 5.3.3 返回参数2：每个DMU 的所有值 (29)5.3.4 返回参数3：增加的松弛变量 ........................................................................................... 29 5.3.5 返回参数4：非DEA 有效DMU 调整后的投入产出矩阵 .............................................. 29 5.3.6 返回参数5：非DEA 有效DMU 各个指标调整值 .......................................................... 29 5.4 返回参数例子 ............................................................................................................................. 29 5.4.1 返回参数1：每个DMU 效率、规模效益、是否弱有效 ................................................ 29 5.4.2 返回参数2：每个DMU 的所有值 (30)5.4.3 返回参数3：增加的松弛变量 ........................................................................................... 30 5.4.4 返回参数4：非DEA 有效DMU 调整后的投入产出矩阵 .............................................. 30 5.4.5 返回参数5：非DEA 有效DMU 各个指标调整值 .......................................................... 30 6 补充知识 ............................................................................................................................................ 30 6.1 自定义MA TLAB 函数 .................................................................................................................. 30 6.2 M A TLAB 向量操作 ....................................................................................................................... 32 6.2.1 读取矩阵第一列 .................................................................................................................. 32 6.3 M A TLAB 操作EXCEL 数据 ........................................................................................................... 32 6.3.1 读入excel 数据 .................................................................................................................... 32 6.3.2 写内容到xls ........................................................................................................................ 33 6.4 M A TLAB 的FOR 循环语句............................................................................................................ 35 7 参考资料 .. (35)λλ1 编写目的1.1 Excel 一次只能计算一个DMUDEA 的CCR 模型，他的对偶模型如下图：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧≥=-+++=-+++=++++=++++=++++=++---无约束θθθθθλλλλλλλλλλλλλλλλλλλλλ,004.165921.266204.165922.93009.219620.144410.18120.144760.4929.17920.443000.46120.44320.24980.40131.84940.144431.84964.58145.98084.93656.130684.93608.58366.932..min 2432114321343212432114321jDs s s s s Vt s 很多人通过EXCEL 提供的一个插件进行计算，如下图所示：但是，这种方法有以下不足：（1）每次只能计算一个DMU ，如果有多个DMU ，那么需要人工重复计算过程多次；（2）通过Excel 计算，只能得到θ，没法得到各个，所以，也无法直接判断是规模效益递增还是递减；λ（3）没发直接得到ss ii、+-的值，也无法直接判断DMU 是弱DEA 有效，还是DEA 有效1.2 Matlab 编程一次性计算所有DMU 的效率、有效性、调整值文章通过编写Matlab 程序，实现一次性对所有DMU 计算效率θ、有效性（根据θ以及所有的汇总值）、调整值（根据ss ii、+-）。

如何使用Matlab进行神经电信号处理与分析

如何使用Matlab进行神经电信号处理与分析引言神经电信号是用于在神经系统中进行信息传递的电信号。

对于神经科学研究人员来说，了解和分析神经电信号对于揭示大脑的功能和机制至关重要。

Matlab作为一种功能强大的编程语言和开发环境，提供了丰富的工具和函数，可用于处理和分析神经电信号。

本文将介绍如何使用Matlab进行神经电信号处理和分析的基本方法和技巧。

1. 数据导入与预处理首先，我们需要将神经电信号数据导入Matlab环境中进行处理和分析。

常见的神经电信号数据包括脑电图（EEG）、脑磁图（MEG）和神经肌电图（EMG）。

Matlab提供了一系列函数和工具箱来读取不同格式的神经电信号数据文件，如EEGLAB和FieldTrip等。

在导入数据之后，我们还需要对数据进行预处理，以去除噪声和伪装信号。

常见的预处理步骤包括滤波、伪迹去除和去除运动伪迹等。

Matlab提供了诸多滤波函数和技术，如带通滤波、低通滤波和高通滤波等。

通过合理运用这些工具，我们可以对神经电信号数据进行有效的预处理。

2. 特征提取与分析在预处理之后，我们可以开始对神经电信号数据进行特征提取和分析。

特征提取是神经电信号处理中的重要步骤，可以从原始信号中提取出有用的信息。

在Matlab中，我们可以使用一系列函数和算法来提取信号的频域特征、时域特征和空域特征。

频域特征可以用于分析信号的频率成分和频率特征，如功率谱密度和频谱特性等。

Matlab提供了FFT和Periodogram等函数，可用于计算信号的频谱与谱密度。

时域特征包括信号的能量、振幅、时延和相位等。

可以使用Matlab的瞬时特征函数来计算信号的瞬时属性。

空域特征用于分析信号在空间上的分布和变化，如空间滤波和空间相关性等。

Matlab提供了一些函数和工具箱，如EEGLAB和FieldTrip，可用于实现这些分析。

3. 数据可视化与结果展示在特征提取和分析之后，我们通常需要将结果进行可视化展示，以便更好地理解和传达。

MATLAB基本操作及环境设置

MATLAB基本操作及环境设置1.MATLAB的基本操作：-启动MATLAB：在计算机上安装MATLAB软件后，可以从开始菜单中或桌面图标启动MATLAB。

-MATLAB命令窗口：启动MATLAB后，可以看到一个命令窗口。

在命令窗口中，可以输入MATLAB命令，并执行它们。

- 基本算术操作：MATLAB可以进行基本的算术操作，如加减乘除。

例如，输入"2+3"，然后按Enter键，MATLAB将计算并显示结果。

- 变量：在MATLAB中，可以定义变量，并将值赋给它们。

例如，输入"x = 5"，然后按Enter键，MATLAB将创建变量x，并将值设为5 - 矩阵操作：MATLAB是以矩阵为基础的语言。

可以使用MATLAB的矩阵操作函数创建、修改和操作矩阵。

例如，可以使用"zeros"函数创建由0组成的矩阵，使用"eye"函数创建单位矩阵，以及使用"inv"函数计算矩阵的逆矩阵。

2.MATLAB的环境设置：- 工作目录：工作目录是MATLAB文件的位置。

可以使用"cd"命令更改工作目录。

可以使用"pwd"命令查看当前工作目录。

- 文件管理：MATLAB提供了一些函数来管理和操作文件。

可以使用"dir"函数列出当前目录中的文件和文件夹，使用"mkdir"函数创建新文件夹，使用"delete"函数删除文件等。

-图形界面：MATLAB还提供了一个图形用户界面（GUI），可以通过点击菜单和按钮来执行操作。

GUI提供了更直观和交互式的方式来使用MATLAB。

- 图形绘制：MATLAB具有强大的图形绘制功能。

可以使用"plot"函数绘制二维曲线，使用"mesh"函数绘制三维曲面等。

MATLAB在超效率DEA模型中的应用

MATLAB在超效率DEA模型中的应用作者：刘展屈聪来源：《经济研究导刊》2014年第03期摘要：利用数学软件MATLAB编写了便于使用超效率DEA模型的计算程序，并利用该程序对河南省2002—2011年财政科技投入的超效率进行计算与分析，实证分析表明该MATLAB计算程序十分的方便、有效。

关键词：MATLAB；超效率DEA模型；财政科技投入中图分类号：F22 文献标志码：A 文章编号：1673-291X（2014）03-0086-03随着时代的发展，超效率数据包络分析模型（SE-DEA）也随之被提出，并被运用得越来越广泛，相应的求解软件的开发也在不断的向前推进。

目前主要有DEA Solver pro、Pioneer、EMS、DEA Excel Solver、等专门用于求解SE-DEA模型的软件，但获得这些软件不太容易，在一般的网站无法下载与购买，需要通过一些专门的渠道。

MATLAB是一门功能强大、简单易学且应用广泛的编程语言，而且MATLAB软件的下载与购买相对来说比较容易。

文献[1]给出了数据包络分析模型（DEA）的基本模型C2R模型的MATLAB计算程序，但对于超效率数据包络分析模型的MATLAB计算程序，目前尚未有文献报道。

本文在文献[1]的基础上，编写超效率数据包络分析模型的计算程序，并进行实证分析。

一、超效率DEA模型超效率数据包络分析模型（Super Efficiency DEA，SE-DEA）是由Andersen&Petersen根据传统DEA模型所提出的新模型。

传统DEA模型如最基本的C2R模型对决策单元规模有效性和技术有效性同时进行评价，BC2模型用于专门评价决策单元技术有效性，但C2R模型和BC2模型只能区别出有效率与无效率的决策单元，无法进行比较和排序。

超效率DEA模型与C2R模型的不同之处在于评价某个决策单元时将其排除在决策单元集合之外，这样使得C2R 模型中相对有效的决策单元仍保持相对有效，同时不会改变在C2R模型中相对无效决策单元在超效率DEA模型中的有效性，可以弥补传统DEA模型的不足，计算出的效率值不再限制在0～1的范围内，而是允许效率值超过1，可以对各决策单元进行比较和排序。

DEA程序

第一步：计算效率与权值clearx=[];y=[];n=size(x', 1);m=size(x, 1);s=size(y, 1);A=[-x' y'];b=zeros(n, 1);LB=zeros(m+s, 1);UB=[];for i=1:n;f=[zeros(1,m) -y(:,i)'];Aeq=[x(:,i)' zeros(1,s)];beq=1;w(:,i)=LINPROG(f, A, b, Aeq, beq, LB, UB);E(i,i)=y(:,i)'*w(m+1:m+s,i);endwEomega=w(l:m,:)mu=w(m+l:m+s,:)第二步：计算剩余变量、松弛变量clearx=[];y=[];n=size(x', 1);m=size(x, 1);s=size(y, 1);epsilon=10^-10;f=[zeros(1, n) -epsilon*ones(1, m+s) 1];A=zeros(1, n+m+s+1);b=0;LB=zeros(n+m+s+1, 1);UB=[];LB(n+m+s+1)=-Inf;for i=1:n;Aeq=[x eye(m) zeros(m,s) -x(:,i); （此处的分号很重要）y zeros(s,m) -eye(s) zeros(s,1)]; （此处的分号很重要） beq=[zeros(m,1);y(:,i)];w(:,i)=LINPROG(f, A, b, Aeq, beq, LB, UB);endlambda=w(1:n,:)s_minus=w(n+1:n+m,:)s_plus=w(n+m+1:n+m+s,:)theta=w(n+m+s+1,:)////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// 传统CCR模型：Function [W,Q,T,I]=deaccr(X,Y)%X行位决策单元，列为指标X=X’;Y=Y;n=size(X’,1);m=size(X,1);s=size(Y,1);A=[-X’,Y’];b=zeros(n,1);LB=zeros(m+s,1);UB=[];for i=1:nAeq=[X(:,i)’,zeros(1,s)];beq=1;f=[zeros(1,m),-Y(:,i)’];w(:,i)=LINPROG(f,A,b,Aeq,beq,LB,UB);E(1,i)=Y(:,i)’*w(m+1:m+s,i);endW=w’;Q=E;[T,I]=sort(E);end包络DEA模型：Function [A,B,D]=diccr(X,Y)X=X’;Y=Y;n=size(X’,1);m=size(X,1);s=size(Y,1);LB=zeros(n+m+s+1,1);UB=[];A=[];b=[];options=optimset(‘maxiter’,100);for i=1:nAeq=[X,eye(m),zeros(m,s),-X(:,i)Y,zeros(s,m),-eye(s),zeros(s,1)];beq=[zeros(m,1)Y(:,1)];f=[zeros(1,n+m+s),1];w(:,i) =LINPROG(f,A,b,Aeq,beq,LB,UB,[], options);endB=w(n+m+1:n+m+s,:);D=w(n+m+s+1,:);end最劣CCR模型：Function [Q,T,I]=zlccr(X,Y)X=X’;Y=Y;n=size(X’,1);m=size(X,1);s=size(Y,1);A=[X’,-Y’];b=zeros(n,1);LB=zeros(m+s,1);UB=[];For i=1:nAeq=[X(:,i)’,zeros(1,s)];beq=1;f=[zeros(1,m),Y(:,i)’];w(:,i)= LINPROG(f,A,b,Aeq,beq,LB,UB);E(1,i)=Y(:,i)’*w(m+1:m+s,i);endQ=E;[T,I]=sort(E);endBCC模型：Function [E,T,I]=bcc(X,Y)X=X’;Y=Y;n=size(X’,1);m=size(X,1);s=size(Y,1);A=[-X’,Y’,-ones(n,1)];b=zeros(n,1);LB=[zeros(m+s,1);[]];UB=[];For i=1:nAeq=[X(:,i)’,zeros(1,s+1)];beg=1;f=[zeros(1,m),-Y(:,i)’,1];w(:,i)= LINPROG(f,A,b,Aeq,beq,LB,UB);E(1,i)=Y(:,i)’*w(m+1:m+s,i)-w(m+s+1: m+s+1,i); EndE;[T,I]=sort(E);endFunction [W,Q,T,I]=deasuper(X,Y)X=X’;Y=Y;n=size(X’,1);m=size(X,1);s=size(Y,1);b=zeros(n-1,1);LB=zeros(m+s,1);UB=[];For i=1:nAeq=[X(:,i)’,zeros(1,s)];beq=1;f=[zeros(1,m),-Y(:,i)’];if i==1A=[-X(:,2:n)’,Y(:,2:n)’];elseif i==nA=[-X(:,1:n-1)’,Y(:,1:n-1)’];elseA=[[-X(:,1:i-1),-X(:,i+1:n)]’,[Y(:,1:i-1),Y(:,i+1:n)]’]; endw(:,i)= LINPROG(f,A,b,Aeq,beq,LB,UB);E(1,i)=Y(:,i)’*w(m+1:m+s,i);endW=w’;Q=E;[T,I]=sort(E);end。

数据包络分析DEA教程(全)

DEA的起源与发展
金融投资
在金融投资领域，DEA用于评估投资组合的相对效率，为投资者提供决策依据。
环境保护
在环境保护领域，DEA用于评估企业的环保投入与产出的相对效率，促进企业绿色发展。
公共部门
DEA也被广泛应用于公共部门，如政府机构、学校、医院等，用于评估其资源利用效率和改进方向。
运营管理
DEA被广泛应用于运营管理领域，用于评估企业的生产效率、资源配置效率和流程改进等方面。
02
随着DEA的应用范围不断扩大，许多学者对DEA模型进行了改进和发展。例如，Banker、Charnes和Cooper提出的BCC模型，解决了CCR模型中固定规模报酬假设的问题。
03
此外，DEA还与其他方法结合，如Malmquist指数、超效率DEA、方向距离函数等，进一步扩展了DEA的应用领域和评估准确性。
除了比率法和角度法，DEA有效性判定还可以采用其他方法，如SBM模型、全局DEA模型等。
03
CHAPTER
DEA的优化与改进
考虑了不同决策单元(DMU)在不同规模下的效率变化，能够更准确地评估DMU的效率。
总结词
规模报酬可变的DEA模型假设生产过程中可能存在规模效应，即随着生产规模的扩大，生产效率可能会提高。该模型通过调整权重来考虑不同规模下的效率变化，从而更准确地评估DMU的效率。
DEA的应用领域
02
CHAPTER
DEA基本模型
CCR模型
CCR模型（Charnes, Cooper和Rhodes模型）是最早提出的数据包络分析模型，用于评估决策单元（DMU）的相对效率。
02
CCR模型假设所有DMU都具有相同的输入和输出指标，并且规模报酬不变。

应用Matlab解决常用DEA模型的评价分析

ＱＩＮＹｉ，ＪＩＡＮＧＪｕｎ－ｙｉ
（ＳｈｅｎｙａｎｇＵｎｉｖｅｒｓｉｔｙｏｆＴｅｃｈｎｏｌｏｇｙ，Ｓｃｈｏｏｌ பைடு நூலகம்ｏｆＭａｎａｇｅｍｅｎｔ，Ｓｈｅｎｙａｎｇ１１０８７０，Ｃｈｉｎａ）
川 … ：．： … ”
㈩
Ｆｈ于模型（１）是非线性的，不利于计算，通过ＣＬ换，将模型（１）变成线性规划模型，如下所示：
变
Ａｈｎ＝ ∑ ｆＪ－１
权值，甚至零权重。随后研究人员相继提出了传统ＣＣＲ模型的对偶模型— — 包络ＤＥＡ模型，规模效应可变的ＢＣＣ模型，与传统ＣＣＲ相对的最劣ＣＣＲ模型以及为克服传统ＣＣＲ模型
电脑编程技巧与维护
应用Ｍａｔｌａｂ解决常用ＤＥＡ模型的评价分析
秦毅，姜钧译
（沈阳工业大学管理学院，沈阳１１０８７０）
摘
要：阐述多种常用的ＤＥＡ评价模型，利用矩阵形式表述模型结构，应用Ｍａｔｌａｂ对这些模型的评价程序进行编
Ａｂｓｔｒａｃｔ：ＴｈｉｓｐａｐｅｒｉｎｔｒｏｄｕｅｅｓｖａｉｏｒｕｓｃｏｍｍｏｎＤＥＡｍｏｄｅｌｓａｎｄｄｅｓｃｉｂｒｅｓｔｈｅｓｔｒｕｃｔｕｒｅｏｆｍｏｄｅｌｓｔｈｒｏｕｇｈｍａｔｒｉｘｆｏｒｍ，ａｆｔｅｒｗａｒｄｓ。ｗｒｉｔｅｓｐｒｏｇｒａｍｓｏｆｔｈｅｓｅｍｏｄｅｌｓｔｈｒｏｕｇｈＭａｔｌａｂ．ＳｏｗｅｃａｎｓｏｌｖｅｔｈｅｅｖａｌｕａｔｉｏｎｏｆｔｈｅｓｅＤＥＡｍｏｄｅｌｓｂｙＭａｔｌａｂｓｏｆｔｗａｒｅ．ａｎｄｏｖｅｒｃｏｍｅｔｈｅｐｒｏｂｌｅｍｏｆｌａｒｇｅａｍｏｕｎｔｏｆｃａｌｃｕｌａｔｉｏｎａｎｄｃｏｍｐｌｅｘｓｔｒｕｃｔｕｒｅｄｕｅｔｏｌｏｏｐｅｖａｌｕａｔｉｏｎｓ．Ｔｈｅｐｒｏ — ｇｒａｍｓｏｆｔｈｅｐａｐｅｒｉｎｃｌｕｄｅｔｒａｄｉｔｉｏｎａｌＤＥＡ— ＣＣＲｍｏｄｅｌａｎｄｉｔｓｄｕａｌｍｏｄｅ１．ＢＣＣｍｏｄｅ１．ｔｈｅｗｏｒｓｔＣＣＲｍｏｄｅｌａｎｄｓｕｐｅｒ — ｅｉｃｆｉｅｎｃｙＤＥＡ．ｗｈｉｃｈｐｒｏｖｉｄｅｃｏｎｖｅｎｉｅｎｃｅｏｒｆｆｕｔｕｒｅＤＥＡｅｖａｌｕａｔｉｏｎａｎｄｍｏｄｅｌｉｍｐｒｏｖｅｍｅｎｔ．Ｋｅｙｗｏｒｄｓ：ＤＥＡｍｏｄｅｌｓ；ＴｈｅｗｏｒｓｔＣＣＲ；Ｓｕｐｅｒｅｉｃｆｉｅｎｃｙ；Ｍａｔｌａｂｓｏｆｔｗａｒｅ；Ｌｉｎｅａｒｐｒｏｇｒａｍｍｉｎｇ

DEA-MATlab

模型((P 的模型C2 R)的MATLAB 程序clearX=[]; %用户输入多指标输入矩阵XY=[]; %用户输入多指标输出矩阵Yn=size(X',1); m=size(X,1); s=size(Y,1); A=[-X' Y'];b=zeros(n, 1);LB=zeros(m+s,1);UB=[];for i=1:n;f= [zeros(1,m) -Y(:,i)'];Aeq=[X(:,i)' zeros(1,s)];beq=1;w(:,i)=LINPROG(f,A,b,Aeq,beq,LB,UB); %解线性规划，得DMU;的最佳权向量w; E(i, i)=Y(:,i)'*w(m+1:m+s,i); %求出DMUi 的相对效率值Eiiendw %输出最佳权向量E %输出相对效率值EiiOmega=w(1:m,:) %输出投入权向量。

mu=w(m+1:m+s,:) %输出产出权向量。

模型(Dε的模型C 2R)的MA TLAB 程序clearX=[]; %用户输入多指标输入矩阵XY=[]; %用户输入多指标输出矩阵Yn=size(X',1); m=size(X,1); s=size(Y,1);epsilon=10^-10; %定义非阿基米德无穷小=10^-10f=[zeros(1,n) -epsilon*ones(1,m+s) 1]; %目标函数的系数矩阵：的系数为0,s-,s+的系数为-e,的系数为1；A=zeros(1,n+m+s+1); b=0; %<=约束；LB=zeros(n+m+s+1,1); UB=[]; %变量约束；LB(n+m+s+1)= -Inf; %-Inf 表示下限为负无穷大。

for i=1:n;Aeq=[X eye(m) zeros(m,s) -X(:,i)Y zeros(s,m) -eye(s) zeros(s,1)];beq=[zeros(m, 1 )Y(:,i)];w(:,i)=LINPROG (f,A,b,Aeq,beq,LB,UB); %解线性规划，得DMU 的最佳权向量w;endw %输出最佳权向量lambda=w(1:n,:) %输出s_minus=w(n+1:n+m,:) %输出ss_plus=w(n+m+1:n+m+s,:) %输出s+ theta=w(n+m+s+1,:) %输出w=1.0000 0.0000 0.0000 0.00000.0000 1.0000 0.0000 0.07130.0000 0.0000 1.0000 0.24950.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 28.50970.0000 0.0000 0.0000 0.00001.0000 1.0000 1.0000 0.8553lambda =1.0000 0.0000 0.0000 0.00000.0000 1.0000 0.0000 0.07130.0000 0.0000 1.0000 0.24950.0000 0.0000 0.0000 0.0000s_minus =0.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 0.00000.0000 0.0000 0.0000 28.5097s_plus =1.0e-005 *0.0000 0.0010 0.0037 0.1474theta = 1.0000 1.0000 1.0000 0.8553面对外需乏力的局面，中国经济增长的动力责无旁贷地落在了内需上，而作为中国最大内需潜力所在的城镇化，则迫切需解决效率不高的问题。

matlab相关代码

matlab相关代码Matlab是一种高级技术计算语言和交互式环境，广泛应用于科学、工程和金融等领域。

它具有强大的数学和图形处理能力，可以快速处理大量数据和进行复杂的算法分析。

以下是一些常用的Matlab相关代码：1. 矩阵操作Matlab中的矩阵操作非常方便，可以使用以下代码实现：a = [1 2 3; 4 5 6; 7 8 9]; % 定义一个3x3的矩阵b = [4 5 6; 7 8 9; 10 11 12]; % 定义另一个3x3的矩阵c = a + b; % 矩阵加法d = a - b; % 矩阵减法e = a * b; % 矩阵乘法f = a .* b; % 矩阵对应元素相乘g = a' % 矩阵转置2. 绘图Matlab中的绘图功能非常强大，可以使用以下代码实现：x = 0:0.1:2*pi; % 定义x轴的范围y = sin(x); % 定义y轴的值plot(x,y); % 绘制sin函数图像xlabel('x'); % 设置x轴标签ylabel('y'); % 设置y轴标签title('sin函数图像'); % 设置图像标题grid on; % 显示网格线3. 数据处理Matlab中的数据处理功能非常强大，可以使用以下代码实现：data = [1 2 3 4 5 6 7 8 9]; % 定义一个数据数组mean_data = mean(data); % 计算平均值std_data = std(data); % 计算标准差max_data = max(data); % 计算最大值min_data = min(data); % 计算最小值median_data = median(data); % 计算中位数4. 机器学习Matlab中的机器学习功能非常强大，可以使用以下代码实现：load fisheriris; % 加载鸢尾花数据集X = meas(:,1:2); % 取前两个特征Y = species; % 取标签svmModel = fitcsvm(X,Y); % 训练SVM模型svmModel.ClassNames % 显示类别名称svmModel.Beta % 显示模型系数总之，Matlab是一种非常强大的工具，可以帮助科学家、工程师和金融分析师等快速处理数据和进行复杂的算法分析。

MATLAB如何使用-教程-初步入门大全资料

运算数学表达式
加 a+b
减
a-b
乘 a×b
除 a÷ b
幂 a^b
MATLAB运算符
+ *
/(右除)或\(左除)
^
MATLAB表达式
a+b a-b a*b a/b或b\a a^b
示例
1+2 5-3 2*3
6/2或2\6 2^3
指出：右除相当于通常的除法。
22
七、MATLAB的变量与函数
1、变量变量就是在程序的运行过程中，其数值可以变化的量
MATLAB是交互式的语言，输入命令即给出运算结果。而命令窗口则是MATLAB的主要交互窗口，用于输入和编辑命令行等信息，显示结果（图形除外）。
当命令窗口中出现提示符“>>”时，表示MATLAB已经准备好，可以输入命令、变量或运行函数。提示符总是位于行首。
在每个指令行输入后要按回车键，才能使指令被 MATLAB执行。
28
矩阵的创建（续）
1、直接输入法－在命令窗口按规则输入方式创建矩阵
例1.在命令窗口创建简单的数值矩阵。
>>A=[1 3 2;3 1 0;2 1 5] 回车后在命令窗口显示如下结果
A=
132
310
215 例2.在命令窗口创建带运算表达式的矩阵，不显示结果。
>>y=[sin(pi/3),cos(pi/6);log(20),exp(2)]; 输入“y”回车，在命令窗口显示出来。
（3）在MATLAB安装目录\MATLAB6p5中双击 MATLAB快捷方式。
（4）在MATLAB安装目录\MATLAB6p5\bin\win32 中双击MATLAB.exe图标。

数据包络法（DEA）matlab程序

a=input('请输入投入数据：','s'); X=str2num(a);%用户输入多指标输入矩阵X b=input('请输入产出数据：','s'); Y=str2num(b);%用户输入多指标输出矩阵Y n=size(X', 1) m=size(X,1); s=size(Y,1); epsilon=10^-10; f=[zeros(1,n) -epsilon*ones(1,m+s) 1]; A=zeros(1,n+m+s+1);b=0; LB=zeros(n+m+s+1,1); UB=[]; LB(n+m+s+1)=-inf; for i=1:n; Aeq=[X eye(m) zeros(m,s) -X(:,i)
原先学长给了一个matlab程阵的输入修改了一下下
数据包络法（ DEA） matlab程序
DEA看了一天，结果学长告诉我说我们用的是方法，不需要去搞懂原理，知道怎么用就行了，我真是。。。唉，只有自己去找matlab程序。原先学长给了一个matlab程序，但是只是给的一个特定例子即特定矩阵的程序，自己上网查找了一下matlab矩阵的输入，修改了一下下。
Y zeros(s,m) -eye(s) zeros(s,1) ones(1,n) zeros(1,m+s+1)]; beq=[zeros(m,1) Y(:,i) 1]; w(:,i)=linprog(f, A, b, Aeq, beq, LB, UB); end w Lambda=w([1:n],:) s_minus=w([n+1:n+m],:) s_plus=w([n+m+1:n+m+s],:) theta=w(n+m+s+1,:)

dea模型 matlab程序

dea模型 matlab程序
DEA（数据包络分析）模型的MATLAB程序如下：
```matlab
% C R 模型（P 2 ）的 MATLAB 程序
clear
X=;%用户输入多指标输入矩阵 X
Y=;%用户输入多指标输出矩阵 Y
n=size(X,1);%DMU 个数
m=size(X,2);%输入指标个数
s=size(Y,2);%输出指标个数
A=-XY;%输入输出矩阵
b=zeros(n, 1);%常数项
LB=zeros(m+s,1);%下限
UB=;%上限
for i=1:n;
f=zeros(1,m) -Y(:,i);
Aeq=X(:,i) zeros(1,s);
beq=1;
w(:,i)=LINPROG(f,A,b,Aeq,beq,LB,UB);%解线性规划，得 DMU 的最佳权向量 w E(i, i)=Y(:,i)*w(m+1:m+s,i);%求出 DMU i 的相对效率值 Eii
end
w%输出最佳权向量
E%输出相对效率值 Eii
Omega=w(1:m,:)%输出投入权向量
mu=w(m+1:m+s,:)%输出产出权向量
```
请注意，这只是一个简单的示例程序，实际应用中可能需要根据具体情况进行调整和修改。

如需了解更多信息，请提供更具体的问题描述。

MATLAB 在DEA-Malmquist 分析中的应用

by Inmaculada C. Álvarez and others, this paper conduct a DEA-Malmquist analysis. The operation results show that the MATLAB
software is competent for DEA-Malmquist's analysis work and can provide the researches on economics and management with a
10.0000
27.0000
1.0000
0.0000
0.0000
0.0000
8
27.0000
22.0000
30.0000
0.7577
0.0000
0.0000
0.0000
9
37.0000
14.0000
31.0000
0.8201
1.6402
0.0000
0.0000
10
42.0000
25.0000
26.0000
指标的值。DEA 等价于解决下列问题：
⑴
min
θ s.t θx i = Xλ, Yλ = y i , λ i ≥ 0
θ,λ
其中 λ = [ λ 1
λ2
…
λ n ] 是一个半正定向量。由于
T
表1
DMU
PTEC、SE 的值，能满足绝大多数场景的 DEA 分析。
将文献 [10]中的 DEA 工具箱下载后，将文件夹
Computer Era No. 7 2021
·42 ·
DOI:10.16644/33-1094/tp.2021.07.011

matlab最优化计算薛定宇程序

一、介绍MATLAB最优化计算薛定宇程序MATLAB是一种用于数学计算、算法开发和数据分析的高级技术计算语言和交互式环境。

在MATLAB中，最优化计算是指寻找函数的最小值或最大值的过程。

薛定宇程序是一种基于MATLAB的最优化计算工具，其灵活性和可扩展性使其成为广泛使用的工具之一。

二、MATLAB最优化计算薛定宇程序的应用领域1. 工程优化：在工程领域，MATLAB最优化计算薛定宇程序可用于优化设计，例如在结构设计中寻找最佳材料使用方案，或者在控制系统设计中调整参数以满足性能指标。

2. 金融领域：在金融领域，MATLAB最优化计算薛定宇程序可用于风险管理、资产组合优化、期权定价等。

3. 生物医学领域：在生物医学领域，MATLAB最优化计算薛定宇程序可用于基因组学、蛋白质结构预测、医学图像处理等方面的研究。

4. 人工智能领域：在人工智能领域，MATLAB最优化计算薛定宇程序可用于优化神经网络的参数，改进机器学习算法等。

三、MATLAB最优化计算薛定宇程序的基本原理MATLAB最优化计算薛定宇程序以薛定宇法为基础，这是一种通过迭代寻找函数最小值的数值方法。

其基本原理包括以下几个步骤：1. 初始化：选择一个初始点作为搜索的起点。

2. 梯度计算：计算目标函数在当前点的梯度，即函数在该点的变化率。

3. 方向选择：根据梯度计算结果选择一个搜索方向。

4. 步长确定：确定在选择的搜索方向上的步长，即在该方向上移动的距离。

5. 更新：根据步长确定的结果，更新当前点的位置。

6. 收敛判断：判断算法是否收敛，即函数值是否趋于最小值。

四、MATLAB最优化计算薛定宇程序的主要特点1. 灵活性：MATLAB最优化计算薛定宇程序支持多种最优化算法和约束条件的设置，用户可以根据具体的问题选择合适的算法和约束条件。

2. 可扩展性：MATLAB最优化计算薛定宇程序支持用户自定义函数和约束条件，可以满足不同领域的需求。

3. 高效性：MATLAB最优化计算薛定宇程序经过优化，具有较高的计算效率和稳定性。

DEA软件利用说明

DEA软件利用说明
一、打开DEA-vsolver ，点击“视图”—“宏”—“查看宏”，弹出如下对话框：
点击“执行”，弹出如下对话框：
二、点击“click here to start”，然后点击“ok”
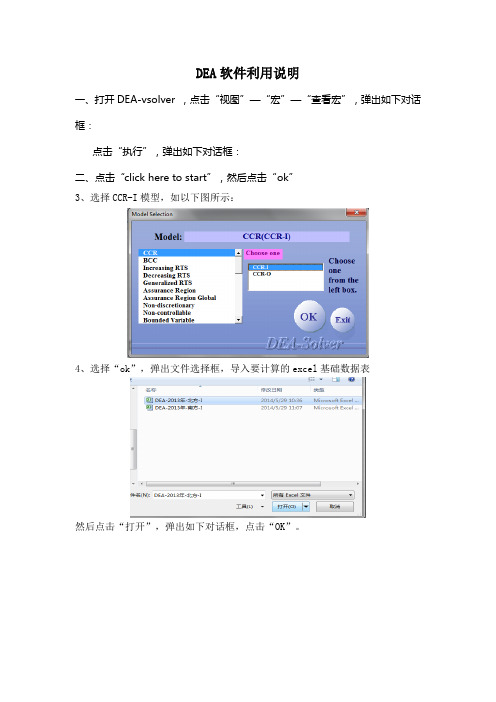
3、选择CCR-I模型，如以下图所示：
4、选择“ok”，弹出文件选择框，导入要计算的excel基础数据表
然后点击“打开”，弹出如下对话框，点击“OK”。

五、现在弹出如下对话框，该对话框表示：选择DEA运行结果的保留途径及文件名，若是选择桌面，文件名为“效率值”，那么会在桌面生成excel文件效率值，即DEA的运营结果。

六、选择好途径和输入要保留的文件名后，点击“保留”，弹出如下对话框：
7、最后点击“run”，软件将自动测算并在第5步当选择的途径处生成名为相应的excel文件。

注意事项
一、上述第4步中：导入要计算的excel基础数据表，该表只能有一个sheet，excel的指标名称格式必需如下：(I)表示投入指标，（O）表示产出指标。

A列本地网的名字无要求，能够随意起名。

二、结果说明：生成的excel文件有多个sheet，sheet“score”中即包括各本地网相对效率值和排名。

DMU列为各个本地网的名字，SCORE为本地网的相对效率值，RANK为本地网的排名。

DEA软件使用说明

DEA软件使用说明
1、打开DEA-vsolver 5.0，点击“视图”—“宏”—“查看宏”，弹出如下对话框：
点击“执行”，弹出如下对话框：
2、点击“click here to start”，然后点击“ok”
3、选择CCR-I模型，如下图所示：
4、选择“ok”，弹出文件选择框，导入要计算的excel基础数据表
然后点击“打开”，弹出如下对话框，点击“OK”。

5、此时弹出如下对话框，该对话框表示：选择DEA运行结果的保存路径及文件名，如果选择桌面，文件名为“效率值”，则会在桌面生成excel文件效率值，即DEA的运营结果。

6、选择好路径以及输入要保存的文件名后，点击“保存”，弹出如下对话框：
7、最后点击“run”，软件将自动测算并在第5步中选择的路径处生成名为相应的excel文件。

注意事项
1、上述第4步中：导入要计算的excel基础数据表，该表只能有一个sheet，excel的指标名称格式必须如下：(I)表示投入指标，（O）表示产出指标。

A列本地网的名字无要求，可以随意起名。

2、结果说明：生成的excel文件有多个sheet，sheet“score”中即包含各本地网相对效率值以及排名。

DMU列为各个本地网的名字，SCORE为本地网的相对效率值，RANK为本地网的排名。

-----精心整理，希望对您有所帮助!。

DEA-solver 软件操作中文版

B.5.1 CCR, BCC, IRS, DRS, GRS, SBM, Super-Efficinecy, Scale Elasticity, Congestion 和FDH 模型
表B.1是这些模型输入数据的例子
1.第一行
第一行是变量的名称，例如A1是我们研究问题的名称（医院），B1是投入变量
（医生），C1是投入变量（护士），D1是产出变量（门诊病人），E1是产出变量
（门诊病人）。

需要注意的是，投入变量（I）和产出变量(O)必须得在变量名称前加I或者O,否则
系统将不识别。

2.第二行及之后行
第二行表示第一个DMU的名称以及投入变量和产出变量的值，第三行往后以此类
推。

3.数据的范围
数据集应该从A1单元往右往下扩展。

4.数据表名称
不要用"Score","Rank", "Projection", "Weight", "WeightedData", "Slack", "RTS", "Window","Decomposition, "Graphl" and "Graph2"这些名称，因为软件中这些名称已
被命名含有不同含义。

B.1
表
在原始的投入（I）和产出（O）中加入坏（非期望）产出（OBad）。

如表B.12所示，这个模型需要通过键盘输入两个供给；好产出的权重和坏产出的权重默认值都为1.。