(经典)2012年全国中考数学试题分类解析汇编(159套63专题)专题59:新定义和跨学科问题
2012年全国中考数学试题分类解析汇编专题52:平面几何的综合
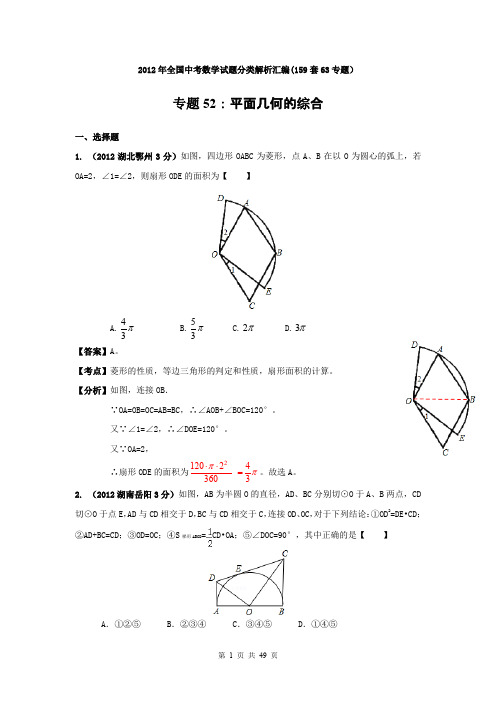
2012年全国中考数学试题分类解析汇编(159套63专题)专题52:平面几何的综合一、选择题1. (2012湖北鄂州3分)如图,四边形OABC 为菱形,点A 、B 在以O 为圆心的弧上,若OA=2,∠1=∠2,则扇形ODE 的面积为【 】A.π34B.π35C.π2D.π3【答案】A 。
【考点】菱形的性质,等边三角形的判定和性质,扇形面积的计算。
【分析】如图,连接OB .∵OA=OB=OC=AB=BC,∴∠AOB+∠BOC=120°。
又∵∠1=∠2,∴∠DOE=120°。
又∵OA=2,∴扇形ODE 的面积为21202 4 3603ππ⋅⋅=。
故选A 。
2. (2012湖南岳阳3分)如图,AB 为半圆O 的直径,AD 、BC 分别切⊙O 于A 、B 两点,CD 切⊙O 于点E ,AD 与CD 相交于D ,BC 与CD 相交于C ,连接OD 、OC ,对于下列结论:①OD 2=DE•CD; ②AD+BC=CD;③OD=OC;④S 梯形ABCD =CD•OA;⑤∠DOC=90°,其中正确的是【 】A .①②⑤ B.②③④ C.③④⑤ D.①④⑤【答案】A 。
【考点】切线的性质,切线长定理,相似三角形的判定与性质。
1052629【分析】如图,连接OE ,∵AD 与圆O 相切,DC 与圆O 相切,BC 与圆O 相切,∴∠DAO=∠DEO=∠OBC=90°,∴DA=DE,CE=CB ,AD∥BC。
∴CD=DE+EC=AD+BC。
结论②正确。
在Rt△ADO 和Rt△EDO 中,OD=OD ,DA=DE ,∴Rt△ADO≌Rt△EDO(HL )∴∠AOD=∠EOD。
同理Rt△CEO≌Rt△CBO,∴∠EOC=∠BOC。
又∠AOD+∠DOE+∠EOC+∠COB=180°,∴2(∠DOE+∠EOC)=180°,即∠DOC=90°。
结论⑤正确。
∴∠DOC=∠DEO=90°。
2012年全国中考数学试题分类解析汇编(159套63专题)专题3_整式2(教师篇)

2012年全国中考数学试题分类解析汇编(159套63专题)专题3_整式2(教师篇)2012年全国中考数学试题分类解析汇编(159套63专题)专题3:整式⼀、选择题1. (2012上海市4分)在下列代数式中,次数为3的单项式是【】A . xy 2B .x 3+y 3C ..x 3yD .3xy 【答案】A 。
2. (2012重庆市4分)计算)2ab 的结果是【】 A .2ab B .2a b C .22a b D .2ab 【答案】C 。
3. (2012安徽省4分)计算32)2(x -的结果是【】A.52x -B. 68x -C.62x -D.58x -【答案】B 。
4. (2012安徽省4分)某企业今年3⽉份产值为a 万元,4⽉份⽐3⽉份减少了10%,5⽉份⽐4⽉份增加了15%,则5⽉份的产值是【】A.(a -10%)(a +15%)万元B. a (1-10%)(1+15%)万元C.(a -10%+15%)万元D. a (1-10%+15%)万元【答案】B 。
5. (2012⼭西省2分)下列运算正确的是【】A .B .C .a 2a 4=a 8D .(﹣a 3)2=a 6【答案】D 。
6. (2012海南省3分)计算23x x ?,正确结果是【】A .6xB .5xC .9xD .8x 【答案】B 。
7. (2012海南省3分)当x 2=-时,代数式x +3的值是【】A .1B .-1C .5D .-5【答案】A 。
8. (2012陕西省3分)计算32(5a )-的结果是【】A .510a -B .610aC .525a -D .625a 【答案】D 。
9. (2012宁夏区3分)下列运算正确的是【】A .223a a =3-B .235(a )=aC .369a a =a ?D .222(2a )=4a 【答案】C 。
10. (2012⼴东佛⼭3分)23a a ?等于【】A .5aB .6aC .8aD .9a 【答案】A 。
2012年全国各地中考数学试题分类解析汇编(有理数)

2012年全国各地中考数学试题分类解析汇编第一章有理数(1)1、(2012•遵义)-(-2)的值是()A.-2 B.2 C.±2 D.4考点:相反数.专题:存在型.分析:根据相反数的定义可知,-(-2)是-2的相反数,由于-2<0,所以-(-2)=2.解答:∵-(-2)是-2的相反数,-2<0,∴-(-2)=2.故选B.点评:本题考查的是相反数的定义,即只有符号不同的两个数叫做互为相反数.2、(2012•遵义)据有关资料显示,2011年遵义市全年财政总收入202亿元,将202亿用科学记数法可表示()A.2.02×102 B.202×108 C.2.02×109 D.2.02×1010考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:将202亿用科学记数法表示为:202亿元=20200000000元=2.02×1010元,故选D.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3、(2012•自贡)|-3|的倒数是()A.-3 B.-1/3 C.3 D.1 /3考点:倒数;绝对值.分析:先计算|-3|=3,再求3的倒数,即可得出答案.解答:∵|-3|=3,∴|-3|的倒数是1 /3 .故选:D.点评:本题考查了倒数、绝对值的概念,熟练掌握绝对值与倒数的意义是解题关键.4、(2012•自贡)自贡市约330万人口,用科学记数法表示这个数为()A.330×104 B.33×105 C.3.3×105 D.3.3×106考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:将330万=3300000用科学记数法表示为:3.3×106.故选:D.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5、(2012•重庆)在-3,-1,0,2这四个数中,最小的数是()A.-3 B.-1 C.0 D.2考点:有理数大小比较.分析:画出数轴,在数轴上标出各点,再根据数轴的特点进行解答即可.解答:这四个数在数轴上的位置如图所示:由数轴的特点可知,这四个数中最小的数是-3.故选A.点评:本题考查的是有理数的大小比较,利用数形结合比较出有理数的大小是解答此题的关键•.6、(2012•肇庆)计算-3+2的结果是()A.1 B.-1 C.5 D.-5考点:有理数的加法.专题:计算题.分析:根据有理数的加法运算法则计算即可得解.解答: -3+2,=-(3-2),=-1.故选B.点评:本题考查了有理数的加法运算,是基础题,熟记运算法则是解题的关键.7、(2012•肇庆)用科学记数法表示5700000,正确的是()A.5.7×106 B.57×105 C.570×104 D.0.57×107考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于5700000有7位,所以可以确定n=7-1=6.解答: 5 700 000=5.7×106.故选A.点评:此题考查科学记数法表示较大的数的方法,准确确定n值是关键.8、(2012•张家界)-2012的相反数是()A.-2012 B.2012 C.-1/2012 D.1 /2012考点:相反数.分析:据相反数的性质,互为相反数的两个数和为0,采用逐一检验法求解即可.解答:根据概念,(-2012的相反数)+(-2012)=0,则-2012的相反数是2012.故选B.点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.9、(2012•湛江)2的倒数是()A.2 B.-2 C.1/2 D.-1 /2考点:倒数.分析:直接根据倒数的定义进行解答即可.解答:∵2×1 /2 =1,∴2的倒数是1 /2 .故选C.点评:本题考查的是倒数的定义,即乘积是1的两数互为倒数.10、(2012•湛江)国家发改委已于2012年5月24日核准广东湛江钢铁基地项目,项目由宝钢湛江钢铁有限公司投资建设,预计投产后年产10200000吨钢铁,数据10200000用科学记数法表示为()A.102×105 B.10.2×106 C.1.02×106 D.1.02×107考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:将10200000用科学记数法表示为:1.02×107.故选:D.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.11、(2012•玉林)计算:22 =()A.1 B.2 C.4 D.8考点:有理数的乘方.分析:利用有理数乘方的意义求得结果即可.解答:原式=2×2=4,故选C.点评:本题考查了有理数的乘方,属于基本运算,比较简单.12、(2012•益阳)-2的绝对值等于()A.2 B.-2 C.1/2 D.±2考点:绝对值.专题:计算题.分析:根据绝对值的性质,当a是正有理数时,a的绝对值是它本身a;即可解答.解答:根据绝对值的性质,|2|=2.故选A.点评:本题考查了绝对值的性质,①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零.13、(2012•义乌市)-2的相反数是()A.2 B.-2 C.±2 D.-1/2考点:相反数.分析:根据相反数的定义进行解答即可.解答:由相反数的定义可知,-2的相反数是-(-2)=2.故选A.点评:本题考查的是相反数的定义,即只有符号不同的两个数叫做互为相反数.14、(2012•宜昌)如图,数轴上表示数-2的相反数的点是()A.点P B.点Q C.点M D.点N考点:数轴;相反数.分析:根据数轴得出N、M、Q、P表示的数,求出-2的相反数,根据以上结论即可得出答案.解答:从数轴可以看出N表示的数是-2,M表示的数是-0.5,Q表示的数是0.5,P表示的数是2,∵-2的相反数是2,∴数轴上表示数-2的相反数是点P,故选A.点评:本题考查了数轴和相反数的应用,主要培养学生的观察图形的能力和理解能力,题型较好,难度不大.15、(2012•宜昌)2012年4月30日,我国在西昌卫星发射中心用“长征三号乙”运载火箭成功发射两颗北斗导航卫星,其中静止轨道卫星的高度约为36000km.这个数据用科学记数法表示为()A.36×103km B.3.6×103km C.3.6×104km D.0.36×105km考点:科学记数法—表示较大的数.分析:科学记数法就是将一个数字表示成(a×10的n次幂的形式),其中1≤|a|<10,n表示整数.n为整数位数减1,即从左边第一位开始,在首位非零的后面加上小数点,再乘以10的n次幂.解答:36000=3.6×104km.故选C.点评:用科学记数法表示一个数的方法是(1)确定a:a是只有一位整数的数;(2)确定n:当原数的绝对值≥10时,n为正整数,n等于原数的整数位数减1;当原数的绝对值<1时,n为负整数,n的绝对值等于原数中左起第一个非零数前零的个数(含整数位数上的零).16、(2012•宜宾)-3的倒数是()A.1/3 B.3 C.-3 D.-1 /3考点:倒数.分析:据倒数的定义,互为倒数的两数乘积为1,-3×(-1 /3)=1.解答:根据倒数的定义得:-3×(-1 /3 )=1,因此倒数是-1/ 3 .故选:D.点评:此题考查的是倒数,关键明确倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.需要注意的是负数的倒数还是负数.17、(2012•扬州)-3的绝对值是()A.3 B.-3 C.-3 D.1/3考点:绝对值.分析:计算绝对值要根据绝对值的定义求解.第一步列出绝对值的表达式;第二步根据绝对值定义去掉这个绝对值的符号.解答:-3的绝对值是3.故选:A.点评:此题主要考查了绝对值的定义,规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.18、(2012•扬州)今年我市参加中考的人数大约有41300人,将41300用科学记数法表示为()A.413×102 B.41.3×103 C.4.13×104 D.0.413×103考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答: 41300=4.13×104,故选:C.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.19、(2012•孝感)我国平均每平方千米的土地上,一年从太阳得到的能量相当于燃烧130000吨煤所产生的能量.130000用科学记数法表示为()A.13×104 B.1.3×105 C.0.13×106 D.1.3×108考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:130000=1.3×105,故选:B.点评:此题主要考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.20、(2012•襄阳)一个数的绝对值等于3,这个数是()A.3 B.-3 C.±3 D.1/3考点:绝对值.分析:根据绝对值的定义即可求解.解答:因为|3|=3,|-3|=3,所以绝对值等于3的数是±3.故选C.点评:规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.本题是绝对值性质的逆向运用,此类题要注意答案一般有2个,除非绝对值为0的数才只有一个为0.21、(2012•襄阳)李阳同学在“百度”搜索引擎中输入“魅力襄阳”,能搜索到与之相关的结果个数约为236 000,这个数用科学记数法表示为()A.2.36×103 B.236×103 C.2.36×105 D.2.36×106考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:236 000=2.36×105,故选:C.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.22、(2012•咸宁)-8的相反数是()A.-8 B.8 C.-1/8 D.1/8考点:相反数.分析:直接根据相反数的定义进行解答即可.解答:由相反数的定义可知,-8的相反数是-(-8)=8.故选B.点评:本题考查的是相反数的定义,即只有符号不同的两个数叫做互为相反数.23、(2012•咸宁)南海是我国固有领海,它的面积超过东海、黄海、渤海面积的总和,约为360万平方千米,360万用科学记数法表示为()A.3.6×102 B.360×104 C.3.6×104 D.3.6×106考点:科学记数法—表示较大的数.分析:单位为“万”,换成计数单位为1的数,相当于把原数扩大10000倍,进而把得到的数表示成a×10n的形式,a为3.6,n为整数数位减去1.解答:360万=3600000=3.6×106,故选D.点评:考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.24、(2012•武汉)在2.5,-2.5,0,3这四个数种,最小的数是()A.2.5 B.-2.5 C.0 D.3考点:有理数大小比较.分析:根据有理数的大小比较法则是负数都小于0,正数都大于0,正数大于一切负数进行比较即可.解答:∵-2.5<0<2.5<3,∴最小的数是-2.5,故选B.点评:本题考查了有理数的大小比较法则的应用,有理数的大小比较法则是:负数都小于0,正数都大于0,正数大于一切负数,两个负数比较大小,其绝对值大的反而小.25、(2012•武汉)某市2012年在校初中生的人数约为23万.数230000用科学记数法表示为()A.23×104 B.2.3×105 C.0.23×103 D.0.023×106考点:科学记数法—表示较大的数.专题:常规题型.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于23万有6位,所以可以确定n=6-1=5.解答:23万=230 000=2.3×105.故选B.点评:此题考查科学记数法表示较大的数的方法,准确确定n值是关键.26、(2012•潍坊)许多人由于粗心,经常造成水龙头“滴水”或“流水”不断.根据测定,一般情况下一个水龙头“滴水”1个小时可以流掉3.5千克水,若1年按365天计算,这个水龙头1年可以流掉()千克水.(用科学记数法表示,保留3个有效数字)A.3.1×104 B.0.31×105 C.3.06×104 D.3.07×104考点:科学记数法与有效数字.分析:先列式表示1年水龙头滴水的重量,再把结果用科学记数法表示.有效数字是从左边第一个不是0的数字起,后面所有的数字都是有效数字.用科学记数法表示的数的有效数字只与前面的a有关,与10的多少次方无关.解答:3.5×24×365=30660=3.066×104≈3.07×104故选D.点评:此题主要考查了有理数的乘法在实际生活中的应用,科学记数法的表示方法,以及用科学记数法表示的数的有效数字的确定方法.27、(2012•铜仁地区)从权威部门获悉,中国海洋面积是299.7万平方公里,约为陆地面积的三分之一,299.7万平方公里用科学记数法表示为()平方公里(保留两位有效数字)A.3×106 B.0.3×107 C.3.0×106 D.2.99×106考点:科学记数法与有效数字.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于299.7万有7位,所以可以确定n=7-1=6.有效数字的计算方法是:从左边第一个不是0的数字起,后面所有的数字都是有效数字.用科学记数法表示的数的有效数字只与前面的a有关,与10的多少次方无关.解答:299.7万=2.997×106≈3.0×106.故选:C.点评:此题主要考查了科学记数法的表示方法,以及用科学记数法表示的数的有效数字的确定方法.28、(2012•天门)2012的绝对值是()A.2012 B.-2012 C.1/2012 D.-1/2012考点:绝对值.专题:计算题.分析:根据绝对值的性质直接解答即可.解答:∵2012是正数,∴|2012|=2012,故选A.点评:本题考查了绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.29、(2012•天门)吸烟有害健康.据中央电视台2012年5月30日报道,全世界每因吸烟引起的疾病致死的人数大约为600万,数据600万用科学记数法表示为()A.0.6×107 B.6×106 C.60×105 D.6×105考点:科学记数法—表示较大的数.分析:首先把600万化为6000000,再用科学记数法表示,科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:600万=6000000=6×106,故选:B.点评:此题主要考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.30、(2012•天津)据某域名统计机构公布的数据显示,截至2012年5月21日,我国“.NET”域名注册量约为560000个,居全球第三位,将560000用科学记数法表示应为()A.560×103 B.56×104 C.5.6×105 D.0.56×106考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于560000有6位,所以可以确定n=6-1=5.解答:560 000=5.6×105.故选C.点评:此题考查科学记数法表示较大的数的方法,准确确定n值是关键.31、(2012•泰州)过度包装既浪费资源又污染环境.据测算,如果全国每年减少10%的过度包装纸用量,那么可减排二氧化碳3120000吨,把数3120000用科学记数法表示为()A.3.12×105 B.3.12×106 C.31.2×105 D.0.312×107考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:将3120000用科学记数法表示为:3.12×106.故选:B.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.32、(2012•泰安)下列各数比-3小的数是()A.0 B.1 C.-4 D.-1考点:有理数大小比较.分析:首先判断出1>-3,0>-3,求出每个数的绝对值,根据两负数比较大小,其绝对值大的反而小,求出即可.解答:根据两负数比较大小,其绝对值大的反而小,正数都大于负数,零大于一切负数,∴1>-3,0>-3,∵|-3|=3,|-1|=1,|-4|=4,∴比-3小的数是负数,是-4.故选C .点评:本题考查了有理数的大小比较法则和绝对值等知识点的应用,注意:正数都大于负数,两负数比较大小,其绝对值大的反而小,题型较好,但是一道比较容易出错的题目.33、(2012•泰安)已知一粒米的质量是0.000021千克,这个数字用科学记数法表示为( )A .21×104-千克B .2.1×106-千克C .2.1×105-千克D .21×104-千克考点:科学记数法—表示较小的数.分析:绝对值小于1的正数也可以利用科学记数法表示,一般形式为a ×10n -,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解答: 0.000021=2.1×105-; 故选:C .点评:本题考查了用科学记数法表示较小的数,一般形式为a ×10n -,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定.34、(2012•台州)计算-1+1的结果是( )A .1B .0C .-1D .-2考点:有理数的加法.专题:常规题型.分析:根据互为相反数的和等于0解答.解答: -1+1=0.故选B .点评:本题考查了有理数的加法运算,是基础题,熟记运算法则是解题的关键.35、(2012•台湾)计算(-100051)×(5-10)之值为何?( )A .1000B .1001C .4999D .5001考点:有理数的乘法.专题:计算题.分析:将-100051化为-(1000+51),然后计算出5-10,再根据分配律进行计算. 解答:原式=-(1000+51)×(-5)=(1000+51)×5 =1000×5+51×5=5000+1=5001.故选D.点评:本题考查了有理数的乘法,灵活运用分配律是解题的关键.36、(2012•台湾)如图是利用短除法求出三数8、12、18的最大公因子的过程.利用短除法,求出这三数的最小公倍数为何?()A.12 B.72 C.216 D.432考点:有理数的除法.专题:常规题型.分析:继续完善短除法,然后根据最小公倍数的求法,把所有的数相乘即可.解答:如图,完成短除法如下最小公倍数为2×2×3×2×1×3=72.故选B.点评:本题考查了短除法求最小公倍数的方法,属于小学内容,比较简单,完善短除过程是解题的关键.37、(2012•台湾)已知某公司去年的营业额为四千零七十亿元,则此营业额可用下列何者表示?()A.4.07×109元 B.4.07×1010元 C.4.07×1011元 D.4.07×1012元考点:科学记数法—表示较大的数.分析:首先将四千零七十亿元可写成407000000000,再利用科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:将四千零七十亿元可写成407000000000,407000000000=4.07×1011,故选:C.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.38、(2012•随州)湿地旅游爱好者小明了解到鄂东南某市水资源总量为42.43亿立方米,其中42.43亿用科学记数法可表示为()A.42.43×109 B.4.423×108 C.4.243×109 D.0.423×108考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:根据42.43亿=4243000000,用科学记数法表示为:4.243×109.故选:C.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.39、(2012•宿迁)-8的绝对值是()A.8 B.1/8 C.-1/8 D.-8考点:绝对值.分析:根据负数的绝对值等于它的相反数解答.解答: -8的绝对值为|-8|=8.故选A.点评:本题考查了绝对值的性质,熟记一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0是解题的关键.40、(2012•沈阳)沈阳地铁2号线的开通,方便了市民的出行.从2012年1月9日到2月7日的30天里,累计客运量约达3040000人次,将3040000用科学记数法表示为()A.3.04×105 B.3.04×106 C.30.4×105 D.0.304×107考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:将3040000用科学记数法表示为3.04×106.故选B.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.41、(2012•深圳)第八届中国(深圳)文博会以总成交额143 300 000 000元再创新高,将数143 300 000 000用科学记数法表示为()A.1.433×1010 B.1.433×1011 C.1.433×1012 D.0.1433×1012考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于143 300 000 000有12位,所以可以确定n=12-1=11.解答:143 300 000 000=1.433×1011.故选B.点评:此题考查科学记数法表示较大的数的方法,准确确定n值是关键.42、(2012•绍兴)3的相反数是()A.3 B.-3 C.1/3 D.-1/3考点:相反数.分析:根据相反数的意义,3的相反数即是在3的前面加负号.解答:根据相反数的概念及意义可知:3的相反数是-3.故选B.点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.43、(2012•绍兴)据科学家估计,地球年龄大约是4 600 000 000年,这个数用科学记数法表示为()A.4.6×108 B.46×108 C.4.6×109 D.0.46×1010考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答: 4 600 000 000用科学记数法表示为:4.6×109.故选:C.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.44、(2012•陕西)如果零上5℃记作+5℃,那么零下7℃可记作()A.-7℃ B.+7℃ C.+12℃ D.-12℃考点:正数和负数.分析:在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.解答:∵“正”和“负”相对,∴零上5℃记作+5℃,则零下7℃可记作-7℃.故选A.点评:此题考查了正数与负数的定义.解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.45、(2012•山西)为了实现街巷硬化工程高质量“全覆盖”,我省今年1-4月公路建设累计投资92.7亿元,该数据用科学记数法可表示为()A.0.927×1010 B.92.7×109 C.9.27×1011 D.9.27×109考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:将92.7亿=9270000000用科学记数法表示为:9.27×109.故选:D.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.46、(2012•日照)-5的相反数是()A.-5 B.-1/5 C.5 D.1/5考点:相反数.分析:根据相反数的定义解答.解答:只有符号不同的两个数称为互为相反数,则-5的相反数为5,故选C.点评:本题考查了相反数的定义,只有符号不同的两个数互为相反数,a的相反数是-a.47、(2012•日照)据新华社报道:在我国南海某海域探明可燃冰储量约有194亿立方米.194亿用科学记数法表示为()A.1.94×1010 B.0.194×1010 C.19.4×109 D.1.94×109考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:194亿=19400000000,用科学记数法表示为:1.94×1010.故选:A.点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.48、(2012•泉州)-7的相反数是()A.-7 B.7 C.-1/7 D.1/7考点:相反数.分析:据相反数的性质,互为相反数的两个数和为0,采用逐一检验法求解即可.解答:根据概念,(-7的相反数)+(-7)=0,则-7的相反数是7.故选B.点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.49、(2012•衢州)下列四个数中,最小的数是( ) A .2 B .-2 C .0 D .-1/2 考点:有理数大小比较. 专题:探究型.分析:根据有理数比较大小的法则进行比较即可. 解答:∵2>0,-2<0,-1/2 <0, ∴可排除A 、C ,∵|-2|=2,|-1 /2 |=1 2 ,2>1/ 2 , ∴-2<-1/ 2 . 故选B .点评:本题考查的是有理数的大小比较,熟知正数都大于0; 负数都小于0; 正数大于一切负数; 两个负数,绝对值大的其值反而小是解答此题的关键.50、(2012•衢州)衢州市是国家优秀旅游城市,吸引了众多的海内外游客.据衢州市2011年国民经济和社会发展统计报显示,全年旅游总收入达121.04亿元.将121.04亿元用科学记数法可表示为( )A .12.104×109元B .12.104×1010元C .1.2104×1010元D .1.2104××1011元 考点:科学记数法—表示较大的数. 分析:科学记数法的表示形式为a ×10n的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.解答:将121.04亿用科学记数法表示为:121.04亿元=12104000000元=1.2104×1010元, 故选;C .点评:此题考查了科学记数法的表示方法.科学记数法的表示形式为a ×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值. 51、(2012•青岛)-2的绝对值是( )A .-1/2B .-2C .1 /2D .2 考点:绝对值.分析:根据绝对值的定义:数轴上某个数与原点的距离叫做这个数的绝对值.则-2的绝对值就是表示-2的点与原点的距离.解答: |-2|=2, 故选:D .点评:此题主要考查了绝对值,关键是掌握:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.52、(2012•黔西南州)-141的倒数是( ) A .-45 B .45 C .-54 D .54考点:倒数.。
2012年全国中考数学试题分类解析汇编专题59:新定义和跨学科问题
2012年全国中考数学试题分类解析汇编(159套63专题)专题59:新定义和跨学科问题一、选择题1. (2012浙江丽水、金华3分)如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是【】A【答案】【考点】【分析】2. (A.B.C.D.【答案】D。
【考点】跨学科问题,反比例函数的图象。
【分析】∵在公式I=UR中,当电压U一定时,电流I与电阻R之间的函数关系不反比例函数关系,且R为正数,∴选项D正确。
故选D。
3. (2012湖北随州4分)定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l 1、l 2的距离分别为a 、b ,则称有序非实数对(a ,b )是点M 的“距离坐标”,根据上述定义,距离坐标为(2,3)的点的个数是【 】A .2B .1C . 4D .3【答案】C 。
【考点】新定义,点的坐标,点到直线的距离。
【分析】画出两条相交直线,到l 1的距离为2的直线有2条,到l 2的距离为3的直线有2条,看所画的这些直线的交点有几个即为所求的点的个数:4. ( 】A .2I=R 【答案】【考点】【分析】5. (2012湖南益阳4分)在一个标准大气压下,能反映水在均匀加热过程中,水的温度(T )随加热时间(t )变化的函数图象大致是【 】A .B .C .D .【答案】B。
【考点】跨学科问题,函数的图象。
【分析】根据在一个标准大气压下水加热到100℃后水温不会继续增加,而是保持100℃不变,据此可以6. (3)=(3,2),g(6,﹣5)【答案】【考点】【分析】7. (20122【】A.32B.25C.425D.254【答案】B。
【考点】新定义,求函数值。
【分析】根据所给的函数关系式所对应的自变量的取值范围,发现:当x=52时,在2≤x≤4之间,所以将x的值代入对应的函数即可求得y的值:112y===5x52。
全国各地2012年中考数学分类解析(159套)专题5分式

2012年全国中考数学试题分类解析汇编(159套63专题)专题5:分式一、选择题1. (2012安徽省4分)化简xx x x-+-112的结果是【 】A.x +1B. x -1C.—xD. x 【答案】D 。
【考点】分式的加法运算【分析】分式的加减,首先看分母是否相同,同分母的分式加减,分母不变,分子相加减,如果分母不同,先通分,后加减,本题分母互为相反数,可以化成同分母的分式加减:222(1)111111xx xx x x x x x x xx x x x --+=-===------。
故选D 。
2. (2012浙江湖州3分)要使分式1x有意义,x 的取值范围满足【 】A .x=0B .x≠0 C.x >0 D .x <0 【答案】B 。
【考点】分式有意义的条件。
【分析】根据分式分母不为0的条件,要使1x在实数范围内有意义,必须x≠0。
故选B 。
3.(2012浙江嘉兴、舟山4分)若分式x 1x+2-的值为0,则【 】A . x=﹣2B . x=0C . x=1或2D .x=1 【答案】D 。
【考点】分式的值为零的条件。
【分析】∵分式x 1x+2-的值为0,∴x 1=0x+2x+20-⎧⎪⎨⎪≠⎩,解得x=1。
故选D 。
4. (2012浙江绍兴4分)化简111xx --可得【 】 A .21x x- B . 21x x--C .221x x x+- D .221x x x--【答案】B 。
【考点】分式的加减法。
【分析】原式=211(1)x x x x x x--=---。
故选B 。
5. (2012浙江义乌3分)下列计算错误的是【 】 A .0.2a b 2a b 0.7a b7a b++=-- B .3223x y x yx y=C .a b 1b a-=-- D .123ccc+=【答案】A 。
【考点】分式的混合运算。
【分析】根据分式的运算法则逐一作出判断:A 、0.2a b 2a 10b 0.7a b 7a 10b++=--,故本选项错误;B 、3223x y x yx y=,故本选项正确;C 、a b b a 1b a b a--=-=---,故本选项正确;D 、123ccc+=,故本选项正确。
2012年全国中考数学试题分类解析汇编(159套63专题)专题58:开放探究型问题

2012年全国中考数学试题分类解析汇编(159套63专题)专题58:开放探究型问题一、选择题二、填空题1. (2012陕西省3分)在同一平面直角坐标系中,若一个反比例函数的图象与一次函数y=2x+6-的图象无.公共点,则这个反比例函数的表达式是 ▲ (只写出符合条件的一个即可). 【答案】5y x=(答案不唯一)。
【考点】开放型问题,反比例函数与一次函数的交点问题,一元二次方程根与系数的关系。
【分析】设反比例函数的解析式为:k y x =, 联立y=2x+6-和k y x=,得k 2x+6x -=,即22x 6x+k 0-= ∵一次函数y=2x+6-与反比例函数k y x= 图象无公共点, ∴△<0,即268k 0<--(),解得k >92。
∴只要选择一个大于92的k 值即可。
如k=5,这个反比例函数的表达式是5y x=(答案不唯一)。
2. (2012广东湛江4分) 请写出一个二元一次方程组 ▲ ,使它的解是x=2y=1⎧⎨-⎩.【答案】x+y=1x+2y=0⎧⎨⎩(答案不唯一)。
【考点】二元一次方程的解。
【分析】根据二元一次方程解的定义,围绕x=2y=1⎧⎨-⎩列一组等式,例如:由x +y=2+(-1)=1得方程x +y=1;由x -y=2-(-1)=3得方程x -y=3;由x +2y=2+2(-1)=0得方程x +2y=0;由2x +y=4+(-1)=3得方程2x +y=3;等等,任取两个组成方程组即可,如x+y=1x+2y=0⎧⎨⎩(答案不唯一)。
3. (2012广东梅州3分)春蕾数学兴趣小组用一块正方形木板在阳光做投影实验,这块正方形木板在地面上形成的投影是可能是▲ (写出符合题意的两个图形即可)【答案】正方形、菱形(答案不唯一)。
【考点】平行投影。
【分析】根据平行投影的特点:在同一时刻,平行物体的投影仍旧平行。
所以,在同一时刻,这块正方形木板在地面上形成的投影是平行四边形或特殊的平行四边形,例如,正方形、菱形(答案不唯一)。
2012年全国中考数学试题分类解析汇编(159套63专题)专题10_分式方程

2012年全国中考数学试题分类解析汇编(159套63专题)专题10:分式方程一、选择题1. (2012海南省3分)分式方程12x +2x 1x+1=-的解是【 】 A .1 B .-1 C .3 D .无解【答案】C 。
【考点】解分式方程。
【分析】首先去掉分母,观察可得最简公分母是(x+1)(x ﹣1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解: ()()()12x +2x+1+2x x 12x+1x 1x 3x 1x+1=⇒-=-⇒=-。
∵x 3=时,(x+1)(x ﹣1)≠0,∴x 3=是原方程的解。
故选C 。
2. (2012浙江丽水、金华3分)把分式方程21=x+4x 转化为一元一次方程时,方程两边需同乘以【 】A .xB .2xC .x +4D .x(x +4)【答案】D 。
【考点】解分式方程。
【分析】根据各分母寻找公分母x(x +4),方程两边乘最简公分母,可以把分式方程转化为整式方程。
故选D 。
3. (2012福建三明4分)分式方程52=x+3x的解是【 】 A .x=2 B .x=1 C .x=12D .x=-2 【答案】A 。
【考点】解分式方程。
【分析】首先去掉分母,观察可得最简公分母是x (x +3),方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解:去分母,得5x=2(x +3),解得x=1。
检验,合适。
故选A 。
4. (2012湖北随州4分)分式方程10060=20+v 20v-的解是【 】 A.v=-20 B. v =5 C. v =-5 D. v =20【答案】B 。
【考点】解分式方程。
【分析】观察可得最简公分母是(20+v )(20-v ),方程两边乘最简公分母,可以把分式方程转化为整式方程求解:方程的两边同乘(20+v )(20-v ),得100(20-v )=60(20+v ),解得:v=5。
2012年全国中考数学试题分类解析汇编(159套63专题)专题60:代数几何综合

2012年全国中考数学试题分类解析汇编(159套63专题)专题60:代数几何综合一、选择题1. (2012浙江义乌3分)一个正方形的面积是15,估计它的边长大小在【 】A .2与3之间B .3与4之间C .4与5之间D .5与6之间【答案】B 。
【考点】算术平方根,估算无理数的大小。
【分析】∵一个正方形的面积是15,∵9<15<16<4。
故选B 。
2. (2012浙江杭州3分)已知抛物线()3y k x 1x k ⎛⎫=+ ⎪⎝⎭-与x 轴交于点A ,B ,与y 轴交于点C ,则能使△ABC 为等腰三角形的抛物线的条数是【 】A .2B .3C .4D .5【答案】B 。
【考点】抛物线与x 轴的交点。
【分析】根据抛物线的解析式可得C (0,﹣3),再表示出抛物线与x 轴的两个交点的横坐标,再根据ABC 是等腰三角形分三种情况讨论,求得k 的值,即可求出答案:根据题意,得C (0,﹣3).令y=0,则()3k x 1x 0k ⎛⎫+= ⎪⎝⎭-,解得x=﹣1或x=3k 。
设A 点的坐标为(﹣1,0),则B (3k,0), ①当AC=BC 时,OA=OB=1,B 点的坐标为(1,0),∴3k =1,k=3; ②当AC=AB 时,点B 在点A 的右面时,∵AC =B 1,0),∴31,k k ==③当AC=AB 时,点B 在点A 的左面时,B 0),∴3k k == 。
∴能使△ABC 为等腰三角形的抛物线的条数是3条。
故选B 。
3. (2012浙江湖州3分)如图,已知点A (4,0),O 为坐标原点,P 是线段OA 上任意一点(不含端点O ,A ),过P 、O 两点的二次函数y 1和过P 、A 两点的二次函数y 2的图象开口均向下,它们的顶点分别为B 、C ,射线OB 与AC 相交于点D .当OD=AD=3时,这两个二次函数的最大值之和等于【 】A C .3 D .4 【答案】A 。
【考点】二次函数的性质,等腰三角形的性质,勾股定理,相似三角形的判定和性质。
2012年全国中考数学试题分类解析汇编专题:38等腰(边)三角形

2012年全国中考数学试题分类解析汇编(159套63专题)专题:38等腰(边)三角形一、选择题1. (2012宁夏区3分)一个等腰三角形两边的长分别为4和9,那么这个三角形的周长是【】A.13 B.17 C.22 D.17或22【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】求等腰三角形的周长,即是确定等腰三角形的腰与底的长;题目给出等腰三角形有两条边长为4和9,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形:①若4为腰长,9为底边长,由于4+4<9,则三角形不存在;②9为腰长,则符合三角形的两边之和大于第三边。
∴这个三角形的周长为9+9+4=22。
故选C。
2. (2012广东肇庆3分)等腰三角形两边长分别为4和8,则这个等腰三角形的周长为【】A.16 B.18 C.20 D.16或20【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】由于题中没有指明哪边是底哪边是腰,则应该分两种情况进行分析:①当4为腰时,4+4=8,故此种情况不存在;②当8为腰时,8-4<8<8+4,符合题意。
∴此三角形的周长=8+8+4=20。
故选C。
3. (2012江苏常州2分)已知三角形三边的长分别为4,9,则这个等腰三角形的周长为【】A.13B.17C.22D.17或22【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】由三角形三边的长分别为4,9,知三角形三边的长分别为4,4,9或4,9,9,但由于4,4,9与三角形的构成条件“两边之和大于第三边,两边之差小于第三边”不符,因此,三角形三边的长只能分别为4,9,9 ,周长为22。
故选C。
4. (2012江苏徐州3分)如果等腰三角形的两边长分别为2和5,则它的周长为【】A.9 B.7 C.12D.9或12【答案】C。
【考点】等腰三角形的性质,三角形三边关系。
【分析】根据等腰三角形的性质,如果等腰三角形的两边长分别为2和5,则另一边可能是2或5。
2012年全国中考数学试题分类解析汇编(159套63专题)专题2_实数的运算无答案版

2012年全国中考数学试题分类解析汇编(159套63专题)专题2:实数的运算一、选择题1. (2012山西省2分)计算:﹣2﹣5的结果是【 】 A . ﹣7B . ﹣3C . 3D . 72. (2012广东佛山3分)与2÷3÷4运算结果相同的是【 】A .4÷2÷3B .2÷(3×4)C .2÷(4÷2)D .3÷2÷43. (2012广东梅州3分)012⎛⎫-- ⎪⎝⎭=【 】A .﹣2B .2C .1D .﹣14. (2012广东肇庆3分)计算 23+- 的结果是【 】A .1B .1-C . 5D . 5- 5. (2012浙江杭州3分)计算(2﹣3)+(﹣1)的结果是【 】 A .﹣2 B .0 C .1 D .26. (2012浙江嘉兴、舟山4分)(﹣2)0等于【 】 A . 1B . 2C . 0D . ﹣27. (2012浙江宁波3分)(﹣2)0的值为【 】 A .﹣2 B .0 C .1 D .28. (2012浙江台州4分)计算-1+1的结果是【 】 A.1 B.0 C.-1 D.-29. (2012浙江宁波3分)如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是【 】A .41B .40C .39D .3810. (2012江苏南通3分)计算6÷(-3)的结果是【 】A .- 12B .-2C .-3D .-1811. (2012江苏泰州3分)13-等于【 】 A .3 B .31-C .-3D .31 12. (2012江苏苏州3分)若m m 1139273⨯⨯=,则m 的值为【 】 A.3 B.4 C.5 D. 613. (2012广东河源3分)021⎪⎭⎫⎝⎛--=【 】A .-2B .2C .1D .-1 14. (2012福建龙岩4分)计算:2-3 =【 】 A .-1B .1C .-5D .515. (2012湖南湘潭3分)文文设计了一个关于实数运算的程序,按此程序,输入一个数后,输出的数比输入的数的平方小1,则输出的结果为【 】 A .5 B .6 C .7 D .816.(2012四川南充3分)计算2-(-3)的结果是【 】.(A )5 (B )1 (C )-1 (D )-517. (2012贵州安顺3分) 】A .±B .C .±3D . 318. (2012贵州黔东南4分)计算﹣1﹣2等于【 】 A .1 B .3 C .﹣1 D .﹣319. (2012贵州黔南4分)计算﹣(﹣5)等于【 】A .5B .﹣5C .15 D .﹣1520. (2012贵州遵义3分)﹣(﹣2)的值是【 】A .﹣2B .2C .±2 D.4 21. (2012山东滨州3分)32- 等于【 】 A .6- B .6 C .8- D .822. (2012山东德州3分)下列运算正确的是【 】A B .(﹣3)2=﹣9 C .2﹣3=8 D .20=0 23. (2012山东聊城3分)计算|﹣31|﹣32的结果是【 】A .﹣31 B .31C .﹣1D .1 24. (2012山东潍坊3分)计算:2-2=【 】.A .14 B C .-14D .4 25. (2012广西河池3分)计算12的结果是【 】 A .-3B .3C .-1D .126. (2012广西玉林、防城港3分)计算:22=【 】A.1B. 2C. 4D.827. (2012甘肃白银3=【 】 A .3 B .-3 C .-2 D .2 28. (2012黑龙江绥化3分)下列计算正确的是【 】A .-|-3|=-3B .30=0C .3-1=-3 D . 39±=29. (2012黑龙江龙东地区3分)若(a -1)2+|b -2|=0,则(a -b )2012的值是【 】A. -1B. 1C. 0D. 2012 二、填空题1. (2012天津市3分)∣-3∣= ▲ .2.(2012上海市4分)计算112-= ▲ . 3. (2012广东肇庆3分)计算5120⋅的结果是 ▲ . 4. (2012广东珠海4分)计算11=32-▲ . 5. (2012浙江杭州4分)某企业向银行贷款1000万元,一年后归还银行1065.6多万元,则年利率高于 ▲ %.6. (2012江苏常州4分)计算:∣-2∣= ▲ ,12--()= ▲ ,22-()=▲ , ▲ 。
2012年全国各地中考数学真题分类汇编

2012年全国各地中考数学真题分类汇编点、线、面、体、角一 .选择题1.(2012南通)已知∠=32o,则∠的补角为【C】A .58o B. 68o C. 148o D. 168o矚慫润厲钐瘗睞枥。
【考点】余角和补角.【专题】惯例题型.【剖析】依据互为补角的和等于180°列式计算即可得解.【解答】解:∵∠ a=32°,∴∠ a 的补角为 180°- 32° =148°.应选 C.【评论】本题考察了余角与补角的定义,熟记互为补角的和等于180°是解题的重点.2.( 2012 中考)如图,直线 a 与直线 c 订交于点 O,∠ 1 的度数是(D)A. 60°B. 50°C. 40° D .30°3.(2012长沙)以下四个角中,最有可能与70°角互补的是()A.B.C.D.【答案】D【评论】解: 70°角的补角 =180°﹣ 70°=110°,是钝角,联合各选项,只有 D 选项是钝角,因此,最有可能与70°角互补的是 D 选项的角.应选 D .4. (2012 嘉兴)已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于()聞創沟燴鐺險爱氇。
A.40 °B.60 °C.80 °D.90 °【分析】∵∠ B = 2∠ A, ∠C=∠ A+20°,∠ A+ ∠ B+ ∠C= 180°,∴∠ A+2 ∠ A+( ∠A+20°)= 180°, ∴∠ A =40°. 应选 A.【答案】 A.【评论】本题考察三角形内角和的应用.送分题 .5.( 2012 滨州)借助一副三角尺,你能画出下边哪个度数的角()A . 65°B. 75°C. 85°D. 95°【分析】利用一副三角板能够画出 75°角,用 45°和 30°的组合即可,【答案】选 B.【评论】本题考察角的计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
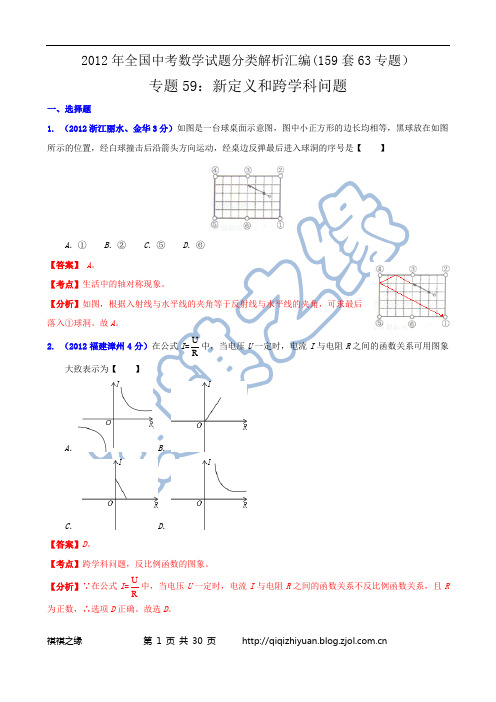
专题59:新定义和跨学科问题一、选择题1. (2012浙江丽水、金华3分)如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是【】A.①B.②C.⑤D.⑥【答案】 A。
【考点】生活中的轴对称现象。
【分析】如图,根据入射线与水平线的夹角等于反射线与水平线的夹角,可求最后落入①球洞。
故A。
2. (2012福建漳州4分)在公式I=UR中,当电压U一定时,电流I与电阻R之间的函数关系可用图象大致表示为【】A. B.C.D.【答案】D。
【考点】跨学科问题,反比例函数的图象。
【分析】∵在公式I=UR中,当电压U一定时,电流I与电阻R之间的函数关系不反比例函数关系,且R为正数,∴选项D正确。
故选D。
3. (2012湖北随州4分)定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,3)的点的个数是【】A.2B.1C. 4D.3【答案】C。
【考点】新定义,点的坐标,点到直线的距离。
【分析】画出两条相交直线,到l1的距离为2的直线有2条,到l2的距离为3的直线有2条,看所画的这些直线的交点有几个即为所求的点的个数:如图所示,所求的点有4个。
故选C。
4. (2012湖南长沙3分)某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.图表示的是该电路中电流I与电阻R之间函数关系的图象,则用电阻R表示电流I的函数解析式为【】A.2I=RB.3I=RC.6I=RD.6I=R【答案】C。
【考点】跨学科问题,待定系数法,曲线上点的坐标与方程的关系。
【分析】设kI=R,那么点(3,2)满足这个函数解析式,∴k=3×2=6。
∴6I=R。
故选C。
5. (2012湖南益阳4分)在一个标准大气压下,能反映水在均匀加热过程中,水的温度(T)随加热时间(t)变化的函数图象大致是【】A.B.C.D.【答案】B。
【考点】跨学科问题,函数的图象。
【分析】根据在一个标准大气压下水加热到100℃后水温不会继续增加,而是保持100℃不变,据此可以得到函数的图象。
故选B。
6. (2012贵州六盘水3分)定义:f(a,b)=(b,a),g(m,n)=(﹣m,﹣n).例如f(2,3)=(3,2),g(﹣1,﹣4)=(1,4).则g等于【】A.(﹣6,5)B.(﹣5,﹣6)C.(6,﹣5)D.(﹣5,6)【答案】A 。
【考点】新定义。
【分析】根据新定义先求出f (﹣5,6),然后根据g 的定义解答即可:∵根据定义,f (﹣5,6)=(6,﹣5), ∴g=g(6,﹣5)=(﹣6,5)。
故选A 。
7. (2012山东东营3分)根据下图所示程序计算函数值,若输入的x 的值为52,则输出的函数值为【 】A .32B .25C .425D .254【答案】B 。
【考点】新定义,求函数值。
【分析】根据所给的函数关系式所对应的自变量的取值范围,发现:当x=52时,在2≤x≤4之间,所以将x 的值代入对应的函数即可求得y 的值:112y===5x 52。
故选B 。
8. (2012山东莱芜3分)对于非零的实数a 、b ,规定a⊕b= 1 b - 1 a.若2⊕(2x-1)=1,则x =【 】A .5 6. 5 4. 3 2 D .- 16【答案】A 。
【考点】新定义,解分式方程。
【分析】∵a⊕b= 1 b - 1 a ,2⊕(2x-1)=1,∴2⊕(2x-1)=11=12x 12--。
∴()135=32x 1=26x 3=26x=5x=2x 126⇒-⇒-⇒⇒-。
检验,合适。
故选A 。
9. (2012广西钦州3分)在平面直角坐标系中,对于平面内任意一点(x ,y ),若规定以下两种变换: ①f(x ,y )=(y ,x ).如f (2,3)=(3,2);②g(x ,y )=(﹣x ,﹣y ),如g (2,3)=(﹣2,﹣3).按照以上变换有:f (g (2,3))=f (﹣2,﹣3)=(﹣3,﹣2),那么g (f (﹣6,7))等于【 】A.(7,6) B.(7,﹣6) C.(﹣7,6) D.(﹣7,﹣6)【答案】C。
【考点】新定义,点的坐标。
【分析】由题意应先进行f方式的变换,再进行g方式的变换,注意运算顺序及坐标的符号变化:∵f(﹣6,7)=(7,﹣6),∴g(f(﹣6,7))=g(7,﹣6)=(﹣7,6)。
故选C。
10. (2012甘肃兰州4分)在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是【】A. B. C. D.【答案】C。
【考点】跨学科问题,函数的图象。
【分析】根据浮力的知识,铁块露出水面前读数y不变,出水面后y逐渐增大,离开水面后y不变。
因为小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度。
故选C。
二、填空题1. (2012陕西省3分)如图,从点A(0,2)发出的一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过路径的长为▲ .2. (2012福建南平3分)设为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”的一次函数是正比例函数,则关于x的方程11+=1x1m-的解为▲ .【答案】x=3。
【考点】新定义,一次函数和正比例函数的定义,解分式方程。
【分析】根据新定义得:y=x+m-2,∵“关联数”的一次函数是正比例函数,∴m﹣2=0,解得:m=2。
则关于x的方程11+=1x1m-即为11+=1x12-,解得:x=3。
检验:把x=3代入最简公分母2(x﹣1)=4≠0,故x=3是原分式方程的解。
5. (2012湖北荆州3分)新定义:为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”的一次函数是正比例函数,则关于x的方程11+=1x1m-的解为▲ .【答案】x=3。
【考点】新定义,一次函数和正比例函数的定义,解分式方程。
【分析】根据新定义得:y=x+m-2,∵“关联数”的一次函数是正比例函数,∴m﹣2=0,解得:m=2。
则关于x的方程11+=1x1m-即为11+=1x12-,解得:x=3。
检验:把x=3代入最简公分母2(x﹣1)=4≠0,故x=3是原分式方程的解。
6. (2012湖南常德3分)规定用符号表示一个实数m的整数部分,例如: =0,=3。
按此规定的值为▲ 。
【答案】4。
【考点】新定义,估计无理数的大小。
【分析】∵9<10<16,∴3445<<< ,。
∴=4⎤⎦。
7. (2012湖南株洲3分)若(x 1,y 1)•(x 2,y 2)=x 1x 2+y 1y 2,则(4,5)•(6,8)= ▲ . 【答案】64。
【考点】新定义,代数式求值。
【分析】将(4,5)•(6,8)中的数字分别替换(x 1,y 1)•(x 2,y 2)即可解答:∵(x 1,y 1)•(x 2,y 2)=x 1x 2+y 1y 2,∴(4,5)•(6,8)=4×6+5×8=64。
8. (2012四川自贡4分)如图,△ABC 是正三角形,曲线CDEF 叫做正三角形的渐开线,其中弧CD .弧DE 、弧EF 的圆心依次是A .B .C ,如果AB=1,那么曲线CDEF 的长是 ▲ .【答案】4π。
【考点】新定义,等边三角形的性质,三角形外角定理,弧长的计算。
【分析】弧CD 是以点A 为圆心,AB=1为半径,∠CAD=1200为圆心角的圆弧,长是12012=1803ππ⋅⋅;弧DE 是以点B 为圆心,BD=2为半径,∠DBE=1200为圆心角的圆弧,长是:12024=1803ππ⋅⋅;弧EF 是以点C 为圆心,CE=3为半径,∠ECF=1200为圆心角的圆弧,长是:1203=2180ππ⋅⋅。
则曲线CDEF 的长是:24++2433ππππ=。
9. (2012山东菏泽4分)将4个数a b c d ,,,排成2行、2列,两边各加一条竖直线记成a b cd,定义a b cdad bc =-,上述记号就叫做2阶行列式.若+11=81+1x x x x -- ,则x = ▲ .【答案】2。
【考点】新定义,整式的混合运算,解一元一次方程。
【分析】根据定义化简+11=81+1x x x x -- ,得:()()22+11=8x x --,整理得:()()22+2+112+=8x x x x --,即4=8x ,解得:=2x 。
三、解答题1. (2012北京市8分)在平面直角坐标系xoy 中,对于任意两点P 1(x 1,y 1)与P 2(x 2,y 2)的“非常距离”, 给出如下定义:若∣x 1-x 2∣≥∣y 1-y 2∣,则点P 1与点P 2的“非常距离”为∣x 1-x 2∣; 若∣x 1-x 2∣<∣y 1-y 2∣,则点P 1与点P 2的“非常距离”为∣y 1-y 2∣.例如:点P 1(1,2),点P 2(3,5),因为∣1-3∣<∣2-5∣,所以点P 1与点P 2的“非常距离”为 ∣2-5∣=3,也就是图1中线段P 1Q 与线段P 2Q 长度的较大值(点Q 为垂直于y 轴的直线P 1Q 与垂直于x 轴的直线P 2Q 的交点)。
(1)已知点A 1(0)2-,,B 为y 轴上的一个动点,①若点A 与点B 的“非常距离”为2,写出一个满足条件的点B 的坐标; ②直接写出点A 与点B 的“非常距离”的最小值; (2)已知C 是直线3y x 34=+上的一个动点,①如图2,点D 的坐标是(0,1),求点C 与点D 的“非常距离”的最小值及相应的点C 的坐标; ②如图3,E 是以原点O 为圆心,1为半径的圆上的一个动点,求点C 与点E 的“非常距离”的最 小值及相应的点E 和点C 的坐标。
【答案】解:(1)①(0,-2)或(0,2)。
②21。
(2)①设C 坐标为003x x 34⎛⎫+ ⎪⎝⎭,,如图,过点C 作CP⊥x轴于点P ,作CQ⊥y 轴于点Q 。
由“非常距离”的定义知,当OP=DQ 时,点C 与点D 的“非常距离”最小,∴003x 0x 314-=+-。
两边平方并整理,得2007x 48x 64=0--,解得,08x 7=-或0x 8=(大于87,舍去)。
∴点C 与点D 的“非常距离”的最小值距离为87,此时815C 77⎛⎫- ⎪⎝⎭,。
②设直线3y x 34=+与x 轴和y 轴交于点A ,B ,过点O作直线3y x 34=+的垂线交直线3y x 34=+于点C ,交圆于点E ,过点C作CP⊥x 轴于点P ,作CQ⊥y 轴于点Q ,过点E 作EM⊥x 轴于点M ,作EN⊥y 轴于点N 。
