三视图(第一课时)_沪科版
沪科版数学九年级下册25.2第1课时三视图的识别与画法

金戈铁骑整理制作
学练优九年级数学下(HK) 教学课件
第25章 投影与视图
25.2 三视图
第1课时 三视图的识别与画法
导入新课
讲授新课
当堂练习
灿若寒星
课堂小结
学习目标
1.理解视图及三视图的概念. 2.会辨别几何体的三种视图,能熟练画出几何体的三种视图. (重点)
灿若寒星
导入新课
问题引入 问题:观察下面图形,假如有一束平形光从正面、左面、上面照 射到物体上,请分别画出不同方向的正投影图形?
左视图
灿若寒星
俯视图
当堂练习
1.关于下面几何体有几种说法,其中说法正确的是( B ) A.它的俯视图是圆 B.它的主视图与左视图相同 C.它的三种视图都相同 D.它的主视图与俯视图都是圆
灿若寒星
2.如下图几何体,请画出这个物体的三视图.
主视图
俯视图
(1)
左视图
主视图
俯视图
(2)
左视图
灿若寒星
课堂小结
灿若寒星
情景引入1
只不 缘识 身庐 在山 此真 山面 中目
远横
近 高 低 各 不
看 成 岭 侧 成
题 苏西 轼林
壁
同峰
诗中说明了怎样的一个数学道理?
灿若寒星
情景引入2
看
猜
问
猜
题
他
不
们
能
是
只
什
看
么
单
关
方
系
面
?
灿若寒星
讲授新课
一 简单几何体的三视图
互动探究 问题1 假如有一束平形光从正面、左面、上面照射到长方体 上,你能画出该长方体不同方向的正投影图形?
沪科版九年级下册数学:25.2 三视图 (共20张PPT)

主视图
左视图
俯视 图
A
B
C
D
组合体的三视图:
主视图
左视图
俯视图
应用提高:
如图:是由7个完全一样的小正方体搭成的几何体 的俯视图,其中小正方形中的数字表示在该位置上 小正方体的个数,请画出该几何体的主视图和左视 图。
13 21
课堂 小结
• 三视图 • 主视图——从前到后得到的视图 • 左视图——从左到右得到的视图 • 俯视图——从上到下得到的视图 • 画物体的三视图时,要满足如下规律: • 长对正,高平齐,宽相等.
从左面看
正面
从正面看
主视图
左视图
高
长
宽
宽
俯视图
将三个互相垂直的投影面展开在同一 个平面内,得到这一物体的三视图。
三视图的画法规律
主视图和俯视图 ----长对正 主视图和左视图 ----高平齐
俯视图和左视图 ----宽相等
主视图
长
左视图
高 宽
宽
俯视图
试一试:
主视图
正面
主视图
左视图
高
长
宽
宽
俯视图
画图步骤:
领悟
也会来也看
有 许 多 闪 光 点 哦 !
发 现 , 你 的 同 学 身 上 有 缺 点 ,
看 , 才 能 看 得 全 面 客 观 。 你
是 一 样 , 要 从 多 个 方 面 综 合
才 看 得 准 确 , 同 学 之 间 相 处
观 察 一 个 物 体 要 从 多 个 方 向
某工厂要加工一批密封罐,设计者给出了密封罐的三视 图,请你按照三视图确定制作每个密封罐所需钢板的面积.
(1)根据长和高画出 主视图
上海沪科版初中数学九年级下册25.2 第1课时 三视图的识别与画法

2.如图(1)所示的是圆台形灯罩的示意图,它的俯视图是如图(2)所示的(
D )
A
B
C
图 图 1图
图 图 2图
3.如图所示的四个几何体中,主视图与其他几何体的主视图不同的是(
D
)
A
B
C
D
4.如图(1)所示的是由 6 个大小相同的正方形组成的几何体,它的俯视图是如图(2)所
示的( )
图 图 1图
A
B
C
D
D
(第 3 题)
TB:小初高题库
上海沪科版初中数学
相信自己,就能走向成功的第一步 教师不光要传授知识,还要告诉学生学会生活。数学思维
可以让他们更理性地看待人生
TB:小初高题库
上海沪科版初中数学
上海沪科版初中数学 重点知识精选
掌握知识点,多做练习题,基础知识很重要! 上海沪科版初中数学 和你一起共同进步学业有成!
TB:小初高题库
29.2 三视图
第 1 课时 三视图的识别与画法
1.如图(1)放置的一个圆柱,则它的左视图是 ( )
上海沪科版初中数学
图 图 1图
A
B
C
图 图 2图
图 图 2图
5.如图(1)所示,放置的一个水管三叉接头,若其主视图如图(2)所示,则其俯视图是
TB:小初高题库
图(3)所示的( )
上海沪科版初中数学
A
B
C
D
图 图 3图
6.在水平的讲台上放置圆柱形水杯和长方形粉笔盒,如图(1)所示,则它的主视图是图
(2)所示的( )
A
B
C
图 图 2图
7.沿圆柱体上面直径截去一部分的物体如图所示,画出它的三视图.
2020年春沪科版九年级数学下册25.2 第1课时 三视图的识别与画法

29.2 三视图
第1课时三视图的识别与画法1.如图(1)放置的一个圆柱,则它的左视图是()
2.如图(1)所示的是圆台形灯罩的示意图,它的俯视图是如图(2)所示的()
3.如图所示的四个几何体中,主视图与其他几何体的主视图不同的是()
4.如图(
1)所示的是由6个大小相同的正方形组成的几何体,它的俯视图是如图(2)所示的()
5.如图(1)所示,放置的一个水管三叉接头,若其主视图如图(2
)所示,则其俯视图是
D
C
B
A
图图2图
D
C
B
A
图图1
图
图图2图
D
C
B
A
图图2图
D
C
B
A
图图1图
图图1图
图(3)所示的( )
6.在水平的讲台上放置圆柱形水杯和长方形粉笔盒,如图(1)所示,则它的主视图是图
(2)所示的( )
7.沿圆柱体上面直径截去一部分的物体如图所示,画出它的三视图.
图图3图D
C B
A 图图2图D
C B
A。
沪科版九下数学第1课时 三视图

Z
X
Y′
Y
画三视图时,看得见部分的轮廓线画 成实线,看不见部分的轮廓线画成虚线.
典例精析
例1 画出下列几何体的三视图.
主视图 左视图 俯视图
主视图
左视图
俯视图
主视图 左视图 俯视图
例2 画出如图所示的支架的三视图, 其中支架的两个台阶的高度和宽度相等.
主视图
左视图
俯视图
随堂练习
1.下列几何体中,主视图、左视图和俯视 图是全等形的几何体是( B )
三视图
自几何体的前方向后投
V W
射,在正面投影面V上得到
的视图称为主视图;
H
自几何体的上方向下投
V W
射,在水平面投影面H上得
到的视图称为俯视图;
H
自几何体的左侧向右投
V W
射,在侧面投影面W上得到
的视图称为左视图;
H
将三个投影面展开在一个平面内,得到这 一物体的一张三视图(由主视图、俯视图和左 视图组成).
A.圆柱 B.正方体 C.棱柱 D.圆锥
2.某长方体的主视图和左视图如图所示 (单位:cm),则其俯视图的面积是多少?
解 俯视图的长等于主视图的宽,为3cm 俯视图的宽等于左视图的宽,为2cm
则 其俯视图的面积为:3×2=6cm2
课后作业
1.从教材习题中选取. 2.完成练习册本课时的习题.
主视图要放在左上方,它的正下方是俯视 图,它的正右方是左视图.
主
左
视
视
图
高高
图
长
宽
长 宽
高平齐
长对正
宽相等
俯视图
主视图与俯视图的长对正,主视图与左视 图的高平齐,左视图与俯视图的宽相等.
沪科版初中数学HK九年级下册数学教案 第25章 投影与视图 第1课时 三视图的识别与画法

25.2 三视图第1课时三视图的识别与画法1.理解视图及三视图的概念;2.会辨别简单几何体的三种视图,能熟练画出简单几何体的三种视图(重点);3.能根据三视图描述基本几何体或实物原型(难点).一、情境导入一个物体从不同的角度观察,看到的形状可能是不相同的.观察一个玩具,我们从三个不同的角度看,得到三个图形,如图所示.你能说出它们是从哪个方向观察得到的吗?二、合作探究探究点一:几何体的三视图【类型一】判断简单几何体的三种视图图中的四个几何体中,主视图、左视图和俯视图都相同的几何体共有( )A.1个 B.2个 C.3个 D.4个解析:圆柱的主视图、左视图都是长方形,而俯视图是圆;圆锥的主视图、左视图都是等腰三角形,而俯视图是带圆心的圆;球的三种视图都是圆;正方体的三种视图都是正方形,故选B.方法总结:常见的几何体有圆柱、圆锥、球以及直棱柱,竖直放置的圆柱、圆锥的主视图、左视图相同,一般的直棱柱的三种视图是不同的,而球和正方体的三种视图都是相同的,它们分别是圆和正方形.【类型二】根据实物确定视图如图,从不同方向看一只茶壶,你认为是俯视效果图的是( )解析:俯视图就是从物体的正上方向下看到的视图,因而能够看到茶壶的顶部、壶把、壶嘴,故选A.方法总结:根据实物确定视图的方法:首先要弄清楚物体的主视图、左视图、俯视图的含义,然后根据实际物体思考三种视图的大体轮廓.探究点二:由三视图想象几何体【类型一】根据三视图判断几何体的形状已知一个几何体的三种视图如图所示,则该几何体是( )解析:A图的主视图、左视图均为等腰三角形,B图的左视图、俯视图均为矩形,C图的俯视图的外轮廓线为四边形,由此可排除A,B,C选项,抓住某个特征采用排除法是解决这类问题的常用方法.故选D.方法总结:主视图能体现物体的左右长度、上下高度;俯视图能体现物体的左右长度、前后宽度;左视图能体现物体的上下高度、前后宽度.通过观察三种视图可以想象出几何体的立体图形.变式训练:见《学练优》本课时练习“课堂达标训练”第8题【类型二】根据两种视图讨论构成几何体的小正方体的个数用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中的字母表示在该位置小正方体的个数,请解答下列问题:(1)a,b,c各表示多少?(2)这个几何体最少由几个小立方体组成,最多又是多少?(3)当d=e=1,f=2时,画出这个几何体的左视图.解:(1)由俯视图知道这个几何体共有三排三列,第三列只有一排,第二列有两排;而从主视图知道第三列的层数为3层,第二列的层数为1层,所以a为3,b,c应为1;(2)d,e,f既可以为1,也可以为2,但至少有一个为2,另外两个为1时,共有9个小立方体;另外两个都为2时,共有11个小正方体;故最少由9个小立方体搭成,最多由11个小立方体搭成;(3)左视图如右图所示.方法:这类问题一般是给出一个由相同的小正方体搭成的立体图形的两种视图,要求想象出这个几何体可能的形状.解答时可以先由三种视图描述出对应的该物体,再由此得出组成该物体的部分个体的个数.变式训练:见《学练优》本课时练习“课后巩固提升”第6题三、板书设计1.三视图主视图:自几何体的前方向后投射,在正面投影面上得到的视图.俯视图:自几何体的上方向下投射,在水平投影面上得到的视图.左视图:自几何体的左侧向右投射,在侧面投影面上得到的视图.2.三视图的画法(1)主视图的长与俯视图的长对正;(2)主视图的高与左视图的高平齐;(3)俯视图的宽与左视图的宽相等.通过观察、操作、猜想、讨论、合作等活动,使学生体会到三视图中位置及各部分之间大小的对应关系.通过具体活动,积累学生的观察、想象物体投影的经验,发展学生的动手实践能力、数学思考能力和空间观念.。
沪科版七年级上册数学资料之三视图第1课时课件

正面
自几何体的前方向后投影,在正面投影面V上 得到的视图,叫主视图(从前面看).
主视图
正面
主视图
V
从正面看
自几何体的上方向下投影,在水平投影面H上 得到的视图,叫俯视图(从上面看) .
主视图
从上面看
正面
主视图
俯视图
H
从正面看
自几何体的左侧向右投影,在侧面投影面W上 得到的视图,叫左视图(从左面看).
高平齐
主视图
左视图
高
长
宽
俯视图和左视图
宽
----宽相等
俯视图
宽相等
三视图能较全面地反映几何体的形状和大小。
长方体的三视图:
ቤተ መጻሕፍቲ ባይዱ
正 视 图
5cm
4cm
4cm
俯
视
图
4cm
3cm
5cm
左 视 图
3cm
5cm
小试 牛刀
画出如图所示圆柱的三视图
解:圆柱的主视图和左视图都是长方
形,俯视图为圆.
正 视 图
左 视 图
25.2 三视图(第1课时)
合肥一六八玫瑰园学校 袁保玉
从正面看 从上面看
从侧面看
飞机 模型
你能说出这三个 视图分别是从哪 个方向观察这本
书得到的吗?
要清楚地刻画一个几何体的形状与大小, 通常需要画出它在三个互相垂直的投影面 (例如墙角的三个面)上的正投影(视图)
其中,正对着我们的面叫正面, 下方的面叫水平面, 右边的面叫做侧面。
虚实:在画图时,看的见部分的轮廓通常画 成实线,看不见部分的轮廓线通常画成虚线.
分析:钢管有内外壁,从一定角度看它时,看不见内 壁,为全面地反映立体图形的现状,画图时规定:看 得见部分的轮廓线画成实线,因被其他部分遮挡而看 不见部分的轮廓线画成虚线.
2020-2021学年九年级下册沪科版数学教学课件 25.2 第1课时 三视图的识别与画法

25.2 三视图
第1课时 三视图的识别与画法
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1. 理解视图及三视图的概念. 2. 会辨别几何体的三个视图,能熟练画出几何体的三
个视图. (重点)
导入新课
情境引入
么缘各“ 原身不横 因在同看 吗此.成 ?山不岭
中识侧 ”庐成 你山峰 能真, 说面远 明目近 是,高 什只低
视图
主视图:从正面得到的视图 三视图的组成 左视图:从左面得到的视图
俯视图:从上面得到的视图
三视图的画法 长对正,高平齐,宽相等
左视图
长长对正
高 高齐 平
宽
宽相等 宽
俯视图
典例精析 例1 (1) 分别找出上述几何体的主视图.
(2) 请完成下表. 几何体 主视图
左视图 俯视图
练一练 找出图中每一物品所对应的主视图.
二 组合体的三视图 例2 画出如图所示的几何体的三视图.
提示:该几何体由两个大小不 等的长方体构成,画三视图时 要注意这两个长方体的上下、 前后的位置关系.
解:作法如下:
(1) 先画互相垂直的辅助
线XY',ZY;
(2) 确定主视图的位置,
画出主视图;
主
(3) 根据“长对正”与几何 视 体宽度画出俯视图; 图
(4) 根据“高平齐”与 X 俯
“宽相等”画出左视 视
图;
图
(5) 擦去辅助线.
用铅笔画,图 画好后可擦去
Z
左
视
图
O
Y'
注意看不见的
轮廓画成虚线
Y
宽
俯视图
将三个投影面展开在一个平面内,得到这个物体 的一张三视图.
三视图教学课件沪科版

内部;从上面看这个圆锥,它的投影是一
个圆及其内部,其中圆锥顶点的投影是这
个圆的圆心.
第13页,共20页。
解
这个圆锥的三视图如下图所示.
第14页,共20页。
例3 如图,这是一个底面为等边三角形的 正三棱柱,画出它的三视图.
第15页,共20页。
分析 从正面看,这个正三棱柱的投影是一个矩形
第4页,共20页。
动脑筋
制造一个圆柱形家具,为了让工人师傅知道 工件的准确形状和大小,设计人员应该如何画出
这个工件的图?
可以采用下述方法来画圆柱的视图.
第5页,共20页。
第一步,从前往后看,画出圆柱在立于它的
后面的竖直平面上的正投影,如图,
这称为“主视图”.通俗地说,就是 从圆柱的正面看这个圆柱.
议一议
如图,在正午的阳光下,一个物体在地面上的影 子是一个圆,你能确定这个物体的形状吗?
第2页,共20页。
影子是圆的物体可以是圆盘,可以 是球,在正午的阳光下, 还可以是立着 的圆柱,……
单凭在地面上的影子, 不可以确定 物体的形状.
第3页,共20页。
因此,只从一个方向看物体,不能确定物体的形状 ,应该从多个方向对物体进行观察.
圆,并且圆的半径与球的半径相等,所
以球的主视图、左视图、俯视图都是半 径与球的半径相等的圆及其内部.
第10页,共20页。
解 这个球的三视图如下图所示.
第11页,共20页。
例2 画圆锥的三视图(如下图所示).
第12页,共20页。
分析 从正面看这个圆锥,它的投影是一个等腰
三角形及其内部;从左面看这个圆锥,它
第6页,共20页。
第二步:从左往右看,画出圆柱在立于它的右边 的竖直平面上的正投影,这称为“左视 图”.通俗地说,就是从圆柱的左面看这 个圆柱.
《三视图》课件1-优质公开课-沪科9下精品

例1 画出图25-7(1)中儿何体的三视图:
图25-7 作法 1.在图25-7(2)中,先画互相垂直的辅助线 XY',ZY(用铅笔画,图画好后可擦去).
2.确定主视图的位置,画出主视图. 3.根据“长对正”与几何体宽度画出俯视图.
4.根据“高平齐”与“宽相等”画出左视图
(宽相等,可通过点O为中心旋转画出).
主视图
左视图
下面图(1)与图(2)是几个小方块所搭几何体俯视图, 小正方形中的数字表示在该位置的小立方块的个 数.请画出这两个几何体的主视图、左视图.
3 4 2
2 1
主视图
左视图
由三视图描述几何体(或实物原 型),一般先根据各视图想像从各个方向 看到的几何体形状, 然后综合起来确定 几何体(或实物原型)的形状, 再根据三 视图“长对正、高平齐、宽相等”的关 系,确定轮廓线的位置,以及各个方向的 尺寸.
图3-25
例2 某工厂要加工一批正六棱柱形状的食品盒, 其三视图如图25-9(单位:cm).问制作这样一个食 品盒所需要硬纸板的面积至少为多少?(精确到 1cm2)
解 这个正六棱柱形状的食品盒有六个侧面(都是 矩形)和两个底而(都是正六边形),因此制作这 样一个食品盒所需要硬纸板的面积至少为
3 S 6 10 36 2 6 10 2 4 2160 300 3 2680(cm )
5.擦去辅助线.
要注意看不见的轮廓线应画成虚线.
已知一个几何体的三视图如图3-23所示,描述该 几何体的形状,量出三视图的有关尺寸,并根据已知的 比例求出它的侧面积(精确到0.1cm2)
6cm 4.5cm 9cm
图3-23
3cm
图3-24
由主视图、左视图知道,这个几何体是直棱 从图上看出有五个面的面积可以直接求出 ,关 柱 , 但不能确定棱的条数. 再由俯视图可以确定它是 键只要求出另个侧面的面积就行了 ,怎样求呢? 直四棱柱,且底面是梯形.
九年级数学下册 25.2 三视图(第1课时)课件 (新版)沪科版

“9”,问四人是怎样的座次? 丁正对着数字(shùzì)“9”;甲坐在丁的 对面; 乙在丁的右手边; 丙在丁的左手边. 第四页,共31页。
6
有关 物体向(y投ǒu影gu(tāónu)yǐng)面 投影(t概óuy念ǐng)所得到的
图如形果称物为体视向图三.个互相垂直
的投影面分别投影,所得到 (dédào)的三个图形摊平 在一个平面上,则就是三视
(zhēnshí)的形状和长、宽、
第十六页,共31页。
体验 (tǐyàn)三 视图的作 法
第十七页,共31页。
三视图的作图步骤
1.确定视图方向
俯视图方向
2.先画出能反映物体
(wùtǐ)真实形状的一 左视图方向
个视图
3.运用长对正、高平齐、
宽相等的原则(yuánzé)
画出其它视图
主视图方向
4.检查
体观察,画出主视图,主视图反 映了物体的长和高及前后两个面 的从实上形向. 下正对着物体观察,画出
俯视图,布置(bùzhì)在主视图的正 下方,俯视图反映了物体的长和宽 及上下两个面的实形.
第十五页,共31页。
三视图表达(biǎodá) 的从意左义向右正对着物体观察,
画出左视图(shìtú),布置在 主视图(shìtú)的正右方,左 视图(shìtú)反映了物体的宽 和高三及视左图右能两反个映面物的体实真形实.
练一练:画 出下列 (xià liè)几 何体的三视 图
第二十三页,共31页。
俯
左
圆锥
第二十四页,共31页。
正六棱柱(léngzhù) 三视图
第二十五页,共31页。
先布局定•作正图五基棱准,柱从俯视图开始 (kāishǐ)(画lé起n,g后zh画ù主)、左视图.
九年级数学下册 第25章 投影与视图 25.2 三视图教案 (新版)沪科版-(新版)沪科版初中九年级

三视图教学反思教学过程教学过一、导入新课、揭示目标(2分钟左右)1.掌握正棱柱的概念;2.能根据三视图想象实物形状.二、学生自学,质疑问难(10分钟左右)阅读教材:1.什么是棱柱(底面、侧面、侧棱)?直棱柱?正棱柱?2如图所示的几何体叫做,它的上下两个面叫做,其余各面叫,相邻侧面的交线叫做,当侧棱垂直于底面时,棱柱称为,图中几何体叫做。
3.如何画正方体、圆柱、圆锥、球的三视图.4.由三视图描述实物形状,画出物体的表面展开图.三、合作探究,解决疑难(15分钟左右)如图所示的几何体的三视图,根据这个三视图,你能说说这种几何体的特点吗?正棱柱:底面是正多边形的直棱柱叫做正棱柱.长方体的三视图如图所示的几何体的三视图,根据这个三视图,你能说说这种几何体的特点吗?解:从三个方向看立体图形,图象都是矩形,可以想象出:整体是长方体,如图所示.讨论补充记录学生自学,对不会的问题要做好批注或随笔,与同学进行合作探究。
教师检查学情,不指导、不提问、不干扰。
讨论补充记录如图所示的几何体的三视图,根据这个三视图,你能说说这种几何体的特点吗?程如图所示的几何体的三视图,根据这个三视图,你能说说这种几何体的特点吗?从正面、侧面看立体图形,图象都是等腰三角形;从上面看,图象是圆;可以想象出,整体图形是圆锥,例根据物体的三视图摸索物体的形状.四、课堂小结: 本节课你有什么收获?还有什么不明白的地方?五、布置作业:(选做两题)必做:教材第3题选做:1.一个几何体的主视图和左视图如图所示,它是什么几何体?请补画这个几何体的俯视图.2.一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.板书设计教学反思。
2017春九年级数学下册 25.2 三视图(第1课时)几何体的三视图学案 (新版)沪科版
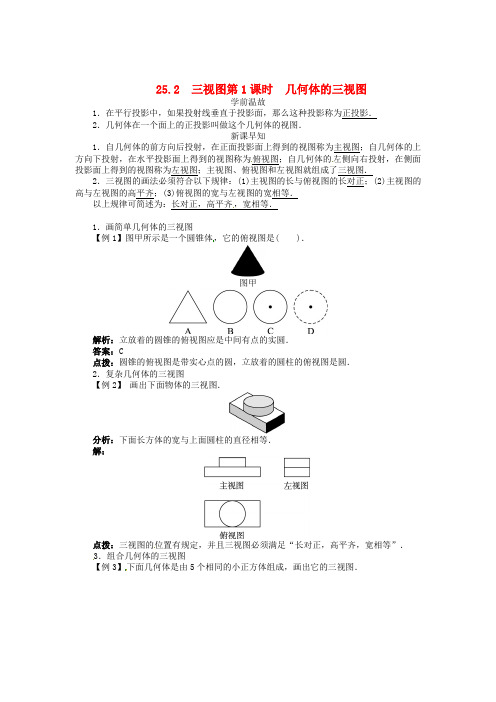
25.2 三视图第1课时几何体的三视图学前温故1.在平行投影中,如果投射线垂直于投影面,那么这种投影称为正投影.2.几何体在一个面上的正投影叫做这个几何体的视图.新课早知1.自几何体的前方向后投射,在正面投影面上得到的视图称为主视图;自几何体的上方向下投射,在水平投影面上得到的视图称为俯视图;自几何体的左侧向右投射,在侧面投影面上得到的视图称为左视图;主视图、俯视图和左视图就组成了三视图.2.三视图的画法必须符合以下规律:(1)主视图的长与俯视图的长对正;(2)主视图的高与左视图的高平齐;(3)俯视图的宽与左视图的宽相等.以上规律可简述为:长对正,高平齐,宽相等.1.画简单几何体的三视图【例1】图甲所示是一个圆锥体,它的俯视图是( ).图甲解析:立放着的圆锥的俯视图应是中间有点的实圆.答案:C点拨:圆锥的俯视图是带实心点的圆,立放着的圆柱的俯视图是圆.2.复杂几何体的三视图【例2】画出下面物体的三视图.分析:下面长方体的宽与上面圆柱的直径相等.解:点拨:三视图的位置有规定,并且三视图必须满足“长对正,高平齐,宽相等”.3.组合几何体的三视图【例3】下面几何体是由5个相同的小正方体组成,画出它的三视图.分析:从不同方向看到的小正方体都是一个面,其三视图画成正方形即可.解:三视图如图.点拨:小正方体的位置是一定的,看不见的不用画出,因此三视图中的小正方体的个数小于(或等于)实际个数.1.从不同方向看一只茶壶,你认为是俯视效果图的是( ).答案:A2.下图所示的几何体的主视图是( ).答案:D3.如图所示,一个斜插吸管的盒装饮料从正面看的图形是( ).答案:A4.如图所示的几何体的左视图是( ).答案:B5.图甲所示的几何体的俯视图是( ).甲答案:D6.四个小正方体组合成的组合体如图,画出它的三视图.解:如下图.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14
简单组合体的三视图
正视图 侧视图
俯视图
注意:不可见的轮廓线,用虚线画出。
15
简单组合体的三视图
正视图 侧视图
俯视图
16
三视图的作图步骤:
1.确定主视图方向
主视图——从正面看到的图 左视图——从左面看到的图 俯视图——从上面看到的图
俯视图方向
左视图方向
2.先画出能反映物体真实形状 的一个视图(一般为主视图) 3.布置视图 位置:主视图 左视图 俯视图 4.画图原则:
正面
长
宽
宽
俯视图
从正面看
5
P116 三视图(2)
主视图
主视图 左视图 高
正面
长 宽 俯视图
宽
6
圆柱
圆锥球ຫໍສະໝຸດ 从正面,侧面,上面看这些几何体,它们的形状各是 什么样的? 正面看:长方体 等腰三角形 圆 左面看:长方体 等腰三角形 圆 上面看: 圆 圆 圆 你能画出各物体的三视图吗?
7
圆柱,圆锥三视图
1
你能指出这些图形分别从哪个角度观察得到的吗?
2
从正面看
从侧面看
从上面看
飞机 模型
3
三视图的形成
物体向投影面投影所得到的图形称为视图。
如果物体向三个互相垂直的投影面分别投影,所得到 的三个图形摊平在一个平面上,称为物体的三视图。
4
P116 三视图(1)
从左面看
从上面看 主视图 左视图 高
主视图
主视图
左视图
俯视图
50
用小立方块搭出符合下列三视图的几何体:
主视图
左视图
俯视图
51
下列是一个物体的三视图,请描述出它的形状
主视图
俯视图
左视图
52
主视图
俯视图
左视图
53
探究
主视图
根据三视图摆出它的立体图形
左视图
俯视图
54
下面图(1)与图(2)是几个小方块所搭几何体俯视图, 小正方形中的数字表示在该位置的小立方块的个数. 请画出这两个几何体的主视图、左视图. 2 4 1 2 3
20
试一试
你会画圆柱的三视图吗?试一试吧!
21
宽相 等
主视图 左视图
俯视图
宽相等:俯视图和左视 图共同反映了物体前 后方向的尺寸.
22
错误的三视图 —长未对正1
23
错误的三视图 —长未对正2
24
错误的三视图 —高不平齐1
25
错误的三视图 —高不平齐2
26
错误的三视图 —宽不相等1
27
错误的三视图 —宽不相等1
28
错误的三视图
29
练习:下面的四组图中,如图所 示的圆柱体的三视图是( )
主视图
左视图
主视图
左视图
A
俯视图
B
俯视图
主视图
左视图
主视图
左视图
C
俯视图
俯视图
D
30
随堂练习
2.将两个圆盘一个茶叶桶,一个皮球和一个 蒙古包模型按如图所云浮的方式摆放在一起, 其主视图是( )。 D
(A)
(B)
(C)
72
P 123
2 画出图中的几何体的三视图:
73
主视图 左视图 主视图 左视图
· 俯视图 俯视图
8
球的三视图
主视图 左视图
俯视图
9
钢管的三视图
主视图
左视图
俯视图
10
练画 出 习下
一
列 : 基 本 几 何 体 的 三 视 图
长方体
圆台
六棱锥
11
长方体
主视图
左视图
长方体
俯视图
12
圆台
主视图
左视图
俯视图
圆台
13
简单组合体的三视图
例3:画出下面几何体的三视图。
(D)
31
练一练: 画出左图 的三视图 请同学 自己做
先布局定作图基准,从主视图 开始画起,后画俯、左视图。
32
主视图
左视图
俯视图
33
例2、画下例几何体的三视图
34
例3、画下例几何体的三视图
35
练习1、画下例几何体的三视图
36
小
结
1、物体向投影面投影所得到的图形称为视图。
2、主视图、俯视图和左视图合称三视图。 3、主视图反映物体的长和高,俯视图反映物 体的长和宽,左视图反映物体的高和宽,在 画三视图时主、俯视图要长对正,主、左视 图要高平齐,左、俯视图要宽相等。
37
38
P116 三视图(2)
主视图
主视图 左视图 高
正面
长
宽
宽
俯视图
39
P116 三视图(2)
主视图
主视图 左视图 高
正面
长 宽 俯视图
宽
40
下面所给的三视图表示什么几何体?
直四棱柱
41
下面所给的三视图表示什么几何体?
直五棱柱
42
下面所给的三视图表示什么几何体?
圆锥
43
下面所给的三视图表示什么几何体?
图3-25
57
想一想,摆一摆
用小方块搭一个几何体,使得它 的主视图和俯视图如图所示:
请你摆一摆,你会发现些什么?
58
做一做:由几个相同的小立方块搭成的几何体的 俯视图如图所示。方格中的数字表示该位置的小 方块的个数.请画出这个几何体的三视图。
1
3 2
59
• ⒉由三视图描述几何体(或实物原型),一
61
课内练习
1.某两个物体的三视图如图所示.请分别说出它们的形状.
直三棱柱
正四棱锥
2.由几个相同的小立方块搭 成的几何体的俯视图如图所 示.方格中的数字表示该位置 的小方块的个数.请画出这个 几何体的三视图.
1
3 2
62
那怎样画一个空间几何体的三 视图呢?请同学们看底下图的三视图.
V
63
1. 在主视图、俯视图中都体现形 体的长度,且长度在竖直方向上是 对正的,我们称之为长对正。
般步骤为: • ① 想象:根据各视图想象从各个方向看到 的几何体形状; • ② 定形:综合确定几何体(或实物原型) 的形状; • ③ 定大小位置:根据三个视图“长对正, 高平齐,宽相等”的关系,确定轮廓线的位 置,以及各个方向的尺寸.
60
由三视图描述几何体(或实物原型), 一般先根据各视图想像从各个方向看到 的几何体形状, 然后综合起来确定几何 体(或实物原型)的形状, 再根据三视图 “长对正、高平齐、宽相等”的关系, 确定轮廓线的位置,以及各个方向的尺 寸.
长对正 高平齐 宽相等
主视图方向
主视图
左视图
要求:俯视图安排在主视图的 正下方,左视图安排在主视图 的正右方。
俯视图
17
你能画出正方体和的三视图吗?
18
想一想,再动手画一画:
高平齐
主视图
左视图
高平齐:主视图和左视 图共同反映了物体上 下方向的尺寸.
俯视图
19
主视图
左视图
长对正
俯视图
长对正:主视图和俯视图共同 反映了物体左右方向的尺寸.
44
下面所给的三视图表示什么几何体?
45
下面所给的三视图表示什么几何体?
46
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
三棱锥
47
下面是一个物体的三视图,试说出它的形状
48
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
俯视图
49
下列是一个物体的三视图,请描述出它的形状
主视图
左视图
55
下面图(1)与图(2)是几个小方块所搭几何体俯视图, 小正方形中的数字表示在该位置的小立方块的个数. 请画出这两个几何体的主视图、左视图.
3 4 2
2 1
主视图
左视图
56
探究活动
用6个相同的小方块搭成一 个几何体,它的俯视图如图3-25所 示.则一共有几种不同形状的搭救 法(你可以用实物模型动手试一 试)?你能用三视图表示你探究的 结果吗?
64
2. 在主视图、左视图上都体现形体 的高度,且高度在水平方向上是平齐的, 我们称之为高平齐。
65
3. 在左视图、俯视图上都体现形体的 宽度,且是同一形体的宽度,是相等的, 我们称之为宽相等。
66
P124
5题
67
P124
6
68
P124
7
69
P124 7
70
P123
2
71
P123 2
