第8章习题解答
初二物理第八章练习题含答案

初二物理第八章练习题含答案1. 选择题(1) 以下属于力的性质是:A. 大小B. 方向C. 作用点D. 面积答案:A、B、C(2) 能够使物体发生位移的只有:A. 摩擦力B. 重力C. 弹力和悬挂力D. 正确答案全部都对答案:C(3) 法拉第一定律指出的是:A. 外力作用于物体上时,物体一定保持静止或匀速直线运动B. 外力作用于物体上时,物体的速度将发生变化C. 物体受到的合力为零时,物体一定保持静止或匀速直线运动D. 物体受到的合力为零时,物体的速度将发生变化答案:C2. 填空题(1) 一个力从右往左作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从左往右(2) 一个力从上往下作用于一个物体,这个物体产生的反作用力的方向是______。
答案:从下往上(3) 一个物体受到A力的作用产生加速度a,如果力A的大小不变,改变作用方向,则产生的加速度为______。
答案:-a3. 解答题(1) 什么是力?力的三要素是什么?解答:力是物体之间相互作用的结果,是导致物体发生变化的原因。
力的三要素包括大小、方向和作用点。
大小表示力的强弱程度,方向表示力作用的直线方向,作用点表示力作用的具体位置。
(2) 什么是合力?如何求合力?解答:合力是同时作用在物体上的多个力的共同效果。
求合力的方法是将所有作用在物体上的力按照大小和方向合成,可以通过向量法或图示法来求解。
(3) 描述牛顿第一定律,并用实例说明其应用。
解答:牛顿第一定律也称为惯性定律,指出在没有外力作用时,物体将保持静止或匀速直线运动的状态。
例如,当我们用力推动一张光滑的桌子上的书时,如果力的大小和方向适当,书就会保持匀速直线运动,直到受到其他力的作用。
这说明物体在没有外力干扰时具有惯性,保持原来的状态不发生变化。
总结:初二物理第八章练习题主要涉及力的性质和作用、法拉第一定律等内容。
通过选择题和填空题加深对知识点的理解,同时通过解答题展开思考和拓展。
运筹学答案(第八章)

page 32 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
page 33 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
心B货1B中,18,心B.22B的0,2,运B某3B输每种3。能天货A力物需1,、由求A2单分个2的位别仓库运为库存费9At量,如1,分5表At别,82运—为64t送每,。到天求各31运仓个3t费库配,最到货9t省中;配
School of Management
运筹学教程
第八章习题解答
解:两条船就够了。
一条船完成:T4→T5→T3; 另一条船完成:T1→T2 。
page 37 2020年5月13日星期三
School of Management
page 25 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
8.15 如图8-59,发点S1,S2分别可供应10和15个 单边位上,数收为c点ij。t1,t2可以接收10和25个单位,求最大流,
page 26 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
8.1 证明在9座工厂之间,不可能每座工厂只与其 他3座工厂有业务联系,也不可能只有4座工厂与偶数 个工厂有业务联系。
解:将有联系的工厂做一条连线。
如果仅有9座工厂只与其他3座工厂有业务联系, 说明顶点次数之和为27,矛盾。
如果只有4座工厂与偶数个工厂有业务联系,其他 5个工厂一定与奇数个工厂有业务联系,说明顶点次 数之和还是奇数,矛盾。
高等数学习题详解-第8章 二重积分

习题8-11. 设有一平面薄片,在xOy 平面上形成闭区域D ,它在点(x ,y )处的面密度为μ(x ,y ),且μ(x ,y )在D 连续,试用二重积分表示该薄片的质量. 解:(,)Dm x y d μσ=⎰⎰.2. 试比较下列二重积分的大小:(1) 2()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰,其中D 由x 轴、y 轴及直线x +y =1围成;(2)ln()Dx y d σ+⎰⎰与2ln()Dx y d σ+⎡⎤⎣⎦⎰⎰,其中D 是以A (1,0),B (1,1),C (2,0)为顶点的三角形闭区域.解:(1)在D 内,()()2301x y x y x y ≤+≤+≥+,故,23()()DDx y d x y d σσ+≥+⎰⎰⎰⎰.(2) 在D 内,212ln()1,ln()ln ()x y x y x y x y ≤+≤≤+≤+≥+,故0从而, 2ln()[ln()]DDx y d x y d σσ+≥+⎰⎰⎰⎰习题8-21. 画出积分区域,并计算下列二重积分:(1) ()Dx y d σ+⎰⎰,其中D 为矩形闭区域:1,1x y ≤≤;(2) (32)Dx y d σ+⎰⎰,其中D 是由两坐标轴及直线x +y =2所围成的闭区域;(3) 22()D xy x d σ+-⎰⎰,其中D 是由直线y =2,y =x ,y =2x 所围成的闭区域;(4) 2Dx y d σ⎰⎰,其中D 是半圆形闭区域:x 2+y 2≤4,x ≥0;(5) ln Dx y d σ⎰⎰,其中D 为:0≤x ≤4,1≤y ≤e ;(6)22Dx d σy ⎰⎰其中D 是由曲线11,,2xy x y x ===所围成的闭区域. 解:(1) 111111()()20.Dx y d dx x y dy xdx σ---+=+==⎰⎰⎰⎰⎰ (2) 222200(32)(32)[3(2)(2)]x Dx y d dx x y dy x x x dx σ-+=+=-+-⎰⎰⎰⎰⎰223202220[224]4.330x x dx x x x =-++=-++=⎰(3) 32222222002193()()()248yy Dy x y x d dy x y x dx y dy σ+-=+-=-⎰⎰⎰⎰⎰43219113.96860y y -= (4) 因为被积函数是关于y 的奇函数,且D 关于x 轴对称,所以20.Dx yd σ=⎰⎰(5) 44201041ln ln (ln ln )2(1)2110e De e e x yd dx x ydy x y y y dx x e σ-==-==-⎰⎰⎰⎰⎰.(6) 122224111311122222119()()124642x x Dx x x x x x d dx dy dx x x dx y y y x σ==-=-=-=⎰⎰⎰⎰⎰⎰.2. 将二重积分(,)Df x y d σ⎰⎰化为二次积分(两种次序)其中积分区域D 分别如下:(1) 以点(0,0),(2,0),(1,1)为顶点的三角形;(2) 由直线y =x 及抛物线y 2=4x 所围成的闭区域;(3) 由直线y =x ,x =2及双曲线1y x=所围成的闭区域;(4) 由曲线y =x 2及y =1所围成的闭区域. 解:(1) 1221201(,)(,)(,).xx y ydx f x y dy dx f x y dy dy f x y dx --+=⎰⎰⎰⎰⎰⎰(2) 2441004(,)(,).y x y dx f x y dy dy f x y dx =⎰⎰⎰⎰(3) 12222111112(,)(,)(,).xyyxdy f x y dx dy f x y dx dx f x y dy +=⎰⎰⎰⎰⎰⎰(4) 21111(,)(,).xdx f x y dy dy f x y dx -=⎰⎰⎰3. 交换下列二次积分的积分次序:(1) 10(,)ydy f x y dx ⎰⎰; (2)2220(,)yydy f x y dx ⎰⎰;(3) ln 10(,)e xdx f x y dy ⎰⎰; (4) 123301(,)(,)y ydy f x y dx dy f x y dx -+⎰⎰⎰⎰.解:(1) 111(,)(,)yxdy f x y dx dx f x y dy =⎰⎰⎰⎰.(2) 222402(,)(,).y x ydy f x y dx dx f x y dy =⎰⎰⎰⎰(3) ln 11(,)(,)y e xeedx f x y dy dy f x y dx =⎰⎰⎰⎰(4) 123323012(,)(,)(,)yyxxdy f x y dx dy f x y dx dx f x y dy --+=⎰⎰⎰⎰⎰⎰.4. 求由平面x =0,y =0,x =1,y =1所围成的柱体被平面z =0及2x +3y +z =6截得的立体体积.解:11100037(623)(62).22V dx x y dy x dx =--=--=⎰⎰⎰5. 求由平面x =0,y =0,x +y =1所围成的柱体被平面z =0及曲面x 2+y 2=6-z 截得的立体体积.解:3111222000(1)34(6)[6(1)(1)).312x x V dx x y dy x x x dx --=--=----=⎰⎰⎰习题8-31. 画出积分区域,把二重积分(,)Df x y d σ⎰⎰化为极坐标系下的二次积分,其中积分区域D是:(1) x 2+y 2≤a 2 (a >0); (2) x 2+y 2≤2x ;(3) 1≤x 2+y 2≤4; (4) 0≤y ≤1-x ,0≤x ≤1. 解:(1) 20(,)(cos ,sin ).aDf x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(2) 2cos 202(,)(cos ,sin ).Df x y d d f r r rdr πθπσθθθ-=⎰⎰⎰⎰(3) 221(,)(cos ,sin ).D f x y d d f r r rdr πσθθθ=⎰⎰⎰⎰(4)12cos sin 0(,)(cos ,sin ).Df x y d d f r r rdr πθθσθθθ+=⎰⎰⎰⎰2. 把下列积分化为极坐标形式,并计算积分值:(1)22220()aa y dy x y dx -+⎰⎰;(2)21220;xxdx x y dx +⎰⎰解:(1)224422320()248aa y aa a dy x y dx d r dr πππθ-+==⋅=⎰⎰⎰⎰. (2) 22sin 3122244cos 600001sin 3cos x x dx x y dx d r dr d πθπθθθθθ+==⎰⎰⎰⎰⎰244466400011cos 111(cos )[(cos )(cos )]33cos cos cos d d d πππθθθθθθθ-=-=--⎰⎰⎰ 532(21)1cos cos 4().3530πθθ--+=--+= 3. 在极坐标系下计算下列二重积分:(1)22x y De d σ+⎰⎰,其中D 是圆形闭区域: x 2+y 2≤1;(2) 22ln(1)Dxy d σ++⎰⎰,其中D 是由圆周x 2+y 2=1及坐标轴所围成的在第一象限内的闭区域;(3)arctanDyd σx⎰⎰,其中D 是由圆周x 2+y 2=1,x 2+y 2=4及直线y =0,y =x 所围成的在第一象限内的闭区域;(4)222DR x y d σ--其中D 由圆周x 2+y 2=Rx (R >0)所围成.解:(1) 22222100112(1).20xy r r De d d e rdr e e πσθππ+==⋅=-⎰⎰⎰⎰(2)23112222221ln(1)ln(1)[ln(1)]221Dr r xy d d r rdr r dr rππσθ++=+=+-+⎰⎰⎰⎰⎰ 212(1)[ln 22](2ln 21)441r r r dr rππ+-=-=-+⎰. (3) 222244010133arctan arctan(tan ).32264Dy d d rdr d rdr x ππππσθθθθ=⋅==⋅=⎰⎰⎰⎰⎰⎰(4)222DR x y d σ--3cos 2222222022cos 12()230R R d R r rdr R r d ππθππθθθ--=-=--⎰⎰⎰3333221(sin )33R R R d πππθθ-=--=⎰.4. 求由曲面z =x 2+y 2与22z x y =+所围成的立体体积.解:两条曲线的交线为x 2+y 2=1,因此,所围成的立体体积为:21222220[()]().6DV x y x y d d r r rdr ππσθ=++=-=⎰⎰⎰⎰习题8-41. 计算反常二重积分()x y De dx dy -+⎰⎰,其中D :x ≥0,y ≥x .2. 计算反常二重积分222()Ddx dyx y +⎰⎰,其中D :x 2+y 2≥1. 解:1.22201()2a aaax yx x aaa xe dx edy eedx e e ---------=-=-+-⎰⎰⎰所以2()211lim ().22a x y a a a De edxdy e e --+--→+∞-=-+-=⎰⎰2. 由232011112()22R d dr r R πθπ=-⎰⎰,得222211lim 2().2()2R Ddxdy x y R ππ→+∞=-=+⎰⎰复习题8(A )1. 将二重积分d d (,)Df x y x y ⎰⎰化为二次积分(两种次序都要),其中积分区域D 是:(1) ︱x ︱≤1,︱y ︱≤2;(2) 由直线y =x 及抛物线y 2=4x 所围成. 解:(1) 12211221(,)(,).dx f x y dy dy f x y dx ----=⎰⎰⎰⎰(2) 2424004(,)(,).xyy xdx f x y dy dy f x y dx =⎰⎰⎰⎰2. 交换下列两次积分的次序: (1)d d 10(,)yyy f x y x ⎰⎰;(2)d d 2220(,)a ax x x f x y y -⎰⎰;(3)d d +d d 12201(,)(,)xxx f x y y x f x y y -⎰⎰⎰⎰.解:(1) 211d (,)d d (,)d y x yxy f x y x x f x y y =⎰⎰⎰⎰.(2) 222222200d (,)d d (,)d aax x aa a y a a y x f x y y y f x y x -+---=⎰⎰⎰⎰.(3)1221201d (,)d +d (,)d d (,)d xxy yx f x y y x f x y y y f x y x --=⎰⎰⎰⎰⎰⎰.3. 计算下列二重积分:(1) e d x y Dσ+⎰⎰, D : ︱x ︱≤1,︱y ︱≤1;(2) d d 2D xy x y ⎰⎰,D 由直线y =1,x =2及y =x 围成;(3) d d (1)Dx x y -⎰⎰,D 由y =x 和y =x3围成;(4) d d 22()Dx y x y +⎰⎰,D :︱x ︱+︱y ︱≤1; (5) d 1sin Dy σy ⎰⎰,D 由22y x π=与y =x 围成; (6)d (4)Dx y σ--⎰⎰,D 是圆域x 2+y 2≤R 2;解: (1) 1111111211111e d ()()()1x y x y x x x x Ddx e dy e e dx e e e e σ+++-+----==-=-=--⎰⎰⎰⎰⎰.(2)5322224211121129d d ()()2253151xDx x xy x y dx x ydy x x dx ==-=-=⎰⎰⎰⎰⎰.(3) 3112430011117(1)d d (1)()325460x x Dx x y dx x dy x x x x dx -=-=--+=--+=-⎰⎰⎰⎰⎰.(4)1122220()d d 4()xDx y x y dx x y dy -+=+⎰⎰⎰⎰33241201412124(2)4()33323330x x x x x x dx x =--+=--+=⎰. (5) 222200sin 12sin d (sin sin )y y Dy y dy dx y y y dy y y πππσπ==-⎰⎰⎰⎰⎰222222sin (cos )1(cos sin )10ydy yd y y y y ππππππ=+=+-=-⎰⎰. (6)322200(4)d (4cos sin )[2(cos sin )]3RDR x y d r r rdr R d ππσθθθθθθ--=--=-+⎰⎰⎰⎰⎰3222[2(sin cos )]430R R R πθθθπ=--=.4. 已知反常二重积分e d 2y Dx σ-⎰⎰收敛,求其值.其中D 是由曲线y =4x 2与y =9x 2在第一象限所围成的区域.解:设2249(0)a D y x y x y a a ===>是由曲线、和在第一象限所围成.则22222200015555ed ()236144144144aaa a y y y y a D x dy dx ye dy e d y e σ-----==⋅=--=-⎰⎰⎰⎰⎰. 所以225e d lime d 144ay ya DD x x σσ--→+∞==⎰⎰⎰⎰. 5. 计算e d 2x x +∞--∞⎰.解:由第四节例2以及2y =e x -是偶函数,可知2e d x x +∞--∞=⎰.6. 求由曲面z =0及z =4-x 2-y 2所围空间立体的体积.解:曲面z =0和z =4-x 2-y 2的交线为x 2+y 2 =4.因此,所围空间立体的体积为:222220016(4)d d (4)2(8)84D x y x y d r rdr πθππ--=-=-=⎰⎰⎰⎰.7. 已知曲线y =ln x 及过此曲线上点(e ,1)的切线ey x 1=.(1) 求由曲线y =ln x ,直线ey x 1=和y =0所围成的平面图形D 的面积;(2) 求以平面图形D 为底,以曲面z =e y 为顶的曲顶柱体的体积.解:(1) 1ln (ln )12221e e e ee S xdx x x x =-=--=-⎰.(2) 221120013()()2220y y e yyyy y ye e V dy e dx e ye dy ye e ==-=-+=-⎰⎰⎰.(B )1. 交换积分次序:(1) 311(,)xxdx f x y dy -⎰⎰; (2)0112(,)y dy f x y dx --⎰⎰;(3) 224(,)x x f x y dy -⎰;(4) 110(,)dx f x y dy ⎰.解:(1) 3111(,)(,)x xydx f x y dy dy f x y dx -=⎰⎰⎰.(2) 01101221(,)(,)yxdy f x y dx dx f x y dy ---=⎰⎰⎰⎰.(3) 2242402(,)(,)(,)x x f x y dy dy f x y dx dy f x y dx -=+⎰⎰⎰.(4) 211121(,)(,)(,)y dx f x y dy dy f x y dx dy f x y dx =+⎰⎰⎰⎰.2. 计算积分2122x xxdx dy x y +⎰⎰.解:222sin sin 144cos cos 2220000cos cos xxx r dx dy d rdr d dr x y r πθπθθθθθθθ==+⎰⎰⎰⎰⎰⎰ 40sin ln 24(ln cos )cos 2d ππθθθθ==-=⎰. 3. 计算积分112201yy dy dx x y ++⎰⎰.解:111114cos 4cos cos 2222000sin sin [sin ]111yy r dy dx d rdr d dr dr x y r r ππθθθθθθθθ==-++++⎰⎰⎰⎰⎰⎰⎰ 44001ln 21(tan sin arctan )arctan (cos )cos 2cos d d ππθθθθθθ=-⋅=+⎰⎰令cos t θ=,则原式211ln 21ln 21ln 211(arctan ln(12222dt dt t t t t t =+=+=+++ln 213ln 213ln ln 22242224ππ=+--=-. 4. 设函数f (x )在区间0,1⎡⎤⎣⎦上连续,且1()f x dx A =⎰,求11()()xdx f x f y dy ⎰⎰. 解:设1'()()()(1)(0)F x f x f x dx F F A ==-=⎰,则.11111()()()[(1)()](1)()()(())xdx f x f y dy f x F F x dx F f x dx F x d F x =-=-⎰⎰⎰⎰⎰21()111(1)(1)[(1)(0)][(1)(0)](1)(1)(0)22220F x F A F A F F F F F A AF AF =-=--+=--21[(1)(0)]22A A F F =-=. 5. 计算2Dx y d σ⎰⎰,其中D 是由直线y =0,y =1及双曲线x 2-y 2=1所围成的闭区域.解:11222022(13Dx yd dy ydx y y σ==+⎰⎰⎰⎰35122222011122(1)(1)(1)1)335150y d y y =++=⋅+=⎰. 6. 计算222y xdx e dy ⎰⎰.解:2222222240000211(1)220y y y y y x dx e dy dy e dx ye dy e e ====-⎰⎰⎰⎰⎰.7. 证明211()()d ()()d 1b x bn n a a adx x y f y y b y f y y n ---=--⎰⎰⎰,其中n 为大于1的正整数. 证:22()()d ()()b x b bn n aaaydx x y f y y dy x y f y dx ---=-⎰⎰⎰⎰11()()1bn b yax y f y dy n -=--⎰11()()d 1bn ab y f y y n -=--⎰。
第8章习题答案

第八章多态1.单选题(1).下列关于运算符重载的描述中,( D )是正确的。
(A) 可以改变参与运算的操作数个数 (B) 可以改变运算符原来的优先级(C) 可以改变运算符原来的结合性(D) 不能改变原运算符的语义(2).下列函数中,不能重载运算符的函数是( b )。
(A) 成员函数(B) 构造函数(C) 普通函数 (D) 友员函数(3).要求用成员函数重载的运算符是( A )。
(A) =(B) == (C) <= (D) ++(4).要求用友员函数重载的运算符是( C )。
(A) = (B) [] (C) <<(D) ()(5).在C++中,要实现动态联编,必须使用( D )调用虚函数。
(A) 类名(B) 派生类指针(C) 对象名(D) 基类指针(6).下列函数中,不能说明为虚函数的是( C )。
(A) 私有成员函数(B) 公有成员函数(C) 构造函数(D) 析构函数(7).在派生类中,重载一个虚函数时,要求函数名、参数的个数、参数的类型、参数的顺序和函数的返回值( A )。
(A) 相同(B)不同(C) 相容(D) 部分相同(8).C++中,根据(D )识别类层次中不同类定义的虚函数版本。
(A) 参数个数(B) 参数类型(C) 函数名(D) this指针类型(9).虚析构函数的作用是(C )。
(A) 虚基类必须定义虚析构函数(B) 类对象作用域结束时释放资源(C)delete动态对象时释放资源(D) 无意义(10).下面函数原型中,( B )声明了fun为纯虚函数。
(A) void fun()=0; (B) virtual void fun()=0;(C) virtual void fun(); (D) virtual void fun(){ };(11).若一个类中含有纯虚函数,则该类称为( C )。
(A) 基类(B)纯基类(C) 抽象类(D) 派生类(12).假设Aclass为抽象类,下列正确的说明语句是( B )。
课后习题答案第8章_存储器和可编程逻辑器件

第8章半导体存储器和可编程逻辑器件8-1存储器按读写功能以及信息的可保存性分别分为哪几类?并简述各自的特点。
解答:存储器按读写功能可分为只读存储器(ROM)和随机存储器(RAM)。
随机存取存储器在工作过程中,既可从其任意单元读出信息,又可以把外部信息写入任意单元。
因此,它具有读、写方便的优点,但由于具有易失性,所以不利于数据的长期保存。
只读存储器在正常工作时其存储的数据固定不变,只能读出,不能随时写入。
ROM为非易失性器件,当器件断电时,所存储的数据不会丢失。
存储器按信息的可保存性可分为易失性存储器和非易失性存储器。
易失性存储器在系统关闭时会失去存储的信息,它需要持续的电源供应以维持数据。
非易失存储器在系统关闭或无电源供应时仍能保持数据信息。
8-2什么是SRAM?什么是DRAM?它们在工作原理、电路结构和读/写操作上有何特点?解答:SRAM(Static Random Access Memory)为静态随机存储器,其存储单元是在静态触发器的基础上附加控制电路构成的。
DRAM(Dynamic Random Access Memory)为动态随机存储器,常利用MOS管栅极电容的电荷存储效应来组成动态存储器,为了避免存储信息的丢失,必须定时地对电路进行动态刷新。
SRAM的数据由触发器记忆,只要不断电,数据就能保存,但其存储单元所用的管子数目多,因此功耗大,集成度受到限制。
DRAM一般采用MOS管的栅极电容来存储信息,由于电荷保存时间有限,为避免存储数据的丢失,必须由刷新电路定期刷新,但其存储单元所用的管子数目少,因此功耗小,集成度高。
SRAM速度非常快,但其价格较贵;DRAM的速度比SRAM慢,不过它比ROM 快。
8-3若RAM的存储矩阵为256字⨯4位,试问其地址线和数据线各为多少条?解答:存储矩阵为256字⨯4位的RAM地址线为8根,数据线为4根。
8-4某仪器的存储器有16位地址线,8位数据线,试计算其最大存储容量是多少?解答:最大存储容量为216⨯8=524288=512k bit(位)8-5用多少片256⨯4位的RAM可以组成一片2K⨯8位的RAM?试画出其逻辑图。
基础电子技术 习题解答 第8章 组合数字电路习题解答
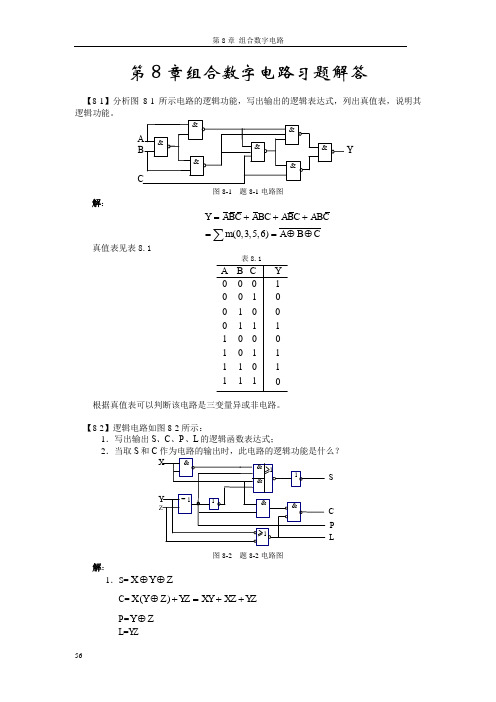
第8章组合数字电路习题解答【8-1】分析图8-1所示电路的逻辑功能,写出输出的逻辑表达式,列出真值表,说明其逻辑功能。
A B &&&&&&&CY图8-1 题8-1电路图解:(0,3,5,6)Y ABC ABC ABC ABC m A B C=+++==⊕⊕∑真值表见表8.1表8.1Y C B A 10001000010011100101110111111000根据真值表可以判断该电路是三变量异或非电路。
【8-2】逻辑电路如图8-2所示:1.写出输出S 、C 、P 、L 的逻辑函数表达式;2.当取S 和C 作为电路的输出时,此电路的逻辑功能是什么?=1&&1&&11&1XYZSC P L图8-2 题8-2电路图解:1.S=X Y Z ⊕⊕C =()X Y Z YZ XY XZ YZ ⊕+=++ P =Y Z ⊕ L =YZ2.当取S 和C 作为电路的输出时,此电路为全加器。
【8-3】 图8-3为由三个全加器构成的电路,试写出其输出F 1,F 2,F 3,F 4的表达式。
A iB iC i-1S i C iA iB iC S i C iA iB iC i-1S i C iX YZ12F 3F 4i-1图8-3 题8-3电路图解:F 1=X Y Z ⊕⊕ 2()F X Y Z =⊕⋅3F XY Z =⊕ 4F XYZ =【8-4】图8-4为集成4位全加器74LS283和或非门构成的电路,已知输入DCBA 为BCD8421码,写出B 2 B 1的表达式,并列表说明输出''''A B C D 为何种编码?A 3A 2A 1A 0S 3 S 2S 1 S 0C 0C 4D' C' B' A'74LS283D C B AB 3 B 2B 1B 041>1>1>图8-4 题8-4电路图解:21B B D B A D C D CB CA ==++++=++若输入DCBA 为BCD8421码,列表可知D 'C 'B 'A '为BCD2421码。
物理学第3版习题解答_第8章光的波动性

. B
解: (1) 以 A 为原点
x1
B
. A
x
A
图 8-35 习题 8-5 用图
-1
本题需补充一平面简谐波以速度 u = 20 m ⋅ s 沿直线传播
t x y = A cos[ 2 π( − ) + ϕ ] λ = uT = 10 m ,根据 T λ , 有
y = A cos[2π(
t x π − )− ] 0.5 10 2
x1 = 0.04 cos(2t + π 6) x 2 = 0.03 cos(2t − π 6)
试写出合振动的表达式。
解 合振动的振幅为
2 A = A12 + A2 + 2 A1 A2 cos(ϕ 2 − ϕ1 )
⎛ π π⎞ = 0.04 2 + 0.03 2 + 2 × 0.03 × 0.04 × cos⎜ − − ⎟ ⎝ 6 6⎠ = 0.06m
第八章习题解答
8-1 一物体沿 x 轴作简谐振动,振幅为 0.12m,周期为 2s。当 t = 0 时,位移为 0.06m,且 向 x 轴正方向运动。求:(1)初相;(2) t = 0.5s 时,物体的位置;(3)在 x = -0.06m 处, 且向 x 轴负向方向运动。物体从这一状态回到平衡位置的最短时间。 解:
−1
8-8 波长为 589.3nm 的钠光照在一双缝上,在距双缝 200cm 的观察屏幕上测量 10 个条纹的 宽度为 2.2cm,试计算双缝之间的距离。
解:根据 ∆x =
D λ 有 d = 0.536 mm d
8-9 在杨氏干涉实验中,若双缝间距为 0.40mm,在距双缝 100cm 的光屏上出现干涉条纹。 现测得相邻两条明纹中心的间距为 1.5mm,求入射光的波长。
第8章思考题和习题解答

第八章变电所二次回路和自动装置8-1 变电所二次回路按功能分为哪几部分各部分的作用是什么答:变电所二次回路按功能分为断路器控制回路、信号回路、保护回路、监测回路、自动控制回路及操作电源回路等。
①断路器控制回路的主要功能是对断路器进行通、断操作,当线路发生短路故障时,相应继电保护动作,接通断路器控制回路中的跳闸回路,使断路器跳闸,起动信号回路发出声响和灯光信号。
②信号回路是用来指示一次电路设备运行状态的二次回路。
信号按用途分,有断路器位置信号、事故信号和预告信号。
③保护回路是用来对变电所设备进行保护。
④监视和测量回路是用来对变电所各线路进行监视和测量,以满足电气设备安全运行的需要。
⑤自动控制回路是用来实现自动重合闸和备用电源自动投入。
⑥操作电源回路是用来提供断路器控制回路、信号回路、保护回路、监测回路、自动控制回路等所需的电源。
8-2 二次回路图主要有哪些内容各有何特点答:二次回路图主要有二次回路原理图、二次回路展开图、二次回路安装接线图。
①二次回路原理图主要是用来表示继电保护、断路器控制、信号等回路的工作原理,在该图中一、二次回路画在一起,继电器线圈和其触点画在一起,有利于叙述工作原理,但由于导线交叉太多,它的应用受到一定的限制。
②二次回路展开图将二次回路中的交流回路与直流回路分开来画。
交流回路又分为电流回路和电压回路,直流回路又有直流操作回路与信号回路,在展开图中继电器线圈和触点分别画在相应的回路,用规定的图形和文字符号表示。
③二次回路安装接线图画出了二次回路中各设备的安装位置及控制电缆和二次回路的连接方式,是现场施工安装、维护必不可少的图纸。
8-3 操作电源有哪几种,直流操作电源又有哪几种各有何特点答:二次回路的操作电源主要有直流操作电源和交流操作电源两类,直流操作电源有蓄电池和硅整流直流电源两种。
蓄电池主要有铅酸蓄电池和镉镍蓄电池两种。
①铅酸蓄电池具有一定危险性和污染性,需要专门的蓄电池室放置,投资大。
《机械制图习题集》习题答案——第8章

0
Φ 40 h7 ( -0.0 25 )
Φ4 0H准制( 基孔制 ) 配合种类(间隙配合) 孔的公差等级代号(8 ) 轴的公差等级代号(7)
公差是( 0.022)。
6、零件的外表面是( 铸造 )面,表面粗糙度代号为“ ”,
含义为( 未去除表面材料获得的表面粗糙度 )。
4、读填料盒零件图,补画左视图。
)
0.015 0.015
+0. ( Φ25k6 015 ) +0. 002
Φ52JS7(+-
8-5 极限与配合
1、根据图中的配合代号,在零件图上分别标出轴和孔的尺寸及 公差带代号,查出偏差数值并填空。
3、说明形位公差的含义 0.03 A ( 齿轮左端面垂直于φ20f7的轴线,其公差为0.03
)。
4、28
0 -0.023
的上偏差(
0
),下偏差( -0.023 ),上极限尺寸
( 28 ),下极限尺寸( 27.977 ),公差( 0.023 )。
2、读支架零件图,回答下列问题,补画D—D剖视图。
宽度方向 尺寸基准
2、找出图中表面表面粗糙度的注写错误,并正确标注。
8-3 标注与识读几何公差
1、解释所注几何公差的含义。
Φ100圆柱面的圆度公差为0.004mm
Φ100圆柱面相对于Φ45轴线的圆跳 动度公差为0.015mm
右端面相对于左端面的平行度公差 为0.01mm
2、标注轴的几何公差
(1)Φ25h7圆柱度公差为0.02; (2)Φ25h7轴线对Φ10H6轴线的同轴度公差为0.03; (3)Φ32h7圆柱面对Φ10H6与Φ20f6的公共轴线的圆跳动度公差为0.04; (4)Φ32h7两端面对Φ10H6与Φ20f6的公共轴线的圆跳动度公差为0.04。
第8章_带传动习题解答

n2'
(1 )
dd1 n1 dd2
332.96r / min
转速误差 n2 n2 n2 ' 0.9%
n2
n2
四.计算带轮转速
在5%允许范围内
v dd1n1 6.28m / s 60 1000
五.计算中心距和带长
5 v 25m / s
1.初定中心距 0.7(dd1 dd2 ) a0 2(dd1 dd2 )
九.计算压轴力
Fp
2F0
sin
1 2
Z
2270N
知识回顾 Knowledge Review
祝您成功!
d d1
57.30
1540
1200
七.计算带根数
作业一
Z
KAP P1
(P0
Pca P0)KK L
式中: P0 1.64kW
P0 0.29kW
K 0.928 KL 0.95
4.94
取Z=5
八.计算预紧力
作业一
作业一
F0
500
Pca zv
2.5 ( K
1)
qv2
500 8.4 ( 2.5 1) 0.17 6.282 233N 5 6.28 0.928
取 a0 dd1 dd2 125 355 480mm
2.初算带长
Ld ' 2a0
2
(d
d1
d
d
2
)
(dd2 dd1)2 4a 0
1742mm
取标准 Ld 1800mm
3.确定中心距
作业一
a
a0
Ld
2
Ld
'
480
1800
第八章习题解答

习题八答案1. 试比较多谐振荡器、单稳态触发器、施密特触发器的工作特点,并说明每种电路的主要用途。
答:多谐振荡器是一种自激振荡电路,不需要外加输入信号,它没有稳定状态,只有两个暂稳态。
暂稳态间的相互转换完全靠电路本身电容的充电和放电自动完成。
改变外接R 、C 定时元件数值的大小,可调节振荡频率。
施密特触发器具有回差特性,它有两个稳定状态,有两个不同的触发电平。
施密特触发器可将任意波形变换成矩形脉冲,输出脉冲宽度取决于输入信号的波形和回差电压的大小。
单稳态触发器有一个稳定状态和一个暂稳态。
输入信号起到触发电路进入暂稳态的作用,其输出脉冲的宽度取决于电路本身 R 、C 定时元件的数值。
改变 R 、C 定时元件的数值可调节输出脉冲的宽度。
多谐振荡器是常用的矩形脉冲产生电路。
施密特触发器和单稳态触发器是两种常用的整形电路。
施密特触发器可用来进行整形、幅度鉴别、构成多谐振荡器等。
单稳态触发器常用于脉冲的延时、定时和整形等。
2.在图8.2所示555集成定时器中,输出电压uo 为高电平UOH、低电平UOL及保持原来状态不变的输入信号条件各是什么?假定UCO端已通过0.01μF 接地,u D 端悬空。
答:当1=R 时, TR U <3V CC ,则C 2输出低电平, 1=Q ,OH o U u =。
当1=R 时, TH U >32V CC ,TR U >3V CC ,则C 1输出低电平、C 2输出高电平,1=Q 、0=Q ,OL o U u =。
当1=R 时, TH U <32V CC,TR U >3V CC ,则C 1C 2输出均为高电平,基本RS 触发器保持原来状态不变,因此o u 保持原来状态不变。
3.在图8.3所示多谐振荡器中,欲降低电路振荡频率,试说明下面列举的各种方法中,哪些是正确的,为什么?1) 加大R 1的阻值; 2) 加大R 2的阻值; 3) 减小C 的容量。
答:根据式(8-2)()ln221121C R R T f +==可知,1)2)两种方法是正确的。
第8、9章习题解答

第8章习题解答8-2下面说法正确的是:()(A )若高斯面上的电场强度处处为零,则该面内必定没有电荷; (B )若高斯面内没有电荷,则该面上的电场强度必定处处为零; (C )若高斯面上的电场强度处处不为零,则该面内必定有电荷; (D )若高斯面内有电荷,则该面上的电场强度必定处处不为零。
解:[答案:D]高斯定理的原意。
8-3一半径为R 的导体球表面的面点荷密度为σ,则在距球面R 处的电场强度()(A )0?/σε (B )0/2σε (C )/4σε0 (D )0/8σε 解:[答案:C]利用均匀带电球面的场强公式计算02004qq r πε==F E r ,其中σπ24R q =, R 2r =8-4下列说法正确的是( )(A) 电场强度为零的点,电势也一定为零 (B) 电场强度不为零的点,电势也一定不为零 (C) 电势为零的点,电场强度也一定为零(D) 电势在某一区域内为常量,则电场强度在该区域内必定为零 解:[答案:D].根据场强与电势的微分关系或积分关系均可以证明。
8-5在静电场中,电势不变的区域,场强必定为 。
解:[答案:0] 根据场强与电势的微分关系或积分关系均可以证明。
8-6一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总通量将 。
解:[答案:0/6q ε, 将为零],第一空:根据高斯定理知:正六面体的六个对称面组成的闭合面总通量为0εq,故每个面是总量的61。
第二空:根据高斯定理:总通量仅与面内电荷有关。
只要将点电荷由中心移动至六面体外,则该点荷对闭合面的总通量将没有贡献。
8-8电量Q 均匀分布在半径为R 的球体内,则球内球外的静电能之比 。
解:[答案:5:6]利用⎰=RV E W 020d 21内内ε及⎰∞=R V E W d 2120外外ε计算。
其中dr r dV 24π=,304R Qr E πε=内,204r QE πε=外。
第8章 直流稳压电源-习题解答

Uz
R1
U 0max R2
R3
R3
U 0max
R1
R2 R3
R3
Uz
24 V
当 R2 滑动头滑到最上方时,调整过程与上述相反,U0 输出将达到最小。
U 0min
R1 R2 R3 R2 R3
Uz
12 V
因此 U0=12~24V
8.14 利用 W7805 固定输出集成稳压器, 通过外接电路来改变输出电压值, 电路
u1
u2
T
C
Ui
IE
IRL
IR
R1
IR1
R
R2 RL
u0
uf
Dz
R3
题 8.13 图
【解】 (1)根据桥式整流电容滤波电路经验公式
U i = 1.2U 2
有
U2
=
Ui 1.2
=
30 1.2
=
25V
(2)当 R2 滑动头滑到最下方时,反馈信号 uf 最弱,运放器净输入信号最强, 其输出信号最强,即调整管 T 的基极电位最高,则 IB 最大,IC 最大,调整管的 UCE 电压最小,所以,此时 U0 输出最大。
②半波 ③桥式
(3)电路如题 8.2(3)图所示,Uz 为稳压管 Dz 的稳定电压,当 UI > Uz 时, 能保持 RL 两端电压为 Uz 的电路为( b )。
8.3 判断题
题 8.2(3)
(1)整流电路可将正弦电压变为脉动的直流电压。( √ )
(2)电容滤波电路适用于小负载电流,而电感滤波电路适用于大负载电流。
(√ )
(3)在单相桥式整流电容滤波电路中,若有一只整流管断开,则输出电压
电子技术习题解答.第8章.触发器和时序逻辑电路及其应用习题解答

第8章 触发器和时序逻辑电路及其应用习题解答8.1 已知基本RS 触发器的两输入端D S 和D R 的波形如图8-33所示,试画出当基本RS 触发器初始状态分别为0和1两种情况下,输出端Q的波形图。
图8-33 习题8.1图解:根据基本RS 触发器的真值表可得:初始状态为0和1两种情况下,Q的输出波形分别如下图所示:习题8.1输出端Q的波形图8.2 已知同步RS 触发器的初态为0,当S 、R 和CP 的波形如图8-34所示时,试画出输出端Q的波形图。
图8-34 题8.2图解:根据同步RS 触发器的真值表可得:初始状态为0时,Q的输出波形分别如下图所示:习题8.2输出端Q的波形图8.3 已知主从JK触发器的输入端CP、J和K的波形如图8-35所示,试画出触发器初始状态分别为0时,输出端Q的波形图。
图8-35 习题8.3图解:根据主从JK触发器的真值表可得:初始状态为0情况下,Q的输出波形分别如下图所示:习题8.3输出端Q的波形图8.4 已知各触发器和它的输入脉冲CP的波形如图8-36所示,当各触发器初始状态均为1时,试画出各触发器输出Q端和Q端的波形。
图8-36 习题8.4图解:根据逻辑图及触发器的真值表或特性方程,且将驱动方程代入特性方程可得状态方程。
即:(a )J =K =1;Qn +1=n Q,上升沿触发 (b)J =K =1;Qn +1=n Q, 下降沿触发 (c)K =0,J =1;Qn +1=J n Q+K Qn =1,上升沿触发 (d)K =1,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0·Qn =n Q,上升沿触发 (e)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,上升沿触发 (f)K =Qn ,J =n Q;Qn +1=J n Q+K Qn =n Qn Q+0=n Q,下降沿触发, 再根据边沿触发器的触发翻转时刻,可得当初始状态为1时,各个电路输出端Q的波形分别如图(a )、(b )、(c )、(d )、(e )和(f )所示,其中具有计数功能的是:(a )、(b )、(d )、(e )和(f )。
第8、9章习题解答分析

第8章习题解答8-2下面说法正确的是:()(A )若高斯面上的电场强度处处为零,则该面内必定没有电荷; (B )若高斯面内没有电荷,则该面上的电场强度必定处处为零; (C )若高斯面上的电场强度处处不为零,则该面内必定有电荷; (D )若高斯面内有电荷,则该面上的电场强度必定处处不为零。
解:[答案:D]高斯定理的原意。
8-3一半径为R 的导体球表面的面点荷密度为σ,则在距球面R 处的电场强度()(A )0?/σε (B )0/2σε (C )/4σε0 (D )0/8σε 解:[答案:C]利用均匀带电球面的场强公式计算02004qq r πε==F E r ,其中σπ24R q =, R 2r =8-4下列说法正确的是( )(A) 电场强度为零的点,电势也一定为零 (B) 电场强度不为零的点,电势也一定不为零 (C) 电势为零的点,电场强度也一定为零(D) 电势在某一区域内为常量,则电场强度在该区域内必定为零 解:[答案:D].根据场强与电势的微分关系或积分关系均可以证明。
8-5在静电场中,电势不变的区域,场强必定为 。
解:[答案:0] 根据场强与电势的微分关系或积分关系均可以证明。
8-6一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总通量将 。
解:[答案:0/6q ε, 将为零],第一空:根据高斯定理知:正六面体的六个对称面组成的闭合面总通量为0εq,故每个面是总量的61。
第二空:根据高斯定理:总通量仅与面内电荷有关。
只要将点电荷由中心移动至六面体外,则该点荷对闭合面的总通量将没有贡献。
8-8电量Q 均匀分布在半径为R 的球体内,则球内球外的静电能之比 。
解:[答案:5:6]利用⎰=RV E W 020d 21内内ε及⎰∞=R V E W d 2120外外ε计算。
其中dr r dV 24π=,304R Qr E πε=内,204r QE πε=外。
仪器分析课后习题第八章答案

精品文档
12.用波长为213.8nm,质量浓度为0.010mg.mL-1的锌标准溶 液和空白溶液交替连续测定10次,用记录仪记录的格数如下. 计算该原子吸收分光光度计测定锌元素的检出限.
3.在原子吸收光度计中为什么不采用连续光源(如钨丝灯或氘灯), 而在分光光度计中则需要采用连续光源?
解:虽然原子吸收光谱中积分吸收与样品浓度呈线性关系,但由于原子 吸收线的半宽度很小,如果采用连续光源,要测定半宽度很小的吸收线 的积分吸收值就需要分辨率非常高的单色器,目前的技术条件尚达不到, 因此只能借助锐线光源,利用峰值吸收来代替.
9.应用原子吸收光谱法进行定量分析的依据是什么?进行定量分析有哪些方法? 试比较它们的优缺点. 解:在一定的浓度范围和一定的火焰宽度条件下,当采用锐线光源时,溶液 的吸光度与待测元素浓度成正比关系,这就是原子吸收光谱定量分析的依据。 常用两种方法进行定量分析: (1)标准曲线法:该方法简便、快速,但仅适用于组成简单的试样。 (2)标准加入法:本方法适用于试样的确切组分未知的情况。不适合于曲 线斜率度,应注意那些问题?怎样 选择原子吸收光谱分析的最佳条件? 解:应该从分析线的选择、光源(空心阴极灯)的工作电流、火焰的 选择、燃烧器高度的选择及狭缝宽度等几个方面来考虑,选择最佳的 测定条件。
11.从工作原理、仪器设备上对原子吸收法及原子荧光法作比较。 解:从工作原理上看,原子吸收是通过测定待测元素的原子蒸气对其特 征谱线的吸收来实现测定的,属于吸收光谱,而原子荧光则是通过测量 待测元素的原子蒸气在辐射能激发下所产生的荧光的强度来实现测定的, 属于发射光谱。
第8章习题解答

第8章思考题及习题8参考答案一、填空1. 单片机存储器的主要功能是存储和。
答:程序、数据。
2.假设外部数据存储器2000H单元的内容为80H,执行下列指令后累加器A中的内容为。
MOV P2,#20HMOV R0,#00HMOVX A,@R0答:80H。
3.在存储器扩展中,无论是线选法还是译码法最终都是为扩展芯片的端提供控制信号。
答:片选。
4.起止范围为0000H~3FFFH的数据存储器的容量是 KB。
答:16KB。
5.在AT89S52单片机中,PC和DPTR都用于提供地址,但PC是为访问存储器提供地址,而DPTR是为访问存储器提供地址。
答:程序、数据。
6.11条地址线可选个存储单元,16KB存储单元需要条地址线。
答:2K,14。
7.4KB RAM存储器的首地址若为0000H,则末地址为 H。
答:0FFF。
8.若单片机外扩32KB 数据存储器的首地址若为4000H,则末地址为 H。
答:BFFF9. 设计一个以AT89S52单片机为核心的系统,如果不外扩程序存储器,使其内部8KB闪烁程序存储器有效,则其引脚应该接。
答:EA*,+5V10.74LS138是具有3个输入的译码器芯片,其输出常作片选信号,可选中片芯片中的任一芯片,并且只有1路输出为电平,其它输出均为电平。
答:8,低,高;二、单选1.区分AT89S51单片机片外程序存储器和片外数据存储器的最可靠方法是。
A.看其位于地址范围的低端还是高端B.看其离AT89S51单片机芯片的远近C.看其芯片的型号是ROM还是RAMD.看其是与RD信号连接还是与PSEN信号连接答:D2.访问片外数据存储器的寻址方式是。
A.立即寻址B.寄存器寻址C.寄存器间接寻址D.直接寻址答:C3.若要同时扩展4片2KB的RAM和4片4KB的ROM,则最少需要根地址线。
A、12B、13C、14D、154.当EA=1时,AT89S52单片机可以扩展的外部程序存储器的最大容量为。
A. 64KB B.60KB C.58KB D.56KB答:D5. 若某数据存储器芯片地址线为12根,那么它的存储容量为。
大学物理3第08章习题分析与解答

习题8-6图IOR 第八章 恒定磁场8-1 均匀磁场的磁感强度B 垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为[ ]。
(A) B r 22π (B) B r 2π (C) 0 (D) 无法确定 分析与解 根据高斯定理,磁感线是闭合曲线,穿过圆平面的磁通量与穿过半球面的磁通量相等。
正确答案为(B )。
8-2 下列说法正确的是[ ]。
(A) 闭合回路上各点磁感强度都为零时,回路内一定没有电流穿过(B) 闭合回路上各点磁感强度都为零时,回路内穿过电流的代数和必定为零 (C) 磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度必定为零(D) 磁感强度沿闭合回路的积分不为零时,回路上任意点的磁感强度必定为零分析与解 由磁场中的安培环路定理,磁感强度沿闭合回路的积分为零时,回路上各点的磁感强度不一定为零;闭合回路上各点磁感强度为零时,穿过回路的电流代数和一定为零。
正确答案为(B )。
8-3 磁场中的安培环路定理∑⎰=μ=⋅nLI1i i0d l B 说明稳恒电流的磁场是[ ]。
(A) 无源场 (B) 有旋场 (C) 无旋场 (D) 有源场分析与解 磁场的高斯定理与安培环路定理是磁场性质的重要表述,在恒定磁场中B 的环流一般不为零,所以磁场是涡旋场;而在恒定磁场中,通过任意闭合曲面的磁通量必为零,所以磁场是无源场;静电场中E 的环流等于零,故静电场为保守场;而静电场中,通过任意闭合面的电通量可以不为零,故静电场为有源场。
正确答案为(B )。
8-4 一半圆形闭合平面线圈,半径为R ,通有电流I ,放在磁感强度为B 的均匀磁场中,磁场方向与线圈平面平行,则线圈所受磁力矩大小为[ ]。
(A) B R I 2π (B)B R I 221π (C) B R I 241π (D) 0 分析与解 对一匝通电平面线圈,在磁场中所受的磁力矩可表示为B e M ⨯=n IS ,而且对任意形状的平面线圈都是适用的。
大学应用物理第八章习题解答

第8章 磁场8-10一均匀密绕直螺线管的半径为 ,单位长度上有 匝线圈,每匝线圈中的电流为 ,用毕奥—萨伐尔定律求此螺线管轴线上的磁场。
分析:由于线圈密绕,因此可以近似地把螺线管看成一系列圆电流的紧密排列,且每一匝圆电流在轴线上任一点的磁场均沿轴向。
解: 取通过螺线管的轴线并与电流形成右旋的方向(即磁场的方向)为x 轴正向,如习题8-10图解(a )所示。
在螺线管上任取一段微元dx ,则通过它的电流为dI nIdx =,把它看成一个圆线圈,它在轴线上O 点产生的磁感应强度dB 为2022322()R nIdxdB R x μ=+ 由叠加原理可得,整个螺线管在O 点产生的磁感应强度B 的大小为由图可知12122212221212cos os ()()x x R x R x ββ==++ c ,代入上式并整理可得式中12ββ和分别为x 轴正向与从O 点引向螺线管两端的矢径r 之间的夹角。
讨论:(1)若螺线管的长度远远大于其直径,即螺线管可视为无限长时,20β=,1βπ=,则有上式说明,无限长密绕长直螺线管内部轴线上各点磁感应强度为常矢量。
理论和实验均证明:在整个无限长螺线管内部空间里,上述结论也适用。
即无限长螺线管内部空间里的磁场为均匀磁场,其磁感应强度B 的大小为0nI μ,方向与轴线平行;(2)若点O 位于半无限长载流螺线管一端,即12πβ=,20β=或12πβ=,2βπ=时,无论哪一种情况均有nI B 021μ=------(8-19) 可见半无限长螺线管端面中心轴线上磁感应强度的大小为管内的一半;综上所述,密绕长直螺线管轴线上各处磁感应强度分布见习题8-10图解(b )所示,从图中也可看出,长直螺线管内中部的磁场可以看成是均匀的。
习题8-10图解(a )习题8-10图解(b )8-11两根长直导线互相平行地放置,导线内电流大小相等,均为I =10A ,方向相同,如图8-49题图(左)所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
并且在理论上有如下的关系
(提示:由范德瓦耳斯方程可写出 的三次方程,对于临界点,以 、 数据代入后对 求解,应得三重根的解。或由 , ,求证亦可)
解:由 解出
设临界状态下 、 、
是方程的根, 展开后
比较两式
(3)/(2)得 ,其余的解是
再由(3)
由于 ,所以
*8-24在标准状态下,氦气(He)的内摩擦系数 =1.89×10-5Pa·s,求:(1)在此状态下氦原子的平均自由程;(2)氦原子半径。
解:标况:
(1)
把 、 代入
得
(2)
*8-25热水瓶胆的两壁间距L=4×10-3m,其间充满温度为27℃的氮气,氮分子的有效直径为d=3.1×10-10m,问瓶胆两壁间的压强降低到多大数值以下时,氮的热传导系数才会比它在一个大气压下的数值小?
解:
(1)
(2)
(3)
(4)
8-8水蒸气分解为同温度的氢气和氧气,即H2O →H2+ O2
也就是1mol水蒸气可分解成同温度的1mol氢和1/2mol的氧。当不计振动自由度时,求此过程的内能增量。
解: ,
若水蒸气温度是100℃时
8-9已知在273 K、1.0×10-2atm时,容器内装有一理想气体,其密度为1.24×10-2kg/m3。求:(1)方均根速率;(2)气体的摩尔质量,并确定它是什么气体;(3)气体分子的平均平动动能和转动动能各为多少?(4)容器单位体积内分子的总平动动能是多少?(5)若该气体有0.3 mol,其内能是多少?
解:
8-3容积V=1 m3的容器内混有N1=1.0×1023个氢气分子和N2=4.0×1023个氧气分子,混合气体的温度为400 K,求:
(1)气体分子的平动动能总和;(2)混合气体的压强。
解:(1)
(2)
8-4储有1mol氧气、容积为1 m3的容器以 =10 m/s的速率运动。设容器突然停止,其中氧气的80%的机械运动动能转化为气体分子热运动动能。问气体的温度及压强各升高多少?(将氧气分子视为刚性分子)
解:1mol氧气的质量 ,
由题意得
8-5一个具有活塞的容器中盛有一定量的氧气,压强为1 atm。如果压缩气体并对它加热,使温度从27℃上升到177℃,体积减少一半,则气体的压强变化多少?气体分子的平均平动动能变化多少?分子的方均根速率变化多少?
解:已知
根据
8-6温度为0 ℃和100 ℃时理想气体分子的平均平动动能各为多少?欲使分子的平均平动动能等于1 eV,气体的温度需多高?
习题
8-1设想太阳是由氢原子组成的理想气体,其密度可当成是均匀的。若此理想气体的压强为1.35×1014Pa。试估计太阳的温度。(已知氢原子的质量m=1.67×10-27kg,太阳半径R=6.96×108m,太阳质量M=1.99×1030kg)
解:
8-2目前已可获得1.013×10-10Pa的高真空,在此压强下温度为27℃的1cm3体积内有多少个气体分子?
解:(1)由速率分布函数的归一化条件可得
(2) 时:
时:
(3)
8-19质点离开地球引力作用所需的逃逸速率为 ,其中r为地球半径。(1)若使氢气分子和氧气分子的平均速率分别与逃逸速率相等,它们各自应有多高的温度;(2)说明大气层中为什么氢气比氧气要少。(取r=6.40×106m)
解:(1)由题意知
又
(2)根据上述分析,当温度相同时,氢气的平均速率比氧气的要大(约为4倍),因此达到逃逸速率的氢气分子比氧气分子多。按大爆炸理论,宇宙在形成过程中经历了一个极高温过程。在地球形成的初期,虽然温度已大大降低,但温度值还是很高。因而,在气体分子产生过程中就开始有分子逃逸地球,其中氢气分子比氧气分子更易逃逸。另外,虽然目前的大气层温度不可能达到上述计算结果中逃逸速率所需的温度,但由麦克斯韦分子速率分布曲线可知,在任一温度下,总有一些气体分子的运动速率大于逃逸速率。从分布曲线也可知道在相同温度下氢气分子能达到逃逸速率的可能性大于氧气分子。
解:(1)
(2)
8-7一容积为10 cm3的电子管,当温度为300 K时,用真空泵把管内空气抽成压强为5×10-4mmHg的高真空,问此时(1)管内有多少空气分子?(2)这些空气分子的平均平动动能的总和是多少?(3)平均转动动能的总和是多少?(4)平均动能的总和是多少?(将空气分子视为刚性双原子分子,760mmHg=1.013×105Pa)
解:热传导系数
由于 , ,所以 与压强无关,即热传导系数与压强无关。然而在抽真空的容器中当压强降到一定程度时,平均自由程 会大于容器本身的线度,这时 取为容器的线度不变,当真空度进一步提高时,因 不变,所以 时, ,则 ,于是热传导系数就小于一个大气压下的数值了。因此当
时传导系数开始发生变化。
*8-26由范德瓦耳斯方程 ,证明气体在临界状态下温度 、压强 及体积 为
*8-20试求上升到什么高度时大气压强减至地面的75%?设空气温度为0℃,空气的摩尔质量为0.0289 kg/mol。
解:由
8-21(1)求氮气在标准状态下的平均碰撞次数和平均自由程;(2)若温度不变,气压降低到1.33×10-4Pa,平均碰撞次数又为多少?平均自由程为多少?(设分子有效直径为10-10m)
(2) 范围内的粒子数
(3)速率小于 的粒子数占总粒子数的百分比
8-14图中 、 两条曲线是两种不同气体(氢气和氧气)在同一温度下的麦克斯韦速率分布曲线。试由图中数据求:(1)氢气分子和氧气分子的最概然速率;(2)两种气体所处的温度。
解:(1)由习题8-14图可知:
(2)由
8-15在容积为3.0×10-2m3的容器中装有2.0×10-2kg气体,容器内气体的压强为5.06104Pa,求气体分子的最概然速率。
解:由
8-16质量 =6.2×10-14g的微粒悬浮在27℃的液体中,观察到悬浮粒子的方均根速率为1.4 cm/s,假设粒子服从麦克斯韦速率分布函数,求阿伏伽德罗常数。
解:
8-17有N个粒子,其速率分布函数为
(1)作速率分布曲线;(2)由 求常数c;(3)求粒子平均速率。
解:(1)
(2)
(3)
8-18有N个粒子,其速率分布曲线如图所示,当 时 。求:(1)常数a;(2)速率大于 和小于 的粒子数;(3)求粒子平均速率。
解:
8-22真空管的线度为10-2m,真空度为1.33×10-3Pa,设空气分子有效直径为3×10-10m,求27℃时单位体积内的空气分子数、平均自由程和平均碰撞频率。
解:
由 ,当容器足够大时,取
代入可得 (真空管线度)
所以空气分子间实际不会发生碰撞,而只能与管壁碰撞,因此平均自由程就是真空管的线度,即
8-23在气体放电管中,电子不断与气体分子碰撞。因电子速率远大于气体分子的平均速率,所以可以认为气体分子不动。设气体分子有效直径为 ,电子的“有效直径”比起气体分子来可以忽略不计,求:(1)电子与气体分子的碰撞截面;(2)电子与气体分子碰撞的平均自由程。(气体分子数密度为 )
解:(1)
(2) 其中 为电子相对于分子的平均相对速率
解: (1)
(2)
所以此气体分子为CO或N2
(3)
(4)
(5)
8-10一容器内储有氧气,其压强为1.01×105Pa,温度为27.0℃,求:(1)分子数密度;(2)氧气的密度;(3)分子的平均平动动能;(4)分子间的平均距离。(设分子间均匀等距排列)
解:(1)
(2)
(3)
(4)
8-11设容器内盛有质量为 和 的两种不同的单原子理想气体,此混合气体处在平衡态时内能相等,均为 ,若容器体积为 。试求:(1)两种气体分子平均速率 与 之比;(2)混合气体的压强。
解:(1)
(2)
8-12在容积为2.0×10-3m3的容器中,有内能为6.75102J的刚性双原子分子理想气体。(1)求气体的压强;(2)设分子总数为5.41022个,求分子的平均平动动能及气体的温度。
解:(1)
(2)
8-13已知 是速率分布函数,说明以下各式的物理意义:
(1) ;(2) ;(3)
解:(1) 范围内的粒子数占总粒子数的百分比;
