08第八章 材料力学习题解答(应力状态分析和强度理论)
《材料力学》第八章课后习题参考答案

解题方法与技巧归纳
受力分析
在解题前首先要对物体进行受力分析, 明确各力的大小和方向,以便后续进 行应力和应变的计算。
图形结合
对于一些复杂的力学问题,可以画出 相应的示意图或变形图,帮助理解和 分析问题。
公式应用
熟练掌握材料力学的相关公式,能够 准确应用公式进行计算和分析。
检查结果
在解题完成后,要对结果进行检查和 验证,确保答案的正确性和合理性。
压杆稳定
探讨细长压杆在压缩载荷作用下的稳定性问题。
解题方法与技巧
准确理解题意
仔细审题,明确题目要求和考查的知识点。
选择合适的公式
根据题目类型和所给条件,选用相应的公式 进行计算。
注意单位换算
在计算过程中,要注意各物理量的单位换算, 确保计算结果的准确性。
检查答案合理性
得出答案后,要检查其是否符合实际情况和 物理规律,避免出现错误。
相关题型拓展与延伸
组合变形问题
超静定问题
涉及多种基本变形的组合,如弯曲与扭转 的组合、拉伸与压缩的组合等,需要综合 运用所学知识进行分析和计算。
超静定结构是指未知力数目多于静力平衡 方程数目的结构,需要通过变形协调条件 或力法、位移法等方法进行求解。
稳定性问题
疲劳强度问题
研究细长压杆在压力作用下的稳定性问题 ,需要考虑压杆的临界力和失稳形式等因 素。
研究材料在交变应力作用下的疲劳破坏行为 ,需要了解疲劳极限、疲劳寿命等概念和计 算方法。
THANKS FOR WATCHING
感谢您的观看
重点知识点回顾
材料的力学性质
包括弹性、塑性、强度、硬度等基本概念和 性质。
杆件的拉伸与压缩
涉及杆件在拉伸和压缩状态下的应力、应变及 变形分析。
材料力学应力状态和强度理论

x 122.5MPa x 64.6MPa
σy 0
τ y 64.6
(122.5 , 64.6)
D1
B2
o
C
B1
(0 , - 64.6)
由 x , x 定出 D1 点 由 y , y 定出 D2 点 以 D1D2 为直径作应力圆。
D2
A1,A2 两点的横坐标分别代表 a 点的两个主应力
1 oA1 150MPa
1 x 136.5MPa
σ x 136.5MPa σy 0
τx0 τy0
2 3 0
D2 (0,0)
D1(136.5,0)
x 136.5MPa
b
σ1
σ x 136.5MPa τ x 0
σy 0
τy0
1 所在的主平面就是 x 平面 , 即梁的横截面 C 。
解析法求 a 点的主平面和主应力
解: x 100MPa, y 20MPa, x 40MPa, 300
20
300
100 40
x 100MPa, y 20MPa, x 40MPa, 300
x
2
y
x
2
y
cos
2
x
sin
2
x
2
y
sin
2
x
cos
2
300
100
(20) 2
100
(20) 2
cos( 600)
m
F
A
F
m
A
F
F
A
A 点 横截面 m—m 上的应力为: F
A
n
m
F
A
F
m
n
F
A
2
材料力学教程习题解答-第八章

M
F2 4 F2 4 15 103 N 2 7.64 Mpa 2 A d 0.05 T 16M e 16 1.2 103 T 48.89 Mpa 2 3 Wp d 0.05
F1l
T
Me
则: r 3
36.67 7.64 4 48.892 Mpa
2
107.35Mpa 160 Mpa 则强度符合要求
8-12
l
A
T F1a
B
a
C F1
F2 M F2 a
1 A截面是危险截面 F
F2
T
r4
M N 3 T 2
2
F1a
FN
M F2
M F1
M合
F2 a F1l
2 1 2 3 1 E D 2 2 1 2 3 1 0 0 E D 45 45 M 2 1 2 1 2 4 1 1 2
2 2
x y
1 38.28Mpa 40 Mpa
则 1 38.28Mpa, 2 0, 3 18.28Mpa则应用第一强度理论进行校核:
8-4
则 1 , 2 0, 3 。根据第一强度理论则: 1 则第一强度理论有: 第二强度理论: r2 1 2 3 0 1 许用切应力为: 脆性材料纯剪切,则 max min
8-22
t
若剪应力采用薄壁圆筒的剪应力公式时有:
x
M
pD pD x , t , T 4 2
材料力学习题应力状态和强度理论
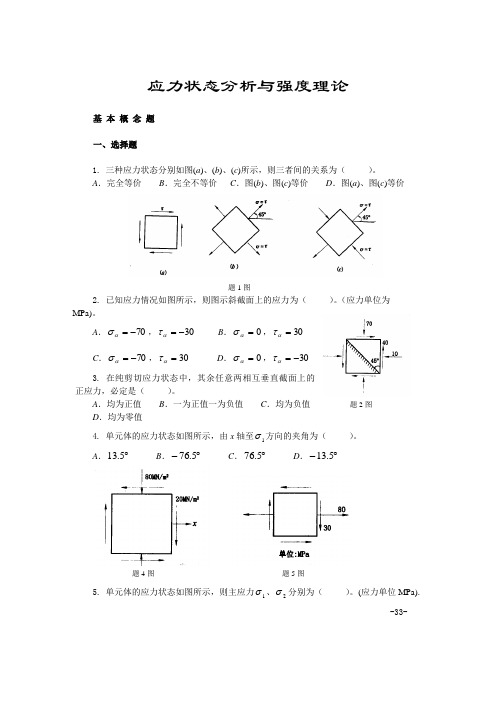
应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示,则三者间的关系为( )。
A .完全等价B .完全不等价C .图(b )、图(c )等价D .图(a )、图(c )等价题1图2. 已知应力情况如图所示,则图示斜截面上的应力为( )。
(应力单位为 MPa)。
A .70-=ασ,30-=ατB .0=ασ,30=ατC .70-=ασ,30=ατD .0=ασ,30-=ατ3. 在纯剪切应力状态中,其余任意两相互垂直截面上的 正应力,必定是( )。
A .均为正值B .一为正值一为负值C .均为负值 题2图D .均为零值4. 单元体的应力状态如图所示,由x 轴至1σ方向的夹角为( )。
A .︒5.13 B .︒-5.76 C .︒5.76 D .︒-5.13题4图 题5图5. 单元体的应力状态如图所示,则主应力1σ、2σ分别为( )。
(应力单位MPa). -33-A .901=σ,102-=σB .1001=σ,102-=σC .901=σ,02=σD .1001=σ,02=σ 6. 如图6所示单元体最大剪应力m ax τ为( )。
A .100 MPaB .50 MPaC .25 MPaD .0题6图 题7图7. 单元体如图所示,关于其主应力有下列四种答案,正确的是( )。
A .1σ>2σ,03=σ B .3σ<2σ<0,03=σ01=σ C .1σ>0,2σ= 0,3σ<0,1σ<3σ D .1σ>0,2σ= 0,3σ<0,1σ>3σ8. 已知应力圆如图7-22所示,图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力,则与应力圆所对应的单元体为( )。
A .图(a )B .图(b )C .图(c )D .图(d )题8图9. 在图示四种应力状态中,其应力圆具有相同的圆心和相同的半径是( )。
-34-题9图A .图(a )、图(d )B .图(b )、图(c )C .图(a )、图(b )、图(c ) 、图(d )D .图(a )、图(d )、图(b )、图(c )10. 如图所示,较大体积的钢块上开有一贯穿的槽,槽内嵌入一铝质立方体,铝块受到均布压力P 作用,假设钢块不变形,铝块处于( )。
材料力学作业及练习题参考答案(8、9章)

八章2题: 解:查槽钢表,每根槽钢,A=25.669 cm2,W=141 cm3, 则两根槽钢制成的梁:A=2A=51.538 cm2, W=2W=282 cm3 在B截面左侧的上边缘处: =-FN/A+M/W=-50×103/(51.538×10-4)+37.5×103/(282×10-6) =123.24×106 Pa, 即在该处为拉应力123.24 MPa ; 在B截面左侧的下边缘处: =-FN/A-M/W=-50×103/(51.538×10-4)-37.5×103/(282×10-6) =-142.72×106 Pa, 即在该处为压应力142.72 MPa ; 在B截面右侧的上边缘处: =M/W=37.5×103/(282×10-6)=132.98×106 Pa, 即在该处为拉应力132.98 MPa ; 在B截面右侧的下边缘处: =-M/W=-37.5×103/(282×10-6)=-132.98×106 Pa, 即在该处为压应力132.98 MPa。
材料力学08(第八章 应力状态分析 第九章 强度理论 第十章 组合变形)PPT课件

D x6.7 3 , 3.7 5
Dy(0, 35.7)
60°
Dx(63.7,-35.7)
E-30°, -30° )
20MPa
Dy0, 3.57
按一定比例,作出应 力圆,并找到斜截面对应 的点,量取其坐标可得:
30 17MPa
30 46MPa
17
3、主平面和主应力
对图a所示应力状态,作出应力圆(图b)。
即: E x 2 y x 2 yc2 o s xs2 i n
同理可得E点的纵坐标为:
E E F x 2 ysi2 n xc2 o s
可见,E点坐标值即为斜截面上的应力分量值。
14
二倍角对应:应力圆半径转过的角度是微体截面方位角 变化的两倍,且二者转向相同。
y
y
n
x x
H( , )
即为斜截面上的应力分量值。
2)证明
对下图所示应力圆可见C点的
横坐标为:
E D1x,x
2
C
D2y,y
E
OC O2BB2C
由于
O
2
A2 B2
0 C F
D 2B 2C D 1B 1C y D2
可得:
x
1
y
x
D1
2 0
B1 A1
12
B2CB1C
则:
O O C 2 B 1 B 2/2 yx 2yx 2y
ta2n0
D1B1 2x C1B xy
19
所以,1主平面方位角0为:
0
1arc 2
tanx 2xy
2
O
A2 B2
E
D1
2 0
CF
B1 A1
y
第八章 应力状态分析和强度理论材料力学

(3)主方向 (4)主应力
(5)主单元体
4 广义胡克定律
1.应变叠加原理
各向同性材料在小变形的情况下,当应力不超过比例极限,则线应变只与正 应力有关,剪应变只与剪应力有关,且由正应力引起的某一方向上的应变 可以叠加;
2.主方向上的广义 胡克定律
由σ1 引起三个主方向的线应变为:
由σ2 引起三个主方向的线应变为:
2 二向应力状态分析
1.应力分量及其符号的规定
正应力规定与截面外法线 方向一致为正,反之为负; 剪应力规定对单元体内任 一点的矩顺时针为正,反 之为负;
2.斜截面上的应力
列出平衡方程: 由剪应力互等定理
整理得:
由上面两式可得:
这是关于σα和τα的圆方程;
圆心坐标是
半径是
3.应力圆 以横坐标表示正应力,纵坐标表示剪应力,画出二向应力状态的应力圆
4.应力圆与单元体之间的对应关系
(1)应力圆上的每一点对应单元体上互成1800的二个面上的应力状态; (2)应力圆上的点按某一方向转动2α角度,单元体上的面按相同方向转动α角度; (3)应力圆与α轴的交点代表主平面上的应力; (4)应力圆上代表主平面的点转动900得到剪应力极值点;单元体上主平面转动450得到剪 应力极值平面;
解: (1)应力分量
应力圆
(2)求主平面位置和主应力大小
例3.已知应力状态如图所示,图中的应力单位为MPa。试求: (1)主应力大小,主平面位置;(2)在单元体上给出主平面位置及主应力方向; (3)最大剪应力。
解:
(2)求主平面位置和主应力大小
(3)最大剪应力
例4.薄壁圆筒的扭转-拉伸示意图如图所示。若P=20kN,T=600NN·m,且d=50mm, =2mm。试求:(1)A点在指定斜截面上的应力。(2)A点主应力的大小及方向, 并用单元体表示。
材料力学课后习题答案8章

由于式中 α 为任意值,故原命题得证。
8-7
已知某点 A 处截面 AB 与 AC 的应力如图所示(应力单位为 MPa) ,试用图解法
求主应力的大小及所在截面的方位。
题 8-7 图 解:根据题图所给的已知应力,可画出应力圆来,如图 8-7 所示。
图 8-7 从所画的应力圆上可以量得两个主应力,它们是:
由
tanα 0 = −
得 σ 1 的方位角为
τx 2.25 =− = −0.07458 σ x − σ min 30.0 + 0.1678
α 0 = −4.27 o
对于应力图 c,其切应力为
τC =
3FS 3 × 20 × 103 N = = 3.00 × 106 Pa = 3.00MPa 2 2 A 2 × 0.050 × 0.200m
σα = (
30 + 10 + 20sin 90 o )MPa = 40.0MPa 2 30 − 10 sin 90 o )MPa = 10.0MPa τα = ( 2
(b)解:由题图所示应力状态可知,
1
σ x = −30MPa,σ y = 10MPa,τ x = 20MPa,α = 22.5 o
(a) (b) (c)
= 350 × 10 −6
将式(a)和(b)代入式(c),得
γ xy = (550 − 700) × 10 −6 = −150 × 10 −6
(d)
将以上所得结果(a),(b)和(d)代入平面应变状态任意方位的正应变公式,计算 ε135o 应有 的测量值为
ε135o =
1 1 (450 + 100) × 10 −6 + (450 − 100) × 10 −6 cos270 o 2 2 1 − × (−150 × 10 −6 )sin270 o = 200 × 10 −6 2
材料力学之应力分析与强度理论

eq4
M 2 0.75T 2 [ ]
W
统一形式:
eq
M eq W
[ ]
M eq3
M
2 z
M2 yT2 NhomakorabeaM eq4
M
2 z
M
2 y
0.75T
2
例1 求图示单元体的主应力及主平面的位置。(
单位:MPa)
解:主应力坐标系如图
25 3 4 5 B 9 5
A
在坐标系内画出点
2
1
0
° 5
25 3
45o
拉伸对应
2E
1
45o
剪切对应值
E
1
现在已测得圆杆表面上一点a沿45方向的线应变 45o=-2×10-4, 是上述两45方向的线应变之和
45o 测试值 45o 剪切对应值 45o 拉伸对应值
E45o 剪切对应值 E 45o 测试值 45o 拉伸对应值 =
1
1
E
2 3
1 3
体积改变比能
vV
1 2
6E
1 2
3 2
形状改变比能
1
vd 6E
1 2 2 2 3 2 1 3 2
5、四个常用强度理论
强度理论的统一形式: eqk [ ]
• 第一强度理论: • 第二强度理论: • 第三强度理论: • 第四强度理论:
eq1 1
eq2 1 2 3
组合变形习题课
一、应力分析和强度理论
1、平面应力状态分析
(1)斜截面上的应力
x x
y 2 y
2
x y
2
sin 2 x
cos cos
2 2
材料力学课件 第八章应力状态与强度理论

单向应力状态(Unidirectional State of Stress): 一个主应力不为零的应力状态。
x B x
zx
xz
x
x
A
§8–2 平面应力状态下的应力分析
y
y
y
xy x
等价 y
x
xy
x z
Ox
一、解析法
30
x
y
2
sin 2
x cos2
80 (40) sin(2 30 ) 60 cos(2 30 ) 2
21.96MPa
确定主平面方位,将单元体已知应力代入 8.3,得
20 45
tan 20
2 x x y
2 (60) 80 (40)
1
0 22.5
0 即为最大主应力1 与 x 轴的夹角。主应力为
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane):
剪应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
1
主应力排列规定:按代数值大小,
1 2 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
解:由于主应力1 ,2 ,3 与主应变1 ,2 ,3 一一对应,故由已知数据可知,
已知点处于平面应力状态且 2 0 。由广义胡克定律
1
1 E
(1
3 )
3
1 E
( 3
1)
联立上式
材料力学应力状态分析和强度理论

材料力学应力状态分析和强度理论材料力学是一门研究物质内部各个部分之间的相互作用关系的科学。
在材料力学中,应力状态分析和强度理论是非常重要的概念和方法,用来描述和分析材料的力学行为和变形性能。
材料的应力状态是指在外力作用下,物体内部各个部分所受到的力的分布情况。
应力有三个分量:法向应力、剪应力和旋转应力。
法向应力是垂直于物体表面的作用力,剪应力是平行于物体表面的作用力,旋转应力则是物体受到扭转力产生的应力分量。
应力状态的描述可以用应力矢量来表示。
应力状态分析的目的是确定材料内部各个部分的应力分布情况,进而推导出物体的变形和破坏行为。
常用的应力状态分析方法有平面应力问题、平面应变问题和三维应力问题。
平面应力问题是指在一个平面上的应变为零,而垂直于该平面的应力不为零;平面应变问题是指在一个平面上的变形为零,而垂直于该平面的应力不为零;三维应力问题则是指在空间中3个方向的应力都不为零。
强度理论是指根据材料的内部应力状态来评估其抗拉强度、抗压强度和抗剪强度等,以判断材料是否能够承受外力而不发生破坏。
常见的强度理论有最大正应力理论、最大剪应力理论和最大扭转应力理论。
最大正应力理论是指在材料的任何一个点,其法向应力都不能超过材料的抗拉强度;最大剪应力理论则是指剪应力不能超过材料的抗剪强度;最大扭转应力理论则是指旋转应力不能超过材料的极限扭转强度。
实际应用中,强度理论通常与材料的断裂理论结合起来,以评估材料的破坏行为。
材料断裂的主要原因是应力超过了材料的强度极限,从而导致材料的破坏。
为了提高材料的强度和抗拉性能,可以通过选择合适的材料、改变材料的结构和制造工艺等方法来实现。
综上所述,材料力学应力状态分析和强度理论是描述和分析材料力学行为和变形性能的重要理论和方法。
通过深入研究应力状态、应力分析和强度理论,可以为材料的设计和制造提供指导和支持,从而提高材料的强度和抗拉性能。
材料力学课后习题解答--配套孙训方教材应力状态和强度理论
V 03D
F V D 03D WD V V V 03D
03D 03D
q
W 03D
R V 03D V [ V \
G V D 03D W D 03D V 03D V V 03D D $c
VD
)V $
FRV D
d >V @
)V
>V @$
FRV D
WD
)W $
VLQ D
d
>W @
>V @ )W
>V @$
VLQ D
D $
)V >V @$ )W f
D $ )V >V @$ )W >V @$
D $ )V >V @$ )W >V @$
V$
0$\ ,]
u u u u
u 1P 03D
W$
)6 6] E, ]
u u u u u u
03D
V 03D
V 03D
V
R V
D V V 03D
D
$%
$%
V
&&
&$ &%
[ [ [
U
V 03D
V 03D
P )
D )
Q
)V )W
>V @$
)W )V
V $ qc
> @
D
D $
VD
) $
FRV
材料力学课件第八章应力状态与强度理论

第八章 应力状态分析与强度理论
第八章 应力状态分析与强度理论
第八章 应力状态分析与强度理论
第八章 应力状态分析与强度理论
第八章 应力状态分析与强度理论
应力状态的分类
单向应力状态:三个主应力中只有一个不等于零 二向应力状态:三个主应力中有二个不等于零 三向应力状态:三个主应力均不等于零
n
x x
y y
x
y
2
x
y
2
cos(2)xsin(2)
x
ห้องสมุดไป่ตู้
y
2
sin(2)xcos(2)
第八章 应力状态分析与强度理论
x 2 y x 2 yco s x 2 si n2
x 2ysin 2 xcos2
应力转轴公式的适用范围? 上述关系式是建立在静力学基础上,与材料性质无关。
换句话说,它既适用于各向同性与线弹性情况,也 适用于各向异性、非线弹性与非弹性问题。
第八章 应力状态分析与强度理论
Fn 0
d A x d A c o s()sin () x d A c o s()c o s() yd A sin ()c o s() yd A sin ()sin () 0
Ft 0
d A x d A c o s()c o s() x d A c o s()sin () yd A sin ()sin () yd A sin ()c o s() 0
40 60
80 60
(-40,60)
C
O
60
10M 2 Pa, 22MPa max10M 5 Pa,min65MPa 0 22.5, max85MPa
单向应力状态也称为 简单应力状态,二向和三向应力 状态统称为 复杂应力状态。
周建方版材料力学第八章习题解答[第八章01-76]
![周建方版材料力学第八章习题解答[第八章01-76]](https://img.taocdn.com/s3/m/e3cb205677232f60ddcca1af.png)
8-1 图8-34所示结构,杆AB 为5号槽钢,许用应力MPa ][1601=σ,杆BC 为矩形截面,mm b 50=,mm h 100=,许用应力MPa ][82=σ,承受载荷kN F 128=,试校核该结构的强度。
题8-1图解:由平衡条件解得, kNF F BC 642/==kN F F AB9.11023= 293.6cm A AB = 23105mm A BC ⨯=[]1231601093.6109.110σσ==⨯⨯==MPa A F AB AB AB[]MPa MPa A F BC BC BC88.121051064233=>=⨯⨯==σσ8-2 在图8-35所示结构中,钢索BC 由一组直径mm d 2=的钢丝组成。
若钢丝的许用应力MPa ][160=σ,AC 梁受有均布载荷m /kN q 30=,试求所需钢丝的根数。
又若将BC 杆改为由两个等边角钢焊成的组合截面,试确定所需等边角钢的型号。
角钢的MPa ][160=σ。
题8-1图解:BC 的内力计算:kN F F C BC10053/60sin /===α []2362516010100mm F A BC BC =⨯==σ 采用钢丝数:根)(19924625422=⨯==ππd A n BC采用两等边角钢,则型号为 ()2172.62086.3440cm A L BC =⨯=⨯8-3 图8-36为一托架,AC 是圆钢杆,许用应力MPa ][160=钢σ;BC 杆是方木杆,许用应力kN F MPa ][604==-,木σ。
试选择钢杆圆截面的直径d 及木杆方截面的边长b 。
题8-3图解:AB 和BC 的内力计算:kN F F BC 2.1081330sin /===α kN tg F F AC 9032/60/===α AC 杆:[]MPa d A F ACAC AC1604109023=≤⨯==钢σπσ d ≥27mmBC 杆:[]MPa b A F BC BC BC 4102.10823=≤⨯==木σσ b ≥165mm8-4 结构受力如图8-37所示,各杆的材料和横截面面积均相等:2200mm A =,MPa ,MPa ,GPa E b s 460280200===σσ。
应力状态分析和强度理论(例题)

例题
3
4
5
2
应力状态分析和 6
1
强度理论
7
11 8
10 9
p.1
例题
例题
例7-1 已知图示单元体上的应力为σx=80MPa,σy=-40MPa,τxy’=-60MPa;求主应力、主平面、剪应 力极值和极值平面,并在单元体上表示出来。
解:(1)求主平面:
tg 2 0
2 xy x y
p.6
例题
例题
例7-4 薄壁锅炉的平均直径D=1060 mm,壁厚t=25 mm,蒸气压力p=2.5 MPa,材料许用应力
[σ]=40 MP;按最大剪应力理论校核锅炉的强度。
σ’ p
σ’
p
σ’’
σ’’
强度不够,重新设计 pD
r3
1
3
2t
t
pD
2
0.033m
(4)在单元体上标出它们的位置;
σ1
τmax
α0
σ3
p.3
例题
例7-2 已知图示正三角形单元体上的应力,求主应力和最大剪应力。 50MPa
解:(1)取出正三角形一半(直角三角形),分析如图;
50MPa 300
86.6MPa
σx
86.6MPa
例题
50MPa 86.6MPa 100MPa
100MPa
(2)求σx的值;
210 109
3.11104
τα σα 300 τxy
p.5
例题
例题
例7-4 薄壁锅炉的平均直径D=1060 mm,壁厚t=25 mm,蒸气压力p=2.5 MPa,材料许用应力
材料力学习题解答[第八章49-76]
![材料力学习题解答[第八章49-76]](https://img.taocdn.com/s3/m/5a67538e8762caaedd33d4fd.png)
8-49现用某种黄铜材料制成的标准圆柱形试件做拉伸试验。
已知临近破坏时,颈缩中心部位的主应力比值为113321::::=σσσ;并已知这种材料当最大拉应力达到770MPa 时发生脆性断裂,最大切应力达到313MPa 时发生塑性破坏。
若对塑性破坏采用第三强度理论,试问现在试件将发生何种形式的破坏?并给出破坏时各主应力之值。
解: 令主应力分别为:σσ31=,σσσ==32脆性断裂时,由第一强度理论=1r σσσ31==770MPa所以,MPa257≈σ塑性破坏时,由第三强度理论=3r σMPa6262313231=⨯==-σσσ所以MPa 313=σ故,试件将发生脆性断裂。
破坏时MPa 7701=σ,MPa 25732==σσ8-50 钢制圆柱形薄壁压力容器(参见图8-13),其平均直径mm d 800=,壁厚mm 4=δ,材料的MPa ][120=σ,试根据强度理论确定容器的许可内压p 。
解:在压力容器壁上取一单元体,其应力状态为二向应力状态。
p pd 504'==δσ ,p pd1002"==δσ 其三个主应力为p 100"1==σσ, p 50'2==σσ,03=σ据第三强度理论=3r σ[]MPap 120100331=≤=-σσσ所以 ,MPa p 2.13≤,许可内压MPa p 2.13= 据第四强度理论()()()[][]MPa p r 1206.862142132322214=≤≈-+-+-=σσσσσσσσ题 8-50 图所以,MPa p 39.14≤,许可内压MPa p 39.14=8-51 空心薄壁钢球,其平均内径mm d 200=,承受内压MPa p 15=,钢的MPa ][160=σ。
试根据第三强度理论确定钢球的壁厚δ。
解:钢球上任一点应力状态如图示 其三个主应力为:σσσ==21,03=σ而MPa MPa d p R R p δδδδππσ4342.0152222=⨯=⋅=⋅⋅=据第三强度理论=3r σ[]MPa 1604331=≤=-σδσσ 所以 mm m 69.41069.41601433=⨯=⨯≥-δ8-52 图8-77所示两端封闭的铸铁圆筒,其直径mm d 100=,壁厚mm 10=δ,承受内压MPa p 5=,且在两端受压力kN F 100=和外扭矩m kN T ⋅=3作用,材料的许用拉应力MPa ][40=+σ,许用压应力MPa ][160=-σ,泊松比250.=ν,试用莫尔强度理论校核其强度。
材料力学 应力状态和强度理论答案

7-1(7-3) 一拉杆由两段杆沿m-n面胶合而成。
由于实用的原因,图中的角限于范围内。
作为“假定计算”,对胶合缝作强度计算时可以把其上的正应力和切应力分别与相应的许用应力比较。
现设胶合缝的许用切应力为许用拉应力的3/4,且这一拉杆的强度由胶合缝的强度控制。
为了使杆能承受最大的荷载F,试问角的值应取多大?解:按正应力强度条件求得的荷载以表示:按切应力强度条件求得的荷载以表示,则即:当时,,,时,,,时,,时,,由、随而变化的曲线图中得出,当时,杆件承受的荷载最大,。
若按胶合缝的达到的同时,亦达到的条件计算则即:,则故此时杆件承受的荷载,并不是杆能承受的最大荷载。
返回7-2(7-7)试用应力圆的几何关系求图示悬臂梁距离自由端为0.72m的截面上,在顶面以下40mm的一点处的最大及最小主应力,并求最大主应力与x轴之间的夹角。
解:=由应力圆得返回7-3(7-8)各单元体面上的应力如图所示。
试利用应力圆的几何关系求:(1)指定截面上的应力;(2)主应力的数值;(3)在单元体上绘出主平面的位置及主应力的方向。
解:(a),,,,(b),,,,(c), , ,(d),,,,,返回7-4(7-9) 各单元体如图所示。
试利用应力圆的几何关系求:(1)主应力的数值;(2)在单元体上绘出主平面的位置及主应力的方向。
解:(a),,,(b),,,(c),,,(d),,,返回7-5(7-10)已知平面应力状态下某点处的两个截面上的应力如图所示。
试利用应力圆求该点处的主应力值和主平面方位,并求出两截面间的夹角值。
解:由已知按比例作图中A,B两点,作AB的垂直平分线交轴于点C,以C为圆心,CA或CB为半径作圆,得(或由得半径)(1)主应力(2)主方向角(3)两截面间夹角:返回7-6(7-13) 在一块钢板上先画上直径的圆,然后在板上加上应力,如图所示。
试问所画的圆将变成何种图形?并计算其尺寸。
已知钢板的弹性常数E=206GPa,=0.28。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σ x +σ y
2 +
+
σ x −σ y
2
cos 2α − τ xy sin 2α
80 + σ y
80 − σ y
2 2 ∴σ y = 40 MPa
(3) 主应力
cos(120o ) − 0
σ 1 = σ x = 80 MPa
τ xy = 0
α = 60o
σα = τα =
σx +σ y σx −σ y
2 2
+
σ x −σ y
2
cos 2α =
75 + 150 75 − 150 + cos120o = 131.3 MPa 2 2
sin 2α =
75 − 150 sin120o = −32.5 MPa 2
3
上海理工大学 力学教研室
(3) 应力圆:为一点圆
σ x +σ y
σ x −σ y
τ
(70,0)
σ
(f) (1) 应力分量
上海理工大学 力学教研室
2
σ x = 100 MPa
(2) 用解析法求斜截面上的应力
σ y = 50 MPa
τ xy = 0
α = 60o
σα =
cos 2α − τ xy sin 2α 2 2 100 + 50 100 − 50 = + cos120° = 62.5 MPa 2 2 σ −σ y τα = x sin 2α + τ xy cos 2α 2 100 − 50 = sin120° = 21.7 MPa 2 +
τ
(35,60.6) 60o -70 70
σx +σ y
σ x −σ y
(3) 应力圆
σ
(e) (1) 应力分量
σ x = 70 MPa
σ y = 70 MPa
τ
xy
=0
α = 30 o
(2) 用解析法求斜截面上的应力
cos 2α − τ x sin 2α 2 2 70 + 70 = = 70 MPa 2 σ −σ y τα = x sin 2α + τ x cos 2α = 0 2 σα = +
l/2
l/2
Q=
P 140 = = 70 kN 2 2
M=
Pl 140 × 4 = = 140 kNm 4 4
(2) A 点的应力状态
σx τxy
(3) 截面几何性质
W = 875cm 3 h = 360mm
(4)应力分量
I z = 15800cm 4 b = 10mm t = 15.8mm
B = 136mm
(6)主方向
σ x −σ y
α 0 = −13.6o
(7)主应力
α 0 + 90o = 76.4o
σ −σ y 2 2 ⎧σ max σ x + σ y ) + τ xy = ± ( x ⎨ 2 2 ⎩σ min
⎧84.7 MPa 79.75 79.75 2 ) + (20.56) 2 = ⎨ ± ( 2 2 ⎩ −5.0 MPa ∴σ 1 = 84.7 MPa σ 2 = 0 σ 3 = −5.0 MPa =
τ xy = 20 MPa
tg 2α 0 = −
σ x −σ y
= −0.5
∴α 0 = −13.3o
α 0 + 90o = 76.7o
σ −σ y 2 2 ⎧σ max σ x + σ y ) + τ xy = ± ( x ⎨ 2 2 ⎩σ min ⎧ 4.7 MPa 80 −80 = ± ( ) 2 + 202 = ⎨ 2 2 ⎩ −84.7 MPa ∴σ 1 = 4.7 MPa σ 2 = 0 σ 3 = −84.7 MPa
τ
(62.5,21.7) 120o 50 100
σ x +σ y
σ x −σ y
(3) 应力圆
σ
8.5. 图示锅炉直径D=1 m,壁厚t=10 mm,锅炉蒸汽压力p=3 MPa。试求:(1)壁内主应力σ1、 σ2及最大切应力τmax;(2)斜截面ab上的正应力及切应力。
60
o
σ2
p
σ1
解:(1) 求主应力
= −120 MPa
τ (1) = 0
应力状态单元:
120MPa
主应力:
σ 1 = σ 2 = 0 σ 3 = −120 MPa
(2) 截面上 2 点的应力:
σ (2) = 0
应力状态单元:
τ (2) = −
3Q 3 120 × 103 =− × = 36 MPa 2 bh 2 0.05 × 0.1
(2) 画主平面位置及主应力方向: σx>σy,α0面对应σmax。
σ3
13.3o
σ1
(3) 最大剪应力
τ max =
(4) 应力圆
σ1 − 3
2
=
4.7 + 84.7 = 44.7 MPa 2
τ
(0,20) 26.6o
-84.7 (-80,-20)
4.7
σ
(f) (1) 应力分量
σ x = −20 MPa
α = 120o σ +σ y σ x −σ y σα = x + cos 2α − τ xy sin 2α
5
(3) 主方向
tg 2α 0 = −
2τ xy
σ x −σ y
=−
2 × ( −70.6) = 2.22 63.7
α 0 = 32.9o
(4) 主应力
α 0 + 90o = 122.9o
σ −σ y 2 ⎧σ max σ x + σ y = ± ( x ) +τ 2 ⎨ xy σ 2 2 ⎩ min ⎧109.3MPa 63.7 63.7 2 ± ( ) + (−70.6) 2 = ⎨ 2 2 ⎩− 45.6 MPa ∴σ 1 = 109.3 MPa σ 2 = 0 σ 3 = −45.6 MPa =
8.2. 已知应力状态如图所示,应力单位为 MPa。试用解析法和应力圆分别求:(1)主应力大 小,主平面位置;(2)在单元体上绘出主平面位置及主应力方向;(3)最大切应力。
80 30
20 20 20
(e)
(f)
解:(e) (1) 应力分量
σx =0
主平面位置和主应力大小
σ y = −80 MPa
2τ xy
8.12. 图示二向应力状态的应力单位为 MPa。试作应力圆,并求主应力。
上海理工大学 力学教研室
7
50 80 60
o
τ
80
τ
50
解:(1) 用水平面截得
50 80 60
o
τ
σy
其中
σ x = 80 MPa
(2) 求应力分量
τ xy = 0
σ α = 50 MPa
α = 60o
σ α = 50 =
1
解:(d) (1) 应力分量
σ x = 70 MPa
σ y = −70 MPa
τ xy = 0
α = 30o
(2) 用解析法求斜截面上的应力
σα =
cos 2α − τ xy sin 2α 2 2 70 − 70 70 + 70 = + cos 60° = 35 MPa 2 2 σ −σ y τα = x sin 2α + τ xy cos 2α 2 70 + 70 = sin 60° = 60.6 MPa 2 +
(5)斜截面上的应力
α = 60o σ +σ y σ x −σ y σα = x + cos 2α − τ xy sin 2α
2 2 79.75 79.75 = + × cos120o − 20.56 × sin120o 2 2 = 2.13MPa σ −σ y sin 2α + τ xy cos 2α τα = x 2 79.75 = × sin120o + 20.56 × cos120o 2 = 24.25 MPa tg 2α 0 = − 2τ xy =− 2 × 20.56 = −0.516 79.75
δ
T P 解:(1) A 点的应力状态 T
30 A
o
d
P
τxy σx
属二向应力状态,应力分量是
P 20000 = = 63.7 × 106 Pa = 63.7 MPa A π × 50 × 2 × 10−6 σy =0
σx =
τ xy = −
T 600 =− = −70.6 × 106 Pa = −70.6 MPa 2 2π r t 2π × 262 × 2 × 10−9
主平面位置和主应力大小
σ y = 30 MPa
2τ xy
τ xy = 20 MPa
tg 2α 0 = −
σ x −σ y
= 0.8
∴α 0 = 19.3o
α 0 + 90o = 109.3o
σ −σ y 2 2 ⎧σ max σ x + σ y ) + τ xy = ± ( x ⎨ 2 2 ⎩σ min
上海理工大学 力学教研室
6
σx =
M×
h 0.36 140 × 103 × 4= 4 = 79.75 MPa −8 Iz 15800 × 10
σy =0 τ xy
2 Q ⎧ b ⎡ ( h − 2t ) h2 ⎤ ⎫ 2 ⎪B ⎡ 2 ⎪ ⎤ = − ⎥⎬ ⎨ ⎣ h − ( h − 2t ) ⎦ + ⎢ Izb ⎪ 8 2⎣ 4 16 ⎦ ⎢ ⎥⎪ ⎩ ⎭ 3 70 × 10 0.136 ⎡ 2 = { 0.362 − ( 0.36 − 2 × 0.0158) ⎤ −8 ⎣ ⎦ 15800 × 10 × 0.01 8 2 0.01 ⎡ ( 0.36 − 2 × 0.0158) 0.362 ⎤ + − ⎢ ⎥} 2 ⎢ 4 16 ⎥ ⎣ ⎦ = 20.56 MPa
