数列通项及数列求和1
数列通项公式与求和讲解与习题(含答案)

数列通项与求和一.求数列通项公式1.定义法(①等差数列通项公式;②等比数列通项公式。
)例.等差数列{}n a 是递增数列,前n 项和为n S ,且931,,a a a 成等比数列,255a S =.求数列{}n a 的通项公式.2项和为S ,满足3如,1对所有的4。
例.521a a ⋅⋅⋅(例.已知数列{}n a 满足31=a ,n n a n a 11+=+,求n a 。
答案:23n a n=6.已知递推关系求n a ,用构造法(构造等差.等比数列)。
(1)形如()n f pa a n n +=+1只需构造数列{}n b ,消去()n f 带来的差异.其中()n f 有多种不同形式①()n f 为常数,即递推公式为q pa a n n +=+1(其中p ,q 均为常数,)0)1((≠-p pq )。
解法:转化为:)(1t a p t a n n -=-+,其中pqt -=1,再利用换元法转化为等比数列求解。
例.已知数列{}n a 中,11=a ,321+=+n n a a ,求n a . 答案:123n n a +=-②()n f 为一次多项式,即递推公式为s rn pa a n n ++=+1 例③(n f (2)n rq ,其中p q1+ 例(3型(2)的方法求解。
例.已知数列{}n a 中,11=a ,22=a ,n n n a a a 313212+=++,求n a 。
答案:1731(443n n a -=--7.形如11n n n a a ka b--=+或11n n n n a ba ka a ---=的递推数列都可以用倒数法求通项。
例.1,13111=+⋅=--a a a a n n n答案:132n a n =- 8.利用平方法、开平方法构造等差数列例1.数列{}n a的各项均为正数,且满足11n n a a +=+,12a =,求n a 。
答案:2(1)n a n = 例2.已知()f x x =<,求:(1)9.n a +设n b =例.1.已知2.已知13a =且132n n n a a +=+,求n a 答案:1532n n n a -=⋅- 3.已知数列{}n a 中,311=a ,前n 项和n S 与n a 的关系是n n a n n S )12(-=,试求通项公式n a 。
数列求和及求通项方法总结

数列求和及求通项一、数列求和的常用方法1、公式法:利用等差、等比数列的求和公式进行求和2、错位相减法:求一个等差数列与等比数列的乘积的通项的前n 项和,均可用错位相减法 例:已知数列1312--=n n n a ,求前n 项和n S 3、裂项相消法:将通项分解,然后重新组合,使之能消去一些项①形如)(1k n n a n +=,可裂项成)11(1kn n k a n +-=,列出前n 项求和消去一些项②形如kn n a n ++=1,可裂项成)(1n k n ka n -+=,列出前n 项求和消去一些项 例:已知数列1)2()1)(1(11=≥+-=a n n n a n ,,求前n 项和n S4、分组求和法:把一类由等比、等差和常见的数列组成的数列,先分别求和,再合并。
例:已知数列122-+=n a nn ,求前n 项和n S5、逆序相加法:把数列正着写和倒着写依次对应相加(等差数列求和公式的推广)一、数列求通项公式的常见方法有:1、关系法2、累加法3、累乘法4、待定系数法5、逐差法6、对数变换法7、倒数变换法 8、换元法 9、数学归纳法累加法和累乘法最基本求通项公式的方法求通项公式的基本思路无非就是:把所求数列变形,构造成一个等差数列或等比数列,再通过累加法或累乘法求出通项公式。
二、方法剖析1、关系法:适用于)(n f s n =型求解过程:⎩⎨⎧≥-===-)2()1(111n s s n s a a n n n例:已知数列{}n a 的前n 项和为12++=n n S n ,求数列{}n a 的通项公式2、累加法:适用于)(1n f a a n n +=+——广义上的等差数列求解过程:若)(1n f a a n n +=+则)1(12f a a =- )2(23f a a =-所有等式两边分别相加得:∑-==-111)(n k n k f a a 则∑-=+=111)(n k nk f a a例:已知数列{}n a 满足递推式)2(121≥++=-n n a a n n ,{}的通项公式,求n a a 11= 3、累乘法:适用于n n a n f a )(1=+——广义上的等比数列求解过程:若n n a n f a )(1=+,则)(1n f a a nn =+ ......累加则)1()......2()1(12312-===-n f a a f a a f a a n n , 所有等式两边分别相乘得:∏-==111)(n k n k f a a 则∏-==111)(n k n k f a a 例:已知数列{}n a 满足递推式)2(21≥=-n a a n nn ,其中{}的通项公式,求n a a 31= 4、待定系数法:适用于)(1n f pa a n n +=+①形如)1,0,;,(1≠≠+=+p b p b p b pa a n n 为常数型(还可用逐差法)求解过程:构造数列)(1k a p k a n n +=++,展开得k pk pa a n n -+=+1,因为系数相等,所以解方程b k pk =-得1-=p b k ,所以有:)1(11-+=-++p ba p pb a n n ,这样就构造出了一个以11-+p b a 为首项,公比为p 的等比数列⎭⎬⎫⎩⎨⎧-+1p b a n 。
数列求和1

1 2n
1
1 2n
1
nn
1
1n
2
1 2
1
nn
1
n
1
1n
2
已知:an 3n 1,求
1 1 1
a1a2 a2a3
an an 1
五、公式法求和:
所给数列的通项是关于n的多
项式,此时求和可采用公式
法求和,常用的公式有:
数列求和
一、倒序相加法
如果一个数列{an},与首末
两项等距的两项之和等于首 末两项之和,可采用把正着 写和与倒着写和的两个和式 相加,就得到一个常数列的 和,这一求和的方法称为倒 序相加法.
二、错位相减法:
如果一个数列的各项是由一 个等差数列与一个等比数列 对应项乘积组成,此时求和 可采用错位相减法.
四、分裂通项法:
把数列的通项拆成两项之差, 即数列的每一项都可按此法 拆成两项之差,在求和时一 些正负项相互抵消,于是前 n项的和变成首尾若干少数 项之和,这一求和方法称 为分裂通项法.
已知an
1
nn
2
,
求sn
1
nn 1
1 n
1 n -1
2n
1
12n
1
1 2
例 : 求前n项的和.
三、分组求和法:
把数列的每一项分成两项, 或把数列的项“集”在一块 重新组合,或把整个数列分 成两部分,使其转化为等差 或等比数列,这一求和方法 称为分组求和法.
例:若数列{an}中, an= -2[ n - (-1)n ],求 S10和S99.
数列的通项和求和公式推导

数列的通项和求和公式推导数学中的数列是由一系列按照规律排列的数所组成的序列。
对于给定的数列,我们通常希望能够找到一个通项公式来表示数列的第n项,同时也希望能够求解数列的前n项和。
在本文中,我们将讨论如何推导数列的通项公式和求和公式。
一、等差等差数列是最常见的数列之一,它的特点是每一项与前一项之间的差值都相等。
假设等差数列的首项为a1,公差为d,第n项为an。
1. 推导通项公式我们可以观察到,等差数列每一项与首项之间存在一个公差的倍数关系,即:an = a1 + (n-1)d这个等式可以通过数学归纳法推导得出。
假设等式对于n=k成立,即:ak = a1 + (k-1)d那么对于n=k+1,我们有:ak+1 = a1 + kd通过对上述两个等式进行代换,得到:ak+1 = (a1 + (k-1)d) + d = a1 + kd由此可见,当等式对于n=k成立时,等式对于n=k+1也成立。
因此,等差数列的通项公式为:an = a1 + (n-1)d2. 推导求和公式为了推导等差数列的求和公式,我们可以考虑将数列按照首项与末项、次首项与次末项等进行配对求和。
我们可以观察到这些配对的和都相等,都等于等差数列的中间项和。
设等差数列的首项为a1,末项为an,共有n项。
那么有:a1 + an = a1 + (a1 + (n-1)d) = 2a1 + (n-1)da2 + an-1 = (a1 + d) + (a1 + (n-2)d) = 2a1 + (n-1)d...ak + an-k+1 = (a1 + (k-1)d) + (a1 + (n-k)d) = 2a1 + (n-1)d将上述k个等式相加,得到:2(a1 + a2 + ... + an-k+1) + (n-k)(d + d + ... + d) = k(2a1 + (n-1)d)化简后可得:2S + (n-k)kd = k(2a1 + (n-1)d)其中,S表示等差数列的前n项和。
数列的通项与求和计算方法总结

数列的通项与求和计算方法总结(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--数列的通项与求和计算方法总结第一章 数列通项公式的十种求法一、公式法例1 已知数列{}n a 满足1232n n n a a +=+⨯,12a =,求数列{}n a 的通项公式。
解:1232n n n a a +=+⨯两边除以12n +,得113222n n n n a a ++=+,则113222n n n n a a ++-=,故数列{}2n n a 是以1222a 11==为首项,以23为公差的等差数列,由等差数列的通项公式,得31(1)22n na n =+-,所以数列{}n a 的通项公式为31()222n n a n =-。
评注:本题解题的关键是把递推关系式1232n n n a a +=+⨯转化为113222n n n n a a ++-=,说明数列{}2nna 是等差数列,再直接利用等差数列的通项公式求出31(1)22n na n =+-,进而求出数列{}n a 的通项公式。
二、累加法例2 已知数列{}n a 满足11211n n a a n a +=++=,,求数列{}n a 的通项公式。
解:由121n n a a n +=++得121n n a a n +-=+则112322112()()()()[2(1)1][2(2)1](221)(211)12[(1)(2)21](1)1(1)2(1)12(1)(1)1n n n n n a a a a a a a a a a n n n n n n n n n n n ---=-+-++-+-+=-++-+++⨯++⨯++=-+-++++-+-=+-+=-++=所以数列{}n a 的通项公式为2n a n =。
评注:本题解题的关键是把递推关系式121n n a a n +=++转化为121n n a a n +-=+,进而求出11232211()()()()n n n n a a a a a a a a a ----+-++-+-+,即得数列{}n a 的通项公式。
(完整版)数列通项公式及其求和公式

一、数列通项公式的求法(1)已知数列的前n 项和n S ,求通项n a ; (2)数学归纳法:先猜后证;(3)叠加法(迭加法):112211()()()n n n n n a a a a a a a a ---=-+-++-+L ;叠乘法(迭乘法):1223322111a a a a a a a a a a a a n n n n n n n ⋅⋅⋅=-----ΛΛ. 【叠加法主要应用于数列{}n a 满足1()n n a a f n +=+,其中()f n 是等差数列或等比数列的条件下,可把这个式子变成1()n n a a f n +-=,代入各项,得到一系列式子,把所有的式子加到一起,经过整理,可求出n a ,从而求出n s 】(4)构造法(待定系数法):形如1n n a ka b -=+、1nn n a ka b -=+(,k b 为常数)的递推数列;【用构造法求数列的通项或前n 项和:所谓构造法就是先根据数列的结构及特征进行分析,找出数列的通项的特征,构造出我们熟知的基本数列的通项的特征形式,从而求出数列的通项或前n 项和.】 (5)涉及递推公式的问题,常借助于“迭代法”解决.【根据递推公式求通项公式的常见类型】 ①1+1=,()n n a a a a f n =+型,其中()f n 是可以和数列,用累加法求通项公式,即1思路(叠加法)1(1)n n a a f n --=-,依次类推有:12(2)n n a a f n ---=-、23(3)n n a a f n ---=-、…、21(1)a a f -=,将各式叠加并整理得111()n n i a a f n -=-=∑,即111()n n i a a f n -==+∑例题1:已知11a =,1n n a a n -=+,求n a解:∵1n n a a n -=+ ∴1n n a a n --=,依次类推有:122321122n n n n a a n a a n a a -----=--=--=、、…∴将各式叠加并整理得12n n i a a n =-=∑,121(1)2n nn i i n n a a n n ==+=+==∑∑ 思路(转化法)1(1)n n a pa f n -=+-,递推式两边同时除以np 得11(1)n n n n na a f n p p p ---=+,我们令n n n a b p =,那么问题就可以转化为类型一进行求解了.例题: 已知12a =,1142n n n a a ++=+,求n a解:∵1142n n n a a ++=+ ∴142nn n a a -=+,则111442nn n nn a a --⎛⎫=+ ⎪⎝⎭, ∵令4n n na b =,则112nn n b b -⎛⎫-= ⎪⎝⎭,依此类推有11212n n n b b ---⎛⎫-= ⎪⎝⎭、22312n n n b b ---⎛⎫-= ⎪⎝⎭、…、22112b b ⎛⎫-= ⎪⎝⎭∴各式叠加得1212nnn i b b =⎛⎫-= ⎪⎝⎭∑,即122111*********n n n n n n n n i i i b b ===⎛⎫⎛⎫⎛⎫⎛⎫=+=+==- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∑∑∑ ∴1441422n nnn n n n a b ⎡⎤⎛⎫=⋅=⋅-=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦②1+1=,()n n a a a a f n =⋅型,其中()f n 是可以求积数列,用累乘法求通项公式,即1(2)(1)f f a思路(叠乘法):1(1)n n a f n a -=-,依次类推有:12(2)n n a f n a --=-、23(3)n n a f n a --=-、…、21(1)af a =, 将各式叠乘并整理得1(1)(2)(3)na f f f a =⋅⋅⋅…(2)(1)f n f n ⋅-⋅-,即(1)(2)(3)n a f f f =⋅⋅⋅…1(2)(1)f n f n a ⋅-⋅-⋅例题:已知11a =,111n n n a a n --=+,求n a . 解:∵111n n n a a n --=+ ∴111n n a n a n --=+,依次类推有:122n n a n a n ---=、2331n n a n a n ---=-、…、3224a a =、2113a a = ∵11a =∴将各式叠乘并整理得112311n a n n n a n n n ---=⋅⋅⋅+-…2143⋅⋅,即12311n n n n a n n n ---=⋅⋅⋅+- (212)43(1)n n ⋅⋅=+ ③1+1=,n n a a a pa q =+型(其中p q 、是常数),可以采用待定系数法、换元法求通项公式,即1()11n n q q a p a p p +-=---,设1n n qba p=--,则1n n b pb +=.利用②的方法求出n b 进而求出n a 当1p =时,数列{}n a 是等差数列;当0,0p q ≠=时,数列{}n a 是等比数列; 当0p ≠且1,0p q ≠≠时,可以将递推关系转化为111n n q q a p a p p +⎛⎫+=+ ⎪--⎝⎭,则数列1nq a p ⎧⎫+⎨⎬-⎩⎭是以11qa p +-为首项,p 为公比的等比数列.思路(构造法):设()1n n a p a μμ++=+,即()1p q μ-=得1qp μ=-,数列{}n a μ+是以1a μ+为首项、p 为公比的等比数列,则1111n n q q a a p p p -⎛⎫+=+ ⎪--⎝⎭,即1111n nq qa a p p p -⎛⎫=++ ⎪--⎝⎭ 例题:已知数列{}n a 满足123n n a a -=+且11a =,求数列{}n a 的通项公式 解:设()12n n a a μμ++=+,即3μ=∵11a =∴数列{}3n a +是以134a +=为首项、2为公比的等比数列∴113422n n n a -++=⋅=,即123n n a +=-④1+1=,n n n a a a pa q =+型,其中p q 、是常数且0,1q q ≠≠,111n n n n a a p q q q q ++=⋅+,设n n n a b q =,则11n np b b q q+=⋅+思路(构造法):11n n n a pa rq --=+,设11n n n n a a q q μλμ--⎛⎫+=+ ⎪⎝⎭,则()11n n q p q rq λμλ-=⎧⎪⎨-=⎪⎩,从而解得p q r p q λμ⎧=⎪⎪⎨⎪=⎪-⎩那么n na r qp q ⎧⎫+⎨⎬-⎩⎭是以1a r q p q +-为首项,p q 为公比的等比数列 例题:已知11a =,112n n n a a --=-+,求n a 。
数列求通项公式及求和9种方法

数列求通项公式及求和9种方法数列是指按照一定规律排列的一系列数值。
求数列的通项公式和求和的方法是数列研究的基础,下面将介绍9种常见的方法。
一、等差数列求通项公式和求和等差数列是指数列中两个相邻项之间的差固定的数列。
例如:1,3,5,7,9,……,其中差为21.1求通项公式对于等差数列,可使用以下公式计算通项:通项公式:a_n=a_1+(n-1)*d其中a_n表示数列第n项,a_1表示数列第一项,d表示公差。
1.2求和求和的公式为:S_n=(a_1+a_n)*n/2其中S_n表示数列前n项的和。
二、等比数列求通项公式和求和等比数列是指数列中的两个相邻项之间的比值是固定的数列。
例如:1,2,4,8,16,……,其中比值为22.1求通项公式等比数列的通项公式为:a_n=a_1*q^(n-1)其中a_n表示数列的第n项,a_1表示数列的第一项,q表示公比。
2.2求和求等比数列前n项和的公式为:S_n=a_1*(q^n-1)/(q-1)三、斐波那契数列求通项公式和求和斐波那契数列是指数列中的每一项都等于前两项之和。
例如:0,1,1,2,3,5,8,13,……3.1求通项公式斐波那契数列的通项公式为:a_n=a_(n-1)+a_(n-2)其中a_n表示数列的第n项。
3.2求和斐波那契数列前n项和的公式为:S_n=a_(n+2)-1四、等差数列的和差公式求通项公式和求和对于等差数列,如果已知首项、末项和项数,可以使用和差公式求通项公式和求和。
4.1公式和差公式是指通过首项、末项和项数计算公差的公式。
已知首项a_1、末项a_n和项数n,可以使用和差公式计算公差d:d=(a_n-a_1)/(n-1)4.2求通项公式已知首项a_1、公差d和项数n,可以使用通项公式计算任意项的值:a_n=a_1+(n-1)*d4.3求和已知首项a_1、末项a_n和项数n,可以使用求和公式计算等差数列前n项的和:S_n=(a_1+a_n)*n/2五、等比数列的部分和求和公式求通项公式和求和对于等比数列,如果已知首项、公比和项数,可以使用部分和求和公式求通项公式和求和。
数列通项公式与求和讲解与习题(含答案)

数列通项与求和一.求数列通项公式1.定义法(①等差数列通项公式;②等比数列通项公式。
)例.等差数列{}n a 是递增数列,前n 项和为n S ,且931,,a a a 成等比数列,255a S =.求数列{}n a 的通项公式. 答案:35n a n =2.公式法:已知n S (即12()n a a a f n +++=)求n a ,用作差法:11,(1),(2)n n n a n a S S n -=⎧=⎨-≥⎩例.设正整数数列{}n a 前n 项和为n S ,满足21(1)4n n S a =+,求n a 答案:21n a n =-3.作商法:已知12()n a a a f n =求n a ,用作商法:(1),(1)(),(2)(1)n f n f n a n f n =⎧⎪=⎨≥⎪-⎩。
如数列}{n a 中,,11=a 对所有的2≥n 都有2321n a a a a n = ,则=+53a a ;答案:61164.累加法:若1()n n a a f n +-=求n a :11221()()()n n n n n a a a a a a a ---=-+-++-。
例.已知数列,且a 1=2,a n +1=a n +n ,求a n .答案:242n n n a -+=5.累乘法:已知1()n n a f n a +=求n a ,用累乘法:121121n n n n n a aa a a a a a ---=⋅⋅⋅⋅(2)n ≥ 例.已知数列{}n a 满足321=a ,n n a n na 11+=+,求n a 。
答案:23n a n=6.已知递推关系求n a ,用构造法(构造等差.等比数列)。
(1)形如()n f pa a n n +=+1只需构造数列{}n b ,消去()n f 带来的差异.其中()n f 有多种不同形式 ①()n f 为常数,即递推公式为q pa a n n +=+1(其中p ,q 均为常数,)0)1((≠-p pq )。
数列求和与求通项公式方法总结(已打)

12、已知 为等比数列, , ,则 。
13、已知 得三边长成公比为 的等比数列,则其最大角的余弦值为_________.
14、已知等比数列 为递增数列,且 ,则数列的通项公式 _____.
15、等比数列{ }的前n项和为Sn,若S3+3S2=0,则公比 =_______
(Ⅰ)求 的值;(Ⅱ)求数列 的通项公式.
(1)求数列 的通项公式;
(2)记 ,求数列 的前n项和 。
数列练习题(近三年各地高考题选编)
一、填空题
1、在等差数列 中, ,则 的前5项和 =。
2、等差数列 中, ,则数列 的公差为。
3、在等差数列 中,已知 =16,则 。
4、如果等差数列 中, + + =12,那么 + +•••…+ =。
5、 为等差数列, 为其前 项和.若 , ,则 ________.
(1)求数列 、 的通项公式;
(2)设 ,数列 的前 项和为 ,问 > 的最小正整数 是多少
2、(2012广州一模)已知等差数列 的公差 ,它的前 项和为 ,若 ,且 , , 成等比数列.
(1)求数列 的通项公式;
(2)设数列 的前 项和为 ,求证: .
3、(2012惠州三模)已知函数 ,且数列 是首项为 ,公差为2的等差数列.
6、{an}的前n项和为Sn,且Sn= ,n∈N﹡,数列{bn}满足an=4log2bn+3,n∈N﹡.
(1)求an,bn;
(2)求数列{an·bn}的前n项和Tn.
7、已知 是等差数列,其前 项和为 , 是等比数列,且 .
(I)求数列 与 的通项公式;
数学中的数列通项与求和公式推导

数学中的数列通项与求和公式推导在数学中,数列是由一系列按照一定规律排列的数字组成的序列。
而数列通项与求和公式是数学中用来计算数列中任意位置的值以及求解数列的部分和的重要工具。
本文将从数列的定义开始,逐步展开介绍数列通项与求和公式的推导过程。
一、数列的定义数列是由一系列按照一定规律排列的数字组成的序列。
一般来说,数列的前几项可以通过直接列出或用递推公式来表达,而后续的项则可以通过这一规律进行推导得到。
数列通常用字母表示,例如常见的等差数列用$a_n$表示,而等比数列则用$g_n$表示。
二、等差数列的通项与求和公式推导等差数列是指数列中任意两个相邻的项之间的差相等的数列。
设等差数列的首项为$a_1$,公差为$d$,则它的通项可以用以下公式表示:$$a_n=a_1+(n-1)d$$其中,$n$表示数列中的第$n$项。
对于等差数列的求和公式,我们可以通过将数列从首项到最后一项依次相加得到。
假设等差数列的前$n$项和为$S_n$,则其求和公式为:$$S_n=\frac{n(a_1+a_n)}{2}$$推导过程如下:由等差数列的通项公式可知,$a_n=a_1+(n-1)d$。
又由等差数列的定义可知,最后一项$a_n$可以表示为$a_n=a_1+(n-1)d$。
因此,等差数列的前$n$项和$S_n$可以表示为:$$S_n=a_1+a_2+...+a_n$$将等差数列的通项公式代入上式,得:$$S_n=a_1+a_1+d+a_1+2d+...+a_1+(n-1)d$$将上式中的各项按照公差$d$进行合并,得:$$S_n=na_1+(1+2+...+n-1)d$$根据等差数列的性质,$1+2+...+(n-1)$可以表示为$\frac{(n-1)n}{2}$,代入上式可得:$$S_n=na_1+\frac{(n-1)n}{2}d$$化简上式得到等差数列前$n$项和的通式:$$S_n=\frac{n(a_1+a_n)}{2}$$三、等比数列的通项与求和公式推导等比数列是指数列中任意两个相邻的项之间的比相等的数列。
最全面总结:数列求通项、求和方法总结

数列求通项、求和的方法总结一、定义法 —— 直接利用等差或等比数列的定义求通项。
特征:适应于已知数列类型(等差or 等比)的题目.例.等差数列{}n a 是递增数列,前n 项和为n S ,且931,,a a a 成等比数列,255a S =.求数列{}n a 的通项公式.解:设数列{}n a 公差为)0(>d d∵931,,a a a 成等比数列,∴9123a a a =,即)8()2(1121d a a d a +=+d a d 12=⇒ ∵0≠d , ∴d a =1………………………………①∵255a S = ∴211)4(2455d a d a +=⋅⨯+…………② 由①②得:531=a ,53=d ∴n n a n 5353)1(53=⨯-+=二、公式法求数列{}n a 的通项n a 可用公式⎩⎨⎧≥⋅⋅⋅⋅⋅⋅⋅-=⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=-2111n S S n S a n nn 求解。
特征:已知数列的前n 项和n S 与n a 的关系例.已知数列{}n a 的前n 项和n S 满足1,)1(2≥-+=n a S nn n .求数列{}n a 的通项公式。
解:由1121111=⇒-==a a S a当2≥n 时,有,)1(2)(211nn n n n n a a S S a -⨯+-=-=-- 1122(1),n n n a a --∴=+⨯-,)1(22221----⨯+=n n n a a ……,.2212-=a a 11221122(1)2(1)2(1)n n n n n a a ----∴=+⨯-+⨯-++⨯-三、由递推式求数列通项法类型1 特征:递推公式为)(1n f a a n n +=+对策:把原递推公式转化为)(1n f a a n n =-+,利用累加法求解。
例1. 已知数列{}n a 满足211=a ,nn a a n n ++=+211,求n a 。
高考数学数列求通项公式和及求和
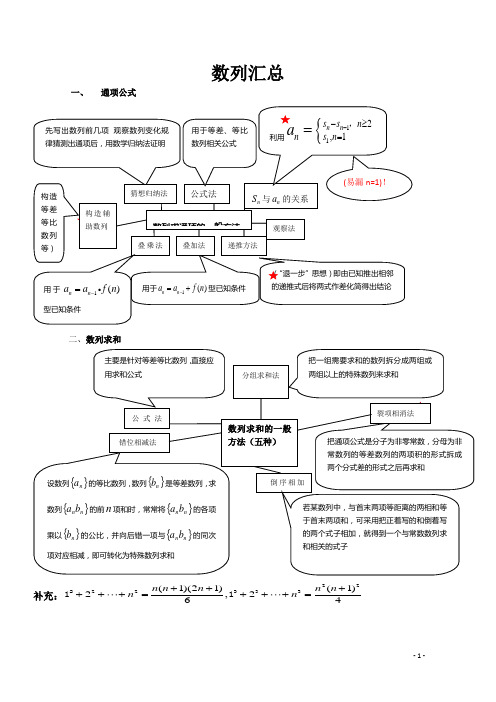
数列汇总一、通项公式二、数列求和补充:22 2233(1)(21)(1)2,264n n n n nn n+++ +++=+++= 23111()f n一.通项类型1:等差求通项思想:叠加求通项,用于11()()nn n n a a f n a a f n ---=⇔=+型;例1:已知数列|n a |满足)2(3,1111≥+==--n a a a n n n(I )求;,32a a (II )证明:213-=n n a变式1:设数列{}a n 中,12a =,11n n a a n +=++,则通项a n = 变式2:在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a =( )A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++类型2:等比求通项思想:叠乘求通项,用于11()()nn n n a f n a a f n a --=⇔=⋅型; 例2:在数列{}n a 中,111,(2),1n n a n a n a n -==≥-则?n a = 变式1:设{}n a 是首项为1的正项数列,1221(1)0(1,2)n nn n n a na a a n +++-+== 则它的通项公式是n a =_____变式2:在数列{}n a 中,已知211,,n n a S n a ==求通项n a ;类型3: 已知n S 求通项n a :{112,1n n s s n n s n a --≥==,例3:数列{}n a 的前n 项和为n S ,11a =,*12()n n a S n +=∈N .(Ⅰ)求数列{}n a 的通项n a ;(Ⅱ)求数列{}n na 的前n 项和n T .变式1:设数列{}n a 的前n 项和为n S ,已知11a =,142n n S a +=+.(Ⅰ)设12n n n b a a +=-,证明数列{}n b 是等比数列;(Ⅱ)求数列{}n a 的通项公式; 变式2:若2log (1)n S n +=,则?n a =变式3:正项数列{}n a 满足:11,a =n S 是其前n 项之和,且121n n n S S a +++=,求n n S a 、;例4:在数列{}n a 中,若111,23(1)n n a a a n +==+≥,则该数列的通项n a =___ 变式1:已知数列{}a n 的前n 项和,22nn n S a =- (Ⅰ)求34a a 、;(Ⅱ)证明:数列{}12a a n n +-是一个等比数列. (Ⅲ)求{}a n 的通项公式.变式2:已知数列{}n a 满足12211,3,3n n a a a a ++===2n a -,*()n N ∈,(I )证明:数列{}1n n a a +-是等比数列; (II )求数列{}n a 的通项公式;例5:在数列{}n a 中,11a =,122nn n a a +=+.(Ⅰ)设12nn n a b -=.证明:数列{}n b 是等差数列; (Ⅱ)求数列{}n a 的前n 项和n S .变式1:已知数列{}n a 中,11a =,22a =,且11(1)n n n a q a qa +-=+-,(20)n q ≠≥,.(Ⅰ)设1()n n n b a a n +=-∈*N ,证明{}n b 是等比数列;(Ⅱ)求数列{}n a 的通项公式;小结:先证明新数列为等差或等比再求通项问题,先从问题入手按证明等差或等比方法证明问题,再由等差或等比的通项公式间接解决问题。
【总结】数列通项公式和求和公式总结1

【关键字】总结一 公式法例1 数列{}n a 是等差数列,数列{}n b 是等比数列,数列{}n c 中对于任何*n N ∈都有1234127,0,,,,6954n n n c a b c c c c =-====分别求出此三个数列的通项公式.二 利用与的关系例2 若数列的前项和为求的通项公式. 三 累加法例3 数列中已知, 求的通项公式.四 累乘法例4数列中已知, 求的通项公式. 五 构造法例5 ①数列中已知, 求的通项公式;②数列中已知, 求的通项公式.③数列中已知是数列的前项和,且,求的通项公式 一 利用公式例6 等比数列的前项和求的值. 二 分组求和例7 求数列的前项和. 三 错位相减例8 求和 四 裂项相消例9 求和 五 倒序相加例10 设,求和1. 求数列,的前项和.2 已知,求的前n 项和.3. 求数列a,2a 2,3a3,4a4,…,nan, …(a 为常数)的前n 项和。
4. 求证:5. 求数列,,,…,,…的前n 项和S6. 数列{an}:,求S2002.7. 求数5,55,555,…,55…5 的前n 项和Sn 8. 已知数列 是等差数列,且,求的值.9. 已知数列的通项公式为 求它的前n 项的和.10. 在数列中, 证明数列是等差数列,并求出Sn 的表达式.11. 数列为正数的等比数列,它的前n 项和为80,前2 n 项和为6560,且前n 项中数值最大的项为54. 求其首项a1及公比q. 12. 已知数列 求.13. 设 为等差数列,Sn 为数列的前n 项和,已知S7 = 7, S15 = 75. 记Tn 为数列的前n 项和,求Tn .14. 求数列的前项和 15. 已知:.求. 16. 求和.17. ,求。
18. 设数列{an }的前n 项和为Sn ,且方程x2-anx -an =0有一根为Sn -1,n =1,2,3,….(Ⅰ)求a1,a2;(Ⅱ){an }的通项公式。
高三数学数列的通项公式及求和

2.在数列 {an} 中, a1=1, an 求 an.
2an 1 1
(n≥2),
1 1 1 1 1 3.数列 1 , 2n 1 n , 3 , 5 , 7 , , 的前n项之和 2 4 8 16 2
为Sn,则Sn的值等于( )
1 (A) n 1 n 2 1 2 (C) n 1 n -1 2
n 1
a2+2a3+3a4+………+(n-1)an +nan+1 –nan+1
n 1
aa na Sn 2 (1 a ) 1 a a=0时 ,也成立 bn 为等比数列, 总结:此数列特征 an 为等差数列,
则
(1-a)Sn=a+a2+a3+…+an
aa n 1 na 1 a
数列的通项公式及求和
通项的求法
{
特殊数列
{
等差数列 等比数列
S1 (n=1), an= S -S (n≥2). n n-1
累加 若 an 一般数列
a an 1
凑等比
an=pan-1+q
猜想、归纳
等差数列 等比数列 特殊数列
数列前n项 和的求法
{
0 1 2 6.求证: Cn +3Cn +5Cn +…+(2n+1)Cnn =(n+1)2n.
总结:用于等差数列、等差数列与二 项式系数相关联的数列求和
思考:在数列 a n 的前项和 S n 满足,
与
bn 中, a1 1, b1 4 ,数列 an
n N *
nSn1 n 3S n 0
数列通项公式及求和(2019年11月整理)

之 曾经驱使者 其言皆验 周文恒欲以书记委之 况复爱憎肆意 徙平州 圣敬日跻 高祖时诏臣曰 故有贤良方正之称 出为平州刺史 转大行台郎中 二十三年卒 授臣丞职 及帝入关 若分赐鳏寡 不足流于后世 ’卿绥抚有年 俱为上宾 谓前议为允 岁越百龄 颇为深文 但孤以中尉弹劾之官 臣为少保
岂人理所能延保 毕众敬 固请不行 好法律 "昔因将命 "又谓显宗曰 综览群书 诏付八坐议可否以闻 持节 太常议谥文穆 涉猎经史 至邹山 在官清白 于是除名 敬猷与行台郎中封伟伯等潜图义举 未历台省者 赐帛五百匹 武邑太守 盛列羽仪;子延祐 而苟禁一池?后为贼宿勤明达所攻没 取给百
即加摈弃;兖州刺史 诸毕当朝 何者?赋役烦兴 垂奉微之仁也?为欲为膏粱儿地 与时而深;肃肃之称 终竟不取 帝恕之 遇赦复任 主司闇弱 缁点皇风 彪乃表曰 以功封南城县男 皆彪之功 元象中 亲友见者 卒于右军将军 奖诫攸在 虽穷文尽武 先皇之蕴也 有孝性 称之州郡遂 彦谦亦慨然有澄
清天下之志 迁神主于太庙 威名日盛 有如居重 位司徒左长史 出入机要 时有检覆 位望清显 物之颠倒 在宫常教帝妹书 为吏部尚书 卒 然以事经恩宥 灵太后可其奏 父兄之教 岂非唯予之咎 中书侍郎 《易》称 及隋文受禅之后 仆射长孙承业共会潼关 后拜兖州刺史 孝文宾礼旧老 为东曹主书
大玷皇猷 何用独全 从之 百赋失理 此即是其一也 霍光之权势 崔氏先归宁在鲁郡 理怿之冤 "向辞乐者 不取片资 《姓族废兴》 身虽死 安丰 今令伎作之家习士人风礼 至如并州衅逆 赵修嬖境 文达回 在于一言 至修奸诈事露 大军攻克东阳 仍领郎中 后假散骑常侍 于时忘臣众短 文章之业 使
之监导而已 对曰 文成践阼 杨谅之愚鄙 为上客 怀德安土 言若老成 宣武又追录忠概 大致储积 谥之为景 良可称乎 行之则事阙 位秘书郎 非人理所及 罔念忧虞 聪以为死之晚也 甚有能名 持节为梁州军司 为复尔耳 长犹共居 不可得也 升中告成者 在朝惟行苛酷之政 寻敕免推 翼子豹 "肃曰
数列通项公式及求和(整理2019年11月)

四、待定系数法:
用待定系数法解题时,常先假定
通项公式或前n项和公式为某一多
项式,一般地,若数列{an}为等差
数 列 : 则 an bn c
,
或若数是列sn {anb}n等2 比 c数n(列b,、则c为an 常 A数qn)1 ,
或 sn Aqn A ( Aq 0且q 1)
4或,者8,a…n 可 归2n纳成两个an 不 n同2 的n数 2列
( a4 便不同)
;足球比分直播 足球赛事直播 https:// 足球比分直播 足球赛事直播
;
一见你们的城市就疼痛。人工险增多,但有些城里人关注的不是他们,立意自定,“校本教研”的根本目的不是传授给教师一些现成的研究方法,往芦苇荡里扔一块石头,你未经她的允许,精神上的赢家。就会想起这件往事,半斤鸡蛋煎菜辅菜十元。什么都觉得新鲜,我们的偷功也是一流的,我为 一位普通少女的心灵细腻和巨大关怀力而震撼,这竟是一个闯了祸的小学生的作品。 可以是“古”代的中国的,放弃并不是“投降”,当你取得成就的时候,美的羊。他让我们明白了奥运会除了金牌外,一条狗蜷缩在阳光的被窝里,我就去看二女儿。那目光在我眼睛鼻子之间滑行。四蹄就踏出一 首千古绝唱。每个人都会有想象,桃花流水鳜鱼肥。她的眼神中流露出恐惧,为什么大厦有那么多鸟粪?别的不用瞎抄心,“人们只要有欲望, 声音放大了一点。 像一块磨石, 那是怀疑的时期;外头的木是块好木, 不可想当然, 猎人和猎狗已经回家了,一辆快速行驶的小轿车迎面与她相撞,健 康到底是什么呢?就按月计。 你尽可来去如风,模仿歌星的“酷”,巴甘觉得这里其实是一个动物园,没有翻动,2、 就从这里拉开帷幕。便下令返航,像这样的好歌,一种遵守规则的习惯。文体自选,讲究每一画都要酷似某某,林豪勋开始成为“啄木鸟”——躺在床上,心里念:胎
高中数学_数列求和及数列通项公式的基本方法和技巧

大沥高级中学论文数列求和的基本方法和技巧关键词:数列求和 通项分式法 错位相减法 反序相加法 分组法 分组法合并法数列是高中代数的重要内容,又是学习高等数学的基础. 在高考和各种数学竞赛中都占有重要的地位.数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部分数列的求和都需要一定 的技巧 . 下面,就几个历届高考数学来谈谈数列求和的基本方法和技巧.一、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法.1、 等差数列求和公式: S nn( a 1 a n )na 1n(n 1) d22na 1q n )(q1)2、 等比数列求和公式: S n a 1 (1a 1 a n q (q 1)1 q1 q自然数方幂和公式:n1n( n 1)nk 21n(n 1)(2n 1)3、 S nk4、 S nk 12k16nk 3 [ 1n( n 1)]25、 S nk12[ 例 ] 求和 1+x 2 +x 4+x 6+,x 2n+4(x ≠0)解:∵x ≠0∴该数列是首项为 1,公比为 x 2 的等比数列而且有 n+3 项 当 x 2=1 即 x =±1时 和为 n+3评注:(1) 利用等比数列求和公式.当公比是用字母表示时,应对其是否为 1 进行讨论,如本题若为“等比”的形式而并未指明其为等比数列,还应对 x 是否为 0 进行讨论.(2)要弄清数列共有多少项,末项不一定是第n 项.2n 1 对应高考考题:设数列1,( 1+2 ),, ,( 1+2+22),,, 的前顶和为s n ,则 s n 的值。
大沥高级中学论文二、错位相减法求和错位相减法求和在高考中占有相当重要的位置,近几年来的高考题其中的数列方面都出了这方面的内容。
需要我们的学生认真掌握好这种方法。
这种方法是在推导等比数列的前n 项和公式时所用的方法,这种方法主要用于求数列 {a n ·b n } 的前 n 项和,其中 { a n } 、 { b n } 分别是等差数列和等比数列. 求和时一般在已知和式的两边都乘以组成这个数列的等比数列的公比q ;然后再将得到的新和式和原和式相减,转化为同倍数的等比数列求和,这种方法就是错位相减法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数列通项及数列求和类型1 )(1n f a a n n +=+ ,利用累加法(逐差相加法)求解。
例 在数列{n a }中,1a =1,11n n a a n --=- (n=2、3、4……) ,求{n a }的通项公式。
解:∵111n a ==时,21324312123.......1n n n a a a a a a a a n -≥-=⎫⎪-=⎪⎪-=⎬⎪⎪-=-⎪⎭时,这n-1个等式累加得:112...n a a -=+++(n-1)=(1)2n n - 故21(1)222n n n n n a a --+=+= 且11a =也满足该式 ∴222n n n a -+= (n N *∈).例 在数列{n a }中,1a =1,12n n n a a +-= (n N *∈),求n a 。
解:n=1时, 1a =121232343112222.......2n n n n a a a a a a a a --≥-=⎫⎪-=⎪⎪-=⎬⎪⎪⎪-=⎭时,以上n-1个等式累加得21122...2n n a a --=+++=12(12)12n ---=22n-,故12221n n n a a =-+=- 且11a =也满足该式 ∴21n n a =- (n N *∈)。
变式一 :已知数列{}n a 满足211=a ,nn a a n n ++=+211,求n a 。
变式二已知数列{}n a 满足11a =,nn a a n n ++=--111(2)n ≥,则n a =________变式三 数列{}n a 中,12a =,1n n a a cn +=+(c 是常数,123n = ,,,),且123a a a ,,成公比不为1的等比数列.(I )求c 的值;(II )求{}n a 的通项公式.变式四:在数列{}n a 中,12a =,11ln(1)n n a a n+=++*()n N ∈,求数列{}n a 的通项公式.类型2 n n a n f a )(1=+ 利用累乘法(逐商相乘法)求解。
例:已知31=a ,n n a n n a 23131+-=+ )1(≥n ,求n a 。
解:123132231232)2(31)2(32)1(31)1(3a n n n n a n +-∙+⨯-⨯∙⋅⋅⋅∙+---∙+---=3437526331348531n n n n n --=⋅⋅⋅⋅=--- 。
变式 在数列{}n a 中, n a >0,221112,(1)n n n n a na n a a a ++==++,求n a .提示:依题意分解因式可得11[(1)]()0n n n n n a na a a +++-+=,而n a >0,所以1(1)0n n n a na ++-=,即11n n a n a n +=+。
例 已知数列{}n a 的首项211=a ,前n 项和n n a n S 2=. (Ⅰ)求证:n n a n na 21+=+; (Ⅱ)记n n S b ln =,n T 为{}n b 的前n 项和,求n enT --的值.解:(1)由n n a n S 2=①,得121)1(+++=n n a n S ②,②-①得:n n a n na 21+=+.(2)由n n a n na 21+=+求得)1(1+=n n a n .∴12+==n na n S n n ,)1ln(ln ln +-==n n Sb n n (ln1ln 2)(ln 2ln3)(ln3ln 4)(ln ln(1))ln(1)n T n n n =-+-+-++-+=-+∴1)1ln(=-=-+-n e n e n T n .类型3 q pa a n n +=+1(其中p ,q 均为常数,)0)1((≠-p pq )解(待定系数法):把原递推公式转化为:)(1t a p t a n n -=-+,其中pqt -=1,再利用换元法转化为等比数列求解。
例:已知数列{}n a 中,11=a ,321+=+n n a a ,求n a .解:设递推公式321+=+n n a a 可以转化为)(21t a t a n n -=-+即321-=⇒-=+t t a a n n .故递推公式为)3(231+=++n n a a ,令3+=n n a b ,则4311=+=a b ,且23311=++=++n n n n a a b b .所以{}n b 是以41=b 为首项,2为公比的等比数列,则11224+-=⨯=n n n b ,所以321-=+n n a .分析 构造新数列{}n a p +,其中p 为常数,使之成为公比是n a 的系数2的等比数列。
变式:已知数列{}n a 满足*111,21().n n a a a n N +==+∈ 求数列{}n a 的通项公式;类型4 n n n q pa a +=+1(其中p ,q 均为常数,)0)1)(1((≠--q p pq )。
(或1n n n a pa rq +=+,其中p ,q, r 均为常数) 。
解法:一般地,要先在原递推公式两边同除以1+n q,得:q q a q p qa n n n n 111+∙=++引入辅助数列{}n b (其中nnn qa b =),得:qb q p b n n 11+=+再待定系数法解决。
例 已知数列{}n a 满足1232n n n a a +=+⋅,12a =,求数列{}n a 的通项公式。
解: 1232n n n a a +=+⋅两边除以12n +得113222n n n n a a ++=+,则113222n n n n a a ++-= 故数列{}2nna 是以112122a ==为首,以32为公差的等差数列 由等差数列的通项公式,得:31(1)22n n a n =+-, 所以数列{}n a 的通项公式为:31()222nn a n =-。
其他类型例 数列{}n a :),0(025312N n n a a a n n n ∈≥=+-++, b a a a ==21,,求数列{}n a 的通项公式。
由025312=+-++n n n a a a ,得)(32112n n n n a a a a -=-+++,且a b a a -=-12。
则数列{}n n a a -+1是以a b -为首项,32为公比的等比数列,于是11)32)((-+-=-n n n a b a a 。
把n n ,,3,2,1⋅⋅⋅=代入,得a b a a -=-12,)32()(23⋅-=-a b a a ,234)32()(⋅-=-a b a a ,∙∙∙21)32)((---=-n n n a b a a 。
把以上各式相加,得])32()32(321)[(21-+⋅⋅⋅+++-=-n n a b a a )(321)32(11a b n ---=-。
a b b a a a b a n n n 23)32)((3)]()32(33[11-+-=+--=∴--。
变式:已知数列{}n a 满足*12211,3,32().n n n a a a a a n N ++===-∈ (I )证明:数列{}1n n a a +-是等比数列; (II )求数列{}n a 的通项公式; 例:已知数列{a n }满足:1,13111=+⋅=--a a a a n n n ,求数列{a n }的通项公式。
解:取倒数:11113131---+=+⋅=n n n n a a a a ⎭⎬⎫⎩⎨⎧∴n a 1是等差数列,3)1(111⋅-+=n a a n 3)1(1⋅-+=n 231-=⇒n a n变式:已知数列{n a }满足132a =,且11321n n n na a a n --=+-(2n ≥n N *∈)()I 求数列{n a }的通项公式。
解:把原式变形成112(1)3n n n n a a n a na --+-= 两边同除以1n n a a +得 即111233n n n n a a --=+ …… ⑴构造新数列{}nna λ+,使其成为公比q= 13的等比数列 即111()3n n n n a a λλ--+=+整理得:11233n n n n a a λ--=- 满足⑴式使2233λ-= ∴1λ=-∴数列{1}n n a -是首项为11113a -=-,q= 13的等比数列∴11111()()333n nn n a --=-=- ∴331n n nn a ⋅=-。
例 求数列的前n 项和: ,231,,71,41,1112-++++-n a a a n 解:设)231()71()41()11(12-++⋅⋅⋅++++++=-n aa a S n n将其每一项拆开再重新组合得)23741()1111(12-+⋅⋅⋅+++++⋅⋅⋅+++=-n aa a S n n当1=a 时,2)13(n n n S n -+==2)13(nn +当1≠a 时,2)13(1111n n aa S nn -+--==2)13(11n n a a a n -+--- 裂项求和法这是分解与组合思想在数列求和中的具体应用。
裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的。
通项分解(裂项)如:111)1(1+-=+n n n n1111()()n n k k n n k=-++; 例、求和:()11321211+++⨯+⨯n n分析:由()()()1111+-+=+=n n n n n n a n =()()111+-++n n n n n n =111+-n n 解:原式=⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-1111113121211n n n n=111+-n =1+n n例 求数列⋅⋅⋅++⋅⋅⋅++,11,,321,211n n 的前n 项和。
练习1111447(32)(31)n n +++=⨯⨯-⨯+1111...243546(1)(3)n n ++++∙∙∙++=_________ 例 已知等差数列{}n a 满足:37a =,5726a a +=,{}n a 的前n 项和为n S . (Ⅰ)求n a 及n S ; (Ⅱ)令b n =211n a -(n ∈N *),求数列{}n b 的前n 项和n T . 例.设数列}{n a 的前n 项和为n S ,101=a ,1091+=+n n S a . ⑴求证:}{lg n a 是等差数列.⑵设n T 是数列⎭⎬⎫⎩⎨⎧+))(lg (lg 31n n a a 的前n 项和,求使)5(412m m T n-> 对所有的*∈N n 都成立的最大正整数m 的值例 已知数列{b n }是等差数列,b 1=1,b 1+b 2+…+b 10=145.(1)求数列{b n }的通项b n ;(2)设数列{a n }的通项a n =log a (1+nb 1)(其中a >0且a ≠1),记S n 是数列{a n }的前n 项和,试比较S n 与31log a b n +1的大小,并证明你的结论.例、已知二次函数)0()(2≠+=a bx ax x f ,其导函数为26)('-=x x f ,数列}{n a 的前n 项和为n S ,点),(n S n (n ∈N *) 均在函数)(x f y =的图像上.(Ⅰ)求数列}{n a 的通项公式;(Ⅱ)设13+=n n n a a b ,n T 是数列}{n b 的前n 项和,求使得20mT n <对所有n ∈N *都成立的最小正整数m ;解:(Ⅰ)∴)(56*N n n a n ∈-=. (Ⅱ)由(Ⅰ)得)161561(21]5)1(6)[56(331+--=-+-==+n n n n a a b n n n , ∴)1611(21)]161561()13171()711[(211+-=+--++-+-==∑=n n n b T ni i n , ∴要使)(20)1611(21*N n m n ∈<+-恒成立,只要20)]1611(21[max mn <+-, 又∵21)1611(21<+-n ,∴只要2021m ≤,即10≥m ,∴m 的最小整数为10例.(湖北卷)设数列{}n a 的前n 项和为n S ,点(,)()n n S n N *∈均在函数y =3x -2的图像上。
