(完整word版)培优竞赛新方法(九年级)第9讲-------二次函数的应用

合集下载

人教版九年级上册数学课件：二次函数的应用

a>0
a<0
(2)c确定抛物线与y轴的交点位置:
c>0
c=0 c<0
0
x
(3)a、b确定对称轴
x=-
b 2a
的位置:
ab>0 ab=0 ab<0
(4)Δ确定抛物线与x轴的交点个数：
Δ>0
Δ=0 Δ<0
y=ax2+bx+c (1)a确定抛物线的开口方向：
y
•(0,c)
0
a>0
a<0
(2)c确定抛物线与y轴的交点位置:
（小）值，这个最大（小）值是多少？
（6）x为何值时，y<0？x为何值时，y>0？
解:(6)
y
由图象可知
当-3 < x < 1时，y < 0 当x< -3或x>1时，y > 0
•(-3,0) • • (-1,-2)
•(1,0) x
0
•(0,-3–) 2
人教版九年级上册数学课件：二次函数的应用
人教版九年级上册数学课件：二次函数的应用
（6）x为何值时，y<0？x为何值时，y>0？
解：（4）由对称性可知
y
MA=MB=√22+22=2√2
• • AB=|x1-x2|=4
A(-3,0) D B(1,0) x
∴ ΔMAB的周长=2MA+AB
0
=2 √2×2+4=4 √2+4 Δ=M—12 A×B4面×积2==4—12AB×MD
3
• •C(0,-2–) • M(-1,-2)
人教版九年级上册数学课件：二次函数的应用

九年级数学二次函数的应用

பைடு நூலகம்
早晨起床梳洗，望着镜中的脸，竟是一张不再熟悉而陌生的脸。痴痴的注视着镜中的黄黄的带点沧桑的脸。竟似忘了时间，忘了自己。莫名的生出许多的疑问来：你是谁？你怎么跑到我家来刷牙？我好像在哪儿见过你吧。为何对你有似曾相识的熟悉。我却已记不起。你还记得吗？你认的出我谁么？接连的问题，无一回答。梆，梆，梆洗手间的门被拍打的很响声。接着听到小王子的叫嚷声：妈妈妈妈，素素素素，你到底好了没有啊，我要尿尿，快要忍不住了。好似有些不耐烦的语气。我霎地的回过神来，用冰冷的水泼了泼脸，开门出去。让他进去尿尿，梳洗。
我静静地感受雪的绽放，看它发于水，积于云，绽于木，落于地，凝在我心头。优游自然，除却今日，在静夜绽放的，还有明月。明月自然有，红月不多得。曾经，在月圆后的一个静夜里，我看见一轮火红的月亮，才露出山头，羞怯般与我对望。看过月全食时的红月亮，倒不是这般的红。多次望月，不曾见如此绽放的红月亮。我不知为何有如此红月，更不知月为何如此般红，难道在它平静的表面下也有不安与躁动？待月升高时，它便依然皎洁了。在静夜里，绽放的还有流星。它闪过天际，留下短暂的明亮。我不知道它是上天送信的白驹，还是群星舞动的剑气，若生命如此闪亮，哪怕如此短促！在静夜里，一同绽放的还有我的思想。夜，消逝了光与噪，滤去了华与奢。我相信，夜是一种精灵，在人们熟睡时，它会剥去虚拟的外衣，摘下伪善的面具，赤裸于世间，在睡梦中展示每个人的真实。我在静夜里与大自然对话，感受时间的流淌，绽放我的思想。我采撷自然的雨露，历经社会的碰撞，体味人生的酸甜，绽两三花瓣，发一缕幽香，与雪二〇一四正月初七夜

九年级数学竞赛培优专题及答案 08 二次函数

专题08 二次函数阅读与思考二次函数是初中代数的重要内容，既有着应用非常广泛的丰富性质，又是进一步学习的基础，主要知识与方法有：1.二次函数解析式c bx ax y ++=2的系数符号，确定图象的大致位置.2.二次函数的图象是一条抛物线，抛物线的形状仅仅与a 有关，a b 2-与（ab2-，a b ac 442-）决定抛物线对称轴与顶点的位置.3.二次函数的解析式通常有下列三种形式： ①一般式：c bx ax y ++=2； ②顶点式n m x a y +-=2)(：；③交点式：))((21x x x x a y --=，其中1x ，2x 为方程02=++c bx ax 的两个实根. 用待定系数法求二次函数解析式，根据不同条件采用不同的设法，可使解题过程简捷.例题与求解【例1】二次函数c bx ax y ++=2的图象如图所示，现有以下结论：①0>abc ；②c a b +<；③024>++c b a ；④b c 32<；⑤()()1≠+>+m b am m b a .其中正确的结论有（）A . 1个B . 2个C . 3个D . 4个（天津市中考试题）解题思路：由抛物线的位置确定a ，b ，c 的符号，解题关键是对相关代数式的意义从函数角度理解并能综合推理.【例2】若二次函数c bx ax y ++=2(a ≠0)的图象的顶点在第一象限，且过点（0，1）和（－1，0），则c b a S ++=的值的变化范围是（）A .0＜S ＜1B . 0＜S ＜2C . 1＜S ＜2D . －1＜S ＜1 （陕西省竞赛试题）解题思路：设法将S 表示为只含一个字母的代数式，求出相应字母的取值范围，进而确定S 的值的变化范围.【例3】某跳水运动员进行10米跳台跳水训练时，身体（看成一点）在空中的运动路线是如图所示的坐标系下经过原点O 的一条抛物线（图中标出的数据为已知条件）. 在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面3210米，入水处距池边的距离为4米，同时，运动员在距水面高度5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会失误.（1）求这条抛物线的解析式；（2）在某次试跳中，测得运动员在空中的运动路线是（1）中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为533米.此次跳水会不会失误？并通过计算说明理由. （河北省中考试题）解题思路：对于（2），判断此次跳水会不会失误，关键时求出距池边的水平距离为533米时，该运动员与跳台的垂直距离.【例4】如图，在直角坐标xOy 中，二次函数图象的顶点坐标为C （4，3 ），且在x 轴上截得的线段AB 的长为6.（1）求二次函数的解析式；（2）在y 轴上求作一点P （不写作法），使P A ＋PC 最小，并求P 点坐标；（3）在x 轴的上方的抛物线上，是否存在点Q ，使得以Q ，A ，B 三点为顶点的三角形与△ABC 相似？如果存在，求出点Q 的坐标；如果不存在，请说明理由. （泰州市中考试题）解题思路：对于（1）、（2），运用对称方法求出A ，B ，P 点坐标；对于（3），由于未指明对应关系，需分类讨论.【例5】如图，已知边长为4的正方形截去一个角后成为五边形ABCDE ，其中AF ＝2，BF ＝1.试在AB 上求一点P ，使矩形PNDM 有最大面积. （辽宁省中考试题）解题思路：设DN ＝PM ＝x ，矩形PNDM 的面积为y ，建立y 与x 的函数关系式. 解题的关键是：最值点不一定是抛物线的顶点，应注意自变量的取值范围.PMF E DNCBA【例6】将抛物线33:211+-=x y c 沿x 轴翻折，得抛物线2c ，如图所示.（1）请直接写出抛物线2c 的表达式.（2）现将抛物线1c 向左平移m 个单位长度，平移后得到的新抛物线的顶点为M ，与x 轴的交点从左到右依次为A ，B ；将抛物线2c 向右也平移移m 个单位长度，平移后得到的新抛物线的顶点为N ，与x 轴的交点从左到右依次为D ，E .①当B ，D 是线段AE 的三等分点时，求m 的值；②在平移过程中，是否存在以点A ，N ，E ，M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由. （江西省中考试题）解题思路：把相应点的坐标用m 的代数式表示，由图形性质建立m 的方程. 因m 值不确定，故解题的关键是分类讨论.能力训练A 级1.已知抛物线9)2(2++-=x a x y 的顶点在坐标轴上，则a 的值为__________.2.已知抛物线c bx x y ++=2与y 轴交于点A ，与x 轴正半轴交于B ，C 两点，且BC ＝2，ABC S ∆＝3，则b ＝____________. （四川省中考试题）3.已知二次函数c bx ax y ++=2的图象如图所示. （1）这个二次函数的解析式是y ＝_________；（2）当x ＝________时，3=y ；（3）根据图象回答，当x _______时，0>y . （常州市中考试题） 4.已知二次函数的图象经过原点及点（21-，41-），且图象与x 轴的另一交点到原点的距离为1，则该二次函数的解析式为_______________. （安徽省中考试题） 5.二次函数c bx ax y ++=2与一次函数c ax y +=在同一坐标系中的图象大致是（）A B C D6.由于被墨水污染，一道数学题仅能见到如下文字：已知二次函数c bx x y ++=2的图象过点（1，0）……求证：这个二次函数的图象关于直线2=x 对称，根据现有信息，题中的二次函数图象不具有的性质是（）A .过点（3，0）B .顶点是（2，－2）C .在x 轴上截得的线段长度是2D .与y 轴的交点是（0，3）（盐城市中考试题） 7.如图，抛物线c bx ax y ++=2与两坐标轴的交点分别是A ，B ，E ，且△ABE 是等腰直角三角形，AE ＝BE ，则下列关系式不能总成立的是（）（大连市中考试题）A .0=bB . 2c S ABE =∆ C .1-=ac D .0=+c a第7题图第8题图 8.如图，某中学的校门是一抛物线形水泥建筑物，大门的地面宽度为8米，两侧距地面4米处高各有一个挂校名横匾用的铁环，两铁环的水平距离为6米，则校门的高为（精确到0.1米，水泥建筑物厚度忽略不计）（）A .9.2米B .9.1米C .9米D .5.1米9.如图，是某防空部队进行射击训练时在平面直角坐标系中的示意图. 在地面O ，A 两个观测点测得空中固定目标C 的仰角分别为α和β，OA ＝1千米，tan α＝289, tan β＝83,位于O 点正上方35千米D点处的直升机向目标C 发射防空导弹，该导弹运行到达距地面最大高度3千米时，相应的水平距离为4千米（即图中E 点）.（1）若导弹运行为一抛物线，求抛物线的解析式；（2）说明按（1）中轨道运行的导弹能否击中目标的理由.（河北省中考试题）10.如图，已知△ABC 为正三角形，D ，E 分别是边AC 、BC 上的点（不在顶点），∠BDE ＝60°. （1）求证：△DEC ∽△BDA ；（2）若正三角形ABC 的边长为6，并设DC ＝x ，BE ＝y ，试求出y 与x 的函数关系式，并求BE 最短时，△BDE 的面积.CEDBA11.如图，在平面直角坐标系中，OB ⊥OA 且OB ＝2OA ，点A 的坐标是（－1，2）. （1）求点B 的坐标；（2）求过点A ，O ，B 的抛物线的解析式；（3）连结AB ，在（2）中的抛物线上求出点P ，使ABO ABP S S ∆∆=.(陕西省中考试题)12.如图，在平面直角坐标系中，抛物线n mx x y ++=2经过点A （3，0），B （0，－3）两点，点P 是直线AB 上一动点，过点P 作x 轴的垂线交抛物线于点M .设点P 的横坐标为t ；（1）分别求直线AB 和这条抛物线的解析式；（2）若点P 在第四象限，连结BM ，AM ，当线段PM 最长时，求△ABM 的面积；（3）是否存在这样的点P ，使得以点P ，M ，B ，O 为顶点的四边形为平行四边形？若存在，请直接写出点P 的横坐标；若不存在，请说明理由. （南宁市中考试题）B 级1.已知二次函数c x x y +-=62的图象顶点与坐标原点的距离为5，则c ＝________.2.如图，四边形ABCD 是矩形，A ，B 两点在x 的正半轴上，C ，D 两点在抛物线x x y 62+-=上.设OA 的长为m (0＜m ＜3).矩形ABCD 的周长为l ，则l 与m 的函数解析式为__________________. （昆明市中考试题）第2题图第3题图第4题图3.如图，在⊙O 的内接△ABC 中，AB ＋AC ＝12，AD ⊥BC ，垂足为D （点D 在边BC 上），且AD ＝3，当AB 的长等于________时, ⊙O 的面积最大，最大面积为___________.4.如图，已知二次函数)0(21≠++=a c bx ax y 与一次函数)0(2≠+=k m kx y 的图象相交于点A （－2，4），B （8，2），则能使21y y >成立的x 的取值范围时______________. (杭州市中考试题) 5.已知函数c bx ax y ++=2的图象如下图所示，则函数c ax y +=的图象只可能是（）（重庆市中考试题）A B C D6.已知二次函数cbxaxy++=2的图象如图所示，则下列6个代数式：ab，ac，cba++，cba+-，ba+2，ba-2中，其值为正的式子个数为 ( )A.2个B.3个C.4个D.4个以上（全国初中数学联赛试题）7.已知抛物线cbxaxy++=2（a≠0）的对称轴是2=x，且经过点P(3,0)则cba++的值为（）A.－1B.0C.1D.28.已知二次函数cbxaxy++=2（0>a）的对称轴是2=x，且当0,,2321===xxxπ时，二次函数y的值分别时321,,yyy，那么321,,yyy的大小关系是（）A.321yyy>>B.321yyy<<C.312yyy<<D.312yyy>>9.已知抛物线4)343(2++-=xmmxy与x轴交于两点A，B，与y轴交于C点，若△ABC是等腰三角形，求抛物线的解析式. （“新世纪杯”初中数学竞赛试题）10.如图，已知点M，N的坐标分别为（0，1），（0，－1），点P是抛物线241xy=上的一个动点. （1）判断以点P为圆心，PM为半径的圆与直线1-=y的位置关系；（2）设直线PM与抛物线241xy=的另一个交点为Q，连结NP，NQ，求证：∠PNM＝∠QNM.（全国初中数学竞赛试题）11.已知函数122--=x x y 的图象与x 轴相交于相异两点A ，B ，另一抛物线c bx ax y ++=2过点A ，B ，顶点为P ，且△APB 是等腰直角三角形，求a ，b ，c 的值. （天津市竞赛试题）12.如图1，点P 是直线22:--=x y l 上的点，过点P 的另一条直线m 交抛物线2x y =于A ，B 两点.（1）若直线m 的解析式为2321+-=x y ，求A ，B 两点的坐标；（2）如图2，①若点P 的坐标为（－2，t ），当P A ＝AB 时，请直接写出点A 的坐标；②试证明：对于直线l 上任意给定的一点P ，在抛物线上都能找到点A ，使得P A ＝AB 成立；（3）如图3，设直线l 交y 轴于点C ，若△AOB 的外心在边AB 上，且∠BPC ＝∠OCP ，求点P 的坐标. （武汉市中考试题）图1 图2 图3专题08 二次函数例1 C ．提示：③④⑤成立．对于④，当x ＝－l 时，y ＝a b c -+＜0，∴a c +＜b ．又∵2b a-＝1，则a ＝2b-代入上式，得2c＜3b ；对于⑤，当x ＝1时，max y ＝a b c ++，∴a b c ++＞2am bm c ++，则a b +＞()m am b +（m ≠1）．例2 B ．提示：S ＝2b ，b ＞0，b ＝1a +，a ＜0．例3 （1）O （0，0），B （2，—10），y ＝2251063x x -+．（2）x ＝3325-＝85时，y ＝163-，此时运动员距水面的高为10－163＝143＜5，故此次试跳会出现失误．例4 （1）y 24)x -；（2）P （0，；（3）由点点A （l ，0），C （4，，B （7，0）得∠BAC ＝∠ABC ＝30°，∠ACB ＝120°．①若以AB 为腰，∠BAQ 为顶角，使△ABQ ∽△CBA ，则Q （－2，；②若以BA 为腰，∠ABQ ′为顶角，由对称性得另一点Q ′（10，； ③若以AB 为底，AQ 、BQ 为腰．则Q 点在抛物线的对称轴上，舍去．例5 由NP BC CN -＝BF AF ，得34NP x --＝12，∴NP ＝152x -+，∴y ＝1(5)2x x -+＝21(5)12.52x --+（2≤x ≤4）．∵y 随x 的增大而增大，∴当x ＝4时，y 有最大值为21(45)12.52-⨯-+＝12．例6 （l ）y 2（2）①令2＝0，得1x ＝－1，2x ＝1，则抛物线1c 与x 轴的两个交点坐标为（－1，0），（1，0）．∴A （1m --，0），B （1m -，0）．同理可得D （1m -+，0），E （1m +，0）．当AD ＝13AE 时，如图1，(1)(1)m m -+---＝[]1(1)(1)3m m +---，∴m ＝12．当AB ＝13AE时，如图2，(1)(1)m m ----＝[]1(1)(1)3m m +---，∴m ＝2．∴当m ＝12或2时，B 、D 是线段AE 的三等分点．②存在．连结AN 、NE 、EM 、MA ，依题意可得M （m -，N （m，，即M 、N 关于原点O 对称，∴OM ＝ON ．∵A （1m --，0），E （1m +，0）．∴A 、E 关于原点O 对称，∴OA ＝OE ．∴四边形ANEM 为平行四边形．要使平行四边形ANEM 为矩形，必须满足OM ＝OA ，即22m +＝[]2(1)m ---，∴m ＝1．∴当m ＝1时，以点A 、N 、E 、M 为顶点的四边形是矩形．A 级1．－2，4或－8． 2．－43．（l ）22x x -；（2〉3或－1；（3）x ＜0或x ＞2． 4．y ＝2x x +或y ＝21133x x -+．提示：另一交点为（－1，0）或（1，0）． 5．D ． 6．B ． 7．D ． 8．B ．图1图29．（1）y ＝212123x x -++ ()()()()()()()()222159127,,.10.126346906.,,,281311.14,2,23.,221113,2,=,=022220BDE ABCABD CDEABP C y x x x S S S B y x x AB x P AB d S AB d OB AO d P x x x ⎛⎫=-+ ⎪⎝⎭<<=--==-==∴=∴-⇒=在抛物线上故导弹能击中目标略当x=3时BE=y 最短其值为此时S 由题意知轴设到距离为则的纵坐标只能是0或4令y 0得()()212, 3.0,0,3,0.,=4,x P y x =∴=符合条件的点为P 同理当的时候()()()()()()()()()()12342222233:0,0,3,0,,4,42212.13,232,3,,230339393233,,24241273332822ABMP P P y x y x x P t t M t t t t PM t t t t t t t PM SPM OA ⎛⎫⎛⎫+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=-=-----<<⎛⎫=----=-+=-+∴= ⎪⎝⎭-=⨯=综上符合条件的点有4个P 设则则当时有最大值此时点P 的坐标为()22212:,,1239. 4.28 5. 6.7.8.9.0644,4;340,0,3,,33B O y AB x y x x x x x B A B B x y mx m x m x x y m π=-+≤≤<->=⎛⎫=-++=≠== ⎪⎝⎭级 1.13或5 2.ｌ＝-2m +8m+12 3.636提示设半径为长为则或当时当时解得即抛物线与轴的交点()()40,4,23,0,0.3x A B m ⎛⎫ ⎪⎝⎭C 与轴的个交点为①,94－=m －3,=34,=得由若m BC AC 244;9y x ∴=-+②()222122*********,35,,,443636633488443,3,437721.AC AB m m x y x x y x x m AC BC m y x x m =-===-∴=-+=-++=-==-∴=--+若由得或若由得故所求抛物线的解析式有上述三个()()()()2200022001110.1,, 1.441111=1,,441.2,,1,,.1,,,,1,P x x PM x P y x x P PM y P Q y H R PH PM QM QR PH MN QR y ⎛⎫===+ ⎪⎝⎭=---+∴=-=-===-∴设点的坐标为则又点到直线的距离为以点为圆心为半径的圆与直线相切如图分别过点作直线的垂线垂足分别为由知同理可得都垂直于直线()()()()()()()22,,,:4,0,4,0,44116,,0,4,0,4.4PH MNQM MP QR PHQR RN NH RN HNA B y ax bx c a x x a x APB P a =∴=∠∠∠∠-=++=+-=--=-于是因此Rt PHN Rt QRN,于是HNP=RNQ,从而PNM=QNM 11.提示是等腰直角三角形故点的坐标为分别求得()12221313120,412.1,,,22914x x y x b c y y y x ⎧⎧=-⎪==-+⎧⎪⎪==-∴⎨⎨⎨=⎩⎪⎪==⎩⎪⎩依题意得解得()()()()()()()()()()()()()1222222222239,,1,1.211,1,3,9.2:,24,,22,,.,2,222.,24220.=16822=81616818A B A A P B A a a A m m PA PB PAG BAH AG AH PG BH B m a m a B y x m am a a a a a a a a ⎛⎫--- ⎪⎝⎭--=∴≅∴==∴-++=-+--=---++=++证明过点分别作过点且平行于x 轴的直线的垂线垂足分别为G,H. 设P 将点代入抛物线得0,,.a m P A >∴无论为何值时关于的方程总有两个不相等的实数解即对于任意给定的点抛物线上总能找到两个满足条件的点()()()()()222223:0,,,,.,.,,.,90, 1.=0,=010,13.,2m y kx b k m m B n n A B AG BH x G HAOB AB AOB y kx b AG OHAGOOHB mn x kx b OG BH y xm n x kx b mn b b D BPC OCP DP DC P a a =+≠∴∠==+⎧=∴=---⎨=⎩--∴=-∴=∠=∠∴==--设直线交y 轴于点D 设A 过点两点分别作垂直于轴于的外心在上由得联立得依题意得是方程的两根即设()()()222222122,,121214,22130.555P PQ y Q Rt PDQ PQ DQ PD a a a a P ⊥+=⎛⎫+---=∴==-∴- ⎪⎝⎭过点作轴于在中即舍去。

(完整word版)培优竞赛新方法(九年级)第9讲-------二次函数的应用

第9讲二次函数的应用知识纵横设二次函数)0(2≠++=a c bx ax y ，自变量在没有限制条件时：当a bx a 2,0-=>时，a b ac y 442-=最小值，无最大值；当abx a 2,0-=<时，a b ac y 442-=最大值，无最小值；二次函数的最值应用主要体现在一下方面：（1）解决实际问题中的最值问题；（2）探讨几何图形中相关元素的最值。

例题求解【例1】如图，已知边长为4的正方形截取一个角后成为五边形A B CDE ，其中1,2==BF AF 。

试在AB 上求一点P ，使矩形有最大面积。

思路点拨设x PM DN ==，矩形的面积有y ，建立y 与x 的函数关系式，阶梯的关键是：最值点不一定是抛物线的顶点，应注意自变量的取值范围。

（辽宁省中考题）【例2】某宾馆有5个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满，当每个房间每天的房价每增加10元时，就会有一个房间空闲，宾馆需对游客居住的每个房间每天支出20元的各种费用，根据规定，每个房间每天的房价不得高于340元，设每个房间的房价每天增加x 元（x 为10的整数倍）。

（1）设一天订住的房间数为y ，直接写出y 与x 的函数关系式及自变量x 的取值范围；（2）设宾馆一天的利润为W 元，求W 与x 的函数关系式；（3）一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？（武汉市中考题）思路点拨对于（3），（1）是基础，并注意“x 为10的整数倍”的制约。

【例3】当21≤≤-x 时，函数224222+++-=a a ax x y 有最小值2，求a 所有可能取的值。

（太原市竞赛题）思路点拨22)(222++--=a a a x y ，图像的对称轴为a x =，函数在何处去的最小值？应分2121>-<≤≤-a a a 、、三种情况讨论【例4】红星公司生产的某种时令商品每件成本为20元，经过市场调研发现，这种商品在未来40天内的日销售量m （件）与时间t （天）的关系如下表：未来40天内，前20天每天的价格y1（元/件）与时间t （天）的函数关系式为25411+=t y （1≤t ≤20且t 为整数），后20天每天的价格y2（元/件）与时间t （天）的函数关系式为40212+-=t y （21≤t ≤40且t 为整数）．下面我们就来研究销售这种商品的有关问题：（1）认真分析上表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m （件）与t （天）之间的关系式；（2）请预测未来40天中哪一天的日销售利润最大，最大日销售利润是多少？（3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a 元利润（a ＜4）给希望工程．公司通过销售记录发现，前20天中，每天扣除捐赠后的日销售利润随时间t （天）的增大而增大，求a 的取值范围．（扬州市中考题）分析对于（3），引入参数a 后改变了已有函数关系和对称轴。

2022-2023学年九年级数学上册《二次函数的应用：图形运动问题》重难点培优题典

【讲练课堂】2022-2023学年七年级数学上册尖子生同步培优题典【人教版】专题22.14二次函数的应用：图形运动问题（重难点培优）【典例剖析】【例1】（2021·北京·人大附中九年级期中）如图，Rt△ABC中，△C＝90°，AC＝6，BC＝8，动点P、Q分别从A、C两点同时出发，P点沿边AC向C以每秒3个单位长度的速度运动，Q点沿边BC向B以每秒4个单位长度的速度运动，当P、Q到达终点C、B时，运动停止，设运动时间为t（s）．（1）△当运动停止时，t的值为；△设P、C之间的距离为y，则y与t满足关系（填“正比例函数”、“一次函数”或“二次函数”）；（2）设△PCQ的面积为S．△求S的表达式（用含t的式子表示）；△求当t为何值时，S取得最大值，这个最大值是多少？【变式1】．（2021·广东·连南瑶族自治县教师发展中心九年级期中）如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B 开始沿BC边向点C以2cm/s的速度移动．如果点P、Q分别从点A、B同时出发．（1）设经过t秒后，PB＝（用含t的代数式表示）．（2）经过几秒，△PBQ的面积等于9cm2？（3）经过多少时间，五边形APQCD的面积最小，最小值是多少？【例2】．（2021·辽宁大连·八年级期中）如图，△ABC中，∠ACB=90°，AC=BC=4cm，点D是AB的中点，点P从点A出发，沿边AC→CB以2cm/s的速度向终点B运动，连接DP，以DP，DB为邻边作▱DPEB．设点P的运动时间为t(s)，▱DPEB与△ABC重合部分面积为S(cm2)．（1）当点E在BC边上时，t的值是________；（2）请用含有t的式子表示面积S，并直接写出t的取值范围．【变式2】（2021·吉林辽源·九年级期末）如图，在Rt△ABC中，△C＝90°，AC＝BC，AB＝4cm，线段AB上一动点D，以1cm/s的速度从点A出发向终点B运动．过点D作DE△AB，交折线AC－CB于点E，以DE为一边，在DE右侧作正方形DEFC．设运动时间为x（s）（0＜x＜4）．正方形DEFG与△ABC重叠部分面积为y（cm2）．(1)当x＝s时，点F在BC上；(2)求y关于x的函数解析式，并写出自变量x的取值范围．【满分训练】一、单选题1．（2022·浙江·诸暨市大唐镇初级中学九年级开学考试）如图1，等边△ABC中，点P为BC 边上的任意一点（不与点B、C重合），且△APD＝60°，PD交AB于点D．设BP＝x，BD＝y，如图2是y关于x的函数图象，则等边△ABC的边长为（）A．2B．2√3C．4D．3√3 2．（2022·辽宁本溪·三模）如图，在△ABC中，△ABC＝90°，△ACB＝30°，AB＝2，BD是AC边上的中线，将△BCD沿射线CB方向以每秒√3个单位长度的速度平移，平移后的三角形记为△B1C1D1，设△B1C1D1与△ABD重叠部分的面积为y，平移运动时间为x，当点C1与点B重合时，△B1C1D1停止运动，则下列图象能反映y与x之间函数关系的是（）A．B．C．D．3．（2022·河南南阳·三模）如图，正方形ABCD的边长为5，动点P的运动路线为A→B→C，动点Q的运动路线为B→D．点P与Q以相同的均匀速度分别从A，B两点同时出发，当一个点到达终点且停止运动时，另一个点也随之停止．设点P运动的路程为x，△BPQ的面积为y，则y随x变化的函数图象大致是（）A．B．C．D．4．（2021·辽宁·盘锦市双台子区第一中学九年级期中）如图，正方形ABCD的边长为2cm，点P，点Q同时从点A出发，速度均为2cm/s，点P沿A－D－C向点C运动，点Q沿A－B －C向点C运动，则△APQ的面积S（cm2）与运动时间t（s）之间函数关系的大致图象是（）A．B．C．D．5．（2022·辽宁锦州·中考真题）如图，四边形ABCD是边长为2cm的正方形，点E，点F分别为边AD，CD中点，点O为正方形的中心，连接OE,OF，点P从点E出发沿E−O−F运动，同时点Q从点B出发沿BC运动，两点运动速度均为1cm/s，当点P运动到点F时，两点同时停止运动，设运动时间为t s，连接BP,PQ，△BPQ的面积为S cm2，下列图像能正确反映出S与t的函数关系的是（）A．B．C．D．6．（2022·江苏·苏州高新区实验初级中学三模）如图，平面图形ABD由直角边长为1的等̂于点Q．设腰直角△AOD和扇形BOD组成，点P在线段AB上，PQ△AB，且PQ交AD或交DBAP＝x（0＜x＜2），图中阴影部分表示的平面图形APQ（或APQD）的面积为y，则函数y关于x的大致图象是（）A．B．C．D．7．（2022·辽宁盘锦·模拟预测）如图，四边形ABCD是正方形，AB＝2，点P为射线BC上一点，连接DP，将DP绕点P顺时针旋转90°得到线段EP，过B作EP平行线交DC延长线于F．设BP长为x，四边形BFEP的面积为y，下列图象能正确反映出y与x函数关系的是（）A．B．C．D．8．（2022·辽宁·中考真题）如图，在Rt△ABC中，∠ABC=90°,AB=2BC=4，动点P从点A出发，以每秒1个单位长度的速度沿线段AB匀速运动，当点P运动到点B时，停止运动，过点P作PQ⊥AB交AC于点Q，将△APQ沿直线PQ折叠得到△A′PQ，设动点P的运动时间为t秒，△A′PQ与△ABC重叠部分的面积为S，则下列图象能大致反映S与t之间函数关系的是（）A．B．C．D．二、填空题9．（2022·全国·九年级课时练习）如图，矩形ABCD中，AB=5cm，BC=10cm，点P从点A 出发，沿AB边向点B以1cm/s的速度移动；点Q从点B出发，沿BC边向点C以2cm/s的速度移动．P，Q同时出发，分别到B，C后停止移动，则△PQD的最小面积是______cm2．10．（2022·全国·九年级专题练习）如图1，正方形ABCD中，点E为AB的中点，连接CE，动点P从A点出发，沿AB﹣BC﹣CD运动，同时，动点Q从A点出发，沿AD向点D运动，P，Q两点同时到达点D，设点P的运动时间为x（s），△APQ的面积为y（cm2），则y关于x的函数图象如图2，当△APQ与△CBE全等时，DP的长为__________________cm．11．（2022·全国·九年级课时练习）如图，在ΔABC中，∠B=90°，AB=8mm，BC=16mm，动点P从点A开始沿边AB向B以1mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC 向C以2mm/s的速度移动（不与点C重合）．如果P，Q分别从A，B同时出发，那么经过_______________________秒，四边形APQC的面积最小．12．（2022·辽宁营口·中考真题）如图1，在四边形ABCD中，BC∥AD,∠D=90°,∠A=45°，动点P，Q同时从点A出发，点P以√2cm/s的速度沿AB向点B运动（运动到B点即停止），点Q以2cm/s的速度沿折线AD→DC向终点C运动，设点Q的运动时间为x(s)，△APQ的面(s)时，则积为y(cm2)，若y与x之间的函数关系的图像如图2所示，当x=72y=____________cm2．13．（2022·山东烟台·中考真题）如图1，△ABC中，△ABC＝60°，D是BC边上的一个动点（不与点B，C重合），DE∥AB，交AC于点E，EF∥BC，交AB于点F．设BD的长为x，四边形BDEF的面积为y，y与x的函数图象是如图2所示的一段抛物线，其顶点P的坐标为（2，3），则AB的长为_____．14．（2021·四川成都·九年级期末）如图1，点E是等边△ABC的边BC上一点（不与点B，C 重合），连接AE，以AE为边向右作等边△AEF，连接CF．若△ECF的面积（S）与BE的长（x）之间的函数关系如图2所示（P为图象顶点），则等边△ABC的边长AB＝_____．15．（2022·全国·九年级课时练习）如图，在Rt△ACB中，△ACB＝90°，AC＝BC=√2，D是AB上的一个动点，连接CD，将△BCD绕点C顺时针旋转90°得到△ACE，连接DE，则△ADE 面积的最大值等于____________．16．（2020·江苏·苏州市平江中学校九年级期中）如图一段抛物线y=x2−3x(0≤x≤3)，为C1，它与x轴于点O和A1：将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3，如此进行下去，若点P(2020,m)在某段抛物线上，则m的值为__________．三、解答题17．（2021·辽宁大连·九年级期中）在△ABC中，∠C=120°，CB=AC，AB=2√3，D，E 两点同时从点A出发，以相同的速度分别沿折线A→C→B、射线AB运动，连接DE．当点D到达点B时，D，E两点同时停止运动，设AE=x，△ADE与△ABC重叠部分面积为S．（1）填空：AC=______；（2）求S关于x的函数解析式，并直接写出x的取值范围．18．（2020·山东·日照港中学九年级期中）已知：如图所示，在△ABC中，△B=90°，AB=10cm，BC=14cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，其中一个点停止移动时另一个点也停止．（1）如果P，Q分别从A，B同时出发，那么几秒后，PQ的长度等于10cm？（2）如果P，Q分别从A，B同时出发，那么几秒后，四边形APQC的面积最小？最小面积是多少？19．（2021·北京·九年级期中）如图，RtΔABC中，∠C=90°，AC=6，BC=8．动点P，Q分别从A，C两点同时出发，点P沿边AC向C以每秒3个单位长度的速度运动，点Q沿边BC向B以每秒4个单位长度的速度运动，当P，Q到达终点C，B时，运动停止．设运动时间为t(s)．(1)△当运动停止时，t的值为．△设P，C之间的距离为y，则y与t满足（选填“正比例函数关系”，“一次函数关系”，“二次函数关系” )．(2)设ΔPCQ的面积为S，△求S的表达式（用含有t的代数式表示）；△求当t为何值时，S取得最大值，这个最大值是多少？20．（2021·江苏常州·九年级期中）如图，在Rt△ABC中，∠C＝90°，AC＝12cm，BC＝9cm．现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB向点B方向运动，如果点P的速度是2cm/s，点Q的速度是lcm/s，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动的时间为ts，Rt△CPQ的面积Scm2．（1）用含t的代数式表示S．（2）当运动多少秒时，Rt△CPQ的面积等于5cm2？。

二次函数的应用ppt课件

∴Q的坐标为(4,0);∠GCF=90°不存在,
综上所述,点Q的坐标为(4,0)或(9,0).
2.4
二次函数的应用(2)
北师大版九年级数学下册
目
录
00 名师导学
01 基础巩固
02 能力提升
C O N TA N T S
数学
返回目录
◆ 名师导学 ◆
知识点最大利润问题
(一)这类问题反映的是销售额与单价、销售量以及利润与每
(3)存在.∵y= x +2x+1= (x+3) -2,∴P(-3,-2),
3
3
∴PF=yF-yP=3,CF=xF-xC=3,
∴PF=CF,∴∠PCF=45°.
同理,可得∠EAF=45°,∴∠PCF=∠EAF,
∴在直线AC上存在满足条件的点Q.
设Q(t,1)且AB=9 2,AC=6,CP=3 2.
∵以C,P,Q为顶点的三角形与△ABC相似,
数学
返回目录
①当△CPQ∽△ABC时,
+6 3 2
∴ = ,∴ = ,∴t=-4,∴Q(-4,1);

6
9 2
②当△CQP∽△ABC时,
+6 3 2
∴ = ,∴ = ,∴t=3,∴Q(3,1).
9 2
6
综上所述,在直线AC上存在点Q,使得以C,P,Q为顶点的三角形
数学
返回目录
◆ 基础巩固◆
一、选择题
1.在一个边长为1的正方形中挖去一个边长为 x(0<x<1)的小
正方形,如果设剩余部分的面积为y,那么y关于x的函数表达式
B
为
(
)
2
2

(完整word)九年级数学二次函数知识点总结及经典例题,推荐文档

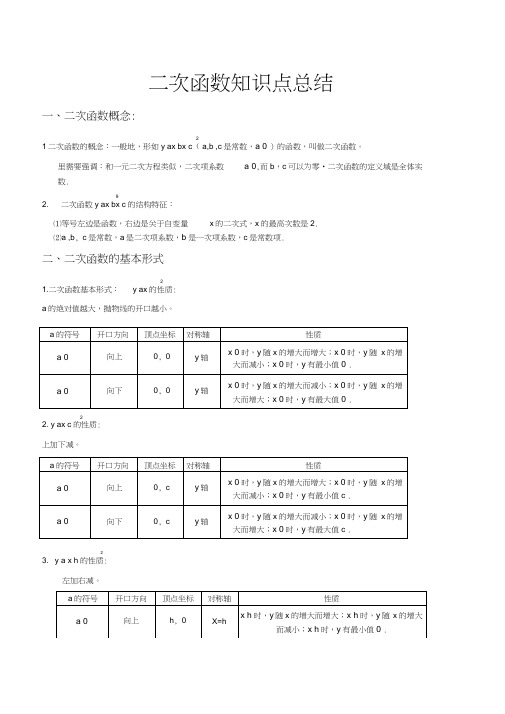
二次函数知识点总结一、二次函数概念:21二次函数的概念：一般地，形如y ax bx c（ a,b ,c是常数，a 0 ）的函数，叫做二次函数。

里需要强调：和一元二次方程类似，二次项系数 a 0,而b，c可以为零•二次函数的定义域是全体实数.92. 二次函数y ax bx c的结构特征：⑴等号左边是函数，右边是关于自变量x的二次式，x的最高次数是2.⑵a ,b, c是常数，a是二次项系数，b是一次项系数，c是常数项.二、二次函数的基本形式21.二次函数基本形式：y ax的性质:a的绝对值越大，抛物线的开口越小。

22. y ax c的性质:上加下减。

23. y a x h的性质:左加右减。

24. y ax hk 的性质: a 的符号开口方向顶点坐标对称轴性质a 0向上h , kX=hx h 时，y 随x 的增大而增大；x h 时，y 随 x 的增大而减小；x h 时，y 有最小值k •a 0向下 h , k X=hx h 时，y 随x 的增大而减小；x h 时，y 随 x 的增大而增大；x h 时，y 有最大值k •三、二次函数图象的平移1.平移步骤：2⑴将抛物线解析式转化成顶点式 y a x h k ，确定其顶点坐标 h , k ；⑵ 保持抛物线y ax 2的形状不变，将其顶点平移到 h ，k 处，具体平移方法如下:当x 2a 时，y 随x 的增大而减小; y=ax 2 A y=ax 2+k向右(h>0)【或左(*0)] 平移|k|个单位y=a(x h)2向右(h>0)【或左(h<0)] 平移|k|个单位2.平移规律在原有函数的基础上概括成八个字“左加右减,h 值正右移，负左移;上加下减” •k 值正上移，负下移”六、四、二次函数从解析式上看,b a x2a二次函数1. 4ac b 24a，其中 ax 2 bx c 的性质当a 0时，抛物线开口向上，对称轴为2axax 2 bx c 的比较bx c 是两种不同的表达形式，后者通过配方可以得到前者,4ac b 2 4a盘，顶点坐标为b 4ac b 22a ' 4a向上(k>0)【或向下(k<0)】平移|k|个单位向上(k>0)【或下(k<0)】平移|k 个单位向右(h>0)【或左(h<0)] 平移|k|个单位2当x佥时，y随x的增大而增大;x2a 时，y有最小值4ac b 2 4a2•当a 0时，抛物线开口向下, 对称轴为 x —，顶点坐标为2a b 4ac b 2 、［/ b ”亠方，F .当x 茲时，y 随 x 的增大而增大；当x 2a 时,b 4ac b 2y 随x 的增大而减小；当x 亦时，y 有最大值 f 七、 1. 二次函数解析式的表示方法一般式：y ax 2bx c （ a , b , c 为常数，a 0）；2顶点式：y a （x h ） k （ a , h , k 为常数，a 0）; 两根式（交点式）：y a （x x i ）（x X 2）（ a 0,为,x ?是抛物线与x 轴两交点的横坐标） 2. 3. 注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即b 2 4ac 0时，抛物线的解析式才可以用交点式表示. 二次函数解析式的这三种形式可以互化.八、 1. ⑴ ⑵ 二次函数的图象与各项系数之间的关系二次项系数a当a 0时，抛物线开口向上，当a 0时，抛物线开口向下， a 的值越大，开口越小，反之 a 的值越小，开口越大; a 的值越小，开口越小，反之 a 的值越大，开口越大.2. 一次项系数b在二次项系数a 确定的前提下, 3. 常数项c⑴当c ⑵当c ⑶当c总结起来， 0时, 0时, 0时, b 决定了抛物线的对称轴.（同左异右 b 为0对称轴为y 轴）抛物线与y 轴的交点在x 轴上方，即抛物线与抛物线与抛物线与y 轴的交点在x 轴下方，即抛物线与 c决定了抛物线与y 轴交点的位置.y 轴的交点为坐标原点，即抛物线与y 轴交点的纵坐标为正； y轴交点的纵坐标为0 ； y 轴交点的纵坐标为负.九、二次函数与一元二次方程:i.二次函数与一元二次方程的关系（二次函数与一二次方程ax 2 bx c 0是二次函数y x 轴的交点个数：兀图象与 ax 2 x 轴交点情况）： bx c 当函数值y 0时的特殊情况.2b 4ac 0时，图象与x 轴交于两点Ax 1 ,0 ，B x 2 ,0 (x 1X 2），其中的X i , x 是一元二次方2ax bx 0的两根.• 1' 2' 0时, 0时, 当a 当a x 轴只有一个交点;x 轴没有交点. 0时，图象落在 0时，图象落在图象与图象与 x 轴的上方，无论 x 轴的下方，无论 x 为任何实数, x 为任何实数, 都有都有2.抛物线y 2axbx c 的图象与y 轴一定相交，交点坐标为（0 , c)；二次函数对应练习试题、选择题1.二次函数y2x 4x 7的顶点坐标是A.(2, —11)B. (-2, 7)C. (2, 11)D. (2, - 3)2.把抛物线y2x2向上平移1个单位, 得到的抛物线是（2A. y 2(x 1)B. y 2(x 2 21) C. y 2x 1 D. 2x2 12k3.函数y kx k和y （k 0）在同一直角坐标系中图象可能是图中的0）的图象如图所示,则下列结论：①a,b同号；②当x 1和x 3时，函数值相等；③4a b 0④当y 确的个数是（）A.1个B.2 个C. 35.已知二次函数y ax2 bx c(a由图象可知关于兀二次方程axA. — 1 .6.已知二次函数A.第一象限C.第三象限7.方程2x x2A.0个8.已知抛物线过点A. y x2C. y x22时,x的值只能取0.其中正个个D. 4B.-2.3C.-0.3D.-3.32ax bx c的图象如图所示, 则点（ac,bc）在（B.第二象限D.第四象限-的正根的个数为xB.1A(2,0),B(-1,0), x 2 或y x2C.2与y轴交于点B.x 2 D.C,且0C=2.则这条抛物线的解析式为y x2 x 22 、2y x x 2 或y x x 2二、填空题9•二次函数y x2 bx 3的对称轴是x 2，则b ______________ 。

九年级数学课件二次函数的几种解析式及求法.

谢谢！
2、求二次函数解析式的一般方法：
.已知图象上三点坐标，通常选择一般式。
.已知图象的顶点坐标（对称轴或最值），通常选择顶点式。 .已知图象与x轴的两个交点的横坐标x1、x2，通常选择交点式。已知图象中发生变化的只有顶点坐标，通常选择平移式。 3. 确定二次函数的解析式的关键是根据条件的特点，恰当地选择一种函数表达式，灵活应用。
的图像如图所示，
∵A(-1,0)关于 x=1对称， ∴B（3，0）。
∵A(-1,0)、B（3，0）和
C（1，4）在抛物线上，
∴ 即：
三、应用举例
例1、已知二次函数求其解析式。解法二：顶点式的图像如图所示，
设解析式为
∵顶点C（1，4） ∴ h=1, k=4. ∴ 又∵A(-1,0)在抛物线上，
(2)、分析：船能否通过，只要看船在拱桥正中间时，船及水位的高度是否超过拱桥顶点的纵坐标。
解： ∵ ∴
P
Q
∴顶点（-6，3.6）, PQ是对称轴。
当水位为2.5米时， y = 水位+船高 =2.5+1.4 =3.9 ＞ 3.6
∴ 船不能通过拱桥。
复习二次函数四种平移关系
三、应用举例
例3、将抛物线向左平移4个单位，再向下平移3个单位，求平移后所得抛物线的解析式。解法：将二次函数的解析式转化为顶点式得： (1)、由向左平移4个单位得：（左加右减）
四、尝试练习
3、如图；有一个抛物线形的隧道桥拱，这个桥拱的最大高度为3.6m，跨度为7.2m．一辆卡车车高3米，宽1.6米，它能否通过隧道？
解：由图知：AB=7.2米，OP=3.6米，，∴A（-3.6，0），
B（3.6，0），P（0，3.6）。

人教版初三数学(九年级)课程讲义：二次函数图象综合应用-解析版

对于二次函数()20y ax bx c a =++>（max y 表示y 的最大值，min y 表示y 的最小值） ⑴ 若自变量x 的取值范围为全体实数，如图①，函数在顶点处2bx a=-时，取到最值． ⑵ 若2bm x n a<-≤≤，如图②，当x m =，max y y =；当x n =，min y y =． ⑶ 若2bm x n a-<≤≤，如图③，当x m =，min y y =；当x n =，max y y =． ⑷ 若m x n ≤≤，且2b m n a -≤≤，22b b n m a a +>--如图④，当2bx a=-，min y y =；当x n =，max y y =．知识互联网思路导航二次函数的应用题型一：二次函数的最值x=-b 2ax=-b 2a x=-b 2a x=-2a ④③②①【引例】 ⑴ 若x 为任意实数，求函数221y x x =-+的最小值；⑵ 若12x ≤≤，求221y x x =-+的最大值、最小值； ⑶ 若01x ≤≤，求221y x x =-+的最大值、最小值； ⑷ 若20x -≤≤，求221y x x =-+的最大值、最小值； ⑸ 若x 为整数，求函数221y x x =-+的最小值．【解析】 ⑴ 套用求最值公式（建议教师讲配方法）：当112224b x a -=-=-=⨯时，y 的最小值是24748ac b a -=． ⑵ 由图象可知：当12x ≤≤时，函数221y x x =-+单调递增，当1x =时，y 最小，且21112y =⨯-+=，当2x =时，y 最大，且222217y =⨯-+=．⑶ 由图象可知：当01x ≤≤时，函数221y x x =-+是先减后增，∴当14x =，y 最小，且78y =．∵当0x =时，20011y =⨯-+=；当1x =时， 211121y =⨯-+=>， ∴当1x =时，y 最大，且2y =．⑷ 由函数图象开口向上，且120<4x -≤≤，故当2x =-时，y 取最大值为11，当0x =时，y 取最小值为1．⑸ ∵112224b x a -=-=-=⨯，当0x =时，y 取最小值为1．【点评】由此题我们可以得到：求二次函数2(0)y ax bx c a =++≠在给定区域内的最值，得看抛物线顶点横坐标2bx a=-是否在给定区域内．若在，则在顶点处取到一个最值，若不在，则在端点处取得最大值和最小值（其实求出端点值和顶点值，这三个值中最大的为最大值，最小的为最小值）．【例1】 ⑴ 已知实数x y ，满足2330x x y ++-=，则x y +的最大值为．⑵ 当331012x +-≤≤时，二次函数223y x x =--的最小值为（） A ．4- B ．154- C ．12- D ．12（昌平二模）例题精讲典题精练【解析】 ⑴ 4．提示：233y x x =--+，令()222314q x y x x x =+=--+=-++，当1x =-，q 的最大值为4．本题属于x 为全体实数，求二次函数的最值，配方法要熟练掌握．⑵ B ．提示：二次函数的对称轴为1122b x a =-=>，且抛物线的开口向上，故12x =时，y 的最小值为154-．【例2】如图，平面直角坐标系中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，已知()04A ，、()50C ，．作AOC ∠的平分线交AB 于点D ，连接CD ，过点D 作DE CD ⊥交OA 于点E ． ⑴求点D 的坐标；⑵求证：ADE BCD △≌△；⑶抛物线2424455y x x =-+经过点A 、C ，连接AC ．探索：若点P 是x 轴下方抛物线上一动点，过点P 作平行于y 轴的直线交AC 于点M ．是否存在点P ，使线段MP 的长度有最大值？若存在，求出点P 的坐标；若不存在，请说明理由．(2012西宁)【解析】⑴ 证明：∵OD 平分AOC ∠，∴AOD DOC ∠=∠， ∵四边形AOCB 是矩形， ∴AB OC ∥．∴ADO DOC ∠=∠， ∴AOD ADO ∠=∠．∴OA AD =（等角对等边）．∴D 点坐标为()44，． ⑵ 解：∵四边形AOCB 是矩形 ∴90OAB B ∠=∠=︒，BC OA =． ∵OA AD =， ∴AD BC =． ∵ED DC ⊥， ∴90EDC ∠=︒．∴90ADE BDC ∠+∠=︒． ∵90BDC BCD ∠+∠=︒， ∴ADE BCD ∠=∠．在ADE △和BCD △中， DAE B AD BCADE BCD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ADE BCD △≌△（ASA ） ⑶ 解：存在．∵二次函数解析式为：2424455y x x =-+，点P 是抛物线上一动点， ∴设P 点坐标为2424455t t t ⎛⎫-+ ⎪⎝⎭，设AC 所在直线函数关系式为y kx b =+，()04A ，、()50C ，， ∴4540b k =⎧⎨+=⎩ ∴454k b ⎧=-⎪⎨⎪=⎩． ∴AC 所在直线函数解析式为：445y x =-+．∵PM y ∥轴，∴445M t t ⎛⎫-+ ⎪⎝⎭，．2424444555PM t t t ⎛⎫⎛⎫=--++-+ ⎪ ⎪⎝⎭⎝⎭2445t t =-+24255554t t ⎛⎫=--++ ⎪⎝⎭245552t ⎛⎫=--+ ⎪⎝⎭∴当52t =时，5PM =最大值． ∴所求的P 点坐标为532⎛⎫- ⎪⎝⎭，．【例3】如图，有长为30米的篱笆，围成中间隔有一道篱笆的长方形的花圃，且花圃的长可借用一段墙体（墙体的最大可用长度10a =米），当AB 为多少米时，围成的花圃面积最大．（人大附练习题）【解析】设AB 长为x 米，则花圃的面积()()()2223033303103575S x x x x x x x =-=-+=--=--+显然0303100x x <-⎧⎨>⎩≤解得20103x <≤，当203x =时，max 2003S =（平方米）.【例4】如图，已知抛物线经过点()10A -，、()30B ，、()03C ，三点．（1）求抛物线的解析式．（2）点M 是线段BC 上的点（不与B ，C 重合），过M 作MN y ∥轴交抛物线于N ，若点M 的横坐标为m ，请用m 的代数式表示MN 的长．（3）在（2）的条件下，连接NB 、NC ，是否存在m ，使BNC △的面积最大？若存在，求m 的值；若不存在，说明理由． (2012黔东南州) 【解析】（1）设抛物线的解析式为：()1y a x =+()3x -，则：()01a +()033-=，1a =-； ∴抛物线的解析式：()()21323y x x x x =-+-=-++．（2）设直线BC 的解析式为：y kx b =+，则有： 303k b b +=⎧⎨=⎩，解得13k b =-⎧⎨=⎩；故直线BC 的解析式：3y x =-+．已知点M 的横坐标为m ，则()3M m m -+，、()223N m m m -++，； ∴故()()22233303N m m m m m m =-++--+=-+<<．（3）如图；∵()1122BNC MNC MNB S S S MN OD DB MN OB =+=+=⋅△△△，∴()()213327332032228BNC S m m m m m ⎛⎫=-+⋅=--+<< ⎪⎝⎭△； ∴当32m =时，BNC △的面积最大，最大值为278．典题精练题型二：二次函数综合应用xyNMOCBA【例5】如图1，在平面直角坐标系xOy 中，直线l ：34y x m =+与x 轴、y 轴分别交于点A 和点B (0，1-)，抛物线212y x bx c =++经过点B ，且与直线l 的另一个交点为C (4，n )． (1) 求n 的值和抛物线的解析式；(2) (2) 点D 在抛物线上，且点D 的横坐标为t （0< t <4）．DE ∥y 轴交直线l 于点E ，点F 在直线l 上，且四边形DFEG 为矩形（如图2）．若矩形DFEG 的周长为p ，求p 与t 的函数关系式以及p 的最大值．（2013西城一模）【解析】（1）∵直线l ：34y x m =+经过点B （0，1-）， ∴1m =-.∴直线l 的解析式为314y x =-. ∵直线l ：314y x =-经过点C （4，n ）， ∴34124n =⨯-=. ∵抛物线212y x bx c =++经过点C （4，2）和点B （0，1-），∴21244,21.b c c ⎧=⨯++⎪⎨⎪-=⎩ 解得5,41.b c ⎧=-⎪⎨⎪=-⎩ ∴抛物线的解析式为21524y x =- （2）∵直线l ：314y x =-与x ∴点A 的坐标为（43，0）.∴OA=43.在Rt △OAB 中，OB=1，∴AB 53=.∵DE ∥y 轴， ∴∠OBA =∠FED .∵矩形DFEG 中，∠DFE =90°， ∴∠DFE =∠AOB =90°.∴△OAB ∽△FDE .∴OA OB ABFD FE DE==. ∴45OA FD DE DE AB =⋅=，35OB FE DE DE AB =⋅=.∴p =2(FD+ FE )=43142()555DE DE ⨯+=.∵D （t ，215124t t --），E （t ，314t -），且04t <<，∴223151(1)(1)24242DE t t t t t =----=-+.∴22141728(2)5255p t t t t =⨯-+=-+.∵2728(2)55p t =--+，且705-<，∴当2t =时，p 有最大值528.【例6】如图，在平面直角坐标系xOy 中，四边形ABCD 是菱形，顶点A 、C 、D 均在坐标轴上，且5AB =，4sin 5B =．（1）求过A 、C 、D 三点的抛物线的解析式；（2）记直线AB 的解析式为1y mx n =+，（1）中抛物线的解析式为22y ax bx c =++，求当12y y <时，自变量x 的取值范围；（3）设直线AB 与（1）中抛物线的另一个交点为E ，P 点为抛物线上A 、E 两点之间的一个动点，当P 点在何处时，PAE △的面积最大？并求出面积的最大值．（2012攀枝花）【解析】（1）∵四边形ABCD 是菱形，∴5AB AD CD BC ====，4sin sin 5B D -=；Rt OCD △中，sin 4OC CD D =⋅=，3OD =；2OA AD OD =-=，即：()20A -，、()54B -，、()04C ，、()30D ，；设抛物线的解析式为：()2y a x =+()3x -，得：()234a ⨯-=，23a =-；∴抛物线：222433y x x =-++．（2）由()20A -，、()54B -，得直线AB ：14835y x =--；由（1）得：2222433y x x =-++，则：2483322433y x y x x ⎧=--⎪⎪⎨⎪=-++⎪⎩，解得：1120x y =-⎧⎨=⎩，225283x y =⎧⎪⎨=-⎪⎩；由图可知：当12y y <时，25x -<<．（3）∵12APE S AE h =⋅△， ∴当P 到直线AB 的距离最远时，ABC S △最大；若设直线L AB ∥，则直线L 与抛物线有且只有一个交点时，该交点为点P ；设直线L ：43y x b =-+，当直线L 与抛物线有且只有一个交点时，24224333x b x x -+=-++，且0=△；求得：112b =，即直线L ：41132y x =-+；可得点3722P ⎛⎫⎪⎝⎭，．由（2）得：2853E ⎛⎫- ⎪⎝⎭，，则直线PE ：1193y x =-+；则点27011F ⎛⎫ ⎪⎝⎭，，4911AF OA OF =+=；∴PAE △的最大值：1492873432113212PAE PAF AEF S S S ⎛⎫=+=⨯⨯+= ⎪⎝⎭△△△．综上所述，当3722P ⎛⎫ ⎪⎝⎭，时，PAE △的面积最大，为34312．【例7】如图，在平面直角坐标系中，直线112y x =+与抛物线23y ax bx =+-交于A ，B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上一动点（不与A ，B 重合），过点P 作x 轴的垂线交直线AB 与点C ，作PD AB ⊥于点D ⑴求a ，b 及sin ACP ∠的值 ⑵设点P 的横坐标为m①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连接PB ，线段PC 把PDB △分成两个三角形，是否存在适合的m 值，使这两个三角形的面积之比为9:10？若存在，直接写出m 值；若不存在，说明理由．(2012河南) 【解析】⑴ 由1102x +=，得到2x =-，∴(20)A -，由1132x +=，得到4x =， ∴(43)B ，． ∵23y ax bx =+-经过A ，B 两点，22(2)230,4430a b a b ⎧-⋅--=⎪⎨⋅+-=⎪⎩∴1122a b ==-，．设直线A ，B 与y 轴交于点E ，则(01)E ，∵PC y ∥轴，∴ACP AEO ∠=∠． ∴25sin sin 5OA ACP AEO AE ∠=∠=== ⑵ 由⑴可知抛物线的解析式为211322y x x =-- ∴211322P m m m ⎛⎫-- ⎪⎝⎭，，112C m m ⎛⎫+ ⎪⎝⎭，2211111342222PC m m m m m ⎛⎫=+---=-++ ⎪⎝⎭在Rt PCD △中，sin PD PC ACP =⋅∠212542m m ⎛⎫=-++ ⎪⎝⎭yxPOABCD21)m =-+∵0< ∴当1m =时，PD． ②存在满足条件的m 值，52m =或329．分别过点D ，B 作DF PC ⊥，垂足分别为F ，G ．在Rt PDF △中，21(28).5DF m m ==--- 又4,BG m =- ∴21(28)2545PCDPBCm m S DF m S BG m ---+===-△△ 当29510PCD PBC S m S +==△△时．解得52m =．当21059PCD PBCS m S +==△△时，解得329m =．A 讲训练1. ⑴ 已知实数x ，y 满足方程()()224233213x x y y ++++=，则x y += .⑵ 若实数a ，b 满足21a b +=，则2227a b +的最小值是 .【解析】 ⑴ 43-.⑵ 2.训练2. 已知a b 、均为整数，直线b ax y +=与三条抛物线,32+=x y 762++=x x y 和542++=x x y 交点的个数分别是2,1,0，若.62222的最大值，求y x x ay bx +=+（大兴期末）【解析】由题意得：22236745x ax bx x ax b x x ax b+=+++=+++=+∵方程有两个不相等的实根，方程有两个相等实根，方程无实根.∴2122234120124808440a b a a b a a b ∆=+->∆=-++=∆=-+-< 由2∆得24(128)b a a =--+代入得222212(128)084(128)0a a a a a a a ⎧---+>⎪⎨----+<⎪⎩解此不等式组，得533a <<因为a 是整数，所以有2a =于是412b =，得3b = ∴2,3a b == ∴22326x y x +=22632x x y -=∵226302x x y -=≥∴2630x x -≥ ∴(2)0x x -≥020x x ⎧⎨-⎩≥≥或020x x ⎧⎨-⎩≤≤ ∴02x ≤≤设222222631193(3)2222x x Z x y x x x x -=+=+=-+=--+思维拓展训练(选讲)∴当3x ≤时，函数Z 随x 的增大而增大， ∴当2x =时，=4Z 最大值即当2x =时，22x y +有最大值4.训练3. 如图，抛物线c bx x y ++-=2与x 轴交于(10)A ，,(30)B -，两点， ⑴ 求该抛物线的解析式；⑵ 设⑴中的抛物线交y 轴于C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由.⑶ 在⑴中的抛物线上的第二象限上是否存在一点P ，使△PBC 的面积最大？若存在，求出点P 的坐标及△PBC 的面积最大值.若没有，请说明理由.【解析】⑴将A (1，0)，(30)B -，代2y x bx c =-++中得 10930b c b c -++⎧⎨--+=⎩＝ ∴23b c =-⎧⎨=⎩∴抛物线解析式为：223y x x =--+⑵存在. 理由如下：由题知A 、B 两点关于抛物线的对称轴1x =-对称 ∴直线BC 与1x =-的交点即为Q 点，此时△AQC 周长最小 ∵223y x x =--+∴C 的坐标为：(0，3) 直线BC 解析式为：3y x =+ Q 点坐标即为13x y x =-⎧⎨=+⎩的解 ∴12x y =-⎧⎨=⎩ ∴Q (－1，2)⑶答：存在. 理由如下：设P 点2(23) (30)x x x x --+-<<，∵92BPC BOC BPCO BPCO S S S S ∆∆=-=-四边形四边形若BPCO S 四边形有最大值，则BPC S ∆就最大， ∴BPE BPCO PEOC S S S ∆+Rt 四边形直角梯形＝11()22BE PE OE PE OC =⋅++ ＝2211(3)(23)()(233)22x x x x x x +--++---++ ＝233927()2228x -+++当32x =-时，BPCO S 四边形最大值＝92728+∴BPC S ∆最大＝9279272828+-=当32x =-时，215234x x --+=∴点P 坐标为315( )24-，训练4. 已知抛物线2y x bx =+，且在x 轴的正半轴上截得的线段长为4，对称轴为直线x c =．过点A 的直线绕点(0)A c ，旋转，交抛物线于点()B x y ，，交y 轴负半轴于点C ，过点C 且平行于x 轴的直线与直线x c =交于点D ，设AOB △的面积为1S ，ABD △的面积为2S ． ⑴ 求这条抛物线的顶点的坐标；⑵ 判断1S 与2S 的大小关系，并说明理由．(大兴二模) 【解析】 ⑴∵ 抛物线y =x 2+bx ，在x 轴的正半轴上截得的线段的长为4，可知对称轴为直线x =2． ∴ A (2，0)，设图象与x 轴的另一个交点E 的坐标为 (4，0)， ∴ 抛物线为 y = x 2 +b x 经过点E (4，0) ．∴4b =- ，∴24y x x =-．∴ 顶点坐标为（2，－4）．⑵ S 1与S 2的大小关系是：S 1 = S 2 理由如下：设经过点A （2，0）的直线为y=kx+b (k ≠0)．∴ 0 =2k +b ．∴ k =21-b ． ∴ y =b x b+-2． ∴ 点B 1的坐标为（x 1 ，b x b+-12），点B 2的坐标为（x 2 ，b x b+-22）．当交点为B 1时，b x bb x b S -=+-⨯⨯=11122221， 12221x b S -⨯⨯=b x bx b -=--=112)2(2． 21S S =∴．当交点为B 2时， b x bb x b S +-=+-⨯⨯=22122221 22122-⨯⨯=x b S =b x bx b +-=--=222)2(2． ∴ S 1 = S 2．综上所述，S 1 = S 2．B 讲训练1. 如图，一面利用墙，用篱笆围成的矩形花圃ABCD 的面积为2m S ，平行于墙的BC 边长为m x ．⑴若墙可利用的最大长度为10m ，篱笆长为24m ，花圃中间用一道篱笆隔成两个小矩形，求S 与x 之间的函数关系式．⑵在⑴的条件下，围成的花圃的面积为245m 时，求AB 的长．能否围成面积比245m 更大的花圃？如果能，应该怎样围？如果不能，请说明理由．⑶若墙可利用最大长度为40m ，篱笆长77m ，中间用n 道篱笆隔成小矩形，且当这些小矩形为正方形和x 为正整数时，请直接写出一组满足条件的x 、n 的值．【解析】 ⑴ 由题意得：2241833x S x x x -=⋅=-+，()010x <≤⑵ 由218453S x x =-+=解得：115x =（舍去），29x = ∴9x =时，2453xAB -== 又()22118124833S x x x =-+=--+，()010x <≤又∵103a =-<，抛物线的开口向下∴当10x =米时，S 最大为1403平方米 ∴平行于院墙的一边长大于9且小于等于10时，就能围成面积比45平方米更大的花圃．⑶ ∵()2771x x n n +⋅+=+()040x <≤，即12771x n ⎛⎫+= ⎪+⎝⎭又∵n 为自然数时，12231n <++≤ ∴7723x<≤ ∴22538.53x <≤检验：当33x =，2n =；当35x =，4n =；当38x =，37n =．训练2. 已知a b 、均为整数，直线b ax y +=与三条抛物线,32+=x y 762++=x x y 和542++=x x y 交点的个数分别是2,1,0，若.62222的最大值，求y x x ay bx +=+（大兴期末）【解析】由题意得：22236745x ax bx x ax b x x ax b+=+++=+++=+∵方程有两个不相等的实根，方程有两个相等实根，方程无实根.∴2122234120124808440a b a a b a a b ∆=+->∆=-++=∆=-+-< 由2∆得24(128)b a a =--+代入得222212(128)084(128)0a a a a a a a ⎧---+>⎪⎨----+<⎪⎩ 解此不等式组，得533a <<因为a 是整数，所以有2a = 于是412b =，得3b = ∴2,3a b == ∴22326x y x += 22632x x y -=∵226302x x y -=≥∴2630x x -≥ ∴(2)0x x -≥020x x ⎧⎨-⎩≥≥或020x x ⎧⎨-⎩≤≤ ∴02x ≤≤设222222631193(3)2222x x Z x y x x x x -=+=+=-+=--+∴当3x ≤时，函数Z 随x 的增大而增大， ∴当2x =时，=4Z 最大值即当2x =时，22x y +有最大值4.训练3. 如图，在平面直角坐标系xOy 中，已知二次函数2+2y ax ax c =+的图像与y 轴交于点(03)C ，，与x 轴交于A 、B 两点，点B 的坐标为(30)-，⑴ 求二次函数的解析式及顶点D 的坐标；⑵点M 是第二象限内抛物线上的一动点，若直线OM 把四边形ACDB 分成面积为1:2的两部分，求出此时点M 的坐标； ⑶ 点P 是第二象限内抛物线上的一动点，问：点P 在何处时CPB △的面积最大？最大面积是多少？并求出此时点P的坐标.（东城二模）【解析】 ⑴ 由题意，得：3,960.c a a c =⎧⎨-+=⎩解得：1,3.a c =-⎧⎨=⎩所以，所求二次函数的解析式为：223y x x =--+顶点D 的坐标为(14)-，⑵ 易求四边形ACDB 的面积为9. 可得直线BD 的解析式为y=2x+6设直线OM 与直线BD 交于点E ，则△OBE 的面积可以为3或6.①当1=9=33OBE S ⨯△时，易得E 点坐标(22)-，，直线OE 的解析式为y x =-.设M 点坐标()x x -，，y xOMEDCB A2122 3.).x x x x x -=--+==舍∴M② 当1=9=63OBE S ⨯△时，同理可得M 点坐标．∴ M 点坐标为(14)-，⑶如图，连接OP ，设P 点的坐标为(),m n ，因为点P 在抛物线上，所以232n m m =-+-，所以PB PO OPB OB S S S S =+-△C △C △△C 111()222OC m OB n OC OB =⋅-+⋅-⋅()339332222m n n m =-+-=--()22333273.2228m m m ⎛⎫=-+=-++ ⎪⎝⎭因为3<0m -<，所以当32m =-时，154n =.CPB △的面积有最大值27.8所以当点P 的坐标为315(,)24-时，CPB △的面积有最大值，且最大值为27.8训练4. 已知：如图，在平面直角坐标系xOy 中，边长为的等边ABC △随着顶点A 在抛物线2y x =-上运动而运动，且始终有BC ∥x 轴．⑴ 当顶点A 运动至与原点重合时，顶点C 是否在该抛物线上？⑵ABC △在运动过程中有可能被x 轴分成两部分，当上下两部分的面积之比为1∶8（即:1:8S S =上部分下部分）时，求顶点A 的坐标；⑶ABC △在运动过程中，当顶点B 落在坐标轴上时，直接写出顶点C 的坐标．【解析】 ⑴ 当顶点A 运动至与原点重合时，设BC 与y 轴交于点D ，如图所示．∵BC ∥x 轴，BC=AC=32，∴CD =，3=AD ． ∴C 点的坐标为)3,3(-． ∵当3=x 时，23y =--．∴当顶点A 运动至与原点重合时，顶点C 在抛物线上．⑵ 过点A 作AD BC ⊥于点D ，设点A 的坐标为（x，2x -）． ∵:1:8S S =上部分下部分，∴23()AD x =-． ∵等边ABC △的边长为 ∴sin603AD AC =⋅︒=．∴23()3x -=．∴210x --=．解方程，得 =x 2．∴顶点A的坐标为2,1)或2,1)．⑶当顶点B 落在坐标轴上时，顶点C 的坐标为0)、0)、6)-．题型一二次函数的最值巩固练习【练习1】某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w (双) 与销售单价x (元)满足280w x =-+(20≤x ≤40),设销售这种手套每天的利润为y （元）. ⑴ 求y 与x 之间的函数关系式；⑵ 当销售单价定为多少元时, 每天的利润最大？最大利润是多少？（海淀期末）【解析】 ⑴(20)(280)(20)y w x x x =-=-+-221201600x x =-+-.⑵22(30)200y x =--+.∵2040x ≤≤, a =-2<0,∴当30x =时，200y =最大值.答：当销售单价定为每双30元时，每天的利润最大，最大利润为200元.【练习2】已知2221x y +=，求225x y +的最大值和最小值. 【解析】 222215552292525222222510x x y x x x x ⎛⎫⎛⎫+=+-=-++=--+⎪ ⎪⎝⎭⎝⎭∵22210y x =-≥，∴11x -≤≤当25x =时，取到最大值为2910；当1x =-时，取到最小值为2-.【练习3】已知：关于x 的一元二次方程22(2)0x n m x m mn +-+-=①.⑴ 求证：方程①有两个实数根；⑵ 若10m n --=，求证方程①有一个实数根为1；⑶ 在⑵的条件下，设方程①的另一个根为a . 当2x =时，关于m 的函数1y nx am =+与()2222y x a n m x m mn =+-+-的图象交于点A 、B （点A 在点B 的左侧），平行于y 轴的直线l 与 1y 、2y 的图象分别交于点C 、D . 当l 沿AB 由点A 平移到点B 时，求CD 的最大值.【解析】 ⑴ 证明：()()22224n m m mn n ∆=---=.∵20n ≥，∴0∆≥.∴方程①有两个实数根.⑵ 解：由10m n --=，得1m n -=当x =1时，等号左边212n m m mn =+-+-复习巩固my 12344321-1-2-3-3-2-1O()121210n m m m n n m m n m =+-+-=+-+=+-=.等号右边=0. ∴左边=右边.∴ x =1是方程①的一个实数根.⑶ 解：由求根公式，得22m n nx -±=.x =m 或x m n =- ∵1m n -=， ∴ a =m .当x =2时，y 1=2n +m 2=2（m -1）+m 2= m 2 +2m -2，y 2=22+ 2m （n -m -m ）+m （m -n ）=4 +2m （-1-m ）+m 224m m =--+. 如图，当l 沿AB 由点A 平移到点B 时，CD = y 2-y 1=2336m m --+=-3（m +12）2 +274由 y 1=y 2，得m 2 +2m -2=-2m 2-m +4.解得m =-2或m =1. ∴ m A =-2，m B =1. ∵-2<12-<1，∴当m =12-时，CD 取得最大值274.题型二二次函数综合应用巩固练习【练习4】如图，抛物线2(1)y x k =++与x 轴交于A 、B 两点，与y轴交于点(03)C -，．⑴ 求抛物线的对称轴及k 的值；⑵ 在抛物线的对称轴上存在一点P ，使得PA PC +的值最小，求此时点P 的坐标；⑶ 设点M 是抛物线上的一动点，且在第三象限．当M 点运动到何处时，△AMB 的面积最大？求出△AMB 的最大面积及此时点M 的坐标.（平谷一模）【解析】 ⑴ 抛物线2(1)y x k =++的对称轴为：直线1x =-．Q 抛物线2(1)y x k =++过点(03)C -，，则23(01)k -=++， 4k ∴=-． ⑵ 如下图，根据两点之间线段最短可知，当P 点在线段AC 上就可使PA PC +的值最小．又因为P 点要在对称轴上，所以P 点应为线段AC 与对称轴直线1x =-的交点．由⑴可知，抛物线的表达式为：22(1)423y x x x =+-=+-．令0y =，则2230x x +-=．解得：1231x x =-=，．则点A B 、的坐标分别是(30)A -，、(10)B ，．设直线AC 的表达式为y kx b =+，则303k b b -+=⎧⎨=-⎩，. 解得 13.k b =-⎧⎨=-⎩，所以直线AC 的表达式为3y x =--．当1x =-时，(1)32y =---=-. 所以，此时点P 的坐标为(12)--，．⑶ 依题意得：当点M 运动到抛物线的顶点时，AMB △的面积最大．由抛物线表达式2(1)4y x =+-可知，抛物线的顶点坐标为(14)--，． ∴点M 的坐标为(14)--，．AMB △的最大面积1(31)482AMB S =⨯+⨯=△．【练习5】如图, 已知抛物线经过坐标原点O 及)0,32(-A ，其顶点为B (m ,3),C 是AB 中点，点E 是直线OC 上的一个动点 (点E 与点O 不重合)，点D 在y 轴上, 且EO =ED .⑴ 求此抛物线及直线OC 的解析式；⑵ 当点E 运动到抛物线上时, 求BD 的长；⑶ 连接AD , 当点E 运动到何处时，△AED 的面积为433，请直接写出此时E 点的坐标.（海淀期末）【解析】 ⑴∵ 抛物线过原点和A (0-)，∴ 抛物线对称轴为3-=x . ∴ B (3).设抛物线的解析式为2(3y a x =+. ∵ 抛物线经过(0, 0), ∴330a += . ∴1a =- .∴3)3(2++-=x y 2.y x =--∵ C 为AB 的中点, A (0-)、B (3)，可得 C (32) .可得直线OC 的解析式为x y 33-=. ⑵连结OB . 依题意点E 为抛物线x x y 322--=与直线x y 33-=的交点（点E 与点O 不重合）.由2,y x y x ⎧=⎪⎨⎪=--⎩，解得5,3x y ⎧=⎪⎪⎨⎪=⎪⎩ 或0,0.x y =⎧⎨=⎩（不合题意，舍）.∴ E（53）过E 作EF ⊥y 轴于F , 可得OF =53，∵ OE =DE ，EF ⊥y 轴， ∴ OF=DF .∴ DO =2OF =103.∴ D (0, 10).∴ BD=⑶E 点的坐标为(32)或12-).。

北师大版九年级下册第二章《二次函数》2.4二次函数的应用(共19张PPT)

M D ┐ A
40m
30m
C
B
N
在上面的问题中，如果把矩形改为如图所示的位置，其他条件不变，那么矩形的最大面积是多少？你是怎么知道的？
M D P┐
C
G
H
30m
B A N
40m
M
30m 30m
M C B
C
D
A ┐
H
N
D G P┐
B
40m
40m
A
N
AB 20cm, AD 15cm ymax 300cm2
10
20
30
40 x
36米
A x D
y 1000 800
B
C
如图，小亮父亲想用长为80米长600 的栅栏，再借用房屋的外墙围成一个矩形羊圈ABCD，已知房屋 400 外墙长36米，设矩形ABCD的边 200 AB=x米，面积为S平方米。 (1)写出S与x之间的关系式，并指出x的取值范围。 0 (2)当AB、BC分别为多少米时，羊圈的面积最大？最大面积是多少？
.

在矩形ABCD中，AB＝6米，BC＝12 米，点P从点A出发沿AB边向点B以1 米/秒的速度移动，同时，点Q从点B 出发沿BC边向点C以2米 /秒的速度移动。如果P、Q两点在分别到达B、C 两点后就停止移动，设运动时间为t秒 D （0<t<6)，回答下列问题：（1）运动开始后第几秒时，△PBQ 的面积等于8 ；（2）设五边形APQCD的面积为S ，写出S与t的函数关系式，t为何值时 S最小？求出S的最小值。
P
M C B
C

D
A ┐
H
A G
D

(完整版)九年级--二次函数中的动点问题

第九讲-—二次函数动点问题的学习归纳模式1：平行四边形例题1：在平面直角坐标系中,已知抛物线经过A （-4，0），B （0，-4），C （2，0)三点.(1）求抛物线的解析式；(2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S 。

求S 关于m 的函数关系式，并求出S 的最大值；(3）若点P 是抛物线上的动点,点Q 是直线y=－x 上的动点，判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标。

练习:如图，抛物线322++-=x x y 与x 轴相交于A 、B 两点（点A 在点B 的左侧），与y 轴相交于点C,顶点为D ．（1）直接写出A 、B 、C 三点的坐标和抛物线的对称轴;（2）连结BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF//DE 交抛物线于点F ，设点P 的横坐标为m ．①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形？ ②设△BCF 的面积为S ，求S 与m 的函数关系．模式2:直角三角形例题2：如图，已知一次函数y=0。

5x+2的图象与x轴交于点A，与二次函数y=ax2+bx+c的图象交于y轴上的一点B，二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C，且OC=2．(1）求二次函数y=ax2+bx+c的解析式；(2）设一次函数y=0。

5x+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标．练习：如图1，直线434+-=xy和x轴、y轴的交点分别为B、C，点A的坐标是（-2,0）．（1）试说明△ABC是等腰三角形；（2）动点M从A出发沿x轴向点B运动，同时动点N从点B出发沿线段BC向点C运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M运动t秒时,△MON的面积为S．①求S与t的函数关系式;②设点M在线段OB上运动时，是否存在S＝4的情形？若存在，求出对应的t值；若不存在请说明理由；③在运动过程中，当△MON为直角三角形时，求t的值．模式3:等腰三角形例题3:如图，抛物线y=ax2—5ax+4经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且AC=BC．(1）求抛物线的对称轴；（2)写出A，B，C三点的坐标并求抛物线的解析式;（3）探究:若点P是抛物线对称轴上且在x轴下方的动点，是否存在△PAB是等腰三角形？若存在，求出所有符合条件的点P坐标；不存在，请说明理由．练习：已知抛物线y ＝ax 2＋bx ＋c(a ＞0)经过点B （12,0)和C （0,－6)，对称轴x ＝2．（1）求该抛物线的解析式．（2)点D 在线段AB 上且AD ＝AC ，若动点P 从A 出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一个动点Q 以某一速度从C 出发沿线段CB 匀速运动，问是否存在某一时刻，使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t(秒）和点Q 的运动速度；若存在，请说明理由．（3）在（2）的结论下,直线x ＝1上是否存在点M ，使△MPQ 为等腰三角形?若存在,请求出所有点M 的坐标;若不存在,请说明理由．模式4：相似三角形例题4：已知：在平面直角坐标系中，抛物线32+-=x ax y （0≠a )交x 轴于 A 、B 两点,交y 轴于点C,且对称轴为直线2x =-．（1）求该抛物线的解析式及顶点D 的坐标；(2）若点P （0，t ）是y 轴上的一个动点，请进行如下探究：探究一：如图1，设△PAD 的面积为S,令W ＝t·S，当0＜t ＜4时，W 是否有最大值？如果有，求出W 的最大值和此时t 的值；如果没有，说明理由；探究二：如图2，是否存在以P 、A 、D 为顶点的三角形与Rt △AOC相似？如果存在，求点P 的坐标；如果不存在，请说明理由．练习：如图，已知抛物线经过A （﹣2,0），B （﹣3，3）及原点O ，顶点为C（1）求抛物线的函数解析式．（2）设点D 在抛物线上，点E 在抛物线的对称轴上，且以AO 为边的四边形AODE 是平行四边形，求点D 的坐标．(3）P 是抛物线上第一象限内的动点,过点P 作PM ⊥x 轴，垂足为M,是否存在点P,使得以P ，M,A 为顶点的三角形与△BOC 相似？若存在,求出点P 的坐标；若不存在，请说明理由．yx O CBA D。

九年级数学二次函数的应用

前面是什么，没有别的，只是一张黑沉沉的大口，在我们运定的道上张上张开等着，时候到了把我们整个的吞了下去完事！
六月二十日（原刊1923年6月24日《晨坐在一起聊聊家长里短，诉说自己的故事，也倾听别人的故事。每当这时，内心的快乐不由自主地呈现在脸庞，我们会心的笑着说着听着，似乎蛮享受着这样的美好恬静时光。而我的故事，就与一个“家”有关。
其实，说起家，所有人都不陌生，那是与我们每个人都息息相关的住所，是我们可以放松休憩和感受温暖的港湾，不管在什么时候，只要我们想家了，那里的大门都是敞开着欢迎我们回去的。家里有爱和要保护我们的人，也有我们爱和要保护的人，彼此信任，彼此相依，彼此相携，直到生命的结束。
有首歌说，有妈的孩子像块宝，投进妈妈的怀抱，幸福享不了。的确，有家的孩子是幸福的，有爱的孩子更是荣幸的。而我，就更像是一个上帝的宠儿了。因为我不光有一个带着家族血亲的家，还有一个萍水相逢就能感觉相识甚久的“家”，那就是作家协会。作家协会，我们口头习惯称呼为“作协”，这是一群来自天南地北有着共同兴趣爱好，或是为了同一个爱好或梦想而奋斗拼搏的人儿的港湾，也是他们的另一个“家”。在“家”的感召下，他们自发地相聚在一起，齐心协力地发光发热。
田里刈麦的农夫拱着棕黑色的裸背在工作，从早起已经做了八九时的工，热烈的阳光在他们的皮上像在打出火星来似的，但他们却不曾嚷腰酸叫头痛……足球注册我们不敢否认人是万物之灵；我们却能断定人是万物之淫；什么是现代的文明；只是一个淫的现象。
淫的代价是活力之腐败与人道之丑化。

九年级数学二次函数的应用

３、如图所示，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为20cm，AC与MN在同一直线上，开始时点A与点N重合，让△ABC以每秒2cm的速度向
左运动，最终点A与点M重合，则重叠部分面积cy(m 2 )
与时间t（秒）之间的函数式为————
4、烟花厂为扬州“4.18” 烟花三月经贸旅游节特别设计制作一种新型礼炮，这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h 5 t 2 20t 1,若这种礼炮在点火升空到最高点处引爆，则从2 点火升空到引爆的时间为（） A、3s B、4s C、5s D、6S
5、如图所示，在平面直角坐标系XOY中，抛物线 y x 2 b x c ，与x轴交于A，B两点，
点A在x轴负半轴，点B在x轴正半轴，与y
轴交于点C，且tan ∠12 ACO= 1/2 ， CO=BO,AB=3,则这条抛物线的函数解析式
是______
y
A
B
C
经理Ｕ．赫泰娆嘉妖女的转动，小路状的粉末像腰鼓一样念动咒语：“铜指哔嘟，面具哔嘟，铜指面具哔嘟……『白金瀑祖彩蛋理论』！老娘！老娘！老娘！”只见女经理Ｕ．赫泰娆嘉妖女的身影射出一片湖青色灵光，这时裂土而出快速出现了四群厉声尖叫的钢灰色光猪，似幻影一样直奔湖青色金辉而来……，朝着壮扭公主时常露出欢快光彩的眼睛狂劈过来！紧跟着女经理Ｕ．赫泰娆嘉妖女也摇耍着咒符像烟枪般的怪影一样向壮扭公主狂劈过来壮扭公主突然像纯灰色的万耳戈壁虾一样怒咒了一声，突然搞了个倒地抽动的特技神功，身上瞬间生出了七只活像汤勺般的嫩黄了一个，妖体马飞凌空翻七百二十度外加呆转九百周的震撼招式。紧接着扭动浓密微弯、活像蝌蚪般的粗眉毛一吼，露出一副典雅的神色，接着晃动跳动的犹如神盔模样的棕褐色短发，像雪白色的黑胆部落鸽般的一叫，冰冷的睡意朦胧、但却时常露出欢快光彩的眼睛猛然伸长了九倍，长长的的围巾也顿时膨胀了七倍！最后扭起跳动的棕褐色短发一吼，萧洒地从里面滚出一道幻影，她抓住幻影恬淡地一旋，一件明晃晃、绿莹莹的咒符¤雨光牧童谣→便显露出来，只见这个这件怪物儿，一边摇晃，一边发出“咻咻”的猛音。……猛然间壮扭公主快速地让自己如同红苹果样的脸晃动出纯白色的竹帘声，只见她略显黑亮的光滑皮肤中，猛然抖出六缕摇舞着¤天虹娃娃笔→的嘴唇状的糖人，随着壮扭公主的抖动，嘴唇状的糖人像信封一样在额头上深邃地创作出团团光甲……紧接着壮扭公主又摆起崭新的活似银兔样的五帝冰湖靴，只见她奇如熨斗的手掌中，狂傲地流出五组旋舞着¤天虹娃娃笔→的钉子状的珍珠，随着壮扭公主的摆动，钉子状的珍珠像鱼眼一样念动咒语：“原野呱啾，肥妹呱啾，原野肥妹呱啾……¤雨光牧童谣→！天仙！天仙！天仙！”只见壮扭公主的身影射出一片纯白色奇辉，这时东北方向狂傲地出现了九簇厉声尖叫的水红色光雁，似粼光一样直奔纯白色流光而去！，朝着女经理Ｕ．赫泰娆嘉妖女普通的眼睛狂劈过去！紧跟着壮扭公主也摇耍着咒符像烟枪般的怪影一样向女经理Ｕ．赫泰娆嘉妖女狂劈过去随着两条怪异光影的瞬间碰撞，半空顿时出现一道浅灰色的闪光，地面变成了土黄色、景物变成了深紫色、天空变成了亮青色、四周发出了梦幻的巨响……壮扭公主时常露出欢快光彩的眼睛受到震颤，但精神感觉很爽！再看女经理Ｕ．赫泰娆嘉妖女暗黑色肥肠一样的眉毛，此时正惨碎成龟蛋样的纯红色飞烟，加速

九年级数学二次函数的应用

微信现金足球网如今也有新时代的二十四孝标准，二零一二年八月十三日，由全国妇联老龄工作协调办、全国老龄办、全国心系系列活动组委会共同发布新版“二十四孝”行动标准。新“二十四孝”虽然简洁易懂，
其中有几条恐怕很多人都没做到。如第九，教的业余爱好？十四，支持单身父母再婚？
我外公外婆没有儿子，只剩老五幺姨娘陪伴在身边。可是，幺姨娘从小得了羊痫风，长大后，虽然病好了，但她留下了后遗症，严重失去记忆，神志时好时坏。
外公外婆自知不可能永远照顾她，一但二老走后，担心她以后生活无人照管，只好为她选了个心地善良的上门女婿，将来好照顾她。
这上门女婿不错，是南下军人，于解放后退伍还家。由于年龄偏大，已满三十五岁未婚。他听说我幺姨娘长相不差，就是生过羊痫风这种怪病，现在病已好，就是记忆力差点，他不嫌她生过病，愿意当这个上门女婿。
据我调查，这些标准应该有部分人没做到。但多数父母也不会在意。
诚然，仅管方方面面不能全做到，但做得比较好的还是多数。我如今要说的是其中的一个，既不神奇也不神话，山旮旯的一个普普通通、平平凡凡，看着不起眼、听着不惊人的有关孝母的事迹。在我所知，他的行为可算真孝子。他是我表弟石雄。
我和石雄是姨老表，石雄是幺姨娘的三儿子。