三输入变量判奇电路的真值表及表达式
组合逻辑电路设计应用题

组合逻辑电路设计题1、试设计一个三人多数表决器组合逻辑电路。
2、已知某工厂电源允许功率容量为35KW,厂内有三台设备A、B、C,其额定功率分别为10KW,20KW,30KW,它们投入运行为随机组合,为超出工厂电源允许功率容量则安全运行,试求工厂用电安全运行组合逻辑电路。
3、已知某工厂电源允许功率容量为100KW,厂内有三台大功率设备,其额定功率分别为30KW,50KW,65KW,它们投入运行为随机组合,为超出工厂电源允许功率容量则安全运行,超过时为超负荷运行,电路自动报警。
试求超负荷运行报警的组合逻辑电路。
4、某企业有两台电动机,试用门电路设计一个故障指示电路,要求:(1)若两台电动机正常工作,绿灯亮,其余灯暗(2)若其中一台发生故障,黄灯亮,其余灯暗(3)若两台电动机均有故障,则红灯亮。
5、自动控制地铁列车,在关门和下一段路轨空出条件下,列车可以开出,其中关门可分自动关门或者手动关门,试用门电路,设计列车可以开出的逻辑电路。
6、试用门电路实现3变量奇校电路,即输入“1”的个数为奇数时,输出为1,否则为0,要求列出真值表,画出用门电路组成的组合逻辑电路。
7、已知输入信号A、B、C和输出信号Y,如图所示,试用最少呢数量与非门实现该波形要求。
8、某工厂有3个用电量相同的车间和一大一小的两台发电机,若只有一个车间开工,小发电机可以满足供电要求,若两个车间同时开工,大发电机可以满足供电要求,若3个车间同时开工,需要大、小两台发电机同时起动才能满足供电要求,试用与非门设计一个控制器,以实现对两台发电机的控制。
9、设计一个电路,用3个开关控制一个灯,即任何一个开关都可以控制灯的开关,即一个开时就亮,两个开时就熄灭,3个开时就亮。
10、某年级毕业统考,要求总分达到9分可以毕业,其中课程A,及格5分,不及格0分;课程B,及格4分,不及格0分;课程C,及格3分,不及格0分;课程D,及格2分,不及格0分;设计一个判断能毕业的电路。
数字电路实验报告

数字电路实验报告姓名:张珂班级:10级8班学号:2010302540224实验一:组合逻辑电路分析一.实验用集成电路引脚图1.74LS00集成电路2.74LS20集成电路二、实验内容1、组合逻辑电路分析逻辑原理图如下:U1A 74LS00NU2B74LS00NU3C74LS00N X12.5 VJ1Key = Space J2Key = Space J3Key = Space J4Key = SpaceVCC5VGND图1.1组合逻辑电路分析电路图说明:ABCD 按逻辑开关“1”表示高电平,“0”表示低电平; 逻辑指示灯:灯亮表示“1”,灯不亮表示“0”。
真值表如下: A B C D Y 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 1 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 0 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1表1.1 组合逻辑电路分析真值表实验分析:由实验逻辑电路图可知:输出X1=AB CD =AB+CD ,同样,由真值表也能推出此方程,说明此逻辑电路具有与或功能。
2、密码锁问题:密码锁的开锁条件是:拨对密码,钥匙插入锁眼将电源接通,当两个条件同时满足时,开锁信号为“1”,将锁打开;否则,报警信号为“1”,则接通警铃。
试分析下图中密码锁的密码ABCD 是什么? 密码锁逻辑原理图如下:U1A74LS00NU2B74LS00NU3C 74LS00NU4D 74LS00NU5D 74LS00NU6A74LS00N U7A74LS00NU8A74LS20D GNDVCC5VJ1Key = SpaceJ2Key = SpaceJ3Key = SpaceJ4Key = SpaceVCC5VX12.5 VX22.5 V图 2 密码锁电路分析实验真值表记录如下:实验真值表 A B CD X1 X2 0 0 0 0 0 1 0 0 0 1 0 1 0 0 1 0 0 1 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 0 0 0 1 1 0 0 1 1 0 1 0 1 0 0 1 1 0 1 1 0 1 1 1 0 0 0 1 1 1 0 1 0 1 1 1 1 0 0 1 1 11 10 1表1.2 密码锁电路分析真值表实验分析:由真值表(表1.2)可知:当ABCD 为1001时,灯X1亮,灯X2灭;其他情况下,灯X1灭,灯X2亮。
数字电子技术第四章课后习题答案(江晓安等编)

第四章组合逻辑电路1. 解: (a)(b)是相同的电路,均为同或电路。
2. 解:分析结果表明图(a)、(b)是相同的电路,均为同或电路。
同或电路的功能:输入相同输出为“1”;输入相异输出为“0”。
因此,输出为“0”(低电平)时,输入状态为AB=01或103. 由真值表可看出,该电路是一位二进制数的全加电路,A为被加数,B为加数,C为低位向本位的进位,F1为本位向高位的进位,F2为本位的和位。
4. 解:函数关系如下:SF++⊕=+ABSABS BABS将具体的S值代入,求得F 312值,填入表中。
A A FB A B A B A A F B A B A A F A A F AB AB F B B A AB F AB B A B A B A AB F B A A AB F B A B A B A F B A AB AB B A B A F B B A B A B A B A B A B A F AB BA A A B A A B A F F B A B A F B A B A F A A F S S S S =⊕==+==+⊕===+⊕===⊕===⊕===+⊕===+=+⊕===⊕==+==⊕==Θ=+=+⊕===+++=+⊕===+=⊕===⊕==+=+⊕==+=+⊕===⊕==01111111011010110001011101010011000001110110)(01010100101001110010100011000001235. (1)用异或门实现,电路图如图(a)所示。
(2) 用与或门实现,电路图如图(b)所示。
6. 解因为一天24小时,所以需要5个变量。
P变量表示上午或下午,P=0为上午,P=1为下午;ABCD表示时间数值。
真值表如表所示。
利用卡诺图化简如图(a)所示。
化简后的函数表达式为D C A P D B A P C B A P A P DC A PD B A P C B A P A P F =+++=用与非门实现的逻辑图如图(b )所示。
2006年江苏省普通高校对口单独招生统一考试机电试卷

江苏省2006年普通高校单独招生统一考试试卷机电专业综合理论一、判断题(14题,每题2分,共28分。
若命题正确,请将答题卡上A涂黑;若命题不正确,将答题卡上B涂黑)1、通常,照明电路中灯开得越多,负载电阻越大。
2、直流电路中,元件中无电流流过,元件的两端一定无电压。
3、电气设备或元件所受的实际电压不能超过其额定电压。
4、两根靠得很近的平行直导线,若通以相同方向的直流电流,则它们相互排斥。
5、用普通指针式万用表测量电阻时,应将万用表转换开关置于电阻挡上,选择适当的量程,再将两表笔接在一起,调节调零旋钮,使指针位于电阻刻度的零位上后,才能开始测量。
6、某同学做荧光灯实验时,测得灯管两端电压为106 V,镇流器两端电压为198 V,两电压之和大于电源电压220 V,说明该同学测量数据有误。
7、同一铁心上的两个线圈的端点分别为1、2和3、4,若1和与3为同名端,则2与4也为同名端。
8、两个空心线圈之间的互感系数与线圈中的电流大小无关。
9、(1010111)2 >(142)1010、二极管和三极管一样,具有开关特性和放大特性。
11、在选购V带时,只要说明带的型号和基准长度,就可以购得正确适用的V带。
12、链传动在任一时刻的瞬时传动比都是恒定的。
13、传动齿轮在轴上必须作轴向固定和周向固定。
14、机床上的丝杠,螺旋千斤顶等使用的螺纹都是三角形螺纹。
二、选择题(19题,每题3分,共57分。
在每题列出的选项中,只有一项符合题目要求。
)15、单位不相同的两个物理量是。
A. 电压、电位B. 电压、电流C.电位、电动势D. 电压、电动势16、交流电压u =102sin(6280t-30o) V,其相量U=V。
A.102∠-30o B.102∠30o C.10∠30o D.10∠-30 o17、R-L-C串联电路发生谐振时,电路的恒等于零。
A.有功功率B.无功功率C.视在功率D.瞬时功率18、三相交流异步电动机采用降压起动,主要是为了降低起动时的。
丁志杰《数字电路》课后习题解答

(2Байду номын сангаас 证明“自等律” A ⋅ 1 = A , A + 0 = A 。真值表如下: 真值表 A 0 1 F = A·1 0 1 A 0 1 真值表 F = A+0 0 1
习题
(3) 证明“互补律” A ⋅ A = 0 , A + A = 1 。真值表如下: 真值表 A 0 1 F = A·A 0 0 A 0 1 真值表 F = A+A 1 1
第一章
习题
第一章习题 1-1 例 1.2.12 中转换前后两个数的绝对值哪个大?为什么? 答:转换前大。因为转换后舍去了后边的小数位。 1-2 将下列二进制数分别转换为八进制数、十六进制数和十进制数。 11001101.101,10010011.1111 解:(11001101.101)2 =(11 001 101.101)2= ( 315.5)8 =(1100 1101.1010)2 =( CD.A)16 =(128+64+8+4+1+0.5+0.125)10=(205.625)10 (10010011.1111)2 =(1001 0011.1111)2= (93.F)16 =(10 010 011.111 100)2 =( 223.74)8 =(128+16+2+1+0.5+0.25+0.125+0.0625)10=(147.9375)10 1-3 将下列十进制数转换为二进制、八进制和十六进制数。 121.56,73.85 解:1. 0Å1Å3Å7Å15Å30Å60Å121 0.56Æ0.12Æ0.24Æ0.48Æ0.96Æ0.92 1 1 1 1 0 0 1 1 0 0 0 1 所以: (121.56)10=(1111001.10001)2=(171.42)8=(79.88)16 2. 0Å1Å2Å4Å9Å18Å36Å73 0.85Æ0.7Æ0.4Æ0.8Æ0.6Æ0.2Æ0.4 1 0 0 1 0 0 1 1 1 0 1 1 0 (73.85)10=(1001001.11011)2=(111.66)8=(49.D8)16 1-4 将下列十六进制数转换为二进制、八进制和十进制数。 89.0F,E5.CD 解:(89.0F)16=(10001001.00001111)2=(211.036)8=(8*16+9+15/256)10=(137. 0.05859375)10 1-5 试求例 1.2.17 的转换误差,比较例 1.2.12 的转换误差,哪个大?为什么? 答:例 1.2.12 的误差大。例 1.2.17 实际上转换了 15 位二进制小数,而例 1.2.12 只转换了 5 位。 1-6 用十六位二进数表示符号数。试分别写出原码、反码和补码可表示的数值范围。 解: 原码 –(215-1) ~ +(215-1); 反码 –(215-1) ~ +(215-1); 补码 –215 ~ +(215-1) 1-7 设 n=8,求下列二进制数的反码: 101101,-101101,10100,-10100 解:先补齐 8 位,再求反;正数的反码是原码,负数的反码需求反。 (101101)反 =00101101 (-101101)反=11010010 (10100)反 =00010100 (-101101)反=11101011 1-8 设 n=8,求下列二进制数的补码: 101101,-101101,10100,-10100,101.001,-101.001 解:先补齐 8 位,再求补;正数的补码是原码,负数的补码需求补。 (101101)补 =00101101 (-101101)补=11010011 (10100)补=00010100 (-101101)补=11101100 (101.001)补 =00000101.001
数字电子技术基础课后答案(李雪飞)

(1)
(2)
[题2.11]
(1)
(2)
[题2.12]
Y1为高电平,Y2为低电平,Y3为低电平,Y4为高阻态,Y5为低电平,Y6为高阻态,Y7为低电平,Y8为低电平,Y9为高电平,Y10为低电平
[题2.13]
Y1为低电平,Y2为低电平,Y3为低电平,Y4为低电平
[题2.14]
这种扩展输入端的方法不能用于TTL门电路。CMOS门电路的内部结构决定了其输入端的个数不能太多,由于其输入信号的范围较宽(0~VDD),因此,可以采用本题的扩展方式。而TTL门的输入输出信号的高低电平分别为3.6V和0.3V。
对于Y3和Y4来说,采用此连接方式后,不能满足TTL电路输出电平的要求,无法驱动后级TTL门工作。
[题2.15]
(a)错。TTL门电路不能直接驱动晶体管,否则在与非门输出高电平3.6V时,会将晶体管和门电路损坏。应在晶体管基极接一个电阻Rb,电路如图(a)所示。
(b)错。集电极开路门应用中必须在电源与其输出端之间加一个外接电阻,正确的电路如图(b)所示。
[题3.18]
电路如下图
当M=0时,
当M=1时,
[题3.19]
[题3.20]
解:设两个5位二进制数分别为A( )和B( )。依据题意,将两个5位二进制数的高4位,即 和 分别接入比较器的数据输入端,将 和 比较的结果 , 和 分别接入级联输入的 , 和 端,其函数表达式为
[题3.21]
解:由电路写出输出Y的逻辑函数式为
[题1.4]
(1)(2942)D(2)(10010010.01110101)BCD
[题1.5]
(1)原码和补码都是01001(2)原码是11101,补码是10011
[数字电子技术及应用(第2版)习题答案第2单元习题答案

自我检测题一、填空题2-1如果对键盘上108个符号进行二进制编码,则至少要 7 位二进制数码。
2-2共阳LED 数码管应由输出 低 电平的七段显示译码器来驱动点亮,而共阴LED 数码管应采用输出为 高 电平的七段显示译码器来驱动点亮。
2-3采用54LS138完成数据分配器的功能时,若把S 1作为数据输入端接D ,则应将使能端2S 接 低 电平,3S 接 低 电平。
2-4对N 个信号进行编码时,需要使用的二进制代码位数n 要满足条件 N ≤2n 。
二、选择题2-5一个8选1的数据选择器,其地址输入端有几个 B 。
A 、1 B 、3 C 、2 D 、42-6可以用 B 、C 电路的芯片来实现一个三变量组合逻辑函数。
A 、编码器 B 、译码器 C 、数据选择器2-7要实现一个三变量组合逻辑函数,可选用 A 芯片。
A 、74LS138 B 、54LS148 C 、74LS147 三、判断题2-8 54/74LS138是输出低电平有效的3线-8线译码器。
( ✓ )2-9当共阳极LED 数码管的七段(a ~g )阴极电平依次为1001111时,数码管将显示数字1。
(✓ )练习题2-1试分析图题2-10所示各组合逻辑电路的逻辑功能。
图题2-1解:(a )图,)()(D C B A Y ⊕⊕⊕=,真值表如表题2-1(a)所示:表题2-1(a)A B C DYABY(a )(b )(a )图为四变量奇校验器,当输入变量中有奇数个为1,输出为1。
(b )图,AB B A B A B A Y +=+++=,真值表如表题2-1(b)所示:(b )图为同或门电路,当输入变量状态相同时出1,相反时出0。
2-2试分析图题2-2所示各组合逻辑电路的逻辑功能,写出函数表达式。
图题2-2解:(a)图0=+++=CD C B AB Y(b)图C B A Y C B A AB C B A AB Y ⊕⊕=⊕+=⊕∙=21,)()(2-3试采用与非门设计下列逻辑电路:(1)三变量非一致电路;(2)三变量判奇电路(含1的个数); (3)三变量多数表决电路。
数字电路实验报告

数字电路实验报告实验一组合逻辑电路分析一.实验目的1.熟悉基本逻辑电路的特点。
2.熟悉各类门的实物元件以及元件的使用和线路连接。
3.学会分析电路功能。
二.实验原理1.利用单刀双掷开关的双接点,分别连接高电平和低电平,开关的掷点不同,门电路输入的电平也不同。
2.门电路的输出端连接逻辑指示灯,灯亮则输出为高电平,灯灭则输出低电平。
3.依次通过门电路的输入电平与输出电平,分析门电路的逻辑关系和实现的逻辑功能。
三.实验元件1.74LS00D2.74LS20D四、实验内容⑴组合逻辑电路分析XLC1组合逻辑电路分析真值表由实验逻辑电路图可知:输出CD AB CD AB X +=∙=1 ,同样,由真值表也能推出此方程,说明此逻辑电路具有与或功能。
⑵密码锁问题密码锁的开锁条件是:拨对密码,钥匙插入锁眼将电源接通,当两个条件同时满足时,开锁信号为“1”,将锁打开。
否则,报警信号为“1”,则接通警铃。
试分析密码锁的密码ABCD 是什么?VCC实验结果分析:由真值表可知:当ABCD 为1001时,灯X1亮,灯X2灭;其他情况下,灯X1灭,灯X2亮。
由此可见,该密码锁的密码ABCD 为1001。
因而,可以得到:D C B A X =1,12X X =。
实验二 组合逻辑实验(一)半加器和全加器一、实验目的1.熟悉用门电路设计组合电路的原理和方法步骤。
二、预习内容1.复习用门电路设计组合逻辑电路的原理和方法步骤。
2.复习二进制数的运算。
(1)用“与非”门设计半加器的逻辑图。
(2)完成用“异或”门、“与或非”门、“与非”门设计全加器的逻辑图。
(3)完成用“异或”门设计的3变量判奇电路的原理图。
三、参考元件1.74LS283(集成超前4位进位加法器)2.74LS00 (四2输入与非门)3.74LS51 (双与或非门)4.74LS136(四2输入异或门)四、实验内容⑴用与非门组成半加器 由理论课知识可知:i i i i i i i i i i i i i B B A A B A B A B A B A S ∙∙∙=+=⊕= i i i i i B A B A C ==根据上式,设计如下电路图:得到实验数据表格所得如下:⑵用异或门、与或非门、与非门组成全加器 由理论课知识可知:i S =1i i i A B C -⊕⊕i C =1()i i i i i A B A B C -+⊕ 根据上式,设计如下电路:XLC1实验数据表格所得如下:0 1 0 1 0 1 00 1 1 0 0 1- 0 0 0 0 1 1 0 1 1 0 1 0 011⑶用异或门设计3变量判奇电路,要求变量中1的个数为奇数时,输出为1,否则为0。
第4章 组合逻辑电路课后答案
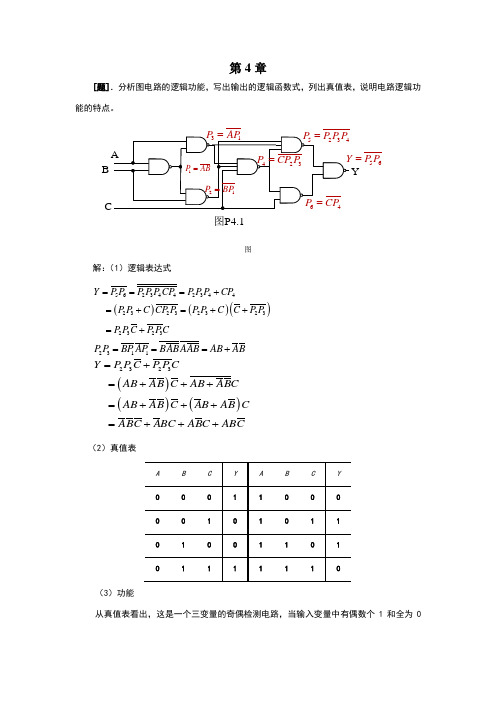
第4章[题].分析图电路的逻辑功能,写出输出的逻辑函数式,列出真值表,说明电路逻辑功能的特点。
图P4.1B YAP 56P P =图解:(1)逻辑表达式()()()5623442344232323232323Y P P P P P CP P P P CP P P C CP P P P C C P P P P C P PC ===+=+=++=+ 2311P P BP AP BABAAB AB AB ===+()()()2323Y P P C P P CAB AB C AB ABC AB AB C AB AB CABC ABC ABC ABC=+=+++=+++=+++(2)真值表(3)功能从真值表看出,这是一个三变量的奇偶检测电路,当输入变量中有偶数个1和全为0时,Y =1,否则Y=0。
[题] 分析图电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式,列出真值表,指出电路完成什么逻辑功能。
图P4.3B1Y 2[解]解: 2Y AB BC AC =++12Y ABC A B C Y ABC A B C AB BC AC ABC ABC ABC ABC =+++=+++++=+++()())真值表:由真值表可知:、C 为加数、被加数和低位的进位,Y 1为“和”,Y 2为“进位”。
[题] 图是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1、Z=0、和COMP=0、Z=0时,Y 1~Y 4的逻辑式,列出真值表。
图P4.4[解](1)COMP=1、Z=0时,TG 1、TG 3、TG 5导通,TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===, 4324A A A Y ++=(2)COMP=0、Z=0时,Y 1=A 1, Y 2=A 2, Y 3=A 3, Y 4=A 4。
、COMP=1、Z=0时的真值表COMP=0、Z=0的真值表从略。
[题]用与非门设1,输入为其他状态时输出为0。
[数字电子技术及应用(第2版)习题答案第2单元习题答案

[数字电子技术及应用(第2版)习题答案第2单元习题答案自我检测题一、填空题2-1如果对键盘上108个符号进行二进制编码,则至少要 7 位二进制数码。
2-2共阳LED 数码管应由输出 低 电平的七段显示译码器来驱动点亮,而共阴LED 数码管应采用输出为 高 电平的七段显示译码器来驱动点亮。
2-3采用54LS138完成数据分配器的功能时,若把S 1作为数据输入端接D ,则应将使能端2S 接 低 电平,3S 接 低 电平。
2-4对N 个信号进行编码时,需要使用的二进制代码位数n 要满足条件 N ≤2n 。
二、选择题2-5一个8选1的数据选择器,其地址输入端有几个 B 。
A 、1B 、3C 、2D 、42-6可以用 B 、C 电路的芯片来实现一个三变量组合逻辑函数。
A 、编码器B 、译码器C 、数据选择器2-7要实现一个三变量组合逻辑函数,可选用 A 芯片。
A 、74LS138B 、54LS148C 、74LS147 三、判断题2-8 54/74LS138是输出低电平有效的3线-8线译码器。
( ✓ )2-9当共阳极LED 数码管的七段(a ~g )阴极电平依次为1001111时,数码管将显示数字1。
(✓ ) 练习题2-1试分析图题2-10所示各组合逻辑电路的逻辑功能。
A B C DYABY图题2-1解:(a)图,)⊕=,真值表如表题2-1(a)A⊕Y⊕B)((DC所示:表题2-1(a)(a)图为四变量奇校验器,当输入变量中有奇数个为1,输出为1。
(b )图,AB B A B A B A Y +=+++=,真值表如表题2-1(b)所示:(b )图为同或门电路,当输入变量状态相同时出1,相反时出0。
2-2试分析图题2-2所示各组合逻辑电路的逻辑功能,写出函数表达式。
图题2-2解:(a)图0=+++=CD C B AB YA BCYD 12A B C(a )(b )(b)图CB A YC B A AB C B A AB Y ⊕⊕=⊕+=⊕•=21,)()(2-3试采用与非门设计下列逻辑电路: (1)三变量非一致电路;(2)三变量判奇电路(含1的个数); (3)三变量多数表决电路。
数字电子技术教案

【例1】设计A具有否决权的三人多数表决电路
(先一起讨论真值表;学生各自完成逻辑图。找出典型电路画在黑板上,讨论优劣及工程实际意义。)
2。多端输出组合逻辑电路的设计
【例2】试设计“故障指示电路”
(要求独立最简)
【归纳总结】
【布置作业】
教学方式方法
讲授法、讨论研究式、问题教学法、实例教学法
【归纳总结】
【布置作业】
教学方式方法
讲授法、讨论法、问题教学法、实例教学法
教学手段及用具
多媒体;电子课程设计实验箱,芯片
作业
作业:习题6;预习P100
教学参考书
杨志忠《数字电子技术》;阎石《数字电子技术基础》
《数字电子技术》教案
课题名称
模块三 3。2时序逻辑电路的分析
授课地点
教室
教学目标
理解时序逻辑电路的分析方法;两类电路比较
教学手段及用具
多媒体;
作业
作业:P49—习题20;预习P122
教学参考书
杨志忠《数字电子技术》;阎石《数字电子技术基础》
《数字电子技术》教案
课题名称
模块四 数字逻辑电路的设计 4。2同步时序逻辑电路的设计
授课地点
教室
教学目标
了解时序逻辑电路的设计步骤
教学参考书
杨志忠《数字电子技术》;阎石《数字电子技术基础》
《数字电子技术》教案
课题名称
模块二2.3集成触发器及其应用
授课地点
教室
教学目标
①掌握触发器的符号及功能.
②理解触发器的应用.
教学
重点
边沿触发器
难点
触发器的应用
教学基本内容与教学设计
数字逻辑(科学出版社 第五版)课后习题答案

(1)
化简得F=
(2)
化简得F=
(3)F(A,B,C,D)=∑m(0,1,2,5,6,7,8,9,13,14)
化简得F=
(4) F(A,B,C,D)=∑m(0,13,14,15)+∑ (1,2,3,9,10,11)
化简得F=
11.利用与非门实现下列函数,并画出逻辑图。
(1)F= =
12.用适当门电路,设计16位串行加法器,要求进位琏速度最快,计算一次加法时间。
解:全加器真值表如下
Ai
Bi
Ci-1
Si
Ci+1
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
0
1
1
0
0
1
0
1
0
1
0
1
1
1
0
0
1
1
1
1
1
1
可以写出以下表达式
要使进位琏速度最快,应使用“与或非”门。具体连接图如下。
若“与或非”门延迟时间为t1,“非门”延迟时间为t2,则完成一次16位加法运算所需时间为:
G的卡诺图
化简得:
第三章时序逻辑
1.写出触发器的次态方程,并根据已给波形画出输出Q的波形。
解:
2.说明由RS触发器组成的防抖动电路的工作原理,画出对应输入输出波形
解:
3.已知JK信号如图,请画出负边沿JK触发器的输出波形(设触发器的初态为0)
4.写出下图所示个触发器次态方程,指出CP脉冲到来时,触发器置“1”的条件。
组合逻辑电路题解
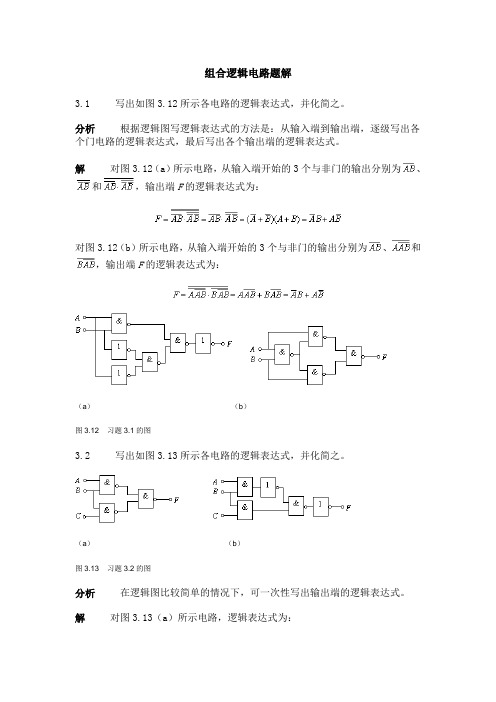
组合逻辑电路题解3.1 写出如图3.12所示各电路的逻辑表达式,并化简之。
分析根据逻辑图写逻辑表达式的方法是:从输入端到输出端,逐级写出各个门电路的逻辑表达式,最后写出各个输出端的逻辑表达式。
解对图3.12(a)所示电路,从输入端开始的3个与非门的输出分别为、和,输出端F的逻辑表达式为:对图3.12(b)所示电路,从输入端开始的3个与非门的输出分别为、和,输出端F的逻辑表达式为:(a)(b)图3.12 习题3.1的图3.2 写出如图3.13所示各电路的逻辑表达式,并化简之。
(a)(b)图3.13 习题3.2的图分析在逻辑图比较简单的情况下,可一次性写出输出端的逻辑表达式。
解对图3.13(a)所示电路,逻辑表达式为:对图3.13(b)所示电路,逻辑表达式为:3.3 证明如图3.14所示两个逻辑电路具有相同的逻辑功能。
(a)(b)图3.14 习题3.3的图分析如果两个逻辑电路的逻辑表达式或真值表完全相同,则它们具有相同的逻辑功能。
解对图3.14(a)所示电路,逻辑表达式为:对图3.14(b)所示电路,逻辑表达式为:因为两个逻辑电路的逻辑表达式完全相同,所以它们具有相同的逻辑功能。
3.4 分析如图3.15所示两个逻辑电路的逻辑功能是否相同?要求写出逻辑表达式,列出真值表。
(a)(b)图3.15 习题3.4的图解对图3.15(a)所示电路,逻辑表达式为:对图3.15(b)所示电路,逻辑表达式为:真值表如表3.12所示。
因为两个逻辑电路的逻辑表达式以及真值表完全相同,所以它们具有相同的逻辑功能。
表3.12 习题3.4的真值表A B C F1F20 0 0 0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1 011113.5 分析如图3.16所示两个逻辑电路,要求写出逻辑式,列出真值表,然后说明这两个电路的逻辑功能是否相同。
(a)(b)图3.16 习题3.5的图解对图3.16(a)所示电路,逻辑表达式为:对图3.16(b)所示电路,逻辑表达式为:真值表如表3.13所示。
数字逻辑(第二版)毛法尧课后题答案(1-6章)

习题一1.1 把以下不同进制数写成按权展开式:⑴(4517.239)10= 4×103+5×102+1×101+7×100+2×10-1+3×10-2+9×10-3⑵(10110.0101)2=1×24+0×23+1×22+1×21+0×20+0×2-1+1×2-2+0×2-3+1×2-4⑶(325.744)8=3×82+2×81+5×80+7×8-1+4×8-2+4×8-3⑷(785.4AF)16=7×162+8×161+5×160+4×16-1+A×16-2+F×16-31.2 完成以下二进制表达式的运算:1.3 将以下二进制数转换成十进制数、八进制数和十六进制数:⑴(1110101)2=(165)8=(75)16=7×16+5=(117)10⑵(0.110101)2=(0.65)8=(0.D4)16=13×16-1+4×16-2=()10⑶(10111.01)2=(27.2)8=(17.4)16=1×16+7+4×16-1=(23.25)101.4 将以下十进制数转换成二进制数、八进制数和十六进制数,准确到小数点后5位:⑴(29)10=(1D)16=(11101)2=(35)8⑵(0.207)10=(0.34FDF)16=(0.001101)2=(0.15176)8⑶(33.333)10=(21.553F7)16=(100001.010101)2=(41.25237)81.5 如何判断一个二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除?解: 一个二进制正整数被(2)10除时,小数点向左挪动一位, 被(4)10除时,小数点向左挪动两位,能被整除时,应无余数,故当b1=0和b0=0时, 二进制正整数B=b6b5b4b3b2b1b0能否被(4)10整除.1.6 写出以下各数的原码、反码和补码:⑴[0.1011]原=0.1011; [0.1011]反=0.1011; [0.1011]补=0.1011⑵[0.000]原=0.0000; [0.0000]反=0.0000; [0.0000]补=⑶-10110[-10110]原=110110; [-10110]反=101001; [-10110]补=1010101.7 [N]补=1.0110,求[N]原,[N]反和N.解:由[N]补得: [N]反=[N]补-1=1.0101, [N]原=1.8 用原码、反码和补码完成如下运算:⑴0000101-0011010[0000101-0011010]原=10010101;∴0000101-0011010=-0010101。
《数字电子技术》课后习题答案

第1单元能力训练检测题(共100分,120分钟)一、填空题:(每空0.5分,共20分)1、由二值变量所构成的因果关系称为逻辑关系。
能够反映和处理逻辑关系的数学工具称为逻辑代数。
2、在正逻辑的约定下,“1”表示高电平,“0”表示低电平。
3、数字电路中,输入信号和输出信号之间的关系是逻辑关系,所以数字电路也称为逻辑电路。
在逻辑关系中,最基本的关系是与逻辑、或逻辑和非逻辑。
4、用来表示各种计数制数码个数的数称为基数,同一数码在不同数位所代表的权不同。
十进制计数各位的基数是10,位权是10的幂。
5、8421 BCD码和2421码是有权码;余3码和格雷码是无权码。
6、进位计数制是表示数值大小的各种方法的统称。
一般都是按照进位方式来实现计数的,简称为数制。
任意进制数转换为十进制数时,均采用按位权展开求和的方法。
7、十进制整数转换成二进制时采用除2取余法;十进制小数转换成二进制时采用乘2取整法。
8、十进制数转换为八进制和十六进制时,应先转换成二进制,然后再根据转换的二进数,按照三个数码一组转换成八进制;按四个数码一组转换成十六进制。
9、逻辑代数的基本定律有交换律、结合律、分配律、反演律和非非律。
10、最简与或表达式是指在表达式中与项中的变量最少,且或项也最少。
13、卡诺图是将代表最小项的小方格按相邻原则排列而构成的方块图。
卡诺图的画图规则:任意两个几何位置相邻的最小项之间,只允许一位变量的取值不同。
14、在化简的过程中,约束项可以根据需要看作1或0。
二、判断正误题(每小题1分,共10分)1、奇偶校验码是最基本的检错码,用来使用PCM方法传送讯号时避免出错。
(对)2、异或函数与同或函数在逻辑上互为反函数。
(对)3、8421BCD码、2421BCD码和余3码都属于有权码。
(错)4、二进制计数中各位的基是2,不同数位的权是2的幂。
(对)3、每个最小项都是各变量相“与”构成的,即n个变量的最小项含有n个因子。
(对)4、因为逻辑表达式A+B+AB=A+B成立,所以AB=0成立。
数字逻辑考试题.(优选)

数字逻辑考试题(一)一、填空(每空1分,共17分)1. (1011.11)B =( ) D =( )H2. (16)D =( )8421BCD 码。
3. 三态门的输出有 输出高电平 、输出低电平 、 输出高阻态 三种状态。
4. 试举出CMOS 三个电路的优点 、 、 。
5. )(CD B B A Y +=则其对偶式Y ’为 。
6. ABC C B A C AB C B A Y ++=),,( 的最简式为Y= 。
7. 由n 位寄存器组成的扭环型移位寄存器可以构成 进制计数器。
8. 半导体存储器对存储单元的寻址一般有 和矩阵译码两种方式。
9. 一片8K ×8位的ROM 存储器有 个字,字长为 位。
10. 四位环型计数器初始状态是1000,经过5个时钟后状态为 。
11. 在RS 、JK 、T 和D 触发器中, 触发器的逻辑功能最多。
12. 设一个包围圈所包围的方格数目为S ,消去的变量数目为N ,那么S 与N 的关系式应是 。
13. 在卡诺图化简逻辑函数时,圈1求得 的最简与或式,圈0求得 的最简与或式。
二、选择(5分) 1. DE BC A Y +=的反函数为Y =( )。
A. E D C B A Y +++⋅= B. E D C B A Y +++⋅=C. )(E D C B A Y +++⋅=D. )(E D C B A Y +++⋅=2. 下列哪个元件是CMOS 器件( )。
A. 74S00B. 74LS00C. 74HC00D. 74H003. 十进制数25用8421BCD 码表示为( )。
A. 10101B. 0010 0101C. 100101D. 101014. 若用1表示高电平,0表示低电平,则是( )。
A. 正逻辑B. 负逻辑C. 正、负逻辑D. 任意逻辑5. 下逻辑图的逻辑表达式为( )。
A. AC BC AB Y =B. BC AC AB Y ++=C. BC AC AB Y ++=D. BC AC AB Y =6. 三态门的逻辑值正确是指它有( )。
用与非门设计三变量判奇电路

用与非门设计三变量判奇电路在数字电路中,判断奇数是一个常见的问题。
常常使用三变量判奇电路进行解决。
而这种电路的设计非常基础,运用了与门、或门和反相器三种不同类型的逻辑门进行组合。
本文将分步骤具体阐述用与非门设计三变量判奇电路的过程。
第一步:电路的总体架构设计首先,需要根据题目要求,设计出一个三变量判奇电路。
在这个电路中,每个变量只能为0或1。
这样,电路的输出就应该是1或0,来判断变量的奇偶性。
考虑到不同逻辑门的特性,需要采用适当的逻辑门组合,才能得到正确的输出。
因此,在总体设计阶段,需要确定适合解决该问题的逻辑门组合。
第二步:使用与非门完成电路的设计接下来,我们将使用与非门设计三变量判奇电路。
这个电路的总体结构非常简单,只需要使用一个与非门和两个反相器。
如图所示,三个变量A、B、C 分别与三个反相器相连,然后再将三个变量和三个反向的变量的输出连接到与非门的两个输入端。
这些反向的变量输出值对应变量的补码,因此可以使用与非门来完成补码的计算。
当所有输入值为1时,输出为0.否则,输出为1。
此时,我们已经设计完了用与非门实现三变量判奇的数字电路。
第三步:使用模拟器进行模拟在实际使用中,为了确保设计的电路没有问题,我们需要使用数字电路模拟器进行模拟。
通过这个工具,我们可以在计算机上模拟电路的运行,检查其输出是否符合预期。
如果输出值符合题目要求,说明电路设计成功。
总之,使用与非门设计三变量判奇电路,只需要使用适合的逻辑门和反相器的组合即可实现。
在实际操作中,需要严格按照设计流程进行,发现问题及时调整和修正,从而确保电路的正确性和可靠性,为科技进步贡献自己的一份力量。
三变量判奇电路

三变量判奇电路电路设计与实现是一门非常重要的工程科学,在大家日常的生活中,我们经常使用各种电器、电子设备来解决生活当中的问题,而这些电器、电子设备的实现离不开各种电路的设计与实现。
而“三变量判奇电路”是一种非常有用的电路设计方案,接下来我们将详细介绍“三变量判奇电路”是如何设计与实现的。
首先我们需要明确“三变量判奇电路”的设计原理。
这种电路的本质是将三个二进制变量输入电路,根据输入数据的奇偶性,输出一个二进制变量,用于表示奇偶性(1为奇数,0为偶数)。
在这个过程中我们需要定义三个逻辑输入变量A、B、C,并定义一个逻辑输出变量Y,Y的输出将与A、B、C中的二进制状态相关。
进一步深入,就需要了解“三变量判奇电路”的设计方法。
我们可以采用卡诺图的方法设计这个电路,这也是比较普遍和常见的方法。
具体来说,我们需要按照真值表的方式,以2的幂(1,2,4)递增来定义输入和输出的值。
然后我们可以通过Karnaugh映射方法来推导出逻辑表达式,将逻辑表达式通过门电路实现。
举例来说,如果我们要设计一个能够判断3个二进制变量的奇偶性的电路,我们可以这样操作:1.定义AB和C的状态,一共有23=8种输入状态,分别表示为000、001、010、011、100、101、110、111。
2.定义输出Y的值,赋值为1(表示奇数)或0(表示偶数),并根据真值表的相关规律,将可能的值用表格列出。
这里我们可以得到一个表格,共3列(A、B、C)、1列(Y)。
3.画出卡诺图,卡诺图是代表一组布尔表达式的二维图形。
我们按照实际情况将Y列中的“1”和“0”两种值分别填在图中适当的位置。
4.通过卡诺图的方法,求出逻辑表达式。
在这一步,我们首先要将同一行或同一列上的所有单元格分为尽可能大的组合形状,并将不同组别用不同的颜色标记;然后我们可以用组合内的变量来枚举每个组,并将组中每个元素的相反状态取反。
5.将逻辑表达式转化为电路。
当我们得到了逻辑表达式之后,我们可以根据它来选择合适的门电路。
硬声三变量判奇偶电路

硬声三变量判奇偶电路
第一:三个变量每次输入相加求
第二:所求的和除二,
第三:整除的判为1(偶数),有小数的判为0(奇数)。
用一个电路实现对之前的一个计数器里面所记的数是奇数或是偶数的的判定。
列真值表,设输入ABC三个端钮,输出Y,把三变量的八种取值全部罗列,偶数个一时,Y为1,其他为零。
根据真值表列表达式,用与非门实现需要对表达式取非,再利用摩根定律将与或关系变换成与非即可。
扩展资料:
任何时刻输出信号的逻辑状态仅取决于该时刻输入信号的逻辑状态,而与输入信号和输出信号过去状态无关的逻辑电路。
由于组合逻辑电路的输出逻辑状态与电路的历史情况无关,所以它的电路中不包含记忆性电路或器件。
门电路,组合逻辑电路的基本单元。
当前组合逻辑电路都已制成标准化、系列化的中、大规模集成电路可供选用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三输入变量判奇电路的真值表及表达式
摘要:以三输入判奇为例,通过对其输出函数表达式的形式变换,分别
采用多种门电路及译码器、数据选择器等74 系列器件进行电路设计,给出了7 种电路实现形式,并分析了各种电路实现的优缺点。
此例说明了组合逻辑电路
设计的灵活性及电路实现的多样性,所采用的设计方法对其他组合逻辑电路设
计具有一定的启发与指导意义。
目前数字基础课程的实验内容包括验证性实验、综合性实验、设计性实验
三部分,每一部分实验内容安排的侧重点不同。
比如设计性实验的关键是设计,要求学生依据设计要求,设计合理的实验电路,并选择器件、安装调试完成实
验内容。
从教学实践来看,多数学生能够顺利完成实验要求,但解决问题的思
路单一,设计过程灵活性差,不注意创新思维能力的锻炼。
这就要求教师在合
理安排实验内容的同时,不断通过各种途径,引导学生拓宽知识面,创新思维
方式,对待同一问题,积极探索多种解决问题的路径。
组合逻辑电路的设计多
种多样,笔者选择一种奇偶校验电路实现进行详细阐述。
奇偶校验电路在组合逻辑电路的分析与设计中具有一定的典型性和实用性,熟悉判奇电路的逻辑功能及电路实现,有助于加深对组合逻辑电路的理解与掌握。
以判奇电路实现为例,分别讨论了用门电路、译码器、数据选择器的多种
实现方案,用实例说明了组合逻辑电路设计的灵活性与多样性。
1 三输入变量判奇电路的真值表及表达式
对于三输入变量的判奇问题,设其输入变量分别用A、B、C 表示,输出
函数用F 表示。
当输入变量的取值组合中有奇数个1 时,输出函数值为1;当
输入变量的取值组合中1 的个数为偶数时,输出函数值为0,依据这种逻辑关
系可列写出三输入变量判奇电路的真值表如表1 所示。
表1 三输入判奇电路的真值表
由真值表1 可见,有4 组输入变量取值组合使输出函数值为1,即分别为。
所以,三输入变量判奇逻辑问题的输出函数表达式为:
2 采用门电路实现三输入变量判奇电路
门电路实现三输入变量判奇电路的方法有很多,文中列举如下。
方法一:与或表达式(1)可用反相器、与门、或门直接实现,作其电路图如图1 所示。
图1 采用反相器、与门、或门实现。
用反相器、与门、或门实现三输入判奇电路,其特点是表达式基本没有变化,实现途径简单明了,缺点是连线较多,电路复杂。
方法二:与或表达式(1)也可用反相器、与或门实现,电路图如图2 所示。
图2 采用反相器、与或门实现
由上述两种不同门方法实现三输入变量判奇电路可以得出,方法一和方法二虽然实现逻辑简单,但是都连线太多,浪费资源。
同一逻辑问题的逻辑函数表达式是不具备唯一性的。
对三变量输入判奇逻辑问题的输出函数表达式(1)进行变换如下所示:
方法三:根据上述表达式(2)得出,三输入变量判奇电路也可采用异或门实现,其电路如图3 所示。
图3 采用异或门实现
由图3 所示电路可见,对于三输入变量判奇的逻辑问题,当采用异或门实
现时,相比于方法一和方法二,电路中的连线较少,电路简单明了,实现简单。
对于异或逻辑表达式也可以稍作变换得出:
即一个异或门可用4 个2 输入与非门实现,所以三输入判奇电路又可用
8 个2 输入与非门实现,电路如图4 所示。
图4 采用2 输入与非门实现
3 采用74138 译码器实现三输入变量判奇电路
译码器的电路结构表明,在适当的连接条件下,译码器实际上是一个最小
项发生器。
依据逻辑代数的基本原理,任何一个逻辑函数表达式都可以变换为
最小项表达式。
因此,译码器与适当的门电路结合,可以实现给定的逻辑函数。
对于三输入变量的判奇问题,利用74138 译码器并配备适当的门电路亦可实现。
由74138 译码器的功能表可知:
在(4)式中,当G1=1,G2A=G2B=0 时,有Yi=m軓i.如果把给定逻辑函数的输入变量连与74138 译码器的A2A1A0输入端相连接,比如取A2A1A0=ABC,
则逻辑函数表达式(1)可变换为:
(5)式表明,三输入变量判奇电路可以利用74138 译码器和四输入与非门实现,其电路如图5 所示。
图5 三输入判奇电路的译码器和与非门实现
4 采用数据选择器实现三输入变量判奇电路
数据选择器的输出与输入关系的一般表达式为:
(式)6 中EN 是输入使能控制信号,mi是地址输入变量构成的最小项,Di表示数据输入。
当使能输入信号有效时,如果把数据输入作为控制信号,则当Di= 1 时,其对应的最小项mi在表达式中出现,当Di= 0 时,其对应的最小项mi在表达式中就不出现。
所以,数据选择器的输出表达式事实上是受数据输入端控制的最小项之和表达式。
考虑到任何一个逻辑函数表达式都可以变换为最小项表达式,因此,只要逻辑函数的输入变量接到数据选择器的地址选择输入端,就可以实现组合逻辑函数。
利用数据选择器这一特点,亦可实现三输入变量的判奇电路。
如果选用八选一数据选择器实现三输入变量的判奇电路,此时,函数的输
入变量个数与数据选择器的地址变量个数相同。
如果令A2A1A0 =ABC,使能输
入端接地,则(6)式变为:
比较(1)与(7)式,可见只要D0=D3=D5=D6=0,D1=D2=D4=D7=1,则有
Y=F.由此可作电路图如图6(a)所示。
也可以采用四选一数据选择器实现,其
电路之一如图6(b)所示。
图6 采用数据选择器实现
5 采用反函数取非的方式设计判奇电路
在上述的判奇中,是按照输出函数的原函数进行分析。
逻辑代数的基本定理表明:F=F ,由此可得出组合逻辑电路设计的另一途径,即先求出F軈再反相。
这样做看起来是麻烦一点,但对于某些应用场合,设计过程并不增加麻烦,反而提供了解决问题的一种途径。
对于三输入变量的判奇电路,在真值表1 中
对0 写出F 的反函数有:
对式(8)两边取反有:
对于(9)式,可采用反相器、与或非门实现,其电路如图7所示。
(9)式同样可采用74138 译码器或者数据选择器实现。
图7 采用反相器及与或非门实现
6 结束语
设计性实验的关键在于设计过程,正确的设计以熟悉基本知识为前提。
对于具体的应用问题,由于组合逻辑电路元器件的多样性,为实现途径提供了多种可能的选择,文中以三输入变量的判奇逻辑问题为例,分析讨论了多种电路实现的途径,给出了7 种电路实现方案,用实例说明了逻辑电路设计的灵活性与多样性。
三输入变量判奇逻辑电路的设计仅仅是个例,通过其设计途径的讨论在其他逻辑电路设计中举一反三是目的。
利用文中提出的设计思路,同样可以设计全加器、全减器等其它组合逻辑电路,开阔组合逻辑电路设计的视野,培养创新思维能力,指导数字逻辑电路的设计与实验。
