单级倒立摆的PID控制

合集下载

基于MATLAB的直线一级倒立摆的PID控制研究

基于MATLAB的直线一级倒立摆的PID控制研究一、内容概述本文旨在研究基于MATLAB的直线一级倒立摆的PID控制策略。

倒立摆系统作为控制理论中的重要实验对象，具有非线性、不稳定性以及快速运动等特点，对于控制系统的设计与实现提出了较高要求。

PID控制作为一种经典的控制方法，在倒立摆系统中具有广泛的应用价值。

本文利用MATLAB软件平台，对直线一级倒立摆的PID控制进行深入研究和探讨。

文章对直线一级倒立摆系统的基本原理进行介绍，包括其物理模型、运动方程以及稳定性分析等方面。

在此基础上，详细阐述了PID 控制器的基本原理、参数整定方法及其在倒立摆系统中的应用。

通过对比不同PID参数下的控制效果，分析了PID控制器在倒立摆系统中的性能特点。

文章重点介绍了基于MATLAB的直线一级倒立摆PID控制系统的设计与实现过程。

利用MATLAB的Simulink仿真工具，搭建了直线一级倒立摆的仿真模型，并设计了PID控制器进行仿真实验。

通过不断调整PID控制器的参数，观察系统的动态响应和稳态性能，得到了较优的控制参数。

文章还讨论了在实际应用中可能遇到的挑战与问题，并提出了相应的解决方案。

针对倒立摆系统的非线性特性，可以采用模糊PID控制或神经网络PID控制等智能控制方法进行改进；针对干扰和噪声的影响，可以采用滤波技术或鲁棒控制策略来提高系统的抗干扰能力。

文章总结了基于MATLAB的直线一级倒立摆PID控制研究的主要成果和贡献，并展望了未来研究方向和应用前景。

通过本文的研究，不仅加深了对倒立摆系统和PID控制方法的理解，也为实际工程应用提供了有益的参考和借鉴。

1. 直线一级倒立摆系统的介绍直线一级倒立摆系统，作为一个复杂且典型的非线性不稳定系统，历来被视为控制理论教学及实验的理想平台。

它不仅能够有效地反映出控制中的多种问题，如非线性、鲁棒性、镇定等，还因其在多个领域中的实际应用价值而备受关注。

直线一级倒立摆系统主要由小车、摆杆等部件构成，它们之间通过自由连接形成一个整体。

单级倒立摆稳定控制

单级倒立摆稳定控制摘要单级倒立摆是一种受控系统，在工业控制和机器人技术中有着广泛的应用。

这篇文档将介绍单级倒立摆的结构、原理和控制方法，特别是借助PID控制系统来实现单级倒立摆的稳定控制。

单级倒立摆是一种类人形机器人，它通常由一个水平旋转的轮子和一个通过电机传动的滑移杆组成，最后再由摆杆上的陀螺控制实现倒立。

这种结构使得单级倒立摆成为了机器人应用领域中的一个挑战问题。

为了实现单级倒立摆的稳定控制，需要在控制系统中引入一个合适的控制机制。

PID控制算法是一种最为通用的控制算法之一，常被用于像单级倒立摆这样的机器人平衡控制。

PID控制PID控制是一种基于反馈的控制系统，在工业和机器人技术中得到了广泛的应用。

PID控制通过比较实际的输出值与期望的输入值之间的差异，来作出对输出值的控制。

PID控制可以对输出值的稳定性、可靠性和精度进行控制，适用于不同类型的工业和机器人控制系统。

PID控制通常由三个部分组成：比例(P)、积分(I)和微分(D)控制。

比例控制反馈调整输出值，使得实际输出值逼近期望输入值。

积分控制记录过去所有误差，并将这些误差相乘来调整输出值。

微分控制通过记录过去的误差变化率，来防止输出值的快速变化。

在单级倒立摆稳定控制中，采用PID控制可以较好地解决因摩擦力、惯性、重心偏移等因素导致的系统不稳定问题，进而实现系统的平衡控制。

单级倒立摆的稳定控制实现单级倒立摆的稳定控制需要进行以下步骤：步骤1：系统建模将单级倒立摆系统建模，根据运动学和动力学原理，得到系统的运动方程。

步骤2：PID参数调节通过对PID控制算法中比例、积分、微分三个部分的参数进行调整，得到较好的控制效果。

步骤3：PID控制实现将PID控制器与单级倒立摆系统进行连接，实现单级倒立摆的稳定控制。

本文档介绍了单级倒立摆的结构、原理和控制方法，分析了PID控制算法在单级倒立摆稳定控制中的应用。

通过对步骤进行深入的解析，得到了单级倒立摆的稳定控制方法。

基于双闭环PID控制的一阶倒立摆控制系统设计

基于双闭环PID控制的一阶倒立摆控制系统设计一阶倒立摆是一种常见的控制系统，它由一个旋转臂和一个悬挂在旋转臂末端的摆杆组成。

控制目标是使摆杆保持垂直位置并保持在指定的角度范围内。

本文将基于双闭环PID控制设计一阶倒立摆控制系统，并对其进行详细的分析和讨论。

首先，我们需要明确控制系统的结构。

一阶倒立摆控制系统可以分为两个闭环：内环和外环。

内环用于控制旋转臂的角度，并将输出作为外环的输入。

外环用于控制摆杆的角度，并根据测量的摆杆角度和设定的目标角度来调整内环的输入。

在进行控制系统设计之前，我们需要先建立一阶倒立摆的数学模型。

假设倒立摆的质量集中在摆杆的一端，摆杆的长度为L，质量为m，摩擦系数为b，重力加速度为g。

通过应用牛顿第二定律，可以得到如下动力学方程：mL²θ¨ + bLθ˙ + mgLsinθ = u其中，θ是旋转臂的角度，u是旋转臂的扭矩。

为了简化方程，我们进行恒定参数修正和线性化处理，得到线性方程：θ¨ + 2ξωnθ˙ + ωn²θ = kru其中，ξ是阻尼比，ωn是无阻尼自然频率，kr是旋转臂的增益。

接下来，我们将按照以下步骤设计基于双闭环PID控制的一阶倒立摆控制系统：1.内环设计：-选择合适的内环闭环控制器类型。

对于一阶倒立摆，可以选择PID控制器。

-根据倒立摆的特性和性能要求，选择合适的PID参数。

可以使用试错法、经验法、系统辨识等方法进行参数调整。

-将PID控制器的输入设置为旋转臂角度误差，输出为旋转臂的扭矩。

2.外环设计：-选择合适的外环闭环控制器类型。

对于一阶倒立摆，可以选择PID控制器。

-根据倒立摆的特性和性能要求，选择合适的PID参数。

-将PID控制器的输入设置为摆杆角度误差，输出为旋转臂的角度设定值。

3.进行系统仿真和调试：-使用MATLAB等仿真工具建立一阶倒立摆的数学模型，并将设计的控制器与模型进行集成。

-调整控制器的参数，以满足性能指标和系统稳定性的要求。

直线一级倒立摆PID控制实验报告

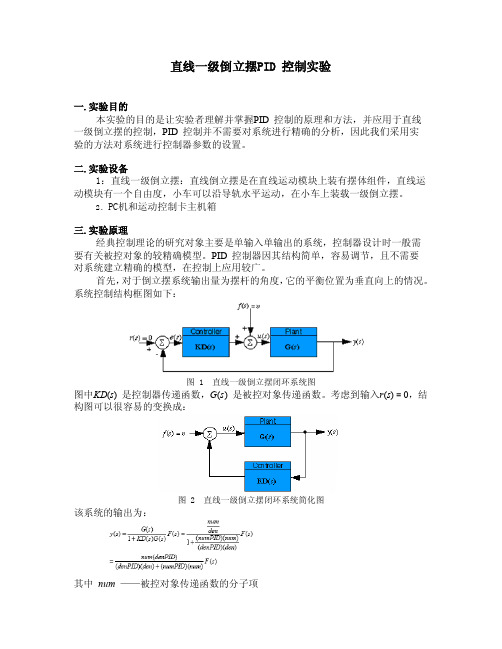
直线一级倒立摆PID 控制实验一.实验目的本实验的目的是让实验者理解并掌握PID 控制的原理和方法，并应用于直线一级倒立摆的控制，PID 控制并不需要对系统进行精确的分析，因此我们采用实验的方法对系统进行控制器参数的设置。

二.实验设备1：直线一级倒立摆：直线倒立摆是在直线运动模块上装有摆体组件，直线运动模块有一个自由度，小车可以沿导轨水平运动，在小车上装载一级倒立摆。

2．PC机和运动控制卡主机箱三.实验原理经典控制理论的研究对象主要是单输入单输出的系统，控制器设计时一般需要有关被控对象的较精确模型。

PID 控制器因其结构简单，容易调节，且不需要对系统建立精确的模型，在控制上应用较广。

首先，对于倒立摆系统输出量为摆杆的角度，它的平衡位置为垂直向上的情况。

系统控制结构框图如下：图 1 直线一级倒立摆闭环系统图图中KD(s) 是控制器传递函数，G(s) 是被控对象传递函数。

考虑到输入r(s) = 0，结构图可以很容易的变换成：图 2 直线一级倒立摆闭环系统简化图该系统的输出为：其中num ——被控对象传递函数的分子项den ——被控对象传递函数的分母项numPID ——PID 控制器传递函数的分子项denPID ——PID 控制器传递函数的分母项通过分析上式就可以得到系统的各项性能。

由(3-13)可以得到摆杆角度和小车加速度的传递函数：PID 控制器的传递函数为：需仔细调节PID 控制器的参数，以得到满意的控制效果。

在控制的过程中，小车位置输出为：通过对控制量v 双重积分即可以得到小车位置。

四.仿真步骤及结果图 3 直线一级倒立摆PID 控制MATLAB 仿真模型其中PID Controller 为封装（Mask ）后的PID 控制器，双击模块打开参数设置窗口先设置PID 控制器为P 控制器，令0,0,===kd ki kp ，得到以下仿真结果图4从图4中可以看出，闭环控制系统持续振荡，周期约为0.7s 。

PID控制的一阶倒立摆控制系统设计

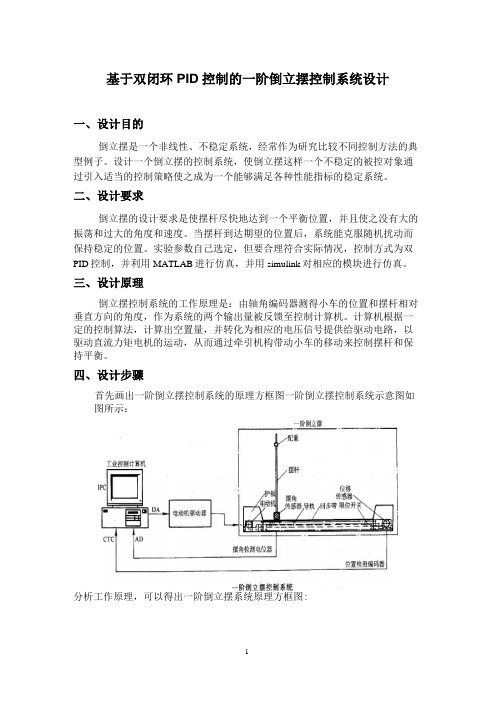
基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统，经常作为研究比较不同控制方法的典型例子。

设计一个倒立摆的控制系统，使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。

二、设计要求倒立摆的设计要求是使摆杆尽快地达到一个平衡位置，并且使之没有大的振荡和过大的角度和速度。

当摆杆到达期望的位置后，系统能克服随机扰动而保持稳定的位置。

实验参数自己选定，但要合理符合实际情况，控制方式为双PID控制，并利用MATLAB进行仿真，并用simulink对相应的模块进行仿真。

三、设计原理倒立摆控制系统的工作原理是：由轴角编码器测得小车的位置和摆杆相对垂直方向的角度，作为系统的两个输出量被反馈至控制计算机。

计算机根据一定的控制算法，计算出空置量，并转化为相应的电压信号提供给驱动电路，以驱动直流力矩电机的运动，从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。

四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示：分析工作原理，可以得出一阶倒立摆系统原理方框图:一阶倒立摆控制系统动态结构图 F 面的工作是根据结构框图，分析和解决各个环节的传递函数!1•一阶倒立摆建模在忽略了空气流动阻力，以及各种摩擦之后，可将倒立摆系统抽象成小车和匀质杆组成的系统，如下图所示，其中：M ：小车质量 m ：为摆杆质量J ：为摆杆惯量F ：加在小车上的力 x ：小车位置。

：摆杆与垂直向上方向的夹角l ：摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律, (1) 摆杆绕其重心的转动方程为J 0=F/sin 0-F/cos 0(1)yx'/(2) 摆杆重心的运动方程为d 2=m-d 2t工业控制计算机电动机驰动器一阶倒立摆—Lb D 购*.—dl卜DI ⑸J bD I 即可知: (x +1sin 0)(l cos0)d 2t(3) 小车水平方向上的运动为d 2x d 2t联列上述4个方程，可以得出一阶倒立精确气模型：J +ml 2)F +mlG +ml 2)(M +m )-m 2/2cos 20+m )m lgsin 0ml 2)""若只考虑e 在其工作点附近e=0附近(-10°<0<10。

直线一级倒立摆系统的PID控制算法设计

摘要直线一级倒立摆由直线运动模块和一级摆体组件组成，是最常见的倒立摆之一。

设计直线一级倒立摆前,首先要应清楚直线一级倒立摆的定义及它的特性,其次用数学建模的方法建立直线一级倒立摆模型。

再次PID控制器的结构与参数设计，将直线一级倒立摆当作简单的单输入单输出系统（忽略了小车位移的控制），采用了 PID控制器设计方法进行了控制器结构设计和参数设计。

确定PID控制器主要参数KP、KI、KD,通过改变这三个参数的值,使直线一级倒立摆由开环不稳定系统变为闭环稳定系统。

直线一级倒立摆系统在PID控制器下用MATLAB进行仿真,通过改变控制器PID主要参数,使得仿真曲线更接近理论曲线。

这些便是直线一级倒立摆系统的PID控制算法设计的主要内容。

关键词：直线一级倒立摆；Matlab仿真；PID控制ABSTRACTInverted pendulum linear 1-stage stands upside down suspends is composed by the translation module and the level pendulum mass module, is most common stands upside down suspends one Front the design straight line level stands upside down suspends, first must be supposed the clear straight line level to stand upside down the definition and its characteristic which suspends, next stands upside down with mathematics modelling method establishment straight line level suspends the model. Once more the PID controller structure and the parameter design, stood upside down Inverted pendulum linear 1-stage suspends the regard simple single input list output system (to neglect car displacement control), used the PID controller design method to carry on the controller structural design and the parameter design. Determined PID controller main parameter KP, KI, KD, through change these three parameters the value, causes the straight line level to stand upside down suspends becomes the closed loop stable system by the split-ring unstable system. Inverted pendulum linear 1-stage stands upside down suspends the system to carry on the simulation under the PID controller with MATLAB, through the change controller PID main parameter, causes the simulation curve closer theoretical curve.These then are the straight line level stands upside down suspends the system the PID control algorithm design primary coverage.Keywords:Inverted pendulum linear；Matlab Simulation; PID control目录第1章绪论 (1)第2章倒立摆系统 (2)2.1 系统的组成 (3)2.1.1 倒立摆本体 (3)2.1.2 电控箱 (4)2.1.3 电机 (4)2.1.4 编码器 (4)2.1.5 控制卡 (5)2.2 系统使用说明 (5)2.2.1 直线一级摆硬件操作系统 (5)2.2.2 一级摆软件操作说明 (5)第3章自动控制及MATLAB软件介绍 (7)3.1自动控制概念 (7)3.2 自动控制系统的类型 (8)3.2.1 随机系统与自动调整系统 (8)3.2.2 线性系统和非线性系统 (9)3.2.3 连续系统和离散系统 (9)3.2.4 单输入单输出系统和多输入多输出系统 (9)3.2.5 确定系统与不确定系统 (9)3.2.6 集中参数系统和分布参数系统 (9)3.3 自动控制理论概要 (10)3.3.1 自动控制系统所要分析的问题 (10)3.3.2 自动控制系统的设计问题 (10)3.4 MATLAB实验软件 (10)3.5.1 MATLAB的基本介绍 (11)3.5.2 MATLAB程序设计基础 (12)第4章 PID控制 (13)4.1 PID控制原理 (13)4.2 数字PID控制 (14)4.2.1 位置式PID控制算法 (14)4.2.2 增量式PID控制算法 (15)4.3 常见的PID控制系统 (15)4.3.1 串级PID控制 (15)4.3.2 纯滞后系统的大林控制算法 (16)4.3.3 纯滞后系统的smith控制算法 (17)第5章直线一级倒立摆的牛顿—欧拉方法建模 (19)5.1 微分方程的推导 (19)5.2 传递函数 (21)5.3 状态方程 (21)5.4 实际系统模型 (23)5.5 采用MATLAB语句形式进行仿真 (24)第6章直线一级倒立摆控制器设计及仿真 (27)6.1 PID参数的调整 (28)6.2 PID控制回路运行 (28)6.3直线一级倒立摆PID控制器设计 (29)6.4直线一级倒立摆PID控制器设计MATLAB仿真 (32)结论 (37)参考文献 (38)致谢 (39)附录 (40)第1章绪论计算机的诞生和发展给自动控制增添了先进的工具，现代控制理论的发展，又给自动控制提供了新的理论支柱。

基于PID控制的一级倒立摆系统的研究

基于PID控制的一级倒立摆系统的研究一级倒立摆系统是控制理论中常用的一个实验模型，它能够很好地展示PID控制器的性能和效果。

本文将介绍一级倒立摆系统的建模过程、PID控制器的设计以及实验结果和分析。

一、一级倒立摆系统的建模为了进行控制系统设计，首先需要对一级倒立摆系统进行建模。

可以利用动力学方程来描述一级倒立摆系统的行为。

设系统的输入为电机的扭矩τ，输出为杆的角度θ。

根据牛顿第二定律，可以得到如下的动力学方程：mL²θ¨ + mgsinθL = τ其中，m是摆的质量，L是摆的长度，g是重力加速度，θ¨是杆的角加速度。

将动力学方程进行线性化，得到如下形式：θ¨=(g/L)θ+(τ/(mL²))这是一个二阶常微分方程，可以通过PID控制器进行控制。

二、PID控制器的设计PID控制器是一种经典的控制器，由比例、积分和微分三部分组成。

PID控制器的输出和输入之间的关系如下：u(t) = Kp e(t) + Ki ∫e(t)dt + Kd de(t)/dt其中，u(t)是控制器的输出，e(t)是控制误差，Kp、Ki和Kd分别是比例、积分和微分增益。

利用PID控制器，可以将控制器的输出u(t)作为电机的扭矩输入τ，实现对杆角度θ的控制。

具体的PID参数选择需要根据实际情况和控制要求进行调整和优化。

三、实验结果和分析通过实验，可以得到一级倒立摆系统的实际响应曲线。

利用PID控制器对系统进行控制，将杆保持在倒立状态。

实验结果显示，PID控制器可以有效控制一级倒立摆系统。

通过调整PID参数，可以调节系统的稳定性、响应速度和抗干扰性能。

总结本文基于PID控制，对一级倒立摆系统进行了研究。

通过建模和控制器设计，实现了对杆角度的控制。

实验结果证明了PID控制器在一级倒立摆系统中的良好性能和效果。

未来的研究可以进一步探索其他控制算法在一级倒立摆系统中的应用，以及优化控制器参数的方法。

单级移动倒立摆建模及串联PID校正-课程设计

单级移动倒立摆建模及串联PID校正-课程设计武汉理工大学《自动控制原理》课程设计说明书课程设计任务书学生姓名: 专业班级: 自动化0807班指导教师: 刘志立工作单位: 自动化学院题目: 单级移动倒立摆建模及串联PID校正初始条件:图示为一个倒立摆装置，该装置包含一个小车和一个安装在小车上的倒立摆杆。

由于小车在水平方向可适当移动，因此，控制小车的移动可使摆杆维持直立不倒。

2Mkgmkglmgms,,,,1.2,0.3,0.8,10/要求完成的主要任务: (包括课程设计工作量及其技术要求，以及说明书撰写等具体要求)1、研究该装置的非线性数学模型，并提出合理的线性化方法，建立该装置的线性数学模型,传递函数(以u为输入，为输出); ,,%,4.3%,t,1.5s,2、要求系统输出动态性能满足试设计串联PIDs校正装置。

3、用Matlab对校正后的系统进行仿真分析，比较校正装置加在线性化前的模型上和线性化后的模型上的时域响应有何区别，并说明原因。

时间安排:任务时间(天)审题、查阅相关资料 2分析、计算 3编写程序 2撰写报告 2论文答辩 1指导教师签名: 年月日系主任(或责任教师)签名: 年月日武汉理工大学《自动控制原理》课程设计说明书目录摘要 ...............................................................1 1 单级移动倒立摆系统建模 (2)1.1 倒立摆系统建模 (2)1.2 求倒立摆系统的传递函数 (4)2 绘制校正前系统的Bode图和Nyquist图 (4)2.1 绘制Bode图 (4)2.2 绘制Nyquist图 (6)3 PID控制器设计 (7)3.1 设计PID控制器装置 (7)4 用MATLAB对校正后的系统进行仿真分析 (10)4.1 绘制校正后的系统Bode图 (10)4.2 绘制校正后系统的Nyquist图 (11)4.3 系统校正前后的比较 (11)5 结束语 (12)参考文献 (12)本科生课程设计成绩评定表 (13)武汉理工大学《自动控制原理》课程设计说明书摘要倒立摆系统是一个典型的非线性多变量强耦合不稳定的非最小相位系统，在航天航空和机电一体化等领域得到了广泛的应用，如在火箭箭身的姿态稳定控制及机器人多自由运动稳定的设计都用到了倒立摆系统。

浅谈单级倒立摆的先进PID控制

浅谈单级倒立摆的先进PID控制摘要：倒立摆系统是非线性、强耦合、多变量和自然不稳定的系统。

本文以控制方法中最常用的PID控制算法进行研究，研究模糊PID控制的控制规律，并对其作出仿真。

关键词:倒立摆、数学模型、PIDAbstract: inverted pendulum system is nonlinear, strong coupling, many variables and natural not stable system. This paper to control method is the most commonly used in PID control algorithm is studied, the fuzzy PID control the control law, and to make the simulation.Keywords: inverted pendulum, mathematical model and PID1、倒立摆系统简介倒立摆是典型的高阶非线性不稳定系统。

小车可以自由地在限定的轨道上左右移动，小车上的倒立摆一端被绞链在小车顶部，另一端可以在小车轨道所在的垂直平面上自由转动，控制目的是通过电机推动小车运动，使倒立摆平衡并保持小车不和轨道两端相撞（图1为单级倒立摆的模型本论文的研究对象）。

在此基础上，在摆杆的另一端再绞连摆杆，可以组成二级、三级倒立摆系统。

该系统是一个多用途的综合性实验装置，它和火箭的飞行及机器人关节运动有许多相似之处，其原理可用于控制火箭稳定发射，且对揭示定性定量转换规律和策略具普遍意义。

图1单级倒立摆原理结构图2、控制方法中的典范—PIDPID控制是众多控制方法中应用最为广泛也是最为容易被人们所掌握的一种控制方法。

随着科学技术的不断发展，控制技术的不断成熟，传统的PID 控制已被人们注入了先进的控制思想。

使得PID控制方法不断丰富，控制性能不断加强。

PID控制的一阶倒立摆控制系统设计

PID控制的一阶倒立摆控制系统设计一阶倒立摆是一种基本的控制系统，在工业及自动化领域有广泛的应用。

PID控制是一种常用的控制算法，可以有效地控制系统的输出，使其稳定在期望值附近。

本文将介绍如何设计一个PID控制器来控制一阶倒立摆。

一阶倒立摆是一个简化的倒立摆系统，由一个质量为m的小球通过一个无摩擦杆连接到一个固定支撑点上。

系统的输入是杆的角度，输出是小球的位置。

我们的目标是通过调节杆的角度来控制小球的位置。

首先，我们需要建立一阶倒立摆的动力学方程。

根据牛顿第二定律和杆的力学特性，可以得到以下方程：m * x'' = m * g * sin(theta) - k * x' + u其中，x是小球的位置，theta是杆的角度，u是控制输入，k是杆的阻尼系数，g是重力加速度。

为了简化问题，我们可以假设杆的阻尼系数k为零，即忽略杆的阻尼。

此外，我们可以将上述方程转换为状态空间方程形式，可以得到以下方程：x'=vv' = g * sin(theta) + u / m其中，v是小球的速度。

接下来，我们需要设计PID控制器来控制系统的输出。

PID控制器由比例项（P项）、积分项（I项）和微分项（D项）组成。

PID控制器的输出可以通过以下公式计算：u = Kp * e + Ki * ∫e + Kd * de/dt其中，e是系统的误差（期望值与实际值之差），Kp、Ki和Kd分别是比例项、积分项和微分项的系数。

在一阶倒立摆控制中，我们可以将系统的误差定义为小球的位置与期望位置之差。

因此，可以将控制器的输出计算公式改写为：u = Kp * (x_d - x) + Ki * ∫(x_d - x) + Kd * d(x_d - x) / dt 其中，x_d为期望位置。

接下来，我们需要调整PID控制器的参数，以使系统稳定在期望位置附近。

调整参数的方法包括手动调整和自动调整。

手动调整需要根据经验和观察来选择参数，而自动调整可以通过一些专门的调参算法来实现，例如Ziegler-Nichols方法和遗传算法等。

(完整版)倒立摆实验报告(PID控制)

专业实验报告3. 实验装置直线单级倒立摆控制系统硬件结构框图如图1所示，包括计算机、I/O设备、伺服系统、倒立摆本体和光电码盘反馈测量元件等几大部分，组成了一个闭环系统。

图1 一级倒立摆实验硬件结构图对于倒立摆本体而言，可以根据光电码盘的反馈通过换算获得小车的位移，小车的速度信号可以通过差分法得到。

摆杆的角度由光电码盘检测并直接反馈到I/O设备，速度信号可以通过差分法得到。

计算机从I/O设备中实时读取数据，确定控制策略（实际上是电机的输出力矩），并发送给I/O设备，I/O设备产生相应的控制量，交与伺服驱动器处理，然后使电机转动，带动小车运动，保持摆杆平衡。

图2是一个典型的倒立摆装置。

铝制小车由6V的直流电机通过齿轮和齿条机构来驱动。

小车可以沿不锈钢导轨做往复运动。

小车位移通过一个额外的与电机齿轮啮合的齿轮测得。

小车上面通过轴关节安装一个摆杆，摆杆可以绕轴做旋转运动。

系统的参数可以改变以使用户能够研究运动特性变化的影响，同时结合系统详尽的参数说明和建模过程，我们能够方便地设计自己的控制系统。

图2 一级倒立摆实验装置图上面的倒立摆控制系统的主体包括摆杆、小车、便携支架、导轨、直流伺服电机等。

主图7 直线一级倒立摆PD控制仿真结果图从上图可以看出，系统在1.5秒后达到平衡，但是存在一定的稳态误差。

为消除稳态误差，我们增加积分参数Ki，令Kp=40，Ki=60，Kd=2，得到以下仿真结果：图8 直线一级倒立摆PID控制仿真结果图从上面仿真结果可以看出，系统可以较好的稳定，但由于积分因素的影响，稳定时间明显增大。

双击“Scope1”，得到小车的位置输出曲线为：图9 施加PID控制器后小车位置输出曲线图由于PID 控制器为单输入单输出系统，所以只能控制摆杆的角度，并不能控制小车的位置，所以小车会往一个方向运动，PID控制分析中的最后一段，若是想控制电机的位置，使得倒立摆系统稳定在固定位置附近，那么还需要设计位置PID闭环。

PID控制的一阶倒立摆控制系统设计

PID控制的一阶倒立摆控制系统设计一阶倒立摆控制系统是一种常见的控制系统，通过PID控制器对倒立摆系统进行稳定控制，使其在一定的时间内达到平衡位置。

本文将详细介绍一阶倒立摆控制系统的设计流程和方法。

1.引言一阶倒立摆控制系统是一类具有非线性动力学特性的控制系统。

其基本结构包含一个摆杆和一个摆杆在垂直方向上运动的小车。

该控制系统的目标是通过调节小车的运动，使摆杆能够在垂直方向上保持平衡。

为了实现这个目标，我们需要设计一个有效的控制方案，并使用PID控制器对系统进行控制。

2.模型建立首先，我们需要建立一阶倒立摆系统的数学模型。

假设摆杆的长度为L，摆杆与水平线的夹角为θ，小车与水平线的位置为x，小车与水平线的速度为v。

根据牛顿运动定律和平衡条件，可以得到如下模型：m*x'=m*a=F(1)M*x'' = -F*l*sin(θ) - b*v (2)I*θ'' = F*l*cos(θ) - M*g*l*sin(θ) (3)其中，m是小车的质量，M是摆杆的质量，l是摆杆的长度，b是摩擦系数，g是重力加速度，I是摆杆的转动惯量。

将式(3)对时间t求导得到：I*θ''' = -b*l*θ' - M*g*l*cos(θ) (4)3.控制设计为了设计PID控制器，我们需要首先将系统模型线性化。

可以将非线性的动力学模型近似为线性模型，并在静态平衡点附近进行线性化。

静态平衡点是系统的平衡位置，满足以下条件：x=0,v=0,θ=0,θ'=0。

我们可以对系统模型进行泰勒级数展开，保留一阶项，得到如下线性化模型：m*x'=F(5)M*x''=-F*l*θ(6)I*θ''=F*l(7)经过线性化，系统的动力学模型变为了一组线性微分方程。

接下来，我们使用PID控制器对系统进行控制。

4.PID控制器设计PID控制器由比例项、积分项和微分项组成，用于校正系统输出与目标值之间的差异。

(完整版)倒立摆实验报告(PID控制)

图1 一级倒立摆实验硬件结构图对于倒立摆本体而言，可以根据光电码盘的反馈通过换算获得小车的位移，小车的速度信号可以通过差分法得到。

摆杆的角度由光电码盘检测并直接反馈到I/O设备，速度信号可以通过差分法得到。

图2是一个典型的倒立摆装置。

铝制小车由6V的直流电机通过齿轮和齿条机构来驱动。

小车可以沿不锈钢导轨做往复运动。

小车位移通过一个额外的与电机齿轮啮合的齿轮测得。

小车上面通过轴关节安装一个摆杆，摆杆可以绕轴做旋转运动。

系统的参数可以改变以使用户能够研究运动特性变化的影响，同时结合系统详尽的参数说明和建模过程，我们能够方便地设计自己的控制系统。

图2 一级倒立摆实验装置图上面的倒立摆控制系统的主体包括摆杆、小车、便携支架、导轨、直流伺服电机等。

主图7 直线一级倒立摆PD控制仿真结果图从上图可以看出，系统在1.5秒后达到平衡，但是存在一定的稳态误差。

单级倒立摆的PID控制

自动化专业综合设计报告设计题目：单级倒立摆的PID控制器设计所在实验室：运动控制实验室 ________指导教师：杨世勇学生姓名：刘新班级：文自082-2 学号：200890517216 撰写时间：2012318成绩评定： _________________、设计目的掌握PID控制器设计、整定及其在MATLAB环境下的实现方法二、设计要求设计倒立摆的PID控制系统三、设计内容建立单级倒立摆的数学模型；设计倒立摆的控制器；仿真实现倒立摆(角度)的稳定控制四、设计分析1.倒立摆系统数学模型的建立基于以下假设：(1)摆杆及小车都是刚体。

(2)皮带轮与皮带之间无相对滑动，传动皮带无伸长现象。

(3)小车的驱动力与直流放大器的输入成正比，而且无滞后，忽略交流伺服电机电枢组中的电感。

(4)实验过程中的库仑摩擦、各种动摩擦等所有摩擦力足够小，在建模过程中可忽略不计。

对摆杆进行受力分析，建立一级倒立摆系统的数学模型。

对摆杆的受力分解如图3所示。

图中!为摆杆与竖直方向的夹角。

FJ为小车对摆杆的水平分力，片2‘为小车对摆杆的竖直分力。

水平方向的方程为:F11 ' F 22 m i d2x1dt2m1d2dt2(x I1 sin)g(x 111 COS 1 )m1x m1l1 1 cos 1m1l1 sin 1竖直方向的方程为:m i g F12' F 21 m i2y idm1£dt2(l i COS i) m i ( l i i sin i)m i l i i sin i m i l i i cos i2 ・I ml mgl Sinmlxcos当摆杆与垂直向上方向之间的夹角相比很小时, 则可以进行如下处理：cos i,s in 0为了得到控制理论的习惯表达,即u为一般控制量，用u代G i s ⑵将两个方程合并：表控制量的输入力F,线性化得到数学模型方程为:2I ml mgl mlx (4)M m x bx mlx u (5) 将(4)，(5)进行拉普拉斯变化为:2 2 2I ml s s mgl s mlX s s⑹2 2 ' 7M m X s s bXss ml s s U s整理后得以u为输入量，以摆杆摆角为输出量的传递函数，将上式整理得:ml 2sq _______________________________2 2 24 b I ml 3 M m mgls bmgls s sq q q其中q M m I ml2ml2.单级倒立摆系统物理参数M 小车质量 1.096KgM 摆杆质量0.109Kgb 小车摩擦系数0.1N/m/secl 摆杆转动轴心到质心的长度0.25mI 摆杆质量0.0034Kg*m*m 将上述参数代入，就可以得到系统的实际模型。

一阶直线倒立摆双闭环PID控制仿真报告

目录摘要 (2)一、一阶倒立摆系统建模 (3)1、对象模型 (3)2、电动机、驱动器及机械传动装置的模型 (4)二、双闭环PID控制器设计 (5)1、仿真验证 (6)2、内环控制器的设计 (9)3、系统外环控制器设计 (12)三、仿真实验 (15)1、绘图子程序 (15)2、仿真结果 (16)四、结论 (18)摘要本报告旨在借助Matlab 仿真软件，设计基于双闭环PID 控制的一阶倒立摆控制系统。

在如图0.1所示的“一阶倒立摆控制系统”中，通过检测小车的位置与摆杆的摆动角，来适当控制驱动电动机拖动力的大小，控制器由一台工业控制计算机（IPC ）完成。

图0.1 一阶倒立摆控制系统分析工作原理，可以得出一阶倒立摆系统原理方框图：图0.2 一阶倒立摆控制系统动态结构图本报告将借助于“Simulink 封装技术——子系统”，在模型验证的基础上，采用双闭环PID 控制方案，实现倒立摆位置伺服控制的数字仿真实验。

一、一阶倒立摆系统建模1、对象模型如图1.1所示，设小车的质量为m 0，倒立摆均匀杆的质量为m ，摆长为2l ，摆的偏角为θ，小车的位移为x ，作用在小车上的水平方向的力为F ，O 1为摆角质心。

θxyOFF xF x F yF yllxO 1图1.1 一阶倒立摆的物理模型根据刚体绕定轴转动的动力学微分方程，转动惯量与角加速度乘积等于作用于刚体主动力对该轴力矩的代数和，则 1）摆杆绕其中心的转动方程为θθθcos sin y l F l F J x-= （1-1） 2）摆杆重心的水平运动可描述为)sin (22x θl x dtd m F += （1-2）3）摆杆重心在垂直方向上的运动可描述为)cos (22y θl dtd m mg F =- （1-3）4）小车水平方向上的运动可描述为220dtxd m F F x =- （1-4）由式（1-2）和式（1-4）得F ml x m m =⋅-⋅++)sin (cos )(20θθθθ (1-5) 由式（1-1）、（式1-2）和式（1-3）得θθθsin g cos 2ml x ml ml J =⋅++ ）（（1-6）整理式（1-5）和式（1-6），得⎪⎪⎩⎪⎪⎨⎧++-+-⋅+⋅=-++-⋅+++=))((cos sin )(cos sin cos cos ))((cos sin sin )()(x 2022202222220222222m l J m m l m m l m m l m F m l l m m m m l J g l m m l J lm F m l J θθθθθθθθθθθθ（1-7）以上式1-7为一阶倒立摆精确模型。

状态反馈的倒立摆PID控制

基于LMI的单级倒立摆的状态反馈PID控制摘要本文以单级倒立摆为研究对象，通过物理规律得到系统的传递函数和状态方程，并结合状态反馈的概念，将约束条件转化为线性矩阵不等式求解反馈矩阵并得到PID控制器，最后进行MATLAB仿真得到仿真曲线进行对比分析指出该方法的优缺点。

关键字单级倒立摆PID MATLAB LMI状态反馈前言倒立摆系统是一种典型的非线性的，不稳定的复杂系统。

是控制理论教学与科研中研究诸如鲁棒问题、非线性系统的控制等问题的良好实验对象。

同时，倒立摆系统作为机器人行走中平衡控制、火箭垂直姿态控制和卫星飞行中姿态控制的最简单模型在航空航天以及军工等领域有着广泛的用处。

倒立摆可以根据摆杆数量的不同分为一级、二级和三级等，多级摆杆间采用自由连接。

一级倒立摆的仿真与控制已广泛应用于教学科研，而二级倒立摆也已在大部分实验室中实现，至于三级倒立摆的控制问题则是国际上公认的难题。

然而我国学者李洪兴教授在2002年实现了国际上首次四级倒立摆实物系统的控制，这是我国学者采用自己提出的理论完成世界性难题的重大科学成就。

本文中以单级倒立摆为研究对象，根据物理定律进行建模得到数学模型，在此基础上进行PID控制，并通过MATLAB仿真对比加入PID控制器前后的响应曲线进行分析。

数学模型的建立直线一级倒立摆是由小车、摆杆等部件构成。

现假设有一个一级倒立摆系统，其中摆杆的长度为L，2=，质量为m，小车质量为M，u为作用在小车上的外L l力，θ为摆杆与垂直向上方向的夹角，x为小车的水平位移。

若不考虑小车与导轨，摆杆与小车之间的摩擦并且不计各种空气阻力，则倒立摆系统的受力分析如图1所示。

Figure 1规定摆杆重心的坐标为(),G G x y ，则sin cos G Gx x l y l θθ=+⎧⎨=⎩ 采用隔离法，对小车有212d xu T M dt-= (1)其中1T 为摆杆所受沿水平方向的力。

对于摆杆，在水平方向上有()212sin d x l T m dt θ+= (2)在竖直方向上有()222cos d l mg T m dt θ-= (3)其中2T 为摆杆所受沿垂直方向的力。

单级移动倒立摆建模及串联PID控制器设

题目: 单级移动倒立摆建模及串联PID 控制器设计初始条件：要求完成的主要任务:（包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）（1）研究该装置的非线性数学模型，并提出合理的线性化方法，建立该装置的线性数学模型－传递函数（以u 为输入，θ为输出）；（2）要求系统输出动态性能满足,5.1%,3.4%s t s ≤≤σ试设计串联PID 校正装置。

（3）用Matlab 对校正后的系统进行仿真分析，比较校正装置加在线性化前的模型上和线性化后的模型上的时域响应有何区别，并说明原因。

（4）对上述任务写出完整的课程设计说明书，说明书中必须进行原理分析，写清楚分析计算的过程及其比较分析的结果，并包含Matlab 源程序或Simulink 仿真模型，说明书的格式按照教务处标准书写。

时间安排：任务时间（天）指导老师下达任务书，审题、查阅相关资料2 分析、计算 2 编写程序 1 撰写报告 2 论文答辩1指导教师签名：年月日系主任（或责任教师）签名：年月日图示为一个倒立摆装置，该装置包含一个小车和一个安装在小车上的倒立摆杆。

由于小车在水平方向可适当移动，因此，控制小车的移动可使摆杆维持直立不倒。

2/10,5.0,2.0,1s m g m l kg m kg M ====目录摘要 (I)1 单级移动倒立摆系统建模 (1)1.1 倒立摆系统建模 (1)1.2 倒立摆系统的传递函数 (2)2 系统校正前性能分析 (3)2.1 未校正移动倒立摆系统时域响应 (3)2.2 绘制bode图 (3)2.3 绘制根轨迹图 (4)2.4 系统校正前的阶跃响应及性能分析 (5)3 PID控制器设计 (6)3.1 PID控制器参数选择 (6)3.2 校正后系统性能指标 (8)3.3 系统校正前后性能比较 (9)4 小结体会 (10)参考文献............................................................................................................................... 错误!未定义书签。