二次函数存在性——直角三角形
二次函数存在性——直角三角形

3.如图,现将一块等腰直角三角板ABC放在第二象限, 斜靠在两坐标轴上,且点A(0,2),点C(-1,0), 如图所示:抛物线y=ax2+ax-2经过点B. (1)求点B的坐标; (2)求抛物线的解析式; (3)抛物线的对称轴上是否存在点P,使△ACP是以 AC为直角边的直等腰角直三角角三角形形?若存在,求出所有点P的 坐标;若不存在,请说明理由.
第27题图
3.如图,抛物线yx22xk 与x轴交于A、B两 点,与y轴交于点C(0,-3)
①点A的坐标为 ,点B的坐标为 ;
②设抛物线的顶点为M,求四边形ABMC的面积;
③在x轴下方的抛物线上是否存在一点D,使四边 形ABDC的面积最大?若存在,请求出点D的坐标 ;若不存在,请说明理由;
④在抛物线上求点Q,使△BCQ是以BC为直角边的 直角三角形.
回顾:如图,四边形OABC为直角梯形,A(4,0),
B(3,4),C(0,4)。点M从O出发以每秒2个单
位长度的速度向A运动;点N从B同时出发,以每秒1
个单位长度的速度向C运动。其中一个动点到达终点
时,另一个动点也随之停止运动。过点N作NP垂直x
轴于点P,连结AC交M或N)能到达终点;
yx22xk
yx22xk
4.如图,矩形OABC的顶点A在x轴的正半轴上,点B的坐 标为(1,3),把矩形绕点B旋转一定的角度,使它的 顶点O落在x轴的点D处,已知M是第四象限内纵坐标为-1 的点,以M为顶点的抛物线正好过O、D两点. (1)求点D的坐标; (2)求抛物线的解析式; (3)在抛物线上是否存在点N,使以O、M、N为顶点的 三角形为直角三角形?若存在,求出所有满足条件的点 N的坐标;若不存在,请说明理由.
5A
4 3
(完整版)二次函数与三角形的存在性问题的解法

二次函数与三角形的存在性问题一、预备知识1、坐标系中或抛物线上有两个点为P (x1,y ),Q (x2,y )(1)线段对称轴是直线2x 21x x +=(2)AB 两点之间距离公式:221221)()(y y x x PQ -+-=中点公式:已知两点()()2211y ,x Q ,y ,x P ,则线段PQ 的中点M 为⎪⎭⎫ ⎝⎛++222121y y ,x x 。
2、两直线的解析式为11b x k y +=与 22b x k y +=如果这两天两直线互相垂直,则有121-=⋅k k3、平面内两直线之间的位置关系:两直线分别为:L1:y=k1x+b1 L2:y=k2x+b2(1)当k1=k2,b1≠b2 ,L1∥L2(2)当k1≠k2, ,L1与L2相交(3)K1×k2= -1时, L1与L2垂直二、三角形的存在性问题探究:三角形的存在性问题主要涉及到的是等腰三角形,等边三角形,直角三角形(一)三角形的性质和判定:1、等腰三角形性质:两腰相等,两底角相等,三线合一(中线、高线、角平分线)。
判定:两腰相等,两底角相等,三线合一(中线、高线、角平分线)的三角形是等腰三角形。
2、直角三角形性质:满足勾股定理的三边关系,斜边上的中线等于斜边的一半。
判定:有一个角是直角的三角形是直角三角形。
3、等腰直角三角形性质:具有等腰三角形和等边三角形的所以性质,两底角相等且等于45°。
判定:具有等腰三角形和等边三角形的所以性质的三角形是等腰直角三角形4、等边三角形性质:三边相等,三个角相等且等于60°,三线合一,具有等腰三角形的一切性质。
判定:三边相等,抛物线或坐标轴或对称轴上三个角相等,有一个角是60°的等腰三角形是等边三角形。
总结:(1)已知A 、B 两点,通过“两圆一线”可以找到所有满足条件的等腰三角形,要求的点(不与A 、B 点重合)即在两圆上以及两圆的公共弦上(2)已知A 、B 两点,通过“两线一圆”可以找到所有满足条件的直角三角形,要求的点(不与A 、B 点重合)即在圆上以及在两条与直径AB 垂直的直线上。
二次函数背景下的直角三角形的存在性问题修订版

请说明理由。
y HP
C
A
OM
B
x
例3. 如图,抛物线y=ax2+bx+c经过A(-3,0)、C(0,4),点B在抛物线上, CB∥x轴,且AB平分∠CAO. (1)求抛物线的解析式; (2)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三 角形?如果存在,求出点M的坐标;如果不存在,说明理由. (3)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段 PQ的最大值;
(3)若点 Q 是 y 轴上一点,且 APQ 为直角三角形,求点 Q 的坐标。
y
P
O
C A
D
ቤተ መጻሕፍቲ ባይዱ
B
x
5.抛物线 y 1 x2 bx c 与 x 轴交于 A(-2,0),B(4,0)两点,与 y 轴交于点 C,顶 2
点为 P (1)求抛物线解析式; (2)动点 M,N 从点 O 同时出发,都以每秒 1 个单位长度的速度分别在线段 OB,OC 上向点 B, C 方向运动,过点 M 做 x 轴的垂线交 BC 于点 F,交抛物线于点 H ①当四边形 OMHN 为矩形时,求点 H 的坐标;
3:如图,已知直线 y=kx-6 与抛物线 y ax2 bx c 相交于 A,B 两点,且点 A(1,-4)为
抛物线的顶点,点 B 在 x 轴上。 (1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图像上是否存在一点 P,使 POB与POC 全等?若存在,
求出点 P 坐标,若不存在,请说明理由;
一、课前小测: 1.直角三角形的两边长分别是3和4,则第三边的长是
二次函数压轴之直角三角形的存在性问题,方法集锦

②
AF BG
BF CG
得
3 m
3
3 (m2 3m)
解得m1 2 7(舍去), m 2 7
C2 (2 7,5 7)
方法一:一线三角构相似
① ②合并
第一种情况
E
设C(m, m2 3m)如图可得AOB : BEC
C
AO BO 得
3
3
BE EC |m2 3m 3| |m|
①
解得m1 2 7, m 2 7
C=900, AC2 CB2 AB2 (m 3)2 (m2 3m)2 m2 (m2 3m 3)2 18
m1
0,
m2
3 2
17
,
m3
3 2
17
C(0, 0),C(3 17 , 2)C(3 17 , 2)
2
2
ቤተ መጻሕፍቲ ባይዱ
方法三:利用勾股定理
设C(m,m2 -3m)A(3,0)B(0,3) AB2 18, AC 2 (m 3)2 (m2 3m)2 BC 2 m2 (m2 3m 3)2
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
如图,抛物线y x2 3x,与x轴交于O、A,直线y=-x+3与y轴交于点B, 与抛物线交于A、D, 问:抛物线上是否存在点P使ABC为直角三角形,并求出P点的坐标
二次函数中直角三角形的存在性问题

知识讲解
〔难点突破〕
在两定点,确定第三点构成直角三角形时,要么以两定点为直角顶点,要么以动点为直角顶点。以定点为直角顶点时,构造两条直线与直线垂直;以动点为直角顶点时,以线段为直径构造圆找点。
小结
数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休。平时一定要利用数形结合思想去解决实际问题。
教师姓名
肖金凤
单位名称
填写时间
2021年8月23日
学科
ห้องสมุดไป่ตู้数学
年级/册
九年级
教材版本
人教版
课题名称
第22章二次函数-二次函数中直角三角形存在性问题
难点名称
如何把存在的点找全
难点分析
从知识角度分析为什么难
因为学生不会分类讨论,考虑问题不全面,不会用图形的方法找存在的点。不会用数形结合思想解决问题。
从学生角度分析为什么难
二次函数做为压轴题出现,学生想当然的认为难,而直接放弃。会用代数方法计算,但是不会用图像法找点。
难点教学方法
1、通过分类思想,先把复杂问题简单化;
2、通过用希沃白板5的画板作图,直观的找到存在的点在“两线一圆〞上;
3、通过例题的讲解让学生更好的理解数形结合思想。
教学环节
教学过程
导入
1、如图,抛物线y=a +bx+c〔a≠0〕的对称轴为直线x=﹣1,且抛物线经过B〔-3,0〕,C〔0,3〕两点,与x轴交于点A.
【中考数学压轴题专题突破12】二次函数中的直角三角形存在性问题

【中考压轴题专题突破】二次函数中的直角三角形存在性问题1.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C(0,3),且OB=OC.直线y=x+1与抛物线交于A、D两点,与y轴交于点E,点Q是抛物线的顶点,设直线AD上方的抛物线上的动点P的横坐标为m.(1)求该抛物线的解析式及顶点Q的坐标.(2)连接CQ,直接写出线段CQ与线段AE的数量关系和位置关系.(3)连接P A、PD,当m为何值时S△APD=S△DAB?(4)在直线AD上是否存在一点H,使△PQH为等腰直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.2.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式.(2)在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)设点P为该抛物线的对称轴x=﹣1上的一个动点,直接写出使△BPC为直角三角形的点P的坐标.提示:若平面直角坐标系内有两点P(x1,y1)、Q(x2,y2),则线段PQ的长度PQ=).3.如图,已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0)、B(3,0),顶点为M.(1)求抛物线的解析式和点M的坐标;(2)点E是抛物线段BC上的一个动点,设△BEC的面积为S,求出S的最大值,并求出此时点E的坐标;(3)在抛物线的对称轴上是否存在点P,使得以A、P、C为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.4.综合与探究如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣3,0)、B两点,与y轴相交于点.当x=﹣4和x=2时,二次函数y=ax2+bx+c(a≠0)的函数值y相等,连接AC,BC.(1)求抛物线的解析式;(2)判断△ABC的形状,并说明理由;(3)若点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,其中一个点到达终点时,另一点也随之停止运动,当运动时间为t秒时,连接MN,将△BMN沿MN翻折,B点恰好落在AC边上的P处,则t的值为,点P的坐标为;(4)抛物线对称轴上是否存在一点F,使得△ACF是以AC为直角边的直角三角形?若不存在,请说明理由;若存在,请直接写出点F的坐标.参考答案与试题解析1.【分析】(1)直线y=x+1与抛物线交于A 点,则点A(﹣1,0)、点E(0,1),可得出点B、C的坐标分别为:(3,0)、(0,3),用待定系数法求出二次函数解析即可求解;(2)求出CQ和AE的长,可得出CQ=AE,由两直线的解析式k相等可得出CQ 与AE平行;(3)联立直线y=x+1与抛物线的表达式,并解得x=﹣1或2.故点D(2,3),过点P作y轴的平行线交AD于点K,设点P(m,﹣m2+2m+3),则点K(m,m+1),根据面积关系可求出m的值;(4)分∠QOH=90°、∠PQH=90°、∠QHP=90°三种情况,分别求解即可.【解答】(1)直线y=x+1与抛物线交于A点,则点A(﹣1,0)、点E(0,1).∵OB=OC,C(0,3),∴点B的坐标为(3,0),故抛物线的表达式为y=a(x+1)(x﹣3)=a(x2﹣2x﹣3),将点C的坐标代入,得﹣3a=3,解得a=﹣1,∴抛物线的表达式为y=﹣x2+2x+3,∴函数的对称轴为x=1,故点Q的坐标为(1,4).(2)CQ=AE,且CQ∥AE,理由:∵Q(1,4),C(0,3),∴CQ ==,CQ的解析式为y=x+3,又∵AE ==,直线AE的解析式为y=x+1,∴CQ=AE,CQ∥AE,(3)∵,∴,,∴点D的坐标为(2,3).如图1,过点P作y轴的平行线,交AD 于点K,设点P(m,﹣m2+2m+3),则点K(m,m+1)∴===.解得m=0或1.(4)存在,点P的坐标为(2,3)或(0,3)或.设点H(t,t+1),点P(m,n),n=﹣m2+2m+3,而点Q(1,4),①当∠QPH=90°时,如图2,过点P作y轴的平行线,过点H、点Q作x轴的平行线,交过点P且平行于y轴的直线于点M、G,∵∠GQP+∠QPG=90°,∠QPG+∠HPM=90°,∴∠HPM=∠GQP,∠PGQ=∠HMP=90°,PH=PQ,∴△PGQ≌△HMP(AAS),∴PG=MH,GQ=PM,即4﹣n|=|t﹣m|,|1﹣m|=|n﹣(t+1)|,解得m=2或n=3.当n=3时,3=﹣m2+2m+3,解得m1=0,m2=2,∴点P(2,3)或(0,3).②当∠PQH=90°时,如图3所示,同理可得m1=0,m2=3(舍去),故点P为(0,3).③当∠PHQ=90°时,同理可得n=2,解得(舍去),.故点P 为.综上可得,点P的坐标为(2,3)或(0,3)或.【点评】本题是二次函数综合题,主要考查了待定系数法求函数解析式(包括二次函数解析式,一次函数解析式),三角形面积,全等三角形的判定与性质,等腰直角三角形的判定与性质,坐标与图形的性质,正确进行分类是解题的关键.2.【分析】(1)用待定系数法即可求出直线BC和抛物线的解析式;(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.把x =﹣1代入直线y=x+3得y的值,即可求出点M坐标;(3)设P(﹣1,t),又因为B(﹣3,0),C(0,3),所以可得BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.【解答】(1)由题意得:,解得:,∴抛物线解析式为y=﹣x2﹣2x+3,∵对称轴为x=﹣1,且抛物线经过A(1,0),∴把B(﹣3,0)、C(0,3)分别代入直线y=mx+n,得,解得:,∴直线y=mx+n的解析式为y=x+3;(2)设直线BC与对称轴x=﹣1的交点为M,则此时MA+MC的值最小.把x=﹣1代入直线y=x+3得,y=﹣1+3=2,∴M(﹣1,2),即当点M到点A的距离与到点C的距离之和最小时M的坐标为(﹣1,2);(3)如图,设P(﹣1,t),又∵B(﹣3,0),C(0,3),∴BC2=18,PB2=(﹣1+3)2+t2=4+t2,PC2=(﹣1)2+(t﹣3)2=t2﹣6t+10,①若点B为直角顶点,则BC2+PB2=PC2即:18+4+t2=t2﹣6t+10解之得:t=﹣2;②若点C为直角顶点,则BC2+PC2=PB2即:18+t2﹣6t+10=4+t2解之得:t=4,③若点P为直角顶点,则PB2+PC2=BC2即:4+t2+t2﹣6t+10=18解之得:t1=,t2=;综上所述P的坐标为(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).【点评】本题是二次函数的综合题,考查了二次函数的图象与性质,待定系数法求函数的解析式,利用轴对称性质确定线段的最小长度,两点间的距离公式的运用,直角三角形的性质等知识点,熟练掌握二次函数的性质是解题的关键.3.【分析】(1)将点A、B的坐标代入函数解析式,列出方程组,通过解方程组求得a、b的值即可;利用配方法将函数解析式转化为顶点式,即可得到点M的坐标;(2)利用待定系数法确定直线BC解析式,由函数图象上点的坐标特征求得点E、F的坐标,然后根据两点间的距离公式求得EF长度,结合三角形的面积公式列出函数式,根据二次函数最值的求法求得点E的横坐标,易得其纵坐标,则点E的坐标迎刃而解了;(3)需要分类讨论:点A、P、C分别为直角顶点,利用勾股定理求得答案.【解答】(1)∵抛物线y=ax2+bx+3与x 轴交于点A(﹣1,0)、B(3,0),∴.解得.∴y=﹣x2+2x+3=﹣(x﹣1)2+4,则M (1,4);(2)如图,作EF∥y轴交BC于点F∵B(3,0),C(0,3),∴直线BC解析式为:y=﹣x+3.设E(m,﹣m2+2m+3),则F(m,﹣m+3).∴EF=(﹣m2+2m+3)﹣(﹣m+3)=﹣m2+3m.∴S =EF•OB =(﹣m2+3m)×3=﹣(m ﹣)2+.当m =时,S最大=.此时,点E 的坐标是(,);(3)设P(1,n),A(﹣1,0)、C(0,3),∴AC2=10,AP2=4+n2,CP2=1+(n﹣3)2=n2﹣6n+10.①当AC⊥AP时,AC2+AP2=CP2,即10+4+n2=n2﹣6n+10.解得n =﹣.②当AC⊥CP时,AC2+CP2=AP2,即10+n2﹣6n+10=4+n2.解得n =.③当AP⊥CP时,AP2+CP2=AC2,即4+n2+n2﹣6n+10=10.解得n=1或2.综上所述,存在,符合条件的点P的坐标是(1,﹣)或(1,)或(1,1)或(1,2),【点评】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.4.【分析】(1)由对称性先求出点B的坐标,可设抛物线的解析式为y=a(x+3)(x﹣1),将C坐标代入y=a(x+3)(x﹣1)即可;(2)先判断△ABC为直角三角形,分别求出AB,AC,BC的长,由勾股定理的逆定理可证明结论;(3)因为点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC边运动,所以BM=BN=t,证四边形PMBN是菱形,设PM与y轴交于H,证△CPN∽△CAB,由相似三角形的性质可求出t的值,CH的长,可得出点P纵坐标,求出直线AC的解析式,将点P纵坐标代入即可;(4)求出直线BC的解析式,如图2,当∠ACF=90°时,点B,C,F在一条直线上,求出直线BC与对称轴的交点即可;当∠CAF=90°时,求出直线AF的解析式,再求其与对称轴的交点即可.【解答】(1)∵在抛物线y=ax2+bx+c中,当x=﹣4和x=2时,二次函数y=ax2+bx+c的函数值y相等,∴抛物线的对称轴为x ==﹣1,又∵抛物线y=ax2+bx+c与x轴交于A (﹣3,0)、B两点,由对称性可知B(1,0),∴可设抛物线的解析式为y=a(x+3)(x ﹣1),将C(0,)代入y=a(x+3)(x﹣1),得,﹣3a =,解得,a =﹣,∴此抛物线的解析式为y =﹣(x+3)(x﹣1)=﹣x2﹣x +;(2)△ABC为直角三角形,理由如下:∵A(﹣3,0),B(1,0),C(0,),∴OA=3,OB=1,OC =,∴AB=OA+OB=4,AC ==2,BC ==2,∵AC2+BC2=16,AB2=16,∴AC2+BC2=AB2,∴△ABC是直角三角形;(3)∵点M、N同时从B点出发,均以每秒1个单位长度的速度分别沿BA、BC 边运动,∴BM=BN=t,由翻折知,△BMN≌△PMN,∴BM=PM=BN=PN=t,∴四边形PMBN是菱形,∴PN∥AB,∴△CPN∽△CAB,设PM与y轴交于H,∴==,即==,解得,t =,CH =,∴OH=OC﹣CH =﹣=,∴y P =,设直线AC的解析式为y=kx +,将点A(﹣3,0)代入y=kx +,得,k =,∴直线AC的解析式为y =x +,将y P =代入y =x +,∴x=﹣1,∴P(﹣1,),故答案为:,(﹣1,);(4)设直线BC的解析式为y=kx +,将点B(1,0)代入y=kx +,得,k =﹣,∴直线BC的解析式为y =﹣x +,由(2)知△ABC为直角三角形,∠ACB =90°,如图2,当∠ACF=90°时,点B,C,F在一条直线上,在y =﹣x +中,当x=﹣1时,y=2,∴F1(﹣1,2);当∠CAF=90°时,AF∥BC,∴可设直线AF的解析式为y=﹣x+n,将点A(﹣3,0)代入y =﹣x+n,得,n=﹣3,∴直线AF的解析式为y =﹣x﹣3,在y =﹣x﹣3中,当x=﹣1时,y =﹣2,∴F2(﹣1,﹣2);∴点F的坐标为F1(﹣1,2),F2(﹣1,﹣2).【点评】本题考查了待定系数法求解析式,勾股定理,相似三角形的判定与性质,直角三角形的性质等,解题关键是注意分类讨论思想在解题过程中的运用.。
二次函数存在性问题——直角三角形

二次函数存在性问题——直角三角形例一:如图,抛物线()2230y mx mx m m =-->与x 轴交于A B 、两点,与y 轴交于C 点. (1)请求出抛物线顶点M 的坐标(用含m 的代数式表示),A B 、两点的坐标;(2)经探究可知,BCM △与ABC △的面积比不变,试求出这个比值;(3)是否存在使BCM △为直角三角形的抛物线?若存在,请求出;如果不存在,请说明 理由.例二、如图,抛物线y=-x2+mx+n与x轴分别交于点A(4,0),B(-2,0),与y轴交于点C.(1)求该抛物线的解析式;(2)M为第一象限内抛物线上一动点,点M在何处时,△ACM的面积最大;(3)在抛物线的对称轴上是否存在这样的点P,使得△PAC为直角三角形?若存在,请求出所有可能点P的坐标;若不存在,请说明理由.2.如图,抛物线y=x2-2mx (m>0)与x轴的另一个交点为A,过P(1,-m)作PM⊥x轴与点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.(1)若m=2,求点A和点C的坐标;(2)令m>1,连接CA,若△ACP为直角三角形,求m的值;(3)在坐标轴上是否存在点E,使得△PEC是以P为直角顶点的等腰直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.3. 如图,抛物线y=ax2+bx+2与x轴交于点A(1,0)和B(4,0).(1)求抛物线的解析式;(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC∥x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使△OCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.4、在平面直角坐标系中,抛物线y=x2+( k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧.(1)如图1,当k=1时,直接写出A,B两点的坐标;(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP 面积的最大值及此时点P的坐标;(3)如图2,抛物线y=x2+( k-1)x-k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.5、如图,直线y=x+2与抛物线y=ax 2+bx+6(a≠0)相交于A (12,52)和B(4,m),点P 是线段AB 上异于A 、B 的动点,过点P 作PC ⊥x 轴于点D ,交抛物线于点C .(1)求抛物线的解析式;(2)是否存在这样的P 点,使线段PC 的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC 为直角三角形时点P 的坐标.6、如图,抛物线y=ax2+bx+c经过A(-3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.(1)求抛物线的解析式;(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.。
2019数学中考复习——二次函数中直角三角形存在性问题

二次函数中直角三角形存在性问题
解题方法
一、代数法:
(1)根据条件用坐标表示三边或三边的平方
(2)以直角顶点分三种情况,根据勾股定理列方程,解方程
(3)根据题目条件及方程解确定坐标
二、几何法:
(1)先分三种情况进行构造:若已知边做直角边,过直角边的两端点作垂线,则第三个顶点在垂线上,若已知边为斜边,可取斜边为直径作圆,直角顶点在圆上
(2)计算:注意题目的几何背景,如有直接的相似则表示线段长度,进行相似求解,无直接相似则围绕顶点分别做坐标轴的平行线,构造一线三角模型进行相似求解。
专题训练
例1.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且经过A(1,0),C(0,3)两点,与x轴的另一个交点为B.设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
几何法:
例2.如图,在平面直角坐标系中,已知点A 的坐标是(4,0),并且OA=OC=4OB ,动点P 在过A ,B ,C 三点的抛物线上.
(1)求抛物线的解析式;
(2)是否存在点P ,使得△ACP 是以AC 为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,说明理由;
例3.如图,在平面直角坐标系中,直线交轴于点,交轴于点,抛物线的图象过点,并与直线相交于、两点. 求抛物线的解析式(关系式);
过点作交轴于点,求点的坐标;
除点外,在坐标轴上是否存在点,使得是直角三角形?若存在,请求出点的坐标,若不存在,请说明理由.
123y x =-
+x P y A 212
y x bx c =-++(1,0)E -A B ⑴⑵A AC AB ⊥x C C ⑶C M MAB ∆M。
【 21】第22章 二次函数中的存在性问题-重难点题型总结(学生版)

第22章二次函数中的存在性问题-重难点题型总结【】【题型1 二次函数中直角三角形存在性问题】【例1】(2021•罗湖区校级模拟)如图,已知抛物线y=﹣x2+2x+3与x轴交于点A、B,与y轴交于点C,点P是抛物线上一动点,连接PB,PC.(1)点A的坐标为,点B的坐标为;(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.【变式1-1】(2021春•望城区校级月考)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x 轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),连接AC,点P为第二象限抛物线上的动点.(1)求a、b、c的值;(2)连接P A、PC、AC,求△P AC面积的最大值;(3)在抛物线的对称轴上是否存在一点Q,使得△QAC为直角三角形,若存在,请求出所有符合条件的点Q的坐标;若不存在,请说明理由.【变式1-2】(2021•长沙模拟)如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.点P为线段MB上一个动点,过点P作PD⊥x轴于点D,若OD=m.(1)求二次函数解析式;(2)设△PCD的面积为S,试判断S有最大值或最小值?若有,求出其最值,若没有,请说明理由;(3)在MB上是否存在点P,使△PCD为直角三角形?若存在,请写出点P的坐标;若不存在,请说明理由.【变式1-3】(2021•长沙模拟)如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.(1)求抛物线的表达式;(2)直接写出点C的坐标,并求出△ABC的面积;(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;(4)若点M在直线BH上运动,点N在x轴上运动,是否存在以点C、M、N为顶点的三角形为等腰直角三角形?若存在,请直接写出此时点M的坐标,若不存在,请说明理由.【题型2 二次函数中等腰三角形存在性问题】【例2】(2020秋•曾都区期末)如图,抛物线y=ax2+4x+c经过A(﹣3,﹣4),B(0,﹣1)两点,点P是y轴左侧且位于x轴下方抛物线上一动点,设其横坐标为m.(1)直接写出抛物线的解析式;(2)将线段AB绕点B顺时针旋转90°得线段BD(点D是点A的对应点),求点D的坐标,并判断点D是否在抛物线上;(3)过点P作PM⊥x轴交直线BD于点M,试探究是否存在点P,使△PBM是等腰三角形?若存在,求出点m的值;若不存在,说明理由.【变式2-1】(2020秋•云南期末)如图,直线y=−12x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(﹣1,0).(1)求B,C两点的坐标.(2)求该二次函数的解析式.(3)若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD 为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.【变式2-2】(2021•南充)如图,已知抛物线y=ax2+bx+4(a≠0)与x轴交于点A(1,0)和B,与y轴交于点C,对称轴为直线x=5 2.(1)求抛物线的解析式;(2)如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ,当线段PQ长度最大时,判断四边形OCPQ的形状并说明理由;(3)如图2,在(2)的条件下,D是OC的中点,过点Q的直线与抛物线交于点E,且∠DQE=2∠ODQ.在y轴上是否存在点F,得△BEF为等腰三角形?若存在,求点F的坐标;若不存在,请说明理由.【变式2-3】(2021•建华区二模)综合与探究如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A、C两点,且与x轴交于另一点B(点B在点A右侧).(1)求抛物线的解析式及点B坐标;(2)设该抛物线的顶点为点H,则S△BCH=;(3)若点M是线段BC上一动点,过点M的直线ED平行y轴交x轴于点D,交抛物线于点E,求ME 长的最大值及点M的坐标;(4)在(3)的条件下:当ME取得最大值时,在x轴上是否存在这样的点P,使得以点M、点B、点P 为顶点的三角形是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.【题型3 二次函数中平行四边形存在性问题】【例3】(2020秋•元阳县期末)如图,直线y=−12x+c与x轴交于点A(﹣3,0),与y轴交于点C,抛物线y=12x2+bx+c经过点A,C,与x轴的另一个交点为B(1,0),连接BC.(1)求抛物线的函数解析式.(2)M为x轴的下方的抛物线上一动点,求△ABM的面积的最大值.(3)P为抛物线上一动点,Q为x轴上一动点,当以B,C,Q,P为顶点的四边形为平行四边形时,求点P的坐标.【变式3-1】(2020秋•泰山区期末)如图,抛物线y=12x2+bx+c经过点A(﹣4,0),点M为抛物线的顶点,点B在y轴上,且OA=OB,直线AB与抛物线在第一象限交于点C(2,6),如图.(1)求直线AB和抛物线的表达式;(2)在y轴上找一点Q,使得△AMQ的周长最小,在备用图中画出图形并求出点Q的坐标;(3)在坐标平面内是否存在点N,使以点A、O、C、N为顶点且AC为一边的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【变式3-2】(2021春•雨花区期末)如图,已知抛物线y=ax2+bx+c的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.(1)求抛物线的解析式;(2)若点P从点B出发,沿着射线BC运动,速度每秒√2个单位长度,过点P作直线PM∥y轴,交抛物线于点M.设运动时间为t秒.①在运动过程中,当t为何值时,使(MA+MC)(MA﹣MC)的值最大?并求出此时点P的坐标.②若点N同时从点B出发,向x轴正方向运动,速度每秒v个单位长度,问:是否存在t使点B,C,M,N构成平行四边形?若存在,求出t,v的值;若不存在,说明理由.【变式3-3】(2021•北碚区校级模拟)如图1,在平面直角坐标系中,抛物线y=ax2+bx﹣6与x轴交于A,C(﹣6,0)两点(点A在点C右侧),交y轴于点B,连接BC,且AC=4.(1)求抛物线的解析式.(2)若P是BC上方抛物线上不同于点A的一动点,连接P A,PB,PC,求当S△PBC−12S△P AC有最大值时点P的坐标,并求出此时的最大值.(3)如图2,将原抛物线向右平移,使得点A刚好落在原点O,M是平移后的抛物线上一动点,Q是直线BC上一动点.当A,M,B,Q组成的四边形是平行四边形时,请直接写出此时点Q的坐标.【题型4 二次函数中菱形存在性问题】【例4】(2020秋•巴南区期末)如图,抛物线y=﹣x2+bx+c与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.(1)求b,c的值;(2)如图1,点P为直线BC上方抛物线上的一个动点,设点P的横坐标m.当m为何值时,△PBC的面积最大?并求出这个面积的最大值.(3)如图2,将该抛物线向左平移2个单位长度得到新的抛物线y=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点D,点M为直线BC上的一点,点N是平面坐标系内一点,是否存在点M,N,使以点B,D,M,N为顶点的四边形为菱形,若存在,请直接写出点M的坐标;若不存在,请说明理由.【变式4-1】(2021•湘潭)如图,一次函数y=√33x−√3图象与坐标轴交于点A、B,二次函数y=√33x2+bx+c图象过A、B两点.(1)求二次函数解析式;(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.【变式4-2】(2021春•无棣县月考)如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的一个动点.(1)求二次函数解析式;(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP'C.是否存在点P,使四边形POP'C为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.【变式4-3】(2020秋•南岸区期末)如图,在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴交于点A(4,0)和B(﹣1,0),交y轴于点C.(1)求二次函数y=x2+bx+c的表达式;(2)将点C向右平移n个单位得到点D,点D在该二次函数图象上.点P是直线BD下方该二次函数图象上一点,求△PBD面积的最大值以及此时点P的坐标;(3)在(2)中,当△PBD面积取得最大值时,点E是过点P且垂直于x轴直线上的一点.在该直角坐标平面内,是否存在点Q,使得以点P,D,E,Q四点为顶点的四边形是菱形?若存在,直接写出满足条件的点Q的坐标;若不存在,请说明理由.【题型5 二次函数中矩形存在性问题】【例5】(2021春•九龙坡区校级期末)如图1,若二次函数y=﹣x2+3x+4的图象与x轴交于点A、B,与y轴交于点C,连接AC、BC.(1)求三角形ABC的面积;(2)若点P是抛物线在一象限内BC上方一动点,连接PB、PC,是否存在点P,使四边形ABPC的面积为18,若存在,求出点P的坐标;若不存在,说明理由;(3)如图2,若点Q是抛物线上一动点,在平面内是否存在点K,使以点B、C、Q、K为顶点,BC为边的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.【变式5-1】(2021•齐齐哈尔)综合与探究如图,在平面直角坐标系中,抛物线y=ax2+2x+c(a≠0)与x轴交于点A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.(1)求抛物线的解析式;(2)抛物线上C、D两点之间的距离是2√2;(3)点E是第一象限内抛物线上的动点,连接BE和CE,求△BCE面积的最大值;(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.【变式5-2】(2021春•杏花岭区校级月考)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.(2)若点P为直线BC下方抛物线上一动点,当点P运动到某一位置时,△BCP的面积最大,求△BCP 的最大面积及此时点P的坐标;(3)点M为抛物线对称轴上一动点,点N为坐标平面内一点,若以点B,C,M,N为顶点的四边形是矩形,直接写出点M的坐标.【变式5-3】(2021•北碚区校级模拟)如图,已知抛物线y=ax2+bx﹣4与x轴交于A,B两点,与y轴交于点C,且点A的坐标为(﹣2,0),直线BC的解析式为y=12x﹣4.(2)如图1,过点A作AD∥BC交抛物线于点D(异于点A),P是直线BC下方抛物线上一点,过点P作PQ∥y轴,交AD于点Q,过点Q作QR⊥BC于点R,连接PR.求△PQR面积的最大值及此时点P 的坐标.(3)如图2,点C关于x轴的对称点为点C′,将抛物线沿射线C′A的方向平移2√5个单位长度得到新的抛物线y′,新抛物线y′与原抛物线交于点M,原抛物线的对称轴上有一动点N,平面直角坐标系内是否存在一点K,使得以D,M,N,K为顶点的四边形是矩形?若存在,请直接写出点K的坐标;若不存在,请说明理由.【题型6 二次函数中正方形存在性问题】【例6】(2021•渝中区校级二模)在平面直角坐标系xOy中,抛物线y=ax2+bx+3与y轴交于点C,与x 轴交于A,B两点(点A在点B的左侧),其中A(﹣2,0),并且抛物线过点D(4,3).(1)求抛物线的解析式;(2)如图1,点P为直线CD上方抛物线上一点,过P作PE∥y轴交BC于点E,连接CP,PD,DE,求四边形CPDE面积的最值及点P的坐标;(3)如图2,将抛物线沿射线CB方向平移得新抛物线y=a1x2+b1x+c1(a1≠0),是否在新抛物线上存在点M,在平面内存在点N,使得以A,C,M,N为顶点的四边形为正方形?若在,直接写出此时新抛物线的顶点坐标,若不存在,请说明理由.【变式6-1】(2020秋•高明区期末)如图,抛物线y=x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y 轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.(1)求该抛物线的函数表达式;(2)点Q在该抛物线的对称轴上,若△ACQ是以AC为腰的等腰三角形,求点Q的坐标;(3)若P为BD的中点,过点P作PF⊥x轴于点F,G为抛物线上一动点,GM⊥x轴于点M,N为直线PF上一动点,当以F、M、G、N为顶点的四边形是正方形时,直接写出点M的坐标.【变式6-2】(2021•合川区校级模拟)如图,在平面直角坐标系.xOy中,直线y=x﹣4与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(﹣2,0).(1)求抛物线解析式;(2)如图1,点F是直线AB下方抛物线上一动点,连接F A,FB,求出四边形F AOB面积最大值及此时点F的坐标.(3)如图2,在(2)问的条件下,点Q为平面内y轴右侧的一点,是否存在点Q及平面内任意一点M 使得以A,F,Q,M为顶点的四边形是正方形?若存在,直接写出点Q的坐标;若不存在,说明理由.【变式6-3】(2021•海南模拟)如图,平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A(﹣3,0),B (4,0),交y轴于点C(0,4).(1)求抛物线的函数表达式;(2)直线y=34x+94与抛物线交于A、D两点,与直线BC交于点E.若点M(m,0)是线段AB上的动点,过点M作x轴的垂线,交抛物线于点F,交直线AD于点G,交直线BC于点H.①当S EOG=12S△AOE时,求m的值;②在平面内是否存在点P,使四边形EFHP为正方形?若存在,请求出点P的坐标,若不存在,请说明理由.。
专题06 二次函数中三角形存在性问题(解析版)--2023 年中考数学压轴真题汇编

挑战2023年中考数学解答题压轴真题汇编专题06二次函数中三角形存在性问题一.相似三角形的存在性1.(2022•陕西)已知抛物线y=ax2+bx﹣4经过点A(﹣2,0),B(4,0),与y 轴的交点为C.(1)求该抛物线的函数表达式;(2)若点P是该抛物线上一点,且位于其对称轴l的右侧,过点P分别作l,x轴的垂线,垂足分别为M,N,连接MN.若△PMN和△OBC相似,求点P 的坐标.【解答】解:(1)把A(﹣2,0),B(4,0)代入y=ax2+bx﹣4得:,解得,∴抛物线的函数表达式为y=x2﹣x﹣4;(2)如图:∵y=x2﹣x﹣4=(x﹣1)2﹣,∴抛物线y=x2﹣x﹣4的对称轴是直线x=1,在y=x2﹣x﹣4中,令x=0得y=﹣4,∴C(0,﹣4),∴OB=OC=4,∴△BOC是等腰直角三角形,∵△PMN和△OBC相似,∴△PMN是等腰直角三角形,∵PM⊥直线x=1,PN⊥x轴,∴∠MPN=90°,PM=PN,设P(m,m2﹣m﹣4),∴|m﹣1|=|m2﹣m﹣4|,∴m﹣1=m2﹣m﹣4或m﹣1=﹣m2+m+4,解得m=+2或m=﹣+2或m=或m=﹣,∵点P是该抛物线上一点,且位于其对称轴直线x=1的右侧,∴P的坐标为(+2,+1)或(,1﹣).2.(2022•绵阳)如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.(1)求抛物线的解析式;(2)在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°,若存在,求出点P的坐标,若不存在,请说明理由;(3)过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与△ADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.【解答】解:(1)∵顶点D的横坐标为1,∴抛物线的对称轴为直线x=1,∵A(﹣1,0),∴B(3,0),∴设抛物线的解析式为:y=a(x+1)(x﹣3),将C(0,3)代入抛物线的解析式,则﹣3a=3,解得a=﹣1,∴抛物线的解析式为:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)存在,P(0,﹣1),理由如下:∵∠APB+∠ACB=180°,∴∠CAP+∠CBP=180°,∴点A,C,B,P四点共圆,如图所示,由(1)知,OB=OC=3,∴∠OCB=∠OBC=45°,∴∠APC=∠ABC=45°,∴△AOP是等腰直角三角形,∴OP=OA=1,∴P(0,﹣1).(3)存在,理由如下:由(1)知抛物线的解析式为:y=﹣x2+2x+3,∴D(1,4),由抛物线的对称性可知,E(2,3),∵A(﹣1,0),∴AD=2,DE=,AE=3.∴AD2=DE2+AE2,∴△ADE是直角三角形,且∠AED=90°,DE:AE=1:3.∵点M在直线l下方的抛物线上,∴设M(t,﹣t2+2t+3),则t>2或t<0.∴EF=|t﹣2|,MF=3﹣(﹣t2+2t+3)=t2﹣2t,若△MEF与△ADE相似,则EF:MF=1:3或MF:EF=1:3,∴|t﹣2|:(t2﹣2t)=1:3或(t2﹣2t):|t﹣2|=1:3,解得t=2(舍)或t=3或﹣3或(舍)或﹣,∴M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).综上,存在点M,使以M,F,E三点为顶点的三角形与△ADE相似,此时点M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).3.(2022•恩施州)在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+c与y 轴交于点P(0,4).(1)直接写出抛物线的解析式.(2)如图,将抛物线y=﹣x2+c向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)直线BC与抛物线y=﹣x2+c交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与△ABC 相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)若将抛物线y=﹣x2+c进行适当的平移,当平移后的抛物线与直线BC 最多只有一个公共点时,请直接写出抛物线y=﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标.【解答】解:(1)∵抛物线y=﹣x2+c与y轴交于点P(0,4),∴c=4,∴抛物线的解析式为y=﹣x2+4;(2)△BCQ是直角三角形.理由如下:将抛物线y=﹣x2+4向左平移1个单位长度,得新抛物线y=﹣(x+1)2+4,∴平移后的抛物线顶点为Q(﹣1,4),令x=0,得y=﹣1+4=3,∴C(0,3),令y=0,得﹣(x+1)2+4=0,解得:x1=1,x2=﹣3,∴B(﹣3,0),A(1,0),如图1,连接BQ,CQ,PQ,∵P(0,4),Q(﹣1,4),∴PQ⊥y轴,PQ=1,∵CP=4﹣3=1,∴PQ=CP,∠CPQ=90°,∴△CPQ是等腰直角三角形,∴∠PCQ=45°,∵OB=OC=3,∠BOC=90°,∴△BOC是等腰直角三角形,∴∠BCO=45°,∴∠BCQ=180°﹣45°﹣45°=90°,∴△BCQ是直角三角形.(3)在x轴上存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似.∵△ABC是锐角三角形,∠ABC=45°,∴以B、N、T三点为顶点的三角形与△ABC相似,必须∠NBT=∠ABC=45°,即点T在y轴的右侧,设T(x,0),且x>0,则BT=x+3,∵B(﹣3,0),A(1,0),C(0,3),∴∠ABC=45°,AB=4,BC=3,设直线BC的解析式为y=kx+b,则,解得:,∴直线BC的解析式为y=x+3,由,解得:,,∴M(﹣,),N(,),∴BN=×=,①当△NBT∽△CBA时,则=,∴=,解得:x=,∴T(,0);②当△NBT∽△ABC时,则=,∴=,解得:x=,∴T(,0);综上所述,点T的坐标T(,0)或(,0).(4)抛物线y=﹣x2+4的顶点为P(0,4),∵直线BC的解析式为y=x+3,∴直线BC与y轴的夹角为45°,当抛物线沿着垂直直线BC的方向平移到只有1个公共点时,平移距离最小,此时向右和向下平移距离相等,设平移后的抛物线的顶点为P′(t,4﹣t),则平移后的抛物线为y=﹣(x﹣t)2+4﹣t,由﹣(x﹣t)2+4﹣t=x+3,整理得:x2+(1﹣2t)x+t2+t﹣1=0,∵平移后的抛物线与直线BC最多只有一个公共点,∴Δ=(1﹣2t)2﹣4(t2+t﹣1)=0,解得:t=,∴平移后的抛物线的顶点为P′(,),平移的最短距离为.二.直角三角形的存在性4.(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.【解答】解:(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)存在.理由:如图1中,设D(t,t2+t﹣4),连接OD.令y=0,则x2+x﹣4=0,解得x=﹣4或2,∴A(﹣4,0),C(2,0),∵B(0,﹣4),∴OA=OB=4,=S△AOD+S△OBD﹣S△AOB=×4×(﹣﹣t+4)+×4×(﹣t)﹣×∵S△ABD4×4=﹣t2﹣4t=﹣(t+2)2+4,∵﹣1<0,∴t=﹣2时,△ABD的面积最大,最大值为4,此时D(﹣2,﹣4);(3)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M(﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).5.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC 于点F,连接DF.(1)求抛物线的解析式;(2)当点D在第二象限且=时,求点D的坐标;(3)当△ODF为直角三角形时,请直接写出点D的坐标.【解答】解:(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,∴,解得,∴y=﹣x2﹣3x+4;(2)过点D作DG⊥AB交于G,交AC于点H,设直线AC的解析式为y=kx+b,∴,解得,∴y=x+4,设D(n,﹣n2﹣3n+4),H(n,n+4),∴DH=﹣n2﹣4n,∵DH∥OC,∴==,∵OC=4,∴DH=3,∴﹣n2﹣4n=3,解得n=﹣1或n=﹣3,∴D(﹣1,6)或(﹣3,4);(3)设F(t,t+4),当∠FDO=90°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,∵∠DOF=45°,∴DF=DO,∵∠MDF+∠NDO=90°,∠MDF+∠MFD=90°,∴∠NDO=∠MFD,∴△MDF≌△NOD(AAS),∴DM=ON,MF=DN,∴DN+ON=﹣t,DN=ON+(﹣t﹣4),∴DN=﹣t﹣2,ON=2,∴D点纵坐标为2,∴﹣x2﹣3x+4=2,解得x=或x=,∴D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,∵∠KFD+∠LFO=90°,∠KFD+∠KDF=90°,∴∠LFO=∠KDF,∵DF=FO,∴△KDF≌△LFO(AAS),∴KD=FL,KF=LO,∴KL=t+4﹣t=4,∴D点纵坐标为4,∴﹣x2﹣3x+4=4,解得x=0或x=﹣3,∴D(0,4)或(﹣3,4);综上所述:D点坐标为(,2)或(,2)或(0,4)或(﹣3,4).三.等腰三角形的存在性6.(2022•百色)已知抛物线经过A(﹣1,0)、B(0,3)、C(3,0)三点,O 为坐标原点,抛物线交正方形OBDC的边BD于点E,点M为射线BD上一动点,连接OM,交BC于点F.(1)求抛物线的表达式;(2)求证:∠BOF=∠BDF;(3)是否存在点M,使△MDF为等腰三角形?若不存在,请说明理由;若存在,求ME的长.【解答】(1)解:设抛物线的表达式为y=ax2+bx+c,把A(﹣1,0)、B(0,3)、C(3,0)代入得:,解得,∴抛物线的表达式为:y=﹣x2+2x+3;(2)证明:∵正方形OBDC,∴∠OBC=∠DBC,BD=OB,∵BF=BF,∴△BOF≌△BDF,∴∠BOF=∠BDF;(3)解:∵抛物线交正方形OBDC的边BD于点E,∴令y=3,则3=﹣x2+2x+3,解得:x1=0,x2=2,∴E(2,3),①如图,当M在线段BD的延长线上时,∠BDF为锐角,∴∠FDM为钝角,∵△MDF为等腰三角形,∴DF=DM,∴∠M=∠DFM,∴∠BDF=∠M+∠DFM=2∠M,∵BM∥OC,∴∠M=∠MOC,由(2)得∠BOF=∠BDF,∴∠BDF+∠MOC=3∠M=90°,∴∠M=30°,在Rt△BOM中,BM=,∴ME=BM﹣BE=3﹣2;②如图,当M在线段BD上时,∠DMF为钝角,∵△MDF为等腰三角形,∴MF=DM,∴∠BDF=∠MFD,∴∠BMO=∠BDF+∠MFD=2∠BDF,由(2)得∠BOF=∠BDF,∴∠BMO=2∠BOM,∴∠BOM+∠BMO=3∠BOM=90°,∴∠BOM=30°,在Rt△BOM中,BM=,∴ME=BE﹣BM=2﹣,综上所述,ME的值为:3﹣2或2﹣.7.(2022•山西)综合与探究如图,二次函数y=﹣x2+x+4的图象与x轴交于A,B两点(点A在点B 的左侧),与y轴交于点C.点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m.过点P作直线PD⊥x轴于点D,作直线BC交PD于点E.(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;(2)当△CEP是以PE为底边的等腰三角形时,求点P的坐标;(3)连接AC,过点P作直线l∥AC,交y轴于点F,连接DF.试探究:在点P运动的过程中,是否存在点P,使得CE=FD,若存在,请直接写出m的值;若不存在,请说明理由.【解答】解:(1)在y=﹣x2+x+4中,令x=0得y=4,令y=0得x=8或x=﹣2,∴A(﹣2,0),B(8,0),C(0,4),设直线BC解析式为y=kx+4,将B(8,0)代入得:8k+4=0,解得k=﹣,∴直线BC解析式为y=﹣x+4;(2)过C作CG⊥PD于G,如图:设P(m,﹣m2+m+4),∴PD=﹣m2+m+4,∵∠COD=∠PDO=∠CGD=90°,∴四边形CODG是矩形,∴DG=OC=4,CG=OD=m,∴PG=PD﹣DG=﹣m2+m+4﹣4=﹣m2+m,∵CP=CE,CG⊥PD,∴GE=PG=﹣m2+m,∵∠GCE=∠OBC,∠CGE=90°=∠BOC,∴△CGE∽△BOC,∴=,即=,解得m=0(舍去)或m=4,∴P(4,6);(3)存在点P,使得CE=FD,理由如下:过C作CH⊥PD于H,如图:设P(m,﹣m2+m+4),由A(﹣2,0),C(0,4)可得直线AC解析式为y=2x+4,根据PF∥AC,设直线PF解析式为y=2x+b,将P(m,﹣m2+m+4)代入得:﹣m2+m+4=2m+b,∴b=﹣m2﹣m+4,∴直线PF解析式为y=2x﹣m2﹣m+4,令x=0得y=﹣m2﹣m+4,∴F(0,﹣m2﹣m+4),∴OF=|﹣m2﹣m+4|,同(2)可得四边形CODH是矩形,∴CH=OD,∵CE=FD,∴Rt△CHE≌Rt△DOF(HL),∴∠HCE=∠FDO,∵∠HCE=∠CBO,∴∠FDO=∠CBO,∴tan∠FDO=tan∠CBO,∴=,即=,∴﹣m2﹣m+4=m或﹣m2﹣m+4=﹣m,解得m=2﹣2或m=﹣2﹣2或m=4或m=﹣4,∵P在第一象限,∴m=2﹣2或m=4.8.(2022•东营)如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C.(1)求抛物线的表达式;(2)在对称轴上找一点Q,使△ACQ的周长最小,求点Q的坐标;(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当△PMB是以PB为腰的等腰直角三角形时,请直接写出所有点M的坐标.【解答】解:(1)将点A(﹣1,0),点B(3,0)代入y=ax2+bx﹣3,∴,解得,∴y=x2﹣2x﹣3;(2)连接CB交对称轴于点Q,∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴为直线x=1,∵A、B关于对称轴x=1对称,∴AQ=BQ,∴AC+AQ+CQ=AC+CQ+BQ≥AC+BC,当C、B、Q三点共线时,△ACQ的周长最小,∵C(0,﹣3),B(3,0),设直线BC的解析式为y=kx+b,∴,解得,∴y=x﹣3,∴Q(1,﹣2);(3)当∠BPM=90°时,PM=PB,∴M点与A点重合,∴M(﹣1,0);当∠PBM=90°时,PB=BM,如图1,当P点在M点上方时,过点B作x轴的垂线GH,过点P作PH⊥GH 交于H,过点M作MG⊥HG交于G,∵∠PBM=90°,∴∠PBH+∠MBG=90°,∵∠PBH+∠BPH=90°,∴∠MBG=∠BPH,∵BP=BM,∴△BPH≌△MBG(AAS),∴BH=MG,PH=BG=2,设P(1,t),则M(3﹣t,﹣2),∴﹣2=(3﹣t)2﹣2(3﹣t)﹣3,解得t=2+或t=2﹣,∴M(1﹣,﹣2)或(1+,﹣2),∵M点在对称轴的左侧,∴M点坐标为(1﹣,﹣2);如图2,当P点在M点下方时,同理可得M(3+t,2),∴2=(3+t)2﹣2(3+t)﹣3,解得t=﹣2+(舍)或t=﹣2﹣,∴M(1﹣,2);综上所述:M点的坐标为(1﹣,﹣2)或(1﹣,2)或(﹣1,0).9.(2022•枣庄)如图①,已知抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.(1)求抛物线的关系式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE内(包括△OAE的边界),求h的取值范围;(4)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),∴,解得,∴抛物线的解析式为:y=x2﹣4x+3;(2)如图,过P作PG∥y轴,交OE于点G,设P(m,m2﹣4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3),∴直线OE的解析式为:y=x,∴G(m,m),∴PG=m﹣(m2﹣4m+3)=﹣m2+5m﹣3,=S△OPG+S△EPG∴S△OPE=PG•AE=×3×(﹣m2+5m﹣3)=﹣(m2﹣5m+3)=﹣(m﹣)2+,∵﹣<0,∴当m=时,△OPE面积最大,此时,P点坐标为(,﹣);(3)由y=x2﹣4x+3=(x﹣2)2﹣1,得抛物线l的对称轴为直线x=2,顶点为(2,﹣1),抛物线L向上平移h个单位长度后顶点为F(2,﹣1+h).设直线x=2交OE于点M,交AE于点N,则E(3,3),∵直线OE的解析式为:y=x,∴M(2,2),∵点F在△OAE内(包括△OAE的边界),∴2≤﹣1+h≤3,解得3≤h≤4;(4)设P(m,m2﹣4m+3),分四种情况:①当P在对称轴的左边,且在x轴下方时,如图,过P作MN⊥y轴,交y 轴于M,交l于N,∴∠OMP=∠PNF=90°,∵△OPF是等腰直角三角形,∴OP=PF,∠OPF=90°,∴∠OPM+∠NPF=∠PFN+∠NPF=90°,∴∠OPM=∠PFN,∴△OMP≌△PNF(AAS),∴OM=PN,∵P(m,m2﹣4m+3),则﹣m2+4m﹣3=2﹣m,解得:m=(舍)或,∴P的坐标为(,);②当P在对称轴的左边,且在x轴上方时,同理得:2﹣m=m2﹣4m+3,解得:m1=(舍)或m2=,∴P的坐标为(,);③当P在对称轴的右边,且在x轴下方时,如图,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,∴PN=FM,则﹣m2+4m﹣3=m﹣2,解得:m1=或m2=(舍);P的坐标为(,);④当P在对称轴的右边,且在x轴上方时,如图,同理得m2﹣4m+3=m﹣2,解得:m=或(舍),P的坐标为:(,);综上所述,点P的坐标是:(,)或(,)或(,)或(,).方法二:作直线DE:y=x﹣2,E(1,﹣1)是D点(2,0)绕O点顺时针旋转45°并且OD缩小倍得到,易知直线DE即为对称轴上的点绕O点顺时针旋转45°,且到O点距离缩小倍的轨迹,联立直线DE和抛物线解析式得x2﹣4x+3=x﹣2,解得x1=,x2=,同理可得x3=或x4=;综上所述,点P的坐标是:(,)或(,)或(,)或(,).10.(2023•澄城县一模)如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B,与y轴交于点C(0,3),直线l是抛物线的对称轴.(1)求抛物线的函数解析式;(2)在对称轴l上是否存在点M,使△MAC为等腰三角形,若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【解答】解:(1)把点A(﹣1,0)、点C(0,3)分别代入y=﹣x2+bx+c,得.解得.故该抛物线解析式为:y=﹣x2+2x+3;(2)由(1)知,该抛物线解析式为:y=﹣x2+2x+3.则该抛物线的对称轴为直线x=﹣=1.故设M(1,m).∵A(﹣1,0)、点C(0,3),∴AC2=10,AM2=4+m2,CM2=1+(m﹣3)2.①若AC=AM时,10=4+m2,解得m=±.∴点M的坐标为(1,)或(1,﹣);②若AC=CM时,10=1+(m﹣3)2,解得m=0或m=6,∴点M的坐标为(1,0)或(1,6).当点M的坐标为(1,6)时,点A、C、M共线,∴点M的坐标为(1,0);③当AM=CM时,4+m2=1+(m﹣3)2,解得m=1,∴点M的坐标为(1,1).综上所述,符合条件的点M的坐标为(1,)或(1,﹣)或(1,0)或(1,1).11.(2023•碑林区校级一模)二次函数y=ax2+bx+2的图象交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.(1)求二次函数y=ax2+bx+2的表达式;(2)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标.【解答】解:(1)将点(﹣1,0),B(4,0)代入y=ax2+bx+2,∴a=﹣,b=,∴y=﹣x2+x+2;(2)∵BM=5﹣2t,∴M(2t﹣1,0),设P(2t﹣1,m),∵PC2=(2t﹣1)2+(m﹣2)2,PB2=(2t﹣5)2+m2,∵PB=PC,∴(2t﹣1)2+(m﹣2)2=(2t﹣5)2+m2,∴m=4t﹣5,∴P(2t﹣1,4t﹣5),∵PC⊥PB,∴×=﹣1,∴t=1或t=2,∴M(1,0)或M(3,0),∴D(1,3)或D(3,2).12.(2023•东洲区模拟)抛物线y=ax2+bx+3经过A(﹣1,0),B(3,0)两点,与y轴正半轴交于点C.(1)求此抛物线解析式;(2)如图①,连接BC,点P为抛物线第一象限上一点,设点P的横坐标为m,△PBC的面积为S,求S与m的函数关系式,并求S最大时P点坐标;(3)如图②,连接AC,在抛物线的对称轴上是否存在点M,使△MAC为等腰三角形?若存在,请直接写出符合条件的点M的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+3经过A(﹣1,0),B(3,0)两点,∴,解得:,∴抛物线解析式为y=﹣x2+2x+3;(2)点P作PF⊥x轴于点F,交BC于点E,设BC直线解析式为:y=kx+b,∵B(3,0),C(0,3),∴,解得,∴y=﹣x+3,由题意可知P(m,﹣m2+2m+3),E(m,﹣m+3),S=S△PBE+S△PCE,S=PE•OB=(﹣m2+2m+3+m﹣3)×3,,∵,∴当时,S有最大值,此时P点坐标为;(3)存在,M 1(1,0),,,M4(1,1),①当AC=AM时,如图,设对称轴l与AB交于点E,则,∵AM2=AE2+EM2,∴,解得:,∴M点的坐标为或,②当AC=MC时,则OC为AM的垂直平分线.因此M与E重合,因此,M点的坐标为(1,0),③当AM=CM时,如图,设M点的坐标为(1,n),则AM2=22+n2=4+n2,CM2=12+(3﹣n)2,∴4+n2=12+(3﹣n)2,解得:n=1,∴M点的坐标为(1,1),综上可知,潢足条件的M点共四个,其坐标为M1(1,0),,,M 4(1,1).13.(2023•三亚一模)如图,抛物线y =ax 2+3x +c (a ≠0)与x 轴交于点A (﹣2,0)和点B ,与y 轴交于点C (0,8),顶点为D ,连接AC ,CD ,DB ,直线BC 与抛物线的对称轴l 交于点E .(1)求抛物线的解析式和直线BC 的解析式;(2)求四边形ABDC 的面积;(3)P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =S △ABC 时,求点P 的坐标;(4)在抛物线的对称轴l 上是否存在点M ,使得△BEM 为等腰三角形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y =ax 2+3x +c (a ≠0)过点A (﹣2,0)和C (0,8),∴,解得,∴抛物线的解析式为y =﹣x 2+3x +8.令y =0,得.解得x 1=﹣2,x 2=8.∴点B 的坐标为(8,0).设直线BC 的解析式为y =kx +b .把点B (8,0),C (0,8)分别代入y =kx +b ,得,解得,∴直线BC 的解析式为y =﹣x +8.(2)如图1,设抛物线的对称轴l 与x 轴交于点H .∵抛物线的解析式为,∴顶点D 的坐标为.∴S 四边形ABDC =S △AOC +S 梯形OCDH +S △BDH ===70.(3)∵.∴.如图2,过点P作PG⊥x轴,交x轴于点G,交BC于点F.设点.∵点F在直线BC上,∴F(t,﹣t+8).∴.∴.∴.解得t1=2,t2=6.∴点P的坐标为(2,12)或P(6,8).(4)存在.∵△BEM为等腰三角形,∴BM=EM或BE=BM或BE=EM,设M(3,m),∵B(8,0),E(3,5),∴BE==5,EM=|m﹣5|,BM==,当BM=EM时,=|m﹣5|,∴m2+25=(m﹣5)2,解得:m=0,∴M(3,0);当BE=BM时,5=,∴m2+25=50,解得:m=﹣5或m=5(舍去),∴M(3,﹣5);当BE=EM时,5=|m﹣5|,解得:m=5+5或m=5﹣5,∴M(3,5+5)或(3,5﹣5),综上所述,点M的坐标为(3,0)或(3,﹣5)或(3,5+5)或(3,5﹣5).14.(2023•南海区一模)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a >0)与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P为直线BC下方抛物线上的一动点,PM⊥BC于点M,PN∥y轴交BC于点N.求线段PM的最大值和此时点P的坐标;(3)点E为x轴上一动点,点Q为抛物线上一动点,是否存在以CQ为斜边的等腰直角三角形CEQ?若存在,请直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)将A(﹣1,0),B(3,0)代入函数y=ax2+bx﹣3(a>0)中,得,解得,∴解析式为y=x2﹣2x﹣3,故抛物线解析式为y=x2﹣2x﹣3;(2)当x=0时,y=3,∴C(0,﹣3),∵B(3,0),∴∠OCB=∠OBC=45°,∵PN∥y轴,∴∠MNP=45°,∵PM⊥BC,∴PM=PN,则当PN最大时,PM也最大,设BC的解析式为y=mx+n,∴,解得,∴BC解析式为y=x﹣3,设P(x,x2﹣2x﹣3),N(x,x﹣3),∴PN=x﹣3﹣(x2﹣2x﹣3)=﹣(x﹣)2+,当x=时,PN最大,则PM=PN=×=,∴P(,),故PM最大值为,P点坐标为(,﹣);(3)存在,点E的坐标为(﹣5,0),(,0),(0,0),(,0).∵CEQ是以CQ为斜边的等腰直角三角形,∴设Q(x,x2﹣2x﹣3),①如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,∵∠CEQ=90°,∴∠QEM+∠CEN=90°,∵∠QEM+∠MQE=90°,∴∠EQM=∠CEN,∵∠CNE=∠QME=90°,EC=EQ,∴△EMQ≌△CNE(AAS),∴CN=EM=x2﹣2x﹣3,MQ=EN=3,∴|x Q|+MQ=CN,﹣x+3=x2﹣2x﹣3,解得x=﹣2,x=3(舍去),∴OE=CM=2+3=5,E(﹣5,0),②如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,同理:△EMC≌△QNE(AAS),CM=EN=x2﹣2x﹣3,NQ=EM=3,∴﹣x+x2﹣2x﹣3=3,解得x=,x=(舍去),∴OE=CM=,E(,0),③如图,点E和点O重合,点Q和点B重合,此时E(0,0),④如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,同理:△EMC≌△QNE(AAS),CM=EN=x2﹣2x﹣3,NQ=EM=3,∴x+3=x2﹣2x﹣3,解得x=,x=(舍去),∴OE=CM=,E(,0),综上所述,点E的坐标为(﹣5,0),(,0),(0,0),(,0).41。
二次函数中直角三角形存在性

【2019•阜新】如图,抛物线y=ax2+bx+2交x轴于点A(-3,0)和点B(1,0),交y轴于点C.(1)求这个抛物线的函数表达式.(2)点D的坐标为(-1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使A MNO为等腰直角【2019•铁岭】如图1,抛物线y=ax2+bx+6与x轴交于点A(-2,0),B(6,0),与y轴交于点C,顶点为D,直线AD交y轴于点E.(1)求抛物线的解析式.(2)如图2,将A AOE沿直线AD平移得到△NMP.①当点M落在抛物线上时,求点M的坐标.②在A NMP移动过程中,存在点M使A MBD为直角三角形,请直接写出所有符合条件的点M的坐标.【2019•淄博】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(-1,0)两点,与y轴交于点C.(1)求这条抛物线对应的函数表达式;(2)问在y轴上是否存在一点P,使得A PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.(3)若在第一象限的抛物线下方有一动点D,满足DA=OA,过D作DG丄x轴于点G,设△ADG的内心为I,试求CI的最小值.【2019•甘肃兰州】二次函数y=ax2+bx+2的图象交x轴于点(-1,0),B(4,0)两点,交y轴于点C.动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN丄x轴交直线BC于点N 交抛物线于点D,连接AC,设运动的时间为t秒.(1)求二次函数y=ax2+bx+2的表达式;(2)连接BD,当t=时,求A DNB的面积;(3)在直线MN上存在一点P,当A PBC是以Z BPC为直角的等腰直角三角形时,求此时点D的坐标;(4)当t=,时,在直线MN上存在一点Q使得Z AQC+Z OAC=90。
,求点Q的坐标.【2019•荆门】已知抛物线y=ax2+bx+c顶点(2,-1),经过点(0,3),且与直线y=x-1交于A,B两点.八、、•(1)求抛物线的解析式;(2)若在抛物线上恰好存在三点Q,M,N满足S A QAB=S^MAB=S^NAB=S,求S的值;(3)在A,B之间的抛物线弧上是否存在点P满足Z APB=90°?若存在,求点P的横坐标;若不存在,请说明理由.(坐标平面内两点M(x1,y1),N(x2,y2)之间的距离MN=〔(工厂玄舟色+匕J?)【2019•内蒙古•鄂尔多斯】如图,抛物线y=ax2+bx-2(a M O)与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C,直线y=-x与该抛物线交于E,F两点.(1)求抛物线的解析式.(2)P是直线EF下方抛物线上的一个动点,作PH丄EF于点H,求PH的最大值.(3)以点C为圆心,1为半径作圆,O C上是否存在点M,使得A BCM是以CM为直角边。
数学人教版九年级上册二次函数图像中直角三角形的存在性问题

课题:二次函数图像中直角三角形的存在性问题一、教学目标1、掌握求二次函数表达式的方法。
2、掌握判断直角三角形可以从边和角两个角度入手。
3、掌握二次函数与直角三角形结合的动点问题的解决方法。
二、重、难点重点:线段的表示与分类讨论难点:分类讨论三、教学过程情境创设:存在性问题是中考中的热点问题,所涉知识点多,难度较大,也是学生比较荆手的问题,但它也是有解题方法可循的。
比如我们本节课将复习的直角三角形存在性问题,就可利用坐标系中两点的距离公式,正确得到所求三角形三边长的平方的代数式;根据勾股定理的逆定理得到方程,并解方程即可。
知识梳理:1、二次函数的表达式有哪些?一般式:对轴称为顶点坐标(,)项点式:对轴称为顶点坐标(,)交点(两根)式:对轴称为顶点坐标(,)(设计意图:让学生能根据所给条件选用恰当的表达式求二次函数解析式)2、直角三角形的判定方法有哪些?(设计意图:让学生知道判断一个三角形是直角三角形可从边和角两个角度入手,重点是对勾股定理逆定理的运用)3、已知点P(x,y),则点P到x轴的距离为,到y轴的距离为。
(设计意图:让学生知道点的坐标的实际意义)4、两点间的距离公式:用A,B两点的坐标来表示线段AB的长。
(设计意图:让学生知道用两点坐标来表示该两点的线段长)习题展示:oy B( x2,y2)A( x1,y1)x如图,已知抛物线y=-x 2+bx+c 与x 轴交于点A 、B (3,0),与y 轴交于点C (0,3),直线l 经过点B 、C 两点,抛物线的顶点为D 。
(1)求此抛物线和直线l 的解析式;(2)判断ΔBCD 的形状并说明理由;(3)如图,在抛物线的对称轴上求点P ,使ΔPBC 为直角三角形;思考题:如图,在对称轴右侧的抛物线上,是否存在点P ,使ΔPDC 为等腰三角形。
若存在,请求出符合条件点P 的坐标,若不存在,请说明理由;C B A O y xD CBDA yLO C B A O y xD 思路分析:将B (3,0),C (0,3)代入y=-x 2+bx+c 中,得关于b ,c 的二元一次方程组,解出b ,c 的值,从而得到抛物线的解析式;设y=kx+z,将B (3,0),C (0,3)代入y=kx+z ,得关于k ,z 的二元一次方程组,解出k ,z 的值,从而得到直线l 的解析式。
二次函数中直角三角形存在性问题.doc

二次函数中直角三角形存在性问题1. 找点:在己知两定点,确定第三点构成直角三角形时,要么以两定点为直角顶点,要么以动点为直角顶点•以定点为直角顶点时,构造两条直线与已知直线垂直;以动点为直角顶点时,以已知线段为直 径构造圆找点2. 方法:以两定点为直角顶点时,两直线互相垂直,则k1*k2=-1以已知线段为斜边时,利用K 型图,构造双垂直模 型,最后利用相似求解,或者三条边分别表示Z 后,利用勾股定理求解例一:如图,抛物线y =加空一2加兀+3加 与x 轴交于A 、B 两点,与y 轴交于C 点.(1) 请求出抛物线顶点M 的坐标(用含m 的代数式表示),A 、B 两点的坐标;(2) 经探究可知,A BC M 与A ABC 的而积比不变,试求出这个比值;(1) 求该抛物线的解析式; (2) M 为第一象限内抛物线上一动点,点M 在何处时,△ ACM 的面积最大;(3) 在抛物线的对称轴上是否存在这样的点P,使得△ PAC 为直角三角形?若存在,请求出所有可能点P 的坐标; 若不存在,请说明理由.(3)是否存在使A BCM 为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由0), B(4, 0),与y 轴交于点C.练习:1.如图.C知抛物线y=ar±bx+c (a«)的顶点M在第一象限,抛物线bx轴相交FA、B两点(点A 住点B的左边),f jy轴交万点C, O为唯标原点,如果ZkABM是何角二角形,AB=2, OM= J5(1)求点M的坐标;(2)求抛物线y=ax2+bx+c的解析式;(3)在抛物线的对称轴匕是否存在点P,使W APAC为直角三角形?若存在.请求出所有符合条件的点P 的坐标:若不存在•请说明理由.2.如图,抛物线y =〒一2加兀(m>0)与x轴的另一个交点为A,过P(l, -m)作PM丄x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.(1)若m二2,求点A和点C的坐标;(2)令m>l,连接CA,若AACP为直角三角形,求m的值;(3)在坐标轴上是否存在点E,使得APEC是以P为直角顶点的等腰直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.3.如图,抛物线y =衣+分+2与x轴交于点A(l, 0)和B(4, 0).(1)求抛物线的解析式;(2)若抛物线的对称轴交x轴于点E,点F是位于x轴上方对称轴上一点,FC〃x轴,与对称轴右侧的抛物线交于点C,且四边形OECF是平行四边形,求点C的坐标;(3)在(2)的条件下,抛物线的对称轴上是否存在点P,使AOCP是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.4、在平面直角坐标系中,抛物线y = ++仗一1)兀一比与直线y二kx+1交于A, B两点,点A在点B的左侧.(1)如图1,当k二1吋,直接写出A, B两点的坐标;(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求岀AABP面积的最大值及此时点P 的坐标;(3)如图2,抛物线y =兀2+仗_1)兀一比(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y二kx+1 使得Z0QC=90° ?若存在,请求出此吋k的值;若不存在,请说明理由.5.如图,直线y=x+2与抛物线y = ajc^-bx^6 (a#0)相交于A (2, 2)和B(4, m),点P是线段AB上异于A、B的动点,过点P作PC丄x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;(3)求厶PAC为直角三角形时点P的坐标.6、如图,抛物线y = ci^+bx+c经过A(-3, 0)、C(0, 4),点B在抛物线上,。
第二讲--二次函数中有关三角形存在性问题
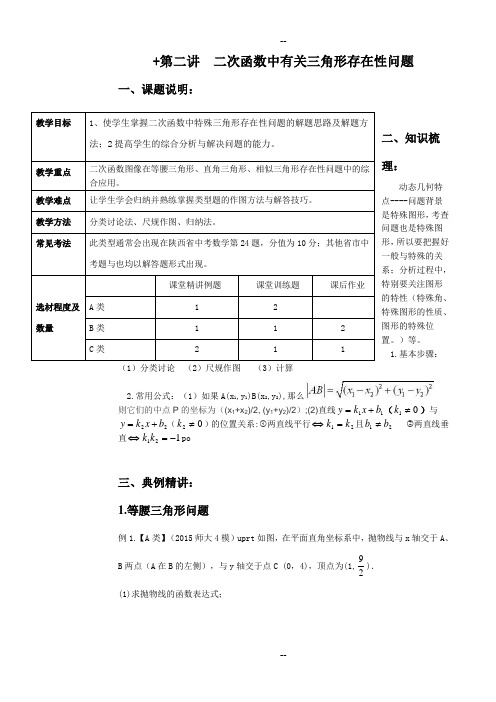
+第二讲 二次函数中有关三角形存在性问题一、课题说明:二、知识梳理:动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)等。
1.基本步骤:(1)分类讨论 (2)尺规作图 (3)计算 2.常用公式:(1)如果A(x 1,y 1)B(x 2,y 2),那么则它们的中点P 的坐标为((x 1+x 2)/2, (y 1+y 2)/2);(2)直线11b x k y +=(01≠k )与22b x k y +=(02≠k )的位置关系:①两直线平行⇔21k k =且21b b ≠ ②两直线垂直⇔121-=k k po三、典例精讲: 1.等腰三角形问题例1.【A 类】(2015师大4模)uprt 如图,在平面直角坐标系中,抛物线与x 轴交于A 、B 两点(A 在B 的左侧),与y 轴交于点C (0,4),顶点为(1,29). (1)求抛物线的函数表达式;教学目标1、使学生掌握二次函数中特殊三角形存在性问题的解题思路及解题方法;2提高学生的综合分析与解决问题的能力。
教学重点 二次函数图像在等腰三角形、直角三角形、相似三角形存在性问题中的综合应用。
教学难点 让学生学会归纳并熟练掌握类型题的作图方法与解答技巧。
教学方法 分类讨论法、尺规作图、归纳法。
常见考法此类型通常会出现在陕西省中考数学第24题,分值为10分;其他省市中考题与也均以解答题形式出现。
选材程度及数量课堂精讲例题课堂训练题课后作业A 类 1 2B 类 1 1 2C 类211(2)设抛物线的对称轴与x 轴交于点D ,试在对称轴上找出点P ,使△CDP 为等腰三角形,请直接写出满足条件的所有点P 的坐标;【教法参考】(1).分类讨论:分类标准:讨论顶角的位置或者底边的位置例如:本题第二问:在抛物线上找一点p ,使得P D C 、、三点构成等腰三角形,则可分成以下几种情况:(1)当C ∠为顶角时,CP CD = (2)当D ∠为顶角时,DP DC = (3)当P ∠为顶角时,PD PC =(2).尺规作图:两圆一线(①当C ∠为顶角时,以C 为圆心CD 为半径画圆,与对称轴交点即为所求点P ,②当D ∠为顶角时,以D 为圆心DC 为半径画圆,与对称轴交点即为所求点P ,③当P ∠为顶角时,线段DC 的垂直平分线与对称轴交点即为所求点P 。
二次函数与直角三角形有关的问题

二次函数的综合——与直角三角形有关的问题一.知识回顾(一)证明直角三角形(或直角)的定理:1.勾股定理的逆定理:如果三角形的三边长a ,b ,c 满足a 2+b 2=c 2, 那么这个三角形是直角三角形;两腰的夹角叫做顶角,腰和底边 的夹角叫做底角.2.半圆(或直径)所对的圆周角是直角. (二)与直角三角形(或直角)有关的线段关系:1. 勾股定理:如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么a 2+b 2=c 2 ;2. 辅助线构造“一线三垂直”相似三角形模型(如下图),对应边的比相等.二.例题解析例1.如图,在平面直角坐标系xOy 中,抛物线y =-x 2+2x +3与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线的顶点为D ,连接BC 、CD 、BD .证明:△BCD 是直角三角形. 解:x =0时,y =3;y =0时,x 1=-1,x 2=3; ∴C 为(0,3),点B 为(3,0).∵y =-x 2+2x +3=-(x -1)2+4,∴抛物线的顶点D 为(1,4),方法一:∵BC 2=(3-0)2+(0-3)2=18,CD 2=(1-0)2+(4-3)2=2,BD 2=(3-1)2+(0-4)2=20, ∴BC 2+CD 2=BD 2,即∠DCB =90°,△BCD 是直角三角形.方法二:过点D 做DE ⊥y 轴于点E , 则DE =CE =1,OB =OC =3,∴∠DCE =∠BCO =45°,即∠BCD =90°,△BCD 是直角三角形.方法三:过点D 做DE ⊥y 轴于点E ,则DE =CE =1,OB =OC =3,∴CE DEBO CO =,又∵∠CED =∠BOC =90°,∴△CED ∽△BOC ,∠ECD =∠OBC , 而∠OBC+∠OCB =90°,∴∠BCD =180°-(∠ECD+∠OCB )=90°, △BCD 是直角三角形.已知三个顶点判断直角三角的方法:(1) 用勾股定理逆定理证明;(2)构造“一线三垂直”相似证明;(3)根据坐标判断某些特殊角,求出直角.交于点C ,点E 是抛物线对称轴上一点,若△ACE 是直角三角形,求出点E 的坐标. 解:x =0时,y =3,y =0时,x 1=-1,x 2=3; ∴C 为(0,3),点A 为(-1,0). ∵y =-x 2+2x +3=-(x -1)2+4, ∴抛物线的的对称轴为直线x =1. 设点E 的坐标为(1,a ), 方法一:AC 2=[0-(-1)]2+(3-0)2=10, EA 2=[1-(-1)]2+(a -0)2=a 2+4, CE 2=(1-0)2+(a -3)2=a 2-6a +10, 若∠CAE =90°,则CE 2=AC 2+EA 2, 即a 2-6a +10=10+a 2+4,解得:a =-32,点E 为(1,-32); 若∠ACE =90°,则AE 2=AC 2+CE 2,即a 2+4=10+a 2-6a +10,解得:a =38,点E 为(1,38);若∠CEA =90°,则AC 2=CE 2+EA 2,即10=a 2-6a +10+a 2+4,解得:a 1=1,a 2=2,点E 为(1,1)或(1,2);综上所述,点E 为(1,-32),(1,38),(1,1)或(1,2).方法二:若∠CAE =90°,过点A 作直线l //y 轴,分别过点C 、点E 作CM ⊥l 于点M ,EN ⊥l 于点N , 可证△AMC ∽△ENA , ∴MA NECM NA =,即3)1(11−−=−a , 解得:a =-32,∴点E 为(1,-32);若∠ACE =90°,过点C 作直线l //x 轴,分别过点A 、点E 作AM ⊥l 于点M ,EN ⊥l 于点N , 可证△AMC ∽△CNE ,∴AMCNMC NE =,即3113=−a ,解得:a =38,∴点E 为(1,38); 若∠AEC =90°,过点E 作直线l //y 轴,分别过点A 、点C 作AM ⊥l 于点M ,CN ⊥l 于点N ,可证△AME ∽△ENC ,∴EN AM NC ME =,即aa −=321, 解得:a 1=1,a 2=2,点E 为(1,1)或(1,2); 综上所述,点E 为(1,-32),(1,38),(1,1)或(1,2). 直角三角形已知两个顶点,求第三个顶点坐标的方法:(1)按直角顶点分类(“一圆两垂直”);(2)用勾股定理或构造“一线三垂直”相似列方程计算.交于点C ,连接BC ,点M ,N 分别是线段AB ,BC 上的动点,且AM =BN ,连接MN .当△BMN 是直角三角形时,求点M 的坐标. 方法一:解:x =0时,y =3;y =0时,x 1=-1,x 2=3; ∴A 为(-1,0),B 为(3,0),C 为(0,3). 设点M 坐标为(m ,0),∴BN =AM =m -(-1)=m +1,BM =3-m , ∵OB =OC =3,∠BOC =90°, ∴∠CBO =∠BCO =45°. 若∠MNB =90°, △BMN ∽△BCO ,则BN BM 2=,即()123+=−m m ,解得524−=m , ∴点M 的坐标为(524−,0); 若∠NMB =90°,△BMN ∽△BOC ,则BM BN 2=, 即()m m −=+321,解得247−=m ,∴点M 的坐标为(247−,0);综上所述,点M 坐标为(524−,0)或(247−,0).方法二:解:x =0时,y =3;y =0时,x 1=-1,x 2=3; ∴A 为(-1,0),B 为(3,0),C 为(0,3). ∴直线BC 的解析式为y =-x +3, ∵OB =OC =3,∠BOC =90°, ∴∠CBO =∠BCO =45°. 设点A M =BN=m ,过点N 作NG ⊥x 轴于点G , 在Rt △BNG 中,m BN BG NG 2222===, ∴点M 为(m -1,0),N 为(m 223−,m 22), ∴BM 2=(3-m +1)2=m 2-8m +16, BN 2=2222m =m 2, MN 2=22222231+ +−−m m m=162482222+−−+m m m m , 若∠MNB =90°,则MN 2+BN 2=MB 2,G即162482222+−−+m m m m +m 2=m 2-8m+16, 解得m 1=0(舍去),m 2=424−, ∴点M 的坐标为(524−,0); 若∠NMB =90°, 则MN 2+BM 2=NB 2,即162482222+−−+m m m m +m 2-8m+16=m 2, 解得m 1=4(舍去),m 2=248−, ∴点M 的坐标为(247−,0);综上所述,点M 坐标为(524−,0)或(247−,0).直角三角形已知一个顶点,另两个点伴随运动,求动点坐标的方法: (1)按直角顶点分类;(2)用勾股定理或相似列方程计算.三.方法总结:四.变式训练:1.如图,已知抛物线经过原点O ,顶点为A (1,1),且与直线y =x ﹣2交于B ,C 两点. (1)求抛物线的解析式及点C 的坐标; (2)求证:△ABC 是直角三角形.【分析】(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C 点坐标;(2)分别过A 、C 两点作x 轴的垂线,交x 轴于点D 、E 两点,结合A 、B 、C 三点的坐标可求得∠ABO =∠CBO =45°,可证得结论;解:(1)∵顶点坐标为(1,1), ∴设抛物线解析式为y =a (x ﹣1)2+1, 又抛物线过原点,∴0=a (0﹣1)2+1,解得a =﹣1, ∴抛物线解析式为y =﹣(x ﹣1)2+1, 即y =﹣x 2+2x ,联立抛物线和直线解析式可得,解得或,∴B (2,0),C (﹣1,﹣3);(2)如图,分别过A、C两点作x轴的垂线,交x轴于点D、E两点,则AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3,∴∠ABO=∠CBO=45°,即∠ABC=90°,∴△ABC是直角三角形.2.如果抛物线C1的顶点在拋物线C2上,抛物线C2的顶点也在拋物线C1上时,那么我们称抛物线C1与C2“互为关联”的抛物线.如图1,已知抛物线C1:y1=x2+x与C2:y2=ax2+x+c是“互为关联”的拋物线,点A,B分别是抛物线C1,C2的顶点,抛物线C2经过点D(6,﹣1).(1)直接写出A,B的坐标和抛物线C2的解析式;(2)抛物线C2上是否存在点E,使得△ABE是直角三角形?如果存在,请求出点E的坐标;如果不存在,请说明理由.【分析】(1)由抛物线C1:y1=x2+x可得A(﹣2,﹣1),将A(﹣2,﹣1),D(6,﹣1)代入y2=ax2+x+c,求得y2=﹣+x+2,B(2,3);(2)易得直线AB的解析式:y=x+1,①若B为直角顶点,BE⊥AB,E(6,﹣1);②若A为直角顶点,AE⊥AB,E(10,﹣13);③若E为直角顶点,设E(m,﹣m2+m+2)不符合题意;解:由抛物线C1:y1=x2+x可得A(﹣2,﹣1),将A(﹣2,﹣1),D(6,﹣1)代入y2=ax2+x+c得,解得,∴y2=﹣+x+2,B(2,3);(2)易得直线AB的解析式:y=x+1,①若B为直角顶点,BE⊥AB,k BE•k AB=﹣1,∴k BE=﹣1,直线BE解析式为y=﹣x+5联立,解得x=2,y=3或x=6,y=﹣1,∴E(6,﹣1);②若A为直角顶点,AE⊥AB,同理得AE解析式:y=﹣x﹣3,联立,解得x=﹣2,y=﹣1或x=10,y=﹣13,∴E(10,﹣13);③若E为直角顶点,设E(m,﹣m2+m+2)由AE⊥BE得k BE•k AE=﹣1,即,,,(m﹣2)2(m﹣6)(m+2)=﹣16(m+2)(m﹣2),(m+2)(m﹣2)[(m﹣2)(m﹣6)+16]=0,∴m+2=0或m﹣2=0,或(m﹣2)(m﹣6)+16=0(无解)解得m=2或﹣2(不符合题意舍去),∴点E的坐标E(6,﹣1)或E(10,﹣13).3.如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C (0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN.(1)求抛物线的解析式及点D的坐标;(2)当△CMN是直角三角形时,求点M的坐标.【分析】(1)利用待定系数法求抛物线解析式;利用等腰三角形的性质得B(3,0),然后计算自变量为3所对应的二次函数值可得到D点坐标;(2)利用勾股定理计算出BC=5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,由于∠MCN=∠OCB,根据相似三角形的判定方法,当=时,△CMN∽△COB,于是有∠CMN=∠COB=90°,即=;当=时,△CMN∽△CBO,于是有∠CNM=∠COB=90°,即=,然后分别求出m的值即可得到M点的坐标;解:(1)把A(﹣3,0),C(0,4)代入y=ax2﹣5ax+c得,解得,∴抛物线解析式为y=﹣x2+x+4;∵AC=BC,CO⊥AB,∴OB=OA=3,∴B(3,0),∵BD⊥x轴交抛物线于点D,∴D点的横坐标为3,当x=3时,y=﹣×9+×3+4=5,∴D点坐标为(3,5);(2)在Rt△OBC中,BC===5,设M(0,m),则BN=4﹣m,CN=5﹣(4﹣m)=m+1,∵∠MCN=∠OCB,∴当=时,△CMN∽△COB,则∠CMN=∠COB=90°,即=,解得m =,此时M点坐标为(0,);当=时,△CMN∽△CBO,则∠CNM=∠COB=90°,即=,解得m=,此时M点坐标为(0,);综上所述,M点的坐标为(0,)或(0,).4.如图1,在平面直角坐标系中,直线l1:y=x+1与直线l2:x=﹣2相交于点D,点A是直线l2上的动点,过点A作AB⊥l1于点B,点C的坐标为(0,3),连接AC,BC.设点A 的纵坐标为t,△ABC的面积为s.(1)当t=2时,请直接写出点B的坐标;(2)在l2上是否存在点A,使得△ABC是直角三角形?若存在,请求出此时点A的坐标和△ABC的面积;若不存在,请说明理由.【分析】(1)先根据t=2可得点A(﹣2,2),因为B在直线l1上,所以设B(x,x+1),利用y=0代入y=x+1可得G点的坐标,在Rt△ABG中,利用勾股定理列方程可得点B 的坐标;(2)先把(7,4)代入s=中计算得b的值,计算在﹣1<t<5范围内图象上一个点的坐标值:当t=2时,根据(1)中的数据可计算此时s=,可得坐标(2,),代入s=a(t+1)(t﹣5)中可得a的值;解:(1)如图1,连接AG,当t=2时,A(﹣2,2),设B(x,x+1),在y=x+1中,当x=0时,y=1,∴G(0,1),∵AB⊥l1,∴∠ABG=90°,∴AB2+BG2=AG2,即(x+2)2+(x+1﹣2)2+x2+(x+1﹣1)2=(﹣2)2+(2﹣1)2,解得:x1=0(舍),x2=﹣,∴B(﹣,);(2)存在,设B(x,x+1),分两种情况:①当∠CAB=90°时,如图4,∵AB⊥l1,∴AC∥l1,∵l1:y=x+1,C(0,3),∴AC:y=x+3,∴A(﹣2,1),∵D(﹣2,﹣1),在Rt△ABD中,AB2+BD2=AD2,即(x+2)2+(x+1﹣1)2+(x+2)2+(x+1+1)2=22,解得:x1=﹣1,x2=﹣2(舍),∴B(﹣1,0),即B在x轴上,∴AB==,AC==2,∴S△ABC===2;②当∠ACB=90°时,如图5,∵∠ABD=90°,∠ADB=45°,∴△ABD是等腰直角三角形,∴AB=BD,∵A(﹣2,t),D(﹣2,﹣1),∴(x+2)2+(x+1﹣t)2=(x+2)2+(x+1+1)2,(x+1﹣t)2=(x+2)2,x+1﹣t=x+2或x+1﹣t=﹣x﹣2,解得:t=﹣1(舍)或t=2x+3,Rt△ACB中,AC2+BC2=AB2,即(﹣2)2+(t﹣3)2+x2+(x+1﹣3)2=(x+2)2+(x+1﹣t)2,把t=2x+3代入得:x2﹣3x=0,解得:x=0或3,当x=3时,如图5,则t=2×3+3=9,∴A(﹣2,9),B(3,4),∴AC==2,BC==,∴S△ABC===10;当x=0时,如图6,此时,A(﹣2,3),AC=2,BC=2,∴S△ABC===2.。
解直角三角形在二次函数中的应用

解直角三角形在二次函数中的应用解直角三角形在二次函数中的应用直角三角形是初中数学中比较基础的概念之一,二次函数则是高中数学中比较重要的一个概念,两者貌似毫无联系,但实际上它们之间却有着紧密的联系。
接下来,我们将通过以下几个方面来探讨解直角三角形在二次函数中的应用。
一、直角三角形的勾股定理勾股定理是解直角三角形中最重要的公式之一。
根据此定理,我们可以得到判断一个三角形是否为直角三角形的方法。
在二次函数中,我们可以通过勾股定理来求解关于二次函数的方程。
这个过程主要是利用勾股定理将三角形的边长转化为二次函数表达式中平方项的系数,从而解出方程。
二、三角函数的基本关系式三角函数是解直角三角形的重要工具,二次函数中也有许多与三角函数相关的公式。
三角函数中的正弦、余弦函数定义中包含直角三角形的边长,通过推导,我们可以得到正弦、余弦函数中另一个角度的值。
在求解包含三角函数的二次函数中,我们可以通过将其化简成标准形式后,利用三角函数的基本关系式,将方程转化为仅包含正弦或余弦函数的方程,从而解出方程。
三、二次函数的最值问题二次函数的图像是一个带有对称轴的抛物线,它的最值点为对称轴上的顶点。
在计算直角三角形的过程中,我们经常需要求解最大值或最小值,因此我们可以将这个过程与二次函数的最值问题联系起来。
通过将直角三角形中的某一个角度和对应的边长代入已知的二次函数中,我们可以得到二次函数的顶点坐标。
这个过程既可以被用来求解最大值和最小值的问题,也可以用于计算直角三角形中中位线的长度。
综上所述,在二次函数中,解直角三角形的知识和技能将起到重要的作用。
通过解三角函数和二次函数的方程来确定直角三角形中的角度和边长,通过二次函数的最值问题来计算直角三角形的某些特殊值,这些都是我们为了更好地理解和掌握二次函数而应该掌握的重要技巧。
二次函数直角三角形存在性问题解题技巧2019年河南中考

二次函数直角三角形存在性问题解题技巧2019年河
南中考
该问题还可以引生为等腰和直角共存的问题,但是无论什么样的情况,我们都需要先掌握基本的等腰三角形及直角三角形存在性问题的解法。
解这两类存在性问题,一般分三个步骤,一是寻找分类标准,而是列方程,三是解方程并验根。
(突出利用两点间距离公式的思路)。
探究等腰三角形的存在性问题时需将情况考虑全面,题目中未指定哪条边是腰或底边时,需分类讨论哪两条边是腰的情况.当有两个点是定点,一个是动点时,即"两定一动"型,有两种解决方法:①"两圆一线"法;②分类讨论法.
对于直角三角形的存在性问题,应充分利用图形的几何关系,需要常常和相似三角形,锐角三角形函数提供的三角比解决,但无论是哪种方法,分类标准是共通的,而分类时寻找确定的直角顶点往往需要用到圆周角的知识。
一般情况下,按照直角顶点或者斜边分类,然后按照勾股定理或者三角比列方程,有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便。
中考二次函数与直角三角形有关的问题知识解读

二次函数与直角三角形有关的问题知识解读【专题说明】二次函数之直角三角形存在性问题,主要指的是在平面直角坐标系下,已知一条边(或两个顶点)的直角三角形存在,求第三个顶点的坐标的题型.主要考察学生对转化思想、方程思想、几何问题代数化的数形结合思想及分类讨论思想的灵活运用。
【解题思路】直角三角形的存在性问题1.找点:在已知两定点,确定第三点构成直角三角形时,要么以两定点为直角顶点,要么以动点为直角顶点.以定点为直角顶点时,构造两条直线与已知直线垂直;以动点为直角顶点时,以已知线段为直径构造圆找点2.方法:(1)以两定点为直角顶点时,两直线互相垂直,则k1*k2=-1(2)以已知线段为斜边时,利用K型图,构造双垂直模型,最后利用相似求解,或者三条边分别表示之后,利用勾股定理求解下面主要介绍2种常用方法:【方法1 几何法】“两线一圆”(1)若∠A 为直角,过点A 作AB 的垂线,与x 轴的交点即为所求点C;(2)若∠B 为直角,过点B 作AB 的垂线,与x 轴的交点即为所求点C;(3)若∠C 为直角,以AB 为直径作圆,与x 轴的交点即为所求点C.(直径所对的圆周角为直角)如何求得点坐标?以C2为例:构造三垂直.),坐标为(故代入得:坐标得、由,易证0213232222C C C BN AM B A N MB BN AM BN AMB ===∆≈∆()),坐标为(,,坐标为故或故又即代入得:设,,坐标得、由求法相同,如下:易证、040231a ,4a ,3ab ,3ab 1N a,31,4333333343C C C C C C C C C C b b M BN AM B A NBM N AMNB AM ==+=======∆≈∆【方法2 代数法】点-线-方程23m 20352235110,m 135-m 1-m 35-m 11-m 22222122111=+=+=+=+==,解得:)代入得方程(,,,)表示线段:();,()、,(),又坐标为()表示点:设(:不妨来求下)()()()(BC C C C A AB B A【典例分析】【方法1 勾股定理】【典例1】(2021秋•建华区期末)抛物线y=x2+bx+c经过A、B(1,0)、C(0,﹣3)三点.点D为抛物线的顶点,连接AD、AC、BC、DC.(1)求抛物线的解析式;(2)在y轴上是否存在一点E,使△ADE为直角三角形?若存在,请你直接写出点E的坐标;若不存在,请说明理由.【解答】解(1)∵抛物线y=x2+bx+c经过B(1,0)、C(0,﹣3),∴,解得,∴抛物线的解析式为:y=x2+2x﹣3.(4)在y轴上存在点E,使△ADE为直角三角形,理由如下:∵抛物线的解析式为y=x2+2x﹣3=(x+1)2﹣4,∴D(﹣1,﹣4),设E点坐标为(0,m),∴AE2=m2+9,DE2=m2+8m+17,AD2=20,当∠EAD=90°时,有AE2+AD2=DE2,∴m2+9+20=m2+8m+17,解得m=,∴此时点E的坐标为(0,);当∠ADE=90°时,DE2+AD2=AE2,m2+8m+17+20=m2+9,解得m=﹣,∴此时点E的坐标为(0,﹣);当∠AED=90°时,AE2+DE2=AD2,m2+9+m2+8m+17=20,解得m=﹣1或m=﹣3,∴此时点E的坐标为(0,﹣1)或(0,﹣3).【变式1-1】(2022•灞桥区校级模拟)如图,抛物线与x轴交于点A(1,0),B(3,0),与y轴交于点C(0,3).(1)求二次函数的表达式及顶点坐标;(2)连接BC,在抛物线的对称轴上是否存在一点E,使△BCE是直角三角形?若存在,请直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)设抛物线的解析式为y=a(x﹣1)(x﹣3),将点C(0,3)代入y=a(x﹣1)(x﹣3),∴3a=3,∴a=1,∴y=(x﹣1)(x﹣3)=x2﹣4x+3,∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点为(2,﹣1);(2)存在一点E,使△BCE是直角三角形,理由如下:∵y=x2﹣4x+3=(x﹣2)2﹣1,∴抛物线的对称轴为直线x=2,设E(2,t),∵△BCE是直角三角形,∴BE⊥CE,∵B(3,0),C(0,3),∴BC=3,BE=,CE=,①当BC为斜边时,∴18=()2+()2,解得t=,∴E点坐标为(2,)或(2,);②当BE为斜边时,∴18+()2=()2,解得t=5,∴E点坐标为(2,5);③当CE为斜边时,∴18+()2=()2,解得t=﹣1,∴E点坐标为(2,﹣1);综上所述:E点坐标为(2,)或(2,)或(2,5)或(2,﹣1)【变式1-2】(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C坐标为(2,0).(1)求此抛物线的函数解析式.(2)点P为该抛物线对称轴上的动点,使得△P AB为直角三角形,请求出点P的坐标.【解答】解:(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)如图2中,设抛物线的对称轴交x轴于点N,过点B作BM⊥抛物线的对称轴于点M.则N(﹣1.0).M(﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).【方法2 构造“K”字型利用相似作答】【典例2】(2022•碑林区校级四模)如图,在平面直角坐标系中,抛物线C1:y=ax2+bx+c 交x轴于点A(﹣5,0),B(﹣1,0),交y轴于点C(0,5).(1)求抛物线C1的表达式和顶点D的坐标.(2)将抛物线C1关于y轴对称的抛物线记作C2,点E为抛物线C2上一点若△DOE是以DO为直角边的直角三角形,求点E的坐标.【解答】解:(1)将点A(﹣5,0),B(﹣1,0),C(0,5)代入y=ax2+bx+c,∴,解得,∴y=x2+6x+5,∵y=x2+6x+5=(x+3)2﹣4,∴顶点D(﹣3,﹣4);(2)设抛物线C2上任意一点(x,y),则(x,y)关于y轴对称的点为(﹣x,y),∵点(﹣x,y)在抛物线C1上,∴抛物线记作C2的解析式为y=x2﹣6x+5,设E(t,t2﹣6t+5),过点D作DG⊥x轴交于点G,过点E作EH⊥x轴交于点H,∵∠DOE=90°,∴∠GOD+∠HOE=90°,∵∠GOD+∠GDO=90°,∴∠HOE=∠GDO,∴△GDO∽△HOE,∴=,∵DG=4,GO=3,HE=﹣t2+6t﹣5,OH=t,∴=,∴t=4或t=,∴E(4,﹣3)或E(,﹣).【变式2-1】(2022•济南)抛物线y=ax2+x﹣6与x轴交于A(t,0),B(8,0)两点,与y轴交于点C,直线y=kx﹣6经过点B.点P在抛物线上,设点P的横坐标为m.(1)求抛物线的表达式和t,k的值;(2)如图1,连接AC,AP,PC,若△APC是以CP为斜边的直角三角形,求点P的坐标;【解答】解:(1)将B(8,0)代入y=ax2+x﹣6,∴64a+22﹣6=0,∴a=﹣,∴y=﹣x2+x﹣6,当y=0时,﹣t2+t﹣6=0,解得t=3或t=8(舍),∴t=3,∵B(8,0)在直线y=kx﹣6上,∴8k﹣6=0,解得k=,∴y=x﹣6;(2)作PM⊥x轴交于M,∵P点横坐标为m,∴P(m,﹣m2+m﹣6),∴PM=m2﹣m+6,AM=m﹣3,在Rt△COA和Rt△AMP中,∵∠OAC+∠P AM=90°,∠APM+∠P AM=90°,∴∠OAC=∠APM,∴△COA∽△AMP,∴=,即OA•MA=CO•PM,3(m﹣3)=6(m2﹣m+6),解得m=3(舍)或m=10,∴P(10,﹣);【变式2-2】(2022•滨州)如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接AC、BC.(1)求线段AC的长;(2)若点M为该抛物线上的一个动点,当△BCM为直角三角形时,求点M的坐标.【解答】解:(1)针对于抛物线y=x2﹣2x﹣3,令x=0,则y=﹣3,∴C(0,﹣3);令y=0,则x2﹣2x﹣3=0,∴x=3或x=﹣1,∵点A在点B的左侧,∴A(﹣1,0),B(3,0),∴AC==;(2)由(1)知,B(3,0),C(0,﹣3),∴OB=OC=3,设M(m,m2﹣2m﹣3),∵△BCM为直角三角形,∴①当∠BCM=90°时,如图1,过点M作MH⊥y轴于H,则HM=m,∵OB=OC,∴∠OCB=∠OBC=45°,∴∠HCM=90°﹣∠OCB=45°,∴∠HMC=45°=∠HCM,∴CH=MH,∵CH=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,∴﹣m2+2m=m,∴m=0(不符合题意,舍去)或m=1,∴M(1,﹣4);②当∠CBM=90°时,过点M作M'H'⊥x轴,同①的方法得,M'(﹣2,5);③当∠BMC=90°时,如图2,Ⅰ、当点M在第四象限时,过点M作MD⊥y轴于D,过点B作BE⊥DM,交DM的延长线于E,∴∠CDM=∠E=90°,∴∠DCM+∠DMC=90°,∵∠DMC+∠EMB=90°,∴∠DCM=∠EMB,∴△CDM∽△MEB,∴,∵M(m,m2﹣2m﹣3),B(3,0),C(0,﹣3),∴DM=m,CD=﹣3﹣(m2﹣2m﹣3)=﹣m2+2m,ME=3﹣m,BE=﹣(m2﹣2m﹣3)=﹣m2+2m+3,∴,∴m=0(舍去)或m=3(点B的横坐标,不符合题意,舍去)或m=(不符合题意,舍去)或m=,∴M(,﹣),Ⅱ、当点M在第三象限时,M(,﹣),即满足条件的M的坐标为(1,﹣4)或(﹣2,5)或(,﹣),或(,﹣).。
二次函数与直角三角形的存在性问题

课题:二次函数中直角三角形的存在性问题教学目标:知识与技能1、 知道并会推导三垂直性质,能正确找出对应边,能准确写出三垂直中的对应边成比例.2、 准确掌握平面直角坐标系中三垂直性质使用条件和操作程序.过程与方法通过对平面直角坐标系中不同位置的直角三角形活动探究出构造三垂直性质应如何添加辅助线,并会利用三垂直性质解决二次函数中直角三角形的存在性问题.情感态度与价值观通过对解析几何产生的背景介绍及三垂直性质在二次函数中直角三角形存在性问题的应用感受数形结合思想的重要性及意义;通过对不确定直角顶点的直角三角形存在性问题的解决,感受分类思想在学习中的必要性.教学重点:探究如何构造三垂直模型,并会利用三垂直性质解决直角三角形的存在性问题.教学难点:探究使用三垂直性质的操作程序.教学过程:一、 情景设计讲述解析几何产生的背景,说明数形结合思想的重要性, 引出课题。
二、 预习思考),(1b x ),(2b x ),(1y a ),(2ya1、如图1,水平线上各点的___坐标相同,水平线上的两点间的距离等于_______________________________。
2、如图2,竖直线上各点的___坐标相同,竖直线上的两点间的距离等于_______________________________。
3、 如何设函数图像上的动点坐标?如何设二次函数对称轴上的动点坐标?教学要点1、 分组提问,调动学生积极性.2、 引导学生由图找答案,并用自己的语言叙述结论.3、 对学生的结论补充强调.三、 探索问题问题1:(1) 图3是什么模型?(2) 该模型的已知条件是什么?结论是什么?你可以证明你的结论吗?(3) 图3、图4的已知条件和结论的区别与联系是什么?教学要点1、问题1的设置是对本节课的应用知识点重点巩固,可齐声回答.2、教师分析:三垂直模型还可看作,已知一直角三角形,过其直角顶点在直角三角形的外部做一条直线,并过直角三角形的另外两个顶点引上述直线的垂线段.问题2:(1) 如果需要求一条线段的长,你希望在坐标系中是什么样的线段?(2) 如果平面直角坐标系中随意放置了一个直角三角形,过其直角顶点在其外部做一条什么方向的直线,能保证构成的三垂直模型中相似的两个直角三角形的四条直角边不是水平方向就是竖直方向?(3) 总结在平面直角坐标系中构造三垂直模型的操作步骤. 教学要点1、针对(1),能预料到学生的答案是竖直方向或水平方向,如果不是这个答案,再继续询问他们的结论的理由.2、对于(2),教师引导学生在平面直角坐标系中画出任意三角形,并让学生观察、尝试符合要求的直线.3、教师引导学生总结平面直角坐标系中构造三垂直模型操作步骤.4、教师课件展示详细操作步骤.(1)平面直角坐标系中构造三垂直模型的操作步骤.(2)过另外两个顶点向水平线或竖直线作垂线段(3)根据条件求出各点坐标及四条直角边长度(4)根据对应边相等或成比例,列出四条直角边之间的数量关系,进而求出未知数,求出动点坐标问题3:例、(2015本溪)如图,抛物线 ( ≠0)经过点A (2,0),点B (3,3)(1)求抛物线的解析式并直接写出它的对称轴;(2)点P 是抛物线对称轴上一点,当△ABP 是直角三角形时,请求出所有符合条件的点P 坐标.教学要点1、学生回答解决第(1)问的方法,学生完成(1)解答过程,教师巡视指导并讲评2、教师引导:(1)构造三垂直模型需要有一个直角,谁是Rt △ABP 的直角呢?(生:不知道)bx ax y +=2a(2)怎么办?(生:分类讨论)(3)分几类?是哪几类?(生:3类,分别是当∠ABP=90°,当∠APB=90°,∠BAP=90°)3、师生共同探究当∠ABP=90°时的情况解:如图,当∠ABP=90°时,过点P作PM⊥BC交BC的延长线于点M,设点P(1,a),则M(3,a),C(3,0)∴PM=3-1=2,MB=a-3,BC=3,AC=3-2=1∵∠MPB+∠MBP=90°,∠MBP+∠ABC=90°,∴∠MPB=∠ABC,又∵∠PMB=∠ACB=90°∴△PM B∽△BCA∴PM/MB=BC/AC,2/(a-3)=3/1解得:a=11/3∴点P(1,11/3)4、剩下两种情况,让学生小组讨论,并找两位学生上台分别讲解,主讲学生可以自己需要选择要不要带小帮手,之后师生共同点评总结.四、课堂小结通过本节课的学习,你有什么收获?五、课后作业除了利用三垂直性质解决二次函数中直角三角形的存在性问题,你还有其它的方法吗?并试用你想到的方法解决今天的例题.教学反思:本节课是二次函数中直角三角形的存在性问题,此类问题通常在河南中招卷中作为压轴题出现,一般是23题的第(2)问或第(3)问,其知识覆盖面较广,综合性较强,是数形结合思想及分类思想的典型题。
中考数学 二次函数存在性问题 及参考答案

中考数学二次函数存在性问题及参考答案中考数学二次函数存在性问题及参考答案一、二次函数中相似三角形的存在性问题1.如图,把抛物线 $y=x^2$ 向左平移1个单位,再向下平移4个单位,得到抛物线 $y=(x-h)^2+k$。
所得抛物线与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D。
1)写出h、k的值;2)判断△ACD的形状,并说明理由;3)在线段AC上是否存在点M,使△AOM∽△ABC?若存在,求出点M的坐标;若不存在,说明理由。
2.如图,已知抛物线经过A($-2,0$),B($-3,3$)及原点O,顶点为C。
1)求抛物线的解析式;2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;3)P是抛物线上的第一象限内的动点,过点P作PM⊥x 轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由。
二、二次函数中面积的存在性问题3.如图,抛物线 $y=ax^2+bx$ ($a>0$)与双曲线$y=\frac{k}{x}$ 相交于点A,B。
已知点B的坐标为($-2,-2$),点A在第一象限内,且 $\tan\angle AOX=4$。
过点A作直线AC∥x轴,交抛物线于另一点C。
1)求双曲线和抛物线的解析式;2)计算△ABC的面积;3)在抛物线上是否存在点D,使△ABD的面积等于△ABC的面积。
若存在,请写出点D的坐标;若不存在,请说明理由。
4.如图,抛物线 $y=ax^2+c$ ($a>0$)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A($-2,0$),B($-1,-3$)。
1)求抛物线的解析式;2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;3)在第(2)问的结论下,抛物线上的点P使$\triangle PAD=4\triangle ABM$ 成立,求点P的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(-1,0) A
O
(0,-2)C
自学指导4(4分钟)
在抛物线y=x2-x-2上是否存在点P ,使△PAC是以AC为 直角边的三角形?若存在,求出所有符合条件的点P的 坐标; 情况一: 当PCA 900时 y=x2-x-2 3 7 P 1 ( , ) 2 2 情况二: 当PAC 900时
3、如图,矩形OABC中,点O为原点,点A的坐标为 (0,8),点C的坐标为(6,0).抛物线y=4/9x2+bx+c经过A、C两点,与AB边交于点D. ①求 S关于m的函数表达式,并求出m为何值时,S取 (1)求抛物线的函数表达式; 得最大值; (2)点P为线段BC上一个动点(不与点C重合),点Q 2+bx+c ②当 S最大时,在抛物线 y=-4/9x 的对称轴 l上若 , 为线段 AC上一个动点, AQ=CP ,连接 PQ,设CP=m 存在点 F,使△ FDQ △CPQ 的面积为 S为直角三角形,请直接写出所有符 . 合条件的F的坐标;若不存在,请说明理由.
3.如图,现将一块等腰直角三角板ABC放在第二象限, 斜靠在两坐标轴上,且点A(0,2),点C(-1,0), 如图所示:抛物线y=ax2+ax-2经过点B. (1)求点B的坐标; (2)求抛物线的解析式; (3)抛物线的对称轴上是否存在点P,使△ACP是以 等腰直角三角形 AC为直角边的直角三角形?若存在,求出所有点 P的 坐标;若不存在,请说明理由. (4)若点D是抛物线在第三象限 内的一个动点,连接BD、 CD.当△BCD的面积最大时, 求点D的坐标. (5)若点P是抛物线上一个动点, 以线段AB、BP为邻边作平行四边 形ABPQ.当点Q落在x轴上时, 直接写出点P的坐标.
第27题图
3.如图,抛物线y x 2x k 与x轴交于A、B两 点,与y轴交于点C(0,-3) ①点A的坐标为 ,点B的坐标为 ; ②设抛物线的顶点为M,求四边形ABMC的面积; ③在x轴下方的抛物线上是否存在一点D,使四边 形ABDC的面积最大?若存在,请求出点D的坐标; 若不存在,请说明理由; ④在抛物线上求点Q,使△BCQ是以BC为直角边的 直角三角形.
由△BCD∽△BAC得: BC2=BD· BA
2.直角三角形相似----K型图
C
A
D
B
E
已知:在直角梯形ADEC中,∠D=90°B是DE边 上一点,∠ABC=90° 求证: BD· BE=AD· CE
3.直角三角形斜边上的中线 CD是RT△ABC斜边AB上的中线。
A
D
C
B
自学指导2(6分钟) 已知:O为坐标原点,A(2,4)
4、如图,在平面直角坐标系中,△ABC是直角三角 形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线 y=x2+bx+c经过A,B两点,抛物线的顶点为D. ( )求b2 , c的值; ( 31 )在( )的条件下: (2)点E是直角三角形 ABC斜边AB上一动点(点A、 ①求以点 、B、F、D为顶点的四边形的面积; B除外),过点E作x 轴的垂线交抛物线于点 F ,当 ②在抛物线上是否存在一点 P,使△EFP是以EF 为直角 线段EF的长度最大时,求点E的坐标; 边的直角三角形?若存在,求出所有点 P的坐标;若不 存在,说明理由.
回顾:如图,四边形OABC为直角梯形,A(4,0), B(3,4),C(0,4)。点M从O出发以每秒2个单 位长度的速度向A运动;点N从B同时出发,以每秒1 个单位长度的速度向C运动。其中一个动点到达终点 时,另一个动点也随之停止运动。过点N作NP垂直x 轴于点P,连结AC交NP于Q,连结MQ。求: (1)点 (填M或N)能到达终点; ( 2)求△AQM的面积 S与运动时间 t的函数关系式, ( 3)是否存在点 M,使得△ AQM为直角三角形?若存 并写出自变量 t和取值范围,当 t为何值时,S的值最 在,求出点 M的坐标,若不存在,说明理由。 y 大;
当堂训练(6分钟)
16.已知抛物线y=a(x+1)2+c与x轴交于点A(-3,0) (1)直接写出抛物线与x轴的另一个交点B的坐标; (2)若直线过抛物线顶点M及抛物线与y轴的交点C(0, 3). ①求直线MC所对应的函数关系式; ②若直线MC与x轴的交点为N,在抛物线上是否存在点P, 使得△NPC是以NC为直角边的直角三角形?若存在,求出 点P的坐标;若不存在,请说明理由.
5 7 P2 ( , ) 2 4
(-1,01(5分钟)
1、已知:A(4,0),B(0,4),C(-2,0).设抛物线上是否 存在点E,使△BCE是以BC为直角边的直角三角 形?若存在,请求出所有点E的坐标,若不存在, 请说明理由。
y
B
C O
A
x
2、如图所示,矩形OABC位于平面直角坐标系中, AB=2,OA=3,点P是OA上的任意一点,PB平分 ∠APD,PE平分∠OPF,且PD、PF重合. ( 1 )设 OP=x,OE=y ,求y关于x的函数解析式,并求 ( 3 )请探究:在( 2)的条件下,抛物线上是否存在 x为何值时, yEPM 的最大值; 一点 M,使得△ 为直角三角形?若存在,求出M ( 2)当PD⊥OA时,求经过E、P、B三点的抛物线的 点的坐标;若不存在,请说明理由. 解析式;
3.如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交 点,那么以该抛物线的顶点和这两个交点为顶点的三 角形称为这条抛物线的“抛物线三角形”. (1)“抛物线三角形”一定是 三角形; (2)若抛物线y=-x2+bx(b>0)的“抛物线三角形” 是等腰直角三角形,求b的值; (3)如图,△OAB是抛物线y=-x2+b′x(b′>0)的 “抛物线三角形”,是否存在以原点O为对称中心的矩 形ABCD?若存在,求出过O、C、D三点的抛物线的 表达式;若不存在,说明理由.
(2012•赤峰改编)如图,抛物线y=x2-bx-5与x轴交于A、 B两点(点A在点B的左侧),与y轴交于点C,点C与点 F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|: |OA|=5:1. (1)求抛物线的解析式; (2)求直线AF的解析式; (3)在直线AF上是否存在 点P,使△CFP是直角三角形? 若存在,求出P点坐标;若不 存在,说明理由. (4)在抛物线上是否存在点M, 使△ACM是以AC为直角边的三 角形?若存在,求出M点坐标; 若不存在,说明理由.
y
9 8 7 6 5 4 3 2
1
点P坐标轴上 是y x轴上一动点, 当△AOP是直角三 角形求P点坐标 A
3 2 1 O0 1 2 3 4 5 1 2
x
自学指导3(6分钟) 已知:O为坐标原点,A(2,4)
y
9 8 7 6 5 4 3 2
1
A
点P是直线x=3上一 动点,当△AOP是 直角三角形求P点坐 标.
3 2 1 O0 1 2 3 4 5 1 2
x
自学检测3(5分钟)
在直线x=0.5上是否存在点P ,使△PAC为直角三角形? 若存在,求出所有符合条件的点P的坐标;
情况一: 当PCA 900时 1 7 P 1 ( , ) 2 4 情况二: 当PAC 900时
1 3 P2 ( , ) 2 4
C N ←B Q
O
M →P
A
x
二次函数与直角三角形
学习目标(1分钟)
1.会解直角三角形存在性问题(点在直线 上) 2.会解直角三角形存在性问题(点在抛物 线上)
自学指导1(5分钟)
1. 射影定理 CD是RT△ABC斜边AB上的高。
c
A
D
B
DB 由△ACD∽△CBD得: DC2=DA·
由△ACD∽△ABC得: AC2=AD· AB
1 2 2 5.如图,抛物线 y x x 2 2 2
与x轴交于A,B
两点,与y轴交于c点.
y
C
A
O
B
x
2.已知:如图一次函数y=0.5x+1的图象与x轴交于点A, 与y轴交于点B;二次函数y=0.5x2+bx+c的图象与一次 函数y=0.5x+1的图象交于B、C两点,与x轴交于D、E 两点且D点坐标为(1,0) (1)求二次函数的解析式; (2)在x轴上是否存在点P,使得△PBC是以P为直角顶点 的直角三角形?若存在,求出所有的点P,若不存在,请 说明理由.
2
y x 2x k
2
y x 2x k
2
4.如图,矩形OABC的顶点A在x轴的正半轴上,点B的坐 标为(1,3),把矩形绕点B旋转一定的角度,使它的 顶点O落在x轴的点D处,已知M是第四象限内纵坐标为-1 的点,以M为顶点的抛物线正好过O、D两点. (1)求点D的坐标; (2)求抛物线的解析式; (3)在抛物线上是否存在点N,使以O、M、N为顶点的 三角形为直角三角形?若存在,求出所有满足条件的点 N的坐标;若不存在,请说明理由.
