【精编文档】山西省晋中市和诚高中2018-2019学年高二数学周练试卷5.11理.doc
山西省晋中市和诚高中有限公司2018-2019学年高二周练(4.20)数学(文)试题
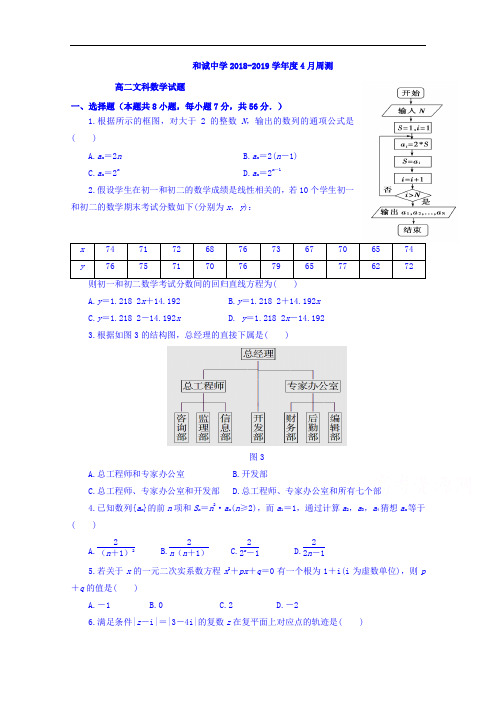
和诚中学2018-2019学年度4月周测高二文科数学试题一、选择题(本题共8小题,每小题7分,共56分.)1.根据所示的框图,对大于2的整数N ,输出的数列的通项公式是( ) A.a n =2n B.a n =2(n -1) C.a n =2nD.a n =2n -12.假设学生在初一和初二的数学成绩是线性相关的,若10个学生初一和初二的数学期末考试分数如下(分别为x ,y ):65 74 A.y =1.218 2x +14.192 B.y =1.218 2+14.192x C.y =1.218 2-14.192x D. y =1.218 2x -14.192 3.根据如图3的结构图,总经理的直接下属是( )图3A.总工程师和专家办公室B.开发部C.总工程师、专家办公室和开发部D.总工程师、专家办公室和所有七个部4.已知数列{a n }的前n 项和S n =n 2·a n (n ≥2),而a 1=1,通过计算a 2,a 3,a 4猜想a n 等于( )A.2(n +1)2B.2n (n +1)C.22n -1D.22n -15.若关于x 的一元二次实系数方程x 2+px +q =0有一个根为1+i(i 为虚数单位),则p +q 的值是( )A.-1B.0C.2D.-26.满足条件|z -i|=|3-4i|的复数z 在复平面上对应点的轨迹是( )A.一条直线B.两条直线C.圆D.椭圆7.设a ,b ,c 均为正实数,P =a +b -c ,Q =b +c -a ,R =c +a -b ,则“PQR >0”是“P ,Q ,R 同时大于0”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.在正整数数列中,由1开始依次按如下规则将某些数染成红色.先染1,再染2个偶数2,4;再染4后面最邻近的3个连续奇数5,7,9;再染9后面最邻近的4个连续偶数10,12,14,16;再染16后面最邻近的5个连续奇数17,19,21,23,25.按此规律一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,….则在这个红色子数列中,由1开始的第60个数是( )A.103B.105C.107D.109 二、填空题(本题共3小题,每小题8分,共24分)9.若复数z =7+a i2-i 的实部为3,则z 的虚部为________. 10.某工程的工序流程图如图4所示,现已知工程总工时数为10天,则工序c 所需工时为________天.图4 11.某考察团对中国10个城市进行职工人均工资水平x (千元)与居民人均消费水平y (千元)调查,y 与x 具有相关关系,回归方程为y ^=0.66x +1.562,若A 城市居民人均消费水平为7.765(千元),估计该城市人均消费额占人均工资收入的百分比约为________.三、解答题(共2小题,每题10,共20分)12.(本小题满分12分)对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行了3年的跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示:(参考1-2课本13页表1-11)13.已知a ,b ,c 是全不相等的正实数,求证:b +c -a a +a +c -b b +a +b -cc >3.。
「精品」山西省晋中市和诚高中2018-2019学年高二数学上学期周练7
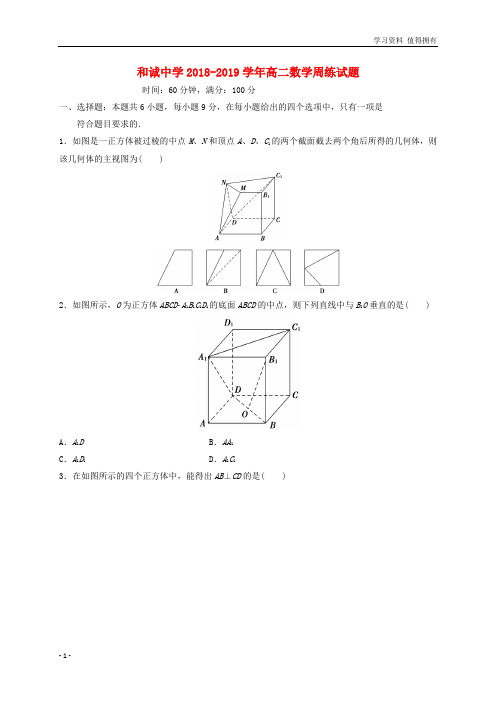
和诚中学2018-2019学年高二数学周练试题时间:60分钟,满分:100分一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图是一正方体被过棱的中点M、N和顶点A、D、C1的两个截面截去两个角后所得的几何体,则该几何体的主视图为( )2.如图所示,O为正方体ABCDA1B1C1D1的底面ABCD的中点,则下列直线中与B1O垂直的是( )A.A1D B.AA1C.A1D1D.A1C13.在如图所示的四个正方体中,能得出AB⊥CD的是( )4.已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( ) A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l5.将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图2),则在空间四面体ABCD中,AD与BC的位置关系是( )A.相交且垂直B.相交但不垂直C.异面且垂直D.异面但不垂直6.已知三棱锥SABC的所有顶点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为( )A.26B.36C.23D.22二、填空题:本题共2小题,每小题9分.7.如图,在正方体ABCDA1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥PABC的正视图与侧视图的面积的比值为________.8.如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为________.三、解答题:9.(本小题满分14分) 10.如图,四棱锥PABCD中,底面ABCD是平行四边形,若Q是PC的中点,求证:PA∥平面BDQ;10.(本小题14分) 在如图所示的正方体中,分别棱是的中点,求异面直线与所成角的余弦值和诚中学2018-2019学年高二数学周练试题(时间:60分钟,满分:100分命题人:)一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图是一正方体被过棱的中点M、N和顶点A、D、C1的两个截面截去两个角后所得的几何体,则该几何体的主视图为( )解析:选B.还原正方体,如图所示,由题意可知,该几何体的主视图是选项B.2.如图所示,O为正方体ABCDA1B1C1D1的底面ABCD的中点,则下列直线中与B1O垂直的是( )A.A1D B.AA1C.A1D1D.A1C1解析:选D.由题意知,A1C1⊥平面DD1B1B,又OB1⊂面DD1B1B,所以A1C1⊥OB1.3.在如图所示的四个正方体中,能得出AB⊥CD的是( )解析:选A.A选项中,∵CD⊥平面AMB,∴CD⊥AB,B选项中,AB与CD成60°角;C选项中,AB与CD成45°角;D选项中,AB与CD夹角的正切值为 2.4.已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( ) A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l解析:选D.根据所给的已知条件作图,如图所示.由图可知α与β相交,且交线平行于l.5.将图1中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图2),则在空间四面体ABCD中,AD与BC的位置关系是( )C.异面且垂直D.异面但不垂直解析:选C.在题图1中的等腰直角三角形ABC 中,斜边上的中线AD 就是斜边上的高,则AD ⊥BC ,翻折后如题图2,AD 与BC 变成异面直线,而原线段BC 变成两条线段BD 、CD ,这两条线段与AD 垂直,即AD ⊥BD ,AD ⊥CD ,且BD ∩CD =D ,故AD ⊥平面BCD ,所以AD ⊥BC .6.已知三棱锥S ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.26 B.36 C.23D.22解析:选A.在直角三角形ASC 中,AC =1,∠SAC =90°,SC =2,所以SA =4-1=3;同理SB =3.过A 点作SC 的垂线交SC 于D 点,连接DB ,因为△SAC ≌△SBC ,所以BD ⊥SC ,故SC ⊥平面ABD ,且平面ABD 为等腰三角形,因为∠ASC =30°,所以AD =12SA =32,则△ABD 的面积为12×1×AD 2-⎝ ⎛⎭⎪⎫122=24,则三棱锥的体积为13×24×2=26. 二、填空题:本题共2小题,每小题9分.7.如图,在正方体ABCD A 1B 1C 1D 1中,点P 是上底面A 1B 1C 1D 1内一动点,则三棱锥P ABC 的正视图与侧视图的面积的比值为________.解析:如题图所示,设正方体的棱长为a ,则三棱锥P ABC 的正(主)视图与侧(左)视图都是三角形,且面积都是12a 2,所以所求面积的比值为1.答案:18. 如图,矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图,其中O ′A ′=6,O ′C ′=2,则原图形OABC 的面积为________.解析:由题意知原图形OABC 是平行四边形,且OA =BC =6,设平行四边形OABC 的高为OE ,则OE ×12×22=O ′C ′, ∵O ′C ′=2,∴OE =42,∴S ▱OABC =6×42=24 2.答案:24 2三、解答题:9.(本小题满分14分) 10.如图,四棱锥PABCD中,底面ABCD是平行四边形,若Q是PC的中点,求证:PA∥平面BDQ;解:证明:连接AC,交BD于点O,连接OQ.(图略),因为O是AC的中点,Q是PC的中点,所以OQ∥PA,又PA⊄平面BDQ,OQ⊂平面BDQ,所以PA∥平面BDQ.10.(本小题14分) 在如图所示的正方体中,分别棱是的中点,求异面直线与所成角的余弦值【答案】【解析】如下图,过E点作EM//AB,过M点作MN//AD,取MN中点G,所以面EMN//面ABCD,EG//BF, 异面直线与所成角,转化为,不妨设正方形边长为2,GE=,,在中,由余弦定理。
山西省晋中市和诚高中2018-2019学年高二数学8月月考试题

和诚中学2018-2019学年度高二8月月考数学试题考试时间:120分钟 满分:150分 命题人:一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={x |x 2-x -2<0,x ∈R },B ={x |x 2-1≥0,x ∈R },则A ∩B 等于( ) A .{x |-1<x <2} B .{x |x ≤-1或1≤x <2} C .{x |1<x <2} D .{x |1≤x <2} 2.若a <1,b >1,那么下列不等式中正确的是( ) A.1a >1b B .b a>1 C .a 2<b 2D .ab <a +b3.若f (x )=-x 2+mx -1的函数值有正值,则m 的取值范围是( ) A .m <-2或m >2 B .-2<m <2 C .m ≠±2 D .1<m <34.已知z =2x +y ,x ,y 满足⎩⎪⎨⎪⎧y ≥x ,x +y ≤2,x ≥a ,且z 的最大值是最小值的4倍,则实数a 的值是( )A.13 B .14 C.15 D .165.若log a 5<log a 2,则不等式(a -x )⎝⎛⎭⎪⎫x -1a >0的解集为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪a <x <1a B .⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1a <x <a C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >1a 或x <a D .⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <1a 或x >a 6.不等式组⎩⎪⎨⎪⎧-2(x -3)>10,x 2+7x +12≤0的解集为( )A .[-4,-3]B .[-4,-2]C .[-3,-2]D .∅7.在坐标平面上,不等式组⎩⎪⎨⎪⎧y ≥x -1,y ≤-3|x |+1所表示的平面区域的面积为( )A. 2 B .32 C.322D .28.已知x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0x +y -4≤0,y ≥1则z =-2x +y 的最大值是( )A .-1B .-2C .-5D .19.已知x >0,y >0.若2y x +8x y>m 2+2m 恒成立,则实数m 的取值范围是( )A .m ≥4或m ≤-2B .m ≥2或m ≤-4C .-2<m <4D .-4<m <210.已知-1≤x +y ≤4,且2≤x -y ≤3,则z =2x -3y 的取值范围是( ) A .[3,8] B .[3,6] C .[6,7] D .[4,5]11.若x ,y 满足条件⎩⎪⎨⎪⎧3x -5y +6≥0,2x +3y -15≤0,y ≥0,当且仅当x =y =3时,z =ax +y 取得最大值,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-23,35B.⎝ ⎛⎭⎪⎫-∞,-35∪⎝ ⎛⎭⎪⎫23,+∞C.⎝ ⎛⎭⎪⎫-35,23D.⎝ ⎛⎭⎪⎫-∞,-23∪⎝ ⎛⎭⎪⎫35,+∞12.若不等式x 2+ax +1≥0对一切x ∈⎝ ⎛⎦⎥⎤0,12恒成立,则实数a 的最小值为( )A .0B .-2C .-52 D .-3二、填空题:本题共4小题,每小题5分.13.设x ,y ∈R ,且xy ≠0,则(x 2+1y 2)(1x2+4y 2)的最小值为________.14.若a >0,b >0,a +b =2,则下列不等式对一切满足条件的a ,b 恒成立的是________(写出所有正确不等式的编号).①ab ≤1;②a +b ≤2;③a 2+b 2≥2;④1a +1b≥2.15.函数y =2-x -4x(x >0)的值域为________.16.设x >5,P =x -4-x -5,Q =x -2-x -3,则P 与Q 的大小关系是__________. 三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数f (x )=x 2+2x,解不等式f (x )-f (x -1)>2x -1.18.(本小题满分10分)已知方程ax 2+bx +2=0的两根为-12和2.解不等式ax 2+bx -1>0.19.(本小题满分12分)正数x ,y 满足1x +9y=1.(1)求xy的最小值;(2)求x+2y的最小值.20.(本小题满分12分)已知函数f(x)=log3(x2-4x+m)的图像过点(0,1).解不等式:f(x)≤1.21.(本小题满分12分)已知函数f(x)=x2-2x-8,g(x)=2x2-4x-16.(1)求不等式g(x)<0的解集;(2)若对一切x>2,均有f(x)≥(m+2)x-m-15恒成立,求实数m的取值范围.22.(本小题满分12分)某蔬菜基地种植甲、乙两种无公害蔬菜.生产一吨甲种蔬菜需用电力9千瓦时,耗肥4吨,3个工时;生产一吨乙种蔬菜需用电力5千瓦时,耗肥5吨,10个工时,现该基地仅有电力360千瓦时,肥200吨,工时300个.已知生产一吨甲种蔬菜获利700元,生产一吨乙种蔬菜获利1 200元,在上述电力、肥、工时的限制下,问如何安排甲、乙两种蔬菜种植,才能使利润最大?最大利润是多少?和诚中学2018-2019学年度高二8月月考数学试题答案考试时间:120分钟 满分:150分一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是 符合题目要求的.1.已知集合A ={x |x 2-x -2<0,x ∈R },B ={x |x 2-1≥0,x ∈R },则A ∩B 等于( ) A .{x |-1<x <2} B .{x |x ≤-1或1≤x <2} C .{x |1<x <2} D .{x |1≤x <2}解析:选D.因为A ={x |-1<x <2},B ={x |x ≥1或x ≤-1},所以A ∩B ={x |1≤x <2}.2.若a <1,b >1,那么下列不等式中正确的是( ) A.1a >1bB .b a>1 C .a 2<b 2D .ab <a +b解析:选D.利用特值法,令a =-2,b =2,则1a <1b ,A 错;b a<0,B 错;a 2=b 2,C 错.3.若f (x )=-x 2+mx -1的函数值有正值,则m 的取值范围是( ) A .m <-2或m >2 B .-2<m <2 C .m ≠±2D .1<m <3解析:选A.因为f (x )=-x 2+mx -1有正值, 所以Δ=m 2-4>0,所以m >2或m <-2.4.已知z =2x +y ,x ,y 满足⎩⎪⎨⎪⎧y ≥x ,x +y ≤2,x ≥a ,且z 的最大值是最小值的4倍,则实数a 的值是( )A.13 B .14 C.15D .16解析:选B.在坐标平面内画出题中的不等式组表示的平面区域及直线2x +y =0,平移该直线,当相应直线分别经过该平面区域内的点(a ,a )与(1,1)时,相应直线在x 轴上的截距达到最小与最大,此时z =2x +y 取得最小值与最大值,于是有2×1+1=4(2a +a ),a =14.5.若log a 5<log a 2,则不等式(a -x )⎝⎛⎭⎪⎫x -1a >0的解集为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪a <x <1a B .⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1a <x <a C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >1a或x <a D .⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <1a或x >a 解析:选A.由log a 5<log a 2知0<a <1,所以a <1a;不等式(a -x )⎝⎛⎭⎪⎫x -1a >0⇔(x -a )⎝ ⎛⎭⎪⎫x -1a <0,解得a <x <1a.6.不等式组⎩⎪⎨⎪⎧-2(x -3)>10,x 2+7x +12≤0的解集为( )A .[-4,-3]B .[-4,-2]C .[-3,-2]D .∅解析:选A.⎩⎪⎨⎪⎧-2(x -3)>10,x 2+7x +12≤0⇒⎩⎪⎨⎪⎧x -3<-5,(x +3)(x +4)≤0 ⇒⎩⎪⎨⎪⎧x <-2,-4≤x ≤-3⇒-4≤x ≤-3. 7.在坐标平面上,不等式组⎩⎪⎨⎪⎧y ≥x -1,y ≤-3|x |+1所表示的平面区域的面积为( )A. 2 B .32 C.322D .2解析:选B.由题意得,图中阴影部分面积即为所求.B 、C 两点横坐标分别为-1、12,A 、D 两点纵坐标分别为1,-1.所以S △ABC =12×2×⎪⎪⎪⎪⎪⎪12-(-1)=32.8.已知x ,y 满足约束条件⎩⎪⎨⎪⎧x -y ≥0x +y -4≤0,y ≥1则z =-2x +y 的最大值是( )A .-1B .-2C .-5D .1解析:选A.作出可行域,如图中阴影部分所示,易知在点A (1,1)处,z 取得最大值,故z max =-2×1+1=-1.9.已知x >0,y >0.若2y x +8x y>m 2+2m 恒成立,则实数m 的取值范围是( )A .m ≥4或m ≤-2B .m ≥2或m ≤-4C .-2<m <4D .-4<m <2解析:选D.因为x >0,y >0,所以2y x +8x y ≥8(当且仅当2y x =8xy时取“=”).若2y x +8x y>m 2+2m 恒成立,则m 2+2m <8,解之得-4<m <2.10.已知-1≤x +y ≤4,且2≤x -y ≤3,则z =2x -3y 的取值范围是( ) A .[3,8] B .[3,6] C .[6,7]D .[4,5]解析:选A.设2x -3y =λ(x +y )+μ(x -y ), 则(λ+μ)x +(λ-μ)y =2x -3y , 所以⎩⎪⎨⎪⎧λ+μ=2,λ-μ=-3,解得⎩⎪⎨⎪⎧λ=-12,μ=52, 所以z =-12(x +y )+52(x -y ).因为-1≤x +y ≤4, 所以-2≤-12(x +y )≤12.①因为2≤x -y ≤3,所以5≤52(x -y )≤152.②①+②得,3≤-12(x +y )+52(x -y )≤8,所以z 的取值范围是[3,8].11.若x ,y 满足条件⎩⎪⎨⎪⎧3x -5y +6≥0,2x +3y -15≤0,y ≥0,当且仅当x =y =3时,z =ax +y 取得最大值,则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-23,35B.⎝ ⎛⎭⎪⎫-∞,-35∪⎝ ⎛⎭⎪⎫23,+∞ C.⎝ ⎛⎭⎪⎫-35,23D.⎝ ⎛⎭⎪⎫-∞,-23∪⎝ ⎛⎭⎪⎫35,+∞ 解析:选C.直线3x -5y +6=0和直线2x +3y -15=0的斜率分别为k 1=35,k 2=-23,且两直线的交点坐标为(3,3),作出可行域如图所示,当且仅当直线z =ax +y 经过点 (3,3)时,z 取得最大值,则直线z =ax +y 的斜率-a 满足-23<-a <35,解得-35<a <23,故选C.12.若不等式x 2+ax +1≥0对一切x ∈⎝ ⎛⎦⎥⎤0,12恒成立,则实数a 的最小值为( )A .0B .-2C .-52D .-3解析:选C.因为不等式x 2+ax +1≥0对一切x ∈⎝ ⎛⎦⎥⎤0,12恒成立,所以对一切x ∈⎝ ⎛⎦⎥⎤0,12,ax ≥-x 2-1,即a ≥-x 2+1x恒成立.令g (x )=-x 2+1x =-⎝ ⎛⎭⎪⎫x +1x .易知g (x )=-⎝ ⎛⎭⎪⎫x +1x 在⎝ ⎛⎦⎥⎤0,12内为增函数.所以当x =12时,g (x )max =-52,所以a 的取值 范围是⎣⎢⎡⎭⎪⎫-52,+∞,即a 的最小值是-52.故选C.二、填空题:本题共4小题,每小题5分.13.设x ,y ∈R ,且xy ≠0,则(x 2+1y 2)(1x2+4y 2)的最小值为________.解析:⎝ ⎛⎭⎪⎫x 2+1y 2⎝ ⎛⎭⎪⎫1x 2+4y 2=1+4+4x 2y 2+1x 2y 2≥1+4+24x 2y 2·1x 2y2=9,当且仅当4x 2y 2=1x 2y 2,即|xy |=22时等号成立. 答案:914.若a >0,b >0,a +b =2,则下列不等式对一切满足条件的a ,b 恒成立的是________ (写出所有正确不等式的编号).ab ≤1;②a +b ≤2;③a 2+b 2≥2;④1a +1b≥2.解析:两个正数,和为定值,积有最大值,即ab ≤(a +b )24=1,当且仅当a =b 时取等号,故①正确;(a +b )2=a +b +2ab =2+2ab ≤4,当且仅当a =b 时取等号,得a +b ≤2,故②错误;由于a 2+b 22≥(a +b )24=1,故a 2+b 2≥2成立,故③正确;1a +1b =⎝ ⎛⎭⎪⎫1a +1b a +b 2=1+a 2b +b2a ≥1+1=2,当且仅当a =b 时取等号,故④正确. 答案:①③④ 答案:315.函数y =2-x -4x(x >0)的值域为________.解析:当x >0时,y =2-⎝⎛⎭⎪⎫x +4x ≤2-2x ×4x =-2.当且仅当x =4x,x =2时取等号.答案:(-∞,-2]16.设x >5,P =x -4-x -5,Q =x -2-x -3,则P 与Q 的大小关系是__________. 解析:P =x -4-x -5=1x -4+x -5,Q =x -2-x -3=1x -2+x -3,而0<x -4+x -5<x -2+x -3,所以必有P >Q .三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分1 0分)已知函数f (x )=x 2+2x,解不等式f (x )-f (x -1)>2x -1.解:由题意可得x 2+2x -(x -1)2-2x -1>2x -1,化简得2x (x -1)<0,即x (x -1)<0,解得0<x <1.所以原不等式的解集为{x |0<x <1}.18.(本小题满分10分)已知方程ax 2+bx +2=0的两根为-12和2.解不等式ax 2+bx -1>0.解:因为方程ax 2+bx +2=0的两根为-12和2.由根与系数的关系,得⎩⎪⎨⎪⎧-12+2=-b a,-12×2=2a ,解得a =-2,b =3.可知ax 2+bx -1>0,即2x 2-3x +1<0,解得12<x <1.所以不等式ax 2+bx -1>0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12<x <1. 19.(本小题满分12分)正数x ,y 满足1x +9y=1.(1)求xy 的最小值; (2)求x +2y 的最小值. 解:(1)由1=1x +9y≥21x ·9y 得xy ≥36,当且仅当1x =9y,即y =9x =18时取等号,故xy 的最小值为36.(2)由题意可得x +2y =(x +2y )·⎝ ⎛⎭⎪⎫1x +9y =19+2y x +9x y≥19+22y x ·9xy=19+62,当且仅当2y x =9x y,即9x 2=2y 2时取等号,故x +2y 的最小值为19+6 2.20.(本小题满分12分)已知函数f (x )=log 3(x 2-4x +m )的图像过点(0,1). 解不等式:f (x )≤1.解:由已知有f (0)=log 3m =1,所以m =3.f (x )=log 3(x 2-4x +3).由x 2-4x +3>0,得x <1或x >3,所以函数的定义域为(-∞,1)∪(3,+∞). 因为log 3(x 2-4x +3)≤1且y =log 3x 为增函数, 所以0<x 2-4x +3≤3, 所以0≤x <1或3<x ≤4,所以不等式的解集为{x |0≤x <1或3<x ≤4}.21.(本小题满分12分)已知函数f (x )=x 2-2x -8,g (x )=2x 2-4x -16. (1)求不等式g (x )<0的解集;(2)若对一切x >2,均有f (x )≥(m +2)x -m -15恒成立,求实数m 的取值范围. 解:(1)g (x )=2x 2-4x -16<0, 所以(2x +4)(x -4)<0,所以-2<x <4, 所以不等式g (x )<0的解集为{x |-2<x <4}. (2)因为f (x )=x 2-2x -8.当x >2时,f (x )≥(m +2)x -m -15恒成立, 所以x 2-2x -8≥(m +2)x -m -15, 则x 2-4x +7≥m (x -1).所以对一切x >2,均有不等式x 2-4x +7x -1≥m 成立.又x 2-4x +7x -1=(x -1)+4x -1-2≥2(x -1)×4x -1-2=2(当x =3时等号成立). 所以实数m 的取值范围是(-∞,2].22.(本小题满分12分)某蔬菜基地种植甲、乙两种无公害蔬菜.生产一吨甲种蔬菜需 用电力9千瓦时,耗肥4吨,3个工时;生产一吨乙种蔬菜需用电力5千瓦时,耗肥 5吨,10个工时,现该基地仅有电力360千瓦时,肥200吨,工时300个.已知生产 一吨甲种蔬菜获利700元,生产一吨乙种蔬菜获利1 200元,在上述电力、肥、工时 的限制下,问如何安排甲、乙两种蔬菜种植,才能使利润最大?最大利润是多少?解:设种植甲种蔬菜x 吨,乙种蔬菜y 吨,利润为z 元,根据题意可得⎩⎪⎨⎪⎧9x +5y ≤360,4x +5y ≤200,3x +10y ≤300,x ≥0,y ≥0,目标函数为:z =700x +1 200y ,作出二元一次不等式组表示的平面区域,即可行域,如图,作直线:700x +1 200y =0, 即7x +12y =0,平移直线,当直线过A 点时目标函数取最大值.解方程组⎩⎪⎨⎪⎧4x +5y =200,3x +10y =300,得x =20,y =24. 所以点A 的坐标为(20,24).所以z max =700×20+1 200×24=42 800.即种植甲种蔬菜20吨,乙种蔬菜24吨,才能使利润最大,最大利润为42 800元.。
山西省晋中市和诚高中有限公司2018-2019学年高二周练英语试题(6.1-6.2)

和诚中学2018-2019学年高二知识清单、易错题目定时训练(29)时间:60分钟总分100分 2019年6月2日一、阅读理解(每题4分,共40分)AI was never very neat, while my roommate Kate was extremely organized. Each of her objects had its place, but mine always hid somewhere. She even labeled(贴标签)everything. I always looked for everything. Over time, Kate got neater and I got messier. She would push my dirty clothing over, and I would lay my books on her tidy desk. We both got tired of each other.War broke out one evening. Kate came into the room. Soon, I heard her screaming, “Take your shoes away! Why under my bed! ” Deafened, I saw my shoes flying at me.I jumped to my feet and started yelling. She yelled back louder.The room was filled with anger. We could not have stayed together for a single minute but for a phone call. Kate answered it. From her end of the conversation, I could tell right away her grandma was seriously ill. When she hung up, she quickly crawled (爬)under her covers, sobbing.Obviously, that was something she should not go through alone. All of a sudden, a warm feeling of sympathy rose up in my heart.Slowly, I collected the pencils, took back the books, made my bed, cleaned the socks and swept the floor, even on her side. I got so into my work that I even didn’t notice Kate had sat up. She was watching, her tears dried and her expression one of disbelief. Then, she reached out her hands to grasp mine. I looked up into her eyes. She smiled at me, “Thanks. ”Kate and I stayed roommates for the rest of the year. We didn’t al ways agree, but we learned the key to living together: giving in, cleaning up and holding on.1. What made Kate so angry one evening?A. She couldn’t find her books.B. She heard the author shouting loud.C. She got the news that her grandma was ill.D. She saw the authors shoes beneath her bed.2. The author tidied up the room most probably because .A. she was scared by Kate’s angerB. she hated herself for being so messyC. she wanted to show her careD. she was asked by Kate to do so3. How is Paragraph 1 mainly developed?A. By analyzing causes.B. By showing differences.C. By describing a process.D. By following time order.4. What might be the best title for the story?A. My Friend KateB. Hard Work Pays OffC. How to Be OrganizedD. Learning to Be RoommatesBThere have always been a lot of commonly believed but false ideas about being fat and doing exercise. Some people believe that they can’t help putting on weight as they get older, while others hold that if they stop exercising, their muscles will turn into fat. Here are some more myths:I’ll never lose weight--I come from a fat familyWrong! While we can't change the body type we are born with, we can't blame our genes for making us fat. There's plenty of evidence that fatness runs in families, and the main reason is that they share the same habit of eating too much and exercise too little.I am fat because I burn calories slowlyWrong! Fatness is not caused by a slow metabolism(新陈代谢).In fact, although fat people consume more energy than slim people, they also fail to realize how much they eat! Keeping a diary can help you work out your daily food intake mom accurately.Exercise is boringWrong! Anything will become boring if you do it repetitively. The key is to develop a balanced and varied program that's fun as well as progressive. If you enjoy a Sunday walk, take a different mute. If you do yoga, try a Tai chi class. If you like swiping, set yourself a distance or time challenge.No pain, no gainWrong! Exercise is not meant to hurt. Indeed, pain is you body telling you something's wrong, and continuing to exercise could lead to serious injury. You may experience mild discomfort as you begin to exercise regularly, but this is your body adapting to the positive changes in your lifestyle and the aches should disappear relatively quickly. If they don't, rest and seek medical advice.5. What does the author think about being fat?A. It is the family genes that make people fat.B. People are fat because they consume too little energy.C. A diary of exercise can prevent people from becoming fat.D. It is the consequence of people's unbalanced lifestyle.6. According to the author, how can we make exercise mom interesting?A. By taking varied exercise.B. By choosing simple exercise.C. By doing regular exercise.D. By sticking to outdoor exercise.7. What is the author's opinion about "No pain, no gain" in exercising?A. Keeping lit is essentially a painful experience.B. Exercise should be stopped if continuous pain is felt.C. Pain in exercise is a precondition for reaching your goal.D. Getting used to pain leads to positive changes in your body.CThe idea of being able to walk on water has long interested humans greatly. Sadly, biological facts prevent us ever accomplishing such a thing without artificial aid---we simply weigh too much, and all our mass pushes down through our relatively small feet, resulting in a lot of pressure that makes us sink.However, several types of animals can walk on water. One of the most interesting is the common basilisk Basilicus basilicus, a lizard (蜥蜴)native to Central and South America. It can run across water for a distance of several meters, avoiding getting wet by rapidly hitting the water’s surface wi th its feet. The lizard will take as many as 20 steps per second to keep moving forward. For humans to do this, we,d need huge feet that we could bring up to our ears in order to create adequate w hitting. ’’But fortunately there is an alternative : cornflour. By adding enough of this common thickening agent to water (and it does take a lot), you can create a“non-Newtonian” liquid that doesn’t behave like normal water. Now, if the surface of the water is hit hard enough, particles(粒子)in the water group together for a moment to make the surface hard. Move quickly enough and put enough force into each step, and you really can walk across the surface of an adequately thick Liquid of cornflour.Fun though all this may sound, it’s still rather messy and better read about in theory than carried out in practice. If you must do it, then keep the water wings handy in case you start to sink--and take a shower afterward!8. What do we know about Basilicus basilicus from the passage?A. It is light enough to walk on water.B. Its huge feet enable it to stay above water.C. It can run across water at a certain speed.D. Its unique skin keeps it from getting wet in water.9. What is the function of the cornflour according to the passage?A. To create a thick liquid.B. To turn the water into solid.C. To help the liquid behave normally.D. To enable the water to move rapidly.10. What is the author’s attitude toward the idea of humans’ walking on water?A. It is risky but beneficial.B. It is interesting and worth trying.C. It is crazy and cannot become a reality.D. It is impractical though theoretically possible.二、完形填空(每题2分,共40分)A gentle breeze blew through Jennifer’s hair. The golden red sun was___11___. She was on the beach, looking up at the fiery ball. She was ___12___ by its color, deep red in the middle, softly fading into yellow. She could hear nothing but the waves and the seagulls ___13___up above in the sky.The atmosphere ___14___her. After all she had been through, this was what she needed." It's getting ___15___," she thought, "I must go home. My parents will be ___16___where I am." She wondered how her parents would___17___, when she got home after the three days she was___18___.She kept on walking,___19___herself to the bungalow where she spent every summer holiday. The road was deserted. She walked slowly and ___20___. Just in a few hundred meters she would be safe in her house.It was really getting dark now. The sun had set a few minutes before and it was getting cold too. She wished she ___21___her favorite sweater on---it kept her really warm. She imagined having it___22___her. This thought disappeared when she finally saw her front door. It seemed ___23___. The outside garden seemed___24___. She was shocked: her father was usually so strict about keeping everything clean and tidy.She entered the house. First, she went into the kitchen where she saw a___25___written by her father. It said: "Ellen, there is some coffee ___26___ . I went looking." Ellen was her mother but-where was she? She entered her parent’s home. Then she saw her. Her mother, lying on the bed, ___27___.Jennifer would have wanted to wake her up but she looked too tired. So Jennifer just fell asleep beside her. When Jennifer___28___, something was different. She was in her cozy bed in her pajamas.It felt so good being back home. ___29___she heard a voice, "Are you feeling better now? You know you got us very, very ___30___."11. A. disappearing B. setting C. rising D. shining12. A. amazed B. excited C. disappointed D. frightened13. A. moving B. flying C. stepping D. flowing14. A. surprised B. confused C. relaxed D. exhausted15. A. early B. cold C. warm D. late16. A. wondering B. knowing C. ignoring D. finding17. A. say B. take C. like D. react18. A. working B. missing C. spending D. traveling19. A. pointing B. enjoying C. directing D. teaching20. A. easily B. silently C. happily D. willingly21. A. believed B. wished C. guessed D. judged22. A. with B. for C. at D. in23. A. same B. familiar C. difficult D. different24. A. crowded B. tidy C. deserted D. clean25. A. text B. letter C. note D. sentence26. A. ready B. gone C. present D. available27. A. cried B. laughed C. coughed D. slept28. A. woke up B. stayed up C. broke up D. held up29. A. Fortunately B. Similarly C. Suddenly D. Constantly30. A. moved B. lost C. inspired D. scared三、语法填空(共10小题;每小题1分,满分10分)A little boy invited his mother to attend his elementary school's first teacherparent meeting. To the little boy's __31__(happy), she said she would go. This would be the first time that his classmates and teacher met his mother and he was embarrassed by her __32__(appear). Although she was a beautiful woman, there was a severe scar __33__ covered nearly the whole right side of her face. The boy never wanted to talk about why or how she got the scar.At the meeting, the people __34__(impress) by the kindness and natural beauty of his mother though she had a scar on her face, but the little boy was still embarrassed and __35__(hide) himself from everyone. He did, however, get within earshot of a conversation __36__ his mother and his teacher, and heard them speaking.“How did you get the scar on your face?” The teacher asked.The mother replied, “When my son was a baby, he was in a room that caught on fire. Everyone was too afraid to go in __37__ the fire was out of control, so I went in. As I was rushing toward his bed, I saw a beam coming down and I placed myself over him trying to protect him. I was knocked unconscious but __38__(fortunate), a fireman came in and saved both of us.” She touched the burned side of her face. “Th is scar will be on my face for ever, but to this day, I have never regretted doing __39__ I did.”At this point, the little boy came out __40__(run) towards his mother with tears in his eyes. He hugged her and felt a great sense of the sacrifice that his mother had made for him. He held her hand tightly for the rest of the day.四、短文改错:见答题卡部分(共10处错误,共10分)和诚中学2018-2019学年高二知识清单、易错题目定时训练答题卡(29)班级:考号:姓名:第一部分:选择题第二部分:三、语法填空31、32、 33、34、35、36、37、38、39、40、四、短文改错Recently the students in our class have had a heated discussion on if people should keep pets at home in cities. We have two different opinions.Some students thought it’s a good idea to keep pets because many old people who will live alone at home can get some comfort from them. Besides, get along well with animals will make our life interesting. However, other students are against the idea. In their opinions, if too many people keep pets at home, it’s harmful for the environment. What is worse, pets may make too many noise and even attack people.As for me, I’m in favor of the former. I don’t think it’s bad for us to keep pets at home. But you must take some measures to prevent them from serious polluting our environment.和诚中学2018-2019学年高二知识清单、易错题目定时训练答案(29)第一部分:选择题第二部分:短文改错三、语法填空31.unhappiness 32.appearance 33.that/which 34.were impressed 35.hid36.between 37.because 38.fortunately 39.what 40.running四、短文改错。
山西省晋中市和诚高中有限公司2018-2019学年高二周练(

和诚2018-2019学年度高二物理知识清单、易错题定时训练考试时间:45分钟命题人:满分:100分一、判断题(将题后括号内打上“√”或“×”每题2分,共20分)1、2g氢气所含的原子数目为阿伏伽德罗常数。
()2、分子直径的数量级为10-10m. ( )3、温度升高,物体分子的热运动变剧烈。
()4、悬浮微粒的布朗运动,说明了微粒内部分子做无规则热运动。
()5、分子间作用力的合力表现为引力时,分子间不存在斥力。
()6、分子间距离减小时,引力和斥力都增大,当斥力比引力增加的快。
()7、分子动理论是在一定实验基础上提出的。
()8、只要温度不变且处处相等,系统就一定处于平衡态。
()9、温度变化10C,也就是温度变化1K。
()10、摄氏温度与热力学温度的关系为:t=273+T ()二、选择题((本题共12小题,每小题4分,1--8题单选,9—12题多选,共计48分)1、下列各种说法中错误的有 ( )A.普朗克在研究黑体的热辐射问题中提出了能量子假说B.一束光照射到某种金属上不能发生光电效应,是因为该束光的照射时间太短C.在光的单缝衍射实验中,狭缝越窄,光子动量的不确定量越大D.任何一个运动物体,无论是大到太阳、地球,还是小到电子、质子,都与一种波相对应,这就是物质波,物质波是概率波2、甲、乙两铁球质量分别是m 1=1kg,m2=2kg,在光滑平面上沿同一直线运动,速度分别是v1=6m/s、v2=2m/s。
甲追上乙发生正碰后两物体的速度有可能是 ( ) A.v1′=7m/s,v2′=1.5m/s B.v1′=2m/s,v2′=4m/sC.v1′=3.5m/s,v2′=3m/s D.v1′=4m/s,v2′=3m/s3、一个质量为m、电荷量为q的带电粒子,由静止开始经加速电场加速后(加速电压为U),该粒子的德布罗意波长为 ( )A.h2mqUB.h2mqUC.h2mqU2mqU D.hmqU4、人眼对绿光最为敏感,正常人的眼睛接收到波长为530nm 的绿光时,只要每秒有6个绿光的光子射入瞳孔,眼睛就能察觉,普朗克常量为6.63×10-34J·s,光速为3.0×108m /s ,则人眼能察觉到绿光时所接收到的最小功率是 ( )A .2.3×10-18W B .3.8×10-19WC .7.0×10-10WD .1.2×10-18W 5、关于下列四幅图说法正确的是 ( )A .玻尔原子理论的基本假设认为,电子绕核运行轨道的半径是任意的B .光电效应产生的条件为:光强大于临界值C .电子束通过铝箔时的衍射图样证实了运动电子具有波动性D .发现少数α粒子发生了较大偏转,说明金原子质量大而且很坚硬6、如图所示,实线表示金原子核电场的等势线,虚线表示α粒子在金核电场中散射时的运动轨迹。
山西省晋中市和诚高中2019-2020高二数学上学期周练8

山西省晋中市和诚高中2018-2019学年高二数学上学期周练8(时间:60分钟,满分:100分 命题人:)一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,l α,l β,则( ).A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l2.已知正四棱柱ABCD -A 1B 1C 1D 1中,AB =2,1CC =E 为CC 1的中点,则直线AC 1与平面BED 的距离为( )A .2B D .13.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为163B.169 C.83 D.3294.如图,平面α⊥平面β,A ∈α,B ∈β,AB 与两平面α,β所成的角分别为4π和6π.过A ,B 分别作两平面交线的垂线,垂足为A ′,B ′,则AB ∶A ′B ′等于∶B.3∶C.3∶D.4∶5.设三棱柱ABC —A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B —APQC 的体积为( )A .16VB .14VC .13VD .12V6.正方体1111ABCD A B C D -中,P 、Q 、R 分别是AB 、AD 、11B C 的中点.那么,正方体的过P 、Q 、R 的截面图形是( )(A) 三角形 (B) 四边形 (C) 五边形 (D) 六边形二、填空题:本题共2小题,每小题9分.7.已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB =6,BC =O ABCD 的体积为__________.8.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有 .(填写所有正确命题的编号)三、解答题:9.(本小题满分14分) △ABC的内角A,B,C的对边分别为a,b,c,已知cos(A-C)+cos B=1,a=2c,如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=PA=2,E是PC上的一点,PE=2EC.(1)证明:PC⊥平面BED;(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.10.(本题14分) (本小题满分12分)如图,四棱锥P ABCD-中,底面ABCD为矩形,PD⊥底面ABCD,=,E、F别为CD、PB的中点.AD PD(Ⅰ) 求证:EF⊥平面PAB;(Ⅱ) 设AB=,求AC与平面AEF所成的角的大小.(求出所求角的一个三角函数值即可)和诚中学2018-2019学年高二数学周练试题(时间:60分钟,满分:100分 命题人:)一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β.直线l 满足l ⊥m ,l ⊥n ,l α,l β,则( ).A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l 【答案】:D【解析】因为m ⊥α,l ⊥m ,lα,所以l ∥α.同理可得l ∥β.又因为m ,n 为异面直线,所以α与β相交,且l 平行于它们的交线.故选D.2.已知正四棱柱ABCD -A 1B 1C 1D 1中,AB =2,1CC E 为CC 1的中点,则直线AC 1与平面BED 的距离为( )A .2B D .1 【答案】 D又△AC C 1为等腰直角三角形,∴CH =2.∴HM =1.3.过球的一条半径的中点,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为163B.169 C.83 D.329【答案】4.如图,平面α⊥平面β,A ∈α,B ∈β,AB 与两平面α,β所成的角分别为4π和6π.过A ,B 分别作两平面交线的垂线,垂足为A ′,B ′,则AB ∶A ′B ′等于∶B.3∶C.3∶D.4∶【答案】5.设三棱柱ABC —A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B —APQC 的体积为( )A .16VB .14VC .13VD .12V【答案】C【解析】连接11,BA BC ,在侧面平行四边形11AAC C 中,∵1PA QC =, ∴ 四边形APQC 的面积1S =四边形11PQA C 的面积2S , 记B 到面11AAC C 的距离为h ,∴113B APQC V S h -=,11213B PQAC V S h -=, ∴11B APQC B PQA C V V --=,∵11113B A B C V V -=,∴11233B APQC B PQA C V V V V V --+=-=,∴3B APQC V V -=.6.正方体1111ABCD A B C D -中,P 、Q 、R 分别是AB 、AD 、11B C 的中点.那么,正方体的过P 、Q 、R 的截面图形是( )(A) 三角形 (B) 四边形(C) 五边形(D) 六边形【答案】D二、填空题:本题共2小题,每小题9分.7.已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且AB =6,BC =O ABCD 的体积为__________.【答案】【解析】8.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有 .(填写所有正确命题的编号)【答案】②③④三、解答题:9.(本小题满分14分) △ABC的内角A,B,C的对边分别为a,b,c,已知cos(A-C)+cos B=1,a=2c,如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,AC=PA=2,E是PC上的一点,PE=2EC.(1)证明:PC⊥平面BED;(2)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.【解析】解法一:(1)证明:因为底面ABCD为菱形,所以BD⊥AC.又PA⊥底面ABCD,所以PC⊥BD.设AC∩BD=F,连结EF.因为AC=PA=2,PE=2EC,故PC=EC=,FC=从而PC FC =,ACEC =, 因为PC ACFC EC=,∠FCE =∠PCA , 所以△FCE ∽△PCA ,∠FEC =∠PAC =90°, 由此知PC ⊥EF .PC 与平面BED 内两条相交直线BD ,EF 都垂直,所以PC ⊥平面BED .10.(本小题14分) (本小题满分12分)如图,四棱锥P ABCD -中,底面ABCD 为矩形,PD ⊥底面ABCD ,AD PD =,E 、F 分别为CD 、PB 的中点.(Ⅰ) 求证:EF ⊥平面PAB ;(Ⅱ) 设AB =,求AC 与平面AEF 所成的角的大小.(求出所求角的一个三角函数值即可)∵PB、FA为平面PAB内的相交直线∴EF⊥平面PAB。
山西省晋中市和诚高中有限公司2018-2019学年高二上学期周练数学试题(3) Word版含答案

和诚中学2018-2019学年高二数学周练试题一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若x ≠-2且y ≠1,则M =x 2+y 2+4x -2y 的值与-5的大小关系是( )A .M >-5B .M <-5C .M ≥-5D .M ≤-52.设x ,y >0,且x +2y =3,则1x +1y的最小值为( ) A .2B.32 C .1+223 D .3+2 23.若不等式ax 2+bx +c >0的解集是(-4,1),则不等式b (x 2-1)+a (x +3)+c >0 的解集为 ( ) A.⎝ ⎛⎭⎪⎫-43,1 B .(-∞,1)∪⎝ ⎛⎭⎪⎫43,+∞ C .(-1,4) D .(-∞,-2)∪(1,+∞)4.已知实数x ,y 满足x 2+y 2=1,则(1-xy )(1+xy )有( )A .最小值12和最大值1B .最小值34和最大值1C .最小值12和最大值34D .最小值15.【2015高考湖北,文6】函数256()lg 3x x f x x -+=+-的定义域为( )A .(2,3)B .(2,4]C .(2,3)(3,4] D .(1,3)(3,6]-6.设10()2,0x x f x x ⎧≥⎪=⎨<⎪⎩,则((2))f f -=( ) A .1- B .14 C .12 D .32二、填空题:本题共2小题,每小题9分.7.若a =ln 22,b =ln 33,c =ln 55,则a ,b , c 的大小关系是________(由小到大排列).8.函数125x y x -=+的值域是___________三、解答题:9.(本小题满分14分) 求函数12++=x x y 的值域.10.(本小题14分) 求函数1212xx y -=+的值域。
和诚中学高二数学知识清单定时训练不等式、函数答案 2018、8、26(时间:60分钟,满分:100分)一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若x ≠-2且y ≠1,则M =x 2+y 2+4x -2y 的值与-5的大小关系是( )A .M >-5B .M <-5C .M ≥-5D .M ≤-5 解析:M -(-5)=x 2+y 2+4x -2y +5=(x +2)2+(y -1)2,∵x ≠-2,y ≠1,∴(x +2)2>0,(y -1)2>0,因此(x +2)2+(y -1)2>0.故M >-5. 答案:A2.设x ,y >0,且x +2y =3,则1x +1y的最小值为( ) A .2 B.32 C .1+223 D .3+2 2解析:1x +1y =13(3x +3y )=13(x +2y x +x +2y y )=13(2y x +x y +3)≥13(22+3)=232+1, 当且仅当2y x =x y ,即x =32-3,y =3-322时取等号.答案:C 3.若不等式ax 2+bx +c >0的解集是(-4,1),则不等式b (x 2-1)+a (x +3)+c >0 的解集为 ( ) A.⎝ ⎛⎭⎪⎫-43,1 B .(-∞,1)∪⎝ ⎛⎭⎪⎫43,+∞ C .(-1,4) D .(-∞,-2)∪(1,+∞)答案:A4.已知实数x ,y 满足x 2+y 2=1,则(1-xy )(1+xy )有( )A .最小值12和最大值1B .最小值34和最大值1C .最小值12和最大值34D .最小值1 解析:选B. 因为x 2y 2≤⎝ ⎛⎭⎪⎫x 2+y 222=14,当且仅当x 2=y 2=12时,等号成立,所以 (1-xy )(1+xy )=1-x 2y 2≥34.因为x 2y 2≥0,所以34≤1-x 2y 2≤1.5.【2015高考湖北,文6】函数256()lg 3x x f x x -+=+-的定义域为( ) A .(2,3)B .(2,4]C .(2,3)(3,4]D .(1,3)(3,6]-【解析】由函数()y f x =的表达式可知,函数()f x 的定义域应满足条件:2564||0,03x x x x -+-≥>-,解之得22,2,3x x x -≤≤>≠,即函数()f x 的定义域为(2,3)(3,4],故应选C .6.设10()2,0x x f x x ⎧≥⎪=⎨<⎪⎩,则((2))f f -=( )A .1-B .14 C .12 D .32【答案】C 【解析】因为21(2)24f --==,所以111((2))()11422f f f -===-=, 二、填空题:本题共2小题,每小题9分.7.若a =ln 22,b =ln 33,c =ln 55,则a ,b ,c 的大小关系是________(由小到大排列). 解析:因为a -b =3ln 2-2ln 36=ln 8-ln 96<0,所以a <b . 因为a -c =5ln 2-2ln 510=ln 32-ln 2510>0,所以a >c . 所以c <a <b . 答案:c <a <b8.函数125x y x -=+的值域是___________ 解:∵177(25)112222525225x x y x x x -++-===-++++, ∵72025x ≠+,∴12y ≠-, ∴函数125x y x -=+的值域为1{|}2y y ≠-。
山西省晋中市和诚高中高二数学上学期周练7

和诚中学2018-2019学年高二数学周练试题时间:60分钟,满分:100分6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.M N 和顶点A 、D G 的两个截面截去两个角后所得的几何体,则该几何体的主视图为 ( )B . AA、选择题:本题共 1.如图是一正方体被过棱的中点2.如图所示,O 为正方体ABCEA 1B 1CD 的底面 ABCD 勺中点,则下列直线中与 BO 垂直的是A. ADC. ADA BA B G DD. AQ3•在如图所示的四个正方体中,能得出ABL CD的是()则()A. a // 3 且 I 〃aB. a 丄3且I 丄3C. a 与3相交,且交线垂直于ID. a 与3相交,且交线平行于l5.将图1中的等腰直角三角形 ABC 沿斜边BC 的中线折起得到空间四面体 ABCD 如图 在空间四面体 ABCDK AD 与 BC 的位置关系是()4.已知m n 为异面直线, mL 平面 a , n 丄平面 3 .直线l 满足I 丄m l 丄n , l ? a ,l ? 3,2),则A.相交且垂直B. 相交但不垂直C.异面且垂直D.异面但不垂直6 .已知三棱锥S - ABO 的所有顶点都在球 0的球面上,△ ABC 是边长为1的正三角形,SC 为球B0的直径,且SC= 2,则此棱锥的体积为()A. C.二、填空题:本题共 2小题,每小题9分.7.如图,在正方体 ABCDABCD 中,点P 是上底面 ABQD 内一动点,则三棱锥 PABC 勺正视 图与侧视图的面积的比值为 _______________ .& 如图,矩形 O A B' C'是水平放置的一个平面图形的直观图,其中O A'= 6 ,O C = 2,则原图形 OABC 勺面积为 ____________ .三、解答题:9.(本小题满分14分)10 •如图,四棱锥 P-ABC [中,底面ABC [是平行四边形,若Q 是PC 的中点,求证:PA//平面BDQ 10.(本小题14分)在如图所示的正方体“V 中,■分别棱是。
山西省晋中市和诚高中高二数学上学期周练8

(时间:60分钟,满分:100分命题人:)BED 的距离为(4.如图,平面a 丄平面卩,A € a , B€卩,AB 与两平面a ,卩所成的角分别为一和一•过A B 4 6 分别作两平面交线的垂线,垂足为A , B',则AB : A B'等于A.2 : 1B.3 : 1C.3 : 2D.4 : 35.设三棱柱 ABC-A 1B 1C 1的体积为V, P 、Q 分别是侧棱 AA 、CC 上的点,且PA=QC 则四棱锥B- APQC 勺体积为()A . 1V6B. *4C. \31 D. -V 26.正方体 ABCD AB1GD 1 中,P 、Q 、 过P 、Q 、R 的截面图形是()R 分另【J 是 AB 、AD 、 BG 的中点.那么,正方体的(A)三角形 (B)四边形(C)五边形(D)六边形、填空题:本题共 2小题,每小题9 分.、选择题:本题共 6小题,每小题 9分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知m n 为异面直线, I 芒a ,丨严|卩,则( mL 平面 n 丄平面卩.直线I 满足I 丄m I 丄n,A . a // 卩且 I 〃a a 丄卩且I 丄卩C. a 与卩 相交,且交线垂直于 a 与卩相交,且交线平行于I2.已知正四棱柱 ABC D ABCD 中, AB= 2, CC i2 2 , E 为CC 的中点,则直线AC 与平面A. 2 B. 、3 C .23.过球的一条半径的中点,作垂直于该半,则所得截面的面积与球的表面积的比为A. 16B. C . 3D.169 327.已知矩形ABCD勺顶点都在半径为4的球0的球面上,且AB= 6, BC= Z 3 ,则棱锥OABCD 的体积为_________________ .& a,卩是两个平面,m n是两条直线,有下列四个命题:①如果mb n, ml a, n//卩,那么a丄卩.②如果mb a , n // a,那么m b n.③如果a / 3 , m a ,那么m//卩.④如果m// n, a // 3,那么m与a所成的角和n与卩所成的角相等其中正确的命题有.(填写所有正确命题的编号)三、解答题:9. (本小题满分14分)△ ABC的内角A, B, C的对边分别为a, b, c,已知cos(A—C)+ cos B =1, a= 2c,如图,四棱锥P— ABCD^,底面ABC西菱形,PAL底面ABCD AC 2迈,PA=2, E是PC上的一点,PE= 2EC(1)证明:PC L平面BED⑵设二面角A—PB- C为90°,求PD与平面PBC所成角的大小.10. (本题14分)(本小题满分12分)如图,四棱锥P ABCD中,底面ABCD为矩形,PD底面ABCD , AD PD , E、F别为CD、PB的中点.(I )求证:EF 平面PAB ;(求出所求角的一个三角函数(n )设AB , '2BC,求AC与平面AEF所成的角的大小.值即可)和诚中学2018-2019学年高二数学周练试题(时间:60分钟,满分:100分命题人:)一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知m n为异面直线,ml平面a , n丄平面卩.直线I满足I丄m l丄n,1 L—a,I 已,贝叫).A. a// 卩且1//aB. a丄卩且1丄3C. a与卩相交, 且交线垂直于D. a与卩相交, 且交线平行于【答案】:D【解析】因为ml a , I丄m |Q匚a ,所以I //a.同理可得I //卩.又因为m n为异面直线,所以a与卩相交,且I平行于它们的交线.故选 D.2.已知正四棱柱ABC D ABGD中,AB= 2, CG 2丘,E为CC的中点,则直线BED的距离为()A. 2 B .「3 C .D . 1【答案】D【解析】连结M交肋于点©连结陶又cq二2血_,则良作于点已交加于点庇由磁为&4CC1的中位综知,C^yOE? M为CH的中点.由BD1AC,卫口丄月迅知,,迟D丄面EQG.\CM1BD.面氐也二为直线.4CjiJ平面BDE的距离•AC与平面A 8又A A©为等腰直角三角形,•••CH=2. ••• HM1.3.过球的一条半径的中点 ,作垂直于该半径的平面,则所得截面的面积与球的表面积的比为5.设三棱柱 ABC- A 1B 1C 1的体积为V,P 、Q 分别是侧棱AA 、CG 上的点,且 PA=QC 则四棱锥【解析】:设球半径为E 截面半轻丸rjv f 侄在RTM 阳中卫二亍如〜亍妙 j.j r I 1 在中,——= -AA^-AB. AB 2 2二任RTU4®中显迟一45一A. 216B.9 16C. 38 D. 232^A -4.如图,平面a 丄平面 卩,A € a , B€卩,AB 与两平面 a ,卩所成的角分别为—和一•过A B4 6分别作两平面交线的垂线,垂足为A B'等于A.2 : 1B.3 : 1D.4 : 3【答案】:AC.3 : 2勺体积为(A. 1V B 1V C-V D. 1V6 4 3 2 【答案】C【解析】连接BA-, BC-,在侧面平行四边形AAC-C中,••• PA QC-,四边形APQC勺面积3=四边形PQA1C1的面积S2,记B到面AAC1C的距离为h, --V B APQC-Sh ,3V B PQA I C1…V B APQC V B PQA I C1 ,'V B A1B1C11匚V ,…V B APQC3V B PQA1C1V V32V,.••3VV B APQC二36•正方体ABCD AB-C-D-中,P、Q、R分别是AB、AD、BC-的中点•那么,正方体的过P、Q、R的截面图形是()(A)三角形(四边形(C)五边形(D)六边形【答案】D【解析】如虱作RG // PQ交CiDi于G连结QP与CB交于屹连结皿交BB1于瓦连结PE、瓯豹截面的咅吩?囑.同理琏结PQ交B于皿连结盹交D6于F,连結QF、面PQERE为六边形一勺体积二、填空题:本题共2小题,每小题9分.为(7.已知矩形ABCD勺顶点都在半径为4的球0的球面上,且AB= 6, BC= ^3,则棱锥OABCD 的体积为. 【答案】8.3【解析】矩形的对角红国长为:胪+口奇=4心」所以球到矩形的K瞎为;以豳―, 所以棱锥O-ABCD旳体积为:ix6x2^>2=8^ .故答秦为:8J3& a,卩是两个平面,m n是两条直线,有下列四个命题:①如果mln, ml a, n//卩,那么a丄卩.②如果ml a , n // a,那么mL n.③如果a / 3 , m a ,那么m卩.④如果m// n, a // 3,那么m与a所成的角和n与卩所成的角相等•其中正确的命题有.(填写所有正确命题的编号)【答案】②③④【解析】试题分析:对于①,膈丄禺™I丄隅则比”的位置关系无袪确忌故错误』对于②厨科忖所以■过直钱川作平面$与平面直相交于宜线6则川匕因为朋丄区所以jn丄匚所以加丄忙故②正确■对于③,由两个平面平行的性质可知正确・对于④,由线面所成角的走哭和等角走理可去嗔正晦故正确的命题有②③④.三、解答题:9. (本小题满分14分)△ ABC的内角A, B, C的对边分别为a, b, c,已知cos(A—C)+ cos B=1, a= 2c,如图,四棱锥P— ABCD^,底面ABCD为菱形,PAL底面ABCD AC 2^2 , PA=2, E是PC上的一点,PE= 2EC⑴证明:P®平面BED⑵设二面角A—PB- C为90°,求PD与平面PBC所成角的大小. 【解析】解法一:⑴ 证明:因为底面ABCD^菱形,所以BDL AC又PAL底面ABCD所以PC L BD设A8 BD=F,连结EF因为AC 2 2 , PA=2, PE=2EC故PC 2 .3 , EC , FC 、2 ,3从而匹,6,也.6,FC ECPC AC因为匚一——,/ FCE=Z PCAFC EC所以△ FC0A PCA / FE(=Z PAC90° ,由此知PC X EFPC与平面BE»两条相交直线BD EF都垂直,所以PC X平面BED⑺在平面期5内过点丄作丄隔G为垂足.因为二面^A-PB-C为帥%所以平面她丄平面?又平面胃婕门平面PBC-PB,故』G丄平面PEG AG±£C.砂与平面PAB内两条相5直线開恥都垂直,故6C丄平面PAB,于是BC1AB,所次底面ABCD为正方形,AD=2J PD =』Pf+ 3 =辺.设刀到平面PBC的距离为也因为ADI/BC,且QX平面PBC t ECC平面PBC f故平面PBC,乩Q两点到平面RBC的亜离相等,即J IG—.谡加与平面PM所成的角为酝则Sifii2t= —=-.PD 2所以PD与平面期C所成的角为30°.10. (本小题14分)(本小题满分12分)如图,四棱锥P ABCD中,底面ABCD为矩形,PD 底面ABCD,AD PD,E、F 分别为CD、PB的中点.(I )求证:EF 平面PAB ;(II)设AB 2BC,求AC与平面AEF所成的角的大小.(求出所求角的一个三角函数值即可)-11 -【解析】方法一:⑴证明:连结EPTPD丄底面ABCD』DE在平面ABCD内/.PD1DE;又CE=ED, PD-AD-BC /.RlABCE^RriPDE.\PE=BETF为PB的中点二EF 丄PBTDA 丄AB由三垂线定理得PA丄AB二在R IA PAB中PF=AF,又PE=BE=EA/.AEFP^AEFA•\EF1FA••• PB FA为平面PAB内的相交直线••• EF丄平面PAB-12 -QI]解:不妨设EC=1, f?]PI>AD=l J AB-血」AC= ^3 AAPAB^等股直角三角砒且PBT, F为苴斜边中駄BIT目AF丄PE TPB与平面AEF内两条相交直线EF. AF 都垂直J.PB丄平面AEF连结EE交AC于②作GH/;BP交EF干也则GH"平面AEFZGAH为AC与平面AEF所成的角由AEGC<^ABGA可知EG=1GIX,EG=-EB, AG=-AC=^^'■AC与平面AEF所成的角为afc^in-ii --3 -。
山西省晋中市和诚高中有限公司2018-2019学年高二周练(20)数学(理)试题

和诚中学2018-2019学年度高二理科数学知识清单易错题目训练考试时间:60分钟 满分:100分一、选择题(本题共8小题,每小题7分,共56分.)1. 已知函数()π,0,cos ∈+=x x x y ,那么下列说法正确的是( ) A. 2π=x 是极大值点 B.2π=x 是极小值点 C. 没有极值点 D. 有且只有一个极值点2.已知函数()21ln x x y +-=,则函数的极值情况是( )A .有极小值B .有极大值C .既有极大值又有极小值D .无极值3. 已知()()x g x f ,是定义在R 是的连续函数(图象连续不断),如果()()x g x f ,当且仅当0=x 时函数值为0,且()()x g x f ≥,则下列情形不可能...的是( ) A .0是()x f 的极大值,也是()x g 的极大值 B . 0是()x f 的极大值,不是()x g 的极值C .0是()x f 的极小值,也是()x g 的极小值D .0是()x f 的极小值,不是()x g 的极值4.已知函数()qx px x x f --=23的图象与x 轴切于()0,1点,则函数()x f 的极值是( ) A .极大值为427,极小值为0 B .极大值为0,极小值为427C .极大值为0,极小值为-427D .极大值为-427,极小值为0 5. 设函数()x f 定义域为R ,()000≠x x 是()x f 的极大值点,以下结论正确的是( )A .()()0,x f x f R x ≤∈∀B .0x -是()x f -的极小值点C .0x -是()x f -的极小值点D .0x -是()x f --的极小值点6.已知e 为自然对数的底数,设函数()()()()2,111=--=k x e x f k x ,则( ) A .当1=k 时,()x f 在1=x 处取到极小值 B .当1=k 时,()x f 在1=x 处取到极大值C .当2=k 时,()x f 在1=x 处取到极小值D .当2=k 时,()x f 在1=x 处取到极大值7.函数331x x y -+=有( )A .极小值-2,极大值2B .极小值-2,极大值3C .极小值-1,极大值1D .极小值-1,极大值38.对于函数()233x x x f -=,给出命题: ①()x f 是增函数,无极值; ②()x f 是减函数,无极值;③()x f 的递增区间为()()+∞∞-,2,0,,递减区间为()2,0; ④()00=f 是极大值,()42-=f 是极小值.其中正确的命题有( )A .1个B .2个C .3个D .4个二、填空题(本题共3小题,每小题8分,共24分)9.函数122+=x x y 当_____=x 时,有极大值______. 10.已知函数()x x x f 33-=的图象与直线a y =有相异三个公共点,则a 的取值范围是________.11.函数a ax x y +-=23在()1,0内有极小值,则实数a 的取值范围是____________. 三、解答题(共2小题,每题10,共20分)12. 设函数()()0323>+++=a d cx bx x a x f ,且方程()09=-'x x f 的两个根分别为1和4.若()x f 在()+∞∞-,内无极值点,求a 的取值范围.13.已知函数2ln )(bx x a x f +=图像上点))1(,1(f P 处的切线方程为032=--y x(1)判断方程21)(-=x f 解的个数 (2)若函数4ln )()(-+=m x f x g 在]2,1[e 上恰有两个零点,求实数m 的取值范围。
【精编文档】山西省晋中市和诚高中2018-2019学年高二数学周练试卷5.18理.doc

山西省晋中市和诚高中2018-2019学年高二数学周练试题(5.18)理(无答案)一、选择题(本题共8小题,每小题7分,共56分.)1.的展开式中各项的二项式系数之和为()A.-1 B.1 C.-512 D.5122.已知两个正态分布密度函数的图象如图所示,则()A.B.C.D.3.若函数,为常数,则()A.B.C.D.4.若函数在时取得极值,则()A.2 B.3 C.4 D.55.用数学归纳法证明时,由时的假设到证明时,等式左边应添加的式子是()A.B.C.D.6.设,则A.2 B.C.D.7.吃零食是中学生中普遍存在的现象,吃零食对学生身体发有有诸多不利影响,影响学生的健康成长,如表是性别与吃零食的列联表:附:K2=,根据以上数据,你有多大把握认为“喜欢吃零食与性别有关”()A.95%以上B.97.5%以上C.99%以上D.85%以上8.改革开放以来,中国经济飞速发展,科学技术突飞猛进。
高铁、核电、桥梁、激光、通信、人工智能、航空航天、移动支付、量子通讯、特高压输电等许多技术都领先于世界。
厉害了,我的国!把“厉害了我的国”这六个字随机地排成一排,其中“厉”、“害”这两个字必须相邻(可以交换顺序),“了”、“的”这两个助词不能相邻,则不同排法的种数为()。
A.72 B.108 C.144 D.288二、填空题(本题共3小题,每小题8分,共24分)9.已知变量之间具有良好的线性关系,若通过10组数据得到的回归方程为,且,则__________.10.已知,若为互质的正整数),由以上等式,可推测 的值,则 ________.11.已知()f x 为偶函数,当0x <时, ()()ln 3f x x x =-+,则曲线()y f x =在点()1,3-处的切线方程是__________.三、解答题(共2小题,每题10,共20分)12.若二项式n的展开式中的常数项为第5项.(1)求的值; (2)求展开式中系数最大的项;13.现有甲、乙、丙三名学生参加某大学的自主招生考试,考试分两轮,第一轮笔试,第二轮面试,只有第一轮笔试通过才有资格进入第二轮面试,面试通过就可以在高考录取中获得该校的优惠加分,两轮考试相互独立.根据以往多次的模拟测试,甲、乙、丙三名学生能通过笔试的概率分别为0.4,0.8,0.5,能通过面试的概率分别为0.8,0.4,0.64.根据这些数据我们可以预测:(1)甲、乙、丙三名学生中至少有两名学生通过第一轮笔试的概率; (2)甲、乙、丙三名学生能获得该校优惠加分的人数X 的数学期望.。
山西省晋中市和诚高中高二数学8月月考试题(2021年整理)

山西省晋中市和诚高中2018-2019学年高二数学8月月考试题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山西省晋中市和诚高中2018-2019学年高二数学8月月考试题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山西省晋中市和诚高中2018-2019学年高二数学8月月考试题的全部内容。
和诚中学2018-2019学年度高二8月月考数学试题考试时间:120分钟满分:150分命题人:一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x2-x-2<0,x∈R},B={x|x2-1≥0,x∈R},则A∩B等于( ) A.{x|-1<x〈2} B.{x|x≤-1或1≤x<2} C.{x|1<x〈2} D.{x|1≤x〈2} 2.若a<1,b>1,那么下列不等式中正确的是( )A。
错误!>错误! B.错误!>1 C.a2<b2 D.ab<a+b3.若f(x)=-x2+mx-1的函数值有正值,则m的取值范围是( )A.m<-2或m〉2 B.-2〈m〈2 C.m≠±2 D.1<m〈34.已知z=2x+y,x,y满足错误!且z的最大值是最小值的4倍,则实数a的值是( )A.错误!B.错误! C.错误! D.错误!5.若log a5〈log a2,则不等式(a-x)错误!〉0的解集为( )A。
错误!B.错误!C。
错误!D.错误!的解集为( )6.不等式组{-2(x-3)>10,x2+7x+12≤0A.[-4,-3] B.[-4,-2] C.[-3,-2] D.∅7.在坐标平面上,不等式组错误!所表示的平面区域的面积为()A。
山西省晋中市和诚高中2018_2019学年高二数学周练试题(5.11)文(无答案)

山西省晋中市和诚高中2018-2019学年高二数学周练试题(5.11)文(无答案)一选择题(本题共8小题,每小题7分,共56分.)1.(2018·湖南六校联考)下列有关命题的说法正确的是( )A.命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”B.命题“若xy=0,则x=0”的逆否命题为真C.命题“∃x0∈R,使得x20+x0+1<0”的否定是“∀x∈R,均有x2+x+1≥0”D.“m=1”是“直线x-my=0和直线x+my=0互相垂直”的充要条件2.(2018·河南洛阳二模)设全集U=R,集合A={x|log2x≤1},B={x|x2+x-2≥0},则A∩∁U B=( )A.(0,1] B.(-2,2) C.(0,1) D.[-2,2]3.已知命题p:有的四边形是平行四边形,则( )A.非p:有的四边形不是平行四边形 B.非p:有的四边形是非平行四边形C.非p:所有的四边形都是平行四边形 D.非p:所有的四边形都不是平行四边形4.(2019·唐山模拟)设集合A={x∈Z|y=log2(9-x2) },B={x|x∈N},则A∩B中元素的个数为( )A.5 B.4 C.3 D.25.给出以下四个命题:①若2≤x<3,则(x-2)(x-3)≤0;②已知x,y∈R,若x=y=0,则x2+y2=0;③若x2-3x+2=0,则x=1或x=2;④若x,y都是偶数或x,y都是奇数,则x+y是偶数.则下列判断正确的是( )A.①的否命题为真 B.②的逆命题为假C.③的否命题为真 D.④的逆否命题为假6.(2018·湖南八市联考)已知数列{a n}是等差数列,m,p,q为正整数,则“p+q=2m”是“a p+a q=2a m”的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件7.(2018·湖南衡阳联考二)下列说法错误的是( )A.“若x≠2,则x2-5x+6≠0”的逆否命题是“若x2-5x+6=0,则x=2”B.“x>3”是“x2-5x+6>0”的充分不必要条件C.“∀x∈R,x2-5x+6≠0”的否定是“∃x0∈R,x20-5x0+6=0”D.命题“在锐角△ABC中,sin A<cos B”为真命题8.(2018·山西太原期末)已知a,b都是实数,那么“2a>2b”是“a2>b2”的( ) A.充分不必要条件 B.必要不充分条件C .充要条件D .既不充分也不必要条件二、填空题(本题共3小题,每小题8分,共24分)9.(2018·衡水金卷A 信息卷五)命题p :若x >0,则x >a ;命题q :若m ≤a -2,则m <sin x (x ∈R )恒成立.若p 的逆命题,q 的逆否命题都是真命题,则实数a 的取值范围是________.10.设函数f (x )=a x +b x -c x ,其中c >a >0,c >b >0.记集合M ={(a ,b ,c )|a ,b ,c 不能构成一个三角形的三条边长,且a =b },则(a ,b ,c )∈M 所对应的f (x )的零点的取值集合为________.11.某校高三(1)班50个学生选择选修模块课程,他们在A ,B ,C 三个模块中进行选择,且至少需要选择1个模块,具体模块选择的情况如下表:则三个模块都选择的学生人数是________.三、解答题(共2小题,每题10,共20分)12.已知m ∈R ,设p :∀x ∈[-1,1],x 2-2x -4m 2+8m -2≥0;q :∃x 0∈[1,2],log 12(x 20-mx 0+1)<-1.如果“p ∨q ”为真,“p ∧q ”为假,求实数m 的取值范围.13.(2018·河北邢台一中月考)已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于x=1对称,当x∈[0,1]时,f(x)=2x-1.(1)当x∈[1,2]时,求f(x)的解析式;(2)计算f(0)+f(1)+f(2)+…+f(2018)的值.。
山西省晋中市2018-2019学年高二数学上学期周练试题(2)

山西省晋中市2018-2019学年高二数学上学期周练试题(2)(时间:60分钟,满分:100分)一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 、c ∈R ,a >b ,则下列不等式成立的是( )A.1a <1bB .a 2>b 2 C.ac 2+1>b c 2+1 D .a |c |>b |c | 2.若a ,b ,c 是不全相等的正数.给出下列判断:①(a -b )2+(b -c )2+(c -a )2≠0;②a >b 与b <a 及a =b 中至少有一个成立;③a ≠c ,b ≠c ,a ≠b 不能同时成立.其中正确判断的个数为( )A .0B .1C .2D .33.直线3x +2y +5=0把平面分成两个区域,下列各点与原点位于同一区域的是( )A .(-3,4)B .(-3,-4)C .(0,-3)D .(-3,2)4.若实数x ,y 满足⎩⎪⎨⎪⎧ x -y +1≥0x +y ≥0x ≤0,则z =3x +2y 的最小值是( )A .0B .1 C. 3 D .9 5.不等式ax 2+bx +2>0的解集是(-12,13),则a -b 等于( ) A .10B .14C .-4D .-106.已知z =2x +y ,x ,y 满足⎩⎪⎨⎪⎧y ≥x ,x +y ≤2,x ≥a ,且z 的最大值是最小值的4倍,则实数a 的值是( )A.13B .14 C.15 D .16二、填空题:本题共2小题,每小题9分.7.x ≥0,y ≥0,x +y ≤4所围成的平面区域的周长是________.8.若角α,β满足-π2<α<β<π2,则2α-β的取值范围是__________. 三、解答题:9.(本小题14分)已知a >0,试比较a 与1a的大小.10.(本小题14分)某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A 、B 两种规格的金属板,每张面积分别为2 m 2与3 m 2.用A 种规格的金属板可造甲种产品3个,乙种产品5个;用B 种规格的金属板可造甲、乙两种产品各6个.问A 、B 两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?和诚学校高二数学知识清单定时训练不等式(2)试题与答案 2018、8、12 (时间:60分钟,满分:100分)一、选择题:本题共6小题,每小题9分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a 、b 、c ∈R ,a >b ,则下列不等式成立的是( )A.1a <1b B .a 2>b 2 C.a c 2+1>b c 2+1 D .a |c |>b |c |解析:根据不等式的性质,知C 正确;若a >0>b ,则1a >1b,A 不正确;若a =1,b =-2,则B 不正确;若c =0,则D 不正确,所以选C. 答案:C2.若a ,b ,c 是不全相等的正数.给出下列判断:①(a -b )2+(b -c )2+(c -a )2≠0;②a >b 与b <a 及a =b 中至少有一个成立;③a ≠c ,b ≠c ,a ≠b 不能同时成立.其中正确判断的个数为( )A .0B .1C .2D .3答案:D3.直线3x +2y +5=0把平面分成两个区域,下列各点与原点位于同一区域的是( )A .(-3,4)B .(-3,-4)C .(0,-3)D .(-3,2) 解析:当x =y =0时,3x +2y +5=5>0,所以原点一侧的平面区域对应的不等式是3x +2y +5>0,可以验证,仅有点(-3,4)的坐标满足3x +2y +5>0. 答案:A4.若实数x ,y 满足⎩⎪⎨⎪⎧ x -y +1≥0x +y ≥0x ≤0,则z =3x +2y 的最小值是( ) A .0 B .1 C. 3 D .9解析:在坐标平面内画出已知不等式组表示的平面区域,此区域是以O (0,0),A (0,1),B (-12,12)为顶点的三角形内部(含边界).当x =y =0时,x +2y 取最小值0,所以z =3x +2y 的最小值是1. 答案:B5.不等式ax 2+bx +2>0的解集是(-12,13),则a -b 等于( ) A .10 B .14 C .-4 D .-10解析:∵2a =(-12)×13=-16,∴a =-12.又-b a =-12+13=-16,∴b =-2,∴a -b =-10.答案:D6.已知z =2x +y ,x ,y 满足⎩⎪⎨⎪⎧y ≥x ,x +y ≤2,x ≥a ,且z 的最大值是最小值的4倍,则实数a 的值是( )A.13 B .14 C.15 D .16解析:选B.在坐标平面内画出题中的不等式组表示的平面区域及直线2x +y =0,平移该直线,当相应直线分别经过该平面区域内的点(a ,a )与(1,1)时,相应直线在x 轴上的截距达到最小与最大,此时z =2x +y 取得最小值与最大值,于是有2×1+1=4(2a +a ),a =14. 二、填空题:本题共2小题,每小题9分.7.x ≥0,y ≥0,x +y ≤4所围成的平面区域的周长是________.解析:图1如下图1中阴影部分所示,围成的平面区域是Rt △OAB .可求得A (4,0),B (0,4),则OA =OB =4,AB =42,所以Rt △OAB 的周长是4+4+42=8+4 2.答案:8+4 28.若角α,β满足-π2<α<β<π2,则2α-β的取值范围是__________. 解析:∵-π2<α<β<π2, ∴-π<α-β<0.∴2α-β=α+α-β.∴-3π2<2α-β<π2. 答案:⎝ ⎛⎭⎪⎫-3π2,π2三、解答题:9.(本小题14分)已知a >0,试比较a 与1a的大小. 解:a -1a =a 2-1a =(a -1)(a +1)a.因为a >0,所以当a >1时,(a -1)(a +1)a >0,有a >1a ;当a =1时,(a-1)(a +1)a=0,有a =1a ;当0<a <1时,(a -1)(a +1)a <0,有a <1a. 综上,当a >1时,a >1a ;当a =1时,a =1a ;当0<a <1时,a <1a. 10.(本小题14分)某工厂生产甲、乙两种产品,其产量分别为45个与55个,所用原料分别为A 、B 两种规格的金属板,每张面积分别为2 m 2与3 m 2.用A 种规格的金属板可造甲种产品3个,乙种产品5个;用B 种规格的金属板可造甲、乙两种产品各6个.问A 、B 两种规格的金属板各取多少张,才能完成计划,并使总的用料面积最省?解图2设A ,B 两种金属板各取x 张,y 张,用料面积为z ,则约束条件为⎩⎪⎨⎪⎧ 3x +6y ≥45,5x +6y ≥55,x ≥0,y ≥0,目标函数z =2x +3y .作出可行域,如右图2所示的阴影部分.目标函数z =2x +3y 即直线y =-23x +z 3,其斜率为-23,在y 轴上的截距为z 3,且随z 变化的一族平行线.由图知,当直线z =2x +3y 过可行域上的点M 时,截距最小,z 最小.解方程组⎩⎪⎨⎪⎧ 5x +6y =55,3x +6y =45,得M 点的坐标为(5,5),此时z min =2×5+3×5=25(m 2),即两种金属板各取5张时,用料面积最省.。
山西省晋中市和诚高中2018_2019学年高二数学周练试题(21)文(无答案)

山西省晋中市和诚高中2018-2019学年高二数学周练试题(21)文(无答案)一、选择题(本题共8小题,每小题7分,共56分.)1:若复数221z ii=++,其中i是虚数单位,则复数z的模为()2D. 22:已知复数1z i=-,则221z zz-=-()A. 2iB. 2i- C. 2 D. 2-3:设i是虚数单位,且20141i kiki-=-,则实数k等于()A. 2B. 0C. 1D. 1-4:复数321iz ii=-+,在复平面上对应的点位于()A.第一象限 B.第二象限 C.第三象限 D.第四象限5:若1a izi+=-是纯虚数,则实数a的值是()A. 1- B. 0 C. 1 D. 2 6:若复数()()2321a a a i-++-是纯虚数,则实数a的值是()A. 1B. 2C. 1或2D. 1-7:已知复数1z=-,z是z的共轭复数,则z z⋅=()A.14B.12C. 1D. 28:函数xxy ln=在()5,0上的单调性为( )A.单调增函数 B.单调减函数C.在⎪⎭⎫⎝⎛e10,上单调递减,在⎪⎭⎫⎝⎛5,1e上单调递增 D.在⎪⎭⎫⎝⎛e10,上单调递增,在⎪⎭⎫⎝⎛5,1e上二、填空题(本题共3小题,每小题8分,共24分)9:设117,,12ia b R a bii-∈+=-(i是虚数单位),则a b+的值是____________10:设1z 是复数,211z z iz =-(其中1z 表示1z 的共轭复数),已知2z 的实部是1-,则2z 的虚部是___________11:已知复数1z 满足()()1211z i i -+=-(i 是虚数单位),复数2z 的虚部为2,且12z z ⋅是实数,则2z =____________三、解答题(共2小题,每题10,共20分)12.已知函数()()x e k x x f -=.(1)求()x f 的单调区间; (2)求()x f 在区间[]1,0上的最小值.13、已知函数x x x f ln )(⋅=(1)求函数)(x f 的最小值;(2)若对所有1≥x 都有1)(-≥ax x f ,求实数a 的取值范围.。
晋中市高中2018-2019学年高二上学期第二次月考试卷数学

晋中市高中2018-2019学年高二上学期第二次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1. 已知椭圆C :+=1(a >b >0)的左、右焦点为F 1、F 2,离心率为,过F 2的直线l 交C 于A 、B两点,若△AF1B 的周长为4,则C 的方程为( )A .+=1B .+y 2=1C .+=1D .+=12. 已知一三棱锥的三视图如图所示,那么它的体积为( )A .13 B .23C .1D .2 3. 设()f x 是奇函数,且在(0,)+∞内是增函数,又(3)0f -=,则()0x f x ⋅<的解集是( )A .{}|303x x x -<<>或B . {}|3003x x x -<<<<或 C .{}|33x x x <->或 D . {}|303x x x <-<<或4. 已知等差数列{a n }满足2a 3﹣a +2a 13=0,且数列{b n } 是等比数列,若b 8=a 8,则b 4b 12=( )A .2B .4C .8D .165. 数列{a n }满足a 1=3,a n ﹣a n •a n+1=1,A n 表示{a n }前n 项之积,则A 2016的值为( )A .﹣B .C .﹣1D .16. 函数f (x )=Asin (ωx+φ)(A >0,ω>0,)的部分图象如图所示,则函数y=f (x )对应的解析式为( )A .B .C .D .7. 已知集合M={1,4,7},M ∪N=M ,则集合N 不可能是( )A .∅B .{1,4}C .MD .{2,7}8. 在《张邱建算经》中有一道题:“今有女子不善织布,逐日所织的布比同数递减,初日织五尺, 末一日织一尺,计织三十日”,由此推断,该女子到第10日时,大约已经完成三十日织布总量的( ) A .33% B .49% C .62% D .88% 9. 已知PD ⊥矩形ABCD 所在的平面,图中相互垂直的平面有( )A .2对B .3对C .4对D .5对10.α是第四象限角,,则sin α=( )A .B .C .D .11.已知f (x )在R 上是奇函数,且f (x+4)=f (x ),当x ∈(0,2)时,f (x )=2x 2,则f (7)=( ) A .﹣2 B .2 C .﹣98 D .9812.2016年3月“两会”期间,有代表提出适当下调“五险一金”的缴存比例,现拟从某工厂职工中抽取20名代表调查对这一提案的态度,已知该厂青年,中年,老年职工人数分别为350,500,150,按分层抽样的方法,应从青年职工中抽取的人数为( ) A. 5 B.6 C.7D.10【命题意图】本题主要考查分层抽样的方法的运用,属容易题.二、填空题13.如图是一个正方体的展开图,在原正方体中直线AB 与CD 的位置关系是 .14.函数y=a x +1(a >0且a ≠1)的图象必经过点 (填点的坐标)15.小明想利用树影测量他家有房子旁的一棵树的高度,但由于地形的原因,树的影子总有一部分落在墙上,某时刻他测得树留在地面部分的影子长为1.4米,留在墙部分的影高为1.2米,同时,他又测得院子中一个直径为1.2米的石球的影子长(球与地面的接触点和地面上阴影边缘的最大距离)为0.8米,根据以上信息,可求得这棵树的高度是 米.(太阳光线可看作为平行光线)16.以点(1,3)和(5,﹣1)为端点的线段的中垂线的方程是 .17.(sinx+1)dx 的值为 .18.当0,1x ∈()时,函数()e 1xf x =-的图象不在函数2()g x x ax =-的下方,则实数a 的取值范围是___________.【命题意图】本题考查函数图象间的关系、利用导数研究函数的单调性,意在考查等价转化能力、逻辑思维能力、运算求解能力.三、解答题19.(本题满分13分)已知圆1C 的圆心在坐标原点O ,且与直线1l :062=+-y x 相切,设点A 为圆上 一动点,⊥AM x 轴于点M ,且动点N 满足OM OA ON )2133(21-+=,设动点N 的轨迹为曲线C . (1)求曲线C 的方程;(2)若动直线2l :m kx y +=与曲线C 有且仅有一个公共点,过)0,1(1-F ,)0,1(2F 两点分别作21l P F ⊥,21l Q F ⊥,垂足分别为P ,Q ,且记1d 为点1F 到直线2l 的距离,2d 为点2F 到直线2l 的距离,3d 为点P到点Q 的距离,试探索321)(d d d ⋅+是否存在最值?若存在,请求出最值.20.某公司春节联欢会中设一抽奖活动:在一个不透明的口袋中装入外形一样号码分别为1,2,3,…,10的十个小球.活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖;奖金30元,三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金. (1)员工甲抽奖一次所得奖金的分布列与期望;(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数的方差是多少?21.19.已知函数f (x )=ln.22.已知数列{a n}满足a1=a,a n+1=(n∈N*).(1)求a2,a3,a4;(2)猜测数列{a n}的通项公式,并用数学归纳法证明.23.已知y=f(x)的定义域为[1,4],f(1)=2,f(2)=3.当x∈[1,2]时,f(x)的图象为线段;当x∈[2,4]时,f(x)的图象为二次函数图象的一部分,且顶点为(3,1).(1)求f(x)的解析式;(2)求f(x)的值域.24.已知等差数列{a n}满足a2=0,a6+a8=10.(1)求数列{a n}的通项公式;(2)求数列{}的前n项和.晋中市高中2018-2019学年高二上学期第二次月考试卷数学(参考答案)一、选择题1. 【答案】A【解析】解:∵△AF1B 的周长为4,∵△AF 1B 的周长=|AF 1|+|AF 2|+|BF 1|+|BF 2|=2a+2a=4a ,∴4a=4,∴a=,∵离心率为,∴,c=1,∴b==,∴椭圆C 的方程为+=1.故选:A .【点评】本题考查椭圆的定义与方程,考查椭圆的几何性质,考查学生的计算能力,属于基础题.2. 【答案】 B【解析】解析:本题考查三视图与几何体的体积的计算.如图该三棱锥是边长为2的正方体1111ABCD A B C D -中的一个四面体1ACED ,其中11ED =,∴该三棱锥的体积为112(12)2323⨯⨯⨯⨯=,选B . 3. 【答案】B 【解析】试题分析:因为()f x 为奇函数且()30f -=,所以()30f =,又因为()f x 在区间()0,+∞上为增函数且()30f =,所以当()0,3x ∈时,()0f x <,当()3,x ∈+∞时,()0f x >,再根据奇函数图象关于原点对称可知:当()3,0x ∈-时,()0f x >,当(),3x ∈-∞-时,()0f x <,所以满足()0x f x ⋅<的x 的取值范围是:()3,0x ∈-或()0,3x ∈。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山西省晋中市和诚高中2018-2019学年高二数学周练试题(5.11)
理(无答案)
一、选择题(本题共8小题,每小题7分,共56分.)
1.将2封信随意投入3个邮箱,不同的投法有
A.3种
B.6种
C.8种
D.9种
2.已知函数,则
3.设随机变量,则
4.两名男生和两名女生随机站成一排照相,则两名男生相邻的概率为
5.袋中有三个红球,两个蓝球,现每次摸出一个球,不放回地摸取两次,则在第一次摸到蓝球的条件下,第二次摸到红球的概率为
6.由数字0,1,2,3,4,5组成的奇偶数字相间且无重复数字的六位数的个数是
A.60
B.48
C.36
D.24
7.若函数在R上有小于0的极值点,则实数a的取值范围是
8.已知函数. ,若对,都有
成立,则a的取值范围是
二、填空题(本题共3小题,每小题8分,共24分)
9.已知离散型随机变量X的分布列为
则m=
_________________
10.已
知,
则
11.甲乙两名选手进行一场羽毛球比赛,采用三局二胜制,先胜两局者赢得比赛,
比赛随即
结束,已知任一局甲胜的概率为p,若甲赢得比赛的概率为q,则q-p取得最大值
时p=
_________________
三、解答题(共2小题,每题10,共20分)
12. 某地区为调查新生婴儿健康状况,随机抽取6名8个月龄婴儿称量体重(单位:千
克),称量结果分别为6, 8,9,9,9.5,10.已知8个月龄婴儿体重超过7.2千克,不超过9.8千克为“标准体重”,否则为“不标准体重”.
(1)根据样本估计总体思想,将频率视为概率,若从该地区全部8个月龄婴儿中任取3名进行称重,则至少有2名婴儿为“标准体重”的概率是多少?
(2)从抽取的6名婴儿中,随机选取4名,设X表示抽到的“标准体重”人数,求X的
分布列和数学期望.
13.某市举办数学知识竞赛活动,共5000名学生参加,竞赛分为初试和复试,复试环节共3道题,其中2道单选题,1道多选题,得分规则如下:参赛学生每答对一道单选题得2分,答错得0分,答对多选题得3分,答错得0分,答完3道题后的得分之和为参赛学生的复试成绩.
(1)通过分析可以认为学生初试成绩X服从正态分布,其中
144,试估计初试成绩不低于90分的人数;
(2)已知小强已通过初试,他在复试中单选题的正答率为,多选题的正答率为且每道题回答正确与否互不影响.记小强复试成绩为y,求y的分布列及数学期望. 附:。
