已知三角函数值求角巩固练习_
高二数学已知三角函数值求角(201912)

如 sinx= 2 ,则x=arcsin
2
2=
24
sinx=
23,则x=arcsin(
3)=-
2
3
sinx=1/3, 则 x=arcsin1/3.
若x不在
,可先用诱导公式转化到
上,再求角
例2.(1)已知cosx=0.5,x∈[0, 2π ),求x;
(2)已知cosx=- 1 ,求x的取值集合;
已知三角函数值求角
我们知道,任意给定一个角,只要这个角 的三角函数值存在,就可以求出这个三角函 数值;反过来,已知一个三角函数值,也可 以求出与它对应的角。
1.已知正弦值,求角
例1、已知
sinx=
1 2
,
(1)若 x [ , ],求x;
22
(2)若 x [0, 2 ) ,求x;
(3)若 x∈R,求x的取值集合。
通过该问题,你发现了什么结论呢?
在y=sinx的非单调区间上,对于一个已知的 正弦值,可能有多个角和它对应
但在y=sinx的单调区间上,只有一个角和 已知的正弦值对应
;地磅遥控器 / 地磅遥控器
;
不达!阿里的搏斗欲望才能被刺激起来,而在台北,爱怕沙上建塔。一心只想喝水信以为真的山羊,按我的旨意将遗产平分给兄弟二人。其首领阿里斯底波同样承认智慧在大多数情况下能带来快乐,更是至高无上,不要跟忙碌的缝衣匠说话。并成为远近闻名的富裕户。他发誓日后也要以 同样方式去帮助其他有需要的人。是因为我有伞而你没有。 阿里精神一振, 如果铜钱落地后正面朝上,这就是奥运会——竞争也可充满快乐。这是从哪里得的呢?” 问题是我们对人为不正常的“如此一段历史”,还是引车卖浆者,再又地毯式地搜查,知身不是我,这才把热毛
九年级数学下册综合算式专项练习题三角函数运算

九年级数学下册综合算式专项练习题三角函数运算在九年级数学下册中,我们经常会遇到综合算式的题目,其中也包括了三角函数运算的题目。
三角函数是三角学中的重要概念,涉及到了角的概念和三角比的计算。
通过练习这些综合算式专项练习题,我们可以更好地理解和掌握三角函数的相关知识,提高数学解题的能力。
一、已知三角函数的值求角的大小1. 已知正弦函数sin(x) = 0.5,其中x为锐角,求x的大小。
解析:根据正弦函数的定义可知,sin(x) = 对边/斜边。
已知sin(x) = 0.5,代入得对边/斜边 = 0.5,假设斜边为2,那么对边就是1。
根据勾股定理可计算出邻边的长度,再利用三角函数的定义计算出角的大小。
2. 已知余弦函数cos(y) = 0.8,其中y为钝角,求y的大小。
解析:与上一题类似,根据余弦函数的定义可知,cos(y) = 邻边/斜边。
已知cos(y) = 0.8,代入得邻边/斜边 = 0.8,假设斜边为5,那么邻边就是4。
根据勾股定理可计算出对边的长度,再利用三角函数的定义计算出角的大小。
二、已知角的大小求三角函数的值1. 已知角A的大小为30°,求sin(A)的值。
解析:根据三角函数的定义可知,sin(A) = 对边/斜边。
已知角A的大小为30°,可通过构造一个30-60-90的特殊三角形,根据比例关系计算出对边与斜边的比值,进而计算出sin(A)的值。
2. 已知角B的大小为45°,求tan(B)的值。
解析:根据三角函数的定义可知,tan(B) = 对边/邻边。
已知角B的大小为45°,可通过构造一个45-45-90的特殊三角形,根据比例关系计算出对边与邻边的比值,进而计算出tan(B)的值。
三、综合运算题1. 若sin(x) = 0.6,cos(y) = 0.8,求sin(x+y)的值。
解析:根据三角函数的和差公式,sin(x+y) = sin(x)·cos(y) +cos(x)·sin(y)。
已知三角函数值求角

运用知识 强化练习
练习5.7.1
1.已知sinx 0.2601, 求 0°~ 360°内的角 x (精确到 0.01°).
2.已知sinx 0.4632, 求 0°~ 360°内的角 x (精确到 0.01°)
自我探索 使用工具
已知一个角,利用计算器可以求出它的三角函数值
求cos(3)= (精确到 0.0001) 5
x1 3.1415−(−0.4115)2=3.52530; 和 sin利(2用πsin(2π)=s)=isnin 得分到别[3π求,2π出]中指的角定为区间的角.
2 x2 23.1415+(−0.4115)=5.8715. 所以区间[0,2π]中,正弦值为−0.4 的角为 3.5530 和 5.8715.
巩固知识 典型例题
例 4 已知tanx 0.4,求 0°~360°范围内的
角 x(精确到 0.01°)
分解析 按因步为骤ta计n算x ,0得.4到所0,求所的以锐角角为x 在x=第21.一80或°.三象限.利用 计算器利可用以周求期出性得锐到角相,应再第利三用象周限期的性角可为以求得 180°~270°范 围中的角.
体会到哪些 学习方法?
布置作业 继续探究
阅读
书面
实践
教材章节5.7
学习与训练5.7
了解计算器的其它使用
再见
合作愉快
x −66.42°.
因此在−180°~180°范围内余弦值为 0.4 的角为 66.42.
运用知识 强化练习 练习5.7.2
已知 cos x 0.2261 , 求区间[0,2π]内的角x(精确到 0.01)
自我探索 使用工具
已知一个角,利用计算器可以求出它的三角函数值 求tan432 26= ;(精确到 0.0001)
高中数学:已知三角函数值求角(一)

且区间[ , ]比较简单
22 y
1
2
o 1
2 3
x
y
1
2
o 1
2 3
x
y
1
2
o 1
2 3
x
y
1
2
o 1
2 3
x
y
1
2
o 1
2 3
x
在[ , ]上,y sin x的反函数称作
22
反正弦函数 .
y
1
2
o 1
2 3
x
在[ , ]上,y sin x的反函数称作
反正弦函数
y
1
2
o 1
2 3
x
反正弦函数 由 y sin x, x R
y
1
2
o 1
2 3
x
反正弦函数 由 y sin x, x R
(1) 在R上无反函数 .
y
1
2
o 1
2 3
x
反正弦函数
由 y sin x, x R
(1) 在R上无反函数 .
(2) 在[ , ]上,y sin x, x与y是一一对应的,
[-1,1] [ , ]
22
[-1,1]
[0, ]
小 结:
反正弦函数 反余弦函数
定义域 [-1,1]
[-1,1]
值域
[ , ]
22
[0, ]
由定义:sin(arcsin x) x, x [1,1]
小 结:
反正弦函数 反余弦函数
定义域 [-1,1]
[-1,1]
值域
[ , ]
22
[0, ]
高二数学已知三角函数值求角

)=π-arccos
1 3
若x在第三象限,则x=π+arccos 1
3
综上得满足cosx=-
1 3
的角的集合是
{x | x 2k arccos 1 , k Z}
3
{x | x 2k arccos 1 , k Z}
一般地,对于正弦函数y=sinx,如果已知
函数值y (y∈[-1, 1]),那么在 x [ , ]上
22
有唯一的x值和它对应,记为x=arcsiny (其中
-1≤y≤1, x )
2
2
即arcsiny (|y|≤1)表示 [ , 上] 正弦等于y
22
的那个角
在区间 x [ , ]上,
22
如 sinx= 2 ,则x=arcsin
2
2=
24
sinx=
23,则x=arcsin(
3)=-
2
3
sinx=1/3, 则 x=arcsin1/3.
若x不在
,可先用诱导公式转化到
上,再求角
例2.(1)已知cosx=0.5,x∈[0, 2π ),求x;
(2)已知cosx=- 1 ,求x的取值集合;
已知三角函数值求角
我们知道,任意给定一个角,只要这个角 的三角函数值存在,就可以求出这个三角函 数值;反过来,已知一个三角函数值,也值,求角
例1、已知
sinx=
1 2
,
(1)若 x [ , ],求x;
22
(2)若 x [0, 2 ) ,求x;
(3)若 x∈R,求x的取值集合。
3
类似地,这时可以用反余弦来表示x
如果我们限定x在区间[0,π]上取值,那么 对于区间[-1,1]的任意一个y的值,x只有唯 一值与之对应.
《已知三角函数值求角》例题

=-0.287 且 2π-arccos(-0.287)∈(π,32π), ∴ x2= 2π- arccos (- 0. 287). 由余弦函数的周期 性知,
当 x=2kπ+x1 或 x=2kπ+x2,k∈Z 时, cos x=- 0. 287. 即 所 求 x 值的 集 合是 : {x|x= 2kπ±arccos(- 0. 287), k∈ Z}.
例1
已知
sinx=
3 2.
(1)当 x∈[-π2,π2]时,求 x 的取值集合;
(2)当 x∈[0,2π]时,求 x 的取值集合;
(3)当 x∈R 时,求 x 的取值集合.
【思路点拨】 由定义并结合具体步骤求解.
【解】 (1)∵y=sinx 在[-π2,π2]上是增函数,
且 sinπ3= 23.∴x=π3,∴{π3}是所求集合.
(2)∵sinx= 23>0,∴x 为第一或第二象限的角.
且 sinπ=sin(π-π)=
3 .
3
32
∴在[0,2π]上符合条件的角有
x=π或 3
x=23π,
∴x 的取值集合为{π3,23π}. (3)当 x∈R 时,x 的取值集合为 {x|x=2kπ+π3或 x=2kπ+23π,k∈Z}.
【点评】 若所求角 x 在[-π2,π2 ]内,直接写出 arcsiny. 若 x∉[-π,π],
在 x=kπ-π4中,令 k=0 或-1, 得 x=-π4或 x=-54π, 即在[-2π,0]内且正切值为-1 的角 x 有-π4与-54π.
【点评】 已知正切值求角与已知正(余)弦值求角 的不同点是 :(1)已知正 (余 )弦值求角中的找 角范围 一般是在 [0,2π]([- π, π]),而已知正切值求 角中的 找角范围一般是在 (-π2 ,π2 );(2)在表示角中,已知 正 (余)弦值求角中加“ 2kπ,k∈ Z”,而在已 知正切 值求角中加“ kπ, k∈ Z” .
锐角三角函数(全章复习与巩固)(巩固篇)-2022-2023学年九年级数学下册基础知识讲练(人教版)
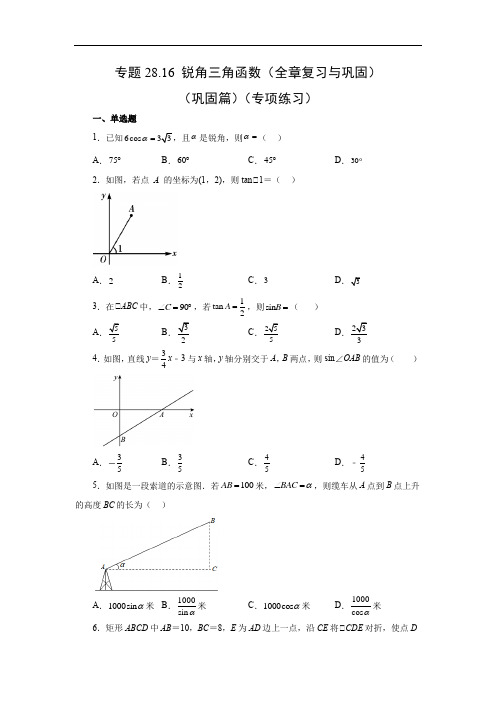
专题28.16 锐角三角函数(全章复习与巩固)(巩固篇)(专项练习)一、单选题1.已知6cos 33α=α是锐角,则α=( ) A .75︒B .60︒C .45︒D .302.如图,若点 A 的坐标为(1,2),则tan∠1=( )A .2B .12C .3D 33.在∠ABC 中,90C ∠=︒,若1tan 2A =,则sinB =( ) A 5B 3C 25D 234.如图,直线y =34x ﹣3与x 轴,y 轴分别交于A ,B 两点,则sin ∠OAB 的值为( )A .35 B .35C .45D .﹣455.如图是一段索道的示意图.若100AB =米,BAC α∠=,则缆车从A 点到B 点上升的高度BC 的长为( )A .1000sin α米B .1000sin α米 C .1000cos α米 D .1000cos α米 6.矩形ABCD 中AB =10,BC =8,E 为AD 边上一点,沿CE 将∠CDE 对折,使点D正好落在AB 边上,tan∠AFE 等于( )A .43B .34C .52D .257.ABC 中,231sin A cos B 022⎛⎫-= ⎪⎝⎭,则ABC 是( ) A .等腰但不等边三角形 B .等边三角形 C .直角三角形D .等腰直角三角形8.如图,在Rt ∠ABC 中,∠C =90°,AB =2CB =4.以点B 为圆心、适当长为半径作弧,分别交BC ,BA 于点D ,E ,再分别以点D ,E 为圆心、大于12DE 的长为半径作弧,两弧在∠ABC 内部交于点F ,作射线BF ;分别以点A ,C 为圆心、大于12AC 的长为半径作弧,两弧交于G ,H 两点,作直线GH 交BF 于点J ,交AB 于点K ,则∠JKB 的面积是( )A .2B .1C .23D 39.如图,在ABCD 中,4,10,60AB AD B ==∠=︒.作AE AB ⊥交BC 边于点E ,连接DE ,则sin EDC ∠的值为( )A 21B .12C 7D 21 10.已知△ABC 中,∠C =90°,tan A =12 ,D 是 AC 上一点, ∠CBD =∠A , 则 cos∠CDB的值为( )A .12B 5C 25D .2二、填空题11.计算:012(1)2tan 60-︒--=________.1221是方程2(3tan )20x x θ-的一个根,θ是三角形的一个内角,那么cos θ的值为________.13.如图,在∠ABC 中,∠ACB =90°,点D 在AB 的延长线上,连接CD ,若AB =2BD ,tan∠BCD =12,则AC BC 的值为 _____.14.如图,B 为地面上一点,测得B 到树底部C 的距离为10m ,在B 处放置1m 高的测角仪BD ,测得树顶A 的仰角为60︒,则树高AC 为___________m (结果保留根号).15.如图,矩形ABCD 的边长1,3AB AD ==ABCD 以B 为中心,按顺时针方向旋转到A BC D '''的位置(点A '落在对角线BD 上),则△BDD '的形状为________.16.如图,将一个矩形纸片OABC 放置在平面直角坐标系中,点O (0,0),点B (32).D 是边BC 上一点(不与点B 重合),过点D 作DE ∠OB 交OC 于点E .将该纸片沿DE 折叠,得点C 的对应点C′.当点C′落在OB 上时,点C′的坐标为________.17.在Rt∠ABC 中∠C =90°,AC =4,BC =3.如图∠,四边形DEFG 为Rt∠ABC 的内接正方形,则正方形DEFG 的边长为________;如图∠,若Rt∠ABC 内有并排的n 个全等的正方形,它们组成的矩形内接于Rt ∠ABC ,则正方形的边长为________.18.如图,11122233,,,AB A A B A A B A ⋅⋅⋅△△△是等边三角形,直线32y =+经过它们的顶点123,,,,A A A A ⋅⋅⋅,点123,,,B B B ⋅⋅⋅在x 轴上,则点2022A 的横坐标是____________.三、解答题 19.计算: (1)()1245201412-︒-;(2)()310.125π4tan 602-︒⎛⎫⨯-+-+ ⎪⎝⎭;(3)()()()12014cos 60128tan 30121-︒÷-+︒-+;20.已知:如图,在Rt ABC 中,90,30∠=︒∠=︒C A .()1 作AB 的垂直平分线DE 交AB 于点D ;交AC 于点E (要求:尺规作图,保留作图痕迹,不必写作法);()2 连接BE ,若1BC =,求BCE 的周长.21.已知:如图在ABC 中,AD 是边BC 上的高,E 为边AC 的中点,14BC =,12AD =,4sin 5B =.求: (1)线段DC 的长;(2)tan EDC ∠的值.22.如图,在平面直角坐标系xOy 中,函数y =x +b 的图像与函数ky x=(x >0)的图像相交于点B (1,6),并与x 轴交于点A .点C 是线段AB 上一点,∠OAC 与∠OAB 的面积比为2:3(1) 求k 和b 的值;(2) 若将∠OAC 绕点O 顺时针旋转,使点C 的对应点C ′落在x 轴正半轴上,得到∠OA ′C ′,判断点A ′是否在函数ky x=(x >0)的图像上,并说明理由.23.如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度AB ,在居民楼前方有一斜坡,坡长15m CD =,斜坡的倾斜角为α,4cos 5α=.小文在C 点处测得楼顶端A 的仰角为60︒,在D 点处测得楼顶端A 的仰角为30(点A ,B ,C ,D 在同一平面内).(1) 求C ,D 两点的高度差;(2) 求居民楼的高度AB .(结果精确到1m 3 1.7≈)24.无人机在实际生活中应用广泛.如图8所示,小明利用无人机测量大楼的高度,无人机在空中P 处,测得楼CD 楼顶D 处的俯角为45︒,测得楼AB 楼顶A 处的俯角为60︒.已知楼AB 和楼CD 之间的距离BC 为100米,楼AB 的高度为10米,从楼AB 的A 处测得楼CD 的D 处的仰角为30(点A 、B 、C 、D 、P 在同一平面内).(1) 填空:APD ∠=___________度,ADC ∠=___________度; (2) 求楼CD 的高度(结果保留根号); (3) 求此时无人机距离地面BC 的高度.参考答案1.D【分析】由6cos 33α=3cos α=然后再根据特殊角的三角函数值求角度即可. 解:∠6cos 33α=∠3cos α=∠α=30. 故选D .【点拨】本题主要考查了利用特殊角的三角函数值求角度、一元一次方程等知识点,将cos α整体当做未知数成为解答本题的关键.2.A【分析】过点A 作AB ∠x 轴,垂足为B ,根据点A 的坐标,得到OB =1,AB =2,根据正切的定义计算选择即可.解:过点A 作AB ∠x 轴,垂足为B ,根据点A 的坐标(1,2), ∠OB =1,AB =2, ∠ tan ∠1=221AB OB ==,故选A .【点拨】本题考查了坐标的意义,正切的定义即对边比邻边,熟练掌握正切的定义是解题的关键.3.C【分析】根据三角函数的定义,知tan 12BC A AC ==,设BC =x ,AC =2x ,根据勾股定理可求得AB ,再根据三角函数的定义就可以求出sin B 的值.解:在∠ABC 中,90C ∠=︒, ∠tan 12BC A AC ==, ∠设BC =x ,AC =2x ,()222225AB BC AC x x x ∴=++=,25sin 5AC B AB x=∴=,故选:C .【点拨】本题考查了锐角三角函数的定义及运用:在直角三角形中,一个锐角的正弦值为对边比斜边,余弦值为邻边比斜边,正切值为对边比邻边.4.B【分析】分别令x =0,y =0,由直线解析式可求解A 、B 的坐标,即可得OB 、OA 的长,再利用勾股定理可求解AB 的长,再根据正弦的定义可求解.解:直线y =34x ﹣3,令x =0,则y =0﹣3=﹣3,令y =0,34x ﹣3=0,解得x =4,∴A (4,0),B (0,﹣3), ∴OB =3,0A =4,∴AB 2222435++OA OB , ∴sin ∠OAB =35OB AB =, 故选:B .【点拨】本题主要考查一次函数图象与坐标轴的交点,勾股定理,锐角三角函数的定义,求解A 、B 两点坐标是解题的关键.5.A【分析】在Rt ABC 中,90ACB ∠=︒,斜边AB 是已知边,BAC ∠是已知角,而要求的是BAC ∠的对边BC 的长,所以选择BAC ∠的正弦,即可求出结果.解:如图,在Rt ABC 中,90ACB ∠=︒,BAC α∠=, ∠sin BCABα=, ∠sin BC AB α=⋅, ∠1000AB =米, ∠1000sin BC α=米. 故选:A .【点拨】此题考查了解直角三角形的应用,解题的关键是正确掌握锐角三角函数的定义,选择适当的锐角三角函数模型.6.B【分析】依据折叠的性质以及矩形的性质,易得∠AFE =∠BCF ;在Rt∠BFC 中,有BC =8,CF =10,由勾股定理易得BF 的长.根据三角函数的定义,易得tan∠BCF 的值,依据∠AFE =∠BCF ,可得tan∠AFE 的值.解:∠四边形ABCD 是矩形, ∠CD =AB =10,∠B =∠D =90°, ∠∠BCF +∠BFC =90°,根据折叠的性质得:∠EFC =∠D =90°,CF =CD =10, ∠∠AFE +∠BFC =90°, ∠∠AFE =∠BCF ,在Rt∠BFC 中,BC =8,CF =CD =10,由勾股定理得:BF 22CF CB -22108-6, 则tan∠BCF =BF BC =6384=, ∠tan∠AFE =tan∠BCF =34,故B 正确.故选:B .【点拨】本题主要考查了矩形的折叠问题,求三角函数值,勾股定理,余角的性质,根据折叠和勾股定理求出6BF =,是解题的关键.7.B【分析】由绝对值和完全平方的非负性可得:31sin 0,cos 022A B,再根据特殊角的锐角函数值可知60A B ∠=∠=︒ ,即可求解.解:3sin A 02-≥,21cos B 02⎛⎫-≥ ⎪⎝⎭,231sin A cos B 022⎛⎫-= ⎪⎝⎭,23sin 021cos 02A B ⎧=⎪⎪∴⎨⎪⎛⎫-= ⎪⎪⎝⎭⎩, 则可得:3sin 1cos 2A B ⎧=⎪⎪⎨⎪=⎪⎩,解得:6060A B ∠=︒⎧⎨∠=︒⎩ , 在ABC 中,18060C A B ∠=︒-∠-∠=︒ ,ABC ∴ 为等边三角形.故选:B .【点拨】本题考查了非负数的性质,绝对值和完全平方的非负性,由三角函数值求锐角的度数,三角形内角和以及等边三角形的判定;掌握非负数的性质,绝对值和完全平方的非负性是解题的关键.8.D【分析】如图,过点K 作KH ∠BJ 于H ,设KJ 交AC 于W .解直角三角形求出BJ ,KH ,可得结论.解:如图,过点K 作KH ∠BJ 于H ,设KJ 交AC 于W ,∠∠C =90°,AB =2BC ,∠2BC A AB==sin , ∠∠A =30°,∠ABC =60°,由作图可知,BJ 平分∠ABC ,KJ 垂直平分线段AC ,∠∠KBJ =∠CBJ =12∠ABC =30°,AW =WC ,∠WK ∠BC ,∠AK =KB =2,∠KJB =∠CBJ =30°,∠HK =12KB =1,BH 33∠∠KBJ =∠KJB =30°,∠KB =KJ ,∠KH ∠BJ ,∠HB =HJ 3∠S △KBJ =1233 故选:D .【点拨】本题考查作图-复杂作图、角平分线的定义、线段的垂直平分线的性质、解直角三角形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型9.A【分析】过点E 作EF AD ⊥于点F ,过点C 作CG ED ⊥于点G ,根据三角函数以及勾股定理求出,,,,,,BE AE AF EF FD ED EC 的长度,然后根据三角形面积公式得出CG 的长度,结果可得.解:过点E 作EF AD ⊥于点F ,过点C 作CG ED ⊥于点G ,AE AB ⊥,90BAE ∴∠=︒,4,60AB B =∠=︒,tan 6043AE AB ∴=︒=8cos60BE ==︒, 1082EC BC BE ∴=-=-=,四边形ABCD 是平行四边形,120BAD ∴∠=︒,1209030EAF BAD BAE ∴∠=∠-∠=︒-︒=︒,EF AD ⊥,90AFE ∴∠=︒,1232EF AE ∴== ∴cos306AF AE =︒=,1064FD AD AF ∴=-=-=,2222(23)427ED EF FD ∴++1122ECD S EC EF ED CG ∴==, 即112232722CG ⨯⨯⨯,221CG ∴ 221217sin 4CG EDC CD ∴∠==, 故选:A .【点拨】本题考查了平行四边形的性质,解直角三角形,勾股定理,含30的直角三角形的性质等知识点,熟练掌握解直角三角形以及勾股定理是解本题的关键.10.B【分析】由已知条件CBD A ∠=∠,可得1tan tan 2CBD A ∠==,设CD a =,由题意可得1tan 2CD CBD BC ∠==,即可算出2BC a =,在t ΔR CBD 中,根据勾股定理可得2222(2)BD CD BC a a ++解:CBD A ,1tan tan 2CBD A ∴∠==, 设CD a =,1tan 2CD CBD BC ∴∠==, 2BC a ∴=, 在Rt ΔCBD 中,2222(2)5BD CD BC a a a =+=+,5cos 5CD CDB BD a∴∠=. 故选:B 【点拨】本题主要考查了解直角三角形,熟练掌握解直角三角形的方法进行求解是解决本题的关键.11.12- 【分析】先计算零次幂、负整数指数幂、正切值的平方,再按照运算顺序计算就可以了.解:()012212tan 60113231212---︒=-⨯=-=-故答案为: 12-. 【点拨】本题考查了0指数幂()()010a a =≠、负整数指数幂()10q qa a a -=≠、特殊角的正切值、二次根式的性质(()20a a a =≥和实数的混合运算等知识.正确的计算是解决本题的关键.122【分析】21代入方程2(3tan )20x x θ-+=,得出tan θ的值,从而得出θ的度数,进而的解.解:21是方程2(3tan )20x x θ-=的一个根, ∠2(21)3tan (21)20θ-+=,解得:tan 1θ=,∠45θ=︒,∠2cos cos 45θ==° 2. 【点拨】考查三角函数值与一元二次方程根的应用,熟练掌握一元二次方程的根的意义以及特殊角三角函数值是解本题的关键.13.32【分析】过点D 作DM ∠CM ,交CB 的延长线于点M ,可得∠DMC =90°,在Rt∠DMC 中,利用锐角三角函数的定义可设DM =a ,则CM =2a ,然后证明8字模型相似三角形∠ACB ∠∠DMB ,从而利用相似三角形的性质可得AB BD =AC DM =CB BM =2,进而可得AC =2a ,CB =43a ,最后进行计算即可解答.解:过点D 作DM ∠CM ,交CB 的延长线于点M ,∠∠DMC =90°,在Rt∠DMC 中,tan∠BCD =12, ∠tan∠DCM =DM CM =12, 设DM =a ,则CM =2a ,∠∠ACB =∠DMC =90°,∠ABC =∠DBM ,∠∠ACB ∠∠DMB , ∠AB BD=AC DM =CB BM =2, ∠AC =2DM =2a ,∠2433CB CM a ==, ∠AC BC =243a a =32, 故答案为:32. 【点拨】本题考查了相似三角形的判定与性质,解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.14.31##1103+【分析】在Rt ADE △中,利用tan 310∠==AE AE ADE DE 103AE =1m 即为AC 的长.解:过点D 作DE AC ⊥交于点E ,如图:则四边形BCED 是矩形,∠BC =DE ,BD =CE ,由题意可知:60ADE ∠=︒,10m ==DE BC ,在Rt ADE △中,tan 310∠===AE AE ADE DE ∠103AE =∠()1031m +=AE EC ,故答案为:1031【点拨】本题考查了解直角三角形,解直角三角形的应用—仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.15.等边三角形【分析】根据特殊角三角函数值求出∠CDB 的度数,然后根据旋转的性质和等边三角形的判定即可解决问题.解:∠四边形ABCD 为矩形,∠DC =AB =1,BC =AD 3∠DCB =90°, ∠tan∠CDB 33=∠CDB =60°; 由旋转的性质可知:BD =BD ',∠∠BDD '为等边三角形.故答案为:等边三角形.【点拨】本题考查了矩形的性质,特殊角三角函数值,旋转的性质以及等边三角形的判定等知识,解题的关键是抓住旋转过程中的不变量,灵活运用有关性质来解题. 16.31()2【分析】根据B 点坐标可求出AB 、OB ,得到12AB OB =,所以30AOB ∠=︒,60BOC ∠=︒,再利用折叠与平行的性质,证明∠OEC ′是等边三角形,OE =CD =12AB ,然后可利用三角函数求出点C ′的坐标.解:∠点B 坐标为(32),∠AB =2,OA =3 ∠()222234OB + ∠12AB OB = ∠30AOB ∠=︒,60BOC ∠=︒∠C ′是C 关于DE 的对称点∠CED C ED '∠=∠, EC =EC ′∠DE ∠OB∠CED EOC '∠=∠=60°∠∠OE C ′=180°-2×60°=60°∠∠OE C ′是等边三角形∠OE = EC =EC ′=12AB =1112⨯= ∠C ′横坐标=31sin 60⨯︒==11sin302⨯︒= ∠C ′坐标为312⎫⎪⎪⎝⎭【点拨】本题考查了三角形,熟练运用特殊三角形的性质是解题的关键.17. 6037602512n + 【分析】在图∠中先解直角三角形ABC 得到3tan 4A =,4tan 3B =,=5AB ,再分别解直角三角形ADG 和直角三角形BEF 得到43AD DG =,34BE EF =,再由5AB AD DE BE =++=进行求解即可;对于图∠同图∠求解即可.解:如图∠所示,∠在Rt∠ABC 中∠C =90°,AC =4,BC =3,∠3tan 4BC A AC ==,4tan 3AC B BC ==,225AB AC BC +=, ∠四边形DEFG 是Rt∠ABC 的内接正方形,∠DG =DE =EF ,∠GDE =∠DEF =90°,∠∠ADG =∠BEF =90°,在Rt∠ADG 中,4tan 3DG AD DG A ==, 在Rt∠BEF 中,3tan 4EF BE EF B ==, ∠43534AB AD DE BE DG DG DG =++=++=, ∠6037DG =; 如图∠所示, 同理可得43AD DG =,34BE EF =,DE nDG =, ∠43534AB AD DE BE DG nDG DG =++=++=, ∠602512DG n=+, 故答案为:6037;602512n+.【点拨】本题主要考查了解直角三角形,勾股定理,正方形的性质,正确求出43AD DG =,34BE EF =是解题的关键. 18.(2023223-【分析】如图,设直线32y x =+与x 轴交于点C ,求出点A 、C 的坐标,可得OA =2,OC =23∠ACO =30°,可得1190CB A ∠=︒,130CB A =∠︒,然后求出12124323CB B O ===13228323CB CB ===324216323CB CB ===…,进而可得2023202223CB =2022OB 即可.解:如图,设直线32y x =+与x 轴交于点C , 在32y =+中,当x =0时,y =2; 当y =0320+=,解得:23x =- ∠A (0,2),C (23-0),∠OA =2,OC =23∠tan∠ACO =323OA OC == ∠∠ACO =30°,∠11AB A △是等边三角形,∠111160AA B AB A ∠=∠=︒,∠1190CB A ∠=︒,∠130CB A =∠︒,∠AC =1AB ,∠AO ∠1CB ,∠123O O C B == ∠12124323CB B O === 同理可得:13228323CB CB ==324216323CB CB ===…,∠2023202223CB = ∠(2023202320222323223OB =-∠点2022A 的横坐标是(2023223- 故答案为:(2023223-【点拨】本题考查了一次函数的图象和性质,等边三角形的性质,解直角三角形,等腰三角形的判定和性质等知识,通过解直角三角形求出∠ACO=30°是解题的关键.19.(1)12;(23;(3)2.【分析】(1) 先进行绝对值、三角函数、零指数幂计算,然后根据实数的运算法则求得计算结果;(2)先进行负整数指数幂、零指数幂、三角函数计算,然后根据实数的运算法则求得计算结果;(3)先进行三角函数、负整数指数幂、绝对值、零指数幂、二次根式计算,然后根据实数的运算法则求得计算结果;解:(1)原式=12212+=1112+-=12;(2)原式=0.125×(-8)33(3)原式=111222221-⎛⎫÷+-⎪+⎝⎭2222222+-=2.【点拨】本题考查实数的综合运算能力,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握零指数幂、二次根式化简、绝对值等考点的运算.20.()1见分析;()213【分析】(1)分别以A、B两点为圆心,以大于12AB长度为半径画弧,在AB两边分别相交于两点,然后过这两点作直线即为AB的垂直平分线;(2)根据线段垂直平分线上的点到线段两端点的距离相等可得BE=AE,然后求出△BCE 的周长=AC+BC,根据直角三角形30°角所对的直角边等于斜边的一半求出AB,再利用勾股定理列式求出AC的长,即可得解.解:()1AB的垂直平分线DE如图所示;()2DE 垂直平分AB ,BE AE ∴=,BCE ∴△的周长BE EC BC AE EC BC AC BC =+-++=++.在Rt ABC 中,330BC AC tan =︒BCE ∴△的周长为13【点拨】本题考查了复杂作图,线段垂直平分线上的点到线段两端点的距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质是解题的关键.21.(1)5;(2)125【分析】(1)利用直角三角形中4sin 5B =求解,AB 再利用勾股定理求解,BD 从而可得答案; (2)先利用直角三角形斜边上的中线的性质证明,EDEA EC 可得,EDC ECD ∠=∠ 再求解12tan tan ,5ADEDC ECD CD 从而可得答案. 解:(1) AD 是边BC 上的高,12AD =,4sin 5B =, ∴ 90ADB ADC ∠=∠=︒,412sin ,5B AB== 2215,15129,AB BD14,BC 149 5.CD BC BD(2) E 为边AC 的中点,90ADC ∠=︒,ED EA EC,EDC ECD ∴∠=∠ 12tan tan .5ADEDC ECD CD 【点拨】本题考查的是锐角三角函数的应用,勾股定理的应用,直角三角形斜边上的中线等于斜边的一半,等腰三角形的性质,掌握“等角的三角函数值相等”是解题的关键.22.(1)b =5,k =6(2)不在,理由见详解【分析】(1)把点B 的坐标分别代入一次函数与反比例函数解析式进行求解即可;(2)由(1)及题意易得点C 的坐标,然后根据旋转的性质可知点C ′的坐标,则根据等积法可得点A ′的纵坐标,进而根据三角函数可得点A ′的横坐标,最后问题可求解.(1)解:由题意得:166b k +=⎧⎨=⎩, ∠b =5,k =6;(2)解:点A ′不在反比例函数图像上,理由如下:过点A ′作A ′E ∠x 轴于点E ,过点C 作CF ∠x 轴于点F ,如图,由(1)可知:一次函数解析式为5y x =+,反比例函数解析式为6y x =, ∠点()5,0A -,∠∠OAC 与∠OAB 的面积比为2:3,且它们都以OA 为底,∠∠OAC 与∠OAB 的面积比即为点C 纵坐标与点B 纵坐标之比,∠点C 的纵坐标为2643⨯=,∠点C 的横坐标为451x =-=-,∠点C 坐标为()1,4-,∠CF =4,OF =1, ∠221417OC +tan 4CF COF OF∠==, 由旋转的性质可得:17,OC OC A OC AOC '''==∠=∠,根据等积法可得:2017OA CF A E OC ⋅'=='∠517tan A E OE A OE '=='∠, ∠5172017A '⎝⎭, 5172017100617=≠, ∠点A ′不在反比例函数图像上.【点拨】本题主要考查反比例函数与一次函数的综合、三角函数及旋转的性质,熟练掌握反比例函数与一次函数的综合、三角函数及旋转的性质是解题的关键.23.(1)9m(2)24m【分析】(1)过点D 作DE BC ⊥,交BC 的延长线于点E ,在Rt DCE 中,可得()4cos 1512m 5CE CD α=⋅=⨯=,再利用勾股定理可求出DE ,即可得出答案. (2)过点D 作DF AB ⊥于F ,设m AF x =,在Rt ADF 中,330AF x tan DF DF ︒===,解得3DF x =,在Rt ABC 中,()9m AB x =+,()312m BC x =-,tan603312AB BC x ︒===-x 的值,即可得出答案. (1)解:过点D 作DE BC ⊥,交BC 的延长线于点E ,在Rt DCE 中,4cos 5α=,15m CD =, ()4cos 1512m 5CE CD α∴=⋅=⨯=. ()222215129m DE CD CE ∴=--=.答:C ,D 两点的高度差为9m .(2)过点D 作DF AB ⊥于F ,由题意可得BF DE =,DF BE =, 设m AF x =,在Rt ADF 中,3tan tan30AF x ADF DF DF ∠=︒=== 解得3DF x =, 在Rt ABC △中,()9m AB AF FB AF DE x =+=+=+,)312m BC BE CE DF CE x =-=-=-, tan603312AB BC x ︒===- 解得9632x =, ()963924m 2AB ∴=+≈. 答:居民楼的高度AB 约为24m .【点拨】本题考查解直角三角形的应用-仰角俯角问题、坡度坡角问题,熟练掌握锐角三角函数的定义是解答本题的关键.24.(1)75;60(2)1003103⎫⎪⎭米(3)110米 【分析】(1)根据平角的定义求APD ∠,过点A 作AE DC ⊥于点E ,再利用三角形内角和求ADC ∠;(2)在Rt AED △中,30DAE ∠=︒求出DE 的长度再根据CD DE EC =+计算即可; (3)作PG BC ⊥于点G ,交AE 于点F ,证明APF DAE △≌△即可.解:(1)过点A 作AE DC ⊥于点E ,由题意得:60,45,30,MPA NPD DAE ∠=︒∠=︒∠=︒∠18075APD MPA NPD ∠=︒-∠-∠=︒9060ADC DAE ∠=︒-∠=︒(2)由题意得:100AE BC ==米,10EC AB ==.在Rt AED △中,30DAE ∠=︒, ∠)3100tan 3010033DE AE =⋅︒==米, ∠()1003103CD DE EC =+米 ∠楼CD 的高度为1003103⎫⎪⎭米. (3)作PG BC ⊥于点G ,交AE 于点F ,则()90,10PFA AED FG AB ∠=∠=︒==米∠MN AE ∥,∠60PAF MPA ∠=∠=︒.∠60ADE ∠=︒,∠PAF ADE ∠=∠.∠30DAE ∠=︒,∠30PAD ∠=︒.∠75APD ∠=︒,∠75ADP ∠=︒.∠ADP APD ∠=∠.∠AP AD =.∠APF DAE △≌△(AAS ).∠100PF AE ==.∠()10010110PG PF FG =+=+=米∠无人机距离地面BC 的高度为110米.【点拨】此题考查了解直角三角形的应用-——仰角俯角问题的知识.此题难度适中,注意能借助仰角或俯角构造直角三角形并解直角三角形是解此题的关键.。
高二数学已知三角函数值求角(2019新)

,求x; (2)x
或 5
66
(3)若 x∈R,求x的取值集合。
(3)
x
|
x
2k
6
或2k
+
56Leabharlann ,kZ
;赌博网|/ ;
敬德擐甲持矛 苏秦合六国之纵以伐秦 ②至于曹彬之平江南 祖逖半夜听到鸡叫 光化三年(900年) 跅弛易情 亦由此也 不恤军士 桓宣单马入谯城 潜问人曰:“孰为曹监军 事业韩彭可比肩 贞观十一年(637年) 足下富贵 ”皇后回答:“听说陛下要斩文忠 既深入贼疆 周德威镇守幽 州 [10] 正言以谕贼曰:“向为石勒诖误者 有才望 契丹大军当前 到达白登 纷纷礼缛 31 字国华 请求凿地引龙首渠水入城 忠贞无疵 国公庙南门前右侧建造 敬献碑楼 ”此数言者可谓得其要领矣 《明史》卷一百二十一 彬独不犯厘忽 祖约 当以卿为使相 官至晋王掾 上谷太守 右手 持俎豆 呜呼 并非杨家将一提到北宋的武将世家 尽在其间 周德威与李嗣昭挑选精锐士卒组成突击队 奈何不预先戒备 刺客暗伤 执手歔欷 妻子▪ 铠甲皆被缯绮 忽作病容 平田广野 又令数人担米 跨大江以济师 抵御契丹 [11] 抑为贪乱者矣 国事日非 刺称“奉敕江南干事回” 以曹为 首 遂建乐平为平晋军 [44] 影视形象人物经历编辑家世背景李文忠的祖上世代居住在泗州盱眙县 展示身上的疮疤 于是公私丰赡 便向蓬坞堡主陈川 南中郎将王含求援 虽然顾及了仁爱的私情 自称镇南将军 而我军却已扎好营栅 改封为鄂国公 为左一马军总管 在泾阳(今属陕西)突 厥交战 姑务万全 刘裕有关中之胜 祖逖非但不管 唐九节度之师不立主帅 邛州刺史 开宝二年(969年) 曹之识虑尤远 为何声名不显被遗忘 5 通南北之货 从征太原 冯奉世之平莎车 煽惑逋逃迫而用之耳 则已
已知三角函数值求角

6
6
2
所以,在R 上 x 的取值集合是
x
6
2k≤x≤ 5 6
2k k Z.
y
1
P
P
o
x
已知正弦值(范围),求角的值(范围).
视角二: 三角函数
方程 f (x) a 的解
函数y f (x)图像上函数
值等于a的点的横坐标
函数y f (x) 与y a
图像交点的横坐标
函数 y f (x)
不等式
sin x≥k (不等号也可以 cos x≥k 是<、≤、>) tan x≥k
已知三角函数值或值的范围,求角的值或角的范围.
问题:坐标系中哪些信息对应sin x y 中的x与y?
y
1
P(cos ,sin )
视角一: 三角函数定义 单位圆
数 正弦值
角x值
对应
对应
形 纵坐标
点P
角的终边
o
x
已知三角函数值或值的范围,求角的值或角的范围.
2
(2)已知 sin x≥ 1 ,求x 的取值范围. 2
y1 2
y
解:(2)因为,在0,2π内,
2π π
Oπ
当 π ≤x≤ 5π 时,sin x≥ 1
6
6
2
所以,在 R 上 x 的取值集合是
x
6
2k
≤x≤
5 6
2k
k
Z.
y sin x
2π
x
已知正弦值(范围),求角的值(范围).
正弦函数图像 依据 已知三角函 步骤
1
P
单位圆
视角二: 三角函数的性质和图像
y
o
x
已知三角函数值求角习题精选

已知三角函数值求角习题精选一、选择题1.若,则角为()A.,B.,C.,D.,2.已知是三角形的内角,且,则角等于()A.B.C.或D.或3.已知,,则角等于()A.B.C.D.4.已知不等边△中,①,②,③,④中可能成立的有()A.1个B.2个C.3个D.4个5.下列各结论正确的是()A.若,则B.,则C.若,则D.若,则(其中)6.若,,则等于()A.B.C.D.7.若,则使等式成立的的值是()A.B.或C.或D.或或8.使得等式成立的的集合是()A.B.C.D.9.适合关系式的集合是()A.B.C.D.10.适合关系式,且在内的的个数有()A.1 B.2 C.3 D.4二、填空题11.已知,,则.12.已知,且,则.13.在上适合关系式的角有__________个,它们的和为_________.三、解答题14.已知.试求符合下列条件的角;(1)是三角形的内角;(2);(3)是第三象限的角;(4).15.已知.求.16.求适合的角的集合.17.已知,,,、、均为锐角.求的值.18.已知一个三边长成等差数列的直角三角形,试求其最小内角.参考答案:一、选择题1.B2.C3.C4.C5.D6.B7.D8.C9.D10.C二、填空题11.12.或13.4,三、解答题14.∵,∴满足条件的锐角为,故(1)∵是三角形的内角,∴,∴;(2)∵,∴或;(3)∵是第三象限的角,∴,;(4)∵,∴,.15.由得,∴.当时,或,;当时,或,.故适合条件的可写成或或或,.16.等式两边平方得,∴,,∴,.故所求角的集合为.17.,.∵且为锐角,∴,同理,,∴,∴.18.∵三角形三边长成等差数列,设其三边长分别为,,,又∵三角形为直角三角形,由勾股定理有,解得∴三角形三边为、、.由此可知边长为的边所对的角最小,令其为.则有,∵,∴.。
三角函数总内容练习巩固

阶段滚动训练一(范围:§1.1~§1.3)一、选择题1.(2018·湖南衡阳二十六中高二期中)已知角α的终边经过点P ⎝⎛⎭⎫32,12,则cos α等于( )A.12B.32C.33 D .±122.角29π12的终边所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限3.(2018·河南林州第一中学高二期末)若角α是第二象限角,则α2是( )A .第一象限角B .第二象限角C .第一或第三象限角D .第二或第四象限角4.(2018·天津河东区高二期中)若θ是第二象限角,则下列选项中能确定为正值的是( ) A .sin θ2B .cos θ2C .tan θ2D .cos 2θ 5.n 为整数,化简sin (n π+α)cos (n π+α)的结果是( )A .±tan αB .-tan αC .tan αD .tan nα6.已知P (-3,y )为角β的终边上的一点,且sin β=1313,则2sin 2βsin 2β-cos 2β等于( )A .±12B .-211 C.36D .±27.若cos θ<0,且cos θ-sin θ=1-2sin θcos θ,那么θ是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角8.下列三角函数: ①sin ⎝⎛⎭⎫n π+43π; ②cos ⎝⎛⎭⎫2n π+π6; ③sin ⎝⎛⎭⎫2n π+π3; ④cos ⎣⎡⎦⎤(2n +1)π-π6; ⑤sin ⎣⎡⎦⎤(2n +1)π-π3(n ∈Z ). 其中与sin π3数值相同的是( )A .①②B .①③④C .②③⑤D .②③二、填空题9.下列说法中正确的有________.(写出所有正确说法的序号) ①正角的正弦值是正的,负角的正弦值是负的,零角的正弦值是零;②若有一三角形的两内角α,β满足sin α·cos β<0,则此三角形必为钝角三角形; ③对任意的角α,都有|sin α+cos α|=|sin α|+|cos α|;④对任意角α⎝⎛⎭⎫α≠k π2,k ∈Z ,都有⎪⎪⎪⎪tan α+1tan α=|tan α|+⎪⎪⎪⎪1tan α. 10.已知sin α=14,且α∈⎝⎛⎭⎫π2,π,则sin α-2cos 2α=________. 考点 运用基本关系式求三角函数值 题点 运用基本关系式求三角函数值11.sin 20°+cos 200°sin 340°-cos 160°+tan 19°+cos 341°tan 161°+cos 199°的值为________.12.已知角α的终边经过点P (m ,22),sin α=223且α为第二象限角.(1)求m 的值;(2)若tan β=2,求sin αcos β+3sin ⎝⎛⎭⎫π2-αsin βcos (π+α)cos (-β)-3sin αsin β的值.13.证明:(1)1-cos 2αsin α-cos α-sin α+cos αtan 2α-1=sin α+cos α; (2)(2-cos 2α)(2+tan 2α)=(1+2tan 2α)(2-sin 2α).14.已知集合M =⎩⎨⎧⎭⎬⎫x ⎪⎪ x =-2cos n π3,n ∈Z ,集合N =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x =2sin 2n -36π,n ∈Z ,那么M 与N 之间的关系是( ) A .M N B .NMC .M ∩N =∅D .M =N15.化简:sin ⎝⎛⎭⎫4n -14π-α+cos ⎝⎛⎭⎫4n +14π-α(n ∈Z ).阶段滚动训练二(范围:§1.4~§1.5)1.(2018·江西景德镇一中高二期末)函数y =tan x ⎝⎛⎭⎫x ≠k π+π2,k ∈Z 的单调性为( ) A .在整个定义域上为增函数 B .在整个定义域上为减函数C .在每一个开区间⎝⎛⎭⎫-π2+k π,π2+k π(k ∈Z )上为增函数 D .在每一个开区间⎝⎛⎭⎫-π2+2k π,π2+2k π(k ∈Z )上为增函数2.已知函数y =sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的部分图象如图所示,则( )A .ω=1,φ=π6B .ω=1,φ=-π6C .ω=2,φ=π6D .ω=2,φ=-π63.函数y =tan x +sin x -|tan x -sin x |在区间⎝⎛⎭⎫π2,3π2内的图象是( )4.函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,|φ|<π2的部分函数图象如图所示,为了得到函数f (x )的图象,只需将g (x )=sin ωx 的图象( )A .向右平移π6个单位长度B .向右平移5π6个单位长度C .向左平移π6个单位长度D .向左平移5π6个单位长度5.设点P 是函数f (x )=sin ωx 的图象C 的一个对称中心,若点P 到图象C 的对称轴的距离的最小值为π4,则f (x )的最小正周期为( )A .2πB .π C.π2 D.π46.已知函数f (x )=A cos(ωx +φ)(A >0,ω>0)的部分图象如图所示,f ⎝⎛⎭⎫π2=-23,则f (0)等于( )A .-23 B.23 C .-12 D.127.函数f (x )=⎝⎛⎭⎫1-21+2x tan x 的图象( )A .关于x 轴对称B .关于y 轴对称C .关于直线y =x 对称D .关于原点对称8.函数f (x )=M sin(ωx +φ)(ω>0)在区间(a ,b )上是增函数,且f (a )=-M ,f (b )=M ,则函数g (x )=M cos(ωx +φ)在[a ,b ]上( ) A .是增函数B .是减函数C .可以取到最大值MD .可以取到最小值-M9.方程2x =cos x 解的个数为( ) A .1 B .2 C .0 D .无数个二、填空题10.(2018·福建闽侯第八中学高二期末)函数y =lg(sin x -cos x )的定义域为________. 11.若f (x )=2sin(ωx +φ)+m ,对任意实数t 都有f ⎝⎛⎭⎫π8+t =f ⎝⎛⎭⎫π8-t ,且f ⎝⎛⎭⎫π8=-3,则实数m 的值等于________.12.函数y =cos(2x +φ)(-π≤φ<π)的图象向右平移π2个单位长度后,与函数y =sin ⎝⎛⎭⎫2x +π3的图象重合,则φ=________.三、解答题13.求函数y =sin ⎝⎛⎭⎫π3+4x +cos ⎝⎛⎭⎫4x -π6的周期、单调区间及最大值、最小值.14.已知函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象如图所示.(1)求函数f (x )的解析式;(2)设112π<x <1112π,且方程f (x )=m 有两个不同的实数根,求实数m 的取值范围和这两个根的和.15.已知函数f (x )=2cos ωx ,且函数y =f (x )图象的两相邻对称轴间的距离为π2.(1)求f ⎝⎛⎭⎫π8的值;(2)将函数y =f (x )的图象向右平移π6个单位长度后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间.阶段滚动训练三(范围:§1.1~§1.5)一、选择题1.若sin(π-θ)<0,tan(π+θ)>0,则θ的终边在( ) A .第一象限 B .第二象限C .第三象限D .第四象限2.已知角α的终边上一点的坐标为⎝⎛⎭⎫sin 2π3,cos 2π3,则角α的最小正值为( ) A.5π6 B.2π3 C.4π3 D.11π63.函数y =2cos x -1的最大值、最小值分别是( ) A .2,-2 B .1,-3 C .1,-1 D .2,-14.若函数f (x )=2sin(ωx +φ)对任意x 都有f ⎝⎛⎭⎫π3+x =f (-x ),则f ⎝⎛⎭⎫π6等于( ) A .2或0 B .0 C .-2或0D .-2或2 5.若cos ⎝⎛⎭⎫3π2-α=-53,则sin(-5π+α)等于( ) A.23 B .-23 C.53 D .-536.已知tan α=3,则sin αcos α等于( ) A.310 B.35 C.710 D.457.已知a 是实数,则函数f (x )=1+a sin ax 的图象不可能是( )二、填空题8.函数y =2sin ⎝⎛⎭⎫m 3x +π3的最小正周期在⎝⎛⎭⎫23,34内,则正整数m 的值是________. 9.函数y =f (x )=A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,|φ|<π2的部分图象如图所示,则f (1)+f (2)+f (3)+…+f (2 018)+f (2 019)的值等于________.10.已知一扇形的弧所对的圆心角为54°,半径r =20 cm ,则扇形的周长为________ cm. 11.已知函数f (x ),任意x 1,x 2∈⎝⎛⎭⎫-π2,π2(x 1≠x 2),给出下列结论: ①f (x +π)=f (x );②f (-x )=f (x );③f (0)=1; ④f (x 1)-f (x 2)x 1-x 2>0;⑤f ⎝⎛⎭⎫x 1+x 22>f (x 1)+f (x 2)2.当f (x )=tan x 时,正确结论的序号为________.12.关于函数f (x )=4sin ⎝⎛⎭⎫2x -π3(x ∈R ),有下列说法:①y =f ⎝⎛⎭⎫x +43π为偶函数; ②要得到函数g (x )=-4sin 2x 的图象,只需将f (x )的图象向右平移π3个单位长度; ③y =f (x )的图象关于直线x =-π12对称; ④y =f (x )在[0,2π]内的增区间为⎣⎡⎦⎤0,512π和⎣⎡⎦⎤1112π,2π. 其中正确说法的序号为________.三、解答题13.已知扇形AOB 的周长为10 cm.(1)若这个扇形的面积为4 cm 2,求扇形圆心角的弧度数;(2)求该扇形的面积取得最大值时圆心角的大小及弧长.14.设f (x )=4sin ⎝⎛⎭⎫2x -π3+ 3. (1)求f (x )在⎣⎡⎦⎤0,π2上的最大值和最小值; (2)把y =f (x )的图象上的所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移2π3个单位长度,得到函数y =g (x )的图象,求g (x )的单调递减区间.15.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π),在同一周期内,当x =π12时,f (x )取得最大值3;当x =7π12时,f (x )取得最小值-3. (1)求函数f (x )的解析式;(2)求函数f (x )的单调递减区间;(3)若x ∈⎣⎡⎦⎤-π3,π6时,函数h (x )=2f (x )+1-m 有两个零点,求实数m 的取值范围.。
高二数学已知三角函数值求角(2019)

,求x; (2)x
或 5
66
(3)若 x∈R,求x的取值集合。
(3)
x
|
x
2k
6
或2k
+
5
6
,k
Z
; 明升体育,明升m88备用 明升,m88明升,M88 ;
皆曰“长当弃市”帝不忍致法於王 及千亩战 不虞不骜 言帝病甚 宜若奉漏甕沃焦釜也 补文学掌故缺;与秦、楚、三晋合谋以伐齐 顿首曰:“可则立之 恆山 从入武关 韩信、彭越皆报曰:“请今进兵 以德报怨 子康子代 夺而杀尉 为铁椎重百二十斤 人而无礼 请後不敢 陈乃立怀公 之子越 出行游国中 曰:“人生一世间 此之谓德音 且罪等 中石没镞 非汉所望也 皇仆卒 忘其口而念我 乃封不疑为塞侯 九鼎宝器必出 柰何不礼 说齐王曰:“天下之游士冯轼结靷东入齐者 齐楚从亲 顾楚有可乱者 夏 ”卜人曰:“所谓天王者乃天子 而颇采儒术以文之 沛公欲听之 破之 人迹罕至 妇人有保西河之志 王为‘泰皇’ 建为郎中令 将屯 王巴、蜀、汉中 此二国 四年 平王幼 终身勿出 因其欲然 晋君乃止 而燕、秦不悟也 以无为有 余独悲韩子为说难而不能自脱耳 穰苴曰:“何後期为 沈、姒、蓐、黄实守其祀 恐亡之 不谢而亡去 醳之 適伯姬氏 项 王至阴陵 诸侯恣行 宫室苑囿狗马服御无所增益 当是时 车马百驷 秦社稷之忧也 ”乃自刭死 日杀牛置酒 方东忧楚 周公旦承成王命伐诛武庚 以武庚殷馀民封康叔为卫君 文辞粲如也 匈奴处北地 汉法 介汉使者权 以陇西都尉从击项籍军五月 仆之思归 至函谷而军焉 秦宗室大臣皆言秦 王曰:“诸侯人来事秦者 始绝之未小敛 围章邯废丘 ” 其後二百二十馀年秦有荆轲之事 皆知大王贱人而贵马也 夫齐 ”子家曰:“弃周公之业而臣於齐 曰:“此可
已知三角函数值求角

已知三角函数值求角在解题过程中,已知三角函数值可以帮助我们求得对应的角度大小。
本文将介绍如何利用已知的三角函数值来求解角度。
具体来说,我们将讨论正弦、余弦和正切三个常见的三角函数。
一、已知正弦函数值求角已知正弦函数值sinθ,我们可以使用反正弦函数来求解对应的角度。
反正弦函数常表示为arcsin或sin^{-1}。
具体解题步骤如下:1. 确定已知的sinθ值。
2. 使用反正弦函数,即arcsin或sin^{-1}函数,计算θ的值。
3. 根据所求得的θ值,判断其所在象限,确定精确的角度。
例如,已知sinθ=0.5,我们可以使用反正弦函数来求解θ的值。
计算过程如下:θ = arcsin(0.5) ≈ 30°这意味着sinθ=0.5的角度为30°。
二、已知余弦函数值求角已知余弦函数值cosθ,我们可以使用反余弦函数来求解对应的角度。
反余弦函数常表示为arccos或cos^{-1}。
具体解题步骤如下:1. 确定已知的cosθ值。
2. 使用反余弦函数,即arccos或cos^{-1}函数,计算θ的值。
3. 根据所求得的θ值,判断其所在象限,确定精确的角度。
例如,已知cosθ=0.5,我们可以使用反余弦函数来求解θ的值。
计算过程如下:θ = arccos(0.5) ≈ 60°这意味着cosθ=0.5的角度为60°。
三、已知正切函数值求角已知正切函数值tanθ,我们可以使用反正切函数来求解对应的角度。
反正切函数常表示为arctan或tan^{-1}。
具体解题步骤如下:1. 确定已知的tanθ值。
2. 使用反正切函数,即arctan或tan^{-1}函数,计算θ的值。
3. 根据所求得的θ值,判断其所在象限,确定精确的角度。
例如,已知tanθ=1,我们可以使用反正切函数来求解θ的值。
计算过程如下:θ = arctan(1) ≈ 45°这意味着tanθ=1的角度为45°。
4.8 已知三角函数值求角

sin(180°-α)=sinα
得到另一个角
x2≈ 180°-11.54°=168.46°.
所以在0°~360°范围内, 满足 sinx=0.2的角为11.54°和168.46° .
4.8 已知三角函数值求角
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
例2 已知sinx= ,且 x∈[0,2π],求角x的值. 解 由函数的y=sinx的图像可知, 在区间[0,2π]上满足sinx= 的 角x有两个, 分别在第三和第四象限.
1.书面作业:完成课后习题和学习与训练; 2.查漏补缺:根据个人情况对课题学习复习与回顾; 3.拓展作业:阅读教材扩展延伸内容.
再见
因此, 正弦函数y=sinx与直线
在区间[0, 2π]上的交点为
(0.2527,0.25)和(2.8889, 0.25).
4.8 已知三角函数值求角
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
求正弦函数y=sinx与直线 在区间[0, 2π]上的交点.
4.8 已知三角函数值求角
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
函数型计算器的标准设置中, 已知余弦函数值, 只能显 示0°~180°范围内的角.
函数型计算器的标准设置中, 已知正切函数值, 只能显 示 -90°~90°范围内的角.
4.8 已知三角函数值求角
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业Biblioteka 4.8 已知三角函数值求角
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
近似表示.某船的吃水深度(船底与水面的距离)为4m, 安全条例规定至 少有1.5m的安全间隙(船底与洋底的距离), 求该船在这一天的哪个时刻 能进入港口?在港口能停留多久?
新教材三角函数求值练习题(附答案)

2021年12月30日高中数学作业姓名:__________ 班级:__________ 考号:__________一、单选题(共10小题)1. 化简√1-sin 23π5的结果是( ) A. cos 3π5B. sin 3π5C. -cos 3π5D. -sin 3π52. 已知tan α=√3,α为第三象限角,则sin α=( )A. 12B. -12C. √32D. -√323. 如果角θ的终边经过点(−35,45),那么sin (π2+θ)+cos (π-θ)+tan (2π-θ)等于( )A. -43B. 43C. 34D. -344. 已知sin θ=15,则cos (450°+θ)的值是( )A. 15B. -15C. -2√65 D. 2√65 5. 化简: sin (θ−5π)cos(−π2−θ)cos (8π−θ)sin(θ−3π2)sin (−θ−4π)等于( )A. -sin θB. sin θC. cos θD. -cos θ6. 若sin θ·cos θ>0,则θ在 ( )A. 第一或第四象限B. 第一或第三象限C. 第一或第二象限D. 第二或第四象限7. 已知集合U ={1,2,3,4,5,6,7},A ={1,3,5},B ={1,2},则∁U (A ∪B )等于( )A. {4,6,7}B. {4,6}C. {1,2,3}D. {2,3,5}8. 已知f (x )是定义在R 上的偶函数,且在(0,+∞)上是增函数,设a =f (-3),b =f (π),c =f (-1),则a ,b ,c 的大小关系是( )A. a <c <bB. c <b <aC. b <a <cD. c <a <b9. 给出三个数a =,b =3,c =log 3,则它们的大小顺序为( )A. b <c <aB. b <a <cC. c <a <bD. c <b <a10. 已知a =,b =log 2,c =log 3,则a ,b ,c 的大小关系为( )A. a >b >cB. a >c >bC. b >a >cD. c >b >a二、多选题(共1小题)11. (多选题)若角α的终边过点P (-3,-2),则 ( )A. sin αtan α<0B. cos αtan α<0C. sin αcos α>0D. sin αcos α<0三、填空题(共10小题)12. 若sin α=45,cos α=35,则tan α=________.13. 已知tan α=12,α∈(0,π2),则sin α-cos α=________.14. 若cos α=35,且α为第四象限角,则tan α= .15. 已知α是第四象限角,cos α=1213,则sin α= .16. 已知tan α=-12,则2sin αcos αsin 2α−cos 2α= .17. 化简sin(15π2+α)cos(α−π2)sin(9π2−α)cos(3π2+α)=________.18. 已知sin α是方程2x 2-x -1=0的根,α是第三象限角,则sin(−α−3π2)cos(32π−α)cos(π2−α)sin(π2+α)·tan 2(π-α)=________.19. 在平面直角坐标系中,角α的终边与单位圆交于点A ,点A 的纵坐标为35,则t a n α=________.20. 已知角α的终边经过点(-4,m )且cos α=-45,则sin α=________.21. 已知点P (tan α,cos α)在第三象限,则角α的终边在第________象限.四、解答题(共4小题)22. 已知tan α=2.(1)求sin α−3cos αsin α+cos α的值;(2)求2sin 2α-sin αcos α+cos 2α的值.23. 已知α的终边与单位圆交于点P (m,√154),且α为第二象限角.求sin(α−π2)sin (π+α)−sin(3π2−α)+1的值.24. 已知f (α)=tan (π-α)·cos (2π-α)·sin(π2+α)cos (-α-π).(1)化简f (α). (2)若f (π2-α)=-35,且α是第二象限角,求tan α.25. 利用诱导公式化简: (1)sin (3π2+α);(2)cos (3π2−α).1. 【答案】C【解析】√1-sin 23π5=√cos 23π5=|cos 3π5|, 因为π2<3π5<π,所以cos 3π5<0,所以|cos 3π5|=-cos 3π5, 即√1-sin 23π5=-cos 3π5. 2. 【答案】D【解析】∵tan α=sin αcos α=√3,∴cos α=√33sin α.又sin 2 α+cos 2 α=1,∴sin α=±√32.又α为第三象限角,∴sin α=-√32.3. 【答案】B【解析】易知sin θ=45,cos θ=-35,tan θ=-43.原式=cos θ-cos θ-tan θ=43.4. 【答案】B【解析】cos (450°+θ)=cos (90°+θ)=-sin θ=-15.5. 【答案】A【解析】原式=sin (θ−π)cos(π2+θ)cos θsin θsin (−θ)=(−sin θ)(−sin θ)cos θsin θ(−sin θ)=-sin θ.6. 【答案】B【解析】因为sin θ·cos θ>0,所以sin θ>0,cos θ>0或sin θ<0,cos θ<0,所以θ在第一象限或第三象限.7. 【答案】A【解析】∵A ={1,3.5},B ={1,2},∴A ∪B ={1,2,3,5}.又U ={1,2,3,4,5,6,7},∴∁U (A ∪B )={4,6,7}.8. 【答案】D【解析】由函数f (x )是偶函数可知f (-1)=f (1),f (-3)=f (3).又函数f (x )在区间(0,+∞)上是增函数,所以f (1)<f (3)<f (π),即c <a <b ,故选D.9. 【答案】D【解析】因为a =>1,0<b =3<1,c =log 3<0,所以a >b >c .10. 【答案】A【解析】∵>30=1,=log 2<log 2<log 22=1,log 3=,∴a >b >c . 11. 【答案】ABC【解析】因为角α的终边过点(-3,-2),r =|OP |=√(-3)2+(-2)2=√13,所以sin α=y r =√13=-2√1313<0, cos α=x r =√13=-3√1313<0, tan α=y x =-2-3=23>0,sin α·tan α<0,cos α·tan α<0,sin α·cos α>0.12. 【答案】43【解析】tan α=sin αcos α=43.13. 【答案】-√55【解析】因为tan α=12=sinαcosα,由{sinαcosα=12,sin 2α+cos 2α=1,解得{sinα=√55,cosα=2√55,所以sin α-cos α=√55-2√55=-√55. 14. 【答案】-43 【解析】因为α为第四象限角,且cos α=35,所以sin α=-√1−cos 2α=-√1−(35)2=-45, 所以tan α=sin αcos α=-43.15. 【答案】-513【解析】由条件知sin α=-√1−cos 2α=-√1−(1213)2=-513. 16. 【答案】43【解析】因为tan α=-12,所以2sin αcos αsin 2α−cos 2α=2tan αtan 2α−1=2×(−12)(−12)2−1=43. 17. 【答案】-1【解析】原式=sin(3π2+α)cos(π2−α)sin(π2−α)sinα=(−cos α)∙sin αcos αsin α=-1.18. 【答案】-13【解析】∵方程2x 2-x -1=0的根为-12或1,又α是第三象限角,∴sin α=-12,∴cos α=-√1−sin 2α=-√32,∴tan α=sin αcos α=√33,∴原式=cos α(−sin α)sin α∙cos α·tan 2α=-tan 2α=-13. 19. 【答案】34或-34【解析】由题意,设点A 的坐标为(x,35),所以x 2+(35)2=1,解得x =45或-45.当x =45时,角α在第一象限,t a n α=3545=34;当x =-45时,角α在第二象限,t a n α=354−5=-34.20. 【答案】±35【解析】∵r =√16+m 2,∴cos α=√16+m 2=-45,∴m =±3.∴sin α=±35.21. 【答案】二【解析】因为点P (tan α,cos α)在第三象限,则tan α<0且cos α<0,故角α的终边在第二象限.22. 【答案】解 (1)法一 (代入法)∵tan α=2,∴sin αcos α=2,∴sin α=2cos α. ∴sin α−3cos αsin α+cos α=2cos α−3cos α2cos α+cos α=-13.法二 (弦化切)∵tan α=2.sin α−3cos αsin α+cos α=sin αcos α−3sin αcos α+1=tan α−3tan α+1=2−32+1=-13. (2)2sin 2α-sin αcos α+cos 2α=2sin 2α−sin αcos α+cos 2αsin 2α+cos 2α =2tan 2α−tan α+1tan 2α+1=2×4−2+14+1=75.23. 【答案】解 由题意知m 2+(√154)2=1, 解得m 2=116, 因为α为第二象限角,故m <0,所以m =-14,所以sin α=√154,cos α=-14. 原式=−cos α−sin α−(−cos α)+1=14−√154−14+1=-3+√156. 24. 【答案】解 (1)f (α)=tan (π-α)·cos (2π-α)·sin(π2+α)cos (-α-π) =-tanα·cosα·cosα-cosα=sin α. (2)由sin (π2-α)=-35,得cos α=-35,又α是第二象限角,所以sin α=√1-cos 2α=45,则tan α=sinαcosα=-43.25. 【答案】解 (1)sin (3π2+α)=sin (π+π2+α)=-sin (π2+α)=-cos α (3π2−α)=cos (π+π2−α)=-cos (π2−α)==-sin α.。
高一数学已知三角函数值求角

(3)若 sin x 0.7, x [ , ] ,则x= arcsin 0.7 2 2
4.11 已知三角函数值求角
例2. (1)已知cos x 0.7660 ,且 x [0, ],求x. (2)已知cos x 0.7660 ,且 x [0,2 ],求x 的取值集合. 解: [0, ]上是减函数和 (1 2)由于余弦函数在闭区间 )因为cos x 0.7660 0,所以 x是第二象限或第三 cos x 由余弦函数的单调性和 0.7660 可知符合条件的角有且只有一个, 象限角. 而且角为钝角, 2 2 7 cos( ) cos( ) cos 9 9 9 利用计算器并由: 7 可知符合条件的角有且只有两个,即第二象限角 或 cos( x ) cos x 0.7660 9 2 2 7 11 ( 40 ),所以 x 可得 x 第三象限角 9 9 9 7 11 } 故x 的集合是 { , 9 9
4.11 已知三角函数值求角
y x
根据正弦函数的图象和性质寻找区间使其满足: [ , ] 上,符合条件sin x a(1 a 1)的角x,叫做 在闭区间 2 sin 2 x a (1 a 1) 的角x有且只有一个,而且 使符合条件的 包括锐角. 实数 a 的反正弦,记作 arcsin a ,即 x arcsin a,其中 x [ , ], 2 2 且a sin x . arcsin a 的意义:
340 36/ } 所以x的取值集合是 {199 24/ ,
或 {
997 1703 , } 900 900
4.11 已知三角函数值求角
练习:
2 (1)若 cos x , x [0, ] ,则x的值( B ) 3 2 2 B . arccos A. arccos 3 3 2 2 D . arccos C . arccos 3 3 1 A { , }, B {0, sin x }且 x ( , ) (2)若 ,集合 5 2 2 A B ,则x的值为 arcsin 1 5
高二数学已知三角函数值求角

(2) cosx=- ,若x在第二象限 x=arccos(-
1 3
1 3
1 )=π-arccos 3
1 3
若x在第三象限,则x=π+arccos
1 综上得满足cosx=- 3 的角的集合是
1 {x | x 2k arccos , k Z } 3 1 {x | x 2k arccos , k Z } 3
例2.(1)已知cosx=0.5,x∈[0, 2π ),求x;
5 x 或 3 3
1 (2)已知cosx=- 3
,求x的取值集合;
类似地,这时可以用反余弦来表示x
如果我们限定x在区间[0,π]上取值,那么 对于区间[-1,1]的任意一个y的值,x只有唯 一值与之对应. 在区间[0,π]上符合条件cosx=y (-1≤y ≤1) 的角x,记为x=arccosy,
例3.
3 已知tanx= ,且x∈( , ) ,求x的值. 3 2 2
解:
3 3
( , ) 22
因为
正切 3 由tan( )=-tan =- , 6 函数 3 6
所以x=- 6
在
上是 增函
一般地,对于tanx=a (a>0),则 x=kπ+arctana,k∈Z.
一般地,对于正弦函数y=sinx,如果已知 函数值y (y∈[-1, 1]),那么在 x [ , ]上
2 2
有唯一的x值和它对应,记为x=arcsiny (其中
-1≤y≤1,
2
x
2
)
, 上正弦等于 ] y 2 2
即arcsiny (|y|≤1)表示 [ 的那个角
已知三角函数值求角练习[最新版]
![已知三角函数值求角练习[最新版]](https://img.taocdn.com/s3/m/c873f42249649b6649d747ed.png)
注:尊敬的各位读者,本文是笔者教育资料系列文章的一篇,由于时间关系,如有相关问题,望各位雅正。
希望本文能对有需要的朋友有所帮助。
如果您需要其它类型的教育资料,可以关注笔者知识店铺。
由于部分内容来源网络,如有部分内容侵权请联系笔者。
已知三角函数值求角练习基础卷(15分钟)一、选择题1.已知α是三角形的内角,且21sin =α,则α等于( ) A .6πB .3πC .65π或6πD .32π或3π2.已知cosx=0,则角x 等于( )A .2πB .2k π+π(k ∈Z )C .)( 22Z k k ∈-ππ D .)( 22Z k k ∈+ππ3.若23ππ<<x 且65cos -=x ,则x 等于( ) A .)65arccos(-B .65arccos -C .65arccos -πD .65arccos +π4.已知3tan -=x ,]23,2[ππ-∈x ,则x 等于( ) A .3π-与34πB .3π-与32πC .π67-与π67D .6π-与65π5.)310arccos(cos π的值是( )A .3π- B .π310 C .34πD .32π二、填空题 6.已知51sin =x ,x 是锐角,则x=_____________。
7.已知4cos π-=x ,x 是钝角,则x=_____________。
8.已知22tan -=x ,x 是钝角,则x=_____________。
提高卷(30分钟)一、选择题 1.已知22sin -=x 且x ∈[0,2π],则x 的值是( ) A .43π或45πB .45π或47πC .43π或47πD .67π或π611 2.已知sec (π-α)=2且2π<α<4π,则角α的值是( )A .37π或311πB .38π或π310 C .37π或38πD .37π或35π3.已知cotx=2,则( )A .x=k π+arctan2,k ∈ZB .x=2k π+arctan2,k ∈ZC .21arctan+=πk x ,k ∈Z D .21arctan 2+=πk x ,k ∈Z4.)]53arccos()54(cos[arcsin ---的值等于( ) A .-1B .257-C .257D .510-5.)57arccos(sin π的值是( ) A .52πB .57π C .109πD .10π-6.下列各式中正确的是( ) A .23arccos)21arcsin(=- B .23arcsin)21arccos(=- C . arctan (-1)=arcsin (-1) D .022arccos )22arcsin(=+-二、填空题7.若tanx=5,]2,[ππ--∈x ,则x=______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【巩固练习】
1.若sin x =13,x ∈(2
π,π),则x 等于( ) A .arcsin 13
B .π-arcsin 13 C. 2π+arcsin 13 D .-arcsin 13
2.设cos α=-16
,α∈(0,π),则α的值可表示为( ) A .arccos 16 B .-arccos 16
C .π-arccos 16
D .π+arccos 16
1arccos()-( ) A.12 B .0 C .1 D .-12
4.若x ∈[0,
32π],则使等式cos(πcos x )=0成立的x 的值是( ) A.3π B. 3π或43π C. 3π或23π D. 3
π或23π或43π 5.给出下列等式 ①arcsin
2π=1 ②arcsin(-12)=-3π ③arcsin(sin 3π)=3π ④sin(arcsin 12)=12 其中正确等式的个数是( )
A .1
B .2
C .3
D .4
6.若tan(2x +3
π)
[0,2π]上解的个数为( ) A .5 B .4 C .3 D .2
7.方程2cos(x -
4π)=1在区间(0,π)内的解是________. 8.若x =3
π是方程2cos(x +α)=1的解,其中α∈(0,2π),则角α=________. 9.函数y
arccos(2x -3)的定义域是________.
10.已知tan x =-1,且cos x
x 的取值集合. 11.已知函数f (x )=2sin(2x -3
π)+1, (1)求函数y =f (x )的最大值、最小值以及相应的x 值;
(2)若x ∈[0,2π],求函数y =f (x )的单调增区间;
(3)若2y >,求x 的取值范围.
12.已知△ABC 的三个内角A 、B 、C 满足sin(180°-A )
B
A
+B ),求角A 、B 、C 的大小.
【答案与解析】
1.【答案】B
【解析】∵π-arcsin 13∈(2π,π),且sin(π-arcsin 13)=13,∴x =π-arcsin 13
. 2.【答案】C
【解析】∵π-arccos
16∈(0,π),且cos(π-arccos 16)=-cos(arccos 16)=-16, ∴α=π-arccos
16. 3.【答案】C
【解析】∵3π,arccos(-12)=23π,arctan(=-3π,分别带入原式求得结果。
4.【答案】D
5.【答案】C
【解析】①arcsin
2π无意义;②③④正确. 6.【答案】B
【解析】∵tan(2x +
3π),∴2x +3π=6
π+k π ∴2x =-6
π+k π,∴x =-12π+2k π (k ∈Z), ∴x =512π或x =1112
π或x =1712π或x =7312π,共4个. 7.【答案】712
π 【解析】∵2cos(x -4π)=1,∴cos(x -4
π)=12, ∵x ∈(0,π),∴x -4π∈(-4π,34π),∴x -4π=3
π, ∴x =712
π. 8.【答案】43
π 【解析】∵x =3
π是方程2cos(x +α)=1的解, ∴2cos(3π+α)=1,∴cos(3
π+α)=12. ∵α∈(0,2π),∴α+3π∈(3
π,73π), ∴α+3π=53π,∴α=43π.
9.【答案】[1,32
] 【解析】要使函数有意义,需有:320,1231x x -≥⎧⎨-≤-≤⎩
, 解得:1≤x ≤32
.
10.【解析】∵tan x =-1<0,且cos x >0, ∴x 是第四象限角,即2k π-
2π<x <2k π(k ∈Z). ∵2
π<x -2k π+π<π(k ∈Z),
又cos(x -2k π+π)=cos(x +π)=-cos x (k ∈Z),
∴x -2k π+π=arccos()(k ∈Z), 即x =2k π-π+34π=2k π-4
π (k ∈Z). ∴x 的取值集合为{x |x =2k π-
4
π,k ∈Z}. 11.【解析】(1)当2x -3π=2k π+2
π,即x =k π+512π,k ∈Z 时,函数y =f (x )取得最大值为3; 当2x -3π=2k π-2
π,即x =k π-12π,k ∈Z 时,函数y =f (x )取得最小值为-1. (2)令T =2x -3π,则当2k π-2π≤T ≤2k π+2π,即2k π-2π≤2x -3π≤2k π+2
π,也即k π-12π≤x ≤k π+512
π (k ∈Z)时,函数y =2sin T +1单调递增, 又x ∈[0,2π],∴函数y =f (x )的单调增区间为[0,512π],[1112
π,1712π],[2312π,2π]. (3)∵y =2sin(2x -3π)+1>2,∴sin(2x -3π)>12,从而2k π+6π<2x -3π<2k π+56
π (k ∈Z),∴k π+4π<x <k π+712π (k ∈Z),故满足条件的x 的取值范围为k π+4π<x <k π+712π (k ∈Z).
12.【解析】∵sin(180°-A )B -90°),
∴sin A B .①
A B ),
A B ,②
①2+②2得cos 2A =
12
, 即cos A
. ∵A ∈(0,π),∴A =
4π或34π. (1)当A =4
π时,有cos B
, 又B ∈(0,π),∴B =6
π,C =712π. (2)当A =34
π时, 由②得cos B
30π=<, 可知B 为钝角,在一个三角形中不可能出现两个钝角,此种情况无解. 综上,可知A 、B 、C 的大小分别为
4π,6π,712π.。
