多状态网络可靠度的d_最小割_路_集转换算法
Edmonds-karp算法

1. 最大流最小割定理介绍:把一个流网络的顶点集划分成两个集合S和T,使得源点s ∈S且汇点t ∈T,割(S,T)的容量C(S,T) =∑Cuv, 其中u∈S且v∈T。
从直观上看,截集(S,T)是从源点s到汇点t的必经之路,如果该路堵塞则流从s无法到达t。
于是我们可以得到下面的定理:最大流最小割定理:任意一个流网络的最大流量等于该网络的最小的割的容量。
这个定理的证明这里就不给出了,可以参考图论方面的资料。
2. 求最大流的Edmonds-Karp算法简介:若给定一个可行流F=(Fij),我们把网络中使Fij=Cij的弧称为饱和弧,Fij<Cij的弧称为未饱和弧。
如果流网络中从i到j没有弧,我们添加一条从i到j且容量Cij=0的弧,这样整个流网络变成一个完全图。
如果从i到j有流量Fij,则从j到i的流量定义为Fji = -Fij 。
考虑一条从源点s出发到汇点t的路径p,如果对于每一段弧(i,j)属于p都有Fij < Cij,即每一条属于p的弧都是未饱和弧,则我们可以向这条路径上压入更多的流,使得其中的一条弧达到饱和。
这样的路径p叫做可改进路,可压入的流量叫做该可改进路的可改进流量。
重复这个过程,直到整个网络找不到一条可改进路,显然这时候网络的流量达到最大。
Edmonds-Karp算法就是利用宽度优先不断地找一条从s到t的可改进路,然后改进流量,一直到找不到可改进路为止。
由于用宽度优先,每次找到的可改进路是最短的可改进路,通过分析可以知道其复杂度为O(VE2)。
Edmonds-Karp算法的伪代码如下:设队列Q--存储当前未检查的标号点,队首节点出队后,成为已检查的标点;path -- 存储当前已标号可改进路经;repeatpath置空;源点s标号并进入path和Q;while Q非空and 汇点t未标号dobegin移出Q的队首顶点u;for 每一条从u出发的弧(u,v) doif v未标号and 弧(u,v)的流量可改进then v进入队列Q和path;end whileif 汇点已标号then 从汇点出发沿着path修正可改进路的流量;until 汇点未标号;Edmonds-Karp算法有一个很重要的性质:当汇点未标号而导致算法结束的时候,那些已经标号的节点构成集合S,未标号的节点构成集合T,割(S,T)恰好是该流网络的最小割;且这样求出的最小割(S,T)中集合S的元素数目一定是最少的。
【国家自然科学基金】_最小路_基金支持热词逐年推荐_【万方软件创新助手】_20140731
科研热词 最小路集 黑启动 节点恢复成功率 网络重构 端端可靠性 有效最小路集 时延 容量 分区优化
推荐指数 2 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
2013年 科研热词 可靠性 最小路集法 配电网 道路网络 继电保护系统 直接不交化算法 畅通可靠度 数字化变电站 敏感度 孤岛 季节性特征 大型网络 城市道路 分布式发电 光伏电源 信息流 交通工程 推荐指数 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
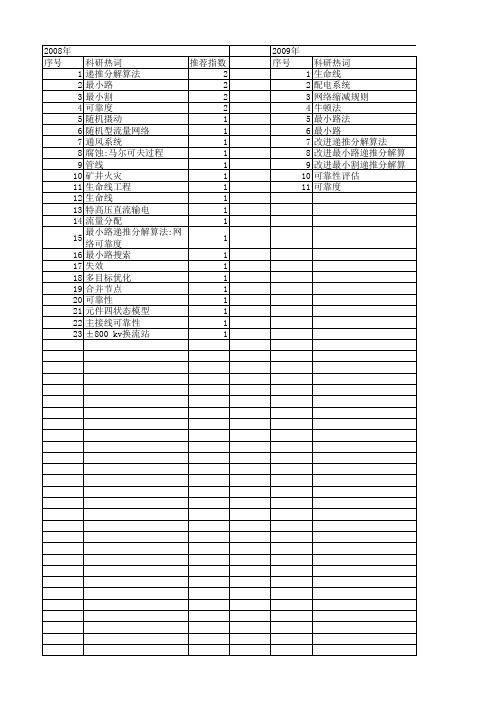
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词 推荐指数 递推分解算法 2 最小路 2 最小割 2 可靠度 2 随机摄动 1 随机型流量网络 1 通风系统 1 腐蚀:马尔可夫过程 1 管线 1 矿井火灾 1 生命线工程 1 生命线 1 特高压直流输电 1 流量分配 1 最小路递推分解算法:网络可靠度 1 最小路搜索 1 失效 1 多目标优化 1 合并节点 1 可靠性 1 元件四状态模型 1 主接线可靠性 1 ±800 kv换流站 1
科研热词 评估 网络可靠性 结构函数 端端可靠性 概率模型 最小路集 最小路 故障序列 可靠性 动态可靠性 供应链 仿真 二元决策图 不交路 下界 上界 petri网
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2012年 序号 1 2 3 4 5 6 7 8 9
2009年 序号 1 2 3 4 5 6 7 8 9 10 11
科研热词 生命线 配电系统 网络缩减规则 牛顿法 最小路法 最小路 改进递推分解算法 改进最小路递推分解算法 改进最小割递推分解算法 可靠性评估 可靠度
可靠性理论-模拟题

《可靠性理论》模拟题一.单选题1. 可靠性定义为:产品在规定的条件下和()内完成规定功能的能力A. 规定的工作时间B. 规定的时间C. 规定的工作范围D. 规定的设备[答案]:B2. 提高人机系统可靠性的有效人机结合形式不包括:()A. 串联冗长式B. 并联冗长式C. 待机冗长式D. 监督校核式[答案]:A3. 读电压表时,人读表的可靠度是0.9940,而把读数记录下来的可靠度为0.9971,若某个作业操作只需要读表和记录数据,那么这个作业操作中,人的失误率是()A. 0.006B. 0.0089C. 0.9911D. 0.0089[答案]:D4. 故障树中代表当全部输入事件发生时,输出事件才发生的逻辑符号是:()A. 条件与门B. 与门C. 条件或门D. 或门[答案]:B5. 简单求解网络可靠度的常用方法有状态枚举法,(),最小割集法,最小径集法,不交布尔代数运算规则A. 蒙特卡洛法B. 全概率分解法C. 事故树法D. 均方根偏差法[答案]:B6. 从学术研究上分,下面哪种不是可靠性研究的内容:()A. 可靠性评价B. 可靠性工程C. 可靠性物理D. 可靠性数学[答案]:A7•工作到某时刻t时尚未失效做障)的产品,在该时刻t以后的下一个单位时间内发生失效(故障)的概率是指()A. 不可靠度B. 故障率C. 失效率D. 失效密度[答案]:C8•在一个正处于基坑施工阶段的建筑工地,新近送来一批钢材,钢材的失效率为常数,则可靠度为R=99.9%的中位寿命t(0.5)为:()A. 25B. 25000C. 17328.7D. 无法求解[答案]:C9•已知某产品可靠性的表达式为R(t)=E.-入,当入=5*104/h时,工作100h,则该产品的MTTF 是:()A. 2000hB. IOOhC. IOOOhD. 1500h[答案]:A10. 对于不可修复的产品,该产品从开始使用到失效前的工作时间(或工作次数)的平均值称为_______ ,()A. 可靠度B. 失效率C. 平均寿命D. 可靠寿命[答案]:C11. 为了使系统达到规定的可靠度水平,不考虑各单元的重要度等因素而给所有的单元分配相等的可靠度,这种分配方法称为:()A. 阿林斯分配法[答案]:DB. A.GRE.E.分配法C. 条件极值法D. 等同分配法[答案]:D12•由三种形态的失效率曲线组成,反映了产品在其全部工作过程中的三个不同阶段或时期的是()A. 正弦曲线B. 浴盆曲线C•凹凸曲线D.恒定型曲线[答案]:B13•反映了由许多零件构成的机器,设备或系统,在不进行预防性维修时,或者对于不可修复的产品,在其全部工作过程中的不同阶段或时期的失效率曲线是()A. 浴盆曲线B. 递减型曲线C•递增型曲线D.恒定型曲线[答案]:A14•某系统的平均无故障工作时间,在该系统1500h的工作期内需有备件更换,现有3个备件供使用,求系统能达到的可靠度是()A. 0.223B. 0.531C. 0.669D. 0.989[答案]:B15•可靠性设计是使产品的可靠性要求在设计中得以落实的技术,可靠性设计决定了产品的()A. 事故率B. 失效率C. 可靠寿命D. 固有可靠性[答案]:D16. 当串联系统的设计不能满足产品可靠性设计指标要求时,可以采用增加一些同样的部件(单元)将这些同样部件组成并联成分系统,以提高系统的可靠性,这种提高可靠性的作法在工程上称:()A. 降额设计B. 概率设计C. 冗余设计D. 容差与漂移设计[答案]:C17. 一操作人员正在完成一项时间连续的任务,操作人员的差错率为0.02次/小时,试求在3小时的任务内操作人员的不可靠度()A. 0.06B. 0.9418[答案]:B D. 0.94 [答案]:C18. 下面哪种逻辑关系表示多输入事件不仅同时发生 ,而且还必须满足某一条件 ,才会有输出事件发生:() A •条件或门 B. 条件与门 C •或门 D.与门 [答案]:B19. 在生产过程中已经确立了的 ,与产品的材料,设计与制造工艺及检验精度等有关的是产品的:() A. 狭义可靠性 B. 固有可靠性 C. 广义可靠性 D. 使用可靠性 [答案]:B20. 已知某事故的事故树的布尔代数表达式为 T=(abc+f)[(a+b)f ](a+be),化简表达式为()A. af+bfeB. (af+bf)(a+be)C. (a+be)fD. af+be [答案]:A21. 与产品的使用条件密切相关 ,并且受到环境,操作水平,保养与维修等因素影响的是产品的()A. 狭义可靠性B. 固有可靠性C. 广义可靠性D. 使用可靠性 [答案]:D22. 广义可靠性是指产品在其 ()内完成规定功能的能力,它包括可靠性(即狭义可靠性)与维修性A. 某一稳定的时间B. 整个寿命期限C. 规定的工作范围23•可靠度水平时所对应的时间称为:()[答案]:B[答案]:B B. 中位寿命 C. 可靠寿命 D. 特征寿命 [答案]:B24. 四个相同单元组成的如下系统中 ,哪种系统的可靠度最高:()A. 四个单元构成的串联系统B. 四个单元构成的并联系统C. 串并联系统(m=2,n=2)D. 并串联系统(m=2,n=2) [答案]:B25.下面的描述属于串联系统的是 :()A. 系统的失效概率低于各单元的失效概率B. 系统的可靠度高于各单元的可靠度C. 系统的平均寿命高于各单元的平均寿命D. 系统的各单元服从指数寿命分布,该系统也服从指数寿命分布 [答案]:D26. 使元器件或设备工作时所承受的工作应力 (电应力或温度应力定的额定值,从而达到降低基本故障率 ,提高使用可靠性的目的程上称:() A. 降额设计 B. 概率设计 C. 冗余设计 D. 容差与漂移设计 [答案]:A 27.下面四种曲线中不属于失效率曲线的是 :()A. 递减型失效率曲线B. 正弦型失效率曲线C. 递增型失效率曲线D. 恒定型失效率曲线 [答案]:B28.影响人的可靠性因素中的自身因素不包括 :()A. 生理因素B. 管理方法C. 心理因素),适当低于元器件或设备规 ,这种提高可靠性的作法在29. 某人连续工作的失效率入=0.003/h式计算他工作25h的可靠度()[答案]:BA. 0.9277B. 0.0723C. 0.5D. 0.075[答案]:A30•可靠性框图中的并联系统对应于故障树图中的逻辑关系是:()A•条件或门B. 条件与门C•或门D.与门[答案]:D31.故障树中代表顶上事件的是:()A. 圆形符号B. 矩形符号C•菱形符号D.椭圆形符号[答案]:B32•故障树中一个或多个输入事件发生,即发生输出事件的逻辑符号是:() A•条件与门B. 与门C•条件或门D.或门[答案]:D33•按照元器件性能参数可能出现的极限值来设计电路的方法是:()A•降额设计B. 冗余设计C. 最坏情况设计D. 概率设计[答案]:C34•可靠性元器件的指数分布的平均寿命和失效率,两者互为()A. 倒数B. 余数C. 相反数D. 以上都不对[答案]:A35•下面哪种不是可靠性理论中经常遇到的失效分布()A. 威布尔分布B. 正态分布C. 指数分布D. 平均分布[答案]:D36. 系统进行可靠度分配时,若已知各元件的预计失效率,而进行分配的方法称为_________ ,()A. 等同分配法B. 均方根偏差分配法C. 阿林斯分配法D. A.GRE.E.分配法[答案]:C37. 系统的整体失效率是各组成单元失效率之和的系统是:()A•并联系统B. 表决系统C. 串联系统D. 混联系统[答案]:C38. 当要求系统的可靠度Rs=0.850,选择三个复杂程度相似的元件串联工作,则每个元件的可靠度应是()A. 0.469B. 0.947C. 0.85D. 0.531[答案]:B39. 下面不属于漂移设计方法的是:()A. 最小径集法B. 最坏情况设计法C. 蒙特卡洛法D. 均方根偏差设计法[答案]:A40. 元器件很多时,漂移设计方法中最适合使用的是:()A. 最小径集法B. 最坏情况设计法C. 均方根偏差设计法D. 蒙特卡洛法[答案]:C二.多选题1. 对于产品来说,可靠性问题和人身安全,经济效益密切相关,因此,研究产品的可靠性问题,显得十分重要,非常迫切;下列属于提高产品的可靠性的重要意义的是 :() A. 防止故障和事故的发生B. 减少停机时间,提高产品可用率 C •规定了系统的固有可靠性 D.减少产品责任赔偿案件的发生 E •可以贯穿于产品的整个寿命周期 [答案]:ABD 2.影响人的可靠性因素中的自身因素包括 :()A. 生理因素B. 管理方法C. 心理因素D. 训练因素E. 环境因素 [答案]:ACD3.人因差错表现类型可由人的行为特征来划分 ,下列选项中属于按人的行为特征划分的是 :()A. 意识差错B. 识别差错C. 管理差错D. 力度差错E. 违章操作 [答案]:ABDE 4.故障树分析中定量分析的内容包括 :()A. 求最小割集B. 求顶上事件概率C. 求概率重要度D. 求最小径集 [答案]:BCA. 状态枚举法B. 最小割集法C. 全概率分解法D. 最小径集法E. 蒙特卡洛法 [答案]:AC 6.矿山通风系统是矿井生产的重要系统,为生产系统5. 网络系统的可靠度计算一般比较复杂 法中仅适用于小型网络求解可靠度,可以进行简单求解网络可靠度的方法很多:,但下列方的安全运行提供可靠的保证,通风系统的功能包括:()A. 在生产时期利用通风动力,以最经济的方式,向井下各用风地点供给保质保量的新鲜风流B. 保证作业空间有良好的气候条件c•冲淡或稀释有毒有害气体和矿尘D. 在发生灾变时,能有效,及时地控制风向及风量E. 与其它措施结合,控制灾害的发生,进而消灭事故[答案]:ABCD7•产品可能会失效的原因有很多,要预知所有这些原因是不切实际的,所以还必须考虑到所涉及的不确定性;发生失效的主要原因在于:()A. 设计可能先天不足B. 变异也可能导致失效C•磨损能导致失效D.潜在现象导致的失效E•正确的规范,设计或软件编码等错误导致的失效[答案]:ABCD8•可靠性工作的目的是实现并保持系统或者产品的最高可靠性水平,因此可靠性预计的目的士亜阜・UA. 设计人员明确产品可靠性设计的要求B. 论证方案所提出的可靠性指标是否合理C•设计人员可以发现设计中的薄弱环节D. 是整体和部分之间的可靠性定量要求协调一致E. 避免设计的盲目性[答案]:BCE9•可靠性的定义包括哪几方面的内容,()A. 对象B. 故障率C. 使用条件D. 规定的功能E•使用期限[答案]:ACDE10•产品运行时的可靠性,称为工作可靠性,它包含了产品的制造和使用两方面因素,分别用___________ 禾廿_________ 来反映,()A. 工程可靠性B. 广义可靠性C. 狭义可靠性D. 固有可靠性E. 使用可靠性[答案]:DE11. 从系统控制的功能方面来看___________ ,故障安全结构主要包括:, _____________________________ 和______ ,()A. 系统综合式B. 消极被动式C. 积极主动式D. 运行操作式E. 运行控制式[答案]:BCD12. 并联系统是表示当组成系统的n个单元同时失效时,系统才失效,即当系统的任一单元正常工作时,系统都能够正常工作,其主要性质有:()A. 并联系统的失效概率低于各单元的失效概率B. 并联系统的可靠度高于各单元的可靠度C. 并联不可以提高系统的可靠度D. 并联系统的平均寿命高于各单元的平均寿命E. 并联系统的各单元服从指数寿命分布,该系统不再服从指数寿命分布[答案]:ABDE13. 可靠性设计的基本内容和设计过程包括哪几个方面,()A. 建立可靠性模型B. 进行可靠性指标的预计和分配C. 进行各种可靠性分析D. 采取各种有效的可靠性设计方法E. 进行系统的可靠性设计评价[答案]:ABCD14. 影响人的可靠性因素主要包括:()A. 人的自身因素B. 环境因素C. 操作规范的设计,使用规程等因素D. 管理方法及规章制度方面的因素E. 家庭成员[答案]:ABCD15. 故障树树形结构正确与否,直接影响到故障树的分析及其可靠程度,因此,为了成功地建造故障树,属于其建树遵循的基本规则的是:()A. 直接原因原理B. 间接原因原理C. 完整门规则D. 非门规则E. 系统性规则[答案]:ACD16. 由失效率曲线所反应,表现产品在其全部工作过程中的不同时期分别是:()A. 早期失效期B. 磨合失效期C. 偶然失效期D. 耗损失效期E. 晚期失效期[答案]:ACD17•下列关于最小割集与最小径集说法正确的是:()A. 最小割集表示系统的危险性B. 最小径集表示系统的安全性C•利用最小割不能集进行结构重要度分析D. 利用最小径集进行结构重要度分析E. 利用最小割集,最小径集进行定量分析和计算顶上事件的概率[答案]:ABDE18•故障树分析法和可靠性框图分析法都可用来分析系统的可靠性,并且两者的结果是互补的但也存在比较大的区别,下列关于两者的说法正确的是:()A. FTA.是以系统故障为导向,以不可靠度为分析对象;而可靠性框图分析法是以系统正常为导向,以可靠度为分析对象B•两者均能分析分析硬件而且可分析人为因素,环境,硬件以及软件的影响C. 可靠性框图能分析两态单调关联系统,两态非单调关联系统和多态系统;而FTA.分析法仅限于分析两态单调关联系统D. FTA.能将导致系统故障的基本原因和中间过程利用故障树清楚地表示出来;而可靠性框图分析法仅能表示系统和部件之间的联系E. 在故障状态的表现方面,FTA.很明显地表示出各种故障状态,可靠性框图不如故障树清晰明了[答案]:ADE19. 简单求解网络可靠度的常用方法有:()A. 状态枚举法B. 全概率分解法C. 最小割集法D. 最小径集法E. 蒙特卡洛法[答案]:ABCD20. ___________________________ 矿井通风系统一般包括方面,()A. 通风网路B. 通风管理规程C. 通风动力设施D. 通风应急系统E. 通风构筑物[答案]:ACE21. 在人机系统中计算可靠度时,不属于人的作业方式的是:()A. 单人作业B. 间歇性作业C. 多人作业D. 连续作业[答案]:ACE22. 由失效率曲线所反应,不能表现产品在其全部工作过程中的不同时期分别是:()A. 早期失效期B. 磨合失效期C•偶然失效期D. 耗损失效期E. 晚期失效期[答案]:BE23•人机系统可靠性设计的原则主要有:()A. 加强可靠性管理原则B. 系统的整体可靠性原则C. 高可靠性组成单元要素原则D. 具有安全系数的设计原则E. 事先进行试验和进行评价的原则[答案]:BCDE24•可靠性工程中用来表示产品总体可靠性高低的各种可靠性数量指标主要有()A. 可靠度B. 失效率C. 平均寿命D. 可靠寿命E. 失效密度[答案]:ABCD25. 产品失效率曲线一般可分为()A. 递减型B. 恒定型C. 递增型D. 正弦型E. 指数型[答案]:ABC26. 在边坡工程中,衡量可靠度的三种尺度分别是()A. 稳定概率B. 坡面厚度C. 破坏概率E. 可靠指标[答案]:ACE27. 可靠性指标分配是可靠性工作中不可缺少的一部分,也是可靠性工程的决策性问题,下列属于可靠性分配方法的是:() A. 阿林斯分配法 B. A.GRE.E.分配法 C. 条件极值法 D. 等同分配法 E •上下限法 [答案]:ABD 28. 可靠性设计是系统总体工程设计的重要组成部分,它是通过工程设计与结构设计等方法 保证系统的可靠性而进行的一系列分析与设计技术 ,其重要性主要为()A. 设计规定了系统的固有可靠性B. 使可靠性贯穿于产品的整个寿命周期 C •产品可靠性设计直接关系人的生命安全 D. 进行系统的可靠性设计评价E. 可靠性设计直接关系产品的投入成本费用 [答案]:ABCE29•产品在长期工作中,它的特性参数会出现漂移 ,当参数漂移超出允许范围时 ,就不能完成规定的功能,其主要原因是:()A. 管理上的缺陷,对机器设备维护不当B. 随着环境条件的变化会使元器件的参数发生漂移 C •人员的操作失误,使机器设备处于不正常的状态D.机械零部件,电子元器件的特性参数实际值都有一定的公差范围 E •机器设备本身存在着缺陷 [答案]:BD31.要进行可靠性指标分配时,由于具体情况不同,可靠性指标的分配方法也不同 ,但无论何种情况下,可靠性指标分配必须遵循的准则是 ()A. 对于复杂度高的分系统,设备等,应分配较低的可靠性指标B. 对于技术上不成熟的产品,分配较高的可靠性指标C. 对于处于恶劣环境条件下工作的产品,应分配较低的可靠性指标D. 对于需要长期工作的产品,分配较低的可靠性指标30.人机系统是指人与其所控制的机器相互配合 作系统;则人机结合方式的方式有 ()A. 串联B. 并联 C •串,并联混合 D. 旁联 E. 冗余:,相互制约,并以人为主导完成规定功能的工E. 对于重要度高的产品,应分配较高的可靠性指标[答案]:ACDE32. 人的操作故障受多种因素的影响,下列属于造成人因差错影响情况的是:()A. 在预定时间内完成某项工作B. 环境的不良导致操作错误C. 没按管理目标完成某项工作D. 没忘记做某项工作,做错了某项工作E. 采取了不应采取的工作步骤[答案]:ABDE33•故障树分析中定量分析的内容包括: ______ ,()A. 求顶上事件概率B. 求结构重要度C. 求概率重要度D. 求最小割集和径集E. 割集和径集[答案]:AC34•产品运行时的可靠性,称为工作可靠性,从可靠性定义的范围上分析,可靠性可分为()A. 工程可靠性B. 广义可靠性C. 狭义可靠性D. 固有可靠性E. 使用可靠性[答案]:BC35•通过分析可知提高人机系统的可靠性,主要应从机器本身技术上和人员管理两方面来进行综合考虑;下列属于从机器本身技术方面考虑,常用的方法有:()A. 将系统的复杂程度降至最低限度B. 减额使用C. 提高系统中的元器件,零部件的可靠性D. 让员工了解工作对象的设计,制造缺陷E. 采用储备系统,即用一个或多个储备部件[答案]:ABCE36•可靠性是一门新兴的边缘学科,从学术研究上分,主要研究的内容包括()A. 可靠性化学B. 可靠性物理C. 可靠性数学D. 可靠性工程E. 可靠性设计[答案]:BCDE37.由n个单元组成的串联系统表示当这n个单元都正常工作时,系统才正常工作,即当系统任一单元失效时,就引起系统失效,其主要性质有:()A. 串联系统的可靠度低于该系统的每个单元的可靠度B. 随着串联单元数量的增大而迅速降低C. 串联系统的失效率大于该系统的各单元的失效率D. 并联系统的失效概率低于各单元的失效概率E•串联系统的各单元寿命服从指数分布,该系统寿命也服从指数分布[答案]:ABCE38•影响可靠性的因素包括:()A. 人的自身因素B. 环境因素C. 操作对象的设计,使用规程等因素D. 管理方法及规章制度方面的因素E. 时间及空间因素[答案]:ABCD39•下列属于人机系统可靠性设计原则的是:()A. 系统的整体可靠性原则B. 标准化原则C. 低维修度原则D. 预测和预防的原则E. 审查原则[答案]:ABDE40. 系统可靠性计算中的模型包括:()A. 并联系统B. 串联系统C. 串并联系统D. 表决系统E. 储备系统[答案]:ABCD41. 故障树分析法的优点包括()A. 工作量小,既经济又省时B. 易于处理多种状态事件C. 便于人们对系统进行定性或定量评价,且有选择评价目标和方法的自由D. 可以利用演绎法帮助人们寻找故障原因所在E. 在一般条件下,对待机储备和可修系统可以分析[答案]:CD42. 下面的描述属于并联系统的是:()A. 并联系统的可靠度高于各单元的可靠度B. 并联系统的失效概率高于各单元的失效概率C. 并联系统的失效概率低于各单元的失效概率D. 并联系统的平均寿命高于各单元的平均寿命E. 并联系统的各单元服从指数寿命分布,该系统不再服从指数寿命分布[答案]:ACDE43•下列属于可靠性工程应用目的和任务的是()A. 可靠性物理B. 可靠性试验C. 可靠性设计D. 可靠性数学E. 系统可靠性[答案]:BCE44•提高人机系统可靠性的有效人机结合形式包括()A. 串联冗长式B. 并联冗长式C. 开机冗长式D. 待机冗长式E. 监督校核式[答案]:BDE45.下列影响可靠性因素中不属于人的自身因素的是()A. 生理因素B. 环境因素C. 心理因素D. 训练因素E. 管理因素[答案]:BE46•目前我国已经对电子元器件划分质量等级,下列属于电子元器件划分类别的是:()A. 特军品B. 厂用级C. 普军品D. 民用品E. 家用级[答案]:ACD47•下列对可靠性指标分配的准则描述正确的是()A. 对于复杂度高的分系统,设备等,应分配较高的可靠性指标B. 对于技术上不成熟的产品,分配较低的可靠性指标C. 对于处于恶劣环境条件下工作的产品,应分配较高的可靠性指标D. 对于需要长期工作的产品,分配较低的可靠性指标E. 对于重要度高的产品,应分配较高的可靠性指标[答案]:BDE48•求解网络可靠度的方法包括()A.状态枚举法B. 全概率分解法C. 最小割集法D. 最小径集法E. 蒙特卡洛法[答案]:ABCD49. 由三种失效率曲线所反应,表现产品在其全部工作过程中的三个不同时期是()A.晚期失效期B•早期失效期C•偶然失效期D. 必然失效期E. 耗损失效期[答案]:BCE50. 下列不属于故障树中常用的事件符号的是()A.矩形符号B•屋形符号C. 正方形符号D. 圆形符号E. 半圆形符号[答案]:CE51. 下列叙述中正确的是()A. 故障树图是一种图形化设计方法,但不可作为可靠性框图的替代方法B. 故障树图是一种逻辑因果关系图C•故障树图不必根据元部件状态(基本事件)来显示系统的状态D. 故障树图是从下到上逐级建树并且根据事件逻辑关系而联系E. 故障树图是表示一个系统从一种可预知的(或不可预知的)失效出发,利用标准的逻辑符号将基本事件相联系的模型”[答案]:BE52. 下列描述中错误的是()A. 最小割集表示系统的安全性B. 最小径集表示系统的危险性C. 可以利用最小割集,最小径集进行结构重要度分析D. 可以利用最小割集,最小径集进行定量分析和计算顶上事件的概率E. 最小径集的求法是利用它与最小割集的对偶性[答案]:AB53•可靠性设计过程包括哪些方面()A. 确定总体方案B. 建立可靠性模型C. 进行可靠性指标的预计和分配D. 进行可靠性分析E. 采取有效的可靠性设计方法[答案]:BCDE54.所谓设备的降额设计主要思想是使元器件或设备工作时所承受的工作应力(电应力或温度应力),适当低于元器件或设备规定的额定值;则下列关于降额设计的说法正确的是:()A. 元器件降额幅度越大,设备可靠性将提高的越多B. 有些元器件降额太大,易产生低电平失效C. 考虑到当环境应力改变,但降额幅值不应相应地改变D•应注意到,有些元器件的某些参数是不能降额的E. 降额幅值过大,将带来设备的体积,重量的增加[答案]:BDE三.判断题1•贝叶斯定理的内容就是将一个复杂的网络系统分解为若干个相当简单的子系统,先求系统的可靠度,再利用全概率公式计算各子系统的可靠度[答案]:F2•系统可靠性设计是指在遵循系统工程规范的基础上,在系统设计过程中,采用一些专门技术将可靠性设计”到系统中去,以满足系统可靠性的要求[答案]:T3•常规设计的平均安全系数与可靠度没有联系,而可靠性设计的平均安全系数与可靠度直接联系起来[答案]:T4•对于大多数武器装备,其寿命周期费用中的使用保障费用要比研制和生产费用高[答案]:T5•如果规定的系统故障率指标是每单位时间0.16,考虑分配余量,可以按每单位时间0.2进行可靠性分配[答案]:F6•系统的工程结构图是表示组成系统的单元之间的可靠性功能关系,而可靠性框图则表示系统的功能与组成系统的单元之间的物理关系和工作关系[答案]:F7•电子元器件降额设计的降额度越大越好[答案]:F8•最小径集表示的是系统的安全性[答案]:T 9•串联系统的可靠度是各独立单元可靠度的乘积[答案]:T10•当可靠度函数为正态分布时,平均寿命等于失效率的倒数[答案]:F11. 当可靠水平小于0.5时,一个单元系统的可靠寿命高于2/3(G)系统的可靠寿命[答案]:T12. 对于处于恶劣环境条件下工作的产品,应分配较高的可靠性指标[答案]:F13. 各单元可靠度大致相同,复杂程度也差不多时适合使用的分配方法是阿林斯分配法[答案]:F14. 全概率分解法的基本思想是:系统的可靠度等于系统中某一个选定的单元正常条件下系统的可靠度乘以该单元的可靠度,再加上该单元失效条件下系统的可靠度乘以该单元的不可靠度[答案]:T15. 系统可靠性与维修性决定了系统的可用性和可信性[答案]:T16•为简化故障树,可将逻辑门之间的中间事件省略[答案]:F17•阿林斯分配法和A.GRE.E.分配方法均考虑了各部件的复杂性和重要程度和工作时间等差别,明确了部件和系统失效之间的关系[答案]:F18.在系统寿命周期的各阶段中,可靠性指标是不变的[答案]:F。
可靠性理论模拟题

《可靠性理论》模拟题一.名词解释1.可靠性:产品在规定的条件下和规定的时间内完成规定功能的能力。
2. 可靠性设计:系统可靠性设计是指在遵循系统工程规范的基础上,在系统设计过程中,采用一些专门技术,将可靠性“设计”到系统中去,以满足系统可靠性的要求。
3. 最小割集和最小径集:最小割集就是引起顶上事件发生所必需的最低限度的割集。
最小径集就是顶上事件不发生所需的最低限度的径集。
4. 网络:连接不同点之间的路线系统或通道系统。
5.广义可靠性:广义可靠性是指产品在其整个寿命期限内完成规定功能的能力,它包括可靠性(即狭义可靠性)与维修性。
6.可靠性指标分配:指根据系统设计任务书中规定的可靠性指标(经过论证和确定的可靠性指标),按照一定的分配原则和分配方法,合理的分配给组成该系统的各分系统、设备、单元和元器件,并将它们写入相应的设计任务书或经济技术合同中。
7. 降额设计:使元器件或设备工作时所承受的工作应力(电应力或温度应力),适当低于元器件或设备规定的额定值,从而达到降低基本故障率、提高使用可靠性的目的。
8. 人机系统:指人与其所控制的机器相互配合,相互制约,并以人为主导而完成规定功能的工作系统。
二.填空题1.可靠性的定义包含有五个方面的内容,它们是:对象、使用条件、使用期限、规定的功能、概率等。
2.由三种失效率曲线所反应,表现产品在其全部工作过程中的三个不同时期分别是:早期失效期、偶然失效期、耗损失效期。
3.对于可修复的产品,其平均无故障工作时间或平均故障间隔称为平均寿命。
4.失效率函数为常数λ时,可靠度函数表达式可写为:tetRλ-=)(。
5.系统进行可靠度分配时,若已知各元件的预计失效率,而进行分配的方法称为阿林斯分配法。
6.简单求解网络可靠度的常用方法有状态枚举法、全概率分解法、最小割集法、最小径集法、不交布尔代数运算规则。
7.割集和径集中反应导致顶上事件发生所必需的最低限度的是最小割集;反应顶上事件不发生所需的最低限度的是最小径集。
最小割集计算

最小割集计算:T=A1+A2+A3=B1B2+X6X7+X8X9=(X1+X2+X3)(X4+X5)+X6X7+X8X9= X1X4+X1X5+X2X4+X2X5+X3X4+X3X5+X6X7+X8X9则最小割集有8个,即K1={X1,X4};K2={X1,X5};K3={X2,X4};K4={X2,X5};K5={X3,X4};K6={X3,X5};K7={X6,X7};K8={X8,X9}。
最小径集计算:T′=A1′·A2′·A3′=(B1′+B2′)(X6′+X7′)(X8′+X9′)=(X1′X2′X3′+X4′X5′)(X6′+X7′)(X8′+X9′)=(X1′X2′X3′X6′+X1′X2′X3′X7′+X4′X5′X6′+X4′X5′X7′)(X8′+X9′)= X1′X2′X3′X6′X8′+ X1′X2′X3′X6′X9′+ X1′X2′X3′X7′X8′+ X1′X2′X3′X7′X9′+ X4′X5′X6′X8′+ X4′X5′X6′X9′+ X4′X5′X7′X8′+ X4′X5′X7′X9′则故障树的最小径集为8个,即P1={X1,X2,X3,X6,X8};P2={X1,X2,X3,X6,X9};P3={X1,X2,X3,X7,X8};P4={X1,X2,X3,X7,X9};P5={X4,X5,X6,X8};P6={X4,X5,X6,X9};P7={X4,X5,X7,X8};P8={X4,X5,X7,X9};起重钢丝绳断裂事故发生概率计算:根据最小割集计算顶上事件的概率即g=1-(1-qk1)(1-qk2)(1-qk3)(1-qk4)(1-qk5)(1-qk6)(1-qk7)(1-qk8)=1-(1-q1q4)(1-q1q5)(1-q2q4)(1-q2q5)(1-q3q4)(1-q3q5)(1-q6q7)(1-q8q9)由于q1=q2=q3=q4=q5=q6=q7=q8=q9=0.1则g=1-(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)(1-0.1×0.1)=1-(1-0.1×0.1)8=1-0.998=0.07726山东科技大学2005年招收硕士学位研究生入学考试安全系统工程试卷(共2页)一、问答题(共25分)1、说明事故法则的概念,它对安全工作的启示是什么?分析其在安全工作中的应用。
最小割集、最小径集的定义

最小割集、最小径集的定义最小割集和最小径集是图论中常用的概念,可以用来解决最小割和最小循环的问题。
1.最小割集:最小割集是指在一个图中,将图的顶点划分成两个不相交的集合A 和B,使得割(A,B)的权重之和达到最小。
其中,割(A,B)是指A中的顶点与B中的顶点之间的边的集合。
割的权重之和是指割中边的权重之和。
最小割集的定义可以用来解决最小割问题。
最小割问题是指在一个图中找到一条割使得割的权重之和最小。
最小割集是指将图中所有割的集合中,权重之和最小的割。
最小割集可以通过最大流算法来计算。
最大流算法是一种用来求解网络流问题的算法,网络流问题是指在一个图中,找到从源点到汇点的最大流量。
2.最小径集:最小径集是指在一个有向图中,将有向边删去一部分后,使得从源点到汇点的路径长度之和最小。
路径长度是指从起始点到终止点经过的边的数量。
最小径集的定义可以用来解决最小循环问题。
最小循环问题是指在一个有向图中找到一个循环使得循环的路径长度之和最小。
最小径集是指将图中所有循环的集合中,路径长度之和最小的循环。
最小径集可以通过拓扑排序和动态规划来计算。
拓扑排序是一种将有向图中的顶点按照拓扑顺序进行排序的算法,拓扑顺序是指如果存在一条从顶点i到顶点j的路径,则i一定排在j的前面。
动态规划是一种将一个问题分解成多个子问题,并将子问题的解结合起来得到原问题的解的算法。
最小割集和最小径集在实际应用中有广泛的应用。
例如,在社交网络中,最小割集可以用来找到社区结构,将一个社交网络划分成多个相互独立的社区。
在电力网络中,最小割集可以用来找到电网中最容易发生故障的部分,从而进行相应的改进和维护。
在运输网络中,最小径集可以用来找到最短路径,以减少运输成本和时间。
总之,最小割集和最小径集是图论中重要的概念,可以帮助解决最小割和最小循环的问题。
它们在实际应用中具有广泛的应用价值,可以帮助我们更好地理解和优化各种网络结构。
网络可靠性分析

网络综合可靠度
为了进一步分析网络的可靠度,需要考 虑网络承载的业务。
下面以电话网为例,考虑网络平均呼损 的计算。在4.4中已讨论电话网络平均呼 损的计算方法,不过在4.4中并没有考虑 网络故障因素。考虑故障因素的电话网 络平均呼损也可被称之为综合不可靠度。
n
连通度的辅助指标
为了更加细致地描述图的可靠性,引入 三个辅助指标。它们的定义如下:
定义7.3 C =最小割端集的数目; B =最小割边集的数目; A =最小混合割集的数目;
可靠性指标的计算
例7.5 下图中(a) ,(b) ,(c)三个图,分别计算它 们的各种可靠性指标。
(a)
(b)
网络在只有端故障下的近似可靠度
首先,假设网络仅有端故障,Ci (i ) 表示 有 i 个割端的割端集的数目。此时,网 络的不可靠集可以按照割端集来分类, 由于各个端点的故障独立,网络可靠度 可以计算如下:
n
R(n) 1 Ci qi (1 q)ni i
网络近似可靠度
由于 q 1,保留最大的项,则有:
两端之间的可靠度
考虑图的某两个端s和t,所谓s和t之间的 可靠度是指s和t之间有路径相通的概率。
这个概率的近似计算类似网络可靠度的 计算。如果各边、端的可靠度不一样, 并且网络规模不大,也可以对可靠度做 准确计算。
7.4 网络综合可靠度
在7.2中讨论了通信网的各种连通度以及一些辅 助指标,这些指标仅仅依赖于拓扑结构,是对 可靠性的确定性度量。
的混接系统,若第 i 个子系统的可靠度
最小割集、最小径集的定义

最小割集、最小径集的定义文章一:最小割集的定义在图论中,最小割集是指将图分为两个不相交的子图,使得两个子图之间的边的权重之和最小。
最小割集是一个被广泛应用于网络流问题中的概念。
具体而言,最小割集可以用来解决最大流最小割定理的相关问题。
最小割集的定义可以通过以下步骤进行:1. 给定一个图G=(V,E),其中V表示节点集合,E表示边集合。
2. 在图G中选择两个不相交的子集A和B,即A∪B=V,A∩B=∅。
3. 最小割集可以被定义为边集合E的一个子集,其中这些边连接A和B之间的节点。
4. 最小割集的权重是指连接A和B之间的边的权重之和,即连接A和B之间的边的权重之和最小。
最小割集的应用非常广泛,特别是在网络流问题中。
最小割集可以被用来解决最大流最小割定理的相关问题。
最大流最小割定理指出,网络中的最大流量等于网络中的最小割集的权重。
因此,通过求解最小割集,我们可以得到网络中的最大流量。
此外,最小割集还可以应用于图像分割、社交网络分析等领域。
在图像分割中,最小割集可以被用来将图片分割为不同的区域,从而实现物体识别和图像处理等任务。
在社交网络分析中,最小割集可以被用来识别不同群组之间的连接情况,从而帮助我们理解社交网络的结构和特征。
综上所述,最小割集是将图分为两个不相交子图的一种方法,其权重表示连接两个子图之间的边的权重之和。
最小割集在网络流问题、图像分割和社交网络分析等领域有广泛的应用。
文章二:最小径集的定义在图论中,最小径集是指将图中所有节点分为两个不相交的子集,使得这两个子集之间的最短路径的长度最小。
最小径集是一个常用的概念,它能够帮助我们理解图的结构和性质,并且在很多实际问题中有着重要的应用。
最小径集的定义可以通过以下步骤进行:1. 给定一个图G=(V,E),其中V表示节点集合,E表示边集合。
2. 在图G中选择两个不相交的子集A和B,即A∪B=V,A∩B=∅。
3. 最小径集可以被定义为连接A和B之间的最短路径的集合,即找到使得连接A和B之间的最短路径的长度最小的路径集合。
二单项选择题

二单项选择题二、单项选择题1、我国安全系统工程的研究开发式从()开始的。
A、20世纪80年代末B、20世界70年代末C、20世纪60年代末D、20世纪50年代末2、在危险因素等级中,Ⅳ级表示的含义是()A、危险的,可能导致事故发生,造成人员伤亡或财产损失,必须采取措施进行控制;B、灾难的,会导致事故发生,造成人员严重伤亡或财产巨大损失;C、安全的,暂时不能发生事故,可以忽略;D、临界的,偶导致事故的可能,事故处于临界状态,可能会造成人员伤亡和财产损失,应该采取措施予以控制;3、关于最小径集和最小割集说法正确的是()A、多事件的最小割集较少事件的最小割集容易发生;B、最小割集越多,系统的危险性越大;C、一个最小径集中所有的基本事件都不发生,顶事件仍有可能发生;D、最小径集是引起顶事件发生的充要条件;4、绘制事故树时,当所有输入事件都发生时,输出事件E才发生,应使用()来表示三者之间的逻辑关系。
A、或门B、与门C、异或门D、与或门5、以下各种评价方法中不属于定量评价方法的有:()A. 故障类型及影响分析B. 事故树分析C. 作业条件危险性评价法D. 危险指数评价法6、在事故树分析中,反映基本事件发生概率的增减对顶事件发生概率影响的敏感程度的是()。
A.结构重要度 B.临界重要度C.概率重要度 D.最小径集7、已知系统事故发生率P,风险率R,事故损失严重度S,则()A. P= RSB. R=PSC. S =RPD. P = R +S8.对于事故的预防与控制,安全技术对策着重解决()。
A.人的不安全行为B.管理的缺陷C.物的不安全状态D.有害的作业环境9.《矿山安全法》规定的矿山建设工程的“三同时”,是指矿山建设工程的安全设施必须和主体工程()。
A.同时设计、同时勘察、同时施工B.同时施工、同时修复、同时投入生产和使用C.同时审批、同时设计、同时施工D.同时设计、同时施工、同时投入生产和使用10.DOW火灾爆炸指数评价法中计算暴露半径的公式是()。
安全系统工程试题

安全系统⼯程试题试卷⼀⼀、填空题1、安全系统⼯程的基本内容包括________、风险评价和________。
2、按照国家安全⽣产监督管理局第“安监管技装字[2002]45号”⽂件,安全评价分为________、安全验收评价、________和专项安全评价。
3、安全预评价是根据________的内容,分析和预测该建设项⽬存在的危险、危害因素的种类和程度,提出合理可⾏的安全技术设计和安全管理建议的过程。
4、“三同时”是指⽣产经营单位的新建、________、扩建⼯程项⽬的________,必须与主体⼯程同时设计、同时施⼯、________。
5、防⽌⼈失误的技术措施有⽤机器代替⼈、________、耐失误设计、警告和________等。
6、安全教育的三个阶段是安全知识教育、________ 和________。
7.根据安全对策措施的制定原则,评价报告提出的安全对策措施应具有________,可操作性和________。
8.狭义的危险是指系统中特定的危险事件发⽣________和________的结合。
9.按照国家安全⽣产监督管理局第“安监管技装字[2002]45号”⽂件,安全评价分为________、安全验收评价、________和专项评价。
10.防⽕墙应采⽤________构成,耐⽕极限不应低于4⼩时。
⼆、选择题1、海因⾥希最初提出的事故因果连锁过程包括如下五个因素:遗传及社会环境;⼈的缺点;________A.⼈的不安全⾏为或物的不安全状态B.事故C.破坏D.伤害2、安全评价是⼀个⾏为过程,该过程包括:________A.项⽬⼯程的可⾏性研究B.评价危险程度。
C.确定危险是否在可承受的范围D.项⽬的施⼯图设计。
3、进⾏建设项⽬安全验收评价依据的设计⽂件是项⽬________A.可⾏性研究报告B.建议书C.施⼯图设计D.设计说明书4.进⾏建设项⽬安全预评价依据的⽂件是项⽬________A. 可⾏性研究报告B. 建议书C. 施⼯图设计D. 设计说明书5.下列属于特种设备的是________A. 电梯B. 压⼒容器C. 客运索道D. 防爆电器设备三、判断题(下列说法有的是正确的、有的是错误的,正确的在题⽬后⾯的括号中打“√”,错误的在题⽬后⾯的括号中打“×”。
离散优化在网络流问题中的应用

离散优化在网络流问题中的应用网络流问题是离散优化领域中的一个重要问题,它涉及到在网络中寻找最优的流量分配方案。
在实际应用中,网络流问题广泛存在于交通运输、通信网络、供应链管理等领域。
离散优化方法在解决网络流问题中发挥着重要的作用,并取得了显著的成果。
一、最大流问题最大流问题是网络流问题中的一类经典问题,其目标是在网络中找到从源点到汇点的最大流量。
离散优化方法中常用的解决最大流问题的算法有Edmonds-Karp 算法、Ford-Fulkerson算法等。
Edmonds-Karp算法基于广度优先搜索的思想,通过不断寻找增广路径来增加流量,直到无法找到增广路径为止。
这一算法的时间复杂度为O(VE^2),其中V 和E分别表示网络中的节点数和边数。
Ford-Fulkerson算法则是通过不断寻找增广路径,并对路径上的边进行反向操作来增加流量。
这一算法的时间复杂度与Edmonds-Karp算法相同,但其实际运行效率更高。
二、最小割问题最小割问题是网络流问题中的另一类重要问题,其目标是在网络中找到一个割集,使得割集上的边的容量之和最小。
离散优化方法中常用的解决最小割问题的算法有Ford-Fulkerson算法、Dinic算法等。
Ford-Fulkerson算法在解决最大流问题的同时,也可以得到最小割问题的解。
该算法通过不断寻找增广路径,并对路径上的边进行反向操作来增加流量,直到无法找到增广路径为止。
最终,割集中的边即为最小割问题的解。
Dinic算法则是一种基于分层图的改进算法,通过预处理网络,构建分层图,并在分层图上进行增广操作,从而提高了算法的效率。
三、多源汇最小费用流问题多源汇最小费用流问题是网络流问题中的一种扩展问题,其目标是在网络中找到从多个源点到多个汇点的最小费用流量分配方案。
离散优化方法中常用的解决多源汇最小费用流问题的算法有费用流算法、最短路算法等。
费用流算法通过引入费用函数,将流量和费用的关系进行建模,从而求解最小费用流问题。
网络可靠性评估方法综述

2网络连通可靠性评估
2.1问题的提出
本文就网络可靠性评估方法这一问题对近10年的相关 文献进行了整理、分类和综述。
根据这些文献的研究内容,网络可靠性评估主要分为3
网络可以抽象为由一组节点集V={矶,功,…,‰}与一 组链路集E一(吼,ez,…,‰}构成的图G(V,D。1955年,Lee
为了简化问题,突出研究重点,研究中往往假设网络中节 点完全可靠,只有链路可能发生故障。近10年的研究中,主 要通过对经典算法的改进来提高评估效率。
①基于不交积和的算法 使用不交积和法的前提是已知网络的所有最小割集或者
・】O・
万方数据
储空间,不足之处是该算法仅适用于且尤其适用于对复杂串
法,因为基于马尔可夫链的方法通过扩展状态空间来定位
network This paper divided the related 1iteratures into three
main types:connecting reliability,capacity reliability and performance reliability,and introduced the new application Id访 bility which is based
的基础上提出了一种确定无向^端网络可靠性的方法。该方
展,原有的一些网络模型和假设并不能很好地体现真实网络
的特点。
因此,10年来在网络可靠性评估方面研究者们主要致力
于解决以下几个问题:
(1)精确计算网络可靠性的效率太低。如何减少计算复 杂度及提高计算效率? (2)近似算法所得界不能使人满意。怎样获得更为准确
④基于0BDD的算法
f鑫I ’’…
不赤
最大流算法解决最小割问题及网络流问题

最大流算法解决最小割问题及网络流问题最大流算法(maximum flow algorithm)是解决网络流问题的一种常用方法。
网络流问题是指在一个有向图中,每条边都有一个容量限制,要求在源点和汇点之间找到一条路径,使得路径上每条边的流量都不超过其容量限制,同时保证从源点流出的总流量最大。
最小割问题(minimum cut problem)是网络流问题的一个相关概念。
在一个有向图中,边上的容量表示其最大流量限制,我们需要找到一条割(cut),将图分为两个部分,并使得割的容量最小。
割的容量是指割中每条边的容量之和。
最大流算法可以解决最小割问题。
常用的最大流算法包括Ford-Fulkerson算法和Edmonds-Karp算法。
Ford-Fulkerson算法是一种经典的最大流算法。
它通过不断寻找增广路径来更新流的值,直到无法找到增广路径为止。
增广路径是一条从源点到汇点的路径,其上每条边的剩余容量都大于0,并且路径上的流量不超过容量限制。
Edmonds-Karp算法是基于Ford-Fulkerson算法的一种优化方法。
它使用广度优先搜索(BFS)来寻找增广路径,可以保证在每次寻找增广路径时更新的流量最小。
最大流算法的应用非常广泛。
例如,可以使用最大流算法来优化交通流量,解决作业分配问题,以及在计算机网络中进行路由和流量控制等。
总结起来,最大流算法是解决最小割问题和网络流问题的一种常用方法。
通过寻找增广路径来更新流的值,最大流算法可以在保证路径上每条边的流量不超过容量限制的前提下,使得从源点流出的总流量最大化。
最小径集和最小割集的区别

最小径集和最小割集的区别最小径集和最小割集是图论中两个重要的概念,它们分别用于解决不同的问题。
本文将围绕这两个概念展开,逐步回答关于它们的区别,解释它们的定义、性质、应用以及算法。
首先,我们先来详细介绍最小径集(Minimum Path Set)。
最小径集是指图中连接两个给定节点的最小路径集合。
在一个有权图(weighted graph)中,每条路径都有一个权重(或称为长度),最小径集即为连接两个节点的路径中的最短路径集合。
最小径集可以用来解决许多实际问题,比如网络通信中的最短路径选择、导航系统中的最优路径规划等。
为了更好地理解最小径集,我们可以使用Dijkstra算法来计算最短路径。
Dijkstra算法是一种贪婪算法,用于解决单源最短路径问题。
它从起点开始,一步一步地扩展路径,直到找到目标节点或遍历完所有可能的路径。
Dijkstra算法的基本思想是维护两个集合:一个是已知最短路径的节点集合,另一个是未知最短路径的节点集合。
通过不断更新节点的最短路径长度,Dijkstra算法可以找到两个节点之间的最短路径。
接下来,让我们来介绍最小割集(Minimum Cut Set)。
最小割集是指将一个图分割为两个不相交子图的最小边集合。
在一个有权图中,每条边都有一个容量,最小割即为将图分割为两个子图的边中容量最小的边集合。
最小割问题是图论中的经典问题,它具有广泛的应用,比如网络流量控制、电路布线、社交网络分析等。
FordFulkerson算法是一种常用的算法,用于解决最小割问题。
该算法基于图的流网络(flow network)模型,通过不断寻找增广路径(augmenting path)来求解最小割。
增广路径是从源节点到汇节点的一条路径,它上的边容量都还没有被饱和。
通过不断寻找增广路径,并更新路径上的边的容量,FordFulkerson算法可以找到图的最小割。
最小径集和最小割集的区别可以从以下几个方面来说明:1. 定义:最小径集是图中连接两个给定节点的最短路径集合,而最小割集是将图分割为两个子图的最小边集合。
求解最大流问题的算法和模型

求解最大流问题的算法和模型最大流问题是图论中的一个基本问题,涉及到网络流的计算和优化。
在实际应用中,最大流问题的求解涉及到诸多算法和模型,如增广路径算法、Ford-Fulkerson算法、Dinic算法、最小割定理等。
本文将从这些方面进行论述。
1. 增广路径算法增广路径算法是求解最大流问题的经典算法,其基本思想是不断地寻找增广路径,通过增加路径上的流量来增加整个网络的流量。
具体来说,首先通过深度优先搜索或广度优先搜索找到一条从源点到汇点的增广路径,然后确定路径上的最小流量d,将当前流量增加d,将反向边的流量减少d,同时计算当前网络的流量。
2. Ford-Fulkerson算法Ford-Fulkerson算法是一种经典的增广路径算法,其基本理念与增广路径算法相同,但采用不同的策略来确定增广路径。
具体来说,Ford-Fulkerson算法采用贪心策略,在每次迭代中选择路径上的最小容量,从而确定增加的流量。
此外,Ford-Fulkerson算法还引入了残量图的概念,用于计算增广路径的容量。
3. Dinic算法Dinic算法是一种高效的增广路径算法,其主要优点是采用了分层图的策略来确定增广路径,使得每次迭代的搜索范围大为缩小。
具体来说,Dinic算法首先利用BFS算法确定每个节点的分层,然后在分层图上通过DFS算法查找增广路径,在路径上增加流量,更新分层图,重复此过程直至求解最大流。
4. 最小割定理最小割定理是求解最大流问题的重要定理,其核心思想是将网络分成两个不相交部分,并将其最小的割称为最小割。
最小割定理指出,在任意网络中,最大流等于最小割。
因此,求解最大流可以转化为求最小割问题,即在网络中寻找一组最小割,使得所有的割中容量最小的一组割。
总之,求解最大流问题是图论中的一个重要问题,其求解涉及到诸多算法和模型,如增广路径算法、Ford-Fulkerson算法、Dinic 算法、最小割定理等。
在实际应用中,不同情况下可能需要采用不同的算法和模型来求解,需要灵活应用。
公路交通网络可靠度的最小路集算法

Ab ta t I s lt n f n t r rl bl y, t e ls o t - e meh d s ey f cie fr i a d sr c : n oui o ewok ei it o a i h at ru e s t to i v r ef t o bg n e v c mpe ewok T eeoe, i i p a t a rs n remeh d rs ligls o t— e nteta s ott n o lxn t r . h rfr t s rci l op ee t h e to sf ovn at ue sti rn p rai c t t o r h o n t o k a d g tte rl blyo a s o ainn t r ytm c odn epo a i t e r. ew r , n e h ei it fr n p r t ewoks s a i t t o e a c ri gt t rb bl yt o oh i h y Ke r y wo d: hg w y n t ok r l it ih a ew r ei l y;ls o t— e to b a i a true st meh d; as cain mar so it t x o i
S ONG a - h n,Z Xi n z e HANG T o CHEN Ya g a, n
( c o lo rfc a d Ta s ott n,S uh s Ja tn iest S h o fT af n r np r i i ao o twet ioo g Unv ri y,C e g u 6 0 3 ,Chn ) h nd 10 1 ia
2 求解 网络 最小 路 的方法
图是 节 点 和 弧 的 集合 ,记 为G= , l { E ,其 中 为节 点 ,E 弧或 边 。 网络 图则 是 根据 系统 的可靠 为 性框 图 ,即把表 示单 元 的每个 框用 弧表 示并 标 明方 向 度 ,因 此交 通 网 络 可靠 度 的 大 小 应 是 适 应 的。交通 管理 者可 借助 对路 网可 靠度 的分析 ,确 定 敏 感 路 段 ,优 化 管 理 员 配 置 .预 防 交 通 事 故 的发
06-多失效模式体系可靠度计算方法

6 多失效模式结构体系可靠度分析在上章中介绍了单一失效模式的结构构件的各种可靠度分析方法。
但一般情况下,任何一种结构都是由不同单元或构件组成的体系。
因此,结构失效模式不止一个,而是多个,即使是一个构件也是如此。
如对于钢筋混凝土受弯构件,在外荷载作用下,可能发生弯曲破坏,也可能发生剪切破坏,如有扭矩作用还可能发生扭剪破坏。
对于静定结构,每一构件的破坏都会导致结构整体失效。
所以结构失效模式的数目等于或多于构件的数目;而对于超静定结构,一个构件的失效不一定会立即导致整个结构失稳,而是使得结构发生内力重分布。
不断的内力重分布,使结构的状态不断发生变化,当结构达到某一特定状态时(如形成机构),整个结构才失效。
从结构开始发生内力重新分布,到整个结构失效的路径称为失效路径。
由于结构抗力和荷载的随机性,结构的失效路径也是不确定的,这种不确定的失效路径导致结构出现多个失效模式。
在这种情况下,多失效模式结构可靠度的计算方法是一个需要研究的问题。
以往多将多失效模式的结构可靠度分析问题归结为结构体系可靠度问题,这是不全面的。
尽管结构体系的可靠度分析研究涉及多构件、多失效模式问题,但是实际上结构体系的可靠度分析极为复杂,尤其岩土工程问题,不仅涉及多构件体系失效模式,而且还涉及连续体稳定和失效问题。
这不仅涉及多种失效模式的失效路径,而且常面临着失效模式的确定和功能函数的建立。
为此,本章将介绍多失效模式的结构体系可靠度问题,对于复杂的多失效模式的可靠度分析将在下章探讨[1-10]。
6.1 结构体系概念与特点6.1.1 结构体系可靠度概念[11]具有多于一个相关失效模式的结构或构件的可靠度,或多于一个相关结构构件的结构体系的可靠度称为体系可靠度。
考虑一简支梁结构,讨论此梁在弯矩max M 与剪力max Q 同时作用下的整体承载能力的可靠度。
因其即可能发生弯曲失效,又可能发生剪切失效,故此梁为具有多个相关失效模式的结构构件,其承载能力可靠度属体系可靠度。
配电网可靠性算法

元件模型: 认为所有元件的故障和修复时间服从于指数分布。 负荷模型:计及用户负荷随季节而变化,以小时为单位模拟一年8760 h 的负荷。 配电网潮流算法: (1)网络各节点电压赋初值,取节点所在馈线的根节点电压。 (2)固定环网节点电压,调用辐射网络潮流程序计算各环网节点下游辐射分支等值到环网 节点上的注入电流。 (3)固定环网节点上的等值注入电流,递推求解环网支路电流。 (4)递推求解环网节点电压 (5)相邻两次迭代环网节点电压差的模的最大值小于给定收敛标准,则潮流收敛,停止计 算,否则转步骤(2)。 概念 1, 支持馈线:指通过联络开关与非故障失电区直接相连的馈线; 2, 有效联络开关: 指一端接在正常供电馈线上、 另一端连在等待恢复供电区上的联络开关; 3, 主支持馈线:指闭合有效联络开关的首先对等待恢复供电区进行供电的支持馈线。 电网故障后供电恢复方法:用启发式推导算法 (1)计算闭合有效联络开关冗余载流量最大的支持馈线的潮流并进行安全校验,若电流越 限则继续步骤(2);否则检验电压是否越限。若电压越限,则选择联络开关冗余载流量次 之的联络开关闭合, 以消除电压越限。 若能消除电压越限, 则全部恢复供电成功, 结束流程; 否则仍然闭合联络开关冗余量最大的联络开关,然后继续步骤(2)。 (2)按照有效联络冗余载流量从大到小的顺序,逐个寻找相匹配的分段开关并进行操作, 将部分等待恢复供电区的负荷转移给其它支持馈线。 每操作一次开关对, 对操作开关对的支 持馈线要进行一次安全校验。若安全越限,则提取下一个有效联络开关;否则对主支持馈线 进行安全校验。若越限则提取下一个有效联络开关,否则结束流程。若有效联络开关循环完 毕,主支持馈线仍存在安全越限,则进入步骤(3)。 (3)取消步骤(2)的操作。将支持馈线的负荷转移到下一级支持馈线,以增大支持馈线上 有效联络开关的冗余载流量。 然后再重新操作有效联络开关和分段开关, 分担等待恢复供电 区的负荷,以缓解或消除电流和电压越限。若无安全越限则结束流程;否则切负荷,进入步 骤(4)。 (4)按照所采用的目标函数决定停运负荷点。传统的启发式推导法是采用一条主支持馈线 给失电区恢复供电, 闭合主支持馈线的有效联络开关形成对等待恢复供电区的供电回路。 但 是对于一些负荷比较重的馈线, 采用这种方法就需要操作多个开关对, 才能转移等待恢复供 电区的负荷。这样不仅耽误时间,增加开关的损耗,而且也不一定能达到恢复供电的目的。
可靠性工程每章基本概念及复习要点知识讲解

可靠性工程每章基本概念及复习要点知识讲解复习要点:可靠性广义可靠性失效率MTTF(平均寿命)MTBF(平均事故间隔)维修性有效性修复度最小路集及求解最小割集及求解可靠寿命中位寿命特征寿命研究可靠性的意义可靠性定义中各要素的实际含义浴盆曲线可靠性中常见的分布简述串联系统特性简述并联系统特性简述旁联系统特性简述r/n系统的优势并-串联系统与串-并联系统的可靠性关系马尔可夫过程可靠性设计的重要性建立可靠性模型的一般步骤降额设计的基本原理冗余(余度)设计的基本原理故障树分析优缺点广义可靠性:包括可靠性、维修性、耐久性、安全性。
可靠性:产品在规定时期内规定条件规定的时间完成规定功能能力。
耐久性:产品在规定的使用和维修条件下,达到某种技术或经济指标极限时,完成规定功能能力。
安全性:产品在一定的功能、时间、成本等制约条件下,使人员和设备蒙受伤害和损失最小的能力可靠度R(t):产品在规定条件下和规定时间内完成规定功能的概率累积失效概率F(t):也称不可靠度,产品在规定条件下和规定时间内失效的概率失效概率密度f(t):产品在包含t的单位时间内发生失效的概率失效率λ(t):工作到t时刻尚未失效的产品,在该时刻t后的单位时间内发生失效的概率。
基本:实验室条件下。
应用:考虑到环境,利用,降额和其它因素的实际使用环境条件下。
任务:元器件在执行任务期间,即工作条件下的基本不可修产品平均寿命MTTF:指产品失效前的平均工作时间可修MTBF:指相邻两次故障间的平均工作时间,称为平均无故障工作时间或平均故障间隔时间维修性:在规定的条件下使用的可维修产品,在规定的时间内,按规定的程序和法进行维修时,保持或恢复到能完成规定功能的能力维修度M(t):是指在规定的条件下使用的产品发生故障后,在规定的时间(0,t)内完成修复的概率。
修复率μ(t):修理时间已达到某一时刻但尚未修复的产品在该时刻后的单位时间内完成修理的概率。
平均修复时间MTTR:可修复的产品的平均修理时间,其估计值为修复时间总和和修复次数之比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计 算 机 应 用 研 究 Application Research of Computers
Vol. 28 No. 11 Nov. 2011
* 多状态网络可靠度的 d最小割 ( 路 ) 集转换算法
李
北京 100085 ) 摘 要: 为寻求计算多状态网络系统可靠度更为简明的方法, 提出了一种 d最小割、 路集转换算法。 该算法在
Abstract: This paper proposed a transition algorithm of dmincuts and dminpaths in order to effectively compute multistate minpaths ( dmincuts ) through expanding network reliability. Based on Boolean algebra theory,the algorithm generated all dproductofsum expression,with knowing all dmincuts ( dminpaths) in advance,then calculated network reliability by appmincut or lying inclusionexclusion principle to dminpaths or dmincuts,whose amount was fewer. Furthermore,denoting a ddminpath through a set pair composed of unsaturated or nonzero edges and corresponding value,respectively,based on membership relationship between assembles and changing the assemble operation sequence from inversemerging to merging inverse , proposed several lemmas to simplify algorithm. The proposed algorithm was efficient and effective,followed by the analysis of associated computational complexities. The provided example shows correctness and applicability of the algorithm. Key words: multistate network; stochasticflow network; dmincuts; dminpaths; reliability
Algorithm for computing multistate network reliability based on transition of dmincuts and dminpaths
LI Zhen1 ,SUN Xinli1 ,JI Guoxun1 ,LIU Haojie2 ,LIU Zhiyong3
作者简介: 李振( 1983-) , 男, 山东枣庄人, 博士, 主要研究方向为多状态网络系统可靠性评估及优化( true_zhenli@ 163. com ) ; 孙新利 ( 1963-) , 男, 导弹专家, 教授, 博导, 主要研究方向为可靠性评估 、 数值仿真; 姬国勋( 1976-) , 男, 讲师, 博士, 主要研究方向为数值仿真 ; 刘好杰 ( 1983-) , 男, 助教, 硕士, 主要研究方向为信息工程 ; 刘志勇( 1982-) , 男, 助理研究员, 硕士, 主要研究方向为数值仿真.
i =1 j =1
( 5)
( X ) = 1 - ∑ ( φ ( x j ≥ p i, j) ) =
i =1 j =1
σP
| E|
1 - ( φ ( x j ≥ p i, j ) ) = 1 - ( ∑ ( φ ( x j ≥ p i, j) ) ) =
i =1 j =1 | E| i =1 j =1 σP
第 11 期
李
振, 等: 多状态网络可靠度的 d最小割( 路) 集转换算法
( X ) = ∑ ( φ ( x j ≤ c i, j) ) =
i =1 j =1 σC | E|
· 4271·
1
符号、 定义
σC | E|
| · | 表示集合“ ·” 中元素的个数。 G( V, E ) 表 示 节 点 集 合 为 V = { v1 ( s ) , v2 , …, vi , …, v | V| ( t) } ( s、 t 分别表示源点和汇点) , e2 , …, 边集合为 E = { e1 , ei , …, e | E | } 的网络。 M = ( m1 , m2 , …, mi , …, m | E | ) 表示每条边的最大容量构成 的状态向量。 X = ( x1 , x2 , …, xi , …, x | E | ) 表示网络的一个状态, 其中 x i 0 ≤x i ≤m i 。 表示边 e i 的当前容量, d 表示从源点 s 到汇点 t 的需求流量。 f( X) 表示状态为 X 时网络允许通过的最大流量 。 ( X) 表示网络结构函数, ( X ) =
进程, 网络系统可靠性研究的应用价值日益凸显 。有关网络系 统可靠性的研究常假设网络中的元素具有成功和失效两种模 态。而现实生活中的很多情况下 , 多种模态的多状态网络 ( 也 称随机流量网络) 能更好地体现实际系统的工作状态 , 其可靠 并取得了很多成果, 其中, 研究 性评估己成为国内外研究热点 , 最多的是基于 d最小路集
i =1 j =1 σC | E|
( φ ( x j ≤ c i, j ) ) = ( ∑ ( φ ( x j ≤ c i, j) ) ) =
i =1 j =1 σC | E|
σC
| E|
i =1 j =1
( ∑ ( φ ( x j > c i, j ) ) ) = ( ∑ ( φ( x j ≥ c' i, j) ) )
d网络中边的数量为 m, 最小路 ( 割 ) 的数量为 σ, 直接应用容 ), 应用改进的容斥原理, 时 - σ - 2 ) ) 。 可见, 复杂度与 d最小路
收稿日期: 2011-04-10 ; 修回日期: 2011-05-09
基金项目: 第二炮兵工程学院创新性探索研究项目( XY2010ห้องสมุดไป่ตู้JB23 )
1 1 1 2 3 振 ,孙新利 ,姬国勋 ,刘好杰 ,刘志勇
( 1. 第二炮兵工程学院, 西安 710025 ; 2. 第二炮兵士官学院, 山东 青州 262500 ; 3. 第二炮兵装备研究院二所,
已知 d最小割( 路) 集的基础上, 基于逻辑代数理论, 通过展开和之积表达式获得 d最小路 ( 割 ) 集, 再基于两者 中数量较少的一个运用容斥原理, 得到网络可靠度。同时, 分别利用容量未取最大和不为 0 的边及对应取值组 成的集合对表示 d最小割( 路) , 基于集合之间的隶属关系及将集合运算中正常的先取逆再合并的运算顺序变 提出相关引理, 简化算法。通过复杂度分析, 证明算法有效。算例证明了算法的有效性 为先合并再取逆的思想, 和适用性。 关键词: 多状态网络; 随机流量网络; d最小割集; d最小路集; 可靠度 中图分类号: TP202. 1 ; TP301. 6 文献标志码: A 文章编号: 1001-3695 ( 2011 ) 11-4270-04 doi:10. 3969 / j. issn. 1001-3695. 2011. 11. 073
0
引言
随着社会和科学技术的不断发展 , 人类社会加快了网络化
( 割) 的数量息息相关, d而对一个具体的多状态网络而言 , 最 小路( 割) 的数量不仅与网络拓扑结构有关 , 还与需求流量 d 有关, 且无法提前判断、 比较 d最小路 ( 割 ) 的数量。 因此, 同 时获得 d最小路( 割) 集, 才能根据其数量的多少加以选择 , 降 d最小 低应用容斥原理获得网络可靠度的计算复杂性 。 此外, 路( 割) 集在多状态网络的故障诊断 、 系统优化中各具作用, 为 了全面评估网络可靠性 , 有时两者都需要。 分别求取 d最小路( 割) 集的过程较复杂且需以网络最小 路( 割) 集为基础。d最小路( 割 ) 本质上是通过向量表示状态 空间中的一些子空间 ( d最小路 ( 割 ) 分别为各自子空间的下 边界和上边界) , 基于多维状态空间的互补思想 , 在已得到 d最小路集或 d最小( 割) 集的基础上, 本文基于逻辑代数理论 , 研究了 d最小路( 割) 集的转换算法。 阐述、 证明了算法原理, 给出算法步骤, 分析了算法的时间复杂度 , 最后通过实例证明 了算法的正确性及适用性 。
( 1 . The Second Artillery Engineering University,Xi ’ an 710025 ,China; 2 . The Second Artillery Sergeant College,Qingzhou Shandong 262500 ,China; 3 . The Second Research Institute,The Second Artillery Equipment Academy,Beijing 100085 ,China)
[1 ~ 5 ] [6 ~ 14 ] ( 也称多 或 d最小 ( 割 ) 集
最小 状态最小路( 割) 集 ) 的各种算法。 这些算法首先求取 d路( 割) 集, 再基于容斥原理求得网络可靠度 斥原理的时间复杂度为 O( mσ2 间复杂度为 O( m ( 2
σ +1 σ -1 [15 ]
。 假设多状态
