高考数学理试题研究数学—杨军
推荐-陕西省咸阳市永寿中学2018-2018年上学期高三第三次月考数学(理)(附答案) 精品

陕西省咸阳市永寿中学高三第三次月考试题数学(理)考试时间:2018年11月28日 命题人:杨宏军本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,把正确的选项填在第Ⅱ卷答案栏中.) 1.命题“若0ab =,则0a =或0b =”的逆否命题是( )(A )若0a =或0b =,则0ab = (B )若0ab ≠,则0a ≠或0b ≠ (C )若0a ≠或0b ≠,则0ab ≠(D)若0a ≠且0b ≠,则0ab ≠2. 在首项为81,公差为-7的等差数列{a n }中,最接近零的是第 ( )(A )11项 (B )12项 (C )13项 (D )14项 3.设Zx ∈(Z 是整数集),则x x f 3c o s )(π=的值域是( )(A){-1,21} (B){-1,-21,21,1} (C){-1,-21,0,21,1}(D){21,1} 4.22-+=x x y 在点M 处切线斜率为3,则点M 的坐标为( )(A)(0,-2) (B)(1,0) (C )(0,0) (D)(1,1) 5. 曲线)4cos()4sin(2ππ-+=x x y 和直线21=y 在y 轴右侧的交点按横坐标从小到大依次记为P 1,P 2,P 3,…,则|P 2P 4|等于( ) (A )π (B )2π (C )3π (D )4π 6.从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列个数为 ( )(A )3 (B )4 (C )6 (D )8 7. 在△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边.如果a 、b 、c 成等差数列,∠B=30°, △ABC 的面积为23,那么b =( )(A )231+ (B )31+(C )232+ (D )32+8.若ABC ∆的内角满足,0sin tan ,0cos sin <->+A A A A 则角A 的取值范围是 ( )(A )⎪⎭⎫⎝⎛4,0π (B ) ⎪⎭⎫ ⎝⎛2,4ππ (C ) ⎪⎭⎫ ⎝⎛43,2ππ (D ) ⎪⎭⎫ ⎝⎛ππ,43 9. 设偶函数b x x f a -=log )(在(-∞,0)单调递增,则)1(+a f 与)2(+b f 的大小关系是( )(A )f(a+1)<f(b+2) (B )f(a+1)>f(b+2) (C )f(a+1)=f(b+2) (D )不能确定 10.已知R 为实数集,Q 为有理数集,设函数0()()1()R x Q f x x Q ∈⎧=⎨∈⎩ð,则( )(A )函数y =f (x )的图象是两条平行直线 (B )函数y =f (x ) 是奇函数(C )函数f [f (x )]恒等于0 (D )函数f [f (x )]的导函数恒等于0 11. 已知函数)(x f y =图象如图甲,则x x f y sin )2(-=π在区间[0,π]上大致图象是( )12.已知函数时当构造函数)()(:)(,2)(,23)(2x g x f x F x x x g x x f ≥-=-=,()();()(),()().()F x g x f x g x F x f x F x =<=当时那么( )(A) 有最大值3,有最小值-1(B) 有最大值727-,无最小值(C) 有最大值3,无最小值 (D )无最小值,也无最大值陕西省咸阳市永寿中学高三第三次月考试题数学(理)班级 考号 姓名第Ⅱ卷(非选择题,共90分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,把正确的选项填在下面的答案栏中.)二、填空题(本题共4小题,每小题4分,共16分. 把答案填在题中横线上.) 13.已知4sin 5θ=,且sin cos 1θθ->,则sin 2θ=___________. 14.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列是等和数列,且,公和为5,那么的值为______________.15.给出下列命题:(1)正切函数图象的对称中心是唯一的; (2)若函数)(x f 的图象关于直线2π=x 对称,则这样的函数)(x f 是不唯一的;(3)若21,x x 是第Ⅰ象限角,且2121sin sin ,x x x x >>则; (4)若)(x f 是定义在R 上的奇函数,它的最小正周期是T ,则0)2(=-Tf 其中正确命题的序号是 .16.定义集合A 和B 的运算:{},A B x x A x B *=∈∉且. 试写出含有集合运算符号“*”、“ ”、“ ”,并对任意集合A 和B 都成立的一个等式:_______________ . 三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)已知a R a a x x x x f ,(cos )6sin()6sin()(∈++-++=ππ为常数) (1)求函数)(x f 的最小正周期; (2)若)(x f 在]2,2[ππ-上最大值与最小值之和为3,求a 的值.18.(本小题满分12分)设P :关于x 的不等式:a x x <-+-|3||4|的解集是φ.Q :函数 )lg(2a x ax y +-=的定义域为R. 如果P 和Q 有且仅有一个正确,求a 的取值范围.19(本小题满分12分)已知定义在区间]32,[ππ-上的函数)(x f y =的图象关于直线6π-=x 对称,当]32,6[ππ-∈x 时,函数)22,0,0()sin()(πϕπωϕω<<->>+=A x A x f ,其图象如图所示.(1) 求函数)(x f y =在]32,[ππ-(2) 求方程22)(=x f 的解.20.(本小题满分12分)假设你正在某公司打工,根据表现,老板给你两个加薪的方案:(i)每年年末....加1000元;(ii)每半年...结束时加300元。
2014年湖北高考数学试题评析

2014年湖北高考数学试题评析孝感一中潘俊军今年湖北高考数学试卷继续贯彻“坚持以稳定为主,注重基础知识的考查,突出能力,体现创新”的命题指导思想,坚持发扬“彰显湖北试卷特色,有利于高校选拔人才,有利于推动高中数学新课程改革”的精神,根据新课改要求,以2014年湖北省高考数学《考试说明》为依据,全面考查学生对高中数学知识和方法的掌握与运用能力。
一、试题特点今年是湖北省高中学校实施新课标后的第三年高考,经过前两年的高考探索,今年的高考数学试卷在命题结构上更加规范和成熟,在知识内容和难度上更能引领高中数学教学。
命题体现了新课程理念基本要求,注重考查学生的数学基础知识、基本技能和思想方法,考查学生对数学本质知识的理解水平和应用数学知识分析问题和解决问题的能力。
(1)以稳定为主。
2014年文理科试卷结构、题型、题量以及赋分方式与2013年完全相同,文理科解答题的考查内容与顺序也没有变化,先易后难,层次分明,理科应用题仍然考查概率统计知识在实际生活中的应用,难度中等偏上,文科立体几何解答题没有与应用题结合考查,难度降低不少,有利于稳定学生情绪。
(2)以数学知识为考查点,加大应用题考查力度。
试卷重视数学知识的应用,富有浓厚的生活气息,通过数学知识与实际生活接轨,反映数学来源于生活又应用于生活,例如理科T17,T20,文科T5,T11,T16,T18。
(3)以考查思维能力为出发点,注重基础,淡化技巧,强化计算。
试卷对基本知识的考查比较全面,文理科试卷基础题所占比例较大,客观试题的命题背景学生比较熟悉,入手比较容易,同时,试卷要求学生深入理解基本概念、基本公式、基本结论以及基本的数学思想,以达到举一反三的效果。
在注重考察基础概念的同时,对学生的计算能力也提出了很高的要求,从试卷的第一题开始到最后一题都会有不同程度和不同类型的计算。
(4)以教材为参考,通过教材试题改编,凸显教材的地位。
试卷突出对基本知识和方法的考查的同时,引导老师和学生回归课本,关注课本本质的知识,如理科T6,T17(文科T18),T21(文科T22)等均源于教材,这些题熟悉而自然,让学生容易上手,对考场上稳定学生心态、发挥学生实际水平有一定意义。
高考数学第三轮复习讲座

高考数学第三轮复习讲座鹤壁高中段红星第一轮复习以纵向为主,侧重于“落实课本,夯实基础”。
以本为本,把握通性通法在构建学科知识体系的同时,兼顾能力渗透。
必须落实“三基”,将课本“由薄读厚”。
第二轮复习以横向为主,建构网络。
适度综合,归类整理,对有关重点、难点做专题复习,注意章节间的联系,由第一轮“复习什么巩固什么”向“解那类题有那些方法”过渡,将课本“由厚读薄”。
第三轮复习是纵横交错,强化训练,以考代学,查漏补缺,提高应试技能。
一轮、二轮复习已经过去,三轮复习已经开始,在三轮复习期间,我们需要从哪些方面做起,又应该如何做,我想谈以下几点:一、先练后讲,少讲多练,对高考重点题型和综合试题强化训练,提高解题能力。
二、每一位同学都要制定数学科目的目标分,确定得分区,强调数学思想方法在问题解决中的指导意义。
既然是目标分,它就不是你现在经常能够考到的分数,但是还要通过自己的努力将来有可能得到的分数。
比如某位同学的目标分是120分,那么在一套试卷中,你就要明确你的主要的分区在哪里。
我希望同学们在最后阶段除了要花相当一部分时间去巩固你的基础知识,还能够针对我们高中阶段七种数学思想,进行认真地落实。
(一)函数与方程思想:(1)函数思想是对函数内容在更高层次上的抽象,概括与提炼,在研究方程、不等式、数列、解析几何等其他内容时,起着重要作用;(2)方程思想是解决各类计算问题的基本思想,是运算能力的基础。
函数与方程是贯穿中学数学的主线。
(二)数形结合思想:(1)数学研究的对象是数量关系和空间形式,即数与形两个方面;(2)在一维空间,实数与数轴上的点建立一一对应关系;在二维空间,实数对与坐标平面上的点建立一一对应关系。
数形结合中,选择、填空题侧重突出考查数到形的转化,在解答题中,考虑推理论证严密性,突出形到数的转化。
(三)分类与整合思想:(1)分类是自然科学乃至社会科学研究中的基本逻辑方法;(2)从具体出发,选取适当的分类标准;(3)划分只是手段,分类研究才是目的;(4)有分有合,先分后合,是分类整合思想的本质属性;(5)含字母参数数学问题进行分类与整合的研究,重点考查学生思维严谨性与周密性。
名师点评2020年高考数学卷(伍海军选编)

日期:2020年7月15日目录NO1:2020年高考数学点评!命题组专家揭秘高考数学出题思路 NO2:整体稳中有变突出核心素养——2020年高考全国I卷数学试题分析NO3:哈六中名师评析2020年高考数学试卷(全国Ⅱ卷)NO4:重视数学思维体现时代特色(全国Ⅲ卷)NO1:2020年高考数学点评!命题组专家揭秘高考数学出题思路来源:光明日报发布时间:2020-07-08 06:54:53 整理:一品高考网2020年高考数学试题落实立德树人根本任务,贯彻德智体美劳全面发展教育方针,坚持素养导向、能力为重的命题原则,体现了高考数学的科学选拔和育人导向作用。
试题重视数学本质,突出理性思维、数学应用、数学探究、数学文化的引领作用,突出对关键能力的考查。
试题展现了我国社会主义建设成就与科学防疫的成果,紧密联系社会实际,设计真实的问题情境,具有鲜明的时代特色。
试卷体现了基础性、综合性、应用性和创新性的考查要求,难度设计科学合理,很好把握了稳定与创新、稳定与改革的关系,对协同推进高考综合改革、引导中学数学教学都将起到积极的作用。
发挥学科特色,“战疫”科学入题揭示病毒传播规律,体现科学防控。
用数学模型揭示病毒传播规律,如新高考Ⅰ卷(供山东省使用)第6题,基于新冠肺炎疫情初始阶段累计感染病例数的数学模型的研究成果,考查了相关的数学知识和从资料中提取信息的能力,突出数学和数学模型的应用;全国Ⅲ卷文、理科第4题以新冠肺炎疫情传播的动态研究为背景,选择适合学生知识水平的Logistic 模型作为试题命制的基础,考查学生对指数函数基本知识的理解和掌握,以及使用数学模型解决实际问题的能力。
展现中国抗疫成果。
全国疫情防控进入常态化后,各地有序推进复工复产复学。
新高考Ⅱ卷(供海南省使用)第9题以各地有序推动复工复产为背景,取材于某地的复工复产指数数据,考查学生解读统计图以及提取信息的能力。
体现志愿精神。
如全国Ⅱ卷理科第3题(文科第4题)是以志愿者参加某超市配货工作为背景设计的数学问题,考查学生对基本知识的掌握程度及运用所学知识解决实际问题的能力。
高考数学理试题研究数学新杨军

高考数学理试题研究数学新杨军The final edition was revised on December 14th, 2020.2018高考理科数学(全国卷Ⅲ)试题研究云南杨军一、对2018年高考理科数学(全国卷Ⅲ)试题的分析总体来看,主干知识中,函数与导数22分,立体几何22分,直线与圆和圆锥曲线27分,三角函数与解三角形15分,概率统计与模拟方法17分,数列约17分,不等式及其应用约15分,平面向量约5分,算法5分,集合5分、复数5分,二项式定理5分。
知识点覆盖比较全面,重点内容几乎全都考查到了,特别是解析几何加大了知识点的考查,总体分值比往年有所增加。
试题总体上还有一个特点,就是知识点间相互的交汇和融合非常自然,如20题圆锥曲线、平面向量与等差数列融汇在一起,加大了对学生系统掌握知识的考查。
只有很少的一些非重点知识点没有考查,比如:随机抽样,命题与逻辑联结词,数学归纳法,合情推理,计数原理,算法流程图,线性规划,定积分等。
其中容易题为79分,中档题约为37分,难题约为34分。
易中难比例相对于往年,容易题目略有增加,但试题仍然有一定灵活度,适当对综合能力进行了考查。
所以总体略低于于去年全国Ⅲ卷。
具体来说有以下几个特点:1. 试题起点低,注重基础,突出考查重点2018年全国高考理科数学(全国卷Ⅲ)对基础知识与基本技能的考查既注重全面又突出重点,贴近教学实际,入手简单,计算量适中,需要学生在做题时加倍细心,许多试题都是考查单一知识点或是在最基础的知识交汇点上设置,如选择题的1-10,这对引导中学数学重视基础知识和基本技能教学具有良好的导向作用。
同时,试卷注重确保支撑数学知识体系的主干内容占有较高的比例,如试卷对函数与导数、三角函数与解三角形、立体几何、解析几何、数列、概率统计等内容的考查高达120分,这充分体现了高考对主干知识的重视程度,同时在立足稳定基础上又颇具创新。
2、强调通性通法,坚持能力立意2018年全国高考理科数学(全国卷Ⅲ)注重通性通法在解题中的运用,都是运用基本概念分析问题,基本公式运算求解、基本定理推理论证、基本数学思想方法分析和解决问题。
圆锥曲线切线问题中的一类角度关系

>2019年7月(下旬)投稿邮箱:sxjk@数学教学通讯作者简介:杨军君(1983-),硕士研究生,中学一级教师,从事中学数学教育教学工作,曾获得重庆市第四届青年教师优质课比赛一等奖、第七届全国青年教师优质课展示一等奖.圆锥曲线切线问题中的一类角度关系杨军君重庆南开中学400030[摘要]文章从一道高三质量检测题出发,对试题进行推广、类比,借用圆锥曲线的光学性质,探究圆锥曲线切线问题中的一类角度之间的关系.[关键词]圆锥曲线;切线;光学性质圆锥曲线是解析几何的核心内容,是高中数学的重点、难点,是高考命题的热点之一.很多圆锥曲线试题源于圆锥曲线的某些几何性质,具有一定的几何背景,内涵丰富,其结论可以推广、类比拓展,为研究性学习提供较好的素材,能激活探究思维,激发探究热情.本文将从一道高三质量检测题出发,对试题进行推广、类比拓展,探求圆锥曲线切线问题中的一类角度关系,供大家参考.试题(2019届质量检测16题)如图1,F 1,F 2为椭圆C :x 2a 2+y2b 2=1(a>b >0)的左、右焦点,直线l 过F 1且交椭圆C 于A ,B ,过A ,B 分别作椭圆C 的切线并相交于点P .若∠APB=65°,则∠AF 2B=________.B PF 1F 2xyA图1本题以椭圆的切线为背景,考查与焦点三角形相关的角度关系,可以从解析、几何不同的方向解决问题.试题结构新颖,考查内容丰富,解答入手点多,能有效考查学生的数学抽象、逻辑推理以及直观想象等核心素养.探究高考数学试题多数源于教材,而又高于教材,这道试题取材源自人教版选修2-1第二章《圆锥曲线与方程》章末的一份阅读与思考材料,是椭圆的光学性质的简单应用.椭圆的光学性质为:从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上,也即是以下命题:命题:如图2,F 1,F 2为椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,点P 在椭圆C 上.过P 作椭圆C 的切线l ,则l 为△PF 1F 2的外角平分线.分析:命题的证明可采用解析法和几何法进行,详见参考文献[1][2].考虑到学生熟悉椭圆的焦半径公式以及三角形内角平分线定理,故而可将问题转化为证明过点P 且与l 垂直的直线为△PF 1F 2的内角平分线.证明:过P 作切线l 的垂线交x 轴于点Q ,只需证明PQ 平分∠F 1PF 2.设P (x 0,y 0),则直线l 的方程为x 0x a 2+y 0y b 2=1.因PQ ⊥l ,故PQ 所在直线方程为:y -y 0=a 2y 0b 2x 0(x -x 0).P F 1F 2xy Q图2862019年7月(下旬)<投稿邮箱:sxjk@数学教学通讯令y=0可得Q (e 2x 0,0),其中e=c a.所以,F 1Q =e 2x 0+c ,F 2Q =c -e 2x 0.由焦半径公式可知:PF 1=a+ex 0,PF 2=a -ex 0.所以有F 1Q F 2Q =PF 1PF 2,即PQ 为∠F 1PF 2的角平分线,进而可得l 为△PF 1F 2的外角平分线.比推广已知F 1,F 2为椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,过椭圆外一点P 作椭圆C 的两条切线,分别切于A ,B ,连结AF 1,AF 2,BF 1,BF 2.记∠APB=θ,四边形APBF 1及四边形APBF 2中∠APB 的对角分别为θ1,θ2,那么θ,θ1,θ2三者具有怎样的关系?由于点P 的位置不同导致两切点A ,B 分布的情况也不同,故而分两种情况讨论:(1)A ,B 位于x 轴两侧如图3,当点P 在y 轴左侧时:∠AF 1F 2+∠BF 1F 2+θ1=2π,∠AF 2F 1+∠BF 2F 1=θ2,PF 1F 2xyAB图3令∠PAF 1=α,∠PBF 1=β,则由命题1可知:∠F 1AF 2=π-2α,∠F 1BF 2=π-2β.考虑四边形APBF 1和四边形AF 1BF 2,则有:θ+α+β+θ1=2π,(π-2α)+(2π-θ1)+(π-2β)+θ2=2π,{消去α,β可得:2θ+θ1+θ2=2π.同理,当点P 在y 轴右侧时,可得2θ+θ1+θ2=2π.所以,当切点A ,B 位于x 轴两侧时,2θ+θ1+θ2=2π.(2)A ,B 位于x 轴同侧如图4,当点P 在x 轴上方时:∠AF 1B=θ1,∠AF 2B=θ2.P F 1F 2xyA B 图4令∠PAF 2=α,∠PBF 1=β,则由命题1可知:∠F 1AF 2=π-2α,∠F 1BF 2=π-2β.考虑四边形APBF 1和四边形APBF 2,则有:θ+(π-α)+θ1+β=2π,θ+α+θ2+(π-β)=2π,{两式相加可得:2θ+θ1+θ2=2π.同理,当点P 在x 轴下方时,2θ+θ1+θ1=2π.所以,当切点A ,B 位于x 轴同侧时,2θ+θ1+θ2=2π.综合(1)(2),θ,θ1,θ2三者的关系为2θ+θ1+θ2=2π.结论1:已知F 1,F 2为椭圆C :x 2a 2+y 2b 2=1(a>b>0)的左、右焦点,过椭圆外一点P 作椭圆C 的两条切线,分别切于A ,B ,连结AF 1,AF 2,BF 1,BF 2.记∠APB=θ,四边形APBF 1及四边形APBF 2中∠APB 的对角分别为θ1,θ2,则2θ+θ1+θ2=2π.特别的,当A ,F 1,B 三者共线时,2θ+θ2=π;当A ,F 2,B 三者共线时,2θ+θ1=π.类比椭圆情况,我们可以将上述结论推广到双曲线以及抛物线中.结论2:已知F 1,F 2为双曲线C :x 2a 2-y 2b 2=1(a>0,b>0)的左、右焦点,过双曲线外一点P 作双曲线C 的两条切线,分别切于A ,B ,连结AF 1,AF 2,BF 1,BF 2.(1)当切点A ,B 位于双曲线的同支时,如图5,记∠APB=θ,四边形APBF 1及四边形APBF 2中∠APB 的对角分别为θ1,θ2,则2θ+θ1-θ2=2π;P F 1F 2xyA B图5(2)当切点A ,B 位于双曲线的异支时,如图6,记∠APB=θ,∠AF 1B=θ1,∠AF 2B=θ2,则2θ=θ1+θ2.PF 1F 2xy A B 图6结论3:已知F 为抛物线C :y 2=2px (p>0)的焦点,过抛物线外一点P 作抛物线C 的两条切线,分别切于A ,B .记∠APB=θ,四边形APBF 中∠APB 的对角为θ′,则2θ+θ′=2π.上述结论2与结论3的证明过程可以类比椭圆进行,由于篇幅有限,在此省略.数学教育家傅种孙先生曾言:“几何之务不在知其然,而在知其所以然;不在知其然,而在知何由以知其所以然.”在这道高三质量检测题的引领下,我们由光学性质出发,回避了复杂的运算,找到相应的结论,使问题变得透彻、简单.我们依此而解题,据此而命题,数学之简洁美、深刻美便跃然纸上,呼之欲出.参考文献:[1]甘志国.圆锥曲线光学性质的证明及其应用[J ].数学教学,2017(9):16-18.[2]李凤华.由圆锥曲线光学性质得出的一组优美性质———定值问题[J ].中学数学研究,2012(4):23-25.87。
2025届云南省玉溪市通海三中高考仿真卷数学试题含解析

2025届云南省玉溪市通海三中高考仿真卷数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.陀螺是中国民间最早的娱乐工具,也称陀罗. 如图,网格纸上小正方形的边长为1,粗线画出的是某个陀螺的三视图,则该陀螺的表面积为( )A .(722+πB .(1022+πC .(1042+πD .(1142+π2.若23455012345(21)(21)(21)(21)(21)a a x a x a x a x a x x +-+-+-+-+-=,则2a 的值为( )A .54B .58C .516D .5323.已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β,直线l 满足l ⊥m ,l ⊥n ,,l α⊄,l β⊄则 ( )A .α∥β且l ∥αB .α⊥β且l ⊥βC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l4.已知m ,n 是两条不重合的直线,α,β是两个不重合的平面,则下列命题中错误的是( ) A .若m //α,α//β,则m //β或m β⊂B .若m //n ,m //α,n α⊄,则n //αC .若m n ⊥,m α⊥,n β⊥,则αβ⊥D .若m n ⊥,m α⊥,则n //α5.三棱锥S ABC -中,侧棱SA ⊥底面ABC ,5AB =,8BC =,60B ∠=︒,25SA =,则该三棱锥的外接球的表面积为( ) A .643π B .2563π C .4363π D .2048327π 6.已知是球的球面上两点,,为该球面上的动点.若三棱锥体积的最大值为36,则球的表面积为( ) A .36πB .64πC .144πD .256π7.双曲线C :22221x y a b-=(0a >,0b >)的离心率是3,焦点到渐近线的距离为2,则双曲线C 的焦距为( )A .3B .32C .6D .628.已知复数z 满足32i z i ⋅=+(i 是虚数单位),则z =( ) A .23i + B .23i -C . 23i -+D . 23i --9.已知函数13()sin cos 22f x x x =+,将函数()f x 的图象向左平移(0)m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( ) A .6πB .4π C .3π D .2π 10.设 2.71828...e ≈为自然对数的底数,函数()1xxf x e e -=--,若()1f a =,则()f a -=( )A .1-B .1C .3D .3-11.《九章算术》“少广”算法中有这样一个数的序列:列出“全步”(整数部分)及诸分子分母,以最下面的分母遍乘各分子和“全步”,各自以分母去约其分子,将所得能通分之分数进行通分约简,又用最下面的分母去遍乘诸(未通者)分子和以通之数,逐个照此同样方法,直至全部为整数,例如:2n =及3n =时,如图:记n S 为每个序列中最后一列数之和,则6S 为( ) A .147B .294C .882D .176412.函数()()sin f x x θ=+在[]0,π上为增函数,则θ的值可以是( ) A .0B .2π C .πD .32π 二、填空题:本题共4小题,每小题5分,共20分。
“动”“静”结合,定点永存——赏析2023年高考数学全国乙卷理科第20题

高考数学 试 卷 中 的 一 个 热 点 与 难 点,常 考 常
方法和基本性质等值得探究、
推广与拓展。
真题破解
2.
新,
数学运 算 量 大,逻 辑 推 理 复 杂,难 度 往 往
b=2,
比较高,
有比较好的选拔 性 与 区 分 度,
备受命
题者关注。
c
5
(
解:
,
1)依 题 意,可 得 =
a
高二数学 2023 年 11 月
同理 Q
-2
t +1
2
t -1
8
t+5
4
,可 得
,2
2
t -6
t+1
8 t -6
t+1
8
2
-1
8
t+5
4
-3
2
2
t -6
t+1
8
t
kRQ =
=- 。
2
1
2
-2
t +1
2
t
+2
2
t -6
t+1
8
4.
1 平面解析 几 何 中 定 点 问 题 的 解 法 归
纳
(
—
—一般推理,
2
题中直线 AP ,
AQ 与y 轴的交点分 别 为
,
可设直线 AP 的方 程 为y=k(
M,
N,
x+2)
。
可得 M (
k≠0。此时令 x=0,
0,
2
k)
k,
y=kx+2
联 立 y2 x2
2020_年全国Ⅲ卷理科第12_题新解及命题思路探究

2020年全国Ⅲ卷理科第12题新解及命题思路探究代红军1ꎬ2㊀何㊀波1(1.云南师范大学数学学院ꎬ云南昆明650500ꎻ2.昆明市官渡区第六中学ꎬ云南昆明650500)摘㊀要:文章通过研究2020年全国Ⅲ卷理科第12题的解法ꎬ尝试提出用二分法寻找中间量解决对数比较大小的方法ꎬ探索命题人设置参考数据的心路历程ꎬ为这类试题命制提供参考.关键词:对数ꎻ新解ꎻ命题思路中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)31-0041-03收稿日期:2023-08-05作者简介:代红军(1987.8-)ꎬ男ꎬ四川省安岳人ꎬ硕士ꎬ中学一级教师ꎬ从事数学教学研究ꎻ何波(1990.2-)ꎬ男ꎬ云南省永善人ꎬ本科ꎬ从事数学教学研究.基金项目:昆明市教育科学研究 十四五 规划第二批立项课题 基于GGB软件积件库的中学函数教学案例研究 (项目编号:ZX2022251)㊀㊀对数比较大小是高考的热点和难点题型ꎬ主要以填空题㊁选择题的形式出现ꎬ试题难度大.近几年试题展现出一定的创新性ꎬ考查学生的数学运算㊁数据处理㊁数学抽象等核心素养ꎬ要求学生掌握必备的知识和解决此类问题的关键能力.笔者对«数理化解题研究»2022年第34期文章«对数比较大小试题的解法探究两例»中变式应用环节的变式1解法提出疑问ꎬ指出错误原因并给出新解.1问题提出«数理化解题研究»2022年第34期«对数比较大小试题的解法探究两例»变式应用环节的变式1.变式1㊀设a=log23ꎬb=log35ꎬc=log58ꎬ则(㊀㊀).㊀A.a<b<c㊀㊀㊀B.c<b<aC.a<c<bD.c<a<b原文中的解法ꎬ由糖水不等式ꎬ得log23=ln3ln2<ln3+ln(3/2)ln2+ln(3/2)=ln(9/2)ln3<ln5ln3=log35ꎬ同理可得log35<log58ꎬ即a<b<cꎬ故选A.错因分析㊀从表面上看ꎬ解法不存在问题.实质糖水不等式满足的条件混淆ꎬ这是因为糖水不等式有两种形式ꎬ即(1)当m>n>0ꎬc>0时ꎬmn<m+cn+cꎻ(2)当m>n>0ꎬc>0时ꎬnm>n+cm+cꎬ使用时要注意nm与1的大小关系ꎬ否则会出现原文中变式1的条件与结论错用.此题的正确解法见新解应用环节.原文中提出了一个有创意的观点:不提供参考数据ꎬ能否解决对数比较大小的问题?针对问题ꎬ尝试探究新的解法.142新解探究2.1高考试题再现题目㊀(2020年全国Ⅲ卷理科第12题)已知55<84ꎬ134<85.设a=log53ꎬb=log85ꎬc=log138ꎬ则(㊀㊀).㊀A.a<b<c㊀㊀㊀B.b<a<cC.b<c<aD.c<a<b分析㊀试题命制的创新之处是给出了一组参考数据ꎬ如何运用参考数据是破解此题的关键ꎬ不同的运用方式能带来不同的解法ꎬ我们从三个角度运用参考数据ꎬ提炼出新的解法.解法1㊀因为34<53ꎬ所以4a=4log53=log534<log553=3ꎬ解得a<34.又因为54>83ꎬ所以4b=4log85=log854>log883=3ꎬ解得b>34.由55<84ꎬ得到log855<log884ꎬ所以5b<4ꎬ解得b<45.综上知34<b<45.同理由134<85ꎬ解得c>45.综上所述ꎬa<34<b<45<c.故选A.解法2㊀作差a-b=log53-log85=ln3ln5-ln5ln8=ln3ln8-ln25ln5ln8ꎬ由基本不等式ꎬ得ln3ln8<(ln3+ln82)2=(ln242)2<ln25.所以a<b.因为b=log85ꎬ得8b=5.所以85b=55<84.因此5b<4ꎬ解得b<45.因为c=log138ꎬ所以135c=85>134ꎬ从而得到5c>4ꎬ解得c>45.综上所述ꎬa<b<45<c.故选A.解法3㊀根据糖水不等式知ꎬa=ln3ln5<ln3+ln(8/5)ln5+ln(8/5)=ln(24/5)ln8<ln5ln8=bꎬ同时a=ln3ln5<ln3+ln(13/5)ln5+ln(13/5)=ln(39/5)ln13<ln8ln13=cꎬ用排除法可知ꎬ故选A.解法点评㊀从以上三种解法不难发现ꎬ参考数据实质是为aꎬbꎬc比较大小提供了中间量34和45.解法1直接运用了参考数据ꎬ解法2间接利用了参考数据ꎬ解法3没有利用参考数据ꎬ抓住试题类型ꎬ是解答选择题的特殊解法.针对解法1和解法2ꎬ很难想到134<85和54>83ꎬ这是解决此题的难点.为了突破难点ꎬ解法3提供了一般思路ꎬ不利用参考数据ꎬ此题能解答吗?或者134<85和54>83是如何想到?2.2新解呈现针对上面两个问题ꎬ笔者提出对数比较大小的另一种方法ꎬ叫二分法寻找中间量.方法介绍及操作流程ꎬ笔者通过具体例题呈现.2020年全国Ⅲ卷理科第12题如不用参考数据ꎬ得到如下变式[1].变式㊀设a=log53ꎬb=log85ꎬc=log138ꎬ则(㊀㊀).A.a<b<c㊀B.b<a<c㊀C.b<c<a㊀D.c<a<b解析㊀因为a=log53ꎬb=log85ꎬc=log138ꎬ所以aꎬbꎬcɪ(0ꎬ1)ꎬ由二分法思想可知ꎬ取中间量t1=12.又因为t1=12=log5512=log8812=log131312ꎬ因此比较3与512ꎬ5与812ꎬ8与1312的大小ꎬ转化为比较32与5ꎬ52与8ꎬ82与13的大小ꎬ容易得到32>5ꎬ52>8ꎬ82>13ꎬ所以3>512ꎬ5>812ꎬ8>1312.则log53>12ꎬlog85>12ꎬlog138>12.所以aꎬbꎬcɪ(12ꎬ1).由二分法思想ꎬ取中间量t2=34ꎬ同样t2=34=log5534=log8834=log131334ꎬ比较3与534ꎬ5与834ꎬ824与1334的大小ꎬ转化为比较34与53ꎬ54与83ꎬ84与133的大小ꎬ由于34<53ꎬ54>83ꎬ84>133ꎬ所以3<534ꎬ5>834ꎬ8>1334ꎬ因此log53<34ꎬlog85>34ꎬlog138>34ꎬ则aɪ(0ꎬ34)ꎬbꎬcɪ(34ꎬ1).为了解释命题人设计参考数据的思路ꎬ我们取区间(34ꎬ1)的第1个四等分点作为中间量t3=45ꎬ同样t3=45=log8845=log131345ꎬ比较5与845ꎬ8与1345的大小ꎬ即比较55与84ꎬ85与134的大小.因为55<84ꎬ85>134ꎬ所以5<845ꎬ8>1345ꎬ得到log85<45ꎬlog138>45.所以0<a<34<b<45<cꎬ故选A.点评㊀此题参考数据的作用主要是为解答提供中间量ꎬ考查考生处理数据的能力ꎬ通过对参考数据的利用ꎬ能否类比联想到55<84和85>134.另外ꎬ提供参考数据为考生提供了多样的解题方法ꎬ符合新高考的命题理念ꎬ让不同层次的考生在高考中都能施展自己的才华和能力.如果不提供参考数据ꎬ解题方法单一ꎬ达不到考查目的.没有参考数据ꎬ用二分法寻找中间量求解的过程中ꎬ能清晰地揣摩命题人是如何设置参考数据ꎬ此题至少要用三次二分ꎬt3=45是区间(34ꎬ1)的一个四等分点ꎬ取区间的不同等分点ꎬ也能命制出不同的试题ꎬ为试题的命制提供了思路ꎬ试题的解答过程对上述疑问的回答就不言而喻了.3新解应用应用1㊀«数理化解题研究»2022年第34期文章«对数比较大小试题的解法探究两例»变式应用环节的变式1.正解㊀显然aꎬbꎬcɪ(1ꎬ2).由表1可知cɪ(54ꎬ118)ꎬbɪ(118ꎬ32)ꎬaɪ(32ꎬ2)ꎬ所以c<b<aꎬ故选B.表1㊀应用1的解析过程区间中间值ta与t的大小b与t的大小c与t的大小(1ꎬ2)t=32><<(1ꎬ32)t=54>>(54ꎬ32)t=118><㊀㊀应用2㊀(必修第一册第141页第13题(2))比较log23ꎬlog34ꎬlog45的大小.解析㊀显然log23ɪ(1ꎬ2)ꎬlog34ɪ(1ꎬ2)ꎬlog45ɪ(1ꎬ2).表2㊀应用2的解析过程区间中间值tlog23与t的大小log34与t的大小log45与t的大小(1ꎬ2)t=32><<(32ꎬ2)t=54><㊀㊀由表2知log23ɪ(32ꎬ2)ꎬlog34ɪ(54ꎬ32)ꎬlog45ɪ(1ꎬ54).所以log45<log34<log23.用二分法寻找对数比较大小的中间量的方法ꎬ能明确命题人命制试题的思路和意图ꎬ在教学和考试中可以对试题进行改编ꎬ发挥试题的变式教学功能ꎬ实现一题一课㊁一法多用的教学作用.教学过程要体现学生主体㊁教师主导㊁问题主线㊁思维主攻 的思想[2]ꎬ对数比较大小方法多样ꎬ教师从不同视角提出问题ꎬ引导学生主动探究不同的解法ꎬ发现不同解法之间的关联ꎬ有助于发展学生思维.参考文献:[1]李鸿昌.对数比较大小试题的解法探究两例[J].数理化解题研究ꎬ2022(34):66-69.[2]代钦ꎬ王光明ꎬ吴立宝.新版课程标准解析与教学指导[M].北京:北京师范大学出版社ꎬ2018.[责任编辑:李㊀璟]34。
高考数学理试题研究数学—杨军
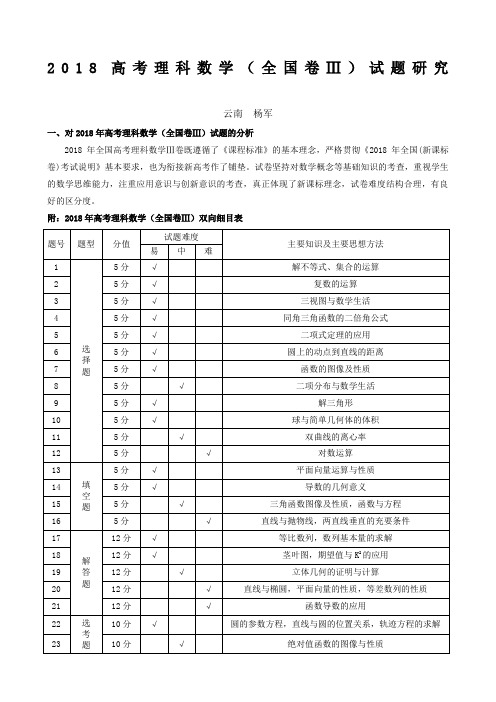
2018高考理科数学(全国卷Ⅲ)试题研究云南杨军一、对2018年高考理科数学(全国卷Ⅲ)试题的分析总体来看,主干知识中,函数与导数22分,立体几何22分,直线与圆和圆锥曲线27分,三角函数与解三角形15分,概率统计与模拟方法17分,数列约17分,不等式及其应用约15分,平面向量约5分,算法5分,集合5分、复数5分,二项式定理5分。
知识点覆盖比较全面,重点内容几乎全都考查到了,特别是解析几何加大了知识点的考查,总体分值比往年有所增加。
试题总体上还有一个特点,就是知识点间相互的交汇和融合非常自然,如20题圆锥曲线、平面向量与等差数列融汇在一起,加大了对学生系统掌握知识的考查。
只有很少的一些非重点知识点没有考查,比如:随机抽样,命题与逻辑联结词,数学归纳法,合情推理,计数原理,算法流程图,线性规划,定积分等。
其中容易题为79分,中档题约为37分,难题约为34分。
易中难比例相对于往年,容易题目略有增加,但试题仍然有一定灵活度,适当对综合能力进行了考查。
所以总体略低于于去年全国Ⅲ卷。
具体来说有以下几个特点:1. 试题起点低,注重基础,突出考查重点2018年全国高考理科数学(全国卷Ⅲ)对基础知识与基本技能的考查既注重全面又突出重点,贴近教学实际,入手简单,计算量适中,需要学生在做题时加倍细心,许多试题都是考查单一知识点或是在最基础的知识交汇点上设置,如选择题的1-10,这对引导中学数学重视基础知识和基本技能教学具有良好的导向作用。
同时,试卷注重确保支撑数学知识体系的主干内容占有较高的比例,如试卷对函数与导数、三角函数与解三角形、立体几何、解析几何、数列、概率统计等内容的考查高达120分,这充分体现了高考对主干知识的重视程度,同时在立足稳定基础上又颇具创新。
2、强调通性通法,坚持能力立意2018年全国高考理科数学(全国卷Ⅲ)注重通性通法在解题中的运用,都是运用基本概念分析问题,基本公式运算求解、基本定理推理论证、基本数学思想方法分析和解决问题。
欣宜市实验学校二零二一学年度高考数学第二轮复习第3讲解答题题型特点与技法指导文试题 2

黔西北州欣宜市实验学校二零二一学年度第3讲解答题题型特点与技法指导高考解答题一般有六大方向:三角函数与平面向量、概率与统计、立体几何、数列与不等式、解析几何、不等式与函数及导数.一般来说,前三题属于中、低档题,第四题属中档偏难题,后两题属难题.三角函数与平面向量、概率与统计、立体几何在前三题中出现的概率较高,掌握解这几类题的解法是大多数学生成功的关键.目前的高考解答题已经由单纯的知识综合型转化为知识、方法和才能的综合型解答题.能否做好解答题,是高考成败的关键.1.三角函数有关三角函数的大题即解答题,主要是考察根底知识、根本技能和根本方法,且难度不大.凸显恒等变换与三角函数图象、性质在三角形内考察.主要考察以下4个方面:①三角函数的图象、性质、图象变换,主要是y=A sin(ωx+φ)+b的图象、性质及图象变换,考察三角函数的概念、奇偶性、周期性、单调性、最值及图象的平移和对称等;②三角恒等变换,主要考察公式的灵敏运用、变换才能,一般需要运用和差角公式、倍角公式,尤其是对公式的应用与三角函数性质的综合考察;③三角函数性质的应用.通过解三角形来考察三角恒等变形及应用三角函数性质的综合才能;④三角函数与平面向量、数列、不等式等知识的综合问题.【例1】向量a=(cosωx-sinωx,sinωx),b=(-cosωx-sinωx,2cosωx),设函数f(x)=a·b+λ(x∈R)的图象关于直线x=π对称,其中ω,λ为常数,且ω∈.(1)求函数f(x)的最小正周期;(2)假设y=f(x)的图象经过点,求函数f(x)在区间上的取值范围.点评利用向量的工具作用,与向量结合在一起命制综合题,表达了在知识交汇点处命题的指导思想.这类问题求解时,首先利用向量的运算,将向量式转化为代数式,再进展有关的三角恒等变换,再研究三角函数的图象与性质.变式训练1(2021·高考,理16)设函数f(x)=cos+sin2x.(1)求f(x)的最小正周期;(2)设函数g(x)对任意x∈R,有g=g(x),且当x∈时,g(x)=-f(x).求g(x)在区间[-π,0]上的解析式.2.立体几何立体几何是高中数学的主干知识之一,命题形式比较稳定,主要考察:(1)三视图:解答题中一般是根据三视图复原几何体模型,然后展开推理;(2)空间线面关系的断定和推理证明:主要是证明平行和垂直,求解这类问题要根据线面关系的断定定理和性质定理进展推理论证;(3)空间几何量(空间角、空间间隔、几何体体积与面积)的计算:求解这类问题,常用方法是根据公理、定理以及性质等经过推理论证,作出所求几何量并求之.一般解题步骤是“作、证、求〞.(2021·八校一联考,18)如图,在多面体ABDEC中,AE⊥平面ABC,BD∥AE,且AC=AB=BC=AE=1,BD =2,F为CD的中点.(1)求证:EF∥平面ABC;(2)求证:EF⊥平面BCD;(3)求多面体ABDEC的体积.点评此题第(1)问是证明线面平行问题,证明直线与平面平行,往往通过证直线与直线平行来实现.第(2)问是证线面垂直问题,往往转化为证线线垂直来实现.第(1)(2)问充分表达了问题的转化思想.第(3)问是几何体的体积计算问题,需要把握锥体的体积计算公式.变式训练2(2021·高考,16)如图,在直三棱柱ABCA1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证:(1)平面ADE⊥平面BCC1B1;(2)直线A1F∥平面ADE.3.概率与统计概率解答题为每年高考的必考内容,主要考察互斥事件和对立事件的关系、古典概型和几何概型.要求学生能准确理解题意,迅速确定是古典概型还是几何概型,然后用概率公式求解.对于古典概型,要准确列出所有根本领件的个数和所求事件包含的根本领件个数.对于几何概型,一定要明确其与面积(体积、长度等)的关系.对于较复杂的问题,可以借助于图形和表格帮助分析.【例3】(2021·统测,文18)为了普及环保知识,增强环保意识,某大学从理工类专业的A班和文史类专业的B班各抽取20名同学参加环保知识测试.两个班同学的成绩(百分制)的茎叶图如下列图:按照大于或者等于80分为优秀,80分以下为非优秀统计成绩.(1)根据以上数据完成下面的2×2列联表:成绩与专业列联表(2)附:K2=点评确读取茎叶图中的数据是解题的关键.变式训练3(2021·高考,文19)假设甲乙两种品牌的同类产品在某地区场上销售量相等,为理解它们的使用寿命,现从这两种品牌的产品中分别随机抽取100个进展测试,结果统计如下:甲品牌乙品牌(1)估计甲品牌产品寿命小于200小时的概率;(2)这两种品牌产品中,某个产品已使用了200小时,试估计该产品是甲品牌的概率.4.数列与不等式高考中数列解答题的求解主要有以下几个特点:(1)与等差、等比数列根本量有关的计算,可根据题意列方程(方程组)或者利用等差、等比数列的性质求解;(2)与求和有关的题目,首先要求通项公式,并根据通项公式选择恰当的求和方法(如错位相减法、裂项相消法、分组求和法等);(3)含S n的式子,要根据题目特征利用a n=进展转化;(4)与递推数列有关的问题,要能合理转化,使之构造出新的等差、等比数列;(5)与数列有关的不等式问题,可根据数列的特征选择方法(如比较法、放缩法等);(6)与函数有关的问题,应根据函数的性质求解.【例4】(2021·二诊,20)数列{a n}和{b n},b1=1,且b n+1-3b n=2n-2,记a n=b n+1-b n+1,n∈N*.(1)证明:数列{a n}为等比数列;(2)求数列{a n}和{b n}的通项公式;(3)记c n=log a n3·log a n+23,数列{c n}的前n项和为T n,假设45T k<29,k∈N*恒成立,求k的最大值.点评第(1)问考察了等比数列的证明,它是为第(2)、(3)问效劳的.第(2)问考察了求数列通项公式的常规方法.第(3)问考察了数列的求和方法,是数列与不等式知识的综合问题.变式训练4(2021·八校二联,19)各项为正数的数列{a n}的前n项和为S n,且满足:S n=a+a n+(n∈N*).(1)求a n;(2)设函数f(n)=c n=f(2n+4)(n∈N*),求数列{c n}的前n项和T n.5.解析几何解析几何解答题主要考察圆锥曲线的根本概念、HY方程及几何性质等根底知识和处理有关问题的根本技能、根本方法,往往以中档偏难题或者以压轴题形式出现,主要考察学生的逻辑推理才能、运算才能,考察学生综合运用数学知识解决问题的才能.打破解答题,应重点研究直线与曲线的位置关系,要充分运用一元二次方程根的判别式和韦达定理,注意运用“设而不求〞的思想方法,灵敏运用“点差法〞解题,要擅长运用数形结合思想分析问题,使数与形互相转化,根据详细特征选择相应方法.【例5】椭圆+=1,点P是椭圆上异于顶点的任意一点,过点P作椭圆的切线l,交y轴于点A,直线l′过点P且垂直于l,交y轴于点B.试判断以AB为直径的圆能否经过定点,假设能,求出定点坐标;假设不能,请说明理由.点评直线与圆锥曲线的位置关系一直是命题的热点,根本方法是联立方程,利用判别式、根与系数关系求解,运算量一般较大,这类综合题中常涉及的问题有弦长问题、面积问题、对称问题、定点定值问题等,是历年高考的热点问题,复习时要注重通性通法的训练.变式训练5(2021·高考,文21)如图,椭圆M:+=1(a>b>0)的离心率为,直线x=±a和y=±b所围成的矩形ABCD的面积为8.(1)求椭圆M的HY方程;(2)设直线l:y=x+m(m∈R)与椭圆M有两个不同的交点P,Q,l与矩形ABCD有两个不同的交点S,T.求的最大值及获得最大值时m的值.6.函数与导数以函数为载体,以导数为工具,以考察函数性质及导数的应用为目的,以导数为工具围绕函数、不等式、方程等综合考察.在知识的交汇处命题,涉及到详细内容较多,如给定解析式求参数值,给定条件求参数范围,以及对参数讨论与证明不等式问题,极值、最值、值域及分析图象交点等问题,都以导数为工具.既考察函数局部的相关知识,又浸透函数与方程、数形结合、化归与转化、分类与整合等数学思想.【例6】(2021·一模,21)函数f(x)=x3-x.(1)假设不等式f(x)<k-2005对于x∈[-2,3]恒成立,求最小的正整数k;(2)令函数g(x)=f(x)-ax2+x(a≥2),求曲线y=g(x)在(1,g(1))处的切线与两坐标轴围成的三角形面积的最小值.点评第(1)问是恒成立求参数范围问题,常用别离参数求最值.第(2)问考察了利用导数的几何意义求切线方程,利用导数求最值问题.变式训练6(2021·广西一模,21)函数f(x)=ax3+bx2+cx+d是定义在R上的奇函数,其图象过点和(2,2).(1)求出函数f(x)的解析式,并求f(x)的单调区间;(2)设g(x)=f(x)-5t,当实数t取何值时,关于x的方程g(x)=0有且只有一个实数根?参考答案方法例析【例1】解:(1)因为f(x)=sin2ωx-cos2ωx+2sinωx·cosωx+λ=-cos2ωx+sin2ωx+λ=2sin+λ.由直线x=π是y=f(x)图象的一条对称轴,可得sin=±1,所以2ωπ-=kπ+(k∈Z),即ω=+(k∈Z).又ω∈,k∈Z,所以k=1,故ω=.所以f(x)的最小正周期是.(2)由y=f(x)的图象过点,得f=0,即λ=-2sin=-2sin=-,即λ=-.故f(x)=2sin-.由0≤x≤,有-≤x-≤,所以-≤sin≤1,得-1-≤2sin-≤2-,故函数f(x)在上的取值范围为[-1-,2-].【变式训练1】解:(1)f(x)=cos+sin2x=+=-sin2x,故f(x)的最小正周期为π.(2)当x∈时,g(x)=-f(x)=sin2x.故①当x∈时,x+∈.由于对任意x∈R,g=g(x),从而g(x)=g=sin=sin(π+2x)=-sin2x.②当x∈时,x+π∈.从而g(x)=g(x+π)=sin[2(x+π)]=sin2x.综合①,②得g(x)在[-π,0]上的解析式为g(x)=【例2】(1)证明:取BC的中点G,连接AG,FG.∵F,G分别为DC,BC的中点,∴FG DB EA.∴四边形EFGA为平行四边形.∴EF∥AG.又因为EF⊄平面ABC,AG⊂平面ABC,∴EF∥平面ABC.(2)证明:因为AE⊥面ABC,BD∥AE,∴DB⊥平面ABC.又∵DB⊂平面BCD,∴平面ABC⊥平面BCD.又∵G为BC的中点且AC=AB=BC,∴AG⊥BC.∴AG⊥平面BCD.又∵EF∥AG,∴EF⊥平面BCD.(3)解:过C作CH⊥AB,那么CH⊥平面ABDE且CH=,∴V CABDE=·S四边形ABDE·CH=××=.【变式训练2】证明:(1)因为ABCA1B1C1是直三棱柱,所以CC1⊥平面ABC.又AD⊂平面ABC,所以CC1⊥AD.又因为AD⊥DE,CC1,DE⊂平面BCC1B1,CC1∩DE=E,所以AD⊥平面BCC1B1.又AD⊂平面ADE,所以平面ADE⊥平面BCC1B1.(2)因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.因为CC1⊥平面A1B1C1,且A1F⊂平面A1B1C1,所以CC1⊥A1F.又因为CC1,B1C1⊂平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.由(1)知AD⊥平面BCC1B1,所以A1F∥AD.又AD⊂平面ADE,A1F⊄平面ADE,所以A1F∥平面ADE.【例3】解:(1)成绩与专业列联表(2)k=≈12>41.所以在犯错误的概率不超过0.05的前提下认为环保知识测试成绩与专业有关.【变式训练3】解:(1)甲品牌产品寿命小于200小时的频率为=,用频率估计概率,所以,甲品牌产品寿命小于200小时的概率为.(2)根据抽样结果,寿命大于200小时的产品有75+70=145(个),其中甲品牌产品是75个,所以在样本中,寿命大于200小时的产品是甲品牌的频率是=,用频率估计概率,所以已使用了200小时的该产品是甲品牌的概率为.【例4】(1)证明:∵b n+1-3b n=2n-2,∴b n-3b n-1=2(n-1)-2,n≥2,n∈N*.两式相减,得b n+1-b n-3b n+3b n-1=2(n≥2,n∈N*).整理,得b n+1-b n+1=3(b n-b n-1+1)(n≥2,n∈N*),即a n=3a n-1(n≥2,n∈N*).∴数列{a n}是公比为3的等比数列.(2)解:∵b2=3,∴a1=3-1+1=3.∴a n=3n(n∈N*).∵a n=b n+1-b n+1=3n,∴b n-b n-1+1=3n-1,b n-1-b n-2+1=3n-2,…,b2-b1+1=31.累加,得b n-b1+n-1=-1.∴b n=-n+(n∈N*).(3)解:c n=logn3·log3n+23==.3∴T n==-.由45T k<29得135-90<116.∴+>=+.∴k<8.又k∈N*,∴k的最大值为7,【变式训练4】解:(1)由S n=a n2+a n+,①得:当n≥2时,S n-1=a2n-1+a n-1+.②①-②,化简得:(a n+a n-1)(a n-a n-1-2)=0.又∵数列{a n}的各项为正数,∴当n≥2时,a n-a n-1=2.故数列{a n}为等差数列,且公差为2.又a1=S1=a12+a1+,解得a1=1,∴a n=2n-1.(2)由分段函数f(n)=可以得到:c1=f(6)=f(3)=a3=5,c2=f(8)=f(4)=f(2)=f(1)=a1=1;当n≥3,n∈N*时,c n=f(2n+4)=f(2n-1+2)=f(2n-2+1)=2(2n-2+1)-1=2n-1+1,故当n≥3时,T n=5+1+(22+1)+(23+1)+…+(2n-1+1)=6++(n-2)=2n+n.n=1时,T1=5不满足T n=2n+n;n=2时,T2=c1+c2=6满足T n=2n+n.故T n=【例5】解:设点P(x0,y0)(x0≠0,y0≠0),直线l的方程为y-y0=k(x-x0),代入+=1,整理得(3+4k2)x2+8k(y0-kx0)x+4(y0-kx0)2-12=0.∵x=x0是方程的两个相等实根,∴2x0=-,解得k=-.∴直线l的方程为y-y0=-(x-x0).令x=0,得点A的坐标为.又∵+=1,∴4y02+3x02=12,∴点A的坐标为.又直线l′的方程为y-y0=(x-x0),令x=0,得点B的坐标为,∴以AB 为直径的圆方程为x ·x +·=0, 整理得x 2+y 2+y -1=0.由得∴以AB 为直径的圆恒过定点(-1,0)和(1,0). 【变式训练5】解:(1)设椭圆M 的半焦距为c , 由题意知 所以a =2,b =1.因此椭圆M 的方程为+y 2=1.(2)由整理得5x 2+8mx +4m 2-4=0,由Δ=64m 2-80(m 2-1)=80-16m 2>0,得-<m <.设P (x 1,y 1),Q (x 2,y 2), 那么x 1+x 2=-,x 1x 2=. 所以|PQ |== =(-<m <).线段CD 的方程为y =1(-2≤x ≤2),线段AD 的方程为x =-2(-1≤y ≤1). ①不妨设点S 在AD 边上,T 在CD 边上,可知1≤m <,S (-2,m -2),D (-2,1), 所以|ST |=|SD |=[1-(m -2)]=(3-m ), 因此=.令t =3-m (1≤m <), 那么m =3-t ,t ∈(3-,2], 所以== =,由于t ∈(3,2],所以1t ∈12⎡⎢⎣⎭,因此当134t =即t =43时,PQ STm =53. ②不妨设点S 在AB 边上,T 在CD 边上,此时-1≤m ≤1,因此,此时PQ ST所以当m =0时,PQ ST③不妨设点S 在AB 边上,T 在BC 边上,m ≤-1,由椭圆和矩形的对称性知PQ STm=53-.综上所述m=±53或者m=0时,PQ ST获得最大值5. 【例6】解:(1)∵f (x )=x 3-x , 令f ′(x )=x 2-1=0,解得x =±1.当x 变化时,f ′(x ),f (x )的变化如下:极大值又f (3)=6,f (-2)=-.比较可得:当x ∈[-2,3]时,f (x )max =f (3)=6. 因为f (x )<k -2005恒成立, 所以k -2005>6,即k >2011, 所以最小的正整数k =2012. (2)g (x )=f (x )-ax 2+x =x 3-ax 2,那么g ′(x )=x 2-ax ,所以g ′(1)=1-a .又因为g (1)=-a ,所以切线方程为y -=(1-a )(x -1). 令x =0,得y =a -,令y =0,得x =, 所以S =.因为a ≥2,那么S =,那么S′=.所以S′>0,即S在[2,+∞)上单调递增,所以a=2时,S min==.【变式训练6】解:(1)∵f(-x)=-f(x),∴-ax3+bx2-cx+d=-ax3-bx2-cx-d.∴b=0,df(x)=ax3+cx.而它的图象过点和(2,2),那么解得故f(x)=x3-x.从而f′(x)=x2-1==.由f′(x)>0,得f(x)的单调增区间为和;由f′(x)<0,得f(x)的单调减区间为.(2)令g(x)=0,得f(x)=5t,要使得方程g(x)=0有且只有一个解,即函数y=f(x)与y=5t的图象有且只有一个交点,而由(1)知,f(x)在x=-时获得极大值,在x=时获得极小值,而f=×3-=,f=-f=-,故要使得y=f(x)与y=5t的图象只有一个交点,那么5t>或者5t<-,即t>或者t<-.。
欣宜市实验学校二零二一学年度高考数学第二轮复习 第1讲 选择题技法指导 理 试题

黔西北州欣宜市实验学校二零二一学年度第1讲选择题技法指导纵观近几年的高考题,无论是全国卷还是自主命题卷,选择题是高考试题的三大题型之一.除卷外,其他高考卷中选择题的个数均在8~12之间,占总分的27%~40%.该题型的根本特点:绝大局部选择题属于低中档题,且一般按由易到难的顺序排列,主要的数学思想和数学方法能通过它得到充分的表达和应用,选择题具有概括性强、知识覆盖面广、小巧灵敏及有一定的综合性和深度等特点,且每一题几乎都有两种或者两种以上的解法.正是因为选择题具有上述特点,所以该题型能有效地检测学生的思维层次及考察学生的观察、分析、判断、推理、根本运算、信息迁移等才能.选择题也在尝试创新,在“形成适当梯度〞“用学过的知识解决没有见过的问题〞“活用方法和应变才能〞“知识的交汇〞等四个维度上不断出现新颖题,这些新颖题成为高考试卷中一道靓丽的风景线.1.直接法与定义法直接从题设条件出发,利用定义、定理、性质、公式等知识,通过变形、推理、运算等过程,直接得到结果,即“小题大做〞,选择正确答案,这种解法叫直接法.直接法是选择题最根本的方法,绝大多数选择题都适宜用直接法解决.它的一般步骤是:计算推理、分析比较、对照选择.直接法又分定性分析法、定量分析法和定性、定量综合分析法.【例1】假设△ABC的内角A,B,C所对边a,b,c满足(a+b)2-c2=4,且C=60°,那么ab的值是().A.B.8-4C.1D.变式训练1=1-n i,其中m,n是实数,i是虚数单位,那么m+n i=().A.1+2iB.1-2iC.2+iD.2-i2.数形结合法根据题设条件作出所研究问题的曲线、有关图形或者草图,借助几何图形的直观性、形状、位置、性质等图象特征作出正确的判断,得出结论.这种方法通过“以形助数〞或者“以数助形〞,使抽象问题直观化、复杂问题简单化.【例2】设函数y=f(x)在(-∞,+∞)内有定义,对于给定的正数K,定义函数f K(x)=取函数f(x)=2-|x|.当K=时,函数f K(x)的单调递增区间为().A.(-∞,0)B.(0,+∞)C.(-∞,-1)D.(1,+∞)变式训练2假设函数f(x)=e x+ln x,g(x)=e-x+ln x,h(x)=e-x-ln x的零点依次为a,b,c,那么a,b,c的大小依次为().A.a>b>c B.a>c>b C.c>a>b D.c>b>a3.特例法与排除法用符合条件的特例来检验各选项,排除错误的,留下正确的一种方法叫特例法(特值法),常用的特例有特殊数值、特殊函数、特殊数列、特殊图形等.排除法就是根据高考数学选择题中有且只有一个答案是正确的这一特点,在解题时,结合估算、特例、逻辑分析等手段先排除一些肯定是错误的选项,从而缩小选择范围,确保答案的准确性,并进步答题速度.【例3】函数f(x)=(0≤x≤2π)的值域是().A.B.[-1,0]C.[-,-1]D.4.估算法由于选择题提供了唯一正确的选择项,解答又无需过程.因此,有些题目,不必进展准确的计算,只需对其数值特点和取值界限作出适当的估计,便能作出正确的判断,这就是估算法.估算法的关键是确定结果所在的大致范围,否那么“估算〞就没有意义,估算法往往可以减少运算量,但是加强了思维的层次.【例4】假设D为不等式组表示的平面区域,那么当a从-2连续变化到1时,动直线x+y=a扫过D 中的那局部区域的面积为().A.B.1 C.D.2参考答案方法例析【例1】A解析:由(a+b)2-c2=4,得a2+b2+2ab-c2=4,由C=60°,得cos C===.解得ab=.【变式训练1】C【例2】C解析:当K=时,f K(x)=12()f x=即12()f x=||1||1, 21|| 1.2xxx⎧⎛⎫≥⎪ ⎪⎪⎝⎭⎨⎪<⎪⎩,,1 2()f x的图象如以下图.由图象可知,所求的单调递增区间为(-∞,-1).【变式训练2】D【例3】B解析:令sin x=0,cos x=1,那么f(x)==-1,排除A,D;令sin x=1,cos x=0,那么f(x)==0,排除C,应选B.【例4】C。
黑龙江省双鸭山市第一中学高考数学二轮复习专项备考讲义:三、“不等式”命题角度及解题技巧例析

“不等式”命题角度及解题技巧例析代数学在近现代数学中占有重要的地位,它的许多理论在数学的发展中都具有重要的应用,作为代数的一个重要组成部分,不等式理论在现在的高考中,乃至在数学奥林匹克竞赛中都扮演着重要的角色,它既是学生学习中的重点,同时也是学好代数学的一个难点,因此我们必须重视不等式知识的研究和学习。
高考中关于不等式知识的考察,不仅仅局限于考察学生解不等式,掌握不等式的简单性质,还注重考察应用不等式求解一些简单的数学问题。
本文以若干高考真题为例,从命题角度及解题技巧方面就“不等式”这一高频考点进行深入剖析,希望作者的拙见能够对广大师生科学备考起到一定的帮助。
命题角度一 解不等式,不等式基本性质的考察【例1】(2015高考山东,理5)不等式152x x ---<的解集是( )(A )(-,4) (B )(-,1) (C )(1,4) (D )(1,5)【答案】A【考查方向】含绝对值的不等式的解法.【解题技巧点拨】本题考查了含绝对值的不等式的解法,重点考查学生利用绝对值的意义将含绝对值的不等式转化为不含绝对值的不等式(组)从而求解的能力,本题属中档题.【解析】原不等式同解于如下三个不等式解集的并集;1155()()()152152152x x x I II III x x x x x x <≤<≥⎧⎧⎧⎨⎨⎨-+-<-+-<--+<⎩⎩⎩解(I )得:1x < ,解(II )得:14x ≤< ,解(III )得:x φ∈ ,所以,原不等式的解集为{}4x x <,故选A.【练习】(2016年上海高考)设x R ∈,则不等式13<-x 的解集为________________【答案】(2,4)【例2】 (2014四川高考) 若0a b >>,0c d <<,则一定有( )A 、a b c d >B 、a b c d <C 、a b d c >D 、a b d c< 【答案】D【考查方向】不等式的基本性质,反比例函数的单调性,代数式比较大小.【解题技巧点拨】本题的解法较多,一方面,可以利用同向正不等式的可乘性,结合函数的单调性求解(即用综合法证明不等式);除此之外,也可以采用分析法进行求解,即从结论出发,寻求其成立的充分条件;另外,本题作为选择题,也可以采用特值法排除选项来得到正确答案.【解析】D cb d ac bd a c d b a c d c d d c 选.0∴0--∴01-1-,001-1-∴011∴0<<>>>>>>>><<<< 【练习】(2013上海高考)如果0a b <<,那么下列不等式成立的是( )A .11a b <B .2ab b <C .2ab a -<-D .11a b-<- 【答案】D命题角度二 线性规划问题【例3】(2016年全国III 高考)若,x y 满足约束条件1020220x y x y x y -+≥⎧⎪-≤⎨⎪+-≤⎩则z x y =+的最大值为_____________. 【答案】32【考查方向】简单的线性规划问题【解题技巧点拨】线性规划问题的求解方法主要有两种,一是利用图象,结合目标函数的几何意义进行求解,二是采用代入点坐标比较大小的方式进行求解.【练习】(2016年天津高考)设变量x ,y 满足约束条件20,2360,3290.x y x y x y -+≥⎧⎪+-≥⎨⎪+-≤⎩则目标函数25z x y=+的最小值为( )(A )4-(B )6(C )10 (D )17【答案】B命题角度三 不等式在求最值中的简单应用【例4】(2015高考浙江,理14)若实数,x y 满足221x y +≤,则2263x y x y +-+--的最小值是.【答案】3.【考查方向】1.线性规划的运用;2.分类讨论的数学思想;3.直线与圆的位置关系【解题技巧点拨】本题主要考查了以线性规划为背景的运用,属于中档题根据可行域是圆 及其内部的特点,结合直线与圆的位置关系的判定,首先可以将目标函数的两个绝对值号 中去掉一个,再利用分类讨论的数学思想去掉其中一个绝对值号,利用线性规划知识求解, 理科试卷的线性规划问题基本考查含参的线性规划问题或者是利用线性规划的知识解决一 些非线性的目标函数或可行域的问题,常需考查目标函数或可行域的几何意义求解,在复 习时应予以关注.【例5】( 2015高考四川,理9)如果函数()()()()21281002f x m x n x m n =-+-+≥≥,在区间122⎡⎤⎢⎥⎣⎦,上单调递减,则mn 的最大值为( ) (A )16 (B )18 (C )25 (D )812 【答案】B【考查方向】 基本不等式,初等函数的性质.【解题技巧点拨】首先弄清抛物线的开口方向和对称轴,结合所给单调区间找到m 、n 满足的条件,然后利用基本不等式求解.本题将函数的单调性与基本不等式结合考查,检测了学生综合运用知识解题的能力.在知识的交汇点命题,这是高考的一个方向,这类题往往以中高档题的形式出现.【解析】2m ≠时,抛物线的对称轴为82n x m -=--.据题意,当2m >时,822n m --≥-即212m n +≤.226,182m n m n mn +⋅≤≤∴≤.由2m n =且212m n +=得3,6m n ==.当2m <时,抛物线开口向下,据题意得,8122n m --≤-即218m n +≤.28129,22n m n m mn +⋅≤≤∴≤.由2n m =且218m n +=得92m =>,故应舍去.要使得mn 取得最大值,应有218m n +=(2,8)m n <>.所以(182)(1828)816mn n n =-<-⨯⨯=,所以最大值为18.选B..命题角度四 不等式与其它知识点间的综合问题【例6】(2015高考陕西,理9)设()ln ,0f x x a b =<<,若p f =,()2a b q f +=,1(()())2r f a f b =+,则下列关系式中正确的是( ) A .q r p =< B .q r p => C .p r q =< D .p r q =>【答案】C【考查方向】1、基本不等式;2、基本初等函数的单调性.【解题技巧点拨】本题主要考查的是基本不等式和基本初等函数的单调性,属于容易题.解题时一定要注意检验在使用基本不等式求最值中是否能够取得等号,否则很容易出现错误.本题先判断2a b +【解析】ln p f ==()ln 22a b a b q f ++==,11(()())ln 22r f a f b ab =+==()ln f x x =在()0,+∞上单调递增,因为2a b +>,所以()2a b f f +>,所以q p r >=,故选C .【练习】(2016北京高考)已知x ,y R ∈,且0x y >>,则( ) A.110x y -> B.sin sin 0x y -> C.11()()022x y -< D.ln ln 0x y +> 【答案】C。
甘肃省武威市第一中学2019年高三上学期10月月考数学(理)试题 Word版含解析

武威一中2019年秋季学期阶段性考试高三年级数学(理科)试卷命题人:杨仑元一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={x|(x-1)2<4,x∈R},N={-1,0,1,2,3},则M∩N=()A. {0,1,2}B. {-1,0,1,2}C. {-1,0,2,3}D. {0,1,2,3}【答案】A【解析】试题分析:求出集合M中不等式的解集,确定出M,找出M与N的公共元素,即可确定出两集合的交集.解:由(x﹣1)2<4,解得:﹣1<x<3,即M={x|﹣1<x<3},∈N={﹣1,0,1,2,3},∈M∩N={0,1,2}.故选A点评:此题考查了交集及其运算,熟练掌握交集定义是解本题的关键.【此处有视频,请去附件查看】2.已知命题p:∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≥0,则⌝p是A. ∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0B. ∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≤0C. ∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0D. ∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0【答案】C【解析】【详解】全称命题的的否定是存在性命题,因为,命题p:∀x1,x2∈R,(f(x2)-f(x1))(x2-x1)≥0,所以,⌝p是∃x1,x2∈R,(f(x2)-f(x1))(x2-x1)<0,故选C.考点:全称命题与存在性命题.点评:简单题,全称命题的的否定是存在性命题.【此处有视频,请去附件查看】3.设a=log36,b=log510,c=log714,则().A. c>b>aB. b>c>aC. a>c>bD. a>b>c【答案】D【解析】试题分析:,,;且;.考点:对数函数的单调性. 【此处有视频,请去附件查看】4.函数()f x =)A. 1(0,)2B. (2,)+∞C. 1(0,)(2,)2+∞UD.1(0,][2,)2+∞U 【答案】C 【解析】由题意得220(log )10x x >⎧⎨->⎩,0,1202x x x 或>⎧⎪⎨><<⎪⎩所以x ∈()10,2,2⎛⎫⋃+∞ ⎪⎝⎭,选C. 5.已知132a -=,21log 3b =,121log 3c =,则( ,, A. a b c >>B. a c b >>C. c a b >>D.c b a >>【答案】C 【解析】试题分析:因为13212112(0,1),log 0,log 1,33a b c -=∈==所以.b a c <<选C . 考点:比较大小【此处有视频,请去附件查看】6.设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=, , A. 3 B. 6C. 9D. 12【答案】C 【解析】()()()()()22log 121log 622221log 223,log 12226,2log 129f f f f -⎡⎤-=+--====∴-+=⎣⎦.故选C.【此处有视频,请去附件查看】7.设a ,b 都是不等于1的正数,则“333a b >>”是“log 3log 3a b <”的( ) A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件【答案】B 【解析】若333a b >>,则1a b >>,从而有log 3log 3a b <,故为充分条件. 若log 3log 3a b <不一定有1a b >>,比如.1,33a b ==,从而333a b >>不成立.故选B. 考点:命题与逻辑.【此处有视频,请去附件查看】8.已知定义在R 上的函数()21()x m f x m -=-为实数为偶函数,记0.5(log 3),a f =2b (log 5),c (2)f f m ==,则,,a b c ,的大小关系为( )A. a b c <<B. c a b <<C. a c b <<D.c b a <<【答案】B 【解析】由()f x 为偶函数得0m = ,所以0,52log 3log 32121312,a =-=-=-=2log 521514b =-=-=,0210c =-=,所以c a b <<,故选B.考点:本题主要考查函数奇偶性及对数运算. 【此处有视频,请去附件查看】9.如图,长方形ABCD 的边2AB =,1BC =,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠=.将动P 到A 、B 两点距离之和表示为x 的函数()f x ,则()y f x =的图像大致为( )A. B.C. D.【答案】B【解析】 【分析】根据函数图象关系,利用排除法进行求解即可.【详解】解:当04x π≤≤时,tan ,BP x AP ===此时()tan f x x =,04x π≤≤,此时单调递增,当P 在CD 边上运动时,344ππ≤≤x 且2x π≠时, 如图所示,1tan tan()tan tan PQ POB POQ x POQ OQ OQπ∠=-∠==-∠=-=-, 1tan OQ x∴=-,111,1tan tan PD AO OQ PC BO OQ x x∴=-=+=+=-,PA PB ∴+=当2x π=时,PA PB +=当P 在DA 边上运动时,3,tan 4x PB x PA ππ≤≤+= 由对称性可知函数()f x 关于2x π=对称,且42f f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,且轨迹为非线型, 排除A ,C ,D , 故选B .【点睛】本题主要考查函数图象的识别和判断,根据条件先求出04x π≤≤时的解析式是解决本题的关键.10.函数()()2ax bf x x c +=+的图象如图所示,则下列结论成立的是( )A. 0a >,0b >,0c <B. 0a <,0b >,0c >C. 0a <,0b >,0c <D. 0a <,0b <,0c < 【答案】C 【解析】试题分析:函数在P 处无意义,由图像看P 在y 轴右侧,所以0,0c c -><,()200,0b f b c =>∴>,由()0,0,f x ax b =∴+=即bx a=-,即函数的零点000.0,0bx a a b c a=->∴<∴<,故选C . 考点:函数的图像【此处有视频,请去附件查看】11.设函数()()()000f x R x x f x ≠的定义域为,是的极大值点,以下结论一定正确的是( )A. ()()0,x R f x f x ∀∈≤B. ()0x f x --是的极小值点C. ()0x f x --是的极小值点D. ()0x f x ---是的极小值点【答案】D 【解析】【详解】对于A 选项函数的极大值不一定是函数的最大值,所以错;对于B 中的()f x -是将()f x 的图象关于y 轴对称,所以0x -是其极大值点,错误;对于C 中的()f x -是将()f x 的图象关x 轴对称,所以0x 才是其极小值点,错误;而对于D 中的()f x --是将()f x 的图象关原点对称,故0x -是其极小值点,正确.故选D.12.已知函数lg ,010()16,102x x f x x x ⎧<≤⎪=⎨-+>⎪⎩,若a ,b ,c 互不相等,且()()()f a f b f c ==,则abc 的取值范围是( ) A. ()1,10B. ()5,6C. ()20,24D.()10,12【答案】D 【解析】 【分析】画出函数的图像,根据对数函数的运算得到1ab =,再根据图像看出c 的范围,也即是abc 的范围.【详解】画出函数图像如下图所示,由于1lg lg lg x x x=-=,故1ab =,即abc c =,由推向可知()10,12c ∈,故选D.【点睛】本小题主要考查分段函数的图像,考查对数的运算,考查数形结合的数学思想方法,属于基础题.【此处有视频,请去附件查看】二、填空题:本题共4小题,每小题5分,共20分.13.若29,Tx dx T =⎰则常数的值为 .【答案】3; 【解析】依题意3301|()933T x T ==,所以3T =【此处有视频,请去附件查看】14.若曲线x y e -=上点P 处的切线平行于直线210x y ++=,则点P 的坐标是________. 【答案】(ln 2,2)- 【解析】试题分析:设切点P (,)a b ,则由xy e -'=-得:2,2,ln 2,2a a a k e e a b e ---=-=-==-==,所以点P 的坐标是(ln 2,2)-.考点:利用导数求切点. 【此处有视频,请去附件查看】15.已知()32,,x x af x x x a⎧≤=⎨>⎩,若存在实数b ,使函数()()g x f x b =-有两个零点,则a 的取值范围是______. 【答案】()(),01,-∞⋃+∞【解析】【分析】由()()g x f x b =-有两个零点可得()f x b =有两个根,即()y f x =与y b =的图象有两个交点,则函数在定义域内不能是单调函数,结合函数图象可求a 的范围 【详解】解:∵()()g x f x b =-有两个零点,∴()f x b =有两个根,即()y f x =与y b =的图象有两个交点, 由32x x =可得,0x =或1x =①当1a >时,函数()y f x =的图象如图所示,此时存在b ,满足题意,故1a >满足题意②当1a =时,由于函数()y f x =在定义域R 上单调递增,故不符合题意 ③当01a <<时,函数()y f x =单调递增,故不符合题意④当0a =时,函数()y f x =单调递增,故不符合题意⑤当0a <时,函数()y f x =的图象如图所示,此时存在b 使得,()y f x =与y b =有两个交点综上可得,0a <或1a > 故答案为()(),01,-∞⋃+∞【点睛】本题考察了函数的零点问题,渗透了转化思想,数形结合、分类讨论的数学思想.16.已知函数()3421f x x x =--+,若对任意实数x 都有()()22f x a f ax -+<,则实数a 的取值范围是________.【答案】()4,0-【解析】 【分析】构造函数342()()1g x f x x x =---=,则函数是奇函数,在R 上单调递减,()()22f x a f ax -+<,等价于()()20g x a g ax -+<,再利用奇偶性和单调性,得到关于x 的不等式,即可得出结论.【详解】解:构造函数342()()1g x f x x x =---=,则函数是奇函数,在R 上单调递减,()()22f x a f ax -+<,等价于()()20g x a g ax -+<,∴2x a ax ->-, ∴20x ax a +->, ∴240a a D=+<∴40a -<<, 故答案为()4,0-.【点睛】本题考查函数的单调性、奇偶性、考查学生解不等式的能力,正确构造函数是关键.三、解答题:共70分。
2025届襄阳市四中高三数学上学期10月考试卷及答案解析

襄阳四中2025届高三上学期10月月考数学试卷命题人:陈国兵 审题人:饶雨一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1. 已知集合31A x x ⎧⎫=∈∈⎨⎬-⎩⎭Z Z ,则用列举法表示A =( )A. {}2,0,1,2,4- B. {}2,0,2,4- C. {}0,2,4 D. {}2,4【答案】B 【解析】【分析】由题意可得1x -可为1±、3±,计算即可得.【详解】由题意可得1x -可为1±、3±,即x 可为0,2,2,4-,即{}2,0,2,4A =-.故选:B.2. 设3i,ia a z +∈=R ,其中i 为虚数单位.则“1a <-”是“z >”的( )A. 充分不必要条件 B. 必要不充分条件C. 充要条件 D. 既不充分也不必要条件【答案】A 【解析】【分析】首先根据复数代数形式的除法运算化简z ,再求出z,令z >a 的取值范围,最后根据充分条件、必要条件的定义判断即可.【详解】因为23i 3i 3i i ia az a +-===-,所以z =令z >>1a >或1a <-,所以1a <-推得出z >,故充分性成立;由z >推不出1a <-,故必要性不成立;所以“1a <-”是“z >的充分不必要条件.故选:A3. 已知向量a ,b 不共线,且c a b λ=+ ,()21d a b λ=++ ,若c 与d 同向共线,则实数λ的值为( )A. 1B.12C. 1或12-D. 1-或12【答案】B 【解析】【分析】先根据向量平行求参数λ,再根据向量同向进行取舍.【详解】因为c与d 共线,所以()2110λλ+-=,解得1λ=-或12λ=.若1λ=-,则c a b =-+,d a b =- ,所以d c =- ,所以c 与d 方向相反,故舍去;若12λ=,则12c a b =+ ,2d a b =+ ,所以2d c = ,所以c与d 方向相同,故12λ=为所求.故选:B4. 已知3322x y x y ---<-,则下列结论中正确的是( )A. ()ln 10y x -+> B. ln0yx> C. ln 0y x +> D. ln 0y x ->【答案】A 【解析】【分析】构造函数()32xf x x -=-,利用()f x 的单调性可得x y <,进而可得.【详解】由3322x y x y ---<-得3322x y x y ---<-,设()32xf x x -=-,因函数3y x =与2x y -=-都是R 上的增函数,故()f x 为R 上的增函数,又因3322x y x y ---<-,故x y <,()ln 1ln10y x -+>=, 故A 正确,因y x,y x +,y x -与1的大小都不确定,故B ,C ,D 错误,故选:A5. 从0,1,2,3,4,5,6这7个数中任选5个组成一个没有重复数字的“五位凹数12345a a a a a ”(满足12345a a a a a >><<),则这样的“五位凹数”的个数为( )A. 126个 B. 112个 C. 98个 D. 84个【答案】A 【解析】【分析】利用分步乘法计数原理可得.【详解】第一步,从0,1,2,3,4,5,6这7个数中任选5个共有57C 种方法,第二步,选出的5个数中,最小的为3a ,从剩下的4个数中选出2个分给12,a a ,由题意可知,选出后1245,,,a a a a 就确定了,共有24C 种方法,故满足条件的“五位凹数”5274C C 126=个,故选:A6. 若数列{}n a 满足11a =,21a =,12n n n a a a --=+(3n ≥,n 为正整数),则称数列{}n a 为斐波那契数列,又称黄金分割数列.在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用.设n S 是数列{}n a 的前n 项和,则下列结论成立的是( )A. 78a = B. 135********a a a a a +++⋅⋅⋅+=C. 754S = D. 24620202021a a a a a +++⋅⋅⋅+=【答案】B 【解析】【分析】按照斐波那契数列的概念,找出规律,得出数列的性质后逐个验证即可.【详解】解析:按照规律有11a =,21a =,32a =,43a =,55a =,68a =,713a =,733S =,故A 、C 错;21112123341n n n n n n n n n n n n n n a a a a a a a a a a a a a S ++--------=+=+++=+++++==+ ,则202020181220183520191352019111a S a a a a a a a a a a =+=++++=++++=++++ ,故B 对;24620202234520182019a a a a a a a a a a a ++++=+++++++ 1234520182019201920211a a a a a a a S a =+++++++==- ,故D 错.故选:B .7. 已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的左,右焦点,A ,B 是椭圆C 上的两点.若122F A F B = ,且12π4AF F ∠=,则椭圆C 的离心率为( )A13B.C.D.23【答案】B 【解析】【分析】设1AF =,结合题意可得2AF,根据椭圆定义整理可得22b c m -=,根据向量关系可得1F A ∥2F B,且2BF =2b c m+=,进而可求离心率.【详解】由题意可知:()()12,0,,0F c F c -,设1,0AF m =>,因为12π4AF F ∠=,则()2,2A c m m -+,可得2AF =由椭圆定义可知:122AF AF a+=,即2a +=,整理可得22b c m-=;又因为122F A F B = ,则1F A ∥2F B,且2112BF AF ==,则(),B c m m +,可得1BF =由椭圆定义可知:|BF 1|+|BF 2|=2a2a =,.2bcm+=;即2c c-=+3c=,所以椭圆C的离心率cea==.故选:B.【点睛】方法点睛:椭圆的离心率(离心率范围)的求法求椭圆的离心率或离心率的范围,关键是根据已知条件确定a,b,c的等量关系或不等关系,然后把b用a,c代换,求e的值.8. 圆锥的表面积为1S,其内切球的表面积为2S,则12SS的取值范围是()A. [)1,+∞ B. [)2,+∞C. )∞⎡+⎣ D.[)4,+∞【答案】B【解析】【分析】选择OBC∠(角θ)与内切球半径R为变量,可表示出圆锥底面半径r和母线l,由圆锥和球的表面积公式可得()122212tan1tanSSθθ=-,再由2tan(0,1)tθ=∈换元,转化为求解二次函数值域,进而得12SS的取值范围.【详解】设圆锥的底面半径为r,母线长为l,圆锥内切球半径为R,如图作出圆锥的轴截面,其中设O为外接圆圆心,,D E为切点,,AB AC为圆锥母线,连接,,,OB OD OA OE.设OBCθ∠=,tanRrθ=,0tan1θ<<tanRrθ∴=.OD AB⊥,OE BC⊥,πDBE DOE∴∠+∠=,又πAOD DOE∠+∠=,2AOD DBE θ∴∠=∠=,tan 2AD R θ∴=,22tan 2tan Rl r AD BD r AD r R θθ∴+=++=+=+,则圆锥表面积()21πππS r rl r l r =+=+,圆锥内切球表面积224πS R =,所求比值为()212222π2tan 21tan 1tan tan 4π2tan 1tan R R R S S R θθθθθθ⎛⎫+ ⎪-⎝⎭==-,令2tan 0t θ=>,则()2211()2122222g t t t t t t ⎛⎫=-=-+=--+ ⎪⎝⎭,则10()2g t <≤,且当12t =时,()g t 取得最大值12,故122S S ≥,即12S S 的取值范围是[)2,+∞.故选:B.【点睛】关键点点睛:求解立体几何中的最值问题一般方法有两类,一是设变量(可以是坐标,也可以是关键线段或关键角)将动态问题转化为代数问题,利用代数方法求目标函数的最值;二是几何法,利用图形的几何性质,将空间问题平面化,将三维问题转化为二维问题来研究,以平面几何中的公理、定义、定理为依据,以几何直观为主要手段直接推理出最值状态何时取到,再加以求解.二、多选题:本题共3小题,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 设A ,B 为随机事件,且()P A ,()P B 是A ,B 发生的概率. ()P A ,()()0,1P B ∈,则下列说法正确的是( )A. 若A ,B 互斥,则()()()P A B P A P B ⋃=+B. 若()()()P AB P A P B =,则A ,B 相互独立C 若A ,B 互斥,则A ,B 相互独立D. 若A ,B 独立,则()(|)P B A P B =【答案】ABD 【解析】【分析】利用互斥事件的概率公式可判断A 选项;由相互独立事件的概念可判断B 选项;由互斥事件和相互独立事件的概念可判断C 选项;由相互独立事件的概念,可判断D 选项.【详解】对于选项A ,若,A B 互斥,根据互斥事件的概率公式,则()()()P A B P A P B ⋃=+,所以选项A 正确,.对于选项B ,由相互独立事件概念知,若()()()P AB P A P B =,则事件,A B 是相互独立事件,所以选项B 正确,对于选项C ,若,A B 互斥,则,A B 不一定相互独立,例:抛掷一枚硬币的试验中,事件A :“正面朝上”,事件B :“反面朝上”,事件A 与事件B 互斥,但()0P AB =,1()()2P A P B ==,不满足相互独立事件的定义,所以选项C 错误,对于选项D ,由相互独立事件的定义知,若A ,B 独立,则()(|)P B A P B =,所以选项D 正确,故选:ABD.10. 已知函数()sin sin cos 2f x x x x =-,则( )A. ()f x 的图象关于点(π,0)对称B. ()f x 的值域为[1,2]-C. 若方程1()4f x =-在(0,)m 上有6个不同的实根,则实数m 的取值范围是17π10π,63⎛⎤⎥⎝⎦D. 若方程[]22()2()1(R)f x af x a a -+=∈在(0,2π)上有6个不同的实根(1,2,,6)i x i = ,则61i i ax =∑的取值范围是(0,5π)【答案】BCD 【解析】【分析】根据(2π)()f f x =-是否成立判断A ,利用分段函数判断BC ,根据正弦函数的单调性画出分段函数()f x 的图象,求出的取值范围,再利用对称性判断D.【详解】因为()sin sin cos 2f x x x x =-,所以(2π)sin(2π)sin(2π)cos 2(2π)sin sin cos 2()f x x x x x x x f x -=----=--≠-,所以()f x 的图象不关于点(π,0)对称,故A 错误;当sin 0x ≥时,()222()sin 12sin 3sin 1f x x x x =--=-,由[]sin 0,1x ∈可得[]()1,2f x ∈-,当sin 0x <时,()222()sin 12sin sin 1f x x x x =---=-,由[)sin 1,0x ∈-可得(]()1,0f x ∈-,的综上[]()1,2f x ∈-,故B 正确:当sin 0x ≥时,由21()3sin 14f x x =-=-解得1sin 2x =,当sin 0x <时,由21()sin 14f x x =-=-解得sin x =,所以方程1()4f x =-在(0,)+∞上的前7个实根分别为π6,5π6,4π3,5π3,13π6,17π6,10π3,所以17π10π63m <≤,故C 正确;由[]22()2()1f x af x a -+=解得()1f x a =-或()1f x a =+,又因为()223sin 1,sin 0sin 1,sin 0x x f x x x ⎧-≥=⎨-<⎩,所以根据正弦函数的单调性可得()f x 图象如图所示,所以()1f x a =-有4个不同的实根,()1f x a =+有2个不同的实根,所以110012a a -<-<⎧⎨<+<⎩,解得01a <<,设123456x x x x x x <<<<<,则1423πx x x x +=+=,563πx x +=,所以615πii x==∑,所以61i i a x =∑的取值范围是(0,5π),故D 正确.故选:BCD.11. 在平面直角坐标系中,定义(){}1212,max ,d A B x x y y =--为两点()11,A x y 、()22,B x y 的“切比雪夫距离”,又设点P 及l 上任意一点Q ,称(),d P Q 的最小值为点P 到直线l 的“切比雪夫距离”,记作(),d P l ,给出下列四个命题,正确的是( )A 对任意三点,,ABC ,都有()()(),,,d C A d C B d A B +≥;B. 已知点()2,1P 和直线:220l x y --=,则()83d P l =,;C. 到定点M 的距离和到M 的“切比雪夫距离”相等的点的轨迹是正方形.D. 定点()1,0F c -、()2,0F c ,动点(),P x y 满足()()()12,,2220d P F d P F a c a =>>-,则点P 的轨迹.与直线y k =(k 为常数)有且仅有2个公共点.【答案】AD 【解析】【分析】对于选项A ,根据新定义,利用绝对值不等性即可判断;对于选项B ,设点Q 是直线21y x =-上一点,且(,21)Q x x -,可得()1,max 2,22d P Q x x ⎧⎫=--⎨⎬⎩⎭,讨论|2|x -,1|2|2x -的大小,可得距离d ,再由函数的性质,可得最小值;对于选项C ,运用新定义,求得点的轨迹方程,即可判断;对于选项D ,根据定义得{}{}max ,max ,2x c y x c y a +--=,再根据对称性进行讨论,求得轨迹方程,即可判断.【详解】A 选项,设()()(),,,,,A A B B C C A x y B x y C x y ,由题意可得:()(){}{},,max ,max ,,A C A CBC B C A C B C A B d C A d C B x x y y x x y y x x x x x x +=--+--≥-+-≥-同理可得:()(),,A B d C A d C B y y +≥-,则:()(){}(),,max ,,A B A B d C A d C B x x y y d A B +≥--=,则对任意的三点A ,B ,C ,都有()()(),,,d C A d C B d A B +≥;故A 正确;B 选项,设点Q 是直线220x y --=上一点,且1,12Q x x ⎛⎫- ⎪⎝⎭,可得()1,max 2,22d P Q x x ⎧⎫=--⎨⎬⎩⎭,由1222x x -≥-,解得0x ≤或83x ≥,即有(),2d P Q x =-,当83x =时,取得最小值23;由1222x x -<-,解得803x <<,即有()1,22d P Q x =-,(),d P Q 的范围是2,23⎛⎫⎪⎝⎭,无最值,综上可得,P ,Q 两点的“切比雪夫距离”的最小值为23,故B 错误;C 选项,设(),M ab {}max ,x a y b =--,若y b x a -≥-,则y b =-,两边平方整理得x a =;此时所求轨迹为x a=(y b ≥或)y b ≤-若y b x a -<-,则x a =-,两边平方整理得y b =;此时所求轨迹为y b=(x a ≥或)x a ≤-,故没法说所求轨迹是正方形,故C 错误;D 选项,定点()1,0F c -、()2,0F c ,动点(),P x y 满足()()12,,2d P F d P F a -=(220c a >>),则:{}{}max ,max ,2x c y x c y a +--=,显然上述方程所表示的曲线关于原点对称,故不妨设x ≥0,y ≥0.(1)当x c yx c y ⎧+≥⎪⎨-≥⎪⎩时,有2x c x c a +--=,得:0x a y a c =⎧⎨≤≤-⎩;(2)当x c y x c y ⎧+≤⎪⎨-≤⎪⎩时,有02a =,此时无解;(3)当x c y x c y⎧+>⎪⎨-<⎪⎩时,有2,x c y a a x +-=<;则点P 的轨迹是如图所示的以原点为中心的两支折线.结合图像可知,点P 的轨迹与直线y k =(k 为常数)有且仅有2个公共点,故D 正确.故选:AD.【点睛】“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.对于此题中的新概念,对阅读理解能力有一定的要求.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.三、填空题:本题共3小题,每小题5分,共15分.12. 若)nax的展开式的二项式系数和为32,且2x -的系数为80,则实数a 的值为________.【答案】―2【解析】【分析】由二项式系数和先求n ,再利用通项53215C ()r r rr T a x -+=-得到2x -的指数确定r 值,由2x -的系数为80,建立关于a 的方程求解可得.【详解】因为)na x-的展开式的二项式系数和为32,所以012C C C C 232nnn n n n ++++== ,解得5n =.所以二项式展开式的通项公式为5352155C ()C ()rr rr r rr a T a x x--+=-=-,由5322r-=-,解得3r =,所以2x -的系数为3335C ()1080a a -=-=,解得2a =-.故答案为:2-.13. 已知函数()()()2f x x a x x =--在x a =处取得极小值,则a =__________.【答案】1【解析】【分析】求得()()()221f x x x x a x =-+--',根据()0f a ¢=,求得a 的值,结合实数a 的值,利用函数的单调性与极值点的概念,即可求解.【详解】由函数()()()2f x x a x x =--,可得()()()221f x x x x a x =-+--',因为x a =处函数()f x 极小值,可得()20f a a a =-=',解得0a =或1a =,若0a =时,可得()(32)f x x x '=-,当0x <时,()0f x '>;当203x <<时,()0f x '<;当23x >时,()0f x '>,此时函数()f x 在2(,0),(,)3-∞+∞单调递增,在2(0,)3上单调递减,所以,当0x =时,函数()f x 取得极大值,不符合题意,(舍去);若1a =时,可得()(1)(31)f x x x '=--,当13x <时,()0f x '>;当113x <<时,()0f x '<;当1x >时,()0f x '>,此时函数()f x 在1(,),(1,)3-∞+∞单调递增,在(0,1)上单调递减,所以,当1x =时,函数()f x 取得极小值,符合题意,综上可得,实数a 的值为1.故答案为:1.14. 数学老师在黑板上写上一个实数0x ,然后老师抛掷一枚质地均匀的硬币,如果正面向上,就将黑板上的数0x 乘以2-再加上3得到1x ,并将0x 擦掉后将1x 写在黑板上;如果反面向上,就将黑板上的数0x 除以2-再减去3得到1x ,也将0x 擦掉后将1x 写在黑板上.然后老师再抛掷一次硬币重复刚才的操作得到黑板上的数为2x .现已知20x x >的概率为0.5,则实数0x 的取值范围是__________.【答案】()(),21,-∞-+∞ 【解析】【分析】构造函数()23f x x =-+,()32xg x =--,由两次复合列出不等式求解即可.【详解】由题意构造()23f x x =-+,()32xg x =--,则有()()43f f x x =-,()()9f g x x =+,()()92g f x x =-,()()342x g g x =-.因为()()f g x x >,()()g f x x <恒成立,又20x x >的概率为0.5,所以必有43,3,42x x x x ->⎧⎪⎨-≤⎪⎩或者43,3,42x x x x -≤⎧⎪⎨->⎪⎩解得()(),21,x ∈-∞-⋃+∞.故答案为:()(),21,-∞-+∞ 四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.15. 在ABC V 中,角,,A B C 所对的边分别为,,a b c ,已知()()()sin sin sin b c B C a c A +-=-.(1)求B ;(2)若ABC,且2AD DC = ,求BD 的最小值.【答案】(1)π3(2.【解析】【分析】(1)利用正弦定理可得()()()b c b c a c a +-=-,再结合余弦定理得2221cos 22a cb B ac +-==,从而可求解.(2)结合ABC V 的面积可求得3ac =,再由112333BD BC CA BA BC =+=+ ,平方后得,()222142993BD c a =++ ,再结合基本不等式即可求解.【小问1详解】由正弦定理得()()()b c b c a c a +-=-,即222a c b ac +-=,由余弦定理可得2221cos 222a cb ac B ac ac +-===,因为()0,πB ∈,所以π3B =.【小问2详解】因为ABC V π3B =,所以1sin 2ac B =,所以3ac =.因为()11123333BD BC CA BC BA BC BA BC =+=+-=+,所以()()()()22222221421441422cos 999999993BD BA BC BA BC c a ac B c a =++⋅⋅=++=++ ,所以2214212222993333c a c a ++≥⋅⋅+=,当且仅当a c ==时取等号,所以BD .16. 已知抛物线2:2(0)E y px p =>与双曲线22134x y -=的渐近线在第一象限的交点为Q ,且Q 点的横坐标为3.(1)求抛物线E 的方程;(2)过点(3,0)M -的直线l 与抛物线E 相交于,A B 两点,B 关于x 轴的对称点为B ',求证:直线AB '必过定点.【答案】(1)24y x = (2)证明见解析【解析】【分析】(1)由双曲线求其渐近线方程,求出点Q 的坐标,由此可求抛物线方程;(2)联立直线AB 的方程与抛物线方程可得关于x 的一元二次方程,设A (x 1,y 1),B (x 2,y 2),()22,B x y '-,根据韦达定理求出12124,12y y m y y +==,求出直线AB '的方程并令0y =,求出x 并逐步化简可得3x =,则直线AB '过定点(3,0).【小问1详解】设点Q 的坐标为()03,y ,因为点Q 在第一象限,所以00y >,双曲线22134x y -=的渐近线方程为y x =,因为点Q在双曲线的渐近线上,所以0y =,所以点Q的坐标为(3,,又点(3,Q 在抛物线22y px =上,所以1223p =⨯,所以2p =,故抛物线E 的标准方程为:24y x =;【小问2详解】设直线AB 的方程为3x my =-,联立243y xx my ⎧=⎨=-⎩,消x 得,24120y my -+=,方程24120y my -+=的判别式216480m ∆=->,即230m ->,设A (x 1,y 1),B (x 2,y 2),则12124,12y y m y y +==,因为点A 、B 在第一象限,所以121240,120y y m y y +=>=>,故0m >,设B 关于x 轴的对称点为()22,B x y '-, 则直线AB '的方程为212221()y y y y x x x x ---+=-,令0y =得:212221x x x y x y y -=+-⨯-122121x y x y y y +=+()()12211233y my y my y y -+-=+()21121223my y y y y y -+=+241212344m m mm m-===.直线AB '过定点(3,0).【点睛】方法点睛:联立直线AB 的方程与抛物线方程可得关于x 的一元二次方程,设A (x 1,y 1),B (x 2,y 2),()22,B x y '-,根据韦达定理求出12124,12y y m y y +==,求出直线AB '的方程并令0y =,求出x 并逐步化简可得3x =,则直线AB '过定点(3,0).17. 如图,已知正方形ABCD 的边长为4,,E F 分别为,AD BC 的中点,沿EF 将四边形EFCD 折起,使二面角A EF C --的大小为60°,点M 在线段AB 上.(1)若M 为AB 的中点,且直线MF 与直线EA 的交点为O ,求OA 的长,并证明直线OD //平面EMC ;(2)在线段AB 上是否存在点M ,使得直线DE 与平面EMC 所成的角为60°;若存在,求此时二面角M EC F --的余弦值,若不存在,说明理由.【答案】(1)2OA =;证明见解析.(2)存在点M ,使得直线DE 与平面EMC 所成的角为60°;此时二面角M EC F --的余弦值为14.【解析】【分析】(1)根据中位线性质可求得OA ,由//MN OD ,结合线面平行判定定理可证得结论;(2)由二面角平面角定义可知60DEA ∠=︒,取AE ,BF 中点O ,P ,由线面垂直的判定和勾股定理可知OD ,OA ,OP 两两互相垂直,则以O 为坐标原点建立空间直角坐标系;设()1,,0M m ()04m ≤≤,利用线面角的向量求法可求得m ;利用二面角的向量求法可求得结果.【小问1详解】,E F 分别为,AD BC 中点,////EF AB CD ∴,且2AE FB ==,又M 为AB 中点,且,AB OE AB BF ⊥⊥,易得OAM FBM ≅ ,2OA FB AE ∴===,连接,CE DF ,交于点N ,连接MN ,由题设,易知四边形CDEF 为平行四边形,N Q 为DF 中点,//,AM EF A 是OE 的中点,M ∴为OF 中点,//MN OD ∴,又MN ⊂平面EMC ,OD ⊄平面EMC ,//OD ∴平面EMC ;【小问2详解】////EF AB CD ,EF DE ⊥ ,EF AE ⊥,又DE ⊂平面CEF ,AE ⊂平面AEF ,DEA ∴∠即为二面角A EF C --的平面角,60DEA ∴=︒∠;取,AE BF 中点,O P ,连接,OD OP ,如图,60DEA ∠=︒ ,112OE DE ==,2414cos 603OD ∴=+-︒=,222OD OE DE +=,OD AE ∴⊥,//OP EF ,OP DE ⊥,OP AE ⊥,又,AE DE ⊂平面AED ,AE DE E = ,OP ∴⊥平面AED ,,OD AE ⊂ 平面AED ,,OD OP AE OP ∴⊥⊥,则以O 为坐标原点,,,OA OP OD方向为,,x y z 轴正方向建立空间直角坐标系如下图所示,则(D ,()1,0,0E -,()1,4,0F -,(0,C ,设()()1,,004M m m ≤≤,则(1,0,DE =-,()2,,0EM m =,(1,EC = ,设平面EMC 的法向量n 1=(x 1,y 1,z 1),则1111111·20·40EM n x my EC n x y ⎧=+=⎪⎨=++=⎪⎩,令12y =,则1x m =-,1z =1,m m ⎛∴=- ⎝,∵直线DE 与平面EMC 所成的角为60o ,·sin 60cos ,·DE n DE n DE n ∴︒==111==1m =或3m =,存在点M ,当1AM =或3AM =时,使得直线DE 与平面EMC 所成的角为60o ;设平面CEF 的法向量()2222,,n x y z=,又(1,EC = ,(FC =,2222222·40·0EC n x y FC n x ⎧=++=⎪∴⎨==⎪⎩,令21z =,则2x =,20y =,()2m ∴=;当1m =时,11,2,n ⎛=- ⎝,121212·1cos ,4·n n n n n n ∴=== ;当3m =时,23,2,n ⎛=- ⎝,121212·1cos ,4·n n n n n n ∴=== ;综上所述:二面角M EC F --的余弦值为14.【点睛】关键点点睛:本题第二步的关键在于证明三线互相垂直,建立空间直角坐标系,设出动点M 的坐标,熟练利用空间向量的坐标运算,求法向量,求二面角、线面角是解题的关键.18. 已知函数()12ex xf x x λ-=-.(1)当1λ=时,求()f x 图象在点(1,f (1))处的切线方程;(2)若1x ≥时,()0f x ≤,求λ的取值范围;(3)求证:()1111111232124e 2e*n n n n nnn ++++-+++->∈N .【答案】(1)0y = (2)[)1,+∞ (3)证明见详解【解析】【分析】(1)利用导数的几何意义求解即可;(2)根据题意,由条件式恒成立分离参数,转化为212ln x x xλ≥+,求出函数()212ln xg x x x =+的最大值得解;(3)先构造函数()12ln x x x x ϕ=-+,利用导数证明11ln 2x x x ⎛⎫<- ⎪⎝⎭,1x >,令11x n=+,可得()111ln 1ln 21n n n n ⎛⎫+-<+ ⎪+⎝⎭,迭代累加可证得结果.【小问1详解】当1λ=时,()12ex xf x x -=-,f (1)=0,的则()12121e x x f x x x -⎛⎫=-+ ⎪⎝'⎭,则()0122e 0f =-=',所以()f x 在点(1,f (1))处的切线方程为0y =.【小问2详解】由1x ≥时,()0f x ≤,即12e0x xx λ--≤,整理得212ln x x xλ≥+,对1x ≥恒成立,令()212ln x g x x x =+,则()()42321ln 222ln x x x x x g x x x x---=-+'=,令()1ln h x x x x =--,1x ≥,所以()ln 0h x x '=-≤,即函数ℎ(x )在1x ≥上单调递减,所以()()10h x h ≤=,即()0g x '≤,所以函数()g x 在1x ≥上单调递减,则()()11g x g ≤=,1λ∴≥.【小问3详解】设()12ln x x x xϕ=-+,1x >,则()()222221212110x x x x x x x xϕ---+-='=--=<,所以φ(x )在(1,+∞)上单调递减,则()()10x ϕϕ<=,即12ln 0x x x-+<,11ln 2x x x ⎛⎫∴<- ⎪⎝⎭,1x >,令11x n=+,*N n ∈,可得1111111ln 1112211n n n n n ⎛⎫⎪⎛⎫⎛⎫+<+-=+ ⎪ ⎪ ⎪+⎝⎭⎝⎭ ⎪+⎝⎭,所以()111ln 1ln 21n n n n ⎛⎫+-<+ ⎪+⎝⎭,()()111ln 2ln 1212n n n n ⎛⎫+-+<+ ⎪++⎝⎭,()()111ln 3ln 2223n n n n ⎛⎫+-+<+ ⎪++⎝⎭,…()()111ln 2ln 212212n n n n ⎛⎫--<+ ⎪-⎝⎭,以上式子相加得()112221ln 2ln 212212n n n n n n n ⎛⎫-<+++++ ⎪++-⎝⎭,整理得,11111ln 2412212n n n n n-<++++++-L ,两边取指数得,11111ln 2412212e e n n n n n -++++++-<L ,即得111114122122e e n n n n n -++++-<L ,()*Nn ∈得证.【点睛】关键点点睛:本题第三问解题的关键是先构造函数()12ln x x x xϕ=-+,利用导数证明11ln 2x x x ⎛⎫<- ⎪⎝⎭,1x >,令11x n=+,得到()111ln 1ln 21n n n n ⎛⎫+-<+ ⎪+⎝⎭.19. 已知整数4n …,数列{}n a 是递增的整数数列,即12,,,n a a a ∈Z 且12n a a a <<<.数列{}n b 满足11b a =,n n b a =.若对于{}2,3,,1i n ∈- ,恒有1i i b a --等于同一个常数k ,则称数列{}n b 为{}n a 的“左k 型间隔数列”;若对于{}2,3,,1i n ∈- ,恒有1i i a b +-等于同一个常数k ,则称数列{}n b 为{}n a 的“右k 型间隔数列”;若对于{}2,3,,1i n ∈- ,恒有1i i a b k +-=或者1i i b a k --=,则称数列{}n b 为{}n a 的“左右k 型间隔数列”.(1)写出数列{}:1,3,5,7,9n a 的所有递增的“左右1型间隔数列”;(2)已知数列{}n a 满足()81n a n n =-,数列{}n b 是{}n a 的“左k 型间隔数列”,数列{}n c 是{}n a 的“右k 型间隔数列”,若10n =,且有1212n n b b b c c c +++=+++ ,求k 的值;(3)数列{}n a 是递增的整数数列,且10a =,27a =.若存在{}n a 的一个递增的“右4型间隔数列{}n b ”,使得对于任意的{},2,3,,1i j n ∈- ,都有i j i j a b b a +≠+,求n a 的关于n 的最小值(即关于n的最小值函数()f n ).【答案】(1)1,2,4,6,9或1,2,4,8,9或1,2,6,8,9或1,4,6,8,9. (2)80k =(3)()()382n n f n -=+【解析】【分析】(1)由“左右k 型间隔数列”的定义,求数列{}:1,3,5,7,9n a 的所有递增的“左右1型间隔数列”;(2)根据“左k 型间隔数列”和“右k 型间隔数列”的定义,由1212n n b b b c c c +++=+++ ,则有1291016a a k a a ++=+,代入通项计算即可;(3)由“右4型间隔数列”的定义,有144i i i b a a +=->-,可知{}3i i b a nn -∈≥-∣,则有()()()232431n n n a a a a a a a a -=+-+-++- ()()()()413216n n ≥-+-+-+-++- ,化简即可.【小问1详解】数列{}:1,3,5,7,9n a 的“左右1型间隔数列”为1,2,4,6,9或1,2,4,8,9或1,2,6,8,9或1,4,6,8,9.【小问2详解】由12101210b b b c c c +++=+++ ,可得239239b b b c c c +++=+++ ,即128341088a a a k a a a k ++++=+++- ,即1291016a a k a a ++=+,即16168988109k +=⨯⨯+⨯⨯,所以80k =.【小问3详解】当{}2,3,,1i n ∈- 时,由144i i i b a a +=->-,可知{}3i i b a nn -∈≥-∣.又因为对任意{},2,3,,1i j n ∈- ,都有i j i j a b b a +≠+,即当{}2,3,,1i n ∈- 时,i i b a -两两不相等.因为()()()232431n n n a a a a a a a a -=+-+-++- ()()()2233117444n n b a b a b a --=++-++-+++- ()()()()223311742n n n b a b a b a --=+-+-+-++- ()()()()413216n n ≥-+-+-+-++- ()382n n -=+.所以n a 的最小值函数()()382n n f n -=+.另外,当数列{a n }的通项()0,1,38,2,2i i a i i i n =⎧⎪=⎨-+≤≤⎪⎩间隔数列{b n }的通项(),1,13,21,2i i a i i n b i i i n ==⎧⎪=⎨-+≤≤-⎪⎩或时也符合题意.【点睛】方法点睛:在实际解决“新定义”问题时,关键是正确提取新定义中的新概念、新公式、新性质、新模式等信息,确定新定义的名称或符号、概念、法则等,并进行信息再加工,寻求相近知识点,明确它们的共同点和不同点,探求解决方法,在此基础上进行知识转换,有效输出,合理归纳,结合相关的数学技巧与方法来分析与解决!。
衡水名师卷2023-2024高考模拟压轴卷(二)数学含答案解析

2024年普通高等学校招生全国统一考试模拟试题数学(二)本试卷共4页,19小题,满分150分.考试用时120分钟.注意事项:1.答题前,考生先将自己的姓名、准考证号码、考场号、座位号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区.2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效.4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑.5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知点()06,P y 在焦点为F 的抛物线2:2(0)C y px p =>上,若152PF =,则p =()A.3B.6C.9D.122.电影《孤注一郑》的上映引发了电信诈骗问题的热议,也加大了各个社区反电信诈骗的宣传力度.已知某社区共有居民480人,其中老年人200人,中年人200人,青少年80人,若按年龄进行分层随机抽样,共抽取36人作为代表,则中年人比青少年多()A.6人B.9人C.12人D.18人3.已知0a b c >>>,则下列说法一定正确的是()A.a b c >+ B.2a bc <C.2ac b > D.2ab bc b ac+>+4.已知向量()()2,3,1,2a b =-=-,则a b +在a b -方向上的投影向量为()A.816,1717⎛⎫-⎪⎝⎭ B.1220,1717⎛⎫-⎪⎝⎭ C.1220,1717⎛⎫-⎪⎝⎭ D.2020,1717⎛⎫-⎪⎝⎭5.已知某正六棱柱的体积为,其外接球体积为205π3,若该六棱柱的高为整数,则其表面积为()A.18+ B.18+ C.24+ D.246.已知甲、乙两地之间的路线图如图所示,其可大致认为是()()cos 03πf x x x =的图像.某日小明和小红分别从甲、乙两地同时出发沿着路线相向而行,当小明到达乙地时,小红也停止前行.若将小明行走轨迹的点记为(),a b ,小红行走轨迹的点记为(),c d ,且满足3π2ac +=,函数()2g a bd =-,则()g a 的一个单调递减区间为()A.4π0,3⎛⎫ ⎪⎝⎭B.π5π,33⎛⎫⎪⎝⎭C.4π8π,33⎛⎫⎪⎝⎭D.()2π,3π7.已知椭圆22:1(09,)9x y C m m m +=<<∈Z 的左、右焦点分别为12,F F ,点P 在C 上但不在坐标轴上,且12PF F 是等腰三角形,其中一个内角的余弦值为78,则m =()A.4B.5C.6D.88.已知函数()()e eln e 1xmf x m x x=++-的定义域为()0,∞+,若()f x 存在零点,则m 的取值范围为()A.1,e ∞⎡⎫+⎪⎢⎣⎭B.(]0,e C.10,e ⎛⎤⎥⎝⎦D.[)e,∞+二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知1232i,4i z z =+=-,则()A.12z z +的虚部为-1B.1243z z -是纯虚数C.12z z 在复平面内所对应的点位于第一象限D.214iz z =+10.已知()7270127(43)13(13)(13)x a a x a x a x -=+-+-++- ,则()A.4945a = B.77141ii a==-∑C.136024622a a a a +++=+ D.613135722a a a a +++=-11.设()M x 是定义在*N 上的奇因函数,是指x 的最大奇因数,比如:()()33,63M M ==,()81M =,则()A.对()()*,212k M k M k ∈-NB.()()2M k M k =C.()()()1263931M M M +++= D.()126363M +++= 三、填空题:本题共3小题,每小题5分,共15分.12.已知集合{}2450,{}A xx x B x x m =-->=>∣∣,若0m =,则()A B ⋂=R ð__________;若A B ⋃=R ,则m 的取值范围为__________.13.某校拟开设“生活中的数学”“音乐中的数学”“逻辑推理论”“彩票中的数学”和“数学建模”5门研究性学习课程,要求每位同学选择其中2门进行研修,记事件A 为甲、乙两人至多有1门相同,且甲必须选择“音乐中的数学”,则()P A =__________.14.定义:对于函数()f x 和数列{}n x ,若()()()10n n n n x x f x f x +-+=',则称数列{}n x 具有“()f x 函数性质”.已知二次函数()f x 图像的最低点为()0,4-,且()()121f x f x x +=++,若数列{}n x 具有“()f x 函数性质”,且首项为1的数列{}n a 满足()()ln 2ln 2n n n a x x =+--,记{}n a 的前n 项和为n S ,则数列52n n S ⎧⎫⎛⎫⋅-⎨⎬ ⎪⎝⎭⎩⎭的最小值为__________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)在ABC 中,内角,,A B C 所对的边分别为,,a b c ,其中c =,且()2tan tan tan b B a B A B =-+.(1)求C ;(2)求22a b +的取值范围.16.(15分)已知函数()ln x f x x a x ⎛⎫=-⎪⎝⎭.(1)讨论()f x 的最值;(2)若1a =,且()e x k xf x x- ,求k 的取值范围.17.(15分)在如图①所示的平面图形中,四边形ACDE 为菱形,现沿AC 进行翻折,使得AB ⊥平面ACDE ,过点E 作EF∥AB ,且12EF AB =,连接,,FD FB BD ,所得图形如图②所示,其中G 为线段BD 的中点,连接FG .(1)求证:FG ⊥平面ABD ;(2)若2AC AD ==,直线FG 与平面BCD 所成角的正弦值为7,求AB 的值.18.(17分)某汽车销售公司为了提升公司的业绩,现将最近300个工作日每日的汽车销售情况进行统计,如图所示.(1)求a 的值以及该公司这300个工作日每日汽车销售量的平均数(同一组中的数据用该组区间的中点值作代表);(2)以频率估计概率,若在所有工作日中随机选择4天,记汽车销售量在区间[)200,250内的天数为X ,求X 的分布列及数学期望;(3)为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:抽奖区有,A B 两个盒子,其中A 盒中放有9张金卡、1张银卡,B 盒中放有2张金卡、8张银卡,顾客在不知情的情况下随机选择其中一个盒子进行抽奖,直到抽到金卡则抽奖结束(每次抽出一张卡,然后放回原来的盒中,再进行下次抽奖,中途可更换盒子),卡片结果的排列对应相应的礼品.已知顾客小明每次抽奖选择两个盒子的概率相同,求小明在首次抽奖抽出银卡的条件下,第二次从另外一个盒子中抽奖抽出金卡的概率.19.(17分)已知双曲线2222:1(0,0)x y C a b a b-=>>的左顶点为A ,直线1:2l y x =-与C 的一条渐近线平行,且与C交于点B ,直线AB 的斜率为13.(1)求C 的方程;(2)已知直线()2:28l y x m m =+≠与C 交于,P Q 两点,问:是否存在满足EA EP EP EQ EA EQ ⋅=⋅=⋅的点()00,E x y ?若存在,求2200x y -的值;若不存在,请说明理由.数学(二)一、选择题1.A【解析】由抛物线的定义可知15622p PF =+=,解得3p =.故选A 项.2.B【解析】设中年人抽取x 人,青少年抽取y 人,由分层随机抽样可知20080,48036480x ==36y,解得15,6x y ==,故中年人比青少年多9人.故选B 项.3.D 【解析】当3,2,1a b c ===时,a b c =+,且2ac b <,故A ,C 项错误;因为0a b >>,0a c >>,所以2a bc >,故B 项错误;()()()20ab bc b ac b c a b +-+=-->,故D 项正确.故选D 项.4.C 【解析】由题意得()()1,1,3,5a b a b +=--=- ,则a b + 在a b - 方向上的投影向量为2()()1220(),1717||a b a b a b a b +⋅-⎛⎫-=- ⎪-⎝⎭,故选C 项.5.D【解析】设该正六棱柱的底面边长为a ,高为h ,其外接球的半径为R,易知34ππ33R =,则R ==①,且264a h ⋅⋅=②,联立①②,因为h ∈Z ,解得1,4a h ==,所以正六棱柱的表面积23126244S a ah =⋅+=.故选D 项.6.A 【解析】依题意得cos ,cos cos 3πcos 22a a b a d c ⎛⎫===-=- ⎪⎝⎭,且03π,03π3π,2a a⎧⎪⎨-⎪⎩解得03πa ,则()2cos 2cos2cos 2cos 1222a a a g a a =+=+-,令cos 2at =,则[]1,1t ∈-,因为2221y t t =+-在区间11,2⎛⎫-- ⎪⎝⎭内单调递减,在区间1,12⎛⎫- ⎪⎝⎭内单调递增,所以()g a 在区间4π8π0,,2π,33⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭内单调递减.故选A 项.7.B 【解析】依题意得126PF PF +=,设12F F n =,不妨设点P 在第一象限,则112PF F F n ==,则26(06)PF n n =-<<,故222122(6)7cos 28n n n PF F n ∠+--==或()22221(6)7cos 268n n n PF F n n ∠+--==-,解得4n =或2411n =,又2,2n m m ⎛⎫∈+= ⎪⎝⎭Z 9,所以4,5n m ==.故选B 项.8.C 【解析】由题意得0m >,令()0f x =,则()ln ln ee ln e eln x mx x m x +++=+.令()e e x g x x =+,易知()g x 单调递增,所以()()ln ln g x m g x +=,即ln ln x m x +=,即ln ln m x x =-.令()ln h x x x =-,则()1xh x x'-=,当()0,1x ∈时,()0h x '>,()h x 单调递增,当()1,x ∞∈+时,()()0,h x h x '<单调递减,又()11h =-,当0x →时,()h x ∞→-,所以ln 1m - ,解得10em < .故选C 项.二、多选题9.BC 【解析】127i z z +=+的虚部为1,故A 项错误;124311i z z -=为纯虚数,故B 项正确;()()1232i 4i 145i z z =+-=+,其在复平面内所对应的点()14,5位于第一象限,故C 项正确;24i 14ii iz -==--=,144z +=+,故D 项错误.故选BC 项.10.AC 【解析】依题意得()77(43)[313]x x -=+-,所以4347C 33527a =⨯=⨯=945,故A 项正确;令13x =,得03a =,令0x =,得774i i a ==∑,所以777143i i a ==-∑,故B 项错误;令23x =,得7012345672a a a a a a a a =-+-+-+-①,又7012345674a a a a a a a a =+++++++②,由①+②可得77135024642222a a a a ++++==+,故C 项正确;同理,由②-①得136135722a a a a +++=-,故D 项错误.故选AC 项.11.ABD 【解析】由题意得()()2M k M k =,故B 项正确;()()()2,2121M k M k k M k k k =-=-,故A 项正确;516312363632632+++++=⨯=⨯ ,所以()()123636363M M ++++== ,故D 项正确;()()()()1263[1M M M M +++=+ ()()][()()36324M M M M ++++++ ()][()6213631M M =+++++()()()1023121M M M ⎤⎡++=++⎦⎣ ()()][()()33124M M M M ++++++ ()108642030]222222M ==+++++=614136514-=-,故C 项错误.故选ABD 项.三、填空题12.()50,14x x ∞⎧⎫<--⎨⎬⎩⎭【解析】集合{1A xx =<-∣或54x ⎫>⎬⎭,所以R A =ð504B x x ⎧⎫=<⎨⎬⎩⎭ .若A B ⋃=R ,结合数轴可知1m <-,故m 的取值范围为(,1)∞--.13.925【解析】若甲、乙两人的选课都不相同则共有1243C C 4312=⨯=种;若甲、乙两人的选课有1门相同,则共有2114432C C C 24+=种.故()225512249C C 25P A +==.14.-5112【解析】由题意知()24(0)f x ax a =->,又()()()12121f x f x a x x +-=+=+,所以1a =,则()24f x x =-.由题意得()()2ln 2ln 2ln2n n n n n x a x x x +=+--=-,由()()()10n n n n x x f x f x +-+=',得()()1n n n n f x x x f x +='-,即2214422n n n nn nx x x x x x +-+=-=,又()()2211222,222n n n n nnx x x x x x +++-+=-=,所以()()21212222n n n n x x x x ++++=--,则1122ln 2ln 22n n n n x x x x ++++=--,即12n n a a +=,故{}n a 是以1为首项,2为公比的等比数列,所以12,21n n n n a S -==-.令n n c S =.()552122n n n ⎛⎫⎛⎫-=-⋅- ⎪ ⎪⎝⎭⎝⎭,则()111822n n nc c n -+-=-⋅-,故当8n 时,1n n c c +<,当9n 时,1n n c c +>,故()9min 5112n c c ==-.四、解答题15.解:(1)因为()()tan tan πtan A B C C +=-=-,所以2tan tan tan b B a B C=+,由正弦定理得sin 2tan sin tan tan B BA B C==+()2sin cos 2sin cos sin cos cos sin sin B C B CB C B C B C ==++2sin cos sin B C A因为sin 0,sin 0A B ≠≠,所以2cos 1C =,则1cos 2C =,又()0,πC ∈,所以π3C =.(2)由余弦定理得223a b ab =+-,因为222a b ab + ,所以22222222,22a b a b a b ab a b +++-+-=即226a b + .当且仅当a b ==.又223a b ab +=+,且0ab >,所以223a b +>.综上,22a b +的取值范围为(]3,6.16.解:(1)由题意得()f x 的定义域为()0,∞+,()11,ax f x a x x-=-='当()0,0,a x ∞∈+时,()0f x '<,所以()f x 在区间()0,∞+内单调递减,无最值;当0a >时,令()0f x '=,得1x a=,当10,x a ⎛⎫∈ ⎪⎝⎭时,()()0,f x f x '<单调递减,当1,x a ∞⎛⎫∈+⎪⎝⎭时,()()0,f x f x '>单调递增.故当1x a=时,()f x 取得最小值,且最小值为11ln f a a ⎛⎫=+ ⎪⎝⎭,无最大值.综上,当0a时,()f x 无最值;当0a >时,()f x 的最小值为1ln a +,无最大值.(2)当1a =时,由()e x k xf x x - ,得e ln x k xx x x-- ,整理得2e ln x k x x x x +- ,即2ln e xx x x x k +- .令()2ln exx x x xh x +-=,则()h x '()()()2221ln 1e ln e e x xxx x x x x x +---+-=()()ln 1e xx x x --=,由(1)知,当1a =时,()ln f x x x =-的最小值为()110f =>,即ln 0x x ->恒成立,所以当()0,1x ∈时,()()0,h x h x '>单调递增;当()1,x ∞∈+时,()()0,h x h x '<单调递减.故当1x =时,()h x 取得最大值()21e h =,即2ek ,故k 的取值范围为2,e ∞⎡⎫+⎪⎢⎣⎭.17.(1)证明:连接CE 交AD 于点O ,连接GO .在菱形ACDE 中,CE AD ⊥,因为AB ⊥平面,ACDE CE ⊂平面ACDE ,所以CE AB ⊥,又,,AB AD A AB AD ⋂=⊂平面ABD ,所以CE ⊥平面ABD .因为,G O 分别为,BD AD 的中点,所以1,2GO AB GO =∥AB ,又1,2EF AB EF =∥AB ,所以GO EF ∥,所以四边形GOEF 为平行四边形,所以FG ∥EO ,所以FG ⊥平面ABD .(2)解:在菱形ACDE 中,因为AC AD =,所以ACD 和ADE 都是正三角形,取ED 的中点H ,连接AH ,则AH AC ⊥,又AB ⊥平面ACDE ,所以,AB AC AB AH ⊥⊥,即,,AB AC AH 两两垂直.以A 为坐标原点,,,AB AC AH 所在直线分别为,,x y z 轴,建立如图所示的空间直角坐标系,设2(0)AB a a =>,则13(0,2,0),(2,0,0),(0,1,(,1,,,22C B a D F a G a ⎛⎫- ⎪ ⎪⎝⎭则()2,2,0,(0,1BC a CD =-=- ,30,,22FG⎛=-⎝⎭.设平面BCD的法向量为(),,m x y z=,则220,0,m BC ax ym CD y⎧⋅=-+=⎪⎨⋅=-+=⎪⎩取1z=,则m a⎛⎫= ⎪⎪⎝⎭.记直线FG与平面BCD所成角为θ,则||sin|cos,|||||FG mFG mFG mθ⋅=〈〉==,7=解得1a=,即AB的值为2.18.解:(1)依题意得(0.0010.0020.00320.006)50 1.a++++⨯=解得0.004a=.所求平均数为250.1750.15125⨯+⨯+⨯0.21750.32250.22750.05150+⨯+⨯+⨯=.(2)依题意得14,5X B⎛⎫~ ⎪⎝⎭,则()442565625P X⎛⎫===⎪⎝⎭,()314142561C55625P X⎛⎫==⨯⨯=⎪⎝⎭()222414962C,55625P X⎛⎫⎛⎫==⨯=⎪ ⎪⎝⎭⎝⎭()33414163C55625P X⎛⎫==⨯=⎪⎝⎭()41145625P X⎛⎫===⎪⎝⎭X01234P 25662525662596625166251625故()14455E X =⨯=.(3)设“选到A 盒”为事件1A ,“选到B 盒”为事件2A ,,摸到金卡”为事件1B ,,摸到银卡”为事件2B ,因为12,B B 是对立事件,所以()119121*********P B =⨯+⨯=.()()219120P B P B =-=由题意得()()1212P A P A ==,所以()()()12122P A B P A B P B ==∣()()()2112111102,9920P B A P A P B ⨯==∣则()()2212819P A B P A B =-=∣∣.故所求的概率89123791091045P =⨯+⨯=.19.解:(1)易知C 的一条渐近线方程为y x =,则a b =.设(),2B t t -,又(),0,0A a a ->,直线AB 的斜率为13,所以213t t a -=+,解得62a t +=,则62,22a a B ++⎛⎫ ⎪⎝⎭,代入222x y a -=中,解得4a =.故C 的方程为2211616x y -=.(2)因为EA EP EP EQ ⋅=⋅ ,所以()0EP EA EQ ⋅-= ,即0EP QA ⋅=,所以PE AQ ⊥,同理可得,AE PQ EQ AP ⊥⊥.设()()1122,,,P x y Q x y ,联立221,16162.x y y x m ⎧-=⎪⎨⎪=+⎩整理得2234160x mx m +++=,由题意知()22Δ1612160m m =-+>,且8m ≠,解得m <-m >8m ≠,所以21212416,33m m x x x x ++=-=.过点A 与2l 垂直的直线的方程为122y x =--,设该直线与C 的右支交于另一点H ,联立221,161612,2x y y x ⎧-=⎪⎪⎨⎪=--⎪⎩整理得238800x x --=,解得203x =或4x =-(舍去).所以2016,33H ⎛⎫- ⎪⎝⎭.因为(1122016,33PH AQ x y x ⎛⎫⋅=---⋅+ ⎪⎝⎭)22121220801644333y x x x x y ⋅=+----(122121220801642333y y x x x x x =+---+()()1212)225(1m x m x m x x -++=--+()()()22128016164802)54233333m m x x m m m m +⎛⎫++--=-⨯-+⋅-+- ⎪⎝⎭222216580168801603333333m m m m m m m -=--+++--=所以PH AQ ⊥,同理可证QH AP ⊥.又AH PQ ⊥,所以H 与E 重合.因为H 在C 上,所以220016x y -=.故存在点E 满足EA EP EP EQ EA EQ ⋅=⋅=⋅ ,且220ij x y -的值为16.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018高考理科数学(全国卷Ⅲ)试题研究
云南杨军
一、对2018年高考理科数学(全国卷Ⅲ)试题的分析
总体来看,主干知识中,函数与导数22分,立体几何22分,直线与圆和圆锥曲线27分,三角函数与解三角形15分,概率统计与模拟方法17分,数列约17分,不等式及其应用约15分,平面向量约5分,算法5分,集合5分、复数5分,二项式定理5分。
知识点覆盖比较全面,重点内容几乎全都考查到了,特别是解析几何加大了知识点的考查,总体分值比往年有所增加。
试题总体上还有一个特点,就是知识点间相互的交汇和融合非常自然,如20题圆锥曲线、平面向量与等差数列融汇在一起,加大了对学生系统掌握知识的考查。
只有很少的一些非重点知识点没有考查,比如:随机抽样,命题与逻辑联结词,数学归纳法,合情推理,计数原理,算法流程图,线性规划,定积分等。
其中容易题为79分,中档题约为37分,难题约为34分。
易中难比例相对于往年,容易题目略有增加,但试题仍然有一定灵活度,适当对综合能力进行了考查。
所以总体略低于于去年全国Ⅲ卷。
具体来说有以下几个特点:
1.试题起点低,注重基础,突出考查重点
2018年全国高考理科数学(全国卷Ⅲ)对基础知识与基本技能的考查既注重全面又突出重点,贴近教学实际,入手简单,计算量适中,需要学生在做题时加倍细心,许多试题都是考查单一知识点或是在最基础的知识交汇点上设置,如选择题的1-10,这对引导中学数学重视基础知识和基本技能教学具有良好的导向作用。
同时,试卷注重确保支撑数学知识体系的主干内容占有较高的比例,如试卷对函数与导数、三角函数与解三角形、立体几何、解析几何、数列、概率统计等内容的考查高达120分,这充分体现了高考对主干知识的重视程度,同时在立足稳定基础上又颇具创新。
2、强调通性通法,坚持能力立意
2018年全国高考理科数学(全国卷Ⅲ)注重通性通法在解题中的运用,都是运用基本概念分析问题,基本公式运算求解、基本定理推理论证、基本数学思想方法分析和解决问题。
试卷强调通性通法,有利于引导中学数学教学回归基础,避免一味的钻偏难怪试题,从而使学生能够在数学学习上获得比较正常的发展。
试卷继续坚持能力立意,全面考查运算求解、空间想象、抽象概括、推理论证、数据处理以及综合运用有关知识分析和解决问题的能力,其中运算求解能力贯穿试卷始终。
3、考查数学素养,关注数学应用
数学素养涵盖数学的基础知识、基本技能和它们所体现的数学思想方法与能力,以及在此基础上的应用意识和创新意识。
2018年全国高考理科数学(全国卷Ⅲ)试题更加注重对学生数学素养的考查,选择题第3题对于三视图的考查,使用了实际问题的题材,拉近数学与生活的距离。
同时,第10题对于概率分布的考查,使用了“移动支付”为背景,让数学与时俱进,体现数学源于生活又高于生活。
第12题对于不等式的考查,类似于简单的比较数的大小,又增加了对数的和与积的运算,增加了题目的难度。
第19题,在考查立体几何证明的同时,增加了动点的干扰,这对学生的运动思想的考查有所创新。
第20题圆锥曲线中加入了平面向量和等差数列,增大了试题覆盖面。
导数题既继承了往年全国卷导数题的显着特点,加强对导数结构的考查,对结构的适当变形,也在衔接新高考前期中下了功夫。
4.难度结构合理,提高区分层次
2018年全国高考理科数学(全国卷Ⅲ)难度结构合理,由易到难,循序渐进,具有一定梯度,能较好区分不同程度的学生,有利于高校选拔:
选择题第1-9题,填空题第13、14题、解答题的第17、18题以及选做题的第22题都属于基础题,起点较低,绝大多数学生都能顺利解答。
选择题第10-11题,填空题15-16,解答题第19题难度中等,对中档程度学生来说,不会构成太大困难。
作为能力把关的第12、20、21题知识综合性较强,能力要求更高,难度较大,但这部分试题也都是由浅入深的设置,上手其实很容易,但要完整解答并非易事。
总体来说,2018年全国高考理科数学(全国卷Ⅲ)对中学数学教学起到很好的导向作用,主要表现于回归课本、扎实基础,重视数学思想方法,加强数学应用与数学空间想象能力、运算能力、思维能力的培养,实现从结果教育到过程教育的转变。
二、2020届的数学教学规划
针对以上分析,应当说2018年的高考试题为我们以后的教学规划以及复习备考指明了方向:课标考纲是依据,教材是蓝本,主抓基础是关键,训练思维是主导,灵活创新是方向。
我们在此对2020届的教学规划提出以下几点建议:
1、重视基础,立足教材,遵循考纲,资源共享
从今年的高考题来看,考查的知识点和基本方法及数学思想都是现行高中数学教材中最基本、最重要的数学知识和数学思想方法。
所以在教学过程中不宜追求“偏、难、怪”的极端做法,还是要回归教材,狠抓基础,不能浮燥,一定要脚踏实地的,一步一步的把课本上的基础知识、基础练习、基本题型、基本方法练到位,认真构建学生的系统知识结构。
教学过程紧扣数学的本质,重视“数学阅读”教学,让学生能读懂数学,重视知识的生成过程,在此基础上培养学生灵活运用知识处理分析问题的能力。
教材是高考命题的基本生长点,“一个人的力量是有限的,大家的智慧是无穷的”,所以我们一线教师应当好好研究、挖掘教材,做好变式教学,实现合作共享。
2、突出重点,与时俱进,贴近生活,大胆创新
从今年高考数学试题来看,不难发现,主干知识还是支撑了整个试卷,命题风格体现了新课标侧重能力与应用意识的考查,鼓励探索创新的特点。
就给我们在今后的教学过程中指明了方向。
所以在教学中,我们需要多收集编纂一些与生活联系密切的命题背景,大胆融合不同知识板块,培养学生灵活的思维能力
3、调节心态,注重细节,控制节奏,提高效率
(1)我们一线教师在教学过程中,从一开始,就要指导学生做到解题规范、细节做到位。
解题不规范是高分卷生成的影响因素之一,我们都知道数学阅卷是拆点给分,完成作业和练习当中,一定要规范、细节要把握好。
(2)争取在常规教学努力做到五个“必须”,即:
①讲必练:克服随意性;
②练必批:了解学生的真实水平;
③批必评:讲解具有针对性;
④评必纠:抓好落实;
⑤纠必考:内化为学生的能力。
(3)作业布置宜精不宜多,给学生留下多一点独立消化和思考的时间和空间,指导学生跳出题海,教会学生进行反思,以致增强适应各种题型的应变能力。
以上内容仅为个人分析及建议,有不正之处还请批评指正!
2018年6月15日。
