极限的求法综述
求极限

浅谈极限的求解方法毕业论文

浅谈函数极限求解方法学生:智年指导老师:守江三峡大学理学院摘要:极限是数学分析的基础,数学分析的基本概念的表述,都可以用极限来描述.如函数在某点处导数的定义,定积分的定义,偏导数的定义,二重积分的定义,三重积分的定义,无穷级数的定义都是用极限来定义的.极限是研究数学分析的基本工具.极限是贯穿数学分析的一条主线.学好极限要从以下两个方面着手: 1)是考察所给函数是否存在极限;2)若函数存在极限,则考虑如何计算此极限.本文主要是对第二个问题即在极限存在的条件下,如何去求极限进行综述. 对于简单的极限的计算,利用定义求值或利用极限的四则运算法则求值都是可行的,但是对于一个比较复杂的极限的计算,例如的值时则不能直接采用一般的定义或者定理,即使采用洛必达法则也是比较繁琐的,然而用泰勒展示则计算简单多了,这就说明为一般地解决极限求值问题时,就必须利用有效有针对性的计算方法,对各个具体问题还要善于发现和利用其特点以简化手续.传统的极限的计算方法不下十几种,但具体到计算不同特征的极限时,究竟采用哪种方法,很多人总感到无从下手.只有将这些方法进行归纳总结,从而才可以针对不同特征的式子选择适当的计算方法,进而简化计算Abstract:Limit is the basis of mathematical analysis , the basic concepts of mathematical analysis of expression , can be used to describe the limit as a function definition derivative at some point , the definition of the definite integral , the definition of partial derivative , the definition of double integrals , triple integral definition , infinite series of definitions are used to define the limits of the limit is the basic tool to study the limits of mathematical analysis is a main theme throughout the mathematical analysis to learn the limits from the following two aspects is to investigate the function if there is a limit .If there is a limit function , then consider how to calculate this limit this article is the second question that under the conditions of the existence of the limit , how to find the limits are reviewed for a simple calculation of the limit of the use . define the limits of the evaluation or the use of four evaluation algorithms are feasible, but for a more complicated limit calculations, such asFind in coslimx when exxx values are not directly using the general definition or theorem, even with the Hospital's Rule is more complicated , however, Taylor shows the calculation is much simpler , which is generally described when the limit is evaluated to solve the problem , we must use effective targeted method of calculation for each specific issues but also good at finding and using its features to simplify procedures. The traditional method of calculating the limit of no less than a dozen, but when calculating the limits specific to different characteristics , whether using either method, a lot of people always feel unable to start . These methods will only besummarized, so that we can choose the appropriate method of calculation formulas for different characteristics , and thus simplify the calculation关键词:极限;极限的定义;极限的性质;罗必达法则;泰勒公式;单调有限法则;积分中值定理;拉格朗日中值定理Keywords :Limit; ultimate limits of nature; Luo's Rule; Taylor formula; monotonous limited law; integral mean value theorem; Lagrange mean value theorem与一切科学方法一样,极限法也是社会实践的产物。
中国古代数学中的极限思想[含论文、综述、开题-可编辑]
![中国古代数学中的极限思想[含论文、综述、开题-可编辑]](https://img.taocdn.com/s3/m/d837b8780722192e4536f685.png)
设计(20 届)中国古代数学中的极限思想所在学院专业班级信息与计算科学学生姓名学号指导教师职称完成日期年月摘要:“极限”是高等数学中最基础和最重要的概念之一,高等数学中许多深层次的理论及其应用都是极限的延拓与深化。
其中,中国古代数学中的极限思想对整个数学的发展起到了非常重要的作用。
本文在中国古代数学中前人研究的基础上,结合国外古代极限思想,介绍极限思想的萌芽、发展到完善的整个过程,并对其相应的应用和影响做较为全面的探讨。
我们首先介绍中国古代的极限思想,接着从三个角度对中西方的极限思想进行比较,最后总结中国古代极限思想对后世数学的影响极其在文学、哲学和实际生活中的应用。
关键字:古代数学;极限思想;割圆术;圆周率;微积分The Ancient Chinese Mathematics Limit Thought Abstract:" Limit " is one of the most basic and most important concepts in the field of higher mathematics, many deep-level mathematics theories and their applications are extension and deepening of limit. Especially the ancient Chinese limit thought plays a very important role during the whole development of mathematics. Based on the ancient Chinese mathematics and previous studies, combined with the ancient limit of foreign ideas, in this paper we will introduce the whole process of limit thought from embryonic, development to perfect and make a comprehensive discussion about its corresponding applications and impact. First of all, we introduce the ancient Chinese limit thought. Then, we compare the Chinese and the west limit thought from three aspects. Last, we summarize the influence of the ancient Chinese mathematics limit thought on mathematics and the application in literature philosophy and actual life.Key words:Ancient mathematics; limit thought; the method of cutting circle; π; calculus .目录1 绪论 (1)1.1 问题的背景和意义 (1)1.2 极限相关概念 (2)1.2.1 数列极限 (2)1.2.2 函数极限 (2)2 中国古代的极限思想 (4)2.1 极限思想的萌芽 (4)2.2 关于数π (4)2.2.1 π的来历 (4)2.2.2 π的数值精确度的发展 (4)3 中西方极限思想的比较 (7)3.1 割圆术与穷竭法 (7)3.2 先秦极限观与古希腊极限观的比较 (8)3.2.1 对无穷大和无穷小认识的比较 (8)3.2.2 对无限可分性、连续性以及无穷数和的认识比较 (8)3.3 从中西方哲学传统看微积分的创立 (9)4 对后世数学的影响及其应用 (10)4.1 对后世数学的影响 (10)4.2 极限思想在文学和哲学方面的影响 (10)4.3 极限思想在古代的应用 (11)5 结论 (13)致谢 (14)参考文献 (15)1 绪论1.1 问题的背景和意义微积分是近代数学产生的标志之一,而其中极限概念与极限方法是近代微积分学的基础。
巧用定积分求极限(数学分析)

定积分在求极限中的应用1、知识准备绪论微积分学在大学的数学学习中占有相当重要的地位.然而,求极限又是微积分学中常常要面临的问题.因此,积累更多求极限的方法应是每位大学生必备的素养.求极限的方法层出不穷,最常用的方法有极限的定义和性质,重要极限的结论,洛必达法则以及泰勒公式等.应用极限的定义时,往往是在极限的结果已经比较明显,只需要根据极限的定义把相关式子进行放缩便可得到相应的结果.但是,这种方法一方面叙述上比较麻烦,另一方面也只适用于看上去容易放缩的式子.重要极限的结论形式上要求非常严格,也只能解决两种形式的极限问题.洛必达法则是用于解决“0”型的极限和“∞∞”型极限的.泰勒公式适宜于解决求分式极限中分子或分母有加减运算的问题,通过泰勒展式后可以达到某些项抵消效果.但若仔细观察这些方法,其特点不是表达较繁琐就是仅仅应用到微分学知识.事实上,微分学和积分学的关系正如中小学时代学习过的加法与减法,乘法与除法,乘方与开方以及幂运算与取对数运算的关系一样,他们互为逆运算.倘若也能用到积分学知识来解决求极限的问题,那么求极限的方法才算完美.而利用定积分求极限正体现了这一理念. 定积分的概念下面首先让我们回顾一下定积分以及极限的定义:定积分:设函数()f x 在闭区间[],a b 上有定义,在闭区间[],a b 内任意插入n-1个分点将[],a b 分成n 个区间[,]x i i x x -,记(1,2,,i i i x x x i n ∆=-=),1[,]i i x x ξ-∀∈,作乘积()i i f x ξ∆(称为积分元),把这些乘积相加得到和式1()ni i i f x ξ=∆∑(称为积分形式)设{}max :1i x i n λ=∆≤≤,若01lim ()ni i i f x λξ→=∆∑极限存在唯一且该极限值与区是[],a b 的分法及分点i ξ的取法无关,则称这个唯一的极限值为函数()f x 在[],a b 上的定积分,记作b a()f x dx ⎰,即01()lim ()nb ai i i f x dx f x λξ→=⎰=∆∑.否则称()f x 在[],a b 上不可积.注1:由牛顿莱布尼兹公式知,计算定积分与原函数有关,故这里借助了不定积分的符号.注2:若()b a f x dx ⎰存在,区间[],a b 进行特殊分割,分点i ξ进行特殊的取法得到的和式极限存在且与定积分的值相等,但反之不成立,这种思想在考题中经常出现,请读者要真正理解.注3:定积分是否存在或者值是多少只与被积函数式和积分区间有关与积分变量用什么字母表示无关,即()()().b b ba a a f x dx f t dt f u du ⎰=⎰=⎰仔细观察定积分的定义,我们一定会发现定积分的极限有以下两个特征.第一,定积分是无穷项和式的极限,容易知道一般项在项数趋近于无穷大时极限值必然趋近于零,否则和式极限不存在.第二,定积分与某一连续函数有紧密的关系,它的一般项受到这一连续函数的约束,它是连续函数在某个区间上进行了无穷的分割,各小区间上任意的函数值与区间长度的乘积的累加.对于极限,大学主要学习了数列的极限和函数的极限.数列的极限是用于解决离散的自然数的相关极限,而函数的极限则主要用于解决连续函数的相关极限.那么就让我们先一一来回忆它们吧! 极限的概念数列的极限设{}n a 为数列, a 为实数,若对任给的正数ε,总存在正整数N ,使得当n N >时有||n a a ε-<, 则称数列{}n a 收敛于a ,实数a 称为数列{}n a 的极限,并记作lim n n a a →∞=或()n a a n →→∞.(读作:当n 趋于无穷大时, n a 的极限等于a 或n a 趋于a ).由于n 限于取正整数,所以在数列极限的记号中把n →+∞写成n →∞,即lim n n a a →∞=或()n a a n →→∞.若数列{}n a 没有极限,则称{}n a 不收敛,或称{}n a 为发散数列.注1:关于ε:①ε的任意性.定义1中的正数ε的作用在于衡量数列通项n a 与常数a 的接近程度,ε越小,表示接近得越好;而正数ε可以任意小,说明n a 与常数a 可以接近到任何程度;②ε的暂时固定性.尽管ε有其任意性,但一经给出,就暂时地被确定下来,以便依靠它来求出N;③ε的多值性.ε既是任意小的正数,那么2,3,2εεε等等,同样也是任意小的正数,因此定义1中的不等式||n a a ε-<中的ε可用2,3,2εεε等来代替.从而“||n a a ε-<”可用“||n a a ε-≤”代替;④正由于ε是任意小的正数,我们可以限定ε小于一个确定的正数.注2:关于N :①相应性,一般地, N 随ε的变小而变大,因此常把N 定义作()N ε来强调, N 是依赖于ε的;ε一经给定,就可以找到一个N ;②N 多值性N 的相应性并不意味着N 是由ε唯一确定的,因为对给定的ε,若100N =时能使得当n N >时,有||n a a ε-<,则101N =或更大的数时此不等式自然成立.所以N 不是唯一的.事实上,在许多场合下,最重要的是N 的存在性,而不是它的值有多大.基于此,在实际使用中的N 也不必限于自然数,只要N 是正数即可;而且把“n N >”改为“n N >”也无妨.函数的极限设函数()f x 在点0x 的某一去心邻域内有定义.如果存在常数A ,对于任意给定的正数ε(不论它有多么小),总存在某正数δ,使得当x 满足不等式00x x δ<-<时,对应的函数值()f x 都满足不等式()f x A ε-<,那么常数A 就叫做函数()f x 当0x x →时的极限,记为00lim ()()()x x f x A f x A x x →=→→或当.可以看出,数列极限与函数极限定义的思想是一致的,都是相应的某个表达上的值无限地接近某个常数值.不同的是数列是离散的,数列中的项在跳跃式地接近,而函数是连续的,函数值在逐渐地接近,但二者都能与相应的常数值以任意程度地接近.2、定积分与极限定积分在求极限中应用概述不难看出,无论是数列的极限还是函数的极限,它们都与定积分的定义存在着千丝万缕的关系,那么就让我们来揭晓它们之间玄机与奥秘吧.事实上,定积分的定义中蕴含着一列数{()i i f x ξ∆}的和,并且只要i x ∆充分地小,和式1()ni i i f x ξ=∆∑就可以任意地接近确定的实数J=()b a f x dx ⎰,这正是极限思想的存在,即1lim ()J ()nb i i a n i f x f x dx ξ→∞=∆==⎰∑.这就为我们求极限提供了一种独特而有力的方法——利用定积分求极限.因为在积分学中有大量的积分公式,所以我们运用之解决众多类型的和式极限.定积分求极限中应用思想的形成先让我们看一个简单的例子:例1.求极限111lim()122n J n n n→∞++=++…. 分析:此极限式的求解,不容易直接用极限的定义解决,因为该法往往是用来一边计算一边证明某个极限结果已经比较明显的问题,因此这里不适合;重要极限的结论显然也在这里没有用武之地,因为形式上根本不同;再考虑洛必达法则,它不是无穷比无穷型的极限也非零比零型的极限,也不可能用到此法;那么泰勒公式呢泰勒公式往往是用来解决连续函数的极限问题,通过泰勒展式往往能把非多项式形式的表达式转化成多项式形式,以简化形式从而求解,看来这里也不适用.那是不是就没有什么合适的办法了呢答案当然是否定的,事实上,它从形式上与定积分的定义还是有一些相像的,那么就让我们尝试用定积分的办法来解决这个问题吧!解:把此极限式转化为某个积分形式,从而计算定积分.为此做如下变形:111lim 1nn i J i n n→∞==+∑.不难看出,其中的和式是函数1()1f x x=+在区间[]0,1上的一个积分和(这里取得是等量分割,11,[,],1,2,i i i i ix i n n n n nξ-∆==∈=…).所以, J=11001ln(1=ln21dx x x=++⎰). 从该例题的解法中可以看出,本题的关键是将极限和转化为积分和,从而利用了定积分将所求极限迎刃而解.于是,我们可以总结出定积分在求极限中应用的一般方法步骤:Sept1将和式极限1lim ()n n i g i →∞=∑经过变形,使其成为积分形式1lim ()ni i n i f x ξ→∞=∆∑.这里常取11,[,],1,2,i i i i i x i n n n n nξ-∆==∈=…;Sept2确定积分函数的上下限.a=lim (i n i ξ→∞取第一个值)lim (i n b i ξ→∞=取最后一个值); Sept3用x 代换i ξ,写出定积分表达式()baf x dx ⎰,并求出原极限的值.通过以上的一般方法步骤,我们在面对无穷项和式的极限问题时就有方可依,有法可循了.现在让我们再来看一个例子,并从中仔细体会以上方法步骤.例2.求极限222222111lim (12n n n n n n →∞+++++…+). 解:Sept1 化和式极限为积分形式.原极限=22211111lim lim 1(nn n n i i i n in n→∞→∞===++∑∑).显然,这里1,(i i i x n n ξ=∆=即是进行N 等分),被积函数可看成()21f x ,1,2,.1+i n x==… Sept2 确定积分函数上下限.1a lim0(,1),lim 0(,).i i n n i n ii b i n n n nξξ→∞→∞======取取n Sept3 写出积分表达式并求出积分值. 原极限=110201arctan 14dx x x π==+⎰.对于本题,我们是紧紧按照刚刚总结出的方法步骤进行的,并顺利地求出了原题的极限值.这是一个具体的例子,那么我们是否可以总结出更为一般性结论呢答案自然是肯定的.3、应用定积分求极限一般性结论的综述及其应用至此,我们可以得出如下结论:结论1如果函数()f x 在区间[],a b 上连续,将区间[],a b 进行n 等分,1[(()],i i i i b ab a b a x n n nξ--∈--∆=),,那么,1lim ()()n b i a n i b a f f x dx n ξ→∞=-=∑⎰. 事实上,连续函数一定可积,而将区间[],a b 进行n 等分也是分割T 的一种特殊情况.根据定积分的定义,上述结论成立.当然,并不是所有的用到定积分求极限的问题中都要严格用到上面总结出的三个步骤,我们可视情况灵活处理,比如无需用到某一步骤或者还需用到其他求极限的思想等.下面我们再看一组求极限的习题,以充分感受结论1的用途.习题组11) 1lim (sin +sin +sin );n n n n nπππ→∞2n-1…2)n →∞3) sinsinsinlim[]1112n n n n n n n nπππ→∞+++++2n …. 这组习题都是无穷项式子和的极限问题,都可以把定积分的思想应用到求极限中去.现在就让我们用结论1来解决这些求极限的问题,并从不同习题中寻找出异同,以加深对结论1的掌握和认识.解: (1) 分析 原极限显然可以看成()sin f x x π=在[]0,1上的定积分.故111011lim (sin +sin +sin )lim sin 12sin cos ;n n n i i n n n n n n xdx x ππππππππ→∞→∞====-=∑⎰2n-1…(2)分析 先通过恒等变形,原极限式=11lim nn i n →∞=,被积函数()f x =,积分区间是[]0,1,于是原极限值=11022(13)33x =+=⎰;(3)分析 原和式极限的通项是sin i n i n nπ+不可以看成是关于i n 的某一个函数,但是注意到: 2sinsinsin1212(sin sin sin )(sin sin sin ).11112n n n n n n n n n n n n n n n n n nπππππππππ+++<+++<+++++++……… 应用结论1,上面不等式左端可以取极限,即111211lim (sin sin sin )lim sin [lim sin ][lim ]1+1+1nn n n n n i i n n i i n n n n n n n n n n n πππππ→∞→∞→∞→∞==+++=⋅⋅=⋅+∑∑…=12[sin ]1xdx ππ⋅=⎰,上面不等式右端可以取极限,即1011212lim (sin sin sin )lim sin sin n n n i n i xdx n n n n nn ππππππ→∞→∞=+++=⋅==∑⎰….于是,由极限的迫敛性可知原极限值=2π. 这组题均典型地运用了定积分的计算,从而求出了各极限.我们发现,只要找到某个连续函数()f x ,并能把这个和式极限1lim ()nn i g i →∞=∑转化成积分形式1limf ()n i n n →∞⋅,我们就只需计算出f(x)在[0,1]上的积分值,从而确定出原极限值.这三个习题中,例题1的式子无需再进行恒等变形,因为其形式上已经是lim n →∞f(i n )1n⋅了;习题2与习题3形式上直观上不是lim n →∞f(i n )1n ⋅的形式,因为式子n →∞与式子sinsinsinlim[]1112n n n n n n n nπππ→∞+++++2n …都不含i n 的项.为此,我们需要对习题2以及习题3极限的式子进行恒等变形,通过提取公因式等手段使其出现in的因子.当然有的题可能不容易找到对应的连续函数()f x ,例如习题3,我们可以用极限的一些性质,如极限的迫敛性,从而间接地求出原和式极限的极限值. 一般性结论的深化及推广接下来,我们对结论1进行适当的推广,以得到更多形式的极限的求法.推论1如果函数(),(),()()f x g x f x g x ⋅均在[],a b 上可积,01111201[,],[,]lim ,max{,,},lim ()()()().n i i i i x nbi i i n i i i ai a x x x b a b x x x x x x x f g x f x g x dx λξηλξη-→∞-→==<<<=∆=-=∆∆∆∆=∑⎰…为区间的任意划分,小区间上任意两点,…则证明:首先, (),(),()()f x g x f x g x ⋅均在[],a b 上可积.又由于1,,i i i i n n ξη-⎡⎤∈⎢⎥⎣⎦,0(i x n ∆→→∞当),所以,lim lim .i i n n ξη→∞→∞=于是,01lim ()()n i i i i f g x λξη→=∆∑=01lim ()()ni i i i f g x λξξ→=∆∑=()()baf xg x dx ⎰.例3.求极限:122lim [sin cos()sin cos()sin cos()]222n n n n n n n n n n n n nπππππππππ→∞-+-++-…. 解:由推论1可知,f(x)=(1)sin ()cos [0,1],[,],0,1,2,(1).2i i i i x g x x i n n n n n nπππππππ-=-∈=-及皆在上可积,且…limlim(),1,2,.2n n i i i n n n nπππ→∞→∞=-=… 于是,原极限式=1210011sin cos sin 02x xdx x ππππ=⋅⋅=⎰. 推论2设10ln ()ln ()0,1]lim.f x dx n f x e →∞⎰=在区间[上可积,则10112lim [ln ()ln ()ln ()]ln (),lim(n n f f f n n n nn f x dxe e →∞++→∞=⎰=…事实上对数的性质)(定积分的定义).例4.试求:112lim()n n n n n n n n n→∞+++⋅⋅…. 2解:直接应用推论11011ln(1)1[ln(1)ln(1)]12lim()lim (1)4.nx dx n n n n i x x x x n n n n i e n n n n e e+→∞→∞=+++-+++⎰⋅⋅=+===∏…推论3如果函数()f x 在区间[]0,1上可积,且()1()11121f x 0,lim[1+()][1+()][1+()]f x dx n nf f f e n n n n n n→∞⎰≥⋅⋅=则…. 证明:记A=11121lim[1+()][1+()][1+()]n n f f f n n n n n n →∞⋅⋅…,则11ln lim ln[1+()]n n i iA f n n →∞==∑1()()11()1011()1111lim ln[1+()]lim ln[1+()]11lim ln lim ()()A .n if i n n nf n nn n i i i nn f n n n i i f x dx i if f n n n nn n i e f f x dxn nn e ⋅→∞→∞==→∞→∞======⋅=⎰=∑∑∑∑⎰于是,例5.计算22212lim(1)(1)(1)333n n n n n→∞+⋅++…. 解:本题也可以直接运用推论3,10113622211211lim(1)(1)(1)lim (1).3333xdxnn n i n ie e n n n n n →∞→∞=⎰+⋅++=+⋅⋅==∏…这三个推论是对结论1的必要补充与完善.形式上我们不仅有无穷项式子和的极限,还衍生出了无穷项式子乘积的极限.它们都是顺着结论1的思路继续进行探索,从形式上丰富了定积分在求极限中应用这一思想,但从本质上讲,它们与结论1是一致的.它们都紧紧抓住了定积分概念的实质,意识到定积分是无穷项和的极限,应用数学的一些基本性质,对各式子进行恒等变形,尽量把不同形式的极限向定积分定义中的和式上去靠拢.最终通过简单明了的定积分公式,求出定积分的值来,以确定出原极限的值.由这三个推论来看,111111111lim (),lim ()(),,[,],lim [()],lim [1+()]n n nnni i i i n n n n i i i i i i i i i f f g f f n n n n n n n n ξηξη→∞→∞→∞→∞====-⋅∈∑∑∏∏对于等形式的极限,我们都有方可循,用定积分的方法容易求出其极限来.对于任何一种数学方法,只要我们仔细地观察与推究,都能将其结论或应用范围加以推广,就像结论 1.现在让我们来看一组习题,以体会以上诸推论.现在,我们已经积累了多种求和式极限的方法,它们是今后应用定积分解决极限类问题的最佳模型与范例.那就再让我们来看一组习题,以熟悉与巩固11111()(),,[,],lim [()],lim [1+()]n nn i i i i n n i i i i i if g f f n n n n n ξηξη→∞→∞==-⋅∈∏∏1111lim (),lim nnn n i i i f nn n →∞→∞==∑∑ 等形式的极限吧.下面这组习题综合用到了以上各结论与推论.习题组2用定积分的方法计算下列各极限.(1)222111lim [](1)(2)()n n n n n n →∞++++++…;(2)11111212111lim [()sin(+()sin(++()sin(]232323n n n n n n n n n n n n n n n n →∞------))…);(3)limn →∞(4)111lim(1)(1)(1)12n n n n n→∞++++++…. 解:分析 以上例题都容易恒等变形,使其满足结论1或者推论1至推论3的条件.于是,(1)122222011111111lim []();(1)(2)()(1)21n n i n dx i n n n n n x n→∞=+++===+++++∑⎰… (2)11111212111lim [()sin(+()sin(++()sin(]232323n n n n n n n n n n n n n n n n →∞------))…)=11sin ni i i nξη=⋅∑,1,[,],1,2,1i i i i i n n n ξη-∈=-…=10sin sin1cos1;x xdx =-⎰(3)1011ln(1)21limlim[(1)]2n x dx n n n i i en ππ-+→∞→∞=⎰=+⋅=∏ 22(1)ln(1)1ππ=++- ;(4)1011111111lim(1)(1)(1)(1)2121n dx x n i e i n n n n n n+→∞=⎰+++=+⋅==++++∏….定积分在求极限中应用思想的转移至此,我们已经深深的体会到了各种形式的定积分在极限中应用的作用.仅仅于此,我们尚不能满足,我们可以把定积分在求极限中的应用思想借鉴到其他方面.例如,利用这种思想方法来证明一些不等式,或者用之解决一些复杂一点的求极限问题.下面将举例说明.例 6.证明:若函数()f x 在[],a b 上连续,且对于[],x a b ∀∈,有()0f x >,则21()()()bb a a f x dx dx b a f x ≥-⎰⎰. 证明:已知()f x 与()g x 在[],a b 上都可积.将[],a b 进行N 等分,分点是01n a x x x b =<<=…<.在第K 个区间上取1,k k k k b a x x x nξ--=-=.由算数平均不小于几何平均,有121111(()1(()()n n k n nk k k k k k k f x f x b a b a f x b a n f x n n n ====--⋅⋅⋅=-⋅⋅≥∑∑∑∑))22(()b a b a -=-) 21()()()b b a a n f x dx dx b a f x →∞≥-⎰⎰当时,有. 体会:本例恰巧反过来,将积分和转化为极限和的形式,并运用了算术平均数不小于几何平均数这一结论,将问题化繁为简.较好地认识与掌握定积分与极限之间的关系是解决本问题的关键.该例题说明,我们应该充分认识到定积分在极限中的作用,并能做到灵活变通,适当情形下,二者可以相互转化,将问题化难为易,从而达到解决问题的目的. 例7.试求极限(21)!!lim[](2)!!n m m →∞-. 分析:该问题似乎不能直接运用结论1或推论1至推论3来求极限.因为极限的表达式不容易化成以上结论或者推论的情形.但是,该问题的解决就真用不到定积分了吗答案是否定的.在解决该问题之前,还是先让我们看一下沃利斯公式的由来吧!沃利斯公式:2(2)!!1lim[](21)!!212m m m m π→∞⋅=-+. 证明:令20sin ,1,2,n n J xdx n π==⎰…,则当2n ≥时用分部积分法容易求得122222*********sin sin cos (1)sin cos (1)sin sin (1)(1.n n n nn n n n n J xdx x x n x xdx n xdx xdx n J n πππππ----==-+-=--=---⎰⎰⎰⎰)J移项并整理后可得递推公式:21, 2.n n n J J n n--=≥由于 220100,sin 1,2J dx J xdx πππ====⎰⎰重复应用上面的递推公式可得 2212123122222()2222121213m m m m J m m m m J m m π+--⎫=⋅⋅⋅⎪⎪-**⎬-⎪=⋅⋅⋅⎪+-⎭……, 又由于2122-1222000sin sin sin m m m xdx xdx xdx πππ+<<⎰⎰⎰,再将**()式代入,便可以得到 22(2)!!1(2)!!1[][](21)!!212(21)!!2m m m m A B m m m mπ=<<=-+-,因为 2(2)!!110[]0()(21)!!2(21)22m m m B A m m m m m π<-=<⋅→→∞-+,根据极限的迫敛性可知lim()0m m m B A →∞-=.而02m m m A B A π<-<-,故得沃利斯公式2(2)!!1lim[](21)!!212m m m m π→∞⋅=-+. 现在让我们来仔细看看沃利斯公式究竟与定积分有什么关系吧!事实上,在计算定积分20sin ,1,2,n n J xdx n π==⎰…时,我们巧妙地运用了定积分的递推表达式,这样我们才正真地寻找到了解决极限问题的金钥匙,看来定积分的运算还是在其中发挥了不可低估的作用.那么就让我们直接运用该公式来探究例8问题吧!根据沃利斯公式2(2)!!1lim[](21)!!212m m m m π→∞⋅=-+,可知1(21)!!21lim lim 0(2)!!2m m m m m π→∞→∞-+==. 从某种程度上讲,我们利用了定积分方法解决了例8中极限的问题.倘若我们采用其方法来求这个极限,恐怕会走一些弯路.定积分在求极限中应用思想的完善我们知道反常积分也是定积分在极限下定义出来的.以上的所有求极限问题都是将极限的表达式整体转化成积分形式,从而应用了定积分巧妙地求出了原极限的结果,那么能不能把定积分在求极限中局部应用呢现在我们再来看一个有趣的问题,以便说明此问题. 例8.证明:1112lim 1ln n n n→∞++=…+. 分析:这个例题不同于前面所有的例题,前面的例题,我们都能迅速地将所求极限的表达式转化成1lim ()ni i n i f x ξ→∞=∆∑,而本例不行,但它形式上与我们讨论的定积分在求极限中应用的例子非常相像,因为式子中有无穷多项和11ni i =∑,所以我们就尝试用定积分的方法来求它吧!把这个极限式子的分子进行适当变形11111nn i i i in n===∑∑.如果根据前面的经验,我们知道101111lim n n i dx i n x n→∞==∑⎰的.可是现在我们对两个问题有所质疑.第一,我们并没有把原极限式直接转化成积分形式;第二,即使局部用到了定积分101dx x ⎰,但我们知道101dx x =∞⎰的.事实上,原式经变形后,我们会发现分子与分母中的无穷大量是等价的.即110001111111lim(ln )lim(ln )ln 2lim lim lim 1ln ln lim ln lim ln lim ln ln n i x x n n x x x x i n dx x x n n x x n n x x x x ++=→→→∞→∞→+∞→+∞→+∞→+∞++-======∑⎰…+(这里我们统一了分子分母中的变量,统一用变量x,这里已经表示变量x 是逐步趋近,由数学分析中归结原理”,这个手段是不影响极限结果的).最后我们求得其结果,1112lim1lnnnn→∞++=…+.由此可以看到,在求极限的问题中,定积分的思想不仅可以对表达式整体使用,也可以对其进行局部使用.总之,只要我们善于思考书本上的一些概念以及分析它们之间联系,我们就往往能够游刃有余地把一种数学思想用于解决其他数学问题上.最后,让我们再来总结一下,定积分在求极限中应用时所应该注意的几个问题.第一,极限必须是无穷项和的极限,并且这些和的极限经过适当的恒等变形之后能转化为定积分的形式.第二,应用定积分求极限时,往往还需要用到其他的一些求极限的方法和手段,例如极限的迫敛性,重要极限的结论,取对数手段等.第三,求极限一类问题往往需要使用各种手段,这样才能做到事半功倍.4、论文总结再认识数学通过以上探讨,我们重新认识了数学.我们在进行推理与应用时,是有深切体会的.数学本身是一门严谨的自然科学,因为它是一种思维的工具,是一种思想方法,它还是一种理性的艺术.数学是一种思维的工具.第一,数学具抽象性.数学概念是以极度抽象的形式出现的.本文中讨论的定积分以及极限更是如此.与此同时,数学的研究方法也是抽象的,这就是说数学命题的真理性不能建立在经验之上,而必须依靠于严格的证明.当数学应用于实际问题的研究时,其关键在于能建立一个较好的数学模型.我们在运用定积分求极限时,就已经拥有了较好的数学模型——函数模型.在一个较好的数学模型上展开数学的推导和计算,以形成对问题的认识,判断和预测.这就是运用抽象思维去解决现实问题的体现.第二,数学赋予科学知识以逻辑的严密性和结论的可靠性,是使认识从感性阶段发展到理性阶段,并使理性认识进一步深化的重要手段.在数学中,每一个公式,定理都要严格地从逻辑上加以证明以后才能够确立.当我们发现了“结论1”之后,相继经过严密的推理与论证后才拓展到了“推论1”至“推论3”.第三,数学是一种辅助工具和表现方式.我们在解决数学问题本身时,还必须依赖于数学中的其他相关方法思路.另外数学反映的是一种复杂而抽象事物内部关系,但是我们仍然有简明的数学符号与形象鲜明的图形等来表示它.无论是定积分还是极限,其中都用到了丰富的数学符号,离开这些数学符号,我们的表达似乎显得寸步难行.数学是一种思想方法.数学是研究量的科学.它研究客观对象量的变化,关系等,并在提炼量的规律性的基础上形成各种有关量的推导和演算的方法.数学的思想方法体现着它作为一般方法论的特征和性质,是物质世界质与量的统一,内容与形式的统一的最有效的表现方式.无论是定积分还是极限都离不开计算,这就意味着它们中都蕴含着量的变化.数学还是一种理性的艺术.一般我们觉得,艺术与数学是两种风格与本质都有着明显不同的事物.它们一个处于高度理性化的峰顶,另一个则位于精神世界的枢纽地带;一个是自然科学的代表,另一个则是美学的杰作.但是,在种种表面上无关甚至完全不同的现象身后却隐藏着艺术与数学相当一致的一般意义.我们进行学术研究纯粹是我们进取以及求知欲的驱使.艺术与数学都是公认的地球语言.艺术与数学在描绘万事万物的过程中,还同时完善了自身的表现形式,这种表现形式最基本的载体便是艺术与数学各自独特的语言特征.其共同特点有(1)超文化性.艺术与数学所表达的是一种带有普遍意义的人类共同的心声,因而它们可以超越时间和地域界限,实现不同文化群体之间的广泛传播和交流.(2)整体性.艺术的整体性来自于其艺术表现的普遍性和广泛性;数学的整体性来自于数学统一的符号体系,各个分支之间的有力联系,共同的逻辑法则和既约的表达方式.(3)简明性.它首先表现为很高的抽象程度,其次是凝冻与浓缩.(4)代表性.艺术与数学语言各自代表性可以诱发某种强烈的情感体验,唤起某种美的享受,而意义则在于把注意力转向思维,上升为理念,成为表现人类内心意图的方式.(5)形式性.在艺术与数学各自进行的符号与信息的含义交换中,其共同的特征就是达到了实体与形式的分离.我们研究的定积分在求极限中的应用,那种思想以及符号呈现方式可被世界人悦纳.艺术与数学具有共同的精神价值.其共同的特点有:(1)自律性.数学价值的自律性是与数学价值的客观性相关联的;艺术的价值也是不能以人的意志而转移.艺术与数学的价值基本上是在自身框架内被鉴别,鉴赏和评价的.(2)超越性.它们可以超越时空,彰显永恒.在艺术与数学的价值超越过程中,现实得以扩张,延伸.艺术与数学的超越性还表现为超前的价值.(3)非功利性.艺术与数学的非功利性是其价值判断异于其他种类文化与科学的显著特征之一.(4)多样化,物质化与广泛化.在现代技术与商业化的推动下,艺术与数学的价值也开始发生升华,出现了各自价值在许多领域内的散射,渗透,应用,交叉等情况.定积分在求极限中的应用,不仅仅贡献于数学本身,它将逐渐在其他领域也发挥一定的作用.结束语我们已经见到了定积分在求极限问题中应用的各种形式.事实上,只要我们对学过的某些概念用心的体会,并加以深刻的思考,我们就可能将其精髓运用到数学的其他领域.正如我们这里把定积分与极限结合起来,并进行了适当推广,得到了较为满意的结论和推论.本文主要给大家介绍了定积分在求极限中应用.一开始我们就回忆了定积分以及极限等大学数学学习中的重要概念.然后剖析它们之间的内在联系,进而寻找到了一种独特的求极限的办法——借助定积分求极限.当然,这种思想也并非空穴来风,它是源于教材中某些例题中具有创新性思想方法或者一些独特的步骤.因为不是所有的数学概念之间经过思考推理,相互之间就能建立起联系来.因此,在平时的数学学习中,我们务必对教材中的基本概念加深体会,尤其是要把相互之间或多或少存在着某种关系的概念加以比较与分析.然后对其进行大胆的假设,并进行一定的逻辑证明.如果我们的假设成立,那就是我们发现的新事物,这对于我们发散思维与创新思维都是大有裨益的;假设不成立,我们也可更好地掌握不同概念之间区别,这对于我们理解知识都是有好处的.所以,在我们平时的学习过程中,我们要积极去思考,并大胆地进行某些适当的假设,以提升我们创新思维能力.求极限的方法可能还有更多,值得大家去思考与挖掘.希望本文能起到抛砖引玉的目的,能激发更多的数学爱好者携起手来探索出更多实用与巧妙的求极限的方法来.欢迎大家对本文进行批评与指正.参考文献。
极值的分析和应用

极值的分析和应用
[5] 华东师范大学数学系. 数学分析上册 [M]. 北京: 高等教育出版社, 2001. [6] 刘书田, 孙慧玲. 微积分 [M]. 北京: 北京大学出版社, 2006. [7] R.B. Davis, S. Vinner. The notion of limit; some seemingly unavoidable Misconception stages [J]. The Journal of Mathematical Behavior, 1986, 5: 281~303. [8] 司清亮. 极限求法分析 [J]. 新乡师范高等专科学校学报, 2002, 16(4): 3~4. [9] 周根立. 求函数极限的方法 [J]. 山西煤炭管理干部学院学报, 2000, 3: 33~36. [10] 马建清, 向彩容, 喻敏. 关于求极限的几种方法 [J]. 高等函授学报, 2006, 19(6): 35~44. [11] 吉米多维奇. 数学分析习题集 [M]. 济南: 山东科学技术出版社, 2008. [12] 刘西垣, 周民强, 李正元等. 微积分题型精讲(经济类) [M]. 北京: 机械工 程出版社, 2004. [13] 卫民波. 关于二元函数极限的讨论 [J]. 山西农业大学学报, 2006, 26(6): 123~124. [14] 任宪林. 多元函数求极限 [J]. 职大学报, 2001, 2: 5~7. [15] D. Tall, S. Vinner. Concept image and concept definition in mathematics with particular reference to limit and continuity [J]. Educational Studies in Mathematics, 1981, 12: 151~169. [16] 陶会强, 罗成广. 二元函数极限的计算方法 [J]. 天中学刊, 2009, 24(2): 3~4. [17] 杨雪宏, 宋振新, 段长存. 二重极限求法探析 [J]. 河北能源职业技术学院 学报, 2002(3): 94~96. [18] 龙永红.概率论与数理统计[M].北京:高等教育出版社.2001,(12),第三版. [19] 韩 新正.“ 概率 为零事 件” 与“不 可 能事件 ”辨 析 [J]. 中小学数 学 ( 初中 版),2011,(11):46.
第一章函数的极限与函数的连续性
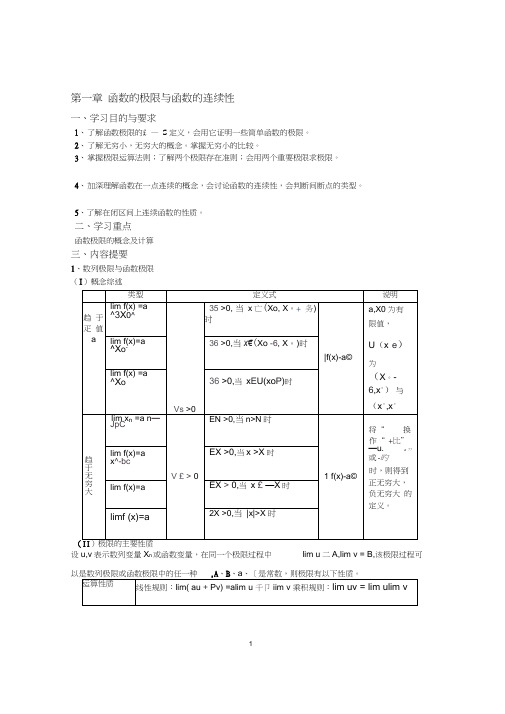
第一章函数的极限与函数的连续性一、学习目的与要求1、了解函数极限的£ —S定义,会用它证明一些简单函数的极限。
2、了解无穷小,无穷大的概念。
掌握无穷小的比较。
3、掌握极限运算法则;了解两个极限存在准则;会用两个重要极限求极限。
4、加深理解函数在一点连续的概念,会讨论函数的连续性,会判断间断点的类型。
5、了解在闭区间上连续函数的性质。
二、学习重点函数极限的概念及计算三、内容提要1、数列极限与函数极限(I)概念综述设u,v表示数列变量X n或函数变量,在同一个极限过程中lim u二A,lim v = B,该极限过程可12商规则:lim _ =lim u / lim v(lim 0)v比较性质(1) 若 u > v ,贝U lim u > lim v(2) 若lim u > lim v ,则在某个范围 X 上有u >v有界性质 (1) 若 {X n }收敛,则{X n }有界(2) 若limu(x)=A ,则u(x)在某个范围X 上有界。
存在性质(1) 单调有界准则:单调有界数列必是收敛数列。
(2) 夹逼准则:若uv ,且u 、v 趋于A ,则⑷亦趋于A (三个变量u 、v 、国极限过程相同)。
注 的形式与极限过程相关,当 U 、v 是数列时,X ={n|n > N} , 是某个自然数;1lxm oxsin ;=,1lim e x 不存在,x(IV )极限之间的联系(1) lim f(x)=A := lim f(x)=A = lim f(x)i x o 十x T x o —(2) lim f (x) = A lim f (x) lim f(x)二 A.X -X ) - .X(3) lim f (x) = —对任意趋于 X o 的数列 X n ,有 ”m_f(X n )二 Av 是函数变量, 极限过程是X — xj 时,X =(Xo - :-,Xo),极限过程是x > X o 时,X 二U(X o ,、J ,其余类推。
极限思想在实际生活中的应用【文献综述】

文献综述信息与计算科学极限思想在实际生活中的应用极限思想的完善与微积分的严格化密切联系. 在很长一段时间里, 许多人尝试解决微积分理论基础的问题, 但都未能如愿. 这是因为数学的研究对象已从常量扩展到变量. 而人们对变量数学特有的规律还不十分清楚. 对变量数学和常量数学的区别和联系还缺乏了解. 对有限和无限的对立统一关系还不明确. 人们使用习惯了的处理常量数学的传统思想方法, 就不能适应变量数学的新需要,仅用旧的概念说明不了这种“零”与“非零”相互转化的辩证关系.早在我国春秋战国时期, 中国就有了极限思想的萌芽. 在《庄子·天下篇》中有名家惠施(约公元前370-310年)提出的“至大无外谓之大一, 至小无内谓之小一”以及“一尺之锤, 日取其半, 万世不竭”的无限观. 在《庄子·秋水》中还有“至精无形, 至大不可围”的说法, 与惠施的观点相同. 在墨家的代表作 《墨经》中, 包含有一定的极限思想. 墨子(约公元前478-392年) 认为:“宇, 弥异所也”(《经上》); 宇, 东、西、家、南、北”(《经说上》); “久, 弥异时也”(《经上》); “久, 古, 今, 旦, 莫”(《经说上》). “弥”有“遍”、“满”的意思, 可用来表示无穷. 墨子认为宇宙无边无际, 时间无始无终, 含有无穷大的观念. 而且, 墨家已用具体、形象的语言给出了“有穷”、“无穷”的定义. “穷, 或有前不容尺”(《经上》) . “穷, 或不容尺, 有穷; 莫不容尺, 无穷”(《经说上》). “或”指“域”, “穷”指一个区域向前量去只剩不到一尺的距离. 一个区域向前量去只剩不到一尺的的距离, 这是有穷; 如果继续量下去, 前面总是长于一尺, 就是无穷. 《墨经》中关于极限思想还有一个精辟的论述:“非半, 勿著斤则不动, 说在端”(《经下》); “非著斤半, 进前取也, 前则中无为半, 犹端也; 前后取, 则端中也, 著斤必半, 毋与非半, 不可著斤也. ”(《经说下》); “著斤”有“斫取”、“分割”的意思. 墨家认为把一段木棒不断地斫去一半, 当这种斫半的过程不能再进行下去的时候, “半”就变成了“非半”, 这是因为有“端”(点)存在的缘故. 而且他们还给出了得到“端”的两种方式: 一是“进前取”, 即设木棒长为, 如图1, 去掉的一半, 得, 去掉的一半AB AB AC AC 得, 去掉的一半得, 依此至无穷次, 便得到端点.1AC 1AC 2AC A图1二是“前后取”. 如图2, 不妨先取的中点, 从前面去掉的一半, 从后面AB O AO 1AA 去掉的一半, 剩下, 然后再去掉的一半, 的一半, 得OB 1BB 11A B 1A O 12A A 1OB 12B B 22A B , 无限进行下去, 则得端点(与重合).O 'O图2公元3世纪, 中国数学家刘徽 (263年左右)成功地把极限思想应用于实践, 其中最典型的方法就是在计算圆的面积时建立的“割圆术”. 由于刘徽所采用的圆的半径为1, 这样圆的面积在数值上即等于圆周率, 所以说刘微成功地创立了科学的求圆周率的方法. 刘徽采用的具体做法是: 在半径为一尺的圆内, 作圆的内接正六边形, 然后逐渐倍增边数, 依次算出内接正6边形、正12边形、…、直至6×192边形的面积. 他利用公式 (为内22n n r l S n ⋅=⋅n l 接正边形的边长, 为内接边形的面积)来求正多边形的面积. 刘徽认为, 割得越细, n 2n S 2n 圆内接正多边形与圆面积之差越小, 即“割之弥细, 所失弥少. 割之又割, 以至于不可割, 则与圆和体, 而无所失矣”.而在国外, 到了l8世纪, 罗宾斯、达朗贝尔与罗依里埃等人先后明确地表示必须将极限作为微积分的基础概念, 并且都对极限作出了各自的定义. 其中达朗贝尔的定义是:“一个量是另一个量的极限, 假如第二个量比任意给定的值更为接近第一个量.”它接近于极限的正确定义. 然而, 这些人的定义都无法摆脱对几何直观的依赖. 事情也只能如此, 因为19世纪以前的算术和几何概念大部分都是建立在几何量的概念上的.首先用极限概念给出导数正确定义的是捷克数学家波尔查诺, 他把函数的导数定义为差商的极限, ()f x y x ∆∆()f x '并强调指出不是两个零的商. 波尔查诺的思想是有价值的, 但关于极限的本质他仍未()f x '说清楚. 到了19世纪, 法国数学家柯西在前人工作的基础上. 比较完整地阐述了极限概念及其理论. 他在《分析教程》中指出:“当一个变量逐次所取的值无限趋于一个定值. 最终使变量的值和该定值之差要多小就多小, 这个定值就叫做所有其他值的极限值, 特别的, 当一个变量的数值(绝对值) 无限地减小使之收敛到极限0, 就说这个变量成为无穷小. ”柯西把无穷小视为以0为极限的变量. 这就澄清了无穷小“似零非零”的模糊认识. 即在变化过程中. 它的值可以是非零, 但它变化的趋向是“零”, 可以无限地接近于零.柯西试图消除极限概念中的几何直观, 作出极限的明确定义, 然后去完成牛顿的愿望. 但柯西的叙述中还存在描述性的词语. 如“无限趋近”、“要多小就多小”等, 因此还保留着几何和物理的直观痕迹, 没有达到彻底严密化的程度. 为了排除极限概念中的直观痕迹 , 维尔斯特拉斯提出了极限的静态的定义.给微积分提供了严格的理论基础. 所谓, 就是指:“如果对任何, 总存在自然数, 使得当时, 不等式lim ()x f x A →∞=0ε>N n N >恒成立. ”()f x A ε-<这个定义借助不等式, 通过和之间的关系, 定量地、具体地刻画了两个“无限过εN 程”之间的联系. 因此, 这样的定义是严格的, 可以作为科学论证的基础, 至今仍在数学分析书籍中使用. 在该定义中, 涉及的仅仅是数及其大小关系, 此外只是给定、存在、任取等词语, 已经摆脱了“趋近”一词, 不再求助于运动的直观.参考文献[1] 张素亮. 《墨经》数学今释[J] . 自然科学史研究, 1994, 13(1) : 1-9.[2] 孙庆华, 王刚. 中国先秦时期与古希腊时期极限思想的比较研究[J] 曲埠师范大学学报, 2000, 2(26): 107-109.[3] E. Keith. Limits of Functions [M]. Springer London, 2005[4] 克莱因M. 古今数学思想(1) [M]. 上海: 上海科技出版社, 1979.[5] 李继阂. 《九章算术》及其刘徽注研究[M]. 西安: 陕西人民教育出版社, 1990.[6] 王晓硕. 极限概念发展的几个历史阶段[M]. 辽宁: 辽宁师范大学数学系, 2001, 40-43.[7] 邹大海. 刘徽的无限思想及其解释[J]. 自然科学史研究, 1995, 14(1): 12~ 21.[8] 李文林. 数学珍宝[M]. 北京: 科学出版社, 1998.[9] 杜石然, 孔国平. 世界数学史[M]. 长春: 吉林教育出版社, 1996.[10] Jobson, Oliver H. Expanding the Boundaries of Self Beyond the Limit of TraditionalThought [M]. Global Pub Assoc Inc, 2011.[11] 邓蜀元. 极限思想的产生和发展[J]. 广西职业技术学院考试周刊, 2009, 28(上): 80-81.。
数学分析中的极限问题毕业论文终稿

数学分析中的极限问题毕业论文目录摘要 (1)关键词 (1)Abstract (1)Key words. (1)引言 (1)1.综述 (2)1.1极限的产生与发展 (2)1.2极限问题的类型 (3)2.常见的极限求解方法 (3)2.1简单求极限的方法 (3)2.2利用两个重要极限公式求极限 (4)2.3利用洛必达法则求极限 (5)2.4利用极限的四则运算法则求极限 (6)2.5利用等价无穷小替换求极限 (6)2.6利用定积分求极限 (7)2.7利用泰勒公式求极限 (8)2.8两边夹法则求极限 (9)2.9利用单侧极限求极限 (10)2. 10利用中值定理求极限 (11)小结 (12)参考文献 (13)数学分析中的极限问题学生:** 学号:*********数学与计算机科学系数学与应用数学专业指导教师:** 职称:**摘要:极限是数学分析这门学科的基础,通过极限思想、借助极限工具使数学分析容更加严谨,贯穿整个数学分析的始末. 本文主要是对数学分析中的极限的产生与发展,以及常见极限的若干常规解法进行了讨论和研究. 本文的重点在第二章,具体介绍了运用四则运算法则、两个重要极限、两边夹法则、等价无穷小替换等方法求解极限.关键词:四则运算法则;洛比达法则;泰勒公式;两边夹法则.Abstract: Limit is the basis of mathematical analysis of the subject, through the of though with the tools of limit, make the content more rigorous mathematical analysis, through the mathematical analysis of events. This article is mainly to limit the emergence and development of mathematical analysis, as well as the common limit of conventional method are disscussed and studied. In the second chapther, the focus of this article, using the laws of arthmetic are analysised in detail, two important limits,between law and equivalent infinitesimal substitution method to solve the limit. Key words:four arithmetic operations; the derivation rule; Taylor formula; both sides grip rule.引言极限是描述数列和函数在无限过程中的变化趋势的重要概念,是从近似认识精确,从有限认识无限,从量变认识质变的一种数学方法,能够通过旧事物的量的变化规律,去计算新事物的量. 因此,极限具有由此达彼的重大创新作用. 同时,极限是研究微积分的理论基础和基本手段,它一直贯穿于该学科的始终. 极限的思想方法不仅在整个分析学的建立和发展中起着基本作用,而且还广泛应用于其他数学分支和自然科学. 同时,考研数学中也少不了有关于极限的题目.极限的思想方法作为人类发现数学问题并解决数学问题的一种重要手段,随着科学技术的不断发展,社会生产力的不断提高,在数学的发展史上将发挥越来越重要的作用. 因此,探讨如何求极限、怎样使求极限变得容易,是一个非常具有现实意义的重要问题. 求极限不仅要准确理解极限的概念、性质和极限存在的条件,而且还要清楚认识各种极限的类型,并熟练应用多种求极限的基本方法.众所周之,求极限的方法繁多且变化灵活,不易掌握. 本文在总结各种常用的求极限方法的同时,更重要的是,也会提出一些创新的极限求解方法,希望能够开拓思路,起到抛砖引玉的作用.1.综述1.1极限的产生与发展早在两千多年前,我国的惠施就在庄子的《天下篇》中有一句著名的话:“一尺之棰,日取其半,万世不竭”,惠施提出了无限变小的过程,这是我国古代极限思想的萌芽.我国三国时期的大数学家徽(约225年~295年)的割圆术,通过不断倍增圆接正多边形的边数来逼近圆周,徽计算了圆接正3072边形的面积和周长,从而推得3.1410243.142704π<<.在国外一千多年以后欧洲人安托尼兹才算到同样精确度的小数.π这扇窗口闪烁着我国古代数学家的数学水平和才能的光辉.徽的割圆术不仅仅是先导,而且是一面旗帜,为研究复杂的逼近数列打开了先河.16世纪前后,欧洲资本主义的萌芽和文艺复兴运动促进了生产力和自然科学的发展. 17世纪,牛顿和莱布尼兹在总结前人经验的基础上,创立了微积分. 随着微积分应用的更加广泛和深入,遇到的数量关系也日益复杂,例如研究天体运行的轨道等问题已超出直观围.在这种情况下,微积分的薄弱之处也越来越暴露出来,严格的极限定义就显得十分迫切需要. 经过近百年的争论,直到19世纪上半叶人们通过对无穷级数的研究和总结,明确的认识了极限的概念.德国著名数学家维尔斯特拉斯通过静态刻板的定义,描述了无限的过程,刻画了极限,对于数列{}n a 如果找到一个实数a ,无论预先指定多么小的正数ε,都能够在数列中找到一项n a ,使得这一项后面的所有项与a 的差的绝对值都小于ε,就把这个实数a 叫做数列{}n a 的极限. 1.2极限问题的类型数列极限定义 设{}n a 为实数数列,a 为定数,任意ε>0,总存在正整数N ,使得当n N >时,有n a a ε-<,则称数列{}n a 收敛于a ,定数a 称为数列{}n a 的极限.不等式n a a ε-<刻画了n a 与a 的无限接近程度,ε愈小,表示接近得愈好;而正数ε可以任意地小,说明n a 与a 可以接近到任何程度. 然而,尽管ε有其任意性,但一经给出正整数,N ε就暂时地被确定下来,以便依靠它来求出ε,又ε既是任意小的正数,那么2ε, ε的平方等等同样也是任意小的正数,因此定义中不定式n a a ε-<中的ε可用2ε, ε的平方等来代替. 同时,正由于ε是任意小正数,我们可限定ε小于一个确定的正数.函数极限定义 设函数()f x 在点0x 的某一去心邻域有定义,如果存在常数A ,对于任意给定的正数ε,总存在正整数d ,当x 满足不等式00x x d <-<时,对应的函数值()f x 都满足不等式()f x A ε-<,那么常数A 就叫做函数()f x 当0x x →时的极限,记作0lim ()x x f x A →=.2.常见的极限求解方法数列极限的求法可谓是多种多样,通过归纳和总结,本章将介绍几种常见的极限求解方法,这些方法均有各自的特点,因为这些常见的方法是研究极限求解的基础,需要我们去深刻的理解并扎实的掌握.我们罗列出一些常用的求法. 2.1简单求极限的方法我们知道,在同一趋近过程中,无穷大量的倒数是无穷小量;有界量乘以无穷小量等于无穷小量;有限个(相同类型)无穷小量之和 、差、积仍为无穷小量,以及利用函数的连续性可以求出某些函数的极限.例1 求极限2147lim32x x x x →--+. 解 当1x →时,分母的极限为0,而分子的极限不为0,可以先求出所给函数的倒数的极限2132132lim04747x x x x →-+-+==--, 利用无穷小量的倒数是无穷大量,故 2147lim32x x x x →-=∞-+. 例2 求极限201sinlimsin x x x x→.解 运用极限运算的四则运算法则,有200001sin11limlim sin lim lim sin sin sin sin x x x x x x x x x x x x x x x→→→→=⋅⋅=⋅, 因为0lim1sin x xx→=,当0x →时,x 为无穷小量,1sinx为有界量,所以 01lim sin 0x x x→⋅=, 故201sin lim0sin x x x x→=.2.2利用两个重要极限公式求极限 我们所熟悉的两个重要极限是 (i)lim ()0x af x →=则sin ()lim1()x a f x f x →=,(ii)lim ()0x af x →=则1()lim(1())f x x af x e →+=,其中,第一个重要极限是“00”型;第二个重要极限是“1∞”型.利用重要极限求函数极限时,关键在于把要求的函数极限化成重要极限的标准型或者它们的变形,这就要抓住重要极限公式的特征,并且能够根据它们的特征,辨认它们的变形,有时会利用到归结原则.例3 求极限10lim(12).xx x →+解 1112220lim(12)lim[(12)(12)]x x xx x x x x e →→+=+⋅+=.例4 求极限211lim(1)nn n n →∞+-.解 2111(1)(1)(n )n n e n n n+-<+→→∞,当1n >时,有2221112221111(1)(1)(1)n n n n n n n n n n n n n-------+-=+≥+,而由归结原则(取2,(n 2,3,)1n n x n ==⋅⋅⋅-)有2221122111lim(1)lim(1)lim(1)n n n n n n n n n n e n n n---→∞→∞→∞--+=+=+=, 于是,由数列极限的迫敛性得211lim(1)nn e n n→∞+-=. 2.3利用洛必达法则求极限定理1 若函数()f x 与()g x 满足 (i) 0lim ()lim ()0();x x x x f x g x →→==∞(ii) 在点0x 的某空心邻域0()U x 两者都可导,且()0g x ≠; (iii) 0()lim()x x f x A g x →'='(A 可为实数,也可为+∞或-∞),则 00()()limlim ()()x x x x f x f x A g x g x →→'=='. 例5 求极限1220(12)limln(1)xx e x x →-++. 解 利用22ln(1)~(0)x x x +→,得 11132222220000(12)(12)(12)(12)limlim limlimln(1)22xxxxx x x x e x e x e x e x x x x--→→→→-+-+-+++===+.应用洛必达法则计算待定型极限需要注意的问题(1)审查计算的极限是不是待定型,如果不是待定型就不能运用洛必达法则,因为它不满足洛必达法则的条件. (2)除计算“”或者“∞∞”两种待定型外,计算其它五种待定型00"0,1,0,,"∞⋅∞∞∞-∞都要用对数或代数运算将它们化为待定型“0”或者“∞∞”,然后再应用洛比达法则.(3)在求极限的过程中,有可约的因子或者极限不是零的因子,可以先约去或从极限符号取出.(4)要特别注意,一般来说,应用洛必达法则计算待定型极限都比较简单.但是对少数的待定型极限应用洛比达法则,并不简单.2.4利用极限的四则运算法则求极限定理2(极限的四则运算法则) 若0lim ()x x f x A →=, 0lim ()x x g x B →=,则(i) 0lim ()lim ()x x x x f x g x A B →→±=±,(ii)0lim[()()]lim ()lim ()x x x x x x f x g x f x g x A B →→→⋅=⋅=⋅,(iii)若0B ≠,则000lim ()()lim ()lim ()x xx x x x f x f x A g x g x B→→→==, 综上所述,函数的和、差、积、商的极限等于函数极限的和、差、积、商.例6 求极限2223lim 4x x x x →+++.解 2223lim 4x x x x →+++=222lim(23)lim(4)x x x x x →→++=+116. 2.5利用等价无穷小替换求极限以下是当0x →时常用的等价无穷小关系sin ~,tan ~,arcsin ~,arctan ~,11~,1~,log (1x)~,ln 11~ln 1~,2(1)1~,ln(1)~.x a x x x x x x x x x x e x n aa x a x x x x x -+-+-+αα等价无穷小代换法 设,,,ααββ'' 都是同一极限过程中的无穷小量,且有~,~,limαααβββ''''存在,则 βαlim 也存在,且有limlim ααββ'='. 例7求极限321(1cos )n n ⋅-.解 因为lim1n →∞=,故321(1cos)n n ⋅-221(1cos )n n ⋅-=2411n n ⋅⋅=1=.例8求极限0lim1x x e →-解 有等价无穷小关系 tan ~,1~ln (0).x x x a x a x -→lim1x x e →-0x →=0x →=21.2x →===2.6利用定积分求极限由于定积分是积分和的极限,因此,某些和式问题可以化为定积分的计算,使运算得以完成.例9 求极限2222221lim 12(n 1)n n nnn n n n →∞⎡⎤++++⎢⎥+++-⎣⎦.解 222222112(n 1)n nnn n n n +++++++-2221111112111()1()1()n n n n n ⎡⎤⎢⎥=+++⎢⎥---⎢⎥+++⎣⎦.可取函数21()1f x x =+,[0,1],x ∈上述和式恰好是21()1f x x =+,在[]0,1上n 等分的积分和,所以2222222221201lim 12(n 1)1111lim 112111()1()1()1.14n n n n n n n n n n n n n n dx x π→∞→∞⎡⎤++++⎢⎥+++-⎣⎦⎡⎤⎢⎥=+++⎢⎥---⎢⎥+++⎣⎦==+⎰2.7利用泰勒公式求极限常用泰勒公式展开235211224221211();2!!sin (1)();3!5!(21)!cos 1(1)();2!4!(2)!ln(1)(1)();2nxn n n n nn n nn n x x e x x n x x x x x x n x x x x x n x x x x x nοοοο--+-=+++⋅⋅⋅++=-++⋅⋅⋅+-+-=-++⋅⋅⋅+-++=-+⋅⋅⋅+-+22(1)(1)(1)(1)1();2!!11().1n n n n n x x x x x n x x x x x--⋅⋅⋅-++=+++⋅⋅⋅++=+++⋅⋅⋅++-αααααααοο例10求极限00)x a →>.解利用泰勒公式,当0x →时1()2xo x =++,于是 0limx x→x →= 01211()()1()22limx x x o x o x a a x→⎤++--⋅-⎥⎣⎦=0()2lim x x o x a x →+=0x →==. 例11 求极限2602cos 2lim x x x e e x x x -→+--.解 应用泰勒公式,将函数x e ,x e -,cos x 展开到6x 项,有2345661(),1!2!3!4!5!6!xx x x x x x e x ο=+++++++2345661(),1!2!3!4!5!6!xx x x x x x ex ο-=-+-+-++2466cos 1().2!4!6!x x x x x ο=-+-+将它们代入上式,整理,得66266004()2cos 246!lim lim 6!xxx x x x e e x x x x ο-→→++--==. 2.8两边夹法则求极限当极限不易求出时,可考虑将所求极限变量,做适当的放大或缩小,是放大或缩小的新变量,易于求极限,且二者的极限值相等,则原极限存在,切等于此公共值.例11 求极限01lim x x x →⎡⎤⎢⎥⎣⎦.解 因为1x ⎡⎤⎢⎥⎣⎦是对1x 取整,则1111(0)x x x x⎡⎤-<≤≠⎢⎥⎣⎦, 当0x >时,111x x x ⎡⎤-<≤⎢⎥⎣⎦,当0x <时,111x x x ⎡⎤->≥⎢⎥⎣⎦, 故1lim 1x x x →⎡⎤=⎢⎥⎣⎦. 例12 设1!2!!,!n n x n ++⋅⋅⋅+=求极限lim .n n x →∞解 当分子2n >时,有2!1!2!(2)!(1)!n n n n -<++⋅⋅⋅+-+-(2)(2)!(1)!!n n n n <--+-+2(1)!!n n <-+,因此,当2n >时,211n x n<<+, 所以lim 1n n x →∞=.2.9利用单侧极限求极限可以用单侧极限求解的问题类型如下(1) 求含xa 的函数x 趋向无穷的极限,或求含1xa 的函数x 趋于0的极限; (2) 求含取整函数的函数极限; (3) 分段函数在分段点处的极限;(4) 含偶次方根的函数以及arctan x 的函数,x 趋向无穷的极限.这种方法还能使用于求分段函数在分段点处的极限,首先必须考虑分段点的左、右极限,如果左、右极限都存在且相等,则函数在分界点处的极限存在,否则极限不存在.例13 设函数21sin ,0()1,0x x f x xx x ⎧>⎪=⎨⎪+≤⎩ ,求()f x 在0x =的极限. 解 由于1lim sin 1x x x+→=,20lim(1)1x x -→+=,故00lim ()lim ()1x x f x f x +-→→==, 从而lim ()1x f x →=.2. 10利用中值定理求极限拉格朗日(Lagrange )中值定理 若函数()f x 满足如下条件 (i) ()f x 在闭区间,a b 上连续 ; (ii) ()f x 在开区间(,)a b 可导, 则在(,)a b 至少存在一点ξ,使得()()()f b f a f b aξ-'=- .例14 求函数极限30sin(sin )sin lim x x xx →- .解 因为sin(sin )sin x x -[](sin )cos (sin )x x x x x θ=-⋅⋅-+ (01)θ<<,所以30sin(sin )sin limx x xx→- []3(sin )cos (sin )lim x x x x x x xθ→-⋅⋅-+=20cos 1lim3x x x →-=0sin lim 6x x x →-=16=-积分中值定理 若()f x 在[,]a b 上连续,则至少存在一点[,]a b ξ∈,使得()()()b af x dx f b a ξ=-⎰.例15 求极限sin lim ,n p nn xdx x+→∞⎰p 为某实数. 解 由积分中值定理,得sin sin n p n nnx dx p x ξξ+=⋅⎰,因为n ξ为介于n 与n p +之间的某值,则111n n n p ξ≤≤+ 或 111n n n pξ≥≥+, 而sin 1n ξ≤,由无穷小量与有界量的乘积仍为无穷小量及迫敛性得sin lim 0n p nn xdx x+→∞=⎰. 定理(推广的积分第一中值定理) 若函数()f x 与()g x 在[],a b 上连续,且()g x 在[],a b 上不变号,则至少有一点[],a b ξ∈,使得()()()()b baaf xg x dx f g x dx ξ=⎰⎰.例16 求函数极限40lim sin n n xdx π→∞⎰.解 由题 ()sin ,()1,n f x x g x ==均在[0,]4π上连续,且()g x 不变号,由推广的积分第一中值定理40limsin nn xdx π→∞⎰40lim sin nn dx πξ→∞=⎰ limsin (0)4n n πξ→∞=⋅-lim(sin )04n n πξ→∞==.小结以上所求极限的方法各有条件、各具特色,因此各种类型所采用的技巧方法都不尽相同,我们必须根据其条件来判断极限的类型,进而根据类型来找到解决问题的方法.当然,有些题目有可能可以用多种方法来解决,此时,我们不可以死搬硬套,要从繁琐中找复杂,在复杂中找简单,而关于如何做到这一点,就必须在做题中不断总结、摸索、领悟各种方法的精髓,才能熟练而有灵活的掌握与运用各种求极限的方法.参考文献[1] 林源渠,方企勤. 数学分析解题指南.[M].:大学,2003.[2] 郝涌,学志,陶有德. 数学分析选讲.[M].:国防工业,2010.[3] 同济大学应用数学系. 高等数学.[M].:高等教育,1996.[4] 玉琏,奎元,伟,吕风. 数学分析讲义学习辅导书.[M].:高等教育,2003.[5] 清华,昊.数学分析容、方法与技巧.[M].华中科技大学, 2003.[6] 华东师大学数学系. 数学分析上册第三版.[M].高等教育,2001.[7] 钱. 数学分析解题精粹.[M].:崇文书局,2003.[8] 梁昌洪. 话说极限.[M].:高等教育,2009.。
中国古代数学中的极限思想文献综述

中国古代数学中的极限思想文献综述文献综述中国古代数学中的极限思想前言部分(说明写作的目的,介绍有关概念、综述范围,扼要说明有关主题争论焦点)极限是数学的一个重要概念。
在数学中,如果某个变化的量无限地逼近于一个确定的数值,那么该定值就叫做变化的量的极限。
极限的思想是近代数学的一种重要思想,数学分析就是以极限概念为基础、极限理论包括级数为主要工具来研究函数的一门学科。
所谓极限的思想,是指用极限概念分析问题和解决问题的一种数学思想。
用极限思想解决问题的一般步骤可概括为:对于被考察的未知量,先设法构思一个与它有关的变量,确认这变量通过无限过程的结果就是所求的未知量;最后用极限计算来得到这结果参见文献[1]。
极限思想是微积分的基本思想,数学分析中的一系列重要概念,如函数的连续性、导数以及定积分等等都是借助于极限来定义的。
如果要问:“数学分析是一门什么学科?”那么可以概括地说:“数学分析就是用极限思想来研究函数的一门学科”。
极限的应用及推广已涉及社会、科学及研究的很多方面。
对其进行研究不仅在理论上也在实践中具有很大的意义。
主题部分(阐明有关主题的历史背景、现状和发展方向,以及对这些问题的评述)早在春秋战国时期(公元前770??前221)道家的代表人物庄子就有了极限思想,据《庄子》“天下篇”中记载:“一尺之棰,日取其半,万事不竭”[2][3]。
意思是说一尺长的木棒每天去下前一天所剩的一半,如此下去,永远也取不完。
这反映了古人对极限的一种思考,它不但表达了我们祖先的极限思想,也提供了一个“无穷小量”的实际例子。
这个经典论断,至今在微积分的教学中还经常使用参见文献[4]。
我国古代的极限思想与方法主要寓于求积面积、体积理论。
刘徽继承和发扬了先秦诸子关于极限的思想用“割圆术”和“阳马术”等成功地解决了求积问题。
在《九章算术》的“圆田术”中给出了计算圆面积的法则:“半周半径相乘得积步。
”即圆的面积S 与一个长为半周C /2,宽为半径的长方形的面积相等:参见文献[5]。
数列上下极限的不同定义方式及相关性质综述

目录数列上下极限的不同定义方式及相关性质摘要 (01)一、数列的上极限、下极限的定义 (01)1. 用“数列的聚点”来定义 (01)2. 用“数列的确界”来定义 (02)3. 数列上、下极限定义的等价性 (02)二、数列的上、下极限的性质及定理 (04)参考文献 (14)英文摘要 (15)数列上下极限的不同定义方式及相关性质摘 要:数列的上、下极限的概念是极限概念的延伸,由于它们在正项级数敛散性的判别法中的重要作用,又成为数学分析中重要的理论部分.本文主要讨论了数列的上下极限的两种定义方式及其等价证明和一些相关定理. 关键词:数列、上极限、下极限、聚点、函数一、数列的上极限、下极限的定义关于数列的上极限、下极限的定义常见的有如下两种形式: 1. 用“数列的聚点”来定义定义 1 若在数a 的任一邻域内都含有数列{}n x 的无限多项,则称a 为数列{}n x 的一个聚点.例1 数列{(1)}1n nn -+有聚点1-与1; 数列{sin}4n π有1,22--和1五个聚点; 数列1{}n只有一个聚点0;常数列{1,1,,1,}只有一个聚点1.定义 2 有界数列{}n x 的最大聚点a 大与最小聚点a 小分别称为数列{}n x 的上极限和下极限,记作lim n a →+∞=大;lim n n a x →∞=小.例2 lim (1)11nn n n →+∞-=+(),lim 111n n n →∞-=-+lim sin14n n π→+∞=,limsin 14n n π→∞=- 11lim lim 0n n n n→+∞→∞==2. 用“数列的确界”来定义定义3 任给数列{}n x ,定义lim limsup{}n k n n k nx x →+∞→∞≥=;lim lim inf{}n k n k nn x x →∞≥→∞= (1)分别称为数列{}n x 的上极限和下极限.若定义1中的a 可允许是非正常点+∞或-∞,则:任一点列{}n x 至少有一个聚点,且存在最大聚点与最小聚点.不难证明:正上(下)界点列的最大(小)聚点为()+∞-∞.于是,无上(下)界点列有非正常上(下)极限()+∞-∞.例3 lim ((1)1)n n n →+∞-+=+∞,lim (1)n n n →+∞-=-∞,lim(1)n n n →∞-=-∞3. 数列上、下极限定义的等价性下面我们来证明一下数列上、下极限定义的等价性,即lim limsup{}n k n n k na x x →+∞→∞≥==大;lim liminf{}n k n k nn a x x →∞≥→∞==小.证明:如果l i m s u p {}k n k nx →∞≥=+∞,由于s u p {}kk nx ≥关于n 单调递减,所以sup{}k k nx ≥=+∞,n N ∀>.于是,可取1n ∈(自然数)1..1n s t x >,又可取2,n ∈221,..2,,n n n s t x >>所以,得到数列{}n x 的子列{}()n k x k →+∞→+∞.这就证明了+∞为数列的聚点,且为最大聚点a 大.由此可得lim limsup{}n k n n k na x x →+∞→∞≥==+∞=大;如果limsup{}k n k nx →∞≥<+∞,则limsup{}k n k nx →∞≥=-∞或实数.设a 数列{}n x 的任一聚点,则必有{}n x 的子列,()i n x a i →→+∞.,n ∀∈,,i i n n i n ≥≥≥当时有sup{}i n k k nx x ≥≤,lim sup{}i n k i k na x x →∞≥=≤,limsup{}k n k na x →∞≥≤,所以,数列{}n x 的最大聚点满足lim limsup{}n k n n k nx x →+∞→∞≥≤.另一方面, lim ,n n y x →+∞∀>易见,[)∞y,+中最多含有数列{}n x 中的有限多项.因此,,N ∃∈当k N >时,有k x y <,从而,当n N >时,有sup{},k k nx y ≥≤由此可得limsup{}k n k nx y →∞≥≤.令()lim nn y x +→+∞→,推出limsup{}lim k n n n k nx x →∞→+∞≥≤.综合上述,有lim limsup{}n k n n k na x x →+∞→∞≥==.类似的可证明或应用上式于{}n x -可证得lim liminf{}n k n k nn a x x →∞≥→∞==小.如果lim inf{}k n k nx →-∞≥=-∞,由于inf{}k k nx ≥关于n 单调递减,所以inf{}k k nx ≥=-∞,对n N ∀>.于是,可取自然数1n 使得11-<n x ,又可取自然数2n 12n n >使得22-<n x ……所以,得到数列{}n x 的子列{k n x }-∞→.这就证明了∞-为数列的聚点,且为最小聚点小a .由此可得lim lim inf{}n k n k nn a x x →-∞≥→∞==小;如果lim inf{}k n k nx →-∞≥>-∞,则lim inf{}k n k nx →-∞≥=+∞或实数.设a 数列{}n x 的任一聚点,则必有{}n x 的子列,()i n x a i →→+∞.任意的n 是自然数,,i i n n i n ≥≥≥当时有k n x ≥inf{}k k nx ≥lim inf{}i n k i k na x x →∞≥=≥lim inf{}k n k na x →+∞≥≥所以,数列{}n x 的最小聚点满足lim n n x →∞≥lim inf{}k n k nx →+∞≥.另一方面,对任意的y ≥lim n n x →∞易见,(-],y ∞中最多含有数列{}n x 中的有限多项.因此,存在N 是自然数当k N >时,有y x k >,从而,当n N >时,有inf{}k k nx ≥y ≥,由此可得lim inf{}k n k nx →+∞≥y ≥.令y →[lim n n x →∞]-,推出lim inf{}k n k nx →+∞≥≥lim n n x →∞.综合上述,有lim lim inf{}n k n k nn a x x →+∞≥→∞==小.下面进一步给出和数列上,下极限定义有关的性质及定理.二、数列的上、下极限的性质及定理设有数列{}n x 与数列{}n y ,则数列的上、下极限有以下性质性质 1 lim lim n n n n x x →+∞→∞≥; (2)性质 2 lim lim lim n n n n n n x A x x A →+∞→+∞→∞=⇔==例 4 用上下极限理论证明:若{}n x 是有界发散数列,则存在{}n x 的两个子列收敛于两个不同的极限.证明:因为数列发散的充要条件是lim lim n n n n x x →+∞→∞≠,于是存在{}n x 的两个子列{}{}''',k k n n x x ,使'l i m l i mk n n n n x x →+∞→+∞=,''lim lim k n n n n x x →+∞→∞=,即存在{}n x 的两个子列收敛于不同的极限.性质 3 (保不等式性质)设有界数列{}n x ,{}n y 满足:存在00N >,当0n N >时有n n x y ≤,则lim lim n n n n x y →+∞→+∞≤;lim lim n n n n x y →∞→∞≤;特别,若,αβ为常数,又存在00N >,当0n N >时有n a αβ≤≤,则lim lim n n n n a a αβ→+∞→∞≤≤≤性质 4 设0,0,(1,2,)n n x y n ≥≥=,则lim lim lim lim lim n n n n n n n n n n n x y x y x y →+∞→∞→∞→∞→∞⋅≤≤⋅ (3)lim lim lim lim lim n n n n n nn n n n n x y x y x y →+∞→+∞→+∞→+∞→∞⋅≤≤⋅(4)例5 证明:若{}n x 收敛,则对任意n y (1,2,)n =,有lim lim lim n n n n n n n x y x y →+∞→+∞→+∞=⋅(0)n x ≥证明:分三种情况讨论1、 若lim 0n n y →+∞>,则{}n y 中有无穷多项大于零,作新序列,0max{,0}00n n n n n y y y y y +>⎧==⎨≤⎩当时,当时则0n y +≥,且lim lim n n n n y y +→+∞→+∞=,对{}n x {}n y +应用(4)有lim lim lim lim lim n n n n n n n n n n n x y x y x y +++→+∞→+∞→+∞→+∞→∞⋅≤≤⋅因{}n x 收敛,所以 lim lim lim n n n n n n x x x →+∞→+∞→∞==,故上式表明 lim lim lim lim lim n n n n n n n n n n n x y x y x y ++→+∞→+∞→+∞→+∞→+∞=⋅=⋅但 lim lim lim n n n n n n n n n x y x y x y ++→+∞→+∞→+∞==()0n x ≥(因)所以 lim lim lim n n n n n n n x y x y →+∞→+∞→+∞=2、 若lim n n y →+∞=-∞,在限制条件下,lim 0n n x →+∞>,因此n 充分大时有0n x >,这时等式明显成立.3、 若lim 0n n y →+∞-∞<≤,可取充分大的正常数C>0,使得l i m ()0n n y C →+∞+>, 如此应用1、的结果, lim ()lim lim ()n n n n n n n x y C x y C →+∞→+∞→+∞+=⋅+再根据(3),此即 lim lim lim lim lim n n n n n n n n n n n x y x C x y x C →+∞→+∞→+∞→+∞→+∞+⋅=⋅+⋅从而 lim lim lim n n n n n n n x y x y →+∞→+∞→+∞=⋅,证毕.性质 5 在不发生()±∞∞)+(情况下,有如下不等式成立:1、lim lim lim ()lim lim n n n n n n n n n n n x y x y x y →+∞→+∞→+∞→+∞→∞+≤+≤+2、lim lim lim()n n n n n n n x y x y →∞→∞→∞+≤+3、lim ()lim lim n n n n n n n x y x y →+∞→+∞→+∞+≤+事实上,这里的等号可以不发生,如对{}{1,0,1,0,1,0,}n x =; {}{0,2,0,2,0,2,}n y =, 这时{}{1,2,1,2,1,2,}n n x y +=lim lim 0lim()1n n n n n n n x y x y →∞→∞→∞+=<+=lim ()2lim lim 3n n n n n n n x y x y →+∞→+∞→+∞+=<+=例6 证明:若{}n x 收敛,则对任意n y (1,2,)n =,有lim ()lim lim n n n n n n n x y x y →+∞→+∞→+∞+=+证:我们已有lim lim lim ()lim lim n n n n n n n n n n n x y x y x y →+∞→+∞→+∞→+∞→∞+≤+≤+注意{}n x 收敛,因此lim lim lim n n n n n n x x x →+∞→+∞→∞==,所以上式即为 lim lim lim ()lim lim n n n n n n n n n n n x y x y x y →+∞→+∞→+∞→+∞→∞+≤+≤+即成立.例7 证明:(1)lim lim lim()lim lim n n n n n n n n n n n x y x y x y →+∞→∞→∞→∞→∞+≤+≤+(2)lim lim lim ()lim lim n n n n n n n n n n n x y x y x y →+∞→+∞→+∞→+∞→∞+≤+≤+证: 先证: lim ()lim n n n n x x →+∞→+∞-=-(1) 设lim n n x a →+∞=,则依上极限定义,0ε∀>,数列{}n x 中至多只有N 项大于a ε+,而有穷项小于a ε-,即对{}n x -,至多有N 项小于a ε--,而有穷项大于a ε-+,所以依下极限定义,有 lim()n n x a →∞-=-,即lim()lim n n n n x x →+∞→∞-=-.设 lim n n x a →∞=,lim n n y b →∞=,lim()n n n x y a b →∞+=+用反证法,设c a b <+,依下极限定义,0ε∀>,N ∃,当n N >时,有n n x y c ε+<+ 不妨设 1()2a b c ε=+-, 则当n N >时, n n x y c a b εε+<+<+- 又有 lim n n x a →∞=,lim n n y b →∞=,依下极限定义,则当1n N >时,2n x a ε<-,当2n N < 时2n y b ε<-,由此推出矛盾,故a b c +≤,即lim lim lim()n n n n n n n x y x y →∞→∞→∞+≤+,又令n n n d x y =+,则()n n n x d x =+-.于是lim lim()lim n n n n n n d y x →∞→∞→∞+-≤,由于 lim()lim n n n n y y →+∞→∞-=-,所以 lim lim()lim lim n n n n n n n n n d x y x y →+∞→∞→∞→∞≤+≤+(2) 以n y -及n x -分别代替题(1)中的n x 与n y ,有lim()lim()lim ()lim lim n n n n n n n n n n n y x x y y x →+∞→∞→∞→∞→∞-+-≤-+≤+-,由 lim()lim n n n n x x →+∞→∞-=-得 lim lim lim ()lim lim n n n n n n n n n n n x y x y x y →+∞→+∞→+∞→+∞→+∞--≤-+≤--,即 lim lim lim ()lim lim n n n n n n n n n n n x y x y x y →+∞→+∞→+∞→+∞→∞+≤+≤+,当{}:0,1,2,0,1,2,n x ;{}:2,3,1,2,3,n y 时,题(1)(2)中仅不等号成立.性质 6lim ()lim n n n n x x →+∞→∞-=-;lim()lim n n n n x x →+∞→∞-=-;性质 7 若 lim 0n n x →∞>,则1lim lim1n n n nx x →+∞→∞⋅=; (7)例7 证:若0,(1,2,)n a n >=且1lim lim1n n n na a →+∞→+∞⋅=,则数列{}n a 收敛.证明:若lim 0n n a →∞=,则∃子列{}k n a ,lim 0k n k a →+∞=,于是有1limkk n a →+∞=+∞,这与1lim lim1n n n na a →+∞→+∞⋅=相矛盾,这样应当有lim 0n n a →+∞>,然后用上下极限等价定义来证明.性质8 当 n x a →,且0n x ≥,则下式右端有意义(不是0⋅∞型)时,有lim lim n n n n n x y a y →∞→∞=;lim lim n n n n n x y a y →+∞→+∞=.证明:以第二式为例给出证明首先设 lim 0n n y b →+∞=>,其中b 为有限数或+∞.令 ,00,0.n n n n y y z y >⎧=⎨≤⎩当;当则lim lim n n n n z y b →+∞→+∞==;lim lim n n n n n n x z x y →+∞→+∞=.由0,0n n x z ≥≥得lim lim lim lim lim n n n n n n n n n n n x z x z x z →+∞→+∞→+∞→+∞→∞≤≤⋅,即lim lim lim n n n n n n n a z x z a z →+∞→+∞→+∞≤≤⋅,也就是lim lim n n n n n x z a z →+∞→+∞=⋅,代回到n y 就得到lim lim n n n n n x y a y →+∞→+∞=⋅.其次设 lim 0n n y b →+∞=≤ (b 为有限数)只要用1n y b +代替n y (其中10b b +>),就可得证. 最后 lim n n y →+∞=-∞,这时即n y →-∞,且0a ≠(否则出现0⋅∞型),显然n n x y →-∞.下面定理指出,对一切数列{}n x 的上、下极限必存在(包括±∞). 定理 1(1)有界数列{}n x 至少有一个聚点,存在最大聚点与最小聚点,且这两个聚点都为实数,它们分别为上极限lim n n x →+∞与下极限lim n n x →∞;(2)如果数列{}n x 无上界,则lim n n x →+∞=+∞,此时+∞为数列{}n x 的最大聚点;如果数列{}n x 有上界b① 若[],,a b a b ∀<中含有数列{}n x 的有限项,则lim lim n n n n x x →+∞→∞=-∞=,此时lim n n x →+∞=-∞;② 若[],,a b a b ∃<中含有数列{}n x 的无限项,则数列{}n x 以实数为最大聚点,它就是lim n n x →+∞;(3) 如果数列{}n x 无下界,则lim n n x →∞=-∞,此时-∞为数列{}n x 的最小聚点;如果数列{}n x 有下界a① 若[],,b a a b ∀>中含有数列{}n x 的有限项,则lim lim n n n n x x →+∞→∞=+∞=,此时lim n n x →+∞=+∞;② 若[],,b a a b ∃>中含有数列{}n x 的无限项,则数列{}n x 以实数为最小聚点,它就是lim n n x →∞.证明: (1) 因数列{}n x 有界,令{}[][]11|,,.n M M a b ∈⊂-=n x 将[]11,a b 两等分,则必有一等分含数列{}n x 的无限多项,记此区间为[]22,a b ,则[][]1122,,a b a b ⊃,且 ()221112b a b a M -=-=; 再将[]22,a b 两等分, 则必有一等分含数列{}n x 的无限多项,记此区间为[]33,a b ,则[][]2233,,a b a b ⊃,且()3322122M b a b a -=-=; 如此下去得到一个递降闭区间套:[][][]1122,,,k k a b a b a b ⊃⊃⊃⊃;10()2k k k Mb a k --=→→+∞, 且每个闭区间[],k k a b 都含有数列{}n x 的无限多项.由闭区间套定理知,[]01|,k k k x a b ∞=∃∈对0x 的任何开领域U,0,..s t ε∃> 000(;)(,)B x x x Uεεε=-+⊂,则N ∃∈,当k N >时,00[,](,)k k a b x x U εε⊂-+⊂,从而U 中含有数列{}n x 的无限多项,所以0x 为数列{}n x 的聚点.至于最大聚点的存在性,只需在上述证明过程中,当每次将区间[]11,k k a b --等分为两个区间时,若右边一个含数列的无限多项,将它取为[],k k a b ;若右边一个含数列的有限项,则取左边的子区间为[],k k a b .于是,所选[],k k a b 都含有数列{}n x 的无限多项,同时在[],k k a b 的右边都至多含有数列的有限项,其中()1111111()022k k k k k b a b a b a ----=-==-→ ()k →+∞ 再根据闭区间套定理知,[]01|,k k k x a b ∞=∃∈.下证0x 为数列{}n x 的最大聚点.(反证) 若不然,设另有数列{}n x 的聚点*00,x x >令*001()0,3x x δ=->则有 ***000(;)(,)B x x x δδδ=-+ 内都含有数列{}n x 的无限多项,但当k 充分大时,***000(;)(,)B x x x δδδ=-+完全落在[],k k a b 的右边,这与上述[],k k a b 的右边都至多含有数列{}n x 的有限项矛盾.类似可证最小聚点的存在性,或用{}n x -代替{}n x .(2) 如果数列{}n x 无上界,则{}n x 必有子列{}k n x ,..lim k n n s t x →+∞=+∞,因此,+∞ 为数列{}n x 的最大聚点,从而lim n n x →+∞=+∞.如果数列{}n x 有上界b① 若[],,a b a b ∀<中含有数列{}n x 的有限项,则根据极限为-∞的定义可知,lim lim n n n n x x →+∞→∞=-∞=;② 若[],,a b a b ∃<中含有数列{}n x 的无限项,由(1)的结果, 数列{}[],n x a b 有最大聚点,显然它也是数列{}n x 的最大聚点,即为lim n n x →+∞; (3) 类似(2)可证明,或用{}n x -代替{}n x .定理 2 lim lim lim n n n n n n x a x x a →+∞→+∞→∞=⇔==.证明:()⇒ 设lim n n x a →+∞=,则对a 的任一邻域U ,N ∃∈,当n N >时,n x U ∈,从而a 为数列{}n x 的一个聚点.b a ∀≠, 则存在a 的开邻域a U ,b 的开邻域b U ,..ab s tU U φ= . 由于lim n n x a →+∞=,故N ∃∈,当n N >时,n a x U ∈,所以n b x U ∉,从而b U 中至多含有数列{}n x 的有限项(如12,,,N x x x )因此,b 不为数列{}n x 的聚点.综上可知,a 为数列{}n x 的唯一聚点,所以lim lim n n n n x a x →+∞→∞==.或者,因lim n n x a →+∞=,故{}n x 的任何子列{}k n x 也必有lim k n n x a →+∞=.因此,数列{}n x 有唯一的聚点,从而lim lim n n n n x a x →+∞→∞==.()⇐ 设lim lim n n n n x x a →+∞→∞==,则数列{}n x 只有一个聚点a ,因此,对a 的任一开邻域U ,在U 外只含有数列{}n x 的有限多项1,,k n n x x (否则数列{}n x 在U 外还有异于a 的聚点,这与数列{}n x 只有一个聚点相矛盾).于是,当{}1max ,,1k n N n n >=时,有n x U ∈,这就证明了lim n n x a →+∞=.定理 3 设{}n x 为有界数列,则下列结论等价:(1) a 大为数列{}n x 的上极限;(2) 0,,..N s t ε∀>∃∈当n N >时,有n x a ε<+大;且存在子列{}k n x ,..s t,k n x a k ε>-∀∈大;(3) ,a a ∀>大 数列{}n x 中大于a 的项至多有限个;,b a ∀<大 数列{}n x 中大于b 的项有无限多个.证明:(1)(2)⇒:因a 大为数列{}n x 的聚点,故0,ε∀>在()a a a εεε=-+大大大;(,)内含有数列{}n x 的无限多项{}12|knx n n <<,则有,kn xa k ε>-∀∈大.又因a 大为数列{}n x 的最大聚点,故在a ε+大的右边至多只含有数列{}n x 的有限多项(否则必有数列{}n x 的聚点a ε≥+大,这与a 大为数列{}n x 的最大聚点相矛盾).设此有限项的最大指标为N ,则当n N >时,有n x a ε<+大.(2)(3)⇒:,a a ∀>大令a a ε=-大,由(2)知,N ∃∈,当n N >时,有n x a ε<+大()a a a a =+-=大大.故数列{}n x 中大于a 的项至多有限个.b a ∀<大,令a b ε=-大,由(2)知,存在数列{}n x 的子列{}k n x ,,k n x a b ε>-=大k ∀∈,故数列{}n x 中大于b 的项有无限多个.(3)(1)⇒:设U 为a 大的任一开邻域,则0,..(;).s t B a a a U εεεε∃>=-+⊂大大大(,)由于a a a ε=+>大大,根据(3),{}n x 中大于a a ε=-大有无限多项.因此a a ε-+大大(, ε)中含有数列{}n x 的无限项,从而U 中含有数列{}n x 的无限项,这就证明了a 大为数列{}n x 的一个聚点.另一方面,a a ∀>大,记1()2a a ε=-大.由(3)知,数列{}n x 中大于()a a ε+>大大的项至多有限个.故a 不为数列{}n x 的一个聚点,这就证明了a 大为数列{}n x 的最大聚点,即a 大为数列{}n x 的上极限.定理 4 设{}n x 为有界数列,则下列结论等价:(1) a 小为数列{}n x 的下极限;(2) 0,,..N s t ε∀>∃∈当n N >时,有n x a ε>-小;且存在子列{}k n x ,..s t,k n x a k ε<+∀∈小;(3) b a∀<小,数列{}n x中小于b的项至多有限个;a a∀>小,数列{}n x中小于a的项有无限多个.证明:类似定理3证明,或用{}n x-代替{}n x.从一些性质和定理的证明可以看出有些步骤用到数列上,下极限定义方面的证明过程.此外,关于不同对象的上、下极限的定义,本质上都起源于数列的上、下极限定义,比如,集合列的上,下限极等,在此就不做介绍了.参考文献:[1] 华东师范大学数学系编.数学分析(上册).北京:高等教育出版社,2001[2] 复旦大学数学系陈传璋等编.数学分析(下册).北京:高等教育出版,1979[3] 李成章,黄玉民编. 数学分析(上册).科学出版社,1998[4] 程其蘘.实变函数与泛函分析基础[M] .2版.北京:高等教育出版社,2003[5] 朱成熹.近世实分析基础[M].天津:南开大学出版社,1993[6] 匡继昌.实分析与泛函分析[M].北京:高等教育出版社,2002[7] 薛昌兴.实变函数与泛函分析:上[M].北京:高等教育出版社,1997[8] 裴礼文.数学分析中的典型问题与方法.北京:高等教育出版社,1993[9] 吴良森,毛羽辉著.数学分析学习指导书(上册).北京:高等教育出版社,2004[10] 胡适耕,张显文著.数学分析原理与方法.北京:科学出版社,2008[11] 陈纪修,於崇华著.数学分析第二版(下册).北京:高等教育出版社.2004The sequence about limit with gathers the row on lower limit collectionHao Li-jiao 200711150652007 grades of mathematics,science college mathematics and the applied mathematicsprofessions 1 classAbstract:Sequence on, under the limit concept is limit concept extending,because they collect in the divergence distinction law in the seriesof positive terms the vital role, also becomes the theory which in themathematical analysis has no alternative but to say to be partial.This article mainly discussed the sequence about limit with to gatherthe row on lower limit collection as well as their a series of natureKey words: Sequence;Limit;Accumulation points;Sequence of sets;Function。
极限计算方法的研究现状

极限计算方法的研究现状一、选题的意义与一切科学的思想方法一样,极限思想也是社会实践的产物。
极限的思想可以追溯到古代,刘徽的割圆术就是建立在直观基础上的一种原始的极限思想的应用;古希腊人的穷竭法也蕴含了极限思想。
到了16世纪,荷兰数学家斯泰文在考察三角形重心的过程中改进了古希腊人的穷竭法,如此,他就在无意中“指出了把极限方法发展成为一个实用概念的方向”。
起初牛顿和莱布尼茨以无穷小概念为基础建立微积分,后来因遇到了逻辑困难,所以在他们的晚期都不同程度地接受了极限思想。
但是,这种定义没有定量地给出两个“无限过程”之间的联系,不能作为科学论证的逻辑基础。
到了18世纪,罗宾斯、达朗贝尔与罗依里埃等人先后明确地表示必须将极限作为微积分的基础概念,并且都对极限作出过各自的定义。
首先用极限概念给出导数正确定义的是捷克数学家波尔查诺,但关于极限的本质他仍未说清楚。
到了19世纪,法国数学家柯西在前人工作的基础上,比较完整地阐述了极限概念及其理论极限的思想方法贯穿数学分析的始终。
可以说数学分析中几乎所有概念离不开极限。
几乎所有数学分析著作都是先介绍极限,然后利用极限的方法给出连续函数,导数,定积分,级数的敛散性,多元函数的偏导性,重积分和曲线积分与曲面积分的概念。
所以掌握极限的技巧和方法是学好高等数学的前提条件。
求极限的方法因题而异,变化多端,有时甚至感到变幻莫测无从下手,本文总结几种常用的求极限的方法以供参考。
二、研究的主要内容,拟解决的主要问题(阐述的主要观点)极限计算的方法与技巧为主要线索,并注释方法的使用范围和使用的常见误区1.明确极限理论的研究意义2.归纳、总结极限的十几种方法3.归纳极限方法的一些技巧并对其注释4.综述三、研究(工作)步骤、方法及措施(思路)本论文设计采取理论研究,网络搜索,文献查阅等多种方法,坚持在老师的指导下单独完成,研究的步骤:1.熟悉、理解和掌握极限理论的思想,方法。
2.通过网络资源,校图书馆途径查阅参考文献。
2013年考研数学复习指导--求函数的极限

求函数的极限一.函数极限的概念1.函数极限的定义定义1: 设函数)(x f y =在0x 的某个去心邻域内有定义,若对0>∀ε,0>∃δ,当δ<-<00x x 时,恒有ε<-a x f )(,则称)(x f y =在0x x →的极限为a ,记为a x f x x =→)(lim 0.(直观地说a x f x x =→)(lim 0:当x 无限趋近0x 时,函数)(x f 无限趋近常数a .)定义2:设函数)(x f y =在0>>E x 内有定义,若对0>∀ε,0>∃M ,使得当M x >时,恒有ε<-a x f )(,则称)(x f y =在∞→x 的极限为a ,记为a x f x =∞→)(lim .2.左、右极限的定义右极限:⇔==+→+a x f x f x x )(lim )(000,0>∃>∀δε当δ<-<00x x 时,恒有ε<-a x f )(. 左极限:⇔==-→-a x f x f x x )(lim )(000>∀ε,0>∃δ当00<-<-x x δ时,恒有ε<-a x f )(.⇔=+∞→a x f x )(lim 0>∀ε,0>∃M ,当M x >时,恒有ε<-a x f )(. ⇔=-∞→a x f x )(lim 0>∀ε,0>∃M ,当M x -<时,恒有ε<-a x f )(.3.极限存在的充要条件:a x f x x =→)(lim 0⇔=+→)(lim 00x f x x a x f x x =-→)(lim 0a x f x =∞→)(lim ⇔=+∞→)(lim x f x a x f x =-∞→)(lim .例1.(1)xx e ∞→lim ; x x e 10lim →; 111lim -→x x e;(2),ln lim 00x x +→ x x ln lim +∞→;(3)x x sin lim ∞→; x x 1sinlim 0→; ∞=→x x 1lim 0;(4)x x arctan lim ∞→;x x tan lim 2π→.二.求极限的方法1.极限的四则运算法则:设)(lim 0x f x x →和)(lim 0x g x x →都存在,则(1)=±→))()((lim 0x g x f x x ±→)(lim 0x f x x )(lim 0x g x x →;(2)=→)()(lim 0x g x f x x )(lim 0x f x x →)(lim 0x g x x →;(3))(lim )(lim )()(lim 00x g x f x g x f x x x x x x →→→=(0)(lim 0≠→x g x x ).例2 (1))1224(lim 22---+++∞→x x x x x =122436lim22--+++++∞→x x x x x x=312124136lim22=--+++++∞→xx x x xx .(2)x x x x x x cos sin 2cos lim 20+→ =x x x x x x x cos sin 2lim cos lim 020⋅+⋅→→=31cos sin 21lim0=+⋅→xxx x .(3)x x x x 220tan cos sin 1lim -+→ xx x x x x cos sin 11cos sin 1lim 2220++⋅-+=→ 220cos sin 1lim 21x x x x -+=→]sin cos 1[lim 212220xx x x x +-=→.43cos 1lim 212120=-+=→x x x (4))sin 12(lim 41xxee xx x +++→. 解)sin 12(lim 4100x x e e x x x ++++→=)sin 12(lim 4100xx e e x xx ++++→=x xx e e 410012lim 1++++→=x x xx x e e ee 444100/)1(/)2(lim 1++++→=1 =+++-→)sin 12(lim 4100x x ee xx x )sin 12(lim 4100xxe e xxx -++-→=1. 所以 1)sin 12(lim 410=+++→xxee xx x .2.利用等价无穷小求极限.(1)无穷小的定义:若0)(lim 0=→x x x α,则称)(x α为0x x →时的无穷小.(2)无穷小的运算.(3)无穷小的比较:若0)(lim 0=→x x x α, 0)(lim 0=→x x x β且l x x x x =→)()(limβα 若0≠l ,则称)(x α与)(x β是同阶无穷小;若1=l ,则称)(x α与)(x β是等价无穷小,记为)(~)(x x βα; 若0=l ,则称)(x α是)(x β的高阶无穷小,记为))(()(x o x βα=.(4)常用等价无穷小(a)当0→x 时,x x ~sin ; 221~cos 1x x -;x x ~)1ln(+;x x ~arcsin ; x x ~arctan ; x e x ~1-;a x a x ln ~1-;x x αα~1)1(-+.(b ))1)((1)(~)(ln →-x f x f x f .(5)利用等价无穷小求极限当0x x →时,)(~)(x x αα',)(~)(x x ββ',则=→)()()()(limx x g x x f x x βα)()()()(lim 0x x g x x f x x βα''→.例3(1)30sin tan limx xx x -→30)1cos 1(sin limxx x x -=→ x x x x x cos )cos 1(sin lim 30⋅-=→20cos 1lim x x x -=→2121lim 220==→x xx .(2))1sin 1(cot lim 0x x x x -→ xx xx x x x sin sin sin cos lim 0-⋅=→30sin lim x x x x -=→203cos 1lim xx x -=→616sin lim 0==→x x x .例4.当+→0x 时,与x 等价的无穷小量是 (A )x e -1;(B )xx-+11ln;(C )11-+x ;(D )x cos 1-.解(A )x ex--~1 (B )x x -+11lnxxx x x -+=--+1111~x x x ~~+ (C )x x 21~11-+ (D ) x x 21~cos 1- 答案(B )例5.设dt t x f x⎰-=cos 102sin )(,65)(65x x x g +=,则当0→x 时,)(x f 是)(x g 的( ). (A)低阶无穷小; (B)高阶无穷小; (C)等价无穷小; (D)同阶但不等价.解 )()(lim 0x g x f x →65sin lim65cos 1020x x dtt xx +=⎰-→5420sin ])cos 1[sin(lim xx xx x +-=→ 4320)cos 1(lim x x x x +-=→041lim 4340=+=→x x xx . 答案)(B 例6.设当0→x 时,)1ln()cos 1(2x x +-是比n x x sin 高阶的无穷小,而n x x sin 是比12-x e 高阶的无穷小,求正整数n .解 n x x x x x sin )1ln()cos 1(lim 20⋅+-→122021lim +→=n x xx x 0lim 2130==-→n x x 303<⇒>-⇒n n . 1sin lim 2-→x nx e x x 210lim xx n x +→=0lim 10==-→n x x 101>⇒>-⇒n n , 2=∴n .例7.())11sin 11(lim 1x x x x --+→πππx x x x x πππππsin )1(sin )1(lim 11---+=→tt t t t πππππsin sin lim10-+=→ 220sin lim 1t t t t ππππ-+=→t t t 202cos lim 1πππππ-+=→ πππππ12sin lim 1220=+=→t t .3.利用洛必达法则求未定式极限的方法 法则I():设函数)(),(x g x f 满足条件: ①()()0lim ,0lim 0==→→x g x f x x x x②)(),(x g x f 在0x 的去心邻域内可导,且0)(≠'x g ; ③()()x g x f x x ''lim→存在(或∞),则()()()()x g x f x g x f x x x x ''lim lim 00→→=.法则Ⅱ⎪⎭⎫⎝⎛∞∞:设函数()()x g x f ,满足条件 ①()()∞=∞=→→x g x f x x x x 0lim ,lim ;②()()x g x f ,在0x 的去心邻域内可导,且()0'≠x g ; ③()()x g x f x x ''lim→存在(或∞),则()()()()x g x f x g x f x x x x ''limlim 00→→=.例8.(1) )sin sin cos 1(lim 220xx x x e x x x +-+→x x e x xx 220sin cos 1lim 1-++=→201lim 1xe x x x -++=→x e xx 21lim 10-+=→x x x -+=→0lim 211=21.(2)x x x x x 40sin )]tan 1ln()[cos 1(lim +--→202)tan 1ln(lim xx x x +-=→x x xx 4tan 1sec 1lim 20+-=→ x x x x 4sec tan 1lim 20-+=→414tan lim 4120=-=→x x .(3) )1ln()cos 1(1cossin 3lim20x x x x x x +++→=23)1cos sin 3(lim 210=⋅+→x x x x x .4.其它未定式:∞⋅0,∞-∞,00,0∞,∞1)(ln )()())((x f x g x g e x f =)例9.(1)xx x e x sin 120)(lim +→)}ln(sin 1lim exp{20xx e x x +=→}1lim exp{20x e x x x -+=→ 320}1lim 1exp{e xe x x =-+=→.(2)xx xxx sin 1)321(lim ++∞→++}sin )321ln(lim exp{xx x x x +++=+∞→ }/)sin (/)321ln(lim exp{xx x xx x x +++=+∞→})321ln(limexp{x x x x ++=+∞→ 3}3213ln 32ln 2lim exp{=+++=+∞→x x x x x .(3)))}ln 1(ln(ln 1lim exp{)}1ln(ln 1lim exp{)1(lim ln 1ln 1x xx e x x x x x x xx x +∞→+∞→+∞→=-=-}1exp{}ln lim exp{}ln ln )ln(ln lim exp{-=-=-=+∞→+∞→ttt x x x t x综述:求极限的问题,主要是求未定型的极限,而它们都可以化为00型或∞∞型: )a 先化简(代数变形、等价无穷小、代换、非零极限因子),最后化成简单函数的00或∞∞; )b 用分子(或分母)同除(或提取)无穷小或无穷大使分母极限存在且非零,再用四则运算; )c 用洛必达法则.三.极限值已知求其中的未知常数例10.(1)83lim2=-++→a x bbx x a x ,求b a ,的值. 解:0)3(lim 2=++→b bx x ax 032=++⇒b ba a .b a bx a x +=+→212lim82=+⇒b a⎩⎨⎧=+=++82032b a b ab a ⎩⎨⎧-==⇒46b a 或⎩⎨⎧=-=164b a .验证这二组数据都符合条件.(2)设当0→x 时,)1(2++-bx ax e x是比2x 高阶的无穷小,求b a ,的值.解 根据题意 0)1(lim 220=++-→xbx ax e x x =++-→220)1(lim x bx ax e x x x bax e x x 22lim 0--→有0)2(lim 0=--→b ax e xx 1=⇒b .x axe x x 221lim 0--∴→a a x e x x -=--=→21]21[lim 0. 从而有021=-a ,所以21=a .(3)当0→x 时,ax x x f sin )(-=与)1ln()(2bx x x g -=是等价无穷小,则(A )61,1-==b a (B )61,1==b a (C )61,1-=-=b a (D )61,1=-=b a解:由于ax x x f sin )(-=与)1ln()(2bx x x g -=为等价无穷小,则有)()(lim 0x g x f x →)1ln(sin lim 20bx x ax x x --=→)(sin lim 20bx x axx x --=→203cos 1lim bx ax a x --=→ 故有0cos 1lim 0=-→ax a x , 所以1=a .)()(lim 0x g x f x →bbx x bx x x x 6132/lim 3cos 1lim 22020-=-=--=→→,有161=-b 得61-=b .高等数学(同济大学第六版)线性代数(同济大学第五版)概率论与数理统计(浙江大学第四版)。
(黄兆麟)等价无穷小量替换法求极限初探综述

等价无穷小量替换法求极限初探天津港 黄兆麟(发表于内部刊物《港口职工教育》1998年第1期)经验告诉我们,借助一个依赖深奥困难的论证的一般定理,我们就能期望在应用此定理的特殊情形中,避免经历同样深奥困难的论证。
求解某些极限时,借助于一些常见的无穷小量等价式,再利用替换定理 (此即等价无穷小量替换法)正是达到了这样的简化。
然而各类教科书对此法介绍不多,笔者愿在此抛砖引玉,谈谈在教学中的体会。
先说明一些符号:若,αβ是在同一变化过程中的无穷小,则lim1αβ= 记作 αβ, 读作:“α与β等价”。
lim0αβ= 记作 0()αβ=,读作:“α比β高阶”。
lim0k αβ=≠,读作:“α与β同阶”。
再给出一些常见的无穷小量等价式: 当0x →时,23sin ,tan ,arcsin ,arctan ,1,1ln ,ln(1),(1)1,1,1cos ,sin 26x x x x x x x x x x e x a x a x x x x x xxxx xnαα--++---这里x 可以为趋于零的函数式。
替换定理:若11,,,αβαβ是同一变化过程中的无穷小,同时11,ααββ且11limαβ存在, 则有 11limlim ααββ= 证:111111111111limlim()lim lim lim 1lim 1lim αβαβαααααβαββαββββ=⋅⋅=⋅⋅=⋅⋅= 等价符号还满足以下规律 (1)自反律 :αα (2)对称律 :若αβ,则βα(3)传递律 :若αβ且βγ,则αγ, (4)弃高律(吸收律) :0()ααα±(5)乘积律 :若1αα且1ββ,则11αβαβ(6)方幂律 :若αβ,则kk αβ,(0)k >需要指出,以上给出的等价式,均可用两个重要极限及连续函数取极限的有关性质加以证明;而六个规律均可用极限四则运算法则给出证明。
所谓弃高律是指替换时可将和差式中的高阶无穷小弃掉。
极限的求法综述

l i m z = a , 则有l i m y = a .
x_ ∞ 。 。
x一
∞
”
利 用 夹 逼 准 则求 极 限关 键 在 T g , x 的表 达 式 中 , 通 常 通 过
放 大 或 缩 小 的 方 法 找 出 两个 有 相 同极 限值 的 数 列 { y } 和{ z l , 使
当变 形 , 使之具有相应的形式 , 有 时也 可 通 过 变 量 替 换 使 问题
简化 . 三、 利 用 夹逼 准则 求 极 限 夹逼 准则 : 若 一 正 整 数 N, 当n > N I t  ̄, " ix f ≤y ≤z  ̄ . 1 i mx =
极 限法 在 现 代 数 学 乃 至 物 理 等学 科 中有 着 广 泛 的应 用 . 这 是 由它 本 身 固有 的 思 维 功 能 所 决 定 的 . 极 限 法 揭 示 了变 量 与常量 、 无 限 与有 限 的对 立统 一 关 系 . 是 唯 物 辩 证 法 的对 立 统 规 律 在 数 学 领 域 中 的应 用 . 借助极 限法 . 人 们 可 以从 有 限认 识无 限 , 从“ 不变 ” 认识 “ 变” , 从 直 线 形 认 识 曲线 形 , 从 量 变 认 识质变 . 从 近似 认 识 准 确 . 极 限的原始思想 可追溯 到古代. 在 中国 , 公 元前4 世 纪 的
ห้องสมุดไป่ตู้
六、 利用 无 穷 小 量 的 性 质 求极 限 无 穷 小量 的性 质 :无 穷 小 量 与 有 界 量 的 乘 积 还 是无 穷小 量. 如果 l i mf ( x ) = 0, g ( x ) 在某 区间( X o -  ̄, x o ) , ( x n , X 0 + 8 ) 有界 , 那
极限的求法综述

求极限的方法摘要:求极限的方法是高等数学的一个重点,而极限概念是微积分学的中心内容。
因此,弄清极限概念,熟练掌握极限的计算方法,对于学好高等数学是十分必要的。
为此,本文将高等数学中各种极限的计算方法,系统地归纳起来,对于在求极限时,能够灵活地运用求极限的法则,较熟练地选择简便的方法,是很有帮助的。
关键词: 正文:极限的概念是由于求某些实际问题的精确解答而产生的。
例如,我国古代数学家刘徽利用圆内接正多边形来推算圆面积的方法—割圆术,就是极限思想在几何学上的应用。
设有一圆,首先作内接正六边形,把它的面积记为A 1;再作内接正十二边形,其面积记为A 2;再作内接正十二边形,其面积记为A 3;循此下去,每次边数加倍,一般把内接正6×2n-1边形的面积记为A n (n ∈N ).这样,就得到一系列内接正多边形的面积:A1,A 2,A 3…,A n ,…..,它们构成一列有次序的数。
当n 越大,内接正多边形与圆的差别就越小,从而以An 作为圆面积的近似值也越精确。
但是无论n 取得如何大,只要n 取定了,An 终究只是多边形的面积,而还不是圆的面积。
因此,设想n 无限增大(记为n →∞),即内接正多边形的边数无限增加,在这个过程中,内接正多边形无限接近于圆,同时A n 也无限接近于某一确定的数值,这个确定的数值在数学上称为上面这列有次序的数(所谓数列)A 1,A 2,A 3,…..,A n ,…..当n →∞时的极限。
极限有两种.:数列极限:∞→n limxn=a ∀ε>0,∃一个正整数N ,当n>N 时,恒有|Xn-a|<ε函数极限:∞→x limf(x)=A ε>0,一个x>0,当|x|>X,恒有|f(x)-A |<ε.limx x →f(x)=A∀ε>0,∃一个δ>0,当0<|x -x 0|<δ时,恒有|f(x)-A|<ε求极限的方法已归纳出15种,分别列举如下: §1 利用极限定义求极限[解题提示]当数列Xn 不单调时,其极限的存在性可考虑用极限的定义证明。
中国古代数学中的极限思想文献综述

中国古代数学中的极限思想文献综述文献综述中国古代数学中的极限思想前言部分(说明写作的目的,介绍有关概念、综述范围,扼要说明有关主题争论焦点)极限是数学的一个重要概念。
在数学中,如果某个变化的量无限地逼近于一个确定的数值,那么该定值就叫做变化的量的极限。
极限的思想是近代数学的一种重要思想,数学分析就是以极限概念为基础、极限理论包括级数为主要工具来研究函数的一门学科。
所谓极限的思想,是指用极限概念分析问题和解决问题的一种数学思想。
用极限思想解决问题的一般步骤可概括为:对于被考察的未知量,先设法构思一个与它有关的变量,确认这变量通过无限过程的结果就是所求的未知量;最后用极限计算来得到这结果参见文献[1]。
极限思想是微积分的基本思想,数学分析中的一系列重要概念,如函数的连续性、导数以及定积分等等都是借助于极限来定义的。
如果要问:“数学分析是一门什么学科?”那么可以概括地说:“数学分析就是用极限思想来研究函数的一门学科”。
极限的应用及推广已涉及社会、科学及研究的很多方面。
对其进行研究不仅在理论上也在实践中具有很大的意义。
主题部分(阐明有关主题的历史背景、现状和发展方向,以及对这些问题的评述)早在春秋战国时期(公元前770??前221)道家的代表人物庄子就有了极限思想,据《庄子》“天下篇”中记载:“一尺之棰,日取其半,万事不竭”[2][3]。
意思是说一尺长的木棒每天去下前一天所剩的一半,如此下去,永远也取不完。
这反映了古人对极限的一种思考,它不但表达了我们祖先的极限思想,也提供了一个“无穷小量”的实际例子。
这个经典论断,至今在微积分的教学中还经常使用参见文献[4]。
我国古代的极限思想与方法主要寓于求积面积、体积理论。
刘徽继承和发扬了先秦诸子关于极限的思想用“割圆术”和“阳马术”等成功地解决了求积问题。
在《九章算术》的“圆田术”中给出了计算圆面积的法则:“半周半径相乘得积步。
”即圆的面积S 与一个长为半周C /2,宽为半径的长方形的面积相等:参见文献[5]。
二元函数重极限和累次极限的关系及其求解【文献综述】

毕业论文文献综述数学与应用数学二元函数重极限和累次极限的关系及其求解1.国内外现状极限思想也是社会实践的产物。
追溯到古代,刘徽的割圆术就是建立在直观基础上的一种原始的极限思想的应用;古希腊人的穷竭法也蕴含了极限思想,但由于希腊人“对无限的恐惧”,他们避免明显地“取极限”,而是借助于间接证法——归谬法来完成了有关的证明。
到了16世纪,荷兰数学家斯泰文在考察三角形重心的过程中在无意中“指出了把极限方法发展成为一个实用概念的方向”。
极限思想的进一步发展是与微积分的建立紧密相联系的。
16世纪的欧洲处于资本主义萌芽时期,要求数学突破只研究常量的传统范围,而提供能够用以描述和研究运动、变化过程的新工具。
牛顿用路程的改变量ΔS与时间的改变量Δt之比ΔS/Δt表示运动物体的平均速度,让Δt无限趋近于零,得到物体的瞬时速度。
他意识到极限概念的重要性试图以极限概念作为微积分的基础,他说:“两个量和量之比,如果在有限时间内不断趋于相等,且在这一时间终止前互相靠近,使得其差小于任意给定的差,则最终就成为相等”。
但牛顿的极限观念也是建立在几何直观上的,因而他无法得出极限的严格表述。
牛顿所运用的极限概念,只是接近于下列直观性的语言描述:“如果当n无限增大时,an无限地接近于常数A,那么就说an以A为极限”。
维尔斯特拉斯提出了极限的静态的定义。
所谓an=A,就是指:“如果对任何ε>0,总存在自然数N,使得当n>N时,不等式|an-A|<ε恒成立”。
这个定义,借助不等式,通过ε和N之间的关系,定量地、具体地刻划了两个“无限过程”之间的联系。
因此,这样的定义是严格的,可以作为科学论证的基础,至今仍在数学分析书籍中使用。
在该定义中,涉及到的仅仅是数及其大小关系,此外只是给定、存在、任取等词语,已经摆脱了“趋近”一词,不再求助于运动的直观。
2.研究方向许汪涛《关于多元极限概念》中强调突出多元函数的重极限与累次极限是两个性质上不同,却又紧密相关的概念。
海涅定理极限

海涅定理极限海涅定理是极限理论中的一个重要概念,它由德国数学家海涅·韦洛斯基提出。
海涅定理在实数域中给出了数列收敛的必要和充分条件,以及收敛数列的性质。
本文将对海涅定理进行详细介绍,并探讨其在极限理论中的应用。
1. 引言极限理论是微积分和数学分析中的基础理论之一,它研究数列和函数的极限性质。
在极限的定义和性质中,海涅定理占据着重要的地位。
海涅定理不仅被广泛应用在数学分析领域,也在物理、工程学等科学领域具有重要作用。
2. 海涅定理的定义在数学中,海涅定理给出了数列收敛的必要和充分条件。
对于一个实数数列{a_n},当存在实数L,对于任意给定的正实数ε,总存在正整数N,使得当n>N时,|a_n - L|<ε成立,即对于任意给定的精度ε,总存在一个正整数N,使得数列的后续项都与实数L的差的绝对值小于ε。
如果满足这个条件,那么数列{a_n}就是收敛的,L为数列的极限。
3. 收敛数列的性质根据海涅定理,我们可以得出一些关于收敛数列的性质。
首先,收敛数列是有界的,即存在一个正实数M,使得对于数列的每一项a_n,都有|a_n|≤M成立。
其次,数列的极限是唯一的,即如果数列收敛,那么它的极限是唯一确定的。
此外,收敛数列的任意子列都收敛于相同的极限。
4. 应用举例:极限计算海涅定理在实际计算中具有重要作用。
例如,我们可以利用海涅定理来计算一些复杂极限。
假设我们需要计算极限lim(n→∞)(1+1/n)^n,可以构造数列{a_n},其中a_n=(1+1/n)^n。
利用数列的性质和海涅定理,我们可以证明这个极限等于常数e≈2.71828。
这个例子展示了海涅定理在极限计算中的应用。
5. 应用举例:泰勒展开海涅定理在泰勒展开中也有重要应用。
泰勒展开是将函数在某一点展开成无穷级数的形式,可以用于近似计算函数的值。
根据海涅定理,我们可以证明如果函数在某一点可导,那么其泰勒展开式在该点处收敛于该函数本身。
这为我们提供了一种近似计算复杂函数的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求极限的方法摘要:求极限的方法是高等数学的一个重点,而极限概念是微积分学的中心内容。
因此,弄清极限概念,熟练掌握极限的计算方法,对于学好高等数学是十分必要的。
为此,本文将高等数学中各种极限的计算方法,系统地归纳起来,对于在求极限时,能够灵活地运用求极限的法则,较熟练地选择简便的方法,是很有帮助的。
关键词: 正文:极限的概念是由于求某些实际问题的精确解答而产生的。
例如,我国古代数学家刘徽利用圆内接正多边形来推算圆面积的方法—割圆术,就是极限思想在几何学上的应用。
设有一圆,首先作内接正六边形,把它的面积记为A 1;再作内接正十二边形,其面积记为A 2;再作内接正十二边形,其面积记为A 3;循此下去,每次边数加倍,一般把内接正6×2n-1边形的面积记为A n (n ∈N ).这样,就得到一系列内接正多边形的面积:A1,A 2,A 3…,A n ,…..,它们构成一列有次序的数。
当n 越大,内接正多边形与圆的差别就越小,从而以An 作为圆面积的近似值也越精确。
但是无论n 取得如何大,只要n 取定了,An 终究只是多边形的面积,而还不是圆的面积。
因此,设想n 无限增大(记为n →∞),即内接正多边形的边数无限增加,在这个过程中,内接正多边形无限接近于圆,同时A n 也无限接近于某一确定的数值,这个确定的数值在数学上称为上面这列有次序的数(所谓数列)A 1,A 2,A 3,…..,A n ,…..当n →∞时的极限。
极限有两种.:数列极限:∞→n limxn=a ⇔∀ε>0,∃一个正整数N ,当n>N 时,恒有|Xn-a|<ε函数极限:∞→x limf(x)=A ⇔ε>0,一个x>0,当|x|>X,恒有|f(x)-A|<ε.limx x →f(x)=A ⇔∀ε>0,∃一个δ>0,当0<|x -x 0|<δ时,恒有|f(x)-A|<ε求极限的方法已归纳出15种,分别列举如下: §1 利用极限定义求极限[解题提示]当数列Xn 不单调时,其极限的存在性可考虑用极限的定义证明。
解题程序是先求出x n 后,再证x n 的存在性。
[例1]设x 1 =2, x n+1 =2+n x 1, n ≥1,求∞→n lim x n [解]令∞→n lim x n =m,则∞→n lim x n+1 =∞→n lim ⎪⎪⎭⎫⎝⎛+n x 12 即m=2+1/m 则m=1±2∵x n ≥2 ∴m≥2 故m=1+2(m=1-2舍去)以下证∞→n limx n 存在 对任意ε>0,|x n - m|=|(2+11-n x )-(2+m1)|=︳11-n x -m 1︱=11---n n mx m x <41m x n --<224m x n --<….<114--n m x=1412--n <ε 由极限定义∞→n lim()m x n -=0,故∞→n lim x n =m=1+2 §2子序列的极限与函数的极限等值即子序列的极限可用函数极限求出。
[例1]∞→n lim tgn ⎪⎭⎫ ⎝⎛+n 14π [解]先求+∞→x lim tanx (4π+1)n=+∞→⎪⎭⎫ ⎝⎛+x x tg l n e14limπ=+∞→-⎪⎭⎫⎝⎛+x x x tg l n e114limπ=()+∞→--•⎪⎭⎫ ⎝⎛+•⎪⎭⎫ ⎝⎛+x x x x x e 114cos 114tan 1lim22ππ=+∞→⎪⎭⎫ ⎝⎛+x x e22sin 2limπ=2e[]2例求+∞→n lim nn arctg ⎪⎭⎫⎝⎛π2[解]先求+∞→n lim 22x arctgx ⎪⎭⎫⎝⎛π极限=+∞→⎪⎭⎫⎝⎛x arctgx x e π2ln lim2(应为原式=)=+∞→⎪⎭⎫⎝⎛-x xarctgx e 22ln lim π=+∞→-+•-x x x arctgx e 322111lim =+∞→•+-x arctgx x x e11lim 2123=0故原极限为0。
§3约简分式的方法即是化简分子分母,能约分的约分,使能求出分式的极限。
[例1]求极限1lim →x 11--n m x x[解]1lim →x 11--n m x x =1lim →x )1)(1()1)(1(2121+++-+++-----ΛΛn n m m x x x x x x = 1lim →x 1.12121+++++----ΛΛn n m m x x x x =项)项)n m (111(111++++++ΛΛ=n m [例2]求极限∞→x limnn n nn -+++42321(n 是正整数变量)[解] 分子、分母各项除以n ,得原式=∞→n lim 111111111422-=-=-+++nn n n注:约简分式的方法实质是分子与分母除以相同的式子,以有利于求极限。
§4 有理化分子或分母即是通过因式分解或根式有理化,消去“0”因子,再用极限运算法则或连续函数极限的求法求解。
所谓根式有理化是指极限中含有b a ±(或b a ±)的题性型,在求极限之前先用它们的共轭根式b a μ(或b a μ)分别乘以分子、分母,使其“0”因子呈现出来的一种运算。
[例1]求+→ax lim )0(22≥--+-a ax ax a x[解]原式=+→a x lim()()()⎥⎥⎦⎤⎢⎢⎣⎡+++-+-a x a x ax a x ax 122=+→a x lim()⎥⎦⎤⎢⎣⎡++++-a x ax a x ax 1=a21[例2]求极限8lim -→x 3231xx +-- [解]分子与分母同乘以()31+-x ()323222x x +-得原式=8lim -→x ()()()x x x x x ++-+---8)31(2491323=8lim -→x ﹣⎪⎪⎭⎫⎝⎛+-+-3124323x x x =2 §5利用夹逼定理(夹逼定理)设在x 0 的邻域内,恒有ϕ(x )≤f (x )ψ≤(x ),且limx x →ϕ(x )=0lim x x →ψ(x )=A ,则0lim x x →f (x )=A [例1]求+∞→n lim ⎰1=x n 3+x dx[解],10≤≤x Θ (233≤+≤x 把含n 的项留下来)n nnx x x x 233≤+≤∴于是⎰1nx 3dx ≤⎰10xn3+x dx ≤⎰12x ndx而∞→n lim ⎰1nx 3dx=∞→n lim 10113++n x n =∞→n lim 13+n =0∞→n lim ⎰12x ndx=∞→n lim 211++n x n 10=∞→n lim 12+n =0故+∞→n lim ⎰1=x n 3+x dx=0[例2]求∞→n lim n nnx x ⎪⎪⎭⎫ ⎝⎛++212 (1)当0≤x 1≤时,1≤n nn x x ⎪⎪⎭⎫ ⎝⎛++212n3≤ Θ∞→n lim n 3=1 ∴当0≤x 1≤时,∞→n lim n nn x x ⎪⎪⎭⎫ ⎝⎛++212=1 (2)当1〈x 2≤时, x 〈n nn x x ⎪⎪⎭⎫ ⎝⎛++212x n3≤ 又∞→n lim x n 3=x ,所以当1〈x 2≤时,∞→n lim n nn x x ⎪⎪⎭⎫ ⎝⎛++212=x (3)当x 〉2时22x 〈 n nn x x ⎪⎪⎭⎫ ⎝⎛++212≤232x n• 又∞→x lim 232x n •=22x 所以,当x 〉2时,∞→n lim n nn x x ⎪⎪⎭⎫ ⎝⎛++212=22x 综上所述,∞→n lim n nnx x ⎪⎪⎭⎫ ⎝⎛++212=⎪⎪⎩⎪⎪⎨⎧>≤<≤≤22211012x x x x x §6利用自然数求和公式即是利用求和公式先算出自然数的和,再求极限。
[例1]求极限∞→n lim⎪⎪⎭⎫ ⎝⎛-++3.212222n n n Λ [解]利用自然数平方和公式:1222.2n Λ++=()()12161++n n n 所以,原式=∞→n lim ()()⎥⎦⎤⎢⎣⎡-++312161n n n n =∞→n lim n n 613+=∞→n lim 613n +=21注:类似地,可用其它求和公式或求和法。
[例2]求极限∞→n lim ⎪⎭⎫ ⎝⎛-+++141351151312n Λ [解]++++ΛΘ351151311412-n = ()()12121751531311+-++•+•+•n n Λ =⎭⎬⎫⎩⎨⎧⎪⎭⎫⎝⎛+--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-121121715151313`1121n n Λ=⎪⎭⎫ ⎝⎛+-121121n21121121=⎪⎭⎫ ⎝⎛+-=∴n 原式 §7 利用基本极限0lim →x xxsin =10lim →x xx sin =1该极限的特点:它是00型未定式,并且正弦函数右边的变量与分数线另一侧的变量形式一致。
注:∞→x lim x x sin =0(∞→x lim xx sin ≠1,为非00型未定式) [例1]求+∞→x lim121sin22-x x x [解]+∞→x lim121sin22-x x x =+∞→x lim •xx 11sin+∞→x lim122-x x =22 [例2]求极限∞→n lim ()⎥⎦⎤⎢⎣⎡-+++22212sin 3sin sin n a n n a n a Λ [解]记An=sin2n a +sin 23n a +()a n n 212sin -Λ a=0时An=0,即有∞→n limAn=0=a设a>0,对于任意给定的正数δ,利用基本极限0lim →x xxsin =1和极限的定义,必存在δ>0,使1sin -x x ∣<aε,当0<x <δ,于是当n>δa2时,由于()δ<<-<<<n a n a n n an a 21232222Λ 故有()()11212sin22---n a k n ak 〈aε, k=1,2,n ,Λ ()()221212sinna k na k ---∴<212nk -ε• k=1,2,n ,Λ利用“和的绝对值不超过绝对值的和”,得()()∑=⎥⎦⎤⎢⎣⎡---nk n a k n a k 1221212sin ()()∑=---≤n k n a k n a k 1221212sin 〈∑=-•nk n k 1212ε ∑=-nk n k 1212Θ=()[]1231`12-+++n n Λ=221n n •=1Θ 前一式化为 δεan a An 2(><-当)按极限定义便得∞→n limAn=a设a<0,则-a>0 并且∞→n limAn=∞→n lim ()⎥⎦⎤⎢⎣⎡--++-+-22212sin 3sin sin n a n n a n aΛ =a§8利用基本极限0lim →x ()x x 11+=∞→x lim xx ⎪⎭⎫ ⎝⎛+11=e该极限的特点:①它是1∞型未定式,②括号中1后的变量(包括符号)与幂互为倒数。
